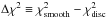| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 24 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322779 | |
| Published online | 31 March 2014 | |
Online material
Estimates of the frequencies and rotational splittings of the detected modes for KIC 12508433 (star A), obtained by fitting Lorentzian functions to the mode profiles.
Inclination angles obtained for the stars of the sample from the final fit (see text).
Appendix A: Computation of asymptotic period spacings from stellar models
According to the asymptotic analysis of g modes (e.g. Christensen-Dalsgaard 2003), the frequencies of two g modes of same degree l and consecutive radial order n verify the following equation: 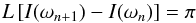 (A.1)where
(A.1)where 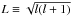 and
and 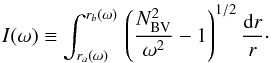 (A.2)The radii ra(ω) and rb(ω) correspond to the turning points of the g-mode cavity for the mode of frequency ω. For red giants, one usually assumes that ω ≪ NBV(r) in the whole g-mode cavity and thus derives
(A.2)The radii ra(ω) and rb(ω) correspond to the turning points of the g-mode cavity for the mode of frequency ω. For red giants, one usually assumes that ω ≪ NBV(r) in the whole g-mode cavity and thus derives 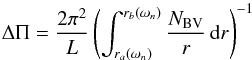 (A.3)from Eq. (A.1). For young giants, this approximation is not legitimate because the core is less dense than in more evolved giants and the integrand of Eq. (A.2) cannot be simplified. In this case, computing the asymptotic period spacing from a model at a frequency ωn requires an iterative method. By definition of the period spacing, we have
(A.3)from Eq. (A.1). For young giants, this approximation is not legitimate because the core is less dense than in more evolved giants and the integrand of Eq. (A.2) cannot be simplified. In this case, computing the asymptotic period spacing from a model at a frequency ωn requires an iterative method. By definition of the period spacing, we have 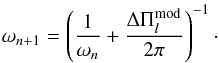 (A.4)This expression of ωn + 1 is then plugged into Eq. (A.1) and we use the Newton method to solve this latter equation for
(A.4)This expression of ωn + 1 is then plugged into Eq. (A.1) and we use the Newton method to solve this latter equation for 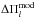 . The obtained values are given in Table 11. They differ from those given by Eq. (A.3) by 3% (for the most evolved targets) to 11% (for the least evolved ones). This shows a posteriori that the usual approximation is not valid for the young red giants.
. The obtained values are given in Table 11. They differ from those given by Eq. (A.3) by 3% (for the most evolved targets) to 11% (for the least evolved ones). This shows a posteriori that the usual approximation is not valid for the young red giants.
Appendix B: Effective number of degrees of freedom for an RLS fit
Estimating the number of degrees of freedom for an RLS fit is not straightforward because this number cannot be interpreted as the dimension of a certain vector subspace, as is the case for ordinary least-squares fits. However, the fitted values (the rotational splittings that correspond to the inverted rotation profile δνRLS in our case) remain linear in the observations δνobs. There exists a matrix H, usually referred to as the hat matrix, such that 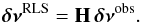 (B.1)We note that both the matrix H and the vector δνRLS depend on the regularization parameter.
(B.1)We note that both the matrix H and the vector δνRLS depend on the regularization parameter.
The number of degrees of freedom of the fit correspond to the expected value of χ2, which is given by Eq. (8). To calculate E(χ2), we assume that the RLS fit is unbiased, that is, we assume that the “true” splittings would be recovered with this method if the observations were noise-free. This assumption is probably not completely justified, but if a bias exists, it will increase the expected value of the χ2. Therefore, by neglecting the bias, we obtain higher values of the reduced χ2 and our assumption is thus conservative. We also consider that the observed splittings are uncorrelated. Under these conditions, we can use the development of Hastie & Tibshirani (1990). The only difference is that in our case the variances of the data points are not all the same. To place ourselves in this particular case, we normalize the rotational splittings by the observed errors by defining 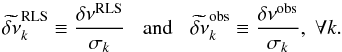 (B.2)We thus have
(B.2)We thus have 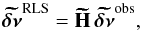 (B.3)where the corresponding hat matrix is such that
(B.3)where the corresponding hat matrix is such that 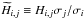 . In this case, Hastie & Tibshirani (1990) have shown that the expected value of χ2 is
. In this case, Hastie & Tibshirani (1990) have shown that the expected value of χ2 is 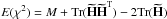 . Finally we obtain
. Finally we obtain 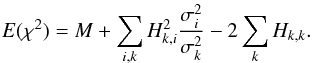 (B.4)
(B.4)
Appendix C: Can we distinguish between a smooth and a discontinuous rotation profile in the stars of the sample?
Appendix C.1: Simulations with a discontinuous rotation profile
To answer this question, we performed simulations by assuming a discontinuous input rotation profile Ωth(r). We took 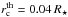 to determine whether or not a discontinuity at this depth can be detected. For each star, the values of Ω1 and Ω2 were fixed to the best-fitting values that were found by assuming rc = 0.04 R⋆ in Sect. 6.3.2. We then used the rotational kernels of the observed modes to compute the theoretical rotational splittings
to determine whether or not a discontinuity at this depth can be detected. For each star, the values of Ω1 and Ω2 were fixed to the best-fitting values that were found by assuming rc = 0.04 R⋆ in Sect. 6.3.2. We then used the rotational kernels of the observed modes to compute the theoretical rotational splittings 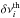 that correspond to Ωth(r). We used the same sets of modes as the observed ones. To simulate the observed splittings, we added to the theoretical splittings
that correspond to Ωth(r). We used the same sets of modes as the observed ones. To simulate the observed splittings, we added to the theoretical splittings 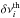 a random noise following a Gaussian distribution with rms
a random noise following a Gaussian distribution with rms 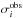 . We then tried to recover the input rotation profile Ωth(r) by performing the same inversion procedures as for the observations. The last two steps were repeated many times (500 iterations per star for each inversion method) to study the statistics.
. We then tried to recover the input rotation profile Ωth(r) by performing the same inversion procedures as for the observations. The last two steps were repeated many times (500 iterations per star for each inversion method) to study the statistics.
We first performed inversions by assuming that the rotation profile is discontinuous. We minimized the χ2 as defined by Eq. (10) for different values of rc. To determine whether or not the input depth of the discontinuity 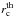 can be recovered, we located the radius rdisc at which the χ2 function is the lowest for each iteration. Correspondingly, the lowest value of the χ2 function is further noted
can be recovered, we located the radius rdisc at which the χ2 function is the lowest for each iteration. Correspondingly, the lowest value of the χ2 function is further noted 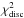 . The distribution of rdisc is shown in Fig. C.1 for all the stars. We remark that for stars D and F, the depth of the discontinuity is correctly recovered in 90% and 97% of the cases, respectively (we arbitrarily considered that the depth of the discontinuity is recovered if
. The distribution of rdisc is shown in Fig. C.1 for all the stars. We remark that for stars D and F, the depth of the discontinuity is correctly recovered in 90% and 97% of the cases, respectively (we arbitrarily considered that the depth of the discontinuity is recovered if 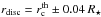 ), which indicates that we should be able to detect a discontinuity in the rotation profile at a depth of
), which indicates that we should be able to detect a discontinuity in the rotation profile at a depth of 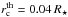 in these stars. For the least evolved stars A and B, the success rate is much lower (28% for both stars). For stars C and E, the correct discontinuity is recovered about 60% of the time.
in these stars. For the least evolved stars A and B, the success rate is much lower (28% for both stars). For stars C and E, the correct discontinuity is recovered about 60% of the time.
 |
Fig. C.1
Distribution of the depth rmin at which a discontinuity in Ω(r) is found to be most probable for simulations considering either a smooth input rotation profile (blue histogram) or discontinuous one at a depth |
| Open with DEXTER | |
 |
Fig. C.2
Distribution of |
| Open with DEXTER | |
We then tried to recover the rotation profile by (incorrectly) assuming that it is smooth for each of the 500 iterations. For this purpose, we used the RLS method with a smoothness condition, as was done for the observations in Sect. 6.3.1. Of course, the resulting profiles contain no discontinuity. For each iteration, the agreement between the simulated splittings and that corresponding to the inverted rotation profile was estimated by computing a χ2, further referred to as 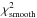 . We compared the values of
. We compared the values of 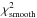 with those of
with those of 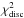 , which were obtained above, assuming that the profile is discontinuous. Figure C.2 shows the distribution of
, which were obtained above, assuming that the profile is discontinuous. Figure C.2 shows the distribution of 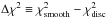 for each star. For stars D and F,
for each star. For stars D and F, 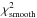 was found larger than
was found larger than 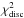 for all the 500 iterations, with Δχ2 = 0.8 ± 0.4 for star D and 1.1 ± 0.6 for star F.
for all the 500 iterations, with Δχ2 = 0.8 ± 0.4 for star D and 1.1 ± 0.6 for star F.
This set of simulations shows that for stars D and F, a discontinuity located at 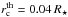 is recovered more than 90% of the time, and the agreement with the input theoretical splittings is better when the rotation profile is assumed to be discontinuous than when it is assumed to be smooth (
is recovered more than 90% of the time, and the agreement with the input theoretical splittings is better when the rotation profile is assumed to be discontinuous than when it is assumed to be smooth (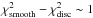 ). To determine whether or not the profile is indeed discontinuous in these stars, we must also show that a smooth profile very probably does not produce the same features.
). To determine whether or not the profile is indeed discontinuous in these stars, we must also show that a smooth profile very probably does not produce the same features.
Appendix C.2: Simulations with a smooth rotation profile
For this purpose, we considered an input rotation profile that is smooth. We took the best-fit profile obtained with the RLS method in Sect. 6.3.1. As before, we computed the theoretical splittings that correspond to this rotation profile, added a random noise to it, and tried to recover the input rotation profile. 500 iterations were performed for each star.
 |
Fig. C.3
Differences between the theoretical splittings that are obtained with a smooth rotation profile and those produced by discontinuous rotation profiles with depths of discontinuity of rc/R⋆ = 0.04 (filled stars), 0.2 (green circles), 0.4 (red circles), 0.6 (blue circles), and 0.8 (purple circles) for star D (KIC 8751420). The differences were normalized by the 1σ errors of the observations to emphasize the contribution of each mode to the χ2. |
| Open with DEXTER | |
We first performed inversions by (incorrectly) assuming that the rotation profile is discontinuous. For each iteration, we determined the radius rdisc at which a discontinuity is most probable and we kept a record of the minimum χ2 (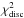 ). The distributions of rdisc that we obtained for all the stars are shown in Fig. C.1 (blue histograms). For stars A, B, C, and E, we observe that rdisc is distributed more or less randomly between 0 and 1. In particular, for stars A and B, the distribution of rdisc is very similar to the one that was obtained when considering a discontinuous input profile, which confirms that it is impossible to detect a discontinuity in the rotation profile for these stars. For stars D and F, some radii are more probable than others (e.g. 0.16, 0.33, 0.50, 0.60, and 0.90 R⋆ for star F). This means that the splittings produced by a smooth rotation profile are quite similar to those produced by discontinuous profiles with specific depths of discontinuity. It would therefore be hopeless to try to detect a discontinuity around these specific radii. However, smooth profiles very seldom produce rotational splittings that are similar to the one corresponding to a discontinuous profile with rc as deep as 0.04 R⋆. Indeed, for stars D and F, a value of rdisc below 0.08 R⋆ was obtained for only 4% and 2% of the iterations, respectively.
). The distributions of rdisc that we obtained for all the stars are shown in Fig. C.1 (blue histograms). For stars A, B, C, and E, we observe that rdisc is distributed more or less randomly between 0 and 1. In particular, for stars A and B, the distribution of rdisc is very similar to the one that was obtained when considering a discontinuous input profile, which confirms that it is impossible to detect a discontinuity in the rotation profile for these stars. For stars D and F, some radii are more probable than others (e.g. 0.16, 0.33, 0.50, 0.60, and 0.90 R⋆ for star F). This means that the splittings produced by a smooth rotation profile are quite similar to those produced by discontinuous profiles with specific depths of discontinuity. It would therefore be hopeless to try to detect a discontinuity around these specific radii. However, smooth profiles very seldom produce rotational splittings that are similar to the one corresponding to a discontinuous profile with rc as deep as 0.04 R⋆. Indeed, for stars D and F, a value of rdisc below 0.08 R⋆ was obtained for only 4% and 2% of the iterations, respectively.
To understand this result, a closer inspection of the theoretical splittings (without noise) is instructive. Figure C.3 shows the difference between the theoretical splittings of the input smooth profile and that of best-fit discontinuous profiles with various values of rc for star D. We observe that for discontinuities between 0.2 and 1, the theoretical splittings does not vary much and is very close to the splitting of the smooth profile. On the other hand, for deeper discontinuities (e.g. around rc = 0.04 R⋆), the splittings of several modes significantly differ from the case of a smooth profile (for example the modes around 454 and 582 μHz for star D, see Fig. C.3), which explains why we can distinguish between these two types of profiles.
For each iteration, we also performed RLS inversions with a smoothness condition and estimated the agreement with the theoretical splittings by computing 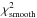 . The distributions of
. The distributions of 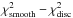 are shown in Fig. C.2 (blue histograms). For all the stars, the values of
are shown in Fig. C.2 (blue histograms). For all the stars, the values of 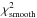 are similar to those of
are similar to those of 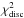 . This was expected since we saw from Fig. C.1 that smooth rotation profiles produce splittings that resemble those of discontinuous profiles with discontinuities at certain depths. However, for stars D and F, if the input profile is smooth,
. This was expected since we saw from Fig. C.1 that smooth rotation profiles produce splittings that resemble those of discontinuous profiles with discontinuities at certain depths. However, for stars D and F, if the input profile is smooth, 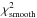 is never larger than
is never larger than 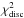 by more than 0.8 and 0.9, respectively, whereas the observed values of Δχ2 are as high as 3.6 and 3.1 for these stars, which is much more consistent with the distribution found for discontinuous input profiles. For all the other stars, the observed Δχ2 are equally consistent with the two types of profiles.
by more than 0.8 and 0.9, respectively, whereas the observed values of Δχ2 are as high as 3.6 and 3.1 for these stars, which is much more consistent with the distribution found for discontinuous input profiles. For all the other stars, the observed Δχ2 are equally consistent with the two types of profiles.
To determine to what extent our results depend on the shape of the smooth rotation profile that is used as an input, we repeated the same simulations considering other smooth profiles (e.g. the best-fit rotation profiles obtained by using the OLA method in Sect. 6.2, or an best-fit linear profile). We obtained results that are quantitatively very similar to those described above.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.