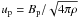| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 20 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201220168 | |
| Published online | 01 February 2013 | |
MHD simulations of accretion onto a dipolar magnetosphere
II. Magnetospheric ejections and stellar spin-down
1 INAF – Osservatorio Astrofisico di Torino, Strada Osservatorio 20, Pino Torinese 10025, Italy
e-mail: zanni@oato.inaf.it
2 UJF – Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
Received: 5 August 2012
Accepted: 16 November 2012
Aims. This paper examines the outflows associated with the interaction of a stellar magnetosphere with an accretion disk. In particular, we investigate the magnetospheric ejections (MEs) due to the expansion and reconnection of the field lines connecting the star with the disk. Our aim is to study the dynamical properties of the outflows and evaluate their impact on the angular momentum evolution of young protostars.
Methods. Our models are based on axisymmetric time-dependent magnetohydrodynamic simulations of the interaction of the dipolar magnetosphere of a rotating protostar with a viscous and resistive disk, using alpha prescriptions for the transport coefficients. Our simulations are designed to model the accretion process and the formation of accretion funnels, the periodic inflation/reconnection of the magnetosphere and the associated MEs, and the stellar wind.
Results. Similar to a magnetic slingshot, MEs can be powered by the rotation of both the disk and the star so that they can efficiently remove angular momentum from both. Depending on the accretion rate, MEs can extract a relevant fraction of the accretion torque and, together with a weak but non-negligible stellar wind torque, can balance the spin-up due to accretion. When the disk truncation approaches the corotation radius, the system enters a “propeller” regime, where the torques exerted by the disk and the MEs can even balance the spin-up due to the stellar contraction.
Conclusions. Magnetospheric ejections can play an important role in the stellar spin evolution. Their spin-down efficiency can be compared to other scenarios, such as the Ghosh & Lamb, X-wind, or stellar wind models. Nevertheless, for all scenarios, an efficient spin-down torque requires a rather strong dipolar component, which has seldom been observed in classical T Tauri stars. A better analysis of the torques acting on the protostar must consider non-axisymmetric and multipolar magnetic components consistent with observations.
Key words: stars: rotation / stars: magnetic field / accretion, accretion disks / ISM: jets and outflows / magnetohydrodynamics (MHD) / methods: numerical
© ESO, 2013
1. Introduction
Classical T Tauri stars (CTTS) are pre-main sequence stars that show clear signatures of accretion from a surrounding accretion disk (Edwards et al. 1994; Hartmann et al. 1998) and ejection in the form of collimated jets (Cabrit et al. 1990; Burrows et al. 1996). The evolution of their rotation period represents an interesting puzzle. As soon as they become visible after the Class 0-I embedded phases, a relevant fraction of CTTS appears to rotate well below their break-up limit, with rotation periods around one to ten days (Bouvier et al. 1993). Besides this, their rotation rate appears to be fairly constant during the accreting evolutionary phases lasting a few million years (Irwin & Bouvier 2009). On the other hand, these protostars are still actively accreting and contracting so that they would be expected to spin-up at break-up in ~106 years. Clearly, CTTS require an efficient spin-down mechanism to explain their rotational evolution.
Since CTTS are known to be magnetically active (see e.g. Johns-Krull 2007; Yang & Johns-Krull 2011), different magnetohydrodynamic (MHD) mechanisms of angular momentum removal have been proposed. In the Ghosh & Lamb (1979) model, originally developed for pulsars, the disk itself extracts angular momentum from the star along the field lines connecting the star with the disk in the region beyond the corotation radius, where the disk rotates slower than the star. On the other hand, it has been shown that the efficiency of the Ghosh & Lamb mechanism is drastically reduced because of the limited size of the connected magnetosphere (Matt & Pudritz 2005a) and of the dilution of the poloidal field beyond the corotation radius (Agapitou & Papaloizou 2000; Zanni & Ferreira 2009, hereafter Paper I).
Other solutions are based on the presence of outflows, drawing out angular momentum from the star-disk system, instead of transferring it back to the disk. Shu et al. (1994) proposed that an “X-wind” launched along the open stellar magnetic surfaces threading the disk around corotation can extract a substantial amount of angular momentum from the disk before it is transferred to the star, so as to cancel at least the spin-up torque due to accretion. Even if models of wide-angle X-winds are feasible (Anderson et al. 2005; Cai et al. 2008), a fully self-consistent calculation of the disk-outflow dynamical connection is currently missing.
Ferreira et al. (2000) investigated a different magnetic configuration, where a magnetic neutral line is formed at the star-disk interface due to the cancellation of the stellar dipolar field by the disk field. Such a reconnection site has been envisioned as driving massive unsteady ejection events, mainly powered by the stellar rotation. These “reconnection X-winds” provide a very efficient spinning down mechanism for early low-mass protostars (Class 0 and I objects), which are able to brake a maximally rotating initial core, slowing it down to observed values. However, this model has not been designed for CTTS and requires a specific magnetic topology, not addressed here.
Stellar winds provide a spin-down torque extracting angular momentum along the open magnetospheric field lines anchored onto the stellar surface (Matt & Pudritz 2005b; Sauty et al. 2011). Matt & Pudritz (2008b) estimate that the wind mass flux is likely to be ~10% of the accretion rate in order to balance at least the torque due to accretion. These stellar winds would carry the entire mass flux typically observed in T Tauri jets, which seems unlikely (Cabrit 2009). Indeed, such high ejection efficiency presents a serious energetic problem (Ferreira et al. 2006): since CTTS are slow rotators and their centrifugal push is not strong enough to drive these outflows, an extra energy input is required. Matt & Pudritz (2005b) propose that it could come from the accretion power carried onto the star by the accreting material. But how to transfer this power to a sizable fraction of ejected material remains a critical issue. It is now clear that the required driving power cannot be of thermal origin (Matt & Pudritz 2007). On the other hand, the push provided by turbulent Alfvén waves, such as those excited by the impact of the accretion streams onto the stellar surface, is likely to remain insufficient to drive massive stellar winds (Cranmer 2008, 2009). But more important, it is quite tricky to assume that some accretion energy would be missing (the fraction that would possibly feed the stellar wind), while still explaining the observed UV luminosity. Indeed, it would imply an even higher mass flux onto the star, hence a higher spinning up torque (Zanni & Ferreira 2011).
Another class of ejection phenomena is expected to arise because of the expansion and subsequent reconnection of the closed magnetospheric field lines. The inflation process is the result of the star-disk differential rotation and the consequent build-up of toroidal magnetic field pressure. This is the same phenomenon that bounds the size of the magnetosphere connecting the star with the disk and limits the efficiency of the Ghosh & Lamb mechanism. While semi-analytical models have foreseen the magnetic field expansion (see e.g. Aly & Kuijpers 1990; Uzdensky et al. 2002), different numerical experiments have shown that plasma ejection is actually associated with the inflation process (Hayashi et al. 1996; Goodson et al. 1997; Miller & Stone 1997; Romanova et al. 2009). Some observable properties of this phenomenon have been discussed, for example, by Hartmann (2009) and Gómez de Castro & von Rekowski (2011). Besides this, Hartmann (2002, 2009) suggests that this mechanism could enhance the angular momentum loss from the star-disk system.
In this paper we present the results of a series of numerical MHD time-dependent simulations to analyze the energetics and dynamics of these magnetospheric ejections in different accretion regimes and evaluate their impact on the angular momentum balance of the star-disk system. At the same time, we are able to include in our models the effects of stellar winds. In Sect. 2 we present the numerical method and provide the initial and boundary conditions employed to carry out the numerical experiments. In Sect. 3 we present the outcome of a reference case in detail: we characterize the dynamical properties of the simulated outflows (Sects. 3.1 and 3.2) and determine their influence on the angular momentum of both the disk (Sect. 3.3) and the star (Sect. 3.4). In Sect. 4 we study the impact of the disk accretion rate onto the dynamics of the outflows and the stellar spin evolution. In Sect. 5 we discuss the outcome of our models making a comparison with the other scenarios proposed to solve the stellar spin conundrum. In Sect. 6 we summarize our conclusions.
2. Numerical setup
The models presented in this paper are numerical solutions of the MHD system of equations, including resistive and viscous effects: ![\begin{eqnarray} \label{eq:mhd} &&\frac{\partial \rho}{\partial t} + \nabla\cdot(\rho \vec {u}) = 0 \nonumber \\ &&\frac{\partial \rho\vec{u}}{\partial t} + \nabla \cdot \left[ \rho \vec{u}\vec{u} + \left( P + \frac{\vec{B}\cdot\vec{B}}{8\pi} \right)\vec{I}- \frac{\vec{B}\vec{B}}{4\pi} - \vec{\tau} \right] = - \rho \nabla \Phi_\mathrm{g} \nonumber \\ &&\frac{\partial E}{\partial t} + \nabla\cdot\left[ \left(E + P + \frac{\vec{B}\cdot\vec{B}}{8\pi}\right)\vec{u}- \frac{\left(\vec{u}\cdot\vec{B}\right)\vec{B}}{4\pi} \right] \\ && \quad\ \ + \nabla\cdot\left[\eta_{\mathrm{m}}\vec{J}\times\vec{B}/4\pi -\vec{u}\cdot\vec{\tau} \right] = - \rho \nabla \Phi_\mathrm{g} \cdot\vec{u}-\Lambda_\mathrm{cool} \nonumber \\ &&\frac{\partial \vec{B}}{\partial t} + \nabla \times \left(\vec{B}\times\vec{u} + \eta_{\mathrm{m}} \vec{J} \right)= 0 \nonumber. \end{eqnarray}](/articles/aa/full_html/2013/02/aa20168-12/aa20168-12-eq4.png) (1)This system expresses the conservation of mass, momentum, and energy and includes the induction equation to describe the evolution of the magnetic field. In the system of Eqs. (1) ρ is the mass density, u the flow speed, P the plasma thermal pressure, B the magnetic field, Φg = −GM⋆/R is the gravitational potential, J = ∇ × B/4π is the electric current, and ηm the magnetic resistivity, where νm = ηm/4π defines the magnetic diffusivity. The total energy density E is defined as
(1)This system expresses the conservation of mass, momentum, and energy and includes the induction equation to describe the evolution of the magnetic field. In the system of Eqs. (1) ρ is the mass density, u the flow speed, P the plasma thermal pressure, B the magnetic field, Φg = −GM⋆/R is the gravitational potential, J = ∇ × B/4π is the electric current, and ηm the magnetic resistivity, where νm = ηm/4π defines the magnetic diffusivity. The total energy density E is defined as
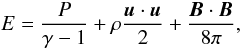 where γ = 5/3 is the polytropic index of the plasma. The viscous stress tensor τ is given by
where γ = 5/3 is the polytropic index of the plasma. The viscous stress tensor τ is given by ![\begin{equation} \tau = \eta_\mathrm{v} \left[ \left(\nabla \vec{u}\right) + \left(\nabla \vec{u}\right)^\mathrm{T} - \frac{2}{3}\left(\nabla\cdot\vec{u}\right) \vec{I} \right], \end{equation}](/articles/aa/full_html/2013/02/aa20168-12/aa20168-12-eq17.png) (2)where ηv is the dynamic and νv = ηv/ρ the kinematic viscosity. The anomalous transport coefficients ηm and ηv are assumed to be of turbulent origin and are parametrized according to an α prescription (Shakura & Sunyaev 1973). The cooling term Λcool = ηmJ·J + Tr(ττT)/2ηv is included to balance the viscous and Ohmic heating, so that the system should evolve adiabatically, modulo numerical dissipative effects. We employed the MHD module provided with the PLUTO code1 (Mignone et al. 2007) to solve the system of Eq. (1). For a precise description of the employed algorithm, we refer the reader to Paper I.
(2)where ηv is the dynamic and νv = ηv/ρ the kinematic viscosity. The anomalous transport coefficients ηm and ηv are assumed to be of turbulent origin and are parametrized according to an α prescription (Shakura & Sunyaev 1973). The cooling term Λcool = ηmJ·J + Tr(ττT)/2ηv is included to balance the viscous and Ohmic heating, so that the system should evolve adiabatically, modulo numerical dissipative effects. We employed the MHD module provided with the PLUTO code1 (Mignone et al. 2007) to solve the system of Eq. (1). For a precise description of the employed algorithm, we refer the reader to Paper I.
2.1. Initial and boundary conditions
We employ the same initial and boundary conditions, computational domain, and resolution of the simulations as presented in Paper I, where a more extensive discussion about the numerical setup can be found. For the sake of completeness, we recall here the main characteristics of our setup.
The two-dimensional simulations are carried out in spherical coordinates (R, θ) assuming axisymmetry around the rotation axis of the star. We indicate the cylindrical radius r = Rsinθ and the height z = Rcosθ with lower-case letters. We initially consider a viscous accretion α-disk surrounded by a rarefied corona threaded by the stellar magnetosphere. The Keplerian accretion disk is modeled after the polytropic solution presented in Kluźniak & Kita (2000, see also Regev & Gitelman 2002; Umurhan et al. 2006). The density, pressure, toroidal and accretion speed, and kinematic viscosity of the disk are given respectively by ![\begin{eqnarray} \rho_\mathrm{d} & = & \rho_\mathrm{d0} \left\{\frac{2}{5\epsilon^2}\left[\frac{R_\star}{R}-\left(1-\frac{5\epsilon^2}{2}\right)\frac{R_\star}{r}\right]\right\}^{3/2} \nonumber \\ P_\mathrm{d} & = & \epsilon^2 \rho_\mathrm{d0} V^2_{\mathrm{K}\star} \left( \frac{\rho_\mathrm{d}}{\rho_\mathrm{d0}} \right)^{5/3} \\ u_{\phi\mathrm{d}} & = & \left[ \sqrt{1-\frac{5\epsilon^2}{2}}+\frac{2}{3}\epsilon^2\alpha^2_\mathrm{v}\Lambda\left(1-\frac{6}{5\epsilon^2\tan^2\theta} \right) \right] \sqrt{\frac{GM_\star}{r}} \nonumber \\ u_{R\mathrm{d}} & = & -\alpha_\mathrm{v}\epsilon^2\left[10-\frac{32}{3}\Lambda\alpha_\mathrm{v}^2-\Lambda\left(5 -\frac{1}{\epsilon^2\tan^2\theta}\right)\right] \sqrt{\frac{GM_\star}{R\sin^3\theta}} \nonumber \\ \nu_\mathrm{v} & = & \frac{2}{3}\alpha_\mathrm{v} \left[ \left. C^2_\mathrm{s}\left(r\right) \right|_{z=0}+\frac{2}{5}\left( \frac{GM_\star}{R}-\frac{GM_\star}{r}\right)\right]\sqrt{\frac{r^3}{GM_\star}} , \nonumber \end{eqnarray}](/articles/aa/full_html/2013/02/aa20168-12/aa20168-12-eq26.png) (3)where αv is the anomalous viscosity coefficient,
(3)where αv is the anomalous viscosity coefficient, 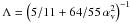 ,
, 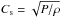 is the isothermal sound speed,
is the isothermal sound speed, 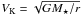 is the Keplerian speed, ϵ = Cs/VK|z = 0 is the disk aspect ratio, ρd0 and VK ⋆ are the density and Keplerian speed on the midplane of the disk at R = R⋆. The magnetic diffusivity is assumed to be proportional to the kinematic viscosity:
is the Keplerian speed, ϵ = Cs/VK|z = 0 is the disk aspect ratio, ρd0 and VK ⋆ are the density and Keplerian speed on the midplane of the disk at R = R⋆. The magnetic diffusivity is assumed to be proportional to the kinematic viscosity: 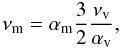 (4)so that the magnetic Prandtl number is equal to
(4)so that the magnetic Prandtl number is equal to 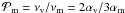 .
.
The corona is represented by a polytropic hydrostatic atmosphere whose density and pressure distributions are given by
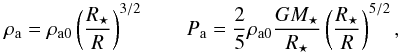 where ρa0 ≪ ρd0 is the density of the corona on the spherical surface R = R⋆.
where ρa0 ≪ ρd0 is the density of the corona on the spherical surface R = R⋆.
We model the stellar magnetosphere as a purely dipolar field aligned with the stellar rotation axis. Given the flux function Ψ⋆, 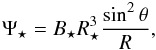 (5)the field components are defined as
(5)the field components are defined as
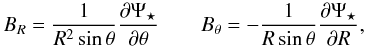 where R⋆ is the stellar radius and B⋆ the magnetic field intensity at the stellar equator. The magnetic flux through one stellar hemisphere is equal to
where R⋆ is the stellar radius and B⋆ the magnetic field intensity at the stellar equator. The magnetic flux through one stellar hemisphere is equal to ![\begin{eqnarray} \label{eq:sflux} \Phi_\star & = & 2 \pi R_\star^2 \int_0^{\pi/2} B_R\left(R_\star ,\theta \right) \sin\theta \, \mathrm{d}\theta \\ & = & 2\pi \left[ \Psi_\star\left(R_\star,\pi/2\right) - \Psi_\star\left(R_\star,0\right) \right] \; = \; 2\pi B_\star R_\star^2. \nonumber \end{eqnarray}](/articles/aa/full_html/2013/02/aa20168-12/aa20168-12-eq44.png) (6)The disk surface is determined by the pressure equilibrium Pd = Pa, while the disk is initially truncated where B2/8π = Pd. To minimize initial transient effects of the differential rotation between the disk and the corona, we set the magnetic surfaces anchored inside the Keplerian disk to corotate with it. The coronal density is corrected so as to nullify the centrifugal acceleration perpendicularly to the magnetic surfaces.
(6)The disk surface is determined by the pressure equilibrium Pd = Pa, while the disk is initially truncated where B2/8π = Pd. To minimize initial transient effects of the differential rotation between the disk and the corona, we set the magnetic surfaces anchored inside the Keplerian disk to corotate with it. The coronal density is corrected so as to nullify the centrifugal acceleration perpendicularly to the magnetic surfaces.
The computational domain encompasses a spherical sector going from the polar axis (θ = 0) to the disk midplane (θ = π/2) and from an inner radius R = R⋆ up to R = 28.6 R⋆. The domain is discretized with a grid of Nθ × NR = 100 × 214 cells. The grid is stretched in the radial direction so that the cell sizes satisfy the condition ΔR ~ RΔθ. Suitable boundary conditions are imposed to satisfy the axial and equatorial symmetries. The boundary conditions on the stellar surface R = R⋆ are carefully chosen to model a perfect conductor rotating with an angular speed Ω⋆ so that, in the rotating frame of reference, the electric field E|Ω = Ω⋆ = B × (u − Ω ⋆ × R) = 0 is zero. Likewise, the boundary is designed to absorb the accretion funnels while forcing the rarefied plasma of the surrounding corona to have a density and enthalpy suitable for driving a light stellar wind. At the outer boundary, the variables are extrapolated, also ensuring that the area of this boundary directly connected to the central star exerts no artificial torques on the latter. A detailed description and discussion of the boundary conditions is given in Paper I.
2.2. Units and normalization
We performed the simulations and now present their outcome in dimensionless units. We here provide the normalization factors needed to express the results in physical units, taking the typical case of a young, forming star into account. The stellar radius R⋆ is employed as unit length, while given the stellar mass and radius, the velocities are expressed in units of the Keplerian speed at the stellar surface 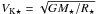 . Taking ρd,0 as the normalization density, the magnetic field is given in units of
. Taking ρd,0 as the normalization density, the magnetic field is given in units of 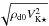 , time in units of t0 = R⋆/VK ⋆ , accretion and ejection rates in units of
, time in units of t0 = R⋆/VK ⋆ , accretion and ejection rates in units of 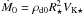 , powers in units of
, powers in units of 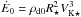 , and torques in units of
, and torques in units of 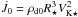 . Assuming M⋆ = 0.5 M⊙, R⋆ = 2 R⊙ and ρd0 = 8.5 × 10-11 g cm-3, we find that
. Assuming M⋆ = 0.5 M⊙, R⋆ = 2 R⊙ and ρd0 = 8.5 × 10-11 g cm-3, we find that 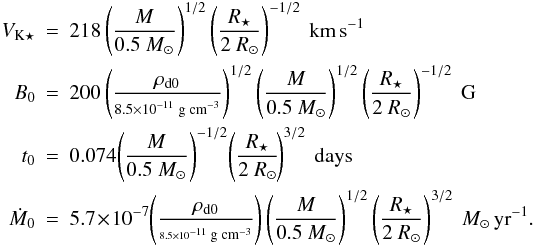 (7)In order to directly provide the characteristic spin-up/spin-down timescales, the torques acting onto the star will be divided by the stellar angular momentum, expressed in units of J ⋆ 0 = M⋆R⋆VK ⋆ . The inverse of the characteristic braking timescale will therefore be expressed in units of2
(7)In order to directly provide the characteristic spin-up/spin-down timescales, the torques acting onto the star will be divided by the stellar angular momentum, expressed in units of J ⋆ 0 = M⋆R⋆VK ⋆ . The inverse of the characteristic braking timescale will therefore be expressed in units of2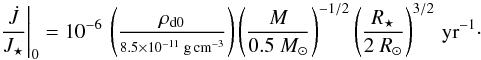 (8)
(8)
Parameters of the simulations.
2.3. The simulations
Once the initial conditions are normalized, the problem depends on six dimensionless parameters: the disk thermal scale height ϵ, the equatorial stellar field intensity B⋆/B0, the stellar rotation rate δ⋆ = R⋆Ω⋆/VK ⋆ , the coronal density contrast ρa0/ρd0, and the viscous and resistive coefficients αv and αm. Except for the transport coefficients, the other parameters are the same as were used in the simulations of Paper I: ϵ = 0.1, B⋆ = 5B0, δ⋆ = 0.1, and ρa0/ρd0 = 10-2. Using the standard normalization given in Sect. 2.2, this corresponds to a stellar magnetic field B⋆ = 1 kG and a period of rotation of the star P⋆ = 2πt0/δ⋆ = 4.65 days with a Keplerian corotation radius 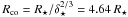 .
.
The transport coefficients αv and αm control, respectively, the intensity of the viscous torque, allowing the disk to accrete, and the strength of the coupling of the stellar magnetic field with the disk material. As discussed, for example, in Uzdensky et al. (2002) and Matt & Pudritz (2005a), the disk magnetic resistivity controls the extent of the disk region that is steadily connected to the star: since the opening of the magnetosphere is determined by the star-disk differential rotation and the consequent buildup of toroidal magnetic pressure, a weaker magnetic coupling (i.e. a higher αm) limits the growth of the toroidal field and therefore increases the size of the connected region. For example, in Paper I we had to assume a value αm = 1 in order to maintain the magnetic connection beyond the corotation radius (“extended” magnetosphere).
Since the main aim of this paper is to study the dynamical processes associated with the inflation and opening of the magnetospheric field lines, we assume a stronger magnetic coupling (αm = 0.1), so that the magnetic configuration opens up closer to the stellar surface (“compact” magnetosphere), where these phenomena can strongly affect both the disk and the stellar dynamics. Besides, we consider different values of the viscosity coefficient αv = 1, 0.3, 0.1 to study the evolution of star-disk systems characterized by different accretion rates. The summary of the cases presented in this paper is given in Table 1. For each simulation we show the viscosity coefficient αv, the magnetic resistivity coefficient αm, the magnetic Prandtl number 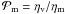 , and the initial viscous accretion rate of the disk Ṁd. We also include the parameters characterizing the reference case of Paper I (case E1) that will be considered to do some comparisons.
, and the initial viscous accretion rate of the disk Ṁd. We also include the parameters characterizing the reference case of Paper I (case E1) that will be considered to do some comparisons.
 |
Fig. 1 Global view of the star-disk interacting system. A logarithmic density map is shown in the background. Poloidal speed vectors are represented as blue arrows. The dotted line marks the Alfvén surface, where |
3. Star-disk interaction and magnetospheric ejections
 |
Fig. 2 Temporal evolution of the periodic inflation/reconnection process which characterizes the dynamics of the magnetospheric ejections in case C03. We show logarithmic density maps with sample field lines (white solid lines) and poloidal speed vectors (blue arrows) superimposed. The yellow solid lines follow the evolution of a single magnetic surface showing clearly the dynamics of the phenomenon. Time is given in units of rotation periods of the central star. |
Using case C03 as a representative example, we analyze the dynamical properties of a interacting star-disk system in which the stellar magnetic field is strongly coupled to the accretion disk. As already pointed out, in such a situation the star-disk differential rotation generates a strong toroidal field component and, due to its pressure, the magnetic structure relaxes by inflating and opening the initial dipolar configuration close to the truncation radius. The overall picture illustrating the outcome of this process is given in Fig. 1. Four groups of field lines can be distinguished: (1) the field lines steadily connecting the disk with the star below the magnetic surface (b); (2) the open field lines anchored on the surface of star at latitudes higher than the position of the surface (a); (3) the open field lines attached to the accretion disk beyond the surface (c); (4) the field lines enclosed between surfaces (a), (b), and (c) connecting the disk with the star, periodically evolving through stages of inflation, reconnection, and contraction. An example of this periodic process is represented in Fig. 2. The periodicity of these phenomena corresponds to about two stellar rotation periods. Since the reconnection processes that are involved are driven by numerical resistivity, this periodicity has to be considered with caution. On the other hand, this almost periodical behavior allows us to use time averages to characterize the long-term evolution of the system and smooth out transient features. For example, Fig. 1 has been obtained by averaging snapshots over 54 rotation periods of the star, and because of the time average, the fleeting reconnection phenomena are not visible.
Different dynamical processes are associated with the four groups of field lines. In the region inside the magnetic surface (b), (“connected disk”) the star and the disk can directly exchange angular momentum, the disk is truncated, and the accretion curtains form. This region extends within the Keplerian corotation radius Rco = 4.64 R⋆ so that, beyond this radius, the disk and the star do not have a direct magnetic connection. Therefore, the Ghosh & Lamb scenario cannot be applied directly: the disk region beyond corotation, which rotates more slowly than the star, cannot exert any direct spin-down torque onto the star. Three classes of outflows correspond to the other groups of field lines. A stellar wind flows along the open magnetic surfaces anchored at high stellar latitudes. A disk wind can be accelerated along the disk open field lines, but only the field lines closer to the star are characterized by a field strong enough for this outflowing component to play a relevant role, as is shown in Sect. 3.3. Finally, the inflation at mid-latitudes of the dipolar field lines is very dynamic, and it is accompanied by outflows that can in principle extract mass, energy, and angular momentum from both the disk and the star. On a relatively large scale (10–20 R⋆, see Fig. 2), these ejections detach from the magnetosphere in a reconnection event and continue their propagation as magnetic islands disconnected from the central part of the star-disk system, in between the open magnetic surfaces anchored into the star and those anchored into the disk. In the following we refer to this type of outflow associated with the process of inflation/reconnection of the magnetospheric field lines as magnetospheric ejections (MEs).
Magnetic flux distribution in the star-disk system.
The different regions outlined in Fig. 1 can also be characterized by the amount of poloidal magnetic flux that participates in each of them. In Table 2 we show, for all the discussed cases, the fraction of magnetic flux Φ = ∫Bp·dS which crosses each region relative to the total stellar flux through one hemisphere, Eq. (6): we display the stellar wind flux ΦSW, also equal to the open magnetic flux of the disk wind, the MEs flux ΦME, the flux of the connected disk ΦCD, and the flux contained in the magnetic cavity inside the truncation radius ΦMC. Obviously we have ΦSW + ΦME + ΦCD + ΦMC = Φ⋆. Since not all the field lines steadily connecting the star to the disk are mass-loaded to form the accretion funnels, we also show the amount of magnetic flux threading the accretion columns ΦAC, which is clearly equal to a fraction of ΦCD, and the corresponding surface covering fraction SAC/S⋆. To give an indication of the size of the different interaction regions, we also provide the position of the disk truncation radius Rt, the anchoring radius Rcm of the outermost steadily connected magnetic surface (labeled as (b) in Fig. 1), and the anchoring radius Rom of the innermost open magnetic surface (labeled as (c) in Fig. 1) at the disk midplane. While the magnetic flux is frozen into the stellar surface, its distribution can change on the disk midplane. Different estimates have been made for the accretion and propeller phases of case C01 (see Sect. 4.2). Besides providing a clear indication of the relative importance of the different dynamical components, these quantities can be directly compared to the predictions of other models, such as the X-wind.
3.1. Dynamical properties of magnetospheric ejections
We now characterize the properties of the MEs by inspecting their mass, angular momentum, and energy fluxes. By defining a surface S perpendicular to the poloidal flow, these are respectively defined as ![\begin{eqnarray} \dot{M} & = & \int_{\vec{S}} \rho \vec{u}_\mathrm{p} \cdot \mathrm{d} \vec{S} \label{eq:mflux} \\[1.5mm] \dot{J} & = & \int_{\vec{S}} \left( r\rho u_\phi \vec{u}_\mathrm{p} - \frac{rB_\phi\vec{B}_\mathrm{p}}{4 \pi} \right) \cdot \mathrm{d} \vec{S} \label{eq:jflux} \\[1.5mm] \dot{E} & = & \int_{\vec{S}} \left[ \left(\frac{1}{2} \rho u^2 + \frac{\gamma P}{\gamma-1}-\frac{GM_\star}{R}\right)\vec{u}_\mathrm{p} + \vec{E}\times\vec{B}\big|_\mathrm{p} \right] \cdot \mathrm{d} \vec{S}. \label{eq:eflux} \end{eqnarray}](/articles/aa/full_html/2013/02/aa20168-12/aa20168-12-eq113.png) As already pointed out, this type of ejection can exchange mass, angular momentum, and energy with both the star and the disk. We can therefore define different contributions to the budget of the MEs. Taking for example the mass flux, we can estimate the stellar mass input as
As already pointed out, this type of ejection can exchange mass, angular momentum, and energy with both the star and the disk. We can therefore define different contributions to the budget of the MEs. Taking for example the mass flux, we can estimate the stellar mass input as 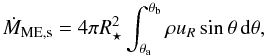 (12)where θa and θb are the anchoring angles onto the stellar surface of the lowest open and the outermost, steadily closed magnetic surfaces, respectively, labeled as (a) and (b) in Fig. 1. The disk contribution can be calculated as
(12)where θa and θb are the anchoring angles onto the stellar surface of the lowest open and the outermost, steadily closed magnetic surfaces, respectively, labeled as (a) and (b) in Fig. 1. The disk contribution can be calculated as 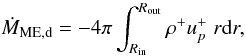 (13)where Rin and Rout are the anchoring radii at the disk surface of the outermost steadily closed magnetic surface and the innermost open field line threading the disk, labeled as (b) and (c) in Fig. 1, whose footpoint radii at the disk midplane are Rcm and Rom, respectively (see Table 2). These radii are marked in the panels of Figs. 7 and 10. The + superscript indicates a quantity evaluated at the disk surface
(13)where Rin and Rout are the anchoring radii at the disk surface of the outermost steadily closed magnetic surface and the innermost open field line threading the disk, labeled as (b) and (c) in Fig. 1, whose footpoint radii at the disk midplane are Rcm and Rom, respectively (see Table 2). These radii are marked in the panels of Figs. 7 and 10. The + superscript indicates a quantity evaluated at the disk surface 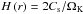 , proportional to the thermal heightscale. The poloidal vectors labeled with a + are defined as the components perpendicular to the surface of the disk: for example, in the case of the speed,
, proportional to the thermal heightscale. The poloidal vectors labeled with a + are defined as the components perpendicular to the surface of the disk: for example, in the case of the speed, 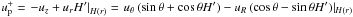 . The total mass flux of the MEs can be evaluated by choosing a surface crossing both magnetic field lines (a) and (c); for example, by selecting a spherical zone with a radius R ≥ 6R⋆, so that it crosses both magnetic surfaces (a) and (c), we define
. The total mass flux of the MEs can be evaluated by choosing a surface crossing both magnetic field lines (a) and (c); for example, by selecting a spherical zone with a radius R ≥ 6R⋆, so that it crosses both magnetic surfaces (a) and (c), we define 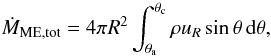 (14)where θa and θc are the angles at which magnetic surfaces (a) and (c) intercept the sphere with radius R. When calculating the time evolution of the previous fluxes, the anchoring angles and radii can vary with time. In a steady situation or considering time-averaged quantities for a system that evolves periodically (as in the considered case), we find that ṀME,tot = ṀME,s + ṀME,d. Analogous expressions can be derived for the angular momentum (
(14)where θa and θc are the angles at which magnetic surfaces (a) and (c) intercept the sphere with radius R. When calculating the time evolution of the previous fluxes, the anchoring angles and radii can vary with time. In a steady situation or considering time-averaged quantities for a system that evolves periodically (as in the considered case), we find that ṀME,tot = ṀME,s + ṀME,d. Analogous expressions can be derived for the angular momentum (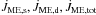 ) and energy fluxes (ĖME,s,ĖME,d,ĖME,tot) by integrating Eqs. (10) and (11) on the same surface elements employed to define the mass fluxes. We exploited the midplane symmetry of our simulations so that the flux integrals are related to two-sided outflows.
) and energy fluxes (ĖME,s,ĖME,d,ĖME,tot) by integrating Eqs. (10) and (11) on the same surface elements employed to define the mass fluxes. We exploited the midplane symmetry of our simulations so that the flux integrals are related to two-sided outflows.
 |
Fig. 3 Temporal evolution of mass fluxes of the different accretion and ejection phenomena present in the system: mass accretion rate measured at the stellar surface (solid line), total mass outflow rate of magnetospheric ejections (dot-dashed line), mass flux fueling the MEs coming from the star only (long-dashed line), stellar wind outflow rate (dashed gray line), disk wind mass outflow rate (dotted line). The image refers to case C03. Time is given in units of rotation periods of the central star. |
3.1.1. Mass fluxes
In Fig. 3 we plot the temporal evolution of the mass-loss rates of the different outflowing components and compare them to the mass accretion rate measured on the surface of the star, defined as 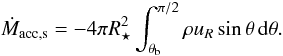 (15)After an initial transient lasting around 20 stellar rotation periods, the total outflow rate of the MEs, calculated using Eq. (14) with R = 7 R⋆, regularly oscillates around a value corresponding to ≈ 18% of the accretion rate at the stellar surface. This corresponds to ≈ 15% of the disk accretion rate measured at Rout. The oscillations correspond to the periodic inflation and reconnection phenomena. The stellar contribution to the MEs, Eq. (12), is a few percent of the accretion rate. This means that MEs are essentially mass-loaded from the disk, and their inertia is dominated by material coming from the accretion disk. The stellar and disk wind mass fluxes plotted in Fig. 3 are defined and discussed in Sect. 3.2.
(15)After an initial transient lasting around 20 stellar rotation periods, the total outflow rate of the MEs, calculated using Eq. (14) with R = 7 R⋆, regularly oscillates around a value corresponding to ≈ 18% of the accretion rate at the stellar surface. This corresponds to ≈ 15% of the disk accretion rate measured at Rout. The oscillations correspond to the periodic inflation and reconnection phenomena. The stellar contribution to the MEs, Eq. (12), is a few percent of the accretion rate. This means that MEs are essentially mass-loaded from the disk, and their inertia is dominated by material coming from the accretion disk. The stellar and disk wind mass fluxes plotted in Fig. 3 are defined and discussed in Sect. 3.2.
 |
Fig. 4 Temporal evolution of the specific angular momentum carried by different accretion and ejection components of the system in case C03: specific angular transported by the accretion flow through Rout (upper panel); total specific angular momentum carried by the MEs (second panel); specific angular momentum extracted by the MEs from the disk only (third panel); specific angular momentum of the stellar wind (lower panel). Dashed lines show the temporal averages of the quantities over the plotted lapse of time. Time is given in units of rotation periods of the star. |
3.1.2. Angular momentum fluxes
Since the MEs are magnetically connected both to the star and the disk, they can potentially extract angular momentum from both. In the second panel from the top in Fig. 4 we plot the temporal evolution of the normalized total specific angular momentum carried by the MEs, defined as 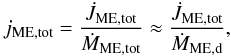 (16)while in the third panel from the top we have evaluated the specific angular momentum extracted by the MEs from the disk only:
(16)while in the third panel from the top we have evaluated the specific angular momentum extracted by the MEs from the disk only: 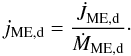 (17)Plots are in units of
(17)Plots are in units of 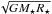 . Both quantities oscillate regularly in time but, if we look at the time averages, we clearly see that the specific angular momentum extracted from the disk is around
. Both quantities oscillate regularly in time but, if we look at the time averages, we clearly see that the specific angular momentum extracted from the disk is around 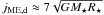 , while the total angular momentum of the MEs is approximately
, while the total angular momentum of the MEs is approximately 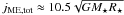 . Clearly, the total angular momentum of the MEs is greater than the angular momentum extracted from the disk alone, meaning that a substantial fraction also comes from the star. In Sects. 3.3 and 3.4 we discuss the effects of these torques on the angular momentum evolution of the disk and the star, respectively.
. Clearly, the total angular momentum of the MEs is greater than the angular momentum extracted from the disk alone, meaning that a substantial fraction also comes from the star. In Sects. 3.3 and 3.4 we discuss the effects of these torques on the angular momentum evolution of the disk and the star, respectively.
3.1.3. Energy fluxes
Concerning the energy budget of the MEs, the power extracted from the disk only corresponds to ĖME,d ≈ 0.2GM⋆Ṁacc,s/Rin ≈ 0.05GM⋆Ṁacc,s/R⋆. It is important to point out that the mechanical power released by the material accreting from Rout down to Rin, defined as 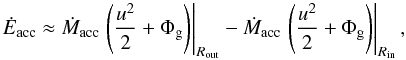 (18)is sufficient to power the part of the MEs coming from the disk. The power extracted from the star is comparable and largely determined by the Poynting flux associated with the spin-down torque
(18)is sufficient to power the part of the MEs coming from the disk. The power extracted from the star is comparable and largely determined by the Poynting flux associated with the spin-down torque 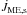 . The enthalpy flux, needed in our simulations to give the initial drive to any stellar outflow, is a small fraction ( ≈ 0.01GM⋆Ṁacc,s/R⋆) of the accretion power. In case C03, the MEs operate as a magnetic sling, powered by both the stellar and disk rotation.
. The enthalpy flux, needed in our simulations to give the initial drive to any stellar outflow, is a small fraction ( ≈ 0.01GM⋆Ṁacc,s/R⋆) of the accretion power. In case C03, the MEs operate as a magnetic sling, powered by both the stellar and disk rotation.
To better understand the asymptotic properties and the acceleration efficiency of MEs, we can inspect the energy conversion along the flow. In Fig. 5 we plot the evolution along the flow of the total specific energy of the MEs as a function of the radial coordinate R: 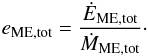 (19)This plot has been obtained by averaging the mass and energy fluxes over 54 stellar periods, and it starts from the cusp of field line (b), located at ≈ 5 R⋆. In a stationary situation this definition obviously corresponds to an average of the Bernoulli invariant over a section of the outflow,
(19)This plot has been obtained by averaging the mass and energy fluxes over 54 stellar periods, and it starts from the cusp of field line (b), located at ≈ 5 R⋆. In a stationary situation this definition obviously corresponds to an average of the Bernoulli invariant over a section of the outflow, 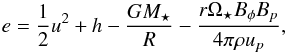 (20)given by the sum of kinetic energy, enthalpy h = γP/(γ − 1)ρ, gravitational and magnetic (Poynting) energy. On the other hand, the more general definition Eq. (18) allows us to define an energy conversion efficiency in the case of nonstationary MEs. We can clearly see that the total energy is not conserved along the flow, mainly because of the dissipation of the magnetic energy owing to the reconnection events. Even if the reconnection is controlled by numerical dissipation and therefore is not physical, it leads to a temperature increase, visible at lower radii in Fig. 5. The outflow cools down subsequently. Since we did not include any realistic cooling function, we simply limited the maximum specific entropy (P/ργ) that can be attained by the outflow in order to preserve code stability. We notice that the kinetic energy stops increasing after ~10 R⋆: this reflects the fact that, after the plasmoids have detached from the inner magnetosphere, the acceleration process stops and the propagation of the outflow becomes ballistic. These aforementioned effects limit the acceleration efficiency of the outflow, whose terminal speed is around 0.5 VK ⋆ . Finally, consistent with their ballistic propagation, MEs cannot be self-collimated thanks to magnetic stresses, as usually envisaged for magnetically driven outflows. This confers the characteristic “conical” shape to these magnetospheric outflows, as already pointed out by Romanova et al. (2009). On the other hand, they can in principle be confined by some external agent, as discussed in Appendix A.
(20)given by the sum of kinetic energy, enthalpy h = γP/(γ − 1)ρ, gravitational and magnetic (Poynting) energy. On the other hand, the more general definition Eq. (18) allows us to define an energy conversion efficiency in the case of nonstationary MEs. We can clearly see that the total energy is not conserved along the flow, mainly because of the dissipation of the magnetic energy owing to the reconnection events. Even if the reconnection is controlled by numerical dissipation and therefore is not physical, it leads to a temperature increase, visible at lower radii in Fig. 5. The outflow cools down subsequently. Since we did not include any realistic cooling function, we simply limited the maximum specific entropy (P/ργ) that can be attained by the outflow in order to preserve code stability. We notice that the kinetic energy stops increasing after ~10 R⋆: this reflects the fact that, after the plasmoids have detached from the inner magnetosphere, the acceleration process stops and the propagation of the outflow becomes ballistic. These aforementioned effects limit the acceleration efficiency of the outflow, whose terminal speed is around 0.5 VK ⋆ . Finally, consistent with their ballistic propagation, MEs cannot be self-collimated thanks to magnetic stresses, as usually envisaged for magnetically driven outflows. This confers the characteristic “conical” shape to these magnetospheric outflows, as already pointed out by Romanova et al. (2009). On the other hand, they can in principle be confined by some external agent, as discussed in Appendix A.
 |
Fig. 5 Radial evolution of the total specific energy carried by the MEs in case C03. The total specific energy (solid line) is given by the sum of Poyinting-to-mass flux ratio (dot-dashed line), kinetic energy (long-dashed line), specific enthalpy (triple-dotted-dashed line) and potential gravitational energy (dotted line, plotted in absolute value). The specific poloidal kinetic energy is also plotted (dashed line). The slow- and fast-magnetosonic surfaces are marked by a vertical line. The plot starts from the cusp of the innermost magnetic surface that steadily connects the disk and the star (labeled as (b) in Fig. 1). The figure has been obtained by time averaging the energy and mass fluxes over 54 rotation periods of the star, from time t = 38 up to t = 92. |
 |
Fig. 6 Forces acting along a field line connecting the star and the disk that is mass-loaded by the MEs in case C03. The left panel refers to the forces acting from the disk midplane up to the cusp of the magnetic surface, while the right panel shows the forces from the stellar surface up to the cusp. We selected a magnetic surface anchored at 4.3 R⋆ on the disk midplane. The plots have been obtained by time averaging the forces over 54 stellar rotation periods. We plot the thermal pressure gradient (solid line), the centrifugal term (dot-dashed line), the Lorentz force (dashed line), and the gravitational pull (dotted line). Vertical lines mark the position of the disk surface (DS) and the slow-magnetosonic point (SM). |
3.1.4. Forces
To complete the analysis of the dynamical properties of the MEs for the reference case C03, we take the forces that drive these outflows into account. Since mass is accelerated both from the disk and the star, we consider an inflating field line anchored in the disk at R = 4.3 R⋆ still connecting the disk and the star: we plot the component of the poloidal forces parallel to this field line from the disk midplane up to the field line cusp (left panel in Fig. 6) and from the stellar surface up to the cusp (right panel in Fig. 6) to analyze the driving mechanism of the MEs from the disk and from the star, respectively. The forces have been obtained from a time-averaged snapshot, in order to smooth out transient features.
In the lefthand panel of Fig. 6 we show that the acceleration of the mass of the MEs coming from the disk is largely due to a combination of centrifugal and magnetic effects, as in a typical disk-driven outflow. In addition, the thermal pressure gradient − ∇∥P is comparable to the centrifugal acceleration at the disk surface (DS, defined as the point where the Lorentz force J × B∥ changes sign) and crucially contributes to the outflow acceleration. As shown in Sect. 3.3, this enhanced thermal pressure gradient is due to the push of the accretion flow against the magnetospheric wall and is responsible for the high mass-load of the MEs coming from the disk. Thermal effects are important since the centrifugal term 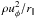 is not sufficient to counteract the gravitational pull ρg∥ at the base of the flow: as more extensively discussed in Sect. 3.3, the disk rotation becomes strongly sub-Keplerian in the disk acceleration region of the MES.
is not sufficient to counteract the gravitational pull ρg∥ at the base of the flow: as more extensively discussed in Sect. 3.3, the disk rotation becomes strongly sub-Keplerian in the disk acceleration region of the MES.
The righthand panel of Fig. 6 shows that the pressure gradient provides the initial thrust of the mass of the MEs coming from the star. Even if this term is most probably not of thermal origin, as assumed in our simulations, it is needed to drive any kind of stellar outflow from slowly rotating stars, where magneto-centrifugal effects are not strong enough to give the initial push. The sudden change in the profile of the forces at r ≈ 7 R⋆ happens when the material accelerated from the star comes across the mass coming from the disk. The latter is characterized by higher density (see, for example, the change in the centrifugal push and gravitational pull), confirming that the MEs inertia is dominated by the mass loaded from the disk, as already discussed in Sect. 3.1.1. The profile of the Lorentz force has some interesting features. We first recall that the Lorentz force parallel to a field line in the poloidal plane is related to the toroidal component of the force, according to the relation
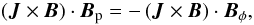 which shows that a Lorentz force accelerating (braking) along a field line also accelerates (brakes) in the toroidal direction. Therefore we can see that the mass loaded from the star is subject to a toroidal acceleration close to the stellar surface, while it is spun down as it gets closer to the part of the MEs coming from the disk, between 5 R⋆ < r < 7 R⋆. This clearly indicates that the star is trying to spin the plasma attached to this field line up, therefore losing angular momentum, while countering the material of the MEs coming from the disk that is trying to spin it down.
which shows that a Lorentz force accelerating (braking) along a field line also accelerates (brakes) in the toroidal direction. Therefore we can see that the mass loaded from the star is subject to a toroidal acceleration close to the stellar surface, while it is spun down as it gets closer to the part of the MEs coming from the disk, between 5 R⋆ < r < 7 R⋆. This clearly indicates that the star is trying to spin the plasma attached to this field line up, therefore losing angular momentum, while countering the material of the MEs coming from the disk that is trying to spin it down.
3.2. Dynamical properties of stellar winds and disk winds
In our simulations, a stellar wind is accelerated along the open field lines anchored in the stellar surface. Due to the energetic limitations illustrated in the Introduction, we limit the mass outflow rate of the stellar wind to a few percent of the mass accretion rate, so that the energy needed to initially drive the outflow corresponds to a small fraction (less than 10%) of the power dissipated by accretion onto the stellar surface. In Fig. 3 the temporal evolution of the stellar wind mass outflow rate is also plotted, calculated as 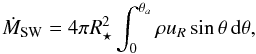 (21)where θa corresponds to the anchoring angle of the last open stellar magnetic surface. The outflow rate corresponds, on average, to ≈ 1.6% of the mass accretion rate measured onto the surface of the star (Eq. (15)). Comparing the mass outflow rate of the reference case with the stellar wind of case E1, we find that the mass loss rate of case C03 corresponds approximately to ~ 30% of the outflow rate of case E1, even though in the two cases we assumed approximately the same injection speed, density, and temperature. The mass ejection rate difference is therefore due to a different size of the launching area. Table 2 shows that in cases C03 and E1 the closed magnetosphere contains approximately the same amount of stellar flux (ΦMC + ΦCD), even if in case C03 this flux is compressed into a much smaller region closer to the star (see Rcm in Table 2); the presence of the MEs, which are almost absent in case E1, reduces the amount of magnetic flux and stellar surface that is available to launch the stellar wind. This example shows that a self-consistent model of stellar winds from accreting protostars must take the presence of the accretion funnels into account, which can strongly affect the geometry of the launching region and the morphology of the magnetic surfaces along which the wind flows.
(21)where θa corresponds to the anchoring angle of the last open stellar magnetic surface. The outflow rate corresponds, on average, to ≈ 1.6% of the mass accretion rate measured onto the surface of the star (Eq. (15)). Comparing the mass outflow rate of the reference case with the stellar wind of case E1, we find that the mass loss rate of case C03 corresponds approximately to ~ 30% of the outflow rate of case E1, even though in the two cases we assumed approximately the same injection speed, density, and temperature. The mass ejection rate difference is therefore due to a different size of the launching area. Table 2 shows that in cases C03 and E1 the closed magnetosphere contains approximately the same amount of stellar flux (ΦMC + ΦCD), even if in case C03 this flux is compressed into a much smaller region closer to the star (see Rcm in Table 2); the presence of the MEs, which are almost absent in case E1, reduces the amount of magnetic flux and stellar surface that is available to launch the stellar wind. This example shows that a self-consistent model of stellar winds from accreting protostars must take the presence of the accretion funnels into account, which can strongly affect the geometry of the launching region and the morphology of the magnetic surfaces along which the wind flows.
We also estimate the specific angular momentum extracted by the stellar winds from the star (lower panel in Fig. 4) defined as 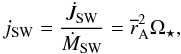 (22)where the stellar wind torque
(22)where the stellar wind torque 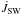 has been obtained by integrating Eq. (10) over the stellar surface from which the wind is launched, as in Eq. (21). This last equation also provides the definition of the average magnetic lever arm
has been obtained by integrating Eq. (10) over the stellar surface from which the wind is launched, as in Eq. (21). This last equation also provides the definition of the average magnetic lever arm 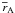 . The average specific angular momentum of the case considered,
. The average specific angular momentum of the case considered, 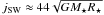 , corresponds to a lever arm
, corresponds to a lever arm 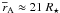 . This value is slightly higher than the value found in case E1 (
. This value is slightly higher than the value found in case E1 (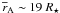 ). Since the mass-to-magnetic flux ratio (η = ρvp/Bp) of the stellar winds of these two cases are comparable, the different topology of the magnetic surfaces due to the interaction with the accretion funnels and the MEs likely determines the different lever arm. We just point out that the magnetic configuration found in case E1 allows wide opening winds, while in case C03 the stellar wind assumes a more conical shape, where the presence of the MEs focuses the open magnetic flux towards the rotation axis.
). Since the mass-to-magnetic flux ratio (η = ρvp/Bp) of the stellar winds of these two cases are comparable, the different topology of the magnetic surfaces due to the interaction with the accretion funnels and the MEs likely determines the different lever arm. We just point out that the magnetic configuration found in case E1 allows wide opening winds, while in case C03 the stellar wind assumes a more conical shape, where the presence of the MEs focuses the open magnetic flux towards the rotation axis.
We can estimate the energy content of the stellar wind by evaluating Eq. (20) at the stellar surface. It can be shown that this expression can be rewritten as 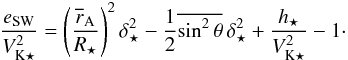 (23)The first term on the righthand side, corresponding to the magnetic flux, is the dominant one. Besides, the stellar boundary conditions on the outflowing material impose
(23)The first term on the righthand side, corresponding to the magnetic flux, is the dominant one. Besides, the stellar boundary conditions on the outflowing material impose 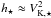 , so that the enthalpy provides the initial drive to the stellar wind: even if this term must have a different origin, it is just meant to mimic the effect of an extra pressure term. Therefore, we find that
, so that the enthalpy provides the initial drive to the stellar wind: even if this term must have a different origin, it is just meant to mimic the effect of an extra pressure term. Therefore, we find that 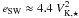 . This specific energy would correspond to a maximum asymptotic speed up,∞ ≈ 2.9VK ⋆ , but the outflow has attained a poloidal speed ≈ VK ⋆ at the end of the computational domain. The stellar wind therefore has the potential to be a light and very fast outflowing component, provided an efficient magnetic-to-kinetic energy conversion can be attained, and this crucially depends on the asymptotic magnetic flux distribution. The total specific energy of the stellar wind is much higher than the one of the MEs (see Fig. 5), almost one order of magnitude, mostly since the MEs are much more massive and therefore have less energy per particle available. This translates into a lower limit on the maximum terminal speed achievable by the MEs.
. This specific energy would correspond to a maximum asymptotic speed up,∞ ≈ 2.9VK ⋆ , but the outflow has attained a poloidal speed ≈ VK ⋆ at the end of the computational domain. The stellar wind therefore has the potential to be a light and very fast outflowing component, provided an efficient magnetic-to-kinetic energy conversion can be attained, and this crucially depends on the asymptotic magnetic flux distribution. The total specific energy of the stellar wind is much higher than the one of the MEs (see Fig. 5), almost one order of magnitude, mostly since the MEs are much more massive and therefore have less energy per particle available. This translates into a lower limit on the maximum terminal speed achievable by the MEs.
We are not going to describe the properties of the disk wind accelerated along the open magnetic surface threading the accretion disk in great detail. Its mass outflow rate, obtained by integrating the mass flux equation Eq. (9) at the disk surface beyond Rout, is rather small, see Fig. 3, and mostly concentrated close to radius Rout, where the magnetic field is stronger. Besides, it is clear from Fig. 1 that the Alfvén surface lies very close to the disk. This means that the disk wind is characterized by a fairly small Alfvén radius, it extracts a limited amount of angular momentum from the disk, and therefore it has a negligible impact on the angular momentum distribution of the star-disk system. This will be shown more quantitatively in the following section.
3.3. The disk’s angular momentum
In this section we analyze the impact of disk-driven outflows, MEs and disk winds, on the angular momentum distribution of the accretion disk. We start our analysis by taking the torques acting on the circumstellar disk into account and their effects on the disk dynamics. Accretion can be triggered (or hampered) by internal torques, which redistribute angular momentum radially inside the disk, or else by external torques, which extract or supply angular momentum at the disk surface. This balance can be expressed in a steady situation by considering the angular momentum conservation inside an annulus of the disk of radial width dr and thickness 2H. Following the notation of Paper I, the angular momentum conservation can be formulated as 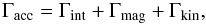 (24)where
(24)where 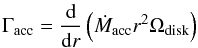 (25)gives the angular momentum advection through the annulus. The mass accretion rate Ṁa is defined as
(25)gives the angular momentum advection through the annulus. The mass accretion rate Ṁa is defined as 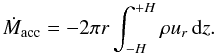 (26)We express the internal torque Γint = Γvisc + ΓB as the sum of the viscous “turbulent” torque:
(26)We express the internal torque Γint = Γvisc + ΓB as the sum of the viscous “turbulent” torque: 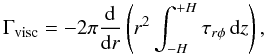 (27)and the radial magnetic transport
(27)and the radial magnetic transport 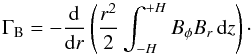 (28)We included this last term for the sake of completeness; nevertheless, the internal torque Γint is dominated by the viscous term. The torque exerted by the large-scale magnetic field, extracting angular momentum at the disk surface, is defined as
(28)We included this last term for the sake of completeness; nevertheless, the internal torque Γint is dominated by the viscous term. The torque exerted by the large-scale magnetic field, extracting angular momentum at the disk surface, is defined as 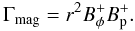 (29)The kinetic torque, determined by the mass exchange at the disk surface, is given by
(29)The kinetic torque, determined by the mass exchange at the disk surface, is given by 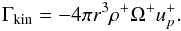 (30)According to these definitions, a positive torque on the righthand side of Eq. (24) extracts angular momentum from the annulus, thus favoring accretion.
(30)According to these definitions, a positive torque on the righthand side of Eq. (24) extracts angular momentum from the annulus, thus favoring accretion.
 |
Fig. 7 Upper panel. Logarithmic density map with sample field lines (yellow solid lines) and speed vectors (blue arrows) superimposed. Middle panel. Radial profiles at the disk midplane of the rotation speed of the accretion disk Ω/Ω⋆ (solid line), accretion sonic Mach number (dot-dashed line) and plasma β (dotted line). The Keplerian and the Ω = Ω⋆ rotation profiles are plotted with a dashed line. Lower panel. Radial profiles of the specific torques acting on the disk (see the text for definitions): magnetic (Γmag, solid line), internal (Γint, dashed line), and kinetic (Γkin, dot-dashed line) torques. In the three panels we marked with vertical lines the position of the truncation radius (Rt) and the anchoring radii at the disk surface of the outermost magnetic surface steadily connecting the star and the disk (Rin) and of the innermost open field line threading the disk (Rout). The panels represent temporal averages over 54 stellar rotation periods. |
In Fig. 7 we show the righthand side torques of Eq. (24) as a function of the radius r (lower panel), in the middle panel the effect of these torques on the disk structure (disk angular speed, accretion sonic Mach number,  and plasma beta, β = 8πB2/P|z = 0), while in the upper panel we display the corresponding density maps with field and stream lines superposed. The three panels are not snapshots at a given time, but have been obtained by averaging over 54 rotation periods of the star, from time t = 38 up to t = 92, in order to smooth out possible transient features. Likewise, we marked three radii corresponding to the truncation radius (Rt), the anchoring radius onto the disk surface of the outermost magnetic field line steadily connecting the disk with the star (Rin), and the innermost open field line threading the disk (Rout). These radii allow three different zones to be distinguished: in the region between Rt and Rin, shaded in red in the middle panel, the disk can directly exchange angular momentum with the star and form the accretion columns; the region between Rin and Rout, shaded in green in the middle panels, despite being magnetically linked to the star, does not exchange angular momentum directly with it, since the magnetic surfaces have expanded too much to be causally connected directly with the star. The material ejected from this region escapes the stellar potential well instead of being accreted, and the angular momentum extracted at the disk surface is transferred to the outflowing material. As already pointed out, this is the region from which the mass coming from the disk is accelerated to fuel the MEs. The disk region outside Rout is threaded by open field lines along which a disk wind can be accelerated, depending on the magnetic field strength.
and plasma beta, β = 8πB2/P|z = 0), while in the upper panel we display the corresponding density maps with field and stream lines superposed. The three panels are not snapshots at a given time, but have been obtained by averaging over 54 rotation periods of the star, from time t = 38 up to t = 92, in order to smooth out possible transient features. Likewise, we marked three radii corresponding to the truncation radius (Rt), the anchoring radius onto the disk surface of the outermost magnetic field line steadily connecting the disk with the star (Rin), and the innermost open field line threading the disk (Rout). These radii allow three different zones to be distinguished: in the region between Rt and Rin, shaded in red in the middle panel, the disk can directly exchange angular momentum with the star and form the accretion columns; the region between Rin and Rout, shaded in green in the middle panels, despite being magnetically linked to the star, does not exchange angular momentum directly with it, since the magnetic surfaces have expanded too much to be causally connected directly with the star. The material ejected from this region escapes the stellar potential well instead of being accreted, and the angular momentum extracted at the disk surface is transferred to the outflowing material. As already pointed out, this is the region from which the mass coming from the disk is accelerated to fuel the MEs. The disk region outside Rout is threaded by open field lines along which a disk wind can be accelerated, depending on the magnetic field strength.
The lower panel shows that the internal turbulent transport is responsible for driving accretion on a large scale (r ≳ 8 R⋆). Even if the disk is threaded by the magnetic flux left by the opening of the dipolar magnetosphere, at this distance from the star the large-scale field is too weak to accelerate a powerful enough disk wind to exert a noticeable torque. Getting closer to the star, the large-scale open magnetic field threading the disk starts to be strong enough to influence the accretion dynamics. Starting already in the region outside Rout, the magnetically-driven disk wind increasingly contributes to drive the accretion flow. Correspondingly, the disk dynamics start to change behavior (middle panels): the rotation profile is still Keplerian but the growing magnetic torque forces the accretion Mach number to increase towards trans-sonic values. Since these outflows do not affect the disk angular momentum distribution in a relevant way (the rotation stays Keplerian) and extract a negligible amount of accreted mass, they will not be discussed in greater detail.
The magnetic torque progressively becomes dominant in the disk region connected to the star from which the MEs arise (Rin < R < Rout). The middle panel shows that, in this region, the accretion Mach number starts to decrease after it has attained a maximum, almost sonic value. This corresponds to an adiabatic compression due to the push of the accretion flow against the stellar magnetosphere, which is acting as a magnetic wall. This compression determines the enhanced mass-loading of the magnetospheric ejections, as the kinetic torque curves show clearly in the lower panel. As already noticed in Paper I, this same effect is crucial for mass-loading the accretion funnels. The ejection torque (kinetic plus magnetic) becomes strong enough so that in this region the disk rotation becomes sub-Keplerian and even sub-stellar. To provide a more precise idea of the amount of angular momentum extracted by the MEs from the star-disk system, we can consider the angular momentum flux carried by the accretion flow through a vertical section of the disk at Rout: 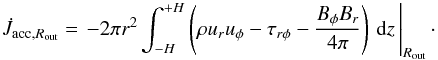 (31)Without any other interaction of the disk with the surroundings inside Rout, this would be the spin-up torque exerted by the accretion flow onto the star. We plot in the upper panel of Fig. 4 the time evolution of the specific angular momentum carried through Rout,
(31)Without any other interaction of the disk with the surroundings inside Rout, this would be the spin-up torque exerted by the accretion flow onto the star. We plot in the upper panel of Fig. 4 the time evolution of the specific angular momentum carried through Rout, 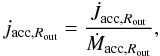 (32)where the disk accretion rate Ṁacc,Rout has been obtained by evaluating Eq. (26) at Rout. The specific angular momentum jacc,Rout is equal, on average, to
(32)where the disk accretion rate Ṁacc,Rout has been obtained by evaluating Eq. (26) at Rout. The specific angular momentum jacc,Rout is equal, on average, to 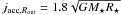 . Since the definition of
. Since the definition of 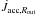 (Eq. (31)) includes the viscous and magnetic torques, jacc,Rout (Eq. (32)) is lower than the specific angular momentum expected from the advection process only ( ≈
(Eq. (31)) includes the viscous and magnetic torques, jacc,Rout (Eq. (32)) is lower than the specific angular momentum expected from the advection process only ( ≈ 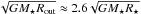 ). Using the estimates done in Sect. 3.1, we can see that the MEs extract directly from the disk a fraction
). Using the estimates done in Sect. 3.1, we can see that the MEs extract directly from the disk a fraction 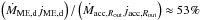 of the angular momentum carried by the disk through Rout, forcing the accretion disk to rotate at a substellar rate. These ejections therefore have the important effect of extracting a relevant fraction of the disk angular momentum and consequently reducing the accretion torque. Besides this, the material ejected from the disk to fuel the MEs clearly rotates slower than the star: since the mass ejected from the disk is also magnetically connected to the star and largely dominates the MEs inertia, it can extract angular momentum from the star thanks to a differential rotation effect.
of the angular momentum carried by the disk through Rout, forcing the accretion disk to rotate at a substellar rate. These ejections therefore have the important effect of extracting a relevant fraction of the disk angular momentum and consequently reducing the accretion torque. Besides this, the material ejected from the disk to fuel the MEs clearly rotates slower than the star: since the mass ejected from the disk is also magnetically connected to the star and largely dominates the MEs inertia, it can extract angular momentum from the star thanks to a differential rotation effect.
The disk region inside Rin can exchange its angular momentum directly with the star. Therefore, all the angular momentum that flows in across Rin is eventually accreted by the star and determines a spin-up torque. In this magnetically connected region, the stellar rotation tries to force the disk to corotate with it. Since in this example the disk rotates slower than the star at Rin, the stellar rotation spins the disk back up to Ω⋆, thus exerting a negative magnetic torque on the disk (see the Γmag curve in the lower panel of Fig. 7) and extracting a fraction of the stellar angular momentum back to the disk. The Γmag curve becomes positive again close to the truncation region and the disk starts to transfer angular momentum to the star. The truncation region is dominated by the kinetic torque, due to the mass loaded onto the base of the accretion funnels3. The external torque (magnetic plus kinetic) is characterized by a double-peaked profile, the inner positive peak being associated with the star-disk angular momentum exchange and the outer one with the torque exerted on the disk by the magnetospheric ejections.
3.4. The stellar angular momentum
In this section we evaluate the impact of accretion and stellar outflows (MEs and stellar winds) on the temporal evolution of the angular momentum of the central star. We can express the time derivative of the stellar angular momentum J⋆ by integrating the angular momentum conservation equation over the stellar volume: 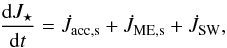 (33)where we separated the contributions to the torque of accretion, magnetospheric ejections and stellar winds. A positive (negative) angular momentum flux on the righthand side of Eq. (33) corresponds to a spin-up (spin-down) torque. The three torques have been obtained by integrating Eq. (10) over three different parts of the stellar surface: the area threaded by open field lines to evaluate the stellar wind torque
(33)where we separated the contributions to the torque of accretion, magnetospheric ejections and stellar winds. A positive (negative) angular momentum flux on the righthand side of Eq. (33) corresponds to a spin-up (spin-down) torque. The three torques have been obtained by integrating Eq. (10) over three different parts of the stellar surface: the area threaded by open field lines to evaluate the stellar wind torque 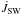 (see Sect. 3.2); the area threaded by magnetic surfaces that undergo periodic inflation/reconnection events to evaluate the MEs contribution
(see Sect. 3.2); the area threaded by magnetic surfaces that undergo periodic inflation/reconnection events to evaluate the MEs contribution 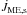 (see Sect. 3.1); the area threaded by field lines steadily connecting the star with the disk to evaluated the accretion torque
(see Sect. 3.1); the area threaded by field lines steadily connecting the star with the disk to evaluated the accretion torque 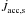 . As already pointed out in Paper I, the contribution of the kinetic terms is completely negligible at the stellar surface, both for accreting and outflowing components, which are completely dominated by the magnetic torque. In the following discussion we will consider the total torques, keeping in mind that the magnetic contribution is prevailing. In Fig. 8 we show the temporal evolution of the torques acting on the star, normalized to the stellar angular momentum J⋆ = I⋆Ω⋆, where
. As already pointed out in Paper I, the contribution of the kinetic terms is completely negligible at the stellar surface, both for accreting and outflowing components, which are completely dominated by the magnetic torque. In the following discussion we will consider the total torques, keeping in mind that the magnetic contribution is prevailing. In Fig. 8 we show the temporal evolution of the torques acting on the star, normalized to the stellar angular momentum J⋆ = I⋆Ω⋆, where 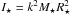 is the stellar moment of inertia. We assumed the typical normalized gyration radius of a fully convective star, i.e. k2 = 0.2. Using this normalization, the curves in Fig. 8 directly provide the inverse of the characteristic braking (or speed-up) timescale. To retrieve the physical units, the plots must be multiplied by Eq. (8) that, expressed in terms of the stellar magnetic field intensity, takes the form
is the stellar moment of inertia. We assumed the typical normalized gyration radius of a fully convective star, i.e. k2 = 0.2. Using this normalization, the curves in Fig. 8 directly provide the inverse of the characteristic braking (or speed-up) timescale. To retrieve the physical units, the plots must be multiplied by Eq. (8) that, expressed in terms of the stellar magnetic field intensity, takes the form 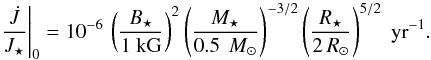 (34)
(34)
 |
Fig. 8 Temporal evolution of the torques acting directly onto the star, normalized to the stellar angular momentum. Plotted are the accretion torque (solid line), the stellar wind torque (dotted line), and the torque exerted by the MEs onto the stellar surface (dashed line). Conventionally, a positive (negative) torque spins the stellar rotation up (down). |
3.4.1. Accretion torque
A rotating accretion disk is likely to exchange angular momentum besides mass with the central object, thus providing a spin-up torque to the latter. The accretion spin-up torque can be parametrized as 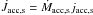 , where jacc,s is the specific angular momentum transported by the accretion streams and along those magnetic surfaces connected to the disk that are not mass-loaded. A common parametrization for the specific accreted angular momentum is
, where jacc,s is the specific angular momentum transported by the accretion streams and along those magnetic surfaces connected to the disk that are not mass-loaded. A common parametrization for the specific accreted angular momentum is 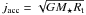 , implying that a Keplerian accretion disk transfers to the star the angular momentum possessed in the truncation region. In our simulations we can estimate the accuracy of this approximation. For example, the specific angular momentum transferred by the disk to the star in case E1 from Paper I is greater than this reference value,
, implying that a Keplerian accretion disk transfers to the star the angular momentum possessed in the truncation region. In our simulations we can estimate the accuracy of this approximation. For example, the specific angular momentum transferred by the disk to the star in case E1 from Paper I is greater than this reference value, 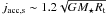 . Since in this case the stellar magnetosphere is connected to the accretion disk over a large extent, even beyond the corotation radius, the star can extract angular momentum from the disk in the entire region from Rt up to Rco. On the other hand, in the “compact” magnetic configuration depicted in Fig. 1, the accretion torque is given by the angular momentum flux through a disk surface from Rt up to Rin < Rco. In case C03, the average accreted angular momentum is approximately equal to 60% of the reference Keplerian value
. Since in this case the stellar magnetosphere is connected to the accretion disk over a large extent, even beyond the corotation radius, the star can extract angular momentum from the disk in the entire region from Rt up to Rco. On the other hand, in the “compact” magnetic configuration depicted in Fig. 1, the accretion torque is given by the angular momentum flux through a disk surface from Rt up to Rin < Rco. In case C03, the average accreted angular momentum is approximately equal to 60% of the reference Keplerian value 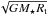 . This effect is due the presence of MEs, which are extracting a consistent fraction of the angular momentum of the accretion disk before it is accreted onto the star.
. This effect is due the presence of MEs, which are extracting a consistent fraction of the angular momentum of the accretion disk before it is accreted onto the star.
3.4.2. Stellar wind torque
In Sect. 3.2 we estimated the mass outflow rate and the specific angular momentum extracted by the stellar wind from the star in the reference case C03. We can now compare the stellar wind torque with the accretion torque. On average, the stellar wind spin-down torque extracts around 66% of the accretion torque. This efficiency seems to be rather high, given the low ejection efficiency of the wind. For example, we recall that the stellar wind of case E1 from Paper I was able to balance only 20% of the accretion torque. Three effects have enhanced the efficiency of the spin-down torque: the mass ejection efficiency in case C03 is slightly higher than in case E1 (1.6% vs. 1.2%); in case C03, the magnetic lever arm is longer (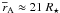 vs.
vs. 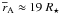 ). But the most important and interesting effect is that, in case C03, the MEs have already extracted a substantial amount of the disk angular momentum, reducing the accretion torque by a factor around 50% (see Sect. 3.3) and therefore enhancing the efficiency of the stellar wind torque.
). But the most important and interesting effect is that, in case C03, the MEs have already extracted a substantial amount of the disk angular momentum, reducing the accretion torque by a factor around 50% (see Sect. 3.3) and therefore enhancing the efficiency of the stellar wind torque.
3.4.3. Magnetospheric ejections torque
As we show in Sect. 3.1, besides reducing the accretion spin-up torque, MEs are able to exchange angular momentum directly with the star. The angular momentum exchange with the star is mainly controlled by the differential rotation between the star and the MEs: if at the cusp of the field line the mass loaded from the disk rotates more slowly (faster) than the star, the MEs exert a spin-down (spin-up) torque. Consistent with that, since we find that in case C03 MEs rotate more slowly than the star (see Sect. 3.3), they exert a net spin-down torque, equal to ≈ 74% of the accretion torque.
Summarizing, in case C03 the combined action of MEs and stellar winds is able to balance the spin-up due to the accretion torque. We notice that, even if MEs represent the dominant effect, by extracting in total ≈ 88% of the disk angular momentum accreted through Rout, the stellar wind can contribute significantly, by extracting, in our example, around 31% of the disk angular momentum flux through Rout. Therefore, in the specific example analyzed in the previous sections, the star is subject to a net spin-down torque: using Eq. (34) to normalize to physical units the sum of the three torques plotted in Fig. 8, we can estimate a characteristic spin-down timescale of ≈ 5.5 × 106 yr.
4. Varying the mass accretion rate
In this section we analyze cases C1 and C01 and compare them with the results obtained from case C03, extensively presented in Sect. 3. We recall that these two cases are characterized by a different disk viscosity coefficient αv (see Table 1), with all the other parameters of the problem left unchanged. Primarily, we use the αv parameter to change the mass accretion rate of the disk. On the other hand, this also modifies the magnetic Prandtl number 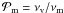 of the disk. Therefore, we bear in mind that our cases are not just characterized by different accretion rates and that other important aspects of the disk physics change. For example, the viscous accretion timescale varies from case to case, while the different Prandtl number can have an impact on the inclination of the field lines at the disk surface and on the advection of the magnetic flux in the part of the disk dominated by the viscous torque. Different accretion rates could also have been obtained by varying the disk density with a fixed Prandtl number, possibly giving somewhat different results.
of the disk. Therefore, we bear in mind that our cases are not just characterized by different accretion rates and that other important aspects of the disk physics change. For example, the viscous accretion timescale varies from case to case, while the different Prandtl number can have an impact on the inclination of the field lines at the disk surface and on the advection of the magnetic flux in the part of the disk dominated by the viscous torque. Different accretion rates could also have been obtained by varying the disk density with a fixed Prandtl number, possibly giving somewhat different results.
4.1. High accretion rate and stellar spin-up
Case C1 is characterized by a value αv = 1, determining an accretion rate around three times higher than the reference case C03, as confirmed by the temporal evolution of the accretion rate measured onto the stellar surface plotted in Fig. 9. There is another feature that is worth noticing: while in case C03 the accretion rate attains a rather constant asymptotic value, in case C1 it slowly grows in time. We have already shown in Sect. 3.3 that the accretion flow is controlled by the internal viscous torque far from the star, while it is determined by the external magnetic torques in the region of magnetospheric interaction. A mismatch between the two torques can trigger long-term variability. For example, it seems that in case C1 the magnetosphere cannot sustain the accretion rate of the outer disk. This determines a density and pressure buildup inside the disk that, due to the α parametrization, causes an increase in the viscous torque and therefore in the accretion rate. The constant asymptotic value of the accretion rate in case C03 is likely to come from a better matching between the inner magnetic and outer viscous torques.
The global magnetic configuration of case C1 is very similar to case C03 (see Fig. 1) and the same dynamical features can be found. Regarding the MEs, their total mass outflow rate corresponds to around 6% of the disk accretion rate, and as in case C03, the mass extracted from the disk largely dominates the mass content of the MEs (see Fig. 9). In the bottom panel of Fig. 10 we can see that the MEs are accelerated from a region of the disk located inside the Keplerian corotation radius, which is more compact than in case C03, probably because of the higher magnetic Prandtl number. Outside Rout, accretion is mainly triggered by the viscous torque, with a relatively small contribution from a weak disk wind, which, nevertheless, accelerates the accretion flow towards an almost sonic accretion speed (middle panel in Fig. 10), without modifying the Keplerian structure of the disk. Inside the launching region of the MEs (Rin < R < Rout), the torque due to the MEs becomes dominant. To estimate the efficiency of this torque, we calculated the specific angular momentum carried by the accretion flow through Rout (see Eq. (31)) and the specific angular momentum extracted by the MEs from the disk (see Eq. (17)) and plotted them in the upper and third panels in Fig. 11, respectively: MEs extract about 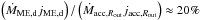 of the angular momentum carried by the disk through Rout. The lower torque efficiency measured in case C1 is due to a lower mass ejection efficiency but also to smaller specific angular momentum extracted from the disk. This is consistent with the fact that in case C1 the magnetic surfaces along which the MEs are accelerated have a larger inclination angle with respect to the disk surface (compare the upper panels of Figs. 7 and 10), thus determining a smaller magnetic lever arm. Nevertheless, the MEs torque is strong enough so that the disk rotation speed becomes sub-Keplerian (middle panel in Fig. 10), but not substellar as in case C03.
of the angular momentum carried by the disk through Rout. The lower torque efficiency measured in case C1 is due to a lower mass ejection efficiency but also to smaller specific angular momentum extracted from the disk. This is consistent with the fact that in case C1 the magnetic surfaces along which the MEs are accelerated have a larger inclination angle with respect to the disk surface (compare the upper panels of Figs. 7 and 10), thus determining a smaller magnetic lever arm. Nevertheless, the MEs torque is strong enough so that the disk rotation speed becomes sub-Keplerian (middle panel in Fig. 10), but not substellar as in case C03.
The angular momentum carried by the disk through Rin is finally transferred to the star and exerts a spin-up torque. In the lower panel of Fig. 10 it is possible to see that, in the disk region directly connected to the star below Rin, the angular momentum is extracted from the disk and transferred to the star by a combination of magnetic and kinetic torques, where the peak of the latter corresponds to the angular momentum loaded onto the base of the accretion funnels. The external torque (magnetic plus kinetic) in the region R < Rout qualitatively presents the same double-peaked profile of case C03, with the inner peak corresponding to the angular momentum exchange with the star, while the outer one representing the torque exerted by the MEs onto the disk. Using the same parametrization as employed in Sect. 3.4.1, we can estimate that the specific angular momentum transferred to the star corresponds to 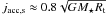 of the reference “Keplerian” value. This clearly shows that also in case C1 one important effect of the MEs is to reduce the amount of angular momentum that the disk transfers to the star, although less efficiently than in case C03.
of the reference “Keplerian” value. This clearly shows that also in case C1 one important effect of the MEs is to reduce the amount of angular momentum that the disk transfers to the star, although less efficiently than in case C03.
The temporal evolution of the accretion torque is plotted in Fig. 12, together with the torques exerted by the MEs and the stellar wind onto the stellar surface. The asymptotic increase in the accretion torque is clearly linked to the temporal growth of the mass accretion rate discussed previously. The spin-down torque exerted by the stellar wind only corresponds to 7.5% of the accretion torque. Despite carrying a specific angular momentum comparable to and even slightly larger than case C03 (see bottom panels of Figs. 4 and 11), the low ejection rate (ṀSW ≈ 2 × 10-3 Ṁacc,s) strongly limits the efficiency of the spin-down torque. By inspecting Table 2, it is possible to notice that the connected magnetosphere contains more magnetic flux (ΦCD + ΦMC) in case C1 and it is even more compressed (see Rcm) than in case C03. The accretion funnels end at slightly higher latitudes, leaving less room for the acceleration area of MEs and stellar winds.
The stellar wind torque slowly drops in time owing to the decrease in the stellar wind specific angular momentum (lower panel in Fig. 11). This is likely associated with the increase in the mass accretion rate, which can modify the shape of the magnetic nozzle at the base of the stellar wind, the acceleration efficiency of the outflow, and therefore its magnetic lever arm. The torque exerted by the MEs directly onto the star is almost completely negligible. It is possible to see in Fig. 12 that for t > 60 it even becomes positive, contributing to the spin-up torque, even if to a very small extent. As pointed out in Sect. 3.4.3, the angular momentum exchange between the MEs and the star depends on a differential rotation effect between the star and the mass loaded from the disk onto the MEs. We saw in Fig. 10 that the base of the MEs rotates at a sub-Keplerian but still super-stellar angular speed in case C1; the MEs do not directly brake the stellar rotation and can actually spin it up. The same effect can be noticed in the two central panels of Fig. 11, which show that the total specific angular momentum carried by the MEs (second panel) is smaller than the specific angular momentum extracted from the disk (third panel). In case C1, unlike case C03, the MEs can extract energy and angular momentum from the disk but then transfer a small fraction back to the star.
Since in this case the spin-down torques are very inefficient, the star experiences a strong spin-up torque due to accretion. Normalizing the torques plotted in Fig. 12 with Eq. (34), we estimate a characteristic spin-up timescale around 5.5 × 105 yr.
 |
Fig. 13 Left panel. Temporal evolution of different mass fluxes in case C01. Plotted are the mass accretion rate onto the stellar surface (solid line), the stellar wind outflow rate (dashed gray line), and the stellar mass flux contribution to the MEs (dashed line). Right panel. Temporal evolution of the torques acting onto the stellar surface, normalized to the stellar angular momentum. Plotted are the spin-up torque associated with accretion (solid line), the spin-down torque exerted along the magnetic surfaces connecting the star and the disk (dashed line) and the spin-down torque due to the stellar wind (dotted line). |
 |
Fig. 14 Time evolution of an accretion cycle during the propeller phase of case C01. We show logarithmic density maps with sample field lines (solid lines) and speed vectors (blue arrows) superimposed. The yellow solid line follows the evolution of a single magnetic surface, clearly showing the periodicity of the accretion-ejection cycles. Time is given in units of the stellar rotation period. |
4.2. Low accretion rate: transition to a “propeller” regime
Case C01 is characterized by a lower disk turbulent viscosity (αv = 0.1), hence a lower mass accretion rate. Consistent with the results of cases C03 and C1, in case C01 the viscous torque likely supports an accretion rate, which is smaller than the one determined by the inner magnetospheric torques. Therefore, the disk tends to empty, reducing its surface density and pressure, thus decreasing the α torque and its accretion rate. Besides, the α-disk model that we employed as initial condition presents a large-scale meridional circulation pattern for low αv values, with the disk accreting only along the surface layers and excreting along the midplane. Especially for low αv values, this model becomes very sensitive to local changes in thermal pressure gradients, and its accretion rate is difficult to control.
Due to these effects, the disk accretion rate in this case is rather low and slowly decreases in time. This is clearly visible in the lefthand panel of Fig. 13, where, after a strong initial transient peak, the accretion rate diminishes steadily, subsequently it starts to oscillate and, at last (t > 60), it becomes highly unsteady and intermittent, varying periodically between relatively high and extremely low values. The system evolution during one of these cycles is depicted in Fig. 14, which clearly shows how the accretion cycles correspond to a periodic oscillation of the truncation radius.
The low-accretion phases correspond to the truncation radius moving close to the Keplerian corotation radius. In this situation it is hard to form the accretion funnels, since the centrifugal barrier raised by the rotating magnetosphere prevents the disk material from falling towards the star, and an extra thermal pressure gradient would be required to cross the barrier (Koldoba et al. 2002). As extensively discussed by Bessolaz et al. (2008), the disk truncation is primarily determined by a pressure equilibrium between the disk and the magnetosphere. Therefore in case C01, as the accretion rate decreases, the disk reduces its push against the magnetosphere and the truncation radius progressively moves outwards closer to corotation. A consequence of the disk being truncated beyond the corotation radius is that, since in this region a Keplerian disk rotates more slowly than the star, the stellar rotation tries to increase (“propel”) the disk angular speed in the region directly connected to the star, hence the appellative “propeller” regime (Illarionov & Sunyaev 1975; Ustyugova et al. 2006). In our simulations, a propeller effect can be present even below the Keplerian corotation radius, whenever the disk rotation becomes substellar, see for example Fig. 7. Despite the propeller effect, the angular momentum extracted from the star is likely not to have enough energy to gravitationally unbind all accreting matter (Spruit & Taam 1993). As the disk moves farther from the star, the stellar magnetic field weakens and the magnetosphere is inflated more and more, losing part of its connection with the disk. As the field lines open up, a massive magnetospheric outflow is launched along the opening magnetic surfaces. These ejections are analogous to the MEs described in the previous sections; in a propeller phase, they can be even stronger and can extract a large fraction of the angular momentum of the disk. Because of the torque exerted by these strong ejections, the disk temporarily increases its accretion rate and its drive against the stellar magnetosphere. The truncation radius can therefore move closer to the star, the funnel flows are fueled again, and the accretion rate onto the surface of the star increases. At the same time, the inflated field lines along which the MEs have been launched tend to close again and quench the outflow (see the lower central panel in Fig. 14). Instead of losing angular momentum to the outflow, the disk can now acquire it from the star along the field lines that are connected to the star, since, due to the action of the MEs, the disk rotation is at least in part substellar, analogous to case C03. The disk therefore decreases its drive against the compressed magnetosphere, which pushes back the disk towards the corotation region and the cycle repeats. The disk can move outwards not only if it becomes super-Keplerian, but since the closed magnetosphere is strongly compressed during the accretion phase (see for example Fig. 8 in Paper I), the poloidal magnetic pressure can also effectively push the disk outwards whenever the latter reduces its thrust.
These accretion/ejection cycles have been observed in other numerical works (e.g. Goodson et al. 1999b; Ustyugova et al. 2006): we notice that the range of timescales and amplitudes of the oscillations observed in these papers can be simply the result of different parameters of the models, i.e. stellar rotation period, magnetic field intensity, and disk accretion rate. The accretion cycles of a disk truncated close to corotation have also been predicted by Spruit & Taam (1993, see also D’Angelo & Spruit 2010). They show how an accretion disk truncated beyond the Keplerian corotation radius can possibly readjust its temperature and density structure so that the viscous stresses get rid of the excess angular momentum coming from the star, and the accretion flow can cross the corotation radius and cyclically form the accretion funnels. The characteristic period of their cycles is obviously associated with the viscous accretion timescale in the corotation region. In our simulation the timescale of the accretion cycles is much shorter. Since the oscillations are mainly driven by the torque exerted by the MEs, the typical period is a few Keplerian orbits around the corotation radius.
The torques exerted onto the star are plotted in the righthand panel of Fig. 13. Clearly, during the “propeller” phases characterized by an extremely low accretion rate, there is no spin-up torque associated with accretion. A strong spin-down torque is exerted along the field lines connected to the disk. Because of the large amount of angular momentum extracted by the magnetospheric ejections, both the accretion disk and the MEs rotate more slowly than the central star, even in the subcorotation region. Therefore the star can be efficiently spun-down along the magnetic surfaces directly connected with the disk and the MEs.
During the high-accretion phases, the disk can deposit its angular momentum along the funnel flows, exerting a small but noticeable spin-up torque. The spin-down torque exerted along the closed magnetosphere is reduced, since the MEs, which are the main cause of this torque, are weaker during the accretion phases; nevertheless, it is still possible to balance the torque due to accretion. The accreting phases of case C01 resemble, at least qualitatively, the steadily accreting case C03.
Finally, it is important to notice that a stellar wind is also present in case C01, exerting a strong spin-down torque onto the star. Table 2 shows that in this case the stellar wind can exploit a larger amount of open stellar flux, which further increases during the nonaccreting phases, when the stellar wind torque seems to become even stronger. This is obviously not consistent with having a stellar wind fueled by the accretion power. In case C01 the stellar wind would require a considerable driving power, even during the phases during which the disk is not accreting. On the other hand, in this case the role played by the stellar wind can be neglected, since the torque exerted by the star-disk-MEs interaction is generally sufficient to brake the stellar rotation. Even neglecting the stellar wind torque, we can estimate that, on average, the characteristic spin-down timescale in case C01 is approximately equal to 8 × 105 yr.
5. Discussion
In this section we compare our findings with works that have described related scenarios and addressed similar issues. First of all, we point out that phenomena qualitatively similar to the MEs have been observed in a number of simulations of magnetic star-disk interaction. In spite of differences in interpreting the results, we have the feeling that these numerical experiments essentially show the same process. For example, Hayashi et al. (1996) observed a plasmoid ejection associated with the expansion of the magnetosphere and associated the reconnection episodes to the X-ray flares observed in young stars. A series of papers (Goodson et al. 1997, 1999a,b; Matt et al. 2002) propose the “episodic magnetospheric inflation” mechanism (EMI, Matt et al. 2003) to explain the origin of jets from young stars. This is probably due to the fact that, besides the presence of uncollimated outflows commonly related to this phenomenon, these simulations show the formation of a dense, axially collimated jet, fueled during the inflation phases by mass coming from the accretion streams and focused on the rotation axis by the expansion of the closed magnetosphere. While their description of this mechanism is very phenomenological, this dense collimated axial feature has not been observed in our numerical models. Additionally, the periodic behavior of the mass accretion rate suggests that these solutions might be in a “propeller” regime. More recently, Romanova et al. (2009) have developed both axisymmetric and three-dimensional nonaxisymmetric simulations that describe the formation of uncollimated outflows (“conical winds”) coming from the boundary of the closed magnetosphere, both for slowly and fast-rotating stars. Despite clear similarities between these results and the scenario proposed in this paper, we have performed a much more detailed analysis of the dynamics and the energetics of MEs, which allowed us to obtain precise results about how they can affect the angular momentum of the star-disk system. For example, we showed how MEs can extract angular momentum from both the disk and the star so that their action can be compared to that of X-winds, on one hand, and stellar winds, on the other.
Similar to X-winds, we showed that MEs can extract a relevant fraction of the disk angular momentum in order to reduce the spin-up torque exerted by accretion. In fact, the X-wind model represents an extreme solution in which all the angular momentum carried by the accretion flow is extracted from the disk, so as to at least cancel the accretion torque. For the MEs we estimated a lower efficiency, e.g. 53% in the fiducial C03 case. Owing to the lower torque efficiency, the energy needed to drive MEs is compatible with the mechanical power released by the accretion flow, while the latter is likely to be insufficient for driving an efficient X-wind (Ferreira & Casse 2013). In addition, the MEs can also extract angular momentum directly from the star, similar to stellar winds. The main difference is that, while the spin-down torque exerted by stellar winds strongly depends on the mass flux of the wind (Matt & Pudritz 2008a), the torque of the MEs is determined by a differential rotation effect between the star and the material ejected from the disk. Therefore, MEs do not seem to suffer the energetic problems associated with the mass-loading of the stellar winds. The idea of having an outflow mass-loaded from the accretion disk capable of extracting angular momentum from the central star is close to the “Reconnection X-wind” model (Ferreira et al. 2000), even if this scenario had been envisaged for a different magnetic configuration.
An important difference between MEs and stationary winds is represented by their asymptotic behavior. While the large-scale acceleration and collimation properties of steady outflows, whether coming from the star or the disk, depend on the global distribution of their poloidal magnetic flux and electric current, we showed that MEs rapidly disconnect from the central region of the disk-star system because of reconnection events and propagate ballistically afterwards, without accelerating any further. Flowing in between a stellar wind and a disk wind (see Fig. 1), the confinement of the MEs depends on the collimating/decollimating behavior of the other two outflows (see discussion in Appendix A).
A final comparison can be made between the poloidal magnetic configuration found in our simulations and the one expected from the X-wind model, at least in its “dipolar” formulation (see e.g. Ostriker & Shu 1995). The amount of magnetic flux contained in the magnetic cavity is fairly consistent with our results (ΦMC in Table 2). The X-wind model also predicts that the remaining flux (see Eq. (11) in Mohanty & Shu 2008) is trapped in the disk in a small region around the corotation radius and is evenly shared among the accretion funnels (ΦAC), the open flux (ΦSW), and the remaining closed field lines that do not accrete (ΦME + ΦCD − ΦAC). In our simulations the flux repartition can noticeably vary from case to case, but it can actually be similar to the X-wind distribution in cases close to the spin equilibrium (e.g., during the accretion phases of case C01). Three important differences can be pointed out: (1) in our simulations the magnetic flux involved in the star-disk interaction is distributed over a sizable region of the disk, as shown by the anchoring radii of the different magnetic surfaces given in Table 2; (2) there is no magnetically “dead zone”, namely a magnetic zone with neither mass nor angular momentum exchanges, as proposed in the X-wind scenario: in contrast, we obtain an extremely active, outbursting zone where MEs take place; (3) the steadily open magnetic surfaces threading the disk, where the X-wind should be accelerated, play a marginal role in our solutions.
In the following section we compare the efficiency of the spin-down torques found in our simulations more quantitatively with the outcome of other scenarios proposed in the literature.
5.1. Zero-torque condition
By progressively lowering the disk accretion rate, the three simulations analyzed in this paper show a transition from a strong spin-up (case C1) to an efficient spin-down state (case C01). This trend also corresponds to a different distribution of the stellar magnetic flux among the spin-down/spin-up phenomena (see Table 2), where the magnetic flux associated with the accretion spin-up torque (ΦAC and ΦCD) decreases at the expenses of the spin-down mechanisms (ΦME and ΦSW). In case C03, the torques exerted by the MEs, with a weaker but non-negligible contribution from a light stellar wind, are able to balance the accretion torque, so that the net total torque is approximately zero (actually slightly negative in this specific case). Correspondingly, the truncation radius moves from Rt ≈ 0.45 Rco (case C1) to Rt ≈ 0.8 Rco (case C01), with the zero-torque configuration located approximately at Rt ≈ 0.6 Rco. The simulations confirmed the results of Bessolaz et al. (2008) and of Paper I, showing that the Alfvén radius for a spherical free-fall collapse (Elsner & Lamb 1977), namely 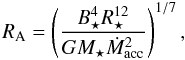 (35)is a good parametrization of the truncation radius. In our simulations we have found Rt ≈ 0.4 RA. Therefore the zero-torque state corresponds roughly to a situation where Rco ≈ 0.67 RA. A proportionality relationship between Rco and RA has been used in different scenarios to estimate the stellar rotation period corresponding to a zero-torque situation:
(35)is a good parametrization of the truncation radius. In our simulations we have found Rt ≈ 0.4 RA. Therefore the zero-torque state corresponds roughly to a situation where Rco ≈ 0.67 RA. A proportionality relationship between Rco and RA has been used in different scenarios to estimate the stellar rotation period corresponding to a zero-torque situation: 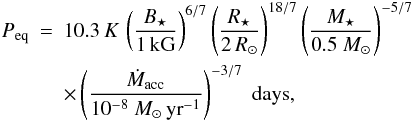 (36)where K = (Rco/RA)3/2. Obviously, the longer the equilibrium rotation period, the more efficient the spin-down mechanism. We have already shown that our simulations suggest a value K ≈ 0.54. We can compare this result with the outcome of other popular scenarios.
(36)where K = (Rco/RA)3/2. Obviously, the longer the equilibrium rotation period, the more efficient the spin-down mechanism. We have already shown that our simulations suggest a value K ≈ 0.54. We can compare this result with the outcome of other popular scenarios.
Applying the classical Ghosh & Lamb scenario to the case of T Tauri stars, Königl (1991) used a value K = 0.87. On the other hand, the corrections brought to the Ghosh & Lamb model by Matt & Pudritz (2005a) provide an upper limit K < 0.3, keeping in mind that, according to Paper I, the Ghosh & Lamb spin-down torque is likely to be even weaker than the Matt & Pudritz (2005a) estimate. In the case of the X-wind model, Ostriker & Shu (1995) employed a value K = 0.89, even if we recall that many properties of the scenario are based on ad-hoc assumptions and are not the result of a detailed dynamical calculation. The results of the time-dependent axisymmetric simulations by Long et al. (2005) have been recently re-examined, suggesting a value K = 0.52 (Romanova, priv. comm.), in good agreement with our findings.
For the accretion-powered stellar wind scenario, it is possible to derive an expression analogous to Eq. (36) by equating the spin-down torque of a stellar wind 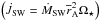 with the accretion torque of the disk
with the accretion torque of the disk 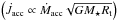 . Using Eq. (12) from Matt & Pudritz (2008a) to determine the average Alfvén radius
. Using Eq. (12) from Matt & Pudritz (2008a) to determine the average Alfvén radius 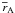 and assuming the accretion torque found in our case E1, since it is not affected by the presence of the MEs
and assuming the accretion torque found in our case E1, since it is not affected by the presence of the MEs 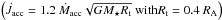 , we obtain
, we obtain 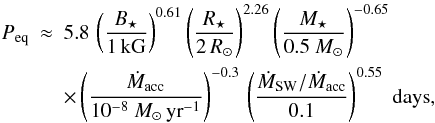 (37)similar to Eq. (17) in Matt & Pudritz (2008b). This equation clearly shows that an ejection efficiency ṀSW/Ṁacc ~ 0.1 is needed to give a characteristic rotation period that is comparable to the other scenarios, as discussed in Matt et al. (2012).
(37)similar to Eq. (17) in Matt & Pudritz (2008b). This equation clearly shows that an ejection efficiency ṀSW/Ṁacc ~ 0.1 is needed to give a characteristic rotation period that is comparable to the other scenarios, as discussed in Matt et al. (2012).
Since Eqs. (36) and (37) describe an equilibrium between accretion and spin-down torques, the same zero-torque condition (i.e. the same Peq) can be obtained by varying the mass accretion rate, proportional to the accretion torque, and the stellar magnetic field intensity, mainly related to the spin-down torque. This implies that stars with a comparatively lower accretion rate need a weaker dipolar field to balance the accretion torque.
5.2. Stellar contraction and spin-down
The zero-torque condition discussed in the previous section is fairly challenging to obtain for all the discussed models, but it is obviously not sufficient to keep the rotation period of a contracting star constant. The time derivative of the stellar angular velocity, 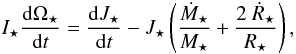 (38)also depends on the temporal evolution of the stellar mass and radius. The righthand side of Eq. (38) defines three timescales: the term Ṁ⋆/M⋆ ~ 1/tacc is associated with the accretion timescale, typically tacc ~ 107 − 1010 yr for a CTTS. The term Ṙ⋆/R⋆ ~ − 1/tKH is associated with the the Kelvin-Helmholtz contraction timescale:
(38)also depends on the temporal evolution of the stellar mass and radius. The righthand side of Eq. (38) defines three timescales: the term Ṁ⋆/M⋆ ~ 1/tacc is associated with the accretion timescale, typically tacc ~ 107 − 1010 yr for a CTTS. The term Ṙ⋆/R⋆ ~ − 1/tKH is associated with the the Kelvin-Helmholtz contraction timescale: 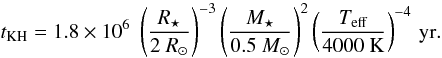 (39)Clearly, it is necessary to exert a net negative torque onto the star with a characteristic spin-down timescale
(39)Clearly, it is necessary to exert a net negative torque onto the star with a characteristic spin-down timescale  that is at least comparable to the contraction timescale to maintain a steady stellar rotation period. In our simulations this condition is clearly satisfied during the propeller phases of case C01. This regime occurs whenever the disk is truncated close enough to the corotation radius (Rt ≳ 0.8 Rco in our simulations); however, this condition is necessary but not sufficient to have a strong enough spin-down torque to balance the stellar contraction. While different B⋆ − Ṁacc combinations can satisfy the condition Rt ≈ 0.8 Rco, as in the case of a null torque configuration, a strong magnetic field is needed to provide a spin-down torque able to balance the stellar contraction. This is clearly shown by Eq. (34), used to normalize the torques plotted in Figs. 8, 12, and 13. In case C01 we must assume a kG dipolar magnetic field to obtain a short enough spin-down timescale. This result shows that, even if stars characterized by a low accretion rate (e.g. < 10-9 M⊙yr-1) need a dipolar field weaker than a kG to cancel the accretion torque, they still need a kG dipole to balance their contraction.
that is at least comparable to the contraction timescale to maintain a steady stellar rotation period. In our simulations this condition is clearly satisfied during the propeller phases of case C01. This regime occurs whenever the disk is truncated close enough to the corotation radius (Rt ≳ 0.8 Rco in our simulations); however, this condition is necessary but not sufficient to have a strong enough spin-down torque to balance the stellar contraction. While different B⋆ − Ṁacc combinations can satisfy the condition Rt ≈ 0.8 Rco, as in the case of a null torque configuration, a strong magnetic field is needed to provide a spin-down torque able to balance the stellar contraction. This is clearly shown by Eq. (34), used to normalize the torques plotted in Figs. 8, 12, and 13. In case C01 we must assume a kG dipolar magnetic field to obtain a short enough spin-down timescale. This result shows that, even if stars characterized by a low accretion rate (e.g. < 10-9 M⊙yr-1) need a dipolar field weaker than a kG to cancel the accretion torque, they still need a kG dipole to balance their contraction.
6. Summary and conclusions
 |
Fig. 15 Poloidal current circuits flowing in the star-disk system in cases C1 (left panel) and C03 (right panel). Dark (red) circuits circulate clockwise along isosurfaces of rBφ > 0. Yellow (light) circuits circulate counterclockwise along isosurfaces of rBφ < 0. Current circuits are superimposed on a logarithmic density map. The figures have been obtained by time averaging over 54 stellar rotation periods. |
In this paper we presented axisymmetric MHD time-dependent simulations of the interaction of a dipolar stellar magnetosphere with a surrounding viscous and resistive accretion disk (using α prescriptions). We assumed a magnetic coupling that is strong enough (i.e. a resistivity sufficiently low) so that the buildup of the toroidal field magnetic pressure due to the star-disk differential rotation inflates and opens up the dipolar structure close to the central star and the truncation region. In particular, the strong coupling prevents the closed magnetosphere to extend beyond the Keplerian corotation radius, so that the Ghosh & Lamb spin-down model, studied in Paper I, can no longer be applied. On the other hand, the simulations showed that magnetospheric ejections naturally arise because of the process of expansion and reconnection of the magnetospheric field lines connected to the disk. We extensively studied the dynamical properties of these ejections with a special focus on their impact on the angular momentum of the star-disk system. At the same time we have included in our models the spin-down torque exerted by a stellar wind. We here summarize the main results of our numerical experiments.
-
1.
MEs can exchange mass, energy and angular momentum withboth the star and the disk. Their inertia and mass content arelargely dominated by the material loaded from the accretion disk.If the mass load rotates more slowly than the star, the ejections canbe powered by both the stellar and disk rotation, as in a hugemagnetic slingshot.
-
2.
MEs cannot explain the jet phenomenon in T Tauri stars: (1) their terminal speed is unlikely to be higher than the gravitational escape speed; (2) after they disconnect from the star-disk system, they propagate ballistically as uncollimated plasmoids. Their confinement depends on the collimation properties of the outflows between which they propagate, stellar and disk winds.
-
3.
MEs crucially contribute to control the stellar rotation period. On one hand, they efficiently extract angular momentum from the disk close to the truncation region so that the spin-up accretion torque is noticeably reduced. On the other hand, if the torque exerted onto the disk is strong enough so that the ejected plasma rotates more slowly than the star, MEs can extract angular momentum directly from the star thanks to a differential rotation effect (slingshot effect). We found a balance between the accretion torque and the spin-down torque for Rt ≈ 0.6 Rco.
-
4.
The efficiency of the spin-down torque of MEs is comparable to other scenarios proposed in the literature, keeping in mind that (1) the Ghosh & Lamb (1979) spin-down torque is highly overestimated (see Matt & Pudritz 2005a; Zanni & Ferreira 2009); (2) a fully self-consistent dynamical model of the X-wind scenario is currently not available; (3) the mass ejection efficiency of a stellar wind capable of balancing at least the accretion torque is energetically very demanding. While the torques exerted by MEs onto the disk and the star share some similarities with the X-wind and stellar wind models, respectively, MEs do not seem to be affected by the energetic limitations that concern the other two scenarios.
-
5.
We limited the mass ejection efficiency of the stellar winds to a few percent. Consistently with the Matt & Pudritz (2008b) results, these winds are not strong enough to balance the spin-up due to accretion and contraction. Nevertheless, we found that for a wind mass flux around 1–2% of the accretion rate, the spin-down torque corresponds to 20–30% of the accretion torque. We found that a light disk wind is launched along the open magnetic surfaces threading the disk but, due to the weakness of the field, the impact of this outflow on the angular momentum structure of the Keplerian disk is negligible.
-
6.
In a propeller phase, when the truncation radius gets close enough to corotation (Rt ≳ 0.8 Rco), the spin-down torque exerted by the disk and the MEs can even balance the spin-up due to contraction. On the other hand, during the propeller phases the accretion becomes intermittent on a dynamical timescale, corresponding to a few rotation periods of the star. Even if this effect is enhanced by the axial symmetry of our models, there is no observational evidence of such behavior.
We want to conclude by pointing out a limit that affects all the scenarios discussed in this work, including the model presented in this paper. All of them are based on axisymmetric models of purely dipolar stellar magnetospheres, and they all lead to the conclusion that, for typical slowly rotating CTTS, a dipolar component around ~ 1 kG is needed to balance, at least, the spin-up torque due to accretion. While this has been observed, for example, in the case of AA Tau (Donati et al. 2010b), such a strong dipolar component does not seem to be a common feature among T Tauri stars (Donati et al. 2007, 2010a, 2011a,b,c; Hussain et al. 2009). While a larger sample of magnetic field measurements is clearly needed, stellar torque models must start to consider more realistic magnetic field configurations, including nonaxisymmetric and multipolar components (see e.g. Long et al. 2011; Romanova et al. 2011; Vidotto et al. 2011).
PLUTO is freely downloadable at http://plutocode.ph.unito.it
This normalization differs from the one employed in Paper I, where we normalized the stellar angular momentum in units of 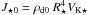 , so that the braking timescale would be given in units of t0.
, so that the braking timescale would be given in units of t0.
For a discussion on the dynamics of the truncation region and the accretion funnels we refer the reader to Bessolaz et al. (2008) and Paper I (Sect. 3.1).
Acknowledgments
The authors thank the referee for insightful comments, Jérôme Bouvier, Sean Matt, Marina Romanova for helpful discussions and Sylvie Cabrit for suggesting the slingshot analogy. C.Z. acknowledges support from the Marie Curie Action “European Reintegration Grants” under contract PERG05-GA-2009-247415.
References
- Agapitou, V., & Papaloizou, J. 2000, MNRAS, 317, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Aly, J. J., & Kuijpers, J. 1990, A&A, 227, 473 [NASA ADS] [Google Scholar]
- Anderson, J. M., Li, Z.-Y., Krasnopolsky, R., & Blandford, R. D. 2005, ApJ, 630, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Bessolaz, N., Zanni, C., Ferreira, J., Keppens, R., & Bouvier, J. 2008, A&A, 478, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Cabrit, S., Fernández, M., Martín, E. L., & Matthews, J. M. 1993, A&A, 272, 176 [NASA ADS] [Google Scholar]
- Burrows, C. J., Stapelfeldt, K. R., Watson, A. M., et al. 1996, ApJ, 473, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S. 2009, in Protostellar Jets in Context, eds. K. Tsinganos, T. Ray, & M. Stute (Berlin: Springer), 247 [Google Scholar]
- Cabrit, S., Edwards, S., Strom, S. E., & Strom, K. M. 1990, ApJ, 354, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, M. J., Shang, H., Lin, H.-H., & Shu, F. H. 2008, ApJ, 672, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R. 2008, ApJ, 689, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R. 2009, ApJ, 706, 824 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, C., & Spruit, H. C. 2010, MNRAS, 406, 1208 [NASA ADS] [Google Scholar]
- Donati., J.-F., Jardine, M. M., Gregory, S. G., et al. 2007, MNRAS, 380, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Donati., J.-F., Skelly, M. B., Bouvier, J., et al. 2010a, MNRAS, 402, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Donati., J.-F., Skelly, M. B., Bouvier, J., et al. 2010b, MNRAS, 409, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Donati., J.-F., Bouvier, J., Walter, F. M., et al. 2011a, MNRAS, 412, 2454 [NASA ADS] [CrossRef] [Google Scholar]
- Donati., J.-F., Gregory, S. G., Alencar, S., et al. 2011b, MNRAS, 417, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Donati., J.-F., Gregory, S. G., Montmerle, T., et al. 2011c, MNRAS, 417, 1747 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, S., Hartigan, P., Ghandour, L., & Andrulis, C. 1994, AJ, 108, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Elsner, R. F., & Lamb, F. K. 1977, ApJ, 215, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 1997, A&A, 319, 340 [NASA ADS] [Google Scholar]
- Ferreira, J., & Casse, F. 2013, MNRAS, 428, 307 [Google Scholar]
- Ferreira, J., Pelletier, G., & Appl, S. 2000, MNRAS, 312, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez de Castro, A. I., & von Rekowski, B. 2011, MNRAS, 411, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Goodson, A. P., & Winglee, R. M. 1999, ApJ, 524, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Goodson, A. P., Winglee, R. M., & Böhm, K.-H. 1997, ApJ, 489, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Goodson, A. P., Böhm, K.-H., & Winglee, R. M. 1999, ApJ, 524, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. 2002, ApJ, 566, 29 [Google Scholar]
- Hartmann, L. 2009, in Protostellar Jets in Context, eds. K. Tsinganos, T. Ray, & M. Stute (Berlin: Springer), 23 [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M. R., Shibata, K., & Matsumoto, R. 1996, ApJ, 468, 37 [Google Scholar]
- Hussain, G. A. J., Collier Cameron, A., Jardine, M. M., et al. 2009, MNRAS, 398, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Irwin, J., & Bouvier, J. 2009, in The Ages of Stars, eds. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse (Cambridge: Cambridge Univ. Press), IAU Symp., 258, 363 [Google Scholar]
- Johns-Krull, C. M. 2007, ApJ, 664, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźniak, W., & Kita, D. 2000 [arXiv:astro-ph/0006266] [Google Scholar]
- Koldoba, A. V., Lovelace, R. V. E., Ustyugova, G. V., & Romanova, M. M. 2002, ApJ, 123, 2019 [Google Scholar]
- Königl, A. 1991, ApJ, 370, 39 [Google Scholar]
- Li, H., Lovelace, R. V. E., Finn, J. M., & Colgate, S. A. 2001, ApJ, 561, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Lii, P., Romanova, M., & Lovelace, R. V. E. 2012, MNRAS, 420, 2020 [NASA ADS] [CrossRef] [Google Scholar]
- Long, M., Romanova, M. M., & Lovelace, R. V. E. 2005, ApJ, 634, 1214 [NASA ADS] [CrossRef] [Google Scholar]
- Long, M., Romanova, M. M., Kulkarni, A. K., & Donati, J.-F. 2011, MNRAS, 413, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2005a, MNRAS, 356, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2005b, ApJ, 632, 135 [Google Scholar]
- Matt, S., & Pudritz, R. E. 2007, in Star-Disk Interaction in Young Stars, eds. J. Bouvier, & I. Appenzeller, IAU Symp., 243, 299 [Google Scholar]
- Matt, S., & Pudritz, R. E. 2008a, ApJ, 678, 1109 [Google Scholar]
- Matt, S., & Pudritz, R. E. 2008b, ApJ, 681, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., Goodson, A. P., Winglee, R. M., & Böhm, K.-H. 2002, ApJ, 574, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., Winglee, R. M., & Böhm, K.-H. 2003, ApJ, 345, 660 [Google Scholar]
- Matt, S. P., Pinzón, G., Greene, T. P., & Pudritz, R. E. 2012, ApJ, 745, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Miller, K. A., & Stone, J. M. 1997, ApJ, 489, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., & Shu, F. H. 2008, ApJ, 687, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., & Shu, F. H. 1994, ApJ, 429, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, E. C., & Shu, F. H. 1995, ApJ, 447, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Regev, O., & Gitelman, L. 2002, A&A, 396, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2009, MNRAS, 399, 1802 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Long, M., Lamb, F. K., Kulkarni, A. K., & Donati, J.-F. 2011, MNRAS, 411, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Sauty, C., Meliani, Z., Lima, J. J. G., et al. 2011, A&A, 533, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shu, F. H., Najita, J. R., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Taam, R. E. 1993, ApJ, 402, 593 [CrossRef] [Google Scholar]
- Umurhan, O. M., Nemirovsky, A., Regev, O., & Shaviv, G. 2006, A&A, 446, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ustyugova, G. V., Koldoba, A. V., Romanova, M. M., & Lovelace, R. V. E. 2006, ApJ, 646, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Uzdensky, D. A., Königl, A., & Litwin, C. 2002, ApJ, 565, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Vidotto, A. A., Jardine, M., Opher, M., Donati, J. F., & Gombosi, T. I. 2011, MNRAS, 412, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., & Johns-Krull, C. M. 2011, ApJ, 729, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., & Ferreira, J. 2009, A&A, 512, 1117 (Paper I) [CrossRef] [EDP Sciences] [Google Scholar]
- Zanni, C., & Ferreira, J. 2011, ApJ, 727, L22 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Global magnetic coupling
 |
Fig. A.1 Poloidal current circuits flowing in the star-disk system in case C01. Color codes are the same as in Fig. 15. The left panel refers to the accretion phases, while the right panel represents the strictly propeller phases. The left (right) panel has been obtained by averaging in time current and density during the maxima (minima) of the accretion rate for t > 60, see Fig. 13. |
Since the star-disk interaction is mainly controlled by magnetic stresses, the best way to have a general view of the magnetic coupling between the different parts of the system, the accretion disk, the star, and the outflows, is to look at the poloidal electric currents Jp, circulating along the rBφ = const. isosurfaces. The poloidal component of the Lorentz force Jp × Bφ is perpendicular to these surfaces, while the toroidal force Jp × Bp is obviously proportional to the magnetic torque. Besides, in the region close to the star, the dominant components of the angular momentum and energy poloidal fluxes are directed along the poloidal magnetic field and are proportional to ∝ − BφBp: the sign of Bφ therefore gives an information about the direction of the Poynting flux. In Fig. 15 we plot sample rBφ = const. isosurfaces to outline the poloidal current circuits characterizing cases C1 and C03. The two panels of Fig. A.1 refer to the current configuration during the high-accretion (left panel) and low-accretion phases (right panel) of the propeller stage (t > 60) of case C01. We can distinguish three main current circuits labeled as A, B, and C in the four panels. In circuits A and C the currents circulates clockwise, and counterclockwise in circuit B. Different colors correspond to negative or positive values of Bφ: dark-red circuits (Bφ > 0) are responsible for extracting angular momentum and energy from the disk, while the light-yellow circuits (Bφ < 0) extract angular momentum and energy from the star.
The electromotive force of A-labeled circuits is due to the star-disk differential rotation: the current flows out from the stellar surface towards the disk, flows back along the accretion funnels and closes inside the star. This current circuit exerts a toroidal braking force inside the disk and the accretion columns and a spinning-up force inside the star, thus transferring angular momentum from the disk and the funnels to the star. It is therefore responsible for the accretion spin-up torque plotted in Figs. 3 and 9. We notice how this circuit becomes smaller and smaller as the accretion torque decreases, going from case C1 to the high accretion phases of case C01, and completely disappears in the low accretion stages of case C01, during which the accretion torque is completely negligible.
Circuit C brakes the disk rotation and is responsible for the magnetic driving of outflows launched from the disk, in particular for the magnetic acceleration of the part of the MEs mass-loaded from the disk. In the launching region of the MEs, it provides a strong vertical force that uplifts matter at the disk surface (see Fig. 6), thus contributing to the high mass-ejection efficiency of these outflows. This circuit corresponds to the innermost part of the butterfly-shaped current circuits characteristic of extended disk winds, see Ferreira (1997).
Current circuit B is associated with the energy and angular momentum extraction from the star. The current flows out from the stellar surface at mid latitudes and flows back to the star at higher latitudes. In Case C1 the current flows mostly along the open field lines anchored onto the stellar surface, therefore fueling the stellar wind. There is no spin-down circuit associated with the MEs or the disk inside the closed magnetosphere. On the other hand, the other cases show clearly that the spin-down circuit B couples the star with the disk, the MEs, and the stellar wind. These three dynamical constituents can in fact extract a fraction of the stellar angular momentum. The current flowing inside the disk, the MEs, and the stellar wind in fact provides a J × B force that tries to spin-up the material rotating at substellar rates, so that the star loses its angular momentum. Circuit B clearly identifies the parts of the disk still magnetically connected to the star that rotate more slowly than the star.
Altogether, the four panels show how the spin-up effects weaken and the spin-down action strengthens going from case C1 to case C01. We can actually see that in case C1 the MEs, which are efficiently extracting angular momentum from the disk, are transferring energy and angular momentum to the star, thus providing a spin-up torque, as we saw in Sect. 4.1. In case C03, MEs extract energy and angular momentum both from the star and the disk, and the two fluxes converge at the cusp of the field line. In the propeller phases of case C01, MEs seem to be powered almost exclusively by the stellar rotation.
Finally, these figures clearly show that MEs tend to propagate on a large scale along the current sheet at the interface between circuits B and C. While circuit B provides a decollimating Lorentz force, circuit C tries to collimate towards the axis. Therefore, since MEs propagate ballistically after they have disconnected, their collimation properties depend on the equilibrium between the decollimating inner field lines and the collimating outer ones, i.e. on the equilibrium between the inner stellar wind and an outer disk wind. A proper treatment of this issue therefore requires simulations covering larger spatial scales, properly treating all the outflows present in the system. For example, the large-scale simulations presented by Goodson et al. (1999a) suggest that an inertial confinement due to a very thick disk and a rather dense corona can help to focus the closed magnetosphere expansion and the propagation of the magnetospheric outflows towards the axis (see also Li et al. 2001). Matt et al. (2003) show how a strong enough outer poloidal magnetic field anchored in the disk can confine the EMIs. More recently, Lii et al. (2012) have shown that, at least for high-mass accretion rates, more typical of EXORs and FUORs, the innermost open disk field lines can be mass loaded enough so that the corresponding disk wind can collimate the inner outflows.
All Tables
All Figures
 |
Fig. 1 Global view of the star-disk interacting system. A logarithmic density map is shown in the background. Poloidal speed vectors are represented as blue arrows. The dotted line marks the Alfvén surface, where |
| In the text | |
 |
Fig. 2 Temporal evolution of the periodic inflation/reconnection process which characterizes the dynamics of the magnetospheric ejections in case C03. We show logarithmic density maps with sample field lines (white solid lines) and poloidal speed vectors (blue arrows) superimposed. The yellow solid lines follow the evolution of a single magnetic surface showing clearly the dynamics of the phenomenon. Time is given in units of rotation periods of the central star. |
| In the text | |
 |
Fig. 3 Temporal evolution of mass fluxes of the different accretion and ejection phenomena present in the system: mass accretion rate measured at the stellar surface (solid line), total mass outflow rate of magnetospheric ejections (dot-dashed line), mass flux fueling the MEs coming from the star only (long-dashed line), stellar wind outflow rate (dashed gray line), disk wind mass outflow rate (dotted line). The image refers to case C03. Time is given in units of rotation periods of the central star. |
| In the text | |
 |
Fig. 4 Temporal evolution of the specific angular momentum carried by different accretion and ejection components of the system in case C03: specific angular transported by the accretion flow through Rout (upper panel); total specific angular momentum carried by the MEs (second panel); specific angular momentum extracted by the MEs from the disk only (third panel); specific angular momentum of the stellar wind (lower panel). Dashed lines show the temporal averages of the quantities over the plotted lapse of time. Time is given in units of rotation periods of the star. |
| In the text | |
 |
Fig. 5 Radial evolution of the total specific energy carried by the MEs in case C03. The total specific energy (solid line) is given by the sum of Poyinting-to-mass flux ratio (dot-dashed line), kinetic energy (long-dashed line), specific enthalpy (triple-dotted-dashed line) and potential gravitational energy (dotted line, plotted in absolute value). The specific poloidal kinetic energy is also plotted (dashed line). The slow- and fast-magnetosonic surfaces are marked by a vertical line. The plot starts from the cusp of the innermost magnetic surface that steadily connects the disk and the star (labeled as (b) in Fig. 1). The figure has been obtained by time averaging the energy and mass fluxes over 54 rotation periods of the star, from time t = 38 up to t = 92. |
| In the text | |
 |
Fig. 6 Forces acting along a field line connecting the star and the disk that is mass-loaded by the MEs in case C03. The left panel refers to the forces acting from the disk midplane up to the cusp of the magnetic surface, while the right panel shows the forces from the stellar surface up to the cusp. We selected a magnetic surface anchored at 4.3 R⋆ on the disk midplane. The plots have been obtained by time averaging the forces over 54 stellar rotation periods. We plot the thermal pressure gradient (solid line), the centrifugal term (dot-dashed line), the Lorentz force (dashed line), and the gravitational pull (dotted line). Vertical lines mark the position of the disk surface (DS) and the slow-magnetosonic point (SM). |
| In the text | |
 |
Fig. 7 Upper panel. Logarithmic density map with sample field lines (yellow solid lines) and speed vectors (blue arrows) superimposed. Middle panel. Radial profiles at the disk midplane of the rotation speed of the accretion disk Ω/Ω⋆ (solid line), accretion sonic Mach number (dot-dashed line) and plasma β (dotted line). The Keplerian and the Ω = Ω⋆ rotation profiles are plotted with a dashed line. Lower panel. Radial profiles of the specific torques acting on the disk (see the text for definitions): magnetic (Γmag, solid line), internal (Γint, dashed line), and kinetic (Γkin, dot-dashed line) torques. In the three panels we marked with vertical lines the position of the truncation radius (Rt) and the anchoring radii at the disk surface of the outermost magnetic surface steadily connecting the star and the disk (Rin) and of the innermost open field line threading the disk (Rout). The panels represent temporal averages over 54 stellar rotation periods. |
| In the text | |
 |
Fig. 8 Temporal evolution of the torques acting directly onto the star, normalized to the stellar angular momentum. Plotted are the accretion torque (solid line), the stellar wind torque (dotted line), and the torque exerted by the MEs onto the stellar surface (dashed line). Conventionally, a positive (negative) torque spins the stellar rotation up (down). |
| In the text | |
 |
Fig. 9 Same as Fig. 3, but for case C1. |
| In the text | |
 |
Fig. 10 Same as Fig. 7, but for case C1. |
| In the text | |
 |
Fig. 11 Same as Fig 4, but for case C1. |
| In the text | |
 |
Fig. 12 Same as Fig. 8, but for case C1. |
| In the text | |
 |
Fig. 13 Left panel. Temporal evolution of different mass fluxes in case C01. Plotted are the mass accretion rate onto the stellar surface (solid line), the stellar wind outflow rate (dashed gray line), and the stellar mass flux contribution to the MEs (dashed line). Right panel. Temporal evolution of the torques acting onto the stellar surface, normalized to the stellar angular momentum. Plotted are the spin-up torque associated with accretion (solid line), the spin-down torque exerted along the magnetic surfaces connecting the star and the disk (dashed line) and the spin-down torque due to the stellar wind (dotted line). |
| In the text | |
 |
Fig. 14 Time evolution of an accretion cycle during the propeller phase of case C01. We show logarithmic density maps with sample field lines (solid lines) and speed vectors (blue arrows) superimposed. The yellow solid line follows the evolution of a single magnetic surface, clearly showing the periodicity of the accretion-ejection cycles. Time is given in units of the stellar rotation period. |
| In the text | |
 |
Fig. 15 Poloidal current circuits flowing in the star-disk system in cases C1 (left panel) and C03 (right panel). Dark (red) circuits circulate clockwise along isosurfaces of rBφ > 0. Yellow (light) circuits circulate counterclockwise along isosurfaces of rBφ < 0. Current circuits are superimposed on a logarithmic density map. The figures have been obtained by time averaging over 54 stellar rotation periods. |
| In the text | |
 |
Fig. A.1 Poloidal current circuits flowing in the star-disk system in case C01. Color codes are the same as in Fig. 15. The left panel refers to the accretion phases, while the right panel represents the strictly propeller phases. The left (right) panel has been obtained by averaging in time current and density during the maxima (minima) of the accretion rate for t > 60, see Fig. 13. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.