| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220060 | |
| Published online | 24 January 2013 | |
Feedback by massive stars and the emergence of superbubbles
I. Energy efficiency and Vishniac instabilities⋆
1
Excellence Cluster Universe, Technische Universität München,
Boltzmannstrasse 2,
85748
Garching,
Germany
e-mail: krause@mpe.mpg.de
2
Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312, Giessenbachstr.,
85741
Garching,
Germany
3
Universitätssternwarte München, Scheinerstr. 1, 81679
München,
Germany
4 Max-Planck-Fellow
5
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, the
Netherlands
6
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
Received: 19 July 2012
Accepted: 5 December 2012
Context. Massive stars influence their environment through stellar winds, ionising radiation, and supernova explosions. This is signified by observed interstellar bubbles. Such feedback is an important factor for galaxy evolution theory and galactic wind models. The efficiency of the energy injection into the interstellar medium (ISM) via bubbles and superbubbles is uncertain, and is usually treated as a free parameter for galaxy scale effects. In particular, since many stars are born in groups, it is interesting to study the dependence of the effective energy injection on the concentration of the stars.
Aims. We aim to reproduce observations of superbubbles, their relation to the energy injection of the parent stars, and to understand their effective energy input into the ISM, as a function of the spatial configuration of the group of parent stars.
Methods. We study the evolution of isolated and merging interstellar bubbles of three stars (25, 32, and 60 M⊙) in a homogeneous background medium with a density of 10mp cm-3 via 3D-hydrodynamic simulations with standard ISM thermodynamics (optically thin radiative cooling and photo-electric heating) and time-dependent energy and mass input according to stellar evolutionary tracks. We vary the position of the three stars relative to each other to compare the energy response for cases of isolated, merging and initially cospatial bubbles.
Results. Mainly due to the Vishniac instability, our simulated bubbles develop thick shells and filamentary internal structures in column density. The shell widths reach tens of per cent of the outer bubble radius, which compares favourably to observations. More energy is retained in the ISM for more closely packed groups, by up to a factor of three and typically a factor of two for intermediate times after the first supernova. Once the superbubble is established, different positions of the contained stars make only a minor difference to the energy tracks. For our case of three massive stars, the energy deposition varies only very little for distances up to about 30 pc between the stars. Energy injected by supernovae is entirely dissipated in a superbubble on a timescale of about 1 Myr, which increases slightly with the superbubble size at the time of the explosion.
Conclusions. The Vishniac instability may be responsible for the broadening of the shells of interstellar bubbles. Massive star winds are significant energetically due to their – in the long run – more efficient, steady energy injection and because they evacuate the space around the massive stars. For larger scale simulations, the feedback effect of close groups of stars or clusters may be subsumed into one effective energy input with insignificant loss of energy accuracy.
Key words: galaxies: ISM / ISM: bubbles / ISM: structure / hydrodynamics / instabilities
The movie associated to Fig. 3 is available at http://www.aanda.org
© ESO, 2013
1. Introduction
The properties of the interstellar medium (ISM) – i.e. its morphology with imprinted bubbles and superbubbles (Gruendl et al. 2000; Arthur 2007; Chu 2008; Sasaki et al. 2011), its molecular-cloud fragments in formation or in dispersal, and its level of turbulence – are strongly affected by the physics and dynamics of stellar feedback (e.g. de Avillez & Breitschwerdt 2004, 2005; Dobbs et al. 2011b,a; Ntormousi et al. 2011).The actual agents of stellar feedback are massive stars, which are born in the denser parts of the ISM (for recent reviews see McKee & Ostriker 2007; Zinnecker & Yorke 2007). The interaction via winds and ionising radiation of a single massive star with its surroundings is usually referred to as an “interstellar bubble” (Weaver et al. 1977). Strong winds are shocked close to the star and produce a hot overpressured bubble, which drives an expanding shell of swept-up, shocked ambient gas. The shell may be partially or completely ionised by the ultraviolet emission of the central star. The increased pressure may additionally push the leading shock front. Interstellar bubbles are usually not energy conserving, because of the radiative losses of the shocked ambient medium (e.g. Weaver et al. 1977). This has been nicely demonstrated by the observations of Gruendl et al. (2000). For some bubbles, they resolve the radiative leading shock wave, with the highly excited [O III] tracing the hottest outermost gas, and Hα tracing a somewhat cooler surface inside of [O III]. This indicates that the leading shock front in these cases is shock ionised rather than photo-ionised. Radiative energy losses are substantial, but hard to quantify in detail (e.g. Garcia-Segura & Mac Low 1995), and they affect wind-blown and supernova related bubbles alike.
Many molecular clouds host massive stars in groups. The bubbles of these stars have to interact, because the sizes of the individual bubbles (parsecs, e.g. Weaver et al. 1977; Gruendl et al. 2000) are comparable to the size of the parent molecular clouds (Kainulainen et al. 2011). Also, in star-forming regions, smaller groups of stars are often located within distances of tens of parsecs (e.g. Orion, Voss et al. 2010). The interaction of individual bubbles leads to the formation of superbubbles (Tenorio-Tagle & Bodenheimer1988; Oey et al.2001; Chu2008; Oey2009, for reviews). The expansion of the combined superbubble is often described by the same model as for individual bubbles. Superbubbles may reach sizes of hundreds of parsecs (e.g. Tenorio-Tagle & Bodenheimer 1988; Breitschwerdt & de Avillez 2006; Sasaki et al. 2011). But they often appear to be too small and too bright in X-rays compared to models (e.g. Oey & García-Segura 2004; Jaskot et al. 2011). Possible explanations include energy dissipation due to mass loading or uncertainties in the stellar wind data, e.g. due to clumping.
Understanding of the physics of bubbles and superbubbles is the key ingredient in order to gauge the efficiency of stellar feedback. It is of particular importance to assess the effective energy input into the ISM. Our group has embarked on this task, and has synthesised the total energy input into molecular clouds for realistic stellar populations based on recent stellar evolution models (Voss et al. 2009): Averaged over all massive stars (8 M⊙ < M < 120 M⊙), the energy input due to winds is of the order of 1050 erg/star. Supernovae contribute about ten times more. The energy injection is extended over several tens of Myr and has a peak near four Myr with a shallow decline afterwards. Winds dominate before the peak and supernovae afterwards. Substantial variations from cluster to cluster are expected due to the sparser sampling at the massive end of the initial mass function.
Stars are born in the densest regions of the ISM. Much of the injected energy is therefore quickly lost to radiation in cooling shock compressed shells. Hydrodynamic simulations have been used to assess the effective energy input into the ISM. The energy deposition efficiency of isolated massive stars in their wind phase has been assessed in 2D hydrodynamic simulations by Freyer et al. (2003, 2006). Though they include the effect of photo-ionisation, they show that the gas dynamical effects are dominated by the mechanical energy input: for example, for a 35 (60) M⊙ star, they expect that only 17 (5) per cent of the energy increase in the ISM in their simulation is due to ionisation. They give their energy deposition efficiency as fractions of the radiative energy input. Scaled to the mechanical energy input, they find that about 38 (9) per cent of the input energy has been added to their ISM at the end of their simulations for the 35 (60) M⊙ star. The dynamics of two wind bubbles (25 M⊙ and 40 M⊙ stars) separated by 16.2 pc has been studied by van Marle et al. (2012). The two bubbles quickly merge, sweeping the colliding parts of the wind shells away into the bubble of the lower mass star, due to the pressure difference in the bubbles. An aspherical superbubble is then formed, which isotropises after a few Myr. More interesting details are observed which we refer to below, when we compare them with our findings in Sect. 3. Ntormousi et al. (2011) have simulated the merging of two superbubbles in 2D with identical stellar content. One of the most interesting findings in the simulations of Ntormousi et al. (2011) and van Marle et al. (2012) is the occurrence of the Vishniac thin shell instability (Vishniac 1983). This instability is strongly suppressed in the simulations of Freyer et al. (2003, 2006) due to the thickening of the shell because of the increased pressure due to the ionisation. The Vishniac instability is interesting as it may create observable filamentary features, and thick filamentary shells, and thus discriminate between models (van Marle & Keppens 2012).
Here, we address the effective energy injection into a homogeneous ISM for three interacting interstellar bubbles with 3D hydrodynamics simulations, using standard ISM thermodynamics. We neglect the effect of ionising radiation, because it is expected to be less important in this context (Freyer et al. (2003), see e.g. Gritschneder et al. (2010) for the effects of ionising radiation). We take as our starting element a group of three coeval massive stars, 25, 32 and 60 M⊙, respectively. We study the deposition efficiency of energy injection as a function of distance between the stars. We find a high efficiency in the wind phase, comparable to the 2D results of Freyer et al. (2003, 2006) and the 2D and 3D results of Fierlinger et al. (2012), details of bubble merging similar to van Marle et al. (2012) and an enhancement of the feedback efficiency by about a factor of two for grouping of the stars closer than about a few tens of pc. The energy of supernovae that explode within superbubbles is dissipated on a timescale of about 1 Myr. Additionally, weshow column density renderings of prominently Vishniac unstable 3D shells, which should give a first approximation of the observational appearance of the Vishniac instability.
 |
Fig. 1 Test simulation of an isolated supernova in a homogeneous environment according to Tenorio-Tagle et al. (1990).This test was run in 1D and spherical coordinates at radial resolutions between 100 and 6400 cells with respective increments of a factor of two and with the standard cooling and heating. Top: density slices at different times (increasing from left to right). Middle: evolution of thermal (thin lines) and kinetic (thick lines) energy for the 100 (orange triple dot-dashed lines), 800 (solid black lines), 6400 (red dashed lines) radial cells simulation. Additionally a simulation with 3200 radial cells and enhanced cooling is shown (blue dot-dashed lines, see text for details). The left part of the plot zooms into the first 2000 yr of the evolution. Bottom: maximum compression at about 20 000 yr as a function of resolution. The expected maximum compression at this time is four for a strong adiabatic shock. |
2. Simulations
We carry out 3D hydrodynamic simulations with the Nirvana 3.5 code (Ziegler 2008, 2011), evolving the conservation equations for mass, momentum and energy. Nirvana 3.5 is a conservative, finite volume code and combines block structured adaptive mesh refinement (AMR) with parallelisation by the message passing interface (MPI) library.
2.1. Numerics and code tests
The main solver modules are an HLLD solver (HLLD_CT), applying the 1D approximate Riemann solver of Miyoshi & Kusano (2005) dimension-by-dimension in 3D, and a second-order Central-Upwind scheme (CU_CT, full details in Ziegler 2011). We work in Cartesian coordinates throughout(apart from the radiative test case in this section). In order to check the isotropy of the solution in this geometry and also for differences between these solvers, we re-run and analysed the adiabatic blastwave test problem that comes with the code with both solvers. Here, a fixed amount of thermal energy is initially deposited in a finite circular region of 22 cells diameter. In both cases, a reasonably spherically symmetric bubble develops, with a forward shock, a contact surface and a backward shock. The contact surface evolves identically for both solvers, forward and backward shock are lead by the solution of the CU_CT solver by at most one cell. Hence, both methods yield a very similar result for symmetrical bubble expansion. For the same solver but different angular directions other than the grid axes, the radii of the different features of interest differ by typically one and up to about three grid cells.
As a radiative (see below for details about radiative cooling and heating) test simulation, we re-run the 1D-supernova test of Tenorio-Tagle et al. (1990, Fig. 1, also in spherical coordinates, but otherwise with the same numerical settings as for the 3D production runs below. Here, 1051 erg are deposited within a radius of 1018 cm. Density and temperature are initially assumed to be 1 cm-3 and 100 K, respectively, throughout the computational domain. We use the CU_CT solver with a uniform mesh with a cell size between 5.6 × 10-3 pc (6400 cells in total) and 0.36 pc (100 cells in total) for this test. The density slices in Fig. 1 (top) show the expected shape for such an explosion. In their 1D test run, Tenorio-Tagle et al. (1990) find the outer shock at 11 pc (24 pc) at 5 300 yr (47 806 yr). Our simulation (10.4 pc at 5483 yr; 25.2 pc at 47 990 yr) reproduces this within expectations. At 47 990 yr, our outer shock is about 5% further out then their solution at 47 806 yr. This is likely related to the differences in the employed cooling functions (more details below). The contact surface at 47 806 yr should be at 8 pc, which agrees well with our result. During the energy conserving phase, i.e. up to say 30 000 yr, we expect 28% of the energy in kinetic form and 72% in thermal form, which is consistent with our energy tracks (Fig. 1, middle, to be compared with Fig. 1a in Tenorio-Tagle et al. 1990) Cooling should become significant around 33 000 yr, which is also in good agreement. After the onset of cooling, the thermal energy should decline strongly, this and the shape of the energy tracks are quite similar to the findings of Tenorio-Tagle et al. (1990). We also find a secondary shock wave in the shocked ambient gas due to the non-uniform cooling of the shell, and a corresponding increase in the track of the kinetic energy, as in Tenorio-Tagle et al. (1990) (another weak shock from reflection at the origin is visible in the shocked ambient gas in Fig. 1, top). The analytically expected compression ratio at the leading shock front is four. Because of the strong decline of the solution inwards, one can however not expect to obtain exactly four in a numerical representation, but the solution should converge towards four with increasing resolution. Our highest resolution run reaches a compression above 3.9 in the adiabatic phase, and we show in Fig. 1 (bottom) that this value converges well with increasing resolution.
The reduced density peak height decreases the cooling rates slightly: The low resolution runs lag behind in thermal energy decrease by at most about 3000 yr at 60 000–90 000 yr. The energy track is entirely converged from about 400 cells. The crossing point of thermal and kinetic energy is around 80 000 yr in our simulation compared to about 46 000 yr in Tenorio-Tagle et al. (1990). This significant difference is due to the employed cooling curve: Tenorio-Tagle et al. (1990) use the cooling curve of Raymond et al. (1976), which features particularly strong cooling around 106–107 K due to highly ionised Fe. The cooling rates are uncertain by a factor of about two (Wiersma et al. 2009). Many, more recent, cooling curves tend to have lower cooling rates than Raymond et al. (1976), including the standard one for the NIRVANA-code, Slyz et al. (2005), which we use. In order to verify that this is the reason for the differences in the energy tracks between Tenorio-Tagle et al. (1990) and our result, we tested a case where we increased the cooling rates ad hoc by a factor of two (Fig. 1, middle). This obviously shifts the result into the right direction. The increased amount of thermal energy probably also leads to the slightly further advanced outer shock (compare above) at late times.
Thus, we reproduce the fundamental properties of the 1D test of Tenorio-Tagle et al. (1990). The 3D nature of our simulations demands some compromise regarding resolution. We expect that this effect should affect energy tracks by at most a few per cent. We account for this in the discussion below.
Simulation parameters.
We initially selected the HLLD_CT solver but encountered severe vacuum formation problems (very low pressure) near contact surfaces for our high resolution runs. For all the simulations presented in this article, we therefore employed CU_CT.
We use standard ISM thermodynamics with radiative cooling and photo-electric heating (see Piontek et al. (2009) for details), employing the standard iterative procedure of Nirvana 3.5. Cooling is always strong for our wind shells, which tend to get thin and eventually also Rayleigh-Taylor and Vishniac-unstable. The instabilities evolve differently for different flux limiters: test simulations with all flux limiters provided (minmod, superbee, monotonised-centred, and Van Leer) showed that for the monotonised-centred and the superbee limiters, the instabilities are systematically different for parts of the shell which move parallel and diagonal to the grid axis. Van Leer and minmod both yield almost isotropic results at our highest resolution, at the expense of being more diffusive, as expected. We correspondingly adopted the minmod flux limiter. Nirvana 3.5 offers an additional multi-dimensional limiter which we also use, and where we adjusted the parameter experimentally to yield optimal isotropy for shell instabilities.
 |
Fig. 2 Cumulative energy (top) and mass (bottom) input. We use the output of a 25 M⊙ (dashed, labels: Ms = M⊙), 32 M⊙ (dotted) and a 60 M⊙ star as input for our simulations, separately or combined. The difference between the total mass output and the initial mass indicates the mass of the dark remnant. The energy is given in “Bethe” = 1051 erg. |
 |
Fig. 3 Column density integrated over Z-direction and Y-direction (left and middle col., respectively) and midplane density (right column) for three different snapshot times from top to bottom for run 3S1-hr. The projections of the three massive stars into the X–Y plane is indicated as small red stars in the density plots on the right. The 60 M⊙ star blows the biggest bubble from the origin. The 32 M⊙ bubble towards its lower left (XY-plots) is only slightly bigger than the one of the 25 M⊙ star above. The shell forms spikes and dense clumps due to the combined action of Vishniac and thermal instability. A movie is provided with the online version. |
2.2. Setup
The computational domain is a cubic Cartesian grid, 400 pc on a side resolved by 24 cells for the base level. The mesh is refined whenever a combined threshold of first and second derivative for density or respectively velocity is exceeded. Additionally, we always keep the wind injection region at the highest refinement level. Effectively, the wind shell and everything inside is always refined to the highest level. For most of our runs we use three levels of adaptive mesh refinement, which would correspond to a uniform grid of 1923 cells with a resolution of 2.1 pc. Simulation 3S1-mr and 3S1-hr use four and five levels of refinement, resulting in 1 and 0.5 pc resolution, respectively. Boundary conditions are formally periodic, but we only use data from snapshots where the shells are entirely contained in the computational domain.
We fill the grid initially with a homogeneous medium. Then we choose one (three) injection regions of eight pc radius in every case. Each injection region gets assigned a star of a particular mass. We inject mass and thermal energy according to the stellar evolutionary tracks of rotating stars of Meynet & Maeder (2005) and wind velocities from Lamers et al. (1995) and Niedzielski & Skorzynski (2002) for the Wolf-Rayet phase, as compiled in Voss et al. (2009). We use 25, 32, and 60 M⊙ stars, with supernovae at 8.6, 7.0 and 4.6 Myr, respectively. The time resolution of the stellar evolution table is 0.1 Myr. Cumulative mass and energy input are shown in Fig. 2. The mass density is initially set to 10mp cm-3 everywhere in the computational domain. The temperature is set in equilibrium between cooling and heating, 121 K. All velocities are initially zero. More details for each individual run are provided in Table 1.
 |
Fig. 5 Maximum density as a function of time for runs 3S1-hr (solid), 3S1-mr (dashed) and 3S1 (dotted). The horizontal lines correspond to the critical compression above which the Vishniac instability is triggered for supernova (lower line) and wind (thicker upper line) shells according to Vishniac & Ryu (1989). The axis on the right shows the overdensity factor over the undisturbed ambient medium. |
 |
Fig. 6 One-dimensional slices in X-direction through run 3S1-hr at time T = 8.53 Myr. The Y and Z coordinates are chosen appropriately for the slices to include the position of the only remaining star at that time (25 M⊙ , at X = −30 pc, indicated by the star in the middle diagram). Top: positive X-velocity (blue, dashed line), negative x-velocity (red dash-dotted line) and sound speed (solid black). Middle: pressure (logarithmic). Bottom: density (logarithmic). See text for details. |
 |
Fig. 7 Shell details for the final snapshot of run 3S1-hr. Shown is an X-Y zoom of density, pressure, temperature and Mach number, as indicated on the individual panels, around the position of the maximum density, which is located at (X, Y, Z) = (−30, −79, −52) pc. Velocity vectors are overlaid on the density plot. The high density region is overpressured and has a temperature below 20 K. See text for more details. |
3. Results
The time evolution of our high resolution run 3S1-hr with three stars at different locations is shown in Figs. 3 and 4. At a given time, the bubble size increases monotonically with the mass of the parent star, with the central 60 M⊙ bubble dominating the gas dynamics. As expected, the shocked ambient medium cools very quickly and consequently gets compressed into a thin shell for each bubble. The shell is subject to a combination of thermal and Vishniac (1983) instabilities1. The bubbles start to merge at around 2 Myr. At the first snapshot in Fig. 3 (1.95 Myr), the shell interface between the 60 M⊙ bubble and the 32 M⊙ bubble has just burst. Up to this point, each bubble has had its individual bubble pressure, which is highest for the 60 M⊙ bubble. Its hot gas can be seen to stream through the hole in the shell. The shell interface then behaves much like a cloud, being ablated by a wind (Pittard et al. 2005): Kelvin-Helmholtz instabilities at the contact surface lead to mixing of the cloud gas into the hot phase. The shell interface has completely dispersed until the next snapshot at 4.05 Myr. We checked the effect of different flux limiters in this phase: Less diffusive ones allow smaller holes, which delays the erosion process compared to the more diffusive case. The final results are however very similar.
The density slice at 4.05 Myr shows the weaker winds of the smaller stars to be pushed aside by the one of the most massive star. The larger part of the 60 M⊙ bubble remains unaffected by the action of the smaller stars. The 60 M⊙ star explodes at 4.6 Myr. The sudden energy injection due to the supernova compresses the shell further (Fig. 5) and accelerates it, triggering the Rayleigh-Taylor instability (RTI). The RTI may cause filamentary structure inside the shell. Also, the outwards directed flow field, centred on the most massive star before its explosion, is no longer present. Thus, from this time on, we find filamentary gas inside the shell, seen in the individual density slices. The effect of the winds of the smaller stars in this phase can hardly be noticed. The second supernova (7.0 Myr) leads to a further acceleration and compression of the shell, causing more RTI filaments. The snapshot at 8.53 Myr shows the superbubble when 2 stars have exploded already, and the third is in its Wolf-Rayet phase. This snapshot demonstrates nicely that our ansatz with thermal energy injection may also cope with situations when the backward shock within the stellar ejecta is unusually far from the star: one can clearly see the declining density away from the star due to adiabatic expansion (1D-slices in Fig. 6). The wind turns supersonic immediately outside the driver and shocks roughly 20 pc away from the star. A second structure is visible at varying distance from the star, up to about 50 pc: This is what we would expect to be the forward shock in the standard picture. Due to the high ambient pressure, it is only a sound wave. The pressure inside of this structure is slightly reduced due to the ongoing expansion. The final supernova at 8.6 Myr causes again mass entrainment into the bubble due to the RTI. The bubble then keeps expanding with decreasing interior density fluctuations until the end of the simulation at 15 Myr.
The highest densities in the shell, around 180 times the ambient density, are reached for roughly 1 Myr after each supernova, where for the later two supernovae, the compression peaks have merged (Fig. 5). At late times the density increases again (see below for details). We show a zoom on the highest density region in the final snapshot in Fig. 7. The density maximum is located in the dense shell, where two humps of the Vishniac instability (compare Sect. 3.1 below) cross, and more towards the interior of the bubble. The velocity field in the shell is still dominantly outwards with substantial Mach numbers. Yet, probably enhanced by the large scale vortices which dominate the shell interior at that time, there is also some non-radial motion. The slightly converging velocity field has to be responsible for the high density, as the region is substantially overpressured compared to the environment. At earlier times (compare above), such maxima in density and pressure could have been in pressure equilibrium with their surroundings. At this late time, the bubble interior is already underpressured with respect to the environment, and so we expect that the maximum is temporary, unless such clumps become self-gravitating. This seems quite likely, given the pc-scale size, low temperature (below 20 K) and high mass (few hundred M⊙ ) of the clump (Jeans length: ≈ 2 pc). Yet, self-gravity is not included in the simulations and therefore details, such as triggered star formation, are beyond the scope of this article.
3.1. Vishniac instability
The shells are subject to various instabilities. The Rayleigh-Taylor instability is especially prominent during the strong acceleration phases after each supernova.The Vishniac instability develops when the shell decelerates. It is an overstability: differences in column density for adjacent regions of a shell cause gas flow from the high column density region into the region with lower column density. This continues in general until the situation is reversed and the region with initially lower column density finally has the greater one. Vishniac & Ryu (1989) derive a critical overdensity for the shell over the unshocked ambient gas of a factor 10 and 25 for a blastwave with initial energy injection and constant energy injection rate, respectively, to become unstable, such that the peak density increases in each cycle. The shell then develops a characteristic spiky pattern (Ntormousi et al. 2011; Drake 2012, Fig. 3), in density slices. The 3D structure of the shell is granular with a regular filamentary pattern (Figs. 3 and 4). The regularity is of course related to the grid structure, because this is the most important perturbation. In column density, we find a web formed of polygons. These polygons have typically four to six sides. The sides are however not always aligned with the coordinate axis or the diagonals, and some are clearly curved. The typical polygon diameter is about 10 pc. At the intersections of the filaments, density and column density achieve their highest values. These points lag behind the shell. Particularly high densities may be achieved, when left and right part of an inwards spike merge. This seems to have happened for the density maximum at the final snapshot we show in Fig. 7. But from a detailed inspection of several snapshots, we conclude that this should happen frequently. The three-dimensional structure of our superbubble shells is very similar to the one of the smaller scale circum-stellar shells of van Marle & Keppens (2012).
 |
Fig. 8 Column density at a comparable late evolution time for runs 3S1 (top) and 3S1-hr (bottom). The high resolution bubble is more spherical, larger, achieves higher peak column densities and the Vishniac instability is more pronounced. |
 |
Fig. 9 Analysis of the non-radial Mach number, i.e. the Mach number perpendicular to the direction of the shell’s expansion. Only the region with positive X-coordinate, which corresponds to the undisturbed part of the 60 M⊙ bubble, is taken into account. Left: 4.05 Myr, right: 7.47 Myr. The upper parts show the non-radial Mach number versus the logarithm of the density. Colour encodes the mass per bin, where each bin spans 0.05 in Mach number and 0.06 dex in logarithmic density. No appreciable non-radial motions are found for the hot bubble interior, whereas the dense shell material shows Mach numbers of the order of unity. The lower parts show mass weighted non-radial Mach number histograms (vertically collapsed versions of the plots above). The plots are dominated by the quiescent ambient medium. The mass with given non-radial Mach number declines strongly around a Mach number of unity towards higher Mach numbers as expected for shells dominated by the Vishniac instability. |
 |
Fig. 10 Top part: input (solid) and retained (dotted) energy for run 3S1-hr. The response ℛ (retained energy divided by input energy) is shown in the bottom part. See text for more details. |
We show the peak density over time in Fig. 5. Clearly, the densest parts of the shell of run 3S1-hr satisfy the criteria of Vishniac & Ryu (1989) from before 2 Myr throughout the simulation, in agreement with Fig. 3. The low resolution simulation 3S1 generally stays below the wind criterion of Vishniac & Ryu (1989). Correspondingly, the Vishniac instability is much less pronounced (Fig. 8). Mac Low & Norman (1993) have shown that the instability is connected to transonic motions in the shell perpendicular to the expansion direction. We evaluate these non-radial velocities for the undisturbed (with respect to the interaction of the bubbles of the other two stars, here we use X > 0) part of the shell in Fig. 9. The 2D mass weighted histogram over logarithmic density and non-radial Mach number, with respect to the local speed of sound, shows that only dense shell gas acquires substantial non-radial Mach numbers. At high densities, indeed most of the gas has Mach numbers around and below unity.
3.2. Energy evolution: general observations
We show the total input energy over time together with the energy retained in the ISM where the initial thermal energy is subtracted in Fig. 10. The retained energy is generally below the input energy because the gas is initially in radiative equilibrium and suffers net radiative losses during the course of the simulation. We define the response ℛ to be the energy retained in the ISM divided by the input energy: 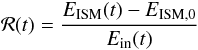 (1)where we define as ISM the whole gas present in the computational domain, including the hot bubble interiors with their stellar ejecta.
(1)where we define as ISM the whole gas present in the computational domain, including the hot bubble interiors with their stellar ejecta.
The response ℛ is generally of the order of ten per cent. It is higher whenever the energy input rate increases. This is especially well visible at the time of the three supernovae at 4.6, 7.0 and 8.6 Myr. Here, ℛ reaches peak values between 20 to 40 per cent. ℛ is lower for phases of decreasing energy input rate. This is particularly well visible after a supernova. About 1 Myr after each supernova, ℛ drops to roughly five per cent. The characteristic decay time of the retained energy increases for each consecutive supernova. When the energy input ceases, the ISM energy is lost to radiation on a timescale of Myr, with ℛ dropping to 2 per cent roughly 4 Myr after the last supernova.
Steady, continuous energy injection is clearly more effective in energising the ISM than sudden bursts such as from infrequent supernovae.
 |
Fig. 11 Resolution effects on the retained energy. Top part: retained energy for run 3S1-hr (solid line, high resolution), 3S-mr (dashed line, intermediate resolution) and run 3S1 (dotted line, low resolution). The bottom part shows the energy ratio 3S1-hr/3S1-mr (solid line), 3S1-mr/3S1 (dashed line) and 3S1-hr/3S1 (dash-dotted line). In each case, the data for the higher resolution run has been interpolated to the data output times of the lower resolution run. The spikes at the supernova times are artefacts of the interpolation process at the discontinuities of the functions. The horizontal dashed line indicates equality for comparison. The energy increases similarly for each doubling of resolution. The general functional behaviour is independent of resolution. See text for more details. |
 |
Fig. 12 Energy tracks for different simulations, where only the positions of the three stars differ. Run labels in the legends are explained in Table 1. S25 + S32 + S60 refers to the sum of the energy tracks of the three simulations of the bubbles of the isolated 25 M⊙, 32 M⊙ and 60 M⊙ stars, respectively, which corresponds to a very large distance. 3S0 is the opposite case, where three stars are in the same region. Top: absolute values. Middle: three-stars simulations relative to the sum of the three isolated bubbles. Interpolations always use the 3S0 time base. Interpolation artefacts are visible at the discontinuities due to the supernovae (4.6, 7.0 and 8.6 Myr). Bottom: difference of the very similar energy tracks of runs 3S1 and 3S0, normalised to 3S0 as a percentage. The solid red line marks zero. The difference has been set to zero for the time intervals 10,000 yr around each supernova in order to mask the interpolation artefacts. See text for details. |
3.3. Resolution effects
We repeated run 3S1-hr at a half and a quarter of the original spatial resolution. Morphologically, the bubbles are less spherical, smaller and the Vishniac instability is less developed at lower resolution (Fig. 8). We compare the energy evolution of the three runs in Fig. 11. The retained energy differs by much less than a factor of two between simulations at different resolution. The differences are more pronounced at later simulation times. Finer spatial resolution always leads to more energy in the ISM. For an increase of the resolution by a factor of two, we find an increase of the retained energy by 20−30 per cent. This agrees with the greater bubble diameter at higher resolution (Fig. 8). The overall functional behaviour is very well converged.
The reason for the changes with resolution is very likely the details of the shell evolution. In the absence of other perturbations, instabilities are triggered on the resolution level. Additionally, the Vishniac instability is only marginally developed at low resolution. This might lead to more non-radial kinetic energy at higher resolution, which is not immediately radiated away. Also, the peak density at a given time depends strongly on resolution (Fig. 5), which also changes the thermodynamics.
3.4. Energy evolution: varying stellar distances
We carried out a set of simulations, where we varied the positions and distances of the same three stars (Fig. 12). Because of computational limitations, these simulations were carried out at 2.1 pc resolution. This is physically justified by the convergence of the general shape of the energy tracks (Fig. 11). For obtaining the large distance limiting case, we simulated each of the three bubbles in a separate simulation (S25, S32 and S60), and added their energy tracks for comparison to the other cases. We model the closely-spaced extreme case, where the bubbles merge instantaneously, by putting the driver regions of the three stars on top of each other at the grid origin (3S0). Additionally, we performed two simulations with intermediate star positions (compare Table 1), where we actually observe the bubble merging during the simulations (3S1 and 3S2).
We see small differences in the energy tracks during the first ≈ 0.5 Myr. They are expected because during this time, the driver region is evacuated and the bubble shape is established. It of course makes a difference if the three stars share the same driver region (3S0), or if each star has its own. Also shifting the driver region on the grid makes the volume of the individual driver regions slightly different, by a few per cent, due to resolution effects at the driver boundary. This translates to a few per cent difference in total energy, which is visible in Fig. 12 (bottom).
Once the bubbles are established properly on the grid, i.e. after about 0.5 Myr, all configurations have essentially the same energy response until the first supernova at 4.6 Myr. The reason for this is the predominance of the energy injection of the 60 M⊙ star. The energy tracks begin to differ slightly after the first star has exploded. The divergence increases abruptly after each supernova. But for very long times after the final explosion, the tracks converge again towards a common value.
Among the four configurations, the energy varies at times by up to a factor of three. A typical value after the second supernova is a factor of two. Throughout the simulation time, the energy is essentially highest for run 3S0 (all stars at same place) and lowest for very large distance (sum of S25, S32 and S60). The two configurations with intermediate distances, where the bubbles merge during the respective simulations, show intermediate energies. The run where the bubbles merge early (3S1) behaves almost identical to the case where the driver regions are on top of each other (3S0).
3.5. Shell widths
We find that our simulated shells are widened due to the Vishniac instability. For the determination of the shell width, we average the column density maps over the angle, and identify the shell as radial interval where the column density is at least five per cent higher than in the undisturbed medium. The shell width is shown in Fig. 13 as a function of time and radius, respectively, for runs 3S1 and 3S1-hr. For this analysis, we only use late snapshots, where the superbubbles are well established.
The shell width is typically in the tens of per cent regime and increases with time. The result does not depend on the resolution.
 |
Fig. 13 Shell width for column density maps. Top: angle-averaged col. density over radius for run 3S1-hr at 12.56 Myr. From such plots, the shell width has been determined as the radial range where the column density is at least five per cent greater than at large radii (undisturbed gas). The shell width determined in this way is shown in the middle plot as a function of time, and in the bottom plot as a function of outer radius. Black pluses are for run 3S1, red stars for run 3S1-hr. The average shell width does not depend significantly on resolution. |
4. Discussion
We investigated the environmental impact of a group of three massive stars via 3D hydrodynamic simulation. Herein, several assumptions and simplifications were necessarily introduced:
We adopted a uniform background density of 10mp cm-3. On scales of ten pc and smaller, the density will in reality be at least a factor of ten higher (e.g. Kainulainen et al. 2011). On scales of 100 pc, the density should become equal to or even smaller than about 1mp cm-3 (e.g. de Avillez & Breitschwerdt 2005). Hence, our choice should be realistic for the tens of pc scales we simulate (compare also Freyer et al. 2003, 2006; van Marle et al. 2012). The real ISM has a rich spatial structure, whereas we use a homogeneous distribution. This is a significant difference. For a porous ISM, the injected wind/SN energy could escape through low density regions making the bubbles smaller (Fierlinger et al. 2012b, in prep.). For such a situation, one should also expect pronounced bubble asymmetries. Indeed, such asymmetries are found in observations (e.g. Churchwell et al. 2006). Yet, in order to be able to compare the effect of different spatial configurations of the stars, and not to be dominated by local environmental effects it is necessary to use a homogeneous background density.
We found that with the standard ISM thermodynamics, the peak shell density does not converge with finer resolution. It is not immediately obvious that this should be so, as the photo-electric heating we take into account could in principle have produced high enough pressure to limit the shell compression. Yet, with our highest resolution of 0.5 pc, this has not been the case. The shell density results from several effects: at a given pressure level, there is a density and a temperature that correspond to thermodynamic equilibrium. When the pressure in the bubble increases, e.g. because a supernova has happened, the shell can however not adjust immediately to the new equilibrium pressure level, because the gas has to be swept together in a finite time. The inverse happens at late times (as demonstrated in Fig. 7) when the bubble pressure strongly decreases, but the clumps in the shell cannot expand fast enough to remain in pressure equilibrium. The compression is of course also limited by the resolution. The non-convergence therefore means that the bubble pressure is high enough for a sufficiently long time so that compression of the shell, or some clumps therein, to even higher densities may occur if one would repeat the simulation with an even higher resolution. For gas on the thermodynamic equilibrium curve in the relevant density regime, higher densities correspond to lower temperatures. Compared to observations (e.g. Preibisch et al. 2012), the ISM in star forming regions rarely reaches temperatures below about 20 K, and 20 K to 100 K are typical for the dense phase. Similar temperatures are also found in our simulated shells. Other effects like magnetic fields, self-gravity or feedback by the new stars, which in reality might form in our dense clouds, may affect the cloud compression, but are not included in our simulation. Thus, even if the compression would increase still further if one would carry out the simulations at yet higher resolution, this would not necessarily be more realistic, as the high density clumps may be regarded as physical systems of their own with some of the physics necessary to describe them properly not being present in our simulations.
The absolute value of the energy deposition is also resolution dependent. It increases by about a factor of 1.2 if we double the resolution. The reason for this is likely related to the Vishniac instability: Vishniac & Ryu (1989) estimate the wavelength at which the growth rate is largest as: 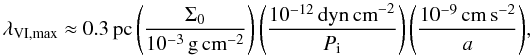 where we plugged in typical values for the column density Σ0, the internal pressure Pi, and the shell deceleration a. This is comparable to our best resolution. Therefore, finer resolution should still trigger strongly unstable Vishniac modes, which seem to have an effect on the result. The minimum unstable wavelength is predicted to be 0.5λVI,max. Unfortunately, for the present study we did not have the computational resources to probe these scales, but this should become possible in future. In contrast to the Vishniac instability, the Rayleigh-Taylor instability continues to grow faster for smaller wavelengths. Thermal conduction would be expected to be important at even smaller scales of about 0.01 pc/n, where n is the number density in the shell (McKee & Cowie 1977). Thus, our absolute efficiency numbers are lower limits.
where we plugged in typical values for the column density Σ0, the internal pressure Pi, and the shell deceleration a. This is comparable to our best resolution. Therefore, finer resolution should still trigger strongly unstable Vishniac modes, which seem to have an effect on the result. The minimum unstable wavelength is predicted to be 0.5λVI,max. Unfortunately, for the present study we did not have the computational resources to probe these scales, but this should become possible in future. In contrast to the Vishniac instability, the Rayleigh-Taylor instability continues to grow faster for smaller wavelengths. Thermal conduction would be expected to be important at even smaller scales of about 0.01 pc/n, where n is the number density in the shell (McKee & Cowie 1977). Thus, our absolute efficiency numbers are lower limits.
At the level of this accuracy, 3D effects might be important, because the shell instabilities should be 3D in nature. Up to the first supernova, our simulations are dominated by the wind of the 60 M⊙ star, and may thus be compared to the 2D results of Freyer et al. (2003). We find an energy response of at least 10 per cent, which compares to 9 per cent in the simulation of Freyer et al. (2003), which is very similar. It might point to some effect in the direction that more energy is retained in the ISM in 3D simulations, but could also be related to numerical details or the slightly higher density they use.
The general shape of the curves is however well converged (compare Fig. 11). As a further check, we also resimulated run 3S0 at the resolution of 3S1-hr. The energy deposition ratio between the two high resolution simulations is very similar to the one at low resolution. We therefore believe that the relative trends of the energy deposition we report here are reliable.
We find that the Vishniac instability dominates the shell evolution. We show that the instability in our simulations is connected to the shells’ overdensity and to non-radial motions in the shells, in agreement with the predictions of Vishniac & Ryu (1989) and Mac Low & Norman (1993). Limiting the shell’s overdensity by e.g. magnetic fields would therefore directly affect the Vishniac instability.
From the column density plots (Figs. 3, 4 and 8), it is obvious that the observational appearance of the shell is dominated by the Vishniac instability: if the shells were smooth, and the maximum density would increase with resolution as seen in our simulations (Fig. 5), one would expect that the shell gets thinner with finer resolution, as the smaller cells allow higher compression. Yet, we find a radially averaged shell width of tens of per cent of the outer radius independent of resolution (Fig. 13). In the low resolution simulation, much of the width is due to the large-scale distortion influenced by the grid directions. For the high resolution simulation the width is due to small wavelength modes.
In their survey of 322 interstellar bubbles, Churchwell et al. (2006) find typical shell widths of 20−40 per cent of the outer radius. Thus, it seems unlikely that the development of the Vishniac instability is frequently impeded by anything, e.g. limited compression due to magnetic fields, as this would again make the shells thin. In other words, in order to study the effects of magnetic fields one probably needs much higher numerical resolution than adopted in our models.
The column density should give a rough indication on observed morphologies. From the corresponding plots, we find that the Vishniac instability should also lead to observable filamentary structure inside the bubbles. This seems to be the case for some shells associated with supernova remnants (e.g. Crab, Hester 2008,compare also the discussion in van Marle & Keppens 2012), which confirms the above analysis. More detailed comparison would of course be interesting.
We find that the best way to inject energy into the ISM, i.e. to achieve a high energy response is a continuous, steady energy injection. Supernovae dissipate their energy within about 1 Myr. We show the kinematics for run 3S0 (all stars at same position) in Fig. 15. After each supernova, the shell accelerates significantly. This means more kinetic energy in the shell. Yet the increased expansion leads to fast adiabatic pressure loss of the shell interior. The increased kinetic energy is quickly dissipated at the leading radiative bow shock, as long as it is strongly supersonic. In contrast, the energy fraction deposited in the ISM in the wind phase remains roughly constant at ten per cent. Thus, retaining the injected energy in an interstellar bubble requires continuous energy injection.
The energy tracks of merging bubbles are entirely dominated by these shell kinematics effects. For example, in run 3S1, the merging process has clearly set in at 2 Myr (compare the high resolution version, Fig. 3) and continues for a few Myr thereafter. Yet, the energy track for this time interval is indistinguishable from run 3S2 (different positions of the stars) and even from 3S0 (no shell merging because drivers are at same location) and the sum of S25, S32 and S60 (no shell merging because the stars are sufficiently far away, realised by having them in different simulations).
Exploding a supernova in a superbubble and not in its own wind bubble leads to weaker radiative losses: each supernova shock heats first the bubble interior. It then makes a difference how large the respective bubble is in communicating the thermal energy to the shell: for larger bubbles, the heat energy is distributed over a greater volume. Thus the overpressure is lower. The force on the shell is correspondingly smaller. Hence, shell acceleration and adiabatic losses of the bubble interior happen on a longer timescale. This is the reason for the longer energy decay timescale for each subsequent supernova. Consequently, after a supernova, the energy decays fastest if the bubbles remain isolated, as each star has a small bubble of its own.
Off-centre explosions are another significant effect for the energy tracks: the first supernova always explodes roughly in the middle of the superbubble. This must of course be so at least for coeval stars, since its parent star also has the highest energy output and is the dominant driver of the superbubble before it explodes. The energy tracks of the simulations with differentspatial configurationsof the stars show little difference up to the point when the second star explodes. This happens necessarily significantly off-centre. The explosion accelerates first and most efficiently the parts of the super-shell which are most nearby (compare the pressure maps in Fig. 14). Yet, if the bubbles are fully merged at the time of the explosion (3S1) the effect is only at the per cent level. This is due to the high sound speed within the bubble, which communicates pressure differences quickly. We notice a considerable effect on the energy track for run 3S2, where the individual bubbles are still well identifiable at the time of the final supernova.
Thus, especially where the shells are not yet fully merged at the time of explosion, the off-centre location leads to a certain extent to a behaviour closer to the isolated bubble case. Therefore, the energy tracks (Fig. 12) of runs 3S1 and 3S2 essentially do not leave the range spanned by the isolated bubbles case (S25 + S32 + S60) and the cospatial parent star case (3S0).
 |
Fig. 14 Pressure maps of run 3S1 (left) and 3S2 (right), shortly after the second (top) and third (bottom) supernova. |
 |
Fig. 15 Shell kinematics (top: radius, middle: velocity, bottom: acceleration), as functions of time for run 3S0. The velocity points are averaged over time intervals of varying length, which correspond to shell radii differences of at least 2 cells. The shell velocity converges towards the ambient sound speed (red line). Each supernova leads to a significant acceleration of the shell (black crosses, bottom plot), followed by a comparably strong deceleration (red stars). |
Another finding which might seem curious is that all the energy tracks in Fig. 12 converge at late times. Long after the energy injection has ceased, the energy of the affected gas is dominated by the kinetic energy of the shell. Because the swept up mass is dominated by the action of the 60 M⊙ star and the final shell velocity is always similar to the sound speed of the ambient medium, the overall energy increase is very similar in all simulations.
Population synthesis of stellar groups/subgroups combined with energy injection data from stellar evolutionary models (Voss et al. 2009) show that the wind energy dominates within the first few Myr after the star formation event. Later, the energy input is dominated by supernovae. Observed subgroups have an age difference of the order of a few Myr (Voss et al. 2010, 2012). Thus, it appears possible that the energy response (compare Eq. (1)) is kept high for ≳10 Myr by the wind contributions of different subgroups coming in at slightly different times. Observations find energy responses of about ten per cent or higher (e.g. Oey & García-Segura 2004; Voss et al. 2012). This agrees very well with the results in the wind phase of our highest resolution run and might suggest that additional effects, which are not taken into account in our simulation and which we believe should only increase the energy response, may not dominate.
A similar energy response has also been inferred observationally for galactic winds (e.g. Veilleux et al. 2005), though only the supernova energy has been taken into account for the calculation. Galactic winds are thought to arise as a final merging stage from central superbubbles in star-forming galaxies. If one wants to keep the energy response high in order to match the constraints from the galactic wind observations, the individual bubbles should be closely spaced and merge early in order to have as constant an energy input rate as possible. This is of course the case for wind galaxies, such as M82, with their star clusters and even super-star clusters (e.g. Förster Schreiber et al. 2003; Westmoquette et al. 2009). The same effect that we observe for individual stars, namely that their energy deposition is higher, if they are closer together, should also apply to clusters of stars: If two clusters are closer together, they should deposit more energy into the ISM as if they were further apart.
5. Conclusions
We simulated isolated interstellar bubbles and emerging superbubbles which form from adjacent interstellar bubbles with stellar distances of the order of 10 pc. Thus, our simulations apply, within the limitations outlined in Sect. 4 above, well to hierarchically clustered star formation complexes like the Orion (Voss et al. 2010), Scorpius-Centaurus (Diehl et al. 2010) or Carina (Voss et al. 2012) regions.
We find in our simulations that up to about the second supernova the total energy of superbubbles is not strongly dependent on the spatial configuration of the group of parent stars, including zero and infinite distance. Off-centre energy injection reduces the ISM energy response significantly only if the individual bubbles are not yet fully merged. Thus, from before the second supernova onwards the energy response is higher for more closely packed configurations. We find on average about a factor of two difference in energy response between the isolated stars-case and the cospatial stellar configuration.
Supernovae increase the ISM energy only for very short timescales of about 1 Myr, increasing with the size of the superbubble at the time of the explosion. After that time, the retained energy is lower than immediately before the supernova (Fig. 10). The energy response drops by a factor of two shortly after the supernova compared to the main sequence wind phase. Our simulations are quite realistic regarding the time intervals in between subsequent supernova events (compare Voss et al. 2009). Thus, we conclude that for realistic star clusters energy is built up in the wind phases. Supernovae lead to large short-term energy variations, but only keep up the bubble energy in the long run, at a roughly constant level.
We also find that supernovae that explode inside larger bubbles have a longer energy decay time. The 60 M⊙ star has produced a bubble of ≳80 pc diameter at the time it explodes. Thus in order to obtain a physically sound feedback model, which is currently lacking in studies of disk galaxies (Scannapieco et al. 2012), it seems essential to account for the wind phase. Further, since the energy deposition does essentially not depend on the spatial configuration of the stars, up to stellar distances of about 30 pc in our simulations, it seems reasonable to use stellar clusters as fundamental feedback units, not individual stars, or in other words superbubbles rather than individual bubbles of individual stars, at least for a clustered star formation mode, which should according to our simulations be more efficient for feedback purposes.
We verified by comparison to theoretical work that the appearance of our wind shells is dominated by the Vishniac instability,which is now for the first time prominently seen in 3D simulations (this article and van Marle & Keppens 2012). High resolution is essential to obtain the necessary shell overdensities which are crucial for the development of the instability. This effect widens the shell significantly in col. density plots, which we suggest may explain the large observed shell widths of 20 per cent of the outer radii and more. It also produces filamentary structure in the shell which is also easily visible in our column density plots. We conclude that filamentary structure inside interstellar bubbles may be related to the Vishniac instability.
Online material
Movie associated to Fig. 3
Access hereAlthough we have carefully chosen the flux limiter, the shell instability evolves still somewhat anisotropically. This is similar to the 2D results of Ntormousi et al. (2011) with the RAMSES code, where even a five times higher spatial resolution could not get the shell instabilities completely isotropic.
Acknowledgments
This research was supported by the cluster of excellence “Origin and Structure of the Universe” (www.universe-cluster.de). We thank the anonymous referee for a very useful report, and Mordecai-Mark Mac Low for very helpful comments.
References
- Arthur, S. J. 2007, Wind-Blown Bubbles around Evolved Stars, eds. T. W., Hartquist, J. M., Pittard, & S. A. E. G., Falle, 183 [Google Scholar]
- Breitschwerdt, D. & de Avillez, M. A. 2006, A&A, 452, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chu, Y.-H. 2008, in IAU Symp. 250, eds. F. Bresolin, P. A. Crowther, & J. Puls, 341 [Google Scholar]
- Churchwell, E., Povich, M. S., Allen, D., et al. 2006, ApJ, 649, 759 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2004, A&A, 425, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2005, A&A, 436, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diehl, R., Lang, M. G., Martin, P., et al. 2010, A&A, 522, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L., Burkert, A., & Pringle, J. E. 2011a, MNRAS, 417, 1318 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., Burkert, A., & Pringle, J. E. 2011b, MNRAS, 413, 2935 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, R. P. 2012, ApJ, 744, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Fierlinger, K. M., Burkert, A., Diehl, R., et al. 2012, in Advances in Computational Astrophysics: Methods, Tools, and Outcome, eds. R. Capuzzo Dolcetta, M. Limongei, A. Tomambe, & G. Giobbi, ASP Conf. Ser., 453 [Google Scholar]
- FörsterSchreiber, N. M., Genzel, R., Lutz, D., & Sternberg, A. 2003, ApJ, 599, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Freyer, T., Hensler, G., & Yorke, H. W. 2003, ApJ, 594, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Freyer, T., Hensler, G., & Yorke, H. W. 2006, ApJ, 638, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Segura, G., & MacLow, M.-M. 1995, ApJ, 455, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Gritschneder, M., Burkert, A., Naab, T., & Walch, S. 2010, ApJ, 723, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Gruendl, R. A., Chu, Y.-H., Dunne, B. C., & Points, S. D. 2000, AJ, 120, 2670 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J. 2008, ARA&A, 46, 127 [Google Scholar]
- Jaskot, A. E., Strickland, D. K., Oey, M. S., Chu, Y.-H., & García-Segura, G. 2011, ApJ, 729, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., Federrath, C., & Henning, T. 2011, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- MacLow, M.-M., & Norman, M. L. 1993, ApJ, 407, 207 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Cowie, L. L. 1977, ApJ, 215, 213 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Niedzielski, A., & Skorzynski, W. 2002, Acta Astron., 52, 81 [Google Scholar]
- Ntormousi, E., Burkert, A., Fierlinger, K., & Heitsch, F. 2011, ApJ, 731, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S. 2009, in AIP Conf. Ser., 1156, eds. R. K. Smith, S. L. Snowden, & K. D. Kuntz, 295 [Google Scholar]
- Oey, M. S., Clarke, C. J., & Massey, P. 2001, in Dwarf galaxies and their environment, eds. K. S. de Boer, R.-J. Dettmar, & U. Klein (Aachen, Germany: Shaker Verlag), 181 [Google Scholar]
- Oey, M. S., & García-Segura, G. 2004, ApJ, 613, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Piontek, R. A., Gressel, O., & Ziegler, U. 2009, A&A, 499, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pittard, J. M., Dyson, J. E., Falle, S. A. E. G., & Hartquist, T. W. 2005, MNRAS, 361, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., Roccatagliata, V., Gaczkowski, B., & Ratzka, T. 2012, A&A, 541, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raymond, J. C., Cox, D. P., & Smith, B. W. 1976, ApJ, 204, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, M., Breitschwerdt, D., Baumgartner, V., & Haberl, F. 2011, A&A, 528, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scannapieco, C., Wadepuhl, M., Parry, O. H., et al. 2012, MNRAS, 423, 1726 [Google Scholar]
- Slyz, A. D., Devriendt, J. E. G., Bryan, G., & Silk, J. 2005, MNRAS, 356, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G., & Bodenheimer, P. 1988, ARA&A, 26, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G., Bodenheimer, P., Franco, J., & Rozyczka, M. 1990, MNRAS, 244, 563 [NASA ADS] [Google Scholar]
- van Marle, A. J., & Keppens, R. 2012, A&A, 547, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Marle, A. J., Meliani, Z., & Marcowith, A. 2012, A&A, 541, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Vishniac, E. T. 1983, ApJ, 274, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Vishniac, E. T., & Ryu, D. 1989, ApJ, 337, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Voss, R., Diehl, R., Hartmann, D. H., et al. 2009, A&A, 504, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voss, R., Diehl, R., Vink, J. S., & Hartmann, D. H. 2010, A&A, 520, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voss, R., Martin, P., Diehl, R., et al. 2012, A&A, 539, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Westmoquette, M. S., Gallagher, J. S., Smith, L. J., et al. 2009, ApJ, 706, 1571 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersma, R. P. C., Schaye, J., & Smith, B. D. 2009, MNRAS, 393, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, U. 2008, Comput. Phys. Commun., 179, 227 [Google Scholar]
- Ziegler, U. 2011, J. Comput. Phys., 230, 1035 [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Test simulation of an isolated supernova in a homogeneous environment according to Tenorio-Tagle et al. (1990).This test was run in 1D and spherical coordinates at radial resolutions between 100 and 6400 cells with respective increments of a factor of two and with the standard cooling and heating. Top: density slices at different times (increasing from left to right). Middle: evolution of thermal (thin lines) and kinetic (thick lines) energy for the 100 (orange triple dot-dashed lines), 800 (solid black lines), 6400 (red dashed lines) radial cells simulation. Additionally a simulation with 3200 radial cells and enhanced cooling is shown (blue dot-dashed lines, see text for details). The left part of the plot zooms into the first 2000 yr of the evolution. Bottom: maximum compression at about 20 000 yr as a function of resolution. The expected maximum compression at this time is four for a strong adiabatic shock. |
| In the text | |
 |
Fig. 2 Cumulative energy (top) and mass (bottom) input. We use the output of a 25 M⊙ (dashed, labels: Ms = M⊙), 32 M⊙ (dotted) and a 60 M⊙ star as input for our simulations, separately or combined. The difference between the total mass output and the initial mass indicates the mass of the dark remnant. The energy is given in “Bethe” = 1051 erg. |
| In the text | |
 |
Fig. 3 Column density integrated over Z-direction and Y-direction (left and middle col., respectively) and midplane density (right column) for three different snapshot times from top to bottom for run 3S1-hr. The projections of the three massive stars into the X–Y plane is indicated as small red stars in the density plots on the right. The 60 M⊙ star blows the biggest bubble from the origin. The 32 M⊙ bubble towards its lower left (XY-plots) is only slightly bigger than the one of the 25 M⊙ star above. The shell forms spikes and dense clumps due to the combined action of Vishniac and thermal instability. A movie is provided with the online version. |
| In the text | |
 |
Fig. 4 Figure 3 continued, but with all scales adapted to the snapshots presented in this figure. |
| In the text | |
 |
Fig. 5 Maximum density as a function of time for runs 3S1-hr (solid), 3S1-mr (dashed) and 3S1 (dotted). The horizontal lines correspond to the critical compression above which the Vishniac instability is triggered for supernova (lower line) and wind (thicker upper line) shells according to Vishniac & Ryu (1989). The axis on the right shows the overdensity factor over the undisturbed ambient medium. |
| In the text | |
 |
Fig. 6 One-dimensional slices in X-direction through run 3S1-hr at time T = 8.53 Myr. The Y and Z coordinates are chosen appropriately for the slices to include the position of the only remaining star at that time (25 M⊙ , at X = −30 pc, indicated by the star in the middle diagram). Top: positive X-velocity (blue, dashed line), negative x-velocity (red dash-dotted line) and sound speed (solid black). Middle: pressure (logarithmic). Bottom: density (logarithmic). See text for details. |
| In the text | |
 |
Fig. 7 Shell details for the final snapshot of run 3S1-hr. Shown is an X-Y zoom of density, pressure, temperature and Mach number, as indicated on the individual panels, around the position of the maximum density, which is located at (X, Y, Z) = (−30, −79, −52) pc. Velocity vectors are overlaid on the density plot. The high density region is overpressured and has a temperature below 20 K. See text for more details. |
| In the text | |
 |
Fig. 8 Column density at a comparable late evolution time for runs 3S1 (top) and 3S1-hr (bottom). The high resolution bubble is more spherical, larger, achieves higher peak column densities and the Vishniac instability is more pronounced. |
| In the text | |
 |
Fig. 9 Analysis of the non-radial Mach number, i.e. the Mach number perpendicular to the direction of the shell’s expansion. Only the region with positive X-coordinate, which corresponds to the undisturbed part of the 60 M⊙ bubble, is taken into account. Left: 4.05 Myr, right: 7.47 Myr. The upper parts show the non-radial Mach number versus the logarithm of the density. Colour encodes the mass per bin, where each bin spans 0.05 in Mach number and 0.06 dex in logarithmic density. No appreciable non-radial motions are found for the hot bubble interior, whereas the dense shell material shows Mach numbers of the order of unity. The lower parts show mass weighted non-radial Mach number histograms (vertically collapsed versions of the plots above). The plots are dominated by the quiescent ambient medium. The mass with given non-radial Mach number declines strongly around a Mach number of unity towards higher Mach numbers as expected for shells dominated by the Vishniac instability. |
| In the text | |
 |
Fig. 10 Top part: input (solid) and retained (dotted) energy for run 3S1-hr. The response ℛ (retained energy divided by input energy) is shown in the bottom part. See text for more details. |
| In the text | |
 |
Fig. 11 Resolution effects on the retained energy. Top part: retained energy for run 3S1-hr (solid line, high resolution), 3S-mr (dashed line, intermediate resolution) and run 3S1 (dotted line, low resolution). The bottom part shows the energy ratio 3S1-hr/3S1-mr (solid line), 3S1-mr/3S1 (dashed line) and 3S1-hr/3S1 (dash-dotted line). In each case, the data for the higher resolution run has been interpolated to the data output times of the lower resolution run. The spikes at the supernova times are artefacts of the interpolation process at the discontinuities of the functions. The horizontal dashed line indicates equality for comparison. The energy increases similarly for each doubling of resolution. The general functional behaviour is independent of resolution. See text for more details. |
| In the text | |
 |
Fig. 12 Energy tracks for different simulations, where only the positions of the three stars differ. Run labels in the legends are explained in Table 1. S25 + S32 + S60 refers to the sum of the energy tracks of the three simulations of the bubbles of the isolated 25 M⊙, 32 M⊙ and 60 M⊙ stars, respectively, which corresponds to a very large distance. 3S0 is the opposite case, where three stars are in the same region. Top: absolute values. Middle: three-stars simulations relative to the sum of the three isolated bubbles. Interpolations always use the 3S0 time base. Interpolation artefacts are visible at the discontinuities due to the supernovae (4.6, 7.0 and 8.6 Myr). Bottom: difference of the very similar energy tracks of runs 3S1 and 3S0, normalised to 3S0 as a percentage. The solid red line marks zero. The difference has been set to zero for the time intervals 10,000 yr around each supernova in order to mask the interpolation artefacts. See text for details. |
| In the text | |
 |
Fig. 13 Shell width for column density maps. Top: angle-averaged col. density over radius for run 3S1-hr at 12.56 Myr. From such plots, the shell width has been determined as the radial range where the column density is at least five per cent greater than at large radii (undisturbed gas). The shell width determined in this way is shown in the middle plot as a function of time, and in the bottom plot as a function of outer radius. Black pluses are for run 3S1, red stars for run 3S1-hr. The average shell width does not depend significantly on resolution. |
| In the text | |
 |
Fig. 14 Pressure maps of run 3S1 (left) and 3S2 (right), shortly after the second (top) and third (bottom) supernova. |
| In the text | |
 |
Fig. 15 Shell kinematics (top: radius, middle: velocity, bottom: acceleration), as functions of time for run 3S0. The velocity points are averaged over time intervals of varying length, which correspond to shell radii differences of at least 2 cells. The shell velocity converges towards the ambient sound speed (red line). Each supernova leads to a significant acceleration of the shell (black crosses, bottom plot), followed by a comparably strong deceleration (red stars). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


