| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219921 | |
| Published online | 28 November 2012 | |
Spectrum of the unresolved cosmic X-ray background: what is unresolved 50 years after its discovery
1
INAF, Osservatorio Astronomico di Brera, via Brera 28,
20121
Milano,
Italy
e-mail: alberto.moretti@brera.inaf.it
2
INAF, Osservatorio Astronomico di Trieste, via Tiepolo 11,
34143
Trieste,
Italy
3
INAF, Istituto di Astrofisica Spaziale e Fisica Cosmica, via E.
Bassini 15, 20133
Milano,
Italy
4
DiSAT, Università dell’Insubria, via Valleggio 11, 22100
Como,
Italy
5
INFN, Sezione di Milano Bicocca, P.za Della Scienza 3,
20126
Milano,
Italy
6
INAF, Osservatorio Astronomico di Brera, via Bologna, via Ranzani
1, 40127
Bologna,
Italy
Received:
29
June
2012
Accepted:
10
October
2012
Aims. We study the spectral properties of the unresolved cosmic X-ray background (CXRB) in the 1.5–7.0 keV energy band with the aim of providing an observational constraint on the statistical properties of those sources that are too faint to be individually probed.
Methods. We made use of the Swift X-ray observation of the Chandra deep field South complemented by the Chandra data. Exploiting the lowest instrument background (Swift) together with the deepest observation ever performed (Chandra) we measured the unresolved emission at the deepest level and with the best accuracy available today.
Results. We find that the unresolved CXRB emission can be modeled by a single power law with a very hard photon index Γ = 0.1 ± 0.7 and a flux of 5-2.6+3.2 erg s-1 cm-2 deg-2 in the 2.0–10 keV energy band (1σ error). Thanks to the low instrument background of the Swift-XRT, we significantly improved the accuracy with respect to previous measurements.
Conclusions. These results point towards a novel ingredient in AGN population synthesis models, namely a positive evolution of the Compton-thick AGN population from local Universe to high redshift.
Key words: X-rays: diffuse background / X-rays: general / galaxies: active
© ESO, 2012
1. Introduction
The flux limit reached by the Chandra deep field South (CDF-S) 4 Ms observation is such that the observed source angular density is four sources per square arcminute (Lehmer et al. 2012). These sources have been found to be mostly unobscured and Compton-thin (NH < 1023 cm -2) active galactic nucleus (AGN) at redshift ≲2 with some contribution at soft energies (<2 keV) from galaxy clusters and starburst galaxies (Brandt & Hasinger 2005; Tozzi et al. 2006; Luo et al. 2008; Xue et al. 2011). Still, it is worth investigating whether a non-negligible contribution to the cosmic X-ray background (CXRB) has not been identified yet. This may be due to an intrinsically diffuse component or to the cumulative contribution of individual sources below the current flux limit. In the latter case, high redshift and Compton-thick AGN (the ones for which the neutral hydrogen column density is higher than the inverse of the Thomson cross-section, NH > 1.5 × 1024), together with star forming galaxies, are expected to be the main contributors.
The very fact that bright quasars, powered by supermassive black holes, have been found at z > 6 (Fan et al. 2006; Willott et al. 2010; Mortlock et al. 2011), implies the existence of a large numbers of less massive AGN at these early epochs (Volonteri 2010). Thus, because no source at z > 6 has been detected in the CDF-S, the unresolved CXRB can be used to probe SMBH formation models at these early epochs (Salvaterra et al. 2012). In the same way, the unresolved CXRB can be used to put some constraints on the contribution of the X-ray sources to re-ionization (Dijkstra et al. 2004; Salvaterra et al. 2005, 2007; McQuinn 2012).
Although CDF-S observation reaches a flux limit such that starburst galaxies match AGN in surface density (Lehmer et al. 2012), most of the galaxies still remain undetected at low redshift, contributing to the unresolved CXRB. Indeed, using the X-ray galaxy luminosity as proxy (Mineo et al. 2012), CXRB can be used to study the evolution of the star formation rate up to redshift z = 6 (Dijkstra et al. 2012; Cowie et al. 2012).
Compton-thick (CT) are expected to be the main contributors to the unresolved X-ray emission in the CDF-S. In fact, while their number is expected to be similar to moderately obscured AGN (Gilli et al. 2007; Treister et al. 2009), only a few have been found among the 740 sources of the CDF-S (Tozzi et al. 2006; Luo et al. 2011).
From an observational point of view two different approaches have been pursued to probe the unresolved emission in the CDF. The first approach consists in calculating the difference between the total CXRB and the integrated flux of all detected sources. Moretti et al. (2003) and Worsley et al. (2006), following this approach, found that the unresolved fraction was 10–20%, and higher at harder energies. Moreover, Worsley et al. (2004) recognized the signature of a highly absorbed AGN in the spectral shape of the unresolved emission. Unlike these, Luo et al. (2011), while measuring similar values in the softer band, found that the unresolved emission is consistent with zero, in the 6–8 keV band, posing a strict upper limit. The main sources of uncertainty here are the total CXRB measure (Revnivtsev et al. 2005; Frontera et al. 2007; Moretti et al. 2009) and the statistical contribution of the rare and bright sources.
The second approach is a direct measure of the unresolved emission: Hickox & Markevitch (2007) found that the flux, with large uncertainties (~200%), was consistent with zero in the 2–5 keV band both in the CDF-S and CDF-N. The source of this huge uncertainty is the very low surface brightness of the unresolved emission, which represents only a small fraction of the Chandra instrument background. In this regime the signal/background ratio is so low that a few percentage points of systematic error in the background measure irreparably affect the measurement accuracy1.
In this paper we work out a different approach, directly measuring the unresolved emission on the Swift-XRT observation of the CDF-S and subtracting the signal of the sources revealed by Chandra. In this way we exploit, at the same time, the low and predictable instrument background of the Swift X-ray telescope (XRT) and the unprecedented depth of the Chandra observation. The paper is organized as follows. In Sect. 2 we briefly describe the Swift-XRT telescope and the datasets we used, showing their distinctive qualities. In particular we dwell on the instrument background comparing Swift-XRT and Chandra in order to emphasize the peculiarity of our work. In Sect. 3 we deal with a wealth of technical details to give the full particulars of the spectral analysis used in this paper. For the sake of clarity the fit procedure and the results are presented in Sect. 4. Finally, in Sect. 5 we discuss our results, first, comparing them with previous measurements and then, with the expectations from one AGN population synthesis model.
Throughout this paper, errors are quoted at the 68% confidence level for the two parameters of interest (Δχ2 = 2.3), unless otherwise specified. We adopt the following cosmology parameter values: Ωm = 0.3, ΩΛ = 0.7, h0 = 0.7.
2. Instrument, data, and reduction procedures
2.1. Swift-XRT
The X-ray telescope (XRT) on board the Swift satellite (Gehrels et al. 2004), uses a Wolter I mirror set, originally designed for the JET-X telescope (Citterio et al. 1994), to focus X-rays (0.2–10 keV) onto a XMM-Newton/EPIC MOS CCD detector (Burrows et al. 2005). The effective area of the telescope (~150 cm2 at 1.5 keV) is about five times smaller than Chandra. The point-spread function (PSF), similar to XMM-Newton, is characterized by a half energy width (HEW) of ~18′′ at 1.5 keV (Moretti et al. 2007). The nominal field of view has a radius of ~11 arcmin, with a pixel scale of 2.37′′.
2.2. XRT observation of the CDFS
Swift observed the CDFS for a total nominal exposure of 563 700 s in the period July 2007 to December 2007. We reduced data using the standard software (HEADAS software, v6.10, CALDB version Sep10) and basically following the procedures described in the instrument user guide2 with some minor modifications for our purposes. In our analysis we excluded the external (detx <90 and detx >510) CCD columns that are affected by the presence of out-of-time-events from corner calibration sources. This corresponds to a nominal field of view (FOV) of 16.5 × 18.9 arcmin (0.087 deg2). To detect sources we ran the task wavedetect (Freeman et al. 2002) with default input parameter values on three different energy bands (0.5–2.0; 2.0–7.0; 0.5–7.0 keV), on a large number of spatial scales (2, 4, 8, 12, 16, 24, 32, 64, 128 pixels, 1 pixel equals 2.36′′). Merging the three catalogs yields a total of 109 sources down to a limit of ~3 × 10-16 erg s-1 cm-2 and ~1 × 10-15 erg s-1 cm-2 in the 0.5–2.0 and 2.–10 keV bands respectively.
2.3. XRT instrument background
For our purposes, the most relevant characteristic of the XRT is the low level and high reproducibility of the instrument background (NXB), which we define as the signal registered on the CCD when focused radiation is excluded. This is mostly contributed by the induced particle emission and the pure instrument electronic noise (Hall et al. 2008).
To estimate the NXB spectrum in the CDF-S observation, we used the signal registered on the small regions in the four CCD corners that are not exposed to the sky (NES regions) and not contaminated by calibration sources. As these data are only available for observations after June 2008, we used observations performed in 2008–2009 for a total of ~7 Ms. For a detailed study of the XRT NXB also see Moretti et al. (2009, 2011). To check at what level of accuracy we can reproduce the XRT instrument background we compared this spectrum with the XRT CDF-S observation in the 7–10 keV energy band. There the effective area is a factor five to ten times lower than the one at energies <2 keV and, at the same time, the instrument background is inflated by the presence of the Ni (Kα and Kβ at 7.478 and 8.265 KeV) and Au (Lα at 9.713 keV) fluorescence lines. Once the detectable sources have been removed, the cosmic signal, is expected to be only ≲1% of the background in this particular energy band.
As shown in Fig. 1 we find that the two spectra coincide very well beyond 7 keV. Indeed, the ratio of the signals between 7–10 keV is XRT-CDF-S/NES = 1.033, while if we restrict to 7 and 8 keV, where the nickel K lines are completely overwhelming, the agreement is even better XRT-CDF-S/NES = 0.993. As such, in the systematic error calculation we conservatively assumed that the instrument background is known at 5% accuracy (1σ). We note that, in some previous works that used Chandra and XMM data (De Luca & Molendi 2004; Hickox & Markevitch 2006), the ratio of the signals at the very end of the energy band has been used to rescale the measurement of the instrument background. Here we find very good agreement between the two datasets, without any ad hoc renormalization. This plainly shows the high level of reproducibility of the XRT instrument background.
2.4. Comparison with Chandra
To compare the Swift-XRT and Chandra instrument backgrounds, we considered the signal registered on the XRT NES regions and the signal registered on the ACIS-I in stowed position3. In the upper panel of Fig. 2 we plot the two instrument background spectra normalized per unit of area, which show the effect of the different environments (orbit plus satellite). The very fact of being in high orbit (assuming negligible effects from the satellite structure differences) produces a particle background in Chandra that is a factor ~5 higher than in XRT, which is in a low orbit. In the spectroscopic study of extended sources, what is relevant is the background per unit of solid angle (middle panel of Fig. 2), which can be calculated from the previous one, by accounting for the pixel scale. Since the ratio of the pixel linear scale between Chandra and Swift is ~4.5, we find that the Chandra background per unit of solid angle is ~50 higher than Swift-XRT. Finally, if we take the effective area into account (which is approximately a factor 5 higher in Chandra), we find that the ratio signal/background for extended sources (for which the angular resolution is not important) is a factor ~10 better in Swift-XRT than in Chandra (lower panel of Fig. 2).
 |
Fig. 1 Energy channel (PI) distribution of the XRT unresolved emission (black) compared with the instrument background (red). In this plot PI channels have been transformed in energy using a single value and not the RMF matrix. |
 |
Fig. 2 Comparison between Chandra and Swift-XRT instrument background spectra. Upper panel: NXB of the two instruments are plotted per unit area, to show the influence of different environments (orbits plus satellite). Middle panel: NXB are plotted per solid angle, to show the influence of different focal lengths. Lower panel: the ratio between Chandra and XRT NXB calculated per solid angle and normalized by the respective effective areas. This shows the improvement in the signal/background ratio for an extended source using XRT instead of Chandra. |
3. Spectral analysis
We restricted our analysis to the sky circular region centered on RA = 53.1092 and Dec = –27.82086 with a radius of 0.1053 degrees (0.03184 deg2), which optimizes the intersection of the two instrument exposure maps. Hereafter we refer to this region as the region of interest (ROI) region. The average effective exposures within this region is 508 ks. Moreover, we restricted our analysis to the 1.5–7.0 keV energy band. We excluded the soft part (<1.5 keV) because in this range our data did not allow us to disentangle the genuine extragalactic CXRB components from the local ones. In fact, in this energy band, the diffuse X-ray emission is expected to be contributed both by the thermal emission from the Galaxy and the local Bubble (Snowden et al. 1998; Kuntz & Snowden 2000) and by the thermal emission from faint galaxy groups and WHIM filaments (Cappelluti et al. 2012; Shull et al. 2012). Above 7 keV, as said in the previous section, the instrument background and, in particular, the particle-induced one overwhelms the cosmic signal.
To study the spectrum of the unresolved CXRB on the Swift-XRT data, first, we excised the signal of all the detected sources, which are 37 within the ROI, with fluxes in the range [1e–15, 1e–14] erg s-1 cm-2 in the 2.0–10.0 keV band. To get rid of most of the source signal without losing too much area, we excluded a circular region with a radius that depends on source counts. We used a radius equal to twice the radius at which the source surface brightness profile matches the background: this means a typical radius of 25 arcsec with values ranging from 20 to 60. Hereafter we refer to this radius as rext.
Besides the instrument background, the unresolved signal on the XRT detector in the 1.5–7.0 energy band is expected to be contributed by the following elements:
-
the sources detected by Chandra and not by XRT;
-
the optically/IR detected (X-ray undetected) sources;
-
PSF residuals from detected sources;
-
the stray-light contamination;
-
the unresolved CXRB that is the goal of the present work.
To perform spectral analysis we subtracted the instrument background and modeled the remaining five components. In the following we describe item by item the way we quantified each single component.
3.1. Chandra sources
We used the public catalog of Xue et al. (2011), which is the result of the cross-correlation of three different energy bands and which consists of 740 sources down to the unprecedented flux limits of 10-17 erg s-1 cm-2 and 10-16 erg s-1 cm-2 in the 0.5–2.0 and 2.0–10.0 keV band. In the selected region the Chandra catalog lists 326 sources that have not been detected by XRT. We summed the pha files of the sources and of the (locally extracted) backgrounds, weighting the response (RMF) and ancillary (ARF) files by the source counts. The full details of the reduction of the X-ray spectral data are described in Vattakunnel et al. (2012).
To quantify the impact of cross-calibration between Chandra and Swift-XRT and source variability (Chandra and Swift-XRT observation were performed in different periods), we compared the summed spectra of the sources detected by both instruments, excluding the five brightest. These are 32 sources with fluxes ranging between 10-16 and 10-14 erg s-1 cm-2 in the [0.5–2.0] band. The spectral analysis of the two stacked spectra yielded results that are consistent within 1σ at the level of 7% (Table 1). This variance can be easily encompassed in the systematic error budget of the analysis. This should be considered as an upper limit as the total flux variation associated to the intrinsic variability of the 294 remaining fainter source sample is expected to be significantly lower than the 32 brighter ones. At the end we conservatively adopted a 7% (1σ) value in the systematic error uncertainties in the cross-calibration between the two telescopes.
Spectral analysis results of 32 stacked XRT sources and corresponding Chandra sources.
3.2. Optical/IR galaxies
Several studies put in evidence that optical/IR galaxies, which are not detected in X-ray, show significant emission once their contribution is averaged (or stacked) over a large sample (Worsley et al. 2006; Hickox & Markevitch 2007). We used the Grazian et al. (2006) multi-wavelength (from 0.3 to 8.0 μm) catalog, which covers the large and deep area in the GOODS Southern Field by combining public data from Hubble VLT, Spitzer, and 2.2ESO. We used the 5683 galaxies detected within the four arcminute radius circular region centered on RA = 53.126 and Dec = –27.820, offset by 1 arcmin to the west from the center of the ROI (Fig. 3). This ensures a coverage of 40% of our ROI. We found that these galaxies make a low, but significant contribution to the X ray emission, with a ratio signal/background of ~3%. To test the systematic uncertainty of this operation we performed the same analysis by varying the region (from 3 to 6 arcmin of radius) and the extraction radius for the single sources (from 2 to 4 pixels). We found that scatter of the result is 10% at 1σ level, which is much less than the statistical error.
3.3. PSF residuals
 |
Fig. 3 Black dots are the 18 296 sources from Grazian et al. (2006) catalog. The green circle indicates our ROI. Red dots are the 5683 optical/IR sources we used in the spectral analysis. |
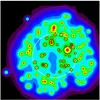 |
Fig. 4 The PSF model of the 109 sources detected in the XRT observation at 2.5 keV energy. The large white circle shows the boundaries of our ROI, while small black circles show regions we excised (rext). The PSF residuals is the small, but not negligible signal outside small circles and within the ROI. |
 |
Fig. 5 Upper-left panel: fraction of the flux of a source outside of the field of view falling within the annulus between 5 and 6 arcmin. Black, red, and blue points represent the fraction measured in the Crab calibration observations in the total (1.5–7.0), soft (1.0–2.0), and hard bands respectively. Lines are the linear interpolation between the measures. Upper-right panel: black line is the calibration measure error histogram. Green dashed line is the histogram of the relative difference, between soft and hard band. Lower-left panel: the stray-light contamination on the XRT detector from a uniform source in different concentric annuli on the detector, accounting for the CDFS exposure map. Right-lower panel: black line is the error histogram. Green dashed line is again the histogram of the soft/hard relative difference. |
As said, from XRT data we excluded most of the signal of the detected sources by excising circular regions, with the size depending on the source flux (rext). This leaves a small fraction (~5%) of source fluence spread on the rest of the field of view, which we evaluated using the PSF analytical model (Moretti et al. 2005). We also considered the small contribution from PSF wings from sources detected outside the ROI (76 objects). This fraction depends on the energy since harder photons are more scattered. We calculated the residuals on a grid of 50 different energies in the 2.0–7.0 keV range. We found that, at 2.5 (6.0) keV, 3.7% (4.0%) of the 109 source flux is diffuse all over the ROI (Fig. 4). To account for this energy dependence we built an ad hoc ARF file, linearly interpolating the grid test energies, such that fitting the stacked spectrum of the 109 sources yields the appropriate corrections. In the systematic error calculation we assumed that the PSF model extrapolated up to ~6 arcmin radii is accurate at the level of 10% accuracy (1σ) (Moretti et al. 2005).
3.4. Stray-light contamination
One of the main components in the unresolved signal in the Swift-XRT data is the stray-light contamination. This is produced by photons coming from sources that are outside the telescope FOV at distances between 25 and 100 arcmin from the optical axis of the telescope. A fraction of the photons produced by these sources reach the detector after only one reflection on the mirror or even directly, passing through the mirror shells without any interaction. Some X-ray telescopes mount baffles on top of the mirrors to prevent this contamination. This is not the case for XRT, for which the stray light is a significant fraction of the diffuse radiation registered on the CCD. This contamination has been accurately calibrated in Moretti et al. (2009) using a set of observations of bright sources (Crab, Sco-X1) observed outside the field of view.
To calculate the stray-light contamination in the XRT CDF-S observation, we first split the detector into 12 concentric annuli (external – internal radius = 1′) and calculated which fraction of the flux of the calibration source, positioned at a given angle outside the field of view, falls within the ith annulus (hereafter frazi(θ)). For example, we found that, when the Crab is positioned at 45′ from the telescope aim, (0.25 ± 0.01)% of its flux falls within the 5–6′ annulus (upper-left panel of Fig. 5). The typical 1σ relative error is ~5% (upper-right panel of Fig. 5). As shown in the same figure we do not detect any dependence of the stray-light fraction on energy: the relative differences between the soft (1.0–2.0 keV) and hard bands (2.0–7.0) keV, defined as abs(frazsoft–frazhard)/frazsoft, are at the level of the statistical error (~5%).
 |
Fig. 6 Five data sets used in this work. The XRT unresolved spectrum (black) has been fit by a sum of 5 different power law: (i) Chandra sources, not detected by XRT (blue); (ii) X-ray emission of optical/IR sources (violet); (iii) XRT sources to model PSF residuals (red); (iv) the CXRB spectrum to model stray-light contamination (green). The XRT unresolved spectrum has been offset up by a factor 8 for clarity. |
Total flux of the 326 Chandra sources not detected in the XRT image: comparison of our best fit to the stacked spectrum with the sum of the Xue et al. (2011) catalog photometric values.
Then, for each annulus we calculated the stray-light contamination produced by a uniform source extended all around the field of view. To do this we linearly interpolated the calibration observations in the 15′ < θ < 120′ interval and integrated frazi(θ) 2πθ dθ (lower-left panel of Fig. 5). In this way we get the contamination measure in terms of CXRB fraction. The histogram of the relative errors of the 12 bins are plotted in the lower right hand panel: typical value is 5%.
After summing different contributions at different off-axis angles and accounting for the effective exposure map of our observation, we found that in our ROI the stray-light contamination is expected to be equivalent to the 0.690 ± 0.020% of the CXRB or (4.9 ± 0.2) × 10-12 erg s-1 cm-2 deg-2 in the 2.0–10.0 keV. This is done in the assumption that the CXRB all around the CDFS is uniform and accurately reproducible. The first assumption is justified by the fact that the master ROSAT catalogs4 do not report bright sources within a two degree radius. This means that we can safely assume that the contamination on our field of view is produced by a typical collection of CXRB sources that are symmetrically distributed. It also follows that the second assumption is fully justified. In fact, although we do not have any direct X-ray observation of the nearby regions (ROSAT observation are limited to energies <2 keV), the cosmic variance is ≲3% because the interested sky area is as large as ~3 deg2 (Moretti et al. 2009). These uncertainties are accounted for in the systematics calculation, see Sect. 4.2.
4. Fit procedure and results
Best fit values of the different components contributing the unresolved signal in the XRT observation.
We used a total of five different datasets (Fig. 6), plus one for the instrument background: (i) the Chandra stacked spectrum of the 326 sources undetected by Swift-XRT; (ii) the Chandra stacked spectrum of the 5683 optical/IR sources; (iii) the XRT stacked spectrum of the 109 detected sources, used with the ad hoc modified response file to model the PSF residuals; (iv) the CXRB spectrum (stacking of 130 XRT observations) used to quantify the stray-light contamination; (v) the fifth dataset is the XRT unresolved spectrum that we assume is given by the sum of the four other (opportunely renormalized), plus the truly unresolved X-ray emission. To correctly propagate the statistical uncertainties of the single components, we fitted the five datasets together. We modeled (i)–(iv) datasets with single absorbed power laws. For the dataset (v) we used the sum of five different power laws (wabs*(pow+pow+pow+pow+pow) in XSPEC syntax): the parameters of the first four power-laws were linked to the best values of the (i)–(iv) dataset fit, while the fifth photon index and normalization were left free to vary. The absorbing column was frozen to the Galactic value derived from the HI Galaxy map (Kalberla et al. 2005) 7.02 × 1019 cm-2. In the fit procedure we used C-statistics grouping the spectrum to have a minimum of one count for each bin. We checked that enhancing the minimum event number for each bin (we tested 3 and 5) does not significantly affect the fit results. We also checked that grouping data with a minimum of 20 counts for each bin and using chi-square statistics does not significantly change the results.
4.1. Results
Considering the five data-sets together, the adopted model provides a good description of the data: chi squared = 2260.25 using 1954 PHA bins; reduced chi-squared = 1.16 for 1944 degrees of freedom. The best values are reported in Table 3, and the best-fit models are plotted in Fig. 7. Instrument background and the stray-light contamination represent ~52% and 15% of the signal respectively. The remaining 33% is essentially contributed by the emission of the Chandra sources and the real unresolved emission at the same level (15% each), while the optical sources represent 2% of the total.
We find that the unresolved emission can be modeled by a hard power law with photon index Γ = 0.1 ± 0.7 and a normalization of 7.6 (+10.0, –5.2) × 10-5 photons s-1 cm-2 deg-2 at 1 keV, corresponding to a flux density of 5 × 10-12 erg s-1 cm-2 deg-2 in the 2.0–10. keV band. We note that excluding fainter and fainter sources makes the unresolved spectrum harder. As shown in Fig. 8, considering the whole signal from the CDF-S, including all the sources, yields a photon index is 1.20 ± 0.05, which is close to the total CXRB (Γ = 1.4). Excluding all the XRT detected source makes the slope 0.84 ± 0.1, while excluding all the Chandra 4 Ms catalog sources brings the photon index down to 0.7 ± 0.3. Finally removing the contribution of optical/IR sources makes the final Γ = 0.1 ± 0.7.
 |
Fig. 7 Results of the fit procedure. We modeled the XRT unresolved spectrum as the sum of five components, each fit by a power law. Colors are the same as in the previous figure: (i) Chandra sources not detected by XRT (blue); x (iii) bright sources PSF residuals (red); (iv) stray-light contamination (green); (iv) X-ray emission of optical/IR sources (violet). The fifth component, the truly unresolved emission, which is our aim, is plotted with its uncertainties as the gray area. |
 |
Fig. 8 Photon index of the unresolved CXRB as function of the flux of the excluded sources. |
In the remainder of this section we detail the results we obtain for the four other components of the XRT unresolved signal.
-
(i)
We find that the integrated emission of the 326 Chandrasources is well constrained both in slope(0.94
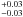 )
and flux (4.94
)
and flux (4.94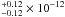 erg s-1 cm-2
in the 2–10 keV band). As expected, the total integrated emission of these faint
sources (flux <10-16 and
10-15 erg s-1 cm-2 in the 0.5–2.0 and 2–10 keV
bands respectively) is harder than the spectrum of brighter sources. As a check we
compared these fluxes with the photometry of Xue
et al. (2011) catalog, which is reported in the 0.5–2.0 keV and
2.0–8.0 keV bands. We find very good agreement between the two measures both in
the soft and hard bands (Table 2).
erg s-1 cm-2
in the 2–10 keV band). As expected, the total integrated emission of these faint
sources (flux <10-16 and
10-15 erg s-1 cm-2 in the 0.5–2.0 and 2–10 keV
bands respectively) is harder than the spectrum of brighter sources. As a check we
compared these fluxes with the photometry of Xue
et al. (2011) catalog, which is reported in the 0.5–2.0 keV and
2.0–8.0 keV bands. We find very good agreement between the two measures both in
the soft and hard bands (Table 2). -
(ii)
Considering the sources detected in XRT to calculate the PSF residuals, we get a photon index of
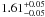 .
.
-
(iii)
The best-fit slope of the 130 XRT stacked observations (to quantify the stray-light contamination) is 1.46
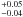 .
.
-
(iv)
The X-ray emission of the optical/IR sources can be modeled well by a relatively soft power law (photon index 1.9) and a flux of 7.2
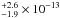 erg s-1 cm-2 deg-2
in the 2–10 keV band. These values are in very good agreement with Cowie et al. (2012), who use the same
optical/IR catalog and report a flux of
~7.0 × 10-13 erg s-1 cm-2 deg-2
in the 2.0–10.0 keV band, (calculated from their Table 1) and a photon index
Γ = 1.7–2.0 based on X-ray colors (Fig. 9).
Our measure is slightly lower but consistent with Hickox & Markevitch (2007) and Luo et al. (2011) (up to 6 keV) who use different catalogs. In the hard
part of the spectrum, we cannot confirm the results of Luo et al. (2011) who find a strong signal equal to
4.8 ± 2.0 erg s-1 cm-2 deg-2 (28% ± 10.0 of the
total CXRB) in the 6–8 keV band. While their measure is in good agreement with our
spectroscopy in the 0.5–6.0 band, consistent with a photon index Γ = 2, their
photometry is an order of magnitude higher than our spectrum in the 6–8 keV
interval. They interpret this strong feature as the signature of a substantial
population of highly absorbed AGN (Xue et al.
2012). The discrepancy with our data cannot be explained by the different
optical/IR adopted catalogs: indeed with their catalog (Giavalisco et al. 2004) we find results that are fully
consistent with our previous finding both in spectral slope and in flux. In order
to go into tho discrepancy thoroughly, we also performed the photometry in the
[0.5–2.0], [2.0–4.0], [4.0–6.0], and [6.0–8.0] keV bands5. While we find agreement with all previous works up to 6 keV,
we do not find any significant flux beyond 4 keV (Fig. 9). Indeed, allowing only for statistical uncertainties our
photometry in the 6–8 keV band yields an upper limit that is inconsistent with the
flux measured by Luo et al. (2011).
However, this discrepancy can be explained by a slight difference in background
estimate. Indeed allowing for only a 2% systematic error in our background value,
we find that our 2σ upper limit becomes consistent with the
photometric point by Luo et al. (2011).
This is because, once all the bright sources have been removed, in the 6–8 keV,
where a strong instrument feature is also present, the ratio between the
instrument background and the cosmic signal is ≲1% (see for example http://cxc.harvard.edu/contrib/maxim/stowed/).
erg s-1 cm-2 deg-2
in the 2–10 keV band. These values are in very good agreement with Cowie et al. (2012), who use the same
optical/IR catalog and report a flux of
~7.0 × 10-13 erg s-1 cm-2 deg-2
in the 2.0–10.0 keV band, (calculated from their Table 1) and a photon index
Γ = 1.7–2.0 based on X-ray colors (Fig. 9).
Our measure is slightly lower but consistent with Hickox & Markevitch (2007) and Luo et al. (2011) (up to 6 keV) who use different catalogs. In the hard
part of the spectrum, we cannot confirm the results of Luo et al. (2011) who find a strong signal equal to
4.8 ± 2.0 erg s-1 cm-2 deg-2 (28% ± 10.0 of the
total CXRB) in the 6–8 keV band. While their measure is in good agreement with our
spectroscopy in the 0.5–6.0 band, consistent with a photon index Γ = 2, their
photometry is an order of magnitude higher than our spectrum in the 6–8 keV
interval. They interpret this strong feature as the signature of a substantial
population of highly absorbed AGN (Xue et al.
2012). The discrepancy with our data cannot be explained by the different
optical/IR adopted catalogs: indeed with their catalog (Giavalisco et al. 2004) we find results that are fully
consistent with our previous finding both in spectral slope and in flux. In order
to go into tho discrepancy thoroughly, we also performed the photometry in the
[0.5–2.0], [2.0–4.0], [4.0–6.0], and [6.0–8.0] keV bands5. While we find agreement with all previous works up to 6 keV,
we do not find any significant flux beyond 4 keV (Fig. 9). Indeed, allowing only for statistical uncertainties our
photometry in the 6–8 keV band yields an upper limit that is inconsistent with the
flux measured by Luo et al. (2011).
However, this discrepancy can be explained by a slight difference in background
estimate. Indeed allowing for only a 2% systematic error in our background value,
we find that our 2σ upper limit becomes consistent with the
photometric point by Luo et al. (2011).
This is because, once all the bright sources have been removed, in the 6–8 keV,
where a strong instrument feature is also present, the ratio between the
instrument background and the cosmic signal is ≲1% (see for example http://cxc.harvard.edu/contrib/maxim/stowed/).
 |
Fig. 9 Comparison among different measures of the contribution of optical/IR (X-ray undetected) to the X-ray background. The gray area represents the best fit to our data. Green, blue, and red points represent the photometry of Hickox & Markevitch (2007), Luo et al. (2011), and Cowie et al. (2012). Black squares and arrows represent our photometric values and 2σ upper limits including systematic error of 2% on the background measure. Gray arrows show the upper limits accounting only for statistical errors. |
4.2. Systematic errors
Because we work in a very low signal/background regime (15%) in the uncertainties calculation we considered the impact of the systematics of the single components of the model. To do this we repeat the fit procedure 1000 times, each time varying the normalization of the different components according to Gaussian distributions with the variances reported above: 5% for the instrument background, 7% for the Chandra source spectrum, 5% for the stray light, and 10% for PSF residuals. We found that the impact of these systematics on the final slope uncertainty is modest, 0.08 (1σ), which is only 10% of the statistical error. The impact on the flux uncertainty is greater at 1.77 erg s-1 cm-2 deg-2, which is 75% of the statistical error.
5. Discussion
5.1. Comparison with previous works
The unresolved emission has been directly measured at faintest level by Hickox & Markevitch (2007) who found that in both the CDF-S and CDF-N it was consistent with zero, although with large uncertainties: in the CDF-S they measured 1.4 ± 3.9 × 10-12 erg s-1 cm-2 deg-2 in the band 2–8 keV. This is nearly a factor three smaller than our measurement, but still consistent within 1σ (Fig. 10). One could find surprising it that the level of unresolved emission we measure in the 4 Ms is three times higher than the one found by a previous work based on 2 Ms. The reason for this is that the sources in the 4 Ms observation that are not detected in 2 Ms supply only a small fraction of the total CXRB flux. Indeed, while there are many sources of the 4 Ms catalog (Xue et al. 2011) that are not included in the 2Ms catalog by Luo et al. (2008) (169 out of 430 in our ROI, that is 40%), their total flux is only ~10-14 erg s-1 cm-2, which represents only 1.5% of the total CXRB or ~7% of the unresolved. However we stress that our measure represents an improvement in the sense that the 1σ upper limit (measured value + 1σ error) is lower than the previous ones.
 |
Fig. 10 Spectrum of the unresolved CXRB: comparison with previous measures. The gray area is the result of the present work. Green points are from Hickox & Markevitch (2007); blue points are from Luo et al. (2011), with the blue arrow indicating the 1σ upper limit; red points from Worsley et al. (2006). The dashed area represents the total CXRB emission as measured by Swift (Moretti et al. 2009). |
In the soft band we find that the spectral fit between 1.5 and 2.0 keV is only marginally consistent with the Hickox & Markevitch (2007) photometry in the band 0.5–2.0. However, we note that a fair comparison between the two measures is not possible because the energy bands do not completely coincide. Moreover, in the 0.5–1.5 keV band the spectrum of the unresolved background is expected to have a thermal component owing to undetected galaxy groups and WHIM emission. This means that in the soft band the extrapolation of our best fit probably underestimates the CDFS unresolved background. As already said we limit our measure to energies higher than 1.5 keV because our data do not allow us to accurately disentangle these thermal extragalactic components from the local thermal emission of the Galaxy and Local Bubble.
In Fig. 10 we also plot the results of Worsley et al. (2006) and Luo et al. (2011), which are in good agreement with our results in the 2–6 keV band. For the reasons already discussed our spectrum is not directly comparable to their photometry in the 0.5–2.0 band.
Luo et al. (2011) find that in the 6–8 keV the unresolved emission is consistent with zero with an upper limit at 10% of the total CXRB at 7 keV. This is essentially due to the measure of the contribution of the optical and infrared sources, which they find at the level of 28% of the total CXRB in this particular energy interval (see Sect. 4.1). At odds with this measure, we do not find any significant feature in the X-ray spectrum of optically/IR detected sources, resulting in a estimate of the unresolved flux at 7 keV which is four times higher than Luo et al. (2011) 1σ upper limit.
In terms of the resolved fraction of the total CXRB, using the Swift measurement of the total CXRB (Moretti et al. 2009), our measurement of the unresolved components corresponds to ~80% in the 2–10 keV band, with 95 ± 3% at 2 keV and 70 ± 16% at 7 keV (lower panel of Fig. 10). We note that this number should be kept with caution and does not really add any significant piece of news once the unresolved emission is directly probed and constrained. This is not only because the spectrum of the total CXRB is highly uncertain (Revnivtsev et al. 2005; Frontera et al. 2007; Moretti et al. 2009), but also because deep fields are limited to a small portion of the sky so they miss the rare and bright population that is responsible for ~20% of the total emission.
To summarize, we can state that, compared to previous works and thanks to the low level of the Swift-XRT instrument background in the hard band (>2 keV) we significantly reduced the uncertainties finding consistent results in terms of absolute flux measurement. After reducing the uncertainties our result left room for a small, but significant component still to be resolved.
5.2. Comparison with AGN population models
 |
Fig. 11 In both panels the dark and light gray areas represent the spectrum of the unresolved and resolved CXRB, respectively. Left panel: the yellow dashed and continuous lines show the expectations of the G07 model for the two components. Right panel: the shaded area represents the total CXRB emission. Blue lines show the G07 model output with the CT (any z, any L, nH > 24) contribution enhanced by a factor 2. Green lines show the G07 model with the only heavily CT contribution enhanced by a factor 5. Red lines show the case where the contribution of high z CT has been enhanced assuming a linear evolution with redshift. Continuous, long-dashed, and short-dashed lines are for CDFS unresolved, CDFS resolved, and total CXRB, respectively. |
To check whether the unresolved spectrum can be accounted for by AGN population synthesis models, we compared our results with Gilli et al. (2007, G07) models6, which provides the integrated spectrum for different AGN subpopulations at given luminosity (L), redshift (z) and absorbing column density (NH).
To compare data and model, first of all, we need to assess which AGN subpopulation can be detected in the CDFS observation. Therefore, for a grid of six nH (1020–1026 cm-2), thirty-six L (1041−1048 erg s-1 cm-2), and twelve z (0–6), we calculated the expected median flux, using the same spectral models as used in G07. For each bin flux we calculated the detection probability by means of the response function of the Xue et al. (2011) catalog. The Xue et al. (2011) catalog is the result of the cross-correlation of three different catalogs built in three different energy bands, while the response function is only provided separately. We calculated the detection probability as the combination of the probability in the soft and hard bands. To ease the calculation we neglected the possibility that a source can only be detected in the total band, while it is undetected either in the soft or in the hard. In our ROI this is only true for 12 out of 430 sources (2.7%).
For example, considering AGN with photon index Γ = 1.9 in the bin 1022 < nH < 1023, 1.0 < z < 1.5 and 1041.9 < L < 1042.1 erg s-1 cm-2, we expect fluxes of 6.0 × 10-17 and 1.8 × 10-16 erg s-1 cm-2 in the 0.5–2.0, and 2.0–8.0 bands, respectively. The catalog response function (Table 7 and Fig. 23 of Xue et al. 2011) gives the source detection probability at these fluxes in the two bands we are interested in, psoft = 0.4 and phard = 0.2. We calculate that, for this AGN, the probability to be included in the CDF-S catalog is pdet = 1.0 − (1 − psoft) × (1 − phard), that is 0.52.
As in G07 a distribution of photon index was considered, we repeated the same procedure using nine different slopes (between 1.5 and 2.3) and weighting the final output by the same distribution used by G07 that is a Gaussian centered on 1.9 with standard deviation 0.2.
The G07 model is fully consistent (7% scatter) with the summed spectrum of all the in Xue et al. (2011) catalog (Fig. 11). We also find that the same model accurately reproduces the soft part (≲3 keV) of the spectrum of the unresolved emission, whereas it falls short in replicating the 3–7 keV emission, hinting that there are some missing hard sources.
5.2.1. AGN and galaxies
To compare our data with the G07 model we assumed that the emission of the
5683 optical/IR sources from the Grazian et al.
(2006) catalog, subtracted from the unresolved spectrum, is dominated by
non-nuclear sources, with a negligible contribution from an AGN component. There is some
evidence of this hypothesis. First, although we cannot measure the X-ray fluxes of the
single sources (which are by definition fainter than the detection limit), we can
estimate the mean luminosity of the sample, using the cataloged photometric redshifts.
We find that a mean luminosity of 2 × 1039 erg s-1 cm-2
in the 0.5–2.0 keV band accounts for the measured total flux of the sample
(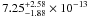 erg s-1 cm-2 deg-2,
see Table 3). Such faint mean luminosity,
together with the softness of the spectrum (photon index ~1.9), is a clear indication
that the galactic emission is prevalent with respect to the nuclear component. While the
mean luminosity by itself can be an indication, it does not rule out the presence of
some AGN. However, integrating (the extrapolation of) the X-ray galaxy number-counts
distribution measured by Lehmer et al. (2012) in
the 2.–10 keV band down to the flux
(3 × 10-19 erg s-1 cm-2) for which the source
density corresponds to the observed (~400 000 galaxies per deg2) and
accounting for the catalog completeness function, we find a value of
6.5 × 10-13 erg s-1 cm-2 deg-2, which is
very close to and consistent with our measure. Moreover, a completely independent
estimate of the galaxy X-ray flux density comes from Dijkstra et al. (2012) who estimate the contribution of the galaxies to the
CXRB. Lacking an accurate measure of the mean galaxy spectral slope in the hard band,
they calculated this contribution by assuming different mean photon indices and using
the star formation history of Hopkins & Beacom
(2006) together with the star formation rate to X-ray luminosity conversion of
Mineo et al. (2012). This estimate is
particularly suitable for our purposes as we have a direct measure of the galaxy mean
spectral slope. In the case of Γ = 1.9, they estimated that the galaxy density flux is
1.2 ± 0.3 × 10-12 erg s-1 cm-2 deg-2 in
the 2–10 keV band, which is slightly higher than our measure and perfectly consistent
with our assumption. These arguments suggest that the emission of the X-ray undetected
optical/IR sources of Grazian et al. (2006)
catalog is mostly of galactic origin with a negligible nuclear contribution.
erg s-1 cm-2 deg-2,
see Table 3). Such faint mean luminosity,
together with the softness of the spectrum (photon index ~1.9), is a clear indication
that the galactic emission is prevalent with respect to the nuclear component. While the
mean luminosity by itself can be an indication, it does not rule out the presence of
some AGN. However, integrating (the extrapolation of) the X-ray galaxy number-counts
distribution measured by Lehmer et al. (2012) in
the 2.–10 keV band down to the flux
(3 × 10-19 erg s-1 cm-2) for which the source
density corresponds to the observed (~400 000 galaxies per deg2) and
accounting for the catalog completeness function, we find a value of
6.5 × 10-13 erg s-1 cm-2 deg-2, which is
very close to and consistent with our measure. Moreover, a completely independent
estimate of the galaxy X-ray flux density comes from Dijkstra et al. (2012) who estimate the contribution of the galaxies to the
CXRB. Lacking an accurate measure of the mean galaxy spectral slope in the hard band,
they calculated this contribution by assuming different mean photon indices and using
the star formation history of Hopkins & Beacom
(2006) together with the star formation rate to X-ray luminosity conversion of
Mineo et al. (2012). This estimate is
particularly suitable for our purposes as we have a direct measure of the galaxy mean
spectral slope. In the case of Γ = 1.9, they estimated that the galaxy density flux is
1.2 ± 0.3 × 10-12 erg s-1 cm-2 deg-2 in
the 2–10 keV band, which is slightly higher than our measure and perfectly consistent
with our assumption. These arguments suggest that the emission of the X-ray undetected
optical/IR sources of Grazian et al. (2006)
catalog is mostly of galactic origin with a negligible nuclear contribution.
5.3. Some speculations
We examine the possibility that the discrepancy between the unresolved spectrum and the G07 model could be explained by the cumulative emission of a number of Compton-thick (CT) which are not included in the model. From an observational point of view the CT luminosity function is highly uncertain both in the local Universe (Della Ceca et al. 2008; Treister et al. 2009; Ballantyne et al. 2011; Severgnini et al. 2012; Ajello et al. 2012) and at higher redshift (Tozzi et al. 2006; Daddi et al. 2007; Alexander et al. 2008; Fiore et al. 2009; Alexander et al. 2011). In G07 the CT luminosity functions at different redshift are indirectly calculated from the difference between the total CXRB and the integrated emission of Compton-thin AGN (21 < NH < 24), under the assumption that the number of mildly CT objects (log NH = 24.5) is equal to that of heavily CT objects (log NH = 25.5) and that they have the same cosmological evolution of Compton-thin AGN.
While the total integrated emission of the CT population by definition agrees with the total CXRB, as we said in the previous section, we found some discrepancies with the constraints placed by the unresolved emission spectrum. Multiplying the whole CT contribution (at any redshift and luminosity) by a factor 2.0 would reconcile model and the observation in the 1.5–7 keV band, but, at the same time, would break through the spectrum of the total CXRB at harder energies ~20–30 keV, where the CT contribution is less affected by absorption (blue line in the right panel of Fig. 11).
Enhancing the contribution of the only heavily CT population by a factor five significantly reduces the distance between data and model; but the number of these sources, which is required to make the model consistent with the data under 7 keV, would result in over predicting the total CXRB at higher energy (green line in right panel of Fig. 11).
On the other hand, high-redshift (z > 2) CT are expected to peak at lower energies and to supply less flux at energies >20 keV. Indeed, while in G07 model a constant fraction of obscured AGN with redshift is assumed, we find that, hypothesizing a linear positive evolution with redshift (1 + z) in the total number of CT objects, corresponding to a (1 + z)a with a ~ 0.5 in terms of CT fraction, would solve the discrepancy between model and observation. With this assumption the overall AGN contribution is still consistent with the CXRB constrain at higher energies (red line in the right panel of Fig. 11).
 |
Fig. 12 Comoving space density of the CT AGN. We report different results for different redshift and luminosity intervals. Different colors indicate different luminosity bins. Continuous lines show the output of the G07 model; dashed lines represent the same outputs modified by applying a linear positive evolution in redshift. The green dotted line displays the output of the composite model by Draper & Ballantyne (2010). |
In Fig. 12 we report different measurements of the CT space density performed with different techniques (most in the infrared band) at different redshift, for different X-ray luminosity intervals, together with the output of the G07 model and imposing a linear evolution as suggested by our observation. This shows that such an evolution of the absolute number of CT AGN is still consistent with the large scatter of the observation results.
Our solution would require an increase in the CT fraction with redshift. The change in the obscured AGN fraction with redshift is a debated issue. A positive evolution has been observed in some studies (La Franca et al. 2005; Treister et al. 2006; Ballantyne et al. 2006; Hasinger 2008), whereas others do not find any significant variation (Ueda et al. 2003; Akylas et al. 2006). While these studies adopted a value of ~1022 cm-2 as pivotal column density to separate obscured and unobscured sources, our data seem to indicate a stronger evolution for only the CT population (>1024 cm-2).
A similar result was found by Brightman & Ueda (2012) that shows a significant increase in the only CT fraction, from 20% in the local universe up to 40% at z = 1–4. An higher number of high-redshift CT have recently been claimed by Gilli et al. (2011) who find a CT AGN at z = 4.76 in the CDF-S area, the detection probability being less than one. A strong positive evolution of the only CT population, has been also discussed in Treister et al. (2009) as a possible explanation to reconcile the difference between IR observations and the expectations from AGN population models normalized to reproduce the local CT density.
From the viewpoint of the population modeling, evolution of the only CT population has been found by Draper & Ballantyne (2010) as a natural consequence of describing the CT AGN by means of a physically motivated Eddington ratio distribution: CT AGN are a composite population accreting either at >90% or <1%. Indeed in this model the predicted evolution of the number density of CT AGN seems to follow the one we propose, although the normalization is a factor 2 lower (Fig. 12).
In the framework of AGN-galaxy coevolution, a positive redshift evolution of heavily obscured AGN is in line with the idea that in the high-redshift Universe SMBH are hosted by gas-rich galaxies. In particular, one of the scenario proposed for the formation and evolution of SMBH and galaxy assumes that major merger can trigger star formation and black hole growth at the same time. Depending on the kind of interaction, different obscuration geometries could be possible around the black hole, but in any case this would increase the probability of observing a SMBH through a very large amount of gas and dust.
6. Conclusions
We exploited the low and predictable instrument background of the Swift-XRT telescope to perform the spectroscopy of the unresolved X-ray emission in the CDF-S. We found a faint, but significant unresolved component that can be modeled by a very hard power-law with photon index Γ = 0.1 ± 0.7 and a flux density of 5 × 10-12 erg s-1 cm-2 deg-2 in the 2.0–10. keV band, corresponding to 20% of the total CXRB. With respect to previous works we significantly improved the accuracy over the 1.5–7.0 keV band. Our measure is in very good agreement with what is expected by the G07 AGN population model in the 1.5–3.0 keV. In the hard band (3–7 keV) the same model falls short when replicating the observed spectrum, pointing toward some missing very hard sources. This discrepancy can be solved hypothesizing a positive evolution with redshift of the contribution Compton-thick AGN population.
This is exactly the same situation as was faced in the study of the external regions of galaxy clusters where the intergalactic medium (ICM) surface brightness is at the same level. In this kind of study telescopes such as Suzaku and Swift are preferred to Chandra and XMM, which have much higher instrument background and a less favorable ratio signal/background (Bautz et al. 2009; Ettori & Molendi 2011).
File acis-D-012367-stowed-psu-evt-041104.fits downloaded from http://cxc.harvard.edu/contrib/maxim/acisbg/
We calculated the signal registered within the 1′′ radius circular regions centered on the positions of the 8637 sources listed by the Giavalisco et al. (2004) catalog within the 4.2′ radius circular region shown in Fig. 3, in the [0.5–2.0], [2.0–4.0], [4.0–6.0], [6.0–8.0] keV bands. To estimate the background we use the mean flux recorded in the same region after excluding of both the X-ray and optical/IR sources. In the 6–8 keV we count 25 385 total events with 25 331 expected background events over a total of 103 973 pixels. To convert these counts in flux, we use a mean exposure time of 3 296 249.2 s and a conversion factor of 1 count s-1 = 7.1 × 10-11 erg s-1 cm-2. Using a larger aperture for the source extraction regions we find consistent results.
Acknowledgments
This work has been supported by ASI grants I/011/07/0 and ASI/INAF I/009/10/0 and has made use of – the XRT Data Analysis Software (XRTDAS) developed under the responsibility of the ASI Science Data Center (ASDC), Italy; – the NASA’s Astrophysics Data System; – the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. We thank the anonymous referee for helpful comments that improved this work. A.M. is grateful to S. Andreon for useful discussions on measure errors handling.
References
- Ajello, M., Alexander, D. M., Greiner, J., et al. 2012, ApJ, 749, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Akylas, A., Georgantopoulos, I., Georgakakis, A., Kitsionas, S., & Hatziminaoglou, E. 2006, A&A, 459, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, D. M., Chary, R.-R., Pope, A., et al. 2008, ApJ, 687, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., Bauer, F. E., Brandt, W. N., et al. 2011, ApJ, 738, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., Shi, Y., Rieke, G. H., et al. 2006, ApJ, 653, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., Draper, A. R., Madsen, K. K., Rigby, J. R., & Treister, E. 2011, ApJ, 736, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bautz, M. W., Miller, E. D., Sanders, J. S., et al. 2009, PASJ, 61, 1117 [NASA ADS] [Google Scholar]
- Brandt, W. N., & Hasinger, G. 2005, ARA&A, 43, 827 [Google Scholar]
- Brightman, M., & Ueda, Y. 2012, MNRAS, 423, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Ranalli, P., Roncarelli, M., et al. 2012, MNRAS, 427, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Citterio, O., Conconi, P., Ghigo, M., et al. 1994, in SPIE Conf. Ser. 2279, eds. R. B. Hoover, & A. B. Walker, 480 [Google Scholar]
- Cowie, L. L., Barger, A. J., & Hasinger, G. 2012, ApJ, 748, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Alexander, D. M., Dickinson, M., et al. 2007, ApJ, 670, 173 [NASA ADS] [CrossRef] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Ceca, R., Caccianiga, A., Severgnini, P., et al. 2008, A&A, 487, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dijkstra, M., Haiman, Z., & Loeb, A. 2004, ApJ, 613, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Gilfanov, M., Loeb, A., & Sunyaev, R. 2012, MNRAS, 421, 213 [NASA ADS] [Google Scholar]
- Draper, A. R., & Ballantyne, D. R. 2010, ApJ, 715, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., & Molendi, S. 2011, Mem. Soc. Astron. It. Supp., 17, 47 [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Puccetti, S., Brusa, M., et al. 2009, ApJ, 693, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, P. E., Kashyap, V., Rosner, R., & Lamb, D. Q. 2002, ApJS, 138, 185 [Google Scholar]
- Frontera, F., Orlandini, M., Landi, R., et al. 2007, ApJ, 666, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilli, R., Su, J., Norman, C., et al. 2011, ApJ, 730, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Fontana, A., de Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, D., Holland, A., & Turner, M. 2008, in SPIE Conf. Ser., 7021 [Google Scholar]
- Hasinger, G. 2008, A&A, 490, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickox, R. C., & Markevitch, M. 2006, ApJ, 645, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Hickox, R. C., & Markevitch, M. 2007, ApJ, 661, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuntz, K. D., & Snowden, S. L. 2000, ApJ, 543, 195 [NASA ADS] [CrossRef] [Google Scholar]
- La Franca, F., Fiore, F., Comastri, A., et al. 2005, ApJ, 635, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmer, B. D., Xue, Y. Q., Brandt, W. N., et al. 2012, ApJ, 752, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Bauer, F. E., Brandt, W. N., et al. 2008, ApJS, 179, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2011, ApJ, 740, 37 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M. 2012, MNRAS, 426, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Mineo, S., Gilfanov, M., & Sunyaev, R. 2012, MNRAS, 426, 1870 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Campana, S., Lazzati, D., & Tagliaferri, G. 2003, ApJ, 588, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Campana, S., Mineo, T., et al. 2005, in SPIE Conf. Ser. 5898, ed. O. H. W. Siegmund, 360 [Google Scholar]
- Moretti, A., Perri, M., Capalbi, M., et al. 2007, in SPIE Conf. Ser. 6688, eds. S. L. O’Dell, & G. Pareschi, 14 [Google Scholar]
- Moretti, A., Pagani, C., Cusumano, G., et al. 2009, A&A, 493, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moretti, A., Gastaldello, F., Ettori, S., & Molendi, S. 2011, A&A, 528, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Revnivtsev, M., Gilfanov, M., Jahoda, K., & Sunyaev, R. 2005, A&A, 444, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvaterra, R., Haardt, F., & Ferrara, A. 2005, MNRAS, 362, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Haardt, F., & Volonteri, M. 2007, MNRAS, 374, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Haardt, F., Volonteri, M., & Moretti, A. 2012, A&A, 545, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Severgnini, P., Caccianiga, A., & Della Ceca, R. 2012, A&A, 542, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shull, J. M., Smith, B. D., & Danforth, C. W. 2012, ApJ, 759, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Egger, R., Finkbeiner, D. P., Freyberg, M. J., & Plucinsky, P. P. 1998, ApJ, 493, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., Gilli, R., Mainieri, V., et al. 2006, A&A, 451, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treister, E., Urry, C. M., Van Duyne, J., et al. 2006, ApJ, 640, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Ohta, K., & Miyaji, T. 2003, ApJ, 598, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Vattakunnel, S., Tozzi, P., Matteucci, F., et al. 2012, MNRAS, 420, 2190 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M. 2010, A&ARv, 18, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Delorme, P., Reylé, C., et al. 2010, AJ, 139, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Barcons, X., et al. 2004, MNRAS, 352, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Bauer, F. E., et al. 2006, MNRAS, 368, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2011, ApJS, 195, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q., Wang, S. X., Brandt, W. N., et al. 2012, ApJ, 758, 129 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectral analysis results of 32 stacked XRT sources and corresponding Chandra sources.
Total flux of the 326 Chandra sources not detected in the XRT image: comparison of our best fit to the stacked spectrum with the sum of the Xue et al. (2011) catalog photometric values.
Best fit values of the different components contributing the unresolved signal in the XRT observation.
All Figures
 |
Fig. 1 Energy channel (PI) distribution of the XRT unresolved emission (black) compared with the instrument background (red). In this plot PI channels have been transformed in energy using a single value and not the RMF matrix. |
| In the text | |
 |
Fig. 2 Comparison between Chandra and Swift-XRT instrument background spectra. Upper panel: NXB of the two instruments are plotted per unit area, to show the influence of different environments (orbits plus satellite). Middle panel: NXB are plotted per solid angle, to show the influence of different focal lengths. Lower panel: the ratio between Chandra and XRT NXB calculated per solid angle and normalized by the respective effective areas. This shows the improvement in the signal/background ratio for an extended source using XRT instead of Chandra. |
| In the text | |
 |
Fig. 3 Black dots are the 18 296 sources from Grazian et al. (2006) catalog. The green circle indicates our ROI. Red dots are the 5683 optical/IR sources we used in the spectral analysis. |
| In the text | |
 |
Fig. 4 The PSF model of the 109 sources detected in the XRT observation at 2.5 keV energy. The large white circle shows the boundaries of our ROI, while small black circles show regions we excised (rext). The PSF residuals is the small, but not negligible signal outside small circles and within the ROI. |
| In the text | |
 |
Fig. 5 Upper-left panel: fraction of the flux of a source outside of the field of view falling within the annulus between 5 and 6 arcmin. Black, red, and blue points represent the fraction measured in the Crab calibration observations in the total (1.5–7.0), soft (1.0–2.0), and hard bands respectively. Lines are the linear interpolation between the measures. Upper-right panel: black line is the calibration measure error histogram. Green dashed line is the histogram of the relative difference, between soft and hard band. Lower-left panel: the stray-light contamination on the XRT detector from a uniform source in different concentric annuli on the detector, accounting for the CDFS exposure map. Right-lower panel: black line is the error histogram. Green dashed line is again the histogram of the soft/hard relative difference. |
| In the text | |
 |
Fig. 6 Five data sets used in this work. The XRT unresolved spectrum (black) has been fit by a sum of 5 different power law: (i) Chandra sources, not detected by XRT (blue); (ii) X-ray emission of optical/IR sources (violet); (iii) XRT sources to model PSF residuals (red); (iv) the CXRB spectrum to model stray-light contamination (green). The XRT unresolved spectrum has been offset up by a factor 8 for clarity. |
| In the text | |
 |
Fig. 7 Results of the fit procedure. We modeled the XRT unresolved spectrum as the sum of five components, each fit by a power law. Colors are the same as in the previous figure: (i) Chandra sources not detected by XRT (blue); x (iii) bright sources PSF residuals (red); (iv) stray-light contamination (green); (iv) X-ray emission of optical/IR sources (violet). The fifth component, the truly unresolved emission, which is our aim, is plotted with its uncertainties as the gray area. |
| In the text | |
 |
Fig. 8 Photon index of the unresolved CXRB as function of the flux of the excluded sources. |
| In the text | |
 |
Fig. 9 Comparison among different measures of the contribution of optical/IR (X-ray undetected) to the X-ray background. The gray area represents the best fit to our data. Green, blue, and red points represent the photometry of Hickox & Markevitch (2007), Luo et al. (2011), and Cowie et al. (2012). Black squares and arrows represent our photometric values and 2σ upper limits including systematic error of 2% on the background measure. Gray arrows show the upper limits accounting only for statistical errors. |
| In the text | |
 |
Fig. 10 Spectrum of the unresolved CXRB: comparison with previous measures. The gray area is the result of the present work. Green points are from Hickox & Markevitch (2007); blue points are from Luo et al. (2011), with the blue arrow indicating the 1σ upper limit; red points from Worsley et al. (2006). The dashed area represents the total CXRB emission as measured by Swift (Moretti et al. 2009). |
| In the text | |
 |
Fig. 11 In both panels the dark and light gray areas represent the spectrum of the unresolved and resolved CXRB, respectively. Left panel: the yellow dashed and continuous lines show the expectations of the G07 model for the two components. Right panel: the shaded area represents the total CXRB emission. Blue lines show the G07 model output with the CT (any z, any L, nH > 24) contribution enhanced by a factor 2. Green lines show the G07 model with the only heavily CT contribution enhanced by a factor 5. Red lines show the case where the contribution of high z CT has been enhanced assuming a linear evolution with redshift. Continuous, long-dashed, and short-dashed lines are for CDFS unresolved, CDFS resolved, and total CXRB, respectively. |
| In the text | |
 |
Fig. 12 Comoving space density of the CT AGN. We report different results for different redshift and luminosity intervals. Different colors indicate different luminosity bins. Continuous lines show the output of the G07 model; dashed lines represent the same outputs modified by applying a linear positive evolution in redshift. The green dotted line displays the output of the composite model by Draper & Ballantyne (2010). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


