| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 16 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201219362 | |
| Published online | 27 November 2012 | |
X-ray variability of pre-main-sequence stars
Toward an explanation of the different X-ray properties of classical and weak-line T Tauri stars ⋆
INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento
1,
90134
Palermo,
Italy
e-mail:
ettoref@astropa.inaf.it
Received: 6 April 2012
Accepted: 24 October 2012
Context. The first million years of the pre-main-sequence (PMS) evolution of low-mass stars are characterized by magnetospheric accretion, a circumstellar proto-planetary disk, and the processes leading to its dispersal. Among these, photo-evaporation caused by strong X-ray emission from the central star is probably significant. Several aspects of the X-ray emission from coronae and accretion shocks remain mysterious, e.g., whether and how much accretion affects coronal emission.
Aims. We studied the X-ray variability of ~1 Myr old low-mass PMS stars as a function of timescale, stellar rotation, and stellar characteristics to gain insights into the working of PMS coronae, their X-ray emission, and the circumstellar environment in which they are immersed.
Methods. We have exploited the ~850 ks long Chandra observation of the Orion Nebula Cluster obtained by the COUP collaboration in January 2003, and statistically analyzed the X-ray lightcurves of low-mass stars in several subsamples. Our main focus was to characterize the different X-ray behavior of stars with and without circumstellar accretion disks, and to infer the physical mechanism responsible for the observed variability.
Results. Accreting stars (classical T Tauri stars, CTTSs) are found to be more variable than non-accreting stars (weak-line T Tauri stars, WTTSs) at all timescales and in all X-ray energy bands considered. Variability is seen to increase with timescale, up to the longest probed, ~10 days. Signatures of rotational modulation are observed for both CTTSs and WTTSs, and most clearly for CTTSs in the soft X-ray band. Lower mass stars are more variable than higher mass stars.
Conclusions. We propose that the difference in variability between CTTSs and WTTSs may be explained assuming that the X-ray emission of CTTS is affected by time-variable absorption due to circumstellar structures, such as warps in the inner disk and/or accretion streams. This suggestion is appealing because, in the hypothesis that the coronae of CTTSs and WTTSs are similar, it may also explain why CTTSs have lower and more scattered X-ray emission levels compared to WTTSs.
Key words: stars: activity / stars: coronae / stars: variables: T Tauri, Herbig Ae/Be / stars: formation / accretion, accretion disks / X-rays: stars
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The evolution of young stars in the first few million years after they emerge from their protostellar dusty envelopes is characterized by the presence of circumstellar disks and intense magnetic fields. These latter crucially regulate the interaction between the star and the disk, they mediate for instance the angular momentum transfer between the two and channel streams of accreting material from the disk onto the stellar surface (e.g. Bouvier et al. 2007b). This material is shocked in the impact, producing optical, UV, and soft X-ray “excesses” (Calvet & Gullbring 1998). Magnetic fields are also responsible for the confinement and heating of X-ray-bright coronae (Feigelson & Montmerle 1999), whose high energy radiation, along with that from accretion shocks, is likely to significantly influence the evolution of circumstellar disks: soft X-rays ionize and heat parts of the disk and may be the main cause of disk photo-evaporation and, consequently, of their eventual dispersal (e.g. Glassgold et al. 2004; Owen et al. 2011).
The above processes are highly dynamical. Strong variability at all wavelengths and on many different timescales is indeed a distinctive trait of young accreting pre-main-sequence (PMS) stars (Alencar et al. 2010; Joy 1945), also known as classical T Tauri stars (CTTS). Weak-line T Tauri stars (WTTS), similarly young stars for which accretion signatures are not observed, represent almost certainly the following stage of PMS evolution, once the circumstellar accretion has stopped and the dusty disk has dissipated or is quickly dissipating (Feigelson & Kriss 1981; Lada 1987). Compared to CTTSs, WTTSs are much much less variable in the optical band and their lightcurves show mostly periodic variations attributable to the modulation of cool stellar spots (Alencar et al. 2010).
The mechanism responsible for the strong and irregular optical variability of CTTSs, although likely related to accretion, remains elusive. The two main hypotheses are i) variability of the emission from the accretion shock(s), both intrinsic and caused by rotational modulation; or ii) variable absorption of the photosphere, or part of the photosphere, from unstable and optically thick accretion streams and/or warps in the circumstellar disk. Grankin et al. (2007, 2008), for example, suggested from a statistical study of CTTS that in about 25% of the cases variable absorption is the likely cause of optical variability, while time-variable accretion is favored in the remaining cases. However, owing to the similar effects of spots and absorption on the broad-band lightcurves, the absorption scenario could not be excluded in most cases. The thorough study of the CTTS AA Tau by Bouvier and collaborators (Bouvier et al. 1999, 2003, 2007a; Grosso et al. 2007; Ménard et al. 2003) has shown that for this near edge-on star-disk system, the strong, irregular optical variability is readily explained by occultation of a significant fraction of the stellar surface by a warp in the inner disk. This warp, located at the corotation radius, produces quasi-periodic eclipses with the period of the stellar rotation. Alencar et al. (2010), using high-quality optical lightcurves of stars in the NGC 2264 region obtained with the CoRoT satellite, have recently proposed that an AA Tau-like scenario might indeed explain the optical variability of at least ~30% of the CTTS. The AA Tau-like phenomenology was also confirmed by Morales-Calderón et al. (2011), from Spitzer/IRAC (3.6/4.5 μm) lightcurves of ONC sources, with a much lower incidence, ~5%, than found by Alencar et al. (2010), however.
In the X-ray band all PMS stars, both CTTS and WTTS, are intense sources (Feigelson & Kriss 1981; Flaccomio et al. 2003b; Preibisch et al. 2005). Thermal emission from magnetically confined plasma (i.e. coronae) at ~10–30 MK accounts for most of the observed emission. Accreting stars (CTTS) also show a softer plasma component at ~2–4 MK that, given its temperature and plasma density, can be interpreted as the direct product of the accretion shock. This component has only been unambiguously detected in the few CTTS for which high-resolution X-ray spectra were obtained (e.g. Argiroffi et al. 2011; Güdel & Telleschi 2007; Kastner et al. 2002), as demonstrated by emission-lines from cool plasma and by density-sensitive He-like triplets. It is natural to think that such a component is a common feature of CTTS. However, for most stars, with the possible exception of TW Hya (Dupree et al. 2012; Kastner et al. 2002), this cool plasma does not contribute significantly to the X-ray flux detected in the 0.3–10 keV energy band covered by present-day imaging detectors, such as those onboard of Chandra and XMM-Newton. In fact, in spite of this additional soft component, CTTS are, on average, two to three times fainter in X-rays compared to WTTSs of the same mass or Lbol (Damiani et al. 1995; Flaccomio et al. 2003a; Neuhaeuser et al. 1995; Preibisch et al. 2005). Moreover, their activity levels at any given mass or Lbol show a larger scatter (Preibisch et al. 2005). These differences cannot be ascribed to differences in stellar rotation, the main factor that determines activity levels on MS stars, and remain largely unexplained. A higher average absorption of CTTS with respect to WTTS, which would lower the observed X-ray fluxes of CTTS (but not the intrinsic ones), was excluded by Preibisch et al. (2005) on the basis of the Chandra Orion Ultra-deep Project (COUP) data (Getman et al. 2005), which allowed determining individual absorption corrections for all stars. These authors, as well as others, instead proposed that accretion might modify the magnetic field structure (and thus coronae, see also Flaccomio et al. 2003b; Telleschi et al. 2007) or the stellar structure in such a way as to influence the stellar dynamo. Telleschi et al. (2007) in particular, based on data from the XMM-Newton Extended Survey of the Taurus molecular cloud (XEST), proposed that the accreting material from the disk cools down part of the coronal plasma to temperatures outside the X-ray regime. Gregory et al. (2007) modeled coronal and accretion structures by extrapolating magnetic field surface maps (from Zeeman-Doppler imaging) and concluded that the lower observed X-ray luminosity of CTTS might indeed be due to the obscuration of large parts of the corona by dense gasseous accretion streams. This scenario is closely related to that invoked to explain the AA Tau-like optical variability, the main difference being that for X-rays the absorbing material would be the gas in the accretion streams rather than the dust in the inner disk warps at the bases of the same accretion steams. The accretion streams would only intercept a fraction of the emitting coronal plasma and the emerging X-ray flux would thus be composed of two components, only one of which is heavily absorbed. As also discussed in this paper, correctly correcting the observed X-ray flux for extinction would be almost impossible, at least with the spectral resolution and sensitivity of present-day instruments.
In addition to the differences in observed X-ray flux, other differences in the X-ray emission of CTTSs and WTTSs have been reported. Flaccomio et al. (2006), for example, reported tentative evidence that CTTSs in the NGC 2264 star-forming regions are more X-ray variable than WTTS. The same data, as well as the XEST data (Telleschi et al. 2007), also indicate that the plasma on CTTSs is, on average, hotter than that on WTTS. At the same time, some CTTSs show evidence for a plasma component cooler than seen on WTTSs. While this latter observation may be attributed to plasma heated in accretion shocks, the harder and more time-variable emission could be consistent with time-variable absorption from circumstellar material (accretion stream and/or disk warps).
From this discussion it is clear that studies of X-ray variability may provide useful information on the mechanism that regulates either the observed or the intrinsic X-ray activity level of PMS stars. All T Tauri stars are strongly variable in the X-ray band on timescales of hours and days: the most prominent form of variability is undoubtedly represented by flares, with short rise phases during which the flux reaches up to ~100 times the pre-flare level, followed by slower decay phases lasting several hours (see e.g. Favata et al. 2005, for a detailed study of bright flares in the COUP observation; Wolk et al. 2005; and Caramazza et al. 2007, for statistical studies). Modulation due to the inhomogeneity of coronal structures and stellar rotation has also been detected by Flaccomio et al. (2010) in the ~13-days long COUP observation (including gaps; the actual exposure time was ~850 ks). This work also highlighted the difficulty in separating flaring from other forms of variability. However, variability on timescales longer than one day has generally not received much attention, partly because of the scarcity of appropriate datasets. Moreover, the highly stochastic nature of the X-ray emission has hindered statistical studies trying to correlate the “average” properties of variability with stellar and circumstellar characteristics.
An interesting result has recently been obtained by us from the correlation of X-ray and optical emission. In a previous study, Stassun et al. (2007) had already searched in vain for a correlation between the COUP X-ray lightcurves and simultaneous ground-based optical multi-band lightcurves. Flaccomio et al. (2010) have instead employed simultaneous space-based observations of NGC 2264 members by Chandra (X-rays) and CoRoT (optical, broad-band). By comparing X-ray and optical fluxes obtained in two 30 ks time windows separated by 16 days, we have found that, for CTTSs only, the X-ray variability in the soft 0.5–1.5 keV band is significantly correlated with the optical variability. This correlation is seen neither for WTTS nor for the harder X-ray band (1.5–8.0 keV). We interpret these findings as caused by the effect of time-variable absorption from circumstellar material. From the relative magnitude of the X-ray and optical variability we conclude, moreover, that the absorbing material must be dust-depleted, thus pointing toward accretion streams within the dust-sublimation radius, as proposed by Gregory et al. (2007).
If the X-ray emission of CTTSs is indeed absorbed by circumstellar structures in co-rotation with the star, their X-ray variability should i) be more extreme than on WTTS; ii) reach maximum amplitudes on the timescale of the stellar rotation; and iii) show clearer signs of rotational modulation. Most X-ray observation of nearby young stars performed with present-day instruments are shorter than ~100 ks (~1 d) and therefore unsuitable for studying variability on the timescale of typical stellar rotations (~1–15 d for stars in the ONC; Herbst et al. 2002). The most notable exception is the almost uninterrupted 850 ks long COUP observation of the ONC. We have thus decided to exploit this dataset once more to investigate X-ray variability as a function of timescale from hours to ~12 days, thus covering the stellar rotation of most ONC stars. In addition to its length, the COUP observation with its ~1600 X-ray sources also provides the advantage of a rich and optically well-characterized sample of PMS stars. Given the highly stochastic nature of variability, large stellar samples are crucial to reliably determine “average” variability properties for different stellar subsamples. We can then try to correlate these average properties with stellar and circumstellar characteristics to investigate the physical origin of variability.
This paper is organized as follows: Sect. 2 describes the COUP dataset; Sect. 3 illustrates the two methods we used to quantify variability, one non-parametric (Sect. 3.1) and one tailored to impulsive flares (Sect. 3.2); Sect. 4 describes the selection of the stellar samples used for the analysis. Section 5 presents the result of the variability analyses, which are then more fully discussed in Sect. 6, along with their implications. Finally, we summarize our main conclusions in Sect. 7.
2. The COUP data
The COUP observation is described in detail by Getman et al. (2005) along with the procedures followed for data preparation, source detection, identifications with optical/NIR catalogs, and photon extraction. We used the products of this analysis and, in particular, the original lists of source and background photons extracted for each source. We also adopted from Getman et al. (2005) the stellar and circumstellar parameters for the COUP sources, both collected from the literature or derived by these authors (e.g. magnitudes, masses, etc.). We updated this database with respect to stellar rotational periods and classifications in terms of near-IR excesses indicative of disks and envelopes. We used the same collection of rotational periods as Flaccomio et al. (2005), with the addition of 48 new periods derived from an ~250 h Spitzer observation of the ONC performed as part of the “Young Stellar Object VARiability” (YSOVAR) program and reported by Morales-Calderón et al. (2011). From this work we also adopted the classification in terms of spectral energy distribution (i.e. Class I, Class II, and Class III).
3. Analysis methods
We first discuss the non-parametric variability analysis that is at the basis of our following discussion, and then the method we used to asses the contribution of X-ray flares to the total source variability.
3.1. Variability amplitudes
To study how the X-ray fluxes vary as a function of timescale, we subdivided the 850 ks COUP observation into shorter segments: we chose to adopt segment lengths of 30 ks, as a compromise between being able to probe short timescales, specifically with respect to the typical stellar rotation periods, and the need to have a sufficient number of detected photons per segment and thus limit Poisson uncertainties. With this choice we selected 25 time segments within the COUP observation, for each of which we measured the background-subtracted photon flux. Figure 1 illustrates, superimposed on a binned light-curve (E = 0.5–8.0 keV) of one of the brighter COUP sources, the time segments we adopted for the following analysis.
 |
Fig. 1 Example X-ray light-curve for a bright COUP source. The horizontal segments, superimposed on the lightcurve (black line), indicate time intervals and relative photon fluxes for the 25 30 ks segments on which the variability analysis is based. |
In general terms, our analysis consists of quantifying the variability between segments separated by a given time interval, Δt, by taking the ratio between the fluxes in the first and second segment, F1/F2 ≡ F(t)/F(t + Δt)1. We then built distributions of these variability measures (i.e. flux ratios) for all segment pairs within the same lightcurve separated by Δt and for all X-ray sources in given subsamples. We then study how the width of the distributions of variability measures obtained for the same subsample varies as a function of timescale, Δt, and compare the trends for different subsamples2. For our purposes the width of the distribution is defined as the difference between the 75% and the 25% quantiles. We refer to this width as the variability amplitude (VA) of the sample at the given Δt. For stars for which we also know the rotation period, we also explore the dependence of VAs on rotational phase differences. To this purpose we construct and compare the widths of distributions of flux ratios taken between segments separated by rotational phase differences: Δφ = Δt/Prot.
The whole analysis was carried out considering three energy bands: the full Chandra band (0.5–8.0 keV), a soft band (0.5–1.5 keV), and a hard band (1.5–8.0 keV). As an example, we plot with a thick broken line in Fig. 2 the differential distributions of log (F1/F2) obtained for the full X-ray spectral range and for Δt ~ 8 days (effectively, 7.1 < Δt < 9.6 days). In this example the stellar sample comprised 167 Class III stars (see below for sample definitions). Given the adopted Δt range, each of these stars contributes 47 flux ratios and the distribution is defined by 7849 datapoints.
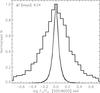 |
Fig. 2 Normalized histogram of all flux ratios, log (F1/F2), taken between 30 ks time intervals separated by Δt = 7.1–9.6 days (logarithmic mean: 8.24 days), for the 167 Class III stars in our flux-limited sample (broken line). The narrower distribution, actually a bundle of ten almost indistinguishable ones, represents the contribution of Poisson statistics to the observed distribution as determined from Monte Carlo simulations (see text). |
The finite width of the log (F1/F2) distributions, i.e. their departure from log (F1/F2) = 0.0, can be caused by two factors: real flux variability, or Poisson uncertainties in the number of detected photons. To isolate this last unwanted contribution, we have taken two approaches: first, we limited our search sample to X-ray sources with “good” statistics; second, we quantified the effect of Poisson noise on the variability distributions through Monte Carlo simulations. More specifically, we imposed a limit of 750 counts within the 25 chosen time segments, i.e. we required >30 counts per segment (or 1 count/ks) on average. This condition reduces the number of available X-ray sources from the initial 1616 to 496, 319, and 361 for the full, soft, and hard band, respectively. As discussed in more detail in Sect. 6.3, this selection introduces a bias on the resulting samples, quite directly in terms of LX, and indirectly, through the correlation of LX with fundamental stellar properties (e.g. Preibisch et al. 2005), in terms of stellar mass and bolometric luminosity.
To evaluate the effect of Poisson uncertainties on the flux-ratio distributions, and ultimately on the VAs, we generated for each of the considered distributions (i.e. for each sample and timescale) 1000 simulated flux-ratio distributions assuming that sources are intrinsically constant and that the measured fluxes only vary because of Poisson fluctuations3. Figure 2 shows ten of the simulated constant-source distributions (the bundle of narrow distributions centered at log (F1/F2) = 0.0). In this case it is quite clear that Poisson uncertainties cannot account for the widths of the actual flux-ratio distributions. In general, we quantified the contribution of Poisson statistics on the VA of each of the considered samples and timescales by recording the medians and 1σ dispersions of the VAs measured from the 1000 simulated constant-source fluxes.
3.2. Flare analysis
Coronal flares, characterized by short rise-phases and slower decays, are an obvious source of variability for our sources. To discuss the contribution of flares to the overall variability amplitudes (Sect. 6.1) we seek to quantify flaring activity statistically for a given stellar sample. X-ray flares in the COUP datasets have already been investigated by at least four studies (Caramazza et al. 2007; Favata et al. 2005; Johnstone et al. 2012; Wolk et al. 2005). We adopted the technique used by Wolk et al. (2005) and Caramazza et al. (2007), that is, we detected individual flares using an automated procedure and then derived their rate of occurrence as a function of their intensities as well as the distribution of “flare durations”. A full description of the method can be found in Caramazza et al. (2007).
4. Sample definitions and selection criteria
As described in the previous section, our parent samples for the three X-ray spectral bands comprise all COUP sources with an average count-rate >1 count/ks in the 25 × 30 ks selected time intervals. We then selected physically relevant and homogeneous stellar samples for our study of variability as a function of timescale and stellar characteristics.
First, we excluded high-mass stars, M > 3 M⊙, the X-ray emission of which is of non-coronal origin, or comes from a different kind of corona, or originates in unresolved lower mass companions (e.g. Damiani et al. 1994; Hamaguchi et al. 2005; Stelzer et al. 2009; Zinnecker & Preibisch 1994). Then, to further restrict the range of masses, and that of absorptions, we excluded stars with Ic > 16, corresponding to M > 0.1−0.2 M⊙ for COUP sources with low optical absorption4 (AV < 2.0). Finally we excluded proper-motion non-members according to the collection of Hillenbrand (1997), unless they had indications of circumstellar accretion or circumstellar material (see below). With these selection our search samples are reduced to 369, 289, and 261 stars for the full, soft, and hard bands, respectively.
Next, we defined the following subsamples of low-mass stars based on their accretion properties, presence of circumstellar disks, and mass:
-
CTTS and WTTS, based on the equivalent width (EW) of the8542 Å Ca II line, following the same approach as Flaccomio et al. (2003b) and Preibisch et al. (2005). Namely, we selected as accreting stars (CTTS) those with the Ca II line in strong emission, EW < −1, and as non-accreting stars (WTTS) those whose Ca II line clearly is in absoption: EW > 1. By excluding intermediate EW values, this approach results in better defined and extreme samples: the selected CTTS, in particular, will be biased toward high accretion rates.
-
Class II and Class III stars, based on the observation of mIR excesses due to warm circumstellar material, as reported by Morales-Calderón et al. (2011).
-
Low- and intermediate-mass Class II and Class III stars, defined as complementing the above selections with the following constraints on mass: M < 0.5 M⊙ and M > 0.8 M⊙.
We considered other possible subsamples, but, since their sizes are too small to derive meaningful results, we will not discuss them. For the samples and X-ray energy bands discussed in the following, Table 1 summarizes the size of the sample and, if relevant, the size of the subsample of stars for which we know the rotational period. Most of our analysis will be based on the samples of CTTSs, WTTSs, Class II, and Class III stars, which we therefore refer to as our main samples5.
In the following we used of the statistical properties of the X-ray sources in our samples to constrain the origin of their X-ray variability. Figure 3 shows the distribution of (full-band) count-rates for our main samples. In spite of our choice of count-rate limited samples, and consistent with the results of Flaccomio (2003) and Preibisch et al. (2005), CTTS have statistically lower count-rates with respect to WTTS (a factor of ~2 in the median). A difference is also seen between Class II and Class III, but it is smaller, possibly owing to the less extreme nature of the selection criteria. Significant differences in median count-rates are also observed between low- and intermediate-mass Class II and Class III stars, with the higher mass samples being systematically brighter than the low-mass ones by a factor of ~2 and ~3 for Class II and Class III, respectively.
Sizes of the analyzed samples.
 |
Fig. 3 Distributions of count rates for our flux-limited samples of CTTS (red), WTTS (green), Class II (orange), and Class III (blue) stars. Sample sizes and median count rates are reported in the legend. Count rates are defined here as the total number of counts detected in the 25 × 30 ks time intervals under consideration, divided by the exposure time, 750 ks. |
5. Results
For the stellar samples introduced in Sect. 4 we first present the results of our non-parametric analysis of variability amplitudes as a function of timescale and rotational phase. Next, as a tool to constrain the origin of variability, we investigate the incidence of flaring activity on the same samples.
5.1. Variability amplitudes
As described in Sect. 3, we defined the representative variability amplitude, VA(Δt), of a given source sample and for a given timescale Δt, as the 50% width (difference between 75% and 25% quantiles) of the distribution of all the F(t)/F(t + Δt) that can be computed from the X-ray light curves of stars in that sample. We now discuss how this quantity depends on Δt and on stellar characteristics by comparing different source samples. Next, we repeat the same comparative analysis as a function of stellar rotational phase (instead of timescale) by normalizing the time-lag Δt by the stellar rotation period, Prot, i.e. by considering VA(Δφ) ≡ VA(Δt/Prot).
 |
Fig. 4 Variability amplitude, VA, as a function of timescale (left column) and rotational phase difference (right column), for CTTS, WTTS, Class II, and Class III stars (see legends within panels), and for three different X-ray energy bands: full (0.5–8.0 keV, top row), soft (0.5–1.5 keV, middle), and hard (1.5–8.0 keV, bottom). As described in Sect. 3, the VA for each sample and x-axis value (Δt or Δφ) is defined as the 50% width of the distribution of log F1/F2 (cf. Fig. 2), i.e. of the difference between the 75% and 25% quantiles. Formal error bars reflect photon statistics and are estimated thorough Monte Carlo simulations. Thick lines refer to the VAs derived from the data, while thin lines with error bars and matching color indicate the contribution of Poisson noise (also estimated with Monte Carlo simulations). |
5.1.1. Timescale
The left-hand column of Fig. 4 shows the run of VA vs. timescale in the interval 0.4–11 days for CTTS, WTTSs, Class II, and Class III stars. The three rows refer to the three X-ray energy bands: full, soft, and hard (from top to bottom). The contribution of Poisson statistics to the VAs, as determined from Monte Carlo simulations, is also shown (both median and 1σ dispersion). Note that this latter contribution is not to be subtracted linearly from the observed VAs. In the hypothesis the distributions of log F1/F2 are Gaussian (which is not far from being true, cf. Fig. 2), the Poisson contribution should be subtracted in quadrature. They thus contribute little to most of the measured VAs. The left-hand panels in Fig. 4 lead to the following conclusions:
-
1.
All samples are significantly variable on all timescales.
-
2.
Variability (VAs) increases strongly with timescale, up to at least 11 days, i.e. the longest timescale probed by the COUP observation. However, for some samples and energy bands (in particular CTTSs in the soft band), VAs may saturate at long timescales.
-
3.
CTTS and Class II stars appear to be systematically more variable than WTTS and Class III stars.
-
4.
The difference in VA between CTTS/Class II and WTTS/Class III stars seems to increase toward long timescales. This is especially true for CTTSs and WTTSs in the soft band.
We also studied the dependence of variability on stellar mass. Figure 5 shows again, repeated from Fig. 4, the run of VA vs. timescale for the two richest samples, Class II and Class III stars, along with the trends obtained for the two mass-segregated subsamples of stars in the same classes. We see that, while the trends for the mass-segregated subsamples are qualitatively the same as for the full samples, low-mass stars of both classes are more variable than their higher mass counterparts.
 |
Fig. 5 Variability amplitude, VA, as a function of timescale for Class II and Class III stars, for the full samples (same as in Fig. 4) and for two mass-segregated subsamples (see caption). |
5.1.2. Rotational phase
The left-hand column of Fig. 4 shows the run of VA vs. the rotational-phase difference Δφ, ranging from 0.05 to 4.0 Prot. The purpose of these plots is to investigate the presence of rotational modulation, as evidenced by peaks at Δφ = 0.5 Prot and Δφ = 1.5 Prot. Other possible peaks at higher Δφ values (e.g. 2.5) cannot be investigated with our data since in order to have a significant number of stars in each Δφ bin we had to choose progressively wider bins with increasing Δφ. We also note that, in contrast to the case of the VA(Δt) plotted on the left, the number of stars entering in the definition of the VA(Δφ), i.e. those that define the distributions of log F(φ)/F(φ + Δφ), generally decreases with Δφ6. For example, given the fixed length of our X-ray observation, the variability at higher Δφ values can only be probed in stars with shorter rotational periods. From these plots we draw the following conclusions:
-
1.
Several samples show, in one or more spectral bands, signs ofrotational modulation. In particular small but statisticallysignificant peaks at Δφ = 1.5 and/or 0.5 Prot are observed in all three bands for WTTS and Class III stars.
-
2.
Less clear signs of rotational modulations are generally seen for CTTS and Class II stars, except in the soft band, and in particular for CTTSs for which a clear modulation signal is revealed by pronounced peaks at both 0.5 and 1.5 Prot. The peaks are significant at the 3.8 and 2.3σ level, when compared to the mean of the two adjacent points7 and suggest apparently larger modulation amplitudes with respect to WTTSs/Class III stars.
5.2. Flare frequencies and lengths
To quantify the flaring activity for the same samples of CTTSs, WTTSs, Class II, and Class III stars discussed above, we applied the direct-detection method discussed in Sect. 3.2. Figure 6 shows the rate of flares as a function of minimum flare counts and the cumulative distribution of measured durations for our four main samples. We conclude that the flares from the four samples have very similar properties, both in terms of rate of occurrence and in their duration.
We note, however, that this observation alone does not allow us to conclude that the contribution of flares to the variability amplitudes, VAs, is the same for all samples. Indeed, VAs are a measure of relative variability while our flare rates indicate that the absolute intensity of flares is the same. However, since we have seen in Sect. 4 that CTTSs (and, to a lesser extent, Class II stars) are on average fainter than WTTSs and Class III stars, the same absolute variability (i.e. flare rate) may translate into a more pronounced relative variability (i.e. VA) in CTTSs than in WTTSs, as is indeed observed. It remains to be seen, however, if this effect is strong enough to justify quantitatively the observed differences in VAs among our samples.
In the following section we resort to Monte Carlo simulations to constrain the contribution of flaring activity to the variability amplitudes as a function of timescale.
 |
Fig. 6 Left: rate of occurrence of flares as a function of minimum number of flare counts for our four main samples. The legend indicates the color of the lines representing each sample as well as the respective numbers of detected flares. Right: cumulative distribution of flare durations for the same four samples. |
 |
Fig. 7 Left: VA vs. rotational phase for simulated lightcurves. The simulations reproduce sinusoidally varying stars, observed with the COUP observation and analyzed in the same way as the real data. Four curves show results for modulation amplitudes from 5% to 30%, as labeled. Right: comparison of the trends observed in the soft band for WTTS and CTTS (green and red lines, respectively) with two simulated VA curves (labeled gray lines) obtained by summing in quadrature the VAs for pure sinusoidal modulation (with amplitudes of 18% and 29%) with constant non-modulated VAs (0.16 and 0.18 dex, see labels). Modulation amplitudes and constant contributions are chosen to reproduce the observed VAs at Δφ = 0.06 (the leftmost points) and Δφ = 0.5 (the first maxima). |
6. Discussion
We now use the results obtained in Sect. 5 to discuss the origin of variability in the X-ray band. We consider two separate mechanisms: magnetic flares and rotational modulation. First, we try to understand to what extent the observed variability and the differences we observe among subsamples can be explained in terms of flares. We then focus on rotational modulation and, finally, discuss the physical implications for the considered samples.
6.1. The contribution of flares
The effect of flares on the fractional variability amplitudes depends, in addition to flare intensity and frequency, also on their durations and on the quiescent or characteristic count-rate on top of which they are observed. For example, for a flare of a given intensity (emitted energy or number of detected counts), a longer duration or a higher characteristic count-rate will result in a lower relative variability amplitude. Moreover, the trend of flare-induced VAs with timescale will depend on flare lengths: since flares are expected to occur stochastically with no particular timescale, rising trends are only possible on timescales shorter than a few decay times, τ.
We have seen that our four main samples share similar frequencies and durations for detectable flares (Sect. 5.2). However, since the samples have mean fluxes (or count-rates) that differ by up to a factor of ~2 (Sect. 4), we cannot straightforwardly conclude that the effect of flares on the VAs is the same. To assess the effect of flares on VAs realistically (even if not rigorously), we ran Monte Carlo simulations of light curves that attempt to reproduce the following observables: i) the time-averaged source count-rates; ii) flare frequencies; and iii) flare durations. These simulations are fully described in Appendix A, and lead to the conclusion that flares are likely not the dominant source of variability as measured by the VAs and cannot explain the differences between our samples. This is particularly true at long timescales. We indeed show that for realistic flares durations the run of VAs with timescale remains rather flat.
6.2. Rotational modulation
We have seen that the run of VA with phase lag shows signatures of rotational modulation, both for WTTS/Class III stars and, most strikingly, for CTTSs in the soft X-ray band. To investigate this scenario in greater detail we computed the expected VA signal for a purely sinusoidal modulation with a given relative amplitude A (Flux = 1.0 + Asinφ).
For this simple experiment we drew rotational periods randomly from either a uniform distribution (between one and ten days) or from the actual distribution of rotational periods in our samples, with almost identical results. Rotational phases at the beginning of the observation were also chosen randomly. Figure 7 (left) shows the VAs vs. phase-lag trends expected for relative amplitudes ranging from 5% to 30%. For better comparison with observations we then added the “modulated” VA signal to a constant VA level, meant to reproduce the contribution of all non-modulated variability sources such as flaring (see Sect. 6.1), as well as Poisson noise. Because the modulated and constant contributions have to be added in quadrature, the absolute value of the latter smaller contribution has an important effect at Δφ values where the modulated VAs are low, but little effect on the peaks at Δφ = 0.5 and 1.5 Prot.
Figure 7 (right) compares the resulting simulated VAs with the observed trends for WTTS and CTTS in the low-energy X-ray band. Modulation amplitudes and constant contributions were chosen to reproduce the observed VAs at Δφ = 0.06 (the leftmost points) and Δφ = 0.5 (i.e. where the first maxima are observed). For both WTTSs and CTTSs, very good agreement with the observed trends can be obtained for Δφ ≤ 0.67 d, i.e. up to the datapoints following the peaks at 0.5 d, by adding in quadrature a constant contributions of ~0.16 dex and ~0.18 dex and for modulation amplitudes of 18% and ~29%, respectively. For higher values of Δφ the agreement is not as good: for CTTSs, even though the maximum predicted at Δφ = 1.5 Prot is indeed observed, the minimum predicted at Δφ = 1.0 Prot is too deep and the one at 2.0 Prot is not observed. Similar considerations apply to WTTSs. The quantitative disagreement may indicate that the actual variability is not sinusoidal, as assumed, and/or, maybe more importantly, that the X-ray modulation periods are not the same as the rotational periods (see below), and/or that the structures responsible for the modulation (e.g. coronal active regions or absorbing circumstellar structures) evolve on timescales of a few rotational periods so that the modulation signal is lost for Δφ > 1–2 Prot. Given the above considerations, we conclude that the clearer modulation signal observed for CTTSs in the soft X-ray band indeed suggests stronger modulation than for WTTSs.
A similar analysis for the hard X-ray band, for which only WTTS show clear indications of rotational modulation, results in a best estimate for the modulation amplitude of WTTS of 24% and a non-modulated contribution to the VAs of ~0.22 dex. For CTTS, instead, our simple model is not able to account for the observed trend, indicating that rotational modulation plays a relatively less important role with respect to other sources of variability such as flares (which cannot account for the increase of VAs with timescale, however) and the evolution of emitting or absorbing structures (i.e. active regions and circumstellar matter).
Our detection of rotational modulation in the soft band is fairly consistent with the conclusions of Flaccomio et al. (2005), who found signatures of rotational modulation in 23 out of the 233 COUP sources in their parent sample, with X-ray amplitudes in the full energy band ranging from 20% to 70%. No evidence was found of a correlation between accretion and the detection of X-ray modulation and/or modulation amplitudes, apparently at odds with our findings that suggest larger modulation amplitudes for CTTSs, at least in the soft X-ray band. The small sample size of Flaccomio et al. (2005), differences in the samples and the fact that only the full X-ray band was considered might very well explain the potential discrepancy.
Our samples significantly overlap with that of Flaccomio et al. (2005), who adopted for their analysis a lower count-rate threshold with respect to ours and excluded stars with short rotational periods, Prot < 2 d. In our sample of CTTSs (WTTSs), for example, 17 (51) out of the 19 (72) stars in our “full band” sample are in common between the two studies. Among these, Flaccomio et al. (2005) claimed the detection of rotational modulation in three CTTSs and ten WTTSs.
Although Flaccomio et al. (2005) did not detect a difference between CTTS and WTTS with regard to the incidence of X-ray rotational modulation or modulation amplitudes, a hint was found at the 1% significance level that CTTSs (and Class II stars) have X-ray modulation periods that are preferentially one half of the optically determined periods. The same hint is present in the subsample in common with the present study, since all three CTTS for which a periodicity was detected by Flaccomio et al. (2005) were found to have PX−ray ~ 0.5 Popt, while the same is true for only two out of ten WTTSs. If, as it seems to be the case for CTTSs, X-ray periods are shorter than the optically determined period in a significant fraction of cases, our interpretation of the peaks in the runs of VA vs. phase lag (these latter computed using Popt) will be affected. In the cases for which PX−ray ~ 0.5 Popt we would indeed expect VA peaks at 0.25 Popt, 0.75 Popt, etc. Although these peaks would not be detectable with the Δφ binning we adopted in our analysis (e.g. Fig. 4), they might fill in the minima between the maxima expected for the PX−ray ~ Popt case (e.g. between the 0.5 Popt and 1.5 Popt). As already mentioned, this might explain why the observed peaks and minima, e.g., in the VAs for CTTSs in the soft X-ray band, are not as pronounced as predicted by our simulations of sinusoidally modulated lightcurves (Fig. 7).
6.3. Implications
Building on the above discussion, we now speculate on the physical mechanisms responsible for the observed X-ray variability, with particular reference to the difference between CTTSs and WTTSs, i.e. by our definition stars undergoing “strong” and “no” accretion, respectively. We focus on the following results: i) flares are a certain source of variability in all our subsamples; ii) most of the variability, however, cannot be explained by flares of the observed duration, especially at long timescales; iii) the higher variability of CTTS/Class II stars with respect to WTTS/Class III stars cannot be explained by different flaring activities; iv) flux modulation due to stellar rotation is a good candidate to explain at least part of the non-flaring variability; v) in the soft X-ray band, in particular, CTTSs show significant signatures of rotational modulation, suggesting higher modulation amplitudes than in WTTSs; vi) no indication of rotational modulation is observed for CTTSs in the harder X-ray band.
6.3.1. The coronae of CTTSs
The enhanced rotational modulation observed for CTTSs in the soft X-ray band with respect to the hard band may indicate that the azimuthal distribution of observable structures emitting soft X-rays is more inhomogeneous than that of those responsible for the hard X-rays. Two scenarios are qualitatively consistent with this conclusion: i) modulation of the X-ray emission from accretion spot(s) or from an accretion-fed corona (as proposed by, e.g. Brickhouse et al. 2010), both expected to be predominantly soft; and ii) modulation of the line-of-sight extinction toward a significant fraction of the coronal structures, again affecting mostly soft X-rays. The first accretion hypothesis builds on the observations of X-ray emission from accretion spots, including recent observations of its rotational modulation (e.g. Argiroffi et al. 2011, 2012). The second absorption hypothesis could be related to the periodic obscuration of large parts of the stellar surface by dusty structures in the inner disk, or by the gaseous accretion streams in co-rotation with the star. Obscuration of the photospheric emission by disk warps has been extensively observed for AA Tau (Bouvier et al. 1999, 2003, 2007a; Grosso et al. 2007; Ménard et al. 2003) and has been inferred to be common in CTTSs by Alencar et al. (2010). Absorption by accretion streams was predicted to be effective in the X-ray regime by Gregory et al. (2007). The same accretion and absorption hypotheses were recently also proposed by Flaccomio et al. (2010) to explain the correlation between the X-ray and optical variability in the NGC 2264 star-forming region, found only for CTTSs and in the soft X-ray band. Flaccomio et al. (2010) favored the absorption/AA Tau-like scenario mainly because the contribution of the accretion shock emission to both the optical and the soft X-ray band was estimated to be too low to explain the large observed variability amplitudes.
The same argument applies here to the X-ray emission from accretion spots: in all cases this emission has been revealed by the observation of emission lines from cool and dense plasma, detected by the Chandra and XMM-Newton high-resolution spectrographs. Even for the most extreme case known, TW Hya, the accretion shock emission is too soft and too faint to contribute a large part of the broad-band X-ray flux detected by imaging instruments, such as the Chandra ACIS (Dupree et al. 2012).
Moreover, the presence of such a significant soft contribution would be evident in the observed CCD spectra and would require, for CTTSs only, a cool thermal component in the X-ray spectral fits. The AA Tau-like hypothesis, i.e. the heavy absorption of part of the emission from the gaseous accretion streams, might instead find support from the time-average CCD spectra if: i) two thermal components of similar temperaure, but subject to very different absorptions, were required to fit the spectra or; ii) the absorptions derived from the fits to the X-ray spectra were significantly higher than those derived from the optical colors and spectral types. The former scenario would indicate the presence of two spatially distinct plasma components of comparable emission measure, only one of which intercepts the additional absorber (disk warp or accretion stream) along the line of sight, while the emission of the other is only subject to interstellar absorption. The latter scenario might instead result if the circumstellar structures absorb the great majority of the emission.
Unfortunately, none of the above predictions is borne out by the CCD spectra of the 11 (19) CTTSs and the 62 (72) WTTSs entering in our VA analysis in the soft (full) X-ray band8. However, we argue that while for the accretion scenario we should indeed expect a detectable soft emission component, if it were responsible for the observed rotational modulation, the non-detection of an absorption “anomaly” in CTTS is actually consistent with the absorption/AA Tau-like scenario. We reach this conclusion through Monte Carlo simulations that aimed to reproduce the observation of X-ray spectra composed of two intrinsically similar thermal components absorbed by different gas columns. These simulations, described in detail in Appendix B, show that the detection of the heavily absorbed component is extremely difficult, if not impossible, using current-quality data. We therefore conclude that the CCD spectra disfavor the accretion scenario as an explanation of the observed X-ray variability, but are compatible with the absorption/AA Tau-like scenario.
6.3.2. Time-averaged activity levels of CTTS and WTTS
The absorption scenario is appealing also because it may provide an explanation not only for the X-ray variability, which is the main subjet of the present study, but also for the previously recognized differences in the time-averaged X-ray activity levels of CTTSs (LX or LX/Lbol) when compared to WTTSs: their on-average lower and more scattered activity levels at any given mass, or Lbol.
Obscuration of large parts of the coronal plasma by the dense accreting columns or disk warps may indeed explain the observation that CTTSs have, on average, 2–3 times lower activity levels than WTTSs, even assuming that their coronae are similar. As shown in Appendix B, the obscured plasma cannot be detected and accounted for with current-quality data. Moreover, for sufficiently high absorbing column densities, NH ≳ 3 × 1022 cm-2, and sufficiently extended absorbing structures, intercepting >1/2 of the coronal plasma, the retrieved X-ray luminosities will indeed be less than one-half of the full coronal luminosity, with no discernible effect on the NH estimated from the spectral fits. The observed magnitude of our VAs, up to ~0.5 dex for timescales of ~10 days and maybe larger for longer timescales, if attributed to periodic obscurations of parts of a corona from circumstellar structures, imply that the obscured fraction is significant.
The estimate for the modulation amplitudes obtained in Sect. 6.2 for the soft X-ray band, ~30%, if attributed to absorption implies a decrease in average flux on the same order. Therefore, to explain a reduction of a factor of ~2 in the observed emission of CTTSs, on average, we would need to assume that an additional fraction, ~20%, of the emission is permanently obscured. This seems reasonable.
 |
Fig. 8 Characteristic LX vs. stellar mass for WTTSs and CTTSs (left and right panels, respectively). The samples are selected in the same way as for our variability study except that in this case we did not impose an X-ray flux (or count-rate) limit. Filled circles refer to the count-rate-limited sample used for the variability study. Linear fits are computed from all points (both filled and empty symbols) within the x-axis range spanned by the gray lines that represent them. |
We now consider the difference in the scatter of the observed activity levels, making the reasonable assumption that the time variability of the stars in our samples is uncorrelated. Regardless of its physical origin, time variability on long timescales will therefore contribute to the observed scatter in activity levels at any given mass or Lbol. Our finding that CTTSs are more variable with respect to WTTSs may therefore explain the observed differences at least qualitatively.
We now aim to assess the contribution of variability to this scatter more quantitatively. Indeed, our measure of variability, the VAs, would translate directly into a contribution to the 50% scatter9 of activity levels (strictly speaking averaged over 30 ks) if they could be measured on the longest timescales (with the reasonable assumption that they level off at some timescale). Since we only measured variability amplitudes for timescales up to ~10 days, we consider our maximum VA for a given sample, VA(10d), as a lower limit to the long-term variability, VA(∞).
VA(10d) is 0.47 dex for CTTS and 0.34 dex for WTTSs (cf. the upper-left panel of Fig. 4). We may compare these numbers with the scatter in the characteristic LX vs. Lbol relation found by Preibisch et al. (2005) for larger samples of CTTS and WTTS in the COUP dataset, where the definition of WTTS and CTTS is the same as adopted here. Preibisch et al. (2005), however, only report the 1σ dispersions (0.72 dex and 0.52 dex for CTTS and WTTS, respectively). To compute 50% dispersions for direct comparisons with our VAs, we repeated the LX vs. Lbol regression analysis with the COUP sources using three sets of X-ray luminosities: the characteristic values, LX,char, the time averages LX,av (over the 850 ks COUP exposure), and those relative to the individual 30 ks segments we employed for our variability analysis, LX,30 ks. These latter values should allow the most direct comparison between VAs and scatter, and were derived by scaling the time-averaged LX to the ratio between the count-rate in each 30 ks segment and the average count-rate. Throughout the regression analysis we used maximum likelihood (χ2) linear fits that, by definition, yield minimum scatter.
Our regression analysis for the LX,char vs. Lbol relation of WTTS and CTTS yields very similar results to those presented by Preibisch et al. (2005, cf. their Fig. 17). Best-fit parameters and 50% dispersions for these regressions and for those computed using LX,av and LX,30 ks are listed in Table 2. The same table also shows the results of regression analyses of the trends of LX with mass for stars with masses below 0.8 M⊙, i.e. for fully radiative stars, as shown in Fig. 8 (for LX,char). Since the dispersions around the maximum likelihood relations are systematically lower (by 0.07–0.15 dex) than for the relation with Lbol, we took these lower values as the measure of the true scatter of activity levels.
Parameters of best-fit linear regressions between LX (three different sets of values, see text) and Lbol or mass (for M < 0.8 M⊙), and resulting 50% scatter.
When comparing these observed scatters in LX with our VAs, we must acknowledge that the VAs are computed from smaller (and biased) subsamples with respect to the scatters. Figure 8 shows with filled and empty symbols the stars belonging and not belonging to the count-rate limited subsample used for VAs (>1 count/ks, or, roughly, log LX > 29.5 erg s -1). In the following we assume that the VAs of X-ray-faint stars, which also have statistically lower Lbol and mass, are similar to those of their brighter counterparts.
All dispersions listed in the last two columns of Table 2 for CTTSs and WTTSs, and in particular those for LX,30 ks which should be more directly comparable to the VAs, are higher than the observed VAs(10 d): 0.34 dex for WTTS and 0.47 dex for CTTSs. In performing this comparison, however, we should consider two facts that might explain this differenece: first, as mentioned above, our VAs are computed for subsamples that, compared to the full samples, are biased toward high masses and bolometric luminosities. An extrapolation of our results on the dependence of VAs on mass (Fig. 5) suggests that low-mass stars not included in our variability study may have higher VAs, and indeed Fig. 8 may suggest an increase of the scatter at low masses. Therefore, our VAs might be underestimated if applied to the whole sample down to the lowest masses and Lbol. Second, and maybe most importantly, part of the observed scatter in the correlations between LX and Lbol or mass will be due to statistical uncertainties in both quantities, e.g. introduced by the correction of the observed X-ray flux for the individual stellar absorptions, and/or by the derivation of stellar masses through placement of the star in the theoretical HR diagram and comparison with PMS evolutionary models, and/or by the inclusion in the samples of unresolved binaries. Following the discussion in Preibisch et al. (2005), we estimate that the 50% scatter introduced by the above uncertainties on the LX vs. mass relation is ~0.43 dex10. This contribution is to be subtracted (in quadrature) from the observed scatters before comparison with VA(10 d).
Given these considerations, we thus argue that for WTTSs, a significant part of the scatter in LX at a given mass might indeed be justified by variability on the timescale of ~10 days11. The scatter for CTTSs is, however, significantly larger than the corresponding VA, even considering uncertainties, and cannot be explained in this way. Variability on longer timescales might, however, be responsible for most of the scatter in this case. A forthcoming study of longer-term variability will aim to address this point. In the absorption (or AA Tau-like) scenario, which we invoked to explain the evidence of significant rotational modulation in the soft X-ray band, this long-term variability might be naturally attributed to the year-over-year evolution of circumstellar structures (disk warps and accretion streams), and the ensuing variability in the amplitude of the shading of coronal structrures (both modulated and unmodulated). This kind of evolution is, indeed, well documented for AA Tau, and may also be inferred from the observed evolution of the structure of the magnetic field in V2129 Oph (Donati et al. 2010).
7. Summary and conclusions
We have performed a study of X-ray variability among the young stars in the ONC, as observed with the 850 ks long COUP observation. By investigating variability for different stellar samples as a function of timescale and rotational phase (for stars with known rotational period), we have found a number of novel results:
-
CTTSs are significantly more variable than WTTSs at alltimescales and in all X-ray spectral bands.
-
For all samples variability amplitudes increase with increasing timescale at least up to ~10 days, i.e. the longest we probed.
-
Signs of rotational modulation are visible, most clearly for CTTSs and in the soft 500–1500 keV band.
-
Among low-mass Class II and Class III stars, variability decreases with increasing stellar mass.
We speculate that the difference in variability between CTTSs and WTTSs may be explained assuming that the X-ray emission of CTTS is affected by time-variable absorption caused by circumstellar structures, such as warps in the inner disk and/or accretion streams, in co-rotation, or close to co-rotation, with the star. This suggestion is appealing because, assuming that the coronae of CTTSs and WTTSs are similar, it may also explain why CTTSs have lower and more scattered X-ray emission levels than WTTSs.
Online material
Appendix A: Monte Carlo flare simulations
As discussed qualitatively in the main text (Sect. 6.1), the effect of flares on the fractional variability amplitudes, the VAs, depends on the intensity, frequency, and duration of flares, as well as on the quiescent or characteristic count-rate on top of which they are observed. In this appendix we employ Monte Carlo simulations to assess, quantitatively and realistically, the contribution of flaring activity to the VAs. We are particularly interested in determining whether flares can explain the observed rising trends of VAs with timescale and the differences among our four main samples (CTTSs, WTTSs, Class II, and Class III stars) .
Although these samples share similar frequencies and durations (Sect. 5.2) for detectable flares, our flare detection algorithm can only identify flares that individually contribute a statistically significant signal to the lightcurves. The VAs may, however, be affected also by smaller flares, either individually or by their superpositions. To assess the effect of flares on VAs realistically, we ran simulations of light curves that attempt to reproduce the following observables: i) the time-averaged source count-rates; ii) flare frequencies; and iii) flare durations. More specifically, following the results of Caramazza et al. (2007), we assumed that the X-ray emission of our sources is produced by a superposition of flares with impulsive rise phases and exponential decays, with a given fixed exponent τ (at least initially). This last assumption is an approximation, since the observed flares clearly show a range of decay times, and was eventually relaxed.
Flares are assumed to occur at an energy-dependent rate, dRfl(E), with a power law dependence: dRfl(C)/dC ∝ C−α, where we substituted the energy with the number of detected flare counts, C. Caramazza et al. (2007) found α ~ −2.2 for low-mass ONC members. We adopted the same value here, which is well-compatible with the bright tail of the flare frequency distribution in Fig. 6 (the turn-off at log C ≲ 3 may be explained by the inefficiency of the flare-detection process). Caramazza et al. (2007) was able to reasonably reproduce the mean characteristics of observed light-curves, as well as the flare frequency distribution, by assuming that the whole stellar X-ray emission is caused by flares, with a source-dependent minimum flare amplitude, Cmin, and total flare frequency, Rfl ≡ ∫dRfl(C). Note that, if α < −2, a given set of α, Cmin and Rfl, directly determines the mean source count-rate, as well as the characteristic one.
Here, we followed a slightly simplified approach with respect to Caramazza et al. (2007): instead of trying to reproduce the characteristics of each individual light curve, i.e. by choosing individual Cmin and Rfl values to fit the mean and characteristic fluxes, we represented all the stars in each of our samples with a single set of Cmin and Rfl values and thus tried to reproduce the median count-rate of the stars in the sample. Moreover, in the last two of the four simulation sets we discuss below, we also allowed for the presence of a quiescent non-flaring emission component to better reproduce the observations, and, in the last set, for a range of flare decay timescales, τ.
All our simulations were run with α = −2.2 and α = −2.4 but we only discuss the case of α = −2.2 since the conclusions are the same for the two cases. We chose Cmin and Rfl so that i) the expected frequency of simulated flares with log C > 3 matches
the observed value in Fig. 6, ~0.4 flares/Ms for all samples; and ii) the simulated lightcurves match the median count-rate of our samples. In particular we ran simulations to reproduce median count-rates of 3, 4, and 6 cnts/ks (cf. Fig. 3).
For each simulation set, i.e. for each set of parameters, α, Cmin, Rfl, and τ, we generated 1000 simulated lightcurves, covering the same temporal observing windows as in the COUP observation (see e.g. Fig. 1), and applied the exact same analysis as previously described for the real COUP sources in our samples, i.e. the VA analysis as a function of timescale and flare detection.
For our first set of simulations we set τ = 10 ks, i.e. similar to that of most observed flares. The top row of Fig. A.1 shows the results. From left to right: the run of VAs vs. timescale, the flare frequency Rfl vs. flare counts, and the distribution of flare durations. In all cases the black lines show the actual observed functions/distributions for our four samples, repeated from Figs. 2 and 6. The three thin red lines instead show the results of the simulations, one for each of the median count-rates, 3, 4, and 6 cnts/ks, that encompass the observed ones12. We conclude that our models, while reproducing the observed flare durations reasonably well, produce light curves that are much more variable and with many more faint flares than observed. A possible solution to reduce both VAs and the frequencies of detected faint flares is to increase τ. The second row in Fig. A.1 shows that for τ = 100 ks we indeed obtain a good match with the observed VAs and flare frequencies. For VAs, we even qualitatively match the observed rising trends with timescale. However, the simulations do not match the measured flare durations, a discrepancy that is clearly supported by simple inspection of the observed and simulated lightcurves.
 |
Fig. A.1 Results of our VA and flare analysis on simulated lightcurves consisting of a superposition of flaring and continuous emission (see text). From left to right we show measured VAs, flare frequencies, and flare durations. In all cases the three red lines refer to simulation sets that reproduce a given median count-rate: 3, 4, and 6 cnts/ks, spanning the median count rates of our four main stellar samples. Observed quantities for these four samples are drawn in black, reproduced from Figs. 2 and 6. The four rows refer to four different simulation sets that differ for the assumed flare decay-times and, in last two cases, for a lower cutoff in flare intensities (in counts), with a corresponding addition of a continuous emission level. From top to bottom: τ = 10 ks (no cutoff/continuum), τ = 100 ks (no cutoff/continuum), τ = 10 ks (>300 counts plus continuum), and τ = 10 ks ± 1 dex (>300 counts plus continuum). |
In our third simulation set we therefore decided to revert τ to 10 ks and, to lower VAs and flare frequencies, to substitute the flux emitted by small flares below a given counts threshold, with a quiescent emission. The third row in Fig. A.1 shows the result of setting the minium flare-counts threshold to 300. We note that i) flare frequencies are now reasonably close to the observations, especially considering that our sharp cut of flare counts at 300 is obviously unrealistic; ii) VAs are significantly smaller than observed, especially for long timescales, which leaves room for other sources of variability such as rotational modulation (of which we found evidence in Sect. 5.1.2); iii), flare durations are on average similar to the observations, even though with a significantly smaller scatter, as would be expected with our simplifying assumption of a single τ value. To correct this single disagreement, in our last set of simulations (fourth row in Fig. A.1) we allowed τ to span a range of values, log-normally distributed with a mean = 10 ks and σ = 1 dex. We are thus able to reproduce the observed distribution and range of measured flare lengths, while the VAs and flare rates remain very similar to those of our previous simulations set.
From the last two sets of simulations, the most successful at reproducing the observed flare statistics, we conclude that flares are likely not the dominant source of variability, as measured by the VAs. This is particularly true at long timescales. In fact, in our last simulation set with a reasonable mix of flare decay-times that well reproduce the measured flare durations, the run of VAs with timescale remains rather flat, which is not compatible with the observed sharp positive trends.
Appendix B: Spectral Monte Carlo simulation
Our preferred interpretation of the higher and more modulated X-ray variability of CTTSs with respect to WTTSs is the intervention of time-variable absorption of part of the X-ray emitting plasma. In this scenario the observable X-ray spectra of CTTSs would be the sum of two intrinsically similar components, undergoing very different attenuations: while the emission of one plasma component would be absorbed by interstellar material only, the emission from the other spatially distinct component would also intercept much thicker circumstellar material. This hypothesis seems to be contradicted by the time-averaged X-ray spectra obtained by the COUP project, showing neither signatures of such composed spectra, nor evidence of significantly higher extinctions for CTTSs (Sect. 6.3).
To verify the significance of this lack of evidence, we have investigated through Monte Carlo simulations whether the two above signatures may or may not actually be detectable with data of the same quality as those in our hands. More specifically, we simulated the expected X-ray spectra in the two-absorptions scenario and verified whether the composite nature of the resulting spectra could be detected with the customary X-ray spectral analysis.
The simulated Chandra ACIS spectra were produced using XSPEC v12.7 (Arnaud 1996), adopting an isothermal model (APEC) with kT = 1.26 keV, quite typical of PMS stars, and assuming zero interstellar extinction. The normalization was chosen so to obtain 1800 and 18 000 counts (in two separate simulation sets). The lower value is somewhat higher than the mean and the median number of counts obtained by COUP for CTTS (as defined in this work): ~450 and ~1500, respectively. The higher value is higher than the number of counts collected for all CTTSs, but one.
For each simulation set, we simulated “1T, two-NH” composed spectra by varying i) fabs, the fraction of the coronal plasma that is absorbed (from 0.1 to 1.0, in 0.1 steps); and ii) NH, the column density of the absorbing material, (from 1021 cm-2 to 3.2 × 1023 cm-2, in 11 logarithmic steps). For each point in this grid, we simulated 100 ACIS spectra, regrouped them so to have SNR ~ 5 per spectral bin, and fit them, within XSPEC, with an usual two-temperature model with a single absorption (“2T, one-NH”). We judge the ability to detect the two absorptions from the goodness of these latter fits, and specifically from the mean value of the null probability, (i.e. the probability of obtaining a higher χ2 value given the model), 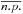 : high
: high 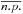 values indicate that a model with a single NH is a good representation of the composite spectrum and that the absorbed component cannot be detected. To reject the single NH hypothesis, we would require low values of
values indicate that a model with a single NH is a good representation of the composite spectrum and that the absorbed component cannot be detected. To reject the single NH hypothesis, we would require low values of 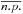 , e.g. <5% (a conservative threshold).
, e.g. <5% (a conservative threshold).
 |
Fig. B.1 Results of the simulations of 1T, two-NH spectra (~18 000 counts for NH = 0) fitted with 2T, one-NH models. The black contours in the upper panel show the average null probability as a function of the fraction of obscured emission measure, fabs, and the column density of the obscuring material, NH. The middle and lower panels show contour plots of the mean unabsorbed flux (in the 0.5–8.0 kV band, in units of 1.3 × 10-13 s-1 cm-2), and of the mean NH (units 1022 cm-2), both obtained from the spectral fits. The two white contours in the upper panel are repeated from the middle panel and show the loci corresponding to a 50% and 70% reduction in measured flux. |
The top panel of Fig. B.1 is a contour plot showing 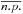 derived from the simulations with the brighter template spectrum (18 000 counts for the unabsorbed case) in the fabs-NH plane. We see that for much of the plane
derived from the simulations with the brighter template spectrum (18 000 counts for the unabsorbed case) in the fabs-NH plane. We see that for much of the plane 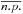 is larger than 5%, indicating that even with high statistics we are unable to detect the existence of two absorption components for most fabs-NH combinations. The same plot for the case of the fainter template spectrum (1800 counts) shows that
is larger than 5%, indicating that even with high statistics we are unable to detect the existence of two absorption components for most fabs-NH combinations. The same plot for the case of the fainter template spectrum (1800 counts) shows that 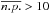 % for all fabs-NH pairs. The middle panel in Fig. B.1 shows the mean unabsorbed flux obtained from the fits with 2T, one-NH spectral models, at each position in the grid and relative to the flux for the NH = 0 case. To obtain a reduction of the flux by a factor of 2–3, i.e. on the order of the mean LX difference between WTTS and CTTSs, NH must be greater than ~3 × 1022 cm-2 and fabs = 0.5–0.7. The contour lines relative to a decrease in flux by a factor of 2 and 3 are also reported in white in the
% for all fabs-NH pairs. The middle panel in Fig. B.1 shows the mean unabsorbed flux obtained from the fits with 2T, one-NH spectral models, at each position in the grid and relative to the flux for the NH = 0 case. To obtain a reduction of the flux by a factor of 2–3, i.e. on the order of the mean LX difference between WTTS and CTTSs, NH must be greater than ~3 × 1022 cm-2 and fabs = 0.5–0.7. The contour lines relative to a decrease in flux by a factor of 2 and 3 are also reported in white in the 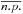 contour plot (upper panel). Note that there is ample room in the fabs-NH plane for having a decrease in retrieved flux on this order, and at the same time being unable to detect the second absorption. The bottom panel of Fig. B.1 shows the mean NH obtained from the spectral fits, showing that in the same region of the parameter space discussed above, not only is it impossible to detect the second NH, but the value of the best fit NH obtained from a single-NH model is very low, basically that of the unabsorbed component. We also note that in the same region of the plane, the values of the two temperatures obtained from the spectral fits with 2T, one-NH models, are in line with observed values (not shown).
contour plot (upper panel). Note that there is ample room in the fabs-NH plane for having a decrease in retrieved flux on this order, and at the same time being unable to detect the second absorption. The bottom panel of Fig. B.1 shows the mean NH obtained from the spectral fits, showing that in the same region of the parameter space discussed above, not only is it impossible to detect the second NH, but the value of the best fit NH obtained from a single-NH model is very low, basically that of the unabsorbed component. We also note that in the same region of the plane, the values of the two temperatures obtained from the spectral fits with 2T, one-NH models, are in line with observed values (not shown).
We did not try to fit the spectra with more than two thermal components or to allow plasma abundances to vary in the
spectral fits. Therefore the combinations of fabs-NH values for which a single-NH model is not adequate to fit the two-NH spectra may be even more limited than found above. Moreover, we neglected systematic uncertainties, e.g. on the models and on the calibration of the spectral responses, which, if considered, might make the rejection of a one-NH model even harder.
We conclude that the scenario in which a large part of the coronal emission is obscured by stable or time-varying gaseous structures is compatible with the observed spectra, showing neither evidence of double absorptions nor substantially higher best fit NH values. Moreover, assuming that WTTS and CTTS have similar coronae and that the difference in observed flux is due to partial obscuration of the corona, we must require that the obscuring material has NH greater than a few 1022 cm-2.
For the low-mass limit we chose to rely on the Ic magnitude instead of the masses estimated from the HR digram and evolutionary models. This is because this latter determination of masses, ultimately based on spectral types, is less complete at the low-mass end. We would thus have lost a number of otherwise useful stars for the following analysis.
There is significant but not complete overlap between CTTS and Class II stars and between WTTS and Class IIIs. In particular, among the 57 CTTSs, 2 are classified as a Class I, 31 as Class II, 14 as Class III and 10 have no nIR classification; among the 110 WTTSs, one is a Class I, 29 are Class II, 70 are Class III, and 10 are have no nIR classification.
As for the presence of a significant accretion-spot contribution, we compared the temperatures of the cool thermal components needed to fit the CCD spectra of CTTS and WTTS, as reported by Getman et al. (2005). We found that CTTSs host, if anything, systematically hotter plasma than WTTS, at odds with the accretion hypotesis. As for the possible evidence of AA Tau-like behavior within our low-energy sample, we found no evidence of double absorptions, both as indicated by Getman et al. (2005), who flagged spectral fits with evidence of this situation, and upon new examination of the spectral fits. We also found no suggestion that CTTS have a peculiar NH-AV relation with respect to WTTS.
Acknowledgments
We thank Jeremy Drake for stimulating discussions and careful reading of the manuscript.
References
- Alencar, S. H. P., Teixeira, P. S., Guimarães, M. M., et al. 2010, A&A, 519, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Argiroffi, C., Flaccomio, E., Bouvier, J., et al. 2011, A&A, 530, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Argiroffi, C., Maggio, A., Montmerle, T., et al. 2012, ApJ, 752, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bouvier, J., Chelli, A., Allain, S., et al. 1999, A&A, 349, 619 [NASA ADS] [Google Scholar]
- Bouvier, J., Grankin, K. N., Alencar, S. H. P., et al. 2003, A&A, 409, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Boutelier, T., et al. 2007a, A&A, 463, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Harries, T. J., Johns-Krull, C. M., & Romanova, M. M. 2007b, Protostars and Planets V, 479 [Google Scholar]
- Brickhouse, N. S., Cranmer, S. R., Dupree, A. K., Luna, G. J. M., & Wolk, S. 2010, ApJ, 710, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Caramazza, M., Flaccomio, E., Micela, G., et al. 2007, A&A, 471, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damiani, F., Micela, G., Sciortino, S., & Harnden, Jr., F. R., 1994, ApJ, 436, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Damiani, F., Micela, G., Sciortino, S., & Harnden, Jr., F. R., 1995, ApJ, 446, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J., Skelly, M. B., Bouvier, J., et al. 2010, MNRAS, 402, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Brickhouse, N. S., Cranmer, S. R., et al. 2012, ApJ, 750, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Favata, F., Flaccomio, E., Reale, F., et al. 2005, ApJS, 160, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Kriss, G. A. 1981, ApJ, 248, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Montmerle, T. 1999, ARA&A, 37, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E. 2003, in Chandra Proposal, 1398 [Google Scholar]
- Flaccomio, E., Damiani, F., Micela, G., et al. 2003a, ApJ, 582, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Damiani, F., Micela, G., et al. 2003b, ApJ, 582, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Micela, G., Sciortino, S., et al. 2005, ApJS, 160, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Micela, G., & Sciortino, S. 2006, A&A, 455, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flaccomio, E., Micela, G., Favata, F., & Alencar, S. P. H. 2010, A&A, 516, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Getman, K. V., Flaccomio, E., Broos, P. S., et al. 2005, ApJS, 160, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Najita, J., & Igea, J. 2004, ApJ, 615, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Grankin, K. N., Melnikov, S. Y., Bouvier, J., Herbst, W., & Shevchenko, V. S. 2007, A&A, 461, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grankin, K. N., Bouvier, J., Herbst, W., & Melnikov, S. Y. 2008, A&A, 479, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregory, S. G., Wood, K., & Jardine, M. 2007, MNRAS, 379, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Grosso, N., Bouvier, J., Montmerle, T., et al. 2007, A&A, 475, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., & Telleschi, A. 2007, A&A, 474, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamaguchi, K., Yamauchi, S., & Koyama, K. 2005, ApJ, 618, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., Mundt, R., Meisenheimer, K., & Wackermann, R. 2002, A&A, 396, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, C. P., Gregory, S. G., Jardine, M. M., & Getman, K. V. 2012, MNRAS, 419, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, A. H. 1945, ApJ, 102, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Kastner, J. H., Huenemoerder, D. P., Schulz, N. S., Canizares, C. R., & Weintraub, D. A. 2002, ApJ, 567, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J. 1987, in Star Forming Regions, eds. M. Peimbert, & J. Jugaku, IAU Symp., 115, 1 [Google Scholar]
- Ménard, F., Bouvier, J., Dougados, C., Mel’nikov, S. Y., & Grankin, K. N. 2003, A&A, 409, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morales-Calderón, M., Stauffer, J. R., Hillenbrand, L. A., et al. 2011, ApJ, 733, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Neuhaeuser, R., Sterzik, M. F., Schmitt, J. H. M. M., Wichmann, R., & Krautter, J. 1995, A&A, 297, 391 [NASA ADS] [Google Scholar]
- Owen, J. E., Ercolano, B., & Clarke, C. J. 2011, MNRAS, 412, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., Kim, Y.-C., Favata, F., et al. 2005, ApJS, 160, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., van den Berg, M., & Feigelson, E. 2007, ApJ, 660, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., Robrade, J., Schmitt, J. H. M. M., & Bouvier, J. 2009, A&A, 493, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Telleschi, A., Güdel, M., Briggs, K. R., Audard, M., & Palla, F. 2007, A&A, 468, 425 [Google Scholar]
- Wolk, S. J., Harnden, Jr., F. R., Flaccomio, E., et al. 2005, ApJS, 160, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Preibisch, T. 1994, A&A, 292, 152 [NASA ADS] [Google Scholar]
All Tables
Parameters of best-fit linear regressions between LX (three different sets of values, see text) and Lbol or mass (for M < 0.8 M⊙), and resulting 50% scatter.
All Figures
 |
Fig. 1 Example X-ray light-curve for a bright COUP source. The horizontal segments, superimposed on the lightcurve (black line), indicate time intervals and relative photon fluxes for the 25 30 ks segments on which the variability analysis is based. |
| In the text | |
 |
Fig. 2 Normalized histogram of all flux ratios, log (F1/F2), taken between 30 ks time intervals separated by Δt = 7.1–9.6 days (logarithmic mean: 8.24 days), for the 167 Class III stars in our flux-limited sample (broken line). The narrower distribution, actually a bundle of ten almost indistinguishable ones, represents the contribution of Poisson statistics to the observed distribution as determined from Monte Carlo simulations (see text). |
| In the text | |
 |
Fig. 3 Distributions of count rates for our flux-limited samples of CTTS (red), WTTS (green), Class II (orange), and Class III (blue) stars. Sample sizes and median count rates are reported in the legend. Count rates are defined here as the total number of counts detected in the 25 × 30 ks time intervals under consideration, divided by the exposure time, 750 ks. |
| In the text | |
 |
Fig. 4 Variability amplitude, VA, as a function of timescale (left column) and rotational phase difference (right column), for CTTS, WTTS, Class II, and Class III stars (see legends within panels), and for three different X-ray energy bands: full (0.5–8.0 keV, top row), soft (0.5–1.5 keV, middle), and hard (1.5–8.0 keV, bottom). As described in Sect. 3, the VA for each sample and x-axis value (Δt or Δφ) is defined as the 50% width of the distribution of log F1/F2 (cf. Fig. 2), i.e. of the difference between the 75% and 25% quantiles. Formal error bars reflect photon statistics and are estimated thorough Monte Carlo simulations. Thick lines refer to the VAs derived from the data, while thin lines with error bars and matching color indicate the contribution of Poisson noise (also estimated with Monte Carlo simulations). |
| In the text | |
 |
Fig. 5 Variability amplitude, VA, as a function of timescale for Class II and Class III stars, for the full samples (same as in Fig. 4) and for two mass-segregated subsamples (see caption). |
| In the text | |
 |
Fig. 6 Left: rate of occurrence of flares as a function of minimum number of flare counts for our four main samples. The legend indicates the color of the lines representing each sample as well as the respective numbers of detected flares. Right: cumulative distribution of flare durations for the same four samples. |
| In the text | |
 |
Fig. 7 Left: VA vs. rotational phase for simulated lightcurves. The simulations reproduce sinusoidally varying stars, observed with the COUP observation and analyzed in the same way as the real data. Four curves show results for modulation amplitudes from 5% to 30%, as labeled. Right: comparison of the trends observed in the soft band for WTTS and CTTS (green and red lines, respectively) with two simulated VA curves (labeled gray lines) obtained by summing in quadrature the VAs for pure sinusoidal modulation (with amplitudes of 18% and 29%) with constant non-modulated VAs (0.16 and 0.18 dex, see labels). Modulation amplitudes and constant contributions are chosen to reproduce the observed VAs at Δφ = 0.06 (the leftmost points) and Δφ = 0.5 (the first maxima). |
| In the text | |
 |
Fig. 8 Characteristic LX vs. stellar mass for WTTSs and CTTSs (left and right panels, respectively). The samples are selected in the same way as for our variability study except that in this case we did not impose an X-ray flux (or count-rate) limit. Filled circles refer to the count-rate-limited sample used for the variability study. Linear fits are computed from all points (both filled and empty symbols) within the x-axis range spanned by the gray lines that represent them. |
| In the text | |
 |
Fig. A.1 Results of our VA and flare analysis on simulated lightcurves consisting of a superposition of flaring and continuous emission (see text). From left to right we show measured VAs, flare frequencies, and flare durations. In all cases the three red lines refer to simulation sets that reproduce a given median count-rate: 3, 4, and 6 cnts/ks, spanning the median count rates of our four main stellar samples. Observed quantities for these four samples are drawn in black, reproduced from Figs. 2 and 6. The four rows refer to four different simulation sets that differ for the assumed flare decay-times and, in last two cases, for a lower cutoff in flare intensities (in counts), with a corresponding addition of a continuous emission level. From top to bottom: τ = 10 ks (no cutoff/continuum), τ = 100 ks (no cutoff/continuum), τ = 10 ks (>300 counts plus continuum), and τ = 10 ks ± 1 dex (>300 counts plus continuum). |
| In the text | |
 |
Fig. B.1 Results of the simulations of 1T, two-NH spectra (~18 000 counts for NH = 0) fitted with 2T, one-NH models. The black contours in the upper panel show the average null probability as a function of the fraction of obscured emission measure, fabs, and the column density of the obscuring material, NH. The middle and lower panels show contour plots of the mean unabsorbed flux (in the 0.5–8.0 kV band, in units of 1.3 × 10-13 s-1 cm-2), and of the mean NH (units 1022 cm-2), both obtained from the spectral fits. The two white contours in the upper panel are repeated from the middle panel and show the loci corresponding to a 50% and 70% reduction in measured flux. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


