| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 16 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201219362 | |
| Published online | 27 November 2012 | |
Online material
Appendix A: Monte Carlo flare simulations
As discussed qualitatively in the main text (Sect. 6.1), the effect of flares on the fractional variability amplitudes, the VAs, depends on the intensity, frequency, and duration of flares, as well as on the quiescent or characteristic count-rate on top of which they are observed. In this appendix we employ Monte Carlo simulations to assess, quantitatively and realistically, the contribution of flaring activity to the VAs. We are particularly interested in determining whether flares can explain the observed rising trends of VAs with timescale and the differences among our four main samples (CTTSs, WTTSs, Class II, and Class III stars) .
Although these samples share similar frequencies and durations (Sect. 5.2) for detectable flares, our flare detection algorithm can only identify flares that individually contribute a statistically significant signal to the lightcurves. The VAs may, however, be affected also by smaller flares, either individually or by their superpositions. To assess the effect of flares on VAs realistically, we ran simulations of light curves that attempt to reproduce the following observables: i) the time-averaged source count-rates; ii) flare frequencies; and iii) flare durations. More specifically, following the results of Caramazza et al. (2007), we assumed that the X-ray emission of our sources is produced by a superposition of flares with impulsive rise phases and exponential decays, with a given fixed exponent τ (at least initially). This last assumption is an approximation, since the observed flares clearly show a range of decay times, and was eventually relaxed.
Flares are assumed to occur at an energy-dependent rate, dRfl(E), with a power law dependence: dRfl(C)/dC ∝ C−α, where we substituted the energy with the number of detected flare counts, C. Caramazza et al. (2007) found α ~ −2.2 for low-mass ONC members. We adopted the same value here, which is well-compatible with the bright tail of the flare frequency distribution in Fig. 6 (the turn-off at log C ≲ 3 may be explained by the inefficiency of the flare-detection process). Caramazza et al. (2007) was able to reasonably reproduce the mean characteristics of observed light-curves, as well as the flare frequency distribution, by assuming that the whole stellar X-ray emission is caused by flares, with a source-dependent minimum flare amplitude, Cmin, and total flare frequency, Rfl ≡ ∫dRfl(C). Note that, if α < −2, a given set of α, Cmin and Rfl, directly determines the mean source count-rate, as well as the characteristic one.
Here, we followed a slightly simplified approach with respect to Caramazza et al. (2007): instead of trying to reproduce the characteristics of each individual light curve, i.e. by choosing individual Cmin and Rfl values to fit the mean and characteristic fluxes, we represented all the stars in each of our samples with a single set of Cmin and Rfl values and thus tried to reproduce the median count-rate of the stars in the sample. Moreover, in the last two of the four simulation sets we discuss below, we also allowed for the presence of a quiescent non-flaring emission component to better reproduce the observations, and, in the last set, for a range of flare decay timescales, τ.
All our simulations were run with α = −2.2 and α = −2.4 but we only discuss the case of α = −2.2 since the conclusions are the same for the two cases. We chose Cmin and Rfl so that i) the expected frequency of simulated flares with log C > 3 matches
the observed value in Fig. 6, ~0.4 flares/Ms for all samples; and ii) the simulated lightcurves match the median count-rate of our samples. In particular we ran simulations to reproduce median count-rates of 3, 4, and 6 cnts/ks (cf. Fig. 3).
For each simulation set, i.e. for each set of parameters, α, Cmin, Rfl, and τ, we generated 1000 simulated lightcurves, covering the same temporal observing windows as in the COUP observation (see e.g. Fig. 1), and applied the exact same analysis as previously described for the real COUP sources in our samples, i.e. the VA analysis as a function of timescale and flare detection.
For our first set of simulations we set τ = 10 ks, i.e. similar to that of most observed flares. The top row of Fig. A.1 shows the results. From left to right: the run of VAs vs. timescale, the flare frequency Rfl vs. flare counts, and the distribution of flare durations. In all cases the black lines show the actual observed functions/distributions for our four samples, repeated from Figs. 2 and 6. The three thin red lines instead show the results of the simulations, one for each of the median count-rates, 3, 4, and 6 cnts/ks, that encompass the observed ones12. We conclude that our models, while reproducing the observed flare durations reasonably well, produce light curves that are much more variable and with many more faint flares than observed. A possible solution to reduce both VAs and the frequencies of detected faint flares is to increase τ. The second row in Fig. A.1 shows that for τ = 100 ks we indeed obtain a good match with the observed VAs and flare frequencies. For VAs, we even qualitatively match the observed rising trends with timescale. However, the simulations do not match the measured flare durations, a discrepancy that is clearly supported by simple inspection of the observed and simulated lightcurves.
 |
Fig. A.1
Results of our VA and flare analysis on simulated lightcurves consisting of a superposition of flaring and continuous emission (see text). From left to right we show measured VAs, flare frequencies, and flare durations. In all cases the three red lines refer to simulation sets that reproduce a given median count-rate: 3, 4, and 6 cnts/ks, spanning the median count rates of our four main stellar samples. Observed quantities for these four samples are drawn in black, reproduced from Figs. 2 and 6. The four rows refer to four different simulation sets that differ for the assumed flare decay-times and, in last two cases, for a lower cutoff in flare intensities (in counts), with a corresponding addition of a continuous emission level. From top to bottom: τ = 10 ks (no cutoff/continuum), τ = 100 ks (no cutoff/continuum), τ = 10 ks (>300 counts plus continuum), and τ = 10 ks ± 1 dex (>300 counts plus continuum). |
| Open with DEXTER | |
In our third simulation set we therefore decided to revert τ to 10 ks and, to lower VAs and flare frequencies, to substitute the flux emitted by small flares below a given counts threshold, with a quiescent emission. The third row in Fig. A.1 shows the result of setting the minium flare-counts threshold to 300. We note that i) flare frequencies are now reasonably close to the observations, especially considering that our sharp cut of flare counts at 300 is obviously unrealistic; ii) VAs are significantly smaller than observed, especially for long timescales, which leaves room for other sources of variability such as rotational modulation (of which we found evidence in Sect. 5.1.2); iii), flare durations are on average similar to the observations, even though with a significantly smaller scatter, as would be expected with our simplifying assumption of a single τ value. To correct this single disagreement, in our last set of simulations (fourth row in Fig. A.1) we allowed τ to span a range of values, log-normally distributed with a mean = 10 ks and σ = 1 dex. We are thus able to reproduce the observed distribution and range of measured flare lengths, while the VAs and flare rates remain very similar to those of our previous simulations set.
From the last two sets of simulations, the most successful at reproducing the observed flare statistics, we conclude that flares are likely not the dominant source of variability, as measured by the VAs. This is particularly true at long timescales. In fact, in our last simulation set with a reasonable mix of flare decay-times that well reproduce the measured flare durations, the run of VAs with timescale remains rather flat, which is not compatible with the observed sharp positive trends.
Appendix B: Spectral Monte Carlo simulation
Our preferred interpretation of the higher and more modulated X-ray variability of CTTSs with respect to WTTSs is the intervention of time-variable absorption of part of the X-ray emitting plasma. In this scenario the observable X-ray spectra of CTTSs would be the sum of two intrinsically similar components, undergoing very different attenuations: while the emission of one plasma component would be absorbed by interstellar material only, the emission from the other spatially distinct component would also intercept much thicker circumstellar material. This hypothesis seems to be contradicted by the time-averaged X-ray spectra obtained by the COUP project, showing neither signatures of such composed spectra, nor evidence of significantly higher extinctions for CTTSs (Sect. 6.3).
To verify the significance of this lack of evidence, we have investigated through Monte Carlo simulations whether the two above signatures may or may not actually be detectable with data of the same quality as those in our hands. More specifically, we simulated the expected X-ray spectra in the two-absorptions scenario and verified whether the composite nature of the resulting spectra could be detected with the customary X-ray spectral analysis.
The simulated Chandra ACIS spectra were produced using XSPEC v12.7 (Arnaud 1996), adopting an isothermal model (APEC) with kT = 1.26 keV, quite typical of PMS stars, and assuming zero interstellar extinction. The normalization was chosen so to obtain 1800 and 18 000 counts (in two separate simulation sets). The lower value is somewhat higher than the mean and the median number of counts obtained by COUP for CTTS (as defined in this work): ~450 and ~1500, respectively. The higher value is higher than the number of counts collected for all CTTSs, but one.
For each simulation set, we simulated “1T, two-NH” composed spectra by varying i) fabs, the fraction of the coronal plasma that is absorbed (from 0.1 to 1.0, in 0.1 steps); and ii) NH, the column density of the absorbing material, (from 1021 cm-2 to 3.2 × 1023 cm-2, in 11 logarithmic steps). For each point in this grid, we simulated 100 ACIS spectra, regrouped them so to have SNR ~ 5 per spectral bin, and fit them, within XSPEC, with an usual two-temperature model with a single absorption (“2T, one-NH”). We judge the ability to detect the two absorptions from the goodness of these latter fits, and specifically from the mean value of the null probability, (i.e. the probability of obtaining a higher χ2 value given the model), 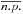 : high
: high 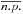 values indicate that a model with a single NH is a good representation of the composite spectrum and that the absorbed component cannot be detected. To reject the single NH hypothesis, we would require low values of
values indicate that a model with a single NH is a good representation of the composite spectrum and that the absorbed component cannot be detected. To reject the single NH hypothesis, we would require low values of 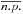 , e.g. <5% (a conservative threshold).
, e.g. <5% (a conservative threshold).
 |
Fig. B.1
Results of the simulations of 1T, two-NH spectra (~18 000 counts for NH = 0) fitted with 2T, one-NH models. The black contours in the upper panel show the average null probability as a function of the fraction of obscured emission measure, fabs, and the column density of the obscuring material, NH. The middle and lower panels show contour plots of the mean unabsorbed flux (in the 0.5–8.0 kV band, in units of 1.3 × 10-13 s-1 cm-2), and of the mean NH (units 1022 cm-2), both obtained from the spectral fits. The two white contours in the upper panel are repeated from the middle panel and show the loci corresponding to a 50% and 70% reduction in measured flux. |
| Open with DEXTER | |
The top panel of Fig. B.1 is a contour plot showing 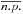 derived from the simulations with the brighter template spectrum (18 000 counts for the unabsorbed case) in the fabs-NH plane. We see that for much of the plane
derived from the simulations with the brighter template spectrum (18 000 counts for the unabsorbed case) in the fabs-NH plane. We see that for much of the plane 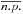 is larger than 5%, indicating that even with high statistics we are unable to detect the existence of two absorption components for most fabs-NH combinations. The same plot for the case of the fainter template spectrum (1800 counts) shows that
is larger than 5%, indicating that even with high statistics we are unable to detect the existence of two absorption components for most fabs-NH combinations. The same plot for the case of the fainter template spectrum (1800 counts) shows that 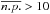 % for all fabs-NH pairs. The middle panel in Fig. B.1 shows the mean unabsorbed flux obtained from the fits with 2T, one-NH spectral models, at each position in the grid and relative to the flux for the NH = 0 case. To obtain a reduction of the flux by a factor of 2–3, i.e. on the order of the mean LX difference between WTTS and CTTSs, NH must be greater than ~3 × 1022 cm-2 and fabs = 0.5–0.7. The contour lines relative to a decrease in flux by a factor of 2 and 3 are also reported in white in the
% for all fabs-NH pairs. The middle panel in Fig. B.1 shows the mean unabsorbed flux obtained from the fits with 2T, one-NH spectral models, at each position in the grid and relative to the flux for the NH = 0 case. To obtain a reduction of the flux by a factor of 2–3, i.e. on the order of the mean LX difference between WTTS and CTTSs, NH must be greater than ~3 × 1022 cm-2 and fabs = 0.5–0.7. The contour lines relative to a decrease in flux by a factor of 2 and 3 are also reported in white in the 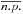 contour plot (upper panel). Note that there is ample room in the fabs-NH plane for having a decrease in retrieved flux on this order, and at the same time being unable to detect the second absorption. The bottom panel of Fig. B.1 shows the mean NH obtained from the spectral fits, showing that in the same region of the parameter space discussed above, not only is it impossible to detect the second NH, but the value of the best fit NH obtained from a single-NH model is very low, basically that of the unabsorbed component. We also note that in the same region of the plane, the values of the two temperatures obtained from the spectral fits with 2T, one-NH models, are in line with observed values (not shown).
contour plot (upper panel). Note that there is ample room in the fabs-NH plane for having a decrease in retrieved flux on this order, and at the same time being unable to detect the second absorption. The bottom panel of Fig. B.1 shows the mean NH obtained from the spectral fits, showing that in the same region of the parameter space discussed above, not only is it impossible to detect the second NH, but the value of the best fit NH obtained from a single-NH model is very low, basically that of the unabsorbed component. We also note that in the same region of the plane, the values of the two temperatures obtained from the spectral fits with 2T, one-NH models, are in line with observed values (not shown).
We did not try to fit the spectra with more than two thermal components or to allow plasma abundances to vary in the
spectral fits. Therefore the combinations of fabs-NH values for which a single-NH model is not adequate to fit the two-NH spectra may be even more limited than found above. Moreover, we neglected systematic uncertainties, e.g. on the models and on the calibration of the spectral responses, which, if considered, might make the rejection of a one-NH model even harder.
We conclude that the scenario in which a large part of the coronal emission is obscured by stable or time-varying gaseous structures is compatible with the observed spectra, showing neither evidence of double absorptions nor substantially higher best fit NH values. Moreover, assuming that WTTS and CTTS have similar coronae and that the difference in observed flux is due to partial obscuration of the corona, we must require that the obscuring material has NH greater than a few 1022 cm-2.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


