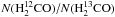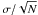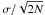| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117664 | |
| Published online | 30 March 2012 | |
Comparative study of CH+ and SH+ absorption lines observed towards distant star-forming regions⋆,⋆⋆,⋆⋆⋆
1 Departamento de Astrofísica, Centro de Astrobiología, CSIC-INTA, Torrejón de Ardoz, Madrid, Spain
e-mail: godard@lra.ens.fr
2 LERMA, CNRS UMR 8112, École Normale Supérieure & Observatoire de Paris, Paris, France
3 California Institute of Technology, Pasadena, CA 91125, USA
4 Department of Earth and Space Sciences, Chalmers University of Technology, Onsala Space Observatory, 43992 Onsala, Sweden
5 The Johns Hopkins University, Baltimore, MD 21218, USA
6 MPI für Radioastronomie, Bonn, Germany
Received: 8 July 2011
Accepted: 13 January 2012
Aims. The HIFI instrument onboard Herschel has allowed high spectral resolution and sensitive observations of ground-state transitions of three molecular ions: the methylidyne cation CH+, its isotopologue 13CH+, and sulfanylium SH+. Because of their unique chemical properties, a comparative analysis of these cations provides essential clues to the link between the chemistry and dynamics of the diffuse interstellar medium.
Methods. The CH+, 13CH+, and SH+ lines are observed in absorption towards the distant high-mass star-forming regions (SFRs) DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51, and towards two sources close to the Galactic centre, SgrB2(N) and SgrA*+50. All sight lines sample the diffuse interstellar matter along pathlengths of several kiloparsecs across the Galactic Plane. In order to compare the velocity structure of each species, the observed line profiles were deconvolved from the hyperfine structure of the SH+ transition and the CH+, 13CH+, and SH+ spectra were independently decomposed into Gaussian velocity components. To analyse the chemical composition of the foreground gas, all spectra were divided, in a second step, into velocity intervals over which the CH+, 13CH+, and SH+ column densities and abundances were derived.
Results. SH+ is detected along all observed lines of sight, with a velocity structure close to that of CH+ and 13CH+. The linewidth distributions of the CH+, SH+, and 13CH+ Gaussian components are found to be similar. These distributions have the same mean (⟨Δυ⟩ ~ 4.2 km s-1) and standard deviation (σ(Δυ) ~ 1.5 km s-1). This mean value is also close to that of the linewidth distribution of the CH+ visible transitions detected in the solar neighbourhood. We show that the lack of absorption components narrower than 2 km s-1 is not an artefact caused by noise: the CH+, 13CH+, and SH+ line profiles are therefore statistically broader than those of most species detected in absorption in diffuse interstellar gas (e.g. HCO+, CH, or CN). The SH+/CH+ column density ratio observed in the components located away from the Galactic centre spans two orders of magnitude and correlates with the CH+ abundance. Conversely, the ratio observed in the components close to the Galactic centre varies over less than one order of magnitude with no apparent correlation with the CH+ abundance. The observed dynamical and chemical properties of SH+ and CH+ are proposed to trace the ubiquitous process of turbulent dissipation, in shocks or shears, in the diffuse ISM and the specific environment of the Galactic centre regions.
Key words: astrochemistry / turbulence / ISM: molecules / ISM: kinematics and dynamics / ISM: structure / ISM: clouds
Based on observations obtained with the HIFI instrument onboard the Herschel space telescope in the framework of the key programmes PRISMAS and HEXOS.
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendices A and B are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Studying the diffuse phases of the interstellar medium (ISM) is essential, not only because they contain a large part of the total gas mass of the cold ISM and are the precursors of dense clouds, but also because they harbour the first steps of interstellar chemistry. Since the detection of the first diatomic molecules CN, CH, and CH+ (see references in the review of Snow & McCall 2006) through their narrow visible absorption lines, the improvement of the observational techniques and instruments has provided a more comprehensive view of the diffuse ISM and led to a better understanding of its dynamical, thermal, and chemical evolution. A wide variety of diatomic and triatomic molecular species has already been observed in the diffuse medium. Moreover, its chemical composition has now been probed in the solar neighbourhood through UV (e.g. Shull & Beckwith 1982; Crawford & Williams 1997; Snow et al. 2000; Rachford et al. 2002; Gry et al. 2002; Lacour et al. 2005), visible (e.g. Crane et al. 1995; Gredel 1997; Thorburn et al. 2003; Weselak et al. 2008; Maier et al. 2001) and radio (e.g. Haud & Kalberla 2007; Liszt et al. 2006, and references therein) spectroscopy, and the inner Galaxy material through submillimetre and radio (millimetre, centimetre) spectroscopy (e.g. Koo 1997; Fish et al. 2003; Nyman & Millar 1989; Greaves & Williams 1994; Neufeld et al. 2002; Plume et al. 2004).
Properties of background sources.
The Herschel space mission has broadened this investigation, giving access to the full submillimetre domain, which has allowed the detection of many molecular species that could not be detected from the ground before because of the high opacity of the atmosphere. In the framework of the HIFI key programme PRISMAS (PRobing InterStellar Molecules with Absorption line Studies) many hydrides such as HF (Neufeld et al. 2010b; Sonnentrucker et al. 2010), OH+, H2O+ (Neufeld et al. 2010a; Gerin et al. 2010a), CH (Gerin et al. 2010b), NH, NH2, NH3 (Persson et al. 2010), and CH+ (Falgarone et al. 2010) were detected in absorption against the strong continuum emission of distant star-forming regions, providing for the first time a good census of these light hydrides in the inner Galaxy.
Of all molecules targeted by PRISMAS, the methylidyne cation CH+ is particularly interesting because its presence in the diffuse ISM remains one of the most intriguing puzzle in astrophysics. The CH+ abundances predicted by steady-state, UV-dominated, PDR-type (photodissociation regions) chemical models are several orders of magnitude lower than the observed values, because all the CH+ formation pathways that are alternative to the highly endothermic C+ + H2 → CH+ + H reaction, are inefficient in balancing its fast destruction by hydrogenation. Indriolo et al. (2010) recently showed that the upper limit on the 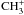 /CH+ abundance ratio observed towards Cyg OB2 can only be reproduced in diffuse molecular clouds with extreme conditions (i.e. fH2 < 0.2, or T > 1000 K). So far, the solution to this puzzle has been to invoke regions of the diffuse gas where a warm chemistry is activated by the release of supra-thermal energy in the cold ISM induced by low-velocity magnetohydrodynamic (MHD) shocks (Draine & Katz 1986; Pineau des Forêts et al. 1986), Alfvén waves (Federman et al. 1996), turbulent mixing (Xie et al. 1995; Lesaffre et al. 2007), or turbulent dissipation (Falgarone et al. 1995; Joulain et al. 1998; Godard et al. 2009). Indriolo et al. (2010) claimed that observations of the excited levels of
/CH+ abundance ratio observed towards Cyg OB2 can only be reproduced in diffuse molecular clouds with extreme conditions (i.e. fH2 < 0.2, or T > 1000 K). So far, the solution to this puzzle has been to invoke regions of the diffuse gas where a warm chemistry is activated by the release of supra-thermal energy in the cold ISM induced by low-velocity magnetohydrodynamic (MHD) shocks (Draine & Katz 1986; Pineau des Forêts et al. 1986), Alfvén waves (Federman et al. 1996), turbulent mixing (Xie et al. 1995; Lesaffre et al. 2007), or turbulent dissipation (Falgarone et al. 1995; Joulain et al. 1998; Godard et al. 2009). Indriolo et al. (2010) claimed that observations of the excited levels of 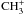 are able to provide the clues necessary to favour one theory over the other.
are able to provide the clues necessary to favour one theory over the other.
A potentially related problem is the existence of sulfanylium (SH+) in the diffuse gas. Because the hydrogenation reaction of S+ has an endothermicity twice as high as that of C+, a measurement of the SH+/CH+ abundance ratio should provide valuable insights about the regions where CH+ is formed. Sought for without success in the local diffuse ISM in absorption against nearby stars in the UV domain since 1988 (Millar & Hobbs 1988; Magnani & Salzer 1989, 1991), this molecular ion was recently detected by Menten et al. (2011) through its ground-state rotational transition in the submillimetre range observed in absorption towards the Galactic centre line of sight SgrB2(M) with the APEX telescope.
In this paper, we report the detection of SH+, CH+, and 13CH+ towards the six distant star-forming regions DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51, and the Galactic centre sight lines1 SgrA*+50 and SgrB2(N), and we perform a cross analysis of the observed properties of those three species. The observations, obtained in the framework of the key programmes PRISMAS and HEXOS, are presented in Sect. 2. The methods used for the analysis and the results obtained are shown in Sects. 3 and 4, respectively. We conclude this work in Sect. 5 with a discussion on the chemical and dynamical properties of the gas seen in absorption. The comparison with the model predictions will be the subject of a forthcoming paper (Godard et al., in prep.).
2. Observations and data reduction
2.1. Observing conditions
CH+X1Σ+, 13CH+X1Σ+, and SH+X3Σ − spectroscopic parameters for the observed pure rotational transitions.
The observations were carried out from March to October 2010 and in April 2011 towards the eight submillimetre background continuum sources listed in Table 1 (with their Galactic coordinates, their distance from the Sun, and their measured single-sideband continuum temperature Tc in K at ~830 and ~530 GHz). Using the dual-beam switch (DBS) mode (with a throw at 3′ from the source) and the wide-band spectrometer (WBS) of Herschel/HIFI (see Roelfsema et al. 2012 for a detailed description of the properties and performances of HIFI), we observed
-
the J = 1 ← 0 absorption lines of CH+ and 13CH+, in the upper and lower sidebands of band 3a;
-
and the F = 3/2 ← 1/2, 5/2 ← 3/2, and 3/2 ← 3/2 hyperfine components of the N,J = 1,2 ← 0,1 absorption line of SH+, in the lower sideband of band 1a.
The data obtained towards SgrB2(N) were part of the full HIFI spectral scan performed by the HEXOS key programme; the corresponding double-sideband spectra were deconvolved into single-sideband spectra, including the continuum (Comito & Schilke 2002). Towards the other sources, the observations were performed in the framework of the PRISMAS key programme; to separate spectral features from upper and lower sidebands of the WBS spectrometer, each transition was observed using three slightly different settings of the local oscillator (LO) frequency, adapted to induce a relative velocity shift of ~30 km s-1 between the two sidebands. The spectroscopic parameters of the observed lines are listed in Table 2, along with the rms noise levels relative to the single-sideband continuum intensities obtained with an on-source integration time ranging from 1 to 20 min. In these frequency ranges, the WBS resolution of 1.1 MHz corresponds to velocity resolutions of ~0.36 km s-1 for the CH+ and 13CH+ transitions, and of ~0.57 km s-1 for the SH+ transitions, and the Herschel HPBW is 26′′ at 835 GHz and 41′′ at 526 GHz.
The data were calibrated with hot and cold blackbodies (Roelfsema et al. 2012), reduced using the standard Herschel pipeline to Level 2, and subsequently analysed using the Herschel Interactive Processing Environment2 (HIPE v5.1, Ott 2010). The final analysis was performed with the GILDAS-CLASS90 software3 (Hily-Blant et al. 2005), and a set of Fortran95 numerical routines that we developed. While the signals measured in the two orthogonal polarizations that were obtained with the three LO settings agreed excellently for both the CH+ and 13CH+ line observations, the SH+ spectra, displayed in Fig. 1, exhibit standing waves (SW) of identified origin4 and removed using the HIPE sine wave fitting task FitHifiFringe (FHF). Since the inferred detected opacities of SH+ are low, and since the period and the amplitude of the waves are similar to the size and the depth of the SH+ absorption features (see Fig. 1), the resulting spectra were sensitive to the FHF input parameters: several plausible solutions were found depending on the number of sub-bands taken into account for the fit, the number of sine waves to remove, and the use of a frequency mask. We estimated a maximal error of 50% on the deepest absorption features of G34.3+0.1 and W51, 30% on those of W33A, and W31C and 10% on the others. The latter value is comparable to that due to the uncertainties on the beam efficiency and the sideband gain ratio (Roelfsema et al. 2012).
 |
Fig. 1 Original SH+ spectra (double-sideband antenna temperature TA before removing the standing waves) observed towards SgrA*+50, W31C, W33A, and W49N in the horizontal polarization and for the three different LO settings (in black, red, and blue). For more clarity the red and blue curves have been shifted from the black curve by 0.2 and 0.4 K (for the SgrA*+50 data), and by 0.1 and 0.2 K (for the W31C, W33A, and W49N data). |
For each transition and both polarizations, we obtained an average spectrum by combining the data from the three observations with different LO settings. Because we are interested in the velocity structure and the properties of the absorbing gas, the spectra in both polarizations were normalized to their respective continuum temperature. As in Falgarone et al. (2010), we used the saturated shape of the CH+ absorption line profiles to measure the sideband gain ratios R at 835.1375 GHz, defined as the ratio of the continuum temperatures in the lower and upper sidebands. For all spectra with saturated absorption lines, we found R ~ 0.9 − 1 and R ~ 0.7−0.8 in the horizontal and vertical polarizations, respectively. We finally used these values at 835 GHz, and R = 1 at 830 GHz and 526 GHz, to combine the data from both polarizations, and obtain the final average spectra (with rms noise levels given in Table 2) shown in Fig. 2 as functions of the LSR (local standard of rest) velocity. This figure illustrates the quality of the baselines over the large bandwidth for most of the spectra. The strong emission lines detected in the spectra shown in Figs. 1 and 2 were identified as the HCO+ (6 → 5) and H2CO (6 → 5) transitions near 535.1 GHz and 525.6 GHz, three methanol lines near 829.9 GHz and 830.3 GHz, and the SO2 emission band near 835 GHz, emitted by the SFRs themselves.
 |
Fig. 2 Spectra observed at the frequencies of the ground-state transitions of CH+ (black), 13CH+ (red), and SH+ (blue) in the direction of DR21(OH), G34.3+0.1, W31C, W33A, W49N, W51, SgrA*+50, and SgrB2(N). All spectra have been normalized to the continuum temperatures. To make the absorption features discernible, the 13CH+ and SH+ signals were mutiplied by a factor of 2 towards SgrA*+50, and SgrB2(N), and by factors of 2 and 3, respectively, towards the other sources. For more clarity the 13CH+ and SH+ spectra were shifted from the CH+ spectra by 0.5 and 1.0. |
2.2. Deconvolution of the SH+ hyperfine structure
 |
Fig. 3 Absorption profiles observed in the direction of DR21(OH), G34.3+0.1, W31C, W33A, W49N, W51, SgrA*+50, and SgrB2(N) in the ground-state transitions of CH+ (black) and 13CH+ (red), and in the main hyperfine component (see Table 2) of the ground-state transition of SH+ (blue). All spectra have been normalized to the continuum temperatures. To make the absorption features discernible, the 13CH+ and SH+ signals were mutiplied by a factor of 2 towards SgrA*+50, and SgrB2(N), and by factors of 2 and 3, respectively, towards the other sources. For more clarity the 13CH+ and SH+ spectra were shifted from the CH+ spectra by 0.5 and 1.0. The x- and y- scales were chosen to display the velocity structure of the absorption features in detail. |
Unfortunately (see Table 2), the velocity shifts Δυh associated with the SH+ hyperfine transitions are smaller than the observed velocity ranges of the SH+ absorption spectra, and prevent us from performing a direct cross comparison of the velocity profiles of the SH+, CH+, and 13CH+ lines. To solve this problem, we developed a numerical procedure to extract the signal associated with each hyperfine transition, solving the following set of equations for τr(υ), over the entire absorption velocity domain, ![\begin{equation} \sum_{k=1}^{N_{\rm h}} I_{\rm h}(k) \, \tau_{\rm r} (\upsilon-\Delta \upsilon_{\rm h}(k)) = -{\rm ln} \left[ T(\upsilon)/T_{\rm c} \right], \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq65.png) (1)where Nh, Ih, τr, and T(υ)/Tc are the number of hyperfine transitions, the intensities relative to the strongest hyperfine component, the opacity of the reference hyperfine transition, and the normalized line profile (line/continuum), respectively. The resulting spectra are shown in Fig. 3, and, as an example, the outcome of the hyperfine decomposition code, applied to the absorption lines observed towards SgrB2(N) and W49N, is shown in Fig. 4. This figure illustrates the excellent agreement between the original data (in black) and the spectra rebuilt after decomposition (in green).
(1)where Nh, Ih, τr, and T(υ)/Tc are the number of hyperfine transitions, the intensities relative to the strongest hyperfine component, the opacity of the reference hyperfine transition, and the normalized line profile (line/continuum), respectively. The resulting spectra are shown in Fig. 3, and, as an example, the outcome of the hyperfine decomposition code, applied to the absorption lines observed towards SgrB2(N) and W49N, is shown in Fig. 4. This figure illustrates the excellent agreement between the original data (in black) and the spectra rebuilt after decomposition (in green).
 |
Fig. 4 Result of the hyperfine structure deconvolution code applied on the SH+ (1,2 ← 0,1) absorption spectrum observed towards SgrB2(N) and W49N. The top panel displays the original data (black) and the resulting decomposition in three hyperfine components, aligned to the same velocity scale. The hyperfine components are shifted by their velocity shift Δυh (see Table 2) in the bottom panels, to show how they can be combined (green line) to reproduce the original data (black line). For more clarity, the hyperfine components were vertically shifted from the original data. |
The 13CH+J = 1 ← 0 line also exhibits a spin-rotation splitting (Amano 2010), although the associated F = 3/2 ← 1/2 and F = 1/2 ← 1/2 transitions are separated by only 1.636 MHz (~0.59 km s-1) and are therefore too close to be individually resolved given the significant velocity dispersion of the gas. This hyperfine structure induces a systematic broadening of the absorption velocity components that depends on their FWHM Δυreal: for Δυreal varying between 2 and 10 km s-1 the broadening ranges5 between 4% and 0.1%. Since this error is far smaller than that imputable to the rms noise levels of the 13CH+ spectra (see Sect. 3), we chose to ignore the hyperfine structure of 13CH+ in the following analysis.
The spectra shown in Fig. 3 are highly structured and have the following remarkable properties: (1) thanks to the high sensitivity of the HIFI receiver, the SH+ ion is seen in absorption along every line of sight; (2) all hydride lines are detected in absorption, and within the limits imposed by the signal/noise (S/N) ratio, CH+ 13CH+ and SH+ absorptions are detected over the whole velocity range of the foreground matter along each line of sight; (3) although the opacity ratios vary from one line of sight to another and from one velocity range to another, the velocity structure of SH+ is similar to those of CH+ and 13CH+. It is the similarity and differences of these absorption line profiles that are the focus of the present study.
3. Analysis of the line profiles
3.1. Multi-Gaussian decomposition
 |
Fig. 5 Top: a) and b) histogram of the linewidths of the CH+, 13CH+, SH+ (this work), and HCO+ (Godard et al. 2010) velocity components obtained with the multi-Gaussian decomposition procedure (see Table A.1); c) linewidth distributions of CH+ and CH observed by Crane et al. (1995) in the local diffuse medium. Bottom: first- (mean) and second- (standard deviation) order moments of the Δυ distributions issued from the combined CH+, 13CH+, and SH+ data (red squares) and from the CH+ data observed in the solar neighbourhood (blue circles); the moments are computed over increasing Δυ intervals: mean = |
As in Godard et al. (2010), the decomposition of the spectra in velocity components was deduced through a multi-Gaussian fitting procedure that we developed, based on the Levenberg-Marquardt algorithm, which takes advantage of the information carried by the hyperfine structure of a given transition. This algorithm is applied to adjust, in the least-squares sense, the minimal number of Gaussians required to describe the data within the observational errors without introducing any systematic effect. The number of Gaussians was increased, for instance, when we visually spotted serpentine curves – characteristic of poor fits in the line wings – in the residuals. Thus, for each transition, the observed normalized line profile (line/continuum) is written ![\begin{equation} \frac{T(\upsilon)}{T_{\rm c}} = {\rm exp}\left[ - \sum_{j\,=\,1}^{N_{\rm c}} \sum_{k\,=\,1}^{N_{\rm h}} I_{\rm h}(k) \, \tau_0(j) \, {\rm e}^{-\frac{1}{2}\left[\frac{\upsilon - \upsilon_{0}(j) - \Delta \upsilon_{\rm h}(k)}{\sigma_0 (j)}\right]^{2}}\right], \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq77.png) (2)where τ0, υ0, and σ0 are the usual Gaussian fit parameters. All spectra were decomposed independently from one another, without imposing any constraints on the Gaussian parameters. The choice of the input parameters, namely the initial values of υ0(j) and σ0(j) for each velocity components j, was guided by the comparison of the different lines observed towards each source. To correctly determine the opacity of weak absorption features blended with saturated lines, as observed in the CH+ spectra, we applied an empirical model constrained by the wings of the saturated line profiles. The results of the multi-Gaussian decomposition procedure and the associated errors on the Gaussian parameters are given in Table A.1, and the resulting fits and models of the saturated line profiles are displayed in Figs. A.1–A.8. Because we aim to compare the kinematic signatures of the CH+, 13CH+, and SH+ spectra, we discuss below the reliability of the extracted Gaussian components in view of the errors on their parameters.
(2)where τ0, υ0, and σ0 are the usual Gaussian fit parameters. All spectra were decomposed independently from one another, without imposing any constraints on the Gaussian parameters. The choice of the input parameters, namely the initial values of υ0(j) and σ0(j) for each velocity components j, was guided by the comparison of the different lines observed towards each source. To correctly determine the opacity of weak absorption features blended with saturated lines, as observed in the CH+ spectra, we applied an empirical model constrained by the wings of the saturated line profiles. The results of the multi-Gaussian decomposition procedure and the associated errors on the Gaussian parameters are given in Table A.1, and the resulting fits and models of the saturated line profiles are displayed in Figs. A.1–A.8. Because we aim to compare the kinematic signatures of the CH+, 13CH+, and SH+ spectra, we discuss below the reliability of the extracted Gaussian components in view of the errors on their parameters.
3.2. Validity and self-consistency of the multi-Gaussian decompositions
Since the decomposition algorithm allows the detection of components with very weak central opacities, the numerical procedure may converge upon Gaussian components whose reality is questionable. To keep only the most reliable velocity components for our subsequent analysis of the linewidths, we applied the following detection criterion: any Gaussian component was considered real if its Gaussian parameters simultaneously verify Δυ > 3σ(Δυ) and τ > 2.5σ(τ), where σ(Δυ) and σ(τ) are the errors on Δυ and τ respectively. The resulting confirmed or uncertain Gaussian components (in the following C-components and U-components) are indicated in Table A.1 (in Cols. 4, 8, and 12), and in Figs. A.1–A.8 (solid red and dashed blue curves).
In total we found that 25 C-components are simultaneously observed in at least two molecular spectra towards DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51. When compared, the positions of these components are found to agree with one another within their respective error for 18 of them, within 0.5 km s-1 for 6 of them, and within 1.3 km s-1 for 1 of them; similarly, out of the 17 common C-components observed towards SgrA*+50 and SgrB2(N), 10 are found to agree with one another within 1 km s-1, 6 within 2 km s-1, and 1 within 3.5 km s-1. Except for the SH+ components at –126 km s-1 observed towards SgrA*+50 these shifts in the central positions are at least four times smaller than the corresponding Gaussian linewidths. Moreover, many of the U-components have corresponding C-components in other species, indicating that the fitting process is robust and that the selection method is severe.
These concordances combined with the strict selection on the Gaussian parameters suggest that all C-components are real detections and not artefacts caused by noise or the standing waves removing procedure.
3.3. Comparison of the Gaussian linewidths
In Fig. 5, we display the distributions of linewidths associated with the C-components extracted from the CH+, 13CH+, and SH+ spectra. To emphasize the differences observed along the Galactic centre sight lines (l ~ 0), these distributions are computed for all sight lines (left panels), and for the l ≠ 0 sight lines only (right panels). As a comparison, the linewidth distributions of the HCO+ ground state radio transition observed by Godard et al. (2010) towards W31C, W49N, W51, and G34.6 are displayed in panels (a), and those of CH and CH+ visible transitions observed at high spectral resolution (~0.3 km s-1) in the local diffuse medium by Crane et al. (1995) are shown in panels (c). Lastly, panels (d) and (e) display the first- and second-order moments of the Δυ-distributions issued from the combined CH+, 13CH+, and SH+ data (red squares) and from the CH+ data observed in the solar neighbourhood (blue circles). In panels (a), the histogram of HCO+ linewidths is narrower and peaks at lower values than those of the submillimetre lines of CH+, 13CH+, and SH+. Conversely, the histogram of the visible CH+ data, characterising the local diffuse interstellar matter, is very similar to that of the submillimetre data. We discuss the validity and the significance of these comparisons below.
To demonstrate that the absence of narrow velocity components in the CH+, 13CH+, and SH+spectra is real and not due to a limitation of our extraction algorithm, we have derived the minimum width of a Gaussian component of optical depth τ0 that can be extracted from a given profile characterised by a noise στ at the velocity resolution δυ. Because στ scales inversely with the square root of the velocity resolution, a component detected at a 3στ level necessarily verifies ![\begin{equation} \Delta \upsilon \geqslant \delta \upsilon \left[3 \sigma_\tau /\tau_0 \right]^2. \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq94.png) (3)While the noise level of the SH+ spectra towards SgrA*+50, DR21(OH), G34.3+0.1, and W33A forbids us to extract components with linewidth smaller than 1 km s-1, that of all the other spectra is small enough to allow us to detect narrow velocity structures down to two velocity channels (0.72 km s-1 for CH+ and 13CH+, and 1.14 km s-1 for SH+). Therefore the scarcity of components in the first bin [0 ; 2 km s-1] of the CH+, 13CH+, and SH+ histograms is not a noise artefact.
(3)While the noise level of the SH+ spectra towards SgrA*+50, DR21(OH), G34.3+0.1, and W33A forbids us to extract components with linewidth smaller than 1 km s-1, that of all the other spectra is small enough to allow us to detect narrow velocity structures down to two velocity channels (0.72 km s-1 for CH+ and 13CH+, and 1.14 km s-1 for SH+). Therefore the scarcity of components in the first bin [0 ; 2 km s-1] of the CH+, 13CH+, and SH+ histograms is not a noise artefact.
Now, can we compare these linewidth distributions with one another? Because the S/N ratios of HCO+ (see Table 1 of Godard et al. 2010) and CH+ (see Table 2) profiles are high and comparable, those two sets of spectra are decomposed with the same level of detection. The noise therefore affects the statistics of the component linewidths at the same level. The same is true for the lines of SH+ and 13CH+, which have comparable, though poorer, S/N ratios. Finally, because CH+ and 13CH+ necessarily bear the same dynamical signatures, all distributions displayed in Fig. 5 can be compared with one another.
We recall that all absorption spectra have been decomposed into Gaussians independently from one another, without imposing the same velocity centroids or width to the different velocity components of a given line of sight. In addition, since the most intense SH+ components are saturated in CH+, and because the moderate S/N ratio of the 13CH+ and SH+ data prevents us from observing the low-opacity structures detected in the CH+ spectra, the respective distributions do not correspond to the same velocity components. It is therefore remarkable that the distributions of the CH+, 13CH+, and SH+ widths of the Gaussian velocity components are so similar, even identical within the statistical uncertainty. They exhibit a common pattern: a peak (hereafter called P1), observed towards all the sources, defined by a first- (mean) and a second- (standard deviation) order moments6 of 4.2 ± 0.2 km s-1 and 1.5 ± 0.1 km s-1, respectively, and an extended tail (hereafter called P2), observed only on the Galactic centre sight lines (left panels), with Δυ-values up to 20 km s-1.
Because the lines of sight sample kiloparsecs of interstellar material in the Galaxy, the patterns P1 and P2 result from the small-scale dynamics of the production processes of CH+ and SH+, the turbulent dynamics of the diffuse ISM, and the Galactic dynamics. The comparison between the left and right (d) and (e) panels of Fig. 5 shows that the first- and second-order moments of the Δυ distributions are the same for the components of the Galactic ISM along the l ≠ 0 sight lines and the visible CH+ lines sampling the solar neighbourhood (defined by first- and second-order moments of 4.3 ± 0.4 km s-1 and 1.85 ± 0.3 km s-1, respectively). Because the latter is unaffected by the Galactic dynamics, this similarity suggests that the peak P1 results from the dynamics of the formation processes of CH+ and SH+ convolved with that of the turbulence of the diffuse gas. Because the tail of the Δυ distributions is observed only on the Galactic centre sight lines, and because the broad absorption dips (Δυ > 8 km s-1) observed on the l ≠ 0 sight lines can be decomposed into many narrow components (as performed by Godard et al. 2010 with the HCO+ spectra), we conclude that P2 is caused by the Galactic dynamics only.
Lastly we note that while the first- and second-order moments of peak P1 both agree with those of the Δυ distribution obtained by Crane et al. (1995) within the statistical uncertainties, they also substantially differ from those of the CH+ Δυ distribution derived in the solar neighbourhood by Pan et al. (2004), who find first- and second-order moments of 3.3 ± 0.04 km s-1 and 0.4 ± 0.03 km s-1. As proposed by Pan et al. (2005), these differences may originate from their profile fitting method: (1) the number of CH+ components and their position were constrained by the observations of other species, possibly unrelated chemically (e.g. CN, CO, Ca); and (2) a maximal value of Δυ of 5.8 km s-1 was set.
Comparison between the column densities of CH+, 13CH+, and SH+obtained with the integrations of the respective opacities over several velocity intervals.
4. Analysis of the integrated opacities
Since the multi-Gaussian decomposition of CH+, 13CH+, and SH+ absorption profiles provides sets of C-components that do not always strictly coincide in velocity and width, and sets of U-components that sometimes clearly correspond to real absorption but with width and depth poorly constrained, our subsequent analysis and comparison of the column densities and abundances of these species is based on integrals of opacities computed over broad velocity intervals corresponding to marked absorption features common to all lines. These broad intervals (typically 5 to 20 km s-1) are given in the two first columns of Table 3. The column densities given in Cols. 4–6 of Table 3 are derived assuming a single excitation temperature of 4.4 K for 12CH+ and 13CH+, and of 3.0 K for SH+ (see Appendix B). Following the method set in Sect. 3.2 to keep only the most reliable absorption features, a 3σ detection level was adopted. Throughout, every measurement below this level is considered as a lower limit. Conversely, we adopt a conservative lower limit of 2.3 on the optical depth for the saturated velocity intervals (Neufeld et al. 2010b).
4.1. Variation of the 12C/13C isotopic ratio across the Galactic disk
 |
Fig. 6 N(12C)/N(13C) column density ratio as a function of the galactocentric distance RG. The red squares are from this work, and therefore evaluated with measurements of the N(12CH+)/N(13CH+) column density ratio. The blue circles are from previous measurements of the N(12CN)/N(13CN), N(12CO)/N(13CO), and |
In Fig. 6, we display the 12C/13C column density ratio derived from the present 12CH+ and 13CH+ data as a function of the Galactocentric distance RG (given in Cols. 7 and 8 of Table 3) which was computed assuming a flat Galactic rotation curve. We compared these results to those deduced from previous observations of CN, CO, H2CO and their respective isotopologues (Milam et al. 2005). We found that the five firm values (indicated in Table 3) derived from the simultaneous detections of 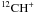 and
and 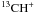 absorption lines over the same velocity range are consistent with those derived from the neutral species. The 25 lower limits inferred from saturated 12CH+ lines (dashed symbols) are also consistent with Milam et al. (2005). This result not only suggests that the isotopic ratios measured with ions and neutrals are not substantially influenced by chemical fractionation processes, but it also validates the use of the empirical relation
absorption lines over the same velocity range are consistent with those derived from the neutral species. The 25 lower limits inferred from saturated 12CH+ lines (dashed symbols) are also consistent with Milam et al. (2005). This result not only suggests that the isotopic ratios measured with ions and neutrals are not substantially influenced by chemical fractionation processes, but it also validates the use of the empirical relation  (4)found by Milam et al. (2005) to infer the 12CH+ column densities from those measured in the 13CH+ spectra. The 12C/13C ratio and N(12CH+) computed from Eq. (4) for the velocity intervals towards DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51 are given in Cols. 9 and 10 of Table 3. Towards SgrA*+50 and SgrB2(N), because most of the gas appears to be associated with the Galactic centre environment (Rodriguez-Fernandez et al. 2006), a 13C/12C abundance ratio of 20 is assumed everywhere except for the velocity interval –20 to +30 km s-1, a velocity domain where the absorption features are also associated with gas in the Galactic plane, and where we use two alternative values, 20 and 60, to bracket the result.
(4)found by Milam et al. (2005) to infer the 12CH+ column densities from those measured in the 13CH+ spectra. The 12C/13C ratio and N(12CH+) computed from Eq. (4) for the velocity intervals towards DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51 are given in Cols. 9 and 10 of Table 3. Towards SgrA*+50 and SgrB2(N), because most of the gas appears to be associated with the Galactic centre environment (Rodriguez-Fernandez et al. 2006), a 13C/12C abundance ratio of 20 is assumed everywhere except for the velocity interval –20 to +30 km s-1, a velocity domain where the absorption features are also associated with gas in the Galactic plane, and where we use two alternative values, 20 and 60, to bracket the result.
The uncertainties given in Eq. (4) correspond to the standard deviation of the best least-squares fit performed by Milam et al. (2005) on the CN, CO, and H2CO data. They do not take into account the uncertainty on RG due to the random motion of interstellar clouds. To do so, we relied on the analysis of the HI emission in the first Galactic quadrant by Elmegreen & Elmegreen (1987): they found that a large part of the mass of the diffuse gas is distributed into ~ 200 pc superclouds, separated along spiral arms by 1.5 kpc. Their one-dimensional internal velocity dispersion of 5.3 km s-1 is the main source of uncertainty on RG. Taking into account the (l,v) location of the absorbing gas observed towards each source (see the equation of RG in the caption of Table 3), we obtain a maximal uncertainty of about 30% on RG. When combined with the errors given in Eq. (4), we find a total uncertainty of about 50% on the 12C/13C ratio and the subsequent N(12CH+) given in Cols. 9 and 10 of Table 3.
4.2. Comparison of the column densities of CH+ and SH+
Figure 7 displays the SH+ and CH+ column densities inferred for each broad velocity interval. The CH+ column densities were derived either from the 12CH+ profile, where unsaturated, or from 13CH+ and the above isotopic ratio in the other case. The data set includes the results of the present study and those obtained by Menten et al. (2011) towards SgrB2(M). While Menten et al. (2011) reported the detection of two absorption components at N(CH+) ~ 3 × 1012 and N(SH+) ~ 1013 cm-2, we removed those points from Fig. 7 because the 13CH+ spectrum in the corresponding velocity range clearly exhibits contamination of the absorption features by a strong and broad emission line. Last, we note that the few points at N(CH+) < 1013 cm-2 correspond to the faintest 12CH+ absorption features. Since they are not detected in SH+, these points weakly constrain our subsequent analysis of the SH+/CH+ratio.
Taking into account the upper and lower limits shown in Fig. 7, we find that N(CH+) and N(SH+) span more than two orders of magnitude and that the SH+/CH+ column density ratio varies from less than 0.01 to 1. Interestingly, the N(SH+)/N(CH+) ratios observed towards SgrB2(M), SgrB2(N), and SgrA*+50 are very similar, with a mean value of 0.28 ± 0.02, ~ 9 times higher than that towards DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51, ⟨ N(SH+)/N(CH+) ⟩ ~ 0.03 ± 0.007. The above difference in the mean SH+/CH+ ratio is much larger than the 50% uncertainty on the computed 12C/13C ratio. Moreover, we obtain the same difference of values if we use only the few points detected in 12CH+. It is therefore unlikely that this difference can be ascribed to an uncertainty on the 12CH+/13CH+ ratio. Last, Daflon & Cunha (2004) found that carbon and sulfur have similar abundance gradients across the Galactic disk (with slopes of –0.037 and –0.040 dex kpc-1, respectively). Consequently, the difference observed in the SH+/CH+ column density ratios measured on the l ~ 0 and l ≠ 0 sight lines is most likely tracing variations of both the physical and chemical conditions of the diffuse gas sampled in each case.
 |
Fig. 7 SH+ column density as a function of the CH+ column density per broad velocity interval (see Table 3). The open squares and open circles are from the present analysis and from Menten et al. (2011), respectively. The blue and purple points are from the absorption lines observed along the Galactic centre sight lines (SgrA*+50, SgrB2(N), and SgrB2(M)) and along the other sight lines (DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51), respectively. The black dashed, dotted, and dashed-dotted lines indicate N(SH+)/N(CH+) ratios of 0.01, 0.1, and 1, respectively. |
Finally, with a correlation coefficient of 0.1, no evident chemical relationship seems to stand out from Fig. 7, a surprising finding in view of the fact that CH+ and SH+ are clearly linked by their dynamics (see Sect. 3.3). However, this lack of correlation applies to the column densities. In the following, we discuss the properties of the abundances relative to hydrogen, a discussion that requires the knowledge of NH.
4.3. Estimation of the hydrogen column densities in the broad velocity intervals
HI, H2, and total hydrogen column densities per velocity interval.
To (1) estimate the mean molecular abundances that are to be compared with the chemical model predictions (Godard et al., in prep.); and (2) to establish a possible relation between the CH+ and SH+ abundances, it is essential to estimate the hydrogen column density NH in the broad velocity intervals over which N(CH+) and N(SH+) are measured. Since the molecular fraction of the gas where CH+ and SH+ are detected is low (0.4 on average, see Appendix C), both atomic and molecular hydrogen HI and H2 are needed to estimate NH.
The method consists in separately evaluating the column densities of HI and H2, using the VLA observations of the λ21 cm absorption line of H (Koo 1997; Fish et al. 2003; Dwarakanath et al. 2004; Pandian et al. 2008; Lang et al. 2010) and a relevant tracer for the molecular hydrogen because H2 is not directly observable. Then, NH = N(HI) + 2N(H2). In Appendix C we discuss the validity of using the HIFI observations of CH and HF to compute the H2 column densities. If available, HF is preferentially used in the following section to infer N(H2) and the ensuing CH+, 13CH+, and SH+ mean abundances. If not, N(H2) is derived from CH, assuming a HF/CH mean abundance ratio of 0.4 (a value defined with a large standard deviation of 0.25), deduced from Cols. 5 and 6 of Table 4. Last, we compare these values of NH to those inferred, as in Godard et al. (2010), from the analysis of the 2MASS survey (Cutri et al. 2003). Marshall et al. (2006) have measured the near infrared colour excess in large areas of the inner Galaxy (|l| < 100°, |b| < 10°) to obtain the visible extinctions (AV ~ 10AK), providing an estimate of the total hydrogen column density along the lines of sight. However, because of the low resolution of the 2MASS extinction analysis (~15 arcmin), the uncertainty on NH (computed as the standard deviation of the extinction measured along the four closest lines of sight surrounding a given source) can be important, and is as high as 50% for DR21(OH), W31C, and W33A. The last columns of Table 4 show that these two independent measurements of NH differ by less than 25%.
5. Results and discussion
5.1. Chemical properties of the gas seen in absorption
 |
Fig. 8 N(SH+)/N(CH+) column density ratio as a function of the CH+ mean abundance. The CH+, SH+, and H column densities are computed from CH+, 13CH+, SH+, HI, HF, and CH opacities integrated over the velocity intervals given in Tables 3 and 4. The blue and purple points are from the absorption lines observed along the Galactic centre sight lines (SgrA*+50 and SgrB2(N)) and along the other sight lines (DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51), respectively. The red line corresponds to a least-squares fit of the latter data. |
In Fig. 8, we display the N(SH+)/N(CH+) column density ratio as a function of the CH+ mean abundance (with respect to the total hydrogen column density NH) integrated over the velocity intervals given in Table 4. Because Menten et al. (2011) used a different method than we did to estimate the H2 column densities7 the data obtained towards SgrB2(M) are not included in this plot. We find that both the mean abundances and the abundance ratios vary by two orders of magnitude in the diffuse ISM sampled by those lines of sight. In addition, Fig. 8 reveals major differences between the results obtained on the l ~ 0 and the l ≠ 0 sight lines. While the CH+ mean abundances span the same range of values in both cases, the SH+/CH+ ratio measured towards SgrA*+50 and SgrB2(N) shows no correlation with N(CH+)/NH. Conversely, the points corresponding to the observations performed on the l ≠ 0 sight lines exhibit a trend ![\begin{equation} N(\SHp)/N(\CHp) \sim 0.09 \,\, \big[ 10^{8} \times N(\CHp)/N_{\rm H} \big]^{-1.4}, \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq173.png) (5)with a correlation coefficient of 0.8. These are the results that have to be compared with the predictions of chemical models applied to the diffuse ISM.
(5)with a correlation coefficient of 0.8. These are the results that have to be compared with the predictions of chemical models applied to the diffuse ISM.
5.2. Carbon and sulfur chemistries in the diffuse ISM
5.2.1. UV-driven chemistry
In a chemistry entirely driven by the UV-radiation field and the cosmic ray particles, the hydrogenation chains of carbon and sulfur, and the subsequent productions of CH+ and SH+ are initiated by the radiative associations of C+ and S+ with molecular hydrogen, ![\begin{equation} \begin{array}{l l l l l l l} {\rm C}^+ & + & {\rm H}_2 & \rightarrow & {\rm CH}_2^+ & + & \gamma \,\, {\rm and} \\[6.0pt] {\rm S}^+ & + & {\rm H}_2 & \rightarrow & {\rm SH}_2^+ & + & \gamma, \\ \end{array} \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq174.png) (6)two reactions with long timescales:
(6)two reactions with long timescales: 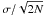 and
and 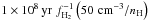 , respectively (Herbst 1985; Herbst et al. 1989), where fH2is the molecular fraction defined as fH2 = 2n(H2)/nH. In comparison, CH+ and SH+ are mainly destroyed by hydrogenation and dissociative recombination8,
, respectively (Herbst 1985; Herbst et al. 1989), where fH2is the molecular fraction defined as fH2 = 2n(H2)/nH. In comparison, CH+ and SH+ are mainly destroyed by hydrogenation and dissociative recombination8, ![\begin{equation} \begin{array}{l l l l l l l} {\rm CH}^+ & + & {\rm H}_2 & \rightarrow & {\rm CH}_2^+ & + & {\rm H} \,\, {\rm and} \\[6.0pt] {\rm SH}^+ & + & e^- & \rightarrow & {\rm S} & + & {\rm H}, \\ \end{array} \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq179.png) (7)two processes with short timescales:
(7)two processes with short timescales: 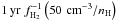 and 5 yr (T/100 K)0.72(1.38 × 10-4/xe − )(50 cm-3/nH), respectively. Because of the lack of efficient production pathways to balance their rapid destruction, the CH+ and SH+ abundances predicted by UV-dominated chemistry are very low. Figure 9 displays the CH+ and SH+ relative abundances computed with two models of PhotoDissociation Regions (PDR)9 illuminated on one side as functions of the shielding from the ISRF AV. For the physical conditions of the diffuse gas, we obtain N(CH+)/NH ~ 1.8 × 10-11 and N(SH+)/NH ~ 1.6 × 10-13, two to four orders of magnitude lower than the observed values, and with a corresponding abundance ratio never higher than 0.01.
and 5 yr (T/100 K)0.72(1.38 × 10-4/xe − )(50 cm-3/nH), respectively. Because of the lack of efficient production pathways to balance their rapid destruction, the CH+ and SH+ abundances predicted by UV-dominated chemistry are very low. Figure 9 displays the CH+ and SH+ relative abundances computed with two models of PhotoDissociation Regions (PDR)9 illuminated on one side as functions of the shielding from the ISRF AV. For the physical conditions of the diffuse gas, we obtain N(CH+)/NH ~ 1.8 × 10-11 and N(SH+)/NH ~ 1.6 × 10-13, two to four orders of magnitude lower than the observed values, and with a corresponding abundance ratio never higher than 0.01.
 |
Fig. 9 Predictions of two PDR models for gas densities nH = 50 and 300 cm-3. The CH+ (in red) and SH+ (in blue) relative abundances are displayed as functions of the shielding AV from the interstellar radiation field for a slab of gas illuminated on one side only. |
5.2.2. Alternative models
In the diffuse interstellar medium sampled by the l ≠ 0 sight lines, the only production pathways efficient enough to balance the fast destruction of CH+ and SH+ are 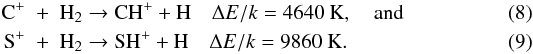 Since these reactions are highly endothermic, it has been proposed that high CH+ and SH+ abundances are the signatures of shock waves propagating through the ISM (Draine 1986; Millar et al. 1986). Comparing the predictions of HD and MHD shocks with the CH+ column density observed towards ζ Oph, Draine (1986) and Pineau des Forêts et al. (1986) favoured the MHD case in which CH+ and SH+ form mainly through ion-neutral friction. Including the sulfur chemistry Millar et al. (1986) and Pineau des Forêts et al. (1986) predicted a SH+/CH+ abundance ratio increasing from 0.01 to 0.4 for a shock speed increasing from 9 to 16 km s-1, a transverse magnetic field of 5 μG and a preshock density of 20 cm-3. These results agree excellently with our observations.
Since these reactions are highly endothermic, it has been proposed that high CH+ and SH+ abundances are the signatures of shock waves propagating through the ISM (Draine 1986; Millar et al. 1986). Comparing the predictions of HD and MHD shocks with the CH+ column density observed towards ζ Oph, Draine (1986) and Pineau des Forêts et al. (1986) favoured the MHD case in which CH+ and SH+ form mainly through ion-neutral friction. Including the sulfur chemistry Millar et al. (1986) and Pineau des Forêts et al. (1986) predicted a SH+/CH+ abundance ratio increasing from 0.01 to 0.4 for a shock speed increasing from 9 to 16 km s-1, a transverse magnetic field of 5 μG and a preshock density of 20 cm-3. These results agree excellently with our observations.
Another scenario, alternative to the shock waves, is the TDR (turbulent dissipation regions) model. In this model the turbulent energy is dissipated in many small-scale magnetized vortices in which the ionized and neutral fluids decouple. Dissipation is caused by both ion-neutral friction and viscous dissipation at the edge of the vortices. Comparing the predictions of TDRs to observations of CH, CH+, OH, and HCO+ in the local diffuse gas, Godard et al. (2009) also favoured models in which the dissipation is dominated by the ion-neutral friction and where the production of CH+ and SH+ via reactions (8) and (9) is triggered by the ambipolar diffusion. An analysis of the SH+/CH+ ratio obtained in the framework of the TDR model will be presented in a forthcoming paper (Godard et al., in prep.).
While the scenarios of shocks and vortices could equally apply to gas sampled by the l ~ 0 sight lines, an alternative chemical process may be at work there. Large amounts of the diffuse gas detected along SgrA*+50, SgrB2(N), and SgrB2(M) belong to the Central Molecular Zone (CMZ). Because the CMZ is pervaded by a strong X-ray radiation field, high CH+ and SH+ abundances could be due to regions where C++ and S++ ions co-exist with H2 and form CH+ and SH+ by the reactions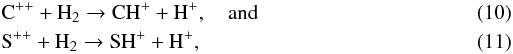 as proposed by Langer (1978). Using the high rate of reaction (11) obtained by Chen et al. (2003), Abel et al. (2008) found that the predicted SH+ column density for molecular gas surrounding an active galactic nucleus is two orders of magnitude higher than that predicted by UV-dominated chemistry. Since rate measurements of reaction (10) point to lower values, this chemical process could account for the high mean SH+/CH+ abundance ratio derived towards SgrA*+50, SgrB2(N), and SgrB2(M) (about nine times higher than that obtained along the other Galactic sight lines, see Sect. 4.2).
as proposed by Langer (1978). Using the high rate of reaction (11) obtained by Chen et al. (2003), Abel et al. (2008) found that the predicted SH+ column density for molecular gas surrounding an active galactic nucleus is two orders of magnitude higher than that predicted by UV-dominated chemistry. Since rate measurements of reaction (10) point to lower values, this chemical process could account for the high mean SH+/CH+ abundance ratio derived towards SgrA*+50, SgrB2(N), and SgrB2(M) (about nine times higher than that obtained along the other Galactic sight lines, see Sect. 4.2).
The above results are in line with the detection of large amounts of warm diffuse gas recently identified with the 3 μm absorption lines of  (Oka et al. 2005; Geballe & Oka 2010) in the CMZ. The temperature (~200–300 K) of the low-density gas phase is found to be considerably higher than that of typical diffuse clouds, and unique to the Galactic CMZ (Goto et al. 2008). They also corroborate the specific dynamics of molecular clouds associated with the Galactic centre regions (e.g. Rodriguez-Fernandez et al. 2006).
(Oka et al. 2005; Geballe & Oka 2010) in the CMZ. The temperature (~200–300 K) of the low-density gas phase is found to be considerably higher than that of typical diffuse clouds, and unique to the Galactic CMZ (Goto et al. 2008). They also corroborate the specific dynamics of molecular clouds associated with the Galactic centre regions (e.g. Rodriguez-Fernandez et al. 2006).
6. Summary and perspectives
We have presented the analysis of Herschel/HIFI observations of the ground-state transitions of CH+, 13CH+, and SH+, all detected in absorption against the submillimetre dust continuum of distant star-forming regions and the Galactic centre sources, SgrA*+50 and SgrB2(N). The velocity range over which the absorption features are detected corresponds to diffuse or transluscent environments. The deconvolution of the hyperfine structure embedded in the SH+ 1,2 − 0,1 spectra, and the independent decomposition of the absorption domains in Gaussian velocity components allowed us to identify many velocity components per sight line and to perform a cross comparison of the dynamical and chemical signatures of those three species.
This study provides the following main results. (1) The linewidth distributions of CH+, 13CH+, and SH+ are found to be similar and likely trace the kinematics of the chemical production processes of these species convolved with that of the turbulent and Galactic dynamics of the diffuse ISM. (2) These lines are broad (~4.2 km s-1), similar to those found in visible absorption lines in the solar neighbourhood, and broader than those of HCO+ and CN along the same lines of sight. (3) The SH+/CH+ abundance ratio covers a broad range of values from 0.01 to more than 1, shows higher values in warmer environments (such as the Galactic centre clouds), and appears to be proportional to (N(CH+)/NH)-1.4 in the diffuse gas sampled by the l ≠ 0 sight lines. (4) As for CH+, the SH+ abundances cannot be reproduced by UV-driven chemistry in the diffuse gas.
The unique properties of the carbon and sulfur chemistries support the framework of a warm chemistry triggered by turbulent dissipation (either in shocks or intense velocity shears) that selectively enhances the production of SH+ for which the formation endothermicity is the highest. A detailed comparison of the TDR model predictions with these observational results will be given in a forthcoming paper (Godard et al., in prep.).
Online material
Appendix A: Gaussian decomposition and calculation of column densities
The results of the Gaussian decomposition procedure applied to the spectra are given in Tables A.1. In turn, Figs. A.1–A.8 display the comparison between the result of the fit and the original data, along with the associated residuals. The uncertainties given in the Table A.1 are the formal 1-σ errors derived from the diagonal elements of the covariance matrix and do not take into account the systematic errors introduced by (1) the finite velocity resolution; (2) the uncertainty on the continuum level; and (3) the error introduced by the decomposition procedure, which depends on its convergence criteria.
According to Godard et al. (2010) (Appendix B), the finite velocity resolution of the spectra introduces an error on the linewidth determination smaller than 8% for the CH+ and 13CH+ components, and smaller than 14% for the SH+ components, if Δυ > 1.3 km s-1 (the smallest observed linewidth). Furthermore, a relative uncertainty ϵ on the continuum temperature leads to an error δτ ~ ϵ − ln(1 + ϵeτ) on the opacity that ranges between 6% and 30% when τ varies between 0.03 and 2.7 (the lowest and highest observed central opacities) and using ϵ = 10% (value corresponding to the error on the beam efficiency and the side band ratio, Roelfsema et al. 2012).
 |
Fig. A.1 Observational data (black lines) compared to the multi-Gaussian decomposition (purple lines) of the SH+ (1,2,5/2 ← 0,1,3/2) (top), 13CH+(1 ← 0) (middle), and CH+ (1 ← 0) (bottom) absorption spectra observed towards DR21(OH). The solid red lines and the dashed blue lines correspond to the confirmed (C) and uncertain (U) Gaussian components, respectively (see main text). The solid green lines are the empirical modelling of the CH+saturated line profiles. |
CH+ (1 ← 0), 13CH+ (1 ← 0), and SH+ (1 ← 0) absorption line analysis results.
Unlike the other numerical fitting methods10 that are devised to find the global minimum of χ2, the Levenberg Marquardt algorithm is a so-called single-shot method: used when the initial conditions are easily fixed, this algorithm takes advantage of the information on the χ2 derivatives with respect to each parameter to converge on the nearest local minimum. However, since the minimum only corresponds to a statistical estimate of the fit parameters, the code can converge on different solutions close to each other depending on the initial condition, the χ2 valley topography, and the criteria to stop the optimization. To estimate the associated error, we analysed the dispersion of the best-fit solutions when varying the initial conditions: for each spectrum, we assumed an uncertainty of 2 km s-1 on the initial guess of the positions and the linewidths of the Gaussians. The resulting 4200 fits are found to bracket the optimum solutions given in Table A.1 with a standard deviation of 10% on the central optical depths and the Gaussian linewidths.
When combined, the robustness of the decomposition procedure, the finite resolution, and the uncertainty on the continuum temperature correspond to maximal errors on the calculation of Δυ and τ of 20% and 30%, respectively.
Appendix B: Determination of the excitation temperatures and of the subsequent column densities
The column densities given in Table 3 are derived assuming a single excitation temperature Tex for all levels of a given molecule as ![\appendix \setcounter{section}{2} \begin{equation} \label{EqDcol} N = Q(T_{\rm ex}) \frac{8 \pi \nu_0^{3}}{c^{3}} \frac{1}{g_{\rm u}} \frac{1}{A_{\rm ul}} \left[1-{\rm e}^{-h\nu_0/k T_{\rm ex}} \right]^{-1} \int \tau \, {\rm d} \upsilon \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq211.png) (B.1)where ν0, gu, gl and Aul are the rest frequency, the upper and lower level degeneracies and the Einstein’s coefficients of the observed transition, Q(Tex) is the partition funtion, and c is the speed of light.
(B.1)where ν0, gu, gl and Aul are the rest frequency, the upper and lower level degeneracies and the Einstein’s coefficients of the observed transition, Q(Tex) is the partition funtion, and c is the speed of light.
To derive the CH+ and SH+J = 1 ← 0 line excitation temperatures Tex, we adopt the recent computation of the CH+ de-excitation rate coefficients by collision with He and e − (Hammami et al. 2009; Lim et al. 1999), and assume a generic SH+ de-excitation rate coefficient by collision with H and H2 of 10-10 cm3 s-1. Because the corresponding critical densities at 100 K, ncrit,He(CH+) ~ 6 × 107 cm-3, ncrit,e − (CH+) ~ 4 × 104 cm-3, and ncrit,H2(SH+) ~ 7 × 106 cm-3, are considerably higher than those of the diffuse ISM, collisions are irrelevant in the excitation of CH+ and SH+, all the more so collisions of CH+ with H2 are its destruction pathway. Therefore, the level populations of these two ions only result from radiative excitation and possible additional excitation processes during their chemical formation. Neglecting the latter, we derive the CH+ and SH+J = 1 ← 0 line excitation temperatures Tex, from statistical equilibrium, using the submillimetre interstellar radiation field measured at l = 45° and b = 0° with the Cosmic Background Explorer (Reach et al. 1995). We obtain low excitation temperatures Tex(835 GHz) = 4.4 K, and Tex(526 GHz) = 3.0 K that agree with the lack of CH+ (2 ← 1) and SH+ (21 ← 11), (22 ← 11), (21 ← 10), and (22 ← 12) detection in absorption at the velocities of the diffuse medium along the same lines of sight (PRISMAS and HEXOS observations, to be published). Note that an error of about 1 K corresponds to an error on the CH+ and SH+ column densities smaller than 1%. While these values of Tex are valid for the velocity components associated with the diffuse interstellar gas, they clearly correspond to lower limits for those associated with the SFRs molecular environments. In the latter case, since the PRISMAS lines of sight target bright IR and submm emitting sources, a complete description of the IR radiative transfer accross the molecular gas surrounding the sources is needed (De Luca et al., in prep.; Vastel et al., in prep.).
For excitation temperatures of 12,13CH+ and SH+ of 4.4 K and 3.0 K, respectively, Eq. (B.1) finally becomes 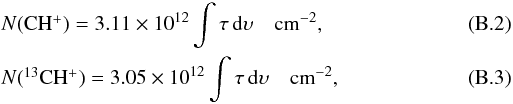 and
and 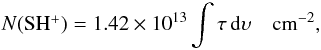 (B.4)using the CH+J = 1 ← 0, 13CH+J = 1 ← 0, and the SH+N,J,F = 1,2,5/2 ← 0,1,3/2 transitions, respectively.
(B.4)using the CH+J = 1 ← 0, 13CH+J = 1 ← 0, and the SH+N,J,F = 1,2,5/2 ← 0,1,3/2 transitions, respectively.
The CH+ line opacity for N(CH+) = 1014 cm-2 and a linewidth of 4 km s-1 is of the order of 15 and the expected line emission is about 4 mK (below the noise level, see Tables 1 and 2). The intensities of the 13CH+ and SH+ lines that are optically thin are even lower.
Appendix C: Tracers of molecular hydrogen in the diffuse ISM
The methylidyne radical CH has often been used as a probe of molecular hydrogen because of its linear relation with H2 observed in the local diffuse medium (Federman 1982) and in dark clouds (Mattila 1986). Compiling the UV and visible data obtained on 48 lines of sight (Savage et al. 1977; Rachford et al. 2002; Crane et al. 1995; Crawford 1995; Allen 1994; Gredel et al. 1993; Federman et al. 1994; Danks et al. 1984; Jenniskens et al. 1992), Liszt & Lucas (2002) derived a mean ratio N(CH)/N(H2) ~ 4.3 × 10-8, while Sheffer et al. (2008) found N(CH)/N(H2) ~ 3.5 × 10-8, using their observations of the absorption profiles of H2 and CH on a sample of 90 diffuse clouds. Although the latter could be used in this work to estimate N(H2), based on the Herschel observations of the six hyperfine components of the CH J = 1/2 − 3/2 absorption line (Gerin et al. 2010b), it raises several problems that have to be taken into account.
-
As quoted by Liszt & Lucas (2002) and Shefferet al. (2008), there is a significantscatter (a dispersion of about a factor of 3) on theN(CH) − N(H2) relation observed in the local diffuse medium, up to N(H2) = 1021 cm-2.
-
Despite the similarity of the CH absorption profiles with those of other tracers of molecular hydrogen (PRISMAS observations, to be published), a N(CH) − N(H2) correlation has never been directly measured in the inner Galactic ISM.
-
Crane et al. (1995) and Lambert et al. (1990) found that the linewidths of CH observed in absorption are highly variable from one diffuse cloud component to another. They reported the detection of CH line profiles either similar to or more Gaussian and less broad than those of CH+. This result was then confirmed by Pan et al. (2005), who divided their observed CH absorption features into two categories: those with CN-like and those with CH+-like line profiles. This implies that the production of CH in the interstellar medium can sometimes be linked to the production of CH+and depends only slightly on the molecular hydrogen abundance (Godard et al., in prep.).
For these reasons, we derive the H2 column densities from observations of the J = 1 ← 0 ground-state rotational transition of hydrogen fluoride (HF) performed with the Herschel/HIFI instrument. If HF is saturated or not available, H2 is deduced from CH, assuming a mean HF/CH abundance ratio of 0.4 (see Cols. 5 and 6 of Table 4). The absorption line analysis performed by Neufeld et al. (2010b) and Sonnentrucker et al. (2010) showed that (1) the HF profiles are similar to those of H2O; and (2) HF accounts for more than 30% of the total fluorine nuclei in the gas-phase along these sight-lines. Since both results agree with the chemical models that predict that the production of HF does not depend on the dynamics of the gas and that HF is the main F-bearing species, we deduce the N(HF) − N(H2) relation from an analytical study of the fluorine chemistry. For the range of parameters defining the diffuse and transluscent gas (Snow & McCall 2006), 10 < nH < 5000 cm-3, 0 < AV < 5, and n(CO)/ [C] < 0.9, the abundance of HF is driven by only four chemical reactions (Neufeld & Wolfire 2009):
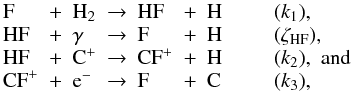 (C.1)where
(C.1)where![\appendix \setcounter{section}{3} \begin{eqnarray} &&k_1 = 1.00 \times 10^{-10} \,\, [{\rm exp}(-450~{\rm K}/T) + 0.078 \, {\rm exp}(-80~{\rm K}/T) \nonumber\\ & & \qquad+ 0.0155 \, {\rm exp} (-10~{\rm K}/T ) ] \,\, {\rm cm}^3{\rm s}^{-1} ,\nonumber \\ &&\zeta_{\rm HF} = 1.17 \times 10^{-10} \,\, {\rm exp}(-2.2 A_V) \,\, {\rm s}^{-1} , \nonumber\\ &&k_2 = 7.20 \times 10^{-09} \,\, (T/300~{\rm K})^{-0.15} \,\, {\rm cm}^3{\rm s}^{-1} , \,\, {\rm and} \nonumber\\ &&k_3 = 5.20 \times 10^{-08} \,\, (T/300~{\rm K})^{-0.80} \,\, {\rm cm}^3{\rm s}^{-1} \end{eqnarray}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq251.png) (C.2)are their respective reaction rate coefficients from the calculations and laboratory measurements (Zhu et al. 2002; Brown & Balint-Kurti 2000; Neufeld et al. 2005; Novotny et al. 2005). Therefore, assuming that there is no depletion of F on interstellar dust, and that the carbon is fully ionized and the sole source of electrons, the HF and H2 abundances are related by
(C.2)are their respective reaction rate coefficients from the calculations and laboratory measurements (Zhu et al. 2002; Brown & Balint-Kurti 2000; Neufeld et al. 2005; Novotny et al. 2005). Therefore, assuming that there is no depletion of F on interstellar dust, and that the carbon is fully ionized and the sole source of electrons, the HF and H2 abundances are related by ![\appendix \setcounter{section}{3} \begin{equation} \label{eqHFHH} \frac{n({\rm HF})}{n({\rm H}_2)} = \frac{ \left[{\rm F}\right] }{ \big( \left[{\rm C}\right]k_2 + \zeta_{\rm HF}/n_{\rm H} \big) / k_1 + 1/2 f_{{\rm H}_2} \big( 1+k_2/k_3 \big)}, \end{equation}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq252.png) (C.3)where [F] and [C] are the fluorine and carbon elemental gas phase abundances relative to H nuclei (assumed to equal those observed in the solar neighbourhood, ~ 1.8 × 10-8 and ~ 1.4 × 10-4 respectively, Savage & Sembach 1996; Sofia & Meyer 2001; Snow et al. 2007), nH is the gas density, and fH2 is the molecular fraction defined as fH2 = 2n(H2)/nH. For nH > 30 cm-3 and AV > 0.2, because F reacts rapidly with H2, the left-hand side of the denominator of Eq. (C.3) can be neglected, more than 90% of the interstellar fluorine being in HF and less than 10% in CF+. We thus assume a n(HF)/n(H2) abundance ratio of 3.6 × 10-8.
(C.3)where [F] and [C] are the fluorine and carbon elemental gas phase abundances relative to H nuclei (assumed to equal those observed in the solar neighbourhood, ~ 1.8 × 10-8 and ~ 1.4 × 10-4 respectively, Savage & Sembach 1996; Sofia & Meyer 2001; Snow et al. 2007), nH is the gas density, and fH2 is the molecular fraction defined as fH2 = 2n(H2)/nH. For nH > 30 cm-3 and AV > 0.2, because F reacts rapidly with H2, the left-hand side of the denominator of Eq. (C.3) can be neglected, more than 90% of the interstellar fluorine being in HF and less than 10% in CF+. We thus assume a n(HF)/n(H2) abundance ratio of 3.6 × 10-8.
Although HF is preferred to CH here as a tracer of molecular hydrogen, relation (C.3) has to be used cautiously because: (1) it has never been proven observationally; (2) this abundance ratio linearly depends on the fluorine elemental abundance, which can vary with the Galactocentric distance (Daflon & Cunha 2004; Rudolph et al. 2006; Abia et al. 2010); and (3) it also depends on the depletion of fluorine onto grains, which can become important in the molecular gas. We note that the H2 molecular fraction computed as 2N(H2)/NH on the velocity intervals given in Table 4 ranges between 0.05 and 1 with an average value of ~ 0.4 (Neufeld et al., in prep.). While this value suggests that the diffuse medium sampled by CH+, 13CH+, and SH+ is on average weakly molecular, it does not preclude the existence within this gas of regions where fH2 = 1. A complete analysis of HF and CH as tracers of molecular hydrogen will be performed by Godard et al. (in prep.).
The SgrA*+50 sight line (GCM-0.02-0.07) corresponds to the 50 km s-1 cloud located in the vicinity of SgrA*, which is known to be a bright submillimetre source (Dowell et al. 1999).
See http://herschel.esac.esa.int/HIPE_download.shtml for more information about HIPE.
See http://www.iram.fr/IRAMFR/GILDAS for more information about GILDAS softwares.
Most of the observed SW have a period of ~90–100 MHz, identified by Roelfsema et al. (2012) as reflections occuring between the mixer focus and the cold and hot black bodies. For two spectra observed towards W49N we had to remove an additional standing wave with a period ~150 MHz.
This result on the line profile broadening is derived from the analysis of 1760 synthetic spectra taking into account the hyperfine structure of 13CH+ (line strength and velocity structure, Amano 2010).
In Menten et al. (2011) the H2 column densities are deduced from those of HCO+, assuming N(HCO+)/N(H2) = 5 × 10-9 (Lucas & Liszt 1996).
The Meudon PDR model employs a one-dimensional chemical code in which a slab of gas with a given density profile is illuminated by the ambient interstellar radiation field (Le Petit et al. 2006).
Acknowledgments
We are most grateful to the referee for providing constructive comments and helping in improving the content of this paper. HIFI has been designed and built by a consortium of institutes and university departments from across Europe, Canada and the United States (NASA) under the leadership of SRON, Netherlands Institute for Space Research, Groningen, The Netherlands, and with major contributions from Germany, France and the US. Consortium members are: Canada: CSA, U. Waterloo; France: CESR, LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland: NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri-INAF; Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronòmico Nacional (IGN), Centro de Astrobiologia; Sweden: Chalmers University of Technology – MC2, RSS & GARD, Onsala Space Observatory, Swedish National Space Board, Stockholm University – Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: CalTech, JPL, NHSC. B.G, E.F., M.G., and M.D.L. acknowledge the support from the Centre National de Recherche Spatiale (CNES), and from ANR through the SCHISM project (ANR-09-BLAN-231). B.G., J.C., and J.R.G. thank the Spanish MICINN for funding support through grants, AYA2009-07304 and CSD2009-00038.
References
- Abel, N. P., Federman, S. R., & Stancil, P. C. 2008, ApJ, 675, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Abia, C., Cunha, K., Cristallo, S., et al. 2010, ApJ, 715, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, M. M. 1994, ApJ, 424, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Amano, T. 2010, ApJ, 716, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A., & Balint-Kurti, G. G. 2000, J. Chem. Phys., 113, 1870 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, D., Gao, H., & Kwong, V. H. 2003, Phys. Rev. A, 68, 052703 [NASA ADS] [CrossRef] [Google Scholar]
- Comito, C., & Schilke, P. 2002, A&A, 395, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crane, P., Lambert, D. L., & Sheffer, Y. 1995, ApJS, 99, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, I. A. 1995, MNRAS, 277, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, I. A., & Williams, D. A. 1997, MNRAS, 291, L53 [NASA ADS] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources., NASA/IPAC Infrared Science Archive [Google Scholar]
- Daflon, S., & Cunha, K. 2004, ApJ, 617, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Danks, A. C., Federman, S. R., & Lambert, D. L. 1984, A&A, 130, 62 [NASA ADS] [Google Scholar]
- Dowell, C. D., Lis, D. C., Serabyn, E., et al. 1999, in The Central Parsecs of the Galaxy, ed. H. Falcke, A. Cotera, W. J. Duschl, F. Melia, & M. J. Rieke, ASP Conf. Ser., 186, 453 [Google Scholar]
- Draine, B. T. 1986, ApJ, 310, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Katz, N. 1986, ApJ, 310, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Dwarakanath, K. S., Goss, W. M., Zhao, J. H., & Lang, C. C. 2004, J. Astrophys. Astron., 25, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Elmegreen, D. M. 1987, ApJ, 320, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Pineau des Forêts, G., & Roueff, E. 1995, A&A, 300, 870 [NASA ADS] [Google Scholar]
- Falgarone, E., Godard, B., Cernicharo, J., et al. 2010, A&A, 521, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federman, S. R., Strom, C. J., Lambert, D. L., et al. 1994, ApJ, 424, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Federman, S. R., Rawlings, J. M. C., Taylor, S. D., & Williams, D. A. 1996, MNRAS, 279, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Fish, V. L., Reid, M. J., Wilner, D. J., & Churchwell, E. 2003, ApJ, 587, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T. R., & Oka, T. 2010, ApJ, 709, L70 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., de Luca, M., Black, J., et al. 2010a, A&A, 518, L110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., de Luca, M., Goicoechea, J. R., et al. 2010b, A&A, 521, L16 [Google Scholar]
- Godard, B., Falgarone, E., & Pineau Des Forêts, G. 2009, A&A, 495, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godard, B., Falgarone, E., Gerin, M., Hily-Blant, P., & de Luca, M. 2010, A&A, 520, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goto, M., Usuda, T., Nagata, T., et al. 2008, ApJ, 688, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Greaves, J. S., & Williams, P. G. 1994, A&A, 290, 259 [NASA ADS] [Google Scholar]
- Gredel, R. 1997, A&A, 320, 929 [NASA ADS] [Google Scholar]
- Gredel, R., van Dishoeck, E. F., & Black, J. H. 1993, A&A, 269, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Gry, C., Boulanger, F., Nehmé, C., et al. 2002, A&A, 391, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammami, K., Owono Owono, L. C., & Stäuber, P. 2009, A&A, 507, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haud, U., & Kalberla, P. M. W. 2007, A&A, 466, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E. 1985, ApJ, 291, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Defrees, D. J., & Koch, W. 1989, MNRAS, 237, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Pety, J., & Guilloteau, S. 2005, IRAM Technical Report 2005-1 [Google Scholar]
- Indriolo, N., Oka, T., Geballe, T. R., & McCall, B. J. 2010, ApJ, 711, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Ehrenfreund, P., & Désert, F. 1992, A&A, 265, L1 [NASA ADS] [Google Scholar]
- Joulain, K., Falgarone, E., Pineau des Forêts, G., & Flower, D. 1998, A&A, 340, 241 [NASA ADS] [Google Scholar]
- Kerr, F. J., & Lynden-Bell, D. 1986, MNRAS, 221, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Koo, B. 1997, ApJS, 108, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Lacour, S., Ziskin, V., Hébrard, G., et al. 2005, ApJ, 627, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Sheffer, Y., & Crane, P. 1990, ApJ, 359, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, C. C., Goss, W. M., Cyganowski, C., & Clubb, K. I. 2010, ApJS, 191, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D. 1978, ApJ, 225, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesaffre, P., Gerin, M., & Hennebelle, P. 2007, A&A, 469, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lim, A. J., Rabadán, I., & Tennyson, J. 1999, MNRAS, 306, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H., & Lucas, R. 2002, A&A, 391, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., Lucas, R., & Pety, J. 2006, A&A, 448, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucas, R., & Liszt, H. 1996, A&A, 307, 237 [NASA ADS] [Google Scholar]
- Magnani, L., & Salzer, J. J. 1989, AJ, 98, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Magnani, L., & Salzer, J. J. 1991, AJ, 101, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, J. P., Lakin, N. M., Walker, G. A. H., & Bohlender, D. A. 2001, ApJ, 553, 267 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattila, K. 1986, A&A, 160, 157 [NASA ADS] [Google Scholar]
- Menten, K. M., Wyrowski, F., Belloche, A., et al. 2011, A&A, 525, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., & Hobbs, L. M. 1988, MNRAS, 231, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., Adams, N. G., Smith, D., Lindinger, W., & Villinger, H. 1986, MNRAS, 221, 673 [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2009, ApJ, 706, 1594 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Kaufman, M. J., Goldsmith, P. F., Hollenbach, D. J., & Plume, R. 2002, ApJ, 580, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Wolfire, M. G., & Schilke, P. 2005, ApJ, 628, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Goicoechea, J. R., Sonnentrucker, P., et al. 2010a, A&A, 521, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A., Sonnentrucker, P., Phillips, T. G., et al. 2010b, A&A, 518, L108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Novotny, O., Mitchell, J. B. A., LeGarrec, J. L., et al. 2005, J. Phys. B Atomic Mol. Phys., 38, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Nyman, L., & Millar, T. J. 1989, A&A, 222, 231 [NASA ADS] [Google Scholar]
- Oka, T., Geballe, T. R., Goto, M., Usuda, T., & McCall, B. J. 2005, ApJ, 632, 882 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX; Proc. Conference held October 4–8, 2009 in Sapporo, Japan, ed. Y. Mizumoto, K. I. Morita, & M. Ohishi (San Francisco: ASP), ASP Conf. Ser., 434, 139 [Google Scholar]
- Pan, K., Federman, S. R., Cunha, K., Smith, V. V., & Welty, D. E. 2004, ApJS, 151, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, K., Federman, S. R., Sheffer, Y., & Andersson, B. 2005, ApJ, 633, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Pandian, J. D., Momjian, E., & Goldsmith, P. F. 2008, A&A, 486, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., Black, J. H., Cernicharo, J., et al. 2010, A&A, 521, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineau des Forêts, G., Roueff, E., & Flower, D. R. 1986, MNRAS, 223, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Plume, R., Kaufman, M. J., Neufeld, D. A., et al. 2004, ApJ, 605, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Rachford, B. L., Snow, T. P., Tumlinson, J., et al. 2002, ApJ, 577, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Reach, W. T., Dwek, E., Fixsen, D. J., et al. 1995, ApJ, 451, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez-Fernandez, N. J., Combes, F., Martin-Pintado, J., Wilson, T. L., & Apponi, A. 2006, A&A, 455, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudolph, A. L., Fich, M., Bell, G. R., et al. 2006, ApJS, 162, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, C., Apponi, A. J., & Ziurys, L. M. 2004, ApJ, 608, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., & Beckwith, S. 1982, ARA&A, 20, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., Rachford, B. L., Tumlinson, J., et al. 2000, ApJ, 538, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., Destree, J. D., & Jensen, A. G. 2007, ApJ, 655, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., & Meyer, D. M. 2001, ApJ, 554, L221 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Neufeld, D. A., Phillips, T. G., et al. 2010, A&A, 521, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thorburn, J. A., Hobbs, L. M., McCall, B. J., et al. 2003, ApJ, 584, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Weselak, T., Galazutdinov, G. A., Musaev, F. A., & Krełowski, J. 2008, A&A, 484, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xie, T., Allen, M., & Langer, W. D. 1995, ApJ, 440, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, C., Krems, R., Dalgarno, A., & Balakrishnan, N. 2002, ApJ, 577, 795 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
CH+X1Σ+, 13CH+X1Σ+, and SH+X3Σ − spectroscopic parameters for the observed pure rotational transitions.
Comparison between the column densities of CH+, 13CH+, and SH+obtained with the integrations of the respective opacities over several velocity intervals.
All Figures
 |
Fig. 1 Original SH+ spectra (double-sideband antenna temperature TA before removing the standing waves) observed towards SgrA*+50, W31C, W33A, and W49N in the horizontal polarization and for the three different LO settings (in black, red, and blue). For more clarity the red and blue curves have been shifted from the black curve by 0.2 and 0.4 K (for the SgrA*+50 data), and by 0.1 and 0.2 K (for the W31C, W33A, and W49N data). |
| In the text | |
 |
Fig. 2 Spectra observed at the frequencies of the ground-state transitions of CH+ (black), 13CH+ (red), and SH+ (blue) in the direction of DR21(OH), G34.3+0.1, W31C, W33A, W49N, W51, SgrA*+50, and SgrB2(N). All spectra have been normalized to the continuum temperatures. To make the absorption features discernible, the 13CH+ and SH+ signals were mutiplied by a factor of 2 towards SgrA*+50, and SgrB2(N), and by factors of 2 and 3, respectively, towards the other sources. For more clarity the 13CH+ and SH+ spectra were shifted from the CH+ spectra by 0.5 and 1.0. |
| In the text | |
 |
Fig. 3 Absorption profiles observed in the direction of DR21(OH), G34.3+0.1, W31C, W33A, W49N, W51, SgrA*+50, and SgrB2(N) in the ground-state transitions of CH+ (black) and 13CH+ (red), and in the main hyperfine component (see Table 2) of the ground-state transition of SH+ (blue). All spectra have been normalized to the continuum temperatures. To make the absorption features discernible, the 13CH+ and SH+ signals were mutiplied by a factor of 2 towards SgrA*+50, and SgrB2(N), and by factors of 2 and 3, respectively, towards the other sources. For more clarity the 13CH+ and SH+ spectra were shifted from the CH+ spectra by 0.5 and 1.0. The x- and y- scales were chosen to display the velocity structure of the absorption features in detail. |
| In the text | |
 |
Fig. 4 Result of the hyperfine structure deconvolution code applied on the SH+ (1,2 ← 0,1) absorption spectrum observed towards SgrB2(N) and W49N. The top panel displays the original data (black) and the resulting decomposition in three hyperfine components, aligned to the same velocity scale. The hyperfine components are shifted by their velocity shift Δυh (see Table 2) in the bottom panels, to show how they can be combined (green line) to reproduce the original data (black line). For more clarity, the hyperfine components were vertically shifted from the original data. |
| In the text | |
 |
Fig. 5 Top: a) and b) histogram of the linewidths of the CH+, 13CH+, SH+ (this work), and HCO+ (Godard et al. 2010) velocity components obtained with the multi-Gaussian decomposition procedure (see Table A.1); c) linewidth distributions of CH+ and CH observed by Crane et al. (1995) in the local diffuse medium. Bottom: first- (mean) and second- (standard deviation) order moments of the Δυ distributions issued from the combined CH+, 13CH+, and SH+ data (red squares) and from the CH+ data observed in the solar neighbourhood (blue circles); the moments are computed over increasing Δυ intervals: mean = |
| In the text | |
 |
Fig. 6 N(12C)/N(13C) column density ratio as a function of the galactocentric distance RG. The red squares are from this work, and therefore evaluated with measurements of the N(12CH+)/N(13CH+) column density ratio. The blue circles are from previous measurements of the N(12CN)/N(13CN), N(12CO)/N(13CO), and |
| In the text | |
 |
Fig. 7 SH+ column density as a function of the CH+ column density per broad velocity interval (see Table 3). The open squares and open circles are from the present analysis and from Menten et al. (2011), respectively. The blue and purple points are from the absorption lines observed along the Galactic centre sight lines (SgrA*+50, SgrB2(N), and SgrB2(M)) and along the other sight lines (DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51), respectively. The black dashed, dotted, and dashed-dotted lines indicate N(SH+)/N(CH+) ratios of 0.01, 0.1, and 1, respectively. |
| In the text | |
 |
Fig. 8 N(SH+)/N(CH+) column density ratio as a function of the CH+ mean abundance. The CH+, SH+, and H column densities are computed from CH+, 13CH+, SH+, HI, HF, and CH opacities integrated over the velocity intervals given in Tables 3 and 4. The blue and purple points are from the absorption lines observed along the Galactic centre sight lines (SgrA*+50 and SgrB2(N)) and along the other sight lines (DR21(OH), G34.3+0.1, W31C, W33A, W49N, and W51), respectively. The red line corresponds to a least-squares fit of the latter data. |
| In the text | |
 |
Fig. 9 Predictions of two PDR models for gas densities nH = 50 and 300 cm-3. The CH+ (in red) and SH+ (in blue) relative abundances are displayed as functions of the shielding AV from the interstellar radiation field for a slab of gas illuminated on one side only. |
| In the text | |
 |
Fig. A.1 Observational data (black lines) compared to the multi-Gaussian decomposition (purple lines) of the SH+ (1,2,5/2 ← 0,1,3/2) (top), 13CH+(1 ← 0) (middle), and CH+ (1 ← 0) (bottom) absorption spectra observed towards DR21(OH). The solid red lines and the dashed blue lines correspond to the confirmed (C) and uncertain (U) Gaussian components, respectively (see main text). The solid green lines are the empirical modelling of the CH+saturated line profiles. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 for the observations towards G34.3+0.1. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 for the observations towards W31C. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1 for the observations towards W33A. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.1 for the observations towards W49N. |
| In the text | |
 |
Fig. A.6 Same as Fig. A.1 for the observations towards W51. |
| In the text | |
 |
Fig. A.7 Same as Fig. A.1 for the observations towards SgrA*+50. |
| In the text | |
 |
Fig. A.8 Same as Fig. A.1 for the observations towards SgrB2(N). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{$\Big[\int_0^{\Delta \upsilon_{\rm max}} (\Delta \upsilon - {\rm mean})^2 N(\Delta \upsilon) {\rm d}(\Delta \upsilon)\Big/\int_0^{\Delta \upsilon_{\rm max}} N(\Delta \upsilon) {\rm d}(\Delta \upsilon)\Big]^{1/2}$}](/articles/aa/full_html/2012/04/aa17664-11/aa17664-11-eq75.png)