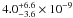| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118415 | |
| Published online | 22 February 2012 | |
Sub-millimetre spectroscopy of Saturn’s trace gases from Herschel/SPIRE
1 Atmospheric, Oceanic & Planetary Physics, Department of PhysicsUniversity of Oxford, Clarendon Laboratory, Parks Road, Oxford, OX1 3PU, UK
e-mail: fletcher@atm.ox.ac.uk
2 Dept. of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
3 Space Science & Technology Department, Science & Technology Facilities Council, Rutherford Appleton Laboratory, Chilton, Didcot, Oxon OX11 0QX, UK
4 Institute for Space Imaging Science, Department of Physics and Astronomy, University of Lethbridge, Lethbridge, Alberta, T1K 3M4, Canada
5 Blue Sky Spectroscopy, 9 / 740 4 Ave S, Lethbridge, Alberta, Canada, T1J 0N9
6 LESIA–Observatoire de Paris, CNRS, Université Paris 06, Université Paris-Diderot, 5 place Jules Janssen, 92195 Meudon, France
7 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
8 Univ. Bordeaux, LAB, UMR 5804, 33270 Floirac, France
9 CNRS, LAB, UMR 5804, 33270 Floirac, France
10 Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
11 Joint Astronomy Centre, 660 N. AÕohoku Place, Hilo, HI 96720, USA
Received: 7 November 2011
Accepted: 31 December 2011
Aims. We provide an extensive new sub-millimetre survey of the trace gas composition of Saturn’s atmosphere using the broad spectral range (15–51 cm-1) and high spectral resolution (0.048 cm-1) offered by Fourier transform spectroscopy by the Herschel/SPIRE instrument (Spectral and Photometric Imaging REceiver). Observations were acquired in June 2010, shortly after equinox, with negligible contribution from Saturn’s ring emission.
Methods. Tropospheric temperatures and the vertical distributions of phosphine and ammonia are derived using an optimal estimation retrieval algorithm to reproduce the sub-millimetre data. The abundance of methane, water and upper limits on a range of different species are estimated using a line-by-line forward model.
Results. Saturn’s disc-averaged temperature profile is found to be quasi-isothermal between 60 and 300 mbar, with uncertainties of 7 K due to the absolute calibration of SPIRE. Modelling of PH3 rotational lines confirms the vertical profile derived in previous studies and shows that negligible PH3 is present above the 10- to 20-mbar level. The upper tropospheric abundance of NH3 appears to follow a vapour pressure distribution throughout the region of sensitivity in the SPIRE data, but the degree of saturation is highly uncertain. The tropospheric CH4 abundance and Saturn’s bulk C/H ratio are consistent with Cassini studies. We improve the upper limits on several species (H2S, HCN, HCP and HI); provide the first observational constraints on others (SO2, CS, methanol, formaldehyde, CH3Cl); and confirm previous upper limits on HF, HCl and HBr. Stratospheric emission from H2O is suggested at 36.6 and 38.8 cm-1 with a 1σ significance level, and these lines are used to derive mole fractions and column abundances consistent with ISO and SWAS estimations a decade earlier.
Key words: Planets and satellites: atmospheres / submillimeter: general / planets and satellites: individual: Saturn / planets and satellites: composition
© ESO, 2012
1. Introduction
Saturn’s atmospheric composition is the end product of a plethora of physicochemical processes (e.g., condensation, vertical transport, thermochemistry, photochemistry and exogenic inputs) supplying molecular species to the regions of the atmosphere accessible to remote sensing (see review by Fouchet et al. 2009). Compositional measurements place constraints on the vertical stratification of the atmosphere (including, for example, the condensation of volatiles and the release of latent heat); the strength of vertical mixing from the deep interior and exogenic flux from the external environment; and provide a window onto the bulk composition of the proto-planetary nebula at the time of Saturn’s formation. In this paper we report new determinations of Saturn’s trace gas abundances using Fourier transform spectroscopy from the Herschel/SPIRE instrument (Spectral and Photometric Imaging Receiver, Griffin et al. 2010). This disc-averaged analysis complements the spatially-resolved sub-millimetre spectroscopy of Saturn from the Cassini Composite Infrared Spectrometer (CIRS, e.g., Fletcher et al. 2009b; Teanby et al. 2006), albeit with a factor of ten improvement in spectral resolution.
Previous studies of Saturn’s sub-millimetre spectrum from space- and ground-based platforms have revealed a great deal about the molecular composition of the gas giant atmosphere. The spectral range investigated by SPIRE (15–51 cm-1, 194–671 μm, or 447–1550 GHz) is largely invisible from the ground, but is characterised by the rotational transitions of the tropospheric species phosphine (PH3), ammonia (NH3) and methane (CH4). Stratospheric emission features of CO and H2O betray the external sources of these oxygen compounds, and several as-yet undetected species are known to have transitions in this spectral range (including the hydrogen halides, HCN, HCP, CS, SO2, H2S and others). These features are superimposed onto a continuum, formed both by collision-induced opacity of H2, He and CH4 and by the pressure-broadened line wings of PH3 and NH3.
Observations from the Caltech Sub-millimeter Observatory (CSO) placed upper limits on a host of species (H2S, hydrogen halides, alkali hydrides, HCN and HCP) and produced vertical profiles of the disequilibrium species, PH3 (Weisstein & Serabyn 1994, 1996; Orton et al. 2000, 2001). The Sub-millimeter Wave Astronomy Satellite (SWAS) and Infrared Space Observatory (ISO) determined the stratospheric abundances of exogenically-supplied H2O (Feuchtgruber et al. 1997; Bergin et al. 2000; Moses et al. 2000b), and a combination of IRAM (Institut de Radio Astronomie Millimétrique) millimetric measurements and JCMT (James Clerk Maxwell Telescope) sub-millimetre observations have been used to investigate the distribution of CO in Saturn’s stratosphere (Cavalié et al. 2008, 2009, 2010). Spatially-resolved Cassini observations between 10–200 cm-1 have been used to map Saturn’s PH3 (Fletcher et al. 2007a, 2009a), determine the abundance of CH4 (Fletcher et al. 2009b) and place new upper limits on the abundances of the hydrogen halides (Teanby et al. 2006).
Ground-based observations are inherently degraded by the limited availability of spectral windows and the variable telluric transmission, which hampers the capability for accurate radiometric calibration. Fourier transform spectroscopy from Herschel/SPIRE, on the other hand, can produce a well-calibrated signal across a broad spectral range. This means that multiple rotational transitions can be used simultaneously to place constraints on Saturn’s chemical composition. Furthermore, the unique epoch of the Herschel observations in June 2010 (soon after Saturn’s ring plane crossing and northern spring equinox in August 2009) means that contamination of the disc average by Saturn’s rings is kept to a minimum. We describe the reduction of the SPIRE data in Sect. 2; the use of an optimal estimation retrieval model to derive temperatures, PH3 and NH3 from the data in Sect. 3; and the derivation of trace gas abundances using a line-by-line forward model in Sect. 4.
2. Herschel/SPIRE observations of Saturn
Herschel/SPIRE (Swinyard et al. 2003; Griffin et al. 2010) comprises an imaging photometer and a Fourier Transform Spectrometer (FTS), both of which use bolometer detector arrays (3 arrays for photometry and 2 for spectroscopy, see Griffin et al. 2010, for an explanation of the SPIRE instrument and observing modes). The spectrometer calibration scheme was described by Swinyard et al. (2010a) and Fulton et al. (2010), and the specific techniques for calibrating a bright, extended source will be discussed below. SPIRE observed Saturn on June 13th 2010 (operational day 395 for Herschel) when the planet subtended 17.75′′ from Herschel’s vantage point. As the full width at half maximum (FWHM) of the beam increases from 17′′ to 45′′ towards the shortest wavenumbers, the measured spectrum can be considered as semi-extended at the longest wavenumbers (50 cm-1) and as a point source disc average at the shortest (15 cm-1). The observations consisted of 8 individual interferograms between 14:14:49 and 14:42:20 UT, a total of 1651 s. During the observation the target was tracked by the Herschel spacecraft in non-sidereal pointing mode. The spectrum was taken as part of the functional and calibration set-up observations used to establish the optimum operating conditions for the instrument.
Figure 1 shows the SPIRE spectrum of Saturn, both in raw units and converted to brightness temperatures, demonstrating the dominance of PH3, NH3 and CH4 features. Saturn was observed with the highest available unapodised spectral resolution on the FTS, corresponding to a FWHM of the instrument spectral response function (a sinc function) of 0.048 cm-1 (or 1.2 GHz). Spectra were recorded on a wavenumber grid with a 0.01 cm-1 spacing.
 |
Fig. 1 Saturn’s sub-millimetre spectrum measured by Herschel/SPIRE in 2010. The spectrum consists of a long-wave channel (14–32 cm-1) and a short-wave channel (32–52 cm-1). Raw flux units of Janskys are shown in panel a); these are converted into radiance units in b) and to brightness temperatures in c), approximately represent the atmospheric temperature at the line-forming region. Key features of the spectrum – PH3, NH3 and CH4 – are labelled in c). |
2.1. Data processing and calibration
The sub-millimetre flux density of Saturn is much higher than that of typical targets for the SPIRE instrument, which was designed to cope with flux densities up to a few hundred Janskys rather than the approximately 5000–25 000 Jy from Saturn. Under nominal detector bias and sensitivity conditions, the power from Saturn would saturate the detectors and conditioning electronics and no useful data would result. We have therefore used a “bright”-source setting for observations of objects brighter than Uranus, which reduces the effective responsivity of the bolometers and the electronics gain to prevent amplifier saturation. This method was first tested and calibrated on Mars (Swinyard et al. 2010b) and is now implemented as a standard observing mode for SPIRE (SPIRE Observers Manual 2011).
The processing applied to “bright” setting data varies from the standard pipeline described in the Observers Manual (SPIRE Observers Manual 2011) and Fulton et al. (2008). Absolute radiometric calibration of the Saturn spectrum used an observation of Uranus taken on Herschel operational day 209 (2009 December 8) and a model of Uranus’ atmospheric structure (based on Spitzer observations, Orton et al., in prep.) to provide a reference. The Uranus model used as the calibration standard is an update to the model of Griffin & Orton (1993), and we estimate it to have an absolute radiometric uncertainty of 5%. Although Uranus’ stratospheric temperature field is thought to be variable (rotational modulation of mid-infrared hydrocarbon emissions was reported by Orton et al. 2010), the Herschel spectrum is mainly sensitive to tropospheric H2-He emission that was unaffected by this variability, allowing us to continue to use the ice giant as a calibration standard.
We convert the voltage interferograms from the detectors into net bolometer temperature for the dark sky and Saturn. Following the standard pipeline procedure the interferograms are linearised (i.e., placed on a common position grid); de-glitched to remove cosmic ray effects; baseline-corrected to remove low frequency temporal variations and phase-corrected before transformation into the spectral domain. At this stage, the eight individual spectra from each of the mechanism scans are kept separate to allow determination of the noise in each spectral bin. The dark-sky observation is subtracted from each scan and the absolute calibration applied by dividing through by the residual spectral response function (RSRF) derived from the Uranus observation. When this procedure was used for the Martian observation it was found that a further gain correction was required (Swinyard et al. 2010b), probably because the detectors are operating at temperatures very far from their nominal range. The final gain correction is found by comparing the signals from the internal calibration source (PCAL, Griffin et al. 2010) taken during the Uranus and Saturn observations. The gain factors found for this observation were 1.29 for the short-wave channel (SSW) and 1.71 for the long-wave channel (SLW), with an overall uncertainty of ± 15% on the applied gain correction. This systematic uncertainty due to the noisy PCAL signal dominates over all other terms and we take the overall absolute uncertainty on the spectrum to be ± 15%.
The spatial response of the SPIRE FTS varies with frequency in a complex manner due to the combination of multi-moded feedhorns on the bolometer detectors and the compact nature of the optics (Ferlet et al., in prep.). This is illustrated by the behaviour of the FWHM of the spatial response versus frequency shown in Fig. 2b. The manner in which the beam couples to sources of varying spatial extent is also complex. In general the approach to solving the coupling integral between the source and the instrument spatial response involves decomposing the beam into a linear superposition of electromagnetic modes (Kogelnik & Li 1966; Martin & Bowen 1993; Padman & Murphy 1991). The efficiency with which these modes couple to the source is not easily modelled in the case of the SPIRE FTS as the optics cause distortion of the primary feedhorn modes, giving a more complex response versus frequency than standard modelling allows. We have found, however, that the intensity pattern of the point spread function can be represented by a combination of Hermite-Gauss (HG) polynomials, which follow the form of the expected native feedhorn modes (Ferlet et al., in prep.). The efficiency with which these couple to point- and fully-extended sources has been estimated using observations of Neptune and Uranus to establish the point source response, and a model of the flux from the Herschel telescope itself to establish the fully extended response. Saturn, at 17.75′′, fills the higher frequency (SSW) beam, but can be considered as a point source in the context of the lower frequency SLW beam (Fig. 2b). For SLW, a small correction for efficiency was made using a power-law interpolation of the coupling efficiency between the two extremes. This correction amounted to no more than 5% at the high-frequency end of the SLW band. Using this corrected efficiency for SLW and the extended source efficiency for SSW, we have then performed the coupling integral between each mode and a circular source the same angular size as Saturn to correct the observed spectrum to the emitted spectrum. It is this corrected spectrum (Fig. 1) that is used for the comparison to the model in the remainder of this paper.
Following removal of the instrument response, the eight individual Saturn spectra can be co-added, removing any remaining outliers, and the noise estimated from the standard deviation between the spectra at each frequency bin. This random error was smaller than 1% of the measured signal for much of the spectral range, with the short wavelength channel (SSW) producing a slightly larger error than the long wavelength channel (SLW). The random error is largest at the long-wavelength ends of each channel, with errors exceeding 1%, so these were omitted from subsequent analysis.
 |
Fig. 2 Observational geometry of Saturn from Herschel, and estimations of the contribution of Saturn’s rings to the disc-averaged spectrum. Panel a) shows the size of the planet in arcseconds and the small ring-opening angle as Saturn’s northern hemisphere passed the spring equinox. The SPIRE FWHM at 50 cm-1 is shown as the dotted line close to Saturn’s limb. The size of the SPIRE beam width is compared to the width of Saturn and the A, B and C rings in panel b). The fractional area of the SPIRE beam occupied by each of the rings is given in panel c), and was used to calculate the contribution of ring emission and absorption to the spectrum as a fraction of the total signal in d). Contributions smaller than 2% are within the estimated uncertainties on the SPIRE data. |
2.2. Estimating Saturn’s ring contribution
Despite the near edge-on view of Saturn’s rings in June 2010, we tested the influence of ring thermal emission and absorption at each wavenumber. The calculation involved a number of individual steps. The ring-opening angle in June 2010 was small (φ = 2.2° from Herschel’s vantage point), so the rings offer only a small surface area to a distant observer, as shown in Fig. 2. The temperatures of the rings were assumed to be 65 K for the A ring, 68 K for the B ring and 80 K for the C ring (e.g., Flandes et al. 2010), with optical depths (τ) of 0.6, 2.0 and 0.1 for the A, B and C rings respectively (e.g., Colwell et al. 2010). We used a simple formulation to estimate the ring emission spectrum (Iem = B(T)(1 − exp( − τ / μ))), where B(T) is the blackbody emission of each ring, and the parameter exp( − τ / μ) accounts for the viewing geometry (μ = sin(φ)) and optical depth (τ). Ring absorption was negligible in this case, but was included via Iabs = Isatexp( − τ / μ), where Isat is the disc-averaged radiance from Saturn.
This ring spectrum was then weighted by the fractional visible surface area of each ring contributing to the beam. The ring area was calculated as ellipse arcs, estimating the fraction obscured by Saturn’s disc. Figure 2 shows that the area of the beam occupied by the rings is largest at the shortest wavenumbers, where the SPIRE FWHM is at its largest (44.7′′). At the largest wavenumbers, the beam size (16.8′′) is smaller than Saturn’s disc, so that only the small portion of the rings eclipsing Saturn can contribute. Thus the ring area was multiplied by the SPIRE beam FWHM (Fig. 2b), and used to estimate the spectrally-variable percentage of the beam area occupied by each ring (Fig. 2c). Finally, the area-weighted ring emission was considered as a fraction of the total signal in the SPIRE disc-averaged spectrum, and found to be approximately 1.5–2.0% at the longest wavenumbers, decreasing to 0.5–1.0% at the shortest (Fig. 2d).
This ring contribution is smaller than systematic errors on the photometry (5%), so can be assumed to be a second-order error in the present analysis. If, however, such disc-averaged observations were undertaken at any other time in Saturn’s seasonal cycle, the ring contribution would be non-negligible. The ring contribution was added to the measurement error as a source of uncertainty in the spectral modelling, and we will further discuss the importance of the Enceladus water torus (Hartogh et al. 2011) in Sect. 4.2. Thus the total calibration uncertainty is comprised of the systematic uncertainty in the Uranus model; the random noise on the measurements; instrumental artefacts and ringing; uncertainties associated with the coupling between the SSW and SLW channels; plus the contribution of Saturn’s rings to the beam.
 |
Fig. 3 Optimal estimation fitting of the SPIRE continuum using a retrieval algorithm (Irwin et al. 2008). Data are shown as black circles, the fit is the continuous line. Radiances in panel a) are converted to brightness temperatures in b), and the residual (black dots) is shown in panel c). The dotted line in c) shows the radiance uncertainty on the SPIRE data, the dashed line shows the zero line. |
3. Saturn continuum modelling: temperatures, PH3, and NH3
The SPIRE data were reproduced in two stages, using an optimal estimation retrieval algorithm (Irwin et al. 2008) to retrieve the atmospheric temperature, PH3 and NH3 mole fractions to fit the continuum, prior to using a line-by-line forward model to place precise estimates on Saturn’s trace-gas abundances (Irwin et al. 1997). Disc-averaged radiances were calculated via an exponential integral method (Goody & Yung 1989a). The sub-millimetre model includes collision-induced absorption of H2-H2, H2-He, H2-CH4 and CH4-CH4 pre-calculated from the tabulations of Borysow (1991, 1993); Borysow et al. (1988); Borysow & Frommhold (1986, 1987) and references therein. The helium mixing ratio He/H2 was set to 0.135 (Conrath & Gautier 2000).
The reference atmospheric structure was defined on 120 pressure levels equally spaced in log (p) between 1 μbar and 10 bar. An a priori temperature profile was estimated as a mean of Cassini/CIRS T(p) profiles between ± 45° latitude from Cassini’s prime mission (sensitive to the 1–800 mbar range, Fletcher et al. 2010). The PH3 profile was initially set to the CIRS-derived mole fraction of 6.4 ppm at p > 0.55 bar, decreasing due to photolysis at lower pressures with a fractional scale height of 0.27 (the ratio of the PH3 scale height to the scale height of the bulk atmosphere, Fletcher et al. 2009a). The vertical distribution of NH3 initially had a reference mole fraction of 60 ppm below 1 bar (Fletcher et al. 2009b), decreasing with altitude following a saturated vapour pressure profile (p > 0.3 bar) and a linear extrapolation to low pressures to represent photolysis (p < 0.3 bar). The CH4 mole fraction was set to a deep value of 4.7 × 10-3 (Fletcher et al. 2009b) and drops with altitude due to both diffusive processes and photochemical reactions throughout the 1–1000 mbar range, as reviewed by Moses et al. (2000a). The inclusion of additional gases into the basic model will be described in Sect. 4.
 |
Fig. 4 Functional derivatives (rate of change of radiance with respect to the model parameter) for the four major contributors to the sub-millimetre spectrum. Figures have been normalised, and each contour represents a change of 0.1. A scale bar is provided in panel c). |
 |
Fig. 5 Retrieved vertical profiles for temperature, PH3 and NH3 in the best-fitting case. The solid line shows the retrieved profile, the dotted line is the uncertainty on the retrieval, estimated by applying a 5% shift in the measured radiances (the absolute calibration uncertainty) and redoing the calculation. The dashed line in the temperature plot a) is a global mean of the T(p) profiles retrieved from the Cassini/CIRS far-infrared focal plane between 2004 and 2008. The dot-dashed grey lines in a) and b) are temperature and PH3 retrievals based on extreme estimates of the calibration uncertainty of ±15%. The NH3 profile in c) was estimated by scaling the saturated vapour pressure profile (see Fig. 8), so the uncertainties are the same at all altitudes. The grey dashed line in c) is the saturated vapour pressure curve of NH3 assuming a relative humidity of 100%, the dot-dashed grey line use the temperature profiles given by the dotted lines in a). The uncertainty in the saturated mole fraction is greater than the uncertainty on the retrieved abundances of NH3. |
 |
Fig. 6 Testing the sensitivity to the pressure knee of the PH3 vertical distribution. The pressure levels (in mbar) are given by the key in the top left corner, but the differences between these curves is hard to distinguish in the top four panels, showing the difficulty we face in trying to constrain the pressure knee from these data. The χ2 / N distributions in the bottom panels show convergence on the 500–650 mbar range. The χ2 estimates do not include the spurious emission peaks from the models (see main text and Fig. 7). The best fitting pressure knee, deep mole fraction and fractional scale height are provided in the lower panels. |
The rotational lines of PH3 originate from an update to the commonly-used GEISA database in the 8–176 cm-1 region by Kleiner (priv. comm.). The PH3 lines were broadened by both H2 and He using γH2 = 0.1078−0.0014J cm-1 atm-1 and γHe = 0.0618−0.0012J cm-1 atm-1 (Levy et al. 1993), and a temperature dependence of Tn where n = 0.702−0.01J (J is the rotational quantum number). For NH3 we use line data from Kleiner et al. (2003), hydrogen- and helium-broadened using the empirical model of Brown & Peterson (1994). A Rosenkrantz Ben-Reuven lineshape was assumed for ammonia (using line coupling from Eq. (13) of Birnbaum et al. 2000, and an appropriate temperature dependence). Experiments with a Van Vleck Weisskopf lineshape for both PH3 and NH3 showed negligible differences at the resolution of the SPIRE observations. Although our preliminary analysis uses spectroscopic line data for methane from the work of Brown et al. (2003) with a multiplicative factor of 1.154 for the line intensities (based on the results of Wishnow et al. 2007, which is also present in the latest HITRAN 2008 compilation), we also use a more recent line list from Boudon et al. (2010) in Sect. 4.1 to show potential uncertainties in the CH4 mole fraction. Both line lists were hydrogen-broadened using a half-width of 0.059 cm-1 atm-1 at 296 K and a temperature dependence, n = 0.44 (Margolis 1993).
 |
Fig. 7 The high spectral resolution of SPIRE is used to place limits on the presence of PH3 in Saturn’s stratosphere. Using the best-fitting parameterised profiles from Fig. 6, we apply upper-level cutoffs between 1 mbar and 300 mbar and test the change in χ2. The upper panels show the data (points) compared to models with high-altitude cut offs at different pressure levels (key shown in mbar in the upper left panel). The lower panels show Δχ2 for the variable cutoff pressure with 1σ and 3σ confidence limits as the dotted horizontal lines. |
 |
Fig. 8 Determining the most plausible fit for the NH3 doublet. The vertical profile is parameterised in terms of a degree of saturation (panel a), with relative humidities given as percentages in the key, based on the best-fitting T(p)), an upper-level cut off (panel c), with pressures between 250–860 mbar given in the key) and a deep mole fraction (panel d)), with mole fractions given in ppm in the key). Of the three parameters, the only way to increase the depth of the absorption features to match the SPIRE data (black circles) is to increase the relative humidity (panel a)). The models in c) and d) do not match the data because they assume a relative humidity of 100%. The Δχ2 for each value of the relative humidity is evaluated for data between the two dotted vertical lines in panel a (i.e., avoiding artefacts in the data near 41.5 cm-1) and displayed in panel b). The best-fit mole fraction at 660 mbar plus the 3σ uncertainty is shown in panel b). |
The spectroscopic data for PH3, NH3 and CH4 were used to generate k-distributions (ranking absorption coefficients, k, according to their frequency distribution, Irwin et al. 2008) using a 0.048 cm-1 FWHM on an evenly sampled wavenumber grid of 0.012 cm-1 spacing. We used a direct sorting method to calculate the k-distribution from line-by-line spectra within each spectral bin (e.g., Goody et al. 1989b). For the continuum fitting, we initially used a triangular function as an approximation to the SPIRE instrument function. Subsequent line-by-line modelling used the appropriate sinc function.
The optimal estimation retrieval algorithm was used to simultaneously derive tropospheric temperatures, a parameterised PH3 profile and a continuous NH3 profile to provide an optimal fit to the 15–50 cm-1 range of the SPIRE data. We experimented with the assumed errors on our a priori assumptions to ensure a smooth vertical T(p) profile which lay close to the Cassini/CIRS reference profile. We found that the SPIRE data could not be reproduced without varying both the temperature and composition, and that fixing the T(p) to that derived by Cassini did not provide an adequate fit to the data. The vertical variation of the ortho/para-H2 ratio, which is known to be seasonably-variable on Saturn due to differing conversion rates and vertical transport (Fletcher et al. 2010), was found to be poorly constrained by the data, and an equally good fit could be obtained by assuming an equilibrium para-H2 fraction. The model fit to the spectra and the residuals are shown in Fig. 3. The spectral region between 28.5–32.5 cm-1 was omitted from our fitting because of the dominance of instrumental artefacts (large-scale oscillations observed in Fig. 1) in the overlap region between the two channels. No additional scalings were required to match the model continua to the observations.
An estimate for the vertical sensitivity of the SPIRE data is provided by the functional derivatives (the rate of change of spectral radiance with a particular model parameter) in Fig. 4. Temperature sensitivity peaks at 500 mbar with a FWHM extending from 220–780 mbar. The functional derivative for PH3 is almost identical, with a range varying from 260–700 mbar. However, when we attempted to reproduce the SPIRE spectrum by varying PH3 alone, we required unrealistic departures of the PH3 vertical profile from previous studies, so fitting the data by varying PH3 alone was deemed inadequate. The spectrum is sensitive to NH3 in the 500–1350 mbar range (with a peak at 660 mbar, although the SPIRE cannot constrain temperatures at the deeper levels) and CH4 in the 100–480 mbar range (peak sensitivity at 250 mbar).
3.1. Temperature profile
The retrieved T(p) is shown in Fig. 5a, where we have also tested the sensitivity of the retrieved profile to uncertainties in the absolute calibration (see Sect. 2) due to (i) 5% errors due to the use of Uranus as the calibration reference (dotted lines) and (ii) an extreme estimate of 15% uncertainty based on the applied gain correction (dot-dashed lines). These calibration uncertainties dominate the error on the thermal profile, exceeding the formal retrieval uncertainties (i.e., those accounting for the degeneracy between temperatures and PH3 and NH3 in our model). We also tested the effects of shifting the long-wavelength spectrum by 2–3% relative to the short-wavelength spectrum (not shown) to assess the coupling between the two spectroscopic arrays, but found that the retrieved T(p) suffered from non-physical oscillations, indicating an inability to fit the resulting spectra.
The extreme range of temperatures suggested by the ± 15% gain correction deviate substantially from previous measurements of Saturn’s tropospheric temperatures (e.g., Lindal 1992), so we consider only solutions within a ±5% calibration uncertainty for the remainder of this manuscript. For the T(p) profiles shown by the solid and dotted lines in Fig. 5a, which differ by 6–7 K in the 0.1–1.0 bar region, the retrieved T(p) appears slightly different to the mean Cassini/CIRS thermal profile (dashed line) in the 0.1–0.8 bar region (using far-IR temperature retrievals from an average of Cassini’s prime mission, 2004–2008, Fletcher et al. 2010), leading to a quasi-isothermal appearance for the tropopause between approximately 60 and 300 mbar. This sort of profile is characteristic of Saturn’s equatorial tropopause, a location of vigorous upwelling and cooling via adiabatic expansion (Fletcher et al. 2007b), but it would be rather surprising if the cool equatorial zone were dominating the disc-averaged emission measured by SPIRE. The difference between the SPIRE and CIRS profiles is within the error associated with the ±5% radiance uncertainty, and we caution that (i) the SPIRE retrieval used an equilibrium para-hydrogen fraction because of the narrow 15–50 cm-1 spectral range is unable to offer adequate constraints on the vertical para-H2 distribution (compared to the broader 10–600 cm-1 range used for the CIRS retrieval of para-H2); and (ii) the retrieval of temperature from SPIRE is not fully independent of the retrieved PH3 and NH3 abundances because of the broad pressure-induced wings of these absorption features. Furthermore, the SPIRE data does not contain information on temperatures outside of the 220–780 mbar range, and we should be cautious of interpreting thermal profiles in regions where the retrieved temperatures relax smoothly back to the a priori profile. It is interesting to note, however, the hints of structure in the 100–150 mbar region reminiscent of the temperature knee discovered by CIRS (Fletcher et al. 2007b), which may be due to localised heating by sunlight-absorbing hazes in the upper troposphere.
3.2. Phosphine, PH3
Four rotational transitions of PH3 dominate the SPIRE spectrum, permitting a test of the vertical parameterisation of the PH3 profile in terms of a deep mole fraction beneath a reference pressure, p0. Using the best-fitting T(p) profile, we independently retrieved the PH3 deep mole fraction and fractional scale height for p0 in the 400–1000 mbar range for each of the four transitions, shown in Fig. 6. The four lines provided deep mole fractions of 5.2–5.5 ppm, with a value of the pressure knee between 500–650 mbar and a fractional scale height of 0.31–0.35. When all four lines were used simultaneously, the best fit profile had a reference p0 = 570 mbar, similar to sub-millimetre studies from CIRS (550 mbar, Fletcher et al. 2007a) and the CSO (650 mbar, Orton et al. 2001), and a deep mole fraction of 5.5 ± 0.4 ppm and a fractional scale height of 0.33 ± 0.03 (shown in Fig. 5b). When we shifted the absolute calibration by ±5% we found that the mole fraction varied from 5.2–6.2 ppm (dashed lines in Fig. 5b). This range is consistent with the 6.4 ± 0.4 ppm estimate from Cassini/CIRS 10-μm observations for the same altitude levels (Fletcher et al. 2009a), and slightly larger than the 2.8–5.0 ppm range cited from Cassini/VIMS (Visual and Infrared Mapping Spectrometer) 5-μm studies for deeper pressures (below 1.3 bar, rather than 0.5 bar used here, Fletcher et al. 2011). The source of the PH3 discrepancies between the pentad polyad at 5 μm and the rotational absorption features in the SPIRE spectral range is a topic of ongoing investigation.
The presence of spurious emission cores in the models in Fig. 6 shows that, with the high spectral resolution of SPIRE, we can also draw tentative conclusions about the upper limits of PH3 penetration into the lower stratosphere. SPIRE does not detect any stratospheric emission lines of PH3, implying that our standard parameterisation of the PH3 profile must be adjusted to prevent the presence of PH3 in the stratosphere. As this requires modelling of narrow stratospheric features, we switched to the line-by-line forward model and convolved the output spectra with a sinc instrument function, testing upper level cut offs for the PH3 distribution between 1 mbar and 300 mbar. The lines at 35.6 and 44.5 cm-1 provided the strongest constraints, and Fig. 7 shows how the goodness-of-fit parameters (χ2) varies for the different PH3 cutoffs. The SPIRE data rule out the presence of PH3 above the 10-mbar level (3σ confidence) due to the absence of narrow emission cores in the data. Similarly, PH3 must be present in the 100–300 mbar region to explain the depths of the absorption features. The multi-lobed behaviour of the χ2 distribution can be explained by comparing models with cutoffs at 20, 50 and 100 mbar in Fig. 7: 50 mbar produces an absorption core that is too strong; whereas 20-mbar permits some stratospheric emission to “fill in” the absorption, partially improving the fits. Nevertheless, models with PH3 cutoffs between 80–100 mbar provide the best reproductions of the SPIRE data, and this profile is shown in Fig. 5b.
3.3. Ammonia, NH3
Reproducing the three ammonia absorption features observed by SPIRE (a single feature near 19 cm-1 plus a doublet feature near 40 cm-1 in Fig. 1) with a physically-plausible NH3 distribution proved more problematic. SPIRE sensitivity to NH3 extends over the 500–1350 mbar range (Fig. 4), but temperatures below the 780-mbar level are under-constrained by the SPIRE data, leaving a degeneracy between temperatures and NH3 abundance at depth. Furthermore, the measured ammonia features all appear deeper than we can account for using a simple model of saturated ammonia vapour throughout the region of sensitivity, based on the best-fitting T(p). Using the retrieval model to fit these spectra requires either (i) a larger tropospheric lapse rate or (ii) supersaturated NH3 abundances (the partial pressure of NH3 exceeding the saturated vapour pressure with a 100% relative humidity) when compared to the nominal T(p) profile in Fig. 5a. The former is inconsistent with the rest of the SPIRE spectrum, so we must evaluate the plausibility of the latter.
Figure 8 highlights the origin of the problem, which shows NH3 spectra calculated for the best-fitting SPIRE T(p). We parameterise the profile in terms of the degree of saturation, a deep mole fraction, and an upper level cutoff. Varying the deep mole fraction (Fig. 8d) has the same effect as varying the pressure level for the transition from well-mixed NH3 at depth to a variation determined by saturation at lower pressures, but we found this to have a negligible effect on the spectrum unless the deep mole fraction was smaller than approximately 50 ppm (i.e., the transition region is around the 1-bar level), which is unlikely when compared to previous studies. It is important to note, therefore, that SPIRE is insensitive to Saturn’s well-mixed NH3 abundance beneath the cloud-condensation region near 1.8 bar (calculated for a fivefold enrichment in heavy elements, Atreya et al. 1999). If we apply arbitrary upper-level cutoffs to the NH3 profile (Fig. 8c) we decrease the absorption depths, worsening the fit to the data. The only way to increase the size of the absorption features for the best-fitting SPIRE T(p) is to increase the relative humidity beyond 100% in Fig. 8a. Although supersaturated conditions could occur in the absence of condensation nuclei (e.g., supersaturation with respect to water ice occurs in some regions of the terrestrial atmosphere), the visibly-hazy appearance of Saturn’s troposphere should provide ample sites to encourage condensation. We therefore deem NH3 supersaturation in this region to be unlikely.
 |
Fig. 9 Testing the line-by-line forward model by fitting the CH4 rotational line. The left hand panel shows the brightness temperatures, with the data given by circles, the smooth spline-fit to the continuum as the dotted line, and the solid grey lines showing the range of mole fractions tested. The central panel converts this to a line-to-continuum ratio relative to the smooth spline. Here, the dotted lines show the error envelope as defined in the main text. The right hand panel shows the Δχ2 for the model, with dotted horizontal lines showing the 1σ and 3σ confidence limits on the results. The derived methane abundance depends upon the choice of line data, with a mole fraction of (4.3 ± 0.3) × 10-3 assuming line intensities from Wishnow et al. (2007) (shown here) and (4.8 ± 0.3) × 10-3 using intensities from Boudon et al. (2010). |
 |
Fig. 10 Marginal detection of two emission features of H2O at 36.6 and 38.8 cm-1 (1097 and 1163 GHz, respectively). The best-fitting mole fractions are |
 |
Fig. 11 Derivations of upper limits on Saturn’s trace gases in the well-mixed case. For all thirteen gases, the left panel shows the line to continuum ratio in the data (circles) compared to a number of models (grey solid lines), and the right panel shows the degradation of the χ2 parameter as we increase the mole fraction. Dashed lines show the 1σ and 3σ confidence limits. For some species we show only the line which provided the best constraints on the upper limit. |
 |
Fig. 12 Derivations of upper limits on Saturn’s trace gases for the case where they are restricted to stratospheric altitudes (p < 1 mbar). For all thirteen gases, the left panel shows the line to continuum ratio in the data (circles) compared to a number of models (grey solid lines), and the right panel shows the degradation of the χ2 parameter as we increase the mole fraction. Dashed lines show the 1σ and 3σ confidence limits. For some species we show only the line which provided the best constraints on the upper limit. |
To investigate this further, we fixed the deep mole fraction at 100 ppm (representative of the conclusions of Courtin et al. 1984; Briggs & Sackett 1989; de Graauw et al. 1997; Orton et al. 2000; Fletcher et al. 2011) and scaled the NH3 relative humidity to fit the absorption features in Fig. 8a. The variation in χ2 is shown in Fig. 8b relative to the mole fraction at 660 mbar (near the peak of the functional derivatives). We find a best fit mole fraction of 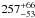 ppb at 660 mbar (errors of 20–25% are 3σ uncertainties based on Fig. 8b), which is consistent with the Cassini/CIRS derivation of 330 ± 30 ppb at the same pressure level (Fletcher et al. 2009b). We avoid oscillatory artefacts in the data that contaminate the wings of the NH3 lines in Fig. 8a. Taking the SPIRE T(p) at face value, this represents a supersaturation of
ppb at 660 mbar (errors of 20–25% are 3σ uncertainties based on Fig. 8b), which is consistent with the Cassini/CIRS derivation of 330 ± 30 ppb at the same pressure level (Fletcher et al. 2009b). We avoid oscillatory artefacts in the data that contaminate the wings of the NH3 lines in Fig. 8a. Taking the SPIRE T(p) at face value, this represents a supersaturation of 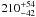 % at 660 mbar (T(660) = 115.5 K). However, the degree of supersaturation diminishes if we assume that the tropospheric temperatures are warmer: the Cassini/CIRS T(660) = 116.8 K suggests a humidity of
% at 660 mbar (T(660) = 115.5 K). However, the degree of supersaturation diminishes if we assume that the tropospheric temperatures are warmer: the Cassini/CIRS T(660) = 116.8 K suggests a humidity of 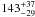 %; and the Voyager radio occultation profile T(660) = 117.5 K (interpolated from Lindal 1992) suggests a humidity of
%; and the Voyager radio occultation profile T(660) = 117.5 K (interpolated from Lindal 1992) suggests a humidity of 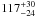 %. Increasing the absolute calibration by 5% served to decrease the amount of NH3 required to fit the data by 30%. Combined with the increased temperature of T(660) = 118.8 K we find sub-saturated conditions of
%. Increasing the absolute calibration by 5% served to decrease the amount of NH3 required to fit the data by 30%. Combined with the increased temperature of T(660) = 118.8 K we find sub-saturated conditions of 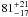 % (quoted humidity errors do not include uncertainty on the temperatures). Indeed, we would need to warm the 660-mbar temperatures to 118 K (ΔT = 2.5 K, within the temperature range suggested by the ± 5% calibration uncertainties) to make the NH3 profile consistent with a 100% relative humidity. Hence, although the derived NH3 mole fraction is accurate to within 20–30% (Fig. 5c), the degree of saturation is highly dependent on the temperature profile. Both sub-saturated and supersaturated conditions are tolerated within the ± 5% absolute calibration uncertainty, so we cannot provide meaningful estimates of the NH3 relative humidity.
% (quoted humidity errors do not include uncertainty on the temperatures). Indeed, we would need to warm the 660-mbar temperatures to 118 K (ΔT = 2.5 K, within the temperature range suggested by the ± 5% calibration uncertainties) to make the NH3 profile consistent with a 100% relative humidity. Hence, although the derived NH3 mole fraction is accurate to within 20–30% (Fig. 5c), the degree of saturation is highly dependent on the temperature profile. Both sub-saturated and supersaturated conditions are tolerated within the ± 5% absolute calibration uncertainty, so we cannot provide meaningful estimates of the NH3 relative humidity.
This discussion also raises the question of how well we know the saturated vapour pressure (psat) curve at the low temperatures of Saturn’s troposphere. Measurements are only available for T > 162.4 K, and must be extrapolated to the 90–130 K conditions of Saturn’s upper troposphere. We calculate the saturated vapour pressure via psat = exp(a + b / T + cT), where the coefficients (a = 23.0868, b = −4263.72 and c = −2.169 × 10-2) were estimated from a fit to data compiled in Lide (1995) and Kaye & Laby (1995) for T > 160 K. This curve is almost identical to those from Briggs & Sackett (1989) and Atreya (1986) for T < 195 K, who both cite Karwat (1924) as their primary source (also used in the compilation of Lide 1995). However, we found that low-temperature estimates of the saturated mole fractions were highly sensitive to the choice of the extrapolation function for psat. In a recent review, Fray & Schmitt (2009) improved this extrapolation between 15 and 195 K by calculating thermodynamic functions based upon the heat capacities of solids and gases, and used a fourth-order polynomial in 1 / T to interpolate psat. Our simple extrapolation based on the measurements is in close agreement with the thermodynamic calculation of Fray & Schmitt (2009) for T > 90 K (and identical at the 660-mbar temperature of 115.5 K), but begins to diverge for lower temperatures (not relevant for Saturn’s tropopause, Fig. 5a).
We must also question the ability of our model to reproduce the far-infrared line shapes, particularly in the wing regions. Following tests of Voigt, Van-Vleck Weisskopf and Rosenkrantz Ben-Reuven line shapes (which made negligible differences to the model spectra), we selected the latter for the NH3 lineshape. Opacity due to tropospheric aerosols is absent from our model as they are not expected to have an effect at these long wavelengths. Foreign broadening of the line intensities (obtained from Kleiner et al. 2003) by H2 and He was calculated using the empirical model of Brown & Peterson (1994), which reproduces experimentally-measured line widths to an 11% accuracy. Furthermore, Table III of Brown & Peterson (1994) suggests an experimental precision of 5–7% on the intensities and 3–6% on line widths for those rotational lines observed by SPIRE. However, even if we increase the NH3 line intensities by a conservative 10%, the derived NH3 abundances still suggest supersaturation based on the best-fit T(p). It is therefore likely that the uncertainties on the absolute calibration (and hence the derived T(p)) dominate the relative humidity estimates, even though the NH3 mole fractions in Fig. 5c are consistent with previous studies.
Finally, the disc-averaged spectrum may be biased towards radiance from warmer regions on the disc, which are typically associated with atmospheric subsidence in belts, leading to sublimation of ices to enhance the abundance of NH3 vapour. However, the relation between tropospheric temperatures and NH3 abundance isn’t always clear – for example, NH3 at Saturn’s cold equator is known to be enhanced by vigorous tropospheric upwelling (Fletcher et al. 2011). Furthermore, this fails to explain why the SPIRE temperature profile is marginally cooler than the Cassini/CIRS disc-average in Fig. 5a. In any case, localised processes may invalidate the comparison of the global-average NH3 profile to saturation based on the global-average T(p) profile. In summary, we find that the SPIRE data can be reproduced with NH3 following a vapour pressure curve in the upper troposphere, although the degree of saturation derived from the global-average T(p) and NH3 mole fraction of 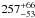 ppb at 660 mbar is highly uncertain.
ppb at 660 mbar is highly uncertain.
4. Trace gas species
In addition to the major absorption features, the SPIRE data are also used to investigate upper limits on a range of trace species expected to be present in Saturn’s atmosphere. We take the retrieved T(p), PH3 and NH3 and use them in a forward model with a sinc instrument function, sequentially increasing the mole fractions of a host of molecular species and assessing the degradation (or improvement) in the quality of the spectral fit. As the retrieved spectrum doesn’t always fit the continuum adequately, we fit a smooth spline interpolation (Teanby 2007) through the measured spectrum (omitting the spectral range affected by the line of interest) to calculate a line-to-continuum ratio. An upper limit is then deduced from a χ2 analysis, using the following sources of uncertainty:
-
measurement errors (variance
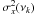 ) due to (i) the standard deviation on the eight successive Saturn scans (smaller than 1%, see Sect. 2); and (ii) the oscillations about the smooth spectral continuum (1.5–2.0% of the signal). The latter constraint assumes that the continuum is smooth at all points away from the line of interest, and that any small-scale structures are due to measurement noise. These instrumental oscillations were found to exceed the rms errors between the 8 scans, and thus dominate the measurement error.
) due to (i) the standard deviation on the eight successive Saturn scans (smaller than 1%, see Sect. 2); and (ii) the oscillations about the smooth spectral continuum (1.5–2.0% of the signal). The latter constraint assumes that the continuum is smooth at all points away from the line of interest, and that any small-scale structures are due to measurement noise. These instrumental oscillations were found to exceed the rms errors between the 8 scans, and thus dominate the measurement error. -
modelling errors (variance
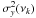 ) due to the residual between the measured and fitted radiance at each wavelength, again masking out the spectral line of interest. We used a mean of the model-data residual over a 3 cm-1 range either side of the line of interest. This is a systematic offset that may arise from an incomplete radiative transfer description in our model, or systematic uncertainties and “ramps” in the SPIRE data.
) due to the residual between the measured and fitted radiance at each wavelength, again masking out the spectral line of interest. We used a mean of the model-data residual over a 3 cm-1 range either side of the line of interest. This is a systematic offset that may arise from an incomplete radiative transfer description in our model, or systematic uncertainties and “ramps” in the SPIRE data.
By taking these sources of errors together, we are able to place conservative confidence limits on the trace gas abundances. Systematic distortions in the measured spectrum have the potential to mask the true measurement statistics in 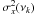 , but solely using the random errors between successive scans would grossly underestimate the uncertainty in the data. Following Teanby et al. (2006), we evaluate a χ2 cost function using the residual between the model line-to-continuum ratio (y(νk)) and the measured ratio (x(νk)) at Nν frequencies, νk, where k = 1,...,Nν.
, but solely using the random errors between successive scans would grossly underestimate the uncertainty in the data. Following Teanby et al. (2006), we evaluate a χ2 cost function using the residual between the model line-to-continuum ratio (y(νk)) and the measured ratio (x(νk)) at Nν frequencies, νk, where k = 1,...,Nν. 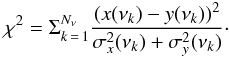 (1)The 1σ (68.3%) and 3σ (99.7%) significance levels are given by a change
(1)The 1σ (68.3%) and 3σ (99.7%) significance levels are given by a change 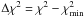 of 1 and 9 respectively (Press et al. 1992).
of 1 and 9 respectively (Press et al. 1992).
In the following analysis we use the 0.048 cm-1 spectral resolution to represent the FWHM of the instrumental sinc function. Rotational broadening due to Doppler shifting of lines resulting from Saturn’s rapid rotation degrades this resolution, but not significantly. Dividing Saturn’s equatorial circumference into 20 bins, we estimated the fractional contribution of each bin to the disc average (smallest for bins near the limb, largest for bins near the equator) and the line-of-sight velocity of each bin (and hence the magnitude of the Doppler shift). The worst-case scenario at 50 cm-1 was an additional broadening of 0.0016 cm-1 at the planetary limb, which contributes little to the disc average. When averaged over the disc, we estimate the rotational broadening at the largest wavenumbers to be no larger than 0.0007 cm-1, smaller than the 0.001 cm-1 sampling of the data and the 0.048 cm-1 FWHM.
Unless otherwise stated, and with the exception of CH4, line data for the following gases was extracted from the HITRAN2004 compilation (Rothman et al. 2005). Line intensities for CS and HCP were extracted from the molecular spectroscopy catalogue maintained by the Jet Propulsion Laboratory (Pickett et al. 1998). All our upper limits use independent uncertainties, meaning that we do not attempt to multiply uncertainties when more than one gas can contribute to a particular spectral region. Where appropriate, we use two different compositional profiles, one where a species is well mixed throughout the atmosphere (Fig. 11), and another where a species is only present above the 1-mbar level (representing a high-altitude source, Fig. 12). The 1-mbar cutoff is not meant to be an accurate representation of the vertical profile of exogenic species, but provides a basis for future detailed chemical studies. Stratospheric temperature constraints were provided by a mean of Cassini measurements (Fletcher et al. 2010), whereas tropospheric temperatures were those derived in Sect. 3. The results are summarised in Table 1.
Summary of Saturn’s trace gas mole fractions derived from Herschel/SPIRE.
4.1. Methane, CH4
CH4 is the principal carbon-bearing species in Saturn’s atmosphere, and the bulk C/H ratio provides a valuable constraint on the heavy-element enrichments in the atmospheres of the giant planets. Over the altitude range of interest (100–480 mbar for SPIRE), CH4 is expected to be well mixed, so we are able to use the rotational feature near 41.9 cm-1 to test the validity of our line-to-continuum approach (Fig. 9). As described in Sect. 3, we estimate the mole fraction of CH4 using two sources of line intensities: (i) the compilation of Brown et al. (2003) with a multiplicative factor of 1.154 based on the new dipole measurements of Wishnow et al. (2007); and (ii) the compilation of Boudon et al. (2010), where the line intensities are weaker by a factor of 0.883. H2 broadening and the temperature dependence were kept the same for both compilations. We find 1σ estimates of the mole fractions of (4.3 ± 0.3) × 10-3 and (4.8 ± 0.3) × 10-3 for the two sources of line data, respectively (3σ error range of ± 0.9 × 10-3). Although the 1σ uncertainties due to the SPIRE measurements do overlap, our dominant source of uncertainty on the CH4 mole fraction is due to the rotational line intensities. The line-to-continuum ratio in Fig. 9 features considerable small-scale oscillatory structure which is not reproduced by the model but which is included in our error budget. Nevertheless, this example demonstrates that we should be cautious about misinterpreting features in the data.
These two SPIRE measurements are broadly consistent (to within one standard deviation) with the results from Cassini/CIRS – (4.7 ± 0.2) × 10-3 (Fletcher et al. 2009b) and (4.5 ± 0.9) × 10-3 (Flasar et al. 2005), which both used the compilation of Brown et al. (2003) with the scaling factor from Wishnow et al. (2007). Converting the two estimates into a C/H ratio for Saturn’s bulk composition, we obtain carbon enrichments (relative to the solar chemical composition of Grevesse et al. 2007) of 9.9 ± 0.7 and 11.1 ± 0.7 for the Wishnow et al. (2007) and Boudon et al. (2010) line intensities, respectively, consistent with the hypothesis that Saturn contains more carbon than Jupiter due to the increasing core-to-envelope ratio as we move away from the Sun (e.g., Owen & Encrenaz 2006).
4.2. Water, H2O
The bulk of Saturn’s H2O is restricted to levels below those accessible to remote sensing due to the condensation of a hypothesised water cloud beneath the 10-bar level (e.g., Atreya & Wong 2005). Sub-saturated tropospheric H2O was detected by de Graauw et al. (1997) in the 5-μm region. However, an external influx of oxygen compounds from micrometeoroid ablation, cometary impacts or a connection to Saturn’s rings and satellites (particularly Enceladus, Hartogh et al. 2011) has long been postulated as a potential source. Water was previously detected in Saturn’s stratosphere in the sub-millimetre by ISO (Feuchtgruber et al. 1997; Moses et al. 2000b) and SWAS (Bergin et al. 2000), but recent observations by Herschel/HIFI (Hartogh et al. 2011) have revealed that an extended cold water vapour torus exists around Saturn’s equatorial plane due to plume activity on Enceladus. During Saturn’s equinox, the inclination of this torus generates a absorption core in the centre of Saturn’s H2O emission lines originating in the fundamental energy levels (including those at 18.6, 32.9 and 37.1 cm-1 in the SPIRE range, or 557, 987 and 1113 GHz, respectively, Hartogh et al. 2011), which would render them undetectable at the SPIRE spectral resolution. However, lines resulting from transitions between higher energy levels should be unaffected by the Enceladus torus, which was shown to be the case at 36.6 cm-1 (1097 GHz) in the Herschel/HIFI observations. The HIFI results showed a ≈13% line to continuum ratio (Fig. 2 of Hartogh et al. 2011), which is consistent with the SPIRE data (line to continuum level of 1%) when convolved with the appropriate instrument lineshape.
We focussed on the three strongest transitions in the SPIRE range at 36.6 cm-1 (1097 GHz), 38.8 cm-1 (1163 GHz) and 47.1 cm-1 (1411 GHz), but the latter was in a region of poor signal-to-noise so was omitted from further study. Emission from water is indicated at 36.6 and 38.8 cm-1 with a 1σ significance level (Fig. 10). We tested two different vertical H2O distributions: (i) a scaling of the theoretical profile of Moses et al. (2000b) (results are shown in Fig. 10); and (ii) a simpler model which has H2O well mixed above the 0.5-mbar level. Both of these profiles were used to model the SWAS and ISO results (Bergin et al. 2000; Moses et al. 2000b), and we quote mole fractions for the 0.5-mbar level in both cases. For model (i), the 36.6-cm-1 line provides a strict 3σ upper limit of 20 ppb, with a 1σ detection of the line with a mole fraction of 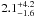 ppb at the 0.5-mbar level. The slightly weaker 38.8-cm-1 line provides a 3σ upper limit of 36.2 ppb, and a 1σ detection of
ppb at the 0.5-mbar level. The slightly weaker 38.8-cm-1 line provides a 3σ upper limit of 36.2 ppb, and a 1σ detection of 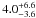 ppb. For reference, the theoretical model of Moses et al. (2000b) had 2.4 ppb at 0.5 mbar, consistent with these SPIRE results. These 1σ detections represent column abundances above 10 mbar of
ppb. For reference, the theoretical model of Moses et al. (2000b) had 2.4 ppb at 0.5 mbar, consistent with these SPIRE results. These 1σ detections represent column abundances above 10 mbar of 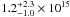 cm2 and
cm2 and 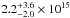 cm2 for the two lines, respectively. These column abundances encompass the (1.4 ± 0.4) × 1015 cm2 range suggested by the ISO/SWS results, and are therefore consistent with the rate of external oxygen influx proposed by Moses et al. (2000b).
cm2 for the two lines, respectively. These column abundances encompass the (1.4 ± 0.4) × 1015 cm2 range suggested by the ISO/SWS results, and are therefore consistent with the rate of external oxygen influx proposed by Moses et al. (2000b).
For the second vertical distribution (well mixed for altitudes above 0.5 mbar), we derive mole fractions of 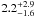 ppb and
ppb and 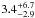 ppb from the 36.6 and 38.8 cm-1 lines, respectively. This is slightly smaller than both the 11 ppb above 0.5-mbar derived from SWAS spectra (Bergin et al. 2000) and the 7 ± 2 ppb from ISO data (Moses et al. 2000b), but given the broad uncertainties on these SPIRE determinations, we conclude that the results are consistent. The two different vertical distributions produced comparable fits to the data and are therefore indistinguishable.
ppb from the 36.6 and 38.8 cm-1 lines, respectively. This is slightly smaller than both the 11 ppb above 0.5-mbar derived from SWAS spectra (Bergin et al. 2000) and the 7 ± 2 ppb from ISO data (Moses et al. 2000b), but given the broad uncertainties on these SPIRE determinations, we conclude that the results are consistent. The two different vertical distributions produced comparable fits to the data and are therefore indistinguishable.
4.3. Carbon monoxide, CO
Externally supplied oxygen molecules are photochemically converted to CO in Saturn’s stratosphere, and the long lifetime of the molecule compared to the Saturnian year means that the CO abundance should be relatively stable over long time periods. Although the SPIRE range encompasses multiple CO transitions, the strongest occurs near 23 cm-1, which provides extremely limited constraints on the stratospheric mole fraction (a 3σ upper limit of 36 ppm above 1 mbar). This stratospheric upper limit is orders of magnitude larger than the stratospheric estimates discussed by Cavalié et al. (2009) (25 ppb above the 15-mbar level), Noll & Larson (1990) and Moses et al. (2000b), so will not be discussed further. Finally, if CO is well mixed (i.e., both an external oxygen supply and transport of CO as a disequilibrium species from the deeper atmosphere), then we find a 3σ upper limit of 7.4 ppb, larger than the 1.0–1.5 ppb range cited by (Moses et al. 2000b) and the 1 ppb estimate of Cavalié et al. (2009). We conclude that SPIRE cannot provide useful upper limits on Saturn’s CO.
4.4. Hydrogen halides
Teanby et al. (2006) reported the best 3σ upper limits for the hydrogen halides to date using far-infrared Cassini/CIRS spectra. The halides are expected to react with NH3 in the troposphere and condense as ammonium salts (e.g., Fegley & Lodders 1994), and so are not expected in the upper troposphere unless strong vertical mixing supplies halides as a disequlibrium species at a rate faster than they can react with NH3. Teanby et al. (2006) estimated upper limits of 8.0 × 10-12, 6.7 × 10-11, 1.3 × 10-10 and 1.4 × 10-9, respectively, for HF, HCl, HBr and HI. The corresponding SPIRE 3σ upper limits are 8.3 × 10-12, 3.8 × 10-11, 1.1 × 10-10 and 3.0 × 10-10 using transitions at 41.1, 20.9, 33.4 and 25.7 cm-1 for HF, HCl, HBr and HI, respectively. The results for HF, HCl and HBr confirm those of Teanby et al. (2006), and support their conclusion that the tentative detection of HCl at 1.1 ppb by Weisstein & Serabyn (1996) is unsupported by the data. We have improved the upper limit on HI by a factor of four because of the excellent low-noise characteristics in this region of the SPIRE spectrum.
An external supply of halide species might be suspected if Enceladus’ plumes contain any proportion of salts (e.g., Postberg et al. 2011), and if those salts could be transported from the rings into Saturn’s upper atmosphere via some mechanism. The SPIRE data provide stratospheric 3σ upper limits of 2.1 × 10-9, 1.3 × 10-7, 1.2 × 10-8 and 2.5 × 10-8 for HF, HCl, HBr and HI, respectively, but no detectable emission lines of any of these four species.
4.5. Methyl chloride, CH3Cl
Showman (2001) described methyl chloride as the best candidate, other than the hydrogen halides, for the transport of chlorine from the deep atmosphere into the troposphere as a disequilibrium species, but suggested that even assuming perfect quenching at equilibrium abundances at the ≈2000-K level, one would not expect mole fractions to exceed 0.01 ppb. The SPIRE data provide access to several transitions between 19–23 cm-1, which provide a 3σ limit of 0.25 ppb in the upper troposphere, an order of magnitude larger than that suggested by the optimistic assumptions of Showman (2001). Finally, photochemical pathways involving CH3 in the stratosphere could recapture exogenically-sourced chlorine, but the SPIRE spectrum limits the mole fraction to 115 ppb above the 1-mbar level.
4.6. Hydrogen cyanide, HCN
On Jupiter, shock-induced chemistry in the aftermath of cometary impacts created substantial perturbations to the composition of the upper atmosphere, generating unusual molecules that persisted for years after the collision (e.g., Moreno et al. 2003). In particular, HCN, CO and CS were important repositories for carbon, oxygen, nitrogen and sulphur in the aftermath of comet Shoemaker-Levy 9 (Lellouch 1996; Harrington et al. 2004). These molecules could also be supplied from external sources such as the rings, satellites or interplanetary dust particles. Alternatively, HCN could be produced in the lower atmosphere, provided a mechanism exists to couple the chemistry of methane and other hydrocarbons to tropospheric ammonia (Moses et al. 2010). This could be due to vertical mixing of HCN thermochemically generated in the deep interior (Lewis & Fegley 1984), or shock chemistry under the extreme environmental conditions of lightning (e.g., Bar-Nun & Podolak 1985), sufficient to dissociate NH3, PH3 and CH4 for the generation of HCN and HCP (see below). The only previously reported estimate of HCN on Saturn comes from Weisstein & Serabyn (1996), who provided 3σ upper limits of 0.1 ppb for well mixed HCN (15 ppb if HCN condensation was accounted for), and a tentative detection of HCN at the 0.4-ppb level from a line at 29.55 cm-1.
SPIRE has access to several lines of HCN, and we choose to focus on the relatively smooth region of the spectrum between 20–24 cm-1. These provide 3σ upper limits of 22 ppb if HCN is restricted to altitudes above the 1-mbar level. However, if we assume HCN is well mixed, we find that the mole fraction cannot exceed 1.6 × 10-11, an order of magnitude smaller than the previous upper limits from Weisstein & Serabyn (1996), and ruling out their 0.4-ppb detection. Unfortunately these upper limits must be improved by another order of magnitude to distinguish between thermochemical and photochemical sources for HCN in Saturn’s atmosphere. This new upper limit may rule out the lightning production postulated by Bar-Nun & Podolak (1985) on Jupiter, but many uncertainties remain as to the production depth and subsequent transport of shock-induced chemical products.
4.7. Methinophosphide, HCP
If shock chemistry were to occur on Saturn, either as the result of cometary impacts or lightning strikes, the substantial presence of PH3 in the upper troposphere could lead to the production of HCP, via the same chemical pathways that link HCN to NH3. Weisstein & Serabyn (1996) deduced an upper limit for well-mixed HCP of 5 ppb, whereas the SPIRE data (with access to several transitions between 20–25 cm-1) provides a 3σ upper limit of 3.3 ppb (well mixed), or 10.3 ppm (using the transition at 22.6 cm-1) if HCP is restricted above the 1-mbar altitude level. However, in the absence of detectable absorption or emission features, we have no evidence of coupled chemistry between CH4 and PH3. The SPIRE results support the conclusion of Weisstein & Serabyn (1996) that the photochemical model of Kaye & Strobel (1984) overestimates the abundance of HCP, which is unsurprising given that the key photolysis regions of CH4 (upper stratosphere) and PH3 (upper troposphere) are well-separated from one another in altitude.
4.8. Carbon monosulphide, CS
CS was also detected in Jupiter’s atmosphere in the aftermath of the SL9 collisions (Lellouch et al. 1995; Moreno et al. 2003), either delivered by the comet or produced by shock chemistry, and can be measured in the sub-millimetre range. Moreno et al. (2003) measured jovian CS in the 4 years after the impact, and then used a diffusion model to predict the depletion of CS in the stratosphere over the ensuing 200 years, with mixing ratios varying between 10-7 and 10-11. No upper limits have been previously determined for Saturn, and SPIRE provides 3σ mole fraction upper limits of 8.9 × 10-11 in the well-mixed case, and 2.5 × 10-7 if CS were restricted to altitudes above 1 mbar (using the 21.2 cm-1 transition). As this is larger than the maximum CS mixing ratio detected in the aftermath of SL9 (May 1995; Moreno et al. 2003), we must await higher spectral resolution observations before meaningful results can be presented.
4.9. Sulphur dioxide, SO2
In the Jupiter system, Io has an SO2 atmosphere and is a source of S and O ions in the plasma torus. Similarly, Saturn’s E-ring torus may contain S ions from the Enceladus plumes (H2S was detected in the plumes by Cassini/INMS, the Ion and Neutral Mass Spectrometer, Waite et al. 2009), and these torii could supply material to the upper atmospheres. However, such a downward flux is considered unlikely (e.g., Showman 2001), and the ultimate fate of stratospheric sulphur is uncertain (e.g., no evidence for SO or SO2 was found in the aftermath of the comet Shoemaker-Levy 9 collisions, despite the expectations of chemical modelling, Harrington et al. 2004). SPIRE places a 3σ upper limit of 1.7 × 10-7 on SO2 in the stratosphere of Saturn, and a well-mixed upper limit of 0.25 ppb. These limits on oxidised sulphur should be compared to similar estimates for Jupiter to investigate the coupling between the central planet and its icy moons.
4.10. Hydrogen sulphide, H2S
H2S is not expected to be present in the upper tropospheres of Jupiter and Saturn due to the a reaction with ammonia to form solid NH4SH aerosols, a predicted (but not yet observed) cloud deck in the deeper atmosphere (around the 4- to 6-bar level for Saturn, Atreya & Wong 2005). Furthermore, H2S would be further depleted by photolysis if it were able to penetrate into the upper troposphere as a disequilibrium species. Thus, it is unsurprising that sub-millimetre searches (including SPIRE) have failed to detect this sulphur-bearing compound. SPIRE provides access to rotational transitions that should be visible in the 21–25 cm-1 spectral region (between two PH3 lines); as well as unobstructed lines at 39.9 cm-1 (between the NH3 doublet features) and 42.7 cm-1. Assuming that H2S is well mixed throughout the troposphere, these three regions provide a 3σ upper limit of 0.36 ppb, improving over the previous 16 ppb upper limit of Weisstein & Serabyn (1996) by an order of magnitude. Furthermore, a stratosphere-only model for H2S places 3σ upper limit of 230 ppb using the transition near 39.9 cm-1. This absence of detectable H2S is consistent with depletion via some mechanism (solid NH4SH formation, for example) in the deeper troposphere.
4.11. Methanol, CH3OH, and formaldehyde, H2CO
Methanol (CH3OH) was considered as one of the most abundant stable oxygen compounds in Saturn’s stratosphere in the photochemical model of Moses et al. (2000b), but no previous upper limits on this molecule have been provided. 23% of the methanol came from meteoritic ablation in the model, the remaining 77% was produced photochemically in Saturn’s upper atmosphere by the reactions of OH with CH3. Methanol would then condense at the cold temperatures of the tropopause. The SPIRE data place a 3σ upper limit of 113 ppb on methanol in the stratosphere (0.3 ppb if well mixed) using features near 21 cm-1, larger than the ≈ 30 ppb maximum stratospheric mole fraction from the models of Moses et al. (2000b). At present, these upper limits are consistent with the photochemical modelling, but are insufficient to distinguish between the different oxygen supply mechanisms (e.g., entirely as H2O, entirely as CO2, or a mixture of both).
Formaldehyde (H2CO) was also a product of the photochemistry in Moses et al. (2000b), due to (i) the reaction of exogenically-supplied CO with atomic H in Saturn’s atmosphere; and (ii) the reaction of H2O with CH3, with a peak mixing ratio of 2 × 10-10. Using a series of transitions between 21–23 cm-1 that should be visible in the SPIRE data, we place a 3σ limit of 56 ppb in Saturn’s stratosphere (6.5 × 10-11 if H2CO were well mixed), two orders of magnitude larger than that predicted by the model. At the present time, neither the methanol nor the formaldehyde upper limits are sufficient to constrain the photochemistry of oxygen molecules in Saturn’s upper atmosphere.
5. Discussion and conclusions
The Herschel/SPIRE instrument combines a broad sub-millimetre range (15–51 cm-1, 194–671 μm, or 447–1550 GHz) with a 0.048 cm-1 resolving power (an order of magnitude improvement over Cassini observations at the same wavelength) to produce an extensive new survey of Saturn’s sub-millimetre spectrum. While the spectral resolution may not compete with some ground-based facilities, the consistently stable calibration and the absence of telluric contamination (most of the SPIRE range is unobservable from the ground) allows us to re-evaluate upper limits on a host of different species in the gas giant’s upper troposphere and stratosphere. Table 1 summarises these new 3σ upper limits, and allows us to draw the following conclusions:
-
1.
Temperatures: Saturn’s upper tropospheric temperaturesbetween 220–780 mbar were retrieved from thedisc-averaged spectrum and show some morphologicaldifferences compared to the global average from Cassini(Fletcher et al. 2010). Thetropopause region appears quasi isothermal between 60 and300 mbar, characteristic of Saturn’s coolequatorial zone.
-
2.
Phosphine: four rotational lines of PH3 dominate the SPIRE spectrum and were used to demonstrate that PH3 begins to be depleted by photolysis above the 570-mbar level, and is well mixed at
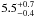 ppm at higher pressures. PH3 must be present up to the 80- to 100-mbar level, but the absence of emission cores rules out its presence above the 10- to 20-mbar level.
ppm at higher pressures. PH3 must be present up to the 80- to 100-mbar level, but the absence of emission cores rules out its presence above the 10- to 20-mbar level. -
3.
Ammonia: the SPIRE data are best reproduced with an NH3 mole fraction of
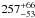 ppb at 660 mbar, and a vertical profile following a vapour pressure distribution in the upper troposphere. The data are insensitive to the deep well-mixed NH3 below the condensation region. Although our best-fit T(p) profile suggests supersaturated conditions, we find that small 2–3 K changes in temperature (tolerated within the ± 5% uncertainty on the absolute calibration) can produce subsaturated conditions, so no meaningful estimates of the relative humidity can be extracted from the SPIRE data.
ppb at 660 mbar, and a vertical profile following a vapour pressure distribution in the upper troposphere. The data are insensitive to the deep well-mixed NH3 below the condensation region. Although our best-fit T(p) profile suggests supersaturated conditions, we find that small 2–3 K changes in temperature (tolerated within the ± 5% uncertainty on the absolute calibration) can produce subsaturated conditions, so no meaningful estimates of the relative humidity can be extracted from the SPIRE data. -
4.
Methane: CH4 at 41.9 cm-1 was used to test our line-by-line technique for estimating the abundances of trace gases in Saturn’s atmosphere. Using two different sources for the rotational line intensities, SPIRE produced 1σ estimates of the mole fraction of (4.3 ± 0.3) × 10-3 using the compilation of Brown et al. (2003) with the dipole measurements of Wishnow et al. (2007); and a mole fraction of (4.8 ± 0.3) × 10-3 with the compilation of Boudon et al. (2010). These results are broadly consistent with the results from Cassini far-infrared observations (Flasar et al. 2005; Fletcher et al. 2009b) and with the enrichment of carbon in Saturn compared to Jupiter.
-
5.
Hydrogen sulphide: SPIRE provides an order-of-magnitude improvement on previous upper limits on tropospheric H2S, supporting the conclusion that H2S is severely depleted by reaction with NH3 to produce solid NH4SH in the deeper atmosphere.
-
6.
Halogen species: upper limits on the hydrogen halides HF, HCl, HBr and HI are all consistent with those of (Teanby et al. 2006), and the upper limit on HI is improved by a factor of four. These results confirm the suggestion that halides are effectively removed in the deeper troposphere by condensation as ammonium salts. Stratospheric upper limits may be used to place constraints on the influx of halides from external reservoirs (e.g., salty water in the Enceladus torus). Furthermore, we provide the first upper limit on methyl chloride, another potential transporter of chlorine upward from the deep atmosphere.
-
7.
External oxygen species: The SPIRE data are consistent with the presence of stratospheric H2O emission lines at 36.6 and 38.8 cm-1 at the 1σ significance level. A H2O mole fraction of
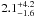 ppb at 0.5 mbar was derived from the strongest line by scaling the photochemical profile of Moses et al. (2000b), equivalent to a column abundance of
ppb at 0.5 mbar was derived from the strongest line by scaling the photochemical profile of Moses et al. (2000b), equivalent to a column abundance of 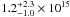 cm2. This estimate is consistent with ISO and SWAS measurements from a decade earlier (Bergin et al. 2000; Moses et al. 2000b), showing the relative stability of Saturn’s stratospheric oxygen flux. SPIRE was unable to provide improved upper limits on CO compared to ground-based observations (e.g., Cavalié et al. 2009), but we were able to provide the first upper limits on other potential oxygen compounds in the stratosphere, including SO2, methanol and formaldehyde. Upper limits on the latter two species are consistent with the expectations of photochemical modelling (Moses et al. 2000b), but they must be improved before they can properly constrain these models.
cm2. This estimate is consistent with ISO and SWAS measurements from a decade earlier (Bergin et al. 2000; Moses et al. 2000b), showing the relative stability of Saturn’s stratospheric oxygen flux. SPIRE was unable to provide improved upper limits on CO compared to ground-based observations (e.g., Cavalié et al. 2009), but we were able to provide the first upper limits on other potential oxygen compounds in the stratosphere, including SO2, methanol and formaldehyde. Upper limits on the latter two species are consistent with the expectations of photochemical modelling (Moses et al. 2000b), but they must be improved before they can properly constrain these models. -
8.
Shock-chemical products: shock-induced chemistry during high-energy processes (asteroidal or cometary impacts; lightning strikes) can couple the chemistry of methane with other trace gases in Saturn’s atmosphere, producing products like HCN, HCP and CS. SPIRE has improved the upper limit on HCN by an order of magnitude, ruling out the tentative detection of this molecule by Weisstein & Serabyn (1996). Our upper limit on HCP supports the conclusion that existing photochemical models (Kaye & Strobel 1984) overestimate the abundance of this molecule. Finally, we provide the first upper limit on the abundance of CS, but this is not currently useful for constraining the rate of impact events in Saturn’s upper atmosphere.
The SPIRE data allow us to close the gap between observational upper limits and theoretical predictions (photochemistry, thermochemistry and vertical transport), but it is clear that further progress requires a reduction of the uncertainties on the sub-millimetre spectrum. This will need both enhanced stability (i.e., reducing instrument-related oscillations on the continuum) and a higher spectral resolution, possibly using heterodyne techniques. But we must also understand the continuum offsets apparent in our Saturn modelling, and the potential for contributions from aerosols or poorly-characterised line wings that may corrupt our interpretation. Nevertheless, the quality of the SPIRE spectrum in Fig. 1 places it among the best sub-millimetre spectra of PH3, NH3 and CH4 observed on a giant planet to date.
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Acknowledgments
SPIRE has been developed by a consortium of institutes led by Cardiff University (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC and UKSA (UK); and NASA (USA). Fletcher was supported during this research by a Glasstone Science Fellowship at the University of Oxford. Cavalié acknowledges for funding from the Centre National d’Études Spatiales (CNES). We thank C. Ferrari for her assistance with the calculation of Saturn’s ring emission spectrum; P. Irwin for the use of the radiative transfer and retrieval codes; and L. Brown and J. Hurley for discussion of Saturn’s ammonia distribution. Orton conducted a portion of this research at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA.
References
- Atreya, S. K. 1986, Phys. Chem. Space, 15, in Atmospheres and Ionospheres of the Outer Planets and their Satellites (Berlin: Springer-Verlag Heidelberg) [Google Scholar]
- Atreya, S. K., & Wong, A.-S. 2005, Space Sci. Rev., 116, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Atreya, S. K., Wong, M. H., Owen, T. C., et al. 1999, Planet & Space Sci., 47, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Bar-Nun, A., & Podolak, M. 1985, Icarus, 64, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Lellouch, E., Harwit, M., et al. 2000, ApJ, 539, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Birnbaum, G., Buechele, A., Jiang, T., et al. 2000, J. Quant. Spectrosc. Radiat. Transf., 64, 661 [CrossRef] [Google Scholar]
- Borysow, A. 1991, Icarus, 92, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A. 1993, Icarus, 106, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., & Frommhold, L. 1986, ApJ, 304, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., & Frommhold, L. 1987, ApJ, 318, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, J., Frommhold, L., & Birnbaum, G. 1988, ApJ, 326, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Boudon, V., Pirali, O., Roy, P., et al. 2010, J. Quant. Spec. Radiat. Transf., 111, 1117 [Google Scholar]
- Briggs, F. H., & Sackett, P. D. 1989, Icarus, 80, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, L. R., & Peterson, D. B. 1994, J. Mol. Spectr., 168, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, L. R., Benner, D. C., Champion, J. P., et al. 2003, J. Quant. Spectr. Radiat. Transf., 82, 219 [Google Scholar]
- Cavalié, T., Billebaud, F., Fouchet, T., et al. 2008, A&A, 484, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavalié, T., Billebaud, F., Dobrijevic, M., et al. 2009, Icarus, 203, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Cavalié, T., Hartogh, P., Billebaud, F., et al. 2010, A&A, 510, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colwell, J. E., Esposito, L. W., Jerousek, R. G., et al. 2010, AJ, 140, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Conrath, B. J., & Gautier, D. 2000, Icarus, 144, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Courtin, R., Gautier, D., Marten, A., Bézard, B., & Hanel, R. 1984, ApJ, 287, 899 [NASA ADS] [CrossRef] [Google Scholar]
- de Graauw, T., Feuchtgruber, H., Bézard, B., et al. 1997, A&A, 321, L13 [NASA ADS] [Google Scholar]
- Fegley, B. J., & Lodders, K. 1994, Icarus, 110, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Feuchtgruber, H., Lellouch, E., de Graauw, T., et al. 1997, Nature, 389, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Flandes, A., Spilker, L., Morishima, R., et al. 2010, Planet. Space Sci., 58, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Flasar, F. M., Achterberg, R. K., Conrath, B. J., et al. 2005, Science, 307, 1247 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fletcher, L. N., Irwin, P. G. J., Teanby, N. A., et al. 2007a, Icarus, 188, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Irwin, P. G. J., Teanby, N. A., et al. 2007b, Icarus, 189, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Orton, G. S., Teanby, N. A., & Irwin, P. G. J. 2009a, Icarus, 202, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Orton, G. S., Teanby, N. A., Irwin, P. G. J., & Bjoraker, G. L. 2009b, Icarus, 199, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Achterberg, R. K., Greathouse, T. K., et al. 2010, Icarus, 208, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Baines, K. H., Momary, T. W., et al. 2011, Icarus, 214, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchet, T., Moses, J. I., & Conrath, B. J. 2009, Saturn: Composition and Chemistry, in Saturn from Cassini-Huygens, ed. M. K. Dougherty, L. W. Esposito, & S. M. Krimigis, 83 [Google Scholar]
- Fray, N., & Schmitt, B. 2009, Planet. Space Sci., 57, 2053 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, T. R., Naylor, D. A., Baluteau, J.-P., et al. 2008, in SPIE Conf. Ser., 7010 [Google Scholar]
- Fulton, T. R., Baluteau, J.-P., Bendo, G., et al. 2010, in SPIE Conf. Ser., 7731 [Google Scholar]
- Goody, R. M., & Yung, Y. L. 1989a, in Atmospheric radiation: theoretical basis ed. R. M. Goody, & Y. L. Yung, 2nd edn. (New York, NY: Oxford University Press) [Google Scholar]
- Goody, R., West, R., Chen, L., & Crisp, D. 1989b, J. Quant. Spect. Radiat. Transf., 42, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Griffin, M. J., & Orton, G. S. 1993, Icarus, 105, 537 [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Harrington, J., de Pater, I., Brecht, S. H., et al. 2004, Lessons from Shoemaker-Levy 9 about Jupiter and planetary impacts (New York: Cambridge Planetary Science, Cambridge Univ. Press), 159 [Google Scholar]
- Hartogh, P., Lellouch, E., Moreno, R., et al. 2011, A&A, 532, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, P. J. G., Calcutt, S. B., & Taylor, F. W. 1997, Adv. Space Res., 19, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, P., Teanby, N., de Kok, R., et al. 2008, J. Quant. Spectrosc. Radiat. Transf., 109, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Karwat, E. 1924, Z. Phys. Chem., 112, 486 [Google Scholar]
- Kaye, G. W. C., & Laby, T. H. 1995, Tables of physical and chemical constants, ed. G. W. C. Kaye, & T. H. Laby [Google Scholar]
- Kaye, J. A., & Strobel, D. F. 1984, Icarus, 59, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Kleiner, I., Tarrago, G., Cottaz, C., et al. 2003, J. Quant. Spectr. Rad. Transf., 82, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Kogelnik, H., & Li, T. 1966, Appl. Opt., 5, 1550 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lellouch, E. 1996, in The Collision of Comet Shoemaker-Levy 9 and Jupiter, ed. K. S. Noll, H. A. Weaver, & P. D. Feldman, IAU Colloq. 156, 213 [Google Scholar]
- Lellouch, E., Paubert, G., Moreno, R., et al. 1995, Nature, 373, 592 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Levy, A., Lacome, N., & Tarrago, G. 1993, J. Mol. Spectrosc., 157, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, J. S., & Fegley, Jr., M. B. 1984, Space Sci. Rev., 39, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Lide, D. R. 1995, CRC Handbook of chemistry and physics, A ready-reference book of chemical and physical data (Boca Raton: CRC Press), 76th edn., ed. D. R. Lide [Google Scholar]
- Lindal, G. 1992, AJ, 103, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Margolis, J. S. 1993, J. Quant. Spectrsc. Rad. Transf., 50, 431 [Google Scholar]
- Martin, D. H., & Bowen, J. W. 1993, IEEE Transactions on Microwave Theory Techniques, 41, 1676 [Google Scholar]
- Moreno, R., Marten, A., Matthews, H. E., & Biraud, Y. 2003, Planet. Space Sci., 51, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J. I., Bézard, B., Lellouch, E., et al. 2000a, Icarus, 143, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J. I., Lellouch, E., Bézard, B., et al. 2000b, Icarus, 145, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J. I., Visscher, C., Keane, T. C., & Sperier, A. 2010, Faraday Discussions, 147, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, K. S., & Larson, H. P. 1990, Icarus, 89, 168 [Google Scholar]
- Orton, G. S., Serabyn, E., & Lee, Y. T. 2000, Icarus, 146, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Orton, G. S., Serabyn, E., & Lee, Y. T. 2001, Icarus, 149, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Orton, G., Fletcher, L., Mousis, O., et al. 2010, in EGU General Assembly Conference Abstracts, 12, 2541 [Google Scholar]
- Owen, T., & Encrenaz, T. 2006, Planet. Space Sci., 54, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Padman, R., & Murphy, J. A. 1991, Infr. Phys., 31, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectrsc. Radiat. Transf., 60, 883 [Google Scholar]
- Postberg, F., Schmidt, J., Hillier, J., Kempf, S., & Srama, R. 2011, Nature, 474, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1992, Numerical Recipes, 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spectrsc. Radiat. Transf., 96, 139 [Google Scholar]
- Showman, A. P. 2001, Icarus, 152, 140 [NASA ADS] [CrossRef] [Google Scholar]
- SPIRE Observers Manual 2011, HERSCHEL-HSC-DOC-0798, v2.4 edn., Herschel Science Centre, http://herschel.esac.esa.int/Documentation.shtml [Google Scholar]
- Swinyard, B. M., Dohlen, K., Ferand, D., et al. 2003, in SPIE Conf. Ser. 4850, ed. J. C. Mather, 698 [Google Scholar]
- Swinyard, B. M., Ade, P., Baluteau, J.-P., et al. 2010a, A&A, 518, L4 [Google Scholar]
- Swinyard, B. M., Hartogh, P., Sidher, S., et al. 2010b, A&A, 518, L151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teanby, N. 2007, Math. Geol., 39, 419 [CrossRef] [MathSciNet] [Google Scholar]
- Teanby, N. A., Fletcher, L. N., Irwin, P. G. J., Fouchet, T., & Orton, G. S. 2006, Icarus, 185, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Waite, Jr., J. H., Lewis, W. S., Magee, B. A., et al. 2009, Nature, 460, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Weisstein, E. W., & Serabyn, E. 1994, Icarus, 109, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Weisstein, E. W., & Serabyn, E. 1996, Icarus, 123, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Wishnow, E. H., Orton, G. S., Ozier, I., & Gush, H. P. 2007, J. Quant. Spectrosc. Radiat. Transf., 103, 102 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Saturn’s sub-millimetre spectrum measured by Herschel/SPIRE in 2010. The spectrum consists of a long-wave channel (14–32 cm-1) and a short-wave channel (32–52 cm-1). Raw flux units of Janskys are shown in panel a); these are converted into radiance units in b) and to brightness temperatures in c), approximately represent the atmospheric temperature at the line-forming region. Key features of the spectrum – PH3, NH3 and CH4 – are labelled in c). |
| In the text | |
 |
Fig. 2 Observational geometry of Saturn from Herschel, and estimations of the contribution of Saturn’s rings to the disc-averaged spectrum. Panel a) shows the size of the planet in arcseconds and the small ring-opening angle as Saturn’s northern hemisphere passed the spring equinox. The SPIRE FWHM at 50 cm-1 is shown as the dotted line close to Saturn’s limb. The size of the SPIRE beam width is compared to the width of Saturn and the A, B and C rings in panel b). The fractional area of the SPIRE beam occupied by each of the rings is given in panel c), and was used to calculate the contribution of ring emission and absorption to the spectrum as a fraction of the total signal in d). Contributions smaller than 2% are within the estimated uncertainties on the SPIRE data. |
| In the text | |
 |
Fig. 3 Optimal estimation fitting of the SPIRE continuum using a retrieval algorithm (Irwin et al. 2008). Data are shown as black circles, the fit is the continuous line. Radiances in panel a) are converted to brightness temperatures in b), and the residual (black dots) is shown in panel c). The dotted line in c) shows the radiance uncertainty on the SPIRE data, the dashed line shows the zero line. |
| In the text | |
 |
Fig. 4 Functional derivatives (rate of change of radiance with respect to the model parameter) for the four major contributors to the sub-millimetre spectrum. Figures have been normalised, and each contour represents a change of 0.1. A scale bar is provided in panel c). |
| In the text | |
 |
Fig. 5 Retrieved vertical profiles for temperature, PH3 and NH3 in the best-fitting case. The solid line shows the retrieved profile, the dotted line is the uncertainty on the retrieval, estimated by applying a 5% shift in the measured radiances (the absolute calibration uncertainty) and redoing the calculation. The dashed line in the temperature plot a) is a global mean of the T(p) profiles retrieved from the Cassini/CIRS far-infrared focal plane between 2004 and 2008. The dot-dashed grey lines in a) and b) are temperature and PH3 retrievals based on extreme estimates of the calibration uncertainty of ±15%. The NH3 profile in c) was estimated by scaling the saturated vapour pressure profile (see Fig. 8), so the uncertainties are the same at all altitudes. The grey dashed line in c) is the saturated vapour pressure curve of NH3 assuming a relative humidity of 100%, the dot-dashed grey line use the temperature profiles given by the dotted lines in a). The uncertainty in the saturated mole fraction is greater than the uncertainty on the retrieved abundances of NH3. |
| In the text | |
 |
Fig. 6 Testing the sensitivity to the pressure knee of the PH3 vertical distribution. The pressure levels (in mbar) are given by the key in the top left corner, but the differences between these curves is hard to distinguish in the top four panels, showing the difficulty we face in trying to constrain the pressure knee from these data. The χ2 / N distributions in the bottom panels show convergence on the 500–650 mbar range. The χ2 estimates do not include the spurious emission peaks from the models (see main text and Fig. 7). The best fitting pressure knee, deep mole fraction and fractional scale height are provided in the lower panels. |
| In the text | |
 |
Fig. 7 The high spectral resolution of SPIRE is used to place limits on the presence of PH3 in Saturn’s stratosphere. Using the best-fitting parameterised profiles from Fig. 6, we apply upper-level cutoffs between 1 mbar and 300 mbar and test the change in χ2. The upper panels show the data (points) compared to models with high-altitude cut offs at different pressure levels (key shown in mbar in the upper left panel). The lower panels show Δχ2 for the variable cutoff pressure with 1σ and 3σ confidence limits as the dotted horizontal lines. |
| In the text | |
 |
Fig. 8 Determining the most plausible fit for the NH3 doublet. The vertical profile is parameterised in terms of a degree of saturation (panel a), with relative humidities given as percentages in the key, based on the best-fitting T(p)), an upper-level cut off (panel c), with pressures between 250–860 mbar given in the key) and a deep mole fraction (panel d)), with mole fractions given in ppm in the key). Of the three parameters, the only way to increase the depth of the absorption features to match the SPIRE data (black circles) is to increase the relative humidity (panel a)). The models in c) and d) do not match the data because they assume a relative humidity of 100%. The Δχ2 for each value of the relative humidity is evaluated for data between the two dotted vertical lines in panel a (i.e., avoiding artefacts in the data near 41.5 cm-1) and displayed in panel b). The best-fit mole fraction at 660 mbar plus the 3σ uncertainty is shown in panel b). |
| In the text | |
 |
Fig. 9 Testing the line-by-line forward model by fitting the CH4 rotational line. The left hand panel shows the brightness temperatures, with the data given by circles, the smooth spline-fit to the continuum as the dotted line, and the solid grey lines showing the range of mole fractions tested. The central panel converts this to a line-to-continuum ratio relative to the smooth spline. Here, the dotted lines show the error envelope as defined in the main text. The right hand panel shows the Δχ2 for the model, with dotted horizontal lines showing the 1σ and 3σ confidence limits on the results. The derived methane abundance depends upon the choice of line data, with a mole fraction of (4.3 ± 0.3) × 10-3 assuming line intensities from Wishnow et al. (2007) (shown here) and (4.8 ± 0.3) × 10-3 using intensities from Boudon et al. (2010). |
| In the text | |
 |
Fig. 10 Marginal detection of two emission features of H2O at 36.6 and 38.8 cm-1 (1097 and 1163 GHz, respectively). The best-fitting mole fractions are |
| In the text | |
 |
Fig. 11 Derivations of upper limits on Saturn’s trace gases in the well-mixed case. For all thirteen gases, the left panel shows the line to continuum ratio in the data (circles) compared to a number of models (grey solid lines), and the right panel shows the degradation of the χ2 parameter as we increase the mole fraction. Dashed lines show the 1σ and 3σ confidence limits. For some species we show only the line which provided the best constraints on the upper limit. |
| In the text | |
 |
Fig. 12 Derivations of upper limits on Saturn’s trace gases for the case where they are restricted to stratospheric altitudes (p < 1 mbar). For all thirteen gases, the left panel shows the line to continuum ratio in the data (circles) compared to a number of models (grey solid lines), and the right panel shows the degradation of the χ2 parameter as we increase the mole fraction. Dashed lines show the 1σ and 3σ confidence limits. For some species we show only the line which provided the best constraints on the upper limit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.