EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 630 (October 2019) A&A, 630 (2019) A87 Full HTML
Open Access
Issue
A&A
Volume 630, October 2019
Article Number A87
Number of page(s) 15
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201935954
Published online 26 September 2019

© T. Cavalié et al. 2019

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

The interiors of giant planets are supposedly rich in oxygen (Owen & Encrenaz 2003; Gautier et al. 2001; Hersant et al. 2004). In the deep hot layers, where thermochemical equilibrium prevails, H2O is the most abundant oxygen species. Oxygen species are transported from deep down toward higher levels, but only CO (and CO2 in Jupiter and Saturn) can reach the stratosphere because of the tropopause cold trap (Lodders & Fegley 1994; Wang et al. 2015; Cavalié et al. 2017). H2O was thus only observed in the tropospheric saturation layers of Jupiter and Saturn (Larson et al. 1975; de Graauw et al. 1997). The detection of oxygen species (H2O, CO, and CO2) in the stratospheres of the giant planets and Titan (Feuchtgruber et al. 1997; Bézard et al. 2002; Lellouch et al. 2002; Coustenis et al. 1998; Samuelson et al. 1983; Noll et al. 1986; Marten et al. 1993; Burgdorf et al. 2006) thus demonstrated that the upper atmospheres of the giant planets are contaminated by external sources from their close and/or more distant environments.

While oxygen-rich interplanetary dust particles (IDP) produced from asteroid collisions and comet activity are a ubiquitous source (Landgraf et al. 2002; Poppe 2016), these particles seem to be the main H2O source only at Uranus and Neptune (Moses & Poppe 2017) and the emerging overall picture however looks more complex. Other sources can actually be at work such as local sources from planetary icy environments (rings and satellites) (Strobel & Yung 1979; Connerney 1986; Prangé et al. 2006; Waite et al. 2018; Mitchell et al. 2018; Hsu et al. 2018) or “Shoemaker-Levy 9” (SL9) type cometary impacts (Lellouch et al. 1995). In Jupiter’s stratosphere, H2O, CO, and CO2 come from SL9 comet fragments (Bézard et al. 2002; Lellouch et al. 2002, 2006; Cavalié et al. 2008a, 2012, 2013). An older comet-impact component was even proposed as the source of the lower stratospheric CO (Bézard et al. 2002), even if IDP are another option (Moses & Poppe 2017). Comets are also the probable source of CO beyond Jupiter (see review in Mandt et al. 2015 and Moses & Poppe 2017), as seen in Saturn (Cavalié et al. 2009, 2010), Uranus (Cavalié et al. 2014), and Neptune (Lellouch et al. 2005, 2010; Luszcz-Cook & de Pater 2013; Moreno et al. 2017).

In Saturn, neither the Infrared Space Observatory (ISO) nor the Submillimeter Wave Astronomy Satellite (SWAS) disk-averaged observations (Feuchtgruber et al. 1997; Bergin et al. 2000) had sufficient spectral resolutions or high enough signal-to-noise ratios (S/N) to identify the source of external H2O. A comet impact is probably not the cause of the observed stratospheric H2O (Moses & Poppe 2017) because of the contradiction between the relatively ancient impacts required to fit the CO observations of Cavalié et al. (2010) and the relatively short diffusion timescale from the deposition level of cometary material in such impacts (Lellouch et al. 1995; Moreno et al. 2003) down to the H2O condensation level (Ollivier et al. 2000; Moses et al. 2000, 2005), which is located between the 1 and a few millibar altitude levels, depending on the latitude. In addition, the H2O/CO in Saturn’s stratosphere (~0.15 – Moses & Poppe 2017) is too large to be characteristic of a cometary impact that delivers mostly CO (H2O/CO < 0.01 in Neptune). This tends to indicate a source that is steadier than a discrete comet impact. Previous observations of Saturn with the Herschel-Heterodyne Instrument for the Far Infrared (HIFI) led to the detection of an H2O torus at the orbit of Enceladus (Hartogh et al. 2011), which is fed by the plumes of this moon (Hansen et al. 2006; Porco et al. 2006; Waite et al. 2006). The fate of H2O from this torus is eventually to spread in Saturn’s system (Cassidy & Johnson 2010) and a fraction is predicted to fall into Saturn’s stratosphere with a distribution centered around the equator. Based on these models, and in comparison with the Herschel observations, Hartogh et al. (2011) tentatively concluded that Enceladus was the source of Saturn’s stratospheric water. It should be noted that a fraction is also expected to feed Titan’s atmosphere as well, and models show that the flux expected at Titan and originating from the Enceladus water torus could explain the observations (Moreno et al. 2012; Lara et al. 2014; Dobrijevic et al. 2014; Rengel et al. 2014; Hickson et al. 2014).

Recent in situ measurements of Cassini during the proximal orbits of its end-of-mission demonstrated the existence of a flux of material from the rings to Saturn’s atmosphere. The Magnetospheric Imaging Instrument (MIMI), the Ion and Neutral Mass Spectrometer (INMS), and the Cosmic Dust Analyzer (CDA) instruments have measured an infall of material originating from the D-ring: (i) neutral icy grains within 2° around the equator, (ii) various gases including H2O (concentrated at the 24% level) in a latitudinal band of 8° centered on the equator (Waite et al. 2018), (iii) and charged grains transported to higher latitudes along the magnetic field lines (Mitchell et al. 2018; Hsu et al. 2018). This latter phenomenon is the long anticipated ring rain phenomenon (Connerney & Waite 1984; Connerney 1986; Prangé et al. 2006; Moore et al. 2010, 2015; O’Donoghue et al. 2017). The mass flux of infalling dust and gas are estimated to be ~5 kg s−1 (Mitchell et al. 2018) and ~ 104 kg s−1 (Waite et al. 2018; Perry et al. 2018), respectively. The sources that can explain the presence of H2O in Saturn’s stratosphere are thus in principle IDP, Enceladus plumes, and Saturn’s rings.

Disentangling the various sources of externally supplied water in giant planet stratospheres, and thus in Saturn, was a key objective of the Herschel key program Herschel Solar System Observations (HssO) (Hartogh et al. 2009). In Sect. 2 of this paper, we present the first disk-resolved mapping observations of H2O in Saturn’s stratosphere and a disk-averaged observation obtained with the Photodetector Array Camera and Spectrometer (PACS) (Poglitsch et al. 2010) and HIFI (de Graauw et al. 2010), respectively; these two instruments were on board the ESA Herschel Space Observatory (Pilbratt et al. 2010). Using a combination of models presented in Sect. 3, we derive the H2O meridional distribution in Saturn’s stratosphere in Sect. 4. We discuss its origin according to our results in Sect. 5 and give our conclusion in Sect. 6.

2 Observations

In Table 1, we present a summary of the observations of Saturn’s stratospheric H2O performed with Herschel-PACS and Herschel-HIFI. We also add the relevant geometry of Saturn, as obtained from the Jet Propulsion Laboratory/Horizons database. In the following sections, we detail the observations and the data reduction.

2.1 PACS observations

We observed Saturn with Herschel-PACS in the framework of the HssO Key Program on January 2, 2011 with the aim of mapping the distribution of H2O in the stratosphere of the planet. We used PACS in its line spectrometry mode (Poglitsch et al. 2010). The integral field spectrometer consists of 5 × 5 spatial pixels (~50′′ × 50′′ on sky), each covering a short instantaneous wavelength range sampled by 16 spectral pixels. Our observation of Saturn consists of a 3 × 3 raster map with 3′′ separation at 66.44 μm. We thus pointed the 25 pixel array over nine different positions to record an oversampled 225 point map of Saturn at 66.44 μm. For the observation of such an intense far-infrared continuum source, we had to use a nonstandard mode, in which the spectrometer readout electronics were configured to the shortest possible reset intervals of 1/32 s, to avoid detector saturation. The half-power beam width (HPBW) of Herschel is 9.4′′ for the PACS observations, which results in covering latitudes from − 23° to 45° for a beam centered on the planet. The spectralresolving power is ~2500–3000.

We ran the basic data reduction with the Herschel Interactive Processing Environment 8.0 (HIPE; Ott 2010) and performed additional processing (flat-fielding, outlier removal, and rebinning) with standard Interactive Data Language (IDL) tools. An example of raw spectra for one of the raster positions of the map in presented in Fig. 1. The 225 spectra corresponding to all raster positions of the map can be found in Fig. A.1. After subtracting the coordinates of Saturn given by the JPL/Horizon ephemeris, we found from the continuum distribution that the map has a residual pointing offset of 2.5′′ in RA and 0.3′′ in dec. The position of the line peak presents some scatter, which results from a combination of two effects: a Doppler shift caused by the rapid rotation of the planet and wavelength shifts induced by the nonuniform illumination of the instrument slit on some of the raster positions (Poglitsch et al. 2010). A baseline, caused by standing waves excited by the strong continuum emission of the planet in the instrument, was then removed from the raw spectra by fitting a polynomial. This step introduces on average a 10–15% uncertainty on the line amplitude. The H2O line is detected in all positions within the disk and on positions within ~one beam from the planetary limb. For the reasons detailed in Cavalié et al. (2013), reasonable uncertainties cannot be achieved on an absolute flux calibration and we have to express the spectra in terms of line-to-continuum ratio (l∕c) to cancel out the absolute response. In addition, the line width is purely instrumental (and Gaussian) and can vary from one position to another because of varying beam filling factors on the detector array. Therefore, the map must be analyzed in terms of line area. We fit the lines with a Gaussian and computed their area from the Gaussian fit parameters. According to the noise on the line peak intensity and line width, we estimated that the line area map can be safely analyzed forpositions within the planetary disk or in the vicinity of the limb (see Fig. 2). We found a 1σ rms of 0.0023 (in units of microns × % of the continuum) when adding quadratically the baseline removal uncertainty and the spectral noise. We used this value in our χ2 ∕N calculations (N is the number of pixels in the map). The resulting continuum and line-area maps are presented in Fig. 2. The average S/N around the limb, i.e., where the lines have the biggest contrast1, is ~15–45 on the line area. There is enhanced emission at low latitudes with respect to mid to high latitudes, and a local minimum around the north pole. This enables us to demonstrate the difference in water emission between the poles and equatorial region despite the limited spatial resolution.

Table 1

Summary of the Herschel-PACS and Herschel-HIFI observations of Saturn and the relevant observation geometry.

thumbnail Fig. 1

Twenty-five raw spectra obtained with the PACS 5 × 5 detector array and extracted from one of the 3 × 3 raster map positions on Saturn at 66.44 μm. The H2O line is detected in all spectra corresponding to pointings on the planetary disk or close to the planetary limb. Spectra without an H2O line correspond to pointings far off the planetary limb. Before fitting the lines with a Gaussian to compute their area, a polynomial baseline was removed from these spectra. The line peak S/N around the limb is ~15–45.

2.2 HIFI observations

In addition, and in an attempt to check the PACS results at the planetary scale, we used the disk-averaged observation of Saturn conducted with the HIFI instrument (de Graauw et al. 2010) at 1097 GHz on December 31, 2010 using a dual beam-switch mode (Roelfsema et al. 2012), which facilitates pointing to the deep sky for calibration by moving the secondary mirror instead of the primary. We chose this strong H2O line because it is not affected by Enceladus torus absorption. This absorption is seen only in lines, such as those at 557 and 1113 GHz (Hartogh et al. 2011), which have a lower state energy relative to the ground state (23.7944 and 0.0 cm−1, respectively); the lower state energy of the 1097 GHz line is 136.7617 cm−1. Given that the Herschel HPBW is 19.3′′ (i.e., bigger than Saturn) and the spectral resolution of the Wide Band Spectrometer (WBS) is 1.1 MHz, the line appears smeared because of the fast rotation of Saturn (9.9 km s−1 at the equator). We processed the data with the standard HIPE 8.2.0 pipeline (Ott 2010) up to level 2 for the H and V polarizations. We then removed standing waves using a Lomb (1976) algorithm before averaging the two polarizations and smoothed the spectral resolution to 10 MHz. This last operation barely changes the line shape as the width of the line is already ~35 MHz because of the aforementioned rotational smearing. The resulting line is shown in Fig. 3 and we note a small asymmetry and the fact that the line-center frequency is not aligned with the line rest frequency. This asymmetry is caused by a pointing offset of 1.5′′ in the planetary western limb direction, which we account for in what follows. We performed no absolute calibration and thus cannot constrain the north-south pointing offset, which must be on the order of a few arcseconds according to the observatory pointing uncertainty at this frequency (Roelfsema et al. 2012). We accounted for the double sideband (DSB) response of the instrument by assuming a normalized sideband ratio GUSB(H + V) = 0.469 ± 0.016 (Higgins et al. 2014)and a ratio of the continuum in the upper to lower sidebands of 1.037 (according to our continuum model) and produced a single sideband (SSB) spectrum that we used for our analyses in this paper in terms of l∕c. The total uncertainty on the l∕c, when accounting for the uncertainties caused by the normalized sideband ratio, baseline removal process, and spectral noise, is 3%, i.e., 0.08 K. All our χ2∕N calculations are based on this rms value, which does not include the absolute calibration uncertainties that are estimated to be 5%.

thumbnail Fig. 2

Water map at 66.44 μm observed bythe PACS spectrometer on January 2, 2011. Saturn is represented by the black ellipse and its rotation axis is shown with a black dashed line. Iso-latitudes are plotted with gray lines. The beam is represented by a blue dashed circle. Each black dot represents the central position of a pixel of the raster map. Top: image of the continuum (in Jy), after the residual pointing offset was corrected. Bottom: the line area in microns × % of the continuum is shown.

3 Modeling

In this section, we present how we modeled the Herschel observations. We first detail how we built a temperature field representative of the epoch of our observations. Then, we describe the radiative-transfer model we applied in our data analysis.

3.1 Thermal model

The pressure-latitude thermal field we used in our radiative-transfer modeling was extracted from the spline interpolation made over time tofill in missing parts of Cassini’s Composite Infrared Spectrometer (CIRS) time series spanning the full mission (Fletcher et al. 2017). We could thus extract the zonally averaged stratospheric temperatures pertinent to the dates of the Herschel observations. At the time of our observations, the CIRS dataset featured significant temperature anomalies associated with the planetary storm that erupted at the end of 2010 (Sánchez-Lavega et al. 2011; Fischer et al. 2011; Fletcher et al. 2011). This storm significantly changed the northern stratospheric temperatures in a 20° latitude band centered on 40° N planetocentric. Two hot stratospheric vortices formed well above the tropospheric storm and were nicknamed “beacons” because of their bright appearance in the infrared and the rapid rotation of Saturn. These beacons eventually merged in April–May 2011 to form a huge vortex in which a temperature increase of up to 80 K was measured at the 2 mbar level. But, because our observationsoccurred very early in the time evolution of the storm and beacons, we first chose to produce a thermal field representative of storm-free conditions by removing any coverage between 20N and 60N and 2011–2012 in the spline smoothing; we include these beacons later in the paper (in Sect. 4.3). We took the thermal field produced for the date closest to our observations, i.e., December 28, 2010. The stratospheric temperatures in the 0.1–10 mbar range, i.e., roughly the range in which the HIFI and PACS lines are sensitive, are quite symmetric in latitude with respect to the equator up to ~40°, with a gradient from 40S to the south pole <5 K and a −10 K gradient from 40N to the north pole, as already hinted for observations at similar LS by Sinclair et al. (2013). The CIRS observations used 600–1400 cm−1 in nadir geometry, therefore probing only the 0.2–5 mbar and 70–250 mbar ranges. Outside of these ranges, the profile goes back to an a priori profile built by averaging Guerlet et al. (2009, 2010) limb observations, which probed higher stratospheric altitudes than the study of Fletcher et al. (2017), between latitudes of 45N and 45S. However, whether this a priori is valid for all latitudes is questionable. Therefore, we chose to extrapolate isothermally the temperature profiles for pressures lower than 0.2 mbar. Between 20S and 20N, we used the thermal profiles of February 2010 derived by Guerlet et al. (2011) from Cassini/CIRS limb viewing geometry observations to benefit from the higher vertical resolution of such observations. With such data, the equatorial quasi-periodic oscillation (Fouchet et al. 2008; Orton et al. 2008; Guerlet et al. 2011) is better resolved than in the nadir data, and the vertical sensitivity in the temperature retrieval is extended to 10−2 mbar. Figure 4 shows the thermal field. We note that the temperatures in the submillibar range are in agreement with temperatures derived from Voyager 2 occultation experiments at several latitudes by Lindal et al. (1985) for a similar LS.

thumbnail Fig. 3

Water line at 1097.365 GHz observed by the HIFI spectrometer on December 31, 2010. The spectrum is expressed in terms of kelvins on the DSB scale. The asymmetry seen in the line shape is caused by a pointing offset of 1.5′′ in the planet western limb direction. The north-south pointing offset is on the order of a few arcseconds, but cannot be constrained further because of calibration uncertainties. The total uncertainty on the l∕c is 3%.
thumbnail Fig. 4

Top: nominal thermal field used in this paper. Zonally averaged temperatures are given as a function of pressure and planetocentric latitude. The data combine retrievals from nadir and limb Cassini/CIRS data (see text for references). Bottom: temperature vertical profiles extracted from the field for a set of latitudes.

3.2 H2O distribution empirical models

In this paper, we test two types of H2O spatial distributions that are representative of two different sources: IDPs and the Enceladus plumes. The IDP source is modeled with a meridionally uniform distribution of H2O. The mole fraction of H2O is uniform above the local condensation level, which is computed following Fray & Schmitt (2009) at each latitude. The Enceladus source is modeled with a two-parameter, Gaussian-shaped latitudinal distribution of H2O, centered on the equator, which has a peak H2O mole fraction at the equator yeq, and a half width at half maximum (HWHM) σ, such that 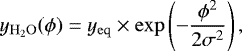(1)

where yeq is the H2O mole fraction above the condensation level at the equator and ϕ is the planetocentric latitude. Latitudinally dependent condensation is computed from our thermal field. The recently observed ring source (Waite et al. 2018; Hsu et al. 2018; Mitchell et al. 2018) shares common properties with the Enceladus source: it is centered on the equator and has, to the first order, a Gaussian shape.

The ring atmosphere (mostly O2, not H2O), another potential source for Saturn’s stratospheric H2O, has lower densities than the Enceladus neutral torus (Johnson et al. 2006; Cassidy & Johnson 2010). Neutral–neutral collisions are therefore inefficient, and even ion–neutral charge exchange collisions are slow. Unlike elsewhere in the magnetosphere, the corotating plasma flow speed is similar to the orbital speed. The ring atmosphere is therefore lost at higher latitudes like ring rain: the atmosphere is lost via photoionization followed by precipitation along field lines (Moore et al. 2015). We note that the neutral component of their H2O distribution is tied to Enceladus. This is why we do not consider the ring atmosphere as a significant enough source to explain our observations and do not include this source in our models.

3.3 Radiative-transfer model

We modeled the observations with a line-by-line non-scattering model that solves the radiative-transfer equation in 1D on several thousand lines of sight, thus highly oversampling our observational spatial resolution. We used the spectral line parameters from the JPL Molecular Spectroscopy Database (Pickett et al. 1998). The spectra of collision-induced absorption caused by H2 –H2, H2 –He, and H2 –CH4 pairs were included following Borysow et al. (1985, 1988) and Borysow & Frommhold (1986). More recent updates to the H2 –H2 absorption from ab initio quantum theory exist (Orton et al. 2007; Fletcher et al. 2018a), but they do not make any significant difference in this spectral region. We adopted mole fractions of 11.8 and 0.47% for He and CH4 respectively, according to Conrath & Gautier (2000) and Fletcher et al. (2009a). We accounted for the absorption caused by the H2O line as well as surrounding NH3 and PH3 broad lines. We took theNH3 and PH3 distributions from Davis et al. (1996) and Fletcher et al. (2009b), respectively. We computed the relevant H2 /He broadening parameters from Levy et al. (1993, 1994) for PH3, from Fletcher et al. (2007) for NH3, and from Brown & Plymate (1996) and Dick et al. (2009) for H2O, for the H2/He mixture described above and the appropriate temperature range. The 1097 GHz line has an opacity of ~0.3 over the HIFI beam in disk-centered conditions and the 66.44 μm line has an opacity that ranges from 0.1 to 0.4 over the PACS beam for disk-centered and limb conditions for the best-fit model H2O profiles given in Sect. 4.4.

We note that, contrary to the 66.4 μm line seen by PACS, the 1097 GHz line seen by HIFI lies on the far wings of a PH3 line. A change in the PH3 abundance therefore influences the l∕c of the H2O line and subsequently on the derived H2O abundance. Increasing the PH3 abundance by a factor of 2 decreases the H2O abundance required to fit the line by ~15%.

This model significantly improves on the model already described in Cavalié et al. (2008b, 2013) regarding the handling of the geometry. The observation plane is sampled with an irregular grid so that the limb and rings, i.e., the regions with the highest variations interms of continuum and line emission, are sufficiently sampled without hampering the computational efficiency. We accounted for the 3D ellipsoidal geometry of Saturn and rings at the time of the observations, using the parameters listed in Table 1. This means we computed the local latitudes, longitudes, and altitudes at each sampled location on each line of sight, and were thus able to use thermal and abundance fields that are fully 3D before applying the beam convolution.

In January 2011, the rings had an inclination of 12.4°, as seen from Herschel. We thus accounted for the contribution of the rings to the continuum emission. The A-B-C ring system brightness temperatures were computed in the wavelength range of our observations by interpolating the observational results obtained in the infrared with Cassini/CIRS (Flandes et al. 2010) and at 2 cm with the Very Large Array (van der Tak et al. 1999), accounting for the brightness temperature roll-off seen around 200 μm by Spilker et al. (2003, 2005). We used the solar elevation as seen from the rings given in Table 1, and the optical depths of the different rings from Altobelli et al. (2014) and Guerlet et al. (2014). Our results are in general agreement with Dunn et al. (2005), when considering averages for the whole ring system. In practice, we geometrically identified the lines of sight that cross the rings and we accounted for the ring absorption and thermal emission, once all the lines of sight on the planet and limb are computed. Beyond the planetary disk, we found the positions of the rings and added their thermal emission. We then created a regular grid of lines of sight from which we computed the beam-averaged spectra in such a way that the beam is highly oversampled by the grid. We produced maps of line integrated emission (for PACS) and disk-averaged spectral line (for HIFI) that can directly be compared with the observation. We present the simulations as well as the residuals resulting from the subtraction of the model from the observations2.

4 Results

4.1 Meridionally uniform distribution

An initial approach was to try to fit the PACS map with a uniform distribution of H2O that would be representative of an IDP source. As shown in Fig. 5, the H2O line-area map is a direct translation of the thermal field and we find a strong gradient between the north and south poles. The minimum χ2 ∕N is obtained for an H2O mole fraction of 6 × 10−10 above the condensation level (roughly a few millibar, varying with latitude), but the χ2 ∕N is as high as 18.9 (i.e., more than 4σ away from the data). The observed decrease of the line area around the southern limb is not reproduced (see Fig. 5), as a results of the warmer stratospheric temperatures in the south compared to the north (see Fig. 4). On the contrary, the strongest emission comes from the south when we use a meridionally uniform distribution of H2O. In addition, there is not enough emission at low latitudes. Such a solution is thus not satisfactory and can be discarded at this stage.

We note that an acceptable fit to the disk-averaged HIFI data can be obtained for a uniform mole fraction of ~3.5 × 10−9, which is consistent with Fletcher et al. (2012) but incompatible with the PACS data. When we simulate the H2O line at 556.936 GHz with this distribution, we obtain a l∕c that is consistent with the previous observation of Bergin et al. (2000). This shows that the disk-averaged H2O influx responsible for our observations of ~ 6 × 105 cm−2 s−1 (Moses & Poppe 2017), which translates into a disk-integrated mass flux of ~8 kg s−1, is surpassedby orders of magnitude by the extraordinarily high flux recently measured by INMS of ~104 kg s−1 coming from the inner ring system. This proves that the ring source observed by Cassini in 2017 cannot be the cause of the H2O observed by Herschel in 2010–2011. The ring source must therefore be more recent than our observations, or at least this source had not been active for long enough (i.e., ~10–15 yr) to diffuse down to observable levels (~0.1–1 mbar). According to Waite et al. (2018), such a large flux is probably linked to the appearance of clumps of material in the D68 ringlet in 2015 (Hedman & Showalter 2016), and is unsustainable for more than 1 Myr without depleting the rings. In conclusion, we will thus not consider the ring source in our subsequent modeling of the Herschel observations.

thumbnail Fig. 5

Top: line-area map at 66.44 μm modeled with a meridionally uniform distribution of H2O. The line area is expressed in microns × percent of the continuum and can thus be directly compared to the observed map of Fig. 2. Bottom: map of the residuals between observations and model (in the same unit as the line-area map). Positive values indicate an excess of emission in the data compared to the model, while negative values indicate a lack of emission compared to the model. The contours are labeled with respect to the 1σ noise level measured in Fig. 2. Above the condensation level, the H2O mole fraction is set to 6 × 10−10. Neither the low latitudes nor the southern latitudes are within 3σ.
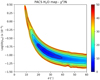thumbnail Fig. 6

χ2∕N as a functionof the H2O meridional Gaussian distribution parameters yeq and σ (Gaussian HWHM in degrees). Acceptable solutions are found for σ ranging from ~20° to ~40°, with a minimum for σ = 25° and yeq = 1.4 ppb. Corresponding line area and residual maps are shown in Fig. 7.

4.2 Meridionally variable distributions

Despite the low spatial resolution of the PACS observations, the contrast observed between the eastern and western limbs and the northern and southern limbs (Fig. 2 bottom), combined with knowledge of the altitude and latitude thermal field (Fig. 4), provides us with a good tool for deriving the meridional distribution of H2O in Saturn’s stratosphere. In what follows, we test several cases of H2O meridional distributions as parametrized in Eq. (1). We first explore the yeq –σ parameter space. Figure 6 shows the χ2∕N obtained as a function of these two parameters. There is a series of marginally acceptable solutions (χ2 ∕N < 9). The best fit is obtained for σ = 25° and yeq = 1.4 ppb, where χ2∕N = 6.3, and the corresponding line area and residual maps are shown in Fig. 7. We cannot obtain better overall fits with this model because of a remaining excess of emission in the northwestern limb (and to a lower extent in the northeastern limb). Minimizing the residuals implies compensating partially for this excess, which results in too much emission in the southern hemisphere. Thus, we first try to improve the fit by reassessing our temperature field in the next section, since the temperature field at the time of the observations was influenced by the onset of Saturn’s Great Storm of 2010–2011.

As in the uniform distribution case, the HIFI data requires a ~5 times higher yeq than the PACS data for σ = 25° to minimize χ2∕N. The fit, shown in Fig. 8 left, is also only marginally acceptable. The line is too broad and not strong enough. This is an indication that models as simple as constant profiles above the condensation level are not optimal. The HIFI line-center contribution function peaks indeed at slightly lower pressures than the PACS line contribution function, which peaks near the condensation level (see Fig. 8). Introducing a positive gradient in the H2O vertical profile above the condensation layer should thus (i) reduce the width of the HIFI line by removing some H2O in the levelsjust above the condensation layer, (ii) increase the HIFI line amplitude by adding some H2O at higher levels to which the HIFI line center is still sensitive, and (iii) help to reconcile the HIFI and PACS data as they probe different altitudes.

In an attempt to improve the fit to the PACS data and to improve the compatibility with the HIFI data, we apply a two-step approach, in which we first account for the temperature changes caused by Saturn’s 2010-2011 Great Storm (Sect. 4.3), and then apply a parametrized gradient in the H2O vertical distribution above its condensation level (Sect. 4.4).

thumbnail Fig. 7

Same as Fig. 5 for a Gaussian distribution of H2O around the equator with yeq = 1.4 ppb and σ = 25°.

4.3 Accounting for Saturn’s Great Storm of 2010–2011

The Herschel observations were conducted a few weeks after the formation of a huge storm system around 40° in the northern hemisphere of the planet (Sánchez-Lavega et al. 2011; Fischer et al. 2011; Fletcher et al. 2011). Between December 2010 and April 2011, this storm system formed a cool region surrounded by two confined warm regions in Saturn’s stratosphere. These are referred to as “beacons” (B1 and B2) given their appearance in the infrared combined with Saturn’s fast rotation.

According to Cassini/CIRS observations made on the same day as the PACS data were recorded (and two days after the HIFI observations), the B1 and B2 beacons were located in the following longitude ranges: 300W–340W for B1 and 220W–250W for B2. The two beacons were thus both in the PACS field of view. Each region was located approximately halfway between the central meridian (289°) and the planetary limb (west for B1 and east for B2). Only B2 was in the HIFI field of view, located around the central meridian (227°). At that time, CIRS only observed the northern edges of these beacons and an increase of ~5–10 K had been measured there at the millibar level (Fletcher et al. 2012). Given the limited spatial coverage of the Cassini data and the absence of ground-based thermal data at that date, we assumed a latitudinal extent of B1 and B2 from 30° N to 50° N (planetocentric), and tried several temperature increase combinations within B1 and B2 compared to adjacent longitudes. As the emission excess seen in the data is more obvious in the northwest than in the northeast, we assume a stronger temperature increase in B1 compared to B2. We tested the following combinations: + 6 K/ + 3 K, + 10 K/ + 5 K, + 15 K/ + 10 K, and + 20 K/ + 15 K for B1/B2, respectively. We applied these temperature increases uniformly above the 10 mbar level at all latitudes/longitudes in B1/B2, following the vertical trends in temperature found in these early development stages of B1 and B2 (see Fig. 8a in Fletcher et al. 2012). The choice of 10 mbar as a cutoff pressure for the temperature increase was guided by the following argument: this level is below the H2O condensation level and thus we do not probe this level, while it is still well above the level where the continuum is generated. It is therefore a pragmatic way to ensure that the temperature changes in the beacon impacts the H2O lines. For B1 and B2, we also account for the longitudinal smearing of 15° caused by the PACS integration time in the modeling of the thermal field. Our thermal field thus becomes a 3D field in our subsequent modeling (see Fig. 9), and we also recompute the condensation level of H2O in the beacons according to this new thermal field (see Fig. 10).

We obtain the best-fit results for the Gaussian meridional distribution of H2O with uniform temperature increases in B1 and B2 of 10 and 5 K, respectively. The resulting 3D temperature field is shown in several latitudinal cross sections in Fig. 9. With this field, we significantly improve the fit to the PACS data, find a range of very good-fit (σ, yeq) combinations, and find a best fit (χ2∕N = 1.1) for σ = 25° and yeq = 1.1 ppb. The line area and residual maps are shown in Fig. 11 and the column density as a function of latitude is shown in Fig. 12. We stress that we did not change the H2O abundance within the beacons in this work; we only changed the pressure of the condensation level. The overall fit is very good, even if, compared to our simulation, the results seem to indicate some enhancement in H2O abundance in the northwest limb from the excess of emission in the observations. Increasing the temperature further in B2 would improve the fit in this region, but degrade the fit at the north pole because of the large beam of PACS. In addition, the temperatureprofile within the beacons was more complex than our idealized isothermal model. Indeed, it had a peak at 0.5 mbar and a drop at lower pressures (Fletcher et al. 2012). This should result in the need for more H2O in the millibar region to compensate for the fainter emission above the temperature peak. We leave this for future analysis of the beacon emissions.

With this model, we can even constrain a background and meridionally uniform flux (e.g., IDP) represented by a variable ymin that can beadded to Eq. (1). We find that it cannot exceed 0.06 ppb at the 2σ limit (Fig. 13), which is an order of magnitude lower than the disk-averaged contribution of the Gaussian distribution. This confirms the small contribution from IDP, as predicted by Moses & Poppe (2017). New photochemical simulations are now required to determine the corresponding IDP H2O flux upper limit. Accounting for the temperature increase in B2, which is in the HIFI field of view does not improve the situation regarding the PACS/HIFI incompatibility, i.e., ~5 times more H2O than in the PACS best-fit model is needed to fit the HIFI line. The best-fit model remains unchanged in terms of yeq for a given σ, compared to Sect. 4.2, and the fit to the HIFI data has the same flaws in that the wings are too broad and line center is too weak.

Now that we have a good fit to the PACS data, we have to briefly turn back to the meridionally uniform distribution model to check whether the improvement in the temperature field induces any improvement in the fit to the data for such a thermal model. Figure 14 shows the line area and residual map obtained for an H2O mole fraction of 4 × 10−10 above the condensation level. With a χ2∕N = 16.2, such a model remains invalid. After leveling out the thermal effects from the line emission map, the uniform distribution still results in high latitudes being too bright and low latitudes being too faint compared to the observations.

Accounting for the effect on the thermal field of Saturn’s Great Storm of 2010–2011 has enabled us to significantly improve the quality of the fit to the PACS data with the Gaussian meridional H2O distribution and confirmed the invalidity of the meridionally uniform distribution.

thumbnail Fig. 8

Left: best fit to the HIFI data for a Gaussian distribution of H2O around the equator with yeq = 7.2 ppb and σ = 25°. The data are shown in black and the model in red; the residuals (observation − model) are plotted at the bottom with the 1σ level of noise in black dashed lines. The synthetic spectrum is too broad and there is a lack of emission at the center. The best-fit model to the PACS data from Fig. 7 is shown in blue for comparison. Right: normalized and beam-averaged contribution functions at the centers of the 66.44 μm line in limb geometry (blue) and at the disk center (green), and of the 1097 GHz line at the disk center (red) are shown. Both functions are computed at their respective observed spectral resolution and the contribution of the continuum emission was subtracted. We note that we rescaled the HIFI contribution function by multiplying it by a factor of 1.45 for an easiercomparison with the PACS value.
thumbnail Fig. 9

Three-dimensional thermal field used in simulations accounting for 10 K temperature increases in B1 and 5 K for B2. B1 is located between 300W–355W; B2 is located between 220W–265W when accounting for longitudinal smearing during the PACS integration; and both are located between 30N and 50N (Fletcher et al. 2012). Top panels: meridional cross sections isolating B1 (left) and B2 (right). Bottom left panel: zonal cross section at 40N. Bottom right: pressure cross section at 2 mbar, in which both beacons can be identified.
thumbnail Fig. 10

H2O vertical profiles of the PACS best-fit model (see Fig. 11), in which the latitudinal distribution is a Gaussian centered around the equator with σ = 25°, and yeq = 1.1 ppb. The effect of the temperature increases in the B1 and B2 beacons is accounted for when computing the condensation level, as shown by the yellow and cyan lines (corresponding to B1 and B2, respectively). The local equatorial minimum at 1 mbar results from condensation at a temperature minimum caused by the Saturn quasi-periodic oscillation (see Fig. 4). The corresponding line area and residual maps are shown in Fig. 11.

4.4 Introducing a gradient in the H2O vertical profile above its condensation layer

In this section, we seek to reconcile the PACS and HIFI observations while building on the improvements in the PACS interpretation, which resulted from including Saturn’s Great Storm effect in our modeling, by introducing a gradient in the H2O vertical distribution above the condensation level.

As the HIFI line probes slightly higher than the PACS line, and as the HIFI line is too broad in the wings and too faint at line center, we introduce a parametrized vertical gradient in the H2O profile at all latitudes to make it less abundant above the condensation level and more abundant at higher altitude. This way, the empirical H2O vertical profiles are closer to physical profiles computed with photochemical models (e.g., Ollivier et al. 2000; Moses et al. 2000). As the PACS data require less H2O than the HIFI data, we see this gradient as a means to reconcile the two datasets. To achieve this, we introduce two additional parameters: a cutoff pressure pgradient, above which the H2O abundance is held constant, and n which is the log(y)∕ log(p) slope of theprofile between the cutoff pressure and the condensation level, as already used in previous works (Marten et al. 2005; Rezac et al. 2014). We test several combinations of pgradient and n: values of pgradient range from 0.01 to 1 mbar, where pgradient is always smaller than the pressure of the condensation level, whatever the latitude; and values of n range from 0.5 to 3 (an example is shown in Fig. 15).

We find that adding a positive gradient in the H2O vertical profile above the condensation layer reduces the incompatibility between the HIFI and PACS yeq values from a factor of ~5 down to a factor of ~2.4 for n = 2–3 and pgradient < 0.3 mbar in the range of values we tested. An example for PACS is shown in Fig. 16 for n = 2, pgradient = 0.1 mbar, yeq = 9 × 10−8 and σ = 25°. The corresponding vertical profiles as a function of latitude are shown in Fig. 15. The corresponding best fit of the HIFI line is obtained for the same set of parameters, except yeq = 2.2 × 10−7 (see Fig. 17).

thumbnail Fig. 11

Same as Fig. 5 for a Gaussian distribution of H2O around the equator with yeq = 1.1 ppb and σ = 25°, after accounting for the temperature increases in the B1 and B2 stratospheric beacons caused by Saturn’s Great Storm of 2010–2011 at the time of the PACS observations.

4.5 Finalremarks on the HIFI/PACS discrepancy

As it stands,we find no H2O distribution that enables us to fully reconcile the HIFI and PACS data in terms of H2O abundance (through the value of yeq) even if introducing a positive gradient above the condensation level significantly improves the situation.

There are some systematic and random errors we have not considered that may explain at least in part the remaining discrepancy between the HIFI and PACS derived abundances. For instance, there is some scatter in the PH3 disk-averaged abundances derived from observations (e.g., Weisstein & Serabyn 1996 vs. Fletcher et al. 2012), its meridional distribution was only measured once by Fletcher et al. (2009b) and any temporal evolution is therefore unconstrained. As noted in Sect. 3.3, the PH3 distribution influences the continuum of the 1097 GHz line (but not of the 66.4 μm line), and thus significantly influences the derivation of the H2O abundance from this line. The thermal field also bears some uncertainties (~3 K at the tropopause and ~4 K at 1–5 mbar,as detailed in Fletcher et al. 2018b). Given that we implement a full 3D thermal field and that the opacities of the observed H2O lines are of the same order but not strictly identical, the uncertainties on the thermal field may be an additional cause of discrepancy between the HIFI and PACS lines.

Finally, we stress that the meridional distribution may be more complicated than that given by Eq. (1), and the vertical gradient may also vary with latitude. This study can thus be seen as a stepping stone for future computations of physical profiles withmore complete altitude-latitude photochemical models.

5 Discussion

In situ measurements carried out by several Cassini instruments during the end-of-mission orbits and final plunge into the atmosphere (all in 2017) have provided strong evidence for material infalling from the rings onto Saturn’s atmosphere whether in gaseous or solid form, or neutral or ionized (Hsu et al. 2018; Mitchell et al. 2018; Waite et al. 2018). While small infalling icy grains, constrained to ±2° around the equatorial plane rain onto Saturn with a modest mass flux of 5 kg s−1 (Mitchell et al. 2018), H2O gas seems to be feeding Saturn’s upper atmosphere at a much higher rate. From INMS on board Cassini, Waite et al. (2018) have found that a global integrated mass flux of 4800–45 000 kg s−1 of gaseous material was raining onto the planet’s atmosphere at the time of the measurements, with 24 ± 5% H2O, within a latitudinal band of 8° centered on the equator. Using data from the same instrument, Perry et al. (2018) have found an even larger influx of 2–20 × 104 kg s−1. This is 2–4 orders of magnitude higher than the influx of H2O of 7–25 kg s−1 derived from previous disk-averaged observations and models (Feuchtgruber et al. 1997; Bergin et al. 2000; Moses et al. 2005; Hartogh et al. 2011). Therefore, this material infalling from the inner ring system, seen in 2017 by Cassini, cannot be the source of the H2O observed by Herschel in December 2010 and January 2011.

An earlier Cassini finding provided another credible candidate: Enceladus and its H2O plumes (Hansen et al. 2006; Porco et al. 2006; Waite et al. 2006). Cassini’s first observations of the plumes at the south pole of the moon venting out significant amounts of H2O triggered a modeling effort to evaluate the fate of the outgassed molecules (Jurac & Richardson 2007; Cassidy & Johnson 2010; Moore et al. 2010). For instance, Cassidy & Johnson (2010) found that neutral/neutral scattering was the main cause of spreading of the molecules in Saturn’s system and predicted that Enceladus plumes formed an H2O neutral torus at the orbital distance of the satellite. This torus was confirmed by the observations of Hartogh et al. (2011). According to Cassidy & Johnson (2010), this torus is likely to be a significant source of H2O for Saturn’s rings, the planet itself, and even Titan. The latter was confirmed by Moreno et al. (2012). At Saturn, the meridional distribution of infalling neutral H2O originating from Enceladus plumes is predicted by Cassidy & Johnson (2010) to be Gaussian and centered on the planet equator with a HWHM σ ~ 15°. The disk-averaged mass flux was estimated to 6 × 105 cm−2 s−1, i.e., ~8 kg s−1, by Hartogh et al. (2011) by fitting the Enceladus source to the absorption caused by the Enceladus torus on the Saturn H2O line at 557 GHz. Comparing this 6 × 105 cm−2 s−1 flux to the required external flux invoked to explain Saturn’s water (1 ± 0.5) × 106 (Moses et al. 2000), Hartogh et al. (2011) concluded that the Enceladus plumes were the likely source of Saturn’s stratospheric H2O.

In this paper, we have analyzed a Herschel-PACS map of H2O emission coming from Saturn’s stratosphere. We presented clear evidence that H2O in Saturn’s stratosphere is not meridionally uniform and that a distribution in which its abundance peaks at the equator and decreases exponentially toward higher latitudes fits the data. This result enables us to identify Enceladus as the main source of Saturn’s stratospheric H2O, and to reject the IDP as a primary source. However, a faint meridionally uniform background flux cannot be ruled out by our observations. Our data indicate that this background is an order of magnitude lower than the disk-averaged contribution of the Enceladus source, which is in agreement with the prediction from Moses & Poppe (2017).

The difference we find between the predicted width of the influx meridional distribution with that observed allows us to compute a rough estimate of meridional eddy mixing at low-to-mid latitudes. If we assume that Kyy ~ L2∕t, we then take L ~ 10500 km as the distance between 15° latitude and 25° latitude. These latitudes correspond to the HWHMs of the input flux from Cassidy & Johnson (2010) and our best model. For the diffusion timescale between those latitudes, we take t equal to the downward diffusion timescale from the top of the atmosphere, where the material is delivered, to the condensation level (150 y according to Moses & Poppe 2017), where H2O was mapped by Herschel. We find that Kyy ~ 2 × 108 cm−2 s−1, and this value is nominally lower by a factor of 10 than early modeling results from Friedson & Moses (2011). A more accurate derivation of the input fluxes as a function of latitude at Saturn that are responsible for the observations will require additional simulation work with 2D photochemical models (Hue et al. 2015, 2016, 2018).

thumbnail Fig. 12

Saturn’s stratospheric H2O meridional distribution as derived from Herschel-PACS mapping observations on January 2, 2011. Left: mole fraction above the local condensation level as a function of latitude. Right: corresponding column density as a function of latitude. The distribution is a Gaussian centered on the equator with yeq = 1.1 ppb and σ = 25°, corresponding to the PACS map best-fit model (see Fig. 11). Background image credits: NASA/JPL-Caltech/Space Science Institute.

6 Conclusion

The findings of our paper can be summarized as follows:

  • We mapped Saturn’s stratospheric H2O emission with Herschel-PACS on January 2, 2011 and obtained a disk-averaged spectrum of the H2O line at 1097 GHz with Herschel-HIFI on December 31, 2010.

  • We find that a meridionally uniform distribution of H2O above its condensation level does not fit the data, which implies that IDP are not the primary source of Saturn’s stratospheric H2O.

  • We find that the data are reasonably well reproduced with a meridional distribution of H2O that is Gaussian-shaped and centered around the equator, when accounting for the 3D temperature field at the time of our observations, including the effect of Saturn’s Great Storm of 2010–2011. The best fit is obtained for an equatorial mole fraction of 1.1 ppb and a HWHM of 25°. This type of distribution points to the Enceladus plumes as the primary source of Saturn’s observed stratospheric H2O.

  • We can place an upper limit on a meridionally uniform background source like IDP about 10 times fainter than the main equatorial source, in agreement with theoretical predictions by Moses & Poppe (2017).

  • We can improve the compatibility between the results obtained from the HIFI and PACS observations by adding a positive gradient above the condensation level in the H2O vertical profiles, in an attempt to bring our profiles closer to physical profiles. However, we do not manage to fully reconcilethe disk-resolved PACS data and the disk-averaged HIFI data with our empirical models, probably because of remaining systematic and random errors and because of the simplicity of our meridional distribution model. Full 2D photochemical modeling is now necessary to move to the next step.

It remains to be seen what meridional distribution of input fluxes are required to reproduce the Herschel observations, and 2D photochemical modeling is required at this stage, starting for example with those of Hue et al. (2015, 2016, 2018). Given their extraordinary sensitivity, bandwidth, and spectral and spatial resolutions, future complementary ALMA and JWST observations will certainly help to shed light on the recent extraordinary influx of exogenic material from the inner ring system to Saturn’s stratosphere, as captured by Cassini in its final orbits (Waite et al. 2018; Perry et al. 2018; Mitchell et al. 2018; Hsu et al. 2018). These future observations (Lellouch 2008; Norwood et al. 2016), as well as possibly direct in situ measurements (Mousis et al. 2014, 2016, 2018), will also help to improve our understanding of the outstanding and more general question of the origin ofexogenic species in giant planet atmospheres.

thumbnail Fig. 13

Same as Fig. 11, in which a uniform component is added to the Gaussian distribution of H2O. The model distribution parameters are yeq = 1.04 ppb, σ = 25°, and ymin = 0.06 ppb. The overall fit is degraded compared to Fig. 11 because of the uniform component of the distribution.
thumbnail Fig. 14

Same as Fig. 5 for a meridionally uniform distribution of H2O with a mole fraction set to 4 × 10−10, after accounting for the temperature increases in the B1 and B2 stratospheric beacons caused by Saturn’s Great Storm of 2010–2011 at the time of the PACS observations. The overall fit is still poor (χ2 ∕N = 16.2) such that accounting for the temperature increases caused by Saturn’s Great Storm of 2010–2011 does not reconcile such an H2O distribution with the data.
thumbnail Fig. 15

H2O vertical profiles of the PACS fit model of Fig. 16, in which the latitudinal distribution is a Gaussian centered around the equator with σ = 25°, and yeq = 9 × 10−8. The effect of the temperature increases in the B1 and B2 beacons is accounted for when computing the condensation level, and a positive gradient is added for pressures higher than pgradient = 0.1 mbar and down to the condensation level, with a slope n = log (y)∕log(p) = 2. The value of yeq applies to p < pgradient. Condensation between 0.1 and 1 mbar occurs in the equatorial region as a result of a local temperature minimum caused by the quasi-periodic oscillation (see Fig. 4). The corresponding line area and residual maps are shown in Fig. 16.
thumbnail Fig. 16

Same as Fig. 5 for a Gaussian distribution of H2O around the equator with yeq = 9 × 10−8 and σ = 25°, after accounting for the temperature increases in the B1 and B2 stratospheric beacons caused by Saturn’s Great Storm of 2010–2011 at the time of the PACS observations, and a positive gradient in the H2O profile abovethe condensation level (with n = 2 and pgradient = 0.1 mbar). More details about the vertical profiles can be found in Fig. 15. The overall fit remains good compared to Fig. 11, and facilitates reducing the inconsistency between the yeq values derived from PACS and HIFI to a factor of ~2.
thumbnail Fig. 17

Best fit to the HIFI data for a Gaussian distribution of H2O around the equator with yeq = 2.2 × 10−7 and σ = 25°, after accounting for the effect of the temperature increases in B1 and B2 and a positive gradient for pressures higher than pgradient = 0.1 mbar and down to the condensation level with a slope n = log (y)∕log (p) = 2. The best-fit model to the PACS data from Fig. 16 is shown for comparison. Same layout as in Fig. 8 left.

Acknowledgements

This work was supported by the Programme National de Planétologie (PNP) of CNRS/INSU, co-funded by CNES. T.C. was supported by a CNES fellowship at the beginning of this work. Support for G.S.O. was provided by NASA through an award issued by the Jet Propulsion Laboratory, California Institute of Technology. PACS was developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). HIFI was designed and built by a consortium of institutes and university departments from across Europe, Canada and the United States under the leadership of SRON Netherlands Institute for Space Research, Groningen, The Netherlands and with major contributions from Germany, France and the USA. Consortium members are: Canada: CSA, U.Waterloo; France: CESR, LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland, NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri-INAF; Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronómico Nacional (IGN), Centro de Astrobiología (CSIC-INTA). Sweden: Chalmers University of Technology – MC2, RSS & GARD; Onsala Space Observatory; Swedish National Space Board, Stockholm University – Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: Caltech, JPL, NHSC. The Herschel spacecraft was designed, built, tested, and launched under a contract to ESA managed by the Herschel/Planck Project team by an industrial consortium under the overall responsibility of the prime contractor Thales Alenia Space (Cannes), and including Astrium (Friedrichshafen) responsible for the payload module and for system testing at spacecraft level, Thales Alenia Space (Turin) responsible for the service module, and Astrium (Toulouse) responsible for the telescope, with in excess of a hundred subcontractors. HCSS/HSpot/HIPE is a joint development (are joint developments) by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS, and SPIRE consortia.

Appendix A Herschel-PACS raw spectra

The 225 raw spectra obtained with Herschel-PACS on the 3 × 3 positions of the raster map are presented in Fig. A.1.

thumbnail Fig. A.1

Two hundred and twenty-five raw spectra obtained with the PACS 5 × 5 detector array on all of the 3 × 3 raster map positions on Saturn at 66.44 μm. The 25 spectra recorded by the detector array are plotted for each of the 9 raster map positions. The H2O line is detected in all spectra corresponding to pointings on the planetary disk or close to the planetary limb. Spectra without an H2O line correspond to pointings far off the planetary limb. Before fitting the lines with a Gaussian to compute their area,a polynomial baseline was removed from these spectra. The line peak S/N around the limb is ~ 15–45.

References

  1. Altobelli, N., Lopez-Paz, D., Pilorz, S., et al. 2014, Icarus, 238, 205 [Google Scholar]
  2. Bergin, E. A., Lellouch, E., Harwit, M., et al. 2000, ApJ, 539, L147 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bézard, B., Lellouch, E., Strobel, D., Maillard, J.-P., & Drossart, P. 2002, Icarus, 159, 95 [NASA ADS] [CrossRef] [Google Scholar]
  4. Borysow, A., & Frommhold, L. 1986, ApJ, 304, 849 [NASA ADS] [CrossRef] [Google Scholar]
  5. Borysow, J., Trafton, L., Frommhold, L., & Birnbaum, G. 1985, ApJ, 296, 644 [NASA ADS] [CrossRef] [Google Scholar]
  6. Borysow, J., Frommhold, L., & Birnbaum, G. 1988, ApJ, 326, 509 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brown, L. R., & Plymate, C. 1996, J. Quant. Spectr. Rad. Transf., 56, 263 [Google Scholar]
  8. Burgdorf, M., Orton, G., van Cleve, J., Meadows, V., & Houck, J. 2006, Icarus, 184, 634 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cassidy, T. A., & Johnson, R. E. 2010, Icarus, 209, 696 [Google Scholar]
  10. Cavalié, T., Billebaud, F., Biver, N., et al. 2008a, Planet. Space Sci., 56, 1573 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cavalié, T., Billebaud, F., Fouchet, T., et al. 2008b, A&A, 484, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cavalié, T., Billebaud, F., Dobrijevic, M., et al. 2009, Icarus, 203, 531 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cavalié, T., Hartogh, P., Billebaud, F., et al. 2010, A&A, 510, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Cavalié, T., Biver, N., Hartogh, P., et al. 2012, Planet. Space Sci., 61, 3 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cavalié, T., Feuchtgruber, H., Lellouch, E., et al. 2013, A&A, 553, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Cavalié, T., Moreno, R., Lellouch, E., et al. 2014, A&A, 562, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Cavalié, T., Venot, O., Selsis, F., et al. 2017, Icarus, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
  18. Connerney, J. E. P. 1986, Geophys. Res. Lett., 13, 773 [NASA ADS] [CrossRef] [Google Scholar]
  19. Connerney, J. E. P., & Waite, J. H. 1984, Nature, 312, 136 [Google Scholar]
  20. Conrath, B. J., & Gautier, D. 2000, Icarus, 144, 124 [NASA ADS] [CrossRef] [Google Scholar]
  21. Coustenis, A., Salama, A., Lellouch, E., et al. 1998, A&A, 336, L85 [NASA ADS] [Google Scholar]
  22. Davis, G. R., Griffin, M. J., Naylor, D. A., et al. 1996, A&A, 315, L393 [NASA ADS] [Google Scholar]
  23. de Graauw, T., Feuchtgruber, H., Bezard, B., et al. 1997, A&A, 321, L13 [NASA ADS] [Google Scholar]
  24. de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dick, M. J., Drouin, B. J., & Pearson, J. C. 2009, J. Quant. Spectr. Rad. Transf., 110, 619 [Google Scholar]
  26. Dobrijevic, M., Hébrard, E., Loison, J. C., & Hickson, K. M. 2014, Icarus, 228, 324 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dunn, D. E., de Pater, I., Wright, M., Hogerheijde, M. R., & Molnar, L. A. 2005, AJ, 129, 1109 [Google Scholar]
  28. Feuchtgruber, H., Lellouch, E., de Graauw, T., et al. 1997, Nature, 389, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Fischer, G., Kurth, W. S., Gurnett, D. A., et al. 2011, Nature, 475, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Flandes, A., Spilker, L., Morishima, R., et al. 2010, Planet. Space Sci., 58, 1758 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fletcher, L. N., Irwin, P. G. J., Teanby, N. A., et al. 2007, Icarus, 188, 72 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fletcher, L. N., Orton, G. S., Teanby, N. A., Irwin, P. G. J., & Bjoraker, G. L. 2009a, Icarus, 199, 351 [NASA ADS] [CrossRef] [Google Scholar]
  33. Fletcher, L. N., Orton, G. S., Teanby, N. A., & Irwin, P. G. J. 2009b, Icarus, 202, 543 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fletcher, L. N., Hesman, B. E., Irwin, P. G. J., et al. 2011, Science, 332, 1413 [NASA ADS] [CrossRef] [Google Scholar]
  35. Fletcher, L. N., Swinyard, B., Salji, C., et al. 2012, A&A, 539, A44 [Google Scholar]
  36. Fletcher, L. N., Guerlet, S., Orton, G. S., et al. 2017, Nat. Astron., 1, 765 [NASA ADS] [CrossRef] [Google Scholar]
  37. Fletcher, L. N., Gustafsson, M., & Orton, G. S. 2018a, ApJS, 235, 24 [NASA ADS] [CrossRef] [Google Scholar]
  38. Fletcher, L. N., Orton, G. S., Sinclair, J. A., et al. 2018b, Nat. Commun., 9, 3564 [NASA ADS] [CrossRef] [Google Scholar]
  39. Fouchet, T., Guerlet, S., Strobel, D. F., et al. 2008, Nature, 453, 200 [NASA ADS] [CrossRef] [Google Scholar]
  40. Fray, N., & Schmitt, B. 2009, Planet. Space Sci., 57, 2053 [NASA ADS] [CrossRef] [Google Scholar]
  41. Friedson, A. J., & Moses, J. I. 2011, AGU Fall Meeting Abstracts, P13C [Google Scholar]
  42. Gautier, D., Hersant, F., Mousis, O., & Lunine, J. I. 2001, ApJ, 550, L227 [NASA ADS] [CrossRef] [Google Scholar]
  43. Guerlet, S., Fouchet, T., Bézard, B., Simon-Miller, A. A., & Michael Flasar, F. 2009, Icarus, 203, 214 [NASA ADS] [CrossRef] [Google Scholar]
  44. Guerlet, S., Fouchet, T., Bézard, B., et al. 2010, Icarus, 209, 682 [NASA ADS] [CrossRef] [Google Scholar]
  45. Guerlet, S., Fouchet, T., Bézard, B., Flasar, F. M., & Simon-Miller, A. A. 2011, Geophys. Res. Lett., 38, L09201 [NASA ADS] [CrossRef] [Google Scholar]
  46. Guerlet, S., Spiga, A., Sylvestre, M., et al. 2014, Icarus, 238, 110 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hansen, C. J., Esposito, L., Stewart, A. I. F., et al. 2006, Science, 311, 1422 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  48. Hartogh, P., Lellouch, E., Crovisier, J., et al. 2009, Planet. Space Sci., 57, 1596 [NASA ADS] [CrossRef] [Google Scholar]
  49. Hartogh, P., Lellouch, E., Moreno, R., et al. 2011, A&A, 532, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Hedman, M. M., & Showalter, M. R. 2016, Icarus, 279, 155 [NASA ADS] [CrossRef] [Google Scholar]
  51. Hersant, F., Gautier, D., & Lunine, J. I. 2004, Planet. Space Sci., 52, 623 [NASA ADS] [CrossRef] [Google Scholar]
  52. Hickson, K. M., Loison, J. C., Cavalié, T., Hébrard, E., & Dobrijevic, M. 2014, A&A, 572, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Higgins, R., Teyssier, D., Borys, C., et al. 2014, Exp. Astron., 37, 433 [NASA ADS] [CrossRef] [Google Scholar]
  54. Hsu, H.-W., Schmidt, J., Kempf, S., et al. 2018, Science, 362, 3185 [NASA ADS] [CrossRef] [Google Scholar]
  55. Hue, V., Cavalié, T., Dobrijevic, M., Hersant, F., & Greathouse, T. K. 2015, Icarus, 257, 163 [NASA ADS] [CrossRef] [Google Scholar]
  56. Hue, V., Greathouse, T. K., Cavalié, T., Dobrijevic, M., & Hersant, F. 2016, Icarus, 267, 334 [NASA ADS] [CrossRef] [Google Scholar]
  57. Hue, V., Hersant, F., Cavalié, T., Dobrijevic, M., & Sinclair, J. A. 2018, Icarus, 307, 106 [NASA ADS] [CrossRef] [Google Scholar]
  58. Johnson, R. E., Luhmann, J. G., Tokar, R. L., et al. 2006, Icarus, 180, 393 [NASA ADS] [CrossRef] [Google Scholar]
  59. Jurac, S., & Richardson, J. D. 2007, Geophys. Res. Lett., 34, L08102 [NASA ADS] [CrossRef] [Google Scholar]
  60. Landgraf, M., Liou, J.-C., Zook, H. A., & Grün, E. 2002, AJ, 123, 2857 [NASA ADS] [CrossRef] [Google Scholar]
  61. Lara, L. M., Lellouch, E., González, M., Moreno, R., & Rengel, M. 2014, A&A, 566, A143 [Google Scholar]
  62. Larson, H. P., Fink, U., Treffers, R., & Gautier, III, T. N. 1975, ApJ, 197, L137 [Google Scholar]
  63. Lellouch, E. 2008, Ap&SS, 313, 175 [Google Scholar]
  64. Lellouch, E., Paubert, G., Moreno, R., et al. 1995, Nature, 373, 592 [Google Scholar]
  65. Lellouch, E., Bézard, B., Moses, J. I., et al. 2002, Icarus, 159, 112 [Google Scholar]
  66. Lellouch, E., Moreno, R., & Paubert, G. 2005, A&A, 430, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Lellouch, E., Bézard, B., Strobel, D. F., et al. 2006, Icarus, 184, 478 [Google Scholar]
  68. Lellouch, E., Hartogh, P., Feuchtgruber, H., et al. 2010, A&A, 518, L152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Levy, A., Lacome, N., & Tarrago, G. 1993, J. Mol. Spectr., 157, 172 [Google Scholar]
  70. Levy, A., Lacome, N., & Tarrago, G. 1994, J. Mol. Spectr., 166, 20 [Google Scholar]
  71. Lindal, G. F., Sweetnam, D. N., & Eshleman, V. R. 1985, AJ, 90, 1136 [Google Scholar]
  72. Lodders, K., & Fegley, Jr. B. 1994, Icarus, 112, 368 [Google Scholar]
  73. Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
  74. Luszcz-Cook, S. H., & de Pater, I. 2013, Icarus, 222, 379 [Google Scholar]
  75. Mandt, K. E., Mousis, O., Marty, B., et al. 2015, Space Sci. Rev., 197, 297 [Google Scholar]
  76. Marten, A., Gautier, D., Owen, T., et al. 1993, ApJ, 406, 285 [Google Scholar]
  77. Marten, A., Matthews, H. E., Owen, T., et al. 2005, A&A, 429, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Mitchell, D. G., Perry, M. E., Hamilton, D. C., et al. 2018, Science, 362, aat2236 [Google Scholar]
  79. Moore, L., Mueller-Wodarg, I., Galand, M., Kliore, A., & Mendillo, M. 2010, J. Geophys. Res. Space Phys., 115, A11317 [Google Scholar]
  80. Moore, L., O’Donoghue, J., Müller-Wodarg, I., Galand, M., & Mendillo, M. 2015, Icarus, 245, 355 [Google Scholar]
  81. Moreno, R., Marten, A., Matthews, H. E., & Biraud, Y. 2003, Planet. Space Sci., 51, 591 [Google Scholar]
  82. Moreno, R., Lellouch, E., Lara, L. M., et al. 2012, Icarus, 221, 753 [Google Scholar]
  83. Moreno, R., Lellouch, E., Cavalié, T., & Moullet, A. 2017, A&A, 608, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Moses, J. I., & Poppe, A. R. 2017, Icarus, 297, 33 [Google Scholar]
  85. Moses, J. I., Lellouch, E., Bézard, B., et al. 2000, Icarus, 145, 166 [Google Scholar]
  86. Moses, J. I., Fouchet, T., Bézard, B., et al. 2005, J. Geophys. Res. Planets, 110, E08001 [Google Scholar]
  87. Mousis, O., Fletcher, L. N., Lebreton, J.-P., et al. 2014, Planet. Space Sci., 104, 29 [Google Scholar]
  88. Mousis, O., Atkinson, D. H., Spilker, T., et al. 2016, Planet. Space Sci., 130, 80 [Google Scholar]
  89. Mousis, O., Atkinson, D. H., Cavalié, T., et al. 2018, Planet. Space Sci., 155, 12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Noll, K. S., Knacke, R. F., Geballe, T. R., & Tokunaga, A. T. 1986, ApJ, 309, L91 [Google Scholar]
  91. Norwood, J., Moses, J., Fletcher, L. N., et al. 2016, PASP, 128, 018005 [Google Scholar]
  92. O’Donoghue, J., Moore, L., Connerney, J. E. P., et al. 2017, Geophys. Res. Lett., 44, 11 [Google Scholar]
  93. Ollivier, J. L., Dobrijévic, M., & Parisot, J. P. 2000, Planet. Space Sci., 48, 699 [Google Scholar]
  94. Orton, G. S., Gustafsson, M., Burgdorf, M., & Meadows, V. 2007, Icarus, 189, 544 [Google Scholar]
  95. Orton, G. S., Yanamandra-Fisher, P. A., Fisher, B. M., et al. 2008, Nature, 453, 196 [Google Scholar]
  96. Ott, S. 2010, PASP, 434, 139 [Google Scholar]
  97. Owen, T., & Encrenaz, T. 2003, Space Sci. Rev., 106, 121 [Google Scholar]
  98. Perry, M. E., Waite Jr. J. H., Mitchell, D. G., et al. 2018, Geophys. Res. Lett., 45, 10, 093 [Google Scholar]
  99. Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [Google Scholar]
  100. Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  101. Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Poppe, A. R. 2016, Icarus, 264, 369 [Google Scholar]
  103. Porco, C. C., Helfenstein, P., Thomas, P. C., et al. 2006, Science, 311, 1393 [Google Scholar]
  104. Prangé, R., Fouchet, T., Courtin, R., Connerney, J. E. P., & McConnell, J. C. 2006, Icarus, 180, 379 [Google Scholar]
  105. Rengel, M., Sagawa, H., Hartogh, P., et al. 2014, A&A, 561, A4 [Google Scholar]
  106. Rezac, L., de Val-Borro, M., Hartogh, P., et al. 2014, A&A, 563, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Samuelson, R. E., Maguire, W. C., Hanel, R. A., et al. 1983, J. Geophys. Res., 88, 8709 [Google Scholar]
  109. Sánchez-Lavega, A., del Río-Gaztelurrutia, T., Hueso, R., et al. 2011, Nature, 475, 71 [Google Scholar]
  110. Sinclair, J. A., Irwin, P. G. J., Fletcher, L. N., et al. 2013, Icarus, 225, 257 [Google Scholar]
  111. Spilker, L., Ferrari, C., Cuzzi, J. N., et al. 2003, Planet. Space Sci., 51, 929 [Google Scholar]
  112. Spilker, L. J., Pilorz, S. H., Edgington, S. G., et al. 2005, Earth Moon Planets, 96, 149 [Google Scholar]
  113. Strobel, D. F., & Yung, Y. L. 1979, Icarus, 37, 256 [Google Scholar]
  114. van der Tak, F., de Pater, I., Silva, A., & Millan, R. 1999, Icarus, 142, 125 [Google Scholar]
  115. Waite, J. H., Combi, M. R., Ip, W.-H., et al. 2006, Science, 311, 1419 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  116. Waite, J. H., Perryman, R. S., Perry, M. E., et al. 2018, Science, 362, 51 [CrossRef] [Google Scholar]
  117. Wang, D., Gierasch, P. J., Lunine, J. I., & Mousis, O. 2015, Icarus, 250, 154 [Google Scholar]
  118. Weisstein, E. W., & Serabyn, E. 1996, Icarus, 123, 23 [NASA ADS] [CrossRef] [Google Scholar]
1

At a given latitude, the increased emission at the limb (compared to the disk center) is a geometrical effect caused by limb brightening in the line and limb darkening in the continuum.

2

In the case of the HIFI spectrum, which was not absolutely calibrated, we have rescaled the spectrum to match our model continuum. The analysis is then done in terms of l∕c.

All Tables

Table 1

Summary of the Herschel-PACS and Herschel-HIFI observations of Saturn and the relevant observation geometry.

In the text

All Figures

thumbnail Fig. 1

Twenty-five raw spectra obtained with the PACS 5 × 5 detector array and extracted from one of the 3 × 3 raster map positions on Saturn at 66.44 μm. The H2O line is detected in all spectra corresponding to pointings on the planetary disk or close to the planetary limb. Spectra without an H2O line correspond to pointings far off the planetary limb. Before fitting the lines with a Gaussian to compute their area, a polynomial baseline was removed from these spectra. The line peak S/N around the limb is ~15–45.
In the text
thumbnail Fig. 2

Water map at 66.44 μm observed bythe PACS spectrometer on January 2, 2011. Saturn is represented by the black ellipse and its rotation axis is shown with a black dashed line. Iso-latitudes are plotted with gray lines. The beam is represented by a blue dashed circle. Each black dot represents the central position of a pixel of the raster map. Top: image of the continuum (in Jy), after the residual pointing offset was corrected. Bottom: the line area in microns × % of the continuum is shown.
In the text
thumbnail Fig. 3

Water line at 1097.365 GHz observed by the HIFI spectrometer on December 31, 2010. The spectrum is expressed in terms of kelvins on the DSB scale. The asymmetry seen in the line shape is caused by a pointing offset of 1.5′′ in the planet western limb direction. The north-south pointing offset is on the order of a few arcseconds, but cannot be constrained further because of calibration uncertainties. The total uncertainty on the l∕c is 3%.
In the text
thumbnail Fig. 4

Top: nominal thermal field used in this paper. Zonally averaged temperatures are given as a function of pressure and planetocentric latitude. The data combine retrievals from nadir and limb Cassini/CIRS data (see text for references). Bottom: temperature vertical profiles extracted from the field for a set of latitudes.
In the text
thumbnail Fig. 5

Top: line-area map at 66.44 μm modeled with a meridionally uniform distribution of H2O. The line area is expressed in microns × percent of the continuum and can thus be directly compared to the observed map of Fig. 2. Bottom: map of the residuals between observations and model (in the same unit as the line-area map). Positive values indicate an excess of emission in the data compared to the model, while negative values indicate a lack of emission compared to the model. The contours are labeled with respect to the 1σ noise level measured in Fig. 2. Above the condensation level, the H2O mole fraction is set to 6 × 10−10. Neither the low latitudes nor the southern latitudes are within 3σ.
In the text
thumbnail Fig. 6

χ2∕N as a functionof the H2O meridional Gaussian distribution parameters yeq and σ (Gaussian HWHM in degrees). Acceptable solutions are found for σ ranging from ~20° to ~40°, with a minimum for σ = 25° and yeq = 1.4 ppb. Corresponding line area and residual maps are shown in Fig. 7.
In the text
thumbnail Fig. 7

Same as Fig. 5 for a Gaussian distribution of H2O around the equator with yeq = 1.4 ppb and σ = 25°.
In the text
thumbnail Fig. 8

Left: best fit to the HIFI data for a Gaussian distribution of H2O around the equator with yeq = 7.2 ppb and σ = 25°. The data are shown in black and the model in red; the residuals (observation − model) are plotted at the bottom with the 1σ level of noise in black dashed lines. The synthetic spectrum is too broad and there is a lack of emission at the center. The best-fit model to the PACS data from Fig. 7 is shown in blue for comparison. Right: normalized and beam-averaged contribution functions at the centers of the 66.44 μm line in limb geometry (blue) and at the disk center (green), and of the 1097 GHz line at the disk center (red) are shown. Both functions are computed at their respective observed spectral resolution and the contribution of the continuum emission was subtracted. We note that we rescaled the HIFI contribution function by multiplying it by a factor of 1.45 for an easiercomparison with the PACS value.
In the text
thumbnail Fig. 9

Three-dimensional thermal field used in simulations accounting for 10 K temperature increases in B1 and 5 K for B2. B1 is located between 300W–355W; B2 is located between 220W–265W when accounting for longitudinal smearing during the PACS integration; and both are located between 30N and 50N (Fletcher et al. 2012). Top panels: meridional cross sections isolating B1 (left) and B2 (right). Bottom left panel: zonal cross section at 40N. Bottom right: pressure cross section at 2 mbar, in which both beacons can be identified.
In the text
thumbnail Fig. 10

H2O vertical profiles of the PACS best-fit model (see Fig. 11), in which the latitudinal distribution is a Gaussian centered around the equator with σ = 25°, and yeq = 1.1 ppb. The effect of the temperature increases in the B1 and B2 beacons is accounted for when computing the condensation level, as shown by the yellow and cyan lines (corresponding to B1 and B2, respectively). The local equatorial minimum at 1 mbar results from condensation at a temperature minimum caused by the Saturn quasi-periodic oscillation (see Fig. 4). The corresponding line area and residual maps are shown in Fig. 11.
In the text
thumbnail Fig. 11

Same as Fig. 5 for a Gaussian distribution of H2O around the equator with yeq = 1.1 ppb and σ = 25°, after accounting for the temperature increases in the B1 and B2 stratospheric beacons caused by Saturn’s Great Storm of 2010–2011 at the time of the PACS observations.
In the text
thumbnail Fig. 12

Saturn’s stratospheric H2O meridional distribution as derived from Herschel-PACS mapping observations on January 2, 2011. Left: mole fraction above the local condensation level as a function of latitude. Right: corresponding column density as a function of latitude. The distribution is a Gaussian centered on the equator with yeq = 1.1 ppb and σ = 25°, corresponding to the PACS map best-fit model (see Fig. 11). Background image credits: NASA/JPL-Caltech/Space Science Institute.
In the text
thumbnail Fig. 13

Same as Fig. 11, in which a uniform component is added to the Gaussian distribution of H2O. The model distribution parameters are yeq = 1.04 ppb, σ = 25°, and ymin = 0.06 ppb. The overall fit is degraded compared to Fig. 11 because of the uniform component of the distribution.
In the text
thumbnail Fig. 14

Same as Fig. 5 for a meridionally uniform distribution of H2O with a mole fraction set to 4 × 10−10, after accounting for the temperature increases in the B1 and B2 stratospheric beacons caused by Saturn’s Great Storm of 2010–2011 at the time of the PACS observations. The overall fit is still poor (χ2 ∕N = 16.2) such that accounting for the temperature increases caused by Saturn’s Great Storm of 2010–2011 does not reconcile such an H2O distribution with the data.
In the text
thumbnail Fig. 15

H2O vertical profiles of the PACS fit model of Fig. 16, in which the latitudinal distribution is a Gaussian centered around the equator with σ = 25°, and yeq = 9 × 10−8. The effect of the temperature increases in the B1 and B2 beacons is accounted for when computing the condensation level, and a positive gradient is added for pressures higher than pgradient = 0.1 mbar and down to the condensation level, with a slope n = log (y)∕log(p) = 2. The value of yeq applies to p < pgradient. Condensation between 0.1 and 1 mbar occurs in the equatorial region as a result of a local temperature minimum caused by the quasi-periodic oscillation (see Fig. 4). The corresponding line area and residual maps are shown in Fig. 16.
In the text
thumbnail Fig. 16

Same as Fig. 5 for a Gaussian distribution of H2O around the equator with yeq = 9 × 10−8 and σ = 25°, after accounting for the temperature increases in the B1 and B2 stratospheric beacons caused by Saturn’s Great Storm of 2010–2011 at the time of the PACS observations, and a positive gradient in the H2O profile abovethe condensation level (with n = 2 and pgradient = 0.1 mbar). More details about the vertical profiles can be found in Fig. 15. The overall fit remains good compared to Fig. 11, and facilitates reducing the inconsistency between the yeq values derived from PACS and HIFI to a factor of ~2.
In the text
thumbnail Fig. 17

Best fit to the HIFI data for a Gaussian distribution of H2O around the equator with yeq = 2.2 × 10−7 and σ = 25°, after accounting for the effect of the temperature increases in B1 and B2 and a positive gradient for pressures higher than pgradient = 0.1 mbar and down to the condensation level with a slope n = log (y)∕log (p) = 2. The best-fit model to the PACS data from Fig. 16 is shown for comparison. Same layout as in Fig. 8 left.
In the text
thumbnail Fig. A.1

Two hundred and twenty-five raw spectra obtained with the PACS 5 × 5 detector array on all of the 3 × 3 raster map positions on Saturn at 66.44 μm. The 25 spectra recorded by the detector array are plotted for each of the 9 raster map positions. The H2O line is detected in all spectra corresponding to pointings on the planetary disk or close to the planetary limb. Spectra without an H2O line correspond to pointings far off the planetary limb. Before fitting the lines with a Gaussian to compute their area,a polynomial baseline was removed from these spectra. The line peak S/N around the limb is ~ 15–45.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.