| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117276 | |
| Published online | 24 October 2011 | |
Will the starless cores in Chamaeleon I and III turn prestellar?⋆,⋆⋆
1
Max-Planck Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: belloche@mpifr-bonn.mpg.de
2
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service d’Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette, France
3
Université de Bordeaux, Laboratoire d’Astrophysique de Bordeaux, CNRS/INSU, UMR 5804, BP 89, 33271 Floirac Cedex, France
Received: 17 May 2011
Accepted: 16 June 2011
Context. The nearby Chamaeleon molecular cloud complex is a good laboratory for studying the process of low-mass star formation because it consists of three clouds with very different properties. Chamaeleon III does not show any sign of star formation, while star formation has been very active in Chamaeleon I and may already be finishing.
Aims. Our goal is to determine whether star formation can proceed in Cha III by searching for prestellar cores, and to compare the results to our recent survey of Cha I.
Methods. We used the Large APEX Bolometer Array (LABOCA) to map Cha III in dust continuum emission at 870 μm. The map is compared with a 2MASS extinction map and decomposed with a multiresolution algorithm. The extracted sources are analyzed by carefully taking into account the spatial filtering inherent in the data reduction process.
Results. Twenty-nine sources are extracted from the 870 μm map, all of them starless. The estimated 90% completeness limit is 0.18 M⊙. The starless cores are found down to a visual extinction of 1.9 mag, in marked contrast with other molecular clouds, including Cha I. Apart from this difference, the Cha III starless cores share very similar properties with those found in Cha I. They are less dense than those detected in continuum emission in other clouds by a factor of a few. At most two sources (<7%) have a mass larger than the critical Bonnor-Ebert mass, which suggests that the fraction of prestellar cores is very low, even lower than in Cha I (<17%). Only the most massive sources are candidate prestellar cores, in agreement with the correlation found earlier in the Pipe nebula. The mass distribution of the 85 starless cores of Cha I and III that are not candidate prestellar cores is consistent with a single power law down to the 90% completeness limit, with an exponent close to the Salpeter value. A fraction of the starless cores detected with LABOCA in Cha I and III may still grow in mass and become gravitationally unstable. Based on predictions of numerical simulations of turbulent molecular clouds, we estimate that at most 50% and 20% of the starless cores of Cha I and III, respectively, may form stars.
Conclusions. The LABOCA survey reveals that Cha III, and Cha I to some extent too, is a prime target to study the formation of prestellar cores, and thus the onset of star formation. Obtaining observational constraints on the duration of the core-building phase prior to gravitational collapse will be necessary to make further progress.
Key words: stars: formation / ISM: individual objects: Chamaleon III / ISM: structure / evolution / dust, extinction / stars: protostars
Based on observations carried out with the Atacama Pathfinder Experiment telescope (APEX). APEX is a collaboration between the Max-Planck Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
The FITS file of Fig. 2 is available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/535/A2
© ESO, 2011
1. Introduction
With the advent of large (sub)mm bolometer arrays, the search for cold dense cores in molecular clouds is becoming more efficient. These dense cores correspond to the earliest stages of the birth of stars and their study is essential for understanding the process of star formation. In particular, unbiased searches for prestellar cores1 and protostars are needed to better understand their formation and derive their lifetimes.
In this respect, the Chamaeleon molecular cloud complex is of particular interest. It is one of the nearest low-mass star-forming regions (150 − 180 pc, Whittet et al. 1997; Knude & Høg 1998; see Appendix B1 of Belloche et al. 2011 for more details) and mainly consists of three molecular clouds, Chamaeleon I, II, and III (hereafter Cha I, II, and III), that have very different degrees of star-formation activity. Their populations of young stellar objects (YSOs) have been well studied from the infrared to X-rays: nearly one order of magnitude more YSOs have been found in Cha I compared to Cha II – while Cha III does not seem to contain any YSO observable at these wavelengths (Persi et al. 2003; Luhman 2008). The three clouds have similar masses as traced with 13CO 1−0 (~1000 M⊙), but the fraction of denser gas traced with C18O 1 − 0 is the highest in Cha I (24%), while it is the lowest in Cha III (4%) (Mizuno et al. 1999, 2001). Finally, several indications of jets/outflows were found in Cha I (Mattila et al. 1989; Gómez et al. 2004; Wang & Henning 2006; Belloche et al. 2006). Only three Herbig-Haro objects are known in Cha II and none has been found in Cha III (Schwartz 1977). Therefore, Cha III is the least active region in the Chamaeleon cloud complex.
Among the three clouds of the Chamaeleon complex, Cha III stands out with a prominent filamentary structure as revealed by the InfraRed Astronomical Satellite (IRAS) at 100 μm (see Figs. 5 and 7 of Boulanger et al. 1998). It consists of a system of interwoven filaments that can be disentangled with velocity information derived from molecular line emission (Gahm et al. 2002). With an angular resolution of 45″, better than that of the 13CO/C18O surveys mentioned above, 38 small clumps embedded in these filaments were detected in C18O 1–0 with the Swedish ESO Submillimeter Telescope (SEST) in the course of a survey targeting the column density peaks of cold dust emission based on IRAS data (Gahm et al. 2002). The clumps have mean densities in the range 1–8 × 104 cm-3 and their internal kinetic energy is dominated by turbulence. Most of them are far from virial equilibrium, suggesting that they are not sites of current star formation.
Because Cha III was mapped in the 1–0 transition of CO and its isotopologues, a transition tracing low densities and a molecule suffering from depletion at high density, only the distribution of its low-density gas is relatively well known. However, in contrast to Cha I (Belloche et al. 2011, hereafter Paper I) and in a limited way Cha II (low-sensitivity 1.3 mm survey of Young et al. 2005), no systematic survey for (sub)mm dust continuum emission has been performed in Cha III. Therefore, the population of dense, prestellar cores in Cha III is completely unknown. On the one hand, the absence of signposts of active star-formation in the protostellar and pre-main-sequence phases in Cha III could be the result of environmental conditions different from those prevailing in, e.g., Cha I, and unfavorable to star formation. On the other hand, star formation could just be starting in Cha III, and finding prestellar cores would favor this interpretation.
To unveil the present status of the earliest stages of star formation in Cha III and compare this cloud to Cha I, we carried out a deep, unbiased dust continuum survey of Cha III at 870 μm with the Large APEX Bolometer Camera at the Atacama Pathfinder Experiment (APEX). The observations and data reduction are described in Sect. 2. Section 3 presents the maps and the method used to extract the detected sources. The properties of these sources are analyzed in Sect. 4. The implications are discussed in Sect. 5. Section 6 gives a summary of our results and conclusions.
2. Observations and data reduction
 |
Fig. 1 Extinction map of Cha III derived from 2MASS in radio projection. The projection center is at (α,δ)J2000 = (12h42m24s, − 79°43′48″). The contours start at AV = 3 mag and increase by steps of 1.5 mag. The dotted lines are lines of constant right ascension. The angular resolution of the map (HPBW = 3′) is shown in the upper right corner. The five fields selected for mapping with LABOCA are delimited with dashed lines. The field of view of LABOCA is displayed in the lower right corner. |
2.1. Extinction map from 2MASS
We derived an extinction map of Cha III from the publicly available 2MASS2 point source catalog in the same way as we did for Cha I (see Paper I), except that no source filtering was applied since there are no known embedded YSOs in Cha III. We used the same resolution of 3′ (FWHM) with a pixel size of 1.5′. With these parameters, most pixels have at least 10 stars within a radius equal to FWHM/2. Only a few pixels contain fewer stars, the minimum being five stars for six pixels. The resulting map is shown in Fig. 1. The typical rms noise level in the outer parts of the map is 0.4 mag, corresponding to a 3σ detection level of 1.2 mag for an FWHM of 3′. This rms noise level is expected to increase toward the higher-extinction regions, however, because of the decreasing number of stars per element of resolution.
2.2. 870 μm continuum observations with APEX
The region of Cha III with a visual extinction higher than 3 mag was selected on the basis of the extinction map derived from 2MASS as described above (Sect. 2.1). It was divided into five contiguous fields labeled Cha3-North, East, Center, South, and West with a total angular area of 0.93 deg2 (see Fig. 1). The five fields were mapped in continuum emission with the Large APEX BOlometer CAmera (LABOCA, Siringo et al. 2009) operating with about 250 working pixels in the 870 μm atmospheric window at the APEX 12 m submillimeter telescope (Güsten et al. 2006). The central frequency of LABOCA is 345 GHz and its angular resolution is 19.2″ (HPBW). The observations were carried out for a total of 88 hours in September and November 2010, under excellent (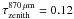 ) to moderate (
) to moderate (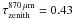 ) atmospheric conditions. The sky opacity was measured every 1 to 2 h with skydips. The focus was optimized on η Carina, Mars, or G34.26+0.15 at least once per day/night. The pointing of the telescope was checked every 1 to 1.5 h on the nearby quasar PKS1057-79and was found to be accurate within 2.5″ (rms). The calibration was performed with the secondary calibrators IRAS 13134-6264, G5.89-0.39, G34.26+0.15, or NGC 2071, which were observed every 1 to 2 h (see Table A.1 of Siringo et al. 2009). Measurements on the primary calibrator Mars were also used.
) atmospheric conditions. The sky opacity was measured every 1 to 2 h with skydips. The focus was optimized on η Carina, Mars, or G34.26+0.15 at least once per day/night. The pointing of the telescope was checked every 1 to 1.5 h on the nearby quasar PKS1057-79and was found to be accurate within 2.5″ (rms). The calibration was performed with the secondary calibrators IRAS 13134-6264, G5.89-0.39, G34.26+0.15, or NGC 2071, which were observed every 1 to 2 h (see Table A.1 of Siringo et al. 2009). Measurements on the primary calibrator Mars were also used.
The observations were performed on-the-fly with a rectangular pattern (“OTF”). The OTF maps were performed with a scanning speed of 2 arcmin s-1and were alternately scanned in right ascension and declination, with a random position angle between − 12° and + 12° to improve the sampling and reduce striping effects.
2.3. LABOCA data reduction
The LABOCA data were reduced with the BoA software3 following the iterative procedure described in Paper I. The only difference is that the baselines of the individual OTF maps scanned in declination had to be removed subscan-wise rather than scan-wise to improve the flatness of the background level. The gridding was done with a cell size of 6.1″ and the map was smoothed with a Gaussian kernel of size 9″ (FWHM). The angular resolution of the final map is 21.2″ (HPBW) and the rms noise level is 11.5 mJy/21.2″-beam (see Sect. 3.1).
The spatial filtering properties of the data reduction and the convergence of the iterative process are analyzed in Appendix A in the same way as was done for Cha I (Paper I). In short, the Cha III dataset that was obtained with rectangular scanning patterns seems to suffer slightly more from spatial filtering than the Cha I dataset that combined rectangular and more compact spiral scanning patterns. The reasons for this counterintuitive result are unclear. It may be related to the slightly smaller number of well-working pixels for the Cha III dataset compared to the Cha I one.
 |
Fig. 2 870 μm continuum emission map of Cha III obtained with LABOCA at APEX. The projection type and center are the same as in Fig. 1. The contour levels are a, 2a, 4a, and 6a with a = 34.5 mJy/21.2″-beam, i.e., three times the rms noise level. The flux density color-scale is shown on the right. The field of view of LABOCA (10.7′) and the angular resolution of the map (HPBW = 21.2″) are shown on the right. The red boxes in the insert are labeled like Figs. 3a–e and show their limits overlaid on the first 870 μm contour. |
3. Basic results and source extraction
In the following, we make the same assumptions as in Paper I (see its Appendix B) to derive the physical properties of the detected sources, in particular we assume a uniform dust temperature of 12 K (see Tóth et al. 2000), a distance of 150 pc (Whittet et al. 1997), a dust mass opacity, κ870, of 0.01 cm2 per gram of gas+dust, a gas-to-dust mass ratio of 100, and a mean molecular weight per free particle, μ, of 2.37. These assumptions are not repeated in the following, except in the few cases where there could be an ambiguity.
3.1. Maps of dust continuum emission in Cha III
The final 870 μm continuum emission map of Cha III obtained with LABOCA is shown in Fig. 2. Pixels with a weight (1/σ2) less than 3500 beam2/Jy2 are masked. The resulting map contains 0.32 megapixels (out of 0.76 that contain some signal), corresponding to a total area of 0.92 deg2 (6.3 pc2). The mean and median weights are 5717 and 5798 beam2/Jy2, respectively. The noise distribution is fairly uniform and Gaussian. The average noise level is 11.5 mJy/21.2″-beam. This translates into an H2 column density of 1.0 × 1021 cm-2, and corresponds to a visual extinction AV ~ 1.1 mag with RV = 3.1 (see the other assumptions in Appendix B of Paper I).
The dust continuum emission map of Cha III reveals many weak, spatially resolved sources. In contrast to Cha I, not a single unresolved, compact source is detected, which is consistent with the absence of signposts of star formation at other wavelengths in Cha III. Figure 3 presents all the detected structures in more detail. The most prominent one is the dense core in the northern part of field Cha3-North (Fig. 3a). All other detected structures are much fainter. Although there is no direct detection of any large-scale, filamentary structure (see Fig. 4b), the distribution of detected sources is much reminiscent of the filamentary structures seen in the far-infrared (see Sect. 1). In field Cha3-East, most detected sources (Cha3-C21, 7, 17, 12, and fainter 3σ compact structures) are distributed along a 1.7 pc long filament (Fig. 3b). A second, shorter (0.3 pc), filamentary structure that may connect to the latter is suggested by the spatial distribution of Cha3-C19, 8, and a fainter 3σ compact structure to the southwest. In field Cha3-Center, Cha3-C3, 4, 13, 5, 16, and 22 are remarkably aligned and nearly equally distributed along a straight line of length 0.9 pc (Fig. 3c). Finally, the sources detected in field Cha3-South also suggest the existence of a filament of length 0.8 pc (Fig. 3d).
Even if the filamentary structure of Cha III is not directly seen with LABOCA, we expect that it will be detected with the Herschel Space Observatory in the frame of the Gould Belt Survey (André et al. 2010). Filaments have been detected in all clouds analyzed from this survey so far, and a close connection between these filaments and the formation of dense cores has been established (André et al. 2010; Men’shchikov et al. 2010; Arzoumanian et al. 2011).
3.2. Masses traced with LABOCA and 2MASS
The total 870 μm flux in the whole map of Cha III is about 42.7 Jy. This translates into a cloud mass of 22.6 M⊙. It corresponds to 1.2% of the total mass traced by CO in Cha III (1890 M⊙, Mizuno et al. 2001), 2.0% of the mass traced by 13CO (1100 M⊙, Mizuno et al. 1999), and 54% of the mass traced by C18O (42 M⊙, Mizuno et al. 1999). In Cha I, these fractions were 5.9%, 7.7%, and 27–32%, respectively (Paper I).
 |
Fig. 3 Detailed 870 μm continuum emission maps of Cha III extracted from the map shown in Fig. 2. The flux density grayscale is shown to the right of each panel and labeled in Jy/21.2″-beam. It has been optimized to reveal the faint emission with a better contrast. The contours start at a and increase with a step of a, with a = 34.5 mJy/21.2″-beam, i.e., three times the rms noise level. The dotted blue contour corresponds to − a. The angular resolution of the map is shown in the lower left corner of each panel (HPBW = 21.2″). The white plus symbols and ellipses show the positions, sizes (FWHM), and orientations of the Gaussian sources extracted with Gaussclumps in the filtered map shown in Fig. 4a. The sources are labeled like in the first column of Table 3. The (red) crosses show the peak position of the 38 clumps detected in C18O 1–0 with SEST (Gahm et al. 2002). a) Field Cha3-North. |
The extinction map shown in Fig. 1 traces larger scales than the 870 μm dust emission map. The median and mean extinctions over the 0.92 deg2 covered with LABOCA are 2.8 and 3.0 mag, respectively. Although our survey was designed to cover the regions above 3 mag, a significant fraction of the resulting map that is based on rectangular fields comprises regions below 3 mag, which explains these low median and mean extinctions. Assuming an extinction-to-H2-column-density conversion factor of 9.4 × 1020 cm-2 mag-1 (for RV = 3.1, see Appendix B.3 of Paper I), we derive a total gas+dust mass of 401 M⊙. However, 96% of this mass, i.e. 386 M⊙, is at AV < 6 mag. With the appropriate conversion factor for AV > 6 mag (see Appendix B of Paper I), the remaining mass is reduced to 9.3 M⊙, yielding a more accurate estimate of 395 M⊙ for the total mass of Cha III traced with the extinction. It is much lower than the masses traced by CO and 13CO mentioned above. Since the latter mass values (at least those derived from CO emission) were based on integrations over much larger areas where CO and 13CO still emit significantly4 (see region VI in Fig. 2 of Mizuno et al. 2001), we consider the mass derived from the extinction map as the best estimate to compare with. Thus the mass traced with LABOCA represents about 5.7% of the cloud mass, which is slightly less than in Cha I (7.5%, see Paper I). Given that the median extinction is 2.8 mag in the extinction map, i.e., about 2.5 times the rms sensitivity achieved with LABOCA, the missing 94% were lost not only because of a lack of sensitivity but also because of the spatial filtering owing to the correlated noise removal (see Sect. A.1). Finally, we estimate the average density of free particles in the field covered with LABOCA. We assume that the depth of the cloud along the line of sight is equal to the square root of its projected surface, i.e. 2.5 pc. This yields an average density of ~420 cm-3. This value is very similar to the average density estimated for Cha I (380 cm-3, see Paper I). Alternatively, if we assume that Cha III is filamentary and that its depth is fairly similar to its typical minor size in the plane of the sky (roughly 1 pc), then its average density becomes 1.1 × 103 cm-3.
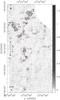 |
Fig. 3 continued. b) Field Cha3 -East. |
The average density derived above corresponds to an average thermal pressure Pth/kB of 0.5–1.3 × 104 cm-3 K, assuming a kinetic temperature of 12 K. The C18O and CO 1–0 linewidths measured in Cha III are on the order of 0.9 and 2.6 km s -1, respectively (Boulanger et al. 1998; Mizuno et al. 1999, 2001). The 13CO 1–0 emission traces gas of densities on the order of 1 × 103 cm-3 in Cha III (Mizuno et al. 1998) and its typical linewidth must be between those of C18O and CO 1–0. We take 1 km s-1 as a representative value, which is the typical value measured by Mizuno et al. (1998) in the small clouds of the Chamaeleon complex. The turbulent pressure is defined as 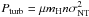 , with μ the mean molecular weight per free particle, mH the atomic mass of hydrogen, n the average free-particle density, and σNT the non-thermal rms velocity dispersion derived from the linewidth. We obtain a turbulent pressure Pturb/kB of 2.1–5.6 × 104 cm-3 K. The turbulent pressure dominates by a factor ~4 over the thermal pressure in Cha III. It is on the same order as the total pressure of the ISM in the mid-plane of the Galaxy (2 × 104 cm-3 K, see Cox 2005). The situation is similar in Cha I.
, with μ the mean molecular weight per free particle, mH the atomic mass of hydrogen, n the average free-particle density, and σNT the non-thermal rms velocity dispersion derived from the linewidth. We obtain a turbulent pressure Pturb/kB of 2.1–5.6 × 104 cm-3 K. The turbulent pressure dominates by a factor ~4 over the thermal pressure in Cha III. It is on the same order as the total pressure of the ISM in the mid-plane of the Galaxy (2 × 104 cm-3 K, see Cox 2005). The situation is similar in Cha I.
3.3. Source extraction and classification
The source extraction from the 870 μm map was performed in the same way as for Cha I (Paper I). The map was first decomposed into different scales with our multiresolution program based on a median filter. The total fluxes measured in the sum maps at scales 3 to 7 (see definition in Appendix C of Paper I) are listed in Table 1, as well as the corresponding masses. About half of the total flux is emitted by structures smaller than ~200″ (FWHM), and only 8% by structures smaller than ~60″. Table 1 shows that the fraction of continuum flux at small scales (<60″) is slightly smaller than in Cha I. This may suggest that the structures in Cha III are less centrally peaked or it could simply be a bias due to the slightly higher sensitivity of the Cha III survey. The sum map at scale 5 and its associated smoothed map are shown in Fig. 4. The sum of these two maps is strictly equal to the original map of Cha III shown in Fig. 2.
 |
Fig. 3 continued. c) Field Cha3-Center. |
 |
Fig. 3 continued. d) Field Cha3-South. |
 |
Fig. 3 continued. e) Field Cha3-West. |
The sources were extracted with the Gaussian fitting program Gaussclumps with the same parameters as for Cha I (see Paper I). The sum maps at scales 1 to 7 were decomposed into 0, 0, 2, 16, 29, 38, and 39 Gaussian sources, respectively, and the full map was decomposed into 39 Gaussian sources. These counts do not include the sources found too close to the noisier map edges (weight < 4400 beam2/Jy2), which we consider as artefacts.
We now consider the results obtained with Gaussclumps for the sum map at scale 5 (i.e., the map shown in Fig. 4a), which is a good scale to characterize sources with FWHM < 120″ as shown in Appendix C of Paper I. The positions, sizes, orientations, and indices of the 29 extracted Gaussian sources are listed in Table 2 in the order in which Gaussclumps found them. We looked for associations with sources in the SIMBAD astronomical database. We used SIMBAD4 (release 1.171) as of February 10th, 2011. None of the 29 Gaussclumps sources is associated with a SIMBAD object within its FWHM ellipse. As a result, we consider that all these 29 sources are starless cores.
4. Analysis
4.1. Comparison with the extinction map
The extinction map derived from 2MASS is overlaid on the 870 μm dust continuum emission map of Cha III in Fig. 5. The overall correspondence is relatively good, most of the continuum emission coincides with the peaks of the extinction map. The 3σ H2 column density sensitivity limit of the 870 μm map is 3.0 × 1021 cm-2, which corresponds to AV ~ 3.2 mag. Most of the continuum emission detected at 870 μm is above the contour level AV = 4.5 mag, and most extended regions with 3 < AV < 4.5 mag traced by the extinction map are not detected at 870 μm. This is partly due to a lack of sensitivity and to the spatial filtering related to the sky noise removal because these low-extinction regions have sizes on the order of 5′–10′, comparable to the field of view of LABOCA. On the other hand, there are also a few 870 μm sources detected below 4.5 mag that are not seen in the extinction map, most likely because of its poor angular resolution (e.g., Cha3-C6 and 23 in fields Cha3-Center and South, respectively).
4.2. Comparison with C18O 1–0
The peak positions of the 38 clumps detected by Gahm et al. (2002) in C18O 1–0 emission are shown as (red) crosses in Figs. 3a–e. One caveat to keep in mind is that the C18O 1–0 survey was biased and covered only parts of the field mapped with LABOCA. For instance, Cha3-C9, 15, and 26 in field Cha3-North, Cha3-C8 and 19 in field Cha3-East, and Cha3-C6 in field Cha3-Center were not covered. A second caveat is that the C18O maps were undersampled by a factor of ~2, with a step of 1′ in fields Cha3-North and East (but 30″ in the brightest regions), and 40″ in fields Cha3-Center, South, and West.
About twenty 870 μm sources only are detected in the fields covered by the C18O observations, which implies a detection rate with LABOCA a factor of 2 lower and shows that the C18O observations were sensitive to lower density gas, as expected. Figures 3a–e show that there is no one-to-one correspondence between the peak positions of the 870 μm and C18O sources. Only seven C18O sources peak within 1′ from the peak position of a 870 μm source. This may partly be caused by the undersampling of the C18O maps, but most likely results from depletion that affects C18O at high density. This confirms that the 870 μm emission traces the high-density regions better than the C18O 1 − 0 emission. The 870 μm map should therefore give a better census of the potential future sites of star formation in Cha III.
4.3. Properties of the starless cores
The properties of the 29 starless sources detected with LABOCA are listed in Table 3 and their distribution is shown in Figs. 6 and 7. The column density (Col. 5) and masses (Cols. 7–9) are computed with the fluxes fitted with Gaussclumps or directly measured in the sum map at scale 5. As a caveat, we remind the reader that the assumption of a uniform temperature may be inaccurate and bias the measurements of the masses and column densities, as well as the mass concentration (or equivalently the density contrast). A dust temperature drop toward the center of starless dense cores is possible (see Appendix B.2 of Paper I and references therein).
4.3.1. Extinction
 |
Fig. 4 a) 870 μm continuum emission sum map of Cha III at scale 5. The contour levels are − a (in dotted blue), a, 2a, and 4a, with a = 34.5 mJy/21.2″-beam, i.e., about 3 times the rms noise level. b) Smoothed map, i.e., residuals, at scale 5. The contour levels are − c (in dotted blue), c, 2c, 4c, and 8c, with c = 8.1 mJy/21.2″-beam, i.e., about 3 times the rms noise level in this map. The grayscales of both maps are different. The sum of these two maps is strictly equal to the original map (Fig. 2). |
Continuum flux distribution in Cha III and comparison to Cha I.
Sources extracted with Gaussclumps in the 870 μm continuum sum map of Cha III at scale 5.
Characteristics of starless sources extracted with Gaussclumps in the 870 μm continuum sum map of Cha III at scale 5.
 |
Fig. 5 Extinction map of Fig. 1 (red contours) overlaid on the 870 μm continuum emission map of Cha III (black contours). The contour levels of the extinction map start at 3 mag and increase by steps of 1.5 mag. The thicker red contours correspond to AV = 4.5 and 7.5 mag. The contour levels of the 870 μm map are the same as in Fig. 2, plus a dotted blue contour at −a. The dotted line delimits the field mapped at 870 μm. The field of view of LABOCA and the angular resolution of the extinction map are shown in the upper right corner. |
The visual extinctions listed in Table 3 and plotted in Fig. 6e are extracted from the extinction map derived from 2MASS (see Sect. 2.1). Given the lower resolution of this map (HPBW = 3′) compared to the 870 μm map, it provides an estimate of the extinction of the environment in which the 870 μm sources are embedded.
The 870 μm sources are found down to a visual extinction, AV, of ~ 1.9 mag (as traced with 2MASS at low angular resolution). This is in marked contrast with the threshold AV ~ 5–7 mag above which starless sources are found in other low-mass star-forming regions such as Cha I (Paper I), Ophiuchus (Johnstone et al. 2004), Perseus (Enoch et al. 2006; Kirk et al. 2006), Taurus (Goldsmith et al. 2008), and Aquila (André et al. 2011). We note, however, that with its high sensitivity, Herschel revealed many starless cores at low extinction in the nearby Polaris flare region, a non-star-forming molecular cloud (André et al. 2010).
About half of the Cha III sources are found at AV < 5 mag (median 4.9 mag), and the distribution peaks at AV ~ 4 mag. Both the median and mean as well as the peak of the distribution are about a factor of 2 lower than in Cha I (see Fig. 6e of Paper I for comparison).
4.3.2. Sizes
The source sizes along the major and minor axes before and after deconvolution are listed in Cols. 6 and 7 of Table 2 and Col. 3 of Table 3, respectively. Their distributions are shown in Figs. 6a and b, respectively, along with the distribution of mean size (geometrical mean of major and minor sizes, i.e. 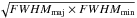 ). The average major, minor, and mean sizes are
). The average major, minor, and mean sizes are 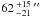 ,
, 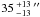 , and
, and 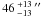 , respectively. These angular sizes correspond to physical sizes of 9300, 5300, and 6900 AU, respectively. Only two sources have a major FWHM size larger than 110″, and no source has a minor or mean FWHM size larger than 90″. The results of the Monte-Carlo simulations of Paper I in the elliptical case (see also Sect. 2.3 and Appendix A.1) imply that these sources, although nearly all of them are faint with a peak flux density lower than 150 mJy/beam, are not significantly affected by the spatial filtering owing to the sky noise removal, with less than 15% loss of peak flux density and size.
, respectively. These angular sizes correspond to physical sizes of 9300, 5300, and 6900 AU, respectively. Only two sources have a major FWHM size larger than 110″, and no source has a minor or mean FWHM size larger than 90″. The results of the Monte-Carlo simulations of Paper I in the elliptical case (see also Sect. 2.3 and Appendix A.1) imply that these sources, although nearly all of them are faint with a peak flux density lower than 150 mJy/beam, are not significantly affected by the spatial filtering owing to the sky noise removal, with less than 15% loss of peak flux density and size.
Like for Cha I (see Paper I), the accuracy to which we can measure the size of a weak ~5σ unresolved source is 4.2″ (21.2/5). Therefore, faint sources with a size smaller than ~25.4″ cannot be reliably deconvolved and we artificially set their size to 25.4″ to perform the deconvolution. As a result the minimum deconvolved FWHM size that we can measure is ~14″ (2100 AU). The average deconvolved mean FWHM size is 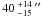 , i.e.
, i.e. 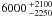 AU (see Fig. 6b). It is only 8% smaller than the average deconvolved mean size of the Cha I sources, so the conclusions of Paper I hold as well: the Cha III sources have similar physical sizes as the Perseus cores, are probably larger than the Serpens cores (maybe by a factor of 1.5–2), are certainly larger than the Ophiuchus cores (by a factor of 2–3), but are significantly smaller than the Taurus cores (by a factor of 3).
AU (see Fig. 6b). It is only 8% smaller than the average deconvolved mean size of the Cha I sources, so the conclusions of Paper I hold as well: the Cha III sources have similar physical sizes as the Perseus cores, are probably larger than the Serpens cores (maybe by a factor of 1.5–2), are certainly larger than the Ophiuchus cores (by a factor of 2–3), but are significantly smaller than the Taurus cores (by a factor of 3).
The comparison to the population of dense cores in the Pipe nebula is less straightforward because these cores were extracted from an extinction map with Clumpfind and only the radii of their lowest contours are available, not their FWHM sizes (Alves et al. 2007; Lada et al. 2008; Rathborne et al. 2009). In addition, the resolution of the extinction map is 1′, i.e. 7800 AU at a distance of 130 pc (Lombardi et al. 2006). Still, because their mean radius is about 19000 AU (Rathborne et al. 2009), it seems very likely that the Pipe dense cores traced by the extinction are larger by a factor of a few compared to the Cha III cores detected with LABOCA.
4.3.3. Aspect ratios and orientations
The distribution of aspect ratios computed with the deconvolved FWHM sizes is shown in Fig. 6c. Based on the Monte Carlo simulations of Paper I, we estimate that a faint source can reliably be considered as intrinsically elongated when its aspect ratio is higher than 1.4. 76% of the sources are above this threshold and can be considered as elongated, which is similar to Cha I. The average aspect ratio is 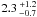 . It is similar to the ones measured in Cha I, Serpens, and Taurus, somewhat larger than in Perseus, and significantly larger than in Ophiuchus (see Table 7 of Paper I).
. It is similar to the ones measured in Cha I, Serpens, and Taurus, somewhat larger than in Perseus, and significantly larger than in Ophiuchus (see Table 7 of Paper I).
The distribution of position angles (Col. 8 of Table 2) does not show any preferred direction. An inspection by eye does not reveal any particular alignment of the elongated sources with the putative filaments mentioned in Sect. 3.1 either, especially in field Cha3-Center (Fig. 3c).
4.3.4. Column densities
The median peak H2 column density of the starless sources in Cha III is 6.4 × 1021 cm-2 (Fig. 6d), nearly identical to the median value found in Cha I (6.5 × 1021 cm-2, see Paper I). However, the average peak H2 column density of the starless sources in Cha III (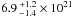 cm-2) is 1.4 times lower than the average peak column density of the starless cores in Cha I. It is five times lower than in Perseus and Serpens, and four to nine times lower than in Ophiuchus (see Table 7 of Paper I). It appears to be significantly lower than in Taurus too (by a factor of 3), but since the Taurus sample is not complete and the source extraction methods differ, we cannot draw any firm conclusion.
cm-2) is 1.4 times lower than the average peak column density of the starless cores in Cha I. It is five times lower than in Perseus and Serpens, and four to nine times lower than in Ophiuchus (see Table 7 of Paper I). It appears to be significantly lower than in Taurus too (by a factor of 3), but since the Taurus sample is not complete and the source extraction methods differ, we cannot draw any firm conclusion.
4.3.5. Masses and densities
The distribution of masses and free-particle densities listed in Table 3 are displayed in Fig. 7. The 5σ sensitivity limit used to extract sources with Gaussclumps corresponds to a peak mass of 0.030 M⊙ and a peak density of 2.7 × 105 cm-3, computed for a diameter of 21.2″ (3200 AU). The median of the peak mass distribution is 0.039 M⊙, implying a median peak density of 3.4 × 105 cm-3 (Figs. 7a and e). We give the mass integrated within an aperture of diameter 50″ (7500 AU) in Col. 9 of Table 3, which is the aperture used for Cha I (Paper I). This aperture is well adapted to the Cha III sample too, for the same three reasons: it nearly corresponds to the average mean, undeconvolved FWHM size (see Sect. 4.3.2 and Fig. 6a), it is not affected by the spatial filtering owing to the sky noise removal (see Appendix A.1 and Table A.1 of Paper I), and it is still preserved in the sum map at scale 5 (see Appendix C and Table C.1 of Paper I). The median of the mass integrated within this aperture is 0.09 M⊙, corresponding to a median mean density of 6 × 104 cm-3 (Figs. 7b and f). The median values of the peak and aperture masses are nearly the same as those of the Cha I sample, but the mean values are lower by about 30%. Within the uncertainties, the mass distributions of Cha I and III are very similar, the only main difference being that the four most massive cores of Cha I have no counterpart in Cha III.
Figure 7c shows the distribution of total masses computed from the Gaussian fits (Col. 8 of Table 3). The completeness limit at 90% is estimated from a peak flux detection threshold at 6.3σ for the average size of the source sample (FWHM = 46″)5. It corresponds to a total mass of 0.18 M⊙, slightly lower than in Cha I (0.22 M⊙, see Paper I). Like in Cha I, the median total mass is very similar (0.20 M⊙), which implies that only 50% of the detected sources are above the estimated 90% completeness limit. The mass completeness limit is slightly better than that obtained by Könyves et al. (2010) for their 11 deg2 sensitive continuum survey of the Aquila Rift cloud complex (distance 260 pc) with Herschel, and about a factor of 6 better than that obtained by Enoch et al. (2008) in Perseus (see Paper I for details). It is however a factor ~20 worse than that obtained with Herschel for the Polaris flare region, which is at the same distance as Cha III (André et al. 2010).
The mean density of each source is estimated from its total mass as derived from the Gaussian fits and a radius set equal to 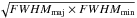 . It is given in Col. 13 of Table 3 and the distribution for the full Cha III sample is shown in Fig. 7g. The average and median mean densities are
. It is given in Col. 13 of Table 3 and the distribution for the full Cha III sample is shown in Fig. 7g. The average and median mean densities are 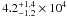 and 3.3 × 104 cm-3, respectively. For Chamaeleon I, the corresponding numbers are
and 3.3 × 104 cm-3, respectively. For Chamaeleon I, the corresponding numbers are 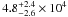 and 3.6 × 104 cm-3, respectively (not given in Paper I). The Cha I and III sources have thus very similar mean densities, a factor of ~5 higher than the mean density of the cores of the Pipe nebula extracted from extinction maps (Lada et al. 2008).
and 3.6 × 104 cm-3, respectively (not given in Paper I). The Cha I and III sources have thus very similar mean densities, a factor of ~5 higher than the mean density of the cores of the Pipe nebula extracted from extinction maps (Lada et al. 2008).
We estimated the mass concentration of the Cha III sources from the ratio of the peak mass to the mass within an aperture of 50″ (Col. 10 of Table 3), which is relatively insensitive to the spatial filtering owing to the data reduction. A similar property is the density contrast measured as the ratio of the peak density to the mean density within this aperture (Col. 15 of Table 3). The statistical rms uncertainties on the peak mass and the mass within 50″ are 0.006 and 0.010 M⊙, respectively, which means a relative uncertainty of up to 25% for the weakest source. The distributions of both ratios are shown in Figs. 7d and h and their rms uncertainties6 are given in parentheses in Cols. 10 and 15 of Table 3. The two outliers with the highest ratios are also those with the highest relative uncertainty (about 30%). The upper axis of Fig. 7d, which can also be used for Fig. 7h, displays the exponent of the density profile under the assumptions that the sources are spherically symmetric with a power-law density profile, i.e., ρ ∝ r − p, and that the dust temperature is uniform. The median mass concentration and density contrast are 0.44 and 5.8, respectively, similar to the Cha I sample. This corresponds to p ~ 2.0, suggesting that most sources are significantly centrally-peaked (see Paper I for the caveats of this estimate). It is similar to the exponent of the singular isothermal sphere.
The upper axis of Fig. 7h, which can also be used for Fig. 7d, deals with an alternate case where the sources have a constant density within a diameter Dflat and a density decreasing as r-2 outside, still with the assumption of a uniform temperature. Under these assumptions, the measurements are consistent with a flat inner region of diameter 16″ at most (2400 AU) for a few sources, but most sources have Dflat < 10″ (1500 AU), or cannot be described with such a density profile.
4.3.6. Mass versus size
The distribution of total masses versus source sizes derived from the Gaussian fits is shown in Fig. 8a. About 50% of the sources are located between the 5σ detection limit (solid line) and the estimated 90% completeness limit (dashed line), suggesting that we most likely miss a significant number of sources with a low peak column density. Figure 8b shows a similar diagram for the deconvolved source size. If we assume that the deconvolved FWHM size is a good estimate of the external radius of each source, then we can compare this distribution to the critical Bonnor-Ebert mass that characterizes the limit above which the hydrostatic equilibrium of an isothermal sphere with thermal support only is gravitationally unstable. This relation 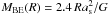 (Bonnor 1956), with MBE(R) the total mass, R the external radius, as the sound speed, and G the gravitational constant, is drawn for a temperature of 12 K as a solid line in Fig. 8b. We define αBE = Mtot/MBE. Only one source (Cha3-C1) has αBE > 1, i.e., is located above the critical mass limit (see Fig. 8b and Col. 11 of Table 3). The threshold αBE = 0.5 approximately defines the limit above which an isothermal sphere is gravitationally bound if it is only supported by thermal pressure and the confinement by the external pressure is negligible. Only one source in addition to Cha3-C1 falls above this limit and may be gravitationally bound (Cha3-C2, see dash-dotted line in Fig. 8b). Most sources, however, have a mass smaller than the critical Bonnor-Ebert mass by a factor of 2 to 6. The uncertainty on the temperature (see Appendix B.2 of Paper I) does not influence these results much since, even in the unlikely case of the bulk of the mass being at a temperature of 7 K, the measured masses would move upward relative to the critical Bonnor-Ebert mass limit by a factor of 1.9 only, because the latter is also temperature-dependent.
(Bonnor 1956), with MBE(R) the total mass, R the external radius, as the sound speed, and G the gravitational constant, is drawn for a temperature of 12 K as a solid line in Fig. 8b. We define αBE = Mtot/MBE. Only one source (Cha3-C1) has αBE > 1, i.e., is located above the critical mass limit (see Fig. 8b and Col. 11 of Table 3). The threshold αBE = 0.5 approximately defines the limit above which an isothermal sphere is gravitationally bound if it is only supported by thermal pressure and the confinement by the external pressure is negligible. Only one source in addition to Cha3-C1 falls above this limit and may be gravitationally bound (Cha3-C2, see dash-dotted line in Fig. 8b). Most sources, however, have a mass smaller than the critical Bonnor-Ebert mass by a factor of 2 to 6. The uncertainty on the temperature (see Appendix B.2 of Paper I) does not influence these results much since, even in the unlikely case of the bulk of the mass being at a temperature of 7 K, the measured masses would move upward relative to the critical Bonnor-Ebert mass limit by a factor of 1.9 only, because the latter is also temperature-dependent.
The critical Bonnor-Ebert mass can also be estimated from the external pressure with 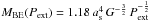 (Bonnor 1956), the external pressure being estimated from the extinction of the environment in which the sources are embedded (see Paper I for the equations and references). The single source with a mass larger than MBE(Pext) is the same as for MBE(R). The agreement between both estimates of MBE suggests that our estimates of the external radius and external pressure are consistent. No additional source falls above the threshold αBE = 0.5 based on MBE(Pext). In summary, only one source is likely above the critical Bonnor-Ebert mass limit (Cha3-C1), and one additional source may be gravitationally bound if it is supported by thermal pressure only (Cha3-C2). The implications of this analysis will be discussed in Sect. 5.
(Bonnor 1956), the external pressure being estimated from the extinction of the environment in which the sources are embedded (see Paper I for the equations and references). The single source with a mass larger than MBE(Pext) is the same as for MBE(R). The agreement between both estimates of MBE suggests that our estimates of the external radius and external pressure are consistent. No additional source falls above the threshold αBE = 0.5 based on MBE(Pext). In summary, only one source is likely above the critical Bonnor-Ebert mass limit (Cha3-C1), and one additional source may be gravitationally bound if it is supported by thermal pressure only (Cha3-C2). The implications of this analysis will be discussed in Sect. 5.
 |
Fig. 6 Distributions of physical properties obtained for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The mean, standard deviation, and median of the distribution are given in each panel. The asymmetric standard deviation defines the range containing 68% of the sample. a) FWHM sizes along the major (solid line) and minor (dashed line) axes. The filled histogram shows the distribution of geometrical mean of major and minor sizes. The mean and median values refer to the filled histogram. The dotted line indicates the angular resolution (21.2″). b) Same as a) but for the deconvolved sizes. c) Aspect ratios computed with the deconvolved sizes. The dotted line at 1.4 shows the threshold above which the deviation from 1 (elongation) can be considered as significant. d) Peak H2 column density. The dotted line at 5.0 × 1021 cm-2 is the 5σ sensitivity limit. e) Visual extinction derived from 2MASS. |
 |
Fig. 7 Distributions of masses and free-particle densities obtained for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The mean, standard deviation, and median of the distribution are given in each panel. The asymmetric standard deviation defines the range containing 68% of the sample. a) Peak mass of the fitted Gaussian. b) Mass within an aperture of diameter 50″. c) Total mass of the fitted Gaussian. The dotted line indicates the estimated completeness limit at 90% for Gaussian sources corresponding to a 6.3σ peak detection limit for the average source size. d) Mass concentration, ratio of the peak mass to the mass within an aperture of diameter 50″. e) Peak density. f) Mean density within an aperture of diameter 50″. g) Mean density derived from the total mass. h) Density contrast, ratio of peak density to mean density. In panels a) and e), the dotted line indicates the 5σ sensitivity limit. The upper axis of panel d), which can also be used for panel h), shows the power-law exponent p derived assuming that the sources have a density profile proportional to r − p and a uniform dust temperature. Alternately, the upper axis of panel h), which can also be used for panel d), deals with the case where the density is uniform within a diameter Dflat and decreases as r-2 outside, still with the assumption of a uniform temperature. |
 |
Fig. 8 a) Total mass versus mean FWHM size for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The angular resolution (21.2″) is marked by the dotted line. The solid line (M ∝ FWHM2) is the 5σ peak sensitivity limit for Gaussian sources. The dashed line shows the 6.3σ peak sensitivity limit which corresponds to a completeness limit of 90% for Gaussian sources. b) Total mass versus mean deconvolved FWHM size. Sizes smaller than 25.4″ were set to 25.4″ before deconvolution (see note b of Table 3). The solid line shows the relation |
The mass concentration CM is plotted versus source size in Fig. 8c. CM is actually equal to the ratio of the peak flux to the flux integrated within the aperture of diameter 50″. When the sources do not overlap, this ratio is nearly independent of the Gaussian fitting because the second and third stiffness parameters of Gaussclumps were set to 1, i.e., Gaussclumps was biased to keep the fitted peak amplitude close to the observed one and the fitted center position close to the position of the observed peak. The dashed line shows the expected ratio if the (not deconvolved) sources were exactly Gaussian and circular and allows us to estimate the departure of the sources from being Gaussian within 50″. Most sources have a mass concentration consistent with the Gaussian expectation, but many of them have a significant uncertainty on CM that prevents a more accurate analysis. The obvious outlier toward the lower left is source Cha3-C18, which has a strong neighbor significantly contaminating its flux within 50″ (source Cha3-C1).
There is no obvious correlation between the total mass or FWHM size of the sources and the visual extinction of the environment in which they are embedded (see Fig. 9). A similar conclusion was drawn for Cha I (Paper I) and for the five nearby molecular clouds Ophiuchus, Taurus, Perseus, Serpens, and Orion based on SCUBA data (Sadavoy et al. 2010).
4.3.7. Core mass distribution (CMD)
The mass distribution of the 29 starless sources is shown in Fig. 10. Its shape looks very similar to the shape of the mass distribution found in other star-forming regions with a power-law-like behavior at the high-mass end and a flattening toward the low-mass end. In our case, the flattening occurs below the estimated 90% completeness limit (0.18 M⊙) and may not be significant. Above this limit, the distribution is consistent with a power-law, but is very noisy. The exponent of the best power-law fit (α = −3.0 ± 0.8 for dN/dM, αlog = −2.0 ± 0.8 for dN/dlog (M)) is consistent, within the uncertainty, with the value of Salpeter (1955) that characterizes the high-mass end of the stellar initial mass function (α = −2.35). However, it is also consistent within 2σ with the exponent of the typical mass spectrum of CO clumps (α = −1.6, see Blitz 1993; Kramer et al. 1998). The sample is too small to distinguish statistically between these two types of mass distribution.
4.4. Spatial distribution
The distribution of nearest-neighbor projected distance is presented in Fig. 11 for both samples of starless sources in Cha III and I. The median distance dm is 0.11 pc in Cha III, a factor of 2 larger than in Cha I (0.056 pc). We follow Gómez et al. (1993) to estimate the corresponding distribution for a sample of sources that would be randomly distributed in the plane of the sky over the same area, assumed to be the surface of a disk of diameter equal to the largest projected distance between two sources (4.9 pc for Cha III and 4.0 pc for Cha I). The median distances of these random distributions are 0.38 pc for Cha III and 0.21 pc for Cha I, i.e., nearly a factor of 4 larger than observed in both cases. The starless sources in both clouds are thus significantly clustered. Assuming that the nearest-neighbor pairs are randomly oriented in the three-dimensional space, the true separation in three dimensions is 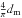 (Gómez et al. 1993), i.e. 0.14 pc for Cha III and 0.07 pc for Cha I.
(Gómez et al. 1993), i.e. 0.14 pc for Cha III and 0.07 pc for Cha I.
Given that the median extinction of the local ambient medium in which the starless sources in Cha III are embedded is a factor of 2 lower than in Cha I (see Sect. 4.3.1), the density of this local ambient medium is most likely also lower, maybe up to a factor of 2. The characteristic length of thermal fragmentation is inversely proportional to the square root of the density. The difference in median nearest-neighbor separation seen between Cha III and I is therefore somewhat more pronounced than what could naively be expected from thermal fragmentation.
The remarkable alignment of six 870 μm sources in field Cha3-Center (see Fig. 3c) deserves some further analysis. The sources are nearly uniformly distributed along a straight line, with a mean projected separation of 0.16 ± 0.03 pc. For a density of the intercore medium of 4 × 103 cm-3 in this region (Gahm et al. 2002), the Jeans length 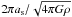 is about 0.36 pc at 12 K. The intercore separation would match this Jeans length if the inclination angle of the putative filament was 26°, which is statistically unlikely. However, the effective scale of fragmentation in a magnetized and/or rotating filament is expected to decrease with increasing magnetic field strength and/or rotation level (e.g., Nakamura et al. 1993; Matsumoto et al. 1994). The measured core separation could be used to estimate the magnetic field strength and/or rotation level as was done for a filament in Orion A (Hanawa et al. 1993). With dFWHM the full width at half maximum of the filament, λ the projected core separation, α and β the ratios of the magnetic pressure and centrifugal force to the thermal pressure, respectively, and i the inclination of the filament along the line of sight, Equation 13 of Hanawa et al. (1993) yields
is about 0.36 pc at 12 K. The intercore separation would match this Jeans length if the inclination angle of the putative filament was 26°, which is statistically unlikely. However, the effective scale of fragmentation in a magnetized and/or rotating filament is expected to decrease with increasing magnetic field strength and/or rotation level (e.g., Nakamura et al. 1993; Matsumoto et al. 1994). The measured core separation could be used to estimate the magnetic field strength and/or rotation level as was done for a filament in Orion A (Hanawa et al. 1993). With dFWHM the full width at half maximum of the filament, λ the projected core separation, α and β the ratios of the magnetic pressure and centrifugal force to the thermal pressure, respectively, and i the inclination of the filament along the line of sight, Equation 13 of Hanawa et al. (1993) yields 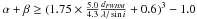 . The equality holds for a pitch angle θ = 0°, with θ characterizing the relative strength of the poloidal to axial magnetic fields. The width of the filament cannot be estimated from the LABOCA map. With the C18O 1–0 map shown in Fig. 9 of Gahm et al. (2002), we roughly estimate dFWHM ~ 0.25–0.40 pc, which is larger than the typical width of the filaments recently detected with Herschel in three other nearby clouds (median width 0.1 pc, see Arzoumanian et al. 2011). Since our estimate from C18O is rather uncertain, we also consider below (in parentheses) the case where the width of the filament is 0.1 pc. If the filament is in the plane of the sky (i = 90°) and θ = 0°, we obtain α + β ~ 53–180 (6 with 0.1 pc). Since there is apparently no significant level of rotation in this filament (Gahm et al. 2002), we derive α ~ 53–180 (6). If the filament is not in the plane of the sky, α would be less than 1 for i ≲ 7.5–12° (31°). An inclination to the line of sight of 7.5–12° is statistically unlikely, so we are left with a very high level of magnetic pressure or an overestimated filament width. If this alignment of six regularly spaced cores is really the result of fragmentation in a filament, then we conclude that either the filament is strongly magnetized, or it is much thinner than it appears in C18O 1–0, or the model of Nakamura et al. (1993) of a magnetized, self-gravitating, isothermal filament in equilibrium does not apply to that filament. Alternatively, the observed regular structure may have nothing to do with fragmentation and simply represent transient periodic overdensities produced by gravitational-magnetoacoustic waves that will be damped away (Langer 1978).
. The equality holds for a pitch angle θ = 0°, with θ characterizing the relative strength of the poloidal to axial magnetic fields. The width of the filament cannot be estimated from the LABOCA map. With the C18O 1–0 map shown in Fig. 9 of Gahm et al. (2002), we roughly estimate dFWHM ~ 0.25–0.40 pc, which is larger than the typical width of the filaments recently detected with Herschel in three other nearby clouds (median width 0.1 pc, see Arzoumanian et al. 2011). Since our estimate from C18O is rather uncertain, we also consider below (in parentheses) the case where the width of the filament is 0.1 pc. If the filament is in the plane of the sky (i = 90°) and θ = 0°, we obtain α + β ~ 53–180 (6 with 0.1 pc). Since there is apparently no significant level of rotation in this filament (Gahm et al. 2002), we derive α ~ 53–180 (6). If the filament is not in the plane of the sky, α would be less than 1 for i ≲ 7.5–12° (31°). An inclination to the line of sight of 7.5–12° is statistically unlikely, so we are left with a very high level of magnetic pressure or an overestimated filament width. If this alignment of six regularly spaced cores is really the result of fragmentation in a filament, then we conclude that either the filament is strongly magnetized, or it is much thinner than it appears in C18O 1–0, or the model of Nakamura et al. (1993) of a magnetized, self-gravitating, isothermal filament in equilibrium does not apply to that filament. Alternatively, the observed regular structure may have nothing to do with fragmentation and simply represent transient periodic overdensities produced by gravitational-magnetoacoustic waves that will be damped away (Langer 1978).
 |
Fig. 9 a) Total mass versus visual extinction AV for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The dashed line shows the estimated 90% completeness limit (0.18 M⊙). b) FWHM size versus visual extinction. The angular resolution (21.2″) is marked by the dotted line. |
 |
Fig. 10 Mass distribution dN/dlog (M) of the 29 starless sources. The error bars represent the Poisson noise (in |
 |
Fig. 11 Distribution of nearest-neighbor projected distance for the starless sources of Cha III (a)) and Cha I (b)). In each panel, the dashed histogram shows the distribution expected for the same number of objects randomly distributed in the same area. The median value of each distribution is marked with a dotted line. |
5. Discussion
5.1. A puzzling population of starless cores in Cha I and III
Based on the comparison to the Bonnor-Ebert mass limit, we estimate that only one (or at most two) source(s) out of 29 is a candidate prestellar core in Cha III (see Sect. 4.3.6). This yields a fraction of candidate prestellar cores of 3–7%, a factor of 2 lower than in Cha I (5–17%, see Paper I). Apart from the few candidate prestellar cores, the population of starless cores in Cha III is very similar to the one in Cha I because they have nearly the same median peak, aperture, and total masses as well as the same median size and aspect ratio (compare Figs. 6 and 7 to Figs. 7 and 8 of Paper I). They also follow the same correlation in an αBE versus Mtot diagram (see Fig. 12). The main striking difference is that the visual extinction of the medium in which the Cha III sources are embedded is on average a factor of 2 lower than in Cha I. Although we a priori cannot exclude that the extinction laws of both clouds may differ or that there may be more contamination by foreground stars toward Cha III leading to an underestimate of the extinction, we rather consider that this difference may come from the density structure or the physical processes at work in the clouds. As mentioned in Sect. 1, Cha III looks much more filamentary in cold dust emission at 100 μm than Cha I (see Fig. 7 of Boulanger et al. 1998). If this is also the case on scales smaller than the resolution of our extinction maps (3′), one could expect lower extinctions for the “ambient” medium in Cha III compared to Cha I. Alternatively, this difference in ambient extinction (and thus ambient density) for two otherwise similar populations of starless cores may indicate that the structuring of the interstellar medium into seeds of cores does not depend much on the local gravity and may be dominated by other processes such as turbulence and magnetic fields (see also André et al. 2010).
 |
Fig. 12 Ratio of total mass to Bonnor-Ebert critical mass as a function of total mass. The filled diamonds and open squares show the Cha I and III sources, respectively. The dashed line shows the limit above which a source is gravitationally unstable. The gravitationally bound sources are located above the dotted line, provided they are supported by thermal pressure only and the external pressure is negligible. |
The sample of starless sources in Cha III being small, the accuracy of the CMD is not sufficient to compare it with the IMF and the CO clump mass spectrum (see Sect. 4.3.7). To enlarge the statistics, the source samples of Cha I and III can be merged, both surveys having nearly the same mass completeness limit and their populations of starless cores having very similar properties. The full sample contains 89 sources (60 in Cha I and 29 in Cha III) and its mass distribution is shown in Fig. 13a. We can also consider only the starless sources of this enlarged sample that are not candidate prestellar cores, i.e., those with αBE < 1. This yields a sample of 85 sources (57 in Cha I and 28 in Cha III), the excluded sources being Cha1-C1–3 and Cha3-C1. The mass distribution of this slightly smaller sample is presented in Fig. 13b. Above the 90% completeness limit, both distributions are well fitted by a single power-law with an exponent αlog = −1.5 ± 0.3 and − 1.7 ± 0.4, respectively. This is steeper than, but still consistent within 1σ with, the Salpeter exponent of the high-mass end of the stellar IMF, and it is definitely much steeper than the CO clump mass distribution that is characterized by αlog = −0.6 (Blitz 1993; Kramer et al. 1998)7. Even if the combined sample of Cha I and III starless sources detected with LABOCA is large (89 sources), there are only about 50 sources above the completeness limit. We thus expect that the ongoing sensitive survey of the Chamaeleon clouds performed with Herschel in the frame of the Gould Belt Survey (André et al. 2010) will provide a more complete sample of starless cores and thus a more robust CMD. In particular, the shape of the mass distribution of the starless sources that are not candidate prestellar cores will be of prime importance.
 |
Fig. 13 Mass distribution dN/dlog (M) of the starless sources of Cha I and III. Panel a) shows all sources while panel b) displays only those with M/MBE < 1.0. The error bars represent the Poisson noise (in |
The population of starless cores detected with LABOCA in Cha I and III is very puzzling: although most of these sources do not appear to be prestellar based on the Bonnor-Ebert criterion, their mass distribution seems to be consistent with the stellar IMF at the high-mass end. For Cha I, we argued that a loss of thermal support via cooling would not be sufficient to bring these cores above the Bonnor-Ebert mass limit, hence that they are unlikely to form stars in the future (Paper I). Along with other arguments, this suggested that star formation is over in Cha I. In the same way, we could a priori conclude (but see the next sections) that, apart from the northern part of the cloud where one candidate prestellar core is found, Cha III does not seem to be able to start the process of star formation.
The level of turbulence is very similar in both clouds, as measured via the linewidths of the J = 1–0 transitions of CO and C18O (see Sect. 5.3 below). Taken at face value, turbulence thus does not seem to be the key parameter promoting star formation because Cha I formed many stars in the past, while Cha III did not. However, the present level of turbulence in Cha I may not reflect the initial conditions when the first stars were formed. On the one hand, the level of turbulence in this cloud may have been lower in the past and have been raised as a result of stellar feedback via, e.g., molecular outflows, possibly preventing the process of star formation to continue at the present epoch. On the other hand, if the feedback of the Cha I (low-mass) YSOs has not been sufficient, the turbulence may have decayed with time. In this case, the same behavior would a priori be expected for both clouds, which would not explain their difference in terms of past star-formation activity.
5.2. Are the Chamaeleon cores similar to the Pipe cores?
At this stage, it is very instructive to compare the population of starless cores in Cha I and III to the one found in the Pipe nebula via extinction maps (Alves et al. 2007; Lada et al. 2008; Rathborne et al. 2009). The Pipe nebula is the only other nearby star-forming region in the pre-Herschel era for which a population of dense cores that are mostly gravitationally unbound has been found, with a mass distribution still consistent with the stellar IMF at the high-mass end. In addition, its CMD departs from a single power law and has a break like the IMF but at a higher mass of 2.7 ± 1.3 M⊙, suggesting a star-formation efficiency of ~ 20% in this cloud (Rathborne et al. 2009). Interestingly, only the sources with a mass higher than this characteristic mass appear to be prestellar based on the Bonnor-Ebert criterion (see Fig. 9 of Lada et al. 2008). Lada et al. (2008) suggest that the gravitationally unbound cores are pressure-confined, the external pressure being most likely provided by the weight of the cloud itself. They thus do not appear to be transient structures. Lada et al. (2008) consider two mechanisms that may turn these stable but unbound cores into prestellar cores: either an increase of the external pressure produced by the contraction of the whole cloud, or a mass increase if these cores have not obtained their final mass yet. The former mechanism would require a decrease of a factor of 2 in cloud radius, which may be possible via the dissipation of its supersonic turbulence but casts a potential timescale problem because the more massive unstable cores would form stars much more rapidly than the less massive ones (see Lada et al. 2008 for details).
The starless cores in Cha I and III that are presently unstable according to the Bonnor-Ebert criterion are also the most massive ones, like in the Pipe nebula, but the transition occurs at a lower mass (~1 versus ~3 M⊙, see Fig. 12). With a median mass of 0.9 M⊙ and a median radius of 0.07 pc (computed from Table 2 of Rathborne et al. 2009), the Pipe cores are bigger than the Chamaeleon ones by a factor of ~4 in mass and ~2.5 in radius (but see the caveats about the radius in Sect. 4.3.2). While this could be an intrinsic property, we believe that it results from the different tracers used to extract the cores: extinction maps are more sensitive to extended, low-density material than 870 μm dust emission maps. The factor of 3 difference between the transition masses mentioned above may therefore simply result from the fact that the LABOCA masses do not include the low-density material surrounding each core.
A major difference exists between the CMDs of the Pipe nebula and the Chamaeleon I and III clouds, however: there is no evidence for a break in the Chamaeleon CMD down to the 90% completeness limit of 0.2 M⊙, while such a break is seen around 2.7 M⊙ in the Pipe nebula. Even the possible mass scaling factor of 4 mentioned above would not be sufficient to explain this difference. However, the low-density material possibly missing in the LABOCA masses could affect the shape of the CMD rather than contributing as just a scaling factor. On the one hand, if the Chamaeleon cores are seeds of prestellar cores in the process of accumulating mass (see Sect. 5.3 below), we may conjecture that the break in the CMD could arise from this mass accumulation process. On the other hand, a large fraction of the lowest mass cores may never become prestellar and they may currently hide the true shape of the prestellar CMD in Chamaeleon.
5.3. Can the starless cores in Cha I and III turn prestellar?
The possibility that the unbound starless cores of the Pipe and Cha I/III clouds are still accumulating mass has been mentioned in Sect. 5.2 and is very attractive in light of the results obtained by recent numerical simulations. In this section, we compare the properties of Cha I and III to several kinds of numerical simulation.
Gómez et al. (2007) study the formation and collapse of quiescent cloud cores induced by focused compressions (or “convergent flows”) in a cloud of diameter 1 pc that initially has a constant sub-Jeans density of 113 cm-3 and a uniform temperature of 11.4 K. The velocity amplitude of the compressing impulse is 0.4 km s-1 (Mach number of 2). A mild shock propagates inward, the material left behind it (the envelope) being set into infall motions. The shock bounces off the center and expands outward, leaving a quiescent core in the inner part. The structure of the core+envelope system then resembles a truncated Bonnor-Ebert sphere with a flat inner density profile and a density falling as ~r-2 in the (infalling) envelope. Depending on the initial conditions (position of the impulse within the cloud), the core can gain enough mass from the envelope to become gravitationally unstable and start collapsing. In this model, the inner quiescent core with a density of ~105 cm-3 is initially unbound and confined by the ram pressure of the inflowing gas. It grows in size and mass until it becomes dominated by gravity. Interestingly, there is a significant time delay of ~5 × 105 yr between the formation of the inner core (when the system starts to look like a pseudo Bonnor-Ebert sphere) and the onset of gravitational collapse, owing to the growth in mass.
The C18O 1–0 linewidths in Cha I and III are on the order of 0.8–0.9 km s-1 at an angular resolution of 2.7′ (Mizuno et al. 1999), implying an rms (turbulent) velocity dispersion of 0.3–0.4 km s-1. The CO 1–0 linewidths, tracing even lower-density material, are a factor of ~2.5 times larger (Boulanger et al. 1998; Mizuno et al. 2001). The initial conditions chosen by Gómez et al. (2007) are therefore plausible for Chamaeleon from a kinematic point of view. The typical densities of the Chamaeleon starless cores are also similar to the density of the inner core formed in these simulations. If this scenario holds for Chamaeleon, a fraction of these presently unbound cores could turn prestellar in the future (in less than ~ 5 × 105 yr) if they gain enough mass to become unstable. We note, however, that there is no evidence for significantly flattened inner density profiles in the Chamaeleon sample (see Sect. 4.3.5 and Paper I), but this may not be a shortcoming for this scenario, the spherically symmetric model and initial conditions of Gómez et al. (2007) being highly idealized. Finally, since some of the simulations of Gómez et al. (2007) do not lead to the formation of an unstable core prone to collapse, a fraction of the Chamaeleon starless cores may never reach the critical mass and simply get dispersed in the future (see their simulation S1).
Another fruitful approach is the one followed by Clark & Bonnell (2005). These authors examine the formation of bound coherent cores in molecular clouds supported by (decaying) turbulence. They model a cloud of mass 32.6 M⊙ and diameter ~0.3 pc at 10 K with an initially uniform density of 5.6 × 104 cm-3 and turbulent velocities characterized by an initial effective Mach number of 5.3 and a power spectrum P(k) ∝ k-4 (their simulation 2). A large number of fragments8 are formed, most of them being initially unbound. Their mass distribution is well fitted by a Salpeter slope at the high-mass end when star formation sets in (at t ~ tff, with tff the initial free-fall time of the cloud). Interestingly, the mass distribution of these mostly unbound fragments is slightly steeper at the high-mass end at an earlier stage (t = 0.6tff, see Fig. 3 of Clark & Bonnell 2005). A second important point is that only the most massive fragments are gravitationally bound (see their Fig. 5). In this simulation, the unbound fragments grow in mass, as a result of coagulation, but only a small fraction of them become gravitationally unstable and can start collapsing. The number of gravitationally unstable cores formed in this way (11 for their simulation 2) is on the same order of magnitude as the initial number of mean Jeans masses in the cloud (33).
The population of starless cores in Cha I and III share similar properties with the simulated fragments of Clark & Bonnell (2005): their CMD resembles the IMF at the high-mass end, most cores are unbound, and only the most massive ones are gravitationally unstable. The slope of the Chamaeleon CMD at the high-mass end is even slightly steeper (but only at the 1σ level) than the Salpeter value, like for the simulated fragments before star formation sets in. However, most objects qualified as fragments in the simulation are much too small and too faint to be detected in our continuum maps. There are more than 1000 fragments formed in the simulated cloud of projected area 0.053 pc2, while we detect only 89 cores in 17 pc2. Because of the limited sensitivity and angular resolution of our maps, the low number of detected starless cores does not really rule out this scenario of turbulence-generated, small, unbound fragments that coagulate with time. We may be seeing only those fragments that have already grown enough by coagulation to be detected. One problem with this analogy may be that the initial level of turbulence assumed in the simulations of Clark & Bonnell (2005) is significantly higher than the one characterizing the regions of Cha I and III that have similar densities of ~5 × 104 cm-3 (Mach number < 2 based on C18O 1–0, see Mizuno et al. 1999; Gahm et al. 2002).
The comparison of the properties of the Chamaeleon starless cores to those produced in the simulations of Clark & Bonnell (2005) and Gómez et al. (2007) leaves open the hypothesis that a fraction of these starless cores may become unstable in the future by accumulating mass from larger scales. Because most Chamaeleon starless cores are located in filamentary structures, the next question is whether this gain in mass could simply occur along the filaments or would require accumulation of material from larger scales. In Cha I, the mass of the filaments traced with LABOCA is, without counting the cores embedded within them, roughly equal to the mass of the starless cores. If this LABOCA mass is representative of the real mass of the filaments, then the mass gain could not be larger than a factor of 2 and would not be sufficient to bring most starless cores above the Bonnor-Ebert limit, provided the product of their temperature and radius does not at the same time decrease by more than a factor of 2 (see the definition of MBE(R) in Sect. 4.3.6). In their simulations of dense core formation in supersonic turbulent converging flows, Gong & Ostriker (2011) report that filaments are formed in post-shock regions at the same time as overdense regions within these filaments condense into cores. It is thus tempting to conclude that the starless cores in Cha I and III may grow in mass at the same time as the filaments do under the influence of turbulence and self-gravity. Interestingly, the simulations of Gong & Ostriker (2011) can produce alignments of nearly regularly spaced cores. For a Mach number of 5, the core separation is on the order of 0.2 code units, i.e. 0.15–0.47 pc for a mean density of free particles of 4000–400 cm-3 (see their Fig. 7, top left and bottom right panels). This is very much reminiscent of the remarkable alignment of regularly spaced cores in Cha3-Center (see Sect. 4.4 and Fig. 3c). The CO linewidths measured on large scales in Cha III are on the order of 2–2.5 km s-1, i.e. a Mach number of 4–5 (Boulanger et al. 1998; Mizuno et al. 2001). Depending on the scale and the assumptions made, the estimates of the mean density range between 400 and 4000 cm-3 for Cha3-Center (see Sect. 3.2 and Gahm et al. 2002). Given the unknown inclination of the filamentary structure, the projected separation of the aligned cores in Cha3-Center could be in rough agreement with the one produced in the simulations of Gong & Ostriker (2011). Because some of the cores become gravitationally unstable in these simulations, this may also be the fate of some of the starless cores in Cha3-Center, and by extension in the full sample of Chamaeleon starless sources.
5.4. A large fraction of “failed” cores in Cha I and III?
In the simulations of Gómez et al. (2007), the phase of mass growth, from the time of central core formation on, lasts about as long as the collapse phase. In their 1D spherically symmetric simulations of converging supersonic flows, Gong & Ostriker (2009) find a duration of the core-building phase about nine times longer than the duration of the collapse phase, which is also confirmed by their three-dimensional simulations (Gong & Ostriker 2011). However, only a fraction of this core-building phase is observable. Gong & Ostriker (2009) estimate that 10–20% of the core building phase is observable if one takes as observability criterion a density contrast between the center and the edge of a core, ρc/ρedge, higher than 5. This means a duration of the observable core-building phase 1–2 times longer than the duration of the collapse phase, which is roughly consistent with the result of Gómez et al. (2007).
If we associate the four9 starless cores of Cha I and III that have αBE > 1 with the collapse phase and the other starless cores (84) with the observable core-building phase, then we would expect only 4–8 additional cores (3–6 in Cha I and 1–2 in Cha III) to become gravitationally unstable in the future, provided the process of star formation occurs at a constant rate and the model prediction of the duration of the core-building phase mentioned in the previous paragraph is correct. If the LABOCA masses are underestimated by a factor of 2, then there are about 10 and 2 candidate collapsing cores at the present time, plus 10–20 and 2–4 additional starless cores that could become gravitationally unstable in Cha I and III, respectively. Given these numbers, at least 29–39 and 23–25 starless cores, i.e., 49–66% and 79–86% of the population of starless cores detected with LABOCA, will most likely never become gravitationally unstable in Cha I and III, respectively. These fractions may even be underestimated if the cores detected with LABOCA have a ratio ρc/ρedge significantly higher than 5, which may well be the case since cn in Table 3 (and Table 6 of Paper I) is likely smaller than the true ratio ρc/ρedge. However, these large fractions of “failed” cores hold only if the simulations of converging flows mentioned above are appropriate descriptions of the physical processes at work in the Chamaeleon molecular clouds. If the observable core-building phase lasts significantly longer than the collapse phase, then the actual fraction of “failed” cores could be smaller.
In light of this new analysis, it cannot be excluded that Cha I will go on forming stars. However, even if mass growth occurs and the number of prestellar cores increases by a factor 2–3 as suggested in the previous paragraphs, this number will still be too low by a factor 2–4 (if the LABOCA masses are correctly estimated) to be consistent with a constant star-formation rate since the time when the current pre-main-sequence stars were formed (2 Myr ago, see Paper I and references therein). In addition, the lack of Class 0 protostars by a factor maybe as large as 10 in Cha I (see Paper I) remains a strong indication that the star-formation rate has decreased with time in this cloud. Cha I may not be at the end of the process of star formation as was suggested in Paper I, but it is at least secure to conclude that its star-formation rate has decreased with time by a factor >2−4 over the last 2 Myr. On top of this overall decrease, it may have significantly fluctuated, by a factor 2 − 5 to account for the lack of Class 0 protostars.
5.5. A prime target to study the formation of prestellar cores
With one candidate prestellar core and one or two additional starless cores that could turn prestellar (see Sect. 5.4), Cha III seems to be able to form stars, even if presently at a very low rate. This is somewhat in contrast with the Polaris flare region, another presently non-star-forming molecular cloud. A large population of starless cores was recently uncovered with Herschel in that cloud but the cores typically lie one to two orders of magnitude below the Bonnor-Ebert mass limit (see Fig. 4 of André et al. 2010). Since the bulk of the population of starless cores detected with LABOCA in Cha III lies a factor 3–4 below the Bonnor-Ebert mass limit, the tip of the Polaris population has αBE lower by a factor ~3 compared to the Cha III starless cores. This suggests that Cha III may be closer to form prestellar cores than Polaris (but see Heithausen et al. 2002 for possible evidence of gravitationally bound cores in the latter).
With a large fraction of starless cores presently not prestellar but still with some evidence that star formation can occur, Cha III becomes a prime target to study the formation of prestellar cores, i.e., the core-building phase when mass is accumulated, and thus the onset of star formation. In particular, it will be essential to obtain observational constraints on the duration of the core-building phase prior to the phase of gravitational collapse. In the previous section, we relied on predictions of numerical simulations to estimate this duration and derive the fraction of “failed” cores, but this needs to be tested observationally.
Finally, on a very speculative level, the factor of 2 difference between the median nearest-neighbor distances of the starless cores in Cha I and III (0.07 pc versus 0.14 pc, respectively, see Sect. 4.4 and Fig. 11) could be interpreted as fragmentation being more efficient or more advanced in Cha I compared to Cha III, which could in turn have played a role in the fact that Cha I has been more efficient than Cha III in forming stars. In that respect, it would be instructive to investigate whether significant differences in, e.g., magnetic field structure exist between both clouds that could explain this speculative difference in their ability to fragment.
6. Conclusions
We performed a deep, unbiased, 870 μm dust continuum survey for starless and protostellar cores in Chamaeleon III with the bolometer array LABOCA at APEX. The resulting 0.9 deg2 map was compared with a map of dust extinction. The analysis was performed by carefully taking into account the spatial filtering properties of the data reduction process following the prescriptions of Paper I. The extracted sources were compared to those found in Cha I (Paper I) and other molecular clouds. Our main results and conclusions are the following:
 |
Fig. A.1 Statistical properties of 100 artificial, circular, Gaussian sources inserted into the raw time signals before data reduction (a) to e)) or directly inserted into the final unsmoothed continuum emission map of Cha I (f) to j). a) and f): ratio of output to input peak flux density as a function of input peak flux density. b) and g): ratio of output to input peak flux density as a function of input size (FWHM). c) and h): ratio of output major size to input size as a function of input size. d) and i): ratio of output minor size to input size as a function of input size. e) and j): ratio of output to input total flux as a function of input size. The size of the black symbols scales with the input peak flux density of the sources. In addition, crosses and plus symbols are for input peak flux densities below and above 150 mJy/19.2″-beam, respectively. The red circles in panels b) to e) and g) to j) show a fit to the data points using the arbitrary 3-parameter function y = log (α/(1 + (x/β)γ)). |
-
1.
The mass detected with LABOCA(23 M⊙) represents only 6%of the cloud mass traced by the dust extinction, and about 54% of the mass traced by the C18O 1–0 emission.
-
2.
Twenty-nine sources were extracted from the 870 μm map, all of them starless. No unresolved source is detected, which is consistent with the absence of any known young stellar object in this cloud.
-
3.
The starless sources are found down to a visual extinction of 1.9 mag. Unexpectedly, about half of the sources are found below 5 mag, which is in marked contrast with other molecular clouds, including Cha I, where starless cores are only found above this threshold. Since the LABOCA surveys toward Cha I and III have the same sensitivity and were analyzed in the same way, this result may point to an intrinsic structural difference between the two clouds.
-
4.
The 90% completeness limit of our 870 μm starless core survey is 0.18 M⊙. Only 50% of the detected starless cores are above this limit, suggesting that we may miss a significant fraction of the existing starless cores.
-
5.
Although the distribution of starless sources suggests the existence of filaments, these filaments are not detected with LABOCA in Cha III, while the LABOCA map of Cha I shows clear evidence of filamentary structures with the same sensitivity.
-
6.
There is a remarkable alignment of six nearly equally spaced sources in Cha III, which may have been produced by turbulent fragmentation of a filament or simply represent transient periodic overdensities.
-
7.
Apart from their distribution of ambient extinction, the Cha III starless cores share very similar properties with those found in Cha I. They are less dense than those in Perseus, Serpens, Ophiuchus, and Taurus by a factor of a few on average.
-
8.
At most two sources (<7%) are above the critical Bonnor-Ebert mass limit in Cha III, which suggests that a large fraction of the starless cores may not be prestellar. Only the most massive cores in Cha I and III turn out to be candidate prestellar cores according to the Bonnor-Ebert mass criterion, in agreement with the correlation observed in the Pipe nebula.
-
9.
The mass distribution of the 85 starless cores of Cha I and III that are not candidate prestellar cores is consistent with a single power law down to the 90% completeness limit, with an exponent close to the Salpeter value. There is no evidence for a break such as the one seen in the core mass distribution of the Pipe nebula, and in the stellar IMF.
-
10.
A fraction of the Cha I and III starless cores that are presently not candidate prestellar cores may still be growing in mass and turn prestellar in the future. Based on predictions of numerical simulations of turbulent molecular clouds concerning the duration of the core-building phase, we estimate that at most 50% and 20% of the starless cores detected with LABOCA in Cha I and III, respectively, may form stars.
Given their large fraction of starless cores that do not appear to be prestellar yet, Cha I and III turn out to be excellent sites to study the formation of prestellar cores. Because we find some evidence that star formation can start in Cha III, this cloud even becomes a prime target to investigate the onset of star formation. The main next step to make further progress will be to obtain observational constraints on the duration of the core-building phase that precedes the gravitational collapse.
A prestellar core is usually defined as a starless core that is gravitationally bound (André et al. 2000; di Francesco et al. 2007). Starless means that it does not contain any young stellar object.
This caveat does not concern the mass derived from C18O 1–0 since the map of Mizuno et al. (1999) has more or less the same size as the LABOCA map.
We note that Ikeda & Kitamura (2011) find α = −2.1 ± 0.2 with C18O 1–0 in S140, the same cloud for which Kramer et al. (1998) derived α = −1.65 ± 0.18 with C18O 2–1. They argue that the study of Kramer et al. (1998) is limited to the central part of the cloud and is likely biased toward high-mass cores (hence yielding a flatter CMD). They also show that a poor spatial resolution leads to underestimating | α | if the resolution is worse than 0.1 pc. The “classical” index α = −1.6 is therefore most likely valid for larger CO clumps only.
Clark & Bonnell (2005) use the word “clumps” for these objects, but we prefer to call them “fragments” because, in the context of observations, the word “clump” is usually given to larger-scale structures that may contain several cores (see, e.g., Williams et al. 2000).
We exclude Cha1-C1, i.e., the candidate first hydrostatic core Cha-MMS1, but we include Cha1-C4 that has αBE > 1 based on the pressure.
Acknowledgments
We thank the APEX staff for their support during the observing sessions and Axel Weiß, Arturo Gómez-Ruiz, Tobias Troost, and Tomasz Kamiński for carrying out part of the observations. A.B. also thanks Patrick Hennebelle and Steve Longmore for enlightening discussions. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. B.P. acknowledges her support by the German Deutsche Forschungsgemeinschaft, DFG Emmy Noether number PA 1692/1-1.
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, Ph., Ward-Thompson, D., & Barsony, M. 2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: University of Arizona Press), 59 [Google Scholar]
- André, Ph., Men’shchikov, A.,Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, Ph., Men’shchikov, A., Könyves, V., & Arzoumanian, D. 2011, in Computational star formation, ed. J. Alves, B. Elmegreen, J. M. Girart, & V. Trimble, IAU Symp., 270, 255 [Google Scholar]
- Arzoumanian, D., André, Ph., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Belloche, A., Parise, B., van der Tak, F. F. S., et al. 2006, A&A, 454, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011, A&A, 527, A145 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blitz, L. 1993, in Protostars and Planets III, ed. E. H. Levy, & J. I. Lunine (Tuscon: Univ. of Arizona Press), 125 [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Boulanger, F., Bronfman, L., Dame, T. M., & Thaddeus, P. 1998, A&A, 332, 273 [NASA ADS] [Google Scholar]
- Chabrier, G. 2005, in The Initial Mass Function 50 Years Later, ed. E. Corbelli, F. Palla, & H. Zinnecker, Astrophysics and Space Science Library, 327, 41 [Google Scholar]
- Clark, P. C., & Bonnell, I. A. 2005, MNRAS, 361, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, D. P. 2005, ARA&A, 43, 337 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- di Francesco, J., Evans, N. J., II, Caselli, P., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 17 [Google Scholar]
- Enoch, M. L., Young, K. E., Glenn, J., et al. 2006, ApJ, 638, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, N. J., II,Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Gahm, G. F., Lehtinen, K., Carlqvist, P., et al. 2002, A&A, 389, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, M., Hartmann, L., Kenyon, S. J., & Hewett, R. 1993, AJ, 105, 1927 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, M., Persi, P., Marenzi, A. R., Roth, M., & Tapia, M. 2004, A&A, 423, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, G. C., Vázquez-Semadeni, E., Shadmehri, M., & Ballesteros-Paredes, J. 2007, ApJ, 669, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, H., & Ostriker, E. C. 2009, ApJ, 699, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, H., & Ostriker, E. C. 2011, ApJ, 729, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanawa, T., Nakamura, F., Matsumoto, T., et al. 1993, ApJ, 404, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Heithausen, A., Bertoldi, F., & Bensch, F. 2002, A&A, 383, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ikeda, N., & Kitamura, Y. 2011, ApJ, 732, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Di Francesco, J., & Kirk, H. 2004, ApJ, 611, L45 [Google Scholar]
- Kirk, H., Johnstone, D., & Di Francesco, J. 2006, ApJ, 646, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Knude, J., & Høg, E. 1998, A&A, 338, 897 [NASA ADS] [Google Scholar]
- Könyves, V., André, Ph., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Muench, A. A., Rathborne, J., Alves, J. F., & Lombardi, M. 2008, ApJ, 672, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D. 1978, ApJ, 225, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2006, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L. 2008, in Handbook of Star Forming Regions Vol., II, ed. B. Reipurth, ASP Monograph Publications, 5, 169 [Google Scholar]
- Matsumoto, T., Nakamura, F., & Hanawa, T. 1994, PASJ, 46, 243 [NASA ADS] [Google Scholar]
- Mattila, K., Liljestrom, T., & Toriseva, M. 1989, in Low Mass Star Formation and Pre-main Sequence Objects, ed. B. Reipurth, ESO Conf. and Workshop Proc., 33, 153 [Google Scholar]
- Men’shchikov, A., André, Ph., Didelon, P., et al. 2010, A&A, 518, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mizuno, A., Hayakawa, T., Yamaguchi, N., et al. 1998, ApJ, 507, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, A., Hayakawa, T., Tachihara, K., et al. 1999, PASJ, 51, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, A., Yamaguchi, R., Tachihara, K., et al. 2001, PASJ, 53, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., André, P., & Neri, R. 1998, A&A, 336, 150 [Google Scholar]
- Nakamura, F., Hanawa, T., & Nakano, T. 1993, PASJ, 45, 551 [NASA ADS] [Google Scholar]
- Persi, P., Marenzi, A. R., & Goméz, M. 2003, in Exploiting the ISO Data Archive. Infrared Astronomy in the Internet Age, ed. C. Gry et al., ESA SP-511, 221 [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., et al. 2009, ApJ, 699, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Sadavoy, S. I., Di Francesco, J., Bontemps, S., et al. 2010, ApJ, 710, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schwartz, R. D. 1977, ApJS, 35, 161 [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tóth, L. V., Hotzel, S., Krause, O., et al. 2000, A&A, 364, 769 [NASA ADS] [Google Scholar]
- Wang, H., & Henning, T. 2006, ApJ, 643, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Prusti, T., Franco, G. A. P., et al. 1997, A&A, 327, 1194 [NASA ADS] [Google Scholar]
- Williams, J. P., Blitz, L., & McKee, C. F. 2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: University of Arizona Press), 97 [Google Scholar]
- Young, K. E., Harvey, P. M., Brooke, T. Y., et al. 2005, ApJ, 628, 283 [Google Scholar]
Appendix A: LABOCA data reduction: spatial filtering and convergence
A.1. Spatial filtering owing to the correlated noise removal
In a previous work, we characterized in detail the spatial filtering of LABOCA data owing to the correlated noise removal and the high-pass filter (Paper I). Because these observations were performed using a combination of rectangular and spiral scanning patterns, the latter being more compact (diameter 6′), the properties of the spatial filtering affecting the Cha III dataset, which was obtained with rectangular scanning patterns only, could a priori differ: the correlated noise removal depends on the size of the camera only, but the baseline removal is performed scan- (or subscan-)wise, i.e., on scales that can be larger than the camera, so it depends on the scanning pattern. We performed Monte Carlo simulations to evaluate the filtering properties following exactly the same procedure as described in Appendix A of Paper I, with four sets of 25 circular, artificial, Gaussian sources each. Figures A.1a–e and Table A.1 present the results. As a control check, we show in Figs. A.1f–j the results of the fits performed on the artificial sources directly inserted in the final unsmoothed continuum emission map of Cha III.
Filtering of artificial Gaussian sources owing to the correlated noise removal depending on the input size (FWHM).
 |
Fig. A.2 a) Convergence of the total 870 μm flux recovered in Cha III by the iterative process of data reduction. b) Relative flux variation between iterations i and i − 1 as a function of iteration number i. |
 |
Fig. A.3 Convergence of the iterative data reduction for artificial, circular, Gaussian sources with a peak flux density larger than 150 mJy beam-1. The first and second columns show the ratio of the output to the input peak flux densities, and its relative variations, respectively. The third and fourth columns show the same for the total flux. The different rows show sources of different widths, as specified in each panel of the first column. The size of the symbols increases with the input peak flux density. In panels n) and p), the noisier curve corresponds to a very large source with a peak flux twice as weak as the other one that has a similar size (see Figs. A.1a and b). |
To first order, the results listed in Table A.1 are very similar to those obtained for Cha I. The difference between strong and weak sources concerning the peak flux density is less pronounced for Cha III than for Cha I, but this may not be statistically significant because the estimate for the weak artificial sources in Cha III is based on very few extended sources: there are only three such sources between 130″ and 260″, two of them behaving like the sample of stronger sources and one being significantly more affected by the filtering (see the outlier point at (145″, 0.63) in Fig. A.1b). However, the size and integrated flux suffer more for Cha III than for Cha I. This is surprising since one would a priori expect the rectangular scanning pattern to be less sensitive to spatial filtering than the more compact spiral scanning pattern. The reasons for this difference are still unclear. It may be caused by a reduction of the number of well-working pixels in 2010 compared to 2007–2008: on average, the Cha III scans had 224 ± 2 well-working pixels while the Cha I scans had 232 ± 18. Alternatively, this could suggest that mixing rectangular and spiral patterns is more robust to spatial filtering than scanning with rectangular patterns only.
A.2. Convergence of the iterative data reduction
Like for Cha I, the iterative process of the data reduction improves the recovery of extended emission. Figure A.2 shows that the convergence of the total astronomical flux is reached within 1% at iteration 20. Figure A.3 shows how the speed of convergence depends on the source size. The convergence in terms of peak flux density and integrated flux for the sources is faster for compact sources than for extended ones. For sources smaller than 320″, the convergence is reached within 1% in peak flux density and 2% in total flux. For the few larger sources, the convergence is reached within 2% and 4% at iteration 20, respectively. These results are very similar to those obtained with the Cha I dataset (see Paper I).
All Tables
Sources extracted with Gaussclumps in the 870 μm continuum sum map of Cha III at scale 5.
Characteristics of starless sources extracted with Gaussclumps in the 870 μm continuum sum map of Cha III at scale 5.
Filtering of artificial Gaussian sources owing to the correlated noise removal depending on the input size (FWHM).
All Figures
 |
Fig. 1 Extinction map of Cha III derived from 2MASS in radio projection. The projection center is at (α,δ)J2000 = (12h42m24s, − 79°43′48″). The contours start at AV = 3 mag and increase by steps of 1.5 mag. The dotted lines are lines of constant right ascension. The angular resolution of the map (HPBW = 3′) is shown in the upper right corner. The five fields selected for mapping with LABOCA are delimited with dashed lines. The field of view of LABOCA is displayed in the lower right corner. |
| In the text | |
 |
Fig. 2 870 μm continuum emission map of Cha III obtained with LABOCA at APEX. The projection type and center are the same as in Fig. 1. The contour levels are a, 2a, 4a, and 6a with a = 34.5 mJy/21.2″-beam, i.e., three times the rms noise level. The flux density color-scale is shown on the right. The field of view of LABOCA (10.7′) and the angular resolution of the map (HPBW = 21.2″) are shown on the right. The red boxes in the insert are labeled like Figs. 3a–e and show their limits overlaid on the first 870 μm contour. |
| In the text | |
 |
Fig. 3 Detailed 870 μm continuum emission maps of Cha III extracted from the map shown in Fig. 2. The flux density grayscale is shown to the right of each panel and labeled in Jy/21.2″-beam. It has been optimized to reveal the faint emission with a better contrast. The contours start at a and increase with a step of a, with a = 34.5 mJy/21.2″-beam, i.e., three times the rms noise level. The dotted blue contour corresponds to − a. The angular resolution of the map is shown in the lower left corner of each panel (HPBW = 21.2″). The white plus symbols and ellipses show the positions, sizes (FWHM), and orientations of the Gaussian sources extracted with Gaussclumps in the filtered map shown in Fig. 4a. The sources are labeled like in the first column of Table 3. The (red) crosses show the peak position of the 38 clumps detected in C18O 1–0 with SEST (Gahm et al. 2002). a) Field Cha3-North. |
| In the text | |
 |
Fig. 3 continued. b) Field Cha3 -East. |
| In the text | |
 |
Fig. 3 continued. c) Field Cha3-Center. |
| In the text | |
 |
Fig. 3 continued. d) Field Cha3-South. |
| In the text | |
 |
Fig. 3 continued. e) Field Cha3-West. |
| In the text | |
 |
Fig. 4 a) 870 μm continuum emission sum map of Cha III at scale 5. The contour levels are − a (in dotted blue), a, 2a, and 4a, with a = 34.5 mJy/21.2″-beam, i.e., about 3 times the rms noise level. b) Smoothed map, i.e., residuals, at scale 5. The contour levels are − c (in dotted blue), c, 2c, 4c, and 8c, with c = 8.1 mJy/21.2″-beam, i.e., about 3 times the rms noise level in this map. The grayscales of both maps are different. The sum of these two maps is strictly equal to the original map (Fig. 2). |
| In the text | |
 |
Fig. 5 Extinction map of Fig. 1 (red contours) overlaid on the 870 μm continuum emission map of Cha III (black contours). The contour levels of the extinction map start at 3 mag and increase by steps of 1.5 mag. The thicker red contours correspond to AV = 4.5 and 7.5 mag. The contour levels of the 870 μm map are the same as in Fig. 2, plus a dotted blue contour at −a. The dotted line delimits the field mapped at 870 μm. The field of view of LABOCA and the angular resolution of the extinction map are shown in the upper right corner. |
| In the text | |
 |
Fig. 6 Distributions of physical properties obtained for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The mean, standard deviation, and median of the distribution are given in each panel. The asymmetric standard deviation defines the range containing 68% of the sample. a) FWHM sizes along the major (solid line) and minor (dashed line) axes. The filled histogram shows the distribution of geometrical mean of major and minor sizes. The mean and median values refer to the filled histogram. The dotted line indicates the angular resolution (21.2″). b) Same as a) but for the deconvolved sizes. c) Aspect ratios computed with the deconvolved sizes. The dotted line at 1.4 shows the threshold above which the deviation from 1 (elongation) can be considered as significant. d) Peak H2 column density. The dotted line at 5.0 × 1021 cm-2 is the 5σ sensitivity limit. e) Visual extinction derived from 2MASS. |
| In the text | |
 |
Fig. 7 Distributions of masses and free-particle densities obtained for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The mean, standard deviation, and median of the distribution are given in each panel. The asymmetric standard deviation defines the range containing 68% of the sample. a) Peak mass of the fitted Gaussian. b) Mass within an aperture of diameter 50″. c) Total mass of the fitted Gaussian. The dotted line indicates the estimated completeness limit at 90% for Gaussian sources corresponding to a 6.3σ peak detection limit for the average source size. d) Mass concentration, ratio of the peak mass to the mass within an aperture of diameter 50″. e) Peak density. f) Mean density within an aperture of diameter 50″. g) Mean density derived from the total mass. h) Density contrast, ratio of peak density to mean density. In panels a) and e), the dotted line indicates the 5σ sensitivity limit. The upper axis of panel d), which can also be used for panel h), shows the power-law exponent p derived assuming that the sources have a density profile proportional to r − p and a uniform dust temperature. Alternately, the upper axis of panel h), which can also be used for panel d), deals with the case where the density is uniform within a diameter Dflat and decreases as r-2 outside, still with the assumption of a uniform temperature. |
| In the text | |
 |
Fig. 8 a) Total mass versus mean FWHM size for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The angular resolution (21.2″) is marked by the dotted line. The solid line (M ∝ FWHM2) is the 5σ peak sensitivity limit for Gaussian sources. The dashed line shows the 6.3σ peak sensitivity limit which corresponds to a completeness limit of 90% for Gaussian sources. b) Total mass versus mean deconvolved FWHM size. Sizes smaller than 25.4″ were set to 25.4″ before deconvolution (see note b of Table 3). The solid line shows the relation |
| In the text | |
 |
Fig. 9 a) Total mass versus visual extinction AV for the 29 starless sources found with Gaussclumps in the sum map of Cha III at scale 5. The dashed line shows the estimated 90% completeness limit (0.18 M⊙). b) FWHM size versus visual extinction. The angular resolution (21.2″) is marked by the dotted line. |
| In the text | |
 |
Fig. 10 Mass distribution dN/dlog (M) of the 29 starless sources. The error bars represent the Poisson noise (in |
| In the text | |
 |
Fig. 11 Distribution of nearest-neighbor projected distance for the starless sources of Cha III (a)) and Cha I (b)). In each panel, the dashed histogram shows the distribution expected for the same number of objects randomly distributed in the same area. The median value of each distribution is marked with a dotted line. |
| In the text | |
 |
Fig. 12 Ratio of total mass to Bonnor-Ebert critical mass as a function of total mass. The filled diamonds and open squares show the Cha I and III sources, respectively. The dashed line shows the limit above which a source is gravitationally unstable. The gravitationally bound sources are located above the dotted line, provided they are supported by thermal pressure only and the external pressure is negligible. |
| In the text | |
 |
Fig. 13 Mass distribution dN/dlog (M) of the starless sources of Cha I and III. Panel a) shows all sources while panel b) displays only those with M/MBE < 1.0. The error bars represent the Poisson noise (in |
| In the text | |
 |
Fig. A.1 Statistical properties of 100 artificial, circular, Gaussian sources inserted into the raw time signals before data reduction (a) to e)) or directly inserted into the final unsmoothed continuum emission map of Cha I (f) to j). a) and f): ratio of output to input peak flux density as a function of input peak flux density. b) and g): ratio of output to input peak flux density as a function of input size (FWHM). c) and h): ratio of output major size to input size as a function of input size. d) and i): ratio of output minor size to input size as a function of input size. e) and j): ratio of output to input total flux as a function of input size. The size of the black symbols scales with the input peak flux density of the sources. In addition, crosses and plus symbols are for input peak flux densities below and above 150 mJy/19.2″-beam, respectively. The red circles in panels b) to e) and g) to j) show a fit to the data points using the arbitrary 3-parameter function y = log (α/(1 + (x/β)γ)). |
| In the text | |
 |
Fig. A.2 a) Convergence of the total 870 μm flux recovered in Cha III by the iterative process of data reduction. b) Relative flux variation between iterations i and i − 1 as a function of iteration number i. |
| In the text | |
 |
Fig. A.3 Convergence of the iterative data reduction for artificial, circular, Gaussian sources with a peak flux density larger than 150 mJy beam-1. The first and second columns show the ratio of the output to the input peak flux densities, and its relative variations, respectively. The third and fourth columns show the same for the total flux. The different rows show sources of different widths, as specified in each panel of the first column. The size of the symbols increases with the input peak flux density. In panels n) and p), the noisier curve corresponds to a very large source with a peak flux twice as weak as the other one that has a similar size (see Figs. A.1a and b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.