| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201015841 | |
| Published online | 18 March 2011 | |
Modeling the evolution of infrared galaxies: a parametric backward evolution model
Univ Paris-Sud, Laboratoire IAS, UMR8617,
91405
Orsay Cedex,
France
CNRS, Orsay,
91405, France
Institut d’Astrophysique de Paris (IAP), UMR 7095 CNRS, UPMC, 98 bis boulevard Arago, 75014 Paris, France
e-mail: matthieu.bethermin@ias.u-psud.fr
Received: 30 September 2010
Accepted: 20 January 2011
Aims. We attempt to model the infrared galaxy evolution in as simple a way as possible and reproduce statistical properties such as the number counts between 15 μm and 1.1 mm, the luminosity functions, and the redshift distributions. We then use the fitted model to interpret observations from Spitzer, AKARI, BLAST, LABOCA, AzTEC, SPT, and Herschel, and make predictions for Planck and future experiments such as CCAT or SPICA.
Methods. This model uses an evolution in density and luminosity of the luminosity function parametrized by broken power-laws with two breaks at redshift ~0.9 and 2, and contains the two populations of the Lagache model: normal and starburst galaxies. We also take into account the effect of the strong lensing of high-redshift sub-millimeter galaxies. This effect is significant in the sub-mm and mm range near 50 mJy. It has 13 free parameters and eight additional calibration parameters. We fit the parameters to the IRAS, Spitzer, Herschel, and AzTEC measurements with a Monte Carlo Markov chain.
Results. The model adjusted to deep counts at key wavelengths reproduces the counts from mid-infrared to millimeter wavelengths, as well as the mid-infrared luminosity functions. We discuss the contribution to both the cosmic infrared background (CIB) and the infrared luminosity density of the different populations. We also estimate the effect of the lensing on the number counts, and discuss the discovery by the South Pole Telescope (SPT) of a very bright population lying at high redshift. We predict the contribution of the lensed sources to the Planck number counts, the confusion level for future missions using a P(D) formalism, and the Universe opacity to TeV photons caused by the CIB. Material of the model (software, tables and predictions) is available online⋆.
Key words: diffuse radiation / galaxies: statistics / galaxies: evolution / galaxies: star formation / infrared: galaxies / submillimeter: galaxies
© ESO, 2011
1. Introduction
The extragalactic background light (EBL) is the relic emission from galaxy formation and accretion processes since the recombination. The infrared (8 μm < λ < 1000 μm) part of this emission called the cosmic infrared background (CIB) was detected for the first time by Puget et al. (1996) and contains about half of the energy of the EBL (Dole et al. 2006; Béthermin et al. 2010a). Nevertheless, in the local universe, the optical/UV emissions is three times brighter than infrared/sub-millimeter ones (Soifer & Neugebauer 1991; Driver et al. 2008). This pseudo-paradox is explained by a strong evolution in the infrared galaxy properties.
The infrared luminosity density is dominated by normal galaxies (LIR,bolometric < 1011 L⊙) in the local Universe (Saunders et al. 1990). At higher redshift, it is dominated by luminous infrared galaxies (LIRG, 1011 L⊙ < LIR,bolometric < 1012 L⊙) at z = 1 (Le Floc’h et al. 2005) and ultra-luminous infrared galaxies (ULIRG, 1012 L⊙ < LIR,bolometric < 1013 L⊙) at z = 2 (Caputi et al. 2007). The infrared luminosity of these galaxies is correlated to the star formation rate (Kennicutt 1998). Thus, modeling this rapid evolution of the infrared galaxies is very important to understand the history of the star formation.
The physical models (such as Lacey et al. 2010; Wilman et al. 2010; Younger & Hopkins 2011, for the latest) use a physical approach based on semi-analytical recipes and dark matter numerical simulations. They use a limited set of physical parameters, but nowadays they poorly reproduce some basic observational constraints such as the infrared-galaxy number counts (Oliver et al. 2010).
The backward evolution models (like Lagache et al. 2004; Franceschini et al. 2010; Rowan-Robinson 2009; Valiante et al. 2009) use an evolution the luminosity function (LF) of the galaxies to reproduce empirically the galaxy counts, and other constraints. These models describe only the evolution and contain little physics. The parameters of these models were tuned manually to fit observational constraints. Le Borgne et al. (2009) used another approach and performed a non-parametric inversion of the counts to determine the LF. Nevertheless, this approach is complex, uses only one population of galaxy, and does not manage to reproduce the 160 μm number counts. An other fully-empirical approach was used by Domínguez et al. (2011). They fitted the SED from UV to mid-infrared of detected galaxies and extrapolated the far-infrared spectral energy distribution of these galaxies and the contribution of faint populations. Nevertheless, their model aims only to reproduce the CIB, although its ability to reproduce other constraints such as the number counts has not been tested.
The Balloon-borne Large-Aperture Submillimeter Telescope (BLAST) experiment (Pascale et al. 2008; Devlin et al. 2009) and the spectral and photometric imaging receiver (SPIRE) instrument (Griffin et al. 2010) onboard the Herchel space telescope (Pilbratt et al. 2010) performed recently new observations in the sub-mm at 250, 350, and 500 μm. In their current version, most of the models fail to reproduce the number counts measured at these wavelengths (Patanchon et al. 2009; Béthermin et al. 2010b; Clements et al. 2010; Oliver et al. 2010). The Valiante et al. (2009) model gives the best results, using a Monte Carlo approach (sources are randomly taken in libraries) to simulate the temperature scatter and the heterogeneity of the active galactic nucleus (AGN) populations, but this model strongly disagrees with the recent measurements of the redshift distribution of the CIB by Jauzac et al. (2011). It is thus necessary to develop new models that reproduce the recent far-infrared and sub-mm observations.
The discovery of very bright and high-redshift dusty galaxies by Vieira et al. (2010) with the South Pole Telescope (SPT) suggests that the contribution of high-redshift galaxies strongly lensed by dark matter halos of massive low-redshift galaxies on the bright sub-millimeter and millimeter counts is non-negligible. This contribution was discussed by Negrello et al. (2007) and observational evidence of this phenomenon was found by Negrello et al. (2010). We can also cite the simplified approach of Lima et al. (2010), who reproduced the AzTEC and SPT counts using a single population of galaxies with a Schechter LF at a single redshift and a lensing model. We can also cite Hezaveh & Holder (2010) on the effect of the lensing on the SPT counts, based on an advanced lensing model.
We present a new simple and parametric model based on Lagache et al. (2004) SED libraries, which reproduces the new observational constraints. The parameters of this model (13 free parameters and eight calibration parameters) were fitted from a large set of recent observations using a Monte Carlo Markov chain (MCMC) method, allowing us to study degeneracies between the parameters. This model also includes the effects of the strong lensing on the observations. We make predictions about the confusion limit for future missions, the high-energy opacity of the Universe, and the effects of strong lensing on the counts. This model is plugged into a halo model to study the spatial distribution of the infrared galaxies in a companion paper (Penin et al., in prep.). We note that another study also using MCMC methods was performed by Marsden et al. (2011) at the same time as ours.
We use the WMAP seven-years best-fit ΛCDM cosmology model (Larson et al. 2011) in this paper. We thus assume that H0 = 71 km s-1 Mpc-1, ΩΛ = 0.734, and Ωm = 0.266.
2. Approach
The backward evolution models are not based on physical parameters. Each model uses different evolving populations to reproduce the observational constraints. Some models (such as Franceschini et al. 2010; Rowan-Robinson 2009) use four galaxy populations evolving separately to reproduce the observations. Valiante et al. (2009) take randomly galaxy SEDs from a very large library of templates and claim that the contribution of the AGNs and the dispersion in the dust temperature of the galaxies must be taken into account to reproduce the observational constraints. Our approach is to keep the model as simple as possible, but to use advanced methods to constrain its free parameters. This new parametric model can be used as an input for halo modeling or P(D) analysis for instance.
As we show, we need neither an AGN contribution nor a temperature dispersion to reproduce the current observational constraints. In the local Universe, the AGNs only dominate in the ULIRG regime (Imanishi 2009). Alexander et al. (2005) estimate an AGN contribution of 8% to the submillimeter galaxies (SMG). Fadda et al. (2010) showed that the proportion of AGN-dominated sources is rather small for LIRGs at z ~ 1 (5%) and ULIRGs around z ~ 2 (12%). Jauzac et al. (2011) demonstrated that the AGN contribution to the CIB is less than 10% at z < 1.5. These categories of luminosity dominate the infrared output at their redshift. The small contribution of AGNs to these categories explains why AGNs are not necessary to reproduce the mean statistical properties of the galaxies. Nevertheless, despite their small contribution to the infrared output, the AGNs play a central role in the physics of galaxies.
Our model takes into account the strong lensing of high redshift galaxies by the dark matter halos of elliptical galaxies. According to the results of Sect. 7.3, the effect of the lensing on the counts we fitted is smaller than 10%. The model of lensing does not have free parameters. It is based on the WMAP seven-years best-fit cosmology and on some parameters taken at values given by the litterature. The lensing is thus not useful to reproduce the current observations, but is necessary to make predictions at bright fluxes (> 100 mJy) in the sub-mm and mm range, where the effects of the lensing are large.
3. Description of the model
3.1. Basic formulae
The flux density Sν at a frequency ν of a source lying at a redshift z is (Hogg 1999) is 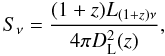 (1)where z is the redshift, DL is the luminosity distance of the source, and L(1 + z)ν is the luminosity at a frequency (1 + z)ν. The comoving volume corresponding to a redshift slice between z and z + dz and a unit solid angle is
(1)where z is the redshift, DL is the luminosity distance of the source, and L(1 + z)ν is the luminosity at a frequency (1 + z)ν. The comoving volume corresponding to a redshift slice between z and z + dz and a unit solid angle is 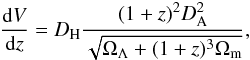 (2)where DH is the Hubble distance (DH = c/H0), DA the angular distance to the redshift z, and Ωm and ΩΛ are the normalized energy density of the matter and the cosmological constant, respectively.
(2)where DH is the Hubble distance (DH = c/H0), DA the angular distance to the redshift z, and Ωm and ΩΛ are the normalized energy density of the matter and the cosmological constant, respectively.
3.2. Bolometric luminosity function and its evolution
We assume that the luminosity function (LF) is a classical double-exponential function (Saunders et al. 1990) ![\begin{equation} \label{eq:lf} \Phi(L_{\rm IR}) = \Phi^\star \, \times \left( \frac{L_{\rm IR}}{L^\star}\right)^{1-\alpha} \, \times \, \exp \left[ -\frac{1}{2\sigma^2} \log_{10}^2\left(1+\frac{L_{\rm IR}}{L^\star}\right) \right], \end{equation}](/articles/aa/full_html/2011/05/aa15841-10/aa15841-10-eq33.png) (3)where Φ(LIR) is the number of sources per logarithm of luminosity and per comoving volume unit for an infrared bolometric luminosity LIR, Φ ⋆ is the normalization constant characterizing the density of sources, L ⋆ is the characteristic luminosity at the break, and 1 − α and 1 − α − 1/σ2/ln2(10) are the slope of the asymptotic power-law behavior at, respectively, low and high luminosity.
(3)where Φ(LIR) is the number of sources per logarithm of luminosity and per comoving volume unit for an infrared bolometric luminosity LIR, Φ ⋆ is the normalization constant characterizing the density of sources, L ⋆ is the characteristic luminosity at the break, and 1 − α and 1 − α − 1/σ2/ln2(10) are the slope of the asymptotic power-law behavior at, respectively, low and high luminosity.
We assume a continuous evolution in luminosity and density of the luminosity function with the redshift of the form L ⋆ ∝ (1 + z)rL and Φ ⋆ ∝ (1 + z)rΦ, where rL and rφ are coefficients driving the evolution in luminosity and density, respectively. It is impossible to reproduce the evolution of the LF with constant rL and rφ. We consequently authorize their value to change at some specific redshifts. The position of these breaks are the same for both rL and rφ. The position of the first redshift break is a free parameter and converges to the same final value for initial values between 0 and 2. To avoid a divergence at high redshift, we also add a second break fixed at z = 2.
 |
Fig. 1 Solid line: local infrared bolometric luminosity function from our best-fit model. Red dotted line: contribution of the normal galaxies. Blue dashed line: contribution of the starburst galaxies. Black vertical long dashed line: luminosity of the transition between the two population (Lpop). |
3.3. Spectral energy distribution (SED) of the galaxies
We use the Lagache et al. (2004) SED library. This library contains two populations: a starburst and a normal one. This library is parametrized only by the infrared bolometric luminosity (LIR). There is no evolution of the SED with redshift. The normal population has that is a spectrum typical of a spiral galaxy. The SED of this population does not evolve with LIR. In contrast, the starburst SED evolves with LIR. The brighter the starburst galaxy, the hotter the dust.
The normal galaxies are dominant at low luminosity and the starburst at high luminosity. We thus chose arbitrarily a smooth function to describe the fraction of starburst galaxies as a function of the bolometric luminosity LIR![\begin{equation} \label{eq:mixpop} \frac{\Phi_{\rm starburst}}{\Phi} = \frac{1+{\rm th} \bigl [ \log_{10}(L_{\rm IR}/L_{\rm pop}) /\sigma_{\rm pop} \bigl ]}{2}, \end{equation}](/articles/aa/full_html/2011/05/aa15841-10/aa15841-10-eq45.png) (4)where th is the hyperbolic tangent function, Lpop is the luminosity at which the number of normal and starburst galaxies are equal, and σpop characterizes the width of the transition between the two populations. At LIR = Lpop, the fraction of starbursts is 50%. The fraction of starbursts is 88% at LIR = Lpop × 10σpop, and 12% at LIR = Lpop × 10 − σpop. The contribution of the different populations to the local infrared bolometric LF is shown in Fig. 1.
(4)where th is the hyperbolic tangent function, Lpop is the luminosity at which the number of normal and starburst galaxies are equal, and σpop characterizes the width of the transition between the two populations. At LIR = Lpop, the fraction of starbursts is 50%. The fraction of starbursts is 88% at LIR = Lpop × 10σpop, and 12% at LIR = Lpop × 10 − σpop. The contribution of the different populations to the local infrared bolometric LF is shown in Fig. 1.
3.4. Observables
The number counts at different wavelengths are an essential constraint of our model. The source extraction biases are in general accurately corrected for these observables. The counts are computed with the formula 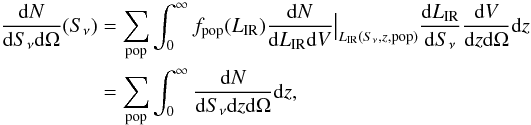 (5)where dN/dSν/dΩ is the number of source per flux unit and per solid angle, fpop(LIR) is the fraction of the sources of a given galaxy population computed with Eq. (4), and dN/dLIR/dV is computed from Eq. (3) to be
(5)where dN/dSν/dΩ is the number of source per flux unit and per solid angle, fpop(LIR) is the fraction of the sources of a given galaxy population computed with Eq. (4), and dN/dLIR/dV is computed from Eq. (3) to be 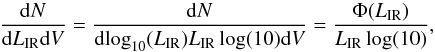 (6)where LIR(Sν,z,pop) and dLIR/dSν were computed on a grid in Sν and z from the cosmology and the SED templates. These grids depend on neither the evolution of the LF nor the population mixing parameters. These grids are thus generated only once and saved to accelerate the computation of the counts. We note that with this method, it is very easy to change the SED templates and/or add other populations.
(6)where LIR(Sν,z,pop) and dLIR/dSν were computed on a grid in Sν and z from the cosmology and the SED templates. These grids depend on neither the evolution of the LF nor the population mixing parameters. These grids are thus generated only once and saved to accelerate the computation of the counts. We note that with this method, it is very easy to change the SED templates and/or add other populations.
Other measurements help us to constrain our model. For example, the monochromatic luminosity Φmono function at a given redshift is 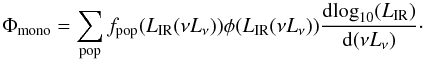 (7)We do not use the bolometric LFs, because they are biased by the choice of the assumed SED of the sources.
(7)We do not use the bolometric LFs, because they are biased by the choice of the assumed SED of the sources.
We can also compute the redshift distribution N(z) for a selection in terms of flux Sν > Sν,cut with 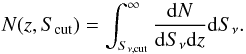 (8)The extragalactic background due to the galaxies at a given wavelength is
(8)The extragalactic background due to the galaxies at a given wavelength is 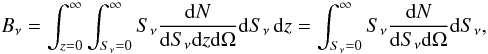 (9)and can be compared to the measurements of the CIB.
(9)and can be compared to the measurements of the CIB.
The level of the non-correlated fluctuations (shot-noise) of the CIB can be easily computed from our model with the equation 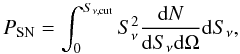 (10)where PSN is the level of the non-correlated fluctuations and Sν,cut the flux limit for the cleaning of the resolved sources.
(10)where PSN is the level of the non-correlated fluctuations and Sν,cut the flux limit for the cleaning of the resolved sources.
3.5. Effect of the strong lensing on the counts
We use a simple strong-lensing model based on Perrotta et al. (2001, 2002), which assumes that the dark matter halos are singular isothermal spheres. The cross-section σ of a halo for a magnification μ larger than μmin is 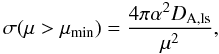 (11)where DA,ls is the angular-diameter distance between the lens and the source and α is given by
(11)where DA,ls is the angular-diameter distance between the lens and the source and α is given by 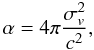 (12)where c is the speed of light and σv the velocity dispersion in the halo, which depends on the cosmology, the redshift, and the mass of the halo.
(12)where c is the speed of light and σv the velocity dispersion in the halo, which depends on the cosmology, the redshift, and the mass of the halo.
The probability P(μmin,zs) that a source at a redshift zs is magnified by a factor greater than μmin is 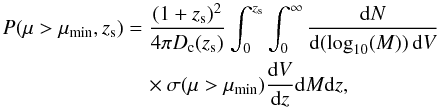 (13)where zs is the redshift of the source, Dc the comoving radial distance,
(13)where zs is the redshift of the source, Dc the comoving radial distance, 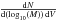 is the halo mass function, and
is the halo mass function, and 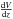 is the comoving volume associated with the redshift slice dz. We use the halo mass function of Reed et al. (2007).
is the comoving volume associated with the redshift slice dz. We use the halo mass function of Reed et al. (2007).
The counts derived by our model take into account the fact that a small fraction of the sources are gravitationally magnified, i.e., the observed number counts taking into account the lensing (dN/dSν/dΩ)lensed are computed from initial counts dSν/dz/dΩ with 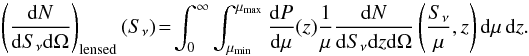 (14)In practice, this operation is performed by multiplying the vector containing the counts for a given redshift slice by a matrix describing the effects of lensing. This lensing matrix has diagonal coefficients values of around 1, and small (<10-3) non-diagonal terms. These non-diagonal terms describe how the magnified faint sources affect the counts at brighter fluxes. The effect of the lensing on the monochromatic luminosity function was computed in the same way. We chose μmin = 2, which corresponds to the limit of the validity of the strong-lensing hypothesis (Perrotta et al. 2001). The spatial extension of the lensed galaxies limits the maximum magnification. According to Perrotta et al. (2002), μmax is in the range 10−30. We chose to use μmax = 20 in this paper. Negrello et al. (2007) used μmin = 2 and μmax = 15.
(14)In practice, this operation is performed by multiplying the vector containing the counts for a given redshift slice by a matrix describing the effects of lensing. This lensing matrix has diagonal coefficients values of around 1, and small (<10-3) non-diagonal terms. These non-diagonal terms describe how the magnified faint sources affect the counts at brighter fluxes. The effect of the lensing on the monochromatic luminosity function was computed in the same way. We chose μmin = 2, which corresponds to the limit of the validity of the strong-lensing hypothesis (Perrotta et al. 2001). The spatial extension of the lensed galaxies limits the maximum magnification. According to Perrotta et al. (2002), μmax is in the range 10−30. We chose to use μmax = 20 in this paper. Negrello et al. (2007) used μmin = 2 and μmax = 15.
Figure 2 illustrates how number counts are affected by lensing. This figure is based on the number counts predicted by the model at 850 μm where the probability of magnification has been multiplied by a factor 10 to enhance the effect. The green dashed line represents contribution of the lensed sources. Owing to the magnification, the peak of this contribution is at higher flux than for non-lensed sources, and because of the small probability of lensing, the peak is lower than for non-lensed sources. This effect of the magnification on the counts become non-negligible when the slope of the counts is very steep, as in the sub-mm and mm domain.
 |
Fig. 2 Effect of the lensing on the number counts at 850 microns. The contribution of lensed sources is multiplied by ten to underline the effect of the lensing on the counts. Red dotted line: counts of non-lensed sources. Green dashed line: counts of lensed sources. Black solid line: total counts. |
4. Fitting the model parameters to the data
Our model has several free parameters. We attempted to use the minimum number of free parameters, which were determined by fitting the model to published measurements of the counts and LFs. We used a Monte Carlo Markov chain (MCMC) to identify the best-fit parameters, their uncertainties, and their degeneracies. We do not fit the measured redshift distributions, because the cosmic variance and the selection effects are currently not accurately enough known.
4.1. Data: extragalactic number counts
4.1.1. Data used for the fit
We chose to fit the following data:
-
Spitzer MIPS counts of Bétherminet al. (2010a) at 24, 70, and160 μm;
-
Herschel SPIRE Oliver et al. (2010) counts at 250, 350, and 500 μm;
-
AzTEC counts of Austermann et al. (2010) and Scott et al. (2010) at 1.1 mm.
4.1.2. Justification of our choice
We fit only the differential number counts since the integral counts are highly correlated and the correlation matrix is rarely estimated.
The number counts were measured at numerous bands between 15 μm and 1.1 mm. We chose a collection of points. We were guided by the reliability of the measurements and their error bars.
Number counts at 15 μm based on Infrared Space Observatory (ISO) data (Elbaz et al. 1999; Gruppioni et al. 2002) and the AKARI data (Pearson et al. 2010; Hopwood et al. 2010) differ by a factor of about 2, and their errors do not include the effects of cosmic variance. The results of these papers were not used for the fit. Nevertheless, we compared a posteriori these measurements to our own results to check for consistency in Sect. 5.4.
We fitted the Spitzer MIPS counts of Béthermin et al. (2010a) at 24, 70, and 160 μm. These points were measured from the data of FIDEL, COSMOS, and SWIRE legacy programs. The errors bars take into account the cosmic variance. These counts agree with the previous Spitzer measurements of Papovich et al. (2004), Shupe et al. (2008), Le Floc’h et al. (2009), and Frayer et al. (2009) and Herschel measurements of Berta et al. (2010) (in which the different fields were not combined).
At 250 μm, 350 μm, and 500 μm, we fitted the Herschel SPIRE counts of Oliver et al. (2010) which take into account the cosmic variance and the deboosting uncertainty. These counts agree with the BLAST measurements of Patanchon et al. (2009) and Béthermin et al. (2010b) and the Herschel measurements of Clements et al. (2010). We chose Oliver et al. (2010) counts because Herschel data are points more accurate than BLAST ones and because Clements et al. (2010) counts use only Poissonian error bars, which could be largely underestimated. For instance, Béthermin et al. (2010a) estimate that the Poissonian uncertainties underestimate the real sample uncertainties by a factor three for counts around 100 mJy at 160 μm in a 10 deg2 field.
We do not fit the 850 μm because of the large discrepancies between the Submillimeter Common-User Bolometer Array (SCUBA) observations (Coppin et al. 2006) and the Large APEX BOlometer CAmera (LABOCA) observations (Weiß et al. 2009). We discuss this problem in the Sect. 5.4.
We fitted the AzTEC measurements at 1.1 mm of Austermann et al. (2010) and Scott et al. (2010). The area covered by AzTEC is small compared to that covered by Spitzer and Herschel. We used two independent measurements of the AzTEC counts to increase the weight of the mm observations in our fit.
4.2. Data: monochromatic luminosity functions
4.2.1. Data used for the fit
We chose to fit the following data:
-
InfraRed Astronomical Satellite (IRAS) local luminosityfunction at 60 μm of Saunders et al. (1990);
-
Spitzer local luminosity function at 24 μm of Rodighiero et al. (2010);
-
Spitzer luminosity function at 15 μm at z = 0.6 of Rodighiero et al. (2010);
-
Spitzer luminosity function at 12 μm at z = 1 of Rodighiero et al. (2010);
-
Spitzer luminosity function at 8 μm at z = 2 of Caputi et al. (2007).
4.2.2. Justification of our choice
We fitted some monochromatic luminosity functions. We chose only wavelengths and redshifts for which no K-corrections are needed. These observations strongly constrain the parameters driving the redshift evolutions of our model.
From the Rodighiero et al. (2010) LFs measured with the Spitzer data at 24 μm, we computed three non K-corrected LFs at z = 0, 0.6, and 1. We used their local LF at 24 μm. At z = 0.6 and 1, instead of directly using their results in their redshift bins, we combined their 15 μm LF at z = 0.6 (respectively, 12 μm LF at z = 1) in the 0.45 < z < 0.6 and 0.6 < z < 0.8 bins (respectively, 0.8 < z < 1.0 and 1.0 < z < 1.4) to obtain our version of the 15 μm LF at z = 0.6 (respectively, 12 μm LF at z = 1). The error in a point is the maximum of the combined statistical errors of the two bins and the difference between the measurements in the two bins. The second value is often larger because of the rapid evolution of the LF and the cosmic variance. We fitted only the points that do not suffer incompleteness to avoid possible biases. We also fitted the 8 μm at z = 2 of Caputi et al. (2007).
We also fitted the local LF at 60 μm determined from IRAS data (Saunders et al. 1990) to better constrain the faint-end slope of the local LF. Owing to the strong AGN contamination at 60 μm in the ULIRG regime, we did not fit the points brighter than 1011.5 L⊙ at 60 μm.
4.3. Data: CIB
The bulk of the CIB is not resolved at SPIRE wavelengths. We thus used the absolute measurement of the CIB level in SPIRE bands as a constraint of our model. We used the Lagache et al. (1999) measurement derived from the far-infrared absolute spectrophotometer (FIRAS) data: 11.7 ± 2.9 nW m2 sr-1 at 250 μm, 6.4 ± 1.6 nW m2 sr-1 at 350 μm, and 2.7 ± 0.7 nW m2 sr-1 at 500 μm. We assume that the CIB is only due to galaxies, thus neglect any possible extragalactic diffuse emission.
4.4. Calibration uncertainties
The calibration uncertainty is responsible for correlated uncertainties between points measured at a given wavelength with the same instrument. A change in the calibration globally modifies both the number counts and the LF. Assuming that the “good” calibration is obtained by multiplying the fluxes by a factor γ, the “good” normalized counts are obtained with Snew = γS and 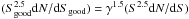 . The effect on the LF in dex per volume unit is more simple. We just have to shift the luminosity in abscissa by a factor γ.
. The effect on the LF in dex per volume unit is more simple. We just have to shift the luminosity in abscissa by a factor γ.
To our free parameters, we added a calibration parameter for each fitted band (see Table 2). We took into account the uncertainties in the calibration estimated by the instrumental team, in our fit (Stansberry et al. 2007; Gordon et al. 2007; Engelbracht et al. 2007; Swinyard et al. 2010; Scott et al. 2010).
4.5. Fitting method
To fit our points, we assumed that the uncertainties in both the measurements and calibrations are Gaussian and uncorrelated. The log-likelihood is then 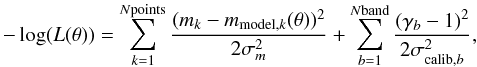 (15)where L is the likelihood, θ the parameters of the model, mk a measurement, mmodel,k the prediction of the model for the same measurement, σm the measurement uncertainty on it, γb the calibration parameter of the band b, and σcalib,b the calibration uncertainty for this band.
(15)where L is the likelihood, θ the parameters of the model, mk a measurement, mmodel,k the prediction of the model for the same measurement, σm the measurement uncertainty on it, γb the calibration parameter of the band b, and σcalib,b the calibration uncertainty for this band.
Parameters of our model fitted to our selection of infrared observations.
We used a Monte Carlo Markov chain (MCMC) Metropolis-Hastings algorithm (Chib & Greenberg 1995; Dunkley et al. 2005) to fit our model. The method consists of a random walk in the parameter space. At each step, a random shift of the parameters is performed using a given fixed proposal density. The new step n is accepted with a probability of 1 if L(θn) > L(θn − 1) or otherwise a probability L(θn)/L(θn − 1). The distribution of the realization of the chain is asymptotically the same as the underlying probability density. This property is thus very convenient to determine the confidence area of the model parameters.
We used the Fisher matrix formalism to determine the proposal density of the chain from initial parameters values that had been set manually. The associated Fisher matrix is 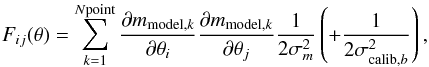 (16)where θ is a vector containing the model and calibration (γb) parameters. The term in brackets appears only for the diagonal terms corresponding to a calibration parameter. We performed a first short chain (10 000 steps) and computed a new proposal density with the covariance matrix of the results. We then executed a second long chain of 300 000 steps. The final chain satisfies the Dunkley et al. (2005) criteria (j ⋆ > 20 and r < 0.01).
(16)where θ is a vector containing the model and calibration (γb) parameters. The term in brackets appears only for the diagonal terms corresponding to a calibration parameter. We performed a first short chain (10 000 steps) and computed a new proposal density with the covariance matrix of the results. We then executed a second long chain of 300 000 steps. The final chain satisfies the Dunkley et al. (2005) criteria (j ⋆ > 20 and r < 0.01).
 |
Fig. 3 a)–f) Differential extragalactic number counts used for the fit. h) Monochromatic LFs at different wavelengths and redshifts. a)–h) The fitted points are thicker. Black solid line: our best-fit model. Black dashed line: 1-σ range of the model. a)–c) Red diamonds: Béthermin et al. (2010a)Spitzer legacy number counts. c) Green triangles: Berta et al. (2010)Herschel/PEP number counts. d)–f) Red diamonds: Oliver et al. (2010)Herschel/Hermes number counts. Green triangles: Glenn et al. (2010)Herschel/Hermes P(D) analysis. Clements et al. (2010)Herschel/ATLAS number counts. Purple cross: Béthermin et al. (2010b) BLAST number counts. g) Green triangles: Scott et al. (2010) AzTEC number counts in the CDFS field. Green triangles: Austermann et al. (2010) AzTEC number counts in the SHADES field. h) Red plus: Rodighiero et al. (2010) local 24 μm LF (not fitted points in grey). Green diamonds: Saunders et al. (1990) local 60 μm LF (shifted by a factor 10 on the y-axis; not fitted points in grey); blue triangles: Rodighiero et al. (2010) 15 μm LF at z = 0.6 (shifted by a factor 100 on the y-axis; not fitted points in grey). Purple squares: Rodighiero et al. (2010) 12 μm LF at z = 1 (shifted by a factor 1000 on the y-axis; not fitted points in grey). Cyan crosses: Caputi et al. (2007) 8 μm LF at z = 2 (shifted by a factor 10 000 on the y-axis). |
5. Results of the fit
5.1. Quality of the fit
Our final best-fit model has a χ2 (χ2 = −2log (L) because all errors are assumed to be Gaussian) of 177 for 113 degrees of freedom. Our fit is thus reasonably good. The parameters found with the fit are given in Table 1 (the uncertainties are computed from the MCMC). The calibration factor are compatible with the calibration uncertainties given by the instrumental teams with a χ2 of 2.89 for seven points (see Table 2). The results are plotted in Fig. 3.
Calibration parameters and 1-σ marginalized errors from our MCMC fit compared with calibration uncertainties given by the instrumental teams.
5.2. Comparison between the model and the observed counts used in the fit
The Béthermin et al. (2010a) points fit globally well, with some exceptions. Our model is lower by about 15% than two points around 300 μJy at 24 μm. These two points where produced combining data for the FIDEL, COSMOS and SWIRE fields. The SWIRE fields are shallow fields and the counts could be affected by the Eddington bias. We also observe a slight under-prediction of the bright (S70 > 50 mJy) counts at 70 μm. We also plotted the Berta et al. (2010) counts at 160 μm measured using the photodetector array camera and spectrometer (PACS) on the Herschel satellite. These counts agree with Béthermin et al. (2010a) and our model.
Our model fits globally well the Oliver et al. (2010) and Béthermin et al. (2010b) counts, apart from a slight under-prediction of the counts between 30 mJy and 100 mJy at 500 μm. There is a mild disagreement with the Clements et al. (2010) counts, but their errors bars do not take into account the cosmic variance and are thus underestimated. We also plotted the results of the P(D) analysis of Glenn et al. (2010). These points and especially the error bars must be interpreted with caution (see the complete discussion in Glenn et al. 2010). We have plotted the knots of the smooth and power-law models, which globally agree with our model.
Our model agrees very well with the AzTEC counts of Austermann et al. (2010) and Scott et al. (2010). The contribution of the strong lensing objects to the AzTEC counts is weak (<10%, see Sect. 7.3).
5.3. Comparison between the model and the observed monochromatic LFs
Our model closely reproduces our collection of LFs (Saunders et al. 1990; Caputi et al. 2007; Rodighiero et al. 2010), apart from the brightest point of Caputi et al. (2007). In Fig. 3, we arbitrarily shifted the different LFs on the y-axis to obtain a clearer plot. Our model underestimates the 60 μm local LF in the ULIRG regime. It is expected because our model does not contain AGNs and confirms our choice of not fitting these points (Sect. 4.2).
 |
Fig. 4 a)–c) Differential extragalactic number counts not used for the fit. Black solid line: our best-fit model. Black dashed line: 1-σ range of the model. a) Red diamonds: Elbaz et al. (1999) ISO counts. Green triangle: Gruppioni et al. (2002) ISO counts. Blue squares: Pearson et al. (2010) AKARI counts. Purple cross: Hopwood et al. (2010) AKARI (lensed) counts. Cyan plus: Teplitz et al. (2011)Spitzer/IRS counts. b) Red diamonds: Hacking & Houck (1987), Lonsdale et al. (1990), Rowan-Robinson et al. (1990), Saunders et al. (1990), Gregorich et al. (1995) and Bertin et al. (1997) IRAS counts. c) Red diamonds: Berta et al. (2010)Herschel/PEP counts. |
5.4. Comparison between the model and the observed counts not used in the fit
We also compared our results with the counts at other wavelengths. They are plotted in Figs. 4 and 5. The 1-σ region of the model includes the γb uncertainty of AKARI at 15 μm (4%, Ishihara et al. 2010), PACS at 110 μm (about 10%, Berta et al. 2010), and LABOCA at 850 μm (8.5%, Weiß et al. 2009). The uncertainty in γb is about the same for LABOCA and SCUBA (~10%, Scott et al. 2006). The uncertainties in the model are larger at these non-fitted wavelengths because the correlations between the model and the calibration parameters are not taken into account by the fit.
At 15 μm, the Elbaz et al. (1999) counts from different fields are incompatible with each other, but our counts coincide with in the cloud of points. The Gruppioni et al. (2002) counts are significantly lower than our model and other works. We marginally agree with the Pearson et al. (2010) counts. The Hopwood et al. (2010) counts measured with AKARI in a field around Abell 2218 are lower than our model by about 25%. Nevertheless, their field is very narrow and their estimation may be affected by cosmic variance. Finally, we agree with the Teplitz et al. (2011) measurements performed with the infrared spectrograph (IRS) onboard the Spitzer space telescope.
We compare our counts to Hacking & Houck (1987), Lonsdale et al. (1990), Rowan-Robinson et al. (1990), Saunders et al. (1990), Gregorich et al. (1995), and Bertin et al. (1997) at 60 μm from IRAS data. There are disagreements between the different observations and some error bars may be underestimated, but our model globally agrees with the cloud of points.
We can also compare the prediction of our model with the Berta et al. (2010) counts at 110 μm. Our model globally agrees with their work, although our model tends to be higher than their measurement near 100 mJy. Observations of several larger fields will help us to see wether this effect is an artifact or not.
At 850 μm, we closely agree with the P(D) analysis of the LABOCA data of Weiß et al. (2009, see Fig. 5). However, the measurements performed with SCUBA (Borys et al. 2003; Scott et al. 2006; Coppin et al. 2006) and LABOCA (Beelen et al. 2008) are significantly higher than our model at 6 and 8 mJy. At low fluxes (<2 mJy), our model agrees very well with the measurement performed in lensed regions (Smail et al. 2002; Knudsen et al. 2008; Zemcov et al. 2010).
 |
Fig. 5 Integral number counts at 850 μm. Black solid line: our best-fit model. Black dashed line: 1-σ range of the model. Grey plus: Zemcov et al. (2010) combined SCUBA lensed counts. Blue dashed line: Weiß et al. (2009) LABOCA P(D) (Schechter model). Red diamonds: Coppin et al. (2006) SCUBA SHADES counts. Cyan square: (Beelen et al. 2008) LABOCA counts around the J2142-4423 Lyα protocluster. Black plus: Knudsen et al. (2008) combined SCUBA lensed counts; green triangles: Scott et al. (2006) revisited SCUBA counts. Purple cross: Borys et al. (2003) SCUBA HDFN counts. Yellow asterisks: Smail et al. (2002) lensed counts. |
We also compare our model predictions with SPT measurements at 1.38 mm (Vieira et al. 2010). At this wavelength, the contribution of the synchrotron emission from the local radio galaxies to the counts is not negligible. Nevertheless, these sources can be separated from dusty galaxies by considering their spectrum. We thus compare our results with the counts of dusty sources. Vieira et al. (2010) measured counts for all the dusty sources and the dusty sources without IRAS 60 μm counterparts. Our model agrees with these two measurements. Figure 6 shows the counts of the non-IRAS dusty sources. The 7.2% calibration uncertainty of SPT is taken into account in the 1-σ region of the model.
 |
Fig. 6 Number counts at 1.38 mm of dusty sources without IRAS 60 μm counterpart. Black diamonds: Vieira et al. (2010) south pole telescope (SPT) measurements. Black solid line: total contribution of S60 < 0.2 Jy sources. Green dot-dashed line: contribution of the non-lensed sources. Red dashed line: contribution of the strongly-lensed sources. Dotted lines 1-σ contours. |
5.5. Comparison with the observed redshift distributions
 |
Fig. 7 Redshift distribution of the S24 > 80 μJy a), S24 > 300 μJy b), S250 > 40 mJy c), S350 > 30 mJy d), S500 > 20 mJy e), S850 > 3 mJy f), and S1100 > 3 mJy g) sources. These measurements are not fitted. Black solid line: our best-fit model. Black dotted line: 1-σ range of the model. Grey solid line: our best-fit model convolved by a Gaussian of σz = 0.125z. Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Red asterisks: Le Floc’h et al. (2009)a), b), Chapin et al. (2011)c)–e), Chapman et al. (2005)f) and Chapin et al. (2009)g) measurements. Blue diamonds: Rodighiero et al. (2010) measurements a), b). Cyan squares: Desai et al. (2008) measurements b). |
In Fig. 7, we compare our model predictions with observed redshift distributions. At 24 μm, our model overpredicts by about 20% the number of sources below z = 1 according to Le Floc’h et al. (2009) observations for the selection S24 > 80 μJy. Nevertheless, these authors excluded 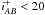 galaxies and their number of sources at low redshift is thus underestimated. Our model also underpredicts the number of sources at z > 3. However, the redshifts of the z > 2 sources are only moderately accurate (σz ≈ 0.25 for
galaxies and their number of sources at low redshift is thus underestimated. Our model also underpredicts the number of sources at z > 3. However, the redshifts of the z > 2 sources are only moderately accurate (σz ≈ 0.25 for 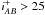 at z ~ 2). Because of the steep slope of the redshift distribution, a significant number of sources measured near z = 3.5 could be sources lying around z = 3 with overestimated redshifts. If we convolve our model with a Gaussian error of σz = 0.125 z to simulate the redshift uncertainties, the model and the measurements agrees (Fig. 7). The Valiante et al. (2009) model poorly reproduces this observation. The Le Borgne et al. (2009) model agrees very well with the measurements, except at z < 0.5 and z > 2.5. The same observables was measured by Rodighiero et al. (2010). Their results agree with Le Floc’h et al. (2009), except at z > 3, where they are higher, perhaps because of a larger σz at high redshift.
at z ~ 2). Because of the steep slope of the redshift distribution, a significant number of sources measured near z = 3.5 could be sources lying around z = 3 with overestimated redshifts. If we convolve our model with a Gaussian error of σz = 0.125 z to simulate the redshift uncertainties, the model and the measurements agrees (Fig. 7). The Valiante et al. (2009) model poorly reproduces this observation. The Le Borgne et al. (2009) model agrees very well with the measurements, except at z < 0.5 and z > 2.5. The same observables was measured by Rodighiero et al. (2010). Their results agree with Le Floc’h et al. (2009), except at z > 3, where they are higher, perhaps because of a larger σz at high redshift.
Level of the non-correlated fluctuations of the CIB at different wavelengths and comparison with the predictions of the model.
We also compare the model with the redshift distribution of S24 > 300 μJy sources measured by Le Floc’h et al. (2009), Rodighiero et al. (2010), and Desai et al. (2008). These different measurements disagree below z = 0.5. This difference could be due to the removal of the brightest optical sources (see previous paragraph). Our model overestimates the number of sources at z < 0.5 by a factor of 2. There is rather close agreements between the model and the measurements between z = 0.5 and z = 2.5, apart from a small overestimation by Valiante et al. (2009) near z = 2. At higher redshifts, the measurements are significantly higher than the models for possibly two reasons: an effect of the redshift uncertainties and the absence of AGNs in our model.
We compare with the Chapin et al. (2011) redshift distributions of the BLAST isolated sources at 250 μm, 350 μm, and 500 μm. This selection of isolated sources does not allow us to determine the effective size of the field. We thus normalized our model and the measured counts to have ∫dN/dzdz = 1. Our predicted redshift distribution globally fits the measurements, except at low z at 250 μm and 350 μm. This difference could be explained by the selection of isolated sources, which could miss sources in structures at low redshift. The other models (Le Borgne et al. 2009; Valiante et al. 2009) underpredict the number of sources at low z. Valiante et al. (2009) also slightly overpredicts the number of sources at z ~ 1.5.
We compared the redshift distribution of the SCUBA sources at 850 μm with the prediction of our model. We used the selection-corrected measurements of Chapman et al. (2005) adopted by Marsden et al. (2011). All the models agree with this measurement.
We also compared the predictions of our model with the redshift distribution of the sources detected at 1.1 mm by AzTEC (Chapin et al. 2009). A significant fraction of the sources detected at this wavelength (10 over 28) are not identified, and the selection is not performed in term of flux, but signal-to-noise ratio. Consequently, the normalization of the redshift distribution is unknown. We thus use the same normalization than for the BLAST redshift distributions (∫dN/dzdz = 1). The behavior predicted by our model agrees well with the observations.
Jauzac et al. (2011) measured the contribution of the S24 > 80 μJy to the CIB at 70 and 160 μm as a function of the redshift. Their stacking analysis allows us to check the total far-infrared (FIR) emission of the faint sources not resolved at these wavelengths. Our model agrees well with their results, except near z = 0.5 (see Fig. 8), where their too low data points could come from a large-scale underdensity in the COSMOS field at this redshift. The Le Borgne et al. (2009) model overpredicts the contribution of the 24 μm sources at z > 1. The Valiante et al. (2009) model does not reproduce the trend of these measurements. Franceschini et al. (2010) underestimate the contribution of the local sources and overestimate the contribution of z ~ 1 sources.
 |
Fig. 8 Differential contribution of the S24 > 80 μJy sources to the CIB as a function of the redshift at 70 μm (upper panel) and 160 μm (lower panel). Red asterisks: measurement by stacking in the COSMOS field (Jauzac et al. 2011). Black solid line: our model (1-σ limit in black dotted line). Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Blue dot-dashed line: Franceschini et al. (2010) model. |
5.6. Comparison with the measured Poisson fluctuations of the CIB
Table 3 summarizes the recent measurements of the non-correlated fluctuations of the CIB (PSN) and the predictions of our model. We note that PSN depends strongly on the Sν,cut, the flux density at which the resolved sources are cleaned. We agree with the measurements of Miville-Deschênes et al. (2002) at 60 μm and 100 μm, Lagache et al. (2007) at 160 μm, and Viero et al. (2009) at 250 μm and 350 μm. We found a value 35% lower than Viero et al. (2009) at 500 μm. This is consistent with the slight underestimation of the counts at 500 μm by our model. Our model is also about 40% lower than the SPT measurements at 1.36 mm (Hall et al. 2010), possibly because of a lack of faint sources at high redshift in our model. We also disagree with the results of Matsuura et al. (2011) at 90 μm within a factor of 2. Nevertheless, they cleaned all the detected sources without using a fixed cut in flux. We took their “mean” value of 20 mJy for the flux cut. The high sensitivity of the measurements to the flux cut could thus explains this difference (for instance, a decrease in the flux cut by 25% leads to a decrease of the fluctuations of 19%).
We also computed the mean redshift at which the fluctuations are emitted with 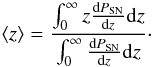 (17)The results are written in Table 3. As expected, the mean redshift increases with the wavelength. Studying the long wavelengths is thus very useful for probing high redshift populations.
(17)The results are written in Table 3. As expected, the mean redshift increases with the wavelength. Studying the long wavelengths is thus very useful for probing high redshift populations.
5.7. Comparison with the pixel histogram of the BLAST maps
The quality of our counts at low fluxes in the sub-mm range can be tested using a P(D) analysis (Condon 1974; Patanchon et al. 2009; Glenn et al. 2010). Without instrumental noise, the probability density of the signal in a pixel of the map, P(D), is given by ![\begin{equation} P(D) = \int_0^\infty \left [ \exp \left ( \int_0^\infty R(x) {\rm e}^{{\rm i} \omega x} {\rm d}x - \int_0^\infty R(x) {\rm d}x \right ) \right ] {\rm e}^{-{\rm i} \omega D} {\rm d}\omega, \end{equation}](/articles/aa/full_html/2011/05/aa15841-10/aa15841-10-eq207.png) (18)where R(x) is defined by
(18)where R(x) is defined by 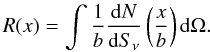 (19)This probability distribution must be convolved with the distribution of the instrumental noise. We also subtract the mean of this distribution.
(19)This probability distribution must be convolved with the distribution of the instrumental noise. We also subtract the mean of this distribution.
 |
Fig. 9 Comparison with the BLAST pixel histogram at 250 μm (upper panel), 350 μm (middle panel) and 500 μm (lower panel). Black histogram: histogram of the values of the central part of the BLAST beam-smoothed map in Jy/beam. Red solid line: distribution predicted by our model using a P(D) analysis. Our analysis does not include the clustering. Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Blue dot-dashed line: Franceschini et al. (2010) model. |
 |
Fig. 10 Diagonal plots: marginalized probability distributions of each parameters deduced from the MCMC. Non-diagonal plots: 1-σ (red), 2-σ (green), and 3-σ (blue) regions for each pair of parameters). From left to right: α, σ, L ⋆ , φ ⋆ , rL ⋆ ,lz, rphi ⋆ ,lz, zbreak,1, rL ⋆ ,mz, rphi ⋆ ,mz, rL ⋆ ,hz, rphi ⋆ ,hz, Lpop, and σpop (cf. Table 1). |
We tested our model by comparing with the deepest part of the observations of the CDFS by the BLAST team. We retained only the pixels in the map with a coverage larger than 90% of the maximum coverage. We smoothed the signal, noise, and beam map by a Gaussian kernel of the same full width at half maximum than the BLAST beam. This smoothing reduces the effect of the instrumental noise (Patanchon et al. 2009). Our model predictions and the BLAST pixel histograms at 250 μm, 350 μm, and 500 μm are shown in Fig. 9. The uncertainties in the model predictions take into account the BLAST calibration uncertainties (Truch et al. 2009). The model agrees rather well with the data. Nevertheless, the measured histogram is slightly broader than the predictions of the model, especially at 500 μm. It is consistent with the slight underestimation by our model of the counts at 500 μm (the higher the counts, the larger the histogram). The clustering of the galaxies (neglected in this analysis) tends to enlarge the histogram by about 10% and could also contribute to this disagreement (Takeuchi & Ishii 2004; Patanchon et al. 2009; Glenn et al. 2010). The Valiante et al. (2009) model reproduce the BLAST pixel histograms very well. Le Borgne et al. (2009) and Franceschini et al. (2010) overpredict the number of bright pixels at 250 μm and 350 μm (Sν > 50 mJy). It is consistent with these authors’ overprediction of the counts at high flux (Oliver et al. 2010; Glenn et al. 2010).
5.8. Degeneracies between parameters
The Pearson correlation matrix of our model is given in Table 4. We found a very strong anti-correlations both between σ and L ⋆ (z = 0) (–0.90) and between L ⋆ (z = 0) and φ ⋆ (z = 0) (− 0.85). These classical strong correlations are due to the choice of the LF parametrisation. There are also very strong degeneracies between the evolution in density and luminosity of the LF: –0.81 between 0 and the first break; –0.67 between the two breaks; and –0.76 after the second break.
There are some slight degeneracies between the calibration factors. The Spitzer calibration parameters are correlated (0.68 between 24 μm and 70 μm, 0.73 between 24 μm and 160 μm, and 0.62 between 70 μm and 160 μm). The other correlations implying a calibration factor are between –0.6 and 0.6.
The marginalized probability distributions of each parameter and the 1, 2, and 3-σ confidence regions for each pair of parameters are plotted in Fig. 10. Some distributions are not Gaussian. It thus justifies the use of a MCMC algorithm.
6. Interpretation of the results
6.1. Evolution of the luminosity function
Our model uses a very strong evolution of the bolometric infrared luminosity function to reproduce the infrared observations. The characteristic luminosity (L ⋆ ) has strongly decreased between z = 2 and now, by about a factor of 50 from z = 2 to 0. The characteristic density (φ ⋆ ) increases strongly between z = 2 and z = 1 and slightly decreases between z = 1 and now. At z > 2, the model is compatible with no evolution in luminosity and a slight decrease in the density as redshift increases. The evolution of these two parameters are plotted in Fig. 11.
We compared our results with the measurements of Caputi et al. (2007) performed from MIPS 24 μm observations and the measurement of Magnelli et al. (2009) obtained using MIPS 70 μm observations. These two works used a stacking analysis to measure the faintest points. The evolutions of L ⋆ and φ ⋆ only marginally agree with these two works. Nevertheless, they use different fixed values of σ and α and an extrapolation from the monochromatic luminosity to LIR. These choices could imply some biases. We found as Caputi et al. (2007) a strong negative evolution in density between z ~ 1 and z ~ 2, these authors finding an evolution in (1 + z)−3.9±1.0 compared to our (1 + z) − 6.2 ± 0.5. Nevertheless, our value is probably biased by our non-smooth parametrization. This evolution is discussed in details by Caputi et al. (2007).
Reddy et al. (2008) claimed that α ~ 1.6 at z > 2. However, we do not need to invoke an evolution of α and σ to reproduce the observations. Nevertheless, the infrared measurements are not sufficiently deep to constrain accurately any evolution of α.
Pearson correlation matrix for our model.
 |
Fig. 11 Evolution of the bolometric infrared luminosity function with redshift. Upper panel: bolometric LF at z = 0 (solid line), z = 0.5 (dot line), z = 1 (dashed line), z = 1.5 (dot-dash line), z = 2 (3-dot-dash line), and z = 3 (long dashed line). Lower panel: Evolution of the L ⋆ (red solid line) and φ ⋆ (blue dot-dash line) parameter as a function of redshift and 1-σ confidence region. The measurement of L ⋆ by Caputi et al. (2007) (triangles) using 24 μm obervations and Magnelli et al. (2009) (diamonds) using 70 μm observations are plotted in red. The measurement of φ ⋆ by Caputi et al. (2007) (cross) and Magnelli et al. (2009) (square) are in blue. |
6.2. Evolution of the dust-obscured star formation rate
The bolometric infrared luminosity density (ρIR) can be deduced from the bolometric infrared LF. Our local value of ρIR ((1.05 ± 0.05) × 108 L⊙ Mpc-3) agrees with the Vaccari et al. (2010) measurements (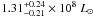 Mpc-3). We also agree well with higher redshift measurements of Rodighiero et al. (2010) and Pascale et al. (2009, see Fig. 12). The infrared luminosity density can be converted into star formation rate density (SFRD) using the conversion factor
Mpc-3). We also agree well with higher redshift measurements of Rodighiero et al. (2010) and Pascale et al. (2009, see Fig. 12). The infrared luminosity density can be converted into star formation rate density (SFRD) using the conversion factor 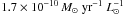 (Kennicutt 1998). The SFRD derived from our model agrees rather well with the Hopkins & Beacom (2006) fit to the optical and infrared measurements.
(Kennicutt 1998). The SFRD derived from our model agrees rather well with the Hopkins & Beacom (2006) fit to the optical and infrared measurements.
 |
Fig. 12 Evolution of the bolometric infrared luminosity density (black solid line) as a function of the redshift. The contribution of normal galaxies (LIR < 1011 L⊙), LIRG (1011 < LIR < 1012 L⊙), ULIRG (1012 < LIR < 1013 L⊙), and HyLIRG (LIR > 1013 L⊙) are plotted with short-dashed, dot-dash, three-dot-dash, and long-dashed line respectively. The measurements of Rodighiero et al. (2010) using the MIPS 24 μm data are plotted with diamonds and Pascale et al. (2009) ones using a BLAST stacking analysis with triangles. The Hopkins & Beacom (2006) fit to the optical and infrared measurement is plotted with a dark grey area (1-σ) and a light grey area (3-σ). |
We also determined the contribution of the different ranges of luminosity to the bolometric infrared luminosity density (normal: LIR < 1011 L⊙, LIRG: 1011 < LIR < 1012 L⊙, ULIRG:1012 < LIR < 1013 L⊙, HyLIRG: LIR > 1013 L⊙). Between z = 0 and 0.5, the infrared luminosity density is dominated by normal galaxies (LIR < 1011 L⊙). Their contribution decreases slowly with redshift because of the evolution of the LF seen in Fig. 11. Between z = 0.5 and 1.5, the infrared output is dominated by the LIRG. At higher redshift, it is dominated by ULIRGs. The HyLIRGs never dominate and account for some percent at high redshift. A physical cutoff at very high luminosity would this not strongly change the infrared density evolution.
Following our model, the number of very bright objects (> 1012.5 L⊙) is maximal around z = 2 (see Fig. 11). These objects could be very massive galaxies observed during their formation in the most massive dark matter halos. Among other analyses, the study of the spatial distribution of the galaxies will help us to confirm or exclude this scenario (Penin et al., in prep.).
Around z = 1, the number of very bright objects is lower than at higher redshift, but the number of LIRGs is about one order of magnitude larger. From z = 1 to now, the infrared output has decreased by about one order of magnitude. Our model describes only this evolution and we need physical models to understand why, in contrast to today, the star formation at high redshift is dominated by a few very-quickly-star-forming galaxies, when the associated dark matter halos grew by hierarchical merging (Cole et al. 2000; Lanzoni et al. 2005). We also need to explain the decrease in the star formation since z = 1, the main candidates being the feedback of AGNs and starbursts (e.g. Baugh 2006) and/or the lack of gas.
6.3. CIB SED
The value of the CIB at different wavelengths predicted by the model is given in Table 5. We found a CIB integrated value (over the 8 − 1000 μm range) of 23.7 ± 0.9 nW m-2 sr-1, which agrees with the 24 − 27.5 nW m-2 sr-1 range of Dole et al. (2006).
We compared the CIB spectrum found with our model with the measurements (see Fig. 13). Our model is always higher than the lower limit given by the stacking. The Marsden et al. (2009) limits are very stringent. Nevertheless, they could be overestimated because of the contamination due to clustering (Bavouzet 2008; Fernandez-Conde et al. 2010; Béthermin et al. 2010b). Our model is compatible with the upper limit given by the absorption of the TeV photons by photon-photon interaction with the CIB (see Sect. 7.2). We globally agree with the DIRBE/WHAM (Lagache et al. 2000) and AKARI (Matsuura et al. 2011) absolute measurement, except at 90 μm (AKARI) and 100 μm (DIRBE/WHAM) where the measurements are significantly higher than our model. These measurements need an accurate subtraction of both the zodiacal light and the galactic emissions and an accurate inter-calibration between DIRBE and FIRAS. A bad removal of the zodiacal light might explain this disagreement (Dole et al. 2006). At longer wavelengths, we closely agree with the FIRAS absolute measurements of Lagache et al. (2000).
 |
Fig. 13 Upper panel: contribution to the CIB per redshift slice. Black solid line: CIB spectrum predicted by the model. Red short-dashed line: contribution of the galaxies between z = 0 and 0.3. Green dot-dash line: same thing between z = 0.3 and 1. Blue three dot-dash line: same thing between z = 1 and 2. Purple long-dashed line: contribution of the galaxies at redshift higher than 2. Black arrows: lower limits coming from the number counts at 15 μm (Hopwood et al. 2010) and 24 μm (Béthermin et al. 2010a) and the stacking analysis at 70 μm (Béthermin et al. 2010a), 100 μm, 160 μm (Berta et al. 2010), 250 μm, 350 μm, 500 μm (Marsden et al. 2009), 850 μm (Greve et al. 2010), and 1.1 mm (Scott et al. 2010) and upper limits coming from absorption of the TeV photons of Stecker & de Jager (1997) at 20 μm and Renault et al. (2001) between 5 μm and 15 μm. Black diamonds: Matsuura et al. (2011) absolute measurements with AKARI. Black square: Lagache et al. (2000) absolute measurements with DIRBE/WHAM. Cyan line: Lagache et al. (2000) FIRAS measurement. Lower panel: contribution to the CIB of the normal galaxies (red short-dashed line), LIRGs (green dot-dash line), ULIRGs (blue three dot-dash line), HyLIRG (purple long-dashed line), and all the galaxies (black solid line). |
We separated the contribution of the infrared galaxies to the CIB to four redshift slices, each slice corresponding to about a quarter of the age of the Universe (Fig. 13). Between 8 and 30 μm, we can see a widely varying behavior of each slice caused by the PAH emission bands. The total CIB is smoother. The 0 < z < 0.3 slice dominates the spectrum only near 8 μm because of the strong PAH emission at this rest-frame wavelength. This slice, where the infrared luminosity density is at its lowest, has a minor contribution at the other wavelengths. The 0.3 < z < 1 slice dominates the spectrum between 10 and 350 μm. The sub-mm and mm wavelengths are dominated by the sources lying at higher redshift (z > 2, see Lagache et al. 2005) because of the redshift effects that shift the peak of emission around rest-frame 80 μm in the sub-mm. The mean redshift of the contribution to the CIB is written in Table 5 and computed with 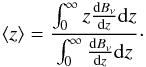 (20)We also separate the contribution of the different infrared luminosity classes. The normal galaxies and LIRGs dominate the background up to 250 μm, which is compatible these populations being dominant ones at low redshift. At longer wavelengths, the redshift effects tend to select high redshift sources, LIRGs and ULIRGs each being responsible for about half of the CIB. The HyLIRG have only a small contribution (< 10%) including in the mm range (Fig. 13, bottom).
(20)We also separate the contribution of the different infrared luminosity classes. The normal galaxies and LIRGs dominate the background up to 250 μm, which is compatible these populations being dominant ones at low redshift. At longer wavelengths, the redshift effects tend to select high redshift sources, LIRGs and ULIRGs each being responsible for about half of the CIB. The HyLIRG have only a small contribution (< 10%) including in the mm range (Fig. 13, bottom).
Surface brightness of the CIB and mean redshift ⟨ z ⟩ of the contribution to the CIB at different wavelengths as predicted by the model.
7. Predictions
7.1. Confusion limit
The confusion limit can be defined in several ways. The radioastronomers classically use a source density criteria, where the confusion limit is the flux cut for which a critical density of sources is reached. The choice of this critical density is not trivial. We follow the approach of Dole et al. (2003). The source density limit NSDC is reached when there is a probability P of having another source in a k θFWHM radius (where θFWHM is the full width at half maximum of the beam profile). Dole et al. (2003) show that 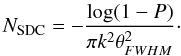 (21)We chose P = 0.1 and k = 0.8 following Dole et al. (2003).
(21)We chose P = 0.1 and k = 0.8 following Dole et al. (2003).
This source density criterion does not take into account the contributions of the sources fainter than the flux limit. We also estimated the photometric confusion noise based on the P(D) analysis (see Sect. 5.7). The P(D) distribution in the absence of instrumental noise is non-Gaussian and have a large tail at bright flux. Thus, the standard deviation is not a good estimator of the confusion noise. We chose to compute the interquartile interval of the P(D) divided by 1.349. With this definition, the value of the confusion noise is exactly σ in the Gaussian case, and we are less sensitive to the bright outliers.
These two estimators can be computed from the counts predicted by our model. We assume that the sources are point-like. The confusion noise found for large telescopes at short wavelengths (<8 μm for a 0.85 m-diameter telescope like Spitzer and <35 μm for a 3.29 m-diameter telescope like Herschel) are thus underestimated. For this reason, we do not estimate the confusion levels for beams smaller than 2 arcsec.
Figure 14 (upper panel) represents the confusion noise, which agrees with the confusion noise measured by Frayer et al. (2009) and Nguyen et al. (2010) with Spitzer/MIPS and Herschel/SPIRE. Weiß et al. (2009) estimate that the confusion noise for a APEX/LABOCA map smoothed by the beam is 0.9 mJy/beam. We find 0.6 mJy/beam with the P(D) approach.
 |
Fig. 14 Upper panel: 1-σ confusion noise as a function of the wavelength for different telescope diameters. We use the confusion noise given by the P(D) method (see Sect. 7.1) for this plot. Red triangles: Frayer et al. (2009)Spitzer/MIPS confusion measurements. Black diamonds: Nguyen et al. (2010): Herschel/SPIRE confusion noise measurements (5-σconf cut). Lower panel: resolved fraction of the CIB by sources brighter than 5-σ confusion noise (fluctuations) and the source density limit. Both panel: Red dotted line: telescope with a diameter of 0.85 m such as Spitzer. Black solid line: 3.29 m telescope such as Herschel. Green dashed line: 12 m telescope such a Atacama pathfinder experiment (APEX). Blue dot-dashed line: 15 m telescope such as the JCMT. Purple three dot-dashed line: 25 m such as the CCAT project. Asterisks: transition between the source density limitation (short wavelengths) and the fluctuation limitation (long wavelengths). |
We also compute the resolved fraction of the CIB by sources brighter than the confusion limit of Dole et al. (2003) (source density criterion) and the 5-σconf given by the P(D). Figure 14 (lower panel) and Tables 6–10 summarize the results. The transition in the confusion regime between the source density limitation (short wavelengths) and the fluctuation limitation (long wavelengths) happens at 100 μm for Spitzer, 220 μm for Herschel, and 1120 μm for the JCMT (asterisks in the lower panel of Fig. 14). For larger antennas below 1.2 mm, the confusion is mainly due to the source density.
Confusion noise and resolved fraction of the CIB at different wavelengths for a 0.85 m telescope(Spitzer like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 3.29 m telescope (Herschel like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 12.00 m telescope (APEX like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 15.00 m telescope (JCMT like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 25.00 m telescope (CCAT-like).
According to these results, at the confusion limit, Herschel can resolve 92%, 84%, 60%, 25.9%, 9.2%, and 3.3% of the CIB at 70 μm, 100 μm, 160 μm, 250 μm, 350 μm, and 500 μm, respectively. Nevertheless, owing to the blackbody emission of the telescope (about 60 K), very long integration times are needed to reach the confusion limit at short wavelengths. The confusion limit in PACS will only be reached in the ultra-deep region of the H-GOODS survey. The confusion limit will probably never be reached at 70 μm. A telescope of the same size as Herschel and a cold (5K) mirror, such as SPICA, could resolve almost all the CIB from the mid-infrared to 100 μm. A 25 m single-dish sub-mm telescope such as the Cornell Caltech Atacama telescope (CCAT) project would be able to resolve more than 80% of the CIB up to 500 μm.
7.2. High energy opacity
The CIB photons can interact with TeV photons. The cross-section between a Eγ rest-frame high-energy photon and an infrared photon with a observer-frame wavelength λIR interacting at a redshift z with an angle θ (and μ = cos(θ)) is (Heitler 1954; Jauch & Rohrlich 1976) ![\begin{eqnarray} \sigma_{\gamma \gamma}(E_\gamma,\lambda_{\rm IR},\mu,z) &=& H\left (1-\frac{\epsilon_{\rm th}}{\epsilon} \right ) \frac{3 \sigma_T}{16} (1-\beta^2) \\ &&\quad \times \left [ 2\beta(\beta^2-2)+(3-\beta^4)\ln\left( \frac{1+\beta}{1-\beta} \right) \right ] \end{eqnarray}](/articles/aa/full_html/2011/05/aa15841-10/aa15841-10-eq346.png) with
with 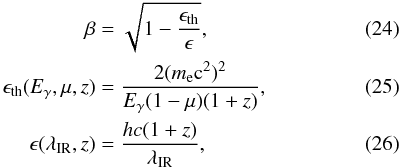 where σT is the Thompson cross-section (6.65 × 10-29 m2), me the mass of the electrons, and H the Heaviside step function (H(x) = 1 if x > 0 and 0 else).
where σT is the Thompson cross-section (6.65 × 10-29 m2), me the mass of the electrons, and H the Heaviside step function (H(x) = 1 if x > 0 and 0 else).
The optical depth τ(Eγ,zs) for a photon observed at energy Eγ and emitted at a redshift zs can be easily computed (Dwek & Krennrich 2005; Younger & Hopkins 2011; Domínguez et al. 2011) with 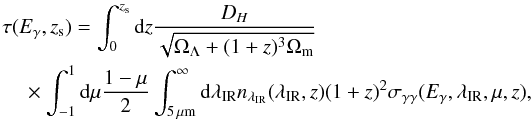 (27)where nλIR(λIR,z) is the comoving number density of photons emitted at a redshift greater than z between λIR and λIR + dλIR. The 5 μm cut corresponds to the limit of the validity of our model. The number density of photons is computed with
(27)where nλIR(λIR,z) is the comoving number density of photons emitted at a redshift greater than z between λIR and λIR + dλIR. The 5 μm cut corresponds to the limit of the validity of our model. The number density of photons is computed with 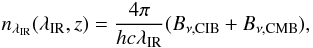 (28)where Bν,CIB is the CIB given by our model and Bν,CMB is the brightness of a blackbody at 2.725 K corresponding to the cosmic microwave background (Fixsen 2009). Our predicted opacities do not take into account the absorption by the cosmic optical background photons (COB, λ < 5 μm). Younger & Hopkins (2011) showed that the contribution of the COB to the opacity is negligible for energies higher than 5 TeV.
(28)where Bν,CIB is the CIB given by our model and Bν,CMB is the brightness of a blackbody at 2.725 K corresponding to the cosmic microwave background (Fixsen 2009). Our predicted opacities do not take into account the absorption by the cosmic optical background photons (COB, λ < 5 μm). Younger & Hopkins (2011) showed that the contribution of the COB to the opacity is negligible for energies higher than 5 TeV.
We can determine up to which redshift the opacity stays lower than 1. We can thus define an horizon as a function of the energy, called the Fazio-Stecker relation. We can see in Fig. 15 that the observed energy cutoff of low-redshift blazars (Mkn 501, Aharonian et al. 1999; Mkn 421, Aharonian et al. 2002; and BL Lac 1ES 1959+650, Aharonian et al. 2003) is compatible with this relation.
 |
Fig. 15 Fazio-Stecker relation: energy at which the opacity reach a given τ as a function of redshift. This plot is done for τ = 1 (red solid line), 2 (blue dashed line) and 5 (green dotted line). The data points are the cutoff energy of Mkn 501 (Aharonian et al. 1999), Mkn 421 (Aharonian et al. 2002) and Lac 1ES 1959+650 (Aharonian et al. 2003). |
7.3. Effect of the strong lensing on the number counts
 |
Fig. 16 Fraction of strongly lensed sources (magnification larger than 2) as a function of the flux at 350 μm (red solid line), at 500 μm (green dashed line), at 850 μm (blue dot-dashed line) and at 1.1 mm (purple three-dot-dashed line). The dotted lines represent the 1-σ confidence area of our model. |
 |
Fig. 17 Differential number counts in the Planck bands. These counts only take into account the individual star-forming galaxies. Black solid line: total contribution. Green dot-dashed line: contribution of the non-lensed sources. Red dashed line: contribution of the strongly-lensed sources. Dotted lines 1-σ contours. Vertical long-dahsed line: 5-σ limits (confusion+instrumental) of Fernandez-Conde et al. (2008) for a bias of 1.5. |
The strongly-lensed fraction is the ratio of the counts of lensed sources to the total observed counts. Because the slope of the counts varies a lot with the flux and wavelength, this fraction depends on the flux and the wavelength (see Fig. 16). The strongly lensed fraction is always smaller than 2% below 250 μm and is thus negligible. At longer wavelengths, we predict a maximum of the strongly lensed fraction near 100 mJy. At 500 μm, about 15% of the sources brighter than 100 mJy are lensed. This fraction increases to 40% near 1 mm.
Our results can be compared with those of the Negrello et al. (2007) model. The two models predict that the lensed fraction as a function of the flux is a bump around 100 mJy. However, the amplitude of this bump predicted by the two models is significantly different. For instance, the maximum of the lensed fraction at 500 μm is 15% for our model and 50% for the Negrello et al. (2007) model. The slope between 10 and 100 mJy is steeper in Negrello et al. (2007) model than in ours and is incompatible with the measurements (Clements et al. 2010; Oliver et al. 2010; Glenn et al. 2010). The steeper the slope, the larger the lensed fraction. This explains why the Negrello et al. (2007) model predicts larger lensed fraction than ours. The probability of a source being lensed increases with its redshift. The differences in the redshift distributions of the models could also explain some of the differences in the lensed fraction.
Figure 6 shows the respective contribution of the lensed and non-lensed sources to the SPT counts of dusty sources without IRAS 60 μm counterparts at 1.38 mm (Vieira et al. 2010). According to the model, these counts are dominated by strongly-lensed sources above 15 mJy. These bright sources are thus very likely to correspond to strongly-lensed sub-mm galaxies.
We predicted on the contribution of the strongly-lensed sources to the Planck number counts (see Fig. 17) using Fernandez-Conde et al. (2008) 5-σ limits, because they take into account the effect of the clustering on the confusion noise. This effect is non-negligible because of the large beam of Planck. We found that the contribution of the lensed sources to the Planck counts is negligible in all the bands (a maximum of 0.47 galaxies sr-1 at 550 μm). At high redshift, Planck will probably detect more small structures such as proto-clusters, than individual galaxies. Planck is thus not the best survey to find lensing candidates. Sub-mm surveys with a sensitivity near 100 mJy are more efficient. For instance, the Herschel-ATLAS survey should find 153 ± 26 and 411 ± 24 lensed sources with S500 > 50 mJy and S350 > 50 mJy, respectively, across 600 deg2.
8. Discussion
8.1. Comparison with other backward evolution models
The evolution of the infrared luminosity density predicted by our model can be compared with the predictions of other backward evolution models. We find, like Franceschini et al. (2010), a strong increase in ρIR from z = 0 to z = 1, a break around z = 1, and a decrease at higher redshift. In contrast, the Valiante et al. (2009) and Le Borgne et al. (2009) models predict a maximum of infrared luminosity density around z = 2.
In a similar way to Le Borgne et al. (2009) and Franceschini et al. (2010), we found that LIRGs dominate infrared luminosity density around z = 1 and that ULIRGs dominate at redshift higher than 1.5. We also found as Le Borgne et al. (2009) that normal galaxies dominates ρIR only up to z ~ 0.5.
Our model and the Valiante et al. (2009) one use a similar parametrization of the LF evolution. Both models found a very strong evolution in luminosity up to z = 2 ((1 + z)3.4 for the Valiante et al. (2009) model, which can be compared with (1 + z)2.9 ± 0.1 from z = 0 to 0.87 ± 0.05 and (1 + z)4.7 ± 0.3 from z = 0.87 ± 0.05 to 2 for our model). At higher redshift, our model is compatible with no evolution and the Valiante et al. (2009) model predicts a slight decrease in (1 + z)-1. Concerning the evolution in density, both models predicts an increase from z = 0 to z ≈ 1 (proportional to (1 + z)2 for the Valiante et al. (2009) model and (1 + z)0.8 ± 0.2 for our model) and a decrease at higher redshift ((1 + z)-1.5 for the Valiante et al. (2009) model, (1 + z) − 6.2 ± 0.5 between z = 0.87 ± 0.5 and z = 2 and (1 + z) − 0.9 ± 0.7 at z > 2 for our model). These two models thus agree on the global shape of the evolution of the LF, but disagree on the values of the coefficient driving it. There is in particular a large difference on the evolution density between z ~ 1 and z ~ 2. This difference could be explained by the different positions of the breaks. Nevertheless, the uncertainties on the Valiante et al. (2009) model are not estimated. It is thus difficult for us to draw any conclusion.
Valiante et al. (2009) and Franceschini et al. (2010) used AGNs to reproduce the infrared observations. Valiante et al. (2009) also used a temperature dispersion of the galaxies. Our model reproduce the same observations using neither AGNs nor temperature dispersion. This demonstrates that the AGN contribution and the temperature scatter cannot be accurately constrained by with this type of modeling.
8.2. Discriminating the models: smoking gun observations?
Although they use different galaxy populations and evolutions, the backward evolution models reproduce the number counts from the mid-IR to the mm domain in a reasonably good way. It is thus important to find new observables to discriminate between models.
The sub-mm redshift distributions of the bright sources are quite straightforward, but very discriminant observations. For instance, Fig. 7 shows a significant difference in the sub-mm redshift distributions predicted by the different models. The Chapin et al. (2011) measurements performed on one small field with a cut at high flux do not enable us to draw strong conclusions. Herschel will help us to increase the accuracy of the measured redshift distributions and estimate the cosmic variance in them. These constraints will be crucial for the next generation of models.
Jauzac et al. (2011) showed that the redshift distribution of the contribution of the 24 microns sources to CIB at 70 and 160 μm (d(νBν)/dz) also provides a strong constraint. Figure 18 shows the d(νBν)/dz at 350 μm. The different models make totally incompatible predictions in the sub-mm. An accurate measurement of d(νBν)/dz will thus be crucial for future models.
 |
Fig. 18 Differential contribution of the S24 > 80 μJy sources to the CIB as a function of the redshift at 350 μm. Black solid line: Our model (1-σ limit in black dotted line). Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Blue dot-dashed line: Franceschini et al. (2010) model. |
8.3. Limits of our model
Our model is a useful tool to make a first interpretation of the observations from the mid-infrared to the mm domain. Nevertheless, it is biased by some structural choice in its construction.
The choice of the parameters biases the results. For example, we have chosen the minimal number of parameters to reproduce the counts. If we had used more breaks in the evolution in both density and luminosity, the evolutions with redshift would have been smoother and the errors in the predictions would have been different. Our errors are just the statistical errors due to the determination of the parameter of a given model using the data. It does not include the uncertainty in our hypothesis about the evolution (such as α fixed) and the biases due to our choice of parameters (evolution in (1 + z)r with breaks). For instance, the strong decrease in density between z ~ 0.9 and z = 2 is probably an artifact caused by our choice of parametrization. In addition, our model of lensing is very simple and should be improved in the future. Nevertheless, the contribution of the lensing in the fitted data is low and the bias is thus negligible.
The backward evolution models gives a very limited interpretation of the data. They provide only a description of the evolution of the statistical properties of the infrared galaxies. The physical processes explaining the strong evolution of these objects are ignored. A more complex physical approach is thus necessary to deeply understand the history of the infrared galaxies. Nevertheless, our model is very useful for providing a rapid interpretation of new observations and predictions for future missions.
8.4. Perspectives
Our models fit the current data when we employ rather simple hypotheses. Nevertheless, the increasing accuracy of infrared observations will probably help us to improve the model. Additional model updates will be possible in the future.
The α and σ parameters are fixed, but it may be necessary to incorporate an evolution of the shape of the LF with the redshift. A Fisher matrix analysis shows that the evolution of α at high redshift cannot be constrained without deeper observations in the sub-mm. An evolution of σ could be constrained, but is not necessary to reproduce the current data.
The evolution of the parameters is very simple in the current version and could be updated by using more breaks or a smoother functional form.
The observations of Herschel will help us to improve the SED used in our model, and maybe enable us to determine the SED evolution with redshift. The temperature of the big grains and its dispersion will be measured more accurately. Nevertheless, this dispersion must be modeled with a limited number of templates to allow us to use an MCMC approach. This will be one of the future challenges of including it in our model.
Nevertheless, each refinement increases the number of free parameters of the model. It is important to limit the number of new parameters in comparison with the number of measurements.
9. Summary
-
Our new parametric backward evolution model has enabled usto reproduce the number counts from 15 μm to 1.1 mm, the monochromatic LF, and the redshift distributions.
-
We have found that our model predicts a strong evolution in the LF characteristic luminosity up to z = 2 and a strong decrease in density from z = 1 to z = 2. We predict that the number of HyLIRG reaches a maximum around z = 2.
-
We have found that normal galaxies, LIRGs, and ULIRGs dominates the infrared output at z = 0, z = 1, and z = 2, respectively. The HyLIRG accounts for a small fraction (< 10%) at all redshifts.
-
We have reproduced the CIB spectrum and predicted the contributions per redshift and luminosity slice. We found that the mid- and far-infrared part of the CIB are mainly emitted by the normal galaxies and LIRG. The sub-mm part is mainly due to LIRGs and ULIRGs at high redshift in accordance with the sub-mm observations of deep fields. We estimated the total flux of the CIB total to be 23.7 ± 0.9 nW m-2 sr-1.
-
We estimated the fraction of lensed sources in the sub-mm as a function of the flux and wavelength. This contribution is low (< 10%) below 500 μm, but high (up to 50%) around 100 mJy in the mm domain.
-
We predicted that the population of very bright dusty galaxies detected by SPT without an IRAS counterpart (Vieira et al. 2010) is essentially composed of lensed sub-mm galaxies. We have also predicted the contribution of the lensed sources to the Planck number counts.
-
We predict the confusion limits for future missions like SPICA or CCAT.
-
We estimated the opacity of the Universe to TeV photons.
-
Material of the model (software, tables and predictions) is available online1.
10. Conclusion
We have demonstrated that it is possible to reproduce the number counts from the mid-IR to the mm domain with a rather simple parametric model that is minimized automatically. Nevertheless, other automatically-tuned models reproduce these counts with different redshift distributions (Le Borgne et al. 2009; Marsden et al. 2011). This suggests that number counts alone are insufficient to uniquely constrain these models. Different observables are thus crucial to discriminate the different parametrizations proposed by the model builders. These constraints are the luminosity functions, the redshift distributions, P(D), and the fluctuations. Future measurements of these quantities and their uncertainties have to be very robust to be used to constrain the next generation of models.
Acknowledgments
We acknowledge Mattia Negrello for explaining us how includes the lensing in our galaxy evolution model, Guillaume Patanchon for pushing us to make a parametric model, Nicolas Taburet and Marian Douspis for their explanations about the MCMC, Julien Grain for his explanations on the photon-photon interaction, Josh Younger for giving us useful references, Axel Weiβ and Alexandre Beelen for their discussion about the counts in the sub-mm, and Morgane Cousin for carefully reading the draft and founding some mistakes. We also thank the BLAST team for the public release of their maps. We finally acknowledge Stefano Berta, Seb Oliver, Dave Clements, Axel Weiβ, Rosalind Hopwood, Joaquin Vieira, Andrew Hopkins, Alexandre Beelen and Kirsten Knudsen and Vandana Desai for providing us quickly their results. We also thanks Gaelen Marsden for our discussion about the comparison of our two models after the submission of our papers. This work was partially supported by the ANR-09-BLAN-0224-02.
References
- Aharonian, F. A., Akhperjanian, A. G., Andronache, M., et al. 1999, A&A, 350, 757 [NASA ADS] [Google Scholar]
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2002, A&A, 393, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2003, A&A, 406, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, D. M., Bauer, F. E., Chapman, S. C., et al. 2005, ApJ, 632, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Austermann, J. E., Dunlop, J. S., Perera, T. A., et al. 2010, MNRAS, 401, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Baugh, C. M. 2006, Reports on Progress in Physics, 69, 3101 [NASA ADS] [CrossRef] [Google Scholar]
- Bavouzet, N. 2008, Ph.D. Thesis, Université Paris-Sud 11 [Google Scholar]
- Beelen, A., Omont, A., Bavouzet, N., et al. 2008, A&A, 485, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, S., Magnelli, B., Lutz, D., et al. 2010, A&A, 518, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Dennefeld, M., & Moshir, M. 1997, A&A, 323, 685 [NASA ADS] [Google Scholar]
- Béthermin, M., Dole, H., Beelen, A., & Aussel, H. 2010a, A&A, 512, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Cousin, M., & Bavouzet, N. 2010b, A&A, 516, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borys, C., Chapman, S., Halpern, M., & Scott, D. 2003, MNRAS, 344, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Caputi, K. I., Lagache, G., Yan, L., et al. 2007, ApJ, 660, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Chapin, E. L., Pope, A., Scott, D., et al. 2009, MNRAS, 398, 1793 [NASA ADS] [CrossRef] [Google Scholar]
- Chapin, E. L., Chapman, S. C., Coppin, K. E., et al. 2011, MNRAS, 411, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Blain, A. W., Smail, I., & Ivison, R. J. 2005, ApJ, 622, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Chib, S., & Greenberg, E. 1995, Amer. Stat., 49, 325 [CrossRef] [Google Scholar]
- Clements, D. L., Rigby, E., Maddox, S., et al. 2010, A&A, 518, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cole, S., Lacey, C. G., Baugh, C. M., & Frenk, C. S. 2000, MNRAS, 319, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1974, ApJ, 188, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Coppin, K., Chapin, E. L., Mortier, A. M. J., et al. 2006, MNRAS, 372, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Desai, V., Soifer, B. T., Dey, A., et al. 2008, ApJ, 679, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Devlin, M. J., Ade, P. A. R., Aretxaga, I., et al. 2009, Nature, 458, 737 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dole, H., Lagache, G., & Puget, J. 2003, ApJ, 585, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Dole, H., Lagache, G., Puget, J., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Popescu, C. C., Tuffs, R. J., et al. 2008, ApJ, 678, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Dunkley, J., Bucher, M., Ferreira, P. G., Moodley, K., & Skordis, C. 2005, MNRAS, 356, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., & Krennrich, F. 2005, ApJ, 618, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Cesarsky, C. J., Fadda, D., et al. 1999, A&A, 351, L37 [NASA ADS] [Google Scholar]
- Engelbracht, C. W., Blaylock, M., Su, K. Y. L., et al. 2007, PASP, 119, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Fadda, D., Yan, L., Lagache, G., et al. 2010, ApJ, 719, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez-Conde, N., Lagache, G., Puget, J., & Dole, H. 2008, A&A, 481, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernandez-Conde, N., Lagache, G., Puget, J., & Dole, H. 2010, A&A, 515, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fixsen, D. J. 2009, ApJ, 707, 916 [Google Scholar]
- Franceschini, A., Rodighiero, G., Vaccari, M., et al. 2010, A&A, 517, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frayer, D. T., Sanders, D. B., Surace, J. A., et al. 2009, AJ, 138, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Glenn, J., Conley, A., Béthermin, M., et al. 2010, MNRAS, 409, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Engelbracht, C. W., Fadda, D., et al. 2007, PASP, 119, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Gregorich, D. T., Neugebauer, G., Soifer, B. T., Gunn, J. E., & Herter, T. L. 1995, AJ, 110, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Greve, T. R., Weiβ, A.,Walter, F., et al. 2010, ApJ, 719, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gruppioni, C., Lari, C., Pozzi, F., et al. 2002, MNRAS, 335, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Hacking, P., & Houck, J. R. 1987, ApJS, 63, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, N. R., Keisler, R., Knox, L., et al. 2010, ApJ, 718, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Heitler, W. 1954, Quantum theory of radiation, ed. W. Heitler [Google Scholar]
- Hezaveh, Y. D., & Holder, G. P. 2010, ApJ, submitted [arXiv:1010.0998] [Google Scholar]
- Hogg, D. W. 1999 [arXiv: 9905116] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hopwood, R., Serjeant, S., Negrello, M., et al. 2010, ApJ, 716, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M. 2009, ApJ, 694, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jauch, J. M., & Rohrlich, F. 1976, The theory of photons and electrons, The relativistic quantum field theory of charged particles with spin one-half, ed. J. M. Jauch, & F. Rohrlich [Google Scholar]
- Jauzac, M., Dole, H., Le Floc’h, E., et al. 2011, A&A, 525, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Knudsen, K. K., van der Werf, P. P., & Kneib, J. 2008, MNRAS, 384, 1611 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2010, MNRAS, 443 [Google Scholar]
- Lagache, G., Abergel, A., Boulanger, F., Désert, F. X., & Puget, J. 1999, A&A, 344, 322 [NASA ADS] [Google Scholar]
- Lagache, G., Haffner, L. M., Reynolds, R. J., & Tufte, S. L. 2000, A&A, 354, 247 [Google Scholar]
- Lagache, G., Dole, H., Puget, J.-L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Bavouzet, N., Fernandez-Conde, N., et al. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzoni, B., Guiderdoni, B., Mamon, G. A., Devriendt, J., & Hatton, S. 2005, MNRAS, 361, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Le Borgne, D., Elbaz, D., Ocvirk, P., & Pichon, C. 2009, A&A, 504, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Le Floc’h, E., Aussel, H., Ilbert, O., et al. 2009, ApJ, 703, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, M., Jain, B., Devlin, M., & Aguirre, J. 2010, ApJ, 717, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Hacking, P. B., Conrow, T. P., & Rowan-Robinson, M. 1990, ApJ, 358, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2009, A&A, 496, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, G., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, G., Chapin, E. L., Halpern, M., et al. 2011, ApJ, submitted [arXiv:1010.1176] [Google Scholar]
- Matsuura, S., Shirahata, M., Kawada, M., et al. 2011, ApJ, submitted [arXiv:1002.3674] [Google Scholar]
- Miville-Deschênes, M., Lagache, G., & Puget, J. 2002, A&A, 393, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Negrello, M., Perrotta, F., González-Nuevo, J., et al. 2007, MNRAS, 377, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Hopwood, R., De Zotti, G., et al. 2010, Science, 330, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, H. T., Schulz, B., Levenson, L., et al. 2010, A&A, 518, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S. J., Wang, L., Smith, A. J., et al. 2010, A&A, 518, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papovich, C., Dole, H., Egami, E., et al. 2004, ApJS, 154, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Pascale, E., Ade, P. A. R., Bock, J. J., et al. 2008, ApJ, 681, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Pascale, E., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Patanchon, G., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1750 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, C. P., Oyabu, S., Wada, T., et al. 2010, A&A, 514, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrotta, F., Baccigalupi, C., Bartelmann, M., De Zotti, G., & Granato, G. L. 2002, MNRAS, 329, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Perrotta, F., Magliocchetti, M., Baccigalupi, C., et al. 2001, unpublished [arXiv:astro-ph/0111239] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Puget, J., Abergel, A., Bernard, J., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., et al. 2008, ApJS, 175, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, D. S., Bower, R., Frenk, C. S., Jenkins, A., & Theuns, T. 2007, MNRAS, 374, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Renault, C., Barrau, A., Lagache, G., & Puget, J. 2001, A&A, 371, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodighiero, G., Vaccari, M., Franceschini, A., et al. 2010, A&A, 515, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rowan-Robinson, M. 2009, MNRAS, 394, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., Hughes, J., Vedi, K., & Walker, D. W. 1990, MNRAS, 246, 273 [NASA ADS] [Google Scholar]
- Saunders, W., Rowan-Robinson, M., Lawrence, A., et al. 1990, MNRAS, 242, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, S. E., Dunlop, J. S., & Serjeant, S. 2006, MNRAS, 370, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, K. S., Yun, M. S., Wilson, G. W., et al. 2010, MNRAS, 405, 2260 [NASA ADS] [Google Scholar]
- Shupe, D. L., Rowan-Robinson, M., Lonsdale, C. J., et al. 2008, AJ, 135, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Ivison, R. J., Blain, A. W., & Kneib, J. 2002, MNRAS, 331, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Soifer, B. T., & Neugebauer, G. 1991, AJ, 101, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J. A., Gordon, K. D., Bhattacharya, B., et al. 2007, PASP, 119, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W., & de Jager, O. C. 1997, ApJ, 476, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Swinyard, B. M., Ade, P., Baluteau, J., et al. 2010, A&A, 518, L4 [Google Scholar]
- Takeuchi, T. T., & Ishii, T. T. 2004, ApJ, 604, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Teplitz, H. I., Chary, R., Elbaz, D., et al. 2011, AJ, 141, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Truch, M. D. P., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1723 [NASA ADS] [CrossRef] [Google Scholar]
- Vaccari, M., Marchetti, L., Franceschini, A., et al. 2010, A&A, 518, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valiante, E., Lutz, D., Sturm, E., Genzel, R., & Chapin, E. L. 2009, ApJ, 701, 1814 [NASA ADS] [CrossRef] [Google Scholar]
- Vieira, J. D., Crawford, T. M., Switzer, E. R., et al. 2010, ApJ, 719, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Weiß, A., Kovács, A., Coppin, K., et al. 2009, ApJ, 707, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, R. J., Jarvis, M. J., Mauch, T., Rawlings, S., & Hickey, S. 2010, MNRAS, accepted [arXiv:1002.1112] [Google Scholar]
- Younger, J. D., & Hopkins, P. F. 2011, MNRAS, 410, 2180 [NASA ADS] [CrossRef] [Google Scholar]
- Zemcov, M., Blain, A., Halpern, M., & Levenson, L. 2010, ApJ, 721, 424 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Calibration parameters and 1-σ marginalized errors from our MCMC fit compared with calibration uncertainties given by the instrumental teams.
Level of the non-correlated fluctuations of the CIB at different wavelengths and comparison with the predictions of the model.
Surface brightness of the CIB and mean redshift ⟨ z ⟩ of the contribution to the CIB at different wavelengths as predicted by the model.
Confusion noise and resolved fraction of the CIB at different wavelengths for a 0.85 m telescope(Spitzer like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 3.29 m telescope (Herschel like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 12.00 m telescope (APEX like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 15.00 m telescope (JCMT like).
Confusion noise and resolved fraction of the CIB at different wavelengths for a 25.00 m telescope (CCAT-like).
All Figures
 |
Fig. 1 Solid line: local infrared bolometric luminosity function from our best-fit model. Red dotted line: contribution of the normal galaxies. Blue dashed line: contribution of the starburst galaxies. Black vertical long dashed line: luminosity of the transition between the two population (Lpop). |
| In the text | |
 |
Fig. 2 Effect of the lensing on the number counts at 850 microns. The contribution of lensed sources is multiplied by ten to underline the effect of the lensing on the counts. Red dotted line: counts of non-lensed sources. Green dashed line: counts of lensed sources. Black solid line: total counts. |
| In the text | |
 |
Fig. 3 a)–f) Differential extragalactic number counts used for the fit. h) Monochromatic LFs at different wavelengths and redshifts. a)–h) The fitted points are thicker. Black solid line: our best-fit model. Black dashed line: 1-σ range of the model. a)–c) Red diamonds: Béthermin et al. (2010a)Spitzer legacy number counts. c) Green triangles: Berta et al. (2010)Herschel/PEP number counts. d)–f) Red diamonds: Oliver et al. (2010)Herschel/Hermes number counts. Green triangles: Glenn et al. (2010)Herschel/Hermes P(D) analysis. Clements et al. (2010)Herschel/ATLAS number counts. Purple cross: Béthermin et al. (2010b) BLAST number counts. g) Green triangles: Scott et al. (2010) AzTEC number counts in the CDFS field. Green triangles: Austermann et al. (2010) AzTEC number counts in the SHADES field. h) Red plus: Rodighiero et al. (2010) local 24 μm LF (not fitted points in grey). Green diamonds: Saunders et al. (1990) local 60 μm LF (shifted by a factor 10 on the y-axis; not fitted points in grey); blue triangles: Rodighiero et al. (2010) 15 μm LF at z = 0.6 (shifted by a factor 100 on the y-axis; not fitted points in grey). Purple squares: Rodighiero et al. (2010) 12 μm LF at z = 1 (shifted by a factor 1000 on the y-axis; not fitted points in grey). Cyan crosses: Caputi et al. (2007) 8 μm LF at z = 2 (shifted by a factor 10 000 on the y-axis). |
| In the text | |
 |
Fig. 4 a)–c) Differential extragalactic number counts not used for the fit. Black solid line: our best-fit model. Black dashed line: 1-σ range of the model. a) Red diamonds: Elbaz et al. (1999) ISO counts. Green triangle: Gruppioni et al. (2002) ISO counts. Blue squares: Pearson et al. (2010) AKARI counts. Purple cross: Hopwood et al. (2010) AKARI (lensed) counts. Cyan plus: Teplitz et al. (2011)Spitzer/IRS counts. b) Red diamonds: Hacking & Houck (1987), Lonsdale et al. (1990), Rowan-Robinson et al. (1990), Saunders et al. (1990), Gregorich et al. (1995) and Bertin et al. (1997) IRAS counts. c) Red diamonds: Berta et al. (2010)Herschel/PEP counts. |
| In the text | |
 |
Fig. 5 Integral number counts at 850 μm. Black solid line: our best-fit model. Black dashed line: 1-σ range of the model. Grey plus: Zemcov et al. (2010) combined SCUBA lensed counts. Blue dashed line: Weiß et al. (2009) LABOCA P(D) (Schechter model). Red diamonds: Coppin et al. (2006) SCUBA SHADES counts. Cyan square: (Beelen et al. 2008) LABOCA counts around the J2142-4423 Lyα protocluster. Black plus: Knudsen et al. (2008) combined SCUBA lensed counts; green triangles: Scott et al. (2006) revisited SCUBA counts. Purple cross: Borys et al. (2003) SCUBA HDFN counts. Yellow asterisks: Smail et al. (2002) lensed counts. |
| In the text | |
 |
Fig. 6 Number counts at 1.38 mm of dusty sources without IRAS 60 μm counterpart. Black diamonds: Vieira et al. (2010) south pole telescope (SPT) measurements. Black solid line: total contribution of S60 < 0.2 Jy sources. Green dot-dashed line: contribution of the non-lensed sources. Red dashed line: contribution of the strongly-lensed sources. Dotted lines 1-σ contours. |
| In the text | |
 |
Fig. 7 Redshift distribution of the S24 > 80 μJy a), S24 > 300 μJy b), S250 > 40 mJy c), S350 > 30 mJy d), S500 > 20 mJy e), S850 > 3 mJy f), and S1100 > 3 mJy g) sources. These measurements are not fitted. Black solid line: our best-fit model. Black dotted line: 1-σ range of the model. Grey solid line: our best-fit model convolved by a Gaussian of σz = 0.125z. Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Red asterisks: Le Floc’h et al. (2009)a), b), Chapin et al. (2011)c)–e), Chapman et al. (2005)f) and Chapin et al. (2009)g) measurements. Blue diamonds: Rodighiero et al. (2010) measurements a), b). Cyan squares: Desai et al. (2008) measurements b). |
| In the text | |
 |
Fig. 8 Differential contribution of the S24 > 80 μJy sources to the CIB as a function of the redshift at 70 μm (upper panel) and 160 μm (lower panel). Red asterisks: measurement by stacking in the COSMOS field (Jauzac et al. 2011). Black solid line: our model (1-σ limit in black dotted line). Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Blue dot-dashed line: Franceschini et al. (2010) model. |
| In the text | |
 |
Fig. 9 Comparison with the BLAST pixel histogram at 250 μm (upper panel), 350 μm (middle panel) and 500 μm (lower panel). Black histogram: histogram of the values of the central part of the BLAST beam-smoothed map in Jy/beam. Red solid line: distribution predicted by our model using a P(D) analysis. Our analysis does not include the clustering. Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Blue dot-dashed line: Franceschini et al. (2010) model. |
| In the text | |
 |
Fig. 10 Diagonal plots: marginalized probability distributions of each parameters deduced from the MCMC. Non-diagonal plots: 1-σ (red), 2-σ (green), and 3-σ (blue) regions for each pair of parameters). From left to right: α, σ, L ⋆ , φ ⋆ , rL ⋆ ,lz, rphi ⋆ ,lz, zbreak,1, rL ⋆ ,mz, rphi ⋆ ,mz, rL ⋆ ,hz, rphi ⋆ ,hz, Lpop, and σpop (cf. Table 1). |
| In the text | |
 |
Fig. 11 Evolution of the bolometric infrared luminosity function with redshift. Upper panel: bolometric LF at z = 0 (solid line), z = 0.5 (dot line), z = 1 (dashed line), z = 1.5 (dot-dash line), z = 2 (3-dot-dash line), and z = 3 (long dashed line). Lower panel: Evolution of the L ⋆ (red solid line) and φ ⋆ (blue dot-dash line) parameter as a function of redshift and 1-σ confidence region. The measurement of L ⋆ by Caputi et al. (2007) (triangles) using 24 μm obervations and Magnelli et al. (2009) (diamonds) using 70 μm observations are plotted in red. The measurement of φ ⋆ by Caputi et al. (2007) (cross) and Magnelli et al. (2009) (square) are in blue. |
| In the text | |
 |
Fig. 12 Evolution of the bolometric infrared luminosity density (black solid line) as a function of the redshift. The contribution of normal galaxies (LIR < 1011 L⊙), LIRG (1011 < LIR < 1012 L⊙), ULIRG (1012 < LIR < 1013 L⊙), and HyLIRG (LIR > 1013 L⊙) are plotted with short-dashed, dot-dash, three-dot-dash, and long-dashed line respectively. The measurements of Rodighiero et al. (2010) using the MIPS 24 μm data are plotted with diamonds and Pascale et al. (2009) ones using a BLAST stacking analysis with triangles. The Hopkins & Beacom (2006) fit to the optical and infrared measurement is plotted with a dark grey area (1-σ) and a light grey area (3-σ). |
| In the text | |
 |
Fig. 13 Upper panel: contribution to the CIB per redshift slice. Black solid line: CIB spectrum predicted by the model. Red short-dashed line: contribution of the galaxies between z = 0 and 0.3. Green dot-dash line: same thing between z = 0.3 and 1. Blue three dot-dash line: same thing between z = 1 and 2. Purple long-dashed line: contribution of the galaxies at redshift higher than 2. Black arrows: lower limits coming from the number counts at 15 μm (Hopwood et al. 2010) and 24 μm (Béthermin et al. 2010a) and the stacking analysis at 70 μm (Béthermin et al. 2010a), 100 μm, 160 μm (Berta et al. 2010), 250 μm, 350 μm, 500 μm (Marsden et al. 2009), 850 μm (Greve et al. 2010), and 1.1 mm (Scott et al. 2010) and upper limits coming from absorption of the TeV photons of Stecker & de Jager (1997) at 20 μm and Renault et al. (2001) between 5 μm and 15 μm. Black diamonds: Matsuura et al. (2011) absolute measurements with AKARI. Black square: Lagache et al. (2000) absolute measurements with DIRBE/WHAM. Cyan line: Lagache et al. (2000) FIRAS measurement. Lower panel: contribution to the CIB of the normal galaxies (red short-dashed line), LIRGs (green dot-dash line), ULIRGs (blue three dot-dash line), HyLIRG (purple long-dashed line), and all the galaxies (black solid line). |
| In the text | |
 |
Fig. 14 Upper panel: 1-σ confusion noise as a function of the wavelength for different telescope diameters. We use the confusion noise given by the P(D) method (see Sect. 7.1) for this plot. Red triangles: Frayer et al. (2009)Spitzer/MIPS confusion measurements. Black diamonds: Nguyen et al. (2010): Herschel/SPIRE confusion noise measurements (5-σconf cut). Lower panel: resolved fraction of the CIB by sources brighter than 5-σ confusion noise (fluctuations) and the source density limit. Both panel: Red dotted line: telescope with a diameter of 0.85 m such as Spitzer. Black solid line: 3.29 m telescope such as Herschel. Green dashed line: 12 m telescope such a Atacama pathfinder experiment (APEX). Blue dot-dashed line: 15 m telescope such as the JCMT. Purple three dot-dashed line: 25 m such as the CCAT project. Asterisks: transition between the source density limitation (short wavelengths) and the fluctuation limitation (long wavelengths). |
| In the text | |
 |
Fig. 15 Fazio-Stecker relation: energy at which the opacity reach a given τ as a function of redshift. This plot is done for τ = 1 (red solid line), 2 (blue dashed line) and 5 (green dotted line). The data points are the cutoff energy of Mkn 501 (Aharonian et al. 1999), Mkn 421 (Aharonian et al. 2002) and Lac 1ES 1959+650 (Aharonian et al. 2003). |
| In the text | |
 |
Fig. 16 Fraction of strongly lensed sources (magnification larger than 2) as a function of the flux at 350 μm (red solid line), at 500 μm (green dashed line), at 850 μm (blue dot-dashed line) and at 1.1 mm (purple three-dot-dashed line). The dotted lines represent the 1-σ confidence area of our model. |
| In the text | |
 |
Fig. 17 Differential number counts in the Planck bands. These counts only take into account the individual star-forming galaxies. Black solid line: total contribution. Green dot-dashed line: contribution of the non-lensed sources. Red dashed line: contribution of the strongly-lensed sources. Dotted lines 1-σ contours. Vertical long-dahsed line: 5-σ limits (confusion+instrumental) of Fernandez-Conde et al. (2008) for a bias of 1.5. |
| In the text | |
 |
Fig. 18 Differential contribution of the S24 > 80 μJy sources to the CIB as a function of the redshift at 350 μm. Black solid line: Our model (1-σ limit in black dotted line). Purple three dot-dashed line: Le Borgne et al. (2009) model. Green dashed line: Valiante et al. (2009) model. Blue dot-dashed line: Franceschini et al. (2010) model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


