| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015477 | |
| Published online | 28 February 2011 | |
Was a cloud-cloud collision the trigger of the recent star formation in Serpens?
1
Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy,
University of Manchester,
Oxford Road,
Manchester
M13 9PL,
UK
e-mail: Ana.Cabral@postgrad.manchester.ac.uk
2
School of Physics, University of Exeter,
Exeter
EX4 4QL,
UK
3
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstraße, 85748
Garching,
Germany
4
Universitäts-Sternwarte München, Scheinerstraße 1, 81679
München,
Germany
5
Laboratoire AIM, CEA/DSM-CNRS-Université Paris
Diderot, IRFU/Service d’Astrophysique, C.E. Saclay,
Orme de merisiers, 91191
Gif-sur-Yvette,
France
Received: 27 July 2010
Accepted: 10 January 2011
Context. The complexity of the interstellar medium (ISM) is such that it is unlikely that star formation is initiated in the same way in all molecular clouds. While some clouds seem to collapse on their own, others may be triggered by an external event such as a cloud/flow collision forming a gravitationally unstable enhanced density layer.
Aims. This work tests cloud-cloud collisions as the triggering mechanism for star formation in the Serpens Main Cluster as has been suggested by previous work.
Methods. A set of smoothed particle hydrodynamics (SPH) simulations of the collision between two cylindrical clouds are performed and compared to (sub)millimetre observations of the Serpens Main Cluster.
Results. A configuration was found that reproduces many of the observed characteristics of Serpens, including some of the main features of the peculiar velocity field. The evolution of the velocity with position throughout the model is similar to the observed one and the column density and masses within the modelled cloud agree with those measured for the SE sub-cluster. Furthermore, our results also show that an asymmetric collision provides the ingredients to reproduce lower density filaments perpendicular to the main structure, similar to those observed. In this scenario, the formation of the NW sub-cluster of Serpens can be reproduced only if there is a pre-existing marginally gravitationally unstable region at the time the collision occurs.
Conclusions. This work supports the interpretation that a collision between two clouds may have been the trigger of the most recent burst of star formation in Serpens. It not only explains the complicated velocity structure seen in the region, but also the temperature differences between the north (in “isolated” collapse) and the south (resulting from the shock between the clouds). In addition it provides an explanation for the sources in the south having a larger spread in age than those in the north.
Key words: stars: formation / stars: individual: Serpens / ISM: clouds / ISM: kinematics and dynamics / methods: numerical
© ESO, 2011
1. Introduction
Observations of molecular clouds indicate that stars form in dense, clumpy filaments (e.g. André et al. 2010; Molinari et al. 2010). However, the processes controlling the formation of these structures and their role in triggering specific star-formation episodes are widely debated. One possible process could simply be a gravity-controlled one: quasi-static or dynamic gravitational collapse of non-spherical clouds can easily generate filamentary structures, which subsequently fragment to form stars (e.g. Palla & Stahler 2002; Hartmann & Burkert 2007). The contraction of an idealised isolated turbulent cloud leads to the formation of small-scale filaments (~0.1 pc long), within which stars begin to form, as shown by simulations from Bate et al. (2003); Klessen et al. (2005); Bate (2009a,b). Alternatively, external triggers can compress molecular gas to generate high-density fragmented filaments. These triggers can be of very different natures: ionisation/shock fronts around OB stars (e.g. Elmegreen & Lada 1977; Dale et al. 2007), large-scale colliding flows generated by supernovae/galactic shear (e.g. Heitsch et al. 2008), or even molecular cloud collisions (e.g. Gittins et al. 2003; Kitsionas & Whitworth 2007; Anathpindika 2009a,b).
Each of these processes have been tested with numerical simulations, and their respective efficiency in forming stars have been investigated. For some local clouds, we are beginning to acquire sufficiently detailed observations to generate a more informed picture of how star formation has progressed in those clouds. With these observations it becomes possible to perform dedicated simulations to model and better understand the processes at work. Only few such studies have been performed so far. For instance, Ballesteros-Paredes et al. (1999) used the results of their turbulent colliding flow simulations to argue that Taurus-Auriga formed through such a process; Peretto et al. (2007) used hydrodynamical simulations to model the global collapse and fragmentation of the NGC 2264-C protocluster; and Heitsch et al. (2009) compared flow-driven models for the formation of isolated molecular clouds with the Pipe nebula. In this paper, we use numerical simulations to investigate whether the recent star-formation episode observed in the Serpens Main Cluster could have been triggered by the collision of two molecular clouds, as proposed in Duarte-Cabral et al. (2010).
Serpens is an interesting region in several aspects. It is a filamentary region with two compact young star-forming clumps. The gas emission reveals an interesting velocity structure and has an unusual temperature structure (Duarte-Cabral et al. 2010). The observations point to remnant signatures of the trigger behind the current young on-going star formation of Serpens. Duarte-Cabral et al. (2010) suggested that this region appears to have been affected by a collision of two clouds or flows. This scenario is also suggested by recent studies of the global dynamics of Serpens and other star-forming regions (e.g. Higuchi et al. 2010; Schneider et al. 2010; Galván-Madrid et al. 2010).
Here we use smoothed particle hydrodynamics (SPH) simulations of cloud-cloud collisions to attempt to reproduce the column density distribution and dynamical properties of the Serpens Main Cluster. A brief summary of the observationally inferred characteristics of Serpens and the motivation for the simulations are presented in Sect. 2. Section 3 explains the SPH code, the initial conditions and the adopted geometrical configurations. The results of the calculations are presented in Sect. 4. Section 5 presents a discussion of these results, where we compare the numerical results with the observations and choose the best-fit scenario to represent the region. The final remarks and conclusion are laid out in Sect. 6. Finally, in Appendix A we present temporal snapshots for all our models.
2. The structure of the Serpens Main Cluster region
The Serpens Main Cluster is a low-mass star-forming region at 260 pc from the Sun (Straižys et al. 1996). It comprises two compact protoclusters, hereafter referred to as sub-clusters, lying in a 0.6 pc long filamentary structure along a NW-SE direction. At first sight, the NW and SE sub-clusters appear fairly similar. The dust emission (Davis et al. 1999,and Fig. 1) shows that they have similar masses within similar sized regions: ~ 30 M⊙ in 0.025 pc2 each, as estimated from the gas emission from C18O (Duarte-Cabral et al. 2010) and the 850 μm continuum emission from SCUBA. Furthermore, both have sources at roughly the same stage of evolution, Class 0 and Class I protostars, which power a number of outflows (Davis et al. 1999; Graves et al. 2010).
 |
Fig. 1 Serpens region as seen in 850 μm dust continuum emission with SCUBA (Davis et al. 1999) in contours, at 0.4, 0.6, 1, 1.4, 1.8, 2.4 and 5 Jy beam-1. In grey scale is the 24 μm from Spitzer MIPS (Harvey et al. 2007). All sources seen in this image, both the 24 μm and the 850 μm sources, are Class 0 and I, with only a few flat-spectrum sources. The 850 μm sources are labelled. |
Previous studies (Kaas et al. 2004; Harvey et al. 2006) have estimated an average age of 105 yr for these sources, which could possibly point to a triggering event. Older sources are also found in the field, but they appear more dispersed, without an obvious connection to the current protostars, and are no longer embedded or surrounded by any cold dust seen at submillimetre wavelengths. Presumably they belong to a different burst of star-formation, which occurred 2 Myr before the current one, and these sources are now in the field as an unbound cluster.
 |
Fig. 2 Position-velocity diagrams at constant declination of C18O J = 1 → 0 (grey scale and contours) as examples of the typical velocity structure in the NW sub-cluster (top) and the SE sub-cluster (bottom) (Duarte-Cabral et al. 2010). Right ascension varies from 18h30m06s to 18h29m46s for all panels. Declinations are 1°16′48′′ (top panel) and 1°12′38′′ (lower panel). The positions of these cuts in the map are shown as white lines in Fig. 3. The dashed lanes labelled as “dust” represent the regions whose 850 μm emission is above 0.6 Jy beam-1. |
In contrast to the similarities of the dust emission, the velocity structure and molecular emission from each sub-cluster are strikingly different. The NW is a well “behaved” sub-cluster with one main velocity throughout, matching the systemic velocity of the cloud with only a smooth velocity shift towards the edges of the sub-cluster. This is shown in the C18O J = 1 → 0 position-velocity (PV) diagram of Fig. 2 (top) and in Fig. 3, which shows the structure of the higher and lower velocity components of Serpens. In this NW sub-cluster, the gas and dust emission have similar distributions, with the gas emission peaks corresponding to the dust emission peaks. In addition, Spitzer 24 μm sources are coincident with many of the 850 μm sources (hereafter submillimetre sources; Fig. 1).
In contrast, the SE sub-cluster is quite different and its velocity structure is more complex. Optically thin tracers show locations with a broad single component (in the north of the SE sub-cluster), which then splits into two clearly separated components (Fig. 3 and lower panel of Fig. 2). At the southern end of the sub-cluster, the filamentary structure is then only visible in one velocity component along the line of sight (lower PV diagram of Fig. 17 of Graves et al. 2010). Furthermore, the gas and submillimetre emission peaks do not coincide. Instead, the gas emission appears to peak between the submillimetre sources (Duarte-Cabral et al. 2010). Finally, there are only a few 24 μm sources associated with the submillimetre dust continuum emission (Fig. 1). The overall picture resembles that of a region where star formation is an on-going process, with some younger sources (the purely submillimetre sources) and others older (the purely 24 μm sources), unlike the NW sub-cluster where the sources appear to be all at the same evolutionary stage.
A final difference between the two Serpens sub-clusters is the gas temperature (Duarte-Cabral et al. 2010). The NW has a very homogeneous temperature around 10 K, while the SE has higher and more varied temperatures, ranging between 10 and 20 K. In addition, the temperature peaks are not coincident with any submillimetre source, but appear between them, in the region where the two velocity components overlap.
 |
Fig. 3 C18O J = 1 → 0 emission separated into blue and red components, using the line fitting and splitting by Duarte-Cabral et al. (2010). The blue emission corresponds to the total integrated intensity of the low-velocity cloud and the red emission corresponds to the high-velocity cloud. The submillimetre sources from the 850 μm emission (Davis et al. 1999) are marked with white triangles and serve as a guide to the location of the dust emission. The positions of the PV diagrams in Fig. 2 are shown by the white solid lines, and the main axis of the blue-shifted and red-shifted cloud is shown as blue and red dashed line, respectively. |
Thus the differences between the two sub-clusters indicate that they have had a complicated history. A scenario capable of explaining what triggered the Serpens star formation has to reproduce the inhomogeneities in the sources’ age, velocity structure, and temperature distribution. The collision of two filament-like clouds, colliding only over part of their length, could provide such a trigger.
3. SPH simulations
To test the proposal that the structure and star formation in the Serpens Main Cluster results from triggering by a cloud-cloud collision, we performed a set of SPH simulations, which are compared in detail with millimetre and submillimetre observations of Serpens.
3.1. Numerical code
The calculations were performed with an SPH code based on a version by Benz et al. (1990), which was subject to substantial modifications including sink particles (Bate 1995), variable smoothing lengths (Price & Monaghan 2005), and magnetic fields (Price & Bate 2007). The code has been frequently used for simulations of star formation (e.g. Dobbs et al. 2006; Bate 2009a).
We performed calculations that include the hydrodynamics and self-gravity, but not magnetic fields. We used sink particles, which are inserted in regions of high density (10-12 g cm-3) that are undergoing collapse, to represent protostars. However, for the whole analysis we used the frame of the simulation when the first sink particle appears, i.e. before stellar feedback is likely to have an effect. Therefore our results are not dependent on the details, or the dynamics of the sink particles.
For all calculations we adopted an isothermal equation of state. Again, we are only interested in the evolution of the clouds up to the point where star formation takes place. This renders a reasonable simplification given that we consider the structure of the gas prior to stellar feedback.
3.2. Initial conditions
Given the elongated appearance of the high- and low-velocity clouds in Serpens, we hypothesised that the velocity structure of the Serpens cluster is caused by the collision of two elongated clouds (~1 pc long). Cloud collisions have long been thought to be an important process in the ISM (since Oort 1954). They are potential triggers for star formation (e.g. Scoville et al. 1986; Vallee 1995), and are frequently found in galactic scale simulations (e.g. Dobbs 2008; Tasker & Tan 2009). We do not suggest that cloud collisions are responsible for all star formation in the Galaxy, but aim to test how well this scenario can model the specific case of Serpens. Taking individual clouds from galactic simulations to model the collision is beyond the scope of this paper, and furthermore does not allow any freedom of the geometry of the clouds or collision. Instead, we assume a simplified initial configuration with cylindrical clouds for our models. The choice of cylinders is reasonable given that the most commonly observed aspect ratio of molecular clouds is ~ 2 (Koda et al. 2006). Thus our model is a simplified but plausible scenario in the local Galaxy.
For our calculations, we based the properties of the cylinders on the observations of Serpens, but with the requirement that the cylinders are not too far from virial equilibrium. We required the star formation to be primarily driven by the collision, and the cylinders should preferably retain their elongated shape as much as possible prior to the collision. Based on the observed spatial distribution of the Serpens’ high- and low-velocity clouds, all simulations we ran involved two cylindrical clouds with radii of 0.25 pc. We kept one cylinder vertical and the other tilted throughout and, with the exception of run D (Table 1), the cylinders have a length of 0.75 and 1 pc respectively.
Configuration of the different simulations.
To ensure the stability of the cylinders prior to the collision, we used the formula for stability of finite cylinders given in Bastien (1983) to estimate the masses of the cylinders, 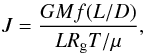 (1)where Rg is the gas constant, G is the gravitational constant, M is the mass of the cylinder, L the length, T the temperature and μ the mean molecular weight (we assumed μ = 2.0 for these calculations). f(L/D) is a function measuring the shape of the cloud, but is of the order of unity for the dimensions of our cylinders. The cylinder is stable providing J ≲ 0.8, a condition which reduces to approximately M(M⊙)/T(K) ≲ 0.8 for a 1 pc cylinder. In addition, we include an external pressure term, which is subtracted from each SPH particle when calculating pressure gradients (Dale et al. 2009). This represents a confining pressure from a low-density medium, which minimises diffusion of the outer parts of the cylinders, particularly in the runs including turbulence.
(1)where Rg is the gas constant, G is the gravitational constant, M is the mass of the cylinder, L the length, T the temperature and μ the mean molecular weight (we assumed μ = 2.0 for these calculations). f(L/D) is a function measuring the shape of the cloud, but is of the order of unity for the dimensions of our cylinders. The cylinder is stable providing J ≲ 0.8, a condition which reduces to approximately M(M⊙)/T(K) ≲ 0.8 for a 1 pc cylinder. In addition, we include an external pressure term, which is subtracted from each SPH particle when calculating pressure gradients (Dale et al. 2009). This represents a confining pressure from a low-density medium, which minimises diffusion of the outer parts of the cylinders, particularly in the runs including turbulence.
To mimic the supra-thermal line widths observed in Serpens, each model was also run for the same initial configuration adopting a turbulent velocity field for the particles. The turbulent field was set up according to the method of Bate et al. (2002), which is described in depth in Dubinski et al. (1995). The energy of the turbulent field E(k) is chosen to follow a power law of E(k) ∝ k-4, with k being the wavenumber. This gives, for a given scale, r, a velocity dispersion, σv, such that σv ∝ r0.5. This is similar to the observed Larson relations for clouds (Larson 1981), although we do not aim to capture the precise details of the internal motion, but rather to compare results with and without turbulence.
From the velocity-space distribution of C18O emission in the Serpens Main Cluster (see Fig. 3 and Duarte-Cabral et al. 2010), we found that the higher velocity component (red in Fig. 3) is tilted at 55° angle from the horizontal plane, and is situated mostly to the east on the map. The lower velocity component (blue in Fig. 3) is roughly vertical and in the west of the map (overlapping only along the SE end of the filament of star formation). To match the observations, the higher velocity component corresponds to the longer and tilted cylinder moving away from us on the right-hand side (see Fig. 4 red cylinder). This cylinder has an elevation angle of 55° above the horizontal plane and an azimuth angle of 0°, i.e. the axis is in a plane parallel to the y′z′ plane. The lower velocity component corresponds to the vertical cylinder, which is coming towards us from the left-hand side (see Fig. 4 blue cylinder).
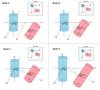 |
Fig. 4 Diagrams showing the starting configuration of the cylinders for the direct collision (model A, top left panel), offset collision (model B, top right panel; and model C, lower left panel) and offset collision with longer cylinders (model D, lower right panel). The black dashed line represents the line of sight, and the green dashed lines are the direction of the motion of the cylinders. On the top right corner of each panel is a sketch with the configuration as viewed from the top. |
The velocities of the cylinders are chosen to agree with the velocity difference of the gas in the Serpens cluster (see lower panel in Fig. 2), which would correspond to the velocities of the clouds during the collision. The initial velocities of each cylinder are v = ± 1 km s-1, i.e. vx′ and vy′ = ± 0.77 km s-1. The cylinders have no initial net velocity in the z direction (and without turbulence the particles have zero velocity in the z direction).
Each of the calculations were run with and without a turbulent velocity field. The differences between the four runs are sketched in Fig. 4 and summarised in Table 1, where “collision” specifies if the collision is off-centred or head-on with respect to the centre of the cylinders; “LOS ∢ V” represents the angle between the line of sight (LOS) and the direction of the cylinders’ motion; “length” is the height of the longer (i.e. the tilted) cylinder in each run; “velocities” specify the initial distribution of velocities: “non-turb” means zero velocity dispersion in the initial conditions, and “turb” indicates a turbulence-generated velocity dispersion amplitude of 0.5 km s-1 (in each direction). This is similar to the observed turbulent velocity dispersion in Serpens, which is of the order of 0.5 km s-1 (Duarte-Cabral et al. 2010)
All other properties of the cylinders, such as the temperatures and densities, are fixed. In the “short-cylinder" runs (A, B, and C) we used 500 000 particles in total, with 250 000 particles in each cylinder. Initially, the particles are uniformly randomly distributed to provide a roughly uniform density distribution within each cylinder.
As discussed in Duarte-Cabral et al. (2010), the NW sub-cluster tends to have a uniform temperature of 10–13 K. On the other hand, the temperature of the SE sub-cluster is more difficult to estimate, given that there are two clumps along the line of sight. Duarte-Cabral et al. (2010) obtained gas temperatures between 10 and 20 K. However, as shown by Eq. (1), a kinetic temperature of 30 K is required for a 30 M⊙ cylinder to be relatively stable. Hence we decided to add this extra internal pressure in the simulations in order to avoid the collapse of the cylinders before the collision. We chose masses of 30 and 45 M⊙ for the two cylinders, and verified that for a temperature of 30 K the cylinders did not collapse prior to the collision. This does not have any impact on the velocity and column density structure discussed in the rest of the paper.
We set the cylinders to collide at an angle of 45° with regard to the line of sight. In addition, we chose to position the cylinders so that either they collided head on (run A), or that their major axis were offset by 0.25 pc (run B). In the direct collision, model A, we centred one cylinder at cartesian coordinates (0,0,0)pc and the second (longer) cylinder at (0.8,0.8,0)pc (Fig. 4 top left panel). For the offset collision, model B, the second cylinder was instead placed at (0.8,1.05,0)pc. We illustrate the offset configuration in Fig. 4 (top right panel).
The results from runs A and B are summarised in Sects. 4.1.1 to 4.1.2. These runs show that by the time sink particles are formed, the two cylinders fully overlap along the line of sight, even though they did not interact everywhere. This means that we can see two velocity components co-existing in most regions (e.g. Fig. 8 top left panel), which is inconsistent with the observations, where the two velocity components overlap only where the collision takes place.
Therefore, we changed the perspective so that the motion of the cylinders is purely along the line of sight, model C (Fig. 4 bottom left panel), to restrict the region where the two components overlap to where the cylinders interact directly. Finally, model D (Fig. 4 bottom right panel) aims to reproduce the whole extent of the observed cloud and, therefore, it is similar to model C, except that the cylinders were made one and half times longer by extending the top and bottom of the cylinders. The number of particles was correspondingly increased in this calculation.
4. Results
As described in Sect. 2, the Serpens Main cluster is divided into two sub-clusters, the SE and NW sub-clusters. All observational evidence tends to show that the SE sub-cluster is at the interface of a cloud-cloud collision, as opposed to the much more quiescent NW sub-cluster. For this reason, in the cloud-cloud collision simulations we present here, we first attempted to reproduce the physical properties of the SE sub-cluster. However, given the obvious physical connection between these two sub-clusters, we also tried in a second set of simulations to trigger the formation of a NW-like sub-cluster as a by-product of the collision.
To compare the velocity structure of the simulations we will use the observational data and results from Duarte-Cabral et al. (2010): IRAM 30 m telescope observations of C18O J = 1 → 0. We also refer to the analysis of Serpens molecular data from the JCMT GBS HARP data of C18O J = 3 → 2 (Graves et al. 2010). For H2 column density comparisons, we used the SCUBA 850 μm emission from JCMT (Davis et al. 1999).
The comparison of the simulations with the observations is primarily focused on observational characteristics of the Serpens SE sub-cluster because this is the region that appears to be directly influenced by the collision. However, even in the short-cylinder runs that do not form the NW sub-cluster, some of the velocity characteristics of the entire cloud are also taken into account. Thus, the following characteristics are the main focus points for a comparison:
-
–
Column density structure: an elongated/filamentary shape aligned in a NW-SE direction, sub-clumped (Fig. 1).
-
The mass and size of the southern clump compared with those of the denser parts of the SE sub-cluster (~30 M⊙ within ~0.025 pc2, measured using the 850 μm emission above 190 mJy beam-1, which corresponds to column densities above 0.1 g cm-2 at a temperature of 10 K).
-
Overall velocity structure: a single red-shifted component in the north, with a fainter blue component spatially offset to the east (top panel of Fig. 2 top panels and Fig. 3). Double (overlapping) components in the south, where the sources are being formed (Fig. 2 lower panel and Fig. 3) with a gradient from east to west of increasing velocities, up to 1.5 km s-1 (Fig. 13). Moving further south, this velocity structure should evolve back into one component along the less dense gas of the filament (Fig. 13, and lower PV diagram of Fig. 17 of Graves et al. 2010).
-
Velocity structure of the less dense material: thin eastern filaments perpendicular to the main filament of Serpens (visible in blue and green on the left-hand side of the main filament in Fig. 13).
 |
Fig. 5 Colour scale and contours of the total column density along the line of sight for the non-turbulent runs: the centred collision, Anon−T, on the left; and off-centred collision, Bnon−T, on the right. The contour levels are 0.01, 0.03, 0.1, 0.3 and 0.5 g cm-2 for both figures. The white horizontal lines show the cuts for the PV diagrams in Fig. 6. |
 |
Fig. 6 Position-velocity diagram at z = −0.02pc (colour scale and contours) for the non-turbulent direct and offset runs, Anon−T and Bnon−T, left and right respectively. The displayed velocity corresponds to the component along the line of sight. Contours at 10-5, 10-4, 5 × 10-4, 10-3, 5 × 10-3, 10-2 and 3 × 10-2 g cm-2. The red crosses represent the column density weighted velocities and are plotted as an auxiliary tool to see the velocity changes along the diagram. Note that the velocities from the direct collision (left) in the central region seem to be more complex than those observed (Fig. 2lower panel), whereas those from the offset collision (right) show a smooth shift in velocities from one component to another, likely because in the offset collision we see the parts of the clouds that do not collide more clearly. |
In order to compare our results with the observations, we first constructed a datacube from the simulated 3D cloud collisions. For each simulation, we define the x direction as the line of sight, so that the plane of the sky is the yz plane. Choosing the time-step of the simulations where the first sink particle is formed, we created a datacube of column density for a space-space-velocity 3D grid. In the spatial planes we convolved the models with a Gaussian with a FWHM of 10 pix (0.02 pc), which corresponds to the 22′′ spatial resolution of the IRAM-30 m telescope observations of C18O J = 1 → 0 at the distance of Serpens. To reproduce the thermal velocity dispersion of Serpens, the velocity space was convolved with a normalised Gaussian of 0.4 km s-1FWHM, corresponding to the thermal line width of H2 at 10 K.
 |
Fig. 7 Colour scale and contours representing the total column density along the line of sight for the turbulent runs: the centred collision, AT, on the left; and off-centred collision, BT, on the right. The contour levels are as in Fig. 5. The white horizontal lines show the cuts for the PV diagrams in Fig. 8. Both turbulent runs show a final cloud which is much more structured and fits the observations better than Fig. 5. |
Gas temperature, density, and abundance all affect the relation between the true column density of a cloud and the emission seen in a molecular line. However, as discussed in Duarte-Cabral et al. (2010) and Graves et al. (2010), in Serpens the C18O appears to be a faithful tracer of the overall velocity structure of the cloud and does not appear to be significantly affected by outflow or infall motions, while the 850 μm emission traces the global mass distribution in the region. To assess the success of the simulations in modelling Serpens, we therefore compare the models with the velocity structure of the C18O and the overall column density distribution from the dust emission.
4.1. Modelling the Serpens SE sub-cluster
We initially tried to reproduce the characteristics of the SE sub-cluster with the short-cylinder calculations: runs A, B, and C. In this section, we describe the results of these simulations. Taking the best-fit configuration for the short-cylinders, we then performed simulations with more extended cylinders that are designed to reproduce the whole cloud (Sect. 4.2).
4.1.1. Non-turbulent runs: Anon−T and Bnon−T
Fundamentally, the only difference between these two simulations is that for Anon−T the centres of gravity of the cylinders are colliding head-on, maximising the loss of kinetic energy in the shock, while for Bnon−T the centres of gravity are shifted and therefore the collision becomes softer, with the gas being able to conserve more of its initial kinetic energy. While the first configuration is a very peculiar one, the second one is very general, corresponding to the most likely situations of cloud-cloud collision. As a result, the formation of sink particles in Bnon−T is slower than in Anon−T, and while it occurs only at the interface region for the latter, in Bnon−T sink particles are more widely distributed, along a dense filament connecting both clouds (see Fig. 5 and Appendix A, Fig. A.1).
The most significant difference between the results of these two simulations is the velocity structure at the collision interface. In Anon−T, three distinct velocity components are present: the two velocities of the individual cylinder, plus an intermediate velocity of the shocked interface gas (Fig. 6 left panel). In Bnon−T, the velocity structure is continuously connecting the initial velocities of the cylinders (Fig. 6 right panel). Thus, the offset collision (B) is better able to reproduce the observations (Fig. 2).
 |
Fig. 8 Position-velocity diagrams in colour scale and contours, at z = 0.16 pc (top), z = −0.06 pc (middle) and z = −0.30 pc (bottom) for the turbulent direct and offset runs, AT and BT, left and right respectively. The contour levels and red crosses are as in Fig. 6. As expected from Fig. 6, the velocities are more complex in the A run than the observed ones. The top panels show that the direct collision (left) produces two velocity components in the northern part of the cloud, whereas the offset collision B (right) and the observations only show one (Fig. 2). From the middle and lower panels, the differences are less obvious, but the middle panel shows that the direct collision exhibits a more “messy” velocity structure rather than a clear transition from high to low velocities. |
4.1.2. Turbulent runs: AT and BT
In these simulations the net effect of turbulence is to render the cylinders inhomogeneous in density and velocity, making them more realistic-looking clouds. One of the important features we see in Fig. 7 (and Appendix A, Fig. A.2), are the channels of material perpendicular to the main filament. These are reminiscent of features often observed in molecular clouds (e.g. Myers 2009). These features will be further discussed in Sect. 5. Another important aspect of injecting turbulence is that is generates density seeds. Before the first sink particles begin to form, we see several regions where the density is beginning to grow. As soon as one of these regions is sufficiently dense, it will attract the remaining less dense sub-clumps to form a major single structure.
At the end of both runs, the material at a column density greater than 0.1 g cm-2 is distributed over similar sized regions to the non-turbulent models, 0.025 pc2 and 0.032 pc2, for runs AT and BT respectively. For AT, a total of 29 M⊙ is in these high column density regions (39% of the total mass of the cylinders), while for BT the mass is 34 M⊙ (45% of the total mass).
In terms of the velocity structure, the direct collision model, AT, still produces too many distinct velocity components without smooth trends (Fig. 8 left panels), for the same reasons as for the Anon−T model. On the other hand, the BT model produces a very interesting velocity structure. To the north (positive z) we mainly see the tilted cylinder and begin to detect the vertical cylinder on the left-hand side. The transition between the two is not sharp nor double-peaked, but a fairly broad smooth transition (Fig. 8 top right panel). A well defined double-peak structure is only detected in the central region of the model, where sink particles have formed (Fig. 8 middle right panel). South of this region, the column density becomes again dominated by one component from the tilted cylinder travelling away from us (Fig. 8 bottom right panel), as also found towards the south end of the Serpens filament by Graves et al. (2010). The results from this run (BT) are more consistent with the observations of the SE sub-cluster of Serpens (Sect. 2), but the change in velocity across the cloud is smaller than the observed one (~0.5 km s-1 instead of ~1 km s-1).
We also ran a model with an intermediate turbulence level (not shown) with a velocity dispersion of 0.3 km s-1. This model showed that the geometric configuration is the dominant factor in determining the main velocity characteristics of the resulting cloud, while the density distribution is sensitive to the level of turbulence. Lower levels of turbulence result in a more filamentary structure, with more sink particles forming along the denser filament. Increased values of initial turbulence tend to disrupt the distribution of cloud’s material, inhibiting the formation of further clumps.
4.1.3. Line of sight, short cylinder run: CT
Model CT is simply a re-projection of model BT so that it is viewed along the axis of the relative motion of the cylinders. The time evolution of CT is shown in Appendix A, Fig. A.3.
From this perspective (Fig. 9) the low-density material is less filamentary and more spatially extended, because the parts of the cylinders that do not interact, do not overlap along the line of sight any longer. Therefore, the extent of the lower density material is greater to the north, where the cylinders do not merge, than in the south (negative z). In this projection, the material at high column density above 0.1 g cm-2 covers a region of 0.02 pc2 in area with a mass of 22 M⊙.
The general shape and trend of the velocity structure (Fig. 10), although slightly more complex, is similar to that seen in BT and consistent with the velocity trend seen in the observational PV diagrams. Overall, this run (C) reproduces Serpens better than run B, because it now shows a more evident velocity change across the cloud.
4.2. Representation of both SE and NW Serpens sub-clusters
4.2.1. Line of sight, long cylinders, run: Dnon−T
Overall, model CT satisfactorily reproduces the observations of the SE sub-cluster. However, it does not have sufficient Jeans masses to form a second sub-cluster comparable to the NW sub-cluster in Serpens, even though the velocity structure of the simulation is very similar to the observed one. Therefore, we increased the length and mass of the cylinders to investigate the possible formation of a separate structure in the north, where the cylinders do not interact. If the non-interacting northern region is massive enough to be close to unstable, the collision in the south of the cylinders may induce its rapid collapse without greatly affecting its systemic velocity.
A non-turbulent model with ~1.5 pc long cylinders, colliding off-centre and along the light of sight (model Dnon−T), does indeed form two sub-clusters. The collision in the south leads to the formation of a sink particle in the south, i.e. the synthetic SE sub-cluster. Later on, a sink particle is formed in the north of the tilted cylinder, along the cylinder axis (time evolution in Appendix A, Fig. A.4). Finally, more sink particles are formed in the south, as the vertical cylinder crosses through the tilted one (Fig. 11). At the end of this run, when sink particles are formed throughout the clouds, the column density distribution is much more filamentary than for the short cylinder calculation. There are two visible sub-clusters: one in the NW and one in the SE. The total mass in these sub-clusters amounts to 57 M⊙, 52% of the total mass in this case, distributed over an area of 0.035 pc2. However, the relative size and mass of each individual sub-cluster is not quite as similar as seen in Serpens. The simulated SE sub-cluster has a mass of about 30 M⊙ in an area of ~0.015 pc2, whereas the NW sub-cluster contains 12 M⊙ in a similar area.
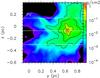 |
Fig. 9 Total column density for the purely along the line of sight turbulent run, CT. Unlike runs A and B, we find a low-density region in the north (large z), because with this orientation we see regions that have not collided. The contour levels are as in Fig. 5. |
The formation of a sink particle in the north occurs at 8 × 105 yr and is mainly due to the initial instability of the cylinder itself. As a test, we ran a simulation with only an isolated non-turbulent cylinder, with the same mass and size as the tilted one. This simulation showed that it would form sink particles along the cylinder axis at 106 yr. Therefore, the collision in the south does not trigger the formation of this sink particle in the north, but only speeds up its collapse.
Interestingly, several different turbulent runs with this configuration failed to induce the collapse of any structure in the north. The collapse only occurs with extremely low levels of turbulence (with amplitude of ~ 0.05 km s-1), almost indistinguishable from the non-turbulent run. This is due to the turbulent velocities that cause the cloud to disperse from its initial configuration andbecome less gravitationally bound than in the absence of turbulence. From this, we conclude that the effect of the collision felt by the north region is quite subtle, and would only have an influence on the collapse there if the region is almost gravitationally unstable prior to the effect of any external perturbation.
The discrepancy in the relative masses of the two sub-clusters in the simulation compared to Serpens, and indeed the failure to form two sub-clusters in the turbulent simulations could be addressed by relaxing the over-simplistic uniform conditions in our initial conditions. Both the density distribution and turbulent velocity distributions are likely to be more inhomogeneous in real colliding clouds than in our models. This discrepancy could also be suggesting that we are missing a physical ingredient such as magnetic pressure, which could help to maintain the filamentary shape of the clouds even with a high level of turbulence. However, we refrained from adding this additional complexity to the models since the nature of the inhomogeneities is poorly constrained and unlikely to provide any further significant physical insight into the processes in this region.
 |
Fig. 10 Position-velocity diagram in colour scale and contours, at z = 0.14 pc (top), z = −0.07 pc (middle) and z = −0.30 pc (bottom), for the turbulent, line of sight, short cylinders run CT. The contour levels and red crosses are as in Fig. 6. Compared with model BT (Fig. 8 right column), we see more evidence of the original velocities of the clouds from the non-interacting parts, because of the change of perspective. This calculation produces the best fit to the observations (Fig. 2). |
In terms of its spatial evolution, the velocity structure of the Dnon−T is similar to the observed one. From Fig. 12 we see as we move from north to south (i.e. from positive z to negative z) two spatially separated components, which then overlap where the collision takes place, to finally end-up with a single velocity component in the south. These PV diagrams can be compared with the more detailed PV diagrams across the entire cloud from Duarte-Cabral et al. (2010) and Graves et al. (2010). Also note that the column densities are higher at velocities corresponding to the tilted cylinder. An increase in the density of the tilted cylinder to produce a more massive NW sub-cluster would increase the difference in column densities between the two velocity components, which would match the observations more closely.
4.3. Timescales
One interesting question for the star-formation history of Serpens is to confirm whether or not the older population of pre-main sequence star of 2 Myr of age could have been formed in the same cloud-cloud collision event. For this we need to estimate a number of characteristic timescales. First, all the simulations correspond to a total elapsed time of ~ 8–9 × 105 years. However, it is only after about 2–3 × 105 years, about a third of the total simulation time, that the two cylinders begin to interact. This time delay is needed, especially in the turbulent cases, to allow the cylinders to relax their initial density distributions. The time from the start of the interaction between the two clouds until they begin to form sink particles is of the order of 6 × 105 years. For the 2 Myr stellar population to be able to form through this collision, the duration of the interaction time has to be at least 2 Myr. In fact, we would need the cloud to be one order of magnitude larger (i.e. a few parsec wide) in order to still have an ongoing collision 2 Myr after the formation of the first protostars. This seems unrealistic and therefore, the cloud collision scenario we present for Serpens is consistent with the idea of two separate bursts of star formation in the region.
 |
Fig. 11 Total column density for the non-turbulent, purely along the line-of-sight run with longer cylinders, Dnon−T, to test the production of both the NW and SE sub-clusters of Serpens. At this stage, sink particles have indeed formed where the collision is happening and in the north-west (within the tilted/longer cylinder). Given the geometry of the collision, the two cylinders do not end up colliding in the north. However, the only perspective where we do not see the cylinders overlap is the one we took for this run, where the line of sight is aligned with the motion of the cylinders. The contour levels are as in Fig. 5. |
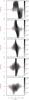 |
Fig. 12 PV diagrams of the long cylinder run Dnon−T at z = 0.16 pc, z = −0.02 pc, z = −0.09 pc, z = −0.21 pc and z = −0.37 pc (from top to bottom). Contour levels and red crosses are as in Fig. 6. Despite the lack of structure typical of a non-turbulent case, these agree with the more detailed PV diagrams from observations from Duarte-Cabral et al. (2010) and Graves et al. (2010). |
 |
Fig. 13 Velocity-coded 3-colour plot of Serpens from the C18O J = 3 → 2 data from the JCMT GBS. Each colour represents the maximum value in the velocity intervals: blue: 5 → 7.7 km s-1; green: 7.7 → 8.3 km s-1; and red: 8.3 → 11 km s-1 (see also Graves et al. 2010). The two sub-clusters of Serpens are indicated by the black ellipses. |
5. Discussion
Overall the simulation that best represents the SE sub-cluster of the Serpens star-forming region is model CT, the offset turbulent model with short cylinders, reprojected so that the line-of-sight coincides with the direction of motion. It has a velocity structure similar to the observed one, both comparing the PV diagrams and the general trend in the velocity coded 3-colour plots (Figs. 13 and 14). Note that this simulation only represents the southern part of Serpens, because the NW sub-cluster is not directly involved in the collision (cf. Sect. 4.1). Despite this, the 3-colour plot of this run (Fig. 14) agrees well with that of the observations (Fig. 13). Model CT shows an overall velocity gradient of ~ 2 km s-1 over 0.2 pc-1, from blue in eastern regions to red in the west (Fig. 14), similar to what is observed.
The 3-colour velocity figures also show the resemblance of the simulation CT with the observations in the way that the filament extending south is mostly represented by the red/green velocities, while the blue part is mainly seen on the denser parts where the stars are being formed. The green-blue component is also seen farther east, forming some less dense filaments perpendicular to the main filament. Note that we do not see these types of filament on the red side.
Understanding the nature of these filaments can be important. If these filaments had been caused by the initial turbulence, we would expect them to exist in both directions. Alternatively, these filaments could be the consequence of some particles left behind as the cylinders move, resembling a tail. However, in simulation C, the cylinders’ motion is along the line of sight, so if these filaments resulted from a tail of material left behind during the collision, they would be behind or in front of the main structure. Their appearance therefore indicates that these perpendicular filaments are caused by the geometry of the collision, in particular, its asymmetric nature. These filaments place a strong constraint on the geometry of the collision. The geometry of simulation A (as well as other tests not shown) do not reproduce them.
In terms of its total column density distribution, 22 M⊙ in 0.02 pc2, model C closely matches the SE sub-cluster. Even the projected distribution of material above a column density of 0.1 g cm-2 resembles the shape of the SE sub-cluster.
To reproduce the NW sub-cluster in addition to the SE sub-cluster requires the longer non-turbulent clouds used in model Dnon−T. In this model a region close to being gravitationally unstable can be perturbed and its collapse hastened by the collision, even though it is not directly involved in the collision. This second sub-cluster forms with the velocity of its native cloud and collapses smoothly and independently of the southern region. If this model is allowed to continue, the NW sub-cluster falls onto the SE sub-cluster. Intriguingly, recent observations of the magnetic field in Serpens (Sugitani et al. 2010) appear to suggest the start of such a collapse, which could result in the merging of the two sub-clusters.
 |
Fig. 14 Velocity-coded 3-colour plot of the simulation CT. Each colour represents the total column density summed over the following line of sight velocities: blue: 0.3 → 2 km s-1; green: − 0.3 → 0.3 km s-1; and red: −2 → − 0.3 km s-1. This figure is to be compared with Fig. 13, particularly around the SE sub-cluster. The synthetic SE sub-cluster is indicated by a black ellipse. |
6. Conclusions
Serpens is a very interesting star-forming region, not only for its youth, but also for the striking differences between the two sub-clusters that compose the active star-forming portion of the cloud. Even though they are at similar stages of evolution, with most sources between Class 0 and Class I protostars and similar dust continuum properties, the gas emission reveals that they have not only different velocity characteristics, but also different temperature distributions (Duarte-Cabral et al. 2010).
Motivated by the two velocity components visible in the southern sub-cluster of Serpens and by the higher temperatures detected there, we performed several SPH calculations of cloud-cloud collisions. The configurations used for these simulations were based on the observed morphologies.
For the SE sub-cluster, a model of two colliding clouds is able to reproduce the column density structure, a centrally condensated filament aligned in a NW-SE direction, and the two velocity components visible where the star formation driven by the collision is occurring. However, the same simulations did not produce a second sub-cluster, similar to the NW sub-cluster of Serpens. Therefore, this sub-cluster does not seem to be the direct result of the collision. This was already suggested by the NW sub-cluster’s well “behaved” temperature profile and velocity structure, as well as by the uniform age of sources within the sub-cluster. Nevertheless, the similar stage of evolution of the sources from the two sub-clusters and their proximity suggests that the two events are not totally independent.
A simulation with more elongated cylinders and increased masses provides a possible explanation. The presence of a marginally stable region in the northern part of one of the colliding clouds can have its collapse induced and quickened by perturbations driven by the cloud-cloud collision.
We consider a cloud-cloud collision scenario to be the best description of the driving of the star-formation history in Serpens. Not only can it reproduce the observed velocities and column densities, it also offers a plausible explanation for why the two sub-clusters are so similar in some aspects and yet so different in others. Although cloud rotation may produce similar general velocity gradients to those observed, the complexity of the region is better explained with such a collision scenario, which is in essence similar to a shear-motion also suggested by Olmi & Testi (2002).
Despite the successful scenario provided by a cloud-cloud collision model, we failed to reproduce all of the Serpens characteristics in one single run. Additional support against gravity is required in order to sustain the existence of two different sub-clusters as in Serpens. The existing magnetic field of the region (Sugitani et al. 2010) could provide this support.
Acknowledgments
Ana Duarte Cabral is funded by the Fundação para a Ciência e a Tecnologia of Portugal, under the grant reference SFRH/BD/36692/2007. A.D.C. would like to thank Jennifer Hatchell for useful discussions and suggestions that initially motivated this work. The calculations reported here were performed using the University of Exeter’s SGI Altix ICE 8200 supercomputer. C.L.D.’s work was conducted as part of the award “The formation of stars and planets: radiation hydrodynamical and magnetohydrodynamical simulations” made under the European Heads of Research Councils and European Science Foundation EURYI (European Young Investigator) Awards scheme and supported by funds from the Participating Organisations of EURYI and the EC Sixth Framework Programme.
References
- Anathpindika, S. 2009a, A&A, 504, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anathpindika, S. 2009b, A&A, 504, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Hartmann, L., & Vázquez-Semadeni, E. 1999, ApJ, 527, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Bastien, P. 1983, A&A, 119, 109 [NASA ADS] [Google Scholar]
- Bate, M. 1995, Ph.D. Thesis, Univ. Cambridge [Google Scholar]
- Bate, M. R. 2009a, MNRAS, 392, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R. 2009b, MNRAS, 397, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Bromm, V. 2002, MNRAS, 332, L65 [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Bromm, V. 2003, MNRAS, 339, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Cameron, A. G. W., Press, W. H., & Bowers, R. L. 1990, ApJ, 348, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Bonnell, I. A., & Whitworth, A. P. 2007, MNRAS, 375, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Wünsch, R., Whitworth, A., & Palouš, J. 2009, MNRAS, 398, 1537 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, C. J., Matthews, H. E., Ray, T. P., Dent, W. R. F., & Richer, J. S. 1999, MNRAS, 309, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L. 2008, MNRAS, 391, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., Bonnell, I. A., & Pringle, J. E. 2006, MNRAS, 371, 1663 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Duarte-Cabral, A., Fuller, G. A., Peretto, N., et al. 2010, A&A, 519, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubinski, J., Narayan, R., & Phillips, T. G. 1995, ApJ, 448, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Lada, C. J. 1977, ApJ, 214, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Galván-Madrid, R., Zhang, Q., Keto, E., et al. 2010, ApJ, 725, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gittins, D. M., Clarke, C. J., & Bate, M. R. 2003, MNRAS, 340, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Graves, S. F., Richer, J. S., Buckle, J. V., et al. 2010, MNRAS, 409, 1412 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., & Burkert, A. 2007, ApJ, 654, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Chapman, N., Lai, S.-P., et al. 2006, ApJ, 644, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Rebull, L. M., Brooke, T., et al. 2007, ApJ, 663, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Hartmann, L. W., Slyz, A. D., Devriendt, J. E. G., & Burkert, A. 2008, ApJ, 674, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Ballesteros-Paredes, J., & Hartmann, L. 2009, ApJ, 704, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Higuchi, A. E., Kurono, Y., Saito, M., & Kawabe, R. 2010, ApJ, 719, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Kaas, A. A., Olofsson, G., Bontemps, S., et al. 2004, A&A, 421, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitsionas, S., & Whitworth, A. P. 2007, MNRAS, 378, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Durán-Rojas, C. 2005, ApJ, 620, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Koda, J., Sawada, T., Hasegawa, T., & Scoville, N. Z. 2006, ApJ, 638, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olmi, L., & Testi, L. 2002, A&A, 392, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oort, J. H. 1954, Bull. Astron. Inst. Netherlands, 12, 177 [Google Scholar]
- Palla, F., & Stahler, S. W. 2002, ApJ, 581, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., Hennebelle, P., & André, P. 2007, A&A, 464, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, D. J., & Monaghan, J. J. 2005, MNRAS, 364, 384 [NASA ADS] [Google Scholar]
- Price, D. J., & Bate, M. R. 2007, MNRAS, 377, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Bontemps, S., et al. 2010, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N. Z., Sanders, D. B., & Clemens, D. P. 1986, ApJ, 310, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Straižys, V., Černis, K., & Bartašiūte, S. 1996, Baltic Astron., 5, 125 [NASA ADS] [Google Scholar]
- Sugitani, K., Nakamura, F., Tamura, M., et al. 2010, ApJ, 716, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Tasker, E. J., & Tan, J. C. 2009, ApJ, 700, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Vallee, J. P. 1995, AJ, 110, 2256 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Time snapshots of the models
 |
Fig. A.1 Three time snapshots of the total column density along the line of sight for the non-turbulent runs: the centred collision, Anon−T (top) and off-centred collision, Bnon−T (bottom). The three frames correspond to the beginning of the simulation (first frame), as soon as the cylinders start to collide (second frame) and when the first sink particle is formed (last frame). |
 |
Fig. A.2 Three time snapshots of the total column density along the line of sight for the turbulent runs: the centred collision, AT (top) and off-centred collision, BT (bottom). The three frames correspond to the beginning of the simulation (first frame), as soon as the cylinders start to collide (second frame) and when the first sink particle is formed (last frame). |
 |
Fig. A.3 Three time snapshots of the total column density along the line of sight for CT. The three frames are as before. Note that this is exactly the same model as BT, but viewed from a different perspective. |
 |
Fig. A.4 Three time snapshots of the total column density along the line of sight for Dnon−T. The three frames are at the beginning of the simulation (left), when the first sink particle forms in the south (middle) and when a sink particle is formed in the north (right). |
Figures A.1 to A.4 show three snapshots to illustrate the time evolution of the models. Each frame is a projected column density plot as seen from the chosen line of sight. The time (in years) is shown in the top-right corner of each frame. Figure A.1 shows three frames for the two non-turbulent runs, Anon−T and Bnon−T. Figure A.2 shows the time evolution for the same models, A and B, but with turbulence. Figure A.3 shows the snapshots of model C, which is essentially the same as model BT, only with a different line of sight. For these three runs, the last frame corresponds to the formation of the first sink particle and is the frame used to construct a datacube for comparison with the observations. Finally, Fig. A.4 shows three snapshots for run D. Note that for this run we are showing frames after the formation of the first sink particle, to demonstrate where and when the second clump in the north is able to form a sink particle. In this case, this last frame was the one used for the comparison with the observations.
All Tables
All Figures
 |
Fig. 1 Serpens region as seen in 850 μm dust continuum emission with SCUBA (Davis et al. 1999) in contours, at 0.4, 0.6, 1, 1.4, 1.8, 2.4 and 5 Jy beam-1. In grey scale is the 24 μm from Spitzer MIPS (Harvey et al. 2007). All sources seen in this image, both the 24 μm and the 850 μm sources, are Class 0 and I, with only a few flat-spectrum sources. The 850 μm sources are labelled. |
| In the text | |
 |
Fig. 2 Position-velocity diagrams at constant declination of C18O J = 1 → 0 (grey scale and contours) as examples of the typical velocity structure in the NW sub-cluster (top) and the SE sub-cluster (bottom) (Duarte-Cabral et al. 2010). Right ascension varies from 18h30m06s to 18h29m46s for all panels. Declinations are 1°16′48′′ (top panel) and 1°12′38′′ (lower panel). The positions of these cuts in the map are shown as white lines in Fig. 3. The dashed lanes labelled as “dust” represent the regions whose 850 μm emission is above 0.6 Jy beam-1. |
| In the text | |
 |
Fig. 3 C18O J = 1 → 0 emission separated into blue and red components, using the line fitting and splitting by Duarte-Cabral et al. (2010). The blue emission corresponds to the total integrated intensity of the low-velocity cloud and the red emission corresponds to the high-velocity cloud. The submillimetre sources from the 850 μm emission (Davis et al. 1999) are marked with white triangles and serve as a guide to the location of the dust emission. The positions of the PV diagrams in Fig. 2 are shown by the white solid lines, and the main axis of the blue-shifted and red-shifted cloud is shown as blue and red dashed line, respectively. |
| In the text | |
 |
Fig. 4 Diagrams showing the starting configuration of the cylinders for the direct collision (model A, top left panel), offset collision (model B, top right panel; and model C, lower left panel) and offset collision with longer cylinders (model D, lower right panel). The black dashed line represents the line of sight, and the green dashed lines are the direction of the motion of the cylinders. On the top right corner of each panel is a sketch with the configuration as viewed from the top. |
| In the text | |
 |
Fig. 5 Colour scale and contours of the total column density along the line of sight for the non-turbulent runs: the centred collision, Anon−T, on the left; and off-centred collision, Bnon−T, on the right. The contour levels are 0.01, 0.03, 0.1, 0.3 and 0.5 g cm-2 for both figures. The white horizontal lines show the cuts for the PV diagrams in Fig. 6. |
| In the text | |
 |
Fig. 6 Position-velocity diagram at z = −0.02pc (colour scale and contours) for the non-turbulent direct and offset runs, Anon−T and Bnon−T, left and right respectively. The displayed velocity corresponds to the component along the line of sight. Contours at 10-5, 10-4, 5 × 10-4, 10-3, 5 × 10-3, 10-2 and 3 × 10-2 g cm-2. The red crosses represent the column density weighted velocities and are plotted as an auxiliary tool to see the velocity changes along the diagram. Note that the velocities from the direct collision (left) in the central region seem to be more complex than those observed (Fig. 2lower panel), whereas those from the offset collision (right) show a smooth shift in velocities from one component to another, likely because in the offset collision we see the parts of the clouds that do not collide more clearly. |
| In the text | |
 |
Fig. 7 Colour scale and contours representing the total column density along the line of sight for the turbulent runs: the centred collision, AT, on the left; and off-centred collision, BT, on the right. The contour levels are as in Fig. 5. The white horizontal lines show the cuts for the PV diagrams in Fig. 8. Both turbulent runs show a final cloud which is much more structured and fits the observations better than Fig. 5. |
| In the text | |
 |
Fig. 8 Position-velocity diagrams in colour scale and contours, at z = 0.16 pc (top), z = −0.06 pc (middle) and z = −0.30 pc (bottom) for the turbulent direct and offset runs, AT and BT, left and right respectively. The contour levels and red crosses are as in Fig. 6. As expected from Fig. 6, the velocities are more complex in the A run than the observed ones. The top panels show that the direct collision (left) produces two velocity components in the northern part of the cloud, whereas the offset collision B (right) and the observations only show one (Fig. 2). From the middle and lower panels, the differences are less obvious, but the middle panel shows that the direct collision exhibits a more “messy” velocity structure rather than a clear transition from high to low velocities. |
| In the text | |
 |
Fig. 9 Total column density for the purely along the line of sight turbulent run, CT. Unlike runs A and B, we find a low-density region in the north (large z), because with this orientation we see regions that have not collided. The contour levels are as in Fig. 5. |
| In the text | |
 |
Fig. 10 Position-velocity diagram in colour scale and contours, at z = 0.14 pc (top), z = −0.07 pc (middle) and z = −0.30 pc (bottom), for the turbulent, line of sight, short cylinders run CT. The contour levels and red crosses are as in Fig. 6. Compared with model BT (Fig. 8 right column), we see more evidence of the original velocities of the clouds from the non-interacting parts, because of the change of perspective. This calculation produces the best fit to the observations (Fig. 2). |
| In the text | |
 |
Fig. 11 Total column density for the non-turbulent, purely along the line-of-sight run with longer cylinders, Dnon−T, to test the production of both the NW and SE sub-clusters of Serpens. At this stage, sink particles have indeed formed where the collision is happening and in the north-west (within the tilted/longer cylinder). Given the geometry of the collision, the two cylinders do not end up colliding in the north. However, the only perspective where we do not see the cylinders overlap is the one we took for this run, where the line of sight is aligned with the motion of the cylinders. The contour levels are as in Fig. 5. |
| In the text | |
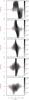 |
Fig. 12 PV diagrams of the long cylinder run Dnon−T at z = 0.16 pc, z = −0.02 pc, z = −0.09 pc, z = −0.21 pc and z = −0.37 pc (from top to bottom). Contour levels and red crosses are as in Fig. 6. Despite the lack of structure typical of a non-turbulent case, these agree with the more detailed PV diagrams from observations from Duarte-Cabral et al. (2010) and Graves et al. (2010). |
| In the text | |
 |
Fig. 13 Velocity-coded 3-colour plot of Serpens from the C18O J = 3 → 2 data from the JCMT GBS. Each colour represents the maximum value in the velocity intervals: blue: 5 → 7.7 km s-1; green: 7.7 → 8.3 km s-1; and red: 8.3 → 11 km s-1 (see also Graves et al. 2010). The two sub-clusters of Serpens are indicated by the black ellipses. |
| In the text | |
 |
Fig. 14 Velocity-coded 3-colour plot of the simulation CT. Each colour represents the total column density summed over the following line of sight velocities: blue: 0.3 → 2 km s-1; green: − 0.3 → 0.3 km s-1; and red: −2 → − 0.3 km s-1. This figure is to be compared with Fig. 13, particularly around the SE sub-cluster. The synthetic SE sub-cluster is indicated by a black ellipse. |
| In the text | |
 |
Fig. A.1 Three time snapshots of the total column density along the line of sight for the non-turbulent runs: the centred collision, Anon−T (top) and off-centred collision, Bnon−T (bottom). The three frames correspond to the beginning of the simulation (first frame), as soon as the cylinders start to collide (second frame) and when the first sink particle is formed (last frame). |
| In the text | |
 |
Fig. A.2 Three time snapshots of the total column density along the line of sight for the turbulent runs: the centred collision, AT (top) and off-centred collision, BT (bottom). The three frames correspond to the beginning of the simulation (first frame), as soon as the cylinders start to collide (second frame) and when the first sink particle is formed (last frame). |
| In the text | |
 |
Fig. A.3 Three time snapshots of the total column density along the line of sight for CT. The three frames are as before. Note that this is exactly the same model as BT, but viewed from a different perspective. |
| In the text | |
 |
Fig. A.4 Three time snapshots of the total column density along the line of sight for Dnon−T. The three frames are at the beginning of the simulation (left), when the first sink particle forms in the south (middle) and when a sink particle is formed in the north (right). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


