| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200911663 | |
| Published online | 25 November 2010 | |
Cosmological radiative transfer for the line-of-sight proximity effect
1
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482
Potsdam, Germany
e-mail: apartl@aip.de
2
Institute of Astronomy, University of Vienna,
Türkenschanzstrasse 17,
1180
Vienna,
Austria
Received: 14 January 2009
Accepted: 20 September 2010
Aims. We study the proximity effect in the Lyα forest around high redshift quasars as a function of redshift and environment employing a set of 3D continuum radiative transfer simulations.
Methods. The analysis is based on dark-matter-only simulations at redshifts 3, 4, and 4.9 and, adopting an effective equation of state for the baryonic matter, we infer the HI densities and temperatures in the cosmological box. The UV background (UVB) and additional QSO radiation with Lyman limit flux of LνLL = 1031 and 1032 erg Hz-1 s-1 are implemented with a Monte Carlo continuum radiative transfer code until an equilibrium configuration is reached. We analyse 500 mock spectra originating at the position of the QSO in the most massive halo, in a random filament, and in a void. The proximity effect is studied using flux transmission statistics, in particular with the normalised optical depth ξ = τeff,QSO/τeff,Lyα, which is the ratio of the effective optical depth in the spectrum near the quasar to that in the average Lyα forest.
Results. Beyond a radius of r > 1 Mpc h-1 from the quasar, we measure a transmission profile consistent with geometric dilution of the QSO ionising radiation. A departure from geometric dilution is only seen when strong absorbers transverse the line-of-sight. The cosmic density distribution around the QSO causes a large scatter in the normalised optical depth. The scatter decreases with increasing redshift and increasing QSO luminosity. The mean proximity effect identified in the average signal over 500 lines of sight provides an average signal that is biased by random large-scale density enhancements on scales up to r ≈ 15 Mpc h-1. The distribution of the proximity effect strength, a parameter that describes a shift in the transmission profile with respect to a fiducial profile, provides a measurement of the proximity effect along individual lines of sight. It shows a clear maximum almost without any environmental bias. This maximum can therefore be used as an unbiased estimate of the UVB. Different spectral energy distributions between the QSO and the UVB modify the profile but this can be reasonably well corrected analytically. A few Lyman limit systems have been identified that prevent the detection of the proximity effect because of shadowing.
Key words: radiative transfer / diffuse radiation / intergalactic medium / quasars: absorption lines / methods: numerical
© ESO, 2010
1. Introduction
The baryon content of intergalactic space is responsible for the large number of absorption lines observed in the spectra of high redshift quasars. This phenomenon, also known as the Lyα forest (Sargent et al. 1980; Rauch 1998), is mainly attributed to intervening H i clouds along the line-of-sight (LOS) towards a QSO. The majority of the H i Lyα systems are optically thin to ionising radiation. The gas is kept in a high ionisation state by the integrated emission of ultraviolet photons originating in the overall populations of quasars and star-forming galaxies: the ultraviolet background field (UVB: Haardt & Madau 1996; Fardal et al. 1998; Haardt & Madau 2001). Accurate estimates of the UVB intensity at the Lyman limit are crucial for the understanding of the relative contribution of stars and quasars to the UVB and also to ensure realistic inputs for numerical simulations of structure formation (Davé et al. 1999; Hoeft et al. 2006).
The intensity of the UVB can be strongly affected by energetic sources such as bright QSOs leading to an enhancement of UV photons in their vicinity. The neutral fraction of H i consequently drops yielding a significant lack of absorption around QSOs within a few Mpc. Knowing the luminosity of the QSO at the Lyman limit, this “proximity effect” has been widely used in estimating the intensity of the UVB (Carswell et al. 1987; Bajtlik et al. 1988) at various redshifts on large samples (Bajtlik et al. 1988; Lu et al. 1991; Scott et al. 2000; Liske & Williger 2001; Scott et al. 2002; but compare Kirkman & Tytler 2008) and also towards individual lines of sight (Lu et al. 1996; Dall’Aglio et al. 2008b).
Principal obstacles in the analysis of the proximity effect are due to several poorly understood effects that in the end might lead to biased estimates of the UVB. The most debated influence is the gravitational clustering of matter around QSOs. Clustering enhances the number of absorption lines on scales of a few proper Mpc, which if not taken into account might lead to an overestimation of the UVB by a factor of a few. Alternatively, star-forming galaxies in the QSO-environment may contribute to an enhancement, or overionisation, of the local ionised hydrogen fraction, i.e., we would underestimate the UVB from the measured QSO luminosity. In the original formalism of the proximity effect theory introduced by Bajtlik et al. (1988, hereafter BDO), the possibility of density enhancements near the QSO redshift was neglected. However, Loeb & Eisenstein (1995) and Faucher-Giguère et al. (2008) found that the UVB may be overestimated by a factor of about 3 because of the high environmental density. Comparing observations and simulations, D’Odorico et al. (2008) found large-scale overdensities over about 4 proper Mpc. The disagreement between the UVB obtained via the proximity effect and from flux transmission statistics has been used to estimate the average density profile around the QSO (Rollinde et al. 2005; Guimarães et al. 2007; Kim & Croft 2008). Dall’Aglio et al. (2008a) showed that a major reason for overestimating the proximity effect is not a general cosmic overdensity around QSOs, but the methodological approach to estimate the UVB intensity by combining the proximity effect signal over several sight lines. Providing a definition of the proximity effect strength for a given LOS, they propose instead to investigate the strength distribution for the QSO sample, with which consistency with the theoretical estimates of the UVB is obtained.
Numerical simulations of structure formation have been a crucial tool in understanding the nature and evolution of the Lyα forest. One of the major challenges in the current development of 3D simulations is the implementation of radiative transfer into the formalism of hierarchical structure formation (Gnedin & Abel 2001; Maselli et al. 2003; Razoumov & Cardall 2005; Rijkhorst et al. 2006; Mellema et al. 2006; Pawlik & Schaye 2008). In particular, the coupling of radiative transfer with the density evolution requires a large amount of computational resources and remains up to now a largely unexplored field. Therefore, most available codes apply radiative transfer as a post-processing step.
Only a couple of radiative transfer studies exist for the Lyα forest (Nakamoto et al. 2001; Maselli & Ferrara 2005). They discuss the influence of radiative transfer on the widely used semi-analytical model of the forest by Hui et al. (1997). Maselli & Ferrara (2005) find that because of the self-shielding of the UVB flux in overdense regions the hydrogen photoionisation rate fluctuates by up to 20 per cent and the helium rate by up to 60 per cent. Since radiative transfer is not negligible for a background field, this should also be true for point sources. Until now numerical studies have dealt with ionisation bubbles in the pre-reionisation era or right at the end of reionisation (Iliev et al. 2007; Kohler et al. 2007; Maselli et al. 2007; Trac & Cen 2007; Zahn et al. 2007). These studies aim to determine the sizes of H ii regions as observed in transmission gaps of Gunn-Peterson troughs (Gunn & Peterson 1965) in high-redshift sources, or in 21 cm emission or absorption signals. By comparing radiative transfer simulations with synthetic spectra, Maselli et al. (2007) showed that the observationally deduced size of the H ii regions from the Gunn-Peterson trough is underestimated by up to 30 per cent.
In the study of the proximity effect at redshifts lower than that of reionisation, the influence of radiative transfer has been neglected up to now, as the universe is optically thin to ionising radiation. We expect that absorption of QSO photons by intervening dense regions might reduce the QSO flux. These dense regions can shield themselves from the QSO radiation field (Maselli & Ferrara 2005) and would not experience the same increase in the ionisation fraction as low density regions. This leads to a dependence of the proximity effect on the QSO environment. Furthermore, the amount of hard photons in the QSO spectral energy distribution (SED) affects the proximity effect profile as suggested by Dall’Aglio et al. (2008b). As in the study of high redshift H ii regions where ionisation fronts are broadened by the ionising flux’s shape of the spectral energy distribution (Shapiro et al. 2004; Qiu et al. 2007), we expect the size of the proximity effect zone to be a function of the spectral hardness. Harder UV photons have smaller ionisation cross-sections and cannot ionise hydrogen as effectively as softer UV photons.
 |
Fig. 1 Cuts through the 25 Mpc h-1 simulation box at redshift z = 4 for a QSO sitting in the void at the lower left corner. In the left panel, the overdensity field 1 + δ is shown. The right panel provides the inverse of the overionisation fraction nHi,Ly − α/nHi,prox due to a LνLL = 1031 erg Hz-1 s-1 QSO. Here nHi,Ly − α and nHi,prox are the neutral hydrogen fractions without and with the influence of the QSO respectively. Clearly visible are the extended overionisation zone and shadowing effects. The scattered white dots arise from numerical noise. The axes are in comoving h-1 Mpc. |
In this study, we employ a three-dimensional radiative transfer simulation to study H ii regions expanding in a pre-ionised intergalactic medium (IGM) at redshifts z = 3,4, and 4.9. We intend to quantify the influence of the above-mentioned effects. To this end, we consider two realistic QSO luminosities. Furthermore, we study the influence of environment by placing the QSO either inside a massive halo, in a random filament, or in an underdense region (void).
The paper is structured as follows. In Sect. 2, we discuss the dark-matter simulation used in this study, and we show that a realistic model of the Lyα forest is found from a semi-analytical model of the IGM. In Sect. 3, we describe the method to solve the radiative transfer equation, and discuss in Sects. 3.2 and 3.3 how the different UV sources are implemented. In Sect. 4, we review the standard approach used to characterise the proximity effect (Bajtlik et al. 1988). In Sect. 5 we describe the different radiative transfer effects on the overionisation profile. Then in Sect. 6, we introduce the proximity effect strength parameter and develop additional models to distinguish the various biases in the signal. In Sect. 7, we present the results for the mean line-of-sight proximity effect as determined from synthetic spectra. In Sect. 8, we discuss the proximity effect strength distribution of our spectra. We finally summarise our findings in Sect. 9.
2. Simulations
2.1. Initial realisation (IGM Model)
We employ a DM simulation in a periodic box1 of 50 Mpc h-1 with 5123 DM particles (von Benda-Beckmann et al. 2008). Using the PM-Tree code GADGET2 (Springel et al. 2005), our simulations yield a force resolution of 2 kpc h-1 and a mass resolution of mp = 7.75 × 107 M⊙ h-1. We fix the cosmological parameters to agree with the 3rd year WMAP measurements (Spergel et al. 2007): the total mass density parameter is Ωm,0 = 0.3, while the baryon mass density is Ωb,0 = 0.04 and the vacuum energy is ΩΛ = 0.7. The dimensionless Hubble constant is h = 0.7, and the power spectrum is normalised by the square root of the linear mass variance at 8 Mpc h-1, σ8 = 0.9.
Simulating the Lyα forest is a challenging task, since a large box is required to capture the largest modes that still influence the mean flux and its distribution (Tytler et al. 2009; Lidz et al. 2010). Furthermore, high resolution is required to capture the properties of single absorbers correctly. Our simulations yield a reasonable representation of the average statistics of the Lyman alpha forest (Theuns et al. 1998; Zhang et al. 1998; McDonald et al. 2001; Viel et al. 2002a) for low redshifts. However, it has been shown by Bolton & Becker (2009) and Lidz et al. (2010) that to resolve the Lyα forest properly at high redshifts, the mass resolution should be higher by two orders of magnitudes for z = 5 and one order of magnitude for z = 4. Given the large box sizes needed, these resolution constraints cannot be fully met with today’s simulations. According to Bolton & Becker (2009), the error in our estimate of the mean flux at z = 4 is around 10%. For z = 3, the simulations will be marginally converged with mass resolution.
We record the state of the simulation at three different redshifts z = 4.9,4, and 3. Using cloud in cell assignment we convert the DM particle distribution into a density and velocity field on a 4003 regularly spaced grid.
We then select three different environments from the highest redshift snapshot: the most massive halo with a mass of Mhalo = (2.6 × 1012,4.0 × 1012,7.9 × 1012,1.0 × 1015) M⊙ h-1 at redshifts z = (4.9,4,3,0), a random filament, and a random void. The last two environments are selected by visual inspection of the particle distribution and their position is tracked down to z = 3. These locations are assumed to host a QSO.
To characterise these environments more precisely, we estimate the volume-averaged overdensities δ5 in r = 5 Mpc h-1 spheres and find that δ5 = (1.7,1.8,2.1) at redshifts z = (4.9,4.0,3.0) for the halo, δ5 = (1.0,0.8,1.1) for the filament, and δ5 = (0.8,0.7,0.7) for the void. Thus the halo resembles a locally overdense region, the void an locally underdense region, and the filament an average environment. Figure 1 illustrates a snapshot of the DM density field at redshift z = 4.
To describe the baryonic component of the IGM, we assume a universe containing hydrogen only, whose density and velocity fields are proportional to those of the dark-matter (Petitjean et al. 1995). To account for pressure effects on baryons, Hui et al. (1997) proposed convolving the density field with a window function cutting off power below the Jeans length. In Viel et al. (2002b), differences in the gas and DM densities between hydrodynamical and DM-only simulations are studied. For δ ≈ 3, baryons follow the DM distribution quite well, i.e. over most of the densities relevant to the Lyman-α forest. However, at higher DM densities, the corresponding gas density is lower because of the smoothing induced by gas pressure. We implicitly smooth our density field with the cloud-in-cell density assignment scheme and cell sizes of 125 h-1 kpc. This is comparable to the Jeans length of ≈150 h-1 kpc at z = 3 and mean density, which scales as δ − 1/2(1 + z) − 1/2.
The hydrogen density at position x is then given by 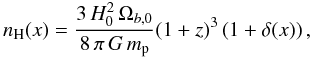 (1)where G is the gravitational
constant, H0 the Hubble constant,
and mp the proton mass. The DM overdensity is
(1)where G is the gravitational
constant, H0 the Hubble constant,
and mp the proton mass. The DM overdensity is
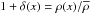 , where the DM density
is ρ(x). Finally the hydrogen velocity
field v(x) is assumed to be equal to the DM one.
, where the DM density
is ρ(x). Finally the hydrogen velocity
field v(x) is assumed to be equal to the DM one.
2.2. Model and calibration of the intergalactic medium
The thermal evolution of the IGM is determined mainly by the equilibrium between photoionisation heating and adiabatic cooling, resulting in a tight relation between the density and temperature of the cosmic gas. This relation is known as the effective equation of state (Hui & Gnedin 1997) and is typically expressed by T = T0(1 + δ)γ − 1. We apply the effective equation of state as an estimate of the baryonic density for overdensities 0.1 < δ < 10 relevant to the Lyman alpha forest. Higher densities correspond to collapsed regions that we approximate by assuming a cut-off temperature Tcut − off = T(δ = 10). Following the formalism of Hui et al. (1997), we can compute an H i Lyα absorption spectrum from the density and velocity fields, once T0, γ, and the UV background photoionisation rate (ΓUVB) are fixed. Thus, by relating simulated to observed H i absorption spectra properties, we can constrain these free parameters. This calibration is crucial in the following to provide realistic representations of the IGM for the radiative transfer calculations.
To calibrate our spectra, we employ three observational constraints sorted by increasing importance: (i) the observed equation of state (Ricotti et al. 2000; Schaye et al. 2000); (ii) the evolution of the UV background photoionisation rate (Haardt & Madau 2001; Bianchi et al. 2001); and (iii) the observed evolution of the effective optical depth in the Lyα forest (Schaye et al. 2003; Kim et al. 2007).
Our catalogues of synthetic spectra consist of 500 lines of sight at each redshift randomly drawn from the cosmological box. The spectra are binned to the typical resolution of UVES spectra of 6.7 km s-1 and convolved with the UVES instrument profile. Random noise with a signal-to-noise ratio (S/N) of 70 is added, the mean S/N in the QSO sample used by Dall’Aglio et al. (2008a). An example of these mock spectra is presented in Fig. 2.
The model parameters of the effective equation of state T0 and γ were chosen according to observations of Ricotti et al. (2000) and Schaye et al. (2000). To obtain values for z > 4, the observed T0 and γ parameters were extrapolated to higher redshifts (see Fig. 3). We constrained our model to yield an observed average effective optical depth τeff(z) = −ln⟨F(z)⟩, where F is the transmitted flux, and the averaging is performed over the whole line of sight. For this, we used observations from Kim et al. (2007). With these constraints, we determined the UVB photoionisation rate ΓUVB for our models.
 |
Fig. 2 Mock spectra synthesised from the z = 3 snapshot with a QSO in a filament. The QSO sits on the right hand side of each spectrum, and the wavelength is in Ångström. The dashed line gives the Lyα forest spectrum without the influence of the QSO, the solid line the spectrum from the radiative transfer simulation of the proximity effect for a QSO with a Lyman limit luminosity of LνLL = 1031 erg Hz-1 s-1. The spectra have a resolution of Δv = 6.7 km s-1 and a signal-to-noise ratio of 70. |
 |
Fig. 3 Upper panel: comparison of our choices for γ (black points) with observationally derived results by Schaye et al. (2000) (grey points). Lower panel: comparison of our model T0 (black points) with observations by Schaye et al. (2000) (grey points). |
Our model parameters are presented in Table 1, and are plotted in Fig. 4 in comparison with different literature results. Both the inferred evolution of the UV background and the effective optical depth agree closely with the results of Haardt & Madau (2001) and Bolton et al. (2005), and high resolution observations by Schaye et al. (2003) and Kim et al. (2007), respectively.
 |
Fig. 4 Upper panel: the evolution of the UV background photoionisation rate in our three snapshots (black points) compared to Bolton et al. (2005) (grey points shifted by z = 0.05 for better visibility) and predictions by Haardt & Madau (2001) (grey line). Lower panel: the effective optical depth of our models (black points) in comparison to measurements by Schaye et al. (2003) (grey points). The continuous line shows the fit by Kim et al. (2007). |
Model parameters of the semi-analytical model.
3. Radiative transfer in cosmological simulations
3.1. Method
We now focus on the method implemented to solve the radiative transfer equation. In developing our Monte-Carlo radiative transfer code (A-CRASH), we closely follow the approach first introduced by Ciardi et al. (2001) and extended by Maselli et al. (2003). While their latest development includes multi-frequency photon packages (Maselli et al. 2009), we only implement the earlier formulation, which uses monochromatic packages2. The advantage of the Monte Carlo scheme is that it accounts for the emission of diffuse recombination photons, which is typically neglected in codes relying on the “on-the-spot” approximation (see Sect. 5.3 for further details).
The idea behind a Monte Carlo radiative transfer scheme is to bundle the radiation flux
field into a discrete amount of radiation energy in the form of photon packages of energy
content 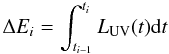 (2)emitted by a source of UV luminosity
LUV between two time
steps ti − 1
and ti. At each time
step ti, we allow the corresponding content
of energy ΔEi to be evenly distributed among
the number of photon packages emitted by the source. In our implementation of the
Monte Carlo scheme, this number can be larger than one. In addition, each photon is
characterised by a given frequency ν following a given SED. Thus, knowing
the source SED and its UV luminosity we are able to infer the number of
photons Nγ,i per package. To guarantee a
proper angular and spatial sampling of the radiative transfer equation, the photon
packages are emitted in random directions.
(2)emitted by a source of UV luminosity
LUV between two time
steps ti − 1
and ti. At each time
step ti, we allow the corresponding content
of energy ΔEi to be evenly distributed among
the number of photon packages emitted by the source. In our implementation of the
Monte Carlo scheme, this number can be larger than one. In addition, each photon is
characterised by a given frequency ν following a given SED. Thus, knowing
the source SED and its UV luminosity we are able to infer the number of
photons Nγ,i per package. To guarantee a
proper angular and spatial sampling of the radiative transfer equation, the photon
packages are emitted in random directions.
Once all the photon packages are produced by the sources, they are propagated through the
computational domain. Each time a package crosses a cell, a certain amount of photons is
absorbed. The absorption probability in the l-th cell is 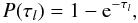 (3)where
τl is the optical depth in the
l-th cell
(3)where
τl is the optical depth in the
l-th cell 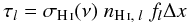 (4)and σHi
is the hydrogen photoionisation cross-section,
nHi,l the neutral hydrogen
number density, and flΔx the
crossing path length of a ray through a cell of size Δx. We calculate the
exact crossing length using the fast voxel traversal algorithm by Amanatides & Woo (1987).
(4)and σHi
is the hydrogen photoionisation cross-section,
nHi,l the neutral hydrogen
number density, and flΔx the
crossing path length of a ray through a cell of size Δx. We calculate the
exact crossing length using the fast voxel traversal algorithm by Amanatides & Woo (1987).
The number of absorbed photons in the cell is
NA,l = Nγ,lP(τl)
where Nγ,l denotes the remaining number of
photons in the package
Nγ,l = Nγ,l − 1 − NA,l − 1
arriving at the l-th cell. In our simple case of pure hydrogen gas, we
can write 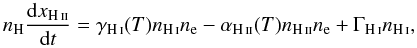 (5)where
xHii = nHii/nH
is the ionisation fraction, nH is the total hydrogen density,
γHi(T) is the collisional
ionisation rate, αHii(T) the
recombination rate, and ΓHi is the photoionisation rate derived from
the number of absorbed photons NA,l. We adopt
γHi(T) and
αHii(T) as in Maselli et al. (2003). We solve this stiff differential
equation using a 4th order Runge-Kutta scheme.
(5)where
xHii = nHii/nH
is the ionisation fraction, nH is the total hydrogen density,
γHi(T) is the collisional
ionisation rate, αHii(T) the
recombination rate, and ΓHi is the photoionisation rate derived from
the number of absorbed photons NA,l. We adopt
γHi(T) and
αHii(T) as in Maselli et al. (2003). We solve this stiff differential
equation using a 4th order Runge-Kutta scheme.
The extent of a time step is defined as the total simulation
time ts divided by the total number of photon
packages Np emitted by each source. The numerical resolution
of the simulation is determined by calculating the mean number of packages crossing a cell
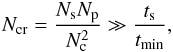 (6)where Ns is the
number of sources, Nc the number of cells in one box
dimension, and tmin the smallest characteristic timescale of
all the processes involved. To efficiently parallelise the scheme, the original rule of
producing one photon per source per time step is dropped; a source is allowed to produce
more than one package per time step as long as
Δt ≪ tmin.
(6)where Ns is the
number of sources, Nc the number of cells in one box
dimension, and tmin the smallest characteristic timescale of
all the processes involved. To efficiently parallelise the scheme, the original rule of
producing one photon per source per time step is dropped; a source is allowed to produce
more than one package per time step as long as
Δt ≪ tmin.
We confirmed that our implementation passes the simple tests described by Maselli et al. (2003) (see Partl 2007, for further details).
3.2. UV background field
The UV background photoionisation rates given in Table 1 need to be modelled in the framework of the radiative transfer scheme. We assume the spectral shape of the UVB to be a power law ναb with αb = −1.3 (Hui et al. 1997), which is a bit lower than measurements by Fechner et al. (2006) yielding αb = −1.99 ± 0.34. From the spectral energy distribution of the UV background field and its intensity, photon packages need to be constructed. To obtain the number of photons in a background package, the total energy content of the background field in the box is mapped to single photon packages; we follow the method of Maselli & Ferrara (2005), but for the hydrogen only case.
To derive the energy content of a single background field photon
package Nγ, the total amount of energy
carried by the background field in the whole simulation box needs to be considered. The
change in the mean ionised hydrogen density nHii by
the UVB is 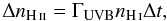 (7)where ΓUVB is the photoionisation
rate of the background field. This is compared to the total amount of absorbed photons in
the box Nγ(1 − exp(− Δτ)),
where
Δτ = σHiΔnHidB
is the total optical depth in the box of length dB. This
corresponds to a mean change in the ionised hydrogen number density of
(7)where ΓUVB is the photoionisation
rate of the background field. This is compared to the total amount of absorbed photons in
the box Nγ(1 − exp(− Δτ)),
where
Δτ = σHiΔnHidB
is the total optical depth in the box of length dB. This
corresponds to a mean change in the ionised hydrogen number density of 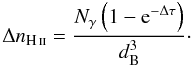 (8)By equating Eqs. (7) and (8) and assuming an optically thin medium Δτ ≪ 1 with
Δτ ≈ (1 − e − Δτ), we derive the photon
number content of a background photon package
(8)By equating Eqs. (7) and (8) and assuming an optically thin medium Δτ ≪ 1 with
Δτ ≈ (1 − e − Δτ), we derive the photon
number content of a background photon package 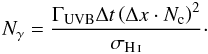 (9)We note that this is only true, if the photon
package is propagated over the distance of exactly one box length.
(9)We note that this is only true, if the photon
package is propagated over the distance of exactly one box length.
Background photons are emitted isotropically from random cells in the box. Dense regions are allowed to shield themselves from the background flux. Thus we emit background photons only from cells below a certain density threshold δUV. In Maselli & Ferrara (2005), a threshold of δUV = 60 was used, corresponding to the density at the virial radius of collapsed haloes. We chose a lower threshold δUV = 1 to ensure that mildly overdense regions have the possibility of shielding themselves from the UV background.
3.3. QSO radiation
As with the UV background, discrete point sources are characterised by a SED and luminosity. We include only one source of radiation other than the UVB. The point source representing the QSO was chosen to follow the composite QSO spectra obtained by Trammell et al. (2007). The mean SED was constructed from over 3000 spectra available in both the Galaxy Evolution Explorer (GALEX) Data Release 1 and the Sloan Digital Sky Survey (SDSS) Data Release 3. It covers a broad wavelength range of about 9000 > λ > 300 Å.
 |
Fig. 5 Lyα absorption along a sight line near a z = 3 LνLL = 1032 erg Hz-1 s-1 QSO simulated with photon numbers Np,QSO = 1 × 108 (solid line), 1 × 109 (dashed line), 2 × 109 (dotted line), and 4 × 109 (dash dotted line). The wavelength is in Ångström and no noise is added to the spectra for better visibility. The lower panel shows the relative deviation from the highest resolution run. |
If a power law ναq is assumed for the UV part of the QSO spectrum, the data of Trammell et al. (2007) leads to αq ≈ −2.5 for λ < 912 Å. Since the scatter in the data of Trammell et al. (2007) is large in the wavelength interval we are interested in, and other authors find harder spectra (Telfer et al. 2002; Scott et al. 2004), we consider in addition a power law SED with a shallower slope of αq = −1.5. The upper energy limit at λ = 300 Å results in a underestimation of the hydrogen photoionisation rate of 0.6% for α = −1.5 and only 0.2% for α = −2.5 with respect to spectra extending to higher energies.
The two QSO Lyman limit luminosities LνLL studied are chosen to bracket the luminosity range of observed QSOs (Scott et al. 2000; Rollinde et al. 2005; Guimarães et al. 2007; Dall’Aglio et al. 2008a). We therefore chose the QSOs to have Lyman limit luminosities of 1031ergHz-1s-1 and 1032 erg Hz-1 s-1. To obtain the total UV luminosity for use with Eq. (2), the high energy part of the SED below 912 Å is scaled to the given Lyman limit luminosity and integrated from 912 > λ > 300 Å. For the Trammell et al. (2007) spectral template and LνLL = 1031 erg Hz-1 s-1, we obtain a total UV luminosity of LUV = 1.15 × 1046 erg s-1, and for LνLL = 1032 erg Hz-1 s-1 a luminosity of LUV = 1.15 × 1047 erg s-1.
3.4. Simulation setup and convergence
Owing to the high precision required to resolve the slight changes in the ionisation fractions governing the proximity effect, a large amount of photon packages had to be tracked. To achieve this, sub-boxes of 25 Mpc h-1 with 2003 cells were selected from the whole box. To ensure that the resulting proximity effect region could be traced to as large a radius as possible, the QSO source was located at the box origin at the cost of analysing only 1/8 of the full sphere around the QSO.
A convergence study was carried out for one of our models with resulting mock spectra shown in Fig. 5. We tested QSO samplings of Np,QSO = 108,109, 2 × 109, and 4 × 109 for a LνLL = 1032 erg Hz-1 s-1 QSO residing in a filament at z = 3. For this test, the α = −2.5 spectrum was used. Simulating the bright QSO at z = 3 provides the most challenging convergence test. The IGM is already highly ionised, and the influence of the quasar results in very small neutral hydrogen fractions and we thus need high numerical resolution. The lower luminosity QSO will not alter the IGM as strongly and therefore resolving the ionisation fractions numerically is easier. The same is true at higher redshift, where the IGM is not yet as strongly ionised as at the low redshifts, and the resulting neutral fractions are larger because of the larger optical depth. The α = −2.5 spectrum is used for this test, since it is more challenging to properly sample the high energy tail than for the harder α = −1.5 model.
It is obvious that 108 photons are insufficient to model the QSO, even if the mean number of photons crossing each cell is around 10. This number has been considered sufficient to resolve Strömgren spheres in a homogeneous medium (Maselli et al. 2003). The solutions for Np,QSO = 2 × 109 and 4 × 109 are similar, with relative differences from the highest resolution run of at most 5 per cent. To achieve good angular sampling of the QSO environment and sufficiently large cell-crossing numbers, we consider the solution for Np,QSO = 2 × 109 as converged. To correctly sample the whole sphere, 1.6 × 1010 packages would be required, which is at the moment beyond the capabilities of our code.
The Monte Carlo radiative transfer method is able to follow photo ionisation heating, although since this effect is already included in the equation of state, we keep the temperatures derived from the equation of state fixed throughout the simulation. This approach neglects any temperature fluctuations caused by He ii photo-heating during He ii reionisation around z ≈ 3 (McQuinn et al. 2009; Meiksin et al. 2010). The simulations are run up to ts = 2.5 × 108 yr and the ionisation fractions were averaged over different outputs at different time steps to reduce the Monte Carlo simulation noise.
4. Line-of-sight proximity effect
 |
Fig. 6 Median overionisation profile as a function of the distance from the QSO (black line, grey area gives upper and lower quartiles) hosted by a halo at z = 3.0 (left) and z = 4.9 (right side) for a QSO luminosity LνLL = 1 × 1031 erg Hz-1 s-1. The analytical overionisation profile including the SED effects is given by the solid line without the grey area. The region affected by oversampling (r < 1 Mpc) is marked with a dotted line. |
In addition to the radiative transfer method for simulating the proximity effect, we also exploit a standard approach to account for the QSO radiation field. This method builds on the work of Bajtlik et al. (1988, also BDO) and Liske & Williger (2001) and we briefly summarise it here. On the basis of the assumption that the IGM is in photoionisation equilibrium with the global UV radiation field, the number density of UV photons produced by bright QSOs is higher in their vicinity than far away and dominate over the UVB. This leads to a reduction in neutral hydrogen, and with it to an opacity deficit of the IGM within a few Mpc from the QSO.
The influence of the QSO onto the surrounding medium leads to an effective optical depth in
the Lyα forest 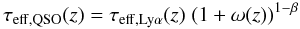 (10)(Liske &
Williger 2001) where
τeff,Lyα(z) represents the
evolution of the effective optical depth in the Lyα forest with redshift,
and τeff,QSO(z) is the effective optical
depth including the alterations by the QSO radiation. Further β is the
slope in the column density distribution and ω(z) is the
ratio between the QSO and the UVB photoionisation rates.
(10)(Liske &
Williger 2001) where
τeff,Lyα(z) represents the
evolution of the effective optical depth in the Lyα forest with redshift,
and τeff,QSO(z) is the effective optical
depth including the alterations by the QSO radiation. Further β is the
slope in the column density distribution and ω(z) is the
ratio between the QSO and the UVB photoionisation rates.
Then following the assumption of pure geometrical dilution of the QSO radiation as proposed
by Bajtlik et al. (1988), we obtain 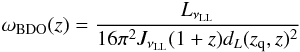 (11)with z as the redshift of
absorbers along the LOS such that z < zq,
and
dL(zq,z) is
the luminosity distance from the absorber to the QSO.
LνLL is the Lyman limit
luminosity of the QSO and JνLL the
UVB flux at the Lyman limit. In observations, the emission redshift of the
QSO zq is subject to uncertainties which propagates through to
the ω scale and increase the uncertainties in the determined
UVB photoionisation rate (Scott et al. 2000). In this
work we consider the emission redshift to be perfectly known.
(11)with z as the redshift of
absorbers along the LOS such that z < zq,
and
dL(zq,z) is
the luminosity distance from the absorber to the QSO.
LνLL is the Lyman limit
luminosity of the QSO and JνLL the
UVB flux at the Lyman limit. In observations, the emission redshift of the
QSO zq is subject to uncertainties which propagates through to
the ω scale and increase the uncertainties in the determined
UVB photoionisation rate (Scott et al. 2000). In this
work we consider the emission redshift to be perfectly known.
We note that this formula is derived assuming identical spectral indices of the QSO and the
UVB. In our simulation we consider two different SEDs for the UVB and the QSO. Therefore in
using Eq. (11) to estimate the proximity
effect, we would introduce a bias. In ω(z) the two
different spectral shapes can be accounted for by the ratio of the photo-ionisation rates of
the QSO as a function of radius ΓQSO(r) and the photo-ionisation
rate of the UVB, ΓUVB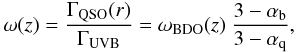 (12)where αb and
αq describe the UVB and the QSO SED, respectively, by
power laws
fν ∝ να.
Further it is assumed that
σHi ∝ ν-3. Finally,
the ω scale is uniquely defined once the QSO Lyman limit flux, redshift,
and the UVB flux are known. In the following analysis, we always use Eq. (12) unless otherwise stated.
(12)where αb and
αq describe the UVB and the QSO SED, respectively, by
power laws
fν ∝ να.
Further it is assumed that
σHi ∝ ν-3. Finally,
the ω scale is uniquely defined once the QSO Lyman limit flux, redshift,
and the UVB flux are known. In the following analysis, we always use Eq. (12) unless otherwise stated.
This correction for differing SEDs has been used in measurements of the UVB photoionisation rate (Dall’Aglio et al. 2009). However, depending on the spectral shape of the QSO, omitting this correction can result in over- or underestimation of the background flux. As stated in Sect. 3.3, we use a QSO spectrum with a rather steep slope of αq = −2.5. Using the original BDO formulation alone would result in an overestimation of the UV background flux by almost 30% assuming αb = −1.3. We later check whether this correction is able to model the SED effect by comparing our simulations with one that uses a shallower QSO spectral slope of αq = −1.5.
As a side note, this spectral effect will alter the QSO’s sphere of influence. We assume as
size of the proximity effect the radius rω = 1
where ΓQSO = ΓUVB. Then 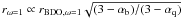 , and the radius is in the case of our steep QSO spectra
13% smaller for equal LνLL.
, and the radius is in the case of our steep QSO spectra
13% smaller for equal LνLL.
5. Radiative transfer effects
5.1. The overionisation profile
The overionisation profile of the proximity effect around the QSO decays radially because of geometric dilution. In addition, differences in the spectral energy distribution between the UVB and the QSO influences the size of the proximity effect zone. Both factors are included in the ω scale. To determine by how much the QSO decreases its surrounding neutral hydrogen density in our simulations, we determine the overionisation profile Ξ(r) = nHi,Ly − α/nHi,Prox, where nHi,Ly − α gives the neutral hydrogen fraction unaffected by the QSO radiation. In addition nHi,Prox denotes the neutral hydrogen density when we include the additional QSO radiation. Assuming ionisation equilibrium, the overionisation profile is directly proportional to the ω scale.
In Fig. 6, we show the median overionisation profile
determined along 200 lines of sight. These have been extracted from the simulation of a
LνLL = 1031 erg Hz-1 s-1
QSO residing in the most massive halo at z = 3 and
z = 4.9. For both redshifts, the simulation data closely follows the
analytical model described in Sect. 4 at radii
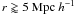 at z = 3 and
at z = 3 and 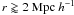 at z = 4.9. However, for the faint QSO,
the simulated overionisation profile begins to deviate from the analytical solution at
smaller radii, where the near host environment leaves an imprint on the profile.
In contrast, for the bright QSO shown in the upper left panel of Fig. 8, the profile more closely follows the analytical model. We need to
emphasise that the spatial resolution of the simulations are limited to
r = 0.125 Mpc h-1. Therefore the
immediate vicinity of the QSO is poorly resolved. Furthermore, all cells up to a radius of
1 Mpc away from the QSO are subject to oversampling in all our cases. Only beyond a radius
of 1 Mpc are cells at most sampled once every time step. Therefore, the solution in this
part of the overionisation profile, which is marked in our plots, is unrealiable.
at z = 4.9. However, for the faint QSO,
the simulated overionisation profile begins to deviate from the analytical solution at
smaller radii, where the near host environment leaves an imprint on the profile.
In contrast, for the bright QSO shown in the upper left panel of Fig. 8, the profile more closely follows the analytical model. We need to
emphasise that the spatial resolution of the simulations are limited to
r = 0.125 Mpc h-1. Therefore the
immediate vicinity of the QSO is poorly resolved. Furthermore, all cells up to a radius of
1 Mpc away from the QSO are subject to oversampling in all our cases. Only beyond a radius
of 1 Mpc are cells at most sampled once every time step. Therefore, the solution in this
part of the overionisation profile, which is marked in our plots, is unrealiable.
5.2. Shadowing by Lyman limit systems
We now focus on the overionisation field and discuss how optically thick regions in the intergalactic medium affect the proximity effect. A slice of the overionisation field is shown in the right panel of Fig. 1 for the LνLL = 1031 erg Hz-1 s-1 QSO residing in a void at z = 4. Again the smooth overionisation profile is seen as expected. However in this smooth transition zone, large shadow cones originating in dense regions are present. The optical depth of these clouds is large enough to absorb most of the ionising photons produced by the QSO. Hence, the ionisation state of the medium behind this absorber remains at the unaltered UVB level.
We determined the hydrogen column density of the shadowing regions in Fig. 1. They lie in the range of 1 × 1017 < NHi < 5 × 1018 cm-2. The regions causing the shadows therefore represent Lyman limit systems. Whether these systems are able to absorb a large amount of QSO photons depends on the one hand on their density and on the other on the QSO flux reaching them. Absorbers further away from the source will receive less flux from the QSO because of geometric dilution. Therefore, they are more likely to remain optically thick. For systems closer to the QSO, the flux field is more intense and a higher density is needed for them to remain optically thick. Thus the number of shadows increases with increasing distance to the source. Moreover, a highly luminous QSO will produce a larger amount of ionising photons and a higher number of absorbers are rendered optically thin. Hence fewer shadows are present in the overionisation field of a highly luminous QSO.
 |
Fig. 7 Mock spectra synthesized from the z = 4 simulation with the QSO in a void. The solid line gives the Lyα forest spectrum without the influence of the QSO, the dashed line the spectrum from the radiative transfer simulation of the proximity effect for a QSO Lyman limit luminosity of LνLL = 1031 erg Hz-1 s-1. The grey line provides the results of a semi-analytical model of the proximity effect that differ significantly from the radiative transfer results behind the strong absorber at the middle of the spectrum. No noise is added to the spectra for better visibility. |
By extracting a spectrum through such an absorber (see Fig. 7), the influence of the Lyman limit system on the proximity effect signature can be seen. Behind the strong absorber on the left hand side, the spectrum follows the unaffected Lyα forest spectrum. Measurements of the proximity effect behind this system do not show any QSO influence. This shadowing is not described by a semi-analytical model where the optical depth in the forest is altered in proportion to 1 + ω(z). We discuss and use this semi-analytical model in Sect. 6. By looking at the semi-analytic model spectrum shown in Fig. 7, it is clear that in this model the proximity effect extends beyond the Lyman limit system.
5.3. Diffuse recombination radiation
 |
Fig. 8 Median overionisation profile as a function of the distance from the QSO hosted by a halo as in Fig. 6. We show the influence of the diffuse field on the H ii region for LνLL = 1032 erg Hz-1 s-1 at z = 3.0. The upper left plot shows the full radiative transfer simulation, the right plot the one without diffusive radiation, and the lower left plot results using the on-the-spot approximation. The analytical overionisation profile including the SED effects is given by the solid line. The region affected by oversampling (r < 1 Mpc) is marked with a dotted line. The lower right histograms gives the distribution of the overionisation fraction at radii r = 10 Mpc h-1 (left) and r = 20 Mpc h-1 (right). The solid lines give radiation transfer results, the dashed lines shows results omitting diffusion, and the dot-dashed distribution illustrates results obtained with the on-the-spot approximation. The solid tick indicates the analytical solution. |
We now discuss the role played by photons produced by recombining electrons with the help of the overionisation profile, since our radiative transfer simulations provide the opportunity to study this diffuse component. With the Monte Carlo scheme we can directly model the radiation field produced by recombination, which in most other schemes is not treated self-consistently. Diffuse radiation produced by recombining electrons plays an important role in radiative transfer problems if the medium is optically thin. Whenever photons originating in recombination events are able to travel over large distances (i.e. larger than one cell size), energy is redistributed on the scale of the photon’s mean free path and the ionisation state is altered over these distances. The importance of diffuse radiation in the simplest of radiative transfer problems, the Strömgren sphere, has been shown in Ritzerveld (2005) where the outer 30% of the Strömgren radius are found to be dominated by recombination photons. In addition Aubert & Teyssier (2008) used their radiative transfer code to discuss how much the on-the-spot approximation, a popular assumption that treats recombination photons as a local process, alters the results of widely used test cases.
Recombination photons to the hydrogen ground level possess enough energy to ionise other hydrogen atoms. If this photon is absorbed by a nearby neutral atom, the on-the-spot approximation can be applied where it is assumed that all recombination photons are absorbed by neighbouring atoms. This is true if the medium is dense and the optical depth high enough for local equilibrium between recombination and absorption to be reached. If however the optical depth is small, the mean free path is longer than the simulation cell size and the recombination photons are absorbed far away from their origin. In this case, the on-the-spot approximation breaks down.
We expect recombination radiation to play an important role in the proximity effect, since the optical depths in the Lyα forest are low. To identify the region where recombination processes influence the solution, we run one simulation without emitting recombination photons. However, we still use case A recombination rates and call this the “no diffusion case”. Furthermore we implement the on-the-spot approximation using case B recombination rates. As before, we do not follow any recombination photons. We expect to see differences at lower redshift, where the mean free paths for ionising photons are large. Therefore, we consider the snapshot at redshift z = 3 with the LνLL = 1032 erg Hz-1 s-1 QSO residing in a halo for this experiment.
The resulting median overionisation profiles are presented in Fig. 8. We also show the overionisation distribution at two radii to more accurately compare the different runs. At radii r > 1 Mpc h-1 we obtain profiles that closely reproduce the theoretical estimates. We see some noisy fluctuations in the profiles. Owing to the larger ionisation fractions for the bright QSO, the ionisation fractions themselves are more susceptible to Monte Carlo noise. Since the neutral hydrogen fractions in the direct vicinity of the QSO are 2 dex lower for the bright QSO than for the faint one, higher precision is needed to more precisely evaluate the extremely low neutral fractions. However, increasing the number of photon packages yet further is at the moment beyond the capabilities of our code.
Comparing the no diffusion run with the full radiative transfer solution shows that recombination greatly contributes to the outer parts of the proximity effect region. The no diffusion solution does not gradually go to unity, but continues to decay rapidly until the QSO’s influence vanishes. At r = 20 Mpc h-1, the difference between the result with and without the diffuse recombination field is 23%. This means that recombination radiation contributes to the photoionisation rate by 23% at this radius, if one assumes that the ionisation fraction is directly proportional to the photoionisation rate.
The on-the-spot solution on the other hand overpredicts the extent of the proximity effect zone by about a factor of 2. This means that keeping the energy produced by recombining electrons locally confined overpredicts the amount of ionised hydrogen. As a result, the QSO’s sphere of influence is overestimated. Furthermore, the on-the-spot solution exhibits a larger dispersion between the lines of sight than the radiative transfer simulation (see Fig. 8 lower right panel). We therefore conclude that the on-the-spot approximation is insufficient when modelling the proximity effect.
6. Radiative transfer on the line-of-sight proximity effect
6.1. Strength parameter
We discuss the imprint of radiative transfer on the line-of-sight proximity effect in Lyα spectra as analysed in observations. To this aim, we study a sample of 500 lines of sight originating in the QSO position with randomly drawn directions. We then measure the proximity effect signature.
First an appropriate ω-scale is constructed for each QSO by applying
Eq. (12) including the SED correction
term. In Sect. 7.2, we discuss how well the
correction term accounts for the SED effect. Given the ω-scale, we then
determine the mean transmission in bins of Δlog ω = 0.5 for each line of
sight. The mean proximity effect signal is calculated by averaging the mean transmission
in each log ω bin over the QSO lines of sight. We determine the mean
optical depth in each bin. The relative change introduced in the optical depth by the QSO
is evaluated by computing the normalised optical depth ξ defined as
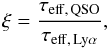 (13)where τeff,QSO is
the effective optical depth in a log ω bin
and τeff,Lyα the effective optical depth
in the Lyα forest without the influence of the QSO.
For Δlog ω < 1, we find the resulting normalised optical depths to
be weakly dependent on the chosen bin size.
(13)where τeff,QSO is
the effective optical depth in a log ω bin
and τeff,Lyα the effective optical depth
in the Lyα forest without the influence of the QSO.
For Δlog ω < 1, we find the resulting normalised optical depths to
be weakly dependent on the chosen bin size.
To quantify any difference in the proximity effect signature to the expected one given by
Eq. (12), we adopt the “strength
parameter” as in Dall’Aglio et al. (2008b,a). The strength parameter a is
defined as 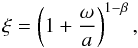 (14)where ω is defined by
Eq. (12). As we know the
UVB photoionisation rates in our models, we use the values given in Table 1 to define the reference ω. Then
values a > 1 or a < 1 describe weaker or stronger
proximity effects, respectively. The SED correction term in Eq. (12) can also be interpreted in the framework
of the proximity strength parameter.
(14)where ω is defined by
Eq. (12). As we know the
UVB photoionisation rates in our models, we use the values given in Table 1 to define the reference ω. Then
values a > 1 or a < 1 describe weaker or stronger
proximity effects, respectively. The SED correction term in Eq. (12) can also be interpreted in the framework
of the proximity strength parameter.
The strength parameter for each line-of-sight can also be measured individually. By obtaining the proximity effect strength for each line of sight, the strength parameter distribution function can be constructed. Studying its properties provides additional insight into the proximity effect signature and was used by Dall’Aglio et al. (2008b) to derive the UVB photoionisation rate. How well this method performs in the present study is discussed in Sect. 8.
6.2. Additional models
In addition to the lines of sight obtained from the radiative transfer simulation, we explored two other models allowing us to characterise the imprint of the cosmological density distribution and radiative transfer in the analysis of the proximity effect. These complementary analyses are used to obtain spectra that can be directly compared to our radiative transfer results.
Semi-analytical model (SAM) of the proximity effect:
from the radiative transfer simulation of only the UV background, we know the ionisation state of hydrogen in the box without the influence of the QSO. We can then semi-analytically introduce the proximity effect along selected lines of sight from the QSO by decreasing the neutral fractions by the factor (1 + ω). We choose the same 500 lines of sight as in the full radiative transfer analysis.
This model includes the imprint of the fluctuating density field on the spectra. Since the semi-analytical model includes only geometric dilution and the influence of the SED, any differences in the results of the full radiative transfer simulations are indicative of additional radiative transfer effects.
Random absorber model (RAM):
in our radiative transfer simulations, we can only cover the proximity effect
signature up to log ω ≥ 0.5 for the faint QSO and to
log ω ≥ 1.0 for the strong one, because of the finite size of our
simulation box. To overcome this limitation, we employ a simple Monte Carlo method to
generate Lyα mock spectra used in observations to study systematic
effects in the data (Fechner et al. 2004; Worseck et al. 2007). The Lyα forest
is randomly populated with absorption lines following observationally derived
statistical properties. The constraints used are: 1) the line number density
distribution approximated by a power law of the form
dn/dz ∝ (1 + z)γ
where γ = 2.65 (Kim et al.
2007); 2) the column density distribution given by 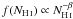 , where the slope is β ≃ 1.5 (Kim et al. 2001); and 3) the Doppler parameter
distribution given by
, where the slope is β ≃ 1.5 (Kim et al. 2001); and 3) the Doppler parameter
distribution given by ![${\rm d}n / {\rm d}b \propto b^{-5} \; {\rm exp}\left[{-{b_{\sigma}^4}/{b^4}} \right]$](/articles/aa/full_html/2010/16/aa11663-09/aa11663-09-eq227.png) , where
bσ ≃ 24 kms-1 (Kim et al. 2001). For a detailed discussion of the
method used, we refer to Dall’Aglio et al.
(2008a,b).
, where
bσ ≃ 24 kms-1 (Kim et al. 2001). For a detailed discussion of the
method used, we refer to Dall’Aglio et al.
(2008a,b).
The random absorber model does not take into account the effects of the clustering of absorption lines due to large-scale fluctuations in the density distribution. Therefore we use this model to determine any possible bias in the analysis method and to infer the effect of absorber clustering. Furthermore, since we can generate spectra of a broad wavelength coverage as in observed spectra, we can quantify the effect introduced by the truncated coverage of the ω scale in the spectra from the radiative transfer simulation. With this simple model, it is possible to study any systematics present in the analysis, such as the influence of the Δlog ω bin size on the resulting proximity effect.
7. Mean proximity effect
Now we discuss the results of the mean proximity effect as measured in the synthesized spectra.
7.1. Mean normalised optical depth
The main results are presented in Figs. 9 and 12. In both plots, we show the analytical model defined by to Eqs. (10) and (13) for comparison. The model predicts that at high ω values, the QSO shows the strongest influence and the normalised optical depth is very low (at the QSO where ω = ∞, the normalised optical depth is ξ = 0). Then in the range 2 > log ω > −1 the influence of the QSO gradually declines because of geometric dilution and reaches ξ = 1 for small ω values. There the Lyα forest is unaffected by the QSO.
The normalised optical depth profile derived from the transfer simulations closely resembles the functional form of the analytical expectations. However, a shift in the profile is present that we quantify using the proximity strength parameter. In observations, the strength parameter is used to measure the UVB photoionisation rate. We therefore faithfully apply the same method to the simulation results. However, since we know the UVB in our models, we can directly compare the photoionisation rate determined using the strength parameter with the model input. The strength parameter is determined by fitting Eq. (14) to the data points using the Levenberg-Marquardt algorithm and a least absolute deviation estimator weighted by the error in the mean. To obtain a reasonable fit, data points deviating strongly from the profile above log ω > 2 were excluded. This also excludes the unreliable region within 1 Mpc of the QSO in the radiation transfer simulation, which translates to an log ω ≥ 2.4 for the faint QSO and log ω ≥ 3.4 for the bright one. We provide the resulting strength parameters in Table 2 and include the fitted profiles in all plots of the mean proximity effect. The shift is due to the large-scale environment around the QSO hosts, which we discuss in more detail in Sect. 7.3.
Parameters of the log a fits to the combined proximity profile for the semi-analytical model (SAM) and the radiative transfer simulation (RT). We indicate the 1σ errors.
For each data point, we show two error bars, the standard deviation in the sample and the 2σ error in the mean. The sample standard deviation indicates the variance between the 500 lines of sight. These variances are very large and extend to values above ξ > 1. Values of ξ > 1 arise when saturated absorption systems dominate the optical depth in a log ω bin and increase the optical depth above the mean effective optical depth in the forest. A detailed illustration is given in the Appendix. Since the real space distance covered by the log ω bins increases with decreasing ω, there the contribution of saturated systems and the variance is lower.
On the other hand, the error in the mean is small because of our sample size of 500 lines of sight, thus the mean profiles are well determined. However, the mean profile does not strictly follow the smooth analytical model, but displays strong fluctuations. These fluctuations are enhanced by our being able to analyse the QSO only in one octant. We also focus our analysis on merely one object, making the signal sensitive to the surrounding density distribution. If multiple halos were combined to one mean profile, the fluctuations would diminish and the profile would follow the smooth analytical profile more closely. Since the data points deviate from the analytical profile, the determination of the strength parameter is quite uncertain. To estimate a formal error in the strength parameter, we applied the Jackknife method. The error values are provided in Table 2.
We verified whether the Monte Carlo noise of the radiation transport simulation contributes to the signal’s variance by reducing the QSO’s photon packages production by half. This does not contribute noticeably to the variance in the signal. The large scatter in the proximity effect signal therefore originates in the distribution of absorption systems along the line of sight. It is a direct imprint of the cosmic density inhomogeneities. The probability distribution of the normalised optical depths in each log ω bin is approximately log-normal as shown in Fig. A.2.
7.2. Performance of the SED correction term
 |
Fig. 9 The normalised optical depth for the LνLL = 1031 erg Hz-1 s-1 QSO with the standard SED residing in a halo at z = 3. Continuous lines show the fitted profiles. The triangles and dash-dotted line indicate the radiation transfer proximity effect without the use of the SED correction term. The circles and dotted line provide the radiation transfer results including the SED correction. The QSO with the hard αq = −1.5 SED is given by the squares and dashed line. The original BDO model is shown as the solid line. The dotted error bars show the sample standard deviation. The solid errors show the 2σ error in the mean. |
With our radiative transfer simulations, we can test whether the SED correction term in Eq. (12) describes the effect of a QSO and UV background that have different spectral shapes. The SED adds to the mentioned shift in the normalised optical depth, ξ, already introduced by the large-scale density distribution around the QSO hosts. To identify the SED influence, we re-simulate the z = 3 faint QSO residing in a halo with a αq = −1.5 power-law SED. With the background’s SED slope of αb = −1.28, we expect to detect only a slight shift caused by the different slopes of Δlog a = 0.02. The softer Trammell et al. (2007) SED used in the rest of the paper yields a shift of Δlog a = 0.11. If the SED correction term performed as intended, the corrected proximity effect profile of the soft SED QSO would lie approximately on top of the one with the hard SED.
In Fig. 9, we present the results of this experiment, where we plot the proximity effect profile of the αq = −1.5 QSO, and SED-corrected and uncorrected profile for the QSO with αq ≈ −2.5. The data points of the corrected α = −2.5 profile lie almost on the αq = −1.5 profile as expected. A similar picture emerges by looking at the strength parameters. The uncorrected soft SED yields a strength parameter of log a = 0.84 ± 0.06. By including the correction term, we obtain log a = 0.70 ± 0.12. For the αq = −1.5 SED, we obtain a strength parameter of log a = 0.65 ± 0.05. The different values of the SED-corrected and the soft QSO results are consistent within the error bars.
7.3. Influence of the large-scale environment
 |
Fig. 10 The mean overdensity profiles of the halo (solid line), filament (dashed line), and void (dash-dotted line) environment at redshift z = 3 as a function of comoving radius. The mean profiles are shown by thick lines. The thin lines indicate the 1σ fluctuations in the density field. An excess in overdensity is seen for all environments in the range of 3 < rc < 10 Mpc h-1, where the profile stays above the average overdensity. |
The environmental density around the QSO has been shown to strongly influence the proximity effect. By studying random DM halos in a mass range of from 1.4 × 1011 M⊙ h-1 to 9 × 1012 M⊙ h-1, Faucher-Giguère et al. (2008) detected an enhancement in the mean overdensity profiles up to a comoving radius of (10 − 15) Mpc h-1. Only at larger radii does the average overdensity profiles exceed the cosmic mean. The overdensity profiles fluctuate strongly between different halos. Since an enhanced density directly translates into an enhancement of the Lyα forest optical depths, the proximity effect measurement is biased accordingly.
 |
Fig. 11 Comparison of the proximity effect at redshift z = 3 of a) the RAM (triangles and dotted line), b) the semi-analytical model (circles and dash dotted line), and c) the results from the radiative transfer simulation (squares and dashed line). The solid line shows the BDO reference analytical model. The dashed vertical line marks the start of the unreliability region of log ω ≥ 2.4 for the faint QSO and log ω ≥ 3.4 for the bright QSO. Results are shown for a QSO sitting in a filament. The left panel is for the low luminosity source, and the right one for the high luminous one. We show only the 2σ errors in the mean. |
We determined the mean overdensity profiles and the fluctuations around the mean for our three QSO host environments. The resulting mean profiles are shown in Fig. 10 for z = 3. Our density profiles show two different influences.
First, the local environment around the QSO host leaves an imprint on the profiles up to a radius of r ≈ 2 Mpc h-1. This is seen in the halo case where the massive host halo is responsible for a strong overdensity that steadily declines up to r ≈ 2 Mpc h-1. The contrary is seen in the void case, where up to r ≈ 3 Mpc h-1 the underdense region of the void is seen. At larger radii, the density increases quite strongly.
All our environments display an overdensity between r ≈ 3 Mpc h-1 and a radius of around r ≈ 15 Mpc h-1. In this region, the density lies above the cosmic mean. We refer to this phenomenon as a large-scale overdensity. Further away from the QSO, the cosmic mean density is reached. The same behaviour is seen at higher redshifts. There, however, the amplitude of the large-scale overdensity is lower. The presence of the large-scale overdensity in the case of the most massive halo is a direct consequence of the most massive halo forming where there is a large overdensity. However, around the filament and the void, this large-scale overdensity is a random selection effect.
An excess in density translates into an excess of Lyα optical depth in this region compared to the mean optical depth. Thus, the normalised optical depth ξ increases and leads to a biased proximity effect. The immediate environment around the quasar extends to log ω ≈ 1.5 for the faint source and to log ω ≈ 2.5 for the bright one. At smaller log ω, the large-scale overdensity influences the proximity effect signal up to log ω ≈ 0.3 for the faint and to log ω ≈ 1.3 for the bright QSO.
Motivated by these considerations, we study the influence of the cosmic density fluctuations on the proximity effect profile. To understand whether radiative transfer effects or the large-scale overdensity are responsible for the shift in the normalised optical depth shown in Fig. 9, we use the reference models introduced in Sect. 6.2.
 |
Fig. 12 The combined proximity effect signature of all 500 lines of sight analysed with the BDO model showing the dependence on environment, luminosity, and redshift. The left column shows the case of a faint LνLL = 1031 erg Hz-1 s-1 QSO, the right one of a luminous LνLL = 1032 erg Hz-1 s-1 QSO. From top to bottom, redshifts are 4.9, 4, and 3. The solid lines show the geometrical dilution model, the other lines are best fits to the measurements with parameters given in Table 2. The circles and dotted lines show the halo cases, the squares and dashed lines the filament case and triangles and dash-dotted lines the void case. Symbols are horizontally shifted by ± 0.05 for better visibility. The dotted error bars show the sample 1σ standard deviation. The solid errors give the 2σ error in the mean. The dashed vertical line marks the start of the unreliability region of log ω ≥ 2.4 for the faint QSO and log ω ≥ 3.4 for the bright QSO. |
We show the resulting proximity effect profiles for the reference models of the faint and bright QSO residing in the filament at z = 3 in Fig. 11. We use the RAM to infer the bias introduced by the analysis method itself because of the finite size of our spectra. In addition, the SAM allows us to determine the influence of the fluctuating density field by omitting any possible radiative transfer effect. On top of that, we show the radiative transfer results.
The data points of the RAM follow the standard BDO profile well for both luminosities. However, a slight shift is seen in the fitted profiles. The strength parameters are log a = 0.06 ± 0.05 in the case of the weak QSO and log a = 0.05 ± 0.10 for the strong QSO. Within the error bars, this is consistent with the analytical predictions. A small shift in the signal was found to be intrinsic to the analysis method because of the asymmetry that it produced in the ξ-distribution (Dall’Aglio & Gnedin 2010).
As for the radiative transfer results, those for the SAM display a strong shift towards the QSO. This is a clear indication that the cosmological density distribution is responsible for the large shift. Comparing the SAM with the radiative transfer results reveals no strong difference. The ratio of the strength parameter of the two models log (aRT/aSAM) for the faint QSO is −0.1 and for the bright one 0.1. Considering the uncertainties in the strength parameters, the two model yield identical results. We provide the ratios of the strength parameters of the two models for all the studied environments and redshifts in Table 2. The ratios vary widely between the different models. However, owing to the uncertainties in the strength parameter, we attribute these differences to the inability of the analytical model to account for the large-scale density distribution.
To strengthen this conclusion, we performed one additional test, where we applied the SAM to 500 randomly selected lines of sight of random origins and directions in the box and not only one specific origin. The resulting proximity effect profile is shown in Fig. 13. The profile now smoothly follows the analytical model without any significant fluctuations around it. The strength parameter of log a = 0.11 ± 0.10 is also consistent with the SED-corrected BDO model. The analytical model is thus a good description of lines of sight with random origins and directions.
Thus the large shift in our simulations is solely due to large-scale overdensities around our sources. We cannot identify significant radiative transfer effects in addition to the one modelled with the SED correction term, since the SAM model gives similar results to the radiative transfer simulations.
7.4. Influence of the host environment
We present the resulting proximity effect profiles for the halo, filament, and void QSO host environments as a function of redshift in Fig. 12. The corresponding strength parameters are given in Table 2. In the analysis, the unreliability region of log ω ≥ 2.4 for the faint QSO and log ω ≥ 3.4 for the bright QSO were excluded. As we have seen in the previous section, the local host environment of the QSO extends to a comoving radius of r ≈ 2 Mpc h-1. Hence, we expect the local environment to affect the proximity effect profiles up to log ω ≈ 1.5 for the faint QSO and to log ω ≈ 2.5 for the bright one.
The effect of the local environment is significant in the halo case. Except for the z = 4.9 bright QSO, the ξ-profile steepens strongly in the direct vicinity of the QSO. The ξ-values start to rise to such an extent, that they lie beyond the plotted region and deviate strongly from the analytical model. In addition, the fluctuations in the normalised optical depth strongly increase. This departure from the analytic profile turns out to pose a problem to the determination of the strength parameter. To obtain a reasonable fit, the region of the local environment needs to be excluded.
 |
Fig. 13 The combined proximity effect signature of the SAM applied to 500 randomly selected lines of sight with random origin. A LνLL = 1031 erg Hz-1 s-1 QSO is assumed. The continuous line shows the fit to the analytical profile to the data. |
For the filament and void environment however, this departure is not seen as expected. Only in the profile of the z = 3 faint QSO in the filament environment is there an enhancement at log ω ≈ 2.5. In the filament and void environments, the scatter in the normalised optical depth decreases. The lack of density enhancements in the immediate surroundings of the host thus reduces the scatter. The influence of the local environment also decreases with increasing luminosity, which is not only because of the lower opacity, but also the larger spatial coverage of each log ω bin.
Beyond the local environment, the ξ-values return to the smooth profile expected from the analytic model. At z = 4.9, the different environments have identical profiles. With decreasing redshift however, the profiles in the different environments start to deviate from the analytical profile without any clear trend. Similar deviations can also be seen in the corresponding strength parameters. For example, the results for the faint halo and void at z = 4 agree. In contrast, for the bright QSO, the strength parameters of the halo and the void disagree. The halo and the filament results agree within the error bars. Owing to the limitations of the analytical model to account for the large-scale overdensity present in the simulation data, the fitted strength parameters exhibit large unsystematic fluctuations. In Sect. 5, we have seen that the local environment does not cause deviations from the geometric dilution model beyond 2 Mpc h-1. The overionisation profile was not found to be influenced by the halo, filament, or void environment at large radii. Therefore we conclude that the local environment does not influence the proximity effect profile at radii larger than the local host environment. Furthermore, the fluctuations in the strength parameter do not correlate with the source environment and solely arise from the analytical model not taking the cosmological density distribution into account.
7.5. Redshift evolution
Studying the strength parameters, no apparent evolution with redshift can be seen, if the fitting errors are taken into account. However, the uncertainties in the strength parameter decrease with increasing redshift. Only in the faint halo case is there a hint of a decrease in proximity strength with increasing redshift.
By looking at the ξ-profiles in Fig. 12, a clear decrease in the fluctuations around the mean profile can be seen with increasing redshift. This is because the density fluctuations of the dark-matter are not as well developed at high redshifts as at lower ones. A minor effect may result from the decreasing transmission of the Lyα forest at higher redshift, i.e. the narrow range of gas densities probed by the Lyα forest. The analysis of the large-scale overdensity discussed in Sect. 7.3 demonstrates however the dominance of the evolution of the density field. There is a slight tendency of the profile to be stronger shifted at low redshifts than at z = 4.9. This is especially prominent in the case of the LνLL = 1032 erg Hz-1 s-1 QSO.
7.6. Luminosity dependence
The environmental bias of the proximity effect signature depends on the QSO luminosity. For all redshifts that we have studied, the shift in the profile is smaller for the bright QSO than for the weak one. The variance in the signal also decreases with increasing QSO luminosity. This can be most clearly seen for redshifts z = 4.9 and z = 3.
The cause of the luminosity dependence is that the ω scale is a function of the QSO luminosity. Therefore an increase in the QSO luminosity translates into larger distances covered by each log ω bin. This dampens the influence of the fluctuating density field and thus the variance in ξ. Hence luminous QSOs help to constrain more tightly the proximity effect signature.
8. Proximity effect strength distribution
We now discuss our results for the distribution of the strength parameter determined on individual lines of sight. The asymmetry of the ξ-distribution and the large-scale overdensity biases the mean proximity effect profiles, as we have discussed in the previous section. To avoid this bias, Dall’Aglio et al. (2008a) used the proximity strength distribution along individual lines of sight to measure the UVB flux, and proposed that the peak of the distribution provides a measure of the UVB. We test the proposed method with our simulations.
The proximity effect strength distribution is obtained by determining the ξ-profile for each individual line of sight and by fitting Eq. (14) to the profile. In contrast to the last section, we use all available ξ data points (except the ones inside the numerically unreliable region) in the fitting procedure. Whenever the simulated data deviates strongly from the analytical model because of the large variance in the ξ-values, it is not possible to determine a strength parameter. This problem is significant for the faint QSO residing in a halo, where the proximity effect profile deviates from the analytical one at log ω ≥ 1.5. There the fitting procedure failed in most cases and we cannot derive a strength parameter distribution.
In Fig. 14, we present the proximity effect strength distribution from our simulations. Only those lines of sights contribute to the distribution, for which a strength parameter could be determined, although we always normalise the distributions P(a) to unity. We employ the comparison models to investigate the various effects that alter the strength distribution. To compare with the results obtained from the mean proximity effect profile, we mark the strength parameters of the mean profiles as given in Table 2.
 |
Fig. 14 The distribution of the strength parameter log a of the proximity effect along the different lines of sight for the radiative transfer simulations (solid histogram), compared with RAM (dotted line) and the SAM (solid line). The mean a-values from the radiative transfer simulations Table 2) and their uncertainties are shown as vertical lines on top of each panel. The upper two panels show the low luminosity case. The lower three panels provide the results for the luminous QSO. From left to right, the redshifts are 4.9, 4, and 3. The vertical dashed line marks log a = 0.0. |
All our models display a strength distribution that is clearly peaked and has a large scatter of σ(log a) = 0.3, 0.4, and 0.7 at redshifts z = 4.9, 4, 3. This scatter is much larger than the variance in the log a values of the mean analysis. All the models show a similar strength distribution as the respective ones of the RAM. In the case of the faint QSO, they all peak around log a = 0. For the bright QSO, the peak is somewhat shifted to negative log a = −0.1. This shift is also present in the RAM results. We therefore suspect that it is due to the small ω scale coverage for the bright QSO and the corresponding uncertain fits. It follows that the peak of the strength distribution can be used to derive unbiased estimates of the proximity effect.
The strength distribution is thus surprisingly not sensitive to the large-scale overdensity environment discussed in the mean analysis. In the averaging process for deriving the mean profile, we are biased by the spherically averaged overdensities shown in Fig. 10. By fitting the strength parameter individually, less weight is given to single log ω bins deviating from the expected profile. This confirms the claim of Dall’Aglio et al. (2008a) that using the proximity effect along individual lines of sight leads to a stable unbiased estimate of the proximity effect and thus of the UVB.
As in the mean analysis, we can investigate the influence of the local environment, the quasar redshift, and the quasar luminosity. The shape of the strength parameter distribution is not influenced by the QSO’s local environment. Whether the QSO resides in a halo, a filament, or a void, the maximum, median, and width of the distribution is not affected. Only for the faint quasar does the halo environment strongly influence the proximity effect profile so that in many cases no reasonable fit could be given. The width of the distribution is found to increase strongly with redshift. This is clearly a consequence of the increasing density inhomogeneities. Overall we find a large uncertainty in the proximity effect along individual sight lines. This is due to the limited ω-scale coverage of the simulated spectra, which are much smaller than in the observations analysed in Dall’Aglio et al. (2008a).
9. Conclusions
We have performed high resolution Monte Carlo radiative transfer simulations of the line-of-sight proximity effect. Using dark-matter-only simulations and a semi-analytic model of the IGM, we have applied our radiative transfer code in a post-processing step. The aim of this paper was to identify radiative transfer influence on the proximity effect for QSOs with different Lyman limit luminosities, different host environments, and at different redshifts.
Owing to the low optical depths in the Lyα forest, we demonstrated that the on-the-spot approximation is insufficient in treating the proximity effect. Diffuse radiation from recombining electrons significantly contribute to the ionising photon budget over large distances and need to be taken into account in the simulations.
In the radiative transfer simulations, we identified Lyman limit systems that cast shadows behind them in the overionisation profile. Any Lyman limit system between the QSO and the observer will result in a suppression of the proximity effect. Behind such a system, the Lyα forest is not affected by the additional QSO radiation and a detection of the proximity effect is not possible. However, Lyman limit systems appear only along rare lines of sight and influence only marginally the proximity effect statistics.
Mock spectra have been synthesized from the simulation results, and methods similar to those used in observations have been applied to extract the observable proximity effect signature. We compared these results with the widely used assumption of the BDO model that only geometric dilution governs the overionisation region around the QSO. We have also used a random absorber model applied extensively in the analysis of observational data. Furthermore, a semi-analytical model was employed to analytically model the proximity effect signal onto spectra drawn from the UVB-only simulations.
We have shown that differences in the shape of the UVB spectral energy distribution function and the spectrum of the QSO introduce a bias in the proximity effect strength. In the original formulation of the BDO model, the SED of the two quantities was assumed to be equal. Differences in the SED of the QSO and the UVB result in a weakening or strengthening of the proximity effect. This bias can be analytically modelled by introducing a correction term in the BDO formalism. We have tested the performance of the correction term. The correction term accounts mostly but not completely for the effect. However, the remaining difference lies within the precision of the determination of the strength parameter.
In all simulations and models, we have confirmed a clear proximity effect profile. However, we found a strong scatter between different lines of sight. Cosmological density inhomogeneities introduced strong fluctuations in the normalised optical depths of the proximity effect. They are caused by individual strong absorbers along the line of sight. The influence is significant near the QSO and can dominate over the standard proximity effect profile if the QSO resides in a massive halo. The fluctuations in the normalised optical depth are smaller, if more luminous QSOs are considered. There the real space coverage of each log ω bin is larger and therefore the fluctuations decrease. In addition the fluctuations decrease with increasing redshift.
We have studied the influence of different QSO host environments on the proximity effect. The QSO was placed in the most massive halo, in a random filament, and in a random void. The local host environment up to a scale of r ≈ 2 Mpc h-1 is responsible for deviations from the BDO model near the QSO. However, it does not affect the proximity effect at radii larger than r ≈ 2 Mpc h-1, and the smooth proximity effect signature was regained.
In the three environments selected for this study, random density enhancement on scales up to r ≈ 15 Mpc h-1 were present. These overdensities introduced a bias in the mean analysis, that decreases the proximity strength. It is a strong effect, clearly seen by averaging the profiles over the 500 lines of sight and then estimating the mean profile. This bias will affect any UVB measurement made using this method. The influence of the bias decreases with increasing QSO luminosity.
Our radiative transfer results complement the analysis of the proximity effect zone performed using a semi-analytical model by Faucher-Giguère et al. (2008). There the authors find a significant dependence of the combined proximity effect on the QSO host halo both by the action of the absorber clustering and the associated gas inflow. Coinciding with our analysis, a stronger proximity effect signal is found at lower redshift because of the higher gas density inhomogeneities. The authors also discuss the nearly log-normal probability distribution of the flux decrement, and they find a strong dependence of the average overionisation in the near zone around the QSO host on the halo mass on scales up to 1 Mpc proper radius.
The proximity effect strength distribution derived along single lines of sight does not show a similar dependence on the large-scale overdensities. The distributions were always consistent with the random absorber model. This is consistent with the results of the analysis of real QSO spectra and the resulting unbiased estimate of the UV-background in Dall’Aglio et al. (2008a). We found that the distributions are slightly shifted to negative log a values, since the ω range covered in the simulation was smaller for the high luminosity QSO. The fluctuations in the normalised optical depth on single lines of sight are responsible for a large scatter in the derived strength distribution. The scatter increases with decreasing redshift. Since the ω scale in our analysis is limited, the fitted strength parameters show large uncertainties. This contributes to the width of the strength parameter distribution. A complete coverage of the proximity effect region will reduce these uncertainties in the strength distributions.
To reliably study all the influences discussed here, the full proximity effect region needs to be simulated and we have to make our radiative transfer code more efficient. It should also be noted that helium was not included in our simulations, which could play an important role in softening the QSO spectra. Helium would absorb a fraction of the hard flux produced by the QSO and increase the influence of the QSO SED.
We finally conclude that the QSO host environment, i.e. whether it sits in a halo, a filament, or a void influences the proximity strength only locally. Apart from shadowing by Lyman limit systems, the proximity effect does not show any radiative transfer influence other then the SED bias.
Our A-CRASH code is OpenMP parallel and publicly available under the GPL license at http://sourceforge.net/projects/acrash/
Acknowledgments
The authors thank Lutz Wisotzki for discussions and useful advice. We are indebted to Tae-Sun Kim and Martin Haehnelt for constructive remarks. We are grateful to the anonymous referee for the careful study and suggestions that helped to improve the paper. The simulations have been carried out at the Konrad-Zuse-Zentrum für Informationstechnik in Berlin, Germany using the AstroGrid-D. A.P. thanks A. Maselli for helpful discussions about CRASH and this study. Further A.P. acknowledges support in parts by the German Ministry for Education and Research (BMBF) under grant FKZ 05 AC7BAA. A.D.A. acknowledges support by the Deutsche Forschungsgemeinschaft under Wi 1369/21-1.
References
- Amanatides, J., & Woo, A. 1987, in Eurographics ’87 (Elsevier Science Publishers), 3 [Google Scholar]
- Aubert, D., & Teyssier, R. 2008, MNRAS, 387, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Bajtlik, S., Duncan, R. C., & Ostriker, J. P. 1988, ApJ, 327, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Cristiani, S., & Kim, T.-S. 2001, A&A, 376, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolton, J. S., & Becker, G. D. 2009, MNRAS, 398, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., Haehnelt, M. G., Viel, M., & Springel, V. 2005, MNRAS, 357, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Carswell, R. F., Webb, J. K., Baldwin, J. A., & Atwood, B. 1987, ApJ, 319, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardi, B., Ferrara, A., Marri, S., & Raimondo, G. 2001, MNRAS, 324, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Aglio, A., & Gnedin, N. Y. 2010, ApJ, 722, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Aglio, A., Wisotzki, L., & Worseck, G. 2008a, A&A, 491, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dall’Aglio, A., Wisotzki, L., & Worseck, G. 2008b, A&A, 480, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dall’Aglio, A., Wisotzki, L., & Worseck, G. 2009, ApJ, submitted [arXiv:0906.1484] [Google Scholar]
- Davé, R., Hernquist, L., Katz, N., & Weinberg, D. H. 1999, ApJ, 511, 521 [NASA ADS] [CrossRef] [Google Scholar]
- D’Odorico, V., Bruscoli, M., Saitta, F., et al. 2008, MNRAS, 389, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Fardal, M. A., Giroux, M. L., & Shull, J. M. 1998, AJ, 115, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., Lidz, A., Zaldarriaga, M., & Hernquist, L. 2008, ApJ, 673, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Fechner, C., Baade, R., & Reimers, D. 2004, A&A, 418, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fechner, C., Reimers, D., Kriss, G. A., et al. 2006, A&A, 455, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gnedin, N. Y., & Abel, T. 2001, New Astron., 6, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Guimarães, R., Petitjean, P., Rollinde, E., et al. 2007, MNRAS, 377, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Peterson, B. A. 1965, ApJ, 142, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 1996, ApJ, 461, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 2001, in Clusters of Galaxies and the High Redshift Universe Observed in X-rays, ed. D. M. Neumann, & J. T. V. Tran [Google Scholar]
- Hoeft, M., Yepes, G., Gottlöber, S., & Springel, V. 2006, MNRAS, 371, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, L., & Gnedin, N. Y. 1997, MNRAS, 292, 27 [Google Scholar]
- Hui, L., Gnedin, N. Y., & Zhang, Y. 1997, ApJ, 486, 599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Iliev, I. T., Mellema, G., Shapiro, P. R., & Pen, U.-L. 2007, MNRAS, 376, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y., & Croft, R. A. C. 2008, MNRAS, 387, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, T.-S., Cristiani, S., & D’Odorico, S. 2001, A&A, 373, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, T.-S., Bolton, J. S., Viel, M., Haehnelt, M. G., & Carswell, R. F. 2007, MNRAS, 382, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkman, D., & Tytler, D. 2008, MNRAS, 391, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Kohler, K., Gnedin, N. Y., & Hamilton, A. J. S. 2007, ApJ, 657, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lidz, A., Faucher-Giguère, C., Dall’Aglio, A., et al. 2010, ApJ, 718, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Liske, J., & Williger, G. M. 2001, MNRAS, 328, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A., & Eisenstein, D. J. 1995, ApJ, 448, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, L., Wolfe, A. M., & Turnshek, D. A. 1991, ApJ, 367, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, L., Sargent, W. L. W., Womble, D. S., & Takada-Hidai, M. 1996, ApJ, 472, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Maselli, A., & Ferrara, A. 2005, MNRAS, 364, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Maselli, A., Ferrara, A., & Ciardi, B. 2003, MNRAS, 345, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Maselli, A., Gallerani, S., Ferrara, A., & Choudhury, T. R. 2007, MNRAS, 376, L34 [NASA ADS] [Google Scholar]
- Maselli, A., Ciardi, B., & Kanekar, A. 2009, MNRAS, 393, 171 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., Miralda-Escudé, J., Rauch, M., et al. 2001, ApJ, 562, 52 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M., Lidz, A., Zaldarriaga, M., et al. 2009, ApJ, 694, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Meiksin, A., Tittley, E. R., & Brown, C. K. 2010, MNRAS, 401, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Mellema, G., Iliev, I. T., Alvarez, M. A., & Shapiro, P. R. 2006, New Astron., 11, 374 [Google Scholar]
- Nakamoto, T., Umemura, M., & Susa, H. 2001, MNRAS, 321, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Partl, A. M. 2007, University of Vienna, Master thesis, http://textfeld.ac.at/pdf/991.pdf [Google Scholar]
- Pawlik, A. H., & Schaye, J. 2008, MNRAS, 389, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Petitjean, P., Mueket, J. P., & Kates, R. E. 1995, A&A, 295, L9 [NASA ADS] [Google Scholar]
- Qiu, J.-M., Feng, L.-L., Shu, C.-W., & Fang, L.-Z. 2007, New Astron., 12, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, M. 1998, ARA&A, 36, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Razoumov, A. O., & Cardall, C. Y. 2005, MNRAS, 362, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Ricotti, M., Gnedin, N. Y., & Shull, J. M. 2000, ApJ, 534, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Rijkhorst, E.-J., Plewa, T., Dubey, A., & Mellema, G. 2006, A&A, 452, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritzerveld, J. 2005, A&A, 439, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rollinde, E., Srianand, R., Theuns, T., Petitjean, P., & Chand, H. 2005, MNRAS, 361, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, W. L. W., Young, P. J., Boksenberg, A., & Tytler, D. 1980, ApJS, 42, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Theuns, T., Rauch, M., Efstathiou, G., & Sargent, W. L. W. 2000, MNRAS, 318, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Aguirre, A., Kim, T.-S., et al. 2003, ApJ, 596, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, J., Bechtold, J., Dobrzycki, A., & Kulkarni, V. P. 2000, ApJS, 130, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, J., Bechtold, J., Morita, M., Dobrzycki, A., & Kulkarni, V. P. 2002, ApJ, 571, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, J. E., Kriss, G. A., Brotherton, M., et al. 2004, ApJ, 615, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, P. R., Iliev, I. T., & Raga, A. C. 2004, MNRAS, 348, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Telfer, R. C., Zheng, W., Kriss, G. A., & Davidsen, A. F. 2002, ApJ, 565, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Theuns, T., Leonard, A., Efstathiou, G., Pearce, F. R., & Thomas, P. A. 1998, MNRAS, 301, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Trac, H., & Cen, R. 2007, ApJ, 671, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Trammell, G. B., Van den Berk, D. E., Schneider, D. P., et al. 2007, AJ, 133, 1780 [Google Scholar]
- Tytler, D., Paschos, P., Kirkman, D., Norman, M. L., & Jena, T. 2009, MNRAS, 393, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Matarrese, S., Mo, H. J., Theuns, T., & Haehnelt, M. G. 2002a, MNRAS, 336, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Matarrese, S., Mo, H. J., Theuns, T., & Haehnelt, M. G. 2002b, MNRAS, 336, 685 [NASA ADS] [CrossRef] [Google Scholar]
- von Benda-Beckmann, A. M., D’Onghia, E., Gottlöber, S., et al. 2008, MNRAS, 386, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., Fechner, C., Wisotzki, L., & Dall’Aglio, A. 2007, A&A, 473, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, O., Lidz, A., McQuinn, M., et al. 2007, ApJ, 654, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Meiksin, A., Anninos, P., & Norman, M. L. 1998, ApJ, 495, 63 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Strong absorber contamination of the normalised optical depth
 |
Fig. A.1 Sample spectra taken from the z = 3 low luminosity QSO located in a void showing the radiative transfer simulations including the proximity effect (solid line) and without it (dashed line). The spectra are given in log ω scale and for better visibility, no noise has been added to the spectra. The normalised optical depths ξ at each log ω bin is overplotted by solid dots to show the effect of absorption features on ξ. The dashed vertical line marks the start of the unreliability region of log ω ≥ 2.4. |
In Sect. 7, we discussed the single line-of-sight variance of the normalised optical depth ξ and its dependency on luminosity and redshift. In this Appendix, we illustrate where and how this variance arises.
 |
Fig. A.2 Normalised optical depth ξ distribution of the void (left panel) and filament QSO (right panel) at redshift z = 3 for three log ω bins. The upper panels show results for the LνLL = 1031 erg Hz-1 s-1 QSOs, the lower one for the LνLL = 1032 erg Hz-1 s-1 QSO. The grey data points give the average normalised optical depths with their variance as shown in Fig. 12. |
The normalised optical depth ξ is the ratio of the effective optical depth in the QSO spectra measured in log ω bins to the effective optical depth present in the unaffected Lyα forest. If the optical depth in a log ω bin is larger than in the unaffected forest, ξ will be larger than unity. The range covered by the log ω bins in the spectra decreases towards the QSO. Therefore any strong absorption system present in the small ranges covered by high log ω bins will bias the optical depth in the bins and therefore increase ξ to values above unity. This bias gives rise to the large variance in ξ at large log ω. It is interesting to note, that an increase in the QSO Lyman luminosity by one dex also increases the proper distance covered in a log ω bin by one dex. Thus the influence of strong absorbers is lower, the more luminous the QSO is.
In Fig. A.1, we show five spectra taken from the z = 3 QSO situated in a void with a luminosity of LνLL = 1031 erg Hz-1 s-1. The spectra are plotted in log ω space and the normalised optical depth measured in the log ω bins is overplotted by solid dots. The spectrum at the bottom panel shows an uncontaminated proximity effect profile. However, all the others panels illustrate the influence of high column density systems on the profile. In the second and third spectra, prominent absorption lines elevate ξ to ξ = 2.
The distribution of ξ in a log ω bin arising from the influence of strong absorbers varies from bin to bin. In Fig. A.2, we show the ξ distribution in three bins for QSOs located in a void and a filament at redshift z = 3. Overplotted are the mean values and the corresponding standard deviations shown in Fig. 12. We note that for the bright QSO the log ω = 0.5 distribution is incomplete, since not all lines of sight reach the proper distance needed for this bin.
The distributions are anisotropic with an extended tail to large optical depth. This behaviour reflects the probability distribution of the simulated density field. The distribution of the high luminosity QSO is narrower than the one of the low luminosity QSO. This is again due to the larger distances covered by the log ω bins in the high luminous case. The width of the distribution covers a large ξ range. The contamination of a single line of sight by strong absorption systems is thus an issue that can only be eliminated by analysing large number of QSO sight lines to reliably determine the mean proximity effect profile.
All Tables
Parameters of the log a fits to the combined proximity profile for the semi-analytical model (SAM) and the radiative transfer simulation (RT). We indicate the 1σ errors.
All Figures
 |
Fig. 1 Cuts through the 25 Mpc h-1 simulation box at redshift z = 4 for a QSO sitting in the void at the lower left corner. In the left panel, the overdensity field 1 + δ is shown. The right panel provides the inverse of the overionisation fraction nHi,Ly − α/nHi,prox due to a LνLL = 1031 erg Hz-1 s-1 QSO. Here nHi,Ly − α and nHi,prox are the neutral hydrogen fractions without and with the influence of the QSO respectively. Clearly visible are the extended overionisation zone and shadowing effects. The scattered white dots arise from numerical noise. The axes are in comoving h-1 Mpc. |
| In the text | |
 |
Fig. 2 Mock spectra synthesised from the z = 3 snapshot with a QSO in a filament. The QSO sits on the right hand side of each spectrum, and the wavelength is in Ångström. The dashed line gives the Lyα forest spectrum without the influence of the QSO, the solid line the spectrum from the radiative transfer simulation of the proximity effect for a QSO with a Lyman limit luminosity of LνLL = 1031 erg Hz-1 s-1. The spectra have a resolution of Δv = 6.7 km s-1 and a signal-to-noise ratio of 70. |
| In the text | |
 |
Fig. 3 Upper panel: comparison of our choices for γ (black points) with observationally derived results by Schaye et al. (2000) (grey points). Lower panel: comparison of our model T0 (black points) with observations by Schaye et al. (2000) (grey points). |
| In the text | |
 |
Fig. 4 Upper panel: the evolution of the UV background photoionisation rate in our three snapshots (black points) compared to Bolton et al. (2005) (grey points shifted by z = 0.05 for better visibility) and predictions by Haardt & Madau (2001) (grey line). Lower panel: the effective optical depth of our models (black points) in comparison to measurements by Schaye et al. (2003) (grey points). The continuous line shows the fit by Kim et al. (2007). |
| In the text | |
 |
Fig. 5 Lyα absorption along a sight line near a z = 3 LνLL = 1032 erg Hz-1 s-1 QSO simulated with photon numbers Np,QSO = 1 × 108 (solid line), 1 × 109 (dashed line), 2 × 109 (dotted line), and 4 × 109 (dash dotted line). The wavelength is in Ångström and no noise is added to the spectra for better visibility. The lower panel shows the relative deviation from the highest resolution run. |
| In the text | |
 |
Fig. 6 Median overionisation profile as a function of the distance from the QSO (black line, grey area gives upper and lower quartiles) hosted by a halo at z = 3.0 (left) and z = 4.9 (right side) for a QSO luminosity LνLL = 1 × 1031 erg Hz-1 s-1. The analytical overionisation profile including the SED effects is given by the solid line without the grey area. The region affected by oversampling (r < 1 Mpc) is marked with a dotted line. |
| In the text | |
 |
Fig. 7 Mock spectra synthesized from the z = 4 simulation with the QSO in a void. The solid line gives the Lyα forest spectrum without the influence of the QSO, the dashed line the spectrum from the radiative transfer simulation of the proximity effect for a QSO Lyman limit luminosity of LνLL = 1031 erg Hz-1 s-1. The grey line provides the results of a semi-analytical model of the proximity effect that differ significantly from the radiative transfer results behind the strong absorber at the middle of the spectrum. No noise is added to the spectra for better visibility. |
| In the text | |
 |
Fig. 8 Median overionisation profile as a function of the distance from the QSO hosted by a halo as in Fig. 6. We show the influence of the diffuse field on the H ii region for LνLL = 1032 erg Hz-1 s-1 at z = 3.0. The upper left plot shows the full radiative transfer simulation, the right plot the one without diffusive radiation, and the lower left plot results using the on-the-spot approximation. The analytical overionisation profile including the SED effects is given by the solid line. The region affected by oversampling (r < 1 Mpc) is marked with a dotted line. The lower right histograms gives the distribution of the overionisation fraction at radii r = 10 Mpc h-1 (left) and r = 20 Mpc h-1 (right). The solid lines give radiation transfer results, the dashed lines shows results omitting diffusion, and the dot-dashed distribution illustrates results obtained with the on-the-spot approximation. The solid tick indicates the analytical solution. |
| In the text | |
 |
Fig. 9 The normalised optical depth for the LνLL = 1031 erg Hz-1 s-1 QSO with the standard SED residing in a halo at z = 3. Continuous lines show the fitted profiles. The triangles and dash-dotted line indicate the radiation transfer proximity effect without the use of the SED correction term. The circles and dotted line provide the radiation transfer results including the SED correction. The QSO with the hard αq = −1.5 SED is given by the squares and dashed line. The original BDO model is shown as the solid line. The dotted error bars show the sample standard deviation. The solid errors show the 2σ error in the mean. |
| In the text | |
 |
Fig. 10 The mean overdensity profiles of the halo (solid line), filament (dashed line), and void (dash-dotted line) environment at redshift z = 3 as a function of comoving radius. The mean profiles are shown by thick lines. The thin lines indicate the 1σ fluctuations in the density field. An excess in overdensity is seen for all environments in the range of 3 < rc < 10 Mpc h-1, where the profile stays above the average overdensity. |
| In the text | |
 |
Fig. 11 Comparison of the proximity effect at redshift z = 3 of a) the RAM (triangles and dotted line), b) the semi-analytical model (circles and dash dotted line), and c) the results from the radiative transfer simulation (squares and dashed line). The solid line shows the BDO reference analytical model. The dashed vertical line marks the start of the unreliability region of log ω ≥ 2.4 for the faint QSO and log ω ≥ 3.4 for the bright QSO. Results are shown for a QSO sitting in a filament. The left panel is for the low luminosity source, and the right one for the high luminous one. We show only the 2σ errors in the mean. |
| In the text | |
 |
Fig. 12 The combined proximity effect signature of all 500 lines of sight analysed with the BDO model showing the dependence on environment, luminosity, and redshift. The left column shows the case of a faint LνLL = 1031 erg Hz-1 s-1 QSO, the right one of a luminous LνLL = 1032 erg Hz-1 s-1 QSO. From top to bottom, redshifts are 4.9, 4, and 3. The solid lines show the geometrical dilution model, the other lines are best fits to the measurements with parameters given in Table 2. The circles and dotted lines show the halo cases, the squares and dashed lines the filament case and triangles and dash-dotted lines the void case. Symbols are horizontally shifted by ± 0.05 for better visibility. The dotted error bars show the sample 1σ standard deviation. The solid errors give the 2σ error in the mean. The dashed vertical line marks the start of the unreliability region of log ω ≥ 2.4 for the faint QSO and log ω ≥ 3.4 for the bright QSO. |
| In the text | |
 |
Fig. 13 The combined proximity effect signature of the SAM applied to 500 randomly selected lines of sight with random origin. A LνLL = 1031 erg Hz-1 s-1 QSO is assumed. The continuous line shows the fit to the analytical profile to the data. |
| In the text | |
 |
Fig. 14 The distribution of the strength parameter log a of the proximity effect along the different lines of sight for the radiative transfer simulations (solid histogram), compared with RAM (dotted line) and the SAM (solid line). The mean a-values from the radiative transfer simulations Table 2) and their uncertainties are shown as vertical lines on top of each panel. The upper two panels show the low luminosity case. The lower three panels provide the results for the luminous QSO. From left to right, the redshifts are 4.9, 4, and 3. The vertical dashed line marks log a = 0.0. |
| In the text | |
 |
Fig. A.1 Sample spectra taken from the z = 3 low luminosity QSO located in a void showing the radiative transfer simulations including the proximity effect (solid line) and without it (dashed line). The spectra are given in log ω scale and for better visibility, no noise has been added to the spectra. The normalised optical depths ξ at each log ω bin is overplotted by solid dots to show the effect of absorption features on ξ. The dashed vertical line marks the start of the unreliability region of log ω ≥ 2.4. |
| In the text | |
 |
Fig. A.2 Normalised optical depth ξ distribution of the void (left panel) and filament QSO (right panel) at redshift z = 3 for three log ω bins. The upper panels show results for the LνLL = 1031 erg Hz-1 s-1 QSOs, the lower one for the LνLL = 1032 erg Hz-1 s-1 QSO. The grey data points give the average normalised optical depths with their variance as shown in Fig. 12. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


