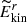| Issue |
A&A
Volume 696, April 2025
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 20 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202451085 | |
| Published online | 08 April 2025 | |
Small-scale and large-scale dynamos in global convection simulations of solar-like stars
1
Department of Computer Science, Aalto University, PO Box 15400 FI-00 076 Espoo, Finland
2
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, D-37077 Göttingen, Germany
3
Nordita, KTH Royal Institute of Technology & Stockholm University, Hannes Alfvéns väg 12, SE-11419 Stockholm, Sweden
4
Wish s.r.l., Via Venezia 24, 87036 Rende, (CS), Italy
5
Sensirion Connected Solutions, Laubisrütistrasse 50, 8712 Stäfa, Switzerland
⋆ Corresponding author; jorn.warnecke@aalto.fi, warnecke@mps.mpg.de
Received:
12
June
2024
Accepted:
14
December
2024
Context. It has recently been shown numerically that a small-scale dynamo (SSD) instability might be possible in solar-like low magnetic Prandtl number plasmas. It was proposed that the presence of SSD might have a significant effect on the dynamics of the large-scale dynamo (LSD) in stellar convection zones. The simultaneous study of these two dynamos, SSD and LSD, in a global magnetoconvection model requires high-resolution simulations and large amounts of computational resources.
Aims. Starting from a well-studied global convective dynamo model that produces cyclic magnetic fields, we systematically increased the resolution and lowered the diffusivities to enter the regime of Reynolds numbers that enable the excitation of SSD in addition to the LSD. We studied the change in the properties of convection, generated differential rotation profiles, and LSD solutions due to the presence of SSD.
Methods. We performed semiglobal convective dynamo simulations in a spherical wedge with the Pencil Code. The resolutions of the models were increased in four steps by a total factor of 16 to achieve maximum fluid and magnetic Reynolds numbers of above 500.
Results. We found that differential rotation is strongly quenched by the presence of the LSD and SSD. Even though the small-scale magnetic field only mildly decreases with increasing Reynolds number, the large-scale field strength decreases significantly. We found no significant quenching of the convective flows by the SSD, as recently claimed by other authors; in contrast, the convective flows first grow and then saturate for increasing Reynolds numbers. Furthermore, the angular momentum transport is highly affected by the presence of small-scale magnetic fields, which are mostly generated by tangling of the LSD. These fields not only change the Reynolds stresses, but also generate dynamically important Maxwell stresses. The LSD evolution in terms of its pattern and field distribution is rather independent of the increase in the fluid and magnetic Reynolds numbers.
Conclusions. At high fluid and magnetic Reynolds numbers, an SSD can be excited in addition to the LSD, and both strongly affect the angular momentum transport. Hence, it is important to study both dynamos and their interplay together to fully understand the dynamics of the Sun and other stars.
Key words: dynamo / magnetic fields / magnetohydrodynamics (MHD) / turbulence / Sun: magnetic fields / stars: activity
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Sun and other cool stars exhibit large-scale magnetic fields that in some cases show cyclic variations (e.g. Baliunas et al. 1995; Boro Saikia et al. 2018; Olspert et al. 2018). This is associated with a large-scale dynamo (LSD) that operates in the stellar convection zones and produces complex magnetic features on the surface (Charbonneau 2014). In addition to the LSD, a small-scale dynamo (SSD) has been proposed to be present in these stars (e.g. Rempel et al. 2023). In contrast to an LSD, the SSD needs no large-scale rotation, shear, or stratification to operate, and the scales of its magnetic field are at or below the characteristic scales of the flow (Brandenburg & Subramanian 2005). There is some debate whether an SSD can operate in solar-like stars. These doubts were supported on one hand by numerical simulations, which showed that an SSD is increasingly harder to excite when approaching the solar parameters (Schekochihin et al. 2005), and on the other hand by the inconclusive results of small-scale field observations on the Sun (Bellot Rubio & Orozco Suárez 2019). Some observational studies showed a cyclic modulation of the internetwork field, that is, a connection to the cyclic large-scale magnetic field, whereas other studies showed that these fields are rather cycle-independent. The doubts based on numerical simulations, however, were recently alleviated by high-resolution simulations at magnetic Prandtl numbers (PrM) that approached the solar value more closely than ever before (Warnecke et al. 2023). These simulations showed that an SSD is not only possible at these very low PrM, but that it becomes even easier to excite in this limit. This indicates a possible dynamical importance of the SSD in the Sun and solar-like stars.
The influence of SSD on the dynamics and LSD was studied with simplified setups (Vainshtein & Cattaneo 1992; Tobias & Cattaneo 2013; Squire & Bhattacharjee 2015; Singh et al. 2017; Väisälä et al. 2021), but global convective dynamo simulations (Käpylä et al. 2023) were only recently able to reach the regime in which both LSD and SSD are excited and can therefore be studied together (Hotta et al. 2016, 2022; Käpylä et al. 2017a; Hotta & Kusano 2021, hereafter HK21, HKS22). Hotta et al. (2016) reported that the SSD suppresses small-scale flows, which mimics the properties of an enhanced magnetic diffusivity. This in turn enhances the LSD. Käpylä et al. (2017a) found on the other hand that the SSD quenches differential rotation. Because this is one of the main dynamo drivers, it consequently suppressed the LSD in some of their cases.
The influence of the magnetic field on the differential rotation has been investigated in many previous analytical and numerical studies. The early global magnetoconvection studies of Gilman (1983) already showed that large-scale magnetism quenched differential rotation, but did not affect the convective motions in a clear manner. Analytical studies in the mean-field (Λ effect) framework produced similar results (e.g. Kitchatinov et al. 1994a). Many other global magnetoconvection studies followed (e.g. Fan & Fang 2014; Karak et al. 2015; Käpylä et al. 2016, 2023; Warnecke et al. 2013, 2016; Brun et al. 2022), but the most relevant for our work is Käpylä et al. (2017a), because it entailed an SSD. These authors reported that an increase in the magnetic Reynolds number ReM leads to a strong suppression of differential rotation. The authors further suggested that the Maxwell stresses become comparable to the Reynolds stresses, and that therefore, only a weak differential rotation can be generated. They found that the increase in Maxwell stresses is partly due to a strong SSD. HK21 and HKS22 reported that the efficient SSD in their simulation was able to reshape an antisolar differential rotation into a solar one for increasing Reynolds numbers Re. Because the results obtained with different approaches diverge quite significantly, it is necessary to further investigate the role of SSD in LSD-active and differentially rotating systems. As magnetic fluctuations originate from different sources, namely SSD-action itself and tangling of the mean field through convective turbulence, it is also important to gain further insights into the role of these two contributions separately. These are the most important goals of this paper.
Since the pioneering work of Brandenburg (2016) and Käpylä et al. (2017b), it has been known that a more realistic description of the radiative heat diffusivity using the Kramers-opacity-based term can lead to the formation of subadiabatic layers at the base of the convection zone (e.g. Käpylä et al. 2019; Viviani & Käpylä 2021). The dependence of the shape and depth of these layers on Re or the presence of SSD and LSD has only been studied in a few Cartesian simulations (Hotta 2017; Käpylä 2019a, 2021), but not in a global setup.
We present a study of a global convective dynamo model in an azimuthal wedge of a spherical shell using the Kramers-opacity-based heat conductivity. We increased the resolution systematically from 128 × 256 × 128 to 2048 × 4096 × 2048 grid points to reach Re and ReM of above 500. This parameter regime allowed us to investigate the LSD and SSD interaction in detail. To separately study the effect of the LSD and SSD on the overall dynamics, we ran for each configuration a full model, in which potentially both LSD and SSD can be excited; a reduced model, in which the large-scale field was removed to allow only for an SSD; and a hydrodynamic model without a magnetic field. The paper is organized as follows: In Sect. 2 we present our model and setup, in Sect. 3 we discuss the results in detail, and in Sect. 4 we present our conclusions. Additional information is given in Appendices A–C.
2. Model and setup
The stellar convection zone was modeled in spherical geometry (r, θ, ϕ) as a shell with a depth D = 0.3R similar to that in the Sun (0.7R ≤ r ≤ R), where R is the radius of the star. We left out the poles (θ0 ≤ θ ≤ π − θ0 with θ0 = 15°) and restricted our model to a quarter of the sphere (a wedge, with 0 ≤ ϕ ≤ π/2), both for numerical reasons. Our model is similar to the models of Käpylä et al. (2013, 2016, 2019) and we refer to these papers for a detailed description.
We solved the fully compressible MHD equations in terms of the vector potential A (ensuring the solenoidality of B), the velocity u, the specific entropy s, and the density ρ, and we employed an ideal-gas equation of state. We included the rotational effects by adding the Coriolis force 2u × Ω0 to the momentum equation, where Ω0 = Ω0(cos θ, −sin θ, 0), and Ω0 is the angular velocity of the corotating frame of the modeled star, in which the plasma has zero total angular momentum. We chose a constant magnetic diffusivity η and kinematic viscosity ν, except near the latitudinal boundaries, where we added ν and η profiles in some of the runs for numerical reasons. These two profiles increased with θ toward the boundaries across an interval Δθ (see Appendix A for details). In our model, the diffusive heat flux has two contributions. The first contribution models the radiative heat flux as Frad = −K∇T with a temperature- and density-dependent radiative heat conductivity K, based on Kramers opacity, so that K is given by
and the reference values ρ0 and T0 were set to the corresponding values at the bottom of the domain in the initial (hydrostatic) state (for details, see Barekat & Brandenburg 2014; Käpylä et al. 2019; Viviani & Käpylä 2021). The second contribution mimics the heat flux of the unresolved or subgrid-scale (SGS) convection and stabilizes the system. This SGS heat flux is given by FSGS = −χSGSρT∇s. As in Käpylä et al. (2013), χSGS followed a smooth radial profile that was zero at the bottom of the domain, constant (χSGS = χmSGS) in the bulk, and maximum near the top, where it transports most of the heat. For some of the hydrodynamic runs, we needed to add a slope-limited diffusion (SLD) that acted on density and velocity to stabilize the system (see Appendix B for details).
The plasma was heated at the bottom by a constant heat flux and cooled at the top by blackbody radiation. The velocity u was stress-free at all radial and latitudinal boundaries, and the entropy s had zero derivatives at the latitudinal boundaries. At the lower radial and at the latitudinal boundaries, we chose the magnetic field B to follow a perfect conductor, while being purely radial at the top. In the ϕ direction, the boundary conditions for all quantities were periodic.
Our runs were defined by the following nondimensional input parameters: We defined a normalized angular frequency and the Taylor number
where Ω⊙ = 2.7 × 10−6 s−1 is the rotation rate of the Sun, while the thermal, SGS-thermal, and magnetic Prandtl numbers were
where χm = K(r = rm)/ρcP is the thermal diffusivity based on the Kramers opacity in the middle of the convection zone (r = rm), see Eq. (1), and cP is the specific heat capacity at constant pressure. As K depends on local density and temperature, we used a one-dimensional hydrostatic model to determine K and ρ for Pr. We note that Pr in the saturated stage can be significantly different from the hydrostatic model. Additionally, we defined two Rayleigh numbers calculated from the same hydrostatic model, one based on the Kramers heat diffusivity χ,
and the other on the SGS heat diffusivity χSGS,
where shs is the specific entropy in the hydrostatic model, G is the gravitational constant, and M is the total mass of the star. Our specific choices of Ra reflect the difficulty of defining a meaningful value for fully compressible convection. To meet the requirement of being determined by input parameters, that is, in the absence of convection, we used a one-dimensional version of our setup and allowed it to equilibrate to the hydrostatic state shs. As the Rayleigh numbers strongly depend on r and are not always positive in the middle of the domain (as in the non-Kramers runs), we averaged them over their logarithmized positive contribution lnRa+,
where the subscript r marks radial averaging.
To estimate the supercriticality, we defined a further Rayleigh number, in which the reduction of supercriticality due to rotation was compensated for by the Taylor number 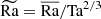 , following (e.g. Chandrasekhar 1961; Roberts 1968; Barik et al. 2023).
, following (e.g. Chandrasekhar 1961; Roberts 1968; Barik et al. 2023).
We further characterized our simulations by the fluid and magnetic Reynolds numbers together with the Coriolis number,
where kf = 2π/D ≈ 21/R is an estimate of the wavenumber of the largest eddies in the domain, and 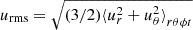 is the rms velocity; the subscripts indicate averaging over r, θ, ϕ, and a time interval covering the saturated state. This definition is a good estimate of the turbulent velocity because the meridional circulation is weak in all of our runs and the 3/2 factor accounts for the omitted azimuthal component of u (see also Käpylä et al. 2013 for more details).
is the rms velocity; the subscripts indicate averaging over r, θ, ϕ, and a time interval covering the saturated state. This definition is a good estimate of the turbulent velocity because the meridional circulation is weak in all of our runs and the 3/2 factor accounts for the omitted azimuthal component of u (see also Käpylä et al. 2013 for more details).
The nondimensional input and solution parameters are given in Table 1 for all runs. In summary, we used the same model as in Käpylä et al. (2016), except that we applied the Kramers heat conductivity instead of a fixed conductivity profile.
Summary of runs.
For our analysis throughout the paper, we decomposed each field into a mean (axisymmetric) and a fluctuating part, which are indicated by an overbar and a prime, respectively. For example, 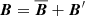 and
and 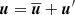 . Restricted to fluctuating fields, we defined an r- and θ-dependent turbulent rms velocity
. Restricted to fluctuating fields, we defined an r- and θ-dependent turbulent rms velocity 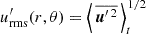 , turbulent rms magnetic field strength
, turbulent rms magnetic field strength 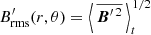 , and turbulent equipartition field strength
, and turbulent equipartition field strength 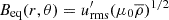 , where μ0 is the magnetic vacuum permeability. The total kinetic energy density is defined as
, where μ0 is the magnetic vacuum permeability. The total kinetic energy density is defined as
which is further decomposed into the energy densities of the fluctuating velocity, the differential rotation, and the meridional circulation,
Here, ⟨ ⋅ ⟩V indicates volume averaging. In a similar way, the total magnetic energy density is defined as
and it can be split into the energy density of the fluctuating field, along with those of the toroidal and poloidal mean fields,
The presented analyses and quantities were performed and calculated from the saturated stage of the simulations. The rescaling to physical units was based on the solar rotation rate Ω⊙ = 2.7 × 10−6 s−1, solar radius R = 7 × 108 m, density at the bottom of the domain ρ(0.7R) = 200 kg/m3, and μ0 = 4π ⋅ 10−7 H m−1. As discussed in Käpylä et al. (2013, 2014), this is one particular choice that gives meaningful results for the input flux, the velocities, and magnetic field strengths in the bulk of the convection zone. All simulations were performed using the PENCIL CODE (Pencil Code Collaboration 2021).
3. Results
Our goal was to study the LSD and SSD together in a setup that includes a physically motivated heat conductivity based on the Kramers opacity. As our starting point, we used the model of Käpylä et al. (2016), with the only difference that we replaced the prescribed heat conductivity by a conductivity based on the Kramers opacity; this represents Run 0M. We then lowered step by step the viscosity ν, the magnetic diffusivity η, and the SGS heat diffusivity χSGS, which caused the simulation to become gradually more turbulent, while keeping PrSGS and PrM constant. At each step, indicated by the number in the run label, the diffusivities were halved, which led to a total reduction by a factor of 16 from Set 0 to Set 4. Technically, this required doubling the resolution and remeshing the run at each step, and finally, running the simulation in the saturation regime for a sufficient time span.
To study the effects of the SSD in isolation and to determine whether it was indeed present, we forked each MHD run into two with identical setups: In the first setup, denoted with S, we removed the mean field 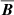 at every fifth1 time step. No LSD was therefore able to develop. When an SSD was sustained, we studied it in detail. In the second setup, denoted by M, we did not remove the mean field, and the LSD was therefore able to develop freely. Finally, we also performed the corresponding hydrodynamic simulations, denoted by H. Run 4M2 was basically the same as 4M, but we did not remesh and restart from 3M, which had an LSD, but restarted from 4S, where only an SSD was present. This again allowed the LSD to grow after the restart. Our motivation was here to study whether an LSD can be excited and grow in the presence of already existing strong magnetic fluctuations. Runs 0M to 2M were similar to Runs G1 to G3 in Käpylä et al. (2017a), whereupon the difference is in the use of the Kramers-opacity-based heat conductivity in our work and in a normal magnetic field condition at the latitudinal boundaries in G2 and G3.
at every fifth1 time step. No LSD was therefore able to develop. When an SSD was sustained, we studied it in detail. In the second setup, denoted by M, we did not remove the mean field, and the LSD was therefore able to develop freely. Finally, we also performed the corresponding hydrodynamic simulations, denoted by H. Run 4M2 was basically the same as 4M, but we did not remesh and restart from 3M, which had an LSD, but restarted from 4S, where only an SSD was present. This again allowed the LSD to grow after the restart. Our motivation was here to study whether an LSD can be excited and grow in the presence of already existing strong magnetic fluctuations. Runs 0M to 2M were similar to Runs G1 to G3 in Käpylä et al. (2017a), whereupon the difference is in the use of the Kramers-opacity-based heat conductivity in our work and in a normal magnetic field condition at the latitudinal boundaries in G2 and G3.
All runs are listed in Table 1 with their control and solution parameters. We note that an SSD is present in Sets 2 − 4, implying that its critical ReM lies between roughly 60 and 130. This is consistent with the study of Käpylä et al. (2017a), who typically found an SSD for ReM > 60. Interestingly, run G2 of Käpylä et al. (2017a) has an SSD with ReM = 66, in contrast to our Run 2M with ReM = 61, which does not excite an SSD. Either the SSD is very close to critical, or the slight differences in the setups are causal. We note here that ReM in their work and ours is only an average, and it hence does not reflect the detailed local dynamics. The critical ReM we found is somewhat higher than what was obtained from theoretical models for smooth velocity fields at low compressibility, which yielded predictions of about 30 − 60 (Brandenburg & Subramanian 2005), and 30 − 50 for simple isothermal forced-turbulence models (e.g. Schekochihin et al. 2005; Väisälä et al. 2021; Warnecke et al. 2023).
When the diffusivities are decreased, the Rayleigh numbers 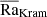 and
and 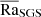 strongly increase by a factor of more than 100. However, because also the Taylor number, Ta, increases significantly by a factor of nearly 300, one needs to inspect the compensated Rayleigh number
strongly increase by a factor of more than 100. However, because also the Taylor number, Ta, increases significantly by a factor of nearly 300, one needs to inspect the compensated Rayleigh number 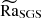 to assess whether the supercriticality increased as well. Indeed,
to assess whether the supercriticality increased as well. Indeed, 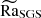 is nearly four times higher in the run with the lowest diffusivities than in the run with the highest diffusivities. The rotational influence on the convection in terms of Co decreased only slightly when the diffusivities were decreased because the turbulent convection becomes slightly stronger. Pr is above unity for Sets 0 and 1 and below unity for Sets 2−4, indicating that heat conduction (in the middle of the convection zone) is dominated by the SGS contribution for Sets 0 and 1 and by the Kramers contribution otherwise. We recall, however, that these two terms involve different gradients.
is nearly four times higher in the run with the lowest diffusivities than in the run with the highest diffusivities. The rotational influence on the convection in terms of Co decreased only slightly when the diffusivities were decreased because the turbulent convection becomes slightly stronger. Pr is above unity for Sets 0 and 1 and below unity for Sets 2−4, indicating that heat conduction (in the middle of the convection zone) is dominated by the SGS contribution for Sets 0 and 1 and by the Kramers contribution otherwise. We recall, however, that these two terms involve different gradients.
All runs reached dynamical saturation in terms of their running time tmax being a multiple of the convective turnover time τ = 1/urmskf; i.e., tmax/τ > 3000 for Sets 0, 1 and 2, tmax/τ > 360 for Set 3, and tmax/τ > 2.4 for Set 4. In terms of the turbulent magnetic diffusion time 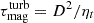 with ηt = urmskf/3, which is important for the evolution of the mean field, all runs from Sets 0−3 reached multiples of
with ηt = urmskf/3, which is important for the evolution of the mean field, all runs from Sets 0−3 reached multiples of 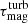 and hence can be considered to be in a steady state (see also the discussion in Sect. 3.2).
and hence can be considered to be in a steady state (see also the discussion in Sect. 3.2).
3.1. Overview of the dynamics
As shown in Fig. 1 for all the M runs, the radial velocity becomes more turbulent and develops progressively more small-scale structures when the diffusivities are decreased and hence the Reynolds numbers increase. For all runs, prominent thermal Rossby waves, also known as Busse columns or banana cells (e.g. Busse 1970, 1976; Featherstone & Hindman 2016; Bekki et al. 2022), were present outside the tangent cylinder in the equatorial regions. This agrees with earlier models and theoretical expectations. Interestingly, the longitudinal degree of these waves did not vary much with increasing Re. It was mostly between m = 32 and m = 40 for all runs (see Appendix C for a more detailed analysis).
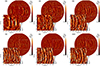 |
Fig. 1. Radial velocity ur at r = 0.98 R with a low-latitude cutout for all M runs in the saturated stage. The wedge is duplicated to form a half-sphere. |
In Fig. 2 we show the corresponding radial magnetic field close to the surface for all the M runs. Near the equator, the radial magnetic field is mostly concentrated in the downflow lanes of the banana cells, where it forms complex structures with small bipolar patches. The radial field is mostly dominated by magnetic fluctuations, while the mean field is not visible near the equator. At higher latitudes in Runs 0M–2M, hints of longitudinal bands of the same polarity as traces of the weak mean radial field are visible. For 3M, 4M, and 4M2, these patterns are no longer as clearly visible.
In Fig. 3 we show the azimuthal magnetic field for Runs 2M, 2S, 3M, 3S, 4M, and 4S. For this component, the difference between Sets S and M is most pronounced. In the M runs, the mean field is clearly visible at all covered latitudes. The magnetic fluctuations in these runs are also present ubiquitously. In Run 2S, the fluctuating magnetic field is more concentrated near the equator. The fluctuations become distributed over progressively wider latitude ranges when the Reynolds numbers are increased (see Runs 3M to 4M). Interestingly, the banana-cell pattern does not produce a strong imprint on the azimuthal magnetic field structure.
 |
Fig. 3. Azimuthal magnetic field Bϕ at r = 0.98 R for all M runs with an SSD and the corresponding S runs. Otherwise the same as Fig. 1. |
3.2. Energies
Next, we studied the total (volume-averaged) energy densities, as shown in Fig. 4 and Table 2. For the H runs, the kinetic energy is generally higher than for the other sets, and it is dominated by the differential rotation at all Re. For the M runs, the contribution of the differential rotation becomes weaker and subdominant with respect to the velocity fluctuations with increasing Re. For the lowest considered diffusivities, however, the contribution of the differential rotation to the total kinetic energy seems to level off at a value of roughly 15%. The contribution of the meridional circulation is tiny for all runs. The energies of the fluctuating velocities remain for roughly constant at increasing Re. for all sets, but are slightly higher for the H runs than for the M runs.
 |
Fig. 4. Dependence of the kinetic and magnetic energy densities on Re. In the top panel, we show |
The S runs with small Re show a similar dominance of differential rotation, but its contribution diminishes for growing Re, similarly to the M runs. The S runs basically show a transition from an almost purely hydrodynamic state (2S) to a fully magnetically dominated state (4S). This has to be attributed to the SSD, which strongly increases with growing Reynolds numbers, as we discuss below.
The magnetic energy increases with increasing Re for the first three M runs. This is mostly due to the increase in the mean field. For higher Re, the energy in the mean field actually decreases, whereas the contribution of the small-scale field increases. The results for the lowest diffusivities (4M, 4M2) need to be taken with caution: Run 4M was restarted from a remeshed earlier stage of 3M, at which the mean-field energy was still high (see Fig. 13 and its discussion in Sect. 3.6). Run 4M was most likely not run long enough for the magnetic field to reach a new saturated stage. For 3M, it took already ∼10 yr to saturate. Run 4M2 was started from 4S to determine how fast the mean field was able to recover after it was removed. After running for ∼0.06 yr, the mean field was still very weak.
For all runs, the mean field is dominated by its toroidal part. For all M runs, the small-scale field contribution dominates the total magnetic energy and shows some tendency to increase for high Re. In the runs without SSD (0M and 1M), the fluctuations contribute roughly 65% to the total magnetic energy. When the SSD starts operating, this contribution increases from 68% (Run 2M) to 75% (4M).
In the S runs, we observe a significant increase in the magnitude of the magnetic fluctuations due to the strengthening SSD. Let us assume that 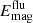 in the S runs represents the strength of the SSD-generated field well also in the corresponding M runs, despite some differences in the flow dynamics. For Re ∼ 130, a quarter of
in the S runs represents the strength of the SSD-generated field well also in the corresponding M runs, despite some differences in the flow dynamics. For Re ∼ 130, a quarter of 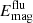 is then due to the SSD, which increases to nearly 80% for Re ∼ 500.
is then due to the SSD, which increases to nearly 80% for Re ∼ 500.
In our interpretation, the quenching of the differential rotation at low Re is caused by the small-scale field that is generated by the tangling of the large-scale magnetic field and not directly by the large-scale field. At higher Re, the SSD also generates a small-scale field, which further quenches the differential rotation.
Disregarding Run 4M because of the issues mentioned above, the total magnetic field energy tends to saturate at high ReM because the increase in the fluctuating-field energy compensates for the decrease in the mean-field magnetic energy. This is in contrast to previous studies (Nelson et al. 2013; Hotta et al. 2016; Käpylä et al. 2017a), where the total field increased monotonically with ReM. However, for the mean field, our study is roughly consistent with the results of Nelson et al. (2013) and Hotta et al. (2016). These authors reported that the mean-field energy decreased with ReM. Our study is inconsistent with our previous work (Käpylä et al. 2017a), however, where the mean field did not decrease.
The total magnetic energy is close to equipartition with the total kinetic energy only at the highest Re (4M) because of the strong mean field and its tangled fluctuating field (see the last two columns of Table 2). In the pure SSD runs, the field reached only 50% of the equipartition value. This disagrees with the results of HKS22, who found superequipartition fields at their highest resolution. The comparison with recent work by Yan & Calkins (2022) on large- and small-scale convective dynamos in plane layers yields several differences: They reported that the ratio of the magnetic to kinetic energy decreased with increasing  , but showed some tendency to saturate from
, but showed some tendency to saturate from 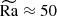 on. In contrast, we found the opposite trend, but in the
on. In contrast, we found the opposite trend, but in the 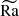 interval [48, 184]. Moreover, we cannot confirm their conclusion that SSDs are likely to yield lower energy ratios. We recall, however, that their simulations were performed at
interval [48, 184]. Moreover, we cannot confirm their conclusion that SSDs are likely to yield lower energy ratios. We recall, however, that their simulations were performed at 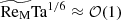 , whereas we covered the
, whereas we covered the 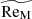 interval [26, 210].
interval [26, 210].
Energy densities for all runs.
3.3. Overshoot and Deardorff layers
Similar as in the work of Käpylä et al. (2019) and Viviani & Käpylä (2021), we found that using a Kramers-based heat conductivity causes the development of subadiabatic but convective layers in addition to the usual convective zone. From top to bottom of the domain, the zones are defined as
where 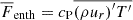 is the radial enthalpy flux, and
is the radial enthalpy flux, and 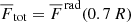 is the total flux, defined by the flux through the bottom boundary. In the definitions above, all fluxes are additionally averaged over latitude, and hence, they only depend on the radius r.
is the total flux, defined by the flux through the bottom boundary. In the definitions above, all fluxes are additionally averaged over latitude, and hence, they only depend on the radius r.
We investigate the dependence of these zones on Re for different runs in Fig. 5. As a first result, we observe that approximately the lower quarter of the domain is convectively stable (even more so for low Re). This is consistent with previous works in similar parameter regimes (Käpylä et al. 2019; Viviani & Käpylä 2021).
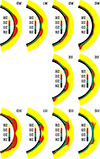 |
Fig. 5. Visualization of the four zones formed in the simulations: buoyancy (BZ, yellow), Deardorff (DZ, red), overshoot (OZ, green), and radiative zone (RZ, dark blue) (see Sect. 3.3 for definitions). |
The DZ is more pronounced near the equator in the high-diffusivity runs, especially in hydro cases. As Re increases, the DZs become narrower near the equator and more uniform over latitude, while their radial extent at high latitudes depends on the presence of magnetic fields. In the M runs, the DZ becomes very thin and is partly replaced by a thin OZ and an extended RZ for high Re. In the S runs, the DZ is more pronounced at low latitudes, even at high Re. For the H runs, it is always pronounced at low latitudes. At high Re, however, most of it is replaced by the overshoot zone.
Regarding the discussion on the dependence of the OZ depth on Re (see Hotta 2017; Käpylä 2019a), our conclusion is complex. For all runs, the depth at high latitudes seems to remain rather constant, which agrees with Käpylä (2019a); Käpylä (2021). At low latitudes, however, the depth decreases with Re for the H runs, which agrees with Hotta (2017), but it increases in the S runs. For the depth of the DZ, Käpylä (2021) reported a weak dependence on Re, which we can confirm for high latitudes, but not throughout.
3.4. Flow and magnetic field distribution
The variation in the fluid and magnetic Reynolds numbers also impacts the distribution of the turbulent velocity and the magnetic fields. In Fig. 6 we illustrate the latitudinally averaged radial profiles of urms′ for all runs and compare them with the values for the Sun, relying on the mixing-length theory (MLT) (see the green line for the Standard Solar Model of Table 6.1 in Stix 2002). As MLT provides only radial velocities, we multiplied them with 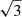 to obtain an estimate of urms assuming isotropy of the flow. These values of the convective velocities need to be taken with caution as they rely on crucial assumptions, such as the value of the MLT parameter. Furthermore, helioseismic analysis has cast doubt on them (e.g. Hanasoge et al. 2012).
to obtain an estimate of urms assuming isotropy of the flow. These values of the convective velocities need to be taken with caution as they rely on crucial assumptions, such as the value of the MLT parameter. Furthermore, helioseismic analysis has cast doubt on them (e.g. Hanasoge et al. 2012).
 |
Fig. 6. Radial profile of the latitudinally averaged turbulent velocity urms′ of all runs. The colors indicate the different run sets with different Re as indicated. The solid lines show M runs, the dotted lines show S runs and the dashed lines show H runs, The thick green line indicates the values from the solar model of Stix (2002) based on mixing-length theory. The inset shows urms′ at a fixed radius r = 0.9 R as a function of Re. There, we overplot urms′ of Hotta & Kusano (2021) using the Re estimated in HKS22 (solid red) and a reestimate according to Eq. (16) (dashed). |
First, our values are somewhat lower than those from the Sun, which is expected because the rotational effects in our simulations are stronger, as indicated by the Coriolis numbers, which range from Co = 8 to 9. Near the surface, significant discrepancies arise that are likely due to the absence of a strong density stratification. The M runs show the poorest agreement, while the H runs exhibit higher velocities than their M counterparts. The S runs fall between these two. We interpret this as suppression of the turbulent velocities by magnetic fields, primarily by those that are generated by the large-scale dynamo.
Upon investigating the turbulent velocity as a function of Re at r = 0.9 R (see inset in Fig. 6), we observed as before that for all H runs, urms′ is larger than for the M runs, with the S runs consistently in between. The velocity fluctuations initially increased for all run sets with Re and then decreased for higher Re. This decrease is not as pronounced as the initial increase, however. The decrease in urms′ in Run 4M might be caused by the magnetic field, but we observed a mild decrease in Run 3H as well and even an increase for Run 4S. Therefore, this interpretation may not be entirely valid.
We also compared our velocities to the results of HK21, who reported that the SSD suppressed the turbulent velocity as their effective Re increased. The authors did not explicitly define Re because they used a SLD scheme without explicit diffusivities, and they therefore estimated Re using the Taylor microscale. As an alternative, we estimated their Re using the grid spacing of our Set 4,
Here, Re4 = 530 is a rough average of all Re in Set 4, Δϕ4 = π/2/2048 is the grid size in this set, and ΔϕHK22 = 2π/(1536, 3072, 6144) is the variable grid size of the three runs of HK21. This approach ensured that Re did not increase much more than by a factor of two when the resolution was doubled, in contrast to the approach of HKS22.
The comparison revealed two significant findings: First, as evident from the inset of Fig. 6, their urms′ values are markedly higher than ours and exceed those of the Standard Solar Model (Stix 2002) for their low and medium resolutions. Second, our simulations do not exhibit a decrease in urms′ with increasing Re, as notable as observed in HK21. Instead, we only observe a mild decrease at high Re. Two explanations for this behavior can be considered: First, it may be linked to the more efficient SSD in the highest-resolution simulation of HK21, which is likely a result of higher turbulent velocities. Second, it might be a consequence of their use of a pure SLD scheme for viscous and magnetic diffusion, as opposed to the constant explicit diffusivities employed in our study. This is supported by the fact that HK21 achieved a more efficient SSD at an even lower resolution than we did.
However, if the turbulent velocities were quenched by the SSD at high Re, we would expect to see a suppression of urms′ as a function of Re only for the M and S runs, but we also observe it for H runs. Another possible cause may be the specific setup of HK21, who fixed the energy fluxes to the solar luminosity at both radial boundaries, forcing the total energy to remain constant at its initial value. This constraint assumes that the initial stage is already very close to the final solution, because large departures from the initial stratification are not possible. This makes the solution intrinsically not self-consistent. We are confident that our model, which allows the thermal energy to adjust to the dynamics, is more self-consistent and hence more realistic.
Next, we examined the latitudinally averaged turbulent magnetic field strength Brms′, normalized by the equipartition field strength in Fig. 7 (see Fig. 6 for the turbulent kinetic energy). As expected, the turbulent magnetic field increased with Re for the M and S runs. Weak superequipartition fields were only observed for Run 4M in the middle of the convection zone. Runs 4M2, 4S, 3M, and 2M reached values above Brms′/Beq = 0.9, but did not exceed unity in the entire convection zone. The pure SSD (S) runs consistently exhibited weaker Brms′ than their M counterparts.
 |
Fig. 7. Radial profile of the normalized latitudinally averaged turbulent magnetic field Brms′/Beq of all runs. The color-coding and line styles are the same as in Fig. 6, with the exception of Run 4M2 (purple dashed line). |
Interestingly, the field increased with Re (=ReM) for the M runs, mostly in the lower half of the convection zone, and it appeared to be mostly independent of ReM in the upper part of the domain. Only the highest ReM run (4M) showed a slightly enhanced field in the upper part of the domain. In contrast, the S runs showed an increase in Brms′ with ReM throughout the domain. We interpret this as follows: In the M runs, where the SSD is still weak, Brms′ is primarily generated by the tangling of the large-scale magnetic field. This process seems independent of Re for the upper part of the domain but becomes more effective in the lower part of the domain as Re increases. As the SSD increases similarly at all radii, it also enhances Brms′ for the highest Re runs, where the SSD field becomes comparable to the tangled field.
In Fig. 8 we present the spherical-harmonic spectra of kinematic and magnetic energies along with their ratio for all runs, calculated from near the surface (r = rs ≡ 0.98 R) θϕ slices. The spectral energies 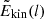 and
and 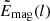 were calculated using the following definitions:
were calculated using the following definitions:
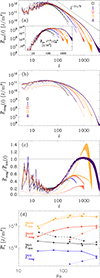 |
Fig. 8. Spectra of kinetic (a) and magnetic (b) energy density along with their ratio (c) near the surface, r = 0.98 R, all excluding the m = 0 contribution. As before the solid lines show M runs, the dotted lines show S runs and the dashed lines show H runs, while different colors indicate run sets with distinct Re. Panel (d) highlights the Re dependence of the kinetic and magnetic spectra for l = 10 and 100. |
where l is the spherical-harmonic degree, and the energy densities are given as
We removed the mean-field contribution (m = 0) and summed over all other m. Because of our wedge approach, l = 4 is the lowest possible l. We refer to Viviani et al. (2018) and Käpylä et al. (2019) for details of computing spherical harmonic decompositions from simulations of the presented type.
For low l, the kinetic energy spectra (Fig. 8a) are similar for all runs – only the hydro runs have slightly higher energies. At the highest resolutions and l > 50, the velocity develops an inertial range, which can be best described by a power law of l−11/5, as illustrated by the compensated spectrum in the inset. This power law was predicted by Bolgiano (1959) and Oboukhov (1959), and was also found in Käpylä (2021). However, as discussed in several studies (e.g., Brandenburg 1992; Rieutord & Rincon 2010; Xie & Huang 2022; Alam et al. 2023), this scaling was obtained for stably stratified media, but not for rotating convection. Moreover, the Bogliani-Obukhov scaling should only appear for those larger scales, which are influenced by the gravity-induced anisotropy, while being followed by a standard Kolmogorov scaling for smaller scales. Furthermore, we observe an extended inertial range only at the highest resolutions, as viscous diffusion affects all l otherwise.
For the magnetic spectra (Fig. 8b), the energies are very similar for all M runs at low l. 4M alone has a lower power at l < 10, which might be caused by some data loss2. We do not observe an inertial range with a clear power law, as in the H runs. For the S runs, the energies are lower at all scales than for the corresponding M runs. However, Run 4S has a higher power than the other S runs, however, in particular at low l, but it appears to be indistinguishable from Run 4M for l > 100. That the field in the S runs is lower than in the M runs, in particular at low l, is consistent with nearly the entire field at l > 500 being due to the SSD, whereas tangling is dominant at l < 500 for the highest ReM. Surprisingly, the shapes of the spectra of the M and S runs are similar in general, which implies that the spectral properties of LSD- and SSD-generated fields are very similar, at least for l ≥ 4. We only observe that amplitude differences are more pronounced at l < 100.
To investigate whether the magnetic field reaches superequipartition at certain scales, we also examined the ratio of the magnetic and kinetic spectra near the surface, as shown in Fig. 8c. Superequipartition is achieved (around l ∼ 1000) only in Run 3S, whereas the corresponding M run has a maximum energy ratio of 0.6. The lowest diffusivity runs only achieve just equipartition for 600 < l < 2000. We note that these spectra were taken close to the surface, where the horizontally averaged magnetic field is well below equipartition, as shown in Fig. 7. We would expect the spectral ratio at larger depths to be higher. The fanning of the spectra, particularly at high l in the kinetic ones, is related to inaccuracies resulting from employing spherical harmonic decomposition on a spherical grid with an incomplete θ range.
To show the Re dependence of the spectral energy more clearly, we plot for l = 10 and 100 the kinetic and magnetic energy as function of Re for all runs (see Fig. 8d). The kinetic energy for l = 10 appears to decrease mildly with increasing Re. Interestingly, this is not only the case for the M or S runs, but also for the H runs and hence cannot be due to a suppression by the magnetic field, as claimed in HK21. The magnetic energy at l = 10 of the M runs seems to be independent of Re, except for a mild decrease for the highest Re. A strong increase is seen only for the S runs. The kinetic and magnetic energy at l = 100 increase continuously. The kinetic energy alone seems to saturate for the highest Re. For this scale, the strong SSD in the highest Re runs has no marked influence on the kinetic energies.
When we compare our results with the spectra provided by HK21 and HKS22, we find two main differences: They observed superequipartition fields at small scales (l > 100) even for their lowest resolution (similar to our Set 2). Additionally, the kinetic energy at large scales is suppressed in their results at high Re because of, as they interpreted it, their very strong SSD. We observe a small decrease in the large-scale energy, but this is also evident in the hydrodynamic runs. It is important to note that HK21 and HKS22 only studied one purely hydrodynamic run, and therefore, there is no Re dependence in their case. Furthermore, their simulations only developed an SSD but no LSD, which means that the influence of a large-scale field on the dynamics was not studied. The differences in the spectral properties might also be related to these two main distinctions in the setup, as discussed above.
3.5. Differential rotation and its generators
Next, we examined the profiles of differential rotation 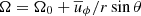 , as shown in Figs. 9 and 10, and investigated the influence of the magnetic fields on their generation terms (see Figs. 11 and 12). As observed from the energy analysis, the differential rotation is most pronounced in the H runs and is suppressed in the M and S runs.
, as shown in Figs. 9 and 10, and investigated the influence of the magnetic fields on their generation terms (see Figs. 11 and 12). As observed from the energy analysis, the differential rotation is most pronounced in the H runs and is suppressed in the M and S runs.
 |
Fig. 9. Differential rotation Ω/Ω0, with |
 |
Fig. 10. Differential rotation of all runs near the surface (r = 0.98 R). At the top we plot Ω/Ω0 as function of latitude. As before, the solid lines show M runs, dotted lines show S runs and the dashed lines show H runs, while the colors indicate the run sets with different Re. At the bottom, we plot Ω/Ω0 at the equator (θ = π/2) as a function of Re. |
 |
Fig. 11. Time-averaged contributions to the differential rotation energy evolution for Runs 0M and 3M, as given in Eqs. (21)–(25). The contributions are shown in units of J/m3s. |
 |
Fig. 12. Contributions to the differential rotation energy evolution averaged in time and latitude for all run sets (0 – 4) as functions of r/R (see Eqs. (21)–(25)). The bottom rightmost panel shows the contributions as functions of Re at r/R = 0.96 (the vertical line in the other panels). |
In the H runs, the contours of constant angular velocity tend to become more cylindrical toward the more turbulent regime, while the maximum Ω values remain roughly constant across Runs 0H, 1H, and 2H. However, for the highest Re (Run 3H), the differential rotation is slightly weaker than in Run 1H. With increasing Re, more jets of opposite sign become visible. Surprisingly, the contours in Run 0H are far less cylindrical than in the H runs with higher Re. We attribute this to the absence of Busse columns (or banana cells) at the lowest Re, as illustrated in Fig. C.1.
As noted previously, the M runs consistently exhibit a weaker differential rotation with Ω profiles strongly influenced by the magnetic field. We observe a tendency for the isorotation contours to become less cylindrical with higher Re. Except for some local minima and maxima near the poles, the differential rotation becomes much weaker in the highly turbulent regime than in the less turbulent regime. Additionally, the differential rotation profile in all cases with active SSD becomes increasingly hemispherically asymmetric with rising Re. This is attributable to the hemispherically asymmetric magnetic field. Notably, the minimum of Ω at mid-latitudes nearly vanishes in the high-Re M runs. For the S runs, the profiles at weak SSD (Run 2S) resemble those of Run 2H. However, Run 3S with stronger SSD exhibits a weaker differential rotation, similar to Run 3M. The profiles of Runs 4S and 4M are almost the same. This might be related to the issues of these runs discussed in Sect. 3.2.
The changes in the differential profile with Re and the presence of the two dynamos become clearer in the plots of the latitudinal distribution and Re dependence (Fig. 10) of Ω. It is evident that it significantly decreases near the equator with increasing Re and in the presence of a magnetic field. Moreover, the jets present in the H runs at mid-latitudes are completely suppressed in the M runs. Interestingly, the differential rotation at the equator is already strongly suppressed in Run 2M, where the SSD is relatively weak, indicating that the suppression is due to the magnetic field generated by the LSD rather than the SSD. However, the SSD in Run 4S is capable of suppressing and shaping the differential rotation, similarly to its corresponding Run 4M.
The reduction of shear at high ReM was also reported by Käpylä et al. (2017a). HK21 and HKS22 found that the differential rotation at high ReM is also strongly influenced by the magnetic field, which is consistent with our work. However, in their cases, the magnetic field was solely due to an SSD, whereas in our case, the change in differential rotation is mainly due to the LSD.
Our modeling strategy prevented us from inspecting the actual generation process of the differential rotation profiles because we restarted from earlier models. We can therefore only address the relaxed states reliably.
The differential rotation follows the mean angular momentum balance (see, e.g. Rüdiger 1989),
where s = r sin θ is the lever arm. As usual, we neglected the compressible term related to 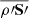 in the equation above.
in the equation above.
To determine which part of the angular momentum flux contributes significantly to the differential rotation, we calculated the contributions to the evolution of differential rotation energy density. This approach has the advantage that generating contributions are shown as positive values, and destructing ones as negative,
Using the right-hand side of Eq. (19) and also averaging over time, we can divide 𝒟 into five different contributions:
Due to our choice of azimuthal averages written out at run time, we calculated 𝒟Mer and 𝒟Rey slightly differently. However, their sum remains the same. For 𝒟Mer, we used
where the second term was calculated by 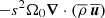 using the conservation of mass flux,
using the conservation of mass flux,
For 𝒟Rey we used
Our choice at the end means that the term 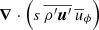 is included in 𝒟Rey instead of in 𝒟Mer, and their sum is therefore the same as in the definitions Eqs. (21) and (22).
is included in 𝒟Rey instead of in 𝒟Mer, and their sum is therefore the same as in the definitions Eqs. (21) and (22).
We show the time-averaged contributions exemplarily for Runs 0M and 3M as a meridional plot in Fig. 11 and for all runs as a line plot from additional averaging over latitude in Fig. 12. For all low Re runs, the main balance is between the contributions of meridional circulation 𝒟mer and Reynolds stresses 𝒟Rey, with a small contribution of 𝒟vis. For most of the domain, 𝒟Rey is generative, whereas 𝒟mer is destructive. At high Re, this balance still holds for the H runs, where 𝒟vis becomes increasingly smaller. For the M runs, we find two main channels through which the magnetic field influences the angular momentum. On one hand, the magnetic field suppresses 𝒟mer and 𝒟Rey to much lower levels, accompanied by some changes in the spatial distribution. On the other hand, the contribution from small-scale Maxwell stresses 𝒟Max becomes comparable to 𝒟Rey, but has mostly negative values. It therefore compensates for 𝒟Rey. Surprisingly, this already occurs at Re ∼ 60, where no SSD is present. The direct influence of the large-scale magnetic field (𝒟BB) appears to be significant only near the surface at high Re, where it has a destructive effect. For the S runs, the contribution of 𝒟Rey is not as effectively quenched as in the corresponding M runs. The magnetic influence primarily comes through the 𝒟Max contribution, which has a destructive effect throughout most of the convection zone. Together with the destructive contribution of 𝒟mer, it balances 𝒟Rey.
From this differential rotation energy balance, we can deduce why the differential rotation is mostly quenched by the LSD and not the SSD alone. The quenching of 𝒟Rey appears to play an important role here. Only the large-scale field can effectively quench this contribution, thus preventing the development of strong differential rotation. Additionally, the small-scale magnetic field, whether generated by tangling or by an SSD, creates a destructive term, 𝒟Max, which further suppresses the generation of differential rotation.
In theory, Maxwell stresses could also act similarly to Reynolds stresses in generating differential rotation; we found that their contribution is always destructive, however. Previous studies by Käpylä et al. (2017a) showed that the contribution of the Reynolds stress is balanced by the contribution of meridional circulation, and that this balance shifts to a balance of Reynolds and Maxwell stress contributions. This finding was confirmed by HK21 and HKS22. However, the latter authors mostly attributed this change in balance to the presence of an SSD, whereas we find that this is already the case at moderate ReM, where no SSD is present.
The finding that large-scale magnetic fields suppress differential rotation dates back to early magnetoconvection models (e.g. Gilman 1983), but also to many theoretical calculations. Quenching of the Λ effect by magnetism was intensively studied in mean-field models (e.g. Kitchatinov et al. 1994a; Kitchatinov 2016; Pipin 2017) and was also confirmed by numerical simulations (Käpylä et al. 2004; Käpylä 2019b). However, the magnetic field will also affect the turbulent viscosity in these mean-field models (e.g. Kitchatinov et al. 1994b), and therefore, differential rotation can also be enhanced (Kitchatinov 2016). Quenching of the Λ effect by SSD was found to be milder than by a corresponding large-scale magnetic field with the same strength in simplified numerical simulations (Käpylä 2019c).
The importance of Busse columns (or banana cells) for the generation of differential rotation was previously pointed out by other authors (e.g. Hotta et al. 2015; Featherstone & Hindman 2016; Matilsky et al. 2020; Bekki et al. 2022; Käpylä 2023). One of their interpretations is that the prominent presence of these large-scale convective structures in simulations hinders the reproduction of the differential rotation of the Sun. Our results are in line with this interpretation because the banana cells seem to cause the differential rotation profile to become more cylindrical, whereas the contours of the Sun’s differential rotation are radial over a considerable range of mid-latitudes (e.g. Schou et al. 1998).
3.6. Magnetic field generation
Next, we studied the evolution of the mean toroidal magnetic field  . We plot in Fig. 13 the butterfly diagrams of Runs 0M, 1M, 2M and 3M; for Run 4M, the time series is too short to form a meaningful diagram. Run 0M shows a very similar mean field evolution as the run of Käpylä et al. (2016): a regular cycle with equatorward migration throughout the convection zone, a fast cycle with poleward migration near the surface close to the equator, and a long cycle that is most pronounced at the bottom of the domain and capable of disturbing the other cycles. This is expected as 0M has the same parameters as the run of Käpylä et al. (2016), except for the use of a Kramers-based heat conduction instead of a prescribed conductivity profile. The dynamo mode with equatorward migration that was first reported in Käpylä et al. (2011b) and further discussed in Käpylä et al. (2013) can clearly be explained by an αΩ Parker dynamo wave (e.g. Warnecke et al. 2014, 2018). However, to obtain the exact period, many other turbulent transport coefficients have to be considered (Warnecke et al. 2021). The fast poleward dynamo mode could be identified as being of α2 type (Käpylä et al. 2016; Warnecke et al. 2021), while the type of the long-period mode is currently unclear (Käpylä et al. 2016; Gent et al. 2017).
. We plot in Fig. 13 the butterfly diagrams of Runs 0M, 1M, 2M and 3M; for Run 4M, the time series is too short to form a meaningful diagram. Run 0M shows a very similar mean field evolution as the run of Käpylä et al. (2016): a regular cycle with equatorward migration throughout the convection zone, a fast cycle with poleward migration near the surface close to the equator, and a long cycle that is most pronounced at the bottom of the domain and capable of disturbing the other cycles. This is expected as 0M has the same parameters as the run of Käpylä et al. (2016), except for the use of a Kramers-based heat conduction instead of a prescribed conductivity profile. The dynamo mode with equatorward migration that was first reported in Käpylä et al. (2011b) and further discussed in Käpylä et al. (2013) can clearly be explained by an αΩ Parker dynamo wave (e.g. Warnecke et al. 2014, 2018). However, to obtain the exact period, many other turbulent transport coefficients have to be considered (Warnecke et al. 2021). The fast poleward dynamo mode could be identified as being of α2 type (Käpylä et al. 2016; Warnecke et al. 2021), while the type of the long-period mode is currently unclear (Käpylä et al. 2016; Gent et al. 2017).
 |
Fig. 13. Time evolution of the mean toroidal magnetic field |
When Re and ReM are increased, the dynamo solutions are affected: The clear equatorward migration vanishes for all runs starting from 1M. This is most likely due to changes in the differential rotation profile (see the discussion below). The two other modes still exist in the higher ReM regime, however. For the highest values of ReM (4M), the time series is unfortunately too short to identify the dynamo cycles safely. The fast dynamo mode is clearly visible in the 1M and 2M runs as well, and even in the 3M run. That this mode is still visible in Run 3M as well supports our interpretation that this is an α2 type dynamo because, as discussed in Sect. 3.5, the differential rotation becomes very weak at these high ReM. The long-cycle dynamo mode is rather irregular and mostly pronounced in field strength, but it also develops polarity reversals. Comparing the butterfly diagrams of 1M and 2M, we find that they look very similar, in particular near the bottom of the domain and at higher latitudes. In summary, an increase in the Reynolds numbers does not strongly affect the short and long cycles, which still generate significant mean magnetic fields, but it causes the equatorward migrating medium-length mode to vanish.
To investigate why this mode vanishes, we inspected the changes in the differential rotation profile in more detail roughly at the latitudinal and radial locations at which the previously found equatorward migrating dynamo mode is generated (see Fig. 14). The minimum of Ω at r = 0.9 and 25° latitude is very pronounced in the 0M run, it is already much weaker in 1M and 2M, but it has vanished completely in the run with the highest ReM (3M). This fits our hypothesis well that the negative shear in this region generates the equatorward migrating dynamo mode seen in 0M (Warnecke et al. 2014, 2018); accordingly, when the shear is sufficiently weakened, this dynamo mode vanishes. To determine which dynamo is at work in these simulations, we need to measure the turbulent transport coefficients as in Warnecke et al. (2018) and analyze them via a mean-field model as in Warnecke et al. (2021). This analysis is currently under development and will be presented in a possible follow-up study.
 |
Fig. 14. Radial profile of the differential rotation Ω/Ω0 of all M runs. We show the radial profile at 25° latitude, which coincides with the local minimum of Ω, causing the equatorward migrating magnetic field pattern in Run 0M. |
To inspect at which locations the LSD and the SSD operate in our runs, we show in Fig. 15 meridional plots of the azimuthally averaged magnetic energy density of the mean and fluctuating fields separately. We recall that the magnetic fluctuations in Runs 0M and 1M are entirely generated by the tangling of the large-scale field, because no SSD operates in these runs. In Run 0M, the large-scale field is mostly generated at medium to high latitudes near the middle of the convection zone, which is consistent with earlier findings of runs with similar parameters (Warnecke et al. 2014, 2018; Käpylä et al. 2016). The weaker field near the bottom of the domain causes the long-term variation shown in Fig. 13. The corresponding small-scale field is also located at medium to high latitudes, as to be expected from the large-scale field. However, near the bottom of the domain, no small-scale field is generated because the convective motions in this area are weak (see Sect. 3.3). For the M runs with higher ReM, the mean field at medium latitudes gradually vanishes and instead becomes dominant near the bottom of the domain. The small-scale field for small ReM is mostly located at high latitudes, but it gradually becomes stronger near the equator. This increase is partly due to tangling as in 1M, but in particular for higher ReM because the SSD operates in this area, as seen in Runs 2S and 3S. At the locations where the small-scale field is strong, the enthalpy flux and the kinetic energy also reach a maximum, as shown in Fig. 16 for the enthalpy flux 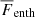 . Such a concentration of
. Such a concentration of 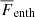 near the equator was also observed in Käpylä et al. (2019) and Viviani & Käpylä (2021). The maximum of the small-scale field in these areas is therefore probably due to the enhanced convective motions. However, this is only true for the S runs. In the M runs, the situation is slightly different. In Run 2M, where an SSD is already present, we indeed see a concentration of small-scale field near the equator, similar to 2S, but also at higher latitudes, where the large-scale field is strong. The small-scale field still seems to be connected with the entropy flux, as the distribution of
near the equator was also observed in Käpylä et al. (2019) and Viviani & Käpylä (2021). The maximum of the small-scale field in these areas is therefore probably due to the enhanced convective motions. However, this is only true for the S runs. In the M runs, the situation is slightly different. In Run 2M, where an SSD is already present, we indeed see a concentration of small-scale field near the equator, similar to 2S, but also at higher latitudes, where the large-scale field is strong. The small-scale field still seems to be connected with the entropy flux, as the distribution of 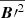 resembles the distribution of
resembles the distribution of 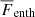 .
.
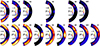 |
Fig. 15. Time-averaged mean magnetic energy of the mean fields |
 |
Fig. 16. Time-averaged radial enthalpy flux |
For the high-ReM runs (3M and 4M), the small-scale field is not concentrated near the equator, as might be expected from their corresponding S runs. However, the distribution of 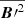 here also somewhat resembles the distribution of
here also somewhat resembles the distribution of 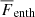 , at least in terms of a minimum near the equator.
, at least in terms of a minimum near the equator.
Furthermore, even though the mean field is very strong near the bottom of the domain, the small-scale field is nearly zero. This is most likely due to the lack of strong convective motions there. Wes can explain the strong mean field at the bottom with the possibility that the field is generated above and then transported down by turbulent pumping or diffusion, and it finally slowly diffuses into this nearly turbulence-free zone, where it can survive for a long time because of the lack of strong turbulent diffusion. As another possibility, the field can be generated locally by the very strong shear flow, which only needs a weak α counterpart to form a dynamo loop.
In Runs 4M, 4M2, and 4S, both the mean field and the small-scale field are mostly concentrated in the northern hemisphere. This is probably due to the short integration time. However, even in these runs, a band of weak small-scale magnetic field appears near the bottom of the domain. Compared to Runs 2S and 3S, the SSD in 4S has a larger volume-filling factor in the northern hemisphere that spreads to higher latitudes and outside the tangent cylinder. To summarize, the SSD is mostly active near the equator in the S runs and 2M, but not in 3M and 4M. The 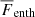 and
and 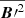 distributions are similar, which indicates that SSD and tangling are both strong where the convection is strong.
distributions are similar, which indicates that SSD and tangling are both strong where the convection is strong.
3.7. Kinetic and current helicities
One of the most important turbulent dynamo processes is the α effect (Steenbeck et al. 1966). Its strength can be estimated by the kinetic helicity density 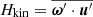 , ω′=curl u′, and the magnetic influence on it by the current helicity density
, ω′=curl u′, and the magnetic influence on it by the current helicity density 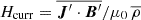 (e.g. Pouquet et al. 1976), here defined with a
(e.g. Pouquet et al. 1976), here defined with a 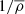 factor,
factor,
where τc is the turbulent correlation time, which in general does not need to be the same for the first and second term. In this work, we only studied these proxies (Figs. 17 and 18) and left the detailed analysis of the α tensor and other turbulent transport coefficients to a future study.
As usual in rotating convection simulations, Hkin is predominantly negative in the upper half of the convection zone and positive below in the northern hemisphere while having the same pattern but opposite sign in the southern hemisphere (see Fig. 17). We find that the profile of Hkin is not much influenced by the increase in Re, nor does it show a large difference between the S and M runs. Only the peak values of Hkin show a tendency to increase with increasing Re, and in Run 0M, the maxima near the equator extend farther into the convection zone.
 |
Fig. 17. Time-averaged kinetic helicity |
The current helicity Hcurr exhibits a different behavior. Similar to earlier results (e.g., Warnecke & Käpylä 2020), it is positive near the surface in the northern hemisphere, negative in the bulk, and again positive near the bottom of the domain for most of the M runs while having an analogous profile but with the opposite sign in the southern hemisphere. When Re is increased, it leaves the profile mostly unchanged, but leads to an increase in the peak values, at least when we compare 0M and 1M with 2M and 3M.
Interestingly, the current helicity Hcurr (see Fig. 18) from the pure SSD runs follows the pattern of Hkin rather than that of Hcurr of the corresponding M runs. The fact that the sign of Hcurr is opposite in the cases with and without LSD is in line with the results of Warnecke et al. (2012), who explained this sign change from simulations (Warnecke et al. 2011) and observations (Brandenburg et al. 2011) by a simple model. This suggests that a sign change in Hcurr is to be expected when an LSD is absent compared to when it is present.
 |
Fig. 18. Time-averaged current helicity |
Hcurr generated by the SSD is clearly lower than the one generated by an LSD. Furthermore, |Hcurr| is always (except for 4M) lower than |Hkin|, and it is therefore not expected to influence the α effect much, following Eq. (29). However, Warnecke & Käpylä (2020) showed that this approximation does not hold when comparing with α determined by the test-field method when the magnitudes of Hcurr and Hkin become comparable.
4. Conclusions
We have conducted global convective dynamo simulations of solar-like stars, wherein we varied the viscosity, magnetic diffusivity, and SGS heat diffusivity to examine how the solutions depend on the fluid and magnetic Reynolds numbers. This enabled us to investigate the interaction between SSD and LSD and their effects on the overall dynamics. As a novel approach, we additionally investigated SSD in LSD-capable systems in isolation by suppressing the large-scale magnetic field.
As an outcome of these simulations, we identified the following results: Magnetic runs with ReM ≥ 140 can excite an SSD, and its magnetic energy becomes comparable to that of the LSD at ReM ≈ 550. The total magnetic field energy appears to reach a maximum at ReM = 120 and decreases for runs with higher ReM. Although the SSD becomes stronger at higher ReM, the energy in the fluctuating field decreases mildly. As the mean field decreases by more than half compared to Runs 2M and 3M, the total magnetic energy is significantly weaker.
The scale of large-scale convective cells, also known as banana cells, does not depend on Re or on the presence of LSD or SSD. The depth of the subadiabatic layers is mostly independent of Re, except at mid-latitudes. However, the Deardorff zone becomes thinner, allowing for a thicker overshoot and radiative zone for higher Re. The turbulent velocity urms′ increases with Re until Re = 120, after which it slightly decreases, even in the H runs. This indicates that the decrease at high Re is not due to SSD or LSD, as found by HK21 and HKS22. The magnetic field in our simulations does not reach strong superequipartition with respect to turbulent kinetic energy. Additionally, at small scales, the magnetic field is mostly at subequipartition. Furthermore, the energy in the large convective scales mildly decreases with Re, but this occurs in the H runs as well, suggesting that it cannot be attributed to the effects of SSD or LSD.
Differential rotation is strongly quenched in M runs with high Re, primarily due to the magnetic field of LSD rather than of SSD. This agrees with many earlier analytical and numerical results (e.g. Gilman 1983; Kitchatinov et al. 1994a; Käpylä et al. 2004; Kitchatinov 2016; Pipin 2017; Käpylä 2019b). The magnetic field affects the angular momentum distribution via the suppression of the Reynolds stresses and the emergence of strong Maxwell stresses. The effects of the Maxwell stresses are dominated by the contributions of the small-scale fields, which are mostly due to tangling of the large-scale field and not the SSD, however. This contradicts the recent findings of (Hotta & Kusano 2021; Hotta et al. 2022), who argued that SSD is the most important driver of fluctuations and that through them, it affects the angular momentum balance.
The evolution of large-scale fields only shows a weak dependence on ReM, with the equatorward migrating field mode disappearing for ReM ≥ 60 due to the weaker shear at mid-latitudes. The irregular low-frequency mode at the bottom of the domain persists, and even the high-frequency mode near the surface is present in all relevant M runs. SSD is strongest in areas where the enthalpy flux is maximum, typically near the equator, where the turbulent energy reaches its peak. The profiles of kinetic and current helicity do not vary much with ReM, but there is a tendency for a mild increase in their peak values with ReM. Interestingly, the current helicity generated by pure SSD has the opposite sign to that of LSD. Our work showed that it is important to study the SSD-LSD interaction to fully understand the dynamics in the Sun and other stars.
Acknowledgments
We thank the anonymous referee for their very useful comments and suggestions. The simulations have been carried out on SuperMUC-NG using the PRACE project Access Call 20 INTERDYNS project, on the Max Planck supercomputer at RZG in Garching and in the facilities hosted by the CSC–IT Center for Science in Espoo, Finland, which are financed by the Finnish ministry of education. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement n:os 818665 “UniSDyn” and 101101005 “SYCOS”), and has been supported from the Academy of Finland Centre of Excellence ReSoLVE (project number 307411). This work was done in collaboration with the COFFIES DRIVE Science Center.
References
- Alam, S., Verma, M. K., & Joshi, P. 2023, Phys. Rev. E, 107, 055106 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [Google Scholar]
- Barekat, A., & Brandenburg, A. 2014, A&A, 571, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barik, A., Triana, S. A., Calkins, M., Stanley, S., & Aurnou, J. 2023, Earth Space Sci., 10, e2022EA002606 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, Y., Cameron, R. H., & Gizon, L. 2022, A&A, 666, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L., & Orozco Suárez, D. 2019, Liv. Rev. Sol. Phys., 16, 1 [Google Scholar]
- Bolgiano, R. J. 1959, J. Geophys. Res., 64, 2226 [NASA ADS] [CrossRef] [Google Scholar]
- Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A. 1992, Phys. Rev. Lett., 69, 605 [CrossRef] [Google Scholar]
- Brandenburg, A. 2016, ApJ, 832, 6 [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Subramanian, K., Balogh, A., & Goldstein, M. L. 2011, ApJ, 734, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Strugarek, A., Noraz, Q., et al. 2022, ApJ, 926, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Busse, F. H. 1970, J. Fluid Mech., 44, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Busse, F. H. 1976, Icarus, 29, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability (Oxford: Clarendon) [Google Scholar]
- Charbonneau, P. 2014, ARA&A, 52, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., & Fang, F. 2014, ApJ, 789, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Featherstone, N. A., & Hindman, B. W. 2016, ApJ, 818, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Gent, F. A., Käpylä, M. J., & Warnecke, J. 2017, Astron. Nachr., 338, 885 [NASA ADS] [Google Scholar]
- Gilman, P. A. 1983, ApJS, 53, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasoge, S. M., Duvall, T. L., & Sreenivasan, K. R. 2012, Proc. Natl. Acad. Sci., 109, 11928 [Google Scholar]
- Hotta, H. 2017, ApJ, 843, 52 [Google Scholar]
- Hotta, H., & Kusano, K. 2021, Nat. Astron., 5, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Hotta, H., Rempel, M., & Yokoyama, T. 2015, ApJ, 798, 51 [Google Scholar]
- Hotta, H., Rempel, M., & Yokoyama, T. 2016, Science, 351, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Hotta, H., Kusano, K., & Shimada, R. 2022, ApJ, 933, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J. 2019a, A&A, 631, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J. 2019b, A&A, 622, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J. 2019c, Astron. Nachr., 340, 744 [CrossRef] [Google Scholar]
- Käpylä, P. J. 2021, A&A, 655, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J. 2023, A&A, 669, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Tuominen, I. 2004, A&A, 422, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., & Hackman, T. 2011a, ApJ, 742, 34 [CrossRef] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2011b, Astron. Nachr., 332, 883 [CrossRef] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Cole, E., Warnecke, J., & Brandenburg, A. 2013, ApJ, 778, 41 [CrossRef] [Google Scholar]
- Käpylä, P. J., Käpylä, M. J., & Brandenburg, A. 2014, A&A, 570, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, M. J., Käpylä, P. J., Olspert, N., et al. 2016, A&A, 589, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Käpylä, M. J., Olspert, N., Warnecke, J., & Brandenburg, A. 2017a, A&A, 599, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Rheinhardt, M., Brandenburg, A., et al. 2017b, ApJ, 845, L23 [CrossRef] [Google Scholar]
- Käpylä, P. J., Viviani, M., Käpylä, M. J., Brandenburg, A., & Spada, F. 2019, Geophys. Astrophys. Fluid Dyn., 113, 149 [CrossRef] [Google Scholar]
- Käpylä, P. J., Browning, M. K., Brun, A. S., Guerrero, G., & Warnecke, J. 2023, Space Sci. Rev., 219, 58 [CrossRef] [Google Scholar]
- Karak, B. B., Käpylä, P. J., Käpylä, M. J., et al. 2015, A&A, 576, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitchatinov, L. L. 2016, Astron. Lett., 42, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., Ruediger, G., & Kueker, M. 1994a, A&A, 292, 125 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., Pipin, V. V., & Rüdiger, G. 1994b, Astron. Nachr., 315, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Mantere, M. J., Käpylä, P. J., & Hackman, T. 2011, Astron. Nachr., 332, 876 [NASA ADS] [Google Scholar]
- Matilsky, L. I., Hindman, B. W., & Toomre, J. 2020, ApJ, 898, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, N. J., Brown, B. P., Brun, A. S., Miesch, M. S., & Toomre, J. 2013, ApJ, 762, 73 [Google Scholar]
- Oboukhov, A. 1959, Akademiia Nauk SSSR Doklady, 128, 1246 [Google Scholar]
- Olspert, N., Lehtinen, J. J., Käpylä, M. J., Pelt, J., & Grigorievskiy, A. 2018, A&A, 619, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pencil Code Collaboration (Brandenburg, A., et al.) 2021, JOSS, 6, 2807 [CrossRef] [Google Scholar]
- Pipin, V. V. 2017, MNRAS, 466, 3007 [Google Scholar]
- Pouquet, A., Frisch, U., & Léorat, J. 1976, J. Fluid Mech., 77, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2014, ApJ, 789, 132 [Google Scholar]
- Rempel, M., Schüssler, M., & Knölker, M. 2009, ApJ, 691, 640 [Google Scholar]
- Rempel, M., Bhatia, T., Bellot Rubio, L., & Korpi-Lagg, M. J. 2023, Space Sci. Rev., 219, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys., 7, 2 [Google Scholar]
- Roberts, P. H. 1968, Phil. Trans. R. Soc. London Ser. A, 263, 93 [Google Scholar]
- Rüdiger, G. 1989, Differential Rotation and Stellar Convection. Sun and Solar-type Stars (Berlin: Akademie Verlag) [Google Scholar]
- Schekochihin, A. A., Haugen, N. E. L., Brandenburg, A., et al. 2005, ApJ, 625, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [Google Scholar]
- Singh, N. K., Rogachevskii, I., & Brandenburg, A. 2017, ApJ, 850, L8 [Google Scholar]
- Squire, J., & Bhattacharjee, A. 2015, Phys. Rev. Lett., 115, 175003 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforsch. Teil A, 21, 369 [Google Scholar]
- Stix, M. 2002, The Sun: An Introduction (Berlin: Springer) [Google Scholar]
- Tobias, S. M., & Cattaneo, F. 2013, Nature, 497, 463 [Google Scholar]
- Vainshtein, S. I., & Cattaneo, F. 1992, ApJ, 393, 165 [Google Scholar]
- Väisälä, M. S., Pekkilä, J., Käpylä, M. J., et al. 2021, ApJ, 907, 83 [Google Scholar]
- Viviani, M., & Käpylä, M. J. 2021, A&A, 645, A141 [EDP Sciences] [Google Scholar]
- Viviani, M., Warnecke, J., Käpylä, M. J., et al. 2018, A&A, 616, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnecke, J., & Käpylä, M. J. 2020, A&A, 642, A66 [EDP Sciences] [Google Scholar]
- Warnecke, J., Brandenburg, A., & Mitra, D. 2011, A&A, 534, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnecke, J., Brandenburg, A., & Mitra, D. 2012, JSWSC, 2, A11 [Google Scholar]
- Warnecke, J., Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2013, ApJ, 778, 141 [Google Scholar]
- Warnecke, J., Käpylä, P. J., Käpylä, M. J., & Brandenburg, A. 2014, ApJ, 796, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., Käpylä, P. J., Käpylä, M. J., & Brandenburg, A. 2016, A&A, 596, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnecke, J., Rheinhardt, M., Tuomisto, S., et al. 2018, A&A, 609, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnecke, J., Rheinhardt, M., Viviani, M., et al. 2021, ApJ, 919, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., Korpi-Lagg, M. J., Gent, F. A., & Rheinhardt, M. 2023, Nat. Astron., 7, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, J.-H., & Huang, S.-D. 2022, J. Fluid Mech., 942, A19 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, M., & Calkins, M. A. 2022, J. Fluid Mech., 951, A24 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Diffusivity profiles
To avoid numerical artifacts near the latitudinal boundaries, we apply a profile for the diffusivities ν and η, increasing towards these boundaries. The profiles’ shape is shown in Fig. A.1, it is determined by its width Δθν and Δθη, respectively, and the ratio between the boundary value and the value at the equator,
We choose the minimal possible values for Δθν, Δθη, and Δνη, which keep the runs stable. It turns out that these adjustments are needed for runs with Re ≥ 61, see Table 1 for details.
Furthermore, for high resolution simulations (Re ≥ 260), the runs have a tendency to produce vortex-like structures at high latitudes. They are as such an interesting phenomenon (Käpylä et al. 2011a; Mantere et al. 2011), but they decrease the time step significantly. Hence, we decided to suppress them in this work by choosing Δθν = 17° and postpone their detailed study to the future.
 |
Fig. A.1. Latitudinal diffusivity profiles shown for viscosity ν with width Δθν = 5° (solid line) and 17° (dashed), indicated by vertical red lines. νm is the equatorial value of ν. |
Appendix B: Slope-limited diffusion
Besides the constant diffusivity ν, the H runs need additional explicit numerical diffusion to be stable. Our choice of using an enhanced luminosity at the bottom boundary, (see Käpylä et al. 2013, for details), causes the local Mach number Ma = |u|/cs to increase near the surface to unusually high values. In the H runs, this can lead to numerical instabilities whereas the M and S runs are stable enough due to the presence of the magnetic field and hence do not need any additional diffusion. To let the numerical diffusion act only in regions, where it is needed, we employ slope-limited diffusion (SLD), newly implemented to the Pencil Code. It turns out that with our choice of parameters as specified below, we are able to stabilize the runs without influencing the overall dynamics much. In the following, we will briefly describe implementation and parameter choice. Thereby, we follow roughly Rempel et al. (2009) and Rempel (2014).
 |
Fig. B.1. Visualization of Eq. (B.9): Q as function of the slope ratio ℛ for various hsld (colored lines) with nsld = 1 (solid) and nsld = 2 (dashed). |
The main idea is to define the diffusive flux f of a velocity component u based on a slope limiter. At the cell interface k + 1/2, it is given by
where the subscript k indicates the cell or grid-point in one particular coordinate direction, 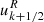 and
and 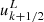 are the right and left values at the cell interface of the velocity component and csld is the characteristic speed, defined below. uR and uL are defined via
are the right and left values at the cell interface of the velocity component and csld is the characteristic speed, defined below. uR and uL are defined via
with the estimated slopes
where the minmod function is defined as
meaning
The diffusive flux is additionally adjusted by the factor
which controls its non-linearity by the power nsld and has values between 0 and 1. The parameter hsld sets the strength of the diffusion for a given slope. If hsld = ∞, i.e. Q = 1, Eq. (B.1) represent a linear 2-order Lax-Friedrichs-scheme. The lower hsld, the less diffusive is the scheme. The power nsld can reduce the diffusion even further for small slopes. The slope ratio ℛ is defined as
It relates the u difference at the cell interface to the difference between the cell centers, therefore indicating the relative slope strength. Equation B.9 implies that in regions where ℛk + 1/2 ≥ 1/hsld, the diffusive flux is maximal and for regions, where ℛk + 1/2 < 1/hsld the diffusive flux is reduced, see Fig. B.1 for an illustration. In this work, we use hsld = 2 and nsld = 1 for the density and hsld = 1 and nsld = 2 for all velocity components. We note here that in Rempel et al. (2009) a similar scheme is used, which corresponds to hsld = 1 and nsld = 2. In the work of Rempel (2014), a different expression for Q(ℛ) is used – see their Eq. (10), employing only one parameter instead of two. Detailed tests indicate no significant differences between his and our scheme.
The characteristic speed is derived from the signal (advection and wave) speeds in the system:
where vA is the Alfvén speed, and the weights w*sld can be chosen depending on the nature of the problem. In this work, we set 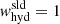 and
and 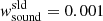 ; there is no magnetic contribution because we use SLD only for purely hydrodynamic runs. The intercell values of csld are calculated by linear interpolation:
; there is no magnetic contribution because we use SLD only for purely hydrodynamic runs. The intercell values of csld are calculated by linear interpolation:
Connecting the strength of the SLD term to the signal speeds via csld makes an extra time step constraint unnecessary.
The calculation of the diffusive fluxes is now performed at each grid point for all three directions separately. With these three fluxes we can for a scalar quantity form a diffusive flux vector fsld = (fq), where q indicates the coordinate direction. If the diffusive fluxes are calculated for a vector quantity, then each vector component builds its own flux vector and these together form a diffusive flux tensor ℱsld.
Finally, the diffusive fluxes are added to the momentum and continuum equations via
where ℱsldu is the SLD tensor for the velocity and fsldρ is the SLD vector for the density. For simplicity, we use 2nd order finite differences for the divergence (∇2nd):
where fsld stands for fsldρ or for one of the column vectors of ℱsldu and q signifies the coordinate, i.e. x, y or z. qk denotes the grid point under consideration in the direction of the coordinate q and qk+ and qk− are short for qk + 1/2 and qk − 1/2, respectively. For brevity, we show only that argument of fq, with respect to which the derivation is performed. For ℱsldu, we calculate the divergence analogously for each component.
For spherical coordinates, Eq. (B.14) is modified and reads for an SLD vector such as fsldρ
for an SLD tensor such as ℱsldu
where the superscripts of f indicate the quantity the diffusive flux is calculated for, e.g. r for ur.
The viscous heat due to SLD, ℋsld, is defined at grid point k as
where p, q denote the Cartesian coordinates. In spherical coordinates, this expression will be modified taking into account the appropriate derivatives. We note here that the viscous heating implementation in MURAM (Rempel et al. 2009; Rempel 2014) only takes into account the derivative of the velocity and not the momentum, i.e. it neglects the changes in the density.
Using a mass diffusion introduces an additional mass flux, for which we compensated in the momentum and energy equations.
Appendix C: Spectra of banana cells
To investigate how the scales of the banana cells depend on the Reynolds numbers, we calculate the power spectra of the kinetic energy density of the radial flow, Ekinr, near the surface (r = rs ≡ 0.98 R). For this, we cut out a thin latitudinal band around the equator (± 7.5°) and calculate the power spectrum of Ekinr, averaged over latitude and time, as a function of the angular order m for each run. We rely on the definition
where the tilde and the operator FFT indicate the Fourier transform. The spectra are shown in Fig. C.1 for all runs, including the Re dependence of the m of their maxima. Only a weak Re dependence is visible. The spectra of the M runs, except M0, peak around m = 40, whereas those of the H runs peak at slightly lower m ≈ 32. The S run spectra peak at m = 32 for moderate ReM and at m = 40 for high ReM.
 |
Fig. C.1. Longitudinal power spectra of the radial kinetic energy density, |
All Tables
All Figures
 |
Fig. 1. Radial velocity ur at r = 0.98 R with a low-latitude cutout for all M runs in the saturated stage. The wedge is duplicated to form a half-sphere. |
| In the text | |
 |
Fig. 2. Radial magnetic field Br at r = 0.98 R for all M runs. Otherwise the same as Fig. 1. |
| In the text | |
 |
Fig. 3. Azimuthal magnetic field Bϕ at r = 0.98 R for all M runs with an SSD and the corresponding S runs. Otherwise the same as Fig. 1. |
| In the text | |
 |
Fig. 4. Dependence of the kinetic and magnetic energy densities on Re. In the top panel, we show |
| In the text | |
 |
Fig. 5. Visualization of the four zones formed in the simulations: buoyancy (BZ, yellow), Deardorff (DZ, red), overshoot (OZ, green), and radiative zone (RZ, dark blue) (see Sect. 3.3 for definitions). |
| In the text | |
 |
Fig. 6. Radial profile of the latitudinally averaged turbulent velocity urms′ of all runs. The colors indicate the different run sets with different Re as indicated. The solid lines show M runs, the dotted lines show S runs and the dashed lines show H runs, The thick green line indicates the values from the solar model of Stix (2002) based on mixing-length theory. The inset shows urms′ at a fixed radius r = 0.9 R as a function of Re. There, we overplot urms′ of Hotta & Kusano (2021) using the Re estimated in HKS22 (solid red) and a reestimate according to Eq. (16) (dashed). |
| In the text | |
 |
Fig. 7. Radial profile of the normalized latitudinally averaged turbulent magnetic field Brms′/Beq of all runs. The color-coding and line styles are the same as in Fig. 6, with the exception of Run 4M2 (purple dashed line). |
| In the text | |
 |
Fig. 8. Spectra of kinetic (a) and magnetic (b) energy density along with their ratio (c) near the surface, r = 0.98 R, all excluding the m = 0 contribution. As before the solid lines show M runs, the dotted lines show S runs and the dashed lines show H runs, while different colors indicate run sets with distinct Re. Panel (d) highlights the Re dependence of the kinetic and magnetic spectra for l = 10 and 100. |
| In the text | |
 |
Fig. 9. Differential rotation Ω/Ω0, with |
| In the text | |
 |
Fig. 10. Differential rotation of all runs near the surface (r = 0.98 R). At the top we plot Ω/Ω0 as function of latitude. As before, the solid lines show M runs, dotted lines show S runs and the dashed lines show H runs, while the colors indicate the run sets with different Re. At the bottom, we plot Ω/Ω0 at the equator (θ = π/2) as a function of Re. |
| In the text | |
 |
Fig. 11. Time-averaged contributions to the differential rotation energy evolution for Runs 0M and 3M, as given in Eqs. (21)–(25). The contributions are shown in units of J/m3s. |
| In the text | |
 |
Fig. 12. Contributions to the differential rotation energy evolution averaged in time and latitude for all run sets (0 – 4) as functions of r/R (see Eqs. (21)–(25)). The bottom rightmost panel shows the contributions as functions of Re at r/R = 0.96 (the vertical line in the other panels). |
| In the text | |
 |
Fig. 13. Time evolution of the mean toroidal magnetic field |
| In the text | |
 |
Fig. 14. Radial profile of the differential rotation Ω/Ω0 of all M runs. We show the radial profile at 25° latitude, which coincides with the local minimum of Ω, causing the equatorward migrating magnetic field pattern in Run 0M. |
| In the text | |
 |
Fig. 15. Time-averaged mean magnetic energy of the mean fields |
| In the text | |
 |
Fig. 16. Time-averaged radial enthalpy flux |
| In the text | |
 |
Fig. 17. Time-averaged kinetic helicity |
| In the text | |
 |
Fig. 18. Time-averaged current helicity |
| In the text | |
 |
Fig. A.1. Latitudinal diffusivity profiles shown for viscosity ν with width Δθν = 5° (solid line) and 17° (dashed), indicated by vertical red lines. νm is the equatorial value of ν. |
| In the text | |
 |
Fig. B.1. Visualization of Eq. (B.9): Q as function of the slope ratio ℛ for various hsld (colored lines) with nsld = 1 (solid) and nsld = 2 (dashed). |
| In the text | |
 |
Fig. C.1. Longitudinal power spectra of the radial kinetic energy density, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



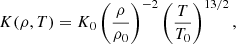
![$$ \begin{aligned} \tilde{\Omega }=\Omega _0/\Omega _\odot , \quad \mathrm{Ta}=\left[2\Omega _0 D^2/\nu \right]^2, \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq2.gif)
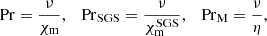
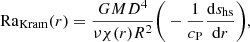
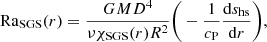
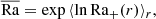
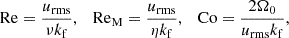
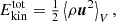
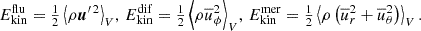
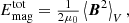
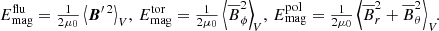
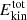
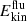
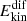
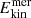
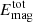
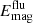
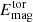
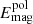
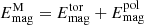
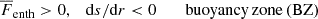
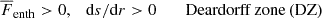
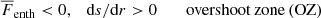
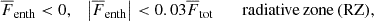
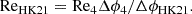
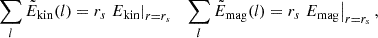
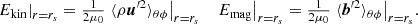
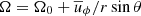
![$$ \begin{aligned} {\partial _t}\left(s^2\overline{\rho }\Omega \right) =-\boldsymbol{\nabla }\cdot s &\left[s\overline{\rho \boldsymbol{u}}\Omega +\overline{{\left(\rho \boldsymbol{u}\right)}^\prime {u}^\prime _\phi } -2\nu \overline{\rho }\overline{{\mathbf S}}\cdot \hat{\boldsymbol{e}}_\phi \right.\nonumber \\&\left.-\mu _0^{-1}\left(\overline{\boldsymbol{B}}\,\overline{B}_{\phi } +\overline{\boldsymbol{B}^{\prime } B_\phi ^{\prime }}\,\right)\right], \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq70.gif)
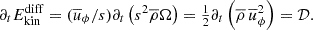
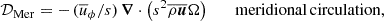
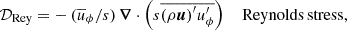
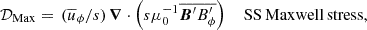
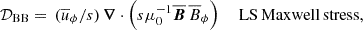
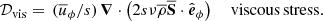
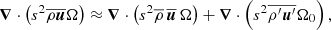
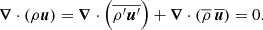
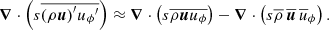
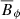
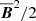
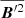
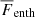
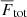
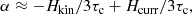
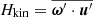
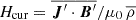
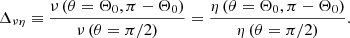
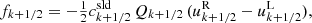
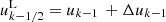
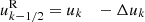
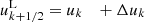
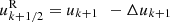
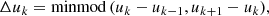
![$$ \begin{aligned} \mathrm{minmod}\,(a,b) = {\textstyle {1\over 2}}\mathrm{sgn}\,(a) \max \left[0,\min \left(|a|,\mathrm{sgn}\,(a)\, b\right)\right], \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq112.gif)
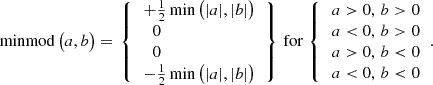
![$$ \begin{aligned} Q_{k+1/2}(\mathcal{R} _{k+1/2}) = \left[\min (1, h_{\rm sld}\,\mathcal{R} _{k+1/2})\right]^{n_{\rm sld}}, \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq114.gif)
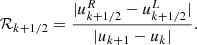
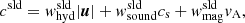
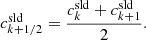
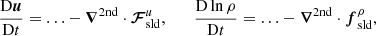
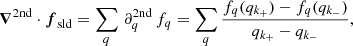
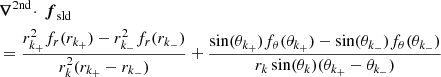
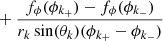
![$$ \begin{aligned}[{\boldsymbol{\nabla }}^{2\mathrm {nd}}\cdot {\boldsymbol{\mathcal{F} }}_{\rm sld}]_r&=\frac{{r_{k_+}^2} f^r_r({r_{k_+}}) - {r_{k_-}^2}f^r_r({r_{k_-}})}{r^2_k ({r_{k_+}}-{r_{k_-}})}\nonumber \\&+\frac{\sin ({\theta _{k_+}})f^r_\theta ({\theta _{k_+}})- \sin ({\theta _{k_-}})f^r_\theta ({\theta _{k_-}})}{r_k\sin (\theta _k) ({\theta _{k_+}}-{\theta _{k_-}})}\nonumber \\&+\frac{f^r_\phi ({\phi _{k_+}}) - f^r_\phi ({\phi _{k_-}})}{r_k\sin (\theta _k) ({\phi _{k_+}} - {\phi _{k_-}})}\\&-\frac{f^\theta _\theta ({\theta _{k_+}}) + f^\theta _\theta ({\theta _{k_-}})}{2 r_k} - \frac{{f^\phi _\phi ({\phi _{k_+}}) + f^\phi _\phi ({\phi _{k_-}})}}{{2 r_k}}\nonumber , \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq124.gif)
![$$ \begin{aligned}[{\boldsymbol{\nabla }}^{2\mathrm nd}\cdot {\boldsymbol{\mathcal{F} }}_{\rm sld}]_\theta&=\frac{{r_{k_+}^2} f^\theta _r({r_{k_+}})- {r_{k_-}^2} f^\theta _r({r_{k_-}})}{r_k^2 ({r_{k_+}}-{r_{k_-}})}\nonumber \\&+\frac{\sin ({\theta _{k_+}})f^\theta _\theta ({\theta _{k_+}})- \sin ({\theta _{k_-}})f^\theta _\theta ({\theta _{k_-}})}{r_k\sin (\theta _k) ({\theta _{k_+}}-{\theta _{k_-}})}\\&+\frac{f^\theta _\phi ({\phi _{k_+}}) -f^\theta _\phi ({\phi _{k_-}})}{r_k\sin (\theta _k) ({\phi _{k_+}}-{\phi _{k_-}})}- \frac{{f^r_\theta ({\theta _{k_+}}) + f^r_\theta ({\theta _{k_-}})}}{{2 r_k}}\nonumber \\&- \frac{{\cot {(\theta _k)}\left(f^\phi _\phi ({\phi _{k_+}}) + f^\phi _\phi ({\phi _{k_-}})\right)}}{{2 r_k}}\nonumber , \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq125.gif)
![$$ \begin{aligned}[{\boldsymbol{\nabla }}^{2\mathrm nd}\cdot {\boldsymbol{\mathcal{F} }}_{\rm sld}]_\phi&= \frac{{r_{k_+}^2} f^\phi _r({r_{k_+}}) - {r_{k_-}^2} f^\phi _r({r_{k_-}})}{r^2_k({r_{k_+}}-{r_{k_-}})}\nonumber \\&+\frac{\sin ({\theta _{k_+}})f^\phi _\theta ({\theta _{k_+}})- \sin ({\theta _{k_-}})f^\phi _\theta ({\theta _{k_-}})}{r_k\sin (\theta _k) ({\theta _{k_+}}-{\theta _{k_-}})}\\&+\frac{f^\phi _\phi ({\phi _{k_+}}) - f^\phi _\phi ({\phi _{k_-}})}{r_k\sin (\theta _k) ({\phi _{k_+}}-{\phi _{k_-}})} - \frac{{f^r_\phi ({\phi _{k_+}}) + f^r_\phi ({\phi _{k_-}})}}{{2 r_k}}\nonumber \\&- \frac{\cot {(\theta _k)}\left(f^\theta _\phi ({\phi _{k_+}}) + f^\theta _\phi ({\phi _{k_-}})\right)}{{2 r_k}},\nonumber \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq126.gif)
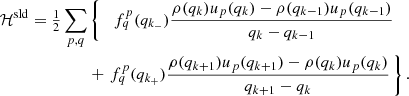
![$$ \begin{aligned} \sum _m \widetilde{E}^r_{\rm kin}(m)&= {\textstyle {1\over 2}}\sum _m \left\langle {\left|\,\mathrm{FFT}\left[\big (u_r\!\sqrt{\rho }\big ) (r_s)\right]\!(m)\right|^2}\right\rangle _{\theta t} \\&= {r_s\over 2}\left\langle {\left(u_r^2\rho \right)(r_s)} \right\rangle _{\theta \phi t}, \nonumber \end{aligned} $$](/articles/aa/full_html/2025/04/aa51085-24/aa51085-24-eq128.gif)