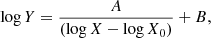| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347190 | |
| Published online | 15 November 2023 | |
Near-infrared emission line diagnostics for AGN from the local Universe to z ∼ 3⋆
1
INAF – Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone, Italy
e-mail: antonello.calabro@inaf.it
2
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
3
NSF’s National Optical-Infrared Astronomy Research Laboratory, 950 N. Cherry Ave., Tucson, AZ 85719, USA
4
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
5
Aix-Marseille Univ., CNRS, CNES, LAM Marseille, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
6
Université Paris-Saclay, Université Paris-Cité, CEA, CNRS, AIM, 91191 Gif-sur-Yvette, France
7
Instituto de Investigación Multidisciplinar en Ciencia y Tecnología, Universidad de La Serena, Raul Bitrán 1305, La Serena 2204000, Chile
8
Departamento de Astronomía, Universidad de La Serena, Av. Juan Cisternas 1200 Norte, La Serena 1720236, Chile
9
Department of Astronomy, The University of Texas at Austin, Austin, TX 78712-1205, USA
10
Dipartimento di Fisica e Astronomia “G. Galilei”, Universitá di Padova, Via Marzolo 8, 35131 Padova, Italy
11
Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
12
George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Texas A& M University, College Station, TX 77843-4242, USA
13
University of Massachusetts Amherst, 710 North Pleasant Street, Amherst, MA 01003-9305, USA
14
Space Telescope Science Institute, 3700 San Martin Dr., Baltimore, MD 21218, USA
15
Institute of Physics, Laboratory of Galaxy Evolution, Ecole Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
16
Laboratory for Multiwavelength Astrophysics, School of Physics and Astronomy, Rochester Institute of Technology, 84 Lomb Memorial Drive, Rochester, NY 14623, USA
17
Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
18
George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
19
Centro de Astrobiología (CAB), CSIC-INTA, Ctra. de Ajalvir km 4, Torrejón de Ardoz, 28850 Madrid, Spain
20
ESA/AURA Space Telescope Science Institute, Baltimore, USA
21
Department of Physics, University of Connecticut, 196 Auditorium Road, Unit 3046, Storrs, CT 06269, USA
22
Department of Physics and Astronomy, University of California, 900 University Ave, Riverside, CA 92521, USA
23
Astronomy Centre, University of Sussex, Falmer, Brighton BN1 9QH, UK
24
Institute of Space Sciences and Astronomy, University of Malta, Msida 2080, Malta
25
Astrophysics Science Division, NASA Goddard Space Flight Center, 8800 Greenbelt Rd, Greenbelt, MD 20771, USA
26
Instituto de Física, Pontificia Universidad Católica de Valparaíso, Casilla, 4059 Valparaíso, Chile
Received:
14
June
2023
Accepted:
5
September
2023
Optical rest-frame spectroscopic diagnostics are usually employed to distinguish between star formation and active galactic nucleus (AGN) powered emission. However, this method is biased against dusty sources, hampering a complete census of the AGN population across cosmic epochs. To mitigate this effect, it is crucial to observe at longer wavelengths in the rest-frame near-infrared (near-IR), which is less affected by dust attenuation and can thus provide a better description of the intrinsic properties of galaxies. AGN diagnostics in this regime have not been fully exploited so far, due to the scarcity of near-IR observations of both AGN and star-forming galaxies, especially at redshifts higher than 0.5. Using Cloudy photoionization models, we identified new AGN – star formation diagnostics based on the ratio of bright near-IR emission lines, namely [SIII] 9530 Å, [CI] 9850 Å, [PII] 1.188 μm, [FeII] 1.257 μm, and [FeII] 1.64 μm to Paschen lines (either Paγ or Paβ), providing simple, analytical classification criteria. We applied these diagnostics to a sample of 64 star-forming galaxies and AGN at 0 ≤ z ≤ 1, and 65 sources at 1 ≤ z ≤ 3 recently observed with JWST-NIRSpec in CEERS. We find that the classification inferred from the near-IR is broadly consistent with the optical one based on the BPT and the [SII]/Hα ratio. However, in the near-IR, we find ∼60% more AGN than in the optical (13 instead of eight), with five sources classified as “hidden” AGN, showing a larger AGN contribution at longer wavelengths, possibly due to the presence of optically thick dust. The diagnostics we present provide a promising tool to find and characterize AGN from z = 0 to z ≃ 3 with low- and medium-resolution near-IR spectrographs in future surveys.
Key words: galaxies: ISM / galaxies: high-redshift / galaxies: evolution / galaxies: Seyfert / galaxies: active
CEERS galaxy sample catalog is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/679/A80
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
For decades, optical spectroscopy of galaxies has been one of the most efficient tools for identifying active galactic nuclei (AGN) in the Universe. This has been possible thanks to a combination of favorable factors. First, optical spectroscopy gives access to the rest-frame ultraviolet (UV) to optical emission of galaxies from z = 0 to z ≃ 6. This spectral range is full of bright emission lines sensitive to the properties of the ionizing sources, and that are exploited to distinguish between ionization driven by an AGN or by young O and B stars (see Kewley et al. 2019 for a review). The best-known star formation (SF) versus AGN diagnostic is the BPT diagram, first introduced by Baldwin et al. (1981), which informs the physical nature of the emitting source by comparing the [N II]/Hα and [O III]/Hβ emission line ratios. Similar diagnostics adopt [S II]/Hα or [O I]/Hα instead of the ionized nitrogen (Veilleux & Osterbrock 1987; Kewley et al. 2001). A second reason is represented by the higher multiplexity and sensitivity reached by optical spectrographs compared to instruments sensitive to other regions of the electromagnetic spectrum. Finally, the atmosphere is mostly transparent in the visible band and thus the observations can be performed mostly from the ground.
Spectroscopy also has the advantage of differentiating the spectral type of AGN and measuring its level of activity, distinguishing between Type 2 and Type 1. The first are characterized by narrow full width at half maximum (FWHM) < 1000 km s−1 emission lines coming from the narrow line region (NLR), and identified through the BPT and similar diagrams. Type 1, in addition to AGN-like narrow emission line ratios, also show broad component (FWHM > 1000 km s−1) permitted lines. These are generated in gas clouds orbiting closer to the accretion disk and dubbed the broad line region (BLR), which in Type 2 AGN are hidden by the dusty torus (Antonucci 1993, but see also Elitzur et al. 2014 for alternative explanations).
These advantages have led in the past decades to find statistical samples of spectroscopically confirmed Type 2 and Type 1 AGN, both in the local Universe, thanks to the Sloan Digital Sky Survey (SDSS; Kauffmann et al. 2003), and at higher redshifts, thanks to large spectroscopic campaigns conducted with multi-object spectrographs (MOS) from the ground, such as zCOSMOS with VIMOS at the VLT (Mignoli et al. 2013, 2019), the FMOS survey at Subaru (Kartaltepe et al. 2015; Kashino et al. 2019), the MOSDEF survey with MOSFIRE at Keck (Coil et al. 2015), and with slitless grism spectroscopy with the Hubble Space Telescope (Trump et al. 2011; Backhaus et al. 2022).
Despite all of these efforts, the census of AGN from optical observations is not complete. Most theoretical models do indeed predict a black-hole accretion rate density that is higher by up to one order of magnitude compared to observational measurements (e.g., Vito et al. 2018, and references therein) at all redshifts from 0 to ∼7, thus suggesting that we are missing a significant population of optically obscured AGN. One physical reason for this is that the rest-frame UV and optical emission might still be severely affected by dust attenuation. Indeed, the accretion disk onto the supermassive black hole (SMBH), powering the AGN emission, typically lies in the central part of a galaxy where the dust attenuation might be higher (Goddard et al. 2017; Wang et al. 2017; Greener et al. 2020; Yung et al. 2021). This effect is more severe for more massive SMBHs, which are hosted in more massive and dustier galaxies. For example, AUV is on the order of ≥3 mag in galaxies with M⋆ > 1010 M⊙ (Pannella et al. 2015), and it can also reach AUV ≃ 15 mag in more luminous AGN according to Yung et al. (2021), with optical lines being highly suppressed by factors of 5 to 1000 assuming the Calzetti et al. (2000) law. There also might be systems in which the dust geometry resembles that of a mixed model, that is, a homogeneous mixture of dust and emitting gas (Calzetti et al. 1996), rather than the typical dust-screen model. In this mixed configuration, we can find AV rising to 30 mag toward the center, as observed in local ultra luminous infrared galaxies (ULIRGs) and massive starbursts at 0.5 ≲ z ≲ 1 (Calabrò et al. 2018, 2019). For the most compact objects, the line of sight toward the central black hole might be completely dominated by dust residing in the host galaxy interstellar medium (ISM) at scales of ≤1 kpc (Calabrò et al. 2018).
To mitigate the problem of dust attenuation, a possible solution is to observe at longer wavelengths in the rest-frame near-infrared (near-IR), where AGN radiation is less susceptible to ISM attenuation, and where our line of sight is less obstructed by dust from the BLR and NLR themselves. In the case of a mixed model, Paschen lines can recover 30% to 40% more of the total SF of the galaxy compared to Hα and Hβ (Calabrò et al. 2018). Since near-IR lines provide a more unbiased view of the systems, the presence of AGN can be assessed with higher reliability, and their intrinsic properties studied more easily.
This approach has successfully discovered hidden broad-line AGN, a type of obscured AGN with narrow Balmer lines but with a broad (> 1000 km s−1) component in Paα and Paβ (Riffel et al. 2006; Onori et al. 2017; Lamperti et al. 2017). den Brok et al. (2022) and Ricci et al. (2022) show that Paα and Paβ are better tracers of black-hole mass compared to Hα. Similarly, metal emission lines at λrest > 1 μm might be better diagnostics than optical ones, especially for identifying Type 2 AGN, given that they typically have larger column densities of dust than Type 1 AGN (Mignoli et al. 2019, and references therein). LaMassa et al. (2019) describe the limitations of the optical BPT analysis, as they find that one-half of mid-infrared color-selected AGN from the WISE survey have optical emission line ratios typical of star-forming galaxies rather than of AGN, which can be due to the highly obscured AGN clouds. Rodríguez-Ardila et al. (2004) and Colina et al. (2015) have proposed H2λ2.121 μm/Brγ versus [Fe II] λ1.257 μm/Paβ and [Fe II] λ1.64 μm/Brγ (respectively), as useful alternatives to standard optical AGN diagnostics, and successfully applied them to study obscured AGN in local galaxy samples. Therefore, going to longer wavelengths could potentially reveal a hidden population of BL and NL AGN, and also better characterize their physical properties.
In this paper, we add to previous efforts in the field by exploring new AGN and SF diagnostics in the near-IR. For these diagnostics to be applied to large samples of galaxies, we need to identify relatively bright emission lines at λrest − frame ≳ 0.8 μm, and to cover a variety of ISM conditions of the galaxies in terms of metallicity, gas density, and ionization. This can be done with the help of Cloudy photoionization models (Ferland et al. 2017), from which we can easily simulate the properties of emission lines emitted by gas clouds (representative of the galaxy ISM) irradiated by different types of ionizing sources, and then compare them to the observational results.
First, this analysis was applied at z ∼ 0, exploiting the near-IR observations and catalogs performed in the last decades and publicly available in the literature. Then, thanks to more recent spectroscopic facilities, we used these diagnostics even beyond the local Universe. In particular, we applied them to a sample of starburst galaxies at intermediate redshifts (0.5 < z < 0.9) observed through Magellan/FIRE. Finally, we exploited the new data coming from JWST/NIRspec, which, after the first light and becoming operational in 2022, started to take spectra from low- to high-resolution mode (30 < R < 2700) in the spectral range from 0.8 to 5.2 μm. The JWST mission (Gardner et al. 2006, 2023) is thus opening a new window by shedding light on the near-IR rest-frame properties of galaxies at high redshift up to at least z ∼ 3. In this paper, we use data from the Cosmic Evolution Early Release Science Survey (CEERS; Finkelstein et al., in prep.), which has thus far collected among the largest samples of galaxies at “cosmic noon” and is thus suited to analyze a sizeable sample of AGN at z > 1.
The paper is organized as follows. In Sect. 2, we describe the dataset of local star-forming galaxies and AGN, and then present the data reduction, redshift measurement, and sample selection of higher redshift sources observed with Magellan/FIRE and JWST/NIRSpec. In Sect. 3, we describe the Cloudy photoionization models that we adopted to study the emission line properties of star-forming galaxies and AGN, and display these models in the classical BPT diagram. We show our results in Sect. 4. First, we present new near-IR diagnostic diagrams that can be used to distinguish between AGN and star-forming driven ionization, providing new separation lines in analytical form. Then, we apply these diagnostics to observations from z = 0 to z = 3, and compare the near-IR classification to the optical one. We discuss our results in Sect. 5, suggesting ideas to improve the statistics of AGN with forthcoming spectroscopic surveys. For our analysis, we adopt a Chabrier (2003) initial mass function (IMF) and, unless stated otherwise, we assume a cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, ΩΛ = 0.7.
2. Observations and data
Given the wide range of cosmic epochs that we want to explore, from the local Universe to redshift ∼3, different instruments and data are required. In this section, we thus describe the various datasets that we use to study the properties of galaxies and AGN with the same near-IR diagnostics. We start by introducing the new JWST/NIRSpec spectra coming from the CEERS survey, which provide physical information for galaxies at 1 < z < 3. At intermediate redshifts (0.5 < z < 1) we use near-IR ground-based spectra taken with the FIRE spectrograph at the Magellan telescope. We supplement this dataset with public spectral compilations of local star-forming galaxies and AGN observed with the Spex-IRTF near-IR spectrograph and several optical instruments.
2.1. JWST/NIRSpec data from CEERS
The data analyzed here are taken from the Cosmic Evolution Early Release Science Survey (CEERS; ERS 1345, PI: S. Finkelstein), a public survey to study galaxy evolution from z ∼ 1 up to the reionization epoch in the Extended Groth Strip (EGS; Noeske et al. 2007) field, which is one of the five fields covered by the Cosmic Assembly Near-Infrared Deep Extragalactic Legacy Survey (CANDELS; Grogin et al. 2011; Koekemoer et al. 2011). The main features of the CEERS program are presented in Arrabal Haro et al. (2023a) and Finkelstein et al. (2023), and will be described in more detail in Finkelstein et al. (in prep.).
The galaxies analyzed in this work were observed with NIRSpec (Jakobsen et al. 2022) during the CEERS epoch 2 observations (December 2022). The spectra were taken with the MOS configuration, which requires precise placement of the sources inside Micro Shutter Arrays (MSA; Ferruit et al. 2022) with size 0.2″ × 0.46″. These NIRSpec observations were divided into 6 different MSA pointings, and performed with the G140M/F100LP, G235M/F170LP, and G395M/F290LP medium resolution (R ∼ 1000) gratings (herewith denoted with “M”), and with the prism in low-resolution mode (R ∼ 100). We use only the M-gratings observations in this paper, to ensure a complete deblending of the [O III] + Hβ and [N II] + Hα emission line triplets in the optical. With this spectroscopic setup, we obtain an almost continuous wavelength coverage from ∼1 to ∼5.2 μm.
The MSA apertures were made of 3-shutter slitlets, and a 3-point nodding pattern was performed along the direction of the longest slitlet side to enable background subtraction, shifting the pointing by a shutter length in each direction. The sources were observed by integrating 14 groups in three exposures (one for each nod position) in NRSIRS2 readout mode, totaling 3107s of integrated time per grating for each MSA pointing.
The targeted sources were chosen among existing catalogs in EGS (Stefanon et al. 2017; Kodra et al. 2023), for which photometric redshifts were already determined in all cases, while for a small subset, the spectroscopic redshifts were also available from 3D-HST grism spectroscopy (Brammer et al. 2012). The final position of the open shutters was defined with the help of the MSA Planning Tool (MPT) to maximize the number of observed targets, preferentially selecting galaxy candidates at z > 1. A more exhaustive description of NIRSpec observations in CEERS is provided by Arrabal Haro et al. (2023a). The details of the aperture position angle (PA), targeted area, and target priority criteria will be fully described in Finkelstein et al. (in prep.).
2.1.1. CEERS spectral reduction
The spectral reduction of NIRSpec observations was performed by the CEERS Collaboration, as described in Arrabal Haro et al. (2023b) and further explained in Arrabal Haro et al. (in prep.). We highlight here the main processing steps based on the JWST Pipeline (Bushouse et al. 2022)1 and on the Calibration Reference Data System (CRDS) mapping 1061.
First, raw images are corrected for the detector 1/f noise, dark current, and bias, and for the “snowball” contamination, which appears as trails in the images, likely produced by high-energy cosmic rays. This yields count-rate maps, from which two-dimensional (2D) spectra are created for each source. We apply to these the flat-field correction, background subtraction (using the 3-nod pattern), and photometric and wavelength calibration. The resulting spectra are also resampled to correct for spectral trace distortions. In the pipeline, a slit loss correction is already performed by default in the pathloss step.
Then, the intermediate background subtracted 2D spectra (one for each nod position) are combined to create the final 2D spectrum of the source. The one-dimensional (1D) spectra are also extracted using customized apertures that are visually determined by CEERS members by collapsing the spectra along the wavelength direction and identifying with high confidence the continuum along the spatial direction. An additional step is performed on the reduced 2D spectra to mask possible hot pixels, detector gaps, and reduction artifacts that are not associated with the main continuum trace or with an emission line. The noise spectrum is automatically calculated by the JWST pipeline, and then corrected as described in Arrabal Haro et al. (2023b) to take into account the spectral resampling performed in the previous stages.
2.1.2. Residual flux scaling and final spectra
Although slit loss correction is performed during the main processing with the JWST pipeline (Sect. 2.1.1), we further check whether additional flux corrections are needed. To this aim, we convolve the previously calibrated, slit-loss-corrected 1D spectra with broadband filters and compare them to the photometric data available for each target through ground-based near-IR imaging, and/or space-based instruments such as HST/WFC3, Spitzer/IRAC, and JWST/NIRCam. This is possible because the continuum is detected with a S/N > 3 per pixel for all our NIRSpec spectra. In particular, for all the selected sources we have HST, IRAC, or ground-based photometry, ensuring at least one band available within each grating, and a maximum number of 14 broadband filters available from λ = 1 μm to 5 μm.
In most cases, the shape of the spectrum is consistent with the broadband photometry across the entire wavelength range 1 μm < λ < 5 μm, indicating that the relative flux calibration between different gratings is generally reliable. We thus multiply the spectra by a single scaling factor to match the photometric data when needed. For a few sources (9%), a different scaling correction factor should be applied to some gratings to match the photometry available in that wavelength range. These issues are not related to a specific grating, or to a particular MSA pointing. We find instead that almost all of these peculiar sources have at least one wavelength gap in the spectrum, which might be responsible for creating jumps in the flux density between different wavelength ranges. These calibration issues will be better described in the survey paper (Finkelstein et al., in prep.), and fixed in future spectroscopic reductions.
In Fig. 1, we show as an example the fully calibrated spectra (normalized to their median flux and converted to a rest-frame reference) of 10 galaxies chosen among our CEERS sample at different redshifts. This highlights the variety of wavelength coverage, continuum shapes, and spectral properties that we are able to probe.
 |
Fig. 1. Rest-frame spectra of 10 sources observed by JWST/NIRSpec in CEERS. The spectra are normalized to their median flux and offset relative to each other to help the visualization. They are colored in black, red, and green, according to whether they are identified, respectively, as optical+near-IR star-forming, optical+near-IR AGN, or hidden AGN (i.e., optical SF and near-IR AGN), according to the diagnostic diagrams presented in this paper (see Sect. 4.3). The CEERS ID and the spectroscopic redshift of each source are written besides each spectrum. The emission lines that can be identified in the range 0.4 μm < λ < 2 μm are highlighted above the top axis (see also Table 1). |
2.1.3. Spectral analysis and sample selection
The spectral analysis is performed as follows. In the first stage, we visually check all the 1D spectra looking for emission lines from 1 μm to 5 μm. In this spectral range, there are subsets of lines that are intrinsically brighter for most galaxies, either star-forming or AGN, such as the Hβ + [O III] triplet and Hα + [N II] triplet in the optical, and the He I + Paγ doublet and the Paβ + [Fe II] triplet in the near-IR. Driven by the visual identification of these groups of lines, we assign a first spectroscopic redshift guess.
We are interested in building a sample of galaxies in the redshift range between 1 and 3. Therefore, in this phase, we select those galaxies in which the spectrum covers at least the Hβ + [O III] triplet and the Paβ + [Fe II] triplet. For the final sample, in addition to the two above triplets, we require the identification of the Hα + [N II] triplet and the [S III] λ9530 Å line, as the presence of all these lines are essential requirements for the analysis of optical and near-IR diagnostics presented in this paper. With these criteria, we automatically select 65 systems between z ∼ 1 and z ∼ 3, among which 27 galaxies have z < 1.75 and thus also have Paα detected in the spectrum. This constitutes our final selected CEERS sample for all the forthcoming analyses. We also note that a few sources (10), despite being at the requested redshift, have been removed, as one of the emission line groups required above falls in detector gaps and is not available.
2.2. Line flux measurements
In addition to the emission lines considered for the first redshift guess and sample selection, we can also identify in many cases other intrinsically fainter lines. The full subset of lines relevant for this work (i.e., from λrest = 0.4 μm to λrest = 2 μm) and that we can detect for at least a subset of galaxies, is summarized in Table 1.
Optical and near-IR rest-frame lines that we are able to detect in our spectra of star-forming galaxies and AGN in the redshift range 0 ≤ z ≤ 3, and that we consider in this paper.
For a more accurate determination of the spectroscopic redshift and for the measurement of emission line fluxes, we use the χ2 minimization based MPFIT 2 routine (Markwardt 2009) to fit all the lines listed in Table 1, assuming single Gaussian functions on top of a linear continuum. We also assume for all the lines a single redshift z and the same line velocity width σv, which are first determined by fitting the highest S/N emission line in the whole spectral range, usually Hα, or [S III] λ9530 Å in case Hα is not present. The Hβ + [O III] and Hα + [N II] triplets are fitted simultaneously with the same underlying continuum, fixing the ratio between the two components of [N II] and [O III] to 0.338 and 0.3356, respectively (Storey & Hummer 1988). In addition, we fit together the following couples of emission lines lying close in wavelength: He I and Paγ, Paβ and [Fe II] λ1.257 μm, without any constraint on their flux ratios.
After the first estimation of z and σv, for the remaining lines we leave a tolerance of 100 km s−1 for both parameters. This provides in all cases a good fit, which we control by requiring a statistical significance of the fit of 95%, as determined from the reduced χ2 (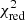 ). The quality of the relative wavelength calibration is excellent, as determined inside the CEERS Collaboration, with precision at the level of less than 5% (Arrabal Haro et al., in prep.). As a further test, we compared our redshifts to those determined by fitting the lines in each grating separately. These measurements were done using the methodology described in Fernández et al. (2023), for the complete sample. We find that they are consistent within 1 standard deviation, suggesting that the wavelength calibration is robust across the three gratings and the full wavelength range of NIRSpec.
). The quality of the relative wavelength calibration is excellent, as determined inside the CEERS Collaboration, with precision at the level of less than 5% (Arrabal Haro et al., in prep.). As a further test, we compared our redshifts to those determined by fitting the lines in each grating separately. These measurements were done using the methodology described in Fernández et al. (2023), for the complete sample. We find that they are consistent within 1 standard deviation, suggesting that the wavelength calibration is robust across the three gratings and the full wavelength range of NIRSpec.
In addition to the spectroscopic redshift and the line velocity width, this MPFIT procedure yields emission line fluxes, underlying continuum, equivalent widths (EW), and their corresponding uncertainties for all the lines3. While for the first line we require a high detection threshold (S/N ≥ 5) to secure the redshift and σv, for the remaining lines we require a S/N ≥ 2 to be detected. This choice was also adopted in Calabrò et al. (2019) to improve the detection of fainter lines while preserving its reliability, given that the fit is performed with a restricted number of free parameters compared to a blind search. For non-detected lines, we adopt a 1σ upper limit. In Fig. 2 we show as an example of our procedure the fit performed for all the emission lines of the source ID 3129 (a broad-line AGN at z = 1.04) that are relevant to this work. We show instead in Fig. 3-top the spectroscopic redshift distribution of our selected targets. They span the entire range from z ≃ 1 to z ≃ 3, with a median redshift zmedian = 2 and 1σ dispersion of ∼0.5.
 |
Fig. 2. Spectrum of the broad-line AGN with CEERS ID 3129 at z = 1.04, around emission lines detected in the full spectral range of NIRSpec, in increasing order of wavelength. The noise spectrum is represented with gray error bars around the observed flux (black line). The emission lines are fitted with multiple Gaussian components, as described in the text. Blue and orange vertical dashed lines highlight the gaussian central wavelength of permitted and forbidden lines, respectively. For broad lines, both the narrow and broad components are shown with a dashed and dotted blue line, respectively. The global best fit profile is drawn with a red dashed line. The S/N of the detection is highlighted in the top left corner of each panel, while the name of each line is written in the top right corner (see also Table 1). |
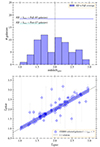 |
Fig. 3. Spectroscopic redshift distribution of emission line galaxies in the CEERS survey in the redshift range between 1 and 3 (top panel), where both optical and rest-frame near-IR lines can be detected, from Hβ to Paβ. The vertical dashed black line highlights the median redshift of our selected sample (zmedian = 2.0). Bottom: comparison between the spectroscopic redshifts estimated from CEERS spectra and previously available photometric redshifts (Kodra et al. 2023). |
We also compare the spectroscopic redshifts zspec to the photometric estimates zphot available from the latest EGS catalog assembled by Kodra et al. (2023). The zphot values are derived by fitting stellar templates to the available UV to near-IR photometry with a Hierarchical Bayesian method. We refer to Kodra et al. (2023) for the detailed photometric analysis. We find in general a good consistency, with a median absolute deviation of 0.11. We find a ∼10% fraction of catastrophic outliers with |zphot − zspec|> 0.5, but no systematic under- or over-estimations across all the explored redshifts (Fig. 3 bottom). We also note that the outliers tend to have larger uncertainties of zphot compared to the whole sample.
In Fig. 4, we show the distribution of the FWHM line velocity widths from the combined Hα, [S III] λ9530 Å, and [O III] λ5007 Å lines. Given the FWHM resolution of our NIRSpec spectroscopic setting (≃300 km s−1) most of the lines appear well resolved. By subtracting in quadrature the instrumental resolution from the observed quantity, we calculate the intrinsic FWHM line widths. We find a median intrinsic FWHMV of 200 km s−1, with standard deviation σ of 130 km s−1 and a tail of galaxies with higher FWHM up to ∼550 km s−1. Furthermore, we find 3 objects for which all the permitted lines, including the Balmer, Paschen, and He I lines, require an additional broader component in the fit, with FWHM > 1000 km s−1, well above the maximum found for the rest of the sample in Fig. 4.
 |
Fig. 4. Distribution of intrinsic FWHM widths (i.e., deconvolved from instrumental broadening) for CEERS galaxies selected at 1 < z < 3 as described in the text. The FWHM is estimated from the Hα line. If Hα is not detected, we use the highest S/N line in the spectrum, that is, [S III] λ9530 Å or [O III] λ5007 Å. The line width is a variable parameter in the fit but is assumed to be the same value for all narrow lines, with a tolerance of 50 km s−1. The median value of the sample (FWHMmedian ≃ 175 km s−1) is represented with a vertical dashed black line. |
For the Balmer and Paschen emission lines, we apply an underlying stellar absorption correction, rescaling their fluxes upward. We apply for this correction the absorption equivalent widths (EWabs) estimated from theoretical stellar population models, namely EWabs = 3.6, 2.7, 2.7, 2.5, and 2 Å for Hβ, Hα, Paγ, Paβ, and Paα, respectively. We note that these values for the optical lines are consistent with Domínguez et al. (2013). In our CEERS galaxies, they produce an increase of the line fluxes of, respectively, 3.4%, 0.5%, 3.7%, 2.1%, and 1% on average, thus would not alter significantly the results of this paper.
Finally, using all the hydrogen recombination lines available (typically those from the Balmer and Paschen series), we also check the quality of the final calibrated spectra by comparing their emission line ratios to the theoretical predictions, considering a variety of dust attenuation laws. While a more detailed analysis of dust attenuation will be presented in a follow-up paper, a representative test is shown in Appendix A. This test suggests that Balmer and Paschen line fluxes across a large range of wavelengths (∼0.4 to ∼2 μm) are physically meaningful and overall consistent with the predictions of typical dust attenuation models, even when the lines reside in different gratings, suggesting that their relative calibration can be trusted at the first order.
2.3. Main physical properties of the CEERS sample
The 65 galaxies selected in Sect. 2.1.3 show a variety of physical properties. They have H-band (F160W) magnitudes ranging between HAB = 21 and 27.2, with a median value of 24.2. Considering previous catalogs published in the CANDELS Collaboration (Stefanon et al. 2017), we can also study the distribution of other main properties of the sample, including the stellar mass and the SFR. We consider here the stellar masses and SFRs obtained through fitting HST, CFHT, and Spitzer photometry (from band u to IRAC channel 4) with BC03 stellar population models, assuming a Chabrier IMF, exponentially declining SFH (τ models), and a solar metallicity (Acquaviva et al. 2012), taking also into account the contribution from emission lines to the observed photometry. While different assumptions in the SED fitting may be applied to specific objects, we aim here at investigating the global properties of the sample that can be compared to other galaxies. Nonetheless, the stellar masses that we consider are in agreement with the median stellar masses reported by Stefanon et al. (2017), which combine estimates from different groups using different prescriptions for the fit.
Representing these quantities in Fig. 5, we notice that our sample is fairly representative of the star-forming main sequence at z ∼ 2 (Schreiber et al. 2015; Whitaker et al. 2014), with stellar masses M⋆ ranging between log M/M⊙ = 7.8 and 11.3 (median M⋆ ≃ 109.5 M⊙). A small subset of CEERS galaxies is also detected at S/N ≥ 5 with Herschel and may host dust-obscured SF, thus we use in these cases the SFRs inferred through fitting the infrared and radio photometry (from Spitzer 24 μm flux to VLA 1.4 GHz flux) as described in Le Bail et al. (in prep.), which adopts a similar methodology to Jin et al. (2018). This subset lies in the upper right part of the diagram with higher stellar masses and higher SFRs, and total infrared luminosities LIR (integrated in the range 8 − 1000 μm) ≳ 1012 L⊙.
 |
Fig. 5. Stellar mass M⋆–SFR diagram of CEERS galaxies selected in this work between redshift 1 and 3. The M⋆ and SFR are taken from Stefanon et al. (2017) as described in the text (cyan triangles) or from Le Bail et al. (in prep.) if Herschel detected (red squares). The sample is representative of the star-forming Main Sequence (MS) at the median redshift of the sample (zmedian = 2). The black dotted line represents the starburst limit, that is, a factor of 4 above the MS of Schreiber et al. (2015). The SFRs shown in this plot are normalized to z = 2 assuming that they scale with redshift as (1 + z)2.8 (Sargent et al. 2014). |
2.4. Magellan/FIRE spectra for starburst galaxies at z ∼ 0.7
To increase the statistics of the sample and the redshift range, we also consider 6 systems at intermediate redshifts between 0.5 and 0.9 (zmedian ≃ 0.7) with both optical and near-IR rest-frame coverage. These systems are presented in Calabrò et al. (2018) and were originally selected in the COSMOS field as infrared bright galaxies representative of a population of highly star-forming galaxies with log (M*/M⊙) > 10 and log (LIR/L⊙) between 11.5 and 12.5.
Their near-IR spectra were observed with the FIRE echelle spectrograph (Simcoe et al. 2013), mounted at the Magellan 6.5 m Baade Telescope, in two observing runs in 2017 and 2018 (PI: P. Cassata and R. Gobat). Thanks to their spectral coverage, from z to the K band, they include at least the Hα and the Paβ emission lines. The optical spectra are instead taken with the VIMOS spectrograph (Le Fèvre et al. 2003) and are publicly available from the zCOSMOS survey (Lilly et al. 2007), and they cover the missing rest-frame range 0.3 < λ < 0.6 μm that includes the [O III] λ5007 Å and Hβ lines.
The observations, data reduction, and final calibrated spectra are fully described in Calabrò et al. (2019). The flux measurements are also presented in the above paper for the Balmer and Paschen lines, while here we also measure with the same approach the other metal lines, including [O III] λ5007 Å, [N II] λ6583 Å, [S III] λ9530 Å, [Fe II] λ1.257 μm, [C I] λ9850 Å, and [P II] λ1.19 μm. For the subset considered here, we are able at least to detect Paβ with S/N ≥ 3 and set upper limits on [S III], [Fe II], [P II], or [C I] in the worst case. Analyzing these sources in the classical BPT diagram, 5 are found to be consistent with star-forming models, while one source (dubbed BPT AGN) lies beyond the maximum separation line of Kewley et al. (2001).
2.5. A comparison sample of local starbursts and AGN
Local samples of galaxies and AGN can provide a useful benchmark to test and apply near-IR rest-frame diagnostics. Spectral compilations in the local Universe were made by Riffel et al. (2006), who present one of the most extensive NIR spectral atlases of AGN. This atlas includes optical/UV and X-ray AGN found from previous surveys, and it is representative of the entire class of AGN at z ∼ 0, with different degrees of nuclear activity. It comprises 27 UV/optically selected sources at z < 0.1, including 12 broad line AGN (Type 1) and 15 narrow line AGN (Type 2), with the addition of 4 starburst galaxies that do not show evidence of nuclear activity through either broad line components, coronal lines, or AGN-like line ratios in optical diagnostics.
To increase the size of the star-forming sample for comparison, we also consider the optical and near-IR spectra of 16 infrared luminous spiral galaxies presented more recently by Riffel et al. (2019). These galaxies are all at z < 0.05 and were originally selected from the IRAS Revised Bright Galaxy Sample with LFIR > 1010.10 L⊙. Their nature (AGN or star-forming) was previously determined through optical spectroscopy: 8 systems are purely star-forming (HII) galaxies, 3 are LINERs, 1 is a Type 1 AGN, and 4 systems have intermediate properties between LINER/HII or Type 2 AGN/HII.
The near-IR spectra of all these sources are taken using the Spex slit spectrograph (Rayner et al. 2003), mounted at the NASA 3 m IRTF telescope at Mauna Kea. For the details of the spectroscopic observations, data reduction, and line measurements, we refer to Riffel et al. (2006, 2019). In the case of Type 1 AGN, they decompose the broad and narrow component of permitted lines, so we only take their narrow component for our purposes.
In addition, we consider the sample of 11 systems from the compilation made more recently by Onori et al. (2017), and for which we have a similar rest-frame spectral coverage to the data presented before and the same subset of detected emission lines from 0.4 to 2 μm rest-frame. These systems are selected as X-ray emitters from the Swift/Burst Alert Telescope 70-month catalog, and include obscured (Type 2) and intermediate type AGN, and starburst galaxies at z < 0.1. Part of this sample (8 systems) is observed at high-resolution (4000 < R < 17 000) with X-shooter at the VLT. For the remaining part of this sample (3 galaxies), similarly high resolution spectra (R > 4000) are taken at LBT with the single slit NIR spectrograph LUCI (Seifert et al. 2003). We refer to Onori et al. (2017) for a complete description of the observations, data reduction, and line measurements. In particular, given the high resolution, they perform a fit with three-Gaussian components, which should be representative of the narrow component (that we use here), and eventually a broad component and an outflow component. Taking the forbidden line fluxes and the narrow component of permitted lines, it is possible to classify spectroscopically the nature of each source in the classical BPT diagram. Following this procedure, almost all the Onori et al. (2017) sources (9) are AGN (1 Type 1, and 8 Type 2), while 1 galaxy is classified as star-forming and an additional 1 lies in the composite BPT region.
In total, we assemble a final local sample of 58 sources, including 14 Type-1 AGN, 26 Type-2 AGN, 13 starburst (purely star-forming) galaxies, 3 LINERs, and 5 sources with mixed line properties. Among the many optical and near-IR lines available in the literature for these galaxies, we select those in Table 1, which we use in the following sections as AGN diagnostics and which can be detected also with NIRSpec in the CEERS sample. In all cases, we directly take the flux measurements available in the above papers.
We note that star-forming systems considered at z < 1 do not cover such a large variety of physical conditions as in the CEERS sample. They rather represent a subset of massive and dusty starbursts, forming stars at higher rates and possibly with higher efficiency than average galaxies in this redshift range. Despite this, they are very useful to constrain the maximum star-forming line ratios as they likely probe extreme ISM conditions among the star-forming galaxy population and the highest metallicities.
3. Emission line modeling with Cloudy
To provide a theoretical basis for interpreting the observations and to build a common ground from which both the optical and the near-IR emission lines of galaxies can be understood, we build a set of photoionization models with Cloudy. We use the python package pyCloudy v.0.9.114 which runs with version 17.01 of the Cloudy code (Ferland et al. 2017). This code assumes a symmetric distribution of gas around or in front of an ionizing source, and then calculates the radiated emission after it is processed by the gas layer. In principle, it is able to predict the emergent continuum and line intensities over the entire electromagnetic spectrum. However, we focus here on emission lines spanning from the optical rest-frame (∼4000 Å) to the near-IR rest-frame (∼2 μm), which can be simultaneously observed with NIRSpec in the redshift range 1 ≲ z ≲ 3. In the following subsections, we describe the star-forming and AGN models adopted in this work.
3.1. SF models
For a theoretical understanding of the radiation emitted by star-forming galaxies, we consider an ionization-bounded, spherically symmetric shell of gas surrounding a population of young (O and B type) stars. We note that this is a simplified picture, where a single shell of gas is representative of the ensemble of HII regions in a galaxy and the emergent spectrum is representative of the whole galaxy emission. Regarding the incident ionizing spectrum, we consider SEDs derived with BPASS stellar population models (Eldridge et al. 2017), assuming a Salpeter IMF with an upper mass limit of 300 M⊙, stellar metallicity equal to the gas phase metallicity of the surrounding gas cloud, and continuous SF history with age ranging from 107 to 109 yr. For representation purposes, we show the prediction relative to a single age of 100 Myr, as other ages would not produce significant variations of the emission line ratios studied in this paper.
We specify the brightness of the incident radiation field, varying the ionization parameter log(U) between −4 and −1, while we assume a hydrogen number density nH for the gas cloud ranging from 102 to 104 cm−3. The gas-phase metallicity Zgas varies from 10% solar to two times solar, where the solar abundance of each element is set as in Savage & Sembach (1996). All the elements are scaled together with metallicity (i.e., by the same factor compared to solar), except nitrogen, which follows the prescription of Feltre et al. (2016) to take into account secondary production. The helium abundance is set as −1 in logarithmic scale (Dopita et al. 2006).
We consider that some elements in the gas phase are depleted onto dust grains. The dust depletion is defined with the standard logarithmic notation system as δ(X) = [X/H] ≡ log(X/H)c − log(X/H)g, where c refers to the cosmic abundance of an element and g to its gas phase component. As shown by Savage & Sembach (1996) and other works, δ(X) can vary significantly as a function of the interstellar environment and grain composition. It is relatively well studied in our Galaxy and nearby systems, such as the Large and Small Magellanic Clouds, while it is still poorly constrained at higher redshifts. In Jenkins (2009), they parameterize the strength of the dust depletion with a factor F* varying between 0 (minimum depletion) and 1 (maximum strength), and it does not depend on the particular element. For this work, we consider average depletion coefficients as reported in Savage & Sembach (1996), which are generally consistent with those estimated from Jenkins (2009) for a medium depletion strength (F* = 0.5). The solar abundances and depletion factors for all the elements are listed in Table 2. We can distinguish between refractive elements with a low δ(X), such as S, O, and C, and non-refractive elements with higher δ(X), such as Fe and Si. In Table 3 we present instead the list of parameters used to model the star-forming galaxies.
Solar abundances and depletion factors for all the models analyzed in this paper.
Full range of parameters used in Cloudy for constructing the grid of star-forming models explored in this work.
3.2. AGN models
The narrow-line region (NLR) of an AGN is modeled as follows. Regarding the ionizing source, the continuum emission from the AGN accretion disk is modeled using multiple prescriptions. First, we use the built-in “AGN” command in Cloudy, with the multiple power law continuum characterized by a “blue bump” temperature of 106 K and a spectral energy index of αUV = −0.5 and αX = −1.35 in UV and X-rays, respectively, as in Risaliti et al. (2000). The spectral index αox of the optical to X-ray SED is free to vary among the following values: −2, −1.7, −1.4, −1.2, spanning the range of observational findings, and consistent with typical values adopted in the literature (e.g., Groves et al. 2004). We also test different and more recent ionizing shapes. In particular, we consider the OXAF models5, which are physically based AGN continuum emission models introduced by Thomas et al. (2016) and further described in Thomas et al. (2018). While we refer to those papers for an exhaustive discussion, we briefly present their main properties. These models are specifically designed for photoionization modeling. Indeed, they are simplified enough to easily reproduce the diversity of observed AGN spectral shapes with only three main parameters: the energy at the peak of the accretion disk emission (Epeak), the power-law index of the nonthermal emission (#x0393;), and the fraction of the total flux coming from the nonthermal component (pNT). The first is a crucial parameter, as it incorporates a dependence on the black hole mass, AGN luminosity, and “coronal” radius, and it is sensitive to contamination from shocks or HII region emission (the higher their contribution to the AGN, the lower the value of Epeak). Moreover, it is not affected by dust screening effects. In our simulations, we vary Epeak from 20 to 100 eV, following Fig. 5 of Thomas et al. (2016). The parameter pNT affects the fraction of photons in the X-ray regime (see Fig. 6), and we consider three possible values: 0.1, 0.25, and 0.4, covering the entire physical range typically found in AGN (Thomas et al. 2016). Finally, we set #x0393; to a median value of +2.0, as it was shown that this parameter does not significantly affect the line ratios (also confirmed in the near-IR regime).
 |
Fig. 6. Top: diagram with the shape of the ionizing radiation field (energy units, normalized to the flux at the Lyman limit) assumed in CLOUDY to model the stellar emission (orange curve) and the AGN emission (black, red, and darkred curves, as described in the legend). For these representative curves we have assumed log(U) = − 2, solar metallicity, and a density of 103 cm−3 in all cases. In the AGN models from Thomas et al. (2016), we identify with the same color (red or darkred) the family with a common Epeak, in which the parameter pNT increases toward the top from the lighter to the darker line. The dashed shaded lines indicate the transmitted continuum. Bottom: zoom-in of the top panel in the energy range between 5 and 100 eV, but with a linear scale on the x-axis and the flux density fν (normalized to the flux density at the Lyman limit) on the y-axis. This version of the plot is inspired by Feltre et al. (2016). The area between the two AGN shapes of Thomas et al. (2016) with the same pNT = 0.25 and varying Epeak (in the range 20 − 100 eV) is filled with a chequered red pattern. |
The brightness of the radiation field is set through the ionization parameter log(U) varying from −4 to −1, as for the star-forming case. Regarding the physical properties and chemical content of the NLR, we vary the gas density from 102 to 104 cm−3, and the gas-phase metallicity from 0.3 to 3 times solar. The element abundances relative to hydrogen are set as for the star-forming galaxies. The helium abundance is set slightly higher (by 0.1 − 0.2 dex) than for star-forming galaxies, following the recent work by Dors et al. (2022). As in Feltre et al. (2016), we adopt an “open geometry” model because it is more appropriate for the low covering fraction of the narrow-line region. In Tables 4 and 5, we present the full list of parameters used to model the NLR of AGN according to the model of Risaliti et al. (2000) and Thomas et al. (2016), respectively.
Full range of parameters used in Cloudy for modeling the emission from an AGN.
Parameters adopted in AGN models from Thomas et al. (2016, 2018), with the custom SED shape injected in pyCloudy through the “table SED” command.
Finally, in both the star-forming and AGN case, we consider dust in the calculation and assume for simplicity the standard grain properties implemented in Cloudy (Mathis et al. 1977), with grains to hydrogen mass ratio scaling linearly with metallicity. We stop the Cloudy calculation when reaching a temperature in the gas of 500 K. In Fig. 6, we show a representative ionizing spectrum and the transmitted continuum radiation for star-forming galaxies and AGN. We can see that the spectral shape obtained with the standard “AGN” command in Cloudy, and adopting the parameter set from Risaliti et al. (2000; black line), does not differ significantly from more recent SEDs, at least up to the soft X-ray regime (∼1 keV), and can be considered as fairly representative of an AGN with median properties (Epeak ≃ 60 eV, pNT = 0.25, and #x0393; = 2.0 in the OXAF models). In the following of the paper, we consider this as our default AGN model, but we discuss potential changes of the line ratios as due to different SEDs. For convenience, we also release the emission line predictions for the entire grid of photoionization models (both star-forming and AGN) analyzed in this paper6.
3.3. Predictions for optical lines: The BPT diagram
We initially test the ability of our models to reproduce the classical BPT diagram, introduced originally by Baldwin et al. (1981), and widely used to separate AGN- and SF-driven ionization from the local Universe to higher redshift. This diagram compares rest-frame optical emission line ratios, namely [O III]/Hβ and [N II]/Hα. The predictions of our Cloudy models are shown in Fig. 7, where the circles are the AGN models for different values of log(U), metallicity, and gas density. Higher gas densities are represented with bigger markers, while the marker colors are indicative of different log(U), as shown in the legend. Triangles represent the star-forming models with varying parameters of the gas shell.
 |
Fig. 7. Prediction from our Cloudy models of the emission line ratios [O III]/Hβ vs [N II]/Hα (BPT diagram). Triangles and circles represent the star-forming and AGN models, respectively. The gas-phase metallicity increases from left to right. The blue continuous line represents the separation line by Kauffmann et al. (2003), while the red dotted line represents the maximum starburst model by Kewley et al. (2001). The cyan and green dashed lines show the average location of star-forming galaxies at z = 0 and z = 2.3, respectively, from Kewley et al. (2013) and Shapley et al. (2015). The big red squares and dashed line highlight the AGN sequence by Richardson et al. (2014), with increasing ionization from bottom to top. |
Models with increasing log(U) tend to occupy a region toward the upper part of the diagram with a higher [O III]/Hβ ratio. At fixed conditions, models with higher metallicity tend instead to move toward the right part of the diagram with higher [N II]/Hα, as the nitrogen abundance also increases with Z. The composite region in Fig. 7 is where the AGN and star-forming models overlap, and where both the NLR and HII (star-forming) regions might contribute to the global emission. While a more detailed analysis of the role of each parameter in the scatter of the BPT diagram has been discussed in many other works (e.g., Brinchmann et al. 2008; Masters et al. 2016; Faisst et al. 2018; Curti et al. 2022, and references therein), we want to remark here that our AGN and star-forming models are globally consistent with observations from z = 0 to z = 3 (Kewley et al. 2013; Shapley et al. 2015; Richardson et al. 2014), and with the typical separation lines adopted in the literature to constrain the AGN location (Kauffmann et al. 2003) and the maximum starburst condition (Kewley et al. 2001). As expected given the similarity of ionizing shapes, the line predictions obtained with the OXAF models occupy a similar parameter space to those derived with our default AGN model. The same trends discussed above as a function of log(U), Z, and gas density, also hold for the models of Thomas et al. (2016). For completeness, we show the location of these additional models in the BPT diagram in the Appendix B. We finally note that our line predictions for AGN in the BPT are similar to those presented by Ji et al. (2020), which are also derived with Cloudy. For the star-forming models, we also checked the predictions assuming a simple black-body with temperature T = 50 000 K as ionizing spectrum, yielding similar results.
The BPT diagram is also routinely used to study the ionizing properties of galaxies well beyond the local Universe. As shown by Topping et al. (2020), star-forming galaxies at 1 < z < 3 have harder ionizing spectra at higher z, lower metallicity, and increased alpha element abundances (i.e., increased O/Fe abundance ratio) compared to local samples. However, the combined effect of this evolution is rather limited in the BPT diagram, with only a slight offset observed for the star-forming population toward the upper right part of the diagram compared to the local BPT (see also Fig. 1 of Bian et al. 2018). Most importantly, they show that normal star-forming galaxies in the above redshift range do not cross the maximum starburst condition of Kewley et al. (2001). Similarly, the separation line introduced by Kewley et al. (2013) to classify AGN and SF sources at z ≃ 1.5 falls entirely on the left of our maximum starburst condition, which thus provides a more stringent condition for AGN.
Hirschmann et al. (2017) also study the evolution of the BPT diagram toward higher redshifts, claiming that the ionization parameter, which is regulated by the SF history, is the main responsible for the enhancement of the [O III]/Hβ ratio compared to local samples, but star-forming galaxies at z < 3 do not typically overcome the maximum starburst separation lines set in previous works in all the optical diagnostics (see Fig. 3 in that paper). Therefore, z ∼ 3 represents the redshift limit up to which the local AGN conditions in the BPT and similar optical diagrams have been tested. Similarly, we consider that our models can also be safely used if we extend our analysis up to at least z ∼ 3. Nevertheless, we discuss in the following sections the possible effects of the α-enhancement and variations of the depletion strengths when considering the emission of iron-like elements. With these models in hand, we analyze the predictions of AGN and star-forming models for emission line ratios in the rest-frame near-IR.
4. Results
In this section, we show the near-IR rest-frame emission line predictions of our star-forming and AGN models. Then we compare them to the 64 + 65 observed sources in the redshift range from z = 0 to z = 3.
4.1. Infrared rest-frame predictions
We utilize the models described in Sect. 3 to analyze the emission line ratios in the rest-frame near-IR, from ∼0.8 to ∼2 μm. Further extending the analysis to longer wavelengths dramatically reduces the number of objects targeted by CEERS. For example, longer wavelength transitions of the ionized hydrogen, like the Brackett emission line series, are more difficult to detect as those lines are significantly fainter than Paα, owing to theoretical Brγ and Brδ to Paα ratios of 0.06 and 0.09, respectively. We focus on near-IR lines in the above spectral range that are intrinsically brighter, as discussed in Sects. 2.1.3 and 2.2, and hence easier to detect for a larger number of galaxies. In particular, we have explored all combinations of close, bright near-IR emission line ratios and how they vary between purely star-forming systems and AGN.
4.1.1. Iron-based diagnostics for AGN
One of the most promising near-IR diagnostic diagrams that we find is the one comparing the [S III] λ9530 Å/Paγ to the [Fe II] λ1.257 μm/Paβ line ratios, which we identify as Fe2S3–β, and is shown in Fig. 8 top-left. The lines involved in each ratio are sufficiently close in wavelength that the dust corrections can be neglected in all conditions. In this parameter space, the AGN and star-forming models, represented respectively as circles and triangles, are clearly separated, with a narrow overlapping region. The star-forming galaxies occupy the bottom left region with log10 [Fe II] λ1.257 μm/Paβ ratios spanning almost 3 orders of magnitude from ∼ − 3.0 to 0, and [S III] λ9530 Å/Paγ showing a similarly large variation between −0.3 and 1.5. The AGN models occupy instead the upper-right part of the diagram with higher [Fe II] λ1.257 μm/Paβ and [S III] λ9530 Å/Paγ line ratios, up to log10 [Fe II]/Paβ ≃ 0.7 and log10 [S III]/Paγ ≃ 1.7, respectively. There is also an intermediate (also dubbed “composite”) region where the two models overlap. The objects lying in this region, while being consistent with pure stellar or pure AGN photoionization, might represent sources with intermediate properties, where we might have the contribution from both photoionization mechanisms.
 |
Fig. 8. Near-IR diagnostic diagrams analyzed in this paper: Top row: [S III]/Paγ as a function of [Fe II]/Paβ (Fe2S3–β), [Fe II]/Paα (Fe2S3–α), [P II]/Paβ (P2S3), and [C I]/Paβ (C1S3). AGN models are represented as circles, colored as a function of log(U), and with sizes increasing with density. Star-forming models are the triangle symbols. The maximum AGN line and the maximum starburst separation limit are defined by a dotted red line and a continuous blue line, respectively. Bottom row: same as above but as a function of the [S III]/Paβ line ratio on the y-axis. |
The theoretical modeling with Cloudy also has the advantage that we can investigate how the different physical properties of the emitting source and surrounding gas cloud influence the observed line ratios. As shown in Fig. 8 top, both the [S III] λ9530 Å/Paγ and the [Fe II] λ1.257 μm/Paβ ratios increase with metallicity, resulting from a higher abundance of coolants. However, while the former line ratio has a turning point at around Z⊙ (depending on log(U)), which mimics the behavior of the R2 (=log [O II] λλ3726 − 3729/Hβ) and S2 (=log [S II] λλ6717 − 6731/Hβ) optical indices (Curti et al. 2020) with Zgas, the latter ratio increases always monothonically, suggesting that it is more sensitive and a better tracer of metallicity in the high Z regime. The overlapping region thus includes star-forming galaxies with higher gas-phase metallicity, AGN with more metal poor NLRs, or sources with both stellar and AGN contribution. An increase of the ionization parameter produces instead an enhancement of [S III]/Paγ but a decrease of [Fe II]/Paβ. However, the [S III]/Paγ line ratio saturates at an ionization parameter log(U)≃ − 2, reaching its maximum in all conditions of density and metallicity. At higher log(U), it starts to slightly decrease, as the emission from higher ionized species of sulfur is favored in these extreme conditions. For representative purposes, we do not show in the figure the predictions from models with log(U) = − 1.5 and −1, as they would overlap with the models at log(U) = − 2. Finally, a higher density has a similar effect to that seen for the ionization parameter, with [S III]/Paγ slightly increasing (and [Fe II]/Paβ slightly decreasing) from ne = 102 to 104 cm−3. These models shed light on new promising diagnostics of metallicity and ionization for dust-enshrouded systems, which will be better investigated in the future. On the other hand, if we can independently measure these parameters from near-IR lines, the star-forming and AGN models would be even more separated, and the classification more precise.
In order to classify the galaxy spectra and provide a clear, quantitative criterion to separate sources dominated by AGN or SF, we derive separation lines in analytical form, as already done in the optical bands in previous works. We first derive a line that encloses all the star-forming models that we have analyzed, by fitting a rectangular hyperbola to regions close and on the upper-right side of the highest metallicity SF models, for each different ionization parameter family, corresponding to triangles with the same colors in Fig. 8. This can be dubbed as the maximum star-forming (or starburst) line, defining a clear boundary for SF models located in the bottom-left corner of the diagram. Similarly, we also derive a boundary, dubbed the maximum AGN line, including the parameter space where the observed line ratios can be explained by an AGN. The points lying outside of the maximum starburst line in the AGN region can be identified as secure narrow-line AGN. The best-fit separation lines are written in general as :
where the coefficients A, B, and log X0 depend on the emission line ratios considered. A summary including all the coefficients used in Eq. (1) is presented in Table 6 for all the diagnostic diagrams.
We also present a diagnostic diagram (dubbed Fe2S3–α) that is based on the measurement of the [Fe II] λ1.64 μm/Paα line ratio on the x-axis. Even though these two lines can be detected in a limited redshift range (z ≲ 1.75) by JWST-NIRSpec (Paα is detected for less than one-half of the CEERS sample), and despite the [Fe II] λ1.64 μm being intrinsically ∼15% fainter than [Fe II] λ1.257 μm, they can provide useful additional contraints on the nature of dust-enshrouded sources as they probe longer wavelengths than the previous near-IR diagnostics. Nevertheless, they could be reached at higher redshifts with MIRI observations.
The model predictions for the Fe2S3–α diagnostic are shown in the second panel of Fig. 8 top as a function of [S III]/Paγ. Considering that the involved ionized species are the same as in the Fe2S3-β diagnostic, the behavior of the models as a function of the various parameters is similar. Considering the intrinsic line ratios between Paα and Paβ, and between [Fe II] λ1.257 μm and [Fe II] λ1.64 μm, the new separation lines can be obtained by translating the Fe2S3–β corresponding lines along the x-axis by −0.35 dex, that is, by setting the X0 coefficient 0.35 dex lower (see Table 6).
The diagnostic diagrams presented above require a measurement of Paγ. Among the recombination lines used in our diagrams, Paγ is usually the faintest for the majority of sources. For this reason, we also present an alternative set of diagrams where we use Paβ to compute the line ratio on the y-axis. These alternative diagrams are shown in Fig. 8 bottom. In contrast with the previous ones, these are slightly more dependent on dust attenuation. However, we have estimated that knowing AV with an uncertainty of ∼0.5 is generally enough to constrain the [S III]/Paβ ratio with an uncertainty of 0.05 dex in case of strong obscuration (AV ≃ 5 mag), or much lower in case of moderate and low attenuation (AV ≤ 2 mag). Therefore, this dust correction does not significantly impact the classification of the source in this diagnostic.
As was done in the first case, for these diagrams we can also derive separation lines to distinguish between the emission from star-forming galaxies and the narrow-line region of AGN. Given the intrinsic ratio between Paγ and Paβ, the new maximum starburst and maximum AGN lines are obtained by simply translating downward the curves described in Eq. (1) by 0.225 (i.e., the intrinsic Paγ/Paβ ratio in logarithm) along the y-axis. In practice, we subtract this constant value from the second member of Eq. (1). The new lines are visible in Fig. 8 bottom with the same color scheme as before. In principle, this approach can be applied to any other Paschen line available in the spectrum. For example, if Paδ or Paϵ are detected, we can use [S III] λ9530 Å/Paδ or [S III] λ9530 Å/Paϵ on the y-axis, in which case we should translate upward the separation lines calculated for [S III] λ9530 Å/Paγ by 0.195 and 0.365 dex, respectively.
Finally, if we consider the AGN models developed by Thomas et al. (2016), they do not significantly alter the line ratio predictions compared to our default AGN SED in both the Fe2S3–β and Fe2S3–α diagnostics, as they tend to occupy a similar parameter space to that shown for AGN in Fig. 8 for all the physical ranges of the three model parameters Epeak, pNT, and #x0393; (see Table 5). The predicted lines show a similar dependence on metallicity, ionization parameter, and gas density to that explained above. The same conclusions also hold for the other near-IR diagnostic diagrams analyzed in this paper and presented in the following subsections. For completeness, we include in Appendix B a more detailed discussion about the effects of those parameters for all the near-IR line ratios considered in this section.
4.1.2. Phosphorus-based AGN diagnostics
In the third panels of each row in Fig. 8, we present another useful diagnostic diagram in which we compare the [S III]/Paγ (or [S III]/Paβ) to the [P II] λ1.19 μm/Paβ line ratio, dubbed P2S3. As in the previous case, we can see that the separation between star-forming and AGN models is rather clear, with the former occupying the lower-left region of the diagrams with lower [S III]/Paγ ([S III]/Paβ) and lower [P II] λ1.19 μm/Paβ, while AGN are located in the upper right corner as due to their higher ratios. We can also see in both panels an intermediate region in the middle where the two models overlap. As for the ratio between [Fe II] and Paschen lines, here the [P II]/Paβ ratio also increases with metallicity, even though it spans a narrower range (∼2 dex), between −2.5 and −0.5 (in logarithmic scale) for star-forming galaxies, and from −1.5 to ∼0 for AGN, suggesting that [P II] is slightly less sensitive to metallicity than [Fe II]. On the other hand, sharing the same y-axis with previous diagrams, the models saturate at log(U)≃ − 2. With the same procedure adopted before, we can define both an AGN and a starburst boundary by applying Eq. (1), from which we can assess the dominant ionizing source in a galaxy. The coefficients derived for the [S III]/Paγ (or [S III]/Paβ) vs [P II]/Paβ diagrams are listed in Table 6.
Compared to the [Fe II] based diagnostics, these diagrams require a measurement of the [P II] λ1.19 μm line, which is fainter than [Fe II] and thus harder to detect, especially for individual star-forming galaxies. Indeed, the [P II]/Paβ ratios span smaller values than [Fe II]/Paβ. Despite this, an upper limit on this ratio would still be very useful to assess a possible AGN contribution.
4.1.3. Carbon-based AGN diagnostics
Finally, we identify a third diagnostic diagram which is based on the measurement of [C I] λ9850 Å. This diagram compares the [S III]/Paγ (or [S III]/Paβ) on the y-axis to the [C I] λ9850 Å/Paβ line ratio on the x-axis, and can be identified as the C1S3 diagram (fourth panels in each row of Fig. 8). The latter quantity can span six orders of magnitudes if we include both star-forming and AGN models, more than any other ratio that we have introduced before. However, in contrast to previous diagrams, this spread is mostly driven by the ionization parameter rather than the gas-phase metallicity. In star-forming galaxies, we can find values of log10 [C I]/Paβ ≃ −4 for models with higher ionization (log(U)∼ − 2), which increase up to ≃ − 0.5 for the lowest ionization models considered (log(U) = − 4). In AGN, we can have [C I] from ∼0.1% of Paβ at log(U)∼ − 2 up to ∼2.5 times brighter than Paβ at log(U) = − 4. Similarly to the previous diagrams, the line ratio in both axis saturates at log(U)∼ − 2. To avoid overcrowding, we do not represent the extreme ionization models, which overlap with those at log(U) = − 2. Overall, while still showing a small secondary dependence on metallicity (i.e., higher Zgas slightly increase [C I]/Paβ), [C I] is a poor tracer of the metal content and a better tracer of log(U) than [Fe II] and [P II], at least in the range of log(U) from −4 to −2. Similarly to the previous elements, also [C I]/Paβ decreases at higher gas densities.
Even considering all possible combinations of chemical composition, ionization parameter, and gas density, the star-forming and the AGN models are in general well separated at log(U)≤ − 3, more than in any other near-IR diagnostic diagram, while overlap between SF and AGN is present at higher ionization (log(U)∼ − 2). However, as we see later, AGN from low to intermediate redshift do not typically populate this parameter space, preferring lower ionization parameters and higher [C I]/Paβ ratios, hence this is not an important limitation for this work. As for [P II], [C I] is mostly detected for individual sources if they are AGN, while in purely star-forming galaxies it can be too faint with [C I]/Paβ ≪ 0.1. Even though a small correction should be preferably applied to the [C I]/Paβ (e.g., using the AV estimated from available Balmer and Paschen lines), the separation between the AGN and star-forming models allows us to assess with enough confidence the ionizing type of the source at log(U)≤3.
4.2. Near-IR AGN diagnostics at low and intermediate redshifts
We first check how the new near-IR diagnostic diagrams perform at z ≤ 1 and their ability to distinguish between local AGN and sources powered by SF. To this aim, we use the observations and the line measurements described in Sects. 2.4 and 2.5. For line ratios including the Paβ line, we correct the fluxes for dust attenuation, using the value of AV estimated from a combination of Paschen and Balmer lines (i.e., from the Paα/Paβ and Paβ/Hα line ratios), or the [Fe II] λ1.257 μm and [Fe II] λ1.64 μm lines, as in Riffel et al. (2006). We adopt the median of the three estimates if all those lines are available.
In Fig. 9, we present the comparison between the observed [Fe II] λ1.257 μm/Paβ, [Fe II] λ1.64 μm/Paβ, [P II] λ1.19 μm/Paβ, and [C I] λ9850 Å/Paβ line ratios as a function of [S III] λ9530 Å/Paγ (top row) and [S III] λ9530 Å/Paβ (bottom row), on top of our Cloudy model predictions. The observed galaxies are divided into three classes of objects, depending on their classification in the optical range: Type 1 AGN, Type 2 AGN, and starburst (i.e., star-forming, infrared bright) galaxies, which are drawn, respectively with green, black, and cyan colors.
 |
Fig. 9. Location of local and intermediate redshift AGN and starbursts in the near-IR diagnostics defined in the paper: the Fe2S3–β, Fe2S3–α, P2S3, and C1S3 diagrams from left to right, as a function of [S III]/Paγ on the y-axis (top row) or [S III]/Paβ (bottom row). Sources coming from Riffel et al. (2006, 2019) are drawn with square symbols and triangles, respectively. Those presented and measured by Onori et al. (2017) are identified with empty stars, while starbursts from Calabrò et al. (2019) are shown with cyan hexagons. The underlying models are the same as described in Fig. 8. |
We can see that, globally, the separation lines defined in Sect. 4.1 are able to separate the two classes of sources. Indeed, all the AGN, either Type 1 or Type 2, have narrow line properties consistent with AGN models, and nearly all of them lie beyond the maximum starburst limit, in a region that cannot be explained by SF alone. These local and intermediate-z AGN span the entire parameter range allowed by the models with different Zgas and log(U), even though the lowest ionization parameters are preferred (−4 ≲ log(U)≲ − 3) in all the four diagnostics. On the other hand, optically selected starbursts, both at z ∼ 0 and at z ∼ 0.7, are overall consistent with the star-forming models, even though they tend to occupy the outer envelope of the SF region toward higher gas-phase metallicities (i.e., close to solar). This is somehow expected, given that they are selected as far-infrared bright sources, therefore they trace a more star-forming, dustier, and more metal-enriched population compared to typical star-forming galaxies at the same redshift. As for the AGN subset, also the starbursts are more in agreement with low ionization models, that is, −4 ≲ log(U) < − 3. Even though we do not have statistical samples of normal, more metal-poor star-forming galaxies at z ≤ 1 with near-IR spectral coverage, the model predictions suggest that their line ratios would span a larger region in the star-forming part toward the lower left, corresponding to lower metallicity models. We can study the normal star-forming galaxy population at higher redshifts with JWST, as we show in the following section. We finally notice that these results are not significantly affected by the exact dust attenuation correction applied. Indeed, they would remain essentially unchanged even if we assume AV = 0 for all the sources.
4.3. Near-IR AGN diagnostics at higher redshifts
We now study the properties of sources at z > 1. This is the redshift range where JWST-NIRSpec is revolutionizing our understanding of galaxy evolution, in particular of dusty galaxies, thanks to its longer wavelength coverage compared to its predecessors. JWST surveys are observing more and more galaxies at cosmic noon with unprecedented sensitivity and spatial resolution, and CEERS provides by far the largest spectroscopic sample of galaxies at this epoch to allow the first statistical studies in the near-IR.
Before investigating our new near-IR spectral diagnostics, we analyze the location of CEERS sources in the classical BPT and [S II] λλ6717 − 6731 based diagram, to get a first understanding of their nature from the optical. The results are shown in Fig. 10 on the left and right sides, respectively. The sources are color-coded based on their position relative to the separation lines of Kewley et al. (2001): blue circles identify the sources consistent with star-forming models (within their 1σ uncertainty), while red circles represent secure AGN (i.e., not consistent with the star-forming region within 1σ) in at least one of the two optical diagnostics. Most of the CEERS galaxies are purely star-forming. However, we also identify 8 optical AGN (∼12% of the whole sample): all these sources lie in the AGN region of the [S II] based diagram, except one system for which [S II] is not available. Six of them are consistently identified as AGN in the BPT. For the remaining two systems, one lies very close to the separation limit. Among the optical AGN, we note that 3 of them also have a broad component detected at S/N > 3 in Hα or Hβ (CEERS ID 2919, 3129, 2904), thus should be considered as Type 1 AGN, while the remaining systems are likely Type 2 AGN in the optical (CEERS ID 2754, 5106, 12286, 16406, and 17496). Two of the broad-line AGN (2919 and 2904) are also detected by Chandra in X-rays (Nandra et al. 2015).
 |
Fig. 10. Position of CEERS galaxies selected at 1 < z < 3 in the BPT diagram (left) and in the [S II]-based optical diagnostic (right). Optical star-forming galaxies and AGN are represented with blue and red circles, respectively. To be identified as an AGN, a source must lie in the AGN region (within its 1σ uncertainty) in at least one of the two optical diagnostics. Cyan crosses are included to highlight hidden AGN, that is, optical star-forming but near-IR AGN, as explained in the text. The green dashed line is a relation representative of star-forming galaxies at z = 2.3, from Shapley et al. (2015). The violet and gray dashed lines are the classification criterion and the maximum starburst condition from Kauffmann et al. (2003) and Kewley et al. (2001), respectively. |
It is interesting to notice that CEERS sources, both star-forming galaxies and AGN with z ranging 1 < z < 3, span almost the entire parameter range of the models. Indeed, we find sources, located in the bottom right of the SF and AGN regions, that are in agreement with low ionization models (down to log(U)≃ − 3.5) and consequently have higher metallicity, while the other galaxies and AGN have increasingly higher log(U). Broad-line AGN show a preference for lower ionization models compared to narrow-line AGN, which are mostly residing in the upper left part of the BPT diagram. We note that the location of our star-forming galaxies in the BPT is broadly consistent with the relation found for typical star-forming systems at z ∼ 2.3 (Shapley et al. 2015). In this star-forming sample, galaxies with upper limits in the [N II]/Hα ratio might have lower metallicity than those with similar [O III]/Hβ ratios.
Moving now to the near-IR rest-frame diagnostics, we analyze the position of our galaxies in the Fe2S3–β, Fe2S3–α, P2S3, and C1S3 diagrams presented in Sect. 4.1. All the results are shown in Fig. 11, where we color code the sources according to their classification in the optical (red = optical AGN, blue = optical star-forming).
 |
Fig. 11. Near-IR diagnostic diagrams applied to our CEERS selected sample at 1 < z < 3. Optical star-forming galaxies and AGN are drawn with blue and red circles, respectively. Hidden AGN (i.e., optical star-forming but near-IR AGN) are identified as cyan crosses. Optical star-forming galaxies with upper limits are drawn without symbols in blue if their line ratios are still consistent with being star-forming. The red dashed and blue continuous lines represent the maximum AGN and starburst limits (respectively) according to our models. The analytical form of the separation lines is described in Eq. (1), using the coefficients listed in Table 6. |
In all the 4 possible versions of the [Fe II] based diagnostics (first and third rows of Fig. 11), most of the optical star-forming galaxies are consistent with star-forming models in these diagrams, while also the optical AGN are globally residing in a parameter space covered by the AGN models, that is, above the maximum AGN line in red. Therefore, these new diagnostics provide in general a consistent picture to that seen at shorter wavelengths. We also notice that, for optical AGN, while the majority lies in the pure AGN region in the Fe2S3–β diagram, they tend to move toward the left to the intermediate region (below the maximum starburst line) in the Fe2S3–α diagnostic, possibly due to a larger contribution in the Paα line from obscured SF. However, we have fewer statistics in this case, as we are limited in redshift.
In the [P II] and [C I] based diagnostics (second and fourth rows of Fig. 11), those lines are undetected for the majority of the optical star-forming galaxies, which is due to their intrinsic faintness compared to the [Fe II] emission lines. On the other hand, we detect them for most of the optical AGN. Also in these diagrams, the near-IR classification is mostly consistent with the optical one. Even more, we can say that for those sources in which we detect [P II] or [C I], there is a more clear separation between optical star-forming galaxies and optical AGN, preferentially falling in the pure SF or AGN region, respectively, with less overlap compared to the [Fe II] based diagrams.
Similarly to the optical case, the CEERS sample spans a wide parameter space in the near-IR diagrams, with star-forming galaxies showing a large variety of [S III]/Paγ or [S III]/Paβ line ratios over almost 2 orders of magnitude, from −0.5 to 1.5 in logarithmic scale. This result further corroborates the presence of sources with different ionization parameters, from log(U) = − 4 to higher values. In principle, the [C I] to Paschen line ratios can better distinguish among the highest ionization parameters, but the upper limits that we have are not sufficiently low to probe different values of log(U) in that regime. Also, the variety of [Fe II] and [P II] to Paschen lines flux ratios of star-forming galaxies might reflect the different metallicity properties of the sample, even though the non-detection of [P II] for a relatively large subset hampers a more precise assessment of their properties.
For the subset of optical AGN, even though they prefer models with low ionization parameters (≤3), some of them only have upper limits on Paγ, Paβ, or [C I], suggesting that they have higher log(U). The narrower range and the higher values of their [P II]/Paβ ratios (compared to star-forming galaxies) indicate instead that they have more uniform metallicity properties, consistent with Zgas at least ≥0.7 times solar on average.
4.4. Hidden AGN displaying from optical to near-IR
In analogy with the criteria adopted in the optical, we classify as near-IR AGN those systems that entirely reside in the pure AGN region in at least one of the 8 near-IR diagnostics, while the remaining systems, which are always consistent with star-forming models within 1σ, are identified as near-IR star-forming galaxies. We find that all optical AGN are also classified as near-IR AGN. However, we also find that 5 optical star-forming galaxies become AGN in the near-IR diagnostics (CEERS ID 2900, 8515, 8588, 8710, 9413). We identify them as hidden AGN, and they are represented as cyan crosses in all the panels in Fig. 11.
All of these hidden AGN are classified as pure AGN in the P2S3 diagram. Three of them also lie in the pure AGN region in the C1S3 diagnostic, while four of them have an enhanced [Fe II]/Paβ line ratio (either the [Fe II] at 1.257 or 1.64 μm) and thus are identified as pure AGN in at least one among the Fe2S3–β and Fe2S3–α diagrams. Even the sources that do not satisfy the pure AGN condition in all four diagrams, lie close to the maximum starburst line in the overlapping region between SF and AGN.
In each of the near-IR diagnostics, the optical SF galaxies whose upper limits do not allow us to put constraints on their near-IR nature (i.e., they could be consistent with either SF or AGN models), we have performed emission line measurements on their spectral stacks, and we have found that their [Fe II], [C I], [P II], and [S III] line properties are similar to the other near-IR star-forming galaxies, and that they are placed in the pure star-forming region in all the new diagnostics. This suggests that we are likely not missing a significant population of hidden AGN below our line detection limit.
In Fig. 12, we show a summary of how our CEERS sources are classified both in the rest-frame optical and the near-IR. Overall, the near-IR classification is in agreement with the optical one, but with 5 optical star-forming systems that show properties similar to AGN in the near-IR diagnostics. These hidden AGN represent a fraction of 8.8% of the population of optical star-forming galaxies, with a 1σ confidence interval of 5.6%−11.8%, estimated following Gehrels (1986). Even though they represent a small fraction of the entire population, they nearly double the total AGN sample going from 8 to 13 objects. We also note that the optical, narrow-line AGN with CEERS ID 5106 is likely a hidden broad-line AGN, showing a broad Paβ component detected at S/N > 2.
 |
Fig. 12. Summary of the AGN and star-forming galaxy classification obtained from the rest-frame optical and near-IR spectroscopic diagnostics for the sample of 65 sources selected in CEERS. |
5. Discussion
The results presented in Sect. 4 show that we can distinguish between AGN and star-forming powered sources by looking at rest-frame near-IR emission lines. In this section, we discuss the physical reason why the new diagnostics are working well for this classification task. We also discuss alternative mechanisms that might be responsible for the emission lines analyzed in this paper, and how the line ratios would evolve at high redshift. We then compare the near-IR diagnostics to the optical ones and provide possible explanations for understanding the class of hidden AGN. Finally, we discuss further improvements that can be made with forthcoming spectroscopic facilities.
5.1. Origin of the line ratio enhancement in AGN
The comparison between optical and near-IR predictions of Cloudy models shows us that we can consistently identify AGN and star-forming powered sources across one order of magnitude in wavelength, using several diagnostics that involve different chemical elements, from the local Universe up to redshift ∼3. This also indicates that the observed lines, both in SF galaxies and in AGN, are all consistent with being produced by photoionization.
All the near-IR diagrams analyzed here are based on the [S III] λ9530 Å to Paschen line ratios. The [S III] λ9530 Å line is one of the brightest available at around λrest ≃ 0.95 μm. It comes from the doubly ionized sulfur (S2+), which is created by photons with energies between 23.3 and 34.8 eV, thus it is produced more efficiently by the harder ionizing radiation of an AGN (see Fig. 6), reaching higher [S III]/Paγ ratios compared to purely star-forming galaxies.
AGN also have enhanced [Fe II], [P II], and [C I] emission compared to the typical star-forming population. The origin of this enhancement is much discussed in the literature. It is due in part to the higher metallicity of the narrow line regions, both at low and high redshift (Kewley & Dopita 2002; Groves et al. 2004), as little evolution is observed up to z ∼ 3 (Nagao et al. 2006; Matsuoka et al. 2009). As claimed by Shields et al. (2010), the strength of the optical [Fe II] line increases almost linearly with the gas-phase iron abundance, which is observed in our models also for the [P II] line.
However, as the AGN and SF predictions differ even at fixed Zgas, the ionization mechanism also plays an important role. The Fe+, P+, and C0 require low ionization or excitation energies, thus usually trace transition regions of partially ionized hydrogen, coexisting with H0, O0, S+, and free electrons, where electron collisions are an important excitation mechanism. As shown in several works (Mouri et al. 1990; Oliva et al. 2001), photoionization by nonthermal continuum radiation, especially by soft X-ray photons, can create such extended regions where the [Fe II] emission and that of other low ionization species can proliferate. The radiation field of an AGN can thus provide such favorable conditions (see also Ferland et al. 2009; Shields et al. 2010; Gaskell et al. 2022). We have verified that by switching off the soft X-ray emission in the incident radiation of the AGN template, also the emission from [Fe II], [P II], and [C I] is significantly reduced to the level of star-forming sources. Overall, this suggests that photoionization models can reproduce the observed emission line ratios.
5.2. Shock-model predictions
It is interesting to understand whether shocks can equally reproduce the observed line ratios in our new near-IR diagnostics. To this aim, we have explored the predictions of shock models as provided by the Mexican Million Models database (3MdB; Morisset et al. 2015). These are produced with the Mappings V code, version 5.1.13 (Sutherland et al. 2018), using the shock parameters of Allen et al. (2008), and assuming a solar abundance for the gaseous phase, a gas density of 1 cm−3, magnetic parameter B/n1/2 of 10−4 to 10 μG cm3/2, and shock velocity between 200 and 1000 km s−1. These are usually identified as fast shocks, in which the ionized front (photoionized by the cooling of hot gas) expands more rapidly than the shock itself, forming a detached HII-like region called precursor. We have analyzed the emission line predictions of both shocks and shock+precursor models in the BPT, in the Fe2S3–β, and in the C1S3 diagrams. However, we note that our star-forming galaxies are sufficiently rich in gas that we likely observe both the shock and its precursor. Seyfert galaxies are also found to be more consistent with shock+precursor models, as opposed to LINERS (Allen et al. 2008).
As we can see in Fig. 13, the shock models produce emission line ratios almost completely overlapping with the AGN models in the BPT and the C1S3 diagnostics. In contrast, they significantly enhance the [Fe II]/Paβ line ratio by almost 1 or 2 orders of magnitude compared to AGN and SF galaxies, respectively. This is because shocks efficiently destroy dust grains by sputtering. Since iron is one of the elements most depleted on dust in the ISM (despite being one of the most abundant in total), this process releases a large amount of iron in the gas phase, which is available to cool.
 |
Fig. 13. Predictions of the shock models described in the text for the BPT diagram, the Fe2S3–β, and the C1S3 diagrams, from top to bottom. The AGN and SF models from Cloudy and the separation lines are the same as in Fig. 8. |
The phosphorus and [P II] line predictions are not included in the original shock models of Allen et al. (2008). However, since it is not heavily depleted, we expect a similar behavior to [N II] and [C I]. Indeed, Storchi-Bergmann et al. (2009) and Oliva et al. (2001) have proposed the [Fe II]/[P II] as a main tracer of shocks. This ratio can rise to ∼20 in shock-dominated regions, significantly higher than the value of 2 observed in photoionized regions. Our CEERS observations and the sample of AGN and SF galaxies at lower redshifts thus suggest that shocks can be excluded as the main contributors of the global emission.
5.3. Redshift evolution of near-IR AGN diagnostics
Our analysis spans a large redshift range, corresponding to almost 12 billion years of cosmic time. It is therefore worth considering possible evolutionary effects on our near-IR emission line properties. The first effect to take into account is the enhancement from low-z to high-z of the fraction of α elements (which include, among all, oxygen, carbon, and sulfur) compared to iron. This is due to galaxies at z > 1 being younger on average than those at z ∼ 0, so that Type 1a supernovae, the main producers of iron, did not have time enough to enrich the surrounding ISM.
Previous studies have found abundance ratios ![$ [\frac{\mathrm{O}}{\mathrm{Fe}}] $](/articles/aa/full_html/2023/11/aa47190-23/aa47190-23-eq3.gif) a factor of 2 (or more) higher than the solar value (Steidel et al. 2016; Topping et al. 2020; Cullen et al. 2021). Assuming a conservative α-enhancement of 2 × [α/Fe]⊙, we find that it would shift the maximum starburst line in the Fe2S3–β and Fe2S3–α diagrams by −0.3 dex along the x-axis. However, at z > 1, the gas-phase metallicity of typical star-forming galaxies with stellar mass ranging 9 < log(M*/M⊙) < 11 is lower than at z = 0 by an amount of ∼0.3 dex (Wuyts et al. 2016; Sanders et al. 2020), while for AGN it is not completely assessed. This means that the depletion factor of iron (the most depleted element) should be also lower, as the dust content is directly proportional to metallicity. Assuming a half solar gas-phase metallicity, one can estimate that the depletion factor is lower by approximately the same order of magnitude (Vladilo et al. 2011), which counterbalances the previous effect, enhancing the [Fe II]/Paβ and [Fe II]/Paα ratios by ∼0.3 dex. For this reason, as a first approximation, and considering the lack of tighter constraints at high-z, we keep at z > 1 the same local relation for separating star-forming galaxies from AGN.
a factor of 2 (or more) higher than the solar value (Steidel et al. 2016; Topping et al. 2020; Cullen et al. 2021). Assuming a conservative α-enhancement of 2 × [α/Fe]⊙, we find that it would shift the maximum starburst line in the Fe2S3–β and Fe2S3–α diagrams by −0.3 dex along the x-axis. However, at z > 1, the gas-phase metallicity of typical star-forming galaxies with stellar mass ranging 9 < log(M*/M⊙) < 11 is lower than at z = 0 by an amount of ∼0.3 dex (Wuyts et al. 2016; Sanders et al. 2020), while for AGN it is not completely assessed. This means that the depletion factor of iron (the most depleted element) should be also lower, as the dust content is directly proportional to metallicity. Assuming a half solar gas-phase metallicity, one can estimate that the depletion factor is lower by approximately the same order of magnitude (Vladilo et al. 2011), which counterbalances the previous effect, enhancing the [Fe II]/Paβ and [Fe II]/Paα ratios by ∼0.3 dex. For this reason, as a first approximation, and considering the lack of tighter constraints at high-z, we keep at z > 1 the same local relation for separating star-forming galaxies from AGN.
For the other near-IR diagrams, since phosphorus and carbon are almost refractive elements, the P2S3 and the C1S3 diagnostics are not significantly altered by this effect. Moreover, phosphorus behaves similarly to an α element like sulfur (Caffau et al. 2011). As a result, we adopt at z > 1 the same separation criteria between SF galaxies and AGN as in the local Universe.
Overall, we remark that, despite the [Fe II] lines being usually brighter than [P II] and [C I], the Fe2S3–β and Fe2S3–α diagnostics have also the highest uncertainties among all near-IR diagrams. A higher α enhancement factor than our conservative value, as suggested by some previous works (e.g., Steidel et al. 2016 report a ratio of 4 − 5 × [O/Fe]⊙), would explain the fraction of optical AGN at z > 1 that in the Fe2S3–β and Fe2S3–α diagrams fall in the intermediate region. On the other hand, the ISM depletion of iron can vary by 1 order of magnitude or more (Shields et al. 2010), sufficient to explain the wide range of [Fe II] strengths in all types of sources compared to the other diagnostics based on [P II] or [C I]. It is important to remind that each diagnostic has its pros and cons, thus we recommend combining all the available near-IR diagnostic diagrams to obtain a more accurate and complete understanding of the nature of sources at 0 < z < 3. The presence of coronal lines and broad components in permitted lines can also help in identifying AGN.
Finally, we also note that near-IR star-forming galaxies in CEERS have typical [Fe II]/Paβ ratios that are lower (with [Fe II] undetected for a large fraction of them) compared to local starbursts. This is likely driven by a combination of the above-mentioned α-enhancement and selection effects: while star-forming galaxies targeted in CEERS are representative of normal star-forming galaxies at mostly M* < 1010 M⊙, local samples are selected as massive (M* > 1010 M⊙) infrared bright sources with higher SFRs and higher specific SFRs, for which we might expect an enhancement of the iron abundance as due to supernovae remnants (Lester et al. 1990).
5.4. Optical versus near-IR diagnostics and hidden AGN
In the near-IR versions of the AGN diagnostics, [S III] λ9530 Å replaces [O III] λ5007 Å on the y-axis, while [Fe II] λ1.257 μm, [Fe II] λ1.64 μm, [P II] λ1.19 μm, and [C I] λ9850 Å are used on the x-axis instead of [N II] λ6583 Å and [S II] λλ6717 − 6731. Comparing the [O III] to the [S III] emission, the production of O2+ requires photons with energies ranging 35.1−54.9 eV, significantly higher than those required to create S2+. At those high energies indeed, a large fraction of sulfur in the gas phase would be triply ionized (S3+), lowering the abundance of S2+. This implies that [S III]/Paβ is not a good tracer of the ionization parameter as the [O III]/Hβ line ratio, as it does not have a monotonic trend over the full range of possible log(U) from −4 up to =−1. The models are thus degenerate, especially at high ionization. However, an advantage is that star-forming galaxies at higher redshifts, despite having typically higher log(U), would not have also extreme [S III]/Paβ line ratios, hence they likely would not cross the maximum starburst lines even at z > 3. The remaining drawback is that the AGN can move to the intermediate part of all the diagnostics (below the maximum star-forming line) if they have metallicities lower than one-half solar. As far as the other lines are concerned, both [Fe II] and [P II] (except [C I]), are very sensitive to metallicity, as [N II] and [S II] in the optical regime. In addition, all the metal emission lines used in the near-IR diagnostics on the x-axis likely have a similar excitation mechanism and a common origin to the low-ionization line [S II] λλ6717 − 6731, as discussed in Sect. 5.1, while [N II] traces slightly higher ionization regions (Mouri et al. 1990). This explains why all AGN identified with the [S II] diagram are also AGN in near-IR diagnostics.
Overall, using the new near-IR diagrams has several advantages compared to the optical ones. First, the Fe2S3–β and Fe2S3–α diagrams, or the [Fe II]/[P II] line ratio, can distinguish between emission lines produced by photoionization or by shocks (Oliva et al. 2001), which is not possible through the classical BPT diagram (see Sect. 5.2). The [Fe II], [S III], and Paβ lines, being among the brightest features in the rest-frame range 0.8 − 1.3 μm, open the possibility to potentially characterize large samples of sources and galactic regions as shock, AGN, or star-forming driven. Secondly, the wavelength separation among the near-IR lines considered in this paper is always larger than the one between Hα and [N II] λ6583 Å, or Hβ and [O III] λ5007 Å. As a consequence, while the optical lines can be resolved only with medium to high-resolution spectrographs (R ≳ 600), we can measure individual near-IR lines also at lower spectral resolutions (100 ≤ R ≤ 600). Finally, and most importantly, [S III] λ9530 Å, [C I] λ9850 Å, [Fe II] λ1.257 μm, [P II] λ1.19 μm, Paγ, and Paβ are significantly less affected by dust attenuation than optical lines. For example, assuming a Calzetti dust law, the attenuation (in magnitudes) at λ ≥ 1 μm is a factor of 4 lower than in the range 0.4 < λ < 0.65 μm (Calzetti et al. 2000). In case of optically thick dust that is well mixed with the emitting gas, the situation is even worse, with optical lines probing only ≤10% of the systems, while Paschen lines can recover up to 30 − 40% more of the total unobscured emission (Calabrò et al. 2018).
This last point provides a clue to the physical interpretation of the class of hidden AGN. In Sect. 4.4 we have found 5 of these systems, with 4 being AGN in the P2S3 diagram and at least one Fe-based diagnostic, while the remaining one is identified as such in P2S3 and C1S3. The host galaxies of all hidden AGN have stellar masses greater than 109.3 M⊙. Having a median log M*/M⊙ = 9.8, they are on average more massive than both the 5 narrow-line optical AGN (M*, med = 109.25 M⊙) and than the parent population of star-forming galaxies selected at 1 < z < 3 (M*, med = 109.26 M⊙). Moreover, we find that in all these systems, the attenuation inferred from the Balmer decrement in the optical (adopting the Calzetti law for simplicity) is systematically lower than the one derived using the Paschen decrement (i.e., Paα + Paβ), or the Paγ/Hα and Paβ/Hα ratio if the longest wavelength line is not available. The AV estimated from Paschen lines is on average ∼0.3 dex higher than those obtained in the optical. This suggests that there might be optically thick dusty regions in or around the narrow-line region of the AGN, or the NLR itself might be partially covered by the dusty torus. In particular, we find that the hidden AGN ID 2900 is a Compton thick AGN with a luminosity log(LX/erg s−1) = 44.07 ± 0.54 and a hydrogen column density NH = 1025 cm−2 (Buchner et al. 2015). The high central density and obscuration might be the reason why it does not show broad lines and it is harder to identify compared to the other X-ray AGN in our sample (ID 2919 and 2904), which have broad lines and a lower NH < 1023 cm−2. To fully understand these trends and the nature of hidden systems, we would need larger statistics. A higher S/N of the spectra would also be necessary to check whether there are hidden broad-line AGN (emerging in the Paschen lines) in the hidden AGN population, as found for the ID 5106.
5.5. Comparison with previous near-IR diagnostics
The idea of using near-IR rest-frame diagnostics to mitigate the problem of dust attenuation in obscured sources is not new in the literature. Rodríguez-Ardila et al. (2004) proposed the diagram comparing [Fe II] λ1.257 μm/Paβ and H2λ2.121 μm/Brγ line ratios as a useful diagnostic to disentangle AGN from star-forming galaxies and LINERs. Since then, this diagram (that we indicate as Fe2H2) has been applied to analyze the ionizing sources in statistical samples of galaxies in the local Universe (e.g., Rodríguez-Ardila et al. 2004; Riffel et al. 2013; Lamperti et al. 2017). A different version of this diagnostic compares the [Fe II] λ1.64 μm/Brγ and H2λ2.121 μm/Brγ line ratios (Colina et al. 2015).
The main difference of these diagnostics compared to those previously analyzed in this paper is that they are based on emission lines (H2 and Brγ) that are in general fainter than Paα. For example, assuming Case B recombination (e.g., Osterbrock 1989), the intrinsic Brγ luminosity is 8% that of Paα and 17% that of Paβ. Furthermore, being at longer wavelengths, we can detect them in our spectra up to redshift ∼1.4, required to include Brγ in the reddest NIRSpec channel. In our sample, we have the coverage of Brγ in 6 galaxies at 1 < z < 1.4, of which 1 is an optical AGN (ID 3129), 1 is a hidden AGN (ID 9413), and the remaining 4 are normal star-forming galaxies from all our previous classifications.
Despite the small sample size, we have checked their position in the two Fe2H2 diagrams, which are shown in Fig. 14. We can see that the optical AGN and the hidden AGN fall in the AGN parameter space identified by Rodríguez-Ardila et al. (2004, 2005) in the first diagram (top panel), and by Colina et al. (2015) in the bottom panel, with the H2/Brγ ratios significantly higher than 1. Regarding the star-forming galaxies, one has lower H2/Brγ placing it in the star-forming region ([Fe II] λ1.64 μm/Brγ is not available), while for the remaining systems H2 and Brγ are both undetected. To conclude, the Fe2H2 diagrams give results that are consistent to those obtained with the four main near-IR diagrams introduced in this paper, confirming our previous classification. This also suggests that the H2 and Brγ-based diagnostics can be reliably used also at z > 1, even though a larger statistics and deeper observations are needed to confirm their effective strengths.
 |
Fig. 14. Top: diagnostic diagram comparing the [Fe II] λ1.257 μm/Paβ and H2λ2.121 μm/Brγ line ratios for CEERS galaxies in the redshift range 1 < z < 1.4 with detection of either H2 or Brγ. The black dashed lines represent the separation lines to distinguish among star-forming sources, AGN, and LINERs, according to Rodríguez-Ardila et al. (2005). Bottom: [Fe II] λ1.64 μm/Brγ vs H2λ2.121 μm/Brγ diagram (Colina et al. 2015) for the same sample. |
5.6. Future observations and facilities
At low redshift, we have been able to characterize large, representative, and almost complete samples of AGN with various degrees of activity, and sizable subsets of near-IR bright starburst galaxies. In the high redshift Universe instead, the number of spectroscopically confirmed AGN with near-IR observations is still small and does not cover all possible conditions of spectral type, black hole mass and obscuration, and level of activity, being limited to a few objects targeted with JWST/NIRSpec from ERS and GO public programs.
Surveys such as FRESCO (Oesch et al. 2023) will soon observe near-IR rest-frame lines in galaxies and AGN at redshifts < 3 with NIRSpec in slitless mode. At higher redshifts, up to the reionization epoch, the brightest near-IR lines can be observed instead with JWST-MIRI, which represents a challenging frontier. Euclid will also perform slitless spectroscopy in a wavelength range between 1.25 and 1.85 μm (Costille et al. 2016), allowing to map the near-IR lines from [S III] to Paβ at z < 0.45 with much larger statistics than JWST. Thanks to the resolving power of ∼450 in the red grism (Euclid Collaboration 2022), star-forming galaxies and AGN can be identified from near-IR diagnostics and broad line components in the brightest cases.
Another opportunity will be offered by the MOONS near-IR (0.6 − 1.8 μm) spectrograph at the VLT (Cirasuolo et al. 2020; Maiolino et al. 2020), which is scheduled to start operations in 2024. This spectrograph will take spectra over a sky area of ∼0.15 deg2 with ∼1000 fibers simultaneously, with a multiplexity performance significantly larger than previous near-IR instruments. This will allow us to detect the near-IR spectral range of thousands of galaxies up to z ∼ 0.4 (for Paβ coverage), identify all types of AGN, and map their 3D distribution, shedding light on their environment. Finally, the Prime Focus Spectrograph (PFS) at the Subaru telescope will carry out multi-fiber spectroscopy in the range 0.38 − 1.3 μm of 2400 targets simultaneously, within an area of 1.3 sq. deg. (Takada et al. 2014). Despite the shorter wavelength coverage, it has a higher resolution (R ≃ 3000), which can be used to study the kinematic properties of local, near-IR selected AGN. These spectroscopic campaigns will allow us to study the properties of both broad line and narrow line AGN even for more obscured systems that are difficult to identify at shorter wavelengths. This will finally provide a more complete census and physical characterization of AGN beyond the local Universe, with the same statistics reached by the SDSS at z < 0.1.
Thanks to the IFU spectroscopic mode of NIRSpec and MIRI we will be able in the future to derive spatially resolved maps of near-IR lines. At the VLT, we should also consider ERIS (Kravchenko et al. 2022), which is a near-IR imager and spectrograph, capable of medium-resolution integral field spectroscopy in J, H, and K bands, and long-slit spectroscopy in band L. It can operate in synergy with a modern adaptive optics system, necessary to spatially resolve the different galaxy components. This will enable a better understanding of the nuclear regions and determine the physical extension where the AGN significantly contributes to the observed line ratios. The resolved [Fe II]/[P II] ratio will be used instead to trace shock-dominated regions and outflows in the outskirts, testing the stellar and AGN feedback on galactic scales.
6. Summary
In this paper, we have investigated new diagnostic diagrams for selecting AGN in the rest-frame near-IR. We have combined model predictions with observations of star-forming galaxies and AGN at z < 3 coming from CEERS and previous spectroscopic surveys. We summarize the main findings as follows:
-
Using Cloudy photoionization models, we present four new diagnostic diagrams, named Fe2S3–β, Fe2S3–α, P2S3, and C1S3, to distinguish between stellar- and AGN-driven photoionization in galaxies, based only on rest-frame near-IR emission lines. These diagnostics share the same [S III] λ9530 Å/Paγ (or [S III] λ9530 Å/Paβ) line ratio on the y-axis, while on the x-axis they have the [Fe II] λ1.257 μm/Paβ, [Fe II] λ1.64 μm/Paα, [P II] λ1.19 μm/Paβ, or [C I] λ9850 Å/Paβ line ratios, respectively. In each case, we derived analytic expressions for the maximum star-forming lines and maximum AGN lines, which can be used to assess the dominant ionizing mechanism contributing to the global emission.
-
These diagnostics were successfully applied from redshift ∼0 to z ∼ 3. The majority of the high redshift sample (z > 1) is made of star-forming galaxies, which were coherently identified as such both in the rest-frame optical and near-IR. We also found eight optical AGN, which are coherently classified as AGN in the near-IR. Previously adopted diagrams including the H2λ2.121 μm and Brγ emission lines at longer wavelengths yield results consistent with our new near-IR diagnostics.
-
We find that five sources, classified as optical star-forming galaxies at z > 1, are identified as AGN from near-IR diagnostics. All of these sources reside in the pure AGN ionization region in the P2S3 diagram, while two and four were also identified as AGN from the C1S3 diagram and at least one iron-based diagnostic (Fe2S3–β or Fe2S3–α), respectively. Within the uncertainties, all of them are consistent with AGN models in the entire set of near-IR diagnostics. The hidden AGN represent a consistent fraction of the AGN population, increasing their total number by ∼60%. They might be systems in which the emission from the narrow-line AGN region is embedded in optically thick dust and thus can be better identified at longer wavelengths. We also find a hidden broad-line AGN candidate, classified as a narrow-line AGN in the optical but for which we tentatively detect a broad Paβ component with S/N > 2.
The near-IR diagnostics presented in this paper are preferable to standard optical diagnostics for several reasons. They are less affected by dust attenuation, require a lower spectral resolution compared to the BPT diagram and the [S II]/Hα based diagram, and finally, they can distinguish shocks from photoionization. Therefore, they represent promising tools for identifying AGN in future spectroscopic surveys.
https://jwst-pipeline.readthedocs.io/en/latest/index.html, version 1.8.5.
GitHub Repository: https://github.com/spacetelescope/stsci.tools/blob/master/lib/stsci/tools/nmpfit.py
A catalog with ID, coordinates, and emission line measurements for the CEERS galaxy sample selected in this work at 1 < z < 3 is available in electronic form at the CDS and on the GitHub page https://github.com/Anthony96/Line_measurements_nearIR.git
The OXAF models are available on the GitHub page: https://github.com/ADThomas-astro/oxaf
The star-forming models can be retrieved on GitHub: https://github.com/Anthony96/star-forming_models.git. The AGN models are available at the following page: https://github.com/Anthony96/AGN_models.git
Acknowledgments
We thank the anonymous referee for the thoughtful and constructive comments that improved the quality of the manuscript. A.C. acknowledges support from the INAF Large Grant for Extragalactic Surveys with JWST. A.F. acknowledges the support from project “VLT-MOONS” CRAM 1.05.03.07, INAF Large Grant 2022 “The metal circle: a new sharp view of the baryon cycle up to Cosmic Dawn with the latest generation IFU facilities” and INAF Large Grant 2022 “Dual and binary SMBH in the multi-messenger era”.
References
- Acquaviva, V., Gawiser, E., & Guaita, L. 2012, Proc. IAU Symp., 284, 42 [NASA ADS] [Google Scholar]
- Allen, M. G., Groves, B. A., Dopita, M. A., et al. 2008, ApJS, 178, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Arrabal Haro, P., Dickinson, M., Kartaltepe, J., et al. 2023a, A&A, 676, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023b, ApJ, 951, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Backhaus, B. E., Trump, J. R., Cleri, N. J., et al. 2022, ApJ, 926, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Bian, F., Kewley, L. J., & Dopita, M. A. 2018, ApJ, 859, 175 [CrossRef] [Google Scholar]
- Bouchet, P., Lequeux, J., Maurice, E., et al. 1985, A&A, 149, 330 [NASA ADS] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., Franx, M., et al. 2012, ApJS, 200, 13 [Google Scholar]
- Brinchmann, J., Pettini, M., & Charlot, S. 2008, MNRAS, 385, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2015, ApJ, 802, 89 [Google Scholar]
- Bushouse, H., Eisenhamer, J., Dencheva, N., et al. 2022, https://doi.org/10.5281/zenodo.7071140 [Google Scholar]
- Caffau, E., Bonifacio, P., Faraggiana, R., et al. 2011, A&A, 532, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calabrò, A., Daddi, E., Cassata, P., et al. 2018, ApJ, 862, L22 [Google Scholar]
- Calabrò, A., Daddi, E., Puglisi, A., et al. 2019, A&A, 623, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1996, ApJ, 458, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Cirasuolo, M., Fairley, A., Rees, P., et al. 2020, The Messenger, 180, 10 [NASA ADS] [Google Scholar]
- Coil, A. L., Aird, J., Reddy, N., et al. 2015, ApJ, 801, 35 [Google Scholar]
- Colina, L., Piqueras López, J., Arribas, S., et al. 2015, A&A, 578, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costille, A., Caillat, A., Rossin, C., et al. 2016, Proc. SPIE, 9912, 99122C [NASA ADS] [Google Scholar]
- Cullen, F., Shapley, A. E., McLure, R. J., et al. 2021, MNRAS, 505, 903 [CrossRef] [Google Scholar]
- Curti, M., Mannucci, F., Cresci, G., et al. 2020, MNRAS, 491, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Curti, M., Hayden-Pawson, C., Maiolino, R., et al. 2022, MNRAS, 512, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- den Brok, J. S., Koss, M. J., Trakhtenbrot, B., et al. 2022, ApJS, 261, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, A., Siana, B., Henry, A. L., et al. 2013, ApJ, 763, 145 [CrossRef] [Google Scholar]
- Dopita, M. A., Fischera, J., Sutherland, R. S., et al. 2006, ApJS, 167, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Dors, O. L., Valerdi, M., Freitas-Lemes, P., et al. 2022, MNRAS, 514, 5506 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, e058 [Google Scholar]
- Elitzur, M., Ho, L. C., & Trump, J. R. 2014, MNRAS, 438, 3340 [Google Scholar]
- Euclid Collaboration (Scaramella, R., et al.) 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faisst, A. L., Masters, D., Wang, Y., et al. 2018, ApJ, 855, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Charlot, S., & Gutkin, J. 2016, MNRAS, 456, 3354 [Google Scholar]
- Ferland, G. J., Hu, C., Wang, J.-M., et al. 2009, ApJ, 707, L82 [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Fernández, V., Amorín, R., Sanchez-Janssen, R., et al. 2023, MNRAS, 520, 3576 [CrossRef] [Google Scholar]
- Ferruit, P., Jakobsen, P., Giardino, G., et al. 2022, A&A, 661, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finkelstein, S. L., Bagley, M. B., Ferguson, H. C., et al. 2023, ApJ, 946, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [Google Scholar]
- Gardner, J. P., Mather, J. C., Abbott, R., et al. 2023, PASP, 135, 068001 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, M., Thakur, N., Tian, B., et al. 2022, Astron. Nachr., 343, e210112 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [Google Scholar]
- Goddard, D., Thomas, D., Maraston, C., et al. 2017, MNRAS, 466, 4731 [NASA ADS] [Google Scholar]
- Greener, M. J., Aragón-Salamanca, A., Merrifield, M. R., et al. 2020, MNRAS, 495, 2305 [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004, ApJS, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Charlot, S., Feltre, A., et al. 2017, MNRAS, 472, 2468 [NASA ADS] [CrossRef] [Google Scholar]
- Jakobsen, P., Ferruit, P., Alves de Oliveira, C., et al. 2022, A&A, 661, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [Google Scholar]
- Ji, X., Yan, R., Riffel, R., et al. 2020, MNRAS, 496, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, S., Daddi, E., Liu, D., et al. 2018, ApJ, 864, 56 [Google Scholar]
- Kartaltepe, J. S., Sanders, D. B., Silverman, J. D., et al. 2015, ApJ, 806, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Kashino, D., Silverman, J. D., Sanders, D., et al. 2019, ApJS, 241, 10 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., et al. 2001, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Maier, C., Yabe, K., et al. 2013, ApJ, 774, L10 [Google Scholar]
- Kewley, L. J., Nicholls, D. C., & Sutherland, R. S. 2019, ARA&A, 57, 511 [Google Scholar]
- Kodra, D., Andrews, B. H., Newman, J. A., et al. 2023, ApJ, 942, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kravchenko, K., Dallilar, Y., Absil, O., et al. 2022, Proc. SPIE, 12184, 121845M [NASA ADS] [Google Scholar]
- LaMassa, S. M., Georgakakis, A., Vivek, M., et al. 2019, ApJ, 876, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Lamperti, I., Koss, M., Trakhtenbrot, B., et al. 2017, MNRAS, 467, 540 [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, Proc. SPIE, 4841, 1670 [NASA ADS] [CrossRef] [Google Scholar]
- Lester, D. F., Carr, J. S., Joy, M., et al. 1990, ApJ, 352, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [Google Scholar]
- Maiolino, R., Cirasuolo, M., Afonso, J., et al. 2020, The Messenger, 180, 24 [NASA ADS] [Google Scholar]
- Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
- Masters, D., Faisst, A., & Capak, P. 2016, ApJ, 828, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- Matsuoka, K., Nagao, T., Maiolino, R., et al. 2009, A&A, 503, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignoli, M., Vignali, C., Gilli, R., et al. 2013, A&A, 556, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignoli, M., Feltre, A., Bongiorno, A., et al. 2019, A&A, 626, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morisset, C., Delgado-Inglada, G., & Flores-Fajardo, N. 2015, Rev. Mex. Astron. Astrofis., 51, 103 [Google Scholar]
- Mouri, H., Nishida, M., Taniguchi, Y., et al. 1990, ApJ, 360, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 447, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nandra, K., Laird, E. S., Aird, J. A., et al. 2015, ApJS, 220, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Oesch, P. A., Brammer, G., Naidu, R. P., et al. 2023, MNRAS, 525, 2864 [NASA ADS] [CrossRef] [Google Scholar]
- Oliva, E., Marconi, A., Maiolino, R., et al. 2001, A&A, 369, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Onori, F., La Franca, F., Ricci, F., et al. 2017, MNRAS, 464, 1783 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Mill Valley: University Science Books) [Google Scholar]
- Pannella, M., Elbaz, D., Daddi, E., et al. 2015, ApJ, 807, 141 [Google Scholar]
- Rayner, J. T., Toomey, D. W., Onaka, P. M., et al. 2003, PASP, 115, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Ananna, T. T., Temple, M. J., et al. 2022, ApJ, 938, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, C. T., Allen, J. T., Baldwin, J. A., et al. 2014, MNRAS, 437, 2376 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R., Rodríguez-Ardila, A., & Pastoriza, M. G. 2006, A&A, 457, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riffel, R., Rodríguez-Ardila, A., Aleman, I., et al. 2013, MNRAS, 430, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R., Rodríguez-Ardila, A., Brotherton, M. S., et al. 2019, MNRAS, 486, 3228 [Google Scholar]
- Risaliti, G., Maiolino, R., & Bassani, L. 2000, A&A, 356, 33 [NASA ADS] [Google Scholar]
- Rodríguez-Ardila, A., Pastoriza, M. G., Viegas, S., et al. 2004, A&A, 425, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Ardila, A., Riffel, R., & Pastoriza, M. G. 2005, MNRAS, 364, 1041 [CrossRef] [Google Scholar]
- Sanders, R. L., Shapley, A. E., Reddy, N. A., et al. 2020, MNRAS, 491, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ApJ, 470, 893 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifert, W., Appenzeller, I., Baumeister, H., et al. 2003, Proc. SPIE, 4841, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Reddy, N. A., Kriek, M., et al. 2015, ApJ, 801, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, G. A., Ludwig, R. R., & Salviander, S. 2010, ApJ, 721, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Simcoe, R. A., Burgasser, A. J., Schechter, P. L., et al. 2013, PASP, 125, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Stefanon, M., Yan, H., Mobasher, B., et al. 2017, ApJS, 229, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Strom, A. L., Pettini, M., et al. 2016, ApJ, 826, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., McGregor, P. J., Riffel, R. A., et al. 2009, MNRAS, 394, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., & Hummer, D. G. 1988, MNRAS, 231, 1139 [NASA ADS] [Google Scholar]
- Sutherland, R., Dopita, M., Binette, L., et al. 2018, Astrophysics Source Code Library [record ascl:1807.005] [Google Scholar]
- Takada, M., Ellis, R. S., Chiba, M., et al. 2014, PASJ, 66, R1 [Google Scholar]
- Thomas, A. D., Groves, B. A., Sutherland, R. S., et al. 2016, ApJ, 833, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, A. D., Dopita, M. A., Kewley, L. J., et al. 2018, ApJ, 856, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Topping, M. W., Shapley, A. E., Reddy, N. A., et al. 2020, MNRAS, 495, 4430 [Google Scholar]
- Trump, J. R., Weiner, B. J., Scarlata, C., et al. 2011, ApJ, 743, 144 [CrossRef] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [Google Scholar]
- Vito, F., Brandt, W. N., Yang, G., et al. 2018, MNRAS, 473, 2378 [Google Scholar]
- Vladilo, G., Abate, C., Yin, J., et al. 2011, A&A, 530, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, W., Faber, S. M., Liu, F. S., et al. 2017, MNRAS, 469, 4063 [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, E., Wisnioski, E., Fossati, M., et al. 2016, ApJ, 827, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Yung, L. Y. A., Somerville, R. S., Finkelstein, S. L., et al. 2021, MNRAS, 508, 2706 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Comparison of Balmer and Paschen line ratios in NIRSpec spectra
In this appendix, we show a representative test performed to assess the quality of the relative flux calibration of our fully reduced spectra across the entire wavelength range from 1μm to 5μm. In this test, we take the recombination lines in our NIRSpec data, and that are available for the highest number of sources, namely Hα, Hβ, Paβ, and Paγ. In Fig. A.1, we compare the optical line ratio Hβ/Hα and the Balmer-Paschen ratio Paβ/Hα (or Paγ/Hα) to the predictions of different dust attenuation laws, including the Calzetti et al. (2000) law, an SMC law from Bouchet et al. (1985), and two mixed model predictions from Calabrò et al. (2018).
 |
Fig. A.1. Diagram comparing the Hβ/Hα emission line ratio to the Paβ/Hα ratio (top panel) and the Paγ/Hα ratio (bottom panel), for CEERS galaxies in the redshift range 1 < z < 3. The predictions of different dust attenuation models are shown with colored lines. The attenuation AV along the line is specified for the Calzetti law. |
Overall, we can see that the observed points occupy a region of the diagrams that is physically allowed by one or more of the above attenuation models, with most galaxies showing relatively low dust attenuations and located in the bottom right part. Other galaxies have slightly different properties and higher attenuations AV, being consistent with either the Calzetti law, an SMC law, or the mixed model. Nearly all outliers in Fig. A.1 have at least one line that is undetected (usually Hβ or Paγ), and thus their line ratios are upper limits and cannot be used for constraining the dust attenuation. As a result, the absence of a significant number of unphysical line ratios, or systematic deviations from model predictions, indicates that the relative flux calibration of the spectra across 2μm in wavelength can be trusted on average. However, we still suggest that each object should be checked individually before computing ratios of distant lines or using their line luminosities for scientific purposes.
Appendix B: Comparison with other AGN model predictions
We analyze in this appendix all the diagnostic diagrams presented in this paper, using emission line predictions obtained with alternative AGN SEDs compared to our default spectral shape (Risaliti et al. 2000). In particular, we analyze the more recent AGN spectral shapes introduced by Thomas et al. (2016), which depend on three parameters: Epeak, pNT, and #x0393;, as discussed in Section 3.2. We first analyze the predictions for the [O III]/Hβ and [N II]/Hα line ratios (BPT diagram), which are shown in Fig. B.1. We can see that the model predictions, at fixed ionization parameter, gas density, and metallicity, occupy a similar region compared to those obtained with our default AGN SED (Fig. 7). Within the same family where those three parameters (log U, Z, and ne) are fixed, we can notice smaller variations as due to the specific properties of the ionizing shape. The stronger variation is produced by Epeak, for which we show for clarity only the predictions obtained with the extreme values considered in this work (Epeak = 20 eV and 100 eV). In detail, a higher Epeak yields on average a higher [O III]/Hβ and [N II]/Hα ratios, with the increase rate depending on Z and log U. The enhancement is almost negligible at small (i.e., subsolar) metallicities and small ionization parameters (log U ≤ 3.5), but it can be up to +0.2 dex at supersolar metallicity and higher log U. This effect was already discussed in Thomas et al. (2016), and is due to more energetic and ionizing photons in SEDs with higher Epeak, which mimics the enhancement of the ionization parameter and gas temperature.
 |
Fig. B.1. BPT diagram, analog of Fig. 7, where the line ratio predictions for AGNs are obtained using the recent models of Thomas et al. (2016, 2018). For AGN models with the same ionization parameter (colored as indicated in the legend), the circles are the predictions obtained with Epeak = 20 eV, while the square symbols are derived assuming Epeak = 100 eV. The marker size varies as a function of gas density (from 102 to 104 cm−3 from the smaller to the larger). The three points with the same marker, size, and color, are the predictions of three different values of pNT: 0.1, 0.25, and 0.4. The lines, markers, and colors for the star-forming models and observations are the same as in Fig. 7. |
On the other hand, pNT produces much smaller variations in the predicted line ratios. A higher pNT increases the fraction of energetic photons in the X-ray part of the spectrum (Fig. 6), including the soft X-rays that are more easily absorbed by the nebula. This causes a more extended partially ionized zone and more emission coming from this region, especially from low-ionization species. However, pNT does not significantly alter the photoionization model predictions in the BPT diagram, with variations of the line ratios typically smaller than 0.1 dex, even smaller than the effects due to varying gas density in the nebula. In Fig. B.1 and all subsequent figures, model predictions with different Epeak are represented with different symbols (circles and squares), while predictions corresponding to different values of pNT are drawn with the same symbol and are almost overlapping.
We also analyze the predictions of the OXAF models for all the near-IR diagrams introduced in Section 4.1. The results are presented in Fig. B.2, which is the analog of Fig. 8. Similarly to the BPT diagram, also in the near-IR diagnostics the models of Thomas et al. (2016) produce line ratios that are comparable to those obtained with our default AGN SED, occupying the same parameter space with the same limits on [S III]/Paγ, [S III]/Paβ, [Fe II]/Paβ, [Fe II]/Paα, [P II]/Paβ, and [C I]/Paβ. If we exclude the influence of metallicity and ionization parameter, Epeak has the third major effect on the emission line intensities. In particular, choosing models with higher Epeak increases all the line ratios listed above, moving all the points toward the upper right part of the plot, by factors that depend on the metallicity, ionization parameter, and on the specific diagram. In detail, for models with log U > −2, the line ratios on both axis increase by 0.2-0.5 dex in the range 20 < Epeak/eV < 100, because of more energetic ionizing photons available at higher Epeak. In the last bin of log U shown in Fig. B.2 (≃ − 2), the [S III]/Paβ and [S III]/Paγ ratios saturate with Epeak, as higher ionization states of sulfur are populated. On the other hand, the ratios on the x-axis still increase, as those low-ionization species are very sensitive to the higher contribution of soft X-ray photons from models with enhanced Epeak (see Fig. 6), as also discussed in Section 5.1. As shown by Thomas et al. (2016), a similar mechanism is responsible for the higher [O I] and [S II] emission in the optical.
 |
Fig. B.2. Near-IR diagnostic diagrams including Fe2S3-β, Fe2S3-α, P2S3, and C1S3. This figure is the analog of Fig. 8, but the emission line predictions for the NLR of AGNs are obtained using the AGN models described in Thomas et al. (2016, 2018). The markers, sizes, and colors of AGN models are the same as described in Fig. B.1. The star-forming models are the same as in Fig. 8. The maximum starburst and AGN lines are defined in Section 4.1 and in Table 6. |
The influence of pNT on the same near-IR line ratios is in general smaller than that produced by Epeak, with variations < 0.1 dex for models with low and intermediate ionization (log U < −2) in all the diagrams in Fig. B.2, except [C I]/Paβ, which can vary by up to ∼0.3 dex from pNT = 0.1 to 0.4. Also for this parameter, at the highest log U considered here, it mostly affects the line ratios on the x-axis by the same mechanism explained above for Epeak, with increments of up to ∼1 dex for [C I]/Paβ and ∼0.5 dex for the remaining ratios. We note that [C I]/Paβ is more sensitive to variations of Epeak and pNT because it is entirely produced in partially ionized regions where electron collisions stimulated by nonthermal continuum radiation are the main excitation mechanism.
Finally, as shown by Thomas et al. (2016), the third parameter #x0393; has a similar behavior to pNT, but produces even smaller variations of the line ratios in all the diagrams analyzed above (both in the optical and near-IR), so we have fixed it to +2.0 in the simulations. We note that a more exhaustive discussion of the effects of each parameter can be found in the introductory paper of the OXAF models. We also remark that the exact line ratio predictions of AGN models do not affect the maximum starburst separation line (derived from star-forming models), hence they do not alter the results of this paper.
All Tables
Optical and near-IR rest-frame lines that we are able to detect in our spectra of star-forming galaxies and AGN in the redshift range 0 ≤ z ≤ 3, and that we consider in this paper.
Solar abundances and depletion factors for all the models analyzed in this paper.
Full range of parameters used in Cloudy for constructing the grid of star-forming models explored in this work.
Parameters adopted in AGN models from Thomas et al. (2016, 2018), with the custom SED shape injected in pyCloudy through the “table SED” command.
All Figures
 |
Fig. 1. Rest-frame spectra of 10 sources observed by JWST/NIRSpec in CEERS. The spectra are normalized to their median flux and offset relative to each other to help the visualization. They are colored in black, red, and green, according to whether they are identified, respectively, as optical+near-IR star-forming, optical+near-IR AGN, or hidden AGN (i.e., optical SF and near-IR AGN), according to the diagnostic diagrams presented in this paper (see Sect. 4.3). The CEERS ID and the spectroscopic redshift of each source are written besides each spectrum. The emission lines that can be identified in the range 0.4 μm < λ < 2 μm are highlighted above the top axis (see also Table 1). |
| In the text | |
 |
Fig. 2. Spectrum of the broad-line AGN with CEERS ID 3129 at z = 1.04, around emission lines detected in the full spectral range of NIRSpec, in increasing order of wavelength. The noise spectrum is represented with gray error bars around the observed flux (black line). The emission lines are fitted with multiple Gaussian components, as described in the text. Blue and orange vertical dashed lines highlight the gaussian central wavelength of permitted and forbidden lines, respectively. For broad lines, both the narrow and broad components are shown with a dashed and dotted blue line, respectively. The global best fit profile is drawn with a red dashed line. The S/N of the detection is highlighted in the top left corner of each panel, while the name of each line is written in the top right corner (see also Table 1). |
| In the text | |
 |
Fig. 3. Spectroscopic redshift distribution of emission line galaxies in the CEERS survey in the redshift range between 1 and 3 (top panel), where both optical and rest-frame near-IR lines can be detected, from Hβ to Paβ. The vertical dashed black line highlights the median redshift of our selected sample (zmedian = 2.0). Bottom: comparison between the spectroscopic redshifts estimated from CEERS spectra and previously available photometric redshifts (Kodra et al. 2023). |
| In the text | |
 |
Fig. 4. Distribution of intrinsic FWHM widths (i.e., deconvolved from instrumental broadening) for CEERS galaxies selected at 1 < z < 3 as described in the text. The FWHM is estimated from the Hα line. If Hα is not detected, we use the highest S/N line in the spectrum, that is, [S III] λ9530 Å or [O III] λ5007 Å. The line width is a variable parameter in the fit but is assumed to be the same value for all narrow lines, with a tolerance of 50 km s−1. The median value of the sample (FWHMmedian ≃ 175 km s−1) is represented with a vertical dashed black line. |
| In the text | |
 |
Fig. 5. Stellar mass M⋆–SFR diagram of CEERS galaxies selected in this work between redshift 1 and 3. The M⋆ and SFR are taken from Stefanon et al. (2017) as described in the text (cyan triangles) or from Le Bail et al. (in prep.) if Herschel detected (red squares). The sample is representative of the star-forming Main Sequence (MS) at the median redshift of the sample (zmedian = 2). The black dotted line represents the starburst limit, that is, a factor of 4 above the MS of Schreiber et al. (2015). The SFRs shown in this plot are normalized to z = 2 assuming that they scale with redshift as (1 + z)2.8 (Sargent et al. 2014). |
| In the text | |
 |
Fig. 6. Top: diagram with the shape of the ionizing radiation field (energy units, normalized to the flux at the Lyman limit) assumed in CLOUDY to model the stellar emission (orange curve) and the AGN emission (black, red, and darkred curves, as described in the legend). For these representative curves we have assumed log(U) = − 2, solar metallicity, and a density of 103 cm−3 in all cases. In the AGN models from Thomas et al. (2016), we identify with the same color (red or darkred) the family with a common Epeak, in which the parameter pNT increases toward the top from the lighter to the darker line. The dashed shaded lines indicate the transmitted continuum. Bottom: zoom-in of the top panel in the energy range between 5 and 100 eV, but with a linear scale on the x-axis and the flux density fν (normalized to the flux density at the Lyman limit) on the y-axis. This version of the plot is inspired by Feltre et al. (2016). The area between the two AGN shapes of Thomas et al. (2016) with the same pNT = 0.25 and varying Epeak (in the range 20 − 100 eV) is filled with a chequered red pattern. |
| In the text | |
 |
Fig. 7. Prediction from our Cloudy models of the emission line ratios [O III]/Hβ vs [N II]/Hα (BPT diagram). Triangles and circles represent the star-forming and AGN models, respectively. The gas-phase metallicity increases from left to right. The blue continuous line represents the separation line by Kauffmann et al. (2003), while the red dotted line represents the maximum starburst model by Kewley et al. (2001). The cyan and green dashed lines show the average location of star-forming galaxies at z = 0 and z = 2.3, respectively, from Kewley et al. (2013) and Shapley et al. (2015). The big red squares and dashed line highlight the AGN sequence by Richardson et al. (2014), with increasing ionization from bottom to top. |
| In the text | |
 |
Fig. 8. Near-IR diagnostic diagrams analyzed in this paper: Top row: [S III]/Paγ as a function of [Fe II]/Paβ (Fe2S3–β), [Fe II]/Paα (Fe2S3–α), [P II]/Paβ (P2S3), and [C I]/Paβ (C1S3). AGN models are represented as circles, colored as a function of log(U), and with sizes increasing with density. Star-forming models are the triangle symbols. The maximum AGN line and the maximum starburst separation limit are defined by a dotted red line and a continuous blue line, respectively. Bottom row: same as above but as a function of the [S III]/Paβ line ratio on the y-axis. |
| In the text | |
 |
Fig. 9. Location of local and intermediate redshift AGN and starbursts in the near-IR diagnostics defined in the paper: the Fe2S3–β, Fe2S3–α, P2S3, and C1S3 diagrams from left to right, as a function of [S III]/Paγ on the y-axis (top row) or [S III]/Paβ (bottom row). Sources coming from Riffel et al. (2006, 2019) are drawn with square symbols and triangles, respectively. Those presented and measured by Onori et al. (2017) are identified with empty stars, while starbursts from Calabrò et al. (2019) are shown with cyan hexagons. The underlying models are the same as described in Fig. 8. |
| In the text | |
 |
Fig. 10. Position of CEERS galaxies selected at 1 < z < 3 in the BPT diagram (left) and in the [S II]-based optical diagnostic (right). Optical star-forming galaxies and AGN are represented with blue and red circles, respectively. To be identified as an AGN, a source must lie in the AGN region (within its 1σ uncertainty) in at least one of the two optical diagnostics. Cyan crosses are included to highlight hidden AGN, that is, optical star-forming but near-IR AGN, as explained in the text. The green dashed line is a relation representative of star-forming galaxies at z = 2.3, from Shapley et al. (2015). The violet and gray dashed lines are the classification criterion and the maximum starburst condition from Kauffmann et al. (2003) and Kewley et al. (2001), respectively. |
| In the text | |
 |
Fig. 11. Near-IR diagnostic diagrams applied to our CEERS selected sample at 1 < z < 3. Optical star-forming galaxies and AGN are drawn with blue and red circles, respectively. Hidden AGN (i.e., optical star-forming but near-IR AGN) are identified as cyan crosses. Optical star-forming galaxies with upper limits are drawn without symbols in blue if their line ratios are still consistent with being star-forming. The red dashed and blue continuous lines represent the maximum AGN and starburst limits (respectively) according to our models. The analytical form of the separation lines is described in Eq. (1), using the coefficients listed in Table 6. |
| In the text | |
 |
Fig. 12. Summary of the AGN and star-forming galaxy classification obtained from the rest-frame optical and near-IR spectroscopic diagnostics for the sample of 65 sources selected in CEERS. |
| In the text | |
 |
Fig. 13. Predictions of the shock models described in the text for the BPT diagram, the Fe2S3–β, and the C1S3 diagrams, from top to bottom. The AGN and SF models from Cloudy and the separation lines are the same as in Fig. 8. |
| In the text | |
 |
Fig. 14. Top: diagnostic diagram comparing the [Fe II] λ1.257 μm/Paβ and H2λ2.121 μm/Brγ line ratios for CEERS galaxies in the redshift range 1 < z < 1.4 with detection of either H2 or Brγ. The black dashed lines represent the separation lines to distinguish among star-forming sources, AGN, and LINERs, according to Rodríguez-Ardila et al. (2005). Bottom: [Fe II] λ1.64 μm/Brγ vs H2λ2.121 μm/Brγ diagram (Colina et al. 2015) for the same sample. |
| In the text | |
 |
Fig. A.1. Diagram comparing the Hβ/Hα emission line ratio to the Paβ/Hα ratio (top panel) and the Paγ/Hα ratio (bottom panel), for CEERS galaxies in the redshift range 1 < z < 3. The predictions of different dust attenuation models are shown with colored lines. The attenuation AV along the line is specified for the Calzetti law. |
| In the text | |
 |
Fig. B.1. BPT diagram, analog of Fig. 7, where the line ratio predictions for AGNs are obtained using the recent models of Thomas et al. (2016, 2018). For AGN models with the same ionization parameter (colored as indicated in the legend), the circles are the predictions obtained with Epeak = 20 eV, while the square symbols are derived assuming Epeak = 100 eV. The marker size varies as a function of gas density (from 102 to 104 cm−3 from the smaller to the larger). The three points with the same marker, size, and color, are the predictions of three different values of pNT: 0.1, 0.25, and 0.4. The lines, markers, and colors for the star-forming models and observations are the same as in Fig. 7. |
| In the text | |
 |
Fig. B.2. Near-IR diagnostic diagrams including Fe2S3-β, Fe2S3-α, P2S3, and C1S3. This figure is the analog of Fig. 8, but the emission line predictions for the NLR of AGNs are obtained using the AGN models described in Thomas et al. (2016, 2018). The markers, sizes, and colors of AGN models are the same as described in Fig. B.1. The star-forming models are the same as in Fig. 8. The maximum starburst and AGN lines are defined in Section 4.1 and in Table 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.