| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141334 | |
| Published online | 19 January 2022 | |
The Fornax Cluster VLT Spectroscopic Survey
III. Kinematical characterisation of globular clusters in the Fornax galaxy cluster⋆
1
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
e-mail: avinash.chaturvedi@eso.org
2
Ludwig Maximilian Universitat, Professor-Huber-Platz 2, 80539 Munich, Germany
3
INAF – Astronomical Observatory of Abruzzo, Via Maggini, 64100 Teramo, Italy
4
School of Physics and Astronomy, Sun Yat-sen University, Zhuhai Campus, 2 Daxue Road, Xiangzhou District, Zhuhai, PR China
5
INAF – Osservatorio Astronomico di Capodimonte, Salita Moiariello, 16, 80131 Napoli, Italy
6
Department of Astrophysics, University of Vienna, Turkenschanzstraße 17, 1180 Wien, Austria
7
Sub-Dep. of Astrophysics, Dep. of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
8
University of Naples Federico II, C.U. Monte Sant’Angelo, Via Cinthia, 80126 Naples, Italy
9
Institute of Astrophysics, Pontificia Universidad Catolica de Chile, Avenida Vicuna Mackenna 4860, Macul, 7820436 Santiago, Chile
Received:
18
May
2021
Accepted:
16
September
2021
The Fornax cluster provides an unparalleled opportunity of investigating the formation and evolution of early-type galaxies in a dense environment in detail. We aim at kinematically characterising photometrically detected globular cluster (GC) candidates in the core of the cluster. We used spectroscopic data from the Visible Multi Object Spectrograph at Very Large Telescope (VLT/VIMOS) from the FVSS survey in the Fornax cluster, covering one square degree around the central massive galaxy NGC 1399. We confirm a total of 777 GCs, almost doubling previously detected GCs, using the same dataset as was used before. Combined with previous literature radial velocity measurements of GCs in Fornax, we compile the most extensive spectroscopic GC sample of 2341 objects in this environment. We found that red GCs are mostly concentrated around major galaxies, while blue GCs are kinematically irregular and are widely spread throughout the core region of the cluster. The velocity dispersion profiles of blue and red GCs show a quite distinct behaviour. Blue GCs exhibit a sharp increase in the velocity dispersion profile from 250 to 400 km s−1 within 5 arcmin (∼29 kpc/∼1 reff of NGC 1399) from the central galaxy. The velocity dispersion profile of red GCs follows a constant value between 200 and 300 km s−1 until 8 arcmin (∼46 kpc/∼1.6 reff), and then rises to 350 km s−1 at 10 arcmin (∼58 kpc/∼2 reff). Beyond 10 arcmin and out to 40 arcmin (∼230 kpc/ ∼8 reff), blue and red GCs show a constant velocity dispersion of 300 ± 50 km s−1, indicating that both GC populations trace the cluster potential. We kinematically confirm and characterise the previously photometrically discovered overdensities of intra-cluster GCs. We found that these substructured intra-cluster regions in Fornax are dominated mostly by blue GCs.
Key words: catalogs / galaxies: clusters: individual: Fornax / galaxies: star clusters: general / galaxies: kinematics and dynamics
The globular cluster radial velocity catalogue (Full Table C.1) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/657/A93
© ESO 2022
1. Introduction
Understanding the assembly of galaxy clusters provides valuable insight into various aspects of cosmology, such as galaxy evolution and formation, gravitational structure formation, and intergalactic medium physics. Galaxy clusters are the largest gravitationally bound systems. Their assembly is driven by early mergers of massive galaxies embedded in large dark matter (DM) halos and sequential accretion of galaxy groups (e.g. Kravtsov & Borgani 2012). During their growth, various physical processes act on the cluster galaxies, such as tidal disturbances, ram pressure stripping, secular evolution, and gas accretion, which all contribute to shape their luminous and DM distributions (Kravtsov & Borgani 2012; Duc et al. 2011; Amorisco 2019). Semi-analytic models of galaxy formation and evolution, combined with cosmological N-body simulations of DM haloes in the ΛCDM framework, have shown that the number of substructures in stellar haloes and their dynamics directly probe two fundamental aspects of galaxy formation: the hierarchical assembly of massive galaxies, and their DM haloes (Cooper et al. 2013; Pillepich et al. 2015).
The interaction processes leave dynamical imprints on the stellar populations of galaxies. In particular, tidal features are preserved and easily identified in the outer halos of galaxies, where the dynamical timescales are longer than in the inner parts (e.g. Napolitano et al. 2003). Observed disturbances include stellar streams and tidal structures in phase space (Romanowsky et al. 2012; Coccato et al. 2013; Longobardi et al. 2015). Therefore stellar halos are crucial in understanding the formation and evolution of galaxies.
Due to the low surface brightness of the outer halos of galaxies, kinematical details from integrated light at large radii are mostly inaccessible with current spectrographs. However, discrete tracers such as globular clusters and planetary nebulae (PNe) play a significant role in learning about the halos kinematics. These are bright sources that are easily detectable in the outskirts of galaxies (Dolfi et al. 2021; Longobardi et al. 2015, 2018a; Hartke et al. 2018). PNe represent a post-main-sequence evolutionary stage of stars and are mainly associated with the stellar populations and integrated light of the galaxies (Douglas et al. 2007; Coccato et al. 2009; Napolitano et al. 2011; Spiniello et al. 2018). Globular clusters (GCs), on the other hand, are massive, compact, and mostly old star clusters that are found in almost all major types of galaxies (e.g. Brodie & Strader 2006). Observations have shown that GCs exist in two major subpopulations: red (metal-rich) GCs, and blue (metal-poor) GCs. The red GCs are found to have radial number density profiles similar to the integrated light of their host galaxies, while blue GCs are spatially more extended into the intergalactic and intra-cluster regions and trace the metal-poor component of the stellar halos (Schuberth et al. 2010; Hilker et al. 2015; Cantiello et al. 2018; Pota et al. 2018).
These two GC subpopulations also show different kinematical characteristics. In most cases, the red GCs follow the stellar population kinematics of their parent galaxies, whereas blue GCs show a more erratic and complex kinematic behaviour (Schuberth et al. 2010; Coccato et al. 2013; Napolitano et al. 2014; Cantiello et al. 2018; Pota et al. 2018). The colour bimodality of GCs is mainly associated with their bimodal metallicity distribution, although the relation between colour and metallicity is not entirely linear (Cantiello et al. 2014; Fahrion et al. 2020a). The colour bi-modality and distinct kinematical behaviour have been explained as the result of a two-stage formation scenario for massive galaxies (Ashman & Zepf 1992; Kundu & Whitmore 2001; Peng et al. 2006). Cosmological simulations suggest that massive early-type galaxies grow and evolve in these two stages: first, rapidly with a high star formation rate and early compact mergers (in situ), and later through the continuous accretion of smaller systems that build up the extended halo populations.
The red metal-rich GCs are thought to have formed during the in situ star formation process, whereas the blue metal-poor GCs are added to the system through the accretion of low-mass objects, such as dwarf galaxies (Forbes et al. 1997; Côté et al. 1998; Hilker et al. 1999a; Kravtsov & Gnedin 2005; Tonini 2013; Forbes & Remus 2018). Various studies of GC populations in galaxy clusters revealed that so-called intra-cluster GCs (ICGCs) exist that are not bound to any individual galaxy (Williams et al. 2007; Bergond et al. 2007; Bassino et al. 2006; Schuberth et al. 2008; Peng et al. 2011; Alamo-Martínez et al. 2013). The ICGCs might represent the first GCs formed in a cluster potential or could be tidally released GCs from multiple galaxy interactions (White 1987; West et al. 1995; Yahagi & Bekki 2005; Madrid et al. 2018; Harris et al. 2020). Although their formation mechanism is still debated (Ramos-Almendares et al. 2018), their kinematics add additional constraints on the accretion and assembly history of their parent galaxy cluster.
These properties of GCs make them privileged discrete tracers for the dynamical study of individual galaxies, as well as of the mass assembly of galaxy clusters. Recent advancements in discrete dynamical modelling such as Jeans dispersion-kurtosis, incorporating high-velocity moments (Napolitano et al. 2014), and chemodynamical modelling methods (Zhu et al. 2016a) allow the unification of several physical properties of discrete tracers at once, such as their positions, velocities, and also colours and metallicities. This has brought a significant improvement and produced better constraints on the mass modelling and orbital anisotropy of the tracers (Watkins et al. 2013; Zhu et al. 2016a,b).
Recently, Li et al. (2020) used GC kinematics to study the mass distribution and kinematics of the giant elliptical galaxy M87 in the centre of the Virgo cluster based on 894 discrete tracers. The M87 GC system (GCS) and the core of the Virgo cluster are a well-explored environment in this respect.
A very interesting and dynamically evolving environment is the Fornax galaxy cluster. It is the most massive galaxy overdensity within 20 Mpc after the Virgo cluster. It is an ideal target for studying the effect of the environment on the structure and assembly of galaxies of any type in detail (Iodice et al. 2016, 2019). The earliest approach to dynamically model the Fornax central galaxy NGC 1399 was made by Kissler-Patig et al. (1999), Saglia et al. (2000), and Napolitano et al. (2002). Later, major and crucial work was presented by Schuberth et al. (2010), who used 700 GCs within 80 kpc of the Fornax cluster as dynamical tracers to place constraints on the properties of the central DM halo.
In the past decade, the GC system of the Fornax cluster has been photometrically examined in great detail. Various imaging surveys such as the ACS Fornax Cluster Survey (ACSFCS) with the Hubble Space Telescope (Jordán et al. 2007, also see Puzia et al. 2014), the Next Generation Fornax Survey (NGFS; Muñoz et al. 2015), and the Fornax Deep Survey (FDS) with the Very Large Telescope Survey Telescope (VST; Iodice et al. 2016) have added a wealth of information about galaxies and GCs in the Fornax cluster. Photometric studies from D’Abrusco et al. (2016), and Iodice et al. (2019) have revealed that despite the regular appearance of the Fornax cluster, its assembly is still ongoing, as evidenced by the presence of stellar and GC tidal streams. Most recently, Cantiello et al. (2020) have produced the largest photometric catalogue of compact and slightly extended objects in the Fornax cluster over an area of ∼27 square degrees.
Due its proximity, Fornax provides a unique opportunity to map its complex kinematics from the core out to at least ∼350 kpc using GCs as kinematic tracers. Based on the radial velocities of GCs and PNe, the Fornax Cluster VLT Spectroscopic Survey (FVSS) has obtained an extended velocity dispersion profile of the central galaxy out to 200 kpc (Pota et al. 2018; Spiniello et al. 2018). This has allowed us to connect the large-scale kinematics of the major galaxies to the small-scale stellar halo kinematics of the central galaxy NGC 1399.
A crucial missing information to comprehend the complete mass assembly of Fornax is to understand the origin and kinematical behaviour of its intra-cluster population and of the disturbed outer halos of interacting cluster galaxies. Several studies have shown that ignoring the presence of substructures, which are generated by accretion and merger events, affects the dynamical mass estimates of clusters, leading to erroneous cosmological inferences (Old et al. 2017; Tucker et al. 2020). For example, studying the kinematics of stellar populations in the core of the Hydra I cluster, Hilker et al. (2018) reported that small-scale variations in the kinematics due to substructures can produce a notable change in the mass modelling, leading to an overestimation of the DM halo mass in the core of that cluster. Therefore the identification and proper kinematical understanding of dynamically cold substructures and outer halos of interacting galaxies in clusters are essential for understanding how these structures formed, assembled, and evolved and have to be taken into account for the mass modelling.
Using a novel cold structure finder algorithm, Gatto et al. (2020) made a first attempt to search for cold kinematical substructures in Fornax based on the GC and PNe data of Pota et al. (2018) and Spiniello et al. (2018). This has revealed at least a dozen candidate streams in the combined kinematical information of the PNe and GCs dataset of the FVSS (Napolitano et al. 2022). These substructures can then be subtracted from the underlying discrete radial velocity field in the Fornax core for unbiased dynamical models. Since the work of Schuberth et al. (2010) about ten years ago, a major dynamical study of the Fornax cluster is still lacking, and so far, no disturbed halo features of central cluster galaxies and no intra-cluster substructures were taken into account in a thorough dynamical model of the Fornax cluster core.
The low recovery fraction of the GC radial velocity measurements from the earlier FVSS results (Pota et al. 2018) and the improvement of the VIMOS ESO pipeline motivated us to reanalyse the VLT/VIMOS data of the Fornax Cluster. Here we present the radial velocity catalogue of GCs in an area of more than two square degrees, corresponding to 250 kpc of galactocentric radius. In forthcoming papers of this series (Chaturvedi et al., in prep.), we will discuss the identification and properties of substructures and the mass modelling of the Fornax cluster, with the final goal to understand its mass assembly and dark matter halo properties.
This paper is organised as follows: In Sect. 2 we describe the observations and data reduction. The radial velocity measurements are presented in Sect. 3 and the results in Sect. 4. In Sect. 5 we discuss the results and present the photometric and spatial distribution of our GC catalogue. Section 6 summarises our results and presents the scope of future work. In Appendices A and B we describe some tests we performed for the radial velocity analysis and an object portfolio used for visual inspection. In Appendix C we show an excerpt of the VIMOS data GC catalogue from this study. The full catalogue is available at the CDS. Throughout the paper, we adopt a distance to NGC 1399 of D ∼ 19.95 Mpc (Tonry et al. 2001), which corresponds to a scale of 5.8 kpc per arcmin.
2. Observations and data reduction
This work examines the detection and kinematical characterisation of GCs in the Fornax cluster core within one square degree. We have reanalysed Fornax cluster VLT/VIMOS spectroscopic data taken in 2014 and 2015 under the ESO program 094.B-0687 (PI: M. Capaccioli). For a detailed description of observations preparation and target selection, we refer to Pota et al. (2018). Here we briefly summarise the observation details and present the new data reduction.
2.1. Photometry and globular cluster selection
The Fornax Deep Survey (FDS, Iodice et al. 2016) and Next Generation Fornax Survey (NGFS, Muñoz et al. 2015) formed the photometric data base for selecting GC candidates for the VIMOS/VLT spectroscopic survey. The FDS deep multiband (u, g, r and i) imaging data from OmegaCAM cover an area of ∼30 square degrees out to the virial radius of the Fornax cluster. NGFS is an optical and near-infrared imaging survey and covers nearly the same area as the FDS survey.
Globular cluster candidates for spectroscopic observations were selected based on dereddened g - and i -band magnitudes from the FDS and preliminary VISTA/VIRCAM photometry in the Ks band from the NGFS. Additionally, wide-field Washington photometry (Dirsch et al. 2004; Bassino et al. 2006) was used to construct the C − i versus i − Ks diagram to select the bona fide GCs. Hubble Space Telescope/ACS photometry was used to find additional GCs in the central regions of NGC 1399 (Puzia et al. 2014). Finally, with a magnitude restriction of 17.0 < i < 23.0 mag, a total of 4340 unique spectroscopic targets were selected. This selection on purpose also includes some background galaxies and compact sources outside the selection criteria whenever there was space for additional VIMOS slits.
2.2. Observations
The spectroscopic observations for this study were carried out with the Visible Multi Object Spectrograph (VIMOS, LeFevre et al. 2013) at the VLT and were acquired in ESO Period 94 between October 2014 and January 2015. A total of 25 VIMOS pointings were defined to cover the central square degree of the Fornax cluster. Each pointing consists of four quadrants of 7 × 8 arcmin2. The MR grism was used together with filter GG475, which allows a multiplexing of two in spectral direction with a spectral coverage of 4750–10 000 Å at resolution with a full width at half maximum (FWHM) of 12Å. Three exposures of 30 minutes each were taken for each pointing.
2.3. Data reduction
The data reduction was performed with the VIMOS pipeline version 3.3.0 incorporated in the ESO Reflex workflow (Freudling et al. 2013). The reduction follows the steps described in Pota et al. (2018). The dataset of each VIMOS pointing consisted of biases, flat fields, scientific spectral images, and arc lamp spectra. The older version of the VIMOS pipeline, used for the analysis performed in Pota et al. (2018), did not correct for flexure-induced wavelength shifts in multiple science exposure before their combination. This caused an incorrect absolute wavelength calibration and line broadening in the stacked spectra. Pota et al. (2018) manually corrected for this limitation by applying the median wavelength shift of the second science exposure to the final stacked spectra. On the other hand, the improved pipeline version we used for our work takes care of wavelength shifts before stacking the individual spectra and prevents the line broadening effects. We confirmed this by reducing the individual exposures of a few VIMOS pointings and compared them with the final stacked reduced spectra.
In Fig. 1 we show the CaT region of the reduced individual spectra and the stacked one for one example case. Red, green, and blue show the three single exposures. The final stacked spectrum is shown in black. We repeated this test for several masks of different pointings, and no significant broadening was noted. We verified this quantitatively by fitting a Gaussian to the CaT line at 8842 Å to the stacked and individual exposures of spectra with different signal-to-noise ratios (S/Ns). The scatter among the mean positions of the CaT at 8842 Å line was found to be within the 10% spaxel resolution limit of 2.58 Å for the used VIMOS grism. In order to obtain the final wavelength calibration, we provided our own skyline catalogue to calculate the residual shifts from the sky emission lines and corrected for them.
 |
Fig. 1. Individual and stacked reduced spectra for one example target. Red, green, and blue show the spectra for the three individual exposures. In black we show the final stacked spectrum. No broadening is observed. |
3. Analysis
In this section, we describe our analysis of the VIMOS data to obtain the line-of-sight (LOS) velocities from the spectra. We discuss our method for disentangling the GCs from background and foreground objects.
3.1. Radial velocity measurements
The radial velocity measurements of GCs were calculated using the python-implemented penalised-PiXel fitting (pPXF) method of Cappellari & Emsellem (2004) and Cappellari (2017). pPXF is a full-spectrum fitting technique that generates a model spectrum by convolving a set of weighted stellar templates to the parametric LOS velocity distribution (LSOVD), modelled as a Gauss-Hermite series. The intrinsic velocity dispersion of GCs (usually ∼20 km s−1) is well below the spectral resolution of the VIMOS grism we used (∼88 km s−1). Our initial test of deriving the radial velocities shows that the velocity dispersion we obtained is always lower than 20 km s−1 (i.e. in most cases, pPXF gives a value of zero if the velocity dispersion is not resolved), which is an expected value for most of the GCs. We derived the mean velocity from pPXF and used the velocity dispersion value as a limiting criterion to select GCs.
For the stellar templates, we used the single stellar population spectra from the extended medium-resolution INT Library of Empirical spectra (E-MILES; Vazdekis et al. 2010, 2016), covering a wavelength range of 1680–50 000 Å. We preferred this stellar library because it provides us flexibility in obtaining the stellar spectrum on a grid of ages ranging from 8 to 14 Gyr and metallicities in the range −2.27 < [M/H]< + 0.04 dex. We used an MW-like double power law (bimodal) initial mass function with a mass slope of 1.30. With these settings, we obtained a set of 84 stellar templates from the E-MILES library at a spectral resolution of 2.51 Å. We convolved the stellar library with a Gaussian filter of standard deviation σ = 12 Å to bring it to the same resolution as the VIMOS spectra.
For the spectral fitting, we used a wavelength region of 4800–8800 Å. This wavelength region covers the major absorption line features, such as Hβ (4862 Å), Mgβ (5176 Å), NaD (5895 Å), Hα (6564 Å), and CaT lines (at 8498, 8548, 8662 Å). We masked several regions to avoid residual sky lines or telluric lines.
pPXF requires starting values of the velocity moment parameter; in our case, its radial velocity and velocity dispersion. pPXF uses the given redshift of an object to make this initial guess (see Cappellari 2017). For the velocity dispersion, we chose a value of 0 km s−1, which is expected for a GC (i.e. its internal velocity dispersion is not resolved). For the Fornax cluster redshift, the initial radial velocity was chosen to be ∼1375 km s−1, which is close to the radial velocity of Fornax central galaxy NGC 1399, which is 1425 km s−1 (taken from Graham et al. 1998). However, pPXF does not produce a meaningful fit with this guess in the case of foreground stars or background galaxies. Moreover, GC in the outer halo of NGC 1399 or in the intra-cluster regions of the Fornax cluster can have radial velocities different from the initial guess by about ±500 km s−1. Therefore it is crucial to test how the pPXF initial velocity guess can affect the resulting radial velocities, especially for GCs lying in the intra-cluster regions. To determine this, we measured the radial velocities of different GCs belonging to the intra-cluster regions as a function of different initial velocity guesses, as shown in Fig. A.1. We found that the change in the resulting radial velocities is within 5%, and this variation is within the measured velocity error. This shows that the initial guess of pPXF does not affect our radial velocity measurements. We present this test in detail in Appendix A.
pPXF allows the use of additive and multiplicative Legendre polynomials to adjust the continuum shape in the spectral calibration. As a first guess, we used a third and fifth order for additive and multiplicative polynomials, respectively. However, when we obtained a radial velocity consistent with the Fornax cluster but a velocity dispersion higher than 20 km s−1, we varied the polynomials such that we were able to obtain a velocity dispersion lower than 20 km s−1. We performed a quantitative analysis to determine how varying polynomials in pPXF can affect the derived mean velocities and dispersions. We performed a test as follows: We defined a grid of additive and multiplicative polynomials in the range from 0 to 6. For each pair of polynomials, we derived the mean velocity and dispersion. First, we ensured that the velocity dispersion was lower than 20 km s−1 and the variation in the mean velocity did not exceed 5% for different pairs of polynomials. Based on these two conditions, we selected the most suitable value of these polynomials. We also verified the effect of higher-order polynomials on the derived radial velocity and that of not using multiplicative polynomials. We found that in all cases, there are only subtle variations in the derived radial velocities; they are all consistent within 5%. We present more details of these tests of varying the order of polynomials in Appendix A.
Figure 2 shows examples of pPXF fits for two GC spectra with different S/Ns. Masked regions are shown in the upper left panels as blue bands, and residuals from the masked regions are plotted in green in the panels below. The right panels show zoomed-in views of individual absorption line features of the GC spectra. Uncertainties on the mean velocity were estimated through Monte Carlo (MC) realisations of the GC spectrum. For each pPXF model fit, we generated 100 realisations of spectra by adding Gaussian noise equivalent to the root mean square (RMS) of the residuals of the best fit. pPXF also returns the weights of template stars that were used to obtain the best fit. To save computational time, we used only template stars with non-zero weights (around ∼7–10) to perform the MC realisations.
 |
Fig. 2. Examples of pPXF fits to two GC spectra with different S/Ns. Top left panel: red and black show the pPXF fit and a GC spectrum with S/N ∼ 25. Masked regions are shown as blue bands. Blue and green dots in the lower subpanel show the residuals for unmasked and masked regions, respectively. Top right panel: a zoom-in view for the absorption features of Hβ, Mgβ, NaD, Hα, and the CaT lines. Orange bands in the subpanels show the expected position of absorption features at the Fornax cluster redshift. Two lower panels: same, but for a spectrum with S/N ∼ 6. |
3.2. Selecting Fornax cluster members
Our VIMOS dataset is contaminated by foreground stars and background galaxies. To distinguish Fornax cluster GCs from the contaminants, we used the expected radial velocity range of 450 < v < 2500 km s−1 from Schuberth et al. (2010) for objects belonging to the Fornax cluster.
We developed a two-step test to separate the GCs from the background galaxies and stars: First, we searched for emission lines in all spectra. In the case of multiple strong emission lines in a spectrum, we classified that object as a background galaxy. Second, the remaining spectra were fitted with an initial velocity guess of zero, and if pPXF returned a velocity lower than 450 km s−1, we classified the object as a star. All the remaining spectra were fitted as mentioned in Sect. 3.1. In this way, we rejected most of the contaminants at the very beginning, before deriving final radial velocity measurements.
To select the final bonafide GCs, we visually inspected the pPXF results for all remaining spectra. To do this, we created a portfolio of each object with its 1D spectrum, pPXF fit with zoomed-in views of major absorption features such as Hβ, Mgβ, NaD, Hα, and CaT lines and a 2D image of the source, with attributes such as the S/N and radial velocity. One example of such a portfolio is shown in Appendix B. Based on these portfolios, we further classified the objects into three quality classes: Class A objects, for which all the above-mentioned absorption features are clearly visible. Class B objects that clearly show CaT and Hα absorption features, but MgB and Hβ are rarely recognisable. Class C objects, for which Fornax cluster radial velocities can be obtained, but hardly any absorption features are visible, although their colours are consistent with being GCs. Figure 3 shows the S/N versus g-magnitude plot for A, B, and C class objects in red, blue and black, respectively. As expected, almost all the class A and B objects have S/N > 3, whereas class C objects are mostly fainter and have a lower S/N on average. Only a few C class objects have S/N > 10, but their absorption features were contaminated by sky lines. We only considered class A and B objects for our kinematic analysis, but we included the class C objects in our catalogue. As the last step, we applied the heliocentric correction to all the bona fide selected GC radial velocities based on the header information of their observation date.
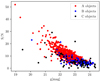 |
Fig. 3. Signal-to-noise ratio vs. g-magnitude for the three classes of objects, as shown in the legend. |
4. Results
A total of 4574 slits were defined in the 25 VIMOS pointings. About 2400 of them were allocated to GC candidates and compact objects, ∼800 slits to background galaxies, and ∼1000 slits to stars (Pota et al. 2018). In our analysis, the Esoreflex pipeline extracted 5131 spectra from the VIMOS data (some slits contained more than one object), and our radial velocity analysis resulted in detecting about 920 possible Fornax cluster GCs. For the remaining spectra, about 1000 are classified as background galaxies, and approximately 700 objects revealed velocities of foreground stars. About 2500 spectra were of poor spectral quality. They either had extremely low S/N or were affected by strong residual telluric and skyline features.
We analysed the possible GC spectra in detail. After visual inspection of the pPXF fits (Sect. 3), we classified 839 spectra as class A and B objects, and 77 were classified as class C objects. After accounting for duplicate objects, we obtained 777 unique GC radial velocity measurements for class A and B objects.
In Appendix C we present an excerpt of our VIMOS GCs catalogue, including all A, B, and C class objects. Despite the radial velocity, the catalogue contains its error and S/N of the spectrum and also the photometric information in the u, g, r, and i bands from the FDS (Cantiello et al. 2020). The full catalogue is available at the CDS. In the following subsections, we present our results, which are based on the new GC catalogue.
4.1. Duplicate measurements
We used the radial velocity measurements of the same objects that were observed in different VIMOS masks as a measure to verify the robustness of the derived radial velocities and as an estimate for the errors. In Fig. 4 we show the radial velocity measurements and their differences for 62 duplicate targets as a function of g magnitude. The root mean square of the velocity difference is 104 km s−1, and the median offset is −11 km s−1. When an object has a velocity difference of more than 3σ of the corresponding uncertainty on the individual measurements, we take the velocity of the higher S/N spectrum; otherwise, we take the error-weighted average velocity of two spectra.
 |
Fig. 4. Velocity comparison of duplicate measurements. Red stars and black dots show the radial velocity from two different measurements of the same object as a function of g magnitude. Bottom panel: velocity difference between the two measurements. The solid and dashed lines are drawn at Δv = 0 and ±100 km s−1, respectively. |
4.2. Comparison with previous measurements
Several previous studies have probed the GC systems in the Fornax cluster. Schuberth et al. (2010) presented a catalogue of 700 GCs from observations with VLT-FORS2 and Gemini-GMOS. Bergond et al. (2007) measured the kinematics of 61 GCs in the intra-cluster space of the cluster based on FLAMES observations. Other studies (e.g. Firth et al. 2007; Chilingarian et al. 2011) have targeted and analysed the most massive compact stellar objects around NGC 1399. These literature velocity measurements of GCs provide us another way to verify and confirm the reliability of our derived radial velocity analysis.
Comparing our sample with Pota et al. (2018), we obtained a match for 369 objects. Out of these, 22 objects were found to have a velocity difference of more than 3σ. Excluding the outliers, the RMS of the velocity difference is 72 km s−1 and the median offset 32 km s−1. Here, the median offset is defined as the median of the velocity difference distribution between our GC radial velocities minus the matched literature GC velocities.
With the GC sample of Schuberth et al. (2010), we obtained a match for 103 objects, of which only 5 were found to have a velocity difference of more than 3σ. Excluding these 5 outliers, we obtain an RMS of 80 km s−1 and median offset of 43 km s−1. We visually inspected all the outliers in both samples and found that our fits to the spectra look very reliable. We therefore neglected the previous measurements of Pota et al. (2018) and Schuberth et al. (2010) for the outliers. In Fig. 5 we show the velocity differences to both samples.
 |
Fig. 5. Velocity measurement comparison with the GC sample of Schuberth et al. (2010) (left panel, blue dots) and that of Pota et al. (2018) (right panel, red dots) as a function of g magnitude. The solid and dashed lines are drawn at Δv = 0 and ±100 km s−1, respectively. |
Finally, we compared our velocity catalogue with all other available literature studies. Table 1 summarises the number of matched objects with our velocity catalogue objects. Figure 6 shows the velocity comparison between velocities measured in this work and from the previously available catalogues. We speculate that the measured mean velocity offsets between our and literature datasets might just be due to systematics in the zero points of the wavelength calibration, as it is common in multi-slit spectroscopy. All offsets are minor and within the overall velocity scatter, and we therefore did not attempt to correct for them.
 |
Fig. 6. Radial velocity comparison with previous measurements. The two dashed lines are drawn at ±100 km s−1. |
Matched number of objects from this study to previous studies, rms scatter and median offset of the comparison (our work−previous work).
4.3. Photometric properties
To obtain the photometric properties of our GC sample, we matched it with the photometric ugri and gri catalogues presented by Cantiello et al. (2020). We obtained a photometric match for 700 and 770 objects with the ugri and gri catalogues, respectively. To separate our GC sample into blue and red GCs, we followed the procedure used by Angora et al. (2019) and Cantiello et al. (2020), namely Gaussian mixture modelling (GMM) implemented through the python library sklearn (Pedregosa et al. 2012). We fitted a bimodal Gaussian distribution to the GC populations in the u − r and g − i colour-colour diagrams. Figure 7 shows the projected distributions of the bivariate Gaussian (and their components for blue and red GCs) on the g − i and u − r colour axes.
 |
Fig. 7. Results of GMM. Left panel: histogram and colour bimodality of the GCs in g − i colour distribution. Blue and red Gaussian curves are obtained from the GMM and represent the blue and red GC populations. Right panel: same as left panel, but for the u − r colour distribution. |
A linear fit between the intersection of blue and red Gaussians for g − i and u − r was used to divide the GCs into the respective samples. Table 2 shows the results of our GMM. Out of 770 objects, our sample has 56% blue and 44% red GCs, as judged from the photometrically complete gri sample.
Bivariate Gaussian parameters using GMM.
4.4. Radial velocity map
Combining our radial velocity measurements with previous literature measurements and the recent catalogue presented by Fahrion et al. (2020b) brings the total number of confirmed GCs in the Fornax cluster to 2341 objects. The catalogue of Fahrion et al. (2020b) is based on integral-field observations of the Fornax3D project (F3D, Sarzi et al. 2018) and provides the GC velocities in the inner regions of 32 Fornax cluster galaxies, many of them located in the cluster outskirts, and thus not shown in Fig. 8, which displays the radial velocity of GCs from our sample within 1.5 square degrees.
 |
Fig. 8. Radial velocity map of GCs within 1.5 square degrees of the Fornax cluster. Major galaxies are shown with green crosses. Left panel: GCs from this work are shown as dots. Squares and stars show GCs from Fahrion et al. (2020b) and previous literature measurements, respectively. Right panel: smooth velocity map using the LOESS technique. The smoothing parameters are given in the legend of the plot. |
The combined sample of GCs provides a representative probe of the whole GC system in the core of Fornax. The GC distribution in the innermost one square degree around NGC 1399 is very uniform and geometrically complete. It amounts to more than 50% of our total GC sample. To better visualize and identify patterns in the velocity distribution, we smoothed the radial velocity with the locally weighted regression method LOESS (Cleveland & Devlin 1988). We implemented it with the python version developed by Cappellari et al. (2013). LOESS tries to estimate the mean pattern by averaging the data into smaller bins. Normally, a linear or quadratic order polynomial is used in the LOESS technique. In our sample, some of the GCs in the phase-space distribution were utterly isolated. Using a lower-order polynomial could cause over-smoothing of distinct kinematic features. To prevent this, we used a third-order polynomial and a low value of the smoothing factor of 0.1 (Cleveland 1979; Cleveland & Devlin 1988). The LOESS-smoothed radial velocity map is shown in the right panel of Fig. 8.
To search for any rotational signature in the GC system, we modelled the GC kinematics with a simple model that describes the rotational amplitude and velocity dispersion, similar to Fahrion et al. (2020b, see their Sect. 4.2.1). To have a homogeneous phase-space distribution of GCs, we considered GCs within 30 arcmin from the central galaxy NGC 1399. In Fig. 9 we show the rotational amplitude and measured velocity dispersion for the full sample as well as red and blue GCs. We find a low rotational velocity of lower than 30 km s−1 for the full sample and the blue GCs. Red GCs show a significant rotational velocity of 60 km s−1 with a rotation axis of PA = 70° (measured north over east). The rotation axis for the entire sample is close to the axis of red GCs and is certainly dominated by them. In Fig. 15 we show the rotation axis (black line) of the red GCs. For the red GCs, the ratio of Vrot/σ is 0.22, meaning a low but significant rotational signature, similar to that of other massive galaxies.
 |
Fig. 9. Rotational velocity of all red and blue GCs within 30 arcmin. We modelled the full sample as well as a restricted sample, excluding the F3D GCs from Fahrion et al. (2020b) as most F3D GCs are bound to their respective host galaxies. |
Only a few studies have examined the kinematics of the stellar body of NGC 1399; for example, Saglia et al. (2000) used longslit observations to obtain the stellar kinematics out to 1.6′ of NGC 1399, giving a value of stellar Vrot/σ ∼ 0.11. This low rotation measure is consistent with the almost round shape of NGC 1399 (ε = 0.1), characterising this galaxy as a slow rotator. The central stellar kinematics of NGC 1399 cannot be straightforwardly compared to the outer GC kinematics and rotation. They most probably reflect the formation of the central stellar spheroid through violent relaxation of early mergers. The photometric PA of the major axis of NGC 1399 is ∼112° degrees (within 1′) and varies between 90–110° at outer radii (up to 20′) (Iodice et al. 2016), which is more or less consistent with the east-west elongation of the extended GC system. More measurements of the outer stellar kinematics around NGC 1399 are needed to understand whether the GCs and stellar halo components are kinematically coupled or decoupled.
Previously, Schuberth et al. (2010) studied the rotation of GCs around NGC 1399 and found a rotation amplitude of 61 ± 35 km s−1 for the red GCs and 110–126 km s−1 for the blue GCs. In contrast to Schuberth et al. (2010), we did not find a strong rotational signature for the blue GCs. This might be due to our large and uniform sample of GCs, whereas the Schuberth et al. (2010) sample was limited to 10 arcmin and was geometrically not complete.
5. Discussion
In this section, we connect the photometrically discovered intra-cluster GCs with the full sample of 2341 confirmed GCs and study their phase-space distribution and radial velocity dispersion profile.
5.1. Colours, phase space, and spatial distribution
We studied the properties of red and blue GCs separately. To divide the entire sample of 2341 GCs into red and blue subpopulations, we used the g − i colour distribution because the shallower u-band photometry does not exist for all GCs. We adopted a value of g − i = 0.978, obtained from the GMM (Fig. 7, left panel), to separate the two subpopulations. The brightest compact objects of our catalogue are a mix of genuine massive globular clusters and stripped nuclei, called ultra-compact dwarf galaxies (UCDs) in the literature (Hilker et al. 1999b; Drinkwater et al. 2000, 2003). To select UCDs, we used a magnitude cut of mi < 20 mag (Mieske et al. 2002) and found a total of 72 UCDs. In Fig. 10 we show the distribution of GCs and UCDs in the magnitude, colour (g − i and g − r), and velocity spaces.
 |
Fig. 10. Distribution of GCs (red dots) and UCDs (yellow dots) in the colour-colour and colour-magnitude diagram. Left panel: distribution of GCs in the (g − r) vs (g − r) space. The lower subplot shows the radial velocity as a function of (g − i) colour. Right panel: same as right panel, but in i mag vs. (g − i) space. |
These plots show that the UCDs are redder than the GCs on average. This confirms the blue tilt of bright GCs and UCDs that was already found in photometric samples of rich GC systems (e.g. Dirsch et al. 2003; Mieske et al. 2010; Fensch et al. 2014). Some very blue and very red GCs exist, with (g − i) < 0.6 and (g − i) > 1.6, respectively. While the blue GCs might be explained by young to intermediate ages, the very red colours point to either very metal-rich populations, dust obscuration, or blends in the photometry. Future investigations are needed to clarify their nature.
In Fig. 11 we show the radial velocity of red (left panel) and blue (right panel) GCs as a function of the cluster-centric distance. Major galaxies around NGC 1399 are shown as green crosses. We observe that most of the red GCs are centrally concentrated on the systematic velocities of these galaxies (taken from Iodice et al. 2019). Within 50 kpc from NGC 1399, red GCs homogenously span a range of relative velocities of ±500 km s−1, and farther outside, they follow a wedge-shaped structure to lower relative velocities until 150 kpc. Schuberth et al. (2010) observed the wedge-shaped feature of the red GCs to be confined within 50 kpc (see their Fig. 9, right panel). However, with the current larger sample of GCs, we note that it extends out to larger distances.
 |
Fig. 11. Phase-space diagrams of radial velocity vs. cluster-centric distance. In both panels the grey dots show the full sample, the green crosses major galaxies within 300 kpc, and the dashed horizontal lines mark the systemic velocity of NGC 1399. Left panel: velocity distribution for red GCs. Right panel: same for blue GCs. Yellow dots indicate UCDs, and the green crosses mark the major galaxies of the Fornax cluster. |
The systemic velocities of most major galaxies at cluster-centric distances larger than 160 kpc are similar to that of NGC 1399. An interesting exception at ∼220 kpc distance is NGC 1380, which has a high systemic velocity of ∼1800 km s−1. Red GCs with similarly high velocities are scattered out to ±50 kpc galactocentric distances in filamentary structures around this galaxy, possibly suggesting a disturbance of its halo. Although most red GCs are concentrated around major galaxies, a noteworthy number of red GCs appears not to be related to any particular galaxy. These are candidates of intra-cluster GCs.
In contrast to red GCs, blue GCs show a more complex and irregular pattern in the phase-space diagram. In particular, between 60–150 kpc, they extend to higher relative velocities and fill the intra-cluster regions between the galaxies. In addition, blue GCs occupy the outer halos of the major galaxies.
We also note different patches of low- (< 1000 km s−1) and high-velocity regions (> 1700 km s−1), elongated in east to west and north-east to south-west structures. We discuss the correlations between the photometric and kinematical properties of the GCs in the subsequent discussion section.
Our UCD sample shows a radial velocity distribution between 750 and 2500 km s−1, with a mean velocity close to the radial velocity of NGC 1399, with a velocity scatter of 312 km s−1, consistent with the fainter GCs. A few red and blue GCs exist at low radial velocities of ∼500 km s−1 at cluster-centric distances between 10 and 220 kpc. This was reported before for the blue GCs by Richtler et al. (2004). Due to their high relative velocity with respect to the Fornax cluster, exceeding 800 km s−1, they might constitute unbound GCs from galaxy encounters with highly radial orbits in the LOS, or a sheet of foreground intra-space GCs.
5.2. Velocity dispersion profile
The large spatial coverage of our sample enables us to measure the velocity dispersion profile of the GCs out to 300 kpc. To do this, we defined circular bins such that each bin had 100 GCs, and measured the velocity dispersion as the standard deviation of radial velocities in that bin. The uncertainty on the velocity dispersion was determined through a bootstrap technique. In each bin, we measured the velocity dispersion 1000 times and took its scatter as the uncertainty. For the total sample, we obtained 23 bins, where the outermost bin has only 41 GCs. We followed the same procedure for red and blue GCs separately. This resulted in 10 and 20 bins, respectively.
In Fig. 12 we show the velocity dispersion profile of our GC sample. The black line indicates the dispersion measurement for the full sample, and the grey band denotes its 1σ uncertainty. Blue and red dots indicate the values for the blue and red GCs. The dashed vertical grey lines show the projected cluster-centric distances of NGC 1404 and other major galaxies. For reference and comparison, we included the velocity dispersion measurements from previous studies as well, as indicated in the legend and caption.
 |
Fig. 12. Velocity dispersion profiles in the Fornax cluster core region as a function of projected distance from NGC 1399. Upper panel: black line denotes the dispersion profile of the complete sample of 2341 GCs. The grey band marks the 1σ uncertainty. Red and blue dots represent the values for the red and blue GCs, with 100 GCs per bin. The dashed blue and red lines represent the dispersion profiles for the GC analysis of the Schuberth et al. (2010) data. The dashed green and orange lines show the PNe and GC dispersion profiles from Spiniello et al. (2018) and Pota et al. (2018), respectively. The horizontal band denotes the velocity dispersion of the Fornax cluster galaxies (Drinkwater et al. 2000). The dashed vertical black line marks the effective radius of NGC 1399 and the dashed vertical grey lines the projected distances of major galaxies (as labelled) from NGC 1399. Lower panel: dispersion profile of ICGC candidates with two different selections. The pink line shows ICGCs and outer halo GCs selected farther than 2reff away from major galaxies, and the light pink band represents the 1σ uncertainty. The dark red line represents ICGCs that were selected outside 4reff around major galaxies (see text for details), and the lighter red band denotes its 1σ uncertainty. |
We also measured the velocity dispersion profile of potential ICGCs within the Fornax core region, shown as a magenta line in the lower panel of Fig. 12, with the light pink band indicating its 1σ uncertainty. The selection of the ICGCs was made by excluding GCs around major galaxies by performing cuts in the phase-space distribution. First, we calculated the scatter in the radial velocities of GCs within two effective radii (reff) of each galaxy, (taken from Iodice et al. 2019). We used ±2σ of this velocity scatter around the galaxy LOS velocity as the lower and upper boundary to select the GCs belonging to each galaxy. The remaining GCs were classified as ICGC candidates, being aware of the fact that this selection might include outer halo GCs that are probably still bound to their parent halos (see below).
Figure 13 shows examples of the ICGC candidate selection for the central galaxy NGC 1399 and the galaxy NGC 1374. For the central galaxy, we clearly see a fraction of GCs with high relative velocities lying inside 2reff, which are identified as the ICGCs. The true central concentration of ICGCs is difficult to access because they might overlap in radial velocity with GCs of the central galaxy. We note that our ICGC selection criteria only provide a rough separation between GCs bound to individual galaxies and those belonging to an unbound or at least disturbed intra-cluster population. Bound GCs might reach out to larger effective radii, but true ICGCs might also be projected at similar velocities in front or behind a galaxy and thus are hidden from detection. Only a detailed dynamical analysis of the mass profile around each galaxy can provide a cleaner sample of ICGCs. This is beyond the scope of this paper.
 |
Fig. 13. Selection of potential ICGCs around NGC 1399 (first row) and NGC 1374 (second row). Left panel: GC distribution within 5reff (dashed blue circle). The radius of 2reff is indicated as a dashed red circle. Middle panel: distribution of GCs in projected phase space. Red dots show the galactic GCs within 2reff, and black dots show the defined ICGCs. Dashed vertical red and blue lines indicate 2reff and 5reff, and the grey horizontal lines give the 1 and 2σ scatter of GC velocities within 2reff around the systemic velocity of NGC 1374. Right panel: velocity histograms of ICGCs (black) and galactic GCs (red). The dashed black line marks the LOS velocity of NGC 1374, and the dashed grey lines show the 1 and 2σ scatter of GC radial velocities, as also shown in the middle panel. |
According to our selection criteria, 719 GCs, almost 31% of the total sample, are classified as ICGCs. This number is probably an upper limit of true ICGSs due to the above-mentioned limitations of our selection criteria. Moreover, the geometrical incompleteness of GC velocities within 2–4reff around the major galaxies plays a role. Whereas the central regions are covered by MUSE observations and thus the GC counts are complete (Fahrion et al. 2020b) there, the outer halo regions are not fully covered by the VIMOS pointings, as can be seen in the uneven distribution of outer GCs around NGC 1374 (Fig. 13, left panel).
To produce a cleaner ICGC sample, we performed a similar selection as mentioned above, but with a phase-space cut at > 4reff. This left us with a sample of only 286 ICGCs (12% of the total sample). The velocity dispersion profile of this set of GCs is shown as the dark red band in the lower panel of Fig. 12.
Figure 14 shows the velocity distribution of the full and ICGC samples. For all three samples, the mean velocity lies close to the radial velocity of NGC 1399. The velocity scatter of the full sample and ICGCs, selected at 2reff, is close to 300 km s−1, whereas ICGCs selected outside 4reff show a larger velocity scatter of 455 km s−1 around a mean velocity of 1400 km s−1. In the following, we describe the features and irregularities noted in the velocity dispersion profiles, starting from the centre outwards.
 |
Fig. 14. Radial velocity histograms of the full sample and the intra-cluster GCs. The dashed vertical green line indicates the radial velocity of NGC 1399. The dashed vertical black, magenta, and dark red lines indicate the mean velocities of fitted Gaussian to the three sets of GCs. |
1) Between 2 and 5 arcmin, the dispersion profile takes a steep rise from 220 to 350 km s−1 within 1reff of NGC 1399. Mostly blue GCs contribute to this rise. This is consistent with the rise previously reported by Schuberth et al. (2010). Red GCs show a constant velocity dispersion of ∼270 km s−1 within 1reff of NGC 1399, in agreement with Schuberth et al. (2010) and Pota et al. (2018).
2) Between 5 and 10 arcmin, the total dispersion profile flattens around a value of ∼300 km s−1. While the dispersion profile of the blue GCs decreases, the profile of the red GCs rises. This rise is caused by the superposition of the GCs of NGC 1404, which has a high systemic velocity of 1944 km s−1. Within these radii limits, Spiniello et al. (2018) have also reported a similar increase in the PNe velocity dispersion profile. The lower velocity dispersion of red GCs from Schuberth et al. (2010) can be explained by the increase in the sample size in our study, which added several GCs with more extreme velocities. For the ICGC velocity dispersion profile, we observe a value of ∼500 km s−1at 8 arcmin. This is artificial and caused by the exclusion of GCs within 2reff of NGC 1399. Thus, we are left with GCs with extreme radial velocities, resulting in the high dispersion value.
3) Beyond 10 arcmin, the dispersion profile remains flat around ∼300 km s−1 until 18 arcmin, consistent with the results of Pota et al. (2018). Farther out, the GCs belonging to individual galaxies dominate the velocity dispersion values of all GCs and cause large variations from < 200 to > 300 km s−1. After a steep decrease from 500 to 300 km s−1, the velocity dispersion profile of ICGCs behaves more smoothly with nearly constant values around 290 km s−1 out to 40 arcmin. This value is relatively consistent with the velocity dispersion of cluster galaxies (Drinkwater et al. 2000). A similar trend with PNe kinematics has been observed by Spiniello et al. (2018) out to 30 arcmin.
Iodice et al. (2016), using the g-band light distribution around NGC 1399, identified a physical break radius at 10 arcmin, separating the total light profile into a central spheroid light of NGC 1399 and an outer exponential halo. The constant value and flattening of the ICGC dispersion profile beyond 12 arcmin kinematically confirms this physical break radius.
5.3. Globular clusters and planetary nebulae
Spiniello et al. (2018) presented the kinematics of 1452 PNe out to 200 kpc in the Fornax cluster core, spatially extending the results presented in McNeil et al. (2010). Although the velocity dispersion profile of PNe overall follows the kinematics behaviour of the red GCs, slight differences in the profiles can be found. In Fig. 12, the green dashed line shows the velocity dispersion profile of PNe taken from Spiniello et al. (2018). Within 5 arcmin, the velocity measurements we obtained for the red GCs show a slightly higher value than the PNe (this was true also in Spiniello et al. (2018), but the difference between the velocity dispersion values was smaller). Between 5–10 arcmin, the PNe show a high dispersion peak value at ∼380 km s−1, unlike our red GCs, and better match the value we measured for blue GCs. Between 10–20 arcmin, the velocity dispersion for both PNe and red GCs, decreases, with the red GCs showing a very low value at the projected distance of NGC 1387. Beyond 20 arcmin, the PNe velocity dispersion shows a flat behaviour at ∼300 km s−1, slightly above that of blue and red GCs. In general, the PNe velocity dispersion profile closely follows that of all GCs beyond 10 arcmin, rather than that of red or blue GCs individually. This might suggest that PNe trace the behaviour of both stellar populations, that of galaxies as well as that of intra-cluster light.
5.4. Intracluster GC kinematics
The first photometric wide-field search for GCs in the Fornax cluster by Bassino et al. (2006) reported an ICGC populations based on GC overdensities in regions between the central galaxy NGC 1399 and neighbouring galaxies. Later, Bergond et al. (2007) and Schuberth et al. (2008) kinematically identified and quantified the properties of some ICGCs. Through the FDS survey, D’Abrusco et al. (2016) reported the discovery of an extended GC density distribution in the Fornax core region with several well-defined overdense regions, and Iodice et al. (2016) discovered a faint stellar bridge coinciding with the GC over density between NGC 1399 and NGC 1387, confirming the interaction between these two galaxies.
Our extended and spatially homogeneous GC catalogue allows us to study the kinematical properties of the enhanced density regions of GCs in Fornax. In Fig. 15 we plot our full GC radial velocity sample on top of a smoothed density distribution of photometric GC candidates by Cantiello et al. (2020). To create the smoothed density map, we used the non-parametric kernel density estimates based on python-scikit-learn kernel density routine by Pedregosa et al. (2011). From the FDS catalogue, a density of 0.75 GCs/arcmin2 is expected within the central region of the Fornax cluster. To include at least some GCs in the density maps and to create the visual impression of the GCs streams, we adopted a Gaussian kernel bandwidth of 0.015 degrees, which is ∼1 arcmin. The top, middle, and lower panels show the distribution of all, red, and blue GC candidates, respectively.
 |
Fig. 15. Globular clusters with confirmed radial velocities (coloured dots) plotted over the surface density map of photometric GC candidates from the FDS (Cantiello et al. 2020). Top panel: full GC radial velocity sample. Middle panel: radial velocity distribution of red GCs. The black line shows the rotation axis of the red GCs at PA = 70°, measured north to east. Major galaxies are labelled in green. Bottom panel: same for blue GCs. The density scale plotted at the bottom represents the number of GCs from the photometric sample per square arcminute. |
Confirming the FDS survey findings of D’Abrusco et al. (2016) and Cantiello et al. (2020), we also observe an elongated distribution of confirmed GCs in the east-west direction, centred on NGC 1399. The radial velocity patterns in the smoothed velocity map in Fig. 8 show that on the west side of NGC 1399, GCs have a relatively higher radial velocity than on the east side. Further on the east side of NGC 1399, in the overdense G and F features, GCs show an extended filamentary spatial distribution.
The azimuthal distribution of ICGCs selected outside 4reff of major galaxies is shown in Fig. 16. It highlights the east-west elongation of ICGCs around NGC 1399. In the two lower panels of this figure, where the azimuthal distribution is shown as a function of cluster-centric distance and radial velocity, respectively, phase-space features in between galaxies become apparent. A detailed dynamical analysis of these features is beyond the scope of this paper.
 |
Fig. 16. Azimuthal distribution of ICGCs selected outside 4reff radii around major galaxies (see text for details). Top panel: histogram of the ICGC position angle (PA), with a bin size of 30°. Middle panel: cluster-centric distance vs PA. Bottom panel: radial velocity vs PA. Green crosses indicate major galaxies. |
We investigated the spatial correlation between the photometric and our radial velocity catalogue. For this, we performed a 2D Kolmogorov-Smirnov (2D-KS) test (Peacock 1983) in the four GC overdensity regions named regions A, C, F, and G following the same naming convention as in D’Abrusco et al. (2016). Figure 17 shows the phase-space distribution of the ICGCs selected with a cut of > 2reff and indicates the rectangular regions around the GC overdensities. For all the regions, we obtain a p-value higher than 0.20, which means that the spatial distributions of photometrically selected and confirmed GCs are correlated with a significance higher than 3σ. Figure 18 shows the radial velocity histograms of ICGCs falling within these four overdense regions. The mean velocities are ∼1450 km s−1, which is close to the radial velocity of NGC 1399 and the Fornax cluster itself. This suggests that the GCs in these regions are ICGCs that are kinematically affected by the Fornax cluster potential. In Table 3 we list the p-values obtained from the 2D-KS tests for all regions and the fitted Gaussian mean and velocity scatter. These selected rectangular regions are populated by both red and blue GC populations, but the blue GCs dominate in numbers on average. In contrast to this, GCs within the 2reff radii of galaxies show a higher fraction of red GCs on average. We list the number ratio of blue to red GCs in Table 3.
 |
Fig. 17. Distribution of ICGCs selected with a phase-space cut at > 2reff. GC overdensity regions are named as in D’Abrusco et al. (2016). The magenta boxes show the regions in which we perform 2D KS tests. Black contours show the visibly selected regions to study the stream properties. |
2D KS test and properties of the ICGCs.
With the small sample size of ICGCs, and given the caveats of the rough ICGC selection criteria mentioned in Sect. 5.2, it is hard to speculate about the nature of the GCs in the overdense regions. Figure 17 shows quite clearly that our spectroscopic sample provides kinematical information about the visible photometric streams in the overdense regions. Our 2D KS test performed for the selected rectangular regions demonstrates that our spectroscopic sample is statistically coherent with the photometric sample. To obtain an indication about the possible progenitor galaxies of ICGCs and their physical properties, specifically those that trace the visible streams (marked in Fig. 17 with the black contours), we plot the radial velocity and g − i colour histograms in Fig. 18. We call these streams A, C, F, and G. In the following, we explain the features we detected within these streams.
 |
Fig. 18. Radial velocity and g − i colour histograms of the intra-cluster regions. Top panel: radial velocity of GCs lying within the rectangular boxes A, C, F, and G (left to right). Middle panel: radial velocity of GCs lying within the streams A, C, F, and G (left to right). The radial velocities of the red GCs are marked in red. Bottom panel: g − i colour histogram of GCs lying within the streams A, C, F, and G (left to right). The dashed vertical black line marks the radial velocity of NGC 1399, and the vertical green lines show the peak positions of the fitted Gaussians. For streams A and C, double Gaussians were fitted. |
Stream A is a feature related to the faint stellar bridge reported by Iodice et al. (2016), connecting NGC 1387 and NGC 1399 (region A). In this stream, the GC radial velocity distribution shows two peaks, one close to the radial velocity of the central galaxy NGC 1399 (at 1374 km s−1), and the other at 1723 km s−1. Both peaks show a low-velocity scatter with values of 127 km s−1 and 56 km s−1, respectively. The second peak might arise from GCs on the east side of NGC 1387, which is interacting with NGC 1399. These GCs might be tidally stripped off the halo of NGC 1387. In the radial velocity histograms, we mark the contribution of red GCs in red. We note that red GCs mostly contribute to the first radial velocity peak, whereas the blue GCs dominate the second peak. This suggests that tidally stipped GCs, those that are outside the systemic Fornax cluster velocity, are mostly blue. In the g − i colour histogram of stream A (bottom panel of Fig. 18), we also observe two peaks, suggesting the presence of red as well as blue GCs. Studying the GC colour distributions of early-type galaxies in the Virgo cluster, Peng et al. (2006) have shown that luminous galaxies (MB ∼ −21 mag) mostly have bimodal GC colour distributions, whereas low-luminosity galaxies (MB ∼ −16) have dominant fractions of blue GCs. In stream A, we see a bimodality in the g − i colour histogram with a larger fraction of red GCs. Comparison of this type of bimodality with results of Peng et al. (2006) suggests that GCs in stream A are mostly generated by the interaction of the luminous galaxy NGC 1387 and NGC 1399.
Stream C in the overdense region C consists of a chain of GCs in the vicinity of NGC 1380 and NGC 1380B. Cantiello et al. (2020) pointed out that this GC overdensity could result from the LOS projection of adjacent GC systems. The GCs in the vicinity of NGC 1380 and NGC 1380B (but beyond 2reff radii) have radial velocities higher than 1700 km s−1, consistent with the systemic velocities of both galaxies. In the GC radial velocity histogram of stream C we also observe two peaks, one close to the radial velocity of NGC 1380, and the other close to the NGC 1399 radial velocity. Similar to stream A, stream C GCs also show a bimodal g − i colour histogram, with a higher fraction of the blue GC population, although the bimodality is not as clear due to the small sample size. In stream C, both radial velocity peaks are dominated by blue GCs with radial velocity scatters of ∼110 km s−1. In stream C, both radial velocity peaks are dominated by the blue GCs with radial velocity scatters of around 110 km s−1. In stream C, blue GCs are almost twice as abundant than red GCs. As shown in the studies of Peng et al. (2006), an asymmetrical distribution of GCs, with an inclination towards blue GCs, suggests that the GCs in stream C are generated by galaxies in the magnitude range −20 < MB < −19 mag.
In stream F, GCs show a radial velocity distribution in between 700–1800 km s−1 with a mean velocity and scatter of 1452 km s−1 and 228 km s−1, respectively. We find an equal fraction of blue to red GCs in stream F.
Stream G harbours GCs in the velocity range 800–2000 km s−1, with a peak velocity close to the systemic velocity of Fornax and is mostly dominated by the blue GCs. These GCs comprise a kinematically coherent group, and in the g − i colour histogram, we observe a peak towards blue GCs, suggesting that the progenitors of GCs in stream G are low-luminosity galaxies (Peng et al. 2006).
We also note that in the south-east of NGC 1404, next to the G feature, some GCs show radial velocities higher than 1700 km s−1, similar to the systemic velocity of NGC 1404. As previously shown by Bekki et al. (2003) and more recently shown through X-ray studies by Su et al. (2017), NGC 1404 suffered from tidal interaction with NGC 1399 in the past few gigayears. Thus, tidally released GCs are expected around NGC 1404, and we now might see the kinematical signature of them for the first time. Detailed dynamical models will be necessary to assess which GCs in the overall phase space distribution might have belonged to NGC 1404 in the past.
Furthermore, we note that GCs around NGC 1427A, on the south-west side of NGC 1399, show a stream-like distribution with a gradual decrease in radial velocity from 1500 km s−1 north of NGC 1427A to 1100 km s−1 south of the galaxy. This kinematic feature might suggest that NGC 1427A is moving in the south-north direction, loosing its GCs during its cruise through the core of the Fornax cluster (e.g. Lee-Waddell et al. 2018).
Finally, we searched for the spatial distribution and numbers of red and blue GC subpopulations in the overdense regions. Figure 15 shows that blue GCs dominate the intra-cluster overdense regions between the Fornax cluster galaxies, whereas red GCs are more concentrated in the galaxies. The dominance of the blue (and thus mostly metal-poor) GCs in the Fornax IC regions and in the visually identified streams suggests that the Fornax IC component results from the accretion of tidally stripped low-mass galaxies. Our results are in accordance with the dominantly blue ICGCs population observed for the Virgo cluster (see Ko et al. 2017; Longobardi et al. 2018b). We list the number ratio of blue to red GCs in each region and the fours streams in Table 3.
6. Conclusions
We have reanalysed VLT/VIMOS data of the central one square degree of the Fornax cluster, based on which, we produced radial velocity measurements of 777 GCs that we present in a catalogue. Adding literature data, this provided the largest and spatially most extended compilation of GC radial velocities in the Fornax cluster. This sample was used to kinematically characterise GCs in the core of the cluster. In the following, we highlight the main results of our work.
1) With the improved VIMOS ESO reflex pipeline 3.3.0 and careful analysis of radial velocity measurements with pPXF over the full spectral range, we have doubled the number of GC radial velocity measurements on the same dataset as was previously analysed by Pota et al. (2018). Combined with previously measured values from the literature, we gathered a sample of 2341 GC radial velocities in Fornax.
2) We used the GMM technique to divide the full sample of 2341 GCs into a blue (56%) and a red (44%) GC subpopulation. The phase-space distribution of red GCs shows that most of them are bound to the major cluster galaxies, in particular, the central galaxy NGC 1399. In contrast, blue GCs are spatially extended and show more irregular kinematics patterns. They occupy the outer haloes of galaxies and the intra-cluster space.
3) Using the radial velocities of GCs, we measured the dispersion profile out to a radius of 300 kpc, covering almost half of the virial radius of the Fornax cluster. Beyond 10 arcmin (∼58 kpc), the dispersion profile of all GCs flattens. This radius is therefore considered as the break radius separating the potential of NGC 1399 from that of the cluster. This result is strongly confirmed by the dispersion profile of potential ICGCs, which shows a flat behaviour beyond 10 arcmin at a value of 300 ± 50 km s−1.
4) The radial velocity map of the full GCs sample kinematically characterises the previously photometrically discovered ICGC population of the Fornax cluster. The different overdense GC regions are marked by streams of higher relative velocity GCs, giving first kinematical evidence of interactions between the central galaxy NGC 1399 and other major galaxies.
5) Finally, we note that mostly blue GCs dominate the intra-cluster regions and trace substructures that connect NGC 1399 to its neighbouring galaxies.
With the future goal to study the Fornax cluster mass distribution and assembly history, the GC radial velocity catalogue we present is of unprecedented value for exploring the dynamical structure and evolution of the Fornax cluster and its member galaxies.
Acknowledgments
Our sincere thanks to the anonymous referee for helpful feedback and suggestions that improved the manuscript’s scientific content. The bulk of the velocities were derived from the FVSS data taken under the ESO programme 094.B-0687 (PI: Capaccioli). Our special thanks goes to Massimo Cappacioli who dedicated INAF GTO time to spectroscopic Fornax cluster projects. Some velocities of our full catalogue (including literature data) are based on so far unpublished FORS2 data taken under ESO programmes 078.B-0632 and 080.B-0337 (PI: Hilker). A. Chaturvedi acknowledges the support from the IMPRS on Astrophysics at the ESO and LMU Munich. A. Chaturvedi also thanks Lodovico Coccato for helpful discussions. M. Cantiello acknowledges support from MIUR, PRIN 2017 (grant 20179ZF5KS). N.R. Napolitano acknowledges financial support from the “One hundred top talent program of Sun Yat-sen University” grant N. 71000-18841229, and from the European Union Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement n. 721463 to the SUNDIAL ITN network. G.v.d. Ven acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 724857 (Consolidator Grant ArcheoDyn). C. Spiniello is supported by a Hintze Fellowship at the Oxford Centre for Astrophysical Surveys, which is funded through generous support from the Hintze Family Charitable Foundation. This research made use of Astropy (https://www.astropy.org)- a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).
References
- Alamo-Martínez, K. A., Blakeslee, J. P., Jee, M. J., et al. 2013, ApJ, 775, 20 [CrossRef] [Google Scholar]
- Amorisco, N. C. 2019, MNRAS, 482, 2978 [Google Scholar]
- Angora, G., Brescia, M., Cavuoti, S., et al. 2019, MNRAS, 490, 4080 [CrossRef] [Google Scholar]
- Ashman, K. M., & Zepf, S. E. 1992, ApJ, 384, 50 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bassino, L. P., Richtler, T., & Dirsch, B. 2006, MNRAS, 367, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., Forbes, D. A., Beasley, M. A., & Couch, W. J. 2003, MNRAS, 344, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Bergond, G., Athanassoula, E., Leon, S., et al. 2007, A&A, 464, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [Google Scholar]
- Cantiello, M., Blakeslee, J. P., Raimondo, G., et al. 2014, A&A, 564, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., D’Abrusco, R., Spavone, M., et al. 2018, A&A, 611, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Venhola, A., Grado, A., et al. 2020, A&A, 639, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2013, MNRAS, 432, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., Mieske, S., Hilker, M., & Infante, L. 2011, MNRAS, 412, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Cleveland, W. S. 1979, J. Am. Stat. Assoc., 74, 829 [Google Scholar]
- Cleveland, W. S., & Devlin, S. J. 1988, J. Am. Stat. Assoc., 83, 596 [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [Google Scholar]
- Coccato, L., Arnaboldi, M., & Gerhard, O. 2013, MNRAS, 436, 1322 [Google Scholar]
- Cooper, A. P., D’Souza, R., Kauffmann, G., et al. 2013, MNRAS, 434, 3348 [Google Scholar]
- Côté, P., Marzke, R. O., & West, M. J. 1998, ApJ, 501, 554 [Google Scholar]
- D’Abrusco, R., Cantiello, M., Paolillo, M., et al. 2016, ApJ, 819, L31 [CrossRef] [Google Scholar]
- Dirsch, B., Richtler, T., Geisler, D., et al. 2003, AJ, 125, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Dirsch, B., Richtler, T., Geisler, D., et al. 2004, AJ, 127, 2114 [NASA ADS] [CrossRef] [Google Scholar]
- Dolfi, A., Forbes, D. A., Couch, W. J., et al. 2021, MNRAS, 504, 4923 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Napolitano, N. R., Romanowsky, A. J., et al. 2007, ApJ, 664, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Drinkwater, M. J., Phillipps, S., Jones, J. B., et al. 2000, A&A, 355, 900 [NASA ADS] [Google Scholar]
- Drinkwater, M. J., Gregg, M. D., Hilker, M., et al. 2003, Nature, 423, 519 [CrossRef] [Google Scholar]
- Duc, P.-A., Cuillandre, J.-C., Serra, P., et al. 2011, MNRAS, 417, 863 [Google Scholar]
- Fahrion, K., Lyubenova, M., Hilker, M., et al. 2020a, A&A, 637, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahrion, K., Lyubenova, M., Hilker, M., et al. 2020b, A&A, 637, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fensch, J., Mieske, S., Müller-Seidlitz, J., & Hilker, M. 2014, A&A, 567, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Firth, P., Drinkwater, M. J., Evstigneeva, E. A., et al. 2007, MNRAS, 382, 1342 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., & Remus, R.-S. 2018, MNRAS, 479, 4760 [Google Scholar]
- Forbes, D. A., Brodie, J. P., & Grillmair, C. J. 1997, AJ, 113, 1652 [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gatto, M., Napolitano, N. R., Spiniello, C., Longo, G., & Paolillo, M. 2020, A&A, 644, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graham, A. W., Colless, M. M., Busarello, G., Zaggia, S., & Longo, G. 1998, A&AS, 133, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E., Brown, R. A., Durrell, P. R., et al. 2020, ApJ, 890, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Hartke, J., Arnaboldi, M., Gerhard, O., et al. 2018, A&A, 616, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilker, M., Infante, L., & Richtler, T. 1999a, A&AS, 138, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilker, M., Infante, L., Vieira, G., Kissler-Patig, M., & Richtler, T. 1999b, A&AS, 134, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilker, M., Baumgardt, H., Infante, L., et al. 2007, A&A, 463, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilker, M., Barbosa, C. E., Richtler, T., et al. 2015, in Galaxies in 3D across the Universe, eds. B. L. Ziegler, F. Combes, H. Dannerbauer, IAU Symp., 309, 221 [NASA ADS] [Google Scholar]
- Hilker, M., Richtler, T., Barbosa, C. E., et al. 2018, A&A, 619, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iodice, E., Capaccioli, M., Grado, A., et al. 2016, ApJ, 820, 42 [Google Scholar]
- Iodice, E., Sarzi, M., Bittner, A., et al. 2019, A&A, 627, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jordán, A., Blakeslee, J. P., Côté, P., et al. 2007, ApJS, 169, 213 [Google Scholar]
- Kissler-Patig, M., Grillmair, C. J., Meylan, G., et al. 1999, AJ, 117, 1206 [CrossRef] [Google Scholar]
- Ko, Y., Hwang, H. S., Lee, M. G., et al. 2017, ApJ, 835, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [Google Scholar]
- Kravtsov, A. V., & Gnedin, O. Y. 2005, ApJ, 623, 650 [Google Scholar]
- Kundu, A., & Whitmore, B. C. 2001, AJ, 121, 2950 [NASA ADS] [CrossRef] [Google Scholar]
- Lee-Waddell, K., Serra, P., Koribalski, B., et al. 2018, MNRAS, 474, 1108 [Google Scholar]
- LeFevre, O., Saisse, M., Mancini, D., et al. 2013, Proc. SPIE, 4841, 1670 [Google Scholar]
- Li, C., Zhu, L., Long, R. J., et al. 2020, MNRAS, 492, 2775 [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., & Mihos, J. C. 2015, A&A, 579, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., Pulsoni, C., & Söldner-Rembold, I. 2018a, A&A, 620, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longobardi, A., Peng, E. W., Côté, P., et al. 2018b, ApJ, 864, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Madrid, J. P., O’Neill, C. R., Gagliano, A. T., & Marvil, J. R. 2018, ApJ, 867, 144 [NASA ADS] [CrossRef] [Google Scholar]
- McNeil, E. K., Arnaboldi, M., Freeman, K. C., et al. 2010, A&A, 518, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mieske, S., Hilker, M., & Infante, L. 2002, A&A, 383, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mieske, S., Hilker, M., Bomans, D. J., et al. 2008, A&A, 489, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mieske, S., Jordán, A., Côté, P., et al. 2010, ApJ, 710, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, R. P., Eigenthaler, P., Puzia, T. H., et al. 2015, ApJ, 813, L15 [Google Scholar]
- Napolitano, N. R., Arnaboldi, M., & Capaccioli, M. 2002, A&A, 383, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napolitano, N. R., Pannella, M., Arnaboldi, M., et al. 2003, ApJ, 594, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Capaccioli, M., et al. 2011, MNRAS, 411, 2035 [Google Scholar]
- Napolitano, N. R., Pota, V., Romanowsky, A. J., et al. 2014, MNRAS, 439, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Gatto, M., Spiniello, C., et al. 2022, A&A, 657, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Old, L., Wojtak, R., Pearce, F. R., et al. 2017, MNRAS, 475, 853 [Google Scholar]
- Peacock, J. A. 1983, MNRAS, 202, 615 [NASA ADS] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2012, ArXiv e-prints [arXiv:1201.0490] [Google Scholar]
- Peng, E. W., Jordán, A., Côté, P., et al. 2006, ApJ, 639, 95 [Google Scholar]
- Peng, E. W., Ferguson, H. C., Goudfrooij, P., et al. 2011, ApJ, 730, 23 [Google Scholar]
- Pillepich, A., Madau, P., & Mayer, L. 2015, ApJ, 799, 184 [Google Scholar]
- Pota, V., Napolitano, N. R., Hilker, M., et al. 2018, MNRAS, 481, 1744 [Google Scholar]
- Puzia, T. H., Paolillo, M., Goudfrooij, P., et al. 2014, ApJ, 786, 78 [Google Scholar]
- Ramos-Almendares, F., Abadi, M., Muriel, H., & Coenda, V. 2018, ApJ, 853, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Richtler, T., Dirsch, B., Gebhardt, K., et al. 2004, AJ, 127, 2094 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., Strader, J., Brodie, J. P., et al. 2012, ApJ, 748, 29 [Google Scholar]
- Saglia, R. P., Kronawitter, A., Gerhard, O., & Bender, R. 2000, AJ, 119, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Iodice, E., Coccato, L., et al. 2018, A&A, 616, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuberth, Y., Richtler, T., Bassino, L., & Hilker, M. 2008, A&A, 477, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiniello, C., Napolitano, N. R., Arnaboldi, M., et al. 2018, MNRAS, 477, 1880 [Google Scholar]
- Su, Y., Nulsen, P. E. J., Kraft, R. P., et al. 2017, ApJ, 851, 69 [Google Scholar]
- Tonini, C. 2013, ApJ, 762, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [Google Scholar]
- Tucker, E., Walker, M. G., Mateo, M., et al. 2020, ApJ, 888, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Vazdekis, A., Koleva, M., Ricciardelli, E., Röck, B., & Falcón-Barroso, J. 2016, MNRAS, 463, 3409 [Google Scholar]
- Watkins, L. L., van de Ven, G., den Brok, M., & van den Bosch, R. C. E. 2013, MNRAS, 436, 2598 [Google Scholar]
- West, M. J., Cote, P., Jones, C., Forman, W., & Marzke, R. O. 1995, ApJ, 453, L77 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. E. 1987, MNRAS, 227, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Ciardullo, R., Durrell, P. R., et al. 2007, ApJ, 654, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Yahagi, H., & Bekki, K. 2005, MNRAS, 364, L86 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L., Romanowsky, A. J., van de Ven, G., et al. 2016a, MNRAS, 462, 4001 [Google Scholar]
- Zhu, L., van de Ven, G., Watkins, L. L., & Posti, L. 2016b, MNRAS, 463, 1117 [Google Scholar]
Appendix A: Test regarding pPXF parameter choices
Effect of initial velocity guesses on the resulting pPXF radial velocity: To determine how strongly the pPXF initial radial velocity guess can affect the resulting radial velocity, we fitted a few spectra with varying initial velocity guesses ranging between 800 and 1800 km s−1 with a step of 200 km s−1. The figure shows three example spectra at S/N = 6, 12, and 17. The resulting radial velocities are mostly consistent, and the variations are less than 5%, which is smaller than the individual velocity measurement errors.
Variation in the derived radial velocity and velocity dispersion as a function of the polynomial degree: Here we present the results of tests mentioned in sect. 3.1. For GCs for which we obtained a radial velocity consistent with the Fornax cluster (450 < v < 2500 km s−1), but a velocity dispersion higher than 20 km s−1, we varied the additive and multiplicative polynomials to quantify the effect on the derived radial velocity and velocity dispersion. Based on consistent values of radial velocity and dispersion, we selected the additive and multiplicative polynomials. In figure A.2 we show the radial velocity (left) and velocity dispersion (right) measured for one spectrum, on a grid of additive and multiplicative polynomials with orders in between 0 and 6. These plots show that the radial velocity remains quite consistent for additive polynomials with orders of 2 to 5 and multiplicative polynomial with orders in between 2 and 5. At the same time, the velocity dispersion remains lower than 20 km s−1 within this polynomial range.
Effect of higher-order pPXF polynomials on radial velocity: To quantify the effect of higher-order polynomials on the inferred radial velocities as well as using only additive polynomials, as is often done when fitting stellar kinematics, we used five sets of additive and multiplicative polynomials denoted as [additive, multiplicative] : [3,5] (our choice), [5,0], [10,0], [15,0], [10,10], [15,15]. The measured radial velocities from pPXF for these sets of polynomials for spectra of three different S/N are shown in figure A.3. The derived radial velocities are always consistent and show only slight variations, which are within 5%.
 |
Fig. A.1. Effect of initial radial velocity guesses on the resulting radial velocity measurements. |
 |
Fig. A.2. Choosing pPXF polynomials. Derived radial velocity (left panel) and the velocity dispersion (right panel) for a GC spectrum of S/N∼5 as a function of additive and multiplicative polynomial degree. Assigning to the additive polynomial a grade equal to -1 means running pPXF without it, i.e. using only multiplicative polynomials. |
 |
Fig. A.3. Effect of higher order polynomials on radial velocity measurements. |
Appendix B: Example of a GC portfolio
 |
Fig. B.1. Example of a GC portfolio. The top panel shows the 1D extracted spectrum from the 2D VIMOS observation (on top). The middle panel shows the pPXF fit and its residuals in the subplot. The lower panel shows zoom-in wavelengths regions of absorption features used to visually select bonafide GCs. The lower right subpanel shows the 2D image of the GC from pre-imaging. |
Appendix C: Catalogue of VIMOS dataset GCs
Table C shows an overview of our VIMOS data GC radial velocity catalogue. Together with the A and B class objects, we also included class C objects in the catalogue, totalling 851 GCs (see the sect. 4 for details.) For each GC, we provide its measured radial velocity and its uncertainty, S/N, and object class (A, B, and C). We also give the magnitude information for each GC in g,r, i, and u band obtained from the matched FDS photometric catalogue presented by Cantiello et al. (2020).
Excerpt of our VIMOS GCs catalogue.
All Tables
Matched number of objects from this study to previous studies, rms scatter and median offset of the comparison (our work−previous work).
All Figures
 |
Fig. 1. Individual and stacked reduced spectra for one example target. Red, green, and blue show the spectra for the three individual exposures. In black we show the final stacked spectrum. No broadening is observed. |
| In the text | |
 |
Fig. 2. Examples of pPXF fits to two GC spectra with different S/Ns. Top left panel: red and black show the pPXF fit and a GC spectrum with S/N ∼ 25. Masked regions are shown as blue bands. Blue and green dots in the lower subpanel show the residuals for unmasked and masked regions, respectively. Top right panel: a zoom-in view for the absorption features of Hβ, Mgβ, NaD, Hα, and the CaT lines. Orange bands in the subpanels show the expected position of absorption features at the Fornax cluster redshift. Two lower panels: same, but for a spectrum with S/N ∼ 6. |
| In the text | |
 |
Fig. 3. Signal-to-noise ratio vs. g-magnitude for the three classes of objects, as shown in the legend. |
| In the text | |
 |
Fig. 4. Velocity comparison of duplicate measurements. Red stars and black dots show the radial velocity from two different measurements of the same object as a function of g magnitude. Bottom panel: velocity difference between the two measurements. The solid and dashed lines are drawn at Δv = 0 and ±100 km s−1, respectively. |
| In the text | |
 |
Fig. 5. Velocity measurement comparison with the GC sample of Schuberth et al. (2010) (left panel, blue dots) and that of Pota et al. (2018) (right panel, red dots) as a function of g magnitude. The solid and dashed lines are drawn at Δv = 0 and ±100 km s−1, respectively. |
| In the text | |
 |
Fig. 6. Radial velocity comparison with previous measurements. The two dashed lines are drawn at ±100 km s−1. |
| In the text | |
 |
Fig. 7. Results of GMM. Left panel: histogram and colour bimodality of the GCs in g − i colour distribution. Blue and red Gaussian curves are obtained from the GMM and represent the blue and red GC populations. Right panel: same as left panel, but for the u − r colour distribution. |
| In the text | |
 |
Fig. 8. Radial velocity map of GCs within 1.5 square degrees of the Fornax cluster. Major galaxies are shown with green crosses. Left panel: GCs from this work are shown as dots. Squares and stars show GCs from Fahrion et al. (2020b) and previous literature measurements, respectively. Right panel: smooth velocity map using the LOESS technique. The smoothing parameters are given in the legend of the plot. |
| In the text | |
 |
Fig. 9. Rotational velocity of all red and blue GCs within 30 arcmin. We modelled the full sample as well as a restricted sample, excluding the F3D GCs from Fahrion et al. (2020b) as most F3D GCs are bound to their respective host galaxies. |
| In the text | |
 |
Fig. 10. Distribution of GCs (red dots) and UCDs (yellow dots) in the colour-colour and colour-magnitude diagram. Left panel: distribution of GCs in the (g − r) vs (g − r) space. The lower subplot shows the radial velocity as a function of (g − i) colour. Right panel: same as right panel, but in i mag vs. (g − i) space. |
| In the text | |
 |
Fig. 11. Phase-space diagrams of radial velocity vs. cluster-centric distance. In both panels the grey dots show the full sample, the green crosses major galaxies within 300 kpc, and the dashed horizontal lines mark the systemic velocity of NGC 1399. Left panel: velocity distribution for red GCs. Right panel: same for blue GCs. Yellow dots indicate UCDs, and the green crosses mark the major galaxies of the Fornax cluster. |
| In the text | |
 |
Fig. 12. Velocity dispersion profiles in the Fornax cluster core region as a function of projected distance from NGC 1399. Upper panel: black line denotes the dispersion profile of the complete sample of 2341 GCs. The grey band marks the 1σ uncertainty. Red and blue dots represent the values for the red and blue GCs, with 100 GCs per bin. The dashed blue and red lines represent the dispersion profiles for the GC analysis of the Schuberth et al. (2010) data. The dashed green and orange lines show the PNe and GC dispersion profiles from Spiniello et al. (2018) and Pota et al. (2018), respectively. The horizontal band denotes the velocity dispersion of the Fornax cluster galaxies (Drinkwater et al. 2000). The dashed vertical black line marks the effective radius of NGC 1399 and the dashed vertical grey lines the projected distances of major galaxies (as labelled) from NGC 1399. Lower panel: dispersion profile of ICGC candidates with two different selections. The pink line shows ICGCs and outer halo GCs selected farther than 2reff away from major galaxies, and the light pink band represents the 1σ uncertainty. The dark red line represents ICGCs that were selected outside 4reff around major galaxies (see text for details), and the lighter red band denotes its 1σ uncertainty. |
| In the text | |
 |
Fig. 13. Selection of potential ICGCs around NGC 1399 (first row) and NGC 1374 (second row). Left panel: GC distribution within 5reff (dashed blue circle). The radius of 2reff is indicated as a dashed red circle. Middle panel: distribution of GCs in projected phase space. Red dots show the galactic GCs within 2reff, and black dots show the defined ICGCs. Dashed vertical red and blue lines indicate 2reff and 5reff, and the grey horizontal lines give the 1 and 2σ scatter of GC velocities within 2reff around the systemic velocity of NGC 1374. Right panel: velocity histograms of ICGCs (black) and galactic GCs (red). The dashed black line marks the LOS velocity of NGC 1374, and the dashed grey lines show the 1 and 2σ scatter of GC radial velocities, as also shown in the middle panel. |
| In the text | |
 |
Fig. 14. Radial velocity histograms of the full sample and the intra-cluster GCs. The dashed vertical green line indicates the radial velocity of NGC 1399. The dashed vertical black, magenta, and dark red lines indicate the mean velocities of fitted Gaussian to the three sets of GCs. |
| In the text | |
 |
Fig. 15. Globular clusters with confirmed radial velocities (coloured dots) plotted over the surface density map of photometric GC candidates from the FDS (Cantiello et al. 2020). Top panel: full GC radial velocity sample. Middle panel: radial velocity distribution of red GCs. The black line shows the rotation axis of the red GCs at PA = 70°, measured north to east. Major galaxies are labelled in green. Bottom panel: same for blue GCs. The density scale plotted at the bottom represents the number of GCs from the photometric sample per square arcminute. |
| In the text | |
 |
Fig. 16. Azimuthal distribution of ICGCs selected outside 4reff radii around major galaxies (see text for details). Top panel: histogram of the ICGC position angle (PA), with a bin size of 30°. Middle panel: cluster-centric distance vs PA. Bottom panel: radial velocity vs PA. Green crosses indicate major galaxies. |
| In the text | |
 |
Fig. 17. Distribution of ICGCs selected with a phase-space cut at > 2reff. GC overdensity regions are named as in D’Abrusco et al. (2016). The magenta boxes show the regions in which we perform 2D KS tests. Black contours show the visibly selected regions to study the stream properties. |
| In the text | |
 |
Fig. 18. Radial velocity and g − i colour histograms of the intra-cluster regions. Top panel: radial velocity of GCs lying within the rectangular boxes A, C, F, and G (left to right). Middle panel: radial velocity of GCs lying within the streams A, C, F, and G (left to right). The radial velocities of the red GCs are marked in red. Bottom panel: g − i colour histogram of GCs lying within the streams A, C, F, and G (left to right). The dashed vertical black line marks the radial velocity of NGC 1399, and the vertical green lines show the peak positions of the fitted Gaussians. For streams A and C, double Gaussians were fitted. |
| In the text | |
 |
Fig. A.1. Effect of initial radial velocity guesses on the resulting radial velocity measurements. |
| In the text | |
 |
Fig. A.2. Choosing pPXF polynomials. Derived radial velocity (left panel) and the velocity dispersion (right panel) for a GC spectrum of S/N∼5 as a function of additive and multiplicative polynomial degree. Assigning to the additive polynomial a grade equal to -1 means running pPXF without it, i.e. using only multiplicative polynomials. |
| In the text | |
 |
Fig. A.3. Effect of higher order polynomials on radial velocity measurements. |
| In the text | |
 |
Fig. B.1. Example of a GC portfolio. The top panel shows the 1D extracted spectrum from the 2D VIMOS observation (on top). The middle panel shows the pPXF fit and its residuals in the subplot. The lower panel shows zoom-in wavelengths regions of absorption features used to visually select bonafide GCs. The lower right subpanel shows the 2D image of the GC from pre-imaging. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


