| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202037493 | |
| Published online | 12 August 2020 | |
Event Horizon Telescope imaging of the archetypal blazar 3C 279 at an extreme 20 microarcsecond resolution⋆
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: jykim@mpifr-bonn.mpg.de
2
Perimeter Institute for Theoretical Physics, 31 Caroline Street North, Waterloo, ON N2L 2Y5, Canada
3
Department of Physics and Astronomy, University of Waterloo, 200 University Avenue West, Waterloo, ON N2L 3G1, Canada
4
Waterloo Centre for Astrophysics, University of Waterloo, Waterloo, ON N2L 3G1, Canada
5
Black Hole Initiative at Harvard University, 20 Garden Street, Cambridge, MA 02138, USA
6
Center for Astrophysics, Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
7
Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
8
California Institute of Technology, 1200 East California Boulevard, Pasadena, CA 91125, USA
9
Princeton Center for Theoretical Science, Jadwin Hall, Princeton University, Princeton, NJ 08544, USA
10
NASA Hubble Fellowship Program, Einstein Fellow, Baltimore, MD, USA
11
National Radio Astronomy Observatory, 520 Edgemont Rd, Charlottesville, VA 22903, USA
12
Massachusetts Institute of Technology Haystack Observatory, 99 Millstone Road, Westford, MA 01886, USA
13
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
14
Institute for Astrophysical Research, Boston University, 725 Commonwealth Ave., Boston, MA 02215, USA
15
Astronomical Institute, St. Petersburg University, Universitetskij pr., 28, Petrodvorets 198504, St.Petersburg, Russia
16
Department of Astrophysics, Institute for Mathematics, Astrophysics and Particle Physics (IMAPP), Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands
17
Steward Observatory and Department of Astronomy, University of Arizona, 933 N. Cherry Ave., Tucson, AZ 85721, USA
18
Data Science Institute, University of Arizona, 1230 N. Cherry Ave., Tucson, AZ 85721, USA
19
Aalto University Department of Electronics and Nanoengineering, PL 15500, 00076 Aalto, Finland
20
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
21
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of Astronomy-Mathematics Building, AS/NTU No. 1, Sec. 4, Roosevelt Rd, Taipei 10617, Taiwan, R.O.C.
22
Departament d’Astronomia i Astrofísica, Universitat de València, C. Dr. Moliner 50, 46100 Burjassot, València, Spain
23
Observatori Astronómic, Universitat de València, C. Catedrático José Beltrán 2, 46980 Paterna, València, Spain
24
East Asian Observatory, 660 N. A’ohoku Place, Hilo, HI 96720, USA
25
Nederlandse Onderzoekschool voor Astronomie (NOVA), PO Box 9513, 2300 RA Leiden, The Netherlands
26
Institute of Astronomy and Astrophysics, Academia Sinica, 645 N. A’ohoku Place, Hilo, HI 96720, USA
27
Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint Martin d’Hères, France
28
Korea Astronomy and Space Science Institute, Daedeok-daero 776, Yuseong-gu, Daejeon 34055, Republic of Korea
29
University of Science and Technology, Gajeong-ro 217, Yuseong-gu, Daejeon 34113, Republic of Korea
30
Kavli Institute for Cosmological Physics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
31
Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
32
Department of Physics, University of Chicago, 5720 South Ellis Avenue, Chicago, IL 60637, USA
33
Enrico Fermi Institute, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
34
Cornell Center for Astrophysics and Planetary Science, Cornell University, Ithaca, NY 14853, USA
35
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
36
Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
37
Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210008, PR China
38
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, 43992 Onsala, Sweden
39
Mizusawa VLBI Observatory, National Astronomical Observatory of Japan, 2-12 Hoshigaoka, Mizusawa, Oshu, Iwate 023-0861, Japan
40
Department of Astronomical Science, The Graduate University for Advanced Studies (SOKENDAI), 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
41
Dipartimento di Fisica “E. Pancini”, Universitá di Napoli “Federico II”, Compl. Univ. di Monte S. Angelo, Edificio G, Via Cinthia, 80126 Napoli, Italy
42
Institut für Theoretische Physik, Goethe-Universität Frankfurt, Max-von-Laue-Straße 1, 60438 Frankfurt am Main, Germany
43
INFN Sez. di Napoli, Compl. Univ. di Monte S. Angelo, Edificio G, Via Cinthia, 80126 Napoli, Italy
44
Department of Physics, University of Pretoria, Lynnwood Road, Hatfield, Pretoria 0083, South Africa
45
Centre for Radio Astronomy Techniques and Technologies, Department of Physics and Electronics, Rhodes University, Grahamstown 6140, South Africa
46
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France
47
JILA and Department of Astrophysical and Planetary Sciences, University of Colorado, Boulder, CO 80309, USA
48
Department of History of Science, Harvard University, Cambridge, MA 02138, USA
49
Department of Physics, Harvard University, Cambridge, MA 02138, USA
50
Department of Physics, University of Illinois, 1110 West Green St, Urbana, IL 61801, USA
51
Department of Astronomy, University of Illinois at Urbana-Champaign, 1002 West Green Street, Urbana, IL 61801, USA
52
Leiden Observatory – Allegro, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
53
CP3-Origins, University of Southern Denmark, Campusvej 55, 5230 Odense M, Denmark
54
CONACYT-Instituto Nacional de Astrofísica, Óptica y Electrónica. Apartado Postal 51 y 216, 72000 Puebla, PUE, México
55
Key Laboratory for Research in Galaxies and Cosmology, Chinese Academy of Sciences, Shanghai 200030, PR China
56
NOVA Sub-mm Instrumentation Group, Kapteyn Astronomical Institute, University of Groningen, Landleven 12, 9747 AD Groningen, The Netherlands
57
Department of Astronomy, School of Physics, Peking University, Beijing 100871, PR China
58
Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, PR China
59
Instituto Nacional de Astrofísica, Óptica y Electrónica. Apartado Postal 51 y 216, 72000 Puebla, PUE, México
60
The Institute of Statistical Mathematics, 10-3 Midori-cho, Tachikawa, Tokyo 190-8562, Japan
61
Department of Statistical Science, The Graduate University for Advanced Studies (SOKENDAI), 10-3 Midori-cho, Tachikawa, Tokyo 190-8562, Japan
62
Kavli Institute for the Physics and Mathematics of the Universe, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 277-8583, Japan
63
ASTRAVEO LLC, PO Box 1668, MA 01931, USA
64
Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstr. 1, 85748 Garching, Germany
65
Joint Institute for VLBI ERIC (JIVE), Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
66
Kogakuin University of Technology & Engineering, Academic Support Center, 2665-1 Nakano, Hachioji, Tokyo 192-0015, Japan
67
Physics Department, National Sun Yat-Sen University, No. 70, Lien-Hai Rd, Kaosiung City 80424, Taiwan, R.O.C.
68
National Optical Astronomy Observatory, 950 North Cherry Ave., Tucson, AZ 85719, USA
69
Key Laboratory for Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, 19B Yuquan Road, Shijingshan District, Beijing, PR China
70
School of Astronomy and Space Science, Nanjing University, Nanjing 210023, PR China
71
Key Laboratory of Modern Astronomy and Astrophysics, Nanjing University, Nanjing 210023, PR China
72
Italian ALMA Regional Centre, INAF-Istituto di Radioastronomia, Via P. Gobetti 101, 40129 Bologna, Italy
73
Department of Physics, National Taiwan University, No.1, Sect.4, Roosevelt Rd., Taipei 10617, Taiwan, R.O.C.
74
Instituto de Radioastronomía y Astrofísica, Universidad Nacional Autónoma de México, Morelia 58089, México
75
Instituto de Astronomía, Universidad Nacional Autónoma de México, CDMX 04510, México
76
Yunnan Observatories, Chinese Academy of Sciences, 650011 Kunming, Yunnan Province, PR China
77
Center for Astronomical Mega-Science, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, Beijing 100012, PR China
78
Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 650011 Kunming, PR China
79
Gravitation Astroparticle Physics Amsterdam (GRAPPA) Institute, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
80
School of Natural Sciences, Institute for Advanced Study, 1 Einstein Drive, Princeton, NJ 08540, USA
81
Astronomy Department, Universidad de Concepción, Casilla 160-C, Concepción, Chile
82
Department of Astronomy, University of Massachusetts, 01003 Amherst, MA, USA
83
Department of Astronomy, Graduate School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
84
Canadian Institute for Theoretical Astrophysics, University of Toronto, 60 St. George Street, Toronto, ON M5S 3H8, Canada
85
Dunlap Institute for Astronomy and Astrophysics, University of Toronto, 50 St. George Street, Toronto, ON M5S 3H4, Canada
86
Canadian Institute for Advanced Research, 180 Dundas St West, Toronto, ON M5G 1Z8, Canada
87
Radio Astronomy Laboratory, University of California, Berkeley, CA 94720, USA
88
Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ 08544, USA
89
Center for Computational Astrophysics, Flatiron Institute, 162 Fifth Avenue, New York, NY 10010, USA
90
CCS-2, Los Alamos National Laboratory, PO Box 1663, Los Alamos, NM 87545, USA
91
Center for Theoretical Astrophysics, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
92
Instituto de Radioastronomía Milimétrica, IRAM, Avenida Divina Pastora 7, Local 20, 18012 Granada, Spain
93
Hiroshima Astrophysical Science Center, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8526, Japan
94
Department of Astronomy, Yonsei University, Yonsei-ro 50, Seodaemun-gu 03722, Seoul, Republic of Korea
95
Netherlands Organisation for Scientific Research (NWO), Postbus 93138, 2509 AC Den Haag, The Netherlands
96
Frontier Research Institute for Interdisciplinary Sciences, Tohoku University, Sendai 980-8578, Japan
97
Astronomical Institute, Tohoku University, Sendai 980-8578, Japan
98
Department of Physics and Astronomy, Seoul National University, Gwanak-gu, Seoul 08826, Republic of Korea
99
Leiden Observatory, Leiden University, Postbus 2300, 9513 RA Leiden, The Netherlands
100
Physics Department, Brandeis University, 415 South Street, Waltham, MA 02453, USA
101
Jeremiah Horrocks Institute, University of Central Lancashire, Preston PR1 2HE, UK
102
School of Physics, Huazhong University of Science and Technology, Wuhan, Hubei 430074, PR China
103
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
104
School of Astronomy and Space Sciences, University of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing 100049, PR China
105
Astronomy Department, University of Science and Technology of China, Hefei 230026, PR China
106
Department of Physics, Faculty of Science, University of Malaya, 50603 Kuala Lumpur, Malaysia
107
University of Vermont, Burlington, VT 05405, USA
108
National Radio Astronomy Observatory, NRAO Technology Center, 1180 Boxwood Estate Road, Charlottesville, VA 22903, USA
109
Department of Physics, Villanova University, 800 E. Lancaster Ave, Villanova, PA 19085, USA
110
Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
111
Fermi National Accelerator Laboratory, PO Box 500, Batavia, IL 60510, USA
112
Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis Enrique Erro 1, Tonantzintla, Puebla 72840, Mexico
113
Consejo Nacional de Ciencia y Tecnología, Av. Insurgentes Sur 1582, Col. Crédito Constructor, CDMX 03940, Mexico
114
National Chung-Shan Institute of Science and Technology, No.566, Ln. 134, Longyuan Rd., Longtan Dist. Taoyuan City 325, Taiwan, R.O.C.
115
Deptartment of Astronomy, University of California Berkeley, 501 Campbell, Berkeley, CA 94720, USA
116
Physikalisches Institut der Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
117
CASA, Department of Astrophysical and Planetary Sciences, University of Colorado, Boulder, CO 80309, USA
118
Western University, 1151 Richmond Street, London, Ontario N6A 3K7, Canada
119
University of Massachusetts Boston, 100 William T, Morrissey Blvd, Boston, MA 02125, USA
120
Research and Development Weather and Climate Models, Royal Netherlands Meteorological Institute, Utrechtseweg 297, 3731 GA De Bilt, The Netherlands
121
Department of Physics, McGill University, 3600 University Street, Montréal, QC H3A 2T8, Canada
122
McGill Space Institute, McGill University, 3550 University Street, Montréal, QC H3A 2A7, Canada
123
CIFAR Azrieli Global Scholar, Gravity & the Extreme Universe Program, Canadian Institute for Advanced Research, 661 University Avenue, Suite 505, Toronto, ON M5G 1M1, Canada
124
Department of Astrophysical and Planetary Sciences and Department of Physics, University of Colorado, Boulder, CO 80309, USA
125
Department of Physical Science, Graduate School of Science, Osaka Prefecture University, 1-1 Gakuen-cho, Nakaku, Sakai 599-8531, Osaka, Japan
126
High Energy Physics Division, Argonne National Laboratory, 9700 S. Cass Avenue, Argonne, IL 60439, USA
127
European Southern Observatory, Alonso de Córdova 3107, Vitacura, Casilla 19001, Santiago de Chile, Chile
128
Institute of Space Sciences (ICE, CSIC), Campus UAB, Carrer de Magrans 08193, Barcelona, Spain
129
ASIAA Hilo Office, 645 N. A‘ohoku Place, University Park, Hilo, HI 96720, USA
130
Square Kilometre Array Organisation, Jodrell Bank Observatory, Lower Withington, Macclesfield, Cheshire SK11 9DL, UK
131
Department of Physics, Ulsan National Institute of Science and Technology, Ulsan 44919, Republic of Korea
132
National Radio Astronomy Observatory, PO Box O, Socorro, NM 87801, USA
133
Joint ALMA Observatory, Alonso de Córdova 3107, Vitacura, 763-0355 Santiago de Chile, Chile
134
ASTRON, Oude Hoogeveensedijk 4, 7991 PD, Dwingeloo, The Netherlands
135
Science Support Office, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
136
University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
137
Center for Detectors, School of Physics and Astronomy, Rochester Institute of Technology, 1 Lomb Memorial Drive, Rochester, NY 14623, USA
138
Physics Dept., CB 1105, Washington University, One Brookings Drive, St. Louis, MO 63130-4899, USA
139
Mizusawa VLBI Observatory, National Astronomical Observatory of Japan, Ohshu, Iwate 023-0861, Japan
140
Systems & Technology Research, 600 West Cummings Park, Woburn, MA 01801, USA
141
Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA
142
MERLAB, 357 S. Candler St., Decatur, GA 30030, USA
143
GWW School of Mechanical Engineering, Georgia Institute of Technology, 771 Ferst Dr., Atlanta, GA 30332, USA
144
Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 452 Lomita Mall, Stanford, CA 94305, USA
145
Dept. of Physics and Astronomy, UCLA, Los Angeles, CA 90095, USA
146
Owens Valley Radio Observatory, California Institute of Technology, Big Pine, CA 93513, USA
147
Dept. of Astronomy, Radio Astronomy Laboratory, Univ. of California Berkeley, 601 Campbell, Berkeley, CA 94720, USA
148
Universidad de las Américas Puebla, Sta. Catarina Mártir S/N, San Andrés Cholula, Puebla 72810, Mexico
Received:
13
January
2020
Accepted:
3
March
2020
3C 279 is an archetypal blazar with a prominent radio jet that show broadband flux density variability across the entire electromagnetic spectrum. We use an ultra-high angular resolution technique – global Very Long Baseline Interferometry (VLBI) at 1.3 mm (230 GHz) – to resolve the innermost jet of 3C 279 in order to study its fine-scale morphology close to the jet base where highly variable γ-ray emission is thought to originate, according to various models. The source was observed during four days in April 2017 with the Event Horizon Telescope at 230 GHz, including the phased Atacama Large Millimeter/submillimeter Array (ALMA), at an angular resolution of ∼20 μas (at a redshift of z = 0.536 this corresponds to ∼0.13 pc ∼ 1700 Schwarzschild radii with a black hole mass MBH = 8 × 108 M⊙). Imaging and model-fitting techniques were applied to the data to parameterize the fine-scale source structure and its variation. We find a multicomponent inner jet morphology with the northernmost component elongated perpendicular to the direction of the jet, as imaged at longer wavelengths. The elongated nuclear structure is consistent on all four observing days and across different imaging methods and model-fitting techniques, and therefore appears robust. Owing to its compactness and brightness, we associate the northern nuclear structure as the VLBI “core”. This morphology can be interpreted as either a broad resolved jet base or a spatially bent jet. We also find significant day-to-day variations in the closure phases, which appear most pronounced on the triangles with the longest baselines. Our analysis shows that this variation is related to a systematic change of the source structure. Two inner jet components move non-radially at apparent speeds of ∼15 c and ∼20 c (∼1.3 and ∼1.7 μas day−1, respectively), which more strongly supports the scenario of traveling shocks or instabilities in a bent, possibly rotating jet. The observed apparent speeds are also coincident with the 3C 279 large-scale jet kinematics observed at longer (cm) wavelengths, suggesting no significant jet acceleration between the 1.3 mm core and the outer jet. The intrinsic brightness temperature of the jet components are ≲1010 K, a magnitude or more lower than typical values seen at ≥7 mm wavelengths. The low brightness temperature and morphological complexity suggest that the core region of 3C 279 becomes optically thin at short (mm) wavelengths.
Key words: galaxies: active / galaxies: jets / galaxies: individual: 3C 279 / techniques: interferometric
The data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/640/A69 and at https://eventhorizontelescope.org/for-astronomers/data
© J.-Y. Kim et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
Relativistic jets in active galactic nuclei (AGN) are believed to originate from the vicinity of a supermassive black hole (SMBH), which is located at the center of the galaxy. Understanding the detailed physical processes of jet formation, acceleration, collimation, and subsequent propagation has been one of the major quests in modern astrophysics (see, e.g., Boccardi et al. 2017; Blandford et al. 2019 and references therein for recent reviews)
Extensive studies on these topics have been carried out over the last several decades, in particular by using the technique of millimeter-wave (mm) very long baseline interferometry (VLBI), which provides especially high angular resolution and can penetrate regions that are opaque at longer wavelengths. Notably, recent Event Horizon Telescope (EHT) observations of M 87 at 1.3 mm (230 GHz) have revealed a ring-like structure on event horizon scales surrounding the SMBH, interpreted as the black hole “shadow” (Event Horizon Telescope Collaboration 2019a,b,c,d,e,f; hereafter Papers I–VI). Although the EHT results for M 87 provide an important step toward understanding jet formation near a BH and in AGN systems in general, the first EHT images of M 87 do not yet provide a direct connection between the SMBH and the large-scale jet. Therefore, imaging of fine-scale structures of AGN jets close to the SMBHs still remains crucial in order to better understand the accretion and outflow activities. Also, a more comprehensive understanding of AGN jet formation will require systematic studies over a wider range of AGN classes, given intrinsic differences such as luminosity, accretion rate, and environmental effects (e.g., Yuan & Narayan 2014). We also note that M 87 and the Galactic Center SMBH Sagittarius A* are relatively weak sources of γ-ray emission (e.g., Lucchini et al. 2019), while many other AGN produce prominent and variable high-energy emission, often from compact regions in their jets (e.g., Madejski & Sikora 2016). Therefore, studies of the high-power, high-luminosity AGN also provide more clues regarding γ-ray emission mechanisms (see, e.g., Blandford et al. 2019 for a review).
Unfortunately, most high-power AGN are located at much larger luminosity distances than M 87 and Sgr A*. Observing frequencies up to 86 GHz have thus limited us in the past to studying relatively large-scale jet morphology and evolution in many different types of AGN. However, it is only with the EHT at 230 GHz and beyond that the finest details at the base of those
gigantic dynamic structures become accessible. Combined with other VLBI arrays, for example the Very Long Baseline Array (VLBA) or Global Millimeter VLBI Array (GMVA) at 86 GHz, the EHT can also connect the innermost regions of jets with the downstream sections, revealing detailed profiles of the jet collimation and locations of the collimation profile changes to better constrain jet collimation and propagation theories (e.g., Asada & Nakamura 2012; Hada et al. 2013).
The blazar 3C 279 (1253−055) is one of the sources that provided the first evidence of rapid structure variability (Knight et al. 1971) and apparent superluminal motions in compact AGN jets (Whitney et al. 1971; Cohen et al. 1971). Since the discovery of the apparent superluminal motions, the detailed structure of the radio jet in 3C 279 has been imaged and its properties have been studied by a number of VLBI observations until the present day. The 3C 279 jet consists of a compact core and straight jet extended from subparsec (sub-pc) to kiloparsec (kpc) scales. The compact core has high apparent brightness temperature at centimeter wavelengths (TB, app ≳ 1012 K; see, e.g., Kovalev et al. 2005). Both the core and the extended jet show high fractional linear polarization (≳10%), and strong circular polarization on the order of ∼1% is also detected in the core region at ≤15 GHz (e.g., Homan & Wardle 1999; Homan & Lister 2006; Homan et al. 2009a) and ≤43 GHz (Vitrishchak et al. 2008). The extended jet components show various propagation speeds (bulk Lorentz factor Γ ∼ 10 − 40; e.g., Bloom et al. 2013; Homan et al. 2015; Jorstad et al. 2017), indicating the presence of not only underlying bulk plasma motions, but also patterns associated with propagating shocks or instabilities. Interestingly, the inner jet components of 3C 279 often display various position angles (see, e.g., Homan et al. 2003; Jorstad et al. 2004 and references therein), but later on such components tend to align with the larger-scale jet direction while propagating toward the jet downstream (e.g., Kellermann et al. 2004; Homan et al. 2009b). Based on the small viewing angle of the 3C 279 jet of θ ∼ 2° (Jorstad et al. 2017), the misaligned jet components are often modeled as spatially bent (and perhaps helical) jet structures, in which the jet Lorentz factor is constant along the outflow but the jet viewing angle changes (e.g., Abdo et al. 2010; Aleksić et al. 2014). We also note that jet bending on VLBI scales is common in many blazar jets (e.g., Hong et al. 2004; Lobanov & Roland 2005; Zhao et al. 2011; Perucho et al. 2012; Fromm et al. 2013). For the innermost region of the 3C 279 jet (≲100 μas ∼0.65 pc projected1), earlier pilot VLBI studies at 230 GHz revealed a complex microarcsecond-scale substructure within the nuclear region of the milliarcsecond scale jet (Lu et al. 2013; Wagner et al. 2015). However, the (u, v) coverage, and therefore the imaging fidelity, of these observations was very limited. We also note that 3C 279 is well known for its highly time-variable flux densities, from radio to γ-rays (e.g., Chatterjee et al. 2008; Abdo et al. 2010; Aleksić et al. 2014; Kiehlmann et al. 2016; Rani et al. 2018; Larionov et al. 2020), while the exact locations of the γ-ray emission zones are often controversial (e.g., Patiño-Álvarez et al. 2018, 2019). In particular, 3C 279 shows flux density variations down to minute timescales, which are often difficult to interpret given the size scales and Doppler factors inferred from radio VLBI observations (e.g., Ackermann et al. 2016).
In April 2017, 3C 279 was observed with a significantly expanded EHT array over four nights. The EHT 2017 observations result in new and more detailed maps of the core region of 3C 279, providing an angular resolution of 20 μas, or ∼0.13 pc (corresponding to ∼1700 Rs for a SMBH of mass MBH ∼ 8 × 108 M⊙; Nilsson et al. 2009). This paper presents the main results from the EHT observation in 2017 and their scientific interpretations. In Sect. 2 we briefly describe the observations, imaging procedures, and model-fitting techniques. In Sect. 3 the source images and model-fit parameters are presented. In Sect. 4 we discuss some physical implications of the peculiar compact jet structure, in relation to the observed rapid variation of the source structure and brightness temperature. Section 5 summarizes our results. Throughout this paper we adopt a cosmology with H0 = 67.7 km s−1 Mpc−1, Ωm = 0.307, and ΩΛ = 0.693 (Planck Collaboration XIII 2016)2.
2. Observations and data processing
2.1. Observations and calibration
3C 279 was observed by the EHT on 2017 April 5, 6, 10, and 11. We refer to Papers II and III, and references therein for details of the scheduling, observations, data acquisition, calibration, and data validation. Here we briefly outline the overall procedures. A total of eight stations at six geographic sites participated in the observations: Atacama Large Millimeter/submillimeter Array (ALMA), Atacama Pathfinder Experiment telescope (APEX), Large Millimeter Telescope Alfonso Serrano (LMT), IRAM 30 m Telescope (PV), Submillimeter Telescope Observatory (SMT), James Clerk Maxwell Telescope (JCMT), Submillimeter Array (SMA), and South Pole Telescope (SPT). The signals were recorded at two 2 GHz bands (centered at 227 and 229 GHz), using dual circularly polarized feeds (RCP and LCP). JCMT observed only in one circular polarization. ALMA observed using dual linear feeds. Because of this, the polconvert software (Martí-Vidal et al. 2016) was applied to the correlated data to convert the ALMA visibilities from linear to circular polarization.
The (u, v) coverage is shown in Fig. 1. The high data recording rate of 32 Gbps (corresponding to a total bandwidth of 2 GHz per polarization per sideband) allowed robust fringe detections up to a ∼8.7 Gλ baseline length, including the SPT, which significantly improved the fringe spacing toward 3C 279 in the north–south direction. The correlated data were then calibrated using various radio astronomical packages and validated through a series of quality assurance tests (see Paper III for details). The flux-calibrated visibility amplitude distributions are shown in Fig. 2.
 |
Fig. 1. Event Horizon Telescope (u, v) coverage of 3C 279 on (from left to right) 2017 April 5, 6, 10, and 11. The color-coding for the corresponding baselines is shown in the legend. The JCMT and APEX baselines are omitted because they repeat the SMA and ALMA baselines, respectively. |
 |
Fig. 2. Flux-calibrated visibility amplitudes of 3C 279 in all epochs. The visibility amplitude distributions are broadly consistent over four days, while the closure phases are not (see Sect. 3). |
2.2. Imaging and model-fitting analysis
For imaging, we used frequency-averaged visibility data from the EHT-HOPS pipeline (see Paper III and Blackburn et al. 2019). We note that image reconstruction with 1.3 mm wavelength EHT data is particularly challenging because of the sparse (u, v) coverage, total loss of absolute atmospheric phase, and large gain fluctuations at some stations. In addition, the 2017 EHT observations lack relatively short baselines at ≲1 Gλ to robustly recover extended emission structure on VLBI scale at ≳100 μas (Paper IV). To ensure that the features we identified in our reconstructed images are robust, the source images were generated by both traditional CLEAN and newer regularized maximum likelihood algorithms implemented in the following programs: Difmap (Shepherd et al. 1994), eht-imaging (Chael et al. 2016, 2018), and SMILI (Akiyama et al. 2017a,b). We used imaging pipelines for these three programs (see Paper IV) to generate a total of 12 images of 3C 279 (i.e., one per epoch per imaging method) within a limited field of view of ∼100 μas due to lack of short EHT 2017 baselines (Paper IV). In all methods, emission from the further extended milliarcsecond-scale jet (Fig. 4), which lies beyond the compact EHT field of view, was represented by a single large-scale Gaussian (see Paper IV for details). We then averaged the three pipeline images to obtain a representative image of the source at each epoch. We refer to Paper IV for the details of the imaging pipelines and image averaging procedures. In order to illustrate the EHT angular resolution toward 3C 279, we show in Table 1 the CLEAN beam sizes of the EHT 3C 279 data calculated by Difmap.
CLEAN beam sizes of the EHT toward 3C 279.
In order to parameterize bright and compact features in the source, we also performed Gaussian model-fitting analyses in two distinct ways. The first is the traditional VLBI model-fitting procedure (DIFMAP modelfit, which employs the Levenberg-Marquardt algorithm for non-linear fits) to reconstruct a static model with more than six components on each observation day. Related components were then identified and the evolution in their relative positions measured.
The second method utilizes THEMIS, an EHT-specific analysis package, using a parallel-tempered, affine invariant Markov chain Monte Carlo sampler (Broderick et al., in prep., and references therein). In this case, a fully time-variable, ten-component (nine compact and one large-scale) Gaussian component model was reconstructed to naturally facilitate the identification of features in subsequent observations and directly reconstruct their evolution. From this time variable model, component parameters and uncertainties are reconstructed for individual days. Additional descriptions of the underlying model and THEMIS analysis can be found in Appendix A (also see Paper VI for more general details for the EHT model-fitting and model-comparison analysis).
In order to examine the reliability of the converged images and models, we also compared antenna gains reconstructed by amplitude self-calibration with both imaging and model-fitting software. Figure B.1 shows plots of antenna gain corrections for all days across different imaging pipelines and THEMIS for LMT, which has the largest systematic gain uncertainties in the EHT 2017 observation (Papers III–VI). Consistent gain corrections across independent imaging methods and model-fitting analysis suggest that the results are robust against possible biases in each algorithm.
3. Results
3.1. First 230 GHz images
Figure 3 shows an overview of the 3C 279 jet structure in April 2017 at 43, 86, and 230 GHz, where the 43 and 86 GHz images are from quasi-simultaneous observations by the VLBA-BU-BLAZAR 43 GHz (Jorstad et al. 2017) and the GMVA blazar monitoring programs3, shown here for an illustration of the larger-scale jet structure. In Fig. 4 we show the final EHT 1.3 mm images of 3C 279 on April 5, 6, 10, and 11 obtained as described in Sect. 2.2. The individual source images for all pipelines and epochs are shown in Fig. C.1. The images show two bright and somewhat extended emission regions, separated by ∼100 μas, with complex substructures within each of them. Hereafter we refer to the northern and southern complexes as C0 and C1, respectively. The C0 feature is substantially elongated in the NW-SE direction by ∼30 − 40 μas, as defined by the separation between its subcomponents (see Sect. 3.3). This elongation is perpendicular to the long-term larger-scale jet direction (SW; see, e.g., Jorstad et al. 2017). We find a prominent and rapid change of the brightness in the center of the C0 region over ∼6 days (see also Sect. 3.3).
 |
Fig. 3. Illustration of multiwavelength 3C 279 jet structure in April 2017. The observing epochs, arrays, and frequencies are noted at the top of each panel. The color bars show the pixel values in Jy beam−1. The white circles in the bottom left corners indicate the convolving beams. The white rectangles shows the field of view of the next panels at the higher 86 and 230 GHz frequencies. We note that the centers of the images (0,0) correspond to the location of the peak of total intensity. (From left to right) the beam sizes are 150 × 380, 50 × 139, and 20 × 20 μas2. For a spatially resolved emitting region, an intensity of 1 Jy beam−1 in the 43, 86, and 230 GHz images correspond to brightness temperatures of 1.16 × 1010, 2.37 × 1010, and 5.78 × 1010 K, respectively. |
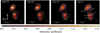 |
Fig. 4. EHT images of 3C 279 on each day, generated by three different pipelines, then aligned and averaged. See Paper IV for details on the method. The circular 20 μas restoring beam is shown in the bottom right corner of each panel. The pixel values are in units of Jy beam−1. In each panel, the contour levels are 5%, 12%, 25%, 50%, and 75% of the peak value. The component identification is shown in the April 11 panel and is only for illustration (see Fig. 6). |
3.2. Inter-day closure phase variations
We show in Fig. 5 the closure phases of several long EHT triangles for all days. Remarkably, the ALMA-SMA-SMT triangle reveals large inter-day closure phase variations of ∼100° in ∼6 days. Comparable closure phase changes are also seen for other large triangles (Fig. 5). We note that similar inter-day closure phase changes were previously found in 3C 279 at 230 GHz by Lu et al. (2013), but the much higher-sensitivity and longer-baseline data presented here reveal much more dramatic closure phase variations. This strongly implies the presence of inter-day variability of the surface brightness distribution and compact structure in the jet.
 |
Fig. 5. Example of the closure phase variation in 3C 279 over four epochs for the large ALMA-SMT-SMA, ALMA-LMT-SMA, and ALMA-LMT-SMT triangles. The points show the data, and their error bars include 1.5% systematic visibility errors (Paper III). The solid lines show the model closure phases corresponding to the images from each pipeline and day, and the dashed lines represent the model closure phases of the average images shown in Fig. 4. Regions constrained by predictions of the three independent image models are shaded. |
3.3. Model-fitting results
Values of parameters resulting from the Gaussian model-fitting analysis for all days, such as component flux densities, sizes, and relative positions are provided in Table D.1. Where these are obtained from THEMIS, they are evaluated from the dynamical model at 6 UTC on each observation day. The component kinematics are displayed in Figs. 6 and 7. Visibility amplitudes and closure phases of the self-calibrated data and the Gaussian model-fit are shown in Fig. D.1.
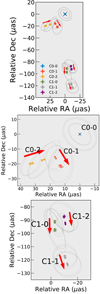 |
Fig. 6. Model-fit component kinematics during April 5–11. Top panel: kinematics for all components. The center positions of different Gaussian components, and their uncertainties are color-coded (see legend). The Gaussian FWHM sizes are shown by dashed gray ellipses. The black cross at (0,0) indicates the kinematic reference (C0-0). Red arrows show the component motions; their lengths are proportional to the apparent velocities. Middle and bottom panel: same as the top panel, but zoomed in to the nuclear (C0) and extended jet regions (C1), respectively. We note that the center (0,0) in all panels is chosen as the center of C0-0, not the peak of total intensity. |
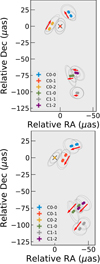 |
Fig. 7. Same as Fig. 6, but using C0-1 (top) and C0-2 (bottom) as kinematic references. We note the more complicated motions of other jet features in both panels compared to Fig. 6. |
Quantitatively similar results were obtained on each day by both Difmap modelfit and THEMIS analyses; hereafter, we focus on the THEMIS results that naturally identify components across observation epochs. We find that the closure phases, closure amplitudes, and visibilities can be consistently described by a model consisting of the ten Gaussian components, with a reduced χ2 of ∼1.3 for the best-fit models with ∼1.5% systematic errors in the visibility amplitudes (and equivalently ∼2° errors in phases; see Paper III).
Six compact and bright features among the nine evolving components are the most robustly constrained across epochs. The other three extra components are much fainter (e.g., by an order of magnitude), and are located outside the intensity distributions reconstructed by imaging methods (Fig. 4). Therefore, we do not discuss these three components hereafter. Figure 8 summarizes the time evolution over all epochs of the parameters of these features. Three of them – C0-0, C0-1, and C0-2 – belong to the C0 region, while the remainder (labeled C1-0, C1-1, and C1-2) belong to the C1 region (see the rightmost panel of Figs. 4 and 6). We note that there are consistent, outward ∼1.1 − 1.2 μas day−1 proper motions of all C1 components when the C0-0 feature is used as a reference. In contrast, C0-1 moves perpendicular to its center position angle with respect to C0-0 with flux density decrease, and C0-2 moves toward C0-0 with a pronounced increase in its flux density (see Sect. 3.4 for more details).
 |
Fig. 8. Model-fit parameters and their time evolution obtained by the THEMIS time-evolving model-fitting (Sect. 2.2). Each row shows a single component. Shaded regions indicate 95% confidence level at each time, the dashed line shows the median value, and the red solid lines indicate the best fit value. Observing epochs are shown by gray vertical bands. The component IDs are shown at the top left corner of the leftmost column. From left: flux density, radial distance with respect to C0-0, RA and Dec offsets with respect to C0-0, core mean FWHM sizes, and apparent brightness temperature. |
Using the jet component parameters, we can compute their apparent brightness temperatures in the frame of the observer (thus not redshift or Doppler-boosting corrected), TB, as TB = 1.22 × 1012F/(ν2dmajdmin) K where for each component F is the flux density in Jy, ν is the observing frequency in GHz, and dmaj, min are the major and minor full width at half maximum (FWHM) sizes of the Gaussians in milliarcseconds, respectively. The TB values for all days are shown in Fig. 8 and Table D.1. The apparent brightness temperatures are in the range of TB ∼ 1010 − 11 K. We note that the C0-1 and C0-2 components show particularly large flux and size variations, which essentially lead to rapid changes in the brightness temperature over the one-week observing period.
3.4. Kinematic reference
Because of the nontrivial, complicated motions of C0-1 and C0-2 with respect to C0-0, we also selected C0-1 and C0-2 as alternative kinematic references and recalculated motions in order to see if the complex kinematics could be described more simply (e.g., simple radial outward motion in all components). We find that the component speeds are still comparable with the alternative references (although the directions of the proper motions are even more complicated), for example the C0 subcomponents moving toward the north (i.e., in the opposite direction to the large-scale jet; see Figs. 7, top panel, and 3) and the C1 subcomponents moving toward the east (Fig. 7, bottom panel) if C0-1 is chosen as the reference. Similar complex motions are seen when C0-2 is chosen as the reference. Therefore, choosing C0-0 as the kinematic reference provides a smoother transition of the kinematics from the inner EHT scale to the outer large jet (see Fig. 3), and also helps avoid unnecessary complexity in the interpretation given the limited available data, although this choice alone does not allow us to determine which of the three C0 subcomponents remains more stationary in time (see Sect. 4.3 for more discussions from a physical perspective).
We also note that adopting C0-0 as the kinematic reference helps avoid false identification of the other C0 subcomponents, such as counterjet features. The expected jet-to-counterjet ratio of discrete emission features in 3C 279 can be computed as ((1 + β cos θ)/(1 − β cos θ))m − α, where β is the jet speed in units of c; m = 2 or 3 for a continuous jet or a single component, respectively (see, e.g., Urry & Padovani 1995); and α is the optically thin spectral index (i.e., flux density S ∝ ν+α). If we adopt α = −0.7, θ = 2°, m = 3, and β = βapp/(sin θ + βapp cos θ), where βapp ≳ 10 based on the observations, the expected brightness ratio is ≳1010; however, the observed brightness ratios of the C0 subcomponents are within an order of magnitude (Table D.1). Therefore, we should expect to find no counterjet features situated to the north of the VLBI “core” (see Fig. 7), although emitting features moving in a helically bent jet could perhaps produce this apparent backward motion if the jet is closely aligned to the line of sight (see Sect. 4 for a discussion).
In addition, we further note that the VLBI core is usually defined as the most compact and brightest jet feature in the obtained images, and thus has the highest brightness temperature. It is interesting to note in Fig. 8 that the brightest component is not C0-0, but either C0-1 or C0-2, depending on the observing epochs. With this criterion, C0-1 and C0-2 might be still classified as the VLBI core. However, long-term and high-resolution observations of blazar jets find that compact and bright jet components near the VLBI core often have higher brightness temperatures than the cores determined by the jet kinematics (see, e.g., Lisakov et al. 2017; Bruni et al. 2017; Jorstad et al. 2017). Thus, identifying C0-1 and C0-2 as the potential VLBI core based on the flux density and brightness temperature may not be strongly supported in our observations. Therefore, we adopt C0-0 as the VLBI core of 3C 279 in the following analysis.
4. Discussion
4.1. Elongated nuclear structure
The nuclear (C0 region) structure of 3C 279 resolved at the highest 20 μas angular resolution is elongated perpendicular to the large-scale jet. This structure is seen in both independent imaging and model-fitting methods, and can be modeled as three bright features separated by ∼30 − 40 μas. This corresponds to a projected spatial scale of ∼2500 − 3400 Rs for MBH = 8 × 108 M⊙. This morphology has not been commonly seen for 3C 279 by VLBA at 15 and 43 GHz (Jorstad et al. 2017; Lister et al. 2018). If the jet emission represents distribution of underlying synchrotron-emitting plasma, this peculiar structure can be interpreted in various ways. Below we provide four possible interpretations.
Standard jet formation scenarios suggest relativistic jet launching by either angular momentum extraction from the spinning SMBH (Blandford & Znajek 1977) or magneto-centrifugal acceleration by an accretion disk (Blandford & Payne 1982), or by both mechanisms at the same time. In this context, a spatially resolved jet base, similar to the jet base morphology found in several nearby radio galaxies, in particular with limb-brightened jets (e.g., 3C 84; Giovannini et al. 2018, Cygnus A; Boccardi et al. 2016) is also possible. However these are viewed at a much larger angle to the line of sight than for 3C 279 and could provide an edge-on view of the limb-brightened jet base or the disk (thus thin elongated geometry if the accretion flow is not a sphere but has a finite height-to-radius ratio of, e.g., H/R ≲ 1; see, e.g., Yuan & Narayan 2014). However, for 3C 279 a nearly face-on view (θ ∼ 2°) and thus a more rounded, thick emission geometry is expected on the sky for the base of a circular jet or the accretion flow, in contrast to the observed images which show a narrow width along the global direction of the jet4.
Alternatively, the large transverse (to the downstream jet) size of the C0 region could correspond to a linear structure such as a site of large-scale magnetic reconnection, which could provide a long linear string of “plasmoids” (see, e.g., Blandford et al. 2017), or some oblique structure, like a shock or an oblique jet filament (e.g., Marscher & Gear 1985; Hardee 2000). The former explanation would require continuous magnetic reconnections along the jet during the observations. Perhaps the simplest and easiest way for this to happen is if the magnetic field in the jet were in the form of loops that become stretched out by cross-jet velocity gradients. Qualitatively, this would provide elongated loops where oppositely directed field lines are adjacent to each other and could reconnect in various locations. In this case, the predicted polarization electric vector position angle would be perpendicular to the elongated emission structure, which can be tested in the future by EHT linear polarization imaging.
It is also important to mention that the above scenarios do not exclude the possibility that the moving emission features are not necessarily associated with motions of the underlying plasma. This implies that the observed emission could only be patterns on the surface of the jet, such as propagating shocks or instabilities (e.g., Lobanov & Zensus 2001). In this case, the observed bright components might represent only a small fraction of the entire broad jet.
For AGN jets such as 3C 279 seen at small viewing angles, however, it should be noted that a propagating component executing a slight bend in three dimensions can cross the line of sight and change the apparent inner jet position angle by a substantial amount. The observed proper motions in the C0 region suggest that non-ballistic (i.e., curved) trajectories are required for C0-1 and C0-2 if they originated from C0-0. That is, the perpendicular motion of C0-1 compared to its position angle with respect to C0-0 could correspond to ∼90° apparent jet bending. It is also worth noting that the contracting component motions within the C0 region are still present even if C0-1 or C0-2 are used as kinematic reference, which could imply a complex three-dimensional structure of the emitting jet plasma in the C0 region. Therefore, we investigate in Sect. 4.2 the kinematics of the inner 3C 279 jet in more detail and constrain the potential three-dimensional jet geometry.
4.2. Jet kinematics on daily and μas scales
As briefly introduced in Sect. 1, the kinematics of the 3C 279 jet revealed by previous interferometric imaging observations is complicated. Previous studies based on VLBA 15 and 43 GHz observations revealed a wide range of observed apparent speeds and jet bulk Lorentz factors at various locations and epochs (e.g., βapp ranging from a few to ∼20 c and Γ ∼ 10 − 40)5, and changing directions of jet proper motions, which is often accompanied by apparent increase of βapp (see references in Sect. 1). There is evidence obtained from studies of large samples (e.g., Homan et al. 2015) that intrinsic jet acceleration (i.e., increasing Γ) is required to explain these phenomena. However, Homan et al. (2003) and Jorstad et al. (2004) show specifically for 3C 279 that the changing motion vectors and increasing βapp can be nicely explained simply by varying the viewing angle along the outflow, without necessarily changing the intrinsic bulk Lorentz factor. In the light of this, we investigate the kinematics of the C0 and C1 regions, focusing on a similar geometrical model (i.e., bent jet) and using the observed component properties. In the following we assume that the dynamical center of the jet system is C0-0 (see Sect. 3.3).
4.2.1. C0 region
Before describing details, we note that the pure jet bending scenario is physically well motivated because (1) the kinematics of C0 subcomponents clearly exclude simple radial outward motions, (2) the separation between C0-1 and C0-2 is small (∼12 − 17 μas ∼0.08 − 0.11 pc projected) and perhaps too short for a significant jet acceleration or deceleration to occur, and (3) the jet bending model requires less fine-tuning than more complicated scenarios in which, for example, a jet changes both the bulk Lorentz factor and viewing angle. Accordingly, we assume that both C0-1 and C0-2 have the same bulk Lorentz factors but different viewing angles.
Using the special relativity relationships (Footnote 5), we show in Fig. 9 possible combinations of viewing angles and Doppler factors for various values of Lorentz factors in the plane of βapp and δ. By inspecting the plot it is clear that Γ = 20 is needed to explain βapp of both C0-1 and C0-2 using a constant Γ. If we take Γ = 20 as a nominal value, it can be seen that a viewing angle of θ ∼ 2.9° is required for C0-2, while θ can be ∼1.5° or ∼5.5° for C0-1. We can then examine whether the viewing angle should be smaller or larger for C0-1 by assuming that the intrinsic flux densities of C0-1 and C0-2 are identical but observed differently only due to Doppler boosting, and then by computing ratios of the Doppler factors for these components.
 |
Fig. 9. Plane of apparent speed (βapp) and Doppler factor (δ). Solid and dashed lines correspond to constant values of bulk Lorenz factors and viewing angles, respectively. The blue and green triangles and red circle show possible values of βapp and δ assuming the same Γ = 20 for C0-1 and C0-2, respectively. The vertical black lines correspond to the βapp values of C0-1 and C0-2. The red and blue shaded areas indicate uncertainties of βapp for C0-1 and C0-2, respectively. |
The flux densities of C0-1, SC0 − 1, and C0-2, SC0 − 2 result in a flux density ratio of SC0 − 1/SC0 − 2 ∼ 0.6 − 5.9 (Table D.1). Since the observed flux density ratio is proportional to δm − α, where m = 2 or 3 as defined in Sect. 3.4, the required Doppler factor ratio should be δC0 − 1/δC0 − 2 = (SC0 − 1/SC0 − 2)1/(m − α). Assuming m = 3 and α = −0.7, we obtain δC0 − 1/δC0 − 2 ∼ 0.87 − 1.62. As shown in Fig. 9, θ = 2.9° could explain C0-2 with Γ = 20, and the corresponding Doppler factor is δC0 − 2 ∼ 20. Similarly for C0-1 and Γ = 20, θ = 1.5° and 5.5° result in Doppler factors of δC0 − 1 ∼ 32 and ∼8, respectively. The Doppler factor ratios are then δC0 − 1/δC0 − 2 ∼ 1.6 or ∼0.4 for the larger and smaller values of θ for C0-2, respectively. Both ratios broadly agree with what is required to explain the observed flux density ratio, considering potentially large uncertainties in those numbers due to our assumptions. Therefore, we could conclude that both viewing angles for C0-2 are consistent with observations, although the rapid time variability of C0-1 may prefer the larger Doppler factor and accordingly smaller viewing angle (Fig. 8). It should be noted, however, that these calculations do not exclude higher Lorentz factors for both components, and therefore we constrain Γ ≥ 20 for both C0-1 and C0-2. Table 2 summarizes the possible values of θ, Γ, and δ for C0-1 and C0-2, as estimated based on the above assumptions.
Importantly, we note that the viewing angles of C0-1 and C0-2 can differ from each other by a few degrees. This amount is similar to the large 3C 279 jet inclination, θ ∼ 2°, which is estimated from long-term VLBA 43 GHz monitoring of the jet kinematics (Jorstad et al. 2017). It appears that these small viewing angle differences could be sufficient to explain the almost 90° position angle offsets of C0-1 and C0-2 relative to the SW-oriented large-scale jet. This means that a deprojection of ∼90° angle difference on the sky to a θ = 2° jet system would correspond to a jet viewing angle change of ∼90° sin(1° −2° ) ∼ 1.6° − 3.1°. This small amount of θ offset is not in contradiction with the estimations of the jet viewing angle differences for C0-1 and C0-2, as shown above.
4.2.2. C1 region
In contrast to the C0 region, the three subcomponents in C1 have comparable apparent speeds (βapp ∼ 13 − 15), and their position angles with respect to C0-0 are all in a narrow range of ∼ − (173° −178°), which are aligned to the directions of their motion vectors (PA ∼ −(160° −180° )). Therefore, we can reasonably presume that these components share common kinematic and geometric properties.
We could extend the analysis in Sect. 4.2.1 to the C1 region, that is assuming a constant Γ = 20 for all the components to estimate their different viewing angles. We show in Fig. 10 the same βapp and δ plane but for the C1 subcomponents, which is used to constrain reasonable ranges of θ and the corresponding δ. For βapp = 13 − 15, there are two possible sets of parameters, which are (i) θ ∼ 6° −8° and δ ∼ 5 − 7, and (ii) θ ∼ 1.0° −1.5° and δ ∼ 33 − 35. We note that there is a similar ambiguity in determining whether the jet bends closer to or away from the line of sight. Nevertheless, we could consider that weaker time variability of the C1-0 and C1-1 components might prefer smaller Doppler factor values (i.e., larger θ), while C1-2 shows stronger variability and thus could have larger Doppler boosting (i.e., smaller θ).
 |
Fig. 10. Same as Fig. 9, but for C1. The vertical solid black lines correspond to βapp values of the C1 subcomponents and the gray shaded area shows their uncertainties. For comparison, the model values for C0 components with Γ = 20 are also shown using the same symbols as in Fig. 9. The ranges of the axes are different from Fig. 9. |
Alternatively, dynamical properties of C1 could be better estimated by simply adopting the viewing angle of the larger-scale jet (θ ∼ 2°; Jorstad et al. 2017) because the motions of the C1 subcomponents are nearly parallel to the jet downstream (Fig. 3). Using θ = 2°, we obtain Γ ∼ 16 − 17 and δ ∼ 24 − 25.
Taken all together, the ranges of Lorentz factors for C1 are comparable to those found from the 3C 279 jet on larger scales and at longer wavelengths (≳103 pc or ≳105 Rs projected; Bloom et al. 2013; Lister et al. 2016; Jorstad et al. 2017; Rani et al. 2018), and also those estimated from radio total flux variability (e.g., Hovatta et al. 2009). The values of θ, Γ, and δ for C1 are also summarized in Table 2.
4.3. Physical implications
In conclusion, it appears that the peculiar C0 structure could be described by a jet closely aligned to the line of sight, but bent by small angles, and the projection of the overall bent geometry to the sky. In this perspective, it is also worth noting that in a previous 230 GHz VLBI experiment on 2011 March 29–April 4, a similar nuclear morphology was found in 3C 279 based on a model-fitting approach (Lu et al. 2013). After 2011 December, this structure became resolved by the VLBA at 43 GHz as a bright moving feature situated at a position angle of initially ∼150°, and later at ∼ − 170° relative to the 43 GHz core (Aleksić et al. 2014; Jorstad et al. 2017), confirming the jet bending scenario (the VLBA 7 mm kinematics is shown in Fig. E.1). Notably, the overall situation of the source in 2011 is similar to the jet geometry we discussed in Sect. 4.2.1. This suggests that the inner jet bending may commonly occur in 3C 279. In this respect it is interesting to note that a similar extremely bent jet morphology is sometimes observed in several AGN on small angular scales, especially when the object is in a flaring state at multiple wavelengths (e.g., 1156+295 – Hong et al. 2004; Zhao et al. 2011; PKS 2136+141 – Savolainen et al. 2006; OJ 287 – Agudo et al. 2012; Hodgson et al. 2017; 3C 345 – Lobanov & Roland 2005; CTA 102 – Fromm et al. 2013; Casadio et al. 2015; 0836+710 – Perucho et al. 2012). The flare is often interpreted as the result of an increase in Doppler beaming of the emission due to the jet bending closer to the line of sight.
There are several possible explanations for the physical origin of the jet bending. First, precession of a jet nozzle, which is induced by propagation of perturbations originating from the accretion disk and BH due to the Lense-Thirring effect (Bardeen & Petterson 1975) or even binary black holes, may display somewhat periodic jet wobbling over time. Abraham & Carrara (1998) and more recently Qian et al. (2019) suggest such a physical model for 3C 279 with a precession period of ∼22 yr. However, we note that the similar erratic inner jet position angle in 2011 and 2017 seen by the EHT implies a precession period of ≲6 yr if the jet wobbling is periodic. The mismatching periods would exclude this possibility. Second, it should be noted that the C0-1 component is moving toward C1 and the jet downstream (Fig. 3), and thus the component is being aligned to the larger scale jet during the observing period. The above-mentioned time evolution of the 3C 279 jet structure during 2011 also suggests that the initially bent jet component in the source later aligned with the downstream emission. The jet alignment in a single preferred direction could indicate that the outflow is being actively collimated to a pre-established channel on these small spatial scales, as similarly observed in other sources as well (see discussions in Homan et al. 2015). Third, an internally rotating jet, in which emission regions are located along strong toroidal magnetic field lines, can also reproduce gradual jet bending features in the images (e.g., Molina et al. 2014). Such a scenario is supported by theoretical studies of jet launching and propagation (see, e.g., Tchekhovskoy 2015 and references therein), and also observations of inner jet dynamics in nearby radio galaxies (e.g., Mertens et al. 2016) and smooth variation of linear polarization of many AGN jets in time and space (e.g., Asada et al. 2002; Marscher et al. 2008; Hovatta et al. 2012; Kiehlmann et al. 2016). Whether one of these scenarios is more favored than others is difficult to determine, however. Joint constraints on the model parameters with additional data, for instance with linear polarization time variability information (Nalewajko 2010), should prove fruitful.
We also note that the apparent jet speed and Lorentz factor of C1 are comparable to those in the outer jet (Sect. 4.2.2). This suggests that intrinsic acceleration of the jet (i.e., increasing Γ) would occur upstream of C1. This puts upper limits on the spatial extension of the intrinsic jet acceleration zone of 3C 279 to be within ≲100 μas from the core, C0-0, which is 0.65 pc ∼8500 Rs projected distances (∼19 pc ∼2.4 × 106Rs deprojected with θ = 2°). If the observed motions of C0-1 and C0-2 can be described by similar bulk Lorentz factors as C1, the intrinsic acceleration zone should be located at much more upstream of the jet, that is within ≲30 − 40 μas core separation ∼0.20 − 0.26 pc ∼2600 − 3400 Rs projected distances (∼6 − 7 pc ∼(7.3 − 9.7)×104 Rs deprojected).
4.4. Low brightness temperature at 230 GHz
The innermost jet brightness temperature provides us with insight about the jet plasma acceleration and radiative evolution further downstream (e.g., Readhead 1994; Marscher 1995; Schinzel et al. 2012; Fromm et al. 2013). The observed brightness temperatures of the subnuclear components within C0 are in the range of TB ∼ 1010 − 1011 K (Fig. 8). We note that these measurements are made in the observer’s frame, while the intrinsic brightness temperature of the plasma in the fluid frame, 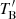 , is lowered by the Doppler factor δ, that is
, is lowered by the Doppler factor δ, that is 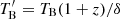 . Considering Doppler factors of δ ∼ 20 or even larger values due to possibly curved jet geometry (Sect. 4.2), an order of magnitude lower intrinsic brightness temperature of
. Considering Doppler factors of δ ∼ 20 or even larger values due to possibly curved jet geometry (Sect. 4.2), an order of magnitude lower intrinsic brightness temperature of 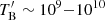 K is possible. This is a significantly lower value compared to the long millimeter or centermeter wavelength VLBI core
K is possible. This is a significantly lower value compared to the long millimeter or centermeter wavelength VLBI core  (e.g., TB > 1012 K and
(e.g., TB > 1012 K and 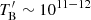 K; Kovalev et al. 2005; Jorstad et al. 2017) and also the inverse Compton limit,
K; Kovalev et al. 2005; Jorstad et al. 2017) and also the inverse Compton limit,  K (Kellermann & Pauliny-Toth 1969).
K (Kellermann & Pauliny-Toth 1969).
It is challenging to make a straightforward interpretation of the low brightness temperature without knowing the level of synchrotron opacity at 230 GHz on 20 μas scales. Nevertheless, we provide two possible implications below.
First, it is worth noting that a trend of decreasing brightness temperature with increasing observing frequencies was previously seen in a number of AGN jet cores in the frequency range of 2 − 86 GHz (e.g., Lee et al. 2016; Nair et al. 2019). This trend is often interpreted as an indication of acceleration of underlying jet outflow, based on the following considerations. In the standard model of relativistic jet (Blandford & Königl 1979), the stationary radio VLBI core structure corresponds to a region with high synchrotron opacity (τ ∼ 1) at the corresponding observing frequency. In multiwavelength VLBI observations, the opacity effect appears as a shift in the apparent core position at different frequencies (i.e., the core located more upstream of the outflow at higher frequencies), which is commonly referred to as a “coreshift” (e.g., Lobanov 1998). In this picture, higher frequency TB measurements reveal physical conditions of the jet closer to its origin, if the core TB represents surface brightness of underlying plasma outflow. In addition, we could further assume that the intrinsic brightness temperature of the plasma underlying the compact core is not frequency-dependent and remains the same over short distances (i.e., the coreshift distances). It then follows that higher TB at lower frequencies could only be explained by higher outflow speed further downstream, and consequent Doppler boosting of the emission to increase the observed TB.
It is tempting to apply this framework to the EHT 230 GHz brightness temperature measurement of 3C 279. The consistent apparent jet speeds of ∼10 − 20 c seen near the EHT core and further downstream in the jet at centimeter wavelengths, however, does not strongly support the jet acceleration scenario. Instead, the brightness temperature can simply decrease with increasing frequency if the observing frequency is higher than the synchrotron self-absorption turn-over frequency (Rybicki & Lightman 1979). The low brightness temperature at 230 GHz can therefore be alternatively understood as a signature of low opacity in the core region at 1.3 mm. The ALMA phased-array data of 3C 279 from our observations show a steep spectral index of α = −(0.6 ± 0.06) at 230 GHz (see Goddi et al. 2019), which supports this conclusion, although the ALMA measurements do not spatially resolve the microarcsecond-scale jet.
If, however, the compact VLBI core region still remains optically thick up to 230 GHz, the observed low TB values could be compared to the energy equipartition brightness temperatures (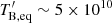 K; Readhead 1994), which is significantly higher than
K; Readhead 1994), which is significantly higher than 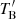 derived from the EHT measurements. The lower
derived from the EHT measurements. The lower 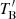 than the particle-to-magnetic field energy density equipartition
than the particle-to-magnetic field energy density equipartition  would then suggest that the innermost jet of 3C 279 may be magnetically dominated, contrary to previous conclusions that the jet plasma has low magnetization in 3C 279 (see, e.g., discussions in Hayashida et al. 2015; Ackermann et al. 2016). While high particle-to-magnetic energy density ratios are seen in other AGN especially during flaring activities (e.g., Jorstad et al. 2017; Algaba et al. 2018), low brightness temperature associated with potentially magnetically dominated jet is also seen in the nuclear region of other nearby AGN jets, such as M 87 (e.g., see discussions in Kim et al. 2018). According to the standard model of jet launching and propagation, magnetic energy density is expected to be dominant in a jet up to central engine distances of ∼105 Rs (see Boccardi et al. 2017 and references therein). Considering the spatial scales of the EHT observations of 3C 279 (20 μas∼1700 Rs), it is not impossible that the observed innermost 3C 279 jet is indeed magnetic energy dominated. Nevertheless, future spectral decomposition and polarimetric analysis on the 20 μas scale with multifrequency EHT observations should determine the jet core opacity at 230 GHz, in order to provide an unambiguous interpretation of the remarkably low
would then suggest that the innermost jet of 3C 279 may be magnetically dominated, contrary to previous conclusions that the jet plasma has low magnetization in 3C 279 (see, e.g., discussions in Hayashida et al. 2015; Ackermann et al. 2016). While high particle-to-magnetic energy density ratios are seen in other AGN especially during flaring activities (e.g., Jorstad et al. 2017; Algaba et al. 2018), low brightness temperature associated with potentially magnetically dominated jet is also seen in the nuclear region of other nearby AGN jets, such as M 87 (e.g., see discussions in Kim et al. 2018). According to the standard model of jet launching and propagation, magnetic energy density is expected to be dominant in a jet up to central engine distances of ∼105 Rs (see Boccardi et al. 2017 and references therein). Considering the spatial scales of the EHT observations of 3C 279 (20 μas∼1700 Rs), it is not impossible that the observed innermost 3C 279 jet is indeed magnetic energy dominated. Nevertheless, future spectral decomposition and polarimetric analysis on the 20 μas scale with multifrequency EHT observations should determine the jet core opacity at 230 GHz, in order to provide an unambiguous interpretation of the remarkably low  values.
values.
4.5. Connection to γ-ray emission in 3C 279
During the EHT observations in April 2017, 3C 279 was in a highly active and variable state at γ-ray energies (see, e.g., Larionov et al. 2020). Here we briefly discuss possible implications of the innermost 3C 279 jet kinematics revealed by the EHT observations on the γ-ray emission of the source. Generally, the jet speeds measured closest to the jet origin are important in order to understand the origin of γ-ray emission in blazars. One of most plausible scenarios explaining γ-ray emission in blazars is inverse Compton (IC) scattering of seed photons from within or around the relativistic jet, while details of the IC models vary depending on the assumptions of the background photon fields (see, e.g., Madejski & Sikora 2016). Observationally, bright γ-ray flares from blazars are often associated with emergence from the VLBI core of new, compact jet features, which travel toward the jet downstream (e.g., Jorstad & Marscher 2016). This association implies that the IC process may occur near (or even upstream of) the VLBI core. Therefore, observational constraints on the innermost jet speed is crucial for an accurate modeling of the IC process.
The EHT measurements of the proper motion suggest a minimum Lorentz factor of Γ ≳ 20 at core separations ≤100 μas. On the other hand, much higher Lorentz factors of Γ ≳ 100 are derived from the observations of rapid γ-ray flares (Ackermann et al. 2016). To accommodate the lower limit of Γ from the EHT observations with the larger Lorentz factors from the jet kinematics and γ-ray variability, viewing angles smaller than θ < 1° in the region C0-1 and C0-2 may be considered. For such small angles, Doppler factors of ∼100 could be reached, which are sufficient to explain the observed γ-ray variability. On the other hand, we note that the continued VLBA 43 GHz monitoring of the source during 2015−2018 now suggests faster motion and higher Lorentz-factors of Γ ≳ 37 than in the past (Larionov et al. 2020). As the authors note, the local values of Γ can be even larger (e.g., ∼70) if fast “mini-jets” are embedded within the main flow (e.g., Giannios et al. 2009) or if multiple, turbulent emitting zones are present (e.g., Narayan & Piran 2012; Marscher 2014). The latter could increase the local Γ values by factors of a few. Future detailed modeling of the broadband spectral energy distribution during the EHT 2017 campaign will provide more detailed tests of the relation between the jet dynamics and the γ-ray emission in 3C 279.
5. Summary
In this paper, we presented the first 1.3 mm VLBI images of the archetypal blazar 3C 279 at the extreme angular resolution of 20 μas. The sharpest-ever images of 3C 279 obtained at four different epochs within a week reveal (i) peculiar substructures in the millimeter VLBI core, which can be interpreted as a bent jet, or perhaps a linear, knotty structure that could result from large-scale magnetic reconnection or plasma instabilities; (ii) rapid day-to-day closure phase variations pronounced in the longest baselines, which are associated with proper motions of ∼1.1 − 1.7 μas day−1 and rapid flux variability; and (iii) low apparent (TB ≲ 1011 K) and intrinsic brightness temperatures ( K) after correcting for Doppler boosting of at least δ ∼ 10 − 20. This suggests that either the jet core is optically thin at 230 GHz, or that the innermost jet of 3C 279 is dominated by magnetic energy if the synchrotron turn-over frequency were close to 230 GHz.
K) after correcting for Doppler boosting of at least δ ∼ 10 − 20. This suggests that either the jet core is optically thin at 230 GHz, or that the innermost jet of 3C 279 is dominated by magnetic energy if the synchrotron turn-over frequency were close to 230 GHz.
More details of the source properties, such as the magnetic field configuration and detailed jet energy balance, will be subject to follow-up studies, for example by EHT full-Stokes imaging of the 3C 279 jet (EHT Collaboration et al., in prep.). As mentioned in Sect. 4.5, 3C 279 was also in a highly active and variable state at γ-ray energies during the EHT observations in April 2017. Follow-up work (EHT Collaboration et al., in prep.), combining the results from this paper with other multiwavelength data obtained close in time, will provide a more detailed understanding of the physical processes in the jet, allowing detailed tests of the potential curvature in the innermost jet, and possible jet acceleration and alternative physical scenarios, as discussed in Sects. 4.3 and 4.5.
At the redshift of 3C 279 (z = 0.536, Marziani et al. 1996), 1 mas corresponds to a linear scale of 6.5 pc. An angular separation rate of 1 mas yr−1 therefore corresponds to an apparent speed of βapp ∼ 33 c.
This holds true, unless the plasma in the jet base moves at highly relativistic speeds. In this case we could effectively observe the jet system in an edge-on view because most of observed radiation would have been emitted perpendicular to the jet in the jet co-moving frame, due to strong relativistic aberration.
Acknowledgments
The authors of the present paper thank the following organizations and programs: the Academy of Finland (projects 274477, 284495, 312496); the Advanced European Network of E-infrastructures for Astronomy with the SKA (AENEAS) project, supported by the European Commission Framework Programme Horizon 2020 Research and Innovation action under grant agreement 731016; the Alexander von Humboldt Stiftung; the Black Hole Initiative at Harvard University, through a grant (60477) from the John Templeton Foundation; the China Scholarship Council; Comisión Nacional de Investigación Científica y Tecnológica (CONICYT, Chile, via PIA ACT172033, Fondecyt projects 1171506 and 3190878, BASAL AFB-170002, ALMA-conicyt 31140007); Consejo Nacional de Ciencia y Tecnología (CONACYT, Mexico, projects 104497, 275201, 279006, 281692); the Delaney Family via the Delaney Family John A. Wheeler Chair at Perimeter Institute; Dirección General de Asuntos del Personal Académico – Universidad Nacional Autónoma de México (DGAPA – UNAM, project IN112417); the European Research Council Synergy Grant “BlackHoleCam: Imaging the Event Horizon of Black Holes” (grant 610058); the Generalitat Valenciana postdoctoral grant APOSTD/2018/177 and GenT Program (project CIDEGENT/2018/021); the Gordon and Betty Moore Foundation (grants GBMF-3561, GBMF-5278); the Istituto Nazionale di Fisica Nucleare (INFN) sezione di Napoli, iniziative specifiche TEONGRAV; the International Max Planck Research School for Astronomy and Astrophysics at the Universities of Bonn and Cologne; the Jansky Fellowship program of the National Radio Astronomy Observatory (NRAO); the Japanese Government (Monbukagakusho: MEXT) Scholarship; the Japan Society for the Promotion of Science (JSPS) Grant-in-Aid for JSPS Research Fellowship (JP17J08829); the Key Research Program of Frontier Sciences, Chinese Academy of Sciences (CAS, grants QYZDJ-SSW-SLH057, QYZDJ-SSW-SYS008, ZDBS-LY-SLH011); the Leverhulme Trust Early Career Research Fellowship; the Malaysian Fundamental Research Grant Scheme (FRGS, grant FRGS/1/2019/STG02/UM/02/6); the Max-Planck-Gesellschaft (MPG); the Max Planck Partner Group of the MPG and the CAS; the MEXT/JSPS KAKENHI (grants 18KK0090, JP18K13594, JP18K03656, JP18H03721, 18K03709, 18H01245, 25120007); the MIT International Science and Technology Initiatives (MISTI) Funds; the Ministry of Science and Technology (MOST) of Taiwan (105-2112-M-001-025-MY3, 106-2112-M-001-011, 106-2119-M-001-027, 107-2119-M-001-017, 107-2119-M-001-020, and 107-2119-M-110-005); the National Aeronautics and Space Administration (NASA, Fermi Guest Investigator grant 80NSSC17K0649 and Hubble Fellowship grant HST-HF2-51431.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555); the National Institute of Natural Sciences (NINS) of Japan; the National Key Research and Development Program of China (grant 2016YFA0400704, 2016YFA0400702); the National Science Foundation (NSF, grants AST-0096454, AST-0352953, AST-0521233, AST-0705062, AST-0905844, AST-0922984, AST-1126433, AST-1140030, DGE-1144085, AST-1207704, AST-1207730, AST-1207752, MRI-1228509, OPP-1248097, AST-1310896, AST-1312651, AST-1337663, AST-1440254, AST-1555365, AST-1715061, AST-1615796, AST-1716327, OISE-1743747, AST-1816420); the Natural Science Foundation of China (grants 11573051, 11633006, 11650110427, 10625314, 11721303, 11725312, 11933007); the Natural Sciences and Engineering Research Council of Canada (NSERC, including a Discovery Grant and the NSERC Alexander Graham Bell Canada Graduate Scholarships-Doctoral Program); the National Youth Thousand Talents Program of China; the National Research Foundation of Korea (the Global PhD Fellowship Grant: grants NRF-2015H1A2A1033752, 2015-R1D1A1A01056807, the Korea Research Fellowship Program: NRF-2015H1D3A1066561); the Netherlands Organization for Scientific Research (NWO) VICI award (grant 639.043.513) and Spinoza Prize SPI 78-409; the New Scientific Frontiers with Precision Radio Interferometry Fellowship awarded by the South African Radio Astronomy Observatory (SARAO), which is a facility of the National Research Foundation (NRF), an agency of the Department of Science and Technology (DST) of South Africa; the Onsala Space Observatory (OSO) national infrastructure, for the provisioning of its facilities/observational support (OSO receives funding through the Swedish Research Council under grant 2017-00648) the Perimeter Institute for Theoretical Physics (research at Perimeter Institute is supported by the Government of Canada through the Department of Innovation, Science and Economic Development and by the Province of Ontario through the Ministry of Research, Innovation and Science); the Russian Science Foundation (grant 17-12-01029); the Spanish Ministerio de Economía y Competitividad (grants PGC2018-098915-B-C21, AYA2016-80889-P); the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709); the Toray Science Foundation; the US Department of Energy (USDOE) through the Los Alamos National Laboratory (operated by Triad National Security, LLC, for the National Nuclear Security Administration of the USDOE (Contract 89233218CNA000001)); the Italian Ministero dell’Istruzione Università e Ricerca through the grant Progetti Premiali 2012-iALMA (CUP C52I13000140001); the European Union’s Horizon 2020 research and innovation programme under grant agreement No 730562 RadioNet; ALMA North America Development Fund; the Academia Sinica; Chandra TM6-17006X; the GenT Program (Generalitat Valenciana) Project CIDEGENT/2018/021. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), supported by NSF grant ACI-1548562, and CyVerse, supported by NSF grants DBI-0735191, DBI-1265383, and DBI-1743442. XSEDE Stampede2 resource at TACC was allocated through TG-AST170024 and TG-AST080026N. XSEDE JetStream resource at PTI and TACC was allocated through AST170028. The simulations were performed in part on the SuperMUC cluster at the LRZ in Garching, on the LOEWE cluster in CSC in Frankfurt, and on the HazelHen cluster at the HLRS in Stuttgart. This research was enabled in part by support provided by Compute Ontario (http://computeontario.ca), Calcul Quebec (http://www.calculquebec.ca) and Compute Canada (http://www.computecanada.ca). We thank the staff at the participating observatories, correlation centers, and institutions for their enthusiastic support. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2016.1.01154.V, ADS/JAO.ALMA#2016.1.01176.V. ALMA is a partnership of the European Southern Observatory (ESO; Europe, representing its member states), NSF, and National Institutes of Natural Sciences of Japan, together with National Research Council (Canada), Ministry of Science and Technology (MOST; Taiwan), Academia Sinica Institute of Astronomy and Astrophysics (ASIAA; Taiwan), and Korea Astronomy and Space Science Institute (KASI; Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, Associated Universities, Inc. (AUI)/NRAO, and the National Astronomical Observatory of Japan (NAOJ). The NRAO is a facility of the NSF operated under cooperative agreement by AUI. APEX is a collaboration between the Max-Planck-Institut für Radioastronomie (Germany), ESO, and the Onsala Space Observatory (Sweden). The SMA is a joint project between the SAO and ASIAA and is funded by the Smithsonian Institution and the Academia Sinica. The JCMT is operated by the East Asian Observatory on behalf of the NAOJ, ASIAA, and KASI, as well as the Ministry of Finance of China, Chinese Academy of Sciences, and the National Key R&D Program (No. 2017YFA0402700) of China. Additional funding support for the JCMT is provided by the Science and Technologies Facility Council (UK) and participating universities in the UK and Canada. The LMT is a project operated by the Instituto Nacional de Astrófisica, Óptica, y Electrónica (Mexico) and the University of Massachusetts at Amherst (USA). The IRAM 30-m telescope on Pico Veleta, Spain is operated by IRAM and supported by CNRS (Centre National de la Recherche Scientifique, France), MPG (Max-Planck-Gesellschaft, Germany) and IGN (Instituto Geográfico Nacional, Spain). The SMT is operated by the Arizona Radio Observatory, a part of the Steward Observatory of the University of Arizona, with financial support of operations from the State of Arizona and financial support for instrumentation development from the NSF. The SPT is supported by the National Science Foundation through grant PLR- 1248097. Partial support is also provided by the NSF Physics Frontier Center grant PHY-1125897 to the Kavli Institute of Cosmological Physics at the University of Chicago, the Kavli Foundation and the Gordon and Betty Moore Foundation grant GBMF 947. The SPT hydrogen maser was provided on loan from the GLT, courtesy of ASIAA. The EHTC has received generous donations of FPGA chips from Xilinx Inc., under the Xilinx University Program. The EHTC has benefited from technology shared under open-source license by the Collaboration for Astronomy Signal Processing and Electronics Research (CASPER). The EHT project is grateful to T4Science and Microsemi for their assistance with Hydrogen Masers. This research has made use of NASA’s Astrophysics Data System. We gratefully acknowledge the support provided by the extended staff of the ALMA, both from the inception of the ALMA Phasing Project through the observational campaigns of 2017 and 2018. We would like to thank A. Deller and W. Brisken for EHT-specific support with the use of DiFX. We acknowledge the significance that Maunakea, where the SMA and JCMT EHT stations are located, has for the indigenous Hawaiian people. This research has made use of data obtained with the Global Millimeter VLBI Array (GMVA), which consists of telescopes operated by the MPIfR, IRAM, Onsala, Metsahovi, Yebes, the Korean VLBI Network, the Green Bank Observatory and the Very Long Baseline Array (VLBA). The VLBA is an instrument of the National Radio Astronomy Observatory. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated by Associated Universities, Inc. The data were correlated at the correlator of the MPIfR in Bonn, Germany. This study makes use of 43 GHz VLBA data from the VLBA-BU Blazar Monitoring Program (VLBA-BU-BLAZAR; http://www.bu.edu/blazars/VLBAproject.html), funded by NASA through the Fermi Guest Investigator Program.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, Nature, 463, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abraham, Z., & Carrara, E. A. 1998, ApJ, 496, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Anantua, R., Asano, K., et al. 2016, ApJ, 824, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Marscher, A. P., Jorstad, S. G., et al. 2012, ApJ, 747, 63 [CrossRef] [Google Scholar]
- Akiyama, K., Ikeda, S., Pleau, M., et al. 2017a, AJ, 153, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Akiyama, K., Kuramochi, K., Ikeda, S., et al. 2017b, ApJ, 838, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2014, A&A, 567, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Algaba, J.-C., Lee, S.-S., Rani, B., et al. 2018, ApJ, 859, 128 [Google Scholar]
- Asada, K., & Nakamura, M. 2012, ApJ, 745, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Asada, K., Inoue, M., Uchida, Y., et al. 2002, PASJ, 54, L39 [NASA ADS] [Google Scholar]
- Bardeen, J. M., & Petterson, J. A. 1975, ApJ, 195, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Blackburn, L., Chan, C.-K., Crew, G. B., et al. 2019, ApJ, 882, 23 [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., Yuan, Y., Hoshino, M., & Sironi, L. 2017, Space Sci. Rev., 207, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, S. D., Fromm, C. M., & Ros, E. 2013, AJ, 145, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Boccardi, B., Krichbaum, T. P., Bach, U., Bremer, M., & Zensus, J. A. 2016, A&A, 588, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccardi, B., Krichbaum, T. P., Ros, E., & Zensus, J. A. 2017, A&ARv, 25, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bruni, G., Gómez, J. L., Casadio, C., et al. 2017, A&A, 604, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casadio, C., Gómez, J. L., Jorstad, S. G., et al. 2015, ApJ, 813, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Chael, A. A., Johnson, M. D., Narayan, R., et al. 2016, ApJ, 829, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Chael, A. A., Johnson, M. D., Bouman, K. L., et al. 2018, ApJ, 857, 23 [Google Scholar]
- Chatterjee, R., Jorstad, S. G., Marscher, A. P., et al. 2008, ApJ, 689, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M. H., Cannon, W., Purcell, G. H., et al. 1971, ApJ, 170, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019a, ApJ, 875, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019b, ApJ, 875, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019c, ApJ, 875, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019d, ApJ, 875, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019e, ApJ, 875, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019f, ApJ, 875, L6 [Google Scholar]
- Fromm, C. M., Ros, E., Perucho, M., et al. 2013, A&A, 551, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannios, D., Uzdensky, D. A., & Begelman, M. C. 2009, MNRAS, 395, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Savolainen, T., Orienti, M., et al. 2018, Nat. Astron., 2, 472 [Google Scholar]
- Goddi, C., Martí-Vidal, I., Messias, H., et al. 2019, PASP, 131, 075003 [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2013, ApJ, 775, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hardee, P. E. 2000, ApJ, 533, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashida, M., Nalewajko, K., Madejski, G. M., et al. 2015, ApJ, 807, 79 [Google Scholar]
- Hodgson, J. A., Krichbaum, T. P., Marscher, A. P., et al. 2017, A&A, 597, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Homan, D. C., & Lister, M. L. 2006, AJ, 131, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., & Wardle, J. F. C. 1999, AJ, 118, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Lister, M. L., Kellermann, K. I., et al. 2003, ApJ, 589, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Lister, M. L., Aller, H. D., Aller, M. F., & Wardle, J. F. C. 2009a, ApJ, 696, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Kadler, M., Kellermann, K. I., et al. 2009b, ApJ, 706, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Lister, M. L., Kovalev, Y. Y., et al. 2015, ApJ, 798, 134 [Google Scholar]
- Hong, X. Y., Jiang, D. R., Gurvits, L. I., et al. 2004, A&A, 417, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., Lister, M. L., Aller, M. F., et al. 2012, AJ, 144, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S., & Marscher, A. 2016, Galaxies, 4, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2004, AJ, 127, 3115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Morozova, D. A., et al. 2017, ApJ, 846, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1969, ApJ, 155, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Kiehlmann, S., Savolainen, T., Jorstad, S. G., et al. 2016, A&A, 590, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, J. Y., Krichbaum, T. P., Lu, R. S., et al. 2018, A&A, 616, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knight, C. A., Robertson, D. S., Rogers, A. E. E., et al. 1971, Science, 172, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Kovalev, Y. Y., Kellermann, K. I., Lister, M. L., et al. 2005, AJ, 130, 2473 [NASA ADS] [CrossRef] [Google Scholar]
- Larionov, V. M., Jorstad, S. G., Marscher, A. P., et al. 2020, MNRAS, 492, 3829 [CrossRef] [Google Scholar]
- Lee, S.-S., Lobanov, A. P., Krichbaum, T. P., & Zensus, J. A. 2016, ApJ, 826, 135 [Google Scholar]
- Lisakov, M. M., Kovalev, Y. Y., Savolainen, T., Hovatta, T., & Kutkin, A. M. 2017, MNRAS, 468, 4478 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2016, AJ, 152, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2018, ApJS, 234, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Lobanov, A. P., & Roland, J. 2005, A&A, 431, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobanov, A. P., & Zensus, J. A. 2001, Science, 294, 128 [Google Scholar]
- Lu, R.-S., Fish, V. L., Akiyama, K., et al. 2013, ApJ, 772, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Lucchini, M., Krauß, F., & Markoff, S. 2019, MNRAS, 489, 1633 [NASA ADS] [Google Scholar]
- Madejski, G. G., & Sikora, M. 2016, ARA&A, 54, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 1995, Proc. Nat. Acad. Sci., 92, 11439 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Martí-Vidal, I., Roy, A., Conway, J., & Zensus, A. J. 2016, A&A, 587, A143 [CrossRef] [EDP Sciences] [Google Scholar]
- Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1996, ApJS, 104, 37 [Google Scholar]
- Mertens, F., Lobanov, A. P., Walker, R. C., & Hardee, P. E. 2016, A&A, 595, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molina, S. N., Agudo, I., Gómez, J. L., et al. 2014, A&A, 566, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nair, D. G., Lobanov, A. P., Krichbaum, T. P., et al. 2019, A&A, 622, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nalewajko, K. 2010, Int. J. Mod. Phys. D, 19, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., & Piran, T. 2012, MNRAS, 420, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, K., Pursimo, T., Villforth, C., Lindfors, E., & Takalo, L. O. 2009, A&A, 505, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patiño-Álvarez, V. M., Fernandes, S., Chavushyan, V., et al. 2018, MNRAS, 479, 2037 [NASA ADS] [CrossRef] [Google Scholar]
- Patiño-Álvarez, V. M., Dzib, S. A., Lobanov, A., & Chavushyan, V. 2019, A&A, 630, A56 [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., Kovalev, Y. Y., Lobanov, A. P., Hardee, P. E., & Agudo, I. 2012, ApJ, 749, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qian, S. J., Britzen, S., Krichbaum, T. P., & Witzel, A. 2019, A&A, 621, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Jorstad, S. G., Marscher, A. P., et al. 2018, ApJ, 858, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Readhead, A. C. S. 1994, ApJ, 426, 51 [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., et al. 2006, ApJ, 647, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Schinzel, F. K., Lobanov, A. P., Taylor, G. B., et al. 2012, A&A, 537, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, Bull. Am. Astron. Soc., 26, 987 [Google Scholar]
- Tchekhovskoy, A. 2015, in The Formation and Disruption of Black Hole Jets, eds. I. Contopoulos, D. Gabuzda, & N. Kylafis, Astrophys. Space Sci. Lib., 414, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vitrishchak, V. M., Gabuzda, D. C., Algaba, J. C., et al. 2008, MNRAS, 391, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, J., Roy, A. L., Krichbaum, T. P., et al. 2015, A&A, 581, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitney, A. R., Shapiro, I. I., Rogers, A. E. E., et al. 1971, Science, 173, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, W., Hong, X. Y., An, T., et al. 2011, A&A, 529, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: THEMIS model-fitting analysis
Using THEMIS, we fit a time variable, ten-component elliptical Gaussian model to the scan-averaged visibility amplitude and closure phase EHT data in both observing bands and across the four observation nights simultaneously using a parallel-tempered, ensemble Markov chain Monte Carlo method. Nine of the components are compact, modeling the structures apparent in the images, and one is large (milliarcsecond scale), representing the extended flux associated with large-scale structures that are detected only by intra-site baselines (ALMA-APEX, JCMT-SMA; see Papers IV and VI).
For THEMIS, all components are characterized by a total flux, size, asymmetry, orientation, position, and their time derivatives (except for orientation). Priors were imposed on the time variability to prevent large changes (e.g., factors of two). A minimum component FWHM of 10 μas was required; the fit quality and parameter estimates are insensitive to decreases in this value. The result of this process is the joint posterior distributions of all of the individual component parameters. The simultaneous fit of the time-variable model produced results consistent with fits on individual days and frequency bands. Of the compact components, only six were robustly recovered on each day individually and simultaneously; we focus on these in Sect. 3.3.
Appendix B: Reconstructed antenna gains from imaging and model-fitting methods
In Fig. B.1 we show the reconstructed antenna gains obtained by using independent images or models from three imaging pipelines and model-fitting analysis. The consistent antenna gains across different methods suggest that the results are robust against possible biases in each analysis.
 |
Fig. B.1. Inverse of the reconstructed multiplicative LMT antenna gain amplitude from imaging and model-fitting analysis. We note larger dispersion of gain amplitudes on April 6, which reflects greater difficulty in the imaging and model-fitting due to limited number of scans and (u, v) coverage. |
Appendix C: Images per day per method
Here we show the 3C 279 images from all days and all the individual methods before averaging.
 |
Fig. C.1. Same as Fig. 4, but for all imaging methods before the averaging. Each row and column corresponds to different imaging pipelines (eht-imaging, SMILI, and Difmap) and observing epochs (April 05, 06, 10, and 11), respectively. We note that these images are not yet aligned with each other. |
Appendix D: Model-fit parameters
In Table D.1 we show the parameters of the Gaussian model-fit components for all epochs. We also show in Fig. D.1 sample
 |
Fig. D.1. Visibility amplitudes (top) and closure phases (bottom) of the data (gray error bars) and Gaussian models (colored diamonds) for all epochs, for both observing frequency bands (HI and LO), and plotted against the baseline length and quadratic sum of the three baseline lengths in triangles (u1, u2, and u3), respectively. In both panels the bottom subpanels show residuals (i.e., differences between data and model) normalized by the uncertainties of each data point. |
Component parameters from dynamical Gaussian model-fitting of 3C 279 evaluated at 6 UTC on each observation day.
plots of visibility amplitudes and closure phases of the data versus the models for April 11.
Appendix E: Long-term 3C 279 jet component positions from VLBA 43 GHz monitoring
 |
Fig. E.1. Positions of jet components in 3C 279 between 2007 and 2013 from VLBA 43 GHz monitoring of the source and reported by Jorstad et al. (2017). Upper and lower panels: overall and inner jet component positions, respectively. The color bars denote the observing epoch in decimal year. The dark cross indicates the core component position. Symbol sizes are proportional to the component flux density. |
All Tables
Component parameters from dynamical Gaussian model-fitting of 3C 279 evaluated at 6 UTC on each observation day.
All Figures
 |
Fig. 1. Event Horizon Telescope (u, v) coverage of 3C 279 on (from left to right) 2017 April 5, 6, 10, and 11. The color-coding for the corresponding baselines is shown in the legend. The JCMT and APEX baselines are omitted because they repeat the SMA and ALMA baselines, respectively. |
| In the text | |
 |
Fig. 2. Flux-calibrated visibility amplitudes of 3C 279 in all epochs. The visibility amplitude distributions are broadly consistent over four days, while the closure phases are not (see Sect. 3). |
| In the text | |
 |
Fig. 3. Illustration of multiwavelength 3C 279 jet structure in April 2017. The observing epochs, arrays, and frequencies are noted at the top of each panel. The color bars show the pixel values in Jy beam−1. The white circles in the bottom left corners indicate the convolving beams. The white rectangles shows the field of view of the next panels at the higher 86 and 230 GHz frequencies. We note that the centers of the images (0,0) correspond to the location of the peak of total intensity. (From left to right) the beam sizes are 150 × 380, 50 × 139, and 20 × 20 μas2. For a spatially resolved emitting region, an intensity of 1 Jy beam−1 in the 43, 86, and 230 GHz images correspond to brightness temperatures of 1.16 × 1010, 2.37 × 1010, and 5.78 × 1010 K, respectively. |
| In the text | |
 |
Fig. 4. EHT images of 3C 279 on each day, generated by three different pipelines, then aligned and averaged. See Paper IV for details on the method. The circular 20 μas restoring beam is shown in the bottom right corner of each panel. The pixel values are in units of Jy beam−1. In each panel, the contour levels are 5%, 12%, 25%, 50%, and 75% of the peak value. The component identification is shown in the April 11 panel and is only for illustration (see Fig. 6). |
| In the text | |
 |
Fig. 5. Example of the closure phase variation in 3C 279 over four epochs for the large ALMA-SMT-SMA, ALMA-LMT-SMA, and ALMA-LMT-SMT triangles. The points show the data, and their error bars include 1.5% systematic visibility errors (Paper III). The solid lines show the model closure phases corresponding to the images from each pipeline and day, and the dashed lines represent the model closure phases of the average images shown in Fig. 4. Regions constrained by predictions of the three independent image models are shaded. |
| In the text | |
 |
Fig. 6. Model-fit component kinematics during April 5–11. Top panel: kinematics for all components. The center positions of different Gaussian components, and their uncertainties are color-coded (see legend). The Gaussian FWHM sizes are shown by dashed gray ellipses. The black cross at (0,0) indicates the kinematic reference (C0-0). Red arrows show the component motions; their lengths are proportional to the apparent velocities. Middle and bottom panel: same as the top panel, but zoomed in to the nuclear (C0) and extended jet regions (C1), respectively. We note that the center (0,0) in all panels is chosen as the center of C0-0, not the peak of total intensity. |
| In the text | |
 |
Fig. 7. Same as Fig. 6, but using C0-1 (top) and C0-2 (bottom) as kinematic references. We note the more complicated motions of other jet features in both panels compared to Fig. 6. |
| In the text | |
 |
Fig. 8. Model-fit parameters and their time evolution obtained by the THEMIS time-evolving model-fitting (Sect. 2.2). Each row shows a single component. Shaded regions indicate 95% confidence level at each time, the dashed line shows the median value, and the red solid lines indicate the best fit value. Observing epochs are shown by gray vertical bands. The component IDs are shown at the top left corner of the leftmost column. From left: flux density, radial distance with respect to C0-0, RA and Dec offsets with respect to C0-0, core mean FWHM sizes, and apparent brightness temperature. |
| In the text | |
 |
Fig. 9. Plane of apparent speed (βapp) and Doppler factor (δ). Solid and dashed lines correspond to constant values of bulk Lorenz factors and viewing angles, respectively. The blue and green triangles and red circle show possible values of βapp and δ assuming the same Γ = 20 for C0-1 and C0-2, respectively. The vertical black lines correspond to the βapp values of C0-1 and C0-2. The red and blue shaded areas indicate uncertainties of βapp for C0-1 and C0-2, respectively. |
| In the text | |
 |
Fig. 10. Same as Fig. 9, but for C1. The vertical solid black lines correspond to βapp values of the C1 subcomponents and the gray shaded area shows their uncertainties. For comparison, the model values for C0 components with Γ = 20 are also shown using the same symbols as in Fig. 9. The ranges of the axes are different from Fig. 9. |
| In the text | |
 |
Fig. B.1. Inverse of the reconstructed multiplicative LMT antenna gain amplitude from imaging and model-fitting analysis. We note larger dispersion of gain amplitudes on April 6, which reflects greater difficulty in the imaging and model-fitting due to limited number of scans and (u, v) coverage. |
| In the text | |
 |
Fig. C.1. Same as Fig. 4, but for all imaging methods before the averaging. Each row and column corresponds to different imaging pipelines (eht-imaging, SMILI, and Difmap) and observing epochs (April 05, 06, 10, and 11), respectively. We note that these images are not yet aligned with each other. |
| In the text | |
 |
Fig. D.1. Visibility amplitudes (top) and closure phases (bottom) of the data (gray error bars) and Gaussian models (colored diamonds) for all epochs, for both observing frequency bands (HI and LO), and plotted against the baseline length and quadratic sum of the three baseline lengths in triangles (u1, u2, and u3), respectively. In both panels the bottom subpanels show residuals (i.e., differences between data and model) normalized by the uncertainties of each data point. |
| In the text | |
 |
Fig. E.1. Positions of jet components in 3C 279 between 2007 and 2013 from VLBA 43 GHz monitoring of the source and reported by Jorstad et al. (2017). Upper and lower panels: overall and inner jet component positions, respectively. The color bars denote the observing epoch in decimal year. The dark cross indicates the core component position. Symbol sizes are proportional to the component flux density. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.