| Issue |
A&A
Volume 695, March 2025
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202450199 | |
| Published online | 14 March 2025 | |
Simulations for the evolution of the chemical clock HC3N/N2H+ in high-mass star-forming regions
1
Purple Mountain Observatory, Chinese Academy of Sciences,
10 Yuanhua Road,
210023
Nanjing, PR China
2
University of Science and Technology of China,
96 Jinzhai Road,
230026
Hefei, PR China
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn, Germany
4
Center for Astrophysics, Guangzhou University,
230 Wai Huan Xi Road,
510006
Guangzhou, PR China
★ Corresponding author; wangyao@pmo.ac.cn
Received:
1
April
2024
Accepted:
10
February
2025
Context. From observations, column density ratios or integrated intensity ratios between some species exhibit monotonic increase or decrease along with the evolution of high-mass star-forming regions (HMSFRs). Such ratios are defined as chemical clocks, which can be used to constrain the evolutionary stage.
Aims. We performed chemical simulations to reproduce the observed column density ratio of HC3N/N2H+ and the abundances of these two species across various evolutionary stages in HMSFRs. Simultaneously, we identified the chemical processes responsible for the observed time-dependent trends in these stages.
Methods. Our simulations utilized the astrochemical code Nautilus and the existing 1D models of HMSFRs that cover four evolutionary stages, accompanied by variations in density and temperature throughout the entire evolution. In addition, to maintain a steady increase in density and temperature over time as predictions of the global hierarchical collapse scenario, we adjusted parameters such as density, temperature, and time spent in each evolutionary stage.
Results. When averaging over large spatial scales, the best model produced successfully matches the observed column density ratio of HC3N/N2H+ and the abundances of the species involved at specific times for each evolutionary stage; that is, the late high-mass starless core stage, the early high-mass protostellar object stage, and the early ultracompact H II stage. HC3N is mainly affected by the warm carbon-chain chemistry (WCCC) and its own thermal desorption, while N2H+ is primarily influenced by the thermal desorption of N2, CO, CH4, NH3, and H2O followed by dissociative recombination and ion-molecule reactions.
Conclusions. The results obtained from the best-fitting model timescales broadly agree with statistical estimates. However, a continuous increasing ratio of HC3N/N2H+ throughout the entire evolution of HMSFRs is not acquired. Some observed ratios between adjacent stages overlap, which could be induced by observational uncertainties (such as those in deriving column densities and abundances, clump classification, and systematic effects), or indicate that the evolution of HC3N/N2H+ may not strictly monotonically increase throughout the entire evolution. Based on our best-fit model, we further examined other 350 ratios involving 27 species, and 178 ratios exhibit an increasing or decreasing evolutionary trend around the best-fit timescales of HC3N/N2H+. Among them, 157 ratios are observable and could be considered as candidate chemical clocks. Our results indicate that 1D models with abrupt jumps in physical parameters have reached their limits in terms of the insights they can provide, and more sophisticated models need to be adopted.
Key words: astrochemistry / stars: formation / ISM: abundances / ISM: molecules
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
High-mass stars are important for the energy generation and the life cycle of the interstellar medium (ISM) in the Universe through radiation, outflows, stellar wind, and supernova events (Motte et al. 2018). Thus, it is crucial to track the evolution of high-mass stars throughout their whole lifetime. However, currently, high-mass star formation is still unclear compared with low-mass star formation, because of the difficulties in observation induced by the small number of targets (∼3%; Kroupa 2001; Wang et al. 2023), large distances from Earth (several kiloparsecs; Urquhart et al. 2018; Gieser et al. 2021), and typically short evolutionary timescales (the order of 105 yr; Mottram et al. 2011; Kuiper & Hosokawa 2018; Motte et al. 2018; Gieser et al. 2021). Nevertheless, based on the observed properties, the evolution of high-mass star-forming regions (HMSFRs) can be roughly divided into four distinct stages, including the high- mass starless core (HMSC) stage, the high-mass protostellar object (HMPO) stage, the hot molecular core (HMC) stage, and the ultracompact HII (UCHII) stage, respectively (e.g., Beuther et al. 2007; Zinnecker & Yorke 2007; Gerner et al. 2014, 2015; Jin et al. 2015; Gieser et al. 2021). The HMSCs are molecular cores of cold dense gas and dust with temperatures of 10–20 K (Pillai et al. 2006; Zinnecker & Yorke 2007; Gieser et al. 2021), which are close to isothermal and radiate mostly at millimeter/submillimeter wavelengths; they commonly belong to infrared dark clouds (IRDCs; Sridharan et al. 2005; Rathborne et al. 2006). Subsequently, HMPOs are formed: gravitational collapse generates protostars that are still accreting mass (>8 M⊙; Beuther et al. 2007; Gerner et al. 2014, 2015), and that can radiate at mid-infrared wavelengths and heat the surrounding environment to become non-isothermal (Beuther et al. 2002; Beltrán & de Wit 2016). Next, a higher temperature (>100 K; Rathborne et al. 2006; Stéphan et al. 2018; Gieser et al. 2021) prompts the formation of HMCs, accompanied by the increased gaseous chemical complexity of various molecules but similar physical conditions compared to HMPOs (Gerner et al. 2014, 2015). Finally, UCHII regions are created by strong radiation from protostars, and are associated with ionized gas, destroyed complex molecules, and free-free emission at centimeter wavelengths (Peters et al. 2010; Sánchez-Monge et al. 2013; Urquhart et al. 2013; Stéphan et al. 2018; Gieser et al. 2021). Due to the smooth evolution, these stages cannot be clearly distinguished, particularly among HMPO, HMC, and UCHII stages (Gerner et al. 2014, 2015; Gieser et al. 2021).
Chemical evolution is a useful tool for further analyzing high-mass star formation. Diverse chemical compositions across various sources can be used to infer physical properties and subsequently constrain different evolutionary conditions (e.g., Herbst & van Dishoeck 2009; Gerner et al. 2014; Jørgensen et al. 2020; McGuire 2022). The column density ratios or integrated intensity ratios between different species are usually used to distinguish different evolutionary stages and constrain lifetimes of HMSFRs, which are defined as chemical clocks (Wakelam et al. 2004; Hoq et al. 2013; Gerner et al. 2015; Yu & Wang 2015; Urquhart et al. 2019; Wang et al. 2023). Such ratios commonly increase or decrease monotonically along with the entire evolution of HMSFRs. For instance, Hoq et al. (2013) derived that the relative abundance ratio of N2H+/HCO+ increased slightly throughout the evolution according to observed 333 sources belonging to the Millimeter Astronomy Legacy Team 90 GHz (MALT90) survey. Ohashi et al. (2014) and Tatematsu et al. (2014) proposed that the column density ratios of N(c-C3H2)/N(C2S), N(NH3 )/N(C2S), N(NH3)/N (HC3N), and N(N2H+)/N(C2S) in starless regions could be lower than those in star-forming regions based on the observations of six molecular clouds in Orion A. Jin et al. (2015) estimated that the abundance ratio of HCN/HNC increased from 0.97 in quiescent IRDC cores, then to 2.65 in active IRDC cores, next to 4.17 in HMPOs, and finally to 8.96 in UCHII regions among a total of 78 sources. Yu & Wang (2015) suggest that the abundance ratios of N2H+/H13CO+ and C2H/H13CO+ decrease from massive young stellar objects (MYSOs) to UCHII regions toward 31 clumps from the MALT90 survey. For the statistics of larger samples, based on 3246 high-mass clumps from the MALT90 survey, Rathborne et al. (2016) found that the integrated intensity ratios of HCO+/HNC, HCN/HNC, HCO+/H13CO+, HNC/HN13C, N2H+/H13CO+, and H13CO+/SiO increase along with the evolution, while the ratios of HCO+/N2H+, HNC/N2H+, and C2H/N2 H+ decrease from quiescent clumps to protostars then increase into UCHII regions. Similarly, Urquhart et al. (2019) propose 13 integrated intensity ratios as candidate chemical clocks among 570 sources from the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL), and that H13CN/N2H+, 13CS/N2H+ , HCN/HNC, HCN/N2H+, HC3N/HN13C, H13CN/HN13C, HC3N/N2H+, C2H/N2H+ , HCO+/N2H+, and C2H/c-C3H2 increase monotonically, while H13CO+/N2H+, H13CO+/HN13C, and C2H/HN13C also exhibit a tendency to increase, except in quiescent clumps. Considering the statistical significance of observed samples and the deviation degree of ratios across different stages, the most promising chemical clocks could include HCO+/HNC, HCN/HNC, 13CS/N2H+, HCN/N2H+, HC3N/HN13C, and HC3N/N2H+ . Among these chemical clocks, N2H+, HCO+, HCN, HNC, and C2H are primarily involved. The two ions are mainly affected by the intensities of ionization and radiation field (e.g., cosmic-ray ionization and dissociation, photoionization, and photodissociation), while the other three molecules are mainly influenced by the temperature and the density (e.g., neutral-neutral reaction, ion-molecule reaction, accretion, and desorption). Therefore, these species can be utilized to research the evolution of HMSFRs.
Recently, Wang et al. (2023) further proposed a candidate chemical clock, N(HC3N)/N(N2H+) (hereafter HC3N/N2H+) in HMSFRs, following the integrated intensity ratio of HC3N/N2H+ proposed by Urquhart et al. (2019). According to their observations concerning 61 UCHII regions via the Insti- tut de Radioastronomie Millimétrique (IRAM) 30 m and the Arizona Radio Observatory (ARO) 12 m telescopes, combined with previous observations toward 17 HMSCs and 28 HMPOs through the Nobeyama 45 m telescope performed by Taniguchi et al. (2019b), the column density ratio increased by a factor of five from ~0.136 at the HMSC stage to ~0.303 at the HMPO stage, and finally to ~0.777 at the UCHII stage (see Table 3). The column density ratio at the HMSC stage is comparable to the integrated intensity ratio (~0.1). However, at the HMPO and UCHII stage, the column density ratio is higher than the integrated intensity ratio by a factor of two or three (~0.13 and ~0.26, respectively; see Fig. 20 in Urquhart et al. 2019). Thus, the column density ratio demonstrates a more distinct increasing trend than the integrated intensity ratio. The properties of these observed sources, including heliocentric distances, temperatures, masses, and the column densities of HC3N and N2H+ , have been provided by Taniguchi et al. (2019b), Wang et al. (2023), and relevant references, which exclude potential biases. However, some observed ratios between HMSC and HMPO stages or between HMPO and UCHII stages can overlap (see Fig. 10 from Taniguchi et al. 2019b and Fig. 6 from Wang et al. 2023), which implies that a particular source may not exhibit a strictly increasing ratio of HC3N/N2H+ throughout the evolution. Besides, the observed HC3N/N2H+ of different sources in each evolutionary stage can fluctuate by over one order of magnitude. This suggests that observed sources in the same stage may span a considerable duration of time, and the value of HC3N/N2H+ during a certain period in the HMSC, HMPO, and UCHII stage could present an increasing trend. Thus, it is necessary to constrain the potential timescales of each stage by fitting the median value of observed HC3N/N2H+ via chemical simulations.
Gerner et al. (2014), (2015) constrained the physical conditions and timescales of each stage in a 1D approximation by fitting the abundances of 18 species (including four deuterated species) toward 59 HMSFRs (19 IRDCs, 20 HMPOs, 11 HMCs, and 9 UCHII regions) through the IRAM 30 m, which can be considered as fiducial physical models in chemical simulations for further comparing other observed ratios during each evolutionary stage. Based on such simulations and observations, 15 column density ratios between different species (excluding deuterated species) were also compared. Only CS/SO, HCN/HNCO, HCO+/N2H+, HNCO/C2H, and N2H+/C2H show monotonic evolutionary trends. However, none of these simulated ratios fit the observed ratios well; indeed, they even exhibit opposite trends, such as HCO+/N2H+ and N2H+/C2H. Additionally, such fiducial models had been further adopted for fitting observed abundances and estimating the lifetime of each HMSFR (e.g., Gieser et al. 2021; Yang et al. 2023). Taniguchi et al. (2019a, 2021, 2023) adopted homogeneous one-point physical models that include a free-fall collapse phase, a warm-up phase, and a hot phase (Garrod & Herbst 2006) to calculate the ratios between several complex organic molecules (COMs; HC5N/CH3OH, C2H/HC5N, HC5N/CH3CN, CH3OH/CH3CN, CH3OCH3/CH3CN, HNCO/CH3CN, CH2CHCN/CH3CN, and CH3CH2CN/CH3CN) toward several MYSOs. These modeled ratios can constrain a hot core stage (T > 100 K) but show no clear evolutionary trend, while the one-point physical models were not sufficient to accurately describe HMSFRs. Thus, a systematic theoretical search for chemical clocks via chemical modeling is necessary.
In this paper, we perform chemical simulations to replicate the observed column density ratio of HC3N/N2H+ and the abundance of these two species across various evolutionary stages of HMSFRs. We focus on this promising chemical clock candidate because it has not been explicitly considered as an evolutionary indicator and analyzed in previous simulations. Simultaneously, we identify the chemical processes responsible for the observed time-dependent trends in these stages. Besides, we analyze other candidate chemical clocks according to numerical simulations. In Sect. 2, we describe adopted chemical models and several physical models for simulating chemical evolution within the range of 105 AU (~0.5pc) in HMSFRs. The 1D models presented by Gerner et al. (2014), (2015) show fluctuations in density and temperature across the entire evolution. To maintain the steady increase in density and temperature over time as predictions of the global hierarchical collapse scenario, we also adjust parameters such as density, temperature, and time spent in each evolutionary stage. In Sect. 3, we compare the modeled average ratio of HC3N/N2H+ within different radii with observed ratios, and present the evolution of HC3N/N2H+ at different locations. In Sect. 4, we discuss key mechanisms affecting the evolution of HC3N/N2H+ , and propose other candidate chemical clocks in HMSFRs according to our simulations. Finally, in Sect. 5 we present our conclusions.
2 Model
2.1 Chemical model
To compare the observations with theoretical predictions in astrochemistry, the evolutions of HC3N and N2H+ were calculated via the astrochemical code Nautilus (Ruaud et al. 2016). In the simulations, both the two-phase (gas and grain surface) model (Hasegawa et al. 1992) and the three-phase (gas, grain surface, and grain mantle) model (Hasegawa & Herbst 1993) were adopted. Since the results adopting the latter one deviate from the observed HC3N/N2H+ because most species in the grain mantles are chemically inert when the temperature is low (<50 K), only the simulations using the two-phase model are discussed. The reaction network is identical to the one proposed by Wang et al. (2021) encompassing 9710 reactions and 947 species, which already includes the photodesorption mechanism (Öberg et al. 2009; Chang & Herbst 2014). To exclude potential bugs, this reaction network was benchmarked against the reaction network from Ruaud et al. (2016) in the Nautilus package (see Appendix A), which includes 717 species and over 11 000 reactions. A higher cosmic ray ionization rate of ζCR = 1.8 × 10−16 s−1 was utilized according to the survey of 20 HMSFRs in the Galactic disk performed by Indriolo et al. (2015); according to these authors, ζCR is supposed to remain constant at a Galactic radius >5 kpc. Given the distances of observed sources from Taniguchi et al. (2019b) and Wang et al. (2023), it is reasonable to adopt this value, which is one order of magnitude higher than the common standard value of 1.3 × 10−17 s−1 for the ISM. This rate is assumed to remain constant throughout the evolution, following the chemical simulations conducted by Gieser et al. (2021). It should be noted that cosmic rays are attenuated inside molecular clouds as a function of column density (Padovani et al. 2022). However, for the inner compact regions of HMSFRs with higher densities and temperatures, several chemical mechanisms become more significant compared to those in the outer diffuse areas. For example, the reaction rates of gaseous reactions and thermal desorption can be several orders of magnitude higher than those in the outer regions. This makes the cosmic ray ionization and dissociation less critical. We compared the results of HC3N and N2H+, adopting ζCR = 1.8 × 10−16s−1 and 1.3 × 10−17 s−1, respectively, using the physical model proposed by Gerner et al. (2014, see our Sect. 2.2). For the inner compact regions, the deviations between these two simulations throughout the entire evolution are fewer than several times. Therefore, for simplicity, a constant ionization rate across HMSFRs was adopted. Similarly, given the potentially stronger FUV radiation field in HMSFRs, χ was assumed to be 10 times higher than the standard value of 1, just like ζCR. Actually, considering the high value of visual extinction, AV (> 10 mag), in the majority of HMSFRs, the impact of such an enhanced radiation field on the results can be ignored. We also adopted the sticking coefficient of adsorption on the grains of Ps = 1, the reactive desorption efficiency of aRRK = 0.01 (Garrod et al. 2007; Vasyunin & Herbst 2013), the grain surface diffusion barrier of Eb1 = 0.5Ed, and the grain mantle diffusion barrier of Eb2 = 0.7Ed (Chang & Herbst 2016), where Ed is the desorption energy of each species. Other parameters can be consulted in Table 1 presented by Wang et al. (2019). In addition, the initial abundances listed in Table 1 approximate the low-metal environment at the start of the HMSC stage (Gerner et al. 2014).
Initial abundances (Gerner et al. 2014).
2.2 Physical model
We adopted the 1D physical model of HMSFRs including four evolutionary stages derived by Gerner et al. (2014), (2015), and their parameters are presented in Table 2, designated as model 1 and model 2, respectively, serving as benchmark physical models. The densities and the temperatures at different radii were calculated with modified power laws,
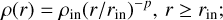 (1)
(1)
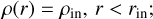 (2)
(2)
which remain constant during each stage. For simplicity, the gas temperature and the grain temperature were assumed to be the same. The UCHII lifetime in model 2 was set to be 1.65 × 104 yr instead of 3.0 × 103 yr for consistency with model 1 and an easy analysis with ttotal = 1.0 × 105 yr. However, simulations adopting these two models cannot fit the observed evolutionary trend of HC3N/N2H+. To improve the fit between simulations and observations without altering the density distribution or the temperature distribution, the timescales of each stage were adjusted considering an uncertainty of a factor of 2–3 for the best-fit ages proposed by (Gerner et al. 2014, 2015). Consequently, models 3 and 4 only modify the duration of each stage to be 3 × 104 yr compared to model 1 and 2, respectively, with prolonged timescales for the HMSC and UCHII stage, but slightly reduced timescales for the HMPO and HMC stage. Such HMSC and HMPO timescales are consistent with the statistical lifetimes for clumps with masses of ~6.3 × 103 M⊙ (see Table 6 from Urquhart et al. 2018), while HMC and UCHII timescales are shorter by a factor of 3–4. Nevertheless, according to the simulated evolutionary trend of HC3N/N2H+ in the HMC and UCHII stage, if we adopt longer HMC and UCHII timescales (e.g., 105 yr), the ratio could be much lower than observed values in UCHII regions. Therefore, the suggested durations of the HMC and UCHII stage remain reasonable nonetheless. Additionally, ρin does not consistently increase throughout the evolution accompanied by the variations in rin in both models 1 and 2. To maintain the same rin with reasonable increasing ρin and Tin throughout the entire evolution, model 5 combines the parameters from the HMSC and HMC stage of model 3 with those from the HMPO and UCHII stage of model 4. A higher Tin in the HMPO stage was adopted to achieve a better agreement with observations. Finally, to have a consistently increased density and temperature within the outer regions (r ~ rout) during the late stages, model 6 adopts reduced values of p and q in the HMC and UCHII stage compared to model 5. Similarly, other test models adopting different values of p (1.5–2.0) and q (0.3–0.4) based on model 5 were calculated but are no longer discussed in this paper, since these results cannot fit the observations well. The visual extinction was calculated by using 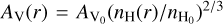 with
with 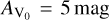 and
and 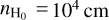 (Taniguchi et al. 2019a), while nH(r) = 2ρ(r). For simplicity, the physical parameters undergo an instantaneous variation at the transition point between two stages, as was proposed by (Gerner et al. 2014, 2015). For each physical model, we selected about 45 different locations from the center to the outmost radius of 105 AU (~0.5 pc) for chemical modeling, then the abundances at different radii and the average abundances within different ranges in an HMSFR could be computed. The average number density of each species is equal to the summed molecule number in each shell divided by the total volume of the same shell; at this point, the average abundance with respect to H2 can be calculated.
(Taniguchi et al. 2019a), while nH(r) = 2ρ(r). For simplicity, the physical parameters undergo an instantaneous variation at the transition point between two stages, as was proposed by (Gerner et al. 2014, 2015). For each physical model, we selected about 45 different locations from the center to the outmost radius of 105 AU (~0.5 pc) for chemical modeling, then the abundances at different radii and the average abundances within different ranges in an HMSFR could be computed. The average number density of each species is equal to the summed molecule number in each shell divided by the total volume of the same shell; at this point, the average abundance with respect to H2 can be calculated.
Physical models of HMSFRs.
 |
Fig. 1 Correlation between the average ratio of HC3N/N2H+ and the average abundance of HC3N with respect to H2 within four different ranges (panel A: 7 × 103 AU, panel B: 104 AU, panel C: 5 × 104 AU, and panel D: 105 AU) around the center by adopting model 4 in chemical simulations compared with observations. The results during the HMSC, HMPO, HMC, and UCHII stages are plotted as squares, circles, diamonds, and triangles, respectively. The evolution of HC3N/N2H+ and HC3N/H2 throughout ttotal during each stage consistently decrease (from right to left and from top to bottom). The observations proposed by Taniguchi et al. (2019b) and Wang et al. (2023, including derived column density of HC3N, N2H+, and H2 simultaneously) are plotted as solid squares, solid circles, and solid triangles, respectively, with error bars. |
3 Results
3.1 Comparison of chemical simulations and observations
The sources observed by Taniguchi et al. (2019b) and Wang et al. (2023) are mainly located at a distance of ~3–10 kpc. Considering the largest 29″ beam size of the IRAM 30 m, the linear resolution corresponds to ~0.4–1.4pc. Since rout = 105 AU is comparable to the linear resolution, and also approximately corresponds to the outermost radius of dense parts of HMSFRs (Gerner et al. 2014), the average abundances of HC3N and N2H+ with respect to H2 within a radius of 105 AU were calculated, and the corresponding ratio HC3N/N2H+ was compared with observed targets (Taniguchi et al. 2019b; Wang et al. 2023). To investigate the correlation between the simulated average ratio of HC3N/N2H+ and HC3N/H2 (the abundance of HC3N with respect to H2) and compare them with observations, we plot them as scatter diagrams in Figs. 1 and 2, within four different ranges (7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU) around the center using models 4 and 6, respectively. These figures show that there is only one radius per model (104 AU for model 4 and 105 AU for model 6) that can reproduce three of the four stages. The detailed comparison between models and observations is discussed below. We note already that due to a lack of observational constraints and observational ambiguities, we did not consider the HMC stage for comparison with our models. Such different ranges were chosen to verify whether the average ratios within certain ranges can fit the observations. The average ratios within 7 × 103 AU usually severely deviate from the observations. The evolution during the HMSC stage, HMPO stage, HMC stage, and UCHII stage is depicted with different symbols, indicating that the correlation consistently evolves from right to left with a decreasing HC3N/N2H+ ratio, while it moves from top to bottom with a decreasing HC3N/H2 ratio in each panel. A line depicting the evolutionary trend is omitted in each panel for concise pictures, since abrupt jumps are induced by discontinuous changes in the physical parameters between the two stages. However, such abrupt jumps do not affect the comparison between modeled and observed ratios. The average ratios within 104 AU around the center can fit the observations at the final HMSC stage (ttotal ~ 2.8–3.0 × 104 yr), the start HMPO stage (ttotal ~ 3.0–3.1 × 104 yr), and the final UCHII stage (ttotal ~ 1.03–1.2 × 105 yr), respectively (see panel B in Fig. 1). Nevertheless, on the one hand, it is noteworthy that a strictly monotonic increase in HC3N/N2H+ over the entire evolution cannot be achieved. On the other hand, such a region only accounts for 10% of the radius and 10−3 of the volume compared to the entire area of HMSFRs, which seems unlikely to reflect the actual conditions. The simulations within the other three ranges cannot fit the observations, with a lower HC3N/H2 ratio in the HMPO stage and a higher HC3N/N2H+ ratio in the UCHII stage within the range of 7 × 103 AU (panel A), a higher HC3N/N2H+ ratio in the HMSC stage and a lower HC3N/N2H+ ratio in the UCHII stage within the range of 5 × 104 AU (panel C), and a lower HC3N/N2H+ ratio in the UCHII stage within the range of 105 AU (panel D). Additionally, for the inner region within 7 × 103 AU, both simulated HC3N/N2H+ and HC3N/H2 ratios can deviate from the observations by over one order of magnitude, because of the high temperature and density. These two simulated ratios can only fit the observations at the late HMSC stage. Thus, such results are no longer plotted.
Similarly, Fig. 2 depicts the comparison between the simulations using model 6 and observations. In panel D, the average ratios within 105 AU from the center can fit observations at the late HMSC stage (ttotal ~ 2.0–3.0 × 104 yr), the early HMPO stage (ttotal ~ 3.0–3.8 × 104 yr), and the early UCHII stage (ttotal ~ 9.4–10.1 × 104 yr), respectively. Therefore, this simulation is more reasonable than the result using model 4, although the strictly monotonic increase in HC3N/N2H+ throughout the entire evolution remains unreplicated. The results within more internal regions deviate from observations more significantly, especially during the HMPO and UCHII stage (see panels A, B, and C), due to the influence of much higher temperature and density in the innermost regions. In addition, the results adopting the other four models are presented in Appendix B, which cannot fit the observations regardless of the radius of the selected regions. Consequently, we propose that the observed increased HC3N/N2H+ ratio from the HMSC stage to the HMPO stage and to the UCHII stage in HMSFRs can be fit during a certain period in each stage in chemical simulations, which may constrain the evolution at the late HMSC stage, the early HMPO stage, and the early UCHII stage.
To individually analyze the time-dependent evolution of average ratios of HC3N/N2H+ , HC3N/H2, and N2H+/H2 in models 4 and 6, we depict the average ratios within the four different aforementioned ranges (7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU) around the center across ttotal in Fig. 3. In model 4, the average ratio of HC3N/N2H+ decreases during the HMSC stage and fits the observations at the final HMSC stage, particularly the ratio within the region of 104 AU. Then an abrupt increase occurs at the start HMPO stage within the innermost 104 AU region, mainly induced by the desorption of HC3N on the grains due to high temperatures. However, the ratio rapidly decreases to be lower than the observations in this region, while within larger regions (5 × 104 AU and 105 AU) the ratio continues to decrease from the HMSC stage. During the HMC stage, the ratio similarly increases at the start because of high temperatures but subsequently decreases within all four regions. The ratio continues to decrease during the UCHII stage, but the values within the innermost 104 AU region can fit the observations, while those within larger regions (5 × 104 AU and 105 AU) can be lower than the observations. For the average abundance of HC3N, the evolutionary tendency is similar to that of HC3N/N2H+, but the results within all four regions can roughly agree with the observations. The average abundance of N2H+ increases during each stage across all four regions (also see Gerner et al. 2014, 2015) in contrast to the observed decreased abundance of N2H+, but only the result within 104 AU can fit the observations. In model 6, the average ratio of HC3N/N2H+ still exhibits a decreasing trend during each stage, with sharp increases at the start of each stage compared with the values at the end of the previous stage. The ratio within 7 × 103 AU or 104 AU is lower than the observations during the HMSC stage, but much higher than the observations during the HMPO and UCHII stage. The ratio within 5 × 104 AU is higher than the observations during the HMSC stage, but can fit the observations during the HMPO and UCHII stage. Only the ratio within 105 AU can fit the observations during all three stages. For the average ratio of HC3N/H2, the results within four regions can agree with the observations during the HMSC and UCHII stage, but only the result within 105 AU can fit the observations during the HMPO stage. For the average ratio of N2H+/H2, the tendency to increase occurs during each stage accompanied by a dramatic decrease at the start of each stage compared to the values at the end of the previous stage. Still, only the result within 105 AU can fit the observations during the UCHII stage. Obviously, a rigorously monotonically increasing ratio of HC3N/N2H+ throughout the evolution of HMSFRs cannot be accurately replicated in simulations.
Due to the current lack of observations of HC3N/N2H+ in HMCs, the evolution of HC3N/N2H+ in chemical simulations is temporarily not regarded as a primary focus in the analysis. However, there are UCHII regions that have the characteristic spectrum of a hot core, and HMPOs can appear as hot cores, depending on the resolution and sensitivity in observations. These observational uncertainties affect the calculation of column densities and abundances, as well as the clump classification. In fact, a scatter of around one dex in the observed ratios appears within any evolutionary stage, which may induce the ratios during the HMC stage to overlap with those in the HMPO and UCHII stages. Additionally, this ratio during the HMC stage indeed follows the increasing trend, considering the integrated intensity ratio of HC3N/N2H+ derived by Urquhart et al. (2019). Consequently, it should be higher than that during the HMPO stage and lower than that during the UCHII stage. In the simulations mentioned above, both HC3N/N2H+ and HC3N/H2 in the HMC stage reach higher values compared to those not only in the HMPO stage but also in the UCHII stage, which contradicts the observations. Such a discrepancy is mainly driven by increased temperatures in the larger areas among HMSFRs during the HMC stage, which induces the thermal desorption of HC3N molecules from the grains and subsequently a rapid increase in HC3N/N2H+ (see Sect. 4.1). Nevertheless, the average HC3N/N2H+ ratio within 105 AU at the late HMC stage already approaches the observed values in UCHII regions (see Fig. 3). Combined with the decreasing trend of HC3N/N2H+ in this stage, adopting a longer duration of this stage (>4 × 104 yr) potentially makes the simulated ratio fit the observed values. In addition, varying temperature distributions across the radius during this stage in physical models could significantly affect the degree of the increase in HC3N/N2H+, as the scale of the area where the thermal desorption of HC3N occurs is directly influenced. Such a comparison could be further explored in a future study, when more observations and simulations are available.
To further constrain the evolutionary timescale in each stage, we calculated the confidence level, κ, of HC3N/N2H+, HC3N/H2, and N2H+/H2 by adopting the “mean confidence level” method (e.g., Garrod et al. 2007; Hassel et al. 2008, 2011; Wang et al. 2019, 2021). For one specific ratio, i, the agreement between the calculated value, Xi, and the observed value, Xobs,i, is defined as the confidence level, κi , which is calculated by
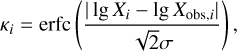 (5)
(5)
with the complementary error function, erfc = 1 − erf, and the standard deviation, σ = 1. A higher value of κi (0−1) indicates a better agreement between the calculated and observed values, while κi = 0.317 corresponds to the calculated value being one order of magnitude higher or lower than the observed value. Subsequently, the average κ across three ratios, HC3N/N2H+, HC3N/H2, and N2H+/H2, during each stage was calculated. By identifying the maximum average κ, the best-fit timescale in each stage can be obtained, which can further constrain the corresponding physical parameters.
Table 3 presents the best-fit timescales for the HMSC stage, HMPO stage, and UCHII stage within 104 AU in model 4 and within 105 AU in model 6, respectively, which can fit all three observed ratios. It is crucial to compare these timescales with previous theoretical studies such as (Gerner et al. 2014, 2015, models 1 and 2), which can evaluate the reliability of these timescales and other physical parameters adopted in our modified models. In the HMSC stage, the best fit occurs at ttotal ~ 3 × 104 yr, which may imply that a lifetime, tHMSC = 3 × 104 yr, a factor of 2–3 longer than models 1 and 2 (Gerner et al. 2014, 2015) is required to decrease the ratio of HC3N/N2H+. A quick evolution within about 103 yr in the HMPO stage (ttotal ~ 3.1 × 104 yr) can fit the observed ratios, which may signify that tHMPO = 3.0 × 104 yr is sufficient compared to the longer timescale of 6.0 × 104 yr in model 1 and the comparable timescale of 3.2 × 104 yr in model 2. Finally, in the UCHII stage, a duration of about 6.7 × 103 yr (ttotal ~ 9.67 × 104 yr) achieves the best fit, which approaches half of tUCHII = 1.2 × 104 yr in model 1 and tUCHII = 1.65 × 104 yr in model 2. Overall, both the best-fit timescale and the total duration of each stage in our models are compatible with those in models 1 and 2 with an uncertainty of a factor of 2–3. The best-fit timescales indicate the order of magnitude of the duration of the process of high-mass star formation, as the modeled chemical composition at these timescales is in broad agreement with statistical estimates. In addition, due to the relatively stable chemical evolutionary trend, certain periods can be confirmed. Different durations of the previous stage mainly influence the abundances at the start of the subsequent stage, with fluctuations by a factor of several times, but do not significantly affect the overall chemical evolutionary trend. Such differences could affect the agreement between simulations and observations at the start of subsequent stages. Overall, our modified physical models incorporating higher densities and temperatures in the outer regions still remain reasonable and provide valuable insights into the evolutionary timescales of HMSFRs, since different HMSFRs could evolve with different physical parameters.
 |
Fig. 3 Time-dependent evolution of the average ratio of HC3N/N2H+ and the average fractional abundance of HC3N and N2H+ with respect to H2 within four different ranges (7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU) around the center using model 4 (left panels) and model 6 (right panels). The four evolutionary stages are labeled in each panel, and the observations are also plotted, with the dashed lines as the median values and the dotted lines as the maximums or minimums of observations. The evolution before 104 yr is excluded to show the changes in different stages more clearly. The results within 7 × 103 AU and 104 AU during the HMSC stage in model 4 completely overlap because of the large rin > 104 AU. |
3.2 Evolution of HC3N/N2H+ at different locations
To investigate potential physical parameters that mainly dominate the evolution of HC3N/N2H+, it is necessary to analyze the agreement between observations and simulated ratios across different layers, spanning from the center to the outermost radius, 105 AU, in the best-fit models. Figure 4 presents the timedependent evolution of HC3N/N2H+, HC3N/H2, and N2H+/H2 at six different radii (102 AU, 103 AU, 7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU) from the center using model 4 and model 6. The evolutionary trends at 7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU in both models resemble those plotted in Fig. 3, but with deviations by a factor of 3–5. Nonetheless, the evolutions at 104 AU in model 4 and at 105 AU in model 6 can still roughly fit the observations at similar aforementioned timescales in each stage. In contrast, the evolutions at 102 AU and 103 AU exhibit greater fluctuations, which can deviate from the observations by several orders of magnitude and can be neglected in our discussion.
Subsequently, we mainly present the densities, the visual extinctions, and the temperatures at large radii of 104 AU and 105 AU in models 4 and 6, which are summarized in Table 4. Firstly, these parameters cannot alter the overall evolutionary trends of HC3N/N2H+, HC3N/H2, and N2H+/H2 in these two models, especially the results at the same radius (see Fig. 4). Next, according to the chemical kinetics, the density primarily influences the overall evolutionary efficiency in the gas phase, while the visual extinction mainly affects the synthesis of ions via photoionization and photodissociation, especially at low values (e.g., <5 mag). Correspondingly, for the evolution during the HMSC stage with the same temperatures in the same model, a higher density at 104 AU induces a more rapid evolution of HC3 N/N2 H+ and HC3N/H2, with larger fluctuations compared with those at 105 AU, whereas N2H+/H2 at both locations evolves steadily. In addition, a higher temperature at 104 AU or 105 AU in model 6 induces lower HC3N/N2H+ and HC3N/H2, but higher N2H+/H2 during the HMSC stage compared with model 4 (20.9 K vs 11.3 K), accompanied by compatible densities and visual extinctions. The discrepancies of these ratios at the same locations in the two models become more distinct during the HMPO stage, as the temperatures in model 6 are higher than those in model 4 by a factor of 3 (36.5 K vs 12.2 K at 104 AU and 14.5 K vs 4.8 K at 105 AU). The abrupt increase in HC3N/N2H+ and HC3N/H2 at the start of the HMPO and HMC stage corresponds to rapidly produced HC3N, which could be induced by the sublimation of CH4 from grains at T ~ 25 K followed by gaseous reactions (see Sect. 4.1). This may indicate that the temperature is more significant than the density and the visual extinction to the evolution of HC3 N/N2 H+ in HMSFRs. For the two best-fit cases, the densities and the visual extinctions at 104 AU in model 4 can be over one order of magnitude higher than those at 105 AU in model 6, but the temperatures are similar except for the HMC stage. The density during each stage probably mainly affects the evolutionary timescale for replicating the observations. The visual extinction mainly influences the evolution of ions via photodissociation in the outer region (several 104 AU – 105 AU) with low AV ~ 5 during the HMSC stage and the HMPO stage. Consequently, a relatively cold diffuse envelope throughout the entire evolution of HMSFRs is essential to replicate the observed ratio of HC3 N/N2 H+, while the inner regions characterized by much higher temperatures are not necessary. Such an analysis suggests that the cold envelope could play a crucial role in maintaining specific chemical conditions.
Observations and best-fit simulations of HC3N/N2H+, HC3N/H2, and N2H+/H2 in HMSFRs.
 |
Fig. 4 Same as Fig. 3, but depicting the ratio of HC3N/N2H+ and the fractional abundance of HC3N and N2H+ with respect to H2 at six different radii (102 AU, 103 AU, 7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU) from the center using model 4 (left panels) and model 6 (right panels). The results at r = 102 AU, 103 AU, 7 × 103 AU, and 104 AU during the HMSC stage in model 4 completely overlap because of the large rin > 104 AU. |
Values of ρ, AV, and T during each stage at two different radii (104 AU and 105 AU) from the center in the best-fit models (model 4 and model 6).
4 Discussion
4.1 Key mechanisms affecting HC3N/N2H+
According to derived physical conditions at the outermost radius in model 6, we discuss the key mechanisms for influencing HC3N/N2H+ in HMSFRs. The major reactions for producing HC3N are:
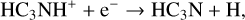 (6)
(6)
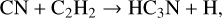 (7)
(7)
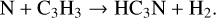 (8)
(8)
Meanwhile, the important reactions for destroying HC3N are:
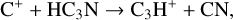 (9)
(9)
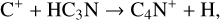 (10)
(10)
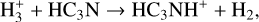 (11)
(11)
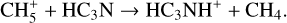 (12)
(12)
Therefore, the evolution of HC3N in HMSFRs can be explained as follows. In the relatively cold HMSC stage with T < 25 K, in the outer diffuse region (several 104 AU – 105 AU), the ion-molecule reactions (9), (10), and (11) mainly destroy HC3N, while the dissociative recombination reaction (6) mainly converts the ion HC3NH+ back to HC3N. These reactions can be further enhanced by more ions (especially C+) and electrons induced by photodissociation due to the low AV . For the inner dense region (r < 104 AU), the neutral-neutral reactions (7) and (8) are more significant for the production of HC3N. They are triggered by carbon-chain species, C2H2 and C3H3 , produced via the reaction of C+ with H2 and subsequent reactions (Sakai & Yamamoto 2013). In addition, reactions (11) and (12) play a major role in the destruction of HC3N in the dense region, but most products can be converted back to HC3N via reaction (6). When T > 25 K during the HMPO, HMC, and UCHII stage, reactions (7) and (8) still remain significant, but driven by the thermal desorption of CH4 and subsequent reactions with C+ for synthesizing C2H2 and C3H3 (Aikawa et al. 2008; Hassel et al. 2008, 2011; Sakai & Yamamoto 2013; Taniguchi et al. 2019a), also known as warm carbon-chain chemistry (WCCC; Sakai et al. 2008, 2009; Sakai & Yamamoto 2013; Wang et al. 2019). For even hotter regions with T > 90 K, the sublimation of HC3N molecules trapped on grains is the only dominating mechanism for increasing gaseous HC3N molecules. Thus, at the start of the HMPO and HMC stage, the average abundance of HC3N increases, as CH4 and HC3N molecules evaporate from the grains in specific regions where T becomes higher than their sublimation temperatures. During the HMPO stage, the sublimation of CH4 and the WCCC mechanism mainly occur within the range of 103−3 × 104 AU, which is smaller than that during the HMC stage within 3 × 103−105 AU. In contrast, the sublimation of HC3N occurs in similar regions during both stages (<103 AU during the HMPO stage and <3 × 103AU during the HMC stage, respectively). A larger warm region during the HMC stage results in a higher increase in HC3N compared to that during the HMPO stage. However, reactions (9)–(12) gradually decrease the abundance of HC3N over time during each stage, since CH4 and HC3 N molecules trapped on the grains are finite.
For N2H+, there is only one major formation reaction,
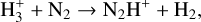 (13)
(13)
and the major destruction reactions are:
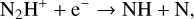 (14)
(14)
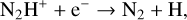 (15)
(15)
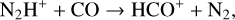 (16)
(16)
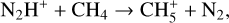 (17)
(17)
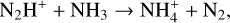 (18)
(18)
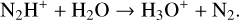 (19)
(19)
During the HMSC stage, T is already higher than the sublimation temperature of N2 (about 19 K), and sublimated N2 molecules drive the formation of N2H+ via reaction (13). In contrast, reactions (14) and (15) mainly destroy N2H+, driven by intense cosmic-ray ionization and photodissociation. During the hotter HMPO, HMC, and UCHII stages, reaction (13) remains significant for forming N2H+. But reactions (16), (17), (18), and (19) can sequentially become important for the destruction of N2H+ when the temperature rises above ~21 K, the sublimation temperature of CO, ~25K for CH4, ~115K for NH3, and ~120K for H2 O, respectively. Consequently, at the start of the HMPO, HMC, and UCHII stages, the thermal desorption of CO, CH4 , NH3, and H2O from the grains enhances reactions (16)–(19) and induces the decrease in N2H+ compared to that at the end of the previous stage. However, the efficiency of reaction (13) always overwhelms the total efficiency of reactions (14)-(19) during each stage, which accumulates more N2H+ ions for increasing the abundance during each stage. As a result, combined with the previous analysis of HC3N, the ratio HC3N/N2H+ can rapidly increase at the start of each stage, accompanied by a decreasing trend as the stages progress. In summary, the evolution of HC3N is mainly affected by the WCCC mechanism and its thermal desorption, whereas the evolution of N2H+ is primarily influenced by the thermal desorption of N2, CO, CH4, NH3, and H2O from the grains, followed by dissociative recombination and ion-molecule reactions.
4.2 Other candidate chemical clocks
Based on the evolution of HC3N and N2H+ during different stages of HMSFRs, carbon-chain species are affected by the WCCC mechanism and their thermal desorption just like HC3N, while ions are mainly influenced by cosmic-ray ionization, photodissociation, and dissociative recombination reactions as N2H+ . Thus, we suggest that the ratio between one carbon- chain species and an ion could be a candidate chemical clock. Other candidate chemical clocks derived from observations (see Sect. 1) can also be further analyzed with our simulations. Therefore, we examined in total 350 ratios involving 27 species, including carbon-chain species (C2H, C3H, C4H, C5H, C2H2, C3H2, C4H2, C5H2, CH3 CCH, HC3N, HC5N, and C2S), simple molecules (CS, NH3 , HCN, HNC, CO, SO, H2CO, and HNCO), COMs (HCOOH, CH3OH, and CH3CN), and ions (N2H+, HCO+, 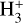 , and C+). Except for the aforementioned HC3N/N2H+, 178 ratios exhibit increasing or decreasing evolutionary trends at the late HMSC stage, the early HMPO stage, and the early UCHII stage according to our simulations. Figure C.1 depicts the evolution of these average ratios within 105 AU from the center adopting model 6, which could be proposed as candidates of chemical clocks from the perspective of chemical evolution. Among them, 157 ratios are observable and can be verified with observations, whereas
, and C+). Except for the aforementioned HC3N/N2H+, 178 ratios exhibit increasing or decreasing evolutionary trends at the late HMSC stage, the early HMPO stage, and the early UCHII stage according to our simulations. Figure C.1 depicts the evolution of these average ratios within 105 AU from the center adopting model 6, which could be proposed as candidates of chemical clocks from the perspective of chemical evolution. Among them, 157 ratios are observable and can be verified with observations, whereas 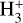 is not observable, and its related ratios cannot be considered as chemical clocks. Thus, such candidate ratios are presented as a foundational database for future observational analysis and simulations. Besides the aforementioned mechanisms affecting carbon-chain species and ions, respectively, for simple molecules, thermal desorption and ion-molecule reactions are significant, and for COMs, two-body reactions on the grains and thermal desorption are important. Nevertheless, the specific reactions affecting the evolution of each ratio can be further discussed in a future study.
is not observable, and its related ratios cannot be considered as chemical clocks. Thus, such candidate ratios are presented as a foundational database for future observational analysis and simulations. Besides the aforementioned mechanisms affecting carbon-chain species and ions, respectively, for simple molecules, thermal desorption and ion-molecule reactions are significant, and for COMs, two-body reactions on the grains and thermal desorption are important. Nevertheless, the specific reactions affecting the evolution of each ratio can be further discussed in a future study.
According to our results, candidate chemical clocks C2H/HCO+ and HC3N/HNC show similar evolutionary trends as observations (Yu & Wang 2015; Urquhart et al. 2019), which may be further confirmed as chemical clocks. In addition, CS/SO, HCN/HNCO, C2H/HNCO, and SO/N2H+ exhibit similar evolutionary trends compared with previous simulations (Gerner et al. 2014) as candidate chemical clocks. In contrast, C2H/N2H+ and C2H/C3H2 display a decreasing tendency along with the evolution, which contradicts the statistics of observations (Rathborne et al. 2016; Urquhart et al. 2019), although the former one, C2H/N2H+, is consistent with previous simulations (Gerner et al. 2014). Except for these candidate chemical clocks based on our simulations, we also depict some ratios in Fig. D.1 that have been suggested as chemical clocks in previous studies. The ratio of N2H+ /HCO+ is indeed lower during the UCHII stage than that during previous stages and in agreement with observations (Yu & Wang 2015; Urquhart et al. 2019), but the ratio during the HMSC stage and HMPO stage does not show clear differences. For C3H2/C2S, NH3/C2S, and N2H+/CS, they increase from the HMSC stage to the HMPO stage and are consistent with observations (Ohashi et al. 2014; Tatematsu et al. 2014), while NH3/HC3 N decreases from the HMSC stage to the HMPO stage and contradicts the observations (Ohashi et al. 2014). However, these four ratios apparently do not exhibit monotonic evolutionary trends when one examines their values across the HMSC, HMPO, and UCHII stages. For HCN/HNC, no obvious difference appears during the whole evolution, which is not consistent with the increased ratio that is observed (Jin et al. 2015; Rathborne et al. 2016; Urquhart et al. 2019) or with previous simulations (Gerner et al. 2014). Also, the evolutionary trends of HCO+/HNC, HNC/N2H+, HCN/N2H+, and CS/N2H+ contradict observations (Rathborne et al. 2016; Urquhart et al. 2019). Such deviations between simulations and observations may be driven by the simplification of the physical models adopted in the simulations. We also compared CH3 CN/C2 H, CH3OH/CO, CH3OH/C2H, CS/C2H, H2CO/CO, N2H+/CO, and CH3 OH/CH3 CN with simulations presented by Gerner et al. (2014). Among them, CH3CN/C2H, CS/C2H, N2H+/CO, and H2CO/CO present roughly similar evolutionary trends across four stages, along with deviations in their values during the same stage. CH3OH/CO, CH3OH/C2H, and CH3OH/CH3CN exhibit opposite evolutionary trends, accompanied by severe deviations in their values. Since most ratios do not exhibit monotonic evolutionary trends, it is not necessary to systematically analyze the reasons inducing the discrepancies between our simulations and results derived by Gerner et al. (2014). We propose that the discrepancies could be attributed to the different physical parameters between our best-fit model and previous models. Such a detailed analysis could be conducted in a future study.
Given the deviations between observations and simulations, some improvements could be considered in the future analysis for our understanding of HMSFRs. Firstly, the 1D physical model of HMSFRs, with constant parameters during each stage and abrupt transitions between two stages, is apparently not sufficiently accurate, although the chemistry can quickly respond to the discontinuities of physical parameters (Gerner et al. 2014). A more sophisticated physical model that incorporates varying parameters and smoother transitions between stages should be developed. An example model is described by Sabatini et al. (2021), which includes a collapse stage and a warm-up stage with continuity between them. The primary distinction between our optimal model 6 and models proposed by Gerner et al. (2014) or Sabatini et al. (2021) is that our model 6 adopts higher densities and temperatures within the range of 105 AU, along with an enhanced cosmic ray ionization rate. Such a physical model could be further analyzed by adopting a larger range of parameters and supplementing the UCHII stage in a future study. Secondly, the chemical model also needs to be further modified by including more updated reactions and mechanisms, especially those related to the grain surfaces. Finally, when comparing simulations with observations, it is important to recognize that only one ratio between two species may not rigorously constrain the evolutionary stage of HMSFRs. This conclusion is mainly based on the results in panel C of Fig. 2 (also see panel C of Fig. B.3 and panel C of Fig. B.4). The average ratio of HC3N/N2H+ within 5 × 104 AU from the center can also replicate similar trends and values in the HMSC, HMPO, and UCHII stages, respectively. However, the average abundance ratio of HC3N/H2 obviously deviates from the observations. If only one ratio between two species were compared, such a discrepancy could go unnoticed. Also, such a ratio could be replicated in different stages in simulations, accompanied by different magnitudes of the abundances of the involved species. Therefore, to rigorously constrain the evolutionary stage of HMSFRs, not only the column density ratio between two species but also the abundances of these two species should be studied. Alternatively, more than two column density ratios should be simultaneously analyzed when the column density of H2 is not derived.
5 Conclusions
In this paper, we have performed chemical simulations to reproduce the observed column density ratio of HC3N/N2H+ and the abundances of these two species across various evolutionary stages in HMSFRs. Observations show an increasing evolutionary trend of HC3N/N2H+, which is considered a chemical clock. Simultaneously, we have identified the chemical processes responsible for the observed time-dependent trends in these stages. Our simulations adopted the astrochemical code Nautilus and the existing 1D models of HMSFRs proposed by (Gerner et al. 2014, 2015), which include four evolutionary stages with constant densities and temperatures during each stage, as well as abrupt transitions between adjacent stages. However, both density and temperature fluctuate throughout the entire evolution. To maintain a steady increase in density and temperature over time as the global hierarchical collapse scenario predicts (e.g., Vázquez-Semadeni et al. 2019), we adjusted parameters such as the density, temperature, and time spent in each stage. The average ratios ofHC3N/N2H+ within different ranges from the center were calculated and compared with observations, as were the average abundances of HC3N and N2H+ with respect to H2. The main conclusions are listed below:
When averaging over large spatial scales (~105AU from the core), the best model produced successfully matches the observed column density ratio of HC3N/N2H+ and the abundances of the species involved at specific times for each evolutionary stage; that is, the late HMSC stage, the early HMPO stage, and the early UCHII stage, respectively. Assuming that thermal desorption occurs instantaneously, the time required to bring the simulated and observed ratios into agreement reflects the time necessary for chemical adjustments following jumps of physical parameters between stages. The agreement is only achieved when averaging over large spatial scales, and indicates that clusterforming regions cannot be modeled without accounting for the extended envelope.
Our simulation fails to demonstrate a continuous and consistent monotonic increase in HC3N/N2H+ throughout the entire evolution. However, some observed ratios between adjacent stages overlap, which could be induced by observational uncertainties (such as those in deriving column densities and abundances, clump classification, and systematic effects), or indicate that the evolution of HC3N/N2H+ may not strictly monotonically increase throughout the entire evolution; for example, because a cluster is being formed in the clump, and different parcels of gas can have different physical properties and thus a different chemistry.
The evolution of HC3N is mainly affected by the WCCC mechanism and its own thermal desorption, while the evolution of N2H+ is primarily influenced by the thermal desorption of N2, CO, CH4 , NH3 , and H2O on the grains, followed by gaseous dissociative recombination and ion-molecule reactions.
We also examined 350 other ratios involving 27 species according to our best-fit model. We find that 178 ratios exhibit an increasing or decreasing evolutionary trend at the late HMSC stage, the early HMPO stage, and the early UCHII stage. Among them, 157 ratios are observable and can be compared with observations, indicating that they could be considered as candidate chemical clocks.
Overall, the results obtained from the best-fitting model timescales broadly agree with statistical estimates. This indicates that 1D models with abrupt jumps in physical parameters have reached their limits in terms of the insights they can provide. Thus, more sophisticated models and advanced approaches are necessary in future studies. For instance, physical models incorporating smoother transitions between evolutionary phases might address some of the discontinuities that cause the current models to deviate from the observational data.
Acknowledgements
We thank our referee’s constructive comments to significantly improve the quality of the manuscript. This work is supported by the National Natural Science Foundation of China (NSFC) grant No. 12303032, the Natural Science Foundation of Jiangsu Province (Grant No. BK20221163), and the Excellent Postdoctoral Talent Program of Jiangsu Province (Grant No. 2022ZB475). F.D. is supported by NSFC grant No. 12041305 and the National Key R&D Program of China grant No. 2023YFA1608000. Y.X.W. is a member of the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne.
Appendix A Benchmark of the chemical reaction network
Our reaction network from Wang et al. (2021) is benchmarked against the reaction network from Ruaud et al. (2016), which is provided as an example network in the Nautilus package. The initial abundances are already listed in Table 1. The TMC1 model proposed by Semenov et al. (2010) is utilized in the benchmark, which is assumed as a stable physical model with the temperature T = 10 K, the hydrogen nuclei density nH = 2 × 104 cm−3, the visual extinction AV = 10 mag, the cosmic ray ionization rate ζCR = 1.8 × 10−16 s−1, and the FUV radiation field χ = 1. Other chemical parameters are the same as those described in Sect. 2. Figure A.1 shows the time-dependent evolution of the fractional abundances of several important species with respect to H2 calculated by the Nautilus code with adopting these two networks, respectively. The comparison shows good agreement between two simulations.
 |
Fig. A.1 Time-dependent evolution of the fractional abundances of several important species (CO, CO2, H2O, CH3 OH, CH4, NH3, HC3N, N2H+, and HCO+) with respect to H2 using the TMC1 model calculated by the Nautilus code. The letter J represents those species on the grains. The black solid lines are the results adopting the reaction network from Wang et al. (2021), and the red crosses represent the results adopting the reaction network from Ruaud et al. (2016), as an example network in the Nautilus package. |
Appendix B Additional simulated HC3N/N2H+
Appendix C Candidate chemical clocks
 |
Fig. C.1 Time-dependent evolution of other average ratios within 105 AU from the center adopting model 6 as candidate chemical clocks. |
Appendix D Other average ratios
 |
Fig. D.1 Other average ratios as in Fig. C.1 but do not exhibit monotonic evolutionary trend throughout the entire evolution. |
References
- Aikawa, Y., Wakelam, V., Garrod, R. T., & Herbst, E. 2008, ApJ, 674, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T., & de Wit, W. J. 2016, A&A Rev., 24, 6 [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945 [Google Scholar]
- Beuther, H., Churchwell, E. B., McKee, C. F., & Tan, J. C. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 165 [Google Scholar]
- Chang, Q., & Herbst, E. 2014, ApJ, 787, 135 [Google Scholar]
- Chang, Q., & Herbst, E. 2016, ApJ, 819, 145 [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerner, T., Beuther, H., Semenov, D., et al. 2014, A&A, 563, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerner, T., Shirley, Y. L., Beuther, H., et al. 2015, A&A, 579, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieser, C., Beuther, H., Semenov, D., et al. 2021, A&A, 648, A66 [EDP Sciences] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [Google Scholar]
- Hassel, G. E., Herbst, E., & Garrod, R. T. 2008, ApJ, 681, 1385 [Google Scholar]
- Hassel, G. E., Harada, N., & Herbst, E. 2011, ApJ, 743, 182 [Google Scholar]
- Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hoq, S., Jackson, J. M., Foster, J. B., et al. 2013, ApJ, 777, 157 [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2015, ApJ, 800, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, M., Lee, J.-E., & Kim, K.-T. 2015, ApJS, 219, 2 [Google Scholar]
- Jørgensen, J. K., Belloche, A., & Garrod, R. T. 2020, ARA&A, 58, 727 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., & Hosokawa, T. 2018, A&A, 616, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, B. A. 2022, ApJS, 259, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Mottram, J. C., Hoare, M. G., Davies, B., et al. 2011, ApJ, 730, L33 [Google Scholar]
- Öberg, K. I., van Dishoeck, E. F., & Linnartz, H. 2009, A&A, 496, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohashi, S., Tatematsu, K., Choi, M., et al. 2014, PASJ, 66, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., Bialy, S., Galli, D., et al. 2022, A&A, 658, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, T., Mac Low, M.-M., Banerjee, R., Klessen, R. S., & Dullemond, C. P. 2010, ApJ, 719, 831 [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., & Menten, K. M. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 [Google Scholar]
- Rathborne, J. M., Whitaker, J. S., Jackson, J. M., et al. 2016, PASA, 33, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [Google Scholar]
- Sabatini, G., Bovino, S., Giannetti, A., et al. 2021, A&A, 652, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, N., & Yamamoto, S. 2013, Chem. Rev., 113, 8981 [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., Burton, M., & Yamamoto, S. 2009, ApJ, 697, 769 [Google Scholar]
- Sánchez-Monge, Á., Kurtz, S., Palau, A., et al. 2013, ApJ, 766, 114 [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sridharan, T. K., Beuther, H., Saito, M., Wyrowski, F., & Schilke, P. 2005, ApJ, 634, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Stéphan, G., Schilke, P., Le Bourlot, J., et al. 2018, A&A, 617, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tatematsu, K., Ohashi, S., Umemoto, T., et al. 2014, PASJ, 66, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, K., Herbst, E., Caselli, P., et al. 2019a, ApJ, 881, 57 [Google Scholar]
- Taniguchi, K., Saito, M., Sridharan, T. K., & Minamidani, T. 2019b, ApJ, 872, 154 [Google Scholar]
- Taniguchi, K., Herbst, E., Majumdar, L., et al. 2021, ApJ, 908, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, K., Majumdar, L., Caselli, P., et al. 2023, ApJS, 267, 4 [CrossRef] [Google Scholar]
- Urquhart, J. S., Thompson, M. A., Moore, T. J. T., et al. 2013, MNRAS, 435, 400 [Google Scholar]
- Urquhart, J. S., König, C., Giannetti, A., et al. 2018, MNRAS, 473, 1059 [Google Scholar]
- Urquhart, J. S., Figura, C., Wyrowski, F., et al. 2019, MNRAS, 484, 4444 [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
- Vázquez-Semadeni, E., Palau, A., Ballesteros-Paredes, J., Gómez, G. C., & Zamora-Avilés, M. 2019, MNRAS, 490, 3061 [Google Scholar]
- Wakelam, V., Caselli, P., Ceccarelli, C., Herbst, E., & Castets, A. 2004, A&A, 422, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., Chang, Q., & Wang, H. 2019, A&A, 622, A185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., Du, F., Semenov, D., Wang, H., & Li, J. 2021, A&A, 648, A72 [EDP Sciences] [Google Scholar]
- Wang, Y. X., Zhang, J. S., Yu, H. Z., et al. 2023, ApJS, 264, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Wang, Y., Jiang, Z., & Chen, Z. 2023, MNRAS, 518, 1472 [Google Scholar]
- Yu, N., & Wang, J.-J. 2015, MNRAS, 451, 2507 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [Google Scholar]
All Tables
Observations and best-fit simulations of HC3N/N2H+, HC3N/H2, and N2H+/H2 in HMSFRs.
Values of ρ, AV, and T during each stage at two different radii (104 AU and 105 AU) from the center in the best-fit models (model 4 and model 6).
All Figures
 |
Fig. 1 Correlation between the average ratio of HC3N/N2H+ and the average abundance of HC3N with respect to H2 within four different ranges (panel A: 7 × 103 AU, panel B: 104 AU, panel C: 5 × 104 AU, and panel D: 105 AU) around the center by adopting model 4 in chemical simulations compared with observations. The results during the HMSC, HMPO, HMC, and UCHII stages are plotted as squares, circles, diamonds, and triangles, respectively. The evolution of HC3N/N2H+ and HC3N/H2 throughout ttotal during each stage consistently decrease (from right to left and from top to bottom). The observations proposed by Taniguchi et al. (2019b) and Wang et al. (2023, including derived column density of HC3N, N2H+, and H2 simultaneously) are plotted as solid squares, solid circles, and solid triangles, respectively, with error bars. |
| In the text | |
 |
Fig. 2 Same as Fig. 1, but adopting model 6. |
| In the text | |
 |
Fig. 3 Time-dependent evolution of the average ratio of HC3N/N2H+ and the average fractional abundance of HC3N and N2H+ with respect to H2 within four different ranges (7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU) around the center using model 4 (left panels) and model 6 (right panels). The four evolutionary stages are labeled in each panel, and the observations are also plotted, with the dashed lines as the median values and the dotted lines as the maximums or minimums of observations. The evolution before 104 yr is excluded to show the changes in different stages more clearly. The results within 7 × 103 AU and 104 AU during the HMSC stage in model 4 completely overlap because of the large rin > 104 AU. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but depicting the ratio of HC3N/N2H+ and the fractional abundance of HC3N and N2H+ with respect to H2 at six different radii (102 AU, 103 AU, 7 × 103 AU, 104 AU, 5 × 104 AU, and 105 AU) from the center using model 4 (left panels) and model 6 (right panels). The results at r = 102 AU, 103 AU, 7 × 103 AU, and 104 AU during the HMSC stage in model 4 completely overlap because of the large rin > 104 AU. |
| In the text | |
 |
Fig. A.1 Time-dependent evolution of the fractional abundances of several important species (CO, CO2, H2O, CH3 OH, CH4, NH3, HC3N, N2H+, and HCO+) with respect to H2 using the TMC1 model calculated by the Nautilus code. The letter J represents those species on the grains. The black solid lines are the results adopting the reaction network from Wang et al. (2021), and the red crosses represent the results adopting the reaction network from Ruaud et al. (2016), as an example network in the Nautilus package. |
| In the text | |
 |
Fig. B.1 Same as Fig. 1, but adopting model 1. |
| In the text | |
 |
Fig. B.2 Same as Fig. 1, but adopting model 2. |
| In the text | |
 |
Fig. B.3 Same as Fig. 1, but adopting model 3. |
| In the text | |
 |
Fig. B.4 Same as Fig. 1, but adopting model 5. |
| In the text | |
 |
Fig. C.1 Time-dependent evolution of other average ratios within 105 AU from the center adopting model 6 as candidate chemical clocks. |
| In the text | |
 |
Fig. D.1 Other average ratios as in Fig. C.1 but do not exhibit monotonic evolutionary trend throughout the entire evolution. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.