EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A355 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A355
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202451554
Published online 22 October 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open Access funding provided by Max Planck Society.

1 Introduction

In recent years, high-resolution near-infrared (NIR) imaging with instruments such as the Very Large Telescope Spectro-Polarimetric High-contrast Exoplanet REsearch (VLT/SPHERE), Gemini South Telescope Gemini Planet Imager (Gemini/GPI), and the Subaru Telescope High-Contrast Coronographic Imager for Adaptive Optics (Subaru/HiCIAO) has revealed large-scale spiral structure in a number of systems (e.g., Shuai et al. 2022, and references therein), including MWC 758 (Grady et al. 2013), SAO 206462/HD 135344B (Muto et al. 2012), and V1247 Ori (Ren et al. 2024). Because planets are ubiquituous in our Galaxy, disk-planet interaction has been suggested as a means of creating a large-scale, multi-armed spiral structure in disks (among other proposals, including the gravitational instability and stellar flybys). Specifically, hydrodynamical simulations (e.g., Fung & Dong 2015; Zhu et al. 2015; Dong et al. 2016) of planetary wave excitation at the Lindblad resonances (Goldreich & Tremaine 1978, 1979, 1980) suggested that the observed scattered-light spirals are consistent with launching by exterior planets with multiple Jupiter masses. These companions, widely separated from their host stars (van der Marel et al. 2021), should be detectable with angular differential imaging (ADI) in the near-infrared (Asensio-Torres et al. 2021; Desidera et al. 2021), in the mid-infrared with the James Webb Space Telescope (JWST) (e.g., Wagner et al. 2019, 2024; Cugno et al. 2024), and in accretion tracers such as Hα and Pa β (Follette et al. 2023; Biddle et al. 2024), but evidence is inconclusive so far. Only in the PDS 70 system are planets confirmed to exist (Müller et al. 2018; Keppler et al. 2018; Haffert et al. 2019) alongside disk substructure of any sort, with additional detections for instance in AB Aur (Currie et al. 2022) and HD 169142 (Hammond et al. 2023).

That such easily-detectable, widely-separated super-Jupiters have proven so elusive raises the question of what mechanisms may be responsible for the observed spirals. Disk illumination and shadowing may have a role to play. Montesinos et al. (2016); Montesinos & Cuello (2018); Cuello et al. (2019), and Su & Bai (2024) ran 2D vertically averaged hydrodynamical simulations of disks with parameterized cooling and included radial dark lanes in their temperature structures to model the effect of a misaligned, shadow-casting inner disk. The resulting strong azimuthal pressure gradient excites m = 2 spiral arms; Monte Carlo radiative transfer (MCRT) post-processing, assuming a Gaussian vertical profile with a scale height governed by the 2D temperature, revealed that arms like this would feature prominently in the NIR. Nealon et al. (2020) used SPH simulations with full radiative transfer, and Qian & Wu (2024) used a parameterized cooling prescription in a grid simulation to simulate the dynamical consequences of shadowing from an inner disk. Separately, in their 3D, grid-based simulations with flux-limited diffusion (FLD; Levermore & Pomraning 1981) and Chrenko & Nesvorný (2020) reported that the outer edge of the gap carved by a 1 MJ planet exhibits unstable non-axisymmetric flow patterns and additional spiral structure, which were absent in their locally isothermal runs. They attributed this outcome to the fact that the temperature profile in the radiative case (with a cooler, shadowed gap region and warmer, directly illuminated outer gap edge) is more favorable for the excitation of the Rossby-wave instability (RWI; Lovelace et al. 1999).

Taken together, these works suggest that even intermediatemass planets could produce prominent, observable spirals, not through direct driving, but by their impact on disk illumination, provided that the shadow corotates with some radius within the disk. To investigate this hypothesis, we ran 3D hydrodynamical simulations of the disk-planet interaction with PLUTO, and postprocessed our results with the RADMC3D Monte Carlo radiative transfer (MCRT) code to generate mock near-infrared images of the simulated disk. In Sect. 2 we describe our methods in more detail, including our implementations of three-temperature radiation hydrodynamics (Muley et al. 2023) and β-cooling to an axisymmetric background. In Sect. 3 we discuss our results, including the structure of the planet-formed gap, excitation of spirals at the gap edge, and post-processed near-infrared images. In Sect. 4 we present our conclusions and questions for future work.

2 Methods

2.1 PLUTO radiation hydrodynamics

For our study of spiral arms, we used a version of the PLUTO hydrodynamical code (Mignone et al. 2007), modified to solve the equations of radiation hydrodynamics (Melon Fuksman & Mignone 2019; Melon Fuksman et al. 2021) with an additional dust internal energy field (Muley et al. 2023). This was thermally coupled to the gas energy (via collision) and radiation energy (via opacity) fields, but it is a passive tracer of the gas velocity without any inertia or back-reaction (implying a Stokes number St ≪ 1 and a globally constant dust-to-gas ratio fd ≪ 1). Radiation transport was computed using the M1 closure, which interpolates between the optically thick (diffusion) and optically thin (free-streaming) regimes (Levermore 1984). We briefly review the most pertinent details below and refer to the aforementioned works (as well as Muley et al. 2024) for a more detailed description of the equations and solution strategy.

2.1.1 Three-temperature simulations

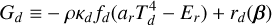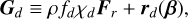Our three-temperature module solves the full set of equations described in Muley et al. (2023). The coupling of dust energy with radiation energy (Gd) and of dust momentum with radiation flux (Gd) is given as follows: Gd≡−ρκdfd(arTd4−Er)+rd(β)${{G_d} \equiv - \rho {\kappa _d}{f_d}\left( {{a_r}T_d^4 - {E_r}} \right) + {r_d}(\beta )}$(1a) Gd≡ρfdχdFr+rd(β),${G_d} \equiv \rho {f_d}{\chi _d}{F_r} + {r_d}(\beta ),$(1b)

where ρ is the dust density, while ar = 4σStefan−Boltzmann/c is the radiation constant. Td refers to the dust temperature, while Er refers to the radiation energy density. κd is a Planck- averaged (and thus, temperature-dependent) dust absorption opacity, while χd is the dust total (absorption plus scattering) opacity. In practice, we equated χd to the greater of the Planck- or Rosseland-averaged dust absorption opacities at a given temperature. rd(β) and rd (β) are relativistic corrections to the above terms, with the vector β ≡ v/c (not to be confused with the β-cooling timescale); these are negligible in the context of protoplanetary disks. We used the tabulated dust absorption opacities from Krieger & Wolf (2020, 2022), while setting the gas opacities to zero.

We also included a dust irradiation term, 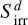Sirrd$S_{{\rm{irr}}}^d$, obtained by frequency-dependent ray-tracing from the central star. Here, the effective dust opacity is a Planck average taken at the stellar surface temperature T*.

The dust-gas collision term X𝑔d is defined as 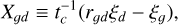Xgd≡tc−1(rgdξd−ξg),${X_{gd}} \equiv t_c^{ - 1}\left( {{r_{gd}}{\xi _d} - {\xi _g}} \right),$(2)

where tc is the dust-gas thermal coupling time, ξ𝑔 and ξd are the internal energy of dust and gas, respectively, and r𝑔d = c𝑔/fdcd is the ratio of the heat capacity per unit volume between gas and dust. cd is the specific heat capacity of dust, while c𝑔 ≡ kB/µmH(γ − 1) is that of the gas. The gas thermal coupling time tc, as a function of the dust-gas stopping time ts, is calculated in the Epstein regime (Burke & Hollenbach 1983; Speedie et al. 2022). 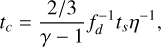tc=2/3γ−1fd−1tsη−1,${t_c} = {{2/3} \over {\gamma - 1}}f_d^{ - 1}{t_s}{\eta ^{ - 1}},$(3)

where we set the accommodation coefficient η to unity.

2.1.2 β-cooling simulations

In our β-cooling simulations, we ignored absorption, emission, scattering (Gd, Gd), and transport (Fr ) of thermalized radiation, as well as dust energy (Ed) and stellar irradiation 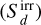(Sdirr)$\left( {S_d^{{\rm{irr}}}} \right)$. To parameterize all of these effects, we replaced Xgd with a term of the form 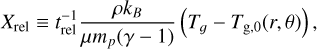Xrel≡trel−1ρkBμmp(γ−1)(Tg−Tg,0(r,θ)),${X_{{\rm{rel}}}} \equiv t_{{\rm{rel}}}^{ - 1}{{\rho {k_B}} \over {\mu {m_p}(\gamma - 1)}}\left( {{T_g} - {T_{{\rm{g}},0}}(r,\theta )} \right),$(4)

where T𝑔,0 is the (axisymmetric) initial condition for gas temperature (see Sect. 2.1.3 for more details), r, θ, ϕ are spherical coordinate positions, and trel can in general be a function of any primitive variables. Following Bae et al. (2021) and Melon Fuksman et al. (2024), we set the cooling (more accurately, thermal relaxation) time 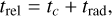trel=tc+trad,${t_{{\rm{rel}}}} = {t_c} + {t_{{\rm{rad}}}},$(5)

where tc is defined as in Eq. (3), and trad is a radiative cooling timescale incorporating both the optically thick diffusion and optically thin free-streaming limits, 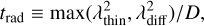trad≡max(λthin2,λdiff2)/D,${t_{{\rm{rad}}}} \equiv \max \left( {\lambda _{{\rm{thin}}}^2,\lambda _{{\rm{diff}}}^2} \right)/D,$(6)

where the thermal diffusivity 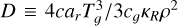D≡4carTg3/3cgκRρ2$D \equiv 4c{a_r}T_g^3/3{c_g}{\kappa _R}{\rho ^2}$. The optically thin cooling effective length scale λthin = (3κRκPρ2)−1/2, while the thick diffusion length is taken to be the local scale height, λdiff ≡ H = cs,isoΩ−1, where Ω is the local Keplerian orbital frequency and 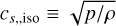cs,, iso ≡p/ρ${c_{s,,{\rm{iso}}}} \equiv \sqrt {p/\rho } $ the isothermal sound speed.

Cooling times were computed self-consistently in each cell of the grid at the start of the simulation. For notational convenience, cooling times can be normalized by the local dynamical time Ω−1, with βd𝑔 = tcΩ, βrad = tradΩ, and the overall β = βrad + βdg.

thumbnail Fig. 1

Initial conditions for gas density ρ (above), and the dust and gas temperatures Td and T𝑔 (below), which are initially equal. The contours for normalized cooling timescales from gas-grain collision (βdg) are plotted above and those from radiation (βrad) below, with white lines. The figure is exactly reproduced from Muley et al. (2024).

2.1.3 Setup and initial conditions

For our simulations, we used the same initial conditions (plotted in Fig. 1) as in Muley et al. (2024), generated with an iterative alternation of radiative and hydrostatic computations. As in that work, we used an extended radial grid with an inner edge at 0.4 au, as well as an additional inner padding prescription to ensure an accurate temperature at the inner edge of our simulated domain. The dust properties remained unchanged between that work and ours, and the dust temperature Td and gas temperature T𝑔 were assumed to be equal in the initial condition. The specific heat capacity for dust is cd = 0.7 J g−1 K−1.

The disk surface density is 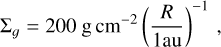Σg=200 g cm−2(R1 au)−1,${{\rm{\Sigma }}_g} = 200\,{\rm{g}}\,{\rm{c}}{{\rm{m}}^{ - 2}}{\left( {{R \over {1\,{\rm{au}}}}} \right)^{ - 1}},$(7)

where R = r sin θ is the cylindrical radius. We used a (Shakura & Sunyaev 1973) α = 0.001.

We fixed the stellar mass M* = 1 M⊙, radius R* = 2.08 R⊙, and temperature T* = 4000 K, giving a total luminosity equal to solar. We tested two thermodynamic prescriptions (β-cooling, 3T) and planet masses (Mp = 3 × 10−4M⊙, 1 × 10−3M⊙), with the planet located at rp = 40 au, θp = π/2, and φp = π/4 in each case. The planets are introduced relatively rapidly into the simulations, with a growth timescale tgr = 10y; this has the potential to strengthen gap-edge effects such as the Rossby-wave instability (Hammer et al. 2017), and thus serves as a caveat of our model. For our hydrodynamic computations, we took a subdomain of the initial disk model generated by our hydrostatic procedure, bounded by r = {0.4, 2.5} × rp, θ = {−0.4, 0.4} + π/2, and ϕ = {0,2π}. We covered this box with 134(r) × 58(θ) × 460(ϕ) cells, logarithmic in radius and uniform in polar and azimuthal angle. This yielded a resolution of ~4.5 cells per scale height at the planet location and is roughly equal to that used in the radiation-hydrodynamic gap-opening simulations of Chrenko & Nesvorný (2020).

We fixed the boundary values of all fields to equal those of the initial condition. To ensure numerical stability near these boundaries, we damped ρ, Er, 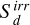Sdirr$S_d^{irr}$, and the components of v to their initial conditions over a timescale tdamp = 2π × 0.1Ω−1. We used an HLL Riemann solver for hydrodynamics and HLLC for radiation; to ensure numerical stability in the presence of fast flows and large density contrasts, we used a piecewise-linear method (PLM) reconstruction to obtain the states at cell boundaries, rather than the WENO3 method used in Muley et al. (2024). We ran each simulation for 250 000 yr (approximately 1000 planetary orbits), then interpolated the result onto a higher- resolution 268(r) × 116(θ) × 919(ϕ) grid; we ran this setup for an additional 2500 yr to study the flow patterns in more detail. A full list of parameters can be found in Table 1.

Table 1

Key simulation parameters.

2.2 RADMC3D Monte Carlo radiative transfer

We used RADMC3D (Dullemond et al. 2012) to generate VLT/SPHERE H-band (λH = 1.62 µm) images from our high- resolution simulation outputs, with Nphot = 2.5 × 107 photon packages launched from the central star. In the post-processing of 3T models, dust temperature was taken directly from the simulation output, whereas for β-cooling, it was assumed to be equal to the gas temperature. To minimize spurious illumination at the inner edge of our hydrodynamic simulation domain, located at rin = 16 au, we padded the disk to rpad = 0.5 au using the initial conditions generated in Sect. 2.1.3.

For simplicity and consistency in our radiative-transfer calculations, we used the tabulated dust opacities in Krieger & Wolf (2020, 2022), including absorption, scattering, and Henyey & Greenstein (1941) 𝑔 parameters to accommodate directional scattering; we expect that a more comprehensive calculation including polarization would yield similar results. In generating our H-band images, we assumed a fiducial line-of-sight distance d = 100 pc and convolved the images with a Gaussian kernel (FWHM ≈ 2.35σ = 0.06 arcsec) to mimic the effects of instrumental beam size.

3 Results

3.1 Temperature structure and thermal spirals

During our simulations, the Lindblad spirals excited by the planet increased the angular momentum of the disk material exterior to the planetary orbit and decreased that of the material interior; the cumulative effect of this over many orbits is to open a gap in the disk. When the gap became sufficiently deep, at roughly 50 orbits for the Jupiter-mass planet and 200 orbits for the Saturn-mass planet, the outer gap edge deviated from axisymmetry, potentially due to hydrodynamic instabilities such as the Rossby-wave instability (see Sect. 3.1.6 of Chrenko & Nesvorný 2020, for a more detailed discussion). With β- cooling, a viscous α = 1 × 10−3 and an axisymmetric background temperature rapidly damp azimuthally asymmetric structures to restore the classical picture of disk-planet interaction (Zhang et al. 2024). With full radiation hydrodynamics, however, the density asymmetries at the outer gap edge couple with the stellar radiation field to create asymmetries in the temperature structure as well, which in turn alters the density, pressure, velocity, and vorticity (Appendix A). Although the vertically integrated temperature deviation is fairly small, typically no more than 10%, the perturbations in the disk atmosphere became substantial because the disk material adjusted its scale height over the course of an orbit and was affected by compression and expansion (via the PdV term). In this region, which we defined to lie at or above the radial τr = 1 surface for stellar irradiation, gas thermal relaxation is dominated by the gas-grain cooling time tc ≈ 0.1–1Ω−1, ensuring that this PdV heating was not immediately radiated away.

The temperature asymmetry leads to a pressure asymmetry at the outer gap edge, which drives strong spiral arms (Montesinos et al. 2016; Cuello et al. 2019, e.g.); in our case, the m = 2 mode predominates. The breakdown of midplane symmetry contributes to the observed nonaxisymmetry in the upper disk layers with a net 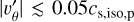| vθ′ |≲0.05cs,iso,p$\left| {v_\theta ^\prime } \right| \mathbin{\lower.3ex\hbox{\buildrel<\over {\smash{\scriptstyle\sim}\vphantom{_x}}}} 0.05{c_{{\rm{s}},{\rm{iso}},{\rm{p}}}}$ in the midplane, but significantly faster in the upper layers of the disk. In Fig. 2 we plot the resulting azimuthal profiles of the density, temperature, and velocity components at high altitude near the outer gap edge t = 252 500 y (~1000 orbits at low resolution, plus ~10 orbits at the doubled resolution). In the bottom panel, the decoupling between dust and gas temperatures in 3T mentioned in the previous paragraph is clearly visible. To better understand this phenomenon, we also conducted a controlled numerical experiment (Appendix B) using β-cooling. We initialized the background temperature profile with asymmetries in azimuth and about the midplane. In this test, a strong spiral structure developed in the disk atmosphere as in the 3T fiducial simulation, where the asymmetric temperature structure developed naturally from illumination and was not prescribed.

In Fig. 3 we plot 2D r –ϕ cuts of the density structure at various polar altitudes, comparing the results obtained with the three-temperature and β-cooling approaches. In both cases, the Lindblad spirals generated by planetary forcing are most prominent at θ = 0.0 and θ = 0.1 above the midplane, but weaken at θ = 0.2 in the disk atmosphere. At these high altitudes, spirals excited by the pressure gradient generated by shadowing, with a somewhat larger corotation radius, become more prominent. Both sets of spiral waves propagate through the disk according to the WKBJ dispersion relation for the radial wavenumber kr and azimuthal wavenumber m (see Bae & Zhu 2018, and references therein), 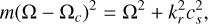m(Ω−Ωc)2=Ω2+kr2cs2,$m{\left( {{\rm{\Omega }} - {{\rm{\Omega }}_c}} \right)^2} = {{\rm{\Omega }}^2} + k_r^2c_s^2,$(8)

in which we assumed that the epicyclic frequency 𝒦 = Ω. From this, the pitch angle δ = arctan(m/krr) can be derived as δ=arctan[ csRΩ(R)((1−Ωc/Ω(R))2−m−2)−1/2 ],$\delta = \arctan \left[ {{{{c_s}} \over {R{\rm{\Omega }}(R)}}{{\left( {{{\left( {1 - {{\rm{\Omega }}_c}/{\rm{\Omega }}(R)} \right)}^2} - {m^{ - 2}}} \right)}^{ - 1/2}}} \right],$(9)

where Ωc is the corotation frequency of the perturbation, and m is the azimuthal wavenumber. The larger corotation radius for shadow-driven spirals accounts for the difference in pitch angles between the spirals and mimics the effect of an external planetary driver.

Over hundreds of orbits, the strong vertical flows shown in Fig. 2 have the effect of depleting the outer disk; in turn, this would reduce the strength of the (inward-directed) outer Lindblad torque on the planet, slowing or even reversing inward Type II planetary migration. However, the precise rate of mass depletion from the domain depends on the strength of vertical damping (see also Appendix C for a discussion of the effect on the spiral strength). Moreover, our simulations did not incorporate other sources of mass depletion that become relevant at high altitude, such as photoevaporation and disk winds. We therefore chose to remain agnostic about the true mass-loss rate and defer this investigation to future work.

Despite sharing similarities with the models presented in Chrenko & Nesvorný (2020), our simulations have important differences. In contrast to our 3T, M1 numerical approach, they employed two-temperature (2T) FLD (e.g., Bitsch et al. 2013), which cannot account for free-streaming and shadowing effects below the radial τ = 1 disk surface or for the delayed response of gas to changes in illumination due to the nonzero collisional coupling time. They also only simulated the upper half of the grid, locking the disk to midplane symmetry, and imposed strong damping of vθ at the upper polar boundary to more strictly conserve mass within the grid (we find in Appendix C that this somewhat strengthens the observed spiral signature). These differences are a consequence of the separate but complementary research goals of each work. their emphasis was on gap structure and planetary torque and migration, while ours is on observational signatures in the upper disk atmosphere.

thumbnail Fig. 2

Azimuthal profiles of various quantities at a fiducial radius of r = 60 au = 1.5 rp, and at an altitude of θ = 0.2 rad above the midplane in our Mp = 3 × 10−4M⊙ simulations. In the 3T case, azimuthal asymmetries of even a few percent in disk illumination that might be induced by the RWI, and are visible in the Td profile lead to strong nonaxisymmetry in ρ, Tg, and the velocity components.
thumbnail Fig. 3

Gas density ρ at t = 1010 orbits (1000 orbits at the fiducial resolution, 10 at the doubled resolution used in Muley et al. 2024) with respect to the initial condition ρ0 for our simulations with a Saturn-mass planet. The green ellipse indicates the planetary Hill radius. With the 3T scheme, the disk atmosphere shows a clear development of m = 2 spiral arms, which are absent in the β-cooling simulations. The white bands at the interior and exterior of the radiative simulation are caused by wave-damping to the initial condition.
thumbnail Fig. 4

Mock H-band (λH = 1.62 µm) total intensity for the disks we simulated, including an inverse-square correction factor. We assumed that the disk is located at a line-of-sight distance dr = 100 pc with a face-on orientation (id = 0°), and convolved the raw image with a Gaussian of FWHM = 0.06 arcsec to mimic the effects of finite telescope resolution. The differences between the radiative and non-radiative cases are clearly visible.

3.2 Radiative transfer post-processing

In Fig. 4 we display face-on simulated NIR images generated with RADMC3D using the procedure described in Sect. 2.2. In order to better show the spiral structure throughout the disk, the intensity was scaled by (R/1 au)2. For the 3T models, the gap-induced spirals are prominently visible in the NIR, far outweighing the planet-driven Lindblad spiral, whose contrast is diluted by beam convolution. By contrast, the β-cooling simulations contain only the Lindblad spiral, which is greatly weakened by the effects of beam convolution.

For a more quantitative view, we plot 1D azimuthal profiles of the brightness contrast at selected radii in Fig. 5. In the outer disk (specifically, router,cut = 60 au), the peak-to-trough brightness contrast across the spiral reaches a factor of ~4 in 3T models, but is negligible for β-cooling models. In the inner disk (rinner,cut = 30 au), the 3T simulations show a contrast of 1.2–1.5, with higher values for a higher planet mass. With β-cooling, the perturbation amplitude is roughly the same, but it is caused by the Lindblad spiral and not by any difference in azimuthal temperature.

thumbnail Fig. 5

H-band intensity in all of our simulations, taken at fiducial radii rinner,cut = 30 au and router,cut = 60 au, and normalized to the azimuthal average. The 3T simulations show a clear m = 2 spiral with a peak-to-trough intensity ratio ~4 in the outer disk and ~ 1.2–1.5 in the inner disk. By contrast, the β-cooling simulations show negligible asymmetry in the outer disk, alongside asymmetries of ~ 1.1–1.5 in the inner disk caused by inner Lindblad spirals.

4 Conclusions

We conducted 3D hydrodynamical simulations of disk-planet interaction by varying both the planet mass (Saturn mass and Jupiter mass) and thermodynamic prescription (three-temperature radiation hydrodynamics and β-cooling). In the radiative case, the deviations from axi- and midplane symmetry at the outer gap edge of a planet-carved gap are amplified by interaction with the radiation field. The resulting strong azimuthal pressure gradients in the upper disk launch spiral density waves (Montesinos et al. 2016) with an m = 2 azimuthal mode structure. Mock H-band images, generated using the RADMC3D Monte Carlo radiative transfer code, showed azimuthal brightness contrasts of a factor of a few, equivalent to those from classical Lindblad spirals generated by planets with multiple Jupiter masses exterior to the spiral (Dong & Fung 2017). This radiative mechanism neither requires the existence of such a massive exterior companion, nor does it create a correspondingly strong spiral structure in the disk midplane, which would concentrate millimeter grains. This is consistent with multiwave-length observations of systems such as V1247 Ori (Ren et al. 2024).

Although our simulations included only Saturn- and Jupiter-mass planets, the spiral-excitation mechanism described here would likewise operate at the outer edge of a gap carved by a super-Jupiter companion. Being interior to the spiral and close to its host star on the sky, a body like this would be more easily concealed by the stellar point-spread function than an exterior companion required by the inner-Lindblad-spiral hypothesis. High-mass interior companions may indeed provide a natural explanation for observations in systems such as MWC 758 (Boehler et al. 2018; Dong et al. 2018) and SAO 206462 (van der Marel et al. 2016), where deep (Fung et al. 2014) eccentric (Goldreich & Sari 2003; Kley & Dirksen 2006) cavities in the millimeter continuum and gas tracers exist alongside large-scale NIR spirals.

In principle, the instability we observed could have been obtained using an orthodox two-temperature approach. However, with 2T, the gas temperature (and consequently, its vertical structure) responds immediately to changes in illumination, which contributes to the development of azimuthal asymmetries at the inner boundary of the disk (also found in Renggli & Szulágyi 2022, priv. comm.). These features in turn affect the temperature structure and generate spiral arms even in the absence of a planet. With 3T, however, the nonzero coupling time between gas and grains suppresses these inner-boundary artifacts, leaving only the spirals generated at the outer gap edge.

With the existing 3T implementation in PLUTO, a parameter study over disk/stellar mass, planet location, and opacity prescription (including molecular opacity) might be conducted to better understand the properties that give rise to large-scale spirals (van der Marel et al. 2021) and to test whether the mechanism we describe can form spiral structures with wavenumbers other than m = 2. Line transfer, a feature of RADMC3D, could be used to model the kinematic signatures expected from such large-scale spirals, and which would potentially be observable in exoALMA and similar large programs. Incorporating multiple dust species (e.g., Krapp et al. 2024), would allow the dynamics of small and large dust grains to be handled simultaneously, ensuring that post-processed near-infrared and submillimeter images are mutually consistent. Radiation-transport methods that allow for beam crossing (such as the discrete-ordinates approach of Jiang 2021) would improve the treatment of shadowing, particularly in the presence of an accreting luminous planet that radiates in all directions. Pursuing these potential future directions would greatly expand scientific understanding of how radiation impacts disk-planet interaction, and in doing so, help us to reproduce observations of real systems.

Acknowledgements

We thank Marcelo Barraza Alfaro, Jiaqing Bi, Ondřej Chrenko, Gabriele Cugno, Ruobing Dong, Mario Flock, Anton Krieger, Nienke van der Marel, Jacksen Narvaez, Rebecca Nealon, Yansong Qian, Richard Teague, Bhargav Vaidya, and Alexandros Ziampras for useful discussions. We thank the anonymous referee for a thorough and insightful report which helped us improve the quality of this work. Numerical simulations were run on the Cobra and Raven clusters of the Max-Planck-Gesellschaft and the Vera Cluster of the Max-Planck-Institut für Astronomie, both hosted by the Max Planck Computing and Data Facility (MPCDF) in Garching bei München. The research of J.D.M.F. and H.K. is supported by the German Science Foundation (DFG) under the priority program SPP 1992: “Exoplanet Diversity” under contract KL 1469/16-1/2.

Appendix A Vorticity of the flow field

The vorticity provides a complementary view to that offered by Fig. 3, emphasizing the gap itself rather than the spiral arms. In Fig. A.1 we plot the polar component of vorticity, 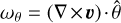ωθ=(∇×v)⋅θ^${\omega _\theta } = (\nabla \times \upsilon ) \cdot \hat \theta $, for our simulations with Mp = 3 × 10−4 M⊙, comparing the β-cooling and 3T prescriptions side-by-side. At t = 200 orbits, right at the onset of the instability described in 3.1, the vorticity profile is similar between simulations. At t = 250 orbits, the gap profile with β-cooling remains intact, but that with 3T is substantially disrupted at the outer edge, causing spiral density waves to be launched.

With 3T, the gap profile bears some resemblance to that caused by the irradiation instability of Fung & Artymowicz (2014). However, the instability that they study is a consequence of radiation pressure directly influencing gas momentum, rather than radiative heating altering the disk’s vertical structure. In this latter respect, the simulated mechanism can be analogized to the self-shadowing instability of Wu & Lithwick (2021).

thumbnail Fig. A.1

θ-component of vorticity at θ = 0.2, with respect to the initial condition, in units of the planet’s orbital frequency Ωp. Between 200 and 250 orbits, the vorticity profile is largely unchanged in the β-cooling simulations, but deviates strongly in the 3T case as radiation couples to the asymmetries generated by disk-planet interaction.

Appendix B β-cooling tests

To validate our hypothesized mechanism for the generation of spirals, we ran β-cooling simulations with no planet. We used the same background temperature profile as in the main text, but multiplied it everywhere by an azimuthally varying factor of 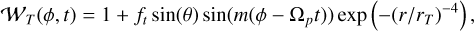WT(ϕ,t)=1+ftsin(θ)sin(m(ϕ−Ωpt))exp(−(r/rT)−4),${{\cal W}_T}(\phi ,t) = 1 + {f_t}\sin (\theta )\sin \left( {m\left( {\phi - {\Omega _p}t} \right)} \right)\exp \left( { - {{\left( {r/{r_T}} \right)}^{ - 4}}} \right),$(B.1)

where ft = 0.25, Ωp is the Keplerian orbital frequency at rp = 40au, and rT = 32 au. We choose an m = 3, as opposed to the m = 2 the observed system settles into, to show the full generality of the mechanism. Although the temperature deviation is at most 10% within the domain, the effect it has on the disk’s vertical structure means that the spiral signature becomes quite substantial in the upper atmosphere.

thumbnail Fig. B.1

Density perturbation in special β-cooling simulations where the planet is removed, and for which the temperature profile in Fig. 1 is multiplied by the azimuthal perturbation factor 𝒲T(ϕ, t) (Eq. B.1). The corotation radius of the temperature profile, equal to the planet radius in the main text, is plotted as a dotted vertical line. Note that the density scale has a much smaller range than in Fig. 3 in the main text.

In Fig. B.1 we plot the resulting density profile at t = 40 orbits, by which the system has settled into a quasi-steady state.

Because the corotation radius of the temperature pattern (rp = 40au) is closer than the outer gap edge in the 3T simulations, the expected outer set of spirals is also contained within the domain. In our self-consistent radiation-hydrodynamics runs, the RWI mediates spiral formation insofar as it creates an analogous non-axisymmetric temperature structure, rather than through direct launching (as in, e.g., Huang et al. 2019).

Appendix C Boundary conditions

Radiation-induced spirals — absent in our β-cooling simulations with axisymmetric background temperatures — induce strong flows in the vertical direction (formally, vθ) in the upper layers of the disk. These, together with with our fixed condition at the upper and lower θ-boundaries of the domain, allow mass to escape from the simulation domain over long periods of time. This complicates radiation-hydrodynamic studies of planetary torques, migration, and transition-disk carving, for which an accurate surface density profile is essential.

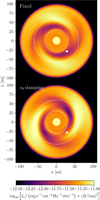thumbnail Fig. C.1

Mock H-band images for different wave-damping prescriptions at the boundary.
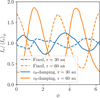thumbnail Fig. C.2

H-band contrast ratios from post-processed simulations with the standard fixed boundary condition, as well as the strong-damping condition.

Mass can be better conserved within the domain by strongly damping vθ to zero in the uppermost and lowermost regions of the simulation domain (see also Chrenko & Nesvorný 2020, who damped vθ to an azimuthal average). However, this would inevitably lead to wave reflection, which could affect the development of radiation-induced spirals. To quantify this effect, we run a test where we take our fiducial low-resolution simulation for a Saturn-mass planet at 1000 orbits, institute an upper wave-damping boundary with an aggressive damping time tdamp = 5 × 10−3 orbits, and run it for another 10 orbits—enough to see changes to the spiral arms.

Figures C.1 and C.2 are analogous to Figs. 4 and 5 but one with the simulation at 1000 orbits with fixed boundaries, and one after 10 more orbits with the wave-damping zone implemented. The spiral is qualitatively similar, but qualitatively somewhat stronger, when reflective boundaries are used. An analogous test with the polar boundaries extended to θ = ±0.6 above and below the midplane, as well as another with the fiducial θ-extent, but where reflective polar boundaries are used from the start — neither shown here — show similar results. This demonstrates the robustness of our conclusions with respect to numerical prescription, and clears the way to use reflecting boundary conditions to model upper-disk and midplane dynamics simultaneously.

References

  1. Asensio-Torres, R., Henning, T., Cantalloube, F., et al. 2021, A&A, 652, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bae, J., & Zhu, Z. 2018, ApJ, 859, 118 [Google Scholar]
  3. Bae, J., Teague, R., & Zhu, Z. 2021, ApJ, 912, 56 [NASA ADS] [CrossRef] [Google Scholar]
  4. Biddle, L. I., Bowler, B. P., Zhou, Y., Franson, K., & Zhang, Z. 2024, AJ, 167, 172 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Boehler, Y., Ricci, L., Weaver, E., et al. 2018, ApJ, 853, 162 [Google Scholar]
  7. Burke, J. R., & Hollenbach, D. J. 1983, ApJ, 265, 223 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chrenko, O., & Nesvorný, D. 2020, A&A, 642, A219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Cuello, N., Montesinos, M., Stammler, S. M., Louvet, F., & Cuadra, J. 2019, A&A, 622, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cugno, G., Leisenring, J., Wagner, K. R., et al. 2024, AJ, 167, 182 [NASA ADS] [CrossRef] [Google Scholar]
  11. Currie, T., Lawson, K., Schneider, G., et al. 2022, Nat. Astron., 6, 751 [NASA ADS] [CrossRef] [Google Scholar]
  12. Desidera, S., Chauvin, G., Bonavita, M., et al. 2021, A&A, 651, A70 [EDP Sciences] [Google Scholar]
  13. Dong, R., & Fung, J. 2017, ApJ, 835, 38 [Google Scholar]
  14. Dong, R., Fung, J., & Chiang, E. 2016, ApJ, 826, 75 [Google Scholar]
  15. Dong, R., Liu, S.-y., Eisner, J., et al. 2018, ApJ, 860, 124 [Google Scholar]
  16. Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
  17. Follette, K. B., Close, L. M., Males, J. R., et al. 2023, AJ, 165, 225 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fung, J., & Artymowicz, P. 2014, ApJ, 790, 78 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fung, J., & Dong, R. 2015, ApJ, 815, L21 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fung, J., Shi, J.-M., & Chiang, E. 2014, ApJ, 782, 88 [NASA ADS] [CrossRef] [Google Scholar]
  21. Goldreich, P., & Sari, R. 2003, ApJ, 585, 1024 [Google Scholar]
  22. Goldreich, P., & Tremaine, S. 1978, ApJ, 222, 850 [NASA ADS] [CrossRef] [Google Scholar]
  23. Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [Google Scholar]
  24. Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [Google Scholar]
  25. Grady, C. A., Muto, T., Hashimoto, J., et al. 2013, ApJ, 762, 48 [Google Scholar]
  26. Haffert, S. Y., Bohn, A. J., de Boer, J., et al. 2019, Nat. Astron., 3, 749 [Google Scholar]
  27. Hammer, M., Kratter, K. M., & Lin, M.-K. 2017, MNRAS, 466, 3533 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hammond, I., Christiaens, V., Price, D. J., et al. 2023, MNRAS, 522, L51 [NASA ADS] [CrossRef] [Google Scholar]
  29. Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [Google Scholar]
  30. Huang, P., Dong, R., Li, H., Li, S., & Ji, J. 2019, ApJ, 883, L39 [NASA ADS] [CrossRef] [Google Scholar]
  31. Jiang, Y.-F. 2021, ApJS, 253, 49 [NASA ADS] [CrossRef] [Google Scholar]
  32. Keppler, M., Benisty, M., Müller, A., et al. 2018, A&A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Kley, W., & Dirksen, G. 2006, A&A, 447, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Krapp, L., Garrido-Deutelmoser, J., Benítez-Llambay, P., & Kratter, K. M. 2024, ApJS, 271, 7 [NASA ADS] [CrossRef] [Google Scholar]
  35. Krieger, A., & Wolf, S. 2020, A&A, 635, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Krieger, A., & Wolf, S. 2022, A&A, 662, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Levermore, C. D. 1984, J. Quant. Spec. Radiat. Transf., 31, 149 [NASA ADS] [CrossRef] [Google Scholar]
  38. Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
  40. Melon Fuksman, J. D., & Mignone, A. 2019, ApJS, 242, 20 [NASA ADS] [CrossRef] [Google Scholar]
  41. Melon Fuksman, J. D., Klahr, H., Flock, M., & Mignone, A. 2021, ApJ, 906, 78 [NASA ADS] [CrossRef] [Google Scholar]
  42. Melon Fuksman, J. D., Flock, M., & Klahr, H. 2024, A&A, 682, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
  44. Montesinos, M., & Cuello, N. 2018, MNRAS, 475, L35 [NASA ADS] [CrossRef] [Google Scholar]
  45. Montesinos, M., Perez, S., Casassus, S., et al. 2016, ApJ, 823, L8 [Google Scholar]
  46. Muley, D., Melon Fuksman, J. D., & Klahr, H. 2023, A&A, 678, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Muley, D., Melon Fuksman, J. D., & Klahr, H. 2024, A&A, 687, A213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Müller, A., Keppler, M., Henning, T., et al. 2018, A&A, 617, L2 [Google Scholar]
  49. Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [Google Scholar]
  50. Nealon, R., Price, D. J., & Pinte, C. 2020, MNRAS, 493, L143 [NASA ADS] [CrossRef] [Google Scholar]
  51. Qian, Y., & Wu, Y. 2024, AAS Journals (submitted) [arXiv:2407.09613] [Google Scholar]
  52. Ren, B. B., Xie, C., Benisty, M., et al. 2024, A&A, 681, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  54. Shuai, L., Ren, B. B., Dong, R., et al. 2022, ApJS, 263, 31 [NASA ADS] [CrossRef] [Google Scholar]
  55. Speedie, J., Booth, R. A., & Dong, R. 2022, ApJ, 930, 40 [NASA ADS] [CrossRef] [Google Scholar]
  56. Su, Z., & Bai, X.-N. 2024, AAS Journals (submitted) [arXiv:2407.12659] [Google Scholar]
  57. van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2016, A&A, 585, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. van der Marel, N., Birnstiel, T., Garufi, A., et al. 2021, AJ, 161, 33 [Google Scholar]
  59. Wagner, K., Stone, J. M., Spalding, E., et al. 2019, ApJ, 882, 20 [Google Scholar]
  60. Wagner, K., Leisenring, J., Cugno, G., et al. 2024, AJ, 167, 181 [NASA ADS] [CrossRef] [Google Scholar]
  61. Wu, Y., & Lithwick, Y. 2021, ApJ, 923, 123 [NASA ADS] [CrossRef] [Google Scholar]
  62. Zhang, M., Huang, P., & Dong, R. 2024, ApJ, 961, 86 [NASA ADS] [CrossRef] [Google Scholar]
  63. Zhu, Z., Dong, R., Stone, J. M., & Rafikov, R. R. 2015, ApJ, 813, 88 [Google Scholar]

All Tables

Table 1

Key simulation parameters.

In the text

All Figures

thumbnail Fig. 1

Initial conditions for gas density ρ (above), and the dust and gas temperatures Td and T𝑔 (below), which are initially equal. The contours for normalized cooling timescales from gas-grain collision (βdg) are plotted above and those from radiation (βrad) below, with white lines. The figure is exactly reproduced from Muley et al. (2024).
In the text
thumbnail Fig. 2

Azimuthal profiles of various quantities at a fiducial radius of r = 60 au = 1.5 rp, and at an altitude of θ = 0.2 rad above the midplane in our Mp = 3 × 10−4M⊙ simulations. In the 3T case, azimuthal asymmetries of even a few percent in disk illumination that might be induced by the RWI, and are visible in the Td profile lead to strong nonaxisymmetry in ρ, Tg, and the velocity components.
In the text
thumbnail Fig. 3

Gas density ρ at t = 1010 orbits (1000 orbits at the fiducial resolution, 10 at the doubled resolution used in Muley et al. 2024) with respect to the initial condition ρ0 for our simulations with a Saturn-mass planet. The green ellipse indicates the planetary Hill radius. With the 3T scheme, the disk atmosphere shows a clear development of m = 2 spiral arms, which are absent in the β-cooling simulations. The white bands at the interior and exterior of the radiative simulation are caused by wave-damping to the initial condition.
In the text
thumbnail Fig. 4

Mock H-band (λH = 1.62 µm) total intensity for the disks we simulated, including an inverse-square correction factor. We assumed that the disk is located at a line-of-sight distance dr = 100 pc with a face-on orientation (id = 0°), and convolved the raw image with a Gaussian of FWHM = 0.06 arcsec to mimic the effects of finite telescope resolution. The differences between the radiative and non-radiative cases are clearly visible.
In the text
thumbnail Fig. 5

H-band intensity in all of our simulations, taken at fiducial radii rinner,cut = 30 au and router,cut = 60 au, and normalized to the azimuthal average. The 3T simulations show a clear m = 2 spiral with a peak-to-trough intensity ratio ~4 in the outer disk and ~ 1.2–1.5 in the inner disk. By contrast, the β-cooling simulations show negligible asymmetry in the outer disk, alongside asymmetries of ~ 1.1–1.5 in the inner disk caused by inner Lindblad spirals.
In the text
thumbnail Fig. A.1

θ-component of vorticity at θ = 0.2, with respect to the initial condition, in units of the planet’s orbital frequency Ωp. Between 200 and 250 orbits, the vorticity profile is largely unchanged in the β-cooling simulations, but deviates strongly in the 3T case as radiation couples to the asymmetries generated by disk-planet interaction.
In the text
thumbnail Fig. B.1

Density perturbation in special β-cooling simulations where the planet is removed, and for which the temperature profile in Fig. 1 is multiplied by the azimuthal perturbation factor 𝒲T(ϕ, t) (Eq. B.1). The corotation radius of the temperature profile, equal to the planet radius in the main text, is plotted as a dotted vertical line. Note that the density scale has a much smaller range than in Fig. 3 in the main text.
In the text
thumbnail Fig. C.1

Mock H-band images for different wave-damping prescriptions at the boundary.
In the text
thumbnail Fig. C.2

H-band contrast ratios from post-processed simulations with the standard fixed boundary condition, as well as the strong-damping condition.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.