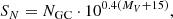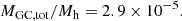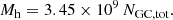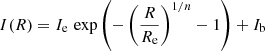EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A339 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A339
Number of page(s) 20
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202449617
Published online 22 October 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Ultra-diffuse galaxies (UDGs) are a sub-class of dwarf galaxies characterised by an exceptionally low surface brightness (LSB) combined with an unusually large physical size. Although a strict numerical threshold for their central surface brightness (μ0) and effective radius (Re) was introduced by van Dokkum et al. (2015) (μ0, g = 24 − 26 mag arcsec−2 and Re > 1.5 kpc), the classification of a LSB galaxy as a UDG is somewhat arbitrary as there is no clear ‘break’ in their physical properties (Venhola et al. 2017, 2022; Lim et al. 2020; Marleau et al. 2021), making their definition somewhat variable in different studies and/or their context with other galaxies. One of the most intriguing aspects of UDGs is their exceptional large size relative to their low luminosity. While the Milky Way has an effective radius of Re = 3.6 kpc (Bovy & Rix 2013; van Dokkum et al. 2015) and a surface brightness μ0, g, MWdisk ≃ 19.8 mag arcsec−2, UDGs can exhibit effective radii that rival or even exceed the effective radius of the Milky Way galaxy, while possessing ∼1/1000 of its stars. However, given that the effective radius depends on how the light is concentrated in these galaxies, alternative size measurement methods have been used to estimate the extent of UDGs, yielding values that are ten times smaller than Milky Way-like galaxies (Trujillo et al. 2020; Chamba et al. 2020). Although we can find some examples of UDGs in our local neighbourhood, namely Andromeda XIX (McConnachie et al. 2008), M81-F8D1 (Caldwell et al. 1998), and Antlia II (Torrealba et al. 2019), the majority of UDGs detected until now are found at larger distances and across a wide range of environments.

Due to the large expense in telescope time necessary to scan large regions of the sky for deep imaging surveys, the overwhelming majority of research into the photometric properties of UDGs was originally limited to select nearby galaxy groups (e.g., M101: Merritt et al. 2016; Bennet et al. 2017; nearby groups: Greco et al. 2018; three nearby isolated groups: Román & Trujillo 2017; NGC 1052: van Dokkum et al. 2018; NGC5846: Forbes et al. 2019), and galaxy clusters (e.g., Coma: van Dokkum et al. 2015; Yagi et al. 2016; Virgo: Mihos et al. 2015; Lim et al. 2020; Perseus: Wittmann et al. 2017; Gannon et al. 2022; Marleau et al. 2024; Fornax: Venhola et al. 2017, 2022; Hydra I: La Marca et al. 2022; six Hubble Frontier Fields galaxy clusters: Janssens et al. 2019), where a high density of low-surface-brightness galaxies could be found. However, since then, other optical imaging surveys have contributed to filling in the gap in our knowledge of properties of UDGs across a range of lower density environments, such as the MATLAS (Mass Assembly of early-Type GaLAxies with their fine Structures) survey (Marleau et al. 2021), the SDSS Stripe 82 (Barbosa et al. 2020), isolated spiral and early-type spiral galaxies (Crnojević et al. 2014; Greco et al. 2018; Müller et al. 2018; For et al. 2019; Román et al. 2019), and other wide-area imaging surveys (DESI Legacy Imaging Survey: Zaritsky et al. 2019, 2021, 2022; Dark Energy Survey: Tanoglidis et al. 2021; GAMA survey Prole et al. 2021; Hyper Suprime-Cam Survey: Greene et al. 2022). Complementary to optical surveys, neutral hydrogen (HI) blind surveys (e.g., Du et al. 2015 using ALFALFA+SDSS, Leisman et al. 2017 using ALFALFA+SDSS,WIYN, Marleau et al. 2021 using WRST+ALFALFA) have established the existence of a sub-population of HI-bearing UDGs in different environments.

As the number of studies identifying UDGs in a variety of environments continues to grow, a more complete determination of their formation and evolution scenario(s) has begun to emerge. One prominent formation scenario suggests that UDGs could be understood as ‘failed galaxies’ (van Dokkum et al. 2015; Peng & Lim 2016). These galaxies would start out just like normal galaxies but would suffer from a sudden halt in star formation (SF) at early cosmic time (z > 2). Early quenching in these ‘underdeveloped’ galaxies could be due to strong tidal forces and interactions within the intracluster medium during an early infall into a dense cluster environment (Yozin & Bekki 2015; Tremmel et al. 2020) or an early, violent, and short-lived star formation episode (Danieli et al. 2022). This violent star-forming episode would also create many GCs which would explain the high number of GCs associated with some UDGs (e.g. MATLAS-2019, Müller et al. 2021; Danieli et al. 2022). Another prominent formation scenario suggests that UDGs could be ‘puffed-up dwarfs’ (Amorisco & Loeb 2016; Burkert 2017; Di Cintio et al. 2017; Chan et al. 2018; Jiang et al. 2019). In this scenario, dwarf galaxies may have undergone tidal stripping and heating or mergers (Carleton et al. 2019; Wright et al. 2021) that would have led to an increase in their effective radii. Alternatively, intrinsic processes such as high halo spins (Amorisco & Loeb 2016; Rong et al. 2017; Amorisco 2018; Benavides et al. 2023) or strong star formation-driven outflows capable of quenching star formation in the galaxies and leading to the expansion and redistribution of the remaining stars to larger radii (Di Cintio et al. 2017; Chan et al. 2018) could form UDGs. In this scenario, gas would remain in the UDGs and hence would explain the blue colours of some UDGs (Román & Trujillo 2017; Marleau et al. 2021) but not necessarily red isolated UDGs. A possible explanation for those would be that they originate as a result of backsplash orbits (Benavides et al. 2021). Finally, another possible scenario for UDG formation is that they could have formed from gas expelled from a massive galaxy after an interaction, becoming tidal UDGs (Duc et al. 2014; Marleau et al. 2021). Tidal UDGs would be outliers in (located above) the mass-metallicity relation (MZR) (Duc et al. 2014) and devoid of dark matter (Lelli et al. 2015). The wide range of properties of UDGs, as described below, could also indicate that UDGs form via multiple pathways (Ferré-Mateu et al. 2018; Lim et al. 2018; Marleau et al. 2021; Toloba et al. 2023).

In terms of their stellar populations, UDGs range in age (∼3–11 Gyr), metallicity ([Z/H] ∼ −1.5 to −0.4), and alpha-element abundance ([α/Fe]≳0.3 dex) (Gu et al. 2018; Ferré-Mateu et al. 2018; Ruiz-Lara et al. 2018; Chilingarian et al. 2019; Fensch et al. 2019; Martín-Navarro et al. 2019; Müller et al. 2020; Rong et al. 2020; Villaume et al. 2022; Heesters et al. 2023). Their stellar populations are generally similar to those of dwarf elliptical galaxies, but some have stellar populations similar to GCs (old age) and dwarf spheroidal galaxies (low metallicity). Also, UDGs found in high-density environments appear to have formed earlier and faster (according to their high [α/Fe] values) than those found in low-density environments (which tend to have lower [α/Fe] values and be younger). The analysis of UDGs using SED fitting has revealed that GC-poor UDGs are more metal-rich, on average younger and more elongated than their GC-rich counterparts (Buzzo et al. 2022, 2024). In these works, the GC richness classification is based directly on GC numbers and the GC-rich UDGs are defined, fairly subjectively, as those with 20 or more GCs. This definition can vary between different works. The GC-poor UDGs have properties similar to those of dwarfs and are consistent with the dwarf MZR, which is consistent with the ‘puffed-up dwarf’ scenario. On the other hand, GC-rich UDGs are located below the dwarf MZR and they are therefore more consistent with early-quenching and, hence, the ‘failed galaxies’ scenario. However, spectral analysis does not show this trend and indicates no GC dependence (Ferré-Mateu et al. 2023). In agreement with the stripped or tidal formation scenario, some UDGs are found to be positive outliers in the MZR (Buzzo et al. 2024).

With respect to their globular cluster population, some studies have found that UDGs tend to host two to three times as many GCs as dwarf galaxies of the same stellar mass (Lim et al. 2018, 2020), whereas others have reported no significant difference in GC numbers between the two types of galaxies (Amorisco et al. 2018; Prole et al. 2019; Marleau et al. 2021). In general, the UDGs have a wide range of GC counts, from GC-poor to GC-rich (e.g. MATLAS-2019) (Lim et al. 2018, 2020; Gannon et al. 2021; Marleau et al. 2021; Müller et al. 2021). Some studies have shown that UDGs in denser environments can have higher specific frequencies (Peng et al. 2008; Mistani et al. 2016; Lim et al. 2018). Other GC properties, such as their colour, luminosity function (LF), and radial distribution (measured in term of the ratio of the GC half-number radius Re, GC to the UDG effective radius Re) seem to match those of dwarf galaxies (Lim et al. 2024). In terms of their radial distribution, UDGs are found to have Re, GC/Re, gal ∼ 0.7 − 1.7 (Peng & Lim 2016; Müller et al. 2021; Montes et al. 2021; Saifollahi et al. 2021, 2022; Danieli et al. 2022; Janssens et al. 2022), compared to dwarfs in local groups and in the Virgo cluster with 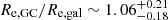R e , GC / R e , gal ∼ 1 . 06 − 0.18 + 0.21 $ R_{\mathrm{e,GC}}/R_{\mathrm{e,gal}} \sim 1.06^{+0.21}_{-0.18} $ and 1 . 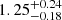25 − 0.18 + 0.24 $ 1.25^{+0.24}_{-0.18} $, respectively (Carlsten et al. 2022). The total mass locked up in GCs compared to the stars are somewhat higher for the UDGs, with MGC/M* up to ∼15%, compared to Virgo dwarfs with MGC/M* up to ∼5%. The GC colours are dominantly blue (0.5 < (mF606W − F814W)0 < 0.9 mag), metal-poor ([Fe/H] ∼ −1.8 to −1.2), and old (∼7.8 − 11.6 Gyr) (Fensch et al. 2019; Müller et al. 2020, 2021). The UDG GC luminosity function (GCLF) is similar to what is found for GCs in dwarf galaxies (Beasley & Trujillo 2016; Peng & Lim 2016; van Dokkum et al. 2017; Amorisco et al. 2018; Prole et al. 2019; Lim et al. 2020; Somalwar et al. 2020; Müller et al. 2021; Saifollahi et al. 2021), with the exception of NGC 1052-DF2 and -DF4 which appear to have GCs that are too bright (van Dokkum et al. 2018). Some studies have reported that HI-rich field UDGs appear to host remarkably few GCs, with many having no candidate GCs (Jones et al. 2023). For the UDGs in the Perseus cluster, GC-rich UDGs appear to have higher velocity dispersions than GC-poor UDGs, resulting in GC-rich UDGs having higher halo masses than GC-poor UDGs (Gannon et al. 2022).

The number of GCs can provide a test to discriminate between different UDG formation scenarios (Saifollahi et al. 2022). For example, if UDGs are more massive galaxies that essentially faded due to a lack of subsequent star formation (the ‘failed galaxies’ model), the number of GCs per stellar mass, NGC/M*, is expected to be larger than that of traditional dwarfs. If UDGs, however, have always been less massive dwarf galaxies (the ‘puffed-up dwarf’ model), the predictions vary depending on the physical mechanisms driving the larger radii. If the UDG formed via tidal interactions, NGC/M* is expected to be comparable to that of other dwarf galaxies, since the LSB is due to the dynamical expansion of the galaxy rather than a lower star formation efficiency, assuming that no GCs are lost during the interaction. For high spins, the expected NGC/M* value is unclear; the stars are more spread out and the star formation efficiency (likely) drops, it is uncertain how this impacts the GC formation. Similarly, the impact of mergers is not well constrained; NGC/M* might be lower than in galaxies with no early-time major mergers if GCs form as a consequence of the merger, but if GCs form only at high redshift, then NGC/M* might be larger in UDGs. Interestingly, if a UDG was formed as a result of stellar feedback from intense star formation, the NGC is not expected to change, but the radial distribution, traced by measuring Re, GC/Re, gal, is likely to. The spatial distribution of GC systems can also provide a way to decipher the galaxy mass and assembly history of the host galaxy, as cosmological simulations are now suggesting (Kruijssen 2015; Renaud et al. 2017; Li & Gnedin 2019; Reina-Campos et al. 2022).

In this paper, we report on the analysis of data taken with the Hubble Space Telescope (HST) of the GC systems of a sample of 74 Mass Assembly of early-Type GaLAxies with their fine Structures (MATLAS) UDGs, selected with a cut of ⟨μe, g⟩> 23.3 mag arcsec−2 and Re > 1.0 kpc, tracing the GCLF two magnitudes below its peak. The MATLAS survey (Duc et al. 2015), reaching a local surface brightness depth of μg ∼ 28.5 − 29 mag arcsec−2, contains a sample of 2210 dwarf galaxies (Habas et al. 2020). Of these, a total of 11% (248 dwarfs) satisfy the selection cut above. In Section 2, we describe the observing strategy and data reduction. The detection of GCs, the counts, background subtraction and completeness correction are described in Section 3, along with the calculation of the specific frequency and halo mass. The spatial distribution is explored in detail in Section 4. In Section 5, our quantitative determination of the key parameters driving the GC count is described. Finally, in Section 6, we summarise our results.

2. Data

2.1. Observations

Our HST images were each obtained through a single orbit in the Cycle 28 and 29 SNAPSHOT programs GO-16257 and GO-16711 (PI: Marleau). We present the observations of 74 MATLAS UDGs selected with a cut at ⟨μe, g⟩> 23.3 mag arcsec−2 and Re > 1.0 kpc, including the data from the Cycle 27 program GO-16082 for MATLAS-2019 (Müller et al. 2021), with the HST Advanced Camera for Surveys (ACS) in both the F606W and F814W filters (see Figure 1). The galaxies were placed at the centre of one of the charge coupled devices (CCDs) to optimise a uniform coverage map of the galaxy and maximise a suitable background sample. Two dithered images (separated by 0.5″) of 412 s each (total exposure time 824 s) were taken in each filter. We used the final, reduced CTE-corrected (Charge Transfer Efficiency corrected) .drc.fits images produced by the standard pipeline that have a spatial sampling of 0.05 arcsec/pixel and a point spread function (PSF) full width half maximum (FWHM) of ∼0.1 arcsec. The list of our HST targets is given in Table A.1.

thumbnail Fig. 1.

F606W+F814W colour images of the 74 MATLAS UDGs, selected with a cut of ⟨μe, g⟩> 23.3 mag arcsec−2 and Re > 1.0 kpc, observed with HST/ACS (top, left to bottom, right) shown by decreasing surface brightness. Due to their low surface brightness, the galaxies in the last rows are difficult to see in the images. The names and distances of the UDGs are displayed on the images. The size of each cutout is 1.3′×1.3′.

Magnitudes were computed using the VEGAmag zeropoints provided by the ACS online documentation1. Aperture corrections were applied according to the ACS documentation2. The magnitudes were corrected for extinction using python ned_extinction_calc3.

2.2. Sample properties

The photometric and structural properties of our HST targets were taken from Poulain et al. (2021). They have assumed or confirmed distances ranging from 12.3 to 45.8 Mpc, g-band absolute magnitude between −15.32 and −11.44, effective radius, Re, in the range of 1.07–3.46 kpc, and central[average] surface brightness ranging from 22.54[23.3] to 26.84[27.6] mag arcsec−2 in the g-band (Poulain et al. 2021, 2022; Heesters et al. 2023). Of the 74 UDGs in our HST sample, a total of 38 fall under the selection criteria from van Dokkum et al. (2015); namely, μ0, g = 24 − 26 mag arcsec−2 and Re > 1.5 kpc (hereafter referred to as “UDGvD15”; Marleau et al. 2021). The remaining 36 are slightly below this selection cut in surface brightness and effective radius, as can be seen in Figure 2. The full UDG sample contains 40 nucleated and 34 non-nucleated UDGs.

thumbnail Fig. 2.

Our sample of 74 MATLAS UDGs, selected with a cut of ⟨μe, g⟩> 23.3 mag arcsec−2 and Re > 1.0 kpc observed with HST (black empty circles), overlaid on the MATLAS dwarfs of Habas et al. (2020) (empty pale blue circles) and UDGs of Marleau et al. (2021) (filled blue circles). Also shown are the dwarfs identified in the Euclid Early Release Observations of the Perseus cluster (grey diamonds; Marleau et al. 2024), Next Generation Virgo Cluster Survey (grey triangles; Ferrarese et al. 2020) and Next Generation Fornax Survey (inverted grey triangles; Eigenthaler et al. 2018) images, as well as Local Group dwarfs (rotated left grey triangles; McConnachie 2012) and Local Volume (rotated right grey triangles; Carlsten et al. 2020). The UDGs found in the Coma (grey cross symbols; van Dokkum et al. 2015) and Virgo cluster (grey plus symbols; Lim et al. 2020) are shown separately. For comparison, we have also included ultra-faint dwarfs (UFDs; grey stars; Simon 2019) and massive ellipticals from the Carnegie-Irvine catalogue (grey large cross symbols; Ho et al. 2011).

3. Analysis

3.1. Detection

To optimise the detection of GCs both near and far from the centre of the UDG, the smooth light profile of the galaxy was first modelled and subtracted using the GALFIT algorithm (Peng et al. 2002). The detection of GCs was then performed on the galaxy-subtracted F814W image using sep.extract, the Source Extractor implementation in python (Bertin & Arnouts 1996), using a 3 sigma threshold and a minimum of 5 adjacent pixels. The detection was done on the full F814W image. The following cuts in size and ellipticity were applied: (1) a semi-major axis a < 30 pc, (transformed in pixels using the distance of the UDG; for instance, in the case of MATLAS-2019 with d = 20.3 Mpc, this corresponds to 6 pix), and (2) an ellipticity of (1 − b/a) < 0.37. The upper limit in size for the GCs was chosen based on the visual extent of the compact GCs around M 31 with half-light radii ∼3 − 5 pc (with maximum sizes of ∼8 arcsec or ∼30 pc at the assumed distance to M 31 of 784 kpc; Huxor et al. 2014).

Photometry was performed with sep.sum_circular with a fixed aperture of 3 pix in radius (background annulus 8 − 23 pix) in both the F814W and F606W images using the F814W image detections. GC candidates were then selected on the basis of their colour, magnitude and concentration index, Δm4 − 8, defined as the difference between 4-pixel and 8-pixel diameter aperture magnitudes in the F606W filter normalised so that point sources have a mean value of zero (Durrell et al. 2014).

The selection cut limits are shown in Figure 3 and were selected based on the measurements obtained for the spectroscopically confirmed GCs in MATLAS-2019 (Müller et al. 2021) and are consistent with the (mF606W − mF814W)0 colours of old (12 Gyr) GCs with metallicities −2.2 < [Fe/H] < 0.0 (Harris 2023), while also allowing for photometric uncertainties in our fainter GC candidates. They consist of a colour cut in colour of 0.5 < (mF606W − mF814W)0 < 1.2, a magnitude cut of −10.4 < (mF606W)0 < −5.1 (assuming a peak at MV = −7.3; Miller & Lotz 2007; Peng & Lim 2016; Lim et al. 2018), and a concentration cut of 0.1 < Δm4 − 8 < 0.5 for UDGs at d < 25 Mpc and −0.1 < Δm4 − 8 < 0.5 for those at larger distances. We did not extend our selection cut any further to the blue to avoid including young GC candidates, which do not offer reliable information about the properties of the galaxy halos, and to exclude star forming clumps. Note that the central compact source, which can either be a nuclear star cluster (NSC) or GC candidate, were included in this catalogue without a colour cut.

thumbnail Fig. 3.

Colour (left) and concentration index (right) cut of all GC detections (black open circles) and the GC detections within 2Re (blue circles), based on the spectroscopically confirmed GCs in MATLAS-2019 (red circles: Müller et al. 2021). The light red region highlights the selection cut we used for colour, 0.5 < (mF606W − F814W)0 < 1.2, and for the concentration index, 0.1 < Δm4 − 8 < 0.5, for galaxies with a distance ≤25 Mpc. For galaxies at larger distances, i.e., > 25 Mpc, the lower concentration index cut was extended to include the unresolved sources, highlighted by the light orange and light red regions, corresponding to a cut of −0.1 < Δm4 − 8 < 0.5.

As our sample of UDGs span a large range of distances, the concentration index was adjusted to include the unresolved GCs at distances greater than 25 Mpc (see Figure 4). The GC counts displayed in Figure 4 have been background- and completeness-corrected (see Section 3.2 below). The comparison between the GC counts measured excluding unresolved GCs and including unresolved GCs as a function of distance shows that below ∼25 Mpc, the GC counts are dominated by the marginally resolved sources whereas above ∼25 Mpc, the counts become dominated by the unresolved sources. At the distance of ∼25 Mpc, the resolution limit of our HST observations corresponds to a radial extent of ∼6 pc.

thumbnail Fig. 4.

Comparison between the GC counts (background and completeness corrected) measured excluding unresolved GCs (tan circles) and including unresolved GCs (red circles) as a function of distance. Below ∼25 Mpc, the GC counts are dominated by the marginally resolved sources (in tan circles) whereas above ∼25 Mpc, the counts become dominated by the unresolved sources (in red circles). Based on this comparison, we included unresolved GCs only at distances greater than 25 Mpc.

Following the arguments in Müller et al. (2021) and Lim et al. (2024), we adopted a radius of 2Re to determine the association of GCs and host UDGs, where Re was measured for each UDG. This was uniformly applied to all UDGs, to allow a direct comparison of the GC distribution in units of effective radius. The number of GCs within that radius is subsequently referred to as Ndet. The GC candidates beyond 2Re were used to determine the background contamination (Nbkg). We identified a total of 676 GC candidates associated with all 74 UDGs within this radius.

3.2. Background and completeness correction

Following the detection of the GCs, a background correction was applied. The number of sources per unit area was computed for the region outside 2Re within the ACS field of view (FoV) for each galaxy. This number was then scaled to the circular area of radius 2Re and removed from Ndet, resulting in a background corrected Ndet, bkg. As an example, Figure 5 shows the distribution of the background corrected Ndet, bkg for MATLAS-2019. To check the validity of our background estimates and compute the uncertainties on the background, the background correction was also computed by i) only including the GC candidates detected in the CCD without the UDG, and ii) by only including the GC candidates detected outside 2Re in the CCD containing the UDG. We find that the median difference between these two latter methods for all UDGs in our sample is only ∼0.04 counts (∼1% of the background value). The standard deviation of all three methods was then used to estimate the error on the background counts.

thumbnail Fig. 5.

GCLF as a function of absolute magnitude MF814W (bottom) and apparent magnitude (mF814W)0 (top) of the detected GCs within 2Re (blue), and the detections outside 2Re (grey) for the UDG MATLAS-2019, which has the largest number of GCs in our sample. The black points are for the raw count within 2Re and the red points show the GC count after background subtraction. The red solid line shows the Gaussian fit with peak absolute magnitude MV = −7.3 mag and a dispersion of 1 mag.

Finally, a completeness correction was applied by assuming a GCLF represented by a Gaussian with peak absolute magnitude MV = −7.3 mag and a dispersion of 1 mag (Miller & Lotz 2007; Peng & Lim 2016; Lim et al. 2018), and taking into account the completeness limit of each HST images. A correcting factor was then applied to the background corrected Ndet, bkg based on the part of the GCLF that is fainter than the observed limit, resulting in the quantity NGC.

After background subtraction and completeness correction, we calculate a total of 387 GCs associated with all 74 UDGs. The final NGC values for each of our sample galaxies are listed in Table A.1 and their distribution shown in Figure 6. We find that 21 UDGs (28%) have NGC values consistent with zero, with the tail of the distribution extending to our most GC-rich galaxy, MATLAS-2019, with NGC = 38. The majority of the sample (47 UDGs or 64%) are measured as having NGC < 3, while the remaining 36% host a GC system with NGC = 3 − 38. Our analysis reveals that the percentage of nucleated UDGs with a large number of GCs (14 UDGs or 35% have NGC ≥ 3) is similar to the one obtained for the whole sample4.

thumbnail Fig. 6.

Distribution of the number of GCs within 2Re for the 74 UDG sample (light grey), the 36 UDGvD15 as defined by van Dokkum et al. (2015) (pale indigo), and the 40 nucleated UDGs (bright coral). The majority of the sample (47 UDGs or 64%) are measured to have NGC < 3, while the remaining 36% is spread across a wider range of values (NGC = 3 − 38). A total of 21 UDGs (28%) have NGC values consistent with zero, with the tail of the distribution extending to our most GC-rich galaxy, MATLAS-2019, with NGC = 38. The percentage of nucleated UDGs with a large number of GCs (14 UDGs or 35% have NGC ≥ 3) is similar to the one for the whole sample.

MATLAS-2019 was the most GC-rich galaxy in the MATLAS dwarfs sample, based on CFHT and HST imaging (Marleau et al. 2021; Müller et al. 2021), and remains the most GC-rich galaxy based on the new sample of galaxies with HST data. With our larger GC population, we confirm the result previously reported in Müller et al. (2021), that MATLAS-2019 does not have an anomalous GCLF, as has been suggested for NGC 1052-DF2 and -DF4, which appear to have GCs that are too bright (van Dokkum et al. 2018). As we re-analysed MATLAS-2019, we compare our results with those of Müller et al. (2021) to check for consistency. For this UDG, we calculated the background and completeness corrected count to be NGC = 38 ± 7, consistent with NGC = 36 ± 6 from (Müller et al. 2021), using a similar method.

We examine how NGC varies as a function of the host galaxy stellar mass for our UDG sample. The results are displayed in Figure 7 along with the GC counts of massive early-type galaxies obtained from the HST ACS Fornax cluster survey (Liu et al. 2019). For dwarf galaxies with stellar masses below M* ∼ 2 × 108 M⊙, the number of GCs per UDG range from zero to 13, while the most massive UDGs with M* > 2 × 108 M⊙ (where a jump in NGC is observed) host, on average, a larger number of GCs (13 − 38 GCs). The galaxies that extend higher at each stellar mass in terms of GC count are mostly those belonging to the UDGvD15 sub-sample, except in the two more massive bins which contain no galaxies from that sub-sample.

thumbnail Fig. 7.

Total number of GCs for the UDG sample (black open circles) and those belonging to the UDGvD15 selection criteria (indigo open circles) as a function of the galaxy stellar mass. The number of GCs is shown to steadily increase with total stellar mass for the full sample of UDGs. The trend continues as the stellar mass increase to massive early-type galaxies, as can be seen using the GC counts obtained from the HST ACS Fornax cluster survey (Liu et al. 2019) (blue open circles). The galaxies in the UDGvD15 sample extend higher at each stellar mass than the galaxies in the non-UDGvD15 sample with the exception of the two most massive bins which contain no galaxies from the UDGvD15 sample.

The comparison between the previously measured GC counts around the MATLAS dwarfs in the CFHT images (Marleau et al. 2021) and those measured from the HST images after background and completeness corrections are shown in Figure 8. The GC detection in the ground-based CFHT images was done using either three (u − g, g − r, g − i), two (g − r, g − i), or one (g − r) colours, depending on the bands available. The GC colour regions and magnitude limits used for the GC selection in the CFHT data are described in Marleau et al. (2021). In particular, a g-band magnitude limit of 24.5, 24.0 and 23.5 was used for fields with three and more filters, two filters, and two filters when the seeing is worse than 1.1 arcsec, respectively.

thumbnail Fig. 8.

Comparison between the GC counts measured in the MATLAS CFHT images and those measured from the HST images after background and completeness corrections have been applied. The light coral, light blue and light green circles are for GC detection in the CFHT images using three (u − g, g − r, g − i), two (g − r, g − i), and one (g − r) colours, respectively. The size of the symbol decreases with increasing distance. We do not find any trend between how many colours were used to identify the GCs in the CFHT images and the agreement with the HST GC numbers. As expected, the scatter is large but there is a clear agreement in the general trend; namely, the UDGs with the largest number of GC candidates in the ground-based images remain the same UDGs that have the largest GC candidates in the higher resolution HST images. The large scatter at the low CFHT NGC values is most likely an effect of distance as the GC selection in the CFHT data was based on a fixed apparent magnitude cut.

For NGC > 2, there is a clear agreement in the general trend at increasing GC richness. However, for NGC ≤ 2, the scatter is large, mostly for low (near zero) CFHT NGC values. The large scatter at the low CFHT NGC values is most likely an effect of distance as the GC selection in the CFHT data was based on a fixed apparent magnitude cut. Therefore, targets at larger distances of ∼40 Mpc (smaller symbols in Figure 8), have a ∼1.5 mag brighter GC selection limit in the CFHT data than those at smaller distances of ∼20 Mpc (larger symbols in the same figure). Moreover, we expect to detect more GCs with increased spatial resolution within the higher surface brightness regions of the galaxy. This effect has been reported in the context NSCs, in which case a higher fraction of NSCs were identified in HST images as compared to lower resolution ground-based images (Côté et al. 2006; Poulain et al., in prep.).

We do not find any trend among how many colours were used to identify the GCs in the CFHT images and the agreement with the GC numbers measured with the HST data. This seems to indicate that a single colour is sufficient to identify the majority of GCs we have identified in the HST data, based on the methodology described above. However, at faint magnitudes (≳24 mag in the g-band), Milky Way halo main sequence stars can become a major contaminant when using a single colour selection (Ferrarese et al. 2012).

3.3. Specific frequency

The specific frequency, SN, for GCs is a measure used to quantify the abundance of GCs in a galaxy relative to its total luminosity. It provides insights into the efficiency of GC formation within a galaxy and the conditions and processes that prevailed during the early stages of galaxy formation and evolution. It is a useful tool for understanding the impact of galaxy interactions and mergers on cluster formation and investigating the interplay between GCs and the overall stellar content of a galaxy. Prior studies of the GC population of UDGs in the Coma and Virgo clusters (Lim et al. 2018, 2020) have claimed that the SN of these UDGs varies dramatically, with the mean SN being higher for UDGs than for classical dwarf galaxies.

The specific frequency SN (Harris & van den Bergh 1981) was computed using the formula:

S N = N GC · 10 0.4 ( M V + 15 ) , $$ \begin{aligned} S_N=N_{\rm GC}\cdot 10^{0.4(M_V+15)}, \end{aligned} $$(1)

where NGC is the total, background- and completeness-corrected number of GCs and MV is the host galaxy absolute magnitude in the V-band. As the number of GCs is a function of the brightness of the host galaxy, we show in Figure 10 the computed values of SN, as a function of the host galaxy absolute magnitude in the V-band, MV, taken from Poulain et al. (2021). The NGC values associated with each UDG are displayed in the top diagram of Figure 10 using the colour map. In particular, there are 7 UDGs (9%) with SN > 30 (MATLAS-405, 585, 658, 1413, 1534, 2019, 2184) and these galaxies are the ones making up the extended tail component of the GC count distribution displayed in Figure 65.

The specific frequency of nucleated UDGs are of special interest, because the NSC could be formed by merging GCs (Fahrion et al. 2021, 2022). However, we find no statistically significant difference between the GC populations of the nucleated and non-nucleated UDGs in our sample. As shown in Figure 9, the nucleated UDGs all have SN < 40, which is consistent with the majority of the MATLAS UDGs.

thumbnail Fig. 9.

Distribution of the specific frequency for the 74 UDG sample (light grey) and the 40 nucleated UDGs (bright coral). The nucleated UDGs are all found to have SN < 40, consistent with the majority of the UDGs. The highest SN values are attributed to UDGs that are not identified as nucleated.

In Figure 10, we compare the SN versus V-band magnitude relation for our UDG sample with the values measured for the UDGs in the Virgo cluster (Lim et al. 2020), the Perseus cluster (Marleau et al. 2024) and the Coma cluster (Lim et al. 2018). We calculate that the median value of our sample with specific frequencies greater than zero, SN = 12.7, is similar to the median value of 10.7 for UDGs in the Perseus cluster but less than the ones for the Virgo and Coma clusters (SN = 42.4 and SN = 30.6, respectively). Furthermore, the range of SN values (with SN > 0) of the MATLAS UDGs (SN = 0.5 − 91.0) extends beyond the Perseus SN values (SN = 1.0 − 60.1) but stays below the highest SN values measured for the Virgo and Coma UDGs (SN = 187.1 and SN = 348.3, respectively). The comparison of the range and median values of the samples are given in Table 1.

thumbnail Fig. 10.

Specific frequency SN as a function of absolute magnitude for the 74 UDGs in our sample. Top: UDGs with NGC > 0 are shown as squares with colours that scale with the value of the background and completeness corrected GC count, NGC. The UDGs with NGC ≤ 0 are shown as small black circles. Bottom: same as the top but now showing the local density parameter, log(ρ10), in the colour bar. In both plots, the specific frequency of the Coma cluster UDGs (Lim et al. 2018; light green symbols), Virgo cluster UDGs (Lim et al. 2020; light blue symbols), and Perseus cluster UDGs (Marleau et al. 2024; light red symbols) are also plotted. The light grey dashed lines correspond to SN with a constant NGC of 1, 10, 20, ..., 90, 100. The error bars are not shown since they are quite large and can be found in Table A.1. The inset plots display the SN values using a logarithmic scale.

Table 1.

Sample comparison of UDG specific frequencies (SN).

Previous studies have shown that low-mass galaxies in denser environments can have higher SN (Peng et al. 2008; Mistani et al. 2016; Lim et al. 2018). This may be due to the formation of more GCs relative to the galaxy luminosity, resulting from an increase in interactions and/or mergers at high redshift. It is also possible that in high density peaks at high redshift (proto-galaxy cluster environments), the SF rate density was higher, and consequently, so was the cluster formation efficiency. To explore this effect for our sample of UDGs, we use the local density parameter ρ10 described in Habas et al. (2020) for the MATLAS sample. The values of log(ρ10) for our UDGs are displayed in the bottom diagram of Figure 10 using the colour map and are in the range −2.86 < log(ρ10) < 0.24. Based on the definition in Cappellari et al. (2011) of log(ρ10) >  − 0.4 for galaxies in the Virgo cluster, we calculate that 69 out of the 74 UDGs (93%) fall in the lower density side of this cut. The five UDGs (MATLAS-1437, 1412, 1400, 1470, 1485) that are located in Virgo-like densities (−0.29 < log(ρ10) < 0.24) are from fields on the outskirts of the Virgo cluster. The UDGs with a high SN at the same given galaxy luminosity as the UDGs in the Virgo and Perseus clusters have low ρ10 values.

3.4. Halo mass

The total number of GCs in a given galaxy has been shown to correlate over six orders of magnitude with the modelled virial mass of the host dark matter halo (Harris et al. 2013; Beasley et al. 2016; Burkert & Forbes 2020). The scaling relation only appears to flatten for halos with virial masses smaller than 1010 M⊙ or NGC ≲ 3 (Burkert & Forbes 2020, see their Figure 1), although the predictive power of the relation is reduced below NGC ∼ 15 due to the increased scatter. There is observational evidence that the correlation holds at these low masses (Zaritsky 2022) but more studies are needed to understand the physical mechanism that drives this trend.

According to Harris et al. (2017), the virial mass Mh of a galaxy is connected to the total mass of the GC system MGC, tot via the following formula:

M GC , tot / M h = 2.9 × 10 − 5 . $$ \begin{aligned} M_{\rm GC,tot}/ M_{\rm h} = 2.9\times 10^{-5}. \end{aligned} $$(2)

As in Marleau et al. (2021), we assume a mean mass of a GC to be 1 × 105 M⊙ for dwarf galaxies (Harris et al. 2017) and then multiply that number by NGC to compute MGC, tot. Therefore:

M h = 3.45 × 10 9 N GC , tot . $$ \begin{aligned} M_{\rm h} = 3.45\times 10^9 \, N_{\rm GC,tot}. \end{aligned} $$(3)

The distribution of the halo masses for the UDGs in our sample are displayed in Figure 11. Based on the higher level of reliability of the scaling relation between halo mass and GC count for NGC > 3, only the 27 UDGs with NGC > 3 are used to produce the distribution shown in the figure. The values range from log(Mh)∼10.05 ± 0.43 to 11.11 ± 0.08 M⊙, with a median value of log(Mh)∼10.54 M⊙. Out of these UDGs, the 7 with the highest specific frequency, defined as SN > 30 (a cut that includes ∼25% of the UDGs), are found to have a range of halo masses, with some at the high end of the distribution. The distributions of halo-to-stellar mass ratios for the 25 out of the 74 UDGs with both NGC > 3 and stellar mass estimates from Habas et al. (2020) are also shown in Figure 11. The values range from Mh ∼ 176 ± 142 to 2542 ± 1430 M* with a median value at ∼472 M*, in agreement with the sample of 59 UDGs of Marleau et al. (2021). Therefore, our UDGs with NGC > 3 are consistent with having significant dark matter halos, although it is important to note that the uncertainties in the halo-to-stellar mass ratios can be substantial, as shown in the values quoted above. The UDGs with the largest SN values are all found to have a halo-to-stellar mass ratios above ∼500.

thumbnail Fig. 11.

Halo and stellar mass measurements for a subsample of our UDGs with NGC > 3. Top: distribution of the halo mass for the 27 out of the 74 UDGs with NGC > 3 (grey) and 6 out of the 27 UDGs with NGC > 3 and SN > 30 (orange). The UDGs with high SN are found to have a range of halo masses, with some at the high end of the distribution. Bottom: same as above but showing the distributions of halo-to-stellar mass ratios. The stellar masses are from Habas et al. (2020). The UDGs with the largest SN values are all found to have a halo-to-stellar mass ratios above ∼500.

4. Spatial distribution

The spatial distribution of GCs, namely, the arrangement and pattern of the GCs relative to their host galaxies, holds valuable insights into the formation history, dynamics, and interactions of both the GCs and their host galaxies (Kruijssen 2015; Renaud et al. 2017; Li & Gnedin 2019; Reina-Campos et al. 2022). Of particular interest are the radial distribution, (a)symmetries, and spatial anisotropy of the GC populations. By separating the GCs in the core and outer regions, the radial distribution may provide clues about the dynamical properties and formation mechanisms of the host and GC population; GCs in the outer regions can also provide information about the underlying dark matter distribution of the host galaxy. Asymmetric distributions, meanwhile, are indicators of recent interactions, mergers, or gravitational influences from nearby companions. Finally, the orientation and elongation of the spatial distribution are expected to trace the rotation and overall shape of the host galaxy, past tidal interactions, and/or indicate preferential directions from which GCs were acquired or formed.

4.1. Density maps

Given the large number of GCs (NGC > 10) for 12 UDGs in our HST sample, we were able to examine the two-dimensional distribution of GCs associated with the following galaxies: MATLAS-1938, 2019 and 799 (all with d < = 25 Mpc) and MATLAS-42, 585, 1413, 1779, 1616, 138, 401, 1332, and 1534 (all with d > 25 Mpc). An example of the projected distribution and density map for MATLAS-2019 is shown in Figure 12. For all 12 UDGs, the density maps are displayed in Figure B.1. The density maps for the 12 UDGs can be classified into the following types:

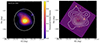thumbnail Fig. 12.

2D density map of the GC distribution for one of the 12 UDGs with NGC > 10, MATLAS-2019. Left: projected distribution (cyan dots) and density map (coloured map) of the GC candidates detected within 2Re (large white circle). Right: density map (white contours) of the GC candidates is overlaid on the HST F814W image of the UDG. The size of each image is 2.5Re × 2.5Re.

Symmetric. MATLAS-1938 and 1413 appear mostly symmetric in their GC and stellar light distributions. MATLAS-1413 has an extremely low surface brightness (μ0 = 26.21 mag/arcsec2) which makes it difficult to see in the figure.

Elongated. MATLAS-799, 1534, 1616 and 2019 have slightly elongated GC distributions. These match well the elongation of the stellar light distribution. MATLAS-1534 has a close (low-mass) neighbour with extended LSB features stretching in its direction and therefore is possibly part of an interacting system. MATLAS-2019 had a slight elongation in the GC distribution towards the massive early-type galaxy NGC 5838.

Off-centre. MATLAS-138 and 1332 have symmetric distribution that are off-centre. Both are classified as nucleated dwarf elliptical. In the case of MATLAS-138, the offset in the distribution is possibly due to the bright galaxy contaminant located to the north-west (NW) of the galaxy, in the opposite direction to the offset. MATLAS-1332 has a bright nucleus and shows a small offset in the GC distribution towards the north.

Asymmetric and off-centre. MATLAS-42, 401, 585 and 1779 show an asymmetric and off-centre GC distribution as compared to the stellar light. All galaxies have a disturbed stellar light morphology and except for MATLAS-585, are classified as dwarf irregulars. In all cases, the GC distribution follows the disturbed stellar distribution. MATLAS-42 is detected in HI (Marleau et al. 2021) and has a nearby dwarf companion (MATLAS-41) situated NW of the galaxy. The large FoV of the CFHT observations allows us to see that MATLAS-1779 displays tidal features extending in the NE and SW directions, i.e. in the direction of the massive early-type galaxy NGC 5493. The GC density clump located in the NE of the UDG follows this tidal feature. In general, a disturbed morphology does not appear to correlate with a high SN value.

It is important to point out that the completeness limits of the detected GCs could introduce some biases in the above results, particularly if the fainter (less massive) GCs have an intrinsically wider spatial distribution than brighter (more massive) GCs, as would be expected from tidal friction (Tremaine et al. 1975). In addition, for UDGs at d < 25 Mpc, the concentration cut might have missed some unresolved compact (with half-light radii ∼2 pc) GCs. This may also cause a bias as compact GCs are usually more spatially concentrated than the more extended clusters found in the outer halos of massive galaxies (Huxor et al. 2014).

4.2. Radial profiles

We characterised the radial profile of GCs in a UDG by counting the number of GCs per unit area in increasing annuli of multiples of 0.25 Re, gal, the effective radius of the galaxy. In order to quantify the radial extent of the GC distribution, the resulting counts were then fitted with a modified Sérsic function of the form:

I ( R ) = I e exp ( − ( R R e ) 1 / n − 1 ) + I b $$ \begin{aligned} I(R) = I_{\rm e} \, \exp \left(-\left(\frac{R}{R_{\rm e}}\right)^{1/n} - 1 \right) + I_{\rm b} \end{aligned} $$(4)

The fitted Sérsic function provides us with an estimate for both the size (Re, GC) and shape (Sérsic index n) of the bright GC system. Because we have to use the uncorrected counts, Ndet, to measure the radial profile of the galaxy, the counts include some contamination; so we included a constant background term, Ib, in our fits.

Using this method, we characterised the stacked radial profile for all GCs detected in the 74 galaxies in our sample (see Figure 13). For the 40 nucleated UDGs, the detection corresponding to the candidate nucleus (or nuclei, in the case of MATLAS-138 and 987) in each galaxy were removed. For the stacked data, we obtain a Sérsic index of 0.3 and Re, GC = 1.0 Re, gal. Based on the error bars associated with the data points, the small dip at small galactocentric radii (at the bin value 0.375 Re) appears to be real and could be related to the dynamical friction infall of massive GCs to create a nucleus/NSC (Tremaine et al. 1975). However, when plotting the stacked radial profile separately for the 40 nucleated and 34 non-nucleated UDGs in our sample, we find that the deficit is seen in both sub-samples, albeit within larger error bars. For the non-nucleated UDGs, the dip is followed by an overdensity of GCs in the next bin. Although the dynamical friction infall of GCs could still be a possible reason for the deficit for the nucleated UDGs, another mechanism must be producing the dip for the non-nucleated UDGs. The presence of a dark matter core and the stalling of GCs at the core radius could potentially be responsible for the observed dip in the radial distribution of GCs. This effect is due to the fact that GCs lose orbital energy through dynamical friction and can stall at the radius where the gravitational potential changes slope, which is typically at the core radius in cored dark matter profiles (Hernandez & Gilmore 1998; Goerdt et al. 2006; Read et al. 2006; Cole et al. 2012; Kaur & Sridhar 2018).

thumbnail Fig. 13.

Radial distributions of the stacked GCs for the UDGs in our HST sample. Top: radial distribution of the stacked GCs for all 74 UDGs in our sample. The black squares are for the GC counts within 2Re while the red squares are the counts outside (background). The counts are also shown with the detection corresponding to the candidate nucleus (or nuclei, in the case of MATLAS-138 and 987) in each galaxy removed (grey points and dotted line). The Sérsic fit is shown with the dash-dot blue line. Middle: same as the top but for the nucleated UDGs only. Bottom: same as the top but for the non-nucleated UDGs only.

For the 12 UDGs with a large number of GCs (NGC > 10), we were also able to characterise their individual GC radial profiles. The results are displayed in Figure C.1. Of these 12 UDGs, 5 galaxies are nucleated (MATLAS-138, 1332, 1616, 1779, 1938). For the UDG MATLAS-1938, which has a bright nucleus and a large number of centrally located GCs, the central (first) bin was not considered in order for the fit to converge. For the UDGs MATLAS-1534, 1616, and 1779, the third, second and second+third bin were not considered, respectively, in order for the fit to converge.

The deficit seen in the stacked radial profile of the 74 UDGs at galactocentric radius of ∼0.4 Re is also seen in the individual radial profiles of 6 UDGs (MATLAS-138, 799, 1332, 1413, 154, 1616). The galaxies MATLAS-42, 401, 585 and 1779 show an even stronger deficit towards the centre of their radial profiles. As can be seen in Figure B.1, the GC density maps of these galaxies are both off-centre and asymmetric, which leads to this deficit. These four galaxies have a disturbed stellar light morphology. The UDG MATLAS-42 is classified as a dwarf irregular and is detected in HI. It appears to have more than one stellar light component: a second component extends along the south-east (SE) direction and is well traced by the GC density extension in that direction. As mentioned above, this UDG has a close nearby dwarf companion, MATLAS-41, which is located NW of the UDG. The UDG MATLAS-401 is also classified as a dwarf irregular and its stellar light appears extended in the same direction as the GC distribution. When comparing the colours of its GCs with the colour distribution of the GCs in all of the UDGs, we do not find a significant bluer population of GCs in this galaxy. MATLAS-585 is classified as a dwarf elliptical but clearly displays a disturbed stellar light morphology and its GC distribution is offset from the centre. As discussed above, the UDG MATLAS-1779 is a nucleated dwarf elliptical which shows extended tidal features in the direction of the massive early-type galaxy NGC 5493. The stretch in the GC distribution along the NE and SW directions seen in the GC density map corroborates the GC deficit annulus region see in the radial profile of this UDG and the fact that this galaxy has suffered from tidal interactions.

4.3. Dependence on the host

We analysed the dependence of the effective radius of the GC system on three host parameters: the host total GC count, the host stellar mass, and the host effective radius. The results are displayed in Figure 14. The relations found for 118 early-type galaxies drawn from the Next Generation Virgo Cluster Survey (NGVS), MATLAS, and ACSVCS surveys from Lim et al. (2024) are shown for comparison.

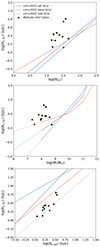thumbnail Fig. 14.

Dependence of the effective radius of the GC system for the 12 UDGs with NGC > 10 (black filled circles) on three host parameters: the total number of GCs associated with the UDG (top), the stellar mass of the host galaxy (middle), and the effective radius of the UDG (bottom). We find that the effective radius of the GC system matches the effective radius of the galaxy (grey dotted line), indicating that the radial distribution of GCs follows the galaxy light. For all plots, the best-fit relations of Lim et al. (2024) are shown by the grey line (all GCs), the blue line (blue GCs), and the red line (red GCs). The error bars are shown for both axes in all plots but are only visible when larger than the symbols.

The effective radii of the GC systems are measured to be 0.8 < Re, GC < 1.9Re, gal (or 1.3 < Re, GC < 6.3 kpc, given the distance to each galaxy), with a median value of 1.2Re, gal (2.5 kpc). The effective radii of the GC systems as a function of the host GC count and host stellar mass are above the relations of Lim et al. (2024) for more massive galaxies (log(M*) > 8.3). Furthermore, we do not find any obvious trend with host total GC count or host stellar mass.

When comparing the effective radius of the GC spatial distribution and the galaxy light profile, we find a simple one-to-one correspondence between them. This means that in our UDG sample, the GCs follow the galaxy light. The relation of Lim et al. (2024) comparing the effective radii of the GC systems to the effective radii of their host galaxies, which includes an environmental effect, sits mostly above our measurements.

Although the scatter is large, the measured Sérsic indices mostly fall in the range 0.01 < n < 0.5 with a median value of n ∼ 0.26, albeit with large measurement errors and sometimes imperfect fits. In comparison, the GC systems of Lim et al. (2024) have Sérsic indices in the range 1 < n < 4, reaching larger Sérsic index values, but this is to be expected as the galaxies in their sample contain more massive hosts and contain galaxies located in higher density environments.

5. Key host properties governing SN

The GC counts have been said to correlate with many host UDG properties, such as its colour, roundness and the local environment it inhabits. We explored the dependence of the GC count per unit galaxy luminosity, i.e. the specific frequency SN, on the host UDG properties in order to determine the key variable(s) governing this UDG property.

Figure 15 displays the behaviour of the specific frequency SN with host galaxy stellar mass, central surface brightness (μ0), local density (log(ρ10)), CFHT g − r colour, axis ratio, and effective radius (Re). As we are using the GC counts per unit host galaxy luminosity, we expect to find no trend with host galaxy stellar mass, as shown in the first plot. There is no clear trend with host galaxy central surface brightness and only weak trends with local density, colour and axis ratio. We note that the colour plot does not contain the same amount of data points as the other plots due to the fact that 10 out of the 74 UDGs do not have CFHT g − r colours. The rise towards blue colours is driven mainly by two blue UDGs (MATLAS-2021 and 2184). Contrary to expectations, we find that the SN values of the UDGs in the lowest density environments appear to be on average slightly higher than those in the highest density environments.

thumbnail Fig. 15.

Behaviour of the specific frequency, SN, as a function of key host properties. Top: dependence of SN on the host galaxy stellar mass, central surface brightness (μ0), and local density (log(ρ10)), shown from left to right. There are no obvious trends, except with ρ10, which shows an increase in specific frequency as the local density becomes less dense. Bottom: dependence of SN on host galaxy g − r colour, axis ratio, and effective radius (Re), shown from left to right. The bottom dependencies show the most prominent trends, with an increase in GC counts with bluer colours, increased roundness, and larger size. For all plots, the running average and standard deviation, computed using only non-zero values of NGC, is shown as the red dashed line and light red region, respectively.

The most prominent trend is seen with host galaxy size. The UDGs with effective radius greater than 2.5 kpc are MATLAS-42, 262, 1413 and 1779. Three of those (MATLAS-42, 262 and 1779 with Re = 3.46, 2.75 and 2.90 kpc, respectively) show signs of disturbed stellar light morphology (MATLAS-42) or tidal features (MATLAS-262 and 1779). This may hint at a connection between a UDG specific frequency and its recent merger and/or tidal interaction history which is accompanied by an increase in the measured effective radius of the UDG.

Although some trends are hinted from our current UDG dataset, more detailed studies of both the host UDGs and their GC populations are needed in order to fully probe and understand the key variable(s) governing SN.

6. Conclusions

Globular clusters (GCs) are key to constructing a complete picture of the formation and evolution of UDGs. Their presence and number reveal important details about the dark matter halos and masses of their host galaxy, and studying their properties can give us insights into past events that shaped these galaxies, helping us uncover their formation histories. Making use of the ACS instrument on the Hubble Space Telescope, we have obtained high resolution images in two filters, F606W and F814W, of 74 UDGs, selected from the MATLAS dwarf sample with cuts in surface brightness and effective radius of ⟨μe, g⟩> 23.3 mag arcsec−2 and Re > 1.0 kpc, respectively. With one of the largest UDG samples observed with HST, we have been able to study the link between GC counts and UDG properties as well as to construct 2D GC density maps. Some of our key findings are summarised below:

  • The number of GCs associated with each UDG in our sample ranges from 0 to 38(±7). The distribution of GC counts is characterised by a prominent peak at extremely small GCs (64% have NGC < 3), while the remaining galaxies populate an extended tail out to the maximum value. More massive UDGs host a larger number of GCs, on average; the UDGs with stellar masses below M* ∼ 2 × 108 M⊙ have GC counts between zero and 13, while the most massive UDGs with M* > 2 × 108 M⊙ have counts ranging from 13 to 38.

  • The distributions of estimated halo masses based on GC counts for the MATLAS UDGs with NGC > 3 range from Mh ∼ 176 ± 142 to 2542 ± 1430 M* with a median value at ∼472 M*. Therefore, our UDGs are consistent with having significant dark matter halos, although the uncertainties in the halo-to-stellar mass ratios can be substantial; therefore, they would require further confirmation.

  • We can also calculate the specific frequency of GCs per galaxy, which allows for a more accurate comparison between galaxies of different stellar masses or luminosities. We find SN values between 0.5 and 91.0 (for SN > 0), with a small population (9%) at high specific frequencies (arbitrarily defined as SN > 30). We note that the median value of our sample with specific frequencies greater than zero, SN = 12.7, is similar to the median value of 10.7 for UDGs in the Perseus cluster but less than the ones for the Virgo and Coma clusters (SN = 42.4 and SN = 30.6, respectively). Furthermore, the range of SN values (for SN > 0) of the MATLAS UDGs extends beyond the Perseus SN values (SN = 1.0 − 60.1) but stays below the highest SN values measured for the Virgo and Coma UDGs (SN = 187.1 and SN = 348.3, respectively). Contrary to expectations, we find that the SN values of the UDGs in the lowest density environments appear to be on average slightly higher than those in the highest density environments.

  • The GC populations of nucleated UDGs are of special interest, because the NSC could be formed by merging GCs. However, we find no statistically significant difference between the GC populations of the nucleated and non-nucleated UDGs in our sample. For both populations, the percentage of galaxies with NGC ≥ 3 is approximately 35%. The nucleated UDGs all have SN < 40, which is also consistent with the majority of the MATLAS UDGs.

  • We also examined density maps for the systems with large enough NGC counts to be meaningful. The 12 UDGs with NGC > 10 show a variety of distributions: symmetric, elongated, and off-centre, as well as asymmetric and off-centre. Both symmetric and elongated GC distributions match well with the stellar distribution. In general, a disturbed morphology does not appear to correlate with a high SN value. Two UDGs show an off-centre (with respect to the stellar light) symmetric density map. In one case, this is likely due to the bright galaxy contaminant located in the opposite direction to the offset. The UDGs with asymmetric and off-centre GC distributions show a disturbed stellar light morphology, with one galaxy exhibiting extended tidal features. The UDGs with disturbed GC density maps also show disturbed stellar light morphology, but no correlation is found with the specific frequency of the system.

  • The spatial distribution of the GCs around the host galaxy is measured for the first time for UDGs. It is derived by fitting a Sérsic profile and characterised by the effective radius of the GC system. For the 12 UDGs with GC counts greater than 10, we find that they are spatially distributed with Re, GC/Re, gal values between 0.8 and 1.9. For these UDGs, the GC radial distribution appears to follow the galaxy light profile. The stacked spatial distribution of the GCs belonging to all UDGs also gives a one-to-one relation with Re, GC/Re, gal = 1.0. For the same sample of 12 UDGs, the GC radial distribution does not seem to correlate with the GC count or the stellar mass of the galaxy.

  • A common feature of the individual radial profiles is a deficit of GCs at small galactocentric radii (∼0.4 Re), followed by an overdensity of GCs in the adjacent higher radial bin. As some of them are nucleated UDGs, this could be due to the dynamical friction infall of massive GCs to create a nucleus/NSC. However, as the stacked profile of the non-nucleated UDGs also show this deficit, the presence of a dark matter core and the stalling of GCs at the core radius could potentially be responsible for the observed dip in the radial distribution of GCs.

  • Based on a trending analysis of the UDG specific frequency SN with the host galaxy properties, we find a relation with host galaxy size, roundness, and g − r colour. These findings, in particular, hint at a connection between the UDG specific frequency and its recent merger and/or tidal interaction history (accompanied by an increase in the size of the UDG). We also find a trend of higher SN values with decreasing local density. This may be a sign that the UDGs in the lowest density environments have not undergone enough major mergers to disrupt their GC populations. However, these possible trends are hampered by large uncertainties due to low statistics, and therefore more data are needed to confirm them.

The imaging data of the Euclid Wide Survey (covering ∼14 000 deg2; Euclid Collaboration 2022) will soon give us access to a much larger statistical sample of UDGs with which we will be able to study in more details the results obtained with the 74 MATLAS UDGs. It will provide high-resolution imaging data for UDGs across a wide range of environments, from clusters to MATLAS-like environments, and even extending to lower local densities. A detailed study of the GC populations of the dwarf and UDGs identified in the Euclid Early Release Observations of the Perseus cluster (Marleau et al. 2024) is currently underway (Saifollahi et al., in prep.) and is already poised to more than double the available number of UDGs having a detailed study of their GC systems.

4

A slightly more elevated fraction (16/38 or 42%) of the most GC-rich UDGs with NGC = 3 − 38 are found to be from the UDGvD15 sample.

5

All of the UDGs in our sample with SN > 30 would be defined as UDGs even when using the stricter selection criteria defined by van Dokkum et al. (2015).

Acknowledgments

We would like to thank the referee for their valuable comments and suggestions, which have greatly improved the quality of this manuscript. This research is based on observations from the NASA/ESA Hubble Space Telescope obtained [from the Data Archive] at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. Support for Program number GO-16257 and GO-16711 was provided through a grant from the STScI under NASA contract NAS5-26555. O.M. is grateful to the Swiss National Science Foundation for financial support. P.R.D. gratefully acknowledges support from grant HST-GO-16257.002-A. S.P. acknowledges support from the Mid-career Researcher Program (No. RS-2023-00208957). S.L. acknowledges the support from the Sejong Science Fellowship Program by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2021R1C1C2006790). M.P. is supported by the Academy of Finland grant No. 347089. R.H. acknowledges funding from the Italian INAF Large Grant 12-2022. This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project No. 534. The work presented in this paper made use of GALFIT (Peng et al. 2002), sep (Barbary 2016), photutils (Bradley et al. 2020), astropy (Astropy Collaboration 2013), as well as Source Extractor (Bertin & Arnouts 1996).

References

  1. Amorisco, N. C. 2018, MNRAS, 475, L116 [NASA ADS] [CrossRef] [Google Scholar]
  2. Amorisco, N. C., & Loeb, A. 2016, MNRAS, 459, L51 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amorisco, N. C., Monachesi, A., Agnello, A., & White, S. D. M. 2018, MNRAS, 475, 4235 [NASA ADS] [CrossRef] [Google Scholar]
  4. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Barbary, K. 2016, J. Open Source Softw., 1, 58 [Google Scholar]
  6. Barbosa, C. E., Zaritsky, D., Donnerstein, R., et al. 2020, ApJS, 247, 46 [Google Scholar]
  7. Beasley, M. A., & Trujillo, I. 2016, ApJ, 830, 23 [CrossRef] [Google Scholar]
  8. Beasley, M. A., Romanowsky, A. J., Pota, V., et al. 2016, ApJ, 819, L20 [NASA ADS] [CrossRef] [Google Scholar]
  9. Benavides, J. A., Sales, L. V., Abadi, M. G., et al. 2021, Nat. Astron., 5, 1255 [NASA ADS] [CrossRef] [Google Scholar]
  10. Benavides, J. A., Sales, L. V., Abadi, M. G., et al. 2023, MNRAS, 522, 1033 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bennet, P., Sand, D. J., Crnojević, D., et al. 2017, ApJ, 850, 109 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bovy, J., & Rix, H.-W. 2013, ApJ, 779, 115 [Google Scholar]
  14. Bradley, L., Sipöcz, B., Robitaille, T., et al. 2020, https://doi.org/10.5281/zenodo.4044744 [Google Scholar]
  15. Burkert, A. 2017, ApJ, 838, 93 [NASA ADS] [CrossRef] [Google Scholar]
  16. Burkert, A., & Forbes, D. A. 2020, AJ, 159, 56 [Google Scholar]
  17. Buzzo, M. L., Forbes, D. A., Brodie, J. P., et al. 2022, MNRAS, 517, 2231 [NASA ADS] [CrossRef] [Google Scholar]
  18. Buzzo, M. L., Forbes, D. A., Jarrett, T. H., et al. 2024, MNRAS, 529, 3210 [NASA ADS] [CrossRef] [Google Scholar]
  19. Caldwell, N., Armandroff, T. E., Da Costa, G. S., & Seitzer, P. 1998, AJ, 115, 535 [NASA ADS] [CrossRef] [Google Scholar]
  20. Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [Google Scholar]
  21. Carleton, T., Errani, R., Cooper, M., et al. 2019, MNRAS, 485, 382 [NASA ADS] [CrossRef] [Google Scholar]
  22. Carlsten, S. G., Greco, J. P., Beaton, R. L., & Greene, J. E. 2020, ApJ, 891, 144 [NASA ADS] [CrossRef] [Google Scholar]
  23. Carlsten, S. G., Greene, J. E., Beaton, R. L., & Greco, J. P. 2022, ApJ, 927, 44 [NASA ADS] [CrossRef] [Google Scholar]
  24. Chamba, N., Trujillo, I., & Knapen, J. H. 2020, A&A, 633, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Chan, T. K., Kereš, D., Wetzel, A., et al. 2018, MNRAS, 478, 906 [NASA ADS] [CrossRef] [Google Scholar]
  26. Chilingarian, I. V., Afanasiev, A. V., Grishin, K. A., Fabricant, D., & Moran, S. 2019, ApJ, 884, 79 [NASA ADS] [CrossRef] [Google Scholar]
  27. Cole, D. R., Dehnen, W., Read, J. I., & Wilkinson, M. I. 2012, MNRAS, 426, 601 [Google Scholar]
  28. Côté, P., Piatek, S., Ferrarese, L., et al. 2006, ApJS, 165, 57 [Google Scholar]
  29. Crnojević, D., Sand, D. J., Caldwell, N., et al. 2014, ApJ, 795, L35 [CrossRef] [Google Scholar]
  30. Danieli, S., van Dokkum, P., Trujillo-Gomez, S., et al. 2022, ApJ, 927, L28 [NASA ADS] [CrossRef] [Google Scholar]
  31. Di Cintio, A., Brook, C. B., Dutton, A. A., et al. 2017, MNRAS, 466, L1 [NASA ADS] [CrossRef] [Google Scholar]
  32. Du, W., Wu, H., Lam, M. I., et al. 2015, AJ, 149, 199 [NASA ADS] [CrossRef] [Google Scholar]
  33. Duc, P.-A., Paudel, S., McDermid, R. M., et al. 2014, MNRAS, 440, 1458 [NASA ADS] [CrossRef] [Google Scholar]
  34. Duc, P.-A., Cuillandre, J.-C., Karabal, E., et al. 2015, MNRAS, 446, 120 [Google Scholar]
  35. Durrell, P. R., Côté, P., Peng, E. W., et al. 2014, ApJ, 794, 103 [NASA ADS] [CrossRef] [Google Scholar]
  36. Eigenthaler, P., Puzia, T. H., Taylor, M. A., et al. 2018, ApJ, 855, 142 [Google Scholar]
  37. Euclid Collaboration (Scaramella, R., et al.) 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Fahrion, K., Lyubenova, M., van de Ven, G., et al. 2021, A&A, 650, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Fahrion, K., Bulichi, T.-E., Hilker, M., et al. 2022, A&A, 667, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Fensch, J., van der Burg, R. F. J., Jeřábková, T., et al. 2019, A&A, 625, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Ferrarese, L., Côté, P., Cuillandre, J., et al. 2012, ApJS, 200, 4 [NASA ADS] [CrossRef] [Google Scholar]
  42. Ferrarese, L., Côté, P., MacArthur, L. A., et al. 2020, ApJ, 890, 128 [Google Scholar]
  43. Ferré-Mateu, A., Alabi, A., Forbes, D. A., et al. 2018, MNRAS, 479, 4891 [CrossRef] [Google Scholar]
  44. Ferré-Mateu, A., Gannon, J. S., Forbes, D. A., et al. 2023, MNRAS, 526, 4735 [CrossRef] [Google Scholar]
  45. For, B. Q., Staveley-Smith, L., Westmeier, T., et al. 2019, MNRAS, 489, 5723 [NASA ADS] [CrossRef] [Google Scholar]
  46. Forbes, D. A., Gannon, J., Couch, W. J., et al. 2019, A&A, 626, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Gannon, J. S., Dullo, B. T., Forbes, D. A., et al. 2021, MNRAS, 502, 3144 [Google Scholar]
  48. Gannon, J. S., Forbes, D. A., Romanowsky, A. J., et al. 2022, MNRAS, 510, 946 [Google Scholar]
  49. Goerdt, T., Moore, B., Read, J. I., Stadel, J., & Zemp, M. 2006, MNRAS, 368, 1073 [Google Scholar]
  50. Greco, J. P., Greene, J. E., Strauss, M. A., et al. 2018, ApJ, 857, 104 [NASA ADS] [CrossRef] [Google Scholar]
  51. Greene, J. E., Greco, J. P., Goulding, A. D., et al. 2022, ApJ, 933, 150 [NASA ADS] [CrossRef] [Google Scholar]
  52. Gu, M., Conroy, C., Law, D., et al. 2018, ApJ, 859, 37 [Google Scholar]
  53. Habas, R., Marleau, F. R., Duc, P.-A., et al. 2020, MNRAS, 491, 1901 [NASA ADS] [Google Scholar]
  54. Harris, W. E. 2023, ApJS, 265, 9 [CrossRef] [Google Scholar]
  55. Harris, W. E., & van den Bergh, S. 1981, AJ, 86, 1627 [NASA ADS] [CrossRef] [Google Scholar]
  56. Harris, W. E., Harris, G. L. H., & Alessi, M. 2013, ApJ, 772, 82 [Google Scholar]
  57. Harris, W. E., Blakeslee, J. P., & Harris, G. L. H. 2017, ApJ, 836, 67 [Google Scholar]
  58. Heesters, N., Müller, O., Marleau, F. R., et al. 2023, A&A, 676, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Hernandez, X., & Gilmore, G. 1998, MNRAS, 297, 517 [NASA ADS] [CrossRef] [Google Scholar]
  60. Ho, L. C., Li, Z.-Y., Barth, A. J., Seigar, M. S., & Peng, C. Y. 2011, ApJS, 197, 21 [Google Scholar]
  61. Huxor, A. P., Mackey, A. D., Ferguson, A. M. N., et al. 2014, MNRAS, 442, 2165 [Google Scholar]
  62. Janssens, S. R., Abraham, R., Brodie, J., Forbes, D. A., & Romanowsky, A. J. 2019, ApJ, 887, 92 [Google Scholar]
  63. Janssens, S. R., Romanowsky, A. J., Abraham, R., et al. 2022, MNRAS, 517, 858 [NASA ADS] [CrossRef] [Google Scholar]
  64. Jiang, F., Dekel, A., Freundlich, J., et al. 2019, MNRAS, 487, 5272 [CrossRef] [Google Scholar]
  65. Jones, M. G., Karunakaran, A., Bennet, P., et al. 2023, ApJ, 942, L5 [CrossRef] [Google Scholar]
  66. Kaur, K., & Sridhar, S. 2018, ApJ, 868, 134 [Google Scholar]
  67. Kruijssen, J. M. D. 2015, MNRAS, 454, 1658 [Google Scholar]
  68. La Marca, A., Iodice, E., Cantiello, M., et al. 2022, A&A, 665, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Leisman, L., Haynes, M. P., Janowiecki, S., et al. 2017, ApJ, 842, 133 [NASA ADS] [CrossRef] [Google Scholar]
  70. Lelli, F., Duc, P.-A., Brinks, E., et al. 2015, A&A, 584, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Li, H., & Gnedin, O. Y. 2019, MNRAS, 486, 4030 [NASA ADS] [CrossRef] [Google Scholar]
  72. Lim, S., Peng, E. W., Côté, P., et al. 2018, ApJ, 862, 82 [Google Scholar]
  73. Lim, S., Côté, P., Peng, E. W., et al. 2020, ApJ, 899, 69 [CrossRef] [Google Scholar]
  74. Lim, S., Peng, E. W., Côté, P., et al. 2024, ApJ, 966, 168 [NASA ADS] [CrossRef] [Google Scholar]
  75. Liu, Y., Peng, E. W., Jordán, A., et al. 2019, ApJ, 875, 156 [NASA ADS] [CrossRef] [Google Scholar]
  76. Marleau, F. R., Habas, R., Poulain, M., et al. 2021, A&A, 654, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Marleau, F. R., Cuillandre, J. C., Cantiello, M., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202450799 [Google Scholar]
  78. Martín-Navarro, I., Romanowsky, A. J., Brodie, J. P., et al. 2019, MNRAS, 484, 3425 [Google Scholar]
  79. McConnachie, A. W. 2012, AJ, 144, 4 [Google Scholar]
  80. McConnachie, A. W., Huxor, A., Martin, N. F., et al. 2008, ApJ, 688, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  81. Merritt, A., van Dokkum, P., Danieli, S., et al. 2016, ApJ, 833, 168 [NASA ADS] [CrossRef] [Google Scholar]
  82. Mihos, J. C., Durrell, P. R., Ferrarese, L., et al. 2015, ApJ, 809, L21 [Google Scholar]
  83. Miller, B. W., & Lotz, J. M. 2007, ApJ, 670, 1074 [NASA ADS] [CrossRef] [Google Scholar]
  84. Mistani, P. A., Sales, L. V., Pillepich, A., et al. 2016, MNRAS, 455, 2323 [NASA ADS] [CrossRef] [Google Scholar]
  85. Montes, M., Trujillo, I., Infante-Sainz, R., Monelli, M., & Borlaff, A. S. 2021, ApJ, 919, 56 [NASA ADS] [CrossRef] [Google Scholar]
  86. Müller, O., Jerjen, H., & Binggeli, B. 2018, A&A, 615, A105 [Google Scholar]
  87. Müller, O., Marleau, F. R., Duc, P.-A., et al. 2020, A&A, 640, A106 [Google Scholar]
  88. Müller, O., Durrell, P. R., Marleau, F. R., et al. 2021, ApJ, 923, 9 [CrossRef] [Google Scholar]
  89. Peng, E. W., & Lim, S. 2016, ApJ, 822, L31 [NASA ADS] [CrossRef] [Google Scholar]
  90. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
  91. Peng, E. W., Jordán, A., Côté, P., et al. 2008, ApJ, 681, 197 [NASA ADS] [CrossRef] [Google Scholar]
  92. Poulain, M., Marleau, F. R., Habas, R., et al. 2021, MNRAS, 506, 5494 [NASA ADS] [CrossRef] [Google Scholar]
  93. Poulain, M., Marleau, F. R., Habas, R., et al. 2022, A&A, 659, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Prole, D. J., Hilker, M., van der Burg, R. F. J., et al. 2019, MNRAS, 484, 4865 [Google Scholar]
  95. Prole, D. J., van der Burg, R. F. J., Hilker, M., & Spitler, L. R. 2021, MNRAS, 500, 2049 [Google Scholar]
  96. Read, J. I., Goerdt, T., Moore, B., et al. 2006, MNRAS, 373, 1451 [NASA ADS] [CrossRef] [Google Scholar]
  97. Reina-Campos, M., Trujillo-Gomez, S., Deason, A. J., et al. 2022, MNRAS, 513, 3925 [NASA ADS] [CrossRef] [Google Scholar]
  98. Renaud, F., Agertz, O., & Gieles, M. 2017, MNRAS, 465, 3622 [NASA ADS] [CrossRef] [Google Scholar]
  99. Román, J., & Trujillo, I. 2017, MNRAS, 468, 4039 [Google Scholar]
  100. Román, J., Beasley, M. A., Ruiz-Lara, T., & Valls-Gabaud, D. 2019, MNRAS, 486, 823 [CrossRef] [Google Scholar]
  101. Rong, Y., Guo, Q., Gao, L., et al. 2017, MNRAS, 470, 4231 [Google Scholar]
  102. Rong, Y., Dong, X.-Y., Puzia, T. H., et al. 2020, ApJ, 899, 78 [NASA ADS] [CrossRef] [Google Scholar]
  103. Ruiz-Lara, T., Beasley, M. A., Falcón-Barroso, J., et al. 2018, MNRAS, 478, 2034 [NASA ADS] [CrossRef] [Google Scholar]
  104. Saifollahi, T., Trujillo, I., Beasley, M. A., Peletier, R. F., & Knapen, J. H. 2021, MNRAS, 502, 5921 [NASA ADS] [CrossRef] [Google Scholar]
  105. Saifollahi, T., Zaritsky, D., Trujillo, I., et al. 2022, MNRAS, 511, 4633 [NASA ADS] [CrossRef] [Google Scholar]
  106. Simon, J. D. 2019, ARA&A, 57, 375 [NASA ADS] [CrossRef] [Google Scholar]
  107. Somalwar, J. J., Greene, J. E., Greco, J. P., et al. 2020, ApJ, 902, 45 [NASA ADS] [CrossRef] [Google Scholar]
  108. Tanoglidis, D., Drlica-Wagner, A., Wei, K., et al. 2021, ApJS, 252, 18 [Google Scholar]
  109. Toloba, E., Sales, L. V., Lim, S., et al. 2023, ApJ, 951, 77 [NASA ADS] [CrossRef] [Google Scholar]
  110. Torrealba, G., Belokurov, V., Koposov, S. E., et al. 2019, MNRAS, 488, 2743 [NASA ADS] [CrossRef] [Google Scholar]
  111. Tremaine, S. D., Ostriker, J. P., & Spitzer, L., Jr 1975, ApJ, 196, 407 [Google Scholar]
  112. Tremmel, M., Wright, A. C., Brooks, A. M., et al. 2020, MNRAS, 497, 2786 [Google Scholar]
  113. Trujillo, I., Chamba, N., & Knapen, J. H. 2020, MNRAS, 493, 87 [NASA ADS] [CrossRef] [Google Scholar]
  114. van Dokkum, P. G., Abraham, R., Merritt, A., et al. 2015, ApJ, 798, L45 [NASA ADS] [CrossRef] [Google Scholar]
  115. van Dokkum, P., Abraham, R., Romanowsky, A. J., et al. 2017, ApJ, 844, L11 [NASA ADS] [CrossRef] [Google Scholar]
  116. van Dokkum, P., Danieli, S., Cohen, Y., et al. 2018, Nature, 555, 629 [Google Scholar]
  117. Venhola, A., Peletier, R., Laurikainen, E., et al. 2017, A&A, 608, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Venhola, A., Peletier, R. F., Salo, H., et al. 2022, A&A, 662, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Villaume, A., Romanowsky, A. J., Brodie, J., et al. 2022, ApJ, 924, 32 [Google Scholar]
  120. Wittmann, C., Lisker, T., Ambachew Tilahun, L., et al. 2017, MNRAS, 470, 1512 [Google Scholar]
  121. Wright, A. C., Tremmel, M., Brooks, A. M., et al. 2021, MNRAS, 502, 5370 [NASA ADS] [CrossRef] [Google Scholar]
  122. Yagi, M., Koda, J., Komiyama, Y., & Yamanoi, H. 2016, ApJS, 225, 11 [CrossRef] [Google Scholar]
  123. Yozin, C., & Bekki, K. 2015, MNRAS, 452, 937 [NASA ADS] [CrossRef] [Google Scholar]
  124. Zaritsky, D. 2022, MNRAS, 513, 2609 [NASA ADS] [CrossRef] [Google Scholar]
  125. Zaritsky, D., Donnerstein, R., Dey, A., et al. 2019, ApJS, 240, 1 [Google Scholar]
  126. Zaritsky, D., Donnerstein, R., Karunakaran, A., et al. 2021, ApJS, 257, 60 [NASA ADS] [CrossRef] [Google Scholar]
  127. Zaritsky, D., Donnerstein, R., Karunakaran, A., et al. 2022, ApJS, 261, 11 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Tables

Table A.1 summarises the number of GCs identified in the HST images for each of the 74 UDGs in our sample, and includes the calculated value of the specific frequency (SN) and the halo mass (Mh). The distance and absolute magnitude (MV) of the UDG is also provided.

Table A.1.

MATLAS UDGs GC counts.

Appendix B: Globular cluster density maps

thumbnail Fig. B.1.

2D density maps of the GC distributions for the 12 UDGs with NGC > 10. Left: The projected distribution (cyan dots) and density map (coloured map) of the GC candidates detected within 2Re (large white circle). Right: The density map (white contours) of the GC candidates is overlaid on the HST F814W image of the UDG. The size of each image is 2.5Re × 2.5Re.

Appendix C: Globular cluster radial profiles

thumbnail Fig. C.1.

Radial distributions of the GCs for the 12 UDGs with NGC > 10. From top left to bottom right: Radial distribution of all detected GCs. The black points are for the GC counts within 2Re while the red points are the counts outside (background). The Sérsic fit is shown with the dash-dotted blue line.

All Tables

Table 1.

Sample comparison of UDG specific frequencies (SN).

In the text
Table A.1.

MATLAS UDGs GC counts.

In the text

All Figures

thumbnail Fig. 1.

F606W+F814W colour images of the 74 MATLAS UDGs, selected with a cut of ⟨μe, g⟩> 23.3 mag arcsec−2 and Re > 1.0 kpc, observed with HST/ACS (top, left to bottom, right) shown by decreasing surface brightness. Due to their low surface brightness, the galaxies in the last rows are difficult to see in the images. The names and distances of the UDGs are displayed on the images. The size of each cutout is 1.3′×1.3′.
In the text
thumbnail Fig. 2.

Our sample of 74 MATLAS UDGs, selected with a cut of ⟨μe, g⟩> 23.3 mag arcsec−2 and Re > 1.0 kpc observed with HST (black empty circles), overlaid on the MATLAS dwarfs of Habas et al. (2020) (empty pale blue circles) and UDGs of Marleau et al. (2021) (filled blue circles). Also shown are the dwarfs identified in the Euclid Early Release Observations of the Perseus cluster (grey diamonds; Marleau et al. 2024), Next Generation Virgo Cluster Survey (grey triangles; Ferrarese et al. 2020) and Next Generation Fornax Survey (inverted grey triangles; Eigenthaler et al. 2018) images, as well as Local Group dwarfs (rotated left grey triangles; McConnachie 2012) and Local Volume (rotated right grey triangles; Carlsten et al. 2020). The UDGs found in the Coma (grey cross symbols; van Dokkum et al. 2015) and Virgo cluster (grey plus symbols; Lim et al. 2020) are shown separately. For comparison, we have also included ultra-faint dwarfs (UFDs; grey stars; Simon 2019) and massive ellipticals from the Carnegie-Irvine catalogue (grey large cross symbols; Ho et al. 2011).
In the text
thumbnail Fig. 3.

Colour (left) and concentration index (right) cut of all GC detections (black open circles) and the GC detections within 2Re (blue circles), based on the spectroscopically confirmed GCs in MATLAS-2019 (red circles: Müller et al. 2021). The light red region highlights the selection cut we used for colour, 0.5 < (mF606W − F814W)0 < 1.2, and for the concentration index, 0.1 < Δm4 − 8 < 0.5, for galaxies with a distance ≤25 Mpc. For galaxies at larger distances, i.e., > 25 Mpc, the lower concentration index cut was extended to include the unresolved sources, highlighted by the light orange and light red regions, corresponding to a cut of −0.1 < Δm4 − 8 < 0.5.
In the text
thumbnail Fig. 4.

Comparison between the GC counts (background and completeness corrected) measured excluding unresolved GCs (tan circles) and including unresolved GCs (red circles) as a function of distance. Below ∼25 Mpc, the GC counts are dominated by the marginally resolved sources (in tan circles) whereas above ∼25 Mpc, the counts become dominated by the unresolved sources (in red circles). Based on this comparison, we included unresolved GCs only at distances greater than 25 Mpc.
In the text
thumbnail Fig. 5.

GCLF as a function of absolute magnitude MF814W (bottom) and apparent magnitude (mF814W)0 (top) of the detected GCs within 2Re (blue), and the detections outside 2Re (grey) for the UDG MATLAS-2019, which has the largest number of GCs in our sample. The black points are for the raw count within 2Re and the red points show the GC count after background subtraction. The red solid line shows the Gaussian fit with peak absolute magnitude MV = −7.3 mag and a dispersion of 1 mag.
In the text
thumbnail Fig. 6.

Distribution of the number of GCs within 2Re for the 74 UDG sample (light grey), the 36 UDGvD15 as defined by van Dokkum et al. (2015) (pale indigo), and the 40 nucleated UDGs (bright coral). The majority of the sample (47 UDGs or 64%) are measured to have NGC < 3, while the remaining 36% is spread across a wider range of values (NGC = 3 − 38). A total of 21 UDGs (28%) have NGC values consistent with zero, with the tail of the distribution extending to our most GC-rich galaxy, MATLAS-2019, with NGC = 38. The percentage of nucleated UDGs with a large number of GCs (14 UDGs or 35% have NGC ≥ 3) is similar to the one for the whole sample.
In the text
thumbnail Fig. 7.

Total number of GCs for the UDG sample (black open circles) and those belonging to the UDGvD15 selection criteria (indigo open circles) as a function of the galaxy stellar mass. The number of GCs is shown to steadily increase with total stellar mass for the full sample of UDGs. The trend continues as the stellar mass increase to massive early-type galaxies, as can be seen using the GC counts obtained from the HST ACS Fornax cluster survey (Liu et al. 2019) (blue open circles). The galaxies in the UDGvD15 sample extend higher at each stellar mass than the galaxies in the non-UDGvD15 sample with the exception of the two most massive bins which contain no galaxies from the UDGvD15 sample.
In the text
thumbnail Fig. 8.

Comparison between the GC counts measured in the MATLAS CFHT images and those measured from the HST images after background and completeness corrections have been applied. The light coral, light blue and light green circles are for GC detection in the CFHT images using three (u − g, g − r, g − i), two (g − r, g − i), and one (g − r) colours, respectively. The size of the symbol decreases with increasing distance. We do not find any trend between how many colours were used to identify the GCs in the CFHT images and the agreement with the HST GC numbers. As expected, the scatter is large but there is a clear agreement in the general trend; namely, the UDGs with the largest number of GC candidates in the ground-based images remain the same UDGs that have the largest GC candidates in the higher resolution HST images. The large scatter at the low CFHT NGC values is most likely an effect of distance as the GC selection in the CFHT data was based on a fixed apparent magnitude cut.
In the text
thumbnail Fig. 9.

Distribution of the specific frequency for the 74 UDG sample (light grey) and the 40 nucleated UDGs (bright coral). The nucleated UDGs are all found to have SN < 40, consistent with the majority of the UDGs. The highest SN values are attributed to UDGs that are not identified as nucleated.
In the text
thumbnail Fig. 10.

Specific frequency SN as a function of absolute magnitude for the 74 UDGs in our sample. Top: UDGs with NGC > 0 are shown as squares with colours that scale with the value of the background and completeness corrected GC count, NGC. The UDGs with NGC ≤ 0 are shown as small black circles. Bottom: same as the top but now showing the local density parameter, log(ρ10), in the colour bar. In both plots, the specific frequency of the Coma cluster UDGs (Lim et al. 2018; light green symbols), Virgo cluster UDGs (Lim et al. 2020; light blue symbols), and Perseus cluster UDGs (Marleau et al. 2024; light red symbols) are also plotted. The light grey dashed lines correspond to SN with a constant NGC of 1, 10, 20, ..., 90, 100. The error bars are not shown since they are quite large and can be found in Table A.1. The inset plots display the SN values using a logarithmic scale.
In the text
thumbnail Fig. 11.

Halo and stellar mass measurements for a subsample of our UDGs with NGC > 3. Top: distribution of the halo mass for the 27 out of the 74 UDGs with NGC > 3 (grey) and 6 out of the 27 UDGs with NGC > 3 and SN > 30 (orange). The UDGs with high SN are found to have a range of halo masses, with some at the high end of the distribution. Bottom: same as above but showing the distributions of halo-to-stellar mass ratios. The stellar masses are from Habas et al. (2020). The UDGs with the largest SN values are all found to have a halo-to-stellar mass ratios above ∼500.
In the text
thumbnail Fig. 12.

2D density map of the GC distribution for one of the 12 UDGs with NGC > 10, MATLAS-2019. Left: projected distribution (cyan dots) and density map (coloured map) of the GC candidates detected within 2Re (large white circle). Right: density map (white contours) of the GC candidates is overlaid on the HST F814W image of the UDG. The size of each image is 2.5Re × 2.5Re.
In the text
thumbnail Fig. 13.

Radial distributions of the stacked GCs for the UDGs in our HST sample. Top: radial distribution of the stacked GCs for all 74 UDGs in our sample. The black squares are for the GC counts within 2Re while the red squares are the counts outside (background). The counts are also shown with the detection corresponding to the candidate nucleus (or nuclei, in the case of MATLAS-138 and 987) in each galaxy removed (grey points and dotted line). The Sérsic fit is shown with the dash-dot blue line. Middle: same as the top but for the nucleated UDGs only. Bottom: same as the top but for the non-nucleated UDGs only.
In the text
thumbnail Fig. 14.

Dependence of the effective radius of the GC system for the 12 UDGs with NGC > 10 (black filled circles) on three host parameters: the total number of GCs associated with the UDG (top), the stellar mass of the host galaxy (middle), and the effective radius of the UDG (bottom). We find that the effective radius of the GC system matches the effective radius of the galaxy (grey dotted line), indicating that the radial distribution of GCs follows the galaxy light. For all plots, the best-fit relations of Lim et al. (2024) are shown by the grey line (all GCs), the blue line (blue GCs), and the red line (red GCs). The error bars are shown for both axes in all plots but are only visible when larger than the symbols.
In the text
thumbnail Fig. 15.

Behaviour of the specific frequency, SN, as a function of key host properties. Top: dependence of SN on the host galaxy stellar mass, central surface brightness (μ0), and local density (log(ρ10)), shown from left to right. There are no obvious trends, except with ρ10, which shows an increase in specific frequency as the local density becomes less dense. Bottom: dependence of SN on host galaxy g − r colour, axis ratio, and effective radius (Re), shown from left to right. The bottom dependencies show the most prominent trends, with an increase in GC counts with bluer colours, increased roundness, and larger size. For all plots, the running average and standard deviation, computed using only non-zero values of NGC, is shown as the red dashed line and light red region, respectively.
In the text
thumbnail Fig. B.1.

2D density maps of the GC distributions for the 12 UDGs with NGC > 10. Left: The projected distribution (cyan dots) and density map (coloured map) of the GC candidates detected within 2Re (large white circle). Right: The density map (white contours) of the GC candidates is overlaid on the HST F814W image of the UDG. The size of each image is 2.5Re × 2.5Re.
In the text
thumbnail Fig. C.1.

Radial distributions of the GCs for the 12 UDGs with NGC > 10. From top left to bottom right: Radial distribution of all detected GCs. The black points are for the GC counts within 2Re while the red points are the counts outside (background). The Sérsic fit is shown with the dash-dotted blue line.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.