| Issue |
A&A
Volume 688, August 2024
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202450018 | |
| Published online | 05 August 2024 | |
Combining Gaia and GRAVITY: Characterising five new directly detected substellar companions
1
European Southern Observatory,
Karl-Schwarzschild-Straße 2,
85748
Garching,
Germany
e-mail: thomas.winterhalder@eso.org
2
LESIA, Observatoire de Paris, PSL, CNRS, Sorbonne Université, Université de Paris,
5 place Janssen,
92195
Meudon,
France
3
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
4
Universidade de Lisboa, Faculdade de Ciências, Campo Grande,
1749-016
Lisboa,
Portugal
5
CENTRA, Centro de Astrofísica e Gravitação, IST, Universidade de Lisboa,
1049-001
Lisboa,
Portugal
6
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
7
Department of Physics & Astronomy, Johns Hopkins University,
3400 N. Charles Street,
Baltimore,
MD
21218,
USA
8
Space Telescope Science Institute,
3700 San Martin Drive,
Baltimore,
MD
21218,
USA
9
Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA) and Department of Physics and Astronomy, Northwestern University,
Evanston,
IL
60208,
USA
10
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstraße 1,
85748
Garching,
Germany
11
Aix Marseille Univ., CNRS, CNES, LAM,
Marseille,
France
12
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS,
Laboratoire Lagrange,
France
13
STAR Institute, Université de Liège,
Allée du Six Août 19c,
4000
Liège,
Belgium
14
Leiden Observatory, Leiden University,
PO Box 9513,
2300
RA
Leiden,
The Netherlands
15
Department of Astrophysical & Planetary Sciences, JILA,
Duane Physics Bldg., 2000 Colorado Ave, University of Colorado,
Boulder,
CO
80309,
USA
16
1. Institute of Physics, University of Cologne,
Zülpicher Straße 77,
50937
Cologne,
Germany
17
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
18
Universidade do Porto, Faculdade de Engenharia,
Rua Dr. Roberto Frias,
4200-465
Porto,
Portugal
19
School of Physics, University College Dublin, Belfield,
Dublin 4,
Ireland
20
Astrophysics Group, Department of Physics & Astronomy, University of Exeter,
Stocker Road,
Exeter
EX4 4QL,
UK
21
Departments of Physics and Astronomy, Le Conte Hall, University of California,
Berkeley,
CA
94720,
USA
22
European Southern Observatory, Casilla
19001,
Santiago 19,
Chile
23
Advanced Concepts Team, European Space Agency, TEC-SF, ESTEC,
Keplerlaan 1,
NL-2201,
AZ
Noordwijk,
The Netherlands
24
University of Exeter, Physics Building,
Stocker Road,
Exeter
EX4 4QL,
UK
25
Fakultät für Physik, Universität Duisburg-Essen,
Lotharstraße 1,
47057
Duisburg,
Germany
26
Institüt für Astronomie und Astrophysik, Universität Tübingen,
Auf der Morgenstelle 10,
72076
Tübingen,
Germany
27
Center for Space and Habitability, Universität Bern,
Gesellschaftsstr. 6,
3012
Bern,
Switzerland
28
Astronomy Department, University of Michigan,
Ann Arbor,
MI
48109,
USA
29
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
30
Academia Sinica, Institute of Astronomy and Astrophysics,
11F Astronomy-Mathematics Building, NTU/AS campus, No. 1, Section 4, Roosevelt Rd.,
Taipei
10617,
Taiwan
31
European Space Agency (ESA), ESA Office, Space Telescope Science Institute,
3700 San Martin Drive,
Baltimore,
MD
21218,
USA
32
Department of Earth & Planetary Sciences, Johns Hopkins University,
Baltimore,
MD,
USA
33
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Straße 1,
85741
Garching,
Germany
34
Excellence Cluster ORIGINS,
Boltzmannstraße 2,
85748
Garching bei München,
Germany
Received:
18
March
2024
Accepted:
10
June
2024
Precise mass constraints are vital for the characterisation of brown dwarfs and exoplanets. Here we present how the combination of data obtained by Gaia and GRAVITY can help enlarge the sample of substellar companions with measured dynamical masses. We show how the Non-Single-Star (NSS) two-body orbit catalogue contained in Gaia DR3 can be used to inform high-angular-resolution follow-up observations with GRAVITY. Applying the method presented in this work to eight Gaia candidate systems, we detect all eight predicted companions, seven of which were previously unknown and five are of a substellar nature. Among the sample is Gaia DR3 2728129004119806464 B, which – detected at an angular separation of (34.01 ± 0.15) mas from the host – is the closest substellar companion ever imaged. In combination with the system’s distance and the orbital elements, this translates to a semi-major axis of (0.938 ± 0.023) AU. WT 766 B, detected at a greater angular separation, was confirmed to be on an orbit exhibiting an even smaller semi-major axis of (0.676 ± 0.008) AU. The GRAVITY data were then used to break the host-companion mass degeneracy inherent to the Gaia NSS orbit solutions as well as to constrain the orbital solutions of the respective target systems. Knowledge of the companion masses enabled us to further characterise them in terms of their ages, effective temperatures, and radii via the application of evolutionary models. The inferred ages exhibit a distinct bias towards values younger than what is to be expected based on the literature. The results serve as an independent validation of the orbital solutions published in the NSS two-body orbit catalogue and show that the combination of astrometric survey missions and high-angular-resolution direct imaging holds great promise for efficiently increasing the sample of directly imaged companions in the future, especially in the light of Gaia’s upcoming DR4 and the advent of GRAVITY+.
Key words: instrumentation: high angular resolution / instrumentation: interferometers / astrometry / planets and satellites: detection
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The knowledge of a given substellar companion’s mass is key to understanding its formation history, interior evolution, and atmosphere (e.g. Mordasini 2013; Marleau & Cumming 2014; D’Angelo et al. 2010; Bowler 2016). Masses being one of the main exoplanetary observables, they are also of central importance for mapping the demographics of the exoplanet and brown dwarf population (e.g. Nielsen et al. 2019; Vigan et al. 2021; Fontanive et al. 2023; Kirkpatrick et al. 2024; Gratton et al. 2024). Estimates of a given companion’s mass are commonly obtained by applying its approximate age and measured luminosity to evolutionary models (e.g. Chabrier et al. 2000; Baraffe et al. 2003, 2015). Such indirect mass constraints must, however, be treated with the utmost care since – in the absence of a large sample of reliably measured masses – the underlying models are as of yet insufficiently benchmarked and do not always agree with one another (Marley et al. 2007; Mordasini 2013). There is thus an urgent need for more directly measured masses of substellar companions. Examples of such dynamical masses obtained for objects in the brown dwarf mass regime are HD 206893 B (Kammerer et al. 2021), HD 72946 B (Maire et al. 2020), and HD 136164 Ab (Balmer et al. 2024). Measured dynamical masses of planetary companion objects, that is, companions with masses below 13 Mjup, include PDS 70 b (Wang et al. 2021), β Pictoris c (Nowak et al. 2020), HR8799 e (Brandt et al. 2021a), AF Lep b (Mesa et al. 2023; Franson et al. 2023; De Rosa et al. 2023), and HD 206893 c (Hinkley et al. 2023). A subset of the cited studies make use of the astrometric data collected by ESA’s Hipparcos and Gaia satellites (Gaia Collaboration 2016). Potential proper motion anomalies, the difference in a star’s proper motion as measured by the two missions, can be suggestive of the presence of an orbiting companion. Catalogues of such anomalous stars can be found in Brandt (2021) or Kervella et al. (2022).
Directly imaging substellar companions is still to unfold its great potential in terms of the number of its successful applications (see The LUVOIR Team 2019; Gaudi et al. 2020; Kasper et al. 2021; Quanz et al. 2022). Yet, even today it can help constrain dynamical masses in a rapid manner. This is the case when it is applied to candidate or confirmed companions whose positions relative to their host stars can be predicted reasonably well and are favourable for such observations. Such an approach has been made possible by Gaia Data Release (DR) 3 (Gaia Collaboration 2023b), opening up a new avenue for searches for substellar companions in Gaia data that do not include the use of proper motion anomalies. As showcased in this work, the synergies between Gaia and GRAVITY (GRAVITY Collaboration 2017) makes this instrument ensemble uniquely suited to pursue this new line of attack.
Gaia is a space-based survey telescope orbiting the Sun at the Sun-Earth Lagrange point L2, mapping the positions, velocities, spectra, and other characteristics of stars in the solar neighbourhood and beyond. Its astrometric accuracy has been shown to be sufficient to detect the reflex motions that stars exhibit as a consequence of orbiting bodies (Perryman et al. 2014; Gaia Collaboration 2023a). In this work, we use the orbits of such host stars to predict the momentary position of the perturbing companion.
The GRAVITY instrument is a near-infrared interferometer at the Very Large Telescope (VLT) on Cerro Paranal. When employed for exoplanet observations, it has been shown to achieve an astrometric accuracy of 50 μas (GRAVITY Collaboration 2019). We used it to follow up on and directly image eight targets identified in the Gaia Non-Single-Star (NSS) catalogue.
The paper is structured as follows: How the Gaia-informed GRAVITY observations are prepared and conducted is described in Sec. 2. The combination of the two data sets as well as further analysis of the GRAVITY observation is presented in Sec. 3. The obtained results are then discussed in Sec. 4, and we present our conclusions in Sec. 5.
2 Observations
2.1 Using Gaia as a signpost
This work makes use of data obtained by the Gaia satellite. The mission’s third data release (DR3; Gaia Collaboration 2023b) contains the NSS two-body orbit catalogue – a collection of hundreds of thousands of orbital solutions of point sources of light that can but are not guaranteed to correspond to individual stars. In principle, they can constitute the combination of two or more unresolved sources and are thus referred to as photocentres. A subset of the photocentre orbits are based on astrometric time-series observations taken by Gaia over several years. The original astrometric measurements in their raw format are not accessible in DR3. Instead, curated orbital fits are presented as sets of Thiele-Innes (TI) elements, which are directly – if not linearly – related to the classical sets of Campbell elements. Additionally, each orbital solution comes with uncertainties associated with the individual elements as well as a correlation matrix. We used nsstools1 (Halbwachs et al. 2023) to perform the conversions between the TI and Campbell space. Dealing with substellar companions, the assumption that the flux seen by Gaia originates entirely from the host star is justified for the targets discussed in this work. The validity of such a zero-companion-Gaia-flux hypothesis, as we shall henceforth call it, is corroborated by the eventual GRAVITY detection of the selected companions and – more substantially – by the later calculation of their synthetic G band magnitudes by means of evolutionary models. As a consequence of the zero-companion-Gaia-flux hypothesis, the photocentre coincides with the position of the host star, and the NSS orbital solution can be interpreted as the star’s orbit around its system’s centre-of-mass (COM). This enables us to compute the Gaia-informed position of the star relative to the COM at any given time. Accordingly, the unresolved companion must be located along the axis connecting the star and the COM and behind the COM as seen from the star. Its exact placement along this axis is determined entirely by the companion-to-host mass ratio. Reflecting on two extreme cases serves as an instructive exercise to make sense of the situation. If the mass ratio approaches 1 (that is the companion has the same mass as the host; the initial zero-companion-Gaia-flux hypothesis would break down for this extreme case) one would expect the companion to be situated at the opposite side of and at the same distance from the COM as the host. If instead the mass ratio approaches 0, we must expect the companion to be far removed from the host. Thus, lower mass ratios imply greater separations between host and companion. Both estimates for the host star and companion mass are provided by Gaia. From the DR3 Binary Masses Table (Gaia Collaboration 2023a), we retrieve the host star’s mass with associated uncertainties. The companion mass is given in the form of an upper and lower limit. Following the reasoning above, by adopting the lower limit as the companion mass we ensure that our eventual host-companion separation is an upper estimate.
Filtering the NSS catalogue according to predefined conditions on different parameters, we can identify favourable targets for a GRAVITY follow-up. Possible filtering conditions are constraints on the RA and Dec positions of the host, its distance, its mass, the companion’s lower mass estimate, or the host-companion separation. Age is another possible criterion. It was not applied in the target selection performed for this work, however. We discuss the consequences of this in Sec. 4.1. The above method enabled us to compile a list of eight target systems viable for a follow up: Gaia DR3 2728129004119806464, Gaia DR3 4986031970629390976, CD-50 869, HD 17155, WT 766, Gaia DR3 4739421098886383872, Gaia DR3 4858390078077441920, and StKM1-1494. Among this sample, only the HD 17155 system is known to host a companion (detected via RV monitoring; see Barbato et al. 2023). For brevity, we shall henceforth shorten the Gaia DR3 IDs to the format G ...wxyz, where wxyz are the last four digits of the ID. To account for the uncertainties of the orbital elements and the correlations between them, we employed a randomisation procedure for each of the companion position predictions. Drawing Nrand = 5 × 105 different sets of orbital parameters from the multivariate distribution in TI space, converting them to Campbell sets, and evaluating the resulting companion position at a defined time of observation, we obtain Nrand different position predictions for each companion candidate. These can be visualised in a two-dimensional histogram of the sky plane as shown for each target system in Fig. 1. We can further quantify the degree of constraint on the companion position prediction by defining a significance metric for the orbital solution. Such a metric can be written as
![$\[(S / N)_{\text {orbit }}=\sqrt{\mathbf{T I}_{\text {Gaia }}^{\mathrm{T}} \cdot \mathbf{C O V}_{\mathrm{TI}, \text { Gaia }}^{-1} \cdot \mathbf{T I}_{\text {Gaia }}},\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq1.png) (1)
(1)
where TIGaia is the vector containing the TI elements A, B, F, and G as reported by Gaia, and COVTI, Gaia is the covariance matrix associated with the four elements. The obtained results are presented in the respective panels of Fig. 1.
 |
Fig. 1 Position probability maps at the time of observation for the observed systems as computed from the respective orbital solutions listed in the Gaia NSS catalogue. The orange cross indicates the mean companion position relative to the mean host position, which is marked by the yellow star. The system’s COM is shown by the grey cross. Randomising the host and companion positions on the basis of the parameter uncertainties and correlations (while keeping the mass ratio, q, fixed to the lower limit; see the main text) yields the predicted spread around the respective mean positions. The contour line encircles 68 % of the randomised companion positions. The grey axis connects the mean host position with the mean companion position to visualise the separation’s dependence on the mass ratio, q. The position at which the companion was detected with GRAVITY is shown as the dark blue cross. For targets that were observed more than once, we show the companion position prediction corresponding to the first epoch and the resulting initial detection. The dark blue uncertainty ellipses associated with the GRAVITY detections are too small to be seen at these scales. The ticks along the panel axes are spaced by 10 mas. Finally, the significance of the individual orbital solutions, (S/N)orbit, is given below the target system name in the top-left corner of each panel. |
2.2 Following-up with GRAVITY
The targets selected from the Gaia NSS two-body orbit catalogue were followed up with GRAVITY between July 2022 and October 2023. Initial observations were conducted on technical time, to demonstrate the validity of the technique. Subsequent observations were conducted within the framework of the Exo-GRAVITY Large Programme (ESO ID 1104.C-0651 Lacour et al. 2020) and within a dedicated open time programme (ESO ID 111.253E, PI A.-L. Maire). An observation log containing observation dates, conditions, exposure times and the fibre placement for each target is presented in Table C.1.
All targets were observed using the dual-field on-axis observation mode comprehensively described in GRAVITY Collaboration (2019). To summarise, this technique places the first instrument fibre on the host star to track fringes (Lacour et al. 2019). The science fibre, on the other hand, alternates between the host and the companion. As this project progressed the observing technique changed slightly. To begin with, the science fibre was placed at the position at which the companion was predicted to be located (as described in Sec. 2.1). Later, we decided to position it slightly off-centre to gain in contrast capabilities (this so-called fibre off-pointing technique is comprehensively discussed in Pourré et al. 2024). The flip side of such an approach is the loss of a fraction of the companion flux. How this throughput loss is corrected for is described in Appendix A.
The data reduction was performed using the ESO GRAVITY Instrument Pipeline 1.6.4b1, from which we obtained the astro-reduced byproduct. The astrometry from these files was then obtained using the standard exoplanet dual field data processing described in Appendix A of GRAVITY Collaboration (2020). The separations in RA and Dec relative to the hosts at which the companions were detected are shown in Table 1. Also note that a metrology jump that occurred on Unit Telescope 3 during the observation of the StKM1-1494 system was corrected for.
One of the detections presented in this work (that of G ...6464 B) as well as a preview of the analysis undertaken below was briefly showcased in Pourré et al. (2024) in order to demonstrate a successful application of the fibre off-pointing observation technique.
Astrometric epochs of the respective companions obtained with GRAVITY.
3 Methods
3.1 Making Gaia and GRAVITY ‘talk’
The synergies between Gaia and GRAVITY are not confined to using the NSS catalogue as a signpost to inform follow-up observations and facilitate detections. By combining the two data sets we can obtain tighter constraints on the orbital elements, break the degeneracy between the host and companion mass that is an inherent feature of Gaia NSS orbital solutions and confirm the initial zero-companion-Gaia-flux hypothesis. To this end, we employed a Bayesian approach. In this sense we can interpret the orbital solution provided by Gaia as the likelihood information from which the posterior distributions of the orbital elements follow. The GRAVITY detection and concomitant relative astrometry measurement can be viewed as an additional likelihood, upon inclusion of which we can update the posteriors. This amounts to re-sampling the posterior distributions by performing a Markov chain Monte Carlo (MCMC) run through the multivariate parameter space, spanned by nine free parameters, namely the TI elements A, B, F, and G, the eccentricity, e, the period, P, the time of periastron passage relative to the Gaia epoch, tp,rel, the parallax, π, and the total mass of the system, Mtot. To avoid external and non-physical constraints on the individual parameters, we defined a broad, uniform prior range for each of them, virtually ranging from minus infinity to infinity. Next, a set of Nw = 100 walkers were initialised. We assigned a unique set of orbital parameter values to each of them. The actual placement was performed by assuming Gaussian distributions around the Gaia NSS orbital elements. To adopt a more conservative initialisation approach and loosen the dependence on the Gaia values, we inflated the distributions’ standard deviations by a factor of two. This introduces a greater spread ensuring that the prior range is more thoroughly sampled by the initial set of walkers. It should be noted that the total mass is initialised around the host mass estimate, M1Gaia, listed in the Gaia DR3 Binary Masses Table. Considering the significantly higher mass of the host compared to the companion, this placement appears reasonable.
The MCMC run and actual building of the posterior sampling was performed using emcee (Foreman-Mackey et al. 2013). At the heart of this procedure lies an ln-likelihood function that reads
![$\[\ln (\mathcal{L})=-\frac{1}{2}\left[\chi_{\text {Gaia }}^2+\chi_{\text {GRAVITY }}^2\right],\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq2.png) (2)
(2)
where χ2 denotes different chi-squared contributions. The first term, χ2Gaia, compares the individual sets of free parameters sampled by the walkers to the set listed in the Gaia NSS catalogue under consideration of the provided covariance matrix. It is thus defined as
![$\[\chi_{\text {Gaia }}^2=\left(\boldsymbol{\theta}_{\text {Sample }}-\boldsymbol{\theta}_{\text {Gaia }}\right)^{\mathrm{T}} \cdot \mathbf{C O V}^{-1} \cdot\left(\boldsymbol{\theta}_{\text {Sample }}-\boldsymbol{\theta}_{\text {Gaia }}\right) .\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq3.png) (3)
(3)
Here, θSample denotes the parameter set vector sampled by the walker, θGaia is the Gaia parameter set as retrieved from the NSS catalogue and COV represents the covariance matrix that follows from the correlation matrix yet again presented in the NSS catalogue. The second term, χ2GRAVITY, introduces the GRAVITY astrometry into the ln-likelihood function and is defined as
![$\[\chi_{\text {GRAVITY }}^2=\sum_{n=1}^{N_{\mathrm{G}}}\left(\boldsymbol{\zeta}_n^{\text {Sample }}-\boldsymbol{\zeta}_n^{\mathrm{G}}\right)^{\mathrm{T}} \cdot \mathbf{C O V}_n^{-1} \cdot\left(\boldsymbol{\zeta}_n^{\text {Sample }}-\boldsymbol{\zeta}_n^{\mathrm{G}}\right),\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq4.png) (4)
(4)
where NG is the number of GRAVITY observations and thus astrometric epochs. The vector ![$\[\boldsymbol{\zeta}_n^{\mathrm{G}}\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq5.png) contains the host-companion separation components in RA and Dec measured during the nth GRAVITY observation.
contains the host-companion separation components in RA and Dec measured during the nth GRAVITY observation. ![$\[\boldsymbol{\zeta}_n^{\text {Sample }}\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq6.png) , on the other hand, represents the separation components resulting from the parameter set probed by the walker. Finally,
, on the other hand, represents the separation components resulting from the parameter set probed by the walker. Finally, ![$\[\mathbf{C O V}_n^{-1}\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq7.png) describes the covariance matrix associated with the n-th GRAVITY observation. Running the MCMC procedure through a burn-in phase of Nburn = 2000 iterations and building the chain in the actual sampling phase over Niter = 10000 iterations yields the posteriors.
describes the covariance matrix associated with the n-th GRAVITY observation. Running the MCMC procedure through a burn-in phase of Nburn = 2000 iterations and building the chain in the actual sampling phase over Niter = 10000 iterations yields the posteriors.
A word of caution: due diligence is required when applying MCMC methods to data from the Gaia NSS two-body orbit catalogue. The orbital solutions contained in the catalogue are presented as sets of TI elements. Related to the classical Campbell elements by a set of non-linear equations (Binnendijk 1960), the TI elements are known to exhibit strong degeneracies and even circular correlations for circular and quasi-circular orbits. This can lead MCMC procedures astray. Local linear approximation (LLA) methods offer a safe way of utilising Gaia NSS orbital solutions (Babusiaux et al. 2023). Information such as the skewness of a posterior distribution or potential multi-modalities, however, is lost when limiting oneself to these inherently Gaussian procedures. Thus, it is desirable to combine the NSS orbital solutions with MCMC methods for such targets where this is possible without misinterpreting the data. We strongly recommend ascertaining the equivalence of LLA and MCMC methods for every target individually. To this end, we used BINARYS (Leclerc et al. 2023), a dedicated LLA implementation specifically designed to handle Gaia NSS orbit solutions in combination with relative astrometry measurements, to compute an independent set of posteriors under inclusion of all available data. The thus obtained consistent results suggest that the NSS solutions for the targets at hand are suitable to be treated with MCMC procedures.
Finally, it should be noted that the procedure as outlined above cannot be applied to the G ...0976 system. This is due to G ...0976 B’s high K band flux relative to its host (see Table 1). Even though the system’s G band flux ratio can be expected to be lower it does not seem reasonable to uphold the zero-companion-Gaia-flux hypothesis. Without it, however, we lose the convenient advantage of assuming the photocentre to coincide with the host. In the absence of a measurement of the system’s G band flux ratio, it is impossible to convert the photocentre orbit into the host orbit.
3.2 Orbital refinements
The MCMC method outlined in Sec. 3.1 is applied twice. First, we ran it while only including the Gaia term, ![$\[\chi_{{Gaia}}^2\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq8.png) , in the ln-likelihood function defined in Eq. (2). By not considering
, in the ln-likelihood function defined in Eq. (2). By not considering ![$\[\chi_{\mathrm{GRAVITY}}^2\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq9.png) , we are ignoring the GRAVITY astrometry. We then ran the MCMC procedure taking both terms into account. This let us visualise the constraining power achievable by the inclusion of GRAVITY data, since we can compare the initial Gaia-only posteriors to the updated ones. Once the two samplings have been created, we conveyed the individual parameter sets from TI to Campbell space. The resulting full corner plots showing both the initial and the updated posteriors are to be found in Appendix C. The marginalised posterior distributions of the free parameters are shown in Fig. 2. The inferred median values and associated uncertainties are listed in Table C.3. The refinements to the orbital solutions also manifest in the orbits’ appearances as projected onto the sky plane. Figure 3 shows how the updated orbits compare to the initial Gaia-only orbits.
, we are ignoring the GRAVITY astrometry. We then ran the MCMC procedure taking both terms into account. This let us visualise the constraining power achievable by the inclusion of GRAVITY data, since we can compare the initial Gaia-only posteriors to the updated ones. Once the two samplings have been created, we conveyed the individual parameter sets from TI to Campbell space. The resulting full corner plots showing both the initial and the updated posteriors are to be found in Appendix C. The marginalised posterior distributions of the free parameters are shown in Fig. 2. The inferred median values and associated uncertainties are listed in Table C.3. The refinements to the orbital solutions also manifest in the orbits’ appearances as projected onto the sky plane. Figure 3 shows how the updated orbits compare to the initial Gaia-only orbits.
3.3 Nailing down dynamical masses
A given host star’s movement around its system’s COM can conceivably be induced by different combinations of the companion’s mass and separation (and when disregarding the zero-companion-Gaia-flux hypothesis also by the host-companion flux ratio). For this reason, the Gaia astrometric time-series data of the host and the resulting orbital fits by themselves are inherently degenerate in terms of the two bodies’ dynamical masses. The columns to the right of Fig. 2 reveal that in addition to enabling significant constraints to be placed on the orbital parameters of target systems, the inclusion of a GRAVITY data point facilitates the breaking of the mass degeneracy. Indeed, one detection suffices to put tight constraints on both absolute masses. Again, the inferred median masses as well as their associated uncertainties are listed in Table C.3.
3.4 Photometric characterisation
Apart from precise relative astrometry measurements between companion and host, the GRAVITY observations of the different target systems also provide so-called contrast spectra in the K band. These measure the flux ratio between companion and host as a function of wavelength. The individual spectra can be found in Fig. C.1. Convolving such a spectrum with a given filter yields the contrast between companion and host as it would appear through the chosen filter. The contrast can then be converted to a magnitude difference. We used species (Stolker et al. 2020) to fit the BT-Settl (CIFIST) atmospheric model (Allard et al. 2003) to stellar photometry from the literature listed in Table C.2. From the resulting fit we then generated a synthetic stellar magnitude in the chosen filter. Finally, the companion magnitude is arrived at by adding the companion-to-host magnitude difference to the synthetic stellar magnitude.
The knowledge of the companion’s dynamical mass alongside its filter magnitude allows us to estimate the object’s age by comparing its position on the mass-magnitude plane with isochrones generated using evolutionary models as shown in Fig. 4. In other words, this procedure amounts to turning the conventional application of evolutionary models to substellar companions on its head. Typically, they are used to obtain mass estimates from a companion’s measured magnitude and its inferred age, which most often is assumed to be similar to that of the stellar association the host belongs to Bowler (2016). As explained above, in our case we can instead obtain constraints on the companion’s age from its magnitude and measured mass. Again, we used species to interpolate isochrones from the ATMO model grid (Phillips et al. 2020). Some companions exhibiting masses above the conventional brown dwarf domain, we included the Baraffe et al. (2015) model to cover the entire mass range of our target sample.
To eventually arrive at a meaningful age estimates, we propagated the posterior distributions in mass and magnitude by means of a bootstrapping method. To this end we interpolated linearly between the isochrones using scipy.interpolate.griddata (Virtanen et al. 2020). This method enables the rapid age determination of mass-magnitude samples randomly drawn from the respective posterior distributions. Computing the ages resulting from Nboot = 10000 mass-magnitude samples for each target yields the age posteriors shown in the left column of Fig. 5 and listed in Table C.3. To showcase the power of possessing a high-precision dynamical mass estimate, we can bootstrap the mass and age sampling further into other parameter spaces. Thus, we can repeat the above procedure to obtain posteriors of the companions’ effective temperatures and radii. The results are shown in the middle and right column of Fig. 5 and are listed in Table C.3.
To further contextualise the detected companions we placed them on a colour-magnitude diagram spanned by the Paranal/SPHERE.IRDIS_B_Ks filter magnitude and the colour between Paranal/SPHERE.IRDIS_D_K12_1 and Paranal/SPHERE.IRDIS_D_K12_1. Such a colour-magnitude diagram, populated with a template dwarfs from the literature (for details see Appendix C of Bonnefoy et al. 2018) and the companion sample presented here, can be found in Fig. 6.
4 Discussion
4.1 On the Gaia–GRAVITY synergy
In the previous sections we showed that the orbit solutions contained in the Gaia NSS catalogue can be used to inform follow-up observations with a high-precision direct imaging instrument such as GRAVITY. The Gaia-based position predictions proved to be sufficiently accurate to facilitate the placement of the GRAVITY science fibre in such a way that the exceedingly small field of view contained the sought-after companion. In this way, we were able to detect and confirm all eight predicted companions.
The complete lack of non-detections is worthy of a short discussion. As the reader will recall, young age was not used as a criterion for target selection. Thus, one would naïvely assume that such an allowance for old targets would cause some of the observations to result in non-detections of the respective companions since the companion-to-host contrast decreases with age. A simple estimation of the companion magnitude at high ages resolves the conundrum. Given the inferred masses, we could compute the magnitudes from evolutionary models. Furthermore, we could compute the limiting magnitude up to which detection with GRAVITY can be achieved for each target system. To this end, we evaluated the GRAVITY contrast curve (Pourré et al. 2024) at the detection separation of each companion and converted the resulting limiting contrasts to a magnitude difference. In combination with the respective K band magnitudes of the hosts this yields the limiting companion magnitudes. Comparison with the companion magnitudes from the evolutionary models reveals that they are all observable independent of their ages. This is a consequence of investigating companions located towards the upper end of the brown dwarf mass range. We are dealing with objects that are sufficiently bright to facilitate successful detection regardless of their age. This is a luxury not afforded to those who plan to apply the procedures outlined here to less massive and therefore fainter companion targets. In such cases one is forced to include age as a selection criterion.
Substellar companions in the NSS catalogue typically reside at separations of a few dozen mas. This makes follow-up observations with classical direct imaging instruments such as SPHERE (Beuzit et al. 2019) or GPI (Macintosh et al. 2014) challenging for the vast majority of these objects due to the inner working angle of their coronagraphs. It is only by the means of GRAVITY and its unique angular resolution that these low-separation companions can be accessed. This will be even more relevant for the numerous Gaia-inferred companions in the planetary-mass regime, which are predicted to be found at even smaller separations (Perryman et al. 2014). To illustrate this point, it is worth noting that among the sample of detected companions presented here is Gaia DR3 2728129004119806464 B, which, observed at a radial separation of 34 mas from the host star, is the closest ever directly detected substellar companion. The inferred companion orbit puts the semi-major axis at (0.938 ± 0.023) AU. Another noteworthy example is that of WT 766 B’s orbit, which exhibits a semi-major axis of (0.676 ± 0.008) AU. The semi-major axes of the entire companion sample are presented in Table 2.
The independent companion detections by GRAVITY provide a rare opportunity to validate and assess the orbital solutions published in the Gaia DR3 NSS two-body orbit catalogue. One way of doing so is by assessing the statistic validity of the Gaia uncertainties. To this end we compared the companion position prediction based on the NSS orbital solutions to the GRAVITY detection. Since the radial separation component depends on the initially unconstrained mass ratio between companion and host, we removed it from the analysis by only considering the position angle component, φ. If the Gaia uncertainties are statistically robust approximately 68 % of the detections should be made at position angles within a 1 σ confidence interval around the median of the Gaia-based position angle prediction, φmed. Figure B.1 shows said position angle distribution for each target system as well as the respective GRAVITY detection position angle, φdet. By taking the absolute difference, Δφ = |φdet − φmed|, between the distribution’s median and the detection value and scaling it by the respective uncertainties, σφ,det and σφ,med, according to
![$\[I=\frac{\Delta \varphi}{\sqrt{\sigma_{\varphi, \text { det }}^2+\sigma_{\varphi, \text { med }}^2}},\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq10.png) (5)
(5)
we can compute an inflation factor, I, that quantifies by how much the Gaia uncertainties need to be ‘blown up’ to make the 1 σ position angle confidence interval encompass the detection. The resulting inflation factors for the individual systems are showcased in Table 2. They indicate that – with the exception of G ...6464 B – all companions were detected outside the respective Gaia-based 1σ position angle confidence interval, suggesting that the Gaia uncertainties are underestimated. We note that as can be seen in Fig. B.1 the inflation factor found for the CD-50 869 system results from a non-Gaussian position angle distribution rendering the value unusable.
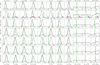 |
Fig. 2 Marginalised posterior distributions of the systems’ orbital parameters for the Gaia-only run (in black) as well as the Gaia-plus-GRAVITY run (in green). Note that the Gaia-plus-GRAVITY chain converges on two different orbital solutions for the CD-50 869 system. The bimodal posterior distribution was separated into the preferred (green) and the secondary solution (purple). The indices 1 denote that the shown parameters describe the host star’s orbit around the respective system’s COM. |
 |
Fig. 3 Orbits of the individual companions relative to their respective host. The black line indicates the orbit as suggested by the orbit solution listed in the Gaia NSS catalogue (assuming the lower companion mass estimate). The black circle shows where the companion was predicted to be located at the time of observation. The blue dot and its uncertainty ellipse indicate where the GRAVITY detection was made. The thick green orbit is based on the median parameter values of the posterior distributions after combining the Gaia and GRAVITY data as described in Sec. 3.1. The thin light green lines show 100 orbits drawn at random from the posterior distribution. Note that CD-50 869’s posterior orbit sampling was separated into a primary and secondary mode, shown here in green and purple, respectively. |
 |
Fig. 4 Mass-magnitude plane with the companions detected in this work and isochrones taken from the ATMO and Baraffe model grids in blue and orange, respectively. Both the data points and the isochrones are presented as 2MASS/2MASS.Ks filter magnitudes. The three potentially under-luminous companions, G ...6464 B, CD-50 869 B, and G ...1920 B, are marked in red. |
 |
Fig. 5 Age, effective temperature, and radius constraints for the individual companions as obtained using the ATMO and Baraffe models in blue and orange, respectively. The horizonal bars show the 1 σ environment around the median of each distribution. |
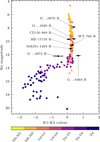 |
Fig. 6 Colour-magnitude diagram showing a template dwarf population compiled in Bonnefoy et al. (2018, for details, see their Appendix C) as well as the companion sample discussed in this work. The colour indicates the spectral type of a given object. |
4.2 Orbital refinements and dynamical masses
By means of a Bayesian inference framework conducted using an MCMC procedure, we were able to combine the orbit solution provided by Gaia with the GRAVITY astrometry measurement. Visual inspection confirmed that, apart from the mass chains, all chains of the Gaia-only runs as well as all chains of the Gaia-plus-GRAVITY runs converged for every target system. The inclusion of the GRAVITY detection resulted in tighter constraints on the orbital elements and the breaking of the mass degeneracy inherent to the NSS orbit solution. With the exception of CD-50 869 B and G ...1920 B, which have both been shown to be of stellar nature, the resulting dynamical masses lie within the respective mass constraints listed in the DR3 Binary Masses Table (Gaia Collaboration 2023a). While the dynamical mass of CD-50 869 B carries a relative uncertainty of 15 %, those of the other targets vary between 0.9 and 5 %.
Furthermore, the posterior sampling of the CD-50 869 system is of bimodal nature. A possible explanation of this circumstance can be found in the geometry of the orbit and epoch of the GRAVITY detection. In order to minimise leakage of the host star flux into the science fibre and the resulting speckle noise it was decided to observe this companion at its furthest separation from the host. In combination with the orbit being almost edge-on, the MCMC chain converges on two different solutions that place the companion before and after the projected turning point, respectively. Such a configuration serves to show the limitation of this method. By observing at the largest separation and thereby maximising the chances of detection, one runs the risk of obtaining an inconclusive posterior due to bi- or even multi-modality. It should be noted, however, that the acquisition of an additional GRAVITY epoch of the companion at a different position along its orbit would likely kill the bimodality and pin down the orbital solution at or close to the primary mode obtained here. Finally, when allowing for additional evidence from proper motion anomaly studies, CD-50 869’s entry in the catalogue put forward in Kervella et al. (2022) suggests a host star mass of (0.90 ± 0.04) M⊙. This estimate is covered by the primary mode’s host mass constraint of ![$\[1.03_{-0.19}^{+0.32} M_{\odot}\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq12.png) . Moreover, using surface brightness to colour relations and the system’s parallax they also obtain a host star radius estimate of (0.87 ± 0.04) RSun, which is incompatible with the secondary mode’s large host mass. The only other system presented here that is also contained in the Kervella et al. (2022) proper motion anomaly catalogue is HD 17155.
. Moreover, using surface brightness to colour relations and the system’s parallax they also obtain a host star radius estimate of (0.87 ± 0.04) RSun, which is incompatible with the secondary mode’s large host mass. The only other system presented here that is also contained in the Kervella et al. (2022) proper motion anomaly catalogue is HD 17155.
While more constrained, on the whole the updated orbit posteriors visualised in Fig. 2 agree with the Gaia NSS orbital solutions. The largest discrepancy between the posteriors before and after inclusion of the GRAVITY astrometry can be seen in the orbital period of G ...3872 B. We note that this period value is particularly large, suggesting that the period estimate presented in the NSS catalogue might have been underestimated due to insufficient orbital coverage.
The almost exactly edge-on orbit of WT 766 B was already indicated by the orbital solution listed in the Gaia NSS catalogue. The updated orbit elements substantiate this orbit configuration and suggest the possibility of observing this substellar companion in transit. The transit probability can be calculated on the basis of the maximum opening angle, ϑ. If a given companion’s orbit exhibits an inclination within the range 90° − ϑ < i < 90° + ϑ it will show a transit. Based on the derivation in Beatty & Seager (2010) the maximum opening angle, ϑ, for an eccentric companion orbit can be computed via
![$\[\vartheta=\arcsin \left(\frac{R_*}{a} \cdot \frac{1+e \sin (\omega)}{1-e^2}\right),\]$](/articles/aa/full_html/2024/08/aa50018-24/aa50018-24-eq13.png) (6)
(6)
where R* is the stellar radius and a, e, and ω are the companion orbit’s semi-major axis, eccentricity, and argument of perias-tron, respectively. For WT 766 B this yields a maximum opening angle of ϑ = (0.236 ± 0.007) °. How this compares to the companion’s inclination posterior is visualised in Fig. 7. Integrating the posterior within the angular transit opening range around 90° yields a transit probability of 84 %.
According to the orbital solution posterior the next transit will occur in February 2025. The symmetry of the orbit as projected onto the sky plane makes it impossible to determine whether this will constitute a primary or secondary eclipse, however. Upon observation it should be fairly obvious which phenomenon is observed, breaking the degeneracy in the orbit symmetry. Alternatively, an additional RV measurement of the system on top of the one listed in Gaia DR3 should enable the derivation of the systematic velocity and in turn resolve the orbit’s directional degeneracy. In any case, such an observation would constitute the first application of imaging and transit techniques to the same object.
In the respective panels of Fig. 3, we can observe that the orbital constraints resulting from the inference procedure also manifest in changes to the geometry of some of the orbits. To prepare for computing reduced chi-squared values of the refined orbits we ran an additional gradient descent procedure starting at the most probable parameter sample as determined by the MCMC run. The minima identified by the gradient descent procedure were then used to compute the chi-squared values presented in Table 2.
Semi-major axes, inflation factors and reduced chi-squared values for the detected companions.
 |
Fig. 7 WT 766 B’s Gaia-plus-GRAVITY inclination posterior compared to the angular transit opening range indicated by the hatched green region. The dashed blue line shows a perfectly edge-on orbit. The percentage values specify the posterior sampling fractions falling within and outside the opening range. |
4.3 Inferring ages from evolutionary models
The first notable feature of Fig. 4 is the potential under-luminosity observed in three of the detected companions, namely G ...6464 B, CD-50 869 B, and G ...1920 B. For two of these (G ...6464 B and CD-50 869 B) the error bars on their dynamical mass estimates still overlap with the oldest isochrones. This is not the case for G ...1920 B, which is significantly removed from the isochrones. Under-luminosity in old brown dwarf companions is a known problem in the literature (e.g. Brandt et al. 2021b). Invoking the possibility of companion binarity offers a potential explanation as to the observed lack in luminosity. A companion to the companion would distort the mass of the primary companion since the treatment as put forward here accounts for the putative pair of bodies as a single point mass located at the astrometric position measured by GRAVITY. This would move the respective companion’s data point in Fig. 4 towards the right into a domain where it appears to be under-luminous when instead its mass was misjudged by assuming the companion system to be a single body.
The presence of a secondary companion could be observable by obtaining several GRAVITY epochs. If the astrometric data can be shown to deviate from the expected orbit and to follow a trajectory that exhibits features reminiscent of epicycles, this would strongly suggest companion binarity. The magnitude of such a feature would depend on the mass ratio between the primary and the secondary companion, which can be estimated to the first order by measuring the excess mass in Fig. 4. Such a follow-up study could not be conducted within the framework of this work since the host-companion separations of the targets at hand have already dropped into a range at which even GRAVITY observations are impossible. Once the separations have sufficiently increased again, a dedicated follow-up should be able to shed light on the question of companion binarity.
A note on the filter magnitudes shown in Fig. 4: to present the isochrones of both evolutionary models in the same filter system, we converted the ATMO isochrones from APO/NSFCam.MKO_K to 2MASS/2MASS.Ks magnitudes (for details on the conversions between the two filter systems, see Hawarden et al. 2001 and Carpenter 2001). The slight divergence of the isochrones towards lower masses can be explained by the fact that the filter system conversion was derived using stellar photometry. It should be noted, however, that the conversion was only performed for visualisation purposes within Fig. 4. The subsequent bootstrapping, which was conducted in the APO/NSFCam.MKO_K and 2MASS/2MASS.Ks filter magnitude space for the ATMO and Baraffe models, respectively, is therefore not affected by any potential isochrone divergence.
Since WT 766 B and StKM1-1494 B lie in a the region of the mass-magnitude plane where both evolutionary models are defined, we were able to use both to infer age, effective temperature and radius. Figure 5 and Table C.3 show that the ages inferred using both models match. While the effective temperature posteriors agree for WT 766 B this is not the case for StKM1-1494 B. Furthermore, the radius posteriors from both models disagree for both targets. For G ...3872 B and HD 17155 B only one model could be used for the characterisation. Due to their placement on the mass-magnitude plane, no such analysis could be conducted for the three potentially under-luminous targets G ...6464 B, CD-50 869 B, and G ...1920 B.
The clustered and thus degenerate nature of isochrones describing older objects within the mass-magnitude plane is reflected in the age posteriors of some of the targets. Their samplings are skewed towards older ages. In general the obtained ages for our target sample companions are remarkably low. This comes as a surprise seeing that the stellar age distribution in the solar neighbourhood peaks at a significantly higher value (at ~5 Gyr according to Gondoin 2023). This bias towards young ages could be caused by an observational overestimation of the companion flux amounting to a photometric calibration error of the GRAVITY data. Investigation into whether or not this is the cause of the observed bias is outside the scope of this work. If confirmed, however, correcting for the resulting magnitude offset would exacerbate the aforementioned under-luminosity observed in three of the companions.
Having acquired the companions’ dynamical masses as well as their ages, we could apply the same evolutionary models as above to generate synthetic companion magnitudes in different wavelength bands. This serves two goals. On the one hand it enables us to verify that our initial zero-companion-Gaia-flux hypothesis was justified, closing the loop and ascertaining that the mass constraints on the hosts and companions are trustworthy. On the other hand these magnitudes will be informative for potential future follow up observations of the companions with other instruments working in different wavelength ranges. The respective synthetic companion magnitudes are listed in Table C.4. Inspection of the G band flux ratio of the target systems for which it could be computed affirms that they are indeed negligible.
Figure 6 establishes that the majority of new companions presented here are spread out along the L-dwarf branch with G ...0976 B, G ...1920 B, and CD-50 869 B consistent with M-L transition bodies (Kirkpatrick et al. 1999). G ...3872 B and G ...6464 B are the only companions discussed here that appear removed from the literature population. In the case of G ...6464 B this could constitute another hint at companion binarity. Alternatively, as Faherty et al. (2014) point out, the strong red colour of G ...6464 B might indicate a thick cloud deck in its atmosphere. G ...3872 B on the other hand sits above the L-T (Kirkpatrick 2005) transition possibly indicating a methane rich atmosphere.
Finally, it is worth remembering that we detected an additional companion, which – judging by its large K band flux relative to its host – is likely of stellar nature. The high contrast was the reason G ...0976 B could not be included in the analysis since the crucial zero-companion-Gaia-flux hypothesis could not be upheld. Since the orbit listed in the Gaia NSS two-body orbit catalogue did facilitate a successful detection, however, there is every reason to expect that such a Gaia-informed observation can be repeated. Obtaining additional epochs of this companion will enable further constraints to be placed on its orbit and thereby its mass, potentially solving the question as to why it is so bright in the K band.
5 Conclusion
In this work, we have demonstrated the synergies between Gaia and GRAVITY by showcasing how the astrometry-based orbital solutions contained in the NSS two-body orbit catalogue can be used to inform high-angular-resolution follow-up observations. We detected and confirmed eight companions, of which seven were previously unknown. Every conducted observation resulted in the successful detection at or close to the predicted position of the inferred companion. It is important to note that the unprecedentedly precise nature of the astrometric data collected by Gaia makes it difficult to follow up on or challenge using other currently available instruments. In most cases, the high contrasts and small angular separations between hosts and companions as suggested by the orbits listed in the NSS catalogue are inaccessible to today’s direct imaging facilities. From this point of view, GRAVITY offers a unique opportunity to test the orbits put forward in the NSS two-body orbit catalogue. We can conclude that the results presented here – both in terms of the 100% success rate in detecting the inferred companions and in terms of how the two data sets can be combined – constitute an independent validation of the Gaia NSS orbital solutions as well as the Gaia binary mass estimates. Applying the Gaia–GRAVITY ensemble to companion candidates of planetary nature will be an intriguing next step in exploring the two instruments’ joint potential.
Combination of the Gaia and GRAVITY data by means of a Bayesian approach revealed more refined orbital solutions as well as tight constraints on the host and companion masses. They suggest that five companions of the sample can be categorised as brown dwarfs, while two, CD-50 869 B and G ...1920 B, are of a stellar nature. The same can be expected for G ...0976 B.
The GRAVITY K band spectra were investigated to further characterise the companions. To this end, evolutionary models were used to obtain constraints on their age, effective temperature, and radius. The possibility of probing for companion binarity by means of a high-resolution astrometric time series with GRAVITY is discussed here and should be considered for the potentially under-luminous targets G ...6464 B, CD-50 869 B, and G ...1920 B. Comparison with a template population from the literature further contextualises the companion sample and indicates that they are consistent with L- to T-type brown dwarfs.
The potential of this method in confirming candidates suggested by Gaia astrometry cannot be overestimated. Rapid direct detections of the inferred companions render the breaking of the mass degeneracy between host and companion a matter of routine. The resulting tight constraints on the companion masses can shed light on formation processes and interior evolution.
The procedures showcased in this work are not confined to brown dwarf companions but can readily be applied to planetary candidates as well. Such candidates are still scarce in DR3 but should be forthcoming in DR4, which is expected to be published in 2026. The astrometric time-series data to be released therein will amount to a treasure trove of planetary candidates accessible with GRAVITY. And finally, with the imminent arrival of GRAVITY+, the possibility of accessing companions at even smaller contrasts bodes well for the future synergies between Gaia and GRAVITY as well as direct imaging in general.
Acknowledgements
This work is based on observations collected at the European Southern Observatory under ESO programmes 60.A-9102, 1104.C-0651 and 111.253E. SL acknowledges the support of the French Agence Nationale de la Recherche (ANR), under grant ANR-21-CE31-0017 (project ExoVLTI). G-DM acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (MA 9185/1) amd from the Swiss National Science Foundation under grant 200021_204847 “PlanetsInTime”. Parts of this work have been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation. J.J.W., A.C., and S.B. acknowledge the support of NASA XRP award 80NSSC23K0280. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the Jean-Marie Mariotti Center Aspro service (available at http://www.jmmc.fr/aspro). This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. Finally, we would like to thank Timothy Brandt for his thorough and insightful referee report. His comments and suggestions have substantially improved the quality of this paper.
Appendix A Correcting for throughput losses
When observing targets in the dual-field on-axis mode of GRAVITY, situations can arise where the companion body is separated from the centre of the science fibre by a certain angular distance. This can be case when the companion’s position relative to the host cannot be constrained well enough to inform the proper placement of the fibre or when the observer deliberately moves the fibre in such a way that the target is not located at its centre anymore. This fibre off-pointing technique (Pourré et al. 2024) can facilitate contrast capability gains rendering it especially useful for such observations where one expects unfavourable contrast conditions between the companion and host. For both these reasons the observations conducted for this work exhibit angular separations between the eventually detected companions and the fibre-centre. Following the procedure outlined in Appendix A of Wang et al. (2021), we computed the normalised coupling efficiency, γ, as a function of the angular separation from the fibre centre. The relation as well as the respective companions’ separations are presented in Fig. A.1. Dividing the observed contrast spectra by the respective coupling efficiency, γ, we can correct for the ensued throughput losses.
 |
Fig. A.1 Normalised coupling efficiency, γ, as a function of the angular separation between the fibre centre and the observed body. |
Appendix B Inflation factors for Gaia uncertainties
As discussed in Sect. 4.1, the companion position angle predictions based on the Gaia NSS two-body orbit catalogue in combination with the true position angle measured with GRAVITY can be used to assess how robust the Gaia uncertainties are. In Fig. B.1 we present the comparison between prediction and detection for each target system.
Appendix C Additional tables and plots
Here, we present additional relevant tables and plots. Table C.1 presents the observation log for every target observed with the GRAVITY instrument. Table C.2 lists the stellar magnitudes used for the spectral fits. Table C.3 showcases the inferred numerical results for each orbital parameter, the host and companion masses as well as the characteristics inferred from evolutionary models for each target system. Table C.4 lists synthetic companion magnitudes resulting from the application of the inferred ages and masses to evolutionary models. Figure C.1 shows the companion-to-host K band contrast spectra measured by GRAVITY. The full corner plots of the respective MCMC runs for each target system are presented in Fig. C.2 to C.8.
 |
Fig. B.1 Position angle distributions of the individual companions as predicted from the Gaia NSS two-body orbit solutions as well as the position angles at which the respective companions were detected using GRAVITY (in green). The inflation factor, I, required to make the 1 σ confidence interval encompass the detection is given in the top-right corner of each panel. Note that the distribution’s non-Gaussian shape in the panel for the CD-50 869 system renders the resulting inflation factor unusable. |
Observation log of the GRAVITY follow-up.
Orbital and evolutionary model parameters of the respective target systems.
Synthetic absolute magnitudes of the different companions.
 |
Fig. C.1 GRAVITY contrast spectra between the companion and host for the different target systems. For targets that were observed multiple times, the spectrum with the highest signal-to-noise ratio is shown. |
 |
Fig. C.2 Corner plot showing the posterior samplings for the G ...6464 system. The Gaia-only and the Gaia-plus-GRAVITY run are presented in black and green, respectively. The indices 1 denote that the shown parameters describe the host star’s orbit around the respective system’s COM. The dashed blue and red lines in the M2 row indicate the upper and lower BD mass boundaries, respectively. |
 |
Fig. C.3 Same as Fig. C.2 but for the CD-50 869 system. This bimodal posterior sampling was separated into the preferred (green) and the secondary mode (purple). |
References
- Allard, F., Guillot, T., Ludwig, H.-G., et al. 2003, in Brown Dwarfs, ed. E. Martín, IAU Symp., 211, 325 [NASA ADS] [Google Scholar]
- Babusiaux, C., Fabricius, C., Khanna, S., et al. 2023, A&A, 674, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balmer, W. O., Pueyo, L., Lacour, S., et al. 2024, AJ, 167, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbato, D., Ségransan, D., Udry, S., et al. 2023, A&A, 674, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beatty, T. G., & Seager, S. 2010, ApJ, 712, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binnendijk, L. 1960, Properties of Double Stars; A Survey of Parallaxes and Orbits (University of Pennsylvania Press) [Google Scholar]
- Bonnefoy, M., Perraut, K., Lagrange, A. M., et al. 2018, A&A, 618, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowler, B. P. 2016, PASP, 128, 102001 [Google Scholar]
- Brandt, T. D. 2021, ApJS, 254, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, G. M., Brandt, T. D., Dupuy, T. J., Michalik, D., & Marleau, G.-D. 2021a, ApJ, 915, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, G. M., Dupuy, T. J., Li, Y., et al. 2021b, AJ, 162, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2021, VizieR On-line Data Catalog: II/328 [Google Scholar]
- D’Angelo, G., Durisen, R. H., & Lissauer, J. J. 2010, in Exoplanets, ed. S. Seager (University of Arizona Press), 319 [Google Scholar]
- De Rosa, R. J., Nielsen, E. L., Wahhaj, Z., et al. 2023, A&A, 672, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faherty, J. K., Beletsky, Y., Burgasser, A. J., et al. 2014, ApJ, 790, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanive, C., Bedin, L. R., De Furio, M., et al. 2023, MNRAS, 526, 1783 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Franson, K., Bowler, B. P., Zhou, Y., et al. 2023, ApJ, 950, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Arenou, F., et al.) 2023a, A&A, 674, A34 [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaudi, B. S., Seager, S., Mennesson, B., et al. 2020, arXiv e-prints [arXiv:2001.06683] [Google Scholar]
- Gondoin, P. 2023, A&A, 678, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R., Bonavita, M., Mesa, D., et al. 2024, A&A, 685, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2017, A&A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Lacour, S., et al.) 2019, A&A, 623, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Nowak, M., et al.) 2020, A&A, 633, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halbwachs, J.-L., Pourbaix, D., Arenou, F., et al. 2023, A&A, 674, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawarden, T. G., Leggett, S. K., Letawsky, M. B., Ballantyne, D. R., & Casali, M. M. 2001, MNRAS, 325, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkley, S., Lacour, S., Marleau, G. D., et al. 2023, A&A, 671, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kammerer, J., Lacour, S., Stolker, T., et al. 2021, A&A, 652, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasper, M., Cerpa Urra, N., Pathak, P., et al. 2021, The Messenger, 182, 38 [Google Scholar]
- Kervella, P., Arenou, F., & Thévenin, F. 2022, A&A, 657, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirkpatrick, J. D. 2005, ARA&A, 43, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Reid, I. N., Liebert, J., et al. 1999, ApJ, 519, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Marocco, F., Gelino, C. R., et al. 2024, ApJS, 271, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Lacour, S., Dembet, R., Abuter, R., et al. 2019, A&A, 624, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Wang, J. J., Nowak, M., et al. 2020, SPIE Conf. Ser., 11446, 114460O [NASA ADS] [Google Scholar]
- Leclerc, A., Babusiaux, C., Arenou, F., et al. 2023, A&A, 672, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, PNAS, 111, 12661 [NASA ADS] [CrossRef] [Google Scholar]
- Maire, A. L., Baudino, J. L., Desidera, S., et al. 2020, A&A, 633, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marleau, G. D., & Cumming, A. 2014, MNRAS, 437, 1378 [Google Scholar]
- Marley, M. S., Fortney, J. J., Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2007, ApJ, 655, 541 [Google Scholar]
- Mesa, D., Gratton, R., Kervella, P., et al. 2023, A&A, 672, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C. 2013, A&A, 558, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nielsen, E. L., De Rosa, R. J., Macintosh, B., et al. 2019, AJ, 158, 13 [Google Scholar]
- Nowak, M., Lacour, S., Lagrange, A. M., et al. 2020, A&A, 642, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M., Hartman, J., Bakos, G. Á., & Lindegren, L. 2014, ApJ, 797, 14 [Google Scholar]
- Phillips, M. W., Tremblin, P., Baraffe, I., et al. 2020, A&A, 637, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourré, N., Winterhalder, T. O., Bouquin, J. B. L., et al. 2024, A&A, 686, A258 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quanz, S. P., Ottiger, M., Fontanet, E., et al. 2022, A&A, 664, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stolker, T., Quanz, S. P., Todorov, K. O., et al. 2020, A&A, 635, A182 [EDP Sciences] [Google Scholar]
- The LUVOIR Team 2019, arXiv e-prints [arXiv:1912.06219] [Google Scholar]
- Tokunaga, A. T., Simons, D. A., & Vacca, W. D. 2002, PASP, 114, 180 [CrossRef] [Google Scholar]
- Vigan, A., Fontanive, C., Meyer, M., et al. 2021, A&A, 651, A72 [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wang, J. J., Vigan, A., Lacour, S., et al. 2021, AJ, 161, 148 [Google Scholar]
All Tables
Semi-major axes, inflation factors and reduced chi-squared values for the detected companions.
All Figures
 |
Fig. 1 Position probability maps at the time of observation for the observed systems as computed from the respective orbital solutions listed in the Gaia NSS catalogue. The orange cross indicates the mean companion position relative to the mean host position, which is marked by the yellow star. The system’s COM is shown by the grey cross. Randomising the host and companion positions on the basis of the parameter uncertainties and correlations (while keeping the mass ratio, q, fixed to the lower limit; see the main text) yields the predicted spread around the respective mean positions. The contour line encircles 68 % of the randomised companion positions. The grey axis connects the mean host position with the mean companion position to visualise the separation’s dependence on the mass ratio, q. The position at which the companion was detected with GRAVITY is shown as the dark blue cross. For targets that were observed more than once, we show the companion position prediction corresponding to the first epoch and the resulting initial detection. The dark blue uncertainty ellipses associated with the GRAVITY detections are too small to be seen at these scales. The ticks along the panel axes are spaced by 10 mas. Finally, the significance of the individual orbital solutions, (S/N)orbit, is given below the target system name in the top-left corner of each panel. |
| In the text | |
 |
Fig. 2 Marginalised posterior distributions of the systems’ orbital parameters for the Gaia-only run (in black) as well as the Gaia-plus-GRAVITY run (in green). Note that the Gaia-plus-GRAVITY chain converges on two different orbital solutions for the CD-50 869 system. The bimodal posterior distribution was separated into the preferred (green) and the secondary solution (purple). The indices 1 denote that the shown parameters describe the host star’s orbit around the respective system’s COM. |
| In the text | |
 |
Fig. 3 Orbits of the individual companions relative to their respective host. The black line indicates the orbit as suggested by the orbit solution listed in the Gaia NSS catalogue (assuming the lower companion mass estimate). The black circle shows where the companion was predicted to be located at the time of observation. The blue dot and its uncertainty ellipse indicate where the GRAVITY detection was made. The thick green orbit is based on the median parameter values of the posterior distributions after combining the Gaia and GRAVITY data as described in Sec. 3.1. The thin light green lines show 100 orbits drawn at random from the posterior distribution. Note that CD-50 869’s posterior orbit sampling was separated into a primary and secondary mode, shown here in green and purple, respectively. |
| In the text | |
 |
Fig. 4 Mass-magnitude plane with the companions detected in this work and isochrones taken from the ATMO and Baraffe model grids in blue and orange, respectively. Both the data points and the isochrones are presented as 2MASS/2MASS.Ks filter magnitudes. The three potentially under-luminous companions, G ...6464 B, CD-50 869 B, and G ...1920 B, are marked in red. |
| In the text | |
 |
Fig. 5 Age, effective temperature, and radius constraints for the individual companions as obtained using the ATMO and Baraffe models in blue and orange, respectively. The horizonal bars show the 1 σ environment around the median of each distribution. |
| In the text | |
 |
Fig. 6 Colour-magnitude diagram showing a template dwarf population compiled in Bonnefoy et al. (2018, for details, see their Appendix C) as well as the companion sample discussed in this work. The colour indicates the spectral type of a given object. |
| In the text | |
 |
Fig. 7 WT 766 B’s Gaia-plus-GRAVITY inclination posterior compared to the angular transit opening range indicated by the hatched green region. The dashed blue line shows a perfectly edge-on orbit. The percentage values specify the posterior sampling fractions falling within and outside the opening range. |
| In the text | |
 |
Fig. A.1 Normalised coupling efficiency, γ, as a function of the angular separation between the fibre centre and the observed body. |
| In the text | |
 |
Fig. B.1 Position angle distributions of the individual companions as predicted from the Gaia NSS two-body orbit solutions as well as the position angles at which the respective companions were detected using GRAVITY (in green). The inflation factor, I, required to make the 1 σ confidence interval encompass the detection is given in the top-right corner of each panel. Note that the distribution’s non-Gaussian shape in the panel for the CD-50 869 system renders the resulting inflation factor unusable. |
| In the text | |
 |
Fig. C.1 GRAVITY contrast spectra between the companion and host for the different target systems. For targets that were observed multiple times, the spectrum with the highest signal-to-noise ratio is shown. |
| In the text | |
 |
Fig. C.2 Corner plot showing the posterior samplings for the G ...6464 system. The Gaia-only and the Gaia-plus-GRAVITY run are presented in black and green, respectively. The indices 1 denote that the shown parameters describe the host star’s orbit around the respective system’s COM. The dashed blue and red lines in the M2 row indicate the upper and lower BD mass boundaries, respectively. |
| In the text | |
 |
Fig. C.3 Same as Fig. C.2 but for the CD-50 869 system. This bimodal posterior sampling was separated into the preferred (green) and the secondary mode (purple). |
| In the text | |
 |
Fig. C.4 Same as Fig. C.2 but for the HD 17155 system. |
| In the text | |
 |
Fig. C.5 Same as Fig. C.2 but for the WT 766 system. |
| In the text | |
 |
Fig. C.6 Same as Fig. C.2 but for the G ...3872 system. |
| In the text | |
 |
Fig. C.7 Same as Fig. C.2 but for the G ...1920 system. |
| In the text | |
 |
Fig. C.8 Same as Fig. C.2 but for the StKM1-1494 system. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


