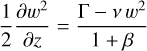| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A274 | |
| Number of page(s) | 24 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245220 | |
| Published online | 23 July 2024 | |
Global climate modeling of the Jupiter troposphere and effect of dry and moist convection on jets
1
Laboratoire de Météorologie Dynamique/Institut Pierre-Simon Laplace (LMD/IPSL), Sorbonne Université, Centre National de la Recherche Scientifique (CNRS), École Polytechnique, École Normale Supérieure (ENS),
Paris,
France
2
Institut Universitaire de France (IUF Paris, France),
Paris,
France
e-mail: aymeric.spiga@sorbonne-universite.fr
3
Laboratoire d’Études Spatiales et d’Instrumentation en Astrophysique (LESIA), Sorbonne Université, Centre National de la Recherche Scientifique (CNRS), Observatoire de Paris, Paris Sciences Lettres (PSL) Research University,
Meudon,
France
4
Université de Paris, Institut de Physique du Globe de Paris, Centre National de la Recherche Scientifique (CNRS),
Paris,
France
5
School of Physics and Astronomy, University of Leicester,
Leicester,
UK
Received:
14
October
2022
Accepted:
1
February
2024
Aims. The atmosphere of Jupiter is characterized by banded jets, including an equatorial super-rotating jet, by an intense moist con-vective activity, and by perturbations exerted by vortices, waves, and turbulence. Even after space exploration missions to Jupiter and detailed numerical modeling of Jupiter, questions remain about the mechanisms underlying the banded jets and the role played by dry and moist convection in maintaining these jets.
Methods. We report three-dimensional simulations of the Jupiter weather layer using a global climate model (GCM) called Jupiter-DYNAMICO, which couples hydrodynamical integrations on an icosahedral grid with detailed radiative transfer computations. We added a thermal plume model for Jupiter that emulates the effect of mixing of heat, momentum, and tracers by dry and moist convec-tive plumes that are left unresolved in the GCM mesh spacing with a physics-based approach.
Results. Our Jupiter-DYNAMICO global climate simulations show that the large-scale Jovian flow, in particular the jet structure, could be highly sensitive to the water abundance in the troposphere and that an abundance threshold exists at which equatorial super-rotation develops. In contrast to our dry (or weakly moist) simulations, simulations that include the observed amount of tropospheric water exhibit a clear-cut super-rotating eastward jet at the equator and a dozen eastward mid-latitude jets that do not migrate poleward. The magnitudes agree with the observations. The convective activity simulated by our thermal plume model is weaker in the equatorial regions than in mid to high latitudes, as indicated by lightning observations. Regardless of whether they are dry or moist, our simulations exhibit the observed inverse energy cascade from small (eddies) to large scales (jets) in a zonostrophic regime.
Key words: hydrodynamics / methods: numerical / planets and satellites: gaseous planets
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Jupiter is a fast-rotating gas giant planet, which means that it is a valuable laboratory for studying geophysical fluid dynamics (Ingersoll 1990; Vasavada & Showman 2005), especially because the terrestrial and Jovian environments differ greatly. In addition to its size, lack of surface, and fast rotation, Jupiter differs from Earth in that its obliquity is only about 3°, implying little seasonal variability. The radiative budget of Jupiter is also highly distinct from that of Earth (Read et al. 2016): it receives an incoming solar flux that is lower by 30 times than that of Earth, and its emitted thermal radiation is twice higher than that absorbed from the Sun at shorter wavelengths. This indicates an internal heat source.
The rich atmospheric dynamics of Jupiter is shown by its system of bright zones and brown belts, caused by narrow zonal jets that alternatively flow eastward and westward. They include a remarkable super-rotating eastward jet at the equator. Jupiter features 27 jets: 14 eastward (prograde) jets, and 13 westward (retrograde) jets (Porco et al. 2003). This jet system is stable with time and only shows sporadic local changes in the colors of the zones and the belts (Fletcher et al. 2011). The intense magnetic field of Jupiter, generated in its metallic hydrogen envelope, is likely to exert a significant drag on the atmospheric flow at depth (Liu et al. 2008), as shown by Juno measurements (Guillot et al. 2018). The Juno gravity measurements determined that the Jupiter jets extend to a depth of 2000–3000 km below the visible cloud deck (Kaspi et al. 2018), which is about 4% of the Jupiter radius.
The Jupiter atmospheric dynamics is also characterized by long-lived vortices (Marcus 2004), which include the Great Red Spot. This is a tropical anticyclone as large as Earth that has lasted for at least three centuries (Fletcher et al. 2010; Sánchez-Lavega et al. 2018; Simon et al. 2014). Furthermore, through its polar orbit, Juno discovered a cluster of eight stable cyclones at the Jupiter northern pole and five stable cyclones at its southern pole. They are regularly spaced around a polar vortex (Adriani et al. 2018; Grassi et al. 2018). In addition to large-scale vortices, the Jupiter atmosphere harbors a wealth of nonaxisym-metric perturbations (called eddies): Salyk et al. (2006) showed that the eddies in the superficial weather layer of Jupiter amount to a significant transfer of kinetic energy toward jets of about 5 to 10% of the Jovian thermal emission. This inverse cascade of energy from small (eddies) to large scales (jets) is also supported by the analysis of observed kinetic energy spectra and energy and enstrophy transfers at Jupiter (Galperin et al. 2014; Young & Read 2017; Read et al. 2020; Cabanes et al. 2020a).
The Jupiter atmosphere is composed of 86% hydrogen and 13% helium, and it is enriched in (most) heavy elements by about a factor of 2 to 4 compared to solar abundances (SA) (Mousis et al. 2019). The oxygen abundance estimated from water measurements by the Galileo probe near the 20 bar level was found to be lower than the solar abundance (Wong et al. 2004), but this was explained by the peculiar dry hot spot into which it plunged. More recently, the Juno spacecraft obtained an enrichment by a factor of 3 for water below the Jupiter cloud deck (Li et al. 2020). Three species are condensible in the Jupiter atmosphere: ammonia NH3 from 0.8 to 0.5 bar (and even 0.2 bar in the equatorial region and the Great Red Spot), ammonium hydrosulfide NH4SH at about 2 bar, and water H2O between 4 and 6 bar. Water and ammonia condensates may combine as partially melted hail-like mushballs through complex thermody-namical pathways permitted by convective storms (Guillot et al. 2020b). All these condensates have a higher mean molecular weight than the main components of the Jupiter atmosphere. This implies convective inhibition, which for large abundances of condensibles may counteract the positive buoyancy allowed by latent heat release (Leconte et al. 2017).
Convective storms on Jupiter (Gierasch et al. 2000), especially those based on the water condensate, are thought to be particularly powerful (the vertical wind reaches 100 m s−1), as shown by observational estimates (Stoker 1986) and studies with convection-resolving models (Hueso et al. 2002; Hueso & Sánchez-Lavega 2006; Sugiyama et al. 2011, 2014; Li & Chen 2019). These storms mostly occur in belts, and their sizes range from 10 to 1000 km. Lightning is frequent in white-patched con-vective storms, whose size exceeds 200 km (Little et al. 1999). The Juno microwave radiometer mapped the meridional distribution of the lightning signatures of the storms to discover that storms are stronger and more frequent between 30° and 70° latitude, but they are almost nonexistent close to the equator (Brown et al. 2018). Guillot et al. (2020a) argued with their mushball mechanism that this dearth of equatorial storms may explain the equatorial maximum in the ammonia abundance discovered by Juno (Bolton et al. 2017), since precipitating ammonia-rich mushballs evaporating at depth are absent at the equator and cannot deplete the Jupiter upper troposphere from its ammonia. Convective storms are thought to play a prominent role in the energy transfer from small to large scales (Siegelman et al. 2022).
It is a long-standing endeavor to interpret the rich weather of Jupiter depicted by observations with modeling. The models can be described as belonging to two classes: Shallow weather-layer models inherited from global climate models (GCMs) used in meteorology and climate research, and deep interior-convection models inherited from dynamo models that are used in geophysics. These two classes of models offer a distinct, if not complementary, picture of the eddies, vortices, and jets that emerge in the fast-rotating Jovian atmosphere. In deep models, the fluid circulations of Jupiter are computed at least down to the transition between molecular and metallic hydrogen, where conductivity increases and implies ohmic drag (Heimpel et al. 2005, 2016; Kaspi et al. 2009; Gastine et al. 2014; Gastine & Wicht 2021). In shallow models, the fluid circulations of Jupiter are resolved in the superficial weather layers, typically several or some dozen bar below the visible cloud deck (middle and upper troposphere) toward the stratosphere (Williams 1978; Dowling et al. 2006; Showman 2007; Schneider & Liu 2009; Young et al. 2019a); deep jets are possible even with a shallow forcing (Showman et al. 2006). The weather layers are represented with an idealized top boundary condition in deep models, and the deeper layers are represented with an idealized bottom boundary condition in shallow models.
Our approach in this paper draws from the weather-layer shallow-model perspective and the development of GCMs for Jupiter. A long-standing topic of interest is how the banded jet system can result from eddies generated by distinct sources in these models. Possibilities that are not mutually exclusive include sunlight-induced baroclinic instabilities and internal-flux-induced convective instability (Schneider & Liu 2009; Liu & Schneider 2010, 2015), moist convective forcing (Showman 2007; Lian & Showman 2010), jet migration, and merging (Young et al. 2019a). In contrast to their terrestrial-planet counterparts, the existing weather-layer GCMs for Jupiter use simple gray radiative computations (Schneider & Liu 2009; Young et al. 2019a) and a simple representation of the moist convection (Lian & Showman 2010) because of the computational cost involved in the modeling of gas-giant atmospheres. More often than not, they simply include a dry convective adjustment scheme as in Schneider & Liu (2009), for example.
Following the approach set up for Saturn (Spiga et al. 2020; Cabanes et al. 2020b; Bardet et al. 2021, 2022), we propose a new weather-layer GCM for Jupiter, called Jupiter-DYNAMICO. A first improvement upon existing Jupiter GCMs is that Jupiter-DYNAMICO couples hydrodynamical computations (Dubos et al. 2015) at an adequate horizontal resolution to resolve Jupiter eddies (half a degree latitude and longitude), with detailed radiative transfer computations, including the effect of both gaseous and aerosol compositions of Jupiter (Guerlet et al. 2020), as was done in our Saturn model (Guerlet et al. 2014). A second improvement upon existing Jupiter GCMs is that Jupiter-DYNAMICO features a physics-based thermal plume model for unresolved subgrid-scale dry and moist convection that is adapted from terrestrial schemes (Hourdin et al. 2002; Rio & Hourdin 2008; Rio et al. 2010) and capable of emulating the transport of heat, momentum, and tracers exerted by subgrid-scale convection. Our aim here with this new Jupiter-DYNAMICO model is to address the question of the possible formation mechanisms for the Jupiter jets, including the equatorial super-rotating jet, and in particular, the impact of moist convection on their formation. We describe the Jupiter-DYNAMICO GCM in Sect. 2 and dedicate Sect. 3 to the description of the thermal plume model (with additional details in Appendix A). The results from dry simulations are included in Sect. 4, and the main results from this study, exploiting moist simulations with Jupiter-DYNAMICO, are included in Sect. 5. We conclude and offer perspectives in Sect. 6.
2 Modeling method
2.1 Building the Jupiter-DYNAMICO global climate model
A GCM is usually composed of two parts: a dynamical core (hydrodynamical solver), and physical parameterizations for subgrid-scale processes (radiative transfer, turbulent mixing, cloud formation, and so on). Our Jupiter GCM, called Jupiter-DYNAMICO, shares many characteristics with the Saturn-DYNAMICO GCM described in Spiga et al. (2020). The reason for this is that the two giant planets have common characteristics.
The dynamical core we use is DYNAMICO (Dubos et al. 2015). It solves the hydrodynamics equation in a rotating spherical shell in an icosahedral mapping. This icosahedral mapping allows for efficient massively parallel computations. A high horizontal resolution is needed to be able to resolve small eddies, which are assumed to supply the jet streams through an inverse energy cascade (Cabanes et al. 2020b). The model outputs are interpolated from the icosahedral grid to a longitude-latitude grid at run time. The equations included in DYNAMICO assume that the atmosphere is hydrostatic and that the atmospheric spherical shell is very thin compared to the planetary radius (i.e., the shallow-atmosphere assumption ɀ ≪ RJ, where ɀ is the altitude above the Jupiter cloud level, and RJ is the Jupiter radius). The vertical coordinates are sigma levels determined by the pressure ratio p/pb, where pb is the bottom pressure. The implementation of dynamical equations in DYNAMICO ensures an exact energy conservation (Dubos et al. 2015).
Physical parameterizations are added to represent the physical processes that are left unresolved by the dynamical core. A complete description of the radiative transfer scheme tailored for the Jupiter atmosphere included in our GCM is detailed in Guerlet et al. (2020). Radiative transfer in our Jupiter GCM is based on the correlated-k method, which includes multiple scattering and Rayleigh scattering from a line-by-line spectrum (HITRAN 2016 database; Gordon et al. 2017). The considered radiatively active species are ammonia, methane, ethane, acetylene, H2-H2, and H2-He collision-induced dimers. Their abundances are assumed constant with time and latitude and are taken from results of the Galileo (H2 and He in Niemann et al. 1998 ; CH4 in Wong et al. 2004) and Juno probes (NH3 in Bolton et al. 2017). The radiative effects of tropospheric hazes and ammonia clouds are important components of the Jupiter atmosphere and are included in the radiative scheme as aerosols. However, they are not transported as a tracer by the dynamical core. Their vertical profiles are set to be horizontally invariant, as described in Guerlet et al. (2020). The diurnal cycle is neglected due to the long radiative timescales on Jupiter; the seasonal cycle is accounted for (both eccentricity and obliquity). As in other published Jupiter GCMs (Schneider & Liu 2009; Lian & Showman 2010; Young et al. 2019a), an internal heat flux is added at the bottom boundary of the model to obtain the correct total emitted power of Jupiter (Li et al. 2018). For simplicity and lack of observations, this flux is taken constant with latitude, even though this might imply a latitudinal temperature gradient that is inconsistent with observations, depending on the efficiency of the dynamical transfer of heat toward the poles (Aurnou et al. 2008).
Convective mixing by turbulence is left unresolved by the dynamical core. This subgrid-scale convective mixing by turbulence can typically be split into two components:
a small-scale part, local turbulence, that may be represented by simple vertical diffusion (in our model, a standard Mellor and Yamada scheme Mellor & Yamada 1982), and
a large-scale part, in which convective mixing is exerted by thermal plumes that appear when the atmosphere is con-vectively unstable with respect to the dry or moist adiabat. This is represented in our model by a specific new scheme (a thermal plume model) that we describe in Sect. 3.
2.2 Settings
The planetary and atmospheric constants used in our Jupiter GCM are summarized in Table 1, together with information on discretization and on the boundary conditions, for which further details are provided below.
Physical constants and parameters used in the Jupiter DYNAMICO GCM simulations.
2.2.1 Discretization
For the purpose of this study with Jupiter-DYNAMICO, as in the work on Saturn by Spiga et al. (2020) and Cabanes et al. (2020b) using the same DYNAMICO dynamical core, the horizontal resolution of the hexagonal-icosahedral grid in our Jupiter GCM must be such that the distance between two neighboring points is smaller than 0.5°. With our settings (see Table 1), we obtain 256 000 grid cells in each vertical layer for a horizontal resolution of about 0.4°.
The vertical dimension was discretized on 32 levels, ranging from 10 bar at the model bottom to 9 mbar at the model top (with the subtlety that the highest layer contains all the remaining mass of the atmosphere, e.g., for radiative transfer integrations). The model top thus lies in the lower stratosphere: While this does not permit stratospheric studies for which the model top needs to be raised significantly (Bardet et al. 2021,2022), resolving the lower stratosphere allows us to prevent the boundary effects from affecting the model predictions lower in the troposphere as much as possible.
To optimize the computational cost of our model, we used three different time steps (Table 1). The dynamical time step, which is applied to the Navier-Stokes equations in the hydro-dynamical core, is very short due to the high spatial resolution and the necessary compliance with numerical stability (Courant–Friedrichs–Lewy CFL criterion). Two distinct time steps were used in the physical parameterizations, one step for the radiative transfer scheme, and the other for the other param-eterizations. Because of the long radiative timescale in Jupiter (Guerlet et al. 2020) and because the radiative scheme is computationally very expensive, the radiative scheme in our Jupiter GCM is called as sparingly as possible while still retaining realistic tendencies by updating the radiative tendencies only once every 20 Jovian days.
2.2.2 Initial and boundary conditions
All the GCM simulations described in this paper started with the same initial wind and temperature conditions. The wind was zero everywhere, and the temperature was set with the same vertical profile at each grid point, regardless of its latitude or longitude. This initial vertical profile was computed in typical global conditions with the one-dimensional radiative-convective model, as described in Guerlet et al. (2020).
At the bottom boundary condition, we used a Rayleigh drag on the velocity field to model the deep magnetohydrodynamics impact on the weather layer as introduced in Schneider & Liu (2009) and also used in Young et al. (2019a). From the Juno probe measurements of the gravitational harmonics, we now know that the jet depth is about 3000 km from the visible cloud layer (Kaspi et al. 2018), where electrical conductivity becomes significant (Guillot et al. 2018). These jets are thought to extend not radially, but along cylinders. Consequently, we can deduce the minimum latitude φR at which the drag is active from this depth. It is indicated in Table 1. To compute the associated relaxation timescale, we used the formula given by Liu & Schneider (2015),
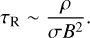
Because we lack knowledge about the inner magnetic field and electric conductivity, we cannot constrain it, but Liu & Schneider (2015) expected that it is between 10 and 40 times shorter on Jupiter than on Saturn. Hence, we chose a relaxation timescale equal to a twentieth of the value used to model the Saturn atmosphere in Spiga et al. (2020), namely 4 × 105 s (about 4.5 terrestrial days).
At the top of the model, a sponge layer that absorbs vertically propagating waves may be included as an option (Lian & Showman 2010; Young et al. 2019a). This is a difficult point: Without this, the waves can be reflected at the top of the model and perturb the equilibrium state in a nonphysical way. With this, the bias in the angular momentum conservation is stronger, which may affect the predicted jet speeds strongly (Shaw & Shepherd 2007). The question is particularly relevant for modeling fast-rotating gas giants that lack a surface, where zonal circulations are strongly controlled by the redistribution of angular momentum (Schneider & Liu 2009). The angular momentum conservation in DYNAMICO for gas giants is satisfactory (see the appendix in Spiga et al. 2020). We therefore adopted the same setting as in Schneider & Liu (2009) and Spiga et al. (2020), where no constraint on the velocity field (sponge layer) was imposed at the top boundary.
As was done in any dynamical core used for atmospheric applications, a dissipation term was added to avoid energy accumulation at the smallest resolved scales. This was implemented in the dynamical core as hyperviscosity (i.e., an iterated Lapla-cian) applied on the vorticity (velocity curl), velocity divergence, and temperature (see the appendix of Spiga et al. 2020 for further details). Each has its own order of Laplacian iteration and relaxation timescale. They were set to 2 and 10 000 s in the three cases, respectively, and we relied on the similar settings in the Saturn-DYNAMICO simulation (Spiga et al. 2020).
3 Thermal plume model adapted to Jupiter
3.1 Motivation and choice of the scheme
In order to improve the subgrid-scale parameterization of convection significantly and to include moist convection processes, we chose a more sophisticated approach than simple convec-tive adjustment. We adopted a parameterization called “thermal plume model”, which was originally developed for dry convection (Hourdin et al. 2002) and was then adapted to moist convection (Rio & Hourdin 2008; Rio et al. 2010) in an Earth GCM boundary layer scheme. The principle of the thermal plume model is to compute an idealized thermal plume induced by convective instability to obtain the mass flux between any atmospheric layer involved in the convective thermal plume. This represents in a physical way the mixing of heat, momentum, and tracers by convective processes that are left unresolved at the mesh spacing of GCMs. These mass fluxes are both horizontal and vertical. The horizontal mass fluxes are called entrainment e or detrainment d, according to whether the flux points lie inward or outward of the plume itself, respectively. Useful diagnostics for subgrid-scale convection were computed as intermediate variables within the thermal plume model, for instance, the surface fraction occupied by the updraft part of the idealized plume. The thermal plume model is dedicated to computing con-vective mass fluxes. For moist convection, this thermal plume scheme has to be coupled with distinct schemes that account for precipitations and cloud microphysics.
The thermal plume model for Earth of Hourdin et al. (2002) and Rio et al. (2010) was previously adapted to another planet than Earth by Colaïtis et al. (2013) for the Martian dry boundary layer convection. In the Martian case, similarly to the terrestrial case, the authors benefited from large eddy simulations to tune the parameters of the thermal plume model. Because we do not have the same tools at our disposal in the Jupiter case, we chose to rely on the generic physics-based approach of the thermal plume model, which ensures adaptability to any possible planetary environment. The thermal plume model is built by design with a small number of free parameters that have a relatively straightforward physical meaning.
3.2 Basic principles
The basics of the thermal plume model are summarized in Fig. 1. The thermal plume model is triggered at any GCM grid point that at a given time step shows a convectively unstable gradient at the bottom of the model. When at least two consecutive levels are convectively unstable, each column is divided into two subcolumns: one column for the ascending plume, and the other for the subsiding environment. The plume is built by iterating over the vertical: the vertical speed and normalized mass fluxes of the plume are computed considering adiabatic expansion, latent heat release from water phase changes, and mean molecular weight. Entrainment, detrainment, and updraft acceleration directly follow in the thermal plume model through simple equations detailed in Appendix A. When the entrainment is positive, we recalculated the acceleration and took the new properties of the plume into account. The updraft stops in the layer in which either its vertical speed or its vertical mass flux vanishes. This permits overshoots to occur in the thermal plume model. Eventually, the height of the idealized thermal plume provides the values of mass fluxes in physical units (i.e., not normalized), which enables us to compute the mixing of heat, momentum, and tracers at the GCM grid scale over the whole vertical profile.
This is provided via the closure relation (which assumes that the lateral entrainment speed approximately equals the maximum of the vertical speed).
In addition to this general framework, several supplementary assumptions underlie the thermal plume model approach:
the mass in each layer is conserved;
the pressure inside the plume is equal to the pressure outside the plume;
the downdraft speed is assumed to be much less than the updraft speed, which allows us to neglect it in the vertical momentum budget;
vertical mass flux variations cannot be simultaneously due to entrainment and detrainment (in other words: either e > v and d = v, or e = v and d > v, where v is a parameter setting the minimum value of entrainment and detrainment);
the idealized thermal plume is assumed to be stationary at the physical time step considered in the GCM.
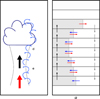 |
Fig. 1 Principles of the thermal plume model. Left panel: schematics of a real convective plume. The bottleneck part is the bulk of the plume, and the puffy upper part is the overshoot. The black arrow represents vertical fluxes in the ascending plume (the red arrow is the bottom source of the plume). The rounded blue arrows represent exchanges between the ascending plume and the environment: entrain-ment e toward the plume, and detrainment d toward the environment. Right panel: schematics of the idealization adopted in the thermal plume model. The gray areas represent the ascending plume subcolumn (see text in Sect. 3.2). The mass fluxes are both vertical (black and gray arrows) and horizontal (entrainment e as blue arrows and detrainment d as red arrows). α is the fraction of the GCM grid mesh that is covered by ascending convective plumes. They are represented as the single plume in the thermal plume model. |
3.3 Adaptation to the Jovian atmosphere
In stark contrast to the boundary layers of terrestrial planets, thermal plumes in the atmosphere of any gaseous planet may start in any tropospheric layer rather than at the first atmospheric layer overlying a warm surface. We therefore modified the thermal plume model borrowed from terrestrial GCMs (Rio et al. 2010) so that the initial plumes triggered by convective instability were not necessarily right above the surface (i.e., the lowest model layer). Nevertheless, we limited the vertical extent over which a thermal plume can be triggered. This upper limit is defined by two parameters: the bottom layer index linf, and the top layer pressure plim (see Table A.2). We set linf to 1 since there are no specific reasons to exclude any bottom layers from the convective scheme.
The second major adaptation to the original version of the thermal plume model is that at any given mesh cell, several thermal plumes can be piled up. In the terrestrial version, the thermal-plume parameterization assumes that only one thermal plume may be triggered above the surface. Above this idealized plume, no possibility for any additional plume is considered. Conversely, on Jupiter, it is not possible to assume that the atmosphere is mixed by a single thermal plume, especially in an atmosphere in which three distinct condensable species create stacked convectively mixed layers.
Thus, wherever there is convective instability between the top of the last computed thermal plume and the plim pressure level, we triggered another plume. We set plim to 1 bar in order to avoid unexpected plumes in the high troposphere while allowing dry convection to be triggered above water clouds. We expect that the simulated plumes starting below the water condensation level will probably stop slightly above it in our GCM moist simulations (see Sect. 5) because only the most powerful plumes are able to reach beyond the condensation level up to the top of the ammonia clouds in the cloud-resolving simulations (see, e.g., Sugiyama et al. 2011, 2014). Triggering a second plume is thus necessary to mix the convectively unstable layer due to the ammonia clouds. Our model currently only accounts for moist convection related to water condensates. This second plume is therefore dry. Future development will include a tracer for ammonia to simulate the associated ammonia-based moist convection. This task is complex owing to the possible formation of mushballs, which involves both ammonia and water condensates (Guillot et al. 2020b,a).
We also note for possible future applications beyond Jupiter that the modifications to the original terrestrial model can be reversed through the parameter settings, so that our adapted parameterization is able to parameterize convective mixing in any (exo)planetary atmosphere.
3.4 Sensitivity study
In order to verify the performance of the thermal plume model and set the free parameters (see Table A.2 in Appendix A), we used the one-dimensional version of our Jovian physical param-eterizations, that is, without the coupling to the dynamical core, for the dry and moist atmospheres. In other words, this is a version of the one-dimension model of Guerlet et al. (2020) with the addition of the thermal plume model. The lack of detailed observational data about the Jupiter water clouds and moist convection prevents us from conducting a tuning similar to what was done in terrestrial thermal plume models (Rio et al. 2010). Instead, the purpose of the sensitivity study was to ensure that the convection was well represented within physics-based bounds in order to understand the qualitative impact of convection on the general circulation. To reduce the complexity of this sensitivity study, we made the following assumptions for Jupiter:
in a given layer, the air can be either entrained or detrained, but not both, that is, the minimum mass flux v was set to 0;
the plume width is twice its height, that is, the aspect ratio r was set to 2;The rationale for this choice is that the size of the numerous small-scale convective storms (subgrid-scale with respect to our model horizontal resolution) is typically about 100 km (see, e.g., Sánchez-Lavega et al. 2018 and Orton et al. 2020), and their depth is about 50 km below cloud deck (see, e.g., Brueshaber et al. 2022 and Fig. 1 in Guillot et al. 2020a), which yields this value for the aspect ratio. Furthermore, an exploration with the one-dimensional version of the thermal plume model suggested that varying the aspect ratio between 0.5 to 5 impacted the plume velocity in the thermal plume model at less than the order of the magnitude level. We therefore decided that it was more important to explore other free parameters, such as buoyancy and friction.
the nature of the convection on Jupiter implies that the horizontal mixing parameter β ≈ 1 (we chose β = 0.9) because this parameter controls the relative contribution of the first layer to entrainment in the whole column. Setting it close to one in practice means that any vertical layer may contribute equally to entrainment, in contrast with Earth’s moist convection, where the contribution of the first layer to entrainment dominates because of the surface.
Eventually, we had two free parameters (hyperparameters) to explore, namely the buoyancy coefficient a, and the fluid friction factor b. Fluid friction b is a model hyperparameter meant to represent small-scale turbulence that affects the plume dynamics. This turbulent viscosity is much higher than the molecular viscosity of molecular hydrogen. This reflects that the friction exerted on convective plumes is mostly that of small-scale turbulence and not that of molecular viscosity, which acts on the smaller scales of turbulence at the end of the Kolomogorov cascade.
3.4.1 Dry case
Using our thermal plume model in the dry configuration, we tested several values for each of the two parameters a and b, as reported in the top panels of Fig. 2. Potential temperature profiles show that regardless of the choice of these parameters, vertical mixing by convection is correctly realized. Every atmospheric layer crossed by the plume becomes convectively neutral and adjusts to the same vertical temperature profile. The mixing layer extends from the bottom of the model at 10 bar up to the 0.4 bar layer. The top of the mixing layer is lower than the tropopause, which is located at 0.1 bar, but it approximately corresponds to the observed ammonia cloud layer (between 0.2 and 0.8 bar).
In contrast to the potential temperature profile, the properties of the idealized plumes in the thermal plume model depend on the tuning parameters (Fig. 2 top right panel). When it is assumed to be less buoyant (low value of a) or more fric-tional (high value of b), the parameterized thermal plume is, as expected, slower and lower. The differences in plume heights are caused by a subtle combination of buoyancy and friction in the various vertical layers of the plume. Counterintuitively, the maximum of the plume vertical speed is located above the p = 1 bar level in the frictional cases (b ≠ 0) but is below the p = 1 bar level in the nonfrictional case (b = 0). The radiative effect of the aerosols simulating the ammonia clouds plays a role, as it impacts the buoyancy above and below p = 1 bar. It creates a stable layer below p = 1 bar and an unstable layer above, thereby giving rise to the two-layer appearance observed in the vertical speed of the plume in most of the cases explored in Fig. 2. We note that a significant vertical speed of the plume and the mass flux only occur at around 5 bar, while imposing an internal heat flux sets a bottom instability in the model at 10 bar. It takes several layers from the bottom instability for the plume to reach significant acceleration. The vertical profile of the buoyancy and plume acceleration depends on the vertical profile of the potential temperature of the environment (relative to the potential temperature of the parcel).
Considering the tests in Fig. 2, we chose to retain a = 0.9, that is, we considered that buoyancy is the main contributor to the thermal plume acceleration, with a loss of 10% typically due to smaller-scale turbulence. We decided to set the fluid friction factor b to a low nonzero value (b = 10−4 m−1 ) for consistency with the principle that buoyancy is the main contributor to thermal plume acceleration, while avoiding unrealistic convective velocities that may arise in several grid points in three-dimensional simulations using the thermal plume model, which significantly perturbs the tropopause level. In other words, we decided to set a = 0.9 and b = 10−4 m−1 to maximize the vertical plume speed while ensuring that the plumes reached realistic levels. The computations from the thermal plume model (notably, the mass fluxes) using these two reference parameters are shown in the bottom panels of Fig. 2. As is the case for any parameter combination tested in Fig. 2 top right (not shown), air is mainly entrained in the deepest layers and detrained in the highest layers. We expect this type of nonlocal vertical mixing from the thermal plume model: This is how convective transport is realized. Nevertheless, entrainment is positive beyond the 1 bar level, concurrently with a decrease in the vertical speed of the plume. This effect is directly associated with the radiative effect of aerosols mentioned above.
The maximum vertical speeds reached by updrafts computed in the thermal plume model are 1.25 m s−1. These simulated vertical speeds of thermal plumes are lower than what is known of Jupiter from observations (Stoker 1986) or cloud-resolving models (Sugiyama et al. 2011). This is in line with the principle of the thermal plume model, which is to compute the characteristics of an idealized average thermal plume over several hundred kilometers (the GCM mesh spacing) from the large-scale fields of temperature and pressure computed by the GCM. The plume speed is representative of the mean transport (of heat, momentum, and chemical species) exerted by plumes and is not the maximum local vertical speed in a realistic convective plume.
 |
Fig. 2 Behavior of the thermal plume model in one-dimensional Jupiter dry simulations (after 1000 Jovian days). The two top plots display the vertical profiles of the potential temperature (left) and vertical plume speed (right). Nine combinations using three values of the buoyancy coefficient a and the fluid friction factor b are shown: a = 0.1/0.5/0.9 (dotted, dashed, and solid lines) and b = 0/10−4/2 × 10−4 m−1 (red, purple, and blue lines). The two bottom plots show the case a = 0.9 and b = 10−4 m−1. They show the vertical plume speed on the left and the mass fluxes on the right (entrainment in blue, detrainment in red, and vertical mass flux in black). |
 |
Fig. 3 Behavior of one-dimensional Jovian modeling using the thermal plume model in the moist case. The sensitivity to the water abundance is explored. The vertical speed (left) and mass fluxes (right) of the plumes are shown for a solar abundance of water of 1 (dotted line), 3 (dashed line) and 9 (solid line). The entrainment is shown in blue, the detainment in red, and the vertical mass flux in black. The variables are plotted as a function of pressure after a run of 1000 Jovian days with a = 0.9 and b = 10−3 m−1. |
3.4.2 Moist case
Of the three condensible species (NH3, NH4SH, and H2O) below the Jupiter cloud deck, water is the only condensible species that is accounted for in this work. Based on the water abundance on Jupiter and the potential related latent heat release (see for instance Table 1 in Guillot 2022), we expect the intensity of water-related moist convective plumes to be strongest and the contribution of water condensation to the Jovian global circulation accordingly to be largest. In our physical parameterizations for Jupiter, the thermal plume model is associated with a simple model for cloud formation, which simply condenses the amount of water vapor in excess to the saturation mixing ratio, then causes it to rain (10% of the amount at each time step) and evaporate (uniformly over all vertical levels in which the environmental air is not saturated). Any remaining liquid water when precipitations reach the lowest layer of the model is evaporated in this layer to ensure water mass conservation.
The results from our one-dimensional Jovian model including the moist thermal plume model and the simple cloud model are shown in Fig. 3. We tested three values for the water abundance, spanning the range of values found in the literature: 1,3, and 9 solar abundances (hereinafter SA). The value of the water abundance was initially set up in the model as a uniform vertical profile of the mixing ratio for the layers with a pressure greater than 2 bar. The main change caused by the addition of water is the vertical extent of the plumes. In the 3 SA and 9 SA cases, the thermal plumes range from p = 8 bar to p = 3 bar and stops above the first layer at which water condenses, because of the impact of the molecular weight of the condensate. In the 1 SA case, the thermal plumes range from 10 bar to 6 bar. They stop lower than in the cases with more water because of the weaker convective instability caused by the lower latent heat release.
Activation of moist convection in the thermal plume model leads to stronger convection (as long as water concentration is low enough to overcome inhibition by mean molecular mass, Leconte et al. 2017), thus requiring a change in the tuning parameters of the thermal plume model compared to the dry case. The parameters chosen in the dry simulations mentioned above result in very fast thermal plumes with a vertical speed of several hundred meters per second. While these vertical wind speeds may be encountered locally and in specific conditions in convec-tive storms of Jupiter, this is not expected in the thermal plume model, which is a parameterization of the mean transport and mixing exerted by convective plumes at the large scale of a GCM grid point. These extreme plume vertical speeds in the thermal plume model in the simulations lead to the disappearance of the Jupiter stratosphere under the influence of unrealistically overshooting plumes. In order to solve this problem, we increased the value of the fluid friction factor b; with b = 10−3 m−1, we obtained a vertical speed of about 1 m s−1 (see Fig. 3). This value of parameter b results in a realistic vertical extension for the plumes; any lower value yields higher vertical speeds, but an unrealistic vertical extent. This adversely affects the simulated upper tropospheric and lower stratospheric profile of Jupiter (in particular, the tropopause altitude). The underlying assumption of representing moist convection with a thermal plume model was made to emphasize the impact on the large-scale circulations in Jupiter of numerous and frequent small-scale moist convective plumes occupying a fraction of a GCM grid (i.e., a region that is about several hundred kilometers across). The impact on the large-scale circulation of the rarest, deepest, and largest-scale moist convective storms on Jupiter are not represented by the thermal plume model; this is a possible area for future modeling work following the present study. In three-dimensional simulations, where atmospheric destabilization is stronger than in one-dimensional simulations due to dynamical activity (eddies), the parameter b = 10−3 m−1 is also found to be more appropriate for the dry case than the setting b = 10−4 m−1 described in Sect. 3.4.1; thus any three-dimensional simulation (dry and moist simulations) below use b = 10−3 m−1. This setting of b = 10−3 m−1 ensures a reasonable vertical speed of the idealized thermal plumes (see Fig. 9) and efficient convective heat and momentum mixing to set an adiabat temperature profile in the troposphere in all simulations (see Figs. 4 and 6). Any value of b above this optimum value would cause friction effects to become dominant over buoyancy effects and hinder convective mixing in the troposphere by thermal plumes.
4 Three-dimensional dry simulations of the Jupiter atmosphere
In this section, we describe the results of a simulation of our Jupiter-DYNAMICO GCM using the thermal plume model for dry convection in the troposphere. The main results ofthis paper are related to the influence of moist convection in Sect. 5, but describing a dry simulation first is an opportunity for us to present the performance of our DYNAMICO GCM in the Jupiter case, as a reference similar to that presented for Saturn in Spiga et al. (2020), before we study the influence of moist convection in Sect. 5. The dry simulation was run for about 40 000 Jovian days (3.7 Jovian years), which is shorter than the 60 000 Jovian days used in the moist simulations.
4.1 Thermal structure
The thermal structure obtained in our three-dimensional Jupiter-DYNAMICO dry simulation is shown in Fig. 4 (temperature T and Brunt-Vaisala frequency N2 proportional to the vertical gradient of the potential temperature). A clear two-layer structure is obtained with a neutral troposphere (N2 = 0) resulting from convective mixing, overlaid by a stable stratosphere (N2 > 0) resulting from radiative processes (Guerlet et al. 2020). This means that the tropopause in the model is located at 200– 250 mbar. We note that this tropopause level is slightly higher than the level of 300 mbar at which the vertical speed of thermal plumes reaches zero (see Figs. 2 and 9), which is expected since mixing occurs by detrainment above the top of the convective layer and the tropopause is located higher because it is defined as the sharp transition from the tropospheric radiative-convective equilibrium to the stratospheric radiative equilibrium.
A 3-K equator-to-pole temperature gradient is produced by the model at the 1 bar pressure level (see also Fig. 7). This is far lower than the 28 K at the same pressure level obtained by Guerlet et al. (2020) with a radiative seasonal model devoid of atmospheric dynamics. The strong reduction of this equator-to-pole temperature gradient in our Jupiter three-dimensional DYNAMICO simulations is caused by resolved atmospheric circulations that transport heat from the equatorial region toward the poles in the troposphere: The dynamics in the weather layer that occurs at pressures lower than 10 bar is already able to remove most of the latitudinal temperature gradient caused by the differential illumination. The seasonal variations, expected to be about 0.5 K in Guerlet et al. (2020) because of the planetary eccentricity and obliquity, are indistinguishable in the three-dimensional simulations.
 |
Fig. 4 Latitude-pressure sections of the (left) zonal-mean temperature T and (right) Brunt-Väisälä frequency N2, i.e., buoyancy frequency, for the dry simulation with our Jupiter-DYNAMICO GCM (average of all simulated years except for the first year, during which the jet structure yet has to be established). |
4.2 Wind fields
The tropospheric dynamics that arises in our Jupiter-DYNAMICO three-dimensional simulations using dry conditions are shown in Fig. 5. At the beginning of the simulation, a dozen eastward jets appear after several thousand Jovian days of integration (Fig. 5a), before they broaden and merge while accelerating continuously. When the merging ceases, the resulting jets start to migrate poleward and continue to broaden until only four eastward jets remain. The additional jets are destroyed when they reach high latitudes. The northern hemisphere shows two simulated prograde jets at 25°N and 55°N, and the southern hemisphere shows three jets at 20°S, 60°S, and a new jet at 45°S, which appears after 30 000 Jovian days of simulation at 35°S. The jet speeds range from 30 m s−1 to 100 m s−1. Throughout the simulation, two eastward (prograde) jets are always separated by a westward (retrograde) jet, unless a merging occurs. The off-equatorial westward jets are slower in magnitude than the eastward jets, with speeds ranging from 10 m s−1 to 25 m s−1. The westward equatorial jet is fastest jet (−100 m s−1 at p = 1 bar) and broadest (22° latitude wide at p = 1 bar). In stark contrast to the equatorial super-rotation observed at Jupiter, Fig. 5a indicates that our three-dimensional GCM simulations with Jupiter-DYNAMICO using dry convection do not exhibit a super-rotating jet in the equatorial region: The simulated equatorial jet is strongly retrograde over the broad subtropical region between 15°S and 15°N.
The top left panel of Fig. 11 (shown in Sect. 5 for comparison with moist cases) exhibits the vertical structure of the jet system simulated by Jupiter-DYNAMICO in its dry configuration. Whether located at the equator or in mid-latitudes, all simulated jets extend vertically from the low stratosphere to the bottom of the model located in the troposphere at 10 bar. The jet speeds are approximately vertically constant in the troposphere, suggesting a barotropic structure. This is not the case in the stratosphere, where the speeds of eastward jets increase with height, while off-equatorial westward jet speeds decrease with height: The stratosphere exhibits a baroclinic structure. The intensity of the equatorial jet also decreases with height, but it also undergoes vertical oscillations, which may be an early stadium an embryo of the Jovian quasi-quadriennal oscillation (Flasar et al. 2004; Antuñano et al. 2021; Benmahi et al. 2021), although our model would need to extend farther up in the stratosphere to allow us to study this phenomenon (see the study by Bardet et al. 2021 for Saturn).
To summarize, in our dry GCM simulations with Jupiter-DYNAMICO, we obtained a quasi-symmetric banded jet structure whose speeds exhibit a satisfactory order of magnitude, although the equatorial jet does not super-rotate and the additional tropical jets are not as numerous as in observations.
4.3 Dynamical analysis
In order to characterize the dynamics further, we investigated several zonal-mean diagnostics (described in more detail in Spiga et al. 2020) that are presented as a dynamical atlas in Fig. 5, which shows the variations with latitude and time of each diagnostic, as listed below.
The zonal jet system described by the zonal wind ū (Fig. 5a, discussed in Sect. 4.2).
Nonaxisymmetric eddies described by the eddy kinetic energy
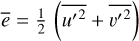 (Fig. 5c).
(Fig. 5c).Forcing of jets by eddies described by the eddy momentum flux
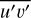 , whose horizontal divergence is related to the zonal wind acceleration (Fig. 5e, Eq. (6) in Spiga et al. 2020).
, whose horizontal divergence is related to the zonal wind acceleration (Fig. 5e, Eq. (6) in Spiga et al. 2020).The Rayleigh-Kuo (hereinafter RK) necessary condition for barotropic instability described by the meridional gradient of the barotropic potential vorticity
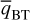 defined in Eq. (14) in Spiga et al. (2020) (the necessary condition for instability is a change of sign in the domain interior; Fig. 5b).
defined in Eq. (14) in Spiga et al. (2020) (the necessary condition for instability is a change of sign in the domain interior; Fig. 5b).The Charney-Stern-Pedlosky (hereinafter CSP) necessary condition for baroclinic instability described by the meridional gradient of the baroclinic potential vorticity
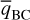 , defined in Eq. (15) in Spiga et al. (2020) (the possible condition CSP 1 for instability is a change of sign in the domain interior; Fig. 5d).
, defined in Eq. (15) in Spiga et al. (2020) (the possible condition CSP 1 for instability is a change of sign in the domain interior; Fig. 5d).An additional criterion for the baroclinic instability described by the vertical wind shear of the zonal wind (condition CSP 2 for instability is the upper boundary same sign as for the PV gradient, condition CSP 3 is the lower boundary same sign as for the PV gradient, condition CSP 4 is zero PV and the same sign shear at both boundaries; see Spiga et al. 2020, Fig. 5f).
Eddies are deviations from the zonal mean flow such as planetary waves (Kelvin, Rossby, and Rossby-gravity waves), large-scale vortices, and smaller-scale vortices and turbulence. Planetary waves may cause jet meandering. For example, in our dry GCM simulation, the equatorial jet is crossed by a long-lived wave with a zonal wave number equal to 5, and planetary waves at higher latitudes have typical wave numbers between 8 and 20 (figures not shown for brevity). Vortices are quite rare and only occur at latitudes higher than ±60°N. Their speed is on the same order of magnitude as that of the jets. The smaller-scale eddies, which consist of all the deviations from zonal mean that are not planetary waves or large-scale vortices, dominate the eddy kinetic energy signal (Fig. 5c). The eddy kinetic energy is significantly higher in the prograde jets, and after 25 000 Jovian days, in the equatorial region (between ±15°N). The eddy activity is also intermittent, with alternating quiet periods and bursts in westward and eastward jets simultaneously. A similar behavior was also noted in the Saturn version of the GCM (Spiga et al. 2020; Cabanes et al. 2020b).
In Fig. 5e, the eddy momentum flux indicates how eddies transfer momentum to the mean flow at various latitudes. When we consider (by convention) transfers of eddy eastward momentum flux u′ > 0, that is, transfers giving rise to the eastward jets of Jupiter, a positive (negative) eddy momentum flux 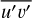 indicates a northward (southward) momentum transfer to the mean flow on average. The equatorial subrotation obtained in our Jupiter-DYNAMICO simulations corresponds to an eastward momentum divergence at the equator that is clearly visible in Fig. 5e. In contrast, additional tropical eastward jets are associated with an eastward momentum convergence in Fig. 5e, denoting a transfer of angular momentum from eddies to jets, as was diagnosed in the Saturn-DYNAMICO simulation by Spiga et al. (2020). In Fig. 15 (top left panel) shown in Sect. 5, the vertical distribution of the eddy momentum flux in our simulations indicates that although the resulting jets appear to be barotropic, eddy forcing has a baroclinic structure with a maximum in the upper troposphere, especially at the equator. In mid-latitudes, the eddy momentum forcing follows a more barotropic structure than at the equator.
indicates a northward (southward) momentum transfer to the mean flow on average. The equatorial subrotation obtained in our Jupiter-DYNAMICO simulations corresponds to an eastward momentum divergence at the equator that is clearly visible in Fig. 5e. In contrast, additional tropical eastward jets are associated with an eastward momentum convergence in Fig. 5e, denoting a transfer of angular momentum from eddies to jets, as was diagnosed in the Saturn-DYNAMICO simulation by Spiga et al. (2020). In Fig. 15 (top left panel) shown in Sect. 5, the vertical distribution of the eddy momentum flux in our simulations indicates that although the resulting jets appear to be barotropic, eddy forcing has a baroclinic structure with a maximum in the upper troposphere, especially at the equator. In mid-latitudes, the eddy momentum forcing follows a more barotropic structure than at the equator.
The poleward migration of the jets described in Sect. 4.2 is expected in a situation in which baroclinic instability plays a prominent role (Kaspi & Flierl 2007; Chemke & Kaspi 2015; Spiga et al. 2020). Baroclinic instabilities (which feed the jets through triggered eddies) are stronger on the poleward sides of the jets, so that the maximum of the zonal wind (i.e., the jet) is shifted poleward. In turn, this affects the baroclinic eddies, and as a result, the jet can migrate over several degrees of latitude. In our Jupiter-DYNAMICO simulation, the mid-latitude jets migrate poleward in both hemispheres, thereby suggesting a leading role of the baroclinic instability. This analysis is strengthened by assessing the CSP criterion for the baroclinic instability and the RK criterion for the barotropic instability (see Figs. 5d and b, respectively). Using these criteria, we have a necessary condition to determine whether a subdomain of the atmosphere may develop barotropic or baroclinic instabilities (see Spiga et al. 2020 or Vallis 2006 for further details). In our Jupiter-DYNAMICO simulations, the stratosphere and the high troposphere are potentially baroclinically unstable over their whole horizontal extent. Moreover, the prograde jets are potentially barotropically unstable on their poleward flank starting from ~ 10 000 Jovian days for the jet closest to the pole and 25 000 Jovian days for the others. This matches the eddy kinetic energy increase at the equator.
 |
Fig. 5 Dynamical atlas of the dry atmosphere simulation with Jupiter-DYNAMICO showing the temporal evolution of the main diagnostics for tropospheric dynamics on Jupiter. Although the model integrations were conducted during 40 000 Jovian days, the temporal axis extends toward 60 000 days for easy comparison with the moist cases described in Sect. 5. The variables shown (see text for further definitions, especially Sect. 4.3) are all zonally averaged. The left column displays the zonal wind (top, panel a), the eddy kinetic energy (middle, panel c), and the eddy momentum flux (bottom, panel e). The right column displays the barotropic potential vorticity [∂q|∂y]bt (top, panel b), the baroclinic potential vorticity [∂q/∂y]bc (middle, panel d), and the zonal wind vertical shear (bottom, panel f). The left column corresponds to flow properties at p = 1 bar, and the right column corresponds to instability diagnostics, shown at p = 0.1 bar for comparison purposes because the baroclinic potential vorticity [∂q/∂y]bc is not defined in the barotropic troposphere. |
5 Three-dimensional moist simulations of the Jupiter atmosphere and effect of the water amount on the global circulation
In this section, we discuss the main results of this paper, using our Jupiter GCM with the thermal plume model representing mixing by moist convection. The settings of the thermal plume model followed what was described in 3.4.2. The choice of the amount of atmospheric water included in the troposphere of our Jupiter GCM was initially guided by the typical enrichment for some other species given by Wong et al. (2004). We chose three different water abundances: 1 SA, 3 SA, and 5 SA. We ran a simulation for 60 000 Jovian days (about 6 Jovian years) in the three cases. These three water abundances are also in line with the recent measurement with the Juno microwave sounder by Li et al. (2020), who reported an atmospheric water abundance of 3 ± 2 solar abundances (SA).
5.1 Thermal structure
The moist simulations using our Jupiter-DYNAMICO GCM with the thermal plume model exhibit the same overall thermal structure as the dry simulation shown in Fig. 4; only subtle differences are found (Fig. 6). The main difference in the temperature field in our Jupiter simulations is shown in Fig. 7 : The moister the simulation, the warmer the troposphere overall. The origin of this effect is not related in a straighforward manner to moist processes: More water vapor may mean more latent heat release, but re-evaporating precipitations that are accounted for in our model induce cooling. The effect is rather indirect: The interplay between convective mixing (which is impacted by the change in moisture; see Fig. 9) and radiative tendencies set the altitude of the tropopause, any slight change of which easily translates into a change of several K in the neutral troposphere. Figure 6 indeed shows that the tropopause is drawn toward slightly higher altitudes (from about 250 mbar to 200 mbar), which drives higher tropospheric temperatures when following the adiabatic gradient down the tropopause. The temperature differences in the stratosphere between our simulations are more subtle and depend on the latitude considered (Fig. 6). We also note in Fig. 7 that the equator-to-pole temperature gradient remains similar at 3 K in all simulations, with a slight reduction to 2.5 K in the moistest 5 SA case. The discussion developed in Sect. 4.1 for the dry GCM case compared to the seasonal radiative model of Guerlet et al. (2020) thus extends to the moist simulations.
5.2 Typical convective activity represented in our model
Based on the thermal plume model formulation (Sect. 3 and Appendix A), the vertical speed of the thermal plumes is an indication of the strength of the convective instability (regardless of whether it is moist or dry convective instability). This vertical speed is a combination of several factors: radiative contributions, internal heat flux, and, for the moist cases, heat exchanges by cloud condensation and precipitation evaporation. In Fig. 8, the zonal-mean vertical speed of plumes parameterized in the thermal plume model included in our GCM are reported for the dry case and the three moist cases. The idealized plume vertical speed is generally stronger in the three moist cases than in the dry case. Furthermore, the moister the simulation, the more frequent vertical wind speeds above 0.8 m s−1 in the thermal plume model. As is shown in Fig. 9, the subgrid-scale convective activity modeled by the thermal plume model is longitudinally heterogeneous, influenced by eddies that are resolved by the model. Locally, the vertical speed of the thermal plume reaches 2 m s−1, which is about twice the value indicated by the zonal-mean diagnostic reported in Fig. 8. Figure 9 shows, however, that higher values for the vertical wind speed in parameterized thermal plumes are more often found for the moister simulations.
Figures 8 and 9 indicate that the zonal-mean intensity of the convective activity varies with latitude. In our three moist simulations (1 SA, 3 SA, and 5 SA) with Jupiter-DYNAMICO, the convective activity follows a similar trend. It is weaker in equatorial regions and stronger in the mid to high latitudes. Subtle differences exist between these three moist cases, but in all of them, the convective activity is strong in the 30° to 75° latitude range in both hemispheres. The convective activity is most different between the quiet equator and convective mid-latitudes in the 3 SA simulation. A similar latitudinal trend is found in the cloud ice column density represented in the model (Fig. 8), where the mid-latitudes are more cloudy than the equatorial and polar regions, which are almost devoid of clouds, showing that the plume moist convective activity is correlated with the formation of clouds at these latitudes. The fact that moist convective clouds mostly form in the mid-latitudes in our simulations is compatible with the latitudinal frequency distribution of lightning, which is assumed to be linked to water clouds, observed by Juno (Brown et al. 2018; Guillot et al. 2020a). This latitudinal contrast in our model might be linked to a latitudinal contrast in water vapor caused by the global circulation, rather than the latitudinal contrast of the temperature conditions. It is difficult to be conclusive, however, because subtle effects also cause the background stability to vary with latitude; moreover, effects such as cloud radiative feedback are not accounted for.
The convective speed in the thermal plume model also varies with pressure level: Figure 9 (left) allows us to describe the layers in our Jupiter-DYNAMICO model in which convective mixing of heat and momentum takes place. As detailed in Sect. 3 and Appendix A, the variations in the plume speed with height relate to horizontal mass fluxes: When the convective speed decreases with height, it means mass transfer toward the environment (detrainment d), and when the convective speed increases with height, it means mass transfer toward the plume (entrainment e). In the dry case, as shown in Fig. 9, a unique convective layer is represented in the Jupiter troposphere, exhibiting entrainment from layers located at several bar and detrainment at approximately 0.6 bar. In the moist cases, two convective layers are represented with a clear separation at about 2 bar (Fig. 9).
Moist air is entrained between 6–10 bar and 3.5 bar and is then detrained between 3.5 bar and 2 bar. Thermal plumes developing from entrainment levels lose buoyancy at the detrainment levels because of the impact of the molecular weight of water (Leconte et al. 2017). These detrainment layers also roughly correspond to the condensation level of water clouds.
Dry air is entrained from 1.5 bar to about 0.6 bar (as in the dry simulation). This layer is poor in water because of mixing within the aforementioned moist layer and precipitation following water condensation. This water-poor mixing layer emulates mixing within the ammonia cloud layer; we recall that no ammonia condensate is considered in the version of the Jupiter-DYNAMICO model described herein.
This two-layer structure in the moist cases is to be understood in a zonal-mean sense. Moist plumes originating from below the cloud deck and developing over the whole tropospheric mixed layer are still sporadically found in specific locations. They are less frequent when the water mixing ratio is high and causes an enhancement of negatively buoyant mean molecular weight effects.
We also find that the deepest layers (below 5 bar) in our model are subsaturated and do not show extensive water-ice clouds. This differs from thermochemical or cloud-resolving models (Hueso et al. 2002; Hueso & Sanchez-Lavega 2006; Sugiyama et al. 2011, 2014) and probably results from the combined impact of complex large-scale atmospheric dynamics and the assumptions of our simple cloud model. Further exploration is needed with convection-resolving modeling coupled with detailed microphysics. Studying the properties of the cloud layers of Jupiter is not the primary goal of this study with the thermal plume model; our goal here is that the thermal plume model plausibly represents the moist convective effects of Jupiter in a GCM, so that the impact of moist convection on the global circulation can be explored. We study this point below.
 |
Fig. 6 Latitude-pressure sections of (left) the zonal-mean temperature T and (right) the Brunt-Väisälä frequency N2 as in Fig. 4, shown for our moist simulations with our Jupiter-DYNAMICO GCM. Top: 1SA. Middle: 3SA. Bottom: 5SA. |
 |
Fig. 7 Typical meridional thermal structure in our Jupiter-DYNAMICO simulations, shown by the zonal-mean temperature at the 1 bar level as a function of latitude (average of all simulated years except for the first year, during which the jet structure is yet to be established). The dry simulation is shown in blue, and the moist simulations are shown in orange (1 SA), green (3 SA), and red (5 SA). |
 |
Fig. 8 Diagnosing the zonal-mean behavior of the thermal plume model in our three-dimensional Jupiter-DYNAMICO simulations. The diagnostics shown are averaged over all simulated years except for the first year, during which the jet structure is yet to be established. The color coding is similar as in Fig. 7: the dry simulation is shown in blue, and moist simulations are shown in orange (1 SA), green (3 SA), and red (5 SA). The top plot in the vicinity of the 3.5 bar level corresponds to the zonal-mean vertical speed of idealized plumes in the thermal plume model, which is an indication of the strength of the subgrid-scale con-vective motions. The bottom plot corresponds to the zonal-mean water ice column density, which is an indication of clouds simulated by our Jupiter model. |
5.3 Simulated Jovian jets
5.3.1 Mid-latitude jets
All the simulations with our Jupiter-DYNAMICO model, regardless of whether they are dry or moist simulations, exhibit a system of several alternating jets in the mid-latitudes (Fig. 10). Furthermore, as is shown in Fig. 11, the jet system in all simulations extends from the low stratosphere to the troposphere, exhibiting a barotropic structure in the troposphere (the zonal wind speed is constant with the pressure level) and a baroclinic structure in the stratosphere (the zonal wind speed increases with altitude, i.e., lower pressure levels). However, the number, width, and speed of the simulated jets with our Jupiter-DYNAMICO model vary with the assumed initial abundance of the water vapor.
The more abundant the water, the more numerous the mid-latitude jets simulated by our Jupiter-DYNAMICO model (Figs. 10 and 11): The prograde (eastward) jets are 5, 7, 10, and 14 in the 0 SA (dry), 1 SA, 3 SA, and 5 SA cases, respectively. Furthermore, the speeds of these mid-latitudes prograde jets significantly decrease when the water abundance increases: at the 1 bar level in the 0 SA, 1 SA, 3 SA, and 5 SA cases, the maximum speeds are 100 m s−1, 80 m s−1, 40 m s−1, and 20 m s−1, respectively. In the moister 3 SA and 5 SA simulations, on each side of the equator, the two prograde jets located in the lower latitudes approach each other in the upper troposphere and lower stratosphere and merge between 70 and 20 mbar and between 200 and 30 mbar, respectively.
Another key contribution of moist convection to the evolution of the jet system in our Jupiter-DYNAMICO simulations is to halt jet migration, which almost disappears in the 3 SA and 5 SA cases (compare the moist simulations reported in Figs. 12a, 13a, 14a with the dry simulation reported in Fig. 5a). As we recalled in Sect. 4.3, Chemke & Kaspi (2015) argued that jet migration occurs as a result of baroclinic instability, implying an asymmetry between the two flanks of a jet; this is also supported by Saturn-DYNAMICO simulations by Spiga et al. (2020) (which did not include the thermal plume model introduced here). A more detailed analysis of large-scale instabilities is developed in Sect. 5.4.
How zonal jets in turn affect the (moist) convective activity is unclear in our Jupiter-DYNAMICO three-dimensional simulations. In the mid-latitudes, there is no obvious link between the extrema of the zonal-mean zonal wind speed and vertical plume speed (Fig. 8). For instance, in the lower troposphere of our Jupiter simulations, while the moist convective activity within the eastward (prograde) jets tends to be strong in the 3 SA case, it is weak in the 5 SA case. A possible cause that we draw from the recent work of Duer et al. (2021) is the Ferrel cells associated with the jet system, which could reinforce convective instability in retrograde jets (subsiding part of the Ferrel cell) and weaken it in prograde jets (ascending part of the Ferrel cell). Identifying Ferrel cells associated with the jet system in our simulations proved to be not straightforward, and this is an area of future work.
 |
Fig. 9 Diagnosing the spatial variability of the vertical speed of idealized plumes in the thermal plume model included in our three-dimensional Jupiter-DYNAMICO simulations. The four-plot arrays on the left and right correspond to the dry (top left) and moist simulations with initial water of 1 SA (top right), 3 SA (bottom left), and 5 SA (bottom right). The left four-plot panel displays the variability of the vertical speed of the zonal-mean plume with pressure and latitude. The right four-plot panel displays the variability of the plume vertical speed with longitude and latitude in the vicinity of the 2 bar level. |
 |
Fig. 10 Jovian jets at the 1 bar level as simulated by our Jupiter-DYNAMICO GCM using the thermal plume model. The diagnostics shown are averaged over all simulated years except for the first year, during which the jet structure is yet to be established). The color coding is similar as in Fig. 7: the dry simulation is shown in blue, and moist simulations are shown in orange (1 SA), green (3 SA), and red (5 SA). This figure may be compared to cloud-tracking observations of Jovian jets (e.g., Fig. 1 in both Porco et al. 2003; Kaspi et al. 2018) and shows that the strong equatorial jet in the troposphere of Jupiter is obtained in our Jupiter-DYNAMICO simulations only in moist conditions with an initial amount of water of 3 SA or 5 SA. |
 |
Fig. 11 Latitudinal and vertical perspective of the Jovian jets simulated by our Jupiter-DYNAMICO GCM using the thermal plume model. This figure shows that a tropospheric super-rotating complements Fig. 10 in showing the impact of moist convection on the Jovian jet system. As in Fig. 10, we show the zonal mean of the zonal wind at the end of the simulated time for 0 SA (top left), 1 SA (top right), 3 SA (bottom left), and 5 SA (bottom right) Jupiter-DYNAMICO GCM simulations. |
5.3.2 Equatorial jets
The equatorial jet (between ± 15°N) is most remarkably impacted by the amount of water vapor assumed in our Jupiter-DYNAMICO simulations.
While the equatorial jet is retrograde and broad in latitudinal range in the 0 SA (dry) and 1 SA simulations, it is prograde (i.e., super-rotating) and narrower in the latitudinal range in the 3 SA and 5 SA simulations, and it is flanked with two retrograde jets at ±10 °N. In the moister cases, the prograde equatorial jet speed is about 60 m s−1 at the 1 bar level, which is on the same order of magnitude as the measurements; this jet speed decays toward the 100 mbar level, above which it becomes retrograde (without clear hints of equatorial oscillations, as expected from the low model top and the coarse stratospheric vertical resolution in our Jupiter-DYNAMICO simulations Bardet et al. 2021). Interestingly, the speed of the prograde equatorial jet is similar in the 3 SA and 5 SA simulations. This means that in our Jupiter-DYNAMICO simulations, the lower troposphere of Jupiter needs to be moist enough for subgrid-scale convection to imply a significant acceleration of a super-rotating jet, but that past this threshold, which lies between 1 SA and 3 SA, the dynamical forcing and resulting jet are similar. Figure 8 indicates that the vertical speeds of the idealized plumes obtained in the thermal plume model are indeed weaker in the 1 SA Jupiter-DYNAMICO simulation than in the 3 SA and the 5 SA simulations, and the amplitudes are similar in the latter two. This may be associated with enhanced convective inhibition when the atmosphere is moister (Leconte et al. 2017), which would make convective activity as strong at 5 SA as at 3 SA. However, Fig. 9 argues against a simple explanation: While zonally averaged plume vertical speeds are slightly weaker in the 5 SA simulation than in the 3 SA simulation (left panel of Fig. 9), stronger maxima of the vertical plume speed, with a much patchier appearance, are found in the 5 SA simulation than the 3 SA simulation (latitude and longitude maps in the right panel of Fig. 9).
Overall, our Jupiter-DYNAMICO simulations demonstrate that the large-scale Jovian flow, in particular, the jet structure, could be highly sensitive to the water abundance in the troposphere and that there exists an abundance threshold at which equatorial super-rotation develops. We note that the appearance of a clear-cut strong super-rotating jet at the equator occurs when the water abundance is raised from 1 SA to 3 SA, which are in the lower and middle range, respectively, of possible observed values according to Li et al. (2020). However, as stated above, we adopt a more qualitative than quantitative conclusion in this context. While our settings of the thermal plume model were chosen to reasonably represent the convective activity of Jupiter (Sects. 3.4.2 and 5.2), there is still space for varying parameters of our thermal plume model, which in turn may impact the SA threshold at which the super-rotating equatorial jet appears. Future refined tropospheric water observations are thus strongly needed to understand the atmospheric dynamics of Jupiter, in addition to the overarching goal of understanding the origin of the Solar System.
For instance, it is important here to highlight that the fluid friction factor b, an unconstrained tunable parameter in our study, influences the vertical speed of the thermal plume and the mixing profile along the vertical. When the fluid friction b is lower, not only is ω larger, but the distribution of mixing along the vertical changes: When a plume is faster, fewer exchanges occur between the environment and the plume, and this results in stronger mixing (of heat, momentum, etc.) at the top and less mixing at the base and middle of the plume. This does not alter the conclusions of our study since the same value for the fluid friction factor b was used in the dry and moist cases, and the main goal of our paper is to explore the sensivitity of large-scale dynamics to moist convection, especially to explore the sensitivity to the water abundance. However, it must be kept in mind that considering a three-dimensional dry simulation with a lower fluid friction factor b than assumed here would lead to stronger convective plumes and to a modified vertical distribution of mixing that could lead to super-rotation as much as the moist cases exhibited here. Considering three-dimensional moist simulations with a different fluid friction factor b than our reference case may modify the threshold of the water abundance at which super-rotation appears, possibly even to the point where dry convection only leads to super-rotation, for instance, as in Schneider & Liu (2009). As a future work, conducting high-resolution cloud-resolving modeling of moist convection in Jupiter in a wide range of cases would allow us to better constrain the typical values of the fluid friction factor b (as well as other tunable parameters) to be set in our thermal plume model.
 |
Fig. 12 Dynamical atlas of the moist atmosphere three-dimensional simulation with Jupiter-DYNAMICO assuming an initial solar abundance of water of 1 (referred to in the text as 1 SA). The figure is organized similarly as Fig. 5 with the diagnostics described in Sect. 4.3 (see also Spiga et al. 2020 for further details). |
 |
Fig. 13 Dynamical atlas of the moist atmosphere three-dimensional simulation with Jupiter-DYNAMICO assuming an initial solar abundance of water of 3 (referred to in the text as 3 SA). The figure is organized similarly as Fig. 5, with the diagnostics described in Sect. 4.3 (see also Spiga et al. 2020 for further details). |
5.4 Eddy activity and instabilities
We reproduce the dynamical atlas, built similarly as Fig. 5 in Sect. 4.3, for the Jupiter-DYNAMICO simulations assuming initial tropospheric water at 1 SA (Fig. 12), 3 SA (Fig. 13), and 5 SA (Fig. 14).
Dynamically speaking, the simulation with 1 SA of water displays similar properties as the dry 0 SA simulation described in Sect. 4: sustained eddy activity, poleward jet migration, and divergent eastward momentum flux at the equator, causing an equatorial westward (retrograde) jet. The noticeable differences in this 1 SA simulation compared to the dry simulation (Fig. 5) are slightly less energetic eddies (Figs. 5c and 12c) and a slower poleward migration of the midlatitudes prograde jets (Figs. 5a and 12a). When the water abundance is increased (3 SA and 5 SA simulations), the eddy activity drops in the high and mid latitudes, but remains strong at the equator (see Figs. 13c and 14c). This decrease in the eddy kinetic energy in the mid-latitudes can be linked to a weakening of large-scale instabilities. This is the case for the barotropic instability, which is only present at the poleward side of jets located at latitudes higher than 60° in 3 SA and 5 SA simulations (Figs. 13b and 14b), as a result of the weakening meridional gradients of the potential vorticity; the similar condition CSP1 for the baroclinic instability follows the same trend (Figs. 13d and 14d).
The other CSP conditions for the baroclinic instability show that it is still present for simulations with a higher water abundance: The vertical wind shear in the mid-latitude troposphere (in equilibrium with the meridional temperature gradient through the thermal wind equation) exhibits a decrease in the moister Jupiter-DYNAMICO simulations, however (Figs. 5f, 12f, 13f, 14f), especially in the 5SA case, in which the meridional gradient of the temperature is consistently reduced (Fig. 7). Thus, the moister simulations (3 SA and 5 SA) feature a weakening of the baroclinic instability in the mid-latitudes. As a result, the poleward migration of the eastward jets is adversely impacted in these simulations (Chemke & Kaspi 2015); jet migration even becomes nonexistent in our 5 SA Jupiter-DYNAMICO simulation. It is important to emphasize that the eddy activity represented in the dynamical atlas is the eddy activity resolved explicitly by the Jupiter-DYNAMICO model, which does not include the subgrid-scale momentum mixing exerted by the thermal plume model with the dry and moist convection (see Fig. 9 and Sect. 5.2). This convective mixing is quite uniform across vertical layers and leads to a more barotropic large-scale structure of the temperature and winds. This might explain why large-scale flows are less prone to baroclinic instability in moister cases. The combination of the two effects (resolved large-scale instabilities and subgrid-scale convective mixing) might be what is needed to represent the observed mid-latitude jets of Jupiter, which do not migrate, in Jovian GCMs. A comparative discussion of the results of our Jupiter-DYNAMICO GCM and other GCMs in the literature is developed in Sect. 5.5.
As a result of the main change in the eddy activity in the moister simulations, the eddy momentum fluxes also change dramatically. Figures 12e, 13e, 14e indicate that in moister Jupiter-DYNAMICO simulations, according to the decrease in eddy activity, the momentum flux decreases in the mid-latitudes, which causes the mid-latitude jets to slow down, as explained above. More importantly, these figures show that when the amount of atmospheric water in our simulations is increased, the eastward momentum flux at the 1 bar layer moves from an equatorial divergence (0 SA and 1 SA simulations) to an equatorial convergence (3 SA and 5 SA simulations), which causes the equatorial super-rotation to appear in the 3 SA and 5 SA simulations (Sect. 5.3.2). This is also shown in Fig. 15, displaying the vertical and latitudinal distribution of the eddy momentum flux, where the reversal from divergence (0SA and 1SA) to convergence (3SA and 5SA) of the eastward eddy momentum flux at the equator is also clear. We highlight that the maximum of the eddy forcing at the equator in all cases is located in the upper troposphere; this baroclinic forcing leads in all cases to a barotropic equatorial jet in the troposphere (Fig. 11), consistent with the conclusion of Showman et al. (2006) that deep jets may result from a shallow forcing. This main change at the equator is associated with a slightly stronger eddy activity at the equator in the 3 SA and 5 SA Jupiter-DYNAMICO simulations (Figs. 13c and 14c), causing subtle momentum transfer exerted by weak-amplitude waves, which act to cause the momentum transfer to converge at the equator (e.g., Rossby waves, for which the equator is the source region; see Schneider & Liu (2009)). We also note, for instance in the last 10 000 simulated days of the 3 SA Jovian simulation, that the equatorial super-rotating jet is prone to baroclinic instability (Fig. 13d) since the vertical wind shear of the zonal wind becomes positive, that is, is of the same sign as the potential vorticity gradient (necessary condition CSP 3; Fig. 13f). As a result, the equatorial eddy activity is strong at the end of the 3 SA simulation. This appears as a supplementary means for the super-rotating jet in our Jupiter-DYNAMICO simulations to be maintained, although the eddy momentum flux analysis draws a probably more complex picture of the situation (Figs. 13c and e).
We provide with Fig. 16 a last element of the dynamical analysis by projecting the simulated Jovian flow from our Jupiter-DYNAMICO model on the spherical harmonics using the method described in Cabanes et al. (2020b). This allows us to study the kinetic energy spectrum with respect to spatial order n (larger n corresponding to smaller horizontal scales) and to compare it to observations using orbital imaging of the Jupiter atmosphere (Galperin et al. 2014; Young & Read 2017). Figure 16 indicates that in our Jupiter-DYNAMICO simulations, jets (i.e., the axisymmetric part of the flow, represented in blue) contains more energy than eddies (i.e., the nonaxisymmetric part of the flow, represented in red) at large scales (small n) and less energy at small scales (large n), except, similarly to what was noted by Cabanes et al. (2020b) for Saturn, at some peculiar large scales corresponding to low-wavenumber planetary waves. The amount of energy contained in each scale decreases rapidly with spatial order n, following two slopes that are compatible with theoretical predictions (Sukoriansky et al. 2002), namely n−5 for the axisymmetric part of the flow (jets), and n−5/3 for the nonaxisymmetric part (eddies). All four Jupiter-DYNAMICO simulations therefore denote an inverse cascade of energy from small (eddies) to large scales (jets), forming what is called a zonostrophic regime, exhibiting kinetic energy spectra similar to the observations at Jupiter of Galperin et al. (2014) and Young & Read (2017).
 |
Fig. 14 Dynamical atlas of the moist atmosphere three-dimensional simulation with Jupiter-DYNAMICO assuming an initial solar abundance of water of 5 (referred to in the text as 5 SA). The figure is organized similarly as Fig. 5, with the diagnostics described in Sect. 4.3 (see also Spiga et al. 2020 for further details). |
 |
Fig. 15 Latitudinal and vertical perspective of the zonal-mean eddy momentum fluxes in our Jupiter-DYNAMICO GCM simulations: 0SA (top left), 1SA (top right), 3SA (bottom left), and 5SA (bottom right). This figure is a complement to Figs. 5e, 12e, 13e, 14e. The diagnostics shown are averaged over all simulated years except for the first year, during which the jet structure is yet to be established. |
 |
Fig. 16 Spectral analysis of the global-scale kinetic energy decomposed into spherical harmonics of spatial order n for our Jupiter-DYNAMICO simulations. The top left plot shows the dry simulation, and the top right, bottom left, and top left shows the 1 SA, 3 SA, and 5 SA moist simulations, respectively. Details on the computations of this diagnostic are reported in Cabanes et al. (2020b). The axisymmet-ric component (i.e., the contribution of zonally averaged zonal jets) is represented in blue, and the nonaxisymmetric component (i.e., the contribution of the eddies) is represented in red. The distribution of the kinetic energy between the axisymmetric (the jets) and nonaxisym-metric (the eddies) parts of the flow can be computed through the decomposition of the horizontal wind fields over the spherical harmonics. The expected regimes for the axisymmetric component (blue) and the eddy component (red) are provided as dashed lines in the figure. |
5.5 Comparison with published models
It is difficult to thoroughly compare our model with results published in the literature (Schneider & Liu 2009; Liu & Schneider 2010, 2015; Lian & Showman 2010; Young et al. 2019a,b) because the models differ. Although they are based on a similar technique employed on Earth for global climate modeling, the dynamical cores in published Jupiter GCM are distinct in their formulation from our model and between one another. Moreover, our bottom boundary condition (Rayleigh friction) is similar to that of Schneider & Liu (2009) and Young et al. (2019a), but distinct from Lian & Showman (2010); our top boundary condition (absence of sponge layer) is similar to that Schneider & Liu (2009), but distinct from Young et al. (2019a) and Lian & Showman (2010). The radiative scheme in our Jupiter-DYNAMICO GCM explicitly computes the radiative transfer in the Jupiter atmosphere, including the impact of aerosols (Guerlet et al. 2020), while models published in the literature either include gray models (Schneider & Liu 2009; Young et al. 2019a) or no radiative model and a Newtonian relaxation (Lian & Showman 2010). Finally, our model alone uses a thermal plume model to represent dry or moist convective mixing of heat and momentum; only Lian & Showman (2010) included moist processes, while the other studies used a dry formulation (Young et al. 2019b presented a Jupiter GCM coupled to moist processes to investigate the impact of the large-scale flow on water and ammonia cycles and cited the impact of the latter on the former as future work).
It is possible, however, to show similarities between the models that are confirmed by our study. All models are shallow-atmosphere weather-layer models, but produce a system of banded jets that extends down to the bottom of the model even when the forcing is superficial (Showman et al. 2006). In all models, the eddies produced by baroclinic instability were identified as the driving force of mid-latitude jets, while eddies associated with convection are the driving force of super-rotation: the former point is better shown in models reproducing a meridional temperature gradient (Schneider & Liu 2009), while the second point is better shown in models emulating moist convection without a meridional temperature gradient (Lian & Showman 2010). Interestingly, the Lian & Showman (2010) Jupiter simulations also feature mid-latitude jets, which indicates that moist convection is sufficient, even without any latitudinal gradient of temperature, to produce them. Eddies may even be produced by different sources and causes in models while giving rise to a similar jet system and dynamical regime (see, e.g., the idealized simulations described in Cabanes et al. (2020b)). Our Jupiter-DYNAMICO model offers especially by means of our 3 SA simulation a synthesis of these previous studies: Our simulation needs both a realistic temperature structure obtained by radiative transfer (and, in particular, meridional temperature gradient) and a plausible moist-convection forcing to reproduce the jet system of Jupiter with both equatorial super-rotation and mid-latitude eastward jets. While the number of jets obtained by published models is close to the observations of Jupiter (in the optimal cases, between 20 and 33 jets), their simulated speeds are too weak either at the equator (e.g., 30 m s−1 in Young et al. 2019a) or at the mid-latitudes (e.g., less than 10 m s−1 in Lian & Showman 2010). With our Jupiter-DYNAMICO simulations with 3 SA of water (the observed averaged value by Juno according to Li et al. 2020), we obtain satisfactory predictions compared to observations: About 20 jets whose speeds range between 10 and 20 m s−1 in the mid-latitudes and equal 60 m s−1 at the equator.
The equatorial super-rotating jet deserves further comment because existing studies state somewhat subtle differences. We already mentioned in the previous paragraph that the study by Lian & Showman (2010) clearly ascribed the equatorial super-rotation of Jupiter to eddies related to moist convection. Schneider & Liu (2009) and Liu & Schneider (2010, 2015) explored dry convection caused by internal heat flux and diagnosed in their simulations a competition at the equator between the eastward momentum flux due to the convection-generated Rossby waves and the westward momentum flux due to the baro-clinic eddies. The results of Young et al. (2019a) also highlight the role played by internal heat flux, but through a distinct mechanism: It causes off-equatorial jets to migrate toward the equator, where they become barotropically unstable and trigger Rossby waves.
Finally, our results tend to confirm the scenario described in Lian & Showman (2010) about the prominence of moist convection in explaining the Jupiter jets, especially the equatorial super-rotating jet. Despite the inclusion of internal heat flux in our Jupiter-DYNAMICO simulations, neither our dry case (0 SA) nor our moderately moist (1 SA) simulations exhibit super-rotation. We obtain an equatorial super-rotation in our Jupiter-DYNAMICO simulations only when the atmosphere is sufficiently moist (3 SA and 5 SA). Although we found a brief period during which the closest off-equatorial prograde jets migrate toward the equator as in Young et al. (2019a), its time of occurrence and brevity make it unlikely to be the main driving force of the super-rotation in our Jupiter-DYNAMICO simulation. The apparent contradiction between our conclusion about the necessary inclusion of moist convection and the fact that Schneider & Liu (2009) and Liu & Schneider (2010) obtained an equatorial super-rotation in a dry atmosphere (with no equatorward migration as in Young et al. (2019a) might be explained by the relaxation time of the convective adjustment in these two studies, which might emulate moist convection.
6 Conclusion
We reported three-dimensional simulations of the Jupiter weather layer using a GCM called Jupiter-DYNAMICO, which couples hydrodynamical integrations on an icosahedral grid to detailed radiative transfer computations. We carried out the crucial addition of a thermal plume model for Jupiter that emulates the impact of mixing of heat, momentum, and tracers by dry and moist convective plumes that are left unresolved at GCM mesh spacing with a physics-based approach. The thermal plume model uses an idealized average plume representative of sub-grid-scale convection in which horizontal and vertical mass fluxes are computed, including overshoots above the unstable region.
Our Jupiter-DYNAMICO dry simulation exhibits a quasi-symmetric (around the equator) banded jet system whose speeds roughly agree with the observed order of magnitude and whose tropospheric vertical structure is barotropic. However, in contrast to observations, the equatorial jet is westward (thus not super-rotating) and the additional tropical eastward jets are less numerous than in observations; furthermore, our dry simulation exhibits strong poleward migration of mid-latitude eastward jets. The simulated jets, whether eastward in the mid-latitudes or westward at the equator, are accounted for by transfer of angular momentum from eddies to jets, with bursts of sustained eddy activity.
Moist simulations with Jupiter-DYNAMICO assuming tro-pospheric water abundances of solar abundances (SA) 3 and 5 suggest that moist processes cause the properties of the simulated jet system to agree better with Jupiter observations: A clear-cut super-rotating eastward jet at the equator, and a dozen eastward mid-latitude jets without poleward migration. In moist Jupiter-DYNAMICO simulations, especially in the 3 SA case, the magnitudes of the equatorial super-rotating jet and that of the mid-latitude jets are close to the observed magnitudes. In the moist simulations, the simulated convective activity is weaker in the equatorial regions than at mid to high latitudes, as indicated by lightning observations. The eddy activity in our Jupiter-DYNAMICO simulations is strongly influenced by the assumed amount of tropospheric water and appears to decrease with increasing water abundance. In contrast to the 3 SA and the 5 SA simulations with Jupiter-DYNAMICO, the jet dynamics developed by the 1 SA simulation is similar to the dry simulation. A threshold appears to exist for the water abundance above which super-rotation develops. This threshold exists between tro-pospheric water abundances of 1 SA and 3 SA, although our assumptions on the thermal plume model may obviously shift this quantitative estimate. Our simulations offer a synthesis of the existing modeling studies by suggesting that both a realistic thermal structure (computed by radiative transfer) and a plausible moist convection forcing (which we chose to represent with the thermal plume model) are needed in weather-layer modeling to reproduce the jet system of Jupiter with both equatorial super-rotation and mid-latitude eastward jets. All our Jupiter-DYNAMICO simulations, regardless of whether they are dry or moist, exhibit kinetic energy spectra that agree with the theoretical and observed slopes, denoting an inverse energy cascade from small (eddies) to large scales (jets) under a zonostrophic regime.
As indicated throughout this paper, several areas for future investigations are highlighted. This study only considered moist convection related to water condensates; ammonia-based processes are clearly an area of future research, especially so with the coupling between water and ammonia in mushball condensates to explain the observed ammonia field by Juno (Guillot et al. 2020b,a). An improved tuning of the thermal plume model used in our Jupiter-DYNAMICO model by comparisons with convection-resolving modeling is also identified as possible future work. Another area of improvement is a broader exploration of the parameter space of our physics-based thermal plume model to represent all possible convective structures at Jupiter. Another choice of our study was the emphasis on tropospheric processes. Extending our Jupiter-DYNAMICO farther up in the stratosphere to study, for instance, the equatorial quasi-quadriennal oscillation (Antuñano et al. 2021), is an area of future work with our model. Ultimately, the usefulness of numerical modeling in planetary science is intimately linked to the observations obtained by planetary missions. The perspectives opened by future Jupiter observations using present and future ground-based telescopes, the still-operating Juno mission, the recently deployed James Webb Space Telescope (JWST), and the future JUpiter ICy moons Explorer (JUICE) ensure a wealth of new ideas to be tested by the type of atmospheric modeling we proposed in this paper. We also suggest that observations of the water abundance in giant planets are not only crucial for understanding the origin of the Solar System and planets, but are also key for understanding their atmospheric dynamics.
Acknowledgements
A. Boissinot, A. Spiga and S. Guerlet acknowledge the essential support (PhD fellowship of A. Boissinot) of Region Île-de-France through the DIM-ACAV+ funding scheme. All authors acknowledge the support of Agence Nationale de la Recherche through grant ANR-17-CE31-0007 grant “EMER-GIANT”. D. Bardet is supported by a European Research Council Consolidator Grant (under the European Union’s Horizon 2020 research and innovation programme, grant agreement No 723890) at the University of Leicester. The authors would like to warmly thank F. Hourdin for guidance on the thermal plume model, E. Millour and T. Dubos for support on running the DYNAMICO model, J. Leconte and T. Guillot for discussions on convection on giant planets, F. Selsis for questions about enstrophy. This modeling work was performed using excellent HPC computing resources from GENCI-CINES (Grants 2021-A0100110391, 2020-A0080110391, 2019-A0060110391 and 2018-A0040110391).
Appendix A Formulation of the thermal plume model
As a complement to Section 3, details of the formulation of the thermal plume model are provided in this appendix. Except for minor modifications and the specific adaptations made to treat the specific case of Jupiter, what follows is taken from Rio et al. (2010). As is explained in the main text, we recall that the thermal plume model is a parameterization that computes an idealized mean plume for each mesh cell, which is thought to be representative of all subgrid-scale convection cells.
A.1 Mass fluxes
The plume vertical mass flux f averaged over the mesh cell is equal to the updraft fraction α times the volumic mass ρ times the vertical speed ω,
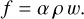 (A.1)
(A.1)
It is counted positive upward. The downdraft vertical mass flux exactly compensates for it to conserve the layer mass.
The horizontal mass flux between the plume and the environment is called entrainment and detrainment depending on whether it is oriented inward or outward of the plume, respectively. According to mass conservation, the vertical variation in the vertical mass flux of the plume is the entrainment minus the detrainment,
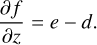 (A.2)
(A.2)
In the same way as in Rio et al. (2010), we chose to express entrainment and detrainment as a linear combination of two extreme cases: One case in which the entrained air exclusively comes from the first unstable layer, and the other case in which the lateral mass fluxes exactly compensate for the variation of ρα. This combination is set by the parameter β, which lies between 0 and 1, β = 0 corresponding to the first situation, and β = 1 to the second situation. Because we also assume that the entrainment and the detrainment cannot simultaneously equal zero, this leads to
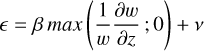 (A.3a)
(A.3a)
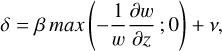 (A.3b)
(A.3b)
where ϵ and δ are the normalized entrainment and detrainment (ϵ = e/f, δ = d/f), respectively. There, v is the part of the mixing that is not linked to the variations in the vertical mass flux. It represents typically geometrical effects because we can reasonably think that for the same average vertical mass flux, mixing may be exerted differently by many small plumes versus a few large plumes. For simplicity and as our first-order approach for Jupiter, we chose to set v to 0.
A.2 Tracer transport
Any tracer ψ transported by the model satisfies
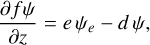 (A.4)
(A.4)
where ψe is the value in the environment, and ψ is the value in the plume.
A.3 Vertical linear momentum budget
The buoyancy B is the acceleration that the thermal plume undergoes as a result of a contrast in density (or, similarly, in the virtual potential temperature) with the environment,
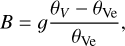 (A.5)
(A.5)
where θV is the virtual potential temperature of the plume, and θVe is the virtual potential temperature of the environment. Buoyancy is the main contribution to the plume acceleration, but the conversion from convective potential energy into kinetic energy is in practice imperfect (owing, e.g., to turbulent effects). Hence, a parameter a ranging between 0 and 1 is introduced to weight the buoyancy. Furthermore, a fluid friction term proportional to the square of the vertical speed is added to the formula with a modulating factor b, which is another free parameter,
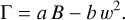 (A.6)
(A.6)
Because we assume that downdrafts are significantly slower than updrafts, the term e ωe is neglected in the vertical linear momentum budget. Furthermore, we took the buoyancy force as a source (or a sink) of momentum into account,
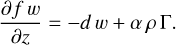 (A.7)
(A.7)
A.4 Vertical speed of the updraft
From the Eq. (A.7), (A.1), and (A.2), we obtain
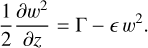 (A.8)
(A.8)
Then we can deduce two new expressions for ϵ and δ,
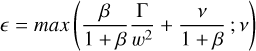 (A.9a)
(A.9a)
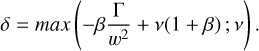 (A.9b)
(A.9b)
which can analytically be solved in each layer of the model (where B is a constant),
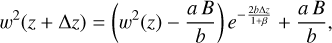 (A.11)
(A.11)
where w2(ɀ) is the value of the vertical speed at the bottom of the layer, and w2(ɀ + ∆ɀ) is this speed at the top of the layer.
A.5 Closure relation
From the equations described above, we can deduce w from the temperature and pressure profiles. Then, the normalized mass flux variations ϵ and δ follow. However, this only grants access to the mass flux normalized by f0 (the value of the vertical mass flux at the bottom of the plume). Hence, an additional formula is needed to close the system of equations. We assume that the average lateral speed of entrainment 〈υ〉 equals the maximum vertical speed wmax. By definition, we have
 (A.12)
(A.12)
where L is the mean size of a convective cell or the average distance between two plumes. Then,
 (A.14)
(A.14)
where r is the aspect ratio L/h of the plume (free parameter), e* = e/f0 is the entrainment normalized by the outgoing vertical mass flux of the first unstable layer (i.e. the entrainment in this layer), wmax is the maximum vertical speed (computed by the model), and h is the plume height (computed by the model).
A.6 Control tests and tracer mixing
When every mass flux is known, some properties were verified to ensure the global consistence of the variables. First, the updraft surface fraction must not be greater than αmax. If this was not the case, we stopped the plume in the lower layer where this relation is not verified, that is, all the incoming mass was detrained and the mass fluxes were set to zero in the layers above. Here, αmax = 0.7. Second, the entrained mass in each layer must not be greater than μmax times the total mass of the layer. If this was not the case, the same amount was subtracted from entrainment and detrainment to reduce the entrainment while conserving the outgoing vertical mass flux. If this was not sufficient, the mass fluxes were renomalized with the maximum value of f0 that respects this constraint.
Finally, assuming that the plumes are stationary and the mixing entirely occurs in a single physical time step, equation A.4 provides us with the equilibrium value of any quantity candidate for mixing, such as horizontal momentum, chemical species, and potential temperature. Finally, we can deduce the variation from the previous time step.
Summary of the equations of the thermal plume model described in appendix A.
List of variables involved in the thermal plume model implemented in the Jupiter-DYNAMICO simulations described in this paper. The values given for the parameters are those that were retained after the one-dimensional sensitivity study described in section 3.
References
- Adriani, A., Mura, A., Orton, G., et al. 2018, Nature, 555, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Antuñano, A., Cosentino, R. G., Fletcher, L. N., et al. 2021, Nat. Astron., 5, 71 [Google Scholar]
- Aurnou, J., Heimpel, M., Allen, L., King, E., & Wicht, J. 2008, Geophys. J. Int., 173, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Bardet, D., Spiga, A., Guerlet, S., et al. 2021, Icarus, 354, 114042 [Google Scholar]
- Bardet, D., Spiga, A., & Guerlet, S. 2022, Nat. Astron., 6, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Benmahi, B., Cavalié, T., Greathouse, T. K., et al. 2021, A&A, 652, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolton, S., Adriani, A., Adumitroaie, V., et al. 2017, Science, 356, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, S., Janssen, M., Adumitroaie, V., et al. 2018, Nature, 558, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Brueshaber, S., Orton, G., Zhang, Z., et al. 2022, in European Planetary Science Congress, 16, EPSC2022–733 [Google Scholar]
- Cabanes, S., Espa, S., Galperin, B., Young, R. M. B., & Read, P. L. 2020a, Geophys. Res. Lett., 47, e88685 [NASA ADS] [CrossRef] [Google Scholar]
- Cabanes, S., Spiga, A., & Young, R. 2020b, Icarus, 345, 113705 [NASA ADS] [CrossRef] [Google Scholar]
- Chemke, R., & Kaspi, Y. 2015, J. Adv. Model. Earth Syst., 7, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Colaïtis, A., Spiga, A., Hourdin, F., et al. 2013, J. Geophys. Res. (Planets), 118, 1468 [CrossRef] [Google Scholar]
- Dowling, T. E., Bradley, M. E., Colón, E., et al. 2006, Icarus, 182, 259 [CrossRef] [Google Scholar]
- Dubos, T., Dubey, S., Tort, M., et al. 2015, Geosci. Model Dev., 8, 3131 [NASA ADS] [CrossRef] [Google Scholar]
- Duer, K., Gavriel, N., Galanti, E., et al. 2021, Geophys. Res. Lett., 48, e95651 [NASA ADS] [CrossRef] [Google Scholar]
- Flasar, F., Kunde, V., Achterberg, R., et al. 2004, Nature, 427, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Orton, G. S., Mousis, O., et al. 2010, Icarus, 208, 306 [CrossRef] [Google Scholar]
- Fletcher, L., Orton, G., Rogers, J., et al. 2011, Icarus, 213, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Galperin, B., Young, R., Sukoriansky, S., et al. 2014, Icarus, 229, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., & Wicht, J. 2021, Icarus, 368, 114514 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., Wicht, J., Duarte, L. D. V., Heimpel, M., & Becker, A. 2014, Geophys. Res. Lett., 41, 5410 [NASA ADS] [CrossRef] [Google Scholar]
- Gierasch, P., Ingersoll, A., Banfield, D., et al. 2000, Nature, 403, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, I. E., Rothman, L. S., Hill, C., et al. 2017, JQSRT, 203, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Grassi, D., Adriani, A., Moriconi, M., et al. 2018, J. Geophys. Res. (Planets), 123, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Guerlet, S., Spiga, A., Delattre, H., & Fouchet, T. 2020, Icarus, 351, 113935 [Google Scholar]
- Guerlet, S., Spiga, A., Sylvestre, M., et al. 2014, Icarus, 238, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2022, Exp. Astron., 54, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Miguel, Y., Militzer, B., et al. 2018, Nature, 555, 227 [Google Scholar]
- Guillot, T., Li, C., Bolton, S., et al. 2020a, J. Geophys. Res. (Planets), 125, e06404 [NASA ADS] [Google Scholar]
- Guillot, T., Stevenson, D., Atreya, S., Bolton, S., & Becker, H. 2020b, J. Geophys. Res. (Planets), 125, e06403 [Google Scholar]
- Heimpel, M., Aurnou, J., & Wicht, J. 2005, Nature, 438, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Heimpel, M., Gastine, T., & Wicht, J. 2016, Nat. Geosci., 9, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hourdin, F., Couvreux, F., & Menut, L. 2002, J. Atmos. Sci., 49, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Hueso, R., & Sánchez-Lavega, A. 2006, in The Many Scales in the Universe: JENAM 2004 Astrophysics Reviews, 6, eds. J. Del Toro Iniesta, E. Alfaro, J. Gorgas, E. Salvador-Sole, & H. Butcher, 211 [Google Scholar]
- Hueso, R., Sánchez-Lavega, A., & Guillot, T. 2002, J. Geophys. Res. (Planets), 107, 5075 [NASA ADS] [CrossRef] [Google Scholar]
- Ingersoll, A. P. 1990, Science, 248, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, Y., & Flierl, G. 2007, J. Atmos. Sci., 64, 3177 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, Y., Flierl, G. R., & Showman, A. P. 2009, Icarus, 202, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, Y., Galanti, E., Hubbard, W., et al. 2018, Nature, 555, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Leconte, J., Selsis, F., Hersant, F., & Guillot, T. 2017, A&A, 598, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, C., & Chen, X. 2019, ApJS, 240, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L., Jiang, X., West, R., et al. 2018, Nat. Commun., 9, 3709 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Ingersoll, A., Bolton, S., et al. 2020, Nat. Astron., 4, 609 [Google Scholar]
- Lian, Y., & Showman, A. 2010, Icarus, 207, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Little, B., Anger, C., Ingersoll, A., et al. 1999, Icarus, 142, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., & Schneider, T. 2010, J. Atmos. Sci., 67, 3652 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., & Schneider, T. 2015, J. Atmos. Sci., 72, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., Goldreich, P. M., & Stevenson, D. J. 2008, Icarus, 196, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Marcus, P. S. 2004, Nature, 428, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Mellor, G., & Yamada, T. 1982, Rev. Geophys. Space Phys., 20, 851 [CrossRef] [Google Scholar]
- Mousis, O., Ronnet, T., & Lunine, J. I. 2019, ApJ, 875, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Niemann, H., Atreya, S., Carignan, G., et al. 1998, J. Geophys. Res., 103, 22831 [NASA ADS] [CrossRef] [Google Scholar]
- Orton, G. S., Tabataba-Vakili, F., Eichstädt, G., et al. 2020, J. Geophys. Res. (Planets), 125, e06369 [NASA ADS] [Google Scholar]
- Porco, C., West, R., McEwen, A., et al. 2003, Science, 299, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Read, P. L., Barstow, J., Charnay, B., et al. 2016, Q. J. Roy. Meteorol. Soc., 142, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Read, P. L., Young, R., & Kennedy, D. 2020, Geosci. Lett., 7, 1 [CrossRef] [Google Scholar]
- Rio, C., & Hourdin, F. 2008, J. Atmos. Sci., 65, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Rio, C., Hourdin, F., Couvreux, F., & Jam, A. 2010, Bound. Layer Meteorol., 135, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Ingersoll, A., Lorre, J., Vasavada, A., & Del Genio, A. 2006, Icarus, 185, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Lavega, A., Hueso, R., Eichstädt, G., et al. 2018, AJ, 156, 162 [CrossRef] [Google Scholar]
- Schneider, T., & Liu, J. 2009, J. Atmos. Sci., 66, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, T. A., & Shepherd, T. G. 2007, J. Atmos. Sci., 64, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P. 2007, J. Atmos. Sci., 64, 3132 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Gierasch, P. J., & Lian, Y. 2006, Icarus, 182, 513 [CrossRef] [Google Scholar]
- Siegelman, L., Klein, P., Ingersoll, A. P., et al. 2022, Nat. Phys., 18, 357 [CrossRef] [Google Scholar]
- Simon, A. A., Wong, M. H., Rogers, J. H., et al. 2014, ApJ, 797, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Spiga, A., Guerlet, S., Millour, E., et al. 2020, Icarus, 335, 113377 [Google Scholar]
- Stoker, C. 1986, Icarus, 67, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Sugiyama, K., Nakajima, K., Odaka, M., et al. 2011, Geophys. Res. Lett., 38, L13201 [Google Scholar]
- Sugiyama, K., Nakajima, K., Odaka, M., Kuramoto, K., & Hayashi, Y. Y. 2014, Icarus, 229, 71 [CrossRef] [Google Scholar]
- Sukoriansky, S., Galperin, B., & Dikovskaya, N. 2002, Phys. Rev. Lett., 89, 124501 [CrossRef] [Google Scholar]
- Vallis, G. K. 2006, Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation (Cambridge University Press) [CrossRef] [Google Scholar]
- Vasavada, A. R., & Showman, A. P. 2005, Rep. Progr. Phys., 68, 1935 [CrossRef] [Google Scholar]
- Williams, G. P. 1978, J. Atmos. Sci., 35, 1399 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, M., Mahaffy, P., Atreya, S., Niemann, H., & Owen, T. 2004, Icarus, 171, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Young, R., & Read, P. 2017, Nat. Phys., 13, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Young, R., Read, P., & Wang, Y. 2019a, Icarus, 326, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Young, R., Read, P., & Wang, Y. 2019b, Icarus, 326, 253 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
List of variables involved in the thermal plume model implemented in the Jupiter-DYNAMICO simulations described in this paper. The values given for the parameters are those that were retained after the one-dimensional sensitivity study described in section 3.
All Figures
 |
Fig. 1 Principles of the thermal plume model. Left panel: schematics of a real convective plume. The bottleneck part is the bulk of the plume, and the puffy upper part is the overshoot. The black arrow represents vertical fluxes in the ascending plume (the red arrow is the bottom source of the plume). The rounded blue arrows represent exchanges between the ascending plume and the environment: entrain-ment e toward the plume, and detrainment d toward the environment. Right panel: schematics of the idealization adopted in the thermal plume model. The gray areas represent the ascending plume subcolumn (see text in Sect. 3.2). The mass fluxes are both vertical (black and gray arrows) and horizontal (entrainment e as blue arrows and detrainment d as red arrows). α is the fraction of the GCM grid mesh that is covered by ascending convective plumes. They are represented as the single plume in the thermal plume model. |
| In the text | |
 |
Fig. 2 Behavior of the thermal plume model in one-dimensional Jupiter dry simulations (after 1000 Jovian days). The two top plots display the vertical profiles of the potential temperature (left) and vertical plume speed (right). Nine combinations using three values of the buoyancy coefficient a and the fluid friction factor b are shown: a = 0.1/0.5/0.9 (dotted, dashed, and solid lines) and b = 0/10−4/2 × 10−4 m−1 (red, purple, and blue lines). The two bottom plots show the case a = 0.9 and b = 10−4 m−1. They show the vertical plume speed on the left and the mass fluxes on the right (entrainment in blue, detrainment in red, and vertical mass flux in black). |
| In the text | |
 |
Fig. 3 Behavior of one-dimensional Jovian modeling using the thermal plume model in the moist case. The sensitivity to the water abundance is explored. The vertical speed (left) and mass fluxes (right) of the plumes are shown for a solar abundance of water of 1 (dotted line), 3 (dashed line) and 9 (solid line). The entrainment is shown in blue, the detainment in red, and the vertical mass flux in black. The variables are plotted as a function of pressure after a run of 1000 Jovian days with a = 0.9 and b = 10−3 m−1. |
| In the text | |
 |
Fig. 4 Latitude-pressure sections of the (left) zonal-mean temperature T and (right) Brunt-Väisälä frequency N2, i.e., buoyancy frequency, for the dry simulation with our Jupiter-DYNAMICO GCM (average of all simulated years except for the first year, during which the jet structure yet has to be established). |
| In the text | |
 |
Fig. 5 Dynamical atlas of the dry atmosphere simulation with Jupiter-DYNAMICO showing the temporal evolution of the main diagnostics for tropospheric dynamics on Jupiter. Although the model integrations were conducted during 40 000 Jovian days, the temporal axis extends toward 60 000 days for easy comparison with the moist cases described in Sect. 5. The variables shown (see text for further definitions, especially Sect. 4.3) are all zonally averaged. The left column displays the zonal wind (top, panel a), the eddy kinetic energy (middle, panel c), and the eddy momentum flux (bottom, panel e). The right column displays the barotropic potential vorticity [∂q|∂y]bt (top, panel b), the baroclinic potential vorticity [∂q/∂y]bc (middle, panel d), and the zonal wind vertical shear (bottom, panel f). The left column corresponds to flow properties at p = 1 bar, and the right column corresponds to instability diagnostics, shown at p = 0.1 bar for comparison purposes because the baroclinic potential vorticity [∂q/∂y]bc is not defined in the barotropic troposphere. |
| In the text | |
 |
Fig. 6 Latitude-pressure sections of (left) the zonal-mean temperature T and (right) the Brunt-Väisälä frequency N2 as in Fig. 4, shown for our moist simulations with our Jupiter-DYNAMICO GCM. Top: 1SA. Middle: 3SA. Bottom: 5SA. |
| In the text | |
 |
Fig. 7 Typical meridional thermal structure in our Jupiter-DYNAMICO simulations, shown by the zonal-mean temperature at the 1 bar level as a function of latitude (average of all simulated years except for the first year, during which the jet structure is yet to be established). The dry simulation is shown in blue, and the moist simulations are shown in orange (1 SA), green (3 SA), and red (5 SA). |
| In the text | |
 |
Fig. 8 Diagnosing the zonal-mean behavior of the thermal plume model in our three-dimensional Jupiter-DYNAMICO simulations. The diagnostics shown are averaged over all simulated years except for the first year, during which the jet structure is yet to be established. The color coding is similar as in Fig. 7: the dry simulation is shown in blue, and moist simulations are shown in orange (1 SA), green (3 SA), and red (5 SA). The top plot in the vicinity of the 3.5 bar level corresponds to the zonal-mean vertical speed of idealized plumes in the thermal plume model, which is an indication of the strength of the subgrid-scale con-vective motions. The bottom plot corresponds to the zonal-mean water ice column density, which is an indication of clouds simulated by our Jupiter model. |
| In the text | |
 |
Fig. 9 Diagnosing the spatial variability of the vertical speed of idealized plumes in the thermal plume model included in our three-dimensional Jupiter-DYNAMICO simulations. The four-plot arrays on the left and right correspond to the dry (top left) and moist simulations with initial water of 1 SA (top right), 3 SA (bottom left), and 5 SA (bottom right). The left four-plot panel displays the variability of the vertical speed of the zonal-mean plume with pressure and latitude. The right four-plot panel displays the variability of the plume vertical speed with longitude and latitude in the vicinity of the 2 bar level. |
| In the text | |
 |
Fig. 10 Jovian jets at the 1 bar level as simulated by our Jupiter-DYNAMICO GCM using the thermal plume model. The diagnostics shown are averaged over all simulated years except for the first year, during which the jet structure is yet to be established). The color coding is similar as in Fig. 7: the dry simulation is shown in blue, and moist simulations are shown in orange (1 SA), green (3 SA), and red (5 SA). This figure may be compared to cloud-tracking observations of Jovian jets (e.g., Fig. 1 in both Porco et al. 2003; Kaspi et al. 2018) and shows that the strong equatorial jet in the troposphere of Jupiter is obtained in our Jupiter-DYNAMICO simulations only in moist conditions with an initial amount of water of 3 SA or 5 SA. |
| In the text | |
 |
Fig. 11 Latitudinal and vertical perspective of the Jovian jets simulated by our Jupiter-DYNAMICO GCM using the thermal plume model. This figure shows that a tropospheric super-rotating complements Fig. 10 in showing the impact of moist convection on the Jovian jet system. As in Fig. 10, we show the zonal mean of the zonal wind at the end of the simulated time for 0 SA (top left), 1 SA (top right), 3 SA (bottom left), and 5 SA (bottom right) Jupiter-DYNAMICO GCM simulations. |
| In the text | |
 |
Fig. 12 Dynamical atlas of the moist atmosphere three-dimensional simulation with Jupiter-DYNAMICO assuming an initial solar abundance of water of 1 (referred to in the text as 1 SA). The figure is organized similarly as Fig. 5 with the diagnostics described in Sect. 4.3 (see also Spiga et al. 2020 for further details). |
| In the text | |
 |
Fig. 13 Dynamical atlas of the moist atmosphere three-dimensional simulation with Jupiter-DYNAMICO assuming an initial solar abundance of water of 3 (referred to in the text as 3 SA). The figure is organized similarly as Fig. 5, with the diagnostics described in Sect. 4.3 (see also Spiga et al. 2020 for further details). |
| In the text | |
 |
Fig. 14 Dynamical atlas of the moist atmosphere three-dimensional simulation with Jupiter-DYNAMICO assuming an initial solar abundance of water of 5 (referred to in the text as 5 SA). The figure is organized similarly as Fig. 5, with the diagnostics described in Sect. 4.3 (see also Spiga et al. 2020 for further details). |
| In the text | |
 |
Fig. 15 Latitudinal and vertical perspective of the zonal-mean eddy momentum fluxes in our Jupiter-DYNAMICO GCM simulations: 0SA (top left), 1SA (top right), 3SA (bottom left), and 5SA (bottom right). This figure is a complement to Figs. 5e, 12e, 13e, 14e. The diagnostics shown are averaged over all simulated years except for the first year, during which the jet structure is yet to be established. |
| In the text | |
 |
Fig. 16 Spectral analysis of the global-scale kinetic energy decomposed into spherical harmonics of spatial order n for our Jupiter-DYNAMICO simulations. The top left plot shows the dry simulation, and the top right, bottom left, and top left shows the 1 SA, 3 SA, and 5 SA moist simulations, respectively. Details on the computations of this diagnostic are reported in Cabanes et al. (2020b). The axisymmet-ric component (i.e., the contribution of zonally averaged zonal jets) is represented in blue, and the nonaxisymmetric component (i.e., the contribution of the eddies) is represented in red. The distribution of the kinetic energy between the axisymmetric (the jets) and nonaxisym-metric (the eddies) parts of the flow can be computed through the decomposition of the horizontal wind fields over the spherical harmonics. The expected regimes for the axisymmetric component (blue) and the eddy component (red) are provided as dashed lines in the figure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.