EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A102 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A102
Number of page(s) 15
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202449434
Published online 03 June 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Ices are abundant in the Solar System and beyond (Schmitt et al. 2012; Boogert et al. 2015; Altwegg et al. 2019). This includes cometary nuclei, which consist of dust and ice, and mainly originate from two reservoirs in the Solar System: the Oort Cloud and the Kuiper Belt (Morbidelli et al. 2008). Due to the large distance to the Sun, cometary ices are thought to be mostly pristine and inherited from the solar nebula, thus offering a unique insight into the building blocks of the planets and potentially also into the emergence of molecular complexity on Earth (Drozdovskaya et al. 2019; Altwegg et al. 2019).

Planetary encounters can result in the injection of comets into the inner Solar System (Morbidelli 2005), approaching the Sun. As the surface temperature of the comet increases, molecules sublimate from the near-surface layer and liberated icy grains (A’Hearn et al. 2011). This results in a cometary gas coma, the observation of which allows one to probe the volatile cometary ices. The most abundant molecules in cometary ices are water (H2O), carbon dioxide (CO2) and carbon monoxide (CO, Mumma & Charnley 2011; A’Hearn et al. 2012), but observations also revealed a plethora of volatile molecules at minor abundances, such as HCN, H2S, CH4, NH3, C2H6, and CH3OH (e.g., Bockelée-Morvan et al. 2004; Bieler et al. 2015). The various ice components of comets desorb at a wide range of temperatures, starting from sublimation temperatures as low as ∼20 K for highly volatile species such as CO and N2, up to the sublimation temperature of water above 140 K (e.g., Fray & Schmitt 2009; Minissale et al. 2022).

67P/Churyumov-Gerasimenko (henceforth 67P) is a Jupiter-family comet and was the target of the Rosetta mission from 2014 to 2016, which followed this object for two years and investigated its nucleus and coma. Among the scientific objectives of the mission were the investigation of outgassing activity and the composition of cometary volatiles (Glassmeier et al. 2007). The coma of 67P is dominated by water vapour, with CO2 being the second largest component at 4.5–7.5% (Rubin et al. 2019a; Läuter et al. 2020). Other volatiles, such as CO, H2S, and O2 are present at the percent level with respect to water (Hässig et al. 2015; Bieler et al. 2015; Rubin et al. 2019b; Läuter et al. 2020). Patches of high concentration CO2 ice were observed on 67P’s night side, which are the result of gas released from the deeper and warmer interior recondensing on the surface (Filacchione et al. 2016).

The Rosetta mission revealed a rich chemical diversity and complexity in the coma of 67P, more than doubling the number of known cometary molecules (Altwegg et al. 2019), including many volatile species, such as O2 and CO, up to complex organics (Hänni et al. 2022, 2023). Another important group of molecules are the nitrogen-bearing species. For comets, an overall nitrogen deficiency is observed compared to the solar value, such as investigated for 1P/Halley (Geiss 1988) and C/1995 O1 (Bockelée-Morvan et al. 2000). The nitrogen reservoir is primarily observed in the form of HCN and NH3 in cometary comae (e.g., Mumma & Charnley 2011; Dello Russo et al. 2016), which are both detected in 67P. Additional, and possible dominant, carriers of nitrogen are ammonium salts and N2.

N2 cannot be detected directly in comets with spectroscopic remote sensing techniques, either due to the spectroscopic inactivity of this molecule in the radio and infrared (e.g., Ehrenfreund & van Dishoeck 1998), or due to equipment not being sensitive enough to detect the optical and ultraviolet transitions (e.g., Opitom et al. 2019, 2022). Therefore, only N 2 + $ \rm{N}_2^+ $ could be detected from ground-based facilities and, for example, revealed comet C/2016 R2 to be nitrogen-rich (Opitom et al. 2019). However, the Rosetta mission marked the first direct detection of N2 with its ROSINA mass spectrometer suite in a cometary coma (Balsiger et al. 2007), which is present at a bulk abundance of 8.9 × 10−4 with respect to water (Rubin et al. 2019b). While ammonium salts are refractory and expected to reside for a long time in or on 67P, N2 is a hyper volatile species (sublimation occurs at ∼20 K), which means that 67P could have lost significant amounts of N2 during past heating events.

The abundances of the volatile molecules in 67P have largely been derived from measurements in the cometary coma as the molecules sublimate. The sublimation of highly volatiles, with sublimation temperatures below the one of CO2, has been shown to correlate with the release of the two major ice components in the comet, H2O and CO2 (Rubin et al. 2023). This indicates that likely a trapping mechanism of highly volatile molecules in the less volatile cometary ice phases took place. Rubin et al. (2023) further state, that no pure ice-phase is needed to explain the cometary abundances of such highly volatile molecules, including N2. These pure ice-phases are suggested to have been lost or to have never been incorporated into the comet.

The trapping of volatiles, including N2, by water ice has been studied extensively in the laboratory in the past (e.g., Bar-Nun et al. 1985, 1987, 2007, 1998; Notesco & Bar-Nun 1996; Collings et al. 2004; Ninio Greenberg et al. 2017; Laufer et al. 2017). N2 has been shown to efficiently trap within amorphous water ice, both if it is deposited on the bottom or on top of the water ice (Collings et al. 2004). In the case of trapping, N2 has been shown to co-desorb with H2O, once at the phase change of amorphous water to crystalline at ∼140 K and when the water itself desorbs at ∼160 K. As a consequence, N2 can be detected well above its free sublimation temperature of ∼20 K (Rubin et al. 2023).

CO2 is a non-negligible component in cometary ices and Simon et al. (2023) have shown that CO2 can act as an efficient trapping agent of volatiles in its own regard. In their study, they have seen trapping of N2 by CO2 ice between 20–60%, depending on the thickness of the ice and CO2:volatile ratio. However, these studies have predominantly employed binary mixtures of H2O:volatile and CO2:volatile, although, as seen in previous trapping experiments, the addition of other molecules can significantly alter the desorption behaviour of a volatile (Collings et al. 2004; Fuchs et al. 2006; Martín-Dománech et al. 2014; Nguyen et al. 2018; Gudipati et al. 2023). To investigate the trapping behaviour of volatiles in a 67P-like cometary ice, ternary mixtures of H2O:CO2:volatiles should be studied.

In this study, we investigate the desorption behaviour of the hypervolatile N2 within H2O:CO2 ice and derive quantitative values for the trapping. Furthermore, complementary investigations on the trapping of 13CO are conducted to verify the results, as it is expected to behave in a similar thermodynamic way as N2. In Sect. 2, the experimental setup and procedures are presented. In Sect. 3, the results of the desorption experiments for various H2O:CO2:volatile ice experiments are shown. In Sect. 4 the results are discussed and connected to the observations of comet 67P.

2. Methods

2.1. ICEBEAR

Experiments performed in this study were conducted with the ICEBEAR setup, which is described in detail in Kipfer et al. (2024). A schematic of the setup is shown in the Appendix A. Here, only a brief description of the setup is given: ICEBEAR consists of a stainless steel high vacuum chamber, which reaches base pressures of < 2 × 10−8 mbar at room temperature. The pressure is monitored via a pressure gauge (PKR 261, Pfeiffer Vacuum), and a quadrupole mass spectrometer (QMS) is attached to the chamber (QMG 250 M2, Pfeiffer Vacuum). The chamber is pumped using a turbomolecular pump (MAG W 400 iP, Pfeiffer Vacuum), backed by an oilfree roughing pump (SC 15 D, ScrollVac).

In the chamber, a copper sample holder is mounted onto the coldhead of a closed cycle helium cryostat (SRDK Series Cryocooler, Sumitomo Cryogenics). The sample holder is heated via resistive heating using a temperature controller (Lakeshore Model 336).

Gas mixtures are prepared by admixing components in a gas mixing system separate from the main chamber. The pressure in the gas mixing system is monitored using a capacitance diaphragm pressure gauge (CMR 362, Pfeiffer Vacuum) and the gas mixing system is pumped with a turbo pump (HiPace 80, Pfeiffer Vacuum), backed by an oil-free roughing pump (MV 2 NT, Vacuubrand). The gas mixture is introduced into the main vacuum chamber by a manually operated high precision leak valve and deposited onto the sample holder via background gas deposition.

2.2. Measurement procedure

The gas mixtures are prepared in the gas mixing backbone, after it has been thoroughly pumped to remove residual water vapour. First, the hypervolatile species, either N2 (99.999%, Messer) or 13CO (Cambridge Isotope Laboratories, 99%), are introduced into the gas mixing system, followed by water vapour (MilliQ-grade water, produced with a local Millipore System), and as a last component CO2 gas (99.995%, Messer). Next, the gases are dosed onto the sample holder, which is cooled to 15 K, with a dosing pressure of 4 × 10−6 mbar for a dosing time of 333 s. We deposit 1000 Langmuir (1.33 × 10−6 mbar s−1 = 1 L (Renner et al. 2007)). We assume that 1 L corresponds to one monolayer of material (1 ML = 1015 molecules cm−2), therefore the deposited ices are approximated as 1000 ML thick. The gas mixture is deposited via background gas deposition onto the cooled down sample holder. This high pressure deposition method, coupled with the low deposition temperature, favours the formation of highly porous, amorphous water ice (e.g., Fayolle et al. 2016), which will be discussed in Sect. 4.

Before and during deposition, the pressure in the chamber is logged, while the QMS records the mass over charge (m/z) with a dwell time of 32 ms (N2 experiments) or 64 ms (13CO experiments) and an electron ionisation energy of 70 eV. An electron current of 2000 μA is used for all experiments and will be discussed in the subsequent section. After gas deposition, the system is left to pump for at least 10 min to remove any gases remaining from the background gas deposition. Afterwards, a temperature programmed desorption (TPD) is started, which is an established technique to study desorption processes of ices and has been applied to the study of cometary ice analogues in previous works (e.g., Burke & Brown 2010; Minissale et al. 2022; Gudipati et al. 2023). During the TPD, the sample holder is heated at a constant heating rate of 2 K min−1 from 15 K to at least 250 K. During the warm up phase, the release of volatiles from the sample holder as a function of the temperature is studied by monitoring the signal with the QMS.

Over the course of the TPD experiment, a maximum of 27 ML of water vapour is calculated to have been accumulated from the background in the chamber. The accreted ice most likely differs slightly in morphology from the deposited ice, but based on the temperature is still expected to be amorphous (Fletcher 1971). This, in combination with the low thickness compared to the deposited ice, likely leads to a negligible effect on the trapping.

2.3. Data correction

The QMS measurements in this study have been observed to be subject to an electron current and pressure effect. At low pressure (≤10−7 mbar), the ratio between electrons emitted by the QMS electron filament and the number of gas particles entering the ionisation region appears to be too large, which results in enhanced fragmentation or double ionisation. In turn, the fragmentation pattern has been observed to vary with pressure, until a high enough pressure (≥10−7 mbar) is reached, where the pattern remains stable. Unfortunately, the default electron emission current could not be modified at the time of the measurement, and therefore the data are corrected to account for this effect whenever applicable.

All prominent fragment ions of H2O, CO2, and N2 are measured during the experiment. Therefore, the main mass m/z = 28 of N2 overlaps with the fragment of CO2, which necessitates the tracing of N2 with the m/z = 14 fragment signal.

To correct the signal for the aforementioned pressure effect, every component of the gas mixtures is individually measured at incremental pressure steps, measuring the current with the QMS and creating a calibration curve from both these data, as well as blank measurements, where an H2O:N2 ice is measured. For the calibration curve, each fragment is corrected to its stable fragmentation pattern (Fx(I)), where I is the total ion current and used as a proxy for the pressure in the system. This correction is applied to all N2 data presented in this paper and allows for the calculation of the m/z = 28 signal from the m/z = 14 data. The corresponding figures and correction values are collected in the Appendix B. The correction factor shows with which factor the signal has to be multiplied to reproduce the stable fragmentation pattern. For the 13CO data, a similar data correction was applied, though in this case the m/z = 29 data could be directly corrected due to no overlapping fragmentation pattern with CO2, as the heavy isotopologue fragments of CO2 only negligibly contribute to this mass channel. All data presented and used for further analysis have been multiplied with the appropriate factor and have had their baseline subtracted, unless mentioned otherwise.

The abundance of CO2 and N2 in the deposited ice with respect to water has been calculated using the formula:

R i = ϕ m / z , H 2 O ϕ m / z , i σ H 2 O σ i A i A H 2 O $$ \begin{aligned} R_{i}=\frac{\phi _{m/z,\mathrm{H_2O}}}{\phi _{m/z,i}}\frac{\sigma _{\rm H_2O}}{\sigma _{i}}\frac{A_{i}}{A_{\rm H_2O}} \end{aligned} $$(1)

where ϕi is the respective fragmentation pattern for the molecule for the selected m/z channel, determined from the stable fragmentation pattern observed at high enough pressures, σi the total electron impact ionization cross section at 70 eV, and Ai the integrated QMS signal over the course of the TPD. The electron-impact ionization cross sections have been referenced from the NIST database1 and are 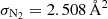σ N 2 = 2.508 Å 2 $ \sigma_{\mathrm{N_2}} =2.508\,{\AA}^2 $, σ CO 2 = 3.521 Å 2 $ \sigma_{\mathrm{CO_2}} ={3.521}\,{\AA}^2 $, and σ H 2 O = 2.275 Å 2 $ \sigma_{\mathrm{H_2O}}={2.275}\,{\AA}^2 $. For the fragmentation pattern, the following values have been experimentally determined: ϕ18, H2O = 0.76, ϕ44, CO2 = 0.79, and ϕ28, N2 = 0.94.

3. Results

3.1. TPD traces

Different H2O:CO2:N2 ice mixtures have been prepared to study the desorption behaviour of N2 from the H2O:CO2 ice matrix, using the desorption traces measured with the QMS during the TPD (see Table 1). A selection of these TPDs is shown in Fig. 1. The amount of CO2 with respect to water increases from left to right, while the amount of N2 is kept constant. Four distinct desorption events are seen for m/z = 28 (N2): a desorption at ∼50 K, a second desorption at ∼85 K, a third desorption at ∼150 K, and a last, small desorption at ∼170 K.

thumbnail Fig. 1.

Desorption traces of N2 and 13CO in H2O:CO2:N2 and H2O:CO2:13CO ices respectively as a function of temperature during the TPD. Top row: desorption traces of N2, (solid, blue), CO2 (grey, dotted) and H2O (grey, dashed) for different ice experiments. For the presented data the N2 contribution has been calculated to be between 3% and 5% with respect to water, therefore assumed to be relatively constant. The CO2 contribution is shown at the top with respect to water and increases from left to right. For N2, the corrected data have been calculated from the m/z = 14 data, corresponding to the N fragment, as described in Appendix B, therefore resulting in more noise than the 13CO data. Neither the CO2 nor the H2O data have been corrected or baseline subtracted for this plot. Bottom row: desorption trace for m/z = 29 (13CO, orange) for different ice experiments, with the CO2 and H2O desorption traces shown as well. The 13CO contributions have been calculated to be between 3% and 4% with respect to water, except for the first experiment, in which the 13CO has been calculated to be ∼2.5%. The 13CO signal has been corrected and baseline subtracted, whereas for the CO2 and H2O traces no corrections have been performed. Please note that for the 13CO measurements, the background pressure has been higher than for the N2 measurements, resulting in a larger background for H2O and CO2.

Table 1.

Fractions of N2 desorbing in the various integration regimes for the different ices.

As the amount of CO2 in the ice increases, another desorption peak emerges for N2, largely coinciding with the CO2 desorption peak at 85 K, pointing to trapping of N2 by CO2. We refer to a volatile as being trapped by CO2 (or H2O) if the volatile co-desorbs with CO2 (or H2O). Lastly, both N2 and CO2 desorb at ∼150 K, which corresponds to the phase change of water from amorphous to crystalline, allowing for previously trapped, more volatile species to desorb. This desorption event is referred to as the ‘volcano desorption’ (Bar-Nun et al. 1985). A lesser desorption can be seen around ∼170 K, which is the H2O co-desorption. The last two desorption events will be collectively referred to as the combined H2O release without explicitly distinguishing between them, as these two regimes are unlikely to be distinguishable in the in-situ measurements performed by ROSINA in the coma of comet 67P (Rubin et al. 2023). The desorption events are collected in three desorption regimes, which have been chosen in keeping with the data in Rubin et al. (2023) and are shown in Table 2.

Table 2.

Different desorption regimes for the volatiles N2 and CO used for the integration, adapted from Rubin et al. (2023).

Figure 2 shows the desorption trends of N2 for selected TPD experiments conducted. The different desorption regimes are indicated as shaded backgrounds. A figure showing all experiments listed in Table 1 can be found in Appendix D. We note here that the selection of different temperature limits for the regimes will result in slightly different values, as the distinction between the CO2 co-desorption and the combined H2O release is not trivial, but the behaviour of the data remains consistent. The fraction of N2 desorbing at the pure N2 desorption peak (30–60 K) is proportional to the N2 present in the ice and appears to be only negligibly affected by the amount of CO2 present. However, a change in the temperature of the desorption onset can be seen, which shifts to higher temperatures as the amount of N2 in the ice decreases. The shift in desorption temperatures due to interactions between the different ice constituents and trapping is a known effect observed in previous TPD experiments (see e.g., Collings et al. 2004). For all ices, a rapid desorption of N2 is observed at the volcano desorption, inversely correlated to the amount of N2 present. Only for small amounts of N2, a noticeable co-desorption with H2O can be observed at > 150 K.

thumbnail Fig. 2.

Normalized desorption behaviour of N2 and 13CO as a function of temperature in the ices. Please note that not all measured data is displayed. A figure showing the complete data is shown in Appendix D. Left: evolution of N2, calculated from the m/z = 14 signal, during the TPD of different ices as a function of the temperature. The data have been sorted with respect to the N2 present in the ice mixture. The shaded regions correspond to the desorption regions in Table 2. A lighter line color corresponds to more N2. The linestyles indicate the amount of CO2 present with respect to water, with the assignment being: x < 1%:dashed, 1 < x < 5%: long dashes, 5 < x < 10%:solid, 10 < x < 15%: dashdot, 15 < x < 20%: dashdotdotted, 20 < x%: dotted. Right: evolution of 13CO, calculated from the m/z = 29 signal, as a function of the temperature. The data have been sorted with respect to the 13CO present in the ice mixture. A lighter color corresponds to more 13CO. The linestyles indicate the amount of CO2 present with respect to water, with the assignment of the linestyles being the same as for the left panel.

3.2. N2 co-desorption with CO2

For increasing amounts of CO2 in the H2O:CO2:N2 ices, the prominence and structure of the CO2 desorption peak at ∼85 K increases as well, see Fig. 1, whereas the peak at the volcano desorption remains relatively constant for CO2 > 5% with respect to water. This indicates that a maximum amount of CO2 can be trapped within the water, while the remainder desorbs at 85 K. Furthermore, for lower amounts of CO2, the temperature of the N2 co-desorption coincides with the CO2 desorption peak, whereas for ices containing ∼15% CO2, N2 is observed to co-desorb at the first onset of CO2 desorption. For CO2 > 10%, the co-desorption of N2 with CO2 can be seen in the normalised desorption trace, see Fig. 2.

Figure 3 shows the signal of N2 co-desorption with CO2 (60–115 K) in more detail. The noise in the signal originates from the calculation of the m/z = 28 signal from the significantly fainter m/z = 14 signal. As the amount of CO2 increases, the co-desorption trace changes from a single peak to three co-desorption events. For the 100:23.1:11.1 ice, a bump in the desorption is seen before the onset of the CO2 desorption. This is also observed for two other TPD measurements containing > 20% CO2 and a bit fainter for the ices containing > 15% CO2. The particular shape is likely not an artefact from the data correction, as shown for 13CO in Fig. B.4. The results of Simon et al. (2023) also show such a three-peak structure between 50 and 100 K in both of their CO2:N2 (3:1) experiments. Furthermore, the N measured by Gudipati et al. (2023) in their CO:O2:CO2:H2O ice also tentatively shows this particular shape.

thumbnail Fig. 3.

Zoom in of the N2 co-desorbing with CO2. The plots have been color coded for the abundance of N2 with respect to water. The linestyles indicate the amount of CO2 present with respect to water, with the assignment being: x < 10%:dotted, 10 < x < 20%: dashed, 20 < x%: solid. For readability, not all data measured are displayed.

This effect is only prominently observed as the amount of CO2 in the ice increases, therefore the behaviour of the volatile is most likely related to diffusion through the CO2 ice. In turn, an increased amount of CO2 in the ice leads to less H2O in the ice mixture, volatiles could be trapped preferentially by the CO2 and then desorb as soon as the desorption of CO2 commences.

3.3. Fraction of desorbing N2

Figure 4 shows the fraction of N2 desorbing depending on the desorbing regime. The fractions have been calculated by integrating the desorption trace between the temperature intervals shown in Table 1 and normalising the values to the total N2 desorption. For the pure N2 desorption peak (T < 60 K), a clear increase in the fraction desorbing as a function of the abundance of N2 present in the ice can be seen, which was already noted in Fig. 2. For > 6% N2 in the ice, more than 40% of N2 is expected to be lost during the pure N2 sublimation peak, whereas for < 2%, less than 25% desorbs in the same temperature regime. Notable outliers are the desorption behaviour from the H2O:N2 ices, which both yield a lower value than expected from the linear fit.

thumbnail Fig. 4.

Desorption behaviour of N2 in the different regimes, colour coded for the abundance of nitrogen in the ice with respect to water. Each column shows the different desorption events for N2 with the integration limits for the desorption events given in Table 2. The data points indicated with a diamond are the H2O:N2 ices, with negligible amounts of CO2 in the mixture. The colour assignment is the same as in Fig. 2. Top row: desorption behaviour of N2 as a function of the total N2 in the mixture, the total CO2 abundance in the mixture, and the H2O abundance respectively. The N2 desorption occurring at the pure N2 desorption peak and the CO2 co-desorption have been fitted with a linear function and the resulting best fit is shown in the corresponding panel (grey, dashed line). The grey shaded region indicates the standard deviation of the fit. For the water co-desorption no overall fit has been done, however, trends for the different N2 abundances have been indicated and colour coded. Bottom row: same data as in the top row, but plotted as a function of the total N2 abundance in the ice mixture.

The data show a clear trend in the desorbing fraction of N2 as a function of the CO2 present in the ice mixture, with no apparent dependence on the amount of N2. It must be noted that for the H2O:N2 ices, an integration has been performed as well, though no increased release of N2 in the temperature region where CO2 normally desorbs can be seen. Instead, the result corresponds to the observed continuous desorption that occurs after the pure N2 desorption peak, see Fig. 1.

The trends for the water co-desorption show, that even though the amount of H2O increases the fraction of N2 trapped, a clear separation can also be seen depending on the amount of N2 present in the ice. Therefore, as opposed to the CO2 co-desorption, not only the amount of H2O, but also the amount of N2 in the ice influences the desorption behaviour during the combined H2O release. However, as CO2 is also desorbing in this regime, the trapping and desorption of N2 is more complex, as most likely N2 is trapped not only within H2O but also within the H2O:CO2 ice matrix.

Figure 5 shows the ratio of N2 co-desorbing with CO2 to the sum of CO2 co-desorption and desorption during the pure N2 desorption peak. For CO2/N2 < 5 the fraction of N2 co-desorbing with CO2 is observed to increase steeply, whereas for even larger CO2/N2 ratios, the slope of the increase reduces significantly. This shows that for all ice mixtures investigated, the pure N2 desorption peak dominates over the CO2 co-desorption.

thumbnail Fig. 5.

Fraction of desorbing N2 during the CO2 co-desorption compared to the sum of the CO2 co-desorption and the pure N2 desorption peak as a function of the CO2 to N2 ratio in the ice. The error bars have been calculated using Gaussian error propagation.

The top row of Fig. 6 shows the ratio of the fraction of N2 desorbing during the combined H2O release, labelled as N2(H2O), to the fraction of N2 co-desorbing with CO2 plus the pure N2 desorption, labelled as N2(CO2)+N2(N2 peak). The bottom row shows the ratio of N2(H2O) to the fraction of N2 co-desorbing with CO2, labelled as N2(CO2). Indicated as a line is the ratio N2(H2O)/N2(CO2) of 1.72 derived for 67P (Läuter et al. 2020; Rubin et al. 2023) from the pre-perihelion period of early February 2015 to early September 2016, assuming CO2/H2O = 0.075. However, a ratio N2(H2O)/N2(CO2) of 3 is also possible, in the case of CO2/H2O = 0.047 (Rubin et al. 2019a). The exact ratio depends on if the mission integrated values or the pre-perihelion values are taken. The plots show the ratios once as a function of the N2 abundance in the ice in the left column and once as a function of the CO2 in the right column.

thumbnail Fig. 6.

Ratios of the N2 fractions desorbing in different desorption regimes. Top row: ratio of the N2 desorption during the combined H2O release to the sum of the CO2 and pure N2 (co-)desorption. The expected ratio of 1.72 for 67P has been indicated (purple, dashed line), as well as the upper limit estimate of 3 (purple, shaded region). Bottom row: ratio of the N2 desorption during the combined H2O release to the N2 co-desorption with CO2. The expected ratio for 67P has been indicated and includes the area between 1.72 (purple, dashed line) and to about 3 (purple, shaded region).

For the N2(H2O)/(N2(CO2)+N2(N2 peak)) desorption, a slight downward trend can be observed as a function of increasing N2 abundance, which is the opposite to the result observed in Fig. 4. Furthermore, for ices with less than 4% N2, a ratio of < 1 can be reached, which indicates that the majority of N2 is lost before the combined H2O release. The same plot as a function of CO2 shows no such clear trend, but instead rather a slight separation depending on the amount of N2 in the ice.

If only the N2(H2O)/N2(CO2) ratio is considered, a downward trend is observed as a function of the CO2 in the ice, with CO2 > 15% leading to values in accordance with observations for 67P, and the combined H2O release is the dominant desorption mechanism. If the same ratio is plotted as a function of N2, no clear trend in the data is seen.

3.4. Comparison between N2 and CO desorption

To verify and complement the N2 data, several measurements have been performed with H2O:CO2:CO ices. A list of the ices prepared is shown in Table C.1. CO is more abundant than N2 in the bulk ice of 67P and is expected to behave in a similar way to N2 due to their comparable binding energies and desorption temperatures (Minissale et al. 2022; Collings et al. 2004). To distinguish the pure CO signal from the CO fragment originating from the CO2 fragmentation, isotopically labelled 13CO was used. However, a correction to the signal intensity still had to be applied, see Appendix B.

The bottom row of Fig. 1 shows the TPD traces of various H2O:CO2:13CO ice mixtures. Qualitatively, a very similar behaviour to the H2O:CO2:N2 experiments can be seen, with four distinct desorption events. First, a desorption peak corresponding to surface bound 13CO is observed at ∼50 K. As the amount of CO2 increases, the co-desorption peak for 13CO with CO2 becomes more prominent. Also similar to the H2O:CO2:N2 ices, the co-desorption of 13CO with CO2 starts before the CO2 desorption for high CO2 concentration. Finally, both the volcano desorption and H2O co-desorption of 13CO are clearly visible. The desorption structure during the CO2 co-desorption observed for N2 and described in Sect. 3.2 is observed for 13CO as well for high abundance of CO2 (> 20%). A slight difference in the temperature of the pure desorption peak between N2 (40–50 K) and 13CO (45–55 K) is noted.

In Fig. 7, the fraction of 13CO desorbing for the different temperature regimes is shown. The integration follows the regimes outlined in Table 2. A very similar trend to the H2O:CO2:N2 ices is observed here, with an increase in the desorbing fraction during the pure 13CO desorption as the amount of 13CO increases. Further, the fraction of 13CO co-desorbing with CO2 also increases as the amount of CO2 in the ice increases. Again, similar to N2, the fraction co-desorbing with CO2 does not appear to depend on the amount of 13CO in the ice but is instead determined by the CO2 present. However, the linear fit indicates that a larger fraction of the 13CO co-desorbs with CO2 than N2 as the amount of CO2 increases.

thumbnail Fig. 7.

Desorption behaviour of 13CO in the different regimes, colour coded for the total abundance of 13CO in the ice. Each column shows the different desorption events for 13CO. Diamond markers indicate the experiments without any CO2. The composition of the ices is collected in Table C.1.

4. Discussion and implications

4.1. Desorption experiments

Figure 4 shows that the presence and abundance of both H2O and CO2 are important to release volatiles in cometary ices. The fraction of N2 co-desorbing with CO2 is a direct function of the CO2 abundance in the ice. Furthermore, the fraction of N2 desorbing during the combined H2O release (that is, volcano and water co-desorption) shows a dependence on the N2 concentration in the ice, with a higher fraction desorbing for lower concentrations of N2. This indicates that there is a maximum amount of N2 that can be trapped in the water ice and for this series of experiments that is approximately 73%, but larger fractions are not ruled out for lower N2 concentrations. For a higher concentration of N2 the likelihood that the direct neighbour of an N2 molecule is neither H2O nor CO2, but instead another N2 increases, resulting in a larger fraction of N2 desorbing in its pure phase instead of being trapped, in line with recent investigations by Simon et al. (2023).

Ninio Greenberg et al. (2017) investigated H2O:CO2:N2 ices with a thickness of 50–100 μm deposited at ≥30 K and subjected to a heating rate of 1 K min−1. They demonstrated that in the case of CO2 being present in the ice, volatiles (such as N2) start to co-desorb with CO2 as well, instead of only with H2O. Furthermore, they reported an increase in the trapping efficiency of N2 in a H2O:CO2:N2 ice compared to a binary H2O:N2 ice. However, we note that Ninio Greenberg et al. (2017) determine trapping differently, by comparing the amount of N2 locked up in the ice after deposition, while we look at fractions of N2 trapped in – or, associated with – CO2 and H2O at 15 K. We conclude that increasing the CO2 content in the ice, increases N2 co-release with CO2, but decreases trapping in the water phase.

Simon et al. (2023) studied thin film (10 and 50 ML) binary mixtures of H2O:N2 and CO2:N2, deposited at 12 K, and determined the trapping of N2 within the two bulk ices. For the mixing ratios of 10:1, they determine that 43 ± 2% of N2 is trapped in H2O for the 10 ML case, and 5 8± 2% of N2 for 50 ML. These values can be compared with our much thicker (1000 ML) ice films, for similar H2O:N2 mixing ratios. The relevant experiments are highlighted in bold in Table 1. Our binary H2O:N2 experiment shows that the N2(H2O) fraction is 52 ± 3%, which is close to the 50 ML values of Simon et al. (2023). We did not investigate ice of thickness between 50 and 1000 ML, but the similarity in trapping fraction suggests that the ice thickness might play a subordinate role in the trapping of N2 within H2O for ices with a thickness of ≥50 ML.

However, a comparison with our ternary mixtures, when CO2 is added, shows that this does affect the N2(H2O) trapping efficiency. For an addition of ∼11% CO2 (w.r.t. H2O), N2(H2O) decreases to 41 ± 3%, while for ∼23% added CO2 N2(H2O) is reduced further to 36 ± 3%. This effect is likely caused by competition for binding sites between different molecular constituents. These experimental observations stress the importance of using realistic ice compositions when investigating cometary or interstellar ice analogues due to the influence the different components have on the overall behaviour of the ice. Nevertheless, binary mixtures are valuable when investigating chemical extremes.

We observe N2 and CO to behave qualitatively similar during the TPDs. However, a comparison between Figs. 4 and 7 shows that a larger portion of CO co-desorbs with CO2 as compared to the ices containing N2 (see the results in Tables 1 and C.1). The results from Simon et al. (2023) show similar entrapment efficiencies for N2 and CO for the 10:1 50 ML experiments in both the CO2 and H2O ices, whereas the results in our study indicate more efficient trapping in CO2 for CO in the H2O:CO2 matrix than for N2. The fractions of CO and N2 trapped in H2O are comparable. Bar-Nun et al. (2007) have linked differences in the N2 and CO desorption behaviour in amorphous water ice to the dipole moment (or lack thereof) of the volatile gases, which is expected to influence their trapping efficiencies in the pores of the amorphous ice. It is possible that a similar effect is taking place with regard to the H2O:CO2 ice, as the N2 molecule does not have a dipole moment.

In Gudipati et al. (2023) a CO:O2:CO2:H2O (1:1:2:6) ice with residual N2 was thermally desorbed. The results show a different behaviour of CO and N2 release, with 70% of CO desorbing during the pure volatile desorption at < 70 K, whereas 38.8% of N2 desorb in the same temperature range. However, care must be taken with the N2 results from their work, as N2 is only a residual component in the gas mixture and was not a controlled contribution in the initial mixture. Nevertheless, extrapolating from the N2 data to CO and vice versa is not trivial and care should be taken when using one as a proxy for the other to derive quantitative values, even though their qualitative behaviour in the H2O:CO2 matrix is similar. Furthermore, future experiments should also consider the four-component ice mixture H2O:CO2:CO:N2, as the qualitatively similar behaviour of N2 and CO in both the binary H2O and CO2 ices, as well as the H2O:CO2 ice suggests that they might be competing for the same binding sites (Simon et al. 2023). Such an effect was observed by Ninio Greenberg et al. (2017) for N2 and argon, where the two volatiles appear to interfere with each other when deposited together, leading to lower trapping efficiencies by H2O. A similar effect might explain the differing desorption behaviour of CO and N2 in Gudipati et al. (2023).

4.2. Implications for comet 67P

As 67P is thought to have inherited most of its volatile material from ice-coated grains in the prestellar cloud that the Solar System formed from (e.g., Altwegg et al. 2017; Drozdovskaya et al. 2019), the present and historic N2 content has astrochemical implications.

The N2 abundances in this study have been chosen high compared to the bulk abundance of N2 in 67P, which is expected to be in the range of 8.9 × 10−4 with respect to water (Rubin et al. 2019a). A realistic CO2/N2 ratio of 52.8–85.7 for 67P (Rubin et al. 2019a,b) can be expected, which is higher than the ratios investigated in this study (maximum of ∼33, see Fig. 5). The maximum fraction of N2 co-desorbing with CO2 in this measurement series has been observed to be ∼20%. However, as addressed in Sect. 3.1, this value might be overestimated due to the continuous desorption of N2 after the N2 peak, therefore the 20% should rather be considered an upper limit.

The temperatures in the outgassing layers of 67P are poorly constrained. Its brightness temperature has been measured to be in the range of 60–180 K (Gulkis et al. 2015) at an orbital distance of 3.2 au and further increases as the comet approaches perihelion. Nevertheless, there might be regions on 67P where the temperature required for the phase transition of water is never reached, resulting in a slow sublimation of the water ice and the trapped volatile species within (Rubin et al. 2023). Thermal heating of up to 0.1 K min−1 (Gulkis et al. 2015), or locally between 2 and 9 K min−1 (Tosi et al. 2019) could be possible on the surface. However, as the field of view is large for ROSINA, the gas could originate from various parts of the surface, in particular the illuminated areas with direct line-of-sight.

Rubin et al. (2023) investigated the desorption behaviour of volatiles in 67P and found that the N2 release correlates with CO2 and H2O outgassing. No unassociated, pure phase N2 is observed. For a CO2/H2O = 0.047 bulk ratio of 67P (Rubin et al. 2019a), 25% of N2 was found to be associated with CO2 and 75% with H2O, while for a CO2/H2O = 0.075 ratio (Läuter et al. 2020) 37% N2 were found to be associated with CO2 and 63% with H2O. Similarly to N2, the CO release in 67P was also observed to correlate with CO2 and H2O (Rubin et al. 2023): For a CO2/H2O = 0.047 ratio, 20% of CO was found to be associated with CO2 and 80% with H2O, while for a CO2/H2O = 0.075 ratio, 30% CO were associated with CO2 and 70% with H2O.

N2 and CO show qualitatively similar behaviour in the observations of 67P, as well as in the analogue ice experiments. However, between 67P observations and experiments, discrepancies become apparent. The bulk behaviour of 67P results in N2(H2O)/N2(CO2) ratios of 3 and 1.7, depending on the value chosen for its CO2 bulk abundance. In our study, a bulk molecular fraction of ≥15% CO2 is needed in the ice to yield this N2(H2O)/N2(CO2) ratio (Fig. 6). A number of explanations are suggested for this discrepancy. First, measurement errors are large for ROSINA measurements of N2, because its mass (m/z = 28.0056) is close to that of CO (m/z = 27.9944), resulting in mass spectrometric interference and larger uncertainties on abundances and correlations. Second, Rubin et al. (2023) showed that there are times in the mission where the CO2 signal dominates over the H2O signal. This could indicate sublimation from regions where the temperature of the sublimating layer is high enough for CO2, but not H2O, enhancing therefore CO2/H2O ratio. In fact, Läuter et al. (2018) showed that the surface emission regions of CO2 on 67P remained nearly constant over the mission, whereas H2O emission regions followed the subsolar latitude, pointing to differences in the CO2/H2O emission over the course of the mission likely being related to the temperature of the sublimating layers. However, the gas phase measurements might not be representative of the bulk ice composition in the interior of the comet. Third, we have seen before that an increase in CO2 content reduces the N2(H2O) fraction, presumably due to competition for binding sites. Other molecules likely have a similar effect on the ice. While CO2 is the second most abundant species in the cometary ice of 67P and therefore has the largest impact, the combined effect of multiple minor species could have a similarly large effect on the competition for binding sites and reduce the trapping of N2 in H2O.

An ongoing and still unresolved question is the morphology of 67Ps ice (e.g., Marboeuf et al. 2012, and references therein). Thomas et al. (2019) summarized the open questions after the Rosetta mission, such as whether the water ice in 67P is in amorphous or crystalline form. Constraints on this question could give information about the formation conditions of 67P, such as if it formed by agglomerating pristine water ice grains from the insterstellar medium (Owen & Bar-Nun 1993), or possibly from grains containing clathrates (Mousis et al. 2000).

The measurement protocol chosen for our experimental campaign favours the formation of highly porous, amorphous ice, which is expected to efficiently trap volatiles (Ayotte et al. 2001) and could be present on 67P if it formed in or inherited its icy material from a cold reservoir, such as a dark cloud. For comet Halley, crystallization of amorphous water ice in the nucleus was theorized to be responsible for an observed outburst (Prialnik & Bar-Nun 1992), though Kouchi & Sirono (2001) have shown that impurities in the amorphous water ice could lead to the transition being endothermic.

Future missions targeting comets, especially missions involving a possible cryogenic sample return of ice, such as the AMBITION mission concept (Bockelée-Morvan et al. 2022), could give valuable insight into the morphology of the ice and guide future laboratory experiments for cometary ice analogues.

4.3. The ‘missing’ nitrogen problem

Rubin et al. (2019a) shows the elemental nitrogen abundance relative to silicon for 67P, which is depleted by about one order of magnitude compared to the solar value for assumed dust-to-ice ratios of 3 and 1 (see their Fig. 5). Similarly, Geiss (1988) suggested a nitrogen depletion in comet 1P/Halley.

Observations of the ice inventories of interstellar clouds have shown that the nitrogen-bearing molecules only account for a fraction of the elemental nitrogen budget (e.g., ∼11% for sources observed with Spitzer, Öberg et al. 2011). The solution to this interstellar ‘missing’ nitrogen problem has been suggested to be found in N2 (Palumbo et al. 2000), which is only weakly spectroscopically active in the infrared wavelength regime that interstellar ices are observed in. This has resulted in the suggestion that the majority of the elemental nitrogen budget is locked up in N2 on ice-coated interstellar dust grains. This hypothesis has been used to explain Jupiter’s super-solar nitrogen abundance, with a scenario where this planet formed outside the N2 snow line (located at ∼30 au in the protosolar nebula), where N2 on ice grains accounted for 90% of the elemental nitrogen budget (Öberg & Wordsworth 2019; Bosman et al. 2019). However, searches for N2 in interstellar ice have resulted in a large range of upper limit abundances (≤0.2–60% w.r.t. H2O, Elsila et al. 1997; Sandford et al. 2001; Boogert et al. 2002, 2015), but no secure detection to date. Currently, the ROSINA detection of N2 in comet 67P provides the only indication of the N2 content in interstellar ice.

The discussion in Sects. 4.1 and 4.2 suggests that 67P, or the ice it is made of originally, could have contained more N2 than observed at the present. During the Centaur-phase of 67P, if the internal temperature increased up to 70 K (Guilbert-Lepoutre et al. 2016), N2 in its pure phase could have been lost. However, the results from Fig. 4 show that the fraction of N2 desorbing during the pure N2 desorption depends on the amount of N2 present in the ice. In other words, the lower the N2 concentration, the smaller the fraction of N2 released in its pure form. Since the current N2 content in 67P (∼0.09% w.r.t. H2O) is lower than the fractions used in this study, this indicates that the fraction lost for 67P is low and probably ≤20%. Furthermore, as shown in Notesco & Bar-Nun (2005), thicker ices (> 5 μm) are more likely to trap impurities such as N2 and other volatiles. Therefore, for cometary ices, their thickness would suggest that the majority of N2 remained trapped.

A neglected aspect in this regard is the timescale. As even the most realistic laboratory experiments cannot reproduce cometary timescales, desorption of trapped N2 might have occurred slowly due to diffusion through the bulk ice, resulting in a steady desorption of N2, in particular upon moderate heating up to 70 K. While this could mean that more N2 was historically present in the ice of 67P, such a scenario would not fit with CO. Carbon monoxide has a similar desorption temperature (desorption parameters) and shows qualitatively similar desorption behaviour to N2. This indicates that both species might have been similarly affected and depleted during the history of 67P. Since 67P at present contains more CO (3.1%) than N2 (0.09%), historic abundances quickly run into limitations. For example, if 67P or the material it formed from started with 1% N2, then, assuming a constant ratio between the species, ∼30% CO was present. While such CO ice abundances are still realistic for comets and interstellar ices (Mumma & Charnley 2011; Boogert et al. 2015), larger factors of increase become increasingly less realistic. Therefore, it is a possibility that N2 was never a major component in 67P or the material it formed from and its loss is not sufficient to account for the missing nitrogen in this comet.

Another explanation for the missing nitrogen is suggested to be the presence of ammonium salts in 67P (Altwegg et al. 2020, 2022). Evidence for such salts in the comet has been detected during a dust impact, where fragments associated with ammonium salts were measured over several hours (Altwegg et al. 2020). Furthermore, VIRTIS-M measurements of 67P show a good agreement between the observed spectrum of the surface and laboratory reference measurements of ammonium salts (Poch et al. 2020).

As the results obtained in the present study suggest that the loss of N2 in 67P might not be sufficient to explain the nitrogen deficiency, this could in turn support the hypothesis of nitrogen being found in the form of ammonium salts. This would allow for the nitrogen to survive at higher temperatures than the sublimation of water ice (Altwegg et al. 2022), but also partly evade detection in the gas phase due to the high sublimation temperature.

More research and observations are required to determine the role ammonium salts can play in the search for the missing nitrogen. For such an endeavour, more sensitive instruments are needed, such as the JWST, which could potentially make a direct, remote detection of such salts possible (Altwegg et al. 2022).

5. Conclusions and outlook

We presented TPD measurements three-component ice mixtures consisting of H2O:CO2:N2 and H2O:CO2:CO. We investigated the desorption behaviour of the volatiles (N2 and CO) as a function of the temperature and ice composition, and contextualised the results within the framework of comet 67P results. Systematic studies of such ternary mixtures containing H2O and CO2 have been neglected by laboratory work to this date. Our findings and outlook are summarised below:

  1. Our experiments with H2O:CO2:N2 ices showed that 15.6–49.0% of N2 desorbs during the pure N2 desorption and that this fraction increases the larger the N2 content in the mixture is. 7.6–21.6% of N2 co-desorbs with CO2 and this amount increases with increasing CO2 content in the ice. Finally, between 36.0–72.3% of N2 desorbs during the combined H2O release (that is, volcano desorption and water co-desorption combined), where lower N2 quantities in the ice result in larger fractions released with H2O. The behaviour of H2O:CO2:CO ice is qualitatively largely identical to its N2 counterpart, but a larger fraction of CO is observed to co-desorb with CO2.

  2. A comparison between binary and ternary H2O-dominated mixtures shows that more complex ice mixtures affect the trapping efficiency of N2 in H2O, which is explained by an increased competition for binding sites when more components are present in the mixture. To assess the trapping behaviour of cometary or interstellar ice, realistic ice mixtures need to be used.

  3. The measured N2(H2O)/N2(CO2) ratio (that is, N2 trapped in water over N2 embedded in CO2) in 67P is in the range of 1.7–3.0. To match such values, the H2O:CO2:N2 ice used in our experiments must contain >15% CO2, while the CO2 bulk value of 67P is likely ≤7.5% (Läuter et al. 2020). For realistic CO2 bulk abundances in 67P, a ratio of N2(H2O)/N2(CO2) between 6 to 9 would be expected based on the present experiments. Local variations in ice composition and temperature of the sublimating layers of 67P are thought to significantly influence the observed gas ratios in the coma during the Rosetta mission.

  4. For realistic bulk N2 abundances in 67P, a maximum of 20% of N2 is expected to desorb before 70 K. Consequently, relatively little N2 has been lost from 67P if it underwent a heating event (that is, Centaur stage). Therefore, loss of N2 likely cannot account for the approximately one order of magnitude elemental nitrogen deficiency of comet 67P compared to the solar elemental composition. Assuming 67P inherited most of its ice from a prestellar environment, the amount of elemental nitrogen locked up in N2 on the ice-coated dust grains forming 67P is suggested to be at most a few percent with respect to H2O.

As a Jupiter-family comet, 67P might have undergone substantial heating in the past before and while it moved to its current orbit. Data from the Comet Interceptor mission (Jones et al. 2024), which will potentially target a pristine and dynamically new comet, can help understand mechanisms that alter the surface and bulk ice composition of comets. Its MANiaC mass spectrometer will be instrumental in detecting highly volatile species. Additional laboratory measurements on more complex and realistic ice mixtures will be necessary to interpret this data.

1

https://www.nist.gov/pml/electron-impact-cross-sections-ionization-and-excitation-database

Acknowledgments

The authors want to thank the Reviewer, Marco Minissale, for his insightful comments which have helped improve the quality of the paper. K.A.K. and N.F.W.L. acknowledge support from the Swiss National Science Foundation (SNSF) Ambizione grant 193453 and NCCR PlanetS. Work by M.R., N.H., and D.R.M. was funded by the Canton of Bern and the Swiss National Science Foundation (SNSF; 200020_207312). S.F.W acknowledges the financial support of the SNSF Eccellenza Professorial Fellowship (PCEFP2_181150).

References

  1. A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2011, Science, 332, 1396 [CrossRef] [Google Scholar]
  2. A’Hearn, M. F., Feaga, L. M., Keller, H. U., et al. 2012, ApJ, 758, 29 [CrossRef] [Google Scholar]
  3. Altwegg, K., Balsiger, H., Berthelier, J. J., et al. 2017, Phil. Trans. Royal Soc. A: Math. Phys. Eng. Sci., 375, 20160253 [Google Scholar]
  4. Altwegg, K., Balsiger, H., & Fuselier, S. A. 2019, ARA&A, 57, 113 [NASA ADS] [CrossRef] [Google Scholar]
  5. Altwegg, K., Balsiger, H., Hänni, N., et al. 2020, Nat. Astron., 4, 533 [NASA ADS] [CrossRef] [Google Scholar]
  6. Altwegg, K., Combi, M., Fuselier, S., et al. 2022, MNRAS, 516, 3900 [NASA ADS] [CrossRef] [Google Scholar]
  7. Ayotte, P., Smith, R. S., Stevenson, K. P., et al. 2001, J. Geophys. Res., 106, 33387 [NASA ADS] [CrossRef] [Google Scholar]
  8. Balsiger, H., Altwegg, K., Bochsler, P., et al. 2007, Space Sci. Rev., 128, 745 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bar-Nun, A., & Owen, T. 1998, in Trapping of Gases in Water Ice and Consequences to Comets and the Atmospheres of the Inner Planets, eds. B. Schmitt, C. De Bergh, & M. Festou (Dordrecht: Springer), 353 [Google Scholar]
  10. Bar-Nun, A., Herman, G., Laufer, D., & Rappaport, M. 1985, Icarus, 63, 317 [CrossRef] [Google Scholar]
  11. Bar-Nun, A., Dror, J., Kochavi, E., & Laufer, D. 1987, Phys. Rev. B, 35, 2427 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bar-Nun, A., Notesco, G., & Owen, T. 2007, Icarus, 190, 655 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, Nature, 526, 678 [Google Scholar]
  14. Bockelée-Morvan, D., Lis, D. C., Wink, J. E., et al. 2000, A&A, 353, 1101 [Google Scholar]
  15. Bockelée-Morvan, D., Crovisier, J., Mumma, M. J., & Weaver, H. 2004, in Comets II, eds. M. C. Festou, H. A. Weaver, & H. U. Keller (Tucson: Univ. of Arizona), 391 [Google Scholar]
  16. Bockelée-Morvan, D., Filacchione, G., Altwegg, K., et al. 2022, Exp. Astron., 54, 1077 [CrossRef] [Google Scholar]
  17. Boogert, A. C. A., Hogerheijde, M. R., Ceccarelli, C., et al. 2002, ApJ, 570, 708 [NASA ADS] [CrossRef] [Google Scholar]
  18. Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
  19. Bosman, A. D., Cridland, A. J., & Miguel, Y. 2019, A&A, 632, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Burke, D. J., & Brown, W. A. 2010, Phys. Chem. Chem. Phys., 12, 5947 [NASA ADS] [CrossRef] [Google Scholar]
  21. Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dello Russo, N., Kawakita, H., Vervack, R. J., & Weaver, H. A. 2016, Icarus, 278, 301 [NASA ADS] [CrossRef] [Google Scholar]
  23. Drozdovskaya, M. N., van Dishoeck, E. F., Rubin, M., Jørgensen, J. K., & Altwegg, K. 2019, MNRAS, 490, 50 [Google Scholar]
  24. Ehrenfreund, P., & van Dishoeck, E. 1998, AdSpR, 21, 15 [NASA ADS] [Google Scholar]
  25. Elsila, J., Allamandola, L. J., & Sandford, S. A. 1997, ApJ, 479, 818 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fayolle, E. C., Balfe, J., Loomis, R., et al. 2016, ApJ, 816, L28 [Google Scholar]
  27. Filacchione, G., Raponi, A., Capaccioni, F., et al. 2016, Science, 354, 1563 [Google Scholar]
  28. Fletcher, N. H. 1971, Rep. Progr. Phys., 34, 913 [CrossRef] [Google Scholar]
  29. Fray, N., & Schmitt, B. 2009, Planet. Space Sci., 57, 2053 [Google Scholar]
  30. Fuchs, G. W., Acharyya, K., Bisschop, S. E., et al. 2006, Faraday Discuss., 133, 331 [Google Scholar]
  31. Geiss, J. 1988, Cosmic Chemistry (New York: Springer), 1 [Google Scholar]
  32. Glassmeier, K.-H., Boehnhardt, H., Koschny, D., Kührt, E., & Richter, I. 2007, Space. Sci. Rev., 128, 1 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gudipati, M. S., Fleury, B., Wagner, R., et al. 2023, Faraday Discuss., 245, 467 [NASA ADS] [CrossRef] [Google Scholar]
  34. Guilbert-Lepoutre, A., Rosenberg, E. D., Prialnik, D., & Besse, S. 2016, MNRAS, 462, S146 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, aaa0709 [Google Scholar]
  36. Hänni, N., Altwegg, K., Combi, M., et al. 2022, Nat. Commun., 13, 3639 [CrossRef] [Google Scholar]
  37. Hänni, N., Altwegg, K., Baklouti, D., et al. 2023, A&A, 678, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Hässig, M., Altwegg, K., Balsiger, H., et al. 2015, Science, 347, aaa0276 [Google Scholar]
  39. Jones, G. H., Snodgrass, C., Tubiana, C., et al. 2024, Space Sci. Rev., 220, 9 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kipfer, K. A., Galli, A., Riedo, A., et al. 2024, Icarus, 410, 115742 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kouchi, A., & Sirono, S.-I. 2001, Geophys. Res. Lett., 28, 827 [NASA ADS] [CrossRef] [Google Scholar]
  42. Laufer, D., Bar-Nun, A., & Ninio Greenberg, A. 2017, MNRAS, 469, S818 [NASA ADS] [CrossRef] [Google Scholar]
  43. Läuter, M., Kramer, T., Rubin, M., & Altwegg, K. 2018, MNRAS, 483, 852 [NASA ADS] [Google Scholar]
  44. Läuter, M., Kramer, T., Rubin, M., & Altwegg, K. 2020, MNRAS, 498, 3995 [Google Scholar]
  45. Marboeuf, U., Schmitt, B., Petit, J. M., Mousis, O., & Fray, N. 2012, A&A, 542, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Martín-Dománech, R., Caro, G., Bueno, J., & Goesmann, F. 2014, A&A, 564 [Google Scholar]
  47. Minissale, M., Aikawa, Y., Bergin, E., et al. 2022, ACS Earth Space Chem., 6, 597 [NASA ADS] [CrossRef] [Google Scholar]
  48. Morbidelli, A. 2005, arXiv e-prints [arXiv:astro-ph/0512256] [Google Scholar]
  49. Morbidelli, A., Levison, H. F., & Gomes, R. 2008, The Solar System beyond Neptune (Tucson: University of Arizona Press), 275 [Google Scholar]
  50. Mousis, O., Gautier, D., Bockelée-Morvan, D., et al. 2000, Icarus, 148, 513 [NASA ADS] [CrossRef] [Google Scholar]
  51. Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
  52. Nguyen, T., Baouche, S., Congiu, E., et al. 2018, A&A, 619, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Ninio Greenberg, A., Laufer, D., & Bar-Nun, A. 2017, MNRAS, 469, S517 [NASA ADS] [CrossRef] [Google Scholar]
  54. Notesco, G., & Bar-Nun, A. 1996, Icarus, 122, 118 [CrossRef] [Google Scholar]
  55. Notesco, G., & Bar-Nun, A. 2005, Icarus, 175, 546 [NASA ADS] [CrossRef] [Google Scholar]
  56. Öberg, K. I., & Wordsworth, R. 2019, AJ, 158, 194 [Google Scholar]
  57. Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [Google Scholar]
  58. Opitom, C., Hutsemékers, D., Jehin, E., et al. 2019, A&A, 624, [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Opitom, C., Snodgrass, C., Forgia, F., et al. 2022, Exp. Astron., 55, 1 [NASA ADS] [Google Scholar]
  60. Owen, T., & Bar-Nun, A. 1993, Nature, 361, 693 [CrossRef] [Google Scholar]
  61. Palumbo, M., Strazzulla, G., Pendleton, Y., & Tielens, A. 2000, ApJ, 534, 801 [NASA ADS] [CrossRef] [Google Scholar]
  62. Poch, O., Istiqomah, I., Quirico, E., et al. 2020, Science, 367, eaaw7462 [Google Scholar]
  63. Prialnik, D., & Bar-Nun, A. 1992, A&A, 258, L9 [NASA ADS] [Google Scholar]
  64. Renner, T., Cohen, E. R., Cvitas, T., et al. 2007, Quantities,Units and Symbols in Physical Chemistry (The Royal Society of Chemistry), 248 [Google Scholar]
  65. Rubin, M., Altwegg, K., Balsiger, H., et al. 2019a, MNRAS, 489, 594 [Google Scholar]
  66. Rubin, M., Bekaert, D. V., Broadley, M. W., Drozdovskaya, M. N., & Wampfler, S. F. 2019b, ACS Earth Space Chem., 3, 1792 [NASA ADS] [CrossRef] [Google Scholar]
  67. Rubin, M., Altwegg, K., Berthelier, J.-J., et al. 2023, MNRAS, 526, 4209 [NASA ADS] [CrossRef] [Google Scholar]
  68. Sandford, S. A., Bernstein, M. P., Allamandola, L. J., Goorvitch, D., & Teixeira, T. V. S. 2001, ApJ, 548, 836 [NASA ADS] [CrossRef] [Google Scholar]
  69. Schmitt, B., de Bergh, C., & Festou, M. 2012, Solar System Ices: Based on Reviews Presented at the International Symposium "Solar System Ices" held in Toulouse, France, on March 27–30, 1995 (Netherlands: Springer), Astrophys. Space Sci. Lib. [Google Scholar]
  70. Simon, A., Rajappan, M., & Öberg, K. I. 2023, ApJ, 955, 5 [NASA ADS] [CrossRef] [Google Scholar]
  71. Thomas, N., Ulamec, S., Kührt, E., et al. 2019, Space Sci. Rev., 215 [CrossRef] [Google Scholar]
  72. Tosi, F., Capaccioni, F., Capria, M. T., et al. 2019, Nat. Astron., 3, 649 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Chamber

The schematic of the chamber is shown in Fig. A.1.

thumbnail Fig. A.1.

Schematic Drawing of the ICEBEAR setup, highlighting the two parts: the main chamber and the separate gas mixing system. The figure was reproduced and adapted from Kipfer et al. (2024).

Appendix B: Correction factor

Both the function and the fitting values for the fractionation curve for N2, CO2 and 13CO are shown in Table B.1. For H2O there was no necessity to perform a correction due to a high enough pressure during its desorption. Figure B.1 shows the correction for m/z = 14 and m/z = 28 and the subsequently fitted factor, with which the data are then multiplied to reproduce the data.

thumbnail Fig. B.1.

Investigation of the fractionation of m/z = 28 and m/z = 14 as a function of the Total Signal measured with the QMS from three different calibration measurements. This highlights the need for a correction of the data. The top panel shows the evolution of the signal measured with the QMS for both mass channels. The middle panel shows the fractionation pattern. The constant value reached at high enough Signal has been marked with a grey dotted line. The bottom panel then shows the factor with which the data have to be multiplied as a function of the total signal to obtain the ’true fragmentation’, which is shown in the middle panel as the dotted line. The details of the fit shown in the middle panel are collected in Table B.1.

Table B.1.

Values for the fit of the fractionation.

Figure B.2 shows the correction factor derived for m/z = 44 for CO2, Fig. B.3 the correction for 13CO. Figure B.4 shows the direct comparison between raw measured data for 13CO versus the corrected data for the CO2 co-desorption regime. Figure B.5 shows the N2 and CO2 correction applied to all data used for this work. The corrected data are then further analysed and integrated.

thumbnail Fig. B.2.

Fractionation of m/z = 44 as a function of the total intensity measured with the QMS for the relevant CO2 mass channel. Three different calibration measurements were used.

thumbnail Fig. B.3.

Fractionation of m/z = 29 as a function of the total intensity measured with the QMS for the relevant 13CO mass channel. Two different calibration measurements were used.

thumbnail Fig. B.4.

Comparison between the raw data measured with the QMS and the corrected data for a H2O:CO2:13CO ice.

thumbnail Fig. B.5.

This figure shows the correction (described in Sect. 2.3) applied to all N2 data (grey, dash-dotted). The m/z = 28 signal consists out of contributions from both N2 and CO2, which necessitates the correction. Furthermore, a simple data correction has been performed, namely only summing the m/z = 28 and m/z = 14 signal and correcting for the expected fractionation pattern (red, dashed), which gives very similar results in the region where the only contribution to m/z = 28 is N2.

Appendix C: CO experiments

Analogous to Table 1 in the main text, the results from the CO ices are collected in Table C.1. TPDs of H2O:CO2:13CO are shown in Fig. C.1. The H2O:13CO experiment has been excluded from the plot.

thumbnail Fig. C.1.

Desorption behaviour of m/z = 29 (13CO, orange), CO2 (grey, dotted), and H2O (grey, dashed). Both the 13CO and CO2 data have been corrected for the fractionation, for H2O this was not necessary. The data was not baseline corrected for the display, but baseline subtraction was performed for further analysis. The figure titles correspond to the theoretical mixing ratio in the gas mixing system.

Table C.1.

Fractions of 13CO desorbing in the various integration regimes for the different ices.

Appendix D: N2 and 13CO desorption plot

Figure D.1 shows the normalized desorption traces of N2 and 13CO as a function of temperature for all measured ices. It is an expanded version of Fig. 2 that contains all experiments shown in Tables 1 and C.1.

thumbnail Fig. D.1.

Plot showing the normalized desorption of N2 and 13CO as a function of temperature for all measured ices in Tables 1 and C.1.

All Tables

Table 1.

Fractions of N2 desorbing in the various integration regimes for the different ices.

In the text
Table 2.

Different desorption regimes for the volatiles N2 and CO used for the integration, adapted from Rubin et al. (2023).

In the text
Table B.1.

Values for the fit of the fractionation.

In the text
Table C.1.

Fractions of 13CO desorbing in the various integration regimes for the different ices.

In the text

All Figures

thumbnail Fig. 1.

Desorption traces of N2 and 13CO in H2O:CO2:N2 and H2O:CO2:13CO ices respectively as a function of temperature during the TPD. Top row: desorption traces of N2, (solid, blue), CO2 (grey, dotted) and H2O (grey, dashed) for different ice experiments. For the presented data the N2 contribution has been calculated to be between 3% and 5% with respect to water, therefore assumed to be relatively constant. The CO2 contribution is shown at the top with respect to water and increases from left to right. For N2, the corrected data have been calculated from the m/z = 14 data, corresponding to the N fragment, as described in Appendix B, therefore resulting in more noise than the 13CO data. Neither the CO2 nor the H2O data have been corrected or baseline subtracted for this plot. Bottom row: desorption trace for m/z = 29 (13CO, orange) for different ice experiments, with the CO2 and H2O desorption traces shown as well. The 13CO contributions have been calculated to be between 3% and 4% with respect to water, except for the first experiment, in which the 13CO has been calculated to be ∼2.5%. The 13CO signal has been corrected and baseline subtracted, whereas for the CO2 and H2O traces no corrections have been performed. Please note that for the 13CO measurements, the background pressure has been higher than for the N2 measurements, resulting in a larger background for H2O and CO2.
In the text
thumbnail Fig. 2.

Normalized desorption behaviour of N2 and 13CO as a function of temperature in the ices. Please note that not all measured data is displayed. A figure showing the complete data is shown in Appendix D. Left: evolution of N2, calculated from the m/z = 14 signal, during the TPD of different ices as a function of the temperature. The data have been sorted with respect to the N2 present in the ice mixture. The shaded regions correspond to the desorption regions in Table 2. A lighter line color corresponds to more N2. The linestyles indicate the amount of CO2 present with respect to water, with the assignment being: x < 1%:dashed, 1 < x < 5%: long dashes, 5 < x < 10%:solid, 10 < x < 15%: dashdot, 15 < x < 20%: dashdotdotted, 20 < x%: dotted. Right: evolution of 13CO, calculated from the m/z = 29 signal, as a function of the temperature. The data have been sorted with respect to the 13CO present in the ice mixture. A lighter color corresponds to more 13CO. The linestyles indicate the amount of CO2 present with respect to water, with the assignment of the linestyles being the same as for the left panel.
In the text
thumbnail Fig. 3.

Zoom in of the N2 co-desorbing with CO2. The plots have been color coded for the abundance of N2 with respect to water. The linestyles indicate the amount of CO2 present with respect to water, with the assignment being: x < 10%:dotted, 10 < x < 20%: dashed, 20 < x%: solid. For readability, not all data measured are displayed.
In the text
thumbnail Fig. 4.

Desorption behaviour of N2 in the different regimes, colour coded for the abundance of nitrogen in the ice with respect to water. Each column shows the different desorption events for N2 with the integration limits for the desorption events given in Table 2. The data points indicated with a diamond are the H2O:N2 ices, with negligible amounts of CO2 in the mixture. The colour assignment is the same as in Fig. 2. Top row: desorption behaviour of N2 as a function of the total N2 in the mixture, the total CO2 abundance in the mixture, and the H2O abundance respectively. The N2 desorption occurring at the pure N2 desorption peak and the CO2 co-desorption have been fitted with a linear function and the resulting best fit is shown in the corresponding panel (grey, dashed line). The grey shaded region indicates the standard deviation of the fit. For the water co-desorption no overall fit has been done, however, trends for the different N2 abundances have been indicated and colour coded. Bottom row: same data as in the top row, but plotted as a function of the total N2 abundance in the ice mixture.
In the text
thumbnail Fig. 5.

Fraction of desorbing N2 during the CO2 co-desorption compared to the sum of the CO2 co-desorption and the pure N2 desorption peak as a function of the CO2 to N2 ratio in the ice. The error bars have been calculated using Gaussian error propagation.
In the text
thumbnail Fig. 6.

Ratios of the N2 fractions desorbing in different desorption regimes. Top row: ratio of the N2 desorption during the combined H2O release to the sum of the CO2 and pure N2 (co-)desorption. The expected ratio of 1.72 for 67P has been indicated (purple, dashed line), as well as the upper limit estimate of 3 (purple, shaded region). Bottom row: ratio of the N2 desorption during the combined H2O release to the N2 co-desorption with CO2. The expected ratio for 67P has been indicated and includes the area between 1.72 (purple, dashed line) and to about 3 (purple, shaded region).
In the text
thumbnail Fig. 7.

Desorption behaviour of 13CO in the different regimes, colour coded for the total abundance of 13CO in the ice. Each column shows the different desorption events for 13CO. Diamond markers indicate the experiments without any CO2. The composition of the ices is collected in Table C.1.
In the text
thumbnail Fig. A.1.

Schematic Drawing of the ICEBEAR setup, highlighting the two parts: the main chamber and the separate gas mixing system. The figure was reproduced and adapted from Kipfer et al. (2024).
In the text
thumbnail Fig. B.1.

Investigation of the fractionation of m/z = 28 and m/z = 14 as a function of the Total Signal measured with the QMS from three different calibration measurements. This highlights the need for a correction of the data. The top panel shows the evolution of the signal measured with the QMS for both mass channels. The middle panel shows the fractionation pattern. The constant value reached at high enough Signal has been marked with a grey dotted line. The bottom panel then shows the factor with which the data have to be multiplied as a function of the total signal to obtain the ’true fragmentation’, which is shown in the middle panel as the dotted line. The details of the fit shown in the middle panel are collected in Table B.1.
In the text
thumbnail Fig. B.2.

Fractionation of m/z = 44 as a function of the total intensity measured with the QMS for the relevant CO2 mass channel. Three different calibration measurements were used.
In the text
thumbnail Fig. B.3.

Fractionation of m/z = 29 as a function of the total intensity measured with the QMS for the relevant 13CO mass channel. Two different calibration measurements were used.
In the text
thumbnail Fig. B.4.

Comparison between the raw data measured with the QMS and the corrected data for a H2O:CO2:13CO ice.
In the text
thumbnail Fig. B.5.

This figure shows the correction (described in Sect. 2.3) applied to all N2 data (grey, dash-dotted). The m/z = 28 signal consists out of contributions from both N2 and CO2, which necessitates the correction. Furthermore, a simple data correction has been performed, namely only summing the m/z = 28 and m/z = 14 signal and correcting for the expected fractionation pattern (red, dashed), which gives very similar results in the region where the only contribution to m/z = 28 is N2.
In the text
thumbnail Fig. C.1.

Desorption behaviour of m/z = 29 (13CO, orange), CO2 (grey, dotted), and H2O (grey, dashed). Both the 13CO and CO2 data have been corrected for the fractionation, for H2O this was not necessary. The data was not baseline corrected for the display, but baseline subtraction was performed for further analysis. The figure titles correspond to the theoretical mixing ratio in the gas mixing system.
In the text
thumbnail Fig. D.1.

Plot showing the normalized desorption of N2 and 13CO as a function of temperature for all measured ices in Tables 1 and C.1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.