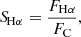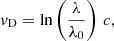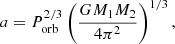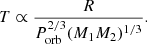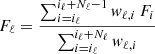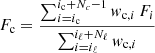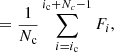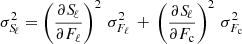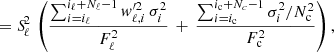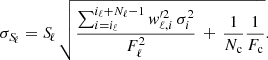EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A93 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A93
Number of page(s) 15
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202349008
Published online 03 June 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open Access funding provided by Max Planck Society.

1. Introduction

A complex dynamo mechanism can be established in the external convective envelope of low-mass stars, where surface magnetic fields are efficiently generated when the rotation period is shorter than the convective turnover time according to dynamo theory (e.g., Skumanich 1972; Charbonneau 2014). Magnetic fields play an important role in stellar evolution, as they are believed to regulate rotation throughout the life of low-mass stars (Vidotto et al. 2014). They can also induce losses of angular momentum through a coupling with the magnetized stellar wind (e.g., Weber & Davis 1967; Gallet & Bouvier 2013). Magnetic fields are also likely to drive the important mass loss observed among red giants (RGs), although the specific mechanisms are still poorly understood (Harper 2018).

Magnetic fields generate various phenomena when they emerge from the outer convective envelope, which are grouped under the name of stellar magnetic activity (Hall 2008). Characterizing stellar activity is crucial for the fields of stellar physics and evolution, as well as exoplanetary science. Indeed, it is an important probe of the magnetic field configuration that can provide clues on the physical dynamo process at work (Reinhold et al. 2019; Metcalfe et al. 2022). Stellar activity also hampers the detection of exoplanetary signals (Borgniet et al. 2015) and affects space weather and planets’ habitability (Airapetian et al. 2020).

In general, as stars age and evolve off the main sequence, they expand, spin down, and become less active (e.g., Wilson & Skumanich 1964; Skumanich 1972). Consequently, the rotational modulation signal caused by stellar spots in corotation with their photosphere tends to become smaller with longer periods, making it difficult to measure the rotation periods of evolved stars (Santos et al. 2021). However, Gaulme et al. (2020) showed that ∼8% of the RGs observed by the NASA Kepler mission (Borucki et al. 2010) display photometric rotational modulation, of which approximately 15% belong to close binary systems. Fast rotation is not the only parameter explaining such enhanced magnetic activity for RGs in close binaries, as Gaulme et al. (2020) also noticed that at a given rotation period, a RG that belongs to a close binary system displays a photometric modulation about one order of magnitude larger than that of a single RG with similar physical properties (mass and radius). This difference in the rotational modulation of binary and single RGs could be due to either a different spot distribution on their photosphere, or a stronger surface magnetic field.

To discriminate between these two possibilities, Gehan et al. (2022) used spectroscopic data from the Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) survey to measure the S-index from the H and K lines of Ca II for 3130 RGs analyzed by Gaulme et al. (2014, 2020) and Benbakoura et al. (2021). The S-index quantifies the level of chromospheric activity (Wilson 1978; Duncan et al. 1991; Karoff et al. 2016; Zhang et al. 2020; Gomes da Silva et al. 2021), and is proportional to the strength of surface magnetic fields (Babcock 1961; Petit et al. 2008; Aurière et al. 2015; Brown et al. 2022). Gehan et al. (2022) found that RGs in close binaries show a significantly larger S-index than single RGs and RGs in wide binaries, indicating that close binaries do display enhanced surface magnetic fields. More specifically, Gehan et al. (2022) showed that the RGs in close binaries with enhanced magnetic activity are either synchronized (with their rotation period being the same as their orbital period), or undergoing spin-orbit resonance (with their rotation period being an integer ratio of their orbital period). This result highlights that tidal locking, rather than close binarity itself, somehow leads to larger magnetic field strengths. Additionally, Gehan et al. (2022) examined the relationship between different stellar activity indicators and found a correlation between the photometric index, the chromospheric S-index, and the detection of rotational modulation due to stellar spots. These investigations provide important information for understanding the mechanisms behind the formation and evolution of stellar magnetic fields (Reinhold et al. 2019).

To fully probe the dynamos and magnetic fields of evolved stars, it is fundamental to be able to classify the active evolved stars, whether they belong to close binary systems or not. Unfortunately, 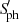S ph ′ $ {S\!}^\prime_{\rm ph} $ and SCa II are not always available and additional indicators from other surveys could help to classify the active RGs. On the one hand, the NUV excess is a relatively unexplored activity proxy that quantifies the NUV flux as measured above the photospheric level, thus providing an indication about chromospheric activity (Findeisen & Hillenbrand 2010; Olmedo et al. 2015; Godoy-Rivera et al. 2021). On the other hand, the Hα (Cincunegui et al. 2007; Newton et al. 2017), Mg I (Sasso et al. 2017), and Ca II infrared (IR) (Busà et al. 2007; Martínez-Arnáiz et al. 2011; Martin et al. 2017) lines have been considered as possible indicators of chromospheric activity for late-type stars. Since the aforementioned spectral lines are located at longer wavelengths compared to the Ca II lines used to measure the S-index, they appear to be more suitable activity indicators for cool late-type stars that have an intrinsically low signal-to-noise ratio (SNR) toward the blue part of their optical spectrum (Cincunegui et al. 2007).

In this paper, we aim to extend the work done by Gaulme et al. (2020) and Gehan et al. (2022) on 4465 single and binary RGs by investigating the possibility of using the following indicators of chromospheric activity: the near-ultraviolet (NUV) excess, measured using data from the Galaxy Evolution Explorer (GALEX) that provided ultraviolet (UV) photometry for about 90 millions stars (Bianchi et al. 2005), as well as the Hα, Mg I, and IR Ca II spectral lines, which can be easily exploited using the optical spectra obtained by LAMOST and encompassing wavelengths between 3690 Å and 9100 Å. We describe our measurement methods in Sect. 2. We explore the relationship between different activity indicators in Sect. 3 and establish links with the amplitude of oscillations in Sect. 4. We discuss in Sect. 5 the impact of close binarity and tidal interactions versus fast rotation on the chromospheric activity indices of RGs. We provide in Sect. 6 criteria to classify the active RGs (single or binary), based on their rotation period and magnetic activity indices. Section 7 is devoted to conclusions.

2. Method and data

The target sample of this work is composed of the 4465 RGs with a measured photometric index, S​ph, from Gaulme et al. (2020, see their Fig. 1) and includes 3130 RGs for which Gehan et al. (2022) also measured the S-index. The characteristics of our sample are summarized in Table 1. Our measurements are publicly available in the database of the Centre de Données de Strasbourg (CDS).

Table 1.

Characteristics of our sample.

2.1. Change of nomenclature

To be consistent with the works of Mathur et al. (2014) and subsequent papers (such as Ceillier et al. 2017; Mathur et al. 2019), we modified the symbol used to describe the photometric modulation as performed by Gaulme et al. (2020), and employed by Benbakoura et al. (2021) and Gehan et al. (2022). Mathur et al. (2014) defined S​ph as the standard deviation of a given light curve over five rotational periods, but do not provide measurements for stars whose light curves do not display rotational modulation. To circumvent this lack of definition, Gaulme et al. (2020) extended the definition of S​ph to stars without rotational modulation by computing it as the moving average of the standard deviation of the light curve over a period of five days. To avoid confusion with the original definition of S​ph by Mathur et al. (2014), we changed the nomenclature by replacing S​ph with 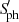S ph ′ $ {S\!}^\prime_{\rm ph} $, defined as

S ph ′ = { S ph with detectable rotational modulation ⟨ σ 5 d ⟩ without detectable rotational modulation , $$ \begin{aligned} {S\!}_{\rm ph}^{\prime } = {\left\{ \begin{array}{ll} {S\!}_{\rm ph}&\text{ with} \text{ detectable} \text{ rotational} \text{ modulation}\\ \langle \sigma _{\rm 5 d}\rangle&\text{ without} \text{ detectable} \text{ rotational} \text{ modulation}, \end{array}\right.} \end{aligned} $$(1)

where ⟨σ5d⟩ is the mean standard deviation of the light curve over five days.

2.2. Measuring the NUV excess

The NUV data used in this work were taken from GALEX (Martin et al. 2005). The GALEX space telescope performed an all-sky imaging survey in the far-UV (FUV, λ ∼ 0.15 μm) and near-UV (NUV, λ ∼ 0.23 μm) bands. Throughout this paper, we focused on the latter of these bands, given its wider availability for our sample.

To calculate the NUV excess, we followed the approach of Dixon et al. (2020) and Godoy-Rivera et al. (2021). We first crossmatched the target sample with the latest GALEX catalogue (Bianchi et al. 2017) (see also Olmedo et al. 2015) using VizieR1. We imposed a maximum angular separation of 2 arcsec, and were left with 842 RGs (∼19% of the initial sample) with measured GALEX NUV magnitudes (with most targets having counterparts within a fraction of 1 arcsec). We used the same procedure to crossmatch with the near-infrared (NIR) 2MASS catalog (Cutri et al. 2003; Skrutskie et al. 2006) and found the entirety of the sample with measured J (λ ∼ 1.25 μm) and K magnitudes (λ ∼ 2.16 μm). We de-reddened the photometry using the extinction values from the Kepler field catalog of Godoy-Rivera et al. (2024) and the coefficients from Dixon et al. (2020) (see also Yuan et al. 2013). Using these data, we constructed the (NUV-J)0 versus (J − K)0 diagram (Fig. 1).

thumbnail Fig. 1.

NUV vs. NIR color-color diagram for the 842 RGs with GALEX NUV magnitudes. From this, the NUV excess was calculated by subtracting the measured (NUV-J)0 magnitudes and the expected values given the fiducial relation from Findeisen & Hillenbrand (2010) and the measured (J − K)0 colors. The targets are color-coded by their NUV excess values, with redder colors indicating stronger excess (more negative values). The gray symbol represents the median error bars.

To be able to detect and characterize an excess of NUV emission, we needed to define a reference level; that is, the NUV magnitude of quiet stars. Such a level, the so-called fiducial relation, was introduced by Findeisen & Hillenbrand (2010) (see their Eq. (2)). This relation parametrizes the behavior of the stellar locus in the NUV-NIR color-color space (the black line in Fig. 1) by tracking expected (NUV-J)0 photospheric flux as a function of the (J − K)0 color. For a given star, the NUV excess, ΔmNUV, is calculated as the difference between the measured (NUV-J)0 color and the value predicted by the fiducial relation evaluated at the corresponding (J − K)0 color. The purpose of this subtraction is to remove the photospheric contribution to the flux in NUV wavelengths. The uncertainty on the NUV excess is calculated by propagating the errors on the fiducial relation, extinction, and measured magnitudes (being dominated by the latter). By definition, a stronger NUV excess corresponds to more negative values; that is, higher NUV fluxes. In Fig. 1, the targets are color-coded by their NUV excess values. The sample of 842 targets for which we measured NUV excess includes 30 confirmed close and wide binaries, where we consider that a close binary system has an orbital period, Porb≤ 150 days, and a wide binary system has Porb> 150 days. Our sample includes three close binaries identified by Gaulme et al. (2020) as well as four close binaries and 23 wide binaries identified by Gaia data release 3 (DR3, Gaia Collaboration 2023b) in the non-single star (NSS) two-body-orbit table (Gaia Collaboration 2023a). Other aspects of the NUV excess are discussed in Appendix A.

2.3. Measuring chromospheric emission from the Hα, Mg I, and Ca II infrared spectral lines

We followed the approach of Cincunegui et al. (2007), who adapted the usual method employed to measure the S-index with the chromospheric emission in the Ca II H&K lines to the Hα line for a sample of late-type main-sequence stars. They defined S​Hα as

S H α = F H α F C , $$ \begin{aligned} {S\!}_{\rm H\alpha } = \frac{F_{\rm H\alpha }}{F_{\rm C}}, \end{aligned} $$(2)

where FHα is the integrated flux in the Hα line centered at 6562.801 Å using a triangular bandpass with a full width at half maximum of 1.5 Å, and FC is the continuum level obtained by integrating the flux comprised of a square bandpass centered on 6605 Å with a width of 20 Å (see Fig. 2). In other words, S​Hα is a proxy of the line depth.

thumbnail Fig. 2.

Example of LAMOST spectrum for KIC 1294122. Top panel: entire spectrum expressed as a function of wavelength (Å). The lines we considered are indicated by arrows. Bottom panels: zoom on the six absorption lines, where the flux is normalized by its average value over the 150-Å range that is displayed in each of the four sub-panels. The portion of the spectrum that was used to compute the continuum level is indicated by a red line.

In a similar way, we used the Mg I line centered at 5184 Å the Ca II IR line centered at 8542 Å and the Fe I line centered at 6495 Å to define the indices SMg I, SCa II IR, and SFe I, respectively (Eq. (2) and Fig. 2). We chose not to make use of the other absorption lines of the Mg I triplet and IR calcium triplet – even the renowned sodium D1, D2 doublet – because they are blended with one another, which makes the pipeline fail quite often. In the same way, we do not report the Mg I at 4571 Å because it belongs to a range packed with spectral lines that are blended, although Sasso et al. (2017) report this line to be sensitive to chromospheric activity. We used a Fe I photospheric line, which is in principle insensitive to magnetic activity (see Sect. 3.1), as a control variable to look for potential systematic biases in the interpretation of our results. We used the Fe I line at 6495 Å because it is close to the Hα line and shows a decent SNR.

In order to lead consistent comparisons between the activity indices mentioned above, we also measured SCa II H&K from the Ca II H&K lines for the 3130 RGs for which Gehan et al. (2022) measured the S-index (see Fig. 2). Here, we chose not to calibrate our SCa II H&K measurements to the Mount Wilson scale, since there is no reference scale to calibrate the other activity indices. Hence, our SCa II H&K measurements are not strictly speaking S-indices, contrarily to the measurements obtained by Gehan et al. (2022).

To improve the accuracy of our results, we modified the algorithm that was used by Gehan et al. (2022), by refining the method to compute the Doppler shift of the spectrum, and the triangular weighted average, FHα. Indeed, Gehan et al. (2022) determined the Doppler shift by comparing the wavelength of the bottom of the Hα line to its theoretical value, and computed the triangular moving average on the LAMOST spectrum interpolated on a finer grid obtained by linear interpolation. Regarding the location of the Doppler shift, basing our measurement only on one line limits its accuracy to the radial velocity resolution of the spectrum, which is about 69 km s−1. Regarding the use of linearly interpolated spectra, discontinuities in the flux caused by discretization introduce noise into the measurements. Our updated method includes improvements on these two aspects.

Firstly, LAMOST spectra, as with most optical spectra, are provided as functions of wavelength but are evenly sampled in radial velocities. The first step consists of selecting a range in which to measure the Doppler shift and attributing a radial-velocity axis to it. With respect to the line of interest of wavelength λ0, the Doppler velocity axis, vD, is expressed as

v D = ln ( λ λ 0 ) c , $$ \begin{aligned} v_{\rm D} = \ln \left(\frac{\lambda }{\lambda _0}\right)\,c ,\end{aligned} $$(3)

where c is the speed of light. The selected range must not include telluric lines and should exclude the noisiest parts of the spectrum. Since not all spectra were good in the complete visible range, we adapted the range used to compute the Doppler shift to the spectral lines that were considered. This means that in some cases we may have a measurement of Hα emission but not of IR Ca II. In case no zeros were present in the selected range, we computed the Doppler shift by computing the cross-correlation of the observed spectrum with a theoretical spectrum provided by the library of PHOENIX stellar atmospheres and synthetic spectra (Husser et al. 2013)2. The location of the correlation maximum was done by picking the maximum of the cross-correlation oversampled by a factor of 1000. In the rare cases in which a chunk of the selected range included zeros, we computed the Doppler shift by picking the minimum of the considered line on an oversampled version of the spectrum. The second step consists of oversampling the spectrum. To avoid being biased by interpolation methods, such as spline or polynomial interpolation, we oversampled the spectra by computing the fast Fourier transform of the selected range and padding it with zeros. The oversampling factor was set to 100. The triangular-weighted value of the line depth was then computed from the oversampled spectrum, as well as the continuum level.

We used LAMOST Data Release 7, which is the same dataset that we used in Gehan et al. (2022) to measure the S-index. Firstly, we validated our activity index measurements only for spectra presenting a high-enough SNR, in a similar way to in Sect. 2.2 of Gehan et al. (2022). Uncertainties were computed by assuming that the noise of the spectra is only due to photon noise (see details in Appendix B). When several spectra were available for a given star, we computed the activity index as the median of all the activity indices measured for each individual spectrum. Our sample includes 185 binaries, among which there are 24 close binaries identified by Gaulme et al. (2020), 9 close binaries identified by Benbakoura et al. (2021), as well as 22 close binaries and 130 wide binaries identified by Gaia DR3 (Gaia Collaboration 2023a).

3. Chromospheric indices of red giants from ultraviolet data and spectral lines

In this section and the next ones, we adopted the measurements of the photometric index, 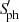S ph ′ $ {S\!}^\prime_{\rm ph} $, the oscillation frequency at maximum amplitude, νmax, the height of the Gaussian envelope employed to model the oscillation excess power, Hmax, and the rotation period, Prot, that were obtained by Gaulme et al. (2020).

3.1. Formation height of spectral lines

As has been shown in previous works, the cores of the spectral lines we used form at different heights in the solar atmosphere, and we can expect the picture to be similar for cool stars. Using radiation-MHD simulations and three-dimensional (3D) non-local thermodynamic equilibrium radiative transfer computations, Bjørgen et al. (2018) showed that the core of the Ca II IR line at 8542 Å forms at a much lower height in the chromosphere (∼1400 km) than the Ca II H&K lines (∼2200 km). Leenaarts & Carlsson (2012) showed that the Hα line also tends to form at a low height of ∼1600 km in the chromosphere. On the other hand, Fe I is a minority species in stellar atmospheres with effective temperatures, Teff > 4500 K (Gray 2008; Mashonkina et al. 2011). The Fe I line at 6495 Å that we use in this work is therefore a photospheric line, and we use it as a control variable, since it is not known to be sensitive to magnetic activity (Wise et al. 2018; Quintero Noda et al. 2021).

3.2. Relation between activity indicators

In the following, we compare the relation between the activity indicators, ΔmNUV, SCa II H&K, S​Hα, SMg I, SFe I, SCa II IR, and S ph ′ $ {S\!}^\prime_{\rm ph} $, for our RG sample. These are shown in Fig. 3, where our sample is split into different subsets, namely single spotless stars (in gray), single spotted stars (in blue), binary spotted stars (in black), and spotted stars with ambiguous binary versus single status (in green). The Pearson correlation coefficients and corresponding p values are indicated in Table 2. We recall here that more NUV-active stars have a more negative NUV-excess value, ΔmNUV.

thumbnail Fig. 3.

Relation between different activity indicators and the photometric modulation, S ph ′ $ {S\!}^\prime_{\rm ph} $, measured by Gaulme et al. (2020) (in log scale), which is an indicator of photospheric activity. The NUV excess, ΔmNUV, is a chromospheric activity indicator measured using GALEX data. The indices, SCa II H&K, S​Hα, SMg I, and SCa II IR, are chromospheric activity indicators measured using LAMOST data. The index, SFe I, measured using LAMOST data is insensitive to stellar activity and used as a control variable. Gray dots refer to regular photometrically inactive RGs (i.e., with no evidence of spot modulation) that display oscillations. Blue dots refer to photometrically active RGs (i.e., those exhibiting spot modulation) with partially suppressed oscillations. Black dots refer to photometrically active and non-oscillating RGs in close binary systems, which were identified by Gaulme et al. (2020). Green dots refer to non-oscillating RGs with ambiguous binary versus single status; we do not have NUV excess data for these stars.

Table 2.

Pearson correlation coefficients, r, and associated p values, p.

Similarly to what Gehan et al. (2022) found for the S-index (see also the upper right panel of Fig. 3), we observe an anticorrelation between ΔmNUV and 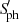S ph ′ $ {S\!}^\prime_{\rm ph} $ for inactive spotless RGs, as well as a marginally significant correlation between ΔmNUV and 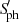S ph ′ $ {S\!}^\prime_{\rm ph} $ for the photometrically active RGs with evidence of spots (upper left panel of Fig. 3). To the extent of our knowledge, the relation between ΔmNUV and 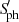S ph ′ $ {S\!}^\prime_{\rm ph} $ has never been checked before, even for main-sequence stars.

Similarly, we observe a correlation between 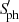S ph ′ $ {S\!}^\prime_{\rm ph} $ and S​Hα (middle left panel of Fig. 3). This is consistent with the findings for M dwarfs of Newton et al. (2017) and García Soto et al. (2023), who reported that the amplitude of photometric variability is correlated with Hα emission. However, the correlation that we observe emerges only when including the very active RGs that mostly belong to close binary systems (black symbols). When discarding the latter, only a marginal trend is left for the stars displaying spots and partially suppressed oscillations (blue symbols), in contrast with the clearer correlation observed with Ca II H&K lines.

Regarding the other spectral lines, we do not observe any significant correlation between 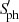S ph ′ $ {S\!}^\prime_{\rm ph} $ and SMg I (middle right panel of Fig. 3), even for close binaries. The same is observed with the SFe I line (bottom left panel of Fig. 3), which was expected, since it is in principle a photospheric line that is insensitive to chromospheric activity. Finally, we observe for SCa II IR (bottom right panel of Fig. 3) similar trends as for ΔmNUV and SCa II H&K (upper right panel of Fig. 3), although the smaller range of values measured for SCa II IR suggests that it is less sensitive to magnetic activity than SCa II H&K.

3.3. Comparisons with other studies

Findeisen et al. (2011) observed a correlation between the NUV excess and chromospheric activity from the H and K lines of Ca II for G dwarfs. Here, we consistently observe a correlation between the NUV excess and SCa II H&K, for both inactive RGs (Pearson correlation coefficient of 0.213 and p value of 6.9 × 10−7) and active RGs (Pearson correlation coefficient of 0.463 and p value of 1.2 × 10−3). Since SCa II H&K is a proxy of the strength of surface magnetic fields (Babcock 1961; Petit et al. 2008; Aurière et al. 2015; Brown et al. 2022), our result indicates that the NUV excess is a proxy for the strength of surface magnetic fields.

In addition, previous works have shown that the correlation between the flux in the Hα and the Ca II H&K lines is still not fully understood (Gomes da Silva et al. 2022). In the case of the Sun, the flux in the Hα and the Ca II H&K lines is known to be correlated with the presence of active regions, and tightly follows the solar magnetic cycle (Livingston et al. 2007). However, the picture is much less straightforward for other stars, where the correlation between the flux in the Hα and the Ca II H&K lines presents a large dispersion (Cincunegui et al. 2007; Walkowicz & Hawley 2009; Gomes da Silva et al. 2011, 2014; Meunier et al. 2022). The correlation appears to be strongly positive for stars with high activity levels, while all types of correlations tend to be observed in the low-activity regime, ranging from negative to positive correlations, including correlations close to 0. Since the cores of the Ca II H&K and Hα lines are formed at different heights in the chromosphere (see Sect. 3.1), we can then expect these two lines to trace different activity phenomena (Cincunegui et al. 2007; Meunier & Delfosse 2009; Gomes da Silva et al. 2022). The different sensitivity of these lines to spots, plages, or filaments could explain the various correlations observed for different stars (Meunier & Delfosse 2009). In particular, Meunier & Delfosse (2009) stated that the contribution of emission in plages in Ca II H&K and Hα should lead to a correlation very close to 1 between the flux in these two lines. However, the presence of dark filaments at the surface, mostly visible in Hα, introduces flux absorption that should decrease the correlation. Moreover, many filaments do not coincide exactly with active regions, which further contributes in decreasing the correlation between the flux in the Ca II H&K and Hα lines. On the other hand, filaments well correlated with plages would lead to an anticorrelation. Here, we observe an anticorrelation between SCa II H&K and the Hα index for inactive RGs, (Pearson correlation coefficient of −0.107 and p value of 1.7 × 10−8). For active RGs, we do not observe any significant correlation or anticorrelation (Pearson correlation coefficient of 0.085 and p value of 0.182). In the case of RGs in close binaries, although the statistics is low (only 21 RGs in close binaries with measured S​Hα), the S-index and the Hα index seem to be positively correlated (Pearson correlation coefficient of 0.803 and p value of 1.2 × 10−5).

For a sample of nearby M dwarfs, Stelzer et al. (2013) found that NUV and X-ray fluxes are correlated, as are Hα and X-ray fluxes, but did not check the relation between NUV and Hα fluxes. Here, we observe an anticorrelation between the NUV excess and the Hα index for inactive RGs (Pearson correlation coefficient of −0.446 and p value of 1.0 × 10−28), while we observe a marginally significant anticorrelation for active RGs (Pearson correlation coefficient of −0.308 and p value of 0.040). Since the NUV excess is a proxy of the chromospheric activity level, and the Hα line is expected to trace activity at a lower height, with an important contribution from filaments, it is not necessarily surprising to observe an anticorrelation between ΔmNUV and S​Hα, in the same way that we observed an anticorrelation between SCa II H&K and S​Hα for inactive RGs.

4. Relation with oscillation amplitude

Magnetic fields tend to inhibit convection, resulting in the partial or total suppression of oscillations (Gaulme et al. 2014, 2016; Beck et al. 2018; Benbakoura et al. 2021). Stars with low-amplitude oscillations or without oscillations are often associated with high S-index values (Bonanno et al. 2014; Gehan et al. 2022, see also upper right panel of Fig. 4) and/or high S​ph values (García et al. 2010; Chaplin et al. 2011; Gaulme et al. 2014, 2020; Mathur et al. 2019; Benbakoura et al. 2021).

thumbnail Fig. 4.

Activity level (color scale) as a function of the oscillation frequency at maximum amplitude, νmax (x axis), and the height of the Gaussian envelope employed to model the oscillation excess power, Hmax (y axis), for the different activity indicators considered in this study.

From Fig. 4, we first observe that the NUV excess is consistent with what was reported by Gehan et al. (2022) about Ca II H&K lines. Even though the trend is less clear than with the index of photometric variability, 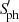S ph ′ $ {S\!}^\prime_{\rm ph} $, a larger UV emission – that is, a lower negative ΔmNUV magnitude difference – corresponds with RG stars that display weaker oscillations. A similar trend is observed for Mg I lines, even though the trend is much smoother than for Ca II H&K and NUV. We comment on that point later in this section. The surprise comes from S​Hα: stars with relatively weak oscillations are associated with low S​Hα. In other words, oscillations are weaker when Hα absorption lines get deeper. A similar but noisier trend is observed with Ca II IR. As regards the control line, SFe I does not exhibit any correlation with the sample of stars that display photometric modulation and weak oscillations.

The trend of S​Hα, then, is opposite to those of ΔmNUV, 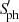S ph ′ $ {S\!}^\prime_{\rm ph} $, S​CaII, and SMg I. As we discussed in Sect. 3.3, this different behavior of S​Hα could come from the larger sensitivity of the Hα line to filaments (Meunier & Delfosse 2009), which appear to be dark in Hα images of the Sun. In the case of the Sun, the number and length of filaments follow the sunspot cycle (Mazumder et al. 2021), implying that higher solar activity levels result in an increased number and length of filaments. If the same is true for RGs, higher activity levels could result in an increase in the filaments’ contribution to S​Hα, and hence in a decrease in S​Hα. In other words, it would mean that in the Hα band the darkening caused by the presence of filaments on the stellar disk dominates the brightness brought by faculae, in contrast to the other spectral bands that we considered.

Besides the cases of stars that display rotational modulation, Fig. 4 shows an interesting new finding. We note that the oscillations’ amplitude at a given νmax is clearly correlated and anticorrelated with S​Hα and SMg I, respectively, regardless of the detection of rotational modulation. The trend is smooth and affects the whole sample, whatever the νmax. Given that the range of effective temperature is quite narrow for RGs and that temperatures are mostly random at a given νmax (see Fig. C.1), a given νmax means a given surface gravity, log g. If the oscillation amplitude is driven by surface magnetic fields, the relative depth of the Hα and Mg I lines is, to some extent, a proxy of surface magnetic fields as well.

In Appendix C, we display the oscillation amplitude versus the νmax, where the color scales are proportional to the stellar effective temperatures, Teff, surface gravity, log g, mass, M, and radius, R, of the sample. We note that similar figures for M are displayed in Vrard et al. (2018). At a given νmax, we see no significant trend between the oscillations’ amplitude, Teff, and log g (see bottom panels of Fig. C.1). On the contrary, the oscillations’ amplitude shows common features with what is observed for S​Hα and SMg I, such as higher masses leading to lower amplitudes (see the upper panels of Fig. C.1). This is consistent with previous works on oscillating RGs, which have also noticed that the maximum mode amplitude decreases with M (Huber et al. 2010, 2011; Mosser et al. 2011, 2012; Stello et al. 2011; Kallinger et al. 2014; Vrard et al. 2018). The fact that the depths of Hα and Mg I spectral lines are correlated with M and R is not totally surprising because surface magnetic fields must depend – besides stellar rotation rates – on stellar structures in the external convective envelope, which are connected to M and R.

5. Close binarity: Impact of tidal interactions versus fast rotation

It has been observed that for a given rotation period, RGs in binary systems undergoing spin-orbit resonance or tidal locking exhibit larger 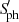S ph ′ $ {S\!}^\prime_{\rm ph} $ (Gaulme et al. 2020) and a larger S-index (Gehan et al. 2022) than single RGs or RGs in binary systems with no special tidal configuration. Since we observe that RGs in close binaries present in average larger values of ΔmNUV, S​Hα, and SCa II IR (see Fig. 3), we checked here the impact of fast rotation and tidal interactions on these indices. The Pearson correlation coefficients between the aforementioned indices and the rotation period, Prot, as well as the corresponding p values are indicated in Table 3.

Table 3.

Number, N, of RGs with measured Prot, as well as the Pearson correlation coefficients, r, and p values, p.

5.1. Impact of surface rotation

The RGs for which Gaulme et al. (2020) measured Prot are active in the sense that they exhibit spots on their photosphere. We observe that ΔmNUV, SCa II H&K and SCa II IR are anticorrelated with Prot (see Fig. 5). This trend is visible whether including the RGs in close binaries or not, although it is less pronounced when discarding the RGs in close binaries. We also find an anticorrelation between S​Hα and Prot, but there is no significant anticorrelation or correlation if we consider only the single RGs and discard the stars in close binaries.

thumbnail Fig. 5.

Activity level as a function of the rotation period, Prot. The RGB and RC stars are represented in red and green, respectively, while RGs with an unidentified evolutionary stage are in blue. Black symbols correspond to non-oscillating RGs in close binaries from Gehan et al. (2022). Triangles and diamonds represent wide (Porb > 150 d) and close (Porb ≤ 150 d) binaries identified by Gaia DR3, respectively. The gray background indicates the distribution of the activity level for inactive stars, where a darker shade corresponds to a larger number of stars. Upper left: ΔmNUV. Upper right: SCa II H&K. Lower left: S​Hα. Lower right: SCa II IR.

Such a decrease in magnetic activity as a function of the rotational period had already been observed using the S-index (Noyes et al. 1984; Aurière et al. 2015, see also upper right panel of Fig. 5). The observed trend for ΔmNUV is consistent with the findings of Dixon et al. (2020) for RGs and Godoy-Rivera et al. (2021) for subgiants, as both works found that the NUV excess increases (i.e., becomes more negative) for faster rotators. We note that one single RG, KIC 11521644, stands among the fastest rotators in our sample, while displaying the smallest ΔmNUV among the RGs with a measured rotation period (blue symbol at the bottom left in the left panel of Fig. 5). However, KIC 11521644 is actually likely a contaminant since we notice the presence of another close bright source on the Target Pixel File of its Kepler light curve. In addition, we observe that its surface modulation is detectable only from the KEPSEISMIC light curve3 but not on the simple aperture photometry (SAP) light curve. Since KEPSEISMIC light curves are built on enlarged photometric apertures with respect to the SAP, it tends to confirm that it is an artifact. Newton et al. (2017) observed a negative correlation between the Hα emission line strength and the rotation period, but they worked on a larger sample (466 stars) of less-evolved stars (dwarfs) that have a different spectral type to the RGs in our sample (M-type stars, while our sample includes G- and K-type stars). A plausible explanation for this difference is that M dwarfs tend to be very active (e.g., Kiraga & Stepien 2007), which could increase the contribution of the chromospheric emission in the core of the Hα line compared to the contribution of filaments in the wings of the Hα line. Overall, our findings provide further evidence for the rotation-activity connection in post-main-sequence stars (Lehtinen et al. 2020).

We also observe that RGs in close binaries present on average larger ΔmNUV, S​Hα, and SCa II IR values than single RGs, for a given rotation period. This is similar to what we observe for the photometric index (Gaulme et al. 2014, 2020; Benbakoura et al. 2021; Beck et al. 2024) and the S-index (Gehan et al. 2022, see also upper right panel of Fig. 5), reinforcing the idea that fast rotation alone is not enough to explain the enhanced magnetic activity observed for RGs in close binaries, and that tidal interactions are actually responsible for it.

5.2. Impact of tidal interactions

To investigate the role of tidal interactions on a chromospheric activity level, Fig. 6 displays the rotational versus orbital periods of the RGs in close binaries in our sample, similarly to Gaulme et al. (2014), Benbakoura et al. (2021), and Beck et al. (2024) for 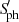S ph ′ $ {S\!}^\prime_{\rm ph} $, as well as Gehan et al. (2022) for the S-index (see also the upper right panel of Fig. 5).

thumbnail Fig. 6.

Rotation period as a function of the orbital period for the close binaries listed by Gaia DR3. The continuous lines represent the 1:1 relation, while the dashed lines represent the 2:1 and 1:2 relations. Upper left: the symbols’ colors in each panel indicate the value of an activity indicator: ΔmNUV (upper left), SCa II H&K (upper right), S​Hα (lower left), and SCa II IR (lower right).

We find no GALEX NUV data for the close binaries studied by Gaulme et al. (2014) and Benbakoura et al. (2021) and we are left with only three RGs in close binaries that have a measured ΔmNUV while also having available a rotation period from Gaulme et al. (2020) and an orbital period from Gaia DR3. Two fast rotators exhibit large ΔmNUV values, namely KIC 7869590 and KIC 11554998, while one slow rotator exhibits a small ΔmNUV, namely KIC 7661609. Notably, we observe that the two fast-rotating RGs belong, respectively, to a tidally locked system (1:1 resonance, KIC 11554998) and to a system in spin-orbit resonance (a rotation period that is twice the orbital period, KIC 7869590), while the system with the slowly rotating RG does not have any special tidal configuration. In a similar fashion, we also observe that RGs in systems that are tidally locked or in spin-orbit resonance display the largest values of SCa II IR and S​Hα compared to the systems that do not have any special tidal configuration.

5.2.1. Comparison with previous studies

Previous studies already noticed a possible relation between NUV emission and binarity for more evolved stars on the asymptotic giant branch (stars undergoing both shell-hydrogen and shell-helium burning, Sahai et al. 2008, 2011; Ortiz & Guerrero 2016; Montez et al. 2017). For less evolved stars on the red giant branch (RGB) and the red clump (RC), Dixon et al. (2020) observed that their binary sample presents larger ΔmNUV values, stating however that this is likely due to fast rotation, since the RGs in binaries are found to be rapidly rotating more often than single RGs. To the extent of our knowledge, the link between large ΔmNUV values and tidal interactions has never been established before. In addition, Montes et al. (1995) reported excess Hα emission for 51 chromospherically active binaries, including both RS Cvn and BY Dra systems. They observed for these systems a slight decrease in the excess Hα emission with the rotation period, as well as a good correlation with the Ca II K line.

Enhanced magnetic activity of RGs in systems that are either tidally locked or undergoing spin-orbit resonance has previously been observed using 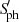S ph ′ $ {S\!}^\prime_{\rm ph} $ (Gaulme et al. 2014; Benbakoura et al. 2021; Beck et al. 2024) and the S-index (Gehan et al. 2022, see also upper right panel of Fig. 5) as activity indicators. Our results show that such systems also exhibit an enhanced NUV excess, Hα index, and Ca II IR index, reinforcing the findings of Gehan et al. (2022) that tidal interactions in close binaries drive abnormally large magnetic fields in RGs, rather than fast rotation by itself.

5.2.2. Candidate mechanisms of tidal dynamo

We here discuss some works that have focused on mechanisms that can in principle generate a tidal dynamo. Tides in stars are generally decomposed into two components (e.g., Zahn 1977; Ogilvie 2013, 2014). The first component is the equilibrium tide, which is a quasi-hydrostatic spheroidal bulge that follows the motion of the companion. This produces a large-scale flow under the form of elliptical streamlines inside the rotating star (Zahn 1966; Remus et al. 2012; Ogilvie 2013). Wei (2022) found that the large-scale tidal flow can in principle induce a magnetic dynamo for solar-like close binaries with Porb up to 2-3 days. This is compatible with the findings of Yu et al. (2024), who find an enhanced magnetic activity, above the saturation level known for single stars, for main-sequence and subgiant stars in close binaries with Porb ≲ 2 days. Although the red giants in close binaries in our sample have much larger orbital periods, the large-scale tidal flow could still be responsible for the enhanced activity that we observe. Indeed, the degree of tidal interactions, T, critically depends on R/a, where a is the orbital distance between the two components of the system (Zahn 1977; Hut 1981). Assuming that the components have Keplerian orbits, the third Kepler law gives

a = P orb 2 / 3 ( G M 1 M 2 4 π 2 ) 1 / 3 , $$ \begin{aligned} a = P^{2/3}_{\rm orb} \left( \frac{G M_{\rm 1} M_{\rm 2}}{4 \pi ^2} \right)^{1/3}, \end{aligned} $$(4)

where M1 and M2 are the masses of the primary and secondary components of the system, respectively. Hence, we obtain

T ∝ R P orb 2 / 3 ( M 1 M 2 ) 1 / 3 . $$ \begin{aligned} T \propto \frac{R}{P^{2/3}_{\rm orb} (M_{\rm 1} M_{\rm 2})^{1/3}}. \end{aligned} $$(5)

We can then evaluate the orbital period at which T is similar for a system including an RG in comparison to a system with an MS star, under the rough assumption that M1 and M2 are similar for both systems, such as

P orb , RG ∼ P orb , MS ( R RG R MS ) 3 / 2 . $$ \begin{aligned} P_{\rm orb, RG} \sim P_{\rm orb, MS} \left( \frac{R_{\rm RG}}{R_{\rm MS}} \right)^{3/2}. \end{aligned} $$(6)

Taking as reference values RRG/RMS = 10 and Porb, MS = 2–3 days, we obtain Porb, RG ∼ 63–95 days. This estimate is compatible with our observations of RGs in close binaries with enhanced activity compared to single RGs (see Fig. 6). This result indicates that the mechanism responsible for the enhanced activity observed by Yu et al. (2024) for MS and subgiant stars in close binaries is likely to be the same as that for the enhanced activity observed by Gehan et al. (2022) and the present work for RGs in close binaries, with the tidal flow as a potential candidate.

The other component of stellar tides is the dynamical tide (Zahn 1975), which represents the tidal excitation of internal waves (e.g. Ogilvie & Lin 2007; Ogilvie 2013; Mathis 2015). For stars with a convective envelope, such as RGs, the dynamical tide is constituted of tidal inertial waves driven by the Coriolis acceleration, which are excited under the condition that Porb > Prot/2 (Beck et al. 2018; Astoul & Barker 2023). Beck et al. (2018) show that due to the large convective envelope of RGs, the dynamical tide is expected to make a negligible contribution to the tidal dissipation that drives spin-orbit evolution, confirming that the equilibrium tide is the main contributor to tidal dissipation (e.g. Zahn 1966; Remus et al. 2012).

However, the equilibrium tide can be subject to parametric instabilities (Barker & Lithwick 2014). One of them is elliptical instability, which affects all rotating fluids with elliptically deformed streamlines (Kerswell 2002; Lacaze et al. 2004; Le Bars et al. 2010; Cébron et al. 2010, 2012). Elliptical instability also drives inertial waves through a parametric resonance and is thought to be important for tidal dissipation in close binary stars (Rieutord 2004). Interestingly, we note that all the RGs in close binaries in our sample that present an enhanced magnetic activity have Porb > Prot/2 (see Fig. 6) and therefore lie in the regime where tidal inertial waves can propagate. It has been predicted and experimentally observed that the flows driven by the elliptical instability can induce a magnetic field (Lacaze et al. 2006; Herreman et al. 2010). Barker & Lithwick (2014) have shown using simulations that the elliptical instability is able to drive a small-scale dynamo in tidally distorted stars, and Cébron & Hollerbach (2014) have shown using magnetohydrodynamic simulations that the elliptical instability is also able to generate a large-scale magnetic field. Hence, the elliptical instability appears to be a potential candidate for the enhanced magnetic activity that we observe in RGs.

6. Classification of active red giants

We here provide criteria to classify the active RGs, which have rotation period measurements resulting from the presence of spots on their photosphere producing photometric rotational modulation. Those criteria come from the findings of Gaulme et al. (2020), Oláh et al. (2021), and the present study and are summarized in Fig. 7.

thumbnail Fig. 7.

Diagram classifying the active RGs, i.e., those exhibiting rotational modulation due to the presence of spots, based on the findings of Gaulme et al. (2020, Prot and S​ph), Oláh et al. (2021, presence of flares for RGs in close binaries), and the present study (SCa II H&K, S​Hα, SCa II IR, and ΔmNUV).

We first focus on fast-rotating RGs (Prot < 50 d). Gaulme et al. (2020) find that RGs belonging to a close binary system (red category in Fig. 7) display S​ph values about one order of magnitude larger than those of single RGs (blue category in Fig. 7). This result suggests two possibilities: either tidal interactions somehow lead to stronger magnetic fields, or the spot distribution differs between binary and single RGs, leading to a different photometric variability. Gehan et al. (2022) could conclude that tidal interactions indeed lead to stronger magnetic fields, by also finding significantly larger chromospheric S-index values for close binaries compared to single RGs. In the present study, we confirm the finding of Gehan et al. (2022) that RGs in close binaries tend to exhibit larger chromospheric SCa II H&K values. We also find that RGs in close binaries tend to exhibit larger chromospheric S​Hα, SCa II IR, and ΔmNUV values than single RGs, reinforcing the conclusions of Gehan et al. (2022). In addition, Oláh et al. (2021) find that a large fraction of the 61 flaring RGs they studied likely belong to close binary systems. Hence, the presence of flares is a possible additional indication of close binarity for RGs.

As regards slower rotating RGs (Prot ≥ 50 d, green category in Fig. 7), they tend to exhibit similar activity levels (S​ph, SCa II H&K, S​Hα, SCa II IR, ΔmNUV, and low flare occurrence) to single fast-rotating RGs, whether they are in a binary or single configuration. Based on Gaulme et al. (2020), slower-rotating RGs have a 85% probability of being single and a 15% probability of being part of a binary system.

7. Conclusions

In the case of RGs, the amplitude of solar-like oscillations has been observed to decrease with increasing photospheric magnetic activity, as probed by measurements of the standard deviation of photometric time series (Chaplin et al. 2011; Huber et al. 2011; Mathur et al. 2019; Gaulme et al. 2020). In particular, based on a sample of about 4500 RGs observed by Kepler, Gaulme et al. (2020) noticed that the photometric modulation of RG light curves is about an order of magnitude larger for RG stars in close binary systems that are tidally locked than for single fast-spinning RGs rotating at the same rate. To understand whether such an increased level of photometric modulation is connected to an increased surface magnetic activity, Gehan et al. (2022) measured the emission of Ca II H&K lines (S-index) from LAMOST spectra of most of the sample used by Gaulme et al. (2020). They unambiguously showed that the larger the photometric rotational modulation, the larger the Ca II H&K emission. In addition, as for photometric variability, there is an enhanced level of chromospheric emission for stars belonging to systems in a state of spin-orbit resonance. Similar results have subsequently been obtained with main-sequence stars observed by Gaia and LAMOST (Yu et al. 2024).

In this paper, we looked for complementary information about active RGs by studying the depth of absorption lines that are known to be sensitive to magnetic fields. What motivated us is the fact that the Ca II H&K lines are at the very blue edge of LAMOST’s spectral range and that the SNR is far from optimal. The main limitation when working with LAMOST spectra is its relatively low resolution, which prevents us from working with any spectral line. Most thin and shallow lines are washed out by the resolution and blended with other lines. After a careful inspection of a sample of LAMOST spectra, we focused on a small set of deep and well-defined absorption lines: Hα at 6563 Å, the last of the Mg I triplet lines at 5184 Å, and the last of the IR Ca II triplet at 8542 Å. In addition, we measured the depth of a Fe line at 6495 Å, which actually is a blend of two iron lines, as a control variable. Finally, besides LAMOST spectra, we analyzed NUV data from the GALEX survey, looking for emission around 2300 Å.

The outcome of our work confirms the general trend that was previously reported, but leads to a few surprises. Firstly, both Hα and Mg I lines display a clear correlation with the oscillation amplitude. However, as was noted in Sect. 4, Hα gets deeper as oscillations get weaker, whereas the opposite trend is observed with Mg I. We note that the observed correlation is much clearer with Hα and Mg I than with Ca II H&K (Gehan et al. 2022). In particular, the correlation between line depth and oscillation amplitude is independent of the detection of photometric rotational modulation caused by spots on the photosphere. The IR Ca II line appears to be less sensitive than Ca II H&K, by showing a very noisy correlation with oscillation amplitude. The control Fe line does not exhibit any correlation with oscillation properties. We checked that there is no significant trend between the depth of the spectral lines studied in this work and the stellar parameters, log g and Teff. On the contrary, we find that the depths of the Hα and Mg I lines are correlated with the stellar mass, M, and radius, R, and hence with the stellar structure. This is not surprising, since the magnetic fields’ properties depend on the stellar structure in the external convective envelope.

Regarding the question of close binarity, Hα shows an enhanced emission for stars in close binaries, whereas no peculiar enhancement can be noticed for active RGs that display partially suppressed oscillations and a relatively low level of photometric modulation. In contrast, the Mg I line does not show any enhancement for close binaries, while Ca II IR does. Similarly to the chromospheric emission, we observe an enhanced level of UV emission for stars in close binary systems. In particular, we observe that RGs in systems that are tidally locked or in spin-orbit resonance display the largest values of ΔmNUV, S​Hα, and SCa II IR compared to the systems that do not have any special tidal configuration. Based on previous works, a potential candidate for enhanced magnetic activity that we observe for RGs in close binaries could be the elliptical instability.

The difference in behavior that is observed between the lines that are known to be sensitive to chromospheric emission is certainly related to differences of altitude in the chromosphere where these lines probe. The fact that Mg and Hα are anticorrelated is puzzling and understanding this is out of the scope of this paper. To go further in analyzing the spectra, we would need 3D atmospheric models of stellar atmospheres, such as CO5BOLD (Freytag et al. 2012) tuned for RG and coupled with a radiative transfer code such as OPTIM3D (Chiavassa et al. 2009). We can imagine that combining asteroseismology, high-resolution spectroscopy, and 3D modeling, with the support of RGs in eclipsing binaries to calibrate the limb darkening, will eventually lead to the possibility of determining the value of the magnetic fields at the surface of RG stars, active or quiet.

3

Mathur, S., Santos, A. R. G., & García, R. A. 2019, Kepler Light Curves Optimized For Asteroseismology (“KEPSEISMIC”), STScI/MAST, doi:10.17909/t9-mrpw-gc07

Acknowledgments

The authors thank B. Mosser, R. A. García, S. Mathur and E. Günther for useful discussions. C.G. was supported by funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under the ERC Synergy Grant WHOLE SUN 810218, as well as by Max Planck Society (Max Planck Gesellschaft) grant “Preparations for PLATO Science” M.FE.A.Aero 0011. D.G.R. acknowledges support from the Spanish Ministry of Science and Innovation (MICINN) with the grant No. PID2019-107187GB-I00. This work has made use of data collected by the NASA Galaxy Evolution Explorer (GALEX). This work has made use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work has made use of data collected by Guoshoujing Telescope (the Large Sky Area Multi-Object Fiber Spectroscopic Telescope LAMOST), a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the LAMOST project has been provided by the National Development and Reform Commission. LAMOST is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences. This work has made use of data collected by the Kepler mission, which data have been obtained from the MAST data archive at the Space Telescope Science Institute (STScI). Funding for the Kepler mission is provided by the NASA Science Mission Directorate. STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5–26555. This work has made use of data collected by the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), which data have been processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Airapetian, V. S., Barnes, R., Cohen, O., et al. 2020, Int. J. Astrobiol., 19, 136 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andrae, R., Rix, H.-W., & Chandra, V. 2023, ApJS, 267, 8 [NASA ADS] [CrossRef] [Google Scholar]
  3. Astoul, A., & Barker, A. J. 2023, ApJ, 955, L23 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aurière, M., Konstantinova-Antova, R., Charbonnel, C., et al. 2015, A&A, 574, A90 [Google Scholar]
  5. Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
  6. Barker, A. J., & Lithwick, Y. 2014, MNRAS, 437, 305 [NASA ADS] [CrossRef] [Google Scholar]
  7. Beck, P. G., Mathis, S., Gallet, F., et al. 2018, MNRAS, 479, L123 [Google Scholar]
  8. Beck, P. G., Grossmann, D. H., Steinwender, L., et al. 2024, A&A, 682, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Benbakoura, M., Gaulme, P., McKeever, J., et al. 2021, A&A, 648, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bianchi, L., Seibert, M., Zheng, W., et al. 2005, ApJ, 619, L27 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bianchi, L., Shiao, B., & Thilker, D. 2017, ApJS, 230, 24 [Google Scholar]
  12. Bjørgen, J. P., Sukhorukov, A. V., Leenaarts, J., et al. 2018, A&A, 611, A62 [Google Scholar]
  13. Bonanno, A., Corsaro, E., & Karoff, C. 2014, A&A, 571, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Borgniet, S., Meunier, N., & Lagrange, A. M. 2015, A&A, 581, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  16. Brown, E. L., Jeffers, S. V., Marsden, S. C., et al. 2022, MNRAS, 514, 4300 [CrossRef] [Google Scholar]
  17. Busà, I., Aznar Cuadrado, R., Terranegra, L., Andretta, V., & Gomez, M. T. 2007, A&A, 466, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Cébron, D., & Hollerbach, R. 2014, ApJ, 789, L25 [Google Scholar]
  19. Cébron, D., Le Bars, M., Leontini, J., Maubert, P., & Le Gal, P. 2010, Phys. Earth Planet. Interiors, 182, 119 [CrossRef] [Google Scholar]
  20. Cébron, D., Le Bars, M., Maubert, P., & Le Gal, P. 2012, Geophys. Astrophys. Fluid Dyn., 106, 524 [CrossRef] [Google Scholar]
  21. Ceillier, T., Tayar, J., Mathur, S., et al. 2017, A&A, 605, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Chaplin, W. J., Bedding, T. R., Bonanno, A., et al. 2011, ApJ, 732, L5 [Google Scholar]
  23. Charbonneau, P. 2014, ARA&A, 52, 251 [NASA ADS] [CrossRef] [Google Scholar]
  24. Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2009, A&A, 506, 1351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 469, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
  27. Dixon, D., Tayar, J., & Stassun, K. G. 2020, AJ, 160, 12 [NASA ADS] [CrossRef] [Google Scholar]
  28. Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [Google Scholar]
  29. Findeisen, K., & Hillenbrand, L. 2010, AJ, 139, 1338 [NASA ADS] [CrossRef] [Google Scholar]
  30. Findeisen, K., Hillenbrand, L., & Soderblom, D. 2011, AJ, 142, 23 [Google Scholar]
  31. Freytag, B., Steffen, M., Ludwig, H. G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
  32. Gaia Collaboration (Arenou, F., et al.) 2023a, A&A, 674, A34 [CrossRef] [EDP Sciences] [Google Scholar]
  33. Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [Google Scholar]
  36. García Soto, A., Newton, E. R., Douglas, S. T., Burrows, A., & Kesseli, A. Y. 2023, AJ, 165, 192 [CrossRef] [Google Scholar]
  37. Gaulme, P., Jackiewicz, J., Appourchaux, T., & Mosser, B. 2014, ApJ, 785, 5 [NASA ADS] [CrossRef] [Google Scholar]
  38. Gaulme, P., McKeever, J., Jackiewicz, J., et al. 2016, ApJ, 832, 121 [NASA ADS] [CrossRef] [Google Scholar]
  39. Gaulme, P., Jackiewicz, J., Spada, F., et al. 2020, A&A, 639, A63 [EDP Sciences] [Google Scholar]
  40. Gehan, C., Gaulme, P., & Yu, J. 2022, A&A, 668, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Godoy-Rivera, D., Tayar, J., Pinsonneault, M. H., et al. 2021, ApJ, 915, 19 [NASA ADS] [CrossRef] [Google Scholar]
  42. Godoy-Rivera, D., Mathur, S., García, R. A., et al. 2024, A&A, submitted [Google Scholar]
  43. Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gomes da Silva, J., Santos, N. C., Boisse, I., Dumusque, X., & Lovis, C. 2014, A&A, 566, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Gomes da Silva, J., Santos, N. C., Adibekyan, V., et al. 2021, A&A, 646, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Gomes da Silva, J., Bensabat, A., Monteiro, T., & Santos, N. C. 2022, A&A, 668, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge, UK: Cambridge University Press) [Google Scholar]
  48. Hall, J. C. 2008, Liv. Rev. Sol. Phys., 5, 2 [Google Scholar]
  49. Harper, G. M. 2018, in Science with a Next Generation Very Large Array, ed. E. Murphy, ASP Conf. Ser., 517, 265 [Google Scholar]
  50. Herreman, W., Cebron, D., Le Dizès, S., & Le Gal, P. 2010, J. Fluid Mech., 661, 130 [NASA ADS] [CrossRef] [Google Scholar]
  51. Huber, D., Bedding, T. R., Stello, D., et al. 2010, ApJ, 723, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  52. Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [Google Scholar]
  53. Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
  55. Kallinger, T., De Ridder, J., Hekker, S., et al. 2014, A&A, 570, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Karoff, C., Knudsen, M. F., De Cat, P., et al. 2016, Nat. Commun., 7, 11058 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kerswell, R. R. 2002, Ann. Rev. Fluid Mech., 34, 83 [Google Scholar]
  58. Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
  59. Lacaze, L., Le Gal, P., & Le Dizès, S. 2004, J. Fluid Mech., 505, 1 [CrossRef] [Google Scholar]
  60. Lacaze, L., Herreman, W., Le Bars, M., Le Dizès, S., & Le Gal, P. 2006, Geophys. Astrophys. Fluid Dyn., 100, 299 [NASA ADS] [CrossRef] [Google Scholar]
  61. Le Bars, M., Lacaze, L., Le Dizès, S., Le Gal, P., & Rieutord, M. 2010, Phys. Earth Planet. Interiors, 178, 48 [CrossRef] [Google Scholar]
  62. Leenaarts, J., & Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [Google Scholar]
  63. Lehtinen, J. J., Spada, F., Käpylä, M. J., Olspert, N., & Käpylä, P. J. 2020, Nat. Astron., 4, 658 [Google Scholar]
  64. Livingston, W., Wallace, L., White, O. R., & Giampapa, M. S. 2007, ApJ, 657, 1137 [CrossRef] [Google Scholar]
  65. Lu, X., Yuan, H., Xu, S., et al. 2023, ApJS, submitted [arXiv:2311.16901] [Google Scholar]
  66. Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
  67. Martin, J., Fuhrmeister, B., Mittag, M., et al. 2017, A&A, 605, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Martínez-Arnáiz, R., López-Santiago, J., Crespo-Chacón, I., & Montes, D. 2011, MNRAS, 414, 2629 [CrossRef] [Google Scholar]
  69. Mashonkina, L., Gehren, T., Shi, J. R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Mathis, S. 2015, A&A, 580, L3 [EDP Sciences] [Google Scholar]
  71. Mathur, S., García, R. A., Ballot, J., et al. 2014, A&A, 562, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Mathur, S., García, R. A., Bugnet, L., et al. 2019, Front. Astron. Space Sci., 6, 46 [Google Scholar]
  73. Mazumder, R., Chatterjee, S., Nandy, D., & Banerjee, D. 2021, ApJ, 919, 125 [NASA ADS] [CrossRef] [Google Scholar]
  74. Metcalfe, T. S., Finley, A. J., Kochukhov, O., et al. 2022, ApJ, 933, L17 [NASA ADS] [CrossRef] [Google Scholar]
  75. Meunier, N., & Delfosse, X. 2009, A&A, 501, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Meunier, N., Kretzschmar, M., Gravet, R., Mignon, L., & Delfosse, X. 2022, A&A, 658, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Montes, D., Fernandez-Figueroa, M. J., de Castro, E., & Cornide, M. 1995, A&A, 294, 165 [NASA ADS] [Google Scholar]
  78. Montez, R. Jr, Ramstedt, S., Kastner, J. H., Vlemmings, W., & Sanchez, E. 2017, ApJ, 841, 33 [NASA ADS] [CrossRef] [Google Scholar]
  79. Mosser, B., Belkacem, K., Goupil, M. J., et al. 2011, A&A, 525, L9 [CrossRef] [EDP Sciences] [Google Scholar]
  80. Mosser, B., Elsworth, Y., Hekker, S., et al. 2012, A&A, 537, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Newton, E. R., Irwin, J., Charbonneau, D., et al. 2017, ApJ, 834, 85 [Google Scholar]
  82. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
  83. Ogilvie, G. I. 2013, MNRAS, 429, 613 [Google Scholar]
  84. Ogilvie, G. I. 2014, ARA&A, 52, 171 [Google Scholar]
  85. Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [Google Scholar]
  86. Oláh, K., Kővári, Z., Günther, M. N., et al. 2021, A&A, 647, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Olmedo, M., Lloyd, J., Mamajek, E. E., et al. 2015, ApJ, 813, 100 [NASA ADS] [CrossRef] [Google Scholar]
  88. Olmedo, M., Olmedo, D., Chávez, M., et al. 2019, Mem. Soc. Astron. It., 90, 680 [NASA ADS] [Google Scholar]
  89. Ortiz, R., & Guerrero, M. A. 2016, MNRAS, 461, 3036 [NASA ADS] [CrossRef] [Google Scholar]
  90. Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [Google Scholar]
  91. Quintero Noda, C., Barklem, P. S., Gafeira, R., et al. 2021, A&A, 652, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Reinhold, T., Bell, K. J., Kuszlewicz, J., Hekker, S., & Shapiro, A. I. 2019, A&A, 621, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Remus, F., Mathis, S., & Zahn, J. P. 2012, A&A, 544, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Rieutord, M. 2004, in Stellar Rotation, eds. A. Maeder, & P. Eenens, 215, 394 [NASA ADS] [Google Scholar]
  95. Sahai, R., Findeisen, K., Gil de Paz, A., & Sánchez Contreras, C. 2008, ApJ, 689, 1274 [NASA ADS] [CrossRef] [Google Scholar]
  96. Sahai, R., Neill, J. D., Gil de Paz, A., & Sánchez Contreras, C. 2011, ApJ, 740, L39 [NASA ADS] [CrossRef] [Google Scholar]
  97. Santos, A. R. G., Breton, S. N., Mathur, S., & García, R. A. 2021, ApJS, 255, 17 [NASA ADS] [CrossRef] [Google Scholar]
  98. Sasso, C., Andretta, V., Terranegra, L., & Gomez, M. T. 2017, A&A, 604, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  100. Skumanich, A. 1972, ApJ, 171, 565 [Google Scholar]
  101. Stello, D., Huber, D., Kallinger, T., et al. 2011, ApJ, 737, L10 [NASA ADS] [CrossRef] [Google Scholar]
  102. Stelzer, B., Marino, A., Micela, G., López-Santiago, J., & Liefke, C. 2013, MNRAS, 431, 2063 [Google Scholar]
  103. Vidotto, A. A., Jardine, M., Morin, J., et al. 2014, MNRAS, 438, 1162 [Google Scholar]
  104. Vrard, M., Kallinger, T., Mosser, B., et al. 2018, A&A, 616, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Walkowicz, L. M., & Hawley, S. L. 2009, AJ, 137, 3297 [NASA ADS] [CrossRef] [Google Scholar]
  106. Weber, E. J., & Davis, L. Jr 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
  107. Wei, X. 2022, MNRAS, 513, 5474 [NASA ADS] [Google Scholar]
  108. Wilson, O. C. 1978, ApJ, 226, 379 [Google Scholar]
  109. Wilson, O. C., & Skumanich, A. 1964, ApJ, 140, 1401 [NASA ADS] [CrossRef] [Google Scholar]
  110. Wise, A. W., Dodson-Robinson, S. E., Bevenour, K., & Provini, A. 2018, AJ, 156, 180 [NASA ADS] [CrossRef] [Google Scholar]
  111. Yu, J., Gehan, C., Bazot, M., et al. 2024, Nat. Astron., submitted [Google Scholar]
  112. Yuan, H. B., Liu, X. W., & Xiang, M. S. 2013, MNRAS, 430, 2188 [NASA ADS] [CrossRef] [Google Scholar]
  113. Zahn, J. P. 1966, Annales d’Astrophysique, 29, 489 [Google Scholar]
  114. Zahn, J. P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
  115. Zahn, J. P. 1977, A&A, 57, 383 [Google Scholar]
  116. Zhang, J., Bi, S., Li, Y., et al. 2020, ApJS, 247, 9 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Details of the NUV excess

A.1. Note on the photometric systems

We note that the GALEX magnitudes are reported in the AB system, and the 2MASS magnitudes are reported in the Vega system. While the GALEX magnitudes can be converted into the Vega system following the transformations of Bianchi et al. (2017, see their Equations 2 and 3), this is not needed when calculating the NUV excess. This is inherited from the definition of the NUV excess by Findeisen & Hillenbrand (2010), who derived the fiducial relation by combining the native GALEX and 2MASS photometric systems (see their Figure 4). Regardless of the above, as the shift from one photometric system to the other is just an additive constant, the activity rank of our targets would remain identical in either of them.

A.2. Impact of metallicity on the NUV excess

Near the submission of this work, Lu et al. (2023) posted a method of obtaining photometric metallicities based on GALEX NUV data. Motivated by this, we tested the influence of metallicity on the NUV excess as follows. As the Lu et al. 2023 catalog was not yet published, we searched for metallicity information for our sample by crossmatching with the catalog of Andrae et al. (2023), which reported stellar parameters (Teff, log g, and [M/H]) derived from the Gaia DR3 BP/RP spectra. Using these [M/H] values, we found our targets to span a range of metallicties centered around a slightly subsolar value (median [M/H] = -0.07 dex), in agreement with the rest of the Kepler field, (e.g., Godoy-Rivera et al. 2024). Indeed, we noted a correlation between the NUV excess and the [M/H] values, which implies that at least part of the NUV activity can be attributed to metallicity (see also Olmedo et al. 2019). Nevertheless, we tested removing this effect via linear regression and found that the majority of the NUV-active targets remain as such after accounting for this metallicity dependence. Thus, the reported NUV excess values are robust against the effect of metallicity.

Appendix B: Error in spectral indices

The spectral index, S​ℓ, of a given line, ℓ, is defined as the ratio of the triangular weighted average flux, Fℓ, in the considered line to the average flux in a selected range of the continuum, Fc. We express them as a function of the discretized spectrum of flux, Fi, per data bin of index, i:

F ℓ = ∑ i = i ℓ i ℓ + N ℓ − 1 w ℓ , i F i ∑ i = i ℓ i ℓ + N ℓ w ℓ , i $$ \begin{aligned} F_\ell&= \frac{\sum _{i=i_\ell }^{i_\ell +N_\ell -1} w_{\ell ,i}\, F_i}{\sum _{i=i_\ell }^{i_\ell +N_\ell } w_{\ell ,i}}\end{aligned} $$(B.1)

F c = ∑ i = i c i c + N c − 1 w c , i F i ∑ i = i ℓ i ℓ + N ℓ w c , i $$ \begin{aligned} F_{\rm c}&= \frac{\sum _{i=i_{\rm c}}^{i_{\rm c}+N_c-1} w_{\mathrm{c} ,i}\, F_i}{\sum _{i=i_\ell }^{i_\ell +N_\ell } w_{\mathrm{c} ,i}}\end{aligned} $$(B.2)

= 1 N c ∑ i = i c i c + N c − 1 F i , $$ \begin{aligned}&= \frac{1}{N_{\rm c}}\sum _{i=i_{\rm c}}^{i_{\rm c}+N_c-1} F_i ,\end{aligned} $$(B.3)

where iℓ and ic are the indices of the starts of the triangular and rectangular windows, Nℓ and Nc the number of bins inside each window, wℓ, i the discretized triangular weighting function, and wc, i the discretized rectangular weighting function such as wc, i = 1,  i ∈ [ic, ic + Nc + 1], or zero elsewhere (Fig B.1). By assuming that data bins of the spectrum are individual random variables of mean flux, Fi, the variance, 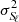σ S ​ l 2 $ \sigma_{{S\!}_\ell}^2 $, of the measurements of S​ℓ is defined by

thumbnail Fig. B.1.

Simulated spectrum of a RG star from a PHOENIX spectrum of a star with an effective temperature of 4800 K, surface gravity of 2.5, and [Fe/H] of 0.0 (gray line). Resolution and sampling were downgraded to that of LAMOST. The red line corresponds with the triangular weighting function, wℓ, of the line, ℓ, and the blue line to the flat weighting function, wc, employed for computing the continuum level. Nℓ (red dots) and Nc (blue dots) indicate the points that belong to the triangular and rectangular weighting functions, respectively.

σ S ℓ 2 = ( ∂ S ℓ ∂ F ℓ ) 2 σ F ℓ 2 + ( ∂ S ℓ ∂ F c ) 2 σ F c 2 $$ \begin{aligned} \sigma _{{S\!}_\ell }^2&= \left(\frac{\partial {S\!}_\ell }{\partial F_\ell }\right)^2\,\sigma _{F_\ell }^2\, +\, \left(\frac{\partial {S\!}_\ell }{\partial F_{\rm c}}\right)^2\,\sigma _{F_{\rm c}}^2 \end{aligned} $$(B.4)

= S ℓ 2 ( ∑ i = i ℓ i ℓ + N ℓ − 1 w ℓ , i ′ 2 σ i 2 F ℓ 2 + ∑ i = i c i c + N c − 1 σ i 2 / N c 2 F c 2 ) , $$ \begin{aligned}&= {S\!}_\ell ^2\, \left(\frac{\sum _{i=i_\ell }^{i_\ell +N_\ell -1} w_{\ell ,i}^{\prime 2}\, \sigma _i^2}{F_\ell ^2} \,+\, \frac{\sum _{i=i_{\rm c}}^{i_{\rm c}+N_c-1} \sigma _i^2/N_{\rm c}^2}{F_{\rm c}^2} \right) ,\end{aligned} $$(B.5)

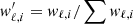where w l,i ′ = w l,i / ∑ w l,i $ w_{\ell,i}^\prime = w_{\ell,i}/\sum{w_{\ell,i}} $. In the case of a purely Gaussian noise, the standard deviation of the measurements is 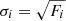σ i = F i $ \sigma_i = \sqrt{F_i} $ for a given data bin of index i. We can easily derive that

σ S ℓ = S ℓ ∑ i = i ℓ i ℓ + N ℓ − 1 w ℓ , i ′ 2 σ i 2 F ℓ 2 + 1 N c 1 F c . $$ \begin{aligned} \sigma _{{S\!}_\ell } = {S\!}_\ell \, \sqrt{\frac{\sum _{i=i_\ell }^{i_\ell +N_\ell -1} w_{\ell ,i}^{\prime 2}\, \sigma _i^2}{F_\ell ^2} \,+\, \frac{1}{N_{\rm c}}\frac{1}{F_{\rm c}} } .\end{aligned} $$(B.6)

We note that assuming the noise to be caused only by photon noise leads to underestimating the errors on the measurements as soon as other sources of noise become significant. This is certainly the case for the Ca II H&K lines, where the detectors are notoriously less sensitive in the near UV than in the mid-visible.

If Nspec spectra are available for a given target, we assume the measurements to be independent. Thus, the noise level of the mean index ⟨S​ℓ⟩ is

σ ⟨ S ℓ ⟩ = 1 N spec ∑ i = 1 N spec σ S ℓ , i 2 . $$ \begin{aligned} \sigma _{\langle {S\!}_\ell \rangle } = \frac{1}{N_{\rm spec}} \, \sqrt{\sum _{i=1}^{N_{\rm spec}} \sigma _{\rm {S\!}_{\ell ,i}}^2}. \end{aligned} $$(B.7)

Appendix C: Mode amplitude versus physical parameters

Here, we display the amplitude of the Gaussian envelope of the oscillations as a function of νmax (as in Fig. 4), where the color scales are related to the masses, radii, surface gravities, and effective temperatures of the stars. Masses, radii, and surface gravities are from Gaulme et al. (2020), and temperatures are from Gaia DR2, as in Gaulme et al. (2020) and Gehan et al. (2022).

thumbnail Fig. C.1.

Physical parameters (color scale) as a function of the oscillation frequency at maximum amplitude, νmax (x axis), and the height of the Gaussian envelope employed to model the oscillation excess power, Hmax (y axis).

All Tables

Table 1.

Characteristics of our sample.

In the text
Table 2.

Pearson correlation coefficients, r, and associated p values, p.

In the text
Table 3.

Number, N, of RGs with measured Prot, as well as the Pearson correlation coefficients, r, and p values, p.

In the text

All Figures

thumbnail Fig. 1.

NUV vs. NIR color-color diagram for the 842 RGs with GALEX NUV magnitudes. From this, the NUV excess was calculated by subtracting the measured (NUV-J)0 magnitudes and the expected values given the fiducial relation from Findeisen & Hillenbrand (2010) and the measured (J − K)0 colors. The targets are color-coded by their NUV excess values, with redder colors indicating stronger excess (more negative values). The gray symbol represents the median error bars.
In the text
thumbnail Fig. 2.

Example of LAMOST spectrum for KIC 1294122. Top panel: entire spectrum expressed as a function of wavelength (Å). The lines we considered are indicated by arrows. Bottom panels: zoom on the six absorption lines, where the flux is normalized by its average value over the 150-Å range that is displayed in each of the four sub-panels. The portion of the spectrum that was used to compute the continuum level is indicated by a red line.
In the text
thumbnail Fig. 3.

Relation between different activity indicators and the photometric modulation, S ph ′ $ {S\!}^\prime_{\rm ph} $, measured by Gaulme et al. (2020) (in log scale), which is an indicator of photospheric activity. The NUV excess, ΔmNUV, is a chromospheric activity indicator measured using GALEX data. The indices, SCa II H&K, S​Hα, SMg I, and SCa II IR, are chromospheric activity indicators measured using LAMOST data. The index, SFe I, measured using LAMOST data is insensitive to stellar activity and used as a control variable. Gray dots refer to regular photometrically inactive RGs (i.e., with no evidence of spot modulation) that display oscillations. Blue dots refer to photometrically active RGs (i.e., those exhibiting spot modulation) with partially suppressed oscillations. Black dots refer to photometrically active and non-oscillating RGs in close binary systems, which were identified by Gaulme et al. (2020). Green dots refer to non-oscillating RGs with ambiguous binary versus single status; we do not have NUV excess data for these stars.
In the text
thumbnail Fig. 4.

Activity level (color scale) as a function of the oscillation frequency at maximum amplitude, νmax (x axis), and the height of the Gaussian envelope employed to model the oscillation excess power, Hmax (y axis), for the different activity indicators considered in this study.
In the text
thumbnail Fig. 5.

Activity level as a function of the rotation period, Prot. The RGB and RC stars are represented in red and green, respectively, while RGs with an unidentified evolutionary stage are in blue. Black symbols correspond to non-oscillating RGs in close binaries from Gehan et al. (2022). Triangles and diamonds represent wide (Porb > 150 d) and close (Porb ≤ 150 d) binaries identified by Gaia DR3, respectively. The gray background indicates the distribution of the activity level for inactive stars, where a darker shade corresponds to a larger number of stars. Upper left: ΔmNUV. Upper right: SCa II H&K. Lower left: S​Hα. Lower right: SCa II IR.
In the text
thumbnail Fig. 6.

Rotation period as a function of the orbital period for the close binaries listed by Gaia DR3. The continuous lines represent the 1:1 relation, while the dashed lines represent the 2:1 and 1:2 relations. Upper left: the symbols’ colors in each panel indicate the value of an activity indicator: ΔmNUV (upper left), SCa II H&K (upper right), S​Hα (lower left), and SCa II IR (lower right).
In the text
thumbnail Fig. 7.

Diagram classifying the active RGs, i.e., those exhibiting rotational modulation due to the presence of spots, based on the findings of Gaulme et al. (2020, Prot and S​ph), Oláh et al. (2021, presence of flares for RGs in close binaries), and the present study (SCa II H&K, S​Hα, SCa II IR, and ΔmNUV).
In the text
thumbnail Fig. B.1.

Simulated spectrum of a RG star from a PHOENIX spectrum of a star with an effective temperature of 4800 K, surface gravity of 2.5, and [Fe/H] of 0.0 (gray line). Resolution and sampling were downgraded to that of LAMOST. The red line corresponds with the triangular weighting function, wℓ, of the line, ℓ, and the blue line to the flat weighting function, wc, employed for computing the continuum level. Nℓ (red dots) and Nc (blue dots) indicate the points that belong to the triangular and rectangular weighting functions, respectively.
In the text
thumbnail Fig. C.1.

Physical parameters (color scale) as a function of the oscillation frequency at maximum amplitude, νmax (x axis), and the height of the Gaussian envelope employed to model the oscillation excess power, Hmax (y axis).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.