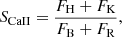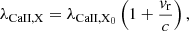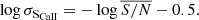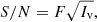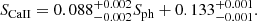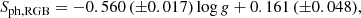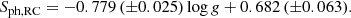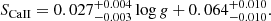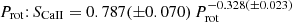| Issue |
A&A
Volume 668, December 2022
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202245083 | |
| Published online | 09 December 2022 | |
Surface magnetism of rapidly rotating red giants: Single versus close binary stars⋆
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: gehan@mps.mpg.de
Received:
28
September
2022
Accepted:
27
October
2022
According to dynamo theory, stars with convective envelopes efficiently generate surface magnetic fields, which manifest as magnetic activity in the form of starspots, faculae, and/or flares, when their rotation period is shorter than their convective turnover time. Most red giants, having undergone significant spin down while expanding, have slow rotation and no spots. However, based on a sample of about 4500 red giants observed by the NASA Kepler mission, a previous study showed that about 8% of them display spots, about 15% of which belong to close binary systems. Here, we shed light on a puzzling fact: for rotation periods less than 80 days, a red giant that belongs to a close binary system displays a photometric modulation about an order of magnitude larger than that of a single red giant with a similar rotational period and similar physical properties. We investigate whether binarity leads to larger magnetic fields when tides lock systems, or if a different spot distribution on single versus close binary stars can explain this fact. For this, we measured the chromospheric emission in the Ca II H & K lines of 3130 of the 4465 stars studied in a previous work thanks to the LAMOST survey. We show that red giants in a close-binary configuration with spin-orbit resonance display significantly larger chromospheric emission than single stars, suggesting that tidal locking leads to larger magnetic fields at a fixed rotational period. Beyond bringing interesting new observables to study the evolution of binary systems, this result could be used to distinguish single versus binary red giants in automatic pipelines based on machine learning.
Key words: asteroseismology / methods: data analysis / techniques: spectroscopic / stars: activity / stars: chromospheres / binaries: general
Full Table 1 is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/668/A116
© The Authors 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model.
This Open access funding provided by Max Planck Society.
1. Introduction
During the main sequence, stars with masses less than 1.3 M⊙ have an external convective envelope that produces a complex dynamo mechanism, whose efficiency depends on the interaction between differential rotation and sub-photospheric convection (Skumanich 1972). According to dynamo theory, surface magnetic fields are efficiently generated when the stellar rotation period is shorter than the convective turnover time (e.g., Charbonneau 2014). Magnetic fields play an important role in stellar evolution. They are believed to regulate the stellar rotation from early to late stages of low-mass stars (Vidotto et al. 2014). Additionally, magnetic fields create a strong coupling between the star and the stellar wind, which leads to loss of angular momentum (e.g., Gallet & Bouvier 2013) during the main sequence, and an important mass loss during the red giant phase (Harper 2018).
Magnetic fields generate various phenomena when emerging from the outer convective envelope, which are grouped under the name of stellar magnetic activity (Hall 2008). Studying stellar activity thus provides information about the physical dynamo process. It is also an important observable for exoplanetary science because it impacts habitability and hampers the detection of planetary signals (Borgniet et al. 2015).
Magnetic activity is a function of stellar evolution, with stars spinning down and becoming less active as they evolve (e.g., Wilson & Skumanich 1964; Skumanich 1972). However, based on a sample of 4465 red giants observed by the NASA Kepler mission, Gaulme et al. (2020) showed that about 8% display a photometric rotational modulation caused by stellar spots. Among these 8%, about 85% are single stars, whereas 15% belong to close binary systems, typically with orbits shorter than 150 days. Red giants in close binaries are expected to display magnetic activity: as they evolve along the red giant branch (RGB), the components can reach a tidal equilibrium where stars are synchronized and orbits are circularized (e.g., Verbunt & Phinney 1995; Beck et al. 2018). Red giant stars are forced to spin faster than they would if they were isolated, which results in surface magnetic fields, and hence spots, sometimes flares, and a larger photometric modulation. This type of close binary including an active evolved star is usually classified as an RS CVn star, from the prototype member RS Canum Venaticorum (e.g., Hall 1976; Strassmeier et al. 1988). This phenomenon is associated with the suppression of the solar-like oscillations, which can be partial or total (Gaulme et al. 2014, 2016; Beck et al. 2018; Benbakoura et al. 2021).
However, the picture is probably more complex than it seems. Indeed, Gaulme et al. (2020) noticed that at a given rotation period, below 80 days, a red giant that belongs to a close binary system displays a photometric modulation about one order of magnitude larger than that of a single red giant with a similar rotation period and similar physical properties (mass, radius). This observation could be explained in two different manners: either tidal locking somehow leads to larger magnetic fields, or the spot distribution differs between binary and single red giants, leading to a different photometric variability. For example, a single large spot can lead to a larger photometric amplitude than a series of smaller spots at all longitudes. It has been shown that stars in RS CVn systems can exhibit special spot distributions, with the presence of active longitudes synchronised with the orbital period in the direction of the line of centers in the binary (e.g., Berdyugina & Tuominen 1998; Kajatkari et al. 2014). This can in turn result in larger photometric amplitudes than observed for single stars exhibiting different spot distributions. In such cases, the larger photometric amplitudes measured for red giants in close binaries are not necessarily due to larger magnetic fields. Unfortunately, photometry alone cannot solve this question.
In this work, we aim to understand whether red giants in close binary systems with a spin-orbit resonance have a larger magnetic field than a single red giant with similar physical and rotational properties. For this, we measured the chromospheric emission in the Ca II H & K lines SCaII (a.k.a. S-index), which is a proxy of the strength of surface magnetic fields, from the spectra of the Large Sky Area Multi-Object Fiber Spectroscopic Telescope survey (LAMOST, Cui et al. 2012). We worked with the sample of 4465 red giants studied by Gaulme et al. (2020).
In Sect. 2, we describe the method we employed to measure chromospheric emission indices from LAMOST spectra. In Sect. 3, we study the correlation between SCaII and the photometric index Sph, which is proportional to the amplitude of the photometric variability. Then, we present SCaII for 3130 red giants measured from LAMOST spectra in Sect. 4. In Sect. 5, we compare the index SCaII between single and binary stars. Finally, we investigate the impact of mass gain on SCaII for stars exhibiting signatures of mass transfer and stellar merging in Sect. 6, before concluding in Sect. 7.
2. Method and data
2.1. Index of chromospheric emission
The chromospheric activity encompasses a wide range of phenomena that produce nonthermal excess emission with respect to a radiative equilibrium atmosphere (Hall 2008), and is a proxy of the strength of surface magnetic fields (Babcock 1961; Petit et al. 2008; Aurière et al. 2015; Brown et al. 2022). The chromospheric activity of cool stars is usually reported in the form of the S-index, which is a measure of the emission-line cores of the Ca II H and K lines that are centered at 3968.470 Åand 3933.664 Å, respectively. A famous long-term survey of stellar surface magnetism is the Mount Wilson project (Baliunas et al. 1995; Duncan et al. 1991), which reported S-indices for a large sample of cool stars from 1966 to the early 2000s.
The S-index SCaII is the flux ratio of the Ca II K & H spectral lines to two nearby bandpasses (Wilson 1978; Duncan et al. 1991; Karoff et al. 2016; Zhang et al. 2020; Gomes da Silva et al. 2021):
where FH and FK correspond to the integrated flux in the Ca II H and K lines, and FB and FR to the integrated flux in the blue and red regions of the pseudo-continuum centered at 3901.070 Å and 4001.070 Å, respectively.
We note that Gomes da Silva et al. (2021) also worked with the modified index of chromospheric emission 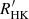 , which essentially gives the fraction of stellar bolometric luminosity radiated in the form of chromospheric H and K emission (Hall 2008), by subtracting the flux in the H and K lines wings, which is mainly from photospheric origin. This parameter was introduced to compare chromospheric activity between stars with different effective temperatures, Teff. However, since we focus on low-RGB and red clump (RC) stars, whose temperatures range from 4700 to 5200 K, we can safely use the SCaII to compare the chromospheric activity within our sample.
, which essentially gives the fraction of stellar bolometric luminosity radiated in the form of chromospheric H and K emission (Hall 2008), by subtracting the flux in the H and K lines wings, which is mainly from photospheric origin. This parameter was introduced to compare chromospheric activity between stars with different effective temperatures, Teff. However, since we focus on low-RGB and red clump (RC) stars, whose temperatures range from 4700 to 5200 K, we can safely use the SCaII to compare the chromospheric activity within our sample.
2.2. From a spectrum to the S-index
The first step consists in determining the line-of-sight velocity (also known as radial velocity) of the considered target before measuring the chromospheric emission. For this, we selected a broad region of the spectrum (6530–6590 Å) surrounding the Hα line, which is located at λHα, 0 = 6562.801 Å in the absence of Doppler effect. We then found the actual center of the Hα line as the wavelength associated with the flux minimum λHα to retrieve the stellar radial velocity vr = c δλHα/λHα, 0, where c is the speed of light in the vacuum and δλHα = λHα − λHα, 0. The Doppler-shifted wavelength of the Ca II H and K lines is given by:
where X = H, K.
The flux in the CaII H and K lines is then integrated using a triangular bandpass, while the flux in the blue and red reference regions is integrated with a square bandpass having a width of 20 Å. We used the same approach as described in Gomes da Silva et al. (2021). The full width at half maximum (FWHM) of the triangular bandpass depends on the resolution of the spectrograph, since it affects the precision one can get on the radial velocity measurement. Hence, we used an FWHM of 1.09 Å for the High Accuracy Radial velocity Planet Searcher (HARPS) data as in Gomes da Silva et al. (2021), while we used an FWHM twice larger (2.18 Å) for the LAMOST data, to ensure that the center of the CaII H and K lines was included in the integrated flux.
Uncertainties were computed from 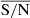 , which is the mean value of the signal-to-noise ratio (S/N) over a wavelength range encompassing the CaII H and K lines, as well as the blue and red regions of the pseudo-continuum between 3881.07 Å and 4021.07 Å such as (Karoff et al. 2016)
, which is the mean value of the signal-to-noise ratio (S/N) over a wavelength range encompassing the CaII H and K lines, as well as the blue and red regions of the pseudo-continuum between 3881.07 Å and 4021.07 Å such as (Karoff et al. 2016)
The S/N is computed as
where F is the flux and Iv is the inverse variance of the flux, provided in the LAMOST spectra files. It should be noted that in case of pure photon noise, Eq. (4) turns into 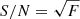 .
.
Because the Ca II H and K lines are located in the blue, where the S/N is lower than at higher wavelengths, the background light correction can result in a nonphysical negative flux. We followed the recommendations of Zhang et al. (2020) and chose to keep the spectra for which less than 1% of the spectrum had negative values in the K and H bandwidths, as well as 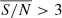 as in Gomes da Silva et al. (2021). We tolerated 1% of negative flux because spectra with a low S/N may have stochastic spikes with negative values, but they remain clearly positive on average.
as in Gomes da Silva et al. (2021). We tolerated 1% of negative flux because spectra with a low S/N may have stochastic spikes with negative values, but they remain clearly positive on average.
When several spectra were available for a given star, we computed the S-index as the median of all the S-indices measured for each individual spectrum. Our method delivers S-index measurements in one to two seconds of computational time on a regular laptop computer.
2.3. Validation on HARPS spectra
We first tested our routine on FGK stars analyzed by Gomes da Silva et al. (2021) using spectroscopic data from HARPS. We made sure to use the same exact spectra as Gomes da Silva et al. (2021) used to derive their S-index measurements. Therefore, we limited our analysis to 15 stars, each having between 1 and 13 spectra from HARPS. Figure 1 emphasizes that we obtained a perfectly linear relation between our measurements and those of Gomes da Silva et al. (2021). We performed a linear fit and found that our measurements needed to be multiplied by a factor of 2.01 ± 0.01 to match those of Gomes da Silva et al. (2021). This factor comes from the calibration of the S-index to the Mount Wilson scale that is usually performed. This factor is usually on the order of ∼1.8 (Karoff et al. 2016), which is globally consistent with what we obtained.
 |
Fig. 1. Comparison between our S-index measurements and those from Gomes da Silva et al. (2021) for 15 FGK stars using HARPS data. The dotted lines represent a 1:1 comparison, while the continuous line represents the best linear fit with a coefficient a = 2.01 ± 0.01. |
2.4. Validation on LAMOST spectra
We additionally applied our method to 1000 red giants analyzed by Zhang et al. (2020) using spectroscopic data from LAMOST, which has already obtained millions of stellar spectra for cool stars in the Milky Way, including many Kepler targets (e.g., Liu et al. 2015; De Cat et al. 2015; Zong et al. 2018). We first retrieved the right ascension α and declination δ of the stars of interest from the Mikulski Archive for Space Telescopes (MAST). We then performed a systematic search of LAMOST spectra associated with these celestial coordinates, within a 6-arcsec radius, among DR4 LAMOST data, as Zhang et al. (2020) did.
Figure 2 shows that we obtained a clear linear trend between our measurements and those of Zhang et al. (2020). We performed a linear fit and found that our measurements needed to be multiplied by a factor of 1.64 ± 0.01 to match those of Zhang et al. (2020). As for HARPS data (Sect. 2.3), this factor is globally consistent with the factor of ∼1.8 usually used to calibrate the S-indices to the Mount Wilson scale.
 |
Fig. 2. Same as for Fig. 1, but for 966 red giants from Zhang et al. (2020) using LAMOST data. The best linear fit corresponds to a coefficient a = 1.64 ± 0.01. Stars with a relative deviation below 10% between S-index measurements are represented in blue, with error bars in gray for visualization purposes. Stars with a relative deviation of at least 10% between S-index measurements are represented in red, as well as the associated error bars. |
We obtained consistent measurements, that is, with a relative deviation below 10% compared to Zhang et al. (2020), in 94% of the cases (blue dots with gray error bars in Fig. 2). We note that among the 1000 red giants we selected, for which Zhang et al. (2020) measured an S-index, we end up with only 989 stars with at least one LAMOST spectrum, while we are using LAMOST DR4 as Zhang et al. (2020) did. This indicates that we obtain different KIC identifications compared to Zhang et al. (2020) in some cases, which results in inconsistencies in the measured S-index.
Additionally, we were able to measure an S-index for 966 stars out of 989, indicating that Zhang et al. (2020) used different criteria than we did to decide whether to discard a spectrum with too low a S/N. This is also a source of inconsistencies between our measurements, since we did not necessarily derive the S-index of a given star relying on the same exact spectra selected by Zhang et al. (2020). These two aspects most probably explain the 58 stars with inconsistent S-index measurements.
2.5. Sample analyzed
We considered the seventh LAMOST data release (DR7) to look for spectra among the 4465 Kepler red giants with radii between 4 and 15 R⊙ that were analyzed by Gaulme et al. (2020). In the absence of stellar names in the LAMOST catalog, we crossmatched the Kepler and LAMOST targets thanks to their coordinates. We identified 3370 stars that have at least one LAMOST spectrum within a 6-arcsec radius on the sky. Then, we discarded 240 stars because their spectra had either nonphysical negative fluxes or exhibited a low S/N near the calcium lines. We measured the chromospheric-emission indices SCaII of 3130 red giants. Table 1 reports the S-index and the associated uncertainties we measured for the 3130 red giants from Gaulme et al. (2020) analyzed in this study (see also Appendix A). The whole table is accessible in the database of the Centre de Données de Strasbourg (CDS). Measurements of the photometric index Sph, the oscillation frequency at maximum amplitude vmax, the height of the Gaussian envelope employed to model the oscillation excess power Hmax, and the rotation period Prot we use in the following sections, were obtained by Gaulme et al. (2020).
Chromospheric emission index SCaII of the 3130 stars from the Gaulme et al. (2020) sample that have exploitable LAMOST spectra.
3. Chromospheric versus photometric indices
The photometric index Sph is defined as the standard deviation of the time series over five times the pseudo-period of the photometric modulation that is measured from the Kepler light curves (Mathur et al. 2014). When no photometric modulation is visible, Sph is the median of the light curve standard deviation over three-day intervals. Figure 3 displays SCaII as a function of Sph and reveals a clear global correlation between them, confirming that the photometric activity is proportional to the strength of surface magnetic fields. A linear fitting of SCaII as a function of Sph leads to:
 |
Fig. 3. Index of chromospheric emission SCaII as a function of photometric modulation Sph (in log scale). Upper panel: results for 3130 red giant stars observed by both LAMOST and Kepler, from the Gaulme et al. (2020) catalog. Gray symbols refer to regular inactive red giants (i.e., with no evidence of spot modulation) that display oscillations, while the other colors refer to photometrically active giants (i.e., exhibiting spot modulation): blue symbols refer to red giants with partially suppressed oscillations; black symbols refer to non-oscillating red giants in close binary systems; and green symbols refer to non-oscillating red giants with ambiguous binary versus single status. The gray line represents the best linear fit given by Eq. (5). Values of Sph are from Gaulme et al. (2020). Bottom panel: zoom on the upper panel for inactive red giants, with the x-axis in linear scale. |
However, by looking closer, we observe a slight anticorrelation between SCaII and Sph for the sample of inactive stars, that is, those where Gaulme et al. (2020) did not report any significant spot modulation after visually inspecting the light curves. We discuss that aspect in Sect. 4.2. We also note that Sph has a much larger dynamical range of values, from about 0.02% to about 8%, whereas SCaII varies from about 0.05 to about 0.9.
4. Chromospheric activity of red giants
4.1. SCaII versus oscillation amplitude
The magnetic field in stellar envelopes reduces the turbulent excitation of pressure waves by partially inhibiting convection. Since spots can also absorb acoustic energy, these two effects lead to a partial or total suppression of oscillations. Bonanno et al. (2014) is the only work to directly confront oscillation amplitude and chromospheric emission, from a set of 19 solar-like pulsators on the main sequence. They showed an anticorrelation between SCaII and the oscillation amplitude. The same was never checked for red giants. Our measurements of SCaII extend the trend observed by Bonanno et al. (2014) to red giants, which is particularly visible for oscillators with frequencies at maximum amplitude vmax > 55 μHz (Fig. 4, left panel). This result is consistent with measurements of photometric modulation Sph, where all of the active stars lay at the bottom of the oscillation amplitude diagram, indicating that red giants with weak oscillations display spots (Fig. 4, right panel, and Gaulme et al. 2020, Fig. 7). The trend we obtain for the S-index is not as clear as for Sph, which likely results from the combination of relatively large errors on SCaII measurements and the smaller range of values explored by SCaII with respect to Sph.
 |
Fig. 4. Impact of the level of magnetic activity on the height of oscillations. Left: chromospheric emission index SCaII (colorscale and symbol size) as a function of oscillations frequency at maximum amplitude vmax (x-axis) and height of the Gaussian envelope employed to model the oscillation excess power Hmax (y-axis) for the 3008 red giants observed both by Kepler and LAMOST, for which Sph and vmax are available. The colorscale was cut at 0.4 for readability purposes, despite a few points reaching SCaII ≈ 0.8. Right: corresponding figure for Sph as measured by Gaulme et al. (2020). |
4.2. Chromospheric emission versus log g
In Sect. 3 (Fig. 3), we noticed that SCaII and Sph are anticorrelated for stars that do not display spots. This fact is related to the way Gaulme et al. (2020) computed Sph: when no spot modulation is detected, Sph is the median standard deviation of the light curve over three-day periods. It is thus much similar to the F8 flicker index introduced by Bastien et al. (2013), which measures the root mean square of the light curve on timescales shorter than 8 h. Bastien et al. (2013, 2016) demonstrated that F8 is correlated with the amplitude of granulation and is anticorrelated with the surface gravity. The latter is confirmed in Fig. 5 (right panel), which shows a clear anticorrelation between Sph and asteroseismic log g (both from Gaulme et al. 2020) for stars that are photometrically inactive, that is, where no spots are detected. We note a different slope for RGB and RC stars. A linear fitting of Sph as a function of log g for RGB and RC groups gives:
 |
Fig. 5. Level of magnetic activity as a function of the surface gravity. Left: chromospheric emission index SCaII as a function of the surface gravity log g. The color indicates the evolution stage: gray symbols refer to stars with an unknown evolution stage; red symbols refer to RGB stars; and green symbols refer to RC stars. Stars with spot modulation are represented by darker dots than stars with no spot modulation. The symbol changes as a function of evolution stage for stars with no spot modulation. The black line represents the best linear fit given by Eq. (8) computed for the red giants where no spot modulation was detected by Gaulme et al. (2020). Right: corresponding figure for Sph as measured by Gaulme et al. (2020). The dashed and the dot-dashed black lines represent the best linear fit of Sph for RGB and RC stars, respectively, given by Eq. (6), computed for the red giants where no spot modulation was measured by Gaulme et al. (2020). |
We note that the photometrically active red giants with oscillations do not follow this trend by having Sph values that stand out of the cohort of inactive stars.
In addition, it is well established that the oscillation amplitude is proportional to the granulation amplitude (Kallinger et al. 2014). Following the anticorrelation between the oscillation amplitude and the chromospheric index, it is normal to find that SCaII is proportional to the surface gravity (see Fig. 5, left panel). That being said, it is remarkable that despite the rather large noise of individual SCaII measurements, a clear trend is visible among the inactive stars. This means that even in the absence of any noticeable surface magnetism – no spot detected –, the chromospheric emission increases as a function of log g. A linear fitting of SCaII as a function of log g performed on the stars with no spots leads to:
A red giant star with log g = 2 has, on average, an SCaII ≈ 0.12, whereas a star with log g = 3.5 has an SCaII ≈ 0.16. A correlation between chromospheric emission and log g was already established by Gomes da Silva et al. (2021, their Fig. 10) from a sample of stars with log g ranging from 2 to 5. Gomes da Silva et al. (2021) used 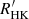 as an indicator of chromospheric activity. No correlation was directly visible among their red giants because of a rather small number of them. To the extent of our knowledge, this is the first time that a direct correlation between SCaII and log g is established for quiet red giants.
as an indicator of chromospheric activity. No correlation was directly visible among their red giants because of a rather small number of them. To the extent of our knowledge, this is the first time that a direct correlation between SCaII and log g is established for quiet red giants.
5. Close binaries versus single red giants
5.1. Close binarity causes enhanced magnetic fields
If we exclude the stars where no spot modulation was reported, the chromospheric emission and photometric modulation are correlated: a large spot modulation means a large SCaII (Fig. 3). We now investigate the impact of close binarity on the chromospheric activity to assess whether there is a significant difference between single fast-rotating red giants and red giants in close binaries. Figure 6 (left panel) displays the chromospheric-emission index SCaII as a function of the rotational period. As was found with Sph (Fig. 6, right panel, and Gaulme et al. 2020), the non-oscillating stars that belong to close binary systems have a significantly larger SCaII (≥0.25) than the inactive oscillating giants. They also have values that are significantly larger than the active red giants that are either single or that belong to systems with relatively long orbits.
 |
Fig. 6. Level of magnetic activity as a function of the rotation period. Left: index of chromospheric emission SCaII as a function of rotational period Prot. The RGB and RC stars are represented in red and green, respectively, while red giants with an unidentified evolutionary stage are in blue. Black symbols correspond to non-oscillating red giants in close binaries. Gray dots indicate non-oscillating red giants with an ambiguous binary signal. Triangles and diamonds represent wide (Porb > 150 d) and close (Porb ≤ 150 d) binaries identified by Gaia DR3, respectively. The gray background indicates the distribution of SCaII for inactive stars, where a darker shade corresponds to a larger number of stars. The gray line represents the best fit of SCaII as a function of |
We observe a difference between the SCaII and Sph diagrams (Fig. 6): the low-activity red giants with partially suppressed oscillations have an Sph clearly above the cohort of inactive red giants, while this is not the case for SCaII. Indeed, SCaII is only slightly larger for the active oscillating giants (median value of 0.17) than for the inactive giants (median value of 0.13). This can be seen from the gray shaded areas that indicate the distribution of SCaII and Sph for the inactive red giants in Fig. 6. That being said, the main message from Fig. 6 is that SCaII is significantly larger, on average, for stars that belong to close binaries than for single stars and for stars in binaries with long orbital periods, meaning that close binarity leads to larger magnetic fields. The few cases that do not follow this trend are listed in Appendix B.
Finally, a correlation between chromospheric emission and rotational period has long been reported, by Noyes et al. (1984) in general, and Aurière et al. (2015) for red giants. We also observe that SCaII decreases as a function of rotational period, but it is mainly due to the stars in close binaries, and is unclear once we remove them. This lack of a clear trend probably originates from the small range of spectral types covered in our study, which is limited to K0, G5, and G8 giants. For example, the sample of Aurière et al. (2015) considers giants with periods from 6 to 600 days, and radii from 5 to 66 R⊙.
5.2. The key role of spin-orbit resonance
From a set of 35 red giants in eclipsing binaries, Benbakoura et al. (2021) report that large magnetic activity and its concomitant oscillation suppression appears in systems whose orbits are either in a state of spin-orbit resonance, or of total tidal synchronization. We sought to verify whether large values of SCaII are connected to spin-orbit resonance. Gaulme et al. (2020) report binary status from radial velocity measurements but do not provide orbital periods because of insufficient amount of data. We looked for information about binarity in the last Gaia data release (DR3, Gaia Collaboration 2022). Among the 3130 giants for which we have a measured SCaII, Gaia identifies 161 binaries (see also Appendix C), 21 of which are already classified as spectroscopic binaries by Gaulme et al. (2020).
Figure 7 (left panel) displays the rotational versus orbital periods of the close binary systems with Porb ≤ 200 days for which both periods are measured, where the sizes and colors of the symbols indicate the values of SCaII. We added the active red giants in eclipsing binaries studied by Gaulme et al. (2014) and Benbakoura et al. (2021) to our sample. In Fig. 7 (right panel), we represent the corresponding plot for Sph as measured by Gaulme et al. (2014, 2020) and Benbakoura et al. (2021). Systems with no oscillations that are tidally locked (1 : 1 resonance) or in spin-orbit resonance display the largest values of SCaII (median values of 0.36 and 0.46, respectively), compared to the systems that do not have any special tidal configuration (median value of 0.22). This result is compatible with the trend obtained with Sph and confirms that close binarity is not enough to cause large magnetic fields: spin orbit resonance in general, and synchronization and circularization in particular, are the driving factors of abnormally large magnetic fields in red giant stars.
 |
Fig. 7. Rotation period as a function of the orbital period for the close binaries listed by Gaia DR3. The continuous lines represent the 1:1 relation, while the dashed lines represent the 2:1 and 1:2 relations. Left: symbols’ sizes and colors indicate the value of SCaII. Right: corresponding figure for Sph as measured by Gaulme et al. (2014, 2020) and Benbakoura et al. (2021). |
6. Beyond tidal interaction: Looking for signatures of mass transfer and stellar merging
Based on asteroseismic measurements, Deheuvels et al. (2022) identified intermediate-mass RGB stars with a degenerate helium core, which was unexpected. They interpreted these stars as being initially low-mass red giants with a degenerate core that underwent mass transfer, becoming intermediate-mass giants with a degenerate core. Similarly, Rui & Fuller (2021) identified higher-mass RGB stars with a degenerate core, which they propose to be merger remnant candidates, with merging occurring after the formation of a degenerate core on the RGB.
To investigate the impact of such a mass gain on the chromospheric activity, we measured the S-index of 34 stars analyzed by Deheuvels et al. (2022), including 21 post-mass transfer candidates and 13 control stars, and 17 stars analyzed by Rui & Fuller (2021). The chromospheric emission of the 21 post-mass transfer candidates was not significantly larger than for the control sample of 13 red giants (median SCaII of 0.145 versus 0.125). As regards the merger remnant candidates, their chromospheric emission is similar, with a median SCaII level of 0.134.
We then verified this apparent lack of enhanced magnetic activity from the Kepler light curves. For the stars that were not part of the Gaulme et al. (2020) catalog, we downloaded the Kepler light curves from MAST and processed them with the same pipeline. We found no significant spot modulation (Sph ≤ 0.1%) for the stars of these two samples. Therefore, we conclude that both samples are magnetically inactive. In other words, these stars have not experienced any significant angular momentum enhancement capable of triggering a dynamo mechanism. However, the non-detection of magnetic activity may reflect a selection bias as stated by Rui & Fuller (2021), because the two studies focus on red giants with high-S/N oscillations. A stronger magnetic activity would result in partially or totally suppressed oscillations, for which their analysis based on interpreting the mixed modes would be compromised.
7. Conclusions
We measured the chromospheric activity of 3130 low-RGB and RC stars observed by Kepler and analyzed by Gaulme et al. (2020), using data from the LAMOST survey (DR7). For stars where spots were detected from the Kepler light curves, we verified that there is a correlation between the chromospheric emission index (S-index) SCaII and the photometric index Sph. This indicates that the intensity of spot modulation is proportional, on average, to the strength of surface magnetic fields, even though stellar inclination can bias this trend. We also noticed that SCaII is correlated with log g for quiet red giants, that is, where no spots are detected.
Regarding the main objective of this work, we conclude that red giants in close binaries that are in a configuration of spin-orbit resonance develop larger magnetic fields than single red giants with similar rotation rates. In other words, the large magnetic field of red giants in close binary systems is not only due to the faster rotation rate induced by tidal interactions, as it has been generally admitted for RS CVn stars (e.g., Shore et al. 1994). Somehow, our work resuscitates an old speculation about a special binary-induced dynamo activity (e.g., Hall 1976), which was discarded a few years later by Morgan & Eggleton (1979), who interpreted it as the result of a selection bias when less than 30 RS CVn stars were known.
In a broader context, we looked for signatures of stellar mergers or post-mass transfer reported by Rui & Fuller (2021) and Deheuvels et al. (2022), but we did not obtain any significant outcome from SCaII and Sph measurements. We also looked for a correlation between chromospheric emission and rotational period, as was observed, for example, by Aurière et al. (2015). We do not confirm their results, likely because of the much smaller range of spectral types covered by our study.
Acknowledgments
C.G. was supported by Max Planck Society (Max Planck Gesellschaft) grant “Preparations for PLATO Science?” M.FE.A.Aero 0011. P.G. was supported by the German space agency (Deutsches Zentrum für Luft- und Raumfahrt) under PLATO data grant 50OO1501. J.Y. acknowledge support from ERC Synergy Grant WHOLE SUN 810218. The authors thank J. Gomes da Silva for providing the HARPS spectra analyzed in this study, as well as J. Zhang for the fruitful discussion. Guoshoujing Telescope (the Large Sky Area Multi-Object Fiber Spectroscopic Telescope LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. LAMOST is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences. P.G. and C.G. hope that Pr. B. Mosser will enjoy reading the first work led by two of his former PhD students.
References
- Aurière, M., Konstantinova-Antova, R., Charbonnel, C., et al. 2015, A&A, 574, A90 [Google Scholar]
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [Google Scholar]
- Bastien, F. A., Stassun, K. G., Basri, G., & Pepper, J. 2013, Nature, 500, 427 [Google Scholar]
- Bastien, F. A., Stassun, K. G., Basri, G., & Pepper, J. 2016, ApJ, 818, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Mathis, S., Gallet, F., et al. 2018, MNRAS, 479, L123 [Google Scholar]
- Benbakoura, M., Gaulme, P., McKeever, J., et al. 2021, A&A, 648, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
- Bonanno, A., Corsaro, E., & Karoff, C. 2014, A&A, 571, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgniet, S., Meunier, N., & Lagrange, A. M. 2015, A&A, 581, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, E. L., Jeffers, S. V., Marsden, S. C., et al. 2022, MNRAS, 514, 4300 [CrossRef] [Google Scholar]
- Charbonneau, P. 2014, ARA&A, 52, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, RAA, 12, 1197 [NASA ADS] [Google Scholar]
- De Cat, P., Fu, J. N., Ren, A. B., et al. 2015, ApJS, 220, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., Ballot, J., Gehan, C., & Mosser, B. 2022, A&A, 659, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [Google Scholar]
- Gaia Collaboration (Arenou F., et al.) 2022, arXiv e-prints [arXiv:2206.05595] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaulme, P., Jackiewicz, J., Appourchaux, T., & Mosser, B. 2014, ApJ, 785, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Gaulme, P., McKeever, J., Jackiewicz, J., et al. 2016, ApJ, 832, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gaulme, P., Jackiewicz, J., Spada, F., et al. 2020, A&A, 639, A63 [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Adibekyan, V., et al. 2021, A&A, 646, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, D. S. 1976, Astrophys. Space Sci. Lib., 60, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. C. 2008, Liv. Rev. Sol. Phys., 5, 2 [Google Scholar]
- Harper, G. M. 2018, in ASP Conf. Ser., 517, 265 [NASA ADS] [Google Scholar]
- Kajatkari, P., Hackman, T., Jetsu, L., Lehtinen, J., & Henry, G. W. 2014, A&A, 562, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., De Ridder, J., Hekker, S., et al. 2014, A&A, 570, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karoff, C., Knudsen, M. F., De Cat, P., et al. 2016, Nat. Commun., 7, 11058 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X.-W., Zhao, G., & Hou, J.-L. 2015, RAA, 15, 1089 [Google Scholar]
- Mathur, S., Salabert, D., García, R. A., & Ceillier, T. 2014, J. Space Weather Space Clim., 4, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgan, J. G., & Eggleton, P. P. 1979, MNRAS, 187, 661 [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Privitera, G., Meynet, G., Eggenberger, P., et al. 2016a, A&A, 593, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Privitera, G., Meynet, G., Eggenberger, P., et al. 2016b, A&A, 593, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rui, N. Z., & Fuller, J. 2021, MNRAS, 508, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- Shore, S. N., Livio, M., & Heuvel, E. P. J. 1994, Interacting Binaries (Berlin: Springer) [CrossRef] [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [Google Scholar]
- Strassmeier, K. G., Hall, D. S., Zeilik, M., et al. 1988, A&AS, 72, 291 [NASA ADS] [Google Scholar]
- Tayar, J., Moyano, F. D., Soares-Furtado, M., et al. 2022, ApJ, 940, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F., & Phinney, E. S. 1995, A&A, 296, 709 [NASA ADS] [Google Scholar]
- Vidotto, A. A., Jardine, M., Morin, J., et al. 2014, MNRAS, 438, 1162 [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [Google Scholar]
- Wilson, O. C., & Skumanich, A. 1964, ApJ, 140, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Bi, S., Li, Y., et al. 2020, ApJS, 247, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Zong, W., Fu, J.-N., De Cat, P., et al. 2018, ApJS, 238, 30 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Median values of SCaII for different categories of red giants
In Table A.1, we report the median S-index measured for each category of red giants listed by Gaulme et al. (2020). We note from Fig. 3 that the clearer the detection of the photometric modulation done by Gaulme et al. (2020), the larger the S-index, on average. We consistently obtain increasing median S-indices for the inactive sample, the low-S/N active sample, and the clearly active sample, respectively.
Median S-index measured for different categories of red giants.
Appendix B: Peculiar cases
From Figs. 6 and 7, it is clear that red giants that belong to close binary systems and that are in a configuration of spin-orbit resonance lead to enhanced magnetic fields with respect to single stars with similar rotational periods, and to binary systems that do not have any special tidal configuration. However, a few cases stand apart.
We note that five oscillating red giants with Prot < 80 days present SCaII > 0.25 (Fig. 6). Among these, two are RC stars that show no evidence for a binary signal in the power spectrum of their light curve (KIC 5372141, 6791309). They might have undergone special events during the previous RGB phase, resulting in an enhanced activity, such as planet engulfment (Privitera et al. 2016a,b; Tayar et al. 2022), mass transfer (Deheuvels et al. 2022), or a stellar merger (Rui & Fuller 2021). Investigating the origin of the enhanced magnetic activity for these two RC stars is beyond the scope of this work. The evolutionary stage of the three remaining red giants with Prot < 80 days and SCaII > 0.25 is unidentified (KIC 5112741, 5471548, 10264774). They exhibit partially suppressed oscillations, which did not allow Gaulme et al. (2020) to identify whether these are RGB or RC stars. Gaulme et al. (2020) found that 15 % of red giants with partially suppressed oscillations belong to binaries. This may also be the case of these three stars, but more data are required to investigate whether they belong to a binary system.
Appendix C: Orbital periods of active red giants
To evaluate whether some red giants belong to binary systems that were missed by Gaulme et al. (2020), we looked for possible binaries from the Gaia DR3 catalog. We found 161 stars that seem to belong to binary systems, with orbital periods up to about 1000 days. Besides, to study the importance of spin-orbit resonance, we added the red giants in eclipsing binaries that were studied by Gaulme et al. (2014) and Benbakoura et al. (2021). Fig. C.1 displays both SCaII and Sph as a function of their orbital periods. As expected, we see that both SCaII and Sph depend on the orbital period. However, this figure also reminds us to not take everything for granted when looking at data from large catalogs, Gaia and Kepler in our case. For example, the targets KICs 4543371, 4761037, 5701850, and 7670875 appear to be binary systems with periods shorter than 5 days and with a low surface magnetism (SCaII < 0.25 and Sph < 0.4 %). Given that their asteroseismic radii are of about 8.4, 8.3, 10.6, and 9.9 R⊙, respectively, these “systems” are likely the result of photometrical blending between short-orbit binaries and red giant stars on the Kepler detector, or triple systems where the red giant component is on a longer orbit.
 |
Fig. C.1. Magnetic activity of red giants in binaries from Gaulme et al. (2020) identified by Gaia DR3 as a function of the orbital period. RGB stars are represented in red, RC stars in green, red giants with an unidentified evolutionary stage in blue, non-oscillating red giants from Gaulme et al. (2020) in black, and red giants from Gaulme et al. (2014), Benbakoura et al. (2021) in magenta. Top panel: S-index SCaII. Bottom panel: Photometric index Sph as measured by Gaulme et al. (2020). |
All Tables
Chromospheric emission index SCaII of the 3130 stars from the Gaulme et al. (2020) sample that have exploitable LAMOST spectra.
All Figures
 |
Fig. 1. Comparison between our S-index measurements and those from Gomes da Silva et al. (2021) for 15 FGK stars using HARPS data. The dotted lines represent a 1:1 comparison, while the continuous line represents the best linear fit with a coefficient a = 2.01 ± 0.01. |
| In the text | |
 |
Fig. 2. Same as for Fig. 1, but for 966 red giants from Zhang et al. (2020) using LAMOST data. The best linear fit corresponds to a coefficient a = 1.64 ± 0.01. Stars with a relative deviation below 10% between S-index measurements are represented in blue, with error bars in gray for visualization purposes. Stars with a relative deviation of at least 10% between S-index measurements are represented in red, as well as the associated error bars. |
| In the text | |
 |
Fig. 3. Index of chromospheric emission SCaII as a function of photometric modulation Sph (in log scale). Upper panel: results for 3130 red giant stars observed by both LAMOST and Kepler, from the Gaulme et al. (2020) catalog. Gray symbols refer to regular inactive red giants (i.e., with no evidence of spot modulation) that display oscillations, while the other colors refer to photometrically active giants (i.e., exhibiting spot modulation): blue symbols refer to red giants with partially suppressed oscillations; black symbols refer to non-oscillating red giants in close binary systems; and green symbols refer to non-oscillating red giants with ambiguous binary versus single status. The gray line represents the best linear fit given by Eq. (5). Values of Sph are from Gaulme et al. (2020). Bottom panel: zoom on the upper panel for inactive red giants, with the x-axis in linear scale. |
| In the text | |
 |
Fig. 4. Impact of the level of magnetic activity on the height of oscillations. Left: chromospheric emission index SCaII (colorscale and symbol size) as a function of oscillations frequency at maximum amplitude vmax (x-axis) and height of the Gaussian envelope employed to model the oscillation excess power Hmax (y-axis) for the 3008 red giants observed both by Kepler and LAMOST, for which Sph and vmax are available. The colorscale was cut at 0.4 for readability purposes, despite a few points reaching SCaII ≈ 0.8. Right: corresponding figure for Sph as measured by Gaulme et al. (2020). |
| In the text | |
 |
Fig. 5. Level of magnetic activity as a function of the surface gravity. Left: chromospheric emission index SCaII as a function of the surface gravity log g. The color indicates the evolution stage: gray symbols refer to stars with an unknown evolution stage; red symbols refer to RGB stars; and green symbols refer to RC stars. Stars with spot modulation are represented by darker dots than stars with no spot modulation. The symbol changes as a function of evolution stage for stars with no spot modulation. The black line represents the best linear fit given by Eq. (8) computed for the red giants where no spot modulation was detected by Gaulme et al. (2020). Right: corresponding figure for Sph as measured by Gaulme et al. (2020). The dashed and the dot-dashed black lines represent the best linear fit of Sph for RGB and RC stars, respectively, given by Eq. (6), computed for the red giants where no spot modulation was measured by Gaulme et al. (2020). |
| In the text | |
 |
Fig. 6. Level of magnetic activity as a function of the rotation period. Left: index of chromospheric emission SCaII as a function of rotational period Prot. The RGB and RC stars are represented in red and green, respectively, while red giants with an unidentified evolutionary stage are in blue. Black symbols correspond to non-oscillating red giants in close binaries. Gray dots indicate non-oscillating red giants with an ambiguous binary signal. Triangles and diamonds represent wide (Porb > 150 d) and close (Porb ≤ 150 d) binaries identified by Gaia DR3, respectively. The gray background indicates the distribution of SCaII for inactive stars, where a darker shade corresponds to a larger number of stars. The gray line represents the best fit of SCaII as a function of |
| In the text | |
 |
Fig. 7. Rotation period as a function of the orbital period for the close binaries listed by Gaia DR3. The continuous lines represent the 1:1 relation, while the dashed lines represent the 2:1 and 1:2 relations. Left: symbols’ sizes and colors indicate the value of SCaII. Right: corresponding figure for Sph as measured by Gaulme et al. (2014, 2020) and Benbakoura et al. (2021). |
| In the text | |
 |
Fig. C.1. Magnetic activity of red giants in binaries from Gaulme et al. (2020) identified by Gaia DR3 as a function of the orbital period. RGB stars are represented in red, RC stars in green, red giants with an unidentified evolutionary stage in blue, non-oscillating red giants from Gaulme et al. (2020) in black, and red giants from Gaulme et al. (2014), Benbakoura et al. (2021) in magenta. Top panel: S-index SCaII. Bottom panel: Photometric index Sph as measured by Gaulme et al. (2020). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.