| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202348398 | |
| Published online | 07 May 2024 | |
Radio surface fluctuations in radio relics⋆
1
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
e-mail: pdominguezfernandez@cfa.harvard.edu
2
Dipartimento di Fisica e Astronomia, Università di Bologna, Via P. Gobetti 93/2, 40129 Bologna, Italy
3
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
4
Department of Physics, College of Natural Sciences UNIST, Ulsan 44919, Republic of Korea
5
Department of Earth Sciences, Pusan National University, Pusan 46241, Republic of Korea
Received:
25
October
2023
Accepted:
15
February
2024
Recent observations have revealed detailed structures of radio relics across a wide range of frequencies. In this work, we performed three-dimensional magnetohydrodynamical (3D MHD) simulations of merger shocks propagating through a turbulent magnetized intracluster medium. We then employed on-the-fly Lagrangian particles to explore the physical processes behind the origination of radio substructures and their appearance in high and low-frequency observations. We employed two cosmic-ray (CR) electron acceleration models, with a fresh injection of electrons from the thermal pool and the re-acceleration of mildly relativistic electrons. We used the relative surface brightness fluctuations, δSν, to define a “degree of patchiness.” First, we found that patchiness is produced if the shock’s surface has a distribution of Mach numbers, rather than a single Mach number. Second, radio relics appear patchier if the Mach number distribution consists of a large percentage of low Mach numbers (ℳ ≲ 2.5). Furthermore, as the frequency increases, the patchiness also becomes larger. Nevertheless, if radio relics are patchy at high frequencies (e.g., 18.6 GHz), they necessarily will also be patchy at low frequencies (e.g., 150 MHz). Then, to produce noticeable differences in the patchiness at low and high frequencies, the shock front should have a Mach number spread of σℳ ≳ 0.3 − 0.4. Finally, the extent of the patchiness depends on the Mach number distribution as well as the CR acceleration model. We propose δSν as a potential tool for extracting merger shock properties and information on particle acceleration processes at shocks in radio observations.
Key words: acceleration of particles / magnetohydrodynamics (MHD) / radiation mechanisms: non-thermal / shock waves / galaxies: clusters: general / galaxies: clusters: intracluster medium
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Galaxy clusters reveal spectacular Mpc-scale diffuse radio emission. It appears that the observed emission is a consequence of merger events accelerating the synchrotron-emitting cosmic ray (CR) electrons (see van Weeren et al. 2011 or Bykov et al. 2019, for a review). The primary focus of this work is on radio relics, which are typically found at the cluster periphery and exhibit elongated morphology with a high polarization fraction (see Brüggen et al. 2012 and van Weeren et al. 2019, for reviews).
The elongated shape of radio relics is believed to be a result of mild merger shocks (ℳs ∼ 1.7 − 4) propagating in the intracluster medium (ICM e.g., Clarke & Ensslin 2006; van Weeren et al. 2010, 2012). Nevertheless, recent high-resolution radio observations have revealed a plethora of additional complex substructures in radio relics (e.g., Rajpurohit et al. 2018, 2020; Owen et al. 2014; van Weeren et al. 2017; Di Gennaro et al. 2018; de Gasperin et al. 2022). Understanding the origin of these radio substructures is challenging due to the lack of available insights into the particle acceleration mechanisms causing the diffuse radio emission.
The preferred mechanism that accelerates relativistic particles at a collisionless shock is the first-order Fermi (Fermi-I) acceleration process of diffusive shock acceleration (DSA e.g. Blandford & Eichler 1987; Drury 1983). In this case, particles need to reach high enough momenta to cross the shock transition zone, which has a thickness of the order of the gyroradius of post-shock thermal ions, and then they can fully participate in the DSA process. It has been widely discussed that there are two types of electron populations in the ICM that can participate in the DSA: thermal electrons and pre-existing mildly relativistic (10 ≲ γ ≲ 104) electrons (e.g. Kang et al. 2012; Pinzke et al. 2013).
Following the idea that thermal electrons are directly injected into the DSA, or what is more commonly referred to as fresh injection, presents certain challenges in our current understanding to explain observed radio relics such as: (1) an unrealistic shock acceleration efficiency in order to explain the observed radio power of some relics (see van Weeren et al. 2019; Botteon et al. 2020); (2) a discrepancy between the Mach numbers inferred from X-ray observations assuming density and/or temperature jump conditions and those inferred from radio observations assuming DSA (e.g. Botteon et al. 2020); (3) a mismatch between our expectations from plasma physics and radio and X-ray observations of very weak shocks. In fact, recent particle-in-cell (PIC) simulations have shown that thermal electrons in the ICM can only be energized to the full DSA regime only in supercritical shocks with a sonic Mach number greater than a critical Mach number, ℳcr ∼ 2.3 (see, e.g., Kang et al. 2019; Ha et al. 2021), which is at odds with several ℳradio ∼ 1.5 − 2.3 shocks detected in the ICM (e.g., van Weeren et al. 2019). Additional factors, such as the presence of pre-existing fossil CR electronsm could potentially explain points 1 and 2 (however, see the discussion in Ha et al. 2022), while pre-existing turbulence could explain point 3 (e.g. Domínguez-Fernández et al. 2020; Wittor et al. 2021). Yet, our understanding on the involved processes still falls short and the details should be further investigated.
Regarding the substructure within relics, there are some observed features that cannot be easily understood. For example, filamentary structures in the form of threads, twisted ribbons, and/or bristles have been consistently observed in various radio relics. Some examples where these filamentary structures of few kpc scales have been found in the Toothbrush (Rajpurohit et al. 2018, 2020), Sausage (Di Gennaro et al. 2018), MACS J7017+35 (van Weeren et al. 2017), Abell 2256 (Rajpurohit et al. 2022), and Abell 3667 (de Gasperin et al. 2022) relics, despite of the very diverse merger scenarios of the host galaxy clusters in which each of these relics have formed. The majority of these filamentary structures point towards sites of shock acceleration (see, e.g., de Gasperin et al. 2022). While repeated DSA events at work in the downstream or in projection could potentially explain their origin, a multiple weak shock scenario in the ICM is yet to be understood.
On the other hand, numerically reproducing shock surfaces and their substructure in the ICM are challenging. A limited knowledge on the merger history of each galaxy cluster, on the ICM conditions at clusters outskirts and/or on the CR budget of clusters add to the challenge. Yet, some radio relics born in binary cluster merger events and observed close to edge-on (i.e., small projection on the plane of the sky) serve as the simplest examples for testing our current theories. For example, the so-called Sausage relic in the CIZA J2242.8+5301 galaxy cluster showing an almost perfect ∼2 Mpc arc-like structure and seen close to edge-on, is one of the most studied radio relics and it has been observed in a very wide range of radio frequencies. The Sausage relic has been primarily studied at low and medium radio frequencies, for instance, from ∼150 MHz to ∼6.5 GHz (see, e.g., van Weeren et al. 2010; Stroe et al. 2013, 2016; Loi et al. 2017; Hoang et al. 2017; Kierdorf et al. 2017; Di Gennaro et al. 2018). On the other end, at high frequencies, the Sausage relic has been observed with single-dish telescopes such as the Effelsberg telescope observing at 14.25 GHz and the Sardinia Radio Telescope (SRT) observing at 18.6 GHz (Loi et al. 2020), and with the Arcminute Microkelvin Imager (AMI) and Combined Array for Research in Millimeter-wave Astronomy (CARMA) interferometers observing at 16 GHz and 30 GHz (Stroe et al. 2014, 2016). We refer to Fig. 20 in Sect. 4.1.3 of Stroe et al. (2013), for a very illustrative example of the variations along the shock front in the Sausage relic at various frequencies.
This wealth of information inspires us to study the surface brightness distribution of a shock front at high and low radio frequencies. Our primary objective in this study is to gain insights into the radio substructures generated by physical conditions. Specifically, radio substructures that arise as a consequence of our current particle shock acceleration theories across a wide range of radio frequencies. Our central emphasis lies in the analysis of radio surface brightness variations or fluctuations.
In Domínguez-Fernández et al. (2020, 2021) it has been shown that a model of thermal electrons injected into DSA in the presence of a turbulent pre-shock magnetized ICM can reproduce some of the morphological small-scale characteristics of radio relics and also their most important observed features in continuum and polarized radio emission. In this work, we follow the numerical approach presented in Domínguez-Fernández et al. (2020), where an ensemble of tracer (Lagrangian) particles represents a whole distribution of electrons embedded in a magneto-hydrodynamical (MHD) fluid. This type of hybrid modeling has been previously applied in post-processing of Eulerian cosmological MHD simulations (e.g., Skillman et al. 2013; Hong et al. 2015; Nuza et al. 2017; Wittor et al. 2019; Roh et al. 2019) and, more recently, implemented in on-the-fly in Lagrangian cosmological MHD simulations (see, e.g., Böss et al. 2023). In this work, we model the cooling processes of each tracer particle at run-time using the MHD code PLUTO (Mignone et al. 2007; Vaidya et al. 2018).
We consider a simplified set-up where a shock tube is present in a turbulent medium that is representative of a small region of the ICM. We then assume that CR electrons are injected instantly at the shock discontinuity and acquire spectral properties according to the DSA theory. We focus on the two plausible models for “injection,” namely thermal electrons injected into DSA (fresh injection) and fossil CR electrons injected into DSA (re-acceleration). In general, the re-acceleration model relies on a source providing the population of fossil electrons such as a radio jet from an AGN or a previous episode of shock or turbulence acceleration (Sarazin 1999; Kang et al. 2012). Therefore, such an electron population is not expected to be distributed uniformly in the ICM, but concentrated instead in fossil clouds or bubbles, for instance.
The paper is structured as follows. In Sect. 2, we describe our numerical set-up and initial conditions. In Sect. 3, we include a description of the particles’ initial spectral distribution and evolution. In this section, we also explain how we obtain the emission maps. Section 4 presents our results and our conclusions are given in Sect. 5.
2. Numerical set-up
2.1. Initial conditions: Modeling the turbulent ICM with FLASH
The turbulent ICM initial conditions were produced using the MHD FLASH code version 4.6.1 (Fryxell et al. 2000; Calder et al. 2002). We use the same set-up used in Domínguez-Fernández et al. (2020, 2021): the unsplit staggered mesh (USM) MHD solver, which employs a constrained transport (CT) method at cell interfaces to maintain the divergence-free magnetic field property on a staggered grid (e.g., Lee et al. 2009). The simulation domain is chosen to be a cubic box of size L = Lx = Ly = Lz, uniformly spaced over a 2563 cells grid, with periodic boundary conditions. We assumed an ideal gas equation of state with γ0 = 5/3.
We employ a spectral forcing method based on the stochastic Ornstein–Uhlenbeck (OU) process with a finite autocorrelation time to generate turbulence (e.g., Eswaran & Pope 1988; Schmidt et al. 2006; Federrath et al. 2010). We use a solenoidal subsonic turbulence forcing with an injection scale of 2L/3. The forcing amplitude, f0, was set to be a paraboloid in Fourier space only containing power on the largest scales: 1 ≤ kL/2π ≤ 2. The autocorrelation timescale was set equal to the dynamical timescale on the scale of energy injection, t2L/3 = 2L/3σv, where σv = 125 km s−1 is the root-mean-square (rms) velocity amplitude of the fluctuations.
We set a magnetic field seed of 0.05 μG on the density 10−4 mp cm−3. The evolution of the rms Mach number and the volume weighted mean plasma beta, βp, is shown on the upper panel of Fig. 1. We selected a snapshot corresponding to 2t2L/3 to act as our initial condition (see Sect. 2.2 and main set-up in Fig. 2). On the lower panel of Fig. 1, we show the probability distribution function (PDF) of the magnetic field strength and Mach number at that time.
 |
Fig. 1. Evolution of the rms Mach number (top) and plasma beta (bottom), shown in the upper panel. The vertical gray line indicates the selected time in the FLASH simulation to be our initial turbulent ICM condition. The selected snapshot has an rms Mach number of ℳs ∼ 0.7 and a plasma beta of βp ∼ 110. Magnetic field strength (darkcyan) and Mach number (purple) PDFs at the selected time in the FLASH simulation, shown in the bottom panel. |
We note that the physical evolution of these turbulence-in-a-box simulations can be fully described by the dimensionless sonic and Alfvén Mach numbers, ℳ and ℳA. Therefore, as long as ℳ and ℳA remain unchanged, all dimensional variables, such as L, ρ, v, B, etc., can be scaled arbitrarily. In the following, we work with L = 200 kpc. We would like to emphasize that our analysis of a final shock with an extent of 3 Mpc is specifically discussed in Sect. 4.4. In this particular case, we employed the stacking of our simulation boxes, made feasible due to our periodic boundary conditions.
2.2. Main PLUTO simulations
To study the synchrotron emission in an MHD shock tube, we use the code PLUTO (Mignone et al. 2007), and follow the same set-up used in Domínguez-Fernández et al. (2020, 2021). The PLUTO code solves the following conservation laws for ideal MHD:
where ρ is the gas mass density, m = ρv is the momentum density, p is the thermal pressure, B is the magnetic field, e the specific internal energy, here the adiabatic index is γ0 = 5/3 as well and Et is the total energy density defined as
For more detailed information on the PLUTO code, we refer to Mignone et al. (2007). Our computational domain is a rectangular box (400 kpc × 200 kpc × 200 kpc with 256 × 128 × 128 cells, respectively), where x∈[–200,200] kpc, y∈[–100,100] kpc, and z∈[–100,100] kpc (see Fig. 2). The right-hand half of the domain is filled with a turbulent medium (see Sect. 2.1), representing a realistic ICM, while the left-hand half contains a uniform medium in which the shock is launched. We define a shock discontinuity at x = −100 kpc (see Fig. 2 for the initial configuration of the magnetic field). This defines three regions in our simulation box: a post-shock uniform region (I), a pre-shock uniform region (II) and a pre-shock turbulent region (III).
 |
Fig. 2. Initial magnetic field configuration in the PLUTO code taken from Domínguez-Fernández et al. (2020). The streamlines are colored according to the magnitude of the magnetic field: green, light colors denote higher values, while dark blue color indicates lower values. Here, I denotes the post-shock region, II the uniform pre-shock region, and III the turbulent pre-shock region (see Sect. 2.1). The left side is a uniform medium with a Bx component matching the mean value of the Bx of the turbulent medium. We have one Lagrangian particle per cell placed in the whole regions II and III. |
The turbulent medium is produced externally, with the procedure outlined in Sect. 2.1. The turbulent fields are then read into PLUTO and interpolated onto the numerical mesh used to evolve shocks with a bi- or tri-linear interpolation at the desired coordinate location at the initial time. The initial boundary conditions of the computational domain are denoted as the “outflow” in x (zero gradient across the boundary) and “periodic” in y and z. We used a piecewise parabolic method (PPM) for the spatial integration, whereas a second-order TVD Runge–Kutta method was used for the time stepping with a Courant–Friedrichs–Lewy (CFL) condition of 0.3. For the Riemann solver in the flux computation, we used the Harten–Lax–van Leer–Discontinuities (HLLD) solver (see Miyoshi & Kusano 2005). We control the ∇ ⋅ B = 0 condition with the hyperbolic divergence cleaning technique where the induction equation is coupled to a generalized Lagrange multiplier (GLM e.g., Dedner et al. 2002). We refer to Appendix A of Domínguez-Fernández et al. (2020) for more details on the effects of the initial interpolation of the external input and handling of the magnetic field divergence under the GLM and constrained transport techniques.
The initial conditions for the density, pressure, and velocity in region II (pre-shock uniform region at [–100,0] kpc) were set to the mean value of the corresponding turbulent fields. In the case of the magnetic field in region II, we set it to be the mean value of the Bx component of the turbulent medium. The initial conditions for region I (post-shock region) were selected according to the Rankine–Hugoniot conditions (e.g., Landau & Lifshitz 1987). We studied shocks propagating into the turbulent medium with different initial sonic Mach numbers. Shocks can be classified as quasi-parallel and quasi-perpendicular if θbn ≤ 45° or θbn > 45°, respectively, where θbn is the angle between the upstream magnetic field and normal of the shock.
In this work, we consider only the quasi-parallel limit, namely, θbn = 0°1. We note that this only defines the initial configuration. Once the shock front reaches region III, θbn can vary. Nevertheless, we do not consider the effects of θbn changing in our CR modeling (see Sect. 3).
Finally, we filled the computational domain from the shock discontinuity up to the right side of the box with one Lagrangian particle per cell. This gives us a total number of 3 145 728 Lagrangian particles for each run. Each particle has its independent energy evolution, as described in detail in the following section.
3. Non-thermal radio emission from shocks
3.1. Particle energy spectrum
Each Lagrangian particle represents an ensemble of CR electrons and is characterized by an energy distribution function,
which gives the number of electrons per fluid number density. These particles evolve according to the CR transport equation defined in Eq. (8) in Vaidya et al. (2018), as follows:
Here, the first term in square brackets accounts for energy losses due to adiabatic expansion, while the second one accounts for the synchrotron and inverse-Compton losses for electrons with isotropically distributed velocity vectors,
where β = ve/c is the velocity of the electrons, me their mass and arad the radiation constant. For the present work, we assume a constant redshift of z = 0. We refer to Vaidya et al. (2018) for a complete description of the numerical implementation and the semi-analytical scheme used for solving Eq. (9).
We study a simplified scenario where the non-thermal spectra of the particles are activated instantly at the shock discontinuity. While the particles follow the fluid flow since t = 0, the particle’s energy distribution starts to evolve only when the particles are at the shock discontinuity. We use a shock finder based on converging flows and pressure jumps in order to tag shock cells and identify the propagating shock. We refer to Domínguez-Fernández et al. (2020) for more details on the shock finder implementation.
Once the Lagrangian particles are activated at the shock discontinuity, they get assigned an initial energy distribution. In this work, we considered two different models. Below, we outline the characteristics of the two initial energy distributions, namely, Finj(E) and Fre(E), associated with each of these models:
-
(1)
Fresh injection model:
where p = q − 2 is what it is usually called the injection spectral index, f0, inj is the normalization constant and n0 is the fluid number density. The power-law index, q, for non-relativistic shocks used in our model is that obtained from the steady state theory of DSA (Drury 1983):
or
where we considered the test particle acceleration at a shock of Mach number ℳ, and for the second equality in Eq. (12), we use γ0 = 5/3. It is relevant to mention that for relativistic shocks, the parameter q will exhibit different behavior with respect to the shock compression ratio (see, e.g., Keshet & Waxman 2005). However, as emphasized in the introduction, this study is exclusively concerned with non-relativistic shocks, which are commonly observed in the ICM (see also Table 1). The normalization factor, f0, inj, is assigned according to the energy contained in the shock. That is, we considered that the total energy per fluid number density is
Table 1.Parameters used in all our simulation runs for the fresh injection and re-acceleration models.
where the CR energy will be considered to be a function of the Mach number, ECR(ℳ). With ECR(ℳ), one can obtain the normalization factor as
The left-hand side of Eq. (14) and the above Eq. (15) depend on the injection energy Emin and the maximum allowed energy Emax. The energy flux of accelerated CRe should be a fraction of the energy dissipated by the shock:
where ϕCR is given in units of [erg cm−2 s−1], ρpre is the pre-shock (upstream) density, vsh is the velocity of the shock and η(ℳ) is the acceleration efficiency as a function that depends only on the shock’s Mach number. The final expression for ECR is obtained by equating the cosmic ray energy flux crossing each particle volume element, and the total energy of cosmic rays advected with a post-shock (downstream) velocity,
where ECR is in units of [erg cm−3]. It is worth noting that the values of ℳ, vsh, ρpre, and vpost are determined through our shock-finding algorithm (see Sect. 3.1 and Domínguez-Fernández et al. 2020, for comprehensive information). We will assume the following toy model for the η(ℳ) function:
where the critical Mach number ℳcr, power law index αη and ηe are parameters of our selection (see Table 1). In this work, we consider Emin and Emax corresponding to γmin = 10 and γmax = 107. The upper boundary is chosen to be arbitrarily high because for ICM shocks, Emax/mec2 ≫ 1, while the lower boundary is selected baring in mind that electrons with momenta p ≳ 3pth, p2, could diffuse across the shock and participate in the DSA process (see the discussion in Kang 2020). The value of ηe is very uncertain for the weak (ℳs ≲ 5) shocks in the ICM (see, e.g., Riquelme & Spitkovsky 2011; Xu et al. 2020). The chosen value agrees with the expectations of DSA for strong shocks (e.g., Kang et al. 2012) and lies in the range of values required to explain observations of radio relics (see Botteon et al. 2020). Nevertheless, we note that, since Emin and Emax are initially fixed, ηe can be treated as a free parameter to re-scale the particle energy distribution such that it matches the observed surface brightness. Although there has been limited advancement in this area, recent findings from PIC simulations indicate that shocks with Mach numbers weaker than ℳs ≃ 2.3 may not possess the capability to facilitate electron acceleration through DSA, as demonstrated by studies such as Kang et al. (2019) and Ha et al. (2021). This serves as the primary motivation behind our choice of the ℳcr parameter. Furthermore, we explore the conservative scenario of ℳcr = 1, which allows for the possibility of even the weakest shocks contributing to electron acceleration via DSA. Our selection of the αη parameter is motivated by fitting functions derived and extensively studied in Kang et al. (2007), Kang & Ryu (2013), Ryu et al. (2019).
-
(2)
Re-acceleration model:
with p given in Eq. (13). Here, fpre is the spectrum of pre-existing fossil electrons. We will consider the following two cases:
where f0, 1 and f0, 2 are normalization constants and s is an energy spectral index3. The Dirac delta function model represents an idealized scenario with a single-burst population of pre-existing electrons. However, it offers us better control over the characteristic energy of these fossil electrons, as discussed in previous studies (see, e.g.,Kang et al. 2012; Pinzke et al. 2013). On the other hand, the power-law model is a more realistic representation of the seed population of electrons, as proposed in Kang & Ryu (2011) (see Eqs. (7) and (8)). In the Dirac delta function model, we consider Ecut corresponding to γmin = 102 and 103, while in the power-law model, we set Emin corresponding to γmin = 10 and s = 2.25 and 3, with the spectrum covering the range of γmin = 10 and γmax = 107, as listed in Table 1. The selected s values are what is typically expected if pre-existing CRe were generated at previous shocks or as a result of turbulent acceleration (see, e.g., Chandran 2005). The energy distribution function of each particle for each corresponding case can be re-written as:
If s ≠ p and for E ≫ Emin, we can re-write the energy distribution function as (see also Eq. (8) of Kang & Ryu 2011):
where r = min(s, p). We note that for both the Dirac delta function and power-law cases, the pre-shock and post-shock CR number densities, NCR, pre = ∫fpre(E)dE and NCR, re = n0∫Fre(E)dE, are mathematically related as follows:
This relation basically reflects the effect of compression, and it is only a function of p. Analogously, the pre-shock and post-shock CR energy densities are related as
The normalization factors, f0, 1 and f0, 2, are usually set by the ratio of upstream CR electron pressure to gas pressure, R = PCR, pre/Pg, pre (see Kang et al. 2012), where Pg = (γ0 − 1)ρe. Here, R is a parameter that will be scaled to match the observed fluxes of radio relics. Nevertheless, it will not be relevant for the research question that we pursue in this work because R effectively only re-scales the particle energy spectrum. Finally, the complete electron distribution at the shock location can be written as a sum of the re-accelerated and freshly injected electron populations,
We point out that the relative significance of the freshly injected and re-accelerated electron populations is ruled by the normalization constants f0 (f0, 1 and f0, 2 for the two cases considered in Eqs. (20a) and (20b)) and f0, inj and the slopes p and s in our model.
3.2. Synchrotron emission
The synchrotron emissivity of a tracer particle in a local magnetic field B′ in the direction 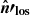 4, per unit solid angle, volume and frequency is given by
4, per unit solid angle, volume and frequency is given by
where 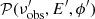 is the synchrotron power per unit frequency and unit solid angle emitted by a single particle that has energy E′ and ϕ′ is the angle that the velocity vector of the particle makes with the direction
is the synchrotron power per unit frequency and unit solid angle emitted by a single particle that has energy E′ and ϕ′ is the angle that the velocity vector of the particle makes with the direction 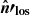 . Following Ginzburg & Syrovatskii (1965), the synchrotron emissivity in units of [erg cm−3 s−1 Hz−1 str−1] is
. Following Ginzburg & Syrovatskii (1965), the synchrotron emissivity in units of [erg cm−3 s−1 Hz−1 str−1] is
where all primed quantities are evaluated in the local comoving frame, and where 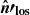 is the unit vector in the direction of the line of sight in the comoving frame and F(ξ) is a Bessel function integral given by
is the unit vector in the direction of the line of sight in the comoving frame and F(ξ) is a Bessel function integral given by
where
where 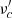 is defined as the critical frequency at which the emission peaks. We note that strictly speaking only those particles with a pitch angle coinciding with the angle between B′ and
is defined as the critical frequency at which the emission peaks. We note that strictly speaking only those particles with a pitch angle coinciding with the angle between B′ and 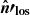 contribute to the emission along the line of sight in Eq. (27). Nevertheless, in this work, we assume an isotropic distribution of pitch angles.
contribute to the emission along the line of sight in Eq. (27). Nevertheless, in this work, we assume an isotropic distribution of pitch angles.
Once the synchrotron emissivity is interpolated back onto the Eulerian grid, the specific intensity maps can then be obtained by integrating along a line of sight as
in units of [erg cm−2 s−1 Hz−1 str−1]. The observed flux is estimated assuming a Gaussian beam with θ width. The surface brightness maps in units of [mJy beam−1] are obtained computing Sν ≈ Iνθ2, where θ2 = πθ1θ2/(4ln(2)) is the beam area of the telescope. Finally, the integrated spectra (or net flux) can be obtained by integrating the specific intensity Iν over the area covered by the source in the plane of the sky, that is
in units of [erg s−1 Hz−1 str−1].
4. Results
4.1. The shock front
We start by displaying the three-dimensional (3D) renderings of the synchrotron emissivity produced by an initial ℳi = 3 shock at t = 184.7 Myr in the fresh-injection and re-acceleration models at low (650 MHz) and very high (18.6 GHz) frequencies in Fig. 3. The turbulent pre-shock ICM (see Sect. 2.1) naturally induces fluctuations at the shock front as it is propagating through the simulation box. These fluctuations determine the variation in the energy spectrum of Lagrangian particles at the shock. However, as illustrated in Fig. 3, it is obvious that thermal and fossil electrons injected into DSA yield different fluctuations. This disparity will be thoroughly examined in the subsequent sections of this paper.
 |
Fig. 3. Volume rendering of the synchrotron emissivity rendering in code units at 650 MHz (left) and 18.6 GHz (right) for the fresh-injection model (top row: case ℳcr = 1; see Sect. 4.2) and the re-acceleration model (bottom row: case s = 2.25). All renderings correspond to the ℳi = 3 case at t = 184.7 Myr. |
It would be instructive to first show how some fluid variables change at the shocked cells as function of time. In the upper row of Fig. 4, we show the evolution of the shock’s Mach number, ℳ, of the shock cells in the 3D computational volume for the three different initial Mach numbers of the shock, ℳi. This evolution is mainly determined by (1) the pre-shock rms Mach number and (2) ℳi. We find that higher ℳi’s produce more extended tails and higher standard deviations in the PDF. In particular, an increment of 0.5 in ℳi results in an increment of ∼0.05 in the standard deviation σℳ (see lower row of Fig. 4).
 |
Fig. 4. 3D Mach number distribution at the shock cells at selected simulation times (top). Standard deviation of the Mach number PDF as function of time (bottom). Each column corresponds to the different initial Mach number of the shock. For the 2D Mach number distribution we used different weights for the projection (see legend). Note: here, Iν is taken from the fresh-injection model (case ℳcr = 1; see Sect. 4.2). See Appendix C for a comparison between weights corresponding to the emission coming from the fresh-injection and re-acceleration models. |
The Mach number we infer from observations is inherently influenced by the projection of phenomena onto the plane of the sky. Consequently, we present the statistical distribution of the projected Mach number in the lower row of Fig. 4. This perspective provides a supplementary understanding of how projected characteristics differ from the actual 3D data. We define the Mach number on the two-dimensional (2D) X − Y plane projected along the Z-axis as
where w is a selected weight. We note here that the projected Mach number weighted with the emission is not the same as the Mach number that can be obtained from radio observations. We recall that the Mach number, as determined from radio observations, relies on a two-step process. Initially, the spectral index of the radio spectra is computed across multiple frequencies. Subsequently, this spectral index is employed to infer the Mach number, utilizing DSA. (see Eq. (28) of Domínguez-Fernández et al. 2020).
As can be seen from the lower row of Fig. 4, the projected Mach number weighted with the radio emission could give rise to a large discrepancy when compared to the projected Mach number weighted with other fluid quantities such as the density or the magnetic field. We see that the standard deviation, σℳ, and mean,  , are larger, if the Mach number is weighted with the radio emission. On the other hand, we do not find significant differences in the projected Mach number when radio emissions at different frequencies are used as weights. Nevertheless, as we will show in the following sections, there is a varying “degree of patchiness” in radio relics with frequency. In Appendix C we additionally show that the σℳ obtained weighting with the emission from the fresh injection model is larger than the σℳ where the radio emission from the re-acceleration model is used. This happens due to the different degrees of patchiness achieved in both the fresh injection and re-acceleration models. We expect that this effect as observed in surface brightness maps can introduce a bias between the real and radio inferred Mach numbers. However, we leave this type of analysis relating the current work to observations to a future work.
, are larger, if the Mach number is weighted with the radio emission. On the other hand, we do not find significant differences in the projected Mach number when radio emissions at different frequencies are used as weights. Nevertheless, as we will show in the following sections, there is a varying “degree of patchiness” in radio relics with frequency. In Appendix C we additionally show that the σℳ obtained weighting with the emission from the fresh injection model is larger than the σℳ where the radio emission from the re-acceleration model is used. This happens due to the different degrees of patchiness achieved in both the fresh injection and re-acceleration models. We expect that this effect as observed in surface brightness maps can introduce a bias between the real and radio inferred Mach numbers. However, we leave this type of analysis relating the current work to observations to a future work.
4.2. Surface brightness maps
We start by showing the normalized surface brightness maps for selected cases of the simulations described in Table 1 at 150 MHz, 1.5 GHz, 14.25 GHz, and 18.6 GHz at two different time steps. In this section, we only show the surface brightness maps corresponding to the ℳi = 3 case, while we recall that our general results also include the ℳi = 2 and ℳi = 2.5 cases. A ℳ ∼ 3 shock should be the most representative example because several radio relics observations have reported similar Mach number values inferred either from radio or X-ray.
In Figs. 5 and A.1, we show the corresponding maps for the fresh-injection model with the two critical Mach numbers studied, namely ℳcr = 1 (left-hand-side) and ℳcr = 2.3 (right-hand-side) in the first row. In the second row, we show the corresponding surface brightness maps for the re-acceleration model assuming a fossil electron population represented by a Dirac delta fpre, 1 (see Eq. (20a)). On the left-hand-side, we show the maps where γcut = 102 and on the right-hand-side, those where γcut = 103. Finally, on the third row, we show the maps corresponding to the fossil electron population that is represented by a power law (fpre, 2 (see Eq. (20b)). On the left-hand-side, we show the case where the parameter s = 2.25 is assumed, while on the right-hand-side, we show the s = 3 case.
 |
Fig. 5. Normalized surface brightness maps of the shock front for the ℳi = 3 case in the fresh-injection model (first row) and re-acceleration model with a Dirac Delta (second row) and a power-law (third row) fossil populations. Each sub-panel shows four different frequencies, namely 150 MHz, 1.5 GHz, 14.25 GHz, and 18.6 GHz. The first (last) four columns correspond to ℳcr = 1 (ℳcr = 2.3), γcut = 102 (γcut = 103), and s = 2.25 (s = 3), respectively. The time-step selected of the simulation is 120.7 Myr (see the top corner of each sub-panel). |
Figure 5 illustrates the early propagation of the radio shock front at t = 102.7 Myr. The shock front is located at x/x0 ∼ 0.5 (see also Fig. 2 for a reference; note that here x0 = 100 kpc) and the extent of the downstream region is ∼30 kpc at 150 MHz. At this stage, we can already observe significant differences comparing the four frequencies, namely, 150 MHz, 1.5 GHz, 14.25 GHz, and 18.6 GHz, for each model considered. From this visualization, we can argue that different observing frequencies may result in different pictures for the radio substructures generated at the shock front. In particular, we observe that both models, namely, the fresh-injection and re-acceleration models, can produce patchiness along the radio shock front. However, as it can be seen from Fig. 5, the fresh-injection model produces more patchy substructures than the re-acceleration model.
It shall be noted that the shock front has a “distribution of Mach numbers”, and it is the Mach numbers distribution that defines the observed morphology in the radio emission; the radio substructures are fully defined by the initial mean strength of the shock in our simulations, hence the mean of the Mach number distribution, namely, 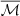 , along with the spread of the Mach number distribution, σℳ (see Sect. 4.1). As we further discuss in Sect. 4.3, the generation of patchy radio structures is more pronounced if the Mach number distribution at the shock front contains a large amount of ℳ ≲ 2.5. This remains true for both the fresh-injection and re-acceleration models. However, the CRe energy spectrum has a different dependency on the Mach number values in the two models, which leads to slightly different radio substructures.
, along with the spread of the Mach number distribution, σℳ (see Sect. 4.1). As we further discuss in Sect. 4.3, the generation of patchy radio structures is more pronounced if the Mach number distribution at the shock front contains a large amount of ℳ ≲ 2.5. This remains true for both the fresh-injection and re-acceleration models. However, the CRe energy spectrum has a different dependency on the Mach number values in the two models, which leads to slightly different radio substructures.
We present identical surface brightness maps to those in Fig. 5, albeit for a different snapshot, in Appendix A. In Fig. A.1, we show the radio shock at t = 184.7 Myr. In this case, the shock front is located almost at the right end of region III at x/x0 ∼ 1.75 and the extent of the downstream region is ∼80 kpc at 150 MHz. Similar to Fig. 5, the Mach number distribution of the shock surface determines the radio substructures generated at the shock front. Further downstream, these substructures are additionally defined by the mixing of emission with different spectral ages. In the following, we use the surface brightness maps from Figs. 5 and A.1 to examine two limiting cases of radio shocks in the ICM. These cases serve as comparative benchmarks, focusing on two distinct downstream widths, with the larger width being most representative of a typical radio relic scenario. We also refer to Appendix A for additional information on the simulated radio emission such as spectral index maps and profiles.
4.3. Degree of patchiness
A good first order approximation to quantify the amount of substructure in radio relics is by computing the relative surface brightness fluctuations or perturbations,
where 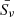 is the mean surface brightness of the selected area. In this work, we use δSν to define the “degree of patchiness or substructure” in radio relics. Within this definition, radio relics will have a higher degree of patchiness or substructure if the spread of δSν is larger. We calculated δSν within a spatial domain of 35 kpc × 200 kpc × 200 kpc at t = 102.7 Myr and extended it to 85 kpc × 200 kpc × 200 kpc at t = 184.7 Myr. With this selection we ensure a through coverage of the downstream region in both snapshots.
is the mean surface brightness of the selected area. In this work, we use δSν to define the “degree of patchiness or substructure” in radio relics. Within this definition, radio relics will have a higher degree of patchiness or substructure if the spread of δSν is larger. We calculated δSν within a spatial domain of 35 kpc × 200 kpc × 200 kpc at t = 102.7 Myr and extended it to 85 kpc × 200 kpc × 200 kpc at t = 184.7 Myr. With this selection we ensure a through coverage of the downstream region in both snapshots.
In Fig. 6 we show the δSν + 1 distributions at t = 184.7 Myr for all the 6 models and 6 frequencies: 150 MHz, 650 MHz, 1.5 GHz, 6.5 GHz, 14.25 GHz and 18.6 GHz. We compare each distribution corresponding to a different frequency with the distribution at the lowest frequency, namely, 150 MHz. In all the models we find that the higher the frequency, the larger the spread of δSν. In other words, the radio shock front has a higher degree of patchiness or substructure at higher frequencies.
 |
Fig. 6. Phase plots of the |
As mentioned before, the substructure will be defined by the Mach distribution at the shock front which in turn depends on the pre-shock medium. Hence, a large standard deviation of δSν, σδSν, is a consequence of a large spread of the Mach number distribution, σℳ.
In Fig. 7 we plot σδSν as function of frequency for all the studied models. We considered again two simulation time-steps, t = 102.7 Myr and t = 184.7 Myr. This figure summarizes all the information from all our models, and we discuss the main findings in the following:
 |
Fig. 7. Standard deviation of the δSν distribution for all our models at all frequencies. Two simulation time-steps are shown: t = 102.7 Myr (higher transparency) and t = 184.7 Myr (no transparency). The first two panels correspond to the fresh injection model (ℳcr = 1 and ℳcr = 2.3 parameters), the third and fourth panels refer to the re-acceleration model, assuming a Dirac Delta pre-existing distribution function (γcut = 102 and γcut = 103 parameters), and the fifth and sixth panels refer to the re-acceleration model assuming a power-law pre-existing distribution function (s = 2.25 and s = 3 parameters). |
(i) Low and high frequencies. A visual inspection of Figs. 5–A.1 reveals a patchier emission at high frequencies compared to lower frequencies. We observe almost no distinction between the surface brightness maps at 14.25 GHz and 18.6 GHz in all our models. This is confirmed in the phase-plots shown in Fig. 6 where we can see that δSν + 1 reaches the highest values at the highest frequencies for both the fresh-injection and re-acceleration models. The largest discrepancies between high (18.6 GHz) and low (150 MHz) frequencies can be more clearly seen in Fig. 7 where the standard deviation of the corresponding distribution can be as large as ∼7 times the standard deviation of the 150 MHz distribution in the fresh-injection model. The same trend follows in the re-acceleration models except that here, the standard deviation of the distribution can be as large as ∼2.5 and ∼2 times the standard deviation of the 150 MHz distributions, respectively for the Dirac delta and power-law fossil electron populations.
(ii) Initial Mach number. The larger ℳi, the less patchy the radio emission. This is expected as a stronger shock can more easily compress and amplify the magnetic field along the shock. This is again reflected in Figs. 6 and 7, where the ℳi = 3 case leads to the lowest values of δSν + 1 and therefore, the lowest values of σδSν. As mentioned in the point above, we observe increasing trends of the standard deviation with the frequency in Fig. 7 for the three ℳi cases. However, the trend can especially steepen for the ℳi = 2 case in the fresh-injection model. This happens because in the fresh-injection model, the differences between the spectral normalization factors corresponding to ℳ ∼ 2 and ℳ ≳ 3 regions can be very large (see Appendix C). Since in this model, the emission will ultimately be biased towards regions where there is higher compression (higher Mach number), then we expect larger variations/fluctuations in the surface brightness maps when the distribution of Mach numbers at the shock front contains a significant amount of low Mach numbers (see first row of Fig. 4 in Sect. 4.1). Finally, we note that the re-acceleration models in the ℳi = 2.5 and ℳi = 3 cases can reproduce similar degrees of patchiness (see last four panels of Fig. 7).
(iii) Fresh-injection model (Critical Mach number). At any ℳi it will be hard (or almost impossible) to visually distinguish only from surface brightness variations different ℳcr models. In the ℳi = 2.5 and ℳi = 3 cases, there is no significant distinction between a model forbidding an acceleration below ℳcr = 1 or ℳcr = 2.3 at all frequencies (see Fig. 5). This is quantitatively better observed in the top row of Fig. 6, where the δSν + 1 values are comparable in both the ℳcr = 1 and ℳcr = 2.3 cases. This changes significantly in the ℳi = 2 case where we see the highest values of the standard deviation in comparison to the stronger shocks with ℳi = 2.5 and ℳi = 3 (see Fig. 7). In fact, in this case we observe the largest discrepancies between the standard deviation of the ℳcr = 1 and ℳcr = 2.3 cases, with the latter yielding higher values. This last result happens due to the fact that only a low percentage of the Mach number distribution at the shock front (see left panel of Fig. 4) is contributing to the emission, namely, the high-end tail of the distribution. Despite the different ℳcr, the discrepancies in the surface brightness are not very pronounced, primarily because the radio emissivity is known to be biased towards higher Mach numbers in the fresh-injection model (see, e.g., Roh et al. 2019; Domínguez-Fernández et al. 2020; Wittor et al. 2021). Therefore, we conclude that the ℳcr parameter has a minor impact in our results.
(iv) Re-acceleration model (Energy of fossil electrons γcut). The smaller the γcut, the larger the fluctuations or the more patchy the substructure will look like. Indeed, the two columns of the middle row in Fig. 7 show that the δSν + 1 values are higher in the γcut = 102 case by less than a factor 2 when compared to the γcut = 103 case. These differences are naturally subtle. Therefore, we conclude that in a re-acceleration model with a fossil population characterized by a Dirac delta, the parameter γcut does not impact our main two results, namely, the higher the frequency and/or the lower the mean strength of the shock (or the parameter ℳi in this study), the larger the surface brightness fluctuations.
(v) Re-acceleration model (Energy spectral index s). The steeper the power-law fossil spectrum is (larger value of s), the larger the fluctuations or the more patchy the substructure will look like. Similar to the other re-acceleration model where we assumed the fossil electron population is characterized by a Dirac delta function, the differences in the δSν + 1 values between the s = 2.25 and s = 3 cases are subtle with less than a factor 2 difference in their values. Yet here, the nature of these differences lies in: (1) the proportion of particles at the shock front which would acquire a re-acceleration spectrum with an s or p power-law index and (2) the normalization factor. For example, for the s = 2.25 case, spectra with index r ∼ s will mainly dominate the emission, whereas for the s = 3 case, spectra with index r ∼ p will dominate. On the other hand, the normalization factors in the s = 2.25 case are larger for the spectra with index r ∼ p while in the s = 3 case, the spectra with index r ∼ s have larger normalization factors.
(vi) Evolution of the shock. In general, the degree of surface brightness fluctuations at the shock front is not expected to be global and will be susceptible to the local environment within the galaxy cluster. For this reason, we analyzed two different time-steps of our simulations. The net result is drawn in Fig. 7 where we show σδSν as function of frequency at t = 120.7 Myr (high transparency) and t = 184.7 Myr (no transparency). At t = 184.7 Myr the shock entails more surface brightness fluctuations and therefore, larger values of the σδSν. This is observed for both the fresh-injection and re-acceleration models. Past studies of shocks in simulated galaxy clusters show that relic shocks should have a broad Mach number distribution (see Ryu et al. 2003). Therefore, we consider our results from this time-step to be a more realistic representation of how can surface brightness fluctuations vary with frequency in different models.
We would like to emphasize that (as mentioned in Sect. 1, shocks with ℳi = 2 are not theoretically expected to be sites of DSA, given that the critical Mach number is typically found to be around ℳcr ∼ 2.3. However, observations often infer Mach numbers using simplified assumptions from both X-ray and radio data, suggest the involvement of such weak shocks, or even weaker, in the DSA process. Our results intriguingly suggest that if this is indeed the case, and the fresh injection model is at play, significant differences in radio morphologies between low and high frequencies should be observable. This is clearly illustrated in the first two panels of Fig. 7, where we observe substantial disparities in σδSν.
Finally, in the context of the fresh injection model, it is widely acknowledged in the literature that η(ℳ) is an increasing function with the Mach number (Kang et al. 2007; Kang & Ryu 2013; Caprioli & Spitkovsky 2014; Ryu et al. 2019). In Appendix B, we additionally explore various toy η(ℳ) models to investigate whether the already found trends can be altered. Physically, it is impossible for the efficiency to increase with weaker shocks, which means η(ℳ) should be a decreasing function with the Mach number. Therefore, in Appendix B, our analysis is restricted to hypothetical models featuring efficiency functions that display more pronounced increases than the currently accepted theoretical models.
We show that steeper models, which assign greater weight to larger Mach numbers, result in a higher degree of patchiness or substructure. Across most of our models, we observe that σδSν increases with the observing frequency, consistent with the findings discussed in this section. However, one exception is our steepest η(ℳ) model, which exhibits minimal change in σδSν when the observing frequency is increased. Nonetheless, both high and low frequencies would render a radio relic notably patchy or with a high degree of patchiness.
In summary, our conclusions regarding the fresh injection model are twofold: (1) steeper η(ℳ) models consistently lead to a higher degree of patchiness and (2) increasing η(ℳ) functions generally reproduce the previously discussed trend, wherein a radio relic appears patchier at higher frequencies. This is in alignment with the results presented in this section.
4.4. Beam and resolution effects
So far, we have shown that under the current accepted theories of particle acceleration, radio relics should appear to be patchier at very high frequencies. While this is a general consequence of the underlying physical processes along with the observing frequency, in this section, we focus on how much the surface brightness variations can change if one takes into account different beam resolutions. At the end of this section, we also discuss the role of numerical resolution.
The linear size of radio relics is of the order of up to a few Mpc. Due to our periodic boundary conditions in the y and z dimensions (as described in Sect. 2.2) and the planar nature of the propagating shock, we can confidently stack our surface brightness maps to mock a larger radio shock without any loss of generality. We stacked our surface brightness maps in the x-direction to mock a 3 Mpc radio shock; that is, we stacked 15 surface brightness maps each with an extension of 200 kpc in the y-direction (see Fig. 5). Taking as an example the CIZA J2242.8+5301 cluster at z = 0.1921 (see Table 2 for the references on different radio telescopes), we considered two beam sizes, 5″ × 5″ and 20″ × 20″. We stress that we do not aim to make a one-to-one comparison with any particular relic. Therefore, the FHWM values in Table 2 are used only as representative values.
Restoring beam sizes assumed for smoothing the emission maps at each observing frequency.
In Fig. 8, we show the standard deviation of the δSν distribution normalized by that at 150 MHz at the shock-front for all our models at all frequencies. We also show the effects of the 5″ × 5″ (dot-dashed line) and 20″ × 20″ (dashed line) beam sizes. As expected, the larger the beam size, the less surface brightness fluctuations are seen along the shock front. We also observe that the trend of increased fluctuations or a patchier radio relic with higher frequencies diminishes considerably when we consider a beam size of 20″ × 20″. In particular, if the shock front is composed of a Mach number distribution that is not broad enough, for instance, when a shock in its early propagation, the relic should be observed with the same degree of patchiness at low and high frequencies. This can be clearly observed in the second and fourth columns of Fig. 8 where the dashed lines denote the results of our analysis with a beam size of 20″ × 20″. Moreover, we note that even if the Mach number distribution is broad as expected from theory, a 20″ × 20″ beam size would not be enough to capture the underlying surface brightness differences at different frequencies. The panorama is slightly better for a 5″ × 5″ beam size, where the trend of having a patchier radio relic as frequency increases could be recovered. This suggests that the shock front should comprise a Mach distribution function with a spread σℳ ≳ 0.3 − 0.4 (see Fig. 4) for us to be able to observe differences between low and high frequencies.
 |
Fig. 8. Standard deviation of the δSν distribution normalized by that at 150 MHz at the shock-front at 184.7 Myr for all our models at all frequencies. The top, middle and bottom rows correspond to the fresh injection model, the re-acceleration model assuming a Dirac Delta pre-existing distribution function and the re-acceleration model assuming a power-law pre-existing distribution function, respectively. The first and third columns show the results from the original maps and the second and fourth columns show the results of the map smoothed with 5″ × 5″ (dot-dashed) and 20″ × 20″ (dashed) beam sizes. |
Next, we plot in Fig. 9 additional statistics of the δSν distribution: skewness (denoted as g) and kurtosis (denoted as G). We use the SciPy package (Virtanen et al. 2020) to compute both. The sample skewness and kurtosis are defined according the Fisher’s definition as
 |
Fig. 9. Skewness (upper row) and kurtosis (lower row) of the δSν/distribution for all our models at all frequencies. We only show the ℳi = 2 and ℳi = 3 cases. The upper solid lines correspond to the unsmoothed data and the dot-dashed and dashed lines correspond to the data smoothed with the 5″ × 5″ and 20″ × 20″ beam sizes, respectively. |
and
respectively, where
is the biased sample ith central moment, and 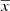 is the sample mean. These higher order statistics show that the higher the frequency the more the δSν distribution is asymmetric and heavy-tailed. In particular, a large kurtosis signals non-Gaussianity and super-Gaussian tails on the PDF. This trend is persistent both in the fresh-injection model and the re-acceleration model with power-law fossil electrons. Nevertheless, it is easy to see that the fresh-injection model leads to larger values of the kurtosis and skewness than the re-acceleration model. A larger difference between these two models can be better seen at lower ℳi (see, e.g., the ℳi = 2 case in Fig. 9). As expected, a larger beam size smooths out the radio substructure leading to lower skewness and kurtosis values, namely, the δSν distribution approaches a normal distribution. Finally, we note that in all cases, the distribution is positively skewed.
is the sample mean. These higher order statistics show that the higher the frequency the more the δSν distribution is asymmetric and heavy-tailed. In particular, a large kurtosis signals non-Gaussianity and super-Gaussian tails on the PDF. This trend is persistent both in the fresh-injection model and the re-acceleration model with power-law fossil electrons. Nevertheless, it is easy to see that the fresh-injection model leads to larger values of the kurtosis and skewness than the re-acceleration model. A larger difference between these two models can be better seen at lower ℳi (see, e.g., the ℳi = 2 case in Fig. 9). As expected, a larger beam size smooths out the radio substructure leading to lower skewness and kurtosis values, namely, the δSν distribution approaches a normal distribution. Finally, we note that in all cases, the distribution is positively skewed.
All these results imply the same findings as described above: (1) the higher the frequency, the larger the degree of patchiness, (2) the larger the initial Mach number of the shock, the less patchy the radio emission and (3) the larger the beam size, the smaller the degree of patchiness. Therefore, the measure of σδSν at different frequencies would suffice to probe the degree of patchiness of radio relics. As such, we propose it as a potential tool for extracting merger shock properties as well as information about particle acceleration processes at shocks.
Finally, we investigate the influence of numerical resolution on our findings. We conducted simulations at three different resolutions: 128 × 64 × 64 cells, 256 × 128 × 128 cells, and 512 × 256 × 256 cells, all for the fresh injection model under the conditions of ℳi = 3 and ℳcr = 1. It is important to note that we did not run simulations at higher resolutions across all our models due to the significant computational demands, particularly when dealing with the energy spectra of 25 165 824 Lagrangian particles in conjunction with the Eulerian code. However, as we go on to demonstrate below, doubling the resolution from our current setting has a minimal impact on our primary outcomes. We also refer to Appendix C of Domínguez-Fernández et al. (2020) for a detailed discussion of the differences between high and medium-resolution runs.
In the left panel of Fig. 10, we show that differences among the three different resolutions are only discernible at high frequencies. At 18.6 GHz, the lowest resolution yields a percentage difference in σδSν/σδS150 compared to the highest resolution of approximately 16%. However, doubling the resolution results in a modest enhancement of approximately 8%. This finding affirms that our chosen resolution is well-suited for the objectives of this study. In the right panel of Fig. 10, we present the corresponding trends obtained from smoothing the surface brightness maps for completeness. We recall that this analysis was analysis was done using also a stacked image, which incorporates the surface brightness map featuring a 3 Mpc radio shock.
 |
Fig. 10. Standard deviation of the δSν distribution normalized by that at 150 MHz at the shock-front for the ℳi = 3 case at all frequencies for the ℳcr = 1 fresh injection model at t = 187.4 Myr. We show the result for three different numerical resolutions. The first column shows the results from the original maps and the second column the results from the smoothed maps, similarly to Fig. 8. |
5. Summary and conclusions
In this work, we aimed at studying the fluctuations of radio surface brightness or what we numerically define as a patchiness among radio relics, at high (≳10 GHz) and low (≲5–6 GHz) frequencies by assuming the two current accepted theories of CR acceleration that we have at hand: (1) the fresh injection model, in which electrons from the thermal pool are injected into the DSA, and (2) the re-acceleration model, in which already mildly relativistic electrons are injected into the DSA. We have studied shock waves with ℳ = 2, 2.5, 3 propagating through a magnetized medium with decaying solenoidal subsonic turbulence representing a small fraction of the ICM. We performed hybrid simulations where the MHD Eulerian grid represents the thermal fluid, while Lagrangian particles represent CR electrons. The CR electrons are injected at the shock discontinuity assuming DSA and evolved according to a simplified cosmic-ray equation including adiabatic, synchrotron and Inverse Compton losses.
The premise of our work is simple, demonstrating that in the presence of pre-shock fluctuations in the ICM, the shock front part of a radio relic is bound to have substructure both at low and high frequencies. However, we find that the radio substructures differ under the assumption of the fresh injection or re-acceleration models as a consequence of the underlying differences between the two physical processes.
Our findings can be summarized as follows:
-
(i)
We find an increasing degree of patchiness with frequency, both in the fresh injection and re-acceleration models. We suggest that quantifying the degree of patchiness with the standard deviation of the relative surface brightness fluctuations, σδSν, suffices to probe this trend across different frequencies. We find that in the fresh injection model, the standard deviation at 18.6 GHz is ∼7 times larger than that at 150 MHz. In contrast, in the re-acceleration models, the standard deviation at 18.6 GHz is ∼2–2.5 times larger than at 150 MHz. Therefore, the re-acceleration model produces smoother radio structures compared to the fresh injection model.
-
(ii)
The Mach number distribution of the shock front plays the main role in the observed surface brightness substructure. We find that the shock front should comprise a Mach number distribution function with a spread σℳ ≳ 0.3 − 0.4 to enable the observation of differences between low and high frequencies at a 5″ × 5″ resolution.
-
(iii)
We find that the larger the mean Mach number of the shock (or ℳi), the less patchy the radio emission. Patchiness arises if the distribution of Mach number characterizing the shock front encompasses a large percentage of low Mach numbers (ℳ ≲ 2.5).
-
(iv)
The projected Mach number weighted with the synchrotron emissivity shows the largest discrepancies with respect to other weights such as the density, temperature or magnetic field. This is particularly shown in the standard deviation of the projected Mach number. This projection effect adds to the problem where larger Mach number values are inferred from radio compared to those inferred from X-ray.
-
(v)
A steeper η(ℳ) model leads to a higher degree of patchiness or more substructure in the radio emission.
Our study shows that comparing the degree of patchiness within radio relics at across a broad range of frequencies allows us to retrieve information about particle acceleration processes at shocks in the ICM. For instance, we have explored its potential to unveil details about the dispersion of the Mach distribution function and the steepness of the acceleration efficiency function. While a more extensive parameter study, incorporating various pre-shock turbulent conditions, is required for formulating a definitive formula for the former, we propose that analyzing the degree of patchiness represents a promising, novel, and robust addition to the traditional observational techniques.
We have shown that, in general, the fresh-injection model can lead to very patchy radio relics while the re-acceleration model leads to smoother ones. Nevertheless, it shall be noted that our modeling is based on a uniformly spaced distribution of fossil electrons. There are few observational examples in which CRe may spread-out up to very large scales in the ICM (see, e.g., Brienza et al. 2021, 2022, for observations showing the late evolution of multiple generations of CRe associated to active-galactic-nuclei bubbles). Yet, this evidence is showing us how complicated and unlikely it would be to get a spatially uniform fossil population such that it reproduces the whole extend of Mpc relics. While this would pose a limitation of our work, this essentially means that it would also be difficult to numerically reproduce very smooth radio relics at low frequencies with the re-acceleration model.
Additionally, we did not consider an acceleration efficiency depending on θB in our fresh-injection model. While this dependency has been considered in other works (see, e.g., Vazza et al. 2016; Pais et al. 2018; Banfi et al. 2020), we restricted ourselves to study only the Mach number dependency because adding another degree of freedom to the acceleration efficiency will further narrow down the locations of emission. As a consequence, this will lead to a more pronounced patchiness in the radio emission along the shock front, ultimately resulting in a heightened degree of patchiness in radio relics. Hence, we anticipate that this variable will not only leave our main result unaffected, but also reinforce it.
It is important to highlight that the main focus of this paper has been to study the physical processes accountable for generating patchiness in radio relics. On top of that, observational factors like sensitivity, resolution image noise, and so on, can influence the perceived surface brightness morphology. Such morphological differences caused by instrumental effects differ conceptually from the physical mechanisms we have explored in this study and therefore, should be studied carefully in future work.
Recent works have started to show high quality data where more statistics beyond integrated quantities are being taken into account (see, e.g., Rajpurohit et al. 2018, 2020, 2021, 2022). While at very high frequencies this may pose more observational challenges due to a limited resolution, conducting similar studies at both low and high frequencies could provide a more robust constraint on radio fluctuations along the shock front. This approach will help us determine whether a frequency-dependent patchiness trend, specifically an increasing σδSν with frequency, is consistently observable in various radio relics. In a future work, we will study the instrumental effects and make a careful comparison with a selection of observations.
The emissivities in the observer frame are obtained by applying the appropriate transformations: 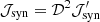 , where 𝒟 is the Doppler factor. Note: for the non-relativistic case, 𝒟 ≈ 1. We refer to Sect. 3 of Vaidya et al. (2018) for more details.
, where 𝒟 is the Doppler factor. Note: for the non-relativistic case, 𝒟 ≈ 1. We refer to Sect. 3 of Vaidya et al. (2018) for more details.
Acknowledgments
We gratefully acknowledge the PLUTO development group with special recognition to our collaborators A. Mignone and D. Mukherjee who provided the particle module of the PLUTO code and extremely helpful comments. The simulations presented in this work made use of computational resources on the JUWELS cluster at the Juelich Supercomputing Centre (JSC), under project No. 24944 CRAMMAG-OUT and CRAMMAG-OUT-2 with P. Domínguez-Fernández as principal investigator. P. Domínguez-Fernández acknowledges the Future Faculty Leaders Fellowship at the Center for Astrophysics, Harvard-Smithsonian, and the financial support from the European Union’s Horizon 2020 programme under the ERC Starting Grant “MAGCOW”, No. 714196 with F. Vazza as principal investigator. All authors acknowledge the support of the National Research Foundation (NRF) of Korea through grant Nos. 2020R1A2C2102800 and 2023R1A2C1003131. We acknowledge useful scientific discussions with R. J. van Weeren, M. Johnston-Hollitt and K. Rajpurohit during the initial phase of this study. We would like to extend our appreciation to P. Nulsen and A. Stroe for their insightful contributions during the last phase of this study. Finally, we acknowledge our anonymous reviewer for helpful comments on the first version of this paper. Software: The source codes used for the simulations of this study, FLASH (Fryxell et al. 2000; Calder et al. 2002) and PLUTO (Mignone et al. 2007) are freely available on https://flash.rochester.edu/site/ and http://plutocode.ph.unito.it. The main tools for our analysis are: Python (Van Rossum & Drake 1995), SciPy (Virtanen et al. 2020) and IDL (Landsman 1993).
References
- Akamatsu, H., van Weeren, R. J., Ogrean, G. A., et al. 2015, A&A, 582, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banfi, S., Vazza, F., & Wittor, D. 2020, MNRAS, 496, 3648 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Böss, L. M., Steinwandel, U. P., Dolag, K., & Lesch, H. 2023, MNRAS, 519, 548 [Google Scholar]
- Botteon, A., Brunetti, G., Ryu, D., & Roh, S. 2020, A&A, 634, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brienza, M., Shimwell, T. W., de Gasperin, F., et al. 2021, Nat. Astron., 5, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Brienza, M., Lovisari, L., Rajpurohit, K., et al. 2022, A&A, 661, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brüggen, M., Bykov, A., Ryu, D., & Röttgering, H. 2012, Space Sci. Rev., 166, 187 [Google Scholar]
- Bykov, A. M., Kaastra, J. S., Brüggen, M., et al. 2019, Space Sci. Rev., 215, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Calder, A. C., Fryxell, B., Plewa, T., et al. 2002, ApJS, 143, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., & Spitkovsky, A. 2014, ApJ, 783, 91 [CrossRef] [Google Scholar]
- Chandran, B. D. G. 2005, Phys. Rev. Lett., 95, 265004 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, T. E., & Ensslin, T. A. 2006, AJ, 131, 2900 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperin, F., Rudnick, L., Finoguenov, A., et al. 2022, A&A, 659, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dedner, A., Kemm, F., Kröner, D., et al. 2002, J. Comput. Phys., 175, 645 [Google Scholar]
- Di Gennaro, G., van Weeren, R. J., Hoeft, M., et al. 2018, ApJ, 865, 24 [Google Scholar]
- Domínguez-Fernández, P., Brüggen, M., Vazza, F., et al. 2020, MNRAS, 500, 795 [Google Scholar]
- Domínguez-Fernández, P., Brüggen, M., Vazza, F., et al. 2021, MNRAS, 507, 2714 [Google Scholar]
- Drury, L. O. 1983, Rep. Progr. Phys., 46, 973 [Google Scholar]
- Eswaran, V., & Pope, S. B. 1988, Phys. Fluids, 31, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M. M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1965, ARA&A, 3, 297 [Google Scholar]
- Ha, J.-H., Kim, S., Ryu, D., & Kang, H. 2021, ApJ, 915, 18 [CrossRef] [Google Scholar]
- Ha, J.-H., Ryu, D., Kang, H., & Kim, S. 2022, ApJ, 925, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, S. E., Kang, H., & Ryu, D. 2015, ApJ, 812, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, D. N., Shimwell, T. W., Stroe, A., et al. 2017, MNRAS, 471, 1107 [Google Scholar]
- Kang, H. 2020, J. Korean Astron. Soc., 53, 59 [NASA ADS] [Google Scholar]
- Kang, H., & Ryu, D. 2011, ApJ, 734, 18 [Google Scholar]
- Kang, H., & Ryu, D. 2013, ApJ, 764, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., Ryu, D., Cen, R., & Ostriker, J. P. 2007, ApJ, 669, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., Ryu, D., & Jones, T. W. 2012, ApJ, 756, 97 [Google Scholar]
- Kang, H., Ryu, D., & Ha, J.-H. 2019, ApJ, 876, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Keshet, U., & Waxman, E. 2005, Phys. Rev. Lett., 94, 111102 [NASA ADS] [CrossRef] [Google Scholar]
- Kierdorf, M., Beck, R., Hoeft, M., et al. 2017, A&A, 600, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landsman, W. B. 1993, ASP Conf. Ser., 52, 246 [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1987, in Fluid Mechanics, eds. L. D. Landau, & E. M. Lifshitz, 2nd Ed. (Butterworth-Heinemann), Course of Theoretical Physics, 6 [Google Scholar]
- Lee, D., Deane, A. E., & Federrath, C. 2009, ASP Conf. Ser., 406, 243 [NASA ADS] [Google Scholar]
- Loi, F., Murgia, M., Govoni, F., et al. 2017, MNRAS, 472, 3605 [NASA ADS] [CrossRef] [Google Scholar]
- Loi, F., Murgia, M., Vacca, V., et al. 2020, MNRAS, 498, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Nuza, S. E., Gelszinnis, J., Hoeft, M., & Yepes, G. 2017, MNRAS, 470, 240 [Google Scholar]
- Owen, F. N., Rudnick, L., Eilek, J., et al. 2014, ApJ, 794, 24 [Google Scholar]
- Pais, M., Pfrommer, C., Ehlert, K., & Pakmor, R. 2018, MNRAS, 478, 5278 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., Oh, S. P., & Pfrommer, C. 2013, MNRAS, 435, 1061 [Google Scholar]
- Rajpurohit, K., Hoeft, M., van Weeren, R. J., et al. 2018, ApJ, 852, 65 [Google Scholar]
- Rajpurohit, K., Hoeft, M., Vazza, F., et al. 2020, A&A, 636, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rajpurohit, K., Wittor, D., van Weeren, R. J., et al. 2021, A&A, 646, A56 [EDP Sciences] [Google Scholar]
- Rajpurohit, K., van Weeren, R. J., Hoeft, M., et al. 2022, ApJ, 927, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Riquelme, M. A., & Spitkovsky, A. 2011, ApJ, 733, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Roh, S., Ryu, D., Kang, H., Ha, S., & Jang, H. 2019, ApJ, 883, 138 [CrossRef] [Google Scholar]
- Ryu, D., Kang, H., Hallman, E., & Jones, T. W. 2003, ApJ, 593, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, D., Kang, H., & Ha, J.-H. 2019, ApJ, 883, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1999, ApJ, 520, 529 [Google Scholar]
- Schmidt, W., Niemeyer, J. C., & Hillebrandt, W. 2006, A&A, 450, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skillman, S. W., Xu, H., Hallman, E. J., et al. 2013, ApJ, 765, 21 [Google Scholar]
- Stroe, A., van Weeren, R. J., Intema, H. T., et al. 2013, A&A, 555, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stroe, A., Rumsey, C., Harwood, J. J., et al. 2014, MNRAS, 441, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Stroe, A., Shimwell, T., Rumsey, C., et al. 2016, MNRAS, 455, 2402 [NASA ADS] [CrossRef] [Google Scholar]
- Vaidya, B., Mignone, A., Bodo, G., Rossi, P., & Massaglia, S. 2018, ApJ, 865, 144 [Google Scholar]
- Van Rossum, G., & Drake, F. L., Jr. 1995, Python Reference Manual (Centrum voor Wiskunde en Informatica Amsterdam) [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Brüggen, M., & Hoeft, M. 2010, Science, 330, 347 [Google Scholar]
- van Weeren, R. J., Brüggen, M., Röttgering, H. J. A., & Hoeft, M. 2011, JApA, 32, 505 [NASA ADS] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Intema, H. T., et al. 2012, A&A, 546, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Ogrean, G. A., Jones, C., et al. 2017, ApJ, 835, 197 [Google Scholar]
- van Weeren, R. J., de Gasperin, F., Akamatsu, H., et al. 2019, Space Sci. Rev., 215, 16 [Google Scholar]
- Vazza, F., Brüggen, M., Wittor, D., et al. 2016, MNRAS, 459, 70 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wittor, D., Hoeft, M., Vazza, F., Brüggen, M., & Domínguez-Fernández, P. 2019, MNRAS, 490, 3987 [Google Scholar]
- Wittor, D., Ettori, S., Vazza, F., et al. 2021, MNRAS, 506, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, R., Spitkovsky, A., & Caprioli, D. 2020, ApJ, 897, L41 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spectral features
In this appendix, we show additional information about the modeled radio emission in our simulations with the purpose of providing a complete view of the simulated radio shock. In Fig. A.1, we show the radio shock at t = 184.7 Myr. In this case, the shock front is located almost at the right end of region III at x ∼ 1.75.
In Fig. A.2, we show the spectral index maps of the ℳi = 3 case. We computed these maps with the following equation:
 |
Fig. A.2. Spectral index maps obtained between 150 MHz and 650 MHz for the ℳi = 3 at t = 184.7 Myr. The first row corresponds to the fresh-injection model and the second and third rows to the re-acceleration model assuming Dirac Delta and power-law fossil electrons, respectively. The first (second) columns correspond to ℳcr = 1 (ℳcr = 2.3), γcut = 102 (γcut = 103) and s = 2.25 (s = 3), respectively. |
where Iν was defined in Eq. 30. In Fig. A.2, we considered ν1 = 150 MHz and ν2 = 650 MHz. We see the expected spectral index gradient starting from the shock front (orange) to the end of the downstream region (blue). The spectral index values range between α ∼ −0.6 and α ∼ −2.1. In Fig. A.3, we show the spectral index profiles between various observing frequencies. We additionally plot the data points from Fig. 10 in Di Gennaro et al. 2018. While in this work we do not aim at reproducing any specific radio relic, we find it useful to make a comparison with observational data. We choose to show the data from this particular relic because it is believed to be observed almost edge-on (see van Weeren et al. 2011). The Mach number of the Sausage relic has been estimated to be ℳX − ray = 2.7 from X-ray observations (Akamatsu et al. 2015). On the radio band, the Mach number has been estimated to be ℳradio = 4.6 (van Weeren et al. 2010), ℳradio = 2.9 (Stroe et al. 2014), ℳradio = 2.7 (Hoang et al. 2017), and ℳradio = 2.58 (Di Gennaro et al. 2018). Some of these estimations would be comparable to the initial Mach number ℳi used in some of our simulations (see the upper or middle panels of Fig. A.3). Nevertheless, as mentioned in the main text, we stress that in this manuscript we do not aim at reproducing any particular observed radio relic.
 |
Fig. A.3. Spectral index profiles for all the models at t = 184.7 Myr. The first row corresponds to the fresh-injection model and the second and third rows to the re-acceleration model assuming Dirac Delta and power-law fossil electrons, respectively. The data points are taken from Fig. 10 of Di Gennaro et al. 2018. |
Appendix B: Extra models
In this appendix, we show the results from extra runs in which we have explored different η(ℳ) efficiency functions in the fresh-injection model. In principle, η(ℳ) remains to be an unknown for weak shocks in the ICM. Nevertheless, various models depending on the Mach number have been proposed in the literature (Kang et al. 2007; Kang & Ryu 2013; Caprioli & Spitkovsky 2014; Ryu et al. 2019). These models have one thing in common, η(ℳ) is an increasing function with the Mach number. In Fig. B.1, we show the resulting standard deviation of the δSν for different runs with different η(ℳ) toy models. We considered only the ℳi = 3 case. The steepest η(ℳ) model (shown in color turquoise in Fig. B.1) leads to the highest level of patchiness as seen by the highest values of σδSν. Yet, this very steep model reveals almost no change in the trend of the standard deviation with frequency. Since steeper η(ℳ) models give even more weight to those regions at the shock front with the largest Mach numbers, the relic would look as patchy at high frequencies as it looks at low frequencies. To summarize, we find that 1) a steeper η(ℳ) model leads to a higher the degree of patchiness or more substructure in the radio emission and 2) if the η(ℳ) model is too steep, the trend where σδSν increases with frequency (see Sect. 4.3) is erased.
 |
Fig. B.1. Standard deviation of the δSν distribution at the shock-front for the ℳi = 3 case at all frequencies for the ℳcr = 1 fresh injection model. In this case, we explore different η(ℳ) functions (see legend). The left (right) panel corresponds to the simulation time-steps t = 102.7 Myr and t = 187.4 Myr. |
Appendix C: Dependence on the Mach number
In this appendix, we show in a simple way how low Mach number shocks lead to the largest discrepancies in the energy spectra of the particles compared to high Mach number shocks. As can be seen from Eq. (27), the synchrotron emission mainly depends on the particle energy spectrum and on the Bessel function integral. Nevertheless, as a first-order approximation, the radio luminosity produced by a given radio source can be estimated as:
where the synchrotron power emitted per unit time is proportional to E2. Thinking about the fresh injection model, the initial energy distribution of the particles is given by Eq. 11 where the injection spectral index p depends on the shock’s Mach number. In Fig. C.1 we show the energy spectra of various particles in one of our simulations. The lower the Mach number, the steeper the spectrum is. Apart from the fact that each Lagrangian particle representing an ensemble of CRe is subject to individual radiative losses or ageing, one can observe that the differences in energy between low and high Mach number spectra can be significant (compare black and red lines in Fig. C.1). Moreover, these differences are enlarged in the radio band which are shown as shaded areas. These differences along with the normalization factors are exactly what gives rise to a high degree of patchiness in the fresh injection model. The radio substructure will be brightest at regions characterized by the highest Mach numbers of the shock’s distribution, that is, the high end tail of the Mach number distribution; it will be patchier if the shock’s Mach number distribution is dominated by a large fraction of low Mach numbers.
 |
Fig. C.1. Energy spectra of 100 randomly selected particles near the shock front in the ℳi = 2 case with ℳcr = 1. The energy spectra are colored by their corresponding Mach numbers. The shaded areas denote the energy range corresponding to the critical frequencies band 0.15–18.6 GHz (see Eq. 29), assuming 0.1 μG (orange), 1 μG (green), and 10 μ G (blue). |
Following Eq. C.1, the ratio of radio emission to the CRe energy can then be estimated in a simplified way via:
In Fig. C.2 we show how this ratio changes considering different energy limits as a function of the shock Mach number. We can see that a steeper energy spectrum (corresponding to low Mach numbers) leads to lower radio luminosity in general. Focusing in a fixed maximum energy with Lorentz factor of γmax = 107 and a minimum of γmin = 10 (solid purple lines in the left panel of Fig. C.2), the difference between ℳ ∼ 2 and ℳ ∼ 3 can be as high as ∼4 orders of magnitude.
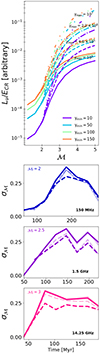 |
Fig. C.2. Ratio of synchrotron and CRe energies as function of the Mach number for different minimum and maximum energy limits (left). A magnetic field of 1 μG was assumed. The right panel shows the same as the bottom row in Fig. 4, but using as weight both the fresh-injection model (solid lines; ℳcr = 2.3 with higher transparency) and the re-acceleration model (dashed lines; s = 3 with higher transparency). |
Finally, in the left panel of Fig. C.2 we show the standard deviation of the projected Mach number of the shock weighted with the radio emission coming from the fresh-injection and the re-acceleration models. This figure is complementary to the panels in the bottom row of Fig. 4. As mentioned before, the fresh injection model produces more patchy radio relics than the acceleration model. As a consequence, the σℳ obtained weighting with the emission from the fresh injection model is larger than the σℳ where the radio emission from the re-acceleration model is used.
All Tables
Parameters used in all our simulation runs for the fresh injection and re-acceleration models.
Restoring beam sizes assumed for smoothing the emission maps at each observing frequency.
All Figures
 |
Fig. 1. Evolution of the rms Mach number (top) and plasma beta (bottom), shown in the upper panel. The vertical gray line indicates the selected time in the FLASH simulation to be our initial turbulent ICM condition. The selected snapshot has an rms Mach number of ℳs ∼ 0.7 and a plasma beta of βp ∼ 110. Magnetic field strength (darkcyan) and Mach number (purple) PDFs at the selected time in the FLASH simulation, shown in the bottom panel. |
| In the text | |
 |
Fig. 2. Initial magnetic field configuration in the PLUTO code taken from Domínguez-Fernández et al. (2020). The streamlines are colored according to the magnitude of the magnetic field: green, light colors denote higher values, while dark blue color indicates lower values. Here, I denotes the post-shock region, II the uniform pre-shock region, and III the turbulent pre-shock region (see Sect. 2.1). The left side is a uniform medium with a Bx component matching the mean value of the Bx of the turbulent medium. We have one Lagrangian particle per cell placed in the whole regions II and III. |
| In the text | |
 |
Fig. 3. Volume rendering of the synchrotron emissivity rendering in code units at 650 MHz (left) and 18.6 GHz (right) for the fresh-injection model (top row: case ℳcr = 1; see Sect. 4.2) and the re-acceleration model (bottom row: case s = 2.25). All renderings correspond to the ℳi = 3 case at t = 184.7 Myr. |
| In the text | |
 |
Fig. 4. 3D Mach number distribution at the shock cells at selected simulation times (top). Standard deviation of the Mach number PDF as function of time (bottom). Each column corresponds to the different initial Mach number of the shock. For the 2D Mach number distribution we used different weights for the projection (see legend). Note: here, Iν is taken from the fresh-injection model (case ℳcr = 1; see Sect. 4.2). See Appendix C for a comparison between weights corresponding to the emission coming from the fresh-injection and re-acceleration models. |
| In the text | |
 |
Fig. 5. Normalized surface brightness maps of the shock front for the ℳi = 3 case in the fresh-injection model (first row) and re-acceleration model with a Dirac Delta (second row) and a power-law (third row) fossil populations. Each sub-panel shows four different frequencies, namely 150 MHz, 1.5 GHz, 14.25 GHz, and 18.6 GHz. The first (last) four columns correspond to ℳcr = 1 (ℳcr = 2.3), γcut = 102 (γcut = 103), and s = 2.25 (s = 3), respectively. The time-step selected of the simulation is 120.7 Myr (see the top corner of each sub-panel). |
| In the text | |
 |
Fig. 6. Phase plots of the |
| In the text | |
 |
Fig. 7. Standard deviation of the δSν distribution for all our models at all frequencies. Two simulation time-steps are shown: t = 102.7 Myr (higher transparency) and t = 184.7 Myr (no transparency). The first two panels correspond to the fresh injection model (ℳcr = 1 and ℳcr = 2.3 parameters), the third and fourth panels refer to the re-acceleration model, assuming a Dirac Delta pre-existing distribution function (γcut = 102 and γcut = 103 parameters), and the fifth and sixth panels refer to the re-acceleration model assuming a power-law pre-existing distribution function (s = 2.25 and s = 3 parameters). |
| In the text | |
 |
Fig. 8. Standard deviation of the δSν distribution normalized by that at 150 MHz at the shock-front at 184.7 Myr for all our models at all frequencies. The top, middle and bottom rows correspond to the fresh injection model, the re-acceleration model assuming a Dirac Delta pre-existing distribution function and the re-acceleration model assuming a power-law pre-existing distribution function, respectively. The first and third columns show the results from the original maps and the second and fourth columns show the results of the map smoothed with 5″ × 5″ (dot-dashed) and 20″ × 20″ (dashed) beam sizes. |
| In the text | |
 |
Fig. 9. Skewness (upper row) and kurtosis (lower row) of the δSν/distribution for all our models at all frequencies. We only show the ℳi = 2 and ℳi = 3 cases. The upper solid lines correspond to the unsmoothed data and the dot-dashed and dashed lines correspond to the data smoothed with the 5″ × 5″ and 20″ × 20″ beam sizes, respectively. |
| In the text | |
 |
Fig. 10. Standard deviation of the δSν distribution normalized by that at 150 MHz at the shock-front for the ℳi = 3 case at all frequencies for the ℳcr = 1 fresh injection model at t = 187.4 Myr. We show the result for three different numerical resolutions. The first column shows the results from the original maps and the second column the results from the smoothed maps, similarly to Fig. 8. |
| In the text | |
 |
Fig. A.1. Same as Fig. 5 but at the simulation time-step of 187.4 Myr. |
| In the text | |
 |
Fig. A.2. Spectral index maps obtained between 150 MHz and 650 MHz for the ℳi = 3 at t = 184.7 Myr. The first row corresponds to the fresh-injection model and the second and third rows to the re-acceleration model assuming Dirac Delta and power-law fossil electrons, respectively. The first (second) columns correspond to ℳcr = 1 (ℳcr = 2.3), γcut = 102 (γcut = 103) and s = 2.25 (s = 3), respectively. |
| In the text | |
 |
Fig. A.3. Spectral index profiles for all the models at t = 184.7 Myr. The first row corresponds to the fresh-injection model and the second and third rows to the re-acceleration model assuming Dirac Delta and power-law fossil electrons, respectively. The data points are taken from Fig. 10 of Di Gennaro et al. 2018. |
| In the text | |
 |
Fig. B.1. Standard deviation of the δSν distribution at the shock-front for the ℳi = 3 case at all frequencies for the ℳcr = 1 fresh injection model. In this case, we explore different η(ℳ) functions (see legend). The left (right) panel corresponds to the simulation time-steps t = 102.7 Myr and t = 187.4 Myr. |
| In the text | |
 |
Fig. C.1. Energy spectra of 100 randomly selected particles near the shock front in the ℳi = 2 case with ℳcr = 1. The energy spectra are colored by their corresponding Mach numbers. The shaded areas denote the energy range corresponding to the critical frequencies band 0.15–18.6 GHz (see Eq. 29), assuming 0.1 μG (orange), 1 μG (green), and 10 μ G (blue). |
| In the text | |
 |
Fig. C.2. Ratio of synchrotron and CRe energies as function of the Mach number for different minimum and maximum energy limits (left). A magnetic field of 1 μG was assumed. The right panel shows the same as the bottom row in Fig. 4, but using as weight both the fresh-injection model (solid lines; ℳcr = 2.3 with higher transparency) and the re-acceleration model (dashed lines; s = 3 with higher transparency). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



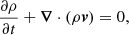
![$$ \begin{aligned}&\frac{\partial \boldsymbol{m}}{\partial t} + \boldsymbol{\nabla } \cdot \left[ \boldsymbol{m} \boldsymbol{v} - \frac{1}{4\pi }\boldsymbol{B}\boldsymbol{B} + \boldsymbol{I} \left( p + \frac{B^2}{8\pi } \right) \right]^T = 0,\end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq2.gif)
![$$ \begin{aligned}&\frac{\partial (E_t)}{\partial t} + \boldsymbol{\nabla } \cdot \left[ \left( \frac{\rho v^2}{2} + \rho e + p \right)\boldsymbol{v} - \frac{1}{4\pi }(\boldsymbol{v} \times \boldsymbol{B}) \times \boldsymbol{B} \right] = 0,\end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq3.gif)
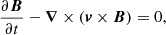
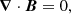
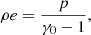
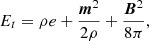
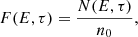
![$$ \begin{aligned} \frac{\mathrm{d} F}{\mathrm{d}\tau } + \frac{\partial }{\partial E} \left[ \left( - \frac{E}{3}\nabla _{\mu }u^{\mu } - c_rE^2 \right) F \right]=0. \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq9.gif)
![$$ \begin{aligned} c_r = \frac{4}{3} \frac{\sigma _Tc\beta ^2}{m_{e}^{2}c^{4}} \left[ \frac{B^2}{8\pi } + a_{\rm rad}T_{\mathrm{CMB}}^4(1+z)^4 \right], \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq10.gif)
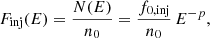
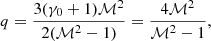
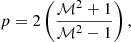
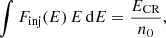
![$$ \begin{aligned} f_{0,\mathrm{inj}} = \left\{ \begin{array}{ll} \frac{E_{\rm CR}(\mathcal{M} )\,(4-q)}{\left[{E_{\rm max}}^{4-q}\, - \, {E_{\rm min}}^{4-q} \right]}&\mathrm{if\ } q \ne 4, \\&\\ E_{\rm CR}(\mathcal{M} ) \log \left( \frac{E_{\rm max}}{E_{\rm min}}\right)&\mathrm{if\ } q=4. \\ \end{array} \right. \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq15.gif)
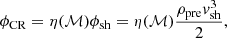
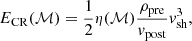
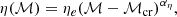
![$$ \begin{aligned} F_{\rm re}(E) = \frac{1}{n_0} \left[ (p+2)E^{-p} \int _{E_{\rm min}}^{E} {E^{\prime }}^{p-1} f_{\rm pre}(E^{\prime }) \mathrm{d}E^{\prime } \right], \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq19.gif)
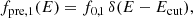
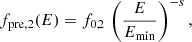
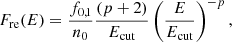
![$$ \begin{aligned}&F_{\rm re}(E) = \left\{ \begin{array}{ll} \frac{1}{n_{0}} \frac{(p+2)}{(p - s)} f_{\mathrm{pre},2}(E) \left[ 1 - \left( \frac{E}{E_{\rm min}} \right)^{s-p} \right]&\mathrm{if}\ s \ne p \\&\\ \frac{1}{n_{0}} (p+2) f_{\mathrm{pre},2}(E) \mathrm{log}\left( \frac{E}{E_{\rm min}} \right)&\mathrm{if }\ s=p. \\ \end{array} \right. \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq23.gif)
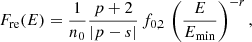
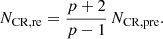
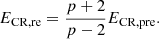
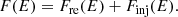
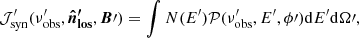
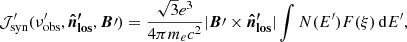
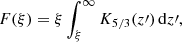
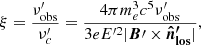
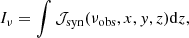
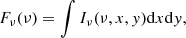
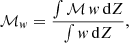
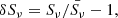
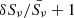
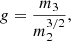
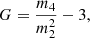
![$$ \begin{aligned} m_i = \frac{1}{N} \, \sum _{n=1}^{N} \left( x[n] - \overline{x} \right)^i \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq48.gif)
![$$ \begin{aligned} - \alpha (x,y) = \frac{\log \left[I_{\nu _{2}}(x,y)/I_{\nu _{1}}(x,y) \right]}{\log (\nu _{2} / \nu _{1})}, \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq51.gif)
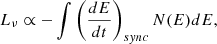
![$$ \begin{aligned} \frac{L_{\nu }}{E_{CR}} \propto \frac{(2 - p)\left[ E_{max}^{3-p} - E_{min}^{3-p} \right]}{(3-p)\left[ E_{max}^{2-p} - E_{min}^{2-p} \right]}. \end{aligned} $$](/articles/aa/full_html/2024/05/aa48398-23/aa48398-23-eq53.gif)