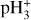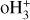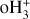| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202346413 | |
| Published online | 07 May 2024 | |
Testing analytical methods to derive the cosmic-ray ionisation rate in cold regions via synthetic observations
1
Centre for Astrochemical Studies, Max-Planck-Institut für extraterrestrische Physik,
Gießenbachstraße 1,
85749
Garching bei München,
Germany
e-mail: eredaelli@mpe.mpg.de
2
Departamento de Astronomía, Facultad Ciencias Físicas y Matemáticas, Universidad de Concepción,
Av. Esteban Iturra s/n Barrio Universitario, Casilla 160,
Concepción,
Chile
3
INAF, Istituto di Radioastronomia – Italian node of the ALMA Regional Centre (It-ARC),
Via Gobetti 101,
40129
Bologna,
Italy
4
Dipartimento di Chimica, Università degli Studi di Roma “La Sapienza”,
P.le Aldo Moro 5,
00185
Roma,
Italy
5
Dipartimento di Scienza e Alta Tecnologia, Università degli Studi dell’Insubria,
via Valleggio 11,
22100
Como,
Italy
6
INFN, Sezione di Milano-Bicocca,
Piazza della Scienza 3,
20126
Milano,
Italy
7
INAF, Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125
Firenze,
Italy
Received:
14
March
2023
Accepted:
15
February
2024
Context. Cosmic rays (CRs) heavily impact the chemistry and physics of cold and dense star-forming regions. However, the characterisation of their ionisation rate continues to pose a challenge from the observational point of view.
Aims. In the past, a few analytical formulas have been proposed to infer the cosmic-ray ionisation rate, ζ2, from molecular line observations. These have been derived from the chemical kinetics of the involved species, but they have not yet been validated using synthetic data processed with a standard observative pipeline. In this work, we aim to bridge this gap.
Methods. We performed a radiative transfer on a set of three-dimensional magneto-hydrodynamical simulations of prestellar cores, exploring different initial ζ2, evolutionary stages, types of radiative transfer (for instance assuming local-thermodynamic-equilibrium conditions), and telescope responses. We then computed the column densities of the involved tracers to determine ζ2, employing a recently proposed method based on the detection of H2D+. We compared this approach with a previous method, based on more common tracers. Both approaches are commonly used.
Results. Our results confirm that the equation based on the detection of H2D+ accurately retrieves the actual ζ2 within a factor of two to three in the physical conditions explored in our tests. Since we have also explored a non-local thermodynamic equilibrium (non-LTE) radiative transfer, this work indirectly offers insights into the excitation temperatures of common transitions at moderate volume densities (n ≈ 105 cm−3). We also performed a few tests using a previous methodology that is independent of H2D+, which overestimates the actual ζ2 by at least two orders of magnitude. We considered a new derivation of this method, however, we found that it still leads to high over-estimations.
Conclusions. The method based on H2D+ is further validated in this work and demonstrates a reliable method for estimating ζ2 in cold and dense gas. On the contrary, the former analytical equation, as already pointed out by its authors, has no global domain of application. Thus, we find that it ought to be employed with caution.
Key words: astrochemistry / radiative transfer / stars: formation / ISM: clouds / cosmic rays / ISM: molecules
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Cosmic rays (CRs) are energetic, ionised particles that are ubiquitously found in the interstellar medium (ISM). In the densest gas phases, they play a key role in triggering the chemistry and regulating the thermodynamical balance. In molecular gas, CRs collide with H2 molecules and usually end up ionising them via the following reaction:
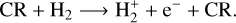
Afterwards, the highly reactive  immediately reacts with another H2 molecule, producing the trihydrogen cation
immediately reacts with another H2 molecule, producing the trihydrogen cation 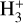 . In doing so, CRs set the ionisation state of dense matter, where the photodissociating UV field is completely attenuated. This, in turn, strongly affects the dynamics of the dense gas. The electron fraction x(e−) determines the degree of coupling between the magnetic fields and the matter and it is therefore linked to the time scale for ambipolar diffusion. This corresponds to the drift between the neutral and the ionised flows, which is one of the proposed mechanisms behind the dissipation of the magnetic flux and enabling gravitational collapse (Mouschovias & Spitzer 1976).
. In doing so, CRs set the ionisation state of dense matter, where the photodissociating UV field is completely attenuated. This, in turn, strongly affects the dynamics of the dense gas. The electron fraction x(e−) determines the degree of coupling between the magnetic fields and the matter and it is therefore linked to the time scale for ambipolar diffusion. This corresponds to the drift between the neutral and the ionised flows, which is one of the proposed mechanisms behind the dissipation of the magnetic flux and enabling gravitational collapse (Mouschovias & Spitzer 1976).
With respect to chemical evolution in the ISM, 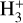 is a pivotal species also since it drives the rich ion chemistry that is ultimately responsible for such phenomena as the production of CO and gas-phase water in cold regions. Furthermore, by reacting with deuterated hydrogen HD,
is a pivotal species also since it drives the rich ion chemistry that is ultimately responsible for such phenomena as the production of CO and gas-phase water in cold regions. Furthermore, by reacting with deuterated hydrogen HD, 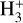 is converted into H2D+, which is the starting point of the deuteration process in the gas phase (see for instance Ceccarelli et al. 2014, and references therein).
is converted into H2D+, which is the starting point of the deuteration process in the gas phase (see for instance Ceccarelli et al. 2014, and references therein).
In summary, CRs are crucial to the physics and chemistry of star-forming regions. The key question is how to measure their effects, particularly their ionisation rate per hydrogen molecule (ζ2). The question of how to infer ζ2 from typical observables has been the focus of several works dating back to the 1970s (see for instance Guelin et al. 1977; Wootten et al. 1979). In the diffuse medium (AV ≲ 1 mag),  can be directly observed in absorption towards bright infrared sources and its relatively simple kinetics can be solved to infer ζ2. This is the approach followed for instance by McCall et al. (2003); Indriolo et al. (2007); Indriolo & McCall (2012), with typical results of the order of ζ2 ≈ 10−16 s−1.
can be directly observed in absorption towards bright infrared sources and its relatively simple kinetics can be solved to infer ζ2. This is the approach followed for instance by McCall et al. (2003); Indriolo et al. (2007); Indriolo & McCall (2012), with typical results of the order of ζ2 ≈ 10−16 s−1.
At higher densities, the absorption lines of 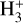 can no longer be detected. To address this situation, Guelin et al. (1977, 1982) proposed an analytic expression containing ζ2, based on the kinetics of DCO+ and HCO+. This work was later expanded by Caselli et al. (1998, hereafter CWT98), who developed a system of two equations to first infer the ionisation fraction x(e−) and then ζ2. Those authors ultimately used a more comprehensive chemical code to infer these parameters in a sample of dense cloud cores (see their Sect. 5.1 and Table 7), resulting in ζ2 values on average lower than with the analytic expression. However, the analytic equations are still used nowadays (for instance Cabedo et al. 2023), due also to the fact that they depend on common observable quantities, such as1 RH = X(HCO+)/X(CO) and the deuteration level of HCO+, RD = X(DCO+)/X(HCO+). It is important to note, however, that this approach was based on several assumptions, such as the abundance of HD. Furthermore, it was derived in specific conditions (for instance at a temperature of TK = 10 K), which prevent its generalisation.
can no longer be detected. To address this situation, Guelin et al. (1977, 1982) proposed an analytic expression containing ζ2, based on the kinetics of DCO+ and HCO+. This work was later expanded by Caselli et al. (1998, hereafter CWT98), who developed a system of two equations to first infer the ionisation fraction x(e−) and then ζ2. Those authors ultimately used a more comprehensive chemical code to infer these parameters in a sample of dense cloud cores (see their Sect. 5.1 and Table 7), resulting in ζ2 values on average lower than with the analytic expression. However, the analytic equations are still used nowadays (for instance Cabedo et al. 2023), due also to the fact that they depend on common observable quantities, such as1 RH = X(HCO+)/X(CO) and the deuteration level of HCO+, RD = X(DCO+)/X(HCO+). It is important to note, however, that this approach was based on several assumptions, such as the abundance of HD. Furthermore, it was derived in specific conditions (for instance at a temperature of TK = 10 K), which prevent its generalisation.
More recently, Bovino et al. (2020, hereafter BFL20) suggested a new analytical approach to determine ζ2 in cold gas, based on the detection of H2D+ (and, in particular, of its ortho spin state, oH2D+, which can be observed from the ground). This method is, in turn, based on the formulation of Oka (2019) and the underlying idea is to infer the abundance of 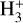 from that of its deuterated forms, together with the deuterium fraction measured from HCO+ isotopologues. It relies on fewer assumptions than CWT98, but it requires oH2D+ data, which are observa-tionally more expensive in terms of observing time. Sabatini et al. (2020) applied this implementation to a sample of highmass star-forming clumps, using observations made with the Atacama Pathfinder EXperiment 12-m submillimeter telescope (APEX; Gusten et al. 2006) and the Institut de Radioastronomie Millimétrique (IRAM) 30m single-dish telescope. Their analysis yielded 7 × 10−18 < ζ2/s−1 < 6 × 10−17, in line with theoretical predictions (Padovani et al. 2018). Sabatini et al. (2023) used the BFL20 equation to estimate ζ2 maps at high resolution in two high-mass clumps, using data from the Atacama Large Millimeter and sub-millimeter Array (ALMA), finding a remarkable agreement with the most recent predictions of cosmic-ray propagation and attenuation (Padovani et al. 2022).
from that of its deuterated forms, together with the deuterium fraction measured from HCO+ isotopologues. It relies on fewer assumptions than CWT98, but it requires oH2D+ data, which are observa-tionally more expensive in terms of observing time. Sabatini et al. (2020) applied this implementation to a sample of highmass star-forming clumps, using observations made with the Atacama Pathfinder EXperiment 12-m submillimeter telescope (APEX; Gusten et al. 2006) and the Institut de Radioastronomie Millimétrique (IRAM) 30m single-dish telescope. Their analysis yielded 7 × 10−18 < ζ2/s−1 < 6 × 10−17, in line with theoretical predictions (Padovani et al. 2018). Sabatini et al. (2023) used the BFL20 equation to estimate ζ2 maps at high resolution in two high-mass clumps, using data from the Atacama Large Millimeter and sub-millimeter Array (ALMA), finding a remarkable agreement with the most recent predictions of cosmic-ray propagation and attenuation (Padovani et al. 2022).
Another possible approach is based on having an underlying chemical model to interpret the observational results, possibly using multiple tracers. This can be done either by comparing the abundances and column densities obtained from observations to the results of chemical codes (as done, for instance, by Caselli et al. 1998; Ceccarelli et al. 2014; Fontani et al. 2017; Favre et al. 2018) or employing radiative transfer analysis. In the latter case, used for instance in Redaelli et al. (2021b), one compares the synthetic spectra of several transitions based on the molecular abundances from the chemical modelling to the observed lines. This approach is more sophisticated, and can potentially constrain ζ2 more accurately, but it also depends on the employed model and the detail of the physics included to study the given source. However, its applicability is limited by the considerable combined runtimes of a chemical code and radiative transfer.
In cases where evaluating ζ2 is required in large surveys, an analytical expression presents a clear advantage in terms of applicability and use of computational resources. The equation from BFL20 was tested on several setups of physicochemical three-dimensional (3D) simulations varying, for instance, the collapse speed or the initial H2 ortho-to-para ratio (OPR). However, a validation based on simulated observations was never performed. It is crucial to test whether (and how) the results are affected by observational effects depending, for instance, on the selected transitions or the line opacities. The same is true for the CWT98, which moreover was never tested, either on a simulation set or on synthetic observations.
In this paper, we aim to: (i) investigate the effects of telescope response and of several possible observational biases and (ii) compare two widely used equations to infer ζ2 from observable tracers and look for the potential applicability limits of the formulas. For these reasons, we have selected two simulation setups of a dense core, where the ζ2 is known by construction, and it varies in the typical range predicted by models at high densities (≈10−18−10−16 s−1). These simulations are used as input for a radiative transfer code, producing synthetic spectra of the chemical tracers involved. These are then post-processed to simulate either single-dish or interferometric-like observations. From this point, the analysis follows the standard procedure to apply the analytical expressions: the datacubes are converted into column densities and abundances maps, on which the formulas can be evaluated. The resulting ζ2 maps are compared to the actual input values of the ionisation rate.
The paper is organised as follows. Section 2 introduces the analytical methods put to the test. Section 3 illustrates the simulation setup, radiative transfer analysis, and the post-processing procedure to infer column density maps. The ζ2 maps are computed and described in Sect. 4. First, we focus on the BFL20 formulation, performing several runs, starting from a reference one (where ζ2 = 2.5 × 10−17 s−1 and the evolutionary time is t = 100 kyr), and then exploring distinct post-processing types, radiative transfer methods, and a set of rotational lines at different evolutionary stages (Sect. 4.1). In Sect. 4.2, we test the CWT98 analytical approach as an alternative approach. Section 4.3 presents the comparison of the two methods on literature values of real observed objects. The results are discussed in Sect. 5. A final summary with concluding remarks is presented in Sect. 6.
2 Retriving ζ2 using analytical expressions
The first analytical expression we aim to test is the one proposed by BFL20. In Appendix A, we present the detailed derivation of the final equation based on observable quantities (namely molecular column densities Ncol), as:
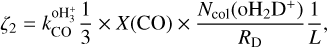 (1)
(1)
where the deuterium fraction of HCO+ is

and the CO abundance (with respect to H2) is

In Eq. (1), 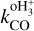 is the destruction rate of
is the destruction rate of  by CO (see reaction rate k7 in Appendix A), assumed here to be the main destruction path for
by CO (see reaction rate k7 in Appendix A), assumed here to be the main destruction path for  , which holds when the CO depletion factor is up to ≈100 assuming x(e−) ≈ 10−8 (see also the discussion in Appendix A for more details). Then, L is the path length over which the column densities are estimated. Note that for tracers that are typically optically thick (CO and HCO+ ), we use the corresponding optically thin isotopologues, assuming standard isotopic ratios for the local ISM: 18O/16O = 557 and 13C/12C = 68 (Wilson 1999). This choice is consistent with that made later in the radiative transfer analysis (see Sect. 3.3). We stress that Eq. (1) can be used only until when H2D+ is the dominant deuterated species of
, which holds when the CO depletion factor is up to ≈100 assuming x(e−) ≈ 10−8 (see also the discussion in Appendix A for more details). Then, L is the path length over which the column densities are estimated. Note that for tracers that are typically optically thick (CO and HCO+ ), we use the corresponding optically thin isotopologues, assuming standard isotopic ratios for the local ISM: 18O/16O = 557 and 13C/12C = 68 (Wilson 1999). This choice is consistent with that made later in the radiative transfer analysis (see Sect. 3.3). We stress that Eq. (1) can be used only until when H2D+ is the dominant deuterated species of  , namely, at the early stages of star-forming regions.
, namely, at the early stages of star-forming regions.
We aim to test the performance of the approach proposed by CWT98 as well, exploring its applicability and comparing it with the BFL20 approach. In these regards, we first used their equations (Eqs. (3) and (4) as they are described in Sect. 4.2). This is motivated by the fact that some papers have been using them in that exact formulation (although CWT98 already employed chemical modelling to interpret the observational results). The numerical constants in those equations, however, were derived at a temperature of 10 K, and without including ortho- and para-states of the involved species. To update the work of CWT98, in Appendix B, we followed the same approach but including the spin-state separation of H2, 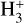 , and H2D+. We also updated the reaction rates involved with the most recent values, and we keep their temperature dependency.
, and H2D+. We also updated the reaction rates involved with the most recent values, and we keep their temperature dependency.
3 Simulations and post-processing
In this work, we performed a post-processing of 3D simulations of prestellar cores to produce the observables needed to test the aforementioned analytical methods. In the following subsections, we describe the set of simulations used in our test, the details of the radiative transfer and the type of post-processing performed afterwards. Finally, we discuss how we recover the molecular column densities and the gas total column density from the synthetic observations.
3.1 The simulation setup
We used a set of three-dimensional magneto-hydrodynamical (3D MHD) simulations of prestellar cores, with constant and variable cosmic-ray ionisation rates, obtained with the code GIZMO (Hopkins 2015). The simulations evolved an isothermal, turbulent, and magnetised Bonnor-Ebert sphere of 20 M⊙ with a radius of 0.17 pc, resembling a collapsing prestellar core. After 100 kyr of evolution, we obtain a low-mass object, with a total mass of ~3 M⊙ in the central 10 000 AU (corresponding to an average density of 〈ra(H2)〉 ~ 105 cm−3). The gas and dust temperatures are Tk = Tdust = 15 K. The size of the total simulation box is 0.6 pc. For the purposes of this work, we focussed on the central 0.3 pc containing the Bonnor-Ebert sphere.
The simulations include a state-of-the-art deuterated and spin-state chemical network, advanced in time alongside hydrodynamics. We refer to Bovino et al. (2019) for the complete description of the physical and chemical initial conditions. We highlight that the chemical code includes molecular depletion and thermal and cosmic-ray-induced desorption, but no further surface chemistry is considered. This assumption is justified since, at the low temperatures considered, the thermal desorption of any species is negligible, and the cosmic-ray-induced desorption timescale is longer than the collapse one (cf. Bovino et al. 2019). Hence, surface chemistry would have negligible effects on the final abundances of gas phase species. The initial H2 ortho-to-para ratio is OPR = 0.1, consistent with the values obtained by large-scale simulations (Lupi et al. 2021).
To investigate different ionisation states, we first used a simulation with constant 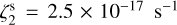 , a value typically assumed for dense regions (this corresponds to the M1 case of Bovino et al. 2019). Throughout this paper, we use the superscript ‘s’ to denote the input
, a value typically assumed for dense regions (this corresponds to the M1 case of Bovino et al. 2019). Throughout this paper, we use the superscript ‘s’ to denote the input 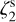 of the simulations, to avoid confusion with the ζ2 retrieved from the synthetic observations. We performed an additional test on a simulation performed with constant
of the simulations, to avoid confusion with the ζ2 retrieved from the synthetic observations. We performed an additional test on a simulation performed with constant  , to expand the range of input ζ2 explored and to be consistent with the tests performed by Bovino et al. (2020). We also simulated a variable
, to expand the range of input ζ2 explored and to be consistent with the tests performed by Bovino et al. (2020). We also simulated a variable 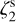 model, by postprocessing the same simulation by employing the framework developed by Ferrada-Chamorro et al. (2021) where ζ2 is varied according to the density-dependent function reported in Ivlev et al. (2019). The details of the latter simulations will be presented in a forthcoming paper (Gaete-Espinoza et al., in prep.). Thus, this set of simulations covers the typical ζ2 values predicted by the most recent models of CR propagation at high densities (for N(H2) ≳ 1022 cm−2 ζ2 ≲ a few × 10−16 s−1; cf. Padovani et al. 2022).
model, by postprocessing the same simulation by employing the framework developed by Ferrada-Chamorro et al. (2021) where ζ2 is varied according to the density-dependent function reported in Ivlev et al. (2019). The details of the latter simulations will be presented in a forthcoming paper (Gaete-Espinoza et al., in prep.). Thus, this set of simulations covers the typical ζ2 values predicted by the most recent models of CR propagation at high densities (for N(H2) ≳ 1022 cm−2 ζ2 ≲ a few × 10−16 s−1; cf. Padovani et al. 2022).
3.2 Description of tested runs
Since our goal is to compare the results of analytic expressions to infer ζ2 from observables, we tested a variety of combinations of types of radiative transfer (assuming or deviating from the local-thermodynamic-equilibrium), of rotational transitions (ground state lines, or higher J transitions), and of post-processing (simulating single-dish or interferometric observations). Starting from a reference run, we modified one parameter at a time, to evaluate its effects. We performed a total of eight tests, reported in Table 1 and described in the following text. The details of how the radiative transfer is performed are discussed in Sect. 3.3, whilst Sect. 3.4 describes how the telescope response is simulated.
Runs 1 and 2 (the latter is considered the reference one throughout the paper) used the simulation with constant  at an evolutionary time of 50 and 100 kyr, respectively. The radiative transfer was performed in local-thermodynamic-equilibrium approximation (LTE), focussing on the molecular lines in the 215–370 GHz range. The postprocessing was single-dish-like, with a final beam size of 27″. Run 3 tested the low-
at an evolutionary time of 50 and 100 kyr, respectively. The radiative transfer was performed in local-thermodynamic-equilibrium approximation (LTE), focussing on the molecular lines in the 215–370 GHz range. The postprocessing was single-dish-like, with a final beam size of 27″. Run 3 tested the low-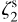 case, where the only difference with respect to the reference run is the value
case, where the only difference with respect to the reference run is the value 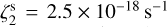 . Run 4 explored the interferometric-like post-processing, (see Sect. 3.4.2). In runs 5 and 6, we modified the kind of radiative transfer, using a non-LTE approach. In particular, in run 5 we simulated again the high-J transition of C18O, DCO+, and H13CO+. In run 6, instead, we aimed to explore the effect of targeting the (1-0) transitions of C18O, H13CO+, and DCO+. This is beneficial to the observational studies that trace the 3 mm lines of these molecules, as in the pioneering work of Caselli et al. (1998). We also adopted a large beam size of ≈70″, to simulate poorly resolved observations, where the beam area is comparable to the source size. The final two runs adopted the LTE analysis and single-dish-like post-processing, performed on the simulation with variable
. Run 4 explored the interferometric-like post-processing, (see Sect. 3.4.2). In runs 5 and 6, we modified the kind of radiative transfer, using a non-LTE approach. In particular, in run 5 we simulated again the high-J transition of C18O, DCO+, and H13CO+. In run 6, instead, we aimed to explore the effect of targeting the (1-0) transitions of C18O, H13CO+, and DCO+. This is beneficial to the observational studies that trace the 3 mm lines of these molecules, as in the pioneering work of Caselli et al. (1998). We also adopted a large beam size of ≈70″, to simulate poorly resolved observations, where the beam area is comparable to the source size. The final two runs adopted the LTE analysis and single-dish-like post-processing, performed on the simulation with variable 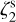 at 50 kyr (run 7) and 100 kyr (run 8), respectively.
at 50 kyr (run 7) and 100 kyr (run 8), respectively.
Properties of the simulations performed in this work.
Properties of the molecular line transitions used for this work.
3.3 Radiative transfer of MHD simulations
The total gas column density distribution and the molecular column densities are involved in the equations to infer ζ2 (see Sect. 2). The radiative transfer of the dust and the molecular lines was performed with the POLARIS code2 (Reissl et al. 2016; Brauer et al. 2017). Concerning the radiative transfer of the dust, we set the gas mean molecular weight to µ = 2.4 (Kauffmann et al. 2008) and the gas-to-dust mass ratio to 100 (Hildebrand 1983). We simulated the dust emission at a wavelength of 870 µm (corresponding to 345 GHz). From an observational perspective, this was the wavelength of the LABOCA instrument mounted on APEX, which was used to perform the all-sky survey ATLASGAL (Schuller et al. 2009). It is also close to the James Clerk Maxwell Telescope (JCMT) SCUBA II longer wavelength (850 µm). Finally, it represents the standard frequency for ALMA continuum observations in Band 7. We stress, however, how the choice of wavelength does not impact the results. For the dust model, we assumed pure silicate grains, with opacities taken from Laor & Draine (1993)3. The grain size distribution is a standard MRN (Mathis et al. 1977), with a power-law index of −3.5 between 5 nm and 0.25 µm. The grain density is 3.5 g cm−3, which is consistent with the value assumed in the simulations. These parameters are likely different from the real dust populations within dense cores, where for instance a mixture of carbonaceous and silicate grains is expected. However, our goal is not to reproduce the exact properties of a real dust population, but to be consistent in the various steps of the analysis, from the simulation to the radiative transfer.
For the molecular tracers, POLARIS needs as input the spec-troscopic description of the simulated transitions, which are summarised in Table 2. In the case of oH2D+, the only line accessible from the ground is the (11,0 − 11,1) one at 372 GHz (Caselli et al. 2003). This can be observed, for instance, by ALMA in Band 7 and by APEX using, for instance, SEPIA345 or LAsMA. Concerning the other tracers (C18O, DCO+, and H13CO+), their transitions at 215–260 GHz are commonly observed. However, several studies have focussed on their lower-J transitions at 3 mm, hence, we also tested these lines in run 6. All molecular transitions were simulated over a total velocity range of 7.5 km s−1 and a velocity resolution of 0.1 kms−1. We assumed that the local standard-of-rest velocity of the source is 0 km −1.
POLARIS is able to perform different approaches of radiative transfer, including LTE and large velocity gradient (LVG). We performed six runs assuming LTE conditions, which allowed us to focus initially on the effect of the radiative transfer itself and of the response of the telescope on the inferred ζ2 values. However, lines with high critical densities (nc ≈ 105−106 cm−3), such as the high-J transitions of H13CO+ and DCO+, and oH2D+, are likely to be sub-thermally excited. Two runs (nos. 5 and 6) hence explored a more realistic case, using the LVG approach.
POLARIS accepts a variety of grid types as input, in particular Voronoi grids. The simulations we consider were obtained with GIZMO, which samples the fluid using a set of discrete tracers representing a sort of cells with smoothed boundaries. In this respect, converting this volume discretisation to a Voronoi tessellation is the most natural and consistent choice, despite some differences existing between the two volume partition schemes4. We, hence, prepared the outputs of the simulations in the form of a Voronoi grid. In order to properly treat boundary cells, we added at the edges of the region of interest a set of virtual particles placed according to a cubic regular grid. We placed virtual particles at 1.5 times the simulated region size to avoid artefacts and we passed them to the SCIPY package (Virtanen et al. 2020) to build the Voronoi cells. We then cut the grid to match the original region, and we passed the information associated with every cell to POLARIS, including the IDs of the cell and its neighbours. In particular, the gas density, gas and dust temperatures, velocity field (3D), and the molecular mass fraction for each species (fmol = ρmol/ρtot) were the input of the radiative transfer. We note that the chemical code does not treat oxygen or carbon fraction-ation. The mass fractions of C18O and H13CO+ were thereby derived from the main ones of the isotopologues (using the same standard isotopic ratios assumed in Sect. 2).
In all radiative transfer analyses, the grid size of the output maps or cubes produced by POLARIS was set to 256 pix × 256 pix. We aimed to produce synthetic observations both for a single dish-like and for an interferometer-like case, with the distance of the source set to 170 pc and 2kpc, respectively5. The final pixel and field-of-views (FoV) are 1″.4 and 6′ × 6′ (single-dish), and 0″.12 and 30″ × 30″ (interferometer-like).
3.4 Post-processing of the POLARIS output
The output of POLARIS consists of bi-dimensional maps (in Jy pix−1), one for each wavelength for the continuum emission (a single one at 870 µm in our case) or one for each velocity channel set for the molecular lines. In the latter case, the first stage is to build the position-position-velocity datacube concatenating all the velocity channels. We now describe the approaches used to simulate a single-dish-like or interferometric response.
3.4.1 Single-dish analysis
In this case, we convolved the continuum maps and the molecular line datacubes to a specific beam size. For all the tests performed with the higher J transitions, we chose a beam size of 27″. This corresponds approximately to the APEX beam size at the lowest frequency in the sample, DCO+ (3−2) at 216 GHz. In the case of run 6, where we simulated the lower J = (1−0) lines (see Sect. 4.1.4 for more details), we selected a beam size of 70″. It is aimed at determining the effects of poorly resolved observations.
We introduced pixel by pixel in the data cubes and in the continuum fluxes some artificial Gaussian noise with zero mean and rms standard deviation. For the continuum maps, we used rms = 15mJybeam−1 and rms = 100mJybeam−1 for the cases at 27″ and 70″ of resolution, respectively. Concerning the line datacubes, we injected a noise with rms = 100 mK. For oH2D+ in run 1, and all lines in run 5, this sensitivity is insufficient for significant detections (see Sect. 4.1.1 and 4.1.4 for more details). In these runs, we reduced the noise level to rms = 50 mK. These values are consistent with the typical rms of observational campaigns with APEX (cf. Sabatini et al. 2020). Run 3, performed with the lowest 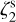 value, present faint lines, and the noise level is reduced to rms = 1 mK (cf. Sect. 4.1.2).
value, present faint lines, and the noise level is reduced to rms = 1 mK (cf. Sect. 4.1.2).
Parameters used in SIMOBSERVE.
3.4.2 Interferometer-like analysis
To simulate interferometer-like observations, we focussed on ALMA, which can cover the frequencies of the transitions analysed here, except for DCO+ (1−0). We hence used the output of POLARIS as input for the task SIMOBSERVE of CASA (version 6.4.3). Due to current limitations of SIMOBSERVE, it is not possible to add total power at the desired sensitivity. We hence simulated only the 12m and 7m-array observations. We chose the Cycle 8 configuration sets. We selected the integration times using the corresponding observing Tool (OT), setting the requested angular resolution to 1″ and the desired noise level to 100 mK and to 5 µJy for the continuum simulations. Table 3 summarises the integration times used in each run of SIMOBSERVE. Concerning the noise, we let the task construct the atmospheric model (using the option THERMAL_NOISE = TSYS-ATM).
The task SIMOBSERVE was called separately to simulate the 12m and the 7 m array observations. We then combined the output visibilities (using CONCAT), making sure that the relative weights are correct6. After that, we imaged the concatenated visibilities using the TCLEAN task. We used the MULTISCALE deconvolver (scales: [0, 5, 15]× pixel size), which is an appropriate choice in case of extended emission, such as in the simulated data. We selected a BRIGGS weighting, with ROBUST = 0.5. The noise threshold was set to 2σ. The final datacubes (or 2D images for continuum observations) have a FoV of 30″ × 30″, sampled with 250 pix × 250 pix.
The lack of total power observations leads to flux losses, due to the filtering of the large-scale emission which is particularly important for extended sources such as the core we simulate. Focussing on run 4, we estimate that between ≈20 and 65% of the flux in a 15″ area around the core is recovered, depending on the tracer. This is in line with simulations regarding the filter-out effect. For instance, Plunkett et al. (2023) found that up to 90% of the original flux can be lost in extended sources when single-dish data are not available.
3.5 Column density computation
The different approaches for computing the cosmic-ray ionisation rate depend on the column densities of the involved species.
To estimate them, we used the approach of Mangum & Shirley (2015):
 (2)
(2)
where h, kB, and c are the Planck constant, the Boltzmann constant, and the speed of light in vacuum; Eu is the upper-level energy, ɡu the upper-level multiplicity, v the line frequency, Aul the Einstein coefficient for spontaneous emission, and Qrot(Tex) the partition function at the excitation temperature Tex. We list the values used for the spectroscopic constant in Table 2. They are taken from the CDMS catalog7. The partition functions are from Giannetti et al. (2019) for oH2D+, the CDMS catalogue for C18O and H13CO+, and Redaelli et al. (2019) for DCO+. To compute the partition function at the requested temperature, we interpolated the values linearly, when necessary. ∫ τvdV is the integral along the velocity axis of the optical depth τv computed channel-by-channel using (cf. Caselli et al. 2002)
![${\tau _v} = - \ln \left[ {1 - {{{T_{{\rm{MB}}}}} \over {{J_v}\left( {{T_{{\rm{ex}}}}} \right) - {J_v}\left( {{T_{{\rm{bg}}}}} \right)}}} \right],$](/articles/aa/full_html/2024/05/aa46413-23/aa46413-23-eq27.png) (3)
(3)
where TMB is the line main beam temperature, Jv(T) is the equivalent Rayleigh-Jeans temperature at the line frequency8, and Tbg = 2.73 K is the background temperature. The obtained optical depth profiles are integrated along the velocity range [−1 : 1] km s−1, which is large enough to include the line emission in all the synthetic cubes analysed for this work.
The excitation temperature for all the transitions is Tex = Tk = 15 K when assuming LTE conditions. For the two non-LTE cases, we selected the excitation temperatures based on the critical densities of the analysed transitions and on available literature data9. The C18O first two rotational lines have relatively low critical densities (nc ≈ 103 cm−3), and it is hence reasonable to assume that they are thermalised by collisions with H2, leading to Tex = Tk = 15 K. The critical density of oH2D+ is higher (nc ≈ 105 cm−3, Hugo et al. 2009), and the line is likely sub-thermally excited, leading to Tex < Tk. We adopt Tex = 10 K, which is frequently employed in the literature. For instance, Caselli et al. (2008) computed Tex = 7–13 K in the envelope of protostellar cores that have gas temperatures of 10–15 K, close to that of our simulations; Friesen et al. (2014) adopted Tex = 12 K; Redaelli etal. (2021a, 2022) used Tex = 10 K. DCO+ and H13CO+ are isotopologues with similar critical densities, and it is reasonable to assume that the same rotational transitions share similar excitation temperatures. However, literature information about these are scarce. Using a full non-LTE modelling of the DCO+ lines in the well-known core L1544, Redaelli et al. (2019) found Tex(1−0) = 5.7 K and Tex(3−2) = 7.8 K. The core L1544 is, however, colder than our simulated cores. We, hence, used the online tool RADEX10 to confirm these values. Using n = 105cm−3, Tk = 15 K, and Ncol = 1012cm −2, we derived Tex ≈ 8–12 K for the lower-J transitions and ≈5 K for the higher-J ones. We therefore set Tex(1−0) = 10 K and Tex(3−2) = 5.5 K for both isotopologues. In Appendix C we show that a 20% variation of these values does not affect our conclusions. The last column of Table 2 summarises the excitation temperature values used in the LVG analysis.
To estimate the uncertainties on the derived column density values (rmsN), we applied standard error propagation on Eq. (2), assuming that the frequency channels are independent and using the small-error approximation. Then, the uncertainty propagation leads to
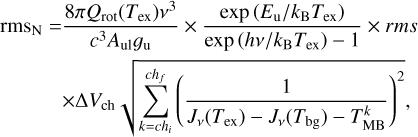 (4)
(4)
where chi and chf are channels corresponding to the velocity interval over which Eq. (3) is computed, 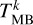 is the intensity of the k-th channel, and ΔVch is the channel width (in km s−1).
is the intensity of the k-th channel, and ΔVch is the channel width (in km s−1).
To estimate the abundances, we derived the total gas column density map from the continuum map as
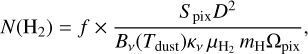 (5)
(5)
where f = 100 is the gas-to-dust mass ratio (Hildebrand 1983), D is the source distance, Bv(Tdust) is the Planck function at the dust temperature Tdust = 15 K, 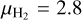 is the mean molecular weight per hydrogen molecule, mH is the mass of the hydrogen atom, Spix is the flux (in units of Jypix−1), Ωpix is the pixel size (in physical units), and κV is the dust opacity. For the latter, we used the output of POLARIS, which tabulates the opacities at the simulated wavelength: κ345 GHz = 0.388 cm2 g−1. We estimated the uncertainties on the total column densities using Eq. (5), with the flux noise level of the continuum map as Spix.
is the mean molecular weight per hydrogen molecule, mH is the mass of the hydrogen atom, Spix is the flux (in units of Jypix−1), Ωpix is the pixel size (in physical units), and κV is the dust opacity. For the latter, we used the output of POLARIS, which tabulates the opacities at the simulated wavelength: κ345 GHz = 0.388 cm2 g−1. We estimated the uncertainties on the total column densities using Eq. (5), with the flux noise level of the continuum map as Spix.
4 Resulting ζ2 maps
We go on to apply the analytical expressions described in Sect. 2 to infer the ζ2 maps. Uncertainties on derived quantities were computed pixel-per-pixel assuming standard error propagation calculated from the uncertainties on the column densities that are considered independent. We neglected, for instance, any source of uncertainty from the reaction rates. With the computed errors, we masked pixels where the signal-to-noise ratio is S/N ≤ 3.
4.1 The Bovino et al. (2020) method
To test the analytical method of Bovino et al. (2020, BFL20), we computed ζ2 in the eight runs described in Table 1, varying the ζ2 model (constant or variable), the type of radiative transfer (LTE or LVG), the post-processing method (single-dish or ALMA-like), and the frequency of the molecular lines. All the simulations are isothermal at 15 K, and, therefore, the rate coefficient in Eq. (1) is 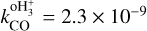 cm3 s−1.
cm3 s−1.
In the following subsections, we discuss in detail the results of each run, showing the obtained ζ2 maps. In order to compare these values with the actual ones, we make use of the ζ2 distributions in Fig. 1. Its panels show the histograms of the ionisation rate values extracted in the densest region of the core (namely where the H2 column density is higher than 50% of its peak value), where the signal-to-noise ratio is higher. The medians of the distributions (vertical dashed lines) are directly compared with the actual value of 2.5 × 10−17 s−1 in the runs with constant 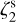 . In runs with variable
. In runs with variable 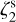 , we compare pixel-by-pixel the ratio between actual and retrieved values, as discussed in Sect. 5.
, we compare pixel-by-pixel the ratio between actual and retrieved values, as discussed in Sect. 5.
 |
Fig. 1 Histogram of the distribution of ζ2 (in units of 10−17 s−1) of the runs as labelled at the top of each panel. We represent the core region where N(H2) > 0.5 × max(N(H2)) (namely the lowest contour in the panels of Figs. 2, 3, and 4). The median value, together with the median uncertainty, is reported in the top-right corner of each panel and shown as a vertical dashed line with a grey-shaded area. Cf. Table 1. |
4.1.1 Runs 1–2: constant 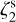 and single-dish like analysis
and single-dish like analysis
The first runs we tested have constant 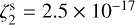 s-1, coupled with LTE radiative transfer of the high-J transitions and single-dish-like analysis. We explored two evolutionary stages, 50 kyr (run 1) and 100 kyr (run 2, the reference run). The resulting ζ2 maps are shown in Fig. 2, top row. We employed Eq. (1) with L = 0.3 pc, which represents the path length (along the line of sight) over which the column densities are integrated. In our case, this corresponds to the size of the simulated box (0.3 pc × 0.3 pc × 0.3 pc). A detailed discussion on how to choose L and the derived uncertainty is presented in Sect. 4.3 and 5.
s-1, coupled with LTE radiative transfer of the high-J transitions and single-dish-like analysis. We explored two evolutionary stages, 50 kyr (run 1) and 100 kyr (run 2, the reference run). The resulting ζ2 maps are shown in Fig. 2, top row. We employed Eq. (1) with L = 0.3 pc, which represents the path length (along the line of sight) over which the column densities are integrated. In our case, this corresponds to the size of the simulated box (0.3 pc × 0.3 pc × 0.3 pc). A detailed discussion on how to choose L and the derived uncertainty is presented in Sect. 4.3 and 5.
The obtained ζ2 values span the range ≈(2–8) × 10−17 s−1, with medians in the denser parts of the core of ζ2 = (3.4 ± 0.6) × 10−17 s−1 (50kyr) and ζ2 = (4.0 ± 0.4) × 10−17 s−1 (100 kyr), as shown in Fig. 1. These values should be compared with the actual  s−1. We conclude that, in these runs, the BFL20 reproduces the
s−1. We conclude that, in these runs, the BFL20 reproduces the  within a factor 1.5–1.6 on average.
within a factor 1.5–1.6 on average.
Concerning the morphology of the retrieved ζ2 maps, the one at 50 kyr shows a smaller scatter around the median value than the run at 100 kyr (see Fig. 1), mainly because we can infer ζ2 only for positions where N(H2) > 4.8 × 1022 cm−2. This is because at this early stage, the oH2D+ abundance is at most X(oH2D+) = 7 × 10−11, producing a line peak intensity of 0.5 K11. For comparison, at 100kyr, the oH2D+ abundance reaches 4 × 10−10, and the transition is as bright as 3 K. This limits the area where ζ2 is computed with S/N > 3 in run 1.
The histogram from run 2 spans a larger range of values than run 1 and presents a tail at higher values, because the retrieved ζ2 map presents an increase with increasing distance from the core centre, especially in the northern and western directions (cf. top-right panel of Fig. 2). A further enhancement up to ζ2 ~ 9 × 10−17 s−1 is visible in the south-eastern part of the source (note that this does not affect the histogram, which focuses on the high H2 column density region to improve the S/N). In Sect. 5, we discuss more in detail the implication of the spatial trends seen in the ζ2 maps.
4.1.2 Run 3: low 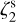 and single-dish like analysis
and single-dish like analysis
To further expand the range of input 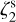 values explored and to be consistent with the tests performed by Bovino et al. (2020), we analysed an additional simulation where the ζ2 is kept constant on the value 2.5 × 10−18 s−1 (low
values explored and to be consistent with the tests performed by Bovino et al. (2020), we analysed an additional simulation where the ζ2 is kept constant on the value 2.5 × 10−18 s−1 (low 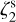 case). We considered the evolutionary time of 100 kyr. The radiative transfer was performed as described in Sect. 3.3, adopting LTE conditions and focusing on the high-J transitions. The post-processing was single-dishlike, with a convolution beam size of 27″. The setup, hence, is identical to the reference run no. 2 except for the input
case). We considered the evolutionary time of 100 kyr. The radiative transfer was performed as described in Sect. 3.3, adopting LTE conditions and focusing on the high-J transitions. The post-processing was single-dishlike, with a convolution beam size of 27″. The setup, hence, is identical to the reference run no. 2 except for the input 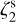 value and the injected noise level. With this
value and the injected noise level. With this 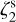 value, the deuteration process is slow, and the abundances of deuterated species (H2D+, DCO+) at 100 kyr are orders of magnitudes lower than in the tests with
value, the deuteration process is slow, and the abundances of deuterated species (H2D+, DCO+) at 100 kyr are orders of magnitudes lower than in the tests with 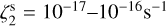 . We reduced the simulated noise level to rms = 1 mK in the post-processing, to compute the column density of all species significantly.
. We reduced the simulated noise level to rms = 1 mK in the post-processing, to compute the column density of all species significantly.
Using the BFL20 method, we obtained the map shown in the bottom-left panel of Fig. 2. The corresponding histogram of the distribution of values is shown in Fig. 1. The computed values are in the range (2–8) × 10−18 s−1, and the median value of (4.8 ± 0.8) × 10−18 s−1 is less than a factor of two higher than the input  .
.
 |
Fig. 2 Resulting ζ2 maps obtained with Eq. (1) in runs 1 to 4. The run ID is reported in the top-left corner, and the key parameters are included at the top of each panel. Run 2 is taken as a reference throughout the rest of this work. The white contours show the 50, 70, and 90% of the N(H2) peaks, which are: 6.67 × 1022 cm−2 (core in single-dish like analysis at 100 kyr); 6.86 × 1022 cm−2 (core in single-dish-like analysis at 50 kyr); 2.51 × 1022 cm−2 (core in ALMAlike analysis at 100 kyr). The beam size and scalebar are shown in the bottom corners of each panel. Note that we show a zoom-in of the central 0.15 pc. |
4.1.3 Run 4: ALMA-like analysis
Here, we focus on the case with constant 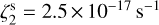 and an ALMA-like post-processing as described in Sect. 3.4.2. It is important to discuss the chosen value of L. In the single-dish-like analysis, the integrated intensity (or optical depth) is computed along the whole simulated line of sight, namely along the whole length of the simulation box (0.3 pc). In the ALMA-like analysis, on the other hand, this is not the case. Once the SIMOBSERVE task is run, the interferometer acts as a low spatial-frequency filter, and the emission over scales larger than the so-called maximum recoverable scale (θmrs) is filtered out. We hence select the θmrs = 15″ that the ALMA OT predicts for the chosen antenna configuration in the oH2D+ (11,0 – 11,1) setup. This corresponds to L = 0.15 pc.
and an ALMA-like post-processing as described in Sect. 3.4.2. It is important to discuss the chosen value of L. In the single-dish-like analysis, the integrated intensity (or optical depth) is computed along the whole simulated line of sight, namely along the whole length of the simulation box (0.3 pc). In the ALMA-like analysis, on the other hand, this is not the case. Once the SIMOBSERVE task is run, the interferometer acts as a low spatial-frequency filter, and the emission over scales larger than the so-called maximum recoverable scale (θmrs) is filtered out. We hence select the θmrs = 15″ that the ALMA OT predicts for the chosen antenna configuration in the oH2D+ (11,0 – 11,1) setup. This corresponds to L = 0.15 pc.
The resulting ζ2 map is shown in the bottom-right panel of Fig. 2. The histogram of run 4 (top-right panel of Fig. 1) is asymmetric, with a global maximum at low ζ2 values (1 × 10−17 s−1), and a tail up to 7 × 10−17 s−1. This is due to the spatial gradient seen in the bottom-right panel of Fig. 2, where ζ2 increases as N(H2) decreases. In the central part of the core, the actual  is well recovered, as confirmed by comparing the median value 〈ζ2〉 = (2.4 ± 0.4) × 10−17 s−1 with
is well recovered, as confirmed by comparing the median value 〈ζ2〉 = (2.4 ± 0.4) × 10−17 s−1 with 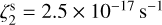 .
.
4.1.4 Runs 5–6: LVG radiative transfer and low-J transition
Runs 5 and 6 explored the effects of the type of radiative transfer performed and of the rotational levels of the lines used in the analysis. Both runs used the LVG option in POLARIS. Run 5 employed the DCO+, H13CO+, and DCO+ transitions at frequencies ≈215–260 GHz. The line intensities are generally lower than in the corresponding LTE calculation. The change is the smallest for the C18O (2−1) line (≈15%), which is expected as this transition is thermalised. On the contrary, the DCO+ and H13CO+ (3−2) fluxes are reduced by a factor of up to 3 and 10, respectively. In fact, due to their high critical densities, these transitions are subthermally excited. This required reducing the simulated noise in this run to 50 mK, to improve the final S/N. Table 2 reports the excitation temperatures used to compute the column densities, following what is stated in Sect. 3.5.
The resulting ζ2 map is shown in the central panel of Fig. 3, and it spans values in the range (0.5–2.5) × 10−17 s−1. The median in the high-density part of the core (see Fig. 1) is 〈ζ2〉 = (1.1 ± 0.2) × 10−17 s−1, hence a factor 2.3 smaller than the actual 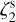 value of the simulations. The ζ2 distribution is asymmetric, as a consequence of the increasing trend of ζ2 with decreasing N(H2) that has also been noted in the previous runs at 100 kyr.
value of the simulations. The ζ2 distribution is asymmetric, as a consequence of the increasing trend of ζ2 with decreasing N(H2) that has also been noted in the previous runs at 100 kyr.
In run 6, we explored the effect of targeting the low-J transitions of C18O, H13CO+, and DCO+, as these lines are often targeted by spectroscopic surveys at 3 mm. We adopt a large beam size of ≈70″, to simulate unresolved observations. The resulting ζ2 map, shown in Fig. 3, presents the flattest distributions of values, with the smallest scatter around the median (see Fig. 1). This happens because the area where we recover the ζ2 map is comparable to the beam size, and hence any spatial trend is smoothed out by the poor resolution. The resulting median 〈ζ2〉 = (3.3 ± 0.7) × 10−17 s−1 agree with the actual 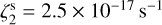 within a factor of 1.3.
within a factor of 1.3.
 |
Fig. 3 Summary of runs performed in LVG approximation, compared with the reference case (run 2, left panel). The central panel refers to the analysis performed on the high-J transitions for DCO+, H13CO+, and C18O, whilst the low-J ones are used in the map in the right panel. The white contours are the same as in Fig. 2. Note that the colour scale is the same across all the panels. The beam size and scalebar are shown in the bottom left and right corners of each panel. |
 |
Fig. 4 Maps of the density-averaged |
4.1.5 Runs 7–8: variable 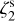
Runs 7 and 8 employed a variable 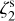 , as described in Sect. 3.1. In this case, it is not straightforward to compare the resulting ζ2 maps with the simulation value, which is a three-dimensional, spatially-dependent quantity. For this comparison, we computed the line-of-sight density-averaged
, as described in Sect. 3.1. In this case, it is not straightforward to compare the resulting ζ2 maps with the simulation value, which is a three-dimensional, spatially-dependent quantity. For this comparison, we computed the line-of-sight density-averaged 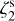 at timesteps 50 and 100 kyr. The results are shown in the top row of Fig. 4. The maps show that the cosmic-ray ionisation rate decreases from ≈2 × 10−16 s−1 at low densities down to ≈1.5 × 10−16 s−1 in the core’s centre, with a variation of 25%. Moreover, the average value in these simulations is almost one order of magnitude larger than in those with constant ζ2, offering us the chance to test a high ζ2 case.
at timesteps 50 and 100 kyr. The results are shown in the top row of Fig. 4. The maps show that the cosmic-ray ionisation rate decreases from ≈2 × 10−16 s−1 at low densities down to ≈1.5 × 10−16 s−1 in the core’s centre, with a variation of 25%. Moreover, the average value in these simulations is almost one order of magnitude larger than in those with constant ζ2, offering us the chance to test a high ζ2 case.
The maps of ζ2 computed using Eq. (1) are shown in Fig. 4 (bottom panels). In general, they tend to underestimate the simulation values, and the disagreement is larger at the earlier timestep. Overall, our results underestimate the actual ζ2 of a factor ≈3. Concerning the decrease of ζ2 with increasing total column density, we note that at 50 kyr the extension of the retrieved ζ2 map corresponds to only a few beams, and no clear spatial trend is seen. In the later timestep, a positive gradient is visible from the core’s centre to the westernmost outskirts, but no symmetric trend is visible in the other directions. A localised enhancement (ζ2 = (7–9) × 10−17 s−1) is seen in the south-east corner of the source, with no clear counterpart in the actual  map, where instead a local decrease is visible in this area. We conclude that the resulting ζ2 map does not reproduce the morphology of the actual one, as we further discuss in Sect. 5.2, but provides an accurate average estimate of
map, where instead a local decrease is visible in this area. We conclude that the resulting ζ2 map does not reproduce the morphology of the actual one, as we further discuss in Sect. 5.2, but provides an accurate average estimate of 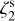 . In addition, we note that the
. In addition, we note that the 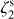 gradient in the original simulations is smaller than the intrinsic error of the analytical formula.
gradient in the original simulations is smaller than the intrinsic error of the analytical formula.
 |
Fig. 5 Maps of the key quantities employed by CWT98: DCO+ deuteration level (top-left panel), CO depletion factor (top-right), electronic fraction (bottom-left), and ζ2 (bottom-right). Note that the colour scales for the last two quantities are in units of 10−6 and 10−13 s−1, respectively. These maps assume the molecular column density and total gas column density derived in run 2. The mean uncertainties are 2.6 × 10−4 (RD), 0.3 (fD), 3 × 10−6 |
4.2 Using the analytical method from Caselli et al. (1998)
We now focus on the analytical method proposed by Caselli et al. (1998, CWT98 hereon) to test the limitations already discussed in Caselli et al. (2002), providing robust evidence via an accurate methodology. The CWT98 approach has the advantage of depending on commonly observed tracers. We note that the equations depend on the H2 volume density, which we estimate as n(H2) = N(H2)/L, where L is set on the same value used for the BFL20 method for each run.
4.2.1 The reference run 2
For the sake of observational applicability, we tested the behaviour of the original equations (Eqs. (3) and (4) of CWT98). Here, we present the results for the reference case (run 2). In Fig. 5, we show the relevant required quantities, in particular, the deuteration level of HCO+ (top left panel), and the CO depletion factor

where Xst(CO) = 1.2 × 10−4 is the CO standard abundance. The HCO+ deuteration level peaks at RD = (6.9 ± 0.3) × 10−3 towards the core’s centre, where the CO depletion reaches fD = (15.8 ± 0.6). Hence, the deuteration level is smaller than the values spanned by the cores of CWT98, but it fulfils the requirement RD < 0.023fD under which the equations can be applied. We further discuss this in Sect. 5. The derived values for the electronic fraction, shown in the bottom-left panel, are in the range (1 – 10) × 10−6. These are overestimated by more than two orders of magnitude compared to the original simulations, where x(e−) ≈ a few × 10−8. This error propagates to the resulting ζ2 map (bottom-right panel of Fig. 5). The equation overestimates the original 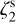 value by more than three orders of magnitudes, especially at the core’s outskirts.
value by more than three orders of magnitudes, especially at the core’s outskirts.
The original method made several simplifications and assumptions, such as, for example, the reaction rates at constant temperature (10 K), and the lack of ortho- and para-state separation. Furthermore, several reaction rates have been updated since then. We have, therefore, derived the equations again using the same theoretical approach of CWT98, but with the formalism of BFL20, to show that the large overestimates produced by the method are not ascribed to these parameters but rather to the approximations made to obtain the formula. The derivation is illustrated in Appendix B. We then computed the electronic fraction and the cosmic-ray ionisation rate using the updated set of Eq. (B.6). We set the HD abundance to X(HD) = 1.5 × 10−5 (Kong et al. 2015), and the para-fraction of 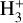 to fpara = 0.7. The latter is consistent with estimates of this parameter in diffuse clouds (see for instance, Crabtree & McCall 2012, and references therein). These values have also been verified in the simulation, and they agree within less than a factor of two (see also Lupi et al. 2021).
to fpara = 0.7. The latter is consistent with estimates of this parameter in diffuse clouds (see for instance, Crabtree & McCall 2012, and references therein). These values have also been verified in the simulation, and they agree within less than a factor of two (see also Lupi et al. 2021).
The resulting maps are shown in Fig. 6. Towards the core’s centre, the x(e−) values are 15–20% lower than those derived with the original equations, but still strongly overestimated. As a consequence, in this area, the new estimates for ζ2 are a factor of ≈2 lower than those from the original derivation, but we still find ζ2 ≈ (1.5 ± 0.2) × 10−13s−1, namely more than three orders of magnitude higher than the actual value.
4.2.2 CWT98 results in all tested runs
We now describe the behaviour of the CWT98 method applied to all the remaining runs. We adopt the new formulation of the method, described in Appendix B. The histograms of the resulting maps, focussing on the central part of the core, are presented in Fig. 7. The most notable feature is that in all tests the retrieved values overestimate the actual ones. The median values in the runs performed on the simulation using 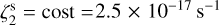 range from (4.8 ± 1.4) × 10–15 s−1 (run 5) to (9.7 ± 1.5) × 10−13 s−1 (run 1), namely an overestimation of two to four orders of magnitude. In the low ζ2 case (run 3), we obtain 〈ζ2〉 = (1.41 ± 0.07) × 10−11 s−1 (overestimated by almost seven orders of magnitude). The two tests performed on simulations with
range from (4.8 ± 1.4) × 10–15 s−1 (run 5) to (9.7 ± 1.5) × 10−13 s−1 (run 1), namely an overestimation of two to four orders of magnitude. In the low ζ2 case (run 3), we obtain 〈ζ2〉 = (1.41 ± 0.07) × 10−11 s−1 (overestimated by almost seven orders of magnitude). The two tests performed on simulations with 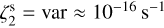 result in (1.68 ± 0.11) × 10−13 s−1 (run 7) and (3.1 ± 0.2) × 10−14 s−1 (run 8), again over-estimating the actual ζ2 by two to three orders of magnitude.
result in (1.68 ± 0.11) × 10−13 s−1 (run 7) and (3.1 ± 0.2) × 10−14 s−1 (run 8), again over-estimating the actual ζ2 by two to three orders of magnitude.
 |
Fig. 6 Electronic fraction (top panel) and ζ2 map (bottom panel) from the reference run 2, using the updated formulation of CWT98. The contours show H2 column density as in Fig. 2. The mean uncertainties are 3 × 10–6 for x(e–) and 0.8 × 10–13 s–1 for ζ2. The beam size and scalebar are shown in the bottom corners of the lower panel. |
4.3 Comparison of the methods on real observations
We now compare the two analytical methods on real observations of prestellar cores found in the literature. We found three sources for which all the needed observables are available: L1544, L183, and TMC-1C. The literature values of the required quantities are listed in Table 4. For these cores, the H2 volume density is well characterised, and we used this quantity directly in the CWT98 Eq. (B.6). For the BFL20 method, a discussion on the parameter L is required. The physical meaning of L is the length of the path on the line-of-sight along which the column densities are computed; in other words, L is the depth of the emitting source. This, in the simulations, is known by construction. In our setup, we cut a (0.3 pc)3 subcube in the initial larger simulation box (0.6 pc) which is initialised with molecular gas; thus, it is full of CO, for instance. Emitting gas, therefore, is found along the whole box, and the choice of L to be equal to the size of the subcube is well justified. If we were to cut a smaller subcube, L should be adjusted accordingly, since the depth of the emitting gas would also be reduced (see also Appendix D for further details). This does not apply to real observations. Real cores are finite, and the length of the emitting gas is limited along the length of the line of sight. Thus, L has to be computed as the source size along the line of sight, which however is unknown. For isolated prestellar cores, we propose to compute L by considering the 20% isocontour of the N(H2) peak. Using this prescription, the sizes of the three analysed cores are 0.20–0.35 pc. The final ζ2 values are also reported in Table 4.
The ζ2 values computed with BFL20 are in the range (0.71.7) × 10−17s−1, whilst with CWT98 we obtain (0.2–2.0) × 10−14 s−1. Note that there are many uncertainties in the analysis. For instance, the literature values have been computed with data from different telescopes (hence at different resolutions). Furthermore, we assume T = 10 K, whilst some of the sources might be colder (cf. Caselli et al. 2008). However, the uncertainties on these quantities cannot explain a difference of three orders of magnitude between the two methods. These examples, hence, confirm that CWT98 tends to produce overestimated results compared to BFL20.
The actual ζ2 value in these objects is not known, however Redaelli et al. (2021b) derived 3.0 × 10−17 s−1 in L1544, and Fuente et al. (2019) found ζ2 = (5−18) × 10−17 s−1 in the translucent cloud associated with TMC1. Both papers used extensive modelling of the sources, coupling chemical models with radiative transfer analysis on a large set of molecular tracers. Pagani et al. (2009) explored the chemistry and structure of L183, assuming ionisation rates in the range (0.1−10) × 10−16 s−1 and, even though a definite best-value for this parameter is not given, the authors used ζ2 = 2 × 10−17 s−1 in their most detailed modelling. Furthermore, the most recent models of CR propagation in the dense gas predict ζ2 values of at most a few 10−16s−1, unless a local source of CR re-acceleration is present (cf. Padovani et al. 2016, 2018, 2022). It is safe to assume, in summary, that values as high as ζ2 = 10−14 s−1 are excluded for these quiescent and dense cores.
5 Discussion
5.1 Results and limitations of the methods
In Fig. 8, we summarise the results obtained with the BFL20 method in the eight runs of Sect. 4.1. In the case of constant 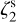 , we show the average ratio between the derived values and the reference
, we show the average ratio between the derived values and the reference 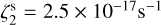 (runs 1, 2, and 4 to 6) or
(runs 1, 2, and 4 to 6) or  (run 3). For runs 7 and 8, where the input
(run 3). For runs 7 and 8, where the input 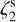 is variable, we show the median of the ratio between the derived values and the input values (see top panels of Fig. 4). Error bars are computed as three times the median uncertainties over the pixels considered to evaluate the median. As for the histograms in Fig. 1, we consider only the densest part of the core.
is variable, we show the median of the ratio between the derived values and the input values (see top panels of Fig. 4). Error bars are computed as three times the median uncertainties over the pixels considered to evaluate the median. As for the histograms in Fig. 1, we consider only the densest part of the core.
Figure 8 shows that the retrieved values are within a factor of 1.5-3 from the actual ones. The offset is not constant, nor systematic. In cases with low and constant 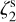 , we see that Eq. (1) overestimates the input value by a factor of up to 1.5 (except run 5). On the other hand, for the two runs with variable
, we see that Eq. (1) overestimates the input value by a factor of up to 1.5 (except run 5). On the other hand, for the two runs with variable 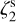 (runs 7 and 8), the resulting ζ2 maps tend to underestimate the actual values by a factor of ≈3. Overall, the BFL20 formula represents a robust and reliable method to estimate the order of magnitude of ζ2 in dense regions. As for similar analytical methods, even if the BFL20 method shows to be accurate within a factor of 2–3, several aspects should be taken into account when it is applied to actual observations. The first one is that the analytic expression depends on the column density of four molecular tracers. If any of these is affected by a systematic error, this will propagate to the ζ2 estimation. Column densities strongly depend on the chosen excitation temperature values. By performing an LTE analysis, we have initially avoided this problem, fixing the Tex for all the molecular tracers to the constant gas temperature. In the LVG runs, we selected Tex looking for literature references and checking the selected values with non-LTE tools (such as RADEX). Indirectly, this work hence provides good estimates of the Tex of several commonly observed transitions, in the considered density (n ≈ 105 cm−3) and gas temperature (TK = 15 K) regimes. In reality, the problem of choosing the correct Tex has no straightforward solution, especially in the case of subthermally-excited lines. We strongly suggest (when possible) using multiple lines of the same tracer, which allows us to constrain their excitation conditions better.
(runs 7 and 8), the resulting ζ2 maps tend to underestimate the actual values by a factor of ≈3. Overall, the BFL20 formula represents a robust and reliable method to estimate the order of magnitude of ζ2 in dense regions. As for similar analytical methods, even if the BFL20 method shows to be accurate within a factor of 2–3, several aspects should be taken into account when it is applied to actual observations. The first one is that the analytic expression depends on the column density of four molecular tracers. If any of these is affected by a systematic error, this will propagate to the ζ2 estimation. Column densities strongly depend on the chosen excitation temperature values. By performing an LTE analysis, we have initially avoided this problem, fixing the Tex for all the molecular tracers to the constant gas temperature. In the LVG runs, we selected Tex looking for literature references and checking the selected values with non-LTE tools (such as RADEX). Indirectly, this work hence provides good estimates of the Tex of several commonly observed transitions, in the considered density (n ≈ 105 cm−3) and gas temperature (TK = 15 K) regimes. In reality, the problem of choosing the correct Tex has no straightforward solution, especially in the case of subthermally-excited lines. We strongly suggest (when possible) using multiple lines of the same tracer, which allows us to constrain their excitation conditions better.
When using optically-thin isotopologues to infer the total column densities of molecular tracers, particular caution has to be paid to the assumed isotopic ratios, since fractionation processes can lead to significant variation from the elemental iso-topic ratios (see, for instance, the discussion of Colzi et al. 2020 on 12C/13C). In this work, we avoided this problem by assuming consistent isotopic ratios throughout the postprocessing analysis (cf. Sects. 3.1 and 3.3).
Another crucial parameter in Eq. (1) is the scale length L employed to obtain the column densities, as discussed in Sect. 4. In our analysis, L is known by construction from the size of the simulation box, since this is a subcube cut out of a larger simulation initialised with molecular gas. We justify this choice further in Appendix D. For observed cores, their size (and, in particular, their depths) are in general unknown. We suggest as a prescription to use the contour where N(H2) is higher than 20% of its peak value to estimate L. In the three real objects we analysed, this approach leads to ζ2 values in agreement with estimations of this quantity derived with completely different methods. Note that applying this rule to the reference run 2 results in L = 0.15 pc, hence overestimating ζ2 by a factor ≈2, still within the uncertainties of the method. This prescription should not be used on interferometric data with a maximum recoverable scale smaller than the actual source size, as this leads to emission filtering. In these cases, we speculate that θmrs is a proper scale to estimate L. This uncertainty on L also affects the approach of CWT98, where however this is mitigated if the gas volume density is known from other observables.
We highlight how the core fraction where we are able to infer ζ2 is different in each case (see Figs. 2, 3, and 4). This is driven, in particular, by the column density of oH2D+. At earlier times, the abundance of this species is lower, hence the extension of the core where it is detected is smaller. This highlights the main limitation of this method, which relies on the detection of oH2D+(11.0 – 11.1) (see also Sect. 5.3 for details).
On the other hand, the analytic method of CWT98 overestimates ζ2 by several orders of magnitudes in the cases explored in this work, where it should not be employed (see also the discussion in Sect. 3 of Caselli et al. 2002). This is due to the overestimation of the electron fraction caused by the neglected kinetics of H2D+ employed to derive Eq. (B.2), in particular, the reactions producing the doubly- and triply-deuterated forms of H+, and other destruction channels involving neutrals. Concerning the importance of D2H+ and  , Caselli et al. (2008) developed analytical equations where the deuteration level of HCO+ is expressed in terms of all the deuterated forms of H+.
, Caselli et al. (2008) developed analytical equations where the deuteration level of HCO+ is expressed in terms of all the deuterated forms of H+.
We note that when ζ2 is derived in the reference case with the analytic expression of CWT98 (10−14−10−13 s-1), its value is one to two orders of magnitude higher than in the original paper (where ζ2 = 10−16−10−14 s−1 was found when assuming ƒD = 5). This is because the simulated core presents relatively low levels of deuteration and a high depletion factor. In Appendix B, we show how the CWT98 formula leads to increasingly high ζ2 values when the deuteration is low, and the CO depletion is high (cf. Fig. B.2). In the reference case (run 2), the core centre presents RD ≈ 0.4–0.7% and ƒD ≈ 10–15. These are not the typical values observed in CWT98, where most sources present a deuteration fraction of a few per cent (see also Butner et al. 1995; Williams et al. 1998). Note that, given the lack of information available back then on the CO depletion, ƒD > 5 was not included in their analysis (catastrophic CO freeze-out was first measured 1 yr later, Caselli et al. 1999). Furthermore, the assumed temperature T = 15 K is higher than typical gas temperatures observed in low-mass prestellar cores (Bergin et al. 2006; Crapsi et al. 2007). However, in run 8, with variable ζ2 at 100 kyr, the core’s centre presents RD ≈ 2% and ƒD ≈ 3–4, closer to the properties of the objects analysed by CWT98. The retrieved ζ2 is (3.1 ± 0.2) × 10−14 s−1 (see Fig. 7), overestimating the actual ζ2 by two orders of magnitudes, confirming the limitation of this approach.
The relatively low deuteration level of the reference case is due to the assumed initial conditions, in particular the initial H2 OPR. By using constant-density one-zone models, we foundthat when OPR = 10−3 (as reported in the dense and evolved prestellar cores, for instance Kong et al. 2015), the HCO+ deuteration level increases by about one order of magnitude, and the derived ζ2 values decrease to ζ2 = 10−16−10−15 s−1, still a factor of 10-100 more than the actual value. These tests show that the CWT98 analytic method has a marked dependence on the initial OPR, conversely to BFL20, which is relatively unaffected by this parameter, as already discussed in Bovino et al. (2020). The scope of this work is to retrieve ζ2 under the typical observational conditions while reproducing the exact physical details of a specific observed object is beyond our aims. The latter was done, for example, by Bovino et al. (2021), where the simulation was designed to reproduce six observed cores in Ophiucus.
 |
Fig. 7 Same as Fig. 1, but the ionisation rate is estimated using the new formulation of the CWT98 method presented in Appendix B, summarised in Eq. (B.6). Note that the ζ2 values are normalised to 10−13 s−1 in all panels. The median (± median uncertainty) is reported in the top-right corner and shown with the vertical dashed line and shaded area in each panel. The reference run is labelled with "Ref" in the bottom-right corner. |
Comparison of ζ2 values obtained with the CWT98 and BFL20 methods towards three prestellar cores, assuming a gas temperature of 10 K.
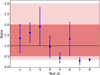 |
Fig. 8 Ratio between ζ2 retrieved in each run (x-axis labels), and the actual value |
5.2 Morphology of the resulting ζ2 maps
The obtained ζ2 maps allow us to comment also on the morphology of the retrieved ionisation rate. By looking at Figs. 2 and 3, it is clear that for most of the runs where ζ2 is computed in an extended part of the source (namely when N(H2) ≲50% of its peak), ζ2 presents a positive gradient with increasing distance from the core’s centre. This is also seen in the histograms in Fig. 1, where asymmetric tails towards the high ζ2 values are seen in runs 2, 4, and 5. Since in these runs, the actual  is constant, these spatial trends are not real. These considerations holds also for CWT98 (see Figs. 5 and 6). The single-dish test performed with the larger beam size (run 6) presents the flattest distribution and the smallest scatter around the median because the core is not spatially resolved. On the contrary, in the tests with variable
is constant, these spatial trends are not real. These considerations holds also for CWT98 (see Figs. 5 and 6). The single-dish test performed with the larger beam size (run 6) presents the flattest distribution and the smallest scatter around the median because the core is not spatially resolved. On the contrary, in the tests with variable  , the retrieved maps do not show the gradient with the increasing density present in the simulation (see Sect. 4.1.5 for more details). We conclude that apparent spatial trends should not be trusted, and averages across the densest regions of the source should be instead considered to express the resulting ζ2.
, the retrieved maps do not show the gradient with the increasing density present in the simulation (see Sect. 4.1.5 for more details). We conclude that apparent spatial trends should not be trusted, and averages across the densest regions of the source should be instead considered to express the resulting ζ2.
5.3 Observational feasibility
This work aims to provide observers with reliable methods to estimate ζ2 in real sources. It is hence important to assess the observability of the proposed tracers. The continuum observations are not particularly challenging and do not represent the limiting aspect of this endeavour. Conversely, the feasibility of the molecular line observations requires a more detailed discussion.
We first focus on single-dish facilities. As reported in Table 2, the H13CO+ (3–2), DCO+ (3–2), ad C18O (2–1) lines can be observed by APEX, namely with the nFLASH23O instrument. Using its observing time calculator12, and standard input values, we compute that on-source times of 1.0–1.4 h are sufficient to reach rms = 100 mK in a 3′ × 3′ FoV and a 0.1 km s–1 channel. The corresponding (1-0) transitions are covered, for instance, by the EMIR receiver mounted on the IRAM 30m telescope. The time estimator13 predicts that, in winter, 1 h of on-source time is enough to reach a sensitivity of 100 mK, with a 3′ × 3′ FoV and using a 0.1 km s–1 resolution.
The oH2D+(110 – 11,1)transition is the most challenging in terms of sensitivity, due to its high frequency when compared to the other transitions analysed here. The same requirements in terms of spectral resolution, sky coverage, and sensitivity made for the other lines would lead to 25 h of on-source time using the multi-beam LAsMA receiver mounted on APEX. However, by relaxing the requirements to a FoV of 2′ × 2′ (still able to cover the portion of the core where N(H2) ≳ 2.5 × 1022 cm–2) and downgrading the resolution to 0.15 km s−1, the on-source time reduces to 7.5 h, which is manageable in a small project. The downgraded spectral resolution does not impact the computation of the column density, since the lines are still resolved by at least 3 channels. The sensitivity required by the low ζ2 case in run 3(1 mK), on the other hand, is currently well beyond the capabilities of existing single-dish facilities, even in the case of single-point observations at the centre of the source.
The observing times required with ALMA are listed in Table 3. Considering that several lines can be observed simultaneously, these observations appear feasible. We conclude that in most cases the observations required to compute ζ2 are feasable, as proved by the increasing number of campaigns recently reported (cf. Giannetti et al. 2019; Sabatini et al. 2020; Redaelli et al. 2021a, 2022).
6 Summary and conclusions
In this work, we tested two analytical methods to retrieve the cosmic-ray ionization rate ζ2 in dense gas. We used synthetic molecular and continuum data, produced via radiative transfer analysis on a set of 3D simulations that include the chemistry of the involved molecular tracers. This allows us to evaluate with accuracy the loss of information (and then the accuracy of the method) when simulating realistic observations.
The method of Caselli et al. (1998) has several limitations by construction, such as RD < 0.029 × ƒD (to avoid x(e) < 0 in the new formulation derived in Appendix B). Furthermore, this analytical approach strongly depends on the H2 initial OPR. This limits its applicability, especially when the OPR is reset to much higher values than those in cold cores by conditions such as shocks or protostellar outflows. In our reference case, this method overestimates  by up to four orders of magnitude. In particular, in tests where the deuteration level is a few %, hence similar to what is observed in several prestellar cores, the Caselli et al. (1998) method overestimates by two orders of magnitude the actual
by up to four orders of magnitude. In particular, in tests where the deuteration level is a few %, hence similar to what is observed in several prestellar cores, the Caselli et al. (1998) method overestimates by two orders of magnitude the actual  .
.
On the contrary, the method of Bovino et al. (2020) is generally accurate (within a factor of 2-3) in retrieving the actual 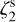 . Its main limitation is linked to the level of total deuteration, since at late evolutionary stages or at very high densities (n ≳ 107 cm–3) H2D+ is converted into doubly and triply deuterated forms, and it is not a reliable tracer of the total
. Its main limitation is linked to the level of total deuteration, since at late evolutionary stages or at very high densities (n ≳ 107 cm–3) H2D+ is converted into doubly and triply deuterated forms, and it is not a reliable tracer of the total 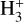 abundance anymore. This leads to underestimating the actual
abundance anymore. This leads to underestimating the actual 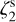 , as already pointed out in the original paper (Bovino et al. 2020).
, as already pointed out in the original paper (Bovino et al. 2020).
As a direct example of the application of the two formulae on observational data, we explored three well-known prestellar objects, with recent literature data on the quantities involved in the calculation. We showed that the ζ2 values obtained with BFL20 are in overall good agreement with estimations of the same quantities obtained with non-analytical methods. The results of CWT98 are two to three orders of magnitude higher, as seen also in the tests on the simulations. We highlight, however, that to establish the methodology proposed by Bovino et al. (2020), a statistical sample of observed cores and a proper comparison with theoretical models of CR propagation are needed.
To conclude, we have discussed the feasibility of the observations necessary to use two commonly employed analytical methods to retrieve ζ2. Despite the observational challenges, they are accessible with currently available radio facilities. When the physical structure of a source is well known, coupling a chemical code with radiative transfer using multiple tracers could be employed to infer the cosmic-ray ionisation rate, even if its results might be affected by the parameters’ degeneracy. For all the other sources (when this approach is not a viable option), the method of Bovino et al. (2020) is a model-independent and reliable analytical method to investigate ζ2 in dense regions.
Acknowledgements
The authors acknowledge the referee’s comments that led to the manuscript’s improvement. E.R. and P.C. acknowledge the support of the Max Planck Society. S.B. is financially supported by ANID Fondecyt Regular (project #1220033), and the ANID BASAL projects ACE210002 and FB210003. A.L. acknowledges funding from MIUR under the grant PRIN 2017-MB8AEZ. G.S. acknowledges the projects PRIN-MUR 2020 MUR BEYOND-2p ("Astro-chemistry beyond the second period elements", Prot. 2020AFB3FX) and INAF-Minigrant 2023 TRIESTE ("TRacing the chemIcal hEritage of our originS: from proTostars to planEts"). The authors acknowledge the Kultrun Astronomy Hybrid Cluster for providing HPC resources that have contributed to the research results reported in this paper.
Appendix A Derivation of Bovino et al. (2020) (BFL20)
Here, we follow the derivation of Eq. (1). The main reactions in our framework, considering the different isomers and isotopologues (but 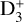 ) for the formation of HCO+ and DCO+ are:
) for the formation of HCO+ and DCO+ are:

For the destruction, we consider only dissociative recombinations, as per:
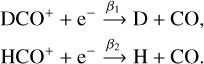
The kinetic equations are expressed as:
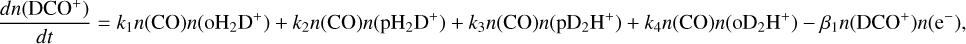
Assuming steady-state14 and taking the ratio between the two equations we obtain
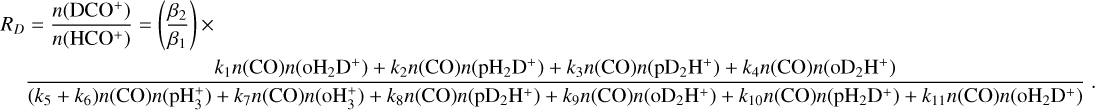
Using the following relations among the reaction rates
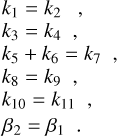
The final equation is expressed as (noting that n(CO) and n(e−) cancel each other out):
![${R_D} = {{n\left( {{\rm{DC}}{{\rm{O}}^ + }} \right)} \over {n\left( {{\rm{HC}}{{\rm{O}}^ + }} \right)}} = {{{k_1}\left[ {n\left( {{\rm{o}}{{\rm{H}}_2}{{\rm{D}}^ + }} \right) + n\left( {{\rm{p}}{{\rm{H}}_2}{{\rm{D}}^ + }} \right)} \right] + {k_3}\left[ {n\left( {{\rm{p}}{{\rm{D}}_2}{{\rm{H}}^ + }} \right) + n\left( {{\rm{o}}{{\rm{D}}_2}{{\rm{H}}^ + }} \right)} \right]} \over {{k_7}\left[ {n\left( {{\rm{oH}}_3^ + } \right) + n\left( {{\rm{pH}}_3^ + } \right)} \right] + {k_8}\left[ {n\left( {{\rm{p}}{{\rm{D}}_2}{{\rm{H}}^ + }} \right) + n\left( {{\rm{o}}{{\rm{D}}_2}{{\rm{H}}^ + }} \right)} \right] + {k_{10}}\left[ {n\left( {{\rm{p}}{{\rm{H}}_2}{{\rm{D}}^ + }} \right) + n\left( {{\rm{o}}{{\rm{H}}_2}{{\rm{D}}^ + }} \right)} \right]}}.$](/articles/aa/full_html/2024/05/aa46413-23/aa46413-23-eq86.png) (A.1)
(A.1)
In order to simplify Eq. (A.1), we can exploit further relations between the reaction rates, mainly linked to their branching ratios: k1/k7 = 1/3, k1/kl0 = 1/2, k8/k3 = 1/2, and k3/k7 = 2/3. Moreover, we neglect the correction for para and ortho species that cannot be observed, the contribution from the doubly deuterated isotopologue, and the formation channel of HCO+ via H2D+, arriving at15
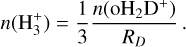 (A.2)
(A.2)
By inserting Eq. (A.2) in (see for instance Oka 2019, and also the derivation in Appendix B) as follows:
 (A.3)
(A.3)
we obtain the final formula for the cosmic-ray ionisation rate
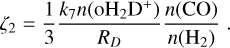 (A.4)
(A.4)
This equation is valid as long as oH2D+ is the dominant deuterated form of 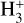 and when the reaction with CO is more important than dissociative recombination in the destruction of H+3. The first limitation implies that when deuteration levels become higher and oH2D+ is converted into its doubly and triply deuterated isotopologues, Eq. (A.4) cannot be used anymore. Concerning the destruction pathways, we can investigate at which CO abundance (as a function of the electronic fraction) its reaction with H3+ dominates over the dissociative recombination (see the right-hand side of Eq. (B.5)). We find that this holds for fD < 9 × l0−7/x(e−) (assuming fpara = 0.7, see also Appendix B). For x(e) = 10−8, close to the values found in the reference run, the reaction with CO is dominant if fD ≲ 90, which is verified in our simulations. However, at very high densities, when fD > 100, this assumption might not hold anymore.
and when the reaction with CO is more important than dissociative recombination in the destruction of H+3. The first limitation implies that when deuteration levels become higher and oH2D+ is converted into its doubly and triply deuterated isotopologues, Eq. (A.4) cannot be used anymore. Concerning the destruction pathways, we can investigate at which CO abundance (as a function of the electronic fraction) its reaction with H3+ dominates over the dissociative recombination (see the right-hand side of Eq. (B.5)). We find that this holds for fD < 9 × l0−7/x(e−) (assuming fpara = 0.7, see also Appendix B). For x(e) = 10−8, close to the values found in the reference run, the reaction with CO is dominant if fD ≲ 90, which is verified in our simulations. However, at very high densities, when fD > 100, this assumption might not hold anymore.
By introducing average quantities integrated over the path L along the line of sight, Eq. (A.4) finally becomes
 (A.5)
(A.5)
We note that 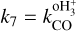 is given in the main text.
is given in the main text.
Appendix B Derivation of Caselli et al. (1998) (CWT98)
We now illustrate the derivation of the equations used in Caselli et al. (1998), which in turn are based on previous works (for instance Guelin et al. 1977, 1982). In particular, we aim to follow the same approach as those papers, including this time the ortho and para separation for all the involved species.
The first part of the equations is the same as illustrated in Appendix A, and involves balancing the destruction and formation pathways of HCO+ and DCO+ , arriving at (see Eq. (A.1))
 (B.1)
(B.1)
where we neglect the reactions involving doubly and triply deuterated 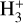 and reactions 10 and 11). In this case, however, we look for a way to express the ratio
and reactions 10 and 11). In this case, however, we look for a way to express the ratio  as a function of the densities of CO, HD, and of the electron fraction. To this aim, we have to write the reactions involved in the formation and destruction of H2D+ (in its ortho and para states). For the formation pathways, we have:
as a function of the densities of CO, HD, and of the electron fraction. To this aim, we have to write the reactions involved in the formation and destruction of H2D+ (in its ortho and para states). For the formation pathways, we have:
The destruction pathways, instead, involve the reactions with CO (with rates k1, k2, k10, and k11, see above)16 and the following dissociative recombinations:
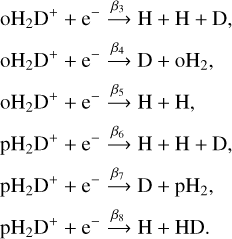
We note that we have neglected all the reactions involving doubly and triply deuterated H+, so as to remain consistent with the simplification done to obtain Eq. (B.1). For several of the involved reaction rates, it is possible to show that
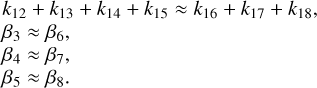
These relations do not hold exactly, but we will show that in the temperature range here considered the agreement is reasonably good. The first relation is reported in the left panel of Fig. B.1. For temperatures ≲ 25 K, the discrepancy is lower than 10%, and in the range 10 − 15 K, the difference is 1 − 3%. We hence assume that equality holds. For the various rates of dissociative recombination (β3 to β8), the difference at 15K is ≈6%, but it quickly rises above 25% outside the range 10 – 20K. We hence suggest extreme caution in using these and the following relations outside this temperature range. However, without these assumptions, it is in practice impossible to properly re-derive and upgrade the formula proposed by CWT98.
We can now write the kinetic equations for the para and ortho species separately as:
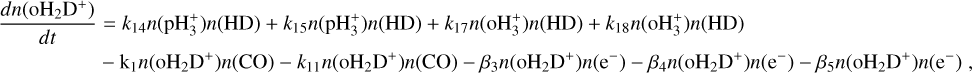
Assuming the steady state, we can re-write the two equations above as:
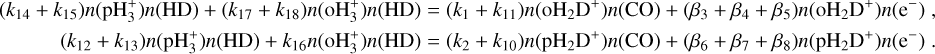
By summing the two equations above and exploiting the relations between the reaction rates, we arrive at:

which allows us to rewrite Eq. (B.1) as:
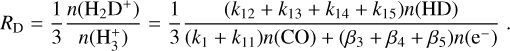 (B.2)
(B.2)
 |
Fig. B.1 Ratio between the sum of the rates of the reactions between |
The next step is to express the quantity RH = n(HCO+)/n(CO) as a function of the cosmic ray ionisation rate and the electronic fraction. First, we solve the kinetic equation for HCO+ in steady-state, again neglecting all terms containing D2H+ and 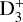 (see above):
(see above):
 (B.3)
(B.3)
To find an expression for n(H+), we solve its kinetics. Its total formation rate is æ2n(H2). The destruction pathways instead are separated in the ortho and para species, and involve the reaction with CO (reactions 5 to 7) and the following dissociative recombinations:

The destruction rates of the two species are then:
![$\eqalign{ & {\left. {{{dn\left( {{\rm{oH}}_3^ + } \right)} \over {dt}}} \right|_{{\rm{destr }}}} = - \left[ {{k_7}n\left( {{\rm{oH}}_3^ + } \right)n({\rm{CO}}) + \left( {{\beta _9} + {\beta _{10}}} \right)\left( {{\rm{oH}}_3^ + } \right)n\left( {{{\rm{e}}^ - }} \right)} \right], \cr & {\left. {{{dn\left( {{\rm{pH}}_3^ + } \right)} \over {dt}}} \right|_{{\rm{destr }}}} = - \left[ {\left( {{k_5} + {k_6}} \right)n\left( {{\rm{pH}}_3^ + } \right)n({\rm{CO}}) + \left( {{\beta _{11}} + {\beta _{12}} + {\beta _{13}}} \right)\left( {{\rm{pH}}_3^ + } \right)n\left( {{{\rm{e}}^ - }} \right)} \right]. \cr} $](/articles/aa/full_html/2024/05/aa46413-23/aa46413-23-eq110.png)
From these equations, we can then compute the destruction rate for the total  density, and set it equal to the total formation rate, obtaining:
density, and set it equal to the total formation rate, obtaining:
![${\zeta _2}n\left( {{{\rm{H}}_2}} \right) = {k_7}n\left( {{\rm{H}}_3^ + } \right)n({\rm{CO}}) + n\left( {{{\rm{e}}^ - }} \right)\left[ {\left( {{\beta _{11}} + {\beta _{12}} + {\beta _{13}}} \right)n\left( {{\rm{pH}}_3^ + } \right) + \left( {{\beta _9} + {\beta _{10}}} \right)\left( {{\rm{oH}}_3^ + } \right)} \right].$](/articles/aa/full_html/2024/05/aa46413-23/aa46413-23-eq112.png) (B.4)
(B.4)
To further simplify Eq. (B.4), we focus on the dissociative recombination rates of ortho- and para- . Their ratio is shown in the right panel of Fig. B.1, where one can see how at low temperatures (T ≲ 20 K), the reaction rates of
. Their ratio is shown in the right panel of Fig. B.1, where one can see how at low temperatures (T ≲ 20 K), the reaction rates of  is about one order of magnitude higher than that of
is about one order of magnitude higher than that of 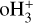 . We will hence neglect the second term, and introduce the para fraction
. We will hence neglect the second term, and introduce the para fraction 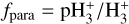 , to write:
, to write:
 (B.5)
(B.5)
where  Equation (B.5) can be solved for
Equation (B.5) can be solved for 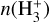 , and then inserted in Eq. (B.3). The system of equations to infer the electron fraction and ζ2 becomes:
, and then inserted in Eq. (B.3). The system of equations to infer the electron fraction and ζ2 becomes:
![$\matrix{ {x\left( {{{\rm{e}}^ - }} \right)} & { = {1 \over {{\beta _3} + {\beta _4} + {\beta _5}}}\left[ {{1 \over 3}{{\left( {{{\rm{k}}_{12}} + {{\rm{k}}_{13}} + {{\rm{k}}_{14}} + {{\rm{k}}_{15}}} \right)X({\rm{HD}})} \over {{R_{\rm{D}}}}} - \left( {{{\rm{k}}_1} + {{\rm{k}}_{11}}} \right)X({\rm{CO}})} \right],} \cr {{\zeta _2}} & { = \left[ {{k_7}X({\rm{CO}}) + {\beta _{{\rm{pH}}_3^ + }}{f_{{\rm{para}}}}x\left( {{{\rm{e}}^ - }} \right)} \right]{{{\beta _2}{R_{\rm{H}}}x\left( {{{\rm{e}}^ - }} \right)n\left( {{{\rm{H}}_2}} \right)} \over {{k_7}}},} \cr } $](/articles/aa/full_html/2024/05/aa46413-23/aa46413-23-eq120.png) (B.6)
(B.6)
where now quantities are expressed in terms of abundances, rather than volume densities.
Equations (B.6) have a mathematical limitation, in that for certain combinations of RD and X(CO) (or, equivalently, of fD) the first one yields negative values for the electron fraction. By computing the reaction rates at 15 K, and assuming X(HD) = 1.5 × 10−5 and fpara = 0.7, we find that the threshold is RD = 0.029 × fD. Note a small variation to the original limitation of RD = 0.023 × fD. For deuteration levels higher than this limit, the equation cannot be applied. At 10 K, the new rates of Eqs. (B.6) 10 – 50% are lower than the original equations (3 and 4) of CWT98. As a result, the updated equations lead to electron fractions lower by 20% and ζ2 values lower by 50% than the original derivation.
Figure B.2 shows the dependency of ζ2 (normalised by the quantity RH × n(H2)) as a function of the deuterium fraction and CO depletion factor. One can see that, for decreasing deuteration levels, the quantity ζ2/(RH × n(H2)) increases by several orders of magnitude. Since ζ2 depends linearly on RH and n(H2), this translates into an equal increase also of this quantity. The plot also shows that for the deuteration values observed in dense prestellar cores (RD = 0.01 – 0.1), there is a strong dependency on the depletion factor, up to fD ≈ 10 – 20.
 |
Fig. B.2 ζ2 values (divided by RH × n(H2)) obtained with Eq. (B.6) at 15 K, as a function of RD and fD. The bottom-right corner is missing because it violates the condition RD < 0.029 × fD. The plot shows that the quantity ζ2/(RH × n(H2)) increases by up to four orders of magnitude when the deuteration fraction decreases from 0.1 to 10−3 and that the CO depletion factor plays a significant role at RD typical for dense gas (0.01 – 0.1). |
Appendix C Tex values for DCO+ and H13CO+ in LVG analysis
In Sect. 3.5 we discussed the choice of Tex values for each transition processed with the LVG radiative transfer. Whilst those for C18O and oH2D+ are well documented in the literature, this is not the case for DCO+ and H13CO+ transitions. We have corroborated the values we chose by using the online tool RADEX. However, in this Appendix, we investigate how a variation of the Tex values of ≈20% affect the inferred ζ2 values. The results are shown in Fig. C.1, where, in the upper panel, we analyse run 5 that uses the DCO+ and H13CO+ (3-2) lines, and in the lower panel we present run 6, which instead focuses on the first rotational transitions.
In run 5, we explore a Tex variation of 1K. The resulting ζ2 values change by ≈25%. Note that the variation is stronger when the Tex is lowered, due to the Tex dependence of Eq. 2. For run 6, the values are changed by 2K, exploring the range 8 – 12 K, which leads to a smaller variation of the inferred ζ2 maps (less than 10%). In all cases, the derived ζ2 values do not change significantly compared to the uncertainties, and the median values are still less than a factor of three from the actual input ζ2 of the simulation.
Appendix D The choice of L in single-dish-like runs
To apply the analytical equations in the case of single-dish-like post-processing of the simulations, we set L = 0.3 pc, corresponding to the size of the analysed cut-out from the original simulation box (0.6 × 0.6 × 0.6 pc3). To support this choice and to show that this is the relevant physical quantity to take into account, we perform a further additional test. We analyse the same simulation as in the reference run n. 2, but this time we halve the size of the cut-out box before the radiative transfer. Hence, L = 0.15 pc. The subsequent steps in terms of radiative transfer and post-processing are identical to those followed in run 2.
 |
Fig. C.1 Histograms of the derived ζ2 values with the BFL20 method in run 5 (upper panel, high-J transitions) and run 6 (lower panel, low-J transitions). The different colours show different assumptions for the excitation temperature of DCO+ and H13CO+ (assumed to be equal). In particular, the reference values used in the main text are shown in red (hence these data are the same presented in Fig. 1), whilst the blue/green curves show a positive/negative variation of ≈20% of that value, respectively (labelled in the top-right corner of each panel). The median values and uncertainties are shown with the vertical dashed lines and shaded areas and with coloured text in each panel. |
Our simulation consists of a box filled with molecular gas. As a consequence, most of the analysed quantities change when L = 0.15 pc. The oH2D+ column density is the only one that is not affected by this change since this molecule is highly concentrated in the densest part of the core and has a high critical density. H13CO+ and C18O suffer the largest change, and their retrieved column densities decrease by a factor of up to 2 – 3. In the simulation, these two molecules are abundant everywhere, and hence cutting a smaller portion of the simulation box affects significantly their total density on the line of sight. The DCO+ column density decreases by 10 – 20%. The total gas density N(H2) derived from the dust thermal emission decreases marginally (~ 5% or less). Because of these changes, RD increases and X(CO) decreases, however not at the same rate. We compare the ζ2 maps obtained in the two tests with distinct L computed with the BFL20 method in Fig. D.1 (left and middle panel). The distributions of values are shown as histograms in the right panel. The maps are similar both in morphology and in the range of values. The histograms confirm these conclusions. The distributions are comparable and the median values (shown with vertical, dashed lines) are consistent with each other: 〈ζ2〉 = (4.0 ± 0.7) × 10−17 s−1 (L = 0.3 pc) and 〈ζ2〉 = (3.7 ± 0.8) × 10−17 s−1 (L = 0.15 pc). If we used the old value L = 0.3 pc in the new test with a smaller box, the blue histogram would shift to the left (towards lower values) by a factor of two.
This test suggests that using the size of the cut-out box to estimate L in these runs is an appropriate choice. We stress again that this is a consequence of the particular simulation we are investigating, which represents a rather dense medium where most of the molecules of interest are abundant in the entire box. This is not the case for isolated cores such as the ones tested in Sect. 4.3 of the manuscript, for which the prescription based on the N(H2) isocontour is appropriate.
 |
Fig. D.1 Comparison of the resulting ζ2 maps (in units of 10−17 s−1) on the two runs with distinct box sizes L but otherwise identical, using the BFL20 method. Panel a) shows the run with L = 0.3 pc (namely the reference run 2), and panel b) shows the results with L = 0.15 pc. The colorbar is kept fixed to ease the comparison. The histogram distributions are compared in panel c), labelled in the top-right corner. The median values (median uncertainties) are shown with the vertical dashed lines (shaded areas). |
References
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Maret, S., van der Tak, F. F. S., et al. 2006, ApJ, 645, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Bovino, S., Ferrada-Chamorro, S., Lupi, A., et al. 2019, ApJ, 887, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Bovino, S., Ferrada-Chamorro, S., Lupi, A., Schleicher, D. R. G., & Caselli, P. 2020, MNRAS, 495, L7 [Google Scholar]
- Bovino, S., Lupi, A., Giannetti, A., et al. 2021, A&A, 654, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, R., Wolf, S., Reissl, S., & Ober, F. 2017, A&A, 601, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butner, H. M., Lada, E. A., & Loren, R. B. 1995, ApJ, 448, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Cabedo, V., Maury, A., Girart, J. M., et al. 2023, A&A, 669, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Walmsley, C. M., Terzieva, R., & Herbst, E. 1998, ApJ, 499, 234 [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002, ApJ, 565, 344 [Google Scholar]
- Caselli, P., van der Tak, F. F. S., Ceccarelli, C., & Bacmann, A. 2003, A&A, 403, L37 [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Vastel, C., Ceccarelli, C., et al. 2008, A&A, 492, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Caselli, P., Bockelée-Morvan, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 859 [Google Scholar]
- Colzi, L., Sipilä, O., Roueff, E., Caselli, P., & Fontani, F. 2020, A&A, 640, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crabtree, K. N., & McCall, B. J. 2012, Philos. Trans. Roy. Soc. Lond. A, 370, 5055 [NASA ADS] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzib, S. A., Loinard, L., Ortiz-León, G. N., Rodríguez, L. F., & Galli, P. A. B. 2018, ApJ, 867, 151 [Google Scholar]
- Favre, C., Ceccarelli, C., López-Sepulcre, A., et al. 2018, ApJ, 859, 136 [Google Scholar]
- Ferrada-Chamorro, S., Lupi, A., & Bovino, S. 2021, MNRAS, 505, 3442 [NASA ADS] [CrossRef] [Google Scholar]
- Fontani, F., Ceccarelli, C., Favre, C., et al. 2017, A&A, 605, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Bourke, T. L., et al. 2014, ApJ, 797, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Navarro, D. G., Caselli, P., et al. 2019, A&A, 624, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, P. A. B., Loinard, L., Bouy, H., et al. 2019, A&A, 630, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannetti, A., Bovino, S., Caselli, P., et al. 2019, A&A, 621, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guelin, M., Langer, W. D., Snell, R. L., & Wootten, H. A. 1977, ApJ, 217, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Guelin, M., Langer, W. D., & Wilson, R. W. 1982, A&A, 107, 107 [NASA ADS] [Google Scholar]
- Gusten, R., Nyman, L. À., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hopkins, P. F. 2015, MNRAS, 450, 53 [Google Scholar]
- Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130, 164302 [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Geballe, T. R., Oka, T., & McCall, B. J. 2007, ApJ, 671, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Ivlev, A. V., Silsbee, K., Sipilä, O., & Caselli, P. 2019, ApJ, 884, 176 [Google Scholar]
- Juvela, M., Mattila, K., Lehtinen, K., et al. 2002, A&A, 382, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, N. J., I., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kong, S., Caselli, P., Tan, J. C., Wakelam, V., & Sipilä, O. 2015, ApJ, 804, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lattanzi, V., Bizzocchi, L., Vasyunin, A. I., et al. 2020, A&A, 633, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lupi, A., Bovino, S., & Grassi, T. 2021, A&A, 654, A6 [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
- McCall, B. J., Huneycutt, A. J., Saykally, R. J., et al. 2003, Nature, 422, 500 [CrossRef] [Google Scholar]
- Mouschovias, T. C., & Spitzer, L., J. 1976, ApJ, 210, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T. 2019, Philos. Trans. Roy. Soc. Lond. A, 377, 20180402 [NASA ADS] [Google Scholar]
- Padovani, M., Marcowith, A., Hennebelle, P., & Ferrière, K. 2016, A&A, 590, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Ivlev, A. V., Galli, D., & Caselli, P. 2018, A&A, 614, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Bialy, S., Galli, D., et al. 2022, A&A, 658, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plunkett, A., Hacar, A., Moser-Fischer, L., et al. 2023, PASP, 135, 034501 [NASA ADS] [CrossRef] [Google Scholar]
- Redaelli, E., Bizzocchi, L., Caselli, P., et al. 2019, A&A, 629, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redaelli, E., Bovino, S., Giannetti, A., et al. 2021a, A&A, 650, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redaelli, E., Sipilä, O., Padovani, M., et al. 2021b, A&A, 656, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redaelli, E., Bovino, S., Sanhueza, P., et al. 2022, ApJ, 936, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Reissl, S., Wolf, S., & Brauer, R. 2016, A&A, 593, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabatini, G., Bovino, S., Giannetti, A., et al. 2020, A&A, 644, A34 [EDP Sciences] [Google Scholar]
- Sabatini, G., Bovino, S., & Redaelli, E. 2023, ApJ, 947, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Sanhueza, P., Contreras, Y., Wu, B., et al. 2019, ApJ, 886, 102 [Google Scholar]
- Schnee, S., Caselli, P., Goodman, A., et al. 2007, ApJ, 671, 1839 [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Williams, J. P., Bergin, E. A., Caselli, P., Myers, P. C., & Plume, R. 1998, ApJ, 503, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L. 1999, Rep. Progr. Phys., 62, 143 [CrossRef] [Google Scholar]
- Wootten, A., Snell, R., & Glassgold, A. E. 1979, ApJ, 234, 876 [NASA ADS] [CrossRef] [Google Scholar]
Latest version available at https://github.com/polaris-MCRT/POLARIS. For this work, we used a custom version, where we corrected an issue in the conversion between mass fractions and number densities.3 These are listed in the file silicate_ld93.nk, available in the POLARIS package.
The former value is within 30 pc from the distance of nearby low-mass star-forming regions, such as parts of Taurus, the Pipe, and Lupus (Dzib et al. 2018; Galli et al. 2019). The larger distance, instead, is consistent with that of some of the closest infrared-dark clouds, see for instance Sanhueza et al. (2019).
Following the instructions at https://casaguides.nrao.edu/index.php/DataWeightsAndCombination
POLARIS does not automatically return the excitation temperature, which in any case is a quantity defined in each Voronoi cell. Computing average values from its 3D distribution is not straightforward (as discussed in Redaelli et al. 2019).
Available at http://var.sron.nl/radex/radex.php (van der Tak et al. 2007).
Version 10.0, available online at http://www.apex-telescope.org/heterodyne/calculator/ns/otf/index.php
Available online at https://oms.iram.fr/tse/
All Tables
Comparison of ζ2 values obtained with the CWT98 and BFL20 methods towards three prestellar cores, assuming a gas temperature of 10 K.
All Figures
 |
Fig. 1 Histogram of the distribution of ζ2 (in units of 10−17 s−1) of the runs as labelled at the top of each panel. We represent the core region where N(H2) > 0.5 × max(N(H2)) (namely the lowest contour in the panels of Figs. 2, 3, and 4). The median value, together with the median uncertainty, is reported in the top-right corner of each panel and shown as a vertical dashed line with a grey-shaded area. Cf. Table 1. |
| In the text | |
 |
Fig. 2 Resulting ζ2 maps obtained with Eq. (1) in runs 1 to 4. The run ID is reported in the top-left corner, and the key parameters are included at the top of each panel. Run 2 is taken as a reference throughout the rest of this work. The white contours show the 50, 70, and 90% of the N(H2) peaks, which are: 6.67 × 1022 cm−2 (core in single-dish like analysis at 100 kyr); 6.86 × 1022 cm−2 (core in single-dish-like analysis at 50 kyr); 2.51 × 1022 cm−2 (core in ALMAlike analysis at 100 kyr). The beam size and scalebar are shown in the bottom corners of each panel. Note that we show a zoom-in of the central 0.15 pc. |
| In the text | |
 |
Fig. 3 Summary of runs performed in LVG approximation, compared with the reference case (run 2, left panel). The central panel refers to the analysis performed on the high-J transitions for DCO+, H13CO+, and C18O, whilst the low-J ones are used in the map in the right panel. The white contours are the same as in Fig. 2. Note that the colour scale is the same across all the panels. The beam size and scalebar are shown in the bottom left and right corners of each panel. |
| In the text | |
 |
Fig. 4 Maps of the density-averaged |
| In the text | |
 |
Fig. 5 Maps of the key quantities employed by CWT98: DCO+ deuteration level (top-left panel), CO depletion factor (top-right), electronic fraction (bottom-left), and ζ2 (bottom-right). Note that the colour scales for the last two quantities are in units of 10−6 and 10−13 s−1, respectively. These maps assume the molecular column density and total gas column density derived in run 2. The mean uncertainties are 2.6 × 10−4 (RD), 0.3 (fD), 3 × 10−6 |
| In the text | |
 |
Fig. 6 Electronic fraction (top panel) and ζ2 map (bottom panel) from the reference run 2, using the updated formulation of CWT98. The contours show H2 column density as in Fig. 2. The mean uncertainties are 3 × 10–6 for x(e–) and 0.8 × 10–13 s–1 for ζ2. The beam size and scalebar are shown in the bottom corners of the lower panel. |
| In the text | |
 |
Fig. 7 Same as Fig. 1, but the ionisation rate is estimated using the new formulation of the CWT98 method presented in Appendix B, summarised in Eq. (B.6). Note that the ζ2 values are normalised to 10−13 s−1 in all panels. The median (± median uncertainty) is reported in the top-right corner and shown with the vertical dashed line and shaded area in each panel. The reference run is labelled with "Ref" in the bottom-right corner. |
| In the text | |
 |
Fig. 8 Ratio between ζ2 retrieved in each run (x-axis labels), and the actual value |
| In the text | |
 |
Fig. B.1 Ratio between the sum of the rates of the reactions between |
| In the text | |
 |
Fig. B.2 ζ2 values (divided by RH × n(H2)) obtained with Eq. (B.6) at 15 K, as a function of RD and fD. The bottom-right corner is missing because it violates the condition RD < 0.029 × fD. The plot shows that the quantity ζ2/(RH × n(H2)) increases by up to four orders of magnitude when the deuteration fraction decreases from 0.1 to 10−3 and that the CO depletion factor plays a significant role at RD typical for dense gas (0.01 – 0.1). |
| In the text | |
 |
Fig. C.1 Histograms of the derived ζ2 values with the BFL20 method in run 5 (upper panel, high-J transitions) and run 6 (lower panel, low-J transitions). The different colours show different assumptions for the excitation temperature of DCO+ and H13CO+ (assumed to be equal). In particular, the reference values used in the main text are shown in red (hence these data are the same presented in Fig. 1), whilst the blue/green curves show a positive/negative variation of ≈20% of that value, respectively (labelled in the top-right corner of each panel). The median values and uncertainties are shown with the vertical dashed lines and shaded areas and with coloured text in each panel. |
| In the text | |
 |
Fig. D.1 Comparison of the resulting ζ2 maps (in units of 10−17 s−1) on the two runs with distinct box sizes L but otherwise identical, using the BFL20 method. Panel a) shows the run with L = 0.3 pc (namely the reference run 2), and panel b) shows the results with L = 0.15 pc. The colorbar is kept fixed to ease the comparison. The histogram distributions are compared in panel c), labelled in the top-right corner. The median values (median uncertainties) are shown with the vertical dashed lines (shaded areas). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.