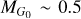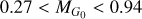| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A173 | |
| Number of page(s) | 16 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202348961 | |
| Published online | 19 April 2024 | |
Variable stars in galactic globular clusters
I. The population of RR Lyrae stars★
Institute of Physics, École Polytechnique Fédérale de Lausanne (EPFL),
Observatoire de Sauverny,
1290
Versoix,
Switzerland
e-mail: mauricio.cruz@correo.nucleares.unam.mx; richard.anderson@epfl.ch
Received:
14
December
2023
Accepted:
12
February
2024
We present a comprehensive catalog of 2824 RR Lyrae stars (RRLs) residing in 115 Galactic globular clusters (GCs). Our catalog includes 1594 fundamental-mode (RRab), 824 first-overtone (RRc), and 28 double-mode (RRd) RRLs, as well as 378 RRLs of an unknown pulsation mode. We cross-matched 481 349 RRLs reported in the third Data Release (DR3) of the ESA mission Gaia and the literature to 170 known GCs. Membership probabilities were computed as the products of a position and shape-dependent prior and a likelihood was computed using parallaxes, proper motions, and, where available, radial velocities from Gaia. Membership likelihoods of RRLs were computed by comparing cluster average parameters based on known member stars and the cross-matched RRLs. We determined empirical RRL instability strip (IS) boundaries based on our catalog and detected three new cluster RRLs inside this region via their excess Gaia G-band photometric uncertainties. We find that 77% of RRLs in GCs are included in the Gaia DR3 Specific Object Study, and 82% were classified as RRLs by the Gaia DR3 classifier, with the majority of the missing sources being located at the crowded GC centers. Surprisingly, we find that 25% of cluster member stars located within the empirical IS are not RRLs and appear to be non-variable. Additionally, we find that 80% of RRab, 84% of RRc, and 100% of the RRd stars are located within theoretical IS boundaries predicted using MESA models with Z = 0.0003, M = 0.7 M⊙, and Y = 0.290. Unexpectedly, a higher Y = 0.357 is required to fully match the location of RRc stars, and lower Y = 0.220 is needed to match the location of RRab stars. Lastly, our catalog does not exhibit an Oosterhoff dichotomy, with at least 22 GCs located inside the Oosterhoff “gap”, which is close to the mode of the distribution of mean RRL periods in GCs.
Key words: catalogs / stars: variables: RR Lyrae / globular clusters: general
Tables 1, 4, A.2 and D.1 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/684/A173
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Globular clusters (GCs) are collections of thousands or even millions of stars with ages that range between ~11 and 12.5 Gyr (VandenBerg et al. 2013) and with a wide range of metallicities (Δ[Fe/H] = −2.3 dex, Harris 2010). They are particularly useful laboratories to understand the properties of pulsating stars because these variable members can be compared with (nearly) coeval non-variable stars, or other types of variables. Although multiple populations of stars (Leitinger et al. 2023; Milone et al. 2020) have been identified, GCs are relatively simple populations that can be used to test stellar models (Eyer & Mowlavi 2008).
Globular clusters are known to host population II variable stars, notably including the RR Lyrae stars (RRLs) studied here, as well as type-II Cepheids and Mira variables. In the 20th century, most studies dedicated to the identification of variable stars in clusters were conducted using photographic plates, which complicated the identification of variable sources with amplitudes smaller than ~0.1 mag. At that time, RRLs were the most commonly detected type of variables due to their high amplitudes and the relatively small baselines required for their characterization, and therefore they were known as cluster variables (Hertzsprung 1912; Shore 2003).
Sawyer (1939) carried out a pioneering work creating the first catalog of variable stars in clusters, which was built by collecting data from existing literature. Following the same approach, Clement (2017, hereafter C17) created the current most complete catalog of variable stars in GCs, which includes Eclipsing binaries (ECLs), SX Phoenicis, Type II Cepheids, slow variables, and RRLs. The catalog of C17 contains, in total, 5604 variables distributed in 122 GCs, out of which 2997 are RRLs and 114 are RRL candidates. At the time the catalog of C17 was created, the main criterion used to assess the membership of an RRL in a cluster relied on the measurement of its angular separation from the cluster center. It was commonly accepted that sources located closer to the center were more likely cluster members than those residing at larger angular separations. This approach was necessary because the vast majority of sources did not have a measured astrometry, and in some cases they did not have color information, making it impossible to identify their position in the color–magnitude diagram. Consequently, it is likely that some of them were incorrectly classified as cluster members.
Bhardwaj (2022) conducted an extensive review of the current observational status of RRLs in GCs, mainly focusing on the photometric properties in both the optical and infrared domains. The review analyzes the light curves of these stars, their relationship with metallicity, and the morphology of the horizontal branch (HB) in the clusters that host them. Additionally, it offers a calibration of the period-luminosity relations for RRLs at multiple wavelengths.
Contributions that focus on obtaining the spectroscopy of individual clusters are crucial for determining the chemical composition of RRLs in GCs. The investigations led by Magurno et al. (2018, 2019) for NGC 3201 and NGC 5139 (ω Cen) and the one led by Clementini et al. (2005) for NGC 6441 have contributed in this direction. These cluster-specific studies have shown that within a single cluster, there are multiple populations of RRLs. Consequently, in order to calibrate the period-luminosity relations for RRLs with maximum precision, it is not sufficient to use the average cluster metallicity, rather, individual measurements are necessary.
Recently, the third Data Release (DR3) of the ESA Gaia mission (Gaia Collaboration 2016, 2021) has delivered unprecedented astrometric measurements (positions, proper motions, and parallaxes) and multiband photometry of 1.8 billion objects. Additionally, Gaia’s coordination unit seven (CU7) dedicated to variability has detected hundreds of thousands of RRLs and provided high-quality chromatic time-series photometry for them (Eyer et al. 2023; Clementini et al. 2023). This wonderful dataset dataset allows for a homogeneous reassessment of the cluster membership of RRLs in GCs in unparalleled detail.
Here, we aim to use the largest possible number of GCs and RRLs in conjunction with astrometry and photometry of from Gaia (DR3) to detect and classify RRLs in GCs. The high source density near the centers of GCs introduces certain challenges for Gaia, notably when sources are no longer fully resolved. Hence, studying variable stars in GCs also allows one to test the limits of Gaia’s performance, for example, in terms of completeness and contamination.
Our study takes advantage of the highly precise cluster parameters to evaluate the consistency of the theoretical instability strip (IS) boundaries with observations and explore whether all stars within the IS pulsate, a particularly interesting aspect considering previous findings indicate that around 30% of stars within the IS boundaries for classical Cepheids do not exhibit pulsations (Narloch et al. 2019). These analyses aim to improve our understanding of the models designed to explain stellar pulsations for RRLs. RRLs in GCs offer a unique laboratory for investigating the purity of the RRL IS because contamination is effectively minimized and because GC populations are much simpler than field populations.
This paper is the first one of a series focused on the study of variable stars within GCs. Section 2 provides a detailed description of the data employed in the membership analysis. Section 3 illustrates the method used to identify RRLs within clusters, in particular Sects. 3.2–3.4 describe the approach utilized for the computation of the membership probabilities. The description of the results of the membership analysis, together with the detection of new RRLs, is presented in Sect. 3.5. Our final sample of RRLs in GCs is presented in Sect. 4. The comparison with the theoretical models for the blue and red edges of the instability strip is shown in Sect. 5, while Sect. 5.1 discuss the non-variable stars located in this region. Section 5.2 explains the Oosterhoff dichotomy and finally, Sect. 6 summarizes the paper and presents our conclusions.
 |
Fig. 1 Distributions of distances, iron abundances, and reddening for our sample of GCs. |
2 Description of the data
This section is divided into two parts: Sect. 2.1 describes the sample of clusters and their parameters, such as proper motion, parallax, metallicities and reddening estimates, whereas Sect. 2.2 describes the sample of RRLs used in our study.
2.1 Cluster sample
Using the astrometry of the Gaia Early Data Release 3 (Gaia Collaboration 2021), Vasiliev & Baumgardt (2021, hereafter VB21) identified the cluster member stars of 170 Milky Way GCs. Our analysis relies on the clusters and the associated members identified by them. The VB21 dataset offers a membership probability for all stars located in regions near the cluster center, irrespective of the quality of their astrometry or photometry. This is extremely useful as it allows us to select the stars that best fit our needs. For example, when determining the central coordinates of a cluster, it is not recommended to remove sources with poor astrometry, as that would remove most of the sources located near the center, leading to an erroneous estimation of the central coordinates. On the other hand, to determine the cluster parameters, it is necessary to ensure that we use the highest quality astrometry, thus requiring strict quality cuts for both astrometry and photometry. We updated the data of VB21 by crossmatching with Gaia DR3 (Gaia Collaboration 2023). All cluster parameters required for our study were recomputed here. A detailed description of the determination of cluster parameters will be presented separately (Cruz Reyes et al., in prep.). An abbreviated version is included in Appendix A. Figure 1 displays the distributions of distances, metallicities, and reddening for the GCs in our sample.
Cluster metallicities and reddening estimates were mainly taken from the catalog of cluster parameters by Harris (1996, 2010, hereafter H10). It is worth noting that H10 employs the metallicity scale provided by Carretta et al. (2009). Seventeen clusters in the VB21 data set are not included in the H10 catalog, and therefore we searched for them in the literature. For FSR 1758, the reddening is E(B − V) = 0.76 ± 0.07 (Romero-Colmenares et al. 2021). The reddening and distance of FSR 1716 were estimated by Bonatto & Bica (2008) using isochrone fitting. However, we deem the resulting color excess unreliable because the derived distance d = 0.8 ± 0.1 kpc is not consistent with the most recent estimate d = 7.43 ± 0.27 kpc (Baumgardt & Vasiliev 2021, hereafter BV21). We were unable to find E(B − V) for the remaining clusters.
Reddening coefficients were computed assuming an RV = 3.3 reddening law from Fitzpatrick (1999) using pysynphot (STScI Development Team 2013) following Anderson (2022) and the following parameters to mimic a typical RRL: E(B − V) = 0.5 (mean of GCs, cf. Fig. 1), Teff = 6800 K, log g = 2.5 and [M/H] = −1.25. We thus obtained RG = 2.855, RRp = 2.047, RBp = 3.576, and 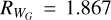 for the reddening-free Wesenheit magnitude. Furthermore, we obtained E(Bp − Rp) = 1.53 × E(B − V) and E(Bp − G) = 0.72 × E(B − V). Given the wide range of color excess values in the GC sample, we recomputed the aforementioned values for E(B − V) = 0.1 and 1.0 for comparison. This changes RG, RRp, and RBp by ±5% (higher R for lower E(B − V)),
for the reddening-free Wesenheit magnitude. Furthermore, we obtained E(Bp − Rp) = 1.53 × E(B − V) and E(Bp − G) = 0.72 × E(B − V). Given the wide range of color excess values in the GC sample, we recomputed the aforementioned values for E(B − V) = 0.1 and 1.0 for comparison. This changes RG, RRp, and RBp by ±5% (higher R for lower E(B − V)), 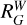 by ±2%, and E(Bp − Rp) by ±3%. Restricting to clusters with E(B − V) ≤ 1.0 limits possible biases in Wesenheit magnitudes to <0.02 mag, in (Bp − Rp)0 < 0.03 mag, and <0.05 mag in single-filter de-reddened magnitudes.
by ±2%, and E(Bp − Rp) by ±3%. Restricting to clusters with E(B − V) ≤ 1.0 limits possible biases in Wesenheit magnitudes to <0.02 mag, in (Bp − Rp)0 < 0.03 mag, and <0.05 mag in single-filter de-reddened magnitudes.
2.2 The RR Lyrae sample
For the convenience of readers and to enhance readability, this section contains all RRLs mentioned in this paper. These include all the RRLs detected by the Gaia Collaboration, the RRLs in the C17 catalog crossmatched with Gaia DR3, and the RRLs detected in this paper.
2.2.1 The Gaia sample
A key objective of the Gaia Collaboration, specifically of the CU7, is the identification and classification of all variable sources observed by Gaia. In the third Data Release of Gaia the CU7 found 10.5 million variable sources (Eyer et al. 2023), which are reported in the table vari_classifier_result, of the Gaia archive1. One million of those sources are active galactic nuclei and the rest are stars divided into 23 variability types, of which 297 778 are RRLs.
The Specific Object Study (SOS; Clementini et al. 2023, vari_rrlyrae) is designed to characterize the properties of Cepheids and RRLs, it contains 271 779 RRLs. The SOS analysis classifies each RRL according to their light curves, Fourier parameters, pulsation modes, and it provides time series photometry for them. We found 26 202 RRLs in the classifier table that are not included in the SOS analysis, and 203 RRLs listed in the SOS analysis that are not present in the classifier list. While the classifier aims to provide an analysis of the largest possible number of RRLs, the SOS analysis provides a more detailed analysis for bona fide RRLs.
The catalog of RRLs of Gaia is among the most extensive ones, but it was not specifically designed to investigate regions with a high density of sources. Holl et al. (2023) demonstrated the presence of spurious periodic signals related with the scanning law of Gaia. These types of signals could result in potential misclassifications in the Gaia catalog, especially for sources with close companions. This study explores Gaia’s ability to observe and characterize RRLs in the extremely dense environments of GCs.
2.2.2 RRLs from the literature
We complement our sample of RRLs using the catalog of Gavras et al. (2023, hereafter G23), a compilation of 7 841 723 sources from 152 variable star catalogs cross-matched to sources reported in Gaia DR3. Among them, 393 030 stars were identified as RRLs, out of which 183 368 were reported neither by the classifier nor by the SOS analysis. The G23 catalog contains a boolean column labeled “selection” that allows the identification of the catalogs for which the classification is of higher quality. It is considered that the sources with “selection = False” are likely misclassified.
For our analysis, we combined the classifier, SOS, G23, and catalogs, to obtain a total of 481 349 unique RRLs. The cluster membership analysis, presented in Sect. 3.5 was applied only to sources that have astrometric solutions with 5 or 6 parameters in Gaia, in the range where systematic corrections to the parallax offset are defined by Lindegren et al. (2021, hereafter L21). This restricts our sample as follows: 6 < phot_g_mean_mag < 21, 1.1 < nu_eff_used_in_astrometry < 1.9 (5-p sources), and 1.24 < pseudocolor < 1.72 (6-p sources).
2.2.3 C17 sample
As mentioned earlier, the C17 catalog contained the largest compilation of RRLs within clusters prior to our study. Section 4 compares it with the results of our membership analysis. We crossmatched the sources in the C17 catalog with Gaia DR3 using a two arcsecond radius. We were able to identify 3015 sources out of the total 3111 candidate RRLs in the C17 catalog. In some occasions multiple stars in the C17 catalog are associated with more than one source in Gaia, in those situations, we decided to prioritize the sources with the smallest angular separation.
2.2.4 Additional RR Lyrae candidates
Three RRLs were detected by analyzing the photometric uncertainties in the G band of all stars located in the HB. These are presented in Sect. 3.6.
3 Identification of RR Lyrae in globular clusters
This section describes the method used to detect RRLs in GCs, which is based on hypothesis testing that is built by comparing the astrometric parameters of RRLs and clusters. Section 3.2 describes the prior that we used for the membership analysis, Sect. 3.3 describes the likelihood and Sect. 3.4 describes the posterior and the criteria that we use to consider an RRL as a likely cluster member.
3.1 Cluster ellipticities
More than 100 yr ago (Pease & Shapley 1917), it was discovered that the geometry of GCs is better described by ellipsoids than by spheres. We measure the ellipticities using the astrometry and photometry of the clusters members identified by VB21.
We start by modeling the two-dimensional geometric shape of clusters in RA and DEC using a principal component analysis (PCA). We decided not to incorporate higher-order principal components, as the structure of our dataset (RA and Dec) was effectively modeled by these components. The axes of each ellipse are given by the eigenvectors ν1, ν2 of the PCA and their lengths by the eigenvalues λ1 and λ2. The largest eigenvalue corresponds to the eigenvector pointing along the major axis of the ellipse (α) and the other eigenvector points in the direction of the minor axis (b). The position angle of the ellipse is measured with respect to its major-axis, with the following equation θ = arctan(νa,y/νa,x), and the ellipticy is determined as 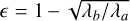 . Details regarding the application of this method to the VB21 dataset are described in Appendix A. In this paper, we use the elliptical shapes only to estimate the prior of membership, and in a separate publication (Cruz & Anderson, in prep.) we present a detailed discussion of the ellipticities.
. Details regarding the application of this method to the VB21 dataset are described in Appendix A. In this paper, we use the elliptical shapes only to estimate the prior of membership, and in a separate publication (Cruz & Anderson, in prep.) we present a detailed discussion of the ellipticities.
 |
Fig. 2 Base-10 logarithm of the number of cluster members divided by the number of field stars as a function of the angular distance from the cluster center for NGC 3201. The red line shows that this quantity decays approximately in a log-linear way. |
3.2 Prior
Our goal is to derive a prior probability function that reflects our level of confidence regarding a star’s membership in a cluster using only the star and cluster positions in the sky, and this information can be combined with the likelihood or considered separately. Since we expect most of the stars located near the core to be cluster members, the prior function should be unit-valued prior near the cluster center. Similarly, the prior should be approximately 1/10 in regions where only one out of ten stars are clusters members. To construct that function, we first defined a core ellipse centered on the cluster core. This core ellipse was aligned with the cluster members eigenvectors such that 66% of stars are cluster members and the rest are background or foreground stars. Inside this core ellipse, we set the prior equal to one. We further defined a limiting ellipse such that only 10% of stars are cluster members. A star falling on this limiting ellipse is assigned a prior probability of 1/10. Since the ratio of cluster to field stars decays approximately exponentially (see Fig. 2), we designed our prior function such that it also exponentially decreases outside the cluster core.
To determine the core and limiting ellipses we use the parameters derived with the PCA and the list of cluster members of VB21 (without astrometric or photometric quality cuts) and consider stars with membership probability greater than 50% (as determined by VB21) as cluster members, and the rest as field stars. We determine the ellipses in two different ways depending on the cluster. Clusters with more than 1000 members are run through a method in which we cut the cluster into different ellipse-slices, starting from a small ellipse around the cluster center and ending at the ellipse where its major axis is 1.2 times bigger than the maximum distance of a cluster star along that axis. To measure the core and limiting ellipses we analyze the ratio of cluster to field stars in each slice, as a function of the distance to the slice on the a-axis aslice. The points where the percentage of cluster stars is 66% and 10%, respectively (that is, the points where the cluster stars outnumber field stars by two, and field stars outnumber cluster stars by nine) are label as ac and alim. Using this definitions, the function that meets our requirements for the prior is
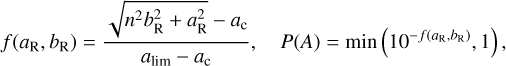 (1)
(1)
where aR and bR are the coordinates of the star of interest in the space (a, b).
Clusters with less than 1000 cluster member stars in VB21 were excluded from this initial analysis, because given the low number of sources we cannot cut them into small enough slices without being susceptible to statistical noise. Instead, we developed a scaling relation based on the well populated clusters that we then apply to the poorly sampled ones. For all clusters, we measure the standard deviation of the distribution of sources on the major axis σa. Subsequently, for each well populated cluster we estimate 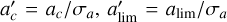 , and then we calculate their mean value
, and then we calculate their mean value 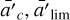 . Finally, for the small clusters we scale their σa, by
. Finally, for the small clusters we scale their σa, by 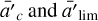 to obtain their core and limiting ellipses.
to obtain their core and limiting ellipses.
3.3 Likelihood
We approach the question of whether a RRL belongs to a cluster by treating it as a null hypothesis test, with the null hypothesis being that of membership. We estimate the probability of membership using the Bayes theorem, which states that the posterior probability of membership P(A|B) is proportional to the product of the likelihood P(B|A) and prior P(A). To estimate the likelihood, we follow the methodology described in Anderson et al. (2013) and Cruz Reyes & Anderson (2023). The likelihood is thus constructed as follows:
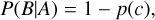 (2)
(2)
where p(c), represents the level of confidence at which we can reject the null hypothesis of cluster membership. The c quantity is defined as c = xTΣ−1x and is constructed using the parallax 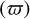 and proper motion
and proper motion 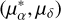 . Radial velocity (υr) measurements were additionally considered if a cluster has more than ten RV measurements and if the average RV of the RRLs was determined by the SOS analysis (table vari_rrlyrae). The vector x is defined as
. Radial velocity (υr) measurements were additionally considered if a cluster has more than ten RV measurements and if the average RV of the RRLs was determined by the SOS analysis (table vari_rrlyrae). The vector x is defined as
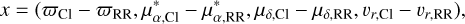 (3)
(3)
and Σ is the diagonal covariance matrix of the combined uncertainties of both RRL and cluster.
The corrections to the parallax systematics of Gaia, provided by Lindegren et al. (2021) provide a good description of the parallax offset for faint sources G > 12. However, additional adjustments are required for brighter sources (Khan et al. 2023; Riess et al. 2022). If these residual corrections are not taken into account in the estimation of the likelihood, then they could lead to artificially low membership probabilities. In the case of RRL, Bhardwaj et al. (2021) found that the residual parallax offset can be as big as −22 µas, this is almost twice as large as the median parallax uncertainty for the clusters in our sample (12 µas). Therefore, before computing the likelihood we added in quadrature 22 µas to the parallax uncertainty of all RRLs.
 |
Fig. 3 Combined color-magnitude diagram of 75 GCs. Cluster members and RRLs meet the quality cuts described in Appendix B. Real RRLs in clusters are located in the HB, around (BP − RP)0 ~ 0.5 mag and |
3.4 Posterior
We consider that a given variable star is a likely cluster member if P(A|B) > 0.0027, which corresponds to an overall difference below 3 standard deviations with respect the cluster parameters, assuming P(A) = 1. It is crucial to emphasize that we cannot use the posterior to prove a matching pair, but only to reject it, if it is sufficiently small.
3.5 Results of the membership analysis
Using the method presented in the previous sections and the RRLs samples described in Sects. 2.2.1 and 2.2.2, we identified 3620 RRLs distributed in 135 clusters, 2260 are included simultaneously in the SOS table and in the classifier, 197 are included only in the classifier and 1163 are present only in the G23 catalog, all of them have a likelihood greater than 0. 0027 and prior larger than 0.001. The stars located outside the HB are removed from the sample in Sect. 4, as most of them are false cluster members, misclassifications, or spurious crossmatches.
Figure 3 displays the color–magnitude diagram for 75 GCs, with low reddening, and high quality cluster parameters, the exact criteria that were used to select them are explained in Appendix B. To plot the color-magnitude diagram we used the distances from BV21. It can be clearly seen that a large number of sources are not located in the HB, which can be due to multiple reasons. For example, it is known that the precision in the astrometry of both RRL and clusters decreases as a function of distance, therefore, our method for computing membership probabilities loses the ability to reject false cluster members at large distances, increasing the contamination in our sample.
Most of the sources in the G23 catalog with the selection flag set to False are located outside the HB. Nearly all of them were originally detected by Sesar et al. (2017), but they were assigned a low probability of being RRLs; G23 classifies them as ECLs. Their location in the color-absolute magnitude diagram shows that the classification by G23 is likely correct, since the majority of them reside on the Main Sequence.
Figure 4 provides a graphical representation of the prior, likelihood, and posterior for the clusters NGC 4833 and NGC 7006. The first cluster contains more than 1000 stars in the VB21 dataset, and thus, the core and limiting ellipses were obtained using the first method described in Sect. 3.2, while the ellipses of the second were obtained using the scaling relation.
3.6 Undetected RRLs
To find the region, where most of the RRLs are located, we decided to use only the stars belonging to the SOS and classifier catalogs. We further restrict our sample to the clusters that meet the quality criteria explained in Appendix B. The 5th and 95th percentile ranges of intrinsic color and absolute magnitude for RRLs in this sample are:
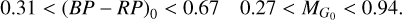 (4)
(4)
Figure 5 shows this region. Not all cluster members located in this area have been reported to be RRLs, neither in Gaia, nor in G23, nor in C17. This either implies that some RRLs have not been detected by any of the catalogs under our consideration, or that not all stars located in the instability strip are RRLs.
To verify whether those cluster members located in the IS are unidentified RRL, we followed the same approach as Mowlavi et al. (2021), which consists in the identification of variable sources using the published weighted mean fluxes (ƒG) and uncertainties 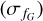 from the Gaia catalog (Riello et al. 2021). Assuming equally weighted measurements, the scatter in the light curves can be approximated as the weighted uncertainty in the flux
from the Gaia catalog (Riello et al. 2021). Assuming equally weighted measurements, the scatter in the light curves can be approximated as the weighted uncertainty in the flux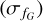 multiplied by the number of observations. For constant stars, the scatter represents an estimate of the quality of the photometry that will vary depending on the magnitude of the source. However, for variable stars the scatters increases due to the astrophysical variability of the sources. Using this as an advantage it was found (Mowlavi et al. 2021) that a good unitless proxy for the amplitudes is given by
multiplied by the number of observations. For constant stars, the scatter represents an estimate of the quality of the photometry that will vary depending on the magnitude of the source. However, for variable stars the scatters increases due to the astrophysical variability of the sources. Using this as an advantage it was found (Mowlavi et al. 2021) that a good unitless proxy for the amplitudes is given by
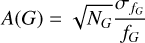 (5)
(5)
where NG is the number of observations in the G band.
We estimated the amplitudes of all cluster members using Eq. (5), the results are shown in Fig. 6. We delimited the region where constant stars are located by searching for the cluster members with the smallest amplitudes in bins of size 0.1 mag, and fitting a fourth order polynomial P(G) to the results. Additionally, we searched for the apparent magnitude (Gmin) of the RRLs from the SOS analysis with the smallest amplitude (Amin) that was identified as a cluster member. We selected as potentially unidentified RRL, to the stars located in the IS with amplitudes A(G) >= limit × P(G), where limit = Amin/P(Gmin).
We found 14 potential RRLs, that are not included in the Gaia catalogs presented in Sect. 2. However, 11 of them were previously identified as RRLs by other catalogs, therefore only three of the 14 are potentially new RRLs in clusters. Our results are summarized in Table C.1. Unfortunately, there is no time-series photometry data available for the three candidates in Gaia DR3.
 |
Fig. 4 Cluster members of NGC 4833 and NGC 7006. The color bar represents the membership probability assigned to the RRLs with our method. All stars were rotated to align the axes of the plot with the minor and major axes of the ellipses obtained with the PCA analysis. The orange ellipse represents the core ellipse and the red one the limiting ellipse. Both of them were obtained using the method presented in Sect. 3.2 and relying on the sample of cluster members determined by VB21. At the limiting ellipse, only 10% of all stars are expected to be cluster members. Field stars are not shown in the plot. |
 |
Fig. 5 Zoom in the region where most of the RRLs from Gaia are located (0.31 < (BP − RP)0 < 0.67 and |
4 Creating the final sample of RRLs in GCs
In this section we present the construction of the final sample of RRLs. As shown in Sect. 3.5, a large number of RRLs reported in the literature are not located on the HB, indicating that they are not real RRLs or not actual cluster members. As discussed in Sect. 2.2.1, some misclassifications may arise from spurious signals associated with the high density of sources in the clusters. Additionally, the likelihood presented in Sect. 3 may fail to reject RRLs with significant uncertainties in their astrometric parameters as cluster members. These stars were thus removed from the sample as described in Sect. 4.1. Meanwhile, in Sect. 4.2 we compare our results with the C17 catalog. Our final set of RRLs in clusters is presented in Sect. 4.3.
 |
Fig. 6 Unitless proxy amplitudes determined using Eq. (5). Cluster members appear in a gray color, while the ones located in the region of the IS appear in turquoise. The yellow triangles denote confirmed RRLs that are not part of the Gaia catalogs presented in Sect. 2. Meanwhile, the black triangles represent RRL candidates first reported here. |
4.1 Removing false identifications
We selected all RRLs within three standard deviations of the median intrinsic color and absolute magnitude derived from the SOS and classifier samples. We have color excess measurements only for 154 clusters, using those values we identified 2422 RRLs as cluster members. For the remaining clusters, we individually inspected their color–magnitude diagram, in BH 140 we identified five RRLs that are likely members and therefore they were added to our final sample, for the rest of the clusters we found that the RRLs are not located on the HB, and thus they are considered as false detections. In total, after including the newly detected RRLs, we were left with 2441 RRLs.
Results of the membership analysis.
 |
Fig. 7 Position in the sky and color–magnitude diagram for ω Cen and M5. Cluster members are represented by gray dots and the red dots indicate the RRLs that were not detected by the variable star analyses of the Gaia Collaboration. We can observe that they are concentrated near the cluster centers. |
4.2 Comparison with the C17 sample
From the 3015 RRLs in the C17 sample, 1806 are included in the sample presented in Sect. 4.1, 66 were rejected from the sample of RRLs in clusters with the method presented in the same section. Nineteen of them have the selection flag equal to False, and 33 are identified with a different type of variability. If we combine all the constraints, there are at least 112 unique RRLs in the C17 catalog that are unlikely cluster members or RRLs. To remove the remaining outliers, we once again reject the three sigma outliers, following the approach presented at the beginning of Sect. 4.1. As a result, we identified 383 RRLs within clusters in the C17 catalog that were not initially detected in Sect. 4.1. Most of them are located in the center of GCs. Twenty-three percent of the sources in this sample do not have parallax measurements in Gaia, hence they were not included in the membership analysis presented in Sect. 3.5. It is likely that our membership analysis failed to detect the remaining sources due to their poorer astrometry, as they exhibit an average ruwe value of 2.7, whereas those identified in Sect. 4.1 have an average ruwe value of 1.5. Figure 7 illustrates the sources in this sample for the clusters NGC 5139 (ω Cen) and NGC 5904 (M5).
4.3 Final sample
Our final set joins the results presented in Sects. 4.1 and 4.2, it contains 2824 RRLs that reside in 115 GCs. The full sample of RRLs in clusters, including the rejected sources is presented in Table 1. This table contains, the Gaia DR3 source id, host cluster, prior, likelihood, and posterior for all sources. The sources that were detected in Sect. 4.2 do not have a likelihood because they were not part of the analysis presented in Sect. 3.5. In Sect. 3.5, we show that our initial sample contained 3620 RRLs in 135 clusters. To distinguish between the stars that pass our selection criteria from those that do not, we introduced a Boolean indicator “Final”. If the indicator is set to True, it means they are considered cluster members, otherwise they were rejected because they are not located in the HB. This boolean column also allows the identification of sources from the C17 catalog that are not in our final sample.
Thirty percent of the RRLs in C17 are not part of our final sample. However, this does not necessarily imply that these sources are not RRLs or cluster members. The C17 catalog is an inhomogeneous compilation of RRLs from various catalogs that includes RRLs detected using a variety of instruments covering optical (UBVI) to near-infrared (J-band) wavelengths. This inho-mogeneity complicates detailed comparisons between the C17 sources and the sources cross-matched within the Gaia catalog, especially if the source was not identified as an RRL by Gaia. Positional cross-matches could be affected by blending, in particular if ground-based telescopes were used to identify RRLs in busy GCs. Since the majority of stars in a cluster are fainter than the HB, issues related to cross-matching would preferentially (but not exclusively) yield stars dimmer than the HB. On the other hand, blending will typically result in overly bright Gaia magnitudes and biased colors according to the type of blended object. Indeed, RRLs from C17 included in our final set have a mean value of ipd_frac_multi_peak = 14, whereas this value is twice larger for the RRLs rejected in this work.
Table 2 shows the number of fundamental mode, first overtone, and double mode RRLs in our sample. Within the entire set of RRLs identified in clusters, 2163 are identified by Gaia’s Specific Object Study (SOS), and 165 additional are identified by the classifier. The approximate completeness of these analyzes, relative to our catalog, is 77% and 82%, respectively. From the sample presented in Sect. 3.5, around 90% of the stars from the SOS and classifier are within our final set. This contrasts sharply with the sources present only in the G23 sample, as only 4% of the RRLs with the selection flag set to False are included, while 60% of the sources with the selection flag set to True are in our final sample. This is interesting as it shows that the majority of stars identified as RRL by the Gaia Collaboration are genuinely located in the HB, highlighting the robustness of the analysis even in areas with high star density.
Figure 8 shows the sky location and color–magnitude diagrams of eight particularly interesting clusters. Among them are the clusters with the highest and lowest number of RRLs in our sample, the particular case of NGC 6715 (M54), a cluster located within the Sagittarius dwarf spheroidal galaxy and finally two well populated clusters with particularly high and low metallicities. The first three clusters, in Fig. 8 are NGC 5272 (M3), ω Cen and NGC 6266, they are the ones with the highest number of RRLs in our sample, with 236, 190, and 162 RRLs respectively. In contrast, some of the clusters with the lowest number of RRLs are 47 Tuc and NGC 6144. The number of RRLs in 47 Tuc has been highly debated in the literature. Keith & Butler (1980) concluded that there are at least three stars of this type in the cluster. However, using radial velocities as membership constraint, Carney et al. (1993) concluded that there is only one RRL member. Based on Gaia astrometry, we conclude that there are at least two RRL member stars. Given Gaia’s limited spatial resolution, we cannot rule out the existence of more RRLs in the center of 47 Tuc. For NGC 6144, it appears that we have detected for the first time an RRL in this cluster. Interestingly, 47 Tuc and NGC 6144 have different iron abundances (Δ[Fe/H] = 1.04) but both have almost zero stars near the HB. Both clusters exhibit distinctive features in their HB morphology. In 47 Tuc, the lack of stars in this region suggests that the stars may not have yet entered this evolutionary phase. Conversely, in NGC 6144, the stars within the HB are too blue to be RRL, as will be shown in Sect. 5 this might be related with a high helium content.
M54 presents a singular challenge. As noted by VB21 is not straightforward to separate the members of the dwarf galaxy from those of the cluster using their membership analysis. The RRLs in our sample extend up to 0.42 degrees from the cluster center. At the cluster’s distance of 26.28 ± 0.33 kpc (BV21), this corresponds to an extension of 192.5 pc, which is clearly far too large given typical half−light radii of ~5 pc (Gratton et al. 2019). Using the prior, P(A), defined in Sect. 3.4, we can remove the sources located at large angular separations from the cluster center. We found that the RRLs within the radius of the cluster obtained with the VB21 data have a prior greater than 0.33. This value might seem unusually large, however, it is important to remember that the prior was estimated using the VB21 dataset, which, in this case, also contains sources from Sgr dSph. This contamination artificially increases the value of the prior. Figure 8 displays the cluster sky location and the combined color–magnitude diagram for the Dwarf Galaxy and cluster.
Within all clusters containing RRLs, those with the highest number of RRLs have an iron abundance of [Fe/H] 1.5 (see Sect. 5.2). In this context, M15 and NGC 6441 are particularly interesting. M3 is the cluster that contains RRLs with the lowest iron abundance in our entire set [Fe/H] = −2.37, yet it hosts 133 RRLs. While, among the metal rich clusters, NGC 6441 ([Fe/H] = −0.46) stands out as the one hosting the highest number of RRLs, reaching a total of 41.
Number of RR Lyrae stars in globular clusters.
 |
Fig. 8 Position in the sky and color-magnitude diagram for some of the most interesting clusters in our sample. Cluster members appear in gray color and RRLs in red. For M54, the RRLs with prior smaller than 0.33 appear in blue, they are likely inside of the Sagittarius dwarf spheroidal galaxy but not inside the cluster. |
Theoretical blue and red edges of the instability strip for RRLs in the (G,BP − RP) plane for pulsations in fundamental mode (RRab) and first overtone (RRc).
5 Models versus observations
We determined the blue and the red edges of the instability strip for pulsations in the fundamental mode (RRab) and the first−overtone (RRc) RRLs using MESA-RSP (Paxton et al. 2019) code with MESA version r23.05.1. We calculated a grid of models for M = 0.7 M⊙, two metal abundances Z = 0.0003, 0.0001 and four helium abundances Y = 0.220, 0.245, 0.290, 0.357 (for details how Y = 0.220, Y = 0.290 and Y = 0.357 were chosen see further in the text). The models were computed in the luminosity range log L/L⊙ ∈ 〈1.5, 1.8〉 with a step of 0.05 dex, and effective temperature Teff ∈ (5600, 8100) K with a step of 50 K. The mixing length parameter, αMLT, was set to 1.5 (the rest of the convective parameters correspond to Set B in Table 4 in Paxton et al. 2019). The OPAL opacities were used (Iglesias & Rogers 1996). The grid of models was transformed into Gaia photometric system using the PARSEC database of bolometric correction (using EDR3 band definitions as in Chen et al. 2019). The linear growth rates for the fundamental and the first-overtone modes were interpolated to obtain the blue and red edges. The models are presented in Table 3.
To compare the models with the observations, we considered only RRLs with mean magnitudes determined by the Gaia DR3 SOS (Clementini et al. 2023). As a result, any sources not present in the SOS sample were not considered in the comparison of IS boundaries. Figure 9 shows that there is a large number of sources with (BP − G)0 < 0, the anomalous color of these stars is likely related with photometric blending, as for them the mean value of ipd_frac_multi_peak is equal to 24, while for sources with (BP − G)0 > 0 the mean ipd_frac_multi_peak is equal to three. To avoid issues with blending and to compare directly with the models, we further restricted our sample of RRLs to those with ipd_frac_multi_peak = 0.
In Fig. 10, we show a comparison of the observations with the models. We find that models with a Y = 0.245 fit relatively well the density contours for RRab stars. However, the same models are too red to fit the RRc stars, which are better described by models featuring a much higher helium abundance of Y = 0.357. NGC 2419 and NGC 6266 (M62) contain simultaneously RRab and RRc stars beyond the IS boundaries predicted by the models with Y = 0.245. However, NGC 2419 is situated at a relatively large distance of 88.47 kpc, and NGC 6266 is located in a region with significant differential reddening (Contreras et al. 2010). Only one cluster (NGC 6362) contains RRc stars outside the boundaries matching RRab types, and three clusters (NGC 6229, NGC 6101, and M5) have RRab stars outside the boundaries matching RRc types. We note that these clusters are not unusually highly reddened, since the mean value for this sample is E(B − V) = 0.04.
We searched for the helium abundance that best matches both RRab and RRc groups. To this end, we defined the IS boundaries using the 68th percentile of the density distribution of RRLs in the color–magnitude diagram. We then varied Y until the difference between the theoretical and empirical IS boundary was minimized. We found that models that minimize this difference for both RRc and RRab stars simultaneously have Y = 0.290. The density contours for RRab stars are reproduced best by the models with a Y = 0. 220.
We note that double mode (RRd) RRLs fall within the predicted IS boundaries for these models (Z = 0.0003, M = 0.7 M⊙, Y = 0.290). Among stars pulsating in the fundamental mode, 80% are located within the predicted blue and red edges, while 84% of stars pulsating in the first overtone are within the boundaries set by the models. In other words, ~80% of RRLs are consistent with this single value of Y. All outlier RRab stars require significantly lower helium content (Y = 0.220), whereas all outlier RRc stars require much higher helium abundance (Y = 0. 357).
Figure 11 displays the color-magnitude diagram for all clusters and RRLs in our catalog with E(B − V) < 1. As can be seen in the left panel, some RRLs are outside the HB, this may be related with blending and that we used the photometry from the gaia_source catalog to make this plot, as not all RRLs have SOS photometry. In the right panel, is interesting to see that clusters lacking RRLs also possess few or no stars on the HB.
Figure 11 shows some cluster RRLs that fall outside the boundaries of the HB. Twenty-four percent of them are part of M62. This cluster is located close to the galactic plane in a region where the differential reddening is not negligible, and therefore, a single reddening value is not enough to characterize this cluster. The rest of the sources outside the HB are characterized by a low posterior probability, with a median value of 0.05. In contrast, the median value for the sources inside the HB is 0.84.
The cluster Pal 4 seems to be particularly interesting, it is located at 101.39 ± 2.57 kpc and the HB of the cluster is visible in Fig. 12, but no RRLs were detected in this study. NGC 6981 has a similar iron abundance (Δ[Fe/H] = 0.005) and hosts 43 RRLs, therefore it is likely that Pal 4 hosts a significant number of RRL, but beyond the capabilities of Gaia for the detection of RRLs.
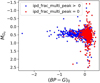 |
Fig. 9 Color–magnitude diagram for the RRLs in our final sample. It can be seen that multiple sources have an unexpected (BP − G)0 color, most of them have a nonzero value of ipd_peak_multi_frac, indicating that their photometry is likely affected by nearby sources. |
 |
Fig. 10 RRLs in the color-magnitude diagram color coded with their pulsation period. The first panel shows the RRc stars and the second panel shows the RRab. The color bar represent the pulsation period of the stars and the contours the 68th and 84th percentiles of density of RRL. All models assume M = 0.7 M⊙. The dotted lines are the theoretical models for the blue and red edge of the instabillity strip of RRc and RRab stars respectively. The solid lines highlight the models that best fit the observations. |
 |
Fig. 11 Color-magnitude diagram for the clusters in our sample E(B − V) < 1, color coded with their mean iron abundance. The plot on the left displays 103 GCs that contain at least one RRL. The right plot shows the same but for 24 clusters without RRLs. The red lines indicate the position of the theoretical blue and red edge of the instability strip for RRab, with Z = 0.0003, M = 0.7M⊙ and Y = 0.290, see Sect. 5. |
 |
Fig. 12 Pal 4, the most distant cluster in our sample with a clearly visible HB, and zero RRL. |
5.1 Purity of the IS
The theoretical models used to describe stellar pulsations, assume that all stars located within the blue and red edge of the IS are pulsating. If this condition is not met, the predictions of stellar populations based on these models would not represent a real population of stars. Interestingly, using ground-based photometry Rozyczka et al. (2018) detected one star in NGC 6254 (M10) located in the IS for RRLs that is not variable at the 0.01 mag level. By crossmatching that star with Gaia DR3 we confirm that within the limits of Gaia that star does not show photometric variability. The dataset of VB21 assigns a membership probability of ~ 1 to this star.
In the case of classical Cepheids in the Large Magellanic Cloud (LMC), it was discovered by Narloch et al. (2019) that up to 30% of the stars located in the classical instability strip do not show photometric variability at the milimag level.
We decided to analyze this effect for RRLs using the cluster sample in Appendix B. The results are shown in Fig. 13. It can be observed that the purity of the IS significantly changes as a function of the intrinsic color and absolute magnitude of the stars. It is highest at the center of the IS, gradually decreases toward the axes, approaching zero near the edges. In the following region
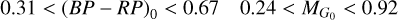 (6)
(6)
and within the limits of the method presented in Sect. 3.6, not all GC member stars are detected as RRLs. We found that 25% of all sources (315 stars) in this region do not exhibit photometric variability. Fifty seven clusters contain at least one non-variable star each inside this region. The median number of non-RRLs in the IS per cluster is four but there are some clusters with an abnormal number of constant stars such as M3 or NGC 6402 that contain 16 and 19 respectively. This stars could be undetected RRLs or interesting new sources. A good way to identify if their photometry is affected by close companions is by using the ipd_frac_multi_peak parameter from Gaia, which provides the fraction of windows for which the Image Parameter Determination (IPD) has identified more than one peak. We do not find evidence of blending in the photometry of the nonvariable sources as the median value of ipd_frac_multi_peak for them is equal to one. Table 4 lists the host cluster, source id, and membership probability computed by VB21 for the non-variable stars. We do not find a clear correlation between the number of non-variable stars and the cluster distance, indicating that this is not an observational bias related with the ability to detect RRLs at large distances. We found that the constant stars are more abundant in clusters with [Fe/H]∽−1.53.
 |
Fig. 13 RRLs (pink open circles) in clusters detected in this study and cluster members (white dots) in the HB detected by VB21 with membership probabilities above 50%. The squares indicate the bins in color and absolute magnitude used to estimate the fraction of RRLs over the number of cluster members detected by VB21. Each bin was color coded according to its specific RRL fraction, the color bar is located at the top of the plot. The purple contours indicate the 68th and 84th percentiles of density of RRLs. |
Nonvariable stars located in the IS for RRLs.
5.2 Oosterhoff dichotomy
The Oosterhoff dichotomy is one of the most well-known conundrums associated with RRLs (Oosterhoff 1939). The dichotomoy refers to RRLs in clusters being divided into two groups based to their average periods. The first group is known as OoI and has an average period) ~ 0.56 and tends to be metal rich ([Fe/H] > −1.5), while the second group has an average period 〈Pab〉 ~ 0.66 and is rather metal-poor ([Fe/H] < −1.5). While the Oosterhoff gap refers to the low number of clusters with RRLs in the region 0.58 < 〈Pab〉 < 0.62. This effect has been detected in the Milky Way but not in the Magellanic Clouds (Smith et al. 2010). Fabrizio et al. (2019) speculates that the lack of clusters in the gap is associated with the absence of metal-intermediate clusters hosting RRLs.
We decided to analyze this effect using the RRLs that pulsate in the fundamental mode from Gaia, in our analysis we used the pulsation periods from the SOS analysis. In Fig. 14, it can be observed that there are 22 clusters out of 97 located in the region known as the Oosterhoff gap. Some of those clusters were previously detected by other studies, such as NGC 6626 (Prieto et al. 2012), Arp 2 (Pritzl et al. 2019), NGC 6864 (Corwin et al. 2005), Rup 106 (Greco et al. 2007), NGC 1851 (Jang et al. 2014), NGC 6402 (Yepez et al. 2022), and M54 (Figuera Jaimes et al. 2016). Given the large dispersion in the mean value of the periods and the high number of clusters located in the region 0.58 < 〈Pab〉 < 0.62 we consider that is not possible to conclude that this region is a real gap.
To verify if the distribution of 〈Pab〉 is described by one or two populations (Oosterhoff types), we fit two models to the observations. The first model is a single Gaussian with three free parameters: mean µ, standard deviation σ, and amplitude A. The second model consists of two Gaussian distributions with three free parameters for each, that is, one Gaussian for each Oosterhoff type. To distinguish which model provides the best fit to the data, we employ the F-test. The purpose of the F-test is to evaluate how well two distinct models fit the data, while taking into account that these models have different degrees of freedom.
The model with two Gaussians must satisfy the following constraints: First, the mean of the Gaussian distribution assigned to OoI must be smaller than 0.58, otherwise, the mean would fall within the Oosterhoff gap. Similarly, the mean of the distribution assigned to OoII must be greater than 0.62, otherwise the mean would be within the gap. Secondly, the amplitude of the Gaussians obtained from fitting the data should be approximately equal to the number of observed clusters in the period where the peak of the Gaussian is reached. This is important because sometimes there are Gaussians that fit the data but have amplitudes inconsistent with the observations.
We chose the difference to be smaller than ten, although the first constraint is sufficient to rule out most models with two Gaussians.
To explore how our results are influenced by the selection of data binning, we repeated our analysis using different bin sizes. We selected the size of the bin with (Pmax − Pmin)/Nbins, where Pmax is the maximum average period of the RRLs hosted by a cluster in our sample, Pmįn is the minimum average period and Nbins is the number of bins. In total, we used 23 different values of Nbins, spanning from 7 to 30, which corresponds to bin size ranging from 0.011 to 0.047 days. The two-Gaussian model never passes the F-test and simultaneously meets the established constraints, therefore we conclude that the one-Gaussian model provides a better description of the data. Our results indicate that is not necessary to separate the cluster population into the classical Oosterhoff types.
Twenty-three percent of the clusters shown in Fig. 14 are located within the gap. One could speculate that these clusters have a limited number of RRab, causing significant uncertainties in their mean period. For this reason, we decided to focus only in clusters with more than ten RRab stars. In this case, we found that 19% of the GCs are within the gap, reaffirming our earlier conclusion that this region is not a gap.
Figure 15 shows the fraction of RRLs pulsating in the fundamental mode over those pulsating in the first overtone as a function of the iron abundance. It can be observed that RRc stars are more abundant than RRab stars in metal-poor clusters, and this trend is reversed for metal-rich clusters. This is expected because RRc stars are bluer than RRab stars, and metal-poor clusters are characterized by having bluer HBs than metal-rich clusters.
The left panel of Fig. 16 shows that the MW clusters with the most RRLs have [Fe/H] = −1.44. However, the number of RRLs can also depend on observational selection effects, such as the number of stars in the clusters and their distance. The right panel of Fig. 16 thus illustrates the number of RRLs divided by the number of stars located on the red giant branch, 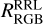 , within one and two magnitudes above the apparent magnitude of RRLs in each cluster. We chose this specific range to estimate the normalization constant because the number of stars in the HB varies significantly among different clusters. Even after introducing the normalization, RRLs remain particularly common in clusters with iron abundance [Fe/H] ≈ −1.5. However, we identify a surprising dichotomy among clusters according to the ratio
, within one and two magnitudes above the apparent magnitude of RRLs in each cluster. We chose this specific range to estimate the normalization constant because the number of stars in the HB varies significantly among different clusters. Even after introducing the normalization, RRLs remain particularly common in clusters with iron abundance [Fe/H] ≈ −1.5. However, we identify a surprising dichotomy among clusters according to the ratio 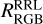 this ratio. The majority of clusters prefers low
this ratio. The majority of clusters prefers low 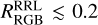 , that is, there typically at least four red giants between one and two magnitudes brighter than RRLs. However,
, that is, there typically at least four red giants between one and two magnitudes brighter than RRLs. However, 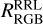 can be significantly larger, reaching up to >l.5, implying more RRL than RGB stars in this magnitude bin. Curiously, there are many clusters with an even ratio,
can be significantly larger, reaching up to >l.5, implying more RRL than RGB stars in this magnitude bin. Curiously, there are many clusters with an even ratio, 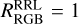 . At present, it is not clear what causes this feature, which could be related to age or observational selection effects.
. At present, it is not clear what causes this feature, which could be related to age or observational selection effects.
 |
Fig. 14 Mean period of the RRLs pulsating in the fundamental mode as a function of the iron abundance of the cluster. The dotted lines indicate the region known as the Oosterhoff gap, we can see that multiple clusters are located in this region. The error bars represent the 16th and 84th percentiles of the distribution of periods. The blue point represents NGC 6388, and the yellow one corresponds to NGC 6441. Both clusters have been classified as Oosterhoff type III in the literature (Pritzl et al. 2003; Bhardwaj 2022). |
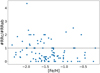 |
Fig. 15 Number of RRLs pulsating in the first overtone divided by the number of the ones pulsating in the fundamental mode. The black dashed line represents unit ratio. |
 |
Fig. 16 Number of RRLs in clusters. The panel illustrates the number of RRLs within each cluster as a function of the iron abundance. The right panel presents the same data, but the number of RRLs is divided by a normalization constant that is calculated individually for each cluster (refer to Sect. 5.2 for more details). |
6 Summary and conclusions
This is the first paper of a series dedicated to study variable stars in GCs. By making use of Gaia s astrometry and photometry, our catalog improves the confidence of membership of multiple RRLs to GCs. Despite the dense stellar environments within GCs, our analysis demonstrated the robustness of the classification methods of the Gaia Collaboration for RRLs, as most of the identified RRLs are located in the HB.
Currently, our catalog is the most comprehensive one obtained with a homogeneous set of astrometry and photometry. However, the limitations of Gaia s angular resolution and its poorer astrometry at the center of GCs pose challenges to our analysis, potentially resulting in an incomplete sample within those regions. It is worth noting that studies dedicated to specific clusters may be more complete than our catalog. For example, Arellano Ferro et al. (2023) has found that there are 18 RRLs in Palomar 2. Whereas we only detected two, some of the stars detected by Arellano Ferro et al. (2023) do not appear in our analysis because they are outside the range where the L21 corrections are defined, and the rest are removed due to a low likelihood or prior. The clusters 2MASS-GC01, 2MASS-GC02, GLIMPSE01, and GLIMPSE02 do not appear in our analysis because they are not listed in the VB21 catalog of GCs, as they are located in highly extincted regions, thus for them, studies in the infrared will be better suited to study their population of RRLs.
We show that more than 80% of RRLs are located within the instability strip boundaries predicted by the MESA models with Z = 0.0003, M = 0.7 M⊙, and Y = 0.290. However, the models that best describe the population of RRab stars feature a lower helium content (Y = 0.220), and the models that best describe the population of RRc stars require a higher helium abundance, Y = 0.357.
The observation that a significant portion (25%) of the stars located in the observational instability strip do not exhibit pulsations challenges our understanding of stellar pulsations models. Further research is needed to explore the reasons behind this behavior, potentially leading to advancements in stellar evolution theories. The finding that the Oosterhoff dichotomy does not exist in our sample suggests that the traditional classification of RRLs based on this dichotomy is not necessary.
In our dataset, there are clusters such as NGC 2419 or Pal 3 which are located at 88.47 ± 2.40 kpc and 94.84 ± 3.23 kpc and contain a significant number of RRLs (52 and 11 respectively) with an average magnitude G ≈ 20.2. The faintest stars that Gaia can detect are of magnitude G ≈ 21, and considering that the amplitude of this type of stars in the V band can reach up to 1.5 magnitudes, it means that we are at the limit of Gaia’s detection capabilities. The next paper of the series will focus on the calibration of the period-luminosity relations for multiple types of pulsating stars.
Acknowledgements
The authors thank the anonymous reviewer whose comments/suggestions helped improve this manuscript. We are thankful for useful discussions with Laurent Eyer. M.C., R.I.A., and H.N. acknowledge support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 947660). R.I.A. is funded by the SNSF through a Swiss National Science Foundation Eccellenza Professorial Fellowship (award PCEFP2_194638). This research was supported by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP) which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of NASA’s Astrophysics Data System; the SIMBAD database and the VizieR catalog access tool (http://cdsweb.u-strasbg.fr/) provided by CDS, Strasbourg; Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Robitaille et al. 2013; Price-Whelan et al. 2018); TOPCAT (http://www.star.bristol.ac.uk/~mbt/topcat/; Taylor 2005).
Appendix A Cluster parameters
Astrometric and photometric constraints that were applied to determine the cluster parameters.
Cluster parameters.
Cluster central positions in the sky were computed as the mean RA and DEC of all sources from the VB21 catalog with membership probabilities above 50% and without using astro-metric or photometric quality cuts. The position angles and ellipticities, are obtained with the method explained in Sect. 2.1 and the uncertainties are estimated using 1000 bootstrap resam-ples. The parameters are recalculated for each resampling and the standard deviation of the resulting distribution is taken as the uncertainty in those parameters.
For the rest of the cluster parameters, we used all five and six parameter solutions from Gaia within the limits of the astro-metric and photometric quality cuts suggested by VB21 with membership probabilities above 90%. To guarantee accurate corrections of the parallax offset, we further limited our analysis to the sources that fall within the magnitude and color range specified by the L21 corrections, all our constraints are summarized in Table A.1.
To compute the cluster parallaxes, we first compute parallax offsets for each cluster member following L21. In turn, we compute the cluster parallax as the weighted mean of the cluster members. The cluster’s parallax uncertainty comprises two terms, the angular covariance and the statistical error following Apellániz et al. (2021). Proper motions are computed as the mean of all cluster members and the uncertainties are the standard deviation on the mean. Given the low number of cluster members with radial velocity measurements, we report the median and the standard error on the median. Table A.2 contains a list of the cluster parameters.
We compared our cluster parameters with the ones estimated by VB21. In general, all parameters argreed with VB21 to within the respective uncertainties. Small differences among our and VB21’s cluster parallaxes are explained by the use of different quality cuts. However, we did not find any indication of values being biased in a particular direction. The difference in the proper motion uncertainties arises because we use the standard error in the mean while they use the weighted error.
Appendix B Purity of the IS
The following defines the sample of clusters used to analyze the population of RRLs within clusters in Sects. 3.5 and 5.1. It is crucial to guarantee that all stars under consideration during the analysis of IS purity are genuinely located within it. Incorrect extinction values can affect the position of stars in the color– magnitude diagram, and therefore we restrict our analysis to clusters with E(B − V) < 1.0 (84th percentile of the distribution of E(B − V)). For cluster members and RRLs, we required a minimum of ten epochs in G, GBP, and GRP. To avoid sources affected by photometric blending, we excluded sources from our analysis for which more than 10% of the transits were contaminated by the light from a nearby star (ipd_frac_multi_peak <10) and we select sources with ruwe< 1.4. To guarantee an accurate determination of the cluster parameters, we select clusters with at least 300 members (median number of members in a cluster after quality cuts). Finally, to avoid potential contamination of background or foreground stars we restrict our sample to clusters at distances smaller than 23 kpc (84th percentile of the distribution of distances). In total, from the 170 initial clusters, only 75 in the VB21 sample meet all constrains. The quality cuts are summarized in Table B.1.
Astrometric and photometric constraints applied to the analysis of the purity of the instability strip.
Appendix C Newly detected RR Lyrae
Table C.1 provides the host cluster, Gaia DR3 source id, the classification determined by Gaia from vari_classifier_result and the additional references for the detected RRLs in Sect. 3.6.
RR Lyrae that were detected using the uncertainties in the Gaia photometry.
Appendix D SOS sources with unrealistic photometric uncertainties
During the creation of this catalog, we detected some issues in the parameters of 63 stars present in vari_rrlyrae, they can be found in Table D.1. Some of them have uncertainties of the order of 10−14 mag in BP (or RP), but this precision is beyond the capabilities of Gaia. Those sources are characterized by less than 10 epochs in BP (or RP). Additionally, we detected some sources with negative apparent magnitudes and this should not be observable by Gaia. We would like to emphasize that the number of stars exhibiting these characteristics is minimal and does not reflect the overall quality of the SOS analysis.
Sources in the Specific Object Study for RRLs with unrealistic photometric uncertainties.
References
- Anderson, R. I. 2022, A&A, 658, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, R. I., Eyer, L., & Mowlavi, N. 2013, MNRAS, 434, 2238 [Google Scholar]
- Apellániz, J. M., González, M. P., & Barbá, R. 2021, A&A, 649, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arellano Ferro, A., Bustos Fierro, I., Muneer, S., & Giridhar, S. 2023, Rev. Mex. Astron. Astrofis., 59, 3 [Google Scholar]
- Baumgardt, H., & Vasiliev, E. 2021, MNRAS, 505, 5957 [NASA ADS] [CrossRef] [Google Scholar]
- Bhardwaj, A. 2022, Universe, 8, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Bhardwaj, A., Rejkuba, M., de Grijs, R., et al. 2021, ApJ, 909, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., & Bica, E. 2008, A&A, 491, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carney, B. W., Storm, J., & Williams, C. 1993, PASP, 105, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S. 2009, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Girardi, L., Fu, X., et al. 2019, A&A, 632, A105 [EDP Sciences] [Google Scholar]
- Clement, C. 2017, Eur. Phys. J. Web Conf., 152, 01021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clement, C. M., & Rowe, J. F. 2001, AJ, 122, 1464 [NASA ADS] [CrossRef] [Google Scholar]
- Clementini, G., Gratton, R. G., Bragaglia, A., et al. 2005, ApJ, 630, L145 [Google Scholar]
- Clementini, G., Ripepi, V., Garofalo, A., et al. 2023, A&A, 674, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contreras, R., Catelan, M., Smith, H. A., et al. 2010, AJ, 140, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras Peña, C., Catelan, M., Grundahl, F., Stephens, A. W., & Smith, H. A. 2018, AJ, 155, 116 [CrossRef] [Google Scholar]
- Corwin, T. M., Scott, N. J., Catelan, M., & Smith, H. A. 2005, AAS Meet. Abstr., 207, 122.14 [NASA ADS] [Google Scholar]
- Cruz Reyes, M., & Anderson, R. I. 2023, A&A, 672, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deras, D., Arellano Ferro, A., Lázaro, C., et al. 2019, MNRAS, 486, 2791 [CrossRef] [Google Scholar]
- Eyer, L. & Mowlavi, N. 2008, J. Phys. Conf. Ser., 118, 012010 [NASA ADS] [CrossRef] [Google Scholar]
- Eyer, L., Audard, M., Holl, B., et al. 2023, A&A, 674, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrizio, M., Bono, G., Braga, V. F., et al. 2019, ApJ, 882, 169 [Google Scholar]
- Figuera Jaimes, R., Bramich, D. M., Kains, N., et al. 2016, A&A, 592, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavras, P., Rimoldini, L., Nienartowicz, K., et al. 2023, A&A, 674, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R., Bragaglia, A., Carretta, E., et al. 2019, A&A Rev., 27, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Greco, C., Clementini, G., Catelan, M., et al. 2007, ApJ, 670, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
- Harris, W. E. 2010, arXiv e-prints [arXiv:1012.3224] [Google Scholar]
- Hertzsprung, E. 1912, Astron. Nachr., 192, 261 [CrossRef] [Google Scholar]
- Holl, B., Fabricius, C., Portell, J., et al. 2023, A&A, 674, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Jang, S., Lee, Y.-W., Joo, S.-J., & Na, C. 2014, MNRAS, 443, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, D. W., & Butler, D. 1980, AJ, 85, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, S., Miglio, A., Willett, E., et al. 2023, A&A, 677, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopacki, G. 2013, Acta Astron., 63, 91 [NASA ADS] [Google Scholar]
- Kunder, A., Stetson, P. B., Cassisi, S., et al. 2013, AJ, 146, 119 [CrossRef] [Google Scholar]
- Leitinger, E., Baumgardt, H., Cabrera-Ziri, I., Hilker, M., & Pancino, E. 2023, MNRAS, 520, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Magurno, D., Sneden, C., Braga, V. F., et al. 2018, ApJ, 864, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Magurno, D., Sneden, C., Bono, G., et al. 2019, ApJ, 881, 104 [Google Scholar]
- Milone, A. P., Marino, A. F., Da Costa, G. S., et al. 2020, MNRAS, 491, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Mowlavi, N., Rimoldini, L., Evans, D. W., et al. 2021, A&A, 648, A44 [EDP Sciences] [Google Scholar]
- Narloch, W., Pietrzynski, G., Kolaczkowski, Z., et al. 2019, MNRAS, 489, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterhoff, P. T. 1939, The Observatory, 62, 104 [NASA ADS] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pease, F. G., & Shapley, H. 1917, PNAS, 3, 96 [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Sipocz, B., Günther, H., et al. 2018, AJ, 156, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, G., Catelan, M., Contreras Ramos, R., et al. 2012, A&A, 543, A148 [EDP Sciences] [Google Scholar]
- Pritzl, B. J., Smith, H. A., Stetson, P. B., et al. 2003, AJ, 126, 1381 [Google Scholar]
- Pritzl, B. J., Gehrman, T. C., Salinas, R., et al. 2019, PASP, 131, 054202 [NASA ADS] [CrossRef] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Breuval, L., Yuan, W., et al. 2022, ApJ, 938, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Tollerud, E. J., Greenfield, P., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero-Colmenares, M., Fernández-Trincado, J. G., Geisler, D., et al. 2021, A&A, 652, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rozyczka, M., Narloch, W., Schwarzenberg-Czerny, A., et al. 2018, Acta Astron., 68, 237 [Google Scholar]
- Sawyer, H. B. 1939, Publ. David Dunlap Observatory, 1, 125 [NASA ADS] [Google Scholar]
- Sesar, B., Hernitschek, N., Mitrovic, S., et al. 2017, AJ, 153, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Shore, S. N. 2003, in Encyclopedia of Physical Science and Technology, 3rd edn., ed. R. A. Meyers (New York: Academic Press), 715 [CrossRef] [Google Scholar]
- Smith, H., Catelan, M., Clementini, G., et al. 2010, AAS Meet. Abstr., 215, 417.11 [Google Scholar]
- STScI Development Team 2013, Astrophysics Source Code Library [record ascl:1303.023] [Google Scholar]
- Taylor, M. B. 2005, Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [NASA ADS] [Google Scholar]
- VandenBerg, D. A., Brogaard, K., Leaman, R., & Casagrande, L. 2013, ApJ, 775, 134 [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
- Yepez, M. A., Arellano Ferro, A., Deras, D., et al. 2022, MNRAS, 511, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Catelan, M., Smith, H. A., et al. 2010, AJ, 139, 357 [CrossRef] [Google Scholar]
All Tables
Theoretical blue and red edges of the instability strip for RRLs in the (G,BP − RP) plane for pulsations in fundamental mode (RRab) and first overtone (RRc).
Astrometric and photometric constraints that were applied to determine the cluster parameters.
Astrometric and photometric constraints applied to the analysis of the purity of the instability strip.
Sources in the Specific Object Study for RRLs with unrealistic photometric uncertainties.
All Figures
 |
Fig. 1 Distributions of distances, iron abundances, and reddening for our sample of GCs. |
| In the text | |
 |
Fig. 2 Base-10 logarithm of the number of cluster members divided by the number of field stars as a function of the angular distance from the cluster center for NGC 3201. The red line shows that this quantity decays approximately in a log-linear way. |
| In the text | |
 |
Fig. 3 Combined color-magnitude diagram of 75 GCs. Cluster members and RRLs meet the quality cuts described in Appendix B. Real RRLs in clusters are located in the HB, around (BP − RP)0 ~ 0.5 mag and |
| In the text | |
 |
Fig. 4 Cluster members of NGC 4833 and NGC 7006. The color bar represents the membership probability assigned to the RRLs with our method. All stars were rotated to align the axes of the plot with the minor and major axes of the ellipses obtained with the PCA analysis. The orange ellipse represents the core ellipse and the red one the limiting ellipse. Both of them were obtained using the method presented in Sect. 3.2 and relying on the sample of cluster members determined by VB21. At the limiting ellipse, only 10% of all stars are expected to be cluster members. Field stars are not shown in the plot. |
| In the text | |
 |
Fig. 5 Zoom in the region where most of the RRLs from Gaia are located (0.31 < (BP − RP)0 < 0.67 and |
| In the text | |
 |
Fig. 6 Unitless proxy amplitudes determined using Eq. (5). Cluster members appear in a gray color, while the ones located in the region of the IS appear in turquoise. The yellow triangles denote confirmed RRLs that are not part of the Gaia catalogs presented in Sect. 2. Meanwhile, the black triangles represent RRL candidates first reported here. |
| In the text | |
 |
Fig. 7 Position in the sky and color–magnitude diagram for ω Cen and M5. Cluster members are represented by gray dots and the red dots indicate the RRLs that were not detected by the variable star analyses of the Gaia Collaboration. We can observe that they are concentrated near the cluster centers. |
| In the text | |
 |
Fig. 8 Position in the sky and color-magnitude diagram for some of the most interesting clusters in our sample. Cluster members appear in gray color and RRLs in red. For M54, the RRLs with prior smaller than 0.33 appear in blue, they are likely inside of the Sagittarius dwarf spheroidal galaxy but not inside the cluster. |
| In the text | |
 |
Fig. 9 Color–magnitude diagram for the RRLs in our final sample. It can be seen that multiple sources have an unexpected (BP − G)0 color, most of them have a nonzero value of ipd_peak_multi_frac, indicating that their photometry is likely affected by nearby sources. |
| In the text | |
 |
Fig. 10 RRLs in the color-magnitude diagram color coded with their pulsation period. The first panel shows the RRc stars and the second panel shows the RRab. The color bar represent the pulsation period of the stars and the contours the 68th and 84th percentiles of density of RRL. All models assume M = 0.7 M⊙. The dotted lines are the theoretical models for the blue and red edge of the instabillity strip of RRc and RRab stars respectively. The solid lines highlight the models that best fit the observations. |
| In the text | |
 |
Fig. 11 Color-magnitude diagram for the clusters in our sample E(B − V) < 1, color coded with their mean iron abundance. The plot on the left displays 103 GCs that contain at least one RRL. The right plot shows the same but for 24 clusters without RRLs. The red lines indicate the position of the theoretical blue and red edge of the instability strip for RRab, with Z = 0.0003, M = 0.7M⊙ and Y = 0.290, see Sect. 5. |
| In the text | |
 |
Fig. 12 Pal 4, the most distant cluster in our sample with a clearly visible HB, and zero RRL. |
| In the text | |
 |
Fig. 13 RRLs (pink open circles) in clusters detected in this study and cluster members (white dots) in the HB detected by VB21 with membership probabilities above 50%. The squares indicate the bins in color and absolute magnitude used to estimate the fraction of RRLs over the number of cluster members detected by VB21. Each bin was color coded according to its specific RRL fraction, the color bar is located at the top of the plot. The purple contours indicate the 68th and 84th percentiles of density of RRLs. |
| In the text | |
 |
Fig. 14 Mean period of the RRLs pulsating in the fundamental mode as a function of the iron abundance of the cluster. The dotted lines indicate the region known as the Oosterhoff gap, we can see that multiple clusters are located in this region. The error bars represent the 16th and 84th percentiles of the distribution of periods. The blue point represents NGC 6388, and the yellow one corresponds to NGC 6441. Both clusters have been classified as Oosterhoff type III in the literature (Pritzl et al. 2003; Bhardwaj 2022). |
| In the text | |
 |
Fig. 15 Number of RRLs pulsating in the first overtone divided by the number of the ones pulsating in the fundamental mode. The black dashed line represents unit ratio. |
| In the text | |
 |
Fig. 16 Number of RRLs in clusters. The panel illustrates the number of RRLs within each cluster as a function of the iron abundance. The right panel presents the same data, but the number of RRLs is divided by a normalization constant that is calculated individually for each cluster (refer to Sect. 5.2 for more details). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.