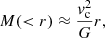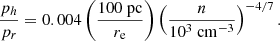| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A207 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202348321 | |
| Published online | 25 April 2024 | |
Super-early JWST galaxies, outflows, and Lyα visibility in the Epoch of Reionization
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
e-mail: andrea.ferrara@sns.it
Received:
19
October
2023
Accepted:
8
February
2024
The overabundance of super-early (redshift z > 10) luminous (MUV < −20) blue galaxies detected by JWST has been explained as being due to negligible dust attenuation in these systems. We show that this model correctly reproduces the UV luminosity function at z > 10 and the star formation rate (SFR) density evolution. The model also predicts, in agreement with data, that the cosmic specific SFR (sSFR) grows as sSFR ∝ (1 + z)3/2. At z ≃ 10, the cosmic sSFR crosses the critical value sSFR⋆ = 25 Gyr−1, and approximately 45% of the galaxies become super-Eddington, driving outflows reaching velocities of ≈830(ϵ⋆/fM)1/2 km s−1, where ϵ⋆ and fM are the star formation efficiency and fraction of the halo gas expelled in the outflow, respectively. This prediction is consistent with the outflow velocities measured in 12 super-Eddington galaxies of the JWST/JADES sample. Such outflows clear the dust, thus boosting the galaxy luminosity. They also dramatically enhance the visibility of the Lyα line from z > 10 galaxies by introducing a velocity offset. The observed Lyα properties in GN-z11 (z = 10.6) are simultaneously recovered by the outflow model if log NHI ≃ 20.1, implying that the outflow is largely ionized. We make analogous predictions for the Lyα visibility of other super-early galaxies, and we compare the model with Lyα surveys at z > 7, finding that essentially all super-Eddington (sub-Eddington) galaxies are (not) detected in Lyα. Finally, the sSFR positively correlates with the LyC escape fraction, as outflows carve ionized transparent channels through which LyC photons leak.
Key words: galaxies: high-redshift
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Among the many tantalizing mysteries the James Webb Space Telescope (JWST) promises to unravel, one of the most captivating is the discovery of super-early (redshift z ≳ 10) galaxies. These galaxies, often endearingly referred to as “blue monsters” (Ferrara et al. 2023; Ziparo et al. 2023; Fiore et al. 2023), show a number of peculiar properties. They are (a) very bright (MUV < −20), (b) more numerous than expected (number density ≈10−5 Mpc−3), (c) very blue (UV spectral slopes β ≲ −2.0), and (d) very compact (size ≈100 pc).
These enigmatic galactic giants represent a critical juncture in the cosmic timeline, bridging the gap between the Big Bang and the formation of the galaxies we see today. The study of super-early galaxies holds the potential to reshape our understanding of the universe’s infancy and shed light on the processes that catalyzed the birth of the first stars and black holes and the emergence of the structures that underpin cosmic tapestry.
After the powerful initial detection boost provided by the public JWST Early Release Science programs (Naidu et al. 2022; Donnan et al. 2023c; Finkelstein & Bagley 2022; Atek et al. 2023; Roberts-Borsani et al. 2022; Castellano et al. 2022, 2023; Santini et al. 2022; Adams et al. 2023; Harikane et al. 2022, 2023a; Topping et al. 2022; Rodighiero et al. 2022; Bradley et al. 2022; Barrufet et al. 2022; Trussler et al. 2022; Leethochawalit et al. 2022; Whitler et al. 2022; Austin et al. 2023; McLeod et al. 2023; Robertson et al. 2023; Fujimoto et al. 2023a) efforts have mostly concentrated on obtaining spectroscopic confirmations of the photometric candidates. These observationally intensive studies (Curtis-Lake et al. 2023; Bunker et al. 2023; Hsiao et al. 2023; Arrabal Haro et al. 2023a; Bradač et al. 2024; Wang et al. 2023; Stiavelli et al. 2023) have not only confirmed the photometric redshifts for the majority of the targets (although with noticeable exceptions, see Arrabal Haro et al. 2023c), but they have also provided key physical insights on the nature of these systems.
The observed large number density of super-early galaxies poses a serious challenge to essentially all galaxy evolution models (Mason et al. 2023; Mirocha & Furlanetto 2023; Di Cesare et al. 2023; Gong et al. 2023; Furlanetto & Mirocha 2023; Kannan et al. 2022; Yajima et al. 2023; Keller et al. 2023; McCaffrey et al. 2023; Mauerhofer & Dayal 2023; Padmanabhan & Loeb 2023; Muñoz et al. 2023), and perhaps to the ΛCDM model itself (Boylan-Kolchin 2023; Lovell et al. 2023; Haslbauer et al. 2022; Steinhardt et al. 2023; Parashari & Laha 2023). Barring modified cosmological scenarios, in order to increase the UV luminosity of a galaxy population at a fixed cosmic number density, there are essentially three possibilities.
Recalling that the UV luminosity of a galaxy is LUV ∝ SFR κ1500 e−τ, where κ1500 is the conversion factor from the star formation rate (SFR) to luminosity and τ is the UV dust optical depth, we can (a) increase the SFR, (b) increase κ1500, or (c) decrease τ. The SFR can be increased if a larger efficiency of gas conversion into stars is assumed (Dekel et al. 2023; Renzini 2023; Sipple & Lidz 2023) or if the SFR is stochastic (Mirocha & Furlanetto 2023; Shen et al. 2023; Pallottini & Ferrara 2023; Sun et al. 2023). Both solutions are unpalatable, as sometimes efficiencies greater than 100% would be required and because the rms of stochastic SFR variations is too small to explain the data (Pallottini & Ferrara 2023; Ciesla et al. 2024). Alternatively, one could postulate the presence of a metal-free (PopIII) stellar population with a larger κ1500 value (Riaz et al. 2022; Wang et al. 2022; Maiolino et al. 2024). Although this cannot be excluded, the absence of prominent He II lines in spectroscopically confirmed z > 10 galaxies, together with their moderately high metallicities (Z ≳ 0.1 Z⊙) make this hypothesis unlikely. Similarly, a significantly top-heavy IMF may partially, but not completely, alleviate the problem (Trinca et al. 2024).
Option (c) can be achieved in two ways. The first is to invoke a spatial segregation of stellar (optical-to-UV) and dust continuum (infrared) emitting regions (Behrens et al. 2018; Sommovigo et al. 2021, 2022; Ferrara et al. 2022; Dayal et al. 2022). In this scenario, the UV radiation mostly comes from the transparent diffuse interstellar medium (ISM), hosting either little or cold dust. The dust-obscured SFR is instead located in giant molecular clouds strongly emitting at IR wavelengths. This hypothesis can be excluded on the basis of the ALMA (Bakx et al. 2022; Popping 2022; Kaasinen et al. 2022; Yoon et al. 2022; Fujimoto et al. 2022) and NOEMA (Fudamoto et al. 2024) far-infrared dust continuum non-detections (Ziparo et al. 2023).
Alternatively, given their typical stellar mass (M⋆ = 109 M⊙) and dust-to-stellar ratio (≈1/1000, Dayal et al. 2022), one would expect 106 M⊙ of dust to be present in these systems. As we later show in Sect. 4, this dust amount would totally obscure the UV light emitted by the galaxy. Thus, some mechanism must expel, or at least lift, the dust off the galaxy main body. We suggest that radiation-driven outflows, developing once the galaxy luminosity becomes super-Eddington, might do the job (Ferrara et al. 2023, see also Tsuna et al. 2023). In this paper, following up the previous work in Ferrara et al. (2023), we study the conditions for early galaxies to develop radiation-driven outflows that increase the galaxy’s luminosity and produce their steep UV spectra.
Thanks to the growing body of JWST observations, it is already possible to test this scenario up to the highest redshifts. The tests include, among others, comparisons with UV luminosity functions, individual and cosmic SFRs, stellar ages, and outflow properties deduced from spectral line information. Once validated, the model can be used to make novel predictions related to the visibility and spectral properties of the Lyα emission from galaxies in the Epoch of Reionization (e.g. Tang et al. 2023; Endsley et al. 2022; Stark et al. 2017). It might also provide information on the escape fraction of LyC photons, a crucial parameter to model the reionization of the intergalactic medium (IGM).
This paper is organized as follows1. In Sect. 2, we derive a specific SFR (sSFR)-based condition for a galaxy to develop a radiation-driven outflow. Section 3 presents the model predictions for the sSFR evolution and various tests of the model using available JWST data. Section 4 discusses the properties of the outflows and compares them with data from the JWST/JADES survey. Predictions for the Lyα visibility in the Epoch of Reionization are given in Sect. 5 and are followed by a general discussion in Sect. 6. A brief summary in Sect. 7 concludes the paper.
2. Super-Eddington galaxies
We started by analyzing the conditions for which high-redshift galaxies might develop a radiatively driven dusty outflow. To this aim, we made two basic assumptions: (a) the stellar component is sufficiently compact such that it can be treated as a point source and (b) the gravity in the central regions is dominated by stars, so the contribution of gas (and dark matter) can be neglected. The first hypothesis is justified by the very small sizes deduced for z > 8 sources (Tacchella et al. 2023; Robertson et al. 2023). The second is supported by the high typical stellar densities of these systems ≈ 1000 M⊙ pc−3 (Charbonnel et al. 2023), which might indicate that most of the gas in these regions has been converted into stars (Dekel et al. 2023).
We also assumed that radiation pressure from the stars acts on dust (Fabian et al. 2006) that is tightly coupled by viscous and Coulomb drag forces to the gas and to which dust transfers the radiation momentum. This implies that the classical Eddington luminosity LE = 4πGmpcM*/σT = 1.26 × 1038(M*/M⊙) erg s−1 is reduced by a boost factor A = σd/σT, the ratio of the dust to Thomson cross section.
Depending on the stellar age, metallicity, dust-to-gas ratio, and radiative transfer effects, the boost factor can be computed from the CLOUDY V13 (Ferland et al. 2013) photoionization code. In particular, the explored ranges are a 10 − 300 Myr starburst, metallicity Z = 0.6 − 3 Z⊙, and a dust-to-gas ratio 0.3 − 1 times the Galactic value, D = 1/162. Fiore et al. (2023) found it to be in the range A = 100 − 600. Such a range brackets uncertainties in the above effects (see Fig. 2 of Fiore et al. 2023). Here, we conservatively use A = 100.
The super-Eddington condition
where Lbol is the source bolometric luminosity, can be equivalently written as 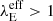 , where the (effective) Eddington parameter
, where the (effective) Eddington parameter 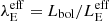 has been introduced. If the galaxy becomes super-Eddington, a radiatively driven outflow will develop, ejecting both dust and gas from the system.
has been introduced. If the galaxy becomes super-Eddington, a radiatively driven outflow will develop, ejecting both dust and gas from the system.
We determined the galaxy (unattenuated) UV luminosity at 1500 Å, L1500, from the SFR via a conversion factor, 𝒦1500 [L⊙/M⊙yr−1], whose value has been chosen so to match the one used by the ALMA REBELS survey (Bouwens et al. 2022a): 𝒦1500 ≡ L1500/SFR = 0.587 × 1010. We then converted the UV luminosity into Lbol using a bolometric correction, fbol = Lbol/L1500 = 2, in agreement with the galaxy templates used to evaluate the boost factor (Fiore et al. 2023).
The super-Eddington condition, 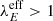 , with the above definitions translates into one on the specific star formation rate, sSFR = SFR/M⋆:
, with the above definitions translates into one on the specific star formation rate, sSFR = SFR/M⋆:
Equation (2) represents the necessary condition for a galaxy to develop a radiation-driven outflow.
3. Specific star formation rate
Given the result in Eq. (2), we turned our attention to the redshift evolution of the sSFR. We followed Ferrara et al. (2023) and wrote the mean SFR in a halo of total mass M as
where ϵ⋆ is the instantaneous star formation efficiency (i.e., at the time of observation) and fb = Ωb/Ωm = 0.158. The gas free-fall time in halos, tff = (4πGρ)−1/2, can be conveniently written as tff = ζH(z)−1, where H(z)−1 is the Hubble time at z and ζ = 0.06. We could then rewrite Eq. (3) as
Before we proceeded, we paused to test the model predictions against the z ≃ 11.5 UV luminosity function and cosmic star formation rate density data. These comparisons are shown in Fig. 1. We note that the blue curves are not a fit to the data, that is, we did not vary any of the parameters of the model provided in Ferrara et al. (2023). In spite of that, the predictions of the model perfectly match both data sets. On this basis, we can confidently use the model to derive the sSFR.
 |
Fig. 1. Results of the Ferrara et al. (2023) model used here. Left panel: Predicted UV luminosity function (blue curve) compared with available data at z ≃ 11.5 (points). The blue curve assumes no dust attenuation, while the gray curve marked as τeff(z = 7) assumes that the dust attenuation at z = 11.5 is the one calibrated at z = 7 using the ALMA REBELS data (Bouwens et al. 2022a; Ferrara et al. 2022). The data are from Castellano et al. (2022, GHZ2), Bunker et al. (2023, GN-z11), McLeod et al. (2023), Adams et al. (2023), and Harikane et al. (2023a) lower limits. Also shown are empirical fits provided by Bouwens et al. (2022b, red dashed), Bowler et al. (2020, yellow dashed), and Finkelstein & Bagley (2022, green dashed). Right panel: Predicted evolution of the cosmic SFR density (blue curve), integrated down to a limiting AB mag M1500 = −17, compared with the data compilation of early JWST measurements in McLeod et al. (2023), also including data from Harikane et al. (2023b), Oesch et al. (2018), Donnan et al. (2023a,b), McLeod et al. (2016), Pérez-González et al. (2023). The other lines refer to different model predictions (Madau & Dickinson 2014; Harikane et al. 2022; Mason et al. 2023; Sun & Furlanetto 2016). |
The galaxy stellar mass, M⋆, can be computed in two different ways. First, one assumes that the star formation proceeds at a constant rate, given by Eq. (3), over the last free-fall time before the observed epoch. At z = 8 − 10, this hypothesis implies a mass assembly of ≃50 Myr, which is consistent with the typical formation times estimated through non-parametric star formation histories (Bouwens et al. 2022b, see their Table 6). It follows that
and
where ⟨ϵ⋆⟩ is the efficiency averaged over a free-fall time. We note that if ϵ⋆ ≃ const. = ⟨ϵ⋆⟩, the sSFR is independent of the mass and star formation efficiency and equal to 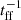 . As the sSFR is a function of redshift only and it grows monotonically, Eq. (2) implies that, on average, galaxies become super-Eddington for z ≳ 10 (see Fig. 2). We refer to Eq. (6) as the “fast formation” model. This result is essentially the same found by Tacchella et al. (2018), but the redshift evolution of the sSFR is shallower than found by Dekel et al. (2013), sSFR ∝ (1 + z)5/2.
. As the sSFR is a function of redshift only and it grows monotonically, Eq. (2) implies that, on average, galaxies become super-Eddington for z ≳ 10 (see Fig. 2). We refer to Eq. (6) as the “fast formation” model. This result is essentially the same found by Tacchella et al. (2018), but the redshift evolution of the sSFR is shallower than found by Dekel et al. (2013), sSFR ∝ (1 + z)5/2.
 |
Fig. 2. Redshift evolution of the sSFR for the two models explored here. The red line corresponds to the fiducial model in which most stars formed over the last free-fall time (Eq. (6)) along with ±1σ uncertainties (red dotted) derived from data in 8 < z < 10. Black lines account for halo mass growth (Eq. (8)) and are shown for present-day halo values of log(M0/M⊙) = 10 − 15 (bottom to top) in 0.5 dex intervals; these curves approximately evolve as (1 + z)5/2. Models are compared with available data points for high-z galaxies from (Bouwens et al. 2022a; Bradley et al. 2022; Strait et al. 2020; Stefanon et al. 2022, 2023; Topping et al. 2022; Tacchella et al. 2022; Smit et al. 2014; Endsley et al. 2021; Roberts-Borsani et al. 2022; Labbé et al. 2013; Robertson et al. 2023; Harikane et al. 2023a). The horizontal dashed line is the critical sSFR (Eq. (2)) above which outflows develop. |
A second way to estimate the stellar mass includes a treatment of the halo mass growth history. We started by writing
where z⋆ is the redshift at which the halo virial temperature reaches Tvir = 104 K, thus enabling Lyα cooling2 and hence star formation. We also used the relation dt/dz = −[H(z)(1 + z)]−1 and substituted Eq. (4) in the equation above. The halo mass growth with redshift can be obtained by time integrating the cosmological accretion of dark plus baryonic matter. A handy fit to M(z) is provided by Correa et al. (2015):
where M0 is the present-day halo mass and (α, β) are parameters that depend on M0, cosmology, and the linear matter power spectrum. These are provided3 in Appendix C of Correa et al. (2015). By combining Eqs. (3) and (7), we obtained the evolution of the sSFR shown in Fig. 2. We refer to such a result as the “slow formation” model. In this case, sSFR depends on halo mass as well as on redshift. In addition, with respect to the previous scenario (Eq. (6)), accounting for halo growth produces a steeper redshift dependence, approximately ∝(1 + z)5/2.
Despite these differences, both models predict that on average high-z galaxies become super-Eddington. In fact, the slow formation model predicts that halos with M0 = 1010 M⊙ (M0 = 1015 M⊙) cross the sSFR = 25 Gyr−1 threshold at z = 14.5 (10).
At this stage, the available data cannot uniquely discriminate between the two models shown in Fig. 2. Arguments in favor of a flatter (1 + z)3/2 evolution have nevertheless been brought by a number of works. Faisst et al. (2016) found that sSFR ∝(1 + z)3/2 at z > 2.2 is consistent with a fast mass build-up in high-z galaxies within e-folding times of ≈100 Myr, consistent with our Eq. (6). A very similar but flatter trend, sSFR ∝ (1 + z)1.6 Gyr−1, has been obtained by Tacchella et al. (2018) and Hsiao et al. (2022). As noted, the different behavior of the models has little impact on the main point here, namely, that a large fraction of z ≳ 10 galaxies should develop an outflow. Hence, in the following we concentrate on the fast formation scenario.
Equation (6) provides a very good match to the mean sSFR trend, but it does not account for the observed sSFR scatter at a fixed redshift. The scatter naturally arises in the model if the efficiency varies over tff, that is, ⟨ϵ⋆⟩≠ϵ⋆. Stated differently, while the SFR depends on the instantaneous star formation efficiency, the stellar mass is sensitive to its past variations. The latter are likely regulated by poorly understood feedback processes, causing the system to experience a stochastic star formation history (Pallottini & Ferrara 2023; Shen et al. 2023; Mirocha & Furlanetto 2023; Sun et al. 2023) or even multiple subsequent phases of quiescent and active star formation (Gelli et al. 2023, 2024; Kobayashi & Ferrara 2023).
For example, Looser et al. (2023) reported the discovery of the quiescent low-mass galaxy JADES-GS-z7-01-QU at redshift z = 7.3 (see also Carnall et al. 2023; Strait et al. 2023 for similar systems). Gelli et al. (2023), using zoom-in simulations (see also Dome et al. 2023), showed that the fraction of time spent in an active phase increases with the stellar mass from fduty ≈ 0.6 at M⋆ ≈ 107.5 M⊙ to ≈0.99 at M⋆ ≥ 109 M⊙, and it is in agreement with the value fduty ≈ 0.75 estimated for JADES-GS-z7-01-QU.
Rather than attempting to model such a complex situation, we resorted to an empirical approach, namely, to calculate the scatter of the model from the observed sSFR of galaxies in the relevant range 8 < z < 10. We used a reduced chi-square to determine the variance of the observed sSFR from the predicted one Eq. (6):
where sSFRi and σi are the N = 23 observational points and errors shown in Fig. 2, respectively. We found that the fractional standard deviation is 83%, and we added it to Eq. (6), assuming it to be redshift independent (red dotted lines in Fig. 2).
Assuming a normal distribution of sSFR with standard deviation σ, we could compute the fraction of galaxies, fλE, at any given redshift for which 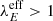 . This is shown in Fig. 3, where fλE is also compared with the observational data collected in Fiore et al. (2023). We observed that fλE increases with redshift following the overall increasing sSFR trend of the mean. At z = 6, we found fλE = 0.2, and at z = 10 (14), fλE reaches 45% (76%).
. This is shown in Fig. 3, where fλE is also compared with the observational data collected in Fiore et al. (2023). We observed that fλE increases with redshift following the overall increasing sSFR trend of the mean. At z = 6, we found fλE = 0.2, and at z = 10 (14), fλE reaches 45% (76%).
 |
Fig. 3. Predicted redshift evolution of the fraction of super-Eddington galaxies (i.e., |
Thus, according to our model, radiation-driven outflows should be very common in Epoch of Reionization galaxies and should become prevalent in galaxies at z ≳ 10. Their presence is solely determined by a high sSFR and is independent of the galaxy mass. We note, however, that super-Eddington conditions might also be found, albeit much more rarely, at lower redshifts provided that sSFR > sSFR⋆.
4. Radiation-driven outflows
We now present how we derived the properties of the radiation-driven outflows from super-Eddington galaxies. We supposed that the radiation from the stars acts on a geometrically thin but initially UV or even IR optically thick dusty gas shell of mass Msh, thus transferring its momentum to both dust and gas. The shell dynamics are governed by the momentum equation
where v is the shell velocity and
is a function of the UV (1500 Å) and IR optical depths (Thompson et al. 2015; Ishibashi et al. 2018; Costa et al. 2018). The first term in Eq. (11) accounts for single-scattering momentum transfer, and the second quantifies the momentum exchange between trapped IR radiation and the outflow.
Adopting a Milky Way extinction curve with a dust-to-gas ratio DMW = 1/162, the dust mass absorption coefficient at 1500 Å is κ1500 = 1.26 × 105 cm2 g−1 (Ferrara et al. 2022). The analogous IR coefficient, κIR(ν) = κ158(ν/ν158)βd, is pivoted at wavelength λ158 = c/ν158 = 158 μm. For a Milky Way curve, κ158 = 10.41 cm2g−1, and βd = 2.03 (Weingartner & Draine 2001). As dust in early galaxies has been found to be increasingly warm at high-z, reaching values of 50 − 70 K at z ≃ 10 (Sommovigo et al. 2022, and references therein), we adopted Td = 60 K as a fiducial value and computed κIR at the peak wavelength of the gray-body spectrum, λp = 0.29/Td = 48 μm. This yielded κIR(νp) = 117 cm2 g−1.
As long as the galaxy is significantly super-Eddington, the gravity term in Eq. (10) can be neglected with respect to f(τ)Lbol/c, and it is easy to see that the outflow reaches a terminal velocity
where rτ = 1 is the radius at which the outflow becomes optically thin due to expansion, that is, max(τ1500, τIR) = τ1500 = 1. Following Ziparo et al. (2023), we write
where ξd = 1/529 is the dust-to-stellar mass ratio due to supernova (SN) dust production for a Salpeter 1 − 100 M⊙ IMF and assuming a dust yield/SN of 0.1 M⊙ and re is the stellar effective radius. Recalling that at high redshifts, re ≈ 0.1 kpc for a galaxy with stellar mass M* ≈ 109 M⊙ (Pallottini et al. 2022; Adams et al. 2023; Bunker et al. 2023; Ono et al. 2022), Eq. (13) numerically yields
The above result shows that super-early massive galaxies are heavily obscured both in the UV, and possibly also in the IR (τIR = τ1500/103) during their initial evolutionary phases, and before the outflow is launched. From Eq. (14), it also follows that rτ = 1 = 2(M⋆/109 M⊙)1/2 kpc.
To evaluate Eq. (12), the final ingredient is Msh. We assumed that a fraction fM of the gas left over from star formation is accelerated in the expanding shell. Hence, Msh = fM[(1 − ⟨ϵ⋆⟩)/⟨ϵ⋆⟩]M⋆ ≡ (fM/gϵ)M⋆. Taking the best studied z > 10 galaxy, GN-z11 (Bunker et al. 2023), from the observed Lyα line profile and displacement (see Sect. 5), we deduced fM = 0.18. We obtained ⟨ϵ⋆⟩ = 0.015 by matching4 the predicted SFR of GN-z11 (Eq. (4)) with the observed one (18.78 M⊙ yr−1). The final expression for the outflow terminal velocity is
having further used the scaling 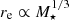 , which implicitly assumes that the effective radius is proportional to the galaxy virial radius, re ≈ 0.01rvir (Shibuya et al. 2015; Ono et al. 2022). We note that we have normalized the sSFR to the critical value, sSFR⋆ = 25 Gyr−1, obtained in Eq. (2). Also, the dependence on stellar mass is very weak,
, which implicitly assumes that the effective radius is proportional to the galaxy virial radius, re ≈ 0.01rvir (Shibuya et al. 2015; Ono et al. 2022). We note that we have normalized the sSFR to the critical value, sSFR⋆ = 25 Gyr−1, obtained in Eq. (2). Also, the dependence on stellar mass is very weak, 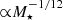 . The terminal velocity increases with the star formation efficiency (via gϵ), and v∞ ∝ ⟨ϵ⋆⟩1/2. Outflows clear the dust and gas from the galaxy main body in a short timescale, tc ≈ rτ = 1/3v∞ = 3.1 (200 km s−1/v∞) Myr, thus making the galaxy UV spectrum very blue, as preliminarily found by Cullen et al. (2023) and Topping et al. (2024).
. The terminal velocity increases with the star formation efficiency (via gϵ), and v∞ ∝ ⟨ϵ⋆⟩1/2. Outflows clear the dust and gas from the galaxy main body in a short timescale, tc ≈ rτ = 1/3v∞ = 3.1 (200 km s−1/v∞) Myr, thus making the galaxy UV spectrum very blue, as preliminarily found by Cullen et al. (2023) and Topping et al. (2024).
Figure 4 shows v∞, derived from Eq. (15), as a function of the UV magnitude of galaxies with stellar masses in the range 107.3−9.1 M⊙. Generally, the outflow velocity increases toward brighter magnitudes, with a moderate scatter introduced by the stellar mass. Outflows can occur at any MUV, but more massive galaxies do not produce an outflow (v∞ = 0) until they reach bright magnitudes.
 |
Fig. 4. Outflow terminal velocity (Eq. (15), assuming ⟨ϵ⋆⟩ = 0.015, fM = 0.18, as appropriate for GN-z11) versus the UV magnitude for different values (colored numbers) of the log of the stellar mass in solar units. We note that v∞ = 0 denotes the sub-Eddington regime in which no radiation-driven outflows are expected. The circles are the predicted values of v∞ for the nine spectroscopically confirmed galaxies presently available at z > 10. Four of these galaxies (GN-z11, MACS0647-JD, Maisie, and GN-z10-0) as well as the photometric candidate GHZ2 are predicted to show outflow signatures. The data are taken from Curtis-Lake et al. (2023), Bunker et al. (2023), Arrabal Haro et al. (2023b), Harikane et al. (2023a), Hsiao et al. (2023), Castellano et al. (2022). Also shown is the lensed (μ = 4.7, Tokuoka et al. 2022) galaxy MACS1149-JD1 (Stiavelli et al. 2023, z = 9.11) specifically discussed in Sect. 6. |
For example, the outflow of a galaxy such as GN-z11 (MUV = −21.5, M⋆ = 108.7 M⊙) is predicted to reach v∞ ≃ 200 km s−1. We note that v∞ is smaller than the circular velocity of GN-z11 halo, vc = = 324 km s−1, having assumed a halo mass5 M ≃ 1011.5 M⊙. This indicates that dust and gas are efficiently removed from the galaxy by the outflow, but they are likely to remain bound to the system as a spatially extended component or a fountain-like flow. This prediction is also consistent with the results by Xu et al. (2023, Fig. 7), who found that in their sample of 30 outflowing galaxies at 3 < z < 9, almost all of the outflows cannot escape from the halo gravitational potential.
In Fig. 4, we consider the nine spectroscopically confirmed galaxies (see Table 1 for a summary of their properties) currently available at z > 10 plus an interesting photometric candidate, GHZ2 (Castellano et al. 2022, z = 12.2). We found that five of these galaxies (i.e., 50%) have super-Eddington luminosities, which is in excellent agreement with the z ≃ 10 − 12 model predictions shown in Fig. 3. Their outflow velocities largely depend on galaxy sSFR and range from 65 km s−1 for GS-z10-0, to 200 km s−1 for GN-z11. The remaining five galaxies are instead in the sub-Eddington (no outflow) regime.
Observed and derived properties of currently available z > 10 spectroscopically confirmed super-Eddington galaxies.
The predicted presence of radiation-driven outflows in high-z galaxies can be confronted with observations. Luckily, and thanks to the advent of JWST, high-quality spectroscopic data have recently become available. Carniani et al. (2024, see also Zhang et al. 2023; Xu et al. 2023) have investigated the ionized gas outflows in 52 galaxies, part of the JADES sample, at 3 < z < 9 with stellar mass 107−9 M⊙. They detected broad line components of optical nebular lines, which they interpreted as an outflow signature, in ≈25 − 40% of the systems. This value represents a lower limit to the incidence if outflows are anisotropic.
Interestingly, the 12 galaxies in the sample that are super-Eddington (sSFR/sSFR⋆ = 1 − 8.5) all show the presence of an outflow with velocities in the range 280 − 925 km s−1 (Fig. 5). This strongly suggests that radiation pressure from young stars in the galaxy drives the outflow. The observed velocities may be used to constrain the fraction of halo gas entrained by the outflow, fM, which is a free parameter in Eq. (15). We found that fM is typically 1 − 10%, with an average value of 4%. Its distribution is shown in the top panel of Fig. 5. This value roughly corresponds to the entire galaxy gas mass.
 |
Fig. 5. Model prediction for outflows. Bottom panel: Outflow terminal velocity (Eq. (15), lines) as a function of the sSFR normalized to the critical value sSFR⋆ (Eq. (2)). The galaxies for which sSFR/sSFR⋆ > 1 are in the super-Eddington regime. Also shown (cyan band) is the sub-Eddington region. The predictions are compared to JWST/JADES data (Carniani et al. 2024, red points) for 12 galaxies in 3 < z < 9 with measured outflow velocity. The data are also used to derive the fraction of halo gas entrained by the outflow, fM (see Eq. (15)), whose (percentage) value is shown by the number on each curve. Top panel: Histogram of the fM values derived in the bottom panel. |
5. Lyα visibility in the Epoch of Reionization
We showed that radiation-driven outflows are common among super-early galaxies. When present, they can dramatically enhance the transmission of the Lyα line emitted by these sources even if the IGM is almost neutral, as expected at z ≳ 10. This fact was already noted by, for example, Dijkstra & Wyithe (2010), who pointed out that scattering off outflows causes the Lyα flux to emerge from galaxies at frequencies where the Gunn–Peterson (GP) optical depth is highly reduced.
To quantify the Lyα visibility, we concentrated on two super-early galaxies, GN-z11 (Bunker et al. 2023, z = 10.6) and Maisie (Finkelstein & Bagley 2022; Arrabal Haro et al. 2023b, z = 11.4) for which exquisite spectroscopic data are available. The results are displayed in Fig. 6. We also considered three other z > 10 super-Eddington galaxies (GHZ2, MACS0647-JD, and GS-z10-0), included in Fig. 4. The results for these five galaxies are summarized in Table 1.
 |
Fig. 6. Predicted profiles of the observed Lyα line from two super-Eddington galaxies GN-z11 (Bunker et al. 2023) at z = 10.6 and Maisie (Finkelstein et al. 2022; Arrabal Haro et al. 2023b) at z = 11.4. In each panel, different curves from left to right refer to the ISM neutral hydrogen column densities NHI = 1020 + 0.1j cm−2, with j = 0, 1, …, 10. The gray lines show the Lyα profile emerging from the galaxy, which also accounts for the outflow velocity. The colored lines represent the observed profile after transmission through the IGM, whose GP damping wing, including the surrounding H II bubble (e−τGP), is shown by the red curve. For each observed curve, we show the values of the line peak velocity shift, vp, FWHM (both in [km s−1]), and EW in [Å]. For GN-z11 the observed values (Bunker et al. 2023; Scholtz et al. 2023) are (vp, FWHM, EW) = (555 ± 32 km s−1, 530 ± 65 km s−1, 18 ± 2 Å), which are very well reproduced by the curve with NHI = 1020.1 cm−2. At the same NHI, we predict that the Lyα EW for Maisie is 7.6 Å. |
To derive the observed Lyα line profile for each galaxy, three steps were required: (a) First was computing the outflow velocity, v∞. This step was performed in Eq. (15). (b) Second was computing the line profile emerging from the galaxy after processing by radiative transfer effects (H I scattering, dust absorption) in the outflow. (c) Last was convolving the emergent line profile with the IGM attenuation due to the GP optical depth τGP in order to determine the observed profile. We describe how steps (b) and (c) were performed in the following sections.
5.1. Emergent Lyα profile
To compute the emergent Lyα profile, we used the results by Orsi et al. (2012). They used a Monte Carlo Lyα radiative transfer code to determine the line properties depending on the outflow velocity, v∞, and H I column density, NHI. As a function of these two quantities6, they provided the emergent Lyα line median velocity shift with respect to systemic (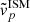 ), full-width half-maximum (FWHMISM), and Lyα escape fraction, (
), full-width half-maximum (FWHMISM), and Lyα escape fraction, (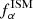 ), that is, the fraction of the line luminosity that escapes the system and goes into the IGM. We linearly interpolated the results given in Orsi et al. (2012, Fig. 2) for
), that is, the fraction of the line luminosity that escapes the system and goes into the IGM. We linearly interpolated the results given in Orsi et al. (2012, Fig. 2) for 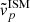 , FWHMISM; Fig. 3 for
, FWHMISM; Fig. 3 for 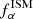 .
.
Moreover, Lyα can also be extincted by dust, whose abundance is approximately ∝Z. Orsi et al. (2012) considered metallicities in the range Z = 0.5 − 1 Z⊙; however, they noted that this choice only affects the results at H I column densities, NHI ≳ 1021 cm−2, which are not relevant for our results. We assumed that the emergent profile is a Gaussian7 centered (in velocity space) at 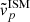 and a full width equal to FWHMISM. Finally, we used
and a full width equal to FWHMISM. Finally, we used 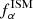 to compute the line EW (see Sect. 5.3 below).
to compute the line EW (see Sect. 5.3 below).
5.2. Observed Lyα profile
The emergent line profile was further processed by the intervening neutral IGM along the line of sight while also considering the fact that LyC photons escaping from GN-z11 carve an approximately spherical ionized bubble around the galaxy8. The bubble radius might be computed from the observed properties of GN-z11 as follows:
where Nion = ξionL1500 is the LyC photon emission rate. The LyC escape fraction, fesc, was obtained from the UV spectral slope β using the Chisholm et al. (2022) relation: log fesc = −4.44 − 1.22β. We slightly corrected the relation to match the GN-z11 value fesc = 0.03 deduced from the Hβ equivalent width (Bunker et al. 2023). The timescale, ts, was taken as the minimum between the stellar age and the recombination time,
where t⋆ ≈ tff (see Sect. 3), αB = 2.6 × 10−13(T/104 K)−3/4 cm3 s−1 is the Case-B recombination coefficient, and ne ≈ nH is the mean (electron) density of the IGM at the redshift of the emitter. Equation (17) accounts for the fact that the stellar population in a galaxy might be too young to fill the galaxy Strömgren sphere. The final Rb values are given in Table 1; they are in the range 0.08 − 0.26 pMpc.
The GP scattering optical depth at the observed wavelength λobs > λα(1 + zem), where λα = 1215.67 Å is the rest-frame Lyα wavelength and zem is the redshift of the source, is
where σα(ν, T) is the Lyα cross section assuming an IGM temperature T = 100 K at z ≈ 10. We assumed that inside Rb, the IGM is fully ionized, that is, we neglected the residual H I in the bubble and wrote the proper cosmological line element as dℓ/dz = c[(1 + z)H(z)]−1. The reionization redshift is fixed to zrei = 6, and zb is defined as the redshift corresponding to the H II bubble radius of each source. Finally, nHI(z) = xHInH is the H I density at redshift z. We set xHI = 1, consistent with recent findings at z ≃ 10 (Bruton et al. 2023).
The observed Lyα profile was then computed by multiplying the emergent profile by e−τGP, that is, the so-called GP damping wing. We also computed the fraction, 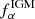 , of the emergent Lyα luminosity that escapes after attenuation by the IGM. The emergent and observed Lyα profiles of GN-z11 and Maisie are shown as an example in Fig. 6, along with the corresponding GP damping wings, as a function of velocity.
, of the emergent Lyα luminosity that escapes after attenuation by the IGM. The emergent and observed Lyα profiles of GN-z11 and Maisie are shown as an example in Fig. 6, along with the corresponding GP damping wings, as a function of velocity.
5.3. Lyα emission from super-Eddington galaxies
From the predicted Lyα profiles of the five super-Eddington galaxies, we extracted four quantities that can be readily compared with observations. These are the Lyα line peak velocity shift, vp; full width half maximum (FWHM); equivalent width (EW); and total escape fraction, 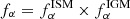 .
.
5.3.1. GN-z11
In this section, we first concentrate on GN-z11, for which the Lyα has been detected by Bunker et al. (2023; Fig. 6, left panel). For the predicted outflow velocity, v∞ = 200 km s−1, the line profile depends on the outflow H I column density, which we allowed to span the range log NHI = 20 − 21. Both the line peak velocity shift and FWHM increase with NHI, whereas the EW decreases due to the increased attenuation. The observed values (vp, FWHM, EW) = (555 ± 32 km s−1, 530 ± 65 km s−1, 18 ± 2 Å) are simultaneously well recovered if log NHI ≃ 20.1 (see Table 1 and Fig. 6). The predicted total Lyα escape fraction is fα = 0.069. We checked that when artificially setting v∞ = 0 (i.e., no outflow) or to larger velocities, v∞ = 500 km s−1, it is impossible to recover the observed line parameters simultaneously. Interestingly, the derived value of NHI is fully consistent with the one measured by Umeda et al. (2023) in 26 JWST-detected galaxies at 7 < z < 12.
From the fit to the GN-z11 Lyα line profile, we found that the outflow shell contains a fraction fM = 0.18 of the baryonic mass of the halo. The total hydrogen column density of the shell measured at the optically thin radius, rτ = 1, is log NH = 22.5. By comparing with the value log NHI = 20.1 found from the Lyα analysis, we concluded that the outflow is largely ionized, with a neutral fraction xHI = NHI/NH = 4.2 × 10−3. Such an ionized state can result from either photoionization, shocks, or a combination of the two. Radiative hydro-dynamical simulations are required to clarify this issue.
The excellent match provided by the model to the observed line properties can be considered as a successful test for the radiation-driven outflows proposed here. It also points toward the importance of outflows in determining the Lyα visibility from z > 10, where in principle the line transmission should be almost completely suppressed by the neutral IGM.
5.3.2. Predictions for Maisie and other galaxies
Beyond explaining the GN-z11 data, our model makes detailed predictions (summarized in Table 1) on the outflow-boosted Lyα emission from the other four super-Eddington galaxies. We started by analyzing Maisie, whose predicted Lyα profile is shown in Fig. 6 (right panel). As the Lyα line for Maisie could have not been detected in the JWST/NIRSpec prism spectra, we cannot put constraints on the H I column density. Rather, the values reported in Fig. 6 and Table 1 can be considered as predictions of the model. For the sake of comparison though, we can consider the curve with log NHI = 20.1 as appropriate for GN-z11. Maisie shows a slightly lower line peak velocity shift of 516 km s−1 and a significantly narrower FWHM (384 km s−1). As a result the line, EW is smaller (7.6 Å), with only 2.8% of the Lyα photons transmitted.
The three other super-Eddington galaxies do not differ considerably in terms of vp, FWHM, and EW from Maisie, with the exception of GHZ2 (photometric redshift z = 12.4), which instead shows properties very similar to GN-z11. Notably, its large EW = 17.6 Å clearly illustrates the boost that outflows can provide to the line visibility. GHZ2 is predicted to have an outflow travelling at v∞ = 182 km s−1, and aided by its blue colors (β = −3.0) and consequently a large LyC escape fraction fesc = 0.16, it manages to transmit 6.5% of its Lyα photons in spite of being located at the highest redshift in the sample.
6. Discussion
The radiation-driven outflow scenario discussed in this work provides a viable interpretation of JWST data that imply (a) an unexpected excess of bright galaxies (b) with very blue colors, (c) some of which are able to transmit their Lyα line through the largely neutral IGM at z > 10. Nevertheless, several aspects of the model need further clarification.
6.1. Outflow physics
We have shown that for dusty outflows, the Eddington luminosity is reduced by a factor A = 100 − 600, making radiation pressure extremely efficient. The super-Eddington condition is equivalent to the requirement that sSFR > sSFR⋆ ≃ 25(100/A) Gyr−1. Thus, a larger value of A would favor the onset of outflows from galaxies with even more modest sSFR (see Fiore et al. 2023, Fig. 2). The value of A is uncertain, as it depends on the galaxy dust-to-gas ratio, interstellar radiation field, and radiative transfer effects (Fabian et al. 2006; Fiore et al. 2023). Although these aspects deserve more study, our choice of A = 100 is very conservative.
We additionally note that even if stars in super-early galaxies formed out of a metal-free gas with no dust, radiation pressure can be initially provided – with comparable strength – by Lyα photons (Tomaselli & Ferrara 2021). This mechanism has been shown to be at work in Green Pea analogs, such as Mrk 71 (Komarova et al. 2021). The interesting feature is that Lyα radiation pressure starts to work immediately after the formation of the first massive stars with no delay (≳3 Myr) associated with SN explosions and dust production. The Lyα feedback might effectively cap the star formation efficiency (Tan & McKee 2008; Dekel et al. 2023).
The Eddington condition, Eq. (2), was derived under the implicit assumptions that (a) gravity is dominated by stars and (b) the system is spherically symmetric. The first assumption is more delicate, as dark matter and gas in the halo might also contribute to the gravitational field. To get a simple estimate of these effects, we assumed that dark matter follows a singular isothermal radial density profile,
where vc is the halo circular velocity. We further assumed that baryons initially follow the same distribution scaled by the cosmological baryon fraction, Mb = fbM.
Considering the case of GN-z11, for which M⋆ = 108.7 M⊙ of stars are located in an effective radius re = 64 pc, and vc = 324 km s−1, the gas mass in that volume, according to Eq. (19), is 108.4 M⊙ < M⋆. This implies that all the gas initially within re (and, formally, up to ≃200 pc) has been turned into stars. Hence, gas outside this region is subject to the gravitational pull of stars and dark matter.
Condition (a) above is satisfied as long as stars dominate the gravitational field, that is, for 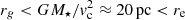 . Hence, outside re, stars are subdominant, and one should replace M⋆ with M⋆ + M(< r) in the gravity term in Eq. (12). However, in the derivation of v∞, we neglected the gravity effects by considering only very super-Eddington systems (i.e., sSFR ≫ sSFR*); in this approximation, our treatment still holds9.
. Hence, outside re, stars are subdominant, and one should replace M⋆ with M⋆ + M(< r) in the gravity term in Eq. (12). However, in the derivation of v∞, we neglected the gravity effects by considering only very super-Eddington systems (i.e., sSFR ≫ sSFR*); in this approximation, our treatment still holds9.
Assumption (b) can be justified with the very compact, almost point-like, size (≲100 pc) of super-early galaxies. Clearly, departures from spherical symmetry are also possible in case of disk formation, for example. One can show that for a thin stellar disk embedded in a more extended gas layer, the super-Eddington condition is the same that we use here as long as gravity is dominated by stars.
Ziparo et al. (2023) have explored the case of a disk geometry assuming a self-gravitating disk. They also concluded that galaxies with high sSFR develop radiation-driven outflows. However, Ziparo et al. (2023) noted that in some extreme cases, the dust production rate might exceed the outflow rate, and dust accumulates faster than it is ejected. This implies that a fraction of super-early galaxies might remain enshrouded in dust for several million years. If spectroscopically confirmed, the sample of galaxies studied by Dressler et al. (2024, see also Rodighiero et al. 2022) might be a notable example of this population.
Outflows with velocities of ≈800 km s−1 have been identified in GN-z11 (Maiolino et al. 2024) from the analysis of CIV. This velocity is compatible with our predictions in Eq. (15) as long as fM is low, although an additional momentum injection from an alleged active galactic nucleus is possible. A low fM might also indicate that the outflow is anisotropic and able to clear dust and gas only in a channel oriented along the line of sight to the galaxy.
As a final remark, it is also worth recalling that the predicted outflow velocities in many cases are lower than the circular velocity of the halo, implying that the dust and gas are not ejected beyond the virial radius. This is not in contrast with our argument, as blue spectral colors can be obtained by pushing the dust beyond the radius rτ = 1 ≈ 2 − 3 kpc (Eq. (14)), at which point it becomes optically thin.
Once the dust distribution is effectively removed from the main body of the galaxy, it will become hard to detect it from its rest-frame UV-optical extinction and/or thermal emission. A recent example can quantify this statement. Stiavelli et al. (2023) obtained JWST/NIRSpec data on the z = 9.11 galaxy MACS1149-JD1 (JD1) and determined its dust content from the Balmer decrement. In spite of a relatively large stellar mass, M⋆ ≈ 108 M⊙, JD1 is consistent with having no dust. The absence of significant amounts of dust is also supported by the non-detection of FIR continuum for this object (Hashimoto et al. 2018; Tokuoka et al. 2022). Interestingly, the sSFR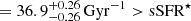 of JD1 indicates that dust has been evacuated by a radiation-driven outflow. We also note that if the measured velocity difference between the blue- and redshifted components of the [O III] 88 μm line (122 ± 30 km s−1, Tokuoka et al. 2022) is interpreted as an outflow, such a velocity is consistent with the predictions of Fig. 4, given the (de-lensed) magnitude of JD1.
of JD1 indicates that dust has been evacuated by a radiation-driven outflow. We also note that if the measured velocity difference between the blue- and redshifted components of the [O III] 88 μm line (122 ± 30 km s−1, Tokuoka et al. 2022) is interpreted as an outflow, such a velocity is consistent with the predictions of Fig. 4, given the (de-lensed) magnitude of JD1.
6.2. Lyα escape
The inferred sizes of the ionized bubbles carved by z > 10 galaxies are actually too small10 (< 0.28 pMpc; see Table 1) to allow for the escape of Lyα photons. Outflows can significantly increase the visibility of the Lyα line from sources at high-z, where in principle the line should be strongly attenuated by the overwhelmingly neutral IGM (Dijkstra & Wyithe 2010; Stark et al. 2017; Mason et al. 2018; Hayes & Scarlata 2023; Bruton et al. 2023). Such a facilitating role of outflows is supported by the evidence reported in Fig. 7, where along with GN-z11, we show the Lya EW versus sSFR for three different samples (Tang et al. 2023; Endsley et al. 2022; Stark et al. 2017) of z > 7 galaxies in which Lyα has been searched for (total of 20 galaxies).
 |
Fig. 7. Lyα EW versus sSFR for 20 galaxies at z ≳ 7. The data points are taken from the following samples: Tang et al. (2023, blue squares), Endsley et al. (2022, red circles), Stark et al. (2017, pink hexagons). The gray points in each sample show non-detections. Also shown is GN-z11 (Bunker et al. 2023, green star). The EW of CEERS-44 has been multiplied by 0.1 for display purposes. The cyan band shows the sub-Eddington regime in which sSFR < 25 Gyr−1 (no outflows expected). The two exceptions (CEERS-498 and COS-zs7-1) to our outflow condition are individually marked and discussed in the text. |
In the Tang et al. (2023) sample, we selected eight galaxies for which Lyα and stellar mass data are simultaneously available. Among these, four were detected in Lyα (CEERS-1019, CEERS-1027, CEERS-698, CEERS-44). All of them have velocity offsets ≳300 km s−1 and meet our super-Eddington condition, having sSFR = (79, 104, 45, 61) Gyr−1 > sSFR⋆. The remaining four non-detected galaxies all show low values of sSFR ≲35 Gyr−1, with the only exception being CEERS-498, which nonetheless has only been observed with the NIRSpec prism at low (R ≃ 100) resolution. Thus, Lyα could still be detected in a higher R grating observation, similar to the case of GN-z11 (Bunker et al. 2023).
Even more striking are the results by Endsley et al. (2022), who searched for Lyα emission in eight galaxies at z ≈ 7 selected from the ALMA REBELS survey (Bouwens et al. 2022a; Ferrara et al. 2022). Using MMT/Binospec spectroscopic data, they detected broad, highly redshifted (mean offset with respect to [C II] line systemic redshift equal to 223 km s−1) Lyα emission from four galaxies. These four systems have sSFR > sSFR* = 25 Gyr−1. In contrast, the four non-detected REBELS sources fall in the sub-Eddington regime in which radiation-driven outflows are not expected.
Finally, Stark et al. (2017) reported Lyα detection from three sources (EGS-zs8-1, EGS-zs8-2, COS-zs7-1). While two of them have an sSFR very close to the critical one, COS-zs7-1 has a low sSFR of 7.2 Gyr−1, and therefore it represents an exception to our criterion. Such an anomaly can be explained by the fact that although outflows clearly favor Lyα escape, other properties, such as low H I column densities, might also produce a large Lyα EW. As a caveat, we reiterate that our calculation of the outflow velocities becomes less accurate close to the sub-super-Eddington transition due to the neglect of gravity in Eq. (12).
In summary, though we found that among the 12 Lyα detected sources, 11 have an sSFR compatible with the presence of an outflow, among the eight non-detected sources, seven are in the sub-Eddington regime where the outflow should not develop. We note that the range 20 < sSFR/Gyr−1 < 35 is populated with both detections and non-detections (Fig. 7), likely as a result of the uncertainties of local variation of the sSFR⋆ value, which in turn depends on the details of dust properties and radiative transfer (see Sect. 2). These results show that outflows play a paramount role for Lyα visibility.
We conclude this section with another potential prediction of our model. According to the discussion in Sect. 4, the terminal velocity v∞ is reached at the radius rτ = 1 = 2(M⋆/109 M⊙)1/2 kpc, where the outflow becomes optically thin and the velocity shift allows Lyα photons to escape. On this basis we expect super-Eddington galaxies to show an extended Lyα halo whose typical size is ≈rτ = 1. Interestingly, Scholtz et al. (2023) reported the detection of a Lyα halo of the size 0.8 − 3.2 kpc around GN-z11. This value is comparable to the value rτ = 1 = 1.4 kpc that we predict for this system. Although a more refined modeling of the Lyα halo properties based on numerical simulations (see, e.g., Hutter et al. 2023) is necessary to draw firm conclusions, it is nevertheless encouraging to see that the model compares well with the data.
6.3. LyC escape
Outflows might also facilitate the escape of LyC photons (Hogarth et al. 2020) by carving highly ionized channels in the galaxy. In fact, we have seen that GN-z11 Lyα modeling requires the H I fraction in the outflow region to be very small, xHI = 4.2 × 10−3. In addition, outflows also decrease the UV opacity by pushing dust on larger radial scales. The fact that the LyC escape fraction, fesc, increases with sSFR has been very convincingly demonstrated by Flury et al. (2022), see their Fig. 17 using the Low-redshift Lyman Continuum Survey (LzLCS). They found that no z ≈ 0.3 LyC emitters with fesc > 10% have sSFR < 10 Gyr−1.
Even more extreme is the case of the three galaxies (EGS-42501, EGS-41419, and EGS-47688) observed with JWST/NIRCam in the redshift range 7.2 < z < 8.4 (Topping et al. 2022). These galaxies exhibit both extremely blue UV slopes (β ≈ −3.1) and very compact (re < 260 pc) sizes11. Noticeably, the LyC escape fraction for these three galaxies is very large (fesc = 0.8, 0.57, 0.65), and their sSFR is clearly super-Eddington, sSFR = (47, 99, 239) Gyr−1.
From this evidence, a coherent picture emerges in which a high sSFR produces radiatively driven outflows that clear the dust (and in turn determining steep UV spectral slopes) and carve ionized dust-transparent channels though which LyC photons can easily leak.
6.4. Supernova explosions
A key feature of high redshift galaxies is that the ISM of these systems is extremely dense, likely as a result of their very compact nature. In a recent study based on JWST/NIRSpec GLASS, ERO, and CEERS programs, Isobe et al. (2023) found that the electron densities of z = 4 − 9 galaxies are ne ≳ 300 cm−3, that is, significantly higher than those of low-z galaxies at a given stellar mass and sSFR. This finding is consistent with the determination of the gas electron density in GN-z11 (z = 10.6) made by Senchyna et al. (2023). From the analysis of the NIV] line, they obtained ne > 105 cm−3.
Under such high-density conditions, SN explosions rapidly lose energy due to radiative losses (the so-called catastrophic cooling, Terlevich et al. 1992; Pizzati et al. 2020), and the shock is quickly (timescale of few ×100 yr) damped into sound waves. Similar conclusions concerning the inefficiency of SN-driven outflows in early massive galaxies were reached in Bassini et al. (2023). Moreover, Nath et al. (2022) found that in high-z galaxies, the gas ejected by SN-driven shocks falls back onto the system.
A second important point is that in dense environments, the radiation pressure, pr, can greatly exceed the thermal pressure, ph, sustained by SN explosions. Following McKee & Ostriker (1977), Thompson et al. (2005) and assuming an SN explosion energy E0 = 1051 erg, a straightforward calculation shows that the ratio of the two pressures is
Grudić et al. (2020) have worked out similar estimates considering the momentum deposition of various sources. These authors concluded that the momentum injected by radiation, SN, and stellar winds are roughly equivalent. One must keep in mind that the result in Eq. (20) is only a first-order estimate of, and possibly a lower limit to, the relative importance of the radiation pressure and SN feedback, as it neglects, for example, the super-linear scaling of momentum deposition by clustered SNe (Gentry et al. 2017) and other more subtle effects.
Although a more robust conclusion on this point has to wait for dedicated studies, for now we can safely conclude that due their compactness and high density, radiation pressure is likely to be the dominant dynamical factor (∼250×) in super-early galaxies. Hence, the contribution from SN explosions in driving outflows can be neglected to the first order.
These arguments are further substantiated by the results in Gelli et al. (2024), who studied the star formation quenching mechanism in two high-z galaxies recently detected by JWST: JADES-GS-z7-01-QU (z = 7.3) and MACS0417-z5BBG (z = 5.2). They found that SN feedback largely fails to reproduce the observed quenched star formation history. They suggested instead that star formation is rapidly suppressed by radiation-driven dusty outflows sustained by the high sSFR (43 Gyr−1 and 25 Gyr−1, respectively) of the two galaxies.
6.5. The possible role of active galactic nuclei
JWST surveys are identifying a potentially large number of active galactic nuclei (AGN) in super-early galaxies (Fudamoto et al. 2022; Larson et al. 2023; Goulding et al. 2023; Maiolino et al. 2023; Fujimoto et al. 2023b). These identifications are mostly based on the presence of a broad component in some emission lines, typically but not exclusively in the Balmer series, with velocities of 400 − 1200 km s−1. However, such detections are sometimes reported with low (2 − 3 σ) significance. Moreover, this approach might bias the observations toward sources whose broad component EW is high and/or whose width is sufficiently broad to be resolved with JWST instruments. In any case, as shown in Sect. 4, comparable velocities can also be achieved (Eq. (15)) by radiation-driven outflows, provided (i) the star formation efficiency, ϵ⋆, is high and/or (ii) the ejected mass fraction, fM, is low.
When also including high ionization line detections and UV LF excess, Fujimoto et al. (2023b) estimated that the AGN fraction at z ≥ 8.5 is about 10 − 35%. On the other hand, Volonteri et al. (2023) pointed out that the number density of JWST candidate galaxies far outnumbers that of the highest-z quasar hosts, thus allowing for only ≃1 high-z AGN for every 1000 of these galaxies.
Thus, together with the virtual lack of X-ray detections (but see Bogdán et al. 2024 for a tentative one), the actual presence of AGN in super-early galaxies remains an intriguing possibility. An additional problem is that the measured AGN UV LF would imply, for a standard AGN spectral template, an X-ray background ≈10× higher than constrained by current experiments (Padnamabhan & Loeb, in prep.). Hence, if present, super-early AGN should show a peculiarly low X-ray-to-UV emissivity.
In terms of the stellar mass, an AGN should largely dominate the UV luminosity in order to affect such a determination. Casey et al. (2023), using the JWST/NIRCam COSMOS-Web survey to study the most luminous (−20.5 > MUV > −22) z ≳ 10 candidates, showed that this would imply a minimum black hole mass of ≈5 × 106 M⊙. Such masses would be unexpectedly large for the downward-revised stellar mass estimates of their host galaxies, ≲109 M⊙.
In the framework of our model, whether the observed UV luminosity driving the outflow has a contribution from an AGN, in addition to that of stars, does not make an actual difference. However, because in that case the same luminosity would correspond to a lower12 SFR while the stellar mass would remain unaltered, the sSFR⋆ value derived in Eq. (2) should be interpreted as an upper limit to the sSFR necessary to drive the outflow.
7. Summary
Radiation-driven outflows should become progressively more common toward high redshifts as a result of the increasing fraction of super-Eddington galaxies at early times. Outflows provide a coherent interpretation of JWST data showing (a) an unexpected excess of super-early bright galaxies (b) with very blue colors, (c) some of which are able to transmit their Lyα line through the largely neutral IGM at z > 10. The main results of this study are the following:
-
Independently of redshift, galaxies with an sSFR > sSFR⋆ ≃ 25 Gyr−1 become super-Eddington and launch an outflow that clears the dust, making the galaxy brighter and bluer (Sect. 2). Such a model successfully reproduces the observed z > 10 UV LF as well as the redshift evolution of the cosmic SFR density and sSFR (Sect. 3).
-
The fraction of galaxies that are in the super-Eddington regime increases with redshift (Fig. 3). It reaches 45% (76%) at z = 10 (14).
-
The outflow velocity is ≈830(ϵ⋆/fM)1/2 km s−1, where ϵ⋆ and fM are the star formation efficiency and the fraction of the halo gas expelled in the outflow, respectively (Eq. (15)). The outflow model is consistent with the outflow measurements in 12 super-Eddington galaxies of the JADES sample, yielding an average value of fM ≈ 0.04 (Fig. 5), roughly corresponding to the entire galaxy gas mass.
-
Outflows can dramatically enhance the Lyα line transmission from high-z sources, even if the IGM is almost neutral, as expected at z ≳ 10. The observed Lyα properties in GN-z11 are simultaneously recovered (Fig. 6) by the outflow model if log NHI ≃ 20.1, implying that the outflow is largely ionized. We make analogous predictions for the Lyα visibility of other super-early galaxies (Table 1).
-
We also compared the model with available Lyα surveys at z > 7, finding that essentially all super-Eddington (sub-Eddington) galaxies are (not) detected in Lyα (Sect. 6.2). Super-Eddington galaxies might also feature Lyα halos, as observed in GN-z11.
-
Based on available low- and high-z data, we show that the sSFR positively correlates with the LyC escape fraction (Sect. 6.3). This is because a high sSFR produces radiation-driven outflows that clear the dust (in turn determining steep UV spectral slopes) and carve ionized dust-transparent channels through which LyC photons leak.
We conclude that radiation-driven outflows are a key factor in understanding the properties and evolution of super-early galaxies.
Throughout the paper, we assume a flat universe with the following cosmological parameters: ΩM = 0.3075, ΩΛ = 1 − ΩM, and Ωb = 0.0486, h = 0.6774, σ8 = 0.826, where ΩM, ΩΛ, and Ωb are the total matter, vacuum, and baryon densities, in units of the critical density; h is the Hubble constant in units of 100 km s−1, and σ8 is the late-time fluctuation amplitude parameter (Planck Collaboration XVI 2014).
We further derived a halo mass of M ≃ 1011.5 M⊙ by abundance matching of the UV luminosity function (LF), see Fig. 1.
Our estimate is based on the halo abundance matching of the LF (Ferrara et al. 2023). Given the measured stellar mass and the extrapolated stellar-halo mass relation in Behroozi et al. (2013), Scholtz et al. (2023) found instead 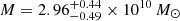 .
.
In principle, Orsi et al. (2012) also give the level of asymmetry of the line. However, the relatively poor sampling and the small values obtained prevented us from robustly including this information in the model.
Other fainter companion galaxies residing in the bubble might also contribute ionizing photons (Castellano et al. 2016, 2022). We neglected this effect, and therefore Rb should be considered as a lower limit to the actual bubble size.
If the halo mass is instead 2.96 × 1010 M⊙ (Scholtz et al. 2023), then rg ≃ 100 pc, essentially validating our approximation.
Alternatively, a larger ionized bubble could be created by the collective contribution of fainter objects clustered around the central luminous one (Castellano et al. 2018; Tilvi et al. 2020; Hu et al. 2021).
Similar conclusions have been reached by Mascia et al. (2024) from an analysis of 70 spectroscopically confirmed star-forming galaxies at 6 < z < 9 from the Cosmic Evolution Early Release Science (CEERS) survey.
As D’Silva et al. (2023) noted, by including an AGN component when fitting spectral energy distributions, the resulting cosmic star formation history decreases by ≃0.9 dex.
Acknowledgments
We thank P. Arrabal-Haro, R. Bouwens, F. Cullen and D. McLeod and M. Stefanon for providing data and useful information in advance of publication; M. Bradač, A. Calabró, S. Carniani, M. Castellano, A. Dekel, V. D’Odorico, F. Fiore, Y. Harikane, A. Inoue, A. Loeb, D. McLeod, M. Ouchi, A. Pallottini, L. Pentericci, H. Padmanabhan, M. Stiavelli, S. Tacchella for useful discussions and comments. Support from the ERC Advanced Grant INTERSTELLAR H2020/740120 is kindly acknowledged. This research is also generously supported by a Carl Friedrich von Siemens-Forschungspreis der Alexander von Humboldt-Stiftung Research Award. Plots in this paper produced with the MATPLOTLIB (Hunter 2007) package for PYTHON.
References
- Adams, N. J., Conselice, C. J., Ferreira, L., et al. 2023, MNRAS, 518, 4755 [Google Scholar]
- Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023a, ApJ, 951, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023b, Nature, 622, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023c, Nature, 622, 7984 [Google Scholar]
- Atek, H., Shuntov, M., Furtak, L. J., et al. 2023, MNRAS, 519, 1201 [Google Scholar]
- Austin, D., Adams, N., Conselice, C. J., et al. 2023, ApJ, 952, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Bakx, T. J. L. C., Zavala, J. A., Mitsuhashi, I., et al. 2022, MNRAS, 519, 5076 [Google Scholar]
- Barrufet, L., Oesch, P. A., Weibel, A., et al. 2022, MNRAS, 522, 449 [Google Scholar]
- Bassini, L., Feldmann, R., Gensior, J., et al. 2023, MNRAS, 525, 5388 [NASA ADS] [CrossRef] [Google Scholar]
- Behrens, C., Pallottini, A., Ferrara, A., Gallerani, S., & Vallini, L. 2018, MNRAS, 477, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdán, Á., Goulding, A. D., Natarajan, P., et al. 2024, Nat. Astron., 8, 126 [Google Scholar]
- Bouwens, R. J., Smit, R., Schouws, S., et al. 2022a, ApJ, 931, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Stefanon, M., Brammer, G., et al. 2022b, MNRAS, 523, 1036 [Google Scholar]
- Bowler, R. A. A., Jarvis, M. J., Dunlop, J. S., et al. 2020, MNRAS, 493, 2059 [Google Scholar]
- Boylan-Kolchin, M. 2023, Nat. Astron., 7, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Strait, V., Mowla, L., et al. 2024, ApJ, 961, L21 [CrossRef] [Google Scholar]
- Bradley, L. D., Coe, D., Brammer, G., et al. 2022, ApJ, 955, 15 [Google Scholar]
- Bruton, S., Lin, Y.-H., Scarlata, C., & Hayes, M. J. 2023, ApJ, 949, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carnall, A. C., McLeod, D. J., McLure, R. J., et al. 2023, MNRAS, 520, 3974 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Venturi, G., Parlanti, E., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202347230 [Google Scholar]
- Casey, C. M., Akins, H. B., Shuntov, M., et al. 2023, ApJ, submitted [arXiv:2308.10932] [Google Scholar]
- Castellano, M., Dayal, P., Pentericci, L., et al. 2016, ApJ, 818, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Castellano, M., Pentericci, L., Vanzella, E., et al. 2018, ApJ, 863, L3 [CrossRef] [Google Scholar]
- Castellano, M., Pentericci, L., Cupani, G., et al. 2022, A&A, 662, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellano, M., Fontana, A., Treu, T., et al. 2023, ApJ, 948, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonnel, C., Schaerer, D., Prantzos, N., et al. 2023, A&A, 673, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chisholm, J., Saldana-Lopez, A., Flury, S., et al. 2022, MNRAS, 517, 5104 [CrossRef] [Google Scholar]
- Ciesla, L., Elbaz, D., Ilbert, O., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348091 [Google Scholar]
- Correa, C. A., Wyithe, J. S. B., Schaye, J., & Duffy, A. R. 2015, MNRAS, 450, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, T., Rosdahl, J., Sijacki, D., & Haehnelt, M. G. 2018, MNRAS, 473, 4197 [Google Scholar]
- Cullen, F., McLure, R. J., McLeod, D. J., et al. 2023, MNRAS, 520, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Curtis-Lake, E., Carniani, S., Cameron, A., et al. 2023, Nat. Astron., 7, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Ferrara, A., Sommovigo, L., et al. 2022, MNRAS, 512, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Zolotov, A., Tweed, D., et al. 2013, MNRAS, 435, 999 [Google Scholar]
- Dekel, A., Sarkar, K. S., Birnboim, Y., Mandelker, N., & Li, Z. 2023, MNRAS, 523, 3201 [NASA ADS] [CrossRef] [Google Scholar]
- Di Cesare, C., Graziani, L., Schneider, R., et al. 2023, MNRAS, 519, 4632 [Google Scholar]
- Dijkstra, M., & Wyithe, J. S. B. 2010, MNRAS, 408, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Dome, T., Tacchella, S., Fialkov, A., et al. 2023, MNRAS, 527, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Donnan, C. T., McLeod, D. J., Dunlop, J. S., et al. 2023a, MNRAS, 518, 6011 [Google Scholar]
- Donnan, C. T., McLeod, D. J., McLure, R. J., et al. 2023b, MNRAS, 520, 4554 [NASA ADS] [CrossRef] [Google Scholar]
- Donnan, C. T., McLeod, D. J., Dunlop, J. S., et al. 2023c, MNRAS, 518, 6011 [Google Scholar]
- Dressler, A., Rieke, M., Eisenstein, D., et al. 2024, ApJ, 964, 150 [NASA ADS] [CrossRef] [Google Scholar]
- D’Silva, J. C. J., Driver, S. P., Lagos, C. D. P., et al. 2023, ApJ, 959, L18 [CrossRef] [Google Scholar]
- Endsley, R., Stark, D. P., Charlot, S., et al. 2021, MNRAS, 502, 6044 [NASA ADS] [CrossRef] [Google Scholar]
- Endsley, R., Stark, D. P., Bouwens, R. J., et al. 2022, MNRAS, 517, 5642 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Celotti, A., & Erlund, M. C. 2006, MNRAS, 373, L16 [NASA ADS] [Google Scholar]
- Faisst, A. L., Capak, P., Hsieh, B. C., et al. 2016, ApJ, 821, 122 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Ferrara, A., Sommovigo, L., Dayal, P., et al. 2022, MNRAS, 512, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A., Pallottini, A., & Dayal, P. 2023, MNRAS, 522, 3986 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., & Bagley, M. B. 2022, ApJ, 938, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Bagley, M. B., Arrabal Haro, P., et al. 2022, ApJ, 940, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Ferrara, A., Bischetti, M., Feruglio, C., & Travascio, A. 2023, ApJ, 943, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Flury, S. R., Jaskot, A. E., Ferguson, H. C., et al. 2022, ApJ, 930, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Fudamoto, Y., Inoue, A. K., & Sugahara, Y. 2022, ApJ, 938, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Walter, F., et al. 2024, MNRAS, 530, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Finkelstein, S. L., Burgarella, D., et al. 2022, ApJ, 955, 21 [Google Scholar]
- Fujimoto, S., Bezanson, R., Labbe, I., et al. 2023a, ApJS, submitted [arXiv:2309.07834] [Google Scholar]
- Fujimoto, S., Wang, B., Weaver, J., et al. 2023b, ApJ, submitted [arXiv:2308.11609] [Google Scholar]
- Furlanetto, S. R., & Mirocha, J. 2023, MNRAS, 523, 5274 [NASA ADS] [CrossRef] [Google Scholar]
- Gelli, V., Salvadori, S., Ferrara, A., Pallottini, A., & Carniani, S. 2023, ApJ, 954, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Gelli, V., Salvadori, S., Ferrara, A., & Pallottini, A. 2024, ApJ, 964, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Gentry, E. S., Krumholz, M. R., Dekel, A., & Madau, P. 2017, MNRAS, 465, 2471 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, Y., Yue, B., Cao, Y., & Chen, X. 2023, ApJ, 947, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Goulding, A. D., Greene, J. E., Setton, D. J., et al. 2023, ApJ, 955, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Grudić, M. Y., Boylan-Kolchin, M., Faucher-Giguère, C.-A., & Hopkins, P. F. 2020, MNRAS, 496, L127 [CrossRef] [Google Scholar]
- Harikane, Y., Ono, Y., Ouchi, M., et al. 2022, ApJS, 259, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Nakajima, K., Ouchi, M., et al. 2023a, ApJ, 960, 56 [Google Scholar]
- Harikane, Y., Ouchi, M., Oguri, M., et al. 2023b, ApJS, 265, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, T., Laporte, N., Mawatari, K., et al. 2018, Nature, 557, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Haslbauer, M., Kroupa, P., Zonoozi, A. H., & Haghi, H. 2022, ApJ, 939, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M. J., & Scarlata, C. 2023, ApJ, 954, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Hogarth, L., Amorín, R., Vílchez, J. M., et al. 2020, MNRAS, 494, 3541 [NASA ADS] [CrossRef] [Google Scholar]
- Hsiao, T. Y. Y., Coe, D., Abdurro’uf, et al. 2022, ApJ, 949, L34 [Google Scholar]
- Hsiao, T. Y.-Y., Abdurro’uf, Coe, D., et al. 2023, ApJ, submitted [arXiv:2305.03042] [Google Scholar]
- Hu, W., Wang, J., Infante, L., et al. 2021, Nat. Astron., 5, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hutter, A., Trebitsch, M., Dayal, P., et al. 2023, MNRAS, 524, 6124 [NASA ADS] [CrossRef] [Google Scholar]
- Ishibashi, W., Fabian, A. C., Ricci, C., & Celotti, A. 2018, MNRAS, 479, 3335 [CrossRef] [Google Scholar]
- Isobe, Y., Ouchi, M., Nakajima, K., et al. 2023, ApJ, 956, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasinen, M., van Marrewijk, J., Popping, G., et al. 2022, A&A, 671, A29 [Google Scholar]
- Kannan, R., Springel, V., Hernquist, L., et al. 2022, MNRAS, 524, 2594 [Google Scholar]
- Keller, B. W., Munshi, F., Trebitsch, M., & Tremmel, M. 2023, ApJ, 943, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., & Ferrara, A. 2023, ApJ, 962, L6 [Google Scholar]
- Komarova, L., Oey, M. S., Krumholz, M. R., et al. 2021, ApJ, 920, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Labbé, I., Oesch, P. A., Bouwens, R. J., et al. 2013, ApJ, 777, L19 [CrossRef] [Google Scholar]
- Larson, R. L., Finkelstein, S. L., Kocevski, D. D., et al. 2023, ApJ, 953, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Leethochawalit, N., Trenti, M., Santini, P., et al. 2022, ApJ, 942, L26 [Google Scholar]
- Looser, T. J., D’Eugenio, F., Maiolino, R., et al. 2023, Nature, submitted [arXiv:2302.14155] [Google Scholar]
- Lovell, C. C., Harrison, I., Harikane, Y., Tacchella, S., & Wilkins, S. M. 2023, MNRAS, 518, 2511 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Maiolino, R., Scholtz, J., Curtis-Lake, E., et al. 2023, A&A, submitted [arXiv:2308.01230] [Google Scholar]
- Maiolino, R., Übler, H., Perna, M., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202347087 [Google Scholar]
- Mascia, S., Pentericci, L., Calabrò, A., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202347884 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, C. A., Treu, T., de Barros, S., et al. 2018, ApJ, 857, L11 [Google Scholar]
- Mason, C. A., Trenti, M., & Treu, T. 2023, MNRAS, 521, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Mauerhofer, V., & Dayal, P. 2023, MNRAS, 526, 2196 [NASA ADS] [CrossRef] [Google Scholar]
- McCaffrey, J., Hardin, S., Wise, J., & Regan, J. 2023, Open J. Astrophys., 6, 47 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, D. J., McLure, R. J., & Dunlop, J. S. 2016, MNRAS, 459, 3812 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, D. J., Donnan, C. T., McLure, R. J., et al. 2023, MNRAS, 527, 5004 [NASA ADS] [CrossRef] [Google Scholar]
- Mirocha, J., & Furlanetto, S. R. 2023, MNRAS, 519, 843 [Google Scholar]
- Muñoz, J. B., Mirocha, J., Furlanetto, S., & Sabti, N. 2023, MNRAS, 526, L47 [CrossRef] [Google Scholar]
- Naidu, R. P., Oesch, P. A., van Dokkum, P., et al. 2022, ApJ, 940, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., Vasiliev, E. O., Drozdov, S. A., & Shchekinov, Y. A. 2022, MNRAS, 521, 662 [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., Labbé, I., & Stefanon, M. 2018, ApJ, 855, 105 [Google Scholar]
- Ono, Y., Harikane, Y., Ouchi, M., et al. 2022, ApJ, 951, 21 [Google Scholar]
- Orsi, A., Lacey, C. G., & Baugh, C. M. 2012, MNRAS, 425, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, H., & Loeb, A. 2023, ApJ, 953, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Pallottini, A., & Ferrara, A. 2023, A&A, 677, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pallottini, A., Ferrara, A., Gallerani, S., et al. 2022, MNRAS, 513, 5621 [NASA ADS] [Google Scholar]
- Parashari, P., & Laha, R. 2023, MNRAS, 526, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzati, E., Ferrara, A., Pallottini, A., et al. 2020, MNRAS, 495, 160 [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popping, G. 2022, A&A, 669, L8 [Google Scholar]
- Pérez-González, P. G., Costantin, L., Langeroodi, D., et al. 2023, ApJ, 951, L1 [CrossRef] [Google Scholar]
- Renzini, A. 2023, MNRAS, 525, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Riaz, S., Hartwig, T., & Latif, M. A. 2022, ApJ, 937, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts-Borsani, G., Morishita, T., Treu, T., et al. 2022, ApJ, 938, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Tacchella, S., Johnson, B. D., et al. 2023, Nat. Astron., 7, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Bisigello, L., Iani, E., et al. 2022, MNRAS, 518, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Fontana, A., Castellano, M., et al. 2022, ApJ, 942, L27 [Google Scholar]
- Scholtz, J., Witten, C., Laporte, N., et al. 2023, A&A, submitted [arXiv:2306.09142] [Google Scholar]
- Senchyna, P., Plat, A., Stark, D. P., & Rudie, G. C. 2023, AAS J., submitted [arXiv:2303.04179] [Google Scholar]
- Shen, X., Vogelsberger, M., Boylan-Kolchin, M., Tacchella, S., & Kannan, R. 2023, MNRAS, 525, 3254 [NASA ADS] [CrossRef] [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [Google Scholar]
- Sipple, J., & Lidz, A. 2023, ApJ, 961, 21 [Google Scholar]
- Smit, R., Bouwens, R. J., Labbé, I., et al. 2014, ApJ, 784, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Carniani, S., et al. 2021, MNRAS, 503, 4878 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2022, MNRAS, 513, 3122 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Charlot, S., et al. 2017, MNRAS, 464, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Stefanon, M., Bouwens, R. J., Labbé, I., et al. 2022, ApJ, 927, 48 [CrossRef] [Google Scholar]
- Stefanon, M., Bouwens, R. J., Labbé, I., et al. 2023, ApJ, 943, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhardt, C. L., Sneppen, A., Clausen, T., et al. 2023, arXiv e-prints [arXiv:2305.15459] [Google Scholar]
- Stiavelli, M., Morishita, T., Chiaberge, M., et al. 2023, ApJ, 957, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Strait, V., Bradač, M., Coe, D., et al. 2020, ApJ, 888, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Strait, V., Brammer, G., Muzzin, A., et al. 2023, ApJ, 949, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, G., & Furlanetto, S. R. 2016, MNRAS, 460, 417 [CrossRef] [Google Scholar]
- Sun, G., Faucher-Giguère, C.-A., Hayward, C. C., et al. 2023, ApJ, 955, L35 [CrossRef] [Google Scholar]
- Tacchella, S., Bose, S., Conroy, C., Eisenstein, D. J., & Johnson, B. D. 2018, ApJ, 868, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Tacchella, S., Finkelstein, S. L., Bagley, M., et al. 2022, ApJ, 927, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Tacchella, S., Eisenstein, D. J., Hainline, K., et al. 2023, ApJ, 952, 15 [Google Scholar]
- Tan, J. C., & McKee, C. F. 2008, Am. Inst. Phys. Conf. Ser., 990, 47 [NASA ADS] [Google Scholar]
- Tang, M., Stark, D. P., Chen, Z., et al. 2023, MNRAS, 526, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Terlevich, R., Tenorio-Tagle, G., Franco, J., & Melnick, J. 1992, MNRAS, 255, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., Quataert, E., & Murray, N. 2005, ApJ, 630, 167 [Google Scholar]
- Thompson, T. A., Fabian, A. C., Quataert, E., & Murray, N. 2015, MNRAS, 449, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Tilvi, V., Malhotra, S., Rhoads, J. E., et al. 2020, ApJ, 891, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Tokuoka, T., Inoue, A. K., Hashimoto, T., et al. 2022, ApJ, 933, L19 [CrossRef] [Google Scholar]
- Tomaselli, G. M., & Ferrara, A. 2021, MNRAS, 504, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Topping, M. W., Stark, D. P., Endsley, R., et al. 2022, MNRAS, 516, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Topping, M. W., Stark, D. P., Endsley, R., et al. 2024, MNRAS, 529, 4087 [NASA ADS] [CrossRef] [Google Scholar]
- Trinca, A., Schneider, R., Valiante, R., et al. 2024, MNRAS, 529, 3563 [NASA ADS] [CrossRef] [Google Scholar]
- Trussler, J. A. A., Adams, N. J., Conselice, C. J., et al. 2022, MNRAS, 523, 3423 [Google Scholar]
- Tsuna, D., Nakazato, Y., & Hartwig, T. 2023, MNRAS, 526, 4801 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., Ouchi, M., Nakajima, K., et al. 2023, arXiv e-prints [arXiv:2306.00487] [Google Scholar]
- Volonteri, M., Habouzit, M., & Colpi, M. 2023, MNRAS, 521, 241 [CrossRef] [Google Scholar]
- Wang, B., Fujimoto, S., Labbe, I., et al. 2023, ApJ, 957, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Cheng, C., Ge, J., et al. 2022, arXiv e-prints [arXiv:2212.04476] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
- Whitler, L., Endsley, R., Stark, D. P., et al. 2022, MNRAS, 519, 157 [CrossRef] [Google Scholar]
- Xu, Y., Ouchi, M., Nakajima, K., et al. 2023, ApJ, submitted [arXiv:2310.06614] [Google Scholar]
- Yajima, H., Abe, M., Fukushima, H., et al. 2023, MNRAS, 525, 4832 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, I., Carilli, C. L., Fujimoto, S., et al. 2022, ApJ, 950, 11 [Google Scholar]
- Zhang, Y., Ouchi, M., Nakajima, K., et al. 2023, arXiv e-prints [arXiv:2306.07940] [Google Scholar]
- Ziparo, F., Ferrara, A., Sommovigo, L., & Kohandel, M. 2023, MNRAS, 520, 2445 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observed and derived properties of currently available z > 10 spectroscopically confirmed super-Eddington galaxies.
All Figures
 |
Fig. 1. Results of the Ferrara et al. (2023) model used here. Left panel: Predicted UV luminosity function (blue curve) compared with available data at z ≃ 11.5 (points). The blue curve assumes no dust attenuation, while the gray curve marked as τeff(z = 7) assumes that the dust attenuation at z = 11.5 is the one calibrated at z = 7 using the ALMA REBELS data (Bouwens et al. 2022a; Ferrara et al. 2022). The data are from Castellano et al. (2022, GHZ2), Bunker et al. (2023, GN-z11), McLeod et al. (2023), Adams et al. (2023), and Harikane et al. (2023a) lower limits. Also shown are empirical fits provided by Bouwens et al. (2022b, red dashed), Bowler et al. (2020, yellow dashed), and Finkelstein & Bagley (2022, green dashed). Right panel: Predicted evolution of the cosmic SFR density (blue curve), integrated down to a limiting AB mag M1500 = −17, compared with the data compilation of early JWST measurements in McLeod et al. (2023), also including data from Harikane et al. (2023b), Oesch et al. (2018), Donnan et al. (2023a,b), McLeod et al. (2016), Pérez-González et al. (2023). The other lines refer to different model predictions (Madau & Dickinson 2014; Harikane et al. 2022; Mason et al. 2023; Sun & Furlanetto 2016). |
| In the text | |
 |
Fig. 2. Redshift evolution of the sSFR for the two models explored here. The red line corresponds to the fiducial model in which most stars formed over the last free-fall time (Eq. (6)) along with ±1σ uncertainties (red dotted) derived from data in 8 < z < 10. Black lines account for halo mass growth (Eq. (8)) and are shown for present-day halo values of log(M0/M⊙) = 10 − 15 (bottom to top) in 0.5 dex intervals; these curves approximately evolve as (1 + z)5/2. Models are compared with available data points for high-z galaxies from (Bouwens et al. 2022a; Bradley et al. 2022; Strait et al. 2020; Stefanon et al. 2022, 2023; Topping et al. 2022; Tacchella et al. 2022; Smit et al. 2014; Endsley et al. 2021; Roberts-Borsani et al. 2022; Labbé et al. 2013; Robertson et al. 2023; Harikane et al. 2023a). The horizontal dashed line is the critical sSFR (Eq. (2)) above which outflows develop. |
| In the text | |
 |
Fig. 3. Predicted redshift evolution of the fraction of super-Eddington galaxies (i.e., |
| In the text | |
 |
Fig. 4. Outflow terminal velocity (Eq. (15), assuming ⟨ϵ⋆⟩ = 0.015, fM = 0.18, as appropriate for GN-z11) versus the UV magnitude for different values (colored numbers) of the log of the stellar mass in solar units. We note that v∞ = 0 denotes the sub-Eddington regime in which no radiation-driven outflows are expected. The circles are the predicted values of v∞ for the nine spectroscopically confirmed galaxies presently available at z > 10. Four of these galaxies (GN-z11, MACS0647-JD, Maisie, and GN-z10-0) as well as the photometric candidate GHZ2 are predicted to show outflow signatures. The data are taken from Curtis-Lake et al. (2023), Bunker et al. (2023), Arrabal Haro et al. (2023b), Harikane et al. (2023a), Hsiao et al. (2023), Castellano et al. (2022). Also shown is the lensed (μ = 4.7, Tokuoka et al. 2022) galaxy MACS1149-JD1 (Stiavelli et al. 2023, z = 9.11) specifically discussed in Sect. 6. |
| In the text | |
 |
Fig. 5. Model prediction for outflows. Bottom panel: Outflow terminal velocity (Eq. (15), lines) as a function of the sSFR normalized to the critical value sSFR⋆ (Eq. (2)). The galaxies for which sSFR/sSFR⋆ > 1 are in the super-Eddington regime. Also shown (cyan band) is the sub-Eddington region. The predictions are compared to JWST/JADES data (Carniani et al. 2024, red points) for 12 galaxies in 3 < z < 9 with measured outflow velocity. The data are also used to derive the fraction of halo gas entrained by the outflow, fM (see Eq. (15)), whose (percentage) value is shown by the number on each curve. Top panel: Histogram of the fM values derived in the bottom panel. |
| In the text | |
 |
Fig. 6. Predicted profiles of the observed Lyα line from two super-Eddington galaxies GN-z11 (Bunker et al. 2023) at z = 10.6 and Maisie (Finkelstein et al. 2022; Arrabal Haro et al. 2023b) at z = 11.4. In each panel, different curves from left to right refer to the ISM neutral hydrogen column densities NHI = 1020 + 0.1j cm−2, with j = 0, 1, …, 10. The gray lines show the Lyα profile emerging from the galaxy, which also accounts for the outflow velocity. The colored lines represent the observed profile after transmission through the IGM, whose GP damping wing, including the surrounding H II bubble (e−τGP), is shown by the red curve. For each observed curve, we show the values of the line peak velocity shift, vp, FWHM (both in [km s−1]), and EW in [Å]. For GN-z11 the observed values (Bunker et al. 2023; Scholtz et al. 2023) are (vp, FWHM, EW) = (555 ± 32 km s−1, 530 ± 65 km s−1, 18 ± 2 Å), which are very well reproduced by the curve with NHI = 1020.1 cm−2. At the same NHI, we predict that the Lyα EW for Maisie is 7.6 Å. |
| In the text | |
 |
Fig. 7. Lyα EW versus sSFR for 20 galaxies at z ≳ 7. The data points are taken from the following samples: Tang et al. (2023, blue squares), Endsley et al. (2022, red circles), Stark et al. (2017, pink hexagons). The gray points in each sample show non-detections. Also shown is GN-z11 (Bunker et al. 2023, green star). The EW of CEERS-44 has been multiplied by 0.1 for display purposes. The cyan band shows the sub-Eddington regime in which sSFR < 25 Gyr−1 (no outflows expected). The two exceptions (CEERS-498 and COS-zs7-1) to our outflow condition are individually marked and discussed in the text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



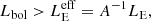
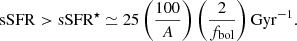
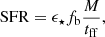
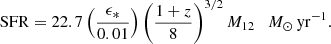
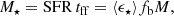
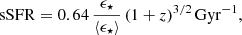
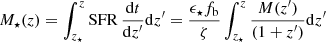
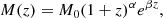
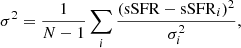
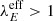
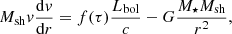
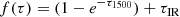
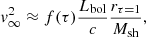
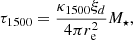
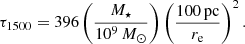
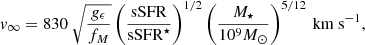
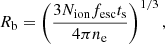
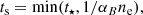
![$$ \begin{aligned} \tau _{\rm GP}(\lambda _{\rm obs}) = \int _{z_{\rm rei}}^{z_{\rm b}} \mathrm{d}z \frac{\mathrm{d}\ell }{\mathrm{d}z} n_{\rm HI}(z) \sigma _\alpha \Big [\nu =\frac{c (1+z)}{\lambda _\alpha } \Big ], \end{aligned} $$](/articles/aa/full_html/2024/04/aa48321-23/aa48321-23-eq32.gif)