| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A197 | |
| Number of page(s) | 25 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202346251 | |
| Published online | 24 April 2024 | |
The diversity of spectral shapes of hydrogen Lyman lines and Mg II lines in a quiescent prominence
1
Astronomical Institute of Slovak Academy of Sciences, 05960 Tatranská Lomnica, Slovak Republic
e-mail: pschwartz@astro.sk
2
Astronomical Institute, Czech Academy of Sciences, 25165 Ondřejov, Czech Republic
3
Center of Excellence – Solar and Stellar Activity, University of Wroclaw, Kopernika 11, 51 622 Wroclaw, Poland
Received:
26
February
2023
Accepted:
3
January
2024
Context. Broad sets of spectroscopic observations comprising multiple lines represent an excellent opportunity for diagnostics of the properties of the prominence plasma and the dynamics of their fine structures. However, they also bring significant challenges when they are compared with synthetic spectra provided by radiative transfer modeling.
Aims. In this work, we provide a statistical spectroscopic analysis of a unique dataset of coordinated prominence observations in the Lyman lines (Lyα to Lyδ) and the Mg II k and h lines. The observed data were obtained by the Solar Ultraviolet Measurements of Emitted Radiation (SUMER) spectrograph on board of the Solar and Heliospheric Observatory (SoHO) satellite and the Interface Region Imaging Spectrograph (IRIS) on 22 October 2013. Only a few similar coordinated datasets of Lyman and Mg II k and h observations have ever been obtained in prominences and we present here the first analysis using these two sets of spectral lines. Moreover, for the first time, we assess the influence of noise on the statistical properties of the studied profile characteristics.
Methods. We focus on the following profile characteristics: the shape of the observed line profiles based on the number of distinct peaks, the integrated line intensity, the center-to-peak ratio describing the depth of the reversal of two-peaked profiles, and the asymmetry of these peaks.
Results. We show that the presence of noise has a negligible effect on the integrated intensity of all observed lines, but it significantly affects the classification of spectral profiles using the number of distinct peaks, the reversal depth, and also the peak asymmetry. We also demonstrate that by taking the influence of noise into account, we can assess which profile characteristics in which spectral lines are suitable for diagnostics of different properties of the observed prominence. For example, we show that the subordinate peaks (peaks below error bars) in the Lyman line profiles are mostly caused by noise, which means that only the dominant peaks should be used for statistical analyses or comparisons with synthetic spectra. On the other hand, in the Mg II k and h profiles, the key role in the distinction between the multi-peaked profiles with low peaks and the profiles with deep reversals is played by the dynamics of multiple fine structures located along a line of sight. The complex, multi-peaked profiles are observed in places where multiple fine structures with different line-of-sight velocities are crossing the line of sight, while the profiles with deep reversals likely correspond to instances when we observe single fine structures or more fine structures but with similar line-of-sight velocities.
Conclusions. This study allows us to conclude that if we are interested in the diagnostics of the dynamics of prominence fine structures, the best approach is to use a combination of profile asymmetry in the Lyman lines together with the complex profiles of Mg II k and h lines. On the other hand, if we want to diagnose the temperature and pressure properties of individual prominence fine structures, we need to focus on the deeply reversed Mg II k and h lines in combination with the Lyman lines and to analyze the depth of the central reversal and the integrated intensities.
Key words: line: profiles / methods: statistical / techniques: spectroscopic / Sun: filaments / prominences / Sun: UV radiation
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Prominences are one of the most common phenomena connected with the solar magnetic fields present in the solar atmosphere. They are relatively dense and cool structures supported against the gravity by coronal magnetic fields occurring in the low-density and hot corona. Concise information on the properties of the prominence plasma and magnetic field and on the prominence modeling can be found in the reviews of Labrosse et al. (2010), Mackay et al. (2010), Gunár (2014), Parenti (2014), and Gibson (2018). For further details, readers can refer to the proceedings of the IAU 300 Symposium edited by Schmieder (2014a) or the book Solar Prominences edited by Vial & Engvold (2015), for example.
Prominences have been observed for more than a hundred years with ground-based instruments in the relatively cool chromospheric spectral lines of hydrogen, helium, and calcium in visual and near-infrared parts of the solar spectrum. Prominences are seen in emission above the solar limb in these lines. On the other hand, they demonstrate themselves as dark filaments visible in absorption against the solar disk. Extensive progress in solar observations from space made it possible to obtain high-quality ultraviolet (UV) and extra-ultraviolet (EUV) spectra of prominences. Such data provided new possibilities for spectroscopic investigations of the properties of their plasma. Spectral observations in the hydrogen Lyman line series plus continuum carried out with the Solar Ultraviolet Measurements of Emitted Radiation (SUMER) spectrograph (Wilhelm et al. 1995) on board the Solar and Heliospheric Observatory (SoHO) represent quite substantial observational material suitable for analyzing the structure and physical properties of quiescent prominences using modelling under deviation from the local thermodynamical equilibrium (non-LTE).
The Interface Region Imaging Spectrograph (IRIS, De Pontieu et al. 2014) is capable of obtaining spectra with almost two times higher spatial resolution than SUMER. Moreover, the IRIS spectrograph can record UV spectra simultaneously with slit-jaw images both in the far-ultraviolet (FUV) and near-ultraviolet (NUV) regions. Several UV lines (mainly Mg II k at 2796 Å, Mg II h at 2803 Å, and C II 1334 Å and 1336 Å) recorded in the IRIS spectra are suitable for studying prominences in great detail and, in combination with modeling using the non-LTE radiative transfer physical properties of prominence, plasma can be derived.
In this work we present a complex statistical spectroscopic analysis of a unique dataset of coordinated prominence observations in the Lyman lines of hydrogen and Mg II k and h lines obtained on 22 October 2013. The observed data were recorded quasi co-spatially and almost simultaneously by SUMER and IRIS. This is the first analysis of high-resolution spectroscopic observations of a prominence in these two sets of spectral lines. Only a few similar coordinated datasets of Lyman and Mg II k and h observations have ever been obtained in prominences. The first joined prominence observations in the Lyα, Lyβ, Mg II k and h, and Ca II UV lines were carried out by the OSO-8/LPSP spectrograph and analyzed by Vial (1982a,b). Except for the SUMER-IRIS observations that took place on 22 October 2013 and are used here, the same prominence was also observed the next day, but obtained spectra were strongly affected by impacts of particles from flaring active regions. Later, another SUMER-IRIS observing campaign for filaments and prominences took place in 2017 from 28 March through 4 April, during which several quiescent prominences and filaments were observed. However, only the Lyα line was observed with the SUMER spectrograph during this campaign (Zhang et al. 2021).
Broad datasets of spectroscopic observations in multiple lines represent an excellent opportunity for diagnostics of the properties of the prominence plasma and the dynamics of their fine structures. This was demonstrated by Gunár et al. (2010). These authors developed a statistical method suitable for comparison of large datasets of spectroscopic observations in different lines with broad sets of synthetic spectra produced by multi-dimensional radiative transfer models. This method was later used by Schwartz et al. (2015a) to analyze SUMER observations in the Lyman line series, with the aim to investigate the temperature and density of the plasma forming the cores of prominence fine structures. Another example is the use of coordinated datasets of Lyman lines observed by SUMER and Hα observations from ground-based instruments by Gunár et al. (2012) to analyze the dynamics of the prominence fine structures. Similarly, coordinated Mg II k and h observations by IRIS, together with other space-borne and ground-based data were used to investigate the plasma properties and dynamics of prominences by, for instance, Schmieder et al. (2014b), Heinzel et al. (2015), Levens et al. (2016), and Ruan et al. (2018, 2019). Thanks to the availability of observations in multiple spectral lines, Gunár et al. (2012) and Heinzel et al. (2015) could demonstrate that the Hα line provides an important constraint on the number of the fine structures present along line of sight (LOS). Levens et al. (2016) were able to analyze the plasma and magnetic field properties of prominence legs resembling tornado-like vertical structures. Ruan et al. (2018, 2019) could also analyze the differences in the LOS velocities of the multiple-component prominence fine structures.
The IRIS observations of the prominence studied here were also the focus of the work by Jejčič et al. (2018). These authors analyzed the Mg II k and h, and C II 1334 Å and 1336 Å spectra and compared them with synthetic spectra produced by the 1D non-LTE models of Heinzel et al. (2014, 2015). Using the temperature-sensitive ratio of integrated intensities of the Mg II k and h lines, Jejčič et al. (2018) concluded that the observed prominence plasma might have kinetic temperature as low as 5000 K. Moreover, these authors found no evidence of global oscillations in the studied prominence, but concluded a likely presence of random motions of fine LOS velocities on the order of ±10 km s−1. The Mg II k and h spectra of other prominences observed by IRIS were used for analyses of the prominence dynamics and plasma properties also by Peat et al. (2021). These authors developed a method for profile-to-profile comparison of the observed Mg II k and h lines with synthetic profiles produced by the 1D non-LTE models of Labrosse & Gouttebroze (2004), some of which included the prominence-corona transition-region (PCTR) extension developed by Levens & Labrosse (2019). Peat et al. (2021) found that when static single-slab models are used, a satisfactory agreement between the synthetic and observed profiles can be found only in the outer layers of the observed prominence, where complex Mg II k and h profiles are not present. These findings were confirmed by Barczynski et al. (2021), who analyzed a different prominence using the method of Peat et al. (2021). Another prominence simultaneously observed in the Mg II k and h and the Hα line was analysed by Jejčič et al. (2022). These authors developed a non-LTE inversion method that relies on a wide grid of 1D non-LTE models and fitting of five parameters of the observed spectra – the integrated intensity of Mg II k and Hα, widths of both lines, and the ratio of integrated intensities of Mg II k and Mg II h lines.
The current paper presents the first statistical analysis of the quasi-simultaneous observations of a quiescent prominence in the Mg II k and h line and the Lyman lines including the Lyα line. Moreover, for the first time, we take into account the influence of the noise on the following profile characteristics: the shape of the observed line profiles based on the number of distinct peaks, the integrated intensity, the depth of the central reversal of two-peaked profiles, and the asymmetry of their peaks.
2. Observations
A quiescent prominence located at the NW limb was observed on 22 October 2013 quasi-simultaneously and almost co-spatially with the SUMER and IRIS space-born spectrographs in the Lyman series of hydrogen and in the Mg II k and h lines, respectively. Basic information on the spectral lines observed by the two spectrographs are listed in Table 1. Position of the observed prominence at the limb is shown in the full-disk image in Fig. 1 recorded in the 304 Å channel of the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012). The helioprojective-Cartesian coordinate system (with abscissa denoted as solar_X and ordinate as solar_Y) is used in this image and hereafter in text and images of this work. In the zoomed image, the field of view (IRIS FOV) of the IRIS spectrograph during its raster observations is marked. Position of IRIS FOV is fixed according to an information given in the data files before any co-alignment was carried out. Because pointing of SUMER during the observations, as given in the data files, is not reliable, the slit position of SUMER can be estimated by co-alignment with IRIS.
 |
Fig. 1. Position and a general shape of the observed prominence at the limb shown in the 304 Å AIA channel. The zoomed image of the prominence reveals its basic structure. The position of the IRIS raster is indicated by the green rectangle. |
Basic information on spectral lines observed by SoHO/SUMER and IRIS spectrographs.
It is important also to note that observed spectral profiles are taken as they are (the level-2 data after basic reduction and radiometric calibration) without applying additional corrections for instrumental effects as deconvolution of instrumental profile, correction for point-spread function, etc. Because methods used for correction for these effects are mathematically complicated and unstable, influence of these effects will be added to synthetic profiles calculated by the non-LTE modeling before comparison with results of analysis of observed data presented here. This will be done in our next paper.
2.1. Lyman line observations
SUMER observations were made between 07:45 and 08:33 UT with a fixed slit position – the so-called sit-and-stare observation mode (hereafter referred to as S&S observations) – pointed at solar_X = 799.94 arcsec and solar_Y = 630.0 arcsec according to headers of the data files. The height and width of the slit were 119.6 arcsec and 0.28 arcsec, respectively. Size of one pixel along the slit corresponds to 1 arcsec in the helioprojective solar_Y coordinate. Due to roll of the satellite during the observations the slit of the spectrograph was inclined by 4.9 deg in counter-clockwise direction from original N–S direction. The S&S observations of the four hydrogen Lyman lines Lyα–Lyδ were made in individual blocks, unlike the observations used in Gunár et al. (2010) and Schwartz et al. (2015a) where individual spectral lines were alternated periodically. The four Lyman lines were observed in five spectral windows: The Lyα spectra were observed roughly divided into their red and blue halves placed on two spectral windows observed simultaneously occurring side-by-side on the bare part of the spectrograph detector B, that is, both outside of attenuator and also outside the KBr-coated part of the detector. Calibration of data recorded at the attenuator, which decreases radiation incident on the detector, is not reliable. On the other hand, KBr coating amplifies the radiation, which would increase danger of damage of the detector by this very intense line. The observed data were reduced and calibrated using standard Solar Soft procedures for the SUMER data reduction (see Schühle 2003 and references therein). Processing of the data was carried out using the procedures in the following order: decompression of binary data, dead-time correction, flat-fielding, local-gain correction, and correction for the geometrical distortion of the detector. Data from the two Lyα spectral windows was joined together before applying correction for the geometrical distortion. Finally, the data were calibrated to radiometric units using respective Solar Soft procedure. To extend lifetime of the detector as much as possible, a lower detector voltage of 5412 V was used instead of the standard 5656 V for all observations. Using this lower voltage affects calibrated Lyman lines specific intensities only marginally; for instance, it was shown by Schwartz et al. (2012) that using of even lower voltage of 5390 V changed calibrated Lα intensities by less than 2%. To better ensure that the detector does not get overburned when not using the attenuator, the aperture door of the instrument was partially closed during the Lyα line observations. Therefore, the specific intensities of this line were multiplied by a geometric factor of five after the radiometric calibration. This factor comes from ratio of area of the instrument entrance when door is fully opened to the area with partially closed door. The wavelength ranges of the two spectral windows were 1213.57–1215.68 Å and 1215.72–1217.82 Å. The three higher Lyman lines Lyβ–Lyδ were observed sequentially each of them in one spectral window on the bare part of the detector B. The wavelength ranges of the spectral windows were 1024.67–1026.82 Å, 971.48–973.64 Å, and 948.68–950.84 Å. Size of one spectral pixel was 0.04 Å in all five spectral windows.
The observations in the individual Lyman lines were performed in blocks in the following sequence: Lyβ, Lyγ, Lyδ, Lyα, Lyβ, Lyγ, and Lyδ. Due to technical problems with the pointing mechanism of the instrument, one cannot be sure whether position of the spectrograph slit is correct when set automatically. Therefore the slit position was set up interactively during the first three blocks of observations in order to position the slit at the prominence within the IRIS raster as reliably as possible. Therefore, data of Lyβ, Lyγ, Lyδ obtained during the first three blocks of observations was not used in the analysis. Then the following four blocks of observations of Lyα–Lyδ were made with final pointing as can be seen in Fig. 2. The figure shows the map of the Lyβ integrated intensities with number of observation on abscissa and position along the slit in the solar_Y coordinates in arcsec (measured from the S pole) on ordinate. The two blocks of the Lyβ observations are shown side-by-side in the map in the left panel of the figure although they were not observed right one after another. In the map of Lyα integrated intensities in the right panel (b) of the figure, it can be seen that the whole Lyα observations were done with the final pointing. More information on all seven blocks of S&S observations is listed in Table 2 where the blocks of observations made with the final pointing are indicated with the word “final” in the last column. Only data from these blocks was taken into our spectroscopic analysis. There are 80 observations of Lyα made with the final pointing and 40 such observations for each of the Lyβ–Lyδ spectral lines.
 |
Fig. 2. Maps of integrated intensities of the Lyβ (a) and Lyα (b) S&S observations of the SUMER spectrograph (left part of each panel). The abscissas show the observation numbers counted from the beginning of the observations of a given spectral line (see observation No. 1 in Table 2). In panel a, both Lyβ blocks of observations are put together, even though they did not follow one after the other, to show that the pointing of the instrument differs between them. The right part of each panel shows an example of the observed spectra of the Lyβ and Lyα lines; the relative wavelength scale according to the laboratory central wavelength (Table 1) is indicated. The horizontal blue lines mark the part along the slit from which the data were taken for the analysis. As for Lyβ, these lines occur only in the latter block of the Lyβ observations (the block of No. 5 observations, see Table 2) because the pointing was not correct during the first block of observations. |
Summary of the SUMER observations of the Lyα – Lyδ lines.
Because direction of dispersion of spectra is not exactly parallel with a detector edge, mutual shifts in positions along the slit between different wavelengths occur. Moreover, effect of nonlinearity of the grating focus-mechanism causes additional contributions to these shifts (Schühle 2003). The shifts for the Lyβ–Lyδ lines with respect to Lyα were estimated by mutual comparing of distributions of their integrated intensities along the slit. Subsequently, positions along the slit for the spectra of the Lyβ–Lyδ were corrected for these shifts. Errors of measured specific intensities were estimated using the Poisson’s statistics. Thus, relative errors of specific intensities are equal to reciprocal of the square root of uncalibrated intensities in counts. An additional error arises from uncertainty of the SoHO/SUMER radiometric calibration. This uncertainty was estimated to be within 15% by Wilhelm et al. (1997) and Schühle et al. (1998) during early years after the SUMER launch. One can assume that the calibration uncertainty in the year 2013 could be larger after almost 20 years of SUMER operation.
Assuming that the width of the instrumental profile is determined mainly by the width of the slit image on the detector, it was found that the instrumental profile is much narrower than the width of the Lyα profiles observed in the prominence when using such a narrow slit of 0.28 arcsec. It was already shown by Gunár et al. (2020) that in a such case observed Lyα profile intensities are modified by deconvolution of the instrumental profile by up to 5%, that is below uncertainty of the radiometric calibration. We found that the intensities of the Lyβ–Lyδ line profiles are modified by the deconvolution by up to 12%, that is also below the uncertainty. Thus, the influence of the instrumental profile on the observed profiles of all four Lyman lines was neglected in our further analysis.
2.2. Observations in the Mg II k and h lines
The IRIS spectrograph observed the prominence between 08:40 and 10:52 UT shortly after the of the SUMER observations. Thirty dense rasters were made by IRIS from which only first nine rasters made between 08:40 and 09:19 UT were taken into our analysis due to the fact that later IRIS observations were affected by impacts of high-energetic particles. These were produced by the C1.0–C1.7 class flares which occurred in the active region AR 11875 located close to the center of the solar disk between 09:07 and 09:24 UT1. Each of the rasters was composed of 16 slit positions with the step in the solar_X direction of 0.34 arcsec and the cadence of 16.5 s and lasted 4 minutes and 24 seconds. Spectra in eight wavelength windows – six of them encompassing the spectral lines of C II 1334 Å, C II 1336 Å, Fe XII 1349 Å, 0I 1356 Å, Si IV 1394 Å, Si IV 1403 Å, and Mg II k and h, and two windows comprising wavelengths around 2832 and 2814 Å – were recorded simultaneously together with slit-jaw images (hereafter referred to as SJ images) in the two channels Mg II k and Si IV 1400 Å. All spectra in all eight spectral windows and also SJ images were recorded with exposure time of 15 s. Both Mg II k and h spectral lines occur in the Mg II 2796 Å window. Spectra of the Mg II lines were extracted from this wavelength window in the wavelength intervals 2795.10–2797.62 and 2802.23–2804.77 Å, respectively. The level-2 IRIS data – data after all corrections were applied including the conversion to DN s−1 but excluding the radiometric calibration – from all wavelength windows was downloaded as multi-extension FITS files with keywords standardly recognized by the Solar Soft (see Sect. 3. IRIS Level 2 Data in the IRIS Technical Note ITN No. 26 by Pereira et al. 2015).
According to information stored in headers of the level-2 IRIS FITS files, pointing of the center of all 30 rasters in Cartesian coordinate system was solar_X = 818.17 arcsec and solar_Y = 603.89 arcsec and their FOV was 5.52 arcsec × 181.65 arcsec (see the green rectangle in Fig. 1). The size of one pixel along the slit (solar_Y direction) is 0.166 arcsec. The spectra and SJ images were taken with native spatial and spectral resolutions. Maps of integrated intensities of the k and h lines in the nine rasters taken into the analysis together with examples of the spectra are shown in Fig. 3.
 |
Fig. 3. Integrated intensities and examples of spectra of Mg II k (a) and Mg II h (b) from the first nine rasters taken into account for the analysis. Time runs from the beginning of the first raster made at 08:40:00 UT. The wavelength scales Δλ are relative to the line center wavelengths λ0 (Table 1). The blue horizontal lines indicate the section from which line profiles were taken into the analysis. In order to achieve a sufficient visibility of both Mg II spectral lines in the spectra at the disk edge, limb and prominence, specific intensities for solar_Y below 550 arcsec (white dotted horizontal line) were decreased by the factor of 0.3. |
The spectral data of both Mg II lines in DN was converted into the physical units W m−2 sr−1 Å −1 according to the method described in sect. 5.2 Radiometric Calibration of ITN No. 26 (Pereira et al. 2015) and Eq. (1) of Liu et al. (2015). The specific intensities were subsequently converted to erg s−1 cm−2 Hz−1, as it is favorable for comparison with synthetic profiles calculated by our non-LTE models. Parameters necessary for the radiometric calibration, especially the effective area for the date of observations, were obtained using the Solar Soft iris_get_response.pro procedure. The parameters defining the solid angle (see, e.g., Gunár et al. 2021) corresponding to one pixel on the detector which also enters in the formula for the radiometric calibration, were inferred from FITS-file headers. The precision of the radiometric calibration, which was determined mainly from uncertainties of the effective area estimated from the cross-calibration with the SORCE/SOLSTICE instrument (McClintock et al. 2005), is within 5% (Gunár et al. 2021). Because this is below the noise in the measured specific intensities, we do not consider this uncertainty in our analysis. Errors of measured specific intensities are combination of photon counting errors and readout noise (dark current). The photon counting errors are obtained using Poisson statistics out of registered signal. Readout noise is function of three detector parameters characterizing number of electrons produced by a photon impact, number of electrons required to record one DN, and readout uncertainty (De Pontieu et al. 2014). Then, errors of measured intensities are calculated as square root of sum of squares of the two errors. Moreover, an additional constant readout noise of the detector is simply added to the errors of measured intensities, as it is shown, for example, in Eq. (3) of Gunár et al. (2021). This additional readout noise is uniform for the whole detector and its value is 3 DN (Schmit et al. 2015).
For comparison of the observed spectra with synthetic spectra produced by modeling it is necessary to take into account that observed profiles are affected by instrumental broadening. To test how much the observed profiles are instrumentally broadened, we deconvolved instrumental profile from several selected Mg II k and h profiles of different shapes and widths observed in the prominence. For instrumental profile of IRIS NUV spectral band (both Mg II lines occur within this band), the Gaussian function of the Full Width at Half Maximum (FWHM) of 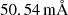 was used as in Tei et al. (2020). For the deconvolution, the Wiener deconvolution numerical method (using the Fast Fourier Transform – FFT – with filtering of high frequencies in power spectra) was applied. After the deconvolution of selected profiles of different types and widths, the specific intensities changed remarkably unlike in the case of the SUMER Lyman-line observations (Sect. 2.1). This is because the FWHM of the IRIS instrumental profile is larger by 77% than that of SUMER. Moreover, the Mg II lines are narrower, on average by 2.4 times, than profiles of the hydrogen Lyman lines Lyα–Lyδ. Because of the complexity and instability of the numerical methods for deconvolution of spectral profiles, we decided not to apply the deconvolution to the observed Mg II line profiles. Instead, the convolution with the instrumental profile, which is more numerically stable and mathematically simpler, will be applied to synthetic profiles produced by modeling in our next paper.
was used as in Tei et al. (2020). For the deconvolution, the Wiener deconvolution numerical method (using the Fast Fourier Transform – FFT – with filtering of high frequencies in power spectra) was applied. After the deconvolution of selected profiles of different types and widths, the specific intensities changed remarkably unlike in the case of the SUMER Lyman-line observations (Sect. 2.1). This is because the FWHM of the IRIS instrumental profile is larger by 77% than that of SUMER. Moreover, the Mg II lines are narrower, on average by 2.4 times, than profiles of the hydrogen Lyman lines Lyα–Lyδ. Because of the complexity and instability of the numerical methods for deconvolution of spectral profiles, we decided not to apply the deconvolution to the observed Mg II line profiles. Instead, the convolution with the instrumental profile, which is more numerically stable and mathematically simpler, will be applied to synthetic profiles produced by modeling in our next paper.
2.3. Co-alignment of the SUMER and IRIS observations
Sophisticated co-alignment of the SUMER slit and IRIS raster positions was carried out in several steps. First, shape and size of the prominence as seen in the IRIS Mg II 2796 Å SJ image (hereafter referred to as IRIS Mg II SJ image) was fitted to its appearance in the AIA 304 Å image. This was made by matching of intensity contours plotted to these two images for different X and Y mutual offsets and different angles of their mutual rotation. It was found that contours match the best for no offsets and no mutual rotation. Thus, this means that the IRIS SJ and AIA 304 Å images are well co-aligned. It is because the coordinate system of the IRIS instrument pointing is fixed according to the full-disk AIA observations (accuracy of the pointing stability using the IRIS guide telescope is better than 1 arcsec, see Pereira et al. 2014). Thus, comparison of the IRIS Mg II SJ and AIA 304 Å images obtained at the times of the nine analyzed IRIS raster observations showed that general shape and position of the prominence is very similar in both of them except of its less bright and rather dynamical peripheries, where shape of the prominence was changing remarkably within time difference between the AIA and IRIS observations. Examples of the IRIS Mg II SJ and AIA 304 Å images obtained during beginning of the IRIS prominence observations are shown in the upper row in Fig. 4. In the second step, the Hα filtrogram observations of the prominence obtained with the High Resolution Hα Imaging System (Otruba & Pötzi 2003) at the Kanzelhöhe Solar Observatory (KSO) were co-aligned with the AIA image in the 211 Å channel. The dark structure visible in the AIA 211 Å image shown in lower left panel of Fig. 4, is an absorption counterpart of the prominence. It is caused by absorption of the EUV coronal radiation in resonance continua of hydrogen and helium and coronal emissivity deficit (see, e.g., Anzer & Heinzel 2005 and Schwartz et al. 2015b). It is clearly distinguishable that its general shape resembles well the prominence in emission as seen in the Hα filtergram (lower right panel of Fig. 4). It was not necessary to perform any special co-alignment of the AIA 211 Å and AIA 304 Å images because AIA observations from different channels are co-aligned during data reduction by the Solar Soft procedure aia_prep.pro. Thus, after completing the second step, the Hα KSO filtergram (Fig. 4 lower right panel) is co-aligned with the IRIS Mg II SJ image (Fig. 4 upper left panel) and subsequently with the Mg II line rasters as position and FOV of the raster can be fixed exactly by tracking position of the spectrograph slit visible as dark vertical line in SJ images. The IRIS FOV is marked by the blue dashed line in all four panels of Fig. 4.
 |
Fig. 4. IRIS Mg II SJ image recorded at 08:40:16 UT (upper left panel) co-aligned by default with the AIA 304 Å channel image obtained at 08:40:19 UT (upper right panel). In the lower left panel is the AIA 211 Å channel image from 08:40:12 UT and in the lower right panel is the KSO Hα filtergram recorded at 07:32:01 UT; both these images are co-aligned with the IRIS observations. Structures visible in the Hα line resemble well the darkest absorption features present in the AIA 211 Å image. The IRIS FOV, the area of possible SUMER slit occurrence within uncertainties, and the analyzed area of the prominence – that is the section along the solar_Y, from which data were taken for the analysis – are marked in all four images. |
In the final step of the co-alignment, position of the SUMER spectrograph slit (hereafter referred simply to as slit position) in the IRIS Mg II SJ image was estimated. This task is rather complicated because SUMER records no slit-jaw images, which could be easily fitted to the filtergrams shown in Fig. 4. Thus, the only possibility was searching for correct slit position by trial-and-error approach placing it in different locations (without changing its length and roll angle) within an area of the whole FOV of IRIS Mg II SJ image and evaluating cross-correlation (hereafter referred to as KSO-SUMER correlation coefficient) between distribution of Hα intensities from the KSO filtergram along the slit position and integrated intensities of the Lyα observed by SUMER. Only positions along the spectrograph slit between 30 and 59 arcsec (measured from the solar south) were used in calculations of the correlation coefficient in order to avoid locations with a lot of dynamics where data are varying remarkably with time – locations close to the solar limb where very dynamical spicules occurred. Either positions at low-dense and very dynamical peripheries of the prominence (above 59 arcsec) are not suitable for including into the co-alignment. The section along the slit taken for the co-alignment is bordered by two blue horizontal lines both in the intensity maps and example spectra in Fig. 2. Vertical positions in this figure are given in the helioprojective-Cartesian Y coordinates (solar_Y) for the SUMER slit location determined by the co-alignment. Solely data from section between these positions is taken into the analysis. This is described in more detail in the next paragraph. The highest KSO-SUMER correlation coefficient of 0.89 was obtained for the slit position located at solar_X = 817.0 arcsec and solar_Y = 608.0 arcsec (slit center). An effort for exact co-alignment based on cross-correlation of 1D data (the Lyα integrated intensities along the SUMER slit) within 2D data (KSO Hα filtergram) cannot be reliable, although rather high value of the KSO-SUMER correlation coefficient was obtained for the above mentioned SUMER slit position. Therefore, it is much more correct in such case to use the co-alignment to estimate of an area which encompasses possible slit positions with acceptable values of the KSO-SUMER correlation coefficient instead of trying to find an exact slit position. The spectrograph slit position was being gradually shifted in both solar_X and solar_Y directions on both sides from the position with the highest value of the KSO-SUMER correlation coefficient. The correlation coefficient was decreasing slowly at first and after reaching the value of ∼0.8 it suddenly dropped down to much lower values. Because a value of the correlation coefficient of 0.8 is sill acceptable, an area of possible slit positions was fixed encompassing those with the KSO-SUMER correlation coefficient equal or higher than 0.8. The area is marked by green line in all four panels of Fig. 4. The area overlaps at least partially with the IRIS raster. Thus, the SUMER slit might lie within the IRIS raster, but it is also possible that it occurred outside but not far. Because the studied prominence appears rather homogeneous within the region of interest (marked by two orange horizontal lines in Fig. 4), such large co-alignment uncertainty should not play a significant role in our analysis.
As was already said in the previous paragraph, only data from the section between positions 30 and 59 arcsec (measured from the solar south) along the SUMER slit was used for the co-alignment. This section corresponds to the solar_Y positions between 575 and 604 arcsec for the slit position with the highest KSO-SUMER correlation coefficient. The observations of SUMER and IRIS do not overlap in time, therefore we decided to take only this section along the solar_Y also into our analysis. Hereafter, this section along the solar_Y is called analyzed area of the prominence. One can clearly see in the maps of integrated intensities constructed for the observations of SUMER and IRIS – Figs. 2 and 3 – that intensity structures inside of this area (bordered by the two blue horizontal lines in both figures) are relatively stable in time, while there is really a lot of dynamics outside of it.
3. Methods of the statistical spectroscopic analysis
3.1. Classification of profiles according to number of peaks
Emission profiles of optically thick spectral lines emitted from the cool prominence plasma and formed by the non-LTE scattering are often reversed in their cores. Moreover, in the case of gradients of LOS velocities of the prominence plasma along LOS, absorption profiles are Doppler-shifted accordingly which can produce profiles with multiple peaks and reversals (see, e.g., Tei et al. 2020). The method for identification of peaks in profiles used in this work is based on searching for local maxima in the profile core. Firstly, profile center is determined by fitting its wings with the Voigt function. Then, the profile is searched for local maxima from the center toward both wings until 30% of the value of global maximum in the profile is reached. To eliminate the influence of noise, profiles were smoothed by running average before searching for peaks. The running average was performed in such a way that for each wavelength point specific intensity in this point is taken with weight of unity and intensities of adjacent points are added with weights of 0.5. Even after the averaging, only peaks with intensities higher than 5% above the adjacent dips are considered.
There is also a possibility of evaluation of credibility of each detected peak – whether it is “above error bars” – which we apply in Sect. 4. The condition for this is that the specific intensity after subtraction of measurement error should be higher than intensities at adjacent reversals after adding measurement errors to them. If it is not the case, the peak is assumed as “lost in noise”. Unlike the peak identification, profiles with original (not smoothed) measured specific intensities with errors at all wavelength points and no other conditions except that above described, are used for evaluation of peak credibility.
3.2. Profile characteristics
In our spectroscopic analysis, we used the same profile characteristics as in Gunár et al. (2010) and Schwartz et al. (2015a) except for the Lyman decrement. The Lyman decrement is defined as the ratio of integrated intensities of a given line to that of Lyβ. However, unlike in Gunár et al. (2010) and Schwartz et al. (2015a), the Lyman-line data used here was obtained in blocks and not sequentially (see Sect. 2.1 for more details). Time delays between observations of individual spectral lines are thus much larger – around 10 min instead of several seconds. We therefore decided not to use the Lyman decrement for the spectral analysis. Designations of all quantities used for calculations of profile characteristics together with their detailed description, are in Table 3.
Designation of quantities used in statistics of the profile characteristics.
The first profile characteristics is the integrated intensity E. Wavelength interval of integration is determined in such a way that whole emission part of the spectral line profile is integrated and in this way blends in the far wings are excluded. This profile characteristics can be used for all types of profiles.
The second characteristics is the depth of central reversal rCP (called center-to-peaks ratio in our previous works). To minimize the influence of noise, average values from three adjacent wavelength points in the reversal and at each peak were considered. This profile characteristics is defined only for 2-peak profiles.
The third profile characteristics used in the analysis is the peak asymmetry rPA. This is also defined only for 2-peak profiles. For better intelligibility of statistics of the peak asymmetry, profiles with higher red peak and with higher blue peak are analyzed separately (see rB − R and rR − B in Table 3). Symmetric profiles are also treated individually because of their much higher count than asymmetric profiles. Influence of noise is again minimized by averaging over three adjacent spectral points in each peak.
As was shown in our previous works (Gunár et al. 2010; Schwartz et al. 2015a), these profiles characteristics are suitable for statistical comparison of observed Lyman-line profiles with synthetic ones obtained by non-LTE modeling. The same three profile characteristics are also used for the Mg II k and h lines.
We note that other, more advanced methods are also suitable for the classifications of line profiles, such as Principal Component Analysis (PCA; Jolliffe 2002) and k-mean clustering (MacQueen et al. 1967). For example, PCA was used by Dineva et al. (2020) for cloud-model diagnostics of a prominence plasma from observed Hα profiles, k-mean clustering for analysis of Doppler velocities in a filament from profiles of Hα and Ca II 8542 Å by Kleint et al. (2015). However, in the current paper we apply the methods used in our previous works to maintain continuity and inter comparability.
3.3. Influence of blends
For precise determination of the profile characteristics, the influence of blends needs to be taken into account. We thus removed their contribution in all profiles included into the analysis. Contributions of blends were estimated similarly as in Schwartz et al. (2015a). Profiles of all six lines averaged from analyzed area of the prominence were fitted by the sum of the Voigt profile and negative Gaussian to reproduce two peaks and reversal in between occurring in the average profiles. Blends are then fitted simply with Gaussians and their contributions are then calculated using these Gaussian fits. The averaged profiles were used to evaluate percentual contributions of blends, although evaluation of influence of blends would be also possible by fitting profiles from each position and time individually. But due to occurrence of multi-peak features in many of them caused by large dynamics and/or noise, fitting of blends could be problematic and contributions to the individual profile characteristics resulting from the fitting could by biased. Average profiles have simple shapes with clearly pronounced two peaks and reversal without any visible manifestation of noise and therefore are more suitable for a reliable fitting. For integrated intensities E, contribution of blends is calculated by summation of integrals of their Gaussian fits. Contributions of the blends to specific intensities at the blue peak, central reversal, and red peak in analyzed profiles are taken from values of their Gaussian fits at these three wavelength points. The contributions of blends in percents to integrated intensities and to specific intensities at the three wavelength points for observed spectral lines are listed in Table 4.
Contributions of blends in percents (CBP) to quantities used in calculations of the profile characteristics for the six spectral lines.
For Lyα, no blends were identified within observed wavelength range. In the case of Lyβ, three blends – He II 1025.27 Å, O I 1025.76 Å, and Fe III 1026.76 Å – are present according to the SUMER spectral atlas (Curdt et al. 2001). The He II and Fe III lines were well distinguishable in the average profile and fitted and thus corrections to the profile characteristics due to these blends were successfully estimated and applied. The O I 1025.76 Å line is too close to the Lyβ core to be reliably fitted and therefore its contributions to the profile characteristics could not be evaluated. But it cannot be neglected, because according to the work of Curdt et al. (1997), upper level of transition emitting this line is in part photo-pumped by the Lyβ photons. This can lead to remarkable increase of its brightness. Although this effect was studied in detail by Carlsson & Judge (1993), unfortunately they have not evaluated specific intensities of the O I 1025.76 Å line relatively to Lyβ. Therefore, contribution of this blend could not be determined and no corrections due to this line were applied. But its presence within the Lyβ profiles should be kept in mind when results of our analysis are compared with the non-LTE modeling. For the Lyγ, profile characteristics were corrected for the blending lines He II 972.12 Å and O I 973.24 Å occurring in its blue and red wings, respectively. In the case of the Lyδ, there is a strong influence of the blends He II 949.36 Å, Si VIII 949.22 Å, and Fe III 950.34 Å on the line profile as can be seen in the Table 4. Other blends of O I and Si IX occur within the Lyδ line core, thus it was not possible to fit them reliably. The O I lines are photo-pumped by the Lyδ photons (Curdt et al. 1997) similarly, as it was for the O I line blending Lyβ. Unfortunately, contributions of these possibly prominent blending lines to Lyδ cannot be specified, because estimations of their intensities lack. But nevertheless, occurrence of these blends within the Lyδ profiles should be kept in mind when comparing with the modeling. According to the SUMER spectral atlas (Curdt et al. 2001), the Si IX lines occurring within the Lyδ profile are faint and their contributions to the Lyδ profile characteristics can be neglected.
According to Schmit et al. (2015), there is a notable blend Mn I 2795.6 Å in the blue wing of the Mg II k line. Fortunately, Mg II k line profiles are narrow enough that the blend occurs in the wing far from the line. We could thus neglect it. In the case of the Mg II h line, no blends were identified within the wavelength interval of its emission profile.
4. Results
4.1. Statistics of profile classification
Peaks in profiles of all six lines within the analyzed area of the prominence were detected regardless noise by the method described in Sect. 3.1. Profiles were classified as 1-peak profiles (also referred to as purely emission profiles), and 2-peak, 3-peak, and 4-peak profiles. Those with unusual shapes without clearly distinguishable peaks by the method are considered as peculiar. Peculiar profiles also include profiles shaped as though they had their top cut off, often containing one narrow unrealistically sharp peak located remarkably asymmetrically from their centers. There are usually also sort of hints of more possible peaks. Although such profiles could be assumed as 1-peak, the method can distinguish them as peculiar. There is most likely more than one peak but those peaks (manifesting themselves just as hints) are too small to rise clearly above adjacent reversals and thus, they cannot be detected. Profiles with more than four distinguishable peaks are not realistic due to large optical thickness in cores of the six lines. For typical LOS velocities up to 20 km s−1 occurring in quiescent prominences, such profiles cannot arise. Moreover, their statistical occurrences within the analyzed area are less than 1%, and their locations are rather scattered (they are not localized in any compact areas). Therefore, these profiles were also included among the peculiar ones. Maps of the integrated intensities were constructed with types of profiles according to number of peaks indicated by different colors in each pixel within the analyzed area. Positions in the prominence outside of the analyzed area (see the last paragraph of Sect. 2.3) are indicated by gray color. The maps for Lyα and Lyβ are shown in the left column of Fig. 5 and for the Mg II k and h lines in the left column of Fig. 6. These maps are hereafter referred to as all-peak maps. In the maps shown in right columns of Figs. 5 and 6, classification of profiles was done taking into account only peaks above error bars. These maps are hereafter called as above-error maps.
 |
Fig. 5. Maps of the integrated intensities of Lyα (top row) and Lyβ (bottom row) overlaid with the colored mosaics classifying profile types (color bar on the right) within the target area. Profile types are classified regardless of noise (left column) and by considering only the peaks safely above error bars (right column). All available Lyα data were employed (see Fig. 2b) while only the Lyβ data with the final pointing were considered in the mosaics (Table 2). |
 |
Fig. 6. Maps of the integrated intensities of the Mg II k (top row) and Mg II h lines (bottom row) overlaid with the colored mosaics classifying profile types (color bar on the right) within the target area. Here only the profile types from first nine rasters are classified regardless of noise (left column) and by considering only the peaks above error bars (right column). |
When inspecting the Lyα all-peak map (upper left panel of Fig. 5), one can see that there are all types of profiles except 1-peak profiles. No clear trend in distributions of different profile types is evident. It can be just stated that the 2-peak profiles occur mainly above solar_Y of approx. 595 arcsec forming several small areas. Below this solar_Y position, the map is dominated by 3- and 4-peak profiles. In the Lyα above-error map (right upper panel of the figure), there are almost only 1-peak and 2-peak profiles with clearly visible trend of their occurrence. The large number of 1-peak Lyα profiles in such a strong line with characteristically pronounced self-absorption is caused by low intensity of one of the peaks, which thus becomes lost in noise. This fact emphasizes the complex issue of the influence of noise on the statistical analysis of even such intense line as Lyα. The 2-peak profiles are gathered mainly in the central part of the analyzed area (section along the slit between approx. solar_Y = 590 and 600 arcsec). At the edges of the analyzed area, the 1-peak profiles dominate. Proportion of peculiar profile is little bit higher than in the all-peak map.
In the case of Lyβ, one can see in the all-peak map (left panel in the second row of Fig. 5) that relative count of the 2-peak profiles is smaller than for Lyα while higher portion of the 3-peak profiles is clearly visible. Neither here any clear trend is seen in distributions of different profile types. There is a small amount of the 1-peak profiles unlike in Lyα where no 1-peak profiles occur in the all-peak map. Similarly as for Lyα, there are only a few peculiar Lyβ profiles. In the Lyβ above-error map (right panel in the second row of Fig. 5), 1-peak and peculiar profiles clearly dominate. There are only few 2-peak and no 3- and 4-peak profiles. Similar all-peak and above-error maps as in the case of Lyβ, were obtained also for Lyγ and Lyδ (not shown in Fig. 5).
There is majority of the 2-peak Mg II k line profiles as can be seen in its all-peak map in the left panel of the first row of Fig. 6. There are several smaller areas with occurrence of purely emission profiles mainly up to solar_Y ≈ 590 arcsec. Count of the profiles with more than 2-peaks is rather low. But there are almost only purely emission and peculiar profiles in the above-error map of this line. Purely emission profiles are gathered mainly in the area between times of approximately 500–1850 s and within positions along the slit above solar_Y of 590 arcsec. Within this area, several small regions with occurrence of the 2-peak profiles are also located. The maps for the Mg II h displayed in the bottom row of Fig. 6 look similar, with purely emission profiles occurring also mainly up to solar_Y ≈ 590 arcsec in the all-peak map but in larger count than for the k line. In the above-error map, there is larger count of peculiar profiles on expense of purely emission profiles and almost no 2-peak profiles contrary to the k line above-error map. Thus, comparing the all-peak and above-error maps for the both Mg II k and h lines indicates that majority of peaks in profiles within the analyzed area are not above error bars.
Examples of all types of profiles (including those assumed as peculiar profiles) of the hydrogen Lyman and Mg II k and h spectral lines are shown in Fig. 7. Profiles of the Lyman lines of a given type (rows of the figure) were not taken from the same position nor at the same time. On the other hand, profiles of Mg II for each of the profile types are from the same place and from the same time.
 |
Fig. 7. Examples of different types of spectral line profiles according to the number of peaks detected regardless of the noise (as in colored maps shown in the columns on the left in Figs. 5 and 6). In columns from the left, spectral profiles of Lyα, Lyβ, Mg II k, and Mg II h are shown. In rows from the top, plots of 1-, 2-, 3-, 4-peak and peculiar profiles are located. Error margins of intensities are shown as gray areas around plot-lines. On abscissas, relative wavelength scales Δλ = λ − λ0 are used (for the λ0 values see Table 1). The relative intensities I/Iref are on ordinates; intensities Iref in erg s−1 cm−2 sr−1 Hz−1 are shown at the top of each column for individual spectral lines. The positions of all peaks are marked with blue vertical dotted lines. For a given type of profile (row of the figure) the Lyman line profiles are not from the same position nor from the same time while Mg II k and h profiles of given type are. |
Comparing the all-peak and above-error maps shown in the left and right panels of Figs. 5 and 6, one can conclude that peaks detected in profiles of the Lyβ and higher analyzed Lyman lines (maps for Lyγ and Lyδ not shown, but are similar to those of Lyβ) and in both Mg II k and h line profiles, are often too small to be taken into account without any doubts caused by the noise. It means that they are not above error bars. This is also manifested in examples of profiles in Fig. 7. Only for Lyα, there are a lot of 2-peak profiles with both of them above error bars and deep reversal in between them or profiles with more peaks but with two of them above error bars. This can be distinguished also on profile examples in the left column of Fig. 7. These findings unambiguously lead to more sophisticated classification, based on different combinations of counts of peaks above error bars and peaks lost in noise. For all six lines, the number of profiles with more than two peaks above error bars in the analyzed area is much lower than the occurrence of profiles with one or two peaks above error bars as it is prominent from the above-error maps shown in the right columns of Figs. 5 and 6. Moreover, the depth of central reversal and peak asymmetry are defined only for 2-peak profiles. Therefore, profiles with more than two peaks above error bars are not classified in any separate groups, instead they are all included in the group containing peculiar profiles. Then, this naturally leads to classification of profiles into the following six groups:
-
1p: one peak
-
1pa & mpb: one peak above error bars (hereafter referred also to as peak above noise) and one or more additional peaks lost in noise (hereafter referred also to as subordinate peaks)
-
2pab: two peaks, each of them above noise or subordinate
-
2pa: two peaks, both above noise
-
2pa & mpb: two peaks above noise plus one or more subordinate ones
-
xp: peculiar profiles (with strange shapes without any clearly distinguishable peaks) plus profiles not belonging to any of the five previous groups.
In these groups, profiles are distinguished by the self-explaining designation encoding the number of peaks (1, 2, or m meaning one or more) and their detectability – above error bars indicated by the subscript a or lost in noise (or below noise) indicated by the subscript b. For instance, the group 2pab involves two-peak profiles, each of the peaks can be above error bars or lost in noise. It should be emphasized that also here the xp group contains, in addition to profiles with no distinguishable peaks, also profiles with more than two peaks above error bars. It was not necessary to develop any special method for this classification, the profiles were classified according to already detected peaks taking into account also their credibility. The groups as they are defined, are not exclusive but their content can overlap. This means that some profiles can belong to two groups at the same time as can be seen in the diagrams in Fig. 8, where two different symbols representing different groups can be located at the same position. We note that the profiles at the position [0, 0] in the diagrams, are the peculiar profiles with strange shapes without any clearly distinguishable peaks. One can notice that there are remarkably larger portions of such profiles in the Mg II lines. Relative counts in percents of profiles classified in each of the six groups are also indicated in this figure. As was already said, definition of the groups is not exclusive, therefore sum of counts of profiles in all groups as shown in each diagram in the figure can exceed 100%. Despite of this, such definitions of groups are more suitable for later comparison with synthetic profiles produced by the non-LTE modeling than classification of profiles simply according to number of peaks marked regardless noise.
 |
Fig. 8. Diagrams showing distributions of profiles of all six spectral lines in a space of the number of all of the detected peaks on the abscissa versus number of peaks above noise on the ordinate. Affiliations to the individual groups are indicated by different colors and symbols; the legend is located on the right. Sizes of the symbols are proportional to numbers of profiles in the individual positions and these numbers are also shown next to the symbols. Further information on the diagrams is given in the text. |
In the case of Lyα, there is 30% of 2-peak profiles with both peaks above noise – the group 2pa. If also profiles, with multiple peaks and two of them are above noise, are added – the group 2pa & mpb, portion of profiles assumed as the 2-peak ones increases by 22% (up to more than 50%). For Lyβ and higher Lyman lines and the Mg II lines, there is much lower number of profiles in the group 2pa (12% for Lyβ, and under 5% for Lyδ and the Mg II lines (even under 1% for Mg II h). Either contributions from the group 2pa & mpb is rather small for the Lyβ–Lyδ lines. It is even under 1% for the Mg II lines, thus portion of profiles in the groups 2pa plus 2pa & mpb does not exceed 4%. Fortunately, there is much larger number of profiles in the IRIS spectral observations within the analyzed area than in the SUMER spectral data (11 times more than in the SUMER spectral data in Lyα and 21 times more than in the SUMER spectral data in Lyβ–Lyδ), thus, number of the Mg II k and h profiles belonging to groups 2pa plus 2pa & mpb is comparable to those of the Lyman lines. For the Lyα–Lyγ and Mg II k lines, portions of profiles with two peaks detected regardless noise (the group 2pab) is between 20 and 40%. Only for the Lyδ and Mg II h lines, it is less (10–12%).
4.2. Statistics of the profile characteristics
Histograms of integrated intensity (E) for profiles of all six spectral lines from analyzed area of the prominence are shown in Fig. A.1. The histograms for three cases are plotted – all profiles, profiles from the groups 1p plus 2pab, and profiles from the groups 1pa & mpb plus 2pa & mpb. The histograms for the Lyα have three maxima while shapes of the histograms for higher Lyman lines are simply single-peaked. Histograms of E for the Mg II k and h lines have similar shape with single peak as those for the Lyman lines and almost no differences occur between histograms for the three cases. Properties of the E histograms for all six spectral lines for the three cases are listed in Table B.1.
In Fig. A.2, histograms of the depth of the central reversal (rCP) for all six lines are plotted. The histograms for each line are plotted for three cases: profiles from the group 2pab, group 2pa & mpb, and the combination of these two groups. Numbers of profiles considered as 2-peak ones in each of the three cases, included in the histograms, are listed in Table B.2 as N(2-peak); numbers of profiles considered as one-peaked – not included in the histograms – are denoted as N(1-peak) in the table. For Lyα, the histogram for the first case contains the lowest count of profiles (N(2-peak)), while for other five lines, the lowest numbers of profiles is contained by the histogram for the second case. The histograms for the Mg II h and k lines for the second case contain even much lower counts of profiles (by one or even two orders of magnitude) than histograms for other two cases. The histograms for the all six lines and all three cases have single peak. For Lyα, the histograms for all three cases are almost the same. On the other hand, the histograms for the higher Lyman lines for the second case differ much from the histograms of other two cases. The histograms for Lyα and Lyβ are more-or-less symmetrical with clearly distinguished maxima unlike those for Lyγ and Lyδ. Maxima of histograms for the all four Lyman lines are at rCP ∼ 0.25–0.50. The Mg II histograms for the second case have maxima at ∼0.75 while the histograms for the first and third cases are strongly asymmetrical with maxima shifted toward values of the rCP ratio above 0.9. Properties of the histograms of rCP for both Lyman and Mg II k and h lines together with number of profiles assumed as 1-peak and 2-peaks in each of the three cases, are listed in Table B.2.
The histograms of peak asymmetry (rPA) for all six spectral lines are presented in Fig. A.3. The peak-asymmetry histograms are also constructed for the same three cases as it was for the rCP histograms. The peak intensity ratios (hereafter called as peak asymmetry) for each line and case are divided into two histograms – one for profiles with higher red peak than blue peak and another for opposite asymmetry. Thus, the rPA values range from zero up to unity in each of the histograms. Only asymmetrical profiles (different heights of the peaks) were taken into the histograms. Relative counts shown on ordinates were calculated according to numbers of asymmetrical profiles (those with red peak dominating plus those with blue peak dominating) which are indicated in Table B.3 as N(2-peak asm). Symmetric profiles (with both peaks of equal height within a tolerance determined by size of one histogram bin) are not included into histograms and their count is shown in the table as N(2-peak sm). Profiles which peak asymmetry exceeds the tolerance are assumed as asymmetrical. Number of 1-peak profiles, neither included into histograms, are denoted as N(1-peak). The histograms constructed for Lyα have typical shape with raise toward the unity although this raise is not strictly monotonous and their maxima need not be at their right edges. The histograms for the first and third cases are almost the same, the histogram for the second case is little bit different. For higher Lyman lines, histograms are gradually loosing this typical shape and more fluctuations also occur. Differences of the histograms for the second case from those for the first and third cases, are also gradually getting larger. The histograms for the Mg II k and h lines for all three cases resemble each other very much. They all are raising nicely monotonously toward higher values of the rPA. Just the histograms for the second case have some fluctuations, while the histograms for the other two cases are nicely smooth. Thus, they reach their maxima at their right edges (toward the unity), just the Mg II k-line rB − R histograms for the first and third cases (group 2pab , groups 2pab and/or 2pa & mpb) have maxima shifted left from right edges. For the k-line rB − R and h-line rR − B histograms, gradient of the raise is not varying much through the whole histogram range. In difference from this, other Mg II histograms raise less steeply first and then, when approaching the unity, the gradient suddenly increases.
5. Discussion
5.1. Profile types
The first characteristics of observed spectral profiles we employ in this statistical analysis, is the shape of the profiles based on the number of distinct peaks (see Sect. 3.1). Although this may seem as a trivial undertaking, we showed in Sect. 4.1 that the classification of profiles based on the number of peaks is strongly influenced by the level of noise. This is true for both the Lyman lines and the Mg II k and h lines, and has several interesting consequences for eventual comparison with synthetic spectra produced by prominence radiative-transfer models. The same classification based on the number of peaks, but without taking into account the effects of noise, was used for the Mg II k and h lines also by Jejčič et al. (2018) and Peat et al. (2021).
When we categorized the observed profiles of Lyman lines without taking into account the influence of noise, we found a large number of profiles that exhibit more than two distinct peaks. An example of such multi-peaked profiles is shown in Fig. 7. These multi-peaked profiles can be a sign of highly dynamic behavior of unresolved prominence fine structures. Indeed, dynamic fine structures can be seen in the peripheral parts of the studied prominence. However, for the current statistical analysis, we used only the compact, dense and less dynamic central part of the prominence (see Fig. 4). Moreover, shapes of the broad Lyman lines are not remarkably influenced by the LOS velocities not exceeding 10–20 km s−1, typically present in quiescent prominences. Another explanation for the multi-peak Lyman profiles can be the influence of noise. As we demonstrated in Fig. 5, that seems to be the correct explanation. This is because when we take into account only those peaks in the spectral profiles of the Lyman lines that extend above the noise level, we obtain a majority of profiles classified as single or double-peaked. This result shows that the subordinate peaks can be caused by noise while the dominant peaks are those that arise from the non-LTE radiative transfer effects. The same result also validates the approach used in our previous statistical analysis of observed Lyman spectra of prominences (Gunár et al. 2010; Schwartz et al. 2015a). In those works, we used double-peaked profiles identified simply by their two dominant peaks, without taking into account neither subordinate peaks nor the influence of the noise.
Interestingly, while in the case of Lyman lines the introduction of the noise helped us to identify most of the observed profiles as single or double-peaked, the situation for the Mg II k and h lines is the opposite. The majority of the Mg II profiles identified as double-peaked when we do not take the noise into account (see Fig. 6) turned out to have rather insignificant peaks that do not extend above the level of noise – examples of Mg II k and h profiles are shown in Fig. 7. When taking the noise into account, these profiles are classified as single-peaked or peculiar profiles due to their strong asymmetry and generally flat tops. Again, broad and complex Mg II k and h profiles are a clear sign of multiple dynamic fine structures present along a LOS (see Tei et al. 2020; Gunár et al. 2022). However, in contrast to the Lyman lines, the narrow Mg II k and h lines are highly sensitive to the LOS velocities not exceeding 10–20 km s−1. Therefore, the hyper-structuring of the Mg II k and h profiles analyzed here is likely realistic and similar to that seen in the synthetic profiles of Tei et al. (2020) or Gunár et al. (2022). Nevertheless, in the observed spectra, the individual peaks cannot be conclusively discerned from the random effects of noise.
Clearly, noise has a significant impact on the classification of spectral profiles using the number of peaks. This means that any method using such profile classification needs to pay a close attention to the fidelity of the peak detection. Due to the ambiguities in the detection of the peaks, it might also be worthwhile to use for comparison with synthetic spectra more robust profile characteristics that are less affected by noise.
5.2. Integrated intensities
The second characteristics of the observed profiles that we study in the current work, is their integrated intensity E. To assess the influence of noise, we use here three sets of profiles. The first set contains all observed profiles, the second set contains 1-peak and 2-peak profiles identified without taking the noise into account (groups 1p and 2pab), and the last set contains only those 1-peak and 2-peak profiles that have peaks extending above the level of noise (groups 1pa & mpb and 2pa & mpb). As expected, noise has a negligible effect on the statistical properties of E of all observed lines. This is demonstrated by the histograms shown in Fig. A.1, which are nearly identical for all assumed sets of profiles.
As we mentioned already, it is interesting that the histograms of E of Lyα have three distinct peaks while the histograms for higher Lyman lines and those of Mg II k and h lines are single-peaked. In our previous statistical analyses of observed Lyman spectra, we obtained histograms of E of all Lyman lines with a single peak (Gunár et al. 2010) or with two peaks (Schwartz et al. 2015a). However, in the latter case, the histograms of all analyzed Lyman line profiles have two peaks and the second peak also appears in the histograms of rCP. In Schwartz et al. (2015a) we thus could assume that the two-peaked histograms indicate the presence of two independent prominence structures crossing the SUMER slit.
In the case of the prominence studied here, only the E histograms of Lyα have three peaks. It is shown in Fig. 9 that positions in the analyzed area of the prominence with the LyαE values belonging to each of the individual peaks are gathered in several compact areas. For the figure, all Lyα profiles from the analyzed area are taken and similar result were obtained when taking into account only profiles from the groups 1p and 2pab, or 1pa & mpb and 2pa & mpb (see Sect. 4.2). The E intensities from the left histogram peak occur closer to edges of the analyzed area. On the other hand, the highest E values (the right histogram peak) occur only inside of the analyzed area. Positions with E values from the middle peak are located mostly in few areas between those containing E values from left and right peaks. This indicates that occurrence of three peaks in the E histograms of Lyα is realistic, not caused by noise. Due to the fact that there are three peaks only in the E histograms of Lyα, it is clear that a simple explanation based on three distinct populations of prominence fine structures with different temperature and/or pressure (as it was in Schwartz et al. 2015a) might not be sufficient. For such a case, the apparent trio of populations of Lyα profiles might help us to shed light on the composition of the prominence-to-corona transition region (PCTR) surrounding the cool prominence material. This is because Lyα line is formed at higher temperatures closer to the surface of the observed prominence material than other Lyman lines (Heinzel et al. 2005) or the Mg II k and h lines. Therefore, a difference in the plasma properties limited to the PCTR might lead to distinct populations only in the case of Lyα. However, such an explanation will need to be supported by detailed radiative transfer modeling, which is planned for our next paper.
 |
Fig. 9. Map (left panel) showing the color mosaic of locations within the analyzed area with the Lyα integrated intensities belonging to the three peaks in the E histogram (right panel). Integrated intensities outside of the analyzed area are shown in shades of gray. The histogram constructed for all Lyα profiles is used (shown also in the upper left panel of Fig. A.1). Color coding in the mosaic corresponds to that used in the histogram: The red is for the left histogram peak, green for the middle, and blue for the right peak of the E histogram. |
5.3. Depths of the central reversal
The third profile characteristics used in this work is the depth of the central reversal that describes the depth of the reversal in 2-peak profiles. This ratio rCP approaches to one when the profiles have shallow reversals and tends toward zero when the reversals are extremely deep.
From the description in Sect. 5.1, it is clear that the identification of 2-peak profiles is significantly influenced by noise. To assess this influence, we use two sets of profiles. The first set contains those profiles in which we have identified two peaks without taking the impact of noise into account (group 2pab). The second set contains profiles in which two peaks extend above the level of the noise (group 2pa & mpb). For calculations of the rCP ratios for profiles in this group, specific intensities at the two peaks above noise and reversal in between are used. Thus, subordinate peaks are excluded from the calculations.
By taking into account the effect of noise, we selected 2-peak profiles with sufficiently deep reversals, which results in histograms of rCP shifted toward lower values (right upper panel and middle two panels of Fig. A.2). This is visible for higher Lyman lines (Lyβ–Lyδ). On the other hand, taking into account noise for Lyα has almost no effect on the histogram (upper left panel of Fig. A.2). All histograms of the depth of the central reversal for Lyman lines presented here are in strong contrast to the histograms for the observed data shown in Gunár et al. (2010). In fact, even without taking the noise into account (i.e., using the Lyman line profiles from group 2pab), the histograms for the prominence studied here show significantly deeper Lyman line profiles than those for the prominence studied in Gunár et al. (2010). This is interesting because the 2D multi-thread non-LTE radiative transfer models in the Gunár et al. (2010) produced similarly deep synthetic profiles as those analyzed in the present work, but which were in stark contrast with the shallow observed profiles used in Gunár et al. (2010). A similar comparison can be done with histograms of the depth of the central reversal from Schwartz et al. (2015a). However, in this case, the situation is more complex because of the two distinct maxima in the histograms for observed data shown in that work. These two maxima likely correspond to two distinct populations of Lyman line profiles, one with deep reversals similar to the case presented here and the other with shallow reversals similar to those of Gunár et al. (2010).
The statistics of rCP becomes even more interesting in the case of the Mg II k and h lines (panels in the bottom row of Fig. A.2). Here, in the case when we do not take the effect of noise into account, we obtained histograms that strongly tend toward shallow profiles. On the other hand, when we select only those Mg II k and h profiles that have peaks extending above the noise level (group 2pa & mpb), we obtained rCP histograms with median values around 0.7. This should not come as a surprise because we have basically selected only a small portion (around 6% for Mg II k) of the observed profiles that have deep reversals. However, the strong difference between the resulting histograms shows the importance of the correct choice of statistical characteristics for any comparison with synthetic profiles.
Histograms constructed for combination of the two groups – 2pab and/or 2pa & mpb – are similar to those constructed for not taking noise into account; for the Mg II lines these histograms are almost identical. This indicates larger number of the 2pab profiles than those from the 2pa & mpb group (see Table B.2). Thus, the 2pab profiles dominate in determining shapes of the histograms.
The main role in the distinction between a large number of shallow profiles and a small number of profiles with deep reversals, which manifests mainly for the Mg II k and h lines, is played by the dynamics of multiple fine structures along a LOS. The shallow profiles are observed in places where multiple fine structures with different LOS velocities are crossing the LOS while the deep profiles likely correspond to instances when we observe single fine structures or more fine structures but with similar LOS velocities (see Tei et al. 2020; Gunár et al. 2022, for more details). This means that when we are interested in the diagnostics of the dynamics of prominence fine structures, we need to use the rCP histograms containing all 2-peak Mg II k and h profiles regardless of noise. On the other hand, if we want to diagnose the temperature and pressure properties of the prominence fine structures, we need to focus on the deep profiles that are minimally affected by the dynamics.
5.4. Peak asymmetry
The last profile characteristics considered in this work is the asymmetry of the peaks rPA of 2-peak profiles. This proved to be helpful for the diagnostics of the LOS dynamics of prominence fine structures in Gunár et al. (2010) and was considered also by Jejčič et al. (2018) and Peat et al. (2021) for the Mg II k and h lines. Since the identification of the peaks is affected by noise, we again use two sets of profiles to assess its influence. The first set contains those profiles in which we have identified two peaks without taking the impact of noise into account (group 2pab) while the second set contains profiles in which two peaks extend above the level of the noise (group 2pa & mpb). Also here, similarly as for the depth of the central reversal, the asymmetry of the peaks is calculated using specific intensities only at the two peaks above noise (subordinate profiles are excluded from the calculations). In the case of the Lyman lines, the histograms of peak asymmetries in both cases – without or with taking noise into account – seem similar (the first part of Fig. A.3). Just for more symmetrical profiles (values of rPA above 0.8), there are larger relative counts in the histograms for the latter case. It can be explained by the fact that the profiles with deeper reversals occurring mostly in the 2pa & mpb group (as already stated in Sect. 5.3), are less sensitive to dynamics of the prominence plasma due to larger optical thickness in cores of these profiles. All histograms presented here are rather different from those obtained in Gunár et al. (2010). In that work, all histograms were monotonously raising toward unity. But some of the histogram presented here have their global maxima at lower values of rPA. This is most probably caused by rather large dynamics of the prominence plasma.
Although histograms of the Mg II k and h lines (second part of Fig. A.3) for the two sets of profiles are very similar, the application of noise leads to significantly smaller sample of profiles used for the statistics (see Table B.3). This causes that the histograms for profiles from the 2pa & mpb group are less smooth than those for the group 2pab. These selected profiles (those with peaks extending above the level of noise) also tend to be more symmetric, having the ratio of one peak to another nearing the unity. This is not surprising. As we discuss in Sect. 5.3, the Mg II k and h profiles with extended peaks likely correspond to arrangements of fine structures with limited LOS dynamics. Such configurations then result in small peak asymmetries. Therefore, when we want to diagnose the dynamics of prominence fine structures (for which rPA is a suitable parameter), we need to use all 2-peak profiles for the statistical comparison with the synthetic spectra.
5.5. Possible biases
Conclusions drawn in this study may be biased by potentially short exposure time of the IRIS Mg II spectra, large imbalance of statistical samples of Lyman and Mg II spectra, and by an ad hoc choice of bin size in the histograms. The first bias manifests itself by the noise resulting in an ambiguity in peak detection even in the brightest region of prominence. The issue can be tackled in the future by an trial-and-error finding of an optimum exposure time for prominence Mg II spectra. The second bias is apparent if we realize an order of difference between the number of profiles (samples) employed in plotting the diagrams for the Lyman and Mg II spectra (Fig. 8). Obviously, this is given by different spatial sampling and duration of SUMER and IRIS spectral data. The pixel sizes along the SUMER and IRIS slits are 1 arcsec (Sect. 2.1) and 0.166 arcsec (Sect. 2.2), respectively. While the SUMER observations in one spectral lines lasted less than 20 min (Table 2), the IRIS observations lasted 39 min (Sect. 2.2). The third bias may influence the appearance of histograms in the Appendix A but should not change much the numerical values in the Appendix B. The issue may be mitigated by employing large statistical samples for which histograms are likely to be less sensitive to bin size.
6. Conclusions
In this work, we present a statistical spectroscopic analysis of a unique dataset of coordinated prominence observations in the Lyman lines (Lyα to Lyδ) and the Mg II k and h lines. The observed data were obtained quasi co-spatially and almost simultaneously by two space spectrographs – SoHO/SUMER and IRIS. Only a few similar coordinated datasets of Lyman and Mg II k and h observations have ever been obtained in prominences and we present here the first analysis using these two sets of spectral lines. Such broad sets of spectroscopic observations in multiple lines represent an excellent opportunity for diagnostics of the properties of the prominence plasma and the dynamics of their fine structures. In the current work, we studied in detail the following profile characteristics: the shape of the observed line profiles based on the number of distinct peaks, the integrated line intensity, the depth of the central reversal of two-peaked profiles, and the asymmetry of these peaks. Moreover, for the first time, we assessed the influence of noise on the statistical properties of these profile characteristics.
As expected, noise has a negligible effect on E of all observed lines. However, the presence of noise significantly affects the classification of spectral profiles using the number of peaks, rCP, and also rPA. By taking the influence of noise into account, we could demonstrate which profile characteristics in which spectral lines are suitable for diagnostics of different properties of the observed prominence.
In the case of the Lyman lines, we showed that subordinate peaks are mostly caused by noise while the dominant peaks are those that arise from the non-LTE radiative transfer effects. This is consistent with the fact that Lyman lines are not strongly sensitive to the typical LOS velocities (10–20 km s−1) exhibited by the fine structures of quiescent prominences. In Lyman lines, such velocities are manifested by the asymmetry of the dominant peaks (see, e.g., Gunár et al. 2008, 2010), but they do not cause multiple peaks (unlike in the case of the Mg II k and h lines, see, e.g., Heinzel et al. 2015). Moreover, the LOS velocities on the order of 10 km s−1 were found to be present in the analyzed prominence by Jejčič et al. (2018). Therefore, noise is the most likely cause of the subordinate peaks in the analyzed Lyman line profiles. This, however, means that only the dominant peaks of the reversed profiles of Lyman lines should be used for statistical analyses or comparisons with synthetic spectra (as in, e.g., Gunár et al. 2010; Schwartz et al. 2015a). The classification of Lyman line profiles based on an overly sensitive identification of peaks can lead to many unnecessarily discarded observed profiles which may significantly degrade the statistical significance of observed datasets. The misclassification of profiles as multi-peaked can also make the fitting of observed and synthetic profiles (which do not suffer from noise) unreliable. These findings mean that any method for the identification of peaks in the observed Lyman line profiles needs to pay close attention to the impact of noise.
The situation is different in the case of the Mg II k and h lines. As we showed, the majority of the Mg II k and h profiles identified as double-peaked when we do not take the noise into account have in fact rather insignificant peaks that do not extend above the level of noise. Therefore, due to the presence of noise, we are unable to unequivocally identify peaks in many Mg II k and h profiles. Often there are simply too many low peaks. However, based on the fact that the Mg II k and h lines are highly sensitive to the LOS velocities on the order of 10–20 km s−1, this hyper-structuring present in the Mg II k and h profiles is likely realistic and similar to that seen in the synthetic profiles of Tei et al. (2020) or Gunár et al. (2022). This means that by taking the impact of noise into account, we effectively selected only those Mg II k and h profiles that have sufficiently high peaks and thus a deep reversal. Such deeply reversed profiles may represent only a small fraction of the observed profiles, but they nevertheless provide a useful diagnostics tool. The key role in the distinction between the multi-peaked Mg II k and h profiles with low peaks and the profiles with deep reversals is played by the dynamics of multiple fine structures located along a LOS. The complex, multi-peaked profiles are observed in places where multiple fine structures with different LOS velocities are crossing the LOS, while the profiles with deep reversals likely correspond to instances when we observe single fine structures or more fine structures but with similar LOS velocities (see Tei et al. 2020; Gunár et al. 2022. for more details). This means that when we are interested in the diagnostics of the dynamics of prominence fine structures, we need to use all Mg II k and h profiles. On the other hand, if we want to diagnose the temperature and pressure properties of individual prominence fine structures, we need to focus on the deep profiles that are minimally affected by the fine-structure dynamics.
Another profile characteristic useful for the diagnostics of dynamics is the profile asymmetry. However, in this case, the Mg II k and h profiles with deep reversals are not very useful because they tend to be more symmetric. This is not surprising. As we discussed above, such Mg II k and h profiles likely correspond to arrangements of fine structures with limited LOS dynamics, resulting in small rPA values. The asymmetry of the peaks in the Lyman lines (when the influence of noise is taken into account) is more suitable for the analysis of the prominence fine-structure dynamics. We want to note here that although the era of SoHO/SUMER observations is over, the Solar-C mission2 (Shimizu et al. 2020, and especially Suematsu et al. 2021, presenting a proposal of instrumental design of the EUV High-Throughput Spectroscopic Telescope planed for Solar-C) will provide new Lyman line observations in the future.
To conclude, the best approach to the analysis of the prominence fine structure dynamics is to use a combination of profile asymmetry in Lyman lines together with complex profiles of Mg II k and h lines. On the other hand, for diagnostics of the prominence plasma parameters, such as temperature or pressure, the best thing is to concentrate on the deeply reversed Mg II k and h lines in combination with Lyman lines and analyze the depth of the central reversal and the integrated intensities.
This study highlights the complexities we encounter when we want to compare the observed spectra with the synthetic spectra provided by models. Previously, three different approaches were used: (i) direct fitting of the shape of the line profiles, (ii) fitting of selected line parameters, and (iii) comparison of statistical properties of selected profile characteristics.
The first approach relies on detailed matching of the actual shapes of observed profiles. Examples of this approach are the ad-hoc fitting of the Lyman line profiles done by Gunár et al. (2007) or the automated Mg II k and h profile fitting procedures of Barczynski et al. (2021) and Peat et al. (2021). However, as we demonstrate in this work, the shape of the observed profiles is strongly influenced by the presence of noise. This means that special attention needs to be paid to the classification of the observed spectra. Moreover, as we have discussed here, the Mg II k and h lines are highly sensitive to the fine-structure dynamics, which results in complex, multi-peaked profiles. Therefore, the best set of Mg II k and h profiles suitable for the direct profile-to-profile comparison is the deeply reversed profiles with peaks unequivocally extending above the level of noise. As shown by Barczynski et al. (2021) and Peat et al. (2021), such Mg II k and h profiles can be matched by synthetic profiles with a good confidence. However, these deeply reversed profiles are typically present only in the outskirts of prominences (see Barczynski et al. 2021; Peat et al. 2021), where the fine-structure dynamics plays a marginal role. There, the direct profile-to-profile fitting provides good diagnostics of the prominence plasma parameters, such as temperature and pressure.
The second approach is the fitting of profile parameters, such as in the non-LTE inversion method of Jejčič et al. (2022). This method allows the use of profile parameters that are not strongly affected by noise (such as integrated intensities); however, it may not lead to a unique solution, especially in the case of complex observed profiles (see Jejčič et al. 2022, for more details).
The third approach does not focus on the individual line profiles but compares the statistical properties of selected profile characteristics of entire observed datasets. Examples of this approach are Gunár et al. (2010) and Schwartz et al. (2015a). The statistical comparison is well suited for analysis of the overall properties of observed prominences, such as the general level of the fine-structure dynamics. However, as we have shown in the present work, due to the impact of noise, close attention needs to be paid to the selection of the profile characteristics used for the comparison.
As we can see, broad datasets comprising many different spectral lines represent a great diagnostic potential but also significant challenges for comparison with synthetic spectra. These challenges are even greater in the case of spectral lines sensitive to the fine-structure dynamics, such as the Mg II k and h lines. Therefore, for future comparison with the results of complex multi-dimensional models with dynamics fine structures, we may need to combine these three approaches. To be less sensitive to the impact of noise in the line profiles without having to reduce it, it could be useful to introduce other profile characteristics that are robust with respect to noise (such as the integrated intensity – see Sect. 5, or the first and second moments of profiles), but that are still capable of describing multi-peak profiles. However, solely using such characteristics may lead to an unwitting introduction of biases. On the other hand, spectroscopic analysis based on the categorization of profiles according to the number of peaks or made using the characteristics for multi-peak profiles, which are defined for two-peak profiles (i.e., two peaks are selected only and others are neglected), can be highly sensitive to the presence of noise. However, selecting peaks above noise only and assuming others as noise might not be correct because some of the subordinate peaks could be real peaks and their occurrence can bear important information on the dynamics of the investigated object. Thus, to distinguish between the real subordinate peak and noise correctly, one has to keep in mind the properties of the observed spectral lines and the dynamics of the observed object (i.e., optical thickness of observed lines and LOS velocities). For the analysis of the quiescent prominence observed in the Lyα–Lyδ and Mg II k and h lines carried out here, as already stated, the LOS velocities should not be large enough so as to cause any multi-peak Lyman-line profiles due to a rather large optical thickness of prominence plasma in the cores of these lines. Conversely, for the less optically thick Mg II lines, multi-peak profiles can also arise for such LOS velocities. In the future, a mitigation of noise using deconvolution techniques removing instrumental effects including noise before the analysis (see, e.g., Peat et al. 2023) will be more effective than the subsequent distinguishing of real peaks from noise. These numerical techniques will continue to improve and conclusions of our present analysis could be an impulse for it. It has to be noted that setting an optimum exposure time can also be important for lowering noise in observed spectroscopic data.
Acknowledgments
P.S. and J.K. acknowledge support from the project VEGA 2/0043/24 of the Science Agency. S.G., P.H., J.K., and P.S. acknowledge support from the grant No. 22-34841S of the Czech Science Foundation (GAČR). S.G., P.S., P.H., and J.K. acknowledge support from the Joint Mobility Project SAV-18-03 of the Academy of Sciences of the Czech Republic and Slovak Academy of Sciences. S.G. and P.H. thank for support from the project RVO:67985815 of the Astronomical Institute of the Czech Academy of Sciences. P.H. acknowledges support by the program ‘Excellence Initiative – Research University’ for years 2020-2026 at University of Wroclaw, project No. BPIDUB.4610.96.2021.KG. Authors are thankful to Dr. W. Curdt for his useful information and advices according to SUMER observations used here. IRIS is a NASA small explorer mission developed and operated by LMSAL with mission operations executed at NASA Ames Research Center and major contributions to downlink communications funded by ESA and the Norwegian Space Center. This research has made use of NASA’s Astrophysics Data System. We are thankful to the anonymous referee for his/her useful comments and suggestions which improved this publication much.
References
- Anzer, U., & Heinzel, P. 2005, ApJ, 622, 714 [Google Scholar]
- Barczynski, K., Schmieder, B., Peat, A. W., et al. 2021, A&A, 653, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., & Judge, P. G. 1993, ApJ, 402, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Curdt, W., Feldman, U., Laming, J. M., et al. 1997, A&AS, 126, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [Google Scholar]
- Dineva, E., Verma, M., González Manrique, S. J., Schwartz, P., & Denker, C. 2020, Astron. Nachr., 341, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. E. 2018, Liv. Rev. Sol. Phys., 15, 7 [Google Scholar]
- Gunár, S. 2014, in Nature of Prominences and their Role in Space Weather, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 300, 59 [Google Scholar]
- Gunár, S., Heinzel, P., Schmieder, B., Schwartz, P., & Anzer, U. 2007, A&A, 472, 929 [Google Scholar]
- Gunár, S., Heinzel, P., Anzer, U., & Schmieder, B. 2008, A&A, 490, 307 [Google Scholar]
- Gunár, S., Schwartz, P., Schmieder, B., Heinzel, P., & Anzer, U. 2010, A&A, 514, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Mein, P., Schmieder, B., Heinzel, P., & Mein, N. 2012, A&A, 543, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Schwartz, P., Koza, J., & Heinzel, P. 2020, A&A, 644, A109 [EDP Sciences] [Google Scholar]
- Gunár, S., Koza, J., Schwartz, P., Heinzel, P., & Liu, W. 2021, ApJS, 255, 16 [CrossRef] [Google Scholar]
- Gunár, S., Heinzel, P., Koza, J., & Schwartz, P. 2022, ApJ, 934, 133 [CrossRef] [Google Scholar]
- Heinzel, P., Anzer, U., & Gunár, S. 2005, A&A, 442, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Vial, J. C., & Anzer, U. 2014, A&A, 564, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Schmieder, B., Mein, N., & Gunár, S. 2015, ApJ, 800, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Jejčič, S., Schwartz, P., Heinzel, P., Zapiór, M., & Gunár, S. 2018, A&A, 618, A88 [Google Scholar]
- Jejčič, S., Heinzel, P., Schmieder, B., et al. 2022, ApJ, 932, 3 [CrossRef] [Google Scholar]
- Jolliffe, I. 2002, Principal Component Analysis (New York: Springer) [Google Scholar]
- Kleint, L., Battaglia, M., Reardon, K., et al. 2015, ApJ, 806, 9 [Google Scholar]
- Labrosse, N., & Gouttebroze, P. 2004, ApJ, 617, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J. C., et al. 2010, Space. Sci. Rev., 151, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Levens, P. J., & Labrosse, N. 2019, A&A, 625, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levens, P. J., Schmieder, B., Labrosse, N., & López Ariste, A. 2016, ApJ, 818, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Heinzel, P., Kleint, L., & Kašparová, J. 2015, Sol. Phys., 290, 3525 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space. Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- MacQueen, J. 1967, in Proc. of the 5th Berkeley Symp. on Mathematical Statistics and Probability 1, eds. L. Cam, & J. Neyman (Berkeley, CA: Univ. California Press), 281 [Google Scholar]
- McClintock, W. E., Snow, M., & Woods, T. N. 2005, Sol. Phys., 230, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Otruba, W., & Pötzi, W. 2003, Hvar Obs. Bull., 27, 189 [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11, 1 [Google Scholar]
- Peat, A. W., Labrosse, N., Schmieder, B., & Barczynski, K. 2021, A&A, 653, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peat, A. W., Labrosse, N., & Gouttebroze, P. 2023, A&A, 679, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., De Pontieu, B., Carlsson, M., et al. 2014, ApJ, 792, L15 [Google Scholar]
- Pereira, T., McIntosh, S., De Pontieu, B., et al. 2015, IRIS Technical Note No.26, A User’s Guide to IRIS Data Retrieval, Reduction& Analysis, Release 1.0, https://iris.lmsal.com/itn26/ [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Ruan, G., Schmieder, B., Mein, P., et al. 2018, ApJ, 865, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Ruan, G., Jejčič, S., Schmieder, B., et al. 2019, ApJ, 886, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Schühle, U. 2003, SUMER Data Cookbook, http://www2.mps.mpg.de/projects/soho/sumer/text/cookbook.html [Google Scholar]
- Schmieder, B., Malherbe, J.-M., & Wu, S. T. 2014a, Nature of Prominences and their role in Space Weather, 300 [Google Scholar]
- Schmieder, B., Tian, H., Kucera, T., et al. 2014b, A&A, 569, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmit, D., Bryans, P., De Pontieu, B., et al. 2015, ApJ, 811, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Schühle, U., Brekke, P., Curdt, W., et al. 1998, Appl. Opt., 37, 2646 [Google Scholar]
- Schwartz, P., Schmieder, B., Heinzel, P., & Kotrč, P. 2012, Sol. Phys., 281, 707 [CrossRef] [Google Scholar]
- Schwartz, P., Gunár, S., & Curdt, W. 2015a, A&A, 577, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, P., Heinzel, P., Kotrč, P., et al. 2015b, A&A, 574, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimizu, T., Imada, S., Kawate, T., et al. 2020, Proceedings of the SPIE, 11444, 114440N [NASA ADS] [Google Scholar]
- Suematsu, Y., Shimizu, T., Hara, H., et al. 2021, Proceedings of the SPIE, 11852, 118523K [NASA ADS] [Google Scholar]
- Tei, A., Gunár, S., Heinzel, P., et al. 2020, ApJ, 888, 42 [Google Scholar]
- Vial, J. C. 1982a, ApJ, 253, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Vial, J. C. 1982b, ApJ, 254, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Vial, J.-C., & Engvold, O. 2015, Astrophys. Space Sci. Libr., 415, 2015 [NASA ADS] [Google Scholar]
- Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189 [Google Scholar]
- Wilhelm, K., Lemaire, P., Curdt, W., et al. 1997, Sol. Phys., 170, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, P., Vial, J. C., Feng, L., Curdt, W., & Zapior, M. 2021, in 43rd COSPAR Scientific Assembly. Held 28 January - 4 February, 43, 1770 [NASA ADS] [Google Scholar]
Appendix A: Histograms of the profile characteristics of hydrogen Lyman and Mg II h and k lines
 |
Fig. A.1. Histograms of the integrated intensities of the Lyα–Lyδ and Mg II k and h lines. Histograms containing all types of profiles are plotted with red, profiles from combination of the groups 1p and 2pab with green, and from combination of the groups 1pa & mpb and 2pa & mpb with the blue color. |
 |
Fig. A.2. Histograms of the depth of the central reversal of the Lyα–Lyδ and Mg II k and h lines. Histogram for profiles from the group 2pab are plotted with red, for profiles from the group 2pa & mpb with green, and for profiles occurring in combination of these groups (2pab and/or 2pa & mpb) with the blue line. |
 |
Fig. A.2. To be continued on the next page |
 |
Fig. A.3. Histograms of the peak asymmetry (rPA) of the Lyα–Lyδ and Mg II k and h lines. Individual histograms are constructed for profiles with dominating red peak (denoted with label rB − R) and dominating blue peak (rR − B). For all six lines, histograms for three cases are plotted with lines of different colors: Those constructed for profiles from the group 2pab with red, for profiles from the group 2pa & mpb with green line. For a combination of profiles from both these groups, the histograms are plotted with the blue line. |
Appendix B: Properties of histograms of the profile characteristics of hydrogen Lyman and Mg II h and k line profiles
Properties of histograms of the integrated intensity E shown in Fig. A.1 in Appendix A for the six studied lines and three cases: 1 – all profiles, 2 – profiles from the groups 1p and 2pab, and 3 – profiles from the groups 1pa & mpb and 2pa & mpb.
Properties of histograms of rCP shown in Fig. A.2 in Appendix A for the six lines and three cases: 1 – 2-peak profiles from the group 2pab, 2 – from the group 2pa & mpb, and 3 – combination of these two groups.
Properties of histograms of rPA shown in Fig. A.3 for the six lines and three cases: 1 – 2-peak profiles from the group 2pab, 2 – from the group 2pa & mpb, and 3 – combination of these two groups.
All Tables
Basic information on spectral lines observed by SoHO/SUMER and IRIS spectrographs.
Contributions of blends in percents (CBP) to quantities used in calculations of the profile characteristics for the six spectral lines.
Properties of histograms of the integrated intensity E shown in Fig. A.1 in Appendix A for the six studied lines and three cases: 1 – all profiles, 2 – profiles from the groups 1p and 2pab, and 3 – profiles from the groups 1pa & mpb and 2pa & mpb.
Properties of histograms of rCP shown in Fig. A.2 in Appendix A for the six lines and three cases: 1 – 2-peak profiles from the group 2pab, 2 – from the group 2pa & mpb, and 3 – combination of these two groups.
Properties of histograms of rPA shown in Fig. A.3 for the six lines and three cases: 1 – 2-peak profiles from the group 2pab, 2 – from the group 2pa & mpb, and 3 – combination of these two groups.
All Figures
 |
Fig. 1. Position and a general shape of the observed prominence at the limb shown in the 304 Å AIA channel. The zoomed image of the prominence reveals its basic structure. The position of the IRIS raster is indicated by the green rectangle. |
| In the text | |
 |
Fig. 2. Maps of integrated intensities of the Lyβ (a) and Lyα (b) S&S observations of the SUMER spectrograph (left part of each panel). The abscissas show the observation numbers counted from the beginning of the observations of a given spectral line (see observation No. 1 in Table 2). In panel a, both Lyβ blocks of observations are put together, even though they did not follow one after the other, to show that the pointing of the instrument differs between them. The right part of each panel shows an example of the observed spectra of the Lyβ and Lyα lines; the relative wavelength scale according to the laboratory central wavelength (Table 1) is indicated. The horizontal blue lines mark the part along the slit from which the data were taken for the analysis. As for Lyβ, these lines occur only in the latter block of the Lyβ observations (the block of No. 5 observations, see Table 2) because the pointing was not correct during the first block of observations. |
| In the text | |
 |
Fig. 3. Integrated intensities and examples of spectra of Mg II k (a) and Mg II h (b) from the first nine rasters taken into account for the analysis. Time runs from the beginning of the first raster made at 08:40:00 UT. The wavelength scales Δλ are relative to the line center wavelengths λ0 (Table 1). The blue horizontal lines indicate the section from which line profiles were taken into the analysis. In order to achieve a sufficient visibility of both Mg II spectral lines in the spectra at the disk edge, limb and prominence, specific intensities for solar_Y below 550 arcsec (white dotted horizontal line) were decreased by the factor of 0.3. |
| In the text | |
 |
Fig. 4. IRIS Mg II SJ image recorded at 08:40:16 UT (upper left panel) co-aligned by default with the AIA 304 Å channel image obtained at 08:40:19 UT (upper right panel). In the lower left panel is the AIA 211 Å channel image from 08:40:12 UT and in the lower right panel is the KSO Hα filtergram recorded at 07:32:01 UT; both these images are co-aligned with the IRIS observations. Structures visible in the Hα line resemble well the darkest absorption features present in the AIA 211 Å image. The IRIS FOV, the area of possible SUMER slit occurrence within uncertainties, and the analyzed area of the prominence – that is the section along the solar_Y, from which data were taken for the analysis – are marked in all four images. |
| In the text | |
 |
Fig. 5. Maps of the integrated intensities of Lyα (top row) and Lyβ (bottom row) overlaid with the colored mosaics classifying profile types (color bar on the right) within the target area. Profile types are classified regardless of noise (left column) and by considering only the peaks safely above error bars (right column). All available Lyα data were employed (see Fig. 2b) while only the Lyβ data with the final pointing were considered in the mosaics (Table 2). |
| In the text | |
 |
Fig. 6. Maps of the integrated intensities of the Mg II k (top row) and Mg II h lines (bottom row) overlaid with the colored mosaics classifying profile types (color bar on the right) within the target area. Here only the profile types from first nine rasters are classified regardless of noise (left column) and by considering only the peaks above error bars (right column). |
| In the text | |
 |
Fig. 7. Examples of different types of spectral line profiles according to the number of peaks detected regardless of the noise (as in colored maps shown in the columns on the left in Figs. 5 and 6). In columns from the left, spectral profiles of Lyα, Lyβ, Mg II k, and Mg II h are shown. In rows from the top, plots of 1-, 2-, 3-, 4-peak and peculiar profiles are located. Error margins of intensities are shown as gray areas around plot-lines. On abscissas, relative wavelength scales Δλ = λ − λ0 are used (for the λ0 values see Table 1). The relative intensities I/Iref are on ordinates; intensities Iref in erg s−1 cm−2 sr−1 Hz−1 are shown at the top of each column for individual spectral lines. The positions of all peaks are marked with blue vertical dotted lines. For a given type of profile (row of the figure) the Lyman line profiles are not from the same position nor from the same time while Mg II k and h profiles of given type are. |
| In the text | |
 |
Fig. 8. Diagrams showing distributions of profiles of all six spectral lines in a space of the number of all of the detected peaks on the abscissa versus number of peaks above noise on the ordinate. Affiliations to the individual groups are indicated by different colors and symbols; the legend is located on the right. Sizes of the symbols are proportional to numbers of profiles in the individual positions and these numbers are also shown next to the symbols. Further information on the diagrams is given in the text. |
| In the text | |
 |
Fig. 9. Map (left panel) showing the color mosaic of locations within the analyzed area with the Lyα integrated intensities belonging to the three peaks in the E histogram (right panel). Integrated intensities outside of the analyzed area are shown in shades of gray. The histogram constructed for all Lyα profiles is used (shown also in the upper left panel of Fig. A.1). Color coding in the mosaic corresponds to that used in the histogram: The red is for the left histogram peak, green for the middle, and blue for the right peak of the E histogram. |
| In the text | |
 |
Fig. A.1. Histograms of the integrated intensities of the Lyα–Lyδ and Mg II k and h lines. Histograms containing all types of profiles are plotted with red, profiles from combination of the groups 1p and 2pab with green, and from combination of the groups 1pa & mpb and 2pa & mpb with the blue color. |
| In the text | |
 |
Fig. A.2. Histograms of the depth of the central reversal of the Lyα–Lyδ and Mg II k and h lines. Histogram for profiles from the group 2pab are plotted with red, for profiles from the group 2pa & mpb with green, and for profiles occurring in combination of these groups (2pab and/or 2pa & mpb) with the blue line. |
| In the text | |
 |
Fig. A.2. To be continued on the next page |
| In the text | |
 |
Fig. A.3. Histograms of the peak asymmetry (rPA) of the Lyα–Lyδ and Mg II k and h lines. Individual histograms are constructed for profiles with dominating red peak (denoted with label rB − R) and dominating blue peak (rR − B). For all six lines, histograms for three cases are plotted with lines of different colors: Those constructed for profiles from the group 2pab with red, for profiles from the group 2pa & mpb with green line. For a combination of profiles from both these groups, the histograms are plotted with the blue line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


