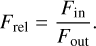| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A242 | |
| Number of page(s) | 23 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202347858 | |
| Published online | 28 March 2024 | |
3D non-LTE modeling of the stellar center-to-limb variation for transmission spectroscopy studies★
Na I D and K I resonance lines in the Sun
1
Department of Astronomy, Stockholm University, AlbaNova University Center,
106 91
Stockholm, Sweden
e-mail: gloria.canocchi@astro.su.se
2
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam, Germany
3
Theoretical Astrophysics, Department of Physics and Astronomy, Uppsala University,
Box 516,
751 20
Uppsala, Sweden
4
Institute for Solar Physics, Dept. of Astronomy, Stockholm University, Albanova University Center,
106 91
Stockholm, Sweden
5
Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University,
Box 43,
221 00
Lund, Sweden
Received:
1
September
2023
Accepted:
8
December
2023
Context. Transmission spectroscopy is one of the most powerful techniques used to characterize transiting exoplanets, since it allows for the abundance of the atomic and molecular species in the planetary atmosphere to be measured. However, stellar lines may bias the determination of such abundances if their center-to-limb variations (CLVs) are not properly accounted for.
Aims. This paper aims to show that three-dimensional (3D) radiation hydrodynamic models and the assumption of non-local ther-modynamic equilibrium (non-LTE) line formation are required for an accurate modeling of the stellar CLV of the Na I D1 and K I resonance lines on transmission spectra.
Methods. We modeled the CLV of the Na I D1 and K I resonance lines in the Sun with 3D non-LTE radiative transfer. The synthetic spectra were compared to solar observations with high spatial and spectral resolution, including new data collected with the CRISP instrument at the Swedish 1-m Solar Telescope between µ = 0.1 and µ = 1.0.
Results. Our 3D non-LTE modeling of the Na I D1 resonance line at 5896 Å and the K I 7699 Å resonance line in the Sun is in good agreement with the observed CLV in the solar spectrum. Moreover, the simulated CLV curve for a Jupiter-Sun system inferred with a 3D non-LTE analysis shows significant differences from the one obtained from a 1D atmosphere. The latter does indeed tend to overestimate the amplitude of the transmission curve by a factor that is on the same order of magnitude as a planetary absorption depth (i.e., up to 0.2%).
Conclusions. This work highlights the fact that to correctly characterize exoplanetary atmospheres, 3D non-LTE synthetic spectra ought to be used to estimate the stellar CLV effect in transmission spectra of solar-like planet hosts. Moreover, since different spectral lines show different CLV curves for the same geometry of the planet-star system, it is fundamental to model the CLV individually for each line of interest. The work will be extended to other lines and FGK-type stars, allowing for synthetic high-resolution spectra to mitigate the stellar contamination of low-resolution planetary spectra, for example, those drawn from JWST.
Key words: line: formation / line: profiles / techniques: spectroscopic / Sun: atmosphere / planets and satellites: atmospheres / planet-star interactions
The SST datasets of the Na I 5896 Å and K I 7699 Å lines are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/683/A242
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Transmission spectroscopy is a powerful tool used to measure the abundances of atomic and molecular species in the atmosphere of transiting exoplanets, especially close-in gas giants or hot Jupiters (Czesla et al. 2015; Casasayas-Barris et al. 2017). When a planet transits across the stellar disk of its host star, the recorded stellar spectrum includes the planetary contribution. The latter can be detected as an extra absorption at specific wavelengths corresponding to the species that are present in the upper layers of the planetary atmosphere, through which the starlight is filtered during the transit. This technique works by subtracting the light recorded out of transit from that recorded during the transit, in order to detect the extra absorption due to the planet. In practice, a high spectral resolution (i.e., R ≈ 100 000) is required to probe such weak features, which are usually on the order of only 0.01–0.1%. Therefore, high-resolution ultra-stable spectrographs such as HARPS (Mayor et al. 2003), HARPS-N (Cosentino et al. 2012), CRIRES+ (Kaeufl et al. 2004; Dorn et al. 2014, 2023), PEPSI (Strassmeier et al. 2015), or ESPRESSO (Pepe et al. 2021) are needed for this kind of research.
To date, the most extensively studied atomic lines in transit spectroscopy are the lines of some alkali metals: the Na I resonance doublet at 5890 Å and 5896 Å, and the near-infrared K I resonance line at 7699 Å. High-resolution studies have allowed for the detection of sodium in the atmospheres of several giant exoplanets, which are either hot Jupiters or Neptunes, such as WASP-166b (e.g., Seidel et al. 2020), WASP-121b (e.g., Hoeijmakers et al. 2020; Cabot et al. 2020; Seidel et al. 2023), WASP-49b (e.g., Wyttenbach et al. 2017), WASP-69b (e.g., Casasayas-Barris et al. 2017), WASP-76b (e.g., Seidel et al. 2019), KELT-9b (e.g., Hoeijmakers et al. 2019), KELT-20b (e.g., Casasayas-Barris et al. 2019), HD 189733b (e.g., Wyttenbach et al. 2015; Yan et al. 2017), and HD 209458b (e.g., Charbonneau et al. 2002; Snellen et al. 2008). The latter is the first exoplanet where an atomic species was detected for the very first time by Charbonneau et al. (2002). These authors detected neutral sodium through in-transit excess absorption in the Na I D1 and D2 lines from observations with the Space Telescope Imaging Spectrograph (STIS) on board the Hubble Space Telescope (HST). Afterward, many other studies also from ground-based telescopes were carried out and several other species were detected including neutral potassium through the 7699 Å resonance line (Casasayas-Barris et al. 2021). The first detections of K I occurred for XO-2b (Sing et al. 2011) and the eccentric hot Jupiter HD 80606b (Colón et al. 2012).
An important effect to consider when analyzing spectra with this technique is the center-to-limb variation (CLV) of the stellar line profiles. Indeed, Casasayas-Barris et al. (2020) stressed the importance of correctly accounting for this effect on the interpretation of the spectra of HD 209458. The CLV describes the change in both strength and shape of the lines forming in the stellar atmosphere as the observer’s line of sight moves from the center to the edge of the stellar disk.
By going toward the limb, the spectral lines are formed in higher layers of the photosphere. Different spectral lines are affected in different ways owing to their sensitivities on depth-dependent quantities such as temperature, electron pressure, and velocity, among others. This CLV effect is closely related to continuum limb darkening: by going toward the limb, the higher, cooler layers of the photosphere are exposed to the observer, decreasing the observed surface brightness. The CLV of stellar lines can affect the correct determination of elemental abundances in the planetary atmospheres if not properly corrected for or even mimic planetary signals, thus leading to a false detection; this is because, in some cases, it is on the same order of magnitude as the planetary absorption feature (Czesla et al. 2015). During a transit, as the planet progresses, it obscures and blocks the light of parts of the stellar disk that contribute differently to the observed stellar line profile, which then varies among the different transit phases. Simply subtracting the out-of-transit light without considering the angle dependence will therefore introduce an error.
Although the CLV effect is recognized as an important and critical factor (e.g., Müller et al. 2013), it is often modeled by adopting the simple assumption of local thermodynamic equilibrium (LTE) and one-dimensional (1D) plane-parallel stellar atmospheres (e.g., Casasayas-Barris et al. 2019; Chen et al. 2020), or sometimes with 1D non-LTE models (e.g., Yan et al. 2017; Casasayas-Barris et al. 2017; Morello et al. 2022; Sicilia et al. 2022). However, several studies have shown that the commonly used 1D LTE models fail to reproduce spatially resolved observations of the solar disk. Specifically, the CLV of several atoms, such as Ca, C, O, Al, and Fe lines, has been investigated in the Sun, finding that they are poorly modeled in 1D LTE, with errors on the line strength that range from strong (100%) to moderate (10%) at µ = 0.2 (e.g., Pereira et al. 2009; Lind et al. 2017; Nordlander & Lind 2017; Bjørgen et al. 2018; Amarsi et al. 2018a, 2019; Bergemann et al. 2021; Pietrow et al. 2023b,a).
The Na I doublet and the K I 7699 Å resonance lines are strongly affected by departures from LTE; in particular over-recombination of the neutral species and photon losses in the resonance lines themselves (e.g., Lind et al. 2011; Reggiani et al. 2019). As such, 3D non-LTE modeling should be used for the highest accuracy.
The Sun is an excellent test bench for observing and studying the CLV of spectral lines (e.g., Pierce & Slaughter 1977; Neckel & Labs 1994). Several solar atlases were recently produced and made publicly available, for example, the NSO/Kitt Peak FTS (Stenflo 2015) and the Gregory Coudé Telescope SS3 (Ramelli et al. 2017, 2019) atlases. There, we can see that the intensity of many spectral lines as a function of wavelength at different viewing angles (µ = cos(θ), with θ the heliocentric angle1) from the limb (i.e., µ = 0) to the solar disk center (i.e., µ = 1.0) is recorded. Specifically, the FTS atlas extends in the range 4084–9950 Å, but it samples only two positions along the solar disk: one at the center and one at the edge (µ = 0.145). Conversely, in the SS3 atlas the intensity at ten different angles, spanning from µ = 0.1 to µ = 1.0 in steps of 0.1, is recorded but the covered spectral range is narrower (4384–6610 Å). Moreover, both these atlases show a noisy continuum (about 3%) and are not corrected for telluric lines. Systematic and significant uncertainties in the continuum of different atlases of the solar disk-center intensity were also investigated in Doerr et al. (2016). An updated high-resolution atlas has been compiled by the Institut für Astrophysik Göttingen (IAG), which includes the CLV of several lines in the wavelength range of 4200-8000 Å (Ellwarth et al. 2023). Nevertheless, it does not reach the very limb, with µ = 0.2 being the farthest angle sampled.
The CLV of stellar lines in stars other than the Sun has only been studied very recently. Dravins et al. (2017, 2018) have tested how to resolve the surface of a K-type star, namely HD 189733A, using a transit of its exoplanet as a probe and performing differential spectroscopy of a strong Fe I line between different transit phases. This technique requires high-resolution spectra as well as very precise observations, but it remains a very promising candidate for spatially resolving the surface of many other stars in the near future. However, it should be noticed that the technique relies on the assumption that the planetary atmosphere contribution for that specific Fe I line is null.
In this work, we study the 3D non-LTE CLV of absorption lines of neutral sodium and potassium in the Sun, and explore the implications for transmission spectroscopy studies. In Sect. 2, we describe the observational data used in this work. Complementing data from the literature, we have carried out observations for the Na I D1 line at 5896 Å and the K I line at 7699 Å between µ = 0.1 and 1.0, obtained with the CRisp Imaging SpectroPolarimeter (CRISP; Scharmer et al. 2008) on the Swedish 1-m Solar Telescope (SST; Scharmer et al. 2003). In Sect. 3, we describe our 3D non-LTE calculations, as well as our 3D LTE, 1D non-LTE, and 1D LTE calculations. In Sect. 4, we use these models to quantitatively analyze the solar observations, and demonstrate the impact of 3D non-LTE modeling on a simulated CLV transmission light curve in a Sun-Jupiter system. Finally, in Sect. 5, we summarize our conclusions and discuss future perspectives.
2 Observations and data processing
For this work, we employed data from the recently published solar intensity atlas obtained with the Fourier Transform Spectrograph (FTS; Schäfer et al. 2020) at the IAG Vacuum Vertical Telescope (VVT), hereafter referred to as IAG FTS CLV Atlas, as well as observations from the SST/CRISP. The spectra from the IAG FTS CLV Atlas show a very high spectral resolution of about R ≈ 700 000 at λ = 6000 Å, or Δv = 0.0024 cm−1 (Reiners et al. 2023) but they have not been corrected for telluric lines from water (H2O) and molecular oxygen (O2).
Therefore, the regions affected by telluric lines were masked out. The IAG Atlas spans from µ = 0.2 to 1.0, in step of 0.1, with additional spectra at the following viewing angles: µ = 0.35, 0.95, 0.97, 0.98, 0.99, with a total of 14 µ-angles covering the wavelength range 4200–8000 Å. These data are described in detail in Ellwarth et al. (2023).
For comparison and completeness, we also took observations with the CRISP instrument at the SST of the Na I D1 resonance line at 5896 Å and the K I 7699 Å resonance line. The datasets for these are described in Sect. 2.1, along with the reduction and calibration processes. A comparison between the two solar datasets, the IAG Atlas and the SST data, is presented in Sect. 2.2.
 |
Fig. 1 Full-disk image of the Sun on 29 April 2023 in the AIA 171 Å filter (Lemen et al. 2012). The black squares show all telescope pointings used during the observation campaigns, spanning from the solar north pole to disk center. |
2.1 SST dataset
We obtained the data for the Na I D1 and K I lines in two campaigns, hereafter referred to as Campaign I and Campaign II, but following the same procedure. We pointed the telescope at several distinct positions on the disk, targeting quiet regions (i.e., without activity), from the solar north pole to the center, recording data for a time period of between 14 and 26 min at each position (i.e., µ-angle). Since the tracking was active for the entire observation time, this method allows us to perform temporal averages in order to correct for p-modes and oscillations. This is a well-established technique used in several previous studies (e.g., Pierce & Slaughter 1982; Ding & Fang 1991; Pereira et al. 2009; Lind et al. 2017). For the Na I D1 line, we pointed the telescope at µ = 0.2, 0.4, 0.6, 0.8 and 1.0, going along the meridian from the solar north pole to the disk center in order to avoid Doppler shifts from rotation. For the K I line, we also pointed at µ = 0.9, but the data from this pointing were not reduced in the end. The pointing positions are highlighted in Fig. 1. For µ = 0.2, 0.4 and 0.6, a wider µ range is covered by each pointing, due to the large Field of View (FoV) of the cameras. The FoV is circular, with a diameter of about 87″ on the solar disk.
In addition to Na I D1 and K I 7699 Å line, we also observed the photospheric magnetically sensitive line of Fe I at 6173 Å in order to check the level of solar activity during measurements. This is the only line for which the polarimetric signal was measured. A summary of the data is reported in Table 1 and the specific wavelength points sampled for each line are shown in Table 2. These positions are given relative to their line center and, especially for the Na I D1 line, they are not all symmetrically sampled2.
The observations were carried out under variable seeing conditions. This is acceptable because our first goal is to take large-scale averages along the FoV and use the fine-scale structure only for the alignment. Indeed, the only constraint was that there had to be at least one frame with high enough seeing to align it to co-temporal SDO/HMI observations, as explained hereunder. Campaign I was performed at the end of August 2022, and specifically, the Na I D1 and Fe I 6173 Å data were taken between 08:15 and 10:41 UT on 27 August 2022 with SST/CRISP, as shown in Table 1. We obtained one scan at five µ-angles on the same day. Just before the start of Campaign I, new detectors were installed at the SST, with a larger FoV compared to the previous set-up (1.5′ radius circular compared to the 1′ × 1′ with the old detectors). The old detectors were from Sarnoff and the new ones are called “Ximea CB262RG-GP-X8G3”. The new detectors also allowed us to solve an issue with the back-scattering light in the red part of the spectrum. The data of Campaign I were the first to be taken with the new detectors.
Campaign II occurred at the end of April 2023, between April 27–30 and we were not able to get one scan in one day due to a very variable seeing. Therefore, different pointings were performed each day depending on the seeing conditions (see Table 1), but the data with the best seeing conditions were taken in the morning of 29 and 30 April 2023 and so these are the K I data analyzed in this work. During this campaign we observed the K I 7699 Å and Fe I 6173 Å lines, obtaining in total two scans at six µ-angles (however, as previously mentioned, the data for µ = 0.9 are not used in this work).
We reduced the data of both Campaigns with the SSTRED pipeline (de la Cruz Rodríguez et al. 2015; Löfdahl et al. 2021), which has been specifically designed to process the data from the SST. It corrects for dark and flat fields but also includes polari-metric calibrations and image restoration that removes optical aberrations due to turbulence in the atmosphere. This step is performed by the Multi-Object Multi-Frame Blind Deconvolution (MOMFBD; Löfdahl 2002; Van Noort et al. 2005) algorithm, which however can fail if the seeing conditions are poor (i.e., Fried parameter, r0 ≤ 5 cm). However, this is not the case with respect to our observations.
The SST pointing and tracking are good but in order to get a very precise estimate of the µ-angle corresponding to each pixel of the FoV, we performed an additional aligning step. Several studies make use of cross-correlation algorithms to align their data (e.g., Cauzzi & Reardon 2012) but they only work well when activity features like sunspots are clearly distinguishable in the FoV. For quiet Sun observations, this is not usually the case, especially at the limb with a lower image contrast. Therefore we use the same method as Pietrow et al. (2023b), which consists of manually aligning the images by looking for patterns among the granules and bright points that match with SDO/HMI continuum images (Lemen et al. 2012) which were enhanced in resolution and contrast by means of a deep learning algorithm (Díaz Baso & Asensio Ramos 2018). Each HMI image was picked to be within half a minute of the highest seeing-quality scan within the first ten scans of each pointing. In this way, we can straightforwardly obtain absolute solar coordinates with respect to the disk center. After that, we assigned a µ value (see Eq. (1)) at each pixel in the images by simply using the Pythagorean theorem to calculate the distance of each pixel from the disk center (r):
where R⊙ is the angular radius of the Sun as seen from the Earth in arcseconds. In Campaign I the solar radius is R⊙ = 949.5″ and it is 953″ in Campaign II3.
Then, as previously mentioned, for the pointing at µ = 0.2, 0.4, and 0.6, a wider µ range is covered due to the large FoV of the cameras. Consequently, we were able to extract average line profiles for more µ-angles. Specifically, from the pointing at µ = 0.2, we obtained the line profiles at µ = 0.1, 0.15, 0.2, and 0.25. Similarly, from the pointing at µ = 0.4, we got the profiles at µ = 0.3, 0.35, 0.4 and 0.45. Lastly, from the pointing at µ = 0.6 we could also extract the profiles at µ = 0.55. Finally, we obtain averaged line profiles for each spectral line, for the following 12 µ-angles: 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.55, 0.6, 0.8, and 1.0. These are computed by averaging over time and over space all the pixels in the frames that are within the selected µ value ±0.02. The CRISP image scale is 0.044″ pixels−1.
After that, we performed another calibration of the disk center intensity (i.e., the µ = 1.0 line profile) using the ISPy4 library (Díaz Baso et al. 2021) by fitting several wavelength points of the averaged disk center profile to the IAG Atlas convolved with CRISP instrumental profile5. The calibration routine was modified because it usually employs the solar atlas by Neckel & Labs (1984). We then applied the intensity and wavelength calibration factors to all the other µ-angle line profiles. This is again the same method employed in Pietrow et al. (2023b).
The resulting limb darkening curves and line profiles of the Na I D1 line taken in Campaign I and of the K I line of Campaign II are shown in Figs. A.2 and A.3, respectively.
Summary of the SST/CRISP data.
FPI tuning positions for each observed line.
2.2 Comparison of solar data
In this section, we compare our new SST/CRISP observations to the IAG FTS Atlas through the measurement of equivalent widths (Wλ) at different µ-angles. First of all, we convolved the Atlas with CRISP instrumental profile in order to degrade it to the same resolution as our SST data, which is about R ≈ 160 000 at 7699 Å. Such convolution is shown in Figs. 2 and 3 where the line profile of the Na I D1 and K I line, respectively, at disk center (i.e., µ = 1.0) is compared between the two datasets. From these figures, it is apparent that the agreement between the two datasets at disk center is excellent, and specifically, it is within 2.5% for the K I line and within 3% for the Na I D1 line.
Next, we computed the Wλ of all the Na line profiles at different µ-angles in the wavelength range 5895.21 – 5896.291 Å (shaded region in Fig. 2) in order to exclude the blending on the right wing due to an uncorrected telluric line that is clearly visible in Fig. 2. It is worth noting that we are not integrating the entire line profile of the Nal D1 line up to the continuum. The Wλ of the Na I D1 line as a function of the µ-angle is shown in Fig. 4.
From the latter, it is apparent that the Wλ of the SST data is slightly lower than the Wλ of the corresponding IAG profile. Even with this small difference linearly increasing toward the limb, the agreement between the two datasets is quite good, and specifically, it is within 0.3% at disk center (µ = 1.0) and about 2.9% at the limb (µ = 0.2). It is worth noting that the SST pointings are more precise than the IAG, especially at the limb because of the method we used to obtain the µ-position of each pixel of the frames, that is the alignment with simultaneous space-based data (i.e., SDO/HMI images) which translates into sub-arcseconds precision at the limb. This procedure is accurately described in Sect. 2.1. Conversely, the limitations of the IAG Atlas come from the use of fibers, which result in increasingly large uncertainties in the μ-positions closer to the limb, as is apparent from the horizontal error bars in Fig. 4.
The same calculations were performed for the K I line, computing the Wλ in the wavelength range 7698.495–7699.415 Å, as highlighted in Fig. 3. The resulting CLV of this line is shown in Fig. 5, where Wλ at different µ-angles are compared between the IAG and SST data. Also in this case the Wλ of the SST data is systematically lower than the IAG data but overall they agree within 1–2% at all µ-angles. Differences in continuum fitting may have contributed to this difference in line strength, but we emphasize that the atlases everywhere agree within the estimated pointing errors.
With regards to the uncertainties on the IAG datapoints, the horizontal error bars on µ-angles were provided by Ellwarth (priv. comm.) whereas the vertical error bars on equivalent widths were estimated from Cayrel’s formula (Cayrel 1988; Cayrel et al. 2004). They are reported in Table A.2. The pointing of the SST is very precise; we estimated the horizontal error bar on µ from the aligning procedure of SST frames with SDO images described in Sect. 2.1. Indeed, the geocentric orbit of SDO leads to a potential error of maximum 1.7″. In µ-space, this translates into a negligible value at disk center (about 10−6) but becomes significant at the limb, reaching 0.02 at µ = 0.1. The vertical error bars on Wλ of the SST data correspond to the standard deviation of the individual pointings (σµ) added to an estimated error due to continuum placement (σcontinuum), which represents the main source of uncertainty for this dataset. These errors were computed by vertically shifting the continuum within 1% and estimating how the Wλ change. Therefore the total error becomes:
These values are shown in Table A.1.
 |
Fig. 2 Intensity profile of the Na I D1 line at disk center. Top: comparison of the Na I D1 line profile at disk center between the SST/CRISP data (black dots) and the IAG Atlas convolved with the instrumental profile (red dashed line). The original profile from the IAG Atlas is also plotted with a black solid line. The grey-shaded region highlights the selected wavelength range for Wλ computation. A telluric spectrum (Hinkle et al. 2000) is overplotted as a grey line in the top panel, to show that there is negligible contamination in the Wλ window. Bottom: difference between the convolved IAG Atlas and the SST data in percentage. |
 |
Fig. 3 Intensity profile of the K I resonance line at disk center. Top: comparison of the K I 7699 line profile at disk center between the SST/CRISP data (black dots) and the IAG Atlas convolved with the instrumental profile (red dashed line). The original profile from the IAG Atlas is also plotted with a black solid line. The grey-shaded region highlights the selected wavelength range for Wλ computation. A telluric spectrum (Hinkle et al. 2000) is overplotted as a grey line in the top panel, to show that there is negligible contamination in the Wλ window. Bottom: difference between the convolved IAG Atlas and the SST data in percentage. |
 |
Fig. 4 Comparison of the SST/CRISP data (black dots) with the IAG FTS CLV Atlas (red squares) convolved with CRISP instrumental profile. Top: equivalent width of the Na I D1 line as a function of the µ-angle. Bottom: difference between the IAG and the SST data in percentage. |
 |
Fig. 5 Comparison of the SST/CRISP data (black dots) with the IAG FTS CLV Atlas (red squares) convolved with CRISP instrumental profile. Top: equivalent width of the K I line at 7699 Å as a function of the µ-angle. Bottom: difference between the IAG and the SST data in percentage. |
3 Radiative transfer calculations
3.1 Synthetic spectra
The synthesis of the solar spectrum was performed with the radiative transfer (RT) MPI-parallelised code Balder (Amarsi et al. 2018b), an extensively modified version of the Multi3d code (Botnen & Carlsson 1999; Leenaarts & Carlsson 2009), which can solve the restricted non-LTE problem for trace elements in 1D and 3D, for user-specified atomic elements. Balder employs the BLUE (Amarsi et al. 2016a,b) opacity package, which computes the line opacity on a grid of wavelength, density, and temperature. A full 3D non-LTE analysis of several elements in the Sun, including Na and K, was performed with the same code by Asplund et al. (2021).
For the model atmosphere, a 3D radiative-hydrodynamics simulation with the Stagger-code (Nordlund & Galsgaard 1995; Stein & Nordlund 1998; Collet et al. 2011) was used. Stagger employs the “box-in-a-star” set-up, meaning that it simulates a rectangular box, vertically open, with periodic horizontal boundaries, located in the upper part of the solar photosphere, without including any chromospheric layer. In this work, we simulate the quiet Sun, without including magnetic fields6. The 3D model is set on a Cartesian grid of size 240×240×240, corresponding to a physical size of 8×8×4 Mm. The vertical dimension is characterized by non-equidistant spacing in order to obtain a higher resolution at the regions of interest and to resolve the strong temperature gradient of the photosphere. In order to decrease the computational time for the spectral synthesis, all the atmospheric snapshots were resized to a resolution of 60×60×101, from their original value of 2403. This approach has been already tested in previous studies, such as Lind et al. (2017) and Lagae et al. (2023).
Ten snapshots were used, from the same simulations discussed already in several earlier analyses of the Sun (Amarsi et al. 2018a, 2019, 2020, 2021; Asplund et al. 2021). We note that this simulation is more recent than that in the Stagger-grid (Magic et al. 2013), with improvements to the opacity binning scheme (Collet et al. 2018) and extending for over one day of solar time. The mean effective temperature of these snapshots is Teff = 5770 ± 5 K7.
An example of the surface image of one of the snapshots of the solar photosphere selected for this work is shown in Fig. 6. It represents the 3D non-LTE to 3D LTE ratio of Wλ of the K I 7699 Å line, showing that the non-LTE effects vary with the convection pattern: under-population in the up-flowing granules and the opposite effect, overpopulation, in the intergranular lanes. Such a variation is expected and is due to the much steeper temperature gradients of the granules compared to those of the intergranular lanes. The granulation pattern of the solar photosphere, which arises from the convective motion of the hot plasma and gas, is clearly recognizable in this figure. This is a natural 3D effect that leads to spectral line broadening and line asymmetries (e.g., Dravins et al. 1981). In the 3D non-LTE models, the broadening effects of these temperature inhomogeneities and convective velocity structures are naturally included; therefore, no extra broadening is required. In 1D, however, the line broadening is instead roughly accounted for by the tunable parameters microturbulence (vmic) and macroturbulence. For the Sun, a microturbulence of 1.0 km s−1 is usually adopted in the literature, and this was the one employed in this work for the 1D simulations, independent of depth or viewing angle. For the macroturbulence velocity (vmac) a value of 3.5 km s−1 was used. The 1D synthetic spectra have been computed with the MARCS (Gustafsson et al. 2008) solar atmosphere.
The synthetic spectra were computed at three different abundances for each snapshot. Then the line profile was spatially and temporally averaged, using all ten snapshots. After that, the diskcenter line profile was fitted to the observed data via a standard χ(2) minimization routine. Linear interpolation between models computed with several values of abundance was applied. In this way, the elemental abundance was fit to the disk-center spectra and then fixed to this value for the other µ-angles. Finally, we computed the line profiles at the other µ-angles with the bestfit model and from those we calculated the Wλ of the synthetic spectra by direct integration of the line within wavelength ranges that were considered blend-free (see Sect. 4.1). For the study of the Na I D1 and K I 7699 Å resonance lines, we also convolved the synthetic spectrum with the CRISP instrumental profile in order to compare Wλ with the observed SST data (see Sect. 4.1).
 |
Fig. 6 Ratio of the NLTE to LTE equivalent width of KI 7699 Å for a single Stagger snapshot. In the up-flowing granules, overionization makes the line weaker in NLTE, whereas in the intergranular lanes the NLTE Wλ is stronger. |
Atomic data of the sodium and potassium lines considered in the CLV analysis, as implemented in the model atoms of Lind et al. (2011) and Reggiani et al. (2019).
3.2 Model atoms
Several studies have shown that both Na I and K I atoms are affected by strong non-LTE effects (i.e. over-recombination of the ground state), meaning that non-LTE line formation is required to correctly reproduce observations. Lind et al. (2011) has shown that Na stellar abundances can be overestimated by up to 0.5 dex if calculations in 1D LTE are performed for saturated lines of metal-poor dwarfs and giants ([Fe/H] = −2). In the case of the Sun, they found a difference of about 0.02 dex between the 1D LTE and non-LTE inferred abundance. Reggiani et al. (2019) showed that the abundance of K in the Sun is overestimated by about 0.3 dex in 1D LTE compared to 1D non-LTE.
The non-LTE of any line is generally determined by the change in formation depth, which is given by the departure coefficient of the lower level, and the change in line source function (Sl), whose ratio with respect to Bv is equal to the ratio between the upper and lower level departure coefficients (neglecting stimulated emission). For the resonance lines (Na D and KI 7699 Å), it has been seen that Sl resembles that of a pure scattering line in a two-level atom at all depths, meaning that Sl is equal to the profile-averaged mean intensity (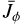 ) and strongly subthermal, that is
) and strongly subthermal, that is 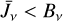 . Over-recombination and over-de-excitation (photon loss) overpopulate the ground levels of Na I and K I compared with LTE, pushing the mean formation depth outwards in the atmosphere. The combined effect is a stronger line in non-LTE compared to LTE, and specifically a deeper line core. For more details about the non-LTE effects of Na I, we refer the reader to Sect. 3.1 of Lind et al. (2011), and for K I to Sect. 4.3 of Reggiani et al. (2019).
. Over-recombination and over-de-excitation (photon loss) overpopulate the ground levels of Na I and K I compared with LTE, pushing the mean formation depth outwards in the atmosphere. The combined effect is a stronger line in non-LTE compared to LTE, and specifically a deeper line core. For more details about the non-LTE effects of Na I, we refer the reader to Sect. 3.1 of Lind et al. (2011), and for K I to Sect. 4.3 of Reggiani et al. (2019).
The model atom used in Balder for the Na atom is the one developed and tested in Lind et al. (2011), characterized by a structure of 23 levels in total: 22 energy levels for Na I and the ionized sodium (Na II) continuum. The lines of the Na doublet originate from the transition between the levels 3s−3p1/2 and 3s−3p3/2. Both fine and hyper-fine structures are accounted for in the model atom. The latter describes both the radiative and collisional transitions among the energy levels and, in particular, detailed quantum mechanical calculations are used for the inelastic collisions of Na respectively with electrons (Park 1971; Allen & Rossouw 1993; Igenbergs et al. 2008) and hydrogen atoms (Belyaev et al. 2010; Barklem et al. 2010). Regarding the latter, in this work, the impact of rate coefficients for the collisions with neutral hydrogens from Kaulakys (1991) was also explored. Indeed in the model atom developed in Lind et al. (2011), these rates were only considered above the ionic limit, but Amarsi et al. (2018a, 2019) argued that it could be necessary to add these rate coefficients even below the ionic limit, at least when asymptotic models such as those of Barklem (2016) or Belyaev (2013) are used. The results of Amarsi et al. (2018a, 2019) for O and C, as well as Bergemann et al. (2019) for Mn, suggest that doing so leads to better agreement of synthetic spectra with observational data.
The model atom of the potassium atom was recently developed by Reggiani et al. (2019), who used the most up-to-date and accurate atomic data, for both the radiative and collisional transitions (e.g., Belyaev & Yakovleva 2017; Yakovleva et al. 2018; Barklem et al. 2017). The atomic model consists of 19 energy levels, including the ionized potassium (K II) continuum. For the collisions with hydrogen atoms, they adopted rate coefficients from Yakovleva et al. (2018), based on the asymptotic models of Barklem (2016). To these data, they also added those from the free electron model of Kaulakys (1991), following Amarsi et al. (2018a, 2019). From Reggiani et al. (2019), the K+H collisions significantly affect the abundance determination. In particular, they produce an abundance difference of about 0.03 dex in the Sun if not taken into account. In the same work, they have shown that the resonance line at 7699 Å has wings insensitive to departures from LTE, but a core that is strongly affected by non-LTE, as it is much deeper than in LTE.
Both these model atoms were employed for full 3D non-LTE calculations in a recent paper by Asplund et al. (2021) to study and update the chemical composition of the Sun. However, the lines selected to compute abundances are not the same as those analyzed in this work. The atomic data of the Na lines and K I resonance line studied here are summarized in Table 3.
4 Analysis of the results
The CLV of solar lines represents a crucial test for line formation modeling since it is an excellent probe of the atmospheric structure. Indeed, the light emitted at different µ-angles probe different heights of the solar atmosphere: shallower layers close to the limb and deeper layers at the disk center (µ = 1.0). The 3D radiative transfer shows that the profiles of the lines emitted from different regions of the solar surface vary in both shape and strength. This is important for transmission spectroscopy studies when the stellar lines are distorted due to the planet transiting in front of its star and blocking the light from different regions of the stellar surface. The deformation of the stellar lines often complicates the interpretation of (chemical) spectral signatures caused by the planet’s atmosphere, even leading to the detection of false positives for some chemical elements or to the wrong derived abundance in some cases. Therefore highresolution ground-based spectra need to be corrected for the CLV signature, using a model that is as realistic as possible.
For this purpose, in Sects. 4.1 and 4.2, we compare the spatially resolved solar observations of the IAG Atlas and of the SST data with several theoretical models assuming different model atmospheres (1D and 3D) and line formation (LTE and non-LTE). Furthermore, in Sect. 4.3 we simulate the impact on transit phase curves for the Sun when the CLV is modeled with different assumptions in a Sun-Jupiter system.
 |
Fig. 7 Center-to-limb variation of the solar Na I lines. Comparison of the equivalent widths of the IAG Atlas (filled squares) and the SST data (open circles) with several different model atmospheres and atomic data, colored as in the figure’s legend. |
4.1 Center-to-limb variation of equivalent widths
In this section, we analyze the CLV of the equivalent widths of four Na I lines and one K I line, presented in Table 3. In transmission spectroscopy studies only the strong Na I D lines are used for the detection of sodium in the planetary atmospheres since they are the only lines strong enough to show a planetary signature. The Na I D2 line at 5890 Å in the IAG Atlas was contaminated by too many telluric lines that were cut out from the dataset; hence, it was not possible to compare it with our synthetic spectra. However, we analyzed the CLV of three other Na I optical lines, respectively at 5688 Å, 6154 Å and 6160 Å, in order to further test our models. The Na I doublet at 6154 Å and 6160 Å is also commonly used for abundance analyses of solar-metallicity stars. The CLV of these two lines was studied by computing the Wλ via direct integration of the line profile over a wavelength region extending ±0.12 Å from the line center, in order to exclude nearby lines from other elements. For the Na I 5688 Å line a wavelength range of ±0.15 Å was adopted instead. The wavelength range for integration is shown in the last column of Table 3. For the Na I D1 and K I resonance lines, the same wavelength range used in Sect. 2.2 was chosen in order to compare the models with both SST and IAG data. For this reason, the convolution of CRISP instrumental profile was applied to the synthetic spectra of these two lines. In all comparisons, the abundance is adjusted to fit the line profile at disk center, as mentioned in Sect. 3.1. The resulting Wλ as a function of µ-angles for the Na I lines and the K I line are shown in Figs. 7 and 8, respectively.
From both these figures, it is clear that 1D LTE modeling (dashed red line) heavily fails in describing the CLV of the solar lines, underestimating the line strengths at the limb as much as 50.1% for the K I and 28.2% for Na I D1 at µ = 0.1, in comparison with the SST data. For the other Na I lines compared with the IAG data at µ = 0.2, the underestimate is as large as 31% for 5688 Å and about 29% for the 6154 and 6160 Å lines. Using a 3D atmosphere with LTE line formation (solid red line) slightly improves the CLV but it still considerably under-performs at the limb, with an equivalent width difference of about 20% for the Na lines and 37% for the K line.
The observations are much better reproduced by the 1D non-LTE model (dashed blue line), which is in agreement with the Na I D1 SST data at µ = 0.1 within about 8%. This demonstrates that the non-LTE effect is a very important feature that must be taken into account in order to accurately model the spectral lines. The agreement with the data improves also for the other Na lines, down to 7.2% for the 5688 Å and about 1% for the 6154 and 6160 Å lines, at µ = 0.2. The equivalent width of the 1D non-LTE model is 17.6% lower than the SST data at µ = 0.1 for the K I resonance line.
A large improvement is obtained by the 3D non-LTE modeling (solid blue line) at the limb (µ = 0.2) for the K I (6%), the 5688 Å (4%) line, and the Na I D1 line (2.5%). The CLV of the latter is also in excellent agreement with the SST data, with a difference of only 0.4% at µ = 0.1. Nevertheless, the 3D non-LTE model slightly overestimates the strength of the other Na I lines by about 8.5% (6154 Å) and 9.8% (6160 Å); that is, performing slightly worse than 1D non-LTE. We stress that the slightly better agreement in 1D non-LTE is likely coincidental, since it is dependent on the various parameters in the 1D models that can be tuned to reproduce observations, such as vmic and vmac. The imperfect agreement of the 3D non-LTE model close to the limb can be explained by several uncertain factors in the modeling, such as the upper layers of the Stagger model atmosphere, as well as the rates for collisions with H and electrons in the model atom.
However, it is worth noting that in general the 3D non-LTE prediction performs extremely well given that it does not rely on any free parameter. Considering that for other stars we cannot take spatially resolved observation of their disk, we would not be able to constrain the parameters for the 1D modeling, like we can do for the Sun.
Moreover, the CLV of the continuum and other observational diagnostics are not well reproduced by 1D models, such as MARCS, not even in the Sun, as shown in Pereira et al. (2013).
For other stars, we cannot resolve the stellar disk, and therefore we cannot take observations at different µ-angles to fit the free parameters of our 1D models with. For this reason, it is important to note how well we can reproduce the solar CLV without any free parameter with our 3D non-LTE models.
 |
Fig. 8 Center-to-limb variation of the K I 7699 Å line. Comparison of the IAG Atlas (filled squares) and the SST data (open circles) with several different model atmospheres and atomic data, colored as in the figure legend. |
4.2 Center-to-limb variation of line profiles
While for some Na I lines, the 1D non-LTE modeling is predicting a very good CLV in terms of equivalent widths (Sect. 4.1), the same is not true anymore for what regards the line profiles. The latter are shown in Figs. 9, and 10 for the Na I D1 and K I line, respectively, displaying the intensity of the µ-pointings in common between the IAG and the SST data, namely µ = 0.2, 0.3, 0.4, 0.6, 0.8, 1.0, and the µ = 0.1 profile in comparison with the SST profile. The line profiles of the other Na lines compared with the IAG data only, are shown in Figs. A.4, A.5 and A.6. Moreover, Figs. A.7 and A.8 show the line profiles of the Na I D1 and K I 7699 Å of the IAG data at original resolution compared with the non-convolved synthetic spectra. In all the figures, from left to right, the panels display the data with the best-fit 1D LTE, 1D non-LTE, 3D LTE and 3D non-LTE synthetic spectra overplotted.
As is apparent from all these figures, the 3D non-LTE modeling is able to consistently reproduce the observed line profiles from the disk center to the limb. On the other hand, the shape and asymmetries of the line profiles are not well modeled by the 1D non-LTE spectra, getting worse at the limb even if the disk center intensity matches the data quite well. The LTE spectra instead fail to correctly reproduce the shape of the lines even at disk center. The Wλ of the observations at different µ-angles are reported in Tables A.1 and A.2 for the SST and IAG data, respectively. The best-fitting abundances are reported in Table 4, from which we notice that the average Na abundance from 3D non-LTE models is in very good agreement with the value of A(Na) = 6.22 ± 0.03, derived by Asplund et al. (2021) even if they used a different line selection. The K I abundance instead, in this work is higher by about 0.14 dex compared to the Asplund et al. (2021) value. However, it is important to note that the Na I D and K I resonance lines are not ideal abundance diagnostics as they are saturated lines. Hence, the values in Asplund et al. (2021) are preferred in the context of the solar chemical composition.
The reason why the 3D non-LTE modeling overestimates the line strengths Wλ at the limb in Na I lines (Fig. 7) is not fully clear and we investigated the impact of collisions with neutral hydrogen (H). As discussed in Sect 3.2, earlier work has argued that it could be necessary to add rate coefficients from asymptotic models such as those of Barklem (2016) or Belyaev (2013), to those from the free electron model of Kaulakys (1991). Motivated by this, the Na model atom tested here includes additional rate coefficients from Kaulakys (1991) for the Na+H collisions, even though the base data are not from an asymptotic model, but come from detailed quantum mechanical calculations. We found that the additional rates have very little influence on the weak 6154 and 6160 Å lines, whereas the effect is more noticeable for the stronger 5688 Å and 5896 Å lines. Specifically, for the latter the 3D non-LTE model matches the CLV of the equivalent widths of the SST data much better, as can be seen from Fig. 7. The comparison with the previous model atom developed in Lind et al. (2011) is shown in Fig. A.1. With the previous model atom, the Wλ of the 3D non-LTE model prefers the IAG data, whereas in the new model atom (the one adopted in this work) the 3D non-LTE model is in better agreement with the SST data. Apart from uncertainties on the H collisions, other factors that might explain why the 3D non-LTE models do not perfectly match observations of some Na lines and the K I line at the limb, could be the uncertainties on the upper layers of the 3D model atmosphere as well as the vertical resolution of the model.
In the next section, we demonstrate the effect of CLV in narrowband transmission spectroscopy with the example of a Jupiter-sized planet orbiting around a Sun-like star. For this purpose, the best-fitting synthetic spectra are used to evaluate the CLV effect in a simulated Sun-Jupiter system in order to analyze the impact of different models and different assumptions on the measurement of planetary atmospheric species. Also, the CLV impact on different geometries of the planet-star system and on different lines is investigated.
 |
Fig. 9 Normalized observed (black dots and blue squares) intensity and synthetic (red lines) center-to-limb profiles for the Na I D1 line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.2 have been incrementally offset vertically by +0.3 for clarity. |
 |
Fig. 10 Normalized observed (black dots and blue squares) intensity and synthetic (red lines) center-to-limb profiles for the K I 7699 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.2 have been incrementally offset vertically by +0.3 for clarity. |
Solar abundances determined from the best-fitting synthetic spectrum at disk center for four Na I lines and one K I line.
4.3 Sun-Jupiter system
The simulation of a transit of a Jupiter-like planet on a circular orbit in front of a Sun-like star is performed by means of a modified version of the StarRotator8 python package. This code simulates how the rotation-broadened stellar spectrum varies during a planetary transit event. As the transit progresses, the planet blocks the light from different parts of the stellar disk, each contributing differently to the line profile. Consequently, the resulting stellar line profile varies in shape and strength during the transit phases in a non-homogeneous way, also depending on the geometry of the star-planet system (i.e., the pattern of the planet across the stellar disk during the transit). We chose to simulate a circular orbit since most hot Jupiters are found in low eccentric orbits that have been circularized due to perturbations from nearby stars or tidal forces (e.g., Fabrycky & Tremaine 2007). In an eccentric orbit, the transit duration would vary, as well as the ingress/egress shape, while the amplitude of the CLV light curve would not significantly change. In the simulation, the stellar disk is divided into a grid of (2×400)×(2×400) cells (i.e., 800×800 square pixels), which provides sufficient spatial resolution for our simulations. Indeed, other works in literature have usually adopted a lower resolution of the grid of (2×100)×(2×100) cells (e.g., Wyttenbach et al. 2015; Yan et al. 2017). However, we performed a simulation with a lower resolution (i.e., (2×100)×(2×100)), finding a maximum difference in the resulting spectra of about 0.01%, which is non-negligible for our CLV study. We also tested a higher resolution grid with (2 × 800) × (2 × 800) elements and we found a maximum difference of only 0.001% among the spectra, which instead is insignificant for our purposes. Therefore, we decided to run our simulations with a (2×400)×(2×400) grid which shows a good balance of resolution and computational time.
Each of the elements of the stellar surface is characterized by its own properties, in terms of µ-angle, corresponding radial velocity (vµ), and intensity (Iµ). The latter comes from the best-fit spectra synthesized with Balder in 3D non-LTE, linearly interpolated at 21 positions between the disk center and the edge, with a spacing of Δµ = 0.05. Other studies employed the same number of spectra at different angles (e.g., Czesla et al. 2015; Sicilia et al. 2022). In order to avoid numerical problems at the edge of the stellar disk, the final angle was chosen to be µ = 0.001 instead of 0. For the cells at intermediate µ-angles, a linear interpolation between the spectra of the grid is performed. This is the main difference with the original StarRotator package, in which the spectra describing the stellar atmospheres are modeled with either the PHOENIX code (Husser et al. 2013), which does not take into account the CLV of the lines, or SPECTRUM (Szente et al. 2019), which considers the CLV effect (i.e., the intensity is given at different µ-angles) but its RT computation is performed in 1D LTE. In the following simulation instead, the stellar spectra are computed in the more realistic 3D non-LTE assumption.
It is important to notice that the planet is only considered as an opaque body without any atmosphere. In the simulation, the stellar flux is computed by summing up the spectra of the regions of the discretized stellar disk that are not obscured by the planet (i.e., the “unobscured” stellar spectrum, Fs), so that the observed line profile varies at different orbital phases. This translates into the following equation at i-th phase of transit:
where Fout is the out-of-transit flux and Fp is the integrated flux that is obscured by the planet during the transit at i-th orbital phase. Then, by dividing Fs by its continuum, the normalized spectrum for each given orbital phase is obtained.
Finally, the transmission curve or CLV curve is obtained as the relative flux (Frel), defined as the ratio of the normalized in (Fin) to out-of-transit stellar flux (Fout) integrated into a given bandwidth centered on the line core, as a function of orbital phase:
The simulations were performed several times with the same set-up, summarised in Table 5, but considering different impact parameters (b), that is varying the planet trajectory from an edge-on transit (b = 0) to a grazing transit (b = 1) in steps of 0.2, as outlined in the illustration in Fig. 11. This was done because previous studies have shown that the CLV curve is affected by planetary parameters, such as the planetary radius and impact parameter. The effect from the former is straightforward: the larger the radius, the stronger the CLV effect since the planet will block more light during the transit. On the other hand, the effect of different trajectories defined by the impact parameter is more complicated to evaluate and we will investigate it further in Sect. 4.3.1.
The final goal of this simulation is to investigate how the CLV of the stellar lines influences the observed spectral line profile during the transit of a Jupiter-sized planet in front of a Sun-like star. This is done by evaluating how the relative flux varies during the transit, that is at different orbital phases. Previous studies on the Na I D lines (e.g., Czesla et al. 2015; Yan et al. 2017) investigated passbands of 0.75, 1.5, and 3.0 Å, noting that the CLV effect is more pronounced in the narrower bandwidth, which is also where the planetary absorption is more prominent. We therefore selected the same three bandwidths to investigate how the line profile changes at different orbital phases during the transit, and with different impact parameters. All the out-of-transit relative flux is normalized to unity.
In the simulations, we considered 66 time steps between orbital phase −0.0005 and +0.0005, where the transit center occurs at phase zero. The CLV light curve, that is the relative flux as a function of the orbital phase, using the best-fit 3D non-LTE model for the Na I D1 line and an edge-on transit is shown in Fig. 12. In this figure, the relative flux in three bandwidths is highlighted in different colors. It can be noted that the CLV curves show a similar shape but the effect is more pronounced for the narrowest passband, that is 0.75 Å (green line in the figure), which is consistent with other studies. However, minimizing the CLV effect by choosing a larger passband might not be the best approach to use, since the absorption from the planet’s atmosphere is usually concentrated in the core of the strong lines. Therefore, in order to better understand how the CLV varies among different trajectories, we analyzed only the flux in the 0.75 Å bandwidth, since the CLV effect is more prominent in this band.
Input parameters for the simulated Sun-Jupiter system.
 |
Fig. 11 Transit schematic with different impact parameters. |
 |
Fig. 12 Transmission curves of the Na I 5896+,Å line for a Jupiter-sized planet transiting a Sun-like star in an edge-on transit (i.e., b = 0), evaluated in different bandwidths around the line center, colored as in legend. 3D non-LTE synthetic spectra are used. |
 |
Fig. 13 Transmission curves of the Na I D1 (top), Na I D2 (middle) and K I line (bottom) for a Jupiter-sized planet transiting a Sun-like star in different trajectories, colored as in legend. The CLV curves are made using synthetic spectra in 3D non-LTE. The relative flux is computed in a bandwidth of 0.75 Å on the line center. |
4.3.1 Different impact parameters
The CLV light curves for transits at different impact parameters are shown in Fig. 13 for the Na I D1, D2 and K I lines from top to bottom, respectively. In Fig. 13, some interesting features in common between the three analyzed lines can be noticed. First of all, as expected, the CLV effect is stronger for an edge-on and almost edge-on transit (i.e., b = 0 or b = 0.2), represented by the blue and yellow solid lines. In particular, it is most pronounced around mid-transit, that is at phase 0, when the planet blocks the light from the very center of the stellar disk, where the intensity of the lines is stronger. Then, varying the impact parameter, the curve varies in a fairly uniform way until b = 0. 6 (red line), and the weakest curve occurs for a grazing transit at b = 1. 0 (brown line), as expected since the planet is obscuring only a small part of the stellar disk during the transit. However, in this specific case, an interesting effect occurs for the Na I D1 and D2 lines, namely that the CLV curve resembles a planetary absorption profile. This means that for a Jupiter-sized planet orbiting a Sun-like star in this trajectory, the CLV effect can mimic a planetary atmospheric absorption, thus leading to a possible misattribution in the planetary elemental abundance of Na if it is not properly corrected. This highlights the importance of properly modeling the stellar CLV in transmission spectroscopy studies.
It is worth noting that even if the CLV curves of Na I D1 and D2 lines have similar shapes at different geometry, the values are still slightly different. For example, in the case of b = 0 (blue line), the CLV curve of the Na I D1 line is about 0.1% lower than the Na I D2 at mid-transit. And the difference between the curve of the Na I D2 and the K I curve at the same point is even larger (about 0.27%). Indeed, the two curves exhibit a completely opposite behavior. For b = 0 to 0.6, the Na I doublet shows a peak with positive values at mid-transit, whereas the peak for the K I line occurs for negative values. This contrast arises from the distinct CLV of the lines (Figs. 7 and 8), with the Na I D1 line weakening as the µ-angles decrease, while the K I line strengthens toward the limb. The different CLV can be explained since the two lines have very different strengths (the Na I D lines are on the damping part of the curve-of-growth whereas the K I resonance line is on the flat, saturated part) and are forming at different layers in the solar atmosphere, characterized by different values of atmospheric depth-dependent quantities, such as temperature, density, and velocity fields. Therefore, since different spectral lines show different CLV light curves for the same geometry of the planetstar system, it is fundamental to model the CLV individually for each line of interest.
4.3.2 Different stellar models
The emergent intensity spectra adopted to simulate the stellar surface of the host star in StarRotator affect the resulting CLV curve. As also noticed in a recent work by Reiners et al. (2023), the amplitude and shape of the curve indeed change with different models, since the center-to-limb line profiles are different (see Sects. 4.1 and 4.2). In order to evaluate the impact of using different stellar models, that is 1D instead of 3D or LTE instead of non-LTE, we performed the same simulations of Sect. 4.3.1 again but using as input the best-fit stellar spectra from Balder computed in 1D LTE, 1D non-LTE and 3D LTE (see Sect. 4.1). We also performed a simulation at b = 0 using the line profiles of the SST data. In Fig. 14 we show the CLV light curves of the analyzed lines with different models and the SST data for an edge-on transit (b = 0), computed in a band of 0.75 Å, since it is the configuration with the strongest feature. The differences between the models depend on each individual line but there are several similar patterns.
Yan et al. (2017) noticed that for the Na I D lines, the CLV effect is less pronounced for a 1D non-LTE model compared to the corresponding 1D LTE model. In this work we find a similar result, that is clearly recognizable in the top panel of Fig. 14, where the relative flux of the 1D LTE model (dashed red line) is larger by about 0.15% than the corresponding 1D non-LTE model (dashed blue line). This is valid also for the K I line in the bottom panel where the difference between the two 1D models is about 0.1%.
For the models computed in non-LTE, in the Na I D1, the difference between a 3D (solid blue line) and a 1D (dashed blue line) atmosphere is that the former produces a less prominent CLV feature of about 0.07%. On the other hand, the situation is reversed for the K I line, where the 3D non-LTE model not only shows a more pronounced feature compared to the 1D non-LTE curve (of about 0.06%) but also an inversion in the relative flux trend with respect to the 1D model, especially noticeable at mid-transit. This is due to the different CLV trend of the synthetic spectra, shown in Fig. 8 in Sect. 4.1, where the 3D non-LTE model gets stronger at the limb, while all the other models exhibit line weakening for decreasing µ-angles. Specifically, the weaker the line gets toward the limb, the larger the amplitude of the CLV curve will be at mid-transit. For both lines, the 1D LTE model is the one that decreases the most in equivalent width (Figs. 7 and 8), and therefore it is producing a higher peak in the CLV light curve in Fig. 14.
In all cases, the 3D LTE model (solid red line) lies in-between the 1D LTE and 1D non-LTE curves. The latter more closely resembles the 3D non-LTE model and the SST data. Consequently, from the analysis, it turns out that using a 1D non-LTE model is more accurate than using a 3D stellar atmosphere with an LTE line formation.
The CLV light curve obtained using the SST line profiles is overplotted in Fig. 14 (open bullets). In both panels, it closely resembles the 3D non-LTE model, with a maximum difference at mid-transit of only 0.003% for the Na I D1. The 3D non-LTE model of K I performs almost as well, with a maximum difference of about 0.008% at mid-transit, reflecting the slightly worse fit to the CLV curve (see Sects. 4.1 and 4.2). In any case, the agreement between the CLV curves of the SST data and the 3D non-LTE spectra is excellent, thus confirming that 3D non-LTE spectra are necessary to model the CLV effect and to get the most accurate results in transmission spectroscopy.
This analysis shows that different assumptions on the computation of the stellar synthetic spectra (1D or 3D, LTE or non-LTE) lead to different CLV curves and consequently to different estimates of the planetary elemental abundances. The differences in the CLV curves between models, even if small, are still important since they are on the same order of magnitude as a planetary absorption depth, which is very weak and typically between 0.01–0.5% (e.g., Snellen et al. 2008; Yan et al. 2017; Mounzer et al. 2022). Using a wrong CLV model could either mimic the presence of a species, thus leading to a false detection, or under(over)-estimate the abundance of a species in the planetary atmosphere. Therefore, a careful modeling as realistic and as precise as possible is required in order to correctly characterize exoplanet atmospheres.
 |
Fig. 14 Transmission curves and residuals of the Na I D1 (top) and K I line (bottom) for a Jupiter-sized planet transiting a Sun-like star at b = 0, using different models and the SST data to compute the stellar spectrum, as in legend. The relative flux is computed in a bandwidth of 0.75 Å around the line center. The residuals are the difference between the curve given by the SST data and the models in percentage. |
4.3.3 Rossiter McLaughlin effect
The Rossiter McLaughlin (RM) effect is an additional source of distortion of the stellar line profile that occurs during an exoplanetary transit and that could be as critical as the CLV effect, especially in fast-rotating stars like KELT-9 (Hoeijmakers et al. 2019). When an exoplanet transits across the stellar disk, it obscures different parts of the stellar surface, each having a local rotational velocity vector that could be pointing toward or away from the observer, depending on the transit phase. Consequently, red- or blue-shifted photons are removed from the total starlight, implying that the averaged wavelength is slightly red or blue-shifted as well. In order to investigate the combined effect of the CLV and the RM on the selected line profiles, we perform simulations of an edge-on transit (b = 0) with a non-zero rotational velocity (vrot) using our 3D non-LTE synthetic spectra of the Na I D1 line. Specifically, one simulation assuming a slow-rotator like a Sun-like star, with a vrot equal to the rotational velocity of the Sun, that is 2069.44 m s−1 at the equator (Meftah et al. 2014), and another simulation for a fast-rotator (i.e., Prot ≤ 10 days), assuming a vrot = 10 km s−1, which for a Sun-like star would correspond to a rotational period of about five days. In these simulations we assume that the star rotates as a solid body, meaning that differential rotation is not implemented in the code, and consequently, it is neglected in our analysis.
The results of these simulations are shown in Figs. 15 and 16, in comparison with the same planet-star configuration with the CLV effect only. The former figure shows the signal imprinted by the planet when transiting the stellar disk, also often referred to as “Doppler shadow”. It usually represents the combination of the stellar CLV and RM, and this signal becomes stronger the faster the star rotates. In Fig. 16, the transmission curve computed in a bandwidth of 0.75 Å is shown for the three models with different stellar rotational velocities. As is apparent, the curve becomes asymmetric due to the RM effect. The asymmetry is more relevant for higher vrot and the amplitude of the curve becomes larger as well. In the Sun case, the CLV is the dominant source of distortion of the stellar lines, and this is also valid for other slow-rotating Sun-like stars, such as HD 189733 (Borsa & Zannoni 2018). On the other hand, in very fast-rotating stars, such as KELT-9 where the lines are very broadened due to the high rotational velocity (v sin(i) = 111.4 km s−1, Gaudi et al. 2017), the RM becomes significantly more important than the CLV.
5 Discussion and conclusions
In this work, we model the CLV of the Na I D1 5896 Å line and K I 7699 Å line using 3D hydrodynamic solar models and non-LTE line formation. We compare our synthetic spectra to solar observations from the high-resolution IAG Atlas as well as to SST/CRISP data taken in two different Campaigns in August 2022 and April 2023. We include in the comparison also 1D LTE, 1D non-LTE, and 3D LTE synthetic spectra. For the model atmosphere, we use ten snapshots from the Stagger solar simulation in 3D and the MARCS solar model in 1D. We investigate the line profile as well as the equivalent width (Wλ) of the lines as a function of the µ-angle. The 3D non-LTE model represents the best match in both cases. It is able to reproduce the line shape from the center to the limb quite well and it is in reasonable agreement with the observed Wλ within 6% and 0.4% at µ = 0.1 for the K I and Na I D1 line, respectively. 1D models are symmetric by design therefore they are not able to reproduce the line asymmetries that are particularly strong in resonance lines. A 3D stellar atmosphere and a proper treatment of convection are required. The LTE models typically produce lines with cores weaker than the observations but wings that are reasonably in agreement, at least for disk center line profiles. However, Wλ is severely underestimated, with differences up to 37% for the K I line at the limb.
With the best-fit synthetic spectra, we also perform simulations of spectral lines of a Sun-like star transited by a Jupiter-sized planet without an atmosphere in order to investigate the impact of the CLV on the inference of planetary absorptions. In transmission spectroscopy the CLV effect can be on the same order of magnitude as the planetary absorption feature, therefore it is fundamental to adopt model spectra as accurate as possible. We compute transmission curves for different trajectories, or impact parameters (b), and evaluate the flux in three different bandwidths centered on the line cores. The LTE models, both with 1D and 3D atmospheres, produce a CLV curve with an amplitude larger than in non-LTE, thus overestimating the effect of CLV. In the presence of a planetary absorption, this would eventually result in an underestimate of the abundance of the analyzed species in the planetary atmosphere. In a recent work by Reiners et al. (2023), they also found that the LTE curve amplitude is overpredicted when evaluating the CLV effect in a simulated planet-star system. They analyzed lines of several atomic species but they stress the fact that for Na I, non-LTE effects are definitely non-negligible in order to reproduce observations. In this work, the differences between models, 1D versus 3D and LTE versus non-LTE, are relatively small but on the same order of magnitude as a planetary absorption depth. The CLV curves also greatly vary in shape for different geometries of the star-planet system and for different lines. Even the CLV curves of lines of the same species, that is Na I D1 and D2 lines, are not identical. The CLV effect is indeed line-dependent and must be modeled line by line individually. We also perform a transit simulation with the SST line profiles and we find that the 3D non-LTE models are able to reproduce the CLV light curve of the observations extremely well.
Since the planetary parameters, such as the planet radius and impact parameter, are also crucial to correctly modeling the shape and strength of the CLV curve (Pietrow & Pastor Yabar 2023), these values need to be known with a high level of accuracy. For instance, in our simulations, the CLV curve of the Na doublet resulting from a grazing transit (b = 1.0) is very similar to a planetary absorption signature and therefore could be mistaken for a sodium detection if not properly corrected for. Nowadays, having accurate planetary parameters is possible thanks to the many ground-based as well as space-based telescopes performing high precision transit photometry, such as TESS (Ricker et al. 2014), CHEOPS (Benz et al. 2021), and also PLATO (Rauer et al. 2014) in the near future.
It is important to note that the simulation presented in this work represents a best-case scenario, given that only the quiet solar photosphere is considered. Inhomogeneities on the stellar surface due to active regions, such as starspots or plages, show a very different spectral line profile from the quiet regions (e.g., Oranje 1983; Dumusque et al. 2014; Pietrow et al. 2020, 2024; Rajhans et al. 2023; Howard et al. 2023; Cretignier et al. 2024). Observational data would allow for the effect of magnetic fields on the line profiles to be investigated. Hence, separate CLV should be measured in active regions in order to correctly incorporate them in the analysis of transmission spectra of active stars (Chakraborty et al. 2024). Future works should also include the modeling of synthetic spectra for active regions of different sizes and at various locations on the stellar disk.
The differences in CLV transmission curves can be larger for different kinds of stars, especially for low-temperature stars, where the effect is stronger as shown in Yan et al. (2017). Consequently, a very good knowledge of the stellar parameters is as important as the precision of the planetary parameters in order to use a model stellar atmosphere as realistic as possible for the modeling of the CLV curves. A significant advance in this direction is given by the recent release of Gaia DR3 (Gaia Collaboration 2021; Katz et al. 2023) and in the very near future by large spectroscopic surveys such as 4MOST (de Jong et al. 2019) and WEAVE (Dalton et al. 2018; Jin et al. 2023), which will target millions of FGK stars providing accurate stellar parameters.
With the continuous improvement of the instrumentation used for transit spectroscopy, such as ESPRESSO on VLT or ANDES on ELT, the CLV effect will soon become crucial not only for the detection but especially for the characterization of exoplanetary atmospheres. At present, some facilities have already achieved the high signal-to-noise ratio necessary for measuring the abundances of atmospheric species in hot Jupiters and other gas giants. Several works have shown that using different models for the stellar spectrum can lead to very different results. For example, the case of the benchmark exoplanet HD 209458b in which the presence of Na was debated in the literature. Initial works detected it in transmission (e.g., Charbonneau et al. 2002; Jensen et al. 2011) but then later analysis argued that it was just an artifact due to the modeled stellar spectrum (Casasayas-Barris et al. 2020, 2021). This highlights the importance of using correct stellar models to evaluate the subtle effects such as the CLV, which could compromise the analysis of transit spectroscopy observations.
The Sun is the only star we can spatially resolve, therefore, developing models able to reproduce solar observations is necessary to improve the CLV model of other stars as well, especially considering that transmission observations are expected to become more and more precise in the coming years. From our analysis, we can conclude that 1D models of Sun-like stars seem to overestimate the CLV signature in transmission curves. We can also say that, in accordance with previous works, the RM effect has an impact on the transmission curve as well which must be taken into account (Reiners et al. 2023). Specifically, it becomes stronger than the CLV effect for fast-rotating stars. For Sun-like stars instead, the CLV remains the main source of distortion of the stellar lines during transit.
However, it is difficult to make predictions about other kinds of stars or even about specific exoplanets, since every planet-star system is different and we show that different configurations lead to very different transmission curves. Consequently, future work includes the analysis of well-known and extensively studied hot Jupiters, such as HD 189733b or HD 209458b, for which several high-resolution observations are already available. The goal is to apply a 3D non-LTE stellar model to evaluate the CLV effect of Na I and K I in these benchmark exoplanets and then compare the results with previous works in the literature (e.g., Yan et al. 2017; Keles et al. 2019, 2020; Sicilia et al. 2022). The methodology presented in this work can be extended as well to other FGK stars using 3D stellar atmospheres from the new full Stagger grid (Rodríguez Díaz et al. 2023). It is worth noting that there are only a few studies where Na I and K I have been detected simultaneously (e.g., Casasayas-Barris et al. 2021). Given the opposite CLV curve of the resonance lines of the two ions, it would be interesting to observe those lines for more planet-star systems.
The impact of a 3D non-LTE modeling of the CLV of the stellar lines needs to be studied in other species and other spectral lines as well. For transmission spectroscopy in particular, interesting species that have been detected in the atmosphere of several exoplanets include Ca I, Ca II (e.g., Yan et al. 2019), Fe I (e.g., Hoeijmakers et al. 2018), Fe II (e.g., Bello-Arufe et al. 2022), and H I Balmer lines (e.g., Fossati et al. 2023).
Finally, with the recent launch of the JWST (Barstow et al. 2015), a new era of low-resolution transit spectroscopy has just begun. This space telescope will allow for the atmospheric characterization of a wide range of exoplanets, from hot Jupiters down to rocky planets and super-Earths. Low-resolution spectra are even more susceptible to the CLV effect in a wavelength-integrated sense than the high-resolution ones. Several studies have showm that high-resolution spectra, if adequately corrected for the RM and CLV effects, can be used to isolate the different spectral components and mitigate the stellar contamination in low-resolution spectra (e.g., Genest et al. 2022). Therefore, exploring the effect of stellar CLV on low-resolution spec-troscopy is an issue that has to be addressed in the near future and this work is a step forward to achieving the best possible results in exoplanet science with JWST.
 |
Fig. 15 Models of the CLV and RM effect of the Na I D1 line for a Sunlike star orbited by a Jupiter-sized planet at b = 0. The upper panel is the CLV effect-only, and the middle panel combines the CLV with the RM effect for a slow-rotator like the Sun. Finally, the bottom panel shows the two effects for a fast-rotator, that is a Sun-like star with a rotational velocity of 10 km s−1. |
 |
Fig. 16 Transmission curves of the Na I D1 line for a Jupiter-sized planet transiting a Sun-like star in an edge-on transit (b = 0), for different rotational velocities of the host star. 3D non-LTE synthetic spectra are used and the relative flux is computed in a bandwidth of 0.75 Å. |
Acknowledgements
We thank the anonymous referee for their comments, which have improved the manuscript. We thank A. Brandeker for the very useful comments on the first draft of the paper. We thank A. Reiners and M. Ellwarth for providing us with the Na I D1 and K I line profiles before the publication of the IAG Atlas, and for the errors on µ-angles. We also thank H. Reggiani for providing the potassium model atom that he developed. G.C. and K.L. acknowledge funds from the Knut and Alice Wallenberg foundation. K.L. and C.L. acknowledge funds from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement no. 852977). A.M.A. acknowledges support from the Swedish Research Council (VR 2020-03940). A.P. was supported at AIP by grants from the European Commission’s Horizon 2020 Program under grant agreements 824064 (ESCAPE – European Science Cluster of Astronomy & Particle Physics ESFRI Research Infrastructures) and 824135 (SOLARNET – Integrating High Resolution Solar Physics). The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX, partially funded by the Swedish Research Council through grant agreement no. 2018-05973. We thank the PDC Center for High Performance Computing, KTH Royal Institute of Technology, Sweden, for providing access to computational resources and support. The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics of Stockholm University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. The Institute for Solar Physics was supported by a grant for research infrastructures of national importance from the Swedish Research Council (registration number 2017-00625). The Swedish 1-m Solar Telescope, SST, is co-funded by the Swedish Research Council as a national research infrastructure (registration number 4.3-2021-00169). This research has made use of NASA’s Astrophysics Data System (ADS) bibliographic services. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. We acknowledge the community efforts devoted to the development of the following open-source packages that were used in this work: numpy (munpy.org), matplotlib (matplotlib.org) and astropy (astropy.org). We also used the CRISPEX analysis tool (Vissers & Rouppe van der Voort 2012) and the ISPy library (Díaz Baso et al. 2021).
Appendix A Additional tables and figures
 |
Fig. A.1 Comparison between 3D non-LTE models of the old Na atom and the new one, with added H rate coefficients from Kaulakys (1991). |
Equivalent widths (in mÅ) measured for the observed spectra of the SST data at different µ-angles via direct integration of the line profiles.
 |
Fig. A.2 Na I D1 data taken in Campaign I. Left: Limb darkening data of each wavelength point in the Na I D1 line on an arbitrary intensity scale. The curves are ordered by wavelength, with the top (red) curve representing the red continuum, the middle (green) curve representing the line core, and the bottom (blue) curve representing the blue continuum. Right: Normalized intensity of the averaged line profiles at different µ-angles. Spectra for µ ≥ 0.15 have been incrementally offset vertically by +0.3 for clarity. |
 |
Fig. A.3 K I data taken in Campaign II. Left: Limb darkening data of each wavelength point in the K I 7699 Å line on an arbitrary intensity scale. The curves are ordered by wavelength, with the top (red) curve representing the red continuum, the middle (green) curve representing the line core, and the bottom (blue) curve representing the blue continuum. Right: Normalized intensity of the averaged line profiles at different µ-angles. Spectra for µ ≥ 0.15 have been incrementally offset vertically by +0.3 for clarity. |
 |
Fig. A.4 Normalized observed (black dots) intensity and synthetic (red lines) center-to-limb profiles for the Na I 5688 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
 |
Fig. A.5 Normalized observed (black dots) intensity and synthetic (red lines) center-to-limb profiles for the Na I 6154 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
 |
Fig. A.6 Normalized observed (black dots) intensity and synthetic (red lines) center-to-limb profiles for the Na I 6160 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
 |
Fig. A.7 Normalized observed (black dots) intensity from the IAG Atlas and synthetic (red lines) center-to-limb profiles for the Na I D1 at 5896 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
 |
Fig. A.8 Normalized observed (black dots) intensity from the IAG Atlas and synthetic (red lines) center-to-limb profiles for the K I 7699 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
References
- Allen, L. J., & Rossouw, C. J. 1993, Phys. Rev. B, 47, 2446 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Asplund, M., Collet, R., & Leenaarts, J. 2016a, MNRAS, 455, 3735 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., & Collet, R. 2016b, MNRAS, 463, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Barklem, P. S., Asplund, M., Collet, R., & Zatsarinny, O. 2018a, A&A, 616, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A. M., Nordlander, T., Barklem, P. S., et al. 2018b, A&A, 615, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A. M., Barklem, P. S., Collet, R., Grevesse, N., & Asplund, M. 2019, A&A, 624, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A. M., Grevesse, N., Grumer, J., et al. 2020, A&A, 636, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A. M., Grevesse, N., Asplund, M., & Collet, R. 2021, A&A, 656, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [Google Scholar]
- Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A&A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S. 2016, Phys. Rev. A, 93, 042705 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Belyaev, A. K., Dickinson, A. S., & Gadéa, F. X. 2010, A&A, 519, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Osorio, Y., Fursa, D. V., et al. 2017, A&A, 606, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barstow, J. K., Aigrain, S., Irwin, P. G. J., Kendrew, S., & Fletcher, L. N. 2015, MNRAS, 448, 2546 [NASA ADS] [CrossRef] [Google Scholar]
- Bello-Arufe, A., Buchhave, L. A., Mendonça, J. M., et al. 2022, A&A, 662, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belyaev, A. K. 2013, Phys. Rev. A, 88, 052704 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, A. K., & Yakovleva, S. A. 2017, A&A, 606, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belyaev, A. K., Barklem, P. S., Dickinson, A. S., & Gadéa, F. X. 2010, Phys. Rev. A, 81, 032706 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
- Bergemann, M., Gallagher, A. J., Eitner, P., et al. 2019, A&A, 631, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Hoppe, R., Semenova, E., et al. 2021, MNRAS, 508, 2236 [NASA ADS] [CrossRef] [Google Scholar]
- Bjørgen, J. P., Sukhorukov, A. V., Leenaarts, J., et al. 2018, A&A, 611, A62 [Google Scholar]
- Borsa, F., & Zannoni, A. 2018, A&A, 617, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botnen, A., & Carlsson, M. 1999, in Astrophys. Space Sci. Lib., 240, Numerical Astrophysics, eds. S. M. Miyama, K. Tomisaka, & T. Hanawa, 379 [Google Scholar]
- Cabot, S. H. C., Madhusudhan, N., Welbanks, L., Piette, A., & Gandhi, S. 2020, MNRAS, 494, 363 [Google Scholar]
- Casasayas-Barris, N., Palle, E., Nowak, G., et al. 2017, A&A, 608, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2019, A&A, 628, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2020, A&A, 635, A206 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Palle, E., Stangret, M., et al. 2021, A&A, 647, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cauzzi, G., & Reardon, K. 2012, IAU Special Session, 6, E5.11 [Google Scholar]
- Cayrel, R. 1988, The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite, (Dordrecht: Kluwer), IAU Symp., 132, 345 [NASA ADS] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chakraborty, H., Lendl, M., Akinsanmi, B., Petit dit de la Roche, D. J. M., & Deline, A. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202347727 [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [Google Scholar]
- Chen, G., Casasayas-Barris, N., Pallé, E., et al. 2020, A&A, 635, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collet, R., Magic, Z., & Asplund, M. 2011, J. Phys. Conf. Ser., 328, 012003 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Nordlund, Å., Asplund, M., Hayek, W., & Trampedach, R. 2018, MNRAS, 475, 3369 [NASA ADS] [CrossRef] [Google Scholar]
- Colón, K. D., Ford, E. B., Redfield, S., et al. 2012, MNRAS, 419, 2233 [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446, 84461V [Google Scholar]
- Cretignier, M., Pietrow, A. G. M., & Aigrain, S. 2024, MNRAS, 527, 2940 [Google Scholar]
- Czesla, S., Klocová, T., Khalafinejad, S., Wolter, U., & Schmitt, J. H. M. M. 2015, A&A, 582, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalton, G., Trager, S., Abrams, D. C., et al. 2018, SPIE Conf. Ser., 10702, 107021B [Google Scholar]
- de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
- de la Cruz Rodríguez, J., Löfdahl, M. G., Sütterlin, P., Hillberg, T., & Rouppe van der Voort, L. 2015, A&A, 573, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz Baso, C. J., & Asensio Ramos, A. 2018, A&A, 614, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz Baso, C., Vissers, G., Calvo, F., et al. 2021, https://doi.org/10.5281/zenodo.5608441 [Google Scholar]
- Ding, M., & Fang, C. 1991, Chin. J. Space Sci., 11, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Doerr, H. P., Vitas, N., & Fabbian, D. 2016, A&A, 590, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorn, R. J., Anglada-Escude, G., Baade, D., et al. 2014, The Messenger, 156, 7 [NASA ADS] [Google Scholar]
- Dorn, R. J., Bristow, P., Smoker, J. V., et al. 2023, A&A, 671, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dravins, D., Lindegren, L., & Nordlund, A. 1981, A&A, 96, 345 [NASA ADS] [Google Scholar]
- Dravins, D., Ludwig, H.-G., Dahlén, E., & Pazira, H. 2017, A&A, 605, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dravins, D., Gustavsson, M., & Ludwig, H.-G. 2018, A&A, 616, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Boisse, I., & Santos, N. C. 2014, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Ellwarth, M., Schäfer, S., Reiners, A., & Zechmeister, M. 2023, A&A, 673, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Biassoni, F., Cappello, G. M., et al. 2023, A&A, 676, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaudi, B. S., Stassun, K. G., Collins, K. A., et al. 2017, Nature, 546, 514 [NASA ADS] [Google Scholar]
- Genest, F., Lafrenière, D., Boucher, A., et al. 2022, AJ, 163, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 A (San Francisco: ASP) [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Heng, K., et al. 2018, Nature, 560, 453 [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Kitzmann, D., et al. 2019, A&A, 627, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoeijmakers, H. J., Seidel, J. V., Pino, L., et al. 2020, A&A, 641, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, W. S., Kowalski, A. F., Flagg, L., et al. 2023, ApJ, 959, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Igenbergs, K., Schweinzer, J., Bray, I., Bridi, D., & Aumayr, F. 2008, At. Data Nucl. Data Tables, 94, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, A. G., Redfield, S., Endl, M., et al. 2011, ApJ, 743, 203 [Google Scholar]
- Jin, S., Trager, S. C., Dalton, G. B., et al. 2023, MNRAS, in press, https://doi.org/10.1093/mnras/stad557 [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, SPIE Conf. Ser., 5492, 1218 [NASA ADS] [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaulakys, B. 1991, J. Phys. B At. Mol. Phys., 24, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Keles, E., Mallonn, M., von Essen, C., et al. 2019, MNRAS, 489, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Keles, E., Kitzmann, D., Mallonn, M., et al. 2020, MNRAS, 498, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Lagae, C., Amarsi, A. M., Rodríguez Díaz, L. F., et al. 2023, A&A, 672, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., & Carlsson, M. 2009, in ASP Conf. Ser., 415, The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, 87 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Amarsi, A. M., Asplund, M., et al. 2017, MNRAS, 468, 4311 [NASA ADS] [CrossRef] [Google Scholar]
- Löfdahl, M. G. 2002, SPIE Conf. Ser., 4792, 146 [Google Scholar]
- Löfdahl, M. G., Hillberg, T., de la Cruz Rodríguez, J., et al. 2021, A&A, 653, A68 [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Meftah, M., Irbah, A., & Hauchecorne, A. 2014, SPIE Conf. Ser., 9143, 91431R [NASA ADS] [Google Scholar]
- Morello, G., Casasayas-Barris, N., Orell-Miquel, J., et al. 2022, A&A, 657, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mounzer, D., Lovis, C., Seidel, J. V., et al. 2022, A&A, 668, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [Google Scholar]
- Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [CrossRef] [Google Scholar]
- Nordlander, T., & Lind, K. 2017, A&A, 607, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, Å., & Galsgaard, K. 1995, A 3D MHD Code for Parallel Computers, Tech. Rep., Astronomical Observatory, Copenhagen University [Google Scholar]
- Oranje, B. J. 1983, A&A, 124, 43 [NASA ADS] [Google Scholar]
- Park, C. 1971, J. Quant. Spec. Radiat. Transf., 11, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Kiselman, D., & Asplund, M. 2009, A&A, 507, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierce, A. K., & Slaughter, C. D. 1977, Sol. Phys., 51, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, A. K., & Slaughter, C. 1982, ApJS, 48, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrow, A. G. M., & Pastor Yabar, A. 2023, arXiv e-prints [arXiv:2311.06200] [Google Scholar]
- Pietrow, A. G. M., Kiselman, D., de la Cruz Rodríguez, J., et al. 2020, A&A, 644, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrow, A. G. M., Hoppe, R., Bergemann, M., & Calvo, F. 2023a, A&A, 672, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrow, A. G. M., Kiselman, D., Andriienko, O., et al. 2023b, A&A, 671, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrow, A. G. M., Cretignier, M., Druett, M. K., et al. 2024, A&A, 682, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [Google Scholar]
- Rajhans, A., Tripathi, D., Kashyap, V. L., Klimchuk, J. A., & Ghosh, A. 2023, ApJ, 944, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Ralchenko, Y. 2005, Mem. Soc. Astron. Ital. Supp., 8, 96 [Google Scholar]
- Ramelli, R., Setzer, M., Engelhard, M., et al. 2017, arXiv e-prints [arXiv:1708.03284] [Google Scholar]
- Ramelli, R., Bianda, M., Setzer, M., et al. 2019, in ASP Conf. Ser., 526, Solar Polariation Workshop 8, eds. L. Belluzzi, R. Casini, M. Romoli, & J. Trujillo Bueno, 287 [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Reggiani, H., Amarsi, A. M., Lind, K., et al. 2019, A&A, 627, A177 [EDP Sciences] [Google Scholar]
- Reiners, A., Yan, F., Ellwarth, M., Ludwig, H. G., & Nortmann, L. 2023, A&A, 673, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rodríguez Díaz, L. F., Lagae, C., Amarsi, A. M., et al. 2023, A&A, submitted [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005 [Google Scholar]
- Schäfer, S., Huke, P., Meyer, D., & Reiners, A. 2020, SPIE Conf. Ser., 11447, 114473Q [Google Scholar]
- Scharmer, G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., & Petterson, B. 2003, SPIE Conf. Ser., 4853, 341 [NASA ADS] [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008, ApJ, 689, L69 [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Wyttenbach, A., et al. 2019, A&A, 623, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Bourrier, V., et al. 2020, A&A, 641, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Borsa, F., Pino, L., et al. 2023, A&A, 673, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sicilia, D., Malavolta, L., Pino, L., et al. 2022, A&A, 667, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sing, D. K., Désert, J. M., Fortney, J. J., et al. 2011, A&A, 527, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Le Poole, R. S. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
- Stenflo, J. O. 2015, A&A, 573, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Ilyin, I., Järvinen, A., et al. 2015, Astron. Nachr., 336, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Szente, J., Landi, E., Manchester, W. B. I., et al. 2019, ApJS, 242, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Van Noort, M., Rouppe Van Der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Vissers, G., & Rouppe van der Voort, L. 2012, ApJ, 750, 22 [Google Scholar]
- Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyttenbach, A., Lovis, C., Ehrenreich, D., et al. 2017, A&A, 602, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yakovleva, S. A., Barklem, P. S., & Belyaev, A. K. 2018, MNRAS, 473, 3810 [CrossRef] [Google Scholar]
- Yan, F., Pallé, E., Fosbury, R. A. E., Petr-Gotzens, M. G., & Henning, T. 2017, A&A, 603, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., Casasayas-Barris, N., Molaverdikhani, K., et al. 2019, A&A, 632, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Atomic data of the sodium and potassium lines considered in the CLV analysis, as implemented in the model atoms of Lind et al. (2011) and Reggiani et al. (2019).
Solar abundances determined from the best-fitting synthetic spectrum at disk center for four Na I lines and one K I line.
Equivalent widths (in mÅ) measured for the observed spectra of the SST data at different µ-angles via direct integration of the line profiles.
All Figures
 |
Fig. 1 Full-disk image of the Sun on 29 April 2023 in the AIA 171 Å filter (Lemen et al. 2012). The black squares show all telescope pointings used during the observation campaigns, spanning from the solar north pole to disk center. |
| In the text | |
 |
Fig. 2 Intensity profile of the Na I D1 line at disk center. Top: comparison of the Na I D1 line profile at disk center between the SST/CRISP data (black dots) and the IAG Atlas convolved with the instrumental profile (red dashed line). The original profile from the IAG Atlas is also plotted with a black solid line. The grey-shaded region highlights the selected wavelength range for Wλ computation. A telluric spectrum (Hinkle et al. 2000) is overplotted as a grey line in the top panel, to show that there is negligible contamination in the Wλ window. Bottom: difference between the convolved IAG Atlas and the SST data in percentage. |
| In the text | |
 |
Fig. 3 Intensity profile of the K I resonance line at disk center. Top: comparison of the K I 7699 line profile at disk center between the SST/CRISP data (black dots) and the IAG Atlas convolved with the instrumental profile (red dashed line). The original profile from the IAG Atlas is also plotted with a black solid line. The grey-shaded region highlights the selected wavelength range for Wλ computation. A telluric spectrum (Hinkle et al. 2000) is overplotted as a grey line in the top panel, to show that there is negligible contamination in the Wλ window. Bottom: difference between the convolved IAG Atlas and the SST data in percentage. |
| In the text | |
 |
Fig. 4 Comparison of the SST/CRISP data (black dots) with the IAG FTS CLV Atlas (red squares) convolved with CRISP instrumental profile. Top: equivalent width of the Na I D1 line as a function of the µ-angle. Bottom: difference between the IAG and the SST data in percentage. |
| In the text | |
 |
Fig. 5 Comparison of the SST/CRISP data (black dots) with the IAG FTS CLV Atlas (red squares) convolved with CRISP instrumental profile. Top: equivalent width of the K I line at 7699 Å as a function of the µ-angle. Bottom: difference between the IAG and the SST data in percentage. |
| In the text | |
 |
Fig. 6 Ratio of the NLTE to LTE equivalent width of KI 7699 Å for a single Stagger snapshot. In the up-flowing granules, overionization makes the line weaker in NLTE, whereas in the intergranular lanes the NLTE Wλ is stronger. |
| In the text | |
 |
Fig. 7 Center-to-limb variation of the solar Na I lines. Comparison of the equivalent widths of the IAG Atlas (filled squares) and the SST data (open circles) with several different model atmospheres and atomic data, colored as in the figure’s legend. |
| In the text | |
 |
Fig. 8 Center-to-limb variation of the K I 7699 Å line. Comparison of the IAG Atlas (filled squares) and the SST data (open circles) with several different model atmospheres and atomic data, colored as in the figure legend. |
| In the text | |
 |
Fig. 9 Normalized observed (black dots and blue squares) intensity and synthetic (red lines) center-to-limb profiles for the Na I D1 line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.2 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. 10 Normalized observed (black dots and blue squares) intensity and synthetic (red lines) center-to-limb profiles for the K I 7699 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.2 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. 11 Transit schematic with different impact parameters. |
| In the text | |
 |
Fig. 12 Transmission curves of the Na I 5896+,Å line for a Jupiter-sized planet transiting a Sun-like star in an edge-on transit (i.e., b = 0), evaluated in different bandwidths around the line center, colored as in legend. 3D non-LTE synthetic spectra are used. |
| In the text | |
 |
Fig. 13 Transmission curves of the Na I D1 (top), Na I D2 (middle) and K I line (bottom) for a Jupiter-sized planet transiting a Sun-like star in different trajectories, colored as in legend. The CLV curves are made using synthetic spectra in 3D non-LTE. The relative flux is computed in a bandwidth of 0.75 Å on the line center. |
| In the text | |
 |
Fig. 14 Transmission curves and residuals of the Na I D1 (top) and K I line (bottom) for a Jupiter-sized planet transiting a Sun-like star at b = 0, using different models and the SST data to compute the stellar spectrum, as in legend. The relative flux is computed in a bandwidth of 0.75 Å around the line center. The residuals are the difference between the curve given by the SST data and the models in percentage. |
| In the text | |
 |
Fig. 15 Models of the CLV and RM effect of the Na I D1 line for a Sunlike star orbited by a Jupiter-sized planet at b = 0. The upper panel is the CLV effect-only, and the middle panel combines the CLV with the RM effect for a slow-rotator like the Sun. Finally, the bottom panel shows the two effects for a fast-rotator, that is a Sun-like star with a rotational velocity of 10 km s−1. |
| In the text | |
 |
Fig. 16 Transmission curves of the Na I D1 line for a Jupiter-sized planet transiting a Sun-like star in an edge-on transit (b = 0), for different rotational velocities of the host star. 3D non-LTE synthetic spectra are used and the relative flux is computed in a bandwidth of 0.75 Å. |
| In the text | |
 |
Fig. A.1 Comparison between 3D non-LTE models of the old Na atom and the new one, with added H rate coefficients from Kaulakys (1991). |
| In the text | |
 |
Fig. A.2 Na I D1 data taken in Campaign I. Left: Limb darkening data of each wavelength point in the Na I D1 line on an arbitrary intensity scale. The curves are ordered by wavelength, with the top (red) curve representing the red continuum, the middle (green) curve representing the line core, and the bottom (blue) curve representing the blue continuum. Right: Normalized intensity of the averaged line profiles at different µ-angles. Spectra for µ ≥ 0.15 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. A.3 K I data taken in Campaign II. Left: Limb darkening data of each wavelength point in the K I 7699 Å line on an arbitrary intensity scale. The curves are ordered by wavelength, with the top (red) curve representing the red continuum, the middle (green) curve representing the line core, and the bottom (blue) curve representing the blue continuum. Right: Normalized intensity of the averaged line profiles at different µ-angles. Spectra for µ ≥ 0.15 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. A.4 Normalized observed (black dots) intensity and synthetic (red lines) center-to-limb profiles for the Na I 5688 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. A.5 Normalized observed (black dots) intensity and synthetic (red lines) center-to-limb profiles for the Na I 6154 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. A.6 Normalized observed (black dots) intensity and synthetic (red lines) center-to-limb profiles for the Na I 6160 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. A.7 Normalized observed (black dots) intensity from the IAG Atlas and synthetic (red lines) center-to-limb profiles for the Na I D1 at 5896 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
 |
Fig. A.8 Normalized observed (black dots) intensity from the IAG Atlas and synthetic (red lines) center-to-limb profiles for the K I 7699 Å line, where the numbers above each spectrum correspond to the µ-angle. In the left corner, the calibrated abundance is shown. Spectra for µ ≥ 0.3 have been incrementally offset vertically by +0.3 for clarity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



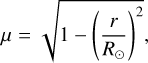
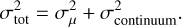
![${F_{\rm{S}}}[i] = {F_{{\rm{out}}}} - {F_{\rm{p}}}[i],$](/articles/aa/full_html/2024/03/aa47858-23/aa47858-23-eq11.png)