| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A248 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347157 | |
| Published online | 22 March 2024 | |
Unveiling the bent-jet structure and polarization of OJ 287 at 1.7 GHz with space VLBI
1
Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
2
Korea Astronomy and Space Science Institute, Daedeok-daero 776, Yuseong-gu, Daejeon 34055, Republic of Korea
e-mail: icho@kasi.re.kr
3
Department of Astronomy, Yonsei University, Yonsei-ro 50, Seodaemun-gu, 03722 Seoul, Republic of Korea
4
INAF – Istituto di Radioastronomia, Via P. Gobetti 101, 40129 Bologna, Italy
5
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
6
Lebedev Physical Institute of the Russian Academy of Sciences, Leninsky prospekt 53, 119991 Moscow, Russia
7
Moscow Institute of Physics and Technology, Institutsky per. 9, Dolgoprudny, Moscow region 141700, Russia
8
Crimean Astrophysical Observatory, 98409 Nauchny, Crimea
9
Joint Institute for VLBI ERIC (JIVE), Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
10
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 HS Delft, The Netherlands
11
Department of Astronomy and Atmospheric Sciences, Kyungpook National University, Daegu 702-701, Republic of Korea
12
Institut de Radioastronomie Millimétrique, Avenida Divina Pastora, 7, Local 20, 18012 Granada, Spain
13
Institute of Astrophysics, Foundation for Research and Technology – Hellas, N. Plastira 100, Voutes, 70013 Heraklion, Greece
Received:
12
June
2023
Accepted:
8
December
2023
We present total intensity and linear polarization images of OJ 287 at 1.68 GHz, obtained through space-based very long baseline interferometry (VLBI) observations with RadioAstron on April 16, 2016. The observations were conducted using a ground array consisting of the Very Long Baseline Array (VLBA) and the European VLBI Network (EVN). Ground-space fringes were detected with a maximum projected baseline length of ∼5.6 Earth’s diameter, resulting in an angular resolution of ∼530 μas. With this unprecedented resolution at such a low frequency, the progressively bending jet structure of OJ 287 has been resolved up to ∼10 parsec of the projected distance from the radio core. In comparison with close-in-time VLBI observations at 15, 43, 86 GHz from MOJAVE and VLBA-BU-BLAZAR monitoring projects, we obtain the spectral index map showing the opaque core and optically thin jet components. The optically thick core has a brightness temperature of ∼1013 K, and is further resolved into two sub-components at higher frequencies labeled C1 and C2. These sub-components exhibit a transition from optically thick to thin, with a synchrotron self-absorption (SSA) turnover frequency estimated to be ∼33 and ∼11.5 GHz, and a turnover flux density ∼4 and ∼0.7 Jy, respectively. Assuming a Doppler boosting factor of 10, the SSA values provide the estimate of the magnetic field strengths from SSA of ∼3.4 G for C1 and ∼1.0 G for C2. The magnetic field strengths assuming equipartition arguments are also estimated as ∼2.6 G and ∼1.6 G, respectively. The integrated degree of linear polarization is found to be approximately ∼2.5%, with the electric vector position angle being well aligned with the local jet direction at the core region. This alignment suggests a predominant toroidal magnetic field, which is in agreement with the jet formation model that requires a helical magnetic field anchored to either the black hole ergosphere or the accretion disk. Further downstream, the jet seems to be predominantly threaded by a poloidal magnetic field.
Key words: galaxies: active / galaxies: jets / quasars: supermassive black holes / radio continuum: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
OJ 287 (0851+202, J0854+2005, z = 0.306; Stickel et al. 1989) is one of the most studied BL Lacertae objects and considered to be a strong candidate for harboring a supermassive black hole binary (SMBHB) system at its center (e.g., Sillanpaa et al. 1988; Lehto & Valtonen 1996). For that reason, it attracts special attention as one of the most promising gravitational wave emitters at nano-hertz frequencies (e.g., Valtonen et al. 2021). In the optical regime, two quasiperiodic outbursts of ∼12 yr and ∼60 yr have been observed, which may be attributed to the gravitationally bound system of SMBHB (e.g., Valtonen et al. 2016; Komossa et al. 2020). Accounting for general relativistic effects, it is predicted that the system consists of primary and secondary supermassive black holes (SMBHs) of ∼1.8 × 1010 M⊙ and ∼1.5 × 108 M⊙, respectively (e.g., Dey et al. 2018), with an orbital major axis of 0.112 pc (∼26 microarcseconds, μas; e.g., Valtonen et al. 2008). However, recently, Komossa et al. (2023) suggested an alternative SMBHB model which involves a primary SMBH of a much lower mass, 108 M⊙, and does not require strong orbital precession. In radio regime, OJ 287 has been intensively studied, especially by means of very long baseline interferometry (VLBI) observations. Owing to its massive central black hole and low redshift, this source has been a very efficient study case for investigating the launching and acceleration mechanism of relativistic jets in active galactic nuclei (AGN) by resolving its innermost structure. Until now, the formation of a jet has been explained by two different mechanisms: (1) by the rotational energy of the black hole (BZ process; Blandford & Znajek 1977), and (2) by the differential rotation of the accretion flow (BP process; Blandford & Payne 1982). In addition the combination of both has been also suggested (e.g., Chiaberge et al. 2000). To probe these mechanisms, it is essential to resolve the fine structure in the vicinity of the black hole, where the jet base is thought to be located. This necessitates observations with extremely high angular resolution. An example of such study has been presented recently by the Event Horizon Telescope (EHT). In combination with multi-wavelength observations by other instruments, the EHT has revealed a potential prevalence of the BZ process in the center of M 87 by resolving its black hole shadow at 230 GHz with angular resolution of ∼20 μas (e.g., Event Horizon Telescope Collaboration 2019). A similar EHT study of OJ 287 will be presented in a forthcoming paper (Gómez et al., in prep.).
Interestingly, many previous studies have found the jet of OJ 287 to be wobbling on parsec (pc) scales, as inferred from the observation of position angle (PA) variations with a period ∼24–30 yr (e.g., Cohen 2017; Britzen et al. 2018). This might support the SMBHB scenario, involving the jet precession by the binary companion (e.g., Dey et al. 2021). However, alternative models cannot still be ruled out, such as the accretion flow instabilities (Agudo et al. 2012) or resonant accretion of magnetic field lines (Villforth et al. 2010), Doppler beaming effects of a precessing jet (Britzen et al. 2018) or jet helicity (Butuzova & Pushkarev 2020), Lense-Thirring effect by the misalignment of black hole and accretion disk spin axis (e.g., Lense & Thirring 1918; Thirring 1918; Liska et al. 2018; Chatterjee et al. 2020), and a helical distortions of the jet by magneto-hydro-dynamic (MHD) instabilities (e.g., current-driven or Kelvin-Helmholtz; Mizuno et al. 2012; Perucho et al. 2012; Vega-García et al. 2019).
It has been also shown that the jet in OJ 287 is bent at de-projected distances from the central black hole of several to tens parsecs. While the innermost jet is mostly extended along the northwest direction (e.g., Zhao et al. 2022), the progressive jet bending towards southwest is found downstream the jet (e.g., Gómez et al. 2022). This might be an indication of the change of the jet launching PA with time “imprinted” in the PA of different sections of the downstream jet. Recently, Lico et al. (2022) have indeed found that the jet structure changes at 86 GHz over the period of ∼2 yr, 2015−2017. These changes can also be investigated in the downstream jet structure through observations at lower frequencies (e.g., ≲1 GHz).
The RadioAstron space VLBI mission (Kardashev et al. 2013) offered an excellent opportunity to probe larger scale jet structures with sub-milliarcsecond (mas) angular resolution. The main component of the mission was a 10-m radio telescope on board the Spektr-R satellite which operated on a highly eccentric orbit with the initial period of ∼9 days. This orbit near the apogee provided the longest interferometric baselines to ground radio telescopes of about 350 000 km. The spaceborne radio telescope (SRT) of this mission was able to observe at four frequency bands (0.32, 1.6, 4.8, and 22 GHz) in the dual polarization mode. A brief comparison of the specifications of the RadioAstron mission with two other space VLBI systems, TDRSS1 and VSOP2, is given in Gurvits (2023). With global VLBI arrays (e.g., the Very Long Baseline Array, VLBA, and the European VLBI Network, EVN) as ground-based elements of the system, the RadioAstron observations could provide interferometric detections on baselines reaching several times the Earth diameter, proportionally exceeding the highest angular resolution accessible to ground-only VLBI networks.
In this study, we have analyzed the RadioAstron observation of OJ 287 at 1.68 GHz with dual polarization mode. The layout of this paper is as follows. We first summarize the RadioAstron observation, data reduction and imaging processes in Sect. 2. In Sect. 3, the results from total intensity and polarization images are presented. Here the independent results from adjacent VLBA observations at 15 and 43 GHz are compared together to derive the spectral index and light curves. In Sect. 4, we further discuss the results and summarize their implications for future studies. The following cosmological parameters are adopted throughout this paper: ΩM = 0.27, ΩΛ = 0.73, H0 = 71 km s−1 Mpc−1 (Komatsu et al. 2009), which result in a luminosity distance (DL) and angular scale of OJ 287 as 1.577 Gpc and 4.48 pc mas−1, respectively.
2. Observation, data reduction, and imaging
2.1. Observations
OJ 287 has been observed by the RadioAstron mission at 1.676 GHz (λ = 18.2 cm; L-band) on 2016 April 16, from UT 05:00 to UT 19:00 (14 h in total; the experiment code GG079B), together with the calibrators 0716+714, 3C 345, 1633+382, 3C 84, NRAO 150, and AO 0235+164. The 19 telescopes on Earth and SRT have participated in the experiment (see Table 1). The ground array consists of 11 telescopes in the US (10 VLBA stations and Green Bank Telescope) and 8 telescopes in Europe, so the longest Earth-based (u, v)-distance was ∼70 Mλ. The SRT provided the baselines longer than the Earth’s diameter (D⊕) resulting in the (u, v)-extension up to ∼380 Mλ (5.6 D⊕; see Fig. 1) corresponding to an angular resolution of ∼0.5 mas. The raw VLBI data were recorded with 16 MHz per intermediate frequency (IF) band ×4 IFs3 for the ground array (i.e., 64 MHz total bandwidth) and ×2 IFs for SRT (IF3 and IF4; 32 MHz total bandwidth), in both left- and right-handed circular polarizations (LCP and RCP, respectively).
 |
Fig. 1. (u, v)-coverage of our observation at 1.68 GHz: full observation with ground+SRT (left) and ground-only array (right). Different color shows the ground stations providing the baseline with the SRT (see Table 1 for station codes). The maximum baseline length of space-baseline (∼5.6 D⊕) and ground-baseline (∼1 D⊕) are shown with broken line circle, which correspond to the angular resolution of ∼530 μas and 3 mas respectively. Each point has been averaged with 5 min interval. |
Stations.
2.2. Data reduction
The observational data consist of two sets corresponding to two Earth-based sub-arrays, the EVN and VLBA. Both arrays consistently observed OJ 287, while the calibrators were observed intermittently by each sub-array. The data were first processed using the DiFX software correlator with a dedicated version for RadioAstron (Bruni et al. 2016).
For the post-correlation data reduction, the NRAO Astronomical Imaging Processing System (AIPS; Greisen 2003) has been used. First, the cross-correlated amplitudes were corrected using the auto-correlated amplitudes (ACSCL) and the bandpass for only amplitudes were corrected (BPASS). Note that the auto-correlation amplitudes at this step have a slight offset from unity so a small adjustment needs to be applied with ACSCL4. For the a priori amplitude calibration, we used the AIPS APCAL task with available system temperature and antenna gain information following the calibration method described in Cho et al. (2017). The atmospheric opacity correction was not applied since the effect is negligible at the frequency of 1.7 GHz. At this step we found that the amplitudes at IF1 showed larger scatter at all stations. The measured system temperatures (Tsys) were also much more scattered than in the other IFs, and the task could not correct the amplitudes properly (see Appendix A). A similar behavior was found in the data from JB (all IFs) and a few VLBA stations (KP, LA, MC in IF4). This station-based problem has been treated later at the self-calibration stage of the processing using the reconstructed image.
As for the phase calibration, the ionospheric effect (only for the ground array) and parallactic angle corrections (VLBATECR and VLBAPANG, respectively) were first applied. The instrumental phase and delay offset correction was made using the best fringe fit solutions on a short segment of data (FRING). The global fringe search was done with the ground array first, and then further searched for the ground-space baselines. Due to the different acceleration of SRT in its orbit, different solution intervals were applied for each scan (e.g., 10−180 s). As a result, the phase delay and fringe frequency solutions were successfully obtained with signal-to-noise ratio (S/N) > 5 up to a baseline length of ∼385 Mλ. With this, the bandpass calibration was done for both amplitudes and phases using the cross-power spectra. The delay between LCP and RCP was obtained through RLDLY.
After the calibrations, the data were averaged within each IF and coherently time averaged over 5 min (Fig. 2 for the visibility amplitudes and phases). Before imaging, outliers and low S/N points (e.g., S/N < 7) were flagged out. The RO station recorded single-polarization at each IF – in particular in the format of RCP-LCP-LCP-RCP at IF1−4, espectively. However, a phase-offset issue was identified at IF1 and IF4, resulting in the utilization of only IF2 and IF3 data with LCP polarization. At the GB station, the L-band receiver encountered an issue that caused a phase difference of ∼90° in each polarization, resulting in near-zero signal for the LCP polarization. As a result, only RCP data were utilized as pseudo Stokes I for imaging. A similar issue was also identified at the IR station, and only RCP data were used accordingly.
 |
Fig. 2. The visibility amplitudes (upper) and phases (lower), as a function of the (u, v)-distance. Each point has been averaged with 5 min interval. Note that only the blue, circle data points are used for CLEAN imaging, and all data including the gray, cross points are self-calibrated with the image (see Sect. 2). |
2.3. Imaging
For imaging, we have applied a conventional VLBI imaging software, Difmap (Shepherd et al. 1994), which is based on the classical CLEAN algorithm. This models the image as a collection of point sources from the inverse Fourier transform of the sampled visibilities.
We first implemented the iterative CLEAN and self-calibration with the ground array. Note that, at this step, the data showing spurious amplitudes (i.e., IF1 at all stations, all IFs at JB, and IF4 at KP, LA, MC) and having receiver issues (i.e., RO, GB, IR) were first flagged out. Then the CLEAN imaging was implemented with the remaining data. After that, full data including the flagged points (i.e., unflag) were self-calibrated with the obtained image. After the phase and amplitude self-calibration for all ground stations with the solution interval down to 5 min, the CLEAN models were removed and the SRT was included for imaging so that we could have the higher angular resolution. In this step, the same CLEAN windows from ground array imaging were used and only the SRT was self-calibrated for both phase and amplitude. This prevents the over-substraction of the CLEAN components. We have tested different uv-weighting parameters for both uniform (UVWEIGHT = [2,0], [2,−1] [2,−2]) and natural (UVWEIGHT=[0,−1], [0,−2]) weighting, and found the best parameter to be UVWEIGHT = [2,−2], providing the lowest 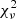 for closure quantities. Note however that the
for closure quantities. Note however that the 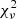 differences are small (e.g., < 0.1) between different choices of the power of UVWEIGHT, while relatively larger difference is found between uniform and natural weighting.
differences are small (e.g., < 0.1) between different choices of the power of UVWEIGHT, while relatively larger difference is found between uniform and natural weighting.
3. Results
3.1. Structure of OJ 287
3.1.1. Stokes I image
Figure 3 (left) shows the Stokes I image of OJ 287 at 1.68 GHz from our observation. Two images at top show the resultant image with the ground-array only (3.5 × 2.3 mas, PA = −27 3) and ground+SRT from uniform-weighted nominal beam (2.2 × 0.4 mas, PA = −50
3) and ground+SRT from uniform-weighted nominal beam (2.2 × 0.4 mas, PA = −50 5). The left, bottom figure shows the ground+SRT image with total intensity (contour), model fitting results (colored circles; see Sect. 3.1.3), linear polarization (gray color; see Sect. 3.3), and electric vector position angle (EVPA). The adjacent higher frequency images are also presented in Fig. 3 (right): (from top to bottom) the 15.35 GHz image in 2016 Jan. 17 from the MOJAVE project5 (Lister et al. 2018), 43.12 GHz image in 2016 Apr. 22 from the VLBA-BU-BLAZAR monitoring project6 (Jorstad et al. 2017; Weaver et al. 2022), and 86.25 GHz image in 2016 May 21 from the GMVA monitoring program7 with the targets of the VLBA-BU-BLAZAR (Lico et al. 2022).
5). The left, bottom figure shows the ground+SRT image with total intensity (contour), model fitting results (colored circles; see Sect. 3.1.3), linear polarization (gray color; see Sect. 3.3), and electric vector position angle (EVPA). The adjacent higher frequency images are also presented in Fig. 3 (right): (from top to bottom) the 15.35 GHz image in 2016 Jan. 17 from the MOJAVE project5 (Lister et al. 2018), 43.12 GHz image in 2016 Apr. 22 from the VLBA-BU-BLAZAR monitoring project6 (Jorstad et al. 2017; Weaver et al. 2022), and 86.25 GHz image in 2016 May 21 from the GMVA monitoring program7 with the targets of the VLBA-BU-BLAZAR (Lico et al. 2022).
 |
Fig. 3. Left: Stokes I images of OJ 287 at 1.68 GHz with a nominal resolution of ground-array only and ground+SRT (top). Bottom panel shows the ground+SRT image with total intensity (contour), model fitting results (colored circles), linear polarization (gray color), and EVPA (ticks). Note that the total intensity contours are set to 4, 8, 16, 32, 64, 90% of the peak intensity. Reliable linear polarization are obtained at where the total intensity is larger than 10σ of the root-mean-squared flux density of residual image. Right: The higher frequency images are shown for comparison: 15.35 GHz image from MOJAVE project (top), 43.12 GHz image from VLBA-BU-BLAZAR project (middle), and 86.25 GHz image from Lico et al. (2022). The field-of-view of image gets smaller at higher frequency which corresponds to the white box in the panels of lower frequency. The restoring beam is shown at the bottom-right corner of each panel. The color scale is in Jy per beam for total intensity images, and in milli-Jy per beam for linear polarization. |
In our RadioAstron image at 1.68 GHz, three main emission features are found: (1) one component at the center, (2) the brightest component at the west, and (3) a distinct component toward south-west at ∼1.6 mas. Due to the elongated (u, v)-coverage (Fig. 1), we have a better resolution in the northeast-southwest direction than to northwest-southeast (i.e., PA of nominal beam = −50 5), which enables us to well resolve the features. The image fidelity, with results from fitting to closure quantities and gain corrections for each telescope, is discussed in Appendix A. Comparing with the images at higher frequencies and considering the bent-jet structure of OJ 287 (e.g., Gómez et al. 2022), the center component is thought to be the core region, while the brightest component at the west is an optically thin jet emission. Note that our identification of the radio core is supported by its compact structure (usually at the most upstream of a jet), a flat spectrum (Sect. 3.1.2), and weak polarization (Sect. 3.3).
5), which enables us to well resolve the features. The image fidelity, with results from fitting to closure quantities and gain corrections for each telescope, is discussed in Appendix A. Comparing with the images at higher frequencies and considering the bent-jet structure of OJ 287 (e.g., Gómez et al. 2022), the center component is thought to be the core region, while the brightest component at the west is an optically thin jet emission. Note that our identification of the radio core is supported by its compact structure (usually at the most upstream of a jet), a flat spectrum (Sect. 3.1.2), and weak polarization (Sect. 3.3).
3.1.2. Spectral index
To confirm the distribution of optical depth, we have obtained the spectral index map by aligning images at two different frequencies. The alignment has been achieved using two-dimensional cross correlation of the optically thin extended jet structure (Walker et al. 2000; Croke & Gabuzda 2008). Since the (u, v)-spacing and the nominal angular resolutions are different in the original images at two different frequencies, the minimum and maximum (u, v)-distances were first matched with each other to be the same (e.g., UVRANGE in Difmap; e.g., Fromm et al. 2013). Next, two images at different frequencies have been convolved with a nominal beam corresponding to the angular resolution at a lower frequency and presented with the same pixel scale (≲1/20 of the lower frequency beam diameter; e.g., Kim & Trippe 2014). After this, the two images have been cross correlated and the higher frequency image has been shifted to achieve the maximum cross correlation. Note that a large field-of-view (FoV) is used so that entire image structure can be shifted within the FoV. Before calculating the cross correlation, the core region which is thought to be partially optically thick (e.g., Pushkarev & Kovalev 2012) has been masked so that the cross correlation is obtained only for the optically thin structures. To limit the effect of residual structures, the flux density cutoff has been applied at the level of 10σ of the root-mean-squared flux density of residual image.
By finding all relative shifts, the images are aligned with each other and the spectral index map is determined (Fig. 4, top). This reveals that the center component at 1.68 GHz (e.g., component C in model-fitting; see Fig. 3 and Sect. 3.1.3) corresponds to the optically thick core region with spectral index α ≳ 1, in Sν ∝ να where Sν and ν are flux density and observing frequency respectively (i.e., an inverted spectrum). This inversion extends up to 43 GHz, and explains the faint nature of the core region at 1.68 GHz due to the opacity effect. The brightest west and the south-west components (i.e., components J3 and J4 in model-fitting) correspond to optically thin jet features with a steep spectrum. Two major uncertainties are considered in the estimation of the spectral index: a systematic error from image alignment and a random error from the image noise (e.g., Pushkarev et al. 2012; Fromm et al. 2013; Hovatta et al. 2014). The former error is mainly affected by the size of core mask. Note that, to obtain a reasonable cross-correlation, the core region needs to be completely masked. For this, 1.5 times the convolution beam size is found as the minimum size of the mask. To estimate the effect of the mask size, the relative image alignments and corresponding spectral index maps are obtained using different sizes of the mask ranging from 1.5 to 2.5 times the convolution beam size. The standard deviation of resultant images are then considered as the systematic error. To account for an additional alignment error, the image providing the highest cross-correlation is manually shifted within 1/3 of beam size, and the standard deviation of the spectral index is further obtained. On the other hand, the random error is estimated from the image noise and flux density measurement error (Lico et al. 2012). As a result, the total error of the spectral index map is obtained by the quadratic sum of these uncertainties (Fig. 4, bottom).
 |
Fig. 4. Spectral index map (top) and corresponding error map (bottom) at three frequencies pairs: 43.12−86.25 GHz (left), 15.35−43.12 GHz (middle), and 1.68−15.35 GHz (right). The color scale indicates the spectral index, α, and its error, σα, as shown at right of top and bottom panels, respectively. The contours of the source structure at each frequency are shown in each panel with gray, broken line for the lower frequency and black, solid line for the higher one. The contours are set to 2, 4, 8, 16, 32, 64% of the peak intensity. Note that the relative position of each image has been aligned according to cross correlation of core-masked images, as described in Sect. 3.1. |
3.1.3. Model fitting
The images at each frequency were modeled with modelfit procedure in Difmap (Table 2), except the 86.25 GHz where the model fitting results were already provided by Lico et al. (2022). With the self-calibrated data from a reconstructed image, the circular Gaussian models were fitted to the complex visibilities using Levenberg-Marquardt non-linear least squares minimization until the residual peak intensity reached less than 5 times the root-mean-squared flux density in residual image. In this way, at 1.68 GHz, we found that three circular Gaussian components, labeled as C, J3 and J4, describe the source’s morphology effectively. The 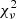 of closure phases for the case with three Gaussian components converges to ∼0.8 from ∼25 for the one Gaussian component case. Note that it was difficult to find more model components beyond three Gaussians, as the initial guess (e.g., based on the residual peak intensity) became uncertain and the result easily converged to negative flux density.
of closure phases for the case with three Gaussian components converges to ∼0.8 from ∼25 for the one Gaussian component case. Note that it was difficult to find more model components beyond three Gaussians, as the initial guess (e.g., based on the residual peak intensity) became uncertain and the result easily converged to negative flux density.
Model fitting results.
Component C is resolved at 15.35 and 43.12 GHz into two sub-components, C1 and C2. In addition, the C1 component is further resolved into two sub-components (C1a and C1b) at 43.12 GHz and three sub-components (C1a, C1b, and C1c) at 86.25 GHz (Fig. 3). That is, the component C is blended with multiple sub-components and has positive spectral index supporting the identification as a core region with optically thick spectrum up to 43.12 GHz. On the other hand, the components J3 and J4 have steep spectra indicating that they are optically thin jet components. Model fitting uncertainties shown in Cols. 5–11 of Table 2 are estimated following the method described by Schinzel et al. (2012). Table 3 summarizes spectral indices of the model components which appear to be consistent with the spectral index distributions shown in Fig. 4.
Spectral analysis of model fitting components
In Fig. 3 (bottom, left), the model components at four frequencies are shown with different colors. Note that the relative position of model components across frequencies are aligned based on the image alignment (see Sect. 3.1.2). With this, the position of the C1a component is well consistent at 43 and 86 GHz (e.g., ≲10 μas) that can be identified as the innermost core. The distances of the other components are then estimated relative to the C1a (Col. 6 in Table 2), which allow us to estimate the frequency dependent radio core position shift, the so called core shift (e.g., Lobanov 1998). At 15 GHz, the core corresponds to the most upstream component C1 so the core shift relative to C1a is obtained as ∼50 μas. At 1.68 GHz, on the other hand, only the blended core component C is found, so the core shifts from 15 and 43 (or 86) GHz are obtained as ∼230 and ∼280 μas, respectively.
By fitting the synchrotron self-absorbed (SSA) spectrum with a power-law energy distribution (e.g., Türler et al. 2000; Gómez et al. 2022), the maximum synchrotron turnover flux density in Jy, Sm, and turnover frequency in GHz, νm, are found for each component (Table 3):
where Sν is the observed flux density in Jy, αthick and αthin are the spectral indices of the optically thick and thin parts of the spectrum, respectively. τm is the optical depth at νm, which is defined as ∼3/2[(1−(8αthin/3αthick))1/2−1]. Note that Sm is defined as 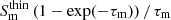 , where
, where 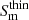 is the extrapolated flux density of optically thin spectrum at νm (e.g., Türler et al. 2000).
is the extrapolated flux density of optically thin spectrum at νm (e.g., Türler et al. 2000).
First, the flux densities of the component C at 15, 43, 86 GHz are assumed as sum of flux densities of sub-components. Since the C2 component is not found at 86 GHz, however, the flux density at 86 GHz is considered as lower limit. With this, the component C shows a transition from optically thick to thin at νm ≥ 28 GHz with Sm ≥ 4.4 Jy (see Table 3 and Fig. 5). As for the sub-components in core region, C1 and C2, the spectral index with 1.68 GHz is obtained assuming the flux density of C as an upper limit. Then the opacity transition is found in the component C1 at νm ≈ 33 GHz with Sm ≈ 4.0 Jy, and in the component C2 at νm ≈ 11.5 GHz with Sm ≈ 0.7 Jy. As for the J3 component, it is optically thin across 1.68–43 GHz so the lower and upper limit of Sm ≳ 1.2 Jy and νm ≲ 0.8 GHz are found, respectively. Note that the optically thick spectral index, αt, in the SSA spectrum for J3 is assumed to be the same as for C (i.e., 0.3). It is also worth noting that the small number of data points and differences in observing dates (up to ∼3 months between 1.6 and 15 GHz) may introduce further uncertainties in the estimates. According to the light curve at 43 GHz (Fig. 6), for instance, the flux variation is stable during Apr.−May 2016 so the uncertainties arising from time gap might be relatively small at 1.68, 43, and 86 GHz. On the other hand, large flux decrease is shown on Jan. 2016 so the uncertainty of 15 GHz may become larger up to ∼30%.
 |
Fig. 5. Spectra of model fitting components identified at 1.68, 15.35, 43.12, and 86.25 GHz: (from left to right) C, C1, C2, and J3. Flux densities are shown with black, circle points with uncertainty (see Table 2), and the blue, solid-line shows the fitting result assuming a SSA spectrum (see Sect. 3.1.3). Fitting errors, due to the flux density uncertainties, are presented with the blue, shaded area. The derived SSA turnover frequencies in C, C1, and C2 are shown with the yellow, shaded area. |
3.2. Brightness temperature
The brightness temperature of each component in the rest frame of the source is then estimated from the fitted flux densities and sizes (e.g., Gómez et al. 2022),
where S is the component flux density in Jy, θobs is the full-width-half-maximum (FWHM) size of the model component in mas, ν is the observing frequency in GHz, and z is the source redshift. Note that the resolution limit has been used for the size of unresolved model components (Lobanov 2005) so that the lower limit of TB is estimated for such cases (see Cols. 8 and 9 of Table 2). Additionally, the minimum and limiting brightness temperatures (TB, min and TB, lim, respectively) are estimated directly from the visibility amplitudes (Lobanov 2015) so that a range of actual TB can be constrained (Fig. 7).
In addition to imaging observations, OJ 287 was regularly monitored by RadioAstron with the visibility tracking mode as part of the AGN survey program (e.g., Kovalev et al. 2020). These snapshot observations provided the angular size and TB of the source by comparing the flux densities at ground-array and space baselines to a simple Gaussian model, if fringes were detected on the space baselines. The OJ 287 survey observations were carried out during 2012−2018, and five experiments at L-band were conducted (2016 Apr. 1, 14, 18, 27, and 28) close to our observation (2016 Apr. 16). The survey observation results provided TB ∼ 2 − 4 × 1012 K, which were well consistent with TB, min at the ground-space baselines of our observation. At their baseline lengths which are longer than our measurement, the TB were slightly lower than the extrapolated TB, min from our observation. Note that the flux densities are mostly consistent in this observing period (see Fig. 6) so the TB difference may not be due to the flux variability but to the different (u, v) sampling of the five adjacent RadioAstron survey observations towards PA ∼ −45°, where there is missing coverage in our imaging observation.
 |
Fig. 6. OJ 287 light curve in 2016 from the VLBA observations at 15 GHz (MOJAVE; green square, solid line) and 43 GHz (VLBA-BU-BLAZAR; black circle, solid line). Our RadioAstron observation at 1.68 GHz is shown with red asterisk, and the GMVA 86 GHz observation is shown with blue diamond. The observations compared in this study are marked with an additional edge. The vertical broken lines show the epochs of adjacent RadioAstron snapshot sessions. |
The estimated TB of C and J3 at 1.68 GHz are ≈1013 K and ≈3 × 1012 K, respectively. These are larger than both the inverse Compton limits of (0.3 − 1.0)×1012 K (Kellermann & Pauliny-Toth 1969) and the equipartition limit of ≈5 × 1010 K (Readhead 1994), which can be explained at the inverse-Compton limit with a jet Doppler boosting factor, δj ≳ 3 − 10. Gómez et al. (2022) suggested the δj ≈ 5 − 15, based on the apparent jet speed, βapp ≤ 15 c at 15 GHz (Lister et al. 2009, 2016) and ∼7 − 12 c at 43 GHz (Weaver et al. 2022), so that the required δj is in agreement with the independent kinematic constraints. With the same kinematic constraint, the TB of J4, ≈5 × 1010 K, provides the intrinsic TB of ∼(0.3 − 1)×1010 K that is slightly lower than the equipartition limit indicating a higher magnetic field energy density compared to the energy density of the relativistic particles (e.g., Zhao et al. 2022). Note however that there are still considerable uncertainties of δj and TB measurements.
Figure 7 shows the independent estimates of TB, including the component model fitting (blue, horizontal lines), TB, min and TB, lim from visibility amplitudes (green and cyan squares), and the adjacent RadioAstron snapshot survey measurements (yellow squares). Note that the TB of component C corresponds to that of space baselines (≳300 Mλ) and is higher than maximum TB, lim of ground baselines. This indicates inherent difficulty in finding this component with the ground-array at 1.68 GHz.
 |
Fig. 7. The brightness temperature as a function of the (u, v)-distance, D. The green, square shows the minimum TB and the cyan, triangle shows the limiting TB. The yellow, square shows the TB, min from five RadioAstron snapshot survey sessions close to our observation. The blue, horizontal lines show the TB at model components C (dotted), J3 (dotted-broken), and J4 (broken). Note that a lower limit is reported for C, since its size is smaller than the resolution limit (see Sect. 3.2). |
3.3. Polarization
For the polarimetric analysis, the instrumental polarization leakage (D-term) was first calibrated using the Stokes I image with the LPCAL procedure in AIPS (see Fig. A.4). Note that the group delay difference between RCP and LCP was already calibrated with the RLDLY, as described in Sect. 2. As a result, linear polarization is detected with a total fractional polarization of m ∼ 2.5% and the EVPA is determined along with the structure (see Fig. 3). The EVPA was calibrated using a nearby single-dish observation with the EF at 2.64 GHz on April 7, 2016, providing m ∼ 3.89% and 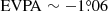 (F-GAMMA/QUIVER program; Myserlis et al. 2018; Angelakis et al. 2019). To account for the Galactic rotation measure (RM) of 31 ± 3 rad m−2 (Rusk 1988) and the local RM in OJ 287 of −7.1 ± 3.4 rad m−2 (Motter & Gabuzda 2017), EVPA rotations of 59 ± 6° and −14 ± 7° were applied, respectively.
(F-GAMMA/QUIVER program; Myserlis et al. 2018; Angelakis et al. 2019). To account for the Galactic rotation measure (RM) of 31 ± 3 rad m−2 (Rusk 1988) and the local RM in OJ 287 of −7.1 ± 3.4 rad m−2 (Motter & Gabuzda 2017), EVPA rotations of 59 ± 6° and −14 ± 7° were applied, respectively.
The linear polarization properties of the model-fitted components are summarized in Table 2. Note that the VLBI model components in total intensity and linear polarization do not correspond exactly to each other. Therefore, the linear polarization of each component is derived from the total intensity model in the image domain by masking the region outside of each model. The core region, C, displays low polarization (m ∼ 0.1%), which is expected for optically thick emission. The EVPA of ∼−24° aligns well with the innermost jet structure of OJ 287 at higher frequencies, indicating a dominant toroidal magnetic field (Gómez et al. 2022). The J3 component also shows low polarization (m ∼ 0.3%), with the EVPA slightly rotated by ∼10° towards the west compared to the core region. Lastly, the J4 component shows higher polarization (m ∼ 2.9%) as it represents an optically thin jet component. The average EVPAs in these jet components are observed to be almost perpendicular to the local jet direction, which support the hypothesis that a poloidal magnetic field is dominant (Myserlis et al. 2018). The uncertainties of the degree of polarization and EVPA are estimated based on the S/N of the total intensity and polarization images, as well as the standard deviation of the instrumental polarization amplitudes (see Lico et al. 2014 and Gómez et al. 2022 for more details). Additionally, for the EVPA, uncertainties arising from RM measurements have also been taken into consideration.
4. Discussions and conclusions
In this study, we have presented our findings on the total intensity and linear polarization structure of OJ 287 at an observing frequency of 1.68 GHz, obtained through the RadioAstron observation on April 16, 2016. Our investigation fills a significant gap in the imaging attempts conducted at low frequencies (e.g., ≲10 GHz), where limited exploration has occurred (Perlman & Stocke 1994; Fey et al. 1996; Fey & Charlot 1997; see also the University College Cork Program8). Notably, the use of the SRT, which possesses a baseline length of approximately ∼5.6 D⊕, has enabled us to achieve the finest angular resolution image to date at this frequency.
Our observation has unveiled the comprehensive jet structure oriented towards the south-west, accompanied by the identification of the optically thick core in its innermost region. This aligns well with the progressive bent-jet structure previously reported for OJ 287 (e.g., Hodgson et al. 2017; Gómez et al. 2022). It is worth noting that the innermost jet structure towards the north-west, which has been observed at higher frequencies (e.g., Gómez et al. 2022; Lico et al. 2022; Zhao et al. 2022), corresponds to the core region and remains unresolved in our study. By employing model fitting and examining the results up to ∼3 mas (i.e., J4; see Table 2), we have determined that the position angle (PA) of the jet, relative to the radio core, is ∼ − 110° (east of north). This is consistent with PA measurements made over the past ∼30 yr (∼ − 112°; Cohen 2017). Especially, as the rotation of the inner jet (e.g., Tateyama & Kingham 2004) has changed from clockwise to counterclockwise in ∼2010, the jet ridgeline can clearly show the bending structure in following years. Therefore, our results support that the bending jet structure primarily arises from the rotation of the jet launching angle, which can also be amplified farther downstream due to the small viewing angle (Gómez et al. 2022). Note that the origin of PA rotation could be the orbital motion of binary black hole system at the center (Dey et al. 2021), although other scenarios cannot be ruled out, as introduced in Sect. 1.
By comparing the adjacent observations at 15, 43, and 86 GHz, we have constructed a spectral index map that confirms the presence of both an opaque core and optically thin jet components. The model fitting has revealed three Gaussian components, corresponding to the core (C), brightest jet component at 1.68 GHz (J3), and the extended faint component (J4). The spectral index of component C indicates that this is the optically thick core region, at least up to 28 GHz, based on the SSA spectrum fitting. The sub-component C1 exhibits clearer transition from optically thick to thin across the frequency range spanning from 1.68 GHz through 86 GHz. This yields an estimated SSA turnover frequency of νm ∼ 33 GHz, accompanied by a turnover flux density Sm ∼ 4.0 Jy (see Table 3 and Fig. 5). Similarly, the sub-component C2 presents the opacity transition from observations up to 43 GHz which provides the SSA turnover frequency and flux density as νm ∼ 11.5 GHz and Sm ∼ 0.7 Jy, respectively.
From the fitted Sm and νm, the magnetic field strength from SSA and assuming equipartition conditions can be estimated (e.g., Pacholczyk 1970; Marscher 1983; Zdziarski 2014; Pushkarev et al. 2019; Lee et al. 2020; Gómez et al. 2022):
In Eq. (3), b(α) is a coefficient as a function of the spectral index (e.g., Marscher 1983; Pushkarev et al. 2019), θm is the emitting region diameter in mas, and δj is the Doppler boosting factor. Note that a factor of 1.8 is multiplied to θm to convert the Gaussian to the spherical shape before estimating the magnetic field strengths (Marscher 1983). In Eq. (4), f is volume filling factor of the emitting plasma, DL, Gpc is the luminosity distance in Gpc, ku is the ratio of total energy to the SSA population of electrons in the emitting region, c12 is a coefficient (e.g., Pacholczyk 1970), and κν is a function of spectral index and frequency cutoffs of the SSA emission. In this study, we adapted the same assumption with Gómez et al. (2022): f = 1, ku = 1 (i.e., an electron-positron flow), κν ≈ (νmax/νm)1 + α/(1 + α) where νmax = 10 THz.
With δj = 10 (e.g., Gómez et al. 2022), the magnetic field strength of component C1 is estimated as Bssa ∼ 3.4 ± 1.4 G and Beq ∼ 2.6 ± 0.2 G. As for the component C2, Bssa ∼ 1.0 ± 0.8 G and Beq ∼ 1.6 ± 0.3 G are obtained. Components J3 and J4 are considered optically thin jet components, and their SSA parameters have not been well constrained. Note that even if C and J3 exhibit TB exceeding the inverse Compton limit, these can still be explained by a jet Doppler boosting factor of δj ≈ 5 − 15, which would be in agreement with kinematic constraints at higher frequencies.
The integrated degree of linear polarization is found as ∼2.5%. As expected, low polarization of ∼0.1% is obtained in the opaque core region, while higher polarization levels of up to ∼3% are observed in more distant jet components. The EVPA of linear polarization is well consistent with the local jet direction in the core region, which may support a toroidal magnetic field structure (Gómez et al. 2022). Farther downstream of the jet, on the other hand, the EVPAs are almost perpendicular to the jet, indicating a predominant poloidal magnetic field structure (Myserlis et al. 2018). However, it is important to note that significant uncertainty remains in the alignment between the local jet axis and the EVPA. This is due to the limited angular resolution, which challenges the determination of a reliable jet ridge line, as well as the substantial error and potential time variation in the RM.
OJ 287 represents a prime candidate for hosting a supermassive black hole binary system, from which a jet from the secondary black hole has been also predicted (e.g., Dey et al. 2021). Despite efforts by Zhao et al. (2022) to search for a secondary jet from the predicted secondary SMBH using GMVA+ALMA observations at 86 GHz, no conclusive detection has been made, potentially due to sensitivity limitations. Similarly, our study at 1.68 GHz, even with the space-ground VLBI observation using RadioAstron, has failed to detect the secondary jet. Therefore, this will be further studied, for instance with the EHT at 230 GHz (Gómez et al., in prep.) and with RadioAstron at 22 GHz (Traianou et al. in prep.; Lico et al., in prep.).
Acknowledgments
We are grateful to anonymous referee, B. Boccardi, T. Savolainen, and J. Park for their helpful comments on the manuscript. The work at the IAA-CSIC is supported in part by the Spanish Ministerio de Economía y Competitividad (grants AYA2016-80889-P and PID2019-108995GB-C21), the Consejería de Economía, Conocimiento, Empresas y Universidad of the Junta de Andalucía (grant P18-FR-1769), the Consejo Superior de Investigaciones Científicas (grant 2019AEP112), and the grant CEX2021-001131-S funded by MCIN/AEI/ 10.13039/501100011033. This publication acknowledges the project M2FINDERS, which is funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 101018682). I.C. is supported by the KASI-Yonsei Postdoctoral Fellowship. R.L. acknowledges financial support from INAF-GO-grant-2021. F.M.P. acknowledges support by the ERC under the HORIZON ERC Grants 2021 programme under grant agreement No. 101040021. J.-Y.K. is supported for this research by the National Research Foundation of Korea (NRF) grant funded by the Korean government (Ministry of Science and ICT; grant no. 2022R1C1C1005255). The RadioAstron project is led by the Astro Space Center of the Lebedev Physical Institute of the Russian Academy of Sciences and the Lavochkin Scientific and Production Association under a contract with the Russian Federal Space Agency, in collaboration with partner organizations in Russia and other countries. The European VLBI Network is a joint facility of independent European, African, Asian, and North American radio astronomy institutes. The VLBA is an instrument of the National Radio Astronomy Observatory, a facility of the National Science Foundation operated under cooperative agreement by Associated Universities. This research is based on observations correlated at the Bonn Correlator, jointly operated by the Max-Planck Institut für Radioastronomie (MPIfR), and the Federal Agency for Cartography and Geodesy (BKG). This research has made use of data from the MOJAVE database that is maintained by the MOJAVE team (Lister et al. 2018). This study makes use of 43 GHz VLBA data from the VLBA-BU Blazar Monitoring Program (VLBA-BU-BLAZAR; http://www.bu.edu/blazars/VLBAproject.html), funded by NASA through the Fermi Guest Investigator grant 80NSSC20K1567. For data correlation, calibration, imaging and analysis, the softwares of DiFX (Bruni et al. 2016), AIPS (Greisen 2003), DIFMAP (Shepherd et al. 1994), and eht-imaging (Chael et al. 2018) are used, respectively.
References
- Agudo, I., Marscher, A. P., Jorstad, S. G., et al. 2012, ApJ, 747, 63 [CrossRef] [Google Scholar]
- Angelakis, E., Fuhrmann, L., Myserlis, I., et al. 2019, A&A, 626, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Britzen, S., Fendt, C., Witzel, G., et al. 2018, MNRAS, 478, 3199 [NASA ADS] [Google Scholar]
- Bruni, G., Anderson, J., Alef, W., et al. 2016, Galaxies, 4, 55 [Google Scholar]
- Butuzova, M. S., & Pushkarev, A. B. 2020, Universe, 6, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Chael, A. A., Johnson, M. D., Bouman, K. L., et al. 2018, ApJ, 857, 23 [Google Scholar]
- Chatterjee, K., Younsi, Z., Liska, M., et al. 2020, MNRAS, 499, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Celotti, A., Capetti, A., & Ghisellini, G. 2000, A&A, 358, 104 [NASA ADS] [Google Scholar]
- Cho, I., Jung, T., Zhao, G.-Y., et al. 2017, PASJ, 69, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M. 2017, Galaxies, 5, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Croke, S. M., & Gabuzda, D. C. 2008, MNRAS, 386, 619 [CrossRef] [Google Scholar]
- Dey, L., Valtonen, M. J., Gopakumar, A., et al. 2018, ApJ, 866, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Dey, L., Valtonen, M. J., Gopakumar, A., et al. 2021, MNRAS, 503, 4400 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [Google Scholar]
- Fey, A. L., & Charlot, P. 1997, ApJS, 111, 95 [Google Scholar]
- Fey, A. L., Clegg, A. W., & Fomalont, E. B. 1996, ApJS, 105, 299 [Google Scholar]
- Fromm, C. M., Ros, E., Perucho, M., et al. 2013, A&A, 557, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, J. L., Traianou, E., Krichbaum, T. P., et al. 2022, ApJ, 924, 122 [Google Scholar]
- Greisen, E. W. 2003, in Information Handling in Astronomy - Historical Vistas, ed. A. Heck, Astrophys. Space Sci. Lib., 285, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gurvits, L. I. 2023, A Brief History of Space VLBI, in 8th IEEE History of Electrotechnology Conference (HISTELCON) [Google Scholar]
- Hodgson, J. A., Krichbaum, T. P., Marscher, A. P., et al. 2017, A&A, 597, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., Aller, M. F., Aller, H. D., et al. 2014, AJ, 147, 143 [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Morozova, D. A., et al. 2017, ApJ, 846, 98 [Google Scholar]
- Kardashev, N. S., Khartov, V. V., Abramov, V. V., et al. 2013, Astron. Rep., 57, 153 [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1969, ApJ, 155, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-Y., & Trippe, S. 2014, J. Korean Astron. Soci., 47, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Grupe, D., Parker, M. L., et al. 2020, MNRAS, 498, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Grupe, D., Kraus, A., et al. 2023, MNRAS, 522, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Kovalev, Y. Y., Kardashev, N. S., Sokolovsky, K. V., et al. 2020, Adv. Space Res., 65, 705 [Google Scholar]
- Lee, J. W., Lee, S.-S., Algaba, J.-C., et al. 2020, ApJ, 902, 104 [Google Scholar]
- Lehto, H. J., & Valtonen, M. J. 1996, ApJ, 460, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lense, J., & Thirring, H. 1918, Phys. Z., 19, 156 [Google Scholar]
- Lico, R., Giroletti, M., Orienti, M., et al. 2012, A&A, 545, A117 [CrossRef] [EDP Sciences] [Google Scholar]
- Lico, R., Giroletti, M., Orienti, M., et al. 2014, A&A, 571, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lico, R., Casadio, C., Jorstad, S. G., et al. 2022, A&A, 658, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2018, MNRAS, 474, L81 [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2016, AJ, 152, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2018, ApJS, 234, 12 [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Lobanov, A. P. 2005, arXiv e-prints [arXiv:astro-ph/0503225] [Google Scholar]
- Lobanov, A. 2015, A&A, 574, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marscher, A. P. 1983, ApJ, 264, 296 [Google Scholar]
- Mizuno, Y., Lyubarsky, Y., Nishikawa, K.-I., & Hardee, P. E. 2012, ApJ, 757, 16 [Google Scholar]
- Motter, J. C., & Gabuzda, D. C. 2017, MNRAS, 467, 2648 [Google Scholar]
- Myserlis, I., Komossa, S., Angelakis, E., et al. 2018, A&A, 619, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pacholczyk, A. G. 1970, Radio Astrophysics. Nonthermal Processes in Galactic and Extragalactic Sources (San Francisco: Freeman) [Google Scholar]
- Perlman, E. S., & Stocke, J. T. 1994, AJ, 108, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Kovalev, Y. Y., Lobanov, A. P., Hardee, P. E., & Agudo, I. 2012, ApJ, 749, 55 [Google Scholar]
- Pushkarev, A. B., & Kovalev, Y. Y. 2012, A&A, 544, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pushkarev, A. B., Hovatta, T., Kovalev, Y. Y., et al. 2012, A&A, 545, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pushkarev, A. B., Butuzova, M. S., Kovalev, Y. Y., & Hovatta, T. 2019, MNRAS, 482, 2336 [NASA ADS] [CrossRef] [Google Scholar]
- Readhead, A. C. S. 1994, ApJ, 426, 51 [Google Scholar]
- Rusk, R. E. 1988, PhD Thesis, University of Toronto, Canada [Google Scholar]
- Schinzel, F. K., Lobanov, A. P., Taylor, G. B., et al. 2012, A&A, 537, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, Bull. Am. Astron. Soc., 26, 987 [Google Scholar]
- Sillanpaa, A., Haarala, S., Valtonen, M. J., Sundelius, B., & Byrd, G. G. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Stickel, M., Fried, J. W., & Kuehr, H. 1989, A&AS, 80, 103 [NASA ADS] [Google Scholar]
- Tateyama, C. E., & Kingham, K. A. 2004, ApJ, 608, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Thirring, H. 1918, Phys. Z., 19, 33 [Google Scholar]
- Türler, M., Courvoisier, T. J. L., & Paltani, S. 2000, A&A, 361, 850 [Google Scholar]
- Valtonen, M. J., Lehto, H. J., Nilsson, K., et al. 2008, Nature, 452, 851 [Google Scholar]
- Valtonen, M. J., Zola, S., Ciprini, S., et al. 2016, ApJ, 819, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Valtonen, M. J., Dey, L., Gopakumar, A., et al. 2021, Galaxies, 10, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vega-García, L., Perucho, M., & Lobanov, A. P. 2019, A&A, 627, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villforth, C., Nilsson, K., Heidt, J., et al. 2010, MNRAS, 402, 2087 [Google Scholar]
- Walker, R. C., Dhawan, V., Romney, J. D., Kellermann, K. I., & Vermeulen, R. C. 2000, ApJ, 530, 233 [Google Scholar]
- Weaver, Z. R., Jorstad, S. G., Marscher, A. P., et al. 2022, ApJS, 260, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A. 2014, MNRAS, 445, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G.-Y., Gómez, J. L., Fuentes, A., et al. 2022, ApJ, 932, 72 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Data issue, image fidelity, and instrumental polarization
In our observation, certain stations and IFs were flagged out due to the poor data quality. First, spurious amplitudes are present at 1) IF1 (1.620-1.636 GHz), 2) all IFs at JB, and 3) IF4 (1.668-1.684 GHz) at KP, LA, and MC. These are also present in the Tsys measurements (see Figure A.1) implying that it is a station-based issue. Note that the large scatter at IF1 may be due to radio interference, since it is affecting all the stations. These data were initially excluded from imaging to avoid any possible bias during the image reconstruction. Once an initial image was obtained these data were self-calibrated in amplitude with that image in an attempt to correct for the issues mentioned before. The same procedure was used for RO, GB, and IR for which only single polarization data could be used. These provide the larger gain correction factor, as shown in Figure A.2 (lower, right), in comparison with the results from a calibrator 0716+714. Figure A.2 shows the observed sources at each station, as a function of total observing time. To compare the gain correction at each station, 0716+714 was the most suitable calibrator as it was observed across all participating stations except SRT. In this regard, the (u, v)-coverage towards 0716+714 and its image are shown together. As a result, it is found that the multiplicative gain correction factor, 1/|g|, is well consistent in OJ 287 and 0716+714. In addition, as expected, larger 1/|g| are derived from the flagged data.
 |
Fig. A.1. The system temperature, Tsys, at all stations for LCP. Each IF is shown with different colors: IF1 (magenta), IF2 (green), IF3 (blue), and IF4 (orange). Note that there is no Tsys measurements at RO so it has been excluded. |
 |
Fig. A.2. (Left) Sources observed at each station, as a function of observing time. OJ 287 is shown with red color, and the other calibrators are also shown with different colors: 3C 345, 1633+382, 0716+714, 0235+164, 3C 84, and NRAO 150. Among them, the 0716+714 is suitable to compare the station-based gain correction with the OJ 287, thanks to its station coverage. (Right, top) The (u, v)-coverage towards 0716+714 and its image are shown. Note that the SRT has not observed this source and the longest baseline length is limited up to ∼50 Mλ so the angular resolution (∼4.5 mas) is much poorer than for OJ 287. (Right, bottom) The multiplicative gain correction factors at each station, derived from OJ 287 (red) and 0716+714 (cyan). Different markers indicate each IF from 1 to 4 at each station. |
Based on the data, the Difmap imaging was implemented with different parameters. The best image has been selected based on the 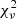 of closure quantities. Figure A.3 shows the example closure phases (upper) and log closure amplitudes (lower) of observed data (gray points) and the model (red, solid line). Note that this shows two representative triangles / quadangles with ground array (left) and with SRT (right). As shown, the model well fits the data with
of closure quantities. Figure A.3 shows the example closure phases (upper) and log closure amplitudes (lower) of observed data (gray points) and the model (red, solid line). Note that this shows two representative triangles / quadangles with ground array (left) and with SRT (right). As shown, the model well fits the data with 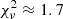 and ≈2.2 for closure phase and log closure amplitude respectively.
and ≈2.2 for closure phase and log closure amplitude respectively.
 |
Fig. A.3. The closure phases (top) and log closure amplitudes (bottom), at the triangle/quadangle of ground array (left) and with the SRT (right). The stations consisting of each triangle and quadangle are shown at the top of each panel. Model from image (red, solid line) well fits the data (gray, circle). |
Lastly, the calibration of the instrumental polarization leakage, so called D-term, is shown in Figure A.4. This is required to obtain reliable polarimetric results. To derive the D-term, the Stokes I data are first self-calibrated with the CLEAN image, as described in section 2. Then the self-calibrated data and image are loaded to AIPS, and the cross polarizations (i.e., LR and RL) are further self-calibrated using CALIB. After that, the polarization structure of OJ 287 is first specified with CCEDT and the D-term calibration is applied with LPCAL. This is because LPCAL assumes that the source consists of sub-components having constant fractional polarization in each. Note that the D-term solution is found for each IF separately, so Figure A.4 shows all these values (square) together with the averaged one (asterisk). The error bar of averaged value indicates the dispersion range of the D-term across different IFs, and the results for LCP and RCP are shown in left- and right-panel respectively.
 |
Fig. A.4. Derived instrumental polarization, D-term, in %. The left and right panels show the solutions in LCP and RCP, respectively. D-terms at each antenna are shown with different colors, and the squares show the solution at each IF. The asterisk with error bar is the averaged D-term across IFs. |
All Tables
All Figures
 |
Fig. 1. (u, v)-coverage of our observation at 1.68 GHz: full observation with ground+SRT (left) and ground-only array (right). Different color shows the ground stations providing the baseline with the SRT (see Table 1 for station codes). The maximum baseline length of space-baseline (∼5.6 D⊕) and ground-baseline (∼1 D⊕) are shown with broken line circle, which correspond to the angular resolution of ∼530 μas and 3 mas respectively. Each point has been averaged with 5 min interval. |
| In the text | |
 |
Fig. 2. The visibility amplitudes (upper) and phases (lower), as a function of the (u, v)-distance. Each point has been averaged with 5 min interval. Note that only the blue, circle data points are used for CLEAN imaging, and all data including the gray, cross points are self-calibrated with the image (see Sect. 2). |
| In the text | |
 |
Fig. 3. Left: Stokes I images of OJ 287 at 1.68 GHz with a nominal resolution of ground-array only and ground+SRT (top). Bottom panel shows the ground+SRT image with total intensity (contour), model fitting results (colored circles), linear polarization (gray color), and EVPA (ticks). Note that the total intensity contours are set to 4, 8, 16, 32, 64, 90% of the peak intensity. Reliable linear polarization are obtained at where the total intensity is larger than 10σ of the root-mean-squared flux density of residual image. Right: The higher frequency images are shown for comparison: 15.35 GHz image from MOJAVE project (top), 43.12 GHz image from VLBA-BU-BLAZAR project (middle), and 86.25 GHz image from Lico et al. (2022). The field-of-view of image gets smaller at higher frequency which corresponds to the white box in the panels of lower frequency. The restoring beam is shown at the bottom-right corner of each panel. The color scale is in Jy per beam for total intensity images, and in milli-Jy per beam for linear polarization. |
| In the text | |
 |
Fig. 4. Spectral index map (top) and corresponding error map (bottom) at three frequencies pairs: 43.12−86.25 GHz (left), 15.35−43.12 GHz (middle), and 1.68−15.35 GHz (right). The color scale indicates the spectral index, α, and its error, σα, as shown at right of top and bottom panels, respectively. The contours of the source structure at each frequency are shown in each panel with gray, broken line for the lower frequency and black, solid line for the higher one. The contours are set to 2, 4, 8, 16, 32, 64% of the peak intensity. Note that the relative position of each image has been aligned according to cross correlation of core-masked images, as described in Sect. 3.1. |
| In the text | |
 |
Fig. 5. Spectra of model fitting components identified at 1.68, 15.35, 43.12, and 86.25 GHz: (from left to right) C, C1, C2, and J3. Flux densities are shown with black, circle points with uncertainty (see Table 2), and the blue, solid-line shows the fitting result assuming a SSA spectrum (see Sect. 3.1.3). Fitting errors, due to the flux density uncertainties, are presented with the blue, shaded area. The derived SSA turnover frequencies in C, C1, and C2 are shown with the yellow, shaded area. |
| In the text | |
 |
Fig. 6. OJ 287 light curve in 2016 from the VLBA observations at 15 GHz (MOJAVE; green square, solid line) and 43 GHz (VLBA-BU-BLAZAR; black circle, solid line). Our RadioAstron observation at 1.68 GHz is shown with red asterisk, and the GMVA 86 GHz observation is shown with blue diamond. The observations compared in this study are marked with an additional edge. The vertical broken lines show the epochs of adjacent RadioAstron snapshot sessions. |
| In the text | |
 |
Fig. 7. The brightness temperature as a function of the (u, v)-distance, D. The green, square shows the minimum TB and the cyan, triangle shows the limiting TB. The yellow, square shows the TB, min from five RadioAstron snapshot survey sessions close to our observation. The blue, horizontal lines show the TB at model components C (dotted), J3 (dotted-broken), and J4 (broken). Note that a lower limit is reported for C, since its size is smaller than the resolution limit (see Sect. 3.2). |
| In the text | |
 |
Fig. A.1. The system temperature, Tsys, at all stations for LCP. Each IF is shown with different colors: IF1 (magenta), IF2 (green), IF3 (blue), and IF4 (orange). Note that there is no Tsys measurements at RO so it has been excluded. |
| In the text | |
 |
Fig. A.2. (Left) Sources observed at each station, as a function of observing time. OJ 287 is shown with red color, and the other calibrators are also shown with different colors: 3C 345, 1633+382, 0716+714, 0235+164, 3C 84, and NRAO 150. Among them, the 0716+714 is suitable to compare the station-based gain correction with the OJ 287, thanks to its station coverage. (Right, top) The (u, v)-coverage towards 0716+714 and its image are shown. Note that the SRT has not observed this source and the longest baseline length is limited up to ∼50 Mλ so the angular resolution (∼4.5 mas) is much poorer than for OJ 287. (Right, bottom) The multiplicative gain correction factors at each station, derived from OJ 287 (red) and 0716+714 (cyan). Different markers indicate each IF from 1 to 4 at each station. |
| In the text | |
 |
Fig. A.3. The closure phases (top) and log closure amplitudes (bottom), at the triangle/quadangle of ground array (left) and with the SRT (right). The stations consisting of each triangle and quadangle are shown at the top of each panel. Model from image (red, solid line) well fits the data (gray, circle). |
| In the text | |
 |
Fig. A.4. Derived instrumental polarization, D-term, in %. The left and right panels show the solutions in LCP and RCP, respectively. D-terms at each antenna are shown with different colors, and the squares show the solution at each IF. The asterisk with error bar is the averaged D-term across IFs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} S_{\nu } = S_\mathrm{m} \left( \dfrac{\nu }{\nu _\mathrm{m} } \right)^{\alpha _\mathrm{thick} } \dfrac{ 1 - \exp [-\tau _\mathrm{m} (\nu / \nu _\mathrm{m} )^{\alpha _\mathrm{thin} - \alpha _\mathrm{thick} }]}{1 - \exp (-\tau _\mathrm{m} ) } ~~~~ [\mathrm{Jy} ], \end{aligned} $$](/articles/aa/full_html/2024/03/aa47157-23/aa47157-23-eq13.gif)
![$$ \begin{aligned} T_{\rm B} = 1.22\times 10^{12} \frac{S}{\theta _{\rm obs}^{2}\nu ^{2}} (1+z)\,\, [\mathrm{K}] \end{aligned} $$](/articles/aa/full_html/2024/03/aa47157-23/aa47157-23-eq16.gif)
![$$ \begin{aligned} B_\mathrm{ssa}&= 10^{-5} b(\alpha ) \, \theta _\mathrm{m} ^{4} \nu _\mathrm{m} ^{5} S_\mathrm{m} ^{-2} \dfrac{\delta _{\rm j}}{1+z} \, [\mathrm{G} ], \end{aligned} $$](/articles/aa/full_html/2024/03/aa47157-23/aa47157-23-eq18.gif)
![$$ \begin{aligned} B_\mathrm{eq}&= 10^{-4} \left[\frac{(1+k_\mathrm{u} )\, c_{12}\, \kappa _{\nu }}{f} \frac{S_\mathrm{m} \, \nu _\mathrm{m} }{\theta ^{3}_\mathrm{m} \,D_\mathrm{L,Gpc} } \frac{(1+z)^{10}}{\delta _{\rm j}^4} \right]^{2/7} \, [\mathrm{G} ]. \end{aligned} $$](/articles/aa/full_html/2024/03/aa47157-23/aa47157-23-eq19.gif)