| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A232 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202243887 | |
| Published online | 22 March 2024 | |
Faint mm NIKA2 dusty star-forming galaxies: Finding the high-redshift population
1
Aix Marseille Univ., CNRS, CNES, LAM (Laboratoire d’Astrophysique de Marseille), Marseille, France
e-mail: binglj94@gmail.com
2
LLR (Laboratoire Leprince-Ringuet), CNRS, École Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
3
School of Physics and Astronomy, Cardiff University, Queen’s Buildings, The Parade, Cardiff CF24 3AA, UK
4
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité, 91191 Gif-sur-Yvette, France
5
Univ. Grenoble Alpes, CNRS, Grenoble INP, LPSC-IN2P3, 53, avenue des Martyrs, 38000 Grenoble, France
6
Institut Néel, CNRS, Université Grenoble Alpes, Grenoble, France
7
Institut de RadioAstronomie Millimétrique (IRAM), Grenoble, France
8
Dipartimento di Fisica, Sapienza Università di Roma, Piazzale Aldo Moro 5, 00185 Roma, Italy
9
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
10
Centro de Astrobiología (CSIC-INTA), Torrejón de Ardoz, 28850 Madrid, Spain
11
High Energy Physics Division, Argonne National Laboratory, 9700 South Cass Avenue, Lemont, IL 60439, USA
12
Instituto de Radioastronomía Milimétrica (IRAM), Granada, Spain
13
Max-Planck-Institut für Extraterrestrische Physik (MPE), Giessenbachstr. 1, 85748 Garching, Germany
14
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université, UPMC, 75014 Paris, France
15
Department of Physics and Astronomy, University of Pennsylvania, 209 South 33rd Street, Philadelphia, PA 19104, USA
16
Laboratoire de Physique de l’École Normale Supérieure, ENS, PSL Research University, CNRS, Sorbonne Université, Université de Paris, 75005 Paris, France
17
INAF-Osservatorio Astronomico di Cagliari, Via della Scienza 5, 09047, Selargius, Italy
18
Institut d’Astrophysique de Paris, CNRS (UMR7095), 98 bis boulevard Arago, 75014 Paris, France
19
University of Lyon, UCB Lyon 1, CNRS/IN2P3, IP2I, 69622 Villeurbanne, France
20
School of Earth and Space Exploration and Department of Physics, Arizona State University, Tempe, AZ 85287, USA
21
Caltech, Pasadena, CA 91125, USA
22
School of Astronomy and Space Science, Nanjing University, Nanjing 210093, PR China
Received:
27
April
2022
Accepted:
1
December
2023
Aims. High-redshift dusty star-forming galaxies (DSFGs) are proposed to be the progenitors of massive quiescent galaxies arising at cosmic noon, providing a crucial insight into the formation, assembly, and early quenching of massive galaxies in the early Universe. However, their high redshift combined with high dust obscuration adds significant difficulties to their redshift measurement, which is mandatory for detailed studies of their physical properties. Blind mm spectral scans are the most unbiased way in prinicple for obtaining accurate spectroscopic redshifts for these sources, but identifying faint molecular and atomic lines within limited telescope time for faint DSFGs is also difficult with these scans.
Methods. We developed a new framework to constrain the source redshift. The method jointly accounts for the detection and/or nondetection of spectral lines and the prior information from the photometric redshift and total infrared luminosity from spectral energy distribution analysis. The method uses the estimated total infrared luminosity to predict the line fluxes at given redshifts and generates model spectra. The redshift-dependent spectral models were then compared with the observed spectra to determine the redshift.
Results. We applied this joint redshift analysis method to four high-z dusty star-forming galaxy candidates selected from the NIKA2 observations of the HLSJ091828.6+514223 (HLS) field that were further observed by NOEMA with blind spectral scans. These sources only have Herschel SPIRE photometry as ancillary data. They were selected because SPIRE counterparts are faint or entirely lacking and thus favor to select the highest-redshift candidates. The method finds a spectroscopic redshift of 4 in the five NOEMA-counterpart detected sources, with z > 3. Based on these measurements, we derived the CO and [CI] lines and mm continuum fluxes from the NOEMA data and studied the properties of their interstellar medium and star formation. We find cold dust temperatures in some of the HLS sources compared to the general population of submm galaxies, which might be related to the bias introduced by the SPIRE-dropout selection. All sources except for one have a short gas-depletion time of a few hundred million years, which is typical of high-z submm galaxies. The only exception shows a longer gas-depletion time of up to a few billion years. This is comparable to the gas-depletion times of main-sequence galaxies at the same redshift. Furthermore, we identify a possible overdensity of dusty star-forming galaxies at z = 5.2 that is traced by two sources in our sample, as well as a lensed galaxy HLSJ091828.6+514223.
Conclusions. We demonstrate that our method when applied to mm-selected DSFGs is able to determine the redshift accurately. This accuracy with only multiple emission lines with a low signal-to-noise ratio shows promising potential for the blind redshift search in large samples of high-z DSFGs, even in the absence of optical to near infrared photometric redshifts.
Key words: methods: data analysis / galaxies: distances and redshifts / galaxies: high-redshift / radio lines: galaxies / submillimeter: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
It is now clearly established that dusty star-forming galaxies (DSFGs) are critical players in the assembly of galaxy stellar mass and the evolution of massive galaxies at z < 3 (e.g. Madau & Dickinson 2014). At higher redshift, observing the dusty star formation and its spatial and redshift distribution undoubtedly requires (sub-)millimeter (submm) experiments and is still very challenging. For example, the limited existing estimates of dust-obscured star formation rate densities (SFRD) at z > 4 are still not consistently measured, as shown in the discrepancy between recent studies (e.g., Gruppioni et al. 2020; Dudzevičiūtė et al. 2020; Fudamoto et al. 2021; Zavala et al. 2021; Fujimoto et al. 2023). This is largely due to difficulties in uncovering a large unbiased sample of high-redshift DSFGs in relatively large cosmic volumes. Bright and faint DSFGs at high redshift have been uncovered by the surveys conducted by the South Pole Telescope (SPT; Reuter et al. 2020) and the Atacama Large Millimeter/submillimeter Array (ALMA; Franco et al. 2018; Zavala et al. 2021; Aravena et al. 2020). However, statistical studies with these sources are hampered because either strongly lensed DSFG samples are not well defined statistically or by the limitation of the covered areas.
It is well known that in the (sub-)mm, high-redshift DSFGs can be found efficiently in a larger area with relatively deep surveys (Béthermin et al. 2015b) when the negative k-correction (e.g., Casey et al. 2014) is combined with the shape of the luminosity functions. These large-area deep surveys are conducted with single-dish telescopes, for instance, with the SCUBA2 instrument on the JCMT (Holland et al. 2013) or the NIKA2 instrument on the IRAM 30m (Perotto et al. 2020). The angular resolutions of these single-dish surveys are 13″, 11.1″, and 17.6″ for SCUBA2 at 850 μm, and NIKA2 at 1.2 and 2 mm respectively. This makes it difficult to unambiguously identify the multiwavelength counterparts of the DSFGs and to search for the high-redshift population. As already shown by the follow-ups of SCUBA2 sources with ALMA (e.g., Simpson et al. 2020), the combination of single-dish and interferometer surveys is by far the most efficient way of constraining the dusty star formation at 2 < z < 6. The high resolution and sensitivity of (sub-)mm interferometers can provide accurate position measurements for DSFGs and can thus identify their multiwavelength counterparts. However, obtaining the photometric redshift from optical-IR is complicated by the lack of sufficiently deep homogeneous multiwavelength data for analyzing large samples. Moreover, DSFGs are subject to significant optical extinction (some of them are even optically dark; see Franco et al. 2018; Williams et al. 2019; Manning et al. 2022), which impacts the quality and reliability of photometric redshift estimates and prevents optical and near-infrared spectroscopic follow-up. Photometric redshifts from far-IR, mm and radio broadband photometry have been used in studies of the cosmic evolution of high-z DSFGs since the discovery of DSFGs (Yun & Carilli 2002; Hughes et al. 2002; Negrello et al. 2010). However, these measurements are even more uncertain than the optical-IR photometric redshift because the spectral energy distributions (SEDs) in the far-IR to mm do not show any spectral features (but a broad peak), and often, only a few data points are available on the SEDs to constrain the model. In addition, there is a strong degeneracy between dust temperature and redshift in distant dusty galaxies, which limits the usefulness of simple photometric redshifts (e.g., Blain 1999). Finally, in the modeling of the far infrared (FIR) emission, optically thin or thick solutions are highly degenerate. The same SED could arise from either cold and optically thin or from a warmer and optically thicker FIR dust emission, and there is no reliable way to distinguish between the two with continuum observations (Cortzen et al. 2020). This often leads to an overestimate of the FIR photometric redshifts because an apparent colder dust temperature is derived from optically thin emission in high-redshift starbursting DSFGs (Jin et al. 2019).
For these galaxies, spectral scans in the mm can be the only way of deriving the spectroscopic redshift, as shown, for example, by Walter et al. (2012), Fudamoto et al. (2017), Strandet et al. (2017), Zavala et al. (2018). The success rate of measuring the redshift using mm spectral scans can be very high, > 70% (Weiß et al. 2013; Strandet et al. 2016) and even up to > 90% (Neri et al. 2020). This success rate is obtained on large samples in a reasonable amount of telescope time, except for bright DSFGs. For example, with a total time of 22.8 h on 13 DSFGs with average 850 μm fluxes of 32 mJy, Neri et al. (2020) measured the redshift of 12 out of 13 sources with NOEMA. Weiß et al. (2013) obtained a ∼90% detection rate for sources with S1.4 mm > 20 mJy. It may clearly become much more difficult to obtain the redshifts for much fainter objects (e.g. Jin et al. 2019).
We are currently conducting a deep survey with NIKA2, the NIKA2 Cosmological Legacy Survey (N2CLS), a guaranteed-time observation (GTO) large program searching for a large sample of high-z DSFGs (Bing et al. 2022, 2023). The observations cover two fields, GOODS-N and COSMOS, and most of the detected DSFGs are submJy sources at 1.2 mm. One of the goals of N2CLS is to place solid new constraints on the obscured SFRD at z > 4. To reach this goal, we first need to obtain the redshift of the N2CLS sources. While deep optical-IR data are available in the two fields and have been extensively used to obtain photometric redshifts, a large fraction of the sources currently lack a secure redshift. The wealth of ancillary data that is available for these two fields means that blind mm spectral scans are the only solution for measuring their spectroscopic redshift. As a pilot program to try to identify the high-redshift population, we selected four high-redshift candidates detected at 1.2 and 2 mm by NIKA2. They were selected from their far-IR to mm SEDs photometric redshift in the HLSJ091828.6+514223 field observed with NIKA2 during the science verification. This paper presents the redshift identification and source properties based on the spectral scans obtained with NOEMA of these sources. It is organized as follows. In Sect. 2, we present the sample and NIKA2 observations. Section 3 describes the NOEMA observations and data reduction, as well as the extraction of continuum fluxes and spectral scans. In Sect. 4, we extensively discuss the redshifts. In particular, we develop a new method that combines far-IR to mm photometric data and spectral scans to measure the redshift. The source properties such as their dust mass and temperature, kinematics, and the excitation of molecular gas, are given in Sect. 5. Section 6 presents the potential discovery of a DSFG overdensity at z = 5.2 in the HLS field. Conclusions based on the main results and the possible implications of our findings for future high-z DSFGs studies are given in Sect. 7. Finally, three appendices describe more details of the method with which the redshift is measured and its validation. Throughout the paper, we adopt the standard flat ΛCDM model as our fiducial cosmology, with cosmological parameters H0 = 67.7 km s−1 Mpc−1, Ωm = 0.31, and ΩΛ = 0.69, as given by Planck Collaboration VI (2020).
2. NIKA2 observation and sample selection
As part of the NIKA2 science verification that took place in February 2017, we observed an area of 185 arcmin2 centered on HLSJ091828.6+514223, a lensed dusty galaxy at z = 5.24 (Combes et al. 2012), for an on-source time of about 3.5 h at the center. This allowed us to reach 1σ sensitivities of about 0.3 mJy at 1.2 mm and 0.1 mJy at 2 mm on HLSJ091828.6+514223. This galaxy is close to the z = 0.22 cluster Abell 773, but is likely lensed by a galaxy at z ∼ 0.63. For our NIKA2 sources, the magnification by the galaxy cluster is < 10%. Therefore, we do not expect the NIKA2 sources to be highly magnified (E. Jullo, priv. comm.).
The NIKA2 field almost entirely overlaps Herschel SPIRE observations at 250, 350, and 500 μm. In contrast, the PACS, IRAC, and HST images only cover a very small part of the field on the west side (where NIKA2 observations have lower signal-to-noise ratios, S/Ns). Thus, only SPIRE data were used to select the high-z candidates. The SPIRE fluxes were measured using FASTPHOT1 (Béthermin et al. 2010) through simultaneous PSF fitting, and NIKA2 source positions were used as priors on the SPIRE maps.
We built a 1.2 and 2 mm catalog using the NIKA2 data reduced using the collaboration pipeline (Ponthieu et al., in prep.). A total of 27 sources are detected with S/N > 5 in at least one band (1.2 or 2 mm). From this catalog, we selected four sources detected at both 1.2 and 2 mm with high S/N (between 5.7 and 9.7) and for which there is a faint (at the level of confusion noise) or no SPIRE counterparts, as to bias the sample towards the highest redshift candidates. Indeed, rough sub-millimeter photometric redshifts, obtained by fitting empirical IR SED templates from Béthermin et al. (2015a) to our SPIRE+NIKA2 data, were zphot ∼ 5 − 7. These sources are named HLS-2, HLS-3, HLS-4, and HLS-22. Their fluxes are between 1.7 and 2.9 mJy at 1.2 mm and 0.28 and 0.60 mJy at 2 mm. The flux measurements and uncertainties are presented in Table 1, where the 1-σ flux uncertainty of SPIRE undetected HLS sources are in parenthesis. The quoted uncertainties account only for uncertainties coming from flux measurements.
Coordinates, millimeter fluxes and SPIRE far-IR fluxes of our NIKA2 HLS sample.
3. NOEMA observations and source identification
3.1. NOEMA observations and data calibration
Follow-up observations were made using NOEMA from 2018 to 2020 with four different programs. The four sources in the HLS field were all observed by NOEMA with the PolyFiX correlator. They were initially targeted by project W17EL (HLS-2/3/4) and W17FA (HLS-22) using the same setups that continuously covered the spectra from 71 GHz to 102 GHz with the D configuration in band1. HLS-22 were further observed in project W18FA with the A configuration in band1, and HLS-2 and HLS-3 were further observed in project S20CL at band2 with the D and C configuration, respectively. The total on-source time of all of the proposals is 44.9 h. The details of the observations for each source are summarized in Table 2.
Information on NOEMA follow-up observations.
NOEMA observations were first calibrated using CLIC and were imaged by MAPPING under GILDAS2. The radio sources 3C454.3, 0716+714, 1156+295, 1055+018, 0851+202, and 0355+508 were used for bandpass calibrations during these observations, and the source fluxes were calibrated using LHKA+101 and MWC349. With the calibrated data, we further generated the uv table with the original resolution of 2 MHz. We also produced the continuum uv table of each source by directly compressing all corresponding lower-sideband (LSB) and upper-sideband (USB) data with the uv_compress function in MAPPING.
3.2. NOEMA continuum flux measurement and source identification
We identified the counterparts of our sample in the NOEMA continuum data. We first generated the continuum dirty map and then cleaned the continuum image of each source with the Clark algorithm within MAPPING. The cleaned image of each source with the highest S/N and (or) the best spatial resolution is shown in Fig. 1. We blindly searched for candidate sources by identifying all of the peaks above four times the rms within the NOEMA primary beam. Their accurate positions were then derived with uv_fit function in MAPPING (with the peak positions as the initial prior and point source as the model), and the continuum fluxes at the other frequencies were estimated with source models fixed to these reference images.
 |
Fig. 1. Cleaned images of the NOEMA observation for our four NIKA2 sources. The effective beam size and shape of each map is shown in the bottom right corner of each panel. The contour levels from orange to dark red correspond to −4, 4, 8, and 12 times the rms of each map, respectively. The red crosses mark the position of detected NOEMA sources from the uv_fit. The two resolved sources associated with HLS-2 are also labeled separately (HLS-2-1 and HLS-2-2). The scale bars in the maps (upper left) correspond to 5 arcsec in the sky. The frequency of the continuum data is given in the lower left corner of each panel. |
The continuum fluxes were measured using uv_fit and the same models as given in Table 3. The four sidebands in the two setups of W17EL and W17FA were combined to generate continuum uv tables centered on 3.6 mm because the S/N of the continuum emission at this long wavelength is low. When data were available, the continuum fluxes at higher frequencies were measured both sideband by sideband and on the combined LSB+USB uv-table. The continuum fluxes are listed in Table 4.
NOEMA continuum source positions and best-fit sizes.
Continuum fluxes from NOEMA observations.
We detected five reliable continuum sources within the primary beam of NOEMA observations as counterparts of the four NIKA2 HLS sources. We further checked the residual rms on the map with source models that were more complex than point sources. This did not improve the level of residuals of three NOEMA sources. For the remaining two sources, HLS-2-1 and HLS-3, the favored simplest models are a circular Gaussian model and an elliptical Gaussian model, respectively. The position and preferred models of each source is listed in Table 3, and we note that the position of these sources does not change significantly for the different models.
We show in Fig. 1 the cleaned images of NOEMA observations. The NIKA2 source HLS-2 is resolved into two continuum sources in our high-resolution NOEMA observation with S/N ∼ 10. The remaining NIKA2 sources are all associated with one single NOEMA source. For these sources (HLS-3, HLS-4, and HLS-22), we compared their positions in the NOEMA and NIKA2 observations. The maximum offset is found in HLS-3 with a value of 1.9 arcsec. The average offset is 0.9 arcsec among these three sources, which suggests that the positional accuracy of NIKA2 in locating sources with relatively high S/N is high.
For HLS-2 and HLS-3, part of our NOEMA observations measured their continuum fluxes at a frequency close to the representative frequencies of the NIKA2 2 mm bands. The NOEMA and NIKA2 fluxes are consistent for HLS-3. The total NOEMA fluxes of the two components of HLS-2 are 50% higher than the flux measured by NIKA2, but they are still consistent with each other within the 3 σ uncertainties. This first comparison is encouraging. A detailed study of NIKA2 and NOEMA fluxes is beyond the scope of this paper and will be conducted with more statistics (e.g., with the NOEMA follow-up of N2CLS sources).
3.3. Extraction of the NOEMA millimeter spectra
We extracted the mm spectra of NOEMA continuum sources from the full uv table. The uv tables were first compressed by the uv_compress function in MAPPING, which makes averages within several channels to enhance the efficiency of the line searching with a higher S/N per channel and a smaller load of data. For observations in band1, we set the number of channels to 15 on average, while the observations in band2 and band3 were averaged every 25 channels, which corresponds to channel widths of 107 km s−1, 100 km s−1, and 59 km s−1 at 84 GHz, 150 GHz, and 255 GHz, respectively. Based on the typical line width (a few hundred to one thousand km s−1) for submm galaxies (Spilker et al. 2014), the compression of the uv tables could still ensure Nyquist sampling by two to three channels on the emission line profiles and preserve the accuracy of line center and redshift measurement.
To extract the spectra, we performed a uv_fit on the compressed spectral uv table with the position and source model fixed to the same values as given in Table 3. For the observations of the W17EL002 setup, we flagged the visibilities associated with one antenna that significantly deviated from the others. Because of the relatively low angular resolution of most of our data for HLS sources (∼5″ in band1 and ∼2″ in band2), these galaxies are unlikely to be significantly resolved, and the uv_fit at a fixed position in the uv tables should therefore be able to uncover most of their line emission.
We further removed the continuum in the extracted spectra, assuming a fixed spectral index of 4. This is equivalent to a modified blackbody spectrum with a fixed emissivity (β) at 2, and is generally consistent with the dust emissivity we derived in Sect. 5.2. We used these continuum-subtracted NOEMA spectra for the redshift search and the emission line flux measurement (see Sect. 4.2 and Sect. 5.1). The extracted spectra and continuum model to be removed are shown in Fig. 2.
 |
Fig. 2. Millimeter spectra of all HLS sources extracted from the uv tables obtained from the NOEMA observations. The continuum models to be subtracted are presented as solid gray lines. The lines we identified to determine the spectroscopic redshift of the sources (see Sect. 4 and Fig. 4 for details) are marked by vertical dashed black lines. |
4. Source redshift from a joint photometric-spectroscopic analysis
An accurate redshift is a prerequisite for an accurate estimate of the physical properties of high-z galaxies. However, the optical-IR SED of high-z DSFGs are often much poorer constrained than those of other high-z galaxies because they are faint at these wavelengths, which poses challenges for an accurate measurement of their photometric redshifts. In the far-IR, the degeneracy between colors, dust temperature, and redshift could also lead to a highly model-dependent estimate of the photometric redshift. In this section, we describe the different methods and summarize the results of the redshift estimate for our sample with the photometric and spectroscopic data described in Sect. 3. Specifically, we introduce a new joint analysis framework to determine the redshifts of NIKA2 sources by combining the probability distribution function of photometric redshifts with the corresponding IR luminosities and blind spectral scans. This helps us identify the low-S/N spectral lines in the NOEMA spectra.
4.1. Photometric redshifts
The lack of deep optical and infrared data for the HLS field makes it impossible to conduct a full SED modeling of NIKA2 detected sources. However, with the NIKA2 and SPIRE photometry, we fit the far-IR SED of HLS sources with dust emission templates to estimate their redshifts and IR luminosities. The angular resolution of the FIR data is very low, and we were therefore unable to obtain the fluxes of each single component resolved by NOEMA observations for HLS-2. We therefore only fit with the integrated fluxes under the assumption that the two components that are blended within the beam of SPIRE and NIKA2 are located at the same redshift.
We used two sets of FIR dust templates: the synthetic infrared SED templates from Béthermin et al. (2015a; hereafter B15), and the MMPZ framework (Casey 2020) using parameterized dust templates from Casey (2012).
B15 templates can be described as a series of empirical dust SEDs of galaxies at different redshifts. The dust SEDs are produced based on the deep observational data from the infrared to mm. It considers two populations of star-forming galaxies: starburst and main-sequence galaxies. It then produces the two corresponding sets of empirical SED templates. We fit our photometric data points with the templates of main-sequence galaxies, which consisted of 13 SEDs at each redshift. These templates included the average SED and the SEDs within ±3σ uncertainties with steps of 0.5σ. The estimated redshift and the 1σ uncertainties based on the fitting using B15 main-sequence and starburst SED templates are listed in Table 5. In the following redshift search involving the B15 templates (see Sects. 4.2 and 4.3), we only used and present the output of the SED fitting based on the main-sequence templates. This is mainly because the output results of the SED fitting based on starburst and main-sequence templates, as shown in Table 5, are highly consistent considering the uncertainty.
Photometric redshift of HLS sources from different methods.
Casey (2012) described the intrinsic FIR dust emission of galaxies using a generalized modified blackbody model in far-IR plus a power-law model at mid-IR. For the SED fitting with the Casey (2012) template, we worked within the framework of the MMPZ algorithm Casey (2020). It considers the intrinsic variation of dust SED at different IR luminosities, as well as the impact of the rising CMB temperature at high redshift. The default set of IR SEDs fixes the mid-infrared spectral slope to 3 and dust emissivity β to 1.8. The template SED also considers the transition from optically thin to optically thick at lower wavelengths, where the wavelength of unity opacity (τ(λ) = 1) is fixed to 200 μm. The redshift, the total infrared luminosity, and the corresponding wavelength at the peak of the IR SED are the main parameters to be considered for the fit. The empirical correlation between the latter two parameters is also taken into account during the fit.
From the analysis and results shown in Fig. 3, we find that the redshifts from MMPZ are systematically lower than those from the B15 template fitting, with a typical Δz/(1 + z) of about 20%. However, the two redshifts are still consistent within their uncertainties. The infrared luminosities returned by MMPZ are also systematically lower by ∼0.3 dex, especially at redshifts beyond 3.
 |
Fig. 3. Results of the IR template fitting of our four HLS sources with the B15 dust templates and MMPZ method using the SPIRE, NIKA2, and NOEMA photometry. The plots in the first column show the probability density distribution (normalized by the peak values) of each source. The second column shows the evolution of the weighted-average infrared luminosity with redshift. The third column shows the best-fit SED models with the observations. The sources from top to bottom are HLS-2, HLS-3, HLS-4, and HLS-22. |
The faintness and large flux uncertainties of our sources in the three SPIRE bands make the constraint on the peak of their IR SEDs much worse than for the brighter and lensed high-z sources, which leads to large uncertainties on the estimated total IR luminosity. Compared to the template fitting with B15, MMPZ further takes the CMB heating and dimming (da Cunha et al. 2013) into consideration. Although this could affect the dust emissivity index β and, as a result of the β-T degeneracy, the dust temperature and IR luminosity, the β values are all fixed to 2 in these two templates. Thus, we consider that the inclusion of the CMB effect is not the main contributor to the differences between the results of the two template-fitting methods.
The difference in the estimated total IR luminosities is propagated to the joint photometric and spectral analysis on the source redshift in Sect. 4.2.
4.2. Joint analysis of the photometric redshifts and NOEMA spectra
As a result of the lack of characteristic spectral features in far-IR, the photometric redshifts of our sample derived from Sect. 4.1 still have large uncertainties. The search for emission lines in the mm spectra provides an approach to constrain our redshifts with a significantly better accuracy. To identify the possible emission lines in the spectra, we performed a blind search in the NOEMA spectra. The NOEMA spectra were first convolved by a box kernel of 500 km s−1 width, which corresponds to the typical molecular line width of bright (sub)mm selected galaxies (e.g., Bothwell et al. 2013). To more completely uncover the possible emission lines in these noisy spectra, we list the five lines (if exist) with the highest S/N in the convolved spectra with S/N > 3 in Table 6. We failed to detect any lines for HLS-2 and HLS-4 with S/N > 3 in our observations. For HLS-3 and HLS-22, we identify one and two detections, respectively. The “detection” at 100.628 GHz in the HLS-22 spectrum is likely to be a glitch or noise spike with an incorrectly estimated uncertainty (see Appendix A and Fig. A.2). With only one significant detection of an emission line, an unambiguous redshift solution is not possible.
S/N > 3 lines blindly detected in the NOEMA spectra.
To find the redshift solutions, we needed to take additional constraints from broadband photometry, in particular, from the total infrared luminosities at any sampled redshift in the SED fitting. From the output χ2 and IR luminosities of all models at one given redshift, we were able to derive the weighted-average value of the total infrared luminosity of the source at this redshift using Eq. (1)
where the σ(j) is a weighting term that accounts for the deviation of the 13 model SEDs from the median of star-forming galaxies at a given redshift in B15. At a given redshift, the B15 template includes one median SED and 12 SEDs within ±3σ uncertainties with a spacing of 0.5σ. When the source IR luminosities at a given redshift is derived, the σ(j) terms should therefore be included to account for the probability that the IR template SEDs deviate from the median in the B15 model. The values of σ(j) are thus between −3 and +3 with steps of 0.5. When we used the output from MMPZ, the σ(j) was set to 0.
With a series of average IR luminosities over the redshift grid from the SED fitting, we linearly interpolated the IR luminosity at any given redshift. We further used the IR luminosity to constrain the fluxes of strong FIR-mm emission lines at any given redshift based on the well-defined almost redshift-invariant LFIR-Lline relations in the form of Eq. (2),
The luminosities and fluxes of the 12CO lines of J(1–0) to J(12–11), two transitions of [CI], and the [CII] line at 158 μm were predicted based on various scaling relations found in the literature. The detailed information is listed in Table 7 and in the references therein. With the estimated fluxes of different line species at a given redshift, we generated a model spectrum in the frequency range of the NOEMA spectral scans and compared this model with the observations3.
Parameters of the log-linear LFIR-Lline scaling relation in our analysis.
When generating the model spectra, we assumed that the emission lines have Gaussian profiles with a fixed full width at half maximum (FWHM) of 500 km s−1. We also linearly interpolated the LFIR, med-z relations from the IR template fitting to a finer redshift grid to avoid missing any possible redshift solutions.
The spacing between adjacent redshifts in the resampled grid satisfies Eq. (3), which is equivalent to a fixed spacing in velocity (Δv) between adjacent redshifts,
We fixed Δv to be one-third of the chosen FWHM, which means that the emission line profile was Nyquist-sampled by the predicted line centers at the corresponding redshifts in the new grid. This ensures that emission lines in the spectra and their corresponding redshift solutions were not missed in our analysis due to poor redshift sampling. The goodness of the model prediction at a given redshift was evaluated by the log-likelihood ln(ℒspec(z)) from the χ2 between the model spectra and the data, as given below in Eqs. (4) and (5),
In addition to the goodness of match between spectra and models, we further accounted for the goodness of the SED fitting at given redshifts,  (z), which is defined similarly to Eq. (5). The joint log-likelihood at each sampled redshift reads
(z), which is defined similarly to Eq. (5). The joint log-likelihood at each sampled redshift reads
As already pointed out, we assumed that the two counterparts for HLS-2 have a similar redshift and share the same FIR SED. Under this assumption, the total infrared luminosity of the two NOEMA sources was thus computed based on their contributions to the total flux at 2 mm, which are used below to derive their final joint-likelihood of the redshift.
4.3. Redshifts measurement
The results of the joint log-likelihood of the redshift from photometry plus spectral scan analysis of the five HLS sources are shown in Fig. 4. For each source, we normalized the ℒspec(z) to the peak value, which helped us to compare the relative goodness of the match between the model predictions and the observed spectra at different redshifts quantitatively. We selected all the peaks in ln(ℒspec(z)) with an amplitude larger than −10 and a width larger than three samples in the redshift grid as the possible redshift solutions of our sources using the “find_peaks” algorithm in SciPy. Considering the large uncertainties on the total infrared luminosity of the HLS sources, we further cross-validated their possible redshift solutions by repeating the joint likelihood analysis using the output IR luminosity at different redshifts from the MMPZ fitting, and we applied the same algorithm to record the possible redshift solutions.
 |
Fig. 4. Joint analysis of the redshift for four NIKA2 HLS sources with the SED-fitting outputs using the B15 dust templates and MMPZ. The first row shows the normalized log-likelihood from the SED fitting and the joint log-likelihood for each source after considering the information obtained from the NOEMA spectral scans. The second and third row show the cutouts of the spectra around candidate spectral lines at the best redshift solutions. The lines shown in the second row are detected in the earliest band1 spectral scans (W17EL and W17FA), and those in the third row are detected in the additional follow-up observations (W18FA and S20CL). The models generated based on the fit with the B15 dust templates and MMPZ at the most probable redshift are plotted as solid and dashed red lines, respectively. |
Compared to the log-likelihood of redshift with photometric constraints alone (see Fig. 3), the joint analysis helped us to highlight significant isolated peaks for the redshift of HLS-2-1, HLS-2-2, HLS-3, and HLS-22 at z = 5.241, 5.128, 3.123, and 3.036, respectively. The redshift with the highest log-likelihood value is not sensitive to the choice of IR templates either. As shown in Fig. 4, the B15 template and MMPZ find almost the same redshift, where the joint log-likelihood value is highest, which further confirms their redshift solutions as listed above. Even though HLS-4 has the most accurate photometric redshift constrained through template fitting, the absence of an emission line detection in the band1 spectral-scan observations means that our analysis is unable to identify significant peaks in the joint log-likelihood. Thus, no reliable redshift solution is found for this source.
With the blindly detected candidate emission lines at S/N > 3, our method successfully confirms the candidate lines for HLS-3 and HLS-22, except for the line at 100 GHz in the HLS-22 spectrum. The extremely narrow profile of the candidate detection suggests that this is likely to be a glitch, which is shown and discussed in Appendix A. For HLS-3, the MMPZ also reveals a secondary redshift solution at z = 2.299 with a slightly lower log-likelihood in the analysis. This means that the most significantly detected emission line at 139.746 GHz is CO(4–3), while the best solution at z = 3.123 means that it is CO(5–4). If HLS-3 has z = 3.123, we also expect to cover the CO(3–2) line in the spectral scan. Although the line is not detected at 3σ (see Sect. 5.1), we cannot simply reject any of the two possible redshift solutions due to the high noise level around the observed frequency. Thus, we consider the redshift of HLS-3 to be less secure than that found for the other sources with at least two lines with S/N > 4 (HLS-2-1, HLS-2-2, and HLS-22, see Table 9), and we provide the estimate of the HLS-3 properties based on the two redshift solutions in the paper. We also note that HLS-2-2 could have a secondary redshift solution at z = 3.385. However, this redshift did not match any of the two most significant emission lines found in the spectrum, which correspond to CO(4–3) and [CI](2–1) at z = 5.128. Thus, we only adopt the z = 5.128 solution in the following analysis.
In Table 8, we summarize the redshifts from the joint analysis method (zjoint), as well as the far-IR photometric redshifts based on the two far-IR templates (zB15, ms and zMMPZ). For sources with ambiguous redshift solutions, we use the two different zfix for the analysis. The uncertainties of z joint are conservatively given and correspond to 0.5 × FWHM of the line (see Table 9). In the following sections, the source properties are estimated at the best solution of redshift of joint analysis, or the most possible photometric redshift when no redshift solution is found in the joint analysis. These choices of redshifts of our sample are listed as zfix in Table 8.
Summary on the joint-analyzed redshifts of NOEMA sources.
4.4. Robustness and self-consistency of the joint-analysis method
The analysis of the source properties of our sample, such as dust mass, temperature, and star formation rate, largely relies on the estimated redshifts from the joint-analysis method, which is subject to the assumptions on the line widths and line luminosities. To test the robustness of the redshift derived from the joint-analysis method, we conducted tests with model spectra of varying line widths, with NOEMA data of a more limited spectral coverage, and with different far-IR templates to derive the photometric redshift and predict the IR luminosity. These tests show that the redshifts of our sources from the joint analysis are reliable. In addition, we also checked the self-consistency of our redshift solution by comparing our LFIR–LCO correlation with the scaling relations and their scatters. These tests and discussions are presented in Appendices A–D.
5. Source properties
5.1. Kinematics and excitation of the molecular gas in the HLS sources
We find redshift solutions for four NOEMA sources associated with three NIKA2 sources. For each of these sources, at least one emission line is detected with S/N > 4 or two lines are detected with S/N at ∼3–4 in the NOEMA spectral scans. With these redshifts, we further measured the flux and line width of the spectral lines covered by the observations and derived the corresponding line luminosities. We started the fitting with a single-Gaussian model on the continuum-subtracted spectra of each source. Regardless of whether they are detected with high significance, all CO or [CI] lines that fall into the frequency coverage of NOEMA were considered. To make a more robust analysis of the line width, we also forced the kinematics of the CO and [CI] lines to be the same during the fit. For the emission line at 139.746 GHz of HLS-3, a double-Gaussian model results in an Akaike information criterion (AIC) of −17.1, compared to the AIC of −11.3 using a single-Gaussian model. This suggests an improved quality of the fit with the double-Gaussian model, and thus, we used this as the model for HLS-3.
The line widths, fluxes, and upper limits of the CO or [CI] lines for each source are listed in Table 9. We measured the total flux or the flux upper limit of each line by integrating the spectra within ±3σline around the best-fit line center for the single-peaked lines. For HLS-3 with a double-peaked line profile (noted as the red and blue peak, respectively), we estimated the line fluxes and upper limits by integrating the spectra in the range of [fcenter, red–3σred, fcenter, blue+3σblue]. The corresponding CO or [CI] line luminosities or 3σ upper limits ( and Lline) were also calculated using the following equations (from Solomon et al. 1997):
and Lline) were also calculated using the following equations (from Solomon et al. 1997):
Emission line fluxes, luminosities, and widths of four sources in the HLS field.
where SlineΔV is the velocity-integrated flux in Jy km s−1, νrest = νobs(1 + z) is the rest frequency in GHz, and DL is the luminosity distance in Mpc.
The [CI](1–0) lines of HLS-2-1 and HLS-2-2 are covered by the spectral scan, but are located at the noisiest edges of the NOEMA sidebands. This means that their upper limits are of little scientific value, and thus, we discarded them from the table. The CO(7–6) line of HLS-2-2 is marginally detected, but only partly covered by our observations. For this line, we used the output parameters from the spectral line fitting to constrain its flux using a complete Gaussian profile.
Figure 5 shows the best-fit models for each CO or [CI] line. The line identification in each panel is presented assuming the best redshift solution of each source, as listed in Table 8. The spectra have the same channel width as those we used for the joint analysis. From the best-fit parameters, we find that the line widths are generally consistent with the assumption we made during the redshift search in Sect. 4.2, with an average FWHM of 500 km s−1. Although previous observations revealed that the integrated [CI] and CO lines from the same high-z galaxies may have different line widths and line profiles (Banerji et al. 2018), fixing or relaxing the velocities and widths of the different lines during our analysis did not significantly change the quality of the best-fit model.
 |
Fig. 5. Observations and best fits of the spectral lines, including both detections and upper limits. The best-fit model of each line is shown with the solid red line. For HLS-3, we show the two lines assuming z = 3.123. |
The observations of the two sources associated with HLS-2 cover both mid-J (CO(4–3) or CO(5–4)) and high-J CO lines (CO(7–6) or CO(8–7)), allowing us to roughly estimate the conditions of their molecular gas and compare them with other DSFGs at similar redshifts using the luminosity ratios (expressed in K km s−1 pc2). For HLS-2-1, the  /
/ is 0.31 ± 0.11, which is consistent with the values found in typical high-z SMGs with low excitation (Bothwell et al. 2013), but it is lower than the reported value of some starburst galaxies and luminous quasars at a similar redshift (Rawle et al. 2014; Li et al. 2020). The
is 0.31 ± 0.11, which is consistent with the values found in typical high-z SMGs with low excitation (Bothwell et al. 2013), but it is lower than the reported value of some starburst galaxies and luminous quasars at a similar redshift (Rawle et al. 2014; Li et al. 2020). The  /
/ and CO(8–7)/CO(4–3) of HLS-2-2 are < 0.17 and < 0.12, respectively. These values are even lower than the typical value of high-z SMGs, but they are still consistent with the low-excitation ISM found in the “Cosmic Eyelash” (Danielson et al. 2011).
and CO(8–7)/CO(4–3) of HLS-2-2 are < 0.17 and < 0.12, respectively. These values are even lower than the typical value of high-z SMGs, but they are still consistent with the low-excitation ISM found in the “Cosmic Eyelash” (Danielson et al. 2011).
In addition to CO detections or upper limits, the detection of [CI](2–1) for HLS-2-2 also provides an additional insight into the state and condition of its molecular gas reservoir. Previous studies suggested that  /
/} $](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq39.gif) could be used to distinguish secular-evolved (low value) and merger-driven (high value) systems. The [CI] dominated systems with
could be used to distinguish secular-evolved (low value) and merger-driven (high value) systems. The [CI] dominated systems with } $](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq40.gif) around or below 1 are generally found for secular-evolved disk-dominated galaxies (Andreani et al. 2018). As neutral carbon could be more easily excited, the low values in secular-evolved systems indicate lower gas excitation or more abundant low-density gas. The low
around or below 1 are generally found for secular-evolved disk-dominated galaxies (Andreani et al. 2018). As neutral carbon could be more easily excited, the low values in secular-evolved systems indicate lower gas excitation or more abundant low-density gas. The low  /
/} $](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq42.gif) suggests a low-excitation molecular gas reservoir in HLS-2-2 and is consistent with the low
suggests a low-excitation molecular gas reservoir in HLS-2-2 and is consistent with the low 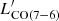 /
/ and
and  /
/ measured in the same galaxy. For HLS-2-1, we estimate
measured in the same galaxy. For HLS-2-1, we estimate  /
/} < 0.9 $](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq48.gif) , which agrees with the values found in secularly evolved galaxies.
, which agrees with the values found in secularly evolved galaxies.
For the remaining two sources with a CO detection of less separated quantum numbers J, our observations find  0.73 in HLS-3 and
0.73 in HLS-3 and  in HLS-22. The value for HLS-22 is generally consistent with the average CO SLED of high-z SMGs in Bothwell et al. (2013), being similar to the case of HLS-2-1. In contrast, HLS-3 has a
in HLS-22. The value for HLS-22 is generally consistent with the average CO SLED of high-z SMGs in Bothwell et al. (2013), being similar to the case of HLS-2-1. In contrast, HLS-3 has a  ratio higher than typical SMGs in Bothwell et al. (2013) and resembles the average of the SPT sample (Spilker et al. 2014) or the local starburst galaxy M82 (Carilli & Walter 2013) with higher excitation. However, the observations of these two sources do not cover higher-J CO lines like for HLS-2, which traces warmer and denser components in the molecular gas reservoir. Thus, with these two line-ratio measurements, it is more difficult to conclude.
ratio higher than typical SMGs in Bothwell et al. (2013) and resembles the average of the SPT sample (Spilker et al. 2014) or the local starburst galaxy M82 (Carilli & Walter 2013) with higher excitation. However, the observations of these two sources do not cover higher-J CO lines like for HLS-2, which traces warmer and denser components in the molecular gas reservoir. Thus, with these two line-ratio measurements, it is more difficult to conclude.
5.2. Dust mass and dust temperature
The far-IR continuum emission of star-forming galaxies is well represented by a single-temperature modified blackbody model from which the dust temperature (Tdust), dust emissivity index (β), and total dust mass (Mdust) can be derived. At high redshift, the increasing temperature of the cosmic microwave background (CMB) reduces the contrast of star-forming galaxy emissions in the (sub-)mm and changes the apparent shape of the spectrum at these frequencies. When we consider the impact of the CMB, the observed modified blackbody emission of a high-z SMG can be expressed as Eq. (9) using the optical-thin assumption (da Cunha et al. 2013),
The dust emissivity κ(ν) in far-IR can be described by a single power law,
where k0 stands for the absorption cross section per unit dust mass at a given specific frequency ν0. We took k0, 850 μm = 0.047 m2 kg−1 from Draine et al. (2014; see also Berta et al. 2021).
We performed an MCMC fitting (using the PyMC3 package) for our far-IR to mm photometric data using the model given in Eq. (9). The two sources associated with HLS-2 were fit using their integrated flux because they have very similar redshifts and their individual fluxes at the far-IR could not be obtained with the low-resolution SPIRE data. We adopted uniform priors for Tdust and Mdust and a flat prior between 1 and 3 for the dust emissivity β. We constrained the temperature to be between TCMB at the given redshifts and 80 K. The redshift values were fixed to zfix given in Table 8. Figure 6 shows as an example the best-fit modified blackbody model for HLS-2, as well as the 1σ and 2σ confidence intervals. For HLS-22, the original fit with free parameters leads to a unphysically low dust temperature at 16 K and a high-β higher than 3, which is due to the poor observational constraints at 3 mm and < 500 μm. Thus, we performed a constrained modified blackbody fit with a fixed β of 1.8, consistent with the average of the other HLS sources. We list the estimated dust temperature, mass, and emissivity index in Table 10.
 |
Fig. 6. Example of a modified blackbody fitting of the far-IR to mm photometric data for one of our galaxies. (a) Photometric data and best-fit model. The ±1σ and ±2σ uncertainties of the model are shown with blue shades of different transparency. (b) Corner plot of the posterior distribution of the three parameters. The contours correspond to 1, 1.5, and 2σ in the 2D histogram. |
Dust properties of the HLS sources from the optically thin modified blackbody fitting.
We derive a dust mass of ∼109 M⊙, which is consistent with the dust masses derived for bright SMGs selected from blind single-dish surveys (Santini et al. 2010; Miettinen et al. 2017). The abundant dust indicates that these high-z dusty star-forming galaxies have already experienced a rapid metal enrichment in the first few billion years of the Universe. The dust emissivity β of our sample (excluding HLS-22) has a median value of 1.75, which is also consistent with the values found in a variety of galaxies across the cosmic time.
We also measured the far-IR luminosities (LFIR) by integrating the model SEDs between 50 and 300 μm at the rest-frame of each source. The LFIR are listed in Table 10. Our observations could not properly constrain and model the mid-IR emission of galaxies. Thus, we extrapolated our LFIR (50–300 μm) to the total infrared luminosity (LIR, 3–1000 μm) by multiplying LFIR by a factor of 1.3, based on the calibrations given in Graciá-Carpio et al. (2008). We further derived the star formation rates, SFR, based on the standard scaling relations from Kennicutt & Evans (2012). The corresponding results are also listed in Table 10.
The dust temperature of our sample varies from 18 to 41 K. Fig. 7 shows the comparison between the dust temperature of our sample with other DSFGs and star-forming galaxies (Roseboom et al. 2013; Riechers et al. 2014, 2017; Pavesi et al. 2018; Béthermin et al. 2020; Faisst et al. 2020; Neri et al. 2020; Bakx et al. 2021; Sugahara et al. 2021) at different redshifts. Similar to our analysis, the literature dust temperatures for comparison here were all derived under the optically thin assumption. The average dust temperature of normal star-forming and starburst galaxies from Béthermin et al. (2015a) and Schreiber et al. (2018) are also shown as baselines of comparison at different redshifts. We find large scatter in the dust temperature of our sample with respect to these empirical Tdust-(z) scaling relations for star-forming and starburst galaxies. Of our HLS and literature sample, HLS-3 shows one of the lowest dust temperatures, 23(18) K, while the other three sources at higher redshifts have a higher dust temperature that is not distinctive of literature DSFGs and the average dust temperature of normal star-forming galaxies. DSFGs with apparently cold temperatures have been reported by some studies in recent years (Jin et al. 2019; Neri et al. 2020). Similarly to these galaxies, the redder and apparently colder far-IR SED of HLS-3 could resemble normal DSFGs at much higher redshift in SED modeling, which explains the significant deviation of its far-IR photometric redshift from its spectroscopic redshift based on the Béthermin et al. (2015a) SED template. At fixed LIR, we expect galaxies with a colder dust temperature to be brighter at 1.2 mm, and thus, these galaxies are more favored by the selection of candidate high-z DSFGs based on red far-IR to mm colors.
 |
Fig. 7. Dust temperature vs. redshift of the high-z DSFGs in our sample, and DSFGs or LBGs from the literature. The dust temperatures of these sources are all measured with the optically thin modified blackbody model. The corresponding references are listed in the legend. We also overlaid the average Tdust-z relation of main-sequence galaxies derived by Schreiber et al. (2018) and Béthermin et al. (2015a) based on observational data. For HLS-4 with a photometric redshift alone, we show the degeneracy between dust temperature and redshift with the dash-dotted gray line. The Tdust of HLS-3 at the two possible redshifts is plotted and connected by the solid red line. |
5.3. Molecular gas mass
Both the CO emission lines and dust continuum in the Rayleigh-Jeans tail of the far-IR SED have been widely used to estimate the amount of molecular gas in galaxies (Carilli & Walter 2013; Hodge & da Cunha 2020). In this section, we measure the molecular gas mass for our sample and cross-validate the results with various methods.
The detections and constraints on CO emission lines enable estimating the molecular gas mass using the conversion factor αCO for the CO luminosity to molecular gas mass. Robust estimates of the conversion factor are mostly made on the lowest J transition, CO(1–0), while CO detections in our sample start from CO(3–2) to CO(5–4). Thus, we need to convert the luminosities of the lowest-J CO line detected in our observations into CO(1–0), in addition to the assumptions on the αCO conversion factor between CO(1–0) luminosity to molecular gas mass. In our case, we took advantage of the multiple line detections and flux upper limits in the NOEMA spectra of each source to find the matching cases in the literature and to roughly estimate the CO(1–0) luminosity and molecular gas mass. As described in Sect. 5.1, we compared the CO luminosity ratios with literature results for each source and determined the cases with CO SLEDs that could reproduce the observed values. For HLS-2-1 and HLS-22, we applied  and
and  from the average SLED of unlensed SMGs in Bothwell et al. (2013). For HLS-2-2 and HLS-3, we find the SLEDs of the “Cosmic Eyelash” (Danielson et al. 2011) and the average of SPT SMGs (Spilker et al. 2014) reproduce the observed luminosity ratios well. We scaled the luminosities of the lowest J CO lines observed in these two sources to their CO(1–0) luminosities by assuming
from the average SLED of unlensed SMGs in Bothwell et al. (2013). For HLS-2-2 and HLS-3, we find the SLEDs of the “Cosmic Eyelash” (Danielson et al. 2011) and the average of SPT SMGs (Spilker et al. 2014) reproduce the observed luminosity ratios well. We scaled the luminosities of the lowest J CO lines observed in these two sources to their CO(1–0) luminosities by assuming  and
and  .
.
Having the  (see Table 11), we then estimated the total molecular gas mass with a fixed conversion factor αCO. Because the derived star formation rates do not reveal solid evidence of ongoing starburst in our sample, we adopted the typical Milky Way value of αCO = 4.36 M⊙ (K km s−1 pc2)−1. The estimated molecular gas are also listed in Table 11.
(see Table 11), we then estimated the total molecular gas mass with a fixed conversion factor αCO. Because the derived star formation rates do not reveal solid evidence of ongoing starburst in our sample, we adopted the typical Milky Way value of αCO = 4.36 M⊙ (K km s−1 pc2)−1. The estimated molecular gas are also listed in Table 11.
Molecular gas properties of the HLS sources.
For all sources, we also provide an estimate of their molecular gas mass using their continuum emission in the Rayleigh-Jeans tail. Following the calibration described in Scoville et al. (2016), we derived the luminosity of the dust emission at a rest-frame of 850 μm. We used the series of optically thin modified blackbody models generated by the combinations of parameters explored by the MCMC fit to interpolate or extrapolate the dust luminosity at a rest-frame of 850 μm, L850 μm. Using the conversion factor for SMGs from Scoville et al. (2016) (L850 μm/Mgas = 8.4 × 1019 erg s−1 Hz−1
 ), we derived the molecular gas mass from the Rayleigh-Jeans dust emission, noted as Mgas, S16, and shown in Table 11. We find that the differences between the molecular gas masses estimated by the two methods are within a factor of 2. Our galaxies have a molecular gas mass of 1–3 × 1011 M⊙, suggesting a gas-rich nature. For HLS-4, we derive a similarly massive molecular gas reservoir as for the four sources with CO detections.
), we derived the molecular gas mass from the Rayleigh-Jeans dust emission, noted as Mgas, S16, and shown in Table 11. We find that the differences between the molecular gas masses estimated by the two methods are within a factor of 2. Our galaxies have a molecular gas mass of 1–3 × 1011 M⊙, suggesting a gas-rich nature. For HLS-4, we derive a similarly massive molecular gas reservoir as for the four sources with CO detections.
One of the primary sources of the uncertainty in molecular gas mass measurement is the CO-to-H2 conversion factor (αCO). We applied a typical Milky Way αCO value of 4.36 to the CO(1–0) luminosities. The alternative estimate, based on Scoville et al. (2016), has a equivalent αCO of 6.5. However, previous studies reported that starburst galaxies can have much lower αCO compared to the Milky Way-like values typical for normal star-forming galaxies (e.g Downes & Solomon 1998; Tacconi et al. 2008). The exact value of αCO at high redshift is still highly uncertain. Although there is evidence that αCO can be as large as for the Milky Way in high-z SMGs, starburst-like values were also prevalently used in previous studies. This would introduce differences of a factor of 5–7 in molecular gas mass measurements. The impact of αCO is accounted for in the values of molecular gas mass and gas-depletion time given in Table 11.
By combining the measurements from Tables 10 and 11, we derived the gas-to-dust ratios of the four sources (HLS-2-1, HLS-2-2, HLS-3, and HLS-22) with relatively secure spectroscopic redshifts and dust-independent molecular gas mass measurements from CO lines. With the assumption of a Milky Way-like αCO, our analysis yields an average gas-to-dust ratio of 113, which is in line with the values found in local and high-z massive galaxies (Santini et al. 2010; Rémy-Ruyer et al. 2014; De Vis et al. 2019; Rujopakarn et al. 2019) and is consistent with the values expected at solar metallicity (Leroy et al. 2011; Magdis et al. 2012; Shapley et al. 2020). A lower starburst-like αCO leads to an average gas-to-dust ratio that is five to eight times lower, which is also consistent with the results of Rowlands et al. (2014) under similar assumptions, but still at the extreme values. Abundant dust in the ISM like this might be difficult to explain unless the sources are already enriched to supersolar metallicity at z = 3 − 5 (Chen et al. 2013; Santini et al. 2014) or (and) are undergoing vigorous merger plus starburst events (Silverman et al. 2018).
We finally derived the depletion time of the molecular gas in each galaxy using the molecular gas mass and the SFR. For the molecular gas mass, we used Mgas, S16 to keep the measurement consistent among all galaxies with or without CO line detections. The results are also given in the last column of Table 11. Figure 8 shows the gas-depletion time of HLS sources compared to high-z main sequence galaxies (Tacconi et al. 2020) and SMGs (Dunne et al. 2022). To consider the uncertainties of αCO, the plot marks the τdep in rectangles, and the upper and lower bounds at the τdep were derived using αCO values of 6.5 and 0.8, respectively. Figure 8 shows that most of the HLS sources have a short gas-depletion time of a few hundred million years, which is typical of high-z SMGs in Dunne et al. (2022). The only exception, HLS-3, shows a possibly long gas-depletion time of up to a few billion years and is comparable to main-sequence galaxies at the same redshift. Remarkably, HLS-3 also has the largest mm continuum size (2.8″ × 0.7″, see Table 3) and the lowest dust temperature ( K at z = 3.123 or
K at z = 3.123 or  K at z = 2.299; see Table 10). These atypical properties among SMGs, in addition to its long gas-depletion time, suggest that HLS-3 is more likely a massive main-sequence galaxy under secular evolution. As reported in Table 3, HLS-2-1 and HLS-3 are already partially resolved in dust continuum with compact NOEMA configurations. This might further suggest extended distributions of the molecular gas reservoir.
K at z = 2.299; see Table 10). These atypical properties among SMGs, in addition to its long gas-depletion time, suggest that HLS-3 is more likely a massive main-sequence galaxy under secular evolution. As reported in Table 3, HLS-2-1 and HLS-3 are already partially resolved in dust continuum with compact NOEMA configurations. This might further suggest extended distributions of the molecular gas reservoir.
 |
Fig. 8. Gas-depletion time of the HLS sample based on the molecular mass from Rayleigh-Jeans dust emission and the star formation rate from far-IR luminosities. The dashed red line shows the redshift evolution of the gas-depletion time of main-sequence galaxies from Tacconi et al. (2020). The gray dots show the gas-depletion time of z > 2 SMGs based on the data summarized in Dunne et al. (2022). |
6. A possible overdensity of DSFGs at z = 5.2
It is found that HLS-2-1 and HLS-2-2, separated by 12 arcsec on the map, both have a redshift of ∼5.2. They are also located within 2 arcmin from HLSJ091828.6+514223 a bright lensed DSFG that was first found in the Herschel Lensing Survey at a similar redshift of z = 5.243 (Egami et al. 2010; Combes et al. 2012; Rawle et al. 2014). At this redshift, their projected separation on the sky corresponds to a physical transverse distance of ∼800 kiloparsec.
Because of the close spectroscopic redshifts of HLS-2-1 and HLSJ091828.6+514223 the physical distance between these two sources is given by their transverse distance Dt = 796 kpc, computed following Dt = DA × θsep. The physical distance between HLS-2-1 (or HLSJ091828.6+514223 ) to HLS-2-2, which are separated in both redshift and sky coordinates, is approximately estimated using the following equations:
We derived physical distances (D) of ∼9.4 Mpc between HLS-2-1/HLSJ091828.6+514223 to HLS-2-24. The distance between HLSJ091828.6+514223 and HLS-2-1 corresponds to 5.0 comoving Mpc, which is comparable to the scale of the z ∼ 5 overdensities found in COSMOS and GOODS-N associated with SMG and DSFGs (Mitsuhashi et al. 2021; Herard-Demanche et al. 2023). When assuming the core of the possible structure has the same redshift as HLS-2-1 and HLSJ091828.6+514223, the deviation of the redshift of HLS-2-2 would correspond to a line-of-sight comoving distance of 58 Mpc. This is an order of magnitude larger than the scale of the SMG over-density in COSMOS, while still being comparable to the protoclusters traced by Ly-α emitters at z = 5–6 (Jiang et al. 2018; Calvi et al. 2021). Although the stochasticity of star formation means that SMG is an unreliable tracer of the most massive halos at intermediate redshift, the high SFR of the three sources at this high redshift could only be produced by the most massive galaxies tracing the densest environments in the early Universe (Miller et al. 2015). A more complete redshift survey of the other NIKA2 sources in the HLS field, as well as deep optical-IR observation in the same region, might reveal more members of this possible galaxy overdensity to confirm its nature and understand its fate in cosmic evolution.
7. Summary and conclusions
We presented the study of four DSFGs selected from the early science-verification observations of NIKA2, the KIDs camera installed on the IRAM 30m telescope.
We developed a new framework to determine the redshift of sources with the joint analysis of multiwavelength photometry and mm spectral scans. Accounting for the additional constraints on IR luminosity from the SED modeling, we predicted the flux of the strongest emission lines from CO, [CI], and [CII], generated the model spectra at given redshifts accordingly, estimated the goodness of match between the broadband SEDs, models, and the observed mm spectra altogether, and quantitatively determined the most probable redshift solutions based on all this information.
Based on the prior selection on red far-IR to mm colors, we identified a sample of four mm NIKA2 sources with mJy fluxes in the HLS field with possible high redshifts, at z = 3 − 7. We conducted deep NOEMA observations on these sources and resolved them into five individual sources. With the NOEMA spectral scans and the newly developed joint-analysis method, we obtained their redshift and confirmed that they all have z > 3. Our analysis revealed that most of their properties, such as the star formation rate, dust temperature, and gas-depletion time, are normal compared to typical high-z DSFGs with very active star formation. However, we also find that one of our sources (HLS-3) shows a significantly low dust temperature and long gas-depletion time, resembling the properties of secularly evolved main-sequence star-forming galaxies. Furthermore, we find two sources at z = 5.2 that are separated by only 5 comoving Mpc and might be linked to a third source lying at a distance comparable to the protocluster size as traced by Ly-α emitters at z = 5 − 6. This might be an indication of an interesting high-z structure in this field.
We demonstrated that our method for constraining the redshift, applied to millimeter-selected DSFGs with far-IR to mm photometry and blind spectral scans alone, is able to determine the true redshift accurately. This accuracy in the redshift determination with multiple low signal-to-noise ratio emission lines shows promising potential in blind redshift searches of a large sample of high-z mm-faint DSFGs, even in the absence of accurate optical-IR photometric redshifts. The method is especially expected to improve the design and efficiency of blind redshift searches for candidate high-z DSFGs detected by the NIKA2 Cosmological Legacy Survey (N2CLS). Most of the N2CLS sources are fainter (submJy) than the four sources discussed here. The new tool we developed will allow us to mitigate the increase in NOEMA or ALMA time that will be needed for these faint DSFGs.
The joint-analysis methods also provide possible implications for the strategy of obtaining an accurate redshift and cosmic evolution of high-z DSFGs. The next-generation single-dish telescopes and instruments, such as the CCAT-prime (CCAT-Prime Collaboration 2023) and LMT TolTEC (Wilson et al. 2020), are planned to devote a substantial fraction of observing time to wide-area deep blind surveys. With thousands of DSFGs expected to be detected, these surveys aim to reveal the role of DSFGs in the formation and evolution of massive galaxies through their cosmic evolution and environment and clustering. However, compared to the existing deep mm surveys, the majority of these planned surveys are not expected to be completely covered by deep surveys in the near-IR at > 2μ (Wang et al. 2019; Williams et al. 2019; Fudamoto et al. 2021; Xiao et al. 2023). The lack of wide and deep near-IR surveys such as COSMOS-Web (Casey et al. 2023) might hinder identification of the counterpart of high-z DSFGs, which further prevents the application of optical-IR SED modeling for efficient and accurate redshift measurements. Our practice for the HLS sources under similar conditions, however, demonstrated that the joint constraints of photometric redshift, IR luminosity, and mm spectra from far-IR SED and blind spectral scans can also provide a promising accuracy and robustness for an efficient redshift search for high-z DSFGs. Further improvement following this strategy, including the application of this method to the redshift identification of a larger sample of DSFGs discovered by the NIKA2 Cosmological Legacy Survey (Bing et al. 2023), is expected to benefit the key scientific objectives of these future wide area (sub)mm surveys.
The aim of this framework is to find the redshift solution and not to measure the line properties precisely. The result of our method is not highly sensitive to different line widths and to a normalization of the LFIR-Lline scaling relation, as shown in the Appendix A.
The bias of the peculiar radial velocity estimate might not be a large effect for HLS-2-2 to the other two sources. For HLS-2-1 to HLSJ091828.6+514223, when we consider a peculiar radial velocity up to 1000 km s−1 along the line of sight, it might introduce a bias in radial distance up to 3.5 Mpc.
Acknowledgments
L.B. warmly acknowledges financial support from IRAM for his first year of PhD thesis and the support from the China Scholarship Council grant (CSC No. 201906190213). We acknowledge financial support from the “Programme National de Cosmologie and Galaxies” (PNCG) funded by CNRS/INSU-IN2P3-INP, CEA and CNES, France, from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project CONCERTO, grant agreement No 788212) and from the Excellence Initiative of Aix-Marseille University-A*Midex, a French “Investissements d’Avenir” programme. This work is based on observations carried out under project numbers W16EE, E16AI, W17EL, W17FA, W18FA, and S20CL with the IRAM NOEMA Interferometer and project numbers 230-14 and 192-16 with the IRAM 30m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). We would like to thank the IRAM staff for their support during the NIKA and NIKA2 campaigns. The NIKA2 dilution cryostat has been designed and built at the Institut Néel. In particular, we acknowledge the crucial contribution of the Cryogenics Group, and in particular Gregory Garde, Henri Rodenas, Jean Paul Leggeri, Philippe Camus. This work has been partially funded by the Foundation Nanoscience Grenoble and the LabEx FOCUS ANR-11-LABX-0013. This work is supported by the French National Research Agency under the contracts “MKIDS”, “NIKA” and ANR-15-CE31-0017 and in the framework of the “Investissements d’avenir” program (ANR-15-IDEX-02). This work has benefited from the support of the European Research Council Advanced Grant ORISTARS under the European Union’s Seventh Framework Programme (Grant Agreement no. 291294). F.R. acknowledges financial supports provided by NASA through SAO Award Number SV2-82023 issued by the Chandra X-Ray Observatory Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of NASA under contract NAS8-03060. In addition to the NIKA2 collaboration pipeline, the NIKA2 data were also processed using the Pointing and Imaging In Continuum (PIIC) software, developed by Robert Zylka at the Institut de Radioastronomie Millimetrique (IRAM) and distributed by IRAM via the GILDAS pages. PIIC is the extension of the MOPSIC data reduction software to the case of NIKA2 data. We warmly thank Véronique Buat for insightful discussions on the results of this paper.
References
- Andreani, P., Retana-Montenegro, E., Zhang, Z.-Y., et al. 2018, A&A, 615, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aravena, M., Boogaard, L., Gónzalez-López, J., et al. 2020, ApJ, 901, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Bakx, T. J. L. C., Sommovigo, L., Carniani, S., et al. 2021, MNRAS, 508, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Banerji, M., Jones, G. C., Wagg, J., et al. 2018, MNRAS, 479, 1154 [Google Scholar]
- Berta, S., Young, A. J., Cox, P., et al. 2021, A&A, 646, A122 [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Cousin, M., & Bavouzet, N. 2010, A&A, 516, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015a, A&A, 573, A113 [Google Scholar]
- Béthermin, M., De Breuck, C., Sargent, M., & Daddi, E. 2015b, A&A, 576, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [Google Scholar]
- Bing, L., Adam, R., Ade, P., et al. 2022, Eur. Phys. J. Web Conf., 257, 00006 [CrossRef] [EDP Sciences] [Google Scholar]
- Bing, L., Béthermin, M., Lagache, G., et al. 2023, A&A, 677, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blain, A. W. 1999, MNRAS, 309, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [Google Scholar]
- Calvi, R., Dannerbauer, H., Arrabal Haro, P., et al. 2021, MNRAS, 502, 4558 [NASA ADS] [CrossRef] [Google Scholar]
- Cañameras, R., Yang, C., Nesvadba, N. P. H., et al. 2018, A&A, 620, A61 [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M. 2012, MNRAS, 425, 3094 [Google Scholar]
- Casey, C. M. 2020, ApJ, 900, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
- Casey, C. M., Kartaltepe, J. S., Drakos, N. E., et al. 2023, ApJ, 954, 31 [NASA ADS] [CrossRef] [Google Scholar]
- CCAT-Prime Collaboration (Aravena, M., et al.) 2023, ApJS, 264, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, B., Dai, X., Kochanek, C. S., & Chartas, G. 2013, arXiv e-prints [arXiv:1306.0008] [Google Scholar]
- Combes, F., Rex, M., Rawle, T. D., et al. 2012, A&A, 538, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortzen, I., Magdis, G. E., Valentino, F., et al. 2020, A&A, 634, L14 [EDP Sciences] [Google Scholar]
- da Cunha, E., Groves, B., Walter, F., et al. 2013, ApJ, 766, 13 [Google Scholar]
- Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2011, MNRAS, 410, 1687 [NASA ADS] [Google Scholar]
- De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Vis, P., Jones, A., Viaene, S., et al. 2019, A&A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [Google Scholar]
- Dudzevičiūtė, U., Smail, I., Swinbank, A. M., et al. 2020, MNRAS, 494, 3828 [Google Scholar]
- Dunne, L., Maddox, S. J., Papadopoulos, P. P., Ivison, R. J., & Gomez, H. L. 2022, MNRAS, 517, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Egami, E., Rex, M., Rawle, T. D., et al. 2010, A&A, 518, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisenhardt, P. R. M., Wu, J., Tsai, C.-W., et al. 2012, ApJ, 755, 173 [Google Scholar]
- Faisst, A. L., Fudamoto, Y., Oesch, P. A., et al. 2020, MNRAS, 498, 4192 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, L., Han, Y., Nikutta, R., Drouart, G., & Knudsen, K. K. 2016, ApJ, 823, 107 [Google Scholar]
- Franco, M., Elbaz, D., Béthermin, M., et al. 2018, A&A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fudamoto, Y., Ivison, R. J., Oteo, I., et al. 2017, MNRAS, 472, 2028 [NASA ADS] [CrossRef] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Schouws, S., et al. 2021, Nature, 597, 489 [CrossRef] [Google Scholar]
- Fujimoto, S., Kohno, K., Ouchi, M., et al. 2023, ApJS, submitted, [arXiv:2303.01658] [Google Scholar]
- Goto, T., & Toft, S. 2015, A&A, 579, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graciá-Carpio, J., García-Burillo, S., Planesas, P., Fuente, A., & Usero, A. 2008, A&A, 479, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greve, T. R., Leonidaki, I., Xilouris, E. M., et al. 2014, ApJ, 794, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Béthermin, M., Loiacono, F., et al. 2020, A&A, 643, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herard-Demanche, T., Bouwens, R. J., Oesch, P. A., et al. 2023, MNRAS, submitted, [arXiv:2309.04525] [Google Scholar]
- Hodge, J. A., & da Cunha, E. 2020, Roy. Soc. Open Sci., 7, 200556a [NASA ADS] [CrossRef] [Google Scholar]
- Holland, W. S., Bintley, D., Chapin, E. L., et al. 2013, MNRAS, 430, 2513 [Google Scholar]
- Hughes, D. H., Aretxaga, I., Chapin, E. L., et al. 2002, MNRAS, 335, 871 [CrossRef] [Google Scholar]
- Jiang, L., Wu, J., Bian, F., et al. 2018, Nat. Astron., 2, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, S., Daddi, E., Magdis, G. E., et al. 2019, ApJ, 887, 144 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [Google Scholar]
- Li, J., Wang, R., Riechers, D., et al. 2020, ApJ, 889, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Gao, Y., Isaak, K., et al. 2015, ApJ, 810, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Manning, S. M., Casey, C. M., Zavala, J. A., et al. 2022, ApJ, 925, 23 [CrossRef] [Google Scholar]
- Miettinen, O., Delvecchio, I., Smolčić, V., et al. 2017, A&A, 606, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, T. B., Hayward, C. C., Chapman, S. C., & Behroozi, P. S. 2015, MNRAS, 452, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuhashi, I., Matsuda, Y., Smail, I., et al. 2021, ApJ, 907, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Hopwood, R., De Zotti, G., et al. 2010, Science, 330, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Neri, R., Cox, P., Omont, A., et al. 2020, A&A, 635, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavesi, R., Riechers, D. A., Sharon, C. E., et al. 2018, ApJ, 861, 43 [Google Scholar]
- Perotto, L., Ponthieu, N., Macías-Pérez, J. F., et al. 2020, A&A, 637, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rawle, T. D., Egami, E., Bussmann, R. S., et al. 2014, ApJ, 783, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [Google Scholar]
- Reuter, C., Vieira, J. D., Spilker, J. S., et al. 2020, ApJ, 902, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Carilli, C. L., Capak, P. L., et al. 2014, ApJ, 796, 84 [Google Scholar]
- Riechers, D. A., Leung, T. K. D., Ivison, R. J., et al. 2017, ApJ, 850, 1 [Google Scholar]
- Roseboom, I. G., Dunlop, J. S., Cirasuolo, M., et al. 2013, MNRAS, 436, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Rowlands, K., Gomez, H. L., Dunne, L., et al. 2014, MNRAS, 441, 1040 [Google Scholar]
- Rujopakarn, W., Daddi, E., Rieke, G. H., et al. 2019, ApJ, 882, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2010, A&A, 518, L154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2014, A&A, 562, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Sheth, K., Aussel, H., et al. 2016, ApJ, 820, 83 [Google Scholar]
- Shapley, A. E., Cullen, F., Dunlop, J. S., et al. 2020, ApJ, 903, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Daddi, E., Rujopakarn, W., et al. 2018, ApJ, 868, 75 [Google Scholar]
- Simpson, J. M., Smail, I., Dudzevičiūtė, U., et al. 2020, MNRAS, 495, 3409 [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Spilker, J. S., Marrone, D. P., Aguirre, J. E., et al. 2014, ApJ, 785, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Strandet, M. L., Weiss, A., Vieira, J. D., et al. 2016, ApJ, 822, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Strandet, M. L., Weiss, A., De Breuck, C., et al. 2017, ApJ, 842, L15 [Google Scholar]
- Sugahara, Y., Inoue, A. K., Hashimoto, T., et al. 2021, ApJ, 923, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Smail, I., et al. 2008, ApJ, 680, 246 [Google Scholar]
- Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Valentino, F., Magdis, G. E., Daddi, E., et al. 2018, ApJ, 869, 27 [Google Scholar]
- Walter, F., Decarli, R., Carilli, C., et al. 2012, Nature, 486, 233 [Google Scholar]
- Wang, T., Schreiber, C., Elbaz, D., et al. 2019, Nature, 572, 211 [Google Scholar]
- Weiß, A., De Breuck, C., Marrone, D. P., et al. 2013, ApJ, 767, 88 [Google Scholar]
- Williams, C. C., Labbe, I., Spilker, J., et al. 2019, ApJ, 884, 154 [Google Scholar]
- Wilson, G. W., Abi-Saad, S., Ade, P., et al. 2020, SPIE Conf. Ser., 11453, 1145302 [NASA ADS] [Google Scholar]
- Wu, J., Tsai, C.-W., Sayers, J., et al. 2012, ApJ, 756, 96 [Google Scholar]
- Xiao, M. Y., Elbaz, D., Gómez-Guijarro, C., et al. 2023, A&A, 672, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yun, M. S., & Carilli, C. L. 2002, ApJ, 568, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, J. A., Montaña, A., Hughes, D. H., et al. 2018, Nat. Astron., 2, 56 [Google Scholar]
- Zavala, J. A., Casey, C. M., Manning, S. M., et al. 2021, ApJ, 909, 165 [CrossRef] [Google Scholar]
Appendix A: Robustness of the joint-likelihood method using different line widths
One of the key assumptions is the width of the emission lines, which we fixed to 500km/s. Previous studies revealed a correlation of the total IR or line luminosity and the far-IR to mm line width that might originate from the regulation of gaseous disk rotation by gravity or (and) feedback from star formation or AGN (Bothwell et al. 2013; Goto & Toft 2015). The assumed line width generally matches the average of the DSFGs with ULIRG-HyLIRG luminosities in infrared, which is similar to the derived IR luminosity of our sample. However, observations also showed significant scatter in IR-luminous DSFGs. Our sample might be a typical example of the variety in the line width of luminous DSFGs, whose line FWHMs range from ∼250km/s (HLS-2-1) to ∼750km/s (HLS-3). In addition, the assumption of aa Gaussian line profile generally holds for most of our sources, but HLS-3, as described in Sect. 5.1, has a significant double-peaked feature in the detected emission line in band2.
The impact on the joint-analysis result of the mismatch between the real and assumed line width and profile is an uncertain prior. Thus, we made the following tests to verify if and how the results of this joint analysis might change with the assumption of different line widths. In addition to the default setting of a 500 km/s FWHM Gaussian line profile, we further performed the joint analysis with line profile FWHMs of 300km/s and 800 km/s, using the redshift and infrared luminosity derived from the fit with Béthermin et al. (2015a). We identified the redshift solutions of the four HLS sources with at least one detected line with these two different assumptions using the same method and criteria described as in Sect. 4.2. The results are listed in Table A.1.
Redshift of HLS sources from the joint analysis with models of different line width
From the results in Table A.1, we conclude that the redshift solutions from the joint analysis method are generally not sensitive to the assumptions on the emission line widths. For all sources but HLS-22, we find little variation in the redshift solutions using different line width assumptions. The differences of Δz ∼ 0.003, as shown in Fig. A.1, mostly originate from the changes in the peak intensity of the emission lines, which could lead to slight variations of χ2(z). However, this small difference is still within the width of the emission lines, and will neither cause a false identification of the emission line, nor affect the analysis of the line fluxes and kinematics in Sect. 5.1 with the corresponding central frequency as an initial guess.
 |
Fig. A.1. The output and comparison between the results of joint redshift analysis under different assumptions of line width. Upper row: Joint log-likelihood of the four HLS sources with model spectra with line widths of 300km/s, 500km/s, and 800km/s. Lower row: Comparison of the models of these the line widths at the corresponding redshift solution and the observed source spectra. |
The only case with a significant inconsistency in redshift from the test is HLS-22, where the procedure using the 300km/s line width strongly favors a redshift solution at z = 2.436. Given the frequency of the two emission lines detected with high S/N, we are confident about the redshift solution at z = 3.036 from the analysis with the model spectra with the 500km/s line width. Therefore, we checked the 300km/s model and the data at z = 2.436 and found that the misidentification is caused by a strong noise spike at 100.64 GHz, as shown in Fig. A.2. The false identification suggests an increased sensitivity to narrow spikes in the spectrum with decreasing model line width. In our calculation of  and correspondingly, the joint log-likelihood, their variation with redshift is dominated by the goodness of match between the model and data within the range of model line profiles. With a narrower line width in the model, the number of data points that dominate the variation of
and correspondingly, the joint log-likelihood, their variation with redshift is dominated by the goodness of match between the model and data within the range of model line profiles. With a narrower line width in the model, the number of data points that dominate the variation of  (z) is smaller than in the cases with a wider line width. This makes the analysis with a narrow line width more sensitive to single spurious data points, such as the noise spike in the HLS-22 spectra, and leads to the misidentification in Fig. A.2. A less aggressive spectral binning along frequency and a preprocessing with sigma clipping could probably reduce this false identification in practice.
(z) is smaller than in the cases with a wider line width. This makes the analysis with a narrow line width more sensitive to single spurious data points, such as the noise spike in the HLS-22 spectra, and leads to the misidentification in Fig. A.2. A less aggressive spectral binning along frequency and a preprocessing with sigma clipping could probably reduce this false identification in practice.
 |
Fig. A.2. Comparison of the observed spectra of HLS-22 and the model spectra with an FHWM of 300 km/s at the best redshift solution z = 2.436. The feature identified as an emission line might be a missing glitch within the data. |
Appendix B: Robustness of the joint-likelihood method with narrower frequency coverage
Millimeter spectral scans made by interferometers are widely used to blindly search for the emission lines from candidate high-redshift DSFGs, determine their spectroscopic redshift, and study the conditions of their cold ISM (Strandet et al. 2016; Fudamoto et al. 2017; Jin et al. 2019; Neri et al. 2020; Reuter et al. 2020). These spectral scan observations are designed to cover a continuous frequency range with several spectral setups. For ALMA and NOEMA, the default setup of the blind spectral scans at their current lowest-frequency band covers ∼ 31 GHz. The earliest observations in 2018 of HLS sources blindly and continuously cover the spectra of HLS sources between 71 GHz and 102 GHz in NOEMA band1 with two setups, which follows this basic strategy of a blind redshift search. To test the joint-analysis method under more realistic conditions in large DSFG redshift survey projects, we applied the method to analyze these band1 spectra and compare their resulting redshifts with those in Sect. 4.2. The results from this analysis are presented in Table B.1 and Fig. B.1.
 |
Fig. B.1. Result of the joint analysis of the four HLS sources with spectroscopic redshifts derived in Sect. 4.2, using only the 31 GHz NOEMA spectral scans observed in 2018. The first row shows the likelihood from the SED fittings and the joint log-likelihood of photometric and spectroscopic data, using the SED-fitting outputs with the Béthermin et al. (2015a) templates and MMPZ. The comparison of the observed spectra and the model spectra predicted by the IR luminosities from the two SED-fitting results are shown in the second and third row. |
Redshift of the HLS sources from the joint analysis for the 31 GHz continuous spectra observed in 2018.
From the comparison of the redshift analysis using the early and full datasets, we find that the best redshift solutions of HLS-2-1 and HLS-2-2 remain stable, while the results of HLS-22 and HLS-3 are affected by the narrowed spectral coverage. This difference in robustness for different spectral coverage can be explained as follows. The joint-analysis method works equivalently to the automatic alignment and stacking of two or more lines in the spectra. If it is at the correct redshift and multiple lines are covered, this method can numerically boost the stacked S/N of emission lines, even if none of the single lines is detected with high significance. At a fixed coverage in frequency, we could expect that more CO lines are covered for sources at higher redshift. Taking our sample as an example, although the lines of HLS-2-1 and HLS-2-2 at z∼ 5.2 are only tentatively detected, their relatively high redshifts ensure that at least two CO and/or [CI] lines are covered by the spectral scan. In contrast, the narrowed spectral coverage leaves only one CO line in the spectral coverage of early observations of HLS-3 and HLS-22, leading to ambiguous redshift solutions regardless of whether the line is detected at high significance. With the comparison of the redshift robustness of these two groups of sources for different spectral coverage, we also emphasize that wide spectral coverage covering at least two strong molecular and/or atomic lines could be even more crucial in the redshift identification of DSFGs compared to reaching high sensitivity.
Appendix C: Cross-validation and difference between different SED modeling
The application of the joint-analysis framework to HLS sources largely relies on the current knowledge of the far-IR SED of high-z galaxies. However, although Herschel provides estimates of the mean far-IR SEDs and the redshift evolution of the main population of star-forming galaxies, these results are also limited by significant source confusion, especially in SPIRE data at longer wavelengths. Moreover, current studies revealed some DSFGs with an apparently low dust temperature (Jin et al. 2019), as well as a significant warm-dust contribution in some starburst galaxies (Eisenhardt et al. 2012; Wu et al. 2012; Fan et al. 2016). These results suggest that a large variation in far-IR SEDs could exist in high-z DSFG populations.
Our choices of template are not free from these issues, and we therefore adjusted our joint-analysis framework to the results of two different far-IR SED templates and modeling framework, and we cross-validated the results of the two. The analysis with the Béthermin et al. (2015a) templates and MMPZ mostly shows consistent redshift solutions. This suggests the relative stability of the joint-analysis method with input information from different SED-fitting results.
However, some discrepancies on HLS-22 when using typical blind spectral scan conditions in Appendix B are also found, which caused us to make an additional check on its origin. From the comparison of the derived IR luminosity in Fig. 3, and the comparison of the model and data in Fig. 4 and Fig. B.1, we note that the estimated infrared luminosity and line fluxes from MMPZ are systematically lower than those from Béthermin et al. (2015a). At the correct redshift, the predicted line fluxes of Béthermin et al. (2015a) match the observed line fluxes better than MMPZ. In contrast, MMPZ generally returns more accurate photometric redshifts, especially on HLS-3, where the photometric redshift from Béthermin et al. (2015a) significantly deviates from the spectroscopic redshift. However, as indicated by the low dust temperatures of the HLS sample, it is possible that the properties of far-IR emission of these galaxies are not representative for high-redshift star-forming galaxies. Thus, we decided not to prefer a dust template and far-IR SED fitting in our framework, and we recommend a cross-validation of the redshift solutions from various methods in application.
In addition, the faint emission of HLS sources in the SPIRE bands introduces large uncertainties on the constraints of the source SEDs around the peak of the far-IR emission. As a result, this might contribute to the difference in IR luminosities derived from methods with different prior constraints (Casey 2020). These issues also further suggest the importance of matching observations at ALMA band 8-10 frequencies to properly reconstruct the far-IR SED, as well as to estimate the IR luminosity and star formation rate of high-z DSFGs selected by mm surveys.
Appendix D: Impact of the scatter of the LFIR-LCO scaling relation
The redshift from the joint analysis was derived based on the goodness of match between the emission line model and observed spectra. As mentioned in Sect. 4.2, in this approach, we predict the expected fluxes of spectral lines based on the LFIR from the SED template fitting using the best-fit scaling relation between LFIR-Lline from the literature (Greve et al. 2014; Liu et al. 2015; Valentino et al. 2018). However, these scaling relations are subject to substantial scatter of up to a factor of a few in observations. To test the possible impact of this scatter on our analysis and the robustness of the joint analysis method against them, we first checked the output best-redshift solution after adding a systematic offset to all LFIR-Lline scaling relations when generating the predicted spectrum models. In this test, we shifted the predicted CO/[CI] line fluxes by four different systematical offsets corresponding to ±0.5 and ±1.0 times of the 1σ scatter of the scaling relations. The exact values of the 1σ scatter for the considered lines are given in Table. 7.
The best-redshift solutions for HLS sources (except for HLS-4) after applying these four different offsets in LFIR-Lline conversion are listed in Table D.1. We find that all offsets in line flux, except for the +1.0σ, result in best-redshift solutions that are similar to the analysis using the median (zero offset) scaling relations. This suggests a good robustness of our joint-analysis method against the existing scatter of LFIR-Lline scaling relations in observations. As for the test with +1.0σ offset, we further determined the reason for the discrepancy in the best-redshift solution. For HLS-22 and HLS-2-2, the application of the +1.0σ offset leads to mismatches between the model and the data due to glitches or noise spikes in the spectra (see Fig. A.2 as an example, where the noise spike matches CO(5-4) at the best-redshift solution of HLS-22 here). For HLS-3, we find this unlikely low redshift solution after applying the +1.0σ offset as the code assigns the only strong emission line in the spectral scan at 139.746 GHz to be CO(2-1). This suggests the stronger demand that the spectral scan be wide enough to cover more than one strong spectral line in the redshift confirmation of DSFGs with moderate redshift (i.e., z∼2-3).
Redshift of HLS sources from the joint analysis when using different numbers of offsets for all LFIR-Lline scaling relations.
To test the self-consistency of the joint-analysis method, we placed the measured CO line fluxes and far-IR luminosities of HLS sources at their best-redshift solutions (the zbest, med in Table D.1) in the corresponding LFIR-LCO diagrams to determine whether they follow the scaling relations used for line flux predictions. The results are shown in Fig. D.1. The plotted CO and far-IR luminosities were derived using the Gaussian-fit line fluxes and modified blackbody fitting (see Table. 9 and Table. 10). In addition to the average LFIR-LCO correlations, we also show the samples from Cañameras et al. (2018) with multiple line transitions from the same sources as a comparison to our sources.
 |
Fig. D.1. Comparison of the LFIR-LCO correlations of different transitions (Greve et al. 2014; Liu et al. 2015) and our sample based on measurements from our observations at the best-redshift solutions. The sources with upper limits on the line luminosities are presented as leftward triangles. |
From Fig. D.1, we find that most of our sources fall within +-2σ of the scaling relation used in our analysis, which is also consistent with the regions occupied by bright submm galaxies in Cañameras et al. (2018). The only exception is HLS-3, which is also highlighted in Fig. D.1. In either the LFIR-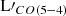 or the LFIR-
or the LFIR- diagram, HLS-3 falls well below the scaling relation even when we consider the scatter of these scaling relations. However, we also note that its SPIRE photometry is one of hte poorest in all of the four HLS sources. As the SPIRE bands close to the peak wavelength of SED predominantly constrain the IR luminosity, it is likely that the IR luminosity of HLS-3 is much less constrained than the other HLS sources, especially compared to HLS-2 and HLS-4.
diagram, HLS-3 falls well below the scaling relation even when we consider the scatter of these scaling relations. However, we also note that its SPIRE photometry is one of hte poorest in all of the four HLS sources. As the SPIRE bands close to the peak wavelength of SED predominantly constrain the IR luminosity, it is likely that the IR luminosity of HLS-3 is much less constrained than the other HLS sources, especially compared to HLS-2 and HLS-4.
All Tables
Emission line fluxes, luminosities, and widths of four sources in the HLS field.
Dust properties of the HLS sources from the optically thin modified blackbody fitting.
Redshift of HLS sources from the joint analysis with models of different line width
Redshift of the HLS sources from the joint analysis for the 31 GHz continuous spectra observed in 2018.
Redshift of HLS sources from the joint analysis when using different numbers of offsets for all LFIR-Lline scaling relations.
All Figures
 |
Fig. 1. Cleaned images of the NOEMA observation for our four NIKA2 sources. The effective beam size and shape of each map is shown in the bottom right corner of each panel. The contour levels from orange to dark red correspond to −4, 4, 8, and 12 times the rms of each map, respectively. The red crosses mark the position of detected NOEMA sources from the uv_fit. The two resolved sources associated with HLS-2 are also labeled separately (HLS-2-1 and HLS-2-2). The scale bars in the maps (upper left) correspond to 5 arcsec in the sky. The frequency of the continuum data is given in the lower left corner of each panel. |
| In the text | |
 |
Fig. 2. Millimeter spectra of all HLS sources extracted from the uv tables obtained from the NOEMA observations. The continuum models to be subtracted are presented as solid gray lines. The lines we identified to determine the spectroscopic redshift of the sources (see Sect. 4 and Fig. 4 for details) are marked by vertical dashed black lines. |
| In the text | |
 |
Fig. 3. Results of the IR template fitting of our four HLS sources with the B15 dust templates and MMPZ method using the SPIRE, NIKA2, and NOEMA photometry. The plots in the first column show the probability density distribution (normalized by the peak values) of each source. The second column shows the evolution of the weighted-average infrared luminosity with redshift. The third column shows the best-fit SED models with the observations. The sources from top to bottom are HLS-2, HLS-3, HLS-4, and HLS-22. |
| In the text | |
 |
Fig. 4. Joint analysis of the redshift for four NIKA2 HLS sources with the SED-fitting outputs using the B15 dust templates and MMPZ. The first row shows the normalized log-likelihood from the SED fitting and the joint log-likelihood for each source after considering the information obtained from the NOEMA spectral scans. The second and third row show the cutouts of the spectra around candidate spectral lines at the best redshift solutions. The lines shown in the second row are detected in the earliest band1 spectral scans (W17EL and W17FA), and those in the third row are detected in the additional follow-up observations (W18FA and S20CL). The models generated based on the fit with the B15 dust templates and MMPZ at the most probable redshift are plotted as solid and dashed red lines, respectively. |
| In the text | |
 |
Fig. 5. Observations and best fits of the spectral lines, including both detections and upper limits. The best-fit model of each line is shown with the solid red line. For HLS-3, we show the two lines assuming z = 3.123. |
| In the text | |
 |
Fig. 6. Example of a modified blackbody fitting of the far-IR to mm photometric data for one of our galaxies. (a) Photometric data and best-fit model. The ±1σ and ±2σ uncertainties of the model are shown with blue shades of different transparency. (b) Corner plot of the posterior distribution of the three parameters. The contours correspond to 1, 1.5, and 2σ in the 2D histogram. |
| In the text | |
 |
Fig. 7. Dust temperature vs. redshift of the high-z DSFGs in our sample, and DSFGs or LBGs from the literature. The dust temperatures of these sources are all measured with the optically thin modified blackbody model. The corresponding references are listed in the legend. We also overlaid the average Tdust-z relation of main-sequence galaxies derived by Schreiber et al. (2018) and Béthermin et al. (2015a) based on observational data. For HLS-4 with a photometric redshift alone, we show the degeneracy between dust temperature and redshift with the dash-dotted gray line. The Tdust of HLS-3 at the two possible redshifts is plotted and connected by the solid red line. |
| In the text | |
 |
Fig. 8. Gas-depletion time of the HLS sample based on the molecular mass from Rayleigh-Jeans dust emission and the star formation rate from far-IR luminosities. The dashed red line shows the redshift evolution of the gas-depletion time of main-sequence galaxies from Tacconi et al. (2020). The gray dots show the gas-depletion time of z > 2 SMGs based on the data summarized in Dunne et al. (2022). |
| In the text | |
 |
Fig. A.1. The output and comparison between the results of joint redshift analysis under different assumptions of line width. Upper row: Joint log-likelihood of the four HLS sources with model spectra with line widths of 300km/s, 500km/s, and 800km/s. Lower row: Comparison of the models of these the line widths at the corresponding redshift solution and the observed source spectra. |
| In the text | |
 |
Fig. A.2. Comparison of the observed spectra of HLS-22 and the model spectra with an FHWM of 300 km/s at the best redshift solution z = 2.436. The feature identified as an emission line might be a missing glitch within the data. |
| In the text | |
 |
Fig. B.1. Result of the joint analysis of the four HLS sources with spectroscopic redshifts derived in Sect. 4.2, using only the 31 GHz NOEMA spectral scans observed in 2018. The first row shows the likelihood from the SED fittings and the joint log-likelihood of photometric and spectroscopic data, using the SED-fitting outputs with the Béthermin et al. (2015a) templates and MMPZ. The comparison of the observed spectra and the model spectra predicted by the IR luminosities from the two SED-fitting results are shown in the second and third row. |
| In the text | |
 |
Fig. D.1. Comparison of the LFIR-LCO correlations of different transitions (Greve et al. 2014; Liu et al. 2015) and our sample based on measurements from our observations at the best-redshift solutions. The sources with upper limits on the line luminosities are presented as leftward triangles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} L_{\mathrm{IR,avg} }(z) = \frac{\sum _{j=1}^{n} L_{\mathrm{IR,j} }(z)\times \exp {\{[\chi ^2(z,j)-\sigma ^2(j)]/2\}}}{\sum _{j=1}^{n}\exp {\{[\chi ^2(z,j)-\sigma ^2(j)]/2\}}} , \end{aligned} $$](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq13.gif)



![$$ \begin{aligned} \chi ^2_{\rm spec}(z) = \sum _{\nu _i}\frac{[f_{\nu _{i,\mathrm {obs}}}-f_{\nu _{i,\mathrm {model}}}(z)]^2}{\sigma ^2_{\nu _i}(z)}. \end{aligned} $$](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq17.gif)
![$$ \begin{aligned} \mathcal{L} _{\rm joint}(z) \propto \mathcal{L} _{\rm spec}(z) \times \exp [-\chi ^2_{\rm SED}(z)/2]. \end{aligned} $$](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq19.gif)


![$$ \begin{aligned} S(\nu ) = \frac{1+z}{d_L^{2}}M_{\rm dust}\kappa (\nu )\left[B\left(\nu , \frac{T_{\rm dust}}{(1+z)}\right)-B\left(\nu ,\frac{T_{\mathrm{CMB},z}}{(1+z)}\right)\right]. \end{aligned} $$](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq52.gif)

![$$ \begin{aligned} D_{\rm los} = [D_c(z1)-D_c(z2)]/(1+\bar{z}), \\ D = \sqrt{{D_t}^2+{D_{\rm los}}^2}. \end{aligned} $$](/articles/aa/full_html/2024/03/aa43887-22/aa43887-22-eq113.gif)