| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 19 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202346185 | |
| Published online | 26 January 2024 | |
Exoplanet detection limits using spectral cross-correlation with spectro-imaging
Analytical model applied to the case of ELT/HARMONI
Institute of Planetology and Astrophysics (IPAG), University of Grenoble Alpes,
414 rue de la Piscine,
Saint-Martin-d’Hères, France
e-mail: alexis.bidot@univ-grenoble-alpes.fr
Received:
19
February
2023
Accepted:
12
October
2023
Context. The combination of high-contrast imaging and medium- to high-resolution spectroscopy offers new possibilities for the detection and characterization of exoplanets. The so-called molecular mapping technique makes use of the difference between the planetary and stellar spectra. While traditional post-processing techniques for high-contrast imaging are quickly limited by speckle noise at short angular separations, we find that molecular mapping efficiently suppresses speckles and offers new detection possibilities.
Aims. The molecular mapping performance depends on multiple parameters such as the star magnitude, adaptive optics residual halo, companion spectrum, and telluric absorption, as well as the telescope and instrument properties. Exploring such a parameter space through end-to-end simulations to predict potential science cases and to optimize future instruments designs is very time-consuming and makes it difficult to draw simple conclusions. We propose quantifying the signal of interest and the noise that propagates in molecular mapping, with explicit dependencies upon the main stellar, planetary, and instrument parameters to define an efficient methodology for such an analysis.
Methods. We derived explicit expressions of the estimates of molecular mapping signal and noise and validated them through comparisons with end-to-end simulations. These expressions provide an understanding of the instrumental dependencies, aiding in the discussion of optimal instrumental choices with regard to the targets of interest. We applied them to the case of the ELT/HARMONI integral field spectrograph as an online tool predicting the contrast performance in various observational cases.
Results. We confirm the potential of molecular mapping for high-contrast detections, especially for cool planets at short separations. We provide guidelines based on quantified estimates for design trade-offs for future instruments. We discuss the planet detection performance of the HARMONI observing modes, with a spectral resolution varying from 3000 to 17 000 and and a range of corresponding spectral bandwidths in the near infrared. While these modes aptly cover the appropriate requirements for high detection capability of warm exoplanets, the high-contrast mode of HARMONI would benefit from a transmission extended down to the J band. A contrast of a few 10−7 at 50 mas should be within reach for bright targets in a photon noise regime with molecular mapping.
Key words: instrumentation: high angular resolution / planets and satellites: detection / techniques: imaging spectroscopy / methods: data analysis
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The spectral information that is carried by the light reflected off or emitted by an exoplanet is of primary importance for studies of its nature. It makes it possible to probe the physical properties and the composition of the atmosphere; this is a proxy for inferring the formation and evolution processes (Oberg & Bergin 2016; Mollière et al. 2022) and a key piece of information in assessing their habitability (Turbet 2018), as well as the potential existence of life (Wang et al. 2018). The brightness of the host star and the huge star-to-planet flux ratio induce noise and systematics on the planet's signature, which are two major challenges to these observations.
Such a detection and characterization of the exoplanetary light can be attempted with or without angularly resolving the planet itself, and, in each case, considering the total, broadband planetary flux or by attempting to focus on some specific spectral features. Each case involves different dominant limitations that lead to different potential ultimate performances, as we briefly review hereafter.
Starting from the spatially unresolved case, in the favorable configuration of transiting planets, the planetary signal can be extracted thanks to temporal differential spectro-photometry (Tinetti et al. 2018), namely, by observing the planet before, during, and after the transit. The performance of this technique is ultimately limited by systematics related to measurement stability and by the limited-time window associated with transits (once every orbit).
The spectral diversity between the star and the planet signal, and/or the use of specific spectral signatures can be used to get rid of these instrumental systematics to the point that even non-transiting planets can be detected and characterized without spatially resolving them. This has enabled the detection and characterization of β-Pic b observed with VLT/CRIRES (Snellen et al. 2014), for instance. The planetary signal detection remains strongly limited by the photon noise associated with the huge stellar flux.
This noise is dramatically reduced if the exoplanet and the star can be spatially separated from each other. It can be further reduced if the star’s diffracted signal at the location of the planet is attenuated using coronagraphic techniques. As for unresolved characterizations, differential signal extraction can be performed without using any prior knowledge of the exoplanet spectrum. The key limitation is associated with systematics on images (in particular, the speckle noise), in spite of various studies and substantial efforts that have been made to handle it (e.g., improved AO correction methods, novel focal plane sensing techniques, improved signal extraction algorithms using data diversity). One way to get rid of the confusion between the speckles in the stellar halo and the planetary signal is the inter-ferometric coherence difference, as used, in particular, in the ExoGRAVITY program (Lacour et al. 2020); this approach is telescope-time expensive, however, since it requires the four UTs of the VLT. In addition, it has a low global transmission. As said before, another way to deal with these systematics is to use the spectral information to look for specific spectral features, over the field of view. This technique referred to as molecular mapping. This requires a high enough spectral resolution (which is discussed below) to distinguish the absorption features of interest from the speckle-induced spectrum modulation. The integral field spectrographs (IFS) used with high-contrast imaging instruments such as VLT/SPHERE (Beuzit et al. 2019), GPI (Macintosh et al. 2014), and Subaru/SCExAO (Lozi et al. 2018) focus on spatial information and have a limited spectral resolution (R = 50). However, molecular mapping has also recently been demonstrated with higher resolution IFS and spectrographs that were not originally dedicated to high-contrast, for instance: with VLT/SINFONI (R = 5000) (Hoeijmakers et al. 2018), Keck/OSIRIS (R = 4000) (Ruffio et al. 2019), and VLT/MUSE (R = 3450) (Haffert et al. 2019). High-dispersion coronagraphy (HDC) has also been proposed and designed to couple high-resolution spectrographs with high-contrast instruments, observing single, diffraction-limited sources, allowing us to characterize exoplanets whose positions are already known: KPIC (R = 37 000) (Delorme et al. 2018; Wang et al. 2021a; Xuan et al. 2022), HiRISE (R = 100 000) (Vigan et al. 2023), and VIPA (R = 80 000) (Carlotti et al. 2022a).
There is a plentiful parameter space to explore when following this approach, with various balances and trade-offs between the spectral information content, noise regimes, and observation context (ground vs. space), as well as star and exoplanet types. We should emphasize the fact that, in practice, when designing an instrument, the main design choices usually favor some capabilities at the expense of others. A classical example is, for instance, the necessary trade-off for an IFS with a given detector size, between its field-of-view (FoV), spectral bandwidth, and spectral resolution. There is certainly not a single, universal sweet spot and the choice depends on various parameters that include the telescope specifications, image quality, stellar type and brightness, total observing time, exoplanet contrast, projected separation, spectral properties, and so on, with the chosen priority given to a given spectral signature. Some IFS using this high spectral resolution approach are already operational, but are not necessarily equipped with the optimal observing modes for the detection of exoplanets (VLT/ERIS (Kravchenko et al. 2022), VLT/MUSE, Keck/OSIRIS, JWST/MIRI (Patapis et al. 2022; Mâlin et al. 2023). Others are currently being designed with these trade-off considerations in mind, such as SPHERE+ MedRES (Boccaletti et al. 2022), ELT/HARMONI, ELT/METIS (Carlomagno et al. 2020), or are planned in the more distant future (ELT/PCS; Kasper et al. 2021). Such discussions on the instrument trade-offs and the different high-resolution instrument modes have already been addressed in some specific cases, such as for space-based, very-high-contrast instruments (Wang et al. 2017) or when coupling VLT/SPHERE with CRIRES+ (Otten et al. 2021). This will need to be extended, and to cover a variety of future instruments.
We argue that a new performance analysis approach is needed to explore this parameter space and we propose the use of a semi-analytical tool that we have developed. Until now, a huge effort has been made to develop end-to-end simulation tools to estimate the performance of various high-contrast imagers; these simulations are necessary to model and to estimate the impact of complex effects (e.g., speckle noise, instrumental instabilities, or correlations generated by the detector) on the final achievable contrast, with various post-processing techniques. A strong drawback of this computationally heavy approach is the difficulty to explore wide parameter spaces and to fully trace and understand the role of each of the various parameters that contribute to the performance budget, however. The approach presented here proposes an answer to this difficulty.
We first recall in Sect. 2 the principles of molecular mapping and how different types of noise limit its efficiency. We verified our analytical model with comparisons with end-to-end simulations in Sect. 3. Section 4 details the bandwidth versus spectral resolution trade-off, and how tellurics, and rotational broadening may influence it. We then consider in Sect. 5 the specific case of the ELT/HARMONI instrument to first compare the performance derived through an end-to-end simulation tool and the one derived with our semi-analytical tool. We then use the latter to discuss the interest of the different observing modes of this instrument with respect to different types of planets. Finally, a conclusion is drawn in Sect. 6.
2 Molecular mapping information and noise
2.1 Molecular mapping core principle
We consider the observational information of spectro-imagers, after the first steps of data reduction and calibration in the form of a 3D collected flux, S, expressed as the measured integrated flux as a function of the wavelength, λ, and spaxel position (x, y). It can be decomposed into several components when the observed scene is a stellar halo as in Eq. (1):
with γatm the atmosphere transmission, Sstar as the star spectrum, Splanet as the planet PSF as a function of wavelength, and n as the noise. The sky background spectrum does not appear here, as we assume that it has been perfectly subtracted from the data. The total noise n is further broken down in Eq. (2) into several standard noise sources: the stellar photon noise, nhalo, the background noise, nbkgd, which is the photon noise coming from the sky emission, the telescope, and the instrument, and the readout noise of the detector, nRON. Also, Mspeckle describes the stellar PSF over the FoV and depends on the wavelength and it is normalized for each spectral channel such that 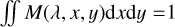 . Spectra quantities (Sstar, Splanet, and consequently also S) are expressed in detected photo-electrons, integrated over the total integration time for each spectral channel. Therefore, those quantities consider the intrinsic star and planet apparent magnitudes, as well as the telescope and instrument transmissions.
. Spectra quantities (Sstar, Splanet, and consequently also S) are expressed in detected photo-electrons, integrated over the total integration time for each spectral channel. Therefore, those quantities consider the intrinsic star and planet apparent magnitudes, as well as the telescope and instrument transmissions.
The PSF and the speckle pattern scale with the wavelength as a first order approximation. Thus, the scaling of the speckle pattern generates a low frequency modulation of the stellar spectrum, in an uncontrolled manner, depending on the location in the field of view. In order to isolate the planetary spectrum from the stellar spectrum, the stellar continuum modulated by the speckles must be estimated and subtracted. This step can be interpreted as high-pass filtering to isolate the uncontaminated frequencies of the planetary spectrum. These frequencies correspond to the absorption lines of the planetary spectrum. To do so, we used the same preprocessing routine as in TexTris (Petrus et al. 2021). It can be summarized in a few steps.
Firstly, models of the observed star spectrum, Ŝstar, and tellurics absorption, 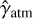 , were chosen. These can either be models derived from libraries such as PHOENIX for the star and Skycalac for tellurics or directly estimated from the data using the brightest spaxels in the FoV uncontaminated by the companion(s) (i.e., the spaxels corresponding to the core of the stellar PSF:
, were chosen. These can either be models derived from libraries such as PHOENIX for the star and Skycalac for tellurics or directly estimated from the data using the brightest spaxels in the FoV uncontaminated by the companion(s) (i.e., the spaxels corresponding to the core of the stellar PSF: 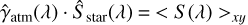 ).
).
These models are needed to estimate the speckle modulations in the FoV, so that stellar light can be subtracted. Indeed, for each spaxel, we can estimate the modulation by low-pass filtering the ratio between the spaxels and a model of the spectrum of the star, multiplied by the transmission of our atmosphere:
We use the notation [.]LF to represent the low-pass filtering operation. Here, it is just a convolution between a spectrum and a Gaussian kernel with a width, σc, homogeneous to nanometer, and defined by the user. This width, σc, will determine the frequency cut-off ƒc, of the filter (homogeneous to nm−1), and it can be also understood as a spectral resolution cut-off, Rc, as in Eq. (4) (see Appendix A):
where λ0 is the central wavelength of the observation bandwidth. The optimal resolution cut, Rc, of this filter is discussed later in Sect. 2.3.2. The high-frequency content of a spectrum [S]HF will represent the difference S − [S]LF. Assuming that the model of the star spectrum with the tellurics absorption is perfect and injecting Eqs. (1) into (3) returns the estimated modulation function:
We note that Eq. (5) should be an approximation in real life, since the model of the spectrum of the star and telluric absorptions cannot be perfect. Then, the modulated stellar spectrum must be removed from the spaxels. We note that the planet’s continuum will be removed, as the estimated modulation 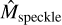 (λ, x, y) will take it into account. Here, Sres(λ, x, y), the residual spectrally high-pass filtered signal after stellar component subtraction is expressed as:
(λ, x, y) will take it into account. Here, Sres(λ, x, y), the residual spectrally high-pass filtered signal after stellar component subtraction is expressed as:
where ![$n'\left( {\lambda ,x,y} \right) = n\left( {\lambda ,x,y} \right) - {\left[ {n\left( {\lambda ,x,y} \right)} \right]_{{\rm{LF}}}} - {{{{\left[ {{\gamma _{{\rm{atm}}}} \cdot \hat S\left( \lambda \right)} \right]}_{{\rm{HF}}}}} \over {{{\left[ {{\gamma _{{\rm{atm}}}} \cdot \hat S\left( \lambda \right)} \right]}_{{\rm{HF}}}}}} \cdot {\left[ {n\left( {\lambda ,x,y} \right)} \right]_{{\rm{LF}}}}.$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq11.png) . [n(λ, x, y)]LF.
. [n(λ, x, y)]LF.
In practice, n′ (λ, x, y) is approximately equal to n(λ, x, y) and we will use this approximation in the rest of the paper. The detailed calculation and discussion can be found in Appendix B.
With these operations, the high-frequency content of the planet (and possibly from the star, if it has a rich absorption lines content) is isolated from the speckles at the location of the planet. We note that the planet signal is still affected by telluric lines due to the atmospheric absorption. Now that the planet is spectrally disentangled from the speckle contamination, molecular mapping (Snellen et al. 2015; Hoeijmakers et al. 2018) consists in cross-correlating, in the spectral dimension, the resulting signal Sres(λ, x, y) in each spaxel (x, y) from the IFS datacube with templates (see Fig. 1) computed in regard to various companion properties (temperature, C/O ratio, metallicity, etc.). When cross-correlating a template with a spaxel corresponding to a companion, a correlation peak can be observed: its position corresponds to the radial velocity and its width can be interpreted as being induced by the spin of the companion (Snellen et al. 2014).
The spectral template, t, used for cross-correlation is user-defined, according to the type of planet atmosphere that is considered. It is expected that various templates will be tested on observation data and they will come either from empirical libraries or from theoretical models. A specific molecular spectrum can also be used to probe the presence of a molecule in the observed atmospheres (Hoeijmakers et al. 2018; Ruffio et al. 2019; Wang et al. 2021b; Cugno et al. 2021). Therefore, at a given radial velocity, the cross-correlation is just the scalar product of the residual signal, Sres, and the Doppler-shifted and normalized template, tRV, such that 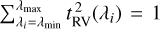 . This operation is described in Eq. (7):
. This operation is described in Eq. (7):
where υRV is the radial velocity, and 〈A,B〈 = ‖A‖‖B‖cos(θ) denotes the scalar product of A and B, and θ is the angle between A and B.
The expression of the correlation signal of interest is derived using Eq. (6) with the approximate expression of the propagated noise n(λ, x, y) and the definition of the scalar product:
where θplanet,RV and θstar,RV are the angle between the high-pass filtered planet spectrum and the template and between the high-pass filtered star spectrum and the template, respectively. Both depend on the input radial velocity. To simplify the notations, we have chosen to note the norm α = ‖γatm · [Splanet]HF‖ and ![$\beta = \left\| {{\gamma _{{\rm{atm}}}} \cdot {{\left[ {{S_{{\rm{star}}}}} \right]}_{{\rm{HF}}}}{{\left[ {{{{S_{{\rm{planet}}}}} \over {{{\hat S}_{{\rm{star}}}}}}} \right]}_{{\rm{LF}}}}} \right\| \cdot \cos \left( {{\theta _{{\rm{star,RV}}}}} \right)$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq15.png) .
.
Hence, we have three terms in this measurement (Eq. (8)). The first one (α) is the total planetary amount of information, including the transmission of telluric absorptions, after the high-pass filtering step. The cosine factor quantifies the similarity between the template and the companion spectrum so that α cos(θplanet,RV) is the actual useful signal coming from the projection of the companion spectrum onto the considered template. The second one (β) is the deterministic projection of the residual stellar spectrum lines onto the template. The last one is related to the noise propagated through the cross-correlation step.
The detection is discussed according to the strength of the correlation peak value. This correlation peak is directly linked to both the α quantity (as it depends on the spectral content of the companion) and to the β term that quantifies the rate of similarity between the star and the planet. This aspect is discussed further in Sect. 2.2. For the detection capability, this correlation peak has to be compared to the noise propagated onto the cross-correlation function (CCF, see Fig. 1). This noise can be empirically estimated with the spatial variance of the correlation map or with the variance of the wings of the CCF, as long as the autocorrelation of the companion spectrum is taken into account to avoid biasing the noise estimate (Cugno et al. 2021). We propose an analytical estimate of this propagated noise level (detailed in Sect. 2.3), and we go on to check that this estimate is consistent with empirical estimation in Sect. 3.2.
 |
Fig. 1 2D correlation map processed on simulated PSF with a fake planet injected, shown in the top-left panel. The colorbar represents the correlation strength between spaxels and the template. The top right panel shows the histogram of the correlation strength map, displaying the distribution of the correlation values in the annulus. Here, µCCF and σCCF denote the mean and the standard deviation of these values, respectively. Also, α(x0, y0) is the correlation at the location of the planet. Bottom panel shows the cross-correlation function on (blue) and off (orange) the planet’s location. |
2.2 Useful information on molecular mapping
We focus here on the two first terms of Eq. (8) and detail the last one in the next subsection. Using the Parseval-Plancherel property of energy conservation in the Fourier domain, α can be expressed as the square root of the sum of the power spectrum density (PSD) of the companion spectrum as in Eq. (9).
where Nλ is the number of spectral channels sampling the spectra, and the Fourier conjugate variable is associated with the spectral resolution, R, because here it is homogeneous to 1/λ.
Using the representation on the Fourier domain, Fig. 2 presents the PSD of the high-pass filtered spectrum for a companion with two different spectral resolutions, while keeping the same bandwidth (from 1 to 3 µm) and the same amount of photons. The area under the PSD curves is then equal to α2. In our study, this visualization allows us to better identify the spectral content location, and to directly compare it with the capabilities of an instrument with any given spectral resolution. Increasing the resolution expands the Fourier spectral range, and thus increases the signal of interest α. Indeed, thin absorption lines in companion spectra induce a very high-resolution content (even if the majority of the information seems at first glance to be found between a resolution of 100 and 10 000). Having such a high resolution thus facilitates companion detection. In the same way, these representations in Fourier space allow us to visualize (in Fig. C.1) a dependencies as a function of planet temperature and spectral range.
Therefore, this factor α quantifies the spectral richness of the companion spectrum and is homogeneous to photons. Analogously to the use of ADI techniques, where the signal of interest is the total number of photons coming from the planet, the signal of interest for molecular mapping lies in this factor. We note that unlike the case of ADI, where the signal remains complete, because we are filtering out the low frequencies here, we sacrifice about 60–90% of the planetary signal. We can define the fraction of the useful high frequency planetary spectrum over the total spectrum as described in Eq. (10). This quantity, as a function of the maximum resolution is expressed as follows (and represented in Fig. 3):
In other words, this ratio quantifies the cost of molecular mapping in terms of signal to be detected; for instance, with respect to ADI, it is used to get rid of the speckle noise limitation.
As seen above, α can vary significantly depending on the planet temperatures (we considered a 500–1700 K range in this study), as the high frequency spectral content is not the same. It can be directly estimated with spectra models, with the resolution and magnitude of the planet as inputs, and it does not require any end-to-end simulations. It depends on the companion spectrum, resolution, bandwidth, and exposure time. We note that the cosine factor is not estimated here and we assume it to be equal to 1 hereafter. However, this could be a limitation of molecular mapping in real life since we have very few data to check the similarity between templates and real spectra. We should always keep in mind that differences likely exist between the template and the signal, and that the detection estimates that are derived when using identical information for the signal and the template are therefore computed in the most optimistic scenario.
However, not all of this information may be usable for detection if the host star has lines in common with the planet. Indeed, subtracting the stellar spectrum will subtract those common lines as well. The term β quantifies this effect, as it expresses the projection of the star’s lines onto the template. Figure 4 shows the proportion of this self-subtraction for M- and A-host stars, and as a function of the planet type. M-stars and T planets have many CO lines, which explains the 30% subtraction factor in K band with a 1700 K planet. In contrast, A-stars have much less content in common with the companion spectra and the subtractive term is almost zero. We note that β can be negative if the cosine between the template and the stellar spectrum is negative, meaning that the spectra have a negative correlation. This explains the negative values in the figure. This negative correlation is very weak, however, as it has no strong physical origin.
Also, various effects may induce some structure in the CCF as a function of radial velocity. The first effect is the intrinsic structure of the template autocorrelation. Radial velocity dependencies on the β term is a secondary potential sources, even though it is minor in most of the cases. These facts are the primary motivation to assess the detection levels in the spatial dimension rather than in the radial velocity dimension. However, these effects can still affect the position of the peak as well as its shape. Therefore, one should take caution when deriving refined estimates of the companion orbital velocity or spin velocity.
 |
Fig. 2 PSD of high-pass filtered (Rc = 100) planet spectrum (T = 500 K, log(g) = 4, [M/H] = 0) for two different resolutions on the total spectral range offered by BT-Settl spectra (0.3–12 µm). The hatched areas correspond to the areas under the curves equal to the quantity α2. Note: the PSD has been smoothed only for better visualization purposes. The y-axis is relative to the total flux of the companions. Only the ratios between the curves explaining the a variation from a given resolution to another one should be taken into consideration. |
 |
Fig. 3 Fraction of the planetary spectrum remaining after high-pass filtering with a resolution cut Rc = 100 as a function of the spectral resolution of the instrument (see text). Templates are chosen for different temperatures but with a constant gravitational surfaces (log(g) = 4) and a constant metallicity ([M/H] = 0). We notice that the colder the planet, the higher content of molecular absorption lines and the larger fraction of signal preserved at high resolution. |
 |
Fig. 4 Percentage of information subtracted from the planetary signal due to the high-frequency content of the host star as a function of spectral resolution for several star and planet types. The stellar spectra that are used here come from the BT-NextGen database. The M-type star was chosen with a temperature of 3200 K, and the A-type star with a temperature of 7200 K. Both have a surface gravity of log(g) = 4, and a metallicity of [M/H] = 0. This signal subtraction is obtained with non-Doppler-shifted spectra to correspond to the worst-case scenario, where absorption lines common to both object are overlaid. |
2.3 Noise
The signal of interest, as quantified above, now has to be compared to the level of the noise term (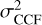 ), which is the variance of the projected noise onto the template 〈n(λ, x, y), tRV〉 in Eq. (8). It corresponds to the expected amount of noise in the correlation map (see Fig. 1). It is paramount to estimating this variance in order to later derive the analytical expression of the signal-to-noise ratio (S/N) and qualifying a detection with a sufficiently high confidence level. Assuming that the PSF is cen-trosymmetric, the noise, n(λ, x, y), will only depend on λ and on the separation, ρ, as the star photon noise is the only source of variable noise in the FoV (Eq. (2)). Therefore,
), which is the variance of the projected noise onto the template 〈n(λ, x, y), tRV〉 in Eq. (8). It corresponds to the expected amount of noise in the correlation map (see Fig. 1). It is paramount to estimating this variance in order to later derive the analytical expression of the signal-to-noise ratio (S/N) and qualifying a detection with a sufficiently high confidence level. Assuming that the PSF is cen-trosymmetric, the noise, n(λ, x, y), will only depend on λ and on the separation, ρ, as the star photon noise is the only source of variable noise in the FoV (Eq. (2)). Therefore, 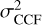 will depend on the separation, ρ, and it can be decomposed with each noise contributor of Eq. (2). We also make the assumption that except for the speckle noise, the noise is uncorrelated at the pixel scale.
will depend on the separation, ρ, and it can be decomposed with each noise contributor of Eq. (2). We also make the assumption that except for the speckle noise, the noise is uncorrelated at the pixel scale.
To facilitate the reading, the first two terms of Eq. (11) are noted as 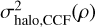 for the projected photon noise from the stellar halo at the separation, ρ, while
for the projected photon noise from the stellar halo at the separation, ρ, while 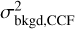 is for the projected photon noise from the sky and instrumental background, respectively.
is for the projected photon noise from the sky and instrumental background, respectively.
2.3.1 S/N derivation
The S/N at the location of the planet can be computed by comparing the signal of interest described earlier with the variance of the CCF values at the same separation as the planet (as shown in the upper panels of Fig. 1). It can be derived as:
where (x0 y0) is the location of the planet and ρ0 is the starplanet separation. Injecting the definition of the projected noise given in Eqs. (11) into (12), the S/N becomes:
With the signal of the planet being spatially distributed on several pixels, we can then integrate on a spatial box that is a few pixels wide (Eq. (14)) to optimize the S/N as done with a matching template technique (Ruffio et al. 2019):
where w is the width of the box.
Assuming here that we cross-correlate planet spectra with a perfect template, the cosine would equal to 1 and we can use Eq. (13) to derive the expression of the highest contrast that leads to a 5σ detection, as a function of separation, and for a given exposure time:
where p is the separation, Nexp is the number of exposures, AFWHM is the area of the FWHM in pixels, and α0 is the companion spectrum PSD integral over the FWHM area for a planet-to-star flux ratio equal to 1. The same applies to β0, which is the projection of the template spectrum over the star spectrum for a planet-to-star flux ratio equal to 1. The typical FWHM size for HARMONI’s apodized PSF is a bit more than 3 pixels wide. This core area covers 20-30% of the total flux from the planet depending on the AO correction.
2.3.2 Discussion of the speckle noise
The result obtained in Eq. (6) is only valid if the estimation of the modulation functions (Eq. (5)) is accurate and if the estimations of the star spectrum, the sky background spectrum, and the tellurics absorption are as well. For the reasons mentioned above, we assumed that these modulations were on a finite frequency support, and that low-pass filtering could effectively separate the modulations from the high-frequency content of the companion. However, if the frequency support of the modulations is not limited and/or a filter with a poor cut-off resolution is applied, residual modulations would result in another stellar residue (which would vary in the FoV this time) and add a new source of noise in Eq. (11). It is therefore important to check whether the assumption is valid by analyzing the PSD of the speckles modulation. This will also allow us to discuss the necessary cut-off resolution.
Figure 5 shows the PSD of a speckle modulation taken at several angular separations, the white noise from photon and read-out noise, as well as from the planet. For illustration purposes, we used the speckles derived from the system analysis of HARMONI, which are based on an end-to-end light propagation diffractive model of the instrument that reproduces their chromatic evolution. This reflects what we would expect to have with a good AO system, and partially calibrated non-common path aberrations (Carlotti et al. 2022b; Jocou et al. 2022). We do not discuss here the relative levels between the curves, which strongly depend on the observation case, but we are here interested in the PSD shapes. The speckle modulation PSD has a large peak at low spectral resolution and often dominates the others. This is why the speckle modulation has to be removed with a high-pass filter with a chosen cut-off frequency. In the same figure, the PSD of the speckle modulation still shows a high-frequency tail. This is because modulation of speckles is observed on a finite bandwidth window. The Fourier transform of this window is responsible for this PSD tail (i.e., the PSD of the speckle is convoluted by a sinc function corresponding to the Fourier transform of the rectangular function) dominating the intrinsic level of the speckle modulation.
To better visualize the frequency content, we propose to study the residual fraction of the speckle modulation and of a planet (T = 1700 K) as a function of the cut-off frequency of the high-pass filter (Fig. 6). To do this, we can use Eq. (10), this time fixing the resolution but varying the cutoff frequency of the high-pass filter. We notice that the fraction of residual speckle modulation increases with separation. This is well understood from the fact that the radial expansion rate of the speckles is proportional to the separation and thus makes the modulations faster at larger separations. We consider that if this parameter was critical, different cut-off frequencies could therefore be chosen depending on the separation. We note that on every curve, regardless of the separation, the main part of the speckle modulation is removed with a frequency cut corresponding to a spectral resolution of 100. This explains that on IFS like SPHERE and GPI (Macintosh et al. 2014), a high-pass spectral filter would be inefficient to disentangle the speckles modulation from the planet features. However, having a spectral resolution greater than a few hundreds makes it feasible. It can also be seen that the planet spectra do indeed have a frequency content over a different frequency domain than the speckle modulations, as the planet PSD ratio decreases slowly as a function of the cut-off resolution.
Thus, frequency cut can be tuned up to optimize the S/N. An overly high frequency cut would remove almost totally the speckles, but also the features of the planet, and thus degrade the S/N. On the contrary, an overly low frequency cut would better preserve the planet, but also the speckle noise, degrading the S/N as well.
Studies of the capability of removing the impact of speckle noise as a function of the cut-off frequency can be done empirically through the test of fake companion detection in a simulated data cube. Under the same astronomical conditions as in Fig. 5, in Fig. 7 we indicate an optimal cut-off frequency slightly above 50. As expected, above a cut-off resolution of 100, speckles are almost entirely removed but the remaining planetary signal to be detected is slowly reduced. On the other hand, when the resolution cut-off is under 30, the influence of speckles is present, which degrades the S/N. For the following, we consider the case of a Rc = 100 cut-off as a reasonable assumption. A second reason to choose a high enough cut-off resolution is the noise statistics. Indeed, every noise component is Gaussian except for the speckle noise, so if the speckles are efficiently removed, the noise would be essentially Gaussian, and we could apply the 5σ threshold to the S/N to validate a detection with a 99.99994% confidence level. The quantile-quantile plot in Fig. 8 is used to compare quantiles from the normal distribution with quantiles empirically estimated from the data. The closer the data are from the Gaussian distribution, the closer the blue dots are from the red line. It shows here that the spatial correlation matches well with a Gaussian distribution after the speckle suppression, and that the 5σ threshold can be applied.
The bottom panel in Fig. 5 represents the PSD of the same components as in the top panel, but after the high-pass filtering. We see that the speckle noise is just under the photon and read-out noise. With this cut-off frequency, one millionth of the speckle PSD remains in the filtered spaxels. The term 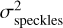 is therefore negligible compared to the other noises. We therefore continue to neglect this noise in the following sections. We go on to check our S/N model with end-to-end simulations in various cases to conclude on the robustness of the validation.
is therefore negligible compared to the other noises. We therefore continue to neglect this noise in the following sections. We go on to check our S/N model with end-to-end simulations in various cases to conclude on the robustness of the validation.
 |
Fig. 5 Effect of high-pass filtering on speckles. Top panel: PSDs of the speckle modulation (taken at a several separations), photon and read-out noise, and planet spectrum. Bottom panel: same PSDs after the highpass filtering with a resolution cut-off of Rc = 100. |
 |
Fig. 6 Residual fraction of the speckle modulation in respect to several angular separation (solid lines) and a planet spectrum (dashed line) as a function of the resolution cut-off. The planet spectrum is a BT-Settl template corresponding to T = 1700 K, log(g) = 4, [M/H] = 0 observed in the K-band degraded to a spectral resolution of 7000. |
3 Testing and validation of the S/N estimation model
We propose to verify here our semi-analytical performance analysis in the specific case of the future ELT/HARMONI spectro-imager. We have a specific interest in this instrument as it is a major upcoming facility for the international community that will combine both a high-contrast imaging capability and medium-to-high resolution spectroscopy. We revisit the high-contrast performance analysis for detections based on molecular mapping and we compare the relative interest of various observing setups to provide useful information for the scientific preparation of future observations and for the final adjustment of the instrument design. This study is also illustrative of other similar studies that can be applied to many other future high-contrast spectro-imagers.
HARMONI is one of the three first-light instruments that are being developed for the ELT, ESO’s 39-m segmented telescope. This visible and near-IR IFS is a general-use workhorse instrument that is designed to address a wide range of science goals (Thatte et al. 2020, 2021, 2022).
The high-contrast module (HCM) takes benefit from the combination of a good AO image quality on bright stars in the NIR and spectral resolutions from 3500 to 17 000. Using a dedicated fine correction of quasi-static instrumental aberrations (N'Diaye et al. 2013; Hours et al. 2022) and a coronagraph, it has been designed to characterize planets as close as 100 mas from their host star (goal 50 mas) and presenting a 10−6 flux ratio with it as described in Carlotti et al. (2022b). It will allow interesting detections of the full (including continuum) spectrum of faint companions thanks to differential imaging and we further discuss the additional capabilities of molecular mapping hereafter.
 |
Fig. 7 Plot shows the empirical S/N obtained with simulations for different cut-off frequencies obtained with the injection of a fake planet with the same HARMONI-like observation conditions as in Fig. 5. |
 |
Fig. 8 Study of noise statistics before and after high-pass filtering. Top panel: quantile-quantile plot without speckle filtering. Bottom panel: quantile-quantile plot with speckle high-pass filtering with a resolution cut-off of 100. |
HARMONI spectral set-ups for high-contrast.
3.1 HARMONI high contrast mode properties
The list of the possible spectral set-ups in the case of NIR high contrast observations are summarized in Table 1.
Concerning the image properties, we used the result of a realistic model of the apodized PSF of the telescope, as seen through the HCM. It considers the adaptive optics turbulence residuals (Neichel et al. 2016) in the case of good or median seeing conditions for which high-contrast observations are considered, resulting in good image quality (Fig. 9), with a Strehl ratio in K-band going from 85% for median seeing to 95% for the best conditions. The model also reproduces the non-common path aberrations by considering the specifications of the optics and the way they are seen (or not) by the wavefront sensors, to reproduce the temporal and spectral evolution of the residual wavefront errors. The detailed end-to-end image formation simulation provides a long exposure time-averaged image (which is sufficient for the estimation of the main noise contributors in our approach); it also produces time-series that can feed an extensive end-to-end simulation (Houllé et al. 2021). In this latter case, fake planets are injected to produce end-to-end contrast curves as a function of separation. We specify that when comparing the obtained planet-to-star contrast in various spectral configurations, the contrast is defined here as the total flux ratio between the faintest detectable planet and the star over a fixed bandwidth from 1.4 to 2.5 μm. We argue that it is the best way to discuss the most favorable observation set-up for a given astronomical target.
In high-contrast observations, one of two coronagraph apodization patterns can be selected depending on the target brightness and separation range of interest (Table 2).
Photon noise and read-out noise were added to background noise from the sky and the instrument estimated with the HARMONI simulator pipeline (HSIM; Zieleniewski et al. 2019). We assume a detector read-out noise of 10 e-/pixel/read, typical of Teledyne’s H4RG (Beletic et al. 2008) for short detector integration times (DIT). Read-out noise can be attenuated if we use the “up-the-ramp” read mode of the detector. This mode allows taking Ni intermediate images without resetting the pixels between the start and the end of the sensor exposure. Within the linear range, a linear regression provides an estimate of the total flux with a resulting read-out noise reduced by the square root of the non-destructive read-outs: 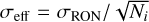 . We take into account this read mode, and select Ni according to the limiting DIT between the saturating DIT and the smearing DIT (i.e., the limit exposure time representing a displacement of the planet of a few tenths of
. We take into account this read mode, and select Ni according to the limiting DIT between the saturating DIT and the smearing DIT (i.e., the limit exposure time representing a displacement of the planet of a few tenths of 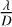 ). This smearing DIT appears in the case of pupil-stabilized observations. It depends on the separation of the planet, and on the position of the object in the sky. As a typical value, we are setting this DIT to 1 min in our further considerations. This would roughly correspond to a minimum read-out noise of 4 e-/pixel/DIT. We also checked that this DIT value ensures that the background noise remains negligible with respect to read-out noise, even in K-band. From these assumptions, the method described in Sect. 2 allows us to rapidly estimate the various noise contributors and resulting contrast curves for a wide diversity of targets and observation cases. This is implemented in the case of HARMONI within a dedicated package, named FastCurves, available on Github1.
). This smearing DIT appears in the case of pupil-stabilized observations. It depends on the separation of the planet, and on the position of the object in the sky. As a typical value, we are setting this DIT to 1 min in our further considerations. This would roughly correspond to a minimum read-out noise of 4 e-/pixel/DIT. We also checked that this DIT value ensures that the background noise remains negligible with respect to read-out noise, even in K-band. From these assumptions, the method described in Sect. 2 allows us to rapidly estimate the various noise contributors and resulting contrast curves for a wide diversity of targets and observation cases. This is implemented in the case of HARMONI within a dedicated package, named FastCurves, available on Github1.
 |
Fig. 9 Monochromatic high contrast long exposure PSFs with the two HARMONI current apodizers. It has been simulated with the best seeing condition (Strehl ratio of 90% in K-band). |
Apodizers specifications.
3.2 Validation of FastCurves with respect to end-to-end simulations
As a first and preliminary step, we want to validate our semi-analytical approach against end-to-end simulations for a specific case. In particular, this is aimed at checking the absolute values of the estimated useful signal of interest α and of the noise variance based on the halo brightness and detector noise, whereas the end-to-end simulation implements many realizations of noisy spectro-images, used as inputs to the molecular mapping signal extraction algorithm. We used several test cases to try out the robustness of the method. We ran end-to-end simulations for different scenarios: 1) in the case of different types of planets and a broad spectral range; 2) in the case of an M-star with numerous absorption lines contaminating the planet spectrum; and 3) in the extreme case of a poor AO correction to test whether speckles are still not limiting.
Figure 10 compares the contrast curves from our own end-to-end simulations and those from FastCurves. Those test cases are an important validation of our general approach and, more specifically, of the quantitative absolute estimates of the useful signal and noise. Finally, it also confirms the assumption that we made, namely, that the residual speckle noise does become negligible after high pass-filtering it in the spectral dimension.
We also compared our estimates to the results published by Houllé et al. (2021). However, Houllé et al. used ATMO templates for fake planets injection and used BT-Settl for the cross-correlation step, as a way to introduce some differences between the planet spectrum and the template spectrum. This leads to the combination of two effects affecting the estimation of detection performance: 1) a lower spectral content for ATMO resulting in a lower signal of interest α and 2) a reduced similarity between templates, leading to a cosine smaller than 1. We took this into account to ensure the coherence of our work. We have computed the term α from the ATMO models, and we have estimated the mismatch with the cosine term which was computed as detailed in Eq. (16):
We found the same orders of magnitude as the above-cited authors reported in their work, as illustrated in Fig. 11. We note that relying only BT-Settl spectra, we would have estimated a deeper contrast by one magnitude.
4 Trade-off for spectro-imaging
We have seen that α, which represents the amount of useful signal of the companion after continuum removal (Eq. (9)), greatly depends on the resolution, the spectral range, and the type of planets. We want to explore this parameter space in regard to various trade-offs and to evaluate the fluctuation of the S/N in the photon-limited case. Considering only the photon noise allows the study to take into account only relative values and to not depend on both a particular star magnitude and integration time. We go on to discuss the case of read-out noise in the HARMONI application case in Sect. 5.
4.1 Quantified high-resolution signal of the exoplanet
Relying on BT-Settl spectra templates (Allard et al. 2012), Fig. 12 shows the variations of S/N for a T = 1700 K planet as a function of the resolution and the spectral range (corresponding to feasible ground-based observations), and assuming a constant 0.5 µm large bandwidth, as described here in Eq. (17):
where λmin = λ0 − 0.25 µm and λmax = λ0 + 0.25 µm.
We note that here the noise factor, as mentioned above, only includes the propagated star photon noise contribution. We have chosen to take an A-star (T = 7200 K) to have a negligible β term. The S/N maps have been normalized to only appreciate the variations of the S/N. The dependency over the resolution (along the y-axis) in Fig 12 is directly related to Fig. 3, showing that the level of useful information increases with the spectral resolution. Quantitatively, in these examples, the gain in detectable signal can be as high as a factor 10 from low to high resolution. This can also be evidenced in Fig. 13, which shows the same spectrum at two different spectral resolutions and the corresponding high number of lines detected at higher resolution. In addition, we point out that this effect is quite inhomogeneous from a bandwidth to another, as there can be large disparities in the S/N gain for the same resolution.
4.2 Trade-off between bandwidth and resolution
The limited pixel resources of a detector imposes a trade-off between resolution, bandwidth, and field of view (discussed later in Sect. 4.3). To respect the Nyquist criterion, a higher resolution mode requires more pixels to sample the spectra correctly and leads to a narrower spectral range. On the one hand, having a wider bandwidth provides a larger total number of photons and more companion absorption lines, which both increase α. On the other hand, higher resolution allows for better separation of absorption peaks, which become more numerous, as well as deeper and more distinct, which also increases α.
This trade-off, under the constraint of a fixed number of pixels, will obviously lead to different S/N variations than those presented in Fig. 12, where the bandwidth was fixed and identical for any resolution. For example, in Fig. 13, it can be seen that the value of α is higher at low resolution than at high resolution, but this factor is to be compared with the photon noise. Thus, a higher resolution coupled with a narrower bandwidth can result in either a better or a worse overall S/N, depending on the local wealth of spectral lines at high resolution, as illustrated in Fig. 13.
Thus, Fig. 14 thus illustrates the variations of the S/N when assuming that the product of the resolution and of the bandwidth remains constant. Black dots represent the location of HARMONI IFU setups for future discussion (see Sect. 5.1). We note that the higher the resolution, the more sensitive we are to the central wavelength. This is because the spectral range is limited; therefore, we must be fully focused on the most interesting lines, and this is what induces the specific triangular shapes. Thus, choosing too high a spectral resolution could be risky. The red area corresponding to the optimal instrumental setup seems to point out a region where the resolution is around 8000 to 20 000 and which moves with temperature from the H-band to the K-band.
We note that in the present trade-offs discussion, the detection boost is the only decision criterion. Obviously, the choice to go to higher resolution can also be motivated by the desire to have a better characterization of the physico-chemical properties of the planet in restricted bandwidths of interest.
 |
Fig. 10 Comparison of contrast curves obtained through our method with respect to end-to-end simulations. The comparison has been made for 1 h exposures with respect to several cases: (top left panel) H-band HARMONI observation mode (Table 1) with an A-star (7200 K, log(g) = 4, [M/H] = 0) magnitude of 6 with T-type planet (500 K, log(g) = 4, [M/H] = 0) and L-type planet (1700 K, log(g) = 4, [M/H] = 0) with median seeing condition (0.65″ for λ = 0.5 µm, Strehl = 94%). Top-right panel: same templates and conditions on K-band HARMONI observation mode. Bottom-right panel: same templates on H-band with JQ3 seeing condition (0.74″ for λ = 0.5 µm, Strehl = 73%). Bottom-left panel: same planetary templates but with an M-star (3200 K, log(g) = 4, [M/H] = 0) on K-band with median seeing condition. The solid lines are the prediction of FastCurves with these parameters, the dashed lines are the result of molecular mapping processing with time-series simulated PSF and fake planets injection. |
4.3 Spatial versus spectral information trade-off
Another parameter involved in the trade-off discussion is the FoV. The larger the FoV, the fewer pixels will be available to either increase the resolution or increase the bandwidth. In the context of a blind search for a planet over a given FoV, one way to provide a quantitative metric for this trade-off is to compare the required total observation time needed to cover the whole FoV with a given S/N goal: either a larger FoV at once (with little spectral information, resolution × bandwidth, inducing a longer integration time per FoV) or mosaïcking over several smaller FoV, with richer spectral information. We show in Fig. 15, the equivalent gain in observation time to reach the same detection level to cover a whole FoV by mosaïcking, either by increasing the resolution, or by increasing the bandwidth.
In these examples, above the modest bandwidth (>0.1 µm), and resolution values (R > 500), the gain of information increases less than linearly with the number of spectral pixels; in such a case, a larger FoV is preferred over more spectral information. This general trend needs to be revisited in each specific case, however, and the proposed metrics make it possible to account for any particular observation and planetary properties. This is also only valid for a blind search over the FoV. On the contrary, there may be external reasons to specifically limit the FoV of interest for molecular mapping. One obvious reason comes from the location of the expected exoplanet that was previously constrained. Another one is statistical, with a strong incentive to focus on small separations where exoplanets are expected to be more numerous and where ADI approaches are more severely speckle-limited.
 |
Fig. 11 Comparison between our approach (right column) and results from Houllé et al. (left column). The comparison was made for the H, K, and K2 high bands observation modes (see Table 1) with a star magnitude of 4.7, L, and T spectral type companions, as well as a rotational broadening of 20 km s−1. These curves are simulated with median seeing conditions with a Strehl ratio of about 80% in K band. The total exposure time is set to 2 h. We note that the green dashed curve on the left panel is the contrast curve obtained with the ADI ANDROMEDA algorithm (Cantalloube et al. 2015), and the orange curve is the raw contrast with a standard deviation of 1σ. |
4.4 Additional interests in high resolution
4.4.1 Telluric absorption lines impact on detection
According to Eq. (6), the telluric absorption still filters the spectrum of the planet after pre-processing. This can filter useful exoplanetary lines, resulting in a smaller value of α. Figure 14 already takes into account the transmission of tellurics in the estimation of α thanks to the ESO simulator Skycalc (Noll et al. 2012). Figure 16 shows the impact of such tellurics on the S/N optimal zones. Despite a slight shift of these optimal zones, the impact of telluric absorption is moderate on young planets emitting their own light. This brings, on average, a degradation of the S/N by a factor of 0.9. This is because the correlation between the telluric absorption lines and those of the young companions is weak.
However, the effect might be stronger when observing planets with an atmospheric composition more similar to the Earth. In such a case, the correlation is much stronger and our telluric absorption becomes troublesome by specifically removing the signal of interest from the exoplanet. Such a problem is partially mitigated if the exoplanet overall radial velocity shifts the spectral features and if the spectral resolution is high enough to deblend the signal of interest from our atmosphere absorption. Relying on molecules opacities from the HITRAN database (Rothman et al. 2009), Fig. 17 illustrates this effect by estimating the gain in detection for spectral absorption lines caused by H2O and CO2 molecules as a function of the exoplanet radial velocity (with respect to Earth). As the resolution increases, the lines of interest appear in between the telluric absorption lines: a higher resolution allows a faster S/N gain (as a function of radial velocity) up to a high plateau value. The gain can even decrease as for some molecules, such as CO2, the absorption lines are almost evenly spaced in the spectral dimension. This is what causes the periodicity of the gain for a resolution of 3000 in Fig 17. On the contrary, in the case of a young giant planet spectrum, there is no strong correlation with the exoplanet spectrum of interest and we found no significant S/N gain with the radial velocity of the planet.
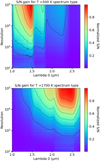 |
Fig. 12 S/N variation (defined in Eq. (17)) as a function of the resolution and the central wavelength of the spectral range, with a constant 0.5 µm large bandwidth. The α quantity has been estimated for a BT-Settl template corresponding to a temperature of 500 (top) and 1700 K (bottom). The S/N has been normalized to the maximum, while the absolute values depend on many observing parameters, starting with the stellar magnitude and planetary contrast. |
 |
Fig. 13 BT-Settl spectrum of a T = 1700 K companion at two different spectral resolutions: R = 7000 (top) and R = 17 000 (bottom). Each red rectangle delimits the observable spectral bands by keeping the same number of pixels for both resolutions. In each case, the corresponding α quantities and the S/N, both normalized to the top panel, are indicated. We note that some areas have more absorption lines, and thus benefit more than others from an increased resolution (e.g., there is a forest of lines corresponding to the presence of CO around 2.3 µm). Both α and the photon noise decrease as the resolution increases and the bandwidth decreases; comparing the two variations may lead to a lower (left rectangle) or higher (right rectangle) resulting S/N. |
 |
Fig. 14 Evolution of the S/N (relative to its maximum) with the spectral resolution, for a fixed number of pixels (3300 pixels per spectrum here, corresponding to the case of HARMONI) and a correspondingly variable bandwidth. The largest spectral range is set to cover the H and K bands H (from 1 to 2.8 µm) for three different templates of planets signature. These maps include only the photon noise, not considering any wavelength-dependant instrumental transmission, which makes this result quite generic, informative of the planetary spectra properties and not of the instrument specificities. Three different planet temperatures are considered: 500 (left), 1200 (middle), and 1700 K (right). |
4.4.2 Exoplanet reflected light vs. stellar spectrum
If we consider the (worst) case of a featureless exoplanetary albedo, the exoplanet’s reflected light is essentially a fraction of the stellar spectrum shifted by the exoplanet orbital velocity (with respect to its host star). Despite the gray albedo, this Doppler shift will also enable molecular mapping to reveal the exoplanet within the stellar halo. Using a high-resolution spectrum of an M3 type star as an example – GJ388, as from the SPIRou database (Donati et al. 2018) – we quantify the interest in going to a higher resolution for this scientific case in Fig. 18. This difficult case of high contrast reflected light exo-planets will definitely push for high spectral resolution at the innermost separations.
4.5 Rotational broadening impact on detection
The exoplanet spin rotation induces a convolution of its intrinsic spectrum, broadening the specific lines. This attenuates the high frequency end of the spectrum PSD and reduces the advantages of observing at higher resolution. This effect is observed in Fig. 19, which compares colormaps representing the relative S/N of the same companion at a temperature of 1200 K, but with two different rotational velocities. As expected, the most interesting region shifts toward lower resolution values as the rotational velocity rises.
5 Application to the ELT/HARMONI high-contrast module
5.1 FastCurves contrast predictions in various observing cases
Here, we explore a few cases of planet or companion types. The point here is not to be exhaustive but to cover a diversity of spectra cases, with very different effective temperatures with the BT-Settl model ranging from 500 to 1700 K. We note that, for these cases, HARMONI modes mainly cover the most interesting part of the parameter space (Fig. 14) and are complementary with respect to different planet temperatures and noise regimes. However, it suffers from not observing in J-band for the coldest companions. In each case, we present the obtained contrast curves for a two-hour exposure and a sixth-magnitude star, for various spectral setups (see Table 1) with the apodizer SP1 (Table 2). The results are displayed in Fig. 20.
These quickly generated contrast curves can be used as an exposure time calculator (ETC). They also help to determine the best observation mode that one should select according to the prior knowledge of the companions.
We find that the ultimate contrast achievable with the actual design seems to be a few 10−7 in two hours of effective integration (without including the system operation overheads). As expected, a given contrast is more rapidly obtained on cool companions: warmer planets have wider and fewer lines, and thus a smaller signal to be detected in molecular mapping. Also, T-type companions are more easily detected in the H band, unlike the L-type companions which are more easily detected in the K band. In addition to the ability of the ELT to observe young planets as close as a few dozens of mas, it might also enable the observation of planets in reflected light (Vaughan et al. 2022).
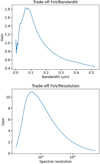 |
Fig. 15 Gain of time as a function of the bandwidth (top panel) or the spectral resolution (bottom panel) at the expense of mosaïcking the FoV for detecting a 500 K planet (log(g) = 4, [M/H] = 0). The spectral range has been chosen to start at λmin = 1.2 µm for the FoV/Bandwidth trade-off and a fixed spectral range between 1.2 and 1.8 µm for the FoV/Resolution trade-off. |
5.2 Discussion
5.2.1 Dominant noise regimes
Since speckle noise is negligible in this approach, detection is either limited by photon noise or by read-out noise. Figure 21 shows the dominant noise regimes as a function of the star magnitude, separation, and spectral resolution in the case of HARMONI. In this plot, we notice that for the high resolution mode (R = 17 385), the frontier between the photon noise limited case and the read-out noise limited case is located around a magnitude of eight in the short-separation, high-contrast region. This frontier is achieved thanks to the up-the-ramp detector read mode, which significantly reduces the impact of read-out noise. Unless the DIT can be significantly increased above 1 min, while remaining compatible with smearing and within the background-limited regime, these plots provide a good indication that the maximum spectral resolution can fully benefit from the collected photons, while avoiding the read-out noise degradation of contrast. Quantitatively, these values will be slightly modified according to the image quality and the corresponding level of the stellar halo.
 |
Fig. 16 Comparison of S/N variations for a planet with temperature of 1700 K with (bottom panel), and without (top panel) telluric absorption. The telluric absorption spectrum has been computed for an airmass of 1 using the ESO Skycalc module. The telluric absorptions do not impact the S/N distribution very much, with the exception of making it slightly more sensitive to the central wavelength, thus delimiting the spectral domains of interest more clearly. For instance, we see that near 2 µm the tellurics separate more the two zones of interest in H band and in K band by making the S/N vary more quickly. |
 |
Fig. 17 S/N gain as a function of radial velocity shift for H2O and CO2 molecules. The three curves represent this gain for different spectral resolutions: 3000, 10 000, and 40 000. |
 |
Fig. 18 S/N gain as a function of a radial velocity shift for featureless exoplanetary albedo. The three curves represent this gain for different spectral resolutions: 3000, 10 000, and 40 000. |
 |
Fig. 19 Evolution of the S/N with the resolution for the same exoplanet spectrum template (1200 K) but with two different rotational broadening results, corresponding to rotational speed of 3 km s−1 and 30 km s−1. The optimal area goes toward lower resolution as the rotational speed of the planet increases. |
5.2.2 Revisit of the coronagraphic set-up
Finally, we revisit the definition and the selection of the optimal coronagraphic setup. The high-contrast module includes two apodizers, designed for the more demanding assumption of ADI post-processing to recover the full companion spectrum. In such a case, it is interesting to minimize the intensity of residual diffracted light in the dark hole, not only to reduce the corresponding photon noise level, but also to limit any pinned speckles associated to the remaining diffraction pattern. This pushes the apodizers design towards higher contrast at the cost of transmission. This trade-off can be revisited in the case of molecular mapping where speckle noise is not anymore the main limitation2. In such a case, a new metric can be applied to design apodizers, comparing the transmission to photon noise, as detailed in Eq. (18).
where S/Napo and S/N0 are the S/N obtained with and without the apodizer, respectively. Also, tapo and t0 are the throughput with and without apodizer. Finally, σapo and σ0 are the brightness levels of the adaptive optics halo for the two setups.
This new metric only takes photon noise into account. In practice, FastCurves provides the comparison of various apodizer cases currently considered for HARMONI (see Fig. 22). At short separations (100 mas), the non-coronagraphic case (no apodizer) actually outperforms the apodized setups with a 0.5 mag contrast gain. The gain becomes even larger at higher angular separation, with a gain of one magnitude.
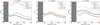 |
Fig. 20 Predicted contrast curves for HARMONI generated with the FastCurves package for three different planet temperatures. The exposure time is set to be 2 h on a 6 mag A-star with a Strehl ratio of about 60% in the H band. |
 |
Fig. 21 Limit star magnitude above which photon noise becomes smaller than read-out noise as a function of separation and spectral resolution. |
6 Conclusions
The proposed explicit expressions of the signal of interest and noise in the molecular mapping detection approach provide very useful support for a number of trade-off studies to optimize future IFS instruments.
We have confirmed the ability of molecular mapping to overcome the dominant limitation of speckle noise in ADI, especially at short separations. We also provide a quantitative estimate of the cost of this approach, which removes the exoplanet continuum and consequently reduces the signal to be detected. As expected, this cost strongly depends on the planet temperature. This approach also helps to discuss the relative interest of various spectral bandwidths as a function of spectral resolution and planet type.
On top of the comparison of various setups relative performance, the application to the specific case of HARMONI and the comparison to end-to-end simulations validate the estimate of absolute S/N values. The corresponding code FastCurves is accessible, and can be used as a direct ETC tool for HARMONI molecular mapping observations. These results provide some quantitative indications for the selection of the optimal set-up depending on the exoplanet type. It also predicts a high-contrast detection capability on bright targets on the order of a few 10−7 at 100 mas in two hours of exposure time.
FastCurves can also be easily adapted for similar studies in the case of other future instruments, by adjusting, in particular, the expected stellar profiles and the transmission. This approach is used to propose an optimized design of the mid-resolution IFS considered for the VLT/SPHERE upgrade (Gratton et al. 2022).
 |
Fig. 22 Contrast curves with and without apodizers. The comparison is made while considering the best seeing conditions (Strehl ratio of 95% in the K band). |
Acknowledgements
The authors thank the people in the HARMONI high-contrast science team, and in particular M. Bonnefoy, E. Choquet, and A. Vigan, for the exchanges they had with them. This project is funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement n°866001 – EXACT).
References
- Allard, F., Homeier, D., & Freytag, B. 2012, Philos. Trans. R. Soc. London Ser. A, 370, 2765 [Google Scholar]
- Beletic, J. W., Blank, R., Gulbransen, D., et al. 2008, SPIE, 7021, 70210H [NASA ADS] [Google Scholar]
- Beuzit, J.-L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Chauvin, G., Wildi, F., et al. 2022, SPIE, 12184, 121841S [NASA ADS] [Google Scholar]
- Cantalloube, F., Mouillet, D., Mugnier, L. M., et al. 2015, A&A, 582, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlomagno, B., Delacroix, C., Absil, O., et al. 2020, J. Astron. Telesc. Instrum. Syst., 6, 035005 [NASA ADS] [Google Scholar]
- Carlotti, A., Bidot, A., Mouillet, D., et al. 2022a, SPIE, 12184, 121841I [NASA ADS] [Google Scholar]
- Carlotti, A., Jocou, L., Moulin, T., et al. 2022b, SPIE, 12185, 121855L [NASA ADS] [Google Scholar]
- Cugno, Patapis, P., Stolker, T., et al. 2021, A&A, 653, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delorme, J. R., Jovanovic, N., Wallace, J. K., et al. 2018, SPIE Conf. Ser., 10703, 107033B [NASA ADS] [Google Scholar]
- Donati, J.-F., Kouach, D., Lacombe, M., et al. 2018, in Handbook of Exoplanets (Berlin: Springer International Publishing), 903 [CrossRef] [Google Scholar]
- Gratton, R., Keller, C., Diolaiti, E., et al. 2022, SPIE Conf. Ser., 12184, 121844F [Google Scholar]
- Haffert, S. Y., Bohn, A. J., de Boer, J., et al. 2019, Nat. Astron., 3, 749 [Google Scholar]
- Hoeijmakers, H. J., Schwarz, H., Snellen, I. A. G., et al. 2018, A&A, 617, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houllé, M., Vigan, A., Carlotti, A., et al. 2021, A&A, 652, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hours, A., Carlotti, A., Mouillet, D., et al. 2022, SPIE Conf. Ser., 12185, 121852E [NASA ADS] [Google Scholar]
- Jocou, L., Rabou, P., Moulin, T., et al. 2022, SPIE, 12185, 121854K [NASA ADS] [Google Scholar]
- Kasper, M., Cerpa Urra, N., Pathak, P., et al. 2021, The Messenger, 182, 38 [Google Scholar]
- Kravchenko, K., Dallilar, Y., Absil, O., et al. 2022, SPIE, 12184, 121845M [NASA ADS] [Google Scholar]
- Lacour, S., Wang, J. J., Nowak, M., et al. 2020, SPIE Conf. Ser., 11446, 114460O [NASA ADS] [Google Scholar]
- Lozi, J., Guyon, O., Jovanovic, N., et al. 2018, SPIE, 10703, 1070359 [NASA ADS] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Natl. Acad. Sci., 111, 12661 [NASA ADS] [CrossRef] [Google Scholar]
- Mâlin, M., Boccaletti, A., Charnay, B., Kiefer, F., & Bézard, B. 2023, A&A, 671, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollière, P., Molyarova, T., Bitsch, B., et al. 2022, ApJ, 934, 74 [CrossRef] [Google Scholar]
- N’Diaye, M., Dohlen, K., Fusco, T., & Paul, B. 2013, A&A, 555, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neichel, B., Fusco, T., Sauvage, J. F., et al. 2016, SPIE Conf. Ser., 9909, 990909 [Google Scholar]
- Noll, S., Kausch, W., Barden, M., et al. 2012, A&A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oberg, K. I., & Bergin, E. A. 2016, ApJ, 831, L19 [CrossRef] [Google Scholar]
- Otten, G. P. P. L., Vigan, A., Muslimov, E., et al. 2021, A&A, 646, A150 [EDP Sciences] [Google Scholar]
- Patapis, Nasedkin, E., Cugno, G., et al. 2022, A&A, 658, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrus, S., Bonnefoy, M., Chauvin, G., et al. 2021, A&A, 648, A59 [EDP Sciences] [Google Scholar]
- Rothman, L., Gordon, I., Barbe, A., et al. 2009, J. Quant. Spectrosc. Radiat. Transf. , 110, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffio, J.-B., Macintosh, B., Konopacky, Q. M., et al. 2019, AJ, 158, 200 [Google Scholar]
- Snellen, I., Brandl, B., Kok, R., et al. 2014, Nature, 509, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I., de Kok, R., Birkby, J. L., et al. 2015, A&A, 576, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thatte, N. A., Bryson, I., Clarke, F., et al. 2020, SPIE Conf. Ser., 11447, 114471W [NASA ADS] [Google Scholar]
- Thatte, N., Tecza, M., Schnetler, H., et al. 2021, The Messenger, 182, 7 [NASA ADS] [Google Scholar]
- Thatte, N. A., Melotte, D., Neichel, B., et al. 2022, SPIE Conf. Ser., 12184, 1218420 [Google Scholar]
- Tinetti, G., Drossart, P., Eccleston, P., et al. 2018, Exp. Astron., 46, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Turbet, M. 2018, Thesis, Sorbonne Université, France [Google Scholar]
- Vaughan, S. R., Birkby, J., Thatte, N., et al. 2022, BAAS, 54, 5 [Google Scholar]
- Vigan, A., El Morsy, M., Lopez, M., et al. 2023, arXiv e-prints [arXiv:2309.12390] [Google Scholar]
- Wang, J., Mawet, D., Ruane, G., Hu, R., & Benneke, B. 2017, AJ, 153, 183 [Google Scholar]
- Wang, J., Mawet, D., Hu, R., et al. 2018, J. Astron. Telesc. Instrum. Syst., 4, 035001 [NASA ADS] [Google Scholar]
- Wang, J., Delorme, J., Ruffio, J., et al. 2021a, AAS Meeting Abstracts, 53, 417.01 [NASA ADS] [Google Scholar]
- Wang, J. J., Ruffio, J.-B., Morris, E., et al. 2021b, AJ, 162, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Xuan, J. W., Wang, J., Ruffio, J.-B., et al. 2022, ApJ, 937, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Zieleniewski, S., Thatte, N., Kendrew, S., et al. 2019, Astrophysics Source Code Library [record ascl:1912.006] [Google Scholar]
Appendix A Frequency cut-off derivation
The chosen Gaussian kernel for the convolution can be written as:
We then have the expression:
We define the frequency cut-off such that:
Using the usual Fourier Transform of a Gaussian we found that 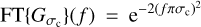 . Using Eq. A.3, we derive the expression of the frequency cut-off as a function of σc:
. Using Eq. A.3, we derive the expression of the frequency cut-off as a function of σc:
The frequency cut-off fc is homogeneous to 1/λ and it can be translated into a spectral resolution cut-off as:
where λ0 is the central wavelength of the spectrum.
Appendix B Stellar subtraction
Here, we seek to express both the residual planetary signal and the noise after molecular mapping preprocessing. Taking Eq. 6 and developing it here, we obtain:
Using the equality of S = [S]LF + [S]HF and assuming that the model of the tellurics transmission is perfect (i.e., 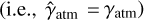 ), we find:
), we find:
While we could apply the full formula, it is convenient to highlight what are the dominant noise terms. We argue that in usual cases, the dominant noise term is n(λ, x, y). Indeed, the total variance of the noise is equal to ![${n^2}(\lambda ,x,y) + [n(\lambda ,x,y)]_{{\rm{LF}}}^2 + {{\left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}(\lambda )} \right]_{{\rm{HF}}}^2} \over {\left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}(\lambda )} \right]_{{\rm{LF}}}^2}} \cdot [n(\lambda ,x,y)]_{{\rm{LF}}}^2$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq42.png) . In practice, the filter cut-off fre-quency is kept small (Rc ≈ 100) so that
. In practice, the filter cut-off fre-quency is kept small (Rc ≈ 100) so that ![$[n]_{{\rm{HF}}}^2 > > [n]_{{\rm{LF}}}^2$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq43.png) . It is however still large enough, considering the steep slope of the stellar DSP, so that
. It is however still large enough, considering the steep slope of the stellar DSP, so that ![$\left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}} \right]_{{\rm{LF}}}^2 > > \left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}} \right]_{{\rm{HF}}}^2$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq44.png) .
.
To illustrate these dominance relationships, Fig B.1 shows the PSD of these four components. Quantitatively, in the case studied in Fig B.1, we find that the variance of the low-frequency noise, ![$\left[ n \right]_{{\rm{LF}}}^2$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq45.png) , represents only 2% of the high-frequency noise
, represents only 2% of the high-frequency noise ![$\left[ n \right]_{{\rm{HF}}}^2$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq46.png) . The fraction
. The fraction ![${{\left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}(\lambda )} \right]_{{\rm{HF}}}^2} \over {\left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}(\lambda )} \right]_{{\rm{LF}}}^2}}$](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq47.png) is also small, and in this example is equal to 0.015.
is also small, and in this example is equal to 0.015.
Therefore, the noise term n(λ, x, y) is the dominant one. We thus find the expression of Eq. 6 as follows:
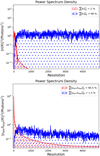 |
Fig. B.1 Relative weight of the low frequency and high frequency part of the noise and stellar signal. Top panel: PSDs of the high-pass filtered noise (in blue) and of the complementary low-pass filtered noise (in red). Bottom panel: Stellar spectrum PSD with the high-frequency part in blue and the low-frequency part in red. The star spectrum corresponds to a M-star and the tellurics to present a case where we have a strong high-frequency content. |
Appendix C Illustration of several signal dependencies
As mentioned in the Section 2.2, the signal of interest depends not only on the spectral resolution of the instrument, but also on the intrinsic characteristics of the companion spectra. The top panel of Fig C.1 quantifies this difference between a spectrum corresponding to an L-type planet and a T-type planet. Here, we find that for the same total photon count, the amount of signal is six times greater for a planet at 500K.
Another significant dependency is the central wavelength of observation. The bottom panel of Fig C.1 shows that we can obtain a difference of a factor of 1.6 for two central wavelengths spaced 400 nm apart.
 |
Fig. C.1 Visualization of the amount of information useful for molecular mapping detection. Top panel: PSD of two high-pass filtered planet spectra (T=500K and T=1200K, log(g)=4, [M/H]=0) at the same resolutions and with the same amount of photons. Bottom panel: PSD of high-pass filtered planet spectra (T=1700K, log(g)=4, [M/H]=0) on two different spectral ranges with a 300 nm bandwidth (center on λ0 = 1.35 µm in red and center on λ0 = 1.75 µm in purple). |
All Tables
All Figures
 |
Fig. 1 2D correlation map processed on simulated PSF with a fake planet injected, shown in the top-left panel. The colorbar represents the correlation strength between spaxels and the template. The top right panel shows the histogram of the correlation strength map, displaying the distribution of the correlation values in the annulus. Here, µCCF and σCCF denote the mean and the standard deviation of these values, respectively. Also, α(x0, y0) is the correlation at the location of the planet. Bottom panel shows the cross-correlation function on (blue) and off (orange) the planet’s location. |
| In the text | |
 |
Fig. 2 PSD of high-pass filtered (Rc = 100) planet spectrum (T = 500 K, log(g) = 4, [M/H] = 0) for two different resolutions on the total spectral range offered by BT-Settl spectra (0.3–12 µm). The hatched areas correspond to the areas under the curves equal to the quantity α2. Note: the PSD has been smoothed only for better visualization purposes. The y-axis is relative to the total flux of the companions. Only the ratios between the curves explaining the a variation from a given resolution to another one should be taken into consideration. |
| In the text | |
 |
Fig. 3 Fraction of the planetary spectrum remaining after high-pass filtering with a resolution cut Rc = 100 as a function of the spectral resolution of the instrument (see text). Templates are chosen for different temperatures but with a constant gravitational surfaces (log(g) = 4) and a constant metallicity ([M/H] = 0). We notice that the colder the planet, the higher content of molecular absorption lines and the larger fraction of signal preserved at high resolution. |
| In the text | |
 |
Fig. 4 Percentage of information subtracted from the planetary signal due to the high-frequency content of the host star as a function of spectral resolution for several star and planet types. The stellar spectra that are used here come from the BT-NextGen database. The M-type star was chosen with a temperature of 3200 K, and the A-type star with a temperature of 7200 K. Both have a surface gravity of log(g) = 4, and a metallicity of [M/H] = 0. This signal subtraction is obtained with non-Doppler-shifted spectra to correspond to the worst-case scenario, where absorption lines common to both object are overlaid. |
| In the text | |
 |
Fig. 5 Effect of high-pass filtering on speckles. Top panel: PSDs of the speckle modulation (taken at a several separations), photon and read-out noise, and planet spectrum. Bottom panel: same PSDs after the highpass filtering with a resolution cut-off of Rc = 100. |
| In the text | |
 |
Fig. 6 Residual fraction of the speckle modulation in respect to several angular separation (solid lines) and a planet spectrum (dashed line) as a function of the resolution cut-off. The planet spectrum is a BT-Settl template corresponding to T = 1700 K, log(g) = 4, [M/H] = 0 observed in the K-band degraded to a spectral resolution of 7000. |
| In the text | |
 |
Fig. 7 Plot shows the empirical S/N obtained with simulations for different cut-off frequencies obtained with the injection of a fake planet with the same HARMONI-like observation conditions as in Fig. 5. |
| In the text | |
 |
Fig. 8 Study of noise statistics before and after high-pass filtering. Top panel: quantile-quantile plot without speckle filtering. Bottom panel: quantile-quantile plot with speckle high-pass filtering with a resolution cut-off of 100. |
| In the text | |
 |
Fig. 9 Monochromatic high contrast long exposure PSFs with the two HARMONI current apodizers. It has been simulated with the best seeing condition (Strehl ratio of 90% in K-band). |
| In the text | |
 |
Fig. 10 Comparison of contrast curves obtained through our method with respect to end-to-end simulations. The comparison has been made for 1 h exposures with respect to several cases: (top left panel) H-band HARMONI observation mode (Table 1) with an A-star (7200 K, log(g) = 4, [M/H] = 0) magnitude of 6 with T-type planet (500 K, log(g) = 4, [M/H] = 0) and L-type planet (1700 K, log(g) = 4, [M/H] = 0) with median seeing condition (0.65″ for λ = 0.5 µm, Strehl = 94%). Top-right panel: same templates and conditions on K-band HARMONI observation mode. Bottom-right panel: same templates on H-band with JQ3 seeing condition (0.74″ for λ = 0.5 µm, Strehl = 73%). Bottom-left panel: same planetary templates but with an M-star (3200 K, log(g) = 4, [M/H] = 0) on K-band with median seeing condition. The solid lines are the prediction of FastCurves with these parameters, the dashed lines are the result of molecular mapping processing with time-series simulated PSF and fake planets injection. |
| In the text | |
 |
Fig. 11 Comparison between our approach (right column) and results from Houllé et al. (left column). The comparison was made for the H, K, and K2 high bands observation modes (see Table 1) with a star magnitude of 4.7, L, and T spectral type companions, as well as a rotational broadening of 20 km s−1. These curves are simulated with median seeing conditions with a Strehl ratio of about 80% in K band. The total exposure time is set to 2 h. We note that the green dashed curve on the left panel is the contrast curve obtained with the ADI ANDROMEDA algorithm (Cantalloube et al. 2015), and the orange curve is the raw contrast with a standard deviation of 1σ. |
| In the text | |
 |
Fig. 12 S/N variation (defined in Eq. (17)) as a function of the resolution and the central wavelength of the spectral range, with a constant 0.5 µm large bandwidth. The α quantity has been estimated for a BT-Settl template corresponding to a temperature of 500 (top) and 1700 K (bottom). The S/N has been normalized to the maximum, while the absolute values depend on many observing parameters, starting with the stellar magnitude and planetary contrast. |
| In the text | |
 |
Fig. 13 BT-Settl spectrum of a T = 1700 K companion at two different spectral resolutions: R = 7000 (top) and R = 17 000 (bottom). Each red rectangle delimits the observable spectral bands by keeping the same number of pixels for both resolutions. In each case, the corresponding α quantities and the S/N, both normalized to the top panel, are indicated. We note that some areas have more absorption lines, and thus benefit more than others from an increased resolution (e.g., there is a forest of lines corresponding to the presence of CO around 2.3 µm). Both α and the photon noise decrease as the resolution increases and the bandwidth decreases; comparing the two variations may lead to a lower (left rectangle) or higher (right rectangle) resulting S/N. |
| In the text | |
 |
Fig. 14 Evolution of the S/N (relative to its maximum) with the spectral resolution, for a fixed number of pixels (3300 pixels per spectrum here, corresponding to the case of HARMONI) and a correspondingly variable bandwidth. The largest spectral range is set to cover the H and K bands H (from 1 to 2.8 µm) for three different templates of planets signature. These maps include only the photon noise, not considering any wavelength-dependant instrumental transmission, which makes this result quite generic, informative of the planetary spectra properties and not of the instrument specificities. Three different planet temperatures are considered: 500 (left), 1200 (middle), and 1700 K (right). |
| In the text | |
 |
Fig. 15 Gain of time as a function of the bandwidth (top panel) or the spectral resolution (bottom panel) at the expense of mosaïcking the FoV for detecting a 500 K planet (log(g) = 4, [M/H] = 0). The spectral range has been chosen to start at λmin = 1.2 µm for the FoV/Bandwidth trade-off and a fixed spectral range between 1.2 and 1.8 µm for the FoV/Resolution trade-off. |
| In the text | |
 |
Fig. 16 Comparison of S/N variations for a planet with temperature of 1700 K with (bottom panel), and without (top panel) telluric absorption. The telluric absorption spectrum has been computed for an airmass of 1 using the ESO Skycalc module. The telluric absorptions do not impact the S/N distribution very much, with the exception of making it slightly more sensitive to the central wavelength, thus delimiting the spectral domains of interest more clearly. For instance, we see that near 2 µm the tellurics separate more the two zones of interest in H band and in K band by making the S/N vary more quickly. |
| In the text | |
 |
Fig. 17 S/N gain as a function of radial velocity shift for H2O and CO2 molecules. The three curves represent this gain for different spectral resolutions: 3000, 10 000, and 40 000. |
| In the text | |
 |
Fig. 18 S/N gain as a function of a radial velocity shift for featureless exoplanetary albedo. The three curves represent this gain for different spectral resolutions: 3000, 10 000, and 40 000. |
| In the text | |
 |
Fig. 19 Evolution of the S/N with the resolution for the same exoplanet spectrum template (1200 K) but with two different rotational broadening results, corresponding to rotational speed of 3 km s−1 and 30 km s−1. The optimal area goes toward lower resolution as the rotational speed of the planet increases. |
| In the text | |
 |
Fig. 20 Predicted contrast curves for HARMONI generated with the FastCurves package for three different planet temperatures. The exposure time is set to be 2 h on a 6 mag A-star with a Strehl ratio of about 60% in the H band. |
| In the text | |
 |
Fig. 21 Limit star magnitude above which photon noise becomes smaller than read-out noise as a function of separation and spectral resolution. |
| In the text | |
 |
Fig. 22 Contrast curves with and without apodizers. The comparison is made while considering the best seeing conditions (Strehl ratio of 95% in the K band). |
| In the text | |
 |
Fig. B.1 Relative weight of the low frequency and high frequency part of the noise and stellar signal. Top panel: PSDs of the high-pass filtered noise (in blue) and of the complementary low-pass filtered noise (in red). Bottom panel: Stellar spectrum PSD with the high-frequency part in blue and the low-frequency part in red. The star spectrum corresponds to a M-star and the tellurics to present a case where we have a strong high-frequency content. |
| In the text | |
 |
Fig. C.1 Visualization of the amount of information useful for molecular mapping detection. Top panel: PSD of two high-pass filtered planet spectra (T=500K and T=1200K, log(g)=4, [M/H]=0) at the same resolutions and with the same amount of photons. Bottom panel: PSD of high-pass filtered planet spectra (T=1700K, log(g)=4, [M/H]=0) on two different spectral ranges with a 300 nm bandwidth (center on λ0 = 1.35 µm in red and center on λ0 = 1.75 µm in purple). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



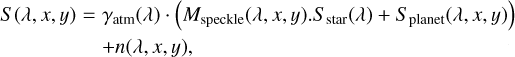
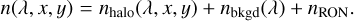
![$ {\hat M_{{\rm{speckle}}}}(\lambda ,x,y) = {\left[ {{{S(\lambda ,x,y)} \over {{{\hat \gamma }_{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]_{{\rm{LF}}}}. $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq6.png)
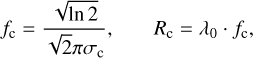
![$ \matrix{ {{{\hat M}_{{\rm{speckle}}}}(\lambda ,x,y) = {M_{{\rm{speckle}}}}(\lambda ,x,y) + {{\left[ {{{{S_{{\rm{planet}}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{\left[ {{{n(\lambda ,x,y)} \over {{{\hat \gamma }_{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}}.} \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq8.png)
![$ \matrix{ {{S_{{\rm{res}}}}(\lambda ,x,y) = S(\lambda ,x,y) - {{\hat M}_{{\rm{speckle}}}}(\lambda ,x,y) \cdot {{\hat \gamma }_{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star}}}}(\lambda ),} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\gamma _{{\rm{atm}}}}(\lambda ) \cdot \left( {{{\left[ {{S_{{\rm{planet}}}}} \right]}_{{\rm{HF}}}}(\lambda ,x,y) - {{\left[ {{{\hat S}_{{\rm{star}}}}} \right]}_{{\rm{HF}}}}(\lambda )} \right.} \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cdot {{\left[ {{{{S_{{\rm{planet}}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \right) + n'(\lambda ,x,y),} \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq10.png)
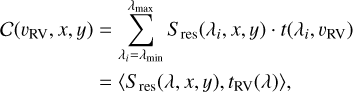
![$ \matrix{ {\left\langle {{S_{{\rm{res}}}}(\lambda ,x,y),{t_{{\rm{RV}}}}(\lambda )} \right\rangle \approx } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\left\langle {{\gamma _{{\rm{atm}}}}(\lambda ) \cdot {{\left[ {{S_{{\rm{planet}}}}(\lambda ,x,y)} \right]}_{{\rm{HF}}}},{t_{{\rm{RV}}}}(\lambda )} \right\rangle } \hfill \cr {\,\,\,\,\,\,\,\, - \left\langle {{\gamma _{{\rm{atm}}}}(\lambda ) \cdot {{\left[ {{{\hat S}_{{\rm{star}}}}} \right]}_{{\rm{HF}}}}(\lambda ) \cdot {{\left[ {{{{S_{{\rm{planet}}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}},{t_{{\rm{RV}}}}(\lambda )} \right\rangle } \hfill \cr {\,\,\,\,\,\,\,\, + \left\langle {n(\lambda ,x,y),{t_{{\rm{RV}}}}} \right\rangle } \hfill \cr { \approx \left\| {{\gamma _{{\rm{atm}}}}(\lambda ) \cdot {{\left[ {{S_{{\rm{planet}}}}(\lambda ,x,y)} \right]}_{{\rm{HF}}}}} \right\| \cdot \left\| {{t_{{\rm{RV}}}}} \right\| \cdot \cos \left( {{\theta _{{\rm{planet,RV}}}}} \right)} \hfill \cr {\,\,\,\,\, - \left\| {{\gamma _{{\rm{atm}}}}(\lambda ) \cdot {{\left[ {{{\hat S}_{{\rm{star}}}}} \right]}_{{\rm{HF}}}}(\lambda ) \cdot {{\left[ {{{{S_{{\rm{planet}}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \right\| \cdot \left\| {{t_{{\rm{RV}}}}} \right\| \cdot \cos \left( {{\theta _{{\rm{star}},{\rm{RV}}}}} \right)} \hfill \cr {\,\,\,\,\, + \left\langle {n(\lambda ,x,y),{t_{{\rm{RV}}}}(\lambda )} \right\rangle } \hfill \cr { \approx \alpha (x,y) \cdot \cos \left( {{\theta _{{\rm{planet,RV}}}}} \right) - \beta (x,y) + \left\langle {n(\lambda ,x,y),{t_{{\rm{RV}}}}(\lambda )} \right\rangle ,} \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq14.png)
![$ \matrix{ {\alpha (x,y) = \sqrt {\mathop {\mathop \sum \nolimits^ }\limits_{{\lambda _i} = {\lambda _{\min }}}^{{\lambda _{\max }}} {{\left( {{\gamma _{{\rm{atm}}}}\left( {{\lambda _i}} \right) \cdot {{\left[ {{S_{{\rm{planet}}}}} \right]}_{{\rm{HF}}}}\left( {{\lambda _i},x,y} \right)} \right)}^2}} } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{1 \over {{N_\lambda }}}\mathop {\mathop \sum \nolimits^ }\limits_{{R_i} = 0}^{{R_{\max }}} {\rm{FFT}}{{\left\{ {{\gamma _{{\rm{atm}}}} \cdot {{\left[ {{S_{{\rm{planet}}}}} \right]}_{{\rm{HF}}}}(x,y)} \right\}}^2}\left( {{R_i}} \right)} } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{1 \over {{N_\lambda }}}\mathop {\mathop \sum \nolimits^ }\limits_{{R_i} = 0}^{{R_{\max }}} {\rm{PSD}}\left\{ {{\gamma _{{\rm{atm}}}} \cdot {{\left[ {{S_{{\rm{planet}}}}} \right]}_{{\rm{HF}}}}(x,y)} \right\}\left( {{R_i}} \right)} ,} \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq16.png)
![$ {F_{{\rm{planet}}{{\rm{}}_{{\rm{HF}}}}}}\left( {{R_{\max }}} \right) = {{\sqrt {\sum\limits_{{R_i} = 0}^{{R_{\max }}} {{\rm{PSD}}\left\{ {{{\left[ {{S_{{\rm{planet}}}}} \right]}_{{\rm{HF}}}}} \right\}\left( {{R_i}} \right)} } } \over {\sqrt {\sum\limits_{{R_i} = 0}^{{R_{\max }}} {{\rm{PSD}}\left\{ {{S_{{\rm{planet}}}}} \right\}\left( {{R_i}} \right)} } }}. $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq17.png)
![$ \matrix{ {\,\sigma _{{\rm{CCF}}}^2(\rho ) = {\rm{Var}}\left[ {\left\langle {n(\rho ),{t_{{\rm{RV}}}}} \right\rangle } \right]} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\rm{Var}}\left[ {\left\langle {{n_{{\rm{halo}}}}(\rho ),{t_{{\rm{RV}}}}} \right\rangle + \left\langle {{n_{{\rm{bkgd}}}},{t_{{\rm{RV}}}}} \right\rangle + \left\langle {{n_{{\rm{RON}}}},{t_{{\rm{RV}}}}} \right\rangle } \right]} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\mathop \sum \nolimits^ }\limits_{{\lambda _i} = {\lambda _{\min }}}^{{\lambda _{\max }}} t_{{\rm{RV}}}^2\left( {{\lambda _i}} \right) \cdot \left( {{\rm{Var}}\left[ {{n_{{\rm{halo}}}}\left( {{\lambda _i},\rho } \right)} \right] + {\rm{Var}}\left[ {{n_{{\rm{bkgd}}}}\left( {{\lambda _i}} \right)} \right]} \right.} \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {\rm{Var}}\left[ {{n_{{\rm{RON}}}}} \right]} \right)} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\mathop \sum \nolimits^ }\limits_{{\lambda _i} = {\lambda _{\min }}}^{{\lambda _{\max }}} t_{{\rm{RV}}}^2\left( {{\lambda _i}} \right) \cdot \sigma _{{\rm{halo}}}^2\left( {{\lambda _i},\rho } \right) + \mathop {\mathop \sum \nolimits^ }\limits_{{\lambda _i} = {\lambda _{\min }}}^{{\lambda _{\max }}} t_{{\rm{RV}}}^2\left( {{\lambda _i}} \right) \cdot {\sigma _{{\rm{bkgd}}}}{{\left( {{\lambda _i}} \right)}^2}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \sigma _{{\rm{RON}}}^2.} \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq20.png)
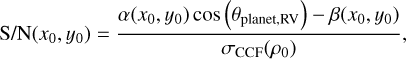
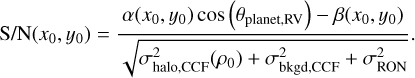
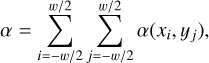
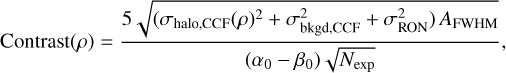
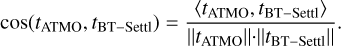
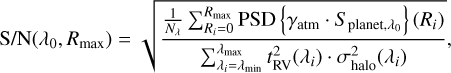
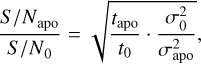
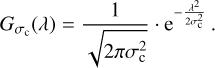
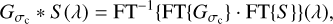
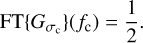
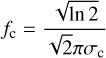
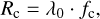
![$ \matrix{ {{S_{{\rm{res }}}}(\lambda ,x,y) = S(\lambda ,x,y) - {{\hat M}_{{\rm{speckle }}}}(\lambda ,x,y) \cdot {{\hat \gamma }_{{\rm{atm }}}}(\lambda ) \cdot {{\hat S}_{{\rm{star }}}}(\lambda )} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\gamma _{{\rm{atm }}}}(\lambda ) \cdot \left( {{M_{{\rm{speckle }}}}(\lambda ,x,y) \cdot {S_{{\rm{star }}}}(\lambda ) + {S_{{\rm{planet }}}}(\lambda ,x,y)} \right)} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + n(\lambda ,x,y) - {{\hat \gamma }_{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star }}}}(\lambda ) \cdot \left( {{M_{{\rm{speckle }}}}(\lambda ,x,y)} \right.} \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{\left[ {{{{S_{{\rm{planet }}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star }}}}(\lambda )}}} \right]}_{{\rm{LF}}}} + {{\left[ {{{n(\lambda ,x,y)} \over {{{\hat \gamma }_{{\rm{atm }}}}(\lambda ) \cdot {{\hat S}_{{\rm{star }}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \right)} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\gamma _{{\rm{atm}}}}(\lambda ) \cdot {S_{{\rm{planet }}}}(\lambda ,x,y) - {{\hat \gamma }_{{\rm{atm}}}}(\lambda )} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cdot {{\hat S}_{{\rm{star }}}}(\lambda ) \cdot {{\left[ {{{{S_{{\rm{planet }}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star }}}}(\lambda )}}} \right]}_{{\rm{LF}}}} + n(\lambda ,x,y)} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {{\hat \gamma }_{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star}}}}(\lambda ) \cdot {{\left[ {{{n(\lambda ,x,y)} \over {{{\hat \gamma }_{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}} \cdot } \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq39.png)
![$ \matrix{ {{S_{{\rm{res }}}}(\lambda ,x,y) = {\gamma _{{\rm{atm }}}}(\lambda ) \cdot {S_{{\rm{planet }}}}(\lambda ,x,y) - {\gamma _{{\rm{atm }}}}(\lambda )} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cdot \left( {{{\left[ {{{\hat S}_{{\rm{star}}}}} \right]}_{{\rm{LF}}}}(\lambda ) + {{\left[ {{{\hat S}_{{\rm{star}}}}} \right]}_{{\rm{HF}}}}(\lambda )} \right) \cdot {{\left[ {{{{S_{{\rm{planet }}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + n(\lambda ,x,y) - {\gamma _{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star}}}}(\lambda ) \cdot {{\left[ {{{n(\lambda ,x,y)} \over {{\gamma _{{\rm{atm}}}}(\lambda ) \cdot {{\hat S}_{{\rm{star}}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\gamma _{{\rm{atm}}}}(\lambda ) \cdot \left( {{{\left[ {{S_{{\rm{planet }}}}} \right]}_{{\rm{HF}}}}(\lambda ,x,y) - {{\left[ {{{\hat S}_{{\rm{star }}}}} \right]}_{{\rm{HF}}}}(\lambda )} \right.} \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cdot {{\left[ {{{{S_{{\rm{planet }}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star }}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \right) + n(\lambda ,x,y) - {{[n(\lambda ,x,y)]}_{{\rm{LF}}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {{{{\left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}(\lambda )} \right]}_{{\rm{HF}}}}} \over {{{\left[ {{\gamma _{{\rm{atm}}}} \cdot {{\hat S}_{{\rm{star}}}}(\lambda )} \right]}_{{\rm{LF}}}}}} \cdot {{[n(\lambda ,x,y)]}_{{\rm{LF}}}}.} \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq41.png)
![$ \matrix{ {{S_{{\rm{res }}}}(\lambda ,x,y) \approx {\gamma _{{\rm{atm }}}}(\lambda ) \cdot \left( {{{\left[ {{S_{{\rm{planet }}}}} \right]}_{{\rm{HF}}}}(\lambda ,x,y) - {{\left[ {{{\hat S}_{{\rm{star }}}}} \right]}_{{\rm{HF}}}}(\lambda )} \right.} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { \cdot {{\left[ {{{{S_{{\rm{planet }}}}(\lambda ,x,y)} \over {{{\hat S}_{{\rm{star }}}}(\lambda )}}} \right]}_{{\rm{LF}}}}} \right) + n(\lambda ,x,y).} \hfill \cr } $](/articles/aa/full_html/2024/02/aa46185-23/aa46185-23-eq48.png)