| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 21 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202347046 | |
| Published online | 12 December 2023 | |
Chemo-dynamical tagging in the outskirts: The origins of stellar substructures in the Magellanic Clouds
1
Instituto Multidisciplinario de Investigación y Postgrado, Universidad de La Serena, Raúl Bitrán 1305, La Serena, Chile
e-mail: cesar.alejandro.munoz.g@gmail.com
2
Departamento de Astronomía, Universidad de La Serena, Av. Cisternas 1200, La Serena, Chile
3
Department of Physics, Montana State University, PO Box 173840, Bozeman, MT 59717, USA
4
Department of Astronomy, University of Virginia, 530 McCormick Road PO Box 400325, Charlottesville, VA 22904, USA
5
National Optical-Infrared Astronomy Research Laboratory (NOIRLab), 950 North Cherry Avenue, Tucson, AZ 85719, USA
6
Department of Astronomy, University of California, Berkeley 501 Campbell Hall 3411, Berkeley, CA 94720-3411, USA
7
IQVIA, 4820 Emperor Blvd, Durham, NC 27703, USA
8
Departamento de Astronomía, Casilla 160-C, Universidad de Concepción, Concepción, Chile
9
Departamento de Astronomía, Universidad de Chile, Camino El Observatorio 1515, Las Condes, Chile
10
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta 1270300, Chile
11
Centro de Investigación en Astronomía, Universidad Bernardo O’Higgins, Avenida Viel 1497, Santiago, Chile
12
Instituto de Astronomía, Universidad Católica del Norte, Av. Angamos 0610, Antofagasta, Chile
Received:
29
May
2023
Accepted:
21
August
2023
We present the first detailed chemical analysis from APOGEE-2S observations of stars in six regions of recently discovered substructures in the outskirts of the Magellanic Clouds extending to 20° from the Large Magellanic Cloud (LMC) center. We also present, for the first time, the metallicity and α-abundance radial gradients of the LMC and the Small Magellanic Cloud (SMC) out to 11° and 6°, respectively. Our chemical tagging includes 13 species including light, α-, and Fe-peak elements. We find that the abundances of all of these chemical elements in stars populating two regions in the northern periphery, along the northern “stream-like” feature, show good agreement with the chemical patterns of the LMC, and thus likely have an LMC origin. For substructures located in the southern periphery of the LMC we find more complex chemical and kinematical signatures, indicative of a mix of LMC-like and SMC-like populations. The southern region closest to the LMC shows better agreement with the LMC, whereas that closest to the SMC shows a much better agreement with the SMC chemical pattern. When combining this information with 3D kinematical information for these stars, we conclude that the southern region closest to the LMC likely has an LMC origin, whereas that closest to the SMC has an SMC origin and the other two southern regions have a mix of LMC and SMC origins. Our results add to the evidence that the southern substructures of the LMC periphery are the product of close interactions between the LMC and SMC, and thus likely hold important clues that can constrain models of their detailed dynamical histories.
Key words: astrochemistry / stars: abundances / Magellanic Clouds / galaxies: kinematics and dynamics
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
According to the standard cosmological paradigm of cosmological structure formation, halos grow in mass hierarchically via the accretion and merger of smaller halos (e.g., White & Rees 1978). Galaxies form inside the more massive halos, where the gas can collapse and form stars. The self-similarity of the ΛCDM paradigm implies that accretion and mergers are expected to also take place in dwarf galaxies (e.g., Diemand et al. 2007), which is the most common type of galaxies in the Universe. However, this prediction is poorly constrained by observations, mostly because dwarf galaxies are intrinsically faint.
The Large and Small Magellanic Clouds (LMC and SMC) are our closest pair of interacting dwarf galaxies, at distances of ∼50 and 64 kpc, respectively (Pietrzyński et al. 2019; Graczyk et al. 2020). They are thus unique and important systems for investigating in great detail not only their formation, but also their interaction history and evolution, and can be used to put constraints on dwarf galaxy formation models. Consequently, they have been the main target of several dedicated surveys (see below).
It is now known that the stellar populations of the Magellanic Clouds (MCs) extend much farther than previously thought (e.g., Nidever et al. 2011; Belokurov & Koposov 2016), and that they underwent close interactions that likely produced both the gaseous Magellanic Bridge (Hindman et al. 1963; Harris 2007) and a likely large amount of as-yet-undetected stellar debris (Besla et al. 2012; Lucchini et al. 2021, but see Gaia Collaboration 2021a for the detection of stars in the Magellanic Bridge). In addition, very precise proper motion (PM) measurements confirmed that the MCs are on their first infall toward the Milky Way (MW; Kallivayalil et al. 2013; Besla et al. 2007). This scenario was supported by several observations, but in particular by the recent observational evidence of a local MW dynamical wake, which was predicted to trail the orbit of the LMC, and a large-scale MW overdensity, also predicted to exist across a large area of the northern Galactic hemisphere (Gómez et al. 2016; Garavito-Camargo et al. 2019, 2021; Conroy et al. 2021; Erkal et al. 2021; Petersen & Peñarrubia 2021).
To understand the hierarchical assembly involving such dwarf galaxies, it is important to study their periphery, which is most affected by tidal interactions and where the fossil record of interaction and past accretion events is most long-lived. Over the last decades large surveys providing both homogeneous, wide-field photometry as well as deep individual fields (e.g., DES: Bechtol et al. 2015, SMASH: Nidever et al. 2017, MagLiteS: Drlica-Wagner et al. 2016, MagES: Cullinane et al. 2020, DELVE: Drlica-Wagner et al. 2021) have been dedicated to imaging the outskirts of the MCs. These observations have revealed the highly disturbed LMC/SMC disks and other faint stellar structures in unprecedented detail, including a northern “stream-like” feature (Mackey et al. 2016, 2018), ring-like structures (Choi et al. 2018a,b), and a diffuse extended stellar component (Nidever et al. 2019).
In addition to dedicated MC surveys, thanks to the Gaia space telescope (Gaia Collaboration 2016), we can now also obtain a homogeneous view (although not as deep) of the MC outskirts by selecting relevant stars using proper motion criteria. Belokurov & Erkal (2019) used red giant branch (RGB) stars from Gaia DR2 and discovered remarkable extended streams of stars in the periphery of the MCs that highlight the complexity of this interacting system. These features could only recently be detected so sharply due to the contiguous uniform coverage of Gaia, which is crucial in order to observe stellar streams that possess very low surface brightness (∼32 mag arcsec−2) and cover a large extent on the sky (∼10 s of degrees). While the discovery of these structures around the LMC provides important insights into the MC system, their exact origin remains unclear. It is possible that both a tidally disturbed disk and a classical accreted halo contribute to the diffuse substructures in the periphery of the MCs.
To help disentangle the nature of these features, we need both stellar kinematical and chemical abundance information of the substructures. The kinematics of these substructures were recently investigated in Cheng et al. (2022, hereafter C22), from new Apache Point Observatory Galactic Evolution Experiment-2S (APOGEE-2S, Majewski et al. 2017, and in prep.) observations of six fields around the MC periphery. The fields were placed on top of the overdensities of stars that have been detected, reaching out to 20° to the north and 15° to the south from the LMC center. C22 performed a detailed kinematical study by combining the APOGEE-2S radial velocities and the proper motions provided by Gaia DR3 data (Gaia Collaboration 2021b) and found that stars in the southern region have extreme space velocities that are distinct from the LMC disk, and not a simple extension of it. On the other hand, the stars in the northern substructure are consistent with being part of the LMC disk (see also Cullinane et al. 2022, who explored the kinematics of the northern arc in the LMC periphery). It was also found in C22 that the combination of LMC and SMC debris produced from their interaction is a plausible explanation for the extreme velocities in the southern periphery of the LMC, although it is not possible to rule out other origins.
To further constrain the origin of these overdense regions, information about their chemical abundances is needed, which is also available from the APOGEE-2S observations. Chemical abundances of the Magellanic system contain relevant information about star formation and evolution, and the stars’ interaction with the interstellar medium (ISM). The detailed chemical characterization of a number of elements available from APOGEE-2S will allow us to better understand the relation between the six regions and the LMC, SMC, and the MW. In addition, we can investigate different starbursts produced in the Magellanic system and how the ISM polluters, such as asymptotic giant branch (AGB) stars and supernovae, among others, influenced the chemical fingerprint currently observed in the Magellanic system and in their periphery. Moreover, we will be able to offer more detailed information about the age–metallicity relation in the LMC (Piatti & Geisler 2013; Carrera et al. 2008).
In this paper we follow up and complement the work done in C22 by presenting a detailed analysis of the chemical abundance patterns of the six fields in the MC periphery. We compare our findings with the abundances of the LMC and SMC studied by Nidever et al. (2020) and with the abundances of other MW dwarf galaxies (Hasselquist et al. 2021) in a consistent and homogeneous way, by using the APOGEE DR17 database (Abdurro’uf et al. 2022) for all the sources analyzed. Our aim is to further constrain the origin of the overdensity regions around the MC periphery and investigate any possible association of the stars in the LMC periphery to those in either the LMC or the SMC.
The outline of this paper is as follows. In Sect. 2 we describe the APOGEE-2S observations and the selection of the sample of stars that we analyze in this work, as well as the sample of MW stars used for comparison. Section 3 presents our general results in terms of the metallicity and α-abundance radial profiles and metallicity distribution function. In Sect. 4 we discuss in detail the abundances for a variety of elements and separately interpret the results for each of the six regions analyzed. Finally, we summarize and conclude our work in Sect. 5.
2. Data
Our study is focused on the chemical analysis of six APOGEE fields placed on substructures identified by Belokurov & Erkal (2019) in the outskirts of the LMC and SMC (see Fig. 1). APOGEE (Majewski et al. 2017) was originally part of Sloan Digital Sky Survey III (SDSS-III, Eisenstein et al. 2011) as a high resolution near-infrared spectroscopic survey of Galactic stars accessible from the Sloan 2.5 m Telescope (Gunn et al. 2006), but the survey was expanded as APOGEE-2 (Majewski et al., in prep.) in SDSS-IV (Blanton et al. 2017) to include measurements made with the du Pont 2.5 m telescope (Bowen & Vaughan 1973) in the southern hemisphere, partly motivated by the desire to probe the MCs. Targeting for the APOGEE surveys, including for the MC program described here, is described in Zasowski et al. (2013, 2017), Beaton et al. (2021), and Santana et al. (2021). We analyzed the chemical abundances measured from spectra that were obtained from the second high resolution, near-IR, APOGEE spectrograph built for APOGEE-2 (Wilson et al. 2019).
 |
Fig. 1. Distribution of the six fields in the substructures as well as LMC and SMC fields observed by APOGEE-2 in Magellanic Stream coordinates (LMS, BMS). |
Our observations were obtained through the Chilean National Telescope Allocation Committee (CNTAC) program CN2019A-30 (PI: A. Monachesi). Table 1 lists the location of the six APOGEE fields, named following the C22 labels, which cover a diameter of 2° each, as well as their field name according to APOGEE-2S and total visits and H magnitude depth. These fields reach out to 20° from the LMC center, which extend the MC program from the APOGEE survey by about 10°. Each APOGEE plate has 300 fibers, and therefore ∼260 science targets and ∼40 calibration targets were observed per field. At the location of our fields (see Table 1), the LMC surface brightness is ∼30 mag arcsec−2, and thus only a few stars on each plate are from the MC system; the vast majority of stars are MW field star contaminants (or “filler” targets; see the APOGEE-2 targeting references cited earlier), which we need to remove from our sample.
Regions, number of stars, coordinates, H magnitude, number of visits, and angular distance from the LMC center for the six substructures analyzed in this article.
The data were reduced with the standard APOGEE reduction pipeline (Nidever et al. 2015), which has been updated for improved calculation of radial velocities, especially for fainter stars similar to those we analyze here. The chemical abundances used here were obtained from the APOGEE Stellar Parameters and Chemical Abundance Pipeline (ASPCAP, García Pérez et al. 2016), as given in SDSS Data Release 17 (DR17, Abdurro’uf et al. 2022). ASPCAP is based on the FERRE2 code of Allende Prieto et al. (2006) and uses a grid of MARCS stellar atmospheres (Gustafsson et al. 2008; Jönsson et al. 2020) with an H-band line list from Smith et al. (2021), an update of the previous version by Shetrone et al. (2015). These atmospheres and the line list are combined to create a grid of synthetic spectra (Zamora et al. 2015) using the Synspec code (Hubeny & Lanz 2011). Some elements, in particular Ca and Mg used here, required the use of non-local thermodynamic equilibrium (LTE) calculations (Osorio et al. 2020). Once created, the library of synthetic spectra were used to find the best match to each observed spectra to determine stellar parameters and chemical abundances.
The APOGEE spectra provide not only chemical abundances, but also precision (to a few hundred m s−1) heliocentric radial velocities. These, together with the proper motions provided by Gaia, can be used to obtain the internal 3D velocities of the stars with respect to the LMC or SMC reference frame. This is relevant to understanding the origin of the stars in the substructures.
Cheng et al. (2022) calculated the 3D velocities of the APOGEE stars in the six substructures, and in the central LMC region, with respect to the LMC, using the model presented in Olsen et al. (in prep.; see also Choi et al. 2022 for a description of this model). In brief, the model follows the formalism by van der Marel et al. (2002, hereafter vdM02), which describes the relationship between the proper-motion vector and the orthogonal velocity components in the plane of the sky (as defined in Eq. (1) of vdM02). The kinematical model was obtained after fitting 12 parameters jointly with the heliocentric velocities and Gaia proper motions of ∼15 000 AGB and RGB stars. The best-fit parameters of the model are found in Table 1 of Choi et al. (2022). Then, using the orientation of the LMC disk obtained from the model and the transformations of the 3D motions to a cylindrical coordinate system (from the equations presented in vdM02), C22 derived Vr and Vϕ, the radial and rotational motions projected onto the LMC disk plane, and the vertical velocity Vz, the motion perpendicular to the disk plane (where a positive Vz is toward the Sun) of all the stars in the substructures.
We repeated this derivation for the substructure stars with respect to the SMC instead of the LMC. To do this, we used the formalism and kinematic model for the SMC presented in Zivick et al. (2021, hereafter Z21), which follows a process similar to the C22 adaption of the vdM02 formalism. However, there are two key differences between the LMC and SMC in the formalism. First, the model of the LMC assumes a thin disk for all stars present, which allows the calculation of the distance of individual stars in the frame of the LMC (a requirement for deriving internal velocities). In the case of the SMC, to calculate the internal velocities, we explored three distance assumptions: 50 kpc, 60 kpc, and 70 kpc for the stars. For simplicity, we chose to calculate the velocities as if all substructure stars are found at 60 kpc, roughly consistent with the distance to the SMC center as determined by RR Lyrae stars (Jacyszyn-Dobrzeniecka et al. 2017). The second difference is that the LMC model assumes a state of equilibrium, which is not the case for the SMC. As shown in Z21, an additional velocity component is required to describe the relative motions of SMC stars, namely the tidal expansion component due to the ongoing tidal disruption occurring in the SMC due to interactions with the LMC. Using the assumed distance of 60 kpc and the Z21 formalism and best-fit kinematic model parameters, we derived the internal velocities, Vr, Vϕ, Vz, with respect to the SMC for all stars in the substructures and in the central SMC region. In this work we use the 3D velocity information jointly with the chemical abundances of the stars in the substructures to understand their origin.
2.1. Selection of MC stars
With the primary goal of studying the chemical abundances of the stars in the MC substructures, which are more challenging to measure than radial velocities and bulk metallicities, we first take the sample of MC stars from the selection made by C22, as briefly described below. The sample used by C22 was selected using parameters delivered by Gaia EDR3 and presented in APOGEE DR17. The specific selection criteria are stars with G < 17.5 within 30° of the center of the Magellanic Stream coordinate system (Nidever et al. 2008) and stars that have similar proper motions to the LMC. This PM selection is shown in Fig. 2 where the stars in our final list in each substructure are color-coded. We can see in that figure that some of the stars in these substructures exhibit a slightly larger proper motion than that of the LMC and/or SMC. Since these stars are located in the outskirts of the MCs, this might be due to differences in velocities and distances from the main bodies. Nevertheless, the position of the stars in proper motion are also in agreement with the selection range made by Cullinane et al. (2022) and can be associated with the MC system.
 |
Fig. 2. Gaia EDR3 proper motions for stars in the six regions analyzed, as well as LMC and SMC stars (top) and Gaia EDR3 proper motion in Magellanic Stream coordinates (LMS, BMS; bottom). |
Additional selection criteria were used by C22 in stellar parameters to constrain the sample to stars along the RGB of the LMC. The specific selection was Teff < 5400 K, log g < 4.0, in addition to the magnitude cut mentioned above. To avoid foreground stars from the MW, stars with parallax π > 0.2 mas or Galactic latitude |b|< 5° were removed. Only stars within the proper motion space of the MCs were considered (see Fig. 2), as well as stars with 100 < VHelio < km s−1, which is the typical heliocentric velocity range for MC stars (see Nidever et al. 2020). Our final sample was very restricted in both Teff and log g (see Fig. 3).
 |
Fig. 3. log g vs. Teff distribution from APOGEE-2 data release (DR17) for the six regions listed in Table 2. The solid gray line represents a Dartmouth RGB isochrone with a metallicity of –1.0 dex and age of 11 Gyr (Dotter et al. 2008). |
For this study we used an additional constraint, not used in C22, related to the signal-to-noise ratio (S/N) of the sample, which is critical to the chemical analysis. Thus, we use in this work a subsample of the C22 sample of stars. Since our sample is very small, and contains few MC-selected stars, we needed a S/N cut that is high enough to perform a chemical analysis, but at the same time not too restrictive, such that we retained as many stars as possible. Nidever et al. (2020) compared the results obtained for metallicity ([Fe/H]) and α-elements ([Ca/Fe], [Si/Fe], [Mg/Fe]) when using a sample of stars with low S/N (∼40) and with a sample of stars with higher S/N > 70. They found that the sample with low S/N was good enough to analyze the chemical patterns of the LMC and SMC, at least for the elements mentioned. Following their approach, we performed a quality check of our data for the elements we use in this work, taking into account a minimum S/N of 35. In Fig. 4 we compare APOGEE-2 DR17 data for LMC stars selected as members by Nidever et al. (2020) and for all the elements analyzed in this study. In this figure we compare each chemical element vs. metallicity for the LMC stars with a S/N greater than 70 (gray in Fig. 4) and for the stars with an S/N between 35 and 75 (red dots in Fig. 4). We divided the metallicity range into four main regions and plotted the results for each of the 13 elements analyzed. In each of these four regions we calculated the median and standard deviation of each group (large filled circle with error bars). We find that for the α- and light elements the medians are in very good agreement when taking into account the dispersion, especially considering that this scatter is greater for the group with more metal-poor stars and with lower S/N. In the case of Fe-peak elements, this difference is more noticeable, and therefore we decided to use only stars with S/N greater than 60 in our analysis of these elements. These results show that a S/N cut of 35 is good enough for our data. It is worth mentioning that while the minimum S/N of our data is 35, the maximum is 192, and 44% of the selected stars listed in Table 2 have an excellent S/N greater than 70.
 |
Fig. 4. Comparison of the APOGEE-2 LMC stars with different S/N. The small red dots are stars with S/N between 35 and 70, and the small gray dots represent stars with S/N > 70. We divided the sample, according to metallicity, into four groups over the range −2.0 to 0.0 dex to obtain the median and dispersion of the stars at different representative metallicities. The filled large red and gray circles with error bars respectively represent these values. |
Basic parameters for the six substructures described in the text.
Our final sample contains 69 stars, in contrast to the 84 stars used in the Cheng et al. (2022) analysis. The number of selected stars in each region is listed in Table 1.
2.2. Milky Way foreground stars
We selected a sample of foreground MW stars, which we use throughout our analysis as a comparison sample. This sample also contains stars from APOGEE DR17, but from two datasets. First we took all stars at distances greater than 10° up to 18° from the center of the LMC (which includes our six regions in the LMC/SMC outskirts), but that did not meet the selection criteria as members of the LMC, the SMC, or the six substructures analyzed here. These stars have observed radial velocity and proper motions consistent with being MW stars. We also included the sample of halo MW stars from Hayes et al. (2018). These stars were selected by Hayes et al. (2018) as halo population members using ASPC parameters using the selection criteria described therein.
3. Results
3.1. Metallicity distribution functions and radial profiles
In Fig. 5 we show the metallicity probability distribution function using kernel density estimation (KDE) for the LMC, the SMC, and the six periphery regions analyzed in this study. For the LMC we subdivide the function into two parts: the inner region (RLMC < 6°) and the outer region (6° ≤RLMC ≤ 11°). There is a small offset in the peak of the outer LMC metallicity compared with that for the inner LMC. This is expected, due to the radial metallicity gradient in the LMC, behavior that has been studied by several authors (Cioni 2009; Feast et al. 2010; Choudhury et al. 2021). The outer region is about 0.1 dex more metal poor than the inner region; this may be because the outer stars are older, as some photometric studies have found in this area of the LMC (Piatti & Geisler 2013; Gatto et al. 2020; Nidever et al. 2019). The peak in metallicity of the SMC is about −1.1 dex. The observed 0.5 dex difference between the two galaxies is in agreement with that found by other studies that determine the metallicity of both MCs (see, e.g., Noël et al. 2009; Meschin et al. 2014). Figure 5 also shows that the foreground MW halo stars (Sect. 2.2) have a higher metallicity than stars in the Magellanic system, including those in the six substructure regions, with a peak at about −0.1 dex, but a wide range of metallicity values. Finally, we find that five of our substructure regions show a peak in metallicity at about −1.0 dex, in agreement with the SMC metallicity peak. However, region O2, with a peak at about −1.3, shows a metallicity distribution function (MDF) that is significantly different; we analyze this difference in more detail in the next section.
 |
Fig. 5. Normalized probability density functions applied to the observed metallicities in each region listed in Table 2, and including APOGEE measurements of more interior parts of the LMC and the SMC. The median metallicity for each region is indicated by a line at the top of the figure. |
It is of particular interest to understand whether the stars in the six peripheral regions originated in the LMC or SMC. One way to gain insight into this question is to see whether the mean chemical abundances of the stars in these fields are more consistent with following radial abundance trends from the LMC vs. the SMC. Figure 6 presents the radial metallicity and α-abundance ([(Mg+Si+Ca)/Fe]) profiles as a function of the distance from the center of the LMC and SMC, respectively, using the LMC and SMC central data points as well as those in the six outskirt regions. We note that this is the first time the metallicity and α-abundance profiles of the MCs have been presented out to these distances, ∼20 deg from the LMC center.
 |
Fig. 6. Metallicity and α-abundance, defined here by [(Mg+Si+Ca)/Fe], radial profiles of our sample from the LMC center (left panel) and SMC center (right panel). Left panels: Median of each region listed in Table 2 (filled large symbols) and the standard deviation (error bars). The solid lines are linear fits made using the APOGEE-2 LMC data inside 11° extrapolated (dashed lines) to show the predicted values from the LMC to its outskirts, where our six APOGEE fields lie (also shown with color-coded points). Right panels: Median values for each region listed in Table 2 (filled large symbols; the error bars represent the standard deviation). The solid lines are linear fits made using the APOGEE SMC data inside 6° extrapolated to show the predicted values from the SMC out to where our six APOGEE fields. |
In this study we decided to use [(Mg+Si+Ca)/Fe] as the alpha-abundance instead of the [α/M] value determined by ASPCAP. The reason for this is twofold. On the one hand, we compare our α-abundance with the results found in Nidever et al. (2020), who used ([(Mg+Si+Ca)/Fe]) as α-abundance. On the other hand, Mészáros et al. (2013) found a correlation between [α/M] and [M/H] in ten globular clusters in APOGEE DR10, which still exists in DR16, according to Nidever et al. (2020). This correlation is mainly due to the second generation of stars being dominated by strong Al lines. Nidever et al. (2020) showed that the correlation is removed by using abundances relative to Fe instead of M.
We find that the LMC metallicity decreases with angular radius (see Fig. 6) from 0 out to ∼11 deg from the LMC center, with a slope of −0.03 dex deg−1 taking into account the median value of each region from the main LMC body (filled gray symbols with error bars in Fig. 6). This behavior is supported by several studies that show that the older and more metal-poor populations of the LMC are mostly in its outskirts (Piatti & Geisler 2013; Carrera et al. 2011; Gatto et al. 2020). Our results are also consistent with those reported by Majewski et al. (2009), who observed a similar metallicity gradient in the LMC, but using a smaller sample size. Regarding the six outer regions of interest here, in general we observe that they closely match the expected metallicity gradient of the LMC, especially regions N1, N2, and O1, even though these regions go beyond the farthest LMC main-body APOGEE stars (see the dashed line in Fig. 6, which shows the extrapolation of the metallicity gradient for the LMC). Region H1 deviates most from the LMC metallicity profile, yet its larger error bars also overlap the extrapolation of the LMC main body.
The α-abundance profile, which we define here as given by the radial gradient of [(Mg+Si+Ca)/Fe], increases slightly for the LMC from 0.02 up to 0.1 dex values at larger radii, taking into account the median value of each region. This is consistent with older (and α-rich) populations dominating the outer LMC. Once again, the regions N1, N2, and O1 exhibit a good match to this trend. On the other hand the discrepancy of region O2, and possibly H1 (which has large error bars that include agreement with the extrapolation), is notable. Because the chemical evolution of the α-element abundance is strongly influenced by the star formation history (SFH) of a galaxy, this discrepancy might suggest that O2 had a different chemical evolution from that of the LMC.
Figure 6 also shows the same radial metallicity and α-abundance profiles for the SMC (right column). We observe that the SMC metallicity decreases sharply, with a slope of −0.04 dex deg−1. In this case we do not observe a good match between the extrapolated radial metallicity trend and the metallicities of stars in the regions in the outskirts, which are significantly more metal rich than the extrapolated trend. However, we do not expect the metallicity trend to follow at such large SMC-centric distances since a galaxy like the SMC is not expected to have stars out to such large radial distances (about 35° or ∼44 kpc from the SMC center; see right panel Fig. 6), considering that its tidal radius is expected to be only ∼5.0 kpc (∼4.5 deg; Massana et al. 2020). We note that Nidever et al. (2011) found an old intermediate-age population at a distance of about 10° from the SMC center that are likely extra-tidal stars, but that could also be a bound stellar halo. Massana et al. (2020) also uncovered a tidally disrupted stellar feature that reaches as far out as 12° from the SMC center. If the stars of interest here at very large radii were stripped SMC stars, they would be expected to have metallicities more like those of the SMC at ∼6°. Only the median metallicities of the stars in H1 and O2 are close to being consistent with that hypothesis. We also note that the inner negative metallicity gradient displayed by the SMC shows signs of stopping, and even of reversing sign in the outer regions, at around 4°, near the limit of the APOGEE data (Parisi et al. 2022).
Regarding the α-abundance profile, as in the case of the LMC, we note an increase in the α-content with distance from the center of the SMC. In this case there is a good match for H2, O1, and H1 to the extrapolated trend. It is important to note that the observed radius of the SMC is about 11 kpc from the center (Nidever et al. 2011); therefore, the comparison with the most extreme regions such as N1 and N2 does not make physical sense unless these regions were very strongly stripped.
3.2. Chemical abundance patterns
Figures 7–9 show 14 different elemental abundances as a function of metallicity for the stars in the substructures, colored as in the previous figures, and for the main body of the LMC (gray dots) and SMC (magenta dots). Table 3 lists the mean and standard deviation of the 14 APOGEE chemical abundances analyzed for each of the six substructure fields. In each panel in Figs. 7–9, the solid black and magenta lines show the best polynomial fit for the LMC and SMC, respectively. In what follows we analyze the chemical abundances per region and compare them with the LMC, SMC, and MW chemical abundances. We note that the determination of the [V/Fe] abundances through the ASPCAP pipeline may lack precision and could be subject to biases in some cases, as evidenced by Hayes et al. (2023). Therefore, analyses that include this element should be approached with caution.
 |
Fig. 7. Distribution of α-abundances vs. metallicity for the LMC (small gray dots) and SMC (small magenta dots). Also included are the density of the Milky Way stars (orange) and the six substructures analyzed in this study (filled colored circles with error bars, which represent the standard deviation of each region). The left panels show the means of our substructure fields, while the right panels show the individual stars in each field. In the top right of each panel the representative errors for the LMC, SMC, and MW stars from the APOGEE pipeline (ASPCAP) are also shown. The solid black line and the solid magenta line represent the best polynomial fit for the LMC and SMC stars, respectively. |
 |
Fig. 8. Similar to Fig. 7, but for the distributions of [C/Fe], [N/Fe], [O/Fe], and [Al/Fe] vs. [Fe/H]. |
 |
Fig. 9. Similar to Fig. 7, but for the distributions of [V/Fe], [Cr/Fe], [Mn/Fe], [Co/Fe], [Ni/Fe], and [Ce/Fe] vs. [Fe/H]. |
Mean and standard deviation of 14 APOGEE chemical abundances for the six substructure fields.
We included the [(C+N)/Fe] abundance in Fig. 8. This abundance in the LMC tends to decrease in the range –2.2 < [Fe/H] < –1.2, as observed and also reported by Hasselquist et al. (2021), and then starts to increase. A similar pattern is observed in the case of the SMC. In the next subsection we analyze this abundance alongside the light elements for each substructure.
3.2.1. Regions N1 and N2
Region N1 is one of the farthest of our six MC APOGEE regions from the center of the LMC (see Fig. 6). It is located on one of the arm-like features discovered by Mackey et al. (2016) in the north of the LMC (see Fig. 1).
The chemical abundance patterns of the APOGEE stars in this region are (out of the six) the most like those of the LMC. N1 exhibits the smallest metallicity spread (σ([Fe/H] = 0.19 dex) of all six regions (see Table 2). Moreover, Fig. 6 shows that the median [Fe/H] of the APOGEE stars in N1 ([Fe/H] = −1.03) follows the extrapolated trend of the LMC metallicity profile (represented by the straight line), taking into account the scatter of the data for this region. This finding in metallicity is in agreement with Majewski et al. (2009) who found a median metallicity for the outer LMC population at radii of 15–20° from the LMC center of [Fe/H] ∼ −1.0, although with a large spread in metallicity. The median N1 metallicity of −1.03 dex matches the predicted value from the Majewski et al. metallicity gradient in the LMC periphery at the radius of N1. Moreover, the N1 metallicity matches the [Fe/H] ≈ −1.0 value derived from isochrone fitting of deep SMASH photometry in the LMC periphery by Nidever et al. (2019). The association of N1 with the LMC is also suggested by the probability density functions (see Fig. 5), where N1 shows a shift in the metallicity distribution toward lower values than the outer LMC population shown there (from 6 to 11°), again in agreement with the LMC metallicity gradient.
The median value of [α/Fe] for N1, represented as the largest color circles with error bars in Fig. 6, also shows a good match to the radial LMC extrapolated trendline (dashed black line) in Fig. 6. We find that the N1 α-element abundances (Mg, Ca, and Si) as a function of metallicity (Fig. 7) show good agreement with the LMC and SMC trends, and are not consistent with the MW abundances trend. We measured the mean orthogonal distance of the stars in N1 to the best fit to the trendlines for the LMC (black line) and SMC (magenta line) and they show similar values (see Tables 4 and 5). In our analysis of the orthogonal distance, we adopt a convention where distances above the curve are considered positive, while distances below are considered negative. This convention helps differentiate and analyze which of these stars, relative to the curve, represents the best fit. In particular, for the α-abundance [(Mg+Si+Ca)/Fe], the mean value for the orthogonal distance to the LMC trend is −0.097 dex and −0.089 dex for the SMC. In Fig. 7 we only observe a slight deviation of the median value for [Si/Fe] in N1, in comparison with the other regions in our analysis.
This conclusion regarding the abundance patterns of N1 also generally holds for other light and iron-peak elements, for which we show the LMC and SMC trends for our data in Figs. 8 and 9, respectively. More specifically, the trends for light elements as a function of metallicity show the stars in N1 to have a good match with the overall trends for the LMC, for the case (C+N), C, and N (Fig. 8). For Al and O we observe offsets with similar values (see Tables 4 and 5) from the LMC and SMC fits. However, the separation from the MW trend is clear, indicating a better match with the MCs. The case of C, O, and Al are especially useful because for these abundance ratios there is a clear difference between the trends of the LMC and SMC and that of the MW. In contrast, the trend of [N/Fe] as a function of metallicity shows an overlap between the LMC, SMC, and MW within the metallicity range of interest in this work (i.e., [Fe/H] < −0.6), which includes all the six outskirt regions analyzed in this work. For C, O, and Al the abundance ratio for N1 is lower by ∼0.35 dex with respect to the MW, and is much closer to the trend for the LMC and SMC.
Finally, for the Fe-peak elements (Fig. 9), we again observe a similarity of the N1 abundance relations to those found in the LMC and SMC trends. However, based on the mean of the orthogonal distances of the stars to the best fit for LMC and SMC, the agreement appears to be slightly better with the LMC (see Tables 4 and 5).
In the particular cases of V, Co, and Ni, there is a clear difference in their trend for LMC and SMC with respect to the MW trend, and so they are particularly useful elements for discriminating MC substructures from MW contaminants. This is in contrast to the abundance ratios involving Mn and Cr, where there is an overlap in the abundance values as a function of metallicity among all the galaxies shown. The abundance ratios for N1 are found to be consistent with the LMC and SMC trends for all of these iron-peak elements, taking into account the scatter of the data, especially for the case of Ni and Co, where there is a significant difference between MCs trends in comparison with the MW.
Because of the general similarity of the SMC and LMC abundances over the metallicities of interest, any similarity of the N1 field to the LMC trendlines implicitly suggests a similarity also to the SMC trendlines. However, the position and distance of the N1 field from the SMC (see Figs. 1 and 6) as well as the radial velocity (RV) observed for the APOGEE stars in this region (see next section) together are simply incompatible with those of the SMC.
The analysis for N2 is almost identical to that for N1, as expected due to the proximity of these two fields. Both are part of the same northern LMC arm and share similar proper motions (see Table 2 and Fig. 1). Furthermore, N2 has a mean metallicity similar to that of N1, ⟨[Fe/H]⟩ = −1.01 (see Table 2 and Fig. 5), and shows a good agreement with the LMC in the radial metallicity and α-gradients presented in Fig. 6. In our analysis presented in Figs. 7–9, N2 shows excellent agreement with the LMC for the light, α-, and Fe-peak elements. Finally, the analysis of cerium (Ce) for N1 and N2 reveals a strong concordance with the LMC and SMC, characterized by minimal dispersion around the trend-lines for the MCs.
3.2.2. Regions H1 and H2
Region H1 is one of the closest to the center of the LMC, at a galactocentric distance of about ∼11.5° (see Fig. 6), and lies in the southeast LMC periphery (see Fig. 1). The proper motions of its MC-related stars show good agreement with the LMC. C22 concluded that their kinematics are associated with the LMC outer disk. In addition, this region is the most metal poor ([Fe/H] = −1.25) and shows the largest spread in metallicity among the six regions (σ([Fe/H] = 0.34 dex), as listed in Table 2. This is also reflected in the LMC radial metallicity profile (see Fig. 6), where H1 has a median metallicity that is the most separated from the trend represented by the straight line. However, the large error bars fall within the extrapolation of the LMC gradient at H1’s distance. For the radial α-abundance profile in Fig. 6, we find that the H1 median value is slightly above the LMC trend represented by the straight light, but again, as in the metallicity profile, it is in agreement within the error bars. We note that the H1 median metallicity and α-abundance would not match the extrapolated values for SMC trends, considering that stars at those distances (about ∼20° from the SMC’s center) should be extra-tidal stars if they were of SMC origin, and their abundances should match those at about ∼6° from the SMC center.
In the case of the α-elements O, Mg, Si, and [(Mg+Si+Ca)/Fe], we find the H1 mean value to be higher than that of the LMC abundance distribution trend, but the trend is just within the error bar for H1 (Figs. 7 and 8). We note that the individual stars have a wide [Fe/H] range in H1, and we can observe that one or two stars (depending on the elements) out of the seven stars in H1 are right on or below the LMC trend for these elements. Ca is the α-element that shows the best agreement with the LMC (see Figs. 7 and 14).
With respect to the light elements (C+N), C, and N (see Fig. 8), the median values for the H1 stars are higher than that for the LMC trend, and a similar behavior is seen for the Fe-peak elements where for the H1 stars the V, Cr, Mn, and Co abundance ratios are higher not only in comparison to the other regions, but even when contrasted with the MW (see Fig. 9). For cerium (Ce) we observe a slightly elevated value for H1 (only one star) in comparison to the trend lines of the MCs. We note, however, that in some cases the number of stars with measurements of these elements and with S/N > 60 is only between one and three stars.
Region H2 is the closest of the six regions of interest to the centers of both the LMC and the SMC, at ∼11° from each galaxy (see Fig. 6) and it has the highest number of member stars of the six regions (27 stars). The vector point diagram of the proper motions (Fig. 2) shows that most of the H2 stars are between the distributions of LMC and SMC stars. Thus, its member stars, due to their distance to the SMC and LMC centers (at about 11° from each) and their PM could be related to either galaxy. However, Nidever et al. (2011) determined a projected galactocentric distance of 10 kpc (10°) as the limit for SMC membership. Therefore, if it belongs to the SMC, H2 could be an extreme outlying SMC field or it could contain extra-tidal stars from the perturbed SMC.
The mean metallicity of H2 is [Fe/H] = −1.0, which, at the position of H2 on the sky, is consistent with the radial metallicity gradients of the LMC and a slightly with the SMC, taking into account the dispersion of H2. (see Fig. 6). However, the probability density function for H2 in Fig. 5 shows a slightly better fit with the SMC profile than with the LMC profile. In the case of the light elements (Fig. 8), we observe a good match with the LMC and SMC trends for most of the H2 stars. However, a few stars show a significant discrepancy, especially for (C+N), C, and N, which show about 0.6 dex difference from the LMC and SMC trends (see Fig. 8). For the α-elements (Fig. 7) there are significant spreads for [Mg/Fe] and [Ca/Fe], the largest spreads among all six of the regions (Table 3).
On the other hand, the H2 abundance ratios for Fe-peak elements (Fig. 9) show good agreement with those for both the LMC and SMC (for the stars with measurements), especially for the elements where there is a clear difference between the MW and MCs, that is for V, Co, and Ni. For Mn and Cr, as we noted previously (Sect. 3.2.1), there is a strong overlap among the MW, LMC, and SMC distributions. For Ni we observe a few stars with extreme values, low and high in comparison with the LMC trend. We also observe two stars in H2, specifically for Cr and V, that exhibit very low abundances. However, these abundances are still in agreement with those found in the LMC and SMC (see Fig. 9). The analysis of cerium (Ce) for H2 also shows a good compatibility with the MCs, although we only have five stars in this field for this element.
3.2.3. Regions O1 and O2
Of the six fields, O1 and O2 are sampling substructures located in the farthest southern portion of the LMC. We have ten selected stars in O1 and five in O2. The metallicity distribution functions of the two regions (see Fig. 5), also analyzed in C221, show that O2 is slightly more metal poor than the SMC mean, but significantly more metal poor than the LMC mean, with a difference of about 0.6 dex in their mean values. This suggests a better match with the SMC than with the LMC. A similar behavior is observed in O1, with a MDF between the outer LMC and SMC values.
Our analysis of the radial metallicity profile for the LMC (Fig. 6) shows a relatively good match in the case of O1, but a difference with the LMC gradient for the case of O2. A similar behavior is observed in the radial α-abundance profile (Fig. 6). O2 stars show a large difference in α-abundance in comparison with the LMC trend, where extrapolation to O1 and O2 distances is shown as a dashed line in Fig. 6. When we place the results of these fields in the radial metallicity profile (see Fig. 6) from the SMC center, we find that region O2 shows the best match with the SMC metallicity radial trend among the six regions. In contrast, the median of region O1 shows a large difference. However, the extrapolated values of SMC α-abundance from its radial trend at the positions of O1 and O2 show a better match for O1 and a larger difference for O2.
We can investigate further the origin of these fields by looking at their chemical abundance patterns. It is interesting to note that region O1, in general, shows a good match in chemical patterns in comparison with both the LMC and SMC. In the particular case of the α-elements (see Fig. 7), we observe good agreement as well, but especially with the SMC (see also Sect. 4, and Figs. 13 and 14).
The case of O2 is more difficult to analyze, mainly due to the small number of stars, only five. Nevertheless, we observe an increase in the α-elements starting from the most metal-poor star in O2, at [Fe/H] = −1.4 dex; the clearest example is for Mg and Ca. For the Fe-peak elements we observe good agreements with the LMC and SMC taking into account the few members for this substructure. We note for Ni the most significant difference, but again in agreement with the LMC and SMC. This behavior for Ni is similar to that in region H1, with similar mean value and scatter (see Table 3).
Finally, the analysis of cerium (Ce) for O1 and O2 reveals a good agreement with the LMC and SMC. However, it is important to note that there is only one star for this element in each region O1 and O2.
3.3. Kinematical analysis
Figure 10 displays the heliocentric radial velocities (RVs) as a function of metallicity for all the stars in the substructures, and for LMC and SMC stars. From this figure, N1 and N2 share similar radial velocities (⟨RVH⟩ ∼ 300 km s−1, see also Table 2), both of which are incompatible with those of the SMC. This is also the case for the stars in H1. In contrast, the bulk of H2 members have metallicities and RVs in agreement with those of SMC stars. The median radial velocity of H2 (⟨RVH⟩ = 168.6 km s−1) is the lowest median value among our fields (see Table 2), although with large scatter of σ([RVH]) = 26.5 km s−1. However, as stated in the previous section, H2 is beyond the limit for SMC membership, which is determined at 10° (Nidever et al. 2011). Therefore, if it belongs to the SMC, H2 could be an extreme outlying SMC field or it could contain extra-tidal stars from the perturbed SMC. O1 and O2 members present RVs and metallicities close to the SMC values, but between the two MCs, as can be seen in Fig. 10.
 |
Fig. 10. Radial velocity vs. metallicity of the stars in the six APOGEE MC periphery regions compared with LMC and SMC stars, with all data from APOGEE-2 DR17. |
In addition to the RVs, thanks to the PMs delivered by Gaia, we can obtain 3D kinematical information of the stars in the substructures by applying the models described in Sect. 2. Figures 11 and 12 show the 3D velocities as a function of metallicity with respect to the LMC and SMC, respectively. The mean 3D velocity values for the six regions are summarized in Table 6.
 |
Fig. 11. Vertical velocity (Vz, LMC), radial velocity (Vr, LMC), and azimuthal velocity (Vϕ, LMC) vs. metallicity of stars in the six targeted substructure regions, and including stars targeted by APOGEE in the central LMC. The velocities were calculated by Cheng et al. (2022) with respect to the assumed LMC disk plane, as described in Sect. 2. |
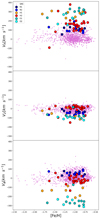 |
Fig. 12. Vertical velocity (Vz, SMC), radial velocity (Vr, SMC), and azimuthal velocity (Vϕ, SMC) vs. metallicity of the stars in the six targeted MC substructures along with stars targeted by APOGEE-2 in the central SMC. The velocities were calculated with respect to the assumed SMC disk plane, as described in Sect. 2, using an assumed distance of 60 kpc and using the formalism and best-fit model parameters presented in Zivick et al. (2021). |
Measured 3D space velocities from the models relative to the LMC and SMC for our six regions.
The C22 analysis of regions N1 and N2 using kinematics and MDFs implies that the APOGEE-targeted stars there have a strong relationship with the outer LMC disk (see also Cullinane et al. 2020); the LMC has mean space velocity values of ⟨Vr⟩ = 4.43 km s−1, ⟨Vϕ⟩ = 61.28 km s−1, and ⟨Vz⟩ = 9.70 km s−1 (see Fig. 11). When comparing N1 and N2 with the 3D LMC velocity distribution, we found that N1 and N2 show relatively good agreement for Vϕ, with a mean for N1 and N2 of ∼52.3 km s−1 and ∼74.8 km s−1, and especially for Vz with a mean for N1 and N2 of ∼47.2 km s−1 and ∼33.8 km s−1, respectively. Additionally, these regions have relatively low velocity dispersions for the azimuthal and vertical velocity components of their stars with respect to the LMC (dark blue symbols, with σ(Vϕ) = 11.00 km s−1 and σ(Vz) = 16.78 km s−1). On the other hand, when comparing N1 and N2 with the 3D SMC velocity distribution (see Fig. 12), the SMC has mean space velocity values of ⟨Vr⟩ = −10.0 km s−1, ⟨Vϕ⟩ = 8.5 km s−1, and ⟨Vz⟩ = −15.2 km s−1, and we find a more significant offset to these values for each velocity component in these regions. For Vr the mean is ∼111.0 km s−1 and ∼113.4 km s−1 for N1 and N2, respectively; for Vϕ the mean is ∼65.3 km s−1 and ∼78.1 km s−1. Finally, for Vz the mean is ∼ − 28.2 km s−1 and ∼ − 53.0 km s−1, respectively. This indicates that N1 and N2 are kinematically more similar to the LMC than to the SMC.
When comparing the 3D velocity distribution of the LMC and SMC (Figs. 11 and 12) with H1 and H2, we also find a generally better agreement of these regions with the LMC. We observe the most significant difference in the case of H1 and H2 when comparing the 3D SMC velocity distribution for the case of Vr, SMC: a mean for H1 and H2 of ∼275.9 km s−1 and ∼157.0 km s−1, respectively. Nevertheless, H2 appears to also be consistent with the SMC when looking at the Vϕ and Vz, SMC velocities.
The O1 and O2 regions are the most complex regions, from a kinematical point of view. The 3D motion of their stars show the most significant discrepancy with both the LMC and SMC (see Figs. 11 and 12). For O1 the mean velocities from the 3D SMC model are Vr, SMC = 293.0 km s−1, Vϕ, SMC = −248.8 km s−1, and Vz, SMC = −74.50 km s−1, while the mean velocities for the same components from the 3D LMC model are Vr, LMC = −82.31 km s−1, Vϕ, LMC = 178.22 km s−1, and Vz, LMC = −92.8 km s−1. Similarly, for O2 the mean velocities from the 3D SMC model are Vr, SMC = 220.78 km s−1, Vϕ, SMC = −254.8 km s−1, and Vz, SMC = −104.6 km s−1, while the mean velocities for the same components from the 3D LMC model are Vr, LMC = −126.67 km s−1, Vϕ, LMC = 121.9 km s−1, and Vz, LMC = −121.1 km s−1 (see Table 6). In C22 we found that these regions show a clear difference in their in-plane velocities, as obtained in C22 from the proper motion of the stars using the same kinematical model described in Sect. 2, with respect to those of the LMC disk stars, with a difference of more than 100 km s−1. This is also observed in the radial velocity (Vr), azimuthal velocity (Vϕ), and vertical velocity (Vz), obtained as described in Sect. 2 (see Fig. 11). By comparing our results with numerical simulations of the MC interactions, we concluded in C22 that the stars in O1 and O2 are not simply an extension of the LMC disk, but most likely a combination of LMC and SMC tidally disrupted stars, although we could not rule out other possible origins. We present in this work a 3D kinematical SMC model. Even though there is discrepancy between the O1 and O2 values and those of the SMC from the 3D model shown in Fig. 12, it is worth noting that the SMC model (albeit with a tidal expansion) is an analytic model that does not completely capture the actual disruption and disturbances that the SMC is undergoing. Thus, this might explain why the 3D kinematical values for O1 and O2 differ from those of the SMC model. Additionally, Fig. 7 in C22 shows the results of two N-body simulations that model the past dynamical evolution and interaction between the MCs performed by Besla et al. (2012). The kinematics of the O1 and O2 stars that we find here in Fig. 12 may be accounted for as SMC tidal debris, according to Fig. 7 in C22.
4. Discussion
Our chemical findings in the regions N1 and N2 (see Sect. 3.2.1) indicate a slightly better agreement with the chemical patterns of the LMC. These findings are reinforced by the proper motion and radial velocity observed in these regions (see Figs. 2 and 10), and with the 3D motions (Figs. 11 and 12), which show a better compatibility with the LMC. This is in line with the complementary work by C22, who find no kinematical difference between these regions and the outer LMC. They are also in agreement with the work by Cullinane et al. (2020, 2022), who studied several regions in the northeast outskirts of the LMC, and analyzed the metallicity and kinematics along the northern arm. They found a strong relationship between the properties in the northern arm and in the outer LMC, and suggest that over the last Gyr the interaction between the LMC and MW produced the northern arm, especially considering the azimuthal velocity with positive out-of-plane values, which we also found in C22 and show here in Fig. 11. It is noteworthy that they found, in the northern arm, that the metallicity decreases from [Fe/H] = −0.9 at 11 kpc to [Fe/H] = −1.2 dex at 22 kpc. This is in agreement with our findings for the LMC and for the northern substructures N1 and N2 (see Fig. 6).
For regions H1 and H2 discussed in Sect. 3.2.2, we find that H1 shows higher abundance values with respect to the LMC and SMC chemical pattern trendlines presented in Figs. 8 and 9. However, region H1 shows a slightly better agreement with the LMC in α-elements (Fig. 7). This is supported by the proper motion and radial velocities observed in H1 (see Figs. 2 and 10), and by the 3D derived velocities, which show a better match with the LMC. We caution that H1 has a small sample size, with only seven stars in total and fewer for the Fe-peak elements.
The sample of H2 stars has chemical abundance patterns related to both the LMC and SMC, and it is the region with the largest chemical abundance dispersion (see Table 3) for most of the elements, in comparison with other regions, specifically for C, N, O, Al, Mg, Ca, V, Cr, Co, and Ni. We also note a clear difference of the stars in H2 with respect to MW halo stars. In C22, we found a strong kinematical relation between stars in H2 with the LMC disk. However, we also find a good resemblance to the SMC from the 3D velocities when comparing them with the model with respect to the SMC motion (see Figs. 11 and 12). We also note that the RVs (Fig. 10) and proper motions (Fig. 2) could be related to either galaxy (LMC or SMC), actually with a larger number of H2 members, in very good agreement with the SMC RVs.
Regarding O1 and O2, we found that O1 has a better agreement in chemical abundance patterns with the SMC than with the LMC; O2 also appears to have similar chemical trends to the SMC, though there is a slight shift in the α-abundance vs. metallicity toward lower metallicity values for O1. This may suggest that the stars in the O2 region belong to another substructure with a slightly different star formation onset time. We note, however, that the analysis in O2 was done with only five stars and their α-abundance values lie within the spread of the SMC values around the α-abundance vs. metallicity trend (see Fig. 7).
To gain more insight into the origins of the stars in the regions analyzed here, we show in Figs. 13 and 14 the chemical evolution tracks of Mg, Si, and [(Mg+Si+Ca)/Fe] presented by Hasselquist et al. (2021) and Nidever et al. (2020) for several galactic systems: the MW, LMC, SMC, Gaia Enceladus (GSE), Sagittarius (Sgr), Fornax (Fnx), and Sculptor (Scl), in addition to our data. These studies also used APOGEE ASPCAP abundances so are very comparable to our study. Each evolutionary track describes the chemical evolution for the different systems presented by each author. The code used to perform the chemical evolution track by Hasselquist et al. (2021) and Nidever et al. (2020) was flexCE (Andrews et al. 2017), which includes as parameters to perform the evolution tracks the initial gas mass, inflow rate, time dependence, and star formation efficiency. Additionally, Fig. 15 presents the orthogonal distance of each star, color-coded according to the corresponding region, to the trendline of each system. The mean and standard deviation of this orthogonal distance are presented in Tables 7 and 8. This orthogonal distance helps us to analyze the agreement of each star, and thus each region, to each of the systems presented in these figures.
 |
Fig. 13. Comparison of distributions of [Mg/Fe] (top panels) and [Si/Fe] (bottom panels) vs. [Fe/H] for our targeted MC substructure regions against those for large Milky Way satellites also using APOGEE data: the LMC, SMC, Sagittarius dSph, Fornax dSph, and the GSE. The left panels show individual stars for each substructure and the right panels show the mean and standard deviation for each substructure region. The overplotted lines show the chemical evolution track for each dwarf galaxy as determined by Hasselquist et al. (2021). |
 |
Fig. 14. Same as Fig. 13, but for [Mg+Si+Ca/Fe] vs. [Fe/H]. Also included are the trendlines derived by Nidever et al. (2020) for the MW, LMC, SMC, Fornax (Fnx), Sagittarius (Sgr), and Sculptor (Scl). |
 |
Fig. 15. Minimum orthogonal distance of each star from the six regions to the best fit for Mg-, Si-, and α-abundance vs. metallicity for each galaxy in Figs. 13 and 14 (MW, LMC, SMC, Fnx, Sgr, Scl, and GSE). The best fit was determined by Hasselquist et al. (2021) for Mg and Si, and by Nidever et al. (2020) for alpha-abundances. Each star from each region is represented by a filled circle and the mean for each region is represented by a filled star symbol (see Table 8). |
Mean and standard deviation of the minimum orthogonal distance for each substructure and each object (MW, LMC, SMC, Fnx, Sgr, Scl, and GSE) represented in Fig. 15 for Mg and Si according to the trendline performed by Hasselquist et al. (2021, see Fig. 13).
The N1 region shows a good agreement with the evolution track of Mg and [(Mg+Si+Ca)/Fe] for the LMC and SMC (Figs. 13 and 14). If we take into account the mean orthogonal distance to the evolution tracks amongst all of the systems analyzed and presented in Tables 7 and 8, N1 shows the best agreement with the LMC for the α-elements, and N2 presents a similar behavior.
Mean and standard deviation of the minimum orthogonal distance for each substructures and each object (MW, LMC, SMC, Fnx, Sgr, Scl) represented in Figs. 14 and 15 for α-elements according to the trendline performed by Nidever et al. (2020).
Comparing the chemical evolution tracks with H1, we find a reasonably good agreement of this region with both the LMC and SMC. However, in Tables 7 and 8, we show that H1 is closer to the LMC model for the case of Mg, Si, and Alpha ([(Mg+Si+Ca)/Fe]). For H2, the minimum distance agrees with the LMC and SMC with a slight difference between them.
The O1 region shows similar behavior to the other regions. The minimum orthogonal distance is to the LMC model in the case of Mg, Si, and α-abundance. However, we note that the most metal-poor star in region O1 (at [Fe/H] ∼ −1.7), is also the most Mg-rich and the most Si-rich among the O1 stars, in complete agreement with the chemical evolution track of the SMC presented by Nidever et al. (2020) and Hasselquist et al. (2021). The bump in the SMC chemical evolution track with a peak in metallicity at [Fe/H] = −0.9 is an indication of the highest star formation rate and that this major SMC burst happened ∼4 Gyr earlier than the burst in the LMC, according to the Hasselquist et al. chemical track models. This bursting was dominated by type II supernova (SNII), and therefore we observe an enhancement in material associated with SNII. After the peak at [Fe/H] = −0.9, we observe a depletion in these materials due to the low contribution from SNII and the onset of SNIa, and this behavior is observed in the most metal-poor star in O1 for Mg and Si. Although one star in Ca shows a significant discrepancy, this star is the most Ca-rich with a metallicity of about [Fe/H] = −0.9 dex, but this star generally exhibits good agreement with both MCs in the other α-elements.
The O2 region exhibits the most peculiar behavior compared to both models. We found that O2 showed the minimum distance in the case of Si with SMC and almost identical to that of the Sgr model, but with a larger standard deviation in this case. For Mg, we observe a similar behavior, and for the α-model we observe that the minimum distance is with Sgr, but again, with only a slight difference and larger standard deviation than that of the SMC model chemical track. For O2, the increase seen in Mg and Ca starting from the most metal-poor star at [Fe/H] = −1.4 is again an indication of the enrichment in α-elements produced mainly by SNII. After that we observe one star at [Fe/H] = −1.1, which is the most α-rich star in O2 and at which we see the increased trend in α-abundance ending (see Figs. 13 and 14). At higher metallicities, there is only one star in O2, the most metal-rich one, that shows a lower α-abundance. This could be an indication of enrichment by SNII in the range of metallicity between [Fe/H] = −1.4 and −1.1 at which point the contribution from SNII starts to decrease. This trend is slightly shifted from the α-abundance vs. metallicity trend found in the SMC (see Fig. 20 in Nidever et al. 2020; Hasselquist et al. 2021) and even more shifted than that in the LMC, such that the contribution of SNIa starts at progressively lower metallicities of [Fe/H] = −0.4, −0.9, −1.1 in the LMC, SMC, and O2, respectively (Fig. 7).
Table 9 summarizes the potential origins of our regions based on combining the results of four different diagnostics: MDF, radial gradients, 3D kinematic modeling, and chemical abundance patterns. It is evident that all of the regions have reasonable connections to both the SMC and LMC, but in particular half of the regions are clearly of LMC origin, namely N1, N2, and H1. These are the two northern regions, along the northern stream-like feature, and the southern region closest to the LMC. Regions H2 and O1 show compatibility with both the LMC and SMC, and thus are likely of tidal origin from both galaxies. The O2 field, located in the southern region closest to the SMC, is less compatible with the LMC, not only from the radial gradients, MDF, and the 3D kinematic model, but also from the chemical abundance pattern analyzed. We conclude that this region contains SMC tidally perturbed stars.
Summary information for the six regions.
5. Summary and conclusions
In this paper we studied the chemistry of six regions located in substructures in the periphery of the Magellanic Clouds, with the main goal of trying to understand the origin of their stars. These regions were previously analyzed in a companion paper from a 3D kinematical point of view (C22), but only from an LMC kinematical reference frame. Our analysis now focuses on the detailed chemical patterns exhibited by different elements in comparison with both of the Magellanic Clouds, and we also add a 3D kinematical model based on the SMC reference frame. We used data from the near-IR APOGEE-2 spectrograph, which allowed us to collect the chemical abundances of 13 different elements, including light, α-, and Fe-peak, with a signal-to-noise ratio from 35 to 192 for a total of 69 red giants in these regions. These data correspond to a subsample of the data presented in the C22 study, where only the high S/N stars are now considered.
Our detailed chemical pattern analysis in conjunction with 3D kinematical information suggests the following:
-
N1 and N2, the two regions along the northern LMC stream-like feature, with 7 and 13 members, respectively, show the strongest relationship with the LMC. We find a good agreement between the chemical patterns of N1 and N2 and those of the LMC for light, α-, and Fe-peak elements which confirm from a chemical point of view that N1 and N2 stars are thus perturbed outer LMC disk stars.
-
H1 and H2, with 7 and 27 members, respectively, belong to the southern periphery of the LMC. We find that H1 is the most metal poor of the six regions, albeit with a large scatter. Overall, we found that the mean abundances of α-, light, and Fe-peak elements exhibit a significant difference, being enhanced compared to the trend observed in the MCs. From the kinematical point of view, we note that H1 shows good agreement with the LMC. On the other hand, H2 shows 3D motions associated with both LMC and SMC. We conclude that H2 is likely populated with stars from both the LMC and SMC.
-
O1 and O2 have ten and five star members, respectively. Their chemical patterns of α-, light, and Fe-peak elements are in broad agreement with both MCs; however, they are more consistent with the SMC chemical evolution track than with the LMC. This is also the case when comparing the MDFs and the radial metallicity profiles. These two regions are more complex regions, in terms of kinematical behavior, showing clear differences in their 3D modeled velocities from both the LMC and SMC reference frames. However, numerical models show that the kinematics of O1 and O2 may be accounted for as SMC tidal debris. This, together with the better chemical pattern agreement with the SMC, leads us to conclude that the stars in these regions, particularly in O2, are of SMC origin.
Additionally, in this work we presented for the first time a metallicity and an alpha-abundance radial profile for the LMC and SMC galaxies, extending to distances of up to 20° and 10°, respectively. The slopes of the metallicity gradients are −0.03 and −0.04 dex deg−1, respectively. We also find positive alpha-abundance gradients in both galaxies, with slopes of 0.04 and 0.01 dex deg−1, respectively (see Fig. 6).
Our findings indicate that regions N1 and N2 are clearly LMC stars, confirming the kinematical analysis by C22, that were removed from the outer disk possibly due to the interactions of the LMC with the MW in its first pericenter passage (see also Cullinane et al. 2022). The southern region H1 is also likely of LMC origin, and H2 is a mix of LMC and SMC stars, with a preference for the region H2 being dominated by SMC stars. It is also probable that H1 has some MW halo stars contaminating our sample. The regions O1 and O2 are populated by a mix of LMC and SMC stars that were likely tidally disrupted due to the interaction of both MCs. The O2 region, in particular, shows a chemical abundance pattern that is very similar to that of the SMC, and velocities that are more similar to SMC debris, and thus we conclude that these stars are of SMC origin. Finally, this study highlights the importance of having chemical abundances in addition to kinematics to help confirm the nature of the stars in the outskirts of the LMC and provide evidence that can be used to better constrain the interaction history of the MCs as well as to improve our knowledge of their orbital history.
Acknowledgments
We thank the anonymous reviewer for their helpful comments, which improved the quality of this paper. C.M. thanks the support provided by FONDECYT Postdoctorado No. 3210144. A.M. gratefully acknowledges support by the ANID BASAL project FB210003, FONDECYT Regular grant 1212046, and funding from the Max Planck Society through a “PartnerGroup” grant. D.L.N. acknowledges support for this research from National Science Foundation (NSF) grant AST-1908331, while X.C., S.R.M., and A.A. acknowledge NSF grant AST-1909497. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High Performance Computing at the University of Utah. The SDSS website is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, Center for Astrophysics | Harvard & Smithsonian, the Chilean Participation Group, the French Participation Group, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. D.G. gratefully acknowledges support from the ANID BASAL project ACE210002. D.G. also acknowledges financial support from the Dirección de Investigación y Desarrollo de la Universidad de La Serena through the Programa de Incentivo a la Investigación de Académicos (PIA-DIDULS). R.R.M. gratefully acknowledges support by the ANID BASAL project FB210003. J.G.F.-T. gratefully acknowledges the grant support provided by Proyecto Fondecyt Iniciación No. 11220340, and also from ANID Concurso de Fomento a la Vinculación Internacional para Instituciones de Investigación Regionales (Modalidad corta duración) Proyecto No. FOVI210020, and from the Joint Committee ESO-Government of Chile 2021 (ORP 023/2021), and from Becas Santander Movilidad Internacional Profesores 2022, Banco Santander Chile.
References
- Abdurro’uf, N., Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, B. H., Weinberg, D. H., Schönrich, R., & Johnson, J. A. 2017, ApJ, 835, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Beaton, R. L., Oelkers, R. J., Hayes, C. R., et al. 2021, AJ, 162, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Bechtol, K., Drlica-Wagner, A., Balbinot, E., et al. 2015, ApJ, 807, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V. A., & Erkal, D. 2019, MNRAS, 482, L9 [Google Scholar]
- Belokurov, V., & Koposov, S. E. 2016, MNRAS, 456, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Besla, G., Kallivayalil, N., Hernquist, L., et al. 2007, ApJ, 668, 949 [Google Scholar]
- Besla, G., Kallivayalil, N., Hernquist, L., et al. 2012, MNRAS, 421, 2109 [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [Google Scholar]
- Bowen, I. S., & Vaughan, A. H., Jr., 1973, Appl. Opt., 12, 1430 [Google Scholar]
- Carrera, R., Gallart, C., Hardy, E., Aparicio, A., & Zinn, R. 2008, AJ, 135, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, R., Gallart, C., Aparicio, A., & Hardy, E. 2011, AJ, 142, 61 [Google Scholar]
- Cheng, X., Choi, Y., Olsen, K., et al. 2022, ApJ, 928, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, Y., Nidever, D. L., Olsen, K., et al. 2018a, ApJ, 866, 90 [Google Scholar]
- Choi, Y., Nidever, D. L., Olsen, K., et al. 2018b, ApJ, 869, 125 [Google Scholar]
- Choi, Y., Olsen, K. A. G., Besla, G., et al. 2022, ApJ, 927, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Choudhury, S., de Grijs, R., Bekki, K., et al. 2021, MNRAS, 507, 4752 [CrossRef] [Google Scholar]
- Cioni, M. R. L. 2009, A&A, 506, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C., Naidu, R. P., Garavito-Camargo, N., et al. 2021, Nature, 592, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Cullinane, L. R., Mackey, A. D., Da Costa, G. S., et al. 2020, MNRAS, 497, 3055 [NASA ADS] [CrossRef] [Google Scholar]
- Cullinane, L. R., Mackey, A. D., Da Costa, G. S., et al. 2022, MNRAS, 510, 445 [Google Scholar]
- Diemand, J., Kuhlen, M., & Madau, P. 2007, ApJ, 667, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [Google Scholar]
- Drlica-Wagner, A., Bechtol, K., Allam, S., et al. 2016, ApJ, 833, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Drlica-Wagner, A., Carlin, J. L., Nidever, D. L., et al. 2021, ApJS, 256, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Erkal, D., Deason, A. J., Belokurov, V., et al. 2021, MNRAS, 506, 2677 [NASA ADS] [CrossRef] [Google Scholar]
- Feast, M. W., Abedigamba, O. P., & Whitelock, P. A. 2010, MNRAS, 408, L76 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Luri, X., et al.) 2021b, A&A, 649, A7 [EDP Sciences] [Google Scholar]
- Garavito-Camargo, N., Besla, G., Laporte, C. F. P., et al. 2019, ApJ, 884, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Garavito-Camargo, N., Besla, G., Laporte, C. F. P., et al. 2021, ApJ, 919, 109 [NASA ADS] [CrossRef] [Google Scholar]
- García Pérez, A. E., Allende Prieto, C., Holtzman, J. A., et al. 2016, AJ, 151, 144 [Google Scholar]
- Gatto, M., Ripepi, V., Bellazzini, M., et al. 2020, MNRAS, 499, 4114 [Google Scholar]
- Gómez, F. A., White, S. D. M., Marinacci, F., et al. 2016, MNRAS, 456, 2779 [Google Scholar]
- Graczyk, D., Pietrzyński, G., Thompson, I. B., et al. 2020, ApJ, 904, 13 [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, J. 2007, ApJ, 658, 345 [Google Scholar]
- Hasselquist, S., Hayes, C. R., Lian, J., et al. 2021, ApJ, 923, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, C. R., Majewski, S. R., Shetrone, M., et al. 2018, ApJ, 852, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, C., Masseron, T., Sobeck, J., et al. 2023, Am. Astron. Soc. Meet. Abstr., 55, 401.07 [NASA ADS] [Google Scholar]
- Hindman, J. V., Kerr, F. J., & McGee, R. X. 1963, Aust. J. Phys., 16, 570 [Google Scholar]
- Hubeny, I., & Lanz, T. 2011, Astrophysics Source Code Library record ascl:1109.022}] [Google Scholar]
- Jacyszyn-Dobrzeniecka, A. M., Skowron, D. M., Mróz, P., et al. 2017, Acta Astron., 67, 1 [NASA ADS] [Google Scholar]
- Jönsson, H., Holtzman, J. A., Allende Prieto, C., et al. 2020, AJ, 160, 120 [Google Scholar]
- Kallivayalil, N., van der Marel, R. P., Besla, G., Anderson, J., & Alcock, C. 2013, ApJ, 764, 161 [Google Scholar]
- Lucchini, S., D’Onghia, E., & Fox, A. J. 2021, ApJ, 921, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., Koposov, S. E., Erkal, D., et al. 2016, MNRAS, 459, 239 [Google Scholar]
- Mackey, D., Koposov, S., Da Costa, G., et al. 2018, ApJ, 858, L21 [Google Scholar]
- Majewski, S. R., Nidever, D. L., Muñoz, R. R., et al. 2009, in The Magellanic System: Stars, Gas, and Galaxies, eds. J. T. Van Loon, J. M. Oliveira, et al., 256, 51 [NASA ADS] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Massana, P., Noël, N. E. D., Nidever, D. L., et al. 2020, MNRAS, 498, 1034 [Google Scholar]
- Meschin, I., Gallart, C., Aparicio, A., et al. 2014, MNRAS, 438, 1067 [Google Scholar]
- Mészáros, S., Holtzman, J., García Pérez, A. E., et al. 2013, AJ, 146, 133 [Google Scholar]
- Nidever, D. L., Majewski, S. R., & Butler Burton, W. 2008, ApJ, 679, 432 [Google Scholar]
- Nidever, D. L., Majewski, S. R., Muñoz, R. R., et al. 2011, ApJ, 733, L10 [Google Scholar]
- Nidever, D. L., Holtzman, J. A., Allende Prieto, C., et al. 2015, AJ, 150, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Olsen, K., Walker, A. R., et al. 2017, AJ, 154, 199 [Google Scholar]
- Nidever, D. L., Olsen, K., Choi, Y., et al. 2019, ApJ, 874, 118 [Google Scholar]
- Nidever, D. L., Hasselquist, S., Hayes, C. R., et al. 2020, ApJ, 895, 88 [Google Scholar]
- Noël, N. E. D., Aparicio, A., Gallart, C., et al. 2009, ApJ, 705, 1260 [CrossRef] [Google Scholar]
- Osorio, Y., Allende Prieto, C., Hubeny, I., Mészáros, S., & Shetrone, M. 2020, A&A, 637, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parisi, M. C., Gramajo, L. V., Geisler, D., et al. 2022, A&A, 662, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petersen, M. S., & Peñarrubia, J. 2021, Nat. Astron., 5, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., & Geisler, D. 2013, AJ, 145, 17 [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [Google Scholar]
- Santana, F. A., Beaton, R. L., Covey, K. R., et al. 2021, AJ, 162, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M., Bizyaev, D., Lawler, J. E., et al. 2015, ApJS, 221, 24 [Google Scholar]
- Smith, V. V., Bizyaev, D., Cunha, K., et al. 2021, AJ, 161, 254 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Alves, D. R., Hardy, E., & Suntzeff, N. B. 2002, AJ, 124, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [Google Scholar]
- Wilson, J. C., Hearty, F. R., Skrutskie, M. F., et al. 2019, PASP, 131, 055001 [NASA ADS] [CrossRef] [Google Scholar]
- Zamora, O., García-Hernández, D. A., Allende Prieto, C., et al. 2015, AJ, 149, 181 [CrossRef] [Google Scholar]
- Zasowski, G., Johnson, J. A., Frinchaboy, P. M., et al. 2013, AJ, 146, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Cohen, R. E., Chojnowski, S. D., et al. 2017, AJ, 154, 198 [Google Scholar]
- Zivick, P., Kallivayalil, N., & van der Marel, R. P. 2021, ApJ, 910, 36 [Google Scholar]
All Tables
Regions, number of stars, coordinates, H magnitude, number of visits, and angular distance from the LMC center for the six substructures analyzed in this article.
Mean and standard deviation of 14 APOGEE chemical abundances for the six substructure fields.
Measured 3D space velocities from the models relative to the LMC and SMC for our six regions.
Mean and standard deviation of the minimum orthogonal distance for each substructure and each object (MW, LMC, SMC, Fnx, Sgr, Scl, and GSE) represented in Fig. 15 for Mg and Si according to the trendline performed by Hasselquist et al. (2021, see Fig. 13).
Mean and standard deviation of the minimum orthogonal distance for each substructures and each object (MW, LMC, SMC, Fnx, Sgr, Scl) represented in Figs. 14 and 15 for α-elements according to the trendline performed by Nidever et al. (2020).
All Figures
 |
Fig. 1. Distribution of the six fields in the substructures as well as LMC and SMC fields observed by APOGEE-2 in Magellanic Stream coordinates (LMS, BMS). |
| In the text | |
 |
Fig. 2. Gaia EDR3 proper motions for stars in the six regions analyzed, as well as LMC and SMC stars (top) and Gaia EDR3 proper motion in Magellanic Stream coordinates (LMS, BMS; bottom). |
| In the text | |
 |
Fig. 3. log g vs. Teff distribution from APOGEE-2 data release (DR17) for the six regions listed in Table 2. The solid gray line represents a Dartmouth RGB isochrone with a metallicity of –1.0 dex and age of 11 Gyr (Dotter et al. 2008). |
| In the text | |
 |
Fig. 4. Comparison of the APOGEE-2 LMC stars with different S/N. The small red dots are stars with S/N between 35 and 70, and the small gray dots represent stars with S/N > 70. We divided the sample, according to metallicity, into four groups over the range −2.0 to 0.0 dex to obtain the median and dispersion of the stars at different representative metallicities. The filled large red and gray circles with error bars respectively represent these values. |
| In the text | |
 |
Fig. 5. Normalized probability density functions applied to the observed metallicities in each region listed in Table 2, and including APOGEE measurements of more interior parts of the LMC and the SMC. The median metallicity for each region is indicated by a line at the top of the figure. |
| In the text | |
 |
Fig. 6. Metallicity and α-abundance, defined here by [(Mg+Si+Ca)/Fe], radial profiles of our sample from the LMC center (left panel) and SMC center (right panel). Left panels: Median of each region listed in Table 2 (filled large symbols) and the standard deviation (error bars). The solid lines are linear fits made using the APOGEE-2 LMC data inside 11° extrapolated (dashed lines) to show the predicted values from the LMC to its outskirts, where our six APOGEE fields lie (also shown with color-coded points). Right panels: Median values for each region listed in Table 2 (filled large symbols; the error bars represent the standard deviation). The solid lines are linear fits made using the APOGEE SMC data inside 6° extrapolated to show the predicted values from the SMC out to where our six APOGEE fields. |
| In the text | |
 |
Fig. 7. Distribution of α-abundances vs. metallicity for the LMC (small gray dots) and SMC (small magenta dots). Also included are the density of the Milky Way stars (orange) and the six substructures analyzed in this study (filled colored circles with error bars, which represent the standard deviation of each region). The left panels show the means of our substructure fields, while the right panels show the individual stars in each field. In the top right of each panel the representative errors for the LMC, SMC, and MW stars from the APOGEE pipeline (ASPCAP) are also shown. The solid black line and the solid magenta line represent the best polynomial fit for the LMC and SMC stars, respectively. |
| In the text | |
 |
Fig. 8. Similar to Fig. 7, but for the distributions of [C/Fe], [N/Fe], [O/Fe], and [Al/Fe] vs. [Fe/H]. |
| In the text | |
 |
Fig. 9. Similar to Fig. 7, but for the distributions of [V/Fe], [Cr/Fe], [Mn/Fe], [Co/Fe], [Ni/Fe], and [Ce/Fe] vs. [Fe/H]. |
| In the text | |
 |
Fig. 10. Radial velocity vs. metallicity of the stars in the six APOGEE MC periphery regions compared with LMC and SMC stars, with all data from APOGEE-2 DR17. |
| In the text | |
 |
Fig. 11. Vertical velocity (Vz, LMC), radial velocity (Vr, LMC), and azimuthal velocity (Vϕ, LMC) vs. metallicity of stars in the six targeted substructure regions, and including stars targeted by APOGEE in the central LMC. The velocities were calculated by Cheng et al. (2022) with respect to the assumed LMC disk plane, as described in Sect. 2. |
| In the text | |
 |
Fig. 12. Vertical velocity (Vz, SMC), radial velocity (Vr, SMC), and azimuthal velocity (Vϕ, SMC) vs. metallicity of the stars in the six targeted MC substructures along with stars targeted by APOGEE-2 in the central SMC. The velocities were calculated with respect to the assumed SMC disk plane, as described in Sect. 2, using an assumed distance of 60 kpc and using the formalism and best-fit model parameters presented in Zivick et al. (2021). |
| In the text | |
 |
Fig. 13. Comparison of distributions of [Mg/Fe] (top panels) and [Si/Fe] (bottom panels) vs. [Fe/H] for our targeted MC substructure regions against those for large Milky Way satellites also using APOGEE data: the LMC, SMC, Sagittarius dSph, Fornax dSph, and the GSE. The left panels show individual stars for each substructure and the right panels show the mean and standard deviation for each substructure region. The overplotted lines show the chemical evolution track for each dwarf galaxy as determined by Hasselquist et al. (2021). |
| In the text | |
 |
Fig. 14. Same as Fig. 13, but for [Mg+Si+Ca/Fe] vs. [Fe/H]. Also included are the trendlines derived by Nidever et al. (2020) for the MW, LMC, SMC, Fornax (Fnx), Sagittarius (Sgr), and Sculptor (Scl). |
| In the text | |
 |
Fig. 15. Minimum orthogonal distance of each star from the six regions to the best fit for Mg-, Si-, and α-abundance vs. metallicity for each galaxy in Figs. 13 and 14 (MW, LMC, SMC, Fnx, Sgr, Scl, and GSE). The best fit was determined by Hasselquist et al. (2021) for Mg and Si, and by Nidever et al. (2020) for alpha-abundances. Each star from each region is represented by a filled circle and the mean for each region is represented by a filled star symbol (see Table 8). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


