EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 671 (March 2023) A&A, 671 (2023) A124 Full HTML
Open Access
Issue
A&A
Volume 671, March 2023
Article Number A124
Number of page(s) 15
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202245133
Published online 15 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The Local Universe provides a unique window into the process of hierarchical mass assembly on all scales, allowing us to investigate a plethora of systems. These systems are satellites of the major assemblies, such as the Milky Way (MW) and M33: for instance, galaxies in relative isolation (e.g. most of the nearby dwarf galaxies), in close interaction with other systems (the Large and Small Magellanic Cloud; LMC and SMC, respectively), or galaxies that are consumed by large galaxies (e.g. the Sagittarius dwarf remnant and the satellites engulfed by the MW). Through their proximity and because individual stars can be resolved, the Magellanic Clouds provide a unique close-up of a pair of interacting dwarf galaxies.

These interacting dwarf galaxies are gas-rich and irregular. They are gravitationally bound to each other and likely at the first peri-Galactic passage with the MW (Besla et al. 2007, 2010; Kallivayalil et al. 2013; Besla 2015). The galaxy discussed in this paper, the SMC, is the second most massive MW satellite after the LMC, with a total mass of ∼2 × 109 M⊙ (Stanimirović et al. 2004). This is about one order of magnitude lower than the mass of the LMC. The stellar mass of the SMC is ∼5 − 6 × 108 M⊙ (van der Marel et al. 2009; Rubele et al. 2018), which is comparable with the mass of the main merger of the MW, the former galaxy Gaia-Enceladus (Helmi et al. 2018). There are several signatures of their mutual interaction and of the interaction between the Clouds and the MW, such as the Magellanic Bridge, which connects SMC and LMC, and the Magellanic Stream, which embraces these two galaxies. The history of the stellar populations of the SMC is intimately linked to the interplay of these three galaxies (Massana et al. 2022): the multiple episodes of star formation (SF) in their history are likely the result of the periodic close encounters between them. The colour-magnitude diagrams (CMD) of different SMC fields (see e.g. Harris & Zaritsky 2004; Noel et al. 2007; Cignoni et al. 2012, 2013) reveal a mixture of stellar populations, with a prominent red giant branch (RGB), which is the signature of stellar populations older than 1–2 Gyr, and an extended blue main sequence, which indicates the presence of younger stars. Our current picture of the SMC SF history (Cignoni et al. 2012, 2013; Rubele et al. 2018; Massana et al. 2022) is that this galaxy formed in isolation, with an SF activity starting ∼13 Gyr ago and a prolonged period of low-level SF activity until ∼3–4 Gyr ago. At this epoch, the SMC likely was tidally captured by the LMC, becoming gravitationally bound to it. This capture should have triggered new, vigorous, and synchronised SF bursts in both the galaxies (see e.g. Bekki & Chiba 2005; Massana et al. 2022) that probably formed most of the stars that we observe today. According to Rubele et al. (2018), the SMC formed (5.31  ±  0.05)×108 M⊙ stars over a Hubble time, two-thirds of which are now found in stellar remnants or living stars.

At variance with the LMC stars, whose chemical composition has been widely studied using high-resolution spectroscopy (Hill et al. 2000; Pompéia et al. 2008; Mucciarelli et al. 2010, 2021b; Lapenna et al. 2012; Van der Swaelmen et al. 2013; Nidever et al. 2020), the chemical composition of the SMC stars has received less attention, despite the proximity of this galaxy (∼62 kpc, Graczyk et al. 2014). For decades, the only high-resolution spectroscopic studies of SMC stars were mainly focused on bright supergiant stars and cepheids. This means that stellar populations younger than ∼200 Myr were sampled (see e.g. Spite et al. 1989a,b; Hill et al. 1997; Romaniello et al. 2008). Most of the information about the metallicity distribution of the SMC RGB stars came from low-resolution spectroscopy in I band, using the calibrated strength of the Ca II triplet as a proxy of [Fe/H] (Carrera et al. 2008; Dobbie et al. 2014a,b; Parisi et al. 2016; De Leo et al. 2020). The metallicity distribution of the SMC stars as derived from these studies displays a main peak around [Fe/H] ∼ –1 dex and a weak metal-poor tail. A clear decrease in mean metallicity has been observed at distance larger than ∼3° from the galaxy centre (Carrera et al. 2008). Evidence of a shallow metallicity gradient within the inner ∼3° of the SMC was found as well, between –0.07 dex deg−1 (Dobbie et al. 2014a) and –0.03 dex deg−1 (Choudhury et al. 2020).

Chemical analyses of high-resolution spectra of SMC RGB stars have been presented only recently (Nidever et al. 2020; Reggiani et al. 2021; Hasselquist et al. 2021). They allow us to investigate the chemical composition of these stellar populations in detail. Nidever et al. (2020) discussed [Mg/Fe], [Si/Fe], and [Ca/Fe] abundance ratios for about 1000 RGB SMC stars, finding a quite flat behaviour of these abundance ratios in the range of [Fe/H] between –1.2 and –0.2 dex, and a knee (the metallicity corresponding to the decrease in [α/Fe] abundance ratios) located at [Fe/H] lower than –2.2 dex. The same sample of SMC stars was discussed by Hasselquist et al. (2021). It also includes the abundances of Al, O, Ni, and Ce. The authors compared them with the abundances of other MW satellites.

Reggiani et al. (2021) discussed the chemical composition of four metal-poor ([Fe/H] < –2.0 dex) SMC stars, finding that the stellar abundances were comparable to those of the MW halo stars for all the main groups of elements. On the other hand, these stars are more enriched in [Eu/Fe] (a pure r-process element) than the MW stars.

This paper is the first of a series dedicated to investigating the chemical properties of the LMC/SMC (field and stellar clusters) stars. In this work, we present the chemical analysis of 206 RGB star members of the SMC that were observed with the high-resolution spectrograph FLAMES, which is mounted at the ESO Very Large Telescope.

2. Observations and data reduction

2.1. SMC sample

A total of 320 stars in the direction of the SMC was observed (ID program 086.D-0665, PI: Mucciarelli) with the multi-object spectrograph FLAMES (Pasquini et al. 2000) in the GIRAFFE-MEDUSA mode. This mode allows us the simultaneous allocation of 132 high-resolution (R ∼ 20 000) fibres over a patrol field with a diameter of about 25 arcmin. Three different fields were observed, centred around three globular clusters (GCs): NGC 121, NGC 339, and NGC 419 (hereafter, these fields are called FLD-121, FLD-339, and FLD-419, respectively). The left panel of Fig. 1 shows the spatial location of the three FLAMES fields superimposed on the map of the SMC stars that was obtained with the early third data release (EDR3) of the Gaia/ESA mission (Gaia Collaboration 2016, 2021). The fields are located in different positions of the SMC. Fields FLD-121, FLD-339, and FLD-419 lie ∼2.4° north-west, ∼1.4° south-east, and ∼1.5° east of the SMC centre (Ripepi et al. 2017), respectively. Ffield FLD-121 partially overlaps the APOGEE field 47Tuc (only two stars in common), field FLD-419 is adjacent to the APOGEE field SMC2 (only one star in common), and field FLD-339 samples a region that was not observed by APOGEE (see Fig. 1 by Nidever et al. 2020).

thumbnail Fig. 1.

Spatial and photometric information of the spectroscopic targets. Left panel: spatial distribution of the three fields observed with FLAMES (red, green, and blue circles for FLD-121, FLD-339, and FLD-419, respectively) superimposed on the map of the SMC RGB stars with G between 16 and 19 from Gaia EDR3 (Gaia Collaboration 2021), revealing the old spheroid of the SMC. The white plus indicates the position of the SMC centre derived by Ripepi et al. (2017). Right panel: Gaia EDR3 CMDs of the three SMC fields (grey points, Gaia Collaboration 2021). The spectroscopic GIRAFFE targets are superposed (same colours as in the left panel). The main sequence of MW GC 47 Tucanae is clearly visible in the CMD of FLD-121.

The adopted GIRAFFE-MEDUSA setups are setup HR11, with a spectral resolution of 24 200, and they range from 5597 to 5840 Å, and setup HR13, with a spectral resolution of 22 500 and a spectral coverage between 6120 and 6405 Å. These two setups allow us to measure the lines of the main groups of elements, such as odd-Z (Na), α (O, Mg, Si, Ca, and Ti), iron-peak (Sc, V, Fe, Ni, and Cu), and s-process elements (Zr, Ba, and La). The UVES fibers were allocated to targets belonging to the three GCs and are discussed in separated papers (Dalessandro et al. 2016, Paper II, in prep.). Table 1 lists the exposure times and the number of individual exposures for each setup and field.

Table 1.

Coordinates of the FLAMES pointing, number of exposures, and exposure times for the two FLAMES setups, adopted colour excess (Schlafly & Finkbeiner 2011), and the number of SMC stars we analysed.

The spectroscopic targets for each field were originally selected from near-infrared (Ks, J − Ks) CMDs, using the catalogues obtained with the near-infrared imager Son of ISAAC (SofI; Moorwood et al. 1998) in the New Technology Telescope catalogues for the region within 2.5 arcmin from the cluster centres (Mucciarelli et al. 2009, for NGC 339 and NGC 419, and unpublished proprietary photometry for NGC 1210), and the 2MASS database (Skrutskie et al. 2006) for the external regions. The targets were selected according to the following criteria: (1) stars fainter than the RGB tip (Ks = 12.62, Cioni et al. 2000). (2) Stars brighter than Ks = 14 for FLD-339 and FLD-419 and brighter than Ks = 14.4 for FLD-121, in order to guarantee a signal-to-noise ratio (S/N) per pixel higher than ∼30 in both setups and in all the observed fields. Because RGB stars in the SMC outskirts are rare, a fainter (by ∼0.4 mag) threshold was adopted for FLD-121 in order to enlarge the number of observed SMC stars. (3) Stars without close stars brighter than 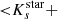< K s star + $ { < }K_{s}^{\mathrm{star}}+ $1.0 within 2″. (4) For the targets from the 2MASS catalogue (the majority of the observed targets) only stars with J and Ks magnitudes flagged as A (photometric uncertainties smaller than 10%) were selected.

All the targets were recovered in the Gaia EDR3 catalog. The right panel of Fig. 1 shows the position in the (G, BP − RP) CMDs of the observed targets that we considered as SMC stars according to their radial velocity (RV); see Sect. 3.3. Table 2 lists the coordinates and the Gaia EDR3 identification number for all SMC targets.

Table 2.

Information about the SMC spectroscopic targets.

The spectra were reduced with the dedicated ESO GIRAFFE pipeline1, including bias-subtraction, flat-fielding, wavelength calibration with a standard Th-Ar lamp, and spectral extraction. The contribution of the sky was subtracted from each spectrum by using a median sky spectrum, as obtained by combining ∼15–20 spectra from fibres allocated to sky positions within each exposure. The final S/N per pixel of the spectra is ∼30–50 for HR11 spectra and ∼40–60 for HR13 spectra. Figure 2 shows the spectra of two SMC giant stars with very similar atmospheric parameters and a large (∼1.5 dex) difference in [Fe/H] as an example of the spectral quality.

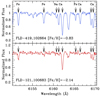thumbnail Fig. 2.

Comparison between the HR13 spectra of the stars FLD-419_102664 (upper panel) and FLD-121_100683 (lower panel). The stars have very similar atmospheric parameters, but different iron content. Arrows mark the position of some metallic lines of interest.

2.2. MW control sample

As discussed in Minelli et al. (2021), the comparison between the chemical abundances obtained from different works can be hampered by various systematics characterising the chemical analyses, for instance the method used to infer the stellar parameters, the adopted atomic data for the analysed transitions, model atmospheres, and solar reference abundances. When chemical analyses of extra-galactic stars are performed (with the aim to compare their abundances with those of MW stars), it is therefore crucial to consider a control sample of MW stars as well that was analysed in a homogeneous way, in order to erase the main systematics quoted above and highlight and quantify possible differences and similarities between the abundance ratios of stars from different galaxies.

We defined a control sample of MW stars that was analysed with the same assumptions used for the SMC stars. We analysed five MW GCs covering the same metallicity range as the SMC stars ([Fe/H] between ∼–2.2 and ∼–0.5 dex) and for which FLAMES spectra obtained with the GIRAFFE HR11 and HR13 setups are available in the ESO archive (ID programs: 072.D-0507 and 083.D-0208, PI: Carretta). The selected GCs are NGC 104, NGC 1851, NGC 1904, NGC 4833, and NGC 5904. The use of the same GIRAFFE setups allowed us to derive chemical abundances in these MW GCs from the same transitions as were used for the SMC stars. We restricted the analysis to the stars whose effective temperatures and surface gravities were comparable with those of the SMC stars studied here: six stars for NGC 104, two stars for NGC 1851, six stars for NGC 5904, three stars for NGC 1904, and four stars for NGC 4833. For O and Na, which exhibit large star-to-star variations in each of these GCs, we analysed stars belonging to the so-called first population that were selected according to Carretta et al. (2009). The O and Na abundances of these first-population stars can be considered as a good proxy of the chemical composition of the MW field at these metallicities.

3. Spectral analysis

3.1. Line selection

We selected an appropriate set of unblended metallic lines for each star. The set was selected by visual inspection of suitable synthetic spectra. The spectra were calculated with the code SYNTHE (Sbordone et al. 2004; Kurucz 2005), using the typical atmospheric parameters of the observed stars (see Sect. 3.2), adopting ATLAS9 model atmospheres (Castelli & Kurucz 2003)2, and including all the atomic and molecular transitions in the Kurucz/Castelli linelist3. The synthetic spectra were convoluted with Gaussian profiles in order to reproduce the observed line broadening, which is mainly dominated by the instrumental resolution. We preferred transitions with laboratory oscillator strengths. We adopted solar oscillator strengths only for the Sc II line at 6245.6 Å, for the Si I lines at 6155.1 and 6237.3 Å, and for the Cu I line at 5782 Å.

Because the level of blending of a given transition depends on the metallicity, which in this case is not known a priori, we adopted an iterative process to define the line list of each target.

A preliminary line list was defined by adopting a metallicity [M/H] = –1.0 dex for all synthetic spectra we used, according to the mean metallicity of the SMC derived from previous studies (Carrera et al. 2008; Dobbie et al. 2014a,b; Parisi et al. 2016; Nidever et al. 2020). After a first chemical analysis, a new set of unblended lines was defined for each star using a synthetic spectrum calculated with the appropriate chemical composition. This procedure was specifically necessary for the most metal-poor stars of our sample, whose [Fe/H] is significantly lower than the mean value of [Fe/H] = –1.0 dex, and for a few stars with enhancement of s-process elements. The average number of selected metallic lines is about 80–90 for most of the stars (with [Fe/H] ∼ –1.0 dex), which decreases to 40–50 for the most metal-poor stars. Most of the lines used in the metal-poor stars are still available for metal-rich stars, while some features are excluded because they are saturated or blended with other lines at higher metallicities. However, we verified that the use of different samples of lines depending on the stellar metallicity does not introduce biases in the abundances at different metallicities.

All the lines we used are listed in Table 3, together with the corresponding log gf and excitation potential χ.

Table 3.

Transitions together with oscillator strengths, the excitation potential, and the reference of the atomic data.

3.2. Atmospheric parameters

The derived atmospheric parameters are listed in Table 2. Effective temperatures (Teff) and surface gravities (log g) were estimated from the photometry. In particular, Teff was obtained from the broad-band colour (G − Ks)0 adopting the (G − Ks)0 − Teff transformation provided by Mucciarelli et al. (2021a). We adopted G magnitudes from Gaia EDR3 and Ks from 2MASS. G magnitudes were corrected for extinction following the prescriptions by Gaia Collaboration (2018), and Ks magnitudes were corrected adopting the extinction coefficient by McCall (2004). The colour excess values E(B − V) are from the infrared dust maps by Schlafly & Finkbeiner (2011) and are listed in Table 1.

Uncertainties in Teff were estimated by propagating the errors in the adopted colour and in the colour excess for each individual star. The typical error in the (G − Ks)0 colours is about 0.03–0.05 mag and is dominated by the uncertainty of the Ks magnitude. This translates into an uncertainty of 20–40 K in Teff. For the colour excess, we adopted a conservative error of 0.01 mag for all the three fields, despite the lower errors quoted by Schlafly & Finkbeiner (2011). This led to a negligible (a few K) uncertainty in Teff. These uncertainties were added in quadrature to the typical error associated with the (G − Ks)0–Teff transformation (46 K), which is estimated as the 1σ dispersion of the fit residuals (Mucciarelli et al. 2021a), and which dominates the total Teff error (typically ∼50–60 K).

The logg values were calculated through the Stefan-Boltzmann relation, adopting the photometric Teff, a true distance modulus (m − M)0 = 18.965 ± 0.025 (Graczyk et al. 2014), the bolometric corrections by Andrae et al. (2018), and a stellar mass of 1.0 M⊙. We recall for the distance modulus that the SMC has a substantial line-of-sight depth that is difficult to take into account properly for each individual target. According to the depth maps provided by Subramanian & Subramaniam (2009), the three fields studied in this study should cover a depth range between 2 and 6 kpc. When we consider a conservative variation in distance of 3 kpc, the quoted uncertainties in log g only increase by 0.02 dex, which translates into variations of less than 0.02 in the abundances of single ionised lines (but without the impact of neutral lines on the abundances). Uncertainties in log g are about 0.1, including the uncertainties in Teff distance modulus and stellar mass. The final error budget in log g is dominated by the uncertainty in the stellar mass, which is assumed to be ±0.2 M⊙ and reflects the possible spread in ages of our targets (older than ∼1–2 Gyr). Microturbulent velocities (vt) are usually derived spectroscopically by erasing any trend between the iron abundance and the reduced equivalent widths (defined as the logarithm of the EW normalised to the wavelength). Because of the relatively small number (∼30–40 or fewer) of available Fe I lines in the adopted spectral ranges, vt obtained spectroscopically risk to be uncertain or unreliable. In order to avoid significant fluctuations in vt (with an impact on the derived abundances), we adopted the log g − vt relations provided by Mucciarelli & Bonifacio (2020) that are based on the spectroscopic vt obtained from high-resolution high-S/N spectra of giant stars in 16 Galactic GCs. The uncertainty in vt was estimated by adding the error arising from the uncertainty in logg in quadrature, and the error of the adopted log g − vt relation and is about 0.2 km s−1.

3.3. Radial velocities

The RVs were measured by using the code DAOSPEC (Stetson & Pancino 2005), which performs a line fitting assuming a Gaussian profile. The code is automatically launched by using the software 4DAO (Mucciarelli 2013), which allows us a visual inspection of all the fitted lines in order to directly evaluate the quality of the fitting procedure. RVs were measured by the position of about 100 metallic lines for each star. The internal uncertainty of the RV for each spectrum was estimated as the standard error of the mean, about 0.1–0.3 km s−1. The final RV for each target was obtained as the weighted mean of the values obtained from the two setups. The accuracy of the wavelength calibration was verified by measuring the position of the strong emission sky line at 6300.3 Å in the HR13 setup. We found no significant offset. No sky emission lines are available in the HR11 setup, and we cannot directly confirm the accuracy of the wavelength calibration. However, the RVs obtained from the two setups agree with each other, with an average difference between the RV from HR11 and HR13 of +0.12  ±  0.06 km s−1 (σ  =  0.8 km s−1). This excludes any offset for the two setups and confirms the accuracy of the RVs from HR11 spectra as well.

3.4. Chemical abundances

The chemical abundances of Na, Mg (from the line at 5711 Å), Si, Ca, Ti, Fe, Ni, and Zr were derived from the measure of the equivalent widths (EWs) of unblended lines by using the code GALA (Mucciarelli et al. 2013). EWs were measured by using the code DAOSPEC (Stetson & Pancino 2005).

The abundances of species whose lines are affected by blending (O and the Mg lines at 6318–19 Å) or by hyperfine/isotopic splitting (Sc, V, Cu, Ba, and La) were derived using our own code SALVADOR, which performs a χ2-minimisation between the observed lines and a grid of synthetic spectra calculated on the fly with the code SYNTHE (Sbordone et al. 2004) and including all the atomic and molecular lines available in the Kurucz/Castelli line lists. For all the species we investigated, we provide upper limits based on the comparison between observed and synthetic spectra when the lines cannot be clearly detected.

The [OI] line at 6300 Å can be also contaminated by telluric lines, depending on the stellar RV. This possible contamination was checked with suitable synthetic spectra of the Earth atmosphere calculated with the tool TAPAS (Bertaux et al. 2014). These synthetic spectra were calculated assuming the appropriate observation date and airmass of our targets, in order to account for the proper weather conditions of the observations. In the case of contamination, the line profile was cleaned by dividing the observed spectrum by the telluric spectrum and by checking visually that no discontinuities were introduced. Figure 3 shows an example of a stellar spectrum around the [OI] line before and after telluric correction.

thumbnail Fig. 3.

Example of telluric correction around the [O I] line in star FLD-339_466. The black curve is the original (not corrected for RV) spectrum, the blue curve is the spectrum corrected for the telluric lines, and the red curve is the synthetic spectrum of the Earth atmosphere (shifted for clarity).

In the calculation of the synthetic spectra used to measure the oxygen abundance, the Ni abundance of each star was included to account for the blending of the O feature with a Ni line.

Mg abundances were obtained for most of the stars from the EW of the line at 5711 Å. As discussed in Minelli et al. (2021), this transition is heavily saturated for giant stars with [Fe/H] > –1.0 dex. For these stars, the Mg triplet at 6318–19 Å should be preferred because these lines are still sensitive to the Mg abundance. For the stars for which the Mg line at 5711 Å is saturated, the Mg abundance was therefore derived from the Mg triplet using spectral synthesis in order to include the contribution of the close auto-ionisation Ca line.

Finally, we corrected the derived abundances for departures from the LTE assumption applying the corrections by Lind et al. (2011) only for the Na lines used here (5682–88 Å and 6154–60 Å).

The abundances were referred to solar abundances, taking as reference the values from Grevesse & Sauval (1998), except for oxygen, for which the adopted value is the value from Caffau et al. (2011).

3.5. Abundance uncertainties

In the determination of the uncertainties in each derived abundance ratio, we took two main sources of error into account, namely the errors arising from the measurement procedure (EW or spectral synthesis), and those arising from atmospheric parameters.

(1) Uncertainties related to the measurement procedure were computed as the dispersion of the mean normalised to the root mean square of the number of used transitions. Properly, this term includes both uncertainties from line fitting and from adopted log gf values. For the elements measured from the EWs and for elements for which only one line is available, the DAOSPEC uncertainty associated with the Gaussian fitting procedure (corresponding to 1σ of the fit residuals) was assumed as the internal error. For the elements (O and La) for which only one transition has been measured using spectral synthesis, the internal error was estimated by means of Monte Carlo simulations, creating a sample of 500 synthetic spectra with a Poissonian noise that reproduces the observed S/N, and the line-fitting procedure was repeated. The dispersion of the abundance distribution obtained from these noisy synthetic spectra was assumed as the 1σ uncertainty.

(2) Uncertainties due to atmospheric parameters were estimated by repeating the analysis by varying a given parameter of the corresponding 1σ error each time and keeping the other parameters fixed.

These two sources of uncertainties were added in quadrature. Since the abundance of the species X is expressed as abundance ratios [X/Fe], the uncertainties in the Fe abundance were also taken into account. The final errors in the [Fe/H] and [X/Fe] abundance ratios were calculated as follows:

σ [ Fe / H ] = σ Fe 2 N Fe + ( δ Fe T eff ) 2 + ( δ Fe log g ) 2 + ( δ Fe v t ) 2 $$ \begin{aligned}&\sigma _{\rm [Fe/H]} = \sqrt{\frac{\sigma _{\rm Fe}^2}{N_{\rm Fe}} + (\delta ^\mathrm{T_{\rm eff}}_{\rm Fe})^2 + (\delta ^{\log \ g}_{\rm Fe})^2 + (\delta ^{{ v}_{\rm t}}_{\rm Fe})^2} \end{aligned} $$(1)

σ [ X / Fe ] = σ X 2 N X + σ Fe 2 N Fe + ( δ X T eff − δ Fe T eff ) 2 + ( δ X log g − δ Fe log g ) 2 + ( δ X v t − δ Fe v t ) 2 , $$ \begin{aligned}&\sigma _{\rm [X/Fe]}=\nonumber \\&\sqrt{\frac{\sigma _{X}^2}{N_{X}} + \frac{\sigma _{\rm Fe}^2}{N_{\rm Fe}} + (\delta ^{T_{\rm eff}}_X - \delta ^{T_{\rm eff}}_{\rm Fe})^2 + (\delta ^{\log \ g}_X - \delta ^{\log \ g}_{\rm Fe})^2 + (\delta ^{{ v}_{\rm t}}_X - \delta ^{{ v}_{\rm t}}_{\rm Fe})^2}, \end{aligned} $$(2)

where σX, Fe is the dispersion around the mean of the chemical abundances, NX, Fe is the number of lines used to derive the abundances, and 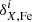δ X , Fe i $ \delta^{i}_{X,\mathrm{Fe}} $ are the abundance variations obtained by modifying the atmospheric parameter i.

3.6. Abundances of the MW control sample

Table 4 lists the average abundance ratios, together with the standard deviation and the average uncertainty in the abundance ratio, for the five GCs of the MW control sample. We compared the atmospheric parameters and [Fe/H] of the analysed stars with those by Carretta et al. (2009, 2014), who analysed the same spectroscopic dataset. The average differences between our analysis and the literature analyses are +52 ± 11 K (σ =  50 K) for Teff, –0.01 ± 0.01 (σ =  0.03) for log g, +0.07±0.04 km s−1 (σ =  0.19 km s−1) for vt, and –0.03 ± 0.02 dex (σ =  0.07 dex) for [Fe/H].

Table 4.

Average abundance ratios, corresponding standard deviation, and average uncertainty for the five GCs of the MW control sample.

4. RV and [Fe/H] distributions

4.1. RV distribution

Following previous spectroscopic studies (Harris & Zaritsky 2006; Carrera et al. 2008; Dobbie et al. 2014a; De Leo et al. 2020; Hasselquist et al. 2021), we identified stars with an RV between +80 and +250 km s−1 as SMC members. The membership was also confirmed by the proper motions measured from Gaia EDR3 (Gaia Collaboration 2021). We excluded from the chemical analysis star members of the GC associated with each field (these stars will be discussed in a forthcoming paper of the series), stars whose spectra were contaminated by prominent TiO or C2 molecular bands, or stars whose S/N was too low. The final sample discussed in this work includes a total of 206 stars out of the 320 observed stars. The RV and [Fe/H] for this sample are listed in Table 2. Figures 4 and 5 show the RV and [Fe/H] discrete and kernel density distributions of the three SMC fields. The advantage of the latter representation is that the distribution is independent of the choice of the bin width and of the starting bin, which is at variance with the discrete distributions.

thumbnail Fig. 4.

RV and [Fe/H] distributions (left and right panel, respectively) of the three fields. Colours indicate the different fields: FLD-121 (red), FLD-339 (green), and FLD-419 (blue).

thumbnail Fig. 5.

RVs plotted against [Fe/H] for target stars in the central panel of the figure. Colour-shaded areas denote the contours of the three clusters RV vs. [Fe/H] distributions. Side plots show the kernel distributions of the RV (right panel) and the [Fe/H] values (top panel) for each cluster. Same colours as in Fig. 4.

The RV distributions of the three fields appear significantly different with each other, in terms of both the main peak and shape. The RV distribution of FLD-121 peaks at RV ≈ +125 km s−1, that of FLD-339 displays a peak at RV ≈ +160 km s−1, and that of FLD-419 exhibits two distinct peaks, the main peak at ≈+150 km s−1, and the second peak at ≈+180 km s−1. A Kolmogorov-Smirnov test performed on these distributions confirmed that the RV distributions of FLD-339 and FLD-419 are significantly different from that of FLD-121 (with a statistic significance larger than 99.9%), while we cannot reject the hypothesis that FLD-339 and FLD-419 may derive from the same population.

The differences in the peaks of these three RV distributions are compatible with the rotation pattern of the SMC as inferred from low-resolution spectroscopic surveys of giant stars (Dobbie et al. 2014a; De Leo et al. 2020), from the HI column density map (Di Teodoro et al. 2019), and from the APOGEE results from 17th Data Release of the Sloan Digital Sky Survey (Abdurro’uf et al. 2022). All these studies show that the velocity in the western side of the SMC, where FLD-121 is located, is lower than in the eastern side. However, the presence of multiple peaks, which is clearly visible in the distribution of FLD-419, seems to suggest a more complex kinematic pattern (as discussed below).

4.2. [Fe/H] distribution

The [Fe/H] distribution of the entire sample peaks at [Fe/H] ∼–1.0 dex; [Fe/H] is between –1.5 and –0.5 dex for about 95% of the stars, and a weak but extended metal-poor tail reaches [Fe/H] ∼ –2.2 dex. This distribution is qualitatively similar to the distributions that were obtained from low-resolution spectra using the Ca II triplet (Carrera et al. 2008; Dobbie et al. 2014a; Parisi et al. 2016) and the distribution based on APOGEE data (Nidever et al. 2020). However, similar to what we see with the RV distributions, the metallicity distributions appear different with each other when individutal fields are considered. The distributions of FLD-339 and FLD-419 are confined between –1.5 and –0.5 dex; only one star per field (∼1%) has [Fe/H] < –1.5 dex. On the other hand, the distribution of FLD-121 ranges from –0.8 dex down to –2.2 dex, and ∼20% of the stars are more metal poor than –1.5 dex. The APOGEE field 47Tuc, superimposed on our field FLD-121, exhibits a lower fraction of metal-poor stars, ∼2%. This probably reflects some selection bias against metal-poor stars in the APOGEE observations.

The peaks of the distributions of FLD-339 and FLD-419 are separated by ∼0.2 dex and are located at [Fe/H] ∼ –0.9 and ∼–1.1 dex, respectively. The two distributions do not seem to be symmetric either: a secondary peak is visible at [Fe/H] ∼ –1.1 dex in FLD-339, and a heavily populated metal-rich tail or a secondary peak is visible in FLD-419 (see Sect. 4.5).

4.3. [Fe/H] distribution and the age-metallicity relation

We tried to interpret the derived [Fe/H] distributions in terms of ages, using the SF histories recovered from Hubble Space Telescope as guidance (Noel et al. 2007; Sabbi et al. 2009; Cignoni et al. 2012, 2013), together with ground-based (Massana et al. 2022) photometry and the theoretical age-metallicity relations available for the SMC (Pagel & Tautvaisiene 1998; Tsujimoto & Bekki 2009; Cignoni et al. 2013).

All the SF histories provided so far in the literature agree that the early epochs of the SMC have been characterised by a significant SF activity, followed by a long quiescent period that was interrupted between ∼3 and ∼4 Gyr ago by significant SF episodes, likely due to some merger events. The oldest SMC GC, NGC 121, has an age of ∼10.5 ± 0.5 Gyr glatt08 and a metallicity of [Fe/H] ∼ –1.2/–1.3 dex (Dalessandro et al. 2016, Paper II, in prep.). This suggests that the SF activity in the first billion years was able to increase the metallicity to values as high as [Fe/H] ∼ –1.2/–1.3 dex. We can consider that the SMC field stars in our sample with [Fe/H] < –1.3 dex (which are almost all located in FLD-121) were formed in the first 1–2 Gyr of the life of the galaxy.

The subsequent evolution of the SMC and the corresponding metallicity distribution can be interpreted in the light of the theoretical age-metallicity relations: Fig. 6 shows the relation by Pagel & Tautvaisiene (1998), who assumed a burst of SF at an age of ∼4 Gyr. After a long period characterised by a low SF efficiency (in which the metallicity remained almost constant), the SF in the SMC re-ignites with a prominent burst, likely triggered by the first close encounter between SMC and LMC (Bekki et al. 2004; Bekki & Chiba 2005). The most recent SF history for the SMC provided by Massana et al. (2022) using the SMASH photometry identified the re-ignition of the SF at ∼3.5 Gyr ago, simultaneously in both the Clouds. The stars with [Fe/H] > –1.3 dex analysed here are thought to be a mixture of stars with different ages (from ∼1 to ∼10–11 Gyr). It is difficult to separate the different populations in terms of age because [Fe/H] is almost constant over a wide age range. Massana et al. (2022) identified five peaks (at ∼3, 2, 1, and 0.45 Gyr ago and one still ongoing) in the SF history of the SMC that simultaneously occur in the LMC as well. A fascinating possibility is that the different peaks in the metallicity distributions of FLD-339 and FLD-419 might be associated with some of these different SF bursts. Finally, we propose that stars with [Fe/H] around –0.6/–0.5 dex likely formed with the burst at 1 Gyr. This is also confirmed by the metallicities of the stellar clusters with ages around 1 Gyr (see e.g. Parisi et al. 2022).

thumbnail Fig. 6.

Main panel: Age-metallicity relation by Pagel & Tautvaisiene (1998). Side panel: Kernel [Fe/H] distributions for the individual SMC field stars.

4.4. Run of [Fe/H] with the distance

Previous spectroscopic studies (Carrera et al. 2008; Dobbie et al. 2014a; Parisi et al. 2016; Choudhury et al. 2020; Grady et al. 2021) found evidence of a shallow (from –0.03 to –0.07 dex/deg) metallicity gradient, within 3°–5°. Figure 7 shows the run of [Fe/H] of the spectroscopic targets with their projected distance from the SMC centre (Ripepi et al. 2017). The mean metallicity in three fields is consistent with the shallow gradient previously proposed by Choudhury et al. (2020). However, two main differences between the external field FLD-121 and the two internal fields are evident. First, the fraction of metal-poor stars ([Fe/H] < –1.5 dex) is about ∼20% in FLD-121, compared with ∼1% in the other two fields. The fraction of metal-poor stars increases outward, reflecting a larger fraction of old stars compared to those that formed subsequently during the long quiescent period and the recent SF bursts, which are preferentially confined in the innermost region of the SMC (see e.g. Rubele et al. 2018).

thumbnail Fig. 7.

Behaviour of [Fe/H] as a function of the projected distance from the SMC centre (Ripepi et al. 2017), with the same colours as in Fig. 1. The thick grey line is the linear fit for the metallicity gradient estimated by Choudhury et al. (2020).

Second, the metallicity distribution of FLD-121 shows a clear lack of stars with [Fe/H] between –0.8 and –0.5 dex, which are instead detected in FLD-339 and FLD-419. Following the discussion above, these stars should have ∼1 Gyr (the youngest stars among the intermediate-age SMC populations). Again, this is consistent with a scenario in which the younger metal-richer populations are progressively more concentrated towards the innermost regions. Age-metallicity gradients of this kind are quite common in dwarf galaxies (see e.g. Taibi et al. 2022, and references therein).

4.5. Possible chemically and kinematic distinct sub-structures?

The distribution of the SMC stars in the RV-[Fe/H] plane seems to suggest sub-structures, in particular, the two different peaks of the [Fe/H] distribution of FLD-339, the large and asymmetric [Fe/H] distribution of FLD-419, and the double peak of the RV distribution of FLD-419.

We used the Gaussian mixture package Mclust (Scrucca et al. 2016), within the R environment, to analyse the distribution of FLD-339 and FLD-419 stars in the [Fe/H] – RV space. Mclust chose the best model, both in terms of number and form (e.g. equal or variable variance and orientation; see Scrucca et al. 2016) of the Gaussian components, by means of the Bayesian information criterion. Since we are interested in sub-structures within the bulk of the metallicity distribution, we excluded the two metal-poor outliers from the analysis, one per field. While for FLD-339, a single elliptical Gaussian model is the preferred solution, the [Fe/H] – RV distribution of FLD-419 is best described with two elliptical Gaussian components with the same variance in [Fe/H] and RV. The gain of this model with respect to a single elliptical Gaussian is only marginal. In practice, they provide an equally good representation of the data. Still, the solution synthesises the properties of the hypothesised two components. The first component has (μ[Fe/H], μRV) = (−0.85 dex, 171.8 km s−1), and it accounts for 33% of the sample. The second component has (μ[Fe/H], μRV) = (−1.13 dex, 154.5 km s−1) and accounts for the remaining 67% of the sample. The standard deviations are σ[Fe/H] =  0.10 dex and σRV =  22.7 km s−1. The most metal-rich component appears to have a higher systemic RV than its metal-poor counterpart.

As additional check, we performed a Kolmogorov-Smirnov test on the RV sub-populations of FLD-419, separated according to the metallicity of their member stars (and assuming [Fe/H]=–1.05 dex as a boundary between the two groups of stars). We obtained that the two RV distributions cannot be extracted from the same population with a significance of 98%.

The size of the FLD-419 sample is not sufficient to put this odd result on sound statistical bases, but it may suggest some chemo-kinematic substructures in the SMC along this line of sight. In this respect, we recall that the SMC has a substantial line-of-sight depth, depending on the tracers that are used, which ranges from a few kiloparsec up to about 20 kpc (see e.g. de Grijs & Bono 2015; Subramanian et al. 2017). When we observe stars in an individual SMC field, we therefore likely cross different depths and sample different populations in terms of kinematics and metallicity.

5. Chemical abundance ratios

We derived abundances of Na, O, Mg, Si, Ca, Sc, Ti, V, Fe, Ni, Cu, Zr, Ba, and La for 206 SMC RGB stars. All the abundances, with the corresponding uncertainties, are available at the CDS (Table 5). With respect to the APOGEE sample by Hasselquist et al. (2021), we measured a larger number of species, in particular Na, Sc, Ti, V, Cu, Zr, Ba, and La, which are not included in that study. Figures 8–11 show the behaviour of derived abundance ratios as a function of [Fe/H] for the analysed SMC stars, highlighting stars belonging to the different fields. These abundance ratios were compared with those obtained for the control sample of five Galactic GCs by adopting the same assumptions in the chemical analysis and therefore removing most of the systematics of the analyses. This comparison allowed us to highlight the real difference between SMC and MW stars of similar [Fe/H]. Additionally, we show abundance ratios for Galactic field stars from the literature as reference. The comparison with the literature is affected by the systematics among the different analyses (in terms of model atmospheres, solar abundance values, NLTE corrections, line lists, and use of dwarf and giant stars). However, it is useful to display the overall trends in the MW based on a large number of stars. In the following, we refer to the MW control sample to quantify the main differences and similarities between MW and SMC stars.

thumbnail Fig. 8.

Behaviour of the light element [Na/Fe] and α-elements [O/Fe], [Mg/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe] abundance ratios as a function of [Fe/H] for SMC stars located in the fields FLD-419, FLD-339, and FLD-121 (blue, green, and red circles, respectively). Arrows indicate upper limits. The error bars in the bottom right corner indicate the typical uncertainties. Grey squares are the average values for the five Galactic GCs of the control sample. Abundances of Galactic stars from the literature are also plotted as a reference (Edvardsson et al. 1993; Gratton et al. 2003; Reddy et al. 2003, 2006; Bensby et al. 2005, 2014 for all the elements, Fulbright 2000; Stephens & Boesgaard 2002; Roederer et al. 2014 for Na, Mg, Si, Ca and Ti, Adibekyan et al. 2012 for Na, Mg, Si and Ca, and Barklem et al. 2005 for Mg).

thumbnail Fig. 9.

Behaviour of the hydrostatic and explosive average [α/Fe] abundance ratios as a function of [Fe/H]. Same symbols as in Fig. 8.

thumbnail Fig. 10.

Behaviour of the iron-element [Sc/Fe], [V/Fe], [Ni/Fe], and [Cu/Fe] abundance ratios as a function of [Fe/H]. Abundances of Galactic field stars are from Reddy et al. (2003, 2006) and Roederer et al. (2014) for all the elements, Gratton et al. (2003) for Sc, V, and Ni, Fulbright (2000) for V and Ni, Adibekyan et al. (2012) for Sc and Ni, Edvardsson et al. (1993), Stephens & Boesgaard (2002) and Bensby et al. (2005) for Ni, and Bihain et al. (2004) and Yan et al. (2015) for Cu. Same symbols as in Fig. 8.

thumbnail Fig. 11.

Behaviour of the neutron capture-elements [Zr/Fe], [Ba/Fe], and [La/Fe] abundance ratios as a function of [Fe/H]. Abundances of Galactic field stars are from Mishenina et al. (2013) and Roederer et al. (2014) for all the elements, Edvardsson et al. (1993), Fulbright (2000) and Reddy et al. (2003) for Zr and Ba, Burris et al. (2000) and Battistini & Bensby (2016) for Zr and La, Stephens & Boesgaard (2002), Barklem et al. (2005) and Bensby et al. (2005) for Ba.

5.1. Na

Sodium is mainly produced in massive stars during the hydrostatic C and Ne burning, with a strong dependence of its yields on the metallicity. Moreover, a smaller contribution is provided by asymptotic giant branch (AGB) stars. In Galactic stars (both in the control sample and in literature data), [Na/Fe] increases by increasing [Fe/H] until it reaches solar values around [Fe/H] > –1 dex. An offset is evident between the values in the control sample and in the literature, especially in the metal-poor regime, and this likely due to the different NLTE corrections. The top left panel of Fig. 8 shows the distribution of [Na/Fe] of the observed targets. The bulk of the SMC stars exhibits sub-solar [Na/Fe] abundance ratios at any metallicities, with an average value of about –0.4/–0.5 dex, similar to the typical [Na/Fe] measured in the LMC stars (Van der Swaelmen et al. 2013; Minelli et al. 2021) but at higher [Fe/H]. The low [Na/Fe] values measured in the SMC stars may indicate a lower contribution by massive stars, in addition to the larger impact of type Ia supernovae (SNe Ia) at low metallicities in dwarf galaxies (Tolstoy et al. 2009). We observe a large scatter of [Na/Fe] that cannot be fully explained within the typical uncertainties and has been detected in spectroscopic samples of LMC and SMC metal-rich stars (Pompéia et al. 2008; Van der Swaelmen et al. 2013; Minelli et al. 2021; Hasselquist et al. 2021). This scatter might reflect multiple sites of Na production. Finally, we note a systematic difference between the median [Na/Fe] values in FLD-339 and FLD-419, where the latter displays [Na/Fe] higher by 0.1–0.15 dex. A systematic difference in [Na/Fe] of different regions of the parent galaxy has been also observed in the LMC (Van der Swaelmen et al. 2013); the stars in the LMC bar are more enriched in [Na/Fe] by 0.2 dex than the LMC disc stars.

5.2. α-elements

The α-elements are produced mainly in short-lived massive stars that explode as core-collapse supernovae (CC-SNe), while a minor fraction (depending on the element) is synthesised in SNe Ia. Because of the time delay between the enrichment of the two classes of SNe, the [α/Fe] abundance ratios are the classical tracers of the relative timescales of the different SNe. In particular, the metallicity of the knee (marking the onset of a significant chemical contribution by SNe Ia) can be used as a proxy of the SF efficiency of the galaxy (Tinsley 1979; Matteucci & Greggio 1986).

O and Mg (the so-called hydrostatic α-elements) are produced mainly in stars with masses higher than ∼30–35 M⊙ and without contribution from SNe Ia. On the other hand, Si, Ca, and Ti (explosive α-elements) are produced in less massive stars (∼15–25 M⊙) and with a smaller (but not negligible) contribution from SNe Ia (see e.g. Kobayashi et al. 2020b). Figure 8 shows the behaviour with [Fe/H] of individual [α/Fe] abundance ratios, and Fig. 9 shows the run of the average values of hydrostatic and explosive [α/Fe]. These abundance ratios in the SMC stars clearly display a decrease by increasing the metallicity, moving from enhanced values for the most metal-poor stars ([Fe/H] < –1.5 dex) down to solar-scaled values in the dominant population. This trend is in contrast with that obtained by the APOGEE survey (Hasselquist et al. 2021), where [Mg/Fe] increases from [Fe/H] ∼ –1.3 dex to [Fe/H] ∼ –1.0 dex, followed by a slight decrease. On the other hand, a similar behaviour is not observed for [O/Fe], [Si/Fe] and [Ca/Fe] that are flat over this [Fe/H] range.

The most metal-poor stars in our sample exhibit enhanced values of [α/Fe], which agrees with the results by Nidever et al. (2020) and Reggiani et al. (2021) for SMC stars of similar metallicity. Oxygen and magnesium, which are mainly produced by stars with masses higher than ∼30 M⊙, are slightly underabundant at low [Fe/H] with respect to the MW sample, however. This indicates a lower contribution from the most massive stars to the overall chemical enrichment of the SMC. The subsequent decrease in [α/Fe] at higher [Fe/H] indicates that these stars formed from a gas that was enriched by SNe Ia. For stars with [Fe/H] > –1.5 dex, the difference in [α/Fe] between SMC and MW stars becomes more significant. In particular, the SMC-MW difference is more pronounced for hydrostatic α-elements, again suggesting a lower contribution by stars with masses higher than 30–35 M⊙ to the chemical enrichment of the SMC.

We note that as for Na, the metal-rich stars in FLD-419 are slightly enhanced in [Ti/Fe] (by ∼0.1 dex) with respect to the stars of the other two fields with similar [Fe/H].

5.3. Iron-peak elements

Iron-peak elements are mainly produced in massive stars through different nucleosynthesis paths (Limongi & Chieffi 2003; Romano et al. 2010; Kobayashi et al. 2020b), and they are ejected in the interstellar medium by normal CC-SNe and hypernovae. These elements are also partly produced by SNe Ia on longer timescales (Leung & Nomoto 2018; Lach et al. 2020).

Sc and V are mainly produced in massive stars, with a small contribution by SN Ia only for V (Kobayashi et al. 2020b). The Sc and V abundances in SMC stars with [Fe/H] < –1.5 dex are compatible with those measured in the control sample. We note some offsets between these abundance ratios in the control sample and in the literature data that are likely attributable to different line lists (in terms of log gf and/or hyperfine structures). On the other hand, the Sc and V abundances of metal-rich SMC stars are significantly lower than those of MW stars (see Fig. 10). For both elements, we observed a decrease of the abundance ratio with increasing [Fe/H] because of the overwhelming delayed contribution to Fe by SNe Ia. This behaviour resembles the behaviour observed in metal-rich stars of dwarf galaxies, such as the LMC and Sagittarius (see e.g. Sbordone et al. 2007; Minelli et al. 2021). We note that [V/Fe] in metal-rich stars of FLD-419 is also systematically higher by ∼0.15 dex than in the stars of FLD-339. A comparable shift was also detected for [V/Fe] in the LMC disc and bar stars (Van der Swaelmen et al. 2013).

Ni is largely produced by SN Ia, and is also produced by CC-SNe, similar to the production of Fe. The [Ni/Fe] values of SMC stars are compatible with those measured in the GCs of the control sample until [Fe/H]∼–1.0 dex, while for higher metallicities, this abundance ratio decreases slightly and reaches values of about [Ni/Fe]∼–0.2 dex (see Fig. 10). A similar behaviour in the SMC stars has been observed by Hasselquist et al. (2021). This mild trend resembles that observed for [Ni/Fe] in the LMC and in Sagittarius at higher [Fe/H] (Minelli et al. 2021). The decrease in [Ni/Fe] at higher metallicities is not observed in MW stars, where [Ni/Fe] remains constant. In this respect, Kobayashi et al. (2020a) suggested a lower contribution by sub-Chandrasekhar mass SN Ia to reproduce the [Ni/Fe] measured in dwarf spheroidal galaxies.

Cu is mainly produced in massive stars through the weak s-process (Romano & Matteucci 2007), with a small contribution by AGB stars (Travaglio et al. 2004) and a negligible contribution by SN Ia (Iwamoto et al. 1999; Romano & Matteucci 2007). The [Cu/Fe] abundance ratio in the SMC stars exhibits a large star-to-star dispersion, and it is difficult to establish its real trend. However, it is clear that [Cu/Fe] is lower in the most metal-rich SMC stars than that measured in MW stars. This again indicates a lower contribution to the chemical enrichment by massive stars. Values of [Cu/Fe] lower than those measured in MW stars were also observed in the LMC (Van der Swaelmen et al. 2013), Sagittarius (Sbordone et al. 2007), and Omega Centauri (Cunha et al. 2002).

5.4. Neutron-capture elements

Elements heavier than the iron-peak group are produced through neutron-capture processes on seed nuclei, followed by β decays (Burbidge et al. 1957). The neutron-capture elements measured here (Zr, Ba, and La) are mainly produced by the slow process occurring in low-mass (1–3 M⊙) AGB stars and in a minor amount in more massive stars (Busso et al. 1999; Cristallo et al. 2015). At low metallicities, these elements are also produced through rapid processes (Truran 1981) that occur in rare and energetic events such as neutron star mergers or collapsars. This spectroscopic dataset contains no transition of pure r-process elements (i.e. Eu), and we cannot discuss the relative contribution of these two production channels. However, Reggiani et al. (2021) analysed four metal-poor SMC giant stars and reported [Eu/Fe] values higher than those of the MW stars. This supports a strong contribution at these metallicities by r-process.

The [Zr/Fe] and [La/Fe] abundance ratios of SMC stars are similar within the star-to-star scatter to those observed in MW stars, and are slightly higher [Ba/Fe]. Generally, these results suggest that the enrichment by AGB stars in the SMC is comparable to that in the MW. [Ba/Fe] in the SMC stars is enhanced (∼+0.3/+0.4 dex) and higher than the values measured in the MW stars. [Ba/Fe] displays a large scatter at all the metallicities, which cannot be explained in light of the typical uncertainties in the abundance ratios (∼0.15 dex). At [Fe/H] ∼ –1.0 dex, the values of [Ba/Fe] of SMC stars are higher than those observed in the MW stars, suggesting that the galaxy-wide initial mass function (IMF) is biased in favour of the low-mass stars in the SMC. A similar behaviour is observed for [La/Fe], and the trend in [Zr/Fe] agrees with that observed for the MW. Similar to what we observe for Na and V, we also found a shift for [Zr/Fe] of ∼0.2 dex between FLD-339 and FLD-419 that resembles the shifts observed for the same ratio between LMC disc and bar stars (Van der Swaelmen et al. 2013). The high values of [Ba/Fa] and [La/Fe], together with the large star-to-star scatter, suggest that the production of s-process elements has been very efficient in the SMC, while the large star-to-star scatter could arise from enrichment from AGB stars of different metallicities, because the yields of AGB stars for these elements are highly dependent on metallicity.

Finally, we identified a few stars with high [Ba/Fe] and [La/Fe] values (> 0.5–0.7 dex, reaching also +1.3 dex). A similar enhancement of s-process elements might be due to mass transfer processes from an AGB companion star in a binary system.

6. Conclusions

The analysis of optical spectra of 206 SMC RGB stars located in three different positions of the parent galaxy has allowed us to highlight some finer details of the complex and still poorly known nature of this galaxy. The main results are summarised below.

The RV and [Fe/H] distributions of the three fields are different. Although the fields FLD-339 and FLD-419 lie at the same distance from the SMC centre, their [Fe/H] distributions peak at different values that are separated by 0.2 dex. These two populations might be connected to different bursts of SF that occurred in the recent life of the SMC (Massana et al. 2022), or they might be the result of a different chemical enrichment path in these regions (despite their similar projected distance from the SMC centre).

The fraction of metal-poor ([Fe/H] < –1.5 dex) stars increases outward. It is ∼1% in the two internal fields and ∼20% in FLD-121. This run likely reflects an age gradient in the SMC, in which the internal regions are dominated by intermediate-age metal-rich stars and the outskirts by the old metal-poor spheroid (see e.g. Rubele et al. 2018).

The RV-[Fe/H] distribution of the observed fields seems to suggest the possible existence of chemically and kinematic distinct substructures. In particular, we potentially identified two groups of stars, one around [Fe/H] ∼ –1.1 dex and RV ∼ +154 km s−1, and the other around [Fe/H] ∼ –0.9 dex and RV ∼ +172 km s−1. More data are needed to confirm the statistical significance of these chemo-kinematical substructures.

Especially for the dominant metal-rich component, the SMC displays distinct abundance patterns with respect to the MW stars. In particular, the abundance ratios of elements that are mainly produced by massive stars (Na, α, Sc, V, and Cu) are lower than those measured in the MW stars. This suggests that the gas from which these stars formed was poorly enriched by the most massive stars. This can be explained in light of the low SF rate expected for a galaxy as small as the SMC, leading to a lower contribution by massive stars to the overall chemical enrichment of the galaxy (Jeřábková et al. 2018; Yan et al. 2020). This is also confirmed by the most metal-poor stars of the sample, whose [O/Fe] and [Mg/Fe] ratios are slightly lower than those in MW stars of similar [Fe/H].

The [s/Fe] abundance ratios are enriched with respect to the MW stars and have a large star-to-star scatter, suggesting that these elements are produced by AGB stars of different masses and metallicities. Moreover, the enhancement of the [s/Fe] abundance ratios in the SMC seems to suggest a galaxy-wide IMF that is biased in favour of the low-mass stars in the SMC.

The possibility that the IMF is not universal but varies with the environment is the subject of lively debate (Bastian et al. 2010; Hopkins 2018; Smith 2020). Theoretically, if stars form in clusters according to IMFs that depend on the metallicity and density of the parent gaseous clumps, it is possible to calculate the integrated galaxy-wide IMF, which in turn depends on the metallicity and star formation rate of the host galaxy (Jeřábková et al. 2018; Yan et al. 2020). Moreover, the abundance ratios of chemical elements that are produced in stars with initial masses falling in narrow and well-detached ranges can be used as powerful indirect probes of the shape of the galaxy-wide IMF (e.g. Romano et al. 2017).

Observationally, the possibility that the Sagittarius dwarf spheroidal galaxy had a stronger contribution from AGB stars to its chemical enrichment than the MW and the LMC is discussed in Hasselquist et al. (2021). Similarly, Hallakoun & Maoz (2021) reported a bottom-heavy IMF for the Gaia-Enceladus progenitor based on data from Gaia DR2. Finally, Mucciarelli et al. (2021b) claimed that the LMC GC NGC 2005 must have formed in an accreted system that experienced an extremely low star formation rate and, hence, an extremely low number of hypernova explosions, in order to explain the peculiarly low Zn abundance of the cluster. On the other hand, Hill et al. (2019) failed to find any clear evidence in favour of a non-standard IMF in the Sculptor dwarf spheroidal galaxy. In a forthcoming paper, we will quantitatively study IMF variations in the SMC by computing chemical evolution models that are specifically tailored to this galaxy (Romano et al., in prep.).

The three fields exhibit similar chemical patterns for all the elements except for Na, V, Zr, and Ti, which are subtly different in the fields. Differences in the same abundance ratios were also observed in the LMC between bar and disc stars (Van der Swaelmen et al. 2013). These differences confirm that the chemical enrichment history in the SMC has been not uniform, but depends on the position within the galaxy.

These promising results clearly show that the properties of the SMC stars need to be studied locally rather than globally, with an effort to enlarge the samples of high-resolution spectra located in different regions of the galaxy. In this respect, the advent of multi-object spectrographs such as MOONS at the Very Large Telescope (Cirasuolo et al. 2020) and 4MOST at the VISTA Telescope (de Jong et al. 2019) will allow us a significant improvement in the investigation of possible chemically distinct sub-structures in the Magellanic Clouds (Gonzalez et al. 2020).

Acknowledgments

We thank the referee, Mathieu Van der Swaelmen, for the useful comments and suggestions. This research is funded by the project “Light-on-Dark”, granted by the Italian MIUR through contract PRIN-2017K7REXT. C. Lardo acknowledges funding from Ministero dell’Universitá e della Ricerca through the Programme Rita Levi Montalcini (grant PGR18YRML1). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [CrossRef] [Google Scholar]
  2. Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [Google Scholar]
  6. Battistini, C., & Bensby, T. 2016, A&A, 586, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bekki, K., & Chiba, M. 2005, MNRAS, 356, 680 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bekki, K., Couch, W. J., Beasley, M. A., et al. 2004, ApJ, 610, L93 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bertaux, J. L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Besla, G. 2015, ArXiv eprints [arXiv:1511.03346] [Google Scholar]
  12. Besla, G., Kallivayalil, N., Hernquist, L., et al. 2007, ApJ, 668, 949 [Google Scholar]
  13. Besla, G., Kallivayalil, N., Hernquist, L., et al. 2010, ApJ, 721, L97 [Google Scholar]
  14. Bensby, T., Feltzing, S., Lundström, I., et al. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bihain, G., Israelian, G., Rebolo, R., et al. 2004, A&A, 423, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Burbidge, E. M., Burbidge, G. R., Fowler, W. A., et al. 1957, Rev. Modern Phys., 29, 547 [NASA ADS] [CrossRef] [Google Scholar]
  17. Burris, D. L., Pilachowski, C. A., Armandroff, T. E., et al. 2000, ApJ, 544, 302 [Google Scholar]
  18. Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [Google Scholar]
  19. Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
  20. Carrera, R., Gallart, C., Aparicio, A., et al. 2008, AJ, 136, 1039 [Google Scholar]
  21. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2014, A&A, 564, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Castelli, F., & Kurucz, R. L. 2003, IAU Symp., 210, poster A20 [NASA ADS] [Google Scholar]
  24. Choudhury, S., de Grijs, R., Rubele, S., et al. 2020, MNRAS, 497, 3746 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cignoni, M., Cole, A. A., Tosi, M., et al. 2012, ApJ, 754, 130 [NASA ADS] [CrossRef] [Google Scholar]
  26. Cignoni, M., Cole, A. A., Tosi, M., et al. 2013, ApJ, 775, 83 [Google Scholar]
  27. Cioni, M.-R.-L., van der Marel, R. P., Loup, C., & Habing, H. J. 2000, A&A, 359, 601 [NASA ADS] [Google Scholar]
  28. Cirasuolo, M., Fairley, A., Rees, P., et al. 2020, The Messenger, 180, 10 [NASA ADS] [Google Scholar]
  29. Cristallo, S., Straniero, O., Piersanti, L., et al. 2015, ApJS, 219, 40 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cunha, K., Smith, V. V., Suntzeff, N. B., et al. 2002, AJ, 124, 379 [NASA ADS] [CrossRef] [Google Scholar]
  31. Dalessandro, E., Lapenna, E., Mucciarelli, A., et al. 2016, ApJ, 829, 77 [NASA ADS] [CrossRef] [Google Scholar]
  32. de Grijs, R., & Bono, G. 2015, AJ, 149, 179 [Google Scholar]
  33. de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, The Messenger, 175, 3 [NASA ADS] [Google Scholar]
  34. De Leo, M., Carrera, R., Noël, N. E. D., et al. 2020, MNRAS, 495, 98 [Google Scholar]
  35. Di Teodoro, E. M., McClure-Griffiths, N. M., Jameson, K. E., et al. 2019, MNRAS, 483, 392 [Google Scholar]
  36. Dobbie, P. D., Cole, A. A., Subramaniam, A., & Keller, S. 2014a, MNRAS, 442, 1663 [Google Scholar]
  37. Dobbie, P. D., Cole, A. A., Subramaniam, A., & Keller, S. 2014b, MNRAS, 442, 1680 [NASA ADS] [CrossRef] [Google Scholar]
  38. Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 500, 391 [NASA ADS] [Google Scholar]
  39. Fuhr, J. R., & Wiese, W. L. 2006, J. Phys. Chem. Ref. Data, 35, 1669 [NASA ADS] [CrossRef] [Google Scholar]
  40. Fuhr, J. R., Martin, G. A., & Wiese, W. L. 1988, J. Phys. Chem. Ref. Data, 17, 383 [Google Scholar]
  41. Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] [Google Scholar]
  42. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Glatt, K., Gallagher, J. S., Grebel, E. K., et al. 2008, AJ, 135, 1106 [NASA ADS] [CrossRef] [Google Scholar]
  46. Gonzalez, O. A., Mucciarelli, A., Origlia, L., et al. 2020, The Messenger, 180, 18 [NASA ADS] [Google Scholar]
  47. Graczyk, D., Pietrzynski, G., Thompson, I. B., et al. 2014, ApJ, 780, 59 [Google Scholar]
  48. Grady, J., Belokurov, V., & Evans, N. W. 2021, ApJ, 909, 150 [Google Scholar]
  49. Gratton, R. G., Carretta, E., Claudi, R., et al. 2003, A&A, 404, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
  51. Hallakoun, N., & Maoz, D. 2021, MNRAS, 507, 398 [NASA ADS] [CrossRef] [Google Scholar]
  52. Harris, J., & Zaritsky, D. 2004, AJ, 127, 1531 [NASA ADS] [CrossRef] [Google Scholar]
  53. Harris, J., & Zaritsky, D. 2006, AJ, 131, 2514 [Google Scholar]
  54. Hasselquist, S., Hayes, C. R., Lian, J., et al. 2021, ApJ, 923, 172 [NASA ADS] [CrossRef] [Google Scholar]
  55. Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
  56. Hill, V., Barbuy, B., & Spite, M. 1997, A&A, 323, 461 [NASA ADS] [Google Scholar]
  57. Hill, V., François, P., Spite, M., et al. 2000, A&A, 364, L19 [NASA ADS] [Google Scholar]
  58. Hill, V., Skúladóttir, Á., Tolstoy, E., et al. 2019, A&A, 626, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Hopkins, A. M. 2018, PASA, 35, e039 [NASA ADS] [CrossRef] [Google Scholar]
  60. Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [Google Scholar]
  61. Jeřábková, T., Hasani Zonoozi, A., Kroupa, P., et al. 2018, A&A, 620, A39 [Google Scholar]
  62. Kobayashi, C., Leung, S.-C., & Nomoto, K. 2020a, ApJ, 895, 138 [CrossRef] [Google Scholar]
  63. Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020b, ApJ, 900, 179 [Google Scholar]
  64. Kallivayalil, N., van der Marel, R. P., Besla, G., et al. 2013, ApJ, 764, 161 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kurucz, R. L. 2005, MSAIS, 8, 14 [NASA ADS] [Google Scholar]
  66. Lach, F., Röpke, F. K., Seitenzahl, I. R., et al. 2020, A&A, 644, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Lapenna, E., Mucciarelli, A., Origlia, L., et al. 2012, ApJ, 761, 33 [NASA ADS] [CrossRef] [Google Scholar]
  68. Leung, S.-C., & Nomoto, K. 2018, ApJ, 861, 143 [Google Scholar]
  69. Limongi, M., & Chieffi, A. 2003, ApJ, 592, 404 [CrossRef] [Google Scholar]
  70. Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Martin, G. A., Fuhr, J. R., & Wiese, W. L. 1988, Atomic transition probabilities. Scandium through Manganese (New York: American Institute of Physics (AIP) and American Chemical Society) [Google Scholar]
  72. Massana, P., Ruiz-Lara, T., Noël, N. E. D., et al. 2022, MNRAS, 513, L40 [CrossRef] [Google Scholar]
  73. Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
  74. McCall, M. L. 2004, AJ, 128, 2144 [Google Scholar]
  75. Minelli, A., Mucciarelli, A., Romano, D., et al. 2021, ApJ, 910, 114 [CrossRef] [Google Scholar]
  76. Mishenina, T. V., Pignatari, M., Korotin, S. A., et al. 2013, A&A, 552, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Moorwood, A., Cuby, J.-G., Biereichel, P., et al. 1998, The Messenger, 94, 7 [NASA ADS] [Google Scholar]
  78. Mucciarelli, A. 2013, ArXiv eprints [arXiv:1311.1403] [Google Scholar]
  79. Mucciarelli, A., & Bonifacio, P. 2020, A&A, 640, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Mucciarelli, A., Origlia, L., Maraston, C., & Ferraro, F. R. 2009, ApJ, 690, 288 [NASA ADS] [CrossRef] [Google Scholar]
  81. Mucciarelli, A., Origlia, L., & Ferraro, F. R. 2010, ApJ, 717, 277 [NASA ADS] [CrossRef] [Google Scholar]
  82. Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
  83. Mucciarelli, A., Monaco, L., Bonifacio, P., & Saviane, I. 2017, A&A, 603, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Mucciarelli, A., Bellazzini, M., & Massari, D. 2021a, A&A, 653, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Mucciarelli, A., Massari, D., Minelli, A., et al. 2021b, Nat. Astron., 5, 1247 [NASA ADS] [CrossRef] [Google Scholar]
  86. Nidever, D. L., Hasselquist, S., Hayes, C. R., et al. 2020, ApJ, 895, 88 [Google Scholar]
  87. Noel, N. E. D., Gallart, C., Costa, E., & Mendez, R. A. 2007, AJ, 133, 2037 [NASA ADS] [CrossRef] [Google Scholar]
  88. Pagel, B. E. J., & Tautvaisiene, G. 1998, MNRAS, 299, 535 [Google Scholar]
  89. Parisi, M. C., Geisler, D., Carraro, G., et al. 2016, AJ, 152, 58 [NASA ADS] [Google Scholar]
  90. Parisi, M. C., Gramajo, L. V., Geisler, D., et al. 2022, A&A, 662, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Pasquini, L., Avila, G., Allaert, E., et al. 2000, SPIE, 4008, 129 [NASA ADS] [Google Scholar]
  92. Pompéia, L., Hill, V., Spite, M., et al. 2008, A&A, 480, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Reddy, B. E., Tomkin, J., Lambert, D. L., et al. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
  94. Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [Google Scholar]
  95. Reggiani, H., Schlaufman, K. C., Casey, A. R., et al. 2021, AJ, 162, 229 [NASA ADS] [CrossRef] [Google Scholar]
  96. Ripepi, V., Cioni, M.-R. L., Moretti, M. I., et al. 2017, MNRAS, 472, 808 [Google Scholar]
  97. Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014, AJ, 147, 136 [Google Scholar]
  98. Romaniello, M., Primas, F., Mottini, M., et al. 2008, A&A, 488, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Romano, D., & Matteucci, F. 2007, MNRAS, 378, L59 [NASA ADS] [Google Scholar]
  100. Romano, D., Karakas, A. I., Tosi, M., et al. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Romano, D., Matteucci, F., Zhang, Z.-Y., et al. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
  102. Rubele, S., Pastorelli, G., Girardi, L., et al. 2018, MNRAS, 478, 5017 [NASA ADS] [CrossRef] [Google Scholar]
  103. Sabbi, E., Gallagher, J. S., Tosi, M., et al. 2009, ApJ, 703, 721 [NASA ADS] [CrossRef] [Google Scholar]
  104. Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, MSAIS, 5, 93 [NASA ADS] [Google Scholar]
  105. Sbordone, L., Bonifacio, P., Buonanno, R., et al. 2007, A&A, 465, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  107. Scrucca, L., Fop, M., Murphy, T. B., & Raftery, A. E. 2016, The R Journal, 8, 289 [NASA ADS] [CrossRef] [Google Scholar]
  108. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  109. Smith, G., & Raggett, D. S. J. 1981, J. Phys. B Atomic Mol. Phys., 14, 4015 [NASA ADS] [CrossRef] [Google Scholar]
  110. Smith, R. J. 2020, ARA&A, 58, 577 [NASA ADS] [CrossRef] [Google Scholar]
  111. Spite, F., Spite, M., & Francois, P. 1989a, A&A, 210, 25 [Google Scholar]
  112. Spite, F., Spite, M., & Barbuy, B. 1989b, A&A, 222, 35 [NASA ADS] [Google Scholar]
  113. Stanimirović, S., Staveley-Smith, L., & Jones, P. A. 2004, ApJ, 604, 176 [Google Scholar]
  114. Stephens, A., & Boesgaard, A. M. 2002, AJ, 123, 1647 [NASA ADS] [CrossRef] [Google Scholar]
  115. Stetson, P. B., & Pancino, E. 2005, PASP, 120, 1332 [Google Scholar]
  116. Subramanian, S., & Subramaniam, A. 2009, A&A, 496, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Subramanian, S., Rubele, S., Sun, N.-C., et al. 2017, MNRAS, 467, 2980 [NASA ADS] [Google Scholar]
  118. Taibi, S., Battaglia, G., Leaman, R., et al. 2022, A&A, 665, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Tinsley, B. M. 1979, ApJ, 229, 1046 [Google Scholar]
  120. Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [Google Scholar]
  121. Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [Google Scholar]
  122. Truran, J. W. 1981, A&A, 97, 391 [NASA ADS] [Google Scholar]
  123. Tsujimoto, T., & Bekki, K. 2009, ApJ, 700, L69 [Google Scholar]
  124. van der Marel, R. P., Kallivayalil, N., & Besla, G. 2009, The Magellanic System: Stars, Gas, and Galaxies, 256, 81 [NASA ADS] [Google Scholar]
  125. Van der Swaelmen, M., Hill, V., Primas, F., et al. 2013, A&A, 560, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Yan, H. L., Shi, J. R., & Zhao, G. 2015, ApJ, 802, 36 [NASA ADS] [CrossRef] [Google Scholar]
  127. Yan, Z., Jerabkova, T., & Kroupa, P. 2020, A&A, 637, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Coordinates of the FLAMES pointing, number of exposures, and exposure times for the two FLAMES setups, adopted colour excess (Schlafly & Finkbeiner 2011), and the number of SMC stars we analysed.

In the text
Table 2.

Information about the SMC spectroscopic targets.

In the text
Table 3.

Transitions together with oscillator strengths, the excitation potential, and the reference of the atomic data.

In the text
Table 4.

Average abundance ratios, corresponding standard deviation, and average uncertainty for the five GCs of the MW control sample.

In the text

All Figures

thumbnail Fig. 1.

Spatial and photometric information of the spectroscopic targets. Left panel: spatial distribution of the three fields observed with FLAMES (red, green, and blue circles for FLD-121, FLD-339, and FLD-419, respectively) superimposed on the map of the SMC RGB stars with G between 16 and 19 from Gaia EDR3 (Gaia Collaboration 2021), revealing the old spheroid of the SMC. The white plus indicates the position of the SMC centre derived by Ripepi et al. (2017). Right panel: Gaia EDR3 CMDs of the three SMC fields (grey points, Gaia Collaboration 2021). The spectroscopic GIRAFFE targets are superposed (same colours as in the left panel). The main sequence of MW GC 47 Tucanae is clearly visible in the CMD of FLD-121.
In the text
thumbnail Fig. 2.

Comparison between the HR13 spectra of the stars FLD-419_102664 (upper panel) and FLD-121_100683 (lower panel). The stars have very similar atmospheric parameters, but different iron content. Arrows mark the position of some metallic lines of interest.
In the text
thumbnail Fig. 3.

Example of telluric correction around the [O I] line in star FLD-339_466. The black curve is the original (not corrected for RV) spectrum, the blue curve is the spectrum corrected for the telluric lines, and the red curve is the synthetic spectrum of the Earth atmosphere (shifted for clarity).
In the text
thumbnail Fig. 4.

RV and [Fe/H] distributions (left and right panel, respectively) of the three fields. Colours indicate the different fields: FLD-121 (red), FLD-339 (green), and FLD-419 (blue).
In the text
thumbnail Fig. 5.

RVs plotted against [Fe/H] for target stars in the central panel of the figure. Colour-shaded areas denote the contours of the three clusters RV vs. [Fe/H] distributions. Side plots show the kernel distributions of the RV (right panel) and the [Fe/H] values (top panel) for each cluster. Same colours as in Fig. 4.
In the text
thumbnail Fig. 6.

Main panel: Age-metallicity relation by Pagel & Tautvaisiene (1998). Side panel: Kernel [Fe/H] distributions for the individual SMC field stars.
In the text
thumbnail Fig. 7.

Behaviour of [Fe/H] as a function of the projected distance from the SMC centre (Ripepi et al. 2017), with the same colours as in Fig. 1. The thick grey line is the linear fit for the metallicity gradient estimated by Choudhury et al. (2020).
In the text
thumbnail Fig. 8.

Behaviour of the light element [Na/Fe] and α-elements [O/Fe], [Mg/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe] abundance ratios as a function of [Fe/H] for SMC stars located in the fields FLD-419, FLD-339, and FLD-121 (blue, green, and red circles, respectively). Arrows indicate upper limits. The error bars in the bottom right corner indicate the typical uncertainties. Grey squares are the average values for the five Galactic GCs of the control sample. Abundances of Galactic stars from the literature are also plotted as a reference (Edvardsson et al. 1993; Gratton et al. 2003; Reddy et al. 2003, 2006; Bensby et al. 2005, 2014 for all the elements, Fulbright 2000; Stephens & Boesgaard 2002; Roederer et al. 2014 for Na, Mg, Si, Ca and Ti, Adibekyan et al. 2012 for Na, Mg, Si and Ca, and Barklem et al. 2005 for Mg).
In the text
thumbnail Fig. 9.

Behaviour of the hydrostatic and explosive average [α/Fe] abundance ratios as a function of [Fe/H]. Same symbols as in Fig. 8.
In the text
thumbnail Fig. 10.

Behaviour of the iron-element [Sc/Fe], [V/Fe], [Ni/Fe], and [Cu/Fe] abundance ratios as a function of [Fe/H]. Abundances of Galactic field stars are from Reddy et al. (2003, 2006) and Roederer et al. (2014) for all the elements, Gratton et al. (2003) for Sc, V, and Ni, Fulbright (2000) for V and Ni, Adibekyan et al. (2012) for Sc and Ni, Edvardsson et al. (1993), Stephens & Boesgaard (2002) and Bensby et al. (2005) for Ni, and Bihain et al. (2004) and Yan et al. (2015) for Cu. Same symbols as in Fig. 8.
In the text
thumbnail Fig. 11.

Behaviour of the neutron capture-elements [Zr/Fe], [Ba/Fe], and [La/Fe] abundance ratios as a function of [Fe/H]. Abundances of Galactic field stars are from Mishenina et al. (2013) and Roederer et al. (2014) for all the elements, Edvardsson et al. (1993), Fulbright (2000) and Reddy et al. (2003) for Zr and Ba, Burris et al. (2000) and Battistini & Bensby (2016) for Zr and La, Stephens & Boesgaard (2002), Barklem et al. (2005) and Bensby et al. (2005) for Ba.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.