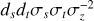| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 21 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202346524 | |
| Published online | 11 December 2023 | |
The CARMENES search for exoplanets around M dwarfs
Telluric absorption corrected high S/N optical and near-infrared template spectra of 382 M dwarf stars★
1
Hamburger Sternwarte,
Gojenbergsweg 112,
21029
Hamburg, Germany
e-mail: evangelos.nagel@hs.uni-hamburg.de
2
Universität Göttingen, Institut für Astrophysik und Geophysik,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
3
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778
Tautenburg, Germany
4
Landessternwarte, Zentrum für Astronomie der Universität Heidelberg,
Königstuhl 12,
69117
Heidelberg, Germany
5
Department of Physics, Ariel University,
Ariel
40700, Israel
6
Centro de Astrobiología (CSIC-INTA), ESAC,
Camino Bajo del Castillo s/n,
28692
Villanueva de la Cañada, Madrid, Spain
7
ISDEFE,
Beatriz de Bobadilla 3,
28040
Madrid, Spain
8
Institut de Ciències de l’Espai (CSIC),
Campus UAB, c/ de Can Magrans s/n,
08193
Bellaterra, Barcelona, Spain
9
Institut d’Estudis Espacials de Catalunya (IEEC),
c/ Gran Capita 2–4,
08034
Barcelona, Spain
10
Instituto de Astrofísica de Andalucía (CSIC),
Glorieta de la Astronomía s/n,
18008
Granada, Spain
11
Instituto de Astrofísica de Canarias,
c/ Vía Láctea s/n,
38205
La Laguna, Tenerife, Spain
12
Departamento de Astrofísica, Universidad de La Laguna,
Avda. Francisco Sánchez s/n,
38206
La Laguna, Tenerife, Spain
13
Departamento de Física de la Tierra y Astrofísica and IPARCOS-UCM (Intituto de Física de Partículas y del Cosmos de la UCM), Facultad de Ciencias Físicas, Universidad Complutense de Madrid,
28040
Madrid, Spain
14
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
15
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen, Germany
16
Department of Physics, University of Warwick,
Gibbet Hill Road,
Coventry
CV4 7AL, UK
17
Centro Astronómico Hispano en Andalucía (CSIC-Junta de Andalucía), Observatorio Astronómico de Calar Alto, Sierra de los Filabres,
04550
Gérgal, Almería, Spain
Received:
28
March
2023
Accepted:
25
September
2023
Light from celestial objects interacts with the molecules of the Earth’s atmosphere, resulting in the production of telluric absorption lines in ground-based spectral data. Correcting for these lines, which strongly affect red and infrared wavelengths, is often needed in a wide variety of scientific applications. Here, we present the template division telluric modeling (TDTM) technique, a method for accurately removing telluric absorption lines in stars that exhibit numerous intrinsic features. Based on the Earth’s barycentric motion throughout the year, our approach is suited for disentangling telluric and stellar spectral components. By fitting a synthetic transmission model, telluric-free spectra are derived. We demonstrate the performance of the TDTM technique in correcting telluric contamination using a high-resolution optical spectral time series of the feature-rich M3.0 dwarf star Wolf 294 that was obtained with the CARMENES spectrograph. We apply the TDTM approach to the CARMENES survey sample, which consists of 382 targets encompassing 22 357 optical and 20 314 near-infrared spectra, to correct for telluric absorption. The corrected spectra are coadded to construct template spectra for each of our targets. This library of telluric-free, high signal-to-noise ratio, high-resolution (ℛ > 80 000) templates comprises the most comprehensive collection of spectral M-dwarf data available to date, both in terms of quantity and quality, and is available at the project website.
Key words: atmospheric effects / instrumentation: spectrographs / methods: data analysis / methods: observational / stars: low-mass / techniques: spectroscopic
Full Table C.1 and the template library spectra are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/680/A73. The template library spectra are further accessible online (http://carmenes.cab.inta-csic.es).
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Cool, low-mass M dwarfs are particularly promising targets for detecting rocky habitable-zone planets because of their relatively short orbital periods of about 20 d and the favorable planet-to-star mass ratios. As M dwarfs are intrinsically faint in the visible wavelength range and emit the bulk of their energy at ~1 µm, a new generation of high-resolution spectrographs, such as CARMENES (Quirrenbach et al. 2020), SPIRou (Donati et al. 2018), HPF (Mahadevan et al. 2014), IRD (Kotani et al. 2018), CRIRES+ (Dorn et al. 2023), and NIRPS (Wildi et al. 2017), have been designed and built to exploit the near-infrared wavelength range for radial velocity (RV) planet searches.
Ground-based spectroscopic observations at optical and, in particular, at near-infrared wavelengths are affected by absorption and emission features produced by the Earth’s atmosphere. Rotational-vibrational transitions of molecules such as water (H2O), oxygen (O2), carbon dioxide (CO2), and methane (CH4) produce numerous absorption lines and broad absorption bands.
The relative strength of individual lines exhibits a considerable range, extending from shallow so-called microtellurics, which present with flux depths of ≲1−2%, to potent lines characterized by completely opaque line cores, signifying a total absence of light transmission. These telluric lines are a common nuisance in ground-based spectroscopy, and in particular, in precise RV measurements (Cunha et al. 2014; Leet et al. 2019; Wang et al. 2022; Latouf et al. 2022).
The atmospheric conditions at the time of observation determine the telluric contribution to a stellar spectrum observed from the ground. The observed strength of the telluric lines depends on the location of the observatory, particularly its elevation, and on the airmass of the target. Furthermore, telluric absorption lines are Doppler shifted and broadened due to turbulent wind motions along the line of sight (e.g., Caccin et al. 1985). The atmospheric temperature and partial-pressure structure have a direct impact on the line profiles. The situation is further complicated by the temporal variability in temperature, pressure, and chemical composition of the Earth’s atmosphere on seasonal, daily, and hourly timescales, which is particularly pronounced for the atmospheric water vapor content (Smette et al. 2015).
To date, several elaborated approaches have been developed to correct for telluric lines. They can roughly be subdivided into empirical, data-driven, and forward-modeling approaches. A widely used empirical technique is telluric division. Here, telluric standard stars (TSS), which usually are rapidly rotating B-to A-type stars, are observed along with the science target observation, preferably similar to the science target in time, airmass, and direction. However, some compromises have to be made regarding these parameters. The drawbacks of the telluric division method have been extensively discussed by, for instance, Vacca et al. (2003), Bailey et al. (2007), Seifahrt et al. (2010), Gullikson et al. (2014), and Smette et al. (2015). Large RV surveys such as those conducted by the HARPS and CARMENES collaborations refrained from frequent TSS observations because a tremendous amount of additional observing time is needed.
An empirical approach, avoiding frequent and repeated TSS observations, was presented by Artigau et al. (2014). These authors created a library of TSS spectra, observed on a dense grid of airmasses and water columns. By carrying out a principal component analysis, they identified independently varying spectral absorption patterns. Thus, telluric spectra were synthesized by using linear combinations of individual absorbances, which Artigau et al. (2014) subsequently removed from HARPS measurements.
A data-driven technique involving machine-learning algorithms was presented by Bedell et al. (2019). Their wobble algorithm incorporates a model for simultaneously deriving the stellar spectra, telluric spectra, and RVs from spectral time series without relying on external information on either the stellar or the telluric transmission spectrum.
While purely data-driven techniques are highly flexible, copious information on the atmosphere of the Earth and its spectrum is available. Synthetic transmission models of the spectrum of the Earth’s atmosphere take advantage of this. They can be generated by radiative transfer codes (for an overview see Seifahrt et al. 2010) in combination with precise molecular line databases, and have become widely used (e.g., Bailey et al. 2007; Seifahrt et al. 2010; Lockwood et al. 2014; Husser & Ulbrich 2014; Gullikson et al. 2014; Rudolf et al. 2016; Allart et al. 2022). Recently, Artigau et al. (2022) introduced a hybrid method in which they first employed the TAPAS1 atmospheric model (Bertaux et al. 2014) to establish a first-order correction, and then computed an empirical correction model derived from a sample of TSSs for the residuals that remain. This approach was implemented into the SPIRou data reduction pipeline APERO (Cook et al. 2022).
The software package molecfit2, developed by Smette et al. (2015) and Kausch et al. (2015), implements a synthetic telluric transmission model and allows correcting observed spectra for telluric contamination. To this end, molecfit incorporates the line-by-line radiative transfer code LBLRTM (Clough et al. 2005) and the HITRAN molecular line list (Rothman et al. 2009). To synthesize a telluric spectrum, molecfit requires a number of parameters such as a model of the instrumental line spread function (LSF), an atmospheric profile describing the meteorological conditions during the observation, and the column density of the molecular species. In turn, the observed spectrum, which contains the telluric transmission spectrum, can be used to find best-fit values for these parameters. molecfit does not consider the actual stellar spectrum, which occurs as a contaminant of the telluric spectrum in this context. Therefore, only a suitable subrange of the observed spectrum is commonly used in the fit, which ideally contains moderately saturated telluric lines with a well-defined continuum. Based on the resulting atmospheric parameters, the telluric spectrum in the remaining range can then be inferred. While this approach works well in many cases, it becomes problematic in objects with ubiquitous intrinsic features such as M dwarfs, where the fitting becomes inaccurate because of numerous blends between stellar and telluric lines.
One of the largest M-dwarf surveys has been conducted by CARMENES. In the course of the guaranteed time observations (GTO) program in 2016 to 2020, more than 19000 high-resolution spectra were obtained in the optical and about the same number in the near-infrared, which is equivalent to about 5000 observing hours (Quirrenbach et al. 2020; Ribas et al. 2023). Meanwhile, the survey is being continued as a legacy program with 300 additional nights until the end of 2023. As telluric contamination is particularly severe in the wavelength range covered by CARMENES (5200–17 100 Å), accurate telluric correction is called for.
To expand the range of applications of molecfit to M-dwarf spectra with strong line crowding, we developed the template division telluric modeling (TDTM) technique. The heart of TDTM is the disentanglement of sections of the telluric and stellar spectra by taking advantage of the relative shift between stellar and telluric lines caused by the Earth’s barycentric motion. We then use molecfit to fit a synthetic transmission model to the extracted telluric spectrum and apply these results to correct for telluric absorption in the entire science spectrum. While the TDTM technique works independently of stellar spectral type, it is only applicable when spectroscopic time series that sample a range of barycentric velocity shifts are available. Time series like this have been provided by the CARMENES survey for more than 300 M-dwarf stars (Reiners et al. 2018). In recent years, our individual telluric-corrected spectra as well as telluric-corrected template spectra have been used in the context of planet detection (e.g., Polanski et al. 2021; Blanco-Pozo et al. 2023; Kossakowski et al. 2023), atmospheric characterization (e.g., Nortmann et al. 2018; Salz et al. 2018; Alonso-Floriano et al. 2019; Palle et al. 2020; Orell-Miquel et al. 2022, 2023), magnetic field measurements (Shulyak et al. 2019; Reiners et al. 2022), photospheric parameter determinations (Passegger et al. 2019, 2020; Marfil et al. 2020, 2021), abundance analyses (Abia et al. 2020; Shan et al. 2021), or chromospheric activity studies (Fuhrmeister et al. 2019, 2020, 2022, 2023; Hintz et al. 2020, 2023). Here, we apply TDTM, which is publicly available3, to the CARMENES survey spectra and subsequently construct telluric-free template spectra with a high signal-to-noise ratio (S/N) for the stars in our sample. As a service to the community, we publish them along with this paper.
Our paper is structured as follows. In Sect. 2, we describe our M-dwarf sample. The TDTM technique and the data preparation are presented in Sect. 3, and our findings are discussed in Sect. 4. Finally, we summarize our results in Sect. 5.
2 M-dwarf sample
The spectra used in this work were taken within the context of the CARMENES4 survey. Constructed by 11 German and Spanish institutions, CARMENES consists of a pair of cross-dispersed fiber-fed échelle spectrographs, mounted on the 3.5 m telescope of the Calar Alto Observatory in Spain (Quirrenbach et al. 2020).
The instrument has two channels. The visual channel (VIS) provides wavelength coverage between 5200 Å and 9600 Å with a resolution of ℛ = 94 600, and the near-infrared channel (NIR) has a resolving power of ℛ = 80 400 and covers the spectral range from 9600 Å to 17 100 Å. Both channels are enclosed in vacuum vessels in the coudé room to ensure long-term stability. The data reduction was carried out using the standard CARMENES reduction pipeline caracal5 (Zechmeister et al. 2014; Caballero et al. 2016b).
We removed 17 spectroscopic binaries and triple systems from the full CARMENES M-dwarf sample of 402 stars, as found by Baroch et al. (2018, 2021). In addition, we excluded three targets that were observed for a period shorter than a month. Our final sample in this work encompasses 382 stars across the full M-dwarf range from M0.0 to M9.0. Additionally, two K5.0 and two K7.0 dwarfs are included in the sample. Insights into target selection, sample characteristics, and data quality were provided by Reiners et al. (2018), Quirrenbach et al. (2020), Ribas et al. (2023), and references therein.
To demonstrate the use of the TDTM technique, we selected 444 VIS and 398 NIR observations of the bright M3.0 dwarf Wolf 294 (HD 265866, GJ 251, J06548+332), obtained between January 2016 and May 2023. Wolf 294 serves as a representative of an object with a feature-rich spectrum. A typical S/N for CARMENES survey observations is 150 in the J band (Reiners et al. 2018), which translates into a median exposure time of 545 s for Wolf 294. We refer to Stock et al. (2020) for more details on the star and its temperate super-Earth.
3 Telluric correction
Fitting telluric transmission models to observed M-dwarf spectra is challenging because the stellar spectrum consists of numerous atomic and molecular lines without a well-defined continuum. The fundamental idea behind the TDTM approach is to construct a template of the stellar spectrum with a high S/N from a spectral time series, which can subsequently be used to eliminate the stellar contribution and to model the residual telluric spectrum.
3.1 Template construction
We used the serval6 code (Zechmeister et al. 2018) to compute the stellar template spectrum based on a time series of input spectra. Following the nomenclature of Zechmeister et al. (2018), we indexed the set of spectra by n = 1,…, N, and each spectrum was composed of discrete flux density measurements fn,i at pixel i with uncertainties ϵn,i and calibrated wavelengths λn,i. We furthermore write the continuous model for the observation in the form
![$f\left( \lambda \right) = \left[ {s\left( \lambda \right) \cdot t\left( \lambda \right)} \right] \otimes L\left( \lambda \right),$](/articles/aa/full_html/2023/12/aa46524-23/aa46524-23-eq1.png) (1)
(1)
where s(λ) denotes the intrinsic stellar spectrum, t(λ) the intrinsic telluric absorption spectrum at the time of observation, L(λ) the LSF, and ⊗ the convolution operator.
In each observation, a stellar spectrum with an a priori unknown RV shift and a telluric spectrum with variable properties, but fixed in the rest frame of the Earth, were superimposed. The ultimate goal of serval is to derive precise measurements of the stellar RV. To this end, a preferably accurate and complete template of the stellar spectrum is required. This template was constructed by serval from the spectral time series, following an iterative and sequential forward-modeling approach.
Template completeness is improved by taking advantage of the relative RV shift of the stellar and telluric spectra induced by Earth’s barycentric motion, which can uncover sections of the stellar spectrum in some observations that may be affected by telluric lines in others with a less favorable relative RV shift. To identify these sections, serval uses a binary mask mn,i, flagging spectral pixels that are affected by known atmospheric absorption features that are typically deeper than 1% (see Sect. 3.2). Additionally, serval employs a bad-pixel map that flags saturated pixels, outliers, pixels providing unphysical (negative) flux densities, and pixels affected by sky emission. The template S/N is improved by coadding the individual spectra after an appropriate RV shift. During this process, the spectra are transformed to the stellar rest frame, that is, they are corrected for barycentric and stellar RVs. serval also accounts for secular acceleration, which is a change in the stellar radial velocity due to the high proper motion of close-by stars (Kürster et al. 2003; Zechmeister et al. 2009).
As a starting point for RV and template calculation, serval calculates preliminary RVs using the highest S/N spectrum of the CARMENES spectral time series as a template. These RVs are subsequently used to improve the stellar template spectrum by coadding the individual spectra and by obtaining higher precision RVs. This process is repeated until convergence is achieved. All masked pixels are excluded, and telluric-affected pixels are heavily downweighted in the process of coadding to isolate the stellar spectrum in the template.
The process of improving the template completeness by taking advantage of the relative shift of the mask is demonstrated in Fig. 1. The upper and middle panels show a segment of the telluric mask position of two observations after the correction for Earth’s barycentric motion. The lower panel shows the resulting mask of the template, assuming that the intrinsic RV shift of the stellar spectrum remained small. In the blue shaded regions, the stellar spectrum is shown in one of the observations, and only the red shaded ranges remain hidden. This results in an improvement of the template wavelength coverage.
Shifting the spectra to the same reference wavelength results in a wavelength sampling that differs for data taken at different nights. serval avoids resampling the spectral data on a new discrete wavelength grid and directly carries out a cubic B-spline regression. In essence, the template is the best-fitting spline through scattered data, and it is a continuous function that can be evaluated at any point within its boundaries, as illustrated in Fig. 2 of Zechmeister et al. (2018). The uniform cubic B-spline has equidistant knots k on a logarithmic wavelength grid ln λk. Typically, the number of template knots is comparable to the number of pixels per spectral order. In the following, sk = s(λk) refers to the stellar template flux density at the knot positions. As an example, a section of the template of Wolf 294 is shown in Fig. 2a.
As a crucial quantity for the TDTM approach, we define Mk as the number of unflagged pixels that contribute to a knot. Mk is stored for each template knot. The link between Mk and the mask can be inferred from the lower panel of Fig. 1. In this specific example with only two observations, Mk = 0 for template knots falling into the red marked wavelength range, Mk = 1 for knots within the blue wavelength range, and Mk = 2 for the remaining part of the spectrum.
Therefore, given one particular template knot k, three situations are possible: (1) all pixels contributing to this knot contain spectral information (i.e., are not masked), (2) all pixels are masked, (3) some pixels contain spectral information, while the remaining pixels are masked. The quantity Mk is maximized in case (1), decreases for knots that are partly affected by tellurics in case (3), and takes a value of Mk = 0 for pixels in case (2). For sampling reasons, spectra can contribute more than one pixel to a template knot, so that Mk can exceed the number N of observations. This is demonstrated in Fig. 2a, where a few template knots have Mk ≳ 500, although the number of observations is NVIS = 444. The red shaded areas show wavelength ranges for which Mk is zero, that is, the stellar spectrum could not be recovered.
As the total masked template fraction γ, we defined the fraction of masked ranges (Mk = 0) compared to the entire wavelength range of the spectrum. As a result, the template completeness corresponds to 1 – γ and depends on barycentric RV of the observer. The wavelength ranges of the stellar spectrum that are characterized by overlapping masked and non-masked regions, indicated by the blue shaded areas in Fig. 1 and recovered in the process, are now additionally available for RV calculation and telluric modeling. We denote the total fraction of these ranges compared to the entire wavelength range of the spectrum by γ′.
 |
Fig. 1 Example of template completion using a binary telluric mask. Upper and middle panels: small section of the telluric binary mask for two observations after the correction for Earth’s barycentric motion. Wavelength ranges with y = 1 are masked as tellurics. Lower panel: resulting mask of the template. The red shaded wavelength ranges correspond to template knots with Mk = 0 and contribute to the total masked template fraction γ. The blue shaded wavelength ranges are used for telluric modeling and contribute to γ′. |
3.2 Mask construction
The telluric mask is an essential ingredient of the TDTM technique. As telluric features are ubiquitous, mask construction needs to balance strictness and achievable template completeness. While a restrictive mask that covers all relevant telluric features is crucial for creating a useful stellar template, an overly strict mask that declares extended chunks of the spectrum unusable jeopardizes the derivation of a template with any practical value.
To construct masks, we computed a synthetic telluric transmission model including H2O, O2, CO2, and CH4 using molecfit. As input parameters, we used the median observational and atmospheric parameters in the data set of each star and adopted the values from the standard atmosphere profile for the column densities of the atmospheric constituents. In the resulting transmission models, we normalized wavelength ranges that were affected by molecular continuum absorption. For each target, we finally computed a binary mask by flagging all model features that were deeper than a specified threshold. In our analysis, we found that thresholds of ~1% provide a reasonable compromise between capturing the vast majority of telluric features and removing critical portions of usable spectrum.
3.3 Extraction of the telluric spectrum
To extract the telluric transmission spectrum, we wish to remove the stellar contribution from the individual observations by division. Following Vacca et al. (2003), we therefore approximated the convolution of the product in Eq. (1) by
![$F\left( \lambda \right) \approx \left[ {s\left( \lambda \right) \otimes L\left( \lambda \right)} \right] \cdot \left[ {t\left( \lambda \right) \otimes L\left( \lambda \right)} \right]$](/articles/aa/full_html/2023/12/aa46524-23/aa46524-23-eq2.png) (2)
(2)
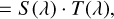 (3)
(3)
which is now a product of the convolved intrinsic stellar flux density and the convolved telluric spectrum,
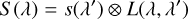 (4)
(4)
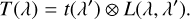 (5)
(5)
We discuss the validity of this approximation in Appendix A.
Dividing the observed spectra by the appropriately shifted template, we derived a residual spectrum that is essentially free of stellar features,
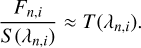 (6)
(6)
As the uncertainty of the template is typically negligible compared to that of the individual observations as Mk ≫ 1, we did not propagate the template uncertainty and used the uncertainty of the observed spectra in the modeling of the individual residual spectra.
The residual telluric transmission spectrum of Wolf 294 is shown in Fig. 2b. Again, the red bands represent template knots for which the residual spectrum could not be constrained. Consequently, these sections are not used to model the telluric lines.
 |
Fig. 2 Illustration of the TDTM method. Panel a: segment of the VIS template spectrum of Wolf 294. The number Mk of exposure pixels that contribute to each template knot is color-coded. The red shaded wavelength ranges mark knots with Mk = 0. Panel b: one residual telluric spectrum Fn,i/S (λn,i) (black dots) after the division of the science spectrum by the template, and the best-fit telluric model (T(λn,i), green line) derived with molecfit. The red shaded wavelength ranges are excluded from the transmission model fit. Panel c: absolute residuals Fn,i/S(λn,i) – T(λn,i) of the fit. Panel d: CARMENES spectrum before (Fn,i, red line) and after (Fn,i/T(λn,i)) correction with the transmission model derived with molecfit (black line). Panel e: telluric free high S/N template spectrum of Wolf 294 (black line) built using 444 telluric absorption- corrected CARMENES observations. The order has a S/N of 2310. |
3.4 Modeling the telluric lines
The residual telluric spectrum was modeled using the molecfit package version 1.5.9 (Smette et al. 2015; Kausch et al. 2015) and the version 3.6 of the aer7 molecular line list. The altitude stratification of temperature, pressure, and molecular abundances served as input for LBLRTM. To create this profile, molecfit merges information from three sources: (1) a reference atmospheric profile, (2) global data assimilation system (GDAS) profiles8, and (3) measurements of the ambient conditions obtained during the time of observations. In this study, we used a nightly midlatitude (45 deg) reference model atmosphere9 as the reference profile. In addition to the pressure and temperature distribution up to an altitude of 120 km as a function of height on a 1 km grid, the profile also provides the abundances of 30 molecules. The GDAS profiles describe the pressure, temperature, and relative humidity as a function of 23 altitude levels up to roughly 26 km.
In the spectral modeling with molecfit, we freely varied the abundances of O2, CO2, CH4, and the atmospheric water vapor content. We carried out the model fitting over broad wavelength ranges that covered large portions of the molecular bands, taking full advantage of numerous unsaturated telluric lines contained in the CARMENES VIS and NIR channels; the selected fitting intervals are given in Table 1. In the modeling, the continuum level within the fitting ranges was approximated with a low-order polynomial. Since small errors in the wavelength calibration result in large residuals in the corrected spectra, we also allowed a Doppler shift of the transmission model to match the observed spectrum. In this way, instrumental drifts can be accounted for in the modeling. Wavelength ranges for which no stellar template was available (Mk = 0) were excluded from the fit, along with sections affected by sky emission features.
molecfit requires the instrumental LSF in the modeling. In the case of CARMENES, the LSF can be represented by a combination of two profiles, one Gaussian and one Lorentzian. We performed an extensive analysis to derive appropriate parameters for the LSFs of the two CARMENES channels based on calibration data (see Sect. 3.5). Therefore, the parameters of the LSF were not free in the modeling.
molecfit fitting ranges used to calibrate the models for CARMENES VIS and NIR spectra.
3.5 CARMENES instrumental line profile
For a proper modeling of the telluric lines, the LSF needs to be well known. In order to characterize the LSF, we analyzed hollow cathode lamp spectra taken for the purpose of calibration before and after the science observations.
An accurate estimation of the line shape is not trivial because the lines are sparsely sampled. Within each échelle order, the coverage of the full width at half maximum (FWHM) of the LSF typically increases from about 2.5 to 4.0 pixels along the main dispersion direction from the blue to the red part of the order. Due to several instrumental effects (e.g., temperature variations), the spectra move across the detector with time. We therefore combined multiple exposures to artificially increase the sampling. A total of 1455 different lamp exposures in the VIS channel and 2605 in the NIR channel were used for this purpose. For each line we investigated in that manner (218 in the VIS and 114 in the NIR), the frames were aligned so that the line was centered. Before they were combined, they were normalized.
These superimposed line profiles are well suited to modeling the shape of the LSF. For this purpose, we tested different profiles, namely Gaussians and Lorentzians, generalized Gaussians and Lorentzians with the exponent treated as an additional free parameter, as well as Voigt profiles, which are defined by the convolution of Lorentzian and Gaussian distributions. The analysis of all fits showed that a Voigt profile is the most appropriate for the LSF modeling. The other profiles were usually not suitable for a proper simultaneous handling of the line cores and lobes.
In addition, we investigated the variations in the measured line widths, Δλ, across the detector and found that except for some secondary but significant features near the detector edges (particularly in the blue part of the VIS CCD), the line widths still can be described in a consistent manner. The dominant effect becomes apparent when the widths of the lines are expressed in terms of wavelength. In the Voigt profile, the overall width can be described by its Gaussian and Lorentzian components. If the resolution remains constant, both components should exhibit a linear trend in wavelength. However, when they are represented in wavelength-independent units using Δλ/λc, where λc represents the central vacuum wavelength of the specific line, these normalized widths are expected to stay constant if the spectrograph resolution is independent of wavelength.
In Fig. 3, we show the measured Gaussian and Lorentzian FWHM components of the Voigt profile for both channels. The NIR channel has a somewhat lower resolution and therefore presents a wider Gaussian component than the VIS channel. However, the widths of the Lorentzian component are very similar for both channels redward of 6000 Å.
To obtain robust estimates of the LSF parameters, we used medians for the FWHM of each component and channel to model the instrumental LSF of CARMENES. These parameters are summarized in Table 2. Due to the clearly visible deviation in the blue part of the visual channel, we considered only lines with a wavelength above 6000 Å. Moreover, the distribution of the Lorentzian component, particularly in the NIR part of the spectrum, shows some conspicuous features. Some outliers cluster around 12 500 Å, while the scatter seems generally increased for wavelengths above 15 000 Å. The reasons for these effects could not consistently and objectively be traced back to line blends or similar effects.
 |
Fig. 3 Measured Gaussian and Lorentzian FWHM components of hollow cathode emission lines as a function of wavelength for the VIS and NIR CARMENES spectrographs. The vertical gray line marks the cutoff wavelength at 6000 Å. The horizontal lines indicate median values of the Gaussian and Lorentzian FWHM components for the VIS (dashed lines) and NIR channel (dotted lines). |
Median averaged Gaussian and Lorentzian FWHMs.
 |
Fig. 4 Distribution of the number of telluric-corrected spectra we used to build the templates for all sample stars in the VIS (left) and NIR (right). The vertical dashed lines indicate the median values at 34 in the VIS and 30 in the NIR. |
3.6 Removing the telluric lines
After fitting a transmission model to the residual telluric spectrum with molecfit, we used the best-fit parameters as input to compute a synthetic transmission model over the entire wavelength range of the observation with the calctrans module of molecfit. To derive the spectrum corrected for telluric lines 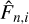 , we finally divided the CARMENES observation by the transmission model T(λn,i),
, we finally divided the CARMENES observation by the transmission model T(λn,i),
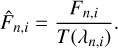 (7)
(7)
As an example, we show one observed and its telluric corrected spectrum of Wolf 294 in Fig. 2d.
4 Telluric-corrected M-dwarf template library
4.1 Sample overview
We applied the TDTM method to each of the 382 targets in our sample and generated a spectrum corrected for telluric absorption for each individual VIS and NIR CARMENES observation. The telluric-corrected spectra for each target were subsequently coadded to create a telluric-free stellar template spectrum with a high S/N with serval. We show the example of Wolf 294 in Fig. 2e, where the displayed order reaches a S/N of 2310.
To construct the library of telluric-free template spectra with a high S/N, we used a total of 22 357 VIS and 20314 NIR observations obtained between 2016 and 2023 that were telluric-corrected with the TDTM method before coaddition. In Table C.1, we present the sample of stars we used in this study and provide information on the targets. In particular, we tabulate the CARMENES identifiers, common names, Gliese-Jahreiss numbers, equatorial coordinates at epoch J2000, spectral types, 2MASS J magnitudes (Alonso-Floriano et al. 2015; Caballero et al. 2016a), the number of telluric-corrected VIS and NIR spectra used to create the telluric-free stellar templates, and the estimated S/N of a reference order at 8600 Å for the VIS templates and at 10 500 Å for the NIR templates. Our template spectra can be downloaded from the CARMENES GTO Data Archive (Caballero et al. 2016b)10.
In the VIS, the number of spectra used for the coadding ranged from 5 up to 774, with a very similar number of spectra in the NIR (from 4 to 756). In the reference orders, the range of the S/N in the VIS varies between 9 and 3057, and in the NIR, it varies between 9 and 3270. We show the distributions of the number of spectra we used for the coaddition in Fig. 4. The median values indicated by the vertical dashed lines in both figures are 34 in the VIS and 30 in the NIR. The distributions of the S/N of the template spectra given in the reference orders are shown in Fig. 5, with median values of 438 in the VIS and 482 in the NIR. Finally, we present the time span of the observations covered for each target in Fig. 6, with median values of 3.83 yr in the VIS and 3.70 in the NIR.
4.2 Correction accuracy
In the following, we examine the accuracy of the telluric correction applied to individual VIS and NIR CARMENES spectra of Wolf 294, using the TDTM approach. Figures B.1–B.7 display examples of the corrections applied to individual lines within a single spectrum, with a focus on specific molecular constituents. For VIS, these molecules include O2 and H2O, while in NIR, they extend to O2, H2O, CO2, and CH4. We assessed the accuracy of these corrections by computing the standard deviation σ of the residuals. In most cases, σ was found to be below the 1% level. An exception was observed in the O2 lines within the VIS spectrum, which generally fell within the 1–2% range. Additionally, some CO2 lines exhibited σ values greater than 2%. These discrepancies may be attributed to an inadequate removal of the stellar spectrum, leading to a distortion in the telluric residual spectrum in the given instance.
To further analyze the variability in the residuals relative to the line depth, an automated procedure was implemented. This procedure detected lines in the telluric residual spectrum, fit a Gaussian model to ascertain the depths, positions (µ), and widths (σGaussian) of the telluric lines, and measured the variability in the residuals within a wavelength range of µ ± 3 σGaussian. The top panel of Fig. 7 illustrates the results for a single spectrum of Wolf 294. In both CARMENES channels, the σ values were confined to a range of 0.3 to 3.0%. Optimal outcomes were observed for line depths up to 30%, where σ was mostly lower than 1%. Our findings indicated a weak or nonexistent correlation between σ and line depth.
Subsequently, we explored the variability in the residuals as a function of airmass for all VIS and NIR spectra of Wolf 294. To this end, we introduced 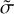 , defined as the median of the measured σ values within a single Wolf 294 spectrum, and we present the results in the middle panel of Fig. 7. Most spectra exhibited a
, defined as the median of the measured σ values within a single Wolf 294 spectrum, and we present the results in the middle panel of Fig. 7. Most spectra exhibited a 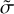 value of approximately 1–2% in the entire airmass range. The discrepancy in ŕ between the VIS and NIR channels is ascribed to the reduced number of usable telluric lines in the NIR spectra relative to the VIS spectra (see the top panel of Fig. 7), leading to reduced scatter and, consequently, a lower value for
value of approximately 1–2% in the entire airmass range. The discrepancy in ŕ between the VIS and NIR channels is ascribed to the reduced number of usable telluric lines in the NIR spectra relative to the VIS spectra (see the top panel of Fig. 7), leading to reduced scatter and, consequently, a lower value for 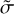 . However, a minor subset of spectra revealed
. However, a minor subset of spectra revealed 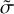 values that reached up to 6– 7%. A visual inspection identified these spectra as characterized by low S/N.
values that reached up to 6– 7%. A visual inspection identified these spectra as characterized by low S/N.
Finally, we calculated 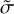 and only included H2O telluric lines. We display the results as a function of precipitable water vapor derived with molecfit, as illustrated in the bottom panel of Fig. 7. Although the
and only included H2O telluric lines. We display the results as a function of precipitable water vapor derived with molecfit, as illustrated in the bottom panel of Fig. 7. Although the 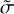 values derived in the NIR exhibit greater scatter than the VIS spectra, the findings in both channels agree and did not disclose any discernible trends.
values derived in the NIR exhibit greater scatter than the VIS spectra, the findings in both channels agree and did not disclose any discernible trends.
Overall, our results indicate that the correction accuracy mostly depends on the S/N of the data and to a much lesser extent on the depth of the telluric features. Most telluric features can be corrected to basically within the noise level. Deep lines are problematic for two reasons. First, the S/N decreases in their cores, and second, lines deeper than 50% can leave comparatively large systematic residuals in the corrected spectra, especially in the line cores. These residuals may be attributed to the fact that small discrepancies between model and observation can result in large residuals, especially in deep lines. These discrepancies may result from uncertainties in the line strengths listed in the HITRAN database, leading to inaccurate column density fits (Seifahrt et al. 2010; Gordon et al. 2011). Potential uncertainties in the line positions affect the wavelength calibration, causing P Cygni-like residuals in the worst cases. Incomplete corrections may also arise from the instrumental line profile model. The Gaussian and Lorentzian profile parameters from different lines show some scatter and are approximated by a constant value (see Sect. 3.5). Another source of uncertainty is the approximation of Eq. (1) by Eq. (3), which becomes particularly relevant for blends between telluric and stellar lines (Sameshima et al. 2018, their Appendix A).
We find that most telluric absorption features are corrected to within 2% or better of the continuum standard deviation, as reported by Smette et al. (2015). For objects with numerous intrinsic features, the authors proposed to apply molecfit to TSSs observations taken with the same instrumental setup as the science object to solve for the polynomial continuum coefficients. These results are then used as fixed input to subsequently apply molecfit for the science observation’s telluric correction. Our approach, however, is able to accurately and directly extract telluric features of various strengths for wavelength ranges with Mk > 0, even for feature-rich objects such as M dwarfs, whose spectra are dominated by numerous molecular features in the VIS and NIR bands.
 |
Fig. 5 Distribution of the S/N of a reference order for the VIS (order 70 around 8600 Å, left) and the NIR (order 52 around 10 500 Å, right). The vertical dashed lines indicate the median values at 438 in the VIS and 482 in the NIR. |
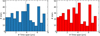 |
Fig. 6 Time-span distribution of the observations for the sample stars for the VIS (left) and NIR spectra (right). The vertical dashed lines indicate the median values at 3.83 yr in the VIS and 3.70 yr in the NIR. |
 |
Fig. 7 Metrics for assessing the quality of the telluric correction. Top panel: residual standard deviation (cx) vs. line depth for a single Wolf 294 VIS (blue) and NIR (red) spectrum. Middle panel: median residual standard deviation ( |
4.3 Visibility constraints
For the TDTM technique to work properly, a good template is essential. While a lack of S/N may be addressed by taking more observations, which may pose a practical but not a fundamental problem, the relative shift between telluric and stellar lines is also crucial for the template construction. In the case of planet-induced reflex motion, the barycentric motion of the Earth and its rotation dominate the sum of relative shifts. The maximum absolute barycentric velocity υbary,max depends on the ecliptic latitude β of a target,
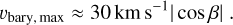 (8)
(8)
The transformation from the ecliptic (λ,β) to the equatorial system (α, δ) with the axial tilt of the Earth ε ≈ 23.44 deg yields
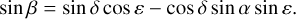 (9)
(9)
Thus, υbary,max as a function of a and δ reads
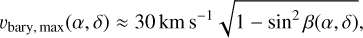 (10)
(10)
which provides a sky map as in the left panel of Fig. 8 showing the maximum offset between telluric lines and stellar lines. Except for objects situated near the ecliptic poles, υbary,max is larger than the natural line width of the tellurics and the instrumental resolution (~3 km s−1), which is required to disentangle the stellar and telluric spectra.
To examine the largest possible improvement on the template completeness, we carried out a simulation of the full amplitude of the barycentric velocity range υbary,max – υbary,min as a function of ecliptic coordinates down to the visibility cutoff for stars with δ < 23 deg, which is also the CARMENES survey limit (Garcia-Piquer et al. 2017). In particular, we computed the dates on which a target is 30 deg above the horizon between the astronomical dusk and dawn for the location of the Calar Alto Observatory, and calculated the barycentric RV at midnight for these dates. In the right panel of Fig. 8, we show the difference between the maximum and minimum barycentric RV υbary,max – υbary,min,min for each pair of coordinates.
The observed barycentric velocity range is further constrained by the visibility. The main contribution to the barycentric velocity is a yearly sinusoid. We considered an object with a half-year visibility period, during which the barycentric Earth RV changes from a maximum to a minimum. In particular, we considered the first half of a cosine
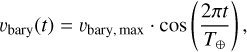 (11)
(11)
where T⊕ is the orbital period of the Earth. When the target is observed at a random time, the probability to observe a barycentric RV shift equal to or smaller than υobs is
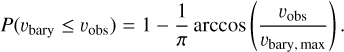 (12)
(12)
The probability density function, PDF(υbary), to observe the target in some interval of barycentric velocity is given by
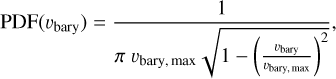 (13)
(13)
which is shown in Fig. 9a.
To study the barycentric velocity distribution as a function of right ascension and declination over 1 yr for the location of the Calar Alto Observatory, we carried out simulations for a set of coordinates with a = 0 h, 6h, 12 h, and 18 h, and δ = 0deg, +30 deg, +60 deg, and +90 deg. In addition, we included a southern coordinate sample with δ = −22 deg, which is near the visibility limit of the CARMENES survey. Assuming that objects can generally only be observed down to an elevation of 30 deg, we determined the nights when the target is observable and computed the barycentric velocity at the time between evening and morning astronomical twilight. Our results are presented in Figs. 9b–e. The simulated distributions show a plateau around υbary = 0 and increasing slopes at both ends where υbary → ±υbary,max. This shape is a consequence of the regular sampling of the yearly sinusoidal barycentric velocity contribution. However, the simulations show that all barycentric velocities between −υberv,max and +υberv,max are covered. We finally present the predicted and observed barycentric velocity distribution of Wolf 294 (Fig. 9f) of our spectroscopic data set.
 |
Fig. 8 Sky maps in Aitoff projection of the maximum absolute barycentric RV υbary,max as derived from Eq. (10) (left panel) and full amplitude of the barycentric RV υbary,max – υbary,min (right panel) for nights when the star is observable above 30deg over the horizon for the location of the Calar Alto Observatory. The positions of the 382 sample stars (purple circles) are indicated. The hatching pattern indicates the visibility cutoff at δ < −23 deg of the CARMENES sample. |
4.4 Total masking fraction
In the case of Wolf 294, a mask that flags telluric features deeper than 1% results in a total masking fraction γmax,VIS = 33.5% for the optical spectral range (0.52–0.96 µm) and γmax,NIR = 62.8% for the NIR (0.96–1.71 µm) when using one observation. As the number of observations with different barycentric velocities is increased, the total masked fraction decreases and converges to a limit of γmin,VIS = 16.5% and γmin,NIR = 42.5% for the 1% mask. These limits are mainly defined by broad telluric features, for example, the strong water bands centered around 1.15 µm and 1.4 µm, which prevent further reduction of masked regions.
The difference between the maximum and minimum masking fraction is the total fraction that is gained for the modeling of the telluric spectrum, which is γ′max,VIS = 17.0% in the optical and γ′max,NIR = 20.3% in the NIR employing the 1% mask. In the VIS, the useable amount of the stellar spectrum was increased from 66.5% to 83.5%, which corresponds to an increase of 25.6%. The increment is even larger in the NIR, where the useable range was increased from 37.2% to 57.5%, which corresponds to a relative growth of 54.6%.
We show the evolution of the total masked fraction using the 1% mask for Wolf 294 Fig. 10. To reach the lower limit of the total masked fraction, it is necessary to cover the full range of barycentric velocities. As shown in Fig. 10, this requirement was fulfilled for Wolf 294 after the first observing season. Additionally, a limited number of observations at approximately ±30 km s−1 substantially reduces the total masked fraction. Our simulations indicate that with six observations that are uniformly distributed across the barycentric velocity space of ±30 km s−1, values of 17.9% in the VIS and 40.3% in the NIR can be achieved. However, for proper telluric correction, a barycentric velocity coverage 2–5 times larger than the minimum 3 km s−1 required to resolve the lines is essential, which means that velocity spans of 6–15 km s−1 are imperative.
5 Summary and conclusions
We presented the TDTM technique, a combination of data-driven (template construction) and forward-modeling (spectral fitting) methods to correct for telluric absorption lines in high-resolution VIS and NIR spectra. After applying a telluric mask to a time series of spectra, we constructed a stellar template with a high S/N and used it to remove the stellar contribution from the observations. We then used molecfit to fit an atmospheric transmission model to the resulting telluric spectrum and finally corrected the target spectrum at all wavelengths. While the telluric correction via spectral modeling with molecfit alone is especially challenging for late-type stars with their high density of molecular lines, the TDTM technique is applicable to spectra of any spectral type. Although we chose the molecfit code to fit the transmission model to the telluric spectra in this work, other software packages that produce synthetic atmospheric transmission spectra, such as TelFit11 (Gullikson et al. 2014) or TAPAS (Bertaux et al. 2014), could be used.
Telluric correction with our method works best with a high number of observations and good coverage of the barycentric velocity space. To demonstrate the performance of our correction method, we applied it to high-resolution optical and NIR CARMENES observations of the M3.0V star Wolf 294. We found that molecfit corrects most telluric lines close to noise level in the residual telluric transmission spectrum obtained with the help of the template. Moreover, we did not find a correlation between the correction accuracy and the depth of telluric lines.
We applied the TDTM approach to the whole CARMENES survey sample, which comprises 382 M-dwarf stars. After correcting for telluric lines, we coadded the individual observations and constructed telluric-corrected high-resolution template spectra with a high S/N for each of our targets. Our spectral library is publicly available and can be found on the CARMENES data archive homepage.
 |
Fig. 9 Barycentric velocity distributions corresponding to various coordinate sets. Panel a: probability density function PDF(υbray) as computed with Eq. (13). Panels b-e: simulated barycentric velocity distributions for targets with a = 0 h, 6 h, 12 h, and 18 h, and δ = −22 deg, 0 deg, +30 deg, +60 deg, +90 deg, assuming one daily measurement over a time span of 1 yr and considering the target visibility. The second entry in the legend is the number of total observing nights. Panel ƒ: simulated barycentric velocity distribution of Wolf 294 (black line). The barycentric velocity distribution for the datasets of Wolf 294 (dashed red line) is overplotted. |
 |
Fig. 10 Evolution of the total masked wavelength fraction color-coded with the barycentric velocity for Wolf 294. The circles represent the VIS channel (bottom) and the triangles the NIR channel (top). The upper and lower dashed black lines mark the maximum and minimum limits of the total masked fraction in the optical wavelength range. The dotted red lines mark the same limits for the NIR wavelength range. |
Acknowledgements
We acknowledge the support of the Deutsche Forschungsgemeinschaft (DFG) priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (CZ 222/3-1, JE 701/5-1). CARMENES is an instrument at the Centra Astronómico Hispano en Andalucía (CAHA) at Calar Alto (Almería, Spain), operated jointly by the Junta de Andalucía and the Instituto de Astrofísica de Andalucía (CSIC). CARMENES was funded by the Max-Planck-Gesellschaft (MPG), the Consejo Superior de Investigaciones Científicas (CSIC), the Mnisterio de Economía y Competitividad (MINECO) and the European Regional Development Fund (ERDF) through projects FICTS-2011-02, ICTS-2017-07-CAHA-4, and CAHA16-CE-3978, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Fandessternwarte Königstuhl, Institut de Cièn-cies de ΓEspai, Institut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Fandessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the MINECO, the DFG through the Major Research Instrumentation Programme and Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. We used data from the CARMENES data archive at CAB (CSIC-INTA). We acknowledge financial support from the Agencia Estatal de Investigación (AEI/10.13039/501100011033) of the Mnisterio de Ciencia e Innovación and the ERDF “A way of making Europe” through projects PID2021-125627OB-C3l, PID2019-109522GB-C5[l:4], and the Centre of Excellence “Severo Ochoa” and “Maria de Maeztu” awards to the Instituto de Astrofísica de Canarias (CEX2019-000920-S), Instituto de Astrofísica de Andalucía (CEX2021-001131-S) and Institut de Ciències de l’Espai (CEX2020-001058-M). This work was also funded by the Generalität de Catalunya/CERCA programme, and the Israel Science Foundation through grant No. 848/16. We thank the anonymous referee for carefully reading our manuscript and for offering constructive comments that substantially helped to improve its quality.
Appendix A Approximation of the convolution equation
In an actual observation, the product of the stellar spectrum, s(λ), and the telluric transmission spectrum, t(λ), is received by the system of telescope and spectrograph, which we call the instrument. The effect of the instrument on the received spectrum is modeled by a convolution with the instrumental LSF, L(λ), so that we obtain the left-hand side of the equation,
![$\left[ {s\left( \lambda \right) \cdot t\left( \lambda \right)} \right] \otimes L\left( \lambda \right) \approx \left[ {s\left( \lambda \right) \otimes L\left( \lambda \right)} \right] \cdot \left[ {t\left( \lambda \right) \otimes L\left( \lambda \right)} \right].$](/articles/aa/full_html/2023/12/aa46524-23/aa46524-23-eq22.png) (A.1)
(A.1)
As the convolution cannot easily be inverted, the left-hand side of Eq. (A.1) is frequently approximated as a product of two spectra separately convolved with the LSF. As previously pointed out, for instance, by Sameshima et al. (2018), the two sides of the equation differ. In their analysis, Sameshima et al. (2018) found that a telluric-corrected spectrum based on this approximation differs noticeably from the stellar spectrum if the width of the stellar lines is comparable to or narrower than the instrumental resolution and if the stellar lines are heavily blended with telluric features.
We analytically investigated the difference between the two sides of Eq. (A.1), making the simplifying assumption of normality for the stellar, telluric, and instrumental line profiles. In particular, we adopted
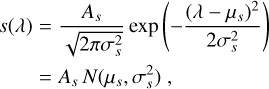 (A.2)
(A.2)
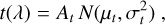 (A.3)
(A.3)
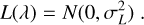 (A.4)
(A.4)
Substitution of s(λ), t(λ), and L(λ) into the left-hand side of Eq. (A.1) leads to
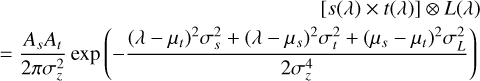 (A.5)
(A.5)
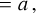 (A.6)
(A.6)
where 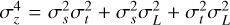 and a abbreviates Eq. (A.5). Using
and a abbreviates Eq. (A.5). Using
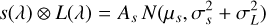 (A.7)
(A.7)
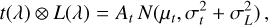 (A.8)
(A.8)
we find that the substitution of s(λ), t(λ), and L(λ) into the right-hand side of Eq. (A.1) leads to
![$\matrix{ \hfill {\left[ {s\left( \lambda \right) \otimes L\left( \lambda \right)} \right] \cdot \left[ {t\left( \lambda \right) \otimes L\left( \lambda \right)} \right] = } \cr \hfill {{{{A_s}{A_t}} \over {2\pi \sqrt {\sigma _z^4 + \sigma _L^4} }}\exp \left( { - {{{{\left( {\lambda - {\mu _s}} \right)}^2}} \over {2\left( {\sigma _s^2 + \sigma _L^2} \right)}} - {{{{\left( {\lambda - {\mu _t}} \right)}^2}} \over {2\left( {\sigma _t^2 + \sigma _L^2} \right)}}} \right) = b,} \cr }$](/articles/aa/full_html/2023/12/aa46524-23/aa46524-23-eq31.png) (A.9)
(A.9)
where b again abbreviates our findings.
A.1 Estimating the difference
The details of the differences between the two sides of Eq. (A.1) depend on the summands represented by a and b and, therefore, the parameters µs,t As,t, and σs,t,L. Some estimates can be obtained in special cases.
 |
Fig. A.1 Approximation of the convolution function for the special case where a stellar line is blended by a telluric line (µs = µt). Upper panel: Artificial line profiles representing a stellar line (red line), a telluric line (dashed green line), and the instrumental line profile (dotted blue line, normalized for the sake of clarity). Middle panel: Left and right side of Eq. (A.1). Lower panel: Difference between the left and right side of Eq. (A.1) expressed by a − b. The dashed line indicates the limit set by the product of the line depths, |
Assuming a perfectly blended stellar and telluric line µs = µt = λ, we obtain for the difference between Eq. (A.5) and Eq. (A.9)
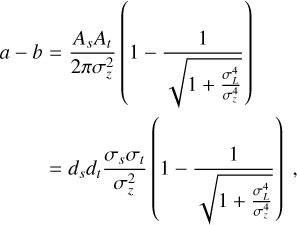 (A.10)
(A.10)
where ds,t denote the line depths,
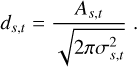 (A.11)
(A.11)
In general, 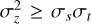 , and we find a − b ≥ 0, from which it follows that
, and we find a − b ≥ 0, from which it follows that 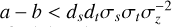 . Under the stated assumptions, we therefore find that the accuracy of the approximation depends on the product of the line depths. This also follows from the linearity of the convolution operator in Eq. (A.1).
. Under the stated assumptions, we therefore find that the accuracy of the approximation depends on the product of the line depths. This also follows from the linearity of the convolution operator in Eq. (A.1).
In Fig. A.1, we illustrate the differences between the two sides of Eq. (A.1) for the special case of a central blend of a stellar and a telluric line (i.e., µs = µt) for parameters appropriate for the CARMENES spectrograph. In our approximation, we consider only normal line profiles. We choose the standard deviation of the instrumental line profile, σL, such that its FWHM matches that of the true VIS channel Voigt line profile of CARMENES (Table 2), which yields σL = 0.048 Å. We assumed stellar and telluric lines located at µs = µt = 10 000 Å with line depths of ds = 0.3 and dt = 0.3. The intrinsic stellar and telluric line widths (before convolution by the instrumental LSF) were estimated from a synthetic PHOENIX spectrum (Husser et al. 2013) and a telluric transmission model, which yields σs = 0.05 Å and σt = 0.01 Å. We present the resulting Gaussian profiles in the upper panel of Fig. A.1, the left and right side of Eq. (A.1) in the middle panel of Fig. A.1, and the difference a − b as well as the limit expressed by 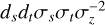 in the lower panel of Fig. A.1. For the adopted parameters, the difference between the left and right side of Eq. (A.1) is approximately 0.5%. This is in the range of 2% cited as the correction accuracy of molecfit. For shallower lines, the effect is less pronounced. In the extreme case of a very high instrument resolution represented by the limit σL → 0, we find that
in the lower panel of Fig. A.1. For the adopted parameters, the difference between the left and right side of Eq. (A.1) is approximately 0.5%. This is in the range of 2% cited as the correction accuracy of molecfit. For shallower lines, the effect is less pronounced. In the extreme case of a very high instrument resolution represented by the limit σL → 0, we find that 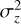 approaches σgσh so that Eq. (A.10) approaches zero and the difference vanishes.
approaches σgσh so that Eq. (A.10) approaches zero and the difference vanishes.
Our results allow obtaining an estimate of the accuracy of the approximation in Eq. (A.1) based on a normal approximation of the line profiles. They are also consistent with the findings of Sameshima et al. (2018).
Appendix B Additional figures
 |
Fig. B.1 Example of telluric line fits for the O2 band in a single Wolf 294 spectrum. The top panel displays the residual telluric spectrum (black dots) after dividing the science spectrum by the stellar template, and the best-fit telluric model (green dots) derived with molecfit. The subplots illustrate the individual telluric lines (top) and the residuals (bottom, black dots), with dashed red lines marking a 2% deviation between data and model. The standard deviation σ of the residuals is also shown in each subplot. |
Appendix C Table of sample stars
CARMENES M-dwarf sample of high S/N template spectra corrected for telluric absorption.
References
- Abia, C., Tabernero, H. M., Korotin, S. A., et al. 2020, A & A, 642, A227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allart, R., Fovis, C., Faria, F., et al. 2022, A & A, 666, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Floriano, F. F., Morales, J. C., Caballero, F. A., et al. 2015, A & A, 577, A128 [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Floriano, F. F., Snellen, I. A. G., Czesla, S., et al. 2019, A & A, 629, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artigau, É., Astudillo-Defru, N., Delfosse, X., et al. 2014, Proa SPIE, 9149, 914905 [NASA ADS] [CrossRef] [Google Scholar]
- Artigau, É., Cadieux, C., Cook, N. F., et al. 2022, AJ, 164, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, F., Simpson, A., & Crisp, D. 2007, PASP, 119, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Baroch, D., Morales, J. C., Ribas, I., et al. 2018, A & A, 619, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baroch, D., Morales, J. C., Ribas, I., et al. 2021, A & A, 653, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedell, M., Hogg, D. W., Foreman-Mackey, D., Montet, B. T., & Fuger, R. 2019, AJ, 158, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Bertaux, F. F., Fallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A & A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanco-Pozo, F., Perger, M., Damasso, M., et al. 2023, A & A, 671, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caballero, J. A., Cortés-Contreras, M., Alonso-Floriano, F. J., et al. 2016a, in 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS19), 148 [Google Scholar]
- Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016b, SPIE, 9910, 0E [Google Scholar]
- Caccin, B., Cavallini, F., Ceppatelli, G., Righini, A., & Sambuco, A. M. 1985, A & A, 149, 357 [NASA ADS] [Google Scholar]
- Clough, S. A., Shephard, M. W., Mlawer, E. J., et al. 2005, J. Quant. Spec. Radiat. Transf., 91, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, N. J., Artigau, É., Doyon, R., et al. 2022, PASP, 134, 114509 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, D., Santos, N. C., Figueira, P., et al. 2014, A & A, 568, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., Kouach, D., Lacombe, M., et al. 2018, SPIRou: A NIR Spectropolarimeter/High-Precision Velocimeter for the CFHT, 107 [Google Scholar]
- Dorn, R. J., Bristow, P., Smoker, J. V., et al. 2023, A & A, 671, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Hildebrandt, L., et al. 2019, A & A, 632, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Hildebrandt, L., et al. 2020, A & A, 640, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Nagel, E., et al. 2022, A & A, 657, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Schmitt, J. H. M. M., et al. 2023, A & A, 678, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia-Piquer, A., Morales, J. C., Ribas, I., et al. 2017, A & A, 604, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordon, I. E., Rothman, L. S., & Toon, G. C. 2011, JQSRT, 112, 2310 [NASA ADS] [CrossRef] [Google Scholar]
- Gullikson, K., Dodson-Robinson, S., & Kraus, A. 2014, AJ, 148, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hintz, D., Fuhrmeister, B., Czesla, S., et al. 2020, A & A, 638, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hintz, D., Peacock, S., Barman, T., et al. 2023, ApJ, 954, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., & Ulbrich, K. 2014, in Astronomical Society of India Conference Series, 11 [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A & A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A & A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kossakowski, D., Kürster, M., Trifonov, T., et al. 2023, A & A, 670, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kotani, T., Tamura, M., Nishikawa, J., et al. 2018, SPIE, 10702, 11 [Google Scholar]
- Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A & A, 403, 1077 [CrossRef] [EDP Sciences] [Google Scholar]
- Latouf, N., Wang, S. X., Cale, B., & Plavchan, P. 2022, AJ, 164, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Leet, C., Fischer, D. A., & Valenti, J. A. 2019, AJ, 157, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, A. C., Johnson, J. A., Bender, C. F., et al. 2014, ApJ, 783, L29 [Google Scholar]
- Mahadevan, S., Ramsey, L. W., Terrien, R., et al. 2014, Proc. SPIE, 9147, 91471G [NASA ADS] [CrossRef] [Google Scholar]
- Marfil, E., Tabernero, H. M., Montes, D., et al. 2020, MNRAS, 492, 5470 [NASA ADS] [CrossRef] [Google Scholar]
- Marfil, E., Tabernero, H. M., Montes, D., et al. 2021, A & A, 656, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nortmann, L., Pallé, E., Salz, M., et al. 2018, Science, 362, 1388 [Google Scholar]
- Orell-Miquel, J., Murgas, F., Pallé, E., et al. 2022, A & A, 659, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orell-Miquel, J., Lampón, M., López-Puertas, M., et al. 2023, A & A, 677, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palle, E., Nortmann, L., Casasayas-Barris, N., et al. 2020, A & A, 638, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Passegger, V. M., Schweitzer, A., Shulyak, D., et al. 2019, A & A, 627, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Passegger, V. M., Bello-García, A., Ordieres-Meré, J., et al. 2020, A & A, 642, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polanski, A. S., Crossfield, I. J. M., Burt, J. A., et al. 2021, AJ, 162, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., CARMENES Consortium, Amado, P. J., et al. 2020, SPIE Conf. Ser., 11447, 114473C [Google Scholar]
- Reiners, A., Zechmeister, M., Caballero, J. A., et al. 2018, A & A, 612, A49 [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., Shulyak, D., Käpylä, P. J., et al. 2022, A & A, 662, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribas, I., Reiners, A., Zechmeister, M., et al. 2023, A & A, 670, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spec. Radiat. Transf., 110, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Rudolf, N., Günther, H. M., Schneider, P. C., & Schmitt, J. H. M. M. 2016, A & A, 585, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A & A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sameshima, H., Matsunaga, N., Kobayashi, N., et al. 2018, PASP, 130, 074502 [NASA ADS] [CrossRef] [Google Scholar]
- Seifahrt, A., Käufl, H. U., Zängl, G., et al. 2010, A & A, 524, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shan, Y., Reiners, A., Fabbian, D., et al. 2021, A & A, 654, A118 [CrossRef] [EDP Sciences] [Google Scholar]
- Shulyak, D., Reiners, A., Nagel, E., et al. 2019, A & A, 626, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A & A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stock, S., Nagel, E., Kemmer, J., et al. 2020, A & A, 643, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vacca, W. D., Cushing, M. C., & Rayner, J. T. 2003, PASP, 115, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S. X., Latouf, N., Plavchan, P., et al. 2022, AJ, 164, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Wildi, F., Blind, N., Reshetov, V., et al. 2017, SPIE, 10400, 18 [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A & A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Anglada-Escudé, G., & Reiners, A. 2014, A & A, 561, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A & A, 609, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Transmissions of the AtmosPhere for AStromomical data, https://tapas.aeris-data.fr/en/home/
SpEctrum Radial Velocity AnaLyser, https://github.com/mzechmeister/serval
All Tables
molecfit fitting ranges used to calibrate the models for CARMENES VIS and NIR spectra.
CARMENES M-dwarf sample of high S/N template spectra corrected for telluric absorption.
All Figures
 |
Fig. 1 Example of template completion using a binary telluric mask. Upper and middle panels: small section of the telluric binary mask for two observations after the correction for Earth’s barycentric motion. Wavelength ranges with y = 1 are masked as tellurics. Lower panel: resulting mask of the template. The red shaded wavelength ranges correspond to template knots with Mk = 0 and contribute to the total masked template fraction γ. The blue shaded wavelength ranges are used for telluric modeling and contribute to γ′. |
| In the text | |
 |
Fig. 2 Illustration of the TDTM method. Panel a: segment of the VIS template spectrum of Wolf 294. The number Mk of exposure pixels that contribute to each template knot is color-coded. The red shaded wavelength ranges mark knots with Mk = 0. Panel b: one residual telluric spectrum Fn,i/S (λn,i) (black dots) after the division of the science spectrum by the template, and the best-fit telluric model (T(λn,i), green line) derived with molecfit. The red shaded wavelength ranges are excluded from the transmission model fit. Panel c: absolute residuals Fn,i/S(λn,i) – T(λn,i) of the fit. Panel d: CARMENES spectrum before (Fn,i, red line) and after (Fn,i/T(λn,i)) correction with the transmission model derived with molecfit (black line). Panel e: telluric free high S/N template spectrum of Wolf 294 (black line) built using 444 telluric absorption- corrected CARMENES observations. The order has a S/N of 2310. |
| In the text | |
 |
Fig. 3 Measured Gaussian and Lorentzian FWHM components of hollow cathode emission lines as a function of wavelength for the VIS and NIR CARMENES spectrographs. The vertical gray line marks the cutoff wavelength at 6000 Å. The horizontal lines indicate median values of the Gaussian and Lorentzian FWHM components for the VIS (dashed lines) and NIR channel (dotted lines). |
| In the text | |
 |
Fig. 4 Distribution of the number of telluric-corrected spectra we used to build the templates for all sample stars in the VIS (left) and NIR (right). The vertical dashed lines indicate the median values at 34 in the VIS and 30 in the NIR. |
| In the text | |
 |
Fig. 5 Distribution of the S/N of a reference order for the VIS (order 70 around 8600 Å, left) and the NIR (order 52 around 10 500 Å, right). The vertical dashed lines indicate the median values at 438 in the VIS and 482 in the NIR. |
| In the text | |
 |
Fig. 6 Time-span distribution of the observations for the sample stars for the VIS (left) and NIR spectra (right). The vertical dashed lines indicate the median values at 3.83 yr in the VIS and 3.70 yr in the NIR. |
| In the text | |
 |
Fig. 7 Metrics for assessing the quality of the telluric correction. Top panel: residual standard deviation (cx) vs. line depth for a single Wolf 294 VIS (blue) and NIR (red) spectrum. Middle panel: median residual standard deviation ( |
| In the text | |
 |
Fig. 8 Sky maps in Aitoff projection of the maximum absolute barycentric RV υbary,max as derived from Eq. (10) (left panel) and full amplitude of the barycentric RV υbary,max – υbary,min (right panel) for nights when the star is observable above 30deg over the horizon for the location of the Calar Alto Observatory. The positions of the 382 sample stars (purple circles) are indicated. The hatching pattern indicates the visibility cutoff at δ < −23 deg of the CARMENES sample. |
| In the text | |
 |
Fig. 9 Barycentric velocity distributions corresponding to various coordinate sets. Panel a: probability density function PDF(υbray) as computed with Eq. (13). Panels b-e: simulated barycentric velocity distributions for targets with a = 0 h, 6 h, 12 h, and 18 h, and δ = −22 deg, 0 deg, +30 deg, +60 deg, +90 deg, assuming one daily measurement over a time span of 1 yr and considering the target visibility. The second entry in the legend is the number of total observing nights. Panel ƒ: simulated barycentric velocity distribution of Wolf 294 (black line). The barycentric velocity distribution for the datasets of Wolf 294 (dashed red line) is overplotted. |
| In the text | |
 |
Fig. 10 Evolution of the total masked wavelength fraction color-coded with the barycentric velocity for Wolf 294. The circles represent the VIS channel (bottom) and the triangles the NIR channel (top). The upper and lower dashed black lines mark the maximum and minimum limits of the total masked fraction in the optical wavelength range. The dotted red lines mark the same limits for the NIR wavelength range. |
| In the text | |
 |
Fig. A.1 Approximation of the convolution function for the special case where a stellar line is blended by a telluric line (µs = µt). Upper panel: Artificial line profiles representing a stellar line (red line), a telluric line (dashed green line), and the instrumental line profile (dotted blue line, normalized for the sake of clarity). Middle panel: Left and right side of Eq. (A.1). Lower panel: Difference between the left and right side of Eq. (A.1) expressed by a − b. The dashed line indicates the limit set by the product of the line depths, |
| In the text | |
 |
Fig. B.1 Example of telluric line fits for the O2 band in a single Wolf 294 spectrum. The top panel displays the residual telluric spectrum (black dots) after dividing the science spectrum by the stellar template, and the best-fit telluric model (green dots) derived with molecfit. The subplots illustrate the individual telluric lines (top) and the residuals (bottom, black dots), with dashed red lines marking a 2% deviation between data and model. The standard deviation σ of the residuals is also shown in each subplot. |
| In the text | |
 |
Fig. B.2 Same as Fig. B.1, but for the H2O band around 8 200 Å. |
| In the text | |
 |
Fig. B.3 Same as Fig. B.1, but for a H2O band around 11 000 Å. |
| In the text | |
 |
Fig. B.4 Same as Fig. B.1, but for a O2 band around 12 600 Å. |
| In the text | |
 |
Fig. B.5 Same as Fig. B.1, but for a H2O band around 15 000 Å. |
| In the text | |
 |
Fig. B.6 Same as Fig. B.1, but for a CO2 band around 15 800 Å. |
| In the text | |
 |
Fig. B.7 Same as Fig. B.1, but for a CH4 band around 16 400 Å. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.