| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202346879 | |
| Published online | 01 November 2023 | |
Circumgalactic Lyα emission around submillimeter-bright galaxies with different quasar contributions
1
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str 1, 85748 Garching bei München, Germany
e-mail: valegl@mpa-garching.mpg.de
2
Academia Sinica Institute of Astronomy and Astrophysics, No. 1, Sec. 4, Roosevelt Rd., Taipei 10617, Taiwan
3
Department of Physics & Astronomy, University of Iowa, Iowa City, IA 52242, USA
4
Universitäts-Sternwarte München, Scheinerstraße 1, 81679 München, Germany
5
Gemini Observatory, NSF’s NOIRLab, 670 N A’ohoku Place, Hilo, Hawai’i 96720, USA
Received:
12
May
2023
Accepted:
28
August
2023
We present VLT/MUSE observations targeting the extended Lyman-α (Lyα) emission of five high-redshift (z ∼ 3-4) submillimeter galaxies (SMGs) with increasing quasi-stellar object (QSO) radiation: two SMGs; two SMGs that host a QSO; and one SMG that hosts a QSO with an SMG companion (QSO+SMG). These sources are predicted to be located in dark matter halos of comparable masses (average mass of MDM ∼ 1012.2 M⊙). We quantified the luminosity and extent of the Lyα emission, together with its kinematics, and examined four Lyα powering mechanisms: photoionization from QSOs or star formation, shocks by galactic and/or QSO outflows, gravitational cooling radiation, and Lyα photon resonant scattering. We find a variety of Lyα luminosities and extents, with the QSO+SMG system displaying the most extended and bright nebula, followed by the SMGs hosting a QSO, and finally the undetected circumgalactic medium of SMGs. This diversity implies that gravitational cooling is unlikely to be the main powering mechanism. We show that photoionization from the QSO and QSO outflows can contribute to power the emission for average densities nH > 0.5 cm−3. Moreover, the observed Lyα luminosities scale with the QSO’s budget of Lyα photons modulo the dust content in each galaxy, highlighting a possible contribution from resonant scattering of QSO radiation in powering the nebulae. We find larger Lyα linewidths (FWHM ≳ 1200 km s−1) than usually reported around radio-quiet systems, pointing to large-scale outflows. A statistical survey targeting similar high-redshift massive systems with known host properties is needed to confirm our findings.
Key words: galaxies: halos / galaxies: high-redshift / intergalactic medium / quasars: emission lines / quasars: general
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
In the Λ cold dark matter paradigm, galaxies form and evolve embedded in a filamentary cosmic web and grow by accretion of material from their surrounding medium. In turn, galaxies are expected to modify and pollute their vicinities through several processes (e.g., photoionization and outflows). The gas interface, extending beyond a galaxy’s interstellar medium but bound to the galaxy’s halo, is often called the circumgalactic medium (CGM; e.g., Tumlinson et al. 2017). The CGM extends over hundreds of kiloparsecs and naturally encodes information on the interactions between a galaxy and its surroundings (e.g., inflows and outflows), making its direct study fundamental for the understanding of galaxy formation and evolution.
The current generation of sensitive integral field unit spectrographs, such as the Multi Unit Spectroscopic Explorer (MUSE; Bacon et al. 2010) at the Very Large Telescope (VLT) and the Keck Cosmic Web Imager (KCWI; Morrissey et al. 2018) at the Keck Observatory, are able to push observations to unprecedented surface brightness (SB) limits (SB ∼ 10−19ergs−1cm−2arcsec−2), allowing us to study the CGM in emission. For example, observations of the hydrogen Lyman-α (Lyα) emission line surrounding high-z (2 < z < 6) quasi-stellar objects (QSOs) are now routinely reported (e.g., Borisova et al. 2016; Arrigoni Battaia et al. 2018, 2019a; Farina et al. 2019; Cai et al. 2019; O’Sullivan et al. 2020; Mackenzie et al. 2021; Fossati et al. 2021). The Lyα emission traces large-scale (∼ 100 kpc), cool (T ∼ 104 K), and massive gas reservoirs within the dark matter halos hosting QSOs at these redshifts, which are expected to have masses in the range M ∼ 1012 − 1013 M⊙ (e.g., Timlin et al. 2018, and references therein).
The main powering mechanism of the extended Lyα glow is frequently invoked as photoionization from the associated bright QSO, followed by recombination in optically thin gas (e.g., Heckman et al. 1991b; Cantalupo et al. 2014; Hennawi et al. 2015; Arrigoni Battaia et al. 2015a, 2018; Cai et al. 2018). However, details regarding the radiative transfer of this resonant line emission, and the balance between different powering mechanisms, are still unclear and debated. Hydrodynamic simulations of z ∼ 2 halos show that photoionization from the central active galactic nucleus (AGN) and star formation from companion galaxies can produce extended Lyα emission (Gronke & Bird 2017). Also, recent simulations of z ≳ 6 QSO nebulae show that scattering of Lyα photons is required to explain the morphology of the extended Lyα emission (Costa et al. 2022). Costa et al. (2022) also show that Lyα photons from the QSO’s broad-line regions, added in post-processing, can contribute to the powering of the extended emission as QSO feedback is able to open channels of least resistance for the propagation of such photons out to CGM scales.
There are at least four possible mechanisms that could act together to power the extended Lyα emission: (i) photoionization from the central AGN or companion galaxies, (ii) shocks powered by galactic and/or AGN outflows, (iii) gravitational cooling radiation, and (iv) resonant scattering of Lyα. Disentangling their relative roles and making a unique interpretation of observations is challenging (e.g., Arrigoni Battaia et al. 2015b; Mackenzie et al. 2021), and it is at the root of the difficulties in firmly constraining the physical properties of the emitting gas. Possible avenues to assess the contribution of different powering mechanisms are polarimetric observations of the Lyα emission (e.g., Hayes et al. 2011; Kim et al. 2020) or constraints on additional emission lines such as Hα, C IVλ15491, and He IIλ1640, which also aid in determining the ionization state and metallicity of the CGM (e.g., Arrigoni Battaia et al. 2015a). For each mechanism, the following expectations hold:
– Photoionization from the central AGN: The AGN illuminates the CGM, which in turn reprocesses the UV emission into a recombination cascade that includes detectable Lyα, Hα, and He II emission (e.g., Heckman et al. 1991a; Christensen et al. 2006; Smith et al. 2009; Geach et al. 2009; Humphrey et al. 2013). If the CGM is already enriched (e.g., from outflows), then extended C IV emission could also be detected.
– Shocks powered by galactic and/or AGN outflows: The Lyα linewidths observed for nebulae around QSOs are generally as expected for quiescent gas in virial equilibrium with the surrounding dark matter halo, with a full width half maximum (FWHM) of ∼600 km s−1 (e.g., Arrigoni Battaia et al. 2019a; Cai et al. 2019; O’Sullivan et al. 2020; Lau et al. 2022). However, broader linewidths at tens of kiloparsecs around some objects (e.g., Ginolfi et al. 2018; Vidal-García et al. 2021) is evidence for greater turbulence likely caused by outflows from the central AGN. Shocks produced by this outflowing material can produce Lyα emission through collisional excitation and ionization (e.g., Taniguchi & Shioya 2000; Taniguchi et al. 2001; Ohyama et al. 2003; Wilman et al. 2005; Mori & Umemura 2006). The same mechanisms could also allow for the emission of C IV and He II lines.
– Gravitational cooling radiation: As gas cools within dark matter halos, it will radiate away the lost gravitational potential energy through cooling channels. The main result is the emission of Lyα photons produced by collisional excitations (e.g., Haiman et al. 2000; Furlanetto et al. 2005; Dijkstra et al. 2006; Faucher-Giguère et al. 2010; Rosdahl & Blaizot 2012). Detecting any other line emission due to this mechanism would be difficult with the current facilities.
– Resonant scattering of Lyα photons originating from compact sources: Lyα photons produced by the QSO, the host galaxy, and companion galaxies can contribute to an extended Lyα glow as they undergo resonant scattering while propagating outward through the CGM (e.g., Dijkstra & Loeb 2008; Hayes et al. 2011; Cen & Zheng 2013; Cantalupo et al. 2014). C IV is also a resonant transition, and it could be detected as extended glow if scattered by a C3+-rich medium. Recombination transitions (e.g., Hα and He II) are expected to be more compact and narrower than Lyα (e.g., Prescott et al. 2015).
In addition, resonant scattering is expected to also take place for the Lyα photons originating from the first three mechanisms. This results in broader lines and larger nebulae due to the diffusion in space and frequency of the Lyα photons (e.g., Dijkstra 2019).
Stacking analyses of several objects have started to reveal extended line emission besides Lyα. Using MUSE data on 80 z ∼ 3 QSOs (1 hour/source), Guo et al. (2020) report average C IV, He II, and CIII[[INLINE87]] SB profiles that imply high metallicities in the inner CGM. Moreover, the latest and deepest (4 hours/source with MUSE) survey targeting high-redshift QSOs was able to reveal extended emission from Lyα and C IV and tentatively from He II (at barely 2σ significance) in their stacked analysis of 27 targets (Fossati et al. 2021). They derived line ratios and highlighted the difficulties in modeling the observed metallicities, but conclude that the CGM gas is metal-polluted at redshift z = 3 − 4.5. In particular, they note that resonant scattering of QSO Lyα photons could be an explanation for the observed ratios and why their sample shows emission that is more extended in resonant lines (Lyα and C IV) than nonresonant lines (He II).
The longer-term goal of our endeavor is to break the degeneracies between different powering mechanisms. In this project, we present the Lyα extended emission around different types of galaxies: unobscured QSOs with a companion submillimeter galaxy (SMG; e.g., Smail et al. 1997), SMGs that host QSOs, and SMGs that do not. While all these objects are predicted to reside in similarly massive dark matter halos as QSOs (1012 − 13 M⊙; e.g., Wilkinson et al. 2017; García-Vergara et al. 2020; Lim et al. 2020) and to have high star formation rates (SFRs), they have different contributions of QSO radiation (from none to bright unobscured QSOs). We stress that the clustering of QSOs is independent of the luminosity of the QSO (−28.7 < Mi < −23.8; Eftekharzadeh et al. 2015), and so looking at different luminosity systems probes the effect of different levels of ionizing radiation in the same environment. Therefore, once corrected for the cosmological SB dimming, we expect that these systems (i) have similar contributions to the total Lyα emission radiated from gravitational cooling (Haiman et al. 2000), (ii) have different contributions from AGN photoionization, star formation, and Lyα resonant scattering that is proportional to the AGN luminosity, star formation activity, and Lyα photon budget in compact sources, respectively, and (iii) have a shock contribution only when evidence of violent kinematics is present on CGM scales.
We emphasize that all our targets have high infrared (IR) luminosities (LFIR ∼ 1012 − 13 L⊙), similar to those of SMGs, which are caused by dust heated by high rates of obscured star formation, with SFR ∼ 100 − 1000 M⊙ yr−1 (Blain et al. 1999; Casey et al. 2014). In particular, recent works have shown that the distribution of dust in some SMGs appears clumpy and displaced from UV regions, which allows a fraction of their UV photons to escape (e.g., Hodge et al. 2015; Chen et al. 2017). Our observations could therefore estimate what fraction of escaping UV photons from star formation impinge on their CGM. In other words, if cool gas is present around these sources, then extended Lyα emission due to star formation might be detected when there are enough escaping UV photons reaching the surrounding gas distribution.
This paper is organized as follows. In Sect. 2 we describe in detail the sample, observations, and data reduction. In Sect. 3 we describe the analysis carried out in order to reveal the extended emission around our sources. In Sect. 4 we present our results, discuss the properties of the detected extended Lyα emission, such as brightness, morphology, and kinematics, and report constraints on additional emission lines. In Sect. 5 we compare our observational results with results in the literature and discuss the Lyα powering mechanisms mentioned above, showing that the firmest constraint is that against the gravitational cooling scenario. We summarize our findings in Sect. 6. We adopt a flat Λ cold dark matter cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7, for which the scale of 1 arcsecond corresponds to 7.0 kpc at the mean redshift of our sources (z ∼ 4).
2. Observations and data reduction
2.1. Sample selection
This project exploits the spectral-imaging capabilities of VLT/MUSE to target five systems with strong star formation, including an SMG that hosts a QSO with an SMG companion (QSO+SMG), two SMGs that host a QSO, and two SMGs that do not. In particular, the non-hosting SMGs are part of the first samples with a firm estimate of their systemic redshifts through the observation of molecular tracers. Our sample is composed as follows:
– One radio-quiet unobscured bright QSO with a submillimeter companion galaxy ∼4″ to the NW of the QSO, BR1202 − 0725 (e.g., Omont et al. 1996b; Drake et al. 2020);
– Two QSOs in SMGs, G09 − 0902 + 0101 and G15 − 1444 − 0044 (Fu et al. 2017). Even though these sources are bright in the submillimeter, their QSO spectra appear unobscured in the rest-frame UV along the line of sight. They are therefore unobscured QSOs hosted by SMGs. They are about one order of magnitude fainter than the QSO in BR1202-0725;
– Two isolated SMGs (with no AGN) with spectroscopic redshift from [CII] and CO, ALESS61.1 and ALESS65.1 (Swinbank et al. 2012; Birkin et al. 2021).
2.2. VLT/MUSE observations and data reduction
The VLT/MUSE data were taken as part of European Southern Observatory programs 0103.A-0296(A) and 0102.A-0403(A) in service modes on UT dates between January 2019 and August 2019 (PI: F. Arrigoni Battaia). The observations were taken in wide field mode, resulting in a 0.2″ spatial sampling of a 1′×1′ field of view. In this configuration MUSE covers the spectral range 4750–9350 Å with a spectral resolution of R ∼ 2230 at 6078 Å (the Lyα wavelength at the mean z of the sample). The observing blocks were organized in three exposures of about 15 minutes each with < 5″ shifts and 90 degree rotations. The observing conditions were clear and the seeing at the expected Lyα wavelength was of 1.13″, on average. In addition, for BR1202 − 0725 we include, re-reduce, and add to our data set the 48 minutes data set from Drake et al. (2020), which was taken with MUSE in the same configuration as part of ESO program 0102.A − 0428(A) (PI: E. P. Farina), with two exposures with a < 5″ shift and a 90 degree rotation. These observations were obtained under good weather conditions and a 0.6″ seeing. In Table 1 we list the total exposure time and the seeing at the Lyα wavelength measured for each field from its final datacube (see Appendix A).
Physical properties of the targeted sample and observing log.
The data reduction was performed using the MUSE pipeline version 2.8.3 Weilbacher et al. (2012, 2014, 2020) as described in Farina et al. (2019), which consist of bias and dark subtraction, flat correction, wavelength calibration, illumination correction and standard star calibration. We continue with the removal of sky emission residuals, which we performed using the Zurich Atmospheric Purge (ZAP) software (Soto et al. 2016). The reduced datacubes contain both the science data cubes and the associated variance cubes. The later are rescaled as usually done in the literature to reflect the empirical variance in the data cubes, since the pipeline underestimates the variance due to correlated noise at pixel level (e.g., Bacon et al. 2015). The scaling factor is found to be on average 1.4, consistent with previous works (e.g., Borisova et al. 2016), and is applied layer by layer to the variance cube. The final variance cubes are used to obtain SB limits and associated errors of our estimates. After data reduction, we manually mask artifacts that appear due to the edges of the MUSE integral field units. This process needs to be performed for each single exposure before combining. During this step, about ∼4% of the pixels are masked on average per exposure. Masking is done by inspection of white images (computed by collapsing the datacube along the spectral axis using the full wavelength range). After masking, each exposure is aligned by performing a 2D Gaussian centroid fitting of point sources (stars) in each field for reference, then a simple offset is computed. Finally, the datacubes were combined using the median, and the variance cubes were combined by performing error propagation.
At the expected wavelength of the Lyα emission, the final 2σ SB limit is on average ∼3 × 10−18 erg s−1 cm−2 arcsec−2 for an aperture of 1 square arcsecond and a 30 Å narrow band. We list these SB limits in Table 1.
Finally, Fig. 1 shows the integrated spectra obtained from our MUSE data inside a 3″ radius aperture for each of the systems studied here, together with SB maps of 30 Å narrow bands centered at the expected Lyα line wavelength before point spread function (PSF) and continuum subtraction. We can already see from this figure that there is no detected emission from the SMGs. We note that for BR1202-0725, the observed He II wavelength is located right before the edge of the spectral range (about 9 Å). In Sect. 3 we discuss in detail these observations and their analysis.
 |
Fig. 1. Overview of the five targeted systems before subtraction of the unresolved QSO’s PSF and continuum sources (see Sect. 3). Left: integrated spectra of the QSOs and SMGs inside a 3″ radius aperture. Vertical dashed lines indicate the positions of the Lyα and QSO broad lines (Si IV, C IV, HeII, and CIII[[INLINE106]]). The gray shaded region indicates the FWHM of the nebular Lyα emission for the QSOs (see Fig. 2 and Table 3) and the 30 Å narrow band used for the SMGs (see Fig. 3). Right: 30 Å SB maps at the expected Lyα wavelength of the targeted QSOs and SMGs before PSF- and continuum-subtraction (see Sect. 3). The maps have a side of 20″, corresponding to about 129, 152, 148, 133, and 132 kpc for BR1202 − 0725, G09 − 0902 + 0101, G15 − 1444 − 0044, ALESS61.1, and ALESS65.1, respectively. |
2.3. Physical properties of the sample
To homogenize our sample, we recomputed some of the galaxies’ physical properties in a consistent way for all sources, namely IR luminosity, SFRs, and dust masses. To do this, we used ancillary submillimeter data. We construct the 8–1000 μm spectral energy distribution (SED) using the data points from Omont et al. (1996a; at 1250 μm with IRAM 30 m) and Iono et al. (2006; at 900 μm with the Submillimeter Array) for BR1202-0725, from Fu et al. (2017; at 250, 350 and 500 μm with Herschel/SPIRE and 870 μm with ALMA) for G09-0902+0101 and G15-1444-0044, and from Swinbank et al. (2012; at 250, 350 and 500 μm with Herschel/SPIRE and 870 μm with ALMA) for ALESS61.1 and ALESS65.1. In Table 2 we summarize the fluxes of these submillimeter observations.
Ancillary data fluxes used to estimate the physical properties of the sample.
We estimated the dust masses of each source assuming a modified black body of the form Sν0 ∝ Bν × [1 − exp( − ν/ν0)β] with ν0 = 2.0 THz and dust emissivity spectral index β = 2.0 (Fu et al. 2017), integrating to obtain the total IR luminosity between λ = 8 − 1000 μm. We then used this integrated IR luminosity to estimate the SFR for each source using the formula ![$ \mathrm{SFR}=[L_{\mathrm{IR}}^{\mathrm{SF}}/(10^{10}\,{L}_{\odot})]\,{{M}_{\odot}}\,\mathrm{yr}^{-1} $](/articles/aa/full_html/2023/11/aa46879-23/aa46879-23-eq5.gif) from Fu et al. (2017), which assumes a Chabrier (2003) initial mass function. This procedure is reasonable as it has been shown that most of the IR emission in these sources is dominated by star formation in the host galaxy (e.g., Iono et al. 2006; Fu et al. 2017). The dust masses are derived using Eq. (3) of Chen et al. (2021), assuming a rest-frame dust mass absorption coefficient κ850 μm = 0.431 cm2 g−1 from Li & Draine (2001). For BR1202-0725 we fix the dust temperature to Tdust = 68 K (Leech et al. 2001) as we only use the two available data points for the QSO, which are not covering the SED peak. For the other sources we find Tdust ∼ 55 K. If we adopt this same temperature for BR1202-0725 we derive a 20% higher dust mass. The derived dust masses (see Table 1) are consistent with dust masses reported in the literature for similar objects. Specifically, the dust masses of ALESS61.1 and ALESS65.1 are in agreement with the values estimated by Birkin et al. (2021).
from Fu et al. (2017), which assumes a Chabrier (2003) initial mass function. This procedure is reasonable as it has been shown that most of the IR emission in these sources is dominated by star formation in the host galaxy (e.g., Iono et al. 2006; Fu et al. 2017). The dust masses are derived using Eq. (3) of Chen et al. (2021), assuming a rest-frame dust mass absorption coefficient κ850 μm = 0.431 cm2 g−1 from Li & Draine (2001). For BR1202-0725 we fix the dust temperature to Tdust = 68 K (Leech et al. 2001) as we only use the two available data points for the QSO, which are not covering the SED peak. For the other sources we find Tdust ∼ 55 K. If we adopt this same temperature for BR1202-0725 we derive a 20% higher dust mass. The derived dust masses (see Table 1) are consistent with dust masses reported in the literature for similar objects. Specifically, the dust masses of ALESS61.1 and ALESS65.1 are in agreement with the values estimated by Birkin et al. (2021).
Furthermore, we provide a rough calculation to show that the halo masses of these systems are within the range expected for QSOs and SMGs at these redshifts (1012 − 1013 M⊙). Specifically, we predict their dark matter halo masses using the halo mass-stellar mass relation by Moster et al. (2018) at their redshifts. We stress that the obtained estimates are affected by large uncertainties given the scatter in this relation. For the two SMGs, ALESS61.1 and ALESS65.1, we can rely on their stellar masses obtained through SED fitting by Birkin et al. (2021), ![$ {\log}(M_{*}/[M_{\odot}])=10.33^{+0.18}_{-0.01} $](/articles/aa/full_html/2023/11/aa46879-23/aa46879-23-eq6.gif) and
and ![$ \mathrm{log}(M_{*}/[M_{\odot}])=10.48^{+0.19}_{-0.13} $](/articles/aa/full_html/2023/11/aa46879-23/aa46879-23-eq7.gif) , respectively. For the three QSO systems, we instead convert their total gas mass to a stellar mass, assuming the gas to stellar mass ratio at their redshift from Birkin et al. (2021; e.g., see their Fig. 9, left panel). For this step, we homogenize all the measurements obtaining gas masses from the far-IR continuum following Eq. (3) in Tacconi et al. (2020), assuming a gas-to-dust ratio of 100 (e.g., Riechers et al. 2013). We find Mgas = 8 × 1010 M⊙ for BR1202-0725, and Mgas = 6.3 × 1010 M⊙ and Mgas = 1.9 × 1010 M⊙ for G09-0902+0101 and G15-1444-0044, respectively. The value for BR1202-0725 is consistent with the value computed from CO emission and assuming an αCO = 0.8 M⊙ K−1 km s−1 pc2 (Riechers et al. 2006). We therefore homogenized the values in Birkin et al. (2021) to this αCO. We stress that they targeted 61 SMGs with no clear sign of AGN activity; therefore, the used ratio may introduce a systematic bias for our QSOs, which are hosted by SMGs. We find stellar masses of
, respectively. For the three QSO systems, we instead convert their total gas mass to a stellar mass, assuming the gas to stellar mass ratio at their redshift from Birkin et al. (2021; e.g., see their Fig. 9, left panel). For this step, we homogenize all the measurements obtaining gas masses from the far-IR continuum following Eq. (3) in Tacconi et al. (2020), assuming a gas-to-dust ratio of 100 (e.g., Riechers et al. 2013). We find Mgas = 8 × 1010 M⊙ for BR1202-0725, and Mgas = 6.3 × 1010 M⊙ and Mgas = 1.9 × 1010 M⊙ for G09-0902+0101 and G15-1444-0044, respectively. The value for BR1202-0725 is consistent with the value computed from CO emission and assuming an αCO = 0.8 M⊙ K−1 km s−1 pc2 (Riechers et al. 2006). We therefore homogenized the values in Birkin et al. (2021) to this αCO. We stress that they targeted 61 SMGs with no clear sign of AGN activity; therefore, the used ratio may introduce a systematic bias for our QSOs, which are hosted by SMGs. We find stellar masses of 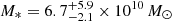 for BR1202-0725, and
for BR1202-0725, and 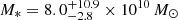 and
and 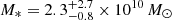 for G09-0902+0101 and G15-1444-0044, respectively. Therefore, the expected dark matter halo masses using the halo mass-stellar mass relation by Moster et al. (2018) for the targeted sources are: log(MDM/[M⊙]) ∼ 12.3 for BR1202-0725, log(MDM/[M⊙]) ∼ 12.5 and log(MDM/[M⊙]) ∼ 11.9 for G09-0902+0101 and G15-1444-0044, and log(MDM/[M⊙]) ∼ 11.9 and log(MDM/[M⊙]) ∼ 12.0 for ALESS61.1, and ALESS65.1, respectively. We quote the halo mass estimates as approximate because of the large uncertainties inherent to the use of the relation in Moster et al. (2018), the use of gas masses to obtain stellar masses, and the uncertainty on the αCO assumed, which could be a factor of 5 higher if αCO is close to the galactic value (Bolatto et al. 2013). Notwithstanding these uncertainties, the values we find are consistent with the range of halo masses from clustering studies (Timlin et al. 2018, and references therein). These estimates are key in placing these systems in the context of galaxy formation, and in quantifying the expected signal for gravitational cooling. Table 1 summarizes most of the properties of our targets (redshift, QSO’s bolometric luminosity, IR luminosity due to star formation, SFR, estimated dust mass, seeing at the Lyα wavelength, exposure time, and type) with their respective references.
for G09-0902+0101 and G15-1444-0044, respectively. Therefore, the expected dark matter halo masses using the halo mass-stellar mass relation by Moster et al. (2018) for the targeted sources are: log(MDM/[M⊙]) ∼ 12.3 for BR1202-0725, log(MDM/[M⊙]) ∼ 12.5 and log(MDM/[M⊙]) ∼ 11.9 for G09-0902+0101 and G15-1444-0044, and log(MDM/[M⊙]) ∼ 11.9 and log(MDM/[M⊙]) ∼ 12.0 for ALESS61.1, and ALESS65.1, respectively. We quote the halo mass estimates as approximate because of the large uncertainties inherent to the use of the relation in Moster et al. (2018), the use of gas masses to obtain stellar masses, and the uncertainty on the αCO assumed, which could be a factor of 5 higher if αCO is close to the galactic value (Bolatto et al. 2013). Notwithstanding these uncertainties, the values we find are consistent with the range of halo masses from clustering studies (Timlin et al. 2018, and references therein). These estimates are key in placing these systems in the context of galaxy formation, and in quantifying the expected signal for gravitational cooling. Table 1 summarizes most of the properties of our targets (redshift, QSO’s bolometric luminosity, IR luminosity due to star formation, SFR, estimated dust mass, seeing at the Lyα wavelength, exposure time, and type) with their respective references.
3. Analysis: Revealing the large-scale emission
While SMGs are faint in rest-frame UV, we need to remove the unresolved QSO’s PSF to reveal the extended emission around them. In the following subsections we describe the method used to reveal the extended Lyα emission. For this, we develop new Python custom routines that construct and subtract the empirical QSO’s PSF, similarly to what is usually done in the literature (e.g., Borisova et al. 2016; Husemann et al. 2018; Farina et al. 2019; O’Sullivan et al. 2020). In summary, we built a wavelength-dependant empirical QSO PSF that we then subtracted from the datacubes; next we subtracted continuum sources in order to obtain datacubes with pure extended line emission. The steps for this method are described below.
3.1. PSF-subtraction
The QSOs in our sample all outshine the host galaxy at the wavelengths targeted by MUSE. As usually done in the literature, the PSF is computed at each wavelength by constructing pseudo narrow-band images of 150 channels (187 Å) centered at the QSO’s position, and inside a box of size 6 times the seeing to ensure that its contribution at the largest radii is negligible. We describe how the seeing is estimated for each observation in Appendix A.
We require that the PSF is not computed where we expect the extended line emission, corresponding to wavelength ranges affected by broad QSO lines (e.g., Lyα, CIV, and HeII). These wavelength ranges are neglected and their PSF is computed at the first available redshifted pseudo narrow band. To identify where these wavelength ranges are, we design a custom routine that automatically detects the location of line emission as explained in detail in Appendix B. In summary, we find the wavelength of local peaks in the spectra that indicate expected line emission and define a conservative spectral window of about Δλ = 430 − 560 Å (Δv = 24 400 − 26 000 km s−1) centered on each line, which is excluded from computing the PSF. Such velocity ranges are much larger than the width of the discovered emission (Sect. 4).
The empirical wavelength-dependent PSF is then rescaled at each layer to match the QSO’s flux within the central 1 arcsec2. Due to possible cosmic rays, the scaling factor is computed from the average sigma clip of the normalization region. We subtract the rescaled PSF from the original datacube layer by layer, after masking negative pixels (at the edges of the PSF where it approaches the background) in order to not introduce spurious signal. In each field, we finally mask the 1 arcsec2 normalization region and exclude it from our analysis.
The resulting PSF subtracted datacubes are already able to highlight the extended emission around the QSOs. However, continuum sources in the field still need to be removed in order to not contaminate the extended emission.
3.2. Continuum subtraction
After subtracting the empirical PSF, we remove the contribution from continuum sources in all spaxels of our datacubes. For this, we first create a sky mask using the PSF-subtracted white light image, for which we estimate the noise floor using an average sigma clip algorithm and identify sources above 5 times this threshold. We estimate the continuum of the identified sources by smoothing their spectra at each spaxel using an order 5 polynomium, as done in the MPDAF Python package from Bacon et al. (2016). Finally, we subtracted the smoothed spectrum from each voxel of the identified sources. This process results in a datacube of only line emission. To check the robustness of our PSF and continuum subtractions, we compared them with the results from Drake et al. (2020) for BR1202-0725 and find consistent results for the Lyα emission (emission morphology and levels), though our data are deeper.
4. Results
The PSF- and continuum-subtracted cubes have been used to extract line emission nebulae associated with the five targets. Below, we focus on the SB maps, integrated spectra, radial profiles and kinematics of the Lyα line emission. We also provide constraints on additional rest-frame UV line emission, C IV, Si IV, He II, and C III]2, when available within the MUSE wavelength range.
4.1. Lyα surface brightness maps and nebula spectra
To ease comparison with early narrow-band studies (e.g., Cantalupo et al. 2014), we obtained SB maps by extracting 30 Å narrow-band maps centered at the peak of the Lyα extended emission from the continuum- and PSF-subtracted cubes. The peak was computed from the Gaussian fit to the integrated spectra inside a 3″ radius aperture centered at the QSO position after masking the 1 arcsec2 normalization region. To test possible deviations from a Gaussian fit due to, for example, radiative transfer effects, we tested our calculation of the peak by estimating it using the first moment of the flux distribution within ±2.5 × FWHM of that fit. We found agreement between the two calculations. The SB maps for the QSO fields in our sample are shown in the right panel of Fig. 2, and highlight the different morphologies and brightness that we find around these sources. Specifically, BR1202 − 0725 shows the largest Lyα luminosity (∼ 3 × 1044 erg s−1, or ∼ 2.7 × 1044 erg s−1 if we mask the Lyα emitter (LAE) inside a 1.6″ diameter aperture) and extent (A = 3062 pkpc2; see Table 3). The two obscured QSOs show a factor of ∼10 lower Lyα luminosity and ∼3 times smaller extent (see Table 3). An extended Lyα halo is not detected around the two SMGs at the current depth. This can be appreciated from the 30 Å SB maps at the expected Lyα wavelength shown in the right column of Fig. 3, and also confirmed by inspecting their integrated spectra within a 2″ radius aperture (see the left column of Fig. 3). Appendix C presents the data shown in Figs. 2 and 3 as χsmooth maps (e.g., Hennawi & Prochaska 2013).
 |
Fig. 2. Integrated spectra and SB maps of the extended Lyα emission around the three systems with AGNs. Left: spectra of the identified Lyα nebulae (black curve), integrated inside the 2σ contour. The gray shaded area shows the channels used to build the SB map. The vertical magenta line indicates the Lyα wavelength from the systemic redshift of the QSOs, while the vertical blue line indicates the wavelength at the peak of the Lyα spectra computed from the first moment of the line. Overlaid in red is a Gaussian fit to the spectra. The velocity shift and FWHM of each system are listed in Table 3. The top axis of the spectra panels show the velocity shift with respect to the systemic redshift in km s−1. Right: Lyα SB maps of BR1202 − 0725 (top), G09 − 0902 + 0101 (middle), and G15 − 1444 − 0044 (bottom) at the expected wavelength from their systemic redshift (Table 1). The maps have a side of 20″, corresponding to about 129, 152, and 148 kpc for BR1202 − 0725, G09 − 0902 + 0101, and G15 − 1444 − 0044, respectively. A scale bar of 20 kpc is indicated on each map. The black contours indicate SB levels of [2, 4, 10, 20, 50] σ (see Table 1). These maps are smoothed using a 2D box kernel with a width of 3 pixels (0.6″). The central 1″ × 1″ region used for the QSO PSF normalization is masked and excluded from analysis. For BR1202 − 0725, we indicate the position of the LAE and SMG companions (Carilli et al. 2013; Drake et al. 2020) with a green and white cross, respectively. |
 |
Fig. 3. Integrated spectra and SB maps of the two observed SMGs. Left: spectra integrated inside the 2″ radius aperture (black circle) of ALESS61.1 (top) and ALESS65.1 (bottom). The gray shaded area shows the channels used to build the SB map, and the vertical magenta line indicates the expected Lyα wavelength. Right: Lyα SB maps of the two SMGs at the expected wavelength from their redshift, listed in Table 1. The maps have a side of 20″, which at their redshifts corresponds to about 133 and 132 kpc for ALESS61.1 and ALESS65.1, respectively. A scale bar is shown for each map. These maps are smoothed using a 2D box kernel with a width of 3 pixels (0.6″). The black circles indicate an aperture of radius 2″ centered at the SMG position. |
Properties of the detected nebulae and upper limits for non-detections.
Given that the detected nebulae are at a different redshifts, we test their extent also by using a common SB threshold corrected for cosmological dimming and compare to another sample presented in Arrigoni Battaia et al. (2023). This work report luminosity–area relations for Lyα nebulae around z ∼ 2 − 3 type-I QSOs obtained using different SB thresholds. Because of the redshift of the targets and the sensitivity of our data, to compare the detected nebulae we used the reference relation, the 2× and 4× higher SB thresholds in that work for G09-0902+0101, G15-1444+0044, and BR1202-0725, respectively. By using these specific SB isophote, we find physical areas of 878, 651, 2651 kpc2 and Lyα nebula luminosities of 7.5 × 1042, 9.0 × 1042, 18.9 × 1043 erg s−1, respectively. These values are in agreement with the relations reported in Arrigoni Battaia et al. (2023), indicating that also type-I QSOs hosted by SMGs sit on these luminosity-area relations. Larger samples are needed to confirm this finding.
Furthermore, we extracted an integrated spectrum for the Lyα emission of each detected nebula by using all the spaxels within the 2σ contour of that nebula, shown in the left column of Fig. 2). We fit a simple Gaussian profile to describe the linewidth of the nebulae spectra. We find that all the spectra have consistent broad (FWHM ∼ 1500 km s−1) line profiles, with the presence of Lyα absorption features. Such broad lines are not frequently seen around QSOs (FWHM ∼ 600 km s−1; e.g., Borisova et al. 2016; Arrigoni Battaia et al. 2019a), possibly indicating more turbulent gas reservoirs in the highly star-forming environments targeted here. Interestingly, BR1202-0725 and G09-0902+0101 show integrated Lyα lines with positive shifts on the order of 300 − 400 km s−1 with respect to the systemic redshift of each system, possibly indicating bulk winds. We note that G15-1444-0044 also show a similar shift when using the maximum of its Lyα line as reference velocity (see Table 3). These shifts are larger than the average positive shift found for QSOs with good systemic redshifts (from, e.g., [CII] 158 μm, 69 ± 36 km s−1; Farina et al. 2019). We examine in detail the presence of an outflow for BR1202-0725 in Sect. 4.3.2.
4.2. Lyα surface brightness radial profiles
In order to describe the morphology and relative brightness of our nebulae, we built circularly averaged radial profiles as usually done in the literature (e.g., Arrigoni Battaia et al. 2019a; Fossati et al. 2021). The radial profiles are extracted from the 30 Å SB maps from Fig. 2, using logarithmically spaced bins starting at about 1.6″. The left panels of Fig. 4 show the circular apertures used to extract the profiles overlaid on the SB maps for the detected sources, while the right panels show the individual extracted profiles. Filled circles represent positive mean SB values, while open circles represent negative mean SB values. In the same figure, the solid red line represents the 2σ SB limit within each ring. From these profiles it is evident that the QSO+SMG system BR1202-0725 has a more extended and bright nebula compared to the two SMGs hosting a QSO. We fit the observed SB profile of BR1202-0725 with both an exponential SBLyα = Cexp( − r/rh) and a power law SBLyα = Crα as usually done in the literature, finding a better agreement with an exponential function. The scale length for the best fit is rh = 11 ± 1 kpc. We do not perform any fit on the other two detected nebulae given the limited radial range covered. We discuss these SB profiles in comparison to other samples in the literature in Sect. 5.2.
 |
Fig. 4. Lyα SB radial profiles extraction. Left: smoothed SB maps of the QSO sample (same as in Fig. 2) with the circular apertures used to extract radial profiles overlaid. The gray circle in each map indicates the 1 arcsec2 region used for the QSO’s PSF normalization, which is neglected in our analysis. Right: extracted radial profiles inside each annulus. Open circles indicate negative values, shown here for completeness. The red line represents the 2σ SB limit rescaled to the area of each annulus. The dashed blue curve in the top panel is the best fit of the data points above the red line using an exponential function with the form SBLyα = Cexp( − r/rh), where C = 85.3 ± 13.8 × 10−18 erg s−1 cm−2 arcsec−2 and rh = 11 ± 1 pkpc. |
4.3. Lyα kinematics
4.3.1. Mean velocity shift and velocity dispersion maps
We computed velocity shift and velocity dispersion maps for our detected sources by building the first and second moment maps within narrow wavelength ranges, which are centered at the peak of their nebula Lyα spectrum and encompass ±FWHM of their Gaussian fit (see Table 3). Figure 5 shows the velocity shift maps and the velocity dispersion maps on the left and right columns, respectively. The velocity shift maps are computed with respect to the Lyα line peak of each nebula and highlight the complex kinematics of the nebulae, likely affected by some Lyα resonant scattering. We select the Lyα line peak as reference to keep our sample homogeneous as we do not have an accurate systemic redshift for the SMGs hosting QSOs. We find that BR1202 − 0725 presents a clear blueshifted and redshifted component at velocities of ∼ ± 400 km s−1. Larger velocity dispersions are seen close to the QSO (FWHM ∼ 1600 − 1800 km s−1), while we observe that the companion SMG (indicated with a white cross) is located, in projection, in a region with more quiescent kinematics with respect to the rest of the nebula (FWHM ∼ 1000 km s−1). This might be due to the fact that this zone is less turbulent or that dust absorbs some of the Lyα photons (e.g., Laursen et al. 2009). However, we stress that there is a substantial velocity shift between the SMG (−142.1 km s−1, with respect to the systemic z; Drake et al. 2020) and the Lyα emission at its projected location (∼ + 400 km s−1), possibly indicating the presence of peculiar velocities between the galaxy and the gas, on top of radiative transfer effects. Similarly, LAE1 shows a velocity offset of +42 km s−1 with respect to BR1202-0725 (Drake et al. 2020), which is smaller than the Lyα velocity offset at its projected location. We further study the large velocity components near the QSO in the BR1202-0725 system in Sect. 4.3.2.
 |
Fig. 5. Kinematics of the detected Lyα nebulae: Velocity shift ΔvLyα maps (left column) with respect to the Lyα peak wavelength of the nebula (see Fig. 2), and velocity dispersion σLyα maps (right column) of the Lyα nebula around the three QSOs, computed from the first and second moment, respectively. The maps are smoothed as in Fig. 2. The moment calculation is performed only inside the 2σ isophote of each nebula. The positions of the LAE and SMG companion of the BR1202-0725 system are marked with a green and white cross, respectively. The side of the map is 20″ for BR1202-0725 and 10″ for G09-0902+0101 and G15-1444-0044. A scale bar is shown for each map. The gray circle in each map indicates the 1 arcsec2 region used for the QSO’s PSF normalization, which is neglected in our analysis. |
The velocity shift and dispersion maps for G09 − 0902 + 0101 and G15 − 1444 − 0044 appear noisy, possibly due to their lower SB levels and the complexity of the gas motions on these scales (e.g., Fig. B1 in Costa et al. 2022). Deeper observations would be needed to study in detail their kinematics.
4.3.2. Evidence of violent kinematics in BR1202-0725
As mentioned in Sect. 4.3.1, we observe large Lyα velocity dispersions near the QSO position in the BR1202-0725 system. Indeed, we estimate a large Lyα FWHM (see Table 3), which could hint to the presence of large-scale outflows due to the QSO and star formation activity. Similarly large Lyα FWHM (> 1000 km s−1) has been observed in the CGM around a broad-absorption line QSO (Ginolfi et al. 2018), suggesting that we observe broader Lyα emission when there are outflow signatures on small scales.
In this section we further explore the aforementioned violent kinematics found in the Lyα nebular emission of BR1202-0725. This nebula is bright and therefore we can access the large velocity wings of its Lyα line. Specifically, we investigate the difference in the Lyα line shape in the regions with positive and negative velocity shifts as seen from its first moment map (see Fig. 5). We show in the top-left panel of Fig. 6 the integrated spectra for regions with negative (blue) and positive (red) velocity shifts, with respect to the peak of the nebular Lyα emission. For the integrated spectrum at positive velocities we subtract the emission coming from a circular region of radius 1.6″ centered at the LAE companion position (from Drake et al. 2020; see the top-right panel of Fig. 6) to be sensitive only to the emission from large-scale gas. Assuming this LAE follows a rescaled version of the average SB profile for LAE presented by Wisotzki et al. (2018), extended emission associated with the LAE outside the chosen aperture should be below our 2σ detection threshold, and therefore negligible.
 |
Fig. 6. Violent kinematics in the Lyα nebula of BR1202-0725. Top left: integrated spectra of regions with negative (blue curve) and positive (red curve) velocity shifts for BR1202-0725, with respect to the peak of the nebular Lyα emission (see Fig. 2). The spectra are taken after masking the 1″ × 1″ region of the QSO’s PSF-subtraction and a circular region with a diameter of 1.6″ at the LAE companion position. We indicate with vertical lines the systemic redshift (solid magenta), the redshift of the SMG (dashed black), and LAE (dot-dashed green) companions (Carilli et al. 2013; Drake et al. 2020). Top middle: residual spectrum between the positive and the negative shift spectrum. We indicate the systemic redshift with a magenta line. Top right: Lyα velocity shift map computed from the first moment using a spectral window of ±FWHM centered at the peak of the nebular Lyα emission (see Table 3) and smoothed as in Fig. 2. The position of the QSO and LAE companion masks are indicated with a hashed gray and a green circle, respectively. Bottom left: Lyα SB map using the spectral channels with the largest negative nebula shifts, indicated with a blue shaded region in the top-left panel. The blue contours indicate the 2σ isophote of the extended emission shown in Fig. 2. Bottom right: Lyα SB map using the spectral channels with the largest positive nebula shifts, indicated with a shaded red region in the top-left panel. Both of the SB maps are smoothed at the bottom as in Fig. 2. All maps have a side of 20″ and black contours indicating SB levels of [2, 4, 10, 20, 50] σ within the respective wavelength ranges. |
We observe that both these spectra display large linewidths with wings at large velocities (Δv > 1000 km s−1). However, the spectrum for the positive velocities shows an excess with a wing out to velocities as high as ∼2500 km s−1 that can be appreciated in the difference spectrum reported in the middle panel of Fig. 6. Also, both spectra show the presence of an absorption feature at velocities −470 km s−1. This feature was also reported in Drake et al. (2020), who suggested that it is due to a shell of outflowing material as usually invoked for the case of high-redshift radio galaxies (e.g., van Ojik et al. 1997) and QSO pairs (e.g., Cai et al. 2018; Arrigoni Battaia et al. 2019b).
Furthermore, we investigated from which spatial region the largest velocity shifts are observable. The bottom panels of Fig. 6 show Lyα SB maps of BR1202-0725 using velocity channels corresponding to the largest velocity shifts, indicated with blue and red shaded regions in the spectra at the top panel, respectively. These maps show that the largest velocity shifts are located closer to the QSO position, extending out to about 20 kpc at the current depth. While all the described features are reminiscent of an outflow, radiative transfer modeling is needed to test this scenario (e.g., Chang et al. 2023). Such a modeling is ongoing and will be presented in a future publication.
4.4. Searching for C IV and He II extended emission
As mentioned in the introduction, the emission lines C IV and He II could be used to constrain the powering mechanism responsible for the observed nebulae, the hardness of the ionizing spectrum of the powering source and shock scenarios, the metallicity, and the extent of the enriched halo. For this reason we searched for these lines in the final datacubes, together with additional rest-frame UV emission lines, Si IV and C III], that could be used to constrain the physical properties of the extended gas. We do not detect extended emission in these transitions for any of the sources in our sample. For completeness, we present χSmooth maps obtained for velocity ranges equivalent to the Lyα 30 Å NB and centered at the expected wavelengths for Si IV, C IV, HeII, and CIII] in Figs. C.1–C.5, respectively. For the BR1202-0725 system, the He II line is within the datacube spectral range, but the equivalent NB falls outside of the spectral range. Therefore, we used the last available channels to compute this χSmooth map. Since there are no detections for any of these additional lines, we computed 2σ SB upper limits and rescaled them to their respective Lyα nebula area, assuming 20 squared arcseconds for the ALESS SMGs; these values are shown in Table 3.
We estimate the C IV/Lyα and He II/Lyα ratio upper limits for the three systems with QSOs and discuss them in the context of the Lyα powering mechanisms in Sect. 5.1. These are estimated from the total Lyα luminosity of each nebula and the luminosity upper limits of C IV and He II (shown in Table 3). For BR1202-0725, the He II velocity range equivalent to the ±FWHM of the Lyα line is outside of the spectral range; therefore, we used the same velocity span encompassing the line but shifted to the last available channels to estimate this limit. Therefore, we caution that this upper limit may not fully represent the noise in the range ±FWHM of the He II line. However, as the He II line is expected to be narrower than the Lyα emission, the range used surely quantifies the absence of a He II detection in the current observation.
5. Discussion
5.1. Extended Lyman-α powering mechanisms
The variety of the systems studied here (one QSO+SMG, two SMGs that host a QSO, and two SMGs that do not) enables us to discuss the different mechanisms through which extended Lyα nebular emission could be produced. We considered the following mechanisms: scattering of Lyα photons produced in compact sources, ionizing and Lyα photons produced by ongoing star formation, gravitational cooling radiation, shocks by galactic and/or AGN outflows, and AGN photoionization followed by recombination. In principle, all these mechanisms could contribute together to the production of the observed extended emission and we discuss their relative roles below. In brief, by revisiting each of the aforementioned mechanisms we show that the firmest conclusion is that gravitational cooling is likely not contributing significantly in powering the observed extended Lyα emission.
5.1.1. Scattering of Lyα photons emitted by compact sources
Lyα photons produced in compact sources can scatter out in the surrounding gas distribution, producing an observable glow. In this scenario, the SB of the extended nebular Lyα emission is therefore expected to be proportional to the Lyα photon budget from the QSO (e.g., Hennawi & Prochaska 2013) and/or embedded galaxies, and no significant extended He II emission should be detected, as it is a recombination line (e.g., Prescott et al. 2015; Arrigoni Battaia et al. 2015a,b).
For the systems studied here, the dominant contribution of Lyα photons in BR1202-0725, G09-0902+0101 and G15-1444-0044 is clearly the AGN. Indeed, in close proximity to the extended Lyα emission BR1202-0725 has three LAEs (FLAE1 = (1.54 ± 0.05)×10−16 erg s−1 cm−2, FLAE2 = (0.54 ± 0.05)×10−16 erg s−1 cm−2 and FLAE3 = (0.24 ± 0.03)×10−16 erg s−1 cm−2; Drake et al. 2020), but their Lyα emission is only 3% of the QSO budget at those wavelengths (see Table 3; (8.661 ± 0.004)×10−15 erg s−1 cm−2). Instead, G09-0902+0101 and G15-1444-0044 do not show LAEs in close proximity to their extended Lyα glow, while in the SMG fields we do not find evidence for any Lyα emitting sources. We compute an indicative number of Lyα photons available for scattering by integrating the QSO’s spectra using the ±FWHM of the nebular emission (luminosities listed in Table 3). We find that for each QSO system these photons would be able to power the observed Lyα nebulae, with the QSO Lyα luminosities exceeding by 6.4, 4.3 and 4.0 the nebular luminosities (computed in the same range; Table 3) for BR1202 − 0725, G09 − 0902 + 0101 and G15 − 1444 − 0044, respectively.
Interestingly, the Lyα luminosity of the QSO in the BR1202-0725 system is 14× greater than G09 − 0902 + 0101 and G15 − 1444 − 0044. In this scenario, if the conditions and environment of these three systems are similar, this would predict a 14× more luminous nebula around BR1202-0725. However, the dust mass in BR1202-0725 is on average 1.3× greater than in the two SMGs hosting QSOs, likely corresponding to a higher probability of Lyα absorption. Therefore, we would only expect a 10× more luminous nebula. This calculation aligns well with the observation that the nebula around BR1202-0725 is 9× more luminous than G09 − 0902 + 0101 and G15 − 1444 − 0044. Accordingly, the two SMGs, where no strong source of Lyα photons is observed, do not have an extended nebula. Therefore, the systems studied here are consistent with a picture in which the extended Lyα level could be regulated by a combination between the QSO’s budget of Lyα photons and the dust content of the host galaxy.
To further test this trend, we obtain the nebula and QSO Lyα luminosities for another system with known extended emission and dust mass estimate (Mdust = (9 ± 3)×108 M⊙; Arrigoni Battaia et al. 2022), finding 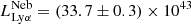 erg s−1 and
erg s−1 and 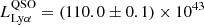 erg s−1. We find that also this system follows the aforementioned tentative trend. To visualize this finding, Fig. 7 shows how the ratio
erg s−1. We find that also this system follows the aforementioned tentative trend. To visualize this finding, Fig. 7 shows how the ratio 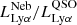 decreases with Mdust.
decreases with Mdust.
 |
Fig. 7. Ratio of the nebula and QSO Lyα luminosities versus the dust mass of the central host galaxy for the three QSOs in our sample (black with IDs) and for the Fabulous system (blue; Arrigoni Battaia et al. 2022). |
We stress that previous works looking at variation of Lyα luminosities for QSO nebulae against the QSO’s budget of Lyα photons and/or the QSO’s luminosity (e.g., Arrigoni Battaia et al. 2019a; Mackenzie et al. 2021) found that if a relation is present, its scatter is large. However, those studies did not have any information on the dust properties of the host galaxies, which could be an important factor in finding a trend. Larger samples of QSO Lyα nebulae with well-studied QSO hosts are required to assess the contribution from this scenario.
Moreover, the detected nebulae present an anisotropic distribution and an offset between the QSO position and the peak of the Lyα emission. For example, BR1202-0725 shows no Lyα emission at the position of the dusty SMG (see the white cross in Fig. 2) and the peak of the Lyα distribution is closer to the LAE (see Fig. 2) where we expect less dust content. The morphological differences and brightest part of the nebulae could therefore be due to the distribution of scattering atoms and dust around each QSO, with the denser regions and the dustier regions showing higher and lower Lyα emission, respectively. Therefore, due to all this, we cannot rule out that resonant scattering of the QSO’s Lyα photons can contribute in powering the detected nebulae.
Finally, we stress two important caveats. First, the same morphological and SB differences observed between the detected nebulae could also be due to variations in the gas physical properties (e.g., density and local dust content) in a photoionization scenario (see Sect. 5.1.5). Secondly, differences in SB could also be produced due to the different local environment in which the extended emission is observed (e.g., presence of companion galaxies) as it is the case for BR1202-0725. We discuss this possibility in Sect. 5.2.
5.1.2. Star formation
The Lyα emission could also be powered by recombination radiation, which follows photoionization from the strong star formation of the targeted sources. As any Lyα emission mechanism this process can be followed by resonant scattering, which we do not take into account in this section. In this scenario, the Lyα luminosity is expected to be proportional to the SFR of the embedded sources, modulo the escape fraction of their ionizing and Lyα photons. We can get a rough estimate of the SFR needed to power the observed extended nebulae by assuming that all of the Lyα luminosity is produced by star formation under case B recombination (LLyα = 8.7LHα) and using Eq. (2) from Kennicutt (1998): SFR(M⊙ yr−1) = LHα/(1.26 × 1041 erg s−1). For the SMGs we do not find any extended Lyα emission; therefore, we report upper limits for their Lyα SFRs. We computed them from their 2σ SB limit (for a 30 Å narrow band) scaled to a similar nebula area as for the two SMGs hosting a QSO (20 arcsec2). All the determined SFR values are listed in Table 3.
We compare these derived instantaneous SFRs (timescales up to ∼10 Myr; Kennicutt & Evans 2012) with the SFRs estimated from the IR (timescales up to ∼100 Myr; Kennicutt & Evans 2012), assuming a constant star formation history. We find that the available star formation is larger than that estimated from the Lyα, implying that it would be enough to power the detected Lyα nebulae, also when a very small (2 − 5%) escape of ionizing photons is taken into account. Interestingly, a similar result was found for z ∼ 6 QSOs (median value ≲1%; Farina et al. 2019). However, the fact that we do not detect emission in the surrounding and proximity of the three SMGs in our sample (the two ALESS sources and the SMG companion of BR1202 − 0725), run counter to the star formation scenario. Indeed, the ratios between the detected nebular emission for the QSOs in our sample (which are all hosted by SMG-like galaxies) and the upper limits for SMGs are > 16 − 160, much larger than the ratios between the SFRs for the targeted objects (4 − 13). In other words, if star formation is the main powering mechanism of extended Lyα the SMGs should have nebulae with LLyα = 4.4 × 1043 erg s−1, which would be detectable in the current data set if they spread out on scales similar to the nebular emission around the two SMGs hosting a QSO. The fact that we do not detect such emission means that most of the UV photons produced by star formation (> 95%, using the 2σ limit) do not escape these galaxies. We stress that the dust contents estimated for the SMGs are the smallest in our sample (Table 1). Therefore, it would require a drastic change in dust geometry and dust grain properties between the different sources to ascribe the diversity of Lyα nebulae in this sample to star formation. Thus, star formation seems to have a minor role in powering the extended emission in these sources.
5.1.3. Gravitational cooling radiation
Large-scale Lyα emission could be produced by gravitational cooling radiation, originating from cold streams accretion. Rosdahl & Blaizot (2012) and Trebitsch et al. (2016) have done radiative transfer calculations to test this scenario, and found that it can reproduce the sizes and luminosities of extended Lyα emission in massive halos, together with their polarization pattern.
In this scenario, for the high dark matter halo masses inferred for our sources (see Sect. 2), uncertain analytical and numerical calculations predict the extended Lyα luminosities to be proportional to the dark matter halo masses, and the peak of the signal to be located at the center of the gravitational potential well (Dijkstra & Loeb 2009; Faucher-Giguère et al. 2010). We stress upfront that the dark matter halo masses currently available are highly uncertain (see the caveats in Sect. 2.3). However, it is of interest to check whether they favor a gravitational cooling scenario, also to make predictions for future observations.
For the inferred dark matter halo masses we would expect G09-0902+0101 to have the brightest Lyα glow, followed by BR1202-0725 (1.6 times dimmer), and then G15-1444-0044 and the SMGs (10 times dimmer). However, the Lyα nebulae around SMGs hosting a QSO are 9 times fainter than the nebula around the QSO+SMG system. Moreover, in this scenario the SMGs should have extended emission only two times dimmer than BR1202-0725, but they are not detected at the current depth. Therefore, there is no clear evidence that gravitational cooling powers these nebulae. This is also supported by recent cosmological simulations of high-redshift QSO halos post-processed with radiative transfer calculations (Costa et al. 2022). the contribution from gravitational cooling is about one order of magnitude lower compared to the effects of recombination and scattering of Lyα photons from the broad-line regions of QSOs. A factor of 10 lower emission with respect to the SMGs hosting a QSO cannot be detected in the current data set.
To search for the gravitational cooling signal one should therefore target obscured isolated galaxies, such as the SMGs studied here. Indeed, in these objects there should be only a very minor contribution from the other mentioned mechanisms. To search for the gravitational cooling signal at a factor of 10 lower SB level than for the SMGs hosting QSO studied here, one would need to be able to detect an average signal on the order of SBLyα ∼ 4 × 10−19 erg s−1 cm−2 arcsec−2. This depth could be achieved at high significance (3σ) with a MUSE 75 hours exposure of an individual system or with a stack of multiple systems with an equivalent total exposure time. The detection of this signal would give an independent indication of the halo mass of SMGs and of its cool gas mass fraction.
5.1.4. Shocks by Galactic and/or AGN outflows
We observe broad Lyα linewidths (FWHM ∼ 1500 km s−1; see Table 3) in all our nebulae around QSOs. These FWHM are broader than usually reported in the literature (FWHM < 940 km s−1; e.g., Borisova et al. 2016; Arrigoni Battaia et al. 2018; Fossati et al. 2021), suggesting the presence of violent kinematics (shocks) driven by the QSO and/or star formation activity. Indeed, the sound speed in the ambient hot medium (T ∼ 5 × 106 K) for a 1012.5 M⊙ dark matter halo is cs ≈ 260 km s−1. Moreover, we observe a positive velocity shift in all our nebulae with respect to the QSO’s systemic redshift (Fig. 2), which could further indicate the presence of bulk outflows as traced by Lyα resonant scattering effects.
In order to build intuition about a shock scenario, we compared C IV/Lyα and He II/Lyα line ratios to those predicted by shock and shock+precursor models from Allen et al. (2008), as done in previous works (e.g., Arrigoni Battaia et al. 2015b; Herenz et al. 2020). When doing this, we imagined the Lyα extended emission as the result of shock fronts propagating at velocity vs in a medium with pre-shock density nH. In such a scenario, the Lyα flux follows 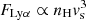 (Allen et al. 2008). We limited the models by Allen et al. (2008) to a realistic set of parameters for the nebulae studied here: nH = 0.01, 0.1, 1.0, 10, 100 cm−3 and vs in the range 100 − 1000 km s−1 in steps of 25 km s−1. We used models with solar metallicity and adopted a magnetic parameter B/n1/2 = 3.23 μG cm3/2, which is expected for interstellar medium gas assuming equipartition of magnetic and thermal energy. However, we stress that the selected models do not vary strongly with either the metallicity or magnetic parameter because of the strong dependence of the ionizing flux on the shock velocity.
(Allen et al. 2008). We limited the models by Allen et al. (2008) to a realistic set of parameters for the nebulae studied here: nH = 0.01, 0.1, 1.0, 10, 100 cm−3 and vs in the range 100 − 1000 km s−1 in steps of 25 km s−1. We used models with solar metallicity and adopted a magnetic parameter B/n1/2 = 3.23 μG cm3/2, which is expected for interstellar medium gas assuming equipartition of magnetic and thermal energy. However, we stress that the selected models do not vary strongly with either the metallicity or magnetic parameter because of the strong dependence of the ionizing flux on the shock velocity.
In more detail, in the shock models the emission is produced within the region ionized and excited by the shock. While in the shock+precursor scenario, it is taken into account also the component ionized by the extreme UV and X-ray emission emitted upstream from the shocked region3. We caution upfront that these models could underestimate the extended Lyα emission since the contribution of resonant scattering is not considered. This effect would therefore shift the grids to lower values for both ratios.
Figure 8 shows the C IV/Lyα versus the He II/Lyα upper limits for our sources in comparison to literature data and the model grids taken from Allen et al. (2008). The QSOs studied here are shown with star symbols. The values are computed from the integrated luminosities within the nebula area (see Table 3). The left panel shows the shock model grids while the right panel shows the shock+precursor model grids. We also compare our data points to literature data for QSOs’ nebulae. Specifically, we indicate the line ratios for z ∼ 3.5 QSO nebulae from Borisova et al. (2016), stacking results for nebulae around z = 3 − 4.5 QSOs inside a radial bin of 10 < R/kpc < 30 from Fossati et al. (2021), and one extremely red QSO at z ∼ 2.3 (Lau et al. 2022). We see that for the systems studied here the shock-only scenario allows for larger shock velocities (vs ≳ 300) than the shock+precursor scenario, which restricts velocities to vs ∼ 300 − 500 km s−1. Most of the upper limits in the literature and our most stringent data would require pre-shock densities nH ≳ 0.5 cm−3 for both models. In the next section we show that similarly dense gas is needed in a photoionization scenario where Lyα scattering from the QSO is neglected (e.g., Arrigoni Battaia et al. 2015a).
 |
Fig. 8. C IV/Lyα and He II/Lyα line ratio upper limits (2σ) for the sources studied here with detected extended Lyα nebulae (star symbols). The line ratios are computed from the nebular luminosities listed in Table 3. The left panel shows the model grids for the shock scenario, while the right panel shows the model grids for the shock+precursor scenario from Allen et al. (2008). Overlaid are derived line ratios and upper limits for QSO nebulae from Borisova et al. (2016) as cyan circles, stacked nebulae around z = 3 − 4.5 QSOs inside a radial bin of 10 < R/kpc < 30 from Fossati et al. (2021) as a white cross, and one extremely red QSO at z ∼ 2.3 (Lau et al. 2022) as a magenta cross. |
5.1.5. Photoionization from AGNs followed by recombination
Unlike the QSOs studied here, the SMGs do not present Lyα emission at the current depth, indicating that AGNs are vital for the powering of the observed extended nebulae. We note that even though all the QSOs in our sample are hosted by SMGs, they have a spectra consistent with the average unobscured QSO templates (e.g., Lusso et al. 2015; see our Appendix D). In Sect. 5.1.1 we discussed the likely contribution of resonant scattering of the AGN Lyα photons in powering the large-scale Lyα emission. Here, instead, we assess the impact of AGN photoionization on the observed Lyα SB following the framework presented in Hennawi & Prochaska (2013). In this scenario, the Lyα signal is produced in the recombination cascade following the gas photoionization due to the central AGN. The cool (T ∼ 104 K) gas is assumed to be organized in small clouds with a single constant hydrogen volume density nH, constant hydrogen column density NH, and uniformly distributed within a spherical halo of radius R, such that the clouds covering factor is fC. The Lyα SB can then be estimated using simple relations for two limiting cases, optically thick (NHI ≫ 1017.2 cm−2) and optically thin (NHI ≪ 1017.5 cm−2) gas to ionizing radiation.
In the optically thick scenario, a thin surface of the gas clouds will emit Lyα photons proportionally to the number of impinging ionizing photons (determined by the specific luminosity at the Lyman edge, LνLL) and decreasing with distance from the QSO as R−2. The Lyα SB in the optically thick regime (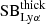 ) is given by Eq. (15) of Hennawi & Prochaska (2013).
) is given by Eq. (15) of Hennawi & Prochaska (2013).
As done in Arrigoni Battaia et al. (2019b), we estimate LνLL of the QSOs assuming a SED described by a power law of the form Lν = LνLL(ν/νLL)αUV and slope αUV = −1.7 as obtained by Lusso et al. (2015). We show a comparison of the QSOs spectra and assumed SEDs in Fig. D.1, and confirm that these standard QSO templates adjust to our data set. In particular, we stress that the two SMGs hosting a QSO in our sample are not obscured in their rest-frame UV along the line of sight, as discovered by Fu et al. (2017). We find log(LνLL/[erg s−1 Hz−1]) values of 31.8, 30.4 and 30.6 for BR1202-0725, G09-0902+0101, and G15-1444-0044, respectively. We estimate the observed 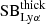 at the same distance R = 13 kpc for all of the nebulae and compare to the observed values at the same distance, which is the maximum projected distance in common to all studied nebulae. We assume a covering factor of fC = 1 for the clouds (fC > 0.5 as favored by the observed diffuse morphologies; e.g., Arrigoni Battaia et al. 2015b) and hydrogen column density of NH = 1020.5 cm−2, as the median value obtained in absorption studies of z ∼ 2 QSO halos (Lau et al. 2016). In principle the covering factor could be even fC > 1, indicating a clumpy medium with a larger volume filling factor. However, we chose a value of 1 to simplify equations and ease comparison with previous works. We derive
at the same distance R = 13 kpc for all of the nebulae and compare to the observed values at the same distance, which is the maximum projected distance in common to all studied nebulae. We assume a covering factor of fC = 1 for the clouds (fC > 0.5 as favored by the observed diffuse morphologies; e.g., Arrigoni Battaia et al. 2015b) and hydrogen column density of NH = 1020.5 cm−2, as the median value obtained in absorption studies of z ∼ 2 QSO halos (Lau et al. 2016). In principle the covering factor could be even fC > 1, indicating a clumpy medium with a larger volume filling factor. However, we chose a value of 1 to simplify equations and ease comparison with previous works. We derive 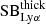 values of 16.5, 2.6 and 2.8 × 10−15 erg s−1 cm−2 arcsec−2 for BR1202-0725, G09-0902+0101, and G15-1444-0044, respectively. These values are a factor of 500 − 600 greater than the observed values at the same distance, which are 24.6, 4.3 and 5.5×10−18 erg s−1 cm−2 arcsec−2 for BR1202-0725, G09-0902+0101, and G15-1444-0044, respectively. Therefore, we conclude that a pure optically thick regime is unlikely to be found in these systems, unless very small covering factors (fC ∼ 0.002) or a very small escape of Lyα photons are considered. This is consistent with several previous works (e.g., Arrigoni Battaia et al. 2015a, 2019b; Farina et al. 2019; Drake et al. 2020).
values of 16.5, 2.6 and 2.8 × 10−15 erg s−1 cm−2 arcsec−2 for BR1202-0725, G09-0902+0101, and G15-1444-0044, respectively. These values are a factor of 500 − 600 greater than the observed values at the same distance, which are 24.6, 4.3 and 5.5×10−18 erg s−1 cm−2 arcsec−2 for BR1202-0725, G09-0902+0101, and G15-1444-0044, respectively. Therefore, we conclude that a pure optically thick regime is unlikely to be found in these systems, unless very small covering factors (fC ∼ 0.002) or a very small escape of Lyα photons are considered. This is consistent with several previous works (e.g., Arrigoni Battaia et al. 2015a, 2019b; Farina et al. 2019; Drake et al. 2020).
Consequently, if the QSO directly shines on the surrounding gas, it is more likely in place an optically thin scenario, where the gas is highly ionized and the Lyα recombination signal depends on the gas properties (nH, NH; Eq. (10) from Hennawi & Prochaska 2013). Considering the Lyα SB in the optically thin regime (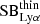 ) as the observed average SB at R = 13 kpc, we estimate the gas volume density nH needed to power the observed Lyα nebulae, assuming once again a covering factor of fC = 1 and hydrogen column density NH = 1020.5 cm−2. We find values for nH of 13.3, 0.6 and 1.0 cm−3 for BR1202-0725, G09-0902+0101 and G15-1444-0044, respectively4. These large interstellar-medium-like values are usually inferred by other observational studies targeting QSO nebulae (see, e.g., Hennawi et al. 2015; Arrigoni Battaia et al. 2015a, 2019b; Cai et al. 2018); however, those studies did not have information on the dust content of the QSO’s host galaxies. The density values are high for CGM gas compared to those found from simulations for z ∼ 3 massive systems (Rosdahl & Blaizot 2012), which are not able to resolve this gas phase.
) as the observed average SB at R = 13 kpc, we estimate the gas volume density nH needed to power the observed Lyα nebulae, assuming once again a covering factor of fC = 1 and hydrogen column density NH = 1020.5 cm−2. We find values for nH of 13.3, 0.6 and 1.0 cm−3 for BR1202-0725, G09-0902+0101 and G15-1444-0044, respectively4. These large interstellar-medium-like values are usually inferred by other observational studies targeting QSO nebulae (see, e.g., Hennawi et al. 2015; Arrigoni Battaia et al. 2015a, 2019b; Cai et al. 2018); however, those studies did not have information on the dust content of the QSO’s host galaxies. The density values are high for CGM gas compared to those found from simulations for z ∼ 3 massive systems (Rosdahl & Blaizot 2012), which are not able to resolve this gas phase.
Recent observational works showed that the high-z CGM has a multiphase nature, with even molecular gas detections on tens of kiloparsecs around some active objects (e.g., high-redshift radio galaxies, Emonts et al. 2016; QSOs and SMGs, Vidal-García et al. 2021). It seems therefore realistic that the simulations need large clumping factors5 to match the observed Lyα SB on CGM scales (e.g., Cantalupo et al. 2014; Arrigoni Battaia et al. 2015a; Cai et al. 2018). However, it is still a matter of debate how strong the clumping needs to be. Large clumping factors are required when assuming only recombination (C ∼ 1000, Cantalupo et al. 2014), while a contribution from other mechanisms (i.e., collisional excitation and/or resonant scattering of QSO Lyα photons) would result in a more moderate clumping.
If the photoionization scenario is the dominant mechanism, we would expect to detect, in deep observations, additional emission lines (e.g., He II) from the QSO’s CGM. In particular, in a recombination-only scenario, the He II/Lyα ratio should be ∼0.3 if helium is fully doubly ionized (Arrigoni Battaia et al. 2015a; Cantalupo et al. 2019). Lower fractions of fully ionized helium and the contribution of additional mechanisms in the budget of Lyα photons would result in lower ratios. Stacking analysis of z ∼ 3 − 4 QSOs clearly detected extended Lyα and C IV, and only marginally He II (e.g., Fossati et al. 2021). That work emphasized that Cloudy photoionization models of gas on CGM scales require scattering of the QSOs’ Lyα photons to match the observed line ratios using reasonable values for CGM metallicities. Since we detect Lyα emission and do not detect He II, resulting in similar upper limits as Fossati et al. (2021; He II/Lyα < 0.03), we cannot provide further insights on this problem. Future works are needed to establish the relative contribution of recombination and QSO Lyα scattered photons to the Lyα glow on CGM scales.
5.2. Comparison with previous Lyα SB radial profiles
Figure 9 shows the SB radial profiles of the three detected targets as red stars, green and yellow diamonds for BR1202 − 0725, G09 − 0902 + 0101 and G15 − 1444 − 0044, respectively, as a function of comoving projected radius, and corrected by cosmological dimming. The profiles are shown only for annulus above the 2σ SB limit for that ring (red line of Fig. 4). Once again, it is evident that the nebulae associated with the SMGs hosting a QSO are dimmer and more compact than the one around the QSO+SMG system. Furthermore, the same figure shows a comparison with different samples from the literature (see the figure caption and legend), highlighting the respective 25 − 75 percentile ranges when available. We find that the sources in our sample are outliers for any of the z ≳ 3 bright QSO samples (Arrigoni Battaia et al. 2019a; Farina et al. 2019; Fossati et al. 2021). However, we find that our faint, but submillimeter-bright z ∼ 3 QSOs present nebulae akin to those found around similarly faint (imag < 19.5) z ∼ 3 QSOs (Mackenzie et al. 2021), and that resemble the median profile from the lower redshift (z ∼ 2.3) sample from Cai et al. (2019). This once again stresses the large difference between nebulae of bright z ∼ 2.3 QSOs and those of bright z ∼ 3 QSOs, which has been argued to be most likely driven by a different halo accretion regime (e.g., Arrigoni Battaia et al. 2019a; Farina et al. 2019; Fossati et al. 2021). For completeness, we also show the observed average SB profile of z = 2.65 Lyman break galaxies (LBGs) from Steidel et al. (2011). These galaxies are sources at the lower end of the halo masses probed by our sample (median halo mass of MDM = 9 × 1011 M⊙; Steidel et al. 2011), and show both signatures of Lyα emission and absorption on galaxy scales, but they do not have an AGN contribution. The LBGs clearly have an SB profile fainter than sources hosting QSOs, further stressing the importance of AGNs in powering strong Lyα emission.
 |
Fig. 9. Circularly averaged SB as a function of comoving projected radius of the nebulae detected in our QSO sample (red stars, green diamonds, and yellow diamonds for BR1202 − 0725, G09 − 0902 + 0101, and G15 − 1444 − 0044, respectively), corrected for cosmological dimming. The red and purple squares with arrows indicate the upper limits for ALESS61.1 and ALESS65.1, respectively. Different profiles from the literature are indicated as colored circles with their respective 25 − 75 percentile ranges when available. The z = 3.17 QSO sample from Arrigoni Battaia et al. (2019a) is shown in yellow. The SB profile (taken from Arrigoni Battaia et al. 2016) of the z = 2.28 Slug ELAN is shown in blue (Cantalupo et al. 2014). The z = 6.2 QSO sample from Farina et al. (2019) is shown in magenta. The z = 3.8 QSO sample from Fossati et al. (2021) is shown in cyan. The z = 2.3 QSO sample from Cai et al. (2019) is shown in orange. The median profile of the faint QSO sample at z = 3 from Mackenzie et al. (2021) is shown with black connected circles. We computed the SB profile of the galaxy group SMMJ02399, which comprises a QSO and an SMG at z = 2.8 from Li et al. (2019; gray connected circles). Finally, the fit to the observed SB profile for z = 2.65 LBGs from Steidel et al. (2011) is shown with the dashed black curve. |
On the other hand, the QSO+SMG system BR1202 − 0725 has clearly an enhanced brightness with respect to all other profiles. This could be due to several factors, such as (i) the merger state of this system with interacting galaxies (an SMG, a QSO host and a LAE), likely providing a larger reservoir of cool gas with respect to individual halos and possible supply for diffuse star formation (e.g., Decarli et al. 2019), (ii) the presence of dense gas on CGM scales, as directly evident from the presence of a bridge of [C II] emission between the QSO and the SMG (Drake et al. 2020), and (iii) presence of galactic and AGN winds or outflows that could enhance densities in their surroundings and/or favor the escape of Lyα photons (e.g., Costa et al. 2022). To confirm whether brighter SB profiles are typical for QSO+SMG systems, we extracted the radial profile for the SMMJ02399 system at z = 2.8 (gray points) from Li et al. (2019). This system is also known to have a multiphase CGM with a cold diffuse molecular phase extending out to at least ∼20 kpc (Vidal-García et al. 2021). We also find that this system is at the high end of the radial profiles, even though its redshift is lower. This finding further suggests that QSO+SMG systems are the pinnacle of Lyα emission at each redshift. Further evidence of this comes from the comparison of the SB radial profile of the z ∼ 2.28 Slug enormous Lyα nebula (ELAN; blue points) from Arrigoni Battaia et al. (2016) with the profiles of similar bright QSOs at z ∼ 2 (Cai et al. 2019). The Slug ELAN is known to host an SMG undergoing ram-pressure stripping within the halo of a bright QSO (Chen et al. 2021). Similar to the aforementioned cases, the SB profile of the Slug ELAN is above the average z ∼ 2 QSOs’ profile. However, its SB profile is not as high as the one found for BR1202 − 0725 and SMMJ02399, possibly indicating a difference in the densities and reservoir of cool material around these systems from high to low redshift (e.g., Arrigoni Battaia et al. 2019a). In the same figure we also indicate the 2σ upper limits for the SB inside each ring for the SMGs, as the red (ALESS61.1) and purple (ALESS65.1) squares with arrows. We find that the Lyα SB for isolated SMGs is at least a factor of 2 fainter than that of QSOs at similar redshifts.
Finally, we compare the scale length rh = 11 ± 1 kpc obtained for BR1202-0725 in Sect. 4.2 with those reported for the average profiles of type-I QSOs at bracketing redshifts z ∼ 3 and z ∼ 6. We find that BR1202-0725 sitting at z = 4.6942 has a scale length smaller (larger) than the sample at z ∼ 3 (z ∼ 6) when looking at physical scales, rh = 15.7 kpc (Arrigoni Battaia et al. 2019a) and rh = 9.4 (Farina et al. 2019), respectively. This would translate to similar scale lengths in comoving units as can be appreciated in Fig. 9. Larger samples of QSO nebulae at z ∼ 5 are needed to firmly constrain these values.
6. Summary
With VLT/MUSE, we targeted five z ∼ 3 − 4 submillimeter-bright systems to unveil extended Lyα emission. In this paper we have discussed the contribution of different powering mechanisms and compared our results to the plethora of z > 2 QSO observations. Specifically, our observations comprise systems with different degrees of QSO illumination: a QSO+SMG system (BR1202-0725), two SMGs that host a QSO (G09-0902+0101 and G15-1444-0044), and two SMGs that do not (ALESS61.1 and ALESS65.1). All these objects are expected to sit in halos as massive as those hosting QSOs (Sect. 2). Below, we summarize our observational findings:
-
We find that our targets have very different Lyα morphologies and brightness levels. The QSO+SMG system presents the highest levels of Lyα emission, probably reflecting the richness of its halo environment in terms of mass and density of the cool gas phase (top panel of Fig. 2 and Sect. 5.2). We do not detect any extended Lyα emission around the two SMGs that do not host a QSO.
-
All the detected Lyα nebulosities present more violent kinematics (FWHM ≳ 1200 km s−1) with respect to nebulae around QSOs at similar redshifts (FWHM ∼ 600 km s−1; Arrigoni Battaia et al. 2019a; Fossati et al. 2021). In particular, we find evidence of large-scale outflows in the BR1202-0725 system (Fig. 4.3.2).
-
None of the targeted systems show extended emission in other rest-frame UV lines besides Lyα down to ∼10−18 erg s−1 cm−2 arcsec−2 (2σ in 30 Å; Sect. 4.4).
-
The two SMGs that host a QSO have CGM Lyα profiles about three times fainter than the typical z ∼ 3 QSO halo, resembling the median profile of similarly faint QSOs from Mackenzie et al. (2021; see our Fig. 9 and Sect. 5.2). We also find that their Lyα emission is at similar levels as the emission around bright z ∼ 2 QSOs, further highlighting the remarkable difference between the Lyα emission around bright z ∼ 2 QSOs and higher-redshift QSOs (e.g., Arrigoni Battaia et al. 2019a; Farina et al. 2019; Fossati et al. 2021).
We have discussed our observational results in the context of the relative roles of the different Lyα powering mechanisms presented in Sect. 1: resonant scattering of Lyα photons for embedded sources, gravitational cooling radiation, shocks by galactic and/or AGN outflows, and photoionization from AGNs or star formation followed by recombination. We briefly summarize our results here.
Cooling radiation is unlikely to be the main powering mechanism, because we would expect the Lyα emission to scale proportionally to the halo mass (see Sect. 5.1.3). Therefore, we should have detected similar levels of Lyα emission for the similar halo masses of our sample (e.g., Haiman et al. 2000; Rosdahl & Blaizot 2012). We propose that more observations of obscured systems, such as isolated SMGs, could provide test cases for this scenario.
We cannot rule out that resonant scattering of Lyα photons emitted by compact sources makes a significant contribution to the observed nebulae. Indeed, we observe that the extended Lyα level is consistent with being regulated by the budget of QSO Lyα photons modulo the dust content on galaxy scales. Sources with no Lyα emission on small scales (i.e., the SMGs) do not show extended Lyα emission. However, due to the small size of our sample, we cannot provide firm constraints on the relationship between the extended Lyα luminosity and the budget of QSO Lyα photons. Therefore, larger samples of QSO Lyα nebulae with information on their host galaxies are needed.
Regarding the star formation scenario, by comparing the inferred SFRLyα between our nebulae (Table 3) and the derived SFR from their total IR luminosity (Table 2), we show that the available star formation in these systems should be enough to power the Lyα nebulae (see Sect. 5.1.2). However, the fact that we do not detect extended Lyα emission around the SMGs suggests that photoionization due to star formation followed by recombination (and resonant scattering) plays a minor role in powering these nebulae, likely because most of the UV and Lyα photons from star formation do not escape these dusty galaxies.
Also, the aforementioned presence of large Lyα linewidths and the positive velocity shifts (Table 3) of the QSO’s nebulae motivated us to test a large-scale outflow scenario (see Sect. 5.1.4). We compared the C IV/Lyα and He II/Lyα line-ratio upper limits with the shock and shock+precursor models from Allen et al. (2008). We find that the ratios for our systems agree with the models with shock velocities vs ≥ 300 km s−1 for the shock-only scenario and vs ∼ 300 − 500 km s−1 for the shock+precursor scenario. Both cases allow for a high pre-shock density of nH ≥ 1 cm−3, usually not resolved in cosmological simulations and expected within the interstellar medium.
Moreover, we find that an AGN presence is essential for powering the observed Lyα halos as only systems with QSOs show an extended Lyα glow, highlighting the importance of photoionization from the central AGN as a contribution to the extended Lyα emission. We tested the contribution of photoionization from the QSO followed by recombination under the assumption of two limiting scenarios: optically thick and optically thin to ionizing radiation (see Sect. 5.1.5). Assuming the QSO is illuminating the gas, we find that our data favor an optically thin scenario, which requires an average volume density of nH ∼ 1 − 10 cm−3, as frequently found in previous studies (e.g., Arrigoni Battaia et al. 2015b; Hennawi et al. 2015; Cai et al. 2018).
Summarizing, we find evidence against gravitational cooling radiation being the main powering mechanism of the detected extended Lyα emission. On the other hand, photoionization, outflows, and resonant scattering of Lyα photons from compact sources are likely contributors to the observed Lyα nebulae. Our pilot work opens the path to analyses of CGM emission around high-z massive systems that take into account the properties of QSO hosts (e.g., Muñoz-Elgueta et al. 2022) and embedded galaxies, frequently overlooked in the study of large-scale emission. Future large statistical samples together with statistical investigations of mock observations are needed to confirm and extend our findings. Moreover, future James Webb Space Telescope observations of extended Hα emission around QSOs could help in disentangling the powering mechanisms discussed in this work.
More details on the physical mechanism at play in each model and on the production of different lines can be found in Allen et al. (2008).
The clumping factor is usually defined as  (e.g., Cantalupo et al. 2014).
(e.g., Cantalupo et al. 2014).
Acknowledgments
The authors thank the anonymous referee for providing constructive comments that have improved our paper. The authors thank Kevin Hall for his useful comments on an advanced draft of this work. Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programmes 0103.A-0296(A), 0102.A-0403(A) and 0102.A-0428(A), available from the ESO Science Archive Facility https://archive.eso.org/. EPF is supported by the international Gemini Observatory, a program of NSF’s NOIRLab, which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation, on behalf of the Gemini partnership of Argentina, Brazil, Canada, Chile, the Republic of Korea, and the United States of America. C.-C.C. acknowledges support from the National Science and Technology Council of Taiwan (NSTC 109-2112-M-001-016-MY3 and 111-2112-M-001-045-MY3), as well as Academia Sinica through the Career Development Award (AS-CDA-112-M02). A.O. is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 443044596. M.G. thanks the Max Planck Society for support through the Max Planck Research Group.
References
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Arrigoni Battaia, F., Hennawi, J. F., Prochaska, J. X., & Cantalupo, S. 2015a, ApJ, 809, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Yang, Y., Hennawi, J. F., et al. 2015b, ApJ, 804, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Hennawi, J. F., Cantalupo, S., & Prochaska, J. X. 2016, ApJ, 829, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Prochaska, J. X., Hennawi, J. F., et al. 2018, MNRAS, 473, 3907 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Hennawi, J. F., Prochaska, J. X., et al. 2019a, MNRAS, 482, 3162 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Obreja, A., Prochaska, J. X., et al. 2019b, A&A, 631, A18 [EDP Sciences] [Google Scholar]
- Arrigoni Battaia, F., Chen, C.-C., Liu, H.-Y. B., et al. 2022, ApJ, 930, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Obreja, A., Costa, T., Farina, E. P., & Cai, Z. 2023, ApJ, 952, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, SPIE Conf. Ser., 7735, 773508 [Google Scholar]
- Bacon, R., Brinchmann, J., Richard, J., et al. 2015, A&A, 575, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Piqueras, L., Conseil, S., Richard, J., & Shepherd, M. 2016, Astrophysics Source Code Library [record ascl:1611.003] [Google Scholar]
- Birkin, J. E., Weiss, A., Wardlow, J. L., et al. 2021, MNRAS, 501, 3926 [Google Scholar]
- Blain, A. W., Smail, I., Ivison, R. J., & Kneib, J. P. 1999, MNRAS, 302, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
- Borisova, E., Cantalupo, S., Lilly, S. J., et al. 2016, ApJ, 831, 39 [Google Scholar]
- Cai, Z., Hamden, E., Matuszewski, M., et al. 2018, ApJ, 861, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, Z., Cantalupo, S., Prochaska, J. X., et al. 2019, ApJS, 245, 23 [Google Scholar]
- Cantalupo, S., Arrigoni-Battaia, F., Prochaska, J. X., Hennawi, J. F., & Madau, P. 2014, Nature, 506, 63 [Google Scholar]
- Cantalupo, S., Pezzulli, G., Lilly, S. J., et al. 2019, MNRAS, 483, 5188 [Google Scholar]
- Carilli, C. L., Riechers, D., Walter, F., et al. 2013, ApJ, 763, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
- Cen, R., & Zheng, Z. 2013, ApJ, 775, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chang, S.-J., Yang, Y., Seon, K.-I., Zabludoff, A., & Lee, H.-W. 2023, ApJ, 945, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C.-C., Hodge, J. A., Smail, I., et al. 2017, ApJ, 846, 108 [Google Scholar]
- Chen, C.-C., Arrigoni Battaia, F., Emonts, B. H. C., Lehnert, M. D., & Prochaska, J. X. 2021, ApJ, 923, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, L., Jahnke, K., Wisotzki, L., & Sánchez, S. F. 2006, A&A, 459, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costa, T., Arrigoni Battaia, F., Farina, E. P., et al. 2022, MNRAS, 517, 1767 [NASA ADS] [CrossRef] [Google Scholar]
- Decarli, R., Dotti, M., Bañados, E., et al. 2019, ApJ, 880, 157 [Google Scholar]
- Dijkstra, M. 2019, Saas-Fee Advanced Course, 46, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., & Loeb, A. 2008, MNRAS, 391, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., & Loeb, A. 2009, MNRAS, 400, 1109 [Google Scholar]
- Dijkstra, M., Haiman, Z., & Spaans, M. 2006, ApJ, 649, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. B., Walter, F., Novak, M., et al. 2020, ApJ, 902, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Eftekharzadeh, S., Myers, A. D., White, M., et al. 2015, MNRAS, 453, 2779 [Google Scholar]
- Emonts, B. H. C., Lehnert, M. D., Villar-Martín, M., et al. 2016, Science, 354, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Farina, E. P., Arrigoni-Battaia, F., Costa, T., et al. 2019, ApJ, 887, 196 [Google Scholar]
- Faucher-Giguère, C.-A., Kereš, D., Dijkstra, M., Hernquist, L., & Zaldarriaga, M. 2010, ApJ, 725, 633 [Google Scholar]
- Fossati, M., Fumagalli, M., Lofthouse, E. K., et al. 2021, MNRAS, 503, 3044 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H., Isbell, J., Casey, C. M., et al. 2017, ApJ, 844, 123 [CrossRef] [Google Scholar]
- Furlanetto, S. R., Schaye, J., Springel, V., & Hernquist, L. 2005, ApJ, 622, 7 [Google Scholar]
- Fusco, T., Bacon, R., Kamann, S., et al. 2020, A&A, 635, A208 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Vergara, C., Hodge, J., Hennawi, J. F., et al. 2020, ApJ, 904, 2 [CrossRef] [Google Scholar]
- Geach, J. E., Alexander, D. M., Lehmer, B. D., et al. 2009, ApJ, 700, 1 [Google Scholar]
- Ginolfi, M., Maiolino, R., Carniani, S., et al. 2018, MNRAS, 476, 2421 [NASA ADS] [CrossRef] [Google Scholar]
- Gronke, M., & Bird, S. 2017, ApJ, 835, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Maiolino, R., Jiang, L., et al. 2020, ApJ, 898, 26 [Google Scholar]
- Haiman, Z., Spaans, M., & Quataert, E. 2000, ApJ, 537, L5 [Google Scholar]
- Hayes, M., Scarlata, C., & Siana, B. 2011, Nature, 476, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Lehnert, M. D., Miley, G. K., & van Breugel, W. 1991a, ApJ, 381, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Lehnert, M. D., van Breugel, W., & Miley, G. K. 1991b, ApJ, 370, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Hennawi, J. F., & Prochaska, J. X. 2013, ApJ, 766, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Hennawi, J. F., Prochaska, J. X., Cantalupo, S., & Arrigoni-Battaia, F. 2015, Science, 348, 779 [Google Scholar]
- Herenz, E. C., Hayes, M., & Scarlata, C. 2020, A&A, 642, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodge, J. A., Riechers, D., Decarli, R., et al. 2015, ApJ, 798, L18 [Google Scholar]
- Humphrey, A., Vernet, J., Villar-Martín, M., et al. 2013, ApJ, 768, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Husemann, B., Worseck, G., Arrigoni Battaia, F., & Shanks, T. 2018, A&A, 610, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iono, D., Yun, M. S., Elvis, M., et al. 2006, ApJ, 645, L97 [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ApJ, 498, 541 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, E., Yang, Y., Zabludoff, A., et al. 2020, ApJ, 894, 33 [CrossRef] [Google Scholar]
- Lau, M. W., Prochaska, J. X., & Hennawi, J. F. 2016, ApJS, 226, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, M. W., Hamann, F., Gillette, J., et al. 2022, MNRAS, 515, 1624 [NASA ADS] [CrossRef] [Google Scholar]
- Laursen, P., Sommer-Larsen, J., & Andersen, A. C. 2009, ApJ, 704, 1640 [Google Scholar]
- Leech, K. J., Metcalfe, L., & Altieri, B. 2001, MNRAS, 328, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Li, Q., Cai, Z., Prochaska, J. X., et al. 2019, ApJ, 875, 130 [CrossRef] [Google Scholar]
- Lim, C.-F., Chen, C.-C., Smail, I., et al. 2020, ApJ, 895, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Worseck, G., Hennawi, J. F., et al. 2015, MNRAS, 449, 4204 [Google Scholar]
- Lyke, B. W., Higley, A. N., McLane, J. N., et al. 2020, ApJS, 250, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Mackenzie, R., Pezzulli, G., Cantalupo, S., et al. 2021, MNRAS, 502, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M., & Umemura, M. 2006, New A Rev., 50, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Morrissey, P., Matuszewski, M., Martin, D. C., et al. 2018, ApJ, 864, 93 [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2018, MNRAS, 477, 1822 [Google Scholar]
- Muñoz-Elgueta, N., Arrigoni Battaia, F., Kauffmann, G., et al. 2022, MNRAS, 511, 1462 [CrossRef] [Google Scholar]
- Ohyama, Y., Taniguchi, Y., Kawabata, K. S., et al. 2003, ApJ, 591, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A., McMahon, R. G., Cox, P., et al. 1996a, A&A, 315, 1 [NASA ADS] [Google Scholar]
- Omont, A., Petitjean, P., Guilloteau, S., et al. 1996b, Nature, 382, 428 [Google Scholar]
- O’Sullivan, D. B., Martin, C., Matuszewski, M., et al. 2020, ApJ, 894, 3 [Google Scholar]
- Prescott, M. K. M., Martin, C. L., & Dey, A. 2015, ApJ, 799, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Walter, F., Carilli, C. L., et al. 2006, ApJ, 650, 604 [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Rosdahl, J., & Blaizot, J. 2012, MNRAS, 423, 344 [Google Scholar]
- Runnoe, J. C., Brotherton, M. S., & Shang, Z. 2012, MNRAS, 422, 478 [Google Scholar]
- Smail, I., Ivison, R. J., & Blain, A. W. 1997, ApJ, 490, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Jarvis, M. J., Simpson, C., & Martínez-Sansigre, A. 2009, MNRAS, 393, 309 [CrossRef] [Google Scholar]
- Soto, K. T., Lilly, S. J., Bacon, R., Richard, J., & Conseil, S. 2016, MNRAS, 458, 3210 [Google Scholar]
- Steidel, C. C., Bogosavljević, M., Shapley, A. E., et al. 2011, ApJ, 736, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Karim, A., Smail, I., et al. 2012, MNRAS, 427, 1066 [Google Scholar]
- Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., & Shioya, Y. 2000, ApJ, 532, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Shioya, Y., & Kakazu, Y. 2001, ApJ, 562, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Timlin, J. D., Ross, N. P., Richards, G. T., et al. 2018, ApJ, 859, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Trebitsch, M., Verhamme, A., Blaizot, J., & Rosdahl, J. 2016, A&A, 593, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tumlinson, J., Peeples, M. S., & Werk, J. K. 2017, ARA&A, 55, 389 [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [Google Scholar]
- van Ojik, R., Roettgering, H. J. A., Miley, G. K., & Hunstead, R. W. 1997, A&A, 317, 358 [NASA ADS] [Google Scholar]
- Vidal-García, A., Falgarone, E., Arrigoni Battaia, F., et al. 2021, MNRAS, 506, 2551 [CrossRef] [Google Scholar]
- Wagg, J., Wiklind, T., Carilli, C. L., et al. 2012, ApJ, 752, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Weilbacher, P. M., Streicher, O., Urrutia, T., et al. 2012, SPIE Conf. Ser., 8451, 84510B [Google Scholar]
- Weilbacher, P. M., Streicher, O., Urrutia, T., et al. 2014, ASP Conf. Ser., 485, 451 [NASA ADS] [Google Scholar]
- Weilbacher, P. M., Palsa, R., Streicher, O., et al. 2020, A&A, 641, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilkinson, A., Almaini, O., Chen, C.-C., et al. 2017, MNRAS, 464, 1380 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, R. J., Gerssen, J., Bower, R. G., et al. 2005, Nature, 436, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Wisotzki, L., Bacon, R., Brinchmann, J., et al. 2018, Nature, 562, 229 [Google Scholar]
Appendix A: Seeing as a function of wavelength
As mentioned in Sect. 3, we subtracted the wavelength-dependent unresolved QSO’s PSF in order to reveal extended Lyα emission. The PSF was subtracted centered at the QSO position and out to six times the seeing; this value was chosen so that the PSF profile becomes consistent with zero. To estimate the seeing, we performed a 2D Moffat fit to pseudo narrow bands (width of 25 Å) of stacked point sources in each field as a function of wavelength.
The 2D Moffat model is given by
where A is the scale amplitude, x0 and y0 are the point source centroid coordinates, γ is the core width of the model, and β is the power of the model. The seeing is obtained from the FWHM of the Moffat profile, given by 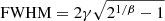 . We show in Table 1 the seeing at the expected Lyα wavelength of each field.
. We show in Table 1 the seeing at the expected Lyα wavelength of each field.
We show in Fig. A.1 an example of the wavelength-dependent FWHM and β of one of the QSO’s empirical PSF, for BR1202-0725. We exclude wavelengths significantly affected by the Lyα forest (< 5600 Å) and indicate with gray shaded regions the wavelength ranges where extended Lyα emission is conservatively expected, and therefore the PSF is kept constant (see Sect. 3.1 and Appendix B). We find an expected decrease with wavelength of the FWHM and a close to constant β parameter consistent with the trend and values found in previous MUSE studies (β ∼ 1.7; e.g., Fusco et al. 2020). In Fig. A.1 we also show a power-law fit to the FWHM as a function of wavelength, which is consistent with the seeing at the Lyα wavelength reported in Sect. 1 from point sources. This fit excludes the gray shaded regions as these are constant by construction.
 |
Fig. A.1. Properties of the wavelength-dependent Moffat fit used to estimate the seeing for BR1202-0725. Top: Seeing (FWHM of the Moffat fit) as a function of observed wavelength of BR1202-0725’s PSF (blue) with its respective 1σ uncertainty (shaded region). The power law fit is shown with a dashed orange line, and the fitted parameters are shown in the legend. Bottom: Beta parameter of the fitted Moffat profile as a function of wavelength with its respective 1σ uncertainty. |
Appendix B: Line emission identification
As mentioned in Sect. 3.1, in order to not subtract the extended emission we are interested in, we construct the wavelength-dependent empirical PSF of each QSO only where there is no line emission. For this, we create a routine that identifies peaks of line emission at the expected wavelengths. This routine is only intended to identify the location in wavelength of the line emissions, instead of characterizing the line emission of the QSO. We detect line emission by integrating a spectrum at the QSO location inside a 1 arcsecond diameter aperture, shown in Fig. B.1. We then use a median filter to create two smoothed spectra, one that highlights the QSO spectrum broad lines (smooth spectrum) and another that smooths out the broad-line features ("continuum" spectrum6). The smooth spectrum uses a median filter of 50 spectral channels (62.5 Å), while the continuum spectrum uses a median filter of 500 spectral channels (625 Å). We find where these two spectra intersect by creating a difference spectrum between the smooth and continuum spectrum, we then identify the lines by finding positive peaks in the difference spectrum that are above a 3σ threshold. The peaks are found using scipy.signal.find_peaks in combination with the 3σ threshold and a minimum separation between the local peaks. The 3σ threshold is computed from the RMS of the difference spectrum redward of the C IV line, because we do not expect to detect more line emissions at these wavelengths due to the redshift of our sources. In Fig. B.1 we show an example of line emission identification for G09-0902+0101. Where the top panel shows the spectrum and the locations of line emission are marked with red crosses, the vertical dashed lines show the regions where we find the wavelength ranges for each line. We excluded these ranges when building the empirical PSF; we instead used the next available PSF redward of the line emission.
 |
Fig. B.1. Example of a QSO broad-line emission identification, for G09-0902+0101. Top: Integrated spectrum inside a 1 arcsecond diameter aperture of G09-0902+0101, shown in black. Overlaid are a smoothed spectrum (blue) and a continuum spectrum (green), constructed using a median filter of 50 and 500 channels, respectively. The red and pink crosses indicate detected peaks of line emission and the intersection between the smooth and continuum spectra, respectively. The vertical gray lines indicate the regions where each line emission is excluded to build the PSF (see Sect. 3.1). Bottom: Difference spectrum between the smooth and continuum spectrum of the top panel. The dashed green line indicates the 3σ threshold for line identification. We indicate with a dashed red line the position of the QSO’s Lyα and broad-line emissions, with their respective labels. |
Appendix C: Si IV, C IV, HeII, and CIII] analysis
We conducted a search for other extended line emission besides Lyα, such as Si IV, C IV, He II and CIII]. However, we do not find extended emission in these lines for any target (Sect. 4.4). For completeness, we built χSmooth maps (e.g., Hennawi & Prochaska 2013) centered at the expected wavelength of each line and using a narrow-band window that reflects the 30 Å narrow band used for Lyα. The χSmooth maps for the systems studied here are shown in Figs. C.1, C.2, C.3, C.4, and C.5, these maps are best suited for visualizing the presence of extended emission (if any), and to appreciate the noise in the data. The χSmooth maps are computed using Eq. (2) from Farina et al. (2019):
 |
Fig. C.1. Lyα, Si IV, CIV, and He IIχSmooth maps using a velocity window equivalent to the 30 Å narrow band used for the Lyα SB maps for BR1202-0725. The side of the maps is 20″, corresponding to 129 kpc. We show with a circle the 1″ × 1″ normalization area of the QSO’s PSF-subtraction. |
 |
Fig. C.2. Lyα, Si IV, C IV, HeII, and CIII]χSmooth maps using a velocity window equivalent to the 30 Å narrow band used for the Lyα SB maps for G09-0902-0101. The side of the maps is 20″, corresponding to 152 kpc. We show with a circle the 1″ × 1″ normalization area of the QSO’s PSF-subtraction. |
 |
Fig. C.4. Lyα, Si IV, C IV, and He IIχSmooth maps using a velocity window equivalent to the 30 Å narrow band used for the Lyα SB maps for ALESS61.1. The side of the maps is 20″, corresponding to 133 kpc. We show with a white cross the position of the SMG. |
where DATAx, y, λ is the original datacube, MODELx, y, λ is the empirical PSF of the QSO obtained in Sect. 3.1, 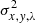 is the variance datacube. CONVOL is a spatial convolution using a 2D box kernel with of 3 pixels width (0.6″) and CONVOL2 is a spatial convolution using the square of the width of the kernel used for CONVOL. Different noise properties depends also on the vicinity to sky lines. For example, the He II velocity range of BR1202-0725 displays sky lines; therefore, we subtracted the residuals from the data before computing the χSmooth map.
is the variance datacube. CONVOL is a spatial convolution using a 2D box kernel with of 3 pixels width (0.6″) and CONVOL2 is a spatial convolution using the square of the width of the kernel used for CONVOL. Different noise properties depends also on the vicinity to sky lines. For example, the He II velocity range of BR1202-0725 displays sky lines; therefore, we subtracted the residuals from the data before computing the χSmooth map.
Appendix D: QSO spectral energy distribution fitting
As mentioned in Sect. 5.1.5, we model the number of QSOs’ ionizing photons impinging on optically thick gas estimating the specific luminosity at the Lyman edge (LνLL) for the three QSOs in our sample. As shown in Arrigoni Battaia et al. (2019b), a QSO SED can be parametrized by different power-laws, with the extreme UV portion described by a power law of the form Lν = LνLL(ν/νLL)αUV with slope αUV = −1.7 (as obtained in Lusso et al. (2015)), and a slope αopt = −0.46 below 1 Ryd (Vanden Berk et al. 2001). Figure D.1 shows a comparison of the MUSE QSO spectra and the assumed SED (following Arrigoni Battaia et al. 2019b), which confirms that a standard QSO template adjust to the sample studied here.
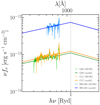 |
Fig. D.1. Comparison of the SED of the three QSOs studied here used as incident radiation field in the modeling. The blue, orange, and green lines indicate the input spectrum with slope αUV = −1.7 (Lusso et al. 2015) for BR1202-0725, G09-0902+0101, and G15-1444-0044, respectively. The curves of the same color indicate the MUSE spectrum of each QSO extracted within a 1.5″ radius aperture. |
All Tables
All Figures
 |
Fig. 1. Overview of the five targeted systems before subtraction of the unresolved QSO’s PSF and continuum sources (see Sect. 3). Left: integrated spectra of the QSOs and SMGs inside a 3″ radius aperture. Vertical dashed lines indicate the positions of the Lyα and QSO broad lines (Si IV, C IV, HeII, and CIII[[INLINE106]]). The gray shaded region indicates the FWHM of the nebular Lyα emission for the QSOs (see Fig. 2 and Table 3) and the 30 Å narrow band used for the SMGs (see Fig. 3). Right: 30 Å SB maps at the expected Lyα wavelength of the targeted QSOs and SMGs before PSF- and continuum-subtraction (see Sect. 3). The maps have a side of 20″, corresponding to about 129, 152, 148, 133, and 132 kpc for BR1202 − 0725, G09 − 0902 + 0101, G15 − 1444 − 0044, ALESS61.1, and ALESS65.1, respectively. |
| In the text | |
 |
Fig. 2. Integrated spectra and SB maps of the extended Lyα emission around the three systems with AGNs. Left: spectra of the identified Lyα nebulae (black curve), integrated inside the 2σ contour. The gray shaded area shows the channels used to build the SB map. The vertical magenta line indicates the Lyα wavelength from the systemic redshift of the QSOs, while the vertical blue line indicates the wavelength at the peak of the Lyα spectra computed from the first moment of the line. Overlaid in red is a Gaussian fit to the spectra. The velocity shift and FWHM of each system are listed in Table 3. The top axis of the spectra panels show the velocity shift with respect to the systemic redshift in km s−1. Right: Lyα SB maps of BR1202 − 0725 (top), G09 − 0902 + 0101 (middle), and G15 − 1444 − 0044 (bottom) at the expected wavelength from their systemic redshift (Table 1). The maps have a side of 20″, corresponding to about 129, 152, and 148 kpc for BR1202 − 0725, G09 − 0902 + 0101, and G15 − 1444 − 0044, respectively. A scale bar of 20 kpc is indicated on each map. The black contours indicate SB levels of [2, 4, 10, 20, 50] σ (see Table 1). These maps are smoothed using a 2D box kernel with a width of 3 pixels (0.6″). The central 1″ × 1″ region used for the QSO PSF normalization is masked and excluded from analysis. For BR1202 − 0725, we indicate the position of the LAE and SMG companions (Carilli et al. 2013; Drake et al. 2020) with a green and white cross, respectively. |
| In the text | |
 |
Fig. 3. Integrated spectra and SB maps of the two observed SMGs. Left: spectra integrated inside the 2″ radius aperture (black circle) of ALESS61.1 (top) and ALESS65.1 (bottom). The gray shaded area shows the channels used to build the SB map, and the vertical magenta line indicates the expected Lyα wavelength. Right: Lyα SB maps of the two SMGs at the expected wavelength from their redshift, listed in Table 1. The maps have a side of 20″, which at their redshifts corresponds to about 133 and 132 kpc for ALESS61.1 and ALESS65.1, respectively. A scale bar is shown for each map. These maps are smoothed using a 2D box kernel with a width of 3 pixels (0.6″). The black circles indicate an aperture of radius 2″ centered at the SMG position. |
| In the text | |
 |
Fig. 4. Lyα SB radial profiles extraction. Left: smoothed SB maps of the QSO sample (same as in Fig. 2) with the circular apertures used to extract radial profiles overlaid. The gray circle in each map indicates the 1 arcsec2 region used for the QSO’s PSF normalization, which is neglected in our analysis. Right: extracted radial profiles inside each annulus. Open circles indicate negative values, shown here for completeness. The red line represents the 2σ SB limit rescaled to the area of each annulus. The dashed blue curve in the top panel is the best fit of the data points above the red line using an exponential function with the form SBLyα = Cexp( − r/rh), where C = 85.3 ± 13.8 × 10−18 erg s−1 cm−2 arcsec−2 and rh = 11 ± 1 pkpc. |
| In the text | |
 |
Fig. 5. Kinematics of the detected Lyα nebulae: Velocity shift ΔvLyα maps (left column) with respect to the Lyα peak wavelength of the nebula (see Fig. 2), and velocity dispersion σLyα maps (right column) of the Lyα nebula around the three QSOs, computed from the first and second moment, respectively. The maps are smoothed as in Fig. 2. The moment calculation is performed only inside the 2σ isophote of each nebula. The positions of the LAE and SMG companion of the BR1202-0725 system are marked with a green and white cross, respectively. The side of the map is 20″ for BR1202-0725 and 10″ for G09-0902+0101 and G15-1444-0044. A scale bar is shown for each map. The gray circle in each map indicates the 1 arcsec2 region used for the QSO’s PSF normalization, which is neglected in our analysis. |
| In the text | |
 |
Fig. 6. Violent kinematics in the Lyα nebula of BR1202-0725. Top left: integrated spectra of regions with negative (blue curve) and positive (red curve) velocity shifts for BR1202-0725, with respect to the peak of the nebular Lyα emission (see Fig. 2). The spectra are taken after masking the 1″ × 1″ region of the QSO’s PSF-subtraction and a circular region with a diameter of 1.6″ at the LAE companion position. We indicate with vertical lines the systemic redshift (solid magenta), the redshift of the SMG (dashed black), and LAE (dot-dashed green) companions (Carilli et al. 2013; Drake et al. 2020). Top middle: residual spectrum between the positive and the negative shift spectrum. We indicate the systemic redshift with a magenta line. Top right: Lyα velocity shift map computed from the first moment using a spectral window of ±FWHM centered at the peak of the nebular Lyα emission (see Table 3) and smoothed as in Fig. 2. The position of the QSO and LAE companion masks are indicated with a hashed gray and a green circle, respectively. Bottom left: Lyα SB map using the spectral channels with the largest negative nebula shifts, indicated with a blue shaded region in the top-left panel. The blue contours indicate the 2σ isophote of the extended emission shown in Fig. 2. Bottom right: Lyα SB map using the spectral channels with the largest positive nebula shifts, indicated with a shaded red region in the top-left panel. Both of the SB maps are smoothed at the bottom as in Fig. 2. All maps have a side of 20″ and black contours indicating SB levels of [2, 4, 10, 20, 50] σ within the respective wavelength ranges. |
| In the text | |
 |
Fig. 7. Ratio of the nebula and QSO Lyα luminosities versus the dust mass of the central host galaxy for the three QSOs in our sample (black with IDs) and for the Fabulous system (blue; Arrigoni Battaia et al. 2022). |
| In the text | |
 |
Fig. 8. C IV/Lyα and He II/Lyα line ratio upper limits (2σ) for the sources studied here with detected extended Lyα nebulae (star symbols). The line ratios are computed from the nebular luminosities listed in Table 3. The left panel shows the model grids for the shock scenario, while the right panel shows the model grids for the shock+precursor scenario from Allen et al. (2008). Overlaid are derived line ratios and upper limits for QSO nebulae from Borisova et al. (2016) as cyan circles, stacked nebulae around z = 3 − 4.5 QSOs inside a radial bin of 10 < R/kpc < 30 from Fossati et al. (2021) as a white cross, and one extremely red QSO at z ∼ 2.3 (Lau et al. 2022) as a magenta cross. |
| In the text | |
 |
Fig. 9. Circularly averaged SB as a function of comoving projected radius of the nebulae detected in our QSO sample (red stars, green diamonds, and yellow diamonds for BR1202 − 0725, G09 − 0902 + 0101, and G15 − 1444 − 0044, respectively), corrected for cosmological dimming. The red and purple squares with arrows indicate the upper limits for ALESS61.1 and ALESS65.1, respectively. Different profiles from the literature are indicated as colored circles with their respective 25 − 75 percentile ranges when available. The z = 3.17 QSO sample from Arrigoni Battaia et al. (2019a) is shown in yellow. The SB profile (taken from Arrigoni Battaia et al. 2016) of the z = 2.28 Slug ELAN is shown in blue (Cantalupo et al. 2014). The z = 6.2 QSO sample from Farina et al. (2019) is shown in magenta. The z = 3.8 QSO sample from Fossati et al. (2021) is shown in cyan. The z = 2.3 QSO sample from Cai et al. (2019) is shown in orange. The median profile of the faint QSO sample at z = 3 from Mackenzie et al. (2021) is shown with black connected circles. We computed the SB profile of the galaxy group SMMJ02399, which comprises a QSO and an SMG at z = 2.8 from Li et al. (2019; gray connected circles). Finally, the fit to the observed SB profile for z = 2.65 LBGs from Steidel et al. (2011) is shown with the dashed black curve. |
| In the text | |
 |
Fig. A.1. Properties of the wavelength-dependent Moffat fit used to estimate the seeing for BR1202-0725. Top: Seeing (FWHM of the Moffat fit) as a function of observed wavelength of BR1202-0725’s PSF (blue) with its respective 1σ uncertainty (shaded region). The power law fit is shown with a dashed orange line, and the fitted parameters are shown in the legend. Bottom: Beta parameter of the fitted Moffat profile as a function of wavelength with its respective 1σ uncertainty. |
| In the text | |
 |
Fig. B.1. Example of a QSO broad-line emission identification, for G09-0902+0101. Top: Integrated spectrum inside a 1 arcsecond diameter aperture of G09-0902+0101, shown in black. Overlaid are a smoothed spectrum (blue) and a continuum spectrum (green), constructed using a median filter of 50 and 500 channels, respectively. The red and pink crosses indicate detected peaks of line emission and the intersection between the smooth and continuum spectra, respectively. The vertical gray lines indicate the regions where each line emission is excluded to build the PSF (see Sect. 3.1). Bottom: Difference spectrum between the smooth and continuum spectrum of the top panel. The dashed green line indicates the 3σ threshold for line identification. We indicate with a dashed red line the position of the QSO’s Lyα and broad-line emissions, with their respective labels. |
| In the text | |
 |
Fig. C.1. Lyα, Si IV, CIV, and He IIχSmooth maps using a velocity window equivalent to the 30 Å narrow band used for the Lyα SB maps for BR1202-0725. The side of the maps is 20″, corresponding to 129 kpc. We show with a circle the 1″ × 1″ normalization area of the QSO’s PSF-subtraction. |
| In the text | |
 |
Fig. C.2. Lyα, Si IV, C IV, HeII, and CIII]χSmooth maps using a velocity window equivalent to the 30 Å narrow band used for the Lyα SB maps for G09-0902-0101. The side of the maps is 20″, corresponding to 152 kpc. We show with a circle the 1″ × 1″ normalization area of the QSO’s PSF-subtraction. |
| In the text | |
 |
Fig. C.3. Same as Fig. C.2, but for G15-1444-0044. The 20″ side of the maps corresponds to 148 kpc. |
| In the text | |
 |
Fig. C.4. Lyα, Si IV, C IV, and He IIχSmooth maps using a velocity window equivalent to the 30 Å narrow band used for the Lyα SB maps for ALESS61.1. The side of the maps is 20″, corresponding to 133 kpc. We show with a white cross the position of the SMG. |
| In the text | |
 |
Fig. C.5. Same as Fig. C.4, but for ALESS65.1. The 20″ side of the maps corresponds to 132 kpc. |
| In the text | |
 |
Fig. D.1. Comparison of the SED of the three QSOs studied here used as incident radiation field in the modeling. The blue, orange, and green lines indicate the input spectrum with slope αUV = −1.7 (Lusso et al. 2015) for BR1202-0725, G09-0902+0101, and G15-1444-0044, respectively. The curves of the same color indicate the MUSE spectrum of each QSO extracted within a 1.5″ radius aperture. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



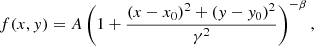
![$$ \begin{aligned} \mathrm{SMOOTH}[\chi _{x,y,\lambda }] = \dfrac{ \mathrm{CONVOL}[\mathrm{DATA}_{x,y,\lambda } - \mathrm{MODEL}_{x,y,\lambda } ] }{ \sqrt{\mathrm{CONVOL^2}[\sigma ^2_{x,y,\lambda }]} }, \end{aligned} $$](/articles/aa/full_html/2023/11/aa46879-23/aa46879-23-eq30.gif)