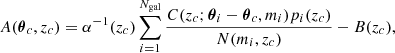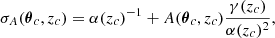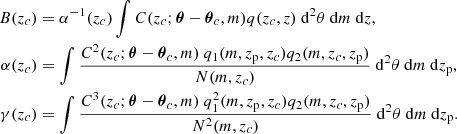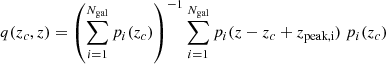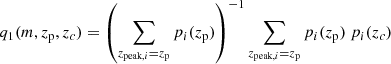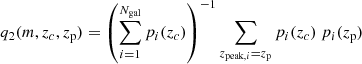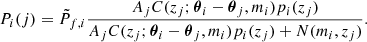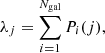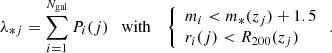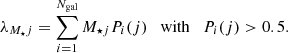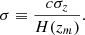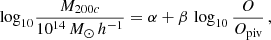EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 678 (October 2023) A&A, 678 (2023) A145 Full HTML
Open Access
Issue
A&A
Volume 678, October 2023
Article Number A145
Number of page(s) 15
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202245323
Published online 16 October 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The formation of structures in the universe is extremely sensitive to cosmic expansion captured by the cosmological parameters, such as the matter density parameter Ωm, the power spectrum normalization σ8, and the equation of state of dark energy whenever high-redshift datasets are available. Notable examples are the study of the large-scale structure through galaxy clustering (Kaiser 1987; Cacciato et al. 2013; Vakili et al. 2023; Pandey et al. 2022), cosmic shear (Blandford et al. 1991; Bernardeau et al. 2010; Hildebrandt et al. 2017), baryonic acoustic oscillations (Hu & Sugiyama 1996; Blake et al. 2011; Hinton et al. 2017; Costa et al. 2019; du Mas des Bourboux et al. 2020), and cosmic microwave background measurements (Pettorino et al. 2012; Hinshaw et al. 2013; Planck Collaboration XIII 2016), which probe the linear regime of the growth of structures. On the other hand, galaxy clusters are found in the exponential tails of the cosmic mass function, being the largest gravitationally bound structures and as such are extremely sensitive to the background cosmology, making them ideal probes for cosmological analysis (Allen et al. 2011; Benson et al. 2013; Planck Collaboration XXIV 2016; Bocquet et al. 2019; Abbott et al. 2020; Finoguenov et al. 2020; Ider Chitham et al. 2020; Costanzi et al. 2021; Marulli et al. 2021; Giocoli et al. 2021; Ingoglia et al. 2022; Lesci et al. 2022a,b; Garrel et al. 2022; Chiu et al. 2023).

For this reason, large campaigns aiming at the detection of large samples of galaxy clusters have been conducted in the last decades at millimetre wavelengths (Bleem et al. 2015; Zubeldia & Challinor 2019; Hilton et al. 2021), in the optical regime (Rykoff et al. 2014, 2016; Maturi et al. 2019), and in the X-rays (Böhringer et al. 2004; Vikhlinin et al. 2009; Finoguenov et al. 2020). Further datasets will be provided in the near future by wide-field surveys such as eROSITA (Merloni et al. 2012; Pillepich et al. 2012; Käfer et al. 2020; Ota et al. 2023), LSST (LSST Science Collaboration 2009), Euclid (Sartoris et al. 2016; Euclid Collaboration 2022), 4MOST (de Jong et al. 2014), and J-PAS (Benitez et al. 2014). In particular, optical surveys are gaining momentum thanks to the availability of the complete wavelength range filling set of narrow-band filters with high uniformity and transmission (Marín-Franch et al. 2012) and refined techniques for the estimation of photometric redshifts (Arnouts & Ilbert 2011; Bilicki et al. 2018; Benítez 2000; Hernán-Caballero et al. 2021), allowing the detection of a large number of clusters with masses lower than those detected with Sunyaev Zel’dovich observations, and redshifts higher than those from typical X-ray observations. In addition, they directly provide accurate redshift and membership estimates without the need of a subsequent follow-up.

Several algorithms for cluster detection have been proposed and used in recent years (see e.g. Farrens et al. 2011; Licitra et al. 2016; Rykoff et al. 2016; Euclid Collaboration 2019), exploiting different cluster optical properties and different methodologies. In this work we discuss the application of the Adaptive Matched Identifier of Clustered Objects (AMICO, Bellagamba et al. 2019; Maturi et al. 2019) algorithm to the miniJPAS dataset (Bonoli et al. 2021) to investigate the prospects for the detection of galaxy clusters in the Javalambre Physics of the Accelerating Universe Astrophysical Survey (J-PAS, Benitez et al. 2014). We construct the cluster sample and we determine mass-proxy scaling relations based on the X-ray mass estimates using Chandra and XMM-Newton data. Furthermore, we provide a catalogue of cluster members based on the probabilistic membership association provided by AMICO itself, we identify the brightest group galaxy (BGG), and we illustrate the power of the 56 J-PAS filters (Marín-Franch et al. 2012). To construct the cluster model used for the cluster detection, we assumed the following cosmological parameters Ωm = 0.3, ΩΛ = 0.7, and h = 0.7.

The plan of the paper is as follows. In Sect. 2 we summarize the properties of the dataset, and in Sect. 3 we describe the detection algorithm and characterize the cluster sample through X-ray and spectroscopic data. In Sect. 4 we present the samples of cluster members and bright group galaxies we produced in the analysis. In Sect. 5 we characterize the cluster sample through spectroscopic redshifts and investigate the accuracy of the probabilistic memberships provided by AMICO. The X-ray counterparts of our sample are discussed in Sect. 6, while in Sect. 7 we discuss the gain provided by the narrow-band J-PAS filters with respect to the broad-band filters. Finally, we give our conclusions in Sect. 8.

2. The dataset

In our study we consider data from the miniJPAS survey (Bonoli et al. 2021), a ∼1 deg2 survey covering the AEGIS field along the Extended Groth Strip and serving as a test of the upcoming much wider J-PAS survey. The data were obtained with the 2.55 m JST telescope at the Javalambre Astrophysical Observatory and an interim camera (J-PAS Pathfinder camera) equipped with a 9k × 9k CCD covering a 0.3 deg2 field of view with a pixel size of 0.23″. The distinctive features of this survey are, in addition to the u, g, r, i SDSS broad-band filters, its 56 J-PAS filters: 54 narrow-band filters (FWHM ∼ 145 Å) and 2 broader filters extending to the near-UV and the near-infrared.

To construct the cluster sample, we selected all objects in the magnitude range 15.0 < r < 22.75, with a SExtractor flag smaller than or equal to 3, a star classification probability below Pstar < 0.5, and a FWHM in the r-band images larger than 0.86, 0.87, 1.01, or 1.03 arcsec according to the criteria FWHMgalaxy > FWHMPSF + 0.11 to avoid any possible contamination due to misclassified stars. The 0.11 additive factor was set heuristically to avoid the loci where stars are located. Here FWHMPSF is the FWHM of the point spread function (PSF) of each individual pointing. We adopted a relatively relaxed constraint on Pstar because we used it in combination with the cutoff at the minimum FWHM values. We also tested a more conservative value of Pstar < 0.95 both with and without FWHM cutoff, and the final results do not change significantly. In Fig. 1 we show the main properties of the photometric sample comprising stars and galaxies. The left panel of the figure shows the distribution of objects classified as stars (in red), galaxies (in blue), and all objects (in green) with a FWHM smaller than the PSF size of each individual pointing plus a tolerance of 0.11 arcsec (indicated by the vertical lines) that were rejected regardless their classification (in green). The presence of the two regions mostly populated by objects classified as stars at low FWHM shows that the PSF quality for the different pointings is bimodal. This dataset provides an ideal playground to test the survey strategy for the detection of galaxy clusters in the final J-PAS survey that will cover an area 8000 times larger.

thumbnail Fig. 1.

Size and magnitude of all sources and photometric redshift of the input galaxies. Left panel: r-band magnitude vs FWHM of the galaxies detected in miniJPAS and used for the analysis (in blue). Shown are objects with a “stellarity” Bayesian probability of being stars higher than 50% (in red) and of being galaxies lower than 50% (in blue). All objects (in green) with a FWHM smaller than the PSF size of each individual pointing plus a tolerance of 0.11 arcsec (indicated by the vertical lines) were rejected regardless their classification. Right panel: average redshift probability distribution of galaxies as measured by AMICO with a peak P(z) located at three different redshifts and for two different magnitudes: r = 20 and r = 22 (in blue and red, respectively). This estimate is produced by AMICO through the input photo-zs and is used in the cluster model construction. The black dashed lines show the typical uncertainty of photo-zs based on broad-band photometry.

Thanks to the availability of the 54 narrow-band filters and the 2 broader-band near-UV and near-IR filters, the photo-zs have an accuracy that is much better with respect to other photometric surveys; they place miniJPAS between low-resolution spectroscopy and typical broad-band photometry. A detailed study of the photo-z characteristics is presented in Hernán-Caballero et al. (2021). In the right panel of Fig. 1 we show the average redshift probability distribution of galaxies of magnitude r = 20 and r = 22 located at different redshifts. The average P(z) is produced by AMICO through the input photo-zs and is used to define the cluster model, as discussed in Maturi et al. (2019). As an illustration, we show the typical photo-z uncertainty of datasets based on broad-band filters, where we assumed σz = 0.03(1 + z) (dashed line). The high accuracy of J-PAS photo-zs provides higher sensitivity towards clusters of lower mass aided by the increase in compactness of cluster members along the redshift direction with decreasing mass. The improved accuracy on photo-zs results is also a better estimation of the clusters richness, which in turn improves the cosmology-relevant mass estimation.

3. The galaxy cluster sample

In this section we summarize the main concepts behind the detection algorithm used in this analysis. We describe the properties of the cluster candidates obtained with the photo-zs based on the 56 J-PAS filters.

3.1. Detection of galaxy groups and clusters with AMICO

We used AMICO (Maturi et al. 2005; Bellagamba et al. 2018) for the detection of galaxy clusters. Thanks to its performance, AMICO was selected as one of the two algorithms tested and implemented in the official scientific data analysis pipeline of the Euclid space mission of the European Space Agency (Euclid Collaboration 2019) and was successfully tested and applied to the data of the Kilo Degrees Survey, allowing both cosmological and astrophysical studies (Maturi et al. 2019; Bellagamba et al. 2019; Radovich et al. 2020; Puddu et al. 2021; Tortora et al. 2020; Sereno et al. 2020; Giocoli et al. 2021; Lesci et al. 2022a; Smit et al. 2022; Ingoglia et al. 2022). Its core stands on an optimal linear matched filtering approach in which the data are convolved with a kernel (called the filter) derived through a constrained minimization approach that minimizes the noise variance under the condition that the estimated signal is unbiased. The two key ingredients of this process are a statistical description of the background noise, N(x), and a template, C(x), characterizing the signal of clusters, S(x) = A C(x), as a function of the properties x and a factor A that scales with the cluster mass (called the amplitude). The statistical properties of the noise N(x) can be derived directly from the data, while the nature of the function C(x) and of the variables x depend on the specific application of the algorithm. Here we restrict ourselves to the case in which x only includes the positions and the r-magnitudes of galaxies. All details about the model are given in Sect. 3.3, where we describe the full-filter formalism.

The result of the filtering applied by AMICO to the data is an estimate of the amplitude,

A ( θ c , z c ) = α − 1 ( z c ) ∑ i = 1 N gal C ( z c ; θ i − θ c , m i ) p i ( z c ) N ( m i , z c ) − B ( z c ) , $$ \begin{aligned} A(\boldsymbol{\theta }_c,z_c) = \alpha ^{-1}(z_c) \sum _{i=1}^{N_{\rm gal}}\frac{C(z_c;\boldsymbol{\theta }_i-\boldsymbol{\theta }_c,m_i)p_i(z_c)}{N(m_i,z_c)} - B(z_c), \end{aligned} $$(1)

where zc and θc are the putative redshift and angular position of a cluster, respectively, while θi, mi and pi(z) are the angular position, the r-band magnitude and the photometric redshift distribution of the i-th galaxy taken from the input catalogue, respectively. The filter normalization is set by the factor α and the average contribution of the field galaxies to the total signal amplitude is given by B. The expected rms of A is given by

σ A ( θ c , z c ) = α ( z c ) − 1 + A ( θ c , z c ) γ ( z c ) α ( z c ) 2 , $$ \begin{aligned} \sigma _A(\boldsymbol{\theta }_c,z_c) = \alpha (z_c)^{-1} + A(\boldsymbol{\theta }_c,z_c)\frac{\gamma (z_c)}{\alpha (z_c)^{2}}, \end{aligned} $$(2)

where the first term captures the stochastic fluctuations of the background and the second term the Poissonian fluctuations due to the cluster members:

B ( z c ) = α − 1 ( z c ) ∫ C ( z c ; θ − θ c , m ) q ( z c , z ) d 2 θ d m d z , α ( z c ) = ∫ C 2 ( z c ; θ − θ c , m ) q 1 ( m , z p , z c ) q 2 ( m , z c , z p ) N ( m , z c ) d 2 θ d m d z p , γ ( z c ) = ∫ C 3 ( z c ; θ − θ c , m ) q 1 2 ( m , z p , z c ) q 2 ( m , z c , z p ) N 2 ( m , z c ) d 2 θ d m d z p . $$ \begin{aligned} B(z_c)&= \alpha ^{-1}(z_c) \int C(z_c;\boldsymbol{\theta } - {\boldsymbol{\theta }}_c, m) q(z_c,z)\ \mathrm{d}^2\theta \ \mathrm{d}m\ \mathrm{d}z, \\ \alpha (z_c)&= \int \frac{C^2(z_c;{\boldsymbol{\theta }} - {\boldsymbol{\theta }}_c, m)\ q_1(m,z_{\rm p},z_c) q_2(m,z_c,z_{\rm p})}{N(m,z_c)}\ \mathrm{d}^2\theta \ \mathrm{d}m\ \mathrm{d}z_{\rm p}, \\ \gamma (z_c)&= \int \frac{C^3(z_c;{\boldsymbol{\theta }} - {\boldsymbol{\theta }}_c, m)\ q^2_1(m,z_{\rm p},z_c) q_2(m,z_c,z_{\rm p})}{N^2(m,z_c)}\ \mathrm{d}^2\theta \ \mathrm{d}m\ \mathrm{d}z_{\rm p}. \end{aligned} $$

These are the filter constants expressing the background level, the filter normalization and the contribution to the noise given by the cluster members, respectively. Here

q ( z c , z ) = ( ∑ i = 1 N gal p i ( z c ) ) − 1 ∑ i = 1 N gal p i ( z − z c + z peak,i ) p i ( z c ) $$ \begin{aligned} q(z_c,z) = \left(\sum _{i=1}^{N_\text{gal}} p_i(z_c) \right)^{-1} \sum _{i=1}^{N_\text{gal}} p_i(z-z_c+z_\text{peak,i})\ p_i(z_c) \end{aligned} $$(3)

expresses the typical redshift probability distribution for a galaxy located at redshift zc;

q 1 ( m , z p , z c ) = ( ∑ z peak , i = z p p i ( z p ) ) − 1 ∑ z peak , i = z p p i ( z p ) p i ( z c ) $$ \begin{aligned} q_1(m,z_{\rm p},z_c) = \left(\sum _{z_{\text{peak},i}=z_{\rm p}} p_i(z_{\rm p}) \right)^{-1} \sum _{z_{\text{peak},i}=z_{\rm p}} p_i(z_{\rm p})\ p_i(z_c) \end{aligned} $$(4)

describes the typical p(z) that peaks at zp; and

q 2 ( m , z c , z p ) = ( ∑ i = 1 N gal p i ( z c ) ) − 1 ∑ z peak , i = z p p i ( z c ) p i ( z p ) $$ \begin{aligned} q_2(m,z_c,z_{\rm p}) = \left(\sum _{i=1}^{N_\text{gal}} p_i(z_c) \right)^{-1} \sum _{z_{\text{peak},i}=z_{\rm p}} p_i(z_c)\ p_i(z_{\rm p}) \end{aligned} $$(5)

describes the probability distribution for the peak, zp, of a galaxy located at redshift zc. All details about these expressions are given in Bellagamba et al. (2018) and Maturi et al. (2019).

As a by-product, the algorithm provides an estimate of the fraction of masked effective area for each detection. This fraction is defined as fj = 1 − B(zj)/Beff(θj, zj), where j refers to the detection; the background B is evaluated as if no mask were present; and Beff is evaluated over the area not covered by masks. We speak of an ‘effective’ area because each unmasked pixel in the evaluation of B is weighted by the amplitude of the cluster model. To illustrate how the filter highlights the density fluctuations, we show the resulting amplitude in Fig. 2 for a redshift slice at z = 0.24 in the miniJPAS data. The complete footprint of the survey is shown together with the masked areas (white contours). In the bottom left and top right boxes we display the g, r, i colour-composite postage stamps based on the miniJPAS images of the two most significant detections at that redshift. The violet contours refer to the extended X-ray emission detected in the deep Chandra data (Erfanianfar et al. 2013). The top left box shows the AMICO response for a background slice at a higher redshift, z = 0.36, where another cluster is detected nearly along the same line of sight of the main central structure visible in the background figure at z = 0.24. The asterisks in the top left panel indicate the position of the cluster visible at redshift z = 0.24. We note the absence in the AMICO maps of cross-contamination between the different redshifts. In addition, the stamp image on the right side shows a case of chance alignment between the two structures. More about this and another case will be discussed in Sect. 3.3.

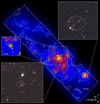thumbnail Fig. 2.

Illustration of the AMICO response amplitude for a redshift slice at z = 0.24. The overdensities highlighted by AMICO are clearly visible as strong enhancements over the background. The survey footprint and masked areas are indicated in white. The two boxes with the miniJPAS images show the two most significant detections at that redshift together with X-ray emission isocontours. The top left box shows the response of AMICO around the main central structure at z = 0.24 and at redshift z = 0.36, where another cluster is clearly visible. There is little cross-contamination between redshift slices. The cluster on the right side is a case of chance alignment between two structures (see left panel of Fig. 6). The asterisks in the figures indicate the position of the cluster visible in the other redshift slice and displaced nearly along the same line of sight.

The same formalism naturally provides a probabilistic association for each galaxy, labelled with the index i, to a specific detection, labelled with the index j,

P i ( j ) = P ∼ f , i A j C ( z j ; θ i − θ j , m i ) p i ( z j ) A j C ( z j ; θ i − θ j , m i ) p i ( z j ) + N ( m i , z j ) . $$ \begin{aligned} P_i(j) = \tilde{P}_{f,i} \frac{A_j C(z_j;{\boldsymbol{\theta }}_i-{\boldsymbol{\theta }}_j,m_i)p_i(z_j)}{A_j C(z_j;{\boldsymbol{\theta }}_i-{\boldsymbol{\theta }}_j,m_i) p_i(z_j) + N(m_i,z_j)}. \end{aligned} $$(6)

Since clusters overlap in the data space, more than one cluster association can be assigned to a galaxy through an iterative approach, in which the 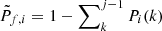P ∼ f , i = 1 − ∑ k j − 1 P i ( k ) $ \tilde{P}_{f,i}= 1-\sum\nolimits_k^{j-1} P_i(k) $ term accounts for the previous memberships assigned to the ith galaxy. This probabilistic membership is relevant for (1) the characterization of galaxy populations in terms of environment (González Delgado et al. 2022; Rodríguez-Martín et al. 2022), (2) the iterative removal of the contribution of larger detections when searching for smaller structures, and (3) the definition of two richness estimates λ and λ* (see Eqs. (7) and (8)).

3.2. Additional mass proxies

In addition to the amplitude, A, which is the direct output of the optimal filtering procedure as given by Eq. (1), the probabilistic membership association provided by AMICO allows us to define two other mass proxies that are directly related to the cluster richness. The first, λ, is defined as the sum of the probabilistic membership association of all galaxies to the jth detection,

λ j = ∑ i = 1 N gal P i ( j ) , $$ \begin{aligned} \lambda _{j} = \sum _{i=1}^{N_{\rm gal}} P_i(j), \end{aligned} $$(7)

and represents the number of visible galaxies belonging to a detection. Consequently it depends on the survey magnitude limit, and it is thus redshift dependent. The second mass proxy, λ*, follows the same definition as λ, but the sum runs only over the galaxies brighter than m* + 1.5, where m* represents the bright-end side cut off of the Schechter luminosity function, and within the virial radius, R200,

λ ∗ j = ∑ i = 1 N gal P i ( j ) with { m i < m ∗ ( z j ) + 1.5 r i ( j ) < R 200 ( z j ) . $$ \begin{aligned} \lambda _{*j} = \sum _{i=1}^{N_{\rm gal}} P_i(j) \quad \mathrm{with}\quad \left\{ \begin{array}{lr} m_i<m_*(z_j)+1.5 \\ r_i(j) < R_{200}(z_j) \end{array} \right. . \end{aligned} $$(8)

The radius R200 and the magnitude m* are given by the model used to construct the filter (see Sect. 3.1). This mass proxy is nearly redshift independent whenever m* + 1.5 is brighter than the survey limit, which for our case is true up to z = 0.56. Mass-scaling relations for these mass proxies are derived in Bellagamba et al. (2019) and in Lesci et al. (2022a) through the use of information coming from weak-gravitational lensing and clustering of galaxy clusters (Sereno et al. 2015; Marulli et al. 2021; Moresco et al. 2021).

The two richness estimates for all detections are displayed in the left and middle panels of Fig. 3. As is clear from the discontinuity at z = 0.56 where the m* + 1.5 limit is reached, the two richness estimates become strongly redshift dependent and their use as mass proxies requires a calibration to correct for this effect. This is not the case for the amplitude, A, because the filtering formalism automatically accounts for and compensates for the survey magnitude limit, and the redshift dependency can be safely neglected (see also Maturi et al. 2019). This is why in this study we favour this mass proxy over λ*, whose redshift dependency cannot be properly calibrated because of the limited statistics offered by the ∼1 deg2 area covered by the miniJPAS data and the large cosmic variance. This limitation will be overcome when the wider area of the J-PAS survey is available.

thumbnail Fig. 3.

Observed richness λ (left panel) and intrinsic richness λ* (central panel) as a function of redshift obtained with AMICO. For redshifts higher than z = 0.56, the cutoff magnitude mcut = m* + 1.5, on which λ* is based, falls below the detection limit and the richness is underestimated, as is clear from the lack of rise in the λ* of detections with z > 0.56. The right panel shows the amplitude, A, of the detections. The blue and red symbols refer to detections with S/N > 3 and S/N < 3, respectively.

In addition to the ‘standard’ mass proxies of AMICO, in this work we defined a mass proxy incorporating the stellar mass, M⋆, of individual galaxies (see e.g. Pereira et al. 2018)

λ M ⋆ j = ∑ i = 1 N gal M ⋆ j P i ( j ) with P i ( j ) > 0.5 . $$ \begin{aligned} \lambda _{M_{\star }j} = \sum _{i=1}^{N_{\rm gal}} M_{\star j} P_i(j) \quad \mathrm{with}\quad P_i(j)>0.5. \end{aligned} $$(9)

The use of this quantity is possible thanks to the 56 J-PAS filters that enable us to perform a reliable spectral energy distribution (SED) fitting for almost all galaxies in the sample, which was done using the BaySEAGal code (González Delgado et al. 2021), placing J-PAS in a unique position. It was in fact possible to evaluate λM⋆ for all groups but one, which was located at z = 0.76.

In Sect. 6 we also obtain X-ray mass estimates (Leauthaud et al. 2010, based on weak lensing calibrations of X-ray luminosity). We use them to define the mass-proxy scaling relations for the amplitude, A; for the intrinsic richness, λ*; and for the total stellar mass, λM⋆ (see Fig. 4). More details are given in Sect. 6.2.

thumbnail Fig. 4.

Scaling relations between different mass proxies (A, top panels; λ*, central panels; and λM⋆, bottom panels) and our X-ray mass estimates for the cluster sample with X-ray fluxes above the X-ray 1σ limit. Results are shown for two different optical significance: S/N > 2.5 and S/N > 3.0, in the left and right panels, respectively. The best-fit scaling relations have been reliably derived for A and λM⋆ but not for λ*. For the fit we used only those detections with an optical mask fraction smaller than 30%, with no X-ray contamination given by interlopers identified with AMICO.

3.3. The catalogue of galaxy clusters

In this work we construct the filter adopting our cluster model, defined as C(zj; θ − θj, m) = R(zj; |θ − θj|) L(zj; m), which is the product of a Schechter luminosity function, L, in the r band given by the combination of a passive and a star-forming population of members with αred = −0.53 and αblue = −1.0, respectively, and a common M* = −20.8. These values, taken from Hansen et al. (2009), refer to clusters with mass M = 1014 M⊙ and richness N200 = 25 as estimated through the weak lensing mass-proxy scaling relation given by Johnston et al. (2007). These values just serve as a guidance to define the template and do not need to be fine-tuned. The same is true for the radial profile, R, describing the projected density distribution of cluster galaxies, here taken from the tabulated values given in Sheldon et al. (2009).

The statistical properties of the noise, N, are extracted directly from the data under the assumption that the number of cluster members is small with respect to that of the overall population of galaxies. This data driven approach is affected by the small area of miniJPAS because of the limited statistics, and the results presented in this work are thus penalized in terms of sensitivity and contamination. Better performance will be certainly obtained when the thousands of square degrees of J-PAS data are available. Despite this limitation, the application of AMICO to miniJPAS allows us to probe groups and clusters of galaxies over a wide range of redshifts and masses, as we show below.

The cluster catalogue provided by AMICO contains 80, 30, and 11 entries for signal-to-noise ratios (defined as S/N = A/σ given by Eqs. (1) and (2)) higher than 2.5, 3.0, and 3.5, respectively, and covers a mass range of approximately 1013 < M < 1014 M⊙ h−1. Assuming this number density of clusters we expect to detect of the order of 2.5  × 105 galaxy clusters with S/N > 3, when all 8000 deg2 of J-PAS have been observed. The redshift distribuion of galaxies and the cluster candidates are shown in the left and central panels of Fig. 5, respectively. The distribution of the signal-to-noise ratios of the detections is shown in the right panel of the same figure. The variations in both galaxy and cluster density are dominated by the physical fluctuations in the distribution of matter along the line of sight (see e.g. the ‘wall’ at z ≈ 0.28).

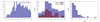thumbnail Fig. 5.

Redshift distribution of miniJPAS galaxies (left panel) and AMICO cluster detections (central panel; blue and red histograms for detections with S/N > 2.5 and S/N > 3, respectively). The large fluctuations in the number of galaxies and clusters are physical and are due to large-scale structure of the field, as confirmed by the spectroscopic redshifts (Bonoli et al. 2021). The right panel shows the distribution of signal-to-noise ratio of the detections.

In Fig. 6 we display some examples of detections. The left panel shows two groups with masses M200c = (6.5 ± 0.5)  ×  1013 M⊙ and M200c = (6.1 ± 0.5)  ×  1013 M⊙ located at different redshifts, z = 0.228 ± 0.005 and z = 0.338 ± 0.005, but close in the observer’s plane. The detection at lower redshift is on the right side of Fig. 2; the mass was derived thanks to X-ray observations, as discussed in Sect. 6. The amplitude maps are shown by the isodensity contours (red and cyan lines for the more and less distant detection, respectively), together with their members having a probabilistic association greater than 50%. These two objects are clearly disentangled by AMICO in contrast with the X-ray analysis in which only the combined flux can be measured (see the X-ray surface brightness displayed by the magenta contours in the right box of Fig. 2). This is a nice example where X-ray mass measurements have to be discarded because of the mutual cross-contamination of two cluster signals. This result is also confirmed by the following analysis of the mass-proxy scaling relations, and as is evident from Fig. 4, the X-ray mass for one of the two clusters, as well as for other cases of line-of-sight alignments, is largely overestimated. In such cases, removing optical counterparts susceptible to chance assignment to X-rays can improve the situation (Klein et al. 2019). The right panel of Fig. 6 shows the most massive object found in miniJPAS, a cluster with an X-ray mass of M200c = (8.6 ± 0.7)  ×  1013 M⊙ located at redshift z = 0.290 ± 0.005. Here the colour of the circles quantifies the probabilistic membership derived with AMICO, as indicated in the colour bar (for a detailed discussion about this cluster and its members, see Rodríguez-Martín et al. 2022). Since the cluster model is based on a luminosity function and a radial density distribution of galaxies in clusters, the probability associated with each galaxy depends not only on the galaxy redshift, but also on their angular separation from the cluster centre and on their magnitude: the closer to the cluster centre and/or the brighter the galaxy, the more likely is its membership to the cluster. The magnitude dependency is given by the difference in the luminosity functions of cluster members and field galaxies, where the first has a more pronounced value at lower magnitudes. The catalogue of galaxy cluster detections is available online1 and the quantities reported in its columns are described in Table 1.

thumbnail Fig. 6.

Examples of detected clusters and associated cluster members. Left panel: two clusters located along the same line of sight, but at two different redshifts (z = 0.233 ± 0.005 and z = 0.391 ± 0.005) displayed together with the map of the amplitude A measured by AMICO (cyan and red isodensity contours, respectively); the galaxy members with a probabilistic association P > 0.5 are indicated by circles. The filter response of AMICO is shown with the isocontours, blue for the lower redshift cluster and red for the higher redshift cluster. Right panel: most massive cluster in the sample having an X-ray mass of M = 8.6 ± 0.7 × 1013 M⊙ and located at z = 0.29. Here the colour of the circles indicate the probabilistic membership association of the members. The white lines represent the masked areas and the survey limit. In both panels the magenta contours show the extended X-ray emission.

Table 1.

Descriptions of the columns for the AMICO galaxy cluster catalogue.

Table 2.

Descriptions of the columns for the AMICO probabilistic association of galaxies to clusters.

thumbnail Fig. 7.

Distribution of radial distance of the BGG candidates with respect to the cluster centre identified by AMICO, given in arcmin (left panel) and Mpc/h (right panel). The BGGs are identified as the brightest and the second brightest galaxies with probabilities greater than 80%.

4. The catalogue of cluster members and BGGs

With this catalogue of galaxy cluster members, its entries detailed in Table 2, we created a sample of the brightest group galaxy (BGG) candidates by selecting the brightest galaxy member with a probabilistic membership greater than 80%. We also listed a second candidate by taking the second most luminous galaxy, again above the 80% probability threshold. This was done because the study of the magnitude gap between the first and second brightest galaxies is of interest (e.g. Gozaliasl et al. 2014); for instance, it might be used to evaluate the presence of fossil groups. Our sample contains several small groups in which it is difficult to identify a clear dominant galaxy. For the most massive systems the presence of two bright central galaxies with a similar luminosity might indicate a recent major merger event where the two galaxies might have been the BGGs of the parent structures. In Fig. 7 we plot the radial distance between the identified BGG and the cluster centre as defined by AMICO. Clearly, the second brightest galaxies (BGG with rank 2) are on average more distant from the cluster centre with respect to the brightest galaxy (BGG with rank 1), as expected.

5. Spectroscopic analysis: Redshift of clusters and probabilistic membership accuracy

The DEEP3 galaxy redshift survey partially overlaps the footprint of the miniJPAS survey (Bonoli et al. 2021). We can then use this dataset to derive a spectroscopic redshift estimate for the AMICO clusters within the DEEP3 region and to select their members. We used these estimates to test the redshift and membership association provided by AMICO.

We started by deriving a list of spectroscopic cluster members using the ‘shifting gapper’ technique in radial bins from the cluster centre (Fadda et al. 1996), as described in Lopes et al. (2009, 2014). The method is based on the application of the gap-technique in radial bins (described in Katgert et al. 1996) to identify gaps in the redshift distribution. Instead of adopting a fixed gap, such as 1000 km s−1 or 0.005(1 + z), we considered a variable gap, called the density gap (Adami et al. 1998; Lopes et al. 2009). The density gap size is given by the expression Δz = fg(1 + exp(−(N − 6)/33))/c, where N is the number of galaxies found in the redshift survey of a cluster (Adami et al. 1998), and c is the speed of light in km s−1. We note that the gap parameter fg replaces the fixed value of 500 adopted in Adami et al. (1998). This gap factor, fg, scales with the velocity range of the galaxies found in each radial bin and is a better choice to work with systems of different masses (Lopes et al. 2009). We considered all galaxies within 2.5 Mpc h−1 (3.57 Mpc for h = 0.7) from the cluster centre and with c |z−zcl| ≤ 4000 km s−1, where c is the speed of light and zcl the cluster redshift. We also used a bin size of 0.42 Mpc h−1 (0.60 Mpc for h = 0.7) or larger if fewer than 15 galaxies were selected. In every radial bin we discarded galaxies not associated with the main body of the cluster (those with a velocity difference exceeding the velocity gap). The procedure was repeated until no more galaxies were rejected as interlopers. One great advantage of this method is that it makes no hypothesis about the dynamical status of clusters that do not need to be virialized. In the end we were able to obtain spectroscopic redshift estimates and spectroscopic memberships for 47 AMICO clusters. Given the relatively low cluster masses and the limited number of members per cluster with spectroscopic redshift it was not possible to derive reliable estimates of clusters properties such as σcl, R200, and M200. The comparison with the redshift returned by AMICO is shown in Fig. 8 (grey circles): the scatter is very small σz = 0.0053(1 + z), dominated by the redshift sampling used in the run rather than by the photo-zs uncertainty, and no bias is present.

thumbnail Fig. 8.

Redshift of AMICO clusters. The data are based on the median miniJPAS photo-z of the galaxies with probabilistic association P > 0.5 (blue circles) and within 10′ from the detection centre compared with the spectroscopic redshift based on DEEP3 data. The uncertainty of our redshift estimates is σz = 0.0037(1 + z) (horizontal dotted lines), which is approximately ten times better than typically achieved with photometric surveys. The improvement of the redshift estimate based on the AMICO probabilistic memberships over the original output (small grey circles) is visible.

To refine the results based on the photometry only and the membership provided by AMICO, we estimated the cluster redshifts as the median of the redshifts of the galaxies with an AMICO probabilistic membership association larger than Pi(j) > 0.5 and within 10′ of the detection centre (see the blue circles in Fig. 8). This approach provides a smaller redshift uncertainty, σz = 0.0037(1 + z), with respect to that directly obtained with AMICO (grey points), which is affected by the relatively coarse redshift resolution, Δz = 0.01, used when running the algorithm. The procedure seems to be stable as the redshift correction is at most half ‘redshift pixel’, as expected. A higher resolution would be demanded by the high accuracy of the miniJPAS photo-zs, but this is not possible since the present limited area of the survey does not provide a reliable noise estimate in more narrow redshift slices, as already discussed. A redshift pixelization with a higher resolution will be adopted for the J-PAS data. We note that the resulting redshift uncertainty is about ten times better than is typically obtained with broad-band filters (see e.g. Maturi et al. 2019).

This high accuracy in redshift makes J-PAS an ideal survey to derive cosmological constraints based on the clustering of galaxy clusters. When performing such studies, the redshift uncertainty introduces an exponential suppression on the redshift-space 2D power spectrum causing a scale-dependent removal of signal over a typical scale k ∼ σ−1, where k is the modulus of the wave-vector components parallel and perpendicular to the line of sight and

σ ≡ c σ z H ( z m ) . $$ \begin{aligned} \sigma \equiv \frac{c\sigma _z}{H(z_m)}. \end{aligned} $$(10)

Here H(zm) is the Hubble function computed at the median redshift of the cluster sample, zm, and σz is the typical photo-z error (see e.g. Sereno et al. 2015; Lesci et al. 2022a). Hence, gaining a factor of 10 in the photo-z accuracy with respect to broad-band filter photometric surveys will allow us to have a stronger clustering signal at scales ten times smaller than is achievable with broad-band photometric surveys (Veropalumbo et al. 2014).

We then used the cluster memberships derived using the spectroscopic information to test the AMICO probabilistic membership association given in Eq. (6). The comparison between the fraction of spectroscopic members with the probabilistic membership associations provided by AMICO is shown in Fig. 9.

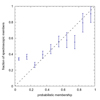thumbnail Fig. 9.

Probabilistic membership association of galaxies to clusters returned by AMICO compared with the fraction of spectroscopic cluster members identified with the ‘shifting gapper’ technique applied to the DEEP3 data. The photometric probabilistic membership is in good agreement with the spectroscopic membership, except for probabilities smaller than P < 0.2.

For the most interesting interval of probabilities (i.e. P > 0.2) the AMICO probabilistic associations appear in very good agreement with the spectroscopic memberships. For lower values, P < 0.2, there is a small discrepancy between spectroscopy and the result provided by AMICO. This might be due to the spectroscopic memberships (not due to AMICO) or to the cluster model used by AMICO during the detection phase, where the scale radius is larger than the typical one for the systems in the sample. While we plan to investigate this issue in more detail in future work, its importance is marginal since the galaxies in question are well below the 50% membership cut in all estimates, are found in the outskirts, and in general are not used in follow-up studies. The effect of this bias on the λ* and λM⋆ estimates, which are based on the membership probabilities, is not so relevant because it affects the galaxies with the lowest probabilistic memberships, which contribute the least and which tend to be faint galaxies, likely excluded by the magnitude cutoff embedded in the definition of these mass-proxies.

6. Analysis of the cluster sample using X-ray data

6.1. X-ray data

The miniJPAS data comprise the area covered by the All-wavelength Extended Groth strip International Survey (AEGIS; Davis et al. 2007). The X-ray data, based on several Chandra and XMM-Newton campaigns, result in one of the deepest X-ray cluster catalogues on the sky (Erfanianfar et al. 2013).

The miniJPAS data cover a larger area compared to the X-ray footprint analysed in Erfanianfar et al. (2013), but the area outside it has been extensively observed by XMM-Newton (PI A. Merloni). We reanalysed all the XMM-Newton observations overlapping with the miniJPAS data using the latest XMMSAS (version 18.0.0) and following the procedures on flare screening, background estimate, point source removal, and image mosaicing outlined in Finoguenov et al. (2010) and Erfanianfar et al. (2013). To measure the X-ray flux of the AMICO clusters, we combined point source cleaned Chandra and XMM-Newton data, and placed a 0.6′ aperture on the central position of each AMICO source. The relatively large aperture is meant to cope with possible miscentring between optical and X-ray positions. This strategy reduces possible biases in the estimates of the X-ray fluxes with the cost of a slightly larger uncertainty on the derived quantities. A subsequent computation of the X-ray luminosity iteratively takes into account the fraction of the flux retained within the aperture, and computes the K-correction, based on the redshift of the source and its spectral shape governed by the temperature estimated using an L − T relation (Finoguenov et al. 2010). The weak lensing calibration of the relation between X-ray luminosity and the total mass (M200c) was derived using similarly derived luminosities (Leauthaud et al. 2010; Taylor et al. 2012), so any biases of the procedure are absorbed by the calibration. The cosmological parameters adopted for this weak lensing calibration are the same as assumed in the cluster detection procedure.

For the non-detected clusters, we place the 1σ upper limit on the X-ray properties. The fraction of optical detections with an X-ray counterpart as a function of redshifts, optical (AMICO) signal-to-noise ratio, amplitude A, and richness λ* is shown in Fig. 10. No particular trend is visible except for a clear increase in this fraction towards detections with higher signal-to-noise ratios, which are more likely to be true positives associated with lower redshift and more massive systems, whose X-ray emission is more likely to be detected. It also seems that there is a difference in the evolution of X-ray versus AMICO efficiency to detect clusters, with X-rays depths yielding to AMICO at z > 0.5. This highlights that in order to fully calibrate the high-z performance of AMICO on J-PAS, much deeper X-ray data are needed, which will only be readily available with future X-ray missions, such as Athena.

thumbnail Fig. 10.

Fraction of optical detections with an X-ray counterpart with S/N > 1 as a function of redshift (top left panel), AMICO signal-to-noise ratio (top right panel), amplitude A (bottom left panel) and intrinsic richness λ* (bottom right panel).

In Fig. 11 we show the relation between the AMICO amplitude, A, and the X-ray luminosity. A strong correlation between these two quantities shows how optical proxies can be used to derive reliable mass scaling relations, which we discuss in Sect. 6.2. From this dataset it appears that clusters down to very small amplitudes (X-ray flux) have a very ‘well-behaved’ relation between their ratio of dark matter, baryonic content (both in terms of gas and number of members), and X-ray fluxes. Only four outliers stand out in the plot, but their X-ray flux is unreliable due to interlopers, objects belonging to pairs or triplets of clusters displaced along the same line of sight within r < 1′ (three of them; see left panel of Fig. 6) or because of an underestimation of the AMICO amplitude due to the non-complete optical coverage of the cluster, more than 30% of its area falls outside the miniJPAS footprint (see right panel of Fig. 6).

thumbnail Fig. 11.

Relation between AMICO amplitude, A, and X-ray luminosity on which the X-ray mass estimates are based (albeit with a redshift-dependent correction). The grey points were rejected from this analysis because they are either heavily masked (more than 30% of the cluster) or their X-ray flux is possibly contaminated by an interloper. Only the systems with a significance of X-ray flux estimate above the 1σ significance are shown. The left and right panel refers to optical detections with S/N > 2.5 and S/N > 3.0, respectively.

6.2. Mass-proxy scaling relations

We model the relation between our X-ray (M200c, obtained for each AMICO cluster following the procedures described in Sect. 6.1) and AMICO (O) mass proxies, discussed in Sect. (3.2) as

log 10 M 200 c 10 14 M ⊙ h − 1 = α + β log 10 O O piv , $$ \begin{aligned} \mathrm{log}_{10}\frac{M_{200c}}{10^{14}\,M_\odot \,h^{-1}} = \alpha + \beta \,\log _{10}\frac{O}{O_{\rm piv}} \,, \end{aligned} $$(11)

where Opiv is a pivot value (Bellagamba et al. 2019). We do not account for any possible redshift dependency because the current sample is too small for its solid assessment, but it will be included when analysing future data releases. The best-fit relations for A and λM⋆ are shown in Fig. 4 for detections with S/N > 2.5 and S/N > 3.0 (left and right panels, respectively). No scaling relation was derived for λ* because of the excessive scatter and strong redshift dependence.

Despite the fact that only four clusters are real outliers, when fitting the scaling laws, we opted to use a hard criteria for the sample selection, meaning that we considered only the clusters with an X-ray flux significance above the 1σ limit and excluded 11 clusters with either significant optical masking or line-of-sight projections affecting the X-ray flux estimate. Four rejected clusters, indicated with open grey circles, are heavily masked (more than 30% of the cluster). Even if AMICO corrects for the masked fraction, one of them remains a clear outlier. The other seven, indicated with grey solid triangles, are systems affected by interlopers. The values of the best-fit parameters based on the mass-proxy scaling relations are reported in Table 3. We only list the results for two mass proxies, namely A and λM⋆, because of the excessive scatter in λ* and because the scaling relation is currently very sensitive to the signal-to-noise ratio cutoff adopted for the cluster sample.

Table 3.

Best-fit values for the mass-proxy scaling relations given by Eq. (11) for the sample with S/N > 2.5 and S/N > 3.0.

thumbnail Fig. 12.

Comparison between properties of the detections derived from the catalogue of galaxies with degraded photo-z, mimicking a typical photometric survey with redshift uncertainty σz = 0.03(1 + z) (broad-band, BB), and of the detections based on the original miniJPAS data exploiting the 56 J-PAS filters. Top left panel: redshift distribution of the detections. The solid boxes refer to the degraded broad-band data and the lines to the original dataset. The detections with S/N > 2.5 and S/N > 3 are in blue and red, respectively. Top right panel: signal-to-noise ratios. Bottom left panel: Amplitude A. Bottom right panel: probabilistic membership association of galaxies to clusters, as provided by AMICO.

For the current release we prefer to use the amplitude, A, as mass proxy because the best-fit parameters of the scaling relations are very stable with respect to the choice of the signal-to-noise ratio adopted to select the clusters. Moreover, the filtering procedure provided by AMICO automatically accounts for the magnitude limit of the survey and the estimate appears unbiased over the entire redshift range under consideration. In contrast, the intrinsic richness, λ* and λM⋆, suffer from the galaxy sample incompleteness for redshifts z > 0.56, as discussed in Sect. (3.2). When it is possible to constrain their redshift dependency, λ* and λM⋆ will also be valuable options, even though they show a larger scatter around the best fit with respect to the amplitude, A. This might be because here we are dealing with a very small system populated by a few bright galaxies. We will investigate in depth this possible issue once data covering a larger area are available. Finally, λM⋆ appears to be very promising as its scatter around the best-fit relation is remarkably smaller than that of λ*; it is very sensitive to the mass and has the additional benefit of providing a physical characterization of clusters in terms of their stellar mass. This is one of the unique features of J-PAS, due to the excellent SED modelling it enables.

We would like to note that for this field we have very deep X-ray data (with a flux limit ranging from 10−15 to 3 × 10−15 erg s−1 cm−2 at the 1σ level), which allows us to derive mass-proxy scaling relations down to very low masses, notably for individual clusters and not only through stacking. Such deep X-ray datasets will not be available for the large number of galaxy groups that J-PAS will provide in the near future. For instance, the ROSAT all-sky survey has a flux limit of 10−13 and 10−12 erg s−1 cm−2 for the deep and faint areas, respectively, and the eRosita survey of 10−14 erg s−1 cm−2 (Merloni et al. 2012). This poses the problem of how to improve the scaling relations for the smaller systems that J-PAS can reach thanks to its sensitivity. This calls for possible targeted X-ray deep observations of the J-PAS galaxy groups, as well as the analysis of archival XMM-Newton data overlapping the J-PAS survey footprint. Weak-gravitational lensing and velocity dispersion measurements will also provide a way out, with large datasets already available within the J-PAS survey footprint from SDSS (e.g. Kirkpatrick et al. 2021), CODEX (Kiiveri et al. 2021), DECaLS (e.g. Phriksee et al. 2020), and in the future from Euclid (Euclid Collaboration 2022) and DESI (Dey et al. 2019).

7. Impact of narrow-band photometry on galaxy cluster detection

To quantify the gain in the cluster detection efficiency provided by the high quality of the photo-zs based on the 56 J-PAS filters, we degraded the data by introducing a final scatter in the photo-z of σz = 0.03(1 + z) to mimic the performance of a typical broad-band survey (see e.g. Maturi et al. 2019). This assumption is optimistic in terms of scatter and, even more importantly, it does not account for possible biases that would affect such surveys. We recall that photo-zs based solely on broad-band filters are more prone to biases caused by features in the galaxy SED, that they cannot resolve the 4000 Å break, for example, when transitioning between the g and r filters (see e.g. Padmanabhan et al. 2005; Maturi et al. 2019; Bonoli et al. 2021; González Delgado et al. 2021). By applying AMICO to this degraded dataset we detect only 46, 26, and 9 clusters for signal-to-noise ratios higher than 2.5, 3.0, and 3.5, respectively, against the 80, 30, and 11 detections in the original catalogue. The increase in sensitivity given by the narrow-band filter is remarkable, as shown by Fig. 12, where we plot the redshift distribution (top left panel) and compare the detection signal-to-noise ratio of the original and degraded samples (top right panel). The gain in sensitivity that the narrow-band filters provide is clear. The amplitude, A, is only minimally affected showing the stability of the algorithm (bottom left panel). Finally, the probabilistic membership of galaxies to clusters is largely improved by the narrow-band filters, as expected (bottom right panel). To prove this last point numerical simulations are needed, but here it is clear that galaxies with relatively high probabilistic membership (P(z) > 0.8) in the BB survey have extremely high probabilities in the miniJPAS data (P(z)∼0.98.

8. Conclusions

We applied the algorithm AMICO for cluster detection to the ∼1 deg2 area of the miniJPAS data detecting 80, 30, and 11 systems with signal-to-noise ratio higher than 2.5, 3.0, and 3.5, respectively, in the redshift range 0.05 < z < 0.8 down to a mass of ∼1013 M⊙ h−1. With this number density of derived galaxy clusters, we expect to detect of the order of 2  × 105 galaxy clusters with S/N > 3 in the upcoming 8000 deg2 of J-PAS, with unprecedented sensitivity in mass and redshift accuracy for a photometric survey.

We derived mass-proxy scaling relations for the native response of AMICO (i.e. the amplitude, A, and a newly defined estimate of the stellar mass λM⋆). The mass estimates for the clusters used for this analysis were obtained using the deep Chandra and XMM data available for the AEGIS field. The best-fit values of the scaling relations parameters are listed in Table 3. We found that the amplitude A has a smaller scatter around the best-fit relation and is more robust with respect to the redshift dependency compared to the other mass proxies because, by directly relying on the filtering formalism, it automatically accounts for and compensates for the survey depth limit. In contrast, λ* and λM⋆ assume a fixed maximum absolute magnitude cutoff, which, for our dataset, cannot be reached for redshifts higher than z = 0.56. Thus, they require a posteriori calibration, which will be possible only when more data (i.e. a larger area) are available.

Furthermore, we produced a catalogue of cluster members based on the probabilistic association of galaxies to clusters provided by AMICO itself. We compared our probabilistic memberships with that based on the shifting gapper approach applied to the spectroscopic DEEP3 survey. Our probabilistic membership appears to be in good agreement for galaxies with probability P > 0.2, with differences observed at lower probabilities, which are of lower interest because they likely do not belonging to clusters. This catalogue of members can be exploited to study galaxy populations and to produce mock catalogues for the estimation of the purity and completeness of the cluster sample with data-driven approaches such as the one implemented in SinFoniA (Maturi et al. 2019). This is crucial information needed for the derivation of cosmological constraints based on the cluster samples. Finally, we used the memberships to identify the BGGs belonging to our cluster sample. We further show how the narrow-band filters of J-PAS provide a substantial gain in sensitivity and an uncertainty on the redshift of clusters of only σz = 0.0037(1 + z) placing J-PAS between photometric and spectroscopic surveys. As an outlook, this might open up the possibility to study the clustering of galaxy clusters as well.

The performance of AMICO and J-PAS we demonstrate in this work will allow us to characterize galaxy groups and clusters down to small groups of ∼103 M⊙ h−1, to identify the BGGs, to split the galaxy population according to the environment, and to derive cosmological constraints. All data products are available online2 together with the miniJPAS data.

1

https://www.j-pas.org/ancillarydata/minijpas_amico_galaxy_clusters

2

https://www.j-pas.org/ancillarydata/minijpas_amico_galaxy_clusters

Acknowledgments

Based on observations made with the JST250 telescope and PathFinder camera for the miniJPAS project at the Observatorio Astrofísico de Javalambre (OAJ), in Teruel, owned, managed, and operated by the Centro de Estudios de Física del Cosmos de Aragón (CEFCA). We acknowledge the OAJ Data Processing and Archiving Unit (UPAD) for reducing and calibrating the OAJ data used in this work. Funding for OAJ, UPAD, and CEFCA has been provided by the Governments of Spain and Aragón through the Fondo de Inversiones de Teruel; the Aragón Government through the Research Groups E96, E103, E16_17R, and E16_20R; the Spanish Ministry of Science, Innovation and Universities (MCIU/AEI/FEDER, UE) with grant PGC2018-097585-B-C21; the Spanish Ministry of Economy and Competitiveness (MINECO/FEDER, UE) under AYA2015-66211-C2-1-P, AYA2015-66211-C2-2, AYA2012-30789, and ICTS-2009-14; and European FEDER funding (FCDD10-4E-867, FCDD13-4E-2685). A.Z. acknowledges support by Grant No. 2020750 from the United States-Israel Binational Science Foundation (BSF) and Grant No. 2109066 from the United States National Science Foundation (NSF), and by the Ministry of Science & Technology, Israel. I.M. acknowledges financial support from the IAA Severo Ochoa Excellence grant CEX2021-001131-S funded by MCIN/AEI/ 10.13039/501100011033. J.A.F.O. acknowledges the financial support from the Spanish Ministry of Science and Innovation and the European Union – NextGenerationEU through the Recovery and Resilience Facility project ICTS-MRR-2021-03-CEFCA. J.M.D. acknowledges the support of projects PGC2018-101814-B-100 and MDM-2017-0765. L.D. acknowledges the scholarship support from the Brazilian federal funding agency Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES). L.M. acknowledges support from the grants PRIN-MIUR 2017 WSCC32 and ASI n.2018-23-HH.0. R.A.D. acknowledges support from the Conselho Nacional de Desenvolvimento Científico e Tecnológico – CNPq through BP grant 308105/2018-4, and the Financiadora de Estudos e Projetos – FINEP grants REF. 1217/13 – 01.13.0279.00 and REF 0859/10 – 01.10.0663.00 and also FAPERJ PRONEX grant E-26/110.566/2010 for hardware funding support for the JPAS project through the National Observatory of Brazil and Centro Brasileiro de Pesquisas Físicas. LM acknowledges support from the grants PRIN-MIUR 2017 WSCC32 and ASI n.2018-23-HH.0. R.G.D. acknowledge financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709), and through PID2019-109067-GB100. S.B. acknowledges support from the project PID2021-124243NB-C21 from the Spanish Ministry of Economy and Competitiveness (MINECO/FEDER, UE) and partial support from the Project of excellence Prometeo/2020/085 from the Conselleria d’Innovació, Universitats, Ciéncia i Societat Digital de la Generalitat Valenciana. V.M. thanks CNPq (Brazil) and FAPES (Brazil) for partial financial support. Y.J.-T. acknowledges financial support from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 898633, the MSCA IF Extensions Program of the Spanish National Research Council (CSIC), and the State Agency for Research of the Spanish MCIU through the Center of Excellence Severo Ochoa award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709).

References

  1. Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2020, Phys. Rev. D, 102, 023509 [Google Scholar]
  2. Adami, C., Mazure, A., Biviano, A., Katgert, P., & Rhee, G. 1998, A&A, 331, 493 [NASA ADS] [Google Scholar]
  3. Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [Google Scholar]
  4. Arnouts, S., & Ilbert, O. 2011, Astrophysics Source Code Library [record ascl:1108.009] [Google Scholar]
  5. Bellagamba, F., Roncarelli, M., Maturi, M., & Moscardini, L. 2018, MNRAS, 473, 5221 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bellagamba, F., Sereno, M., Roncarelli, M., et al. 2019, MNRAS, 484, 1598 [Google Scholar]
  7. Benítez, N. 2000, ApJ, 536, 571 [Google Scholar]
  8. Benitez, N., Dupke, R., Moles, M., et al. 2014, arXiv eprints [arXiv:1403.5237] [Google Scholar]
  9. Benson, B. A., de Haan, T., Dudley, J. P., et al. 2013, ApJ, 763, 147 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bernardeau, F., Bonvin, C., & Vernizzi, F. 2010, Phys. Rev. D, 81, 083002 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bilicki, M., Hoekstra, H., Brown, M. J. I., et al. 2018, A&A, 616, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Blake, C., Kazin, E. A., Beutler, F., et al. 2011, MNRAS, 418, 1707 [NASA ADS] [CrossRef] [Google Scholar]
  13. Blandford, R. D., Saust, A. B., Brainerd, T. G., & Villumsen, J. V. 1991, MNRAS, 251, 600 [NASA ADS] [Google Scholar]
  14. Bleem, L. E., Stalder, B., de Haan, T., et al. 2015, ApJS, 216, 27 [Google Scholar]
  15. Bocquet, S., Dietrich, J. P., Schrabback, T., et al. 2019, ApJ, 878, 55 [Google Scholar]
  16. Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Bonoli, S., Marín-Franch, A., Varela, J., et al. 2021, A&A, 653, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Cacciato, M., van den Bosch, F. C., More, S., Mo, H., & Yang, X. 2013, MNRAS, 430, 767 [Google Scholar]
  19. Chiu, I.-N., Klein, M., Mohr, J., & Bocquet, S. 2023, MNRAS, 522, 1601 [NASA ADS] [CrossRef] [Google Scholar]
  20. Costa, A. A., Marcondes, R. J. F., Landim, R. G., et al. 2019, MNRAS, 488, 78 [NASA ADS] [CrossRef] [Google Scholar]
  21. Costanzi, M., Saro, A., Bocquet, S., et al. 2021, Phys. Rev. D, 103, 043522 [Google Scholar]
  22. Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
  23. de Jong, R. S., Barden, S., Bellido-Tirado, O., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, eds. S. K. Ramsay, I. S. McLean, & H. Takami, SPIE Conf. Ser., 9147, 91470M [NASA ADS] [Google Scholar]
  24. Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168 [Google Scholar]
  25. du Mas des Bourboux, H., Rich, J., Font-Ribera, A., et al. 2020, ApJ, 901, 153 [CrossRef] [Google Scholar]
  26. Erfanianfar, G., Finoguenov, A., Tanaka, M., et al. 2013, ApJ, 765, 117 [NASA ADS] [CrossRef] [Google Scholar]
  27. Euclid Collaboration (Adam, R., et al.) 2019, A&A, 627, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Euclid Collaboration (Scaramella, R., et al.) 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] [Google Scholar]
  30. Farrens, S., Abdalla, F. B., Cypriano, E. S., Sabiu, C., & Blake, C. 2011, MNRAS, 417, 1402 [Google Scholar]
  31. Finoguenov, A., Watson, M. G., Tanaka, M., et al. 2010, MNRAS, 403, 2063 [NASA ADS] [CrossRef] [Google Scholar]
  32. Finoguenov, A., Rykoff, E., Clerc, N., et al. 2020, A&A, 638, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Garrel, C., Pierre, M., Valageas, P., et al. 2022, A&A, 663, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Giocoli, C., Marulli, F., Moscardini, L., et al. 2021, A&A, 653, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. González Delgado, R. M., Díaz-García, L. A., de Amorim, A., et al. 2021, A&A, 649, A79 [Google Scholar]
  36. González Delgado, R. M., Rodríguez-Martín, J. E., Díaz-García, L. A., et al. 2022, A&A, 666, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Gozaliasl, G., Finoguenov, A., Khosroshahi, H. G., et al. 2014, A&A, 566, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Hansen, S. M., Sheldon, E. S., Wechsler, R. H., & Koester, B. P. 2009, ApJ, 699, 1333 [NASA ADS] [CrossRef] [Google Scholar]
  39. Hernán-Caballero, A., Varela, J., López-Sanjuan, C., et al. 2021, A&A, 654, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
  41. Hilton, M., Sifón, C., Naess, S., et al. 2021, ApJS, 253, 3 [Google Scholar]
  42. Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [Google Scholar]
  43. Hinton, S. R., Kazin, E., Davis, T. M., et al. 2017, MNRAS, 464, 4807 [NASA ADS] [CrossRef] [Google Scholar]
  44. Hu, W., & Sugiyama, N. 1996, ApJ, 471, 542 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ider Chitham, J., Comparat, J., Finoguenov, A., et al. 2020, MNRAS, 499, 4768 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ingoglia, L., Covone, G., Sereno, M., et al. 2022, MNRAS, 511, 1484 [NASA ADS] [CrossRef] [Google Scholar]
  47. Johnston, D. E., Sheldon, E. S., Wechsler, R. H., et al. 2007, arXiv e-prints [arXiv:0709.1159] [Google Scholar]
  48. Käfer, F., Finoguenov, A., Eckert, D., et al. 2020, A&A, 634, A8 [Google Scholar]
  49. Kaiser, N. 1987, MNRAS, 227, 1 [Google Scholar]
  50. Katgert, P., Mazure, A., Perea, J., et al. 1996, A&A, 310, 8 [NASA ADS] [Google Scholar]
  51. Kiiveri, K., Gruen, D., Finoguenov, A., et al. 2021, MNRAS, 502, 1494 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kirkpatrick, C. C., Clerc, N., Finoguenov, A., et al. 2021, MNRAS, 503, 5763 [NASA ADS] [CrossRef] [Google Scholar]
  53. Klein, M., Grandis, S., Mohr, J. J., et al. 2019, MNRAS, 488, 739 [Google Scholar]
  54. Leauthaud, A., Finoguenov, A., Kneib, J.-P., et al. 2010, ApJ, 709, 97 [Google Scholar]
  55. Lesci, G. F., Nanni, L., Marulli, F., et al. 2022a, A&A, 665, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Lesci, G. F., Marulli, F., Moscardini, L., et al. 2022b, A&A, 659, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Licitra, R., Mei, S., Raichoor, A., Erben, T., & Hildebrandt, H. 2016, MNRAS, 455, 3020 [NASA ADS] [CrossRef] [Google Scholar]
  58. Lopes, P. A. A., de Carvalho, R. R., Kohl-Moreira, J. L., & Jones, C. 2009, MNRAS, 392, 135 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lopes, P. A. A., Ribeiro, A. L. B., & Rembold, S. B. 2014, MNRAS, 437, 2430 [NASA ADS] [CrossRef] [Google Scholar]
  60. LSST Science Collaboration (Abell, P. A., et al.) 2009, arXiv eprints [arXiv:0912.0201] [Google Scholar]
  61. Marín-Franch, A., Chueca, S., Moles, M., et al. 2012, in Modern Technologies in Space- and Ground-based Telescopes and Instrumentation II, eds. R. Navarro, C. R. Cunningham, & E. Prieto, SPIE Conf. Ser., 8450, 84503S [Google Scholar]
  62. Marulli, F., Veropalumbo, A., García-Farieta, J. E., et al. 2021, ApJ, 920, 13 [Google Scholar]
  63. Maturi, M., Meneghetti, M., Bartelmann, M., Dolag, K., & Moscardini, L. 2005, A&A, 442, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Maturi, M., Bellagamba, F., Radovich, M., et al. 2019, MNRAS, 485, 498 [Google Scholar]
  65. Merloni, A., Predehl, P., Becker, W., et al. 2012, arXiv eprints [arXiv:1209.3114] [Google Scholar]
  66. Moresco, M., Veropalumbo, A., Marulli, F., Moscardini, L., & Cimatti, A. 2021, ApJ, 919, 144 [NASA ADS] [CrossRef] [Google Scholar]
  67. Ota, N., Nguyen-Dang, N. T., Mitsuishi, I., et al. 2023, A&A, 669, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Padmanabhan, N., Budavári, T., Schlegel, D. J., et al. 2005, MNRAS, 359, 237 [Google Scholar]
  69. Pandey, S., Krause, E., DeRose, J., et al. 2022, Phys. Rev. D, 106, 043520 [NASA ADS] [CrossRef] [Google Scholar]
  70. Pereira, M. E. S., Soares-Santos, M., Makler, M., et al. 2018, MNRAS, 474, 1361 [CrossRef] [Google Scholar]
  71. Pettorino, V., Amendola, L., Baccigalupi, C., & Quercellini, C. 2012, Phys. Rev. D, 86, 103507 [CrossRef] [Google Scholar]
  72. Phriksee, A., Jullo, E., Limousin, M., et al. 2020, MNRAS, 491, 1643 [NASA ADS] [CrossRef] [Google Scholar]
  73. Pillepich, A., Porciani, C., & Reiprich, T. H. 2012, MNRAS, 422, 44 [Google Scholar]
  74. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Planck Collaboration XXIV. 2016, A&A, 594, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Puddu, E., Radovich, M., Sereno, M., et al. 2021, A&A, 645, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Radovich, M., Tortora, C., Bellagamba, F., et al. 2020, MNRAS, 498, 4303 [NASA ADS] [CrossRef] [Google Scholar]
  78. Rodríguez-Martín, J. E., González Delgado, R. M., Martínez-Solaeche, G., et al. 2022, A&A, 666, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [Google Scholar]
  80. Rykoff, E. S., Rozo, E., Hollowood, D., et al. 2016, ApJS, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
  81. Sartoris, B., Biviano, A., Fedeli, C., et al. 2016, MNRAS, 459, 1764 [Google Scholar]
  82. Sereno, M., Veropalumbo, A., Marulli, F., et al. 2015, MNRAS, 449, 4147 [NASA ADS] [CrossRef] [Google Scholar]
  83. Sereno, M., Ettori, S., Lesci, G. F., et al. 2020, MNRAS, 497, 894 [NASA ADS] [CrossRef] [Google Scholar]
  84. Sheldon, E. S., Johnston, D. E., Masjedi, M., et al. 2009, ApJ, 703, 2232 [NASA ADS] [CrossRef] [Google Scholar]
  85. Smit, M., Dvornik, A., Radovich, M., et al. 2022, A&A, 659, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Taylor, J. E., Massey, R. J., Leauthaud, A., et al. 2012, ApJ, 749, 127 [NASA ADS] [CrossRef] [Google Scholar]
  87. Tortora, C., Napolitano, N. R., Radovich, M., et al. 2020, A&A, 638, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Vakili, M., Hoekstra, H., Bilicki, M., et al. 2023, A&A, 675, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2014, MNRAS, 442, 3275 [NASA ADS] [CrossRef] [Google Scholar]
  90. Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [Google Scholar]
  91. Zubeldia, Í., & Challinor, A. 2019, MNRAS, 489, 401 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Descriptions of the columns for the AMICO galaxy cluster catalogue.

In the text
Table 2.

Descriptions of the columns for the AMICO probabilistic association of galaxies to clusters.

In the text
Table 3.

Best-fit values for the mass-proxy scaling relations given by Eq. (11) for the sample with S/N > 2.5 and S/N > 3.0.

In the text

All Figures

thumbnail Fig. 1.

Size and magnitude of all sources and photometric redshift of the input galaxies. Left panel: r-band magnitude vs FWHM of the galaxies detected in miniJPAS and used for the analysis (in blue). Shown are objects with a “stellarity” Bayesian probability of being stars higher than 50% (in red) and of being galaxies lower than 50% (in blue). All objects (in green) with a FWHM smaller than the PSF size of each individual pointing plus a tolerance of 0.11 arcsec (indicated by the vertical lines) were rejected regardless their classification. Right panel: average redshift probability distribution of galaxies as measured by AMICO with a peak P(z) located at three different redshifts and for two different magnitudes: r = 20 and r = 22 (in blue and red, respectively). This estimate is produced by AMICO through the input photo-zs and is used in the cluster model construction. The black dashed lines show the typical uncertainty of photo-zs based on broad-band photometry.
In the text
thumbnail Fig. 2.

Illustration of the AMICO response amplitude for a redshift slice at z = 0.24. The overdensities highlighted by AMICO are clearly visible as strong enhancements over the background. The survey footprint and masked areas are indicated in white. The two boxes with the miniJPAS images show the two most significant detections at that redshift together with X-ray emission isocontours. The top left box shows the response of AMICO around the main central structure at z = 0.24 and at redshift z = 0.36, where another cluster is clearly visible. There is little cross-contamination between redshift slices. The cluster on the right side is a case of chance alignment between two structures (see left panel of Fig. 6). The asterisks in the figures indicate the position of the cluster visible in the other redshift slice and displaced nearly along the same line of sight.
In the text
thumbnail Fig. 3.

Observed richness λ (left panel) and intrinsic richness λ* (central panel) as a function of redshift obtained with AMICO. For redshifts higher than z = 0.56, the cutoff magnitude mcut = m* + 1.5, on which λ* is based, falls below the detection limit and the richness is underestimated, as is clear from the lack of rise in the λ* of detections with z > 0.56. The right panel shows the amplitude, A, of the detections. The blue and red symbols refer to detections with S/N > 3 and S/N < 3, respectively.
In the text
thumbnail Fig. 4.

Scaling relations between different mass proxies (A, top panels; λ*, central panels; and λM⋆, bottom panels) and our X-ray mass estimates for the cluster sample with X-ray fluxes above the X-ray 1σ limit. Results are shown for two different optical significance: S/N > 2.5 and S/N > 3.0, in the left and right panels, respectively. The best-fit scaling relations have been reliably derived for A and λM⋆ but not for λ*. For the fit we used only those detections with an optical mask fraction smaller than 30%, with no X-ray contamination given by interlopers identified with AMICO.
In the text
thumbnail Fig. 5.

Redshift distribution of miniJPAS galaxies (left panel) and AMICO cluster detections (central panel; blue and red histograms for detections with S/N > 2.5 and S/N > 3, respectively). The large fluctuations in the number of galaxies and clusters are physical and are due to large-scale structure of the field, as confirmed by the spectroscopic redshifts (Bonoli et al. 2021). The right panel shows the distribution of signal-to-noise ratio of the detections.
In the text
thumbnail Fig. 6.

Examples of detected clusters and associated cluster members. Left panel: two clusters located along the same line of sight, but at two different redshifts (z = 0.233 ± 0.005 and z = 0.391 ± 0.005) displayed together with the map of the amplitude A measured by AMICO (cyan and red isodensity contours, respectively); the galaxy members with a probabilistic association P > 0.5 are indicated by circles. The filter response of AMICO is shown with the isocontours, blue for the lower redshift cluster and red for the higher redshift cluster. Right panel: most massive cluster in the sample having an X-ray mass of M = 8.6 ± 0.7 × 1013 M⊙ and located at z = 0.29. Here the colour of the circles indicate the probabilistic membership association of the members. The white lines represent the masked areas and the survey limit. In both panels the magenta contours show the extended X-ray emission.
In the text
thumbnail Fig. 7.

Distribution of radial distance of the BGG candidates with respect to the cluster centre identified by AMICO, given in arcmin (left panel) and Mpc/h (right panel). The BGGs are identified as the brightest and the second brightest galaxies with probabilities greater than 80%.
In the text
thumbnail Fig. 8.

Redshift of AMICO clusters. The data are based on the median miniJPAS photo-z of the galaxies with probabilistic association P > 0.5 (blue circles) and within 10′ from the detection centre compared with the spectroscopic redshift based on DEEP3 data. The uncertainty of our redshift estimates is σz = 0.0037(1 + z) (horizontal dotted lines), which is approximately ten times better than typically achieved with photometric surveys. The improvement of the redshift estimate based on the AMICO probabilistic memberships over the original output (small grey circles) is visible.
In the text
thumbnail Fig. 9.

Probabilistic membership association of galaxies to clusters returned by AMICO compared with the fraction of spectroscopic cluster members identified with the ‘shifting gapper’ technique applied to the DEEP3 data. The photometric probabilistic membership is in good agreement with the spectroscopic membership, except for probabilities smaller than P < 0.2.
In the text
thumbnail Fig. 10.

Fraction of optical detections with an X-ray counterpart with S/N > 1 as a function of redshift (top left panel), AMICO signal-to-noise ratio (top right panel), amplitude A (bottom left panel) and intrinsic richness λ* (bottom right panel).
In the text
thumbnail Fig. 11.

Relation between AMICO amplitude, A, and X-ray luminosity on which the X-ray mass estimates are based (albeit with a redshift-dependent correction). The grey points were rejected from this analysis because they are either heavily masked (more than 30% of the cluster) or their X-ray flux is possibly contaminated by an interloper. Only the systems with a significance of X-ray flux estimate above the 1σ significance are shown. The left and right panel refers to optical detections with S/N > 2.5 and S/N > 3.0, respectively.
In the text
thumbnail Fig. 12.

Comparison between properties of the detections derived from the catalogue of galaxies with degraded photo-z, mimicking a typical photometric survey with redshift uncertainty σz = 0.03(1 + z) (broad-band, BB), and of the detections based on the original miniJPAS data exploiting the 56 J-PAS filters. Top left panel: redshift distribution of the detections. The solid boxes refer to the degraded broad-band data and the lines to the original dataset. The detections with S/N > 2.5 and S/N > 3 are in blue and red, respectively. Top right panel: signal-to-noise ratios. Bottom left panel: Amplitude A. Bottom right panel: probabilistic membership association of galaxies to clusters, as provided by AMICO.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.