EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A155 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A155
Number of page(s) 17
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202346938
Published online 21 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Supermassive stars (SMSs) and massive Population III (PopIII) stars are thought to be a key intermediate stage in producing black holes with masses in the range 103 M⊙–105 M⊙ in the early Universe. Observations of distant quasars (Willott et al. 2010; Mortlock et al. 2011; Bañados et al. 2018; Wang et al. 2021) powered by supermassive black holes (SMBHs) with masses in excess of 109 M⊙ place extremely tight constraints on the time available to grow seed black holes up to these extreme masses. The recent discovery of a SMBH with a mass of approximately 107 M⊙ by the CEERS survey team at z ∼ 8.7 only exacerbates the problem (Larson et al. 2023).

While the seeds of these early SMBHs could in theory be stellar mass black holes formed from the endpoint of PopIII stars, there are a number of significant challenges to this pathway. Firstly, in order for a typical stellar mass black hole of ≈100 M⊙ to grow by the required 6–8 orders of magnitude within a few hundred million years, it would need to accrete at the Eddington rate for the entire time. In addition, these relatively light black holes would need to sink to the centre of their host galaxy and then find themselves continuously at the centre of a large gas inflow to reach such masses.

A number of authors have carried out numerical studies to investigate this growth pathway (e.g., Milosavljević et al. 2009; Alvarez et al. 2009; Tanaka & Haiman 2009; Jeon et al. 2012; Smith et al. 2018) and in all cases the stellar mass black holes were found to struggle to achieve significant growth because they are rarely surrounded by the high-density gas that is required to trigger rapid growth. Separately, a number of authors have investigated the dynamics of stellar mass black holes inside high-z galaxies, finding that black holes with masses of less than 105 M⊙ produce insufficient dynamical friction and do not fall to the centre of the galaxy (Pfister et al. 2019; Beckmann et al. 2023), instead wandering the host galaxy via a random walk (Bellovary et al. 2010; Tremmel et al. 2018).

As a result of these challenges, recent efforts have focused on investigating the possibility that the early Universe may harbour the correct environmental conditions for SMS and massive PopIII star formation. True SMS formation requires that the star reach the GR instability (Chandrasekhar 1964) due to sustained accretion up to masses of ≈105 − 106 M⊙ (Hosokawa et al. 2013). The stars we study here do not reach such high masses, and so we instead refer to them as massive PopIII stars with typical masses in excess of ≈1000 M⊙. The metal-free or metal-poor nature of the first galaxies is expected to provide ideal conditions that allow massive gravitationally unstable clumps of gas to form, without metal cooling lines to induce fragmentation (Omukai et al. 2008). Massive PopIII star formation is expected to be primarily driven by achieving the critical accretion rate needed to drive the inflation of the photosphere to become a red supergiant. This limits radiative feedback and allows further growth of the massive PopIII stars (e.g., Hosokawa et al. 2013; Woods et al. 2017). The nature and impact of this critical accretion rate is the focus of this work.

Previous studies that investigated this problem did not identify a precise value, but it is expected to be in excess of 10−2 M⊙ yr−1 (e.g., Hosokawa et al. 2013; Haemmerlé et al. 2018). Such high accretion rates may be achieved in atomic cooling haloes (Eisenstein & Loeb 1995; Haiman & Loeb 2001; Oh & Haiman 2002; Haiman 2006) or perhaps also, for short periods, during the merger of mini-haloes just below the atomic limit (e.g., Regan 2023). At larger mass scales, large mass inflows may be realised during major mergers, which may trigger the formation of supermassive discs (Mayer et al. 2023, 2010; Zwick et al. 2023).

In order to achieve this, it may also be necessary to remove, or at least strongly suppress, the abundance of H2 in order to avoid excessive fragmentation, which should (if not limited) lower the initial mass function. If ≲100 M⊙ PopIII stars form first, they may quickly pollute the environment with metals, cutting off the pathway to more massive PopIII star formation. The suppression of H2 can be driven by nearby Lyman-Werner radiation sources (Omukai 2001; Shang et al. 2010; Latif et al. 2014a; Regan et al. 2017), which can readily dissociate H2, allowing larger Jeans masses, and may allow more massive PopIII stars to form. On the other hand, the rapid assembly of the underlying dark matter haloes (Yoshida et al. 2003; Fernandez et al. 2014; Latif et al. 2022) and baryonic streaming velocities (Tseliakhovich & Hirata 2010; Latif et al. 2014b; Schauer et al. 2015, 2017, 2021; Hirano et al. 2017) can promote massive PopIII star formation by creating conditions conducive to rapid mass inflows, which can drive massive PopIII star formation. A combinations of these processes is also possible (Wise et al. 2019; Kulkarni et al. 2021).

The suppression of ≲100 M⊙ PopIII star formation environments in favour of more massive PopIII star formation implies relatively very rare environments in the early Universe are required. However, we note that very massive PopIII stars in the early Universe have been suggested as a means to match the high luminosities observed in distant galaxies by JWST (Chon & Omukai 2020; Trinca et al. 2023; Harikane et al. 2023b,a). A number of recent numerical simulations focussed on the formation of massive objects in relatively modest Lyman-Werner radiation fields, finding that dynamical heating from major and minor mergers produces a small population of very massive (100 s–1000 s of M⊙) stars within a parent dark matter halo (e.g., Wise et al. 2019; Regan et al. 2020b). These more numerous very massive stars undergo episodic rapid accretion (≳10−2 M⊙ yr−1) upon encountering gas overdensities within their host halo, but are otherwise quiescent, suggesting they may only occasionally sustain an inflated photosphere (Regan et al. 2020b; Woods et al. 2021). However, the detailed evolution of very massive and supermassive stars undergoing variable rapid accretion over long timescales remains poorly understood.

A key missing ingredient in current modelling of massive PopIII star formation in cosmological settings are the transitions between inflated ‘red’ and more compact ‘blue’ phases. The exact time in the evolution of the star as well as the exact value of the accretion rate at which this occurs have been a matter of some debate in the community. The focus of this work is to understand the evolution of rapidly accreting massive PopIII stars with variable accretion rates drawn from the cosmological simulations of Regan et al. (2020b). Our understanding of this subject has implications for the stellar luminosity, stellar collision cross sections, radiative feedback, and the observable signatures of such objects. Additionally, such massive stars are expected to directly collapse into massive black holes, seeding a population of intermediate-mass black holes in early galaxies, which are possible progenitors to the recently discovered CEERS SMBH (Larson et al. 2023).

2. Method

2.1. The stellar accretion rates

The stellar accretion rates used in this research are taken from the radiation hydrodynamic simulations of Regan et al. (2020b). While a full discussion of these simulations is outside the scope of this article, we briefly describe the simulations and results here but direct the reader to the original paper for additional details.

The simulations undertaken by Regan et al. (2020b) were zoom-in simulations – using the Enzo code (Bryan et al. 2014; Brummel-Smith et al. 2019) – of atomic cooling haloes originally identified in Wise et al. (2019) and Regan et al. (2020a)1. The haloes remained both pristine (i.e., metal-free) and without previous episodes of PopIII star formation due to a combination of a mild Lyman-Werner flux and a rapid assembly history for the halo (Yoshida et al. 2003; Fernandez et al. 2014; Lupi et al. 2021). The zoom-in simulations allowed for a more in-depth and higher resolution modelling of the gravitational instabilities within the atomic cooling halo and a deeper probe of the subsequent star formation episodes, which were not possible in the original1, somewhat coarser resolution, simulations.

Using the higher resolution (zoom-in) simulations, Regan et al. (2020b) found that one of the haloes formed 101 stars during its initial burst of star formation. The total stellar mass at the end of the simulations (approximately 2 Myr after the formation of the first star) was approximately 90 000 M⊙. The masses of the individual stars ranged from approximately 50 M⊙ up to over 6000 M⊙. The maximum spatial resolution of the simulations was Δx ∼ 1000 au, allowing individual star formation sites to be resolved. Furthermore, accretion onto the stellar surface of each star was tracked and stored for the entirety of the simulation. It is these accretion rates that are used here as input to the stellar evolution modelling.

2.2. Using the stellar accretion rates as input

From the cosmological simulations described above, we select 10 accretion histories out of the 101 available. The choice of accretion histories was based on (i) their variability in accretion rates during the luminosity wave event and subsequent pre-MS stages, (ii) bursts in accretion rates during the hydrogen burning phases, and (iii) a final mass range spanning over an order of magnitude. The ten models, with variable accretion rates, are evolved from the pre-MS up until the end of core helium burning using the Geneva stellar evolution code (GENEC; Eggenberger et al. 2008). The models have a homogeneous chemical composition, with X = 0.7516 and Y = 0.2484, and a metallicity of Z = 0, similar to those used by Ekström et al. (2012) and Murphy et al. (2021). Deuterium, with a mass fraction of X2 = 5 × 10−5, is also included, as in Bernasconi & Maeder (1996, 2001); Haemmerlé et al. (2018). All models are computed with a FITM value of 0.999 (see Appendix C).

Accretion commences onto low-mass hydrostatic cores with a mass of Minit = 2 M⊙ for all ten models. These initial structures correspond to n ≈ 3/2 polytropes with flat entropy profiles, such that models begin their evolution as fully convective seeds. To model accretion, the infall of matter is assumed to occur through a geometrically thin cold disc, with the specific entropy of the accreted material being equivalent to that of the stellar surface (Haemmerlé et al. 2013, 2016). This assumption suggests that any excess entropy in the matter falling onto the star is emitted away before it reaches the stellar surface, in accordance with Palla & Stahler (1992), Hosokawa et al. (2010). To facilitate accretion rates varying as a function of time, in accordance with the hydrodynamic simulations, a new parameter that reads the accretion rates from external files was introduced into GENEC. Moreover, to facilitate numerical convergence amid accretion-rate fluctuations spanning six orders of magnitude, enhancements were made to both the spatial resolution and time discretization to accommodate this effect. Effects of rotation and mass loss are not included in this study.

3. Evolution of accreting massive PopIII stars

We investigated the evolution of accreting massive PopIII stars using the ten models with varying physical parameters (Table 1). The models are referred to by their final mass; for instance the 491 M⊙ star is referred to as model 491. Critical accretion rates during the pre-MS and core hydrogen burning phases significantly impact stellar development. Figure 1 illustrates the general trends as well as the effect that accretion rate has on whether a star will evolve to the red or blue supergiant phase. Figure 2 shows the accretion histories of the ten models computed in this work. The accretion history The critical accretion rate values determined here are explored in detail in the upcoming sections. We begin our evaluation of the critical accretion rate in the pre-MS.

thumbnail Fig. 1.

Illustration depicting the impact of the critical accretion rate (Ṁcrit) on the evolution of a star. The yellow object represents the protostellar seed and the wave pattern depicts the luminosity wave. The contraction towards blue is depicted with blue lines, whereas the expansion towards red is shown in red lines. The white and cloudy rings represent the accretion; this is denser in cases where the accretion rate is higher than Ṁcrit and fainter when the accretion rate drops below Ṁcrit. The black background depicts the pre-MS evolution and the grey background at the top marks the core hydrogen burning phase.

thumbnail Fig. 2.

Accretion rate history of the ten massive PopIII models used in this work. The data for each star are taken from Regan et al. (2020a). The initial accretion rate is similar for each model; however, as the dynamical interaction between the stars and surrounding gas becomes dominant, the stars begin to migrate outwards and away from matter-rich zones and consequently the accretion rate decreases.

Table 1.

Physical parameters of the ten models computed from the start of pre-MS until the end of core helium burning.

3.1. Pre-MS evolution

The evolution onto each star commences with hydrostatic seeds having a mass of 2 M⊙, radius of 26 R⊙, luminosity of log(L/L⊙) = 2.50, effective temperature of log (Teff) = 3.70, and an accretion rate of ≈ 7.5 × 10−2 M⊙ yr−1. In the left panel of Fig. 3, we first display the paths of each star on the Hertzsprung–Russell (HR) diagram and additionally indicate events of particular note with roman numerals I–V, while also paying attention to the variable accretion rates.

thumbnail Fig. 3.

Evolution of accreting PopIII models. Left panel: HR diagram depicting the evolution for ten models with varying accretion rates. The models are labelled according to their final mass. Grey dashed lines represent isoradii. Models 491, 771, 778, 932, 1135, 1331, 1662, and 1923 have near-identical pre-MS accretion histories, unlike models 4477 and 6127. All models except 4477 complete accretion before hydrogen burning starts at log (Teff) = 5.10. Computation stops after core helium burning, with all models in the red at log (Teff)≈3.76. Right panel: evolution of the accretion rate versus the luminosity for the 1662 (solid line) and 4477 (dashed line) models, colour-coded by the effective temperature. Quantities are displayed on a log scale, focusing on a zoomed-in region of the pre-MS. Both models share an identical accretion history until reaching a luminosity of log (L/L⊙) = 5.95. The 1662 model experiences a drop in the accretion rate below 2.5 × 10−2 M⊙ yr−1, while the 4477 model remains above this value.

I. Upon reaching log(L/L⊙) = 2.47 and log (Teff) = 3.77, all models experience the start of the luminosity wave. An increase in central temperature leads to a decrease in central opacity, transitioning the convective core to a radiative core. The lowered opacity boosts luminosity production, allowing the central luminosity to migrate outwards (see e.g., Larson 1972; Stahler et al. 1986; Hosokawa et al. 2010; Haemmerlé et al. 2018). The luminosity wave breaks at the surface, with models migrating to the blue region of the HR diagram (higher effective temperatures). The path length of the knee-like feature at log(L/L⊙) = 5.40 and log (Teff) = 4.35 in the HR diagram (‘I–III’ in Fig. 3) is directly proportional to the accretion rate during this event (for details, see also Fig. E.2. The migration of the luminosity wave is explored further in Appendix D).

II. The start of this event (‘II’) marks the end of the luminosity wave after it has travelled from the centre to the surface over a period of ≈190 yr. Following the brief period of the luminosity wave, almost all models follow near identical paths through the pre-MS. This is due to the accretion rate of all models exceeding 3.1 × 10−2 M⊙ yr−1. Previous works by Woods et al. (2017), Haemmerlé et al. (2018) indicate that an accretion rate greater than 1.0 × 10−3 M⊙ yr−1 after the appearance of the luminosity wave results in a transition to the red. To better explore this narrow critical accretion-rate regime, we performed numerical tests on models 1662 and 4477. A comparison between these two models is presented in the right-hand panel of Fig. 3. By exploring the contrast between these two models in particular, we find that an accretion rate of greater than 2.5 × 10−2 M⊙ yr−1 is needed to transition the models to the red and this value is hereafter referred to as the critical accretion rate during the pre-MS evolution (Ṁcrit,preMS). The accretion timescale during this event (‘II’) remains nearly constant and this is due to the accretion histories we obtain from the hydrodynamic simulations. However, the surface Kelvin–Helmholtz timescale (computed at a given Lagrangian coordinate) increases, preventing the models from adjusting their structures as new matter is deposited on the surface. This results in an increase in radius and all models transition to a radiative core with a large convective envelope, becoming red supergiant protostars (Hosokawa et al. 2012). This transition to red is extremely short and occurs over a span of 4 years, as marked by the ‘III’ in the left panel of Fig. 3. After experiencing the luminosity wave and migrating to red, all of the models follow a near monotonic relationship between luminosity and mass (see left panel of Fig. 4). This relationship of L ∝ M is seen in all accreting models of Hosokawa et al. (2013), Woods et al. (2017), Haemmerlé et al. (2018) and is similar to the mass–luminosity relation for massive stars on the zero-age main sequence (ZAMS; Ekström et al. 2012; Murphy et al. 2021).

thumbnail Fig. 4.

Variation of various physical parameters of accreting PopIII models. Left panel: luminosity–mass relation depicted for all models. The increase in luminosity at 20 M⊙ for all models corresponds to the luminosity wave breaking at the surface. Beyond this, luminosity evolves monotonically vs. mass as L ∝ M until the end of accretion history. Right panel: evolution of radius vs. age (in years) for all models. The colours used to represent models correspond to the label shown in the left panel.

IV. Following the models still in the left-hand panel of Fig. 3, we see that all models begin to diverge in their evolutionary path at log(L/L⊙) = 5.70 and log(Teff) = 3.70. All models except 4477 and 6127 experience a drop in accretion rate below Ṁcrit,preMS and begin their contraction towards the blue. For most models, this drop in the accretion rate only occurs for around 800 years before again increasing in excess of Ṁcrit,preMS, which forces the models to migrate back to red. Models 4477 and 6127 do not follow this particular path. Instead, since their accretion rates remain in excess of Ṁcrit,preMS, they follow the Hayashi line and remain in the red (see also Fig. 1).

V. All ten models converge on the HR diagram at log(L/L⊙) = 6.70 and log(Teff) = 3.73, evolving along the Hayashi line for approximately 20 000 yr. The radius of all models during this stage is between 4000 and 10 000 R⊙ and is clearly shown in the right panel of Fig. 4 as the initial strong spike in the stellar radius at the end of the pre-MS. The large radius and the lack of any nuclear reaction classify these objects as red supergiant protostars (see Hosokawa et al. 2013). Additionally, the radius of each model during this stage is proportional to the current mass, which is in turn determined by the net average accretion rate prior to this stage. All models then begin their subsequent contraction towards the blue and experience a reduction in radius to R < 60 R⊙ (see again the right panel of Fig. 4) until central conditions are optimal for core hydrogen burning. By this stage, each star is experiencing little or no accretion.

In conclusion, the luminosity wave plays a minor role in the pre-MS evolution of massive protostars. However, the critical accretion rate, 2.5 × 10−2 M⊙ yr−1, is crucial in shaping their behavior and structure. Models with accretion rates above this value form red supergiant protostars along the Hayashi limit, while those below contract and migrate blueward. This critical accretion rate is the determining factor in understanding the trajectory of massive protostars on the HR diagram during the pre-MS.

3.2. Core hydrogen burning evolution

Core hydrogen burning commences with all models at log(Teff)≈5.00 and a luminosity range between log(L/L⊙) 7.40 and 8.30 (see left panel of Fig. 3). Numerical tests indicate that for the same values of luminosity and effective temperature at ZAMS, the choice of accretion history does not impact the positions of the models (see Appendix A). We now examine three representative models: 491, 6127, and 4477.

Model 491 is the least massive and experiences no accretion during core hydrogen burning. Hydrogen ignites in the core through pp and 3 − α reactions as the temperature exceeds 1 × 108 K. The CNO cycle becomes the dominant energy source for the rest of this phase (Woods et al. 2017; Haemmerlé et al. 2018). The top left panel of Figs. 5 and 6 show the structure, with a convective core, radiative intermediate zone, and outer convective envelope of this least massive star (491 model). The convective core mass starts at 453 M⊙ and completes the main sequence in 1.82 Myr with a final core mass of 243 M⊙.

thumbnail Fig. 5.

Kippenhahn diagrams showing the evolution of the structure (in Eulerian coordinates) as a function of time (Myr) for the lowest-mass models. The blue and cream regions represent the convective and radiative zones, respectively. The iso-masses are depicted by black lines, whereas the isotherms of log(T[K]) = 5, 6, 7, and 8 are drawn in white lines. The translucent yellow regions show deuterium burning; dotted dark grey zones are hydrogen burning zones; and the dark grey zone highlights helium burning.

thumbnail Fig. 6.

Kippenhahn diagrams depicting the evolution of radius versus mass (both axes represented in log scale) for low-mass models. The details of the diagrams are similar to Fig. 5. In this version of the diagrams, the change in radius during the pre-MS evolution of all models is clearly visible. All models undergo the luminosity wave at log (M/M⊙) = 1.3 and experience a strong increase in radius. The next noteworthy evolutionary trend is at log (M/M⊙) = 1.95 when the models undergo a drop in accretion rate below Ṁcrit,preMS which results in a decrease in radius. Eventually the accretion rate increases above the Ṁcrit,preMS.

Model 6127 has the highest final mass and also stops accreting before H ignition in the core. It starts hydrogen burning in a convective core with an initial mass of 5741 M⊙ and completes the main sequence in 1.25 Myr with a final core mass of 3593 M⊙. When the effective temperature reaches log (Teff) = 4.00, the model still undergoes hydrogen burning with 0.26 Xc left in the core. Core hydrogen exhaustion occurs at the Hayashi limit, followed by structural expansion and the emergence of a convective envelope with intermediate convective zones (see bottom left panel of Figs. 7 and 8).

thumbnail Fig. 7.

Kippenhahn diagrams similar to Fig. 5 but for models with masses of 1331, 1662, 1923, 4477, and 6127 M⊙. The radii of these models is larger than that of the low-mass models. The models depicted here transition to the red and expand their radius before completion of the core hydrogen burning phase. Model 4477 M⊙ shows an exceptional behaviour as it undergoes an expansion in radius during hydrogen burning. This is due to a burst of accretion experienced by this model.

thumbnail Fig. 8.

Kippenhahn diagrams depicting the evolution of radius versus mass (both axes represented in log scale) for high mass models with mass 1331, 1662, 1923, 4477 and 6127 M⊙. The details of these diagrams are similar to Fig. 6.

The 4477 model stands out from the other nine models due to its unique accretion history extending into hydrogen burning, causing multiple blue–red transitions as shown in Fig. 9. It starts hydrogen burning without accretion at log(Teff) = 5.00 and log(L/L⊙) = 8.11. After just 4.0 kyr, it undergoes an accretion episode and climbs the HR diagram to a near-constant log(Teff) = 4.91 and log(L/L⊙) = 8.14. With an accretion rate exceeding 7.0 × 10−3 M⊙ yr−1, the model is unique and migrates towards the red, revealing a critical accretion rate that severely impacts the radius of the model during hydrogen burning. This migration occurs over a Kelvin–Helmholtz timescale (17.5 kyr) that is much shorter than that in all other models, moving at nuclear timescales without accretion. Once the model finishes the redward migration, at log(Teff) = 3.78 and log(L/L⊙) = 8.19, the accretion rate reduces to 5.0 × 10−3 M⊙ yr−1 after 8.5 kyr, starting its final blueward transition for 1.0 kyr. Arriving in the blue at log(L/L⊙) = 8.15 and log(Teff) = 4.94, it exhausts all accreting matter. It then begins its final redward excursion on a nuclear timescale, lasting 0.61 Myr, ending this phase at log(L/L⊙) = 8.21 and log(Teff) = 3.79. The central right panel of Fig. 7 and 8 shows particular trends in this phase, with a radius change at 0.45 Myr corresponding to a 25 kyr burst in accretion rate. See also the right-hand panel of Fig. 4, which shows the near delta-like spike in radius of model 4477 at T ∼ 0.45 Myr. A large outer convective zone appears before the end of core hydrogen burning. Similar to model 6127, core hydrogen burning finishes after this model has already reached the Hayashi line.

thumbnail Fig. 9.

Magnified HR diagram of model 4477 (only the upper part is shown) depicting the migration between blue and red as a result of the variable accretion rate. The colour code follows the central mass fraction of hydrogen. The black arrows represent the evolutionary path taken by the model; the arrows emerge from the bottom right, which marks the pre-MS stage, and end at the top right, which denotes the end of the core hydrogen burning stage.

In summary, we find a critical accretion rate of 7.0 × 10−3 M⊙ yr−1 during the core hydrogen burning phase, as shown in model 4477. This critical accretion rate impacts the radius of the model during hydrogen burning and is responsible for the unique blue–red transitions observed. It is important to note that this critical accretion rate is lower than the critical accretion rate observed during the pre-MS evolution.

3.3. Helium burning

All models follow near identical evolutionary trends during the core helium burning phase, denoted by the grey regions in Figs. 5 and 7. By this time, accretion has completely ceased for all models and the evolution commences and ends in close proximity to the Hayashi line. To further highlight details of this stage, we explore the least massive (model 491) and most massive (model 6127) models below.

The core of model 491 undergoes a contraction until the central temperature reaches 2.80 × 108 K. Helium is ignited in the convective core of mass 242 M⊙. The external layers of the model transition from fully radiative into mostly convective zones; 85% of the model is now convective. Core helium burning lasts 0.23 Myr and the final mass of the helium core at the end of the evolution is 114 M⊙. Model 6127 undergoes a core helium burning phase that is nearly identical to the other models, with one notable difference in its structure; it transitions into a near fully convective structure already at the end of core hydrogen burning. A consequence of the near fully convective structure of all models during helium burning is the ability of the models to transport helium from the core to the surface, even with the absence of any rotational mixing. The duration of core helium burning is 0.15 Myr and the final mass of the helium core is 1262 M⊙. Model 491 has a surface helium abundance of Ysurf = 0.40, whereas model 6127 has an extremely enriched surface, with Ysurf = 0.76, suggesting that its value increases as a function of mass. Additionally, the core mass at the end of this evolutionary phase, as seen in the last column of Table 1, is approximately one-quarter or one-sixth of the total mass. Assuming the final fate of such objects is to form a black hole, the resulting mass would be constrained by two limits. The upper limit corresponds to the scenario where the total mass at the end of the evolution is consumed by the black hole. In this case, the mass of the black hole would be equivalent to the final mass of the star. Alternatively, the lower limit arises when a portion of the outer envelope situated above the helium core is lost, either due to stellar winds or instabilities occurring prior to the final collapse. Under this circumstance, the mass of the black hole would be equivalent to the mass of the helium core.

4. Discussion

4.1. Determining the critical accretion rate

Determining the critical accretion rate that leads to the realisation of the canonical SMS has been the goal of a number of studies over the last two decades. Seminal work by Omukai & Palla (2001, 2003) explored the critical accretion limit in the case of the spherical accretion of matter and found a value of ≈ 4 × 10−3 M⊙ yr−1. Building on this, Schleicher et al. (2013) explored the relationship between the Kelvin–Helmholtz timescale and the accretion timescale, and using this approach determined a mathematical expression for the critical accretion rate. These authors concluded that in the case of spherical accretion, the minimum accretion rate needed to evolve a star along the Hayashi line is the somewhat higher value of 1 × 10−1 M⊙ yr−1. By exploring the more realistic case of accretion via a geometrically thin disc, Hosokawa et al. (2012) found that the critical limit is decreased by an order of magnitude to approximately 1 × 10−2 M⊙ yr−1.

Hosokawa et al. (2013) used the STELLAR code (Yorke & Bodenheimer 2008) to compute models and predicted the critical accretion rate for the cold disc accretion scenario. These authors found that with a choice of three constant accretion rates of 0.01, 0.1, and 1 M⊙ yr−1, the lowest accretion rate required for a star to remain in the red phase is approximately 1 × 10−1 M⊙ yr−1. These results were dependent on the amount of gravitational energy deposited in the centre, which influences the early pre-MS evolution when the Kelvin–Helmholtz timescale is longer than the accretion timescale. The ratio between these two timescales was found to be an important metric when considering the migration towards blue or red. The choice of constant accretion rates was a limiting factor in these studies and was addressed shortly afterwards by Vorobyov et al. (2013), when they performed 2D hydrodynamic simulations to account for a variable accretion rate. Their models underwent a burst (Ṁ = 10−2 − 10−1 M⊙ yr−1) in accretion followed by quiescent phases (Ṁ = 10−5 − 10−4 M⊙ yr−1) due to the migration of fragmented clumps of matter onto the star. Their models hinted at the strong impact of a varying accretion rate on the early evolution of accreting stars. Considering the impact of such accretion histories on the evolution of primordial stars, Sakurai et al. (2015) computed models with variable accretion rate and determined the critical accretion rate needed to produce a red or a blue star to be approximately 4 × 10−2 M⊙ yr−1.

Additionally, these authors found that, as the mass distribution of such objects is mainly concentrated towards the centre, the global Kelvin–Helmholtz timescale provides a poor estimate of the overall thermal timescale. Instead, to determine whether a star would transition into a red or a blue supergiant, Sakurai et al. (2015) noted that it is important to look at the surface Kelvin–Helmholtz timescale of the individual layers.

Using GENEC, Haemmerlé et al. (2018) computed SMS models with constant accretion rates ranging from 10−3 − 101 M⊙ yr−1 and found that the 10−2 M⊙ yr−1 model exhibits an oscillatory behaviour in the HR diagram and eventually settles towards the Hayashi limit with a mass exceeding 600 M⊙. This led the authors to deduce a critical accretion rate of approximately 1 × 10−2 M⊙ yr−1.

Our investigations here go beyond all previous works. By using variable accretion rates drawn from self-consistent cosmological simulations, we are able to vary the accretion rates starting from the advent of the luminosity wave until the end of the pre-MS to obtain a more precise value of the critical accretion rate. Additionally, we perform numerical tests throughout the pre-MS evolution to precisely quantify this value by varying the accretion rate by hand. We determine a value of Ṁ = 2.5 × 10−2 M⊙ yr−1 for the pre-MS, which decreases to Ṁ = 7 × 10−3 M⊙ yr−1 for the Hydrogen burning phase of the stellar evolution. Our Ṁcrit,preMS of 2.5 × 10−2 M⊙ yr−1 is similar to the works of Omukai & Palla (2001, 2003), Sakurai et al. (2015), Haemmerlé et al. (2018). Furthermore, using model 4477, we find the existence of an additional accretion rate, Ṁcrit, during the core hydrogen burning phase, which has not been explored previously in the literature. For the hydrogen burning phase, we find a value of Ṁcrit = 7 × 10−3 M⊙ yr−1.

4.2. Numerical tests to determine Ṁcrit,preMS and Ṁcrit,MS

To precisely determine the critical accretion rate (Ṁcrit,preMS) found in this study, we performed numerical tests on model 932 throughout its pre-MS evolution. This test involved choosing constant accretion rates from 1.0 × 10−3 − 3.1 × 10−2 M⊙ yr−1, and recomputing the evolution of the model from event ‘I’ shown in the left panel of Fig. 3. The choice of lower limit for the accretion rate was motivated by the results of Woods et al. (2017), Haemmerlé et al. (2018) and the upper limit was taken from our hydrodynamic simulations, which is above the Ṁcrit,preMS because this model migrates to red. At accretion rates of 1.0 − 5.0 × 10−3 M⊙ yr−1, the model contracts towards the blue, indicating the accretion timescale is longer than the surface Kelvin–Helmholtz timescale. Moving to a slightly higher accretion rate of 1.0 × 10−2 M⊙ yr−1, the model follows an oscillating behaviour and migrates between the blue and red parts of the HR diagram until it accretes a total of 300 M⊙ over 25 kyr and finally settles in the red. Increasing the accretion rate to 2.0 × 10−2 M⊙ yr−1 leads to a similar oscillating behaviour but the model settles to the red in a shorter time of 12 kyr, with a final mass of 152 M⊙. Finally, the accretion was varied from 2.0 × 10−2 − 3.1 × 10−2 M⊙ yr−1 and we find that at 2.5 × 10−2 M⊙ yr−1, the model directly migrates to red with a mass of 19 M⊙ over 10 years, indicating this value as the Ṁcrit,preMS.

A similar numerical test was performed for the same model at event ‘IV’ (later in the pre-MS), which we show in the left panel of Fig. 3. The model migrates temporarily to blue due to a drop in accretion rate. We find that as the accretion rate drops below the previous critical value of 2.5 × 10−2 M⊙ yr−1, the model migrates to blue over the surface Kelvin–Helmholtz timescale. Based on these tests, we conclude that critical accretion rate during the pre-MS phase is 2.5 × 10−2 M⊙ yr−1.

We also performed similar numerical tests on model 4477 during the core hydrogen burning phase to obtain a better estimate of Ṁcrit,MS. The choice of constant accretion rates this time ranged from 1.0 × 10−6 to 2.5 × 10−2 M⊙ yr−1. We find that accretion rates below 1.0 × 10−3 M⊙ yr−1 have no effect on the position in the HR diagram as the model continues to burn hydrogen in the blue. As the accretion rate approaches 4.0 × 10−3 M⊙ yr−1, the model shows an oscillating behaviour in the effective temperature from Teff = 4.50 to 4.75. Once this rate is set to 7.0 × 10−3 M⊙ yr−1, the model migrates to red over a Kelvin–Helmholtz timescale and stays on the Hayshi limit until this critical rate (Ṁcrit,MS = 7.0 × 10−3 M⊙ yr−1) is maintained. We therefore conclude that the critical accretion rate for the core hydrogen burning phase at a mass of 3984 M⊙ and at a given central hydrogen abundance (0.55 in this case) is Ṁcrit,MS = 7.0 × 10−3 M⊙ yr−1. Basing our understanding of thermal timescale during this stage, we suspect this accretion rate to be dependent on the mass as well as the central mass fraction of hydrogen. However, to provide quantitative answers to this question would require future study, which is outside the scope of this work.

4.3. Luminosity wave and Ṁcrit

The existence of a luminosity wave and its relation to the expansion of protostars was first explored by Larson (1972). Using a 2 M⊙ star, the author highlighted the importance of radiative transfer of entropy in a star once the temperature reaches 9.0 × 106 K. This time in our study corresponds to the early pre-MS phase. The star begins to transport this radiative entropy from the central regions to the outer boundary of the core over the thermal relaxation timescale. As this wave propagates further, the star undergoes a brief expansion of radius due to the wave reaching the surface. The choice of the initial structure of a protostellar seed, that is, whether assumed to be convective or radiative, affects the migration of the luminosity wave from the centre to the surface and furthermore has an impact on the radius as shown by Stahler et al. (1986). These authors explored the extremely short duration of this migration (230 yr) and concluded that such a phenomenon would be difficult to observe. Our results agree with the findings of Stahler et al. (1986) and we find the duration of this migration to be 190 yr. The migration of the luminosity wave was subsequently studied in detail by Hosokawa et al. (2010) in relation to accreting stars. Their choice of accretion rate was 3 × 10−3 M⊙ yr−1 and they concluded that once the luminosity wave is expelled from the surface, the star contracts towards the ZAMS. Further investigations (Hosokawa et al. 2013; Woods et al. 2017; Haemmerlé et al. 2018) expanded on the range of accretion rates, finding that a critical accretion rate exists at the time when the luminosity wave breaks at the surface, which forces the star to transition to either the blue or the red. Our study confirms that the luminosity wave occurs at the very early pre-MS phase of evolution. Secondly, all models, whether accreting or not, undergo an increase in radius when the luminosity wave breaks at the surface. Thirdly, the red or blue evolution is only weakly dependent on the luminosity wave and is instead primarily affected by the accretion rate itself. Crucially, and as discussed above, there exists a critical accretion rate during the pre-MS of Ṁcrit,preMS = 2.5 × 10−2 M⊙ yr−1, above which the models will migrate towards red regardless of other physical processes in operation.

4.4. Variable accretion rates and model comparisons

Departure from a constant accretion rate is expected to occur once the accretion disc around a PopIII star becomes gravitationally unstable and fragments, as shown by Stacy et al. (2010). The migration of such fragments onto the disc and subsequently onto the star could result in a burst of accretion and could give rise to a variable accretion history; see Greif et al. (2012). The evolution of PopIII stars until the end of core silicon burning was modelled by Ohkubo et al. (2009), who employed variable accretion rates from Yoshida et al. (2006, 2007). These models evolved into a blue supergiant phase and concluded their helium burning stage at log(Teff) > 4.6. However, our results differ as our models transition to a red phase with log(Teff)≈3.76 at the start of helium burning and remain there until the end of their evolution. The difference is possibly due to the treatment of energy transport in the outer layers.

The evolution of many of our models with variable accretion rates is similar to that of the models by Woods et al. (2017) and Haemmerlé et al. (2018) with accretion rates above 10−2 M⊙ yr−1, in which the models behave as red supergiant protostars. Despite varying accretion rates, Sakurai et al. (2016) found that the growth of the stellar radius that occurs in the early pre-MS phase (time < 1000 years) is similar to models with constant accretion rate. This result is confirmed in our models, as depicted in the right panel of Fig. 4, and is consistent with the findings of Sakurai et al. (2016).

4.5. Impact of accretion on physical parameters

The accretion history and the episodic burst of accretion have a significant impact on the physical parameters of the models, as shown in Table 1. Although the pre-MS lifetime of all models is nearly identical for all models and follows an inverse relation to the mass, small discrepancies arise due to variation of the accretion rate during this stage, as seen in model 1923. Similarly, the total lifetime of the model is also affected, as evident in models 1135 and 1923. This is due to the models accreting a large proportion of their final mass towards the end of their accretion history, which is longer than in other models. The time spent in the red for each model increases with mass and is due to the higher net average accretion rate during the evolution. However, if the accretion rate history is erratic and above Ṁcrit,preMS, the star may spend a significant fraction of its lifetime in the red. In the case of model 1662, the star spends 59% of its total lifetime in the red. Finally, due to the existence of intermediate convective zones that form early in the evolution of the model and its extended time in the red phase, the surface helium enrichment in this latter model is remarkably high (0.76).

4.6. Kelvin–Helmholtz timescale versus accretion timescale

The correct timescale responsible for dictating the evolutionary tracks of accreting massive stars has been explored by Stahler et al. (1986), Omukai & Palla (2003), Hosokawa & Omukai (2009). These authors describe the Kelvin–Helmholtz timescale as the thermal relaxation timescale over which a star may radiate its gravitational energy (τKH = GM2/RL) and the accretion timescale as the characteristic timescale for stellar growth (τaccr = M/Ṁ). The migration between blue and red follows the interplay between the two timescales; if τaccr < τKH, the models expand and migrate to the red but if τaccr > ;τKH, they instead undergo contraction and move to the blue. However, during the pre-MS evolution, we find that some of our models (e.g., model 4477 in the right panel of Fig. 3) continue to expand and move into the red despite τaccr > ;τKH. There is clearly a problem here.

This effect was first explored by Sakurai et al. (2015), who showed that τKH = GM2/RL is too simplistic a timescale to consider. Sakurai et al. (2015) instead invoked the Kelvin–Helmholtz timescale at the surface layer of the star. If matter is accreted sufficiently quickly onto the surface layers then the surface of the star cannot thermally relax and the star moves to the red; in this case it is correct to consider the timescale for that portion of the star. Sakurai et al. (2015) found that although the star may globally expand due to the offloading of matter at the surface, the interior layers of the star continue to contract during this phase. The two parts of the star therefore become somewhat disconnected and therefore using the global Kelvin–Helmholtz timescale – as defined above – is incorrect.

The Kelvin–Helmholtz timescale of the outer surface layer – which takes into account the actual distribution of mass near the stellar surface – is the more appropriate metric. Sakurai et al. (2015) define this quantity as 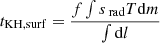, where srad is the entropy of radiation, T is the temperature, m is the mass of the mass of the enclosed region, l is the luminosity of the enclosed region, and f is the fraction of total entropy that is carried away over the timescale. Sakurai et al. (2015) applied this formula over the outer 30% of the star (i.e., from 0.7 M* ≤ m ≤ M*; we refer to this region as the envelope). We also apply this expression to our model and confirm that, in cases where the models expand towards the red, the surface layer Kelvin–Helmholtz timescale is indeed longer than the accretion timescale, i.e., τaccr < τKH, surf. The more simplistic treatment results in τaccr > ;τKH and is misleading.

Additionally, applying the expression of the surface Kelvin–Helmholtz timescale to models at the time of their transitions from red to blue (e.g., model 1662 at log(L/L⊙) = 6.30 in the right panel of Fig. 3), we confirm the value of the critical accretion rate during the pre-MS (Ṁcrit,preMS), which we derive using numerical tests, to be 2.5 × 10−2 M⊙ yr−1 (see Appendix E). At this junction, τaccr ≡ τKH, surf and the critical accretion rate can be written as Ṁcrit,preMS = Menvelope/τKH,surf.

During the pre-MS, the inner regions of the star are undergoing gravitational contraction while the envelope is expanding. As tKH, surf provides a more precise estimate of the timescale at a given Lagrangian coordinate, it is important to use this timescale to determine a red or blue transition during the pre-MS evolution. However, if accretion of matter above Ṁcrit,MS were to occur during the core hydrogen burning stage, as is the case in model 4477, the interior regions of the star contract over a much longer nuclear timescale. Therefore, using the global Kelvin–Helmholtz is sufficient to predict the transition.

5. Conclusion

In this study, we investigated the evolution of massive PopIII stars under the influence of variable accretion rates. We used the GENEC stellar evolution code to model the early stages of stellar evolution and performed a detailed analysis of the critical accretion rate, the impact of the luminosity wave, and the effect of accretion on the physical parameters of the stars. The major findings of this study can be summarised as follows:

  • We determine a critical accretion rate (Ṁcrit,preMS) of 2.5 × 10−2 M⊙, yr−1 for the transition of massive PopIII stars to the red phase under disc accretion conditions during the pre-MS phase. This value is consistent with previous studies and provides a robust benchmark for future work.

  • We discover the existence of a critical accretion rate during hydrogen burning of 7.0 × 10−3 M⊙ yr−1.

  • The timescale over which model 4477 transitions from blue to red during the core hydrogen burning phase is 17.5 kyr. This timescale depends on Ṁcrit,MS and is comparable to the global Kelvin–Helmholtz timescale (τKH ≈ GM2/RL) of the star at the time of transition.

  • We confirm the importance of the surface Kelvin–Helmholtz timescale in determining the transition of a star to the red or blue supergiant during the pre-MS phase, as opposed to the global Kelvin–Helmholtz timescale.

  • The luminosity wave has been shown to only weakly impact the early pre-MS phase of stellar evolution, with the red or blue evolution being more strongly influenced by the accretion rate.

  • Our models demonstrate that variable accretion rates have a significant impact on the physical parameters of PopIII stars, including the total lifetime, time spent in the red phase, and surface helium enrichment

In conclusion, our work contributes to the current understanding of early evolution and the complex processes governing the lives of primordial stars. The results of this study provide a solid foundation for further investigation and refinement of the processes driving the evolution of massive PopIII stars. Given that a robust determination of the critical accretion rate is hugely important for subgrid models in cosmological simulations, we propose that a value of Ṁ = 7 × 10−3 M⊙ yr−1 be used in almost all instances. Where the subgrid modelling can also capture the pre-MS timescale (which will be approximately 10 kyr in duration), the critical accretion rate for this stage should be increased to Ṁ = 2.5 × 10−2 M⊙ yr−1.

Future work in this area could include expansion of the range of accretion rates and exploration of different accretion rate profiles to better understand the various factors that contribute to the observed trends. Additionally, incorporating more sophisticated models of radiative transfer, stellar winds, and mixing processes could lead to a more accurate representation of the complex processes occurring in these early stars. Ultimately, these advancements will contribute to an increasingly comprehensive understanding of the early Universe and the role of primordial stars in shaping the cosmos.

1

The base origin of these simulations is the Renaissance simulation suite (Chen et al. 2014; O’Shea et al. 2015; Xu et al. 2016).

Acknowledgments

D.N., S.E. and G.M. have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 833925, project STAREX). J.R. acknowledges support from the Royal Society and Science Foundation Ireland under grant number URF/R1/191132. J.R. also acknowledges support from the Irish Research Council Laureate programme under grant number IRCLA/2022/1165. E.F. acknowledges support from SNF grant number 200020_212124. T.E.W. acknowledges support from the NRC-Canada Plaskett Fellowship. The authors would like to thank the referee for the constructive feedback and comments during the review process.

References

  1. Alvarez, M. A., Wise, J. H., & Abel, T. 2009, ApJ, 701, L133 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018, Nature, 553, 473 [Google Scholar]
  3. Beckmann, R. S., Dubois, Y., Volonteri, M., et al. 2023, MNRAS, 523, 5610 [NASA ADS] [CrossRef] [Google Scholar]
  4. Behrend, R., & Maeder, A. 2001, A&A, 373, 190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bellovary, J. M., Governato, F., Quinn, T. R., et al. 2010, ApJ, 721, L148 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bernasconi, P. A., & Maeder, A. 1996, A&A, 307, 829 [NASA ADS] [Google Scholar]
  7. Brummel-Smith, C., Bryan, G., Butsky, I., et al. 2019, J. Open Source Softw., 4, 1636 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bryan, G. L., Norman, M. L., O’Shea, B. W., et al. 2014, ApJS, 211, 19 [Google Scholar]
  9. Chandrasekhar, S. 1964, ApJ, 140, 417 [Google Scholar]
  10. Chen, P., Wise, J. H., Norman, M. L., Xu, H., & O’Shea, B. W. 2014, ApJ, 795, 144 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chon, S., & Omukai, K. 2020, MNRAS, 494, 2851 [Google Scholar]
  12. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [Google Scholar]
  13. Eisenstein, D. J., & Loeb, A. 1995, ApJ, 443, 11 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
  15. Fernandez, R., Bryan, G. L., Haiman, Z., & Li, M. 2014, MNRAS, 439, 3798 [CrossRef] [Google Scholar]
  16. Greif, T. H., Bromm, V., Clark, P. C., et al. 2012, MNRAS, 424, 399 [NASA ADS] [CrossRef] [Google Scholar]
  17. Haemmerlé, L., Eggenberger, P., Meynet, G., Maeder, A., & Charbonnel, C. 2013, A&A, 557, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Haemmerlé, L., Eggenberger, P., Meynet, G., Maeder, A., & Charbonnel, C. 2016, A&A, 585, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Haemmerlé, L., Woods, T. E., Klessen, R. S., Heger, A., & Whalen, D. J. 2018, MNRAS, 474, 2757 [Google Scholar]
  20. Haiman, Z. 2006, New Astron. Rev., 50, 672 [CrossRef] [Google Scholar]
  21. Haiman, Z., & Loeb, A. 2001, ApJ, 552, 459 [NASA ADS] [CrossRef] [Google Scholar]
  22. Harikane, Y., Nakajima, K., Ouchi, M., et al. 2023a, ApJ, submitted [arXiv:2304.06658] [Google Scholar]
  23. Harikane, Y., Zhang, Y., Nakajima, K., et al. 2023b, ArXiv e-prints [arXiv:2303.11946] [Google Scholar]
  24. Hirano, S., Hosokawa, T., Yoshida, N., & Kuiper, R. 2017, Science, 357, 1375 [CrossRef] [Google Scholar]
  25. Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [Google Scholar]
  26. Hosokawa, T., Yorke, H. W., & Omukai, K. 2010, ApJ, 721, 478 [Google Scholar]
  27. Hosokawa, T., Omukai, K., & Yorke, H. W. 2012, ApJ, 756, 93 [Google Scholar]
  28. Hosokawa, T., Yorke, H. W., Inayoshi, K., Omukai, K., & Yoshida, N. 2013, ApJ, 778, 178 [Google Scholar]
  29. Jeon, M., Pawlik, A. H., Greif, T. H., et al. 2012, ApJ, 754, 34 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kulkarni, M., Visbal, E., & Bryan, G. L. 2021, ApJ, 917, 40 [NASA ADS] [CrossRef] [Google Scholar]
  31. Larson, R. B. 1972, MNRAS, 157, 121 [NASA ADS] [Google Scholar]
  32. Larson, R. L., Finkelstein, S. L., Kocevski, D. D., et al. 2023, ApJ, 953, L29 [NASA ADS] [CrossRef] [Google Scholar]
  33. Latif, M. A., Niemeyer, J. C., & Schleicher, D. R. G. 2014a, MNRAS, 440, 2969 [NASA ADS] [CrossRef] [Google Scholar]
  34. Latif, M. A., Schleicher, D. R. G., Bovino, S., Grassi, T., & Spaans, M. 2014b, ApJ, 792, 78 [NASA ADS] [CrossRef] [Google Scholar]
  35. Latif, M. A., Whalen, D. J., Khochfar, S., Herrington, N. P., & Woods, T. E. 2022, Nature, 607, 48 [CrossRef] [Google Scholar]
  36. Lupi, A., Haiman, Z., & Volonteri, M. 2021, MNRAS, 503, 5046 [NASA ADS] [CrossRef] [Google Scholar]
  37. Mayer, L., Kazantzidis, S., Escala, A., & Callegari, S. 2010, Nature, 466, 1082 [Google Scholar]
  38. Mayer, L., Capelo, P. R., Zwick, L., & Di Matteo, T. 2023, ApJ, submitted [arXiv:2304.02066] [Google Scholar]
  39. Milosavljević, M., Couch, S. M., & Bromm, V. 2009, ApJ, 696, L146 [CrossRef] [Google Scholar]
  40. Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [Google Scholar]
  41. Murphy, L. J., Groh, J. H., Farrell, E., et al. 2021, MNRAS, 506, 5731 [NASA ADS] [CrossRef] [Google Scholar]
  42. Oh, S. P., & Haiman, Z. 2002, ApJ, 569, 558 [NASA ADS] [CrossRef] [Google Scholar]
  43. Ohkubo, T., Nomoto, K., Umeda, H., Yoshida, N., & Tsuruta, S. 2009, ApJ, 706, 1184 [NASA ADS] [CrossRef] [Google Scholar]
  44. Omukai, K. 2001, ApJ, 546, 635 [NASA ADS] [CrossRef] [Google Scholar]
  45. Omukai, K., & Palla, F. 2001, ApJ, 561, L55 [NASA ADS] [CrossRef] [Google Scholar]
  46. Omukai, K., & Palla, F. 2003, ApJ, 589, 677 [NASA ADS] [CrossRef] [Google Scholar]
  47. Omukai, K., Schneider, R., & Haiman, Z. 2008, ApJ, 686, 801 [Google Scholar]
  48. O’Shea, B. W., Wise, J. H., Xu, H., & Norman, M. L. 2015, ApJ, 807, L12 [CrossRef] [Google Scholar]
  49. Palla, F., & Stahler, S. W. 1992, ApJ, 392, 667 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pfister, H., Volonteri, M., Dubois, Y., Dotti, M., & Colpi, M. 2019, MNRAS, 486, 101 [Google Scholar]
  51. Regan, J. 2023, Open J. Astrophys., 6, 12 [NASA ADS] [CrossRef] [Google Scholar]
  52. Regan, J. A., Visbal, E., Wise, J. H., et al. 2017, Nat. Astron., 1, 0075 [Google Scholar]
  53. Regan, J. A., Wise, J. H., O’Shea, B. W., & Norman, M. L. 2020a, MNRAS, 492, 3021 [NASA ADS] [CrossRef] [Google Scholar]
  54. Regan, J. A., Wise, J. H., Woods, T. E., et al. 2020b, Open J. Astrophys., 3, 15 [NASA ADS] [Google Scholar]
  55. Sakurai, Y., Hosokawa, T., Yoshida, N., & Yorke, H. W. 2015, MNRAS, 452, 755 [Google Scholar]
  56. Sakurai, Y., Vorobyov, E. I., Hosokawa, T., et al. 2016, MNRAS, 459, 1137 [NASA ADS] [CrossRef] [Google Scholar]
  57. Schauer, A. T. P., Whalen, D. J., Glover, S. C. O., & Klessen, R. S. 2015, MNRAS, 454, 2441 [NASA ADS] [CrossRef] [Google Scholar]
  58. Schauer, A. T. P., Regan, J., Glover, S. C. O., & Klessen, R. S. 2017, MNRAS, 471, 4878 [NASA ADS] [CrossRef] [Google Scholar]
  59. Schauer, A. T. P., Glover, S. C. O., Klessen, R. S., & Clark, P. 2021, MNRAS, 507, 1775 [NASA ADS] [CrossRef] [Google Scholar]
  60. Schleicher, D. R. G., Palla, F., Ferrara, A., Galli, D., & Latif, M. 2013, A&A, 558, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  62. Smith, B. D., Regan, J. A., Downes, T. P., et al. 2018, MNRAS, 480, 3762 [NASA ADS] [CrossRef] [Google Scholar]
  63. Stacy, A., Greif, T. H., & Bromm, V. 2010, MNRAS, 403, 45 [NASA ADS] [CrossRef] [Google Scholar]
  64. Stahler, S. W., Palla, F., & Salpeter, E. E. 1986, ApJ, 302, 590 [NASA ADS] [CrossRef] [Google Scholar]
  65. Tanaka, T., & Haiman, Z. 2009, ApJ, 696, 1798 [NASA ADS] [CrossRef] [Google Scholar]
  66. Tremmel, M., Governato, F., Volonteri, M., Pontzen, A., & Quinn, T. R. 2018, ApJ, 857, L22 [Google Scholar]
  67. Trinca, A., Schneider, R., Valiante, R., et al. 2023, MNRAS, submitted [arXiv:2305.04944] [Google Scholar]
  68. Tseliakhovich, D., & Hirata, C. 2010, Phys. Rev. D, 82 [Google Scholar]
  69. Vorobyov, E. I., DeSouza, A. L., & Basu, S. 2013, ApJ, 768, 131 [NASA ADS] [CrossRef] [Google Scholar]
  70. Wang, F., Yang, J., Fan, X., et al. 2021, ApJ, 907, L1 [Google Scholar]
  71. Willott, C. J., Delorme, P., Reylé, C., et al. 2010, AJ, 139, 906 [Google Scholar]
  72. Wise, J. H., Regan, J. A., O’Shea, B. W., et al. 2019, Nature, 566, 85 [NASA ADS] [CrossRef] [Google Scholar]
  73. Woods, T. E., Heger, A., Whalen, D. J., Haemmerlé, L., & Klessen, R. S. 2017, ApJ, 842, L6 [Google Scholar]
  74. Woods, T. E., Willott, C. J., Regan, J. A., et al. 2021, ApJ, 920, L22 [NASA ADS] [CrossRef] [Google Scholar]
  75. Xu, H., Norman, M. L., O’Shea, B. W., & Wise, J. H. 2016, ApJ, 823, 140 [NASA ADS] [CrossRef] [Google Scholar]
  76. Yorke, H. W., & Bodenheimer, P. 2008, ASP Conf. Ser., 387, 189 [Google Scholar]
  77. Yoshida, N., Abel, T., Hernquist, L., & Sugiyama, N. 2003, ApJ, 592, 645 [CrossRef] [Google Scholar]
  78. Yoshida, N., Omukai, K., Hernquist, L., & Abel, T. 2006, ApJ, 652, 6 [NASA ADS] [CrossRef] [Google Scholar]
  79. Yoshida, N., Omukai, K., & Hernquist, L. 2007, ApJ, 667, L117 [NASA ADS] [CrossRef] [Google Scholar]
  80. Zwick, L., Mayer, L., Haemmerlé, L., & Klessen, R. S. 2023, MNRAS, 518, 2076 [Google Scholar]

Appendix A: Impact of accretion history on core hydrogen burning

The left panel of Fig. E.1 depicts the evolutionary track of two 491 models starting at ZAMS (log(L/L⊙) = 7.10 and log(Teff) = 5.08). The second y-axis on the plot represents the central mass fraction of hydrogen. The model with a near straight migration to ZAMS is computed using polytropic criteria with no accretion history, whereas the other model represents the model 491 computed using the accretion history from hydrodynamic simulations. Despite a slight difference in luminosity, which is likely due to the accreting model undergoing a pre-MS evolution where deuterium burning has a minimal impact on luminosity, the tracks are burning hydrogen in the same place on the HR diagram. This is also observed for model 932 as shown in the right panel of Fig. E.1. This shows that the accretion history has near negligible impact on the core hydrogen burning of a star.

Appendix B: Accretion rates and the first 200 years of pre-MS evolution

The left panel of Fig. E.2 depicts a numerical test that explores the impact of changing accretion rates on the path length of the knee-like feature observed in all accreting tracks shown in the left panel of Fig. 3. In this numerical test, the accretion rate at the start of computation is 1 × 10−3 M⊙ yr−1 and is increased by a factor of five every 10 years for the next 110 years. The model shows a near identical evolution in the early pre-MS phase of evolution to that of models 491 and 6127, implying that changing accretion rate during this pre-luminosity wave phase minimally affects the path length of the knee-like feature.

Appendix C: Impact of the choice of FITM on pre-MS evolution

In GENEC, FITM is defined as the mass coordinate inside a stellar model that separates the interior and the envelope and is expressed as a fraction of the actual mass. Envelope is defined as the region where the luminosity is assumed to be constant, convection proceeds non-adiabatically and partial ionisation is allowed. For instance, setting FITM at 0.999 implies the transition from interior to the envelope occurs at 0.999 of the total mass. The choice of FITM is shown to be important when exploring the accretion rates of approximately 1 × 10−2 M⊙ yr−1 as shown by the works of Haemmerlé et al. (2018). Given that all ten models computed in this study have initial accretion rates in the range of 7 × 10−2 M⊙ yr−1, the choice of FITM becomes important as depicted in the right panel of Fig. E.2. The plot depicts an accretion rate of 1 × 10−2 M⊙ yr−1 computed with 0.990 and 0.999. We decided to chose a FITM of 0.999 in accordance with the results of Woods et al. (2017), Haemmerlé et al. (2018).

Appendix D: The breaking of the luminosity wave

Figure 4 depicts the migration of the luminosity wave inside the 932 model during the early pre-MS. This wave originates immediately after the initial contraction and is present in all models during the pre-MS phase. The increase in central temperature reduces central opacity, transitioning the convective core to a radiative core at 12.20 M⊙. The lowered opacity boosts luminosity production, allowing central luminosity to migrate outwards. At 18.50 M⊙, the luminosity approaches the outer layers, as illustrated by the purple line in Fig. 9. This migration, known as the luminosity wave, was described by Larson (1972), Hosokawa et al. (2010), Haemmerlé et al. (2018). The wave breaks at the surface when the mass reaches 19.80 M⊙, with a luminosity of log(L/L⊙) = 5.23 and an effective temperature of log (Teff) = 4.33. All models migrate to the blue region of the HR diagram (log (Teff) > 4.00) 180 years into their pre-MS evolution. The breaking of the luminosity wave has a weak impact on the evolution; it is instead the accretion rate of the model during and after this event that determines the migration to red or blue.

Appendix E: Determining the Ṁcrit,preMS using the surface Kelvin–Helmholtz timescale

To better explore the impact of the surface Kelvin–Helmholtz timescale on the evolution of accreting massive star models described in section 4.6, we study three instances of model 1662 and model 4477 either at or during the time of migration towards the red or the blue. The aim of this analytical test is to first determine the surface Kelvin–Helmholtz timescale 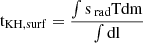and compare it with the surface accretion timescale (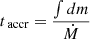). This comparison between timescales was done at log(L/L⊙) = 6.3406, 7.3800, 7.4682 corresponding to model 1662 and model 4477 as depicted in the right panel of Fig. 3. The first comparison at log(L/L⊙) = 6.3406 corresponds to the time when the impact of the critical accretion rate is first described in phase ‘IV’ of section 3.1. Here the values for the global Kelvin–Helmholtz timescale (τKH = GM2/RL) for model 1662 and model 4477 are found to be 150-200 years. The global accretion timescale is instead 3600-4000 years. Upon examining the left and right panels of Fig. 3, we see that τaccr > ;τKH implies both models should migrate to blue, but instead model 4477 stays in the red. However, upon calculating the surface tKH, surf and taccr for the outer 30% of the star, the values for the 4477 model are instead 3298 years and 1439 years, respectively. This shows that to better estimate the blueward or redward migration of a star, it is important to calculate the timescales in the outer envelope. The results also stay consistent when applied to the outer 40% and 50% of the star. This test was then repeated at log(L/L⊙) = 7.3800, 7.4682 and both timescales (now much larger than before, around 30-50kyr) follow a similar trend and provide conclusive results that support the importance of the surface Kelvin–Helmholtz timescale.

A sanity check to explore the critical accretion rate is also performed at a luminosity of log(L/L⊙) = 6.3400. Since numerical tests at this stage provide a value of Ṁcrit,preMS of 2.5 × 10−2 M⊙ yr−1, we can calculate this value again using the analytical relation above. The critical accretion rate is defined as the timescale when τaccr ≡ τKH as explained by Hosokawa et al. (2013), Haemmerlé et al. (2018), we apply this value to tKH, surf instead and obtain 1634 years, which is near identical to taccr. We can use this value to obtain a critical accretion rate using the expression Ṁcrit,preMS = Mcurrent/tKH,surf and find it to be 2.52 × 10−2 M⊙ yr−1.

thumbnail Fig. E.1.

Comparison between accreting and non-accreting models at ZAMS. Left panel: A polytrope model with 491 M⊙ burns hydrogen at the same place in HRD when compared to a 491 M⊙ model with accretion history. Right panel: Same as left panel but for 932 M⊙ .

thumbnail Fig. E.2.

Numerical tests exploring the pre-MS evolution of accreting models. left panel: Zoomed-in region of the pre-MS of three models: Ascending M⊙ (black line), model 491 (red line), and model 6127 (green line) shown in the HR diagram. For the ascending model, the accretion rate begins as 10−3 M⊙/yr, changes every 10 years by a factor of five until it reaches 50M⊙/yr at the age of 110 years. The pre-MS evolution is very similar to that of models 491 and 6127, showing that at least in the early contraction phase, changing the accretion rate has minimal impact on the evolutionary track. Right panel: Impact of FITM on 10−2 M⊙ yr−1 models. The black line represents a FITM of 0.990 and the red line depicts a FITM of 0.999.

thumbnail Fig. E.3.

Propagation of the luminosity wave during the pre-MS evolution of a 932 model. The wave originates deep in the stellar interior when the mass of the model is 12.20 M⊙ and is shown with a blue line. The outward migration of the wave is captured in orange and the model has reached 14.60 M⊙. The wave is about to break at the surface when the mass is 18.50 M⊙ and is shown in purple. If the accretion rate during the breaking of the wave is higher than the critical value, the surface of the model will experience a large expansion in radius and become a red supergiant protostar. If the accretion rate is lower than the critical value, the surface of the model will expand to a much lesser extent and become a blue supergiant protostar. Once the energy is evacuated from the surface, the wave no longer exists and is shown in brown.

All Tables

Table 1.

Physical parameters of the ten models computed from the start of pre-MS until the end of core helium burning.

In the text

All Figures

thumbnail Fig. 1.

Illustration depicting the impact of the critical accretion rate (Ṁcrit) on the evolution of a star. The yellow object represents the protostellar seed and the wave pattern depicts the luminosity wave. The contraction towards blue is depicted with blue lines, whereas the expansion towards red is shown in red lines. The white and cloudy rings represent the accretion; this is denser in cases where the accretion rate is higher than Ṁcrit and fainter when the accretion rate drops below Ṁcrit. The black background depicts the pre-MS evolution and the grey background at the top marks the core hydrogen burning phase.
In the text
thumbnail Fig. 2.

Accretion rate history of the ten massive PopIII models used in this work. The data for each star are taken from Regan et al. (2020a). The initial accretion rate is similar for each model; however, as the dynamical interaction between the stars and surrounding gas becomes dominant, the stars begin to migrate outwards and away from matter-rich zones and consequently the accretion rate decreases.
In the text
thumbnail Fig. 3.

Evolution of accreting PopIII models. Left panel: HR diagram depicting the evolution for ten models with varying accretion rates. The models are labelled according to their final mass. Grey dashed lines represent isoradii. Models 491, 771, 778, 932, 1135, 1331, 1662, and 1923 have near-identical pre-MS accretion histories, unlike models 4477 and 6127. All models except 4477 complete accretion before hydrogen burning starts at log (Teff) = 5.10. Computation stops after core helium burning, with all models in the red at log (Teff)≈3.76. Right panel: evolution of the accretion rate versus the luminosity for the 1662 (solid line) and 4477 (dashed line) models, colour-coded by the effective temperature. Quantities are displayed on a log scale, focusing on a zoomed-in region of the pre-MS. Both models share an identical accretion history until reaching a luminosity of log (L/L⊙) = 5.95. The 1662 model experiences a drop in the accretion rate below 2.5 × 10−2 M⊙ yr−1, while the 4477 model remains above this value.
In the text
thumbnail Fig. 4.

Variation of various physical parameters of accreting PopIII models. Left panel: luminosity–mass relation depicted for all models. The increase in luminosity at 20 M⊙ for all models corresponds to the luminosity wave breaking at the surface. Beyond this, luminosity evolves monotonically vs. mass as L ∝ M until the end of accretion history. Right panel: evolution of radius vs. age (in years) for all models. The colours used to represent models correspond to the label shown in the left panel.
In the text
thumbnail Fig. 5.

Kippenhahn diagrams showing the evolution of the structure (in Eulerian coordinates) as a function of time (Myr) for the lowest-mass models. The blue and cream regions represent the convective and radiative zones, respectively. The iso-masses are depicted by black lines, whereas the isotherms of log(T[K]) = 5, 6, 7, and 8 are drawn in white lines. The translucent yellow regions show deuterium burning; dotted dark grey zones are hydrogen burning zones; and the dark grey zone highlights helium burning.
In the text
thumbnail Fig. 6.

Kippenhahn diagrams depicting the evolution of radius versus mass (both axes represented in log scale) for low-mass models. The details of the diagrams are similar to Fig. 5. In this version of the diagrams, the change in radius during the pre-MS evolution of all models is clearly visible. All models undergo the luminosity wave at log (M/M⊙) = 1.3 and experience a strong increase in radius. The next noteworthy evolutionary trend is at log (M/M⊙) = 1.95 when the models undergo a drop in accretion rate below Ṁcrit,preMS which results in a decrease in radius. Eventually the accretion rate increases above the Ṁcrit,preMS.
In the text
thumbnail Fig. 7.

Kippenhahn diagrams similar to Fig. 5 but for models with masses of 1331, 1662, 1923, 4477, and 6127 M⊙. The radii of these models is larger than that of the low-mass models. The models depicted here transition to the red and expand their radius before completion of the core hydrogen burning phase. Model 4477 M⊙ shows an exceptional behaviour as it undergoes an expansion in radius during hydrogen burning. This is due to a burst of accretion experienced by this model.
In the text
thumbnail Fig. 8.

Kippenhahn diagrams depicting the evolution of radius versus mass (both axes represented in log scale) for high mass models with mass 1331, 1662, 1923, 4477 and 6127 M⊙. The details of these diagrams are similar to Fig. 6.
In the text
thumbnail Fig. 9.

Magnified HR diagram of model 4477 (only the upper part is shown) depicting the migration between blue and red as a result of the variable accretion rate. The colour code follows the central mass fraction of hydrogen. The black arrows represent the evolutionary path taken by the model; the arrows emerge from the bottom right, which marks the pre-MS stage, and end at the top right, which denotes the end of the core hydrogen burning stage.
In the text
thumbnail Fig. E.1.

Comparison between accreting and non-accreting models at ZAMS. Left panel: A polytrope model with 491 M⊙ burns hydrogen at the same place in HRD when compared to a 491 M⊙ model with accretion history. Right panel: Same as left panel but for 932 M⊙ .
In the text
thumbnail Fig. E.2.

Numerical tests exploring the pre-MS evolution of accreting models. left panel: Zoomed-in region of the pre-MS of three models: Ascending M⊙ (black line), model 491 (red line), and model 6127 (green line) shown in the HR diagram. For the ascending model, the accretion rate begins as 10−3 M⊙/yr, changes every 10 years by a factor of five until it reaches 50M⊙/yr at the age of 110 years. The pre-MS evolution is very similar to that of models 491 and 6127, showing that at least in the early contraction phase, changing the accretion rate has minimal impact on the evolutionary track. Right panel: Impact of FITM on 10−2 M⊙ yr−1 models. The black line represents a FITM of 0.990 and the red line depicts a FITM of 0.999.
In the text
thumbnail Fig. E.3.

Propagation of the luminosity wave during the pre-MS evolution of a 932 model. The wave originates deep in the stellar interior when the mass of the model is 12.20 M⊙ and is shown with a blue line. The outward migration of the wave is captured in orange and the model has reached 14.60 M⊙. The wave is about to break at the surface when the mass is 18.50 M⊙ and is shown in purple. If the accretion rate during the breaking of the wave is higher than the critical value, the surface of the model will experience a large expansion in radius and become a red supergiant protostar. If the accretion rate is lower than the critical value, the surface of the model will expand to a much lesser extent and become a blue supergiant protostar. Once the energy is evacuated from the surface, the wave no longer exists and is shown in brown.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.