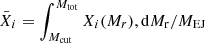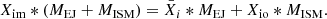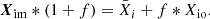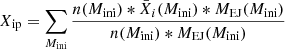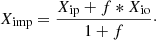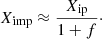| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A156 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202348035 | |
| Published online | 15 March 2024 | |
Explaining the high nitrogen abundances observed in high-z galaxies via population III stars of a few thousand solar masses
1
Département d’Astronomie, Université de Genève, Chemin Pegasi 51, 1290 Versoix, Switzerland
e-mail: deveshnandal@yahoo.com
2
Centre for Astrophysics and Space Sciences Maynooth, Department of Theoretical Physics, Maynooth University, Maynooth, Ireland
3
Department of Physics and Astronomy, Allen Building, University of Manitoba, 30A Sifton Rd, Winnipeg, MB R3T 2N2, Canada
Received:
21
September
2023
Accepted:
30
January
2024
The chemical enrichment of the early Universe is a crucial element in the formation and evolution of galaxies, and Population III (Pop III) stars must play a vital role in this process. In this study, we examine metal enrichment from massive stars in the early Universe’s embryonic galaxies. Using radiation hydrodynamic simulations and stellar evolution modelling, we calculated the expected metal yield from these stars. Specifically, we applied accretion rates from a previous radiation-hydrodynamic simulation to inform our stellar evolution modelling, executed with the Geneva code, across 11 selected datasets, with final stellar masses between 500 and 9000 M⊙. Our results demonstrate that the first generation of Pop III stars within a mass range of 2000−9000 M⊙ result in N/O, C/O and O/H ratios compatible with the values observed in very high-z galaxies GN-z11 and CEERS 1019. The ejecta of these Pop III stars are predominantly composed of 4He, 1H, and 14N. Our Pop III chemical enrichment model of the halo can accurately reproduce the observed N/O and C/O ratios, and, by incorporating a hundred times more zero-metallicity interstellar material with the stellar ejecta, it accurately attains the observed O/H ratio. Thus, a sub-population of extremely massive Pop III stars, with masses surpassing approximately 2000 M⊙, effectively reproduces the CNO elemental abundances observed in high-z JWST galaxies to date. We closely reproduced the observed Ne/O ratio in CEERS 1019 employing a model with several thousand solar masses and non-zero metallicity, and we projected a 12C/13C ratio of 7, substantially lower than the solar ratio of around 90. The significant nitrogen enrichment predicted by Pop III stars with a few thousand solar masses not only reinforces the argument for a heavy seed formation pathway for massive black holes at redshifts as high as z = 10.6 but it also accentuates the need for deeper investigations into their complex nature and pivotal role in the early Universe.
Key words: stars: abundances / stars: evolution / stars: formation / stars: Population II / stars: Population III
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The observation of nitrogen-enhanced high-z galaxies, particularly in GN-z11 (Oesch et al. 2016) and CEERS-1019 (Finkelstein et al. 2017), has sparked a revolution in the study of the Universe’s earliest star and galaxy formation. GN-z11, located at a redshift of z = 10.6 (Bunker et al. 2023), exhibits a N/O abundance ratio in its interstellar medium (ISM) that is more than four times the solar value (log(N/O) > ∼ − 0.25; Cameron et al. 2023; Senchyna et al. 2023). This ratio is not only significantly higher than what is typically found in low-redshift galaxies and HII regions with a comparable metallicity (12 + log(O/H) < ∼ 8.0) but it also slightly exceeds the values observed in galaxies with super-solar metallicities (Vincenzo et al. 2016; Berg et al. 2019). Although the C/O ratio of GN-z11 is consistent with normal values, it is poorly constrained (Cameron et al. 2023).
Similarly, CEERS-1019, at a redshift of z = 8.678, displays strong nitrogen emission lines of N III and N IV, with the N IV] λ1486 being the most intense line in its rest-frame UV spectrum (Tang et al. 2023). This galaxy has an unusually high N/O abundance ratio of log(N/O) = −0.13 ± 0.11, which is approximately 5.6 times the solar ratio. However, its C/O and Ne/O ratios, with values of log(C/O) = −0.75 ± 0.11 and log(Ne/O) = −0.63 ± 0.07 respectively, are relatively normal for its metallicity (Marques-Chaves et al. 2024).
These observations challenge the conventional theories of stellar yields and galactic chemical evolution, necessitating a reexamination of the dynamics of the early Universe. In particular these unusual abundance patterns in high-z galaxies may be a signature of massive, very massive, and supermassive stars (MSs, VMSs, and SMSs)1 in early galaxies. Moreover, these massive objects may well explain the appearance of central massive black holes in these galaxies as well (e.g. Natarajan et al. 2024) and their role in the formation of supermassive black holes (SMBHs) in the early Universe is a subject of ongoing research (Hosokawa et al. 2010; Ekström et al. 2012; Woods et al. 2017, 2021; Haemmerlé et al. 2018).
A number of recent studies have attempted to explain the unusually high Nitrogen abundances (as well as the other metal abundances) observed in these high-z galaxies. Kobayashi & Ferrara (2024) explain these signatures using a rapid chemical enrichment mechanism via a dual-burst model where a quiescent period lasting approximately 100 Myr separates the bursts. In their model, Wolf-Rayet stars become the dominant enrichment source during the second burst – enriching the ISM with heavy elements. Their single burst model, similar to ours described here, requires the presence of massive stars with masses in excess of ∼1000 M⊙. Along similar lines both Charbonnel et al. (2023) and Nagele & Umeda (2023) have studied the impact that metal enriched stars in the mass range of 103 − 105 M⊙ can have in high-z galaxies. In both of these studies the authors have been able to reproduce the high log(N/O) abundance ratios observed in GN-z11. Several other studies have sought to explore different stellar evolution channels on the early chemical evolution of the Universe. For instance, Meynet & Maeder (2006) and Choplin et al. (2018) investigated the impact of fast-rotation on the nucleosynthetic outputs of massive stars. These yields were then used in models for the early chemical evolution of the Milky Way by Chiappini et al. (2003, 2006), Cescutti et al. (2013) showing that the chemical composition of the bulk of halo stars is compatible with yields coming from fast rotating models. The potential role of pair-instability supernovae in the early Universe was analysed by Heger et al. (2002). Although these studies have shed light on different aspects, the exact elemental yields and enrichment potential of VMSs and SMSs remain largely unexplored (Denissenkov & Hartwick 2014).
In this paper, we adopt a novel approach by combining radiation hydrodynamic simulations and stellar evolution modelling to compute the expected metal yield from a population of massive Population III (Pop III) stars. Using the accretion rates from Regan et al. (2020a), we compute eleven Pop III models from the pre-main sequence (PreMS) until the end of core helium burning. We delve into the results of individual stellar models and the integrated halo population, revealing new insights into the N/O, C/O, and O/H number fractions, and taking into account the possibly diluting impact of an additional population of one hundred 20 M⊙ stars. Specifically, we find that chemical enrichment coming from the ejecta of very massive stars, computed with a variety of assumptions can reproduce the observed N/O number fractions, while we successfully match the observed C/O abundances when pulsations from the massive Pop III stars remove all mass above the CO core. Finally to match the O/H number fractions we require a dilution factor (given by the ratio of the mass of the ejecta to that of the interstellar medium with which the ejecta mixed) of 100, entirely consistent with expected ratios chemical abundances in gas rich high-z galaxies. This study not only provides significant insights into the chemical enrichment of the early Universe and the role of supermassive Pop III stars, but also underscores the necessity for further investigations into the complex but pivotal role of massive Pop III stars in the early Universe.
This paper is set out as follows: Sect. 3 first explores the mechanisms invoked for the transport of chemical special and calculates the integrated abundances of the individual stars (we express Xio as the mass fraction of element i in the ejecta a given star) and for the entire halo (Xip, the mean mass fraction of element i in the ejecta coming from a population of stars). Section 4 explores the mass ranges of individual stars that would reproduce the observed results and predicts abundances based on our models, along with comparing our results to previous studies. Section 5 sums up our findings and provides prospects for future work.
2. Methods
2.1. Cosmological context
As discussed in the Introduction, the goal of this study is to calculate the metal enrichement due to pulsational mass loss from massive stars in embryonic haloes in the early Universe. To achieve this goal we utilise the radiation hydrodynamical simulation of Regan et al. (2020a). We previously used the calculated accretion rates from Regan et al. (2020a) to calculate the critical accretion rates onto massive Pop III stars in the study by Nandal et al. (2023). In this study we take the stars found in Regan et al. (2020a) and compute, in post-processing, the expected metal yield from these stars using the same stellar evolution code as used in Nandal et al. (2023).
For an in-depth discussion of both Regan et al. (2020a) and Nandal et al. (2023) we refer readers to the original papers but describe both papers briefly here to provide context. Regan et al. (2020a) employed cosmological zoom-in simulations utilising the Enzo code (Bryan et al. 2014; Brummel-Smith et al. 2019) to investigate pristine, atomic cooling haloes, from the original studies by Wise et al. (2019) and Regan et al. (2020b)2. Using the canonical zoom-in technique Regan et al. (2020a) study showed the formation of 101 (massive) stars in one single halo. The cumulative stellar mass reached roughly 90 000 M⊙ after about 2 Myr of the first star’s inception. Stellar masses ranged between 40 M⊙ to over 6000 M⊙, with a simulation spatial resolution of Δx ∼ 1000 au. Accretion rates onto individual stars ranged from less than 10−3 M⊙ yr−1 to close to 1 M⊙ yr−1 at peak. It is these accretion rates which serve as the input for our stellar evolution modelling and is a key and unique component in this study.
In Nandal et al. (2023) we selected 11 stellar evolution datasets from the underlying cosmological simulations of R20b comprised of a variety of accretion histories and final stellar masses (see Table 1). We use these same 11 datasets here. They contain final stellar masses from 491 M⊙ up to 6127 M⊙. These 11 stellar models, with fluctuating accretion rates, were evolved from the pre-MS to the end of core helium burning using the Geneva code (GENEC; Eggenberger et al. 2008). We adopted a consistent chemical mix (X = 0.7516, Y = 0.2484, Z = 0) and a deuterium mass fraction X2 = 5 × 10−5 as per previous studies. Starting with a 2 M⊙ fully convective seed, accretion is modeled via a thin cold disc (Haemmerlé et al. 2013, 2016), consistent with Palla & Stahler (1992) and Hosokawa et al. (2010). The original study by Nandal et al. (2023) required several code enhancements in GENEC including functionality to cater for variable accretion rates from external files as well as improved spatial and time resolution to account for the variable accretion history. However, effects due to rotation and (explicit) mass loss are not considered, although we note that our model hinges on the assumption that these massive stars do suffer from some degree of mass loss through for example pulsations or due to stellar winds triggered by the increase of the opacity at the surface due to changes of the surface composition here by convection (see Fig. 1 for a graphical illustration). In this work, we do not model the mass loss numerically, but test various hypothesis and assume that some amount occurs during the evolution.
 |
Fig. 1. Illustration depicting the massive Pop III enrichment scenario. From left to right: (1) The formation of a massive Pop III star via accretion which generally occurs during the pre-MS but some stars may undergo short accretion phases during MS. If the accretion rate is below the critical limit described in Nandal et al. (2023), the star migrates to blue. (2) The transition to red at the end of core helium burning leads to the formation of large convective zones and pulsational mass loss as shown by the red mesh. (3) The collapse of a MS may lead to additional mass ejected and the eventual formation of a black hole. (4) Further accretion of ejected material onto the black hole creates the conditions for allowing nitrogen absorption lines to appear, as in the case of GN-z11 and CEERS 1019. |
Mean abundances in the mass fraction of different chemical species in the mass ejected by 11 massive Pop III star models.
We discuss these underlying assumptions further in Sect. 2.2. In addition to the 11 models already computed in Nandal et al. (2023) we computed an additional model with a constant accretion rate of 3.5 × 10−3 M⊙ yr−1 and a final mass of 8904 M⊙ using the same chemical composition as above. This model was computed to serve as a limiting case for halo from the simulations of Regan et al. (2020a) to match the N/O, C/O and O/H values with GN-z11 and CEERS 1019.
2.2. Massive Pop III Star (Nitrogen) Enrichment
To explain the abundances observed in high redshift candidates such as GN-z11 and CEERS1019, we invoke the very and extremely massive Pop III enrichment scenario. In this scenario, a very and extremely massive star begins its evolution as an accreting protostar during the pre-Main Sequence (pre-MS) evolution that lasts for ≲105 yr, see Fig. 1. As the star transitions to the main sequence the core hydrogen burning phase begins in the blue with the star possessing a convective core and a radiative envelope as shown in detail in Nandal et al. (2023). If the star accretes sufficiently rapidly (above approximately 2.5 × 10−3 M⊙ yr−1) then the star can transition to the red during the pre-MS or the MS phase. This transition is included in our modelling. In either case at the end of the MS the star migrates to the red and acquires a near fully convective structure before the start of core helium burning. This allows the efficient transport of chemical species from the interior to the surface. We next make the assumption, that due to the unstable nature of such massive Pop III stars, they are unstable to mass loss, as suggested by Nagele et al. (2022). The quantity of mass lost via winds and/or pulsations is difficult to quantify and instead we parameterise this unknown quantity by examining the impact of different mass loss amounts (see Sect. 3.2)3. Following Helium burning and at the end of core silicon burning, such an object may explode as a supernova (Nagele & Umeda 2023) and produce a black hole or directly collapse into a black hole with mass comparable to the Helium core mass (Montero et al. 2012). For massive stars with masses in excess of approximately 260 M⊙ a direct collapse black hole is always the expected outcome. However, small mass islands leading to a supernova explosions are predicted in some cases (e.g. Chen et al. 2014; Moriya et al. 2021) but there is currently no observational guidance to constrain these islands. For the case of massive Pop III stars with masses in the range of approximately 103 − 104 M⊙ we find that the expulsion of large quantities of surface material, which contains unusually large nitrogen fractions, from the surface can lead to a black hole accretion disc with an unusually large nitrogen abundance. This key signature of massive Pop III mass loss episodes is highly relevant to other recent observations of N-rich quasars as described in the works of Bunker et al. (2023), Cameron et al. (2023).
2.3. Model for the wind enrichment
In this study, we study a scenario where a star enriches the chemical composition of its surrounding interstellar medium (ISM) by shedding some of its mass during its evolution. This mass loss might occur through a series of significant mass-loss episodes prior to the star’s final collapse for example. Our understanding of the mass loss rates of present day massive stars is incomplete (Sabhahit et al. 2023) and in the absence of observational guidance our understanding of early Universe massive stars should certainly be seen as incomplete. We therefore choose to parameterise the mass-loss rates of these stars. We detail our parameterisation as follows.
We assume that the stars lose their mass at or after the core He-burning phase. This is a phase where the star is in the red part of the HR diagram where pulsational instabilities can be large and also a phase where the surface is enriched in heavy elements increasing the opacity. The total mass of element i ejected by the star, denoted as MEJ(i) in solar masses, is given by 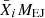 , where
, where 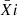 is the mean mass fraction of element i in the ejecta of the star and MEJ is the total mass ejected.
is the mean mass fraction of element i in the ejecta of the star and MEJ is the total mass ejected. 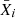 is given by
is given by
where Mcut is the mass coordinate above which we assume the mass to be lost, Mr is the mass coordinate at which Xi is chosen. Here we assume Mcut to take on three separate values: (1) 10% of the total stellar mass; (2) 40% of the total stellar mass; and (3) all the stellar mass above CO core. The CO core is defined as the mass coordinate below which less than 10−3 of Helium mass fraction (Yc) is present. The mass below Mcut is therefore assumed to be locked into the black hole, and Mtot is the total actual mass of the star at the moment of core collapse.
The ejected mass interacts with the interstellar medium (ISM), leading to a mixture of the star’s ejecta and the ISM. The mass of the ISM involved in this interaction is represented as MISM. We introduce a dilution factor f, which is the ratio MISM/MEJ. As noted we treat f as a free parameter as it depends on a number of unknown factors, such as the physics of the explosion and/or the collapse on the one hand and on the exact state of the ISM on the other. To account for our ignorance of both the exact mass lost values and the chemical composition of the ISM we explore different possibilities here considering this f factor as a free parameter, varying from 1 to 1000. We determine Xio as the mass fraction of element i in the ISM at ejection time. The ejection of the mass from a star is assumed to occur in the early stages of the halo evolution. As stars continue to eject matter in their surroundings, the chemical composition changes as a function of time. In other words, the initial chemical composition of the Pop III star is pristine and only consists of hydrogen and helium but as these stars evolve and eject the CNO rich material in the ISM, the chemical composition of the ISM in the halo evolves as a function of time.
Using these parameters, we estimate the final composition of the chemical mixture of the star’s ejecta and the ISM. This is a key objective of our study. We define Xim as the mass fraction of element i in this mixture and calculate it using the principle of mass conservation:
By substituting the dilution factor f = MISM/MEJ into the equation, we can simplify it to:
Furthermore, to extrapolate this to a galaxy containing n stars is straight forward. Let n(Mini) be the number of stars in the galaxy with masses between Mini and Mini + dMini. We obtain the mean mass fraction of element i in the ejecta of all stars in the galaxy as
where Xip is the mass fraction of element i in the ejecta of all the stars. Now again assuming the dilution f as before we can compute the mass fraction in the ISM following the enrichment from the stars as
Finally, we assume the formation of stars in the galaxy occurs at zero metallicity and therefore Xio is taken as zero for C, N, O and 0.7516 for XH, ini. This means that for all elements excluding Hydrogen we have that
Therefore, the mass fraction of element i that exists in the ISM following enrichment is given by the ejected fraction, Xip, divided by the dilution factor, f, if f is much larger than 1. The initial mass function for the halo is given by the simulation, that is, the histograms shown in Fig. 3.
The goal of this paper is to systematically explore the various integrated abundances (i.e. Ximp) expected from very massive Pop III stars in the first galaxies.
3. Results
3.1. Transport of chemical species
The evolution of a typical accreting massive Pop III star is shown in left panel of Fig. 2. The accretion history of this model is artificially generated by assuming a constant accretion rate of 3.5 × 10−3 M⊙ yr−1 to produce a star with mass of 8904 M⊙. The choice of constant accretion rate is motivated by the works of Nandal et al. (2024) where they compare the effects of a constant versus variable accretion rate and find that evolution beyond core hydrogen burning is near identical in both cases. Therefore, we present a new model (in addition to the 11 models with variable accretion rates found in Nandal et al. 2023) that reproduces the same chemical structure in advanced evolutionary stages as the model computed with a variable accretion rate ending with a mass of 8904 M⊙. It must be noted that the accretion history of this model was not obtained from the hydrodynamic simulations and therefore, the contribution of its stellar yields to the entire sub-population of mini halo are not included in the ejecta calculations. We simply use this model to explain the structure of such stars and explore its individual N/O, C/O and O/H ratios later on in this study. After following a pre-MS evolution of ≲105 years, the object commences hydrogen burning in the blue region of HR diagram at log(Teff) = 4.90 (Nandal et al. 2023). During the middle of hydrogen burning, at an age of about 1.5 Myr the star begins its redward migration. The accretion rate during this migration is below the critical value of Ṁcrit,MS = 7.0 × 10−3 found by Nandal et al. (2023), and the star therefore oscillates between red and blue until ≈2 Myr. As the core hydrogen is depleted, the star migrates to the red and attains an effective temperature of log(Teff) = 3.70. During this final crossing of the HR gap, the structure that previously consisted of a convective core and an extended radiative envelope, now consists of a convective core, a series of intermediate convective zones and an extended convective envelope. Such a near-fully convective structure allows the transport of chemical species from the deep interior to the surface, thereby promoting strong enrichment without the need of rotation. It is interesting to note that the near-fully convective structure is only attained at the very end of core hydrogen burning and is absent during the red-blue excursions that occur from 1.5 to 2 Myr, see left panel of Fig. 2. The non-rotating models produced in this study using GENEC show that the structure of such stars is independent of the choice of mass within the mass range of 200−105 M⊙.
 |
Fig. 2. Test model with a final mass of 8904 M⊙ computed using a constant accretion rate of 3.5 M⊙ yr−1 until the end of core helium burning. Left panel: the Kippenhahn diagram showing the evolution of radius versus time. The blue and cream regions represents the convective and radiative zones respectively. Core hydrogen burning is shown in dotted zone and core helium burning in brown zone. The black lines represents the iso-masses and the white lines depict the iso-thermal lines. Right panel: the abundance profile inside the 8904 M⊙ model at the end of core helium burning. The label for each element matches the corresponding line. |
The right panel of Fig. 2 shows the abundance profile of the 8904 M⊙ star at the end of core Helium burning stage. The convective core extends until the mass coordinate of 1142 M⊙ beyond which the effects of large intermediate convective zones become dominant as the profiles of various elements is flat until 5800 M⊙, hinting at strong mixing in these zones. From 5800 to 7800 M⊙, small intermediate convective are present which also promote mixing but to a lesser extent, shown by the negative gradients of the abundance profile of all elements in the right panel of Fig. 2. Finally, a large convective zones extends from a radius of 1600 to 15 848 R⊙ and mass from 8000 to 8904 M⊙, produces a flat abundance profile and affects the surface abundances of the star. As a result of a near-fully convective structure, all chemical species such as 1H, 3He, 4He, 12C, 13C, 14N, 16O, 20Ne, and 22Ne, shown in the right panel of Fig. 2 have their abundances strongly affected compared to their initial abundances. Globally in the zone above the convective core, hydrogen has been depleted (being transformed mainly into helium) and the other chemical species have been synthesised.
Although such massive stars are expected to generate energy via the CNO cycle already during core hydrogen burning, see Woods et al. (2017, 2021), the amount of CNO material available is not sufficient for any significant 14N production during this evolutionary stage. The production of 14N instead occurs during the core helium burning stage. The first step in this process occurs in the 4He rich convective core where 12C is produced via the triple-α reaction. The 12C is then efficiently transported to adjacent hydrogen burning shell via convection. This begins the second step where the presence of 12C in the hydrogen burning shell allows it to capture hydrogen and produce 13N, which emits a positron and produces 13C. In the final step, 13C captures a proton. This produces 14N. The intermediate convective zones are present around the hydrogen burning shell and extend towards the surface, thereby allowing the efficient transport of 14N in the stellar envelope. The variation of the nitrogen abundance in mass fraction inside the star as a function of the lagrangian mass coordinate is denoted by the red line in the right panel of Fig. 2 where the abundance of 14N is highest at the hydrogen burning shell that begins at the mass coordinate of 1142 M⊙ and is the third most abundant element (after 1H and 4He) at the surface. The production of 16O is similarly related to the generation of 12C which for Pop III stars mainly occurs during the core helium burning stage as seen above. Once 12C is produced, it undergoes α capture to produce 16O which is also transported to the surface as shown by purple line in the right panel of Fig. 2. In the envelope we see thus material processed by both H- and He-burning. The CNO cycle is responsible for building nitrogen. The He-burning is responsible for making carbon and oxygen. The final abundances shown in the right panel of Fig. 2 comes out from a complex interplay between nuclear reactions and convection.
3.2. Integrated abundances
In Table 1 we show the mean mass fraction of various isotopes in the ejecta of individual star with different final mass, 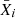 of the 11 model stars as discussed in Sect. 2.1. Firstly we see a clear trend in the ejected abundances for hydrogen and helium that relates to the increasing mass of stars. For example for 10% mass loss parametrisation the integrated mass fraction of 1H left at the end of core hydrogen burning decreases from 0.36 to 0.17. This is due to the near fully convective structure of such stars that allow the mixing of hydrogen and therefore fuse more hydrogen during their lifetimes. As a consequence, the mean mass fraction of 4He increases with increasing mass. The abundance trends for the CNO elements vary significantly for individual models. Taking model 6127 as an example since it provides the most significant contribution amongst the 11 stars. We find that within model 6127, 14N is evenly distributed in the interior and the mean mass fraction varies from 0.039 in the outer 10% of total mass to 0.060 when considering all mass above the CO core. A similar trend is seen for 12C where the mean abundances vary from 0.001 for the 10% case to 0.004 when considering everything above the core. The overall quantity of 12C for all three mass-loss parameterisation is the lowest of all CNO elements and is due to the conversion of 12C to 14N and 16O during the core helium burning stage. The amount of integrated 16O varies from 0.006 at 10% to 0.017 for the mass above the CO core. Once again, this highlights that most of 16O is stored in the interior of the stars. Upon inspecting various integrated mass fractions in Table 1, a general trend concerning the increase or decrease in abundances as a function of mass can be observed, with the exception of models such as 1923. This is likely due to the accretion history of such models where periodic bursts in accretion after a quiescent phase occur well into core hydrogen burning phase. This injects fresh elements, for instance hydrogen in the star which leads to the envelope of such stars exhibiting higher abundance of hydrogen. In summary, high mass stars such as model 6127 have the highest mass fraction of their chemical content in form of 4He and also have a significant mass fraction of 14N when compared to other CNO elements. 1H plays a much larger role in the overall mass fraction content of low mass models such as 491 and these models consist of larger mass fraction of 16O in comparison to 12C and 14N.
of the 11 model stars as discussed in Sect. 2.1. Firstly we see a clear trend in the ejected abundances for hydrogen and helium that relates to the increasing mass of stars. For example for 10% mass loss parametrisation the integrated mass fraction of 1H left at the end of core hydrogen burning decreases from 0.36 to 0.17. This is due to the near fully convective structure of such stars that allow the mixing of hydrogen and therefore fuse more hydrogen during their lifetimes. As a consequence, the mean mass fraction of 4He increases with increasing mass. The abundance trends for the CNO elements vary significantly for individual models. Taking model 6127 as an example since it provides the most significant contribution amongst the 11 stars. We find that within model 6127, 14N is evenly distributed in the interior and the mean mass fraction varies from 0.039 in the outer 10% of total mass to 0.060 when considering all mass above the CO core. A similar trend is seen for 12C where the mean abundances vary from 0.001 for the 10% case to 0.004 when considering everything above the core. The overall quantity of 12C for all three mass-loss parameterisation is the lowest of all CNO elements and is due to the conversion of 12C to 14N and 16O during the core helium burning stage. The amount of integrated 16O varies from 0.006 at 10% to 0.017 for the mass above the CO core. Once again, this highlights that most of 16O is stored in the interior of the stars. Upon inspecting various integrated mass fractions in Table 1, a general trend concerning the increase or decrease in abundances as a function of mass can be observed, with the exception of models such as 1923. This is likely due to the accretion history of such models where periodic bursts in accretion after a quiescent phase occur well into core hydrogen burning phase. This injects fresh elements, for instance hydrogen in the star which leads to the envelope of such stars exhibiting higher abundance of hydrogen. In summary, high mass stars such as model 6127 have the highest mass fraction of their chemical content in form of 4He and also have a significant mass fraction of 14N when compared to other CNO elements. 1H plays a much larger role in the overall mass fraction content of low mass models such as 491 and these models consist of larger mass fraction of 16O in comparison to 12C and 14N.
To determine the mass of the different elements ejected by other initial mass stars (not included among the 11 cases that have been computed here), formed in the simulation of Regan et al. (2020a), we perform linear interpolation for associating a CO core mass and an ejected mass of an isotope to the remaining 90 stars for which we did not compute a detailed evolutionary sequence. Figure 3, we show how the ejected masses of different elements vary as a function of the mass of the different stellar models.
 |
Fig. 3. Mass ejected of various chemical species by each individual star in the halo from Regan et al. (2020a). The first y-axis with lines and dots shows the ejected masses in M⊙ for a given element for all the individual stars in the simulation of Regan et al. (2020a). The dots connect the interpolated values between the 11 computed models and each dot on lines correspond to the 11 models computed until the end of core Helium burning. The second y-axis represents the number of stars in the histogram only. The bins in the histogram cover a width of 100 M⊙ starting from 40 M⊙ and ending at 6200 M⊙. The left panel shows the case when 10% of the total mass is ejected. The middle and right panel, the cases when 40%, and respectively the whole mass above the CO core is ejected. |
Additionally, a histogram representing the mass distribution of all stars from the cosmological simulation is over-plotted at the corresponding mass. A general trend concerning all elements is visible in the three panels; the total amount of any given element ejected (in M⊙) increases as a larger and larger portion of star is considered for mass-loss. This is a quite obvious fact but it also shows that all elements are well mixed in the interior and envelope of all stars. As seen in all three panels of Fig. 3, the integrated ejected mass of 4He (orange line) increases as the mass of stars in the halo increases. This is due to the fact that as the mass of a star increases, larger portions of the convective core are able to sustain temperatures high enough for 1H to fuse into 4He, thereby depleting the star of 1H and producing an excess of 4He. The case of ejecting the entire mass above the CO core can be examined in right panel of Fig. 3, the total helium (orange line) produced by a single 6200 M⊙ bin is an order of magnitude larger than any single 600−700 M⊙ star, or is equal to all 12 stars in the 600−700 M⊙ mass bin.
The trend for ejected mass of 1H (shown as blue line in all panels of Fig. 3) is qualitatively similar to 4He but has a more complex profile for masses ranging from 1000−6000 M⊙. The integrated ejecta mass of 1H increases for the left panel of Fig. 3 but in case of the middle and right panels, the value peaks at around 3000 M⊙ and then decreases. This is due to a more efficient core hydrogen burning shell that produces more 4He in stars with larger masses above 3000 M⊙.
The integrated ejected mass of 14N (shown as red lines in Fig. 3) also shows an increasing trend similar to 4He with the most massive stars producing the majority of 14N. However in the case of integrated ejecta for 16O (purple line), the highest amount is produced by stars of 2000 M⊙ and decreases as mass is further increased. This drop is more significant in 10% and 40% cases and shows that most of 16O is locked in the deep interior of the star and is less mixed when compared to other elements. The integrated ejecta for 12C (green line) also appears to be locked in the deep interior, as seen when the case of CO core (right panel of Fig. 3) is considered. Here 12C integrated ejecta mass follows a trend consistent with other chemical species but is similar to 16O in 10% and 40% cases. These trends are due mainly to the fact that nitrogen results from nuclear processes occurring in the H-burning shell, while carbon and oxygen comes from the deeper He-burning regions and also from the fact that more massive a star is, in general larger mixed zones appear.
Finally, to explore whether such a (progenitor) galaxy could produce the high abundances observed in candidates such as GN-z11 and CEERS 1019, we sum up the contributions of all the individual stars composing the population to one isotopes and obtain the values in Table 2. The first striking feature is the extremely high log10 N/O mass fraction ratio (−0.17 for 10% of total mass and 0.00 for the mass above CO core) and along with high O/H ratios (11.23 for 10% of total mass and 11.54 for the mass above CO core). On the other hand, the C/O ratio is quite low. This is due to the strongly depleted 12C in all models (−1.30 for 10% of total mass and −0.76 for the mass above CO core). Driving the depletion of 12C relative to 14N and 16O is the fusion of 12C to produce the other two elements during the core helium burning stage and is similar to the trend observed in massive stars, as seen in the works of Murphy et al. (2021a).
Abundance ratios of various chemical species of the entire halo.
3.3. Impact of dilution factor
The abundance ratios obtained from individual models and the entire galaxy represent the amount that will be ejected by the respective object(s) and take no account of pre-existing enrichment. However, in order to account for pre-existing enrichment of the ISM, a dilution factor (f = MISM/MEJ) is included in further calculations. Due to the complexity in determining the precise value of the dilution factor, we assume values of 1, 10, 100, 500 and 1000. The results are then compared to the observational data for GN-z11 and CEERS 2019 and are shown in Fig. 4. In Fig. 4 we show a selection of individual models as well as the results from when all of the stars are included. The model with a final mass of 6127 M⊙ reproduces the N/O, C/O and O/H values very well over a wide range of dilution factor (f = 10 → 100). The values for the composition of the ejecta coming from all the stars using three different cutoff values can also reproduce the N/O number fractions of −0.13, −0.04 and 0.05 for 10%, 40% and above the CO core respectively – entirely consistent with observations. However, the C/O number fraction (bottom panel) of −0.64 is the closest of the observed ratios in the two considered high redshift galaxies when the entire mass above the CO core is assumed to be ejected. The O/H number fractions of 7.70, 7.80 and 8.75 for 10%, 40% of total mass and all mass above the CO core for the entire galaxy come close to the observations if a dilution factor of 100 is considered. A dilution factor of 100 is exactly what we expect for a 10% ejection fraction combined with a star formation rate of 0.1. This is compatible with a situation in where the masses of stars represents only 10% of the total mass (stars and gas) of the clusters, and where 10% of the stellar mass is ejected.
 |
Fig. 4. Abundance ratios (in number fractions) in the interstellar medium of the halo as a function of O/H (expressed as log10(O/H) + 12). The dilution factor, f, is given by the colourbar. Dotted lines correspond to the abundance in the ejecta of an individual stellar model. The mass is indicated for each of them. The result for dilution factors equal to 1, 10, 100 and 1000 are shown by coloured circles. The solid lines show the abundances when the ejecta of all the stars in the halo are mixed and mixed also with varying amounts of pristine material: magenta line is for the case when the entire mass above the CO core is assumed to be ejected by each star, brown and red lines for the cases when 40%, respectively 10% of the total mass is ejected. The coloured pentagons on the solid lines show the results for different dilution factors. The grey trapezoid and the orange rectangle represent the conservative and fiducial results for the abundances of GN-z11 by Cameron et al. (2023). The yellow star with error bars correspond to the results of CEERS 1019 as shown in Marques-Chaves et al. (2024). Top panel: N/O abundances as a function of the O/H abundances both in log base 10 scale. The red and brown stars in the top panel are the photoionisation modelling results for GN-z11 by Senchyna et al. (2023). Bottom panel: C/O versus O/H ratios represented in the log base 10 scale. |
3.4. Massive Pop III stars as efficient nitrogen enrichers and the progenitors of high-z N-loud Quasars
The evolution of accreting massive Pop III stars demonstrates profound nitrogen enrichment of the outer envelope, as depicted in Fig. 2. Such enrichment is principally driven during the core helium burning phase, where the presence of 12C advances the production of 14N. However, these stars tend to nearly exhaust their 12C reservoirs in this enrichment process. Delving into the integrated abundances across an entire (sub-)galaxy population, there’s an evident correlation: as stellar mass increases, the remaining fraction of 1H decreases while 4He exhibits the opposite trend. Specifically, in the first galaxy simulations of R20b, the stellar mass range leads to remarkably high N/O and O/H ratios, with a diminished C/O ratio, attributed to the pronounced carbon depletion across models. Introducing the concept of dilution to assess the impact on the interstellar medium, the 6127 M⊙ model aligns very well with observed ratios such as N/O, C/O, and O/H over a dilution factor spectrum of 10−100. Moreover, considering realistic mass cutoffs and a dilution factor of 100, the integrated values from all of the massive stars agrees very closely with observational benchmarks as shown in Fig. 4. What this tells us is that a sub-population of very massive Pop III stars can reproduce the elemental abundances as seen by JWST and in particular explains very well the unusually high nitrogen abundances.
4. Discussion
4.1. Mass ranges
The chemical signatures exhibited by the massive Pop III stars are strongly dependent on their mass during the various mass-loss events and at the time of collapse. Figure 4 shows both the impact from the individual stars from the simulations of Regan et al. (2020a) and those from all of the stars. An individual star with mass less than 1923 M⊙ results in a log10(N/O) ratio of −0.37, which is on the lower end of observed values. The log10(C/O) ratio on the other hand misses the observed values entirely. The next mass in the simulation (not shown in Fig. 4) that produces a log10(N/O) ratio of 0.1 and log10(C/O) ratio of −0.7 is 2479 M⊙. There also exists an upper mass limit for haloA beyond 8904 M⊙ where the log10(N/O) ratio exceeds 0.85 and log10(C/O) reduces below −0.6, thereby missing the observational window for GN-z11 and CEERS 1019. Such a conclusion is strictly time dependent as continual pollution of ISM by the next generations of stars would change the log10(N/O) value. Interestingly supermassive Pop III stars with masses above 100 000 M⊙ cannot produce the observed values as they experience a premature collapse during core hydrogen burning (Haemmerlé et al. 2018). This evolutionary stage, prior to helium burning, is devoid of any substantial production of CNO elements which only occur during the later core helium burning stage. This result demonstrated that there exists both an upper and lower mass limit where massive Pop III are capable of producing the observed signatures. We note that this does imply that such massive stars do not exist – simply that stars in the mass range of approximately 103 − 104 are required to re-produce the abundances signatures seen by JWST.
4.2. Predicted abundances
Here we attempt to predict abundances of additional elements that have not yet been observed so as to make the model falsifiable. The goal here is to provide some additional values to better constrain future observations of objects such as GN-z11 and CEERS 1019. While our study primarily focuses on a specific stellar mass range, it represents only a fraction of the total stellar mass. However, the significance of our work lies in demonstrating the capability of these supermassive stars (SMSs) to both produce substantial amounts of Nitrogen and seed massive black holes. Additionally, various works have shown that Late (z < 7) Pop III star formation might also have occurred in pristine regions due to in-homogeneous metal enrichment of the first galaxies (Tornatore et al. 2007; Salvaterra et al. 2011; Vanzella et al. 2020). With this in mind, we find the integrated ejected mass in our simulated galaxy to be primarily enriched in helium with 0.55 mass fraction for 10% of total mass and 0.65 for all mass ejected above CO core. This mass fraction allows us to predict the undiluted log10(He/H) for 10% and above CO core ratios of all stars for entire halo to be −0.40 and −0.09. Once the helium and hydrogen rich ejecta is exposed to the ISM, we can further predict the diluted log10(He/H) ratios. For an equal contribution from the total stellar ejecta of all stars and the ISM, f = 1, we obtain log10(He/H) = −0.62. For stronger dilutions of f = 0, 100 and 1000, the ratio decreases to −0.99, −1.07 and −1.08 respectively. Given that observing He/H ratios is an important observable signature for massive stars (Schaerer & Pelló 2003), these predicted ratios are useful for future JWST observations.
The log10(12C/13C) is found to be 0.87 for the 10% case and 1.47 for the CO core case. To provide a comparison, the solar composition material shows a ratio 12C/13C around 60 (see Table 2 in Ekström et al. 2012, and references therein). Once these isotopes reach an equilibrium state (i.e. when the process has reached a stationary regime and the abundances of the CNO elements no longer vary) in material that has been processed by CNO burning reactions, the ratio decreases to value around 4. The 12C/13C ratios from the integrated population when considering 10% and all mass above CO cases at the end of core helium burning are found to be 8 and 25 respectively, which clearly show the sign of CNO burning. It is also important to note that the absolute values of both 12C and 13C are boosted by the mixing between the helium and hydrogen burning regions. Fast rotating massive stars would also produce 12C/13C ratios around similar values as the very massive stars considered here (Chiappini et al. 2008).
The right hand panel of Fig. 2 shows that Neon abundance of such stars is strongly dominated by the 22Ne isotope, which is formed via the fusion of 14N. However, such stars also have a high 16O abundance which reduces the overall log10(22Ne/O) ratio to −3.02 for the 10% case and −3.13 for the CO core case. Comparing these values to the log10(Ne/O) ratio of −0.63 obtained by Marques-Chaves et al. (2024), we find that Pop III stars in a halo such as ours cannot produce the observed Ne/O ratios, at least for galaxies such as CEERS 1019. To further explore the possibility of such massive stars producing the required Ne/O ratios, we invoke a scenario where the very and extremely massive stars form in an already enriched halo by previous generations of stars. We compute one model with a final mass of 3200 M⊙ at Z = 10−6 until the end of core helium burning and calculate the mean abundances in mass fractions for various elements in its ejecta, assuming all the mass above the CO core is lost at the end of its evolution. Upon ejection of the chemical species by this model, the ejecta is mixed with the non zero metallicity ISM with a dilution factor ranging from 1 to 1000. The results for a dilution factor 100 show a number fraction ratio of log10(Ne/O) = −0.58. Additional number fractions of CNO are; log10(N/O) = −0.52, log10(C/O) = −1.29 and log10(O/H) + 12 = 8.03. The N/O and C/O ratios for this single model is lower than the observed ratios for GN-z11 and CEERS 1019 but such ratios will likely be different if a population of such stars with different masses are considered in a given halo (as we did for the Pop III case). At least, the numerical example shown here indicates that there is good hope that starting from a non-zero metallicity would still allow strong enrichment in CNO elements compatible with high redshift star forming zones, while also compatible with the high Ne/O ratio.
4.3. Impact of a population of 20 M⊙ stars
Due to the constraints in resolution of the hydrodynamic simulations of Regan et al. (2020a), stars with masses less than 40 M⊙ are likely to be unresolved but should exist in real proto-galaxies of this mass. We can nonetheless estimate their impact on the N/O, C/O and O/H abundances by assuming 100 Pop III stars with 20 M⊙ are born in addition within the halo. This is likely to be a very conservative estimate. Although the outcome of core collapse of 20 M⊙ is realistically unknown, we assume these 20 M⊙ models without rotation to undergo classical core-collapse which we expect will eject a huge portion of the star beyond the CO core, see works by Murphy et al. (2021b).
The ejecta from an individual 20 M⊙ will contain 9.6 M⊙ of 1H, 6.2 M⊙ of 4He, 1.4 M⊙ of 16O, 0.6 M⊙ of 12C and merely 1.2 × 10−7 M⊙ of 13C. Using these values, we can estimate the impact of 100 of 20 M⊙ stars on the mass fraction values of log(N/O), log(C/O) and log(O/H) found in Table 2. For the case of 10% of the total mass ejected from all stars without accounting for dilution (i = 0), we find a value of log(N/O) = −0.27, log(C/O) = −0.87 and log(O/H) + 12 = 11.21. These values when compared to row 1, Cols. 10–12 of Table 2 show a decrease in log(N/O) mass fraction values (from −0.17 to −0.27), an increase in log(C/O) values (from −1.30 to −0.87) and a near identical log(O/H) + 12 values (from 11.23 to 11.21). However, the impact of adding these 100 20 Pop III stars would be smaller for the cases 40% and “above the CO core”. Conclusively, these values are not significantly affected by 100 20 M⊙ stars however if the halo were to contain an excess of a 104 stars, the impact will be enhanced. However, addition of 20 M⊙ Pop III stars would improve our agreement for the log(C/O) and log(Ne/O) ratio in the bottom panel of Fig. 4.
4.4. Comparison with previous studies
The presence of strong NIII] λ1750 and CIII] λλ1909 lines observed in GN-z11 by Bunker et al. (2023) present unusually high N/O ratios at a redshift of z = 10.6. Using the emission line fluxes from Bunker et al. (2023), Cameron et al. (2023) derived the abundance ratios quantitatively and found log(N/O) > −0.25, log(C/O) > −0.78 and log(O/H) ≈ 7.82 for their fiducial model and log(N/O) > −0.49, log(C/O) > −0.95 and log(O/H) ≤ 8.60 for their conservative models as denoted by orange and grey box in Fig. 4.
Using the runaway collision scenario proposed by Gieles et al. (2018), Charbonnel et al. (2023) were the first to explore the N/O, C/O and Ne/O of GN-z11. Using a SMS model with a characteristic mass of 104 M⊙ and metallicities ([Fe/H]) ranging from −1.76 to −0.78. The mechanism of transport of chemical species in their work is the presence of a fully convective SMS that grows via collisions with smaller objects throughout its lifetime. Additionally, they predict the Ne/O in GN-z11 to be higher than other high-z objects when compared to normal galaxies with similar metallicity. In contrast we invoke a more conservative massive Pop III formation scenario where the transition to the later stages of evolution, specifically post H-burning allows the structure to become convective and transport the elements to the surface more efficiently. Our single star models such as 6127 produce a higher N/O and C/O ratio whereas the O/H ratios match for a dilution factor between 10 and 100. Our integrated abundances for our total population of massive stars provide a closer match to the observed values of N/O and C/O, whereas the O/H matches if the dilution factor is around 100. We also find that the 22Ne/16O ratio for the population to be around −3.0 which is much lower than the values of GN-z11 predicted in their work.
Nagele & Umeda (2023) compute metal-enriched SMS models with rotation, stellar winds and SMS explosions to explain the high nitrogen pollution in GN-z11. The four models in their study were generated at ZAMS with initial masses of 103, 104, 5 × 104 and 105. Each model was evolved either until the late carbon burning phase or until the GR instability was reached. The total 12C, 14N and 16O values were 9.91, 17 and 27 M⊙ respectively for the 103 M⊙ model. In comparison, 12C, 14N and 16O values for our 932 M⊙ model are 0.741, 26.76 and 7.657 M⊙ if all the mass above CO core is assumed to be ejected. The difference in the ejected masses is likely due to their inclusion of the effects of mass-loss, rotation and high metallicity in their models; our models are instead computed without mass-loss and rotation and have zero metallicity. Furthermore, Nagele & Umeda (2023) favour their high mass models when explaining the abundances of GN-z11 over a range of dilution factors whereas our models at 105 M⊙ produce a log10(N/O) = 2.2, log10(C/O) = 0.45 and log10(O/H) + 12 varying from -2.3 to 0.8 over a range of dilution factors from 1 to 1000. This difference is possibly due to the difference in metallicity and structure of such objects.
Finally, Kobayashi & Ferrara (2024) advocate for a dual starburst model to explain the high Nitrogen abundances in GN-z11. By assuming that star formation in GN-z11 begins at z ∼ 16.7 and continued for 100 Myr before a quisient phase also lasting approximately 100 Myr Kobayashi & Ferrara (2024) show that WR stars at [Fe/H] = 0, −1, −2 and −3 in the second star burst phase are potential sources of high (C,N)/O ratios. When considering their fiducial model following the dual starburst formation scenario and fixing the star formation age to match the log(O/H) + 12 ratio, the log(N/O) ratio is found to be 0.246. They also conclude that very massive stars (VMS > 100 M⊙) with Z = 0 and 0.0002 as sources do not lead to a sufficient increase in N/O and pair instability supernovae (PISNe) lead to decrease in N/O ratio. They also show a single star burst model which requires stars with masses in excess of 1000 M⊙ to explain the abundances – consistent with what we show here. Kobayashi & Ferrara (2024) also concluded that the impact of adding normal massive stars (typically of 20 M⊙, as we did here) does not affect the overall N/O ratio of GN-z11.
Another high-z JWST galaxy discovered by the CEERS survey team – CEERS 1019 – displays similar abundances to GN-z11. Investigating CEERS 1019 Marques-Chaves et al. (2024) found strong emission of NIII and NIV lines and obtained log(N/O) = −0.13 ± 0.11, log(C/O) = −0.75 ± 0.11, log(O/H) + 12 = 7.78 ± 0.18 and log(Ne/O) = −0.63 ± 0.07. Furthermore, Marques-Chaves et al. (2024) invoke (super-massive) stars with masses in excess of 1000 M⊙ to explain the unusual abundances (consistent also with similar anomalies observed in present day globular clusters; e.g. Denissenkov & Hartwick 2014; Gieles et al. 2018).
5. Conclusion
The research presented here has delved into the intricacies of massive Pop III stars and their pivotal roles in influencing the chemical constitution of specific galaxy environments. Through a meticulous analysis of an expansive dataset and detailed simulations, the study elucidates how the mass, evolution, and environmental interactions of massive Pop III stars are instrumental in deciphering the observed chemical signatures from early epochs of the Universe. Herein, we encapsulate the salient findings and their ramifications for forthcoming research.
Mass ranges’ importance. The mass of the Pop III stars was found to be a determining factor in their resultant chemical signature. Specifically, stars less than ∼1900 M⊙ produce a log10(N/O) ratio of −0.37, which is on the lower end of observed values. Stars beyond 8900 M⊙ exceed the observed ratios for GN-z11 and CEERS 1019 and hence may be rare, at least in these galaxies. Only massive Pop III stars within the range of 1900 M⊙ to 8900 M⊙ appear to align with the observed chemical signatures.
A population of very massive Pop III stars. A sub-population of very massive Pop III stars produces an abundance pattern of nitrogen which is consistent with current observations by JWST of GN-z11 and CEERS 1019. The high nitrogen abundances are driven solely by the most massive stars among that population. Lower mass stars will dilute that abundance pattern as they do not produce sufficient Nitrogen to be consistent with observations. Hence, it appears that some early galaxies must contain a minority population of very massive Pop III stars (i.e. stars with masses in excess of 1000 M⊙) in order to be consistent with observations.
Predicted halo abundance. The mass of individual massive Pop III stars significantly influences the chemical outputs of entire halos. For instance, the integrated ejected mass due to all of the massive stars in our model resulted in enrichment in 4He with a mass fraction of 0.55 for 10% of total mass and 0.65 for all mass ejected above the CO core. As a result, the integrated ejected mass of 1H varied from 0.35 to 0.20. Hence, our model predicts H helium rich environments in these embryonic galaxies. Additionally, low mass (M* ≲ 2000 M⊙) Pop III stars are found to be the strong polluters in 16O whereas the ejecta of stars with masses above 2000 M⊙ are enriched in 14N. Overall, after 4He and 1H, 14N dominates the ejecta of high mass Pop III stars.
Matching abundances with GN-z11 and CEERS 1019. If all massive Pop III stars eject a fraction of their total mass, we can closely reproduce the log(N/O), log(C/O) and log(O/H) + 12 ratios over a range of dilution factor. Our massive Pop III models predict that N-loud quasars should be a key signature of a previous episode of massive Pop III star formation with the seed for the quasars possible originating from one of the Pop III stars responsible for the initial nitrogen enrichment.
The origin of the high Ne/O ratio in CEERS 1019. As mentioned above, our model produces very low Ne/O ratio (−3.02) compared to CEERS 1019 (−0.63). In the present models, neon is under the form of the 22Ne isotopes. It comes from the transformation of the 14N at the beginning of the core He-burning phase. The low value that we obtain indicates that this process alone is not efficient enough to produce Ne/O ratios compatible with the one observed in CEERS 1019. Additionally, we find that stars with mass around 3200 M⊙ at 10−6 Z can reproduce accurately the log10(Ne/O) ratio of −0.58, but the N/O, C/O values are below the observed value. This concludes that it is difficult to reproduce all the observed ratios with just one generation of Pop III models; a more complex analysis of star formation history is needed.
Abundance predictions. It is important to emphasise that the current model predicts the abundances resulting from a first generation of extremely massive stars. As previously mentioned, these predictions are specifically applicable to a unique stage in the evolution of such systems. In this context, we also outline potential abundance signatures characteristic of these systems. Carbon ratios: The log10 (12C/13C) ratio for the 10% case and CO core case was found to be 0.87 and 1.47 respectively, showing a strong signature of CNO cycle. The Ne/O ratios predicted in this study were found to be around −3.0 for the halo. These additional abundance ratios provide an estimated value for future observations of JWST. We encourage observers to seek out for these ratios in future observations.
Impact of 20 M⊙stars. Incorporating 100 stars of 20 M⊙ mass within the stellar population provides pivotal insights into the role of these less massive stars. Specifically, the contribution of these stars leads to log10(N/O) and log10(O/H) + 12 values of −0.27 and 11.21 respectively, indicating their negligible effect on these ratios (i.e. Pop III stars of this mass cannot account for anomalously high N abundances). However, the addition of these stars into the halo increased the log10(C/O) from −1.30 to −0.87 and would likely increase the Ne/O ratio, thereby providing a better fit to the observed values of GN-z11 and CEERS 1019.
As future studies continue to explore the possible scenarios for high red-shift candidates such as GN-z11 and CEERS 1019, our models robustly predict significant N enrichment from massive Pop III stars. If such stars exist, and they eject mass, it would be entirely unsurprising to find strong N-enrichment in the very early Universe. It is important to recognise that nitrogen enrichment can also result from fast-rotating massive stars with masses ranging between 8 and approximately 100 M⊙ (Meynet & Maeder 2006; Chiappini et al. 2003, 2006; Cescutti et al. 2013). Fast rotating models have been suggested to account for the value of about −1.5 (log(N/O)) observed in iron-poor halo stars. This value is more than an order of magnitude lower than what is displayed by high-redshift galaxies such as GN-z11 and CEERS 1019. However, it is worth noting that the chemical enrichment model for the halo of our Galaxy significantly differs from the one discussed here. In future research, it would be insightful to explore the influence of fast-rotating massive, very massive, and even supermassive stars within this context.
The influx of observations by JWST via the JADES (Maiolino et al. 2023a,xb), CEERS (Larson et al. 2023) and UNCOVER (Goulding et al. 2023) surveys have revealed the existence of a population of massive black holes with masses ranging from as low as 4 × 105 M⊙ up to ≲108 M⊙ at redshifts as high as z = 10.6. The masses of these black holes as well as their sub-Eddington accretion rates, in most cases, appears to strengthen the case for a heavy seed formation pathway with the seed being a massive Pop III or SMS the most likely candidate (e.g. Natarajan et al. 2024). Our investigation here adds extra weight to the heavy seed argument by showing that massive Pop III stars enrich the environment surrounding the (mini)-quasar with metal abundances consistent with observations. In light of the above, it is paramount for future investigations to further probe into the multifaceted nature of massive Pop III stars, either to affirm, challenge, or elaborate on the narratives and interpretations offered in this study.
We consider stars to be massive within 10−100 M⊙, very massive within 100−1000 M⊙, extremely massive within 1000−40 000 M⊙ and supermassive with mass above 40 000 M⊙ as described in the work by Woods et al. (2020).
These simulation were themselves rooted in the Renaissance simulation suite (Chen et al. 2014; O’Shea et al. 2015; Xu et al. 2016).
A similar approach has been used by Liu et al. (2021) for investigating the impact of winds of Pop III massive stars.
Acknowledgments
D.N., S.E. and G.M. have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 833925, project STAREX). J.R. acknowledges support from the Royal Society and Science Foundation Ireland under grant number URF/R1/191132. J.R. also acknowledges support from the Irish Research Council Laureate programme under grant number IRCLA/2022/1165. T.E.W. acknowledges support from the National Research Council of Canada’s Plaskett Fellowship. E.F. and G.M. have received funding from the SNF project 200020-212124.
References
- Berg, D. A., Erb, D. K., Henry, R. B. C., Skillman, E. D., & McQuinn, K. B. W. 2019, ApJ, 874, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Brummel-Smith, C., Bryan, G., Butsky, I., et al. 2019, J. Open Source Softw., 4, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. L., Norman, M. L., O’Shea, B. W., et al. 2014, ApJS, 211, 19 [Google Scholar]
- Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, A. J., Katz, H., Rey, M. P., & Saxena, A. 2023, MNRAS, 523, 3516 [NASA ADS] [CrossRef] [Google Scholar]
- Cescutti, G., Chiappini, C., Hirschi, R., Meynet, G., & Frischknecht, U. 2013, A&A, 553, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C., Schaerer, D., Prantzos, N., et al. 2023, A&A, 673, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, P., Wise, J. H., Norman, M. L., Xu, H., & O’Shea, B. W. 2014, ApJ, 795, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Meynet, G. 2003, A&A, 410, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A&A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choplin, A., Hirschi, R., Meynet, G., et al. 2018, A&A, 618, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., & Hartwick, F. D. A. 2014, MNRAS, 437, L21 [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- Finkelstein, S. L., Dickinson, M., Ferguson, H. C., et al. 2017, The Cosmic Evolution Early Release Science (CEERS) Survey, JWST Proposal ID 1345. Cycle 0 Early Release Science [Google Scholar]
- Gieles, M., Charbonnel, C., Krause, M. G. H., et al. 2018, MNRAS, 478, 2461 [Google Scholar]
- Goulding, A. D., Greene, J. E., Setton, D. J., et al. 2023, ApJ, 955, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Haemmerlé, L., Eggenberger, P., Meynet, G., Maeder, A., & Charbonnel, C. 2013, A&A, 557, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haemmerlé, L., Eggenberger, P., Meynet, G., Maeder, A., & Charbonnel, C. 2016, A&A, 585, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haemmerlé, L., Woods, T. E., Klessen, R. S., Heger, A., & Whalen, D. J. 2018, MNRAS, 474, 2757 [Google Scholar]
- Heger, A., Woosley, S., Baraffe, I., & Abel, T. 2002, in Lighthouses of the Universe: The Most Luminous Celestial Objects and Their Use for Cosmology, eds. M. Gilfanov, R. Sunyeav, & E. Churazov, 369 [Google Scholar]
- Hosokawa, T., Yorke, H. W., & Omukai, K. 2010, ApJ, 721, 478 [Google Scholar]
- Kobayashi, C., & Ferrara, A. 2024, ApJ, 962, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. L., Finkelstein, S. L., Kocevski, D. D., et al. 2023, ApJ, 953, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., Sibony, Y., Meynet, G., & Bromm, V. 2021, MNRAS, 506, 5247 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Scholtz, J., Curtis-Lake, E., et al. 2023a, A&A, submitted [arXiv:2308.01230] [Google Scholar]
- Maiolino, R., Scholtz, J., Witstok, J., et al. 2023b, Nature, in press [arXiv:2305.12492] [Google Scholar]
- Marques-Chaves, R., Schaerer, D., Kuruvanthodi, A., et al. 2024, A&A, 681, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2006, in Stars with the B[e] Phenomenon, eds. M. Kraus, & A. S. Miroshnichenko, ASP Conf. Ser., 355, 27 [NASA ADS] [Google Scholar]
- Montero, P. J., Janka, H.-T., & Müller, E. 2012, ApJ, 749, 37 [Google Scholar]
- Moriya, T. J., Chen, K.-J., Nakajima, K., Tominaga, N., & Blinnikov, S. I. 2021, MNRAS, 503, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, L. J., Groh, J. H., Ekström, S., et al. 2021a, MNRAS, 501, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, L. J., Groh, J. H., Farrell, E., et al. 2021b, MNRAS, 506, 5731 [NASA ADS] [CrossRef] [Google Scholar]
- Nagele, C., & Umeda, H. 2023, ApJ, 949, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Nagele, C., Umeda, H., Takahashi, K., Yoshida, T., & Sumiyoshi, K. 2022, MNRAS, 517, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Nandal, D., Regan, J. A., Woods, T. E., et al. 2023, A&A, 677, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nandal, D., Farrell, E., Buldgen, G., Meynet, G., & Ekstrom, S. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202345997 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natarajan, P., Pacucci, F., Ricarte, A., et al. 2024, ApJ, 960, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Brammer, G., van Dokkum, P. G., et al. 2016, ApJ, 819, 129 [NASA ADS] [CrossRef] [Google Scholar]
- O’Shea, B. W., Wise, J. H., Xu, H., & Norman, M. L. 2015, ApJ, 807, L12 [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1992, ApJ, 392, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., Wise, J. H., Woods, T. E., et al. 2020a, Open J. Astrophys., 3, 15 [NASA ADS] [Google Scholar]
- Regan, J. A., Wise, J. H., O’Shea, B. W., & Norman, M. L. 2020b, MNRAS, 492, 3021 [NASA ADS] [CrossRef] [Google Scholar]
- Sabhahit, G. N., Vink, J. S., Sander, A. A. C., & Higgins, E. R. 2023, MNRAS, 524, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Ferrara, A., & Dayal, P. 2011, MNRAS, 414, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & Pelló, R. 2003, in A Massive Star Odyssey: From Main Sequence to Supernova, eds. K. van der Hucht, A. Herrero, & C. Esteban, 212, 747 [NASA ADS] [Google Scholar]
- Senchyna, P., Plat, A., Stark, D. P., & Rudie, G. C. 2023, AAS J., submitted [arXiv:2303.04179] [Google Scholar]
- Tang, M., Stark, D. P., Chen, Z., et al. 2023, MNRAS, 526, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Tornatore, L., Ferrara, A., & Schneider, R. 2007, MNRAS, 382, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Meneghetti, M., Caminha, G. B., et al. 2020, MNRAS, 494, L81 [Google Scholar]
- Vincenzo, F., Belfiore, F., Maiolino, R., Matteucci, F., & Ventura, P. 2016, MNRAS, 458, 3466 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Regan, J. A., O’Shea, B. W., et al. 2019, Nature, 566, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., Heger, A., Whalen, D. J., Haemmerlé, L., & Klessen, R. S. 2017, ApJ, 842, L6 [Google Scholar]
- Woods, T. E., Heger, A., & Haemmerlé, L. 2020, MNRAS, 494, 2236 [Google Scholar]
- Woods, T. E., Willott, C. J., Regan, J. A., et al. 2021, ApJ, 920, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Norman, M. L., O’Shea, B. W., & Wise, J. H. 2016, ApJ, 823, 140 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Impact of evolutionary stages on the integrated abundances
To explore the impact of late stages of evolution on the abundances, we calculated the integrated abundances of Hydrogen, Carbon, Nitrogen and Oxygen for the 3053 M⊙ model as shown in Table A.1. We find that the integrated abundances do no vary significantly beyond the core Helium burning phase. This is due to the very short timescale of the subsequent phases which barely alters the total composition of the model. Therefore the 11 models computed until the end of core Helium burning provide sufficiently accurate results. The core is defined as the mass coordinate in star below which 10−3 mass fraction of the previous chemical species is left. For instance, CO core has 10−3 mass fraction of helium (Yc) is left in the core.
Integrated abundance of various elements inside a 3053 M⊙ model at zero metallicity computed until the end of core Si burning. Column 1 indicates various evolutionary stages. The integrated mass fraction of a given element is presented in columns 2, 3, 4 and 5.
All Tables
Mean abundances in the mass fraction of different chemical species in the mass ejected by 11 massive Pop III star models.
Integrated abundance of various elements inside a 3053 M⊙ model at zero metallicity computed until the end of core Si burning. Column 1 indicates various evolutionary stages. The integrated mass fraction of a given element is presented in columns 2, 3, 4 and 5.
All Figures
 |
Fig. 1. Illustration depicting the massive Pop III enrichment scenario. From left to right: (1) The formation of a massive Pop III star via accretion which generally occurs during the pre-MS but some stars may undergo short accretion phases during MS. If the accretion rate is below the critical limit described in Nandal et al. (2023), the star migrates to blue. (2) The transition to red at the end of core helium burning leads to the formation of large convective zones and pulsational mass loss as shown by the red mesh. (3) The collapse of a MS may lead to additional mass ejected and the eventual formation of a black hole. (4) Further accretion of ejected material onto the black hole creates the conditions for allowing nitrogen absorption lines to appear, as in the case of GN-z11 and CEERS 1019. |
| In the text | |
 |
Fig. 2. Test model with a final mass of 8904 M⊙ computed using a constant accretion rate of 3.5 M⊙ yr−1 until the end of core helium burning. Left panel: the Kippenhahn diagram showing the evolution of radius versus time. The blue and cream regions represents the convective and radiative zones respectively. Core hydrogen burning is shown in dotted zone and core helium burning in brown zone. The black lines represents the iso-masses and the white lines depict the iso-thermal lines. Right panel: the abundance profile inside the 8904 M⊙ model at the end of core helium burning. The label for each element matches the corresponding line. |
| In the text | |
 |
Fig. 3. Mass ejected of various chemical species by each individual star in the halo from Regan et al. (2020a). The first y-axis with lines and dots shows the ejected masses in M⊙ for a given element for all the individual stars in the simulation of Regan et al. (2020a). The dots connect the interpolated values between the 11 computed models and each dot on lines correspond to the 11 models computed until the end of core Helium burning. The second y-axis represents the number of stars in the histogram only. The bins in the histogram cover a width of 100 M⊙ starting from 40 M⊙ and ending at 6200 M⊙. The left panel shows the case when 10% of the total mass is ejected. The middle and right panel, the cases when 40%, and respectively the whole mass above the CO core is ejected. |
| In the text | |
 |
Fig. 4. Abundance ratios (in number fractions) in the interstellar medium of the halo as a function of O/H (expressed as log10(O/H) + 12). The dilution factor, f, is given by the colourbar. Dotted lines correspond to the abundance in the ejecta of an individual stellar model. The mass is indicated for each of them. The result for dilution factors equal to 1, 10, 100 and 1000 are shown by coloured circles. The solid lines show the abundances when the ejecta of all the stars in the halo are mixed and mixed also with varying amounts of pristine material: magenta line is for the case when the entire mass above the CO core is assumed to be ejected by each star, brown and red lines for the cases when 40%, respectively 10% of the total mass is ejected. The coloured pentagons on the solid lines show the results for different dilution factors. The grey trapezoid and the orange rectangle represent the conservative and fiducial results for the abundances of GN-z11 by Cameron et al. (2023). The yellow star with error bars correspond to the results of CEERS 1019 as shown in Marques-Chaves et al. (2024). Top panel: N/O abundances as a function of the O/H abundances both in log base 10 scale. The red and brown stars in the top panel are the photoionisation modelling results for GN-z11 by Senchyna et al. (2023). Bottom panel: C/O versus O/H ratios represented in the log base 10 scale. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.