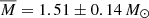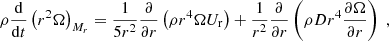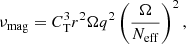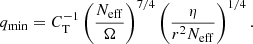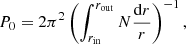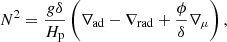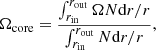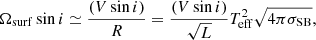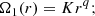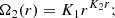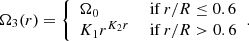| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346548 | |
| Published online | 24 August 2023 | |
Angular momentum transport by magnetic fields in main-sequence stars with Gamma Doradus pulsators
1
Observatoire de Genève, Université de Genève, 51 Ch. Pegasi, 1290 Versoix, Switzerland
e-mail: facundo.moyano@unige.ch
2
Université de Toulouse, CNRS, UPS, CNES, 14 avenue Édouard Belin, 31400 Toulouse, France
Received:
30
March
2023
Accepted:
30
June
2023
Context. Asteroseismic studies show that cores of post-main-sequence stars rotate more slowly than theoretically predicted by stellar models with purely hydrodynamical transport processes. Recent studies of main-sequence stars, particularly Gamma Doradus (γ Dor) stars, have revealed the internal rotation rates for hundreds of stars, offering a counterpart on the main sequence for studies of angular momentum transport.
Aims. We investigate whether such a disagreement between observed and predicted internal rotation rates is present in main-sequence stars by studying angular momentum transport in γ Dor stars. Furthermore, we test whether models of rotating stars with internal magnetic fields can reproduce their rotational properties.
Methods. We computed rotating models with the Geneva stellar evolution code taking into account meridional circulation and shear instability. We also computed models with internal magnetic fields using a general formalism for transport by the Tayler-Spruit dynamo. We then compared these models to observational constraints for γ Dor stars that we compiled from the literature, thus combining the core rotation rates, projected rotational velocities from spectroscopy, and constraints on their fundamental parameters.
Results. We show that combining the different observational constraints available for γ Dor stars enable us to clearly distinguish the different scenarios for internal angular momentum transport. Stellar models with purely hydrodynamical processes are in disagreement with the data, whereas models with internal magnetic fields can reproduce both core and surface constraints simultaneously.
Conclusions. Similarly to results obtained for subgiant and red giant stars, angular momentum transport in radiative regions of γ Dor stars is highly efficient, in good agreement with predictions of models with internal magnetic fields.
Key words: asteroseismology / stars: rotation / stars: interiors / stars: evolution / stars: variables: S Doradus / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Main-sequence (MS) stars are some of the most studied objects in stellar physics. They are numerous, long-lived, and can be found in all types of stellar systems, from binary stars to galaxies. They represent the longest evolutionary phase until they end their lives and become either compact objects or leave no remnant behind, depending on their initial masses. Their accurate characterisation allows us to infer fundamental information, such as ages, masses, and chemical compositions, which are of great importance to other fields from exoplanetary studies to galactic archaeology. This in turn requires accurate stellar structure and evolution models. However, despite our detailed understanding of MS stars there are still many details of their structure still under debate. One current issue in our understanding of stellar interiors in MS stars is the transport of angular momentum (AM). An accurate physical description of AM transport in stellar interiors is crucial to make predictions based on stellar models due to the transport of chemical elements arising from rotational instabilities; this is particularly relevant for massive stars (e.g., Maeder & Meynet 2000). Other long-standing problems remain unsolved, such as convective overshooting, which is thought to be due to the penetration of convective matter beyond the limits imposed by classical convection criteria and is necessary to explain several features from low- to high-mass stars (e.g., Claret & Torres 2019; Martinet et al. 2021). Due to the complex interplay between AM transport, rotational mixing, and other uncertainties such as convective overshooting, it is fundamental to characterise the AM redistribution in stellar interiors.
Thanks to the continuous developments of asteroseismology it is now possible to obtain information about stellar interiors and in particular measurements of internal rotation rates (e.g., Aerts 2021). Thanks to space-borne missions, detailed asteroseismic studies were made possible for a large number of stars in different evolutionary phases and mass-ranges leading to the measurement of rotation rates in stellar interiors (Aerts et al. 2003; Mosser et al. 2012; Deheuvels et al. 2012, 2014, 2015, 2020; Van Reeth et al. 2016; Pápics et al. 2017; Gehan et al. 2018; Tayar et al. 2019; Ouazzani et al. 2019; Li et al. 2020; Garcia et al. 2022). These space missions include CoRoT (Baglin et al. 2009), Kepler (Borucki et al. 2010), TESS (Ricker et al. 2015), and in the future PLATO (Rauer et al. 2014), and they provided us with long and continuous photometry which made possible the characterisation of several pulsation modes for single stars and unprecedented frequency resolution. This would otherwise be difficult to obtain from ground-based observations. In particular, for MS stars this made possible the exploitation of gravity modes, which are known to have relatively long periods compared to pressure modes. These modes are mainly sensitive to the inner regions of MS stars, and thus can give us critical information about their internal structure.
Regarding the theoretical modelling of AM transport in stellar interiors, a first hint of an improper treatment was evidenced by the solar rotation profile. Hydrodynamical processes transport insufficient AM and cannot account for it (Pinsonneault et al. 1989; Chaboyer et al. 1995; Charbonnel & Talon 2005; Eggenberger et al. 2005). This challenges the view of AM transport driven solely by meridional currents and hydrodynamical turbulent processes (Zahn 1992), which were employed in extensive grids of stellar models with rotation (e.g., Ekström et al. 2012). A similar conclusion was obtained for evolved stars, in particular for red giants (Eggenberger et al. 2012; Marques et al. 2013; Ceillier et al. 2013; Moyano et al. 2022). As a consequence, several studies were done to identify an additional process able to transport AM more efficiently and assess its impact on the internal AM redistribution. Some of these processes include small-scale internal magnetic fields (Spruit 2002; Cantiello et al. 2014; Fuller et al. 2019; Eggenberger et al. 2022b), internal gravity waves (e.g., Charbonnel & Talon 2005; Fuller et al. 2014; Pinçon et al. 2017), transport by mixed modes (Belkacem et al. 2015a,b), pumping of AM from convective envelopes (Kissin & Thompson 2015), and magneto-rotational instabilities (e.g., Wheeler et al. 2015; Spada et al. 2016; Griffiths et al. 2022; Moyano et al. 2023), among others. However, despite a great deal of effort, none of them has yet given a satisfactory answer, pointing to a general misunderstanding of the problem.
Among the MS stars, one interesting group of stars for AM studies are the Gamma Doradus (γ Dor) stars, which are variable late F- to early A-type stars. Their pulsation periods are typically P ≃ 1 day, but can range from P ≃ 0.3 to P ≃ 3 days and correspond to high-order non-radial gravity modes. They are found at effective temperatures of Teff ≃ 6700 − 7900 K, surface gravities of log g ≃ 3.9 − 4.3 dex, and slightly subsolar metallicities, and belong mainly to the MS (Kaye et al. 1999; Tkachenko et al. 2013). Their masses are M ≃ 1.4 − 2.0 M⊙, and they are thus expected to have a convective core surrounded by an extensive radiative region and a shallow convective envelope.
Gravity modes (g-modes) are sensitive to the properties of the regions close to the stellar core. For a non-rotating homogeneous star with a convective core and a radiative envelope, high radial order gravity modes of the same angular degree are expected to be equally spaced in period (Tassoul 1980). In particular, Miglio et al. (2008) showed how the internal stratification of chemicals and entropy can lead to differences in the period spacing (ΔP), defined as the difference in period between modes of consecutive radial orders but the same angular and azimuthal degrees. Bouabid et al. (2013) further studied the effects of rotation and chemical mixing, showing that the period spacing changes with the pulsation period when rotation is taken into account. This was further pursued by Ouazzani et al. (2017) who showed how rotation can induce a slope in the period spacing pattern (defined as the relation between the pulsation periods and the period spacing of subsequent radial modes of same angular degree) of g-modes and showed that it is mainly sensitive to the rotation rate of the star. Furthermore, Christophe et al. (2018) developed a method based on the traditional approximation of rotation with which the near-core rotation rate can be obtained by exploiting the properties of high-order g-modes. This methodology was then applied to a sample of 37 stars by Ouazzani et al. (2019), who then obtained their near-core rotation rates (see also Van Reeth et al. 2016). They further studied the internal AM transport due to hydrodynamical processes under different assumptions, concluding that a more efficient process should be present in stellar interiors of MS stars. Later on, Li et al. (2020) studied a larger sample of γ Dor stars and obtained their near-core rotation rates for 611 of them, among other asteroseismic parameters. However, it remains unclear how efficient during the MS the AM transport should be, and if it is consistent with constraints obtained for other stars, in particular regarding transport by the magnetic Tayler instability.
In this paper we study the role of AM transport by internal magnetic fields in MS stars taking advantage of a large sample of γ Dor stars with well-characterised rotational constraints. In particular we combine internal rotation rates measured with asteroseismic techniques, and surface rotational velocities from spectroscopic studies.
The paper is organised as follows. In Sect. 2 we describe the data collected from the literature, and in Sect. 3 we describe the input physics used in our models and the indicators used for comparison with observations. In Sect. 4 we present the various comparisons made with observational data, and discuss the uncertainties present in models that could impact our conclusions in Sect. 5. We provide additional evidence to our analysis in Sect. 6 and discuss our results in the context of more evolved stars in Sect. 7. We summarise and conclude in Sect. 8.
2. Data: Fundamental parameters, core rotation rates, and surface velocities
Our study of internal AM redistribution mainly relies on the sample of γ Dor stars provided by Li et al. (2020), which contains 611 stars with measurements of their core rotation rate. They also provide measurements of the buoyancy radius which we use as a proxy for the evolution during the MS (see Sect. 3.2). In addition to this, since the whole sample of stars lies in the Kepler field, the effective temperature and metallicities are available from the Kepler catalogue of revised stellar properties (Mathur et al. 2017). The distribution of metallicities is shown in Fig. 1, its mean value is [Fe/H] = −0.127 dex with a standard deviation of σ[Fe/H] = 0.191 dex. Approximately 75% of our stars have metallicities between [Fe/H] = −0.3 and [Fe/H] = −0.1 dex (see Fig. 1). We note that we adopt a slightly lower metallicity than the value adopted previously by Ouazzani et al. (2019), who used [M/H] = 0.11 ± 0.17 dex. The cause of this difference was discussed by Gebruers et al. (2021) and is likely due to issues related to the continuum fit in the sample of Van Reeth et al. (2016), which was used by Ouazzani et al. (2019). However, this difference in metallicity does not have a major impact on the conclusions regarding AM transport.
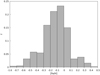 |
Fig. 1. Normalised distribution of metallicities of γ Dor stars used in this work. The histogram contains 572 stars with metallicities from Mathur et al. (2017). The leftmost bin contains all the outliers with [Fe/H] between −1.6 and −0.7 dex. The mean value of the sample is |
In addition to the constraints mentioned above, the bolometric luminosities for nearly all of the γ Dor stars in our sample were determined by Murphy et al. (2019), who rederived the distances for nearly all of them (575 out of 611) based on the parallaxes from Gaia DR2 (Gaia Collaboration 2016). They also gave an estimate of the stellar masses for 575 stars in our sample by comparing stellar evolutionary tracks to the data based on the effective temperatures, bolometric luminosities, and metallicities. This provided us with a distribution of the stellar masses, which we show in Fig. 2, and thus we can make an accurate choice for the initial masses of our models. A Hertzsprung–Russell (HR) diagram comparing our models with rotation computed at Z = 0.01 and the observational data is shown in Fig. 3. We note that although the expected mass range of γ Dor stars is M = 1.4 − 2.0 M⊙, a few stars have inferred masses higher than M = 2.2 M⊙. This could probably occur because of the single-metallicity stellar tracks used by Murphy et al. (2019) and the fact that some stars have quite low metallicities (see Fig. 1), which would mimic a star of lower metallicity but higher mass in the HR diagram, among other possible effects. After removing these stars, the mean value of the stellar mass averaged over the whole sample is M = 1.51 ± 0.14 M⊙.
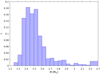 |
Fig. 2. Normalised distribution of stellar masses of γ Dor stars used in this work. The histogram contains 504 stars with masses determined by Murphy et al. (2019). The rightmost bin contains all the outliers with masses between 2.2 and 2.7 M⊙. The mean value of the sample is |
 |
Fig. 3. Hertzsprung–Russell diagram of our models. The data points correspond to the γ Dor stars studied in this work from Li et al. (2020); the points are semi-transparent to illustrate the number density when two or more stars overlap. The typical uncertainty on effective temperature and luminosity is shown in the figure. The stellar models are computed from the ZAMS with an initial metallicity of Z = 0.01 and an initial rotation rate Ω/2π = 20 μHz (no magnetic fields); initial masses are indicated in solar masses for each track. |
To obtain more information on the AM content of our sample of γ Dor stars, we also made a compilation of projected surface rotational velocities (V sin i), determined from medium- to high-resolution spectra from the literature. This gave us information on the AM content both in the core and at the surface for a subsample of our stars, which is a fundamental point in our study. Our subsample of stars with determined surface velocities mainly comes from the study of Gebruers et al. (2021), who determined V sin i for 88 of our stars with high-resolution spectra taken with the HERMES spectrograph (Raskin et al. 2011) and whose resolution reaches R ≃ 85 000. The rest of the stars come from either individual studies or cross-matches with surveys. These include three stars from Van Reeth et al. (2015): KIC5254203, KIC6468987, and KIC9480469; three stars from individual studies: KIC8975515 (Samadi-Ghadim et al. 2020), and KIC10080943A,B (Schmid et al. 2015; Schmid & Aerts 2016); two stars from LAMOST-DR7-MRS (Liu et al. 2020; Luo et al. 2022): KIC8495755 and KIC7448050; five stars from Sun et al. (2021): KIC6780397, KIC7761855, KIC7202395, KIC8759258, and KIC9598448; and three stars from Frasca et al. (2022): KIC9348946, KIC6366512, and KIC7436266. The stars studied by Luo et al. (2022), Sun et al. (2021) and Frasca et al. (2022) come from medium-resolution spectra with a spectral resolution of R ≃ 7500, namely the LAMOST-MRS1 (Liu et al. 2020). For the surface velocities determined from medium-resolution spectra we only chose those stars that were observed with a signal-to-noise ratio higher than one hundred (S/N > 100). Although KIC9598448 has a S/N = 98.6, we decided to include it in our sample. When there is an overlapping star in any of these surveys with the sample of Gebruers et al. (2021), we decided to use the parameters given by these authors due to the higher resolution of the spectra used in their work. Thus, our subsample of stars for which we have both core rotation rates and projected surface rotational velocities contains 104 stars. We note that the measurements of both quantities were obtained with completely different techniques and that we do not make any assumption on any of these quantities.
3. Physical ingredients of stellar models and asteroseismic observables
We compute all of our models with the Geneva stellar evolution code (GENEC; Eggenberger et al. 2008). This code was extensively used to compute grids of models of rotating stars in different mass ranges and metallicities (Ekström et al. 2012; Georgy et al. 2013; Eggenberger et al. 2021; Yusof et al. 2022). Here we mention only the relevant initial conditions and equations for the treatment of AM transport and we refer the reader to the mentioned works for a detailed description of the code and usual input physics adopted.
The mean value of the metallicity distribution given by the data (see Fig. 1) is ![$ \overline{\mathrm{[Fe/H]}} = -0.127 $](/articles/aa/full_html/2023/09/aa46548-23/aa46548-23-eq3.gif) , with a standard deviation of σ[Fe/H] = 0.191 dex, which corresponds to Z ≃ 0.0106 ± 0.0040 in our models. We thus chose an initial metallicity of Z = 0.01 for our models, adopting the chemical mixture of heavy elements from Asplund et al. (2009). We computed the evolution of all of our models from the zero age main sequence (ZAMS) where we assume constant angular velocity along the interior as an initial condition. The initial velocities were chosen to reproduce the range in core rotation rates observed for γ Dor stars at high buoyancy radius that should then be young MS stars. The values chosen are Ω/2π = 10, 20, and 30 μHz, which correspond to surface velocities of V ≃ 60, 120, and 200 km s−1 for our 1.5 M⊙ models at Z = 0.01. These velocities correspond to 16, 32, and 50%, respectively, of their critical velocities at the ZAMS (i.e. the rotational velocities at which the centrifugal force due to rotation counteracts the surface gravity). We adopted an extension of the convective core by the step overshooting formalism (i.e. the overshooting region is assumed to mix instantaneously), and so we chose to extend the convective core by 0.05 times the local pressure scale height Hp for masses 1.25 ≤ M/M⊙ ≤ 1.7 and r = 0.1Hp for masses M > 1.7 M⊙.
, with a standard deviation of σ[Fe/H] = 0.191 dex, which corresponds to Z ≃ 0.0106 ± 0.0040 in our models. We thus chose an initial metallicity of Z = 0.01 for our models, adopting the chemical mixture of heavy elements from Asplund et al. (2009). We computed the evolution of all of our models from the zero age main sequence (ZAMS) where we assume constant angular velocity along the interior as an initial condition. The initial velocities were chosen to reproduce the range in core rotation rates observed for γ Dor stars at high buoyancy radius that should then be young MS stars. The values chosen are Ω/2π = 10, 20, and 30 μHz, which correspond to surface velocities of V ≃ 60, 120, and 200 km s−1 for our 1.5 M⊙ models at Z = 0.01. These velocities correspond to 16, 32, and 50%, respectively, of their critical velocities at the ZAMS (i.e. the rotational velocities at which the centrifugal force due to rotation counteracts the surface gravity). We adopted an extension of the convective core by the step overshooting formalism (i.e. the overshooting region is assumed to mix instantaneously), and so we chose to extend the convective core by 0.05 times the local pressure scale height Hp for masses 1.25 ≤ M/M⊙ ≤ 1.7 and r = 0.1Hp for masses M > 1.7 M⊙.
3.1. AM transport: Hydrodynamical processes and internal magnetic fields
To follow the redistribution of internal AM, we obtained the angular velocity at each layer of the stellar interior under the shellular approximation (Zahn 1992). While in convective zones we assume uniform rotation, in radiative zones the AM transport is treated in an advecto-diffusive way (Zahn 1992), by solving the equation
where r is the radial coordinate, ρ is the density, Ω is the horizontally averaged angular velocity, Ur is the radial component of the meridional circulation velocity, and D is the diffusion coefficient of AM. In our work we consider two types of models: purely hydrodynamical and magneto-hydrodynamical. The former includes only hydrodynamical transport of both AM and chemicals, specifically driven by the shear instability and meridional currents (Zahn 1992). The latter includes the hydrodynamical processes, but also the transport by internal magnetic fields following the formalism of the Tayler-Spruit (TS) dynamo (Spruit 2002) in its calibrated version to reproduce asteroseismic rotation rates of evolved stars (Eggenberger et al. 2022b).
For models without internal magnetic fields, in addition to advective transport by meridional circulation, the diffusive transport by the shear instability is taken into account and the diffusion coefficient is then D = Dshear, following Maeder (1997). For the models with internal magnetic fields, the transport of AM is implemented as an additional source of viscosity which we compute as (Eggenberger et al. 2022b)
where q≡∂lnΩ/∂lnr is the local shear; Neff the effective Brunt–Väisälä frequency, defined as 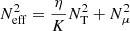 with η the magnetic diffusivity; K the thermal diffusivity; and NT and Nμ the thermal and chemical components. Finally, CT = 216 is a constant that was calibrated to reproduce the core rotation rate of evolved stars (see Eggenberger et al. 2022b). This viscosity is added to the diffusion coefficient, hence the total diffusion coefficient of AM transport is D = Dshear + νmag in our models with internal magnetic fields. The magnetic instability is triggered when the local shear is above a critical value given by
with η the magnetic diffusivity; K the thermal diffusivity; and NT and Nμ the thermal and chemical components. Finally, CT = 216 is a constant that was calibrated to reproduce the core rotation rate of evolved stars (see Eggenberger et al. 2022b). This viscosity is added to the diffusion coefficient, hence the total diffusion coefficient of AM transport is D = Dshear + νmag in our models with internal magnetic fields. The magnetic instability is triggered when the local shear is above a critical value given by
3.2. Evolutionary indicator during the main sequence
Similarly to Ouazzani et al. (2019), we used the buoyancy radius P0 as an evolutionary indicator during the MS. We compute the buoyancy radius in our stellar models as
where N is the Brunt–Väisälä frequency, r is the radial coordinate, and rin and rout are respectively the lower and upper limits of the g-mode cavity. We define the g-mode cavity as the region where the frequency of a high radial order mode, which we take as k = −25, is lower than both the Brunt–Väisälä and Lamb frequencies for dipole modes.
As shown by Ouazzani et al. (2019), the buoyancy radius decreases during the MS in the mass range M = 1.4 − 1.8 M⊙, suitable for γ Dor stars (see their Fig. 2). This occurs because it depends mainly on the size of the convective core and on both thermal and chemical stratification in the radiative layers just above it, which change through evolution because of the hydrogen burning and either expansion or contraction of the inner radiative regions. This can modify the value of the buoyancy radius because it changes the chemical stratification in the near-core regions, specially if the core is retreating. This can be seen by writing the Brunt–Väisälä frequency as
where ∇μ ≡ ∂lnμ/∂lnP is the value of the chemical gradient, ∇rad is the temperature gradient, ∇ad is the adiabatic temperature gradient, g is the local gravity, and ϕ ≡ (∂lnρ/∂lnμ)P, T and δ ≡ −(∂lnρ/∂lnT)P, μ. As shown by Eq. (5), the Brunt–Väisälä frequency depends on the entropy stratification, via the thermal and adiabatic gradients, and on the chemical stratification, via the chemical gradient. We use the buoyancy radius as an evolutionary indicator during the MS, taking advantage of the measurements provided by Li et al. (2020).
3.3. Rotation rate in the gravity-mode cavity
The core rotation rates used in this work are not those of the convective core, but rather an average rotation rate over the g-mode cavity (usually denoted near-core); to compare our models with the data, we computed the near-core rotation rate from our models as (Ouazzani et al. 2019)
where the limits of the integrals are the same as for the buoyancy radius and denote the g-mode cavity. This variable represents the near-core rotation rate as sensed by the gravity modes, which we used to compare to the rotation rates available in our sample. In the following sections we refer to it as the core rotation rate.
4. Models and comparison with data
4.1. Core rotation rate
In our models two physical scenarios are considered (see Sect. 3). In the first transport only by hydrodynamical processes is examined, and in the second we also consider internal magnetic fields. In the following figures and discussion we refer to them as rotation-only and rotation+magnetic fields, respectively. In Fig. 4 we show the core rotation rate as a function of the buoyancy radius for a subset of our models with initial masses of M = 1.5, 1.7, and 1.9 M⊙ and initial rotation rates of Ωcore/2π = 10, 20, and 30 μHz, compared with the data available for our sample of γ Dor stars. In these figures we only include stars for which the uncertainty of the buoyancy radius is less than σP0 = 500 s; models are computed from the ZAMS and the evolution goes from left to right. Both types of models have a decreasing core rotation rate during a large part of the MS, as evidenced by the wide range in buoyancy radius during which the core spins down. However, internal magnetic fields lead to a faster spin down of the core right from the beginning of the evolution, erasing the initial spin-up seen in rotation-only models. In addition, internal magnetic fields lead to a much lower core rotation rate towards the end of the MS, and a rather constant behaviour, while in rotation-only models the core spins up by ∼50% and reaches much higher rates. Because of this, models with internal magnetic fields are in better agreement with the data since there are no fast rotators observed at low buoyancy radii. The upper envelope of the distribution of core rotation rates is also better reproduced when internal magnetic fields are included. Although we cover the mass-range expected for γ Dor stars, the dependence on stellar mass in our models is weak. All this evidence supports the hypothesis of highly efficient AM transport during the MS.
 |
Fig. 4. Core rotation rate as a function of buoyancy radius for models with different initial masses. Left: AM transport driven by hydrodynamical processes alone. Right: same, but including internal magnetic fields. The data points correspond to the γ Dor stars presented by Li et al. (2020). For each initial mass are shown models starting at an initial rotation rate of Ωcore/2π = 10, 20 and 30 μHz. Models are computed from the ZAMS and the evolution goes from left to right. |
4.2. Surface rotational velocity
Since we have a good measurement of the surface rotational velocity for 104 stars in our sample of γ Dor stars, we can also study the evolution of the surface velocity using the buoyancy radius as an evolutionary indicator; the comparison with our models is shown in Fig. 5. The surface velocity of our models is multiplied by a factor π/4 to average over the unknown inclination angle of the observed stars. The factor is equal to the mean value of ⟨sin i⟩, where i is the inclination angle, assuming an isotropic distribution of inclination angles whose probability distribution function is just P(i) = 2π sin i di (Gray 2005).
 |
Fig. 5. Surface rotational velocity as a function of buoyancy radius. The lines correspond to our models with different initial masses, computed at three different initial rotation rates for each initial mass. Left: driven by hydrodynamical processes alone. Right: same, but including internal magnetic fields. The data points correspond to γ Dor stars for which surface velocities are available from the literature (see Sect. 2); buoyancy radii are taken from Li et al. (2020). The surface velocity of the models is multiplied by π/4 to average over the unknown inclination angles of the stars. |
The behaviour of the surface velocities when including internal magnetic fields is opposite to what is seen in Fig. 4 for the rotation rate of the core. Compared to models with only hydrodynamical instabilities, internal magnetic fields lead to higher surface velocities, but the opposite occurs for the core (see Figs. 4 and 5); the core spins more slowly when internal magnetic fields are included. This occurs because internal magnetic fields transport AM efficiently from the core to the surface, increasing the surface angular velocity, and hence (partially) counteracting the progressive slowdown due to the increase in radius during the MS. While rotation-only models have a decreasing surface velocity during most of the evolution, models with internal magnetic fields show a slight increase in the surface velocity at the beginning of their evolution, seen at high buoyancy radii. This mirrors the behaviour of the core when no internal magnetic fields are included (see left panel of Fig. 4); in models with internal magnetic fields, the AM transport is so efficient that the core and surface are coupled, and hence rotate at nearly the same angular velocity through evolution.
There is a lack of fast rotators at low buoyancy radii, which means that in our sample evolved stars are either not observed or do not reach high surface velocities. Still, it remains difficult to definitely conclude from Fig. 5 that models with internal magnetic fields are clearly favoured over models with only hydrodynamical processes.
4.3. Combining surface and core information: Spectroscopic rotational velocities
In the previous sections we presented our individual study of the core rotation rate and surface velocities as a function of the buoyancy radius in models with purely hydrodynamical processes and models with internal magnetic fields, and then compared their rotational properties to the observational data. The effects of internal magnetic fields on the AM redistribution through the MS are illustrated in Fig. 6 for a 1.5 M⊙ model computed with an initial metallicity of Z = 0.01, which closely represents the properties of the γ Dor stars studied in this work (see Figs. 1–3). Now we use our sample of 104 stars for which we have constraints on surface rotational velocities, core rotation rates, and buoyancy radii to distinguish between our two types of models. To do this, we present the diagram of surface velocity as a function of the core rotation rate, containing the data available from our compilation and our models with only hydrodynamical transport of AM, and models which also include internal magnetic fields. We show this diagram in Fig. 7 for models with an initial mass of M = 1.5 M⊙ and three initial rotation rates of Ωcore/2π = 10, 20, and 30 μHz. The models are shifted vertically by multiplying by π/4 the surface velocities to average over the unknown inclination angle of the stars. In this diagram the two types of models start their evolution at the same point, but right from the beginning they evolve in different directions; this is a consequence of the opposite behaviour in core rotation rates and surface velocities obtained when internal magnetic fields are included (see Fig. 6 and Sect. 4.2). We also use the values of the buoyancy radius to highlight the region of the evolutionary tracks that are in agreement with the mean values of the buoyancy radii of the sample of γ Dor stars studied. This is shown by the solid lines, which show the part of the track where the buoyancy radius is P0 = 4092 ± 575 s, where the values correspond to the mean and the standard deviation of the sample, while the dashed lines correspond to buoyancy radii outside of that interval.
 |
Fig. 6. Effect of internal magnetic fields on the redistribution of AM during the MS (evolution goes from left to right). Left: core rotation rate. Right: surface rotational velocity. The surface velocity of the models are multiplied by a factor π/4 to average over the unknown inclination angles of the sample. The models have an initial mass and metallicity of M = 1.5 M⊙ and Z = 0.01, and are computed at three different initial velocities. The data points in the right panel are contained in the data set of the left panel. |
Our models with purely hydrodynamical transport first evolve towards the right, increasing the core rotation rate until a turning point to then evolve towards the left, decreasing their core rotation rate. This behaviour is also seen in the left panel of Fig. 4. Their surface rotational velocity also decreases quite rapidly, which is the reason why, for example for the models with an initial rotation rate of Ωcore/2π ≃ 30 μHz, the first part of the track does not satisfy the constraints on the buoyancy radii. As mentioned in Sect. 4.2, the surface velocity of rotation-only models decreases during most of the MS. It only increases towards the very end of the MS when the core hydrogen content is very low (Xcore ≲ 0.05), and due to the low energy provided by the nuclear reactions in the core the whole star contracts, increasing both surface rotational velocities and core rotation rates. This is why the tracks move upwards and to the right when they approach the end of the MS, and it coincides with the ‘hook’ seen in HR diagrams (see Fig. 3).
Our models with internal magnetic fields start their evolution in the opposite direction, both in core rotation rate and surface velocity. The models evolve to the left because the core rotation rate decreases almost monotonically until the star contracts due to the low central hydrogen content, close to the end of the MS. After this point, the core spins up imperatively since the whole star contracts, but since in this type of model the core and surface are strongly coupled, the spin-up is not so strong as in rotation-only models. Since magnetic models remain more coupled, their surface velocity does not change as much as in models without internal magnetic fields. As mentioned before, this occurs because the extraction of AM from the core to the surface counteracts the slowdown in surface velocity due to the radius’ expansion during the MS. Towards the end of the MS, just after the hook usually seen in the HR diagram, the surface contracts rapidly, leading to a sudden increase in the surface velocity, which is always present in our models irrespective of the efficiency of the internal AM transport.
This roughly describes the reasons of the evolution in opposite directions in the diagram presented in Fig. 7. For the comparison with data, we note that most of the stars lie along a diagonal, indicating that the core rotation rate of the stars is well correlated with their surface rotational velocity. By comparing the behaviour of our rotation-only models we can discard an inefficient transport of AM since the models cannot reproduce the data for any initial rotation rate assumed. This occurs first because the core rotation rate increases at the beginning of the evolution, moving them away from the diagonal traced by the data, but also because the surface velocity decreases during most of the evolution, causing the models to fall below the diagonal. This illustrates the importance of combining different indicators that can also trace the structural evolution of the stars. On the contrary, models with internal magnetic fields can reproduce the data because of the combined effect of a strong spin down of the core and little change in surface velocity, which result from the highly efficient AM transport by internal magnetic fields.
 |
Fig. 7. Projected surface rotational velocity as a function of core rotation rate. The lines correspond to models with an initial mass of M = 1.5 M⊙ and initial metallicity Z = 0.01 shown only during the main sequence, computed with initial rotation rates of Ωcore/2π = 10, 20, and 30 μHz, starting at the ZAMS. The blue and red lines indicate the type of AM transport assumed in each model: only hydrodynamical processes (red) or including internal magnetic fields and hydrodynamical processes (blue). The data points are γ Dor stars with constraints available from the literature (see Sect. 2). The solid lines represent the regions where the buoyancy radius of the models is in agreement with the mean values of the sample. |
We note however that this kind of diagram was already presented by Van Reeth et al. (2018, see their Fig. 7), but was not discussed in evolutionary terms. The behaviour seen for the data in Fig. 7 is striking at first because we have to take into account that the inclination angle poses an uncertainty and should thus produce some random scatter along the natural relationship between the two quantities. Although some stars fall below the diagonal, which could be explained by low inclination angles, the scatter remains weak. This could be also a bias towards high inclination angles as a product of selecting stars that show measurable rotational velocities by means of spectral lines broadening, and detectable g-modes in Kepler light curves. According to Li et al. (2020) the detected modes are mostly sectoral, supporting the fact that probably the scatter in inclination angles is lower than expected from an isotropic distribution. However, even considering that all stars are seen exactly equator-on, models with inefficient transport of angular momentum would be in disagreement with data.
This shows that a highly efficient AM transport is at work during the MS evolution of these stars, such that little to no differential rotation in radiative regions can develop through the whole MS. As we discuss in Sect. 5, this conclusion is obtained independently from the different uncertainties in the input physics used in stellar models.
4.4. Combining surface and core information: Surface rotation rates
Another way to investigate the AM redistribution is by combining projected surface rotational velocities from spectroscopy (V sin i), effective temperatures (Teff), and bolometric luminosities (L). These parameters are available and were obtained with good accuracy for the sample of stars presented in Sect. 2. By combining these parameters, we can estimate the surface rotation rate of the stars as
where Ωsurf is the surface rotation rate of the star and the rest of the symbols have their usual meaning. The stellar radii are then estimated using the luminosities provided by Murphy et al. (2019). Since accuracy is important in this case, we choose the effective temperatures provided by the individual works mentioned in Sect. 2, which were all obtained from medium- to high-resolution spectra. This is because the effective temperature of several of the stars provided by Mathur et al. (2017) were originally estimated with photometric magnitudes and served as input values for the Kepler input catalog (Brown et al. 2011); in some other cases the effective temperature present in that catalogue was taken from results coming from low-resolution spectra (e.g., LAMOST-DR1 Luo et al. 2015). In addition to these choices to compute the stellar radius of the stars in our sample, when available, we used the radius obtained by Mombarg et al. (2021) for 37 of our stars. Hence, we argue that the data presented in this section are accurate and representative of the typical properties of γ Dor stars. We note that for most of the stars presented in this section, the effective temperatures are provided by Gebruers et al. (2021), which were obtained with high-resolution spectra and comprise a homogeneous sample.
In this way we can compare surface-rotation rates with core-rotation rates for the stars in our sample, which is shown in Fig. 8 along with our stellar models. The stars whose radius was derived by Mombarg et al. (2021) are shown by orange squares, and for the rest of the stars represented by circles the radius was computed with the usual black-body relation using Eq. (7). The inclination angle to obtain the exact surface rotation rate remains unknown. The error bars are estimated as the standard deviation with a standard propagation of errors neglecting correlations and taking into account the uncertainties in Teff, V sin i, and L. The data are distributed in a way similar to when comparing core rotation rates with surface rotational velocities; a fast-spinning core is usually related to a fast-spinning surface. Some stars show low surface-rotation rates with rather high core-rotation rates, which could be due to low inclination angles, and almost no stars appear to have a surface that rotates faster than its core. This is shown with the help of the one-to-one line, which would correspond to the location of solid-body rotating stars seen under inclination angles of i = 90°. Stars above the black line in Fig. 8 should have a surface rotating faster than its core, irrespective of its inclination angle. Below this line, stars could either have a core that rotates faster than its surface, with a maximum inclination angle of i = 90°, or could have a surface rotating faster than its core with an inclination angle depending on the rotation contrast between surface and core; for example, for a contrast of Ωsurf/Ωcore ≃ 1.5 an inclination angle of i ≲ 42° would suffice to move the points below the one-to-one line. There are 11 stars that seem to have a surface that rotates faster than its core, seen at both low and high rotation rates. Overall, most of the stars (∼90%) are found below the one-to-one line in Fig. 8, indicating that it is unlikely that in our sample of stars the surface spins faster than their core.
 |
Fig. 8. Surface rotation rates as a function of core rotation rate. The surface rotation rates are obtained by dividing the projected rotational surface velocities by the radius of each star. The dots represent the data set used in this work (see Sect. 2), while the red and blue lines have the same meaning as in Fig. 7, and the black line shows the one-to-one relation. |
In Fig. 8 we show the same stellar models as presented in Fig. 7. The meaning of the different colours and types of lines is the same. The surface rotation rate of the models is also multiplied by a factor π/4 to average over the unknown inclination angles of the stars. Our models with purely hydrodynamical transport (red lines) develop differential rotation during the evolution with a core that rotates faster than its surface, and is the reason why the tracks extend both horizontally and vertically in this diagram. On the other hand, models with internal magnetic fields lie along a diagonal line because the angular velocity in these models is almost uniform, and so they lie along a line of rigid rotation whose slope is determined by the inclination angle assumed. More specifically, what we compare here is the mean rotation rate of the g-mode cavity with the rotation rate at the stellar surface. This means that in these models the angular velocity in the radiative interior is nearly constant. In particular, models with internal magnetic fields would always lie along a diagonal irrespective of their masses because in this figure we compare the rotation rates, so the change in radius due to different masses or metallicities is not seen.
Taking into account this information provided by the models, and since most of the stars lie along a narrow diagonal band, we can interpret this as very efficient AM transport during the evolution. The spread would correspond to different inclination angles, while the diagonal line traced by our model with internal magnetic fields would correspond to an inclination of i ≃ 52°. Otherwise, if models developed strong differential rotation during the evolution, we would expect to see more stars in the lower right part of this diagram as not only the effect of the inclination angle would contribute to populate it, but also the evolution of stars with different properties (such as masses, metallicities, initial velocities) would contribute to populate it. However, this region of the diagram is very weakly populated, which we interpret as evidence against models that develop strong differential rotation during the evolution, and hence against our models with purely hydrodynamical transport. In addition to this, we recall that all the stars studied here are g-mode pulsators and the visibility of the modes is not the same under different inclination angles. Nearly all stars presented in Figs. 7 and 8 are pulsating in sectoral modes, and as pointed out by Li et al. (2020), dipole prograde modes (ℓ = 1, m = 1) have the largest observed amplitudes. This would support the fact that the stars are rather seen at high inclination angles since those modes have larger amplitudes at high inclination angles (Dziembowski et al. 2007). This provides further support to an efficient transport process of AM in stars during the MS.
5. Uncertainties in stellar modelling
Although our study supports the idea of a physical process able to transport AM very efficiently during the MS, we are aware that many uncertainties can impact the properties of stellar models. And even if they are not related to the transport of AM itself, due to the nature of our interdisciplinary study, it could lead to incorrect conclusions. We summarise here the possible uncertainties and their impact on our conclusions.
5.1. Overshooting
One fundamental quantity in the modelling of MS low-mass stars with M ≳ 1.2 M⊙ is the size of their convective core. It determines the luminosity of the star and hence its radius; a larger convective core leads to a more luminous star. Even so, it is an uncertain quantity and many studies point out a discrepancy between data and models computed with the standard Schwarzschild criterion of convection (see e.g., Claret & Torres 2016). To overcome this discrepancy, stellar modellers usually extend the size of the convective core to account for an unknown mixing process between the convective core and radiative regions above it. In our models we extend the size of the convective core by 0.05Hp in our 1.5 M⊙ models and 0.1Hp for M > 1.7 M⊙ adopting the step overshooting formalism. This proved to be a good fit for the observed width of open clusters in previous grids of models (e.g., Ekström et al. 2012). To explore the possible impact of a larger convective core, we recomputed models with an increased overshooting strength of 0.2Hp, which is a large value for the range of stellar masses considered in this work. Its effect on the evolution of the core rotation rate as a function of the buoyancy radius is shown in Fig. 9 for our models with only hydrodynamical processes (red line) and models that also include internal magnetic fields (blue line). A larger overshooting strength leads to a higher buoyancy radius in both types of models and lower core rotation rates during the whole MS. However the evolution of the core rotation rate is not strongly affected. Models with internal magnetic fields still lead to lower core rotation rates towards the end of the MS, while models with purely hydrodynamical transport lead to high core rotation rates at low buoyancy radii. Although a stronger overshooting could help to reduce the core rotation rate of models without internal magnetic fields, it is not supported by the lack of high core-rotation rates at low buoyancy radii. On the other hand, models with internal magnetic fields have a similar behaviour overall, and even a strong increase in the overshooting does not lead to a disagreement with the data.
 |
Fig. 9. Same as Fig. 4, but showing the effect of the overshooting for models with transport only by hydrodynamical processes (red) and models that also include internal magnetic fields (blue). The solid lines correspond to models computed with an overshooting length of 0.05Hp, while the dashed lines have an overshooting length of 0.2Hp. The models have an initial mass of M = 1.5 M⊙. For clarity we only show models computed at two different initial rotation rates. |
We can also verify whether a more efficient overshooting can change our conclusions by comparing simultaneously the surface velocities and core rotation rates with our models. We show this comparison in Fig. 10 in the same way as in Fig. 9, but we include the model with an initial rotation rate of Ωcore/2π = 20 μHz. The models with a more efficient overshooting (dashed lines) can achieve lower surface velocities during the MS because a larger convective core leads to higher luminosities and hence larger radii. The models with a stronger overshooting can approach the diagonal traced by the data due to their lower core rotation rates (see Fig. 9). However, it is not enough for models without internal magnetic fields to reproduce the data. Thus, a different choice of the overshooting cannot counteract the lack of AM transport in models with meridional circulation and shear instabilities during the MS.
 |
Fig. 10. Same as Fig. 7, but showing the effect of overshooting for models with transport only by hydrodynamical processes (red) and models that also include internal magnetic fields (blue). The solid lines correspond to models computed with an overshooting length of 0.05Hp, while the dashed lines have an overshooting length of 0.2Hp. The models have an initial mass of M = 1.5 M⊙. |
5.2. Initial metallicity
In Fig. 1 we show the metallicity distribution of our sample, which we use to choose the initial metallicity of our main models as Z = 0.01. As discussed in Sect. 2, the distribution spans a range of possible values and leads to a small uncertainty. This does not change significantly the behaviour of our evolutionary tracks, or the exact values of the core rotation rate and the surface velocities. In Fig. 11 we show models in the V sin i − Ωcore diagram starting at initial metallicities of Z = 0.0072, 0.01, and 0.014, which correspond to [Fe/H] ≃ −0.3 to 0.
 |
Fig. 11. Same as Fig. 7, but showing effect of different initial metallicities. The cyan, blue, and light blue lines correspond to models computed with internal magnetic fields, whereas the magenta, red, and yellow lines correspond to models computed only with hydrodynamical processes, hence without internal magnetic fields. The models are computed with initial rotation rates of Ωcore/2π = 10, 20, and 30 μHz. The dashed and solid parts of the line have the same meaning as in Fig. 7. |
All models have an initial mass of M = 1.5 M⊙ and initial rotation rates of Ωcore/2π = 10, 20, and 30 μHz. Models with higher metallicities in general have higher initial surface velocities for a fixed initial rotation rate because the radius is larger at the ZAMS. This is why the models seem to be vertically shifted with respect to each other. This shows that the effect of the metallicity is limited (irrespective of whether internal magnetic fields are included) and cannot change the conclusions.
5.3. Initial distribution of AM
Since we compute all of our models from the ZAMS, we must make some assumptions about the initial distribution of internal AM. In our models we assume uniform rotation as an initial condition (i.e. solid-body rotation at the ZAMS). After a few Myr the rotation profile usually reaches an equilibrium state as a consequence of the advective currents and the diffusive turbulent transport by the shear instability, and so the initial conditions do not have a significant impact on the structural evolution; thus, for evolutionary purposes it is not a bad approximation. However, in our study the initial rotation profile is important because it defines the starting point in our V sin i − Ωcore diagram (e.g., Figs. 7 and 10). An initial rotation profile where the core rotates faster than the surface would shift the starting point downwards and to the right in Fig. 7. On the other hand, an initial rotation profile where the surface rotates faster than the core would shift it upwards and to the left.
An initial rotation profile at ZAMS where the core rotates faster than the surface appears to be the most plausible physical scenario (Haemmerlé et al. 2013). Nonetheless, the degree of differential rotation at the ZAMS cannot attain high values, achieving at most a rotation contrast between convective core (cc) and surface of Ωcc/Ωsurf ≃ 1.5 (Haemmerlé et al. 2013). This initial choice would worsen the disagreement between data and models with purely hydrodynamical transport because, as explained above, it would shift the starting point away from the diagonal traced by the data, and afterwards the evolution would be similar to a model starting with a uniform rotation profile. On the other hand, for models with internal magnetic fields the AM transport is so efficient that it returns practically instantaneously to its departure point of solid-body rotation and would follow afterwards a normal evolution. This brings more evidence against models where only hydrodynamical processes transport AM in MS stars.
If we now consider an initial rotation profile where the surface rotates faster than the core, the starting point in Fig. 7 could be shifted upwards and to the left. Under this assumption models without internal magnetic fields could potentially reproduce the data. However, such an initial rotation profile seems unlikely from a physical point of view, so we would expect stars to have rather shallow gradients at the ZAMS, which would then constrain the range of possible initial rotation contrasts in our models. To investigate this question, we constructed initial rotation profiles assuming different rotation laws. First, we employ a simple power law,
a profile with increasing positive shear towards the surface,
and a profile where solid-body rotation is assumed for ≃60% of the star and afterwards the increasing shear law is used,
The variables K, q, K1, K2, and Ω0 are constants that are fixed by the initial angular velocities at the convective core and surface. The rotation profiles are shown in Fig. 12 for three different initial ratios at the ZAMS. These rotation profiles could for example result from accretion of matter in (approximately) Keplerian orbits around the star; in this case even a relatively low content of matter (∼3 − 5 % of the stellar mass) can spin up the surface of the star to critical velocities (Packet 1981). These episodes of accretion could be for example the result of mass-transfer from a companion or accretion of a remnant disk, and depending on the efficiency of the AM redistribution in the near-surface layers, different slopes for the rotation profiles could be expected (e.g., Staritsin 2021). We note that in our framework this would be valid if the star already has a radiative envelope.
 |
Fig. 12. Rotation profiles given by Eqs. (8)–(10) at ZAMS for a 1.5 M⊙ model for three different initial rotation ratios between convective core and surface of Ωsurf/Ωcc = 1, 2, and 3 (dot-dashed, dashed, and solid lines, respectively). The bullets shown on the rotation profiles show the location where the angular velocity is equal to the mean value of the g-mode cavity computed with Eq. (6). |
Since the rotation rate probed by gravity modes is an averaged rotation rate outside of the convective core over the g-mode cavity, the shape of the rotation profile can change the near-core rotation rate computed with Eq. (6). This is illustrated in Fig. 12 by bullets over the rotation profiles; we show the location of the star where the angular velocity would equal the mean angular velocity of the g-mode cavity for each profile. For the flat profile no bullet is shown simply because the mean angular velocity is the same as in the whole star. This shows how the mean core rotation rate probed by g-modes strongly depends on the shape of the profile (but not the region probed) at the ZAMS. This is why it is not enough to consider only a different rotation contrast between the center of the star (i.e. the convective core) and surface at the ZAMS. To verify whether it is possible for our rotation-only models to start their evolution from the left part of the diagonal traced by the data (see Fig. 7) we recomputed both the mean core rotation rate with Eq. (6) and the surface rotational velocity using the structure of the models at the ZAMS for the different rotation profiles assumed.
To achieve a starting point to the left of the diagonal traced by the data, it is necessary to start with a low rotation rate in the convective core. If otherwise we assume a fast rotating convective core, for example spinning at Ωcc/2π ≃ 30 μHz, the surface velocities would be too high, which would lead to a disagreement with the data. Then starting with a model with a convective core rotating at Ωcc/2π ≃ 10 μHz using different initial rotation profiles, we verify whether it is possible to start the evolution on the left part of the diagonal traced by the data in Fig. 7. To achieve this, initial rotation contrasts of at least Ωsurf/Ωcc ≳ 3, 2.5, and 1.8 would be needed with the rotation laws Ω1, Ω2, and Ω3, respectively, with Ωcc the rotation rate of the convective core. This is illustrated in Fig. 13, where we show the ZAMS point in the V sin i − Ωcore diagram for the different rotation profiles explored (see Eqs. (8)–(10)), and initial rotation contrasts of Ωsurf/Ωcc = 1, 1.5, 2, 2.5, and 3. These points converge for a solid-body rotation profile, and thus are located at the ZAMS point of our models computed with an initial rotation rate of Ωcore/2π = 10 μHz. However, starting with a rotation profile where the surface rotates faster than the g-mode cavity would lead to a lack of slow-rotators both in near core-rotation rate and surface rotational velocity. This is not supported by the current data.
 |
Fig. 13. Same as Fig. 7, but assuming different initial rotational profiles. The points correspond to the ZAMS location of models starting with an initial rotation rate of Ωcc/2π = 10 μHz, but assuming different degrees of differential rotation and rotation profiles (see Fig. 12). The points are shown for initial contrasts of Ωsurf/Ωcc = 1, 1.5, 2, 2.5, and 3, where the solid-body rotation profile (Ωsurf/Ωcc = 1) coincides with the starting point of the models (blue and red lines). The red line model starting from the upper green square was computed without internal magnetic fields and with an initial surface rotation rate three times higher than its core. |
Those ratios are rather high and it would remain difficult to invoke a physical scenario leading to these initial distributions, since accretion during the pre-MS would lead to a core spinning only slightly faster than its surface (Haemmerlé et al. 2013). Moreover, once we compute the evolution of models where the initial rotation profile is modified, the evolutionary behaviour of both core rotation rate and surface velocity does not change; rotation-only models still have decreasing surface velocities and increasing core rotation rates, moving them to the lower right in Figs. 7 and 8. Instead, for models with internal magnetic fields, as mentioned before, the transport is so efficient that they quickly lead to uniform rotation and return to their normal evolution, just as if they were computed with a uniform rotation profile at the ZAMS. We also show in Fig. 8 that the data do not support stars with a surface rotating faster than its core. Taking all these arguments into account we deem it unlikely that our models with purely hydrodynamical transport of AM can reproduce the data, and so the conclusions remain robust regardless of the evolutionary history during the stellar formation and further pre-MS evolution.
As an additional test, we checked how a model with an initial strong degree of differential rotation at the ZAMS would evolve and whether it could reproduce the data. We did this by using the Ω1 profile given by Eq. (8) with an initial contrast of Ωsurf/Ωcc = 3 (i.e. surface rotating faster than core) as an initial condition at the ZAMS, and then we computed the evolution with purely hydrodynamical AM transport. This model is shown in Fig. 13 starting from the green point above the diagonal traced by the data, which corresponds to the ZAMS location of a model star with this rotation contrast and rotation law. Although the model can simultaneously reproduce the surface rotational velocities and core rotation rates in the early MS, the buoyancy radius of the model in these parts is not in agreement with the mean observed values and, as shown by the solid lines, in this diagram the regions probed by our rotation-only models remains the same (i.e. below the diagonal traced by the data), and are thus in disagreement with the data. The fact that the buoyancy radius of this model is not in agreement with the data during the early MS occurs because the rotation profile readjusts rapidly during the evolution as a product mainly of the AM advection by meridional circulation, leading to a strong decrease in the surface rotational velocities. The evolution of the rotation profiles is shown in Fig. A.1.
6. Additional evidence and other indicators of evolution
We presented our main results in the previous sections using the buoyancy radius as the main indicator of the evolution during the MS. This is convenient since in the range of metallicities of our sample (see Fig. 1) the buoyancy radius is weakly dependent on the metallicity (see Fig. 2 in Ouazzani et al. 2019), and since we have an estimate of the most likely stellar masses in our sample (see Fig. 2) we can better distinguish between physical scenarios during stellar evolution. However, we can also try to use other indicators and check how well our conclusions hold when compared with independent indicators of evolution during the MS, which we discuss here.
6.1. Stellar clusters and asteroseismic inferences
We checked for membership of the stars in our sample to stellar clusters in the Kepler field and we found 24 stars that belong to the open clusters NGC6811, NGC6866, and ASCC108. All three clusters are well characterised in terms of membership with aid of astrometric information from Gaia-DR2 (Cantat-Gaudin et al. 2018; Cantat-Gaudin & Anders 2020), and thus their ages can be reliably estimated with stellar isochrones. We used the ages derived by Bossini et al. (2019) for the three stellar clusters, and selected only stars with a membership probability higher than 60 %, based on the values given by Cantat-Gaudin & Anders (2020). With this information we can give a reliable estimate of the age for 19 of our γ Dor stars. And since they belong to three different open clusters we can infer the core rotation rate at three different ages for stars of different masses. The ages of the stellar clusters are t ≃ 81.5, 776, and 863 Myr for ASCC108, NGC6866, and NGC6811, respectively, and have metallicities close to solar (Bossini et al. 2019). Then we can compare the core rotation rate of our models as a function of the absolute age, which is shown in Fig. 14.
 |
Fig. 14. Core rotation rate as a function of age. The data points correspond to the γ Dor stars in our sample that belong to the open clusters NGC6811, NGC6866, and ASCC108. The lines correspond to our models with only hydrodynamical processes (solid) and models including internal magnetic fields (dashed). The different colours correspond to models with initial masses of M = 1.5 (red), 1.7 (green), and 1.9 (blue) M⊙, all computed at solar metallicity. |
Although we see that older stars tend to have lower core rotation rates, it is still uncertain whether their cores should be slowing down during evolution and at what rate based solely on Fig. 14. This is because there are very few stars with these constraints available in the literature, and because the absolute age is not a good indicator to distinguish between models with either inefficient or efficient AM transport, as evidenced by the mild difference in core rotation rate between the two types of models in this figure.
Mombarg et al. (2021) estimated the central hydrogen content of 37 stars present in our sample. We compare our two types of models against these constraints in Fig. 15. In this figure we show our models computed with an initial mass of M = 1.5 M⊙ and metallicity of Z = 0.01 since the inferred mass of several of the stars in this sample lies around M ≃ 1.5 M⊙ (see Table B.1 in Mombarg et al. 2021) and the behaviour of the core rotation rate is weakly dependent on the metallicity for the stars in our sample. When comparing the core rotation rate as a function of the central hydrogen content there is an apparent progressive slow down towards the end of the MS, with a clear lack of fast rotators near the end of the MS seen in the data. This favours models with AM transport by magnetic instabilities, but without clearly rejecting rotation-only models.
 |
Fig. 15. Core rotation rate as a function of the mass fraction of hydrogen in the core. The data points correspond to γ Dor stars with inferences on the central hydrogen content from Mombarg et al. (2021). The lines show our models computed at three different initial rotation rates with only hydrodynamical processes (red) or including internal magnetic fields (blue). |
6.2. Evolved stars close to the end of the main sequence
Combining the different indicators presented, we finally selected stars that are most likely to be near the end of the MS. This would be decisive, since depending on the efficiency of the AM transport, stars are expected to evolve differently in core rotation rate and surface velocity, as shown in Fig. 7. In this figure we would expect to find evolved stars mainly on the left part of the diagonal traced by the data if the AM transport was very efficient. On the other hand, if transport were inefficient during the evolution, they would lie mainly below the diagonal. This can also be verified using Fig. 8, but in this diagram, if AM transport were efficient, it could not be distinguished at first since all stars should line up along a diagonal depending on their inclination angles. Nonetheless, they should preferentially be grouped towards the lower left part of the diagram since their core (and hence surface) should spin down through evolution as a result of their increase in size and efficient AM transport.
We only find seven stars likely to be close to the end of the MS, based on their low core-hydrogen content (Schmid et al. 2015; Schmid & Aerts 2016; Mombarg et al. 2021) and on the low values of their buoyancy radii. These stars are KIC6678174, KIC7380501, KIC10467146, KIC11080103, KIC6519869, KIC10080943A, and KIC10080943B. We show their positions with respect to the whole sample in Fig. 16. The first three stars mentioned have an inferred core hydrogen mass fraction lower than Xcore ≃ 0.15 (Mombarg et al. 2021). KIC11080103 and KIC6519869 have buoyancy radii lower than P0 = 3000 s and so they are expected to be close to the end of the MS. The stars in the binary system KIC10080943 have a low core-hydrogen content and a low buoyancy radius (Schmid & Aerts 2016).
 |
Fig. 16. Surface rotation rates as a function of core rotation rate (see Sect. 4.4). The red symbols correspond to stars close to the end of the main sequence. The black solid line indicates the one-to-one line. |
Four of these stars (KIC7380501, KIC11080103, KIC10080943A, and KIC10080943B) are consistent with efficient AM transport because they lie close to the diagonal of solid-body rotation for stars seen at an inclination of i = 90° in Fig. 16. Although this mildly supports efficient transport during the MS, we argue that it strongly rejects inefficient transport during the evolution. If AM transport were inefficient, as in the case of our rotation-only models, we would expect all stars to lie in the lower part of Fig. 16, irrespective of their inclination angles; a low inclination angle would only move them to lower parts of the diagram. This is because differential rotation should then develop, leading to a surface that rotates more slowly than the inner regions, and hence moving the position of the stars to the lower part of Fig. 16. This can be seen for example comparing the expected position of the evolved stars close to the end of the MS in Fig. 8 for our rotation-only models. Another possibility would be that the stars actually began their evolution with strong differential rotation between core and surface, having a surface spinning faster than the core, and are then heading to the right part of the diagrams (i.e. developing a core that rotates faster than the surface). However, we disregard this scenario since, due to meridional circulation, the rotation profile is expected to quickly converge to a profile where the core rotates faster than the surface (see Appendix A and Fig. 13). For a starting rotation contrast of Ωsurf/Ωcore = 1.5, our models achieve this once the hydrogen in the core drops to a mass fraction of just Xcore ≃ 0.65. In addition, since in general the data indicate that the stars do not have a surface spinning faster than their core (see bottom panel of Fig. 16), we find it highly unlikely that near the end of the MS the stars could be in this configuration. We note, however, that KIC10080943B seems to have a surface rotating faster than its core (see Fig. 16).
The other three stars (KIC6678174, KIC10467146, and KIC6519869) have low projected rotational velocities and are consistent with either low inclination angles and efficient AM transport or moderate to high inclination angles and inefficient AM transport. If they were rotating as solid bodies, then their inclination angles would be in the range 15° ≲i ≲ 35°. If we assume that the AM transport was inefficient during the evolution of these three stars and that the inclination angles are moderate to high (i ≳ 52°), then the rotation contrast between the near-core regions and the surface should be in the range Ωcore/Ωsurf ≃ 2.3 − 2.7. This is in fragile agreement with our rotation-only models since the contrast achieved is at most Ωcore/Ωsurf ≃ 2.0 and 2.5 when the central hydrogen mass-fraction reaches Xcore ≃ 0.1 for models with initial rotation rates of Ωcore/2π = 10 and 20 μHz, respectively, and it is roughly independent of the initial mass. Although we are more inclined to say that these stars are not well explained by an evolutionary scenario where the AM transport is inefficient, we cannot entirely rule it out.
None of the stars discussed above have reported rotational modulation in their light curves (Li et al. 2020) and are not reported as eclipsing binaries (Kirk et al. 2016), although KIC10080943 is a double-lined spectroscopic binary system (Schmid & Aerts 2016). To give a more solid conclusion we would need to have more stars likely to be close to the end of the MS. The four stars in agreement with efficient transport, if proved to be true evolved stars with rather high inclination angles, would not only give more support to an efficient transport in the MS, but also to a process able to act during the whole MS. It would still be possible that the efficiency of the physical process decreases at some point during the evolution, but in that case they should quickly develop differential rotation, and hence move to another location in the diagram presented, which is not supported by these stars.
6.3. Surface rotation rate from modulation of light curves
For some γ Dor stars there is evidence of modulation in the light curves that could potentially be a signature of magnetic spots at their surface and so provide direct measurements of their surface rotation rate. This would remove the uncertainty due to the unknown inclination angles present in the surface rotational velocities obtained with spectroscopy. Li et al. (2020) found signatures of surface modulation in the light curves of 58 out of the 611 stars that they analysed, and obtained their respective surface rotation rates concluding that they rotate nearly rigidly. Although this is a precise constraint on the nature of the AM transport in stellar interiors, different interpretations of the cause of the modulation in this group of stars blur the picture (see Lee & Saio 2020; Henriksen et al. 2023). Moreover, the detection of surface modulation in stars with a surface rotating more slowly than the near-core regions may have been overlooked due to selection effects (Li et al. 2020), thus affecting the conclusion on the efficiency of AM transport in stellar interiors; this does not occur if we rely on spectroscopic rotational velocities.
Assuming that the modulation in the light curves corresponds to magnetic spots at the stellar surface, we tested our models with the surface rotation rates provided by Li et al. (2020) as a function of the buoyancy radius in Fig. 17. We excluded the stars labelled as eclipsing binaries in the sample of Li et al. (2020) for this comparison since in those cases the surface rotation rate was assumed to be equal to the orbital period of the system. Our rotation-only models quickly developed internal differential rotation in radiative regions, leading to a disagreement with the data, although at lower initial rotation rates the decoupling occurs more slowly, as evidenced from the model shown by dashed lines in Fig. 17.
 |
Fig. 17. Ratio of core to surface rotation rate as a function of buoyancy radius for models with initial mass and metallicity of M = 1.5 M⊙ and Z = 0.01, respectively. The data points correspond to the data presented by Li et al. (2020). The red and blue lines are models computed with hydrodynamical processes only (red) or both hydrodynamical processes and internal magnetic fields (blue). The models without internal magnetic fields are shown for three different initial rotation rates of Ω/2π = 10, 20, and 30 μHz (dashed, solid, and dot-dashed lines, respectively). For models with internal magnetic fields, only the one starting with Ω/2π = 20 μHz is shown. |
In our models with internal magnetic fields the radiative regions remain strongly coupled and so the ratio of core-to-surface rotation rate is nearly unity during the whole MS, leading only to a slight decoupling as the star approaches the end of the MS as a result of the development of chemical gradients close to the convective core. We obtain this result in our models irrespective of the initial rotation rate assumed. This is why we only show the model with an initial rotation rate of Ω/2π = 20 μHz in Fig. 17 when magnetic fields are included.
Although models without magnetic fields are in disagreement with the data, it is still difficult to reproduce the small degree of differential rotation seen in the data with our models including internal magnetic fields. The apparently decreasing trend seen in Fig. 17 also remains challenging in our models with internal magnetic fields since it is not possible to generate differential rotation in a way that the surface rotates faster than the deep radiative layers through evolution because of the diffusive nature on the AM transport of the magnetic fields studied.
7. Discussion
Overall, our work gives strong support to efficient AM transport during the MS, although its physical nature is debatable. This supports the idea of at least one missing physical process able to transport AM in stellar interiors (Eggenberger et al. 2012; Marques et al. 2013; Ceillier et al. 2013), in addition to the advection of AM by meridional circulation and turbulent transport by shear instabilities. Previous asteroseismic results on single stars obtained by Saio et al. (2015) and Murphy et al. (2016) indicate that the AM transport in main-sequence F-type stars must be highly efficient through evolution (see also Kurtz et al. 2014; Hatta et al. 2022); we support this idea. We believe that the additional process should be active during the whole MS, leading to quasi-rigid rotation in the radiative zones, as is the case for the Sun (Couvidat et al. 2003). We do note however that there could still be some differential rotation between the convective core and the radiative regions in γ Dor stars, which will be the topic of a follow-up study.
Evidence from post-MS stars such as subgiants and red giants points to a general lack of AM transport in stellar models. The TS dynamo seems to satisfy well the rotational evolution of the core during the MS and evolved stages simultaneously, but there are still problems in reproducing the rotation rate of subgiants and young RGB stars simultaneously (Eggenberger et al. 2019). More constraints on the AM content in subgiants would provide crucial information to distinguish between physical scenarios; to date these constraints are available for only eight subgiants (Deheuvels et al. 2014, 2020). The sample of stars studied here represent the MS counterpart of the red giants studied by Gehan et al. (2018; see also Mosser et al. 2012), and future studies on AM redistribution should focus on the connection between the two samples and exploit other indicators, such as chemical abundances. The present work helps us understand the physical process(es) operating in dwarfs, and in connection with the constraints from Deheuvels et al. (2020) for two young subgiants, it gives support to AM transport by the magnetic Tayler instability as the main candidate to resolve the AM transport problem. We also note that other physical processes could contribute to the transport of AM, such as internal gravity waves (Pinçon et al. 2017), mixed modes (Belkacem et al. 2015a,b), or magneto-rotational instabilities (Spada et al. 2016; Moyano et al. 2023).
Another way to study AM redistribution would be to use the periods of rotation of the stellar surface as given by the modulation of the light curve, usually attributed to magnetic spots on the surface of the star. An issue with this approach is the possible misidentification of rotational periods as signatures of pulsations; the modulation seen in the light curve was shown to be possibly due to g-modes excited by the convective core (Lee & Saio 2020), and it remains a possibility despite recent advances (see Henriksen et al. 2023). In that case the rotational period obtained from the modulation of the light curves would actually be the rotation rate of the convective core and although others could reach the same conclusions as we do, the hypotheses would be wrong. We avoid such possible misinterpretations by using the measurements of projected rotational velocities from spectroscopy. Although there are other processes able to broaden the spectral lines (e.g., macroturbulence, pressure broadening), they are expected to be negligible compared to the strong broadening in fast rotators; we recall that some of these stars are rotating at up to 50% of their critical rotational velocities (see Sect. 3).
Moreover, it is possible to study the internal redistribution of AM through evolution with the help of rotational splittings coming from hybrid pulsators with both p- and g-modes (e.g., Dupret et al. 2004; Kurtz et al. 2014; Saio et al. 2015). However this is difficult to achieve for a large sample of stars since stars showing these properties are not abundant. In this work we show that we can avoid this inconvenience by combining data from spectroscopy for a large sample of stars and making coherent assumptions on the modelling of the AM transport.
Future works should verify whether signatures of chemical enrichment in stellar models with strong coupling are in agreement with data. It is also necessary to verify whether our conclusions hold for more massive stars since some targets remain open to different interpretations (see Salmon et al. 2022).
8. Summary and conclusions
We investigated the efficiency of AM transport in MS stars using constraints on both the core rotation rates (Li et al. 2020) and surface rotational velocities from spectroscopy (Sect. 2) of γ Dor stars. We built upon the work of Ouazzani et al. (2019) and our conclusions mainly rely on the data obtained by Li et al. (2020) and Gebruers et al. (2021). We showed how, by combining information from independent techniques, we can better distinguish the different scenarios of AM transport during the MS, which otherwise remain hidden when relying on only information of the core. Our main results are illustrated by Figs. 6–8. For the comparison with stellar models, we chose two types of models, the first in which the AM transport is done only by meridional circulation and the shear instability and another where the action of internal magnetic fields by the Tayler-Spruit dynamo is also included. Internal magnetic fields transport AM very efficiently, and are in better agreement with our whole analysis.
Our strong conclusion is that the transport of AM in radiative zones during the MS of low-mass stars must be efficient. As a corollary, internal magnetic fields are a candidate to the missing physical process in stellar interiors. Our conclusion, in addition to the strong evidence from previous works for the Sun (Couvidat et al. 2003; Eggenberger et al. 2022a) and evolved stars (e.g., Mosser et al. 2012), supports the idea that an efficient process (or at least one able to counteract the development of differential rotation in stellar interiors) must act during the whole evolution of stars.
Acknowledgments
We thank the referee for the constructive feedback and accurate comments that helped improving the manuscript. F.D.M., P.E., S.J.A.J.S., and S.E. have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 833925, project STAREX). J.S.G.M. acknowledges funding from the French National Research Agency (ANR: grant MASSIF, ANR-21-CE3-0018-02). F.D.M. thanks Agostina Filócomo, Matthias Kruckow and Luca Sciarini for useful discussions.
References
- Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]
- Aerts, C., Thoul, A., Daszyńska, J., et al. 2003, Science, 300, 1926 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2009, in Transiting Planets, eds. F. Pont, D. Sasselov, & M. J. Holman, 253, 71 [NASA ADS] [Google Scholar]
- Belkacem, K., Marques, J. P., Goupil, M. J., et al. 2015a, A&A, 579, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Marques, J. P., Goupil, M. J., et al. 2015b, A&A, 579, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Bossini, D., Vallenari, A., Bragaglia, A., et al. 2019, A&A, 623, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouabid, M. P., Dupret, M. A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [Google Scholar]
- Brown, T. M., Latham, D. W., Everett, M. E., & Esquerdo, G. A. 2011, AJ, 142, 112 [Google Scholar]
- Cantat-Gaudin, T., & Anders, F. 2020, A&A, 633, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [Google Scholar]
- Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2013, A&A, 555, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995, ApJ, 441, 865 [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [Google Scholar]
- Christophe, S., Ballot, J., Ouazzani, R. M., Antoci, V., & Salmon, S. J. A. J. 2018, A&A, 618, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2016, A&A, 592, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
- Couvidat, S., García, R. A., Turck-Chièze, S., et al. 2003, ApJ, 597, L77 [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Eggenberger, P., et al. 2020, A&A, 641, A117 [EDP Sciences] [Google Scholar]
- Dupret, M. A., Thoul, A., Scuflaire, R., et al. 2004, A&A, 415, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A., Daszyńska-Daszkiewicz, J., & Pamyatnykh, A. A. 2007, MNRAS, 374, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., den Hartogh, J. W., Buldgen, G., et al. 2019, A&A, 631, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Ekström, S., Georgy, C., et al. 2021, A&A, 652, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Moyano, F. D., & den Hartogh, J. W. 2022a, A&A, 664, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Buldgen, G., Salmon, S. J. A. J., et al. 2022b, Nat. Astron., 6, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- Frasca, A., Molenda-Żakowicz, J., Alonso-Santiago, J., et al. 2022, A&A, 664, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuller, J., Lecoanet, D., Cantiello, M., & Brown, B. 2014, ApJ, 796, 17 [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, S., Van Reeth, T., De Ridder, J., & Aerts, C. 2022, A&A, 668, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gebruers, S., Straumit, I., Tkachenko, A., et al. 2021, A&A, 650, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres (UK: Cambridge University Press) [Google Scholar]
- Griffiths, A., Eggenberger, P., Meynet, G., Moyano, F., & Aloy, M.-Á. 2022, A&A, 665, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haemmerlé, L., Eggenberger, P., Meynet, G., Maeder, A., & Charbonnel, C. 2013, A&A, 557, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatta, Y., Sekii, T., Benomar, O., & Takata, M. 2022, ApJ, 927, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Henriksen, A. I., Antoci, V., Saio, H., et al. 2023, MNRAS, 520, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Kaye, A. B., Handler, G., Krisciunas, K., Poretti, E., & Zerbi, F. M. 1999, PASP, 111, 840 [Google Scholar]
- Kirk, B., Conroy, K., Prša, A., et al. 2016, AJ, 151, 68 [Google Scholar]
- Kissin, Y., & Thompson, C. 2015, ApJ, 808, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [Google Scholar]
- Lee, U., & Saio, H. 2020, MNRAS, 497, 4117 [CrossRef] [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., et al. 2020, MNRAS, 491, 3586 [Google Scholar]
- Liu, C., Fu, J., Shi, J., et al. 2020, ArXiv e-prints [arXiv:2005.07210] [Google Scholar]
- Luo, A. L., Zhao, Y.-H., Zhao, G., et al. 2015, Res. Astron. Astrophys., 15, 1095 [Google Scholar]
- Luo, A. L., Zhao, Y. H., Zhao, G., et al. 2022, ViZieR Online Data Catalog: V/156 [Google Scholar]
- Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinet, S., Meynet, G., Ekström, S., et al. 2021, A&A, 648, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Huber, D., Batalha, N. M., et al. 2017, ApJS, 229, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [Google Scholar]
- Mombarg, J. S. G., Van Reeth, T., & Aerts, C. 2021, A&A, 650, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moyano, F. D., Eggenberger, P., Meynet, G., et al. 2022, A&A, 663, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moyano, F. D., Eggenberger, P., Mosser, B., & Spada, F. 2023, A&A, 673, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, S. J., Fossati, L., Bedding, T. R., et al. 2016, MNRAS, 459, 1201 [Google Scholar]
- Murphy, S. J., Hey, D., Van Reeth, T., & Bedding, T. R. 2019, MNRAS, 485, 2380 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [Google Scholar]
- Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Pápics, P. I., Tkachenko, A., Van Reeth, T., et al. 2017, A&A, 598, A74 [Google Scholar]
- Pinçon, C., Belkacem, K., Goupil, M. J., & Marques, J. P. 2017, A&A, 605, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]
- Salmon, S. J. A. J., Moyano, F. D., Eggenberger, P., Haemmerlé, L., & Buldgen, G. 2022, A&A, 664, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi-Ghadim, A., Lampens, P., Jassur, D. M., & Jofré, P. 2020, A&A, 638, A57 [EDP Sciences] [Google Scholar]
- Schmid, V. S., & Aerts, C. 2016, A&A, 592, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmid, V. S., Tkachenko, A., Aerts, C., et al. 2015, A&A, 584, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spada, F., Gellert, M., Arlt, R., & Deheuvels, S. 2016, A&A, 589, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
- Staritsin, E. 2021, A&A, 646, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, W., Duan, X.-W., Deng, L., et al. 2021, ApJS, 257, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
- Tayar, J., Beck, P. G., Pinsonneault, M. H., García, R. A., & Mathur, S. 2019, ApJ, 887, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Tkachenko, A., Aerts, C., Yakushechkin, A., et al. 2013, A&A, 556, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015, ApJS, 218, 27 [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Mombarg, J. S. G., Mathis, S., et al. 2018, A&A, 618, A24 [NASA ADS] [EDP Sciences] [Google Scholar]
- Wheeler, J. C., Kagan, D., & Chatzopoulos, E. 2015, ApJ, 799, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Yusof, N., Hirschi, R., Eggenberger, P., et al. 2022, MNRAS, 511, 2814 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
Appendix A: Rotation profiles with strong differential rotation
In Fig. A.1 we show the evolution of the rotation profiles during the main sequence of the model presented in Fig. 13 with a strong rotation contrast between convective core and surface of Ωsurf/Ωcc = 3 (i.e. surface rotating faster than the interior). The rotation profile is given as an input for the model and then only transport of angular momentum by hydrodynamical processes (meridional circulation and shear instability) is taken into account. The models quickly invert the initial configuration; as soon as the central hydrogen content reaches Xcore = 0.67 the surface starts rotating slightly slower than the core and then follows a standard evolution, as in models where solid-body rotation is assumed at the ZAMS.
 |
Fig. A.1. Rotation rate as a function of normalised mass-coordinate. The lines correspond to different evolutionary ages during the main sequence, indicated by the abundance of central hydrogen content in mass fraction over each profile. The red line is the initial rotation profile assumed at the ZAMS. |
All Figures
 |
Fig. 1. Normalised distribution of metallicities of γ Dor stars used in this work. The histogram contains 572 stars with metallicities from Mathur et al. (2017). The leftmost bin contains all the outliers with [Fe/H] between −1.6 and −0.7 dex. The mean value of the sample is |
| In the text | |
 |
Fig. 2. Normalised distribution of stellar masses of γ Dor stars used in this work. The histogram contains 504 stars with masses determined by Murphy et al. (2019). The rightmost bin contains all the outliers with masses between 2.2 and 2.7 M⊙. The mean value of the sample is |
| In the text | |
 |
Fig. 3. Hertzsprung–Russell diagram of our models. The data points correspond to the γ Dor stars studied in this work from Li et al. (2020); the points are semi-transparent to illustrate the number density when two or more stars overlap. The typical uncertainty on effective temperature and luminosity is shown in the figure. The stellar models are computed from the ZAMS with an initial metallicity of Z = 0.01 and an initial rotation rate Ω/2π = 20 μHz (no magnetic fields); initial masses are indicated in solar masses for each track. |
| In the text | |
 |
Fig. 4. Core rotation rate as a function of buoyancy radius for models with different initial masses. Left: AM transport driven by hydrodynamical processes alone. Right: same, but including internal magnetic fields. The data points correspond to the γ Dor stars presented by Li et al. (2020). For each initial mass are shown models starting at an initial rotation rate of Ωcore/2π = 10, 20 and 30 μHz. Models are computed from the ZAMS and the evolution goes from left to right. |
| In the text | |
 |
Fig. 5. Surface rotational velocity as a function of buoyancy radius. The lines correspond to our models with different initial masses, computed at three different initial rotation rates for each initial mass. Left: driven by hydrodynamical processes alone. Right: same, but including internal magnetic fields. The data points correspond to γ Dor stars for which surface velocities are available from the literature (see Sect. 2); buoyancy radii are taken from Li et al. (2020). The surface velocity of the models is multiplied by π/4 to average over the unknown inclination angles of the stars. |
| In the text | |
 |
Fig. 6. Effect of internal magnetic fields on the redistribution of AM during the MS (evolution goes from left to right). Left: core rotation rate. Right: surface rotational velocity. The surface velocity of the models are multiplied by a factor π/4 to average over the unknown inclination angles of the sample. The models have an initial mass and metallicity of M = 1.5 M⊙ and Z = 0.01, and are computed at three different initial velocities. The data points in the right panel are contained in the data set of the left panel. |
| In the text | |
 |
Fig. 7. Projected surface rotational velocity as a function of core rotation rate. The lines correspond to models with an initial mass of M = 1.5 M⊙ and initial metallicity Z = 0.01 shown only during the main sequence, computed with initial rotation rates of Ωcore/2π = 10, 20, and 30 μHz, starting at the ZAMS. The blue and red lines indicate the type of AM transport assumed in each model: only hydrodynamical processes (red) or including internal magnetic fields and hydrodynamical processes (blue). The data points are γ Dor stars with constraints available from the literature (see Sect. 2). The solid lines represent the regions where the buoyancy radius of the models is in agreement with the mean values of the sample. |
| In the text | |
 |
Fig. 8. Surface rotation rates as a function of core rotation rate. The surface rotation rates are obtained by dividing the projected rotational surface velocities by the radius of each star. The dots represent the data set used in this work (see Sect. 2), while the red and blue lines have the same meaning as in Fig. 7, and the black line shows the one-to-one relation. |
| In the text | |
 |
Fig. 9. Same as Fig. 4, but showing the effect of the overshooting for models with transport only by hydrodynamical processes (red) and models that also include internal magnetic fields (blue). The solid lines correspond to models computed with an overshooting length of 0.05Hp, while the dashed lines have an overshooting length of 0.2Hp. The models have an initial mass of M = 1.5 M⊙. For clarity we only show models computed at two different initial rotation rates. |
| In the text | |
 |
Fig. 10. Same as Fig. 7, but showing the effect of overshooting for models with transport only by hydrodynamical processes (red) and models that also include internal magnetic fields (blue). The solid lines correspond to models computed with an overshooting length of 0.05Hp, while the dashed lines have an overshooting length of 0.2Hp. The models have an initial mass of M = 1.5 M⊙. |
| In the text | |
 |
Fig. 11. Same as Fig. 7, but showing effect of different initial metallicities. The cyan, blue, and light blue lines correspond to models computed with internal magnetic fields, whereas the magenta, red, and yellow lines correspond to models computed only with hydrodynamical processes, hence without internal magnetic fields. The models are computed with initial rotation rates of Ωcore/2π = 10, 20, and 30 μHz. The dashed and solid parts of the line have the same meaning as in Fig. 7. |
| In the text | |
 |
Fig. 12. Rotation profiles given by Eqs. (8)–(10) at ZAMS for a 1.5 M⊙ model for three different initial rotation ratios between convective core and surface of Ωsurf/Ωcc = 1, 2, and 3 (dot-dashed, dashed, and solid lines, respectively). The bullets shown on the rotation profiles show the location where the angular velocity is equal to the mean value of the g-mode cavity computed with Eq. (6). |
| In the text | |
 |
Fig. 13. Same as Fig. 7, but assuming different initial rotational profiles. The points correspond to the ZAMS location of models starting with an initial rotation rate of Ωcc/2π = 10 μHz, but assuming different degrees of differential rotation and rotation profiles (see Fig. 12). The points are shown for initial contrasts of Ωsurf/Ωcc = 1, 1.5, 2, 2.5, and 3, where the solid-body rotation profile (Ωsurf/Ωcc = 1) coincides with the starting point of the models (blue and red lines). The red line model starting from the upper green square was computed without internal magnetic fields and with an initial surface rotation rate three times higher than its core. |
| In the text | |
 |
Fig. 14. Core rotation rate as a function of age. The data points correspond to the γ Dor stars in our sample that belong to the open clusters NGC6811, NGC6866, and ASCC108. The lines correspond to our models with only hydrodynamical processes (solid) and models including internal magnetic fields (dashed). The different colours correspond to models with initial masses of M = 1.5 (red), 1.7 (green), and 1.9 (blue) M⊙, all computed at solar metallicity. |
| In the text | |
 |
Fig. 15. Core rotation rate as a function of the mass fraction of hydrogen in the core. The data points correspond to γ Dor stars with inferences on the central hydrogen content from Mombarg et al. (2021). The lines show our models computed at three different initial rotation rates with only hydrodynamical processes (red) or including internal magnetic fields (blue). |
| In the text | |
 |
Fig. 16. Surface rotation rates as a function of core rotation rate (see Sect. 4.4). The red symbols correspond to stars close to the end of the main sequence. The black solid line indicates the one-to-one line. |
| In the text | |
 |
Fig. 17. Ratio of core to surface rotation rate as a function of buoyancy radius for models with initial mass and metallicity of M = 1.5 M⊙ and Z = 0.01, respectively. The data points correspond to the data presented by Li et al. (2020). The red and blue lines are models computed with hydrodynamical processes only (red) or both hydrodynamical processes and internal magnetic fields (blue). The models without internal magnetic fields are shown for three different initial rotation rates of Ω/2π = 10, 20, and 30 μHz (dashed, solid, and dot-dashed lines, respectively). For models with internal magnetic fields, only the one starting with Ω/2π = 20 μHz is shown. |
| In the text | |
 |
Fig. A.1. Rotation rate as a function of normalised mass-coordinate. The lines correspond to different evolutionary ages during the main sequence, indicated by the abundance of central hydrogen content in mass fraction over each profile. The red line is the initial rotation profile assumed at the ZAMS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$ \overline{\mathrm{[Fe/H]}} = -0.127 \pm 0.191 $](/articles/aa/full_html/2023/09/aa46548-23/aa46548-23-eq1.gif)