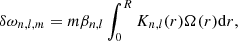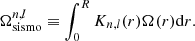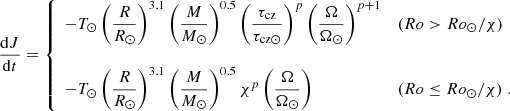EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 673 (May 2023) A&A, 673 (2023) L11 Full HTML
Open Access
Issue
A&A
Volume 673, May 2023
Article Number L11
Number of page(s) 7
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202245764
Published online 12 May 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Oscillations at the surface of stars carry information about the stellar structure. The study of these oscillations permits us to constrain the transport processes occurring inside the star and to characterise its rotation. These studies were first dedicated to helioseismology because of the required data quality, and tremendous successes were achieved. For example, it was shown that the radiative interior of the Sun rotates nearly uniformly (see e.g., Schou et al. 1998; Thompson et al. 2003; Eff-Darwich & Korzennik 2013). Solar models computed with hydrodynamic transport processes in radiative zones alone, such as meridional circulation and shear instability, were then found to predict a high contrast between core and surface rotation rates, which disagrees with helioseismic measurements (Pinsonneault et al. 1989; Chaboyer et al. 1995; Eggenberger et al. 2005; Charbonnel & Talon 2005). Another efficient angular momentum (AM) transport process must then be operating in the solar radiative zone. Different candidates have been invoked for this efficient AM transport in the Sun: internal gravity waves (e.g., Zahn et al. 1997; Charbonnel & Talon 2005), large-scale fossil magnetic fields (e.g., Mestel & Weiss 1987; Charbonneau & MacGregor 1993; Rüdiger & Kitchatinov 1996; Gough & McIntyre 1998), and magnetic instabilities (e.g., Spruit 2002; Eggenberger et al. 2005, 2019). Magnetic instabilities recently demonstrated that they might provide an interesting explanation for the helioseismic measurements of the internal rotation of the Sun simultaneously with the surface abundances of lithium and helium (Eggenberger et al. 2022).

The recent development of space-based photometry missions, such as CoRoT (Baglin et al. 2009), Kepler (Borucki et al. 2010), and TESS (Ricker et al. 2015) in the past two decades enables us to apply these studies to asteroseismology as well. During almost all the phases in the life of a star, the core contracts and the envelope expands, creating differential rotation in which the core rotates faster than the envelope. Moreover, braking of the surface by magnetised winds can create radial differential rotation in solar-type stars with a convective envelope deep enough to host a dynamo. This trend can be mitigated by an efficient AM transport, however. Key observational constraints have been obtained for subgiant and red giant stars with the asteroseismic determination of the core rotation rates for a large sample of these evolved stars (Beck et al. 2012; Deheuvels et al. 2012, 2014, 2015, 2017; Di Mauro et al. 2016, 2018; Mosser et al. 2012; Gehan et al. 2018; Fellay et al. 2021). Comparisons with rotating models have then revealed the need for an efficient AM transport mechanism in addition to meridional circulation and transport by the shear instability (Eggenberger et al. 2012, 2017, 2019; Ceillier et al. 2013; Marques et al. 2013; Moyano et al. 2022). Detailed asteroseismic studies of the internal rotation for some main-sequence (MS) stars, in particular, for γ Dor pulsators, also suggested that an efficient transport of AM operates in the radiative zones of these stars, similarly to the conclusion obtained for the Sun and evolved stars (e.g., Kurtz et al. 2014; Saio et al. 2015, 2021; Murphy et al. 2016; Ouazzani et al. 2019; Li et al. 2020). An important question is related to the internal transport of AM in MS stars less massive than the γ Dor pulsators, with masses typically lower than about 1.5 M⊙. In this context, Benomar et al. (2015, hereafter OB15) studied 22 MS solar-type stars observed by Kepler and found that the average rotation rates deduced from asteroseismic measurements for these stars are very similar to their surface rotation rates. Nielsen et al. (2017, hereafter MN17) reached the same conclusion using an independent approach based on two-zone model fittings of the power spectrum. For the five Kepler targets considered in their work, they found that the radial differential rotation did not exceed 30% between the radiative and convective zones.

In this study, we investigate how these observations can constrain the internal transport of AM in solar-type stars and shed some light on the physical nature of this transport. We considered two AM transport prescriptions, including magnetic Tayler instability or not. We examined how these prescriptions affect internal and surface rotation rates. We give a semi-quantitative assessment of their compatibility with existing measurements from OB15 and MN17, and report whether some scenarios for AM transport can be ruled out. Although our study is based on synthetic models, we still used an advanced modelling to generate models as realistic as possible for the comparisons. The model structure reproduces the classical and (non-rotating) seismic constraints of an actual observed target. We selected four solar-type MS stars from the Kepler LEGACY sample (Lund et al. 2017) that we divided into two categories: Arthur, Barney, and Carlsberg, representative of the hotter region of the Hertzsprung-Russell (HR) diagram, and Doris, representative of the colder regions of the HR diagram (see Fig. 1). This selection was based on the size of the convective envelope, which impacts the efficiency of surface braking. For our hottest targets, the convective envelope is shallow, and inefficient braking is expected for masses above ∼1.2 M⊙ at solar metallicity (Kraft 1967). For Arthur, Barney, and Carlsberg, which lie close to this threshold, the behaviour of the magnetic braking is less clear. We assumed a likely inefficient braking for these targets, and then discuss the relevance of this hypothesis. In Sect. 2 we describe the asteroseismic modelling procedure and the physical input of the models. In Sect. 3 we compare the rotational properties of these different models to the available observational constraints, and the conclusions are given in Sect. 4.

thumbnail Fig. 1.

HR diagram of Arthur, Barney, Carlsberg, Doris, and of the sample of OB15. The tracks correspond to a grid slice with an initial chemical composition of X0 = 0.74 and Z0 = 0.018, and no overshooting.

2. Stellar models

We summarise the observational data in Table 1. The luminosity was estimated from the spectroscopic parameters using the same procedure as for Kepler-93 in Bétrisey et al. (2022, hereafter JB22), but with distances from Bailer-Jones et al. (2021) and based on the parallaxes1 measured by Gaia Collaboration (2021). The frequencies come from Lund et al. (2017) for Barney, Carlsberg, and Doris, and from Roxburgh (2017) for Arthur.

Table 1.

Observed and modelled data of Arthur, Barney, Carlsberg, and Doris.

The modelling procedure is divided in two main steps that are described in detail in Appendix A. The first step, which consists of fitting the seismic information with a Markov chain Monte Carlo (MCMC) in a grid of non-rotating models, serves as a guide for the second step, in which we derive the rotation profiles using rotating models with a detailed and coherent treatment of the AM transport. The modelling procedure of the first step is similar to that of JB22; we used a grid of non-rotating models computed with the Code Liégeois d’Évolution Stellaire (CLES; Scuflaire et al. 2008b), and the frequencies were computed with the Liège Oscillation Code (LOSC; Scuflaire et al. 2008a). The physical ingredients were the same as in JB22 (see Sect. 2.1). The minimisations were conducted with AIMS (Rendle et al. 2019), with a procedure that combines a mean density inversion (Reese et al. 2012) with a fit of frequency separation ratios. This modelling approach provides robust stellar seismic models (see e.g., Buldgen et al. 2019; Bétrisey et al. 2022) whose properties are given in Table 1.

After the targets properties were determined through this detailed asteroseismic modelling, rotating models were computed with the Geneva stellar evolution code (GENEC; Eggenberger et al. 2008). The computation of these rotating models is first based on the initial parameters obtained from the asteroseismic modelling, and these parameters are then adjusted to correctly reproduce the stellar properties given in Table 2. The GENEC code assumes shellular rotation (Zahn 1992), and the internal AM transport is computed along the stellar evolution by accounting for shear instability, meridional circulation, and AM transport by magnetic instability as in Spruit (2002). The advecto-diffusive AM transport in the radiative zone is described by

ρ d d t ( r 2 Ω ) M r = 1 5 r 2 ∂ ∂ r ( ρ r 4 Ω U ( r ) ) + 1 r 2 ∂ ∂ r [ ( D shear + ν TS ) ρ r 4 ∂ Ω ∂ r ] , $$ \begin{aligned} \rho \frac{\mathrm{d}}{\mathrm{d}t}\left(r^2\Omega \right)_{M_r} = \frac{1}{5r^2}\frac{\partial }{\partial r}\left(\rho r^4 \Omega U(r)\right) + \frac{1}{r^2}\frac{\partial }{\partial r} \left[(D_{\rm shear}+\nu _{\rm TS})\rho r^4\frac{\partial \Omega }{\partial r}\right], \end{aligned} $$(1)

where ρ is the mean density, r is the radius, Ω is the mean angular velocity on an isobar, and U is the radial component of the meridional circulation. The AM transport by shear instability is described by the coefficient Dshear following Talon et al. (1997), and the νTS is the diffusion coefficient corresponding to the transport by the Tayler-Spruit dynamo (see e.g., Eggenberger et al. 2019). Two families of rotating stellar models were considered in the present study: models that only include transport by hydrodynamic processes (labelled ‘pure rotation’ in Fig. 2), and models that include both hydrodynamic and magnetic transport processes (labelled ‘Tayler instability’ in Fig. 2). The difference between these models relies on the inclusion of transport by the magnetic Tayler instability for the latter through the coefficient νTS in the equation above. For both families of models, we accounted for the braking of the stellar surface due to magnetised winds according to the prescription by Matt et al. (2015) for models of stars with an extended convective envelope like the Sun, and Doris in this study. For Arthur, Barney, and Carlsberg, which are stars in the hotter part of the HR diagram (see Fig. 1) that are characterised by shallow convective envelopes, we assumed an inefficient braking that is inefficient enough such that it can be modelled by simply neglecting the corresponding term. We discuss the relevance of this assumption in Sect. 3. The zero-age main-sequence initial values of the rotation period are 0.9, 18, 17 and 9 days for Doris, Arthur, Barney and Carlsberg, respectively. We note that using other physical prescriptions for the magnetic instability (e.g., Fuller et al. 2019) or for the magnetic braking (e.g., Garraffo et al. 2018) does not affect the conclusions of this study. In addition, the rotation period of the sample of Benomar et al. (2015) is in the range of ∼3–18 days, which is consistent with gyrochronologic surveys, in which the rotation period of stars of ∼6000 K is mainly observed in the range ∼5–20 days (McQuillan et al. 2014; van Saders et al. 2019). Hence, the rotation periods of Arthur, Barney, and Carlsberg are typical of the period of stars in that temperature range. In this regard, the rotation period of Carlsberg is close to the average value, while the periods of Arthur and Barney lie in the slower half.

thumbnail Fig. 2.

Rotational profiles and splittings of Doris and Arthur considering different AM transport prescriptions. Top line: rotation profiles of Doris (left panel) and Arthur (centre and right panels). The base of the convective zone (BCZ) is shown as a dashed black line. The rotation kernel around the νmax, namely K21, 1, is shown in brown, and is rescaled and shifted vertically for illustration purposes. Bottom line: ratio of the rotation rate predicted by asteroseismology and starsport measurements for Doris (left panel) and Arthur (centre and right panels). The open circles are the theoretical predications, considering different AM transport prescriptions, accounting only for hydrodynamic processes (green circles), or for hydrodynamic processes and magnetic Tayler instability (red circles). The shallow convective envelope of Arthur likely implies an inefficient braking. For Arthur, we also tested extreme cases (right panels) with an AM transport with efficient braking (blue circles) or assuming local AM conservation (purple circles). The error bar corresponds to the precision of the average observational rotational splitting measured by OB18, and the blue area shows a solid-body rotation profile with the observational uncertainty of the surface rate from starspot measurements.

3. Rotational properties

In the upper panels of Fig. 2, we show the rotation profiles of Arthur and Doris considering the two different scenarios. The rotation profiles of Barney and Carlsberg are similar to the profiles of Arthur (see Appendix B). The rotation behaviour is quite different between the hot targets and the cold target Doris. Figure 2 indeed shows a higher degree of radial differential rotation for Doris than for other targets as a direct consequence of the efficient braking of the stellar surface by magnetised winds for this colder star. In the case of Doris, this results in a clear difference in the rotation profile predicted for the model with hydrodynamic transport processes alone (green line in the top left panel of Fig. 2) compared to the one predicted for the model with magnetic instabilities (red line in the same panel of Fig. 2). The efficient magnetic AM transport predicts an almost flat rotation profile for Doris, except in the central layers, where strong chemical gradients reduce the efficiency of this transport. AM transport by meridional circulation and shear instability is much less efficient and is not able to counteract the creation of radial differential rotation in the radiative zone, leading to a core that rotates more than ten times faster than the surface. The situation is different in hotter stars, as shown by the models of Arthur in the top centre panel of Fig. 2. For these models, radial differential rotation results solely from the slight contraction of the central layers and the increase in radius, which leads to a low degree of differential rotation in the radiative interior even for models with only hydrodynamic transport processes (see the top centre panel of Fig. 2). Owing to the very efficient AM transport by the magnetic Tayler instability, models with a Tayler-Spruit dynamo predict an even flatter rotation profile than those with meridional circulation and shear instability alone.

As proposed by OB15, a measurement of the surface rotation rate can be compared to the asteroseismic determination of the mean internal rotation rate of the star as probed by p-modes to shed some light on the radial differential rotation and hence on AM transport in these stars. For slow rotators, the effect of the rotation can be treated as a small perturbation of the pulsation frequency. When spherically symmetric rotation is assumed, the splitting simplifies to (Ledoux 1951; Schou et al. 1994)

δ ω n , l , m = m β n , l ∫ 0 R K n , l ( r ) Ω ( r ) d r , $$ \begin{aligned} \delta \omega _{n,l,m} = m\beta _{n,l}\int _0^R K_{n,l}(r)\Omega (r)\mathrm{d}r, \end{aligned} $$(2)

where m is the azimuthal order, βn, l is a constant that depends on the radial order n and on the harmonic degree l, and Kn, l is the rotation kernel. For a given (n, l) pair, we define the mean asteroseismic rotation rate as

Ω sismo n , l ≡ ∫ 0 R K n , l ( r ) Ω ( r ) d r . $$ \begin{aligned} \Omega _{\mathrm{sismo} }^{n,l} \equiv \int _0^R K_{n,l}(r)\Omega (r)\mathrm{d}r. \end{aligned} $$(3)

We only considered the l = 1 rotational splittings and verified that they were consistent with the l = 2 rotational splittings.

In the lower panels of Fig. 2, we show the ratio of the asteroseismic rotation rate and the surface rotation rate Ωsurf for the different models of Arthur and Doris. The open circles correspond to the theoretical values of 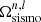Ω sismo n , l $ \Omega_{\mathrm{sismo}}^{n,l} $ computed with Eq. (3) for the different AM transport prescriptions considered in this study. The blue area and the error bars correspond to actual measurements to highlight the detectability of the model differences. The error bars correspond to the precision of the average observational rotational splitting measured by Benomar et al. (2018, hereafter OB18), which is mostly dependent on the signal-to-noise ratio of the modes and of the mode blending width at νmax, and the blue area corresponds to a solid-body rotation profile with the precision of the surface rotation rate from starspots. A value of 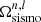Ω sismo n , l $ \Omega_{\mathrm{sismo}}^{n,l} $ that is compatible with the blue area means that asteroseismology does not detect a significant degree of radial differential rotation, as expected from OB15 and MN17. Models with AM transport by magnetic instabilities (red circles) are always compatible with the observations of a similar rotation rate derived from asteroseismic splittings and from an independent measurement of the surface rotation rate, as reported by OB15 and MN17 for stars in the cold part of the HR diagram (Doris) and on the hotter side (Arthur). The efficient AM transport predicted by these models is thus in agreement with the asteroseismic constraints on the internal rotation currently available for various solar-type main-sequence stars, similarly to what is found in the case of the Sun (see Eggenberger et al. 2019, 2022).

For models with hydrodynamic AM transport alone, the situation is different. For targets on the cold side of the HR diagram (Doris), these models predict asteroseismic rotation rates that are significantly higher than surface rotation rates because of efficient braking of the surface by magnetised winds and the low efficiency of AM transport by meridional circulation and shear instability, which leads to a high degree of radial differential rotation in the radiative interior, in particular, close to the base of the convective envelope that can be probed by rotational kernels. These rotating models with transport by hydrodynamic processes alone can then be easily rejected with asteroseismic measurements of solar-type stars on the cold side of the HR diagram, although the observational uncertainties are large (green circles in Fig. 2). For hotter main-sequence stars, the difference between asteroseismic and surface rotation rates expected for models with hydrodynamic transport alone is much lower because surface braking associated with stars with shallow convective envelopes is far less efficient. With the assumption of an inefficient surface braking, the radial differential rotation predicted for these models is too small in the region probed by seismology and falls within the observational uncertainty of the surface rotation rates deduced from starspots (green circles in the bottom centre panel of Fig. 2). Owing to the uncertainties in the knowledge of surface magnetic braking for stars hotter than the Sun, it is difficult to determine exactly above which effective temperature this braking is really inefficient. Stars similar to Arthur are indeed expected to be close to this transition, but it is not absolutely clear whether the assumption of inefficient braking adopted here is fully justified. We thus investigated the impact of introducing a much more efficient braking for stars in the blue part of the HR diagram on the conclusion about internal AM transport obtained for Arthur. We computed a new model for Arthur by using the same prescription for an efficient surface braking by magnetised winds as introduced for the cooler star Doris. This model (labelled ‘efficient braking’ in Fig. 2) is computed with a zero-age main-sequence initial rotation period of 1.6 days and then shows a higher degree of radial differential rotation as a result of this strong braking of the surface and low AM transport efficiency by hydrodynamic processes alone, which can then be discarded using asteroseismic and surface rotation rates observations similarly to the result obtained for the cooler star Doris. For Arthur, we also tested another extreme case for which we assumed local AM conservation (labelled ‘local conservation’ in Fig. 2). This model behaves similarly to the model including hydrodynamic processes alone. We thus observe that for stars in the blue part of the HR diagram, it is difficult to reject rotating models with an inefficient AM transport based on combined asteroseismic and surface rotation rate measurements because only cases with an efficient surface braking by magnetised winds could be detected.

4. Conclusions

We carried out a detailed modelling of four Kepler LEGACY targets, three that lie on the hotter side of the HR diagram and are at different evolutionary stages in the MS, and one on the colder side. In Sect. 2 we described the asteroseismic modelling procedure together with the computation of rotating models with hydrodynamic AM transport alone and models with both hydrodynamic and magnetic transport. The asteroseismic rotation rates were then computed for these different models and were compared with the surface rotation rates deduced from observations of starspots in Sect. 3.

For MS stars in the hotter part of the HR diagram (masses typically above ∼1.2 M⊙ at solar metallicity), models with hydrodynamic transport processes alone, and models with additional transport by magnetic instabilities are found to be consistent with measurements reported by OB15 and MN17, who observed a low degree of radial differential rotation between the radiative and convective zones. For these stars, which constitute a significant fraction of the Kepler LEGACY sample, the combination of asteroseismic constraints from the splitting of pressure modes and of the surface rotation rate does not allow us to conclude that an efficient AM transport is required in addition to the transport by meridional circulation and shear instability alone. Even the model assuming local AM conservation cannot be ruled out. This is because rotational kernels probe a region close below the BCZ, where radial differential rotation can be low for these stars with their shallow convective envelopes. If an unlikely efficient surface braking is assumed for these hotter stars, the degree of radial differential rotation would be incompatible with the observations. Further investigations on that specific point are beyond the scope of this study, but are required to determine whether this signature appears in the available observational data. In the colder part of the HR diagram, the situation is different due to the efficient braking of the stellar surface by magnetised winds. We observed a clear disagreement between the rotational properties of models that only includes hydrodynamic processes and asteroseismic constraints, while models with magnetic fields correctly reproduce the observations, similarly to the solar case. This disagreement allows us to easily rule out models with an inefficient transport of AM in that part of the HR diagram.

1

The Gaia data of Arthur are flagged as unreliable. The estimated observed absolute luminosity should be considered with caution and was not reproduced by our models.

Acknowledgments

J.B. and G.B. acknowledge funding from the SNF AMBIZIONE grant No 185805 (Seismic inversions and modelling of transport processes in stars). P.E. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 833925, project STAREX).

References

  1. Baglin, A., Auvergne, M., Barge, P., et al. 2009, in Transiting Planets, eds. F. Pont, D. Sasselov, & M. J. Holman, IAU Symp., 253, 71 [NASA ADS] [Google Scholar]
  2. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  3. Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [Google Scholar]
  4. Benomar, O., Takata, M., Shibahashi, H., Ceillier, T., & García, R. A. 2015, MNRAS, 452, 2654 [Google Scholar]
  5. Benomar, O., Bazot, M., Nielsen, M. B., et al. 2018, Science, 361, 1231 [Google Scholar]
  6. Bétrisey, J., Pezzotti, C., Buldgen, G., et al. 2022, A&A, 659, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  8. Buldgen, G., Farnir, M., Pezzotti, C., et al. 2019, A&A, 630, A126 [EDP Sciences] [Google Scholar]
  9. Buldgen, G., Bétrisey, J., Roxburgh, I. W., Vorontsov, S. V., & Reese, D. R. 2022, Front. Astron. Space Sci., 9, 942373 [NASA ADS] [CrossRef] [Google Scholar]
  10. Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2013, A&A, 555, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995, ApJ, 441, 865 [Google Scholar]
  12. Charbonneau, P., & MacGregor, K. B. 1993, ApJ, 417, 762 [Google Scholar]
  13. Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [Google Scholar]
  14. Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [Google Scholar]
  15. Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Deheuvels, S., Ouazzani, R. M., & Basu, S. 2017, A&A, 605, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Di Mauro, M. P., Ventura, R., Cardini, D., et al. 2016, ApJ, 817, 65 [NASA ADS] [CrossRef] [Google Scholar]
  19. Di Mauro, M. P., Ventura, R., Corsaro, E., & Lustosa De Moura, B. 2018, ApJ, 862, 9 [Google Scholar]
  20. Eff-Darwich, A., & Korzennik, S. G. 2013, Sol. Phys., 287, 43 [NASA ADS] [CrossRef] [Google Scholar]
  21. Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [Google Scholar]
  23. Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Eggenberger, P., Lagarde, N., Miglio, A., et al. 2017, A&A, 599, A18 [CrossRef] [EDP Sciences] [Google Scholar]
  25. Eggenberger, P., Deheuvels, S., Miglio, A., et al. 2019, A&A, 621, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Eggenberger, P., Buldgen, G., Salmon, S. J. A. J., et al. 2022, Nat. Astron., 6, 788 [NASA ADS] [CrossRef] [Google Scholar]
  27. Farnir, M., Dupret, M. A., Buldgen, G., et al. 2020, A&A, 644, A37 [EDP Sciences] [Google Scholar]
  28. Fellay, L., Buldgen, G., Eggenberger, P., et al. 2021, A&A, 654, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
  30. Furlan, E., Ciardi, D. R., Cochran, W. D., et al. 2018, ApJ, 861, 149 [Google Scholar]
  31. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. García, R. A., Ceillier, T., Salabert, D., et al. 2014, A&A, 572, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Garraffo, C., Drake, J. J., Dotter, A., et al. 2018, ApJ, 862, 90 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Gough, D. O., & McIntyre, M. E. 1998, Nature, 394, 755 [Google Scholar]
  36. Kraft, R. P. 1967, ApJ, 150, 551 [Google Scholar]
  37. Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [Google Scholar]
  38. Ledoux, P. 1951, ApJ, 114, 373 [Google Scholar]
  39. Li, G., Van Reeth, T., Bedding, T. R., et al. 2020, MNRAS, 491, 3586 [Google Scholar]
  40. Lund, M. N., Silva Aguirre, V., Davies, G. R., et al. 2017, ApJ, 835, 172 [Google Scholar]
  41. Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [Google Scholar]
  43. McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [Google Scholar]
  44. Mestel, L., & Weiss, N. O. 1987, MNRAS, 226, 123 [Google Scholar]
  45. Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Moyano, F. D., Eggenberger, P., Meynet, G., et al. 2022, A&A, 663, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Murphy, S. J., Fossati, L., Bedding, T. R., et al. 2016, MNRAS, 459, 1201 [Google Scholar]
  48. Nielsen, M. B., Gizon, L., Schunker, H., & Karoff, C. 2013, A&A, 557, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Nielsen, M. B., Schunker, H., Gizon, L., Schou, J., & Ball, W. H. 2017, A&A, 603, A6 [Google Scholar]
  50. Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [Google Scholar]
  52. Reese, D. R., Marques, J. P., Goupil, M. J., Thompson, M. J., & Deheuvels, S. 2012, A&A, 539, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Reinhold, T., Reiners, A., & Basri, G. 2013, A&A, 560, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Rendle, B. M., Buldgen, G., Miglio, A., et al. 2019, MNRAS, 484, 771 [Google Scholar]
  55. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  56. Roxburgh, I. W. 2017, A&A, 604, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Roxburgh, I. W., & Vorontsov, S. V. 2003, A&A, 411, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Rüdiger, G., & Kitchatinov, L. L. 1996, ApJ, 466, 1078 [NASA ADS] [CrossRef] [Google Scholar]
  59. Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]
  60. Saio, H., Takata, M., Lee, U., Li, G., & Van Reeth, T. 2021, MNRAS, 502, 5856 [Google Scholar]
  61. Schou, J., Christensen-Dalsgaard, J., & Thompson, M. J. 1994, ApJ, 433, 389 [NASA ADS] [CrossRef] [Google Scholar]
  62. Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [Google Scholar]
  63. Scuflaire, R., Théado, S., Montalbán, J., et al. 2008a, Ap&SS, 316, 83 [Google Scholar]
  64. Scuflaire, R., Montalbán, J., Théado, S., et al. 2008b, Ap&SS, 316, 149 [Google Scholar]
  65. Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
  66. Talon, S., Zahn, J.-P., Maeder, A., & Meynet, G. 1997, A&A, 322, 209 [Google Scholar]
  67. Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., & Toomre, J. 2003, ARA&A, 41, 599 [Google Scholar]
  68. van Saders, J. L., Pinsonneault, M. H., & Barbieri, M. 2019, ApJ, 872, 128 [NASA ADS] [CrossRef] [Google Scholar]
  69. Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
  70. Zahn, J.-P., Talon, S., & Matias, J. 1997, A&A, 322, 320 [Google Scholar]

Appendix A: Detailed modelling procedure

The modelling procedure is divided into two main steps. The first step uses non-rotating models to fit the seismic information of the target and to constrain its location in the HR diagram. The second step uses rotating models and follows the HR track to the location identified by the first step to derive the corresponding rotation profile. This modelling procedure outputs a robust stellar structure and its corresponding rotation profile, which can then be used to compute the rotational splittings and the asteroseismic rotation rate. Our targets are slow rotators, which motivated the use of this modelling strategy. For slow rotators, it is possible to use a perturbative treatment of rotation, like for the Sun. In this case, the fit of the internal rotation can be separated from the fit of the structure, and the inferences about rotation are quasi-model-independent from the seismic structure at first order. In this framework, our modelling is appropriate and does not change the conclusions of our study. From the point of view of stellar modelling alone, neglecting rotation in the first step is a simplification that has a small impact on the transport of the chemical elements. It can be associated with a systematic uncertainty that accounts for the uncertainties due to the choice of the physical ingredients (e.g. choice of abundances, opacities, and diffusive formalism) (see JB22). The estimation of this systematic uncertainty is computationally expensive and was performed for some targets in the literature (e.g. Buldgen et al. 2019; Farnir et al. 2020; Bétrisey et al. 2022). For these targets, a rich variety of physical ingredients changes were considered, and the resulting systematic uncertainty was smaller than for the other sources of uncertainties.

The modelling procedure of the first step is similar to that of JB22. It consists of fitting the seismic information with an MCMC in a grid of non-rotating models, coupled with a mean density inversion. We used a grid of non-rotating models computed with the Code Liégeois d’Évolution Stellaire (CLES; Scuflaire et al. 2008b), and the frequencies were computed with the Liège Oscillation Code (LOSC; Scuflaire et al. 2008a). This grid is a high-resolution grid, consiting of 1.3 million models, whose specificities are summarised in Table A.1. The physical ingredients are the same as in Sec. 2.1 of JB22. The minimisations were conducted with AIMS (Rendle et al. 2019), first by fitting the individual frequencies and the classical constraints (effective temperature, metallicity, and luminosity or frequency of maximal power νmax). Then, a mean density inversion (Reese et al. 2012) was performed to constrain the mean density (see e.g. Buldgen et al. 2022, for a review about inversion techniques) that was added to the set of classical constraints, assuming a conservative precision of 0.6%, for a second MCMC, this time with frequency separation ratios (r01 and r02; Roxburgh & Vorontsov 2003) instead of the individual frequencies. We used uniform priors on the estimated stellar parameters. The likelihoods were computed assuming that the true value of the observations were perturbed by some normally distributed random noise (see JB22 for further details).

Table A.1.

Mesh properties of the grid used for the minimisation in the first step of the modelling strategy.

Rotating models were then computed based on the stellar properties determined from this asteroseismic modelling. In addition to the internal transport of AM described in the main text, these rotating models account for the braking of the surface due to magnetised winds following Matt et al. (2015) with the torque

d J d t = { − T ⊙ ( R R ⊙ ) 3.1 ( M M ⊙ ) 0.5 ( τ cz τ cz ⊙ ) p ( Ω Ω ⊙ ) p + 1 ( R o > R o ⊙ / χ ) − T ⊙ ( R R ⊙ ) 3.1 ( M M ⊙ ) 0.5 χ p ( Ω Ω ⊙ ) ( R o ≤ R o ⊙ / χ ) . $$ \begin{aligned} \nonumber \frac{\mathrm{d} J}{\mathrm{d}t} = \left\{ \begin{array}{l l } -T_{\odot } \left({\displaystyle \frac{R}{R_\odot }} \right)^{3.1} \left({\displaystyle \frac{M}{M_\odot } }\right)^{0.5} \left({\displaystyle \frac{\tau _{\rm cz}}{\tau _{\mathrm{cz}\odot }} }\right)^{p} \left({\displaystyle \frac{\Omega }{\Omega _{\odot }} }\right)^{p+1}&(Ro > Ro_{\odot }/\chi ) \\ \nonumber&\\ \nonumber -T_{\odot } \left({\displaystyle \frac{R}{R_\odot }} \right)^{3.1} \left({\displaystyle \frac{M}{M_\odot } }\right)^{0.5} \chi ^{p} \left({\displaystyle \frac{\Omega }{\Omega _{\odot }} }\right)&(Ro \le Ro_{\odot }/\chi ) \; . \end{array} \right. \end{aligned} $$

R and M are the radius and mass of the star, Ro is the Rossby number, and τcz is the convective turnover timescale. Following Eggenberger et al. (2019), the transition from the saturated to the unsaturated regime was defined with the parameter χ = R o⊙/Rosat fixed to 10, the coefficient p was fixed to 2.3, and the solar-calibrated braking constant T⊙ was used.

Appendix B: Supplementary data

In Fig. B.1 we show the rotation profiles of the different models of Barney and Carlsberg. In Fig. B.2 we show the corresponding ratio of the asteroseismic and surface rotation rates.

thumbnail Fig. B.1.

Rotation profiles of Barney and Carlsberg considering different AM transport prescriptions. The rotation profiles of Barney are shown in the upper panel, and the profiles of Carlsberg in the lower panel. The base of the convective zone (BCZ) is shown as a dashed black line. The rotation kernel is shown in brown, with l = 1 and n = 18 or n = 21 to correspond to a frequency around the νmax for Barney and Carlsberg, respectively. It is rescaled and shifted vertically for illustration purposes.

thumbnail Fig. B.2.

Surface rotation predicted by the seismology for Barney and Carlsberg. The results for Barney are shown in the upper panel, and the results for Carlsberg in the lower panel. The error bar corresponds to the precision of the average observational rotational splitting measured by OB18, and the blue area shows a solid-body rotation profile with the observational uncertainty of the surface rate from starspot measurements.

All Tables

Table 1.

Observed and modelled data of Arthur, Barney, Carlsberg, and Doris.

In the text
Table A.1.

Mesh properties of the grid used for the minimisation in the first step of the modelling strategy.

In the text

All Figures

thumbnail Fig. 1.

HR diagram of Arthur, Barney, Carlsberg, Doris, and of the sample of OB15. The tracks correspond to a grid slice with an initial chemical composition of X0 = 0.74 and Z0 = 0.018, and no overshooting.
In the text
thumbnail Fig. 2.

Rotational profiles and splittings of Doris and Arthur considering different AM transport prescriptions. Top line: rotation profiles of Doris (left panel) and Arthur (centre and right panels). The base of the convective zone (BCZ) is shown as a dashed black line. The rotation kernel around the νmax, namely K21, 1, is shown in brown, and is rescaled and shifted vertically for illustration purposes. Bottom line: ratio of the rotation rate predicted by asteroseismology and starsport measurements for Doris (left panel) and Arthur (centre and right panels). The open circles are the theoretical predications, considering different AM transport prescriptions, accounting only for hydrodynamic processes (green circles), or for hydrodynamic processes and magnetic Tayler instability (red circles). The shallow convective envelope of Arthur likely implies an inefficient braking. For Arthur, we also tested extreme cases (right panels) with an AM transport with efficient braking (blue circles) or assuming local AM conservation (purple circles). The error bar corresponds to the precision of the average observational rotational splitting measured by OB18, and the blue area shows a solid-body rotation profile with the observational uncertainty of the surface rate from starspot measurements.
In the text
thumbnail Fig. B.1.

Rotation profiles of Barney and Carlsberg considering different AM transport prescriptions. The rotation profiles of Barney are shown in the upper panel, and the profiles of Carlsberg in the lower panel. The base of the convective zone (BCZ) is shown as a dashed black line. The rotation kernel is shown in brown, with l = 1 and n = 18 or n = 21 to correspond to a frequency around the νmax for Barney and Carlsberg, respectively. It is rescaled and shifted vertically for illustration purposes.
In the text
thumbnail Fig. B.2.

Surface rotation predicted by the seismology for Barney and Carlsberg. The results for Barney are shown in the upper panel, and the results for Carlsberg in the lower panel. The error bar corresponds to the precision of the average observational rotational splitting measured by OB18, and the blue area shows a solid-body rotation profile with the observational uncertainty of the surface rate from starspot measurements.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.