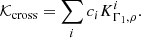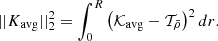| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 26 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346258 | |
| Published online | 26 July 2023 | |
Asteroseismic modelling strategies in the PLATO era
I. Mean density inversions and direct treatment of the seismic information
1
Observatoire de Genève, Université de Genève, Chemin Pegasi 51, 1290 Versoix, Switzerland
e-mail: Jerome.Betrisey@unige.ch
2
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
3
Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, Coventry CV4 7AL, UK
4
Institut d’Astrophysique et Géophysique de l’Université de Liège, Allée du 6 août 17, 4000 Liège, Belgium
5
Institute of Physics, Laboratory of Astrophysics, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Genève, Chemin Pegasi 51, 1290 Versoix, Switzerland
Received:
27
February
2023
Accepted:
5
June
2023
Context. Asteroseismology experienced a breakthrough in the last two decades thanks to the so-called photometry revolution with space-based missions such as CoRoT, Kepler, and TESS. Because asteroseismic modelling will be part of the pipeline of the future PLATO mission, it is relevant to compare some of the current modelling strategies and discuss the limitations and remaining challenges for PLATO. In this first paper, we focused on modelling techniques treating directly the seismic information.
Aims. We compared two modelling strategies by directly fitting the individual frequencies or by coupling a mean density inversion with a fit of the frequency separation ratios.
Methods. We applied these two modelling approaches to six synthetic targets with a patched atmosphere, for which the observed frequencies were obtained with a non-adiabatic oscillation code. We then studied ten actual targets from the Kepler LEGACY sample.
Results. As is well known, the fit of the individual frequencies is very sensitive to the surface effects and to the choice of the underlying prescription for semi-empirical surface effects. This significantly limits the accuracy and precision that can be achieved for the stellar parameters. The mass and radius tend to be overestimated, and the age therefore tends to be underestimated. In contrast, the second strategy, which is based on mean density inversions and on the ratios, efficiently damps the surface effects and allows us to obtain precise and accurate stellar parameters. The average statistical precision of our selection of targets from the LEGACY sample with this second strategy is 1.9% for the mass, 0.7% for the radius, and 4.1% for the age. This is well within the PLATO mission requirements. The addition of the inverted mean density to the constraints significantly improves the precision of the stellar parameters by 20%, 33%, and 16% on average for the stellar mass, radius, and age, respectively.
Conclusions. The modelling strategy based on mean density inversions and frequencies separation ratios showed promising results for PLATO because it achieved a precision and accuracy on the stellar parameters that meet the PLATO mission requirements with ten Kepler LEGACY targets. The strategy also left some margin for other unaccounted systematics, such as the choice of the physical ingredients of the stellar models or the stellar activity.
Key words: stars: solar-type / asteroseismology / stars: fundamental parameters / stars: interiors
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
With the launch of the space-based photometry missions CoRoT (Baglin et al. 2009), Kepler (Borucki et al. 2010), and TESS (Ricker et al. 2015) in the past two decades, asteroseismology experienced a rapid development. The field will further expand with the next-generation instrument of the future PLATO mission (Rauer et al. 2014). The data quality from these missions enables the use of so-called seismic inversion techniques (see Buldgen et al. 2022a), which were restricted to helioseismology so far. In helioseismology, they were applied with tremendous success (see e.g., Basu & Antia 2008; Kosovichev et al. 2011; Buldgen et al. 2019c; Christensen-Dalsgaard 2021, for reviews). One of the key challenges of PLATO is the precision requirements on the stellar parameters (1–2% in radius, 15% in mass, and 10% in age for a Sun-like star). In this context and considering the fact that asteroseismic modelling will be part of the PLATO pipeline, it is relevant to combine the most advanced modelling strategies exploiting seismic data, classical constraints (e.g., interferometric radius, luminosity, metallicity, or effective temperature), and inversion techniques, and to discuss the remaining challenges that could limit the precision and accuracy of the stellar parameters estimated with PLATO data. Among them, we highlight the so-called surface effects (see e.g., Ball & Gizon 2017; Nsamba et al. 2018; Jørgensen et al. 2020, 2021; Cunha et al. 2021), the choice of the physical ingredients (see e.g., Buldgen et al. 2019a; Bétrisey et al. 2022), and the stellar activity, which will be the subject of a future article in this series (see e.g., Broomhall et al. 2011; Santos et al. 2018, 2019a,b, 2021; Howe et al. 2020; Thomas et al. 2021).
Because various modelling strategies have been developed over the years, we provide our discussion in a series of papers. In this first article, we consider techniques that directly treat the seismic information by fitting the individual frequencies or frequency separation ratios. In a future paper of this series, we will consider techniques that treat the seismic information indirectly by studying indicators that are orthogonalised using the Gram-Schmidt procedure (Farnir et al. 2019, 2020). As a side note, we remark that it is also possible to directly treat the seismic information with the εnl matching technique (Roxburgh & Vorontsov 2003; Roxburgh 2015, 2016), and that a comparison between that technique and those presented in this study would be relevant for a future study. In addition, other modelling techniques also exist that can circumvent some of the PLATO challenges, but they are more difficult to implement in a pipeline. To only quote a few examples, it is possible to constrain the stellar structure by applying the differential response technique (Vorontsov et al. 1998; Vorontsov 2001; Roxburgh et al. 2002a,b; Appourchaux et al. 2015), by using inversions based on so-called seismic indicators (Reese et al. 2012; Buldgen et al. 2015a,b, 2018) that are then applied to a variety of targets (Buldgen et al. 2016a,b, 2017, 2019a,b, 2022b; Bétrisey et al. 2022, 2023), or by constraining the properties of the convective core with an inversion of the frequency separation ratios (Bétrisey & Buldgen 2022).
In Sect. 2 we introduce a new high-resolution grid of standard non-rotating stellar models, the Spelaion grid. In Sect. 3 we present the most advanced modelling techniques, which we directly use on the asteroseismic data, together with the classical constraints and inversion techniques. We first apply them to six synthetic targets with a patched atmosphere from Sonoi et al. (2015), and in Sect. 4 we apply them to a selection of ten actual targets from the Kepler LEGACY sample. Finally, we draw our conclusions in Sect. 5.
2. The Spelaion grid
The Spelaion grid is a large high-resolution grid of standard non-rotating models (∼5.1 million models) designed to cover main-sequence stars between 0.8 and 1.6 solar masses. The grid can deal with a large variety of chemical compositions and mixing, with up to three dedicated free parameters (initial hydrogen mass fraction X0, initial metallicity Z0, and overshooting αov). It has a high mesh resolution that brings two advantages. First, the coupling with a minimisation algorithm that can interpolate within the grid allows for a very thorough exploration of the parameter space. Second, the high resolution reduces the issues with the interpolation of higher-mass stars. These stars can have convective cores or mixed modes at low frequency, which are difficult to capture with a grid with a lower resolution. The low-order mixed modes are currently unlikely to be observed in main-sequence stars with the actual instruments because they are in a noisy region of the frequency spectrum. For each model of the grid, we computed the theoretical adiabatic frequencies between fixed boundaries in adimensional angular frequency. This approximately corresponds to the modes with n ∼ 4 − 33 for a solar model and a few more high radial orders for higher-mass stars. This is a broad mode range that extends slightly beyond the actual observational capabilities at low and high radial order. For reference, the radial order of the frequency of maximum power νmax of the targets considered in this work is about n = 21. We considered l = 0, 1, 2 degrees because the grid is ultimately designed to fit the r01 and r02 ratios.
The grid is composed of three subgrids that cover specific types of physics (standard, high metallicity, and overshooting). Their statistics and properties are summarised in Tables 1 and 2. The evolutionary sequences were computed with the Liège evolution code (CLES; Scuflaire et al. 2008b), and for each time-step, the frequencies were computed with the adiabatic Liège oscillation code (LOSC; Scuflaire et al. 2008a). We used the AGSS09 abundances (Asplund et al. 2009), the FreeEOS equation of state (Irwin 2012), and the OPAL opacities (Iglesias & Rogers 1996), supplemented by the Ferguson et al. (2005) opacities at low temperature and the electron conductivity by Potekhin et al. (1999) as physical ingredients of the models. The microscopic diffusion was described using the formalism of Thoul et al. (1994), with the screening coefficients of Paquette et al. (1986) and the nuclear reaction rates are from Adelberger et al. (2011). The mixing-length parameter αMLT was fixed at a solar calibrated value of 2.05, following the implementation of Cox & Giuli (1968). For the atmosphere modelling, we used the T(τ) relation of model C of Vernazza et al. (1981).
Statistics of Spelaion and its subgrids.
Mesh properties of the Spelaion subgrids.
In Fig. 1 we illustrate the Hertzsprung-Russell (HR) diagram of the two sets of targets considered in this work, for the synthetic targets and for the actual targets from the Kepler LEGACY sample (hereafter abbreviated to LEGACY sample; Lund et al. 2017). The evolutionary tracks correspond to a slice of the Spelaion grid with X0 = 0.72, Z0 = 0.018, and αov = 0.00.
 |
Fig. 1. HR diagram of the targets considered in this work. The Sonoi et al. (2015) targets are denoted by the orange stars, and the Kepler LEGACY targets are indicated by the blue stars. The grey lines correspond to the evolutionary tracks from a slice of the Spelaion grid with X0 = 0.72, Z0 = 0.018, and αov = 0.00. |
3. Modelling strategies
In this first paper, we focus on modelling strategies treating directly the seismic information, either in the form of individual frequencies or in the form of frequency separation ratios. Over the years, a variety of methods have been developed, such as Levenberg-Marquardt algorithms (see e.g., Frandsen et al. 2002; Teixeira et al. 2003; Miglio & Montalbán 2005), genetic algorithms (Charpinet et al. 2005; Metcalfe et al. 2009, 2014), Bayesian inference (Silva Aguirre et al. 2015, 2017; Aguirre Børsen-Koch et al. 2022), machine-learning methods (Bellinger et al. 2016, 2019), or Markov chain Monte Carlo methods (MCMC; Bazot et al. 2008; Gruberbauer et al. 2013; Rendle et al. 2019).
In this study, we first investigate the fit of the individual frequencies, with a focus on the impact of the surface effects. Then, we test a more elaborate technique that uses frequency separation ratios coupled with a mean density inversion. This technique has been shown to be effective (Buldgen et al. 2019a; Bétrisey et al. 2022). We also investigate the impact of the correlations between the inverted mean density and the frequency separation ratios, which were neglected in the past studies. For all the minimisations, we used the AIMS software (Rendle et al. 2019), and we applied the two modelling strategies on synthetic targets from Sonoi et al. (2015; models A to F). The frequencies of these simulated targets were computed with the MAD oscillation code. This code includes a non-adiabatic non-local time-dependent convection modelling as detailed in Grigahcène et al. (2005), adapted to the stratification of patched models following the prescriptions of Dupret et al. (2006). For each target and for the sake of realism, we adopted the observational uncertainty of the frequencies of LEGACY targets with similar mode ranges, namely KIC 9206432 (model B), KIC 10162436 (models C and E), and KIC 11081729 (models D and F). For model A, which is a proxy of the Sun, we adopted the uncertainties of Basu et al. (2009) that were partially revised by Davies et al. (2014), degraded by a constant factor to mimic a data quality similar to that of the Kepler mission. The classical constraints are the effective temperature, the metallicity, and the absolute luminosity. When the inverted mean density was added to the constraints, it was treated either as another classical constraint or as a seismic constraint to account for the correlation with the ratios. For the effective temperature, we adopted an uncertainty of 90 K if Teff < 6000 K and 100 K otherwise, and 0.1 dex for the metallicity. For the luminosity, we adopted an uncertainty of 19% when L/L⊙ < = 3, 15% when 3 < L/L⊙ < 4.5, and 11% otherwise. This is in line with the results from Silva Aguirre et al. (2017) for the LEGACY sample, assuming conservative uncertainties considering the impact of extinction, bolometric correction, and uncertainties on the spectral parameters when Gaia parallaxes are used. The uncertainties of the effective temperature and of the metallicity are the typical uncertainties recommended for surveys (see e.g., Furlan et al. 2018), and we assumed that if Teff < 6000 K, a slightly better uncertainty might be expected. We point out that assuming smaller uncertainties on these quantities would not change the results of our study because the fits are mainly driven by the seismic constraints1. Finally, a conservative uncertainty of 0.6% was assumed for the inverted mean density when it was considered a classical constraint (see Sect. 3.3.1).
3.1. AIMS and convergence assessment
The AIMS software (Rendle et al. 2019) is an MCMC-based algorithm that relies on the EMCEE package (Foreman-Mackey et al. 2013), which is an interpolation scheme to sample between the grid points, and on a Bayesian approach to provide the posterior probability distributions of the optimised stellar parameters. The coupling of a high-resolution grid with the interpolation scheme allows a very thorough exploration of the parameter space. For the minimisations of this work, we used the standard MS subgrid of Spelaion, and AIMS therefore included four free variables to optimise (mass, age, and the chemical composition with X0 and Z0). We considered uniform uninformative priors for all the free variables, except for the age, for which we used a uniform distribution with the range [0, 13.8] Gyr. We assumed that the true value of the observations for the observational constraints were perturbed by some Gaussian-distributed random noise for the computation of the likelihoods. AIMS accepts two types of constraints: the seismic constraints (individual frequencies, frequency separation ratios, radial frequency of lower order, inverted mean density, etc.), for which all correlations are accounted for to first order, and the classical constraints (stellar radius, absolute luminosity, effective temperature, metallicity, frequency of maximal power νmax, inverted mean density, etc.), for which the correlations with the seismic constraints are neglected. The inverted mean density is an ambivalent constraint as it can be treated either as a classical constraints or as a seismic constraint if the inversion coefficients are provided (see Sect. 3.3.1).
By design, a run in AIMS is performed in two steps. First, a burn-in phase is computed to identify the relevant part of the parameter space, and then the solution run is performed. By default, AIMS uses 250 walkers, 200 burn-in steps, and 200 steps for the solution. Hence, the stellar parameters are based on 50 000 samples from the production run, which follows the 50 000 probability calculations from the burn-in phase. This choice is a compromise between the required computational power and the control on the autocorrelation time. For individual modelling, we recommend to modify these default values to 800 walkers, 2000 burn-in steps, and 2000 steps for the solution, however. In this configuration, the solution is based on 1.6 million samples from the production run, which follows the 1.6 million probability calculations from the burn-in phase. This ensures that the autocorrelation time is much shorter than the number of steps, at the expense of requiring higher computational power. We opted for this new configuration to have a higher degree of confidence in our results, but some tests would be required to find a good compromise in a pipeline. Along with the solution, AIMS provides several diagnostic plots to ensure that the MCMC converged successfully. These plots notably include a triangle plot of the optimized parameters to confirm that the solution is unique and that the interpolation was smooth, the evolution of the walkers to ensure that they do not drift, and the échelle diagram (Grec et al. 1983). They provide good control on the reliability of the MCMC result, but these checks are manual and not pipeline-friendly. In Appendix D we provide illustrations of the diagnostic plots for a successful convergence (see Fig. D.1) and for the most common issues that may occur (see Figs. D.2–D.6). We separated the convergence issues into five categories for illustration purposes, but a run can be affected by more than one issue. These categories are described in detail in Appendix D, and we point out here that the most frequent issues occurred when the walkers drifted during the sampling or hit the grid boundaries.
3.2. Individual frequencies as constraints
3.2.1. Surface effects
Surface effects are related to the poor treatment of near surface layers. In these regions, the mixing-length theory (MLT) is an inaccurate description of convection because it does not account for compressible turbulence, for example. The simplistic treatment of convection is especially an issue in asteroseismology because the perturbation of turbulent pressure can significantly affect the oscillation frequencies. In addition, the thermal timescales in the near surface layers are similar to the oscillation periods, and the oscillations are thus highly non-adiabatic there (Houdek & Dupret 2015). Semi-empirical prescriptions were proposed to account for the structural contribution of the surface effects (Kjeldsen et al. 2008; Ball & Gizon 2014; Sonoi et al. 2015). These prescriptions are described by one or two free parameters that can be added to the optimised variables during the minimisation.
In the following section, we define νobs as the observed frequency and νmod as the theoretical adiabatic frequency that does not include surface effects. Kjeldsen et al. (2008) treated the surface effects with a power law in frequency,
where a and b are the parameters to be determined, δν = νobs − νmod, and νmax is the frequency of maximum power, computed following the scaling relation (Kjeldsen & Bedding 1995)
where g⊙ ≃ 27 420 cm s−2 (Prša et al. 2016; Tiesinga et al. 2021), Teff, ⊙ = 5777 K (Allen 1976), and νmax, ⊙ = 3090 μHz (Huber et al. 2011). Originally, the parameter b = 4.9 was determined for the Sun, and the parameter a can then be found with a least-squares minimisation. Sonoi et al. (2015) showed that b varies significantly with the surface gravity and the effective temperature and should therefore be determined using the scaling relation
or be treated as an additional free parameter if the prescription is applied to other stars (see e.g., the case of HD 52265; Lebreton & Goupil 2014).
Ball & Gizon (2014) proposed two corrections, a one-term and a two-term correction, based on the mode inertia. The one-term prescription is
and the two-terms prescription is
where ℐ is the normalised mode inertia, and a−1 and a3 are two coefficients to be added in the optimisation procedure. The acoustic cut-off νac is computed using the scaling relation (2) because νmax ∝ νac, as first suggested by Brown et al. (1991), and we used νac, ⊙ = 5100 μHz (Jiménez 2006). Ball & Gizon (2014) found that both corrections produced a good fit of the BiSON frequencies (Broomhall et al. 2009), but Sonoi et al. (2015) pointed out that they only worked well in limited frequency ranges of their models, but not in the whole range.
Sonoi et al. (2015) proposed a correction based on patched models, including averaged 3D hydrodynamical models of the upper layer, allowing it to reproduce realistically the frequencies, and based on the frequencies of the corresponding unpatched models. They proposed a correction based on a Lorentzian function,
where α and β can be determined from the surface gravity and effective temperature using the scaling relations
or be treated as free variables.
These prescriptions were investigated by several works for main-sequence stars (Ball et al. 2016; Nsamba et al. 2018; Jørgensen et al. 2019; Cunha et al. 2021) and for more evolved stars (Ball & Gizon 2017; Jørgensen et al. 2020, 2021) using either observational data or synthetic data based on 3D simulations of the surface layers patching 1D models. These works pointed out that the two-term correction of Ball & Gizon (2014) is the most robust prescription in general, followed by the Sonoi et al. (2015) correction. The Kjeldsen et al. (2008) prescription is less robust and is not recommended in some cases. They also showed that fitting the individual frequencies tends to bias the estimated stellar parameters, especially by overestimating the mass. For post-main-sequence stars, these biases are significant because they are comparable to the PLATO precision requirements (Jørgensen et al. 2021). In addition, Ball & Gizon (2017) showed that the systematic uncertainty due to the choice of the functional form of the surface effects can be up to twice the statistical uncertainty.
We considered the prescriptions summarised in Table 3 when we fitted the individual frequencies. We tested them first with synthetic data whose frequencies were computed using an oscillation code that accounts for non-adiabatic effects2, and then with observational data. For the fit of the frequency separation ratios, the surface effects were neglected because the ratios damp them so efficiently that is not possible to estimate them with the MCMC in this configuration. In this case, we accounted for them in the mean density inversion.
Surface effect prescriptions.
3.2.2. Application to targets (Sonoi et al. 2015)
The direct-modelling strategy consists of fitting the individual frequencies and the classical constraints (surface metallicity, effective temperature, and absolute luminosity). Except for model A, the coefficients of the surface effects were poorly estimated, even though the sampling was high (800 walkers, 2000 steps of burn-in, and 2000 steps for the solution). We therefore extended the burn-in to 8000 steps. This solved the issue for models C, D, and F. The runs for model B still did not converge successfully, and the stellar parameters of model E were significantly biased. As discussed in more detail in Appendix B, the impact of the non-adiabatic effects is much stronger for models B to F than for the solar model (model A). When the non-adiabaticity of oscillations is not taken into account in the targets, which corresponds dealing with adiabatic frequencies from the patched 3D simulations, we obtained similar stellar parameters for models A, E, and F. The results of models B and D are less accurate, and the minimisation failed for model C because the grid boundary was reached. Although it is difficult to draw robust conclusions with a statistics of only six targets, the inaccuracies of models B and D indicate that the non-adiabatic correction may be incompatible with the actual description of surface effects. However, the convergence issues might also be asign that there is a problem with the structure of the targets, for example with the determination of the position of the connection between the 1D structure and the 3D model of the upper layers. To facilitate convergence of the MCMC, we discarded the modes above 2400 μHz for model B and 1500 μHz for model E. This worked for model B, but the stellar parameters of model E were not improved. As we argue below with additional tests, this disagreement likely originates from the structure of model E and not from the surface effect prescription or from the non-adiabatic correction.
In Figs. 2 and 3 we show the results of the fit of the individual frequencies before and after manually discarding the runs with issues. Except for the solar model (model A), only the BG2 and K1 prescriptions produced runs without issues. For the unsuccessful runs, the optimized stellar parameters were surprisingly not significantly biased, as we expected. Although it sounds like an advantage, the spread due to surface effects is much larger than the individual uncertainties, as illustrated in Fig. 2, and it is therefore incompatible with the PLATO precision requirements. From a pipeline perspective, some of the issues, such as histograms that are truncated at the grid boundaries, which was the main issue, can be automatically identified with a high level of confidence. However, other issues, such as an excessively peaked distribution or walker drifts, are harder to identify automatically. This type of problem is well suited for machine-learning methods, however, even though it would be difficult to build a robust and comprehensive training set.
 |
Fig. 2. MCMC results for the targets from Sonoi et al. (2015), using individual frequencies and different prescriptions of the surface effects described in Table 3. Runs with convergence issues are included. For each target, two sets of classical constraints were considered, including the absolute luminosity (upper line) or excluding it (bottom line). The dashed black lines represent the exact value and the grey boxes represent the observational constraints. |
In Figs. 2 and 3 we tested the impact of the luminosity by including or excluding it in the classical constraints, and verifying that both results were consistent. This test is not mandatory for synthetic models, whose absolute luminosity is known exactly (and therefore reliably), but it can point out issues with the bolometric corrections or the extinction maps when the luminosity of an observational target is computed. As expected, all the models in this section consistently reproduce the luminosity.
3.3. Frequency separation ratios as constraints
3.3.1. Mean density inversions
In this section, we present a three-step procedure that couples fits of frequency separation ratios and a mean density inversion to circumvent the issues due to surface effects. We recall that the ratios are constructed by dividing the small separation by the large separation, therefore suppressing the information about the mean density. Our method uses a mean density inversion to recover the lost information in a quasi-model-independent way. We point out that this approach can provide stellar parameters of a PLATO benchmark target whose precision meets the PLATO requirements (Bétrisey et al. 2022). The procedure starts by fitting the individual frequencies and the classical constraints as in Sect. 3.2. Then, a mean density inversion is conducted on the resulting model of this first minimisation. This allows us to constrain the mean density in a quasi-model-independent way and add it to the constraints. If the inverted mean density is treated as a classical constraint in AIMS because no detailed analysis is conducted at this stage, a conservative uncertainty of 0.6% is adopted on that quantity. Then, a second minimisation is conducted, this time by fitting frequency separation ratios (r01 and r02), the classical constraints, and the inverted mean density. The r10 ratios can be used instead of the r01, but they should not be used simultaneously because this will bias the results (Roxburgh 2018). We recall that the surface effects are accounted for in the mean density inversion and are neglected in the fit of the ratios with AIMS.
The inverted mean density is a combination of frequencies, and it is therefore possible to treat it as a seismic constraint to account for the correlations with the other seismic constraints. We computed the inverted mean density using the generalised definition of Reese et al. (2012),
where ci are the inversion coefficients that are optimised by the inversion based on the frequency differences between the reference model (ref) and the observations (obs). The index i denotes the identification pair (n, l) of the corresponding frequency. The inverted mean density is therefore correlated with the frequency separation ratios, as shown in Fig. 4, using model S from Christensen-Dalsgaard et al. (1996) and observational data from Lazrek et al. (1997). We implemented these correlations in AIMS with two subtleties. First, the inversion coefficients should be updated at each iteration of the MCMC. This would require an interpolation of the model structure at each step, however, which is numerically expensive and beyond the actual capabilities of AIMS. Because the variation in the inversion coefficients between similar models is small (see Appendix A), we neglected this effect. We assumed constant coefficients, determined by the original mean density inversion. Second, with the actual definition of s, the covariance matrix needs to be updated each time the likelihood is updated as well, which is also numerically inefficient. We therefore modified the definition of s by switching the reference frequency with the observed frequency,
 |
Fig. 4. Correlations between the inverted mean density and the r02 ratios for our toy model, using model S from Christensen-Dalsgaard et al. (1996) and observational data from Lazrek et al. (1997). |
This switch is only valid if 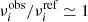 , which occurs in the limit s2 → 1. This amounts to swapping the roles of the observed star and the reference model by determining the required correction for the former to reproduce the mean density of the latter. If it is close to 1, then the two mean densities are similar to each other. This approximation allows us to compute the covariance matrix only once at the beginning of the minimisation, which is numerically much more efficient. In addition, the validity domain of the approximation is well verified because the minimisation converges toward the region where s2 → 1. For completeness, we compute in Appendix A the correlations by implementing the two definitions in AIMS for the toy model. The actual differences are very small and are negligible compared to other sources of uncertainty. We note that this implementation has one drawback. It imposes that s2 → 1, but not that
, which occurs in the limit s2 → 1. This amounts to swapping the roles of the observed star and the reference model by determining the required correction for the former to reproduce the mean density of the latter. If it is close to 1, then the two mean densities are similar to each other. This approximation allows us to compute the covariance matrix only once at the beginning of the minimisation, which is numerically much more efficient. In addition, the validity domain of the approximation is well verified because the minimisation converges toward the region where s2 → 1. For completeness, we compute in Appendix A the correlations by implementing the two definitions in AIMS for the toy model. The actual differences are very small and are negligible compared to other sources of uncertainty. We note that this implementation has one drawback. It imposes that s2 → 1, but not that 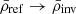 . Depending on the treatment of the surface effects by the inversion, the first condition may imply the second or not. If it does not, the optimal model may converge toward an incorrect mean density while still fulfilling the first condition, or it may simply not converge. To understand further when issues may occur, it is worth recalling what the inversion does. It minimises the following cost function:
. Depending on the treatment of the surface effects by the inversion, the first condition may imply the second or not. If it does not, the optimal model may converge toward an incorrect mean density while still fulfilling the first condition, or it may simply not converge. To understand further when issues may occur, it is worth recalling what the inversion does. It minimises the following cost function:
where ℱStruc accounts for the structural differences, ℱUncert accounts for the observational uncertainties, and ℱSurf accounts for the surface effects. The inversion therefore creates a balance between the extraction of structural differences, in our case, to provide a correction for the mean density of the reference model, while minimising the observational uncertainties and accounting for surface effects. While the first two terms are well understood (see Reese et al. 2012), ℱSurf is semi-empirical, and in practice, it introduces an instability in the inversion because it adds two free variables to the minimisation. The degree of instability depends on the strength of the surface effects, and in the worst-case scenario, all the information from the relative frequency differences can be used in the estimation of the surface effects, and no information is left for extraction of the structural differences. In this case, the inversion coefficients are poorly estimated, resulting in coefficients with high amplitudes and large variations between two consecutive coefficients. Under these conditions, the inversion is unstable, and this instability is then propagated in AIMS, causing the convergence issue we mentioned earlier. Although some techniques exist with which the quality of an inversion can be verified (see Reese et al. 2012; Buldgen et al. 2015a, or Appendix A), they either require manual checks or a knowledge of the structure of the observed target, and they are thus difficult or impossible to adapt in a pipeline. We therefore developed a new test to quantify the quality of an inversion. This test consists of evaluating the Pearson correlation coefficient of the lag plot (with lag = 1) of the inversion coefficients. The Pearson correlation coefficient is defined as the covariance of two random variables divided by the product of their standard deviations. For a sample pair (x, y),
where x = [x1, …, xN], y = [y1, …, yN], and 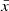 and
and 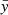 are the mean of the vectors x and y, respectively. For the sake of conciseness, we do not describe lag in detail here, but invite refer to NIST/SEMATECH (2003) and Appendix A, where we provide illustrations of lag plots of targets in different instability regimes, additional tests, and a more complete discussion of the regime boundaries. To summarise, we identified three instability regimes: high (ℛ < 0.5), intermediate (0.5 < ℛ < 0.75), and low (0.75 < ℛ). When a target is in the intermediate- or low-instability regimes, we consider that the mean density inversion can be trusted without further investigations. When a target is in the high-instability regime, the result of the inversion should be treated with caution. We remark that we identified three regimes, but in a pipeline, it would be better to define a unique threshold below which we reject the inversion. Based on the statistics of this work, we would estimate this threshold to be around ℛ ∼ 0.6, but this would benefit from further investigations with larger statistics. In Fig. 5 we show the ℛ coefficient of the targets we considered. Half of the Sonoi et al. (2015) targets lie in the high-instablity regime as a result of the issues mentioned in Sect. 3.2.2 (see also Appendix B), while only one of the ten LEGACY targets is in the high-instability regime.
are the mean of the vectors x and y, respectively. For the sake of conciseness, we do not describe lag in detail here, but invite refer to NIST/SEMATECH (2003) and Appendix A, where we provide illustrations of lag plots of targets in different instability regimes, additional tests, and a more complete discussion of the regime boundaries. To summarise, we identified three instability regimes: high (ℛ < 0.5), intermediate (0.5 < ℛ < 0.75), and low (0.75 < ℛ). When a target is in the intermediate- or low-instability regimes, we consider that the mean density inversion can be trusted without further investigations. When a target is in the high-instability regime, the result of the inversion should be treated with caution. We remark that we identified three regimes, but in a pipeline, it would be better to define a unique threshold below which we reject the inversion. Based on the statistics of this work, we would estimate this threshold to be around ℛ ∼ 0.6, but this would benefit from further investigations with larger statistics. In Fig. 5 we show the ℛ coefficient of the targets we considered. Half of the Sonoi et al. (2015) targets lie in the high-instablity regime as a result of the issues mentioned in Sect. 3.2.2 (see also Appendix B), while only one of the ten LEGACY targets is in the high-instability regime.
 |
Fig. 5. Estimates of the degree of instability in the mean density inversion of the targets. The coefficients of the surface correction were estimated by the inversion using the BG2 prescription. Targets in the high-instability regime would require further investigation, while inversion results in the low and intermediate regimes can be used without further investigation. |
As a side note, we remark that by adding the inverted mean density in the constraints, we re-introduce some uncertainty due to the surface effects, but they only affect one constraint with this approach.
3.3.2. Application to the sample of Sonoi et al. (2015)
By fitting the frequency separation ratios and the classical constraints (metallicity, effective temperature, and luminosity), the relative separations between the frequency ridges can be reproduced, but in general not their position. This results in a horizontal shift in the échelle diagram. The addition of the inverted mean density mitigates this issue but may be insufficient, as was the case for models B and E (see Fig. B.3). In this case, we considered an additional seismic constraint, the lowest-order radial frequency, because this frequency is least affected by the surface effects. This addition fixes the position of the ridges, but can bring (or emphasise) other minimisation issues, notably a drift of walkers that biases the results (see the end of Sect. 4.2 for further details). These issues did not occur with the models of this section.
We tested three prescriptions to include the inverted mean density in the constraints: we did not include it, we included it as a classical constraint, or we included it as a seismic constraint. By classical constraints, we imply that the likelihoods were computed assuming that the true value of the observations were perturbed by some Gaussian-distributed random noise (and we note that other distributions are also supported by the software), while AIMS accounts for all the correlations for a seismic constraint. A comparison of the three prescriptions is shown in Table 4. When the inverted mean density is added to the constraints, the precision of the stellar mass and radius is significantly improved. The precision of the stellar age is mostly dominated by the seismic information contained in the ratios, and a gain in precision is likely to be an indirect consequence of a gain in the precision of the stellar mass and radius. The precision of the stellar parameters by considering the inverted mean density as a classical or seismic constraint is roughly equivalent, but the sources of the uncertainties are different. In the former case, we assumed an arbitrary uncertainty of 0.6% for the inverted mean density, which accounts for the statistical uncertainties (∼0.1 − 0.2%) as well as for the systematic uncertainties due to the choice of the physical ingredients or the prescription for surface effects. Although these effects are difficult to estimate without an individual and detailed analysis of each target, they are unlikely to exceed 0.6%, which is considered as a very large uncertainty for an inversion. As a reference, for Kepler-93, which is a well-behaved target with moderate surface effects, the total uncertainty of the mean density was 0.2% (Bétrisey et al. 2022). Since this arbitrary choice affects the maximum precision that can be achieved for the stellar parameters, a detailed analysis of several benchmark targets could be relevant to refine this choice in certain mass ranges or types of chemical composition, for example. Conversely, when the inverted mean density is treated as a seismic constraint, we can account for the correlations with the ratios, but not for the systematics. As shown in Fig. 6 in orange and green, both prescriptions have an equivalent accuracy. Because both prescriptions lead to a similar precision and accuracy, we would recommend treating the mean density as a classical constraint because it is more stable.
 |
Fig. 6. Accuracy comparison between the results of the modelling strategies that fit the individual frequencies (blue) or the frequency separations ratios by treating the inverted mean density as a classical (orange) or seismic (green) constraint for the Sonoi et al. (2015) targets. For model A, we show the results of the model using the following constraints: [Fe/H],Teff, L, r01, r02. For models B–F, we used the constraints listed in Table 4. |
Precision of the stellar parameters obtained by fitting the frequency separation ratios for the models of Sonoi et al. (2015).
3.4. Comparison and discussion
In Fig. 6 we compare the results between the modelling strategy that fit the individual frequencies and the strategy that fit the frequency separation ratios and the inverted mean density. For the fit of the individual frequencies (blue), we selected the models with the BG2 prescription for the surface effects and the absolute luminosity in the classical constraints because it provided the most robust models, and for the ratios, we selected the results based on the inverted mean density treated as a classical constraint (orange) or as a seismic constraint (green). The stellar parameters are systematically biased with the fit of the individual frequencies. The mass and radius are overestimated, and as a consequence, the age is underestimated. These biases are related to the treatment of the surface effects, which is too simplistic to accurately model the complex processes in upper stellar layers. These biases were expected because they are already documented in the literature for other types of stars (Ball & Gizon 2017; Nsamba et al. 2018; Jørgensen et al. 2020, 2021; Cunha et al. 2021). In addition, the fit of the frequencies has another issue, as was also observed in Rendle et al. (2019), Buldgen et al. (2019a), and Bétrisey et al. (2022). The uncertainty is underestimated because the frequencies constitute a set of constraints that contains too many precise elements, which results in peaked distributions. The fit of the individual frequencies therefore tended to estimate precise but inaccurate stellar parameters. In contrast, the fit of the frequency separation ratios, which damp the surface effects, provided more accurate results. Except for model E, the stellar mass and radius are indeed consistently reproduced. We note some slight inaccuracies in the stellar ages that are likely related to the differences in the physical ingredients between the Sonoi et al. (2015) targets and our grid of models. Especially the abundances are different, as is the value assumed for the mixing-length parameter that is fixed at a solar-calibrated value of 2.05 in our grid. Because the MCMC cannot modify this parameter, it compensates for this by modifying the helium mass fraction and the metallicity, resulting in a bias in the stellar age and absolute luminosity. Although it is tempting to let αMLT be an additional free parameter to avoid this type of issue, it would be numerically extremely expensive, especially if the overshooting is also free. For model E, none of the models of this work was able to reproduce its stellar parameters. No improvements were observed when the non-adiabatic correction of the frequencies was removed. This raises the question whether there is a structural issue with model E, either in the 1D structure of the model itself, in the 3D simulation of the upper layers, or in the connection between the two, or whether the semi-empirical formalism of the surface effects is not suitable for this target.
4. Application to LEGACY targets
In this section, we apply the two modelling strategies of Sect. 3 to ten targets from the Kepler LEGACY sample (Lund et al. 2017) with the best data quality. We divided these targets into two categories that differed by the set of classical constraints considered. The 16 Cyg binary system is one of the best-studied systems from an asteroseismic point of view (see Buldgen et al. 2022b, and references therein). The constraints on 16 Cyg A and B are therefore at another level than the other targets in the LEGACY sample. An interferometric radius was available for these targets (White et al. 2013), and we considered the following classical constraints: effective temperature, metallicity, and interferometric radius. They are summarised in Table 5. We preferred the interferometric radius because it is more constraining and more accurately determined than the absolute luminosity, which depends on the bolometric correction and extinction map considered. For the eight other targets, we considered three sets of constraints summarised in Table 6. As discussed in Sect. 3.2.2, this is to ensure that the luminosity is estimated consistently with the following formula:
Classical constraints and observed luminosity of the 16 Cyg binary system.
Classical constraints for the second category of targets.
where mλ is the magnitude, BCλ is the bolometric correction, and Aλ is the extinction, given a band λ, in our case, the 2MASS Ks-band. We inferred the extinction with the dust map from Green et al. (2018) and computed the bolometric correction following Casagrande & VandenBerg (2014, 2018). We adopted a solar bolometric correction of Mbol, ⊙ = 4.75. The distance d in pc from Gaia EDR3 (Gaia Collaboration 2021) was computed by testing two approaches: by inverting the parallax corrected according to Lindegren et al. (2021), or by using the distance from Bailer-Jones et al. (2021). Both methods led to consistent results, and we adopted the luminosity based on the latter distances as our observational constraint. The precision of the Ks magnitude of Pinocha is very low, which results in a poorly constrained luminosity. In addition, this target and Arthur are flagged as unreliable by Gaia. The RUWE indicator (renormalised unit weight error) is expected to be about one for single-star sources. If this indicator is much larger than one, as is the case for Arthur and Pinocha, it may indicate that the source is not single or that another issue affected the astrometric solution. We summarise the constraints of the second category of targets in Table 7.
Observational constraints for the second category of LEGACY targets.
4.1. Individual frequencies as constraints
In Fig. 7 we show the results of the fit of the individual frequencies and the different sets of classical constraints by considering different prescriptions for the surface effects. We removed the models with convergence issues that result from the treatment of the surface effects. With the K2 and S2 prescriptions, the MCMC could not find optimal values for the free coefficients associated with the surface effects correction. For the other unsuccessful runs, the MCMC hit the grid boundaries by trying to compensate for the other MCMC free parameters (mass, radius, and initial chemical composition with X0 and Z0) to force an inappropriate value for the free parameters of the surface effects. In comparison to the results of Sect. 3.2 with the Sonoi et al. (2015) targets, more prescriptions lead to successful MCMC runs. This difference is most likely due to surface effects, which are weaker with the LEGACY targets and are therefore easier to reproduce. Although some of the results with the BG1 prescription did not show the usual convergence issues, they appear as outliers in Fig. 7. We recommend considering them with caution because they failed to reproduce the high frequencies, which affects the estimate of the mass and radius.
 |
Fig. 7. MCMC results for the LEGACY targets, using different prescriptions of the surface effects described in Table 3. The runs with convergence issues were manually discarded. The modelling of Barney was more challenging, and MCMC runs converged successfully only with the BG2 surface effect prescription. For each target, three sets of classical constraints were considered: set 1 (bottom line), set 2 (middle line), and set 3 (upper line). The grey boxes represent the observational constraints. |
Except for Arthur and Doris, the absolute luminosity estimated by the models is consistent with the observed value, regardless of the set of classical constraints considered. As explained in the previous section, the luminosity of Arthur is flagged as unreliable, but because the fit is mainly driven by the seismic information, the results of the models that include or exclude the luminosity in the constraints are almost identical. This shows that when the luminosity is not very precisely constrained, it plays a small role on the final parameters. If the inverted mean density or/and the radial frequency of lower order are not included in the constraints, the situation may be different and the luminosity should only be included if it is reliable. Because the luminosity of Pinocha is poorly constrained, we did not consider set 1 of the classical constraints because it is equivalent to set 3 in these conditions.
As illustrated in Fig. 7, the systematic uncertainty due to the choice of the prescription for the surface effects is much larger than the individual uncertainties. Except for particular cases that are probably coincidental (e.g., ages of Arthur and Nunny), this systematic is several times larger than the statistical uncertainty. In addition, as for Sonoi et al. (2015), the numerical cost of each minimisation was high because we had to use 8000 steps of burn-in, which is very demanding from the perspective of a pipeline.
4.2. Frequency separation ratios as constraints
As in Sect. 3.3, we fitted the frequency separation ratios along with the classical constraints and considered the same three prescriptions to include the inverted mean density. The results are summarised in Table 8. Just like with the Sonoi et al. (2015) targets, if the inverted mean density is part of the constraints, the precision of the stellar mass and radius is significantly improved. We found comparable precision by treating the mean density as a classical or seismic constraint. However, the convergence of the latter was less stable with real observations, which again favours the recommendation to keep using the mean density as a classical constraint. Moreover, we observed drifts with some of the models that included the radial frequency of lower order. In these cases, we did not include this constraint, which resulted in ridges whose position is slightly less well reproduced. For the model of 16 Cyg A that treats the mean density as a seismic constraint, the estimated mass was too low and incompatible with the literature (see e.g., Buldgen et al. 2022b) or the other set of constraints that we tested. Even though the diagnostic plots did not show any issues, we consider this result unreliable and probably due to an undetected shift during the minimisation linked with the lowest-order radial frequency. These drifts are a recurrent disadvantage of including the lowest-order radial frequency in the constraints. Even when we assume a more conservative uncertainty on this quantity, it does not prevent these drifts from occurring, and if the uncertainty is too large, it no longer constrains the position of the ridges. From the perspective of a pipeline, we do not recommend to use this quantity. The drifts must be detected manually, and this is sometimes difficult even for an experienced modeller. In addition, even though the inverted mean density may lead to an imperfect anchoring of the frequency ridges, it mostly occurs for the most complicated cases, and the resulting slight bias on the stellar parameters is less significant than the bias due to a drift of the walkers.
Precision of the stellar parameters by fitting the frequency separation ratios for our selection of LEGACY targets.
4.3. Comparison and discussion
In Fig. 8 we compare the results between the fit of the individual frequencies, the fit of the frequency separation ratios, and the literature (Silva Aguirre et al. 2015, 2017; Farnir et al. 2020). For the individual frequencies, we selected the models that include the absolute luminosity in the constraints, except for Arthur, Doris, and Pinocha. For these targets, the luminosity estimated with Eq. (13) is considered unreliable, and we selected models that constrain the frequency of the maximum power νmax instead. For the fit of the ratios, we selected the models treating the mean density as a classical constraint, and the literature values come from Farnir et al. (2020) for 16 Cyg A and B, and from the YMCM algorithm (Silva Aguirre et al. 2015, 2017) otherwise. We note that Silva Aguirre et al. (2017) used older references for some of the physical ingredients, in particular, they used the GS98 abundances (Grevesse & Sauval 1998) and the nuclear rates from Adelberger et al. (1998). Hence, although our results are consistent with the literature, we can observe some slight differences that are due the differences in the physics of the models. In addition, as with the Sonoi et al. (2015) targets, the fit of the individual frequencies tends to overestimate the statistical precision of the stellar parameters. Finally, we note that we provide in Table C.1 the optimal stellar parameters of the LEGACY targets studied.
 |
Fig. 8. Comparison between the results of the modelling strategy that fits individual frequencies (blue), the modelling strategy that fits frequency separations ratios and the inverted mean density (orange), and the literature (brown and green). The grey boxes represent the observational constraints. |
5. Conclusions
We introduced in Sect. 2 a new high-resolution grid of stellar models of main-sequence stars with solar masses between 0.8 and 1.6. Then, in Sect. 3, we presented two modelling strategies that focus on a direct exploitation of the seismic information. We discussed the issues occurring with a fit of the individual frequencies, and presented a more elaborate modelling technique that combines mean density inversions and a fit of the frequency separation ratios to damp the surface effects and provide precisely and accurately constrained stellar parameters. We also discussed and compared three options to include the inverted mean density in the constraints. In Sect. 3 we applied the two modelling strategies to six synthetic targets from Sonoi et al. (2015), but including a consistent treatment of non-adiabatic effects, and in Sect. 4, we conducted the same tests on a sample of ten Kepler LEGACY targets.
The current treatment of the surface effects with semi-empirical prescriptions constitutes an important limiting factor in terms of precision, accuracy, and numerical cost. This corroborates what was observed in previous studies for other targets (Ball & Gizon 2017; Nsamba et al. 2018; Jørgensen et al. 2020, 2021). The procedure that combines the mean density inversion and the ratios can significantly improve the precision and accuracy of the stellar parameters, especially the mass and the radius, but would benefit from an improvement in the understanding of surface effects because it would allow us to further improve the maximum precision and accuracy that can be achieved. We recommend to treat the inverted mean density as a classical constraint and to assume a conservative precision. Further studies of benchmark targets would be welcomed to refine this conservative precision in certain mass ranges and to test whether and how it is impacted by the chemical composition and overshooting. The treatment of the inverted mean density as a seismic constraint to account for the correlations with the ratios achieves a comparable precision, but in a less stable manner, and it is therefore less strongly recommended.
We placed this work in the context of PLATO and showed that it was possible to obtain stellar parameters that are precise enough to meet the PLATO precision requirements for ten Kepler LEGACY targets by using the mean density inversions (see Table 8). The numerical cost of the procedure will be challenging for a pipeline. The first step consists of fitting the individual frequencies, thus obtaining a reference model for the mean density inversion in order to circumvent the surface effects. In addition to a better understanding of these effects, PLATO would also benefit from a thorough characterisation of the systematics that are due to the choice of the physical ingredients because it also impacts the maximum precision that can be achieved for the stellar parameters (see e.g., Bétrisey et al. 2022). Finally, we recommend using the following set of constraints if used in a pipeline: r01, r02, [Fe/H], Teff, L if reliable, and 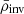 . This was the most robust set, and the benefits from the radial frequency of lowest order are too small in comparison to the biases that it may introduce.
. This was the most robust set, and the benefits from the radial frequency of lowest order are too small in comparison to the biases that it may introduce.
Acknowledgments
We would like to thank Takafumi Sonoi for providing the models and associated data from Sonoi et al. (2015). J.B. and G.B. acknowledge funding from the SNF AMBIZIONE grant No 185805 (Seismic inversions and modelling of transport processes in stars). P.E. and G.M. have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 833925, project STAREX). M.F. acknowledges the support STFC consolidated grant ST/T000252/1. Finally, this work has benefited from financial support by CNES (Centre National des Études Spatiales) in the framework of its contribution to the PLATO mission.
References
- Adelberger, E. G., Austin, S. M., Bahcall, J. N., et al. 1998, Rev. Mod. Phys., 70, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Adelberger, E. G., García, A., Robertson, R. G. H., et al. 2011, Rev. Mod. Phys., 83, 195 [Google Scholar]
- Aguirre Børsen-Koch, V., Rørsted, J. L., Justesen, A. B., et al. 2022, MNRAS, 509, 4344 [Google Scholar]
- Allen, C. W. 1976, Astrophysical Quantities (London: Athlone) [Google Scholar]
- Appourchaux, T., Antia, H. M., Ball, W., et al. 2015, A&A, 582, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Backus, G., & Gilbert, F. 1968, Geophys. J., 16, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Backus, G., & Gilbert, F. 1970, Philos. Trans. R. Soc. London Ser. A, 266, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2009, IAU Symp., 253, 71 [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Ball, W. H., & Gizon, L. 2014, A&A, 568, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ball, W. H., & Gizon, L. 2017, A&A, 600, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ball, W. H., Beeck, B., Cameron, R. H., & Gizon, L. 2016, A&A, 592, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Basu, S., & Antia, H. M. 2008, Phys. Rep., 457, 217 [Google Scholar]
- Basu, S., Chaplin, W. J., Elsworth, Y., New, R., & Serenelli, A. M. 2009, ApJ, 699, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Bazot, M., Bourguignon, S., & Christensen-Dalsgaard, J. 2008, Mem. Soc. Astron. Ital., 79, 660 [Google Scholar]
- Bellinger, E. P., Angelou, G. C., Hekker, S., et al. 2016, ApJ, 830, 31 [Google Scholar]
- Bellinger, E. P., Hekker, S., Angelou, G. C., Stokholm, A., & Basu, S. 2019, A&A, 622, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bétrisey, J., & Buldgen, G. 2022, A&A, 663, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bétrisey, J., Pezzotti, C., Buldgen, G., et al. 2022, A&A, 659, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bétrisey, J., Eggenberger, P., Buldgen, G., Benomar, O., & Bazot, M. 2023, A&A, 673, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Broomhall, A. M., Chaplin, W. J., Davies, G. R., et al. 2009, MNRAS, 396, L100 [Google Scholar]
- Broomhall, A. M., Chaplin, W. J., Elsworth, Y., & New, R. 2011, MNRAS, 413, 2978 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [Google Scholar]
- Buldgen, G., Reese, D. R., & Dupret, M. A. 2015a, A&A, 583, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buldgen, G., Reese, D. R., Dupret, M. A., & Samadi, R. 2015b, A&A, 574, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buldgen, G., Reese, D. R., & Dupret, M. A. 2016a, A&A, 585, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buldgen, G., Salmon, S. J. A. J., Reese, D. R., & Dupret, M. A. 2016b, A&A, 596, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buldgen, G., Reese, D., & Dupret, M. A. 2017, Eur. Phys. J. Web Conf., 160, 03005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buldgen, G., Reese, D. R., & Dupret, M. A. 2018, A&A, 609, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buldgen, G., Salmon, S., & Noels, A. 2019a, Front. Astron. Space Sci., 6, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Buldgen, G., Farnir, M., Pezzotti, C., et al. 2019b, A&A, 630, A126 [EDP Sciences] [Google Scholar]
- Buldgen, G., Rendle, B., Sonoi, T., et al. 2019c, MNRAS, 482, 2305 [Google Scholar]
- Buldgen, G., Bétrisey, J., Roxburgh, I. W., Vorontsov, S. V., & Reese, D. R. 2022a, Front. Astron. Space Sci., 9, 942373 [NASA ADS] [CrossRef] [Google Scholar]
- Buldgen, G., Farnir, M., Eggenberger, P., et al. 2022b, A&A, 661, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [Google Scholar]
- Casagrande, L., & VandenBerg, D. A. 2018, MNRAS, 475, 5023 [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., Green, E. M., & Chayer, P. 2005, A&A, 437, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen-Dalsgaard, J. 2021, Liv. Rev. Sol. Phys., 18, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Dappen, W., Ajukov, S. V., et al. 1996, Science, 272, 1286 [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
- Cunha, M. S., Roxburgh, I. W., Aguirre Børsen-Koch, V., et al. 2021, MNRAS, 508, 5864 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, G. R., Broomhall, A. M., Chaplin, W. J., Elsworth, Y., & Hale, S. J. 2014, MNRAS, 439, 2025 [Google Scholar]
- Dupret, M. A., Goupil, M. J., Samadi, R., Grigahcène, A., & Gabriel, M. 2006, ESA Spec. Pub., 624, 78 [NASA ADS] [Google Scholar]
- Dziembowski, W. A., Pamyatnykh, A. A., & Sienkiewicz, R. 1990, MNRAS, 244, 542 [NASA ADS] [Google Scholar]
- Farnir, M., Dupret, M. A., Salmon, S. J. A. J., Noels, A., & Buldgen, G. 2019, A&A, 622, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farnir, M., Dupret, M. A., Buldgen, G., et al. 2020, A&A, 644, A37 [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Frandsen, S., Carrier, F., Aerts, C., et al. 2002, A&A, 394, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Furlan, E., Ciardi, D. R., Cochran, W. D., et al. 2018, ApJ, 861, 149 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grec, G., Fossat, E., & Pomerantz, M. A. 1983, Sol. Phys., 82, 55 [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space. Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grigahcène, A., Dupret, M. A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruberbauer, M., Guenther, D. B., MacLeod, K., & Kallinger, T. 2013, MNRAS, 435, 242 [CrossRef] [Google Scholar]
- Houdek, G., & Dupret, M.-A. 2015, Liv. Rev. Sol. Phys., 12, 8 [Google Scholar]
- Howe, R., Chaplin, W. J., Basu, S., et al. 2020, MNRAS, 493, L49 [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, A. W. 2012, Astrophysics Source Code Library [record ascl:1211.002] [Google Scholar]
- Jiménez, A. 2006, ApJ, 646, 1398 [CrossRef] [Google Scholar]
- Jørgensen, A. C. S., Weiss, A., Angelou, G., & Silva Aguirre, V. 2019, MNRAS, 484, 5551 [Google Scholar]
- Jørgensen, A. C. S., Montalbán, J., Miglio, A., et al. 2020, MNRAS, 495, 4965 [CrossRef] [Google Scholar]
- Jørgensen, A. C. S., Montalbán, J., Angelou, G. C., et al. 2021, MNRAS, 500, 4277 [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [Google Scholar]
- Kosovichev, A. G. 2011, in Lecture Notes in Physics, eds. J. P. Rozelot, & C. Neiner (Berlin Springer Verlag), 832, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lazrek, M., Baudin, F., Bertello, L., et al. 1997, Sol. Phys., 175, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, Y., & Goupil, M. J. 2014, A&A, 569, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lund, M. N., Silva Aguirre, V., Davies, G. R., et al. 2017, ApJ, 835, 172 [Google Scholar]
- Metcalfe, T. S., Creevey, O. L., & Christensen-Dalsgaard, J. 2009, ApJ, 699, 373 [Google Scholar]
- Metcalfe, T. S., Chaplin, W. J., Appourchaux, T., et al. 2012, ApJ, 748, L10 [Google Scholar]
- Metcalfe, T. S., Creevey, O. L., Doğan, G., et al. 2014, ApJS, 214, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., & Montalbán, J. 2005, A&A, 441, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- NIST/SEMATECH 2003, NIST/SEMATECH e-Handbook of Statistical Methods, https://doi.org/10.18434/M32189 [Google Scholar]
- Nsamba, B., Campante, T. L., Monteiro, M. J. P. F. G., et al. 2018, MNRAS, 477, 5052 [NASA ADS] [CrossRef] [Google Scholar]
- Paquette, C., Pelletier, C., Fontaine, G., & Michaud, G. 1986, ApJS, 61, 177 [Google Scholar]
- Pijpers, F. P., & Thompson, M. J. 1994, A&A, 281, 231 [NASA ADS] [Google Scholar]
- Potekhin, A. Y., Baiko, D. A., Haensel, P., & Yakovlev, D. G. 1999, A&A, 346, 345 [NASA ADS] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [Google Scholar]
- Rabello-Soares, M. C., Basu, S., & Christensen-Dalsgaard, J. 1999, MNRAS, 309, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Reese, D. R., Marques, J. P., Goupil, M. J., Thompson, M. J., & Deheuvels, S. 2012, A&A, 539, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rendle, B. M., Buldgen, G., Miglio, A., et al. 2019, MNRAS, 484, 771 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Roxburgh, I. W. 2015, A&A, 574, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W. 2016, A&A, 585, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W. 2017, A&A, 604, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W. 2018, arXiv e-prints [arXiv:1808.07556] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2002a, ESA Spec. Pub., 485, 337 [NASA ADS] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2002b, ESA Spec. Pub., 485, 349 [NASA ADS] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2003, A&A, 411, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, A. R. G., Campante, T. L., Chaplin, W. J., et al. 2018, ApJS, 237, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, A. R. G., Campante, T. L., Chaplin, W. J., et al. 2019a, ApJ, 883, 65 [CrossRef] [Google Scholar]
- Santos, A. R. G., García, R. A., Mathur, S., et al. 2019b, ApJS, 244, 21 [Google Scholar]
- Santos, A. R. G., Breton, S. N., Mathur, S., & García, R. A. 2021, ApJS, 255, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008a, Ap&SS, 316, 83 [Google Scholar]
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008b, Ap&SS, 316, 149 [Google Scholar]
- Silva Aguirre, V., Davies, G. R., Basu, S., et al. 2015, MNRAS, 452, 2127 [Google Scholar]
- Silva Aguirre, V., Lund, M. N., Antia, H. M., et al. 2017, ApJ, 835, 173 [Google Scholar]
- Sonoi, T., Samadi, R., Belkacem, K., et al. 2015, A&A, 583, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teixeira, T. C., Christensen-Dalsgaard, J., Carrier, F., et al. 2003, Ap&SS, 284, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, A. E. L., Chaplin, W. J., Basu, S., et al. 2021, MNRAS, 502, 5808 [NASA ADS] [CrossRef] [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [Google Scholar]
- Tiesinga, E., Mohr, P. J., Newell, D. B., & Taylor, B. N. 2021, Rev. Mod. Phys., 93, 025010 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [Google Scholar]
- Vorontsov, S. V. 2001, ESA Spec. Pub., 464, 563 [NASA ADS] [Google Scholar]
- Vorontsov, S. V., Jefferies, S. M., Duval, T. L. J., & Harvey, J. W., 1998, MNRAS, 298, 464 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]
Appendix A: Mean density inversion. Numerical treatment and interpretation of the results
For a more complete description of inversions, we refer to Reese et al. (2012), Bétrisey et al. (2022), Bétrisey & Buldgen (2022), or Buldgen et al. (2022a). The mean density inversion used in this work is based on the structure inversion equation, which directly relates the frequency perturbation to the structural perturbation (Dziembowski et al. 1990),
where ν is the oscillation frequency, ρ is the density, 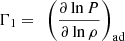 is the first adiabatic exponent, P is the pressure, and
is the first adiabatic exponent, P is the pressure, and 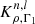 and
and 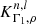 the corresponding structural kernels. We used the definition
the corresponding structural kernels. We used the definition
where ‘ref’ stands for reference and ‘obs’ stands for observed. For a mean density inversion, the idea is then to combine the equations (A.1) to compute a correction of the mean density of the reference model based on the observed frequency differences. In practice, the following cost function is minimised:
where x = r/R, and the averaging kernel 𝒦avg and the cross-term kernel 𝒦cross are related to the structural kernels,
The balance between the amplitudes of the different terms during the fitting is adjusted with trade-off parameters, β and θ. The idea is to obtain a good fit of the target function, in our case, 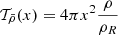 with
with 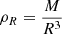 , while reducing the contribution from the cross-term and of the observational errors on the individual frequencies σi. An accurate inversion result is ensured by a good fit of the target function by the averaging kernel. In addition, we defined
, while reducing the contribution from the cross-term and of the observational errors on the individual frequencies σi. An accurate inversion result is ensured by a good fit of the target function by the averaging kernel. In addition, we defined 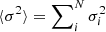 , where N is the number of observed frequencies. The λ symbol is a Lagrange multiplier, and the coefficients ci are the inversion coefficients. The surface term is denoted by ℱSurf(ν) and is implemented using Eq. (5) for the Ball & Gizon (2014) prescription and the linearised version of Eq. (6) for the Sonoi et al. (2015) prescription.
, where N is the number of observed frequencies. The λ symbol is a Lagrange multiplier, and the coefficients ci are the inversion coefficients. The surface term is denoted by ℱSurf(ν) and is implemented using Eq. (5) for the Ball & Gizon (2014) prescription and the linearised version of Eq. (6) for the Sonoi et al. (2015) prescription.
The first term in Eq. (A.3) is the main term, the equivalent of the usual least-squares term in other minimisations techniques. The second term is related to the second structural variable. The structural kernels are based on a structural pair, while we are only interested in one of the variables, in our case, the density. Hence, the idea is to ensure that the contribution of this cross term is as small as possible. The third term is a normalisation term to ensure that the coefficients give the correct result for a homologous transformation, and the fourth term accounts for the observational uncertainty. For the cross term, the idea is to ensure that its contribution is as small as possible. Finally, the last term should be treated with caution because it allows us to take the surface effects into account, but at the expense of the fit of the target function. Asteroseismology works with a limited number of frequencies (about 50 for high-quality targets) compared to helioseismology (a few thousand targets). Hence, the seismic information may be completely used by the additional free variables introduced with the surface term, and no structural differences can be extracted by the inversion. In this case, the target function is poorly reproduced by the averaging kernel, and the inversion coefficients tend to take high amplitudes with large variations between two consecutive coefficients. The target function is also poorly reproduced when the data quality is low, either due to high observational uncertainties or because too few frequencies are observed.
Hence, verifying how the target function is reproduced by the averaging kernels constitutes a good visual test to assess how the inversion behaves. In an effort of automation, we might be tempted to assess the quality of the inversion with the L2 norm similarly to Backus & Gilbert (1968), Backus & Gilbert (1970), Pijpers & Thompson (1994), Rabello-Soares et al. (1999), Reese et al. (2012), or Buldgen et al. (2015a),
However, this approach can only be trusted for inversions with reference models that have a target function with a similar amplitude. This condition was fulfilled in the papers that we quoted, but in our study, we analysed targets that are spread across a wide mass span. The amplitudes of the target functions are therefore not comparable (see e.g. Fig. A.1a and Fig. A.1d), and the absolute value of the L2 norm cannot be used as a quality indicator of the inversion. Hence, we constructed a new test based on the inversion coefficients. When the inversion behaves optimally, the coefficients form smooth structures, as illustrated in Fig. A.1a. Hence, the autocorrelation of the coefficients is relevant because an instability in the inversion tends to destroy these structures. In these conditions, the coefficients seem to be distributed more randomly. To measure the autocorrelation, we produced the lag plot of the coefficients (with lag = 1), where the coefficients present a linear correlation, as illustrated in the third column of Fig. A.1. Physically, we interpret this behaviour as a consequence of the incomplete independence of the frequencies. The frequencies follow an asymptotic behaviour within the same harmonic degree, which implies that the seismic information contained in the frequencies may be redundant. This affects the inversion, which selects some of the same seismic information in multiple frequencies, thus generating the smooth structures in the inversion coefficients. The linear correlation of the coefficients observed with the lag plot is likely related to the linear formalism at the basis of the inversion. To quantify the degree of instability of the inversion, we used the Pearson correlation coefficient ℛ, a low value that corresponds to a high degree of instability. We identified three instability regimes, high (ℛ < 0.5), intermediate (0.5 < ℛ < 0.75), and low (0.75 < ℛ). If ℛ < 0.5, further investigations are required. The boundaries of the different regimes are empirical and were determined based on our limited sample of 16 targets, on the analysis of the averaging kernels, on the lag plots, and on our experience of inversions. We also point out that these regimes were identified for mean density inversions and that further investigations should be conducted for other types of inversions. From a pipeline perspective, we recommend to define a unique threshold, however, below which we reject the result of the inversion, in our case, at ℛ ∼ 0.6, and refine this threshold with a larger statistics.
 |
Fig. A.1. Comparison of the averaging kernels (left column), inversion coefficients (middle column), and lag plots (right column) of models A, E and B, Saxo2, and Dushera by considering different implementations for the surface effects in the inversion. The surface effects are neglected (orange; NoS), the surface effects are treated as free variables in the inversion in InversionKit (green and blue; IK), with the BG2 and S2 prescriptions, respectively, and the frequencies are corrected before the inversion with the optimized coefficients from AIMS (red). |
In Fig. A.1 we illustrate models that are representative of the different instability regimes. The three first rows correspond to results for synthetic models, that is, models A, E, and B, while the last two rows corresponds to LEGACY targets, that is, Saxo2 and Dushera. Model A and Saxo2 are representative of a robust inversion. The instability is low and the target function is well reproduced, regardless of the surface prescription we considered. Model E is representative of an inversion in the intermediate regime. The target function is less well reproduced, especially at the surface, but the main features of the central regions are still captured by the inversion. We note that the S2 prescription is more unstable than the BG2 prescription. Finally, model B and Dushera are representative of high-instability inversions. The target function is poorly reproduced, the central features are missed, and the amplitude of the averaging kernel diverges at the surface. In the lag plot, the coefficients that include surface effects (in green) are significantly different from the coefficients that do not include them (in orange). In these conditions, the inversion could not see the structural differences and therefore did not correct the reference mean density. Hence, using the results of an unstable inversion amounts to admitting that the mean density of the reference model is robust, which is a reasonable assumption because it comes from an MCMC run in a grid. However, some caution should be considered because an unstable inversion can also provide a non-negligible correction of the mean density, which would in that case be a numerical artefact resulting from the poor fit of the target function by the averaging kernel. In our study, we identified four targets in the high-instability regime, models B, D, F, and Dushera, and a numerical artefact only affected the results of model F. To test the impact of using inversion coefficients in the high-instability regime, we did not discard these targets, and we point out that the conservative precision that we adopted when treating the inverted mean density as a classical constraint accounts, at least partially, for this kind of systematics.
In Fig. A.2 we show the inversion coefficients of the models of Kepler-93 from Bétrisey et al. (2022), which include different sets of physical ingredients. Changing the physics slightly shifts the position of the global minimum in the parameter space. Hence, these models generate a scatter of similar models in a confined region of the parameter space. The MCMC generates a scatter of similar models in a confined region of the parameter space with a random walk algorithm. Although the form of the scatter is different in these two cases, the assumption of constant coefficients only requires the models to be similar enough in the parameter space to be valid. As illustrated in Fig. A.2, the variations between the coefficients of Kepler-93 are negligible. It is therefore reasonable to assume constant coefficients for all the MCMC steps. In Table A.1 we show the exact and approximated correlations of the toy model, computed with Eqs. (9) and (10), respectively. The differences are very small, about 0.3% on average, and are therefore negligible compared to other sources of uncertainty. If the set of constraints is changed, it would invalidate our assumption. A different frequency set, even by removing or adding only one frequency, would significantly change the inversion coefficients. This could occur when one of the observed frequencies is not in some of the precomputed frequency sets of the grid. To avoid this issue, we computed extended frequency ranges in our grid, including low- and high-order modes that are currently not observable.
 |
Fig. A.2. Inversion coefficients of the models of Kepler-93 from Bétrisey et al. (2022), for which various physical ingredients were considered. The differences between the coefficients of the different models are very small. Hence, the lines in this figure are nearly-indistinguishable. |
Approximate and exact correlations between the inverted mean density and the r02 ratios for the toy model.
Appendix B: Supplementary data for the targets of Sonoi et al. (2015)
In Figs. B.1 and B.2 we show how the non-adiabatic effects impact the individual frequencies. The adiabatic part of the frequencies comes from a 3D simulation of the upper stellar layers patching a 1D model. For the solar model (model A), the non-adiabatic correction estimated by MAD is small, of the order of a few μHz, while for model B, which is a higher-mass star, the impact is significant, up to 20 μHz for the highest-order frequencies. Models C, D, E, and F have corrections with magnitudes similar to model B. For all the models, the non-adiabatic correction is significantly larger than the observational uncertainties, up to more than an order of magnitude larger in the most extreme cases. We verified that the large separation was correctly estimated by the non-adiabatic oscillation code. Whether corrections as large as this are physically realistic is beyond the scope of this study and would require further investigations.
 |
Fig. B.1. Impact of the non-adiabatic effects on the individual frequencies of model A. |
 |
Fig. B.2. Impact of the non-adiabatic effects on the individual frequencies of model B. |
In Fig. B.3 we show an illustration of an imperfect anchoring. In this example, the inverted mean density was part of the constraints, but proved to be insufficient to perfectly anchor the frequency ridges. This offset in the échelle diagram implies that the stellar parameters are slightly biased. In this example, the offset is small, and the stellar parameters are therefore not significantly affected. We note that adding the frequency of the lowest radial order in this case leads to walker drifts that were more problematic than the imperfect anchoring.
 |
Fig. B.3. Illustration of an imperfect anchoring of the frequency ridges. The observed frequencies are shown in red. The cyan frequencies correspond to the model based on the median of the posterior distributions of the MCMC run, and the orange model shows the best MCMC model, which minimises the χ2. |
In Fig. B.4 we show the impact of different surface effect prescriptions on the mean density. Theoretically, the mean density should not be affected, regardless of the prescription. In practice, however, the choice of the prescription affects the modelled frequencies and therefore the large separation and the mean density. When the mean density is poorly reproduced, it implies that the underlying surface effects prescription performs poorly. For this test, we considered two sets of frequencies by including the non-adiabatic correction (labelled ‘nad’) or excluding it (labelled ‘ad’). For each frequency set, we considered the following ways of determining the mean density:
-
The BG2 prescription, whose coefficients are optimised with AIMS by fitting the individual frequencies (green).
-
The BG2 prescription, whose coefficients are optimised within the mean density inversion (blue).
-
The BG2 prescription, whose coefficients are optimised with AIMS by fitting the individual frequencies, and a mean density inversion is conducted based on the relative difference between the corrected frequencies and the observed frequencies (orange).
-
The S2 prescription, whose coefficients are optimised within the mean density inversion (red).
-
The S2 prescription, whose coefficients are derived with the scaling relations of Sonoi et al. (2015; Eqs. 10 and 11). The individual frequencies from the reference models were corrected before the mean density inversion was carried out.
-
Damping surface effects with AIMS by fitting frequency separation ratios and treating the inverted mean density as a classical constraint (purple).
-
Damping surface effects with AIMS by fitting frequency separation ratios and treating the inverted mean density as a seismic constraint (brown).
 |
Fig. B.4. Mean density of the Sonoi et al. (2015) targets estimated using different techniques to account for the surface effects or damp them. The dashed and dot-dashed black lines correspond to the mean density of the reference model with and without the non-adiabatic correction, respectively. The exact mean density is shown by the solid black line. Each panel is divided into two parts, separated by a solid grey line. The lower part shows the results using the frequencies that include the non-adiabatic correction (labelled nad), and the upper part is based on the frequencies that do not include this correction (labelled ad). For model C, there are no ad results because the MCMC that provides the reference model did not converge successfully with this set of frequencies. |
The synthetic targets fall into four categories. The first category is composed of model A, where all the estimated mean densities are consistent. They all fall within ∼0.2%, which is the precision that we would expect for this type of star (model A is similar to Kepler-93; Bétrisey et al. 2022). The mean density obtained with the fit of the individual frequencies is already very accurate and the inversion confirms this value, as well as the fit of the ratios. There is no significant difference when the non-adiabatic effects are included or excluded. The second category is composed of models E and F. These models have consistent mean densities when the non-adiabatic effects are included or excluded. The dispersion of the mean densities is larger than what we would expect for an actual observed target. This raises the question to which extend synthetic models are representative of actual observed targets, and it questions the performance of the 3D patching. The third category is composed of models B and D. There is a significant difference when the non-adiabatic effects are included or excluded. We interpret this difference as an indication that the non-adiabatic correction is incompatible with the surface effect prescriptions. These results are expected because these prescriptions were not designed to describe corrections as strong as the one predicted by the non-adiabatic effects. Further investigations and statistics are required to test whether the limitations lie in the formalism of the non-adiabatic effects, in the surface effect prescriptions, or in both of them. The last category is composed of model C. The MCMC of fitting the individual frequencies excluding the non-adiabatic correction failed to converge because it hit the grid boundaries. This behaviour was unexpected because the actual stellar parameters of model C should fall within the grid, which raises the question whether there is an issue with the 3D patching. This issue could also originate from differences in the physical ingredients, especially in the mixing-length parameter. Finally, we point out that the fitting frequency separation ratios efficiently damp these issues, as shown by the purple and brown results.
The surface effects can directly be accounted for in the inversion or by correcting the frequencies before carrying out the inversion. Both versions performed equivalently with the BG2 prescription, but not with the S2 prescription. This latter performs poorly with the pre-corrected frequencies because it significantly overestimated the frequencies differences, resulting in a shift towards the left in the HR diagram, which is then interpreted by the inversion as a reference mean density that is too small. The inversion therefore wrongly corrected the model towards a higher mean density. Accounting for the S2 prescription directly in the inversion also performs poorly. The inversion cannot robustly determine the prescription coefficients, and a non-negligible correction would be the result of the poor fit of the target function and not of a difference in the physical structure.
Appendix C: Supplementary data for the LEGACY targets
In Table C.1 we provide the optimal stellar parameters of our subsample of LEGACY targets, determined with the procedure that couples the mean density inversions and frequency separation ratios. For these fits, we treated the inverted mean density as a classical constraint.
Stellar parameters of the targets selected from the LEGACY sample.
Appendix D: Supplementary diagnostic plots for AIMS convergence
In Fig. D.1 we show an illustration of the diagnostic plots of a successful convergence with AIMS. The échelle diagram is consistent and the temporal evolution of the walkers is flat, indicating that the burn-in phase was successful and that the walkers reached the global minimum in the parameter space. The triangle plot of the radius and optimised variables (mass, chemical composition, and age) is consistent and the posterior distributions show uni-modal distributions, which shows that the MCMC found the global minimum.
 |
Fig. D.1. Diagnostic plots of a MCMC run with successful convergence. The median parameters are denoted in cyan, and the best MCMC model, for which the χ2 is lowest, is denoted in orange. |
In Fig. D.2 we show an illustration of an unsuccessful convergence due to a drift of the walkers during the iterations of the MCMC. This issue means that the MCMC is still in the burn-in phase.
 |
Fig. D.2. Illustration of walkers drifting during the MCMC iterations. In this case, the walkers are still drifting after a burn-in of 2000 steps. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
In Fig. D.3 we show an illustration of an unsuccessful convergence due to an issue that occurred while we tried to fit the lowest-order radial frequency. The MCMC sees a second suspicious local minimum and traps the walkers in it, thus biasing the stellar parameters.
 |
Fig. D.3. Illustration of an issue that occurs while trying to fit the lowest -order radial frequency. The MCMC sees a second local minimum and traps the walkers in it. The median parameters are denoted in cyan, and the best MCMC model, for which the χ2 is lowest, is denoted in orange. |
In Fig. D.4 we show an illustration of an unsuccessful convergence due to walkers hitting the grid boundaries during the minimisation. This is the main issue we encountered in our study. Histograms with sharp features are not necessarily a sign that the grid is too small. It can indicate that there are significant physical differences between the grid models and the observed target, and that the MCMC is trying to compensate for this with the free variables at its disposal. A typical indicator of this issue is an excessively high metallicity.
 |
Fig. D.4. Illustration of a run that hit the grid boundaries. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
In Fig. D.5 we show an illustration of an unsuccessful convergence due to excessively peaked posterior distributions. This issue is slightly tricky because excessively peaked posterior distributions do not necessarily imply that the minimisation failed. However, it questions whether the interpolation was successful. In this illustration, the posterior distributions are multi-modal, indicating that the walkers were stuck on grid points and that the interpolation was unsuccessful.
 |
Fig. D.5. Illustration of a run with an excessively peaked posterior distribution. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
In Fig. D.6 we show an illustration of an unsuccessful convergence due to the surface prescription. In this case, the BG1 prescription was used. This prescription is known to have difficulties in reproducing the high frequencies, which is what we observe in the illustration. Although the other diagnostic plots do not show irregularities, the fact that the prescription fails to reproduce the high frequencies can significantly bias the stellar parameters.
 |
Fig. D.6. Illustration of the difficulty with which the BG1 surface prescription reproduces the high frequencies. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
All Tables
Precision of the stellar parameters obtained by fitting the frequency separation ratios for the models of Sonoi et al. (2015).
Precision of the stellar parameters by fitting the frequency separation ratios for our selection of LEGACY targets.
Approximate and exact correlations between the inverted mean density and the r02 ratios for the toy model.
All Figures
 |
Fig. 1. HR diagram of the targets considered in this work. The Sonoi et al. (2015) targets are denoted by the orange stars, and the Kepler LEGACY targets are indicated by the blue stars. The grey lines correspond to the evolutionary tracks from a slice of the Spelaion grid with X0 = 0.72, Z0 = 0.018, and αov = 0.00. |
| In the text | |
 |
Fig. 2. MCMC results for the targets from Sonoi et al. (2015), using individual frequencies and different prescriptions of the surface effects described in Table 3. Runs with convergence issues are included. For each target, two sets of classical constraints were considered, including the absolute luminosity (upper line) or excluding it (bottom line). The dashed black lines represent the exact value and the grey boxes represent the observational constraints. |
| In the text | |
 |
Fig. 3. Same as Fig. 2, but runs with convergence issues were discarded. |
| In the text | |
 |
Fig. 4. Correlations between the inverted mean density and the r02 ratios for our toy model, using model S from Christensen-Dalsgaard et al. (1996) and observational data from Lazrek et al. (1997). |
| In the text | |
 |
Fig. 5. Estimates of the degree of instability in the mean density inversion of the targets. The coefficients of the surface correction were estimated by the inversion using the BG2 prescription. Targets in the high-instability regime would require further investigation, while inversion results in the low and intermediate regimes can be used without further investigation. |
| In the text | |
 |
Fig. 6. Accuracy comparison between the results of the modelling strategies that fit the individual frequencies (blue) or the frequency separations ratios by treating the inverted mean density as a classical (orange) or seismic (green) constraint for the Sonoi et al. (2015) targets. For model A, we show the results of the model using the following constraints: [Fe/H],Teff, L, r01, r02. For models B–F, we used the constraints listed in Table 4. |
| In the text | |
 |
Fig. 7. MCMC results for the LEGACY targets, using different prescriptions of the surface effects described in Table 3. The runs with convergence issues were manually discarded. The modelling of Barney was more challenging, and MCMC runs converged successfully only with the BG2 surface effect prescription. For each target, three sets of classical constraints were considered: set 1 (bottom line), set 2 (middle line), and set 3 (upper line). The grey boxes represent the observational constraints. |
| In the text | |
 |
Fig. 8. Comparison between the results of the modelling strategy that fits individual frequencies (blue), the modelling strategy that fits frequency separations ratios and the inverted mean density (orange), and the literature (brown and green). The grey boxes represent the observational constraints. |
| In the text | |
 |
Fig. A.1. Comparison of the averaging kernels (left column), inversion coefficients (middle column), and lag plots (right column) of models A, E and B, Saxo2, and Dushera by considering different implementations for the surface effects in the inversion. The surface effects are neglected (orange; NoS), the surface effects are treated as free variables in the inversion in InversionKit (green and blue; IK), with the BG2 and S2 prescriptions, respectively, and the frequencies are corrected before the inversion with the optimized coefficients from AIMS (red). |
| In the text | |
 |
Fig. A.2. Inversion coefficients of the models of Kepler-93 from Bétrisey et al. (2022), for which various physical ingredients were considered. The differences between the coefficients of the different models are very small. Hence, the lines in this figure are nearly-indistinguishable. |
| In the text | |
 |
Fig. B.1. Impact of the non-adiabatic effects on the individual frequencies of model A. |
| In the text | |
 |
Fig. B.2. Impact of the non-adiabatic effects on the individual frequencies of model B. |
| In the text | |
 |
Fig. B.3. Illustration of an imperfect anchoring of the frequency ridges. The observed frequencies are shown in red. The cyan frequencies correspond to the model based on the median of the posterior distributions of the MCMC run, and the orange model shows the best MCMC model, which minimises the χ2. |
| In the text | |
 |
Fig. B.4. Mean density of the Sonoi et al. (2015) targets estimated using different techniques to account for the surface effects or damp them. The dashed and dot-dashed black lines correspond to the mean density of the reference model with and without the non-adiabatic correction, respectively. The exact mean density is shown by the solid black line. Each panel is divided into two parts, separated by a solid grey line. The lower part shows the results using the frequencies that include the non-adiabatic correction (labelled nad), and the upper part is based on the frequencies that do not include this correction (labelled ad). For model C, there are no ad results because the MCMC that provides the reference model did not converge successfully with this set of frequencies. |
| In the text | |
 |
Fig. D.1. Diagnostic plots of a MCMC run with successful convergence. The median parameters are denoted in cyan, and the best MCMC model, for which the χ2 is lowest, is denoted in orange. |
| In the text | |
 |
Fig. D.2. Illustration of walkers drifting during the MCMC iterations. In this case, the walkers are still drifting after a burn-in of 2000 steps. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
| In the text | |
 |
Fig. D.3. Illustration of an issue that occurs while trying to fit the lowest -order radial frequency. The MCMC sees a second local minimum and traps the walkers in it. The median parameters are denoted in cyan, and the best MCMC model, for which the χ2 is lowest, is denoted in orange. |
| In the text | |
 |
Fig. D.4. Illustration of a run that hit the grid boundaries. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
| In the text | |
 |
Fig. D.5. Illustration of a run with an excessively peaked posterior distribution. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
| In the text | |
 |
Fig. D.6. Illustration of the difficulty with which the BG1 surface prescription reproduces the high frequencies. The median parameters are denoted in green, and the best MCMC model, for which the χ2 is lowest, is denoted in purple. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



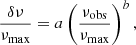
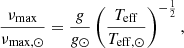
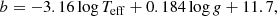
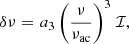
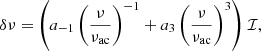
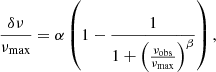
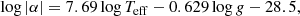
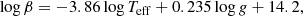
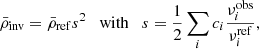
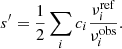
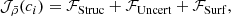
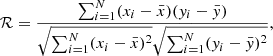
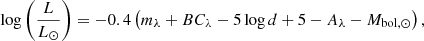
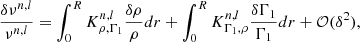
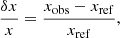
![$$ \begin{aligned} \mathcal{J} _{\bar{\rho }}(c_i)&= \int _0^1 \big (\mathcal{K} _{\mathrm{avg} } - \mathcal{T} _{\bar{\rho }}\big )^2 dx + \beta \int _0^1 \mathcal{K} _{\mathrm{cross} }^2dx + \lambda \left[2-\sum _i c_i\right] \nonumber \\&\quad +\tan \theta \frac{\sum _i (c_i\sigma _i)^2}{\langle \sigma ^2\rangle } + \mathcal{F} _{\mathrm{Surf} }(\nu ), \end{aligned} $$](/articles/aa/full_html/2023/08/aa46258-23/aa46258-23-eq32.gif)