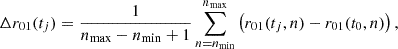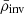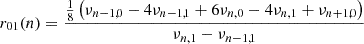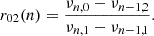EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 699 (July 2025) A&A, 699 (2025) L9 Full HTML
Open Access
Issue
A&A
Volume 699, July 2025
Article Number L9
Number of page(s) 7
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202555930
Published online 16 July 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The convective motions in the outer layers of solar-type stars excite an extended set of stellar oscillations. By examining these oscillations, asteroseismology offers an unparalleled glimpse into the internal structure of stars, allowing us to determine their fundamental parameters with a high level of precision and accuracy. Accurate stellar models are crucial for understanding planetary system evolution and tracing the history of our own galaxy (see e.g. Chaplin & Miglio 2013; García & Ballot 2019; Aerts 2021, for reviews). Building on the success of missions such as CoRoT (Convection, Rotation and planetary Transits; Baglin et al. 2009), Kepler (Borucki et al. 2010), K2 (Howell et al. 2014), and TESS (Transiting Exoplanet Survey Satellite; Ricker et al. 2015), asteroseismic modelling is set to play a pivotal role in upcoming space-based missions such as PLATO (PLAnetary Transits and Oscillations of stars; Rauer et al. 2024), CubeSpec (Bowman et al. 2022), and Roman (Huber et al. 2023). Despite impressive progress in asteroseismology and the modelling of stellar evolution, discrepancies remain between observed data and theoretical models, leading to biases in stellar characterisation. This issue is increasingly becoming pressing given the stringent precision requirements of the PLATO mission (15% in mass, 1–2% in radius, and 10% in age for Sun-like stars).

Three main challenges are impacting asteroseismic modelling: surface effects (e.g. Ball & Gizon 2017; Nsamba et al. 2018; Jørgensen et al. 2020, 2021; Cunha et al. 2021; Bétrisey et al. 2023), stellar magnetic activity (e.g. García et al. 2010; Broomhall et al. 2011; Santos et al. 2018, 2019a,b; Santos et al. 2021, 2023; Pérez Hernández et al. 2019; Howe et al. 2020; Thomas et al. 2021; Bétrisey et al. 2024, 2025), and the physical ingredients used in stellar models (e.g. Buldgen et al. 2019a; Farnir et al. 2020; Bétrisey et al. 2022). We refer for example to Bétrisey (2024) for an in-depth discussion of these challenges. Similar to surface effects, magnetic activity effects induce shifts in the observed oscillation frequencies (see e.g. Broomhall & Nakariakov 2015, for a review). The origin of these shifts remains unclear but two main hypotheses emerge from the dedicated literature: magnetic field variations in the near-surface layers (e.g. Howe et al. 2002; Baldner et al. 2009; García et al. 2024) and structural changes in the acoustic cavity (e.g. Woodard & Noyes 1985; Fossat et al. 1987; Libbrecht & Woodard 1990; Kuhn et al. 1998; Dziembowski & Goode 2005; Basu et al. 2012). Magnetic activity effects are propagated to the asteroseismic characterisation, regardless of whether forward modelling (Creevey et al. 2011; Pérez Hernández et al. 2019; Thomas et al. 2021; Bétrisey et al. 2024) or inverse methods are used (Bétrisey et al. 2025).

Given the non-negligible impact of magnetic activity on asteroseismic characterisation within the current modelling framework, this paper investigates whether conventional methods of effectively suppressing surface effects, which also induce frequency shifts, can mitigate the influence of magnetic activity. In Sect. 2, we assess the impact of magnetic activity on frequency separation ratios, which are the observational constraints employed in these methods. In Sect. 3, we examine whether the effects of magnetic activity are transmitted to the asteroseismic characterisation. Finally, we present the conclusions of our study in Sect. 4.

2. Influence of magnetic activity on observed frequency separation ratios

Similar to Bétrisey et al. (2024) and Bétrisey et al. (2025) (hereafter JB24 and JB25), we based our analysis on two independent datasets of Doppler velocity observations of the Sun as a star: BiSON (Birmingham Solar Oscillations Network; Davies et al. 2014; Hale et al. 2016) and GOLF (Global Oscillations at Low Frequencies; Gabriel et al. 1995). We recall that these datasets correspond to solar observations that were segmented into yearly overlapping snapshots, each offset by a quarter of a year. The original datasets cover solar cycles 23 and 24. In this study, we revised the BiSON dataset using a more sophisticated peak-bagging algorithm (see Appendix A) and extending it to include the first half of the maximum of cycle 25. For this section, similarly to Salabert et al. (2015), we also divided the frequency range into three sub-ranges (see Table 1) to measure whether magnetic activity effects affect certain regimes of the frequency separation ratios, r01 and r02, defined in Appendix B, more.

Table 1.

Frequency ranges considered in the computation of the averaged frequency separation ratio shift due to magnetic activity.

In Fig. 1, we present the temporal evolution of the frequency separation ratios, r01 and r02. To emphasize the impact of the magnetic activity cycle, we employed a method commonly used in the literature for individual frequencies (see e.g. Broomhall & Nakariakov 2015), which involves calculating the shift relative to a reference value – in our case, the value from the first snapshot. We then computed an averaged shift by averaging the shifts across several radial orders, n. For instance, the averaged r01 shift at time tj was determined as follows:

Δ r 01 ( t j ) = 1 n max − n min + 1 ∑ n = n min n max ( r 01 ( t j , n ) − r 01 ( t 0 , n ) ) , $$ \begin{aligned} \Delta r_{01}(t_j) = \frac{1}{n_{\rm max}-n_{\rm min}+1}\sum _{n=n_{\rm min}}^{n_{\rm max}}\left(r_{01}(t_j,n)-r_{01}(t_0,n)\right), \end{aligned} $$(1)

thumbnail Fig. 1.

Influence of the magnetic activity cycle on frequency separation ratios, r01 and r02, observed by BiSON. The grey data represent the averaged shift due to magnetic activity. The full frequency range was considered (n = 14 − 24). The red line was obtained by smoothing the grey data with a Savitzky-Golay filter. The 10.7 cm radio emission flux, a proxy of the solar cycle, is denoted in black. The correlation with the activity proxy is measured with the Spearman rank coefficient, ℛ.

where j is the snapshot number (e.g. 0 to 93 for GOLF datasets). The radial-order boundaries, nmin and nmax, are specified in Table 1. As is shown in Fig. 1, both ratio shifts exhibit a significant (anti-)correlation with the solar activity cycle proxy, the 10.7 cm radio emission flux1, clearly indicating an influence of the activity cycle on the observed frequency separation ratios. Additionally, we observe that this imprint becomes more pronounced with increasing radial order (see Appendix B), as was expected from the literature (Chaplin et al. 2005; Thomas et al. 2019, 2021).

3. Influence of magnetic activity on asteroseismic characterisation

Similar to the effects of magnetic activity, surface effects, which are primarily linked to the inaccurate treatment of convection by the mixing-length theory in the upper stellar layers where acoustic oscillations are excited, also induce frequency shifts. Over the past two decades, significant efforts have been dedicated to understanding these surface effects, leading to the development of several approaches to mitigate the frequency shifts they cause. Among these, two main strategies are commonly employed: semi-empirical corrections to model the shifts (e.g. Kjeldsen et al. 2008; Ball & Gizon 2014; Sonoi et al. 2015) and methods that efficiently damp these shifts (e.g. Roxburgh & Vorontsov 2003; Otí Floranes et al. 2005; Roxburgh 2016). As was discussed in the introduction, the former approach does not prevent magnetic activity effects from biasing the asteroseismic characterisation. In this section, we investigate whether the second approach yields better results.

One of the primary mitigation strategies involves using frequency separation ratios instead of individual frequencies, as these ratios have been shown to effectively suppress surface effects (Roxburgh & Vorontsov 2003; Otí Floranes et al. 2005). To measure the temporal evolution of the asteroseismiccharacterisation based on this approach, we performed asteroseismic characterisations of each snapshot using the r01 and r02 ratios, the mean density determined by JB25 (hereafter inverted mean density), and the same spectroscopic constraints as JB24. We utilised a grid-based global minimisation algorithm that combines an interpolation scheme with a high-resolution grid of stellar models to extensively explore the parameter space and infer robust stellar parameters. For a detailed description of the minimisation process, we refer to Bétrisey et al. (2023). Following JB25, the correlation with the activity proxy is then investigated with the Spearman rank correlation coefficient, ℛ (Spearman 1904).

In the upper panel of Fig. 2, we compare our results (in orange) for the asteroseismic age with those of JB24, who employed semi-empirical corrections (in blue). Stellar age is the most sensitive parameter to magnetic activity effects when semi-empirical corrections are used (JB24). As was demonstrated in the previous section, the observed ratios are sensitive to magnetic activity effects, and this signal is carried through to the asteroseismic characterisation. However, we observe a larger impact of magnetic activity effects, approximately 4.7% compared to about 3% with semi-empirical corrections. Furthermore, a constant bias of about 300 Myr is observed for the asteroseismic age. This bias is primary caused by the abundances used in the models of the high-resolution grid (e.g. Bonanno & Fröhlich 2015), which are based on the determinations of Asplund et al. (2009). This issue, which is more broadly known as the solar modelling problem (see e.g. Basu & Antia 2008; Buldgen et al. 2019b), has no influence on the results of our study.

thumbnail Fig. 2.

Influence of the magnetic activity cycle on the asteroseismic age and mass based on BiSON data. The individual frequencies were used as constraints for the blue data, while the frequency separation ratios (r01 and r02) and the inverted mean density, ρ ¯ inv $ \bar{\rho}_{\mathrm{inv}} $, were used for the orange data. The 10.7 cm radio emission flux, which serves as a proxy of the solar cycle, is denoted in black. The correlation with the activity proxy is measured with the Spearman rank coefficient, ℛ. The purple line was obtained by smoothing the orange data with a Savitzky-Golay filter.

Additionally, most stellar parameters show a weak to moderate imprint of the magnetic cycle (see Appendix C) with correlation coefficients, ℛ, between 0.3 and 0.5, unlike results with semi-empirical corrections, for which magnetic activity effects are limited to certain stellar variables such as age, mean density, and acoustic radius. Notably, stellar mass, displayed in the lower panel of Fig. 2, and radius show a significant correlation with the activity proxy (with ℛ ≃ 0.4). In this case, systematic uncertainties of about 2.9% and 1.0% should be associated with magnetic activity effects, respectively. We note that the mass, age, and initial helium mass fraction, Y0, are free variables of the minimisation and are interconnected. The observed mass variation is thus not solely attributable to changes in age, but also to changes in Y0. The modulation of Y0 across different phases of the activity cycle is substantial and dominates the resulting mass trend.

As has been shown by JB24 and implicitly assuming monotonically increasing magnetic effects, despite their inefficiency, semi-empirical corrections can partially absorb the magnetic activity signal in the free variables introduced to model surface effects, explaining this difference. With frequency separation ratios, surface effects are very efficiently suppressed by construction of the ratios, and no additional free variables are required in the minimisation process to account for these effects. Hence, the full activity signal is propagated to the asteroseismic characterisation. Although this may seem problematic at first, it presents a promising avenue. In the ratio space, surface effects and magnetic activity effects are disentangled, making it possible to define a semi-empirical correction to model magnetic activity effects in this constraint space, similar to how surface effects were modelled in the frequency space (Kjeldsen et al. 2008; Ball & Gizon 2014; Sonoi et al. 2015).

The inverted mean density used as a constraint is also weakly sensitive to magnetic activity. To test which type of constraint transmits the most activity signal, we repeated the computations using a fixed inverted mean density, specifically the optimal value of JB25 based on the averaging of data over two full cycles, and found negligible differences. This indicates that the activity signal comes almost solely from the observed ratios. This is an interesting observation since the mean density determined through seismic inversions is typically used to improve stellar modelling, meaning no additional bias is introduced by this constraint concerning magnetic activity effects.

4. Conclusions

In this study, we have explored whether standard techniques used to mitigate surface effects, specifically fitting frequency separation ratios using a forward modelling algorithm, could also suppress the effects of magnetic activity. We based our analysis on two independent datasets from GOLF and BiSON radial velocity observations of the Sun as a star. In Sect. 2, we assessed the impact of magnetic activity on the observed r01 and r02 ratios, and in Sect. 3, we examined whether magnetic activity effects are propagated to the asteroseismic characterisation.

Our findings indicate that frequency separation ratios do not suppress the effects of magnetic activity. Both r01 and r02 ratios exhibit a clear signature of the magnetic activity cycle. Similar to observations of oscillation frequencies (e.g. Broomhall & Nakariakov 2015, and references therein), the higher the radial order, the more the ratios are affected by magnetic activity. Consequently, when these ratios are used as constraints in asteroseismic modelling, magnetic activity effects propagate to the stellar characterisation. Additionally, most stellar parameters, including mass, age, radius, and initial helium mass fraction, correlate with the solar activity cycle. These findings are consistent across both the GOLF and BiSON datasets. This behaviour differs from when individual frequencies are used as constraints, where magnetic activity effects are partially absorbed by the surface effect prescription, significantly impacting only a limited number of stellar parameters, such as age, mean density, and acoustic radius (Bétrisey et al. 2024, 2025). Unfortunately, these parameters are among the primary stellar parameters of relevance for the PLATO mission (e.g. Rauer et al. 2024). Moreover, the asteroseismic age is more sensitive to magnetic activity effects when ratios are used as constraints. In terms of systematic uncertainty, we observe an increase from about 3% when individual frequencies are used as constraints (Bétrisey et al. 2024) to about 4.7% with frequency separation ratios. For the stellar mass and radius, systematic uncertainties of about 2.9% and 1.0% should be considered, respectively. These values are not negligible considering the PLATO precision requirements for Sun-like stars, especially for the stellar radius.

Within the current modelling framework, magnetic activity effects significantly impact asteroseismic characterisation, regardless of whether forward modelling or inverse methods are used (Creevey et al. 2011; Pérez Hernández et al. 2019; Thomas et al. 2021; Bétrisey et al. 2024, 2025). As is demonstrated in this study, standard techniques to suppress surface effects have proven ineffective against magnetic activity influences. Since phase matching fitting is a variant of our methodology (Roxburgh 2016), we expect similar results but it would be worthwhile carrying out a dedicated study to confirm this extrapolation. In preparation for future space-based photometry missions, it becomes essential to enhance our theoretical understanding of these effects and develop a modelling procedure capable of accounting for or efficiently suppressing them. In this context, we believe that frequency separation ratios may play a crucial role. Since these ratios are designed to efficiently damp surface effects (Roxburgh & Vorontsov 2003; Otí Floranes et al. 2005), they allow for the disentanglement of surface and magnetic effects. It is therefore conceivable to develop semi-empirical corrections to damp magnetic activity effects in this constraint space, similar to what has been done for oscillation frequencies (Kjeldsen et al. 2008; Ball & Gizon 2014; Sonoi et al. 2015).

Acknowledgments

We thank Dr. A.M. Amarsi for the fruitful discussions associated with the accessibility of the paper to non-specialised readers. J.B. acknowledges funding from the SNF Postdoc.Mobility grant no. P500PT_222217 (Impact of magnetic activity on the characterization of FGKM main-sequence host-stars). A.-M.B. has received support from STFC consolidated grant ST/X000915/1. H.D. and A.-M.B. acknowledge support from the Royal Astronomical Society for the Undergraduate Summer Research Bursary. S.N.B acknowledges support from PLATO ASI-INAF agreement no. 2022-28-HH.0 “PLATO Fase D”. R.A.G. acknowledges support from PLATO and GOLF CNES grants. O.K. acknowledges support by the Swedish Research Council (grant no. 2023-03667) and the Swedish National Space Agency.

References

  1. Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]
  2. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Baglin, A., Auvergne, M., Barge, P., et al. 2009, IAU Symp., 253, 71 [Google Scholar]
  4. Baldner, C. S., Larson, T. P., & Basu, S. 2009, ASP Conf. Ser., 416, 477 [NASA ADS] [Google Scholar]
  5. Ball, W. H., & Gizon, L. 2014, A&A, 568, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Ball, W. H., & Gizon, L. 2017, A&A, 600, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Basu, S., & Antia, H. M. 2008, Phys. Rep., 457, 217 [Google Scholar]
  8. Basu, S., Broomhall, A.-M., Chaplin, W. J., & Elsworth, Y. 2012, ApJ, 758, 43 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bétrisey, J. 2024, Ph.D. Thesis, University of Geneva, Switzerland [Google Scholar]
  10. Bétrisey, J., Pezzotti, C., Buldgen, G., et al. 2022, A&A, 659, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bétrisey, J., Buldgen, G., Reese, D. R., et al. 2023, A&A, 676, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bétrisey, J., Farnir, M., Breton, S. N., et al. 2024, A&A, 688, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bétrisey, J., Reese, D. R., Breton, S. N., et al. 2025, A&A, 697, A219 [Google Scholar]
  14. Bonanno, A., & Fröhlich, H. E. 2015, A&A, 580, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  16. Bowman, D. M., Vandenbussche, B., Sana, H., et al. 2022, A&A, 658, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Breton, S. N., Pallé, P. L., García, R. A., et al. 2022, A&A, 658, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Broomhall, A. M., & Nakariakov, V. M. 2015, Sol. Phys., 290, 3095 [NASA ADS] [CrossRef] [Google Scholar]
  19. Broomhall, A. M., Chaplin, W. J., Davies, G. R., et al. 2009, MNRAS, 396, L100 [Google Scholar]
  20. Broomhall, A. M., Chaplin, W. J., Elsworth, Y., & New, R. 2011, MNRAS, 413, 2978 [NASA ADS] [CrossRef] [Google Scholar]
  21. Buldgen, G., Farnir, M., Pezzotti, C., et al. 2019a, A&A, 630, A126 [EDP Sciences] [Google Scholar]
  22. Buldgen, G., Salmon, S., & Noels, A. 2019b, Front. Astron. Space Sci., 6, 42 [NASA ADS] [CrossRef] [Google Scholar]
  23. Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [Google Scholar]
  24. Chaplin, W. J., Elsworth, Y., Miller, B. A., New, R., & Verner, G. A. 2005, ApJ, 635, L105 [Google Scholar]
  25. Creevey, O. L., Salabert, D., & García, R. A. 2011, J. Phys. Conf. Ser., 271, 012054 [Google Scholar]
  26. Cunha, M. S., Roxburgh, I. W., Aguirre Børsen-Koch, V., et al. 2021, MNRAS, 508, 5864 [Google Scholar]
  27. Davies, G. R., Broomhall, A. M., Chaplin, W. J., Elsworth, Y., & Hale, S. J. 2014, MNRAS, 439, 2025 [Google Scholar]
  28. Dziembowski, W. A., & Goode, P. R. 2005, ApJ, 625, 548 [NASA ADS] [CrossRef] [Google Scholar]
  29. Farnir, M., Dupret, M. A., Buldgen, G., et al. 2020, A&A, 644, A37 [EDP Sciences] [Google Scholar]
  30. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  31. Fossat, E., Gelly, B., Grec, G., & Pomerantz, M. 1987, A&A, 177, L47 [NASA ADS] [Google Scholar]
  32. Gabriel, A. H., Grec, G., Charra, J., et al. 1995, Sol. Phys., 162, 61 [Google Scholar]
  33. García, R. A., & Ballot, J. 2019, Liv. Rev. Sol. Phys., 16, 4 [Google Scholar]
  34. García, R. A., Turck-Chièze, S., Boumier, P., et al. 2005, A&A, 442, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [Google Scholar]
  36. García, R. A., Breton, S. N., Salabert, D., et al. 2024, A&A, 691, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Hale, S. J., Howe, R., Chaplin, W. J., Davies, G. R., & Elsworth, Y. P. 2016, Sol. Phys., 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
  38. Howe, R., Komm, R. W., & Hill, F. 2002, ApJ, 580, 1172 [NASA ADS] [CrossRef] [Google Scholar]
  39. Howe, R., Chaplin, W. J., Basu, S., et al. 2020, MNRAS, 493, L49 [Google Scholar]
  40. Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
  41. Huber, D., Pinsonneault, M., Beck, P., et al. 2023, ArXiv e-prints [arXiv:2307.03237] [Google Scholar]
  42. Jørgensen, A. C. S., Montalbán, J., Miglio, A., et al. 2020, MNRAS, 495, 4965 [Google Scholar]
  43. Jørgensen, A. C. S., Montalbán, J., Angelou, G. C., et al. 2021, MNRAS, 500, 4277 [Google Scholar]
  44. Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [Google Scholar]
  45. Kuhn, J. R., Bush, R. I., Scherrer, P., & Scheick, X. 1998, Nature, 392, 155 [NASA ADS] [CrossRef] [Google Scholar]
  46. Libbrecht, K. G., & Woodard, M. F. 1990, Nature, 345, 779 [NASA ADS] [CrossRef] [Google Scholar]
  47. Nsamba, B., Campante, T. L., Monteiro, M. J. P. F. G., et al. 2018, MNRAS, 477, 5052 [NASA ADS] [CrossRef] [Google Scholar]
  48. Otí Floranes, H., Christensen-Dalsgaard, J., & Thompson, M. J. 2005, MNRAS, 356, 671 [Google Scholar]
  49. Pérez Hernández, F., García, R. A., Mathur, S., Santos, A. R. G., & Régulo, C. 2019, Front. Astron. Space Sci., 6, 41 [Google Scholar]
  50. Rauer, H., Aerts, C., Cabrera, J., et al. 2024, ArXiv e-prints [arXiv:2406.05447] [Google Scholar]
  51. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
  52. Roxburgh, I. W. 2016, A&A, 585, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Roxburgh, I. W., & Vorontsov, S. V. 2003, A&A, 411, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Salabert, D., García, R. A., & Turck-Chièze, S. 2015, A&A, 578, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Santos, A. R. G., Campante, T. L., Chaplin, W. J., et al. 2018, ApJS, 237, 17 [NASA ADS] [CrossRef] [Google Scholar]
  56. Santos, A. R. G., Campante, T. L., Chaplin, W. J., et al. 2019a, ApJ, 883, 65 [CrossRef] [Google Scholar]
  57. Santos, A. R. G., García, R. A., Mathur, S., et al. 2019b, ApJS, 244, 21 [NASA ADS] [CrossRef] [Google Scholar]
  58. Santos, A. R. G., Breton, S. N., Mathur, S., & García, R. A. 2021, ApJS, 255, 17 [NASA ADS] [CrossRef] [Google Scholar]
  59. Santos, A. R. G., Mathur, S., García, R. A., et al. 2023, A&A, 672, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Savitzky, A., & Golay, M. J. E. 1964, Anal. Chem., 36, 1627 [Google Scholar]
  61. Sonoi, T., Samadi, R., Belkacem, K., et al. 2015, A&A, 583, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Spearman, C. 1904, Am. J. Psychol., 15, 72 [Google Scholar]
  63. Thomas, A. E. L., Chaplin, W. J., Davies, G. R., et al. 2019, MNRAS, 485, 3857 [Google Scholar]
  64. Thomas, A. E. L., Chaplin, W. J., Basu, S., et al. 2021, MNRAS, 502, 5808 [NASA ADS] [CrossRef] [Google Scholar]
  65. Woodard, M. F., & Noyes, R. W. 1985, Nature, 318, 449 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Observational data

We reused the GOLF datasets (n ≥ 12 and n ≥ 16) from Bétrisey et al. (2024, 2025). We refer to these articles and to García et al. (2005) and Breton et al. (2022), for a detailed explanation of the extraction of the oscillations frequencies from the GOLF observational timeseries. The method for fitting the BiSON data was based on that described in Broomhall et al. (2009), with the key difference that the Affine Invariant Markov Chain Monte Carlo (MCMC) Ensemble sampler emcee (Foreman-Mackey et al. 2013) was used instead of a hill-climbing algorithm. The process was very similar to that described in Santos et al. (2018). To summarise, the modes were fitted in their respective l = 0/2, l = 1/3 pairs. An asymmetric Lorentzian was fitted to each visible peak as well as a flat background term, which is valid over the localized range close to the modes. For stability, the heights of the inner components (m = 0 for l = 2 and |m| = 1 for l = 3) were fixed using average values obtained by Broomhall et al. (2009), which were obtained when fitting a much longer timeseries than those used in this study. While the widths of the peaks were a free parameter in the code, also for stability, the widths were set to be the same for each component observed in the respective l = 0/2, l = 1/3 pairs. Priors for the fits were based on the values obtained by Broomhall et al. (2009). Outputs of the MCMC fitting routine were compared to those obtained by the routine used by Broomhall et al. (2009) and found to be consistent.

Appendix B: Supplementary data for the observed frequency separation ratios

In Table B.1, we present the characteristics of the average shifts induced by magnetic activity for the r01 and r02 ratios, as well as the frequencies of the radial order modes ν0. The frequency separation ratios were computed according to the definitions of Roxburgh & Vorontsov (2003). Specifically,

r 01 ( n ) = 1 8 ( ν n − 1 , 0 − 4 ν n − 1 , 1 + 6 ν n , 0 − 4 ν n , 1 + ν n + 1 , 0 ) ν n , 1 − ν n − 1 , 1 $$ \begin{aligned} r_{01}(n)&= \frac{\frac{1}{8}\left(\nu _{n-1,0}-4\nu _{n-1,1}+6\nu _{n,0}-4\nu _{n,1}+\nu _{n+1,0}\right)}{\nu _{n,1}-\nu _{n-1,1}} \end{aligned} $$(B.1)

and

r 02 ( n ) = ν n , 0 − ν n − 1 , 2 ν n , 1 − ν n − 1 , 1 . $$ \begin{aligned} r_{02}(n)&= \frac{\nu _{n,0}-\nu _{n-1,2}}{\nu _{n,1}-\nu _{n-1,1}}. \end{aligned} $$(B.2)

The correlation between these average shifts and the activity proxy, the 10.7 cm radio emission flux, is assessed using the Spearman rank coefficient ℛ. We consider the data to be uncorrelated, or more precisely, negligibly correlated, when |ℛ|< 0.25. We introduce 𝒜 as a proxy for the amplitude of the average shift, calculated by determining the difference between the maximum and minimum values of the data smoothed with a Savitzky-Golay filter (Savitzky & Golay 1964). The primary purpose of this proxy is to facilitate comparisons between different frequency ranges of the same observable (i.e., Δr01, Δr02, and Δν0).

The results for the radial modes align with the extensive literature on this subject (e.g. Broomhall & Nakariakov 2015, for a review), indicating that higher frequencies experience greater impacts from magnetic activity. Similarly, as observed with oscillation frequencies, higher radial orders show more pronounced effects from magnetic activity. The shifts in ratios also show a latitudinal dependence, as they depend on the harmonic degree of the frequencies used to construct the ratio. For example, for the r02 ratio, the fit of the l = 2 modes is dominated by the |m| = 2 peaks, which are more sensitive to low latitudes than the |m| = 0 component of the nearby l = 0 modes. Since the magnetic field is also predominantly at lower latitudes, the l = 2 modes are shifted by more than the l = 0 modes. This asymmetry in the shift caused by magnetic activity on l = 0 and l = 2 modes explains why the r02 frequency separation ratio is inefficient at damping magnetic activity, unlike surface effects that have a symmetric nature. Similarly, l = 1 modes are more shifted than l = 0 modes, and the r01 ratio is also inefficient at damping magnetic activity. For further details, we refer for example to Fig. B.1 of Salabert et al. (2015), which illustrates the frequency shift induced by magnetic activity for each harmonic degree during solar cycle 23 and the beginning of cycle 24. Additionally, the asymmetry differs between the l = 0/1 and l = 0/2 pairs. Consequently, the r01 and r02 ratios have different sensitivities to magnetic activity, as observed in our datasets. We note that these observations are consistent with existing literature (Chaplin et al. 2005; Thomas et al. 2019, 2021). Figure B.1 provides a qualitative illustration of the results summarised in Table B.1 for BiSON data.

Table B.1.

Characteristics of the averaged shifts due to magnetic activity.

thumbnail Fig. B.1.

Averaged shift due to magnetic activity for frequency separation ratios r01 (left column) and r02 (middle column), and frequencies of radial modes (right column) observed by the BiSON network. Four frequency ranges were investigated: full range, low-frequency range, medium-frequency range, and high-frequency range (from top to bottom). The red line is obtained by smoothing the grey data with a Savitzky-Golay filter. The 10.7 cm radio emission flux, which serves as a proxy of the solar cycle, is denoted in black. The correlation with the activity proxy is measured with the Spearman rank coefficient ℛ.

Appendix C: Supplementary data for the asteroseismic characterisation

In Table C.1, we present the characteristics of the magnetic activity imprint on the asteroseismic characterisation. The correlation between the stellar parameters and the activity proxy, the 10.7 cm radio emission flux, is measured with the Spearman rank coefficient ℛ. The systematic uncertainty σactivity associated to magnetic activity is evaluated using the methodology described in Bétrisey et al. (2025). A systematic uncertainty is only associated to cases with significant correlation coefficient (|ℛ|> 0.25). The averaged statistical uncertainty σstatistical is computed by averaging the statistical uncertainty of each datapoint.

Table C.1.

Characteristics of the magnetic activity imprint on the asteroseismic characterisation.

All Tables

Table 1.

Frequency ranges considered in the computation of the averaged frequency separation ratio shift due to magnetic activity.

In the text
Table B.1.

Characteristics of the averaged shifts due to magnetic activity.

In the text
Table C.1.

Characteristics of the magnetic activity imprint on the asteroseismic characterisation.

In the text

All Figures

thumbnail Fig. 1.

Influence of the magnetic activity cycle on frequency separation ratios, r01 and r02, observed by BiSON. The grey data represent the averaged shift due to magnetic activity. The full frequency range was considered (n = 14 − 24). The red line was obtained by smoothing the grey data with a Savitzky-Golay filter. The 10.7 cm radio emission flux, a proxy of the solar cycle, is denoted in black. The correlation with the activity proxy is measured with the Spearman rank coefficient, ℛ.
In the text
thumbnail Fig. 2.

Influence of the magnetic activity cycle on the asteroseismic age and mass based on BiSON data. The individual frequencies were used as constraints for the blue data, while the frequency separation ratios (r01 and r02) and the inverted mean density, ρ ¯ inv $ \bar{\rho}_{\mathrm{inv}} $, were used for the orange data. The 10.7 cm radio emission flux, which serves as a proxy of the solar cycle, is denoted in black. The correlation with the activity proxy is measured with the Spearman rank coefficient, ℛ. The purple line was obtained by smoothing the orange data with a Savitzky-Golay filter.
In the text
thumbnail Fig. B.1.

Averaged shift due to magnetic activity for frequency separation ratios r01 (left column) and r02 (middle column), and frequencies of radial modes (right column) observed by the BiSON network. Four frequency ranges were investigated: full range, low-frequency range, medium-frequency range, and high-frequency range (from top to bottom). The red line is obtained by smoothing the grey data with a Savitzky-Golay filter. The 10.7 cm radio emission flux, which serves as a proxy of the solar cycle, is denoted in black. The correlation with the activity proxy is measured with the Spearman rank coefficient ℛ.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.