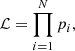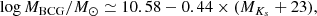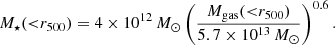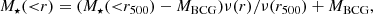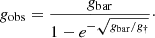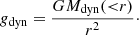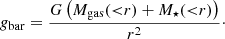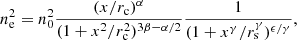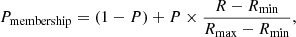| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202346431 | |
| Published online | 25 August 2023 | |
Measuring galaxy cluster mass profiles into the low-acceleration regime with galaxy kinematics
1
Leibniz-Institute for Astrophysics, An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: pli@aip.de
2
Institute of Astronomy, National Central University, Taoyuan 32001, Taiwan
3
Institut für Physik und Astronomie, Universität Potsdam, Karl-Liebknecht-Straße 24/25, 14476 Potsdam, Germany
4
INAF – Arcetri Astrophysical Observatory, Largo Enrico Fermi 5, 50125 Firenze, Italy
5
Department of Astronomy, Case Western Reserve University, 10900 Euclid Avenue, Cleveland, OH 44106, USA
6
Department of Physics, University of Oregon, Eugene, OR 97403, USA
7
Department of Physics, University of Surrey, Guildford GU2 7XH, UK
8
College of General Studies, Yuan-Ze University, Taoyuan 32003, Taiwan
Received:
16
March
2023
Accepted:
12
June
2023
We probed the dynamical mass profiles of ten galaxy clusters from the HIghest X-ray FLUx Galaxy Cluster Sample (HIFLUGCS) using galaxy kinematics. We numerically solved the spherical Jeans equation and parameterize the dynamical mass profile and the galaxy velocity anisotropy profile using two general functions to ensure that our results are not biased toward any specific model. The mass-velocity anisotropy degeneracy is ameliorated by using two “virial shape parameters” that depend on the fourth moment of velocity distribution. The resulting velocity anisotropy estimates consistently show a nearly isotropic distribution in the inner regions, with an increasing radial anisotropy toward large radii. We compared our derived dynamical masses with those calculated from X-ray gas data assuming hydrostatic equilibrium, finding that massive and rich relaxed clusters generally present consistent mass measurements, while unrelaxed or low-richness clusters have systematically larger total masses than hydrostatic masses by, on average, 50%. This might help alleviate current tensions in the measurement of σ8, but it also leads to cluster baryon fractions below the cosmic value. Finally, our approach probes accelerations as low as 10−11 m s−2, comparable to the outskirts of individual late-type galaxies. We confirm that galaxy clusters deviate from the radial acceleration relation defined by galaxies.
Key words: cosmology: observations / dark matter / galaxies: clusters: general / galaxies: clusters: intracluster medium / X-rays: galaxies: clusters
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Clusters of galaxies present the most prominent structures in the Universe given they are the largest self-gravitating objects. Their distribution and abundance provide critical information on the geometry of the Universe and the growth of structures (Böhringer et al. 2014; Planck Collaboration XXIV 2016), which often require measurements of their total mass. Robust estimates of cluster masses rely on constraints from spatially resolved dynamics, which also makes clusters excellent laboratories for testing various dark matter (DM) models and alternative theories of gravity (e.g., Angus et al. 2008).
Hot X-ray-emitting gas under the assumption of hydrostatic equilibrium is the most commonly used dynamical tracer to derive the dynamical mass profiles of galaxy clusters, given that they are generally X-ray-selected and their X-ray surface brightness profiles are usually available. Recent observations have managed to measure radially varying temperature profiles (e.g., Ghirardini et al. 2019; Liu et al. 2023), resulting in more accurate estimates for the total mass. The assumption of hydrostatic equilibrium is sometimes in question due to the existence of nonthermal pressure (Lau et al. 2009; Nelson et al. 2014). Perhaps more interestingly, the cosmological constraints from cluster counts (Planck Collaboration XXIV 2016) is in tension with that from the cosmic microwave background (CMB; Planck Collaboration XIII 2016), which can be resolved by introducing a 40% mass bias. These discrepancies have motivated studies comparing hydrostatic mass with that measured with other approaches, usually gravitational lensing. Gravitational lensing (Postman et al. 2012; Umetsu et al. 2016) measures the deflection of photons from background sources, and this does not assume dynamical equilibrium. As such, it is considered the most reliable method, but it has only be applied to a subset of galaxy clusters and is subject to projection effects.
Historically, using cluster galaxies as dynamical tracers was the very first method to measure the dynamical mass of galaxy clusters and uncover their DM content (Zwicky 1933). However, this approach is relatively less developed and applied, because it requires expensive spectroscopic measurements for a large number of galaxies. On the technical side, it is also challenging to derive 3D dynamical mass profiles from projected galaxy distributions and line-of-sight velocities. There are three mass estimators that have been used in the literature: the virial theorem, caustic approach, and Jeans formula equation. Employing the virial theorem (Limber & Mathews 1960; Biviano et al. 2006) is the easiest, but it only provides the estimate of the virial mass. The caustic approach (Diaferio & Geller 1997; Diaferio 1999; Serra et al. 2011) considers the fact that gravitationally bounded galaxies cannot exceed the escaping velocity, so one would expect a trumpet-shape distribution of galaxies in the projected phase space, given the gravitational field decreases toward large radii. This approach does not rely on dynamical equilibrium. The Jeans equation (van der Marel 1994) relates the phase-space distribution of galaxies to the total gravitational potential. It assumes that galaxies are in dynamical equilibrium. Deviations from the equilibrium are typically accompanied by disturbed gas distributions and thereby can be partially identified from X-ray images (Nagai et al. 2007). Both the caustic approach and the Jeans modeling have to deal with the degeneracy between the density profile and the velocity anisotropy. Strategies that have been implemented include assuming a constant velocity anisotropy (e.g., Biviano et al. 2013), or parameterizing its profile with a single parameter. The latter generally assumes perfect isotropy either in the center (Mamon & Łokas 2005; Tiret et al. 2007) or at the scale radius of DM halos (Biviano et al. 2013). These inevitably introduce some biases. Foëx et al. (2017) compared the cluster mass estimated with these three approaches and found they are generally higher than hydrostatic mass by 20−50%.
With more spectra of cluster galaxies becoming available and especially the advent of SDSS-V (Almeida et al. 2023), it is now worth further developing the approach with galaxy kinematics. In this paper, we numerically solve the Jeans equation and adopt more general functions to describe the dynamical mass profile and velocity anisotropy. Our results are thus not biased toward any specific halo model. We ameliorated the degeneracy between the density profile and velocity anisotropy with fourth moments of velocity distribution, namely two virial shape parameters. We tested the approach using 16 HIFLUGCS clusters and compared them with their hydrostatic mass profiles. Section 2 describes our cluster sample; Sect. 3 introduces the approach we employed; Sect. 4 presents the comparison with hydrostatic mass for six disturbed clusters; and Sect. 5 presents the detailed dynamical analysis for ten X-ray relaxed clusters. We discuss our results and conclude the paper in Sect. 6.
2. HIFLUGCS clusters
2.1. X-ray data
In this paper, we adopted a subsample of HIFLUGCS clusters, which were observed by both the ROSAT All-Sky Survey and XMM-Newton, leading to high-quality X-ray data (Zhang et al. 2011). The complete sample of 63 clusters is X-ray selected and constructed by Reiprich & Böhringer (2002). Chen et al. (2007) provided fits of their surface brightness profiles with the β model (Cavaliere & Fusco-Femiano 1976):
where R is the projected radius, rc is the core radius, S0 is the central surface brightness, and β is the power index. Assuming spherical symmetry, the above function can be de-projected to derive the electron number density profile assuming that X-rays are produced by thermal bremsstrahlung:
where r is the 3D radius and nc is the central electron number density. Chen et al. (2007) adopted H0 = 50 km s−1 Mpc−1 for distance estimates, which is significantly lower than current values. In order to maintain consistency with current estimates, we adopted H0 = 70 km s−1 Mpc−1 and re-scaled their results for core radius and electron number density: nc = nc, original/1.4 and rc = 1.4 rc, original. The enclosed gas mass profile is then
where x = r/rc, mp is the mass of protons, and the mean nuclear mass and charge numbers are A ≃ 1.4 and Z ≃ 1.2 for the intracluster medium (ICM) with 0.3 solar abundance (Anders & Grevesse 1989). Assuming the ICM is in hydrostatic equilibrium and isothermal, the dynamical mass profile can be derived through
where Th is the temperature of the hotter bulk component in the two-phase model. The cooler phase is included to account for the possible cooling core. Chen et al. (2007) pointed out that Th provides a better measure for the gravitational potential and total mass than the single emission-weighted temperature Tm. We therefore used Th when deriving the hydrostatic mass in this work. The mean molecular weight μ is given by
where ngas is the total number density including electrons, protons, ionized helium, and other ionized elements; X, Y, and Z are the mass fractions of hydrogen, helium, and other elements, respectively. For 0.3 solar abundance, X ≃ 0.716 and Y ≃ 0.278. This gives μ ≃ 0.6.
2.2. Optical data
The collection of high-quality spectro-photometric data for the HIFLUGCS clusters is an achievement resulting from decades of dedicated observations, including the compilations in Andernach et al. (2005) and Zhang et al. (2011). In this work, we utilized the compiled sample from Tian et al. (2021), which includes the comprehensive memberships assembled in the literature and organized from SIMBAD (Wenger et al. 2000). This sample was cleaned by excluding uncertain or repeated members. Each cluster in the sample has a single brightest cluster galaxy (BCG), and its position is defined as the optical center. Tian et al. (2021) required the offset between the optical center and X-ray weighted center to be smaller than 60 kpc. Therefore, we do not distinguish between optical or X-ray centers in this paper.
In order to effectively constrain dynamical mass profiles, we required at least three radial bins for each cluster with at least 25 galaxies in each bin. We therefore excluded clusters with fewer than 75 confirmed member galaxies. We also removed two galaxy groups, NGC 4636 and A1060, from our cluster sample. In the end, we retained 16 clusters in the analysis. According to Zhang et al. (2011), six of them are disturbed, so their galaxy kinematics may not trace the gravitational potential. Therefore, we will study disturbed and undisturbed clusters separately in the future.
3. Methodology
3.1. Galaxy kinematics
Using galaxy kinematics to determine the dynamical mass of clusters assumes that galaxies obey the collisionless Boltzmann equation (Binney & Tremaine 2008):
where f(x, v) is the distribution function of galaxies and Φ is the total gravitational potential given by ∇2Φ = 4πGρ. The dynamical equilibrium is a critical assumption. It is also a central question we aim to answer by comparing the results with those using hydrostatic equilibrium. Since we assume spherical symmetry for all the considered clusters, the Boltzmann equation can be simplified as the spherical Jeans equation (Binney & Tremaine 2008):
where ν = ∫fd3v is the number density of tracer galaxies, σr is the radial velocity dispersion, 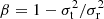 is the velocity anisotropy with σt the tangential anisotropy, and M(< r) is the enclosed total mass. Once ν, σr and β are determined, Eq. (7) provides a direct measurement for the enclosed total mass. In fact, it is more common to use the integrated equation (van der Marel 1994),
is the velocity anisotropy with σt the tangential anisotropy, and M(< r) is the enclosed total mass. Once ν, σr and β are determined, Eq. (7) provides a direct measurement for the enclosed total mass. In fact, it is more common to use the integrated equation (van der Marel 1994),
where 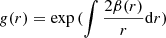 . In observations, only projected distributions of galaxies (Σgal) and line-of-sight velocity dispersion (σlos) are observable. Therefore, it is important to have an equation relating σlos to σr, which has been derived by Binney & Mamon (1982):
. In observations, only projected distributions of galaxies (Σgal) and line-of-sight velocity dispersion (σlos) are observable. Therefore, it is important to have an equation relating σlos to σr, which has been derived by Binney & Mamon (1982):
3.2. GravSphere code
In this work, we used the GravSphere code by Read & Steger (2017), which was written to study the dynamics of star clusters and dwarf galaxies using individual stars as dynamical tracers. Since it solves the same equations (Eqs. (7) and (9)), we can transplant it to galaxy clusters by using individual galaxies as dynamical tracers and changing the corresponding parameters and priors. GravSphere has been carefully validated on a vast array of mock data, including spherical systems (Read & Steger 2017; Read et al. 2021), systems with limited spectroscopic data (Collins et al. 2021), triaxial systems (Read & Steger 2017), tidally disrupting systems (Read et al. 2018; De Leo et al. 2023), and cosmologically realistic mocks (Genina et al. 2020). GravSphere uses parameterized functions to describe the unknown variables in Eqs. (7) and (9). To guarantee that the chosen functions can provide good fits for diverse objects, we choose flexible functions with sufficient number of parameters. Galaxy number density is modeled with three Plummer spheres (Plummer 1911),
where the values of Ni are chosen to make sure ∫ν(r)d3r = 1. We set broad boundaries for the parameters: 10−4 < Ni < 100 and 50 kpc < ai < 2000 kpc. It is possible to include more Plummer spheres and hence more free parameters. However, we found that three Plummer spheres with six parameters are enough for all the considered systems. The values of (Ni, ai) were determined by fitting the projected number density to observed values, which is analytically given by
An example fit with cluster A0085 is given in the left panel of Fig. 1.
 |
Fig. 1. Example fits of projected galaxy number density profiles and line-of-sight velocity dispersion profiles. The cluster shown here is A0085. The galaxy surface number density profile is fit with three Plummer spheres, which are then used as input in the projected Jeans equation. The line-of-sight velocity dispersion profile is used to determine the total mass profile, parameterized using the cNFWt profile with six parameters. Dark and light shadow regions show the 1σ and 2σ confidence intervals, respectively. |
The total enclosed mass M(< r) was modeled with the cNFWt profile (Read et al. 2018), which is based on the Navarro-Frenk-White model (NFW; Navarro et al. 1996):
The cNFWt model modifies the NFW profile at both small and large radii. At small radii, the density profile is described as the cNFW model (Read et al. 2016), and its enclosed mass is given by
where 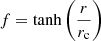 , and the index n controls how cuspy the halo is. An NFW-like cusp has n = 0, while a complete core requires a minimum value of n = 1. The corresponding density profile reads as
, and the index n controls how cuspy the halo is. An NFW-like cusp has n = 0, while a complete core requires a minimum value of n = 1. The corresponding density profile reads as
At r > rt, the enclosed mass is given by
where δ is the outer slope. In total, the cNFWt profile has six parameters, which can accommodate different inner and outer slopes. We set loose boundaries as 13 < log(M200/M⊙) < 20, 0.1 < c200 < 100, 10 kpc < rc < 3000 kpc, −0.5 < n < 2.0, 10 kpc < rt < 5000 kpc, and 0 < δ < 3. The total mass M200 of galaxy clusters generally ranges from 1014 to 3 × 1015 M⊙, and the halo concentration c200 is typically between 1 and 10 (Umetsu et al. 2016). Therefore, the allowed ranges are much wider than the expected values. We allowed rc and rt to vary from galaxy scale to beyond cluster scale. The core-cusp control parameter n is typically within (0, 1). The additional outer slope parameter δ is introduced to accommodate density profiles less steep than the NFW model, which can be switched off by setting a large value of rt if necessary.
By default, the output of the GravSphere code is the enclosed dark matter halo mass, which is calculated by subtracting baryonic mass from the total mass. Since we will have to model stellar mass and gas mass distributions separately, we simply set a negligible baryonic mass in the code. As a result, the output mass profile, as described by the cNFWt model, is the total enclosed mass. The cNFWt model has sufficient freedom to accommodate various mass profiles (see an example fit in the right panel of Fig. 1). This is a critical reason why we do not use the NFW model, which is generally believed to work well in galaxy clusters. Therefore, we treated the cNFWt model simply as a fitting function rather than a halo model and set loose boundaries for its parameters without imposing cosmological priors.
The velocity anisotropy parameter β(r) is also modelled by a fitting function to avoid irregular behavior:
where β0 and β∞ are the values at r = 0 and r = ∞, respectively; and r0 and n are used to characterize the radial shape. The boundary for n was set as 1 < n < 3, while r0 was allowed to vary within 0.5 Rhalf < r0 < 2 Rhalf, where Rhalf is the radius enclosing 50% of the total galaxies. In order to avoid the infinite value for a full tangential velocity dispersion, Read et al. (2006) defined a symmetrized anisotropy parameter:
According to this definition, the full tangential and radial velocity dispersion corresponds to 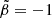 and
and 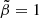 , respectively. Since the velocity distribution is expected to be nearly isotropic in the center of galaxy clusters due to the strong gravitational field, we set the boundary as
, respectively. Since the velocity distribution is expected to be nearly isotropic in the center of galaxy clusters due to the strong gravitational field, we set the boundary as 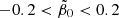 in the center, while we allowed for a larger anisotropy at large radii by setting
in the center, while we allowed for a larger anisotropy at large radii by setting 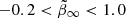 . We find that the set ranges are sufficiently large for all the considered clusters.
. We find that the set ranges are sufficiently large for all the considered clusters.
Notoriously, the velocity anisotropy parameter is degenerated with the density profile, as a larger anisotropy would lead to a larger radial velocity dispersion, which is positively correlated with the enclosed mass profile. The degeneracy can be ameliorated by proper motions, which provide two additional projected equations similar to Eq. (9). However, proper motions are hardly measurable for cluster galaxies. Merrifield & Kent (1990) found that the fourth order of the velocity distribution can be related to the enclosed mass profiles in two separate and independent ways:
where 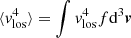 . Therefore, the two Virial Shape parameters can help ameliorate the degeneracy.
. Therefore, the two Virial Shape parameters can help ameliorate the degeneracy.
In total, GravSphere solves the Jeans equation with ten parameters (six in cNFWt and four in β(r)). We impose flat priors on these fitting parameters within the aforementioned hard boundaries. The parameter space was explored using the Markov chain Monte Carlo method with the emcee hammer by Foreman-Mackey et al. (2013). We used 250 walkers and run 50 thousand steps. Raising the number of steps to 100 000 does not affect our results, demonstrating that our chains are converged. In Appendix B, we show some example corner plots for A0085, projected into the space of parameters that are well-constrained by our models.
3.3. Binning data with Binulator
The robust estimate of the dynamical mass is contingent on the accurate calculation of the velocity dispersion, which typically requires a large number of tracers in each bin. This is difficult to achieve in many cases. As such, Collins et al. (2021) introduced a separate routine for data binning – Binulator – prior to running GravSphere. Instead of directly calculating velocity dispersion from measured line-of-sight velocities, Binulator fits a generalized Gaussian function within each bin and estimates the mean, variance, and kurtosis. The generalized function is given by
where α, β, and μ are fitting parameters, the index i labels each individual galaxy, and Γ(x) is the gamma function. As before, we set loose boundaries for these parameters: 50 km s−1 < α < 2000 km s−1, 1 < β < 10, |μ|< 1000 km s−1. Based on the fit, the velocity dispersion is given by 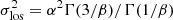 . Since there is no error measurement for line-of-sight velocity in the available catalogs, we assume a 10% uncertainty on the velocity for all cluster galaxies. This is a conservative assumption, since galaxy velocities are measured via spectroscopy with high accuracy. This uncertainty generates an error probability function, which is convolved with the generalized Gaussian function. Eventually, the parameters are determined for each bin by maximizing the likelihood function (with the emcee hammer),
. Since there is no error measurement for line-of-sight velocity in the available catalogs, we assume a 10% uncertainty on the velocity for all cluster galaxies. This is a conservative assumption, since galaxy velocities are measured via spectroscopy with high accuracy. This uncertainty generates an error probability function, which is convolved with the generalized Gaussian function. Eventually, the parameters are determined for each bin by maximizing the likelihood function (with the emcee hammer),
where N is the total number of galaxies in each bin. Collins et al. (2021) showed that the Binulator routine can robustly estimate velocity dispersion with 25 galaxies/bin. We hence set the minimum bin size as 25 galaxies, while for rich clusters we can also choose to use a larger bin size.
4. Disturbed clusters
Galaxy kinematics only traces the gravitational potential if the cluster is relaxed. This is not always the case, as clusters could be undergoing merging, and thereby the distribution and motions of galaxies are disturbed. Unrelaxed clusters can display characteristic signatures in their X-ray images. Nagai et al. (2007) and Ventimiglia et al. (2008) examined some simulated clusters and classified relaxed and unrelaxed clusters based on the morphology of the mock X-ray images. Vikhlinin et al. (2009) applied their procedure to observed clusters and identified unrelaxed clusters as those with secondary maxima, filamentary X-ray structures, or significant isophotal centroid shifts in their X-ray images. These clusters may deviate from hydrostatic equilibrium, as they present a systematic offset from the Mtot − TX relation (Mathiesen & Evrard 2001; Kravtsov et al. 2006). Kravtsov et al. (2006) found that the total mass is higher than the expected mass by 17 ± 5% at the same temperature. Therefore, Vikhlinin et al. (2009) suggested scaling up the total mass from X-ray temperature by 17%. However, the actual offset of observed clusters in the Mtot − TX is unclear, which has to be calibrated through weak-lensing analysis.
In our sample, six clusters are disturbed according to their X-ray images (Vikhlinin et al. 2009; Zhang et al. 2011). We derived their hydrostatic mass from the surface brightness fits using the β function (Eq. (4)), and we plot them in Fig. 2. We also plot the mass profiles derived from the line-of-sight velocity dispersion, which are drawn from the best-fit cNFWt function, but we only show the discrete points with errors rather than the full curve. This is intended to avoid over-constraining where there is no actual data. The points are chosen at the projected radii of the binned data, although the 3D and projected radii do not correspond to each other exactly. The errors are estimated from the Markov chain, so they are formal uncertainties that should be taken with a grain of salt.
 |
Fig. 2. Dynamical mass profiles of six disturbed clusters of galaxies. Solid lines are the hydrostatic mass profiles derived from the surface brightness fits using the β function from Chen et al. (2007). Points with the error bar show the total mass profiles from the line-of-sight velocity dispersion. Vertical dashed lines indicate the positions of r500 measured from X-ray data by Zhang et al. (2011), while dotted lines mark Rhalf enclosing 50% of the total cluster galaxies. 3D radii are chosen according to the binned projected radii to avoid oversampling. That the dynamical mass profiles determined from different tracers are inconsistent presumably indicates nonequilibrium conditions stemming from recent or ongoing mergers. |
Figure 2 shows that the total mass profiles derived from galaxy kinematics for five clusters are above the hydrostatic mass curves at all radii. The differences are larger than 17%, so even if we scale up the hydrostatic mass, as for simulated clusters, the two measurements would not agree. This suggests that the merging process affects cluster galaxies and X-ray gas with different levels of significance. A3526 is the only cluster that presents consistent measurements. Noticeably, its size is significantly smaller than other clusters. This may imply that X-ray gas and satellite galaxies are equally distorted for small clusters, though the sample is too small to make a solid conclusion.
Both measurements of the total mass should not be thought reliable given that their X-ray images present signatures of un-relaxation. We include these clusters in the paper to illustrate how unrelaxed clusters may look in their dynamical mass profiles. We exclude them from our dynamical tests.
5. Undisturbed clusters
5.1. Baryonic mass profiles
The ten clusters identified as undisturbed by Zhang et al. (2011) comprise our main sample of interest. We plot their gas mass, stellar mass, hydrostatic mass, and dynamical mass from galaxy kinematics in Fig. 3. The gas mass profiles are derived by integrating their deprojected surface brightness fits from Chen et al. (2007). Five clusters have measurements in the XMM Cluster Outskirts Project (X-COP; Eckert et al. 2019; Ettori et al. 2019; Ghirardini et al. 2019), so we overplot their results for comparison. The gas mass distributions from X-COP are supposed to be more extended than those from Chen et al. (2007), given that the aim of the X-COP is to explore the outer regions of clusters and study the growth of structures. Three clusters in our plot present more extended gas profiles from the β function fits. These are extrapolations rather than true gas distributions. We extrapolated all the density profiles from the β function fits to the outermost radii with the binned galaxy data. We noticed that the gas mass from the β function is systematically higher than that in X-COP for all five clusters. This is expected given the well-known fact that gas density decreases more quickly than the β function predicts at large radii (Vikhlinin et al. 2006). Therefore, the β function should be used with caution toward larger radii.
 |
Fig. 3. Mass profiles of undisturbed clusters of galaxies. Points with error bars are the total mass profiles from velocity dispersion. Solid and dashed blue lines are the hydrostatic mass and gas mass profiles from the X-COP project, respectively, while solid and dashed black lines show the corresponding results from the surface brightness fits using the β functions in Chen et al. (2007). Green lines show the stellar mass distributions. Vertical dashed lines indicate the positions of r500 measured by Zhang et al. (2011) with X-ray data, while dotted lines mark Rhalf, which equally divide the total cluster galaxies. For these undisturbed clusters, the dynamical mass profiles from galaxy kinematics are generally consistent with hydrostatic mass profiles, but they extend to larger radii in general. Possible reasons for the inconsistency in some clusters are discussed in the text. |
 |
Fig. 3. continued. |
Though gas mass dominates the total baryonic mass in galaxy clusters, the stellar mass contained in galaxies provides significant contributions at small radii. We distinguish BCG and satellite galaxies. Since galaxy kinematics cannot probe the inner regions, we do not need to model the stellar mass distributions of BCGs, but we can simply treat them as a point mass. We derived the stellar mass of each BCG based on their Ks-band absolute magnitude using the relation from Cappellari (2013):
where the absolute magnitude is calculated from the observed apparent magnitude from the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006) using the distance measured by Hubble flow. Cappellari’s relation corresponds to a stellar mass-to-light ratio between 1.3 and 1.6 M⊙/L⊙ for our sample, which is higher than the predicted value (1.2 M⊙/L⊙) of some stellar population models (Schombert et al. 2022).
As mentioned in Sect. 3.2, galaxy number distributions are described by three Plummer spheres ν(r). For simplicity, we assumed that satellite galaxies share the same stellar mass. This should not affect our results as long as the sample of galaxies is sufficiently large. With this assumption, stellar mass distributions are simply galaxy number distributions up to a proportional constant, which can be determined by the total stellar mass. Chiu et al. (2018) reported the correlation between the gas mass and stellar mass within r500:
We took the values of Mgas(< r500) from Zhang et al. (2011) and derived the enclosed stellar mass. The stellar mass distribution is then given by
which is plotted with solid green lines. Figure 3 shows the baryonic mass is generally dominated by stellar mass in the inner regions of clusters.
5.2. Dynamical mass profiles
Similarly to disturbed clusters, we derived the hydrostatic mass from the surface brightness fits using the β function (Chen et al. 2007) with a constant temperature. For the five clusters in the X-COP, we overplot their results from Ettori et al. (2019), which are supposed to be more robust because the radial variations of the temperature are taken into account. Eckert et al. (2022) also included the pressure measurements from the Planck Sunyaev–Zel’dovich (SZ) survey (Planck Collaboration XXIX 2014), so their dynamical mass profiles are more extended than the gas distributions.
Interestingly, though the gas mass profiles from the X-COP and the β function fits differ significantly at large radii, the total mass profiles are quite consistent. This is partially because hydrostatic mass depends on the gas density slope rather than the absolute gas mass density. The slope of the β function is shallower than the true density distribution in the outer regions, while the assumed constant temperature over-predicts the actual values. These two deviations have opposite effects on the measurements of hydorstatic mass. As a result, the hydrostatic mass from the β function fits with a constant temperature is fairly reliable in spite of the apparent technical caveats.
In the inner regions, some clusters have a cool core within 0.1 R500. The positive temperature gradient leads to a smaller pressure gradient, and thereby the derived hydrostatic mass is smaller than that from a constant temperature. On the other hand, the β function is known to underestimate the inner slope of the electron number density. The two opposite effects are competing. As a result, the three cool-core clusters, A0085, A1795, and A2029 present roughly consistent measurements with constant and varying temperatures. A2142 is identified as a non-cool-core cluster by Zhang et al. (2011), but Eckert et al. (2022) show the core temperature is lower than the peak value by 25%. The only non-cool-core cluster, A3158, shows that the hydrostatic mass from the β function fit is apparently lower than that in X-COP at r < 200 kpc, which might be due to the shallower inner slope of the β function. This does not affect the remaining five clusters for which there are no X-COP results, since we mostly focus on the regions beyond 200 kpc.
In Fig. 3, we also plot the dynamical mass profiles measured from the line-of-sight velocity dispersion as discrete points with errors. The corresponding total density profiles are presented in the appendix (Fig. C.1). Among those five clusters in X-COP, four clusters present roughly consistent mass measurements. These are rich and massive clusters, so their spatial dynamics can be well resolved by galaxy kinematics. The galaxy distribution of A2029 is much more extended than its gas distribution. As such, we can only compare our dynamical mass with the extrapolated hydrostatic mass from the β function fit at large radii. The good agreement suggests that the β function extrapolation might be a satisfactory approximation.
The galaxy kinematics of A0085 present consistent dynamical mass within r500, while beyond this radius, they overshoot the hydrostatic mass. This indicates that although the X-ray gas is relaxed, the cluster galaxies in the outskirts are not. It could be that relaxation is quicker at small radii, but it takes longer at large radii. So, after merging, the outskirt galaxies need more time to reach equilibrium. One might think that A0085 is growing its structure by accreting more galaxies. However, if these outskirt galaxies have higher velocity dispersion than allowed by the total gravitational potential, they cannot be gravitationally bounded within the cluster. Therefore, it is more likely that the hydrostatic mass is underestimated at large radii.
The remaining five clusters are low-mass and low-richness. Figure 3 show that the dynamical masses from galaxy kinematics for four clusters overshoot their hydrostatic masses, while only A3571 presents an acceptable agreement. The inconsistency may imply that these cluster galaxies are away from dynamical equilibrium, though their X-ray images do not present abnormal structures. If true, this would suggest that galaxies and ICM have different time scales for relaxation. However, our results are qualitatively consistent with what Foëx et al. (2017) found. This indicates that their hydrostatic masses are likely being underestimated.
In Table 1, we present the mass budget for each relaxed cluster. We also compared the total masses measured from galaxy kinematics and hydrostatic equilibrium. Our results show that the total mass from galaxy kinematics is higher than hydrostatic mass by 3% to 94%. The mean percentage is ∼50%. This could affect the σ8 tension (Blanchard & Ilić 2021). The σ8 parameter describes the magnitude of matter fluctuations in the later Universe, which can be calculated from the CMB fluctuations via extrapolations (Planck Collaboration XIII 2016). It can also be directly measured through cluster counts. The cluster sample for cosmological interests is SZ selected, but the cluster mass is calibrated using hydrostatic mass (Planck Collaboration XXIV 2016). So if the hydrostatic mass is underestimated, the measured σ8 would be lower as well. Blanchard & Ilić (2021) pointed out the tension can be resolved if the hydrostatic mass is scaled up by 40%, which is roughly consistent with our mass estimates. However, our sample is quite small, so it is unclear if the true mass deviation measured from galaxy kinematics and hydrostatic equilibrium is around 40% or not. To completely resolve the σ8 tension, one would also need to understand the cosmic shear analysis from weak-lensing measurements (Asgari et al. 2021), which also presents this tension with the CMB results. Our results could be a step forward if statistically confirmed with larger cluster samples.
Mass budget of each relaxed cluster.
Though promising for the σ8 tension, our measurements result in the baryonic fraction that is in tension with the cosmic value, fb = 0.16. Table 1 shows that most of our clusters have a baryonic fraction much smaller than 0.16. Therefore, the tension between the early-Universe and late-Universe measurements is hardly resolved in the ΛCDM cosmology.
5.3. Completeness of the cluster galaxy sample
The possible incompleteness of the galaxy samples could affect our mass profiles in two ways: (1) smaller samples could make the derived line-of-sight velocity dispersion profiles statistically less robust; (2) it may underestimate the galaxy number density and surface density appearing in Eqs. (7) and (9). The first concern is largely removed by the Binulator approach, which fits a group of galaxies to the generalized Gaussian function, so missing a few galaxies would not seriously affect the statistics. The second concern is alleviated by the fact that the galaxy number density appears in both the numerator and denominator in Eqs. (7) and (9), so a constant fraction of incompleteness is canceled out exactly (in Eq. (9), Σgal carries the same incompleteness constant as ν(r)). As a result, only radially variable incompleteness can affect our results.
Since the clusters in our sample are all at low redshift (z < 0.1, see Table 1), they have been well observed both photometrically and spectroscopically. Their spectroscopically selected galaxy samples are reported to have a relatively high completeness level (see, e.g., Cava et al. 2009), so clusters with less extended galaxy distributions are unlikely to have a completeness profile that varies significantly at different radii. For extended clusters such as A2142, Owers et al. (2011) showed that their completeness remains almost constant for up to 3 Mpc (see their Fig. 2). Our only concern regarding incompleteness is A2029, the most extended cluster in our sample. Sohn et al. (2017) found that its completeness level remains constant up to 1.5 Mpc but decreases by ∼15% at 2 Mpc. In Appendix A, we investigate how the radially varying completeness could possibly bias the mass profile of A2029. We find that even if the completeness decreases by 80% at the outermost region, the mass profile lies well within the 1σ region of that assuming a constant completeness profile. Therefore, incompleteness does not affect our results significantly. Our mass profiles are robust within their errors.
5.4. Velocity anisotropy
Figure 4 plots the radial distributions of the velocity anisotropy parameter for the ten undisturbed clusters. The derivation of their values relies on the two virial shape parameters, vs1 and vs2, which help ameliorate the ρ − β degeneracy. However, vs1 and vs2 are not radially dependent functions, but two single values. As such, they do not put strong constraints. The measured velocity anisotropies hence present large uncertainties. At small radii, the uncertainties are mostly around 0.1, while they could be as large as 0.2 at large radii. The richest cluster, A2029, has the smallest uncertainty, smaller than 0.1, given that the line-of-sight velocity dispersion profile is better measured thanks to the larger sample of galaxy tracers.
 |
Fig. 4. Radial distributions of velocity anisotropy parameter β for the ten undisturbed clusters. Lightly shaded regions show the 1σ confidence intervals. The mean values of β are consistent with an isotropic velocity distribution within the errors at small radii, while at large radii the velocity anisotropies are clearly presented in spite of the large errors. The two big error bars at small and large radii represent the allowed ranges set by the priors on β0 and β∞, respectively. The lower boundary is −0.5 at all radii. |
In spite of the large uncertainties, nine of the ten clusters present similar trends for their mean velocity anisotropies: nearly isotropic in the inner regions while apparently anisotropic in the outskirts. The boundary we imposed on the inner anisotropy is 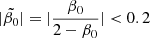 , which corresponds to −0.5 < β0 < 0.33. Figure 4 shows all the inner anisotropies are well within the set range. This justifies our priors and suggests that the isotropy in the inner regions is truly physical rather than artificially imposed. The only cluster presenting a clear velocity anisotropy in the inner region is A2029, which is an extremely extended cluster. Its stronger constraints most likely owe to its large extent, but it is also possible that they are due to our fitting function (Eq. (16)) being too restrictive. We will explore this in future work.
, which corresponds to −0.5 < β0 < 0.33. Figure 4 shows all the inner anisotropies are well within the set range. This justifies our priors and suggests that the isotropy in the inner regions is truly physical rather than artificially imposed. The only cluster presenting a clear velocity anisotropy in the inner region is A2029, which is an extremely extended cluster. Its stronger constraints most likely owe to its large extent, but it is also possible that they are due to our fitting function (Eq. (16)) being too restrictive. We will explore this in future work.
The apparent anisotropies observed at large radii may not be solid either given their larger uncertainties, except for A2029. Even so, our mean values of velocity anisotropy are qualitatively consistent with the expectations. Since the impact of violent relaxation is strongest at small radii, one expects spherically averaged galaxy motions to present a nearly isotropic velocity distribution (e.g., Pontzen et al. 2015); while at large radii, the velocity distribution could be more radially dominated. Our results are also quantitatively consistent with cosmological simulations (Aguirre Tagliaferro et al. 2021).
5.5. Radial acceleration relation
The extended dynamical mass profiles probed by galaxy kinematics put strong constraints on dynamical relations. We tested the radial acceleration relation (RAR; McGaugh et al. 2016; Lelli et al. 2017b), a tight correlation relating the observed acceleration from rotation curves gobs and that from the baryonic distributions gbar:
This relation was established statistically with 153 late-type galaxies (Lelli et al. 2016b) and holds in early-type galaxies (Lelli et al. 2017a; Shelest & Lelli 2020). It also holds in individual galaxies once the uncertainties on stellar mass-to-light ratio, galaxy distances, and disk inclinations are taken into account (Li et al. 2018). The empirical relation is in line with modified Newtonian dynamics (MOND; Milgrom 1983).
The RAR has also been explored on BCG-cluster scales. For example, Tian et al. (2020) employed 20 massive clusters from the Cluster Lensing And Supernova survey with Hubble (CLASH; Postman et al. 2012) with total mass profiles measured from gravitational lensing (Umetsu et al. 2016). They found a correlation between gobs and gbar that it is systematically offset from the RAR observed in galaxies, with a significantly larger acceleration scale. Eckert et al. (2022) investigated the RAR using 12 X-COP clusters with dynamical mass profiles measured from hydrostatic equilibrium and the SZ effect. They also reported higher dynamical accelerations than expected from the RAR.
We calculated the total accelerations from the dynamical mass profiles measured with galaxy kinematics:
Since galaxy distributions can be quite extended, their kinematics help probe lower accelerations than other approaches. The CLASH sample used by Tian et al. (2020) probes accelerations as low as 10−10 m s−2. With the help of the SZ technique, Eckert et al. (2022) extended the acceleration to slightly above 10−11 m s−2, which is similar to that observed in individual clusters (Fig. 5).
 |
Fig. 5. Radial acceleration relation of ten undisturbed galaxy clusters. Black points show the results with both measured dynamical and baryonic masses, while grey points show the radii where there are only measured dynamical masses. The gas masses at these radii are derived from extrapolations based on the surface brightness fits. The dotted line is the line of unity, and the red line is the RAR established with late-type galaxies (McGaugh et al. 2016; Lelli et al. 2017b). Light gray points represent the SPARC galaxies from McGaugh et al. (2016). The total accelerations overshoot the RAR in galaxies, suggesting a missing baryon problem in the inner regions of galaxy clusters for MOND Milgrom (1983). |
It is challenging to derive the corresponding baryonic acceleration, which is the summation of the gas and stellar contributions:
In the outskirts, X-ray surface brightness becomes too low to be observable. Therefore, we can only estimate the gas mass via extrapolations using the β function fits. For the five clusters in the X-COP, we adopted the modified β function from Vikhlinin et al. (2006):
where x = r/r500 and γ = 3 is generally fixed. The free parameter space is comprised of (n0, α, β, ϵ, rc, rs). Ghirardini et al. (2019) claimed that the density profile is universal for the 12 X-COP clusters, so they can be described by a single set of values: lnn0 = −4.44, α = 0.89, β = 0.43, ϵ = 2.86, lnrc = −2.99, lnrs = −0.29. However, their Fig. 3 shows the electron number density profiles are quite diverse in the inner and outer regions. To achieve more accurate extrapolations toward large radii, we only adopt their values of α, β, and rc, but re-fit the outer slope ϵ, scale length rs, and the overall normalization factor n0. The resultant fits properly describe the diversity of the density profiles in the outskirts with greater accuracy, so we extrapolated the gas mass distributions with these fits where X-ray data are absent.
Figure 5 plots the total acceleration measured with the line-of-sight velocity dispersions of cluster member galaxies against the baryonic acceleration for the ten relaxed clusters. Regions where the gas mass is estimated by extrapolating the surface brightness fits should be given less credit. Similar to previous works, we find that the total acceleration is systematically higher than expected from the RAR defined by individual galaxies. This is particularly true at intermediate radii. Black points roughly form a line, parallel to the galactic RAR. A similar behavior was reported by Tian et al. (2020) with the CLASH sample. Tian et al. (2020) found that the higher total acceleration imply a larger critical acceleration (g† ∼ 10−9 m s−2) in clusters than that in galaxies (g† ∼ 10−10 m s−2; McGaugh et al. 2016). The high critical acceleration is a reflection of the missing baryon problem, a well-known problem for MOND in galaxy clusters.
At larger radii and lower acceleration, the data appear to converge with the galactic RAR. This indicates that the missing baryon problem that MOND suffers in clusters is concentrated toward their centers (Sanders 2003; Angus et al. 2008), while at large radii the baryonic mass seems consistent with the MOND prediction. However, we caution that the total baryonic mass in the outskirts are extrapolations from surface brightness fits. As a result, the total baryonic mass may be overestimated. Whether the missing baryon problem appears in the outskirts of galaxy clusters remains an open question that will be explored with more extended X-ray data in the future.
6. Discussion and conclusion
In this work, we applied the spherical Jeans equation to the motions of galaxies in clusters to infer their orbital anisotropies and dynamical mass profiles. We tested this approach with 16 HIFLUGCS clusters and derived the dynamical mass profiles from the observed galaxy distributions and line-of-sight velocity dispersion. We distinguish six clusters with indications of disturbances in their X-ray images and found their dynamical masses measured from galaxy kinematics are systematically larger than the hydrostatic masses. For the X-ray relaxed clusters, half of them present consistent dynamical mass measurements from galaxy kinematics and hydrostatic equilibrium. These are mostly massive and rich clusters. The rest of the clusters present higher dynamical mass, which suggests that the hydrostatic mass might be underestimated. This could be a step toward solving the σ8 tension. The latter requires a higher mass calibration than hydrostatic mass, but it also causes difficulty in reproducing the cosmic baryonic fraction. Alternatively, it could imply that these clusters are not in dynamical equilibrium. Therefore, our approach can also be used to study the dynamical state of galaxy clusters.
A big advantage of using galaxies to constrain cluster dynamics is that they can trace the gravitational potential far beyond X-ray emitting regions, where the acceleration can be extremely low. In this paper, we showed the lowest acceleration probed by the ten HIFLUGCS clusters is slightly below 10−11 m s−2. The low acceleration region is critical for testing some alternative theories of gravity such as MOND, as well as different dark matter models such as superfluid dark matter (Khoury 2015). However, it also raises the concern that galaxies in the outskirts of a cluster may still be on the way to collapsing into the center, so they may have not reached the dynamical equilibrium yet. Since there are no X-ray data in the outskirts, we cannot robustly test the equilibrium; we can only provide a rough investigation by extrapolating the hydrostatic mass profiles with the fits using the β function or modified β function when the actual data are available. The comparison supports the application of galaxy kinematics in the outskirts, which makes our approach promising. A robust calibration can only be carried out by cross-checking the results from weak-lensing measurements. Weak lensing measures the projected mass along the line of sight, which includes any foreground or background mass, whereas our dynamical analysis constrains the spherically averaged 3D mass distribution. As such, a comparison between the two requires both a projection of our 3D mass distribution on the sky and analysis of mock data from full cosmological simulations to test the impact of line-of-sight structures. For these reasons, we will consider detailed comparisons with weak-lensing studies in future work.
Our dynamical analysis refines and reinforces previous results that MOND suffers from a missing baryon problem in rich, X-ray emitting galaxy clusters. This discrepancy is pronounced at intermediate radii where the dynamical acceleration exceeds that predicted by the galaxy-calibrated RAR applied to the observed baryons. Numerous solutions have been proposed for this, such as unseen baryons (Milgrom 2015), massive neutrinos (Sanders 2003), sterile neutrinos (Angus & Diaferio 2011), mixed dark matter/alternative gravity models (Berezhiani & Khoury 2015), making the Lagrangian a function of potential depth as well as acceleration (Hodson & Zhao 2017), tinkering with the MOND interpolation function (Zhao & Famaey 2012), or some combination of these. The cluster data converge toward the galaxy RAR at low accelerations in their outskirts. Therefore, it seems the discrepancy is restricted to cluster cores, while the total baryonic mass may be consistent with that predicted by the Baryonic Tully–Fisher relation (McGaugh 2005; Lelli et al. 2016a; McGaugh et al. 2021). However, our baryonic mass estimates in the outskirts are extrapolations, and only three clusters extend to the low acceleration region. More clusters with robust gas mass measurements in the outskirts are necessary to further examine this behavior.
Acknowledgments
We are grateful for the useful discussion with Johan Comparat. P.L. is supported by the Alexander von Humboldt Foundation. Y.T. is supported by Taiwan National Science and Technology Council NSTC 110-2112-M-008-015-MY3. M.S.P. acknowledges funding of a Leibniz-Junior Research Group (project number J94/2020) and a KT Boost Fund by the German Scholars Organization and Klaus Tschira Stiftung. S.S.M. and J.M.S. are supported in part by NASA ADAP grant 80NSSC19k0570. S.S.M. also acknowledges support from NSF PHY-1911909. C.M.K. is supported by Taiwan NSTC 111-2112-M-008-013.
References
- Aguirre Tagliaferro, T., Biviano, A., De Lucia, G., Munari, E., & Garcia Lambas, D. 2021, A&A, 652, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Almeida, A., Anderson, S. F., Argudo-Fernández, M., et al. 2023, ApJS, 267, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Andernach, H., Tago, E., Einasto, M., Einasto, J., & Jaaniste, J. 2005, ASP Conf. Ser., 329, 283 [NASA ADS] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Angus, G. W., & Diaferio, A. 2011, MNRAS, 417, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., Famaey, B., & Buote, D. A. 2008, MNRAS, 387, 1470 [CrossRef] [Google Scholar]
- Asgari, M., Lin, C.-A., Joachimi, B., et al. 2021, A&A, 645, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berezhiani, L., & Khoury, J. 2015, Phys. Rev. D, 92, 103510 [Google Scholar]
- Binney, J., & Mamon, G. A. 1982, MNRAS, 200, 361 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
- Biviano, A., Murante, G., Borgani, S., et al. 2006, A&A, 456, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Rosati, P., Balestra, I., et al. 2013, A&A, 558, A1 [Google Scholar]
- Blanchard, A., & Ilić, S. 2021, A&A, 656, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Chon, G., & Collins, C. A. 2014, A&A, 570, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappellari, M. 2013, ApJ, 778, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [Google Scholar]
- Cava, A., Bettoni, D., Poggianti, B. M., et al. 2009, A&A, 495, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y., & Zhang, Y. Y. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiu, I., Mohr, J. J., McDonald, M., et al. 2018, MNRAS, 478, 3072 [Google Scholar]
- Collins, M. L. M., Read, J. I., Ibata, R. A., et al. 2021, MNRAS, 505, 5686 [NASA ADS] [CrossRef] [Google Scholar]
- De Leo, M., Read, J. I., Noel, N. E. D., et al. 2023, MNRAS, submitted [arXiv:2303.08838] [Google Scholar]
- Diaferio, A. 1999, MNRAS, 309, 610 [CrossRef] [Google Scholar]
- Diaferio, A., & Geller, M. J. 1997, ApJ, 481, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ghirardini, V., Ettori, S., et al. 2019, A&A, 621, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Ettori, S., Pointecouteau, E., van der Burg, R. F. J., & Loubser, S. I. 2022, A&A, 662, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Ghirardini, V., Eckert, D., et al. 2019, A&A, 621, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foëx, G., Böhringer, H., & Chon, G. 2017, A&A, 606, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Genina, A., Read, J. I., Frenk, C. S., et al. 2020, MNRAS, 498, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirardini, V., Eckert, D., Ettori, S., et al. 2019, A&A, 621, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodson, A. O., & Zhao, H. 2017, A&A, 598, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoury, J. 2015, Phys. Rev. D, 91, 024022 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [Google Scholar]
- Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016a, ApJ, 816, L14 [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016b, AJ, 152, 157 [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2017a, MNRAS, 468, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017b, ApJ, 836, 152 [Google Scholar]
- Li, P., Lelli, F., McGaugh, S., & Schombert, J. 2018, A&A, 615, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limber, D. N., & Mathews, W. G. 1960, ApJ, 132, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, A., Bulbul, E., Ramos-Ceja, M. E., et al. 2023, A&A, 670, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamon, G. A., & Łokas, E. L. 2005, MNRAS, 363, 705 [Google Scholar]
- Mathiesen, B. F., & Evrard, A. E. 2001, ApJ, 546, 100 [CrossRef] [Google Scholar]
- McGaugh, S. S. 2005, ApJ, 632, 859 [Google Scholar]
- McGaugh, S. S., Lelli, F., & Schombert, J. M. 2016, Phys. Rev. Lett., 117, 201101 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Lelli, F., Schombert, J. M., et al. 2021, AJ, 162, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Merrifield, M. R., & Kent, S. M. 1990, AJ, 99, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [Google Scholar]
- Milgrom, M. 2015, MNRAS, 454, 3810 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [Google Scholar]
- Navarro, J. F., Eke, V. R., & Frenk, C. S. 1996, MNRAS, 283, L72 [NASA ADS] [Google Scholar]
- Nelson, K., Lau, E. T., & Nagai, D. 2014, ApJ, 792, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Owers, M. S., Nulsen, P. E. J., & Couch, W. J. 2011, ApJ, 741, 122 [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2016, A&A, 594, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [Google Scholar]
- Pontzen, A., Read, J. I., Teyssier, R., et al. 2015, MNRAS, 451, 1366 [CrossRef] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [Google Scholar]
- Read, J. I., & Steger, P. 2017, MNRAS, 471, 4541 [Google Scholar]
- Read, J. I., Wilkinson, M. I., Evans, N. W., Gilmore, G., & Kleyna, J. T. 2006, MNRAS, 367, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I., Agertz, O., & Collins, M. L. M. 2016, MNRAS, 459, 2573 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I., Walker, M. G., & Steger, P. 2018, MNRAS, 481, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I., Mamon, G. A., Vasiliev, E., et al. 2021, MNRAS, 501, 978 [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [Google Scholar]
- Sanders, R. H. 2003, MNRAS, 342, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J., McGaugh, S., & Lelli, F. 2022, AJ, 163, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, A. L., Diaferio, A., Murante, G., & Borgani, S. 2011, MNRAS, 412, 800 [NASA ADS] [Google Scholar]
- Shelest, A., & Lelli, F. 2020, A&A, 641, A31 [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sohn, J., Geller, M. J., Zahid, H. J., et al. 2017, ApJS, 229, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, Y., Umetsu, K., Ko, C.-M., Donahue, M., & Chiu, I. N. 2020, ApJ, 896, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, Y., Yu, P.-C., Li, P., McGaugh, S. S., & Ko, C.-M. 2021, ApJ, 910, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Tiret, O., Combes, F., Angus, G. W., Famaey, B., & Zhao, H. S. 2007, A&A, 476, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umetsu, K., Zitrin, A., Gruen, D., et al. 2016, ApJ, 821, 116 [Google Scholar]
- van der Marel, R. P. 1994, MNRAS, 270, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Ventimiglia, D. A., Voit, G. M., Donahue, M., & Ameglio, S. 2008, ApJ, 685, 118 [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y. Y., Andernach, H., Caretta, C. A., et al. 2011, A&A, 526, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, H., & Famaey, B. 2012, Phys. Rev. D, 86, 067301 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1933, Helv. Phys. Acta, 6, 110 [NASA ADS] [Google Scholar]
Appendix A: The mass profiles of A2029 assuming different, radially varying, completeness functions
In order to quantitatively study the possible bias due to the radially varying completeness, we derived the mass profiles for A2029 assuming different completeness functions. For simplicity, we assumed the completeness of A2029 linearly decreases from 100% at the innermost radius to 60% and 20% at the outermost radius, which corresponds to 40% and 80% radial variations in the completeness profiles, respectively. Since we cannot add missing galaxies at large radii, we can instead proceed by randomly rejecting some galaxies at small radii to achieve a constant completeness profile. However, rejecting a large number of galaxies could lower the statistical robustness for the velocity dispersion measurements. So, we kept all these galaxies, but lowered the membership probability from 100% to
where P = 40% for a 40% completeness variation, and P = 80% for a, 80% variation; R is the projected radius of each cluster galaxy; and Rmax and Rmin refer to the radii of the innermost and outermost galaxies, respectively. The designed function of membership probability reduces the effective number of cluster galaxies while preserving all the galaxies for velocity dispersion measurements.
Figure A.1 shows the mass profiles of A2029 when assuming different radial variations of completeness. At small radii, the enclosed mass becomes smaller for a larger radial variation of completeness. However, the uncertainties also increase quickly. This is because the galaxy sample becomes smaller after we reduce the effective number of galaxies by lowering the membership probability. The variation in the mass profile is smaller than the uncertainty. At large radii, the mass profiles are even more consistent. This suggests that incompleteness does not affect our mass measurements significantly. Our mass profiles are robust within their errors.
 |
Fig. A.1. Mass profiles of A2029 with radially varying completeness. The black line assumes the completeness is a constant with radius. The red and blue lines assume the completeness decreases from the innermost region to the ourtermost region by 40% and 80%, respectively. Shadow regions present the 1 σ credible intervals. Larger completeness variations show larger uncertainties due to the smaller sample after reducing the effective number of galaxies at small radii. The vertical dashed and dotted lines mark the positions of r500 and Rhalf, respectively. The variations of the mass profiles due to different completeness functions are well with the 1 σ region, suggesting our results are not sensitive to incompleteness. |
Appendix B: Example corner plots for the mass-velocity anisotropy degeneracy
We examined how the two virial shape parameters help ameliorate the mass-velocity anisotropy degeneracy by plotting their posterior distributions in Figure B.1. Since both the enclosed total mass and velocity anisotropy are functions of radius, we present four posterior distributions nearly equally spanning from the innermost to ourtermost radii for the example cluster A0085 (other clusters present similar posterior distributions). Figure B.1 shows that the enclosed total mass is well constrained at all radii, suggesting the two virial shape parameters indeed help ameliorate the degeneracy. In contrast, velocity anisotropy presents wide distributions. At large radii, we observe some Gaussian-like distributions, but they generally have a large standard deviation. This suggests that the degeneracy, though ameliorated by virial shape parameters, is not completely broken.
 |
Fig. B.1. Example corner plots for cluster A0085 showing mass-velocity anisotropy degeneracy. The four panels present the posterior distributions of total enclosed mass and velocity anisotropy at four different radii where binned velocity dispersion data are available: r = 96 kpc (top left), r = 570 kpc (top right), r = 965 kpc (bottom left), and r = 1827 kpc (bottom right). Blue marks regions that are used for parameter estimations. Blue crosses indicate the position of the best-fit parameters and vertical dashed lines outline the 1 σ regions. The total enclosed mass is well determined at all radii, while the velocity anisotropy is less constrained at small radii but improves slightly toward large radii. |
Appendix C: Total density profiles of ten relaxed clusters
 |
Fig. C.1. Density profiles corresponding to the total cumulative mass profiles in Figure 3. Dark and light shaded areas are 1σ and 2σ regions. Vertical dashed and dotted lines indicate the positions of r500 from X-ray data and Rhalf from optical data. Please note that these are not dark matter density profiles but the total density profiles including baryonic contributions. |
 |
Fig. C.1. continued. |
All Tables
All Figures
 |
Fig. 1. Example fits of projected galaxy number density profiles and line-of-sight velocity dispersion profiles. The cluster shown here is A0085. The galaxy surface number density profile is fit with three Plummer spheres, which are then used as input in the projected Jeans equation. The line-of-sight velocity dispersion profile is used to determine the total mass profile, parameterized using the cNFWt profile with six parameters. Dark and light shadow regions show the 1σ and 2σ confidence intervals, respectively. |
| In the text | |
 |
Fig. 2. Dynamical mass profiles of six disturbed clusters of galaxies. Solid lines are the hydrostatic mass profiles derived from the surface brightness fits using the β function from Chen et al. (2007). Points with the error bar show the total mass profiles from the line-of-sight velocity dispersion. Vertical dashed lines indicate the positions of r500 measured from X-ray data by Zhang et al. (2011), while dotted lines mark Rhalf enclosing 50% of the total cluster galaxies. 3D radii are chosen according to the binned projected radii to avoid oversampling. That the dynamical mass profiles determined from different tracers are inconsistent presumably indicates nonequilibrium conditions stemming from recent or ongoing mergers. |
| In the text | |
 |
Fig. 3. Mass profiles of undisturbed clusters of galaxies. Points with error bars are the total mass profiles from velocity dispersion. Solid and dashed blue lines are the hydrostatic mass and gas mass profiles from the X-COP project, respectively, while solid and dashed black lines show the corresponding results from the surface brightness fits using the β functions in Chen et al. (2007). Green lines show the stellar mass distributions. Vertical dashed lines indicate the positions of r500 measured by Zhang et al. (2011) with X-ray data, while dotted lines mark Rhalf, which equally divide the total cluster galaxies. For these undisturbed clusters, the dynamical mass profiles from galaxy kinematics are generally consistent with hydrostatic mass profiles, but they extend to larger radii in general. Possible reasons for the inconsistency in some clusters are discussed in the text. |
| In the text | |
 |
Fig. 3. continued. |
| In the text | |
 |
Fig. 4. Radial distributions of velocity anisotropy parameter β for the ten undisturbed clusters. Lightly shaded regions show the 1σ confidence intervals. The mean values of β are consistent with an isotropic velocity distribution within the errors at small radii, while at large radii the velocity anisotropies are clearly presented in spite of the large errors. The two big error bars at small and large radii represent the allowed ranges set by the priors on β0 and β∞, respectively. The lower boundary is −0.5 at all radii. |
| In the text | |
 |
Fig. 5. Radial acceleration relation of ten undisturbed galaxy clusters. Black points show the results with both measured dynamical and baryonic masses, while grey points show the radii where there are only measured dynamical masses. The gas masses at these radii are derived from extrapolations based on the surface brightness fits. The dotted line is the line of unity, and the red line is the RAR established with late-type galaxies (McGaugh et al. 2016; Lelli et al. 2017b). Light gray points represent the SPARC galaxies from McGaugh et al. (2016). The total accelerations overshoot the RAR in galaxies, suggesting a missing baryon problem in the inner regions of galaxy clusters for MOND Milgrom (1983). |
| In the text | |
 |
Fig. A.1. Mass profiles of A2029 with radially varying completeness. The black line assumes the completeness is a constant with radius. The red and blue lines assume the completeness decreases from the innermost region to the ourtermost region by 40% and 80%, respectively. Shadow regions present the 1 σ credible intervals. Larger completeness variations show larger uncertainties due to the smaller sample after reducing the effective number of galaxies at small radii. The vertical dashed and dotted lines mark the positions of r500 and Rhalf, respectively. The variations of the mass profiles due to different completeness functions are well with the 1 σ region, suggesting our results are not sensitive to incompleteness. |
| In the text | |
 |
Fig. B.1. Example corner plots for cluster A0085 showing mass-velocity anisotropy degeneracy. The four panels present the posterior distributions of total enclosed mass and velocity anisotropy at four different radii where binned velocity dispersion data are available: r = 96 kpc (top left), r = 570 kpc (top right), r = 965 kpc (bottom left), and r = 1827 kpc (bottom right). Blue marks regions that are used for parameter estimations. Blue crosses indicate the position of the best-fit parameters and vertical dashed lines outline the 1 σ regions. The total enclosed mass is well determined at all radii, while the velocity anisotropy is less constrained at small radii but improves slightly toward large radii. |
| In the text | |
 |
Fig. C.1. Density profiles corresponding to the total cumulative mass profiles in Figure 3. Dark and light shaded areas are 1σ and 2σ regions. Vertical dashed and dotted lines indicate the positions of r500 from X-ray data and Rhalf from optical data. Please note that these are not dark matter density profiles but the total density profiles including baryonic contributions. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



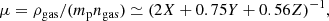
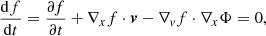
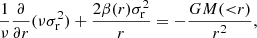
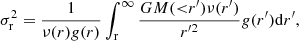
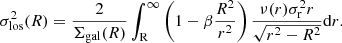
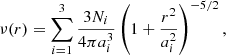
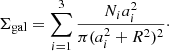
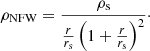
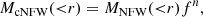
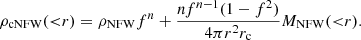
![$$ \begin{aligned} M_{\rm cNFWt}({ < }r) = M_{\rm cNFW}({ < }r_{\rm t}) + 4\pi \rho _{\rm cNFW}(r_{\rm t})\frac{r_{\rm t}^3}{3-\delta }\left[\left(\frac{r}{r_{\rm t}}\right)^{3-\delta }-1\right], \end{aligned} $$](/articles/aa/full_html/2023/09/aa46431-23/aa46431-23-eq18.gif)
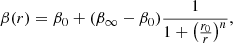
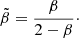
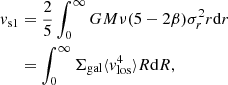
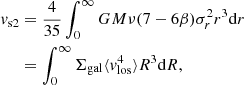
![$$ \begin{aligned} p_i = \frac{\beta }{2\alpha \Gamma (1/\beta )}\exp {\left[-\left(|v_{\mathrm{los},i}-\mu |/\alpha \right)^\beta \right]}, \end{aligned} $$](/articles/aa/full_html/2023/09/aa46431-23/aa46431-23-eq28.gif)