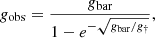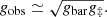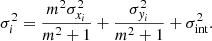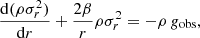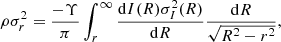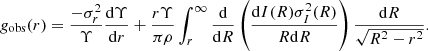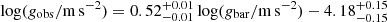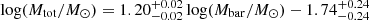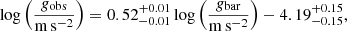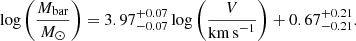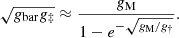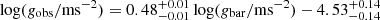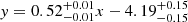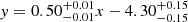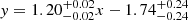EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 684 (April 2024) A&A, 684 (2024) A180 Full HTML
Open Access
Issue
A&A
Volume 684, April 2024
Article Number A180
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202347868
Published online 19 April 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Tight empirical scaling relations are pivotal in physics and astronomy, particularly in the exploration of new fundamental concepts. A prominent example is the dark matter (DM) problem, manifested through the discrepancy between observed gravitational effects (inferred mass) and the mass calculated from luminosity (baryonic matter). However, an intriguing perspective arises when examining the empirical acceleration relation in galaxies. This perspective focuses on the discrepancy between the baryonic acceleration, gbar ≡  GMbar(< r)/r2, and the observed acceleration, gobs, ascertained through methods like gravitational lensing, rotation curve analysis, or the Jeans equation. This inquiry into galactic acceleration uncovers a significant empirical scaling relation, including the identification of a characteristic acceleration scale, a key parameter in understanding these dynamics.

Recent discoveries have unveiled a tight empirical radial acceleration relation (RAR; McGaugh et al. 2016; Lelli et al. 2017) in spiral galaxies, providing a fresh perspective on the DM problem. The correlation can be parameterized between gobs and gbar as

(1)

which exhibits a characteristic acceleration scale, g† = (1.20 ± 0.02)×10−10m s−2 (McGaugh et al. 2016; Lelli et al. 2017; Li et al. 2018). Additionally, the low acceleration limit (gbar ≪ g†) recovers the baryonic Tully–Fisher relation (BTFR; McGaugh et al. 2000; Verheijen 2001; McGaugh 2011; Lelli et al. 2016, 2019), 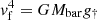, which relates the flat rotation velocity, vf, and the baryonic mass, Mbar. Subsequent studies of the RAR in elliptical galaxies have yielded consistent results, not only in dynamics (Lelli et al. 2017; Chae et al. 2019, 2020) but also in gravitational lensing effects (Tian & Ko 2019; Brouwer et al. 2021). In elliptical galaxies, replacing vf with the velocity dispersion, σ, yields the baryonic Faber–Jackson relation (BFJR; Sanders 2010; Famaey & McGaugh 2012), stating that σ4 ∝ GMbarg†. These findings further emphasize the importance of the RAR in understanding the fundamental concepts behind the observed acceleration discrepancies in galaxies. Coincidentally, the RAR was predicted by MOdified Newtonian Dynamics (MOND; Milgrom 1983) four decades ago.

In addition to galaxies, the “missing mass” problem has also been observed in galaxy clusters (Zwicky 1933; Famaey & McGaugh 2012; Overzier 2016; Rines et al. 2016; Umetsu 2020), which represent the largest gravitationally bound systems in the universe. Within the strong gravitational potential of galaxy clusters, the brightest cluster galaxy (BCG) is typically located at the center. However, even when accounting for the baryonic mass in the form of X-ray gas, the calculated mass remains insufficient when determining gravity using dynamics or gravitational lensing effects.

Upon examining the acceleration discrepancy on BCG-cluster scales, recent studies have revealed a more significant offset from the RAR in galaxy clusters (Chan & Del Popolo 2020; Tian et al. 2020; Pradyumna et al. 2021; Eckert et al. 2022; Tam et al. 2023; Liu et al. 2023; Li et al. 2023). In particular, a tight RAR (Tian et al. 2020) has been investigated in 20 massive galaxy clusters from the Cluster Lensing And Supernova survey with Hubble (CLASH) samples, referred to as the CLASH RAR, expressed as

(2)

This relation features a larger acceleration scale, g‡ = (2.0 ± 0.1)×10−9 m s−2, and a small log-normal intrinsic scatter of 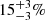. The CLASH RAR implies a parallel baryonic Faber-Jackson relation (BFJR) in galaxy clusters, given by σ4 ∝ GMbarg‡. More recent studies confirm this kinematic counterpart as the mass-velocity dispersion relation (MVDR; Tian et al. 2021a,b), found in 29 galaxy clusters and 54 BCGs. The MVDR exhibits a consistent acceleration scale, g‡ = (1.7 ± 0.7)×10−9 m s−2, with the CLASH samples and a small log-normal intrinsic scatter of .

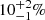In this work, we investigate the dynamical RAR in BCGs to address the second acceleration scale, g‡, on BCG-cluster scales. The confirmation of a distinct RAR necessitates a thorough examination of both gravitational mass and baryonic mass. To accomplish this, we employed integral field spectroscopy (IFS) for the internal kinematics of BCGs and model photometry for the stellar mass. It is intriguing to investigate both acceleration and mass correlations within the same sample. Moreover, by comparing dynamical and lensing samples, a universal acceleration scale can be scrutinized in galaxies, particularly for BCGs.

2. Data and methods

Our primary objective is to investigate the correlation between the dynamical acceleration and the baryonic acceleration in BCGs, as well as their mass correlation. While the RAR in 20 CLASH samples has been examined in gravitational lensing (Tian et al. 2020), the RAR of BCGs in dynamics has not been systematically explored. Furthermore, we assess the consistency of the dynamical and lensing RAR and compare the results between BCGs and clusters.

Investigating the dynamical RAR requires spatially resolved velocity dispersion profiles and the estimation of baryonic mass for individual galaxies. We noted that most of the velocity dispersion profiles within our BCG samples follow linear trends. This observation facilitated a simplified approach to analyzing galactic dynamics through the Jeans equation. Our primary objective was to derive the observed gravitational acceleration, gobs, with an enhanced accuracy. To this end, we employed Abel’s inversion (Binney & Mamon 1982; Binney & Tremaine 2008), an analytic formulation for linear velocity dispersion profiles. This technique, when combined with Bayesian statistics for fitting the velocity dispersion profiles, enabled us to efficiently compute gobs using Abel’s inversion of the Jeans equation. On the other hand, gbar was calculated using the accumulated baryonic mass at the same radius, employing an empirical Sérsic profile.

2.1. Data

The spatially resolved kinematic profiles in the galaxies necessitated using IFS to measure spectra for hundreds of points within each galaxy. At present, MaNGA provides an unprecedented sample of approximately 10 000 nearby galaxies with which to investigate the internal kinematic structure and composition of gas and stars (Bundy et al. 2015). MaNGA is a core program in the fourth-generation Sloan Digital Sky Survey (SDSS; Law et al. 2021). Also, MaNGA offers one of the most extensive samples of BCGs for IFS studies, presenting an unparalleled resource for in-depth analysis.

BCGs are distinguished not only by their luminosity and mass but also by their unique morphological and kinematic characteristics, which set them apart from typical galaxies. Typically located at the centers of galaxy clusters, BCGs often exhibit elliptical or cD galaxy morphologies, characterized by extended, diffuse envelopes indicative of their evolutionary history, which is marked by mergers and accretion within dense cluster environments. Kinematically, BCGs generally exhibit significant velocity dispersion with less pronounced rotational features.

In this study, we investigated 50 MaNGA BCGs with complete IFS and photometry data for dynamical analysis, building upon the previous systematic exploration of their kinematics. The velocity dispersion of MaNGA BCGs has been systematically explored using IFS data (Tian et al. 2021a), so we further investigated these BCG samples for dynamic studies. Most of these BCGs were initially obtained from Yang’s catalog (Yang et al. 2007), which was developed using a halo-based group finder in SDSS Data Release 4 (DR4). Hsu et al. (2022) re-identified them visually in color-magnitude diagrams with corresponding memberships. From their 54-galaxy sample, one BCG, 8943-9102, was excluded due to its morphology singling it out as a spiral galaxy. Because BCGs are generally classified as elliptical galaxies, identifying BCGs with spiral galaxy morphology may be considered a misclassification or misidentification. Additionally, three BCGs, 8613-12705, 9042-3702, and 9044-12703, were excluded due to an uncertain stellar mass estimated from the model photometry in SDSS. Ultimately, we utilized 50 BCGs with complete IFS and photometry data, which are listed with their plateifu IDs in Table A.1.

To examine the baryonic mass contribution of BCGs, we carefully considered the total stellar and gas mass. In our study, the stellar mass within the MaNGA survey was estimated by utilizing photometric data from the SDSS, whereby galaxy luminosities were converted to stellar masses through a constant mass-to-light ratio (Law et al. 2021). Concurrently, the gas mass was ascertained primarily from the analysis of ionized gas emission lines, which were observed using MaNGA’s integral field spectroscopy (Bundy et al. 2015). The gas fraction in our samples accounts for less than 3.2% of the baryonic mass. MaNGA primarily studies ionized gas in galaxies using optical spectroscopy through emission lines like Hα, [NII], [OII], [OIII], and [SII], but it’s not designed for observing neutral atomic (HI) or molecular gas (H2) (Bundy et al. 2015). Its focus on optical wavelengths might miss regions that have high amounts of dust or that are dominated by neutral or molecular gas, possibly resulting in the total galaxy gas content being underestimated. Because the RAR should be estimated at the same radius for both gobs and gbar, we computed the velocity dispersion measured up to approximately the effective radius and the accumulated baryonic mass based on the measured Sérsic profile at the same radius. Furthermore, we explored an alternative scenario regarding the possible gradient in the mass-to-light ratio in Appendix B. This analysis yields a stellar mass variation in the range of approximately 10%–20%.

2.2. Velocity dispersion profile with Bayesian statistics

We adopted the one-dimensional line-of-sight (LOS) velocity dispersion of 50 MaNGA BCGs (Tian et al. 2021a) and employed the profile with a linear fit using Bayesian statistics. Tian et al. (2021a) computed the mean LOS stellar velocity dispersion of each circle relative to its center, using Marvin, which was developed in Python (Cherinka et al. 2019). Surprisingly, those velocity dispersion profiles prove to be remarkably flat, even at the innermost region, in most cases (Tian et al. 2021a). Instead of the flat profile, we improved the fitting with a linear relation and estimated the error for each data point by implementing a maximum likelihood estimation with the orthogonal distance regression (ODR) method suggested in Lelli et al. (2019), Tian et al. (2021a,b). The linear relation with the ODR method was adopted, with the log-likelihood function 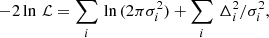, with 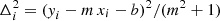, where i runs over all the data points, and σi includes the observational uncertainties (σxi, σyi) and the log-normal intrinsic scatter, σint, by

(3)

We modeled the one-dimensional velocity dispersion using two variables of y ≡ σ/⟨σ⟩ and x ≡ R/Re, which was normalized to the mean velocity dispersion ⟨σ⟩ and the effective radius, Re. In our samples, only the uncertainty of velocity dispersion was obtained for fitting. The slopes and the intercepts with the ODR MLE are presented in Table A.1 and illustrated for three examples in Fig. 1.

thumbnail Fig. 1.

Three examples of MaNGA BCGs with the plateifu of 8554-6102, 8331-12701, and 9888-12703. Upper panel: two-dimensional map plot of Spaxel data for the stellar velocity dispersion. Lower panel: velocity dispersion profiles in terms of the effective radius. The red circles represent the LOS velocity dispersion of concentric circles at different radii with the corresponding error bar. The solid blue lines represent the linear fit with the ODR MLE method.

2.3. Dynamical mass inferred by Abel inversion

In pressure-supported systems such as BCGs, the dynamics in equilibrium are governed by the Jeans equation in spherical coordinates (Binney & Mamon 1982; Binney & Tremaine 2008):

(4)

where 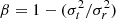represents the anisotropy parameter. For simplicity, we considered the isotropic case to be β = 0 and expressed the projected velocity dispersion, σI(R), in the form of an Abel integral equation with its inverse (Binney & Mamon 1982; Mamon & Łokas 2005; Binney & Tremaine 2008):

(5)

where I(R) represents the surface density and Υ denotes the mass-to-light ratio, depending on R in general. Then, we could conduct gobs through Abel inversion, deducing from Eqs. (4) and (5), expressed as (Binney & Mamon 1982; Mamon & Łokas 2005; Binney & Tremaine 2008)

(6)

In this study, we modeled σI(R) using a linear relation in the velocity dispersion profile due to mostly flat velocity dispersion profiles in our MaNGA BCG samples (see Fig. 1). Consequently, the total mass in Newtonian dynamics was defined as Mtot(< r) = r2gobs(r)/G. Additionally, we estimated the deviation of the anisotropic models in Appendix C, resulting in at most 6% (or a scatter of 0.02 dex) for gobs.

3. Results

Our primary objective is to investigate the dynamical mass and the RAR in MaNGA BCGs and compare the results with the lensing RAR observed in CLASH BCGs and clusters. The observational acceleration was directly computed at the last data point using Abel’s inversion, applied to the velocity dispersion profiles. On the other hand, the baryonic acceleration was estimated from the accumulated stellar mass, which was modeled with a Sérsic profile. Both accelerations were measured independently and presented on different axes. Moreover, we employed Bayesian statistics to assess the tightness of the correlation and examine their residuals with four galactic and cluster properties. Additionally, we illustrate the relationship between dynamical and baryonic mass for comparative purposes.

3.1. Radial acceleration relation and mass correlation

We implemented an ODR Markov chain Monte Carlo (MCMC) analysis, to explore the linear correlation evident in the RAR. Utilizing the Python package (emcee; Foreman-Mackey 2016; Foreman-Mackey et al. 2019), we conducted an ODR MCMC analysis to estimate the slope, m, intercept, b, and intrinsic scatter, σint, with two variables of y ≡ log(gobs/m s−2) and x ≡ log(gbar/m s−2). We employed non-informative flat priors for the slope and intercept within the range of [ − 100, 100], and for the intrinsic scatter with ln(σint)  ∈ [ − 10, 10]. The findings from our ODR MCMC analysis are illustrated in Fig. 2 for various samples.

thumbnail Fig. 2.

RAR and mass correlation of both BCGs and clusters. Left panel: black and green diamonds represent 50 MaNGA and 20 CLASH BCGs, while blue circles indicate data for 64 CLASH galaxy clusters. The solid black line illustrates the resulting RAR of all samples: . The shaded orange area illustrates the 1σ error of the best fit with the ODR MCMC method. The inset panel demonstrates the histograms of the orthogonal residuals of a whole sample (blue). For comparison, the galactic RAR is depicted by the dash-dotted line, while the dotted line represents the line of unity. Right panel: solid black line represents the mass correlation of all samples: . All symbols are the same as those in the left panel.

Our sample, consisting of 50 MaNGA BCGs, shows a linear correlation with a slope of 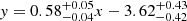, which dominates the higher acceleration region. When we combine MaNGA BCGs with the lensing result of 20 CLASH BCGs, the linear correlation presents a shallow slope of y = (0.54 ± 0.03)x − (4.01 ± 0.29), which extends to a lower acceleration region. Finally, we performed a complete fit including data for all 50 MaNGA BCGs, 20 CLASH BCGs, and 64 clusters, which resulted in the following equation:

(7)

with a tiny uncertainty log-normal intrinsic scatter of (4.9 ± 0.9)%, corresponding to 0.02 dex. The related triangle diagrams of the regression parameters are presented in Appendix D.

In further analysis, we employed the same vertical MCMC method used in the CLASH RAR study (Tian et al. 2020). This approach yielded a shallow slope represented by the relation y = (0.50 ± 0.01)x − (4.30 ± 0.15), along with a similar uncertainty in the log-normal intrinsic scatter of (5.6 ± 1.0)%, corresponding to 0.02 dex. While the fitting result may vary slightly depending on the methods employed, the differences remain minor and are consistent with their respective uncertainties.

We subsequently analyzed the mass correlation in a logarithmic diagram between the accumulated total mass, Mtot, and baryonic mass, Mbar, as is shown in the right panel of Fig. 2. Using the ODR MCMC method for the entire sample to establish a linear correlation, the result yielded log(Mtot/M⊙) = (1.20 ± 0.02)log(Mbar/M⊙)−(1.74 ± 0.24), with a larger uncertainty in the log-normal intrinsic scatter of (19 ± 2)%. Unlike the consistency observed in acceleration correlation, CLASH BCGs and MaNGA BCGs dominate the same mass range but exhibit a larger scatter in mass correlation when combined.

3.2. Residuals

To investigate correlations between the residuals, we computed the orthogonal distance between Eq. (7) and each individual piece of data for four global quantities of BCGs and clusters: the observational acceleration, radius, baryonic mass surface density, and redshift (see Fig. 3). The residuals of all samples are distributed within a tiny range from −0.22 to 0.23 dex. No significant correlations are observed in the residuals diagram, except for a slight correlation of cluster data concerning the outer radius.

thumbnail Fig. 3.

Orthogonal residuals against four global quantities of galaxies and galaxy clusters: the observational acceleration, gobs (upper left), radius, R (upper right), baryonic mass surface density, ΣBar (lower left), and redshift (lower right). The plot displays the residuals for 50 MaNGA BCGs (black diamonds), 20 CLASH BCGs (green diamonds), and 64 data points from CLASH clusters (blue circles), with the dashed line representing zero difference.

3.3. Mimicking the baryonic Tully–Fisher relation

Although the approach may seem conceptual, it is enlightening to analyze the BTFR as the kinematic analog of the tight dynamical scaling relation in this context. Defining the circular velocity as 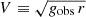, we corresponded V using the total acceleration of both BCG and cluster samples. The BTFR was investigated with both V and the baryonic mass, Mbar. One of the main benefits of examining the BTFR is the expansion of the dynamic range of the distinct RAR concerning the baryonic mass. This range spans approximately 3.5 orders of magnitude in our samples, as is illustrated in Fig. 4.

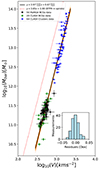thumbnail Fig. 4.

BTFR analysis with ODR MCMC for extended dynamic range. The solid black line illustrates the fitting BTFR of all samples: log(Mbar/M⊙) = (3.97 ± 0.07)log(V/m s−1)−(0.67 ± 0.21). The shaded orange area illustrates the 1σ error of the best fit with the ODR MCMC method. The inset panel demonstrates the histograms of the orthogonal residuals of a whole sample (blue). For comparison, the galactic BTFR (Lelli et al. 2019) is depicted by the dotted red line. The plot displays the residuals for 50 MaNGA BCGs (black diamonds), 20 CLASH BCGs (green diamonds), and 64 data points from CLASH clusters (blue circles).

Because our samples demonstrate a linear correlation, we again adopted the ODR MCMC for the analysis. The resulting BTFR presents a tight relation, with an uncertainty in the log-normal intrinsic scatter of (11 ± 2)%, equivalent to 0.05 dex, and can be expressed as

(8)

The slope of this relation closely aligns with that observed in spiral galaxies (Lelli et al. 2019), being nearly parallel with a value close to four. However, a deviation is noted in the intercept, suggesting a larger acceleration scale. By assuming a fixed slope of four for g‡, the relation simplifies to log(Mbar/M⊙) = 4 log(V/km s−1)+(0.57 ± 0.02), maintaining the intrinsic scatter of 0.05 dex. Because Eq. (2) induced a parallel BTFR, represented as V4 = GMbarg‡, we are able to determine that g‡ = (2.0 ± 0.1)×10−9 m s−2. This value aligns consistently with the g‡ obtained from the distinct RAR.

4. Discussions and summary

In this study, we report four key discoveries that significantly enhance our understanding of the RAR and its implications for BCGs and clusters. Our main findings are as follows: (1) We identified a linear correlation between MaNGA BCGs, CLASH BCGs, and clusters in the RAR; (2) the acceleration scale, g‡, was found to be valid across a range spanning over two orders of magnitude in baryonic acceleration, suggesting that the RAR holds on even larger scales than previously considered; (3) the distribution of residuals within a narrow range highlights a tight correlation between the dynamical and baryonic components in BCGs and clusters; and (4) there is no significant accumulated mass correlation on BCG-cluster scales.

The distinct RAR on BCG-cluster scales provides a fresh perspective on the residual missing mass of MOND in galaxy clusters (Sanders 1999, 2003; Angus et al. 2008, 2010; Milgrom 2008; Famaey & McGaugh 2012), recasting it as an acceleration-dependent residual mass issue. Although MOND successfully explained the missing mass problem in galactic systems (Banik & Zhao 2022), it has been reported that additional mass, such as missing baryons (Sanders 1999, 2003; Milgrom 2008) or sterile neutrinos (Angus et al. 2010; Famaey & McGaugh 2012), is required in galaxy clusters, a phenomenon known as the residual missing mass. When examining the RAR within the context of the MOND framework, we can compute the residual missing mass by comparing it with two RARs, as is described below. Here, gbar represents the baryonic acceleration estimated by the baryonic mass in our samples, while gM denotes the MONDian mass necessary to reproduce a distinct RAR. One can define a missing mass ratio, Q = gM/gbar = MM/Mbar, in MOND when considering the same observational acceleration. To explore the possibility of compensating for the distinct RAR with missing mass, we connect the RAR as in McGaugh et al. (2016) to the same observed acceleration, gobs, by way of

(9)

Using Eq. (9), we can compute the factor, Q, for a given gbar. For example, with a median logarithm of baryonic acceleration in 50 BCGs at log(gbar) = − 9.5, we find that Q = 2.2. However, the value of Q exhibits significant variability with gbar: for the highest acceleration in our MaNGA BCG samples, log(gbar) = − 8.9, Q decreases to 1.2, while for the lowest acceleration, log(gbar) = − 10.4, Q increases to 4.9. This variability indicates that a constant systematic offset in the mass-to-light ratio is insufficient to address the discrepancy. Consequently, the residual missing mass appears to be correlated with the baryonic acceleration, gbar.

In this study, we also evaluated the mass-to-light ratio, Υ, to validate the choice of using the total stellar mass calculated from SDSS model photometry. For 50 MaNGA BCGs, we calculated Υ across the five SDSS bands: u, g, r, i, and z. The average values for these bands are (Υu, Υg, Υr, Υi, Υz) = (9.6, 5.5, 3.1, 2.3, 1.9). Our results indicate that the potential underestimation of the stellar mass is a serious concern. The residual missing mass would result from other matters than the stellar mass, such as the underestimation of the gas mass or sterile neutrinos.

Besides the residual mass on BCG-cluster scales, other possibilities can be further investigated within the framework of relativistic MOND theories. Interestingly, given the consistency between our MaNGA BCGs and the CLASH samples measured by gravitational lensing, relativistic MOND offers a variety of results that extend beyond the standard MOND formulation. One particularly intriguing interpretation involves the acceleration scale being contingent on the depth of the potential well (eMOND; Zhao & Famaey 2012; Hodson & Zhao 2017). In BCGs and galaxy clusters, eMOND implied a stronger observational acceleration that deviates from the RAR suggested by the initial MOND. Moreover, recent advancements in relativistic MOND theories (Skordis & Złośnik 2021; Verwayen et al. 2023) also suggest the feasibility of an enhancement in galaxy clusters.

Investigating the mass consistency in MaNGA BCGs reveals implications for the DM distribution in galaxy clusters. Some MaNGA BCGs exhibit a consistent mass between the dynamical and baryonic mass, suggesting insufficient DM within one effective radius. This finding poses a challenge to the merger model in the cold dark matter (CDM) paradigm, according to which one would expect a significant amount of DM at the center of galaxy clusters due to dynamical friction. To fully comprehend this issue, further analysis of these specific BCG samples is necessary, especially in comparison to computer simulations such as TNG (Springel et al. 2018; Nelson et al. 2019b,a), EAGLE (Schaye et al. 2015; Crain et al. 2015), and BAHAMAS (McCarthy et al. 2017).

Investigating the RAR in the context of BCGs and galaxy clusters is key to understanding the DM problem, particularly in relation to the residual missing mass. MOND, which accurately predicts the RAR’s slope of 0.5, indicates a correlation between the residual missing mass and baryonic acceleration, warranting further exploration. Additionally, the RAR’s application to BCG-cluster scales is crucial for assessing different DM theories, as it notably challenges the self-interacting DM model, especially in light of the BAHAMAS simulation results (Tam et al. 2023). Although our current dynamical RAR studies in BCGs would benefit from improved stellar mass estimation methods that are model-independent and enhanced dynamical mass evaluations using numerical models (Li et al. 2023), these initial findings broaden the scope of baryonic acceleration research and establish a foundation for more detailed future investigations.

Acknowledgments

We sincerely appreciate the referee’s constructive suggestions and valuable comments, which have significantly contributed to enhancing the clarity and overall quality of our work. YT is supported by the Taiwan National Science and Technology Council NSTC 110-2112-M-008-015-MY3. CMK and SLP are supported by the Taiwan NSTC 111-2112-M-008-013 and NSTC 112-2112-M-008-032. PL is supported by the Alexander von Humboldt Foundation. SSM is supported in part by NASA ADAP grant 80NSSC19k0570 and also acknowledges support from NSF PHY-1911909.

References

  1. Angus, G. W., Famaey, B., & Buote, D. A. 2008, MNRAS, 387, 1470 [CrossRef] [Google Scholar]
  2. Angus, G. W., Famaey, B., & Diaferio, A. 2010, MNRAS, 402, 395 [NASA ADS] [CrossRef] [Google Scholar]
  3. Banik, I., & Zhao, H. 2022, Symmetry, 14, 1331 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bernardi, M., Sheth, R. K., Dominguez-Sanchez, H., et al. 2018, MNRAS, 477, 2560 [NASA ADS] [CrossRef] [Google Scholar]
  5. Binney, J., & Mamon, G. A. 1982, MNRAS, 200, 361 [Google Scholar]
  6. Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Princeton: Princeton University Press) [Google Scholar]
  7. Brouwer, M. M., Oman, K. A., Valentijn, E. A., et al. 2021, A&A, 650, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [Google Scholar]
  9. Carlberg, R. G., Yee, H. K. C., Ellingson, E., et al. 1997, ApJ, 485, L13 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chae, K.-H., Bernardi, M., Sheth, R. K., & Gong, I.-T. 2019, ApJ, 877, 18 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chae, K.-H., Bernardi, M., Domínguez Sánchez, H., & Sheth, R. K. 2020, ApJ, 903, L31 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chan, M. H., & Del Popolo, A. 2020, MNRAS, 492, 5865 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cherinka, B., Andrews, B. H., Sánchez-Gallego, J., et al. 2019, AJ, 158, 74 [CrossRef] [Google Scholar]
  14. Colín, P., Klypin, A. A., & Kravtsov, A. V. 2000, ApJ, 539, 561 [CrossRef] [Google Scholar]
  15. Crain, R. A., Schaye, J., Bower, R. G., et al. 2015, MNRAS, 450, 1937 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dekel, A., Stoehr, F., Mamon, G. A., et al. 2005, Nature, 437, 707 [CrossRef] [Google Scholar]
  17. Eckert, D., Ettori, S., Pointecouteau, E., van der Burg, R. F. J., & Loubser, S. I. 2022, A&A, 662, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Relat., 15, 10 [Google Scholar]
  19. Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
  20. Foreman-Mackey, D., Farr, W., Sinha, M., et al. 2019, J. Open Source Softw., 4, 1864 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hodson, A. O., & Zhao, H. 2017, A&A, 598, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hsu, Y.-H., Lin, Y.-T., Huang, S., et al. 2022, ApJ, 933, 61 [NASA ADS] [CrossRef] [Google Scholar]
  23. Law, D. R., Westfall, K. B., Bershady, M. A., et al. 2021, AJ, 161, 52 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016, ApJ, 816, L14 [Google Scholar]
  25. Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017, ApJ, 836, 152 [Google Scholar]
  26. Lelli, F., McGaugh, S. S., Schombert, J. M., Desmond, H., & Katz, H. 2019, MNRAS, 484, 3267 [NASA ADS] [CrossRef] [Google Scholar]
  27. Li, P., Lelli, F., McGaugh, S., & Schombert, J. 2018, A&A, 615, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Li, P., Tian, Y., Júlio, M. P., et al. 2023, A&A, 677, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Liu, A., Bulbul, E., Ramos-Ceja, M. E., et al. 2023, A&A, 670, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Mamon, G. A., & Łokas, E. L. 2005, MNRAS, 363, 705 [Google Scholar]
  31. McCarthy, I. G., Schaye, J., Bird, S., & Le Brun, A. M. C. 2017, MNRAS, 465, 2936 [Google Scholar]
  32. McGaugh, S. S. 2011, Phys. Rev. Lett., 106, 121303 [CrossRef] [Google Scholar]
  33. McGaugh, S. S., Schombert, J. M., Bothun, G. D., & de Blok, W. J. G. 2000, ApJ, 533, L99 [Google Scholar]
  34. McGaugh, S. S., Lelli, F., & Schombert, J. M. 2016, Phys. Rev. Lett., 117, 201101 [NASA ADS] [CrossRef] [Google Scholar]
  35. Milgrom, M. 1983, ApJ, 270, 365 [Google Scholar]
  36. Milgrom, M. 2008, Nat. Astron., 51, 906 [Google Scholar]
  37. Nelson, D., Pillepich, A., Springel, V., et al. 2019a, MNRAS, 490, 3234 [Google Scholar]
  38. Nelson, D., Springel, V., Pillepich, A., et al. 2019b, Comput. Astrophys. Cosmol., 6, 2 [Google Scholar]
  39. Overzier, R. A. 2016, A&A Rev., 24, 14 [NASA ADS] [CrossRef] [Google Scholar]
  40. Pradyumna, S., Gupta, S., Seeram, S., & Desai, S. 2021, Phys. Dark Universe, 31, 100765 [NASA ADS] [CrossRef] [Google Scholar]
  41. Rines, K. J., Geller, M. J., Diaferio, A., & Hwang, H. S. 2016, ApJ, 819, 63 [NASA ADS] [CrossRef] [Google Scholar]
  42. Sanders, R. H. 1999, ApJ, 512, L23 [NASA ADS] [CrossRef] [Google Scholar]
  43. Sanders, R. H. 2003, MNRAS, 342, 901 [NASA ADS] [CrossRef] [Google Scholar]
  44. Sanders, R. H. 2010, MNRAS, 407, 1128 [CrossRef] [Google Scholar]
  45. Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
  46. Skordis, C., & Złośnik, T. 2021, Phys. Rev Lett., 127, 161302 [NASA ADS] [CrossRef] [Google Scholar]
  47. Springel, V., Pakmor, R., Pillepich, A., et al. 2018, MNRAS, 475, 676 [Google Scholar]
  48. Tam, S.-I., Umetsu, K., Robertson, A., & McCarthy, I. G. 2023, ApJ, 953, 169 [CrossRef] [Google Scholar]
  49. Tian, Y., & Ko, C.-M. 2019, MNRAS, 488, L41 [NASA ADS] [CrossRef] [Google Scholar]
  50. Tian, Y., Umetsu, K., Ko, C.-M., Donahue, M., & Chiu, I. N. 2020, ApJ, 896, 70 [NASA ADS] [CrossRef] [Google Scholar]
  51. Tian, Y., Cheng, H., McGaugh, S. S., Ko, C.-M., & Hsu, Y.-H. 2021a, ApJ, 917, L24 [CrossRef] [Google Scholar]
  52. Tian, Y., Yu, P.-C., Li, P., McGaugh, S. S., & Ko, C.-M. 2021b, ApJ, 910, 56 [NASA ADS] [CrossRef] [Google Scholar]
  53. Umetsu, K. 2020, A&A Rev., 28, 7 [NASA ADS] [CrossRef] [Google Scholar]
  54. Verheijen, M. A. W. 2001, ApJ, 563, 694 [NASA ADS] [CrossRef] [Google Scholar]
  55. Verwayen, P., Skordis, C., & Bœhm, C. 2023, arXiv e-prints [arXiv:2304.05134] [Google Scholar]
  56. Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [Google Scholar]
  57. Zhao, H., & Famaey, B. 2012, Phys. Rev. D, 86, 067301 [NASA ADS] [CrossRef] [Google Scholar]
  58. Zwicky, F. 1933, Helvet. Phys. Acta, 6, 110 [Google Scholar]

Appendix A: Table

Table A.1.

Properties and results of 50 MaNGA BCGs.

Appendix B: The gradient in the mass-to-light ratio

To refine our analysis, we incorporated the gradient in the mass-to-light ratio, Υ*, within the inner regions of BCGs. Commonly, analyses employing SDSS model photometry operate under the assumption of a constant mass-to-light ratio, Υ. However, taking into consideration the variation of Υ* within BCGs can have implications. We therefore utilized the mass-to-light gradient (Salpeter-Chabrier model) presented in Bernardi et al. (2018), expressed as Υ*(R) = Υ(1 + 1.29 − 3.33R/Re), valid for R/Re ≤ 1.29/3.33, with the ratio remaining constant thereafter. This modification led to an increase in the stellar mass of approximately 10% to 20% across our sample. We conducted a separate analysis of this effect to illustrate the nuances it introduces to our findings.

Upon meticulous examination of the mass-to-light ratio gradient, our observations indicated an absence of any pronounced enhancement in the dynamical acceleration within our BCG sample. This can be attributed to the fact that the mass-to-light ratio tends to stabilize as a constant when R/Re is sufficiently large. Delving into the Jeans equation, it becomes apparent that the gravitational acceleration, gobs, at a given radius, R, is contingent upon densities and velocity dispersions beyond that radius. Consequently, for gobs in the vicinity of 1Re, variations in the mass-to-light ratio within R < 0.39Re have a negligible influence.

In analyzing the mass-to-light ratio gradient, we also examined the RAR to understand the influence of an increased baryonic acceleration in our sample. This enhancement principally appears as a horizontal shift in the logarithmic space of around 0.04–0.08 dex. Employing ODR with MCMC, we found that this shift gives rise to a shallower slope, represented by the relation 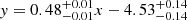(see Fig. B.1). It is noteworthy that this enhancement leads to a small difference between the accumulative dynamical mass and stellar mass in some of the BCG samples, which poses challenges due to the implied deficiency in DM.

thumbnail Fig. B.1.

RAR of both BCGs and clusters when considering the mass-to-light ratio gradient for 50 MaNGA BCGs. All the symbols are the same as those in Fig. 2. The solid black line illustrates the resulting RAR of all samples: . For comparison, the galactic RAR is depicted by the dash-dotted line, while the dotted line represents the line of unity.

Appendix C: Scatters estimated by the anisotropic parameter

In our exploration of potential sources of uncertainty, we diligently assessed the influence of anisotropy. We adopted the anisotropic model given by β = 0.5r/(r + ra), as was introduced by Mamon & Łokas (2005). Additionally, to represent our BCG samples, we utilized a Sérsic profile with Sérsic indices, n, spanning from 2 to 6.

For systems exhibiting anisotropy, we aimed to emulate a nearly flat projected velocity dispersion (within 2%) to mirror the observed VD profiles of our BCG samples. While the observed VD profiles remain flat up to one effective radius in observations, we made an assumption of this flatness extending up to two effective radii. Using the parameter ra = 0.18rv = 14Re for β = 0.03 at one effective radius, Re, recommended by Mamon & Łokas (2005), where rv represents the virial radius, the resulting gobs deviates from the isotropic counterpart by less than 1.2% (or a scatter of 0.005 dex) within one effective radius for all Sérsic indices in the range 2 ≤ n ≤ 6. For an extreme case with ra = 1.4Re for β = 0.21 at 1Re (Mamon & Łokas 2005; Dekel et al. 2005), the gobs deviates by at most 6% (or a scatter of 0.025 dex) within the same radius for all such n values.

Considering alternative anisotropic models, such as 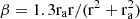from (Carlberg et al. 1997; Colín et al. 2000; Mamon & Łokas 2005), and using ra = 2rv ≈ 156Re for β = 0.008 at 1Re (Mamon & Łokas 2005), the derived gobs lies within a 0.3% deviation (or 0.001 dex scatter) for all Sérsic indices in the given range, when measured within one effective radius. The uncertainties stemming from anisotropy closely match the error bars from the measured velocity dispersion. As a result, our RAR calculations under the isotropy assumption emerge as remarkably robust.

Appendix D: Triangle diagrams of the MCMC method

In our analysis, we employed the MCMC method to investigate the close correlations. The triangle diagrams depicting the regression parameters are presented in Fig. D.1 for four distinct scenarios: (1) the ODR MCMC for the RAR; (2) the vertical MCMC for the RAR; (3) the ODR MCMC for the mass correlation; and (4) the ODR MCMC for the RAR with a fixed slope, m = 0.5.

thumbnail Fig. D.1.

MCMC method in 70 BCGs and 64 CLASH cluster data. Upper right panel: Triangle diagrams of the regression parameters in the ODR MCMC method for the RAR, , with marginalized one-dimensional (histograms) and two-dimensional posterior distributions. The black contours represent 1σ and 2σ confidence regions. Upper left panel: Triangle diagrams of the regression parameters in the vertical MCMC method for the RAR, . Lower right panel: Triangle diagrams of the regression parameters in the ODR MCMC method for the mass correlation, . Lower left panel: Triangle diagrams of the regression parameters in the ODR MCMC method for the RAR with a fixed slope, m = 0.5.

All Tables

Table A.1.

Properties and results of 50 MaNGA BCGs.

In the text

All Figures

thumbnail Fig. 1.

Three examples of MaNGA BCGs with the plateifu of 8554-6102, 8331-12701, and 9888-12703. Upper panel: two-dimensional map plot of Spaxel data for the stellar velocity dispersion. Lower panel: velocity dispersion profiles in terms of the effective radius. The red circles represent the LOS velocity dispersion of concentric circles at different radii with the corresponding error bar. The solid blue lines represent the linear fit with the ODR MLE method.
In the text
thumbnail Fig. 2.

RAR and mass correlation of both BCGs and clusters. Left panel: black and green diamonds represent 50 MaNGA and 20 CLASH BCGs, while blue circles indicate data for 64 CLASH galaxy clusters. The solid black line illustrates the resulting RAR of all samples: . The shaded orange area illustrates the 1σ error of the best fit with the ODR MCMC method. The inset panel demonstrates the histograms of the orthogonal residuals of a whole sample (blue). For comparison, the galactic RAR is depicted by the dash-dotted line, while the dotted line represents the line of unity. Right panel: solid black line represents the mass correlation of all samples: . All symbols are the same as those in the left panel.
In the text
thumbnail Fig. 3.

Orthogonal residuals against four global quantities of galaxies and galaxy clusters: the observational acceleration, gobs (upper left), radius, R (upper right), baryonic mass surface density, ΣBar (lower left), and redshift (lower right). The plot displays the residuals for 50 MaNGA BCGs (black diamonds), 20 CLASH BCGs (green diamonds), and 64 data points from CLASH clusters (blue circles), with the dashed line representing zero difference.
In the text
thumbnail Fig. 4.

BTFR analysis with ODR MCMC for extended dynamic range. The solid black line illustrates the fitting BTFR of all samples: log(Mbar/M⊙) = (3.97 ± 0.07)log(V/m s−1)−(0.67 ± 0.21). The shaded orange area illustrates the 1σ error of the best fit with the ODR MCMC method. The inset panel demonstrates the histograms of the orthogonal residuals of a whole sample (blue). For comparison, the galactic BTFR (Lelli et al. 2019) is depicted by the dotted red line. The plot displays the residuals for 50 MaNGA BCGs (black diamonds), 20 CLASH BCGs (green diamonds), and 64 data points from CLASH clusters (blue circles).
In the text
thumbnail Fig. B.1.

RAR of both BCGs and clusters when considering the mass-to-light ratio gradient for 50 MaNGA BCGs. All the symbols are the same as those in Fig. 2. The solid black line illustrates the resulting RAR of all samples: . For comparison, the galactic RAR is depicted by the dash-dotted line, while the dotted line represents the line of unity.
In the text
thumbnail Fig. D.1.

MCMC method in 70 BCGs and 64 CLASH cluster data. Upper right panel: Triangle diagrams of the regression parameters in the ODR MCMC method for the RAR, , with marginalized one-dimensional (histograms) and two-dimensional posterior distributions. The black contours represent 1σ and 2σ confidence regions. Upper left panel: Triangle diagrams of the regression parameters in the vertical MCMC method for the RAR, . Lower right panel: Triangle diagrams of the regression parameters in the ODR MCMC method for the mass correlation, . Lower left panel: Triangle diagrams of the regression parameters in the ODR MCMC method for the RAR with a fixed slope, m = 0.5.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.