EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A60 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A60
Number of page(s) 18
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202346274
Published online 04 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Our Universe is enriched in different chemical elements on different timescales (due to their different nucleosynthetic origins). This suggests that some chemical abundance ratios can be used to trace different star formation histories. One classical abundance ratio often used in Galactic archaeology is the [α/Fe] ratio (e.g. Matteucci 2021). Other abundance ratios are also expected to vary with age, for instance the ratio of slow neutron-capture process (s-process) to α-elements. These abundance ratios with a strong correlation with age are called chemical clocks. Recent data on open clusters (e.g. Casamiquela et al. 2021; Viscasillas Vázquez et al. 2022), and on field stars (e.g. Spina et al. 2018; Nissen et al. 2020; Morel et al. 2021) for which it was possible to measure ages have confirmed the theoretical expectations in general terms.

S-process elements can be produced in massive stars (weak component, 60 < A< 90, with A being the atomic mass number, Pignatari et al. 2010) or in low- and intermediate-mass asymptotic giant branch (AGB) stars with a main component (90 < A< 204, Lugaro et al. 2003) and/or with a strong component (low-metallicity AGB stars, 204 < A< 209, Gallino et al. 1998). Cerium (Ce) is mostly produced by the main s-process component (83.5 ± 5.9% at solar metallicity, Bisterzo et al. 2014) in low-mass AGB stars (1.5 − 3 M⊙).

The standard view of the s-process in massive stars might be modified in rotating stars because of the rotational mixing operating between the H-shell and He-core during the core helium burning phase. Several observational signatures support an enhancement of s-process elements (up to A  ∼  140) in massive rotating stars (Pignatari et al. 2008; Chiappini 2013; Cescutti et al. 2013; Cescutti & Chiappini 2014). Recently, an overabundance of Ce was observed in metal-poor bulge stars (Razera et al. 2022), which was interpreted as a result of an early enrichment by fast rotating massive stars, or spinstars (Meynet & Maeder 2002; Chiappini et al. 2011; Cescutti et al. 2018).

In the last decade, [Y/Mg] and [Y/Al] have been among the most studied chemical clocks (da Silva et al. 2012; Nissen 2015; Feltzing et al. 2017; Slumstrup et al. 2017; Spina et al. 2018; Delgado Mena et al. 2019; Anders et al. 2018; Casali et al. 2020; Jofré et al. 2020; Nissen et al. 2020). However, recent works have demonstrated not only their metallicity dependence, but also the non-universality of the chemical clock–age relations, with variations in the shape of the relations at different galactocentric distances (Casali et al. 2020; Magrini et al. 2021; Casamiquela et al. 2021; Viscasillas Vázquez et al. 2022).

Owing to the large uncertainties on ages of field stars, these studies have been mostly restricted to clusters. In this context, asteroseismology comes to our aid. Through asteroseismology, we are able to detect solar-like pulsations in thousands of G-K giants using data collected by the COnvection ROtation and planetary Transits (CoRoT, Baglin et al. 2006), Kepler (Gilliland et al. 2010), K2 (Howell et al. 2014), and Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2014) missions. The pulsation frequencies are directly linked to the stellar structure and thus provide tight constraints on stellar properties (radius, mass, age) and evolutionary state (Chaplin & Miglio 2013).

In this paper we focus on the evolution of Ce, one of the least studied s-process elements in the literature, in a sample of field stars for which precise asteroseismic ages are available. The [Ce/Fe]–age (and also [Ce/α]–age) relation has been studied in open clusters and solar twins by Maiorca et al. (2011), Spina et al. (2018), Magrini et al. (2018), Delgado Mena et al. (2019), Tautvaišienė et al. (2021), Casamiquela et al. (2021), Viscasillas Vázquez et al. (2022), Sales-Silva et al. (2022), among others. They all find an increase in [Ce/Fe] with decreasing stellar age, except for Tautvaišienė et al. (2021), who find an almost flat trend.

Here we complement such studies with field stars sampling a larger age baseline than is possible with clusters alone, thanks to asteroseismic ages coming from three different missions (Kepler, TESS, and K2). We use Ce abundances published in the latest data release (DR17) of the high-resolution spectroscopic survey, Apache Point Observatory Galactic Evolution Experiment, APOGEE (Majewski et al. 2017; Abdurro’uf et al. 2022). Our aim is to investigate the time evolution of Ce across the Milky Way; Kepler and TESS are focused on the solar neighbourhood, 7.5 < RGC < 8.5 kpc, but K2 covers a large range in galactocentric radii, 4 < RGC < 12 kpc. With this dataset we investigate the [Ce/Fe] trends as a function of the metallicity [Fe/H] and [α/Fe], its time evolution, and [Ce/α] as a chemical clock.

The paper is structured as follows. In Sect. 2 we describe the data samples; in Sect. 3 we present a comparison between the Ce abundances used in this work and those determined in other surveys; in Sects. 4 and 5 we show our results for the [Ce/Fe] trends and the Ce abundance time evolution; in Sect. 6 we show a quantitative comparison of our results with Galactic chemical evolution models. Finally, in Sect. 7 we summarise and conclude.

2. Stellar samples

Our data samples combine the global asteroseismic parameters measured from light curves obtained by the Kepler (Borucki et al. 2010), K2 (Howell et al. 2014), and TESS (Ricker et al. 2015) missions with stellar parameters and chemical abundances inferred from near-infrared high-resolution spectra taken by the APOGEE DR17 survey (Abdurro’uf et al. 2022). These targets were then cross-matched with the Early Third Data Release of Gaia (Gaia EDR3, Gaia Collaboration 2021).

2.1. Spectroscopic constraints

The atmospheric parameters and abundances used in this paper are produced by the standard data analysis pipeline, the APOGEE Stellar Parameters and Chemical Abundances Pipeline (ASPCAP, García Pérez et al. 2016). A full description of the pipeline is given in Holtzman et al. (in prep.), and a description of an earlier implementation of this pipeline can be found in García Pérez et al. (2016).

2.2. Asteroseismic constraints

We consider three main samples. Our first data sample is composed of ∼5600 Kepler solar-like oscillating giants whose spectroscopic parameters are available from APOGEE DR17 (Abdurro’uf et al. 2022). The list of targets and global asteroseismic constraints corresponds to the reference sample (R1) explored in Miglio et al. (2021), but updated to use photospheric parameters from APOGEE DR17.

The second data sample is composed of data collected by the TESS mission during the first year of observations in its southern continuous viewing zone (SCVZ; see Mackereth et al. 2021 for more details). The sample, which corresponds to the ‘gold sample’ in Mackereth et al. (2021) with APOGEE DR17 parameters available, is composed of ∼1700 stars, with ∼1 yr TESS observations.

The third dataset is composed of data collected by the K2 mission in 20 observational campaigns along the ecliptic. Unlike the previous two missions, K2 observed stars in a wide range of galactocentric radii crucially extending the regions sampled by Kepler and TESS. Atmospheric parameters from APOGEE DR17 stars are available for a total of ∼11 000 stars with asteroseismic constraints from K2. For this sample we used the global parameter νmax, from the Elsworth et al. (2020) pipeline, as the only asteroseismic constraint (see below for more details).

2.3. Inferring stellar masses, ages, and radii

Masses, radii, and ages are computed using the code PARAM (da Silva et al. 2006; Rodrigues et al. 2017), which makes use of a Bayesian estimation method. We input a combination of seismic indices and spectroscopic constraints, such as vmax, Δv, [Fe/H], [α/Fe], and Teff. A detailed explanation of the method is available in Miglio et al. (2021).

For the K2 dataset (80d-long light curves), however, we included as constraint the luminosity, L, instead of Δν, because the latter is affected by significant systematic uncertainties in shorter datasets, as described in Willett at al. (in prep.; see also Tailo et al. 2022). The luminosity is computed using the magnitude Ks from 2MASS (Skrutskie et al. 2006), distance deduced from the Gaia parallax, extinction determined using the Bayestar2019 map (Green et al. 2019) through the dustmaps Python package (Green 2018), and bolometric corrections computed through the code by Casagrande & VandenBerg (2014, 2018a,b). In addition, the luminosity takes into account the global median Gaia parallax zero point offset of −17 μas based on quasars (Lindegren et al. 2021).

When using PARAM, we considered a lower limit of 0.05 dex for the uncertainty on [Fe/H] and a limit of 50 K for Teff. This choice is due to the very small uncertainties present in APOGEE DR17 (typical uncertainties are σTeff ∼ 10 K, σlog g ∼ 0.03 dex and σ[Fe/H] ∼ 0.01 dex) as the quoted uncertainties are internal errors only, and cross-validation against other surveys shows larger systematic differences (see e.g. Rendle et al. 2019; Hekker & Johnson 2019; Anguiano et al. 2018). Moreover, model-predicted Teff suffer from large uncertainties associated with the modelling of outer boundary conditions and near-surface convection, and hence we prefer to downplay the role of Teff. The grid of stellar models used in PARAM for this work is the reference grid adopted in Miglio et al. (2021), labelled G2 in their work.

The distributions of uncertainties in stellar age for the three samples are shown in Fig. 1. While the longer duration of the Kepler time series leads to a lower median age uncertainty (20%) compared to that of TESS (28%), the relatively low median age uncertainty for K2 (18%) can be attributed to the use of a very precise (6%) luminosity instead of Δν. For a more detailed description on all datasets, we refer to the work by Willett et al. (in prep.).

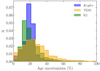thumbnail Fig. 1.

Distribution of the age uncertainties for the three data samples. The area under each histogram is integrated to 1.

Finally, to investigate whether using L instead Δν while inferring ages could lead to a significant bias, we compared ages based on νmax and L with those obtained from νmax and Δν for the Kepler and TESS samples (where Δν is not affected by systematic uncertainties). As a result, we found no significant difference between the two inferred ages for the two samples (difference ≲1σ).

2.4. Selection criteria

In this section we describe how we selected stars with robust spectroscopy and age estimates. Specifically, we kept stars with S/N > 100 and σ(Ce) < 0.2 dex. Then we removed stars with the following flags from the APOGEE survey: STARFLAG = VERY_BRIGHT_NEIGHBOR, LOW_SNR, PERSIST_HIGH, PERSIST_JUMP_POS, PERSIST_JUMP_NEG, SUSPECT_RV_COMBINATION or ASPCAPFLAG = STAR_BAD, STAR_WARN and ELEMFLAG = GRIDEDGE_BAD, CALRANGE_BAD, OTHER_BAD, FERRE_FAIL for Ce.

We also restricted the sample to stars with estimated radii smaller than 11 R⊙ (following the same cut present in Miglio et al. 2021). This avoids the contamination by early AGB stars and removes stars with relatively low νmax, a domain where seismic inferences have not been extensively tested so far. Moreover, we computed the distribution of age uncertainties over the whole population, and removed stars whose uncertainties lie in the top 5%.

Finally, the K2 sample contains very metal-poor stars with respect to those of Kepler and TESS. In order to have samples in the same range of metallicity, we selected stars in −1 ≤ [Fe/H]< 0.4 dex. These selection criteria reduce the initial Kepler sample of ∼5600 stars to ∼2700, the TESS sample of ∼1700 stars to ∼900 and the K2 sample of ∼11 000 stars to ∼4000.

3. Comparison with the literature

In order to validate the Ce abundances we used in this study, we compared the stars in common between APOGEE DR17 (used in this work) and the optical counterpart from the Gaia-ESO DR5 survey (Randich et al. 2022). Moreover, we also compared the Ce abundances measured from APOGEE spectra using three different pipelines: ASPCAP, the standard pipeline used to obtain the abundances in the APOGEE DR17 survey, the Brussels Automatic Code for Characterizing High Accuracy Spectra (BACCHUS; Masseron et al. 2016) used in Sales-Silva et al. (2022), and its updated version for weak and blended lines, the BACCHUS Analysis of Weak Lines in APOGEE Spectra (BAWLAS) used in Hayes et al. (2022). Sales-Silva et al. (2022) redetermined the Ce abundances from the measurements of Ce II lines in the APOGEE DR16 spectra of the member stars of the open clusters present in the Open Cluster Chemical Abundances and Mapping (OCCAM) sample (Donor et al. 2020), using the BACCHUS pipeline. Hayes et al. (2022), instead, reanalysed ∼120 000 APOGEE DR17 spectra with BAWLAS.

For the APOGEE DR17 sample, we selected stars with high-quality Ce abundances (the same selection in σ(Ce), S/N, and APOGEE flags shown in Sect. 2.4). Instead, for Gaia-ESO, we kept stars with Ce measurements from at least two lines in their spectra. In Fig. 2 we compare the 298 stars in common between APOGEE DR17 with Gaia-ESO DR5. The mean difference in [Ce/Fe] is Δ[Ce/Fe](APOGEE − GES) = − 0.07 ± 0.15 dex. The scatter is larger at lower metallicity (see Fig. 2).

thumbnail Fig. 2.

Comparison between [Ce/Fe] using the abundances in APOGEE DR17 (this work) and the Gaia-ESO abundances (Randich et al. 2022). The dashed line indicates the median, whereas the solid line indicates the zero difference.

Comparing instead the APOGEE DR17 with Sales-Silva et al. (Sales-Silva et al.), we found 162 member stars in common. They have a mean difference Δ[Ce/Fe](APOGEE − SS) of −0.13 ± 0.09 dex (see Fig. 3).

thumbnail Fig. 3.

Comparison between [Ce/Fe] using the abundances in APOGEE DR17 (this work) and the abundances from Sales-Silva et al. (2022). The dashed line is the median, whereas the solid line indicates the zero difference.

Finally, the comparison between APOGEE DR17 and Hayes et al. (2022) shows a difference of Δ[Ce/Fe](APOGEE − BAWLAS) = − 0.09 ± 0.13 dex. The chemical abundance patterns of Ce from ASPCAP and BAWLAS are relatively similar. However, Hayes et al. (2022) find a trend in the differences between the two Ce measurements as a function of [Fe/H] at lower metallicities. Figure 4 shows the density plot of the Δ[Ce/Fe](APOGEE − BAWLAS) for 94 522 stars in common. This metallicity-correlated offset seems to primarily be a result of using different Teff and log g, calibrated for ASPCAP and uncalibrated for BAWLAS. Nevertheless, the stars in our sample do not cover these metallicities, so we can overlook this trend.

thumbnail Fig. 4.

Comparison between [Ce/Fe] using the abundances in APOGEE DR17 (this work) and the BAWLAS abundances (Hayes et al. 2022). The dashed line is the median, whereas the solid line indicates the zero difference.

In all these cases, the measurements from APOGEE DR17 show a systematic offset of ∼0.1 dex with a larger scatter at lower metallicity. This offset may be due to the different pipelines, spectral range, and linelists used in the different surveys. Moreover, the uncertainties on the Ce abundance present in the APOGEE DR17 survey are larger than the uncertainties from the analyses in the Gaia-ESO survey, in Sales-Silva et al. (2022), and in Hayes et al. (2022; see their distributions in Fig. 5). Despite a large standard deviation of the Ce abundance differences among the samples, we can conclude that the measurements from the APOGEE DR17 show a rather good agreement with the Gaia-ESO, Sales-Silva et al. (2022), and Hayes et al. (2022) studies.

thumbnail Fig. 5.

[Ce/Fe] uncertainty distributions in APOGEE DR17, Sales-Silva et al. (2022), Hayes et al. (2022), and Gaia-ESO DR5.

Open clusters. To understand whether the use of the BAWLAS pipeline can provide an advantage to our work with respect to ASPCAP, we computed the mean and standard deviation of [Ce/Fe] for the member stars of open clusters in common between the two pipelines. The list of the open clusters and the catalogue of their members can be found in Myers et al. (2022). The values are shown in Fig. 6. We can see that the average values of [Ce/Fe] computed with the BAWLAS results are larger than those computed with ASPCAP, except in a few cases. This discrepancy is related to the offset that we discussed in the previous section. In both pipelines, the standard deviation is large (σ ∼ 0.1 dex) for almost all clusters, showing a spread in the Ce measurements among the member stars of the same cluster, which is not expected since they should be homogeneous. Such large standard deviations indicate that the Ce uncertainties are likely underestimated by both pipelines. Moreover, our results are similar using one or the other pipeline. Therefore, we chose to use the ASPCAP results for the following section.

thumbnail Fig. 6.

Mean and standard deviation of [Ce/Fe] for the open clusters in common between ASPCAP (black) and BAWLAS (red) pipelines. The [Ce/Fe] mean in each cluster is represented with a dot and the standard deviation with the error bar. The number near the cluster names represents the number of stars in each cluster.

4. The [Ce/Fe] abundance ratio trends

In this section we show the Kepler, TESS, and K2 stars selected following the criteria presented in Sect. 2.4. These samples contain stars with a distribution in age and metallicity spanning [0, 14] Gyr and [−1,+0.4] dex, respectively. In addition, we removed outliers using a Huber regression (Huber 1964), with a hyperparameter set to 3.

In the next subsections we present two different planes to present the samples: [Ce/Fe]–[α/M] and [Ce/Fe]–[Fe/H].

4.1. [Ce/Fe] versus [α/M]

Figure 7 shows the [Ce/Fe]–[α/M] for our three datasets, colour-coded by age. We used the ASPCAP [α/M] as a proxy for [α/Fe]. In our dataset the difference between [α/M] and an average [α/Fe] defined using O, Mg, Si, S, and Ca over Fe is negligible (with a mean offset equal to −0.002 dex and a standard deviation of 0.016 dex). In all datasets, we have two samples of stars that display two stellar populations: the low-α sequence ([α/M] ≲ 0.15 dex) and the high-α sequence ([α/M] ≳ 0.15 dex). The number of high-α stars is larger for the K2 sample and lower for the TESS sample. Additionally, the high-α sequence also contains the oldest stars in all three samples with a mean age ∼10 − 11 Gyr (see e.g. Miglio et al. 2021 for the age of the high-α population). The other sequence, instead, spans a large range in the stellar age, and with a gradient in age with increasing [Ce/Fe] and [α/M]. Finally, the high-α sequence has an average of [Ce/Fe] around −0.2 dex, while the low-α sequence has an average of [Ce/Fe] around −0.1 dex.

thumbnail Fig. 7.

[Ce/Fe] vs. [α/M]. Shown are Kepler (top panel), TESS (middle panel), and K2 (bottom panel) stars. The stars are colour-coded by stellar age.

In the next sections we focus on the low-α sequence since low- and intermediate-mass AGB stars polluted mainly this stellar population. Moreover, it is more numerous with respect to the high-α sequence, and allows us to compare our field stars with open clusters present in the literature (e.g. Sales-Silva et al. 2022; Viscasillas Vázquez et al. 2022; Casamiquela et al. 2021). Furthermore, we did not make a selection in z, the height on the Galactic plane, because this cut would remove the old stars from our samples.

Here we adopted a separation in [α/M], using a piece-wise function to divide the populations. The function is an adjustment of the separation curve proposed by Adibekyan et al. (2012) for our data:

(1)

We chose this division following the most-adopted functions to separate low- and high-α sequences present in the literature (see e.g. Adibekyan et al. 2012; Mikolaitis et al. 2014).

4.2. [Ce/Fe] versus [Fe/H] in the low-α sequence

In Fig. 8 we show the [Ce/Fe] trend in the low-α sequence as a function of metallicity for the three samples. They show the same shape: an increasing [Ce/Fe] at increasing [Fe/H] with a maximum at ∼ − 0.2 dex in [Fe/H], and a drop in [Ce/Fe] at higher metallicities. The stars are also colour-coded by stellar age. At a given metallicity, the younger field stars show a [Ce/Fe] content that is larger than the older stars. A better visualisation of this trend is shown in the histograms in Fig. B.1. These histograms display the [Ce/Fe] binned in different ranges of stellar ages. The peaks of the histograms move towards lower [Ce/Fe] with increasing age.

thumbnail Fig. 8.

[Ce/Fe] vs. [Fe/H] in low-α sequence. Shown are Kepler (top panel), TESS (middle panel), and K2 (bottom panel) stars. The stars are colour-coded by stellar age.

A similar behaviour is also shown in the samples of open clusters present in Viscasillas Vázquez et al. (2022) and Sales-Silva et al. (2022). In the former, they analyse 62 open clusters observed by the Gaia-ESO DR5 survey, while in the latter, they study 42 open clusters observed by the APOGEE DR16 survey (with spectral analysis using BACCHUS).

As described in the introduction, the predominant fraction of s-process elements, such as Ce, is produced by long-lived stars (1.5 − 3.0 M⊙; see e.g. Cristallo et al. 2009, 2011). This, together with the secondary nature (dependence on metallicity) of the s-process elements, determines the behaviour shown in the figure. Chemical evolution models present in literature (Prantzos et al. 2018; Grisoni et al. 2020; the three-infall model in Contursi et al. 2023) show a banana shape with a rise in [Ce/Fe], a peak, and then a decline, similar to that seen in Fig. 8.

In addition, the s-process production of Ce in AGB stars is strongly dependent on the metallicity (Busso et al. 2001; Vescovi et al. 2020). It depends on the number of iron nuclei as seeds for the neutron captures and on the flux of neutrons. The former decreases with decreasing metallicity, while the latter increases because it depends (approximately) on 13C/56Fe, which increases with decreasing metallicity (13C is a primary element, and does not depend on metallicity). This means there are more neutrons per seed in low-metallicity AGB stars and fewer in high-metallicity AGB stars. Therefore, stellar evolution models predict lower [Ce/Fe] in higher-metallicity AGB stars (Cristallo et al. 2015; Karakas & Lugaro 2016; Battino et al. 2019), implying the trend that we see in Fig. 8.

5. Time evolution of Ce abundance in the low-α sequence

In this section we study the temporal evolution of the Ce abundance in the low-α sequence. We explore the [Ce/Fe] and [Ce/α] trends as a function of age and position in the Galactic disc.

5.1. [Ce/Fe] versus age

Figure 9 shows the correlation of [Ce/Fe] with stellar age for our three samples, colour-coded by metallicity. The three lines in the figure represent the mean [Ce/Fe] in three different bins of [Fe/H]: [Fe/H] < −0.1, −0.1 ≤ [Fe/H] ≤ 0.1, [Fe/H] > 0.1 dex. These three lines clearly illustrate the metallicity dependence of the [Ce/Fe]–age relation. In particular, at a given age metal-poor stars have a higher [Ce/Fe] ratio than the metal-rich stars. Moreover, [Ce/Fe] increases with decreasing age, and becomes almost flat for ages older than 6 Gyr. The same behaviour is shown in Sales-Silva et al. (2022) for the open clusters. However, in this figure and in the work of Sales-Silva et al. (2022), the location of the stars in the Galactic disc is not taken into account.

thumbnail Fig. 9.

[Ce/Fe] vs. stellar age for the three samples. The data are colour-coded by metallicity. The three lines represent the [Ce/Fe] mean in different bins of metallicity and age. The error budget of stellar age is shown at the top of each panel.

The majority of our stars are located in the solar neighbourhood (7.5 < RGC < 8.5 kpc). Nonetheless, they could have come from the inner or outer regions of the Galactic disc and transited in the solar vicinity, or could have migrated in previous epochs due to the change in their eccentricity through radial heating or in their angular momentum. To better understand their provenance, we can compute the guiding radius Rg, which is the radius of a circular orbit with specific angular momentum Lz. Moreover, the adoption of Rg instead of the galactocentric radius RGC can mitigate the blurring effect due to epicyclic oscillations around the guiding radius (Schönrich & Binney 2009). However, it cannot overcome the migrating effect due to the churning, which can change Rg due to interactions with spiral arms or bars (Sellwood & Binney 2002; Binney & Tremaine 2008).

The guiding radius is computed from the stellar orbits obtained using the GalPy package of Python, in which the model MWpotential2014 for the gravitational potential of the Milky Way is assumed (Bovy 2015). Through the astrometric information by Gaia EDR3, distances from Bailer-Jones et al. (2021), an assumed solar galactocentric distance R0 = 8 kpc, a height above the plane z0 = 0.025 kpc (Jurić et al. 2008), a circular velocity at the solar galactocentric distance equal to Vc = 220 km s−1, and the Sun’s motion with respect to the local standard of rest [U⊙,V⊙,W⊙] = [11.1,12.24,7.25] km s−1 (Schönrich et al. 2010), we obtained the orbital parameters, among which the guiding radius Rg. The distribution of Rg of the three datasets is shown in Fig. 10. The K2 sample shows a larger distribution with respect to those of Kepler and TESS; those of the latter are located between 5 ≲ Rg ≲ 10 kpc, while K2 reaches Rg ∼ 4 kpc in the inner disc and Rg ∼ 12 kpc in the outer disc, as expected from the different field locations and distances reached.

thumbnail Fig. 10.

Distribution of Rg of the three selected samples.

Figure 11 shows the same plane of Fig. 9 for the Kepler, TESS and K2 samples, divided in three different bins of guiding radius: Rg < 7 kpc, 7 ≤ Rg ≤ 8 kpc, Rg > 8 kpc. Since K2 has a larger range in Rg with respect to Kepler and TESS (see Fig. 10), we added two more bins for this dataset, not covered by the other two data samples: Rg < 5 kpc and Rg > 10 kpc.

thumbnail Fig. 11.

[Ce/Fe] vs. stellar age in different bins of Rg. The Kepler sample is shown in the upper panel, the TESS sample in the middle panel, and the K2 one in the bottom panel. The data are colour-coded by metallicity. The dash-dotted line represents the best fit, and the shaded area the 68% confidence interval plus intrinsic scatter.

In order to visualise in a more quantitative way the different trends in the different bins and the flattening at old age, we modelled the distribution of [Ce/Fe] versus stellar age through a broken-line as follows:

(2)

Through a Markov chain Monte Carlo (MCMC) procedure we derived the posterior distributions of the parameters of the fitting m1, c, n1, and k, where k is the switch point of the fitting line. In our model we took into account the uncertainties on [Ce/Fe] and stellar age. We also included in our calculation an intrinsic scatter of the relation, ϵ.

In this procedure, we used uniform priors for m1, c, n1, k, and ϵ, with limits for k (4 < k < 10 Gyr) and ϵ (ϵ > 0). We ran the simulation with 10 000 samples, 1000 of which are used for burn-in. The script is written in Python using the emcee package (Foreman-Mackey et al. 2013).

In order to decide if the broken-line was the best model for our data, we compared a broken-line and a single-line given the data by computing the Bayesian information criterion (BIC). The model with the lowest BIC is generally the most reasonable one. In the bins with Rg larger than 7 kpc, the broken-line provides a lower BIC, while in the bins of Rg < 7 kpc for the Kepler and TESS samples and Rg < 5 kpc for the K2 sample, the single-line provides the lowest BIC. For the range 5 ≤ Rg < 7 kpc of the K2 sample, the broken-line provides a marginally lower BIC than the single-line. In each region we adopted the model with the lowest BIC.

The convergence of the Bayesian inference is checked against the traces of each parameter and their auto-correlation plots. The spread (68% confidence interval plus intrinsic scatter) of the models resulting from the posteriors are represented in Fig. 11 with the red shaded area, while their values are reported in Table 1.

Table 1.

Parameters of the MCMC fitting for the [Ce/Fe]–age relations in the Kepler, TESS, and K2 samples.

The [Ce/Fe] trends in the three samples show different behaviours, in particular in the young regime, between inner and outer regions. The latter usually have higher [Ce/Fe] than the former at a given age (the slope is more negative; see the second column on Table 1). Moving towards the outer regions the [Ce/Fe]–age trends become increasingly steep in all our datasets. Dividing the samples by guiding radius makes it clear that there is a strong dependence of the [Ce/Fe] abundances on the location of the stars. The behaviour of [Ce/Fe] with Rg seems to be complex and likely related to different star formation histories and to metallicity dependency of the stellar yields.

In more detail, the left panels of Fig. 11 (Rg < 7 kpc) show a large fraction of Kepler and K2 stars coming from the inner disc with respect to the TESS stars. Moreover, the trends of [Ce/Fe] with stellar age in these bins of Rg are quite flat, with a slope of ∼ − 0.01 dex Gyr−1 against the slopes in the outer regions of ∼ − 0.02, ∼ − 0.03 dex Gyr−1. These trends could be due to the more intense star formation efficiency (SFE) in the inner regions of the Galactic disc, where high values of [Ce/Fe] are reached at earlier epochs.

In the other panels with Rg > 7 kpc, there is a clear increasing trend with decreasing age. The slope in the young regime becomes steeper towards the outer regions (Rg > 8 kpc) in all datasets. In the solar vicinity and outer disc, where the star formation rate is less intense with respect to the inner regions, the increasing trends with decreasing age can be due to the recent contribution of low- and intermediate-mass AGB stars to the Galactic enrichment. Instead, the flattening of the slope at ages older than 6–8 Gyr (see the parameter k in Table 1) might reflect the lower contribution of low- and intermediate-mass AGB stars in early epoch of Galaxy formation because they have not yet started to contribute significantly. We also tested whether the flattening of the data in the oldest regime could be due to their larger uncertainties on age. We generated mock data with a distribution similar to ours, an uncertainty of 30% on age, and an intrinsic scatter of 0.05 dex using a single-line model (see Appendix A). Applying the same MCMC procedure as for the two models (broken-line and single-line), we obtained a lower BIC for the single-line. This suggests that the flattening is not a consequence of the larger uncertainties on the oldest age, but a consequence of the Galactic chemical evolution.

5.2. [Ce/α] as a chemical clock

The ratios of s-process elements to α-elements are widely studied as age indicators because they show a steeper trend with age than [s/Fe]. In this section we investigate [Ce/α]–age trends for the low-α sequence stars in the Kepler, TESS, and K2 samples in the same Rg bins shown in Sect. 5.1. The α-elements we take into account in this work are the same as studied by Sales-Silva et al. (2022) for their open clusters: O, Mg, Si, and Ca. In this way we can compare the trends present in our low-α sequence stars with their open clusters.

In order to study the [Ce/α] trends in a more quantitative way, we modelled their distributions at different Rg, also taking into account the [Fe/H] dependence (following the work by Delgado Mena et al. 2019; Casali et al. 2020; Viscasillas Vázquez et al. 2022) as follows:

(3)

In our calculation, we also took into account the uncertainties on [Ce/α], [Fe/H], and stellar age. We adopted a single-line for the bin of Rg < 7 kpc for Kepler and TESS and the bin of Rg < 5 kpc for K2 where their BIC is lower.

The best fits with the spread (68% confidence interval plus intrinsic scatter) of the models resulting from the posteriors are represented in Figs. 12 and 13 with a black line and a red shaded area. Their values are shown in Table 2.

thumbnail Fig. 12.

[Ce/α]–age planes for Kepler (top panels) and TESS (bottom panels). The points are colour-coded by [Fe/H]. The black dash-dotted line represents the best fit, and the red shaded area the 68% confidence interval plus intrinsic scatter.

thumbnail Fig. 13.

[Ce/α]–age planes for the K2 sample. The symbols are the same as in Fig. 12.

Table 2.

Parameters of the MCMC fitting for the [Ce/α]–[Fe/H]-age relations in the Kepler, TESS, and K2 samples.

The [Fe/H] colour-coding of these stars show a dependence on metallicity. We can see that stars with lower metallicity have higher [Ce/α] at a given age. Furthermore, the stars at higher metallicity show an almost flat trend with respect to the metal poor ones (see Fig. B.2 for a better visualisation of these trends). The same behaviour is displayed by Sales-Silva et al. (2022) and Viscasillas Vázquez et al. (2022) for their samples of open clusters.

This result was already shown in Feltzing et al. (2017), Delgado Mena et al. (2019), Casali et al. (2020), and Magrini et al. (2021) for [Y/α]. Casali et al. (2020), Magrini et al. (2021), and Viscasillas Vázquez et al. (2022) suggested that the metallicity dependence is due to the different star formation history and the non-monotonic dependence of s-process yields on [Fe/H]. In particular, Magrini et al. (2021) investigated the different metallicity dependence of s-process AGB yields if we include or not the magnetic-buoyancy-induced mixing (Vescovi et al. 2020). This mixing can cause a change in the metallicity dependence of the s-process production due to a change in the 13C pocket in AGB stars, specifically for metal-rich stars in the inner regions. Therefore, the s-process yields including the mixing are lower than s-process yields without mixing. This scenario is a signature of the complexity of the s-process yields and, consequently, of the chemical evolution models of these elements. For this reason, a comparison between the observed age versus chemical composition trends, and predictions from chemical evolution models can help us to understand the Ce production in our Galaxy.

Moreover, looking at the [Ce/α]–age relations at different Rg, it is clear how their slopes become steeper moving towards the outer regions: m1 becomes more negative with increasing Rg (see Table 2). This behaviour is a suggestion of the late enrichment of Ce in the Galaxy evolution due to the low- and intermediate-mass AGB stars and indicates a [Ce/α] gradient in the Galactic disc. Moreover, there is a flattening at the oldest ages, a trend hinted at by Sales-Silva et al. (2022) for all studied α-elements. However, we have the advantages of exploiting a homogeneous sample of stars with precise age, spanning the entire range in age and a large interval in metallicity. This is not possible using open clusters because they have ages typically younger than 7 Gyr and metallicity in the range [−0.4, +0.4] dex.

To conclude, the [Ce/α] trends with stellar age, metallicity, and Rg are consistent in all data samples within 3σ. The slight difference among the fitting parameters, particularly for K2, is likely due to the selection effects: our K2 targets have a broader z distribution (where z is the height from the Galactic mid-plane) with respect to the Kepler and TESS targets. For a given Rg bin, stars in K2 are located, on average, at greater distances from the Galactic plane. This different z distribution implies a different distribution in age since stars with higher z are older. A larger number of old stars in the K2 sample can slightly change the fitting parameters with respect to the TESS and Kepler datasets.

Application to field stars. The chemical clock relations obtained from a sample of stars with well-known ages (e.g. stars with asteroseismic age) are usually applied to other field stars of which we know the abundances, but we cannot derive age using standard techniques (e.g. isochrone fitting, asteroseismology). There are some examples in the literature, for instance Casali et al. (2020) and Viscasillas Vázquez et al. (2022) for the [s-/α] ratios, but also Casali et al. (2019), Masseron & Gilmore (2015), Martig et al. (2016), and Ness et al. (2016) for [C/N].

Unfortunately, the large spread in the Ce abundances does not permit us to apply the relations in Table 2 to a sample of field stars. At a given age, there are stars with a difference in [Ce/α] of the order of 0.5 dex, and the intrinsic scatter of these relations is of the order of ∼0.1 dex. Part of this scatter can be ascribed to radial migration. By using Rg we can mitigate the scatter associated with the blurring effect alone, not accounting for churning. To consider the full effect of radial migration, we would need to estimate the birth radii of stars (e.g. by interpolating the position of the stars in the age–metallicity relation in comparison with the chemical evolution curves for each radius from the models). In this way the scatter would most likely be reduced. Nevertheless, this treatment is beyond the scope of this work.

In addition to the expected scatter due to radial migration, there is also the fact that additional scatter is due to Ce measurement uncertainties. The uncertainties on the Ce abundances are likely underestimated, as is the case for most of the uncertainties on other abundances and atmospheric parameters in APOGEE DR17. This is also proved by the large standard deviation in the average abundances of star clusters in the Sect. 3. A better treatment of the Ce uncertainties might reduce the intrinsic scatter in the model and make these chemical clock relations useful to be applied to samples of field stars. We tested the sum in quadrature of the mean of the standard deviations measured for the open clusters shown in Fig. 6 (σ  ∼  0.1 dex) to Ce uncertainties. The result is a significant reduction of the intrinsic scatter (∼50%) of the relations, while the fit parameters remain unaltered.

All these sources of scatter make impossible to apply the [Ce/α]-[Fe/H]-age relations to derive the ‘chemical age’ of other field stars. Furthermore, the [Ce/α]–age trends become flat for age > 6 Gyr, so this chemical clock cannot be applied to old stars.

6. Comparison with Galactic chemical evolution models

Here we interpret our observational results in the light of chemical evolution models, showing in particular the effect of different star formation efficiencies on the chemical evolution of Ce. A more quantitative analysis on Galactic chemical evolution (GCE) models and radial migration effects will be given in a future paper.

We compared the [Ce/α] trends with the predictions of a GCE model. We focused on the [Ce/O] ratio since O is the most representative α-element with the highest percentage of production from Type II Supernovae.

We considered the reference model of Grisoni et al. (2017, 2020) to follow the evolution of the Galactic thin disc. In this model Ce is produced by both the s- and r-process. Low- and intermediate-mass AGB stars in the range 1.3 − 6 M⊙ are responsible for most of the s-process, and the corresponding yields are taken from the database FRUITY (Cristallo et al. 2009, 2011). Moreover, we also included the s-process contribution from rotating massive stars, considering the nucleosynthesis prescriptions of Frischknecht et al. (2016) for these stars. The r-process yields for Ce are obtained by scaling the Eu yields adopted in Cescutti & Chiappini (2014), according to the abundance ratios observed in r-process-rich stars (Sneden et al. 2008). For core-collapse supernovae we considered the yields of Kobayashi et al. (2006).

In Fig. 14 we show the observed and predicted [Ce/O] versus age in different bins of Rg, where Ce and O have different timescales of production, with Ce being mainly produced by low-mass AGB stars and O by massive stars. The predictions are for the reference model of the Galactic thin disc (Grisoni et al. 2020), with three different star formation histories, reference case A (SFE = 0.5 Gyr−1), and model B (SFE = 0.2 Gyr−1) and model C (SFE = 0.1 Gyr−1) for the less efficient star formation efficiency. In order to better understand the fundamental contribution of AGB stars for the Ce production, we also show the model without AGB contribution. This shows a lower limit, where the contribution to the Ce abundance derives from the massive stars only. The chemical evolution of Ce is very sensitive to the star formation history since the yields of Ce are very dependent on mass and metallicity. By assuming a more efficient star formation history (case A in Fig. 14), we obtained a faster chemical evolution, reaching high values of [Ce/O] at earlier epochs; the slope [Ce/O] versus age then flattens. Instead, a milder star formation history shows an increase in [Ce/O] towards younger ages, due to the fact that AGB stars contribute at later times with respect to the massive ones.

thumbnail Fig. 14.

Observed and predicted [Ce/O] vs. age for the K2 sample in five bins of Rg. The Galactic chemical evolution models are labelled as follows: A for the most efficient star formation history, B and C for the less efficient star formation histories, and the dashed line for the model without AGB star contribution.

Because of the large scatter due to the uncertainties on the Ce measurements and to stellar radial migration, the three models A, B, and C can only be used to describe the trends of our data in each bin of guiding radius. Model A represents better the [Ce/O] trend in the inner regions, while the models with a milder SFE (model B and C) describes the [Ce/O] behaviour in the outer regions, as expected also from the inside-out scenario (Matteucci & Francois 1989; Chiappini et al. 2001; Grisoni et al. 2018; Spitoni et al. 2021). In agreement with the inside-out scenario, we assume that the inner Galactic regions form more quickly than the outer ones: in this way, the larger number of stars per unit time in the inner regions reaches the maximum [Ce/O] value earlier with respect to the outer regions, which evolve with a milder SFE. To conclude, the inside-out scenario, combined with the metallicity dependence of AGB yields, can explain the findings discussed in the previous sections.

Moreover, the increasing trends of the observed [Ce/O] moving towards the outer regions is a possible signature of a [Ce/O] gradient in the Galactic disc. This gradient is made less clear because of the large scatter of the data. The reason for this scatter could be related to the uncertainties of the Ce measurements and radial migration. Even though we used the Rg to mitigate the blurring effect, there is still the churning component, which makes the study of abundance gradients in the Galactic disc very complicated. The treatment of the radial migration is beyond the scope of this work, but we can overcome this problem by focusing on the youngest ages (< 1 Gyr). It is expected that radial migration does not affect young stars (or at least only slightly) because they have not had time to migrate yet.

In Fig. 15 we plot the K2 stars with age < 1 Gyr, which is the age bin least affected by radial migration1. There is still scatter in this age bin, but we can see a [Ce/O] gradient in the data. The fit is shown in the figure and is compared with the points at the present time of the GCE model at different galactocentric distances (Grisoni et al. 2018) and the intercepts of the MCMC models shown in Table 2 at different bins of radii. The linear regression is obtained using a MCMC simulation. We can see good agreement between the fit of the data with the gradient predicted by models at the present time. Nevertheless, the spread of the linear regression is very large. Our goal is neither to give a robust theoretical explanation of these trends nor to study in detail the gradients at this stage, but to present the results from an observational point of view.

thumbnail Fig. 15.

[Ce/O] gradient for K2 stars with age < 1 Gyr (cyan circles). The blue dashed line represents the best fit and the blue shaded area the 68% confidence interval plus intrinsic scatter. The black line is the intercept of the MCMC simulation studied in Table 2 at the present time in the five Rg bins; the red line the GCE models at the present time at 4, 6, 8, 10, and 12 kpc.

7. Summary and conclusions

The study of the abundance trends of s-process elements in our Galaxy is very important for constraining theoretical models. Thanks to the data collected by the Gaia mission; by large spectroscopic surveys such as Gaia-ESO, GALAH, and APOGEE; and space missions such as Kepler, TESS, K2, and CoRoT, we can start exploiting the orthogonal constraints offered by age and chemistry to infer the history of s-process elements, and consequently the formation and evolution of the Milky Way.

In this work we focus on the heavy s-process element Ce for three different datasets: Kepler, TESS SCVZ, and K2. For all of them, we have abundances from the APOGEE DR17, where Ce is the only measured s-process element in this survey. Currently, APOGEE is the only high-resolution large spectroscopic survey that can be cross-matched with the TESS and Kepler dataset.

The TESS and Kepler samples observed stars in the solar neighbourhood, while K2 observed different regions of our Galaxy, spanning a wide range of galactocentric distances. Furthermore, using these three datasets of field stars, we were able to cover the oldest age, not covered by open clusters (see e.g. Sales-Silva et al. 2022; Casamiquela et al. 2021; Viscasillas Vázquez et al. 2022) and benefit from the improved statistics of a larger sample. Open clusters can cover ages up to 7 Gyr, with the bulk of them around 1 Gyr. Finally, the number of observed (spectroscopically) open clusters is less than ∼150 (see e.g. open clusters in the Gaia-ESO survey, OCCAM, OCCASO, Randich et al. 2022; Myers et al. 2022; Casamiquela et al. 2016).

In this study, we investigated the [Ce/Fe] abundance ratio trends and the temporal evolution of Ce. Here are our main findings:

  • In the [Ce/Fe]–[α/M] plane we see how the two population with high- and low-α content have different ages and a different average [Ce/Fe]. The high-α sequence contains older stars with lower mean [Ce/Fe], while the low-α sequence displays a wide range of stellar ages with higher mean [Ce/Fe]. We focused on the low-α sequence only since the low- and intermediate-mass AGB stars polluted mainly this stellar population.

  • In the [Ce/Fe]–[Fe/H] plane we see a peak in [Ce/Fe] ratio at around −0.2 dex in [Fe/H] with a consequent decrease in [Ce/Fe] towards lower and higher metallicity. This is related to a non-monotonic metallicity dependence of the s-process stellar yields, and a decreasing efficiency of the s-process at high metallicity. Moreover, at a given [Fe/H], younger stars have a higher [Ce/Fe] content than the older stars. A similar behavoiur is studied in open clusters by Sales-Silva et al. (2022) and Viscasillas Vázquez et al. (2022), among others.

  • To study the time evolution of Ce, we divided the samples in different bins of guiding radius Rg. The [Ce/Fe]–age plane shows how metal-poor stars have a higher [Ce/Fe] content than metal-rich stars at a given age in all bins of Rg. Stars with Rg < 7 kpc show a flattening trend with age. This is a possible signature of the high SFE in the inner regions. In the other bins of Rg (Rg > 7 kpc), [Ce/Fe] decreases with increasing age with a different slope. Moreover, for ages < 6 − 8 Gyr the trend is steeper, while for ages > 6 − 8 Gyr the trend is almost flat, confirming the results for open clusters in Sales-Silva et al. (2022). This is a possible signature of the latest enrichment of low-mass AGB stars for Ce (i.e. the inside-out scenario), combined with metal-dependent AGB yields. This late enrichment takes a few Gyr to pollute the interstellar medium. Furthermore, the [Ce/Fe]–age slope becomes steeper and steeper moving towards the outer regions.

  • Then, we studied the [Ce/α] as a chemical clock for the low-α sequence in the same bins of Rg. The ratio of Ce to an α-element maximises the correlation with the stellar age. The trend is decreasing with age, showing that younger stars have a higher content of [Ce/α] than the older ones. Moreover, we can see different behaviours at different metallicities, as we already saw in the literature, and a change in slope at 6–8 Gyr for these ratios. As we have already seen for [Ce/Fe]–age, the [Ce/α]–age trends also show a steeper slope in the young regime moving towards the outer disc. However, the large scatter due to the underestimate of the Ce uncertainties and radial migration does not allow us to apply the [Ce/α]-age-[Fe/H] relations to date stars for which we cannot derive age with other stellar age dating methods.

  • Finally, we compared the [Ce/O]–age relations with the predictions of Galactic chemical evolution models. This comparison supports the interpretation that the [Ce/O] trends with Rg seen in the observational data, but also [Ce/α] in general, are indeed related to the evolution of the Galactic disc: the observed behaviour is in agreement with the metallicity dependence of the AGB yields and the inside-out scenario, where the inner parts of the Galaxy form more quickly than the outer ones. GCE models with a more intense SFE represent better the observed [Ce/O] trend in the inner regions, while models with a less efficient SFE describe the [Ce/O] behaviour in the outer regions. These GCE models also allow us to reproduce the present-day [Ce/O] gradient.

To conclude, our results show a strong dependence of Ce on metallicity, stellar age, and position in the Galactic disc. Moreover, Ce, a heavy s-process element, is mainly produced by low-mass AGB stars. Their longer lifetime implies a delayed ejection with respect to intermediate and massive stars, and a late contribution to the Galactic chemical evolution. Finally, the uncertainties on s-process yields due to the metallicity dependence, treatment of the 13C-pocket, convection, mass-loss rates, among other factors, require further investigation. These investigations are likely to shed light on the trends of Ce abundances, and those of the other s-process elements, with age.

1

See Anders et al. (2017) who found the metallicity gradients for CoRoT stars younger than 1 Gyr to be similar to the value traced by Cepheids and HII regions.

Acknowledgments

G.C., V.G., A.M., M.M., E.W., A.S., M.M., J.S. acknowledge support from the European Research Council Consolidator Grant funding scheme (project ASTEROCHRONOMETRY, G.A. n. 772293, http://www.asterochronometry.eu. The authors thank Thomas Masseron to providing us with the BAWLAS catalogue for the comparison. L.M. and G.C. acknowledge support from INAF with the Grant “Checs, (CHEmical ClockS) Seeking a theoretical foundation for the use of chemical clocks”.

References

  1. Abdurro’uf, Accetta, K., Aerts, C.-, et al. 2022, ApJS, 259, 35 [CrossRef] [Google Scholar]
  2. Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Anders, F., Chiappini, C., Minchev, I., et al. 2017, A&A, 600, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Anders, F., Chiappini, C., Santiago, B. X., et al. 2018, A&A, 619, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Anguiano, B., Majewski, S. R., Allende-Prieto, C., et al. 2018, A&A, 620, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in 36th COSPAR Scientific Assembly, 36, 3749 [Google Scholar]
  7. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  8. Battino, U., Tattersall, A., Lederer-Woods, C., et al. 2019, MNRAS, 489, 1082 [Google Scholar]
  9. Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton University Press) [Google Scholar]
  10. Bisterzo, S., Travaglio, C., Gallino, R., Wiescher, M., & Käppeler, F. 2014, ApJ, 787, 10 [NASA ADS] [CrossRef] [Google Scholar]
  11. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  12. Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
  13. Busso, M., Gallino, R., Lambert, D. L., Travaglio, C., & Smith, V. V. 2001, ApJ, 557, 802 [CrossRef] [Google Scholar]
  14. Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [Google Scholar]
  15. Casagrande, L., & VandenBerg, D. A. 2018a, MNRAS, 479, L102 [NASA ADS] [CrossRef] [Google Scholar]
  16. Casagrande, L., & VandenBerg, D. A. 2018b, MNRAS, 475, 5023 [Google Scholar]
  17. Casali, G., Magrini, L., Tognelli, E., et al. 2019, A&A, 629, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Casali, G., Spina, L., Magrini, L., et al. 2020, A&A, 639, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Casamiquela, L., Carrera, R., Jordi, C., et al. 2016, MNRAS, 458, 3150 [NASA ADS] [CrossRef] [Google Scholar]
  20. Casamiquela, L., Soubiran, C., Jofré, P., et al. 2021, A&A, 652, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Cescutti, G., & Chiappini, C. 2014, A&A, 565, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Cescutti, G., Chiappini, C., Hirschi, R., Meynet, G., & Frischknecht, U. 2013, A&A, 553, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Cescutti, G., Chiappini, C., & Hirschi, R. 2018, in Rediscovering Our Galaxy, eds. C. Chiappini, I. Minchev, E. Starkenburg, & M. Valentini, 334, 94 [NASA ADS] [Google Scholar]
  24. Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [Google Scholar]
  25. Chiappini, C. 2013, Astron. Nachr., 334, 595 [NASA ADS] [CrossRef] [Google Scholar]
  26. Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  27. Chiappini, C., Frischknecht, U., Meynet, G., et al. 2011, Nature, 472, 454 [Google Scholar]
  28. Contursi, G., de Laverny, P., Recio-Blanco, A., et al. 2023, A&A, 670, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
  31. Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
  32. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. da Silva, R., Porto de Mello, G. F., & Milone, A. C. 2012, A&A, 542, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Delgado Mena, E., Moya, A., Adibekyan, V., et al. 2019, A&A, 624, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Donor, J., Frinchaboy, P. M., Cunha, K., et al. 2020, AJ, 159, 199 [NASA ADS] [CrossRef] [Google Scholar]
  36. Elsworth, Y., Themeßl, N., Hekker, S., & Chaplin, W. 2020, Res. Notes Am. Astron. Soc., 4, 177 [Google Scholar]
  37. Feltzing, S., Howes, L. M., McMillan, P. J., & Stonkutė, E. 2017, MNRAS, 465, L109 [Google Scholar]
  38. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  39. Frischknecht, U., Hirschi, R., Pignatari, M., et al. 2016, MNRAS, 456, 1803 [Google Scholar]
  40. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [Google Scholar]
  42. García Pérez, A. E., Allende Prieto, C., Holtzman, J. A., et al. 2016, AJ, 151, 144 [Google Scholar]
  43. Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [Google Scholar]
  44. Green, G. 2018, J. Open Source Softw., 3, 695 [NASA ADS] [CrossRef] [Google Scholar]
  45. Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
  46. Grisoni, V., Spitoni, E., Matteucci, F., et al. 2017, MNRAS, 472, 3637 [Google Scholar]
  47. Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
  48. Grisoni, V., Cescutti, G., Matteucci, F., et al. 2020, MNRAS, 492, 2828 [Google Scholar]
  49. Hayes, C. R., Masseron, T., Sobeck, J., et al. 2022, ApJS, 262, 34 [NASA ADS] [CrossRef] [Google Scholar]
  50. Hekker, S., & Johnson, J. A. 2019, MNRAS, 487, 4343 [NASA ADS] [CrossRef] [Google Scholar]
  51. Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
  52. Huber, P. J. 1964, Ann. Math. Stat., 35, 73 [CrossRef] [Google Scholar]
  53. Jofré, P., Jackson, H., & Tucci Maia, M. 2020, A&A, 633, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [Google Scholar]
  55. Karakas, A. I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
  56. Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
  57. Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  58. Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
  59. Lugaro, M., Herwig, F., Lattanzio, J. C., Gallino, R., & Straniero, O. 2003, ApJ, 586, 1305 [NASA ADS] [CrossRef] [Google Scholar]
  60. Mackereth, J. T., Miglio, A., Elsworth, Y., et al. 2021, MNRAS, 502, 1947 [NASA ADS] [CrossRef] [Google Scholar]
  61. Magrini, L., Spina, L., Randich, S., et al. 2018, A&A, 617, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Magrini, L., Vescovi, D., Casali, G., et al. 2021, A&A, 646, L2 [EDP Sciences] [Google Scholar]
  63. Maiorca, E., Randich, S., Busso, M., Magrini, L., & Palmerini, S. 2011, ApJ, 736, 120 [NASA ADS] [CrossRef] [Google Scholar]
  64. Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [Google Scholar]
  65. Martig, M., Fouesneau, M., Rix, H.-W., et al. 2016, MNRAS, 456, 3655 [NASA ADS] [CrossRef] [Google Scholar]
  66. Masseron, T., & Gilmore, G. 2015, MNRAS, 453, 1855 [CrossRef] [Google Scholar]
  67. Masseron, T., Merle, T., & Hawkins, K. 2016, Astrophysics Source Code Library [record ascl:1605.004] [Google Scholar]
  68. Matteucci, F. 2021, A&ARv, 29, 5 [NASA ADS] [CrossRef] [Google Scholar]
  69. Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [Google Scholar]
  70. Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Miglio, A., Chiappini, C., Mackereth, J. T., et al. 2021, A&A, 645, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Mikolaitis, Š., Hill, V., Recio-Blanco, A., et al. 2014, A&A, 572, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Morel, T., Creevey, O. L., Montalbán, J., Miglio, A., & Willett, E. 2021, A&A, 646, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Myers, N., Donor, J., Spoo, T., et al. 2022, AJ, 164, 85 [NASA ADS] [CrossRef] [Google Scholar]
  75. Ness, M., Hogg, D. W., Rix, H. W., et al. 2016, ApJ, 823, 114 [NASA ADS] [CrossRef] [Google Scholar]
  76. Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Nissen, P. E., Christensen-Dalsgaard, J., Mosumgaard, J. R., et al. 2020, A&A, 640, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Pignatari, M., Gallino, R., Meynet, G., et al. 2008, ApJ, 687, L95 [Google Scholar]
  79. Pignatari, M., Gallino, R., Heil, M., et al. 2010, ApJ, 710, 1557 [Google Scholar]
  80. Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [Google Scholar]
  81. Randich, S., Gilmore, G., Magrini, L., et al. 2022, A&A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Razera, R., Barbuy, B., Moura, T. C., et al. 2022, MNRAS, 517, 4590 [CrossRef] [Google Scholar]
  83. Rendle, B. M., Miglio, A., Chiappini, C., et al. 2019, MNRAS, 490, 4465 [NASA ADS] [CrossRef] [Google Scholar]
  84. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, SPIE Conf. Ser., 9143, 914320 [Google Scholar]
  85. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1, 014003 [Google Scholar]
  86. Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
  87. Sales-Silva, J. V., Daflon, S., Cunha, K., et al. 2022, ApJ, 926, 154 [NASA ADS] [CrossRef] [Google Scholar]
  88. Schönrich, R., & Binney, J. 2009, MNRAS, 399, 1145 [Google Scholar]
  89. Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [Google Scholar]
  90. Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [Google Scholar]
  91. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  92. Slumstrup, D., Grundahl, F., Brogaard, K., et al. 2017, A&A, 604, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [Google Scholar]
  94. Spina, L., Meléndez, J., Karakas, A. I., et al. 2018, MNRAS, 474, 2580 [NASA ADS] [Google Scholar]
  95. Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021, A&A, 647, A73 [EDP Sciences] [Google Scholar]
  96. Tailo, M., Corsaro, E., Miglio, A., et al. 2022, A&A, 662, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Tautvaišienė, G., Viscasillas Vázquez, C., Mikolaitis, Š., et al. 2021, A&A, 649, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Vescovi, D., Cristallo, S., Busso, M., & Liu, N. 2020, ApJ, 897, L25 [Google Scholar]
  99. Viscasillas Vázquez, C., Magrini, L., Casali, G., et al. 2022, A&A, 660, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Mock data

We generated mock data using a uniform distribution for [Fe/H], between −0.5 and 0.3 dex, and a truncated Gaussian for the age distribution, with a median of 7 Gyr, bound between 1 and 12 Gyr, and a σ-value of 3.5 Gyr. These choices aim to broadly reproduce the observed distributions.

Then we defined a function to generate [Ce/Fe] based on a single-line model (see Sect. 5.1). Then we added a scatter, and afterwards the uncertainties on [Fe/H], [Ce/Fe], and relative age: σ[Fe/H] = 0.05 dex; σ[Ce/Fe] = 0.05 dex; σAge = 30% (see Fig. A.1).

thumbnail Fig. A.1.

Distribution of mock data using single-line model. The top right panel is the model including the intrinsic scatter, the bottom left panel is the model with intrinsic scatter and age uncertainties, the bottom right panel is the model including the intrinsic scatter and all uncertainties.

Finally, we performed the MCMC simulations applying the broken-line and the single-line model to the data (with scatter and uncertainties included) generated using a single-line. We did this to understand which of the two models can reproduce the mock data better. If the broken-line reproduces the mock data better, this means the change in slope in the [Ce/Fe]–age plane that we see in our data is due to the larger age uncertainties of older stars. If, instead, the single-line reproduces the observational data better, this implies the change in slope might be due to the Galactic evolution.

To determine which model fits the mock data better, we used the Bayesian information criterion (BIC) parameter. The model with the lowest BIC is the most reasonable one. We obtained a BIC of −803.13 for the broken-line and of −813.68 for the single-line. Following the rules by Kass & Raftery (1995), we can thus compute ΔBIC= BICi − BICmin. Given i models, the magnitude of the ΔBIC can be interpreted as evidence against a candidate model being the best model. The rules of thumb are the following: (i) less than 2, it is barely worth mentioning; (ii) between 2 and 6, the evidence against the candidate model is positive; (iii) between 6 and 10, the evidence against the candidate model is strong; (iv) greater than 10, the evidence is very strong. In our case the ΔBIC is larger than 10. This shows that the single-line model is the most reasonable one.

Appendix B: Additional figures

In this Appendix we present some additional figures for a better understanding of our work. Figure B.1 displays the [Ce/Fe] uncertainties distributions for the Kepler, TESS, and K2 stars in different bins of age, while Fig. B.2 shows the [Ce/α]–age planes for the three data samples in different bins of Rg. The three different lines in Fig. B.2 represent the [Ce/α] average in three different bins of metallicity: [Fe/H] < −0.1, −0.1 ≤ [Fe/H] ≤ + 0.1, [Fe/H] > +0.1. For the K2 stars in the interval Rg < 5 kpc, we do not plot the [Ce/α] average because there are too few stars.

thumbnail Fig. B.1.

[Ce/Fe] distributions of the low-α sequences of Kepler (top, blue), TESS (middle, orange), and K2 (bottom, green) in different bins of stellar age.

thumbnail Fig. B.2.

[Ce/α]–age planes for the low-αKepler (top), TESS (middle), and K2 (bottom) stars in different bins of Rg. The three lines represent the [Ce/α] average in three different bins of metallicity: [Fe/H] < −0.1, −0.1 ≤ [Fe/H] ≤ +0.1, [Fe/H] > +0.1.

All Tables

Table 1.

Parameters of the MCMC fitting for the [Ce/Fe]–age relations in the Kepler, TESS, and K2 samples.

In the text
Table 2.

Parameters of the MCMC fitting for the [Ce/α]–[Fe/H]-age relations in the Kepler, TESS, and K2 samples.

In the text

All Figures

thumbnail Fig. 1.

Distribution of the age uncertainties for the three data samples. The area under each histogram is integrated to 1.
In the text
thumbnail Fig. 2.

Comparison between [Ce/Fe] using the abundances in APOGEE DR17 (this work) and the Gaia-ESO abundances (Randich et al. 2022). The dashed line indicates the median, whereas the solid line indicates the zero difference.
In the text
thumbnail Fig. 3.

Comparison between [Ce/Fe] using the abundances in APOGEE DR17 (this work) and the abundances from Sales-Silva et al. (2022). The dashed line is the median, whereas the solid line indicates the zero difference.
In the text
thumbnail Fig. 4.

Comparison between [Ce/Fe] using the abundances in APOGEE DR17 (this work) and the BAWLAS abundances (Hayes et al. 2022). The dashed line is the median, whereas the solid line indicates the zero difference.
In the text
thumbnail Fig. 5.

[Ce/Fe] uncertainty distributions in APOGEE DR17, Sales-Silva et al. (2022), Hayes et al. (2022), and Gaia-ESO DR5.
In the text
thumbnail Fig. 6.

Mean and standard deviation of [Ce/Fe] for the open clusters in common between ASPCAP (black) and BAWLAS (red) pipelines. The [Ce/Fe] mean in each cluster is represented with a dot and the standard deviation with the error bar. The number near the cluster names represents the number of stars in each cluster.
In the text
thumbnail Fig. 7.

[Ce/Fe] vs. [α/M]. Shown are Kepler (top panel), TESS (middle panel), and K2 (bottom panel) stars. The stars are colour-coded by stellar age.
In the text
thumbnail Fig. 8.

[Ce/Fe] vs. [Fe/H] in low-α sequence. Shown are Kepler (top panel), TESS (middle panel), and K2 (bottom panel) stars. The stars are colour-coded by stellar age.
In the text
thumbnail Fig. 9.

[Ce/Fe] vs. stellar age for the three samples. The data are colour-coded by metallicity. The three lines represent the [Ce/Fe] mean in different bins of metallicity and age. The error budget of stellar age is shown at the top of each panel.
In the text
thumbnail Fig. 10.

Distribution of Rg of the three selected samples.
In the text
thumbnail Fig. 11.

[Ce/Fe] vs. stellar age in different bins of Rg. The Kepler sample is shown in the upper panel, the TESS sample in the middle panel, and the K2 one in the bottom panel. The data are colour-coded by metallicity. The dash-dotted line represents the best fit, and the shaded area the 68% confidence interval plus intrinsic scatter.
In the text
thumbnail Fig. 12.

[Ce/α]–age planes for Kepler (top panels) and TESS (bottom panels). The points are colour-coded by [Fe/H]. The black dash-dotted line represents the best fit, and the red shaded area the 68% confidence interval plus intrinsic scatter.
In the text
thumbnail Fig. 13.

[Ce/α]–age planes for the K2 sample. The symbols are the same as in Fig. 12.
In the text
thumbnail Fig. 14.

Observed and predicted [Ce/O] vs. age for the K2 sample in five bins of Rg. The Galactic chemical evolution models are labelled as follows: A for the most efficient star formation history, B and C for the less efficient star formation histories, and the dashed line for the model without AGB star contribution.
In the text
thumbnail Fig. 15.

[Ce/O] gradient for K2 stars with age < 1 Gyr (cyan circles). The blue dashed line represents the best fit and the blue shaded area the 68% confidence interval plus intrinsic scatter. The black line is the intercept of the MCMC simulation studied in Table 2 at the present time in the five Rg bins; the red line the GCE models at the present time at 4, 6, 8, 10, and 12 kpc.
In the text
thumbnail Fig. A.1.

Distribution of mock data using single-line model. The top right panel is the model including the intrinsic scatter, the bottom left panel is the model with intrinsic scatter and age uncertainties, the bottom right panel is the model including the intrinsic scatter and all uncertainties.
In the text
thumbnail Fig. B.1.

[Ce/Fe] distributions of the low-α sequences of Kepler (top, blue), TESS (middle, orange), and K2 (bottom, green) in different bins of stellar age.
In the text
thumbnail Fig. B.2.

[Ce/α]–age planes for the low-αKepler (top), TESS (middle), and K2 (bottom) stars in different bins of Rg. The three lines represent the [Ce/α] average in three different bins of metallicity: [Fe/H] < −0.1, −0.1 ≤ [Fe/H] ≤ +0.1, [Fe/H] > +0.1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.