| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346196 | |
| Published online | 25 August 2023 | |
Investigating Gaia EDR3 parallax systematics using asteroseismology of Cool Giant Stars observed by Kepler, K2, and TESS
I. Asteroseismic distances to 12 500 red-giant stars⋆
1
Institute of Physics, Laboratory of Astrophysics, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
e-mail: saniya.khan@epfl.ch
2
Dipartimento di Fisica e Astronomia, Universitä degli Studi di Bologna, Via Gobetti 93/2, 40129 Bologna, Italy
3
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
4
School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
5
LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université, Université Paris-Cité, 92195 Meudon, France
6
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
7
Leiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
8
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
9
Research School of Astronomy and Astrophysics, The Australian National University, Canberra ACT 2611, Australia
10
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Stromlo, Australia
Received:
20
February
2023
Accepted:
10
April
2023
Gaia EDR3 has provided unprecedented data that has generated a great deal of interest in the astrophysical community, even though systematics affect the reported parallaxes at the level of ∼10 μas. Independent distance measurements are available from asteroseismology of red-giant stars with measurable parallaxes, whose magnitude and colour ranges more closely reflect those of other stars of interest. In this paper we determine distances to nearly 12 500 red-giant-branch and red clump stars observed by Kepler, K2, and TESS. This was done via a grid-based modelling method, where global asteroseismic observables, and constraints on the photospheric chemical composition and on the unreddened photometry are used as observational inputs. This large catalogue of asteroseismic distances allows us to provide a first comparison with Gaia EDR3 parallaxes. Offset values estimated with asteroseismology show no clear trend with ecliptic latitude or magnitude, and the trend whereby they increase (in absolute terms) as we move towards redder colours is dominated by the brightest stars. The correction model proposed by Lindegren et al. (2021a) is not suitable for all the fields considered in this study. We find a good agreement between asteroseismic results and model predictions of the red clump magnitude. We discuss possible trends with the Gaia scan law statistics, and show that two magnitude regimes exist where either asteroseismology or Gaia provides the best precision in parallax.
Key words: asteroseismology / astrometry / parallaxes / stars: distances / stars: low-mass / stars: oscillations
Catalogues described in Appendix A are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/677/A21
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In December 2020, the early third intermediate data release of Gaia (Gaia EDR3; Gaia Collaboration 2021) was published, with an updated source list, astrometry, and broad-band photometry in the G, GBP, and GRP bands. This release represents a significant improvement in both the precision and accuracy of the astrometry and photometry, with respect to Gaia DR2. While quasars yielded a median parallax of −29 μas in DR2, this is now reduced to about −17 μas in Gaia EDR3, with variations at a level of ∼10 μas depending on position, magnitude, and colour (Lindegren et al. 2021b).
With the EDR3 release, Lindegren et al. (2021a, hereafter L21) proposed two offset functions, Z5(G, νeff, β) and 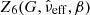 , applicable to five- and six-parameter astrometric solutions, respectively, that give an estimate of the systematics in the parallax measurement as a function of the G-band magnitude, effective wavenumber νeff or pseudo-colour
, applicable to five- and six-parameter astrometric solutions, respectively, that give an estimate of the systematics in the parallax measurement as a function of the G-band magnitude, effective wavenumber νeff or pseudo-colour 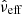 , and ecliptic latitude β. Their zero-point correction model is based on quasars and is complemented with indirect methods involving physical binaries and stars in the Large Magellanic Cloud1.
, and ecliptic latitude β. Their zero-point correction model is based on quasars and is complemented with indirect methods involving physical binaries and stars in the Large Magellanic Cloud1.
Despite the availability of this correction, L21 still encourage users of Gaia EDR3 data to derive their own zero-point estimates whenever possible. Some studies dedicated to the comparison between EDR3 parallaxes and independent measurements have found that the inclusion of the L21 offset could lead to an overcorrection of the parallaxes. All the values reported below give the difference between the corrected EDR3 parallaxes and the other measurements. Hence, positive values correspond to an overcorrection, as a result of applying the L21 values2. This includes samples based on classical Cepheids (+14 ± 5 μas, Riess et al. 2021; +18 ± 5 μas and +22 ± 3 μas, based on NIR HST and optical Gaia bands, respectively, Cruz Reyes & Anderson 2023; +22 ± 4 μas, Molinaro et al. 2023) and RR Lyrae stars (+22 ± 2 μas; Bhardwaj et al. 2021). Even so, there are other studies that did not report this overestimation of the parallax zero point, as can be seen from eclipsing binaries (−15 ± 18 μas; Stassun & Torres 2021), red clump stars (+4.04 μas, the uncertainty is not reported; Huang et al. 2021), and WUMa-type eclipsing binary systems (+4.2 ± 0.5 μas; Ren et al. 2021).
Following on from our Gaia DR2 study (Khan et al. 2019, hereafter K19), we extend our catalogue of distances using asteroseismic data in the Kepler, K2, and TESS southern continuous viewing zone (TESS-SCVZ) fields, allowing for a first comparison with Gaia EDR3. The asteroseismic and spectroscopic surveys used are briefly described in Sect. 2. The method for estimating asteroseismology-based parallaxes is introduced in Sect. 3. Section 4 presents our parallax zero-point results for Kepler, K2, and TESS separately, and provides a first discussion of global trends seen in ecliptic latitude, magnitude, and effective wavenumber. In Sect. 5 we discuss the magnitude of the red clump as an independent validation of the method, the impact of Gaia scanning law statistics for K2, and the existence of two regimes in magnitude where either the precision of asteroseismology or Gaia dominates. Our conclusions are reported in Sect. 6.
2. Observational framework
Our sample is divided into three main parts, summarised in Table 1, and the location of the various fields is illustrated in Fig. 1. The full datasets with asteroseismic, spectroscopic, and astrometric information are provided along with the paper, and details about the columns are given in Appendix A.
 |
Fig. 1. Skymap in Galactic coordinates. Shown are the location and coverage resulting from the crossmatch between the various asteroseismic fields considered in this study and APOGEE DR17. This figure has been generated using the Python package mw-plot (http://milkyway-plot.readthedocs.io/). The background image comes from ESA/Gaia/DPAC. |
Overview of the properties of the different datasets.
2.1. Asteroseismic information
We first have first-ascent red-giant-branch (RGB) stars and red clump (RC) stars observed by Kepler (Borucki et al. 2010), for which the observation length is the longest: four years. The second part of our sample consists of red giants observed by K2, Kepler’s follow-up mission (Howell et al. 2014). Compared to the two campaigns analysed in K19, we now have data available for 17 campaigns: C01-08, C10-18. The observations of K2 campaigns have a much shorter duration of 80 days. We further analysed very bright (G < 11) red-giant stars in the TESS-SCVZ (Ricker et al. 2015). The TESS full-frame images, from which the asteroseismic data are extracted, are based on one year of observations.
For all three surveys, we use the frequency of maximum oscillation power νmax and the average large frequency spacing ⟨Δν⟩, and consider two different asteroseismic pipelines: Mosser & Appourchaux (2009, hereafter MA09) and Elsworth et al. (2020, hereafter E20). We keep stars for which both pipelines return a νmax value in the range [15, 200] μHz. Beyond these limits the νmax estimates are more uncertain and can deviate significantly between MA09 and E20.
2.2. Spectroscopic information
For K2, two different surveys are considered for constraints on the photospheric chemical composition (i.e. Teff and [Fe/H], and, if available, [α/Fe]): APOGEE DR17 with near-infrared (NIR) all-sky spectroscopic observations and a resolution of R ∼ 22 500 (Abdurro’uf et al. 2022), and GALAH DR3 with southern hemisphere spectroscopic observations in the optical/NIR and R ∼ 28 000 (Buder et al. 2021). For Kepler and TESS, we only use APOGEE constraints. Additional flags are also applied following recommendations specific to each spectroscopic survey3. Another survey that could be considered is the all-sky Gaia DR3 GSP-Spec observing in the NIR and with R ∼ 11 500 (Recio-Blanco et al. 2023), but this is beyond the scope of this work.
3. Asteroseismic parallaxes
Asteroseismic parallaxes are estimated with the Bayesian tool PARAM (Rodrigues et al. 2017). For a given set of observational inputs: νmax, ⟨Δν⟩, Teff, log g, [Fe/H], and [α/Fe] (when available), as well as photometric measurements, the code determines the best-fitting stellar parameters by searching amongst a grid of models. The outputs are given in the form of probability density functions, from which the median and 68% credible intervals lead to the final parameters of interest and their uncertainties. We refer the reader to Miglio et al. (2021) for a more extensive discussion of the importance of uncertainties related to stellar models.
In particular, asteroseismic and spectroscopic constraints are combined to derive absolute magnitudes in the different passbands using bolometric corrections from Girardi et al. (2002). Extinction coefficients are computed by adopting the reddening laws of Cardelli et al. (1989) and O’Donnell (1994) with RV = 3.1. It is then assumed that extinctions in all filters Aλ are related by a single interstellar extinction curve expressed in terms of its V-band value, that is Aλ(AV). The total extinction AV and the distance d can then be derived simultaneously. Parallaxes are obtained by inverting the said distances (with a relative uncertainty below ∼5%), and the error on the distance is propagated to obtain the uncertainty on the parallax. We provide a comparison with Gaia DR3 GSP-Phot distances in Appendix B.
4. First comparison to Gaia EDR3 parallaxes
To simplify the discussion and figures, we focus on one combination of asteroseismic and spectroscopic constraints. For most K2 fields, the offsets measured using the MA09 or E20 seismic observables agree to within a few microarcseconds. For TESS-SCVZ targets, Mackereth et al. (2021) found the ⟨Δν⟩ values returned by the E20 pipeline to be more consistent with individual-mode frequencies (and thus to the method employed in models). Hence, we use the E20 asteroseismic pipeline for all three fields. Systematic differences in the spectroscopic parameters published by different surveys affect our results at the level of 5–10 μas (also partly due to the samples being different). We therefore adopt a single homogeneous spectroscopic dataset (APOGEE DR17) to ensure the greatest precision.
A summary of the parallax zero points derived is given in Table 2, whilst individual offsets for all combinations of seismic and spectroscopic constraints are provided in Appendix C. More detailed checks on how the asteroseismic method and the choice of spectroscopy affect the analysis of Gaia systematics will be presented in a forthcoming paper (Khan et al., in prep.).
Summary of the different combinations of asteroseismic and spectroscopic constraints used in this study for the fields considered: Kepler, K2 (C01-08, C10-18), and TESS-SCVZ.
4.1. Separate analyses for Kepler, K2, and TESS
In the following, our results are based on five-parameter astrometric solutions only. We estimate the parallax offset for each field, before and after applying L21 corrections to Gaia parallaxes, and study potential trends with asteroseismic, spectroscopic, and photometric parameters. We had initially compared our results with the Zinn (2021) analysis of Kepler targets. However, the results are not directly comparable because versions 0.0.1 and 0.0.2 of the Gaia-provided Python implementation of the correction zero_point incorrectly applied the ecliptic latitude term.
We investigate the parallax difference Δϖ=ϖEDR3 − ϖPARAM as a function of G, and verify that Δϖ is negative for all fields, in the sense that Gaia parallaxes are smaller (Fig. 2). We apply the same analysis as in K19 on the Kepler sample, but this time with Gaia EDR3 parallaxes and updated APOGEE constraints. The quantity Δϖ shows fairly flat trends as a function of the ecliptic latitude, the effective wavenumber, the frequency of maximum oscillation, the mass inferred from PARAM, and the metallicity, but not for the G magnitude, which displays a non-linear feature (see bottom left panel of Fig. 2). This relation with G is expected due to changes in the gating scheme or in the window size (see Fig. 17 in Fabricius et al. 2021). Despite the larger scatter and a higher proportion of fainter stars compared to Kepler, we also observe a non-linear trend as a function of G if we combine all K2 fields together, which have an ecliptic latitude near zero (see bottom middle panel of Fig. 2). However, our TESS-SCVZ sample is too bright for us to see this trend.
 |
Fig. 2. Parallax difference ϖEDR3 − ϖPARAM as a function of G magnitude for the full sample (top), Kepler (bottom left), K2 (bottom middle), and TESS (bottom right), using E20 and APOGEE DR17. The colour scale indicates the density of stars, increasing from black to white. The red, yellow, and blue shaded areas show the median parallax difference binned by magnitude for Kepler, K2, and TESS, respectively. |
Figure D.1 is similar to Fig. 2, but shows instead the parallax offset residuals Δϖcorr = ϖEDR3, corr − ϖPARAM, with Z5-corrected Gaia EDR3 parallaxes. This removes the non-linear trend with G. It is also clear from Fig. D.1 that L21 corrections underestimate the parallax offset in the case of TESS, and overestimate it for the K2 fields. However, in Kepler the residual parallax offset gets very close to zero. This suggests that L21 corrections are not universally suited for different types of sources, spanning a wide range of positions, magnitudes, and colours.
For some of the K2 campaigns (and independently of the spectroscopy used), we note a significant trend of the parallax difference with the stellar mass. As we do not observe such a trend with mass for Kepler and TESS, we suspect that it could be related to, for instance, different noise levels in the various K2 campaigns. We tried using scaling relations to compute the mass and the asteroseismic parallax instead of PARAM, tested different asteroseismic pipelines and spectroscopic surveys, and removed high νmax stars. Unfortunately, none of these made a difference and this is still being investigated (by BM and YE) as it might directly be related to the accuracy of seismically inferred parameters.
4.2. Global picture
In Fig. 3 we show the offset estimates Δϖ suggested from the difference between the uncorrected Gaia EDR3 and PARAM parallaxes in the Kepler, the individual K2 campaigns, and the TESS-SCVZ fields. We analyse the relation between the parallax zero point and the ecliptic latitude β, the G magnitude, and the effective wavenumber νeff, which are the three parameters constituting the L21 correction model.
 |
Fig. 3. Global trends for our parallax zero points as a function of the three quantities defining the L21 correction. Top: Median parallax offsets estimated from asteroseismology (E20+APOGEE) as a function of the sine of ecliptic latitude. Kepler and TESS are plotted as white and black symbols, respectively. The coloured symbols correspond to the various K2 fields, and follow the colour scheme adopted in Fig. 1. Middle and bottom: Median parallax difference binned by G magnitude (middle) and effective wavenumber (bottom). Kepler and TESS are plotted as black solid and dashed lines, respectively. The median uncertainty on the parallax difference is shown in the lower part of each panel. C15 does not appear in the two bottom panels as there are not enough stars to bin in G and νeff. |
We first note that the offsets measured from asteroseismology are either close to zero or negative, and lie (at most) a few tens of μas away from the zero point suggested by quasars (∼ − 17 μas). All the K2 campaigns have a similar sin β, close to zero, which is expected as the K2 survey observed solar-like oscillators all along the ecliptic.
For individual K2 campaigns, the parallax difference also follows a non-linear relationship with G, in line with what is discussed in Sect. 4.1. The bottom panel of Fig. 3 suggests that the parallax difference becomes more negative as we go towards lower νeff, that is redder colours. This is also apparent for νeff ≲ 1.40, where we have fewer campaigns. One should keep in mind, however, that this trend is dominated by bright stars, for which other caveats exist (see e.g. Sect. 5.3), which tend to drag the parallax difference towards substantially negative values (as can be seen from the middle panel of Fig. 3).
5. Discussion
5.1. Magnitude of the red clump
As a way to validate our findings, we also analyse the information provided by the magnitude of the red clump. In Fig. 4 we show different estimates of the absolute magnitude of the clump as a function of the galactic latitude b. The first estimate is based on the Ks-band absolute magnitude computed by PARAM, which is thus representative of our asteroseismic samples. For the other two estimates, we select Gaia EDR3 sources centred around the coordinates of each field and with 1 < G < 15: one estimate is calculated with the inverted Gaia uncorrected parallaxes and the other with corrected parallaxes (using the L21 correction model). In order to be able to safely use inverted parallaxes, we restrict our samples to Gaia sources with a relative parallax uncertainty lower than 10%. Extinctions are calculated with the combined map (Marshall et al. 2006; Green et al. 2019; Drimmel et al. 2003) from mwdust4 (Bovy et al. 2016), and should only have a minor effect on the current analysis as we are working with Ks-band magnitudes. For each dataset we then compute the mode of the magnitude of the red clump using a kernel density estimation with a fixed bandwidth (equal to 0.1) on the corresponding histogram.
 |
Fig. 4. Magnitude of the red clump in Ks band estimated from our asteroseismic sample (circles, same colour scheme as in Fig. 1), and Gaia EDR3 samples before applying L21 corrections (filled triangles) and after (open triangles), as a function of the sine of the galactic latitude. The lines show predictions from modelling: purple and orange respectively for a metal-poor (−0.4 dex) and metal-rich model (+0.2 dex); dashed and dotted respectively for a young (5 Gyr) and old model (12 Gyr; see Fig. 8 in Girardi 2016). These values were chosen to be representative of the lower and upper bounds of the metallicity and age distributions in the asteroseismic fields. |
The magnitude of the red clump shows a trend with galactic latitude. Figure 3 of Ren et al. (2021) shows that the parallax offset is observed to be more negative for sin b ∼ 0, which could explain why the filled triangles are more luminous in our Fig. 4. On the other hand, a brighter red clump luminosity would result from a younger and more metal-rich population. This trend is visible when using the seismic sample or the Gaia EDR3 sample without applying L21 parallax corrections. Instead, the corrected Gaia EDR3 sample shows a flat trend, which again supports the idea that the L21 zero-point model is not suitable for every kind of star (see also Sect. 4.1). In addition, results from asteroseismology agree well with model predictions (see e.g. Girardi 2016).
5.2. Impact of Gaia scanning law statistics for K2
We look into whether the spread in parallax zero points suggested by the K2 fields could be related to Gaia scan law statistics. For this we extracted both the average number of scans and spread of scans throughout the year for Gaia EDR3 (see Fig. 1 of Everall et al. 2021 for the all-sky distribution of these quantities in Gaia DR2). The high ecliptic latitude fields, Kepler and TESS, show a high number of scans and an important spread of scans. On the other hand, for K2 we find fewer scans that are often concentrated at a single time of the year, which is consistent with the fact that these fields are located unfavourably with respect to the Gaia scanning law. As a result, the uncertainty on Gaia EDR3 parallaxes is larger for K2 compared to Kepler and TESS. Apart from these obvious differences, we do not observe any trend of the parallax offset with the scan law statistics between the various K2 campaigns (see Fig. 5).
 |
Fig. 5. Parallax offset, measured as difference between uncorrected Gaia EDR3 and asteroseismic parallaxes as a function of number of scans over spread of scans. A low value suggests fewer scans clustered at one time of the year, and hence an astrometry of lesser quality, while a higher value corresponds to a greater number of scans better separated in time. The colour scheme is the same as in Fig. 1. |
5.3. Existence of two magnitude regimes
Figure 6 illustrates the biases arising from asteroseismology or Gaia’s point of view as a function of the G-band apparent magnitude. The asteroseismic bias corresponds to a fractional systematic uncertainty in radius and hence in distance, while the Gaia bias would be related to the effect of a systematic (absolute) uncertainty in parallax.
 |
Fig. 6. Bias in the parallax difference as a function of the apparent magnitude. Two mock stars are considered for the asteroseismic bias: a RGB star (blue) and a RC star (red; see text for details). We show the asteroseismic bias that would result from a 1–3% systematic uncertainty in radius. The Gaia bias, ±10–40 μas in parallax, is shown as a yellow hatched region. Kepler observations are shown in the background after subtracting the mean parallax offset. |
In order to test this we considered two mock stars: a RGB star with L = 30 L⊙, Teff = 4630 K, [Fe/H] = 0.0 dex, log g = 2.6, and a RC star with L = 50 L⊙, Teff = 4740 K, [Fe/H] = 0.0 dex, log g = 2.4. We then estimated the absolute magnitude in the G-band. We considered a range of apparent magnitude values [9, 15], and computed a parallax value for each magnitude. ‘Biased’ parallaxes are then estimated either by adding a constant to the distance modulus, which would correspond to a fractional uncertainty in radius (asteroseismic bias), or by adding a constant to the parallax itself (Gaia bias). For the former we considered a ±1–3% bias in radius, which corresponds to the 16th and 84th percentiles for the Kepler dataset, while for the latter we used a range of ±10–40 μas.
We show in Fig. 6 how such biases can affect the estimation of the parallax zero point. The Kepler dataset is also shown in the background (after subtracting the mean parallax offset) to see how the order of magnitude of these biases compares with the actual observations. The existence of two regimes becomes quite clear. At the bright end the comparisons in terms of parallax difference are dominated by systematics affecting the seismic parallax; at the faint end the systematics from asteroseismology are much less dominant, and one can potentially expose Gaia’s. This division stems from the fact that the fractional uncertainty on asteroseismic distances (or parallaxes) is largely distance independent, but the absolute precision (in pc or mas) is very much distance dependent, so it becomes worse than Gaia’s in nearby objects. Similar comparisons of fractional versus constant offset effect as a function of magnitude and other parameters are shown in Figs. 4–7 of Zinn et al. 2019, to which we refer the reader for further discussion.
6. Conclusions
We carried out a follow-up of our 2019 study (Khan et al. 2019) to investigate the Gaia EDR3 parallax zero point, for a significantly larger number of asteroseismic fields: Kepler, 17 K2 campaigns, and the TESS-SCVZ. Our analysis is similar to that of Zinn (2021) for the Kepler field, but goes beyond theirs with the addition of K2 and TESS. In combining results across Kepler, K2, and TESS, we have made sure to combine asteroseismic and spectroscopic constraints in a fully homogeneous way. This has the benefit of exploring Gaia parallax systematics for the same type of objects but with a wide range of positions over the sky within a single study. A quick comparison of asteroseismic distances with the Gaia DR3 GSP-Phot estimates shows that a reasonable agreement is found for objects within 2 kpc.
Firstly, we confirm the positional dependence of the Gaia parallax zero point: Kepler has an offset of ∼ − 20 μas, K2 campaigns span a wide range between ∼ − 39 and +1 μas, and TESS shows an offset of ∼ − 41 μas when using E20 and APOGEE constraints.
The inclusion of the Lindegren et al. (2021a) zero-point estimates improves the agreement between Gaia and asteroseismology in the case of Kepler and, to a much lesser extent, TESS. However, in most K2 fields it can significantly overcorrect the parallax difference, sometimes resulting in large positive parallax offsets. This underlines the need to consistently determine the parallax systematics applicable to the sample of interest, taking into account the distributions in position, magnitude, and colour. This overcorrection had already been suggested by previous studies (e.g. Bhardwaj et al. 2021; Riess et al. 2021).
Lastly, in terms of magnitude and colour dependence, we show that asteroseismology provides us with strong constraints on the Gaia EDR3 parallax zero point, in ranges that are not necessarily well sampled by L21 corrections. There are no clear trends with the ecliptic latitude or the G magnitude, but the zero-point values tend to increase (in absolute terms) towards redder colours (lower νeff). Although this trend seems to be dominated by caveats associated with stars at brighter magnitudes. Moreover, we find that seismic-based estimates of the red clump magnitude are consistent with theoretical predictions of 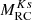 , and that the inclusion of the L21 offset tends to make the red clump too faint. We do not find any correlation between Gaia scan law statistics and parallax offset estimates for the K2 fields. We also use two mock stars to illustrate the existence of two regimes: bright magnitudes, where Gaia’s precision is better than asteroseismology’s; and faint magnitudes, where we can expose Gaia’s limits thanks to seismology’s precision.
, and that the inclusion of the L21 offset tends to make the red clump too faint. We do not find any correlation between Gaia scan law statistics and parallax offset estimates for the K2 fields. We also use two mock stars to illustrate the existence of two regimes: bright magnitudes, where Gaia’s precision is better than asteroseismology’s; and faint magnitudes, where we can expose Gaia’s limits thanks to seismology’s precision.
With this study, we present asteroseismology as a powerful tool for constraining Gaia systematics. Red giants come with several benefits: they are single stars with measurable parallaxes and without large-amplitude photometric variations, and thus differ substantially from eclipsing binaries, quasars, RR Lyrae, and Cepheids. Further progress is expected with Gaia DR4, which will have improved parallax uncertainties and reduced systematics. In a forthcoming paper we will look in more detail at the uncertainties potentially affecting parallax estimates from asteroseismology and Gaia, and investigate how we can define the best sample to study parallax systematics in Gaia.
Python implementations of both functions are available on the Gaia web pages: https://www.cosmos.esa.int/web/gaia/edr3-code
We used the STAR_WARN and STAR_BAD flags to clean the APOGEE sample (https://www.sdss.org/dr17/irspec/parameters/) and flag_sp == 0, flag_fe_h == 0, flag_alpha_fe == 0 for the GALAH sample (https://www.galah-survey.org/dr3/flags/).
Acknowledgments
This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. R.I.A. and S.K. are funded by the Swiss National Science Foundation (SNSF) through an Eccellenza Professorial Fellowship (award PCEFP2_194638). A.M. and E.W. acknowledge support from the ERC Consolidator Grant funding scheme (project ASTEROCHRONOMETRY, G.A. n. 772293). This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #490, SHoT: The Stellar Path to the Ho Tension in the Gaia, TESS, LSST and JWST Era. We also wish to thank the referee who provided a very positive report.
References
- Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Bhardwaj, A., Rejkuba, M., de Grijs, R., et al. 2021, ApJ, 909, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Bovy, J., Rix, H.-W., Green, G. M., Schlafly, E. F., & Finkbeiner, D. P. 2016, ApJ, 818, 130 [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Cruz Reyes, M., & Anderson, R. I. 2023, A&A, 672, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elsworth, Y., Hekker, S., Basu, S., & Davies, G. R. 2017, MNRAS, 466, 3344 [NASA ADS] [CrossRef] [Google Scholar]
- Elsworth, Y., Themeßl, N., Hekker, S., & Chaplin, W. 2020, Res. Notes Am. Astron. Soc., 4, 177 [Google Scholar]
- Everall, A., Boubert, D., Koposov, S. E., Smith, L., & Holl, B. 2021, MNRAS, 502, 1908 [CrossRef] [Google Scholar]
- Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fouesneau, M., Frémat, Y., Andrae, R., et al. 2023, A&A, 674, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L. 2016, ARA&A, 54, 95 [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [Google Scholar]
- Huang, Y., Yuan, H., Beers, T. C., & Zhang, H. 2021, ApJ, 910, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, S., Miglio, A., Mosser, B., et al. 2019, A&A, 628, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021a, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021b, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Mackereth, J. T., Miglio, A., Elsworth, Y., et al. 2021, MNRAS, 502, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Chiappini, C., Mackereth, J. T., et al. 2021, A&A, 645, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinaro, R., Ripepi, V., Marconi, M., et al. 2023, MNRAS, 520, 4154 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Palicio, P. A., et al. 2023, A&A, 674, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ren, F., Chen, X., Zhang, H., et al. 2021, ApJ, 911, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2021, ApJ, 908, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
- Stassun, K. G., & Torres, G. 2021, ApJ, 907, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, J. C. 2021, AJ, 161, 214 [Google Scholar]
- Zinn, J. C., Pinsonneault, M. H., Huber, D., & Stello, D. 2019, ApJ, 878, 136 [Google Scholar]
Appendix A: Catalogues of asteroseismic, spectroscopic, and astrometric properties for Kepler, K2, and TESS red giants
Description of the columns used in the catalogues we release in this work.
Appendix B: Comparison with Gaia DR3 Apsis GSP-Phot distances
Figure B.1 compares distances from asteroseismology (based on E20 and APOGEE) and Gaia DR3 Apsis GSP-Phot for Kepler, K2, and TESS. As noted by Fouesneau et al. (2023), a good agreement is found to about 2 kpc; beyond this distance GSP-Phot tends to overestimate distances, as in Kepler, or on the contrary to systematically underestimate them at even further distances (see K2). No issues are found for TESS nearby targets.
 |
Fig. B.1. Comparison of Gaia DR3 Apsis GSP-Phot distances with asteroseismic values computed using E20 and APOGEE for Kepler (left), K2 (middle), and TESS (right). The bottom panels show the relative difference in distance. The colour scale indicates the Gaia parallax-to-error ratio. See Fig. 9 in Fouesneau et al. (2023) for a similar comparison with other asteroseismic datasets. |
Appendix C: Parallax zero-point estimates from asteroseismology
Table C.1 gives a summary of the parallax offsets measured with the various combinations of asteroseismology and spectroscopy in the Kepler, K2 campaigns, and TESS fields.
Parallax zero points, measured as the difference between the Gaia EDR3 and the asteroseismic parallaxes (ϖGEDR3 − ϖPARAM) for the asteroseismic fields considered in this study.
Appendix D: Impact of L21 corrections on parallax offset estimation
All Tables
Summary of the different combinations of asteroseismic and spectroscopic constraints used in this study for the fields considered: Kepler, K2 (C01-08, C10-18), and TESS-SCVZ.
Parallax zero points, measured as the difference between the Gaia EDR3 and the asteroseismic parallaxes (ϖGEDR3 − ϖPARAM) for the asteroseismic fields considered in this study.
All Figures
 |
Fig. 1. Skymap in Galactic coordinates. Shown are the location and coverage resulting from the crossmatch between the various asteroseismic fields considered in this study and APOGEE DR17. This figure has been generated using the Python package mw-plot (http://milkyway-plot.readthedocs.io/). The background image comes from ESA/Gaia/DPAC. |
| In the text | |
 |
Fig. 2. Parallax difference ϖEDR3 − ϖPARAM as a function of G magnitude for the full sample (top), Kepler (bottom left), K2 (bottom middle), and TESS (bottom right), using E20 and APOGEE DR17. The colour scale indicates the density of stars, increasing from black to white. The red, yellow, and blue shaded areas show the median parallax difference binned by magnitude for Kepler, K2, and TESS, respectively. |
| In the text | |
 |
Fig. 3. Global trends for our parallax zero points as a function of the three quantities defining the L21 correction. Top: Median parallax offsets estimated from asteroseismology (E20+APOGEE) as a function of the sine of ecliptic latitude. Kepler and TESS are plotted as white and black symbols, respectively. The coloured symbols correspond to the various K2 fields, and follow the colour scheme adopted in Fig. 1. Middle and bottom: Median parallax difference binned by G magnitude (middle) and effective wavenumber (bottom). Kepler and TESS are plotted as black solid and dashed lines, respectively. The median uncertainty on the parallax difference is shown in the lower part of each panel. C15 does not appear in the two bottom panels as there are not enough stars to bin in G and νeff. |
| In the text | |
 |
Fig. 4. Magnitude of the red clump in Ks band estimated from our asteroseismic sample (circles, same colour scheme as in Fig. 1), and Gaia EDR3 samples before applying L21 corrections (filled triangles) and after (open triangles), as a function of the sine of the galactic latitude. The lines show predictions from modelling: purple and orange respectively for a metal-poor (−0.4 dex) and metal-rich model (+0.2 dex); dashed and dotted respectively for a young (5 Gyr) and old model (12 Gyr; see Fig. 8 in Girardi 2016). These values were chosen to be representative of the lower and upper bounds of the metallicity and age distributions in the asteroseismic fields. |
| In the text | |
 |
Fig. 5. Parallax offset, measured as difference between uncorrected Gaia EDR3 and asteroseismic parallaxes as a function of number of scans over spread of scans. A low value suggests fewer scans clustered at one time of the year, and hence an astrometry of lesser quality, while a higher value corresponds to a greater number of scans better separated in time. The colour scheme is the same as in Fig. 1. |
| In the text | |
 |
Fig. 6. Bias in the parallax difference as a function of the apparent magnitude. Two mock stars are considered for the asteroseismic bias: a RGB star (blue) and a RC star (red; see text for details). We show the asteroseismic bias that would result from a 1–3% systematic uncertainty in radius. The Gaia bias, ±10–40 μas in parallax, is shown as a yellow hatched region. Kepler observations are shown in the background after subtracting the mean parallax offset. |
| In the text | |
 |
Fig. B.1. Comparison of Gaia DR3 Apsis GSP-Phot distances with asteroseismic values computed using E20 and APOGEE for Kepler (left), K2 (middle), and TESS (right). The bottom panels show the relative difference in distance. The colour scale indicates the Gaia parallax-to-error ratio. See Fig. 9 in Fouesneau et al. (2023) for a similar comparison with other asteroseismic datasets. |
| In the text | |
 |
Fig. D.1. Same as Fig. 2, but including L21 corrections in the Gaia EDR3 parallaxes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


