| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 26 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346050 | |
| Published online | 13 September 2023 | |
Investigating the visible phase-curve variability of 55 Cnc e★,★★
1
Center for Space and Habitability, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern,
Switzerland
e-mail: erik.meiervaldes@csh.unibe.ch
2
Space Telescope Science Institute,
Baltimore, MD
21218,
USA
3
Physikalisches Institut, University of Bern,
Sidlerstrasse 5,
3012
Bern,
Switzerland
4
Department of Astronomy, Stockholm University, AlbaNova University Center,
10691
Stockholm,
Sweden
5
Observatoire Astronomique de l’Université de Genève,
Chemin Pegasi 51,
1290
Versoix,
Switzerland
6
Instituto de Astrofisica e Ciencias do Espaco, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto,
Portugal
7
INAF, Osservatorio Astrofisico di Catania,
Via S. Sofia 78,
95123
Catania,
Italy
8
Ludwig Maximilian University, University Observatory Munich,
Scheinerstrasse 1,
Munich
81679,
Germany
9
University of Warwick, Department of Physics, Astronomy & Astrophysics Group,
Coventry
CV4 7AL,
UK
10
University of Bern, ARTORG Center for Biomedical Engineering Research,
Murtenstrasse 50,
3008
Bern,
Switzerland
11
Université Paris-Saclay, Université Paris Cité, CEA, CNRS, AIM,
91191
Gif-sur-Yvette,
France
12
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz,
Austria
13
Jet Propulsion Laboratory, California Institute of Technology,
Pasadena,
USA
14
Departamento de Fisica e Astronomia, Faculdade de Ciencias, Universidade do Porto, Rua do Campo Alegre,
4169-007
Porto,
Portugal
15
Instituto de Astrofisica de Canarias,
38200
La Laguna, Tenerife,
Spain
16
Departamento de Astrofisica, Universidad de La Laguna,
38206
La Laguna, Tenerife,
Spain
17
Institut de Ciencies de l’Espai (ICE, CSIC), Campus UAB,
Can Magrans s/n,
08193
Bellaterra,
Spain
18
Institut d’Estudis Espacials de Catalunya (IEEC),
08034
Barcelona,
Spain
19
European Space Agency (ESA), European Space Research and Technology Centre (ESTEC),
Keplerlaan 1,
2201
AZ Noordwijk,
The Netherlands
20
Admatis,
5. Kandó Kálmán Street,
3534
Miskolc,
Hungary
21
Depto. de Astrofisica, Centro de Astrobiologia (CSIC-INTA), ESAC campus,
28692
Villanueva de la Cañada (Madrid),
Spain
22
Université Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
23
INAF, Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
24
Institute of Planetary Research, German Aerospace Center (DLR),
Rutherfordstrasse 2,
12489
Berlin,
Germany
25
Université de Paris, Institut de physique du globe de Paris, CNRS,
75005
Paris,
France
26
Centre for Exoplanet Science, SUPA School of Physics and Astronomy, University of St Andrews,
North Haugh,
St Andrews
KY16 9SS,
UK
27
INAF, Osservatorio Astrofisico di Torino,
Via Osservatorio, 20,
10025
Pino Torinese To,
Italy
28
Centre for Mathematical Sciences, Lund University,
Box 118,
221 00
Lund,
Sweden
29
Aix Marseille Univ, CNRS, CNES, LAM,
38 rue Frédéric Joliot-Curie,
13388
Marseille,
France
30
Astrobiology Research Unit, Université de Liège,
Allée du 6 Août 19C,
4000
Liège,
Belgium
31
Space sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège,
Allée du 6 Août 19C,
4000
Liège,
Belgium
32
Centre Vie dans l’Univers, Faculté des sciences, Université de Genève,
Quai Ernest-Ansermet 30,
1211
Genève 4,
Switzerland
33
Leiden Observatory, University of Leiden,
PO Box 9513,
2300
RA Leiden,
The Netherlands
34
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala,
Sweden
35
Dipartimento di Fisica, Universita degli Studi di Torino,
via Pietro Giuria 1,
10125
Torino,
Italy
36
Department of Astrophysics, University of Vienna,
Türkenschanzstrasse 17,
1180
Vienna,
Austria
37
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
1121
Budapest,
Konkoly Thege Miklós út 15–17,
Hungary
38
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
1117
Budapest,
Hungary
39
IMCCE, UMR8028 CNRS, Observatoire de Paris, PSL Univ., Sorbonne Univ.,
77 av. Denfert-Rochereau,
75014
Paris,
France
40
Institut d’astrophysique de Paris, UMR7095 CNRS, Université Pierre & Marie Curie,
98bis blvd. Arago,
75014
Paris,
France
41
Astrophysics Group, Keele University,
Staffordshire
ST5 5BG,
UK
42
Institute of Optical Sensor Systems, German Aerospace Center (DLR),
Rutherfordstrasse 2,
12489
Berlin,
Germany
43
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Universita degli Studi di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova,
Italy
44
Department of Physics, University of Warwick, Gibbet Hill Road,
Coventry
CV4 7AL,
UK
45
ETH Zurich, Department of Physics,
Wolfgang-Pauli-Strasse 2,
8093
Zurich,
Switzerland
46
Cavendish Laboratory, JJ Thomson Avenue,
Cambridge
CB3 0HE,
UK
47
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstr. 36,
10623
Berlin,
Germany
48
Institut für Geologische Wissenschaften, Freie Universität Berlin,
12249
Berlin,
Germany
49
ELTE Eötvös Loránd University, Gothard Astrophysical Observatory,
9700
Szombathely,
Szent Imre h. u. 112,
Hungary
50
MTA-ELTE Exoplanet Research Group,
9700
Szombathely,
Szent Imre h. u. 112,
Hungary
51
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
Received:
1
February
2023
Accepted:
4
July
2023
Context. 55 Cnc e is an ultra-short period super-Earth transiting a Sun-like star. Previous observations in the optical range detected a time-variable flux modulation that is phased with the planetary orbital period, whose amplitude is too large to be explained by reflected light and thermal emission alone.
Aims. The goal of the study is to investigate the origin of the variability and timescale of the phase-curve modulation in 55 Cnc e. To this end, we used the CHaracterising ExOPlanet Satellite (CHEOPS), whose exquisite photometric precision provides an opportunity to characterise minute changes in the phase curve from one orbit to the next.
Methods. CHEOPS observed 29 individual visits of 55 Cnc e between March 2020 and February 2022. Based on these observations, we investigated the different processes that could be at the origin of the observed modulation. In particular, we built a toy model to assess whether a circumstellar torus of dust driven by radiation pressure and gravity might match the observed flux variability timescale.
Results. We find that the phase-curve amplitude and peak offset of 55 Cnc e do vary between visits. The sublimation timescales of selected dust species reveal that silicates expected in an Earth-like mantle would not survive long enough to explain the observed phase-curve modulation. We find that silicon carbide, quartz, and graphite are plausible candidates for the circumstellar torus composition because their sublimation timescales are long.
Conclusions. The extensive CHEOPS observations confirm that the phase-curve amplitude and offset vary in time. We find that dust could provide the grey opacity source required to match the observations. However, the data at hand do not provide evidence that circumstellar material with a variable grain mass per unit area causes the observed variability. Future observations with the James Webb Space Telescope (JWST) promise exciting insights into this iconic super-Earth.
Key words: stars: individual: 55 Cnc / techniques: photometric / planets and satellites: individual: 55 Cnc e
The raw and detrended photometric time-series data are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/677/A112
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The super-Earth 55 Cnc e is the only transiting planet of the five planets that are known to be orbiting its star. The star is one of the brightest stars known to host planets (V = 6). Because of its short orbital period (P = 0.74 days), 55 Cnc e is catalogued as an ultra-short period (USP) planet. Among the population of discovered USP planets, 55 Cnc e is one of the most frequently studied close-in exoplanets. However, the vast number of observations across the entire spectrum, from the ultra-violet (UV; Bourrier et al. 2018b) to the infrared (IR; Demory et al. 2011), did not lead to a conclusive understanding of this object.
55 Cnc e was discovered via radial velocity (RV) observations at McDonald Observatory with the Hobby-Eberly Telescope (HET; McArthur et al. 2004) with an RV solution pointing to a 2.808-day period. Later, Dawson & Fabrycky (2010) argued that the reported period was an alias, and they computed a true orbital period of 0.74 days. Winn et al. (2011) and Demory et al. (2011) independently discovered the planet to be transiting its host star and confirmed the previously predicted period with the Microvariability and Oscillations of Stars (MOST) telescope and the Spitzer space telescope, respectively.
The first photometric observations in the optical revealed that the measured flux at different phases of the planetary orbit could not be explained by thermal emission and reflected light alone (Winn et al. 2011). An extensive observation campaign between 2011 and 2015 with MOST concluded that the phase modulation and phase offset change over time (Dragomir et al. 2012; Sulis et al. 2019). The occultation was not detected in the MOST dataset. Spitzer observed 55 Cnc e multiple times, revealing a significant variability in the occultation depth between 2012 and 2013 (Demory et al. 2015) that was later confirmed by Tamburo et al. (2018). However, a recent analysis using the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014) observations indicated weak evidence of variability in the occultation depth in the optical range across the sectors (Meier Valdés et al. 2022).
The phase-curve of an exoplanet measures the light of a star and planet throughout an orbit. It exposes different sides of the planet to the observer (Knutson et al. 2007; Borucki et al. 2009; Heng 2017). Between transit and occultation (secondary eclipse), the measured flux varies because a different phase of the planet is observed. Here we focus on tidally locked planets that transit their host star. In the absence of atmospheric dynamics, the flux will reach its lowest point when the planet transits and peak at the secondary eclipse, where the flux corresponds to the star alone. If the phase-curve peak has a phase offset, this could imply atmospheric winds or dynamics.
Atmospheric dynamics and weather can produce variability in the shape and amplitude of a phase curve, but all other time-varying sources must be ruled out. There is a precedent of observed phase-curve variability of an exoplanet in addition to 55 Cnc e. Armstrong et al. (2016) claimed evidence for variability in the atmosphere of the hot Jupiter HAT-P-7 b, but a reassessment by Lally & Vanderburg (2022) concluded that stellar noise might entirely cause the claimed variability. Stars with convective outer envelopes have granules that vary stochastically in time. Supergranulation is a similar dynamical phenomenon that involves horizontal flows that occur on longer timescales, and it displays larger photometric amplitudes (Lally & Vanderburg 2022). In future work, asteroseismic predictions of the variability amplitude at each frequency as a function of the stellar properties may help extrapolate the stellar phenomena of HAT-P-7 (F6V) to 55 Cnc (G8V).
A thermal map of the planet derived with Spitzer observations in the IR revealed a hot spot that is offset 41 degrees east of the substellar point (Demory et al. 2016). This phase offset can be explained by a narrow region of volcanic activity or by a circulating atmosphere. Moreover, the night-side brightness temperature is about 1400 K, while the hottest region on the day-side is approximately 1300 K hotter. The high temperature gradient indicates inefficient heat redistribution from the day-side to the night-side. The temperature contrast and the offset hot spot are consistent with an optically thick atmosphere in which atmospheric recirculation mostly occurs on the day-side, or a planet without atmosphere with magma flows at the surface. The Spitzer observations were further analysed by Angelo & Hu (2017), who concluded that the phase curve favours a substantial atmosphere on 55 Cnc e. A recent reanalysis of the Spitzer dataset found a phase offset consistent with zero, with a markedly higher day-side temperature of 3770 K and a gradient of 2700 K to the night-side temperature (Mercier et al. 2022).
The phase curve of another USP planet was obtained with Spitzer and Kepler. K2-141 b is a small rocky planet discovered by Kepler, orbiting its host star every 6.7 h. The observations in the IR and optical are consistent with thermal emission and reflected light. The phase offset of this exoplanet is negligible (Zieba et al. 2022).
Some effort was expended to identify certain atmospheric species on 55 Cnc e. So far, there is no evidence of H Ly α absorption (Ehrenreich et al. 2012; Tabernero et al. 2020), He (Zhang et al. 2021), H2O, TiO (Esteves et al. 2017; Jindal et al. 2020), CO, CO2, HCN, NH3, and C2H2 (Deibert et al. 2021). Ridden-Harper et al. (2016) found hints of CaII H&K and NaD, but did not claim detection due to the low significance of the signal and variable CaII. A recent survey (Keles et al. 2022) of a single transit concluded no detection of absorption of O, Si, Al, Na, Mg, K H, P, F, Sr, S, C, Cl, V, Cr, as well as Fe, Ca, Ti, Mn, Ba, Zr, and its singularly ionized forms. This extensive list of no detections strengthens the hypothesis of a heavyweight atmosphere, if any is present at all.
The process that causes the puzzling observations remains unknown. Temporal variability in UV transit observations suggests star-planet interactions (SPIs) as the possible origin (Bourrier et al. 2018b). Because of the short orbital distance, the planet and its host star might be magnetically connected (Folsom et al. 2020). However, more recent work showed that the energy budget seems too low to cause the measured signal (Morris et al. 2021). Other hypotheses include active volcanism or an inhomogeneous circumstellar dust torus.
In this paper, we present the results of an extensive campaign with CHEOPS to observe the phase curve of 55 Cnc e. First, we present the observations, the detrending of the systematics, and the phase-curve model fit to the data in Sect. 2. Then we present the results for the phase-curve amplitude and phase offset in Sect. 3. Based on the results, a discussion follows in Sect. 4. We conclude in Sect. 5 and highlight future projects that explore this fascinating system.
2 Methods
2.1 CHEOPS
The CHaracterising ExOPlanet Satellite (CHEOPS; Benz et al. 2021) is an on-axis Ritchey-Chrétien telescope with a primary mirror with a diameter of 320 mm. CHEOPS is designed to operate nadir-locked in a Sun-synchronous orbit at an altitude of 700 km above the Earth’s surface. The exposures have a distinctive three-pointed point-spread function (PSF) due to the partial obscuration of the primary mirror by the secondary mirror and its three supports and because the telescope is intentionally defo-cused (Benz et al. 2021). The photometer operates in the visible and near-IR range (0.33 µm to 1.1 µm) using a back-illuminated charge-coupled device (CCD) detector.
CHEOPS performed 29 photometric visits of 55 Cnc between 23 March 2020 and 26 February 2022, each visit observing at least one orbital period of planet e. The duration of each visit ranged between 25 and 40 h. Each frame had an exposure time of 44.2 s obtained by stacking 20 individual readout of 2.2 s. The observation log is given in Table 1. The first visit was analysed by Morris et al. (2021). Before stacking, small images (called imagettes) of 30 pixels in radius were extracted that contain the PSF of the target star. For each individual frame (referred to as subarray), 10 imagettes were downlinked. The observations were reduced with the data reduction pipeline (DRP; Hoyer et al. 2020). Complementary to the DRP, PIPE (Brandeker et al., in prep.; see also descriptions in Brandeker et al. 2022, Morris et al. 2021 and Szabó et al. 2021) is a photometry-extraction Python package that uses PSF photometry on the 30-pixel imagettes. The results using the subarrays and imagettes are consistent, and thus we chose to use the subarray dataset in this work for computational efficiency.
To prepare our data, we first discarded all observations flagged by PIPE (caused by cosmic rays, contamination from a satellite passing through the field of view, or passage above the South Atlantic Anomaly (SAA); Brandeker et al. 2022). We normalised the flux by dividing all measurements by their median value and removed all points above 3σ and below 6σ from the median of the absolute deviations. The observations that occur before and after Earth occultation often exhibit a significant offset of the star position on the CCD, which is caused by refraction of the light in the upper Earth atmosphere. Therefore, we masked out all measurements with centroids above 3.5σ away from the median centroid. Additionally, we removed high-background level above 4σ from the median. The background level usually increases before or after Earth occultation. We also determined whether light from the nearby star 53 Cnc might affect the flux measurements by leaking into the aperture. While 53 Cnc falls within the full frame of the CCD of 1024x1024 pixels, the 200-pixel aperture is not affected by leaking flux. The DRP report included in every CHEOPS observation file estimates a mean flux due to nearby stars of approximately 0.001% relative to the flux of the target and thus contributes negligibly to the light curves. The orbital configuration of CHEOPS means that its field of view (FOV) rotates. Any significant flux contamination would therefore be apparent on the CHEOPS orbit timescales of 100 min.
CHEOPS observation logs on 55 Cnc.
2.2 Detrending basis vectors
The spacecraft introduces several systematics to photometry. Previous works with CHEOPS datasets have corrected these trends via linear regression (e.g. Morris et al. 2021; Delrez et al. 2021; Jones et al. 2022), Gaussian process (e.g. Lendl et al. 2020; Bonfanti et al. 2021; Leleu et al. 2021; Deline et al. 2022), or a PSF detrending method (Parviainen et al. 2022; Wilson et al. 2022). The last method consists of determining vectors associated with changes in the PSF shape by conducting a principal component analysis (PCA) on the subarray images and selecting the vectors that contribute most for use in the light-curve model. For this work, we performed a correction via polynomial regression.
Because of the orbital configuration of CHEOPS, the field of view of the telescope rotates once per orbit. It is necessary to detrend the flux of the star against the roll angle to ensure that the rotating field of view does not introduce correlated noise. We implemented the effect of the roll angle as the following Fourier series (Deline et al. 2022):
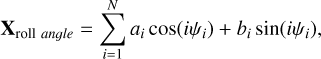 (1)
(1)
where ψ is the roll angle, and ai and bi are the best-fit weights of the roll angle components to the polynomial fit. We limited the series up to fourth order (N = 4).
A strong increase or decrease in flux at the beginning of a visit has been observed in many datasets, the so-called “ramp effect”. This is presumably caused by the change in pointing orientation from one target to the next and is related to the temperature of the spacecraft recorded by the thermistor readout called ThermFront 2. We added a linear term of this thermistor readout as a basis vector to detrend the flux. For some visits, as detailed in the next paragraph, we deemed it necessary to add a quadratic term of ThermFront 2.
Morris et al. (2021) performed an exhaustive search through different combinations of basis vectors that are correlated with the flux of 55 Cnc and concluded that the combination of the cosine and sine of the roll angle, a unit vector representing the normalised stellar flux and the ThermFront 2 thermistor readout, are the best set for their study. We also performed a statistical comparison based on the Bayesian information criterion (BIC; Schwarz 1978) for different combinations of basis vectors in a first fit with a linear regression. The reason for using the BIC and not another more robust information criterion is computational efficiency because the fit was only preliminary for the selection of the basis vectors. By definition, the BIC gives a larger penalty per parameter for large datasets and thus favours simpler models (Gelman et al. 2014). For our current purpose, it suffices. We considered the same set of basis vectors as Morris et al. (2021) for all visits. In addition to these vectors, we included the background level, quadratic terms of time and thermistor readout, and harmonics of the cosine and sine of the roll angle of Eq. (1) when the BIC favoured the selection (∆BIC>10). The set of basis vectors used in each visit is listed in Table A.1. We constructed an independent design matrix X for each visit with the selected basis vectors. The basis vector coefficients β were obtained via polynomial regression and were stored for a later stage. The uncertainties σβ on the coefficients were obtained from the covariance matrix.
2.3 Phase-curve model
We modelled the flux variation as a sum of terms,
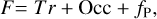 (2)
(2)
where Tr is the transit model, Occ is the occultation model, and fP is the phase-curve model. The transit model was based on Mandel & Agol (2002), implemented in the exoplanet Python package (Foreman-Mackey et al. 2021). The occultation function was implemented in exoplanet as an eclipse model without limb darkening. To perform a statistical model comparison, we used multiple functional forms for fP. First, we modelled the variation in out-of-transit flux with a simple sinusoidal function with a period matching the orbital period of planet e,
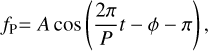 (3)
(3)
where P is the planetary orbital period, and A and ϕ are the phase-curve amplitude and offset, respectively. We define the orbital phase on [−π, π], where ϕ = π is at the time of mid-transit and ϕ = 0 is the occultation. A strong sinusoidal modulation of the flux of 55 Cnc phased with the orbital period of planet e was reported by Winn et al. (2011) and more recently by Sulis et al. (2019). Further studies also used a sinusoidal function, among other models (Demory et al. 2016; Morris et al. 2021).
We also considered a phase function based on the assumption that the planet is a Lambertian sphere that scatters isotropically or emits thermally, defined as
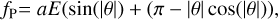 (4)
(4)
with a the amplitude, E the occultation function, and θ the orbital phase. This phase function has no phase offset by construction.
Hu et al. (2015) presented a semi-analytical model1 for planets in a circular orbit with asymmetric phase variations. This piecewise-Lambertian sphere is suitable for phase-curve observations in the optical range, constructed with significant reflection or emission between two longitudes. This model adds two parameters corresponding to the longitudes ξ1 and ξ2. Local longitudes ranging between these values have a lower reflectivity than other longitudes on the planet. Our last functional form for the phase curve is a flat line outside of transit and occultation, which implies a constant baseline flux. We tried two variations of a constant continuum, one fitting for the occultation depth, and another assuming an occultation depth fixed to zero.
Each CHEOPS visit was analysed individually. Based on previous studies (Nelson et al. 2014; Demory et al. 2016; Bourrier et al. 2018a; Tamburo et al. 2018), we assumed a circular orbit. We further assumed a quadratic limb-darkening law, where the priors on the coefficients specific to the CHEOPS transmission were retrieved from tables containing computed values by Claret (2021) using the ATLAS (Castelli & Kurucz 2003) and PHOENIX stellar models (Husser et al. 2013). For 55 Cnc A, we used a PHOENIX stellar model with an effective temperature of 5200 K and surface gravity log(ɡ) = 4.5 (von Braun et al. 2011). In our model, we fitted for the time of the mid-transit t0, the impact parameter b, the quadratic limb-darkening coefficients u0 and u1 the planet-to-star radius ratio Rp/R⋆, the occultation depth δocc, the phase-curve parameters, and the best-fit estimators of the basis vectors selected in Sect. 2.2 and presented in Table A.1. To deal with the systematics, we implemented a hierarchical model (also known as multilevel model; Yao et al. 2022; McElreath 2016), where the parameters themselves are described by parameters called hyperparameters. In particular, the mean µH and σH are distributions instead of a fixed numerical value. The priors on µH use the information of the polynomial regression made previously, while σH is an exponential distribution. The use of hierarchical models allows for an efficient estimate of the uncertainties in the basis vector coefficients, thus avoiding arbitrary scaling of the covariance matrix uncertainties from the polynomial regression. In Table 2 we list detailed information about the priors we used. The transit depth was obtained by two different formulations: As the planet-to-star radius ratio squared and for a given stellar limb-darkening law and impact parameter, we implemented the analytic solutions from Heller (2019). In our model, the occultation depth parameter was free to explore negative values as well. We set Gaussian priors on the stellar radius and mass based on von Braun et al. (2011). The model was implemented in a Markov chain Monte Carlo (MCMC) using the no u-turn sampler (NUTS; Hoffman & Gelman 2011), a variant of Hamiltonian Monte Carlo. We sampled the posterior distributions for the parameters with the probabilistic programming package PyMC3 (Salvatier et al. 2016), with 32000 draws and 4000 burn-in iterations. After each run, we checked that the chains were well mixed and that the Gelman-Rubin statistic was below 1.01 for all parameters (Gelman & Rubin 1992).
Parameters in the MCMC.
3 Results
We present the results assuming a sinusoidal shape for the phase curve based on the fact that this model is preferred in most visits (see Sect. 3.5 for details). The detrended flux and samples of the fitted phase-curve model for every CHEOPS visit are shown in a gallery in Fig. 1, while Table 3 presents the best-fit values of the phase-curve parameters with 1σ uncertainty and the residual root mean square (RMS) of each visit. The overlapping phase-curve model and confidence interval in Fig. 1 exhibit sharp curves in the transit and spikes due to stitching between the gaps. Appendix B presents the residual flux.
3.1 Transit and occultation depth
The transit depth across visits, shown in Fig. 2, agree within 3σ with a mean transit depth of 348 ppm, except for visits 8, 18, and 29. Visual inspection of the residuals of these visits reveals trends that remain in the data, especially in visit 18, which exhibits a strong trend out of transit. In general, these visits are noisier than others, as indicated by the residual RMS. The moderate evidence of variability in the transit depth agrees with Demory et al. (2015), Bourrier et al. (2018a), Tamburo et al. (2018), Sulis et al. (2019), and Meier Valdés et al. (2022).
The occultation depth (Fig. 3) varies by more than 3σ in some visits, notably visits 5, 10, 24, and 28. The best-fit occultation depth is negative in many cases, which lacks physical meaning. There seems to be a temporal correlation in the trend between the transit depth and occultation depth, which is especially clear in the first six visits. It is possible that fitting each visit independently for the orbital parameters, such as the impact parameter or mid-transit time, causes this trend. Our results are consistent with those in Demory et al. (2023), who used the same CHEOPS dataset. In Appendix C we present plots of the relation between relevant phase-curve parameters.
Best-fit phase-curve parameters and residual RMS.
3.2 Amplitude
The phase-curve amplitude initially observed by Morris et al. (2021) is seen in most of the CHEOPS visits, but the magnitude changes. The highest modulation was observed during the first visit. For visits 8, 9, 19, 21, 23, 24, 25, 28, and 29, the amplitude is consistent with zero at 2σ significance. The difference between the lowest and highest phase-curve amplitude is 48 ppm. The phase-curve amplitude for each visit is displayed in Fig. 4. A weak correlation between the phase-curve amplitude and both the transit and occultation depth is observed (see Figs. C.2 and Figs. C.4), which likely arises from the model construction. As in Morris et al. (2021), we do not assume that the origin of the sinusoidal signal in the flux is planetary. As a consequence, the sinusoidal signal can alter the flux level before and after a transit or occultation.
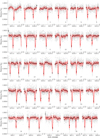 |
Fig. 1 Detrended photometry of 55 Cnc e for every visit. The detrended flux is plotted in grey, the best-fit phase-curve model in red, and the 1σ uncertainty from the posterior distribution in shaded light red. The black squares represent the binned data per CHEOPS orbit. The integer close to the bottom right corner of each panel indicates the number of the CHEOPS visit (see Table 1). |
 |
Fig. 2 Transit depth in ppm for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
 |
Fig. 3 Occultation depth for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
3.3 Phase offset
Our observations reveal a changing phase offset for the visits that varies over the complete phase parameter space. The phase offset for each visit is shown in Fig. 5. The small phase-curve amplitude and the huge uncertainty in the offset are related, as shown in Fig. C.6. If a sinusoidal function has a small amplitude, it converges in practice to a straight line, and any point is good as the peak of a sinusoid. This is the case for visits 8, 23, 24, and 28.
The best-fit median phase offset of visits 5, 6, 12, 13, 17, 19, 21, and 25 shifts the phase peak close to the transit. This has two possible ramifications: Either the sinusoidal function, which has no physical interpretation, is a poor fit to the data, or an astro-physical event occurred during these visits that caused an excess flux during transit. If the phase offset originates at the planet, then a maximum of reflected light on the night-side would be implied if the best-fit values peaked during transit or close to it. While analysing the wide uncertainty in visits 19 and 25, we realised that the reason for is that the ingress and egress of the transit were not observed by CHEOPS. As a consequence, the mid-transit time parameter has a bimodal distribution. The same phenomenon is observed in visits 9 and 24, although in these cases, the phase peak is not close to the transit. In Appendix D we show the joint posterior distributions of a CHEOPS visit that covered the transit ingress and egress and a visit where these events could not be observed. The sinusoidal model is statistically preferred over physically motivated models (Sect. 3.5) in most CHEOPS visits. This suggests that it is not a poor fit to the data.
 |
Fig. 4 Phase-curve amplitude for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
 |
Fig. 5 Phase-curve offset for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
3.4 Consecutive CHEOPS visits
Some visits were scheduled to start immediately after a previous observation of 55 Cnc had ended. These continuous visits provide useful information on the phase-curve change and its rimescale. The consecutive visits are numbers 3 and 4, 5 and 6, 8 and 9, 10 and 11, 12 and 13, and 24 to 27. We compare consecutive visits by overplotting the posterior distributions of the transit depth, occultation depth, phase-curve amplitude, and offset to properly estimate the significance between each parameter and their joint correlations. Figure 6 shows the posterior distribution functions of phase-curve parameters and joint correlation plots of visits 3 and 4. The values of the transit depth differ at 1.9σ between visits 3 and 4, and the significance is at 2.9σ between visits 26 and 27. For the rest of the visit pairs, the difference is below 1.6σ. The occultation depth varies over 3σ between visits 3 and 4. The strong variability in the occultation depth between visits 3 and 4 is shown in the top left panel in Fig. 6, where the two posterior distributions barely overlap. The occultation depth varies significantly at 4.6σ between visits 10 and 11 and at 3σ between visits 24 and 25. The rest of the visit pairs show a difference below 2σ. The phase-curve amplitude differs at 1.9σ and 2σ between visits 3 and 4 and between visits 10 and 11, respectively. The sequential increase in amplitude from visits 25 to 27 exceeds 2.5σ from one visit to the next. Other pairs are consistent below 1.5σ. Finally, the phase offset exhibits change over 3σ between visits 8 and 9, 25 to 27, and between 26 and 27. Incidentally, the joint correlation plots show no significant correlation between the transit depth and phase-curve amplitude. There is low evidence of a variable transit depth and phase-curve amplitude between consecutive visits, but the occultation depth and phase offset vary significantly over 3σ in some cases. The 2D posterior distribution correlation plot between the phase-curve amplitude and offset (third panel in Fig. 6 at the bottom from left to right) does not overlap at the 3σ level, revealing an overall phase-curve change due to the joint change in amplitude and offset between visits 3 and 4. The same is true for visits 8 and 9, 25 and 26, and 26 and 27. Because a CHEOPS visit of 55 Cnc e lasts approximately 1.5 orbital periods, we conclude that the joint change in the parameters describing the phase curve occurs on the order of the planetary orbital timescale or approximately on the order of a day.
 |
Fig. 6 Posterior distributions and joint correlations plot for visit 3 in blue and visit 4 in red. δt stands for the transit depth, δocc is the occultation depth, and the amplitude and offset refer to the phase-curve amplitude and offset, respectively. |
3.5 Model comparison
The considered models for the phase curve were compared using the leave-one-out (LOO) cross-validation (Vehtari et al. 2016), which is a method for estimating the pointwise out-of-sample prediction accuracy from a Bayesian model. The LOO is similar to the widely applicable information criterion (WAIC), but it is more robust when the observations contain weak priors or sensitive outliers, at the cost of being computationally more expensive. It consists essentially of estimating the relative likelihood for one model to be preferred over other models in a set using the posterior samples of the MCMC.
The top-ranked model has the lowest LOO value. The higher the difference in the LOO between models, the better the top-ranked model. In practice, the threshold of ∆LOO to consider a model significantly better than others is subjective and debated (McElreath 2016), but it is common convention to consider a model significantly better if the ∆LOO to the second-ranked model is greater than 10. Another relevant parameter in the model comparison is the statistical weight, which can be interpreted as an estimate of the probability that the model will make the best predictions on future data among the considered models. The values range between 0 and 1, and the sum of the weights for a set of models is equal to 1.
Because we considered five phase-curve models for a total of 29 CHEOPS visits, we present the information of the model comparison summarised in Fig. 7. The y-axis represents the CHEOPS visits, where each row depicts the model comparison for a specific visit. Each marker represents a phase-curve model, as indicated in the legend in Fig. 7. The x-axis shows the LOO relative to the top-ranked model. Thus, the top-ranked model appears leftmost in the plot with ∆LOO = 0. The error bars are the standard error of the difference in the expected log-predictive density between each model and the top-ranked model. Complementary to the figure, Table E.1 reports the statistical weight of the top-ranked model.
The simple sinusoidal modulation of the phase curve is preferred in 18 out of 29 visits, while the flat phase curve is favoured by the LOO in 6 visits. A flat phase curve without occultation is ranked best in 4 visits. The piecewise-Lambertian is preferred only in visit 22. It is worth mentioning that for the cases when a flat phase curve is preferred by the LOO, the rest of the models follow close behind. To elaborate further, in visits 8, 9, 11, 21, 23, and 25, the difference in the LOO between the best and worst model is below 5. However, the flat model takes most of the statistical weight in visits 8, 9, and 23. The best-fit results of the sinusoidal model show that the amplitude for the above-mentioned visits is consistent with zero within 2σ. The small difference between the models reported by the LOO can be explained by the fact that at small amplitudes, the functions converge to a flat line. Visit 4 stands out due to its low amplitude, but it nonetheless slightly favours the sinusoidal model by the LOO. A flat phase curve without occultation is favoured in visit 28, even though the occultation depth is significant. This is even one of the deepest occultations of the dataset. While the piecewise-Lambertian is preferred only in visit 22, there is no strong indication that the observations are described best by a planet with an asymmetric albedo.
3.6 Thermal emission
We estimated the thermal contribution in the CHEOPS bandpass by retrieving a theoretical stellar spectrum from the PHOENIX stellar model (Husser et al. 2013) with an effective temperature of 5200 K, surface gravity log(ɡ) = 4.5 (von Braun et al. 2011), and a planet temperature of 2697 ± 270 K, which is the maximum hemisphere-averaged temperature measured by Demory et al. (2016) with Spitzer observations. When the uncertainty in the brightness temperature is taken into account, the thermal contribution in the CHEOPS bandpass ranges between 3 and 11 ppm.
 |
Fig. 7 Model comparison based on the LOO criterion. The best-ranked model has a ∆LOO of zero. The x-axis shows the difference in the LOO for the models considered in each visit (y-axis). The error bars represent the standard error of the difference in the expected log-predictive density between each model and the top-ranked model. By definition, the standard error of the top-ranked model is zero. In visit 1, the ∆LOO to the second-ranked model is above 50 and thus is not visible in the plot. The red diamond represents a sinusoidal phase curve, the green cross is the piecewise-Lambertian model, the cyan hexagon is the Lambertian sphere, the orange star is a flat baseline without an eclipse, and the violet circle is a flat baseline with the eclipse as a free parameter. |
4 Discussion
The CHEOPS observations of 55 Cnc e present a puzzling case. The phase-curve amplitude and phase offset change from one visit to the next by up to 50 ppm and span a wide range of offset angles. Consecutive visits reveal changes on the timescale of at least the orbital period.
When we attribute the mechanism that causes this to activity of some sort, then the change between high and low phase-curve amplitude can be ascribed to periods of activity and inactivity, depending on the nature of the mechanism (Sulis et al. 2019). A sufficiently strong grey absorber could obscure the dayside enough to produce a flat phase-curve signal and might produce flux variation due to scattering (Tamburo et al. 2018).
When the process behind the change in the phase-curve amplitude and offset of the signal comes from the planet or is bounded in its vicinity, then we would expect the occultation depth to be approximately twice the phase-curve amplitude. Most visits do not satisfy 2A ≈ δocc. Additionally, the sinusoidal model infers a phase offset close to the transit or during transit for some visits. It is hard to conceal an event on the night-side of the planet to cause a stronger signal than at any other orbital phase. Thus, the origin of the variable signal is probably not at the planet.
4.1 Power spectrum
We characterised the periodic signals in the residuals with a Lomb-Scargle periodogram (see VanderPlas 2018 for a review). In Fig. 8, the blue points are unprocessed flux measurements, and the darker blue curve shows the binned data. Similarly, the red points represent the power of residual data, while the darker red curve shows the binned data. The residuals consist of the CHEOPS observations after removing systematics, transit, occultation, and phase-curve model. We identified the corresponding frequency of the known periodicities such as the orbital period of planet e and the CHEOPS orbital period. Because a single CHEOPS visit of 27 h translates into approximately 10 µHz, we did not consider frequencies below this value. The power spectrum searches for periodicities in the time-series observations. Periodic signals can only be measured reliably for periods shorter than the visit duration (Martins et al. 2020).
In the residuals, no strong signals remain at the orbital period of the planet. The power at the CHEOPS orbital period also shows an absence of power. However, the Lomb-Scargle periodogram in Fig. 8 exhibits strong peaks at higher-order harmonics of the CHEOPS orbital period at frequencies starting around 1000 µHz. This can be indicative of an improper removal of systematic noise induced by the spacecraft. To analyse this in depth, we performed tests on simulated data.
We constructed 29 sets, each one consisting of 2000 points with an observing efficiency of 56% (see Table 1), lasting for 1.5 orbital periods. The gaps of 100 min in the dataset simulate the CHEOPS occultation caused by Earth. Between two consecutive sets, which represent CHEOPS visits, we added gaps of random durations. The points were randomly drawn from a normal distribution representing white noise on a level comparable to the real CHEOPS observations. In addition, we added correlated noise with a ID Gaussian filter with a period that matched the stellar rotation period of 38.8 days (Bourrier et al. 2018a). The resulting power spectra show peaks at a frequency corresponding to the 100-min duration of the gaps due to the CHEOPS orbital configuration and its higher harmonics. The peaks in our residuals might therefore be explained by the CHEOPS orbital configuration and do not necessarily imply an insufficient systematics detrending. Moreover, the absence of power in the periodogram at the CHEOPS orbital period shows that there are no strong signals at this frequency in the residuals.
Another source of time-correlated astrophysical noise that we expect in the power spectrum is stellar granulation of the host 55 Cnc, which occurs at multiple time and length scales (Rast 2003). A granulation phenomenon called supergranulation has a characteristic timescale similar to the orbital period of 55 Cnc e, and this could give rise to the apparent phase variations that change in amplitude and phase over time. It is difficult to reliably measure the excess power on the supergranulation timescale with these CHEOPS observations because the duration of each visit in this work is about one granulation timescale. Future observations with longer visit durations, or theoretical advances in modeling the long-timescale granulation phenomenon, can address this hypothesis.
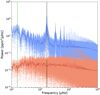 |
Fig. 8 Power spectrum computed with the Lomb-Scargle technique as a function of frequency. The blue dots show raw flux measurements of all CHEOPS visits, while the red dots represent the detrended flux after the phase-curve model was removed. The dark blue and dark red curves represent the binned data. The dashed green vertical line corresponds to the orbital period of 55 Cnc e, and the vertical dashed black line corresponds to the CHEOPS orbital period of 101 min. |
 |
Fig. 9 Phase-curve amplitude of every CHEOPS visit phase-folded at the best-fit period of 51.9 days. The sinusoidal function is overplotted in red. |
4.2 Phase-curve amplitude variability
Motivated by the 47.3-day periodicity in the occultation depth of 55 Cnc e found by Demory et al. (2023), we investigated the putative variability timescale of the phase-curve amplitude. Similar to Tamburo et al. (2018) and Demory et al. (2023), we constructed three different models to reproduce the amplitude as a function of time. The first model consists of a flat line. The second model is a linear function, where the free parameters are the slope and intercept. The last model is a sine function of the form A sin(2πt/P + В) + С, where t is BJD time, and P is the variability period. The caveat of this analysis is that there is no precise timing associated with the amplitude of the phase, in contrast to the precise mid-eclipse time used in Demory et al. (2023). As an approximation, we used the mean BJD time of each CHEOPS visit. The periodogram of the amplitude of each CHEOPS visit shows a maximum peak at 52.25 days. This peak has no dominant power compared to other peaks, and thus, we used the maximum value only as a reference to set a uniform prior between 40 and 70 days. We fitted our models in an MCMC routine. The sine function is favoured by the LOO because it carries all the statistical weight, and with a ΔLOO = 11 to the linear function, ranked second. The flat line is ranked last, with ΔLOO = 14. We find a period of 51.9 + 1.4 days, A = 11.1 + 2.3 ppm, В = 73.85 + 21.84 degrees, and С = 16.2 + 1.6 ppm. The amplitudes of each visit are phase-folded at the best-fit period and are shown in Fig. 9. From the best-fit sinusoidal model, we infer an estimate reference timing of the local maximum at 2458934.98 BJD.
The period is similar to the 47.3-day periodicity on the occultation depth (Demory et al. 2023). At the present time, it is unclear whether the periodicity in the occultation depth in Demory et al. (2023) and in the phase-curve amplitude are related. The 51.9-day period is absent from the power spectrum of the CHEOPS residuals (Fig. 8). The rotation period of the star of 38.8 days from combined photometry and spectroscopy (Bourrier et al. 2018a) and 42.7 from photometry (Fischer et al. 2008) appear close to the 51.9-day period. We also note that the orbital period of the non-transiting planet c is 44.4 days. An approximate computation of the reflected light that planet c could contribute yields a maximum value of 2.7 ppm. For this estimate, we assumed no thermal emission and a geometric albedo of unity to obtain an upper limit. Because planet c is not transiting and its inclination is unknown, RV measurements (Bourrier et al. 2018a) estimate a mass comparable to the mass of Saturn, and thus, we used the nominal radius of Saturn for the calculation. The estimated reflected light that could leak into the field of view of CHEOPS is too low to match the 11 ppm amplitude found in the periodic signal of the phase-curve amplitude, and it is thus unlikely to be the sole cause for the signal. The origin of our 51.9-day signal is unknown.
Identified flux drops in the observations and their estimated depth.
4.3 Observed flux dips
Visual inspection of the detrended flux and bins in Fig. 1 reveals a decrease in flux, so-called dips, outside of the transit and occultation of 55 Cnc e. The most conspicuous dip is found in visit 17 after the second occultation, approximately at BJD time 2459251.98. Other identified dips occur during visits 26, 27, and 28 at BJD time 2459595.3, 2459595.95, and 2459630.28, respectively. In Table 4, we summarise the identified dips with an estimated time of the event and depth.
Another interesting case is visit 10, where the residuals in Fig. B.1 show three small dips that occur roughly every 0.5 days at approximately BJD time 2459229.1, 2459229.59, and 2459230. However, inspection of the power spectrum on the complete dataset of the residuals does not reveal a significant periodicity at 0.5 days (the corresponding frequency of 23.1 µHz).
We checked whether another planet in addition to planet e might be transiting during the CHEOPS visits. 55 Cnc A is known to host five planets, of which planet e is the only transiting planet. We used the ephemeris of the remaining planets in Table 3 of Bourrier et al. (2018a) to compute predicted transit times. Only during visit 4 did a predicted possible transit of planet b coincide with the observing time. Phase-folding of the observations provided no hint of a transit, and running an MCMC searching for the planet was negative. The dips are not related to a transit or occultation of planets b, c, d, or f. After carefully inspecting the dips and each frame of the corresponding visit, we note that the dip durations coincide exactly with the duration of a CHEOPS orbit. We therefore suspect that they are systematic.
Based on the analysis of the observations on the phase-curve, we discuss possible mechanisms that might have caused the phase-curve amplitude and shift variability. Previous research suggested that refractory material (Tamburo et al. 2018) or an inhomogeneous circumstellar dust torus (Demory et al. 2015; Sulis et al. 2019; Morris et al. 2021) might explain the observations, as might volcanic activity (Demory et al. 2015) or star-planet interaction (Demory et al. 2015; Sulis et al. 2019; Folsom et al. 2020; Morris et al. 2021).
4.4 Dust in the environment of 55 Cnc e
In the following sections, we build a toy model to study dust in the orbital environment of 55 Cnc e. First, we estimate the required material to obscure the stellar light by an arbitrary fraction. Then we constrain the composition of the material by estimating its characteristic sublimation timescale and comparing this to the variability timescales in the data. Finally, we compute the motion of the dust in the system after it escapes the planet to determine whether the ejected material could form a circumstellar torus.
Because of the uncertainty on the composition and interior of the planet, we consider characteristic species for a rocky planet and lava worlds: silicon monoxide, fayalite (iron-rich end-member2 of olivine), enstatite (an end-member of pyroxene), forsterite (magnesium-rich end-member of olivine), α-quartz and amorphous quartz, corundum, silicon carbide, and graphite. The silicates pyroxene and olivine are expected in rocky exoplan-ets because they predominate in Earth’s mantle (Perez-Becker & Chiang 2013). α-quartz refers to quartz with a trigonal structure, which is a crystalline unit that looks like an oblique cube whose angles in the corners are equal, but not rectangular. Table 5 lists the selected species.
4.4.1 Estimated mass loss
The amplitude change in the phase curve reveals a maximum difference of approximately 50 ppm, as shown in Fig. 4. We investigated the estimated amount of material required to produce a 50 ppm change in flux. For the purpose of this computation, we assumed instead of considering material causing variation out of transit that the material composed of grey absorbing grains transited the star. We determined the material that is required to obscure the star by 50 ppm.
Following Perez-Becker & Chiang (2013), we first computed the total mass required to absorb or scatter a certain fraction f of the starlight. We assumed that the dust is optically thin (otherwise, the surface of the planet would cool down enough so that the material would not be produced in the first place Rappaport et al. 2012). We let the dust cover an area A of the stellar disk 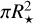 and have an optical depth
and have an optical depth 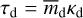 , where the subscript d represents the dust,
, where the subscript d represents the dust, 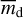 is the grain mass per unit area, and κd is the opacity. Then the fraction of starlight is given by
is the grain mass per unit area, and κd is the opacity. Then the fraction of starlight is given by
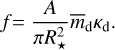 (5)
(5)
When we consider the grains to be spherical with radii s and internal density ρint, the opacity is given as
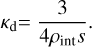 (6)
(6)
The total mass in dust covering the star is given as a function of the grain mass per unit area 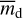 and total covered area A as
and total covered area A as
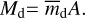 (7)
(7)
Substituting Eq. (6) into Eq. (5), solving for 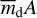 , and substituting into Eq. (7), we obtain a total mass of
, and substituting into Eq. (7), we obtain a total mass of
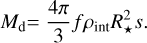 (8)
(8)
To obtain a numerical estimate, we first took possible grain sizes into account that are opaque in the CHEOPS bandpass and transparent in the Spitzer bandpass (Morris et al. 2021), resulting in a plausible range of particle radii 0.1 ≤ s ≤ 0.7 µm. The grain density was chosen to be 3 g cm−3, similar to the density of forsterite and enstatite. The radius of the star was R⋆ = 0.94 R⊙. For a fraction of obscured starlight of f = 50 ppm, we estimate a mass between 2.7 × 109 and 1.88 × 1011 kg. Finally, the mass-loss rate was estimated by dividing by the planetary orbital period of 0.74 days, yielding a rate Ṁd between 1.33 × 1012 and 9.32 × 1013 kgyr−1.
To place this value in perspective, we compared it to the mass loss due to photoevaporation of the planetary atmosphere driven by the combined X-ray and extreme ultra-violet (EUV) flux from the host star, abbreviated as XUV. In this case, the mass-loss rate due to photoevaporation is (Rappaport et al. 2014)
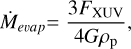 (9)
(9)
where FXUV is the XUV flux from the host star at the planet, ρp is the bulk density of the planet, and G is the gravitational constant. The estimate was made without an assumption on the planetary atmosphere. Sanz-Forcada et al. (2011) collected X-ray luminosities for 82 stars and inferred EUV luminosities using coronal models. The star 55 Cnc A has available X-ray observations. The XUV flux at 55 Cnc e is 870.96 erg s−1 cm−2 (see Table 6 of Sanz-Forcada et al. 2011). Using appropriate parameters for the bulk density of 55 Cnc e (Bourrier et al. 2018a), we obtain a mass-flux rate due to photoevaporation of 4.64 × 1013 kg yr−1.
Our estimated mass loss due to the amount of material obscuring the star is comparable to the mass-loss rate due to photoevaporation, which suggests that the amount of material required to cause a 50 ppm change is plausible. However, photoevaporation is not the only mechanism leading to atmospheric escape. Tidally driven volcanism, as well as Jeans escape (Oza et al. 2019) and plasma-driven atmospheric sputtering feeding a plasma torus, are mass-loss processes that could occur on a super-Earth (Gebek & Oza 2020). The main challenge for the required mass to escape the planet is the high escape velocity of approximately 24 km s−1. However, violent plumes such as those observed in Io (Jessup & Spencer 2012) could provide the material to the circumstellar environment. The plume speeds in Io are approximately 0.5 km s−1 (Lellouch et al. 1996), which is lower than the Io escape velocity of 2.6 km s−1. Even so, plume material escapes the atmosphere with the aid of additional mechanisms such as sputtering by charged particles (Geissler & Goldstein 2007). A complex model combining different mass-loss processes is required to determine whether the amount of material can reach the escape velocity.
4.4.2 Characteristic sublimation timescales
Due to the close-in orbit of 55 Cnc e and its likely tidally locked configuration, the silicates vaporise at the day-side surface temperature of ~2700 K (Demory et al. 2016) and form an atmosphere whose equilibrium vapour pressure is given by the Clausius-Clapeyron equation,
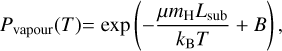 (10)
(10)
where µ is the molecular mass of gas released from dust due to sublimation, mH is the atomic mass unit (Kimura et al. 2002), Lsub is the latent heat of sublimation, kB is Boltzmann’s constant, and B is a constant composition-dependent sublimation parameter. We express Eq. (10) as
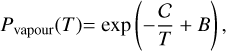 (11)
(11)
The sublimation parameters for the selected species are shown in Table 5.
The mass-loss rate of dust particles due to sublimation is given by (Kimura et al. 2002)
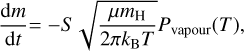 (13)
(13)
where S is the surface area of the aggregate particle. We assumed that a dust grain is composed of N identical spheres with radius s, so that S = 4πNs2.
We calculated the equilibrium temperature T of the dust in local thermodynamic equilibrium through an energy balance between the absorption rate of stellar radiation and the thermal emission and energy loss through sublimation (Gail & Sedlmayr 2013),
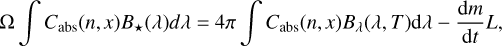 (14)
(14)
where B⋆(λ) is the solar radiance, and Bλ(λ, T) is the Planck function of the dust (Kimura et al. 2002). The solid angle subtended by the star at a distance r is given by
![$ {\rm{\Omega = 2}}\pi \left[ {1 - \sqrt {1 - {{\left( {{{{R_ \star }} \over r}} \right)}^2}} } \right]. $](/articles/aa/full_html/2023/09/aa46050-23/aa46050-23-eq78.png) (15)
(15)
The absorption cross sections Cabs in Eq. (14) depend on the complex refractive index n, the size parameter x = 2πs/λ, and the structure of the particle. These cross sections were computed using the Mie theory. We used the program LX-MIE (Kitzmann & Heng 2018) to retrieve the absorption cross sections for each species listed in Table 5 for dust radii 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, and 0.7 µm and for a wide discrete range of wavelength values available in the LX-MIE collection. This narrow range of particle sizes satisfies the conditions of being opaque in the optical (Morris et al. 2021), but transparent in the IR (Demory et al. 2015). The dataset of LX-MIE contains optical properties of 32 condensates (see Table 1 of Kitzmann & Heng 2018 for more details). The equilibrium temperature for each grain size was pretabulated according to Eq. (14).
Finally, after the temperature of the grains reached a state of equilibrium, the characteristic timescales for sublimation were estimated. For this purpose, we considered the grain mass as a function of its density and volumen of spheres. Taking the first derivative, we obtain
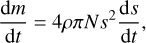 (16)
(16)
and rewriting Eq. (13) results in
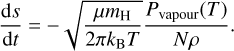 (17)
(17)
The advantage of Eq. (17) is that it relates the grain radii and time explicitly. The right-hand side of the equation only depends on the temperature and properties of the grain. After tabulating all relevant values, we solved the differential equation numerically to estimate the required time for a dust grain of a given size to sublimate. We integrated numerically using a trapezoidal method for an initial grain radius until it reached a threshold value of s = 0.001 µm.
For a single sphere (N = 1), the characteristic sublimation timescale of the selected species is shown in Table 6. Silicates made of pyroxene, olivine, and fayalite survive less than a minute. Silicon monoxide and corundum have an even shorter sublimation timescale on the order of a second. An α-quartz grain remains in the environment for up to approximately 11 h before sublimating, while for amorphous quartz, the sublimation time is around 2 h. Silicon carbide has a survival time between 4 and h. The range of characteristic sublimation timescales of graphite spans a wide range of values for different grain radii, translating into sublimation times of between 4 s and up to 46 h. Because the phase variation of 55 Cnc e is observed at least on the orbital timescale of around 17. h, most of the species for the radius range sublimate long before they would be able to produce the phase-curve variability. Only graphite and α-quartz between 0.3 and 0. µm, as well as a 0. µm grain of silicon carbide, survive over multiple hours. Ultimately, larger grains composed of graphite and α-quartz have a sublimation time comparable to the orbital period of the planet. For an Earth-like mantle, the short sublimation lifetimes of pyroxene and olivine would require the planet to continuously supply material to the atmosphere to produce variability on the timescale of hours. Such a continuous replenishment of material to the circumstellar environment would result in comet-like tail shape in the transit, which has not been observed. Because the composition of the outgassed material is connected to the composition of the planetary mantle (Gaillard & Scaillet 2014), it seems unlikely that these elements originate from the planet and reach the circum-stellar environment or at least are abundant enough to cause the observed variability.
Sublimation parameters for the selected dust species (van Lieshout et al. 2014).
Characteristic sublimation timescales in seconds of a single dust grain of the selected species with radii between 0.1 and 0.7 µm.
4.4.3 Stellar radiation pressure
We considered the scenario of material that is ejected from the planet through, for example, explosive volcanism or high-altitude condensation (Mahapatra et al. 2017). As soon as the dust leaves the planet, it will be subject to radiation pressure by the star. The ratio of radiation pressure to gravity acting on a dust particle with mass md is given by (Kimura et al. 2002)3
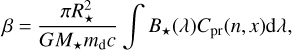 (18)
(18)
where M⋆ is the mass of the host star, с is the speed of light, and Срr(n, х) is the radiation pressure cross section, defined as Cpr = Cabs + (1 − ɡ0)Csca, with Cabs and Csca the absorption and scattering cross section, respectively; and ɡ0 is the scattering asymmetry parameter. The ɡ0 parameter describes how isotropic or anisotropic the scattering is. It is usually tabulated as a function of the wavelength and particle size. For ɡ0 = 0, light is scattered equally in all directions4. A positive value of the asymmetric parameter indicates forward scattering, while for a negative value, backscattering prevails. We computed these quantities with LX-MIE. By examining the output of LX-MIE, the asymmetry parameter in the CHEOPS bandpass for particle sizes between 0.1 and 0.7 µm shows that forward scattering dominates for all considered species in the shorter wavelengths. However, forward scattering is not dominant for the small grain sizes. For the smallest grains, the asymmetry parameter tends asymptotically to a symmetric phase function for longer wavelengths in the CHEOPS range.
A ratio of radiation pressure to gravity above 0.5 leads to an unbounded trajectory, while values below this threshold correspond to closed orbits. In the presence of radiation pressure and gravity, we can interpret the two opposing forces as an effective reduced gravitational field compared to the planet and defined as ɡeff = GM⋆(1 −β)/r2. Material in bounded orbits moves in a Keplerian ellipse with the periastron at the location where it was released. Conservation of energy and angular momentum between the grain and the planet provide information regarding the eccentricity and semi-major axis of the grain (Rappaport et al. 2014),
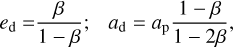 (19)
(19)
where ap is the semi-major axis of the planet. With Kepler’s third law, we then computed the period of a grain released by the planet and subject to radiation pressure.
We used Eq. (18) to estimate the ratio of radiation pressure to gravity for our range of grain radii and compositions. In Fig. 10, the ratio of radiation pressure to gravity for each considered species is shown. Grains with a ratio above 0.5 will be blown away, while grains below this ratio will orbit the star. The latter case is of particular interest because of the possibility of forming a circumstellar torus of dust. Most silicates within our size range move in a closed orbit, while graphite and silicon carbide grains smaller than 0.5 µm experience a radiation pressure that is too strong and are blown away. The same occurs to silicon carbide smaller than 0.4 µm.
For the grain radii that lead to a Keplerian orbit, we computed the eccentricity and semi-major axis using Eq. (19) to obtain the trajectory of a grain during its characteristic sublimation timescale after escaping the planet. A grain of a specific species and size with periastron at the location it escaped the planetary Hill sphere radius initially moves at the same speed as the planet (Rappaport et al. 2012). It is fair to assume this initial speed value because the ratio of the escape speed to the orbital speed is approximately 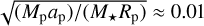 . A higher ratio of the radiation pressure to gravity leads to more eccentric and longer orbits. Figure 11 shows the motion of the dust during its characteristic sublimation lifetime. Based on the timescales, most species will stay bounded to the planet or follow closely behind, forming a comet-like tail. So far, there is no evidence of a comet-like transit shape in observations of 55 Cnc e. No asymmetry in the transit shape is observed in the CHEOPS observations, as shown in the phase-folded light curve in Fig. 12.
. A higher ratio of the radiation pressure to gravity leads to more eccentric and longer orbits. Figure 11 shows the motion of the dust during its characteristic sublimation lifetime. Based on the timescales, most species will stay bounded to the planet or follow closely behind, forming a comet-like tail. So far, there is no evidence of a comet-like transit shape in observations of 55 Cnc e. No asymmetry in the transit shape is observed in the CHEOPS observations, as shown in the phase-folded light curve in Fig. 12.
Graphite, α-quartz, and silicon carbide travel at least one-fourth of an entire orbit during their lifetime. Whilst the process of supplying material could be stochastic in nature, if the dust is replenished frequently enough, an inhomogeneous torus around the star could form. It would consist of regions that are more densely packed than others, and in theory, it would vary in opacity, producing measurable flux variation. While this could explain the variability in the phase-curve amplitude, it remains to be seen why this is not observed during transit. The material could be an inefficient forward-scatterer but might efficiently scatter at other angles. However, the asymmetry parameter of our considered species indicates that forward scattering mostly dominates in the CHEOPS bandpass for most of the grain sizes. If the ejecta of material occur during transit, the material would float close behind the planet and manifest in the transit shape as a less pronounced flux increase during egress and even after egress of the planet. It is possible that none of the CHEOPS visits coincided with an event like this during transit, which might explain why we did not see a comet-like transit shape (Rappaport et al. 2012) in the data. Even more, the fact that such a transit due to a comet-like tail is not observed suggests that the replenishment of material to the torus is not an uninterrupted process.
 |
Fig. 10 Ratio of radiation pressure to gravity β as a function of grain radius. The values below the horizontal dashed black line (β = 0.5) lead to closed orbits, while the values above the line lead to unbounded motion. |
 |
Fig. 11 Motion of dust for a selected composition subject to gravity and radiation pressure. The time interval of the trajectory is the characteristic sublimation timescale of the compound. The orange circle represents 55 Cnc A, and the dashed black circle is the orbit of 55 Cnc e scaled in units of stellar radius. The zoomed-in panel shows the trajectory of short-lived species. Different lines of the same colour represent different grain sizes of a species. |
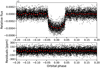 |
Fig. 12 Detrended flux measurements of 55 Cnc e, phase-folded at the planet orbital period. The top panel shows the relative flux, and the bottom panel presents the residuals in ppm. The plots show a portion of the phase centred around the transit. The red squares represent the binned data. |
4.5 Star-planet interactions
Magnetic star-planet interactions have been already considered in previous works as a possible origin of the chromospheric hot spots in 55 Cnc. Folsom et al. (2020) modelled the environment of 55 Cnc based on the magnetic field constrained by Zeeman-Doppler imaging carried out in 2017, and found that 55 Cnc e is extremely likely to orbit within the sub-Alfvénic region of the stellar wind. This implies that a direct magnetic connection can be established between planet e and 55 Cnc (Saur et al. 2013), channelling energy from the planet vicinity to the star along the magnetic topology of the stellar environment (Strugarek 2016). Morris et al. (2021) further considered this possibility and estimated the strongest power that could be associated with such an interaction (Zarka 2007) using the data from the wind model of Folsom et al. (2020). They found that any star-planet magnetic interaction signal could not exceed 10−10 L⋆. This optimistic estimate predicts a very low power and thus rules out any detectable magnetic star-planet interaction between 55 Cnc and 55 Cnc e.
In addition, the characteristics of the 55 Cnc system also allow us to rule out such a detection. Any magnetic star-planet interaction signal will be modulated by the orbital period of the planet and the rotation rate of the star that entrains its low corona (for an example for HD 189733, see Strugarek et al. 2022). 55 Cnc rotates in about 40 days (Henry et al. 2000; Fischer et al. 2008; Bourrier et al. 2018a), while the planet orbits in about 0.74 days. If the star possesses a large-scale magnetic topology similar to the topology it had in April 2017, that is, an inclined dipole (Folsom et al. 2020), the location of the origin of the signal would circulate around the magnetic poles of the star as the planet orbits. Because the star rotates more slowly than the orbital motion, the signal would be visible at all times (one magnetic pole would always face Earth) and should correlate with the orbital period of 55 Cnc e. In addition to this signal, radio emission from the hypothetical magnetosphere of 55 Cnc e would also be expected, again correlated with the orbital period of the planet (Turner et al. 2021). No such signals have been detected so far. We can therefore safely reject this hypothesis for 55 Cnc e.
Other types of star-planet interactions could nevertheless occur between the two bodies. Tidal interactions have also been proposed as a source of enhanced stellar activity (e.g. Cuntz et al. 2000; Lanza 2008). In the case of 55 Cnc, the low mass of planet e renders this scenario nevertheless implausible. The last type of star-planet interaction that could be acting in 55 Cnc would be the infall of escaping material from the planet atmosphere down to the stellar corona, producing a detectable signal (e.g. Matsakos et al. 2015). In this case, dedicated studies (beyond the scope of the present paper; e.g. Daley-Yates & Stevens 2019) are needed to assess both the energetics and the relative phase of such a signal.
5 Conclusions
CHEOPS observations reveal a changing phase curve at least on the orbital timescale of the planet. The phase modulation varies by up to 50 ppm. Additionally, we found a 51.9-day period of the time-dependent phase-curve amplitude of each CHEOPS visit. The origin of this is unknown. The fact that the peak of the phase curve for some visits occur during transit or close to transit rule out the planet as the source of the signal. The results motivated a deeper study on whether dust might be the cause. Our toy model allowed us to explore possible compositions of dust. The short lifetimes of some compounds such as pyroxene and olivine, whose abundance is expected to dominate at the surface of Earth-like exoplanets, mean that they are unlikely to cause a variability in the order of hours. Only a narrow range of dust sizes of graphite, silicon carbide, and quartz satisfy the required timescale. Additionally, only certain particle sizes of these species remain candidates to form a torus around the star, as suggested by past research. An argument against forming a circumstellar torus of dust is the escape velocity of approximately 24 km s−1 of the planet.
Previous research attributed the puzzling observations on 55 Cnc e to be caused by an individual phenomenon. Instead of searching for a single process, a complex model including dust dynamics, magnetohydrodynamics, and atmospheric radiative transfer should provide a self-consistent model of the planet. A model should take this into account to realistically model the motion of a grain and its influence on the observations and provide conclusive answers.
Recently, JWST observed 55 Cnc e in the framework of two accepted programs for Cycle 1. The first set of observations aims to study the possibility of a 3:2 spin-orbit resonance as an explanation for the variable occultation depth (Brandeker et al. 2021). The second program will characterise the atmosphere of 55 Cnc e via spectral features of H20, CO, C02, and SiO (Hu et al. 2021). These observations promise exciting new insights in the IR range. Moreover, simultaneous observations of CHEOPS and JWST, accompanied by other instruments such as a spectropolarimeter, would provide a unique opportunity for resolving the nature of this fascinating exoplanet.
Acknowledgements
We are grateful to the anonymous referee for the careful reading and thoughtful suggestions that improved this paper. He made the submission process an enjoyable experience. CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the United Kingdom. The CHEOPS Consortium would like to gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of this mission. EMV acknowledges support from the Centre for Space and Habitability (CSH). This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. EMV acknowledges the financial support of the SNSF. EMV thanks Beatriz Campos Estrada for insightful discussion on the sublimation timescales of dust in disintegrating exoplanets. B.-O.D. acknowledges support from the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number MB22.00046. ABr was supported by the SNSA. S.G.S. acknowledges support from FCT through FCT contract no. CEECIND/00826/2018 and POPH/FSE (EC). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project SPICE DUNE, grant agreement no. 947634). LBo, VNa, IPa, GPi, RRa, GSc, VSi, and TZi acknowledge support from CHEOPS ASI-INAF agreement no. 2019-29-HH.0. DJB acknowledges financial support from the CSH, University of Bern. ML acknowledges support of the Swiss National Science Foundation under grant number PCEFP2_194576. ASt acknowledges support from the PLATO/CNES grant at CEA/IRFU/DAp and the French Programme National de Planétologie (PNP). This work was supported by FCT - Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 - Programa Operacional Competitividade e Internacionalizacão by these grants: UID/FIS/04434/2019, UIDB/04434/2020, UIDP/04434/2020, PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113, PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953, PTDC/FIS-AST/28987/2017 & POCI-01-0145-FEDER-028987, O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. YAl acknowledges the support of the Swiss National Fund under grant 200020_172746. We acknowledge support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grants ESP2016-80435-C2-1-R, ESP2016-80435-C2-2-R, PGC2018-098153-B-C33, PGC2018-098153-B-C31, ESP2017-87676-C5-1-R, MDM-2017-0737 Unidad de Excelencia Maria de Maeztu-Centro de Astrobiología (INTA-CSIC), as well as the support of the Generalitat de Catalunya/CERCA programme. The MOC activities have been supported by the ESA contract no. 4000124370. S.C.C.B. acknowledges support from FCT through FCT contracts nr. IF/01312/2014/CP1215/CT0004. X.B., S.C., D.G., M.F. and J.L. acknowledge their role as ESA-appointed CHEOPS science team members. ACC acknowledges support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. This project was supported by the CNES. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation. L.D. is an F.R.S.-FNRS Postdoctoral Researcher. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project FOUR ACES. grant agreement no. 724427). It has also been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). DE acknowledges financial support from the Swiss National Science Foundation for project 200021_200726. M.F. and C.M.P. gratefully acknowledge the support of the Swedish National Space Agency (DNR 65/19, 174/18). DG gratefully acknowledges financial support from the CRT foundation under grant no. 2018.2323 “Gaseous or rocky? Unveiling the nature of small worlds”. M.G. is an F.R.S.-FNRS Senior Research Associate. MNG is the ESA CHEOPS Project Scientist and Mission Representative, and as such also responsible for the Guest Observers (GO) Programme. M.N.G. does not relay proprietary information between the GO and Guaranteed Time Observation (GTO) Programmes, and does not decide on the definition and target selection of the GTO Programme. S.H. gratefully acknowledges CNES funding through the grant 837319. KGI is the ESA CHEOPS Project Scientist and is responsible for the ESA CHEOPS Guest Observers Programme. She does not participate in, or contribute to, the definition of the Guaranteed Time Programme of the CHEOPS mission through which observations described in this paper have been taken, nor to any aspect of target selection for the programme. This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. P.M. acknowledges support from STFC research grant number ST/M001040/1. This work was also partially supported by a grant from the Simons Foundation (PI Queloz, grant number 327127). IRI acknowledges support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grant PGC2018-098153-B-C33, as well as the support of the Generalitat de Catalunya/CERCA programme. GyMSz acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a PRODEX Experiment Agreement No. 4000137122, the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. V.V.G. is an F.R.S.-FNRS Research Associate. N.A.W. acknowledges UKSA grant ST/R004838/1. A.C.C. and T.W. acknowledge support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. NCS acknowledges funding by the European Union (ERC, FIERCE, 101052347). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. This research made use of exoplanet (Foreman-Mackey et al. 2021) and its dependencies (Agol et al. 2020; Kumar et al. 2019; Astropy Collaboration 2013, 2018; Kipping 2013; Luger et al. 2019; Salvatier et al. 2016; Theano Development Team 2016). We acknowledge the use of further software: batman (Kreidberg 2015), NumPy (Harris et al. 2020), matplotlib (Hunter 2007), corner (Foreman-Mackey 2016), astroquery (Ginsburg et al. 2019), seaborn (Waskom 2021) and scipy (Virtanen et al. 2020).
Appendix A Detrending basis vectors
Table A.1 provides information of the basis vectors we used to correct for systematics from the flux measurements in each CHEOPS visit. The selection is based on the combination of basis vectors that minimise the BIC.
Basis vectors used to detrend each visit.
Appendix B Residuals
The residuals correspond to the flux after systematics, transit, occultation model, and the sinusoidal signal of the phase curve are removed. The gallery in Figs. B.1 and Figs. B.2 contains the residuals of all CHEOPS visits. Complementary to this, the density distribution of the residuals is shown next to the time series.
 |
Fig. B.1 Residual flux in ppm assuming a sinusoidal shape of the phase curve for CHEOPS visits 1 to 15. The number in each panel corresponds to the CHEOPS visit, where the subscript a) refers to the residuals vs. BJD time-2450000 in the x-axis. The subscript b) refers to the density distribution, with density in the x-axis and residuals in the y-axis. All panels share the same y-axis scale. |
Appendix C Phase-curve parameters
Here we present pairwise relations between relevant phase-curve parameters: transit and occultation depth, and phase-curve amplitude and offset. The transit depth is compared with the occultation depth (Fig. C.1), phase-curve amplitude (Fig. C.2), and phase offset (Fig. C.3). Then the occultation depth is compared with amplitude (Fig. C.4) and offset (Fig. C.5). The remaining combination relates the phase-curve amplitude with the offset (Fig. C.6).
 |
Fig. C.1 Transit depth vs. occultation depth. |
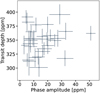 |
Fig. C.2 Transit depth vs. phase-curve amplitude. |
 |
Fig. C.3 Transit depth vs. phase offset. |
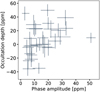 |
Fig. C.4 Occultation depth vs. phase-curve amplitude. |
 |
Fig. C.5 Occultation depth vs. phase offset. |
 |
Fig. C.6 Phase-curve amplitude vs. phase offset. |
Appendix D Selected corner plots
Figure D.1 and Figure D.2 show the full joint posterior correlation plots of visits 2 and 9, respectively, b is the impact parameter, t0 is the mid-transit time relative to the reference time, Rp/R⋆ is the ratio of the planetary radius to the stellar radius, (Rp/R⋆)2 is the transit depth, δt is the analytical expression of the transit depth (Heller 2019), R⊙ and M⊙ are the stellar radius and mass, roll refers to the roll angle, δocc is the occultation depth, Phi is the phase offset in degrees, and log(s) is the natural logarithm of the flux uncertainty for each measurement. Visit 9 clarifies the nature of the high uncertainty in the phase offset reported in Table 3. Since ingress or egress were not observed by CHEOPS, the MCMC infers a bimodal distribution on the mid-transit time.
 |
Fig. D.1 Posterior distributions and joint correlations plot corresponding to CHEOPS visit 2. |
Appendix E Model comparison
For each visit, we performed a comparison between different models for the phase curve: sinusoid function, Lambertian sphere, piecewise-Lambertian, constant baseline flux, and constant baseline flux without occultation (set to zero). Table E.1 shows the top-ranked model and the difference in the LOO between the first and second ranked model. The last column is the statistical weight of the top-ranked model.
Statistical weight of the preferred model for each visit based on the LOO.
References
- Agol, E., Luger, R., & Foreman-Mackey, D. 2020, AJ, 159, 123 [Google Scholar]
- Angelo, I., & Hu, R. 2017, AJ, 154, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, D. J., de Mooij, E., Barstow, J., et al. 2016, Nat. Astron., 1 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
- Bonfanti, A., Delrez, L., Hooton, M. J., et al. 2021, A&A, 646, A157 [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Jenkins, J., et al. 2009, Science, 325, 709 [Google Scholar]
- Bourrier, V., Dumusque, X., Dorn, C., et al. 2018a, A&A, 619, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Ehrenreich, D., des Etangs, A. L., et al. 2018b, A&A, 615, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandeker, A., Alibert, Y., Bourrier, V., et al. 2021, Is it raining lava in the evening on 55 Cancri e?, JWST Proposal. Cycle 1, 2084 [Google Scholar]
- Brandeker, A., Heng, K., Lendl, M., et al. 2022, A&A, 659, A4 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, Proc. IAU Symp., 210, poster A20 [Google Scholar]
- Claret, A. 2021, RNAAS, 5, 13 [NASA ADS] [Google Scholar]
- Cuntz, M., Saar, S. H., & Musielak, Z. E. 2000, ApJ, 533, L151 [Google Scholar]
- Daley-Yates, S., & Stevens, I. R. 2019, MNRAS, 483, 2600 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., & Fabrycky, D. C. 2010, ApJ, 722, 937 [Google Scholar]
- Deibert, E. K., de Mooij, E. J. W., Jayawardhana, R., et al. 2021, AJ, 161, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Deline, A., Hooton, M. J., Lendl, M., et al. 2022, A&A, 659, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Ehrenreich, D., Alibert, Y., et al. 2021, Nat. Astron., 5, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Gillon, M., Deming, D., et al. 2011, A&A, 533, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demory, B.-O., Gillon, M., Madhusudhan, N., & Queloz, D. 2015, MNRAS, 455, 2018 [Google Scholar]
- Demory, B.-O., Gillon, M., de Wit, J., et al. 2016, Nature, 532, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B. O., Sulis, S., Meier Valdés, E., et al. 2023, A&A, 669, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dragomir, D., Matthews, J. M., Winn, J. N., & J. F. R. 2012, Proc. Int. Astron. Union, 8, 52 [CrossRef] [Google Scholar]
- Ehrenreich, D., Bourrier, V., Bonfils, X., et al. 2012, A&A, 547, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esteves, L. J., de Mooij, E. J. W., Jayawardhana, R., Watson, C., & de Kok, R. 2017, AJ, 153, 268 [Google Scholar]
- Fischer, D. A., Marcy, G. W., Butler, R. P., et al. 2008, ApJ, 675, 790 [Google Scholar]
- Folsom, C., Fionnagáin, D. Ó., Fossati, L., et al. 2020, A&A, 633, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
- Foreman-Mackey, D., Savel, A., Luger, R., et al. 2021, https://doi.org/10.5281/zenodo.4737444 [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 2013, Approaches to the Temperature Equations, Cambridge Astrophysics (Cambridge University Press), 216 [Google Scholar]
- Gaillard, F., & Scaillet, B. 2014, Earth Planet. Sci. Lett., 403, 307 [Google Scholar]
- Gebek, A., & Oza, A. V. 2020, MNRAS, 497, 5271 [Google Scholar]
- Geissler, P. E., & Goldstein, D. B. 2007, Plumes and their Deposits (Berlin, Heidelberg: Springer Berlin Heidelberg), 163 [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Gelman, A., Hwang, J., & Vehtari, A. 2014, Stat. Comput., 24, 997 [Google Scholar]
- Ginsburg, A., Sipocz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Heller, R. 2019, A&A, 623, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heng, K. 2017, Exoplanetary Atmospheres: Theoretical Concepts and Foundations (Princeton University Press) [Google Scholar]
- Henry, G. W., Baliunas, S. L., Donahue, R. A., Fekel, F. C., & Soon, W. 2000, ApJ, 531, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, M. D., & Gelman, A. 2011, The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo [Google Scholar]
- Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A&A, 635, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, R., Demory, B.-O., Seager, S., Lewis, N., & Showman, A. P. 2015, ApJ, 802, 51 [Google Scholar]
- Hu, R., Brandeker, A., Damiano, M., et al. 2021, Determining the Atmospheric Composition of the Super-Earth 55 Cancri e, JWST Proposal. Cycle 1, 1952 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., von Berg, S. W., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jessup, K. L., & Spencer, J. R. 2012, Icarus, 218, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Jindal, A., de Mooij, E. J. W., Jayawardhana, R., et al. 2020, AJ, 160, 101 [Google Scholar]
- Jones, K., Morris, B. M., Demory, B. O., et al. 2022, A&A, 666, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keles, E., Mallonn, M., Kitzmann, D., et al. 2022, MNRAS, 513, 1544 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., Mann, I., Biesecker, D. A., & Jessberger, E. K. 2002, Icarus, 159, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., Mann, I., Biesecker, D. A., & Jessberger, E. K. 2004, Icarus, 169, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kitzmann, D., & Heng, K. 2018, MNRAS, 475, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
- Kumar, R., Carroll, C., Hartikainen, A., & Martin, O. A. 2019, J. Open Source Softw., 4, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Lally, M., & Vanderburg, A. 2022, AJ, 163, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2008, A&A, 487, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leleu, A., Alibert, Y., Hara, N. C., et al. 2021, A&A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lellouch, E., Strobel, D. F., Belton, M. J. S., et al. 1996, ApJ, 459, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Lendl, M., Csizmadia, Sz., Deline, A., et al. 2020, A&A, 643, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luger, R., Agol, E., Foreman-Mackey, D., et al. 2019, AJ, 157, 64 [Google Scholar]
- Mahapatra, G., Helling, C., & Miguel, Y. 2017, MNRAS, 472, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
- Martins, B. L. C., Gomes, R. L., Messias, Y. S., et al. 2020, ApJS, 250, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Matsakos, T., Uribe, A., & Königl, A. 2015, A&A, 578, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McArthur, B. E., Endl, M., Cochran, W. D., et al. 2004, ApJ, 614, L81 [Google Scholar]
- McElreath, R. 2016, Statistical Rethinking: A Bayesian Course with Examples in R and Stan, Chapman & Hall/CRC Texts in Statistical Science (CRC Press) [Google Scholar]
- Meier Valdés, E. A., Morris, B. M., Wells, R. D., Schanche, N., & Demory, B.-O. 2022, A&A, 663, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mercier, S. J., Dang, L., Gass, A., Cowan, N. B., & Bell, T. J. 2022, AJ, 164, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, B. M., Delrez, L., Brandeker, A., et al. 2021, A&A, 653, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, B. E., Ford, E. B., Wright, J. T., et al. 2014, MNRAS, 441, 442 [Google Scholar]
- Oza, A. V., Johnson, R. E., Lellouch, E., et al. 2019, ApJ, 885, 168 [Google Scholar]
- Parviainen, H., Wilson, T. G., Lendl, M., et al. 2022, A&A, 668, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perez-Becker, D., & Chiang, E. 2013, MNRAS, 433, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Levine, A., Chiang, E., et al. 2012, ApJ, 752, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Barclay, T., DeVore, J., et al. 2014, ApJ, 784, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Rast, M. P. 2003, ApJ, 597, 1200 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, J. Astron. Telescopes Instrum. Syst., 1, 1 [NASA ADS] [Google Scholar]
- Ridden-Harper, A. R., Snellen, I. A. G., Keller, C. U., et al. 2016, A&A, 593, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvatier, J., Wiecki, T. V., & Fonnesbeck, C. 2016, PeerJ Comput. Sci., 2, e55 [Google Scholar]
- Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saur, J., Grambusch, T., Duling, S., Neubauer, F. M., & Simon, S. 2013, A&A, 552, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Strugarek, A. 2016, ApJ, 833, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Strugarek, A., Fares, R., Bourrier, V., et al. 2022, MNRAS, 512, 4556 [NASA ADS] [CrossRef] [Google Scholar]
- Sulis, S., Dragomir, D., Lendl, M., et al. 2019, A&A, 631, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szabó, G. M., Gandolfi, D., Brandeker, A., et al. 2021, A&A, 654, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabernero, H. M., Allende Prieto, C., Zapatero Osorio, M. R., et al. 2020, MNRAS, 498, 4222 [Google Scholar]
- Tamburo, P., Mandell, A., Deming, D., & Garhart, E. 2018, AJ, 155 [Google Scholar]
- Theano Development Team 2016, arXiv e-prints, [arXiv:abs/1605.02688] [Google Scholar]
- Turner, J. D., Zarka, P., Grießmeier, J.-M., et al. 2021, A&A, 645, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Lieshout, R., Min, M., & Dominik, C. 2014, A&A, 572, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Lieshout, R., Min, M., Dominik, C., et al. 2016, A&A, 596, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VanderPlas, J. T. 2018, ApJS, 236, 16 [Google Scholar]
- Vehtari, A., Gelman, A., & Gabry, J. 2016, Stat. Comput., 27, 1413 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- von Braun, K., Boyajian, T. S., ten Brummelaar, T. A., et al. 2011, ApJ, 740, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Waskom, M. L. 2021, J. Open Source Softw., 6, 3021 [CrossRef] [Google Scholar]
- Wilson, T. G., Goffo, E., Alibert, Y., et al. 2022, MNRAS, 511, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Matthews, J. M., Dawson, R. I., et al. 2011, ApJ, 737, L18 [Google Scholar]
- Yao, Y., Pirš, G., Vehtari, A., & Gelman, A. 2022, Bayesian Anal., 17, 1043 [CrossRef] [Google Scholar]
- Zarka, P. 2007, Planet. Space Sci., 55, 598 [Google Scholar]
- Zhang, M., Knutson, H. A., Wang, L., et al. 2021, AJ, 161, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zieba, S., Zilinskas, M., Kreidberg, L., et al. 2022, A&A, 664, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
For details about the derivation, see Appendix A in Hu et al. (2015).
The correct formulation of the solid angle used here to calculate the ratio of radiation pressure to gravity, 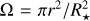 , can be found in Kimura et al. (2004).
, can be found in Kimura et al. (2004).
An asymmetry parameter of ɡ0 = 0 does not necessarily imply isotropic scattering (Kitzmann & Heng 2018). To be precise, it corresponds to a symmetric phase function (Heng 2017).
All Tables
Characteristic sublimation timescales in seconds of a single dust grain of the selected species with radii between 0.1 and 0.7 µm.
All Figures
 |
Fig. 1 Detrended photometry of 55 Cnc e for every visit. The detrended flux is plotted in grey, the best-fit phase-curve model in red, and the 1σ uncertainty from the posterior distribution in shaded light red. The black squares represent the binned data per CHEOPS orbit. The integer close to the bottom right corner of each panel indicates the number of the CHEOPS visit (see Table 1). |
| In the text | |
 |
Fig. 2 Transit depth in ppm for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
| In the text | |
 |
Fig. 3 Occultation depth for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
| In the text | |
 |
Fig. 4 Phase-curve amplitude for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
| In the text | |
 |
Fig. 5 Phase-curve offset for each CHEOPS visit. The error bars represent the 1σ uncertainty. |
| In the text | |
 |
Fig. 6 Posterior distributions and joint correlations plot for visit 3 in blue and visit 4 in red. δt stands for the transit depth, δocc is the occultation depth, and the amplitude and offset refer to the phase-curve amplitude and offset, respectively. |
| In the text | |
 |
Fig. 7 Model comparison based on the LOO criterion. The best-ranked model has a ∆LOO of zero. The x-axis shows the difference in the LOO for the models considered in each visit (y-axis). The error bars represent the standard error of the difference in the expected log-predictive density between each model and the top-ranked model. By definition, the standard error of the top-ranked model is zero. In visit 1, the ∆LOO to the second-ranked model is above 50 and thus is not visible in the plot. The red diamond represents a sinusoidal phase curve, the green cross is the piecewise-Lambertian model, the cyan hexagon is the Lambertian sphere, the orange star is a flat baseline without an eclipse, and the violet circle is a flat baseline with the eclipse as a free parameter. |
| In the text | |
 |
Fig. 8 Power spectrum computed with the Lomb-Scargle technique as a function of frequency. The blue dots show raw flux measurements of all CHEOPS visits, while the red dots represent the detrended flux after the phase-curve model was removed. The dark blue and dark red curves represent the binned data. The dashed green vertical line corresponds to the orbital period of 55 Cnc e, and the vertical dashed black line corresponds to the CHEOPS orbital period of 101 min. |
| In the text | |
 |
Fig. 9 Phase-curve amplitude of every CHEOPS visit phase-folded at the best-fit period of 51.9 days. The sinusoidal function is overplotted in red. |
| In the text | |
 |
Fig. 10 Ratio of radiation pressure to gravity β as a function of grain radius. The values below the horizontal dashed black line (β = 0.5) lead to closed orbits, while the values above the line lead to unbounded motion. |
| In the text | |
 |
Fig. 11 Motion of dust for a selected composition subject to gravity and radiation pressure. The time interval of the trajectory is the characteristic sublimation timescale of the compound. The orange circle represents 55 Cnc A, and the dashed black circle is the orbit of 55 Cnc e scaled in units of stellar radius. The zoomed-in panel shows the trajectory of short-lived species. Different lines of the same colour represent different grain sizes of a species. |
| In the text | |
 |
Fig. 12 Detrended flux measurements of 55 Cnc e, phase-folded at the planet orbital period. The top panel shows the relative flux, and the bottom panel presents the residuals in ppm. The plots show a portion of the phase centred around the transit. The red squares represent the binned data. |
| In the text | |
 |
Fig. B.1 Residual flux in ppm assuming a sinusoidal shape of the phase curve for CHEOPS visits 1 to 15. The number in each panel corresponds to the CHEOPS visit, where the subscript a) refers to the residuals vs. BJD time-2450000 in the x-axis. The subscript b) refers to the density distribution, with density in the x-axis and residuals in the y-axis. All panels share the same y-axis scale. |
| In the text | |
 |
Fig. B.2 Same as Fig. B.1 for CHEOPS visits 16 to 29. |
| In the text | |
 |
Fig. C.1 Transit depth vs. occultation depth. |
| In the text | |
 |
Fig. C.2 Transit depth vs. phase-curve amplitude. |
| In the text | |
 |
Fig. C.3 Transit depth vs. phase offset. |
| In the text | |
 |
Fig. C.4 Occultation depth vs. phase-curve amplitude. |
| In the text | |
 |
Fig. C.5 Occultation depth vs. phase offset. |
| In the text | |
 |
Fig. C.6 Phase-curve amplitude vs. phase offset. |
| In the text | |
 |
Fig. D.1 Posterior distributions and joint correlations plot corresponding to CHEOPS visit 2. |
| In the text | |
 |
Fig. D.2 Same as Fig. D.1, but corresponding to CHEOPS visit 9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.